2010年各省市中考数学试题分类汇编-相似形

合集下载

2010年中考数学试题分类汇编

2010年中考数学试题分类汇编整式的乘除（幂的运算性质,乘法，除法，公式，因式分解）（2010哈尔滨）1。

把多项式2a2－4ab＋2b2分解因式的结果是2(a-b)2（2010珠海）２．分解因式=________________. a(x+y)(x-y)（2010年镇江市）3．化简：= a3；a4 .（2010年镇江市）5．分解因式：=；化简：= .(2010遵义市) 计算的结果是Ａ．Ｂ．Ｃ．Ｄ．答案：D(2010台州市)下列运算正确的是(▲)A．B．C．D．答案：C(2010遵义市) 分解因式: = ▲ .答案：(2010遵义市) 已知，则▲ .答案：2010(2010台州市)因式分解：= ▲．答案：（2010年无锡）2．下列运算正确的是（▲）A．B．C．D．答案 D（2010年无锡）13．分解因式：▲．答案(2a+1) (2a-1)（2010年连云港）2．下列计算正确的是（）A．a＋a＝x2B．a·a2＝a2C．(a2) 3＝a5D．a2 (a＋1)＝a3＋1答案B（2010年连云港）19.（本题满分8分）计算：（2）已知x＝－1，求x2＋3x－1的值( 2 ) 法一：当时，=.............................................................7分= ..........................................................................................8分法二:即:..............................................................7分...........................8分（2010宁波市）2．下列运算正确的是A．x·x2＝x2 B．(xy) 2＝xy2 C．(x2) 3＝x6 D．x2＋x2＝x4（2010宁波市）4．据《中国经济周刊》报道，上海世博会第四轮环保活动投资总金额高达820亿元，其中820亿用科学记数法表示为A．0.82×1011 B．8.2×1010 C．8.2×109D．82×108（2010宁波市）17．若x＋y＝3，xy＝1，则x2＋y2＝_________________．7（2010年金华）分解因式▲.答案：(x-3)(x+3)；7．（2010年长沙）下列计算正确的是 CA．B．C．D．（2010年湖南郴州市）4.下列运算，正确的是A．B． C．D．答案：A（2010年湖南郴州市）10. 分解因式： .答案：(2010湖北省荆门市)11．如图是一个包装纸盒的三视图(单位：cm)，则制作一个纸盒所需纸板的面积是( )(A)75(1＋)cm2(B)75(1＋)cm2(C)75(2＋)cm2(D)75(2＋)cm2答案：C2．（2010湖北省咸宁市）下列运算正确的是A．B．C．D．答案：C4.（2010年郴州市）下列运算，正确的是A．B． C．D．答案：A10. （2010年郴州市）分解因式：.答案：17．（2010年郴州市）计算：.答案：17. 解：原式＝2+2+1218．（2010年郴州市）先化简再求值：，其中x=2.答案：原式===当x=2时，原式==3．（2010年怀化市）若，，则的值是（）．Ａ．2 Ｂ．4 Ｃ．Ｄ．答案：B10．（2010年怀化市）若，则、、的大小关系是（）A．B．C．D．答案：C4．（2010年济宁市)把代数式分解因式，结果正确的是A．B．C．D．答案：D12．（2010年济宁市)若代数式可化为，则的值是．答案：5（2010年成都）2．表示（）（A）（B）（C）（D）答案：C（2010年眉山）5．把代数式分解因式，下列结果中正确的是A． B． C． D．答案：D（北京）10. 分解因式：m2 4m= 。

2010年全国各地数学中考试题分类汇编

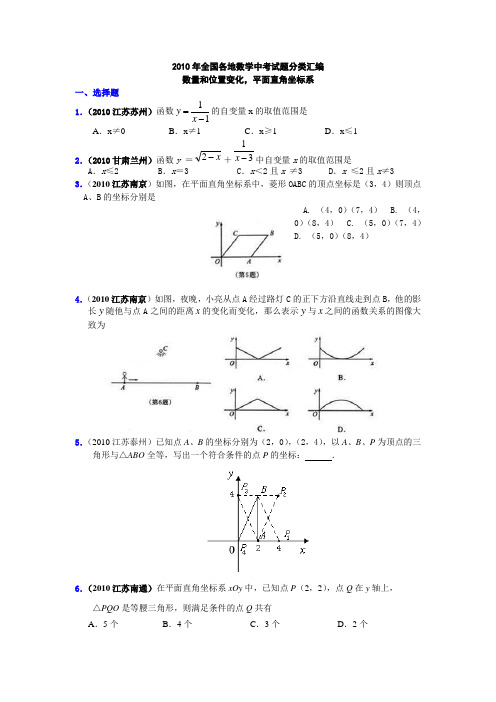
2010年全国各地数学中考试题分类汇编数量和位置变化，平面直角坐标系一、选择题1．（2010江苏苏州）函数11y x =-的自变量x 的取值范围是 A ．x ≠0 B ．x ≠1 C ．x ≥1 D ．x ≤12．（2010甘肃兰州）函数y ＝x -2＋31-x 中自变量x 的取值范围是A ．x ≤2B ．x ＝3C ．x ＜2且x ≠3D ．x ≤2且x ≠3 3．（2010江苏南京）如图，在平面直角坐标系中，菱形OABC 的顶点坐标是（3，4）则顶点A 、B 的坐标分别是A. （4，0）（7，4）B. （4，0）（8，4）C. （5，0）（7，4）D. （5，0）（8，4）4．（2010江苏南京）如图，夜晚，小亮从点A 经过路灯C 的正下方沿直线走到点B ，他的影长y 随他与点A 之间的距离x 的变化而变化，那么表示y 与x 之间的函数关系的图像大致为5．（2010江苏泰州）已知点A 、B 的坐标分别为（2，0），（2，4），以A 、B 、P 为顶点的三角形与△ABO 全等，写出一个符合条件的点P 的坐标：．6．（2010江苏南通）在平面直角坐标系xOy 中，已知点P （2，2），点Q 在y 轴上，△PQO 是等腰三角形，则满足条件的点Q 共有 A ．5个B ．4个C ．3个D ．2个8．（2010 山东省德州）某游泳池的横截面如图所示，用一水管向池内持续注水，若单位时间内注入的水量保持不变，则在注水过程中，下列图象能反映深水区水深h 与注水时间t 关系的是（Ａ）（Ｂ）（Ｃ）（Ｄ）10．（2010 河北）一艘轮船在同一航线上往返于甲、乙两地．已知轮船在静水中的速度为15 km /h ，水流速度为5 km /h ．轮船先从甲地顺水航行到乙地，在乙地停留一段时间后，又从乙地逆水航行返回到甲地．设轮船从甲地出发后所用时间为t （h ），航行的路程为s （km ），则s 与t 的函数图象大致是11．（2010辽宁丹东市）如图，在平面直角坐标系中，以O （0，0），A （1，1）， B （3，0）为顶点，构造平行四边形，下列各点中不能．．作为平行四边形顶点坐标的是（）A ．（－3，1）B ．（4，1）C ．（－2，1）D ．（2，－1）12．（2010山东济宁）如图，是张老师出门散步时离家的距离y 与时间x 之间的函数关系的图象，若用黑点表示张老师家的位置，则张老师散步行走的路线可能是13．（2010山东威海）在平面直角坐标系中，正方形ABCD 的位置如图所示，点A 的坐标为（1，0），点D 的坐标为（0，2）．延长CB 交x 轴于点A 1，作正方形A 1B 1C 1C ；延长C 1B 1交x 轴于点A 2，作正方形A 2B 2C 2C 1…按这样的规律进行下去，第2010个正方形的面积yxO.AB.第7题图 sOAsOBsOCsODt hOt hO t hO htO 第5题图深水区浅水区••••ABCDyxO（第7题）为A ．2009235⎪⎭⎫ ⎝⎛B ．2010495⎪⎭⎫ ⎝⎛ C ．2008495⎪⎭⎫⎝⎛D ．4018235⎪⎭⎫ ⎝⎛14．（2010山东青岛）如图，△ABC 的顶点坐标分别为A （4，6）、B （5，2）、C （2，1），如果将△ABC 绕点C 按逆时针方向旋转90°，得到△''A B C ，那么点A 的对应点'A 的坐标是（）． A ．（－3，3） B ．（3，－3） C ．（－2，4） D ．（1，4）16．（2010 山东莱芜）在一次自行车越野赛中，甲乙两名选手行驶的路程y （千米）随时间x （分）变化的图象（全程）如图，根据图象判定下列结论不正确．．．的是 A ．甲先到达终点B ．前30分钟，甲在乙的前面C ．第48分钟时，两人第一次相遇D ．这次比赛的全程是28千米18．（2010四川凉山）如图，因水桶中的水有图①的位置下降到图②的位置的过程中，如果水减少的体积是y ，水位下降的高度是x ，那么能够表示y 与x 之间函数关系的图像是CB ①②A（第12题图）乙甲第7题图19．（2010四川眉山）某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程（工作前洗衣机内无水），在这三个过程中洗衣机内水量y（升）与时间x（分）之间的函数关20．（2010台湾）坐标半面上，在第二象限内有一点P，且P点到x轴的距离是4，到y轴的距离是5，则P点坐标为何？(A) (-5，4) (B) (-4，5) (C) (4，5) (D) (5，-4) 。

(免费)2010年部分省市中考数学试题分类汇编综合型问题(含答案)

2010年部分省市中考数学试题分类汇编综合型问题20、（2010年浙江省东阳县）如图，BD 为⊙O 的直径，点A 是弧BC 的中点，AD 交BC 于E 点，AE=2，ED=4.（1）求证: ABE ∆～ABD ∆；(2) 求tan ADB ∠的值；（3）延长BC 至F ，连接FD ，使BDF ∆的面积等于求EDF ∠的度数.【关键词】圆、相似三角形、三角形函数问题【答案】（１）∵点A 是弧BC 的中点 ∴∠ＡＢＣ＝∠ＡＤＢ又∵∠ＢＡＥ＝∠ＢＡＥ ∴△ＡＢＥ∽△ＡＢＤ（２）∵△ＡＢＥ∽△ＡＢＤ ∴ＡＢ２＝２×６＝１２ ∴ＡＢ＝２3在Ｒｔ△ＡＤＢ中，ｔａｎ∠ＡＤＢ＝33632=（３）连接ＣＤ，可得ＢＦ＝８，ＢＥ＝４，则ＥＦ＝４，△ＤＥＦ是正三角形， ∠ＥＤＦ＝６０°20．（2010年山东省青岛市）某学校组织八年级学生参加社会实践活动，若单独租用35座客车若干辆，则刚好坐满；若单独租用55座客车，则可以少租一辆，且余45个空座位．（1）求该校八年级学生参加社会实践活动的人数；（2）已知35座客车的租金为每辆320元，55座客车的租金为每辆400元．根据租车资金不超过1500元的预算，学校决定同时租用这两种客车共4辆（可以坐不满）．请你计算本次社会实践活动所需车辆的租金．【关键词】不等式与方程问题【答案】解：（1）设单独租用35座客车需x 辆，由题意得：3555(1)45x x =--,解得：5x =.∴35355175x =⨯=（人）.答：该校八年级参加社会实践活动的人数为175人． ········· 3分（2）设租35座客车y 辆，则租55座客车（4y -）辆，由题意得：3555(4)175320400(4)1500y y y y +-⎧⎨+-⎩≥≤， ······· 6分解这个不等式组，得111244y ≤≤．∵y 取正整数， ∴y = 2.∴4－y = 4－2 = 2.∴320×2＋400×2 = 1440（元）.所以本次社会实践活动所需车辆的租金为1440元． (2010年安徽省B 卷)23.（本小题满分１２分）如图， Rt ABC △内接于O ⊙，AC BC BAC =∠，的平分线AD 与O ⊙交于点D ，与BC 交于点E ，延长BD ，与AC 的延长线交于点F ，连接CD G ，是CD 的中点，连结OG ．（1）判断OG 与CD 的位置关系，写出你的结论并证明；（2）求证：AE BF =；（3）若3(2OG DE = ，求O ⊙的面积．【关键词】圆等腰三角形三角形全等三角形相似勾股定理【答案】（1）猜想：OG CD ⊥．证明：如图，连结OC 、OD ． ∵OC OD =，G 是CD 的中点，∴由等腰三角形的性质，有OG CD ⊥．（2）证明：∵AB 是⊙O 的直径，∴∠ACB ＝90°．而∠CAE ＝∠CBF （同弧所对的圆周角相等）．在Rt △ACE 和Rt △BCF 中， ∵∠ACE =∠BCF ＝90°，AC =BC ，∠CAE =∠CBF ， ∴Rt △ACE ≌Rt △BCF （ASA ） ∴ AE BF =．（3）解：如图，过点O 作BD 的垂线，垂足为H ．则H 为BD 的中点．∴OH ＝12AD ，即AD =2OH ．又∠CAD ＝∠BAD ⇒CD =BD ，∴OH =OG ．在Rt △BDE 和Rt △ADB 中， ∵∠DBE ＝∠DAC ＝∠BAD ， ∴Rt △BDE ∽Rt △ADB∴BD DE AD DB=，即2BD AD DE =·AA∴226(2BD AD DE OG DE ===·· 又BD FD =，∴2BF BD =．∴22424(2BF BD == … ① 设AC x =，则BC x =，．∵AD 是∠BAC 的平分线， ∴FAD BAD ∠=∠．在Rt △ABD 和Rt △AFD 中， ∵∠ADB =∠ADF ＝90°，AD =AD ，∠F AD ＝∠BAD ， ∴Rt △ABD ≌Rt △AFD （ASA ）． ∴AF =AB，BD =FD ． ∴CF =AF -AC1)x x -= 在Rt △BCF 中，由勾股定理，得2222221)]2(2BF BC CF x x x =+=+= …②由①、②，得22(224(2x =． ∴212x =．解得x =-．∴AB ===∴⊙O∴π6πO S =⋅2⊙＝(2010年安徽省B 卷)24.（本小题满分12分）已知：抛物线()20y ax bx c a =++≠的对称轴为1x =-与x 轴交于A B ，两点，与y 轴交于点C ，其中()30A -，、()02C -，．（1）求这条抛物线的函数表达式．（2）已知在对称轴上存在一点P ，使得PBC △的周长最小．请求出点P 的坐标．（3）若点D 是线段OC 上的一个动点（不与点O 、点C 重合）．过点D 作DE PC ∥交x 轴于点E ．连接PD 、PE ．设CD 的长为m ，PDE △的面积为S ．求S 与m 之间的函数关系式．试说明S 是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．【关键词】二次函数解析式对称点相似三角形三角形面积【答案】（1）由题意得129302b a a bc c ⎧=⎪⎪⎪-+=⎨⎪⎪=-⎪⎩解得23432a b c ⎧=⎪⎪⎪=⎨⎪=-⎪⎪⎩∴此抛物线的解析式为224233y x x =+- （2）连结AC 、BC .因为BC 的长度一定，所以PBC △周长最小，就是使PC PB +最小.B 点关于对称轴的对称点是A 点，AC 与对称轴1x =-的交点即为所求的点P .设直线AC 的表达式为y kx b =+则302k b b -+=⎧⎨=-⎩，解得232k b ⎧=-⎪⎨⎪=-⎩∴此直线的表达式为223y x =--．把1x =-代入得43y =-∴P 点的坐标为413⎛⎫--⎪⎝⎭，（3）S 存在最大值理由：∵DE PC ∥，即DE AC ∥． ∴OED OAC △∽△．∴OD OE OC OA =，即223m OE-=． ∴332OE m =-，连结OPOAC OED AEP PCD S S S S S =---△△△△=()1131341323212222232m m m m ⎛⎫⨯⨯-⨯-⨯--⨯⨯-⨯⨯ ⎪⎝⎭ =()22333314244m m m -+=--+ ∵304-<∴当1m =时，34S =最大（2010年福建省晋江市）已知：如图，把矩形OCBA 放置于直角坐标系中，3=OC ，2=BC ，取AB 的中点M ，连结MC ，把MBC ∆沿x 轴的负方向平移OC 的长度后得到DAO ∆.(1)试直接写出点D 的坐标；(2)已知点B 与点D 在经过原点的抛物线上，点P 在第一象限内的该抛物线上移动，过点P 作x PQ ⊥轴于点Q ，连结OP .①若以O 、P 、Q 为顶点的三角形与DAO ∆相似，试求出点P 的坐标；②试问在抛物线的对称轴上是否存在一点T ，使得TB TO -的值最大.【关键词】二次函数、相似三角形、最值问题答案：解：(1)依题意得：⎪⎭⎫ ⎝⎛-2,23D ；(2) ① ∵3=OC ，2=BC ， ∴()2,3B .∵抛物线经过原点，∴设抛物线的解析式为bx ax y +=2()0≠a又抛物线经过点()2,3B 与点⎪⎭⎫⎝⎛-2,23D∴⎪⎩⎪⎨⎧=-=+22349,239b a b a 解得：⎪⎪⎩⎪⎪⎨⎧-==32,94b a ∴抛物线的解析式为x x y 32942-=. ∵点P 在抛物线上， ∴设点⎪⎭⎫ ⎝⎛-x x x P 3294,2. 1)若PQO ∆∽DAO ∆，则AO QO DA PQ =， 22332942x xx =-，解得：01=x (舍去)或16512=x ，∴点⎪⎭⎫⎝⎛64153,1651P . 2)若OQP ∆∽DAO ∆，则AO PQ DA OQ =， 23294232xx x -=，解得：01=x (舍去)或292=x ，∴点⎪⎭⎫⎝⎛6,29P . ②存在点T ，使得TO TB -的值最大. 抛物线x x y 32942-=的对称轴为直线43=x ，设抛物线与x 轴的另一个交点为E ，则点⎪⎭⎫⎝⎛0,23E . ∵点O 、点E 关于直线43=x 对称， ∴TE TO =要使得TB TO -的值最大，即是使得TB TE -的值最大，根据三角形两边之差小于第三边可知，当T 、E 、B 三点在同一直线上时，TB TE -的值最大.设过B 、E 两点的直线解析式为b kx y +=()0≠k ，∴⎪⎩⎪⎨⎧=+=+023,23b k b k 解得：⎪⎩⎪⎨⎧-==2,34b k∴直线BE 的解析式为234-=x y . 当43=x 时，124334-=-⨯=y . ∴存在一点⎪⎭⎫⎝⎛-1,43T 使得TO TB -最大.2. （2010年福建省晋江市）如图，在等边ABC ∆中，线段AM 为BC 边上的中线. 动点D 在直线．．AM 上时，以CD 为一边且在CD 的下方作等边CDE ∆，连结BE .(1) 填空：______ACB ∠=度；(2) 当点D 在线段．．AM 上(点D 不运动到点A )时，试求出BEAD的值； (3)若8=AB ，以点C 为圆心，以5为半径作⊙C 与直线BE 相交于点P 、Q 两点，在点D 运动的过程中(点D 与点A 重合除外)，试求PQ 的长.(2)∵ABC ∆与DEC ∆都是等边三角形∴BC AC =，CE CD =，︒=∠=∠60DCE ACB ∴BCE DCB DCB ACD ∠+∠=∠+∠ ∴BCE ACD ∠=∠CAB 备用图(1) AB C备用图(2)∴ACD ∆≌BCE ∆()SAS∴BE AD =，∴1=BEAD. (3)①当点D 在线段AM 上（不与点A 重合）时，由(2)可知ACD ∆≌BCE ∆，则︒=∠=∠30CAD CBE ，作BE CH ⊥于点H ，则HQ PQ 2=，连结CQ ，则5=CQ .在CBH Rt ∆中，︒=∠30CBH ，8==AB BC ，则421830sin =⨯=︒⋅=BC CH . 在CHQ Rt ∆中，由勾股定理得：3452222=-=-=CH CQ HQ ，则②当点D 在线段AM 的延长线上时，∵ABC ∆与DEC ∆都是等边三角形 ∴BC AC =，CE CD =，︒=∠=∠60DCE ACB ∴DCB ACB =∠+∠∴BCE ACD ∠=∠ ∴ACD ∆≌BCE ∆(∴=∠=∠CAD CBE ③当点D 在线段MA ∵ABC ∆与DEC ∆∴BC AC =，CD =∴=∠+∠ACE ACD ∴BCE ACD ∠=∠ ∴ACD ∆≌BCE ∆(∴CAD CBE ∠=∠∵︒=∠30CAM∴︒=∠=∠150CAD CBE ∴︒=∠30CBQ . 同理可得：6=PQ . 综上，PQ 的长是6.1.（2010年浙江省东阳市）如图，P 为正方形ABCD 的对称中心，A （0，3），B （1，0），直线OP 交AB 于N ，DC 于M ，点H 从原点O 出发沿x 轴的正半轴方向以1个单位每秒速度运动，同时，点R 从O 出发沿OM 方向以2个单位每秒速度运动，运动时间为t 。

2010年部分省市中考数学试题分类汇编(共28专题)17[1(精)

2010年部分省市中考数学试题分类汇编 (1平行四边形、矩形、菱形与正方形1. (2010重庆市潼南县如图24,四边形ABCD 是边长为2的正方形,点G 是BC 延长线上一点,连结AG ,点E 、F 分别在AG 上,连接BE 、DF ,∠1=∠2 , ∠3=∠4. (1证明:△AB E ≌△DAF ;(2若∠AGB =30°,求EF 的长. 解:(1∵四边形ABCD 是正方形∴AB=AD在△ABE 和△DAF 中⎪⎩⎪⎨⎧∠=∠=∠=∠3412DA AB ∴△ABE ≌△DAF -----------------------4分(2∵四边形ABCD 是正方形∴∠1+∠4=900∵∠3=∠4∴∠1+∠3=900∴∠AFD=900----------------------------6分在正方形ABCD 中, AD ∥BC∴∠1=∠AGB=300在Rt △ADF 中,∠AFD=900AD=2∴AF=3 DF =1----------------------------------------8分由(1得△ABE ≌△ADF∴AE=DF=1∴EF=AF-AE=13- -----------------------------------------10分2. (2010年青岛已知:如图,在正方形ABCD 中,点E 、F 分别在BC 和CD 上,AE = AF .(1求证:BE = DF ;(2连接AC 交EF 于点O ,延长OC 至点M ,使OM = OA ,连接EM 、FM .判断四边形AEMF是什么特殊四边形?并证明你的结论.【答案】证明:(1∵四边形ABCD 是正方形,∴AB =AD ,∠B = ∠D = 90°.∵AE = AF ,∴Rt Rt ABE ADF △≌△.∴BE =DF .(2四边形AEMF 是菱形.∵四边形ABCD 是正方形,∴∠BCA = ∠DCA = 45°,BC = DC .∵BE =DF ,题图24A D B E F O CM第21题图∴BC -BE = DC -DF . 即CE CF =. ∴OE OF =. ∵OM = OA ,∴四边形AEMF 是平行四边形. ∵AE = AF ,∴平行四边形AEMF 是菱形.3.(2010福建龙岩中考20.(10分如图,平行四边形ABCD 中,E 、F 是对角线BD 上的点,且BE =DF . (1请你写出图中所有的全等三角形(2试在上述各对全等三角形中找出一对加以证明.4.(2010年益阳市如图7,在菱形ABCD 中,∠A =60°,AB =4,O 为对角线BD 的中点,过O 点作OE ⊥AB ,垂足为E . (1 求∠ABD 的度数; (2求线段BE 的长.【关键词】菱形性质、等边三角形、【答案】解:⑴在菱形ABCD 中,AD AB =,︒=∠60A∴ABD ∆为等边三角形∴︒=∠60ABD⑵由(1可知4==AB BD又∵O 为BD 的中点∴2=OB 又∵AB OE ⊥,及︒=∠60ABD ∴︒=∠30BOE ∴1=BE5.(2010年山东省青岛市已知:如图,在正方形ABCD 中,点E 、F 分别在BC 和CD 上,AE = AF .(1求证:BE = DF ;(2连接AC 交EF 于点O ,延长OC 至点M ,使OM = OA ,连接EM 、FM .判断四边形AEMF 是什么特殊四边形?并证明你的结论.7图【关键词】菱形的判定【答案】证明:(1∵四边形ABCD 是正方形,∴AB =AD ,∠B = ∠D = 90°. ∵AE = AF ,∴Rt Rt ABE ADF △≌△. ∴BE =DF .(2四边形AEMF 是菱形.∵四边形ABCD 是正方形,∴∠BCA = ∠DCA = 45°,BC = DC . ∵BE =DF ,∴BC -BE = DC -DF . 即CE CF =. ∴OE OF =. ∵OM = OA ,∴四边形AEMF 是平行四边形. ∵AE = AF ,∴平行四边形AEMF 是菱形.6. (2010年浙江省绍兴市 (1 如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,AE ,BF 交于点O ,∠AOF =90°. 求证:BE =CF .(2 如图2,在正方形ABCD 中,点E ,H ,F ,G 分别在边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,∠FOH =90°, EF =4.求GH 的长.(3 已知点E ,H ,F ,G 分别在矩形ABCD 的边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,∠FOH =90°,EF =4. 直接写出下列两题的答案:①如图3,矩形ABCD 由2个全等的正方形组成,求GH 的长; ②如图4,矩形ABCD 由n 个全等的正方形组成,求GH 的长(用n的代数式表示.【答案】(1 证明:如图1,∵四边形ABCD 为正方形,∴ AB =BC ,∠ABC =∠BCD =90°, ∴∠EAB +∠AEB =90°. ∵∠EOB =∠AOF =90°, ∴∠FBC +∠AEB =90°,∴∠EAB =∠FBC ,∴△ABE ≌△BCF , ∴ BE =CF .(2 解:如图2,过点A 作AM //GH 交BC 于M ,第23题图1第23题图3 第23题图 4 第23题图1第23题图2O ′N AD BEFOC第21题图过点B 作BN //EF 交CD 于N ,AM 与BN 交于点O /, 则四边形AMHG 和四边形BNFE 均为平行四边形, ∴ EF=BN ,GH=AM ,∵∠FOH =90°, AM //GH ,EF//BN , ∴∠NO /A =90°, 故由(1得, △ABM≌△BCN , ∴ AM =BN , ∴ GH =EF =4. (3 ① 8.② 4n .7.(2010年宁德市(本题满分13分如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD (不含B 点上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM. ⑴求证:△AMB ≌△ENB ;⑵①当M 点在何处时,AM +CM 的值最小;②当M 点在何处时,AM +BM +CM 的值最小,并说明理由; ⑶当AM +BM +CM 的最小值为13【答案】解:⑴∵△ABE 是等边三角形, ∴BA =BE ,∠ABE =60°. ∵∠MBN=60°,∴∠MBN -∠ABN =∠ABE -∠ABN. 即∠BMA =∠NBE. 又∵MB =NB ,∴△AMB ≌△ENB (SAS .⑵①当M 点落在BD 的中点时,AM +CM 的值最小. ②如图,连接CE ,当M 点位于BD 与CE 的交点处时, AM +BM +CM 的值最小. ………………9分理由如下:连接MN.由⑴知,△AMB ≌△ENB , ∴AM =EN.∵∠MBN =60°,MB =NB , ∴△BMN 是等边三角形. ∴BM =MN.∴AM +BM +CM =EN +MN +CM.根据“两点之间线段最短”,得EN +MN +CM =EC 最短∴当M 点位于BD 与CE 的交点处时,AM +BM +CM 的值最小,即等于EC 的长.⑶过E 点作EF ⊥BC 交CB 的延长线于F , ∴∠EBF =90°-60°=30°.A DB C F A DB CABC DFED CB AO E设正方形的边长为x ,则BF =23x ,EF =2x . 在Rt △EFC 中,∵EF 2+FC 2=EC 2, ∴(2x 2+(23x +x 2=(213+.解得,x =2(舍去负值. ∴正方形的边长为2.8.(2010年四川省眉山市如图,O 为矩形ABCD 对角线的交点,DE ∥AC ,CE ∥BD .(1试判断四边形OCED 的形状,并说明理由;(2若AB =6,BC =8,求四边形OCED 的面积.【关键词】平行四边形的判定、菱形的性质与判定和面积、矩形的性质【答案】解:(1四边形OCED 是菱形.∵DE ∥AC ,CE ∥BD ,∴四边形OCED 是平行四边形, 又在矩形ABCD 中,OC =OD , ∴四边形OCED 是菱形.(2连结OE .由菱形OCED 得:CD ⊥OE , ∴OE ∥BC 又 CE ∥BD∴四边形BCEO 是平行四边形∴OE =BC =8 ∴S 四边形OCED =11862422OE CD ⋅=⨯⨯=9.(2010年浙江省东阳市(6分如图,已知BE ⊥AD ,CF ⊥AD ,且BE =CF . (1 请你判断AD 是△ABC 的中线还是角平分线?请证明你的结论.(2连接BF 、CE ,若四边形BFCE 是菱形,则△ABC 中应添加一个条件▲ 【关键词】三角形的全等【答案】(1AD 是△ABC 的中线.................................1分理由如下:∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°.........1分又∵BE=CF,∠BDE=∠CFD ∴△BDE≌△CFD(AAS.......2分(2AB=AC或∠ABC=∠ACB或AD⊥BC或AD平分∠BAC.......2分10. (2010年安徽中考如图,AD ∥FE ,点B 、C 在AD 上,∠1=∠2,BF =BC⑴求证:四边形BCEF 是菱形⑵若AB =BC =CD ,求证:△ACF ≌△BDE 。

(免费)2010年部分省市中考数学试题分类汇编阅读理解型(含答案)

2010年部分省市中考数学试题分类汇编阅读理解型15．（2010年浙江省东阳县）阅读材料，寻找共同存在的规律：有一个运算程序a ⊕b = n ，可以使：（a+c ）⊕b= n+c ，a ⊕（b+c ）=n －2c ，如果1⊕1=2，那么2010⊕2010 = ．【关键词】阅读理解【答案】-200722．（2010年山东省青岛市）某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y （件）与销售单价x （元）之间的关系可近似的看作一次函数：10500y x =-+．（1）设李明每月获得利润为w （元），当销售单价定为多少元时，每月可获得最大利润？（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？（成本＝进价×销售量）【关键词】函数的应用【答案】解：（1）由题意，得：w = (x －20)·y=(x －20)·(10500x -+) 21070010000x x =-+-352b x a=-=.答：当销售单价定为35元时，每月可获得最大利润． ········ 3分（2）由题意，得：210700100002000x x -+-= 解这个方程得：x 1 = 30，x 2 = 40．答：李明想要每月获得2000元的利润，销售单价应定为30元或40元. ···· 6分（3）法一：∵10a =-<0，∴抛物线开口向下. ∴当30≤x ≤40时，w ≥2000． ∵x ≤32， ∴当30≤x ≤32时，w ≥2000．设成本为P （元），由题意，得： 20(10500)P x =-+ 20010000x =-+ ∵200k =-<0，∴P 随x 的增大而减小.∴当x = 32时，P 最小＝3600.答：想要每月获得的利润不低于2000元，每月的成本最少为3600元．1．（2010年浙江省东阳市）阅读材料，寻找共同存在的规律：有一个运算程序a ⊕b = n ，法二：∵10a =-<0， ∴抛物线开口向下. ∴当30≤x ≤40时，w ≥2000． ∵x ≤32，∴30≤x ≤32时，w ≥2000． ∵10500y x =-+，100k =-<， ∴y 随x 的增大而减小. ∴当x = 32时，y 最小＝180. ∵当进价一定时，销售量越小，成本越小，∴201803600⨯=（元）.可以使：（a+c ）⊕b= n+c ，a ⊕（b+c ）=n －2c ，如果1⊕1=2，那么2010⊕2010 = ▲ ．关键词：阅读理解答案：-20071、（2010年宁波市）《几何原本》的诞生，标志着几何学已成为一个有着严密理论系统和科学方法的学科，它奠定了现代数学的基础，它是下列哪位数学家的著作（） A 、欧几里得 B 、杨辉 C 、费马 D 、刘徽【关键词】数学阅读知识【答案】A(2010年浙江省绍兴市)在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形, 叫做此一次函数的坐标三角形.例如，图中的一次函数的图象与x ,y 轴分别交于点A ,B ,则△OAB 为此函数的坐标三角形.（1）求函数y ＝43-x ＋3的坐标三角形的三条边长；（2）若函数y ＝43-x ＋b （b 为常数）的坐标三角形周长为16求此三角形面积.【答案】解：(1) ∵ 直线y ＝43-x ＋3与x 轴的交点坐标为（4,0），与y 轴交点坐标为（0,3）， ∴函数y ＝43-x ＋3的坐标三角形的三条边长分别为3,4,5. (2) 直线y ＝43-x ＋b 与x 轴的交点坐标为（b 34,0），与y 轴交点坐标为（0,b ），当b >0时,163534=++b b b ，得b =4，此时,坐标三角形面积为332；当b <0时，163534=---b b b ，得b =－4，此时,坐标三角形面积为332.综上,当函数y ＝43-x ＋b 的坐标三角形周长为16时,面积为332．2010年益阳市）我们把对称中心重合，四边分别平行的两个正方形之间的部分叫“方形环”，易知方形环四周的宽度相等．．．．. 一条直线l 与方形环的边线有四个交点M 、'M 、'N 、N ．小明在探究线段'MM 与N N ' 的数量关系时，从点'M 、'N 向对边作垂线段E M '、F N '，利用三角形全等、相似及锐角三角函数等相关知识解决了问题．请你参考小明的思路解答下列问题： ⑴当直线l 与方形环的对边相交时（如图18-），直线l 分别交AD 、D A ''、C B ''、BC 于M 、'M 、'N 、N ，小明发现'MM 与N N '相等，请你帮他说明理由； ⑵当直线l 与方形环的邻边相交时（如图28-），l 分别交AD 、D A ''、C D ''、DC于M 、'M 、'N 、N ，l 与DC 的夹角为α，你认为'MM 与N N '还相等吗？若相等，说明理由；若不相等，求出NN MM ''的值（用含α的三角函数表示）.第21题图【关键词】正方形性质、相似三角形、三角函数值【答案】⑴解: 在方形环中，∵AD BC F N AD E M ,',⊥⊥'∥BC ∴NF N M EM FN N EM M F N E M ',90','∠='∠=∠='∠='︒ ∴△E MM '≌△F NN '∴N N M M '='⑵解法一：∵α='∠='∠︒='∠='∠M M E N FN M ME N NF ,90 ∴N NF '∆∽EM M '∆ ∴NF EM N N M M '='' ∵F N E M '='∴αtan ''='=NF F N N N MM （或ααcos sin ） ①当︒=45α时，tan α=1,则N N M M '=' ②当︒≠45α时，N N M M '≠'则 αtan =''N N M M （或ααcos sin ）解法二：在方形环中，︒=∠90D又∵CD F N AD E M ⊥⊥'', ∴E M '∥E M F N DC '=', ∴α=∠='∠NF N E M M ' 在F N N Rt '∆与E M M Rt '∆中， MM EM N N F N ''='=ααcos ,'sin N N M M E M M M N N F N ''=''⋅'=='cos sin tan ααα 即 αtan =''N N M M （或ααcos sin ）B18-图28-图①当︒=45α时，N N M M '=' ②当︒≠45α时，N N M M '≠'则 αtan =''N N M M （或ααcos sin ）。

2010年部分省市中考数学试题分类汇编(共28专题)统计

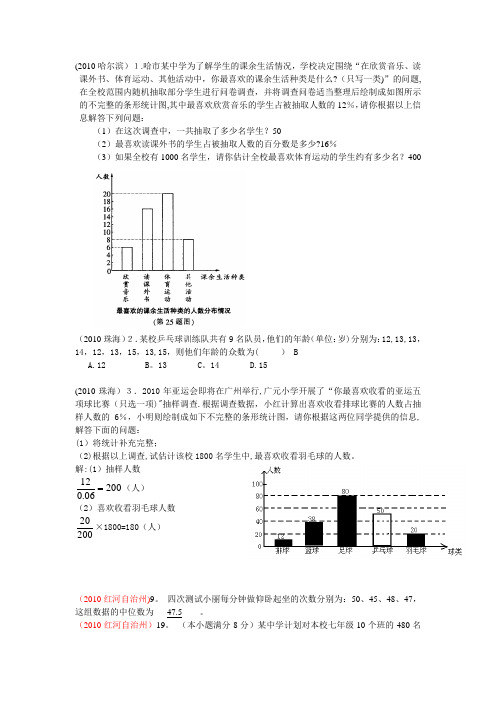
(2010哈尔滨）１.哈市某中学为了解学生的课余生活情况，学校决定围绕“在欣赏音乐、读课外书、体育运动、其他活动中，你最喜欢的课余生活种类是什么?（只写一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查，并将调查问卷适当整理后绘制成如图所示的不完整的条形统计图,其中最喜欢欣赏音乐的学生占被抽取人数的12％，请你根据以上信息解答下列问题：（1）在这次调查中，一共抽取了多少名学生？50（2）最喜欢读课外书的学生占被抽取人数的百分数是多少?16％（3）如果全校有1000名学生，请你估计全校最喜欢体育运动的学生约有多少名？400（2010珠海）２．某校乒乓球训练队共有9名队员，他们的年龄（单位：岁)分别为：12,13,13，14，12，13，15，13,15，则他们年龄的众数为( ） B A.12 B 。

13 C 。

14 D.15(2010珠海）３．2010年亚运会即将在广州举行,广元小学开展了“你最喜欢收看的亚运五项球比赛（只选一项)"抽样调查.根据调查数据，小红计算出喜欢收看排球比赛的人数占抽样人数的6％，小明则绘制成如下不完整的条形统计图，请你根据这两位同学提供的信息,解答下面的问题： (1）将统计补充完整；（2)根据以上调查,试估计该校1800名学生中,最喜欢收看羽毛球的人数。

解:(1）抽样人数20006.012（人）（2）喜欢收看羽毛球人数20020×1800=180（人）（2010红河自治州)9。

四次测试小丽每分钟做仰卧起坐的次数分别为：50、45、48、47，这组数据的中位数为___47.5____。

（2010红河自治州）19。

（本小题满分8分）某中学计划对本校七年级10个班的480名学生按“学科”、“文体"、“手工”三个项目安排课外兴起小组,小组小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下所示的表和图7.（1)请将统计表、统计图补充完整；(2)请以小明的统计结果来估计该校七年级480图7图7项目手工文体学科学生人数51015202530解：（1）统计表、统计图补充如上;（2）七年级480名学生参加个项目人数约为:学科:480×50%=240（人）文体:480×20％=96(人）手工:480×30%=144（人)答：该校七年级480名学生参加“学科"、“文体”、“手工"三个项目的人数分别约为240人，96人,144人.(2010年镇江市）6．一组数据按从小到大顺序排列为:3,5,7,8,8，则这组数据的中位数是 7 ，众数是 8 。

2010年各地中考数学试题分类选编(中)

字是（
）
工Ａ
Ｂ
Ａ上
Ｂ海．Ｃ世．
Ｄ．博
第２题图１
第１题图５
■，． ● 主视． ● ●● ２．湛江）察下列几何体－ｔ一图、视２（观左
１．临沂）图，面几何体的俯视图６（如下
ＡＢ
Ｏ／，
Ａ．－ａ。６（一）Ｂ（ａ，６１．－一一）Ｃ．－ａ，６１（一＋）Ｄ．－ａ，６２（一 — ）
第４图题
２（．天津）列图形中，可以看做是轴对下既称图形，可以看做是中心对称图形的又
ｌｍｃ
）
第９图题
口
１．兰州）察下列银行标志，０（观从是轴对称图形又是中心对称图形的有
√２ｃｍ
口
第１题图４
Ｃ
第ｌ图Ｏ题
试题类编
１．连云港）图所示的几何体的左视图５（如
是（）
教
是（）
图和俯视图都是矩形的是（
）
田ｃ
③ 。目匝
第１题图６
块搭成的几何体，么这个几何体的左视图那
是（）
则该几何体
Ｄ．４个）
１．昆明）右图是某个几何体的三视图，１（若
邑口曲［［日日］
Ａ
第６图题
△棱ＢＢ．柱三
的体验．

(免费)2010年部分省市中考数学试题分类汇编点线面角(含答案)

（第3题）2010年部分省市中考数学试题分类汇编点、线、面、角1．(2010年福建晋江) 附加题：若︒=∠35A ，则A ∠的余角等于度. 答案：552010年广东省广州市）将图1所示的直角梯形绕直线l 旋转一周，得到的立体图开是（）lA ．B ．C ．D ．图1 【关键词】面动成体【答案】C2．（2010年浙江台州市）如图，△ABC 中，∠C =90°，AC =3，点P 是边BC 上的动点，则AP 长不可能．．．是(▲) A ．2.5 B ．3 C ．4 D ．5 【关键词】点到直线的距离【答案】A3．（2010年益阳市）如图3，已知△ABC ，求作一点P ，使P 到∠A 的两边的距离相等，且P A ＝PB ．下列Ａ．P 为∠A 、∠B 两角平分线的交点Ｂ．P 为∠A 的角平分线与AB 的垂直平分线的交点Ｃ．P 为AC 、AB 两边上的高的交点Ｄ．P 为AC 、AB 两边的垂直平分线的交点【关键词】角平分线、垂直平分线、三角形的高【答案】B4.（2010年台湾省）如图(十二)，直线CP 是AB 的中垂线且交AB 于P ，其中AP =2CP 。

甲、乙两人想在AB 上取两点D 、E ，使得AD =DC =CE =EB ，其作法如下：(甲) 作∠ACP 、∠BCP 之角平分线，分别交AB 于D 、E ，则D 、E 即为所求(乙) 作AC 、BC 之中垂线，分别交AB 于D 、E ，则D 、 E 即为所求对于甲、乙两人的作法，下列判断何者正确？ABCP 图(十二)AB3图(A) 两人都正确 (B) 两人都错误 (C) 甲正确，乙错误 (D) 甲错误，乙正确。

【关键词】垂线【答案】D5、（2010年宁波）《几何原本》的诞生，标志着几何学已成为一个有着严密理论系统和科学方法的学科，它奠定了现代数学的基础，它是下列哪位数学家的著作（） A 、欧几里得 B 、杨辉 C 、费马 D 、刘徽答案：A4. (金华)下图所示几何体的主视图是（ ▲ ） A . B . C . D .正面。

2010年中考数学试题汇编之相似

中考试题专题之——相似形一、选择题1．如图所示，给出下列条件：①B ACD ∠=∠；②ADC ACB ∠=∠；③AC ABCD BC=；④2AC AD AB = ．其中单独能够判定ABC ACD △∽△的个数为（）A ．1B ．2C ．3D ．42.如图，已知AB CD EF ∥∥，那么下列结论正确的是（） A ．AD BCDF CE= B ．BC DFCE AD= C ．CD BCEF BE= D ．CD ADEF AF=3.已知△ABC∽△DEF，且AB ：DE=1：2，则△ABC 的面积与△DEF 的面积之比为（） (A)1：2 (B)1：4 (C)2：1 (D)4：14. 如图，已知等边三角形ABC 的边长为2，DE 是它的中位线，则下面四个结论：（1）DE=1，（2）△CDE ∽△CAB ，（3）△CDE 的面积与△CAB 的面积之比为1：4.其中正确的有：( ) A ．0个 B ．1个 C ．2个D ．3个5.如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3和4及x ，那么x 的值（）A 只有1个 B 可以有2个 C 有2个以上但有限D ．有无数个6. 小明在一次军事夏令营活动中，进行打靶训练，在用枪瞄准目标点B 时，要使眼睛O 、准星A 、目标B 在同一条直线上，如图4所示，在射击时，小明有轻微的抖动，致使准星A 偏离到A ′，若OA=0.2米，OB=40米，AA ′=0.0015米，则小明射击到的点B ′偏离目标点B 的长度BB ′为 ( ）A ．3米B ．0.3米C ．0.03米 D ．0.2米7.如图，在ABC △中，C ∠9060B D =∠=°，°，是AC 上一点，DE AB ⊥于E ，且21CD DE ==，，则BC 的长为（）A ．2 B ．433C ．23D ．43 8.在ABC △和DEF △中，22AB DE AC DF A D ==∠=∠，，，如果ABC △的周长是16，面积是12，那么DEF △的周长、面积依次为（）A ．8，3B ．8，6C ．4，3D ４，6①1A ∠=∠，②CD DBAD CD=，③290B ∠+∠=°，④345BC AC AB =∶∶∶∶，⑤ CD AC BD AC ∙=∙A ．1 B ．2 C ．3 D ．410. 在△ABC 中，AB =12，AC =10，BC =9，AD 是BC 边上的高.将△ABC 按如图所示的方式折叠，使点A 与点D 重合，折痕为EF ，则△DEF 的周长为( ) A ．9.5 B ．10.5 C ．11 D ．15.511.如图，△ABC 中，A ，B 两个顶点在x 轴的上方，点C 的坐标是(-1，0)．以点C 为位似中心，在x 轴的下方作△ABC 的位似图形，并把△ABC 的边长放大到原来的2倍，记所得的像是△A ′B ′C ．设点B 的对应点B ′的横坐标是a ，则点B 的横坐标是( )A ．12a -B ．1(1)2a -+C ．1(1)2a -- D ．1(3)2a -+12.如图，在长为8 cm 、宽为4 cm 的矩形中，截去一个矩形，使得留下的矩形（图中阴影部分）与原矩形相似，则留下矩形的面积是（）A. 2 cm 2 B. 4 cm 2 C. 8 cm 2 D. 16 cm213. 若一个图形的面积为2，那么将它与成中心对称的图形放大为原来的两倍后的图形面积为（）A. 8 B. 6 C. 4 D. 2 14.如图，正方形ABCD 中，E 为AB 的中点，AF ⊥DE 于点O ，则DOAO等于（） A ．352 B ．31 C ．32 D ．21 15.如图，在正三角形ABC 中，D ，E ，F 分别是BC ，AC ，AB 上的点，DE AC ⊥，EF AB ⊥，FD BC ⊥，则DEF △的面积与ABC △的面积之比等于（）A ．1∶3B ．2∶3C ．3∶2D ．3∶316．如图，AB 是O ⊙的直径，AD 是O ⊙的切线，点C 在O ⊙上，BC OD ∥，23AB OD ==，,则BC 的长为（） A ．23B ．32 C 32 D ．2217．如图，在Rt ABC △中，90ACB ∠=°，3BC =，4AC =，AB 的垂直平分线DE 交BC 的延长线于点E ，则CE 的长为（）A ．32 B ．76C ．D ．2 18. 如图，AB 是O ⊙的直径，点C 在圆上，CD AB DE BC ⊥，∥，则图中与ABC △相似的三角形的个数有（）CBDO AE二、填空题1.锐角△ABC 中，BC ＝6,,12=∆ABC S 两动点M 、N 分别在边AB 、AC 上滑动，且MN ∥BC ，以MN 为边向下作正方形MPQN ，设其边长为x ，正方形MPQN 与△ABC 公共部分的面积为y （y ＞0）,当x ＝，公共部分面积y 最大，y 最大值＝ ,2.在平面直角坐标系中，ABC △顶点A 的坐标为(23)，，若以原点O 为位似中心，画ABC△的位似图形A B C '''△，使ABC △与A B C '''△的相似比等于12，则点A '的坐标为． 3.如图，OAB △的顶点B 的坐标为（4，0），把OAB △沿x 轴向右平移得到CDE △，如果1,CB =那么OE 的长为．4.如图，ABC △与AEF △中，AB AE BC EF B E AB ==∠=∠，，，交EF 于D ．给出下列结论：①AFC C ∠=∠；②D F C F =；③A D E F D B △∽△；④BFD CAF ∠=∠．其中正确的结论是（填写所有正确结论的序号）．5.如图，点M 是△ABC 内一点，过点M 分别作直线平行于△ABC 的各边，所形成的三个小三角形△1、△2、△3（图中阴影部分）的面积分别是4，9和49．则△ABC 的面积是．6.Rt ABC △中，90ACB ∠=°，直线EF BD ∥，交AB 于点E ，交AC 于点G ，交AD 于点F ，若13AEG EBCG S S =△四边形，则CFAD= ． 7. 已知A B C A B '''△∽△且1:2ABC A B C S S '''=△△:，则:A B A B ''= ．8.在□ABCD 中，E 在DC 上，若:1:2DE EC =，则:BF BE = ．三、解答题1.如图，在矩形A B C D 中，点E F 、分别在边A D D C 、上，A B E D E F △∽△，692AB AE DE ===，，，求EF 的长．2．如图，在ABCD中，32BAD ∠=°，分别以BC CD 、为边向外作BCE △和DCF △，使BE BC DF DC EBC CDF ==∠=∠，，．延长AB 交边EC 于点H ，点H 在E C 、两点之间，连结AE AF 、．（1）求证：ABE FDA △≌△．（2）当A E A F ⊥时，求EBH ∠的度数．3.如图，M 为线段AB 的中点，AE 与BD 交于点C ，∠DME ＝∠A ＝∠B ＝α，且DM 交AC 于F ，ME 交BC 于G ．（1）写出图中三对相似三角形，并证明其中的一对；（2）连结FG ，如果α＝45°，AB ＝42，AF ＝3，求FG 的长．4.如图，△ABC 内接于⊙O ，AD 是△ABC 的边BC 上的高，AE 是⊙O 的直径，连接BE ，△ABE 与△ADC 相似吗？请证明你的结论．5.如图，已知抛物线与x交于A(－1，0)、E(3，0)两点，与y轴交于点B(0，3)。

2010中考数学试题分类汇编--相似

2010中考数学试题分类汇编--相似（2010哈尔滨）1 .已知：在△ ABC中AB = AC,点D为BC边的中点，点F是AB边上一点，点E在线段DF 的延长线上，/ BAE =Z BDF，点M在线段DF上，/ ABE = Z DBM .（1）如图1，当/ ABC = 45° 时，求证：AE = 2 MD ;（2）如图2，当/ ABC = 60°时，则线段AE、MD之间的数量关系为： _____________________ 。

（3）在（2）的条件下延长BM到P,使MP= BM，连接CP，若AB = 7, AE = 2 7 ,求tan/ ACP的值.（2010珠海）2 .如图，在平行四边形ABCD中,过点A作AE丄BC垂足为E,连接DE, F为线段DE上一点，且/ AFE=/ B.(1) 求证：△ ADF^A DEC(2) 若AB= 4,AD = 3 .3,AE = 3,求AF 的长.(1) 证明：•••四边形ABCD是平行四边形••• AD// BC AB // CD•••/ ADF=/ CED / B+/ C=180°•// AFE+/ AFD=180 / AFE=/ B•••/ AFD=/ C• △ADF^A DEC⑵解：•••四边形ABCD是平行四边形• AD// BC CD=AB=4又••• AE丄BC • AE 丄AD在Rt △ ADE中, DE=.、AD2 AE2二,(3 .. 3)2 32 =6•/△ADF^A DECAD AF.3、.3 _ AF—rtr—z. v aDE CD64C旁边一颗树在阳光下”十青（2010珠海）3。

一天，小青在校园内发现：的影子和她本人的影子在同一直线上，树顶的影子和她头顶的影子恰好落在地面的同一点，同时还发现她站立于树影的中点（如图所示）•如果小青的峰高为1.65米，由此可推断出树高是____________ 米.3.3（2010年兰州）19.如图，上体育课，甲、乙两名同学分别站在 C D的位置时，乙的影子恰好在甲的影子里边，已知甲，乙同学相距1米.甲身高1.8米，乙身高1.5米，则甲的影长是____________ 米.答案6（2010宁波市）26.如图1,在平面直角坐标系中，0是坐标原点，口ABCD的顶点A的坐标为（一2, 0）, 点D的坐标为（0, 2羽），点B在x轴的正半轴上，点E为线段AD的中点，过点E的直线I与x轴交于点F，与射线DC交于点G.（1）求/ DCB的度数；（2）当点F的坐标为（一4, 0）,求点的坐标；（3）连结0E,以0E所在直线为对称轴，△ OEF经轴对称变换后得到△ OEF '，记直线EF '与射线DC 的交点为H.①如图2,当点G在点H的左侧时，求证：△ DEG DHE ;②△若EHG的面积为3 ,3,请你直接写出点F的坐标24. （2010年金华）（本题12分）与厶ABC的面积比为(BA . 1: 2B.1:C. 2: 1D. 4:（桂林2010）6.如图，已知△（罠"【件厠图）如图，把含有30。

(免费)2010年部分省市中考数学试题分类汇编_分式与分式方程(含答案)

2010年部分省市中考数学试题分类汇编分式与分式方程11．（2010年山东省青岛市）某市为治理污水，需要铺设一段全长为300 m 的污水排放管道．铺设120 m 后，为了尽量减少施工对城市交通所造成的影响，后来每天的工效比原计划增加20%，结果共用30天完成这一任务．求原计划每天铺设管道的长度．如果设原计划每天铺设m x 管道，那么根据题意，可得方程．【关键词】分式方程【答案】()()12030012030120%120180301.2x xxx-+=++=或7．（2010年益阳市）货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x 千米/小时,依题意列方程正确的是Ａ．203525-=x x Ｂ．x x 352025=- Ｃ．203525+=x x Ｄ．xx 352025=+【关键词】分式方程【答案】C（2010年广东省广州市）已知关于x 的一元二次方程)0(012≠=++a bx ax有两个相等的实数根，求4)2(222-+-b a ab的值。

【关键词】分式化简，一元二次方程根的判别式【答案】解：∵)0(012≠=++a bx ax有两个相等的实数根，∴⊿＝240b ac -=，即240b a -=． ∵2222222222244444)2(aab ba a abb a a abb a ab=+-=-++-=-+-∵0a ≠，∴4222==ab aab21．(2010重庆市)先化简，再求值：（x 2＋4x －4）÷ x 2－4x 2＋2x，其中x ＝－1解：原式=4244222-+⋅+-x x x xx x =)2)(2()2()2(2-++⋅-x x x x xx =2-x当x ＝－1时，原式=2-x =-1.6．（2010江苏泰州，6，3分）下列命题：①正多边形都是轴对称图形；②通过对足球迷健康状况的调查可以了解我国公民的健康状况；③方程1312112-=+--x x x 的解是0=x ；④如果一个角的两边与另一个角的两边分别平行，那么这两个角相等．其中真命题的个数有（）A.1个B.2个C.3个D.4个【答案】B 【关键词】轴对称与中心对称随机抽样分式方程的解法简单的推理21．(2010重庆市)先化简，再求值：（x 2＋4x －4）÷ x 2－4x 2＋2x，其中x ＝－1解：原式=4244222-+⋅+-x x x xx x =)2)(2()2()2(2-++⋅-x x x x xx =2-x当x ＝－1时，原式=2-x =-1.3.（2010年福建省晋江市）先化简，再求值：x x x x x x11132-⋅⎪⎭⎫ ⎝⎛+--，其中22-=x【关键词】分式运算、化简求值【答案】解一：原式=()()()()()()x x x x x x x x x x 111111132-⋅⎥⎦⎤⎢⎣⎡+---+-+ =()()xxx x xxx x11133222-⋅+-+-+=()()xxx x xx1114222-⋅+-+=()()()()()xx x x x x x 111122-+⋅+-+=()22+x 当22-=x 时，原式=()2222+-=22解二：原式=xx x x xx x x 1111322-⋅+--⋅-= ()()()()xx x x xxx x x x 1111113+-⋅+-+-⋅-= ()()113--+x x = 133+-+x x =42+x 当22-=x 时，原式=224+）=224.（2010年辽宁省丹东市）进入防汛期后，某地对河堤进行了加固．该地驻军在河堤加固的工程中出色完成了任务．这是记者与驻军工程指挥官的一段对话:【关键词】分式方程的实际应用【答案】解：设原来每天加固x 米，根据题意，得926004800600=-+xx ．去分母，得 1200+4200=18x （或18x =5400）解得 300x =．检验：当300x =时，20x ≠（或分母不等于0）． ∴300x =是原方程的解．答：该地驻军原来每天加固300米．通过这段对话,请你求出该地驻军原来每天加固的米数.。

(免费)2010年部分省市中考数学试题分类汇编频数与频率(含答案)

频数分布直方图2010年部分省市中考数学试题分类汇编频数与频率1．（2010山东德州）为了了解某校九年级学生的体能情况，随机抽查了其中50名学生，测试1分钟仰卧起坐的成绩（次数），进行整理后绘制成如图所示的频数分布直方图（注：15~20包括15，不包括20，以下同），请根据统计图计算成绩在20~30次的频率是（A ）0.4（B ）0.5 （C ）0.6 （D ）0.7【关键词】频率、频数分布直方图【答案】D1.（2010年台湾省）自连续正整数10~99中选出一个数，其中每个数被选出的机会相等。

求选出的数其十位数字与个位数字的和为9的机率为何？ (A)908 (B) 909 (C) 898 (D) 899 【关键词】频率【答案】B1. (2010重庆市潼南县)根据市教委提出的学生每天体育锻炼不少于1小时的要求，为确保阳光体育运动时间得到落实，某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查，其中部分结果记录如下：频数分布表：请你将频数分布表和频数分布直方图补充完整.5.2频数分布直方图题图20 第6题图2. (2010年福建晋江)某校为了了解九年级女生的体能情况，随机抽查了部分女生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图和不完整的统计表（每个分组包括左端点，不包括右端点）. 请你根据图中提供的信息,解答以下问题: (1) 分别把统计图与统计表补充完整；位数”，请你写出小敏仰卧起坐次数所在的范围.(3)若年段的奋斗目标成绩是每个女生每分钟23次，问被抽查的所有女生的平均成绩是否达到奋斗目标成绩？解: (1) 5 ，52…………………………………………（2分）补图正确得2分. ………………………………………（4分） (2) 25~30.………………………………………………（7分） (3) 被抽查的所有女生的平均成绩至少是：2.233053012251020315≈⨯+⨯+⨯+⨯(次) ………………（9分）∵23.2>23∴被抽查的所有女生的平均成绩达到奋斗目标成绩. …………（10分）3. (2010浙江衢州)黄老师退休在家，为选择一个合适的时间参观2010年上海世博会，他查阅了5月10日至16日(星期一至星期日)每天的参观人数，得到图1、图2所示的统计图，其中图1是每天参观人数的统计图，图2是5月15日(星期六)这一天上午、中午、下午和晚上四个时间段参观人数的扇形统计图．请你根据统计图解答下面的问题： (1) 5月10日至16日这一周中，参观人数最多的是哪一天？有多少人？参观人数最少的又是哪一天？有多少人？(2) 5月15日(星期六)这一天，上午的参观人数比下午的参观人数多多少人 (精确到1万人)？ (3) 如果黄老师想尽可能选择参观人数较少的时间去参观世博会，你认(次)(次)为他选择什么时间比较合适？解：(1) 参观人数最多的是15日(或周六)，有34万人； ……2分参观人数最少的是10日(或周一)，有16万人． ……2分 (2) 34×(74%-6%)=23.12≈23．上午参观人数比下午参观人数多23万人． ……2分 (3) 答案不唯一，基本合理即可，如选择星期一下午参观等． ……2分4.（2010年日照市）为增强学生的身体素质，教育行政部门规定学生每天参加户外活动的平均时间不少于1小时。

2010年各地中考数学试题分类选编(下)

ｌ．南京）图，晚，１（如夜小亮从点Ａ经过路灯Ｃ的正下方沿直线走到点Ｂ，的影长Ｙ随他他与点Ａ之间的距离．ｚ的变化而变化，么表那１：桂林）图，５（如已知正方形ＡＢＤ的边长Ｃ为４Ｅ是Ｂ，Ｃ边上的一个动点ＡＥ上ＥＥＦ，Ｆ交ＤＣ于Ｆ，Ｂ＝ｘ，Ｃ，当点Ｅ从点Ｂ运动设ＥＦ＝ｙ则
水航行到乙地，乙地停留一段时间后，在又从乙）
１（．北京）二次函数 — 一２＋３化为将ｚ
一
（一矗）十足的形式，果为（结
Ａ．＝（＝＋１＋４Ｂ．＝（～１＋４＝）＝＝）Ｃ．一（＋１＋２Ｄ．一（～１。２））＋
＋ｃＯ（．
Ｉ
ｔ
．／
。Ｚ￣
。
其中，确结论的个数正
第４图题
ＡＢＣＤ
试ｌ匿蕙
— —
试题类编
８（．陕西）已知抛物线Ｃ：２＋３１，一．Ｃｘ一Ｏ
将抛物线Ｃ平移得到抛物线Ｃ．两条抛物线若Ｃ、于直线一１对称，下列平移方法中，Ｃ关则
地逆水航行返回到甲地．轮船从甲地出发后设
所用时间为ｆｈ，（）航行的路程为ｓｋ，ｓ（ｍ）则与ｔ函数图象大致是（的）
２（海）平面直角坐标系中，比例函．上在反

2010年部分省市中考数学试题分类汇编-图形的相似与位似(含答案)

20XX 年部分省市中考数学试题分类汇编图形的相似与位似1. （20XX 年福建省德化县）如图，小“鱼”与大“鱼”是位似图形，如果小“鱼”(a, b)，那么大“鱼”上对( )E 、( 2a , b) D 、(2b, 2a)【关键词】位似中心是原点的坐标之间的关系（若相似比为则坐标之比同侧为 k 异侧为-k ）【答案】C2.（ 2010江苏泰州，）一个铝质三角形框架三条边长分别为24cm 、30cm 、36cm ,要做一个与它相似的铝质三角形框架，现有长为27cm 、45cm 的两根铝材，要求以其中的一根为一边，从另一根上截下两段（允许有余料）作为另外两边.截法有（）A.0种B. 1 种C. 2 种D. 3 种【答案】B【关键词】相似三角形的判定3. （20XX 年宁德市）如图，在口 ABCD 中，AE = EB AF = 2,贝U FC 等于 ______ .【答案4】5.（2010福建泉州市惠安县）两个相似三角形的面积比是 9:16，则这两个三角形的相似比是（）A.9:16B. 3:4C.9: 4D.3:16【关键词】相似三角形的性质【答案】B6. （20XX 年兰州市）如图，上体育课，甲、乙两名同学分别站在C 、D 的位置时，乙的影子恰好在甲的影子里边, 的影长是米.【关键词】图形的相似上一个"顶点”的4. （20XX 年台湾省）图（一）表示D 、E 、F 、G 四点在△ABC 三边上的位置，其中交于H 点。

若 ABC= 一组三角形相似？（A ） △ BDG , △ CEF （C ） △ ABC , △ BDG 【关键词】相似【答案】BEFC=70 , (B) △ ABC , △ CEF (D) △ FGH , △ ABC 。

DG 与 EFB【答案】6已知甲，乙同学相距1米.甲身高1.8米，乙身高1.5米，则甲7. （2010辽宁省丹东市）如图，△ ABC与厶ABC是位似图形，且位似比是1: 2，若AB=2cm,则A B cm并在图中画出位似中心O.【关键词】位似【答案】.4 （填空2分，画图1分）& （20XX年安徽省芜湖市）如图，光源P在横杆AB的正上方，AB在灯光下的影子为CD , AB// CD, AB = 2m, CD = 6m，点P至U CD的距离是2.7m，贝U AB与CD间的距离是 _________ m ./ \tZ ----------------------- D筒13世圏【关键词】投影相似三角形【答案】1.89. （2010重庆市）已知△ ABC与厶DEF相似且对应中线的比为2:3，则△ ABC与厶DEF的周长比为_______________ .解析：由相似三角形的对应线段比等于相似比知，△ABC与厶DEF的周长比为2:3答案：2: 3.10. （2010山东德州）如图，小明在A时测得某树的影长为2m, B时又测得该树的影长为8m,若两次日照的光线互相垂直，则树的高度为________ m.第14题图【关键词】三角形相似【答案】411. （2010重庆潼南县）12. △ ABC与厶DEF的相似比为3: 4,则厶ABC与厶DEF的周长第11题图比为____________ .答案：3: 412. （2010重庆市潼南县）△ ABC 与厶DEF 的相似比为 3: 4，则△ ABC 与厶DEF 的周长比答案：3:4.13.. （2010浙江衢州）如图，方格纸中每个小正方形的边长为〔，△ ABC 和厶DEF的顶点都在方格纸的格点上.（1）判断△ ABC 和厶DEF 是否相似，并说明理由；（2） P 1 , P 2, P 3, P 4, P 5, D , F 是厶DEF 边上的7个格点，请在这 7个格点中选取 3 个点作为三角形的顶点，使构成的三角形与△ABC 相似（要求写出2个符合条件的三角形，并在图中连结相应线段，不必说明理由）•14. （2010江西）图1所示的遮阳伞，伞炳垂直于水平地面，起示意图如图2•当伞收紧时，点P 与点A 重合；当三慢慢撑开时，动点 P 由A 向B 移动；当点P 到达点B 时，伞张得最开。

2010中考数学试题分类汇编-相似

年中考数学试题分类汇编——相似（哈尔滨）１．已知：在△中＝，点为边的中点，点是边上一点，点在线段的延长线上，∠＝∠，点在线段上，∠＝∠．（）如图，当∠＝°时，求证：＝2；（）如图，当∠＝°时，则线段、之间的数量关系为：。

（）在（）的条件下延长到，使＝，连接，若＝，＝72，求∠的值．（珠海）２．如图，在平行四边形中，过点作⊥，垂足为，连接，为线段上一点，且∠＝∠. (1) 求证：△∽△(2) 若＝＝3＝,求的长. （）证明：∵四边形是平行四边形 ∴∥ ∥∴∠∠ ∠∠° ∵∠∠ ∠∠ ∴∠∠ ∴△∽△()解：∵四边形是平行四边形 ∴∥又∵⊥ ∴ ⊥ 在△中，63)33(2222=+=+AE AD∵△∽△ ∴ CDAFDE AD =∴4633AF = 32（珠海）３。

一天，小青在校园内发现：旁边一颗树在阳光下的影子和她本人的影子在同一直线上，树顶的影子和她头顶的影子恰好落在地面的同一点，同时还发现她站立于树影的中点（如图所示）.如果小青的峰高为米，由此可推断出树高是米.（桂林）．如图，已知△与△的相似比为：，则△ 与△的面积比为（）．．：．：．：．：（年兰州）. 如图，上体育课，甲、乙两名同学分别站在、的位置时，乙的影子恰好在甲的影子里边，已知甲，乙同学相距米.甲身高米，乙身高米，则甲的影长是米. 答案（宁波市）．如图，在平面直角坐标系中，是坐标原点，□的顶点的坐标为（－，），点的坐标为（，），点在轴的正半轴上，点为线段的中点，过点的直线与轴交于点，与射线交于点．（）求∠的度数；（）当点的坐标为（－，），求点的坐标；（）连结，以所在直线为对称轴，△经轴对称变换后得到△′，记直线′与射线的交点为．① 如图，当点在点的左侧时，求证：△≌△； ② △若的面积为，请你直接写出点的坐标. （年金华）(本题分)AD E B C如图，把含有°角的三角板置入平面直角坐标系中，，两点坐标分别为（，）和(，.(长度单位秒)﹒一直尺的上边缘从轴的位置开始以 (长度单位秒)的速度向上平行移动（即移动过程中保持∥轴），且分别与，交于，两点﹒设动点与动直线同时出发，运动时间为秒，当点沿折线运动一周时，直线和动点同时停止运动．请解答下列问题：（）过，两点的直线解析式是 ▲ ；（）当﹦时，点的坐标为 ▲ ；当 ﹦ ▲ ，点与点重合；（）① 作点关于直线的对称点′. 在运动过程中，若形成的四边形′为菱形，则的值是多少？② 当﹦时，是否存在着点，使得△请说明理由．解：（）333+-=x y ；………分（）（,3（）①当点P 在线段AO 上时，过F 作FG ⊥x 轴，G 为垂足（如图） ∵FG OE =,FP EP =,∠=EOP ∠=FGP ° ∴△EOP ≌△FGP ，∴PG OP =﹒又∵t FG OE 33==,∠=A °,∴t FG AG 3160tan 0== (图)而t AP =，∴t OP -=3,t AG AP PG 32=-=由t t 323=-得 59=t ；………………………………………………………………分当点在线段OB 上时，形成的是三角形，不存在菱形；当点在线段BA 上时，过作PH ⊥EF ，PM ⊥OB ，H 、M∵t OE 33=,∴t BE 3333-=,∴3360tan 0t BE EF -== ∴6921tEF EH MP -===，又∵)6(2-=t BP 在△BMP 中，MP BP =⋅060cos 即6921)6(2tt -=⋅-，解得745=t ．…………………………………………………分 ②存在﹒理由如下：∵2=t ，∴332=OE ,2=AP ，1=OP 将△BEP 绕点E 顺时针方向旋转°，得到 △EC B '（如图）∵OB ⊥EF ，∴点B '在直线EF 上，点坐标为（332，332－）过F 作FQ ∥C B '，交EC 于点,则△FEQ ∽△EC B '由3=='=QE CE FE E B FE BE ，可得的坐标为（－32，33）………………………分根据对称性可得，关于直线的对称点Q '（－32，3）也符合条件．……分．（年长沙）如图，在平面直角坐标系中，矩形的两边分别在轴和轴上，OA =，，现的速度匀速运动，在线段上沿方向以每秒的速度匀速运动．设运动时间为秒．（）用的式子表示△的面积；（）求证：四边形的面积是一个定值，并求出这个定值；（）当△与△和△相似时，抛物线214y x bx c =++经过、两点，过线段上一动点作y 轴的平行线交抛物线于，当线段的长取最大值时，求直线把四边形分成两部分的面积之比．(图)解：()∴－∴△＝21(8)22t t -=-+（＜＜）…………………分 () ∵四边形＝矩形－△－△＝1188)22⨯⨯-⨯⨯………… 分 …………分（）当△与△和△相似时, △必须是一个直角三角形，依题意只能是∠＝°又∵与不平行∴∠不可能等于∠，∠不可能等于∠∴根据相似三角形的对应关系只能是△∽△∽△………………分 8=解得：＝经检验：＝是方程的解且符合题意（从边长关系和速度）此时（，）∵（214y x bx c =++经过、两点， ∴抛物线是2184y x =-+，直线是：8y =- …………………分设（8-）、(，2184m -+)∵在上运动∴m ≤≤∵21184y x =-+与28y-交于、两点且抛物线的顶点是 ∴当m ≤≤时，12y y > ………………………………分∴12MN y y =-＝21(24m --+∴当m = 第题图∴设与交于点则M、H ∴△＝132⨯⨯∴△ ：五边形＝＝∴当取最大值时两部分面积之比是：． …………………分（年湖南郴州市）.如图，已知平行四边形ABCD ，E 是AB 延长线上一点，连结DE 交BC 于点F ，在不添加任何辅助线的情况下，请补充一个条件，使CDF BEF △≌△，这个条件是．（只要填一个）答案DC EB =或CF BF =或DF EF = 或为的中点或为的中点或AB BE =或为的中点(湖北省荆门市)．(本题满分分)如图，圆的直径为，在圆上位于直径的异侧有定点和动点，已知∶＝∶，点在半圆弧上运动(不与、重合)，过作的垂线交的延长线于点 ()求证：·＝·；()当点运动到弧中点时，求的长；()当点运动到什么位置时，△的面积最大？并求这个最大面积．答案．解：()∵为直径，∴∠＝°．又∵⊥，∴∠＝°．而∠＝∠，∴△∽△．∴AC BCCP CD=．∴·＝·；………………………………………………………………………分第题图第题FEC BB'C'()当点运动到弧中点时，过点作⊥于点． ∵是中点，∴∠＝°．又∠＝∠，∴∠＝∠＝43．∴＝tan BE CPB ∠＝3)4．由()得＝43()当点在上运动时，△＝12·．由()可知，＝43． ∴△＝23．故最大时，△取得最大值；而为直径时最大，∴△的最大值＝23×＝503．………………………………分（年眉山）．如图，△ ' ' 是由△绕点顺时针旋转得到的，连结 ' 交斜边于点， ' 的延长线交' 于点．（）证明：△∽△；（）设∠α，∠ ' β，试探索α、β满足什么关系时，△与△是全等三角形，并说明理由．答案：．（）证明：∵△ ' ' 是由△绕点顺时针旋转得到的， ∴ '， '，∠∠ ' ' ………………（分） ∴∠ '∠ '∴∠ '∠ ' ……………………………………（分）又∠∠∴△∽△ ……………………………………（分）（）解：当2βα=时，△≌△． …………………（分）在△'中，∵ '， ∴180'180'9022CAC ACC βα︒-∠︒-∠===︒- ………（分）在△中，第题图FEC BAB'C' ∠'∠°，即9090BCE α︒-+∠=︒， ∴∠α． ∵∠α，∴∠∠ ……………………（分） ∴由（）知：△∽△，∴△≌△．………………………（分）．(重庆潼南县)△与△的相似比为：，则△与△的周长比为．：、（年杭州市）如图，，，又∥，点，，在同一条直线上.() 求证：△∽△；() 如果， 22，设，求的长.答案：() ∵ ∥，点，，在同一条直线上， ∴ ∠ ∠, 又∵3==AEBDAC AB , ∴ △∽△. () ∵ ， 2 ， ∴ ， ∴∠ °, 由（）得 ∠ ∠ °, ∵31 , 31232, ， ∴在△中， ( ) (31 ) (322) 9108 ,∴ 32 .（陕西省）、如图在△中是边上一点，连接，要使△与△相似，应添加的条件是 ∠∠ ∠∠AD ACAC AB=（年天津市）（）如图，等边三角形ABC 中，D 、E 分别为AB 、BC 边上的点，AD BE =，AE 与CD 交于点F ，AG CD ⊥于点G ，则AGAF的值为．（山西．在 △中，∠＝º，若将各边长度都扩大为原来的倍，则∠的正弦值（）．扩大倍．缩小倍．扩大倍．不变（宁夏．关于对位似图形的表述，下列命题正确的是 ②③ ．（只填序号）2．相似图形一定是位似图形，位似图形一定是相似图形； 3．位似图形一定有位似中心；4．如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么，这两个图形是位似图形；5．位似图形上任意两点与位似中心的距离之比等于位似比．（宁夏．(分)已知：正方形中，、分别是边、上的点，且，与交于点．（）求证：△≌△；（）找出图中与△相似的所有三角形（不添加任何辅助线）．．()证明：在正方形中： , 且∠∠090 ∵∴ 即：在△与△中⎪⎩⎪⎨⎧=∠=∠=已证）已证）已证）(((DE AF ADE BAF DA AB ∴△≌△（）分（）与△相似的三角形有：△; △; △分（山西．在直角梯形中，∥，∠＝º，＝，＝，＝．分别以、边所在直线为轴、轴建立如图（第题） MFE D CBAM FE D C BA第（）题所示的平面直角坐标系．（）求点的坐标；（）已知、分别为线段、上的点，＝，＝，直线交轴于点．求直线的解析式；（）点是（）中直线上的一个动点，在轴上方的平面内是否存在另一个点．使以、、、为顶点的四边形是菱形？若存在，请求出点的坐标；若不存在，请说明理由．．（四川宜宾）如图，在△中，∠°，∠°，⊥于点.则△与△的周长之比为（）．︰．︰．︰．︰答案：（年安徽）.如图，已知△∽△111C B A ，相似比为k （1>k ），且△的三边长分别为a 、b 、c （c b a >>），△111C B A 的三边长分别为1a 、1b 、1c 。

2010年部分省市中考数学相似练习

2010相似分类1.（2010某某）如图，D ，E 分别是△ABC 的边AC 和BC 的中点，已知DE =2，则AB =( D )A ．1B ．2C ．3D ．42.（2010某某）在△ABC 中，D 、E 分别是边AB 、AC 的中点，若BC ＝5，则DE 的长是（A ） A ．．5C ．10D ．153.（2010某某）在△ABC 中，D 、E 分别是AB 、AC 的中点，若DE =2cm ，则BC 的长是（ C ） A ．2cm B ．3cm C ．4cm D ．5cm4.（2010某某）如图，在Rt △ABC 中，∠ACB=90°，∠A=30°，CD ⊥AB 于点D .则△BCD 与△ABC 的周长之比为（ A ）A ．1︰2B ．1︰3C ．1︰4D ．1︰55.(2010义乌)如图，将三角形纸片ABC 沿DE 折叠，使点A 落在BC 边上的点F 处，且DE ∥BC ，下列结论中，一定正确的个数是( C )①BDF ∆是等腰三角形 ②BC DE 21=③四边形ADFE 是菱形④2BDF FEC A ∠+∠=∠ A ．1B ．2C ．3D ．46.(2010某某）如图,EF 是△ABC 的中位线，将△AEF 沿中线AD 方向平移到△A 1E 1F 1的位置，使E 1F 1与BC 边重合，已知△AEF 的面积为7，则图中阴影部分的面积为（B ） A. 7 B. 14 C. 21 D. 287.（2010某某）如图，在△ABC 中，CD 是∠ACB 的平分线，∠A =80°，∠ACB=60°，那么∠BDC=（ D ） A ．80° B ．90° C ．100° D ．110°8.(2010红河)下列命题错误的是（ B ）A. 四边形内角和等于外角和B. 相似多边形的面积比等于相似比C. 点P （1,2）关于原点对称的点的坐标为（-1，-2）D. 三角形的中位线平行于第三边，且等于第三边的一半 9.（2010某某）下列命题中，是真命题的为（ D ） A .锐角三角形都相似 B .直角三角形都相似 C .等腰三角形都相似 D .等边三角形都相似10.(2010某某)如图，已知△ADE 与△ABC 的相似比为1：2，则△ADE 与△ABC 的面积比为（ B ）．A ．1：2B ．1：4C ．2：1D ．4：111. (2010黄冈)如图，过边长为1的等边△ABC 的边AB 上一点P ，作PE ⊥AC 于E ，Q 为 BC 延长线上一点，当PA ＝CQ 时，连PQ 交AC 边于D ，则DE 的长为（ B ）A ．13 B ．12 C ．23D ．不能确定12．(2010 达州 )如图，在一块形状为直角梯形的草坪中，修建了一条由A →M →N →C 的AD EB C小路（M 、N 分别是AB 、CD 中点）.极少数同学为了走“捷径”，沿线段AC 行走，破坏了草坪，实际上他们仅少走了( B )A. 7米B. 6米C. 5米D. 4米13.ABCD 沿EF 对开后，再把矩形EFCD 沿MN 对开，依此类推.若各种开本的矩形都相似，那么ABAD等于（ B ） A ．0.618 B.22C.2D.21.(2010某某)如图，在△ABC 中，AB ＝AC ＝13，BC ＝10，D 是AB 的中点，过点D 作DE ⊥AC 于点E ，则DE 的长是______________．60132.(2010某某)如图在△ABC 中D 是AB 边上一点，连接CD ，要使△ADC 与△ABC 相似，应添加的条件是 ∠ACD=∠B ∠ADC=∠AOBAD ACAC AB3.(2010某某)在△ABC 中，AB=AC=12cm ，BC=6cm ，D 为BC 的中点，动点P 从B 点出发，以每秒1cm 的速度沿B →A →C 的方向运动．设运动时间为t 秒，过D 、P 两点的直线将△ABC 的周长分成两个部分，使其中一部分是另一部分的2倍，那么t 的值为.7秒或17秒 4.（2010某某）如图，在△ABC 中，点D 、E 、F 分别是AB 、BC 、CA 的中点，若△ABC 的周长为10cm ，则△DEF 的周长是cm ．55.(2010某某)如图，在平行四边形ABCD 中，CD=10，F 是AB 边上一点，DF 交AC 于点E ，且的面积的面积则CDE AEF EC AE ∆∆=,52=，BF=.6,2546.(2010某某)如图，小明在A 时测得某树的影长为2m ，B 时又测得该树的影长为8m ，若两次日照的光线互相垂直，则树的高度为_____m.47.（2010某某）如图，△ABC 中，点D 在边AB 上，满足∠ACD =∠ABC ，若AC = 2，AD= 1，则DB = __3________.8.(2010某某)关于对位似图形的表述，下列命题正确的是．（只填序号）②③① 相似图形一定是位似图形，位似图形一定是相似图形； ② 位似图形一定有位似中心；DA BCA 时B 时③ 如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么，这两个图形是位似图形；④ 位似图形上任意两点与位似中心的距离之比等于位似比．9.(2010某某)如图，上体育课，甲、乙两名同学分别站在C 、D 的位置时，乙的影子恰好在甲的影子里边，已知甲，乙同学相距1米，乙身高10.(2010滨州)如图，A 、B 两点被池塘隔开，在AB 外取一点c ，连结AC 、BC ，在AC 上取点M ，使AM=3MC ，作MN ∥AB 交BC 于N ，量得MN=38m ，则AB 的长为____________．152m11.(2010某某)如图，梯形ABCD 中，AD ∥BC ，EF 是梯形的中位线，对角线AC 交EF于G ，若BC=10cm ，EF=8cm ，则GF 的长等于cm ．312.(2010某某)如图，在△ABC 中，AB ＝AC ＝8，AD 是底边上的高，E 为AC 中点，则DE ＝． 4GF E D CBAAE13.(2010某某) 如图，ABC △与A B C '''△是位似图形，且位似比是1:2，若AB =2cm ，则A B ''=cm ，并在图中画出位似中心O ．414．(2010 达州 )如图，△ABC 中，CD ⊥AB ，垂足为D.下列条件中，能证明△ABC 是直角三角形的有（多选、错选不得分）. ①②④①∠A+∠B=90°②222AB AC BC =+ ③AC CD AB BD=④2CD AD BD =⋅ 15．（2010某某）如图，一根直立于水平地面的木杆AB 在灯光下形成影子，当木杆绕点A 按逆时针方向旋转直至到达地面时，影子的长度发生变化.设AB 垂直于地面时的影子为AC （假定AC>AB ），影长的最大值为m.最小值为n,那么下列结论：①m>AC;②m ＝AC;③n ＝AB;④影子的长度先增大后减小. 其中，正确结论的序号是. ①③④（多填或错填的得0分，少填的酌情给分）16.（2010某某）如图，在□ ABCD 中，点E 在边BC 上，BE ：EC =1：2，连接AE 交BD 于点F ，则△BFE 的面积与△DF A 的面积之比为1：9′A BC AB C′ ′′A BC AB C′ ′ODA16.（2010某某）在同一时刻，身高的小强在阳光下的影长为，一棵大树的影长为米，则这棵树的高度为米 17.（2010某某）如果两个相似三角形的一组对应边分别为3cm 和5cm ，且较小三角形的周长为15cm ，则较大三角形的周长为__________cm ．251.(2010滨州)如图，在△ABC 和△ADE 中，∠BAD=∠CAE ，∠ABC=∠ADE 。

部分省市中考数学试题分类汇编

2010年部分省市中考数学试题分类汇编二元一次方程组及其应用16.（ 1）（ 2010年山东省青岛市）解方程组:【关键词】二元一次方程组的解法解：②X 4得：4x 4y 16，③①+③得：7x = 35 , 解得：x = 5. 把x = 5代入②得，y = 1.•••原方程组的解为根据以下对话，可以求得小红所买的笔和笔记本的价格分别是（小红，你上周买的笔和笔记本的价格是多少啊?哦，…，我忘了！只记得先后买了两次，第一次买了 5支笔和10本笔记本共花了 42元钱，第二次买了 10支笔和5本笔记本共花了 30元钱。

13. （2010江西）某班有40名同学去看演出，购买甲、乙两种票共用去 370元，其中甲种票每张 10元，乙种票每张8元，设购买了甲种票 x 张，乙种票y 张，由此可列出方程组： ________________________________________________________________________ . 【分析】根据题意可找到等量关系：甲种票数量 +乙种票数量=40,甲种票总费用+乙种票总费用=370。

【关键词】列二兀一次方程组【答案】x y 40 10x 8y 370（2010年广东省广州市）解方程组【关键词】解方程组x 2y 1 ①【答案】y —3x 4y 19 x y 4【答案】（1） 3x 4y 19 ① x y 4②A. 0.8元/支，2.6元/本 C. 1.2元/支，2.6元/本【关键词】二元一次方程组【答案】D.0.8元/支，3.6元/本 .1.2元/支，3.6元/本8. （2010浙江省喜嘉兴市）x 2y 1,3x 2y 113x 2y 11②①+②，得4x= 12,解得：x = 3.将x = 3代入①，得9-2y= 11,解得y=—1.所以方程组的解是16. （2010年重庆）含有同种果蔬但浓度不同的A,B 两种饮料，A 种饮料重40千克，E 种饮料重 60千克•现从这两种饮料中各倒出一部分，且倒出部分的重量相同，再将每种饮料所倒出的部分与另一种饮料余下的部分混合.如果混合后的两种饮料所含的果蔬浓度相同，那么从每种饮料中倒出的相同重量是 ________ 千克.【答案】2413. （2010江苏泰州，13, 3分）一次函数y kx b （ k 为常数且k 0 ）的图象如图所示，则使 y 0成立的x 的取值范围为 .【答案】X V -2【关键词】一次函数与二元一次方程的关系（2010年宁德市）（本题满分10分）据宁德网报道：第三届海峡两岸茶业博览会在宁德市的成功举办，提升了闽东茶叶的国内外知名度和市场竞争力，今年第一季茶青（刚采摘下的茶叶）每千克的价格是去年同期价格的10倍•茶农叶亮亮今年种植的茶树受霜冻影响，第一季茶青产量为198.6千克，比去年同期减少了87.4千克，但销售收入却比去年同期增加 8500元.求茶农叶亮亮今年第一季茶青的销售收入为多少元？【答案】解法设去年第一季茶青每千克的价格为 X 元，则今年第一季茶青每千克的价格为 10X 元，…2分依题意，得:（198.6 + 87.4 ） x + 8500 = 198.6 X 10x.解得x = 5.198.6 X 10X 5 = 9930 （元）.答：茶农叶亮亮今年第一季茶青的总收入为 9930元.解法二：设今年第一季茶青的总收入为 x 元,依题意，得:x=10X x 8500答：茶农叶亮亮今年第一季茶青的总收入为 9930 元.198. 6198.6 87.4解得x=9930.1. （2010年福建省晋江市）（10分）2010年春季我国西南大旱，导致大量农田减产，下图是一对农民父子的对话内容，请根据对话内容分别求出该农户今年两块农田的花生产量分别是多少千克？【答案】解一：设去年第一块田的花生产量为x 千克，第二块田的花生产量为 y 千克，根据题意，得x y 470 (1 80%)x (1 90%)y 572.（ 2010年辽宁省丹东市）某校春季运动会比赛中，八年级（1）班、（5）班的竞技实力相当，关于比赛结果，甲同学说：（1）班与（5）班得分比为6:5;乙同学说：（1）班得分比（5）班得分的2倍少40分•若设（1）班得 x 分，（5）班得y 分，根据题意所列的方程组应为（）【关键词】二元一次方程组【答案】D解得x 100y 370100 (1 80%) 20，370 (1 90%) 37答：该农户今年第一块田的花生产量是 20千克，第二解二：设今年第一块田的花生产量为x 千克，第二块田的花生产量为y 千克，根据题意，得x y 57解得x y1 80% 1 90% 470x 20 y 37答：该农户今年第一块田的花生产量是20千克，第二块田的花生产量是 37千克。

2010年中考数学试题分类大全36_相似形

一、选择题1．（2010山东烟台）手工制作课上，小红利用一些花布的边角料，剪裁后装饰手工画，下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边，其中，每个图案花边的宽度都相等，那么，每个图案中花边的内外边缘所围成的几何图形不相似的是【答案】D2．（2010山东烟台）如图，△ ABC 中，点D 在线段BC 上，且△ ABC ∽△ DBA ，则下列结论一定正确的是A 、AB 2=BC ·BD B 、AB 2=AC ·BD C 、AB ·AD=BD ·BC D 、AB ·AD=AD ·CD 【答案】A3．（2010台湾）图(一)表示D 、E 、F 、G 四点在△ABC 三边上的位置，其中DG 与EF交于H 点。

若?ABC =?EFC =70?，?ACB =60?，?DGB =40?，则下列哪一组三角形相似？(A) △BDG ，△CEF (B) △ABC ，△CEF(C) △ABC ，△BDG (D) △FGH ，△ABC 。

【答案】B4．（2010浙江嘉兴）如图，已知AD 为△ABC 的角平分线，AB DE //交AC 于E ，如果32=ECAE ，那么=ACAB （ ▲ ）（A ）31 （B ）32A BCD E FG H图(一)（C ）52 （D ）53【答案】B5．（2010 福建德化）下列各组线段（单位：㎝）中，成比例线段的是（）A 、1、2、3、4B 、1、2、2、4C 、3、5、9、13D 、1、2、2、3 【答案】B6．（2010江苏泰州）一个铝质三角形框架三条边长分别为24cm 、30cm 、36cm ，要做一个与它相似的铝质三角形框架，现有长为27cm 、45cm 的两根铝材，要求以其中的一根为一边，从另一根上截下两段（允许有余料）作为另外两边．截法有（） A.0种 B. 1种 C. 2种 D. 3种【答案】B7．（2010年上海）下列命题中，是真命题的为（）A.锐角三角形都相似B.直角三角形都相似C.等腰三角形都相似D.等边三角形都相似【答案】D8．（2010山东潍坊）如图所示，一般书本的纸张是原纸张多次对开得到的，矩形ABCD 沿EF 对开后，再把矩形EFCD 沿MN 对开，依次类推，若各种开本的矩形都相似，那么ABAD等于（）． AB CDE（第7题）A ．0．618B ．22C ．2D ．2【答案】B9．（2010北京）如图，在△ABC 中，点D 、E 分别在AB 、AC 边上，DE ∥BC ，若AD ∶AB =3∶4，AE =6，则AC 等于( )A ．3B ．4C ．6D ． 8 【答案】D10．（2010年上海）下列命题中，是真命题的为（）A.锐角三角形都相似B.直角三角形都相似C.等腰三角形都相似D.等边三角形都相似【答案】D11．（2010云南楚雄）下列说法不正确的是（） A ．在选举中，人们通常最关心的数据是众数． B ．掷一枚骰子，3点朝上是不确定事件． C ．数据3，5，4，1，－2的中位数是3．D ．有两边对应成比例且有一个角对应相等的两个三角形相似．【答案】D12．（2010河南）如图，在△ABC 中，点D 、E 分别是AB 、AC 的中点，则下列结论：①BC=2DE ；②△ADE ∽△ABC ；③AD ABAE AC.其中正确的有 (A)3个 (B)2个ABC D E(C)1个（D ）0个【答案】A13．（2010 四川绵阳）如图，梯形ABCD 的对角线AC 、BD 相交于O ，G 是BD 的中点．若AD = 3，BC = 9，则GO : BG =（）．A ．1 : 2B ．1 : 3C ．2 : 3D ．11 : 20【答案】A14．（2010广西桂林）如图，已知△ADE 与△ABC 的相似比为1：2，则△ADE与△ABC 的面积比为（）． A ． 1：2 B ． 1：4 C ． 2：1 D ． 4：1 【答案】B15．（2010辽宁沈阳）如图，在等边△ABC 中，D 为BC 边上一点，E 为AC 边上一点，且∠ADE=60°，BD=3，CE=2，则△ABC 的边长为A ．9B ．12C ．15D ．18 【答案】A16．（2010福建省南平）下列说法中，错误的是( )G A BDCOA ．等边三角形都相似B ．等腰直角三角形都相似C ．矩形都相似D ．正方形都相似【答案】C17．（2010吉林）如图，在△ABC 中，∠C=900，D 是AC 上一点，DE⊥AB 于点E ，若AC=8，BC=6，DE=3，则AD 的长为（） A ．3 B ．4 C ．5 D ．6 【答案】C18．（2010内蒙赤峰）如图，有一矩形纸片ABCD ，AB=6，AD=8，将纸片折叠，使AB 落在AD 边上，折痕为AE ，再将△AEB 以BE 为折痕向右折叠，AE 与DC 交于点F ，则CDFC 的值是（）【答案】C19．（2010广西百色）下列命题中，是假命题的是（）A.全等三角形的对应边相等B.两角和一边分别对应相等的两个三角形全等C.对应角相等的两个三角形全等D.相似三角形的面积比等于相似比的平方【答案】C20．（2010广西百色）如图，△ABC 中，D 、E 分别为AC 、BC 边上的点，AB ∥DE ，CF 为AB 边上的中线，若AD =5，CD =3，DE=4，则BF 的长为（）A. 332 B. 316 C. 310 D. 38【答案】B二、填空题1．（2010江苏南通）若△ABC ∽△DEF ， △ABC 与△DEF 的相似比为1∶2，则△ABC 与△DEF 的周长比为 ▲ ．【答案】1∶22．（2010 嵊州市）如图，射线AM ，BN 都垂直于线段AB ，点E 为AM 上一点，过点A 作BE 的垂线AC 分别交BE ，BN 于点F,C ，过点C 作AM 的垂线CD ，垂足为D ，若CD ＝CF ，则=ADAE。