中考数学几何综合题汇总.doc

合集下载

2023年数学中考试题精选：几何综合证明(一)

1.（2023.营口24题）在平行四边形ABCD中，∠ADB=90°,点E在CD 上，点G在AB上，点F在BD的延长线上，连接EF，DG, ∠FED=∠ADG，ADBD =DG EF=k.（1）如图1，当k=1时，请用等式表示线段AG与线段DF的数量关系________；（2）如图2，当k=√(3)时，写出线段AD，DE和DF之间的数量关系,并说明理由；（3）在（2）的条件下，当点G是AB的中点时，连接BE，求tan∠EBF的值2.（2023.本溪铁岭辽阳25题）在Rt△ABC中，∠ACB=90°，CA=CB，点O为AB的中点，点D在直线AB上（不与点A，B重合），连接CD，线段CD绕点C逆时针旋转90°，得到线段CE，过点B作直线l⊥BC，过点E作EF⊥l，垂足为点F，直线EF交直线OC于点G.（1）如图1，当点D与点O重合时，请直接写出线段AD与线段EF 的数量关系；（2）如图2，当点D在线段AB上时，求证：CG+BD=√2BC；（3）连接DE，△CDE的面积记为S1，△ABC的面积记为S2，当EF:BC=1:3时，请直接写出S1S2的值.3.(2023.大连25题)综合与实践问题情境：数学活动课上，王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质。

已知AB=AC，∠A>90°，点E为AC上一动点，将△ABE以BE为对称轴翻折，同学们经过思考后进行如下探究：独立思考：小明：“当点D落在BC上时，∠EDC=2∠ACB.”小红：“若点E为AC中点，给出AC与DC的长，就可求出BE的长.”补足探究：奋进小组的同学们经过探究后提出问题1，请你回答：问题1：在等腰△ABC中，AB=AC，∠A>90°，△BDE由△ABE翻折得到.（1）如图1，当点D落在BC上时，求证：∠EDC=2∠ACB；（2）如图2，若点E为AC中点，AC=4，CD=3，求BE的长.问题解决：小明经过探究发现：若将问题1中的等腰三角形换成∠A<90°的等腰三角形，可以问题进一步拓展.问题2：如图3，在等腰△ABC中，∠A<90°，AB=AC=BD=4，2∠D=∠ABD.若CD=1，则求BC的长.4.(2023.牡丹江26题)平行四边形ABCD中，AE⊥BC，垂足为E，连接DE，将ED绕点E逆时针旋转90°，得到EF，连接BF.（1）当点E在线段BC上，∠ABC=45°时，如图1，求证：AE+EC=BF；（2）当点E在线段BC延长线上，∠ABC=45°时，如图2，当点E在线段CB延长线上，∠ABC=135°时，如图3，请猜想并直接写出线段AE，EC,BF的数量关系；（3）在（1）、（2）的条件下，若BE=3，DE=5，则CE=______.5.（2023.贵州省25题）如图1，小红在学习了三角形相关知识后，对等腰直角三角形进行了探究，在等腰直角三角形ABC中，CA=CB,∠C=90°,过点B作射线BD⊥AB，垂足为B，点P在CB上.（1）【动手操作】如图2，若点P在线段CB上，画出射线PA，并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图中画出图形，图中∠PBE的度数为______度；（2）【问题探究】根据（1）所画图形，探究线段PA与PE的数量关系，并说明理由；（3）【拓展延伸】如图3，若点P在射线CB上移动，将射线PA绕点P逆时针旋转90°与BD将于点E，探究线段BA，BP，BE之间的数量关系，并说明理由.6.(2023.沈阳24题)如图1.在平行四边形纸片中，AB=10，AD=6，∠DAB=60°，点E为BC边上的一点（点E不与点C重合），连接AE，将平行四边形ABCD纸片沿AE所在直线折叠，点C，D的对应点分别为C`，D`，射线C`E与射线AD将于点F.（1）求证：AF=EF；（2）如图2，当EF⊥AF时，DF的长为______;（3）如图3，当CE=2时，过点F作FM⊥AE，垂足为点M，延长FM 交C`D`于点N，连接AN，EN，求△ANE的面积。

历年中考数学(典型)几何中长度的计算综合试题汇总

历年中考数学（典型）几何中长度的计算综合试题汇总1如图，在等边三角形ABC 中，点D 、E 分别是边AC 、BC 上两点，将三角形ABC 沿DE 翻折，点C 正好落在线段AB 上的点F 处，使得AF ：BF=2：3，若BE=16，则CE的长度为（）A.18B.19C.20D.212如图，△BAC 中，AB=AC=10，tan 2A =，BE ⊥AC 于点E ，D 是线段BE 上一动点，则5CD BD +的最小值（） A 25 B 45 C 53 D 103如图，已知在△ABC 中，90BAC ∠>,13AB =,BC=10，点D 是BC 中点，点E 在AC 上，将△CDE 沿着 DE 翻折，使得点C 恰好落在BA 的延长线上的点F 处，连接AD ，5=2EDF S △，这AD 的长度为（） A 52B 22C 734D 41354如图，在等腰三角形纸片ABC 中，∠ABC=120,BC=6，点D 、E 分别在边AC 、BC 上，连接DE ，将△CDE 沿着DE 翻折使得点C 恰好落在点B处，则AE 的长为（）A 372B 152C 37D 675如图，在△ABC 中，点D 是BC 边上一点，连接AD ，把△ABD 沿着AD 翻折，得到'AB D △,'B D 与AC 交于点E ，连接'B B 交AD 于点F ，若'=3B D DE ,213AB ,AF=6，'AB E △的面积为12，则点B 到'B D 的距离为（）A 65B 125C 245D 4576如图，在三等腰△ABC 中，AB=AC=2，∠ABC=120，点D 为边BC 的中点，将△ACD 沿着AC 折叠，使得点D 落在了点E 处，则点B 到直线CE 的距离是（）A 1B 3C 2D 37如图，在四边形ABCD 中，AD//BC ，90A ∠=,120ADC ∠=,连接BD ，把△ABD 沿着BD 翻折，得到'A BD △，连接'A C ,若AB=3，∠ABC=60，则点D 到直线'A C 的距离为（） A 7 B 9714 C 977 D 18778如图，在△ABC 中，AB=AC=5，BC=8，点D 是BC 上一点，（点D 不与B,C 重合），将△ACD 沿着AD 翻折，点C 的对应点为E ，AE 交BC 于点F ，若DE//AB ，则点B 到线段AD 的距离为（） A.255 B.3102 C.552 D.71029如图，把一张矩形纸片折叠使点A 与点C 重合，折痕为EF ，再将△CDF 沿着CF折叠，点D 恰好哦落在EF 上的点M 处，若BC=6厘米，则EF 的长为（）里面A.1.5B.3C.23D.410如图四边形ABEC 中，∠BEC 和∠BAC 都是直角，且AB=AC ，现将△BEC 沿BC 翻折，点E 的对应点'E ,BE 与AC 边相交于点D 点，恰好'BE 是∠ABC 的角平分线，若CE=1，则BD 的长为（）A 1.5B 2C 2D 311如图，在四边形ABCD 中，90ABC BCD ∠=∠=,,3,3AB BC ==,把Rt △ABC沿着AC 翻折得到Rt △AEC ，若23tan CED ∠=,则线段DE 的长度A.63 B.7373 C.32 D.275。

中考数学专题《一次函数与几何综合》高分必刷原卷

（培优特训）专项19.3 一一次函数与几何综合高分必刷1．（2023春•普兰店区期中）已知△ABC中，∠C＝90°，AC＝3，CD＝4，BD ＝AD．点F从点A出发，沿AC﹣CD运动，速度为1cm/s，同时点E从点B 出发，沿BD﹣DA运动，运动速度为1cm/s，一个点到达终点，另一点也停止运动．（1）求BD的长；（2）设△AEF的面积为S，点P、Q运动时间为t，求S与的函数关系式，并写出的取值范围．2．（2023春•鼓楼区期中）如图1，已知直线l1：y＝ax﹣6a交x轴于点A，交轴y于点B，直线l2：y＝bx﹣18a交x轴于点C，交y轴于点D，交直线l1于点E．（1）求点A的坐标；（2）若点B为线段AE的中点，求证：EC＝EA；（3）如图2，已知P（0，m），将线段P A绕点P逆时针方向旋转90°至PF，连接OF，求证：点F在某条直线上运动，并求OF的最小值．3．（2023春•苍南县期中）如图，在平面直角坐标系中，▱OABC的顶点A落在x轴上，点B的坐标为（7，4），AB＝2，点D是OC的中点，点E是线段AD上一动点，EF⊥BC于点F，连结DF．（1）求点A、C的坐标．（2）求直线AD的函数表达式．（3）若△DEF是等腰三角形，求CF的长．4．（2023•佳木斯一模）如图，将矩形纸片OABC放在平面直角坐标系中，O为坐标原点．点A在y轴上，点C在x轴上，OA，OB的长是x2﹣16x+60＝0的两个根，P是边AB上的一点，将△OAP沿OP折叠，使点A落在OB上的点Q处．（1）求点B的坐标；（2）求直线PQ的解析式；（3）点M在直线OP上，点N在直线PQ上，是否存在点M，N，使以A，C．M，N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．5．（2023春•顺德区校级月考）如图，请根据图象所提供的信息解答下列问题：（1）当x时，kx+b≥mx﹣n；（2）不等式kx+b＜0的解集是；（3）求两个一次函数表达式；（4）若直线l1分别交x轴、y轴于点M、A，直线l2分别交x轴、y轴于点B、N，求点M的坐标和四边形OMPN的面积．6．（2023春•北碚区校级期中）如图，在平面直角坐标系中，直线y＝2x﹣2与x 轴、y轴分别交于点A、点B，与直线CD：y＝kx+b（k≠0）交于点P，OC ＝OD＝4OA．（1）求直线CD的解析式；（2）连接OP、BC，若直线AB上存在一点Q，使得S△PQC ＝S四边形OBCP，求点Q的坐标；（3）将直线CD向下平移1个单位长度得到直线，直线l与x轴交于点E，点N为直线l上的一点，在平面直角坐标系中，是否存在点M，使以点O，E，N，M为顶点的四边形是矩形？若存在，请直接写出点M的坐标；若不存在，请说明理由．7．（2023春•宜兴市期中）如图，在平面直角坐标系中，已知A（0，4），点B、C都在x轴上，BC＝12，AD∥BC，CD所在直线的函数表达式为y＝﹣x+9，E是BC的中点，点P是BC边上一个动点．（1）当PB＝时，以点P、A、D、E为顶点的四边形为平行四边形；（2）点P在BC边上运动过程中，以点P、A、D、E为顶点的四边形能否构成菱形？试说明理由．8．（2023春•工业园区校级期中）如图，在平面直角坐标系中，点A、点B分别在x轴与y轴上，直线AB的解析式为，以线段AB、BC为边作平行四边形ABCD．（1）如图1，若点C的坐标为（3，7），判断四边形ABCD的形状，并说明理由；（2）如图2，在（1）的条件下，P为CD边上的动点，点C关于直线BP的对称点是Q，连接PQ，BQ．①当∠CBP＝°时，点Q位于线段AD的垂直平分线上；②连接AQ，DQ，设CP＝x，设PQ的延长线交AD边于点E，当∠AQD＝90°时，求证：QE＝DE，并求出此时x的值．9．（2023•沈阳一模）如图，在平面直角坐标系中，直线y＝kx+b与x轴交于点B（﹣5，0），与y轴交于点A，直线过点A，与x轴交于点C，点P 是x轴上方一个动点．（1）求直线AB的函数表达式；（2）若点P在线段AB上，且S△APC ＝S△AOB，求点P的坐标；（3）当S△PBC ＝S△AOB时，动点M从点B出发，先运动到点P，再从点P运动到点C后停止运动．点M的运动速度始终为每秒1个单位长度，运动的总时间为t（秒），请直接写出t的最小值．10．（2023春•鼓楼区期中）如图1，已知函数与x轴交于点A，与y轴交于点B，点C与点A关于y轴对称．（1）求直线BC的函数解析式；（2）设点M是x轴上的一个动点，过点M作y轴的平行线，交直线AB于点P，交直线BC于点Q．①若△PQB的面积为，求点M的坐标；②连接BM，如图2，若∠BMP＝∠BAC，求点P的坐标．11．（2023春•顺德区校级期中）一次函数y＝kx+b的图象经过点A（﹣2，0）、B（﹣1，1），且和一次函数y＝﹣2x+a的图象交于点C，如图所示．（1）填空：不等式kx+b＜0的解集是；（2）若不等式kx+b＞﹣2x+a的解集是x＞1，求点C的坐标；（3）在（2）的条件下，点P是直线y＝﹣2x+a上一动点．且在点C上方，当∠P AC＝15°时，求点P的坐标．12．（2023春•重庆期中）如图，已知函数y＝x+1的图象与y轴交于点A，一次函数y＝kx+b的图象经过点B（0，﹣1），与x轴以及y＝x+1的图象分别交于点C，D，且点D的坐标为（1，n）．（1）则k＝，b＝，n＝；（2）求四边形AOCD的面积；（3）在x轴上是否存在点P，使得以点P，C，D为顶点的三角形是直角三角形，请求出点P的坐标．13．（2023春•崇川区校级月考）模型建立：如图1，等腰直角三角形ABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过A作AD⊥ED于D，过B作BE⊥ED于E．（1）求证：△BEC≌△CDA；（2）模型应用：已知直线l1：y＝﹣x﹣4与y轴交于A点．将直线l1绕着A 点逆时针旋转45°至l2，如图2，求l2的函数解析式．14．（2023春•崇川区校级月考）如图，在平面直角坐标系中，直线l1：y＝﹣x+4分别与x轴，y轴交于点B，C．直线l2：y＝x．（1）直接写出点B，C的坐标：B，C．（2）若D是直线l2上的点，且△COD的面积为6，求直线CD的函数表达式；（3）在（2）的条件下，且当点D在第一象限时，设P是射线CD上的点，在平面内存在点Q．使以O，C，P，Q为顶点的四边形是菱形，请直接求点Q的坐标．15．（2023•城固县模拟）如图，A、B两个长方体水箱放置在同一水平桌面上，开始时水箱A中没有水，水箱B盛满水，现以6dm3/min的流量从水箱B中抽水注入水箱A中，直至水箱A注满水为止．设注水时间为t（min），水箱A 的水位高度为y A（dm），水箱B中的水位高度为y B（dm）．（抽水水管的体积忽略不计）（1）分别求出y A，y B与t之间的函数表达式；（2）当水箱A与水箱B中的水的体积相等时，求出此时两水箱中水位的高度差．16．（2022秋•常州期末）在平面直角坐标系中，一次函数的图象l1与x轴交于点A，一次函数y＝x+6的图象l2与x轴交于点B，与l1交于点P．直线l3过点A且与x轴垂直，C是l3上的一个动点．（1）分别求出点A、P的坐标；（2）设直线PC对应的函数表达式为y＝kx+b，且满足函数值y随x的增大而增大．若△PCA的面积为15，分别求出k、b的值；（3）是否存在点C，使得2∠PCA+∠P AB＝90°？若存在，直接写出点C的坐标；若不存在，请说明理由．17．（2023春•靖江市期中）如图，平面直角坐标系中，已知点A（0，a）在y 轴正半轴上，点B（0，b）（a＞b），点C（c，0）在x轴正半轴上，且a2﹣2ab+b2（1）如图1，求证：AB＝OC；（2）如图2，当a＝3，b＝1时，过点B的直线与AC成45°夹角，试求该直线与AC交点的横坐标；（3）如图3，当b＜0时，点D在OC的延长线上，且CD＝OB，连接AD，射线BC交AD于点E．当点B在y轴负半轴上运动时，∠AEB的度数是否为定值？如果是，请求出∠AEB的度数；如果不是，请说明理由．18．（2023春•沙坪坝区校级期中）如图，在平面直角坐标系xOy中，直线AB：与直线CD：y＝kx﹣2相交于点M（4，a），分别交坐标轴于点A，（1）求直线CD的解析表达式；（2）如图，点P是直线CD上的一个动点，当△PBM的面积为20时，求点P的坐标；（3）直线AB上有一点F，在平面直角坐标系内找一点N，使得以BF为一边，以点B，D，F，N为顶点的四边形是菱形，请直接写出符合条件的点N的坐标．19．（2023春•揭西县校级月考）在平面直角坐标系中，直线y1＝kx+b经过点P （2，2）和点Q（0，﹣2），与x轴交于点A，与直线y2＝mx+n交于点P．（1）求出直线y1＝kx+b的解析式；（2）当m＜0时，直接写出y1＜y2时自变量x的取值范围；（3）直线y2＝mx+n绕着点P任意旋转，与x轴交于点B，当△P AB是等腰三角形时，请直接写出符合条件的所有点B的坐标．20．（2023春•溧阳市校级月考）如图，四边形OABC是矩形，点A、C在坐标轴上，△ODE是由△OCB绕点O顺时针旋转90°得到的，点D在x轴上，直线BD交y轴于点F，交OE于点H，线段BC、OC的长是2和4；（1）求直线BD的表达式；（2）求△OFH的面积；（3）点M在坐标轴上，平面内是否存在点N，使以点D、F、M、N为顶点的四边形是矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由．21．（2023春•江都区月考）如图，在平面直角坐标系中，直线y＝﹣x+3与x 轴、y轴相交于A、B两点，动点C在线段OA上，将线段CB绕着点C顺时针旋转90°得到CD，此时点D恰好落在直线AB上时，过点D作DE⊥x轴于点E．（1）求证：△BOC≌△CED；（2）求点D的坐标；（3）若点P在y轴上，点Q在直线AB上，是否存在以C、D、P、Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的Q点坐标；若不存在，请说明理由．22．（2023春•新城区校级月考）如图，在平面直角坐标系中，直线l1的解析式为y＝x，直线l2的解析式为，与x轴、y轴分别交于点A、点B，直线l1与l2交于点C．（1）若直线l2上存在点P（不与B重合），满足S△COP＝S△COB，求出点P的坐标；（2）在y轴右侧有一动直线平行于y轴，分别与l1，l2交于点M、N，且点M 在点N的下方，y轴上是否存在点Q，使△MNQ为等腰直角三角形？若存在，请直接写出满足条件的点Q的坐标；若不存在，请说明理由．23．（2022秋•宿豫区期末）如图，直线l分别与x轴、y轴交于点A（4，0）、B （0，5），把直线l沿y轴向下平移3个单位长度，得到直线m，且直线m分别与x轴、y轴交于点C、D．（1）求直线l对应的函数表达式；（2）求四边形ABDC的面积．24．（2022秋•临淄区期末）如图，在直角坐标系中，四边形ABCD的顶点坐标分别为A（﹣1，0），B（0，2），C（2，3），D（4，0）．（1）求直线BC的表达式；（2）线段AB与BC相等吗？请说明理由；（3）求四边形ABCD的面积；（4）已知点M在x轴上，且△MBC是等腰三角形，求点M的坐标．25．（2022秋•金牛区期末）如图1，在平面直角坐标系xOy中，直线AB：y＝2x+b 与x轴交于点A（﹣2，0），与y轴交于点B．（1）求直线AB的解析式；（2）若直线CD：y＝﹣x+与x轴、y轴、直线AB分别交于点C、D、E，求△BDE面积；（3）如图2，在（2）的条件下，点F为线段AC上一动点，将△EFC沿直线EF翻折得到△EFN，EN交x轴于点M．当△MNF为直角三角形时，求点N 的坐标．26．（2022秋•婺城区期末）如图，直线y＝x+4与x轴、y轴分别交于点A、点B，点P是射线BO上的动点，过点B作直线AP的垂线交x轴于点Q，垂足为点C，连结OC．（1）当点P在线段BO上时，①求证：△AOP≌△BOQ；②若点P为BO的中点，求△OCQ的面积．（2）在点P的运动过程中，是否存在某一位置，使得△OCQ成为等腰三角形？若存在，求点P的坐标；若不存在，请说明理由．27．（2022秋•郫都区期末）在直角坐标系xOy中，直线l1：y＝﹣x+4与x轴、y 轴分别交于点A，点B．直线l2：y＝mx+m（m＞0）与x轴，y轴分别交于点C，点D，直线l1与l2交于点E．（1）若点E坐标为（，n）．ⅰ）求m的值；ⅱ）点P在直线l2上，若S△AEP＝3S△BDE，求点P的坐标；（2）点F是线段CE的中点，点G为y轴上一动点，是否存在点F使△CFG 为以FC为直角边的等腰直角三角形．若存在，求出m的值，若不存在，请说明理由．28．（2022秋•市中区期末）如图，直线y＝kx+b经过点，点B（0，25），与直线交于点C，点D为直线AB上一动点，过D点作x轴的垂线交直线OC于点E．（1）求直线AB的表达式和点C的坐标；（2）当时，求△CDE的面积；（3）连接OD，当△OAD沿着OD折叠，使得点A的对应点A'落在直线OC 上，直接写出此时点D的坐标．29．（2022秋•新都区期末）如图1，在平面直角坐标系中，点A的坐标为（4，4），点B的坐标为（﹣4，0）．（1）求直线AB的表达式；（2）点M是坐标轴上的一点，若以AB为直角边构造Rt△ABM，请求出满足条件的所有点M的坐标；（3）如图2，以A为直角顶点作∠CAD＝90°，射线AC交x轴的正半轴于点C，射线AD交y轴的负半轴于点D，当∠CAD绕点A旋转时，求OC﹣OD 的值．30．（2022秋•皇姑区期末）如图，在平面直角坐标系中，直线AD：y＝﹣x+4交y轴于点A，交x轴于点D．直线AB交x轴于点B（﹣3，0），点P为直线AB上的动点．（1）求直线AB的关系式；（2）连接PD，当线段PD⊥AB时，直线AD上有一点动M，x轴上有一动点N，直接写出△PMN周长的最小值；（3）若∠POA＝∠BAO，直接写出点P的纵坐标．31．（2022秋•新都区期末）如图所示，直线l1：y＝x﹣1与y轴交于点A，直线l2：y＝﹣2x﹣4与x轴交于点B，直线l1与l2交于点C．（1）求点A，C的坐标；（2）点P在直线l1上运动，求出满足条件S△PBC＝S△ABC且异于点A的点P的坐标；（3）点D（2，0）为x轴上一定点，当点Q在直线l1上运动时，请直接写出|DQ﹣BQ|的最大值．32．（2022秋•鸡西期末）如图，直角三角形ABC在平面直角坐标系中，直角边BC在y轴上，AB，BC的长分别是一元二次方程x2﹣14x+48＝0的两个根，AB＜BC，且BC＝2OB，P为BC上一点，且∠BAP＝∠C．（1）求点A的坐标；（2）求直线AP的解析式；（3）M为x轴上一点，在平面内是否存在点N，使以A，C，M，N为顶点的四边形为矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由．33．（2022秋•锦江区校级期末）如图，直线y＝kx+b与x轴、y轴分别交于点A 和点B，点C在线段AO上，将△ABC沿BC所在直线折叠后，点A恰好落在y轴上点D处，若OA＝4，OD＝2．（1）求直线AB的解析式．（2）求S△ABC ：S△OCD的值．（3）直线CD上是否存在点P使得∠PBC＝45°，若存在，请直接写出P的坐标．34．（2022秋•福田区校级期末）已知：如图，一次函数的图象分别与x 轴、y轴相交于点A、B，且与经过点C（2，0）的一次函数y＝kx+b的图象相交于点D．点D的横坐标为4，直线CD与y轴相交于点E．（1）直线CD的函数表达式为：；（2）点Q为线段DE上的一个动点，连接BQ．①若直线BQ将△BDE的面积分为1：2两部分，求点Q的坐标；②点Q是否存在某个位置，将△BQD沿着直线BQ翻折，使得点D恰好落在直线AB下方的坐标轴上？若存在，请直接写出点Q的坐标；若不存在，请说明理由．35．（2022秋•抚州期末）如图，在平面直角坐标系xOy中，直线AP交x轴于点P（p，0），与y轴交于点A（0，a），且a，p满足＝0．（1）求直线AP的解析式；（2）如图1，直线x＝﹣2与x轴交于点N，点M在x轴上方且在直线x＝﹣2上，若△MAP的面积等于6，请求出点M的坐标；（3）如图2，已知点C（﹣2，4），若点B为射线AP上一动点，连接BC，在坐标轴上是否存在点Q，使△BCQ是以BC为底边，点Q为直角顶点的等腰直角三角形，若存在，请直接写出点Q坐标；若不存在，请说明理由．36．（2022秋•天桥区期末）如图1，在平面直角坐标系xOy中，点O是坐标原点，直线AB：y＝kx+与直线AC：y＝﹣2x+b交于点A，两直线与x轴分别交于点B（﹣3，0）和C（2，0）．（1）求直线AB和AC的表达式．（2）点P是y轴上一点，当P A+PC最小时，求点P的坐标．（3）如图2，点D为线段BC上一动点，将△ABD沿直线AD翻折得到△ADE，线段AE交x轴于点F，若△DEF为直角三角形，求点D坐标．37．（2023•桐乡市校级开学）如图，一次函数y＝x+6的图象与x轴交于点A，与y轴交于点B，OC⊥AB于点C，点P在直线AB上运动，点Q在y轴的正半轴上运动．（1）求点A，B的坐标；（2）求OC的长；（3）若以O，P，Q为顶点的三角形与△OCP全等，求点Q的坐标．38．（2022秋•秦都区期末）如图，平面直角坐标系中，直线AB与x轴交于点A （﹣3，0）与y轴交于点B（0，6），点C是直线AB上的一点，它的坐标为（m，4），经过点C作直线CD∥x轴交y轴于点D．（1）求点C的坐标；（2）已知点P是直线CD上的动点，①若△POC的面积为4，求点P的坐标；②若△POC为直角三角形，请求出所有满足条件的点P的坐标．39．（2022秋•南海区期末）如图，在平面直角坐标系中，直线y＝x+1分别交x 轴，y轴于点A、B．另一条直线CD与直线AB交于点C（a，6），与x轴交于点D（3，0），点P是直线CD上一点（不与点C重合）．（1）求a的值．（2）当△APC的面积为18时，求点P的坐标．（3）若直线MN在平面直角坐标系内运动，且MN始终与AB平行，直线MN 交直线CD于点M，交y轴于点N，当∠BMN＝90°时，求△BMN的面积．40．（2023•丰顺县校级开学）问题提出：如图，等腰Rt△ABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过点A作AD⊥ED于点D，过点B作BE⊥ED于点E，求证：△BEC≌△CDA；问题探究：如图2，在平面直角坐标系中，一次函数与x轴交于点A，与y轴交于点B，以AB为腰在第二象限作等腰直角△ABC，∠BAC＝90°，求点C的坐标；问题解决：古城西安已经全面迎来地铁时代！继西安地铁2号线于2011年9月16日通车试运行以来，共有八条线路开通运营，极大促进了西安市的交通运输，目前还有多条线路正在修建中．如图，地铁某线路原计划按OA﹣AB的方向施工，由于在AB方向发现一处地下古建筑，地铁修建须绕开此区域．经实地勘测，若将AB段绕点A顺时针或逆时针方向旋转45°至AC或AD方向，则可以绕开此区域．已知OA长为1千米，以点O为原点，OA所在直线为x轴，1千米为单位长度，建立平面直角坐标系，且射线AB与直线y＝﹣2x平行，请帮助施工队计算出AC和AD所在直线的解析式．41．（2022秋•碑林区校级期末）（1）模型建立：如图1，在等腰直角三角形ABC中，∠ACB＝90°，CA＝CB，直线ED经过点C，过点A作AD⊥ED于点D，过点B作BE⊥ED于点E，请直接写出图中相等的线段（除CA＝CB）；模型应用：（2）如图2，在平面直角坐标系xOy中，直线与x，y轴分别交于A、B两点，C为第一象限内的点，若△ABC是以AB为直角边的等腰直角三角形，请求出点C的坐标和直线BC的表达式；探究提升：（3）如图3，在平面直角坐标系xOy中，A（3，0），点B在y轴上运动，将AB绕点A顺时针旋转90°至AC，连接OC，求CA+OC的最小值，及此时点B坐标．42．（2023•南岸区校级开学）如图，已知直线l1：y＝﹣x+b与直线l2：y＝kx+3相交于y轴的B点，且分别交x轴于点A、C，已知OC＝OA．（1）如图，求点C的坐标及k的值；（2）如图，若E为直线l1上一点，且E点的横坐标为，点P为y轴上一个动点，求当|PC﹣PE|最大时，点P的坐标；（3）若M为x轴上一点，当△ABM是等腰三角形时，直接写出点M的坐标．43．（2022秋•驿城区校级期末）（1）操作思考：如图1，在平面直角坐标系中，等腰直角△ACB的直角顶点C在原点，将其绕着点O旋转，若顶点A恰好落在点（1，2）处．则：①OA的长为；②点B的坐标为．（直接写结果）（2）感悟应用：如图2，在平面直角坐标系中，将等腰直角△ACB如图放置，直角顶点C（﹣1，0），点A（0，4），试求直线AB的函数表达式．（3）拓展研究：如图3，在直角坐标系中，点B（4，3），过点B作BA⊥y 轴，垂足为点A，作BC⊥x轴，垂足为点C，P是线段BC上的一个动点，点Q是直线y＝2x﹣8上一动点，存在以点P为直角顶点的等腰直角△APQ，请直接写出点P的坐标．。

中考数学几何题总汇

1.三角形的有关概念知识考点：理解三角形三边的关系及三角形的主要线段（中线、高线、角平分线）和三角形的内角和定理。

关键是正确理解有关概念，学会概念和定理的运用。

应用方程知识求解几何题是这部分知识常用的方法。

【例1】已知一个三角形中两条边的长分别是a 、b ，且b a >，那么这个三角形的周长L 的取值范围是（） A 、b L a 33>> B 、a L b a 2)(2>>+ C 、a b L b a +>>+262 D 、b a L b a 23+>>- 变式与思考：在△ABC 中，AC ＝5，中线AD ＝7，则AB 边的取值范围是（） A 、1＜AB ＜29 B 、4＜AB ＜24 C 、5＜AB ＜19 D 、9＜AB ＜19 【例2】如图，已知△ABC 中，∠ABC ＝450，∠ACB ＝610，延长BC 至E ，使CE ＝AC ，延长CB 至D ，使DB ＝AB ，求∠DAE 的度数。

一、填空题：1、三角形的三边为1，a -1，9，则a 的取值范围是。

2、已知三角形两边的长分别为1和2，如果第三边的长也是整数，那么第三边的长为。

3、在△ABC 中，若∠C ＝2（∠A ＋∠B ），则∠C ＝度。

4、如果△ABC 的一个外角等于1500，且∠B ＝∠C ，则∠A ＝。

5、如果△ABC 中，∠ACB ＝900，CD 是AB 边上的高，则与∠A 相等的角是。

6、如图，在△ABC 中，∠A ＝800，∠ABC 和∠ACB 的外角平分线相交于点D ，那么∠BDC ＝。

7、如图，CE 平分∠ACB ，且CE ⊥DB ，∠DAB ＝∠DBA ，AC ＝18cm ，△CBD 的周长为28 cm ，则DB ＝。

8、纸片△ABC 中，∠A ＝650，∠B ＝750，将纸片的一角折叠，使点C 落在△ABC 内（如图），若∠1＝200，则∠2的度数为。

中考数学-几何综合压轴问题(共40题)(学生版)

几何综合压轴问题(40题)1(2023·四川自贡·统考中考真题)如图1，一大一小两个等腰直角三角形叠放在一起，M，N分别是斜边DE，AB的中点，DE=2,AB=4．(1)将△CDE绕顶点C旋转一周，请直接写出点M，N距离的最大值和最小值；(2)将△CDE绕顶点C逆时针旋转120°(如图2)，求MN的长．2(2023·山东烟台·统考中考真题)如图，点C为线段AB上一点，分别以AC,BC为等腰三角形的底边，在AB的同侧作等腰△ACD和等腰△BCE，且∠A=∠CBE．在线段EC上取一点F，使EF=AD，连接BF,DE．(1)如图1，求证：DE=BF；(2)如图2，若AD=2，BF的延长线恰好经过DE的中点G，求BE的长．3(2023·浙江绍兴·统考中考真题)在平行四边形ABCD中(顶点A,B,C,D按逆时针方向排列)，AB= 12,AD=10,∠B为锐角，且sin B=45．(1)如图1，求AB边上的高CH的长．(2)P是边AB上的一动点，点C,D同时绕点P按逆时针方向旋转90°得点C ,D ．①如图2，当点C 落在射线CA上时，求BP的长．②当△AC D 是直角三角形时，求BP的长．4(2023·甘肃武威·统考中考真题)【模型建立】(1)如图1，△ABC和△BDE都是等边三角形，点C关于AD的对称点F在BD边上．①求证：AE=CD；②用等式写出线段AD，BD，DF的数量关系，并说明理由．【模型应用】(2)如图2，△ABC是直角三角形，AB=AC，CD⊥BD，垂足为D，点C关于AD的对称点F在BD边上．用等式写出线段AD，BD，DF的数量关系，并说明理由．【模型迁移】(3)在(2)的条件下，若AD=42，BD=3CD，求cos∠AFB的值．5(2023·江西·统考中考真题)课本再现思考我们知道，菱形的对角线互相垂直．反过来，对角线互相垂直的平行四边形是菱形吗？可以发现并证明菱形的一个判定定理；对角线互相垂直的平行四边形是菱形．(1)定理证明：为了证明该定理，小明同学画出了图形(如图1)，并写出了“已知”和“求证”，请你完成证明过程．己知：在▱ABCD中，对角线BD⊥AC，垂足为O．求证：▱ABCD是菱形．(2)知识应用：如图2，在▱ABCD中，对角线AC和BD相交于点O，AD=5，AC=8，BD=6．①求证：▱ABCD是菱形；②延长BC至点E，连接OE交CD于点F，若∠E=12∠ACD，求OFEF的值．6(2023·湖北随州·统考中考真题)1643年，法国数学家费马曾提出一个著名的几何问题：给定不在同一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最小的点的位置，意大利数学家和物理学家托里拆利给出了分析和证明，该点也被称为“费马点”或“托里拆利点”，该问题也被称为“将军巡营”问题．(1)下面是该问题的一种常见的解决方法，请补充以下推理过程：(其中①处从“直角”和“等边”中选择填空，②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空，③处填写角度数，④处填写该三角形的某个顶点)当△ABC的三个内角均小于120°时，如图1，将△APC绕，点C顺时针旋转60°得到△A P C，连接PP ，由PC=P C，∠PCP =60°，可知△PCP 为三角形，故PP =PC，又P A =PA，故PA+PB+PC =PA +PB+PP ≥A B，由可知，当B，P，P ，A在同一条直线上时，PA+PB+PC取最小值，如图2，最小值为A B，此时的P点为该三角形的“费马点”，且有∠APC=∠BPC=∠APB=；已知当△ABC有一个内角大于或等于120°时，“费马点”为该三角形的某个顶点．如图3，若∠BAC≥120°，则该三角形的“费马点”为点．(2)如图4，在△ABC中，三个内角均小于120°，且AC=3，BC=4，∠ACB=30°，已知点P为△ABC的“费马点”，求PA+PB+PC的值；(3)如图5，设村庄A，B，C的连线构成一个三角形，且已知AC=4km，BC=23km，∠ACB=60°．现欲建一中转站P沿直线向A，B，C三个村庄铺设电缆，已知由中转站P到村庄A，B，C的铺设成本分别为a 元/km，a元/km，2a元/km，选取合适的P的位置，可以使总的铺设成本最低为元．(结果用含a的式子表示)7(2023·山东枣庄·统考中考真题)问题情境：如图1，在△ABC中，AB=AC=17，BC=30，AD是BC边上的中线．如图2，将△ABC的两个顶点B，C分别沿EF,GH折叠后均与点D重合，折痕分别交AB,AC,BC于点E，G，F，H．猜想证明：(1)如图2，试判断四边形AEDG的形状，并说明理由．问题解决；(2)如图3，将图2中左侧折叠的三角形展开后，重新沿MN折叠，使得顶点B与点H重合，折痕分别交AB, BC于点M，N，BM的对应线段交DG于点K，求四边形MKGA的面积．8(2023·湖南·统考中考真题)(1)[问题探究]如图1，在正方形ABCD中，对角线AC、BD相交于点O．在线段AO上任取一点P(端点除外)，连接PD、PB．①求证：PD=PB；②将线段DP绕点P逆时针旋转，使点D落在BA的延长线上的点Q处．当点P在线段AO上的位置发生变化时，∠DPQ的大小是否发生变化？请说明理由；③探究AQ与OP的数量关系，并说明理由．(2)[迁移探究]如图2，将正方形ABCD换成菱形ABCD，且∠ABC=60°，其他条件不变．试探究AQ与CP的数量关系，并说明理由．9(2023·湖南岳阳·统考中考真题)如图1，在△ABC中，AB=AC，点M,N分别为边AB,BC的中点，连接MN．初步尝试：(1)MN与AC的数量关系是，MN与AC的位置关系是．特例研讨：(2)如图2，若∠BAC=90°,BC=42，先将△BMN绕点B顺时针旋转α(α为锐角)，得到△BEF，当点A,E,F在同一直线上时，AE与BC相交于点D，连接CF．(1)求∠BCF的度数；(2)求CD的长．深入探究：(3)若∠BAC<90°，将△BMN绕点B顺时针旋转α，得到△BEF，连接AE，CF．当旋转角α满足0°<α<360°，点C,E,F在同一直线上时，利用所提供的备用图探究∠BAE与∠ABF的数量关系，并说明理由．10(2023·湖北黄冈·统考中考真题)【问题呈现】△CAB和△CDE都是直角三角形，∠ACB=∠DCE=90°,CB=mCA,CE=mCD，连接AD，BE，探究AD，BE的位置关系．(1)如图1，当m=1时，直接写出AD，BE的位置关系：；(2)如图2，当m≠1时，(1)中的结论是否成立？若成立，给出证明；若不成立，说明理由．【拓展应用】(3)当m=3,AB=47,DE=4时，将△CDE绕点C旋转，使A,D,E三点恰好在同一直线上，求BE的长．11(2023·河北·统考中考真题)如图1和图2，平面上，四边形ABCD中，AB=8,BC=211,CD=12, DA=6,∠A=90°，点M在AD边上，且DM=2．将线段MA绕点M顺时针旋转n°(0<n≤180)到MA ,∠A MA的平分线MP所在直线交折线AB-BC于点P，设点P在该折线上运动的路径长为x(x>0)，连接A P．(1)若点P在AB上，求证：A P=AP；(2)如图2．连接BD．①求∠CBD的度数，并直接写出当n=180时，x的值；②若点P到BD的距离为2，求tan∠A MP的值；(3)当0<x≤8时，请直接写出点A 到直线AB的距离．(用含x的式子表示)．12(2023·四川达州·统考中考真题)(1)如图①，在矩形ABCD的AB边上取一点E，将△ADE沿DE翻折，使点A落在BC上A 处，若AB=6,BC=10，求AEEB的值；(2)如图②，在矩形ABCD 的BC 边上取一点E ，将四边形ABED 沿DE 翻折，使点B 落在DC 的延长线上B 处，若BC ⋅CE =24,AB =6，求BE 的值；(3)如图③，在△ABC 中，∠BAC =45°,AD ⊥BC ，垂足为点D ,AD =10,AE =6，过点E 作EF ⊥AD 交AC 于点F ，连接DF ，且满足∠DFE =2∠DAC ，直接写出BD +53EF 的值．13(2023·湖南郴州·统考中考真题)已知△ABC 是等边三角形，点D 是射线AB 上的一个动点，延长BC 至点E ，使CE =AD ，连接DE 交射线AC 于点F ．(1)如图1，当点D 在线段AB 上时，猜测线段CF 与BD 的数量关系并说明理由；(2)如图2，当点D 在线段AB 的延长线上时，①线段CF 与BD 的数量关系是否仍然成立？请说明理由；②如图3，连接AE ．设AB =4，若∠AEB =∠DEB ，求四边形BDFC 的面积．14(2023·湖北宜昌·统考中考真题)如图，在正方形ABCD 中，E ，F 分别是边AD ，AB 上的点，连接CE ，EF ，CF ．(1)若正方形ABCD 的边长为2，E 是AD 的中点．①如图1，当∠FEC =90°时，求证：△AEF ∽△DCE ；②如图2，当tan ∠FCE =23时，求AF 的长；(2)如图3，延长CF ，DA 交于点G ，当GE =DE ,sin ∠FCE =13时，求证：AE =AF ．15(2023·湖北武汉·统考中考真题)问题提出：如图(1)，E 是菱形ABCD 边BC 上一点，△AEF 是等腰三角形，AE =EF ，∠AEF =∠ABC =αa ≥90° ,AF 交CD 于点G ，探究∠GCF 与α的数量关系．问题探究：(1)先将问题特殊化，如图(2)，当α=90°时，直接写出∠GCF 的大小；(2)再探究一般情形，如图(1)，求∠GCF 与α的数量关系．问题拓展：(3)将图(1)特殊化，如图(3)，当α=120°时，若DG CG =12，求BECE的值．16(2023·山西·统考中考真题)问题情境：“综合与实践”课上，老师提出如下问题：将图1中的矩形纸片沿对角线剪开，得到两个全等的三角形纸片，表示为△ABC 和△DFE ，其中∠ACB =∠DEF =90°,∠A =∠D ．将△ABC 和△DFE 按图2所示方式摆放，其中点B 与点F 重合(标记为点B )．当∠ABE =∠A 时，延长DE 交AC 于点G ．试判断四边形BCGE 的形状，并说明理由．(1)数学思考：谈你解答老师提出的问题；(2)深入探究：老师将图2中的△DBE 绕点B 逆时针方向旋转，使点E 落在△ABC 内部，并让同学们提出新的问题．①“善思小组”提出问题：如图3，当∠ABE =∠BAC 时，过点A 作AM ⊥BE 交BE 的延长线于点M ,BM 与AC 交于点N ．试猜想线段AM 和BE 的数量关系，并加以证明．请你解答此问题；②“智慧小组”提出问题：如图4，当∠CBE=∠BAC时，过点A作AH⊥DE于点H，若BC=9,AC=12，求AH的长．请你思考此问题，直接写出结果．17(2023·湖北十堰·统考中考真题)过正方形ABCD的顶点D作直线DP，点C关于直线DP的对称点为点E，连接AE，直线AE交直线DP于点F．(1)如图1，若∠CDP=25°，则∠DAF=°；(2)如图1，请探究线段CD，EF，AF之间的数量关系，并证明你的结论；(3)在DP绕点D转动的过程中，设AF=a，EF=b请直接用含a,b的式子表示DF的长．18(2023·辽宁大连·统考中考真题)综合与实践问题情境：数学活动课上，王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质．已知AB=AC,∠A>90°，点E为AC上一动点，将△ABE以BE为对称轴翻折．同学们经过思考后进行如下探究：独立思考：小明：“当点D落在BC上时，∠EDC=2∠ACB．”小红：“若点E为AC中点，给出AC与DC的长，就可求出BE的长．”实践探究：奋进小组的同学们经过探究后提出问题1，请你回答：问题1：在等腰△ABC中，AB=AC,∠A>90°,△BDE由△ABE翻折得到．(1)如图1，当点D落在BC上时，求证：∠EDC=2∠ACB；(2)如图2，若点E为AC中点，AC=4,CD=3，求BE的长．问题解决：小明经过探究发现：若将问题1中的等腰三角形换成∠A<90°的等腰三角形，可以将问题进一步拓展．问题2：如图3，在等腰△ABC中，∠A<90°,AB=AC=BD=4,2∠D=∠ABD．若CD=1，则求BC的长．19(2023·山东·统考中考真题)(1)如图1，在矩形ABCD中，点E，F分别在边DC，BC上，AE⊥DF，垂足为点G．求证：△ADE∽△DCF．【问题解决】(2)如图2，在正方形ABCD中，点E，F分别在边DC，BC上，AE=DF，延长BC到点H，使CH=DE，连接DH．求证：∠ADF=∠H．【类比迁移】(3)如图3，在菱形ABCD中，点E，F分别在边DC，BC上，AE=DF=11，DE=8，∠AED=60°，求CF 的长．20(2023·福建·统考中考真题)如图1，在△ABC中，∠BAC=90°,AB=AC,D是AB边上不与A,B重合的一个定点．AO⊥BC于点O，交CD于点E．DF是由线段DC绕点D顺时针旋转90°得到的，FD,CA的延长线相交于点M．(1)求证：△ADE∽△FMC；(2)求∠ABF的度数；(3)若N是AF的中点，如图2．求证：ND=NO．21(2023·四川·统考中考真题)如图1，已知线段AB，AC，线段AC绕点A在直线AB上方旋转，连接BC，以BC为边在BC上方作Rt△BDC，且∠DBC=30°．(1)若∠BDC=90°，以AB为边在AB上方作Rt△BAE，且∠AEB=90°，∠EBA=30°，连接DE，用等式表示线段AC与DE的数量关系是；(2)如图2，在(1)的条件下，若DE⊥AB，AB=4，AC=2，求BC的长；(3)如图3，若∠BCD=90°，AB=4，AC=2，当AD的值最大时，求此时tan∠CBA的值．22(2023·广西·统考中考真题)【探究与证明】折纸，操作简单，富有数学趣味，我们可以通过折纸开展数学探究，探索数学奥秘．【动手操作】如图1，将矩形纸片ABCD对折，使AD与BC重合，展平纸片，得到折痕EF；折叠纸片，使点B 落在EF上，并使折痕经过点A，得到折痕AM，点B，E的对应点分别为B ，E ，展平纸片，连接AB ，BB ，BE ．请完成：(1)观察图1中∠1，∠2和∠3，试猜想这三个角的大小关系；(2)证明(1)中的猜想；【类比操作】如图2，N为矩形纸片ABCD的边AD上的一点，连接BN，在AB上取一点P，折叠纸片，使B ，P 两点重合，展平纸片，得到折痕EF ；折叠纸片，使点B ，P 分别落在EF ，BN 上，得到折痕l ，点B ，P 的对应点分别为B ，P ，展平纸片，连接，P B ．请完成：(3)证明BB 是∠NBC 的一条三等分线．23(2023·重庆·统考中考真题)在Rt △ABC 中，∠ACB =90°，∠B =60°，点D 为线段AB 上一动点，连接CD ．(1)如图1，若AC =9，BD =3，求线段AD 的长．(2)如图2，以CD 为边在CD 上方作等边△CDE ，点F 是DE 的中点，连接BF 并延长，交CD 的延长线于点G ．若∠G =∠BCE ，求证：GF =BF +BE ．(3)在CD 取得最小值的条件下，以CD 为边在CD 右侧作等边△CDE ．点M 为CD 所在直线上一点，将△BEM 沿BM 所在直线翻折至△ABC 所在平面内得到△BNM ．连接AN ，点P 为AN 的中点，连接CP ，当CP 取最大值时，连接BP ，将△BCP 沿BC 所在直线翻折至△ABC 所在平面内得到△BCQ ，请直接写出此时NQ CP的值．24(2023·湖南·统考中考真题)如图，在等边三角形ABC 中，D 为AB 上的一点，过点D 作BC 的平行线DE 交AC 于点E ，点P 是线段DE 上的动点(点P 不与D 、E 重合)．将△ABP 绕点A 逆时针方向旋转60°，得到△ACQ ，连接EQ 、PQ ,PQ 交AC 于F ．(1)证明：在点P 的运动过程中，总有∠PEQ =120°．(2)当AP DP为何值时，△AQF 是直角三角形？25(2023·黑龙江·统考中考真题)如图①，△ABC和△ADE是等边三角形，连接DC，点F，G，H分别是DE,DC和BC的中点，连接FG,FH．易证：FH=3FG．若△ABC和△ADE都是等腰直角三角形，且∠BAC=∠DAE=90°，如图②：若△ABC和△ADE都是等腰三角形，且∠BAC=∠DAE=120°，如图③：其他条件不变，判断FH和FG之间的数量关系，写出你的猜想，并利用图②或图③进行证明．26(2023·黑龙江齐齐哈尔·统考中考真题)综合与实践数学模型可以用来解决一类问题，是数学应用的基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．(1)发现问题：如图1，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=30°，连接BE，CF，延长BE交CF于点D．则BE与CF的数量关系：，∠BDC=°；(2)类比探究：如图2，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=120°，连接BE，CF，延长BE，FC交于点D．请猜想BE与CF的数量关系及∠BDC的度数，并说明理由；(3)拓展延伸：如图3，△ABC和△AEF均为等腰直角三角形，∠BAC=∠EAF=90°，连接BE，CF，且点B，E，F在一条直线上，过点A作AM⊥BF，垂足为点M．则BF，CF，AM之间的数量关系：；(4)实践应用：正方形ABCD中，AB=2，若平面内存在点P满足∠BPD=90°，PD=1，则S△ABP=．27(2023·广东深圳·统考中考真题)(1)如图，在矩形ABCD中，E为AD边上一点，连接BE，①若BE=BC，过C作CF⊥BE交BE于点F，求证：△ABE≌△FCB；=20时，则BE⋅CF=．②若S矩形ABCD(2)如图，在菱形ABCD中，cos A=13，过C作CE⊥AB交AB的延长线于点E，过E作EF⊥AD交AD =24时，求EF⋅BC的值．于点F，若S菱形ABCD(3)如图，在平行四边形ABCD中，∠A=60°，AB=6，AD=5，点E在CD上，且CE=2，点F为BC上一点，连接EF，过E作EG⊥EF交平行四边形ABCD的边于点G，若EF⋅EG=73时，请直接写出AG的长．28(2023·内蒙古·统考中考真题)如图，在菱形ABCD中，对角线AC,BD相交于点O，点P,Q分别是边BC，线段OD上的点，连接AP,QP,AP与OB相交于点E．(1)如图1，连接QA．当QA=QP时，试判断点Q是否在线段PC的垂直平分线上，并说明理由；(2)如图2，若∠APB=90°，且∠BAP=∠ADB，①求证：AE=2EP；②当OQ=OE时，设EP=a，求PQ的长(用含a的代数式表示)．29(2023·内蒙古赤峰·统考中考真题)数学兴趣小组探究了以下几何图形．如图①，把一个含有45°角的三角尺放在正方形ABCD中，使45°角的顶点始终与正方形的顶点C重合，绕点C旋转三角尺时，45°角的两边CM ，CN 始终与正方形的边AD ，AB 所在直线分别相交于点M ，N ，连接MN ，可得△CMN ．【探究一】如图②，把△CDM 绕点C 逆时针旋转90°得到△CBH ，同时得到点H 在直线AB 上．求证：∠CNM =∠CNH ；【探究二】在图②中，连接BD ，分别交CM ，CN 于点E ，F ．求证：△CEF ∽△CNM ；【探究三】把三角尺旋转到如图③所示位置，直线BD 与三角尺45°角两边CM ，CN 分别交于点E ，F ．连接AC 交BD 于点O ，求EFNM的值．30(2023·山东东营·统考中考真题)(1)用数学的眼光观察．如图，在四边形ABCD 中，AD =BC ，P 是对角线BD 的中点，M 是AB 的中点，N 是DC 的中点，求证：∠PMN =∠PNM ．(2)用数学的思维思考．如图，延长图中的线段AD 交MN 的延长线于点E ，延长线段BC 交MN 的延长线于点F ，求证：∠AEM =∠F ．(3)用数学的语言表达．如图，在△ABC 中，AC <AB ，点D 在AC 上，AD =BC ，M 是AB 的中点，N 是DC 的中点，连接MN 并延长，与BC 的延长线交于点G ，连接GD ，若∠ANM =60°，试判断△CGD 的形状，并进行证明．31(2023·甘肃兰州·统考中考真题)综合与实践【思考尝试】(1)数学活动课上，老师出示了一个问题：如图1，在矩形ABCD中，E是边AB上一点，DF⊥CE于点F，GD⊥DF，AG⊥DG，AG=CF．试猜想四边形ABCD的形状，并说明理由；【实践探究】(2)小睿受此问题启发，逆向思考并提出新的问题：如图2，在正方形ABCD中，E是边AB上一点，DF⊥CE于点F，AH⊥CE于点H，GD⊥DF交AH于点G，可以用等式表示线段FH，AH，CF的数量关系，请你思考并解答这个问题；【拓展迁移】(3)小博深入研究小睿提出的这个问题，发现并提出新的探究点：如图3，在正方形ABCD中，E是边AB上一点，AH⊥CE于点H，点M在CH上，且AH=HM，连接AM，BH，可以用等式表示线段CM，BH的数量关系，请你思考并解答这个问题．32(2023·贵州·统考中考真题)如图①，小红在学习了三角形相关知识后，对等腰直角三角形进行了探究，在等腰直角三角形ABC中，CA=CB,∠C=90°，过点B作射线BD⊥AB，垂足为B，点P在CB上．(1)【动手操作】如图②，若点P在线段CB上，画出射线PA，并将射线PA绕点P逆时针旋转90°与BD交于点E，根据题意在图中画出图形，图中∠PBE的度数为度；(2)【问题探究】根据(1)所画图形，探究线段PA与PE的数量关系，并说明理由；(3)【拓展延伸】如图③，若点P在射线CB上移动，将射线PA绕点P逆时针旋转90°与BD交于点E，探究线段BA,BP, BE之间的数量关系，并说明理由．33(2023·辽宁·统考中考真题)在RtΔABC中，∠ACB=90°，CA=CB，点O为AB的中点，点D在直线AB上(不与点A,B重合)，连接CD，线段CD绕点C逆时针旋转90°，得到线段CE，过点B作直线l⊥BC，过点E作EF⊥l，垂足为点F，直线EF交直线OC于点G．(1)如图，当点D与点O重合时，请直接写出线段AD与线段EF的数量关系；(2)如图，当点D在线段AB上时，求证：CG+BD=2BC；(3)连接DE，△CDE的面积记为S1，△ABC的面积记为S2，当EF:BC=1:3时，请直接写出S1S2的值．34(2023·四川成都·统考中考真题)探究式学习是新课程倡导的重要学习方式，某兴趣小组拟做以下探究．在Rt△ABC中，∠C=90°,AC=BC，D是AB边上一点，且ADBD=1n(n为正整数)，E是AC边上的动点，过点D作DE的垂线交直线BC于点F．【初步感知】(1)如图1，当n=1时，兴趣小组探究得出结论：AE+BF=22AB，请写出证明过程．【深入探究】(2)①如图2，当n=2，且点F在线段BC上时，试探究线段AE，BF，AB之间的数量关系，请写出结论并证明；②请通过类比、归纳、猜想，探究出线段AE，BF，AB之间数量关系的一般结论(直接写出结论，不必证明)【拓展运用】(3)如图3，连接EF，设EF的中点为M．若AB=22，求点E从点A运动到点C的过程中，点M运动的路径长(用含n的代数式表示)．35(2023·江苏徐州·统考中考真题)【阅读理解】如图1，在矩形ABCD中，若AB=a,BC=b，由勾股定理，得AC2=a2+b2，同理BD2=a2+b2，故AC2+BD2=2a2+b2．【探究发现】如图2，四边形ABCD为平行四边形，若AB=a,BC=b，则上述结论是否依然成立？请加以判断，并说明理由．【拓展提升】如图3，已知BO为△ABC的一条中线，AB=a,BC=b,AC=c．求证：BO2=a2+b22-c24．【尝试应用】如图4，在矩形ABCD中，若AB=8,BC=12，点P在边AD上，则PB2+PC2的最小值为．36(2023·四川南充·统考中考真题)如图，正方形ABCD中，点M在边BC上，点E是AM的中点，连接ED，EC．(1)求证：ED=EC；(2)将BE绕点E逆时针旋转，使点B的对应点B 落在AC上，连接MB′．当点M在边BC上运动时(点M 不与B，C重合)，判断△CMB′的形状，并说明理由．(3)在(2)的条件下，已知AB=1，当∠DEB′=45°时，求BM的长．37(2023·安徽·统考中考真题)在Rt△ABC中，M是斜边AB的中点，将线段MA绕点M旋转至MD 位置，点D在直线AB外，连接AD,BD．(1)如图1，求∠ADB的大小；(2)已知点D和边AC上的点E满足ME⊥AD,DE∥AB．(ⅰ)如图2，连接CD，求证：BD=CD；(ⅱ)如图3，连接BE，若AC=8,BC=6，求tan∠ABE的值．38(2023·浙江宁波·统考中考真题)定义：有两个相邻的内角是直角，并且有两条邻边相等的四边形称为邻等四边形，相等两邻边的夹角称为邻等角．(1)如图1，在四边形ABCD中，AD∥BC,∠A=90°，对角线BD平分∠ADC．求证：四边形ABCD为邻等四边形．(2)如图2，在6×5的方格纸中，A，B，C三点均在格点上，若四边形ABCD是邻等四边形，请画出所有符合条件的格点D．(3)如图3，四边形ABCD是邻等四边形，∠DAB=∠ABC=90°，∠BCD为邻等角，连接AC，过B作BE∥AC交DA的延长线于点E．若AC=8,DE=10，求四边形EBCD的周长．39(2023·江苏扬州·统考中考真题)【问题情境】在综合实践活动课上，李老师让同桌两位同学用相同的两块含30°的三角板开展数学探究活动，两块三角板分别记作△ADB和△A D C,∠ADB=∠A D C=90°,∠B=∠C=30°，设AB=2．【操作探究】如图1，先将△ADB和△A D C的边AD、A D 重合，再将△A D C绕着点A按顺时针方向旋转，旋转角为α0°≤α≤360°，旋转过程中△ADB保持不动，连接BC．(1)当α=60°时，BC=；当BC=22时，α=°；(2)当α=90°时，画出图形，并求两块三角板重叠部分图形的面积；(3)如图2，取BC的中点F，将△A D C绕着点A旋转一周，点F的运动路径长为．40(2023·四川乐山·统考中考真题)在学习完《图形的旋转》后，刘老师带领学生开展了一次数学探究活动【问题情境】刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容：如图，将一个三角形纸板△ABC绕点A逆时针旋转θ到达△AB C 的位置，那么可以得到：AB=AB ，AC =AC ，BC=B C ；∠BAC=∠B AC ，∠ABC=∠AB C ，∠ACB=∠AC B ()刘老师进一步谈到：图形的旋转蕴含于自然界的运动变化规律中，即“变”中蕴含着“不变”，这是我们解决图形旋转的关键；故数学就是一门哲学．【问题解决】(1)上述问题情境中“( )”处应填理由：；(2)如图，小王将一个半径为4cm，圆心角为60°的扇形纸板ABC绕点O逆时针旋转90°到达扇形纸板A BC 的位置．①请在图中作出点O；②如果BB =6cm，则在旋转过程中，点B经过的路径长为；【问题拓展】小李突发奇想，将与(2)中完全相同的两个扇形纸板重叠，一个固定在墙上，使得一边位于水平位置，另一个在弧的中点处固定，然后放开纸板，使其摆动到竖直位置时静止，此时，两个纸板重叠部分的面积是多少呢？如图所示，请你帮助小李解决这个问题．。

中考数学几何压轴题(有关三角形、四边形)的综合专题(含答案解析)

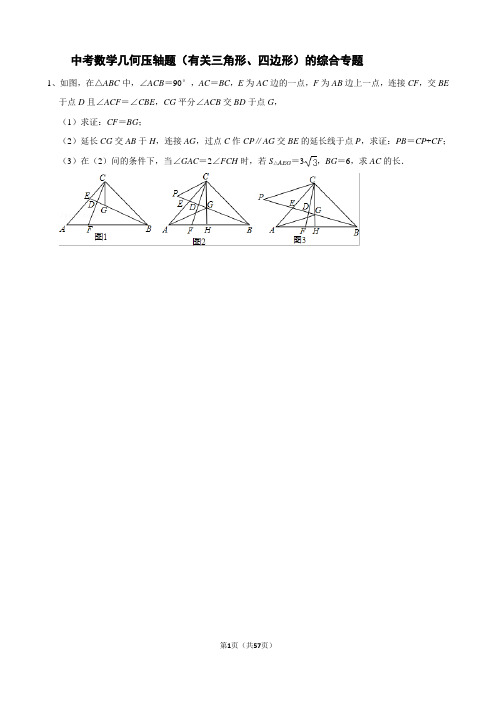
中考数学几何压轴题（有关三角形、四边形）的综合专题1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△，可推证△CEF是三角形，从而求得∠DCE＝．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．3、（2019秋•锦江区校级期末）在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．4、（2019•镇平县三模）如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为；∠EFC的度数为；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．5、（2017春•西城区校级期末）如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．7、（1）如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．9、（2018•大东区一模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于时，线段BC的长取得最大值，且最大值为（用含b，c的式子表示）（直接填空）.模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线上时，线段PC、PG又有怎样的数量关系，请直接写出你的结论，并画出论证过程中需要添加的辅助线．17、在△ABC中，∠BAC＝60°，点D、E分别在边AC、AB上，AD＝AE，连接CE、BD相交于点F，且∠BEC＝∠ADF，连接AF．（1）如图1，连接ED，求证：∠ABD＝∠CED；（2）如图2，求证：EF+FD＝AF；（3）如图3，取BC的中点G，连接AG交BD于点H，若∠GAC＝3∠ABD，BH＝7，求△ABH的面积．18、点D，E分别在△ABC的边AC，BD上，BD，CE交于点F，连接AF，∠F AE＝∠F AD，FE＝FD．（1）如图1，若∠AEF＝∠ADF，求证：AE＝AD；（2）如图2，若∠AEF≠∠ADF，FB平分∠ABC，求∠BAC的度数；（3）在（2）的条件下，如图3，点G在BE上，∠CFG＝∠AFB若AG＝6，△ABC的周长为20，求BC长．中考数学几何压轴题（有关三角形、四边形）的综合专题参考答案1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．证明：（1）如图1，∵∠ACB＝90°，AC＝BC，∴∠A＝45°，∵CG平分∠ACB，∴∠ACG＝∠BCG＝45°，∴∠A＝∠BCG，在△BCG和△CAF中，∵，∴△BCG≌△CAF（ASA），∴CF＝BG；（2）如图2，∵PC∥AG，∴∠PCA＝∠CAG，∵AC＝BC，∠ACG＝∠BCG，CG＝CG，∴△ACG≌△BCG，∴∠CAG＝∠CBE，∵∠PCG＝∠PCA+∠ACG＝∠CAG+45°＝∠CBE+45°，∠PGC＝∠GCB+∠CBE＝∠CBE+45°，∴∠PCG＝∠PGC，∴PC＝PG，∵PB＝BG+PG，BG＝CF，∴PB＝CF+CP；（3）解法一：如图3，过E作EM⊥AG，交AG于M，∵S△AEG＝AG•EM＝3，由（2）得：△ACG≌△BCG，∴BG＝AG＝6，∴×6×EM＝3，EM＝，设∠FCH＝x°，则∠GAC＝2x°，∴∠ACF＝∠EBC＝∠GAC＝2x°，∵∠ACH＝45°，∴2x+x＝45，x＝15，∴∠ACF＝∠GAC＝30°，在Rt△AEM中，AE＝2EM＝2，AM＝＝3，∴M是AG的中点，∴AE＝EG＝2，∴BE＝BG+EG＝6+2，在Rt△ECB中，∠EBC＝30°，∴CE＝BE＝3+，∴AC＝AE+EC＝2+3+＝3+3．解法二：同理得：∠CAG＝30°，AG＝BG＝6，如图4，过G作GM⊥AC于M，在Rt△AGM中，GM＝3，AM＝＝＝3，∵∠ACG＝45°，∠MGC＝90°，∴GM＝CM＝3，∴AC＝AM+CM＝3+3．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△ADB，可推证△CEF是等腰直角三角形，从而求得∠DCE＝135°．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．解：[问题初探]如图2，过点E作EF⊥BC交直线BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝135°，故答案为：ADB，等腰直角，135；[继续探究]如图3，过点E作EF⊥BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝45°；[拓展延伸]如图4，在△ABC中，∠ABC＝90°，AB＝BC＝，∴∠ACB＝45°当点D在射线BC上时，由[问题初探]知，∠BCM＝135°，∴∠ACM＝∠BCM﹣∠ACB＝90°，当点D在线段CB的延长线上时，由[继续探究]知，∠BCE＝45°，∴∠ACN＝∠ACB+∠BCM＝90°，∴点E是过点C垂直于AC的直线上的点，∴当BE⊥MN时，BE最小，∵∠BCE＝45°，∴∠CBE＝45°＝∠BCE，∴BE＝CE，∴BE最小＝BC＝，即：BE的最小值为．3、在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．证明：（1）如图1，过点D作DE⊥AB，∵BD是△ABC的角平分线，DE⊥AB，∠ACB＝90°，∴DC＝DE，∵∠A＝30°，DE⊥AB，∴AD＝2DE，∴AD＝2DC；（2）如图2，过点M作ME∥BD，∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∵BD是△ABC的角平分线，∴∠ABD＝∠DBC＝30°，∵BM平分∠CBD，∴∠CBM＝15°＝∠DBM，∵ME∥BD，∴∠MEC＝∠CBD＝30°，∠EMB＝∠DBM＝∠MBE，∴ME＝BE，∵∠MEC＝30°，∠C＝90°∴CE＝MC＝，ME＝2MC＝2＝BE，∴BC＝+2，∵∠CBD＝30°，∠C＝90°，∴BC＝CD，∴CD＝1+，∴DM＝，∴△DBM的面积＝××（+2）＝1+；（3）若点N在CD上时，AD＝DG+DN，理由如下：如图3所示：延长ED使得DW＝DN，连接NW，∵∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线，DE⊥AB于点E，∴∠ADE＝∠BDE＝60°，AD＝BD，∵DN＝DW，且∠WDN＝60°∴△WDN是等边三角形，∴NW＝DN，∠W＝∠WND＝∠BNG＝∠BDN＝60°，∴∠WNG＝∠BND，在△WGN和△DBN中，∴△WGN≌△DBN（SAS），∴BD＝WG＝DG+DN，∴AD＝DG+DN．（3）若点N在AD上时，AD＝DG﹣DN，理由如下：如图4，延长BD至H，使得DH＝DN，连接HN，由（1）得DA＝DB，∠A＝30°．∵DE⊥AB于点E．∴∠2＝∠3＝60°．∴∠4＝∠5＝60°．∴△NDH是等边三角形．∴NH＝ND，∠H＝∠6＝60°．∴∠H＝∠2．∵∠BNG＝60°，∴∠BNG+∠7＝∠6+∠7．即∠DNG＝∠HNB．在△DNG和△HNB中，∴△DNG≌△HNB（ASA）．∴DG＝HB．∵HB＝HD+DB＝ND+AD，∴DG＝ND+AD．∴AD＝DG﹣ND．4、如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为EF＝CF；∠EFC的度数为120°；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．解：（1）如图1中，∵DE⊥AB，∴∠BED＝90°，∵∠BCD＝90°，BF＝DF，∴FE＝FB＝FD＝CF，∴∠FBE＝∠FEB，∠FBC＝∠FCB，∴∠EFC＝∠EFD+∠CFD＝∠FBE+∠FEB+∠FBC+∠FCB＝2（∠FBE+∠FBC）＝2∠ABC＝120°，故答案为：EF＝CF，120°．（2）结论成立．理由：如图2中，取AB的中点M，AD的中点N，连接MC，MF，ED，EN，FN．∵BM＝MA，BF＝FD，∴MF∥AD，MF＝AD，∵AN＝ND，∴MF＝AN，MF∥AN，∴四边形MFNA是平行四边形，∴NF＝AM，∠FMA＝∠ANF，在Rt△ADE中，∵AN＝ND，∠AED＝90°，∴EN＝AD＝AN＝ND，同理CM＝AB＝AM＝MB，在△AEN和△ACM中，∠AEN＝∠EAN，∠MCA＝∠MAC，∵∠MAC＝∠EAN，∴∠AMC＝∠ANE，又∵∠FMA＝∠ANF，∴∠ENF＝∠FMC，在△MFC和△NEF中，，∴△MFC≌△NEF（SAS），∴FE＝FC，∠NFE＝∠MCF，∵NF∥AB，∴∠NFD＝∠ABD，∵∠ACB＝90°，∠BAC＝30°，∴∠ABC＝60°，△BMC是等边三角形，∠MCB＝60°∴∠EFC＝∠EFN+∠NFD+∠DFC＝∠MCF+∠ABD+∠FBC+∠FCB＝∠ABC+∠MCB＝60°+60°＝120°．（3）如图3中，作EH⊥AB于H．在Rt△ABC中，∵∠BAC＝30°，BC＝3，∴AB＝2BC＝6，在Rt△AED中，∠DAE＝30°，AD＝2，∴DE＝AD＝1，在Rt△DEH中，∵∠EDH＝60°，DE＝1，∴EH＝ED•sin60°＝，DH＝ED•cos60°＝，在Rt△EHG中，EG＝＝．5、如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．解：（1）BC＝2BD，理由：如图2，连接CD，由旋转可得，CP＝DP，∠CPD＝60°，∴△CDP是等边三角形，∴∠CDP＝60°＝∠PCD，又∵P是AB的中点，AB＝AC，∠A＝60°，∴等边三角形ABC中，∠PCB＝30°，CP⊥AB，∴∠BCD＝30°，即BC平分∠PCD，∴BC垂直平分PD，∴∠BDC＝∠BPC＝90°，∴Rt△BCD中，BC＝2BD．（2）如图3，取BC中点F，连接PF，∵∠A＝90°，AB＝AC，∴△ABC是等腰直角三角形，∵P是AB的中点，F是BC的中点，∴PF是△ABC的中位线，∴PF∥AC，∴∠PFB＝∠ACB＝45°，∠BPF＝∠A＝90°，∴△BPF是等腰直角三角形，∴BF＝BP，BP＝PF，∵∠DPC＝∠BPF＝90°，∴∠BPD＝∠FPC，又∵PD＝PC，∴△BDP≌△FCP，∴BD＝CF，∵BC＝BF+FC，∴BC＝BD+BP．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．【发现问题】解：延长CA到M，作∠MAC的平分线AN，在AN上截取AD＝AC，连接CD，即可得到等腰直角△ACD；连接BD、CE，如图1所示：∵△ABE与△ACD都是等腰直角三角形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE，【拓展探究】解：BD＝CE；理由如下：∵四边形AEFB与四边形ACGD都是正方形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；【解决问题】解：以AB为边向外作等边三角形ABE，连接CE，如图3所示：则∠BAE＝60°，BE＝AB＝AE＝8，∵AD＝CD，∠ADC＝60°，∴△ACD是等边三角形，∴∠CAD＝60°，AC＝AD，∴∠CAD+∠BAC＝∠BAE+∠BAC，即∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；当C、B、E三点共线时，CE最大＝BC+BE＝15+8＝23，∴BD的最大值为23．7、如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为a+b（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．（1）解：∵点C为线段AB外一动点，且AC＝b，AB＝a，∴当点C位于BA的延长线上时，线段BC的长取得最大值，且最大值为AC+AB＝a+b，（2）①证明：如图2中，∵△ACD与△BCE是等边三角形，∴CD＝AC，CB＝CE，∠ACD＝∠BCE＝60°，∴∠DCB＝∠ACE，在△CAD与△EAB中，，∴△CAD≌△EAB（SAS），∴AE＝BD．②∵线段AE长的最大值＝线段BD的最大值，由（1）知，当线段BD的长取得最大值时，点D在BA的延长线上，∴最大值为AD+AB＝3+10＝13；（3）如图3中，连接BN，∵将△AMN绕着点M顺时针旋转90°得到△PBM，连接AP，则△APM是等腰直角三角形，∴MA＝MP＝2，BP＝AN，∴P A＝2，∵AB＝6，∴线段AN长的最大值＝线段BP长的最大值，∴当P在线段BA的延长线时，线段BP取得最大值最大值＝AB+AP＝6+2．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是∠BAE+∠F AD＝∠EAF；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．解：（1）∠BAE+∠F AD＝∠EAF．理由：如图1，延长FD到点G，使DG＝BE，连接AG，根据SAS可判定△ABE≌△ADG，进而得出∠BAE＝∠DAG，AE＝AG，再根据SSS可判定△AEF≌△AGF，可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF．故答案为：∠BAE+∠F AD＝∠EAF；（2）仍成立，理由：如图2，延长FD到点G，使DG＝BE，连接AG，∵∠B+∠ADF＝180°，∠ADG+∠ADF＝180°，∴∠B＝∠ADG，又∵AB＝AD，∴△ABE≌△ADG（SAS），∴∠BAE＝∠DAG，AE＝AG，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；（3）∠EAF＝180°﹣∠DAB．证明：如图3，在DC延长线上取一点G，使得DG＝BE，连接AG，∵∠ABC+∠ADC＝180°，∠ABC+∠ABE＝180°，∴∠ADC＝∠ABE，又∵AB＝AD，∴△ADG≌△ABE（SAS），∴AG＝AE，∠DAG＝∠BAE，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠F AE＝∠F AG，∵∠F AE+∠F AG+∠GAE＝360°，∴2∠F AE+（∠GAB+∠BAE）＝360°，∴2∠F AE+（∠GAB+∠DAG）＝360°，即2∠F AE+∠DAB＝360°，∴∠EAF＝180°﹣∠DAB．9、如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．解：（1）CP＝BQ，理由：如图1，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°⊅∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（2）CP＝BQ，理由：如图2，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（3）如图3，在Rt△ABC中，∠A＝30°，AC＝，∴BC＝AC•tan∠A＝，过点O作OH⊥BC，∴∠OHB＝90°＝∠BCA，∴OH∥AB，∵O是AB中点，∴CH＝BC＝，OH＝AC＝，∵∠BPQ＝45°，∠OHP＝90°，∴∠BPQ＝∠PQH，∴PH＝OH＝，∴CP＝PH﹣CH＝﹣＝，连接BQ，同（1）的方法得，BQ＝CP＝．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于线段BA的延长线上时，线段BC的长取得最大值，且最大值为b+c（用含b，c的式子表示）（直接填空）模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为5．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．解：当点C位于线段BA的延长线上时，线段BC的长取得最大值，最大值为b+c，故答案为：线段BA的延长线上；b+c；模型应用：（1）证明：∵△ACD、△BCE都是等边三角形，∴CD＝CA＝AD，CB＝CE，∠ACD＝60°，∠BCE＝60°，∴∠DCB＝∠ACE，在△DCB和△ACE中，，∴△DCB≌△ACE（SAS）∴BD＝AE；（2）当点D位于线段BA的延长线上时，线段BD的长取得最大值，最大值为AB+AD＝AB+AC＝3+2＝5，∵AE＝BD，∴线段AE长的最大值为5，模型拓展：取AB的中点G，连接OG、CG，在Rt△AOB中，G为AB的中点，∴OG＝AB＝4，在Rt△CAG中，CG＝＝＝5，当点O、G、C在同一条直线上时，OC最大，最大值为4+5＝9．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．（1）证明：如图1中，∵BE⊥AD于E，∴∠AEF＝∠BCF＝90°，∵∠AFE＝∠CFB，∴∠DAC＝∠CBF，∵BC＝CA，∴△BCF≌△ACD，∴BF＝AD．（2）结论：BD＝2CF．理由：如图2中，作EH⊥AC于H．∵∠AHE＝∠ACD＝∠DAE＝90°，∴∠DAC+∠ADC＝90°，∠DAC+∠EAH＝90°，∴∠DAC＝∠AEH，∵AD＝AE，∴△ACD≌△EHA，∴CD＝AH，EH＝AC＝BC，∵CB＝CA，∴BD＝CH，∵∠EHF＝∠BCF＝90°，∠EFH＝∠BFC，EH＝BC，∴△EHF≌△BCF，∴FH＝CF，∴BD＝CH＝2CF．（3）如图3中，同法可证BD＝2CM．∵AC＝3CM，设CM＝a，则AC＝CB＝3a，BD＝2a，∴＝＝．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF上截取BK＝AF，连接AK．∵∠BFE＝∠2+∠BAF，∠CFE＝∠4+∠1，∴∠CFB＝∠2+∠4+∠BAC，∵∠BFE＝∠BAC＝2∠EFC，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB＝AC，∴△ABK≌CAF，∴∠3＝∠4，S△ABK＝S△AFC，∵∠1+∠3＝∠2+∠3＝∠CFE＝∠AKB，∠BAC＝2∠CEF，∴∠KAF＝∠1+∠3＝∠AKF，∴AF＝FK＝BK，∴S△ABK＝S△AFK，∴＝2．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．（1）解：如图1中，在AB上取一点M，使得BM＝ME，连接ME．在Rt△ABE中，∵OB＝OE，∴BE＝2OA＝2，∵MB＝ME，∴∠MBE＝∠MEB＝15°，∴∠AME＝∠MBE+∠MEB＝30°，设AE＝x，则ME＝BM＝2x，AM＝x，∵AB2+AE2＝BE2，∴（2x+x）2+x2＝22，∴x＝（负根已经舍弃），∴AB＝AC＝（2+）•，∴BC＝AB＝+1．方法二：作EH⊥BC于H，求出BH，CH即可解决问题．（2）证明：如图2中，作CP⊥AC，交AD的延长线于P，GM⊥AC于M．∵BE⊥AP，∴∠AHB＝90°，∴∠ABH+∠BAH＝90°，∵∠BAH+∠P AC＝90°，∴∠ABE＝∠P AC，在△ABE和△CAP中，，∴△ABE≌△CAP，∴AE＝CP＝CF，∠AEB＝∠P，在△DCF和△DCP中，，∴△DCF≌△DCP，∴∠DFC＝∠P，∴∠GFE＝∠GEF，∴GE＝GF，∵GM⊥EF，∴FM＝ME，∵AE＝CF，∴AF＝CE，∴AM＝CM，在△GAH和△GAM中，，∴△AGH≌△AGM，∴AH＝AM＝CM＝AC（3）解：结论：AG＝EF．理由：如图3中，作CM⊥AC交AD的延长线于M，连接PG交AC于点O．由（2）可知△ACM≌△BAE，△CDF≌△CDM，∴∠AEB＝∠M＝∠GEF，∠M＝∠CFD＝∠GFE，AE＝CM＝CF，∴∠GEF＝∠GFE，∴GE＝GF，∵△EFP是由△EFG翻折得到，∴EG＝EP＝GF＝PF，∴四边形EGFP是菱形，∴PG⊥AC，OE＝OF，∵AE＝CF，∴AO＝OC，∵AB∥OP，∴BP＝PC，∵PF∥BE，∴EF＝CF＝AE，∵PB＝PC，AO＝OC，∴PO＝OG＝AB，∴AB＝PG，AB∥PG，∴四边形ABPG是平行四边形，∴AG∥BC，∴∠GAO＝∠ACB＝45°，设EO＝OF＝a，则OA＝OG＝3a，AG＝3a，∴＝＝，∴AG＝EF14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．解：（1）∵E为AC中点，作ED⊥AC交AB于D，∴AD＝CD，∵∠ACB＝90°，∴BC∥DE，∴AD＝BD，∴CD＝BD，∴AB＝2CD；（2）如图2，连接CH，∵点E是AC的中点，∴AE＝CE，∵DE⊥AC，∴CH＝AH，∴∠ACH＝∠CAH，∵∠ACB＝90°，∴∠B+∠BAC＝90°，∵CF⊥AB，∴∠BAC+∠ACF＝90°，∴∠ACF＝∠B，∴∠HCG＝∠ACH+∠ACF＝∠CAH+∠B，∠AHG＝2∠B∴在四边形AHGF中，∠AFG+∠FGH+∠AHG+∠F AH＝360°，∴∠FGH＝360°﹣（∠AFG+∠AHG+∠F AH）＝360°﹣（90°+2∠B+∠CAH+∠BAC）＝360°﹣（90°+2∠B+∠CAH+90°﹣∠B）＝360°﹣（180°+∠B+∠CAH）＝180°﹣（∠B+∠CAH），∵∠CGH＝180°﹣∠FGH＝∠B+∠CAH＝∠HCG，∴CH＝GH，∵CH＝AH，∴AH＝GH；（3）如图3，由（1）知，DE∥BC，∴∠B＝∠ADE，在△BFC和△DEA中，，∴△BFC≌△DEA，∴BC＝AD，∵AD＝BD＝CD，∴BC＝BD＝CD，∴△BCD是等边三角形，∴∠B＝60°，在Rt△ABC中，AC＝6，∴BC＝2，AB＝4，∵CF⊥BD，∴DF＝，CF＝3，∵∠BAC＝30°，∴∠ADE＝60°，∵∠EDG＝90°，∠FDG＝30°，在Rt△DFG中，DF＝，∴FG＝1，DG＝2，∴CG＝CF﹣FG＝2过点H作HN⊥CF，由（2）知，CH＝GH，∴NG＝CG＝1，∴FN＝NG+FG＝2，过点H作HM⊥AB，∴∠FMH＝∠NFM＝∠HNF＝90°，∴四边形NFMH是矩形，∴HM＝FN＝2，在Rt△DMH中，∠ADE＝60°，HM＝2，∴DH＝，在Rt△HDG中，根据勾股定理得，HG＝＝．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）（1）证明：∵AC＝BC，∠ACB＝90°，∴∠A＝∠B＝45°，∵CD⊥AB，∴∠CDB＝90°，∴∠DCB＝45°，∵∠ECF＝∠DCB+∠1＝45°+∠1，∠EFC＝∠B+∠2＝45°+∠2，∠1＝∠2，∴∠ECF＝∠EFC，∴CE＝EF，∵CD⊥AB，FG⊥AB，∴∠CDE＝∠EGF＝90°，在△CDE和△EGF中，，∴△CDE≌△EGF（AAS）；（2）证明：由（1）得：CE＝EF，∠A＝∠B，∵CE平分∠ACD，∴∠ACE＝∠1，∵∠1＝∠2，∴∠ACE＝∠2，在△ACE和△BEF中，，∴△ACE≌△BEF（AAS），∴AE＝BF；（3）AE＝BF，作EH⊥BC与H，如图3所示：设DE＝x，根据题意得：BE＝DE＝x，AD＝BD＝2x，CD＝AD＝2x，AE＝3x，根据勾股定理得：BC＝AC＝2x，∵∠ABC＝45°，EH⊥BC，∴BH＝x，∴CH＝BC﹣BH＝x，∵EC＝EF，∴FH＝CH＝x，∴BF＝x﹣x＝x，∴＝，∴AE＝．16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线。

中考数学模拟题《几何综合》专项测试题(附带参考答案)

中考数学模拟题《几何综合》专项测试题(附带参考答案)学校:___________班级：___________姓名：___________考号：___________考点解读在中考数学中有这么一类题它是以点线几何图形的运动为载体集合多个代数知识几何知识及数学解题思想于一题的综合性试题它就是动态几何问题。

动态几何问题经常在各地以中考试卷解答压轴题出现也常会出现在选择题最后一题的位置考察知识面较广综合性强可以提升学生的空间想象能力和综合分析问题的能力但同时难度也很大令无数初中学子闻风丧胆考场上更是丢盔弃甲解题思路1 熟练掌握平面几何知识﹕要想解决好有关几何综合题首先就是要熟练掌握关于平面几何的所有知识尤其是要重点把握三角形特殊四边形圆及函数三角函数相关知识．几何综合题重点考查的是关于三角形特殊四边形（平行四边形矩形菱形正方形）圆等相关知识2 掌握分析问题的基本方法﹕分析法综合法“两头堵”法﹕1）分析法是我们最常用的解决问题的方法也就是从问题出发执果索因去寻找解决问题所需要的条件依次向前推直至已知条件例如我们要证明某两个三角形全等先看看要证明全等需要哪些条件哪些条件已知了还缺少哪些条件然后再思考要证缺少的条件又需要哪些条件依次向前推直到所有的条件都已知为止即可综合法﹕即从已知条件出发经过推理得出结论适合比较简单的问题3）“两头堵”法﹕当我们用分析法分析到某个地方不知道如何向下分析时可以从已知条件出发看看能得到什么结论把分析法与综合法结合起来运用是我们解决综合题最常用的办策略3 注意运用数学思想方法﹕对于几何综合题的解决我们还要注意运用数学思想方法这样会大大帮助我们解决问题或者简化我们解决问题的过程加快我们解决问题的速度毕竟考场上时间是非常宝贵的．常用数学思想方法﹕转化类比归纳等等模拟预测1 （2024·江西九江·二模）如图在矩形()ABDC AB AC >的对称轴l 上找点P 使得PAB PCD 、均为直角三角形则符合条件的点P 的个数是（）A ．1B ．3C ．4D ．52 （2024·江西吉安·模拟预测）如图在平面直角坐标系中边长为23ABC 的顶点A B ，分别在y 轴的正半轴 x 轴的负半轴上滑动连接OC 则OC 的最小值为（）A ．2B ．3C ．33D ．333 （2024·江西吉安·一模）如图矩形ABCD 中 4AB = 6AD = 点E 在矩形的边上则当BEC 的一个内角度数为60︒时符合条件的点E 的个数共有（）A ．4个B ．5个C ．6个D ．7个4 （2023·江西·中考真题）如图在ABCD 中 602B BC AB ∠=︒=，将AB 绕点A 逆时针旋转角α（0360α︒<<︒）得到AP 连接PC PD ．当PCD 为直角三角形时旋转角α的度数为．5 （2024·江西吉安·二模）如图在矩形ABCD 中 6,10,AB AD E ==为CD 的中点点P 在AE 下方矩形的边上．当APE 为直角三角形且P 为直角顶点时 BP 的长为．6 （2024·江西九江·二模）如图在平面直角坐标系中已知矩形OABC 的顶点()20,0A ()0,8C D 为OA 的中点点P 为矩形OABC 边上任意一点将ODP 沿DP 折叠得EDP △ 若点E 在矩形OABC 的边上则点E 的坐标为．7 （2024·江西·模拟预测）如图 ABC 中 AB AC = 30A ∠=︒ 射线CP 从射线CA 开始绕点C 逆时针旋转α角()075α︒<<︒ 与射线AB 相交于点D 将ACD 沿射线CP 翻折至A CD '△处射线CA '与射线AB 相交于点E ．若A DE '是等腰三角形则α∠的度数为．8 （2024·江西赣州·二模）在Rt ABC △中已知90C ∠=︒ 10AB = 3cos 5B = 点M 在边AB 上点N 在边BC 上且AM BN = 连接MN 当BMN 为等腰三角形时 AM = ．9 （2024·江西吉安·模拟预测）如图在矩形ABCD 中 6,10AB AD == E 为BC 边上一点 3BE = 点P 沿着边按B A D →→的路线运动．在运动过程中若PAE △中有一个角为45︒ 则PE 的长为．10 （2024·江西吉安·三模）如图在ABC 中 AB AC = 30B ∠=︒ 9BC = D 为AC上一点 2AD DC = P 为边BC 上的动点当APD △为直角三角形时 BP 的长为．11 （2024·江西吉安·一模）如图矩形ABCD 中 4AB = 6AD = E 为CD 的中点连接BE 点P 在矩形的边上且在BE 的上方则当BEP △是以BE 为斜边的直角三角形时 BP 的长为．12 （2024·江西九江·二模）如图在等腰ABC 中 2AB AC == 30B ∠=︒ D 是线段BC 上一动点沿直线AD 将ADB 折叠得到ADE 连接EC ．当DEC 是以DE 为直角边的直角三角形时则BD 的长为．13 （2024·江西·模拟预测）如图在菱形ABCD 中对角线AC BD 相交于点O 23AB = 60ABC ∠=︒ E 为BC 的中点 F 为线段OD 上一动点当AEF △为等腰三角形时 DF 的长为．14 （2024·江西上饶·一模）如图在三角形纸片ABC 中 90,60,6C B BC ∠=︒∠=︒= 将三角形纸片折叠使点B 的对应点B '落在AC 上折痕与,BC AB 分别相交于点E F 当AFB '为等腰三角形时 BE 的长为．15 （2024·江西抚州·一模）课本再现（1）如图1 CD 与BE 相交于点,A ABC 是等腰直角三角形 90C ∠=︒ 若DE BC ∥ 求证：ADE 是等腰直角三角形．类比探究（2）①如图2 AB 是等腰直角ACB △的斜边 G 为边AB 的中点 E 是BA 的延长线上一动点过点E 分别作AC 与BC 的垂线垂足分别为,D F 顺次连接,,DG GF FD 得到DGF △ 求证：DGF △是等腰直角三角形．②如图3 当点E 在边AB 上且①中其他条件不变时 DGF △是等腰直角三角形是否成立？_______（填“是”或“否”）．拓展应用（3）如图4 在四边形ABCD 中 ,90,BC CD BCD BAD AC =∠=∠=︒平分BAD ∠ 当1,22AD AC == 求线段BC 的长．16 （2023·江西·中考真题）课本再现思考我们知道菱形的对角线互相垂直．反过来对角线互相垂直的平行四边形是菱形吗？可以发现并证明菱形的一个判定定理对角线互相垂直的平行四边形是菱形．(1)定理证明：为了证明该定理小明同学画出了图形（如图1）并写出了“已知”和“求证”请你完成证明过程．已知：在ABCD中对角线BD AC⊥垂足为O．求证：ABCD是菱形．(2)知识应用：如图2在ABCD中对角线AC和BD相交于点O586AD AC BD===，，．①求证：ABCD是菱形②延长BC至点E连接OE交CD于点F若12E ACD∠=∠求OFEF的值．17 （2022·江西·中考真题）问题提出：某兴趣小组在一次综合与实践活动中提出这样一个问题：将足够大的直角三角板()90,60PEF P F ∠=︒∠=︒的一个顶点放在正方形中心O 处并绕点O 逆时针旋转探究直角三角板PEF 与正方形ABCD 重叠部分的面积变化情况（已知正方形边长为2）．(1)操作发现：如图1 若将三角板的顶点P 放在点O 处在旋转过程中当OF 与OB 重合时重叠部分的面积为__________ 当OF 与BC 垂直时重叠部分的面积为__________ 一般地若正方形面积为S 在旋转过程中重叠部分的面积1S 与S 的关系为__________(2)类比探究：若将三角板的顶点F 放在点O 处在旋转过程中 ,OE OP 分别与正方形的边相交于点M N ．①如图2 当BM CN =时试判断重叠部分OMN 的形状并说明理由②如图3 当CM CN =时求重叠部分四边形OMCN 的面积（结果保留根号）(3)拓展应用：若将任意一个锐角的顶点放在正方形中心O 处该锐角记为GOH ∠（设GOH α∠=）将GOH ∠绕点O 逆时针旋转在旋转过程中 GOH ∠的两边与正方形ABCD 的边所围成的图形的面积为2S 请直接写出2S 的最小值与最大值（分别用含α的式子表示）（参考数据：6262sin15tan1523-+︒=︒=︒=18 （2024·江西吉安·二模）如图在ABC 和ADE 中 (),AB AC AD AE AD AB ==< 且BAC DAE ∠=∠．连接CE BD ．(1)求证：BD CE =．(2)在图2中点B D E 在同一直线上且点D 在AC 上若,AB a BC b == 求AD CD的值（用含a b 的代数式表示）．19 （2024·江西九江·二模）初步探究（1）如图1 在四边形ABCD 中 ,AC BD 相交于点O AC BD ⊥ 且ABD CBD S S = 则OA 与OC 的数量关系为．迁移探究（2）如图2 在四边形ABCD 中 ,AC BD 相交于点O ABD CBD SS = （1）中OA 与OC 的数量关系还成立吗？如果成立请说明理由．拓展探究（3）如图3 在四边形ABCD 中 ,AC BD 相交于点O 180,ABD CBD BAD BCD S S ∠∠+=︒=△△ 且 33OB OD == 求AC 的长．20 （2024·江西九江·二模）课本再现如图1 四边形ABCD 是菱形 30ACD ∠=︒ 6BD =．（1）求,AB AC 的长．应用拓展（2）如图2 E 为AB 上一动点连接DE 将DE 绕点D 逆时针旋转120︒ 得到DF 连接EF ．①直接写出点D 到EF 距离的最小值②如图3 连接,OF CF 若OCF △的面积为6 求BE 的长．21 （2024·江西赣州·三模）某数学小组在一次数学探究活动过程中经历了如下过程：AB=P为对角线AC上的一个动点以P为直角顶问题提出：如图正方形ABCD中8△．点向右作等腰直角DPM(1)操作发现：DM的最小值为_______ 最大值为_______(2)数学思考：求证：点M在射线BC上=时求CM的长．(3)拓展应用：当CP CM22 （2024·江西赣州·二模）【课本再现】思考我们知道角的平分线上的点到角的两边的距离相等反过来角的内部到角的两边的距离相等的点在角的平分线上吗？可以发现并证明角的平分线的性质定理的逆定理角的内部到角的两边的距离相等的点在角的平分线上．【定理证明】（1）为证明此逆定理某同学画出了图形并写好“已知”和“求证” 请你完成证明过程．已知：如图1 在ABC ∠的内部过射线BP 上的点P 作PD BA ⊥ PE BC ⊥ 垂足分别为D E 且PD PE =．求证：BP 平分ABC ∠．【知识应用】（2）如图2 在ABC 中过内部一点P 作PD BC ⊥ PE AB ⊥ PF AC ⊥ 垂足分别为D E F 且PD PE PF == 120A ∠=︒ 连接PB PC ．①求BPC ∠的度数②若6PB=23PC=求BC的长．23 （2024·江西吉安·模拟预测）一块材料的形状是锐角三角形ABC下面分别对这块材料进行课题探究：课本再现：（1）在图1中若边120mmBC=高80mmAD=把它加工成正方形零件使正方形的一边在BC上其余两个顶点分别在AB AC上这个正方形零件的边长是多少?类比探究（2）如图2 若这块锐角三角形ABC材料可以加工成3个相同大小的正方形零件请你探究高AD与边BC的数量关系并说明理由．拓展延伸（3）①如图3 若这块锐角三角形ABC材料可以加工成图中所示的4个相同大小的正方形零件则ADBC的值为_______（直接写出结果）②如图4 若这块锐角三角形ABC材料可以加工成图中所示的()3n m≥相同大小的正方形零件求ADBC的值．24 （2024·江西吉安·三模）课本再现矩形的定义有一个角是直角的平行四边形是矩形．定义应用(1)如图1 已知：在四边形ABCD 中 90A B C ∠=∠=∠=︒用矩形的定义求证：四边形ABCD 是矩形．(2)如图2 在四边形ABCD 中 90A B ∠=∠=︒ E 是AB 的中点连接DE CE 且DE CE = 求证：四边形ABCD 是矩形．拓展延伸(3)如图3 将矩形ABCD 沿DE 折叠使点A 落在BC 边上的点F 处若图中的四个三角形都相似求AB BC的值．25 （2024·江西吉安·一模）课本再现在学习了平行四边形的概念后进一步得到平行四边形的性质：平行四边形的对角线互相平分．=（1）如图1 在平行四边形ABCD中对角线AC与BD交于点O 求证：OA OC =．OB OD知识应用=延长AC到E 使得（2）在ABC中点P为BC的中点．延长AB到D 使得BD AC∠=︒请你探究线段BE与线段AP之间的BACCE AB=连接DE．如图2 连接BE若60数量关系．写出你的结论并加以证明．26 （2024·江西九江·二模）问题提出在综合与实践课上某数学研究小组提出了这样一个问题：如图1 在边长为4的正方形ABCD 的中心作直角EOF ∠ EOF ∠的两边分别与正方形ABCD 的边BC CD 交于点E F （点E 与点B C 不重合）将EOF ∠绕点O 旋转．在旋转过程中四边形OECF 的面积会发生变化吗？爱思考的浩浩和小航分别探究出了如下两种解题思路．浩浩：如图a 充分利用正方形对角线垂直相等且互相平分等性质证明了OEC OFD ≌ 则OEC OFD S S = OEC OCF OFD OCF OCD OECF S S S S S S =+=+=四边形．这样就实现了四边形OECF 的面积向OCD 面积的转化．小航：如图b 考虑到正方形对角线的特征过点O 分别作OG BC ⊥于点G OH CD ⊥于点H 证明OGE OHF ≌△△ 从而将四边形OECF 的面积转化成了小正方形OGCH 的面积．（1）通过浩浩和小航的思路点拨﹐我们可以得到OECF S =四边形__________ CE CF +=__________．类比探究（2）①如图⒉ 在矩形ABCD 中 3AB = 6AD = O 是边AD 的中点 90EOF ∠=︒ 点E 在AB 上点F 在BC 上则EB BF +=__________．②如图3 将问题中的正方形ABCD 改为菱形ABCD 且45ABC ∠=︒ 当45EOF ∠=︒时其他条件不变四边形OECF 的面积还是一个定值吗？若是请求出四边形OECF 的面积若不是请说明理由．拓展延伸（3）如图4 在四边形ABCD 中 7AB = 2DC = 60BAD ∠=︒ 120BCD ∠=︒ CA 是BCD ∠的平分线求四边形ABCD 的面积．27 （2024·江西九江·模拟预测）【课本再现】（1）如图1 四边形ABCD 是一个正方形 E 是BC 延长线上一点且AC EC = 则DAE ∠的度数为．【变式探究】（2）如图2 将（1）中的ABE 沿AE 折叠得到AB E ' 延长CD 交B E '于点F 若2AB = 求B F '的长．【延伸拓展】（3）如图3 当（2）中的点E 在射线BC 上运动时连接B B ' B B '与AE 交于点P ．探究：当EC 的长为多少时 D P 两点间的距离最短？请求出最短距离．28 （2024·江西上饶·一模）课本再现：（1）如图1 ,D E 分别是等边三角形的两边,AB AC 上的点且AD CE =．求证：CD BE =．下面是小涵同学的证明过程：证明：ABC 是等边三角形,60AC BC A ACB ∴=∠=∠=︒．AD CE =()SAS ADC CEB ∴≌CD BE ∴=．小涵同学认为此题还可以得到另一个结论：BFD ∠的度数是______迁移应用：（2）如图2 将图1中的CD 延长至点G 使FG FB = 连接,AG BG ．利用（1）中的结论完成下面的问题．①求证：AG BE ∥②若25CF BF = 试探究AD 与BD 之间的数量关系．参考答案考点解读在中考数学中有这么一类题它是以点线几何图形的运动为载体集合多个代数知识几何知识及数学解题思想于一题的综合性试题它就是动态几何问题。

中考数学真题分类汇编——几何综合题(含答案)

中考数学真题分类汇编——几何综合题(含答案)类型1 类比探究的几何综合题类型2 与图形变换有关的几何综合题类型3 与动点有关的几何综合题类型4 与实际操作有关的几何综合题类型5 其他类型的几何综合题类型1 类比探究的几何综合题（2018苏州）（2018烟台）（2018东营）（1）某学校“智慧方园”数学社团遇到这样一个题目：如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO=33，BO：CO=1:3，求AB的长．经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．请回答：∠ADB= °，AB= ．（2）请参考以上解决思路，解决问题：如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO=33，∠ABC=∠ACB=75°， BO：OD=1:3，求DC的长．（2018长春）(第24题图1) (第24题图2) (第24题图3)（2018陕西）（2018齐齐哈尔）（2018河南）（2018仙桃）问题：如图①，在Rt△ABC中，AB=AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A 逆时针旋转90°得到AE，连接EC，则线段BC，DC，EC之间满足的等量关系式为；探索：如图②，在Rt△ABC与Rt△ADE中，AB=AC，AD=AE，将△ADE绕点A旋转，使点D落在BC边上，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；应用：如图③，在四边形ABCD中，∠ABC=∠ACB=∠ADC=45°．若BD=9，CD=3，求AD的长．（2018襄阳）如图(1)，已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．(1)证明与推断：①求证：四边形CEGF是正方形；的值为；②推断：AGBE(2)探究与证明：将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°)，如图(2)所示，试探究线段AG与BE 之间的数量关系，并说明理由；(3)拓展与运用正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图(3)所示，延长CG交AD于点H．若AG=6，GH=22，则BC= ．（2018淮安）（2018咸宁）（2018黄石）在△ABC 中，E 、F 分别为线段AB 、AC 上的点（不与A 、B 、C 重合）. （1）如图1，若EF ∥BC ，求证：AEF ABC S AE AFS AB AC∆∆= （2）如图2，若EF 不与BC 平行，（1）中的结论是否仍然成立？请说明理由；（3）如图3，若EF 上一点G 恰为△ABC 的重心，34AE AB =,求AEFABC S S ∆∆的值.BBB（2018山西）（2018盐城）【发现】如图①，已知等边ABC ，将直角三角形的60角顶点D 任意放在BC 边上（点D 不与点B 、C 重合），使两边分别交线段AB 、AC 于点E 、F .（1）若6AB=，4AE=，2BD=，则CF=_______；（2）求证：EBD DCF∆∆.【思考】若将图①中的三角板的顶点D在BC边上移动，保持三角板与AB、AC的两个交点E、F都存在，连接EF，如图②所示.问点D是否存在某一位置，使ED平分BEF∠且FD平分CFE∠？若存在，求出BDBC的值；若不存在，请说明理由.【探索】如图③，在等腰ABC∆中，AB AC=，点O为BC边的中点，将三角形透明纸板的一个顶点放在点O处（其中MON B∠=∠），使两条边分别交边AB、AC于点E、F（点E、F均不与ABC∆的顶点重合），连接EF.设Bα∠=，则AEF∆与ABC∆的周长之比为________（用含α的表达式表示）.（2018绍兴）（2018达州）（2018菏泽）（2018扬州）问题呈现如图1，在边长为1的正方形网格中，连接格点D、N和E、C，DN与EC相交于点P，求tan CPN∠的值.方法归纳求一个锐角的三角函数值，我们往往需要找出（或构造出）一个直角三角形.观察发现问题中CPN∠不在直角三角形中，我们常常利用网格画平行线等方法解决此类问题.比如连接格点M、N，可得∠就变换到中Rt DMN∆.∠=∠，连接DM，那么CPNMN EC，则DNM CPN//问题解决（1）直接写出图1中tan CPN ∠的值为_________；（2）如图2，在边长为1的正方形网格中，AN 与CM 相交于点P ，求cos CPN ∠的值；思维拓展（3）如图3，AB BC ⊥，4AB BC =，点M 在AB 上，且AM BC =，延长CB 到N ，使2BN BC =，连接AN 交CM 的延长线于点P ，用上述方法构造网格求CPN ∠的度数.（2018常德）已知正方形ABCD 中AC 与BD 交于O 点，点M 在线段BD 上，作直线AM 交直线DC 于E ,过D 作DH AE ⊥于H ,设直线DH 交AC 于N .（1）如图14，当M 在线段BO 上时，求证：MO NO =；（2）如图15，当M 在线段OD 上，连接NE ,当//EN BD 时，求证：BM AB =；（3）在图16，当M 在线段OD 上，连接NE ,当NE EC ⊥时，求证：2AN NC AC =⋅.（2018滨州）（2018湖州）（2018自贡）如图，已知AOB 60∠=,在AOB ∠的平分线OM 上有一点C ,将一个120°角的顶点与点C 重合，它的两条边分别与直线OA OB 、相交于点D E 、 .⑴当DCE ∠绕点C 旋转到CD 与OA 垂直时（如图1），请猜想OE OD +与OC 的数量关系，并说明理由；⑵当DCE ∠绕点C 旋转到CD 与OA 不垂直时，到达图2的位置，⑴中的结论是否成立？并说明理由； ⑶当DCE ∠绕点C 旋转到CD 与OA 的反向延长线相交时，上述结论是否成立？请在图3中画出图形，若成立，请给于证明；若不成立，线段OD OE 、与OC 之间又有怎样的数量关系？请写出你的猜想，不需证明.（2018嘉兴、舟山）O BOO B图3.（2018淄博）（1）操作发现：如图①，小明画了一个等腰三角形ABC ，其中AB AC =，在ABC ∆的外侧分别以,AB AC 为腰作了两个等腰直角三角形ABD ACE ，，分别取,BD CE ，BC 的中点,,M N G ，连接,GM GN .小明发现了：线段GM 与GN 的数量关系是；位置关系是 . （2）类比思考：如图②，小明在此基础上进行了深入思考.把等腰三角形ABC 换为一般的锐角三角形，其中AB AC >，其它条件不变，小明发现的上述结论还成立吗？请说明理由. （3）深入研究：如图③，小明在（2）的基础上，又作了进一步的探究.向ABC ∆的内侧分别作等腰直角三角形,ABD ACE ，其它条件不变，试判断GMN ∆的形状，并给与证明.类型2 与图形变换有关的几何综合题（2018宜昌）在矩形ABCD 中，12AB =，P 是边AB 上一点，把PBC 沿直线PC 折叠，顶点B 的对应点是点G ，过点B 作BE CG ⊥，垂足为E 且在AD 上，BE 交PC 于点F . (1)如图1，若点E 是AD 的中点，求证:AEB DEC ∆∆≌； (2) 如图2，①求证: BP BF =；②当AD 25=，且AE DE <时，求cos PCB ∠的值； ③当BP 9=时，求BE EF 的值.图1 图2 图2备用图 23.(1)证明：在矩形ABCD 中，90,A D AB DC ∠=∠==, 如图1，又AE DE =，图1∆≅∆,ABE DCE(2)如图2，图2①在矩形ABCD中，90∠=,ABC∆沿PC折叠得到GPC∆BPC∠=∠∴∠=∠=,BPC GPC PGC PBC90⊥BE CG∴,BE PG//∴∠=∠GPF PFBBPF BFP∴∠=∠∴=BP BFAD=时，②当25∠=BEC90∴∠+∠=,90AEB CED90AEB ABE ∠+∠=,CED ABE ∴∠=∠ 又90A D ∠=∠=,ABE DEC ∴∆∆∽AB DEAE CD∴=∴设AE x =，则25DE x =-，122512xx -∴=，解得19x =，216x =AE DE <9,16AE DE ∴==, 20,15CE BE ∴==,由折叠得BP PG =，BP BF PG ∴==,//BE PG , ECF GCP ∴∆∆∽EF CEPG CG∴=设BP BF PG y ===，152025y y -∴=253y ∴=则253BP = 在Rt PBC ∆中，PC =,cos 10BC PCB PC ∠=== ③若9BP =,解法一：连接GF ，（如图3）90GEF BAE ∠=∠=, //,BF PG BF PG =∴四边形BPGF 是平行四边形BP BF =,∴平行四边形BPGF 是菱形//BP GF ∴, GFE ABE ∴∠=∠, GEF EAB ∴∆∆∽EF ABGF BE∴=129108BE EF AB GF ∴==⨯= 解法二：如图2，90FEC PBC ∠=∠=,EFC PFB BPF ∠=∠=∠, EFC BPC ∴∆∆∽EF CEBP CB∴=又90BEC A ∠=∠=, 由//AD BC 得AEB EBC ∠=∠,AEB EBC ∴∆∆∽AB CEBE CB∴=AE EFBE BP∴=129108BE EF AE BP ∴==⨯=解法三：（如图4）过点F 作FH BC ⊥，垂足为HBPF PFEGS BF BFS EF PG BE∆==+四边形图41212BFC BEC S BF EF BC EFBE S BC ∆∆⋅===⨯ 912EFBE ∴=129108BE EF ∴=⨯=（2018邵阳）（2018永州）（2018无锡）（2018包头）（2018赤峰）（2018昆明）（2018岳阳）（2018宿迁）（2018绵阳）（2018南充）（2018徐州）类型3 与动点有关的几何综合题（2018吉林）（2018黑龙江龙东）（2018黑龙江龙东）（2018广东）已知Rt△OAB，∠OAB=90o，∠ABO=30o，斜边OB=4，将Rt△OAB绕点O顺时针旋转60o，如图25-1图，连接BC.（1）填空：∠OBC=_______o；（2）如图25-1图，连接AC，作OP⊥AC，垂足为P，求OP的长度；（3）如图25-2图，点M、N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止.已知点M的运动速度为1.5单位/秒，点N的运动速度为1单位/秒.设运动时间为x秒，△OMN的面积为y，求当x为何值时y取得最大值？最大值为多少？（结果可保留根号）（2018衡阳）（2018黔东南）如图1，已知矩形AOCB，6cm s的AB cm=，动点P从点A出发，以3/=，16BC cm速度向点O运动，直到点O为止；动点Q同时从点C出发，以2/cm s的速度向点B运动，与点P同时结束运动.（1）点P 到达终点O 的运动时间是________s ，此时点Q 的运动距离是________cm ；（2）当运动时间为2s 时，P 、Q 两点的距离为________cm ；（3）请你计算出发多久时，点P 和点Q 之间的距离是10cm ；（4）如图2，以点O 为坐标原点，OC 所在直线为x 轴，OA 所在直线为y 轴，1cm 长为单位长度建立平面直角坐标系，连结AC ，与PQ 相交于点D ，若双曲线ky x=过点D ，问k 的值是否会变化？若会变化，说明理由；若不会变化，请求出k 的值.（2018青岛）已知：如图，四边形ABCD ，//,AB DC CB AB ⊥，16,6,8AB cm BC cm CD cm ===，动点P 从点D 开始沿DA 边匀速运动，动点Q 从点A 开始沿AB 边匀速运动，它们的运动速度均为2/cm s .点P 和点Q 同时出发，以QA QP 、为边作平行四边形AQPE ，设运动的时间为()t s ，05t <<.根据题意解答下列问题：（1）用含t 的代数式表示AP ；（2）设四边形CPQB 的面积为()2S cm ，求S 与t 的函数关系式；（3）当QP BD ⊥时，求t 的值；（4）在运动过程中，是否存在某一时刻t ，使点E 在ABD ∠的平分线上？若存在，求出t 的值；若不存在，请说明理由.（2018广州）如图12，在四边形ABCD 中，∠B=60°，∠D=30°，AB=BC. (1)求∠A+∠C 的度数（2）连接BD,探究AD,BD,CD 三者之间的数量关系，并说明理由。

中考数学专题复习：几何综合题

【考点总结】四、全等三角形的性质与判定
1．概念：能够完全重合的两个三角形叫做全等三角形． 2．性质：全等三角形的对应边、对应角分别相等． 3．判定：(1)有三边对应相等的两个三角形全等，简记为(SSS)； (2)有两边和它们的夹角对应相等的两个三角形全等，简记为(SAS)； (3)有两角和它们的夹边对应相等的两个三角形全等，简记为(ASA)； (4)有两角和其中一角的对边对应相等的两个三角形全等，简记为(AAS)； (5)有斜边和一条直角边对应相等的两个直角三角形全等，简记为(HL)．
三角形专题
1，掌握三角形相关基础知识（2课时）
目标
2，掌握三角形有关模型的全等或相似证明（3课时） 3，完成三角形有关模型的全等或相似证明（3课时）
三角形
模型
手拉手模型
三垂直模型
相似模型
三角形有关的知识
【考点总结】一、三角形中的重要线段 1．三角形的高线：从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段叫做三角形的高线，简称高．特性：三角形的三条高线相交于一点． 2．三角形的中线：在三角形中，连接一个顶点和它对边中点的线段叫做三角形的中线．特性：三角形的三条中线交于一点． 3．三角形的中位线：连接三角形两边中点的线段叫做三角形的中位线．定理：三角形的中位线平行于第三边，且等于它的一半 4．三角形的角平分线：三角形一个角的平分线和这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线．特性：三角形的三条角平分线交于一点，这点叫做三角形的内心．性质：角平分线上的点到角的两边的距离相等．
小组合作
1.在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D．
（1）如图1，点M，N分别在AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝2时，求线段

《几何综合探究问题》(共48题)中考专项配套练习(重庆专用)

5年（2016-2020）中考1年模拟数学试题分项详解（重庆专用）专题13 几何综合探究问题（共48题）一．解析题（共10小题）1．（2020•重庆）如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D是BC边上一动点，连接AD，把AD绕点A逆时针旋转90°，得到AE，连接CE，DE．点F是DE的中点，连接CF．（1）求证：CF=√22AD；（2）如图2所示，在点D运动的过程中，当BD＝2CD时，分别延长CF，BA，相交于点G，猜想AG 与BC存在的数量关系，并证明你猜想的结论；（3）在点D运动的过程中，在线段AD上存在一点P，使P A+PB+PC的值最小．当P A+PB+PC的值取得最小值时，AP的长为m，请直接用含m的式子表示CE的长．2．（2020•重庆）△ABC为等边三角形，AB＝8，AD⊥BC于点D，E为线段AD上一点，AE＝2√3．以AE 为边在直线AD右侧构造等边三角形AEF，连接CE，N为CE的中点．（1）如图1，EF与AC交于点G，连接NG，求线段NG的长；（2）如图2，将△AEF绕点A逆时针旋转，旋转角为α，M为线段EF的中点，连接DN，MN．当30°＜α＜120°时，猜想∠DNM的大小是否为定值，并证明你的结论；（3）连接BN，在△AEF绕点A逆时针旋转过程中，当线段BN最大时，请直接写出△ADN的面五年中考真题积．3．（2019•重庆）如图，在平行四边形ABCD中，点E在边BC上，连接AE，EM⊥AE，垂足为E，交CD 于点M，AF⊥BC，垂足为F，BH⊥AE，垂足为H，交AF于点N，点P是AD上一点，连接CP．（1）若DP＝2AP＝4，CP=√17，CD＝5，求△ACD的面积．（2）若AE＝BN，AN＝CE，求证：AD=√2CM+2CE．4．（2019•重庆）在▱ABCD中，BE平分∠ABC交AD于点E．（1）如图1，若∠D＝30°，AB=√6，求△ABE的面积；（2）如图2，过点A作AF⊥DC，交DC的延长线于点F，分别交BE，BC于点G，H，且AB＝AF．求证：ED﹣AG＝FC．5．（2018•重庆）如图，在平行四边形ABCD中，点O是对角线AC的中点，点E是BC上一点，且AB＝AE，连接EO并延长交AD于点F．过点B作AE的垂线，垂足为H，交AC于点G．（1）若AH＝3，HE＝1，求△ABE的面积；（2）若∠ACB＝45°，求证：DF=√2CG．6．（2018•重庆）如图，在▱ABCD中，∠ACB＝45°，点E在对角线AC上，BE＝BA，BF⊥AC于点F，BF的延长线交AD于点G．点H在BC的延长线上，且CH＝AG，连接EH．（1）若BC＝12√2，AB＝13，求AF的长；（2）求证：EB＝EH．7．（2017•重庆）在△ABM中，∠ABM＝45°，AM⊥BM，垂足为M，点C是BM延长线上一点，连接AC．（1）如图1，若AB＝3√2，BC＝5，求AC的长；（2）如图2，点D是线段AM上一点，MD＝MC，点E是△ABC外一点，EC＝AC，连接ED并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF＝∠CEF．8．（2017•重庆）如图，△ABC中，∠ACB＝90°，AC＝BC，点E是AC上一点，连接BE．（1）如图1，若AB＝4√2，BE＝5，求AE的长；（2）如图2，点D是线段BE延长线上一点，过点A作AF⊥BD于点F，连接CD、CF，当AF＝DF时，求证：DC＝BC．9．（2016•重庆）在△ABC中，∠B＝45°，∠C＝30°，点D是BC上一点，连接AD，过点A作AG⊥AD，在AG上取点F，连接DF．延长DA至E，使AE＝AF，连接EG，DG，且GE＝DF．（1）若AB ＝2√2，求BC 的长；（2）如图1，当点G 在AC 上时，求证：BD =12CG ；（3）如图2，当点G 在AC 的垂直平分线上时，直接写出ABCG 的值．10．（2016•重庆）已知△ABC 是等腰直角三角形，∠BAC ＝90°，CD =12BC ，DE ⊥CE ，DE ＝CE ，连接AE ，点M 是AE 的中点．（1）如图1，若点D 在BC 边上，连接CM ，当AB ＝4时，求CM 的长；（2）如图2，若点D 在△ABC 的内部，连接BD ，点N 是BD 中点，连接MN ，NE ，求证：MN ⊥AE ；（3）如图3，将图2中的△CDE 绕点C 逆时针旋转，使∠BCD ＝30°，连接BD ，点N 是BD 中点，连接MN ，探索MNAC 的值并直接写出结果．一．解答题（共38小题）1．（2020•渝中区校级二模）如图，CA ＝CB ，∠ACB ＝90°，点D 为AB 的中点，连接CD ；点E 为CD 的中点，EF ＝EG ＝EC ，且∠FEG ＝90°；点O 为CB 的中点，直线GO 与直线CF 交于点N ．（1）如图1，若∠FCD ＝30°，OC =√2，求CF 的长；（2）连接BG 并延长至点M ，使BG ＝MG ，连接CM ．①如图2，若NG ⊥MB ，求证：AB =√10CM ；②如图3，当点G 、F 、B 共线时，BM 交AC 于点H ，AH =14AC ，请直接写出FCMH 的值．一年模拟新题2．（2020•渝中区二模）如图，在△ABC中，∠ACB＝90°，AC＝BC，CD⊥AB于点D，E为线段CD上一点（不含端点），连接AE，设F为AE的中点，作CG⊥CF交直线AB于点G．（1）猜想：线段AG、BC、EC之间有何等量关系？并加以证明；（2）如果将题设中的条件“E为线段CD上一点（不含端点）”改变为“E为直线CD上任意一点”，试探究发现线段AG、BC、EC之间有怎样的等量关系，请直接写出你的结论，不用证明．3．（2020•沙坪坝区校级一模）在△ABC中，AE⊥CD且AE＝CD，∠CAE+2∠BAE＝90°．（1）如图1，若△ACE为等边三角形，CD＝2√3，求AB的长；（2）如图2，作EG⊥AB，求证：AD=√2BE；（3）如图3，作EG⊥AB，当点D与点G重合时，连接BF，请直接写出BF与EC之间的数量关系．4．（2020•南岸区模拟）如图，在△ABC中，∠BAC＝90°，AB＝AC＝6，AD⊥BC于点D．点G是射线AD上一点．（1）若GE⊥GF，点E，F分别在AB，AC上，当点G与点D重合时，如图①所示，容易证明AE+AF=√2AD．当点G在线段AD外时，如图②所示，点E与点B重合，猜想并证明AE，AF与AG存在的数量关系．（2）当点G在线段AD上时，AG+BG+CG的值是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．5．（2020•南岸区校级模拟）△ABC与△ADE都是等边三角形，DE与AC交于点P，点P恰为DE的中点，延长AD交BC于点F，连结BD、CD，取CD的中点Q，连结PQ．求证：PQ=12BD．（1）如图1，理清思路，完成解答：本题证明的思路可以用下列框图表示：根据上述思路，请你完整地书写本题的证明过程；（2）如图2，特殊位置，求线段长：若点P为AC的中点，连接PF，已知PQ=√3，求PF的长．（3）知识迁移，探索新知：若点P是线段AC上任意一点，直接写出PF与CD的数量关系．6．（2020•九龙坡区校级模拟）【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF ＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F 在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．7．（2019•渝中区校级一模）已知△ABC和△ADE都是等腰直角三角形，∠ACB＝∠ADE＝90°，点F为BE中点，连结DF，CF．（1）如图1，点D在AC上，请你判断此时线段DF，CF的关系，并证明你的判断；（2）如图2，在（1）的条件下将△ADE绕点A顺时针旋转45时，若AD＝DE＝2，AB＝6，求此时线段CF的长．8．（2019•重庆模拟）一节数学课后，老师布置了一道课后练习：△ABC是等边三角形，点D是线段BC上的点，点E为△ABC的外角平分线上一点，且∠ADE＝60°，如图①，当点D是线段BC上（除B，C 外）任意一点时，求证：AD＝DE（1）理清思路，完成解答本题证明思路可以用下列框图表：根据上述思路，请你完整地书写本题的证明过程；（2）特殊位置，计算求解当点D为BC的中点时，等边△ABC的边长为6，求出DE的长；（3）知识迁移，探索新知当点D在线段BC的延长线上，且满足CD＝BC时，若AB＝2，请直接写出△ADE的面积（不必写解答过程）9．（2020•南岸区校级模拟）如图1，直角三角形△ABC中，∠ACB＝90°，AC＝4，∠A＝60°，O为BC中点，将△ABC 绕O 点旋转180°得到△DCB ．一动点P 从A 出发，以每秒1的速度沿A →B →D 的路线匀速运动，过点P 作直线PM ⊥AC 交折线段A ﹣C ﹣D 于M ．（1）如图2，当点P 运动2秒时，另一动点Q 也从A 出发沿A →B →D 的路线运动，且在AB 上以每秒1的速度匀速运动，在BD 上以每秒2的速度匀速运动，过Q 作直线QN ∥PM 交折线段A ﹣C ﹣D 于N ，设点Q 的运动时间为t 秒，（0＜t ＜10）直线PM 与QN 截四边形ABDC 所得图形的面积为S ，求S 关于t 的函数关系式，并求出S 的最大值．（2）如图3，当点P 开始运动的同时，另一动点R 从B 处出发沿B →C →D 的路线运动，且在BC 上以每秒√32的速度匀速运动，在CD 上以每秒2的速度匀速运动，是否存在这样的P 、R ．使△BPR 为等腰三角形？若存在，直接写出点P 运动的时间m 的值，若不存在请说明理由．10．（2019秋•沙坪坝区校级期末）如图，在菱形ABCD 中，∠ABC ＝60°，连接AC ，动点P 从A 点出发沿射线AB 方向运动，同时动点Q 从B 点出发以与P 点相同的速度沿射线BC 方向运动，连接AQ ，CP ，直线AQ 与直线CP 交于点H ．（1）如图1，当P ，Q 两点分别在线段AB 和线段BC 上时，直接写出∠CHQ 的度数；（2）如图2，当P ，Q 两点分别运动到线段AB 和线段BC 的延长线上时，试问（1）问中的结论是否成立：若成立请说明理由，若不成立，请求出∠CHQ 的度数；（3）如图3，在（2）问的前提下，连接DH ，过点D 作DE ⊥PH 交PH 延长线于点E ．求证：AH ﹣CE =12DH ．11．（2020春•沙坪坝区校级月考）如图，正方形ABCD 中，对角线AC ，BD 交于点O ，点E ，点F 分别在线段OB ，线段AB 上，且AF ＝OE ，连接AE 交OF 于G ，连接DG 交AO 于H ．（1）如图1，若点E为线段BO中点，AE=√5，求BF的长；（2）如图2，若AE平分∠BAC，求证：FG＝HG；（3）如图3，点E在线段BO（含端点）上运动，连接HE，当线段HE长度取得最大值时，直接写出cos ∠HDO的值．12．（2020•沙坪坝区自主招生）在▱ABCD中，AF平分∠BAD交BC于点F，∠BAC＝90°，点E是对角线AC上的点，连结BE．（1）如图1．若AB＝AE，BF＝3，求BE的长；（2）如图2，若AB＝AE，点G是BE的中点，∠F AG＝∠BFG，求证：AB=√10FG；（3）如图3，以点E为直角顶点，在BE的右下方作等腰直角△BEM，若点E从点A出发，沿AC运动到点C停止，设在点E运动过程中，BM的中点N经过的路径长为m，AC的长为n，请直接写出nm的值．13．（2020•巴南区自主招生）已知，在矩形ABCD中，AB＝2，点E在边BC上，且AE⊥DE，AE＝DE，点F是BC的延长线上一点，AF与DE相交于点G，DH⊥AF，垂足为H，DH的延长线与BC相交于点K．（1）如图1，求AD的长；（2）如图2，连接KG，求证：AG＝DK+KG；（3）如图3，设△ADM与△ADH关于AD对称，点N、Q分别是MA、MD的中点，请直接写出BN+NQ 的最大值．14．（2020•南岸区自主招生）如图1，在正方形ABCD中，点E是边BC上一点，连接AE，过点E作EM ⊥AE，交对角线AC于点M，过点M作MN⊥AB，垂足为N，连接NE．（1）求证：AE=√2NE+ME；（2）如图2，延长EM至点F，使EF＝EA，连接AF，过点F作FH⊥DC，垂足为H．猜想CH与FH存在的数量关系，并证明你的结论；（3）在（2）的条件下，若点G是AF的中点，连接GH．当GH＝CH时，直接写出GH与AC之间存在的数量关系．15．（2020•北碚区自主招生）如图1，在正方形ABCD中，对角线AC、BD相交于点O，点E为线段BO上一点，连接CE，将CE绕点C顺时针旋转90°得到CF，连接EF交CD于点G．（1）若AB＝4，BE=√2，求△CEF的面积．（2）如图2，线段FE的延长线交AB于点H，过点F作FM⊥CD于点M，求证：BH+MG=√22BE；（3）如图3，点E为射线OD上一点，线段FE的延长线交直线CD于点G，交直线AB于点H，过点F 作FM垂直直线CD于点M，请直接写出线段BH、MG、BE的数量关系．16．（2019秋•九龙坡区校级期末）已知，在平行四边形ABCD中，∠D＝60°，点F，G在边BC上，且AF＝AG．（1）如图1，若AG平分∠F AC，∠AFC＝5∠BAF，且AF＝4，求线段AC的长；（2）如图2，点E在边AB上，且BE＝EF，证明：AE＝BG；（3）在（2）的条件下，连接CE（如图3），若∠AEC＝∠ACD，你能得到AD，FG，BE怎样的数量关系？试证明你的猜想．17．（2020春•沙坪坝区校级月考）如图，已知在矩形ABCD中，AD＝8，CD＝4，点E从点D出发，沿线段DA以每秒1个单位长的速度向点A方向移动，到达A点停止运动；同时点F从点C出发，沿射线CD方向以每秒2个单位长的速度移动，到达D点停止运动，设点E移动的时间为t（秒）．（1）当t＝1时，求四边形BCFE的面积；（2）设四边形BCFE的面积为S，求S与t之间的关系式，并写出t的取值范围；（3）若F点到达D点后立即返回，并在线段CD上往返运动，当E点到达A点时它们同时停止运动，求当t为何值时，以E，F，D三点为顶点的三角形是等腰三角形，并求出此的等腰三角形的面积S△EDF．18．（2020春•沙坪坝区校级月考）已知，在▱ABCD中，AB⊥BD，AB＝BD，E为射线BC上一点，连接AE 交BD于点F．（1）如图1，若点E与点C重合，且AF＝2√5，求AD的长；（2）如图2，当点E在BC边上时，过点D作DG⊥AE于G，延长DG交BC于H，连接FH．求证：AF＝DH+FH；（3）如图3，当点E在射线BC上运动时，过点D作DG⊥AE于G，M为AG的中点，点N在BC边上且BN＝1，已知AB＝4√2，请直接写出MN的最小值．19．（2020春•沙坪坝区校级月考）已知：在△ABC中，∠C＝90°，BC＝AC．（1）如图1，若点D、E分别在BC、AC边上，且CD＝CE，连接AD、BE，点O、M、N分别是AB、AD、BE的中点．求证：△OMN是等腰直⻆三角形；（2）将图1中△CDE绕着点C顺时针旋转90°如图2，O、M、N分别为AB、AD、BE中点，则（1）中的结论是否成⽴，并说明理由；（3）如图3，将图1中△CDE绕着点C顺时针旋转，记旋转⻆为α（0＜α＜360°），O、M、N分别为AB、AD、BE中点，当MN=√10，请求出四边形ABED的⽴积．20．（2019秋•九龙坡区期末）（1）如图1，四边形EFGH中，FE＝EH，∠EFG+∠EHG＝180°，点A，B分别在边FG，GH上，且∠AEB=12∠FEH，求证：AB＝AF+BH．（2）如图2，四边形EFGH中，FE＝EH，点M在边EH上，连接FM，EN平分∠FEH交FM于点N，∠ENM＝α，∠FGH＝180°﹣2α，连接GN，HN．①找出图中与NH相等的线段，并加以证明；②求∠NGH的度数（用含α的式子表示）．21．（2019秋•吉州区期末）【问题情境】如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．【探究展示】（1）直接写出AM、AD、MC三条线段的数量关系：；（2）AM＝DE+BM是否成立？若成立，请给出证明；若不成立，请说明理由．【拓展延伸】（3）若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否成立？请分别作出判断，不需要证明．22．（2019春•江北区校级期中）如图，在平面直角坐标系中，平行四边形ABCD的边AB在x轴上，点A （﹣2，0），线段AB＝8，线段AD＝6，且∠BAD＝60°，AD与y的交点记为E，连接BE．（1）求▱ABCD的面积．（2）如图2，在线段BE上有两个动点G、K（G在K点上方），且KG=√3，点F为BC中点，点P为线段CD上一动点，当FG+GK+KP的值最小时，求出此时P点的坐标；此时在y轴上找一点H，x轴上线一点M，使得PH+HM−√22AM取得最小值，请求出PH+HM−√22AM的最小值．（3）如图3，将△AOE沿射线EB平移到△A′O'E'的位置，线段E′A′的中点N落在x轴上，此时再将△A′O'E'绕平面内某点W旋转90°，旋转后的三角形记为△A''O''E''，若△A''O''E'恰好只有两个顶点同时落在直线BC和直线BE上，且△A''E''B''的边均不在直线BC或直线BE上，请求出满足条件的W的坐标．23．（2019秋•北碚区校级月考）已知平行四边形ABCD中，N是边BC上一点，延长DN、AB交于点Q，过A作AM⊥DN于点M，连接AN，则AD⊥AN．（1）如图①，若tan∠ADM=34，MN＝3，求BC的长；（2）如图②，过点B作BH∥DQ交AN于点H，若AM＝CN，求证：DM＝BH+NH．24．（2019秋•沙坪坝区校级月考）如图，在平行四边形ABCD中，过A作AE⊥CD于点E，点G，F分别为AD，BC上一点，连接CG交AE于点H，连接AF，AF＝AH，∠GCF＝∠F AE＝45°．（1）若tan∠DAE=23，GH＝4，求AF的长；（2）求证：AG+√2GH＝GC．25．（2020春•北碚区校级期末）已知在△ABC和△ADE中，∠ACB+∠AED＝180°，CA＝CB，EA＝ED，AB＝3．（1）如图1，若∠ACB＝90°，B、A、D三点共线，连接CE：①若CE=5√22，求BD长度；②如图2，若点F是BD中点，连接CF，EF，求证：CE=√2EF；（2）如图3，若点D在线段BC上，且∠CAB＝2∠EAD，试直接写出△AED面积的最小值．26．（2020春•重庆期末）已知三角形ABC中，∠ACB＝90°，点D（0，﹣4），M（4，﹣4）．（1）如图1，若点C与点O重合，A（﹣2，2）、B（4，4），求△ABC的面积；（2）如图2，AC经过坐标原点O，点C在第三象限且点C在直线DM与x轴之间，AB分别与x轴，直线DM交于点G，F，BC交DM于点E，若∠AOG＝55°，求∠CEF的度数；（3）如图3，AC经过坐标原点O，点C在第三象限且点C在直线DM与x轴之间，N为AC上一点，AB分别与x轴，直线DM交于点G，F，BC交DM于点E，∠NEC+∠CEF＝180°，求证：∠NEF＝2∠AOG．27．（2020春•沙坪坝区校级月考）已知Rt△ABC中，∠ACB＝90°，以AC为斜边作Rt△AEC，∠AEC＝90°，AB与CE相交于点D．（1）如图1，AB平分∠CAE，BD＝4，CD＝5，求AC；（2）如图2，若AC＝BC，点F在EA的延长线上，连接FB、FC，FB与CE相交于点G，且∠EAD＝∠ACF，求证：AF＝2GE；（3）如图3，在（2）的条件下，CE的中垂线与AB相交于点Q，连接EQ，若∠DEQ+2∠ACE＝90°，请直接写出线段FC、ED、EQ的关系．28．（2020春•沙坪坝区校级月考）已知等腰直角△ABC中，AB＝AC，∠BAC＝90°，点D是AC边上一点，以BD为边作等腰直角△BDE，其中BD＝BE，∠DBE＝90°，边AB与DE交于点F，点G是BC上一点．（1）如图1，若DG⊥DE，连接FG．①若∠ABD＝30°，DE=√6+√2，求BF的长度；②求证：DG＝EF﹣FG；（2）如图2，若DG⊥BD，EP⊥BE交BA的延长线于点P，连接PG，请猜想线段PG，DG，PE之间的数量关系，并证明．29．（2020春•沙坪坝区校级月考）如图，在等边△ABC中，延长AB至点D，延长AC交BD的中垂线于点E，连接BE，DE．（1）如图1，若DE＝3√10，BC＝2√3，求CE的长；（2）如图2，连接CD交BE于点M，在CE上取一点F，连接DF交BE于点N，且DF＝CD，求证：AB=12EF；（3）在（2）的条件下，若∠AED＝45°，直接写出线段BD，EF，ED的等量关系．30．（2020春•沙坪坝区校级月考）在△ABC中，AC＝BC，点G是直线BC上一点，CF⊥AG，垂足为点E，BF⊥CF于点F，点D为AB的中点，连接DF．（1）如图1，如果∠ACB＝90°，且G在CB边上，设CF交AB于点R，且E为CR的中点，若CG＝1，求线段BG的长；（2）如图2，如果∠ACB＝90°，且G在CB边上，求证：EF=√2DF；（3）如图3，如果∠ACB＝60°，且G在CB的延长线上，∠BAG＝15°，请探究线段EF、BD之间的数量关系，并直接写出你的结论．31．（2020春•沙坪坝区校级月考）如图所示，△ABC为等边三角形，点D，点E分别在CA，CB的延长线上，连接BD，DE，DB＝DE．（1）如图1，若CA：AD＝3：7，BE＝4，求EC的长；（2）如图2，点F在AC上，连接BE，∠DBF＝60°，连接EF，①求证：BF+EF＝BD；②如图3，若∠BDE＝30°，直接写出EFBF的值．32．（2020春•沙坪坝区校级月考）在△ABC，△CDE中，∠BAC＝∠DEC＝90°，连接BD，F为BD中点，连接AF，EF．（1）如图1，若A，C，E三点在同一直线上，∠ABC＝∠EDC＝45°，已知AB＝3，DE＝5，求线段AF的长；（2）如图2，若∠ABC＝∠EDC＝45°，求证：△AEF为等腰直角三角形；（3）如图3，若∠ABC＝∠EDC＝30°，请判断△AEF的形状，并说明理由．33．（2019秋•渝中区校级期末）如图，在△ABC中，∠ABC＝30°，以AC为边作等边△ACD，连接BD．（1）如图1，若∠ACB＝90°，AB＝4，求△BCD的面积；（2）如图2，若∠ACB＜90°，点E为BD中点，连接AE、CE，且AE⊥CE，延长BC至点F，连接AF，使得∠F＝30°，求证：AF＝CE+√3AE．34．（2020春•南岸区期末）把△ABC绕着点A逆时针旋转α，得到△ADE．（1）如图1，当点B恰好在ED的延长线上时，若α＝60°，求∠ABC的度数；（2）如图2，当点C恰好在ED的延长线上时，求证：CA平分∠BCE；（3）如图3，连接CD，如果DE＝DC，连接EC与AB的延长线交于点F，直接写出∠F的度数（用含α的式子表示）．35．（2020春•渝中区期末）如图，在正方形ABCD中，E为CD边上一点，以DE为边向外作正方形DEFG，将正方形DEFG绕点D顺时针旋转，连接AG．（1）如图1，若AD＝2√3、DE＝2，当∠ADG＝150°时，求AG的长；（2）如图2，正方形DEFG绕点D旋转的过程中，取AG的中点M，连接DM、CE，猜想：DM和CE 之间有何等量关系？并利用图2加以证明．36．（2020春•沙坪坝区校级月考）在菱形ABCD中，∠ABC＝60°，点M是对角线BD上一动点，将线段CM绕点C顺时针旋转120°到CN，连接DN，连接NM并延长，分别交AB、CD于点P、Q．（1）如图1，若CM⊥BD且PQ＝4√3，求菱形ABCD的面积；（2）如图2，求证：PM＝QN．37．（2019秋•江津区期末）如图，四边形ABCD是平行四边形，AC＝CD，∠BAC＝90°，点E为BC边上一点，将AE绕点A顺时针旋转90°后得到线段AF，连接FB，FB⊥BC．且FB的延长线与AE的延长线交于点G，点E是AG的中点．（1）若BG＝2，BE＝1，求FG的长；（2）求证：√2AB＝BG+2BE．38．（2020春•渝北区期中）如图1，光线照射在光滑表面上时会发生反射现象，入射光线与镜面的夹角等于出射光线与镜面的夹角，即∠1＝∠2．（1）如图1，AB、BC为两个平面镜，∠B＝90°，一束光线l经两次反射后，经点D，由从点E射出，求证：DM∥EN；（2）如图2，AB、BC为两个平面镜，∠B＝122°，一束光线l经两次反射后，经点D，且由从点E射出，且EN⊥AB，求∠ADM的度数；（3）如图3，已知FL∥GS，FG⊥GS，∠LPK＝∠SQK＝30°，∠PKQ绕点K顺时针旋转，旋转速度为5°/秒，记旋转角α（0＜α≤360°），同时，射线FG绕点F顺时针旋转，旋转速度为3°/秒，记旋转角β（0＜β≤360°），当FG所在直线平行于∠PKQ边所在直线时，直接写出对应时间t的所有值．。

初三数学几何综合-中考必做题(详解版)

中，点是边的中点，延长至点，使
，连接
，．将
绕点按顺时针方向旋转．当点恰好落在上的点处时，连接、
、，则的长是
．
答案
解析如图，过作
于，过作
于，过作
．
∵
，
，
∵四边形
是正方形，
∴
，
∴
，
由勾股定理得：
，
∵
，
，
∴
，
∴
，
∴
，
∴
，
∴
，
由旋转得
，
∵
，
∴
，
∴
，
∴
，
∴
，
∴
，
∴
，
，交于，交于
和
，连接、，与的延长线交于点，下列结论：①
；②
；③
是
的中线；④
，其中，正确结论的个数是（）．
A.
B.
答案 A
解析在正方形
和
中，
C.
，
，
D. ，
∴
，
即
，
∵在
和
中，
，
∴
≌
，
∴
，（故①正确）；
设、相交于点，
∵
≌
，
∴
，
∵
，
∴
，
∴
，（故②正确）；
过点作
的延长线于，过点作
于，
∵
，
∴
圆圆的基础知识圆心角、弧、弦的关系
，不一定成立，因此④不正确．
10
如图，已知是⊙ 的直径，点在上，过点的直线与的延长线交于点，

中考数学几何综合题练习(附答案)

几何专题综合训练1如图，四边形ABCD 是正方形，△ECF 是等腰直角三角形，其中CE=CF ，G 是CD 与EF 的交点．（1）求证：△BCF ≌△DCE ．（2）若BC=5，CF=3，∠BFC=900，求DG ：GC 的值．2正方形ABCD 边长为4，M 、N 分别是BC 、CD 上的两个动点，当M 点在BC 上运动时，保持AM 和MN 垂直，（1）证明：Rt Rt ABM MCN △∽△；（2）设BM x ，梯形ABCN 的面积为y ，求y 与x 之间的函数关系式；当M 点运动到什么位置时，四边形ABCN 面积最大，并求出最大面积；（3）当M 点运动到什么位置时Rt Rt ABM AMN △∽△，求x 的值．NDA CBM第2题图3在图3-1至图3-3中，点B是线段AC的中点，点D是线段CE的中点．四边形BCGF和CDHN都是正方形．AE的中点是M．（1）如图3-1，点E在AC的延长线上，点N与点G重合时，点M与点C重合，求证：FM = MH，FM⊥MH；（2）将图3-1中的CE绕点C顺时针旋转一个锐角，得到图3-2，求证：△FMH是等腰直角三角形；（3）将图3-2中的CE缩短到图3-3的情况，△FMH还是等腰直角三角形吗？（不必说明理由）图3-1AHC(M) D E BF G(N)G图3-2AHCDEBF NMAHCDE图3-3BF GMN4如图（1），已知正方形ABCD 在直线MN 的上方，BC 在直线MN 上，E 是BC 上一点，以AE 为边在直线MN 的上方作正方形AEFG ．（1）连接GD ，求证：△ADG ≌△ABE ；(4分) （2）连接FC ，观察并猜测∠FCN 的度数，并说明理由；(4分)（3）如图（2），将图（1）中正方形ABCD 改为矩形ABCD ，AB =a ，BC =b （a 、b 为常数），E 是线段BC 上一动点（不含端点B 、C ），以AE 为边在直线MN 的上方作矩形AEFG ，使顶点G 恰好落在射线CD 上．判断当点E 由B 向C 运动时，∠FCN 的大小是否总保持不变，若∠FCN 的大小不变，请用含a 、b 的代数式表示tan ∠FCN 的值；若∠FCN 的大小发生改变，请举例说明N M B E A C D F G图（1）图（2） M B E A C D F G N5如图2－5－7，矩形ABCD中，AB＝8，BC＝6，对角线AC上有一个动点P（不包括点A和点C）．设AP＝x，四边形PBCD的面积为y．（1）写出y与x的函数关系，并确定自变量x的范围．（2）有人提出一个判断：“关于动点P，⊿PBC面积与⊿PAD面积之和为常数”．请你说明此判断是否正确，并说明理由．．答案1. 分析与解答（1）∵四边形 ABCD 是正方形，∴∠BCF+∠FCD=900，BC=CD ．∵△ECF 是等腰直角三角形，CF=CE ．∴∠ECD+∠FCD=900．∴∠BCF=∠ECD ．∴△BCF ≌△DCE（2）在△BFC 中，BC=5，CF=3，∠BFC=900． ∴4==．∵△BCF ≌△DCE ，∴DE=BF=4，∠BFC=∠DEC=∠FCE=900． ∴DE ∥FC ．∴△DGE ∽△CGF ．∴DG ：GC=DE ：CF=4：3．2. ．解：（1）在正方形ABCD 中，490AB BC CD B C ===∠=∠=，°， AM MN ⊥ ，90AMN ∴∠=°，90CMN AMB ∴∠+∠=°．在Rt ABM △中，90MAB AMB ∠+∠=°， CMN MAB ∴∠=∠，Rt Rt ABM MCN ∴△∽△． ······················································· 2分（2）Rt Rt ABM MCN △∽△，44AB BM xMC CN x CN∴=∴=-，， 244x x CN -+∴=， ···················································································································· 4分22214114428(2)102422ABCNx x y S x x x ⎛⎫-+∴==+=-++=--+ ⎪⎝⎭梯形，当2x =时，y 取最大值，最大值为10． ··················································································· 6分（3）90B AMN ∠=∠= °，∴要使ABM AMN △∽△，必须有AM ABMN BM=， ································································ 7分由（1）知AM ABMN MC=， BM MC ∴=，∴当点M 运动到BC 的中点时，ABM AMN △∽△，此时2x =． ···································· 9分3（1）证明：∵四边形BCGF 和CDHN 都是正方形，又∵点N 与点G 重合，点M 与点C 重合，∴FB = BM = MG = MD = DH ，∠FBM =∠MDH = 90°． ∴△FBM ≌ △MDH ． ∴FM = MH ．NDA CBM答案第2题图∵∠FMB =∠DMH = 45°，∴∠FMH = 90°．∴FM ⊥HM ．（2）证明：连接MB 、MD ，如图2，设FM 与AC 交于点P ． ∵B 、D 、M 分别是AC 、CE 、AE 的中点， ∴MD ∥BC ，且MD = BC = BF ；MB ∥CD ，且MB =CD =DH ．∴四边形BCDM 是平行四边形． ∴ ∠CBM =∠CDM ．又∵∠FBP =∠HDC ，∴∠FBM =∠MDH ． ∴△FBM ≌ △MDH ． ∴FM = MH ，且∠MFB =∠HMD ．∴∠FMH =∠FMD －∠HMD =∠APM －∠MFB =∠FBP = 90°． ∴△FMH 是等腰直角三角形．（3）是．。

(完整版)中考数学几何综合题

几何综合题复习几何综合题是中考试卷中常见的题型，大致可分为几何计算型与几何论证型综合题，它主要考查考生综合运用几何知识的能力。

、几何论证型综合题例1、（盐城）如图，已知：⊙ O1与⊙O2 是等圆，它们相交于A、B 两点，⊙ O2在⊙O1 上，AC 是⊙ O2的直径，直线CB交⊙O1于D，E为AB 延长线上一点，连接DE。

（1）请你连结AD ，证明：AD 是⊙ O1 的直径；（2）若∠ E=60°，求证：DE 是⊙ O1 的切线。

分析：解几何综合题，一要注意图形的直观提示，二要注意分析挖掘题目的隐含条件，不断地由已知想可知，发展条件，为解题创条件打好基础。

证明：1）连接AD ，∵ AC 是⊙ O2的直径，AB⊥DC ∴∠ ABD=90° ,∴ AD 是⊙ O1 的直径2）证法一：∵ AD 是⊙ O1的直径，∴O1 为AD 中点连接O1O2，∵点O2 在⊙O1上，⊙ O1与⊙O2 的半径相等，∴O1O2=AO1=AO 2E ∴△AO 1O2是等边三角形，∴∠AO 1O2=60° 由三角形中位线定理得：O1O2∥DC ，∴∠ ADB= ∠AO 1O2=60 °∵AB⊥DC，∠ E=60，∴∠ BDE=30 ，∠ ADE= ∠ADB+ ∠BDE=60° +30°=90° 又AD 是直径，∴DE 是⊙ O1的切线证法二：连接O1O2，∵点O2在⊙O1上，O1与O2的半径相等，∴点O1 在⊙O2∴O1O2=AO 1=AO 2，∴∠ O1AO 2=60°∵ AB 是公共弦，∴ AB ⊥ O1O2，∴∠ O1AB=30°∵∠ E=60°∴∠ ADE=180°-（60°+30°）=90°由（1）知：AD 是的⊙ O1直径，∴DE 是⊙ O1的切线.说明：本题考查了三角形的中位线定理、圆有关概念以及圆的切线的判定定理等。

(整理版)中考数学专题复习之十二几何综合题

中考数学专题复习之十二几何综合题
几何综合题一般以圆为根底，涉及相似三角形等有关知识；这类题虽较难，但有梯度，一般题目中由浅入深有1～3个问题，解答这种题一般用分析综合法．
【范例讲析】：
1. ⊿ABC中，AB＝AC，以AC为直径的⊙O与AB相交于点E，点F是BE的中点．
〔1〕求证：DF是⊙O的切线．
〔2〕假设AE＝14，BC＝12，求BF的长．
2. 如图，AB是⊙O的直径，直线l与⊙O 相切于点C，过点A作直线l的垂线，垂足为点D，连结AC .
(1)求证：AC平分∠DAB；
(2)假设AD=3，AC=23，求直径AB的长。

【闯关夺冠】
1.：如图，AB 为⊙O 的直径，⊙O 过AC 的中点D ，DE ⊥BC 于点E ．〔1〕求证：DE 为⊙O 的切线；
〔2〕假设DE =2，tan C =21
，求⊙O 的直径．
4.如图，⊙O 的两条弦AC 、BD 相交于点Q ，OA ⊥BD ．
〔1〕求证：AB 2=AQ ·AC ：
〔2〕假设过点C 作⊙O 的切线交DB 的延长线于点P ，
求证：PC=PQ ．。

中考数学真题几何综合2

∴∠EOD=180°-∠POC=120°，
∴S扇EOD= = ．
【点睛】本题考查了全等三角形的性质和判定，三角形的外角，切线的性质，扇形面积的计算，掌握知识点灵活运用是解题关键．
5.如图，在中，，平分交于点，点在上，以点为圆心，为半径的圆恰好经过点，分别交、于点、．
（1）试判断直线与的位置关系，并说明理由；
（1）①求证：；
②写出∠1，∠2和三者间的数量关系，并说明理由．
（2）若，当最大时，直接指出与小半圆的位置关系，并求此时（答案保留）．
【答案】（1）①见详解；②∠2=∠C+∠1；（2）与小半圆相切，．
【解析】
【分析】
（1）①直接由已知即可得出AO=PO，∠AOE=∠POC，OE=OC，即可证明；
（2）如图（见解析），设圆O的半径为，先根据圆周角定理得出，再根据直角三角形的性质可得，从而可得，然后在中，利用勾股定理求解即可得．
【详解】（1）如图，连接OA
设
，
AE是圆O的切线
，即
在中，由三角形的内角和定理得：
即
解得
则由圆周角定理得：
故的度数为；
（2）如图，连接AD
设圆O的半径为，则
【详解】解：(1)证明:∵四边形ABCD为菱形，
∴点O为BD的中点，
∵点E为AD中点，
∴OE为△ABD的中位线，
∴OE∥FG，
∵OG∥EF，∴四边形OEFG为平行四边形
∵EF⊥AB，∴平行四边形OEFG为矩形．
(2)∵点E为AD的中点，AD=10，
∴AE=
∵∠EFA=90°，EF=4，
∴在Rt△AEF中，．

【超级精练】中考数学：几何综合题

几何综合题（旋转为主的题型）一、知识梳理二、教学重、难点三、作业完成情况四、典题探究例1 已知：如图，点P 是线段AB 上的动点，分别以AP 、BP 为边向线段AB 的同侧作正△APC和正△BPD ，AD 和BC 交于点M.（1）当△APC 和△BPD 面积之和最小时，直接写出AP : PB 的值和∠AMC 的度数；（2）将点P 在线段AB 上随意固定，再把△BPD 按顺时针方向绕点P 旋转一个角度α，当α<60°时，旋转过程中，∠AMC 的度数是否发生变化？证明你的结论.（3）在第（2）小题给出的旋转过程中，若限定60°<α<120°，∠AMC 的大小是否会发生变化？若变化，请写出∠AMC 的度数变化范围；若不变化，请写出∠AMC 的度数.例2 探究：（1）如图1，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45°，试判断BE 、DF 与EF 三条线段之间的数量关系，直接写出判断结果：；（2）如图2，若把(1)问中的条件变为“在四边形ABCD 中，AB ＝AD ，∠B ＋∠D ＝180°，E 、F 分别是边BC 、CD 上的点，且∠EAF=21∠BAD ”，则（1）问中的结论是否仍然成立？若成立，请给出证明，若不成立，请说明理由；（3）在（2）问中，若将△AEF 绕点A 逆时针旋转，当点分别E 、F 运动到BC 、CD 延长线上时，如图3所示，其它条件不变，则（1）问中的结论是否发生变化？若变化，请给出结论并予以证明..例3 已知：△ABC 和△ADE 是两个不全等的等腰直角三角形，其中BA =BC ，DA =DE ，联结EC ，取EC 的中点M ，联结BM 和DM ．（1）如图1，如果点D 、E 分别在边AC 、AB 上，那么BM 、DM 的数量关系与位置关系是；（2）将图1中的△ADE 绕点A 旋转到图2的位置时，判断（1）中的结论是否仍然成立，并说明理由．DCB AEMMEABCD图1 图2例4 在ABCD Y中，A DBC ∠=∠，过点D 作DE DF =，且EDF ABD =∠，连接EF ，EC ，N 、P 分别为EC ，BC 的中点，连接NP . （1）如图1，若点E 在DP 上，EF 与DC 交于点M ，试探究线段NP 与线段NM 的数量关系及ABD ∠与MNP ∠满足的等量关系，请直接写出你的结论；（2）如图2，若点M 在线段EF 上，当点M 在何位置时，你在（1）中得到的结论仍然成立，写出你确定的点M 的位置，并证明（1）中的结论.五、演练方阵A 档（巩固专练）1．（1）如图1，△ABC 和△CDE 都是等边三角形，且B 、C 、D 三点共线，联结AD 、BE 相交于点P ，求证： BE = AD .（2）如图2，在△BCD 中，∠BCD ＜120°，分别以BC 、CD 和BD 为边在△BCD 外部作等边三角形ABC 、等边三角形CDE 和等边三角形BDF ，联结AD 、BE 和CF 交于点P ，下列结论中正确的是（只填序号即可）①AD=BE=CF ；②∠BEC=∠ADC ；③∠DPE=∠EPC=∠CPA =60°；（3）如图2，在（2）的条件下，求证：PB+PC+PD=BE .2. 已知：2AD =，4BD =，以AB 为一边作等边三角形ABC .使C 、D 两点落在直线AB 的两侧. （1）如图，当∠ADB=60°时，求AB 及CD 的长；（2）当∠ADB 变化，且其它条件不变时，求CD 的最大值，及相应∠ADB 的大小.3. 如图，△ABC 中，∠ACB=90°，AD=AC,AB=AN,连结CD 、BN,CD 的延长线交BN 于点F ．（1）当∠ADN 等于多少度时，∠ACE=∠EBF,并说明理由；（2）在（1）的条件下，设∠ABC=α，∠CAD =β，试探索α、β满足什么关系时，△ACE ≌△FBE ，并说明理由．4. 在△ABC 中，AB =4，BC =6，∠ACB =30°，将△ABC 绕点B 按逆时针方向旋转，得到△A 1BC 1．（1）如图1，当点C 1在线段CA 的延长线上时，求∠CC 1A 1的度数；（2）如图2，连接AA 1，CC 1．若△CBC 1的面积为3，求△ABA 1的面积；（3）如图3，点E 为线段AB 中点，点P 是线段AC 上的动点，在△ABC 绕点B 按逆时针方向旋转的过程中，点P 的对应点是点P 1，直接写出线段EP 1长度的最大值与最小值．图2PDECABP PFDCAEB B图1C1CBA1A图2A1C1ABC图1图3PP1EA1A C1CB5. 问题1：如图1，在等腰梯形ABCD中，AD∥BC，AB=BC=CD，点M，N分别在AD，CD上，若∠MBN=12∠ABC，试探究线段MN，AM，CN有怎样的数量关系？请直接写出你的猜想，不用证明；问题2：如图2，在四边形ABCD中，AB=BC，∠ABC+∠ADC=180°，点M，N分别在DA，CD的延长线上，若∠MBN=12∠ABC仍然成立，请你进一步探究线段MN，AM，CN又有怎样的数量关系？写出你的猜想，并给予证明.6. 如图，四边形ABCD、1111A B C D是两个边长分别为5和1且中心重合的正方形．其中，正方形1111A B C D可以绕中心O旋转,正方形ABCD静止不动．（1）如图1，当11D D B B、、、四点共线时，四边形11DCC D的面积为 __；（2）如图2，当11D D A、、三点共线时，请直接写出11CDDD= _________；（3）在正方形1111A B C D绕中心O旋转的过程中，直线1CC与直线1DD的位置关系是______________,请借助图3证明你的猜想．B档（提升精练）1. 如图，△ABC 中，∠90ACB =︒, 2=AC ，以AC 为边向右侧作等边三角形ACD ．（1）如图24-1,将线段AB 绕点A 逆时针旋转︒60，得到线段1AB ，联结1DB ，则与1DB 长度相等的线段为（直接写出结论）；（2）如图24-2，若P 是线段BC 上任意一点（不与点C 重合），点P 绕点A 逆时针旋转︒60得到点Q ,求ADQ ∠的度数；（3）画图并探究：若P 是直线BC 上任意一点（不与点C 重合），点P 绕点A 逆时针旋转︒60得到点Q ,是否存在点P ，使得以 A 、 C 、 Q 、 D 为顶点的四边形是梯形，若存在,请指出点P 的位置，并求出PC 的长；若不存在，请说明理由．2. 如图1，△ABC 是等腰直角三角形，四边形ADEF 是正方形，D 、F 分别在AB 、AC 边上，此时BD=CF ，BD ⊥CF 成立．（1）当正方形ADEF 绕点A 逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF 成立吗？若成立，请证明；若不成立，请说明理由．（2）当正方形ADEF 绕点A 逆时针旋转45°时，如图3，延长BD 交CF 于点G ． ①求证：BD ⊥CF ； ②当AB=4，AD=时，求线段BG 的长．3. 已知：在△AOB 与△COD 中，OA ＝OB ，OC ＝OD ，︒=∠=∠90COD AOB ．（1）如图1，点C 、D 分别在边OA 、OB 上，连结AD 、BC ，点M 为线段BC 的中点，连结OM ，则线段AD 与OM 之间的数量关系是，位置关系是；（2）如图2，将图1中的△COD 绕点O 逆时针旋转，旋转角为α (︒<<︒900α)．连结AD 、BC ，点M 为线段BC 的中点，连结OM ．请你判断（1）中的两个结论是否仍然成立．若成立，请证明；若不成立，请说明理由；（3）如图3，将图1中的 △COD 绕点 O 逆时针旋转到使 △COD 的一边OD 恰好与△AOB 的边OA 在同一条直线上时，点C 落在OB 上，点M 为线段BC 的中点．请你判断（1）中线段AD 与OM 之间的数量关系是否发生变化，写出你的猜想，并加以证明．4. 在Rt △ABC 中，AB =BC ，∠B =90°，将一块等腰直角三角板的直角顶点O 放在斜边AC 上，将三角板绕点O 旋转．（1）当点O 为AC 中点时，①如图1，三角板的两直角边分别交AB ，BC 于E 、F 两点，连接EF ，猜想线段AE 、CF 与EF 之间存在的等量关系（无需证明）；②如图2，三角板的两直角边分别交AB ，BC 延长线于E 、F 两点，连接EF ，判断①中的猜想是否成立．若成立，请证明；若不成立，请说明理由；（2）当点O 不是AC 中点时，如图3,，三角板的两直角边分别交AB ，BC 于E 、F 两点，若14AO AC ，求OE OF的值．5. 如图1，四边形ABCD ，将顶点为A 的角绕着顶点A 顺时针旋转，若角的一条边与DC 的延长线交于点F ，角的另一条边与CB 的延长线交于点E ，连接EF ．（1）若四边形ABCD 为正方形，当∠EAF=45°时，有EF=DF －BE ．请你思考如何证明这个结论（只思考，不必写出证明过程）；（2）如图2，如果在四边形ABCD 中，AB=AD ，∠ABC=∠ADC=90°，当∠EAF=21∠BAD 时，EF 与DF 、BE 之间有怎样的数量关系？请写出它们之间的关系式（只需写出结论）；（3）如图3，如果四边形ABCD 中，AB=AD ，∠ABC 与∠ADC 互补，当∠EAF=21∠BAD 时，EF 与DF 、BE 之间有怎样的数量关系？请写出它们之间的关系式并给予证明．（4）在（3）中，若BC=4，DC=7，CF=2，求△CEF 的周长（直接写出结果即可）．C 档（跨越导练）1. 已知：正方形ABCD 中，45MAN ∠=o，绕点A 顺时针旋转，它的两边分别交CB 、DC （或它们的延长线）于点M 、N ．（1）如图1，当MAN ∠绕点A 旋转到BM DN =时，有BM DN MN +=．当MAN ∠ 绕点A 旋转到BM DN ≠时，如图2，请问图1中的结论还是否成立？如果成立，请给予证明，如果不成立，请说明理由；（2）当MAN ∠绕点A 旋转到如图3的位置时，线段BM DN ，和MN 之间有怎样的等量关系？请写出你的猜想，并证明．2. 如图，已知四边形ABCD 是正方形，对角线ACBD 相交于O .（1）如图1，设 E 、F 分别是AD 、AB 上的点，且∠EOF =90°，线段AF 、BF 和EF 之间存在一定的数量关系．请你用等式直接写出这个数量关系；（2）如图2，设 E 、F 分别是AB 上不同的两个点，且∠EOF =45°，请你用等式表示线段AE 、BF 和EF 之间的数量关系，并证明.3. 问题：如图1，在Rt △ABC 中，90C ∠=︒，30ABC ∠=︒，点D 是射线CB 上任意一点，△ADE 是等边三角形，且点D 在ACB ∠的内部，连接BE ．探究线段BE 与DE 之间的数量关系．请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明.（1）当点D 与点C 重合时（如图2），请你补全图形．由BAC ∠的度数为，点E落在，容易得出BE 与DE 之间的数量关系为；（2）当点D 在如图3的位置时，请你画出图形，研究线段BE 与DE 之间的数量关系是否与（1）中的结论相同，写出你的猜想并加以证明．4. 在△ABC 中，AB=AC ，∠BAC=α（︒<<︒600α），将线段BC 绕点B 逆时针旋转60°得到线段BD 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

如图 8，在Rt ABC中，CAB 90，AC 3 ， AB 4 ，点 P 是边 AB 上任意一点，过点 P 作PQ AB 交BC于点E，截取 PQ AP ，联结 AQ ，线段 AQ 交BC于点D，设 AP x ，DQ y ．【2013徐汇】（1）求y关于x的函数解析式及定义域；（ 4 分）（2）如图 9，联结CQ，当CDQ和ADB相似时，求x的值；（ 5 分）（3）当以点C为圆心，CQ为半径的⊙C和以点B为圆心，BQ为半径的⊙B相交的另一个交点在边 AB 上时，求 AP 的长．（ 5 分）CQDEA P B（图 8）CQDEA（图 9）P BCA B（备用图）【2013 奉贤】如图，已知AB是⊙O的直径，AB=8，点C在半径OA上（点C与点O、A不重合），过点 C作 AB的垂线交⊙ O于点 D，联结 OD，过点 B 作 OD的平行线交⊙ O于点 E、交射线CD于点 F．（1）若⌒EDBE⌒，求∠ F 的度数；（2）设CO x, EF y,写出y 与x之间的函数解析式，并写出定义域；（3）设点 C 关于直线 OD 的对称点为 P ，若△ PBE 为等腰三角形，求 OC 的长．第 25 题【 2013 长宁】△ ABC 和△ DEF 的顶点 A 与 D 重合，已知∠ B = 90 . ，∠ BAC = 30 . ， BC=6，∠FDE = 90 ， DF=DE=4.（1）如图①，EF 与边、分别交于点，且 . 设 DF a ，在射线上取AC AB G 、H FG=EHDF一点 P ，记： DP xa ，联结 CP. 设△ DPC 的面积为 y ，求 y 关于 x 的函数解析式，并写出定义域；（2）在（ 1）的条件下，求当x 为何值时 PC // AB ；（ 3）如图②，先将△ DEF 绕点 D 逆时针旋转，使点 E 恰好落在 AC 边上，在保持 DE 边与 AC 边完全重合的条件下，使△ DEF 沿着 AC 方向移动 . 当△ DEF 移动到什么位置时，以线段AD 、FC 、BC 的长度为边长的三角形是直角三角形.图①图②【 2013 嘉定】已知 AP 是半圆 O 的直径，点 C 是半圆 O 上的一个动点（不与点 A 、P 重合），联结 AC ，以直线 AC 为对称轴翻折 AO ，将点 O 的对称点记为 O 1 ，射线 AO 1 交半圆 O 于点 B ，联结 OC .（1）如图 8，求证： AB ∥ OC ；（2）如图 9，当点 B 与点 O 1 重合时，求证： AB CB ；（3）过点 C 作射线 AO 1 的垂线，垂足为 E ，联结 OE 交 AC 于 F . 当 AO5 ，O 1 B 1 时，求CF的值 .AFB（ 1）BCCOO 1【2013 金山】如图，在ABC 中， AB AC 2 ， A90 ， P 为 BC 的中点， E 、 FAOPAOP AO分别是 AB 、 AC 上的动点，EPF图 9备用图图 8(1) 求证：BPE ∽ CFP ．A(2) 设 BEx ， PEF 的面积为 y ．求 y 关EF于 x 的函数解析式，并写出 x 的取值范围．(3) 当 E 、 F 在运动过程中，EFP 是否可能BCP等于 60 ，若可能请求出 x 的值，若不可能请说明理由．【 2013 静安】已知 AB 是⊙ O 的直径，弦 CD ⊥ AB ，垂足为 H ， AH =5， CD = 4 5 ，点 E 在⊙ O 上，射线与射线相交于点，设= ， = y ．FAECDFAE xDF（1）求⊙ O 的半径；ED（ 2）如图，当点 E 在 AD 上时，求 y 与 x 之间的函数解析式，并写出函数的定义域；（3）如果= 3AOHB，求的长．2C（第 24 题图）ADC【 2013 松江】如图，已知在 Rt △ ABC 中，EBFPG（第 25 题图）∠BAC=90°， AB=4，点 D在边 AC上，△ ABD沿 BD翻折，点 A与 BC边上的点 E重合，过点 B 作 BG∥ AC交 AE的延长线于点G，交 DE的延长线于点F．(1)当∠ ABC=60°时，求 CD的长；(2)如果 AC=x，AD=y，求 y 关于 x 的函数解析式，并写出函数定义域；(3)联结 CG，如果∠ ACB=∠ CGB，求 AC的长．【 2013 闸北】已知：如图七，在梯形ABCD中， AD∥BC，∠A＝90°， AD＝ 6， AB＝ 8， sinC ＝4，点 P 在射线 DC上，5点Q在射线 AB 上，且 PQ⊥CD，设 DP＝ x， BQ＝ y．（1）求证：点 D 在线段 BC的垂直平分线上；（2）如图八，当点 P 在线段 DC上，且点 Q在线段AB上时，求 y 关于 x 的函数解析式，并写出定义域；A D（P图Q八）B C（ 3）若以点 B 为圆心、 BQ为半径的⊙B 与以点 C为圆心、 CP为半径的⊙C 相切，求线段DP的长．A D （备用）B C【2013 黄浦】如图，在梯形ABCD中，AD=BC=10，tanD=4，E是腰AD上一点，且AE∶ED=1∶33.（1）当AB∶CD=1∶ 3 时，求梯形ABCD的面积；（2）当∠ABE=∠BCE时，求线段BE的长；A B（ 3）当△BCE是直角三角形时，求边AB的长. ED C【 2013 闵行】如图，在平行四边形ABCD中， AB 8 ， tan B 2， CE⊥ AB，垂足为点E （点 E 在边 AB上），F 为边 AD的中点，联结EF，CD．（1）如图 1，当点E是边AB的中点时，求线段EF的长；（2）如图 2，设BC x，△CEF的面积等于y，求y与x的函数解析式，并写出函数定义域；（ 3）当BC16时，∠ EFD与∠ AEF的度数满足数量关系：EFD k AEF ，其中k≥ 0，求 k 的值．F FA D A DEEB C B C（图 1）（图 2）A F DEB C（第 25 题图）1 【 2013 浦东】已知：如图，在Rt△ABC中， C 90 ， BC 4 ， tan CAB ，2 点 O 在边 AC 上，以点 O 为圆心的圆过A、 B 两点，点 P 为 AB上一动点.（1）求⊙O的半径；（2）联结AP并延长，交边CB 延长线于点 D，设 AP x ， BD y ，求y关于 x 的函数解析式，并写出定义域；（3）联结BP，当点P是AB的中点时，求△ABP的面积与△ABD的面积比SS ABP的值．ABD备用图第 25 题图【2013 普陀】如图，在 Rt △ABC中，∠ACB=90°，AC=6cm，BC=8cm.点 P 为 BC的中点，动点 Q从点 P 出发， A延射线 PC方向以2cm/s的速度运动，以点 P 为圆心，PQ长为半径作圆.设点 Q运动的时间为 t 秒，O（ 1）当 t =时，判断直线 AB与⊙ P 的位置关系，C Q P B并说明理由； (6 分 )（ 2）当△ AQP是等腰三角形时，求 t 的值；(4分) 第 25 题（3）已知⊙O为ABC的外接圆，若⊙P与⊙O相切，求t 的值. (4分)【2013 杨浦】如图 1，已知⊙O的半径长为3，点A是⊙O上一定点，点P 为⊙ O上不同于点A 的动点。

（1）当tan A 1时，求 AP的长；2（2）如果⊙Q过点P、O，且点Q在直线AP上（如图2），设AP=x，QP=y，求y关于x的函数关系式，并写出函数的定义域；（3）在（ 2）的条件下，当tan A 43），存在⊙M与⊙O相内切，同时与⊙Q相时（如图3外切，且 OM⊥ OQ，试求⊙ M的半径的长。

（图 1）（图2）（图3）（第 25 题图）【 2012 虹口】如图，△ABC中，∠ABC=90°，AB=BC=4，点O为AB边的中点，点M是BC边上一动点（不与点 B、C重合），AD⊥ AB，垂足为点 A.联结 MO，将△ BOM沿直线 MO翻折，点B 落在点 B1处，直线 M B1与 AC、AD分别交于点 F、N..（1）当∠CMF=120°时，求BM的长；（）设 BM x ，y CMF的周长，求y关于 x 的函数关系式，并写出自变量x 的2ANF的周长取值范围；（ 3）联结NO，与AC边交于点E，当△ FMC∽△ AEO时，求BM的长.CDF MB1NA O B第 25 题图【 2012 宝山】已知△ ABC 中， ACB 90 （如图 8），点 P 到 ACB 两边的距离相等，且 PA =PB ．（ 1）先用尺规作出符合要求的点 P （保留作图痕迹，不需要写作法），然后判断△ ABP 的形状，并说明理由；2m ， PC n ，试用 m 、 n 的代数式表示 ABC 的周长和面积；（）设 PA（ 3）设 CP 与 AB 交于点 D ，试探索当边 AC 、BC 的长度变化时， CD CD的值是否发生AC BC变化，若不变，试求出这个不变的值，若变化，试说明理由．C（图）8C（备用图）ABAB【 2012 闵D 行】已A 知：如图， AB ⊥ BC ， ADADRt ABC CC90 AC6 sin B3COMPB B CB P O AB B P 180 M M AB5 CPy OAx y x x y yNOA N BC NB N OA O NBx （ 1）如图 1，当点 E 在线段 BC 上时，PPOBAB AB .AO试猜想线段OEF 、 BE 、DF 有怎样的数量关系？并证明你的猜想ECBO图 9图 8题图）（备用图）（第 25（ 2）设 BE=x ，DF=y ，当点 E 在线段 BC 上运动时（不包括点 B 、C ），如图 1，求 y 关于A CD 图 10 B x 的函数解析式，并指出x 的取值范围 .（第 25 题图）（ 3）当点 E 在射线 BC 上运动时（不含端点 B ），点 F 在射线 CD 上运动 . 试判断以 E 为圆心以 BE 为半径的⊙ E 和以 F 为圆心以 FD 为半径的⊙ F 之间的位置关系 .（ 4）当点 E 在 BC 延长线上时，设 AE 与 CD 交于点 G ，如图 2. 问⊿ EGF 与⊿ EFA 能否相似，若能相似，求出BE 的值，若不可能相似，请说明理由.【 2012 市抽样】已知：在Rt △ABC中，∠C=90°，AC=4，∠A=60°，CD是边AB上的中线，直线 BM∥ AC，E是边 CA延长线上一点， ED交直线 BM于点 F，将△ EDC沿 CD翻折得△E DC ，射线 DE 交直线 BM于点 G．（1）如图 1，当CD⊥EF时，求BF的值；（2）如图 2，当点G在点F的右侧时；①求证：△ BDF∽△ BGD；②设 AE=x，△ DFG的面积为 y，求 y 关于 x 的函数解析式，并写出x 的取值范围；（ 3）如果△DFG的面积为 6 3，求AE的长．B F M B F G MED DE A C E A C（第 25 题图 1）（第25题图2）B MDA C（第 25 题备用图）【2012 长宁】在Rt△ ABC中, AB=BC=4,∠ B=90,将一直角三角板的直角顶点放在斜边AC的中点 P 处 , 将三角板绕点P 旋转 , 三角板的两直角边分别与边 AB 、BC 或其延长线上交于D 、E 两点 ( 假设三角板的两直角边足够长 ), 如图 (1) 、图 (2) 表示三角板旋转过程中的两种情形 .(1) 直角三角板绕点 P 旋转过程中 , 当 BE = ▼ 时 , △ PEC 是等腰三角形；(2) 直角三角板绕点 P 旋转到图 (1) 的情形时 , 求证 : PD =PE ； (3) 如图 (3), 若将直角三角板的直角顶点放在斜边AC 的点 M 处 , 设 AM : MC =m : n ( m 、n 为正数 ), 试判断 MD 、ME 的数量关系 , 并说明理由 .图（ 1）图（ 2）图（ 3）【 2012 奉贤】已知：半圆 O 的半径 OA =4，P 是 OA 延长线上一点，过线段OP 的中点 B 做垂线交⊙ 于点，射线交⊙ O 于点，联结．O C PCDOD（1）若 AC =CD ，求弦 CD 的长。