(优辅资源)山西省应县一中高二上学期期中考试数文试卷Word版含答案

合集下载

山西省应县高二上学期语文期中考试试卷

山西省应县高二上学期语文期中考试试卷姓名:________ 班级:________ 成绩:________一、现代文阅读 (共3题；共27分)1. （6分） (2018高一上·嘉兴期中) 阅读下面选文，完成各题。

中国道家学派的代表人物老子首倡“朴素”观。

“朴”是没有雕琢的木，“素”是没有染色的丝。

老子用它们代表事物原本的状态，即自然的状态。

老子从哲学的高度提出“道法自然”的思想，认为自然才是事物的极致，也是人精神所应追求的极致，“见素抱朴”是“道法自然”的美学表达。

朴素观首创于道家学派，亦为儒墨等学派采用并融入自身学说。

在现实生活层面，朴素观与主要由墨家与儒家创立的节俭观结合，成为中华民族共同奉行的道德观、审美观。

中国农业社会倡导由道家创立的朴素观，在精神上发展出一种以自然为本位的崇真尚善臻美的哲学观、道德观、美学观。

具体来说主要包括以下几方面：一是本色观，崇尚天然，崇尚纯真，以本色为真，以本色为美，如《论语》引《诗经》中所描绘的那位姑娘“巧笑倩兮，美目盼兮，素以为绚兮”；二是恬淡观，不慕繁华，不贪名利，以清廉为贵，以平淡为美；三是清新观，不繁复，不艳丽，清雅，简洁，充满生气，如苏轼所云“其身与竹化，无穷出清新”；四是精诚观，《庄子》中云“不精不诚，不能动人”。

此外，朴素观还导出重实质轻修饰、重内容轻形式等观念。

就中国传统美学来说，朴素是最高的美。

这种美灵动而无限，既是美之极致，又是美之根源。

其实，视朴素为美不独中华民族为然，世界各民族也大都如此。

法国雕塑家罗丹崇奉自然，他说他最喜欢的一句箴言就是“自然总是美的”。

他还说：“美只有一种，即宣示真实的美。

”罗丹这里说的“自然”“真实”，均可以理解成“朴素”。

进入工业社会，朴素观被工业社会追求财富、追求享受的价值导向所排挤，奢华生活也成为个人炫耀的资本，进而腐蚀人心，催生腐败，引发严重社会问题。

以大量浪费资源、污染环境为代价的奢华生活方式可以说是工业文明发展之“殇”。

2018-2019学年山西省朔州市应县一中高二(上)期中数学试卷(文科)(附答案详解)

2018-2019学年山西省朔州市应县一中高二（上）期中数学试卷（文科）一、单选题（本大题共12小题，共60.0分）1.点(−2,3)到直线l：3x+4y+3=0的距离是()A. 2B. 95C. 85D. 752.直线2x−y+k=0与4x−2y+1=0的位置关系是()A. 平行B. 不平行C. 平行或重合D. 既不平行也不重合3.直线x+y=5与直线x−y=1交点坐标是()A. (1,2)B. (2,3)C. (3,2)D. (2,1)4.圆(x−2)2+(y+3)2=2的圆心和半径分别是()A. (−2,3)，1B. (2,−3)，3C. (−2,3)，√2D. (2,−3)，√25.下列命题正确的是()①平行于同一平面的两直线平行；②垂直于同一平面的两直线平行；③平行于同一直线的两平面平行；④垂直于同一直线的两平面平行．A. ①②B. ③④C. ①③D. ②④6.某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为()A. 2√17B. 2√5C. 3D. 27.已知圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为()A. 12√2πB. 12πC. 8√2πD. 10π8.下列命题中正确的是()A. 经过点P0(x0,y0)的直线都可以用方程y−y0=k(x−x0)表示B. 经过定点A(0,b)的直线都可以用方程y=kx+b表示C. 经过任意两个不同点P1(x1,y1)，P2(x2,y2)的直线都可用方程(x2−x1)(y−y1)=(y2−y1)(x−x1)表示D. 不经过原点的直线都可以用方程xa +yb=1表示9.已知A(5,2)，B(−1,4)，则AB的垂直平分线方程为()A. x−3y+7=0B. 3x−y−3=0C. 3x+y−7=0D. 3x−y−7=010.若直线y=−2x+3k+14与直线x−4y=−3k−2的交点位于第四象限，则实数k的取值范围是()A. −6<k<−2B. −5<k<−3C. k<−6D. k>−211.已知直线l:kx−y+2−k=0过定点M，点P(x,y)在直线2x+y−1=0上，则|MP|的最小值是()A. √10B. 3√55C. √6D. 3√512.在三棱锥S−ABC中，三侧面两两互相垂直，侧面△SAB，△SBC，△SAC的面积分别为1，32，3，则此三棱锥的外接球的表面积为()A. 14πB. 12πC. 10πD. 8π二、单空题（本大题共4小题，共20.0分）13.直线x+ky=0，2x+3y+8=0和x−y−1=0三条直线交与一点，则k=______．14.无论m为何值，直线l：(m+1)x−y−7m−4=0恒过一定点P，则点P的坐标为______．15.已知A(2,3)、B(1,0)，动点P在y轴上，当|PA|+|PB|取最小值时，则点P的坐标为_____．16.如图所示，点P在正方形ABCD所在平面外，PD⊥平面ABCD，PD=AD，则PA与BD所成角的度数为______．三、解答题（本大题共6小题，共70.0分）17.已知两直线l1：x+8y+7=0和l2：2x+y−1=0．(1)求l1与l2交点坐标；(2)求过l1与l2交点且与直线x+y+1=0平行的直线方程．18.求过三点O(0,0)，A(1,1)，B(4,2)的圆的方程，并求这个圆的半径和圆心坐标．19.已知平行四边形ABCD的三个顶点坐标为A(−1,2)，B(0,−1)，C(4,1)．(Ⅰ)求顶点D的坐标；(Ⅱ)求四边形ABCD的面积．20.如图，在正方体ABCD−A1B1C1D1中，O是AC的中点．(1)求证：AD1//平面DOC1；(2)求异面直线AD1和OC1所成角的大小．21.已知四棱锥P−ABCD，底面ABCD是菱形，∠DAB=60°，PD⊥平面ABCD，PD=AD，点E为AB中点，点F为PD中点．(1)证明：平面PED⊥平面PAB；(2)求二面角P−AB−F的平面角的余弦值．22.已知三点A(1,3)，B(−1,−1)，C(2,1)，直线l平行于BC，分别交AB、AC于点P、Q，，求直线l的方程．若△APQ的面积是△ABC面积的19答案和解析1.【答案】B【解析】解：点(−2,3)到直线l ：3x +4y +3=0的距离d =√9+16=95．故选：B ．利用点到直线的距离公式直接求解．本题考查点到直线的距离的求法，考查点到直线的距离公式等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．2.【答案】C【解析】解：∵由方程组{2x −y +k =04x −2y +1=0，得2k −1=0，当k =12时，方程组由无穷多个解，两条直线重合，当k ≠12时，方程组无解，两条直线平行，综上，两条直线平行或重合，故选 C ．化简方程组得到2k −1=0，根据k 值确定方程组解的个数，由方程组解得个数判断两条直线的位置关系．本题考查方程组解得个数与两条直线的位置关系，方程有唯一解时，两直线相交，方程组有无穷解时，两直线重合，方程组无解时，两直线平行．3.【答案】C【解析】解：由题意可得{x +y =5x −y =1，解得{x =3y =2，两条直线的交点坐标为：(3,2)．故选：C ．直接利用联立方程组求解即可．本题考查直线的交点坐标的求法，是基础题．4.【答案】D【解析】解：∵圆的标准方程为(x−2)2+(y+3)2=2∴圆的圆心坐标和半径长分别是(2,−3)，√2故选：D．根据圆的标准方程，即可写出圆心坐标和半径．本题考查圆的标准方程，考查学生分析解决问题的能力，属于基础题．5.【答案】D【解析】解：①平行于同一平面的两直线平行，错误，有可能相交，如图：AC//面A1B1C1D1，AB//面A1B1C1D1，AB∩AC=A．②垂直于同一平面的两直线平行，正确，垂直于同一平面的直线都和该平面的法线平行，因此它们之间必然平行．除非两条直线重合；③平行于同一直线的两平面平行，不正确；证明：假设有一条直线l和它的两条平行线a，b，a，b确定一个平面p，过a作任何一个平面，只要不过l，肯定和l平行，却和原来的平面相交于a．④垂直于同一直线的两平面平行．正确．证明：假设两个面相交．假设这条直线与第一个面相交于A点，与第二个面相交于B点．两面相交直线为CD，在直线CD上任取一点E，则ABE应该为一个三角形．然而，与∠ABE 与∠BAE均为直角不符，所以，两个面不可以相交，两个面平行．故选：D．结合公理及正方体模型可以判断，可以利用反证法证明结论，也可以从具体的实物模型中去寻找反例证明．本题主要考查了空间中直线与直线之间的位置关系，直线与平面垂直的性质，考查空间想象能力和思维能力，属于基本知识的考查．6.【答案】B【解析】【分析】本题考查空间几何体的三视图，考查计算能力，属于中档题．根据题意，利用侧面展开图，转化求解即可．【解答】解：由题意可知，该几何体是圆柱，底面周长16，高为2，直观图以及侧面展开图如图：圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度：√22+42=2√5．故选B．7.【答案】B【解析】解：设圆柱的底面直径为2R，则高为2R，圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，可得：4R2=8，解得R=√2，则该圆柱的表面积为：π⋅(√2)2×2+2√2π×2√2=12π．故选：B．利用圆柱的截面是面积为8的正方形，求出圆柱的底面直径与高，然后求解圆柱的表面积．本题考查圆柱的表面积的求法，考查圆柱的结构特征，截面的性质，是基本知识的考查．8.【答案】C【解析】解：A选项中过P0的方程为直线的点斜式方程，当直线与y轴平行即斜率不存在时例如x=5，就不能写成此形式，此选项错；B选项中过A点的直线方程为直线的斜截式方程，当直线与y轴平行时即斜率不存在时例如x =8，就不能写成此形式，此选项错；C 选项中经过任意两个不同点P 1(x 1,y 1)，P 2(x 2,y 2)的直线P 1P 2，都可以用方程(y −y 1)(x 2−x 1)=(x −x 1)(y 2−y 1)来表示，所以此选项正确； D 选项中当直线与坐标轴平行时例如y =2，与x 轴没有交点且不过原点，但是不能直线的截距式，此选项错．故选CA 、B 、D 选项中都是有条件限制才能写出直线方程的，条件是斜率存在或与坐标轴的截距存在，C 选项中的方程不受限制只需两点坐标即可，得到正确答案．此题考查学生掌握直线的点斜式、斜截式及截距式方程所满足的条件，会利用两点坐标过两点直线的两点式方程，是一道中档题．9.【答案】B【解析】解：设线段AB 的中点坐标为(x,y)，则x =5−12=2，y =2+42=3，中点坐标为(2,3)，直线AB 的斜率k =4−2−1−5=−13，所以AB 垂直平分线的斜率为3，则AB 的垂直平分线方程为y −3=3(x −2)化简得3x −y −3=0 故选：B ．设出AB 的中点坐标(x,y)，利用中点坐标公式求出x 和y 得到中点坐标，然后根据AB 的垂直平分线与线段AB 垂直得到斜率乘积为−1，所以先根据A 与B 的坐标求出直线AB 的斜率即可求出垂直平分线的斜率，根据中点坐标和求出的斜率写出直线的方程即可．本题考查学生灵活运用中点坐标公式化简求值，掌握两直线垂直时斜率的关系，会根据一点坐标和斜率写出直线的点斜式方程．10.【答案】A【解析】解：解方程组{y =−2x +3k +14x −4y =−3k −2，得，x =k +6，y =k +2∵直线y =−2x +3k +14与直线x −4y =−3k −2的交点位于第四象限， ∴k +6>0且k +2<0， ∴−6<k <−2．解方程组{y =−2x +3k +14x −4y =−3k −2，得，x =k +6，y =k +2，由此能求出实数k 的取值范围．本题考查两条直线的交点坐标的求法，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．11.【答案】B【解析】【分析】本题主要考查直线经过定点问题，两点间的距离公式的应用，二次函数的性质，属于中档题．令直线l 的参数k 的系数等于零，求得定点M 的坐标，利用两点间的距离公式、二次函数的性质，求得|MP|的最小值．【解答】解：直线l ：kx −y +2−k =0，即k(x −1)−y +2=0，过定点M(1,2)，点P(x,y)在直线2x +y −1=0上，∴y =1−2x ，∴|MP|=√(x −1)2+(1−2x −2)2=√5x 2+2x +2=√5(x +15)2+95，故当x =−15时，|MP|取得最小值为3√55，故选：B ．12.【答案】A【解析】【分析】本题给出特殊三棱锥，求它的外接球表面积，着重考查了空间垂直关系的性质和多面体的外接球等知识，属于中档题．先根据题意得出侧棱SA ，SB ，SC 两两垂直，再根据三角形面积公式，解方程组得SA =2，SB =1，SC =3，进而算出以SA 、SB 、SC 为长、宽、高的长方体的对角线长为√14，从而得到三棱锥外接球R =√142，最后用球的表面积公式，可得此三棱锥外接球表面积．解：由题意得，侧棱SA ，SB ，SC 两两垂直，设SA =x ，SB =y ，SC =z ，则因为△SAB ，△SBC ，△SAC 都是以S 为直角顶点的直角三角形，得{xy =2yz =3xz =6，解之得：x =2，y =1，z =3即SA =2，SB =1，SC =3， ∵侧棱SA ，SB ，SC 两两垂直，∴以SA 、SB 、SC 为过同一顶点的3条棱作长方体，该长方体的对角线长为√4+1+9=√14，恰好等于三棱锥外接球的直径，由此可得外接球的半径R =√142，得此三棱锥外接球表面积为S =4πR 2=14π，故选A ．13.【答案】−12【解析】解：∵直线x +ky =0，2x +3y +8=0和x −y −1=0三条直线交与一点，解方程组{2x +3y +8=0x −y −1=0，得{x =−1y =−2，∴直线x +ky =0过点(−1,−2)，解得k =−12．故答案为：−12．解方程组{2x +3y +8=0x −y −1=0，得直线x +ky =0过点(−1,−2)，由此能求出k 的值．本题考查实数值的求法，是基础题，解题时要认真审题，注意直线与直线的交点的合理运用．14.【答案】(7,3)【解析】解：直线l ：(m +1)x −y −7m −4=0化为：m(x −7)+x −y −4=0，令{x −7=0x −y −4=0，解得x =7，y =3． ∴直线恒过一定点P(7,3)，故答案为：(7,3)，直线l ：(m +1)x −y −7m −4=0化为：m(x −7)+x −y −4=0，令{x −7=0x −y −4=0，解出即可得出．本题考查了直线系的应用，考查了推理能力与计算能力，属于基础题．15.【答案】(0,1)【解析】【分析】本题考查距离之和取最小值的情况，注意运用对称思想，考查运算能力，属于基础题．作出A 关于y 轴的对称点A′(−2,3)，连接A′B ，与y 轴交于P ，即为所求．求出直线A′B 的方程，可令x =0，可得P 的坐标．【解答】解：作出A 关于y 轴的对称点A′(−2,3)，连接A′B ，与y 轴交于P ，即为所求．此时|PA|+|PB|取最小值|A′B|，由A′B 的斜率为3−0−2−1=−1，可得方程：y =−(x −1)，令x =0，可得y =1，即为P(0,1)，故答案为：(0,1)． 16.【答案】60°【解析】解：如图，以D 为坐标原点，DA 所在直线为x 轴，DC 所在线为y 轴，DP 所在线为z 轴，建立空间坐标系，∵点P 在正方形ABCD 所在平面外，PD ⊥平面ABCD ，PD =AD ，令PD =AD =1 ∴A(1,0,0)，P(0,0,1)，B(1,1,0)，D(0,0,0)∴PA ⃗⃗⃗⃗⃗ =(1,0,−1)，BD⃗⃗⃗⃗⃗⃗ =(−1,−1,0)∴cosθ=PA ⃗⃗⃗⃗⃗ ⋅BD ⃗⃗⃗⃗⃗⃗ |PA⃗⃗⃗⃗⃗ |×| BD ⃗⃗⃗⃗⃗⃗ |=−1√2×√2=−12 故两向量夹角的余弦值为12，即两直线PA 与BD 所成角的度数为60°．故答案为：60°本题求解宜用向量法来做，以D 为坐标原点，建立空间坐标系，求出两直线的方向向量，利用数量积公式求夹角即可本题考查异面直线所角的求法，由于本题中所给的背景建立空间坐标系方便，故采取了向量法求两直线所成角的度数，从解题过程可以看出，此法的优点是不用作辅助线，大大降低了思维难度．17.【答案】解：(1)联立两条直线的方程可得：{x +8y +7=02x +y −1=0解得x =1，y =−1所以l 1与l 2交点坐标是(1,−1)．(2)设与直线x +y +1=0平行的直线l 方程为x +y +c =0因为直线l 过l 1与l 2交点(1,−1)所以c =0所以直线l 的方程为x +y =0．【解析】(1)联立两条直线的方程可得：{x +8y +7=02x +y −1=0，解得x =1，y =−1． (2)设与直线x +y +1=0平行的直线l 方程为x +y +c =0因为直线l 过l 1与l 2交点(1,−1)，所以c =0．解决此类问题的方法是联立两条直线的方程进行计算，要细心仔细，两条直线平行时注意未知直线的设法x 与y 的系数相同，只是常数不同而已．18.【答案】解：设圆的方程为：x 2+y 2+Dx +Ey +F =0，则{F =0D +E +F +2=04D +2E +F +20=0，解得D =−4，E =3，F =0，∴圆的方程为x 2+y 2−8x +6y =0，化为(x −4)2+(y +3)2=25，可得：圆心是(4,−3)、半径r =5．【解析】设出圆的一般方程，把点的坐标代入，求解D、E、F，即可求得圆的方程，并进一步求得圆心坐标与半径．本题考查圆的一般方程与标准方程，考查直线与圆位置关系的应用，是基础题．19.【答案】解：(Ⅰ)如图，设AC∩BD=M，因为四边形ABCD为平行四边形，所以对角线互相平分，又A(−1,2)，C(4,1).∴M(32,32 )，又B(0,−1)，所以顶点D的坐标为(3,4)．(Ⅱ)依题意可得k BC=−1−10−4=12，故直线BC的方程为y=12x−1，即x−2y−2=0，又|BC|=√(4−0)2+(−1−1)2=2√5，点A到直线BC的距离d=|−1−2×2−2|√12+(−2)2=7√55．所以四边形ABCD的面积S=|BC|⋅d=2√5×7√55=14．【解析】本题考查了平行四边形的性质、点到直线的距离公式、中点坐标公式、四边形的面积，考查了推理能力与计算能力，属于基础题．(Ⅰ)如图，设AC∩BD=M，因为四边形ABCD为平行四边形，所以对角线互相平分，利用中点坐标公式可得M，进而得到D的坐标．(Ⅱ)依题意可得k BC，可得点斜式可得直线BC的方程，利用两点之间的距离公式可得：|BC|.利用点到直线的距离公式可得点A到直线BC的距离d，即可得出．20.【答案】(1)证明：如图，连接D1C交DC1于点O1，连接OO1，∵O、O1分别是AC和D1C的中点，∴OO1//AD1．又OO1⊂平面DOC1，AD1⊄平面DOC1，∴AD1//平面DOC1；(2)解：由(1)知，OO1//AD1，∴∠O1OC1为异面直线AD1和OC1所成角，设正方体ABCD−A1B1C1D1的棱长为2，则O1C1=O1O=√2，OC1=√22+(√2)2=√6，∴cos∠O1OC1=(√2)2+(√6)2−(√2)22×√2×√6=√32，∴∠O1OC1=π6．即异面直线AD1和OC1所成角的大小为π6．【解析】(1)连接D1C交DC1于点O1，连接OO1，则OO1//AD1.再由线面平行的判定可得AD1//平面DOC1；(2)由(1)知，OO1//AD1，可得∠O1OC1为异面直线AD1和OC1所成角，设正方体ABCD−A1B1C1D1的棱长为2，求解三角形得答案．本题考查直线与平面平行的判定，考查空间想象能力与思维能力，训练了空间角的求法，是中档题．21.【答案】(1)证明：连接BD.∵AB=AD，∠DAB=60°，∴△ADB为等边三角形．∵E是AB中点，∴AB⊥DE.(2分)∵PD⊥面ABCD，AB⊂面ABCD，∴AB⊥PD．∵DE⊂面PED，PD⊂面PED，DE∩PD=D，∴AB⊥面PED.(4分)∵AB⊂面PAB，∴面PED⊥面PAB.(6分)(2)解：∵AB⊥平面PED，PE⊂面PED，∴AB⊥PE．连接EF，∵EF⊂PED，∴AB⊥EF.∴∠PEF为二面角P−AB−F的平面角．(9分)设AD=2，那么PF=FD=1，DE=√3．在△PEF中，PE=√7,EF=2,PF=1，∴cos∠PEF=(√7)2+22−12×2√7=5√714，即二面角P−AB−F的平面角的余弦值为5√714.(12分)【解析】(1)先由已知条件证明∴△ADB为等边三角形，AB⊥DE，易证AB⊥PD，得到AB⊥面PED，进而证明面PED⊥面PAB．(2)先由二面角的定义找出二面角的平面角，把二面角的平面角放在一个三角形中，求出此角的余弦值．本小题主要考查空间中的线面关系，四棱锥的有关概念及余弦定理等基础知识，考查空间想象能力和推理能力．22.【答案】解：过A 点作BC 边的高AE ，交PQ 于点F ，因为l//BC ，所以k l =k BC =23，∵S △APQ S △ABC =19，∴AF AE=13．由于直线BC 的方程为2x −3y −1=0，所以|AE|=√4+9=8√1313，所以|AF|=8√1339，所以|EF|=|AE|−|AF|=16√1339 设直线l 的方程为y =23x +b ，即2x −3y +3b =0，因为两条平行线间的距离为16√1339，∴√4+9=16√1339，解得b =139或b =−199(舍去)，所以直线l 的方程是y =23x +139，即6x −9y +13=0．【解析】先求出直线BC 的方程，由三角形面积间的关系求出直线l 与直线BC 之间的距离，由直线l 平行于BC ，设出直线l 的方程，再利用两平行线间的距离公式求出待定系数，从而得到直线l 的方程．本题考查直线的点斜式方程，两平行线间的距离公式，用到顶系数法求直线的方程的方法是一种常用的重要方法，属于基础题．。

高二上学期期中试题_3 34(共23页)

应县第一中学2021-2021学年高二语文上学期期中(qī zhōnɡ)试题时间是：150分钟满分是：150分一、课内阅读阅读下面的文字，完成下面小题。

〔此题一共3小题，9分〕“袅袅兮秋风，洞庭波兮木叶下。

〞〔?九歌?〕自从屈原吟唱出这动人的诗句，它的鲜明的形象，影响了此后历代的诗人们，许多为人传诵的诗篇正是从这里得到了启发，如谢庄?月赋?说：“洞庭始波，木叶微脱。

〞陆厥的?王节士歌?又说：“木叶下，江波连，秋月照浦云歇山。

〞“木叶〞是那么突出地成为诗人们笔下钟爱的形象。

“木叶〞是什么呢？按照字面的解释，“木〞就是“树〞，“木叶〞也就是“树叶〞，可是我们在古代的诗歌中为什么很少看见用“树叶〞呢？一般的情况，大概遇见“树叶〞的时候就都简称之为“叶〞，这可以说是由于诗人们文字洗炼的缘故，但一遇见“木叶〞的时候，诗人们似乎都不再考虑文字洗炼的问题，而是尽量争取通过“木叶〞来写出流传人口的名句，例如“九月寒砧催木叶，十年征戍忆。

〞〔沈佺期?古意?〕可见洗炼并不能作为“叶〞字独用的理由。

这里关键显然在“木〞这一字。

“木〞要比“树〞更显得单纯，所谓“枯桑知天风〞这样的树，似乎才更近于“木〞；它仿佛本身就含有一个落叶的因素，这正是“木〞的第一个艺术特征。

要说明“木〞它何以会有这个特征，就不能不触及诗歌语言中暗示性的问题，这暗示性仿佛是概念的影子，常常躲在概念的背后，我们不留心就不会发觉它的存在。

“木〞作为“树〞的概念的同时，却正是具有着一般“木头〞“木板〞等的影子，这潜在的形象常常影响着我们会更多地想起了树干，而很少会想到了叶子，因为叶子原不是属于木质的，“叶〞因此常被排挤到“木〞的疏朗的形象以外去，这排挤也就是为什么会暗示着落叶的缘故。

而“树〞呢？它是具有繁茂的枝叶的，它与“叶〞都带有密密层层浓阴的联想。

至于“木叶〞呢，那么全然不同。

这里又还需要说到“木〞在形象上的第二个艺术特征。

“木〞不但(bùdàn)让我们容易想起了树干，而且还会带来了“木〞所暗示的颜色性。

山西省朔州市应县第一中学高二上学期期中考试语文试题.doc

山西省朔州市应县第一中学高二上学期期中考试语文试题阅读下面的文字，完成下列小题。

谈起法律工具主义，还要追溯到公元前5世纪左右，管仲提出依法治国。

此后，法律就被公认为是治理国家的工具。

所谓治世之具，也可以叫治国之具，法律的工具主义从这儿就开始了。

到唐朝，魏征做了一个形象的比喻。

他说国家好像是一匹奔马，骑在马上的骑手就是皇帝，皇帝手中拿的鞭子就是法律，这样就把法律工具主义更加形象化。

既然古代的法律是君主手中的鞭子，这个法律必然受到君主的影响。

遇有开明的君主就能够发挥法律治世功能的作用，遇到昏君那就没有办法发挥法律的治世功能。

历史事实也确实如此。

唐太宗时期就是个讲究法制的时代。

当时，针对官吏假冒伪造履历，唐太宗说了一句话，以后再遇到假冒履历的官员必死不赦。

不久，又发现了假冒履历的事情，大理寺少卿戴胄据法断流，没有断死刑，唐太宗就非常不高兴，说我说过以后再有一定要处死。

这时戴胄讲了一句话，他说什么是法，法是“国家布大信于天下”，不能因为皇帝一时喜怒的意见，使法丧失了大信，这样说服了唐太宗。

唐太宗说了一句话，法乃天下之法非朕一人之法。

所以皇帝也遵法了，这就发挥了法律的工具主义的作用，这是遇到了明主。

遇到了昏君的时候，就是法制的败坏。

隋文帝本来是很重视法律的，但是到晚年任意为法。

比如说六月天要判处犯人死刑，大家就劝解他从汉以来都秋冬行刑，六月天不能判死刑。

他说六月天为什么不能判死刑呢?六月天还有雷霆震怒，雷还会击人呢，我是皇帝我也可以杀人。

所以法律工具主义是人治下的法制，遇到明主确实起到了治世的功能，但是遇到昏君的时候便不能发挥积极作用。

法律工具主义不仅影响了整个古代社会，也包括近代社会。

想起用法就把法拿出来，不想用法就把法收起来。

所以今天我们要牢固树立依法治国的法律权威主义的观念，就必须肃清法律工具主义的残余影响。

法与改革的关系就是古人所说的改制与更法。

春秋战国时期处于社会大变动时期，其经济体制改革和政治体制改革是联在一起的。

山西省应县第一中学2018-2019学年高二数学上学期期中试题文

山西省应县第一中学2018-2019学年高二数学上学期期中试题文时间：120分钟满分：150分一．选择题（共12题，每题5分）1．点（﹣2，3）到直线l：3x+4y+3=0的距离是（）A．2 B． C． D．2．直线2x﹣y+k=0与4x﹣2y+1=0的位置关系是（）A．平行 B．不平行C．平行或重合 D．既不平行也不重合3．直线x+y=5与直线x﹣y=1交点坐标是（）A．（1，2） B．（2，3） C．（3，2） D．（2，1）4．圆（x﹣2）2+（y+3）2=2的圆心和半径分别是（）A．（﹣2，3），1 B．（2，﹣3），3 C．（﹣2，3）， D．（2，﹣3），5．下列命题正确的是( )①平行于同一平面的两直线平行；②垂直于同一平面的两直线平行；③平行于同一直线的两平面平行；④垂直于同一直线的两平面平行．A．①② B．③④ C．①③ D．②④6．某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为（）A．2 B．2 C．3 D．27．已知圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为（）A．12π B．12π C．8πD．10π8．下列命题中正确的是（）A．经过点P0（x0，y0）的直线都可以用方程y﹣y0=k（x﹣x0）表示B．经过定点A（0，b）的直线都可以用方程y=kx+b表示C．经过任意两个不同点P1（x1，y1），P2（x2，y2）的直线都可用方程（x2﹣x1）（y﹣y1）=（y2﹣y1）（x﹣x1）表示D．不经过原点的直线都可以用方程表示9．已知A（5，2），B（﹣1，4），则AB的垂直平分线方程为（）A．x﹣3y+7=0 B．3x﹣y﹣3=0 C．3x+y﹣7=0 D．3x﹣y﹣7=010．若直线y=﹣2x+3k+14与直线x﹣4y=﹣3k﹣2的交点位于第四象限，则实数k的取值范围是（）A．﹣6＜k＜﹣2 B．﹣5＜k＜﹣3 C．k＜﹣6 D．k＞﹣211．已知直线l：kx﹣y+2﹣k=0过定点M，点P（x，y）在直线2x+y﹣1=0上，则|MP|的最小值是（）A． B． C． D．312．在三棱锥S﹣ABC中，三侧面两两互相垂直，侧面△SAB，△SAC的面积分别为1，，3，则此三棱锥的外接球的表面积为（）A．14πB．12π C．10π D．8π二．填空题（共4题，每题5分）13．直线x+ky=0，2x+3y+8=0和x﹣y﹣1=0三条直线交于一点，则k= ．14．无论m为何值，直线l：（m+1）x﹣y﹣7m﹣4=0恒过一定点P，则点P的坐标为．15．已知A（2，3）、B（1，0），动点P在y轴上，当|PA|+|PB|取最小值时，则点P的坐标为．16.如图，点P在正方形ABCD所在的平面外，PD⊥ABCD，PD=AD，则PA与BD所成角的度数为..三．解答题（共6题，第17题为10分，其余各题每题为12分）17．已知两直线l1：x+8y+7=0和l2：2x+y﹣1=0．（1）求l1与l2交点坐标；（2）求过l1与l2交点且与直线x+y+1=0平行的直线方程．18．求过三点O（0，0），A（1，1），B（4，2）的圆的方程，并求这个圆的半径和圆心坐标．19．已知平行四边形ABCD的三个顶点坐标为A（﹣1，2），B（0，﹣1），C（4，1）．（Ⅰ）求顶点D的坐标；（Ⅱ）求四边形ABCD的面积．20．(本小题满分12分)如图，在正方体ABCD－A1B1C1D1中，O是AC的中点．(1)求证：AD1∥平面DOC1；(2)求异面直线AD1和DC1所成角的大小．21. 已0知四棱锥P －ABCD ，底面ABCD 是菱形，∠DAB＝60°，PD⊥平面ABCD ，PD ＝AD ，点E 为AB 中点，点F 为PD 中点．（1）证明：平面PED⊥平面PAB ；（2）求二面角P －AB －F 的平面角的余弦值．22．已知三点A （1，3），B （﹣1，﹣1），C （2，1），直线l 平行于BC ，分别交AB 、AC 于点P 、Q ，若△APQ 的面积是△ABC 面积的，求直线l 的方程．F PDAC高二期中文数答案2018.10123456789101112B C C D D B B C C A B A13. ﹣． 14.（7，3） 15.（0，1） 16. 60°17．解：（1）联立两条直线的方程可得：解得x=1，y=﹣1 , 所以l1与l2交点坐标是（1，﹣1）．（2）设与直线x+y+1=0平行的直线l方程为x+y+c=0因为直线l过l1与l2交点（1，﹣1） , 所以c=0 , 所以直线l的方程为x+y=0．18．解：设圆的方程为：x2+y2+Dx+Ey+F=0，则，解得D=﹣4，E=3，F=0，∴圆的方程为x2+y2﹣8x+6y=0，化为（x﹣4）2+（y+3）2=25，可得：圆心是（4，﹣3）、半径r=5．19．解：（Ⅰ）如图，设AC∩BD=M，因为四边形ABCD为平行四边形，所以对角线互相平分，又A（﹣1，2），C（4，1）．∴M，又B（0，﹣1），所以顶点D的坐标为（3，4）．（Ⅱ）依题意可得k BC==，故直线BC的方程为y=x﹣1，即x﹣2y﹣2=0，又|BC|==2，点A到直线BC的距离d==．所以四边形ABCD的面积S=|BC|•d=2=14．20．【解】(1)证明：如图，连接D1C交DC1于点O1，连接OO1，∵O、O1分别是AC和D1C的中点，∴OO1∥AD1.又OO1⊂平面DOC1，AD1⊄平面DOC1，∴AD1∥平面DOC1.(2)由OO 1∥AD 1知，AD 1和DC 1所成角等于OO 1和DC 1所成的锐角或直角．设正方体的棱长为1.在△OO 1D 中，DO 1＝22，DO ＝22，OO 1＝12AD 1＝22， ∴△OO 1D 是等边三角形．∴异面直线AD 1与DC 1所成的角为60°.21. （1）证明：连BD ．∵AB＝AD ，∠DAB＝60°，∴△ADB 为等边三角形，∴E 是AB 中点．∴AB⊥DE ，∵PD⊥面ABCD ，AB ⊂面ABCD ，∴AB⊥PD． ∵DE ⊂面PED ，PD ⊂面PED ，DE∩PD＝D ，∴AB⊥面PED ，∵AB ⊂面PAB ．∴面PED⊥面PAB ．（2）解：∵AB⊥平面PED ，PE ⊂面PED ，∴AB⊥PE．连结EF ，∵ EF ⊂面PED ，∴AB⊥EF． ∴ ∠PEF 为二面角P －AB －F 的平面角．设AD ＝2，那么PF ＝FD ＝1，DE ＝3．在△PEF 中，PE ＝7，EF ＝2，PF ＝1 ∴cos∠PEF＝147572212)7(22=⨯-+ 即二面角P －AB －F 的平面角的余弦值为1475． 22．解：过A 点作BC 边的高AE ，交PQ 于点F ，因为l ∥BC ，所以，∵，∴．由于直线BC 的方程为2x ﹣3y ﹣1=0，所以|AE|=，所以|A F|=，所以|EF|=|AE|﹣|AF|=设直线l 的方程为y=x+b ，即2x ﹣3y+3b=0，因为两条平行线间的距离为，∴，解得b=或b=（舍去），所以直线l 的方程是y=x+，即6x ﹣9y+13=0．欢迎您的下载，资料仅供参考！。

高二数学上学期期中试题文_1 10

应县第一中学2021-2021学年高二数学上学期期中试题文创作人：历恰面日期：2020年1月1日时间是：120分钟满分是：150分一．选择题〔一共12题，每一小题5分〕1．点〔﹣2，3〕到直线l：3x+4y+3=0的间隔是〔〕A．2 B． C． D．2．直线2x﹣y+k=0与4x﹣2y+1=0的位置关系是〔〕A．平行 B．不平行C．平行或者重合 D．既不平行也不重合3．直线x+y=5与直线x﹣y=1交点坐标是〔〕A．〔1，2〕 B．〔2，3〕 C．〔3，2〕 D．〔2，1〕4．圆〔x﹣2〕2+〔y+3〕2=2的圆心和半径分别是〔〕A．〔﹣2，3〕，1 B．〔2，﹣3〕，3 C．〔﹣2，3〕， D．〔2，﹣3〕，5．以下命题正确的选项是( )①平行于同一平面的两直线平行；②垂直于同一平面的两直线平行；③平行于同一直线的两平面平行；④垂直于同一直线的两平面平行．A．①② B．③④ C．①③ D．②④6．某圆柱的高为2，底面周长为16，其三视图如图．圆柱外表上的点M在正视图上的对应点为A，圆柱外表上的点N在左视图上的对应点为B，那么在此圆柱侧面上，从M到N的途径中，最短途径的长度为〔〕A．2 B．2 C．3 D．27．圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，那么该圆柱的外表积为〔〕A．12π B．12π C．8πD．10π8．以下命题中正确的选项是〔〕A．经过点P0〔x0，y0〕的直线都可以用方程y﹣y0=k〔x﹣x0〕表示B．经过定点A〔0，b〕的直线都可以用方程y=kx+b表示C．经过任意两个不同点P1〔x1，y1〕，P2〔x2，y2〕的直线都可用方程〔x2﹣x1〕〔y﹣y1〕=〔y2﹣y1〕〔x﹣x1〕表示D．不经过原点的直线都可以用方程表示9．A〔5，2〕，B〔﹣1，4〕，那么AB的垂直平分线方程为〔〕A．x﹣3y+7=0 B．3x﹣y﹣3=0 C．3x+y﹣7=0 D．3x﹣y﹣7=010．假设直线y=﹣2x+3k+14与直线x﹣4y=﹣3k﹣2的交点位于第四象限，那么实数k的取值范围是〔〕A．﹣6＜k＜﹣2 B．﹣5＜k＜﹣3 C．k＜﹣6 D．k＞﹣211．直线l：kx﹣y+2﹣k=0过定点M，点P〔x，y〕在直线2x+y﹣1=0上，那么|MP|的最小值是〔〕A． B． C． D．312．在三棱锥S﹣ABC中，三侧面两两互相垂直，侧面△SAB，△SAC的面积分别为1，，3，那么此三棱锥的外接球的外表积为〔〕A．14πB．12π C．10π D．8π二．填空题〔一共4题，每一小题5分〕13．直线x+ky=0，2x+3y+8=0和x﹣y﹣1=0三条直线交于一点，那么k= ．14．无论m为何值，直线l：〔m+1〕x﹣y﹣7m﹣4=0恒过一定点P，那么点P的坐标为．15．A〔2，3〕、B〔1，0〕，动点P在y轴上，当|PA|+|PB|取最小值时，那么点P的坐标为．16.如图，点P在正方形ABCD所在的平面外，PD⊥ABCD，PD=AD，那么PA与BD所成角的度数为..三．解答题〔一共6题，第17题为10分，其余各题每一小题为12分〕17．两直线l1：x+8y+7=0和l2：2x+y﹣1=0．〔1〕求l1与l2交点坐标；〔2〕求过l1与l2交点且与直线x+y+1=0平行的直线方程．18．求过三点O〔0，0〕，A〔1，1〕，B〔4，2〕的圆的方程，并求这个圆的半径和圆心坐标．19．平行四边形ABCD的三个顶点坐标为A〔﹣1，2〕，B〔0，﹣1〕，C〔4，1〕．〔Ⅰ〕求顶点D的坐标；〔Ⅱ〕求四边形ABCD的面积．20．(本小题满分是12分)如图，在正方体ABCD－A1B1C1D1中，O是AC的中点．(1)求证：AD1∥平面DOC1；(2)求异面直线AD1和DC1所成角的大小．21. 已0知四棱锥P －ABCD ，底面ABCD 是菱形，∠DAB＝60°，PD⊥平面ABCD ，PD ＝AD ，点E 为AB 中点，点F 为PD 中点．〔1〕证明：平面PED⊥平面PAB ；〔2〕求二面角P －AB －F 的平面角的余弦值．22．三点A 〔1，3〕，B 〔﹣1，﹣1〕，C 〔2，1〕，直线l 平行于BC ，分别交AB 、AC 于点P 、Q ，假设△APQ 的面积是△ABC 面积的，求直线l 的方程．F PDAC1 2 3 4 5 6 7 8 9 10 11 12B C C D D B B C C A B A13. ﹣． 14.〔7，3〕 15.〔0，1〕 16. 60°17．解：〔1〕联立两条直线的方程可得：解得x=1，y=﹣1 , 所以l1与l2交点坐标是〔1，﹣1〕．〔2〕设与直线x+y+1=0平行的直线l方程为x+y+c=0因为直线l过l1与l2交点〔1，﹣1〕 , 所以c=0 , 所以直线l的方程为x+y=0．18．解：设圆的方程为：x2+y2+Dx+Ey+F=0，那么，解得D=﹣4，E=3，F=0，∴圆的方程为x2+y2﹣8x+6y=0，化为〔x﹣4〕2+〔y+3〕2=25，可得：圆心是〔4，﹣3〕、半径r=5．19．解：〔Ⅰ〕如图，设AC∩BD=M，因为四边形ABCD为平行四边形，所以对角线互相平分，又A〔﹣1，2〕，C〔4，1〕．∴M，又B〔0，﹣1〕，所以顶点D的坐标为〔3，4〕．〔Ⅱ〕依题意可得k BC==，故直线BC的方程为y=x﹣1，即x﹣2y﹣2=0，又|BC|==2，点A到直线BC的间隔 d==．所以四边形ABCD 的面积S=|BC|•d=2=14．20．【解】 (1)证明：如图，连接D 1C 交DC 1于点O 1，连接OO 1，∵O 、O 1分别是AC 和D 1C 的中点， ∴OO 1∥AD 1.又OO 1⊂平面DOC 1，AD 1⊄平面DOC 1， ∴AD 1∥平面DOC 1.(2)由OO 1∥AD 1知，AD 1和DC 1所成角等于OO 1和DC 1所成的锐角或者直角．设正方体的棱长为1.在△OO 1D 中，DO 1＝22，DO ＝22，OO 1＝12AD 1＝22， ∴△OO 1D 是等边三角形．∴异面直线AD 1与DC 1所成的角为60°. 21. 〔1〕证明：连BD ．∵AB＝AD ，∠DAB＝60°，∴△ADB 为等边三角形，∴E 是AB 中点．∴AB⊥DE，∵PD⊥面ABCD ，AB ⊂面ABCD ，∴AB⊥PD． ∵DE ⊂面PED ，PD ⊂面PED ，DE∩PD＝D ，∴AB⊥面PED ，∵AB ⊂面PAB ．∴面PED⊥面PAB ．〔2〕解：∵AB⊥平面PED ，PE ⊂面PED ，∴AB⊥PE．连结EF ，∵ EF ⊂面PED ，∴AB⊥EF． ∴ ∠PEF 为二面角P －AB －F 的平面角．设AD ＝2，那么PF ＝FD ＝1，DE ＝3．在△PEF 中，PE ＝7，EF ＝2，PF ＝1 ∴cos∠PEF＝147572212)7(22=⨯-+ 即二面角P －AB －F 的平面角的余弦值为1475． 22．解：过A 点作BC 边的高AE ，交PQ 于点F ，因为l ∥BC ，所以，∵，∴．由于直线BC的方程为2x﹣3y﹣1=0，所以|AE|=，所以|AF|=，所以|EF|=|AE|﹣|AF|=设直线l的方程为y=x+b，即2x﹣3y+3b=0，因为两条平行线间的间隔为，∴，解得b=或者b=〔舍去〕，所以直线l的方程是y=x+，即6x﹣9y+13=0．创作人：历恰面日期：2020年1月1日。

山西省朔州市应县一中高二上学期期中考试语文试题.pdf

阅读积累（一）（完成---4题）（1分）於是论次其文。

七年而太史公遭李陵之祸，幽於缧绁。

乃喟然而叹曰：“是余之罪也夫！是余之罪也夫！身毁不用矣。

”退而深惟曰：“夫诗书隐约者，欲遂其志之思也。

昔西伯拘里，演周易；孔子陈蔡，作春秋；屈原放逐，著离骚；左丘失明，厥有国语；孙子膑脚，而论兵法；不韦迁蜀，世传吕览；韩非囚秦，说难、孤愤；诗三百篇，大抵贤圣发愤之所为作也。

此人皆意有所郁结，不得通其道也，故述往事，思来者。

”於是卒述陶唐以来，至于麟止，自黄帝始。

、下列句子中加点的词语解释（?）（分） A、于是论次其文。

?次：编次、整理。

B、孔子陈蔡。

?：遭受困厄。

C、厥有《国语》。

厥：才。

D、欲遂其志之思也。

?遂：、。

、对下列句子中加点词语的意义和用法判断正确的一项：（?）(?分) 乃喟然而叹曰②孙子膑脚，而论兵法。

? 是余之罪也夫夫《诗》《书》隐约者。

A、?两个“而”不同，两个“夫”也不同。

B、两个“而”不同，两个“夫”相同。

C、两个“而”相同，两个“夫”不同。

?D、两个“而”不同，两个“夫”相同。

、对选文内容分析概括不正确的一项是（?）（分） A、司马迁的感叹表明，他对自己在武帝面前为李陵辩护一事深感后悔。

B、“身毁不用”的叹息表明，司马迁在遭祸前还有著述以外的志向。

C、昔圣贤发愤著述的故事，给了司马迁巨大的精神动力。

D、司马迁列举古圣先贤的事迹，也从一个侧面表明了他想像古圣先贤一样创造不朽业绩。

、请翻译下列句子：（6分）（1）《诗》《书》隐约者，欲遂其志之思也。

（2）《诗》三百篇，大底圣贤发愤之所为作也。

（分）’。

今之燕，必经赵，臣不可以行。

”文信侯不快，未有以强也。

甘罗曰：“君侯何不快之甚也？”文信侯曰：“吾令刚成君蔡泽事燕三年，燕太子丹已入质矣。

吾自请张卿相秦而不肯行”。

甘罗曰：“臣请行之。

”文信侯叱曰：“去！我身自请之而不肯，汝焉能行之？”甘罗曰：“大项橐生七岁为孔子师，今臣生十二岁于兹矣，君其试臣，何遽叱乎？”于是甘罗见张卿曰：“卿之功孰与武安君？”卿曰：“武安君南挫强楚，北威燕、赵，战胜攻取，破城堕邑，不知其数，臣之功不如也。

山西省应县一中2021-2022学年高二上学期期中考试英语试卷 Word版含答案

应县一中高二年级期中考试英语试题2021.10时间：120分钟满分：150分命题人：第I卷（三部分，共100分）第一部分: 听力（共两节，满分20分）第一节（共5小题；每小题1分，满分5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C、三个选项中选出最佳答案，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What does the woman advise the man to do?A. Learn to use a new camera.B. Take the camera back to the shop.C. Clean the camera when taking pictures.2.Where will the woman probably live next year?A. In a rented room.B. In the dormitory.C. At home.3. What does the man not like about the blue shirt?A. Its style.B. Its color.C. Its size.4. Who paid 2, 330 dollars for a car?A. The woman.B. The man.C. Linda.5. What time is it by the man's watch?A. 1 : 40.B. 1 : 30C. 1 : 00.其次节：（共15小题；每小题1分，满分15分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所A、B、C、三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话或独白前后，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟作答时间。

每段对话或独白读两遍。

听第6段材料，回答第6、7题6. How much is a ticket?A. 2 pounds.B. 3 pounds.C. 5 pounds.7. Why does the woman tell the man to get off the bus?A. They're at the last stop.B. They're at Woodford Green.C. The bus broke down.听第7段材料，回答第8、9题8. What did an Italian waiter teach the man to do?A. Say some words in Italian.B. Read Italian newspaper.C. Write in Italian.9. Where did the man spend the last day?A. In a museum.B. In a garden.C. In his hotel.听第8段材料，回答第10至12题。

山西省应县高二上学期语文期中考试试卷

山西省应县高二上学期语文期中考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共1题；共6分)1. （6分） (2019高二上·成都开学考) 阅读下面的文字，完成下面小题。

巴黎圣母院失火，在网上引发激烈争论。

（）它的焚毁不仅是法国文明的消损，更是人类历史文明的重大遗憾。

然而，在巴黎圣母院失火的新闻下面，竟有不少网民拍手称快，更是称这场大火是当初法军烧圆明园的报应，相关微博评论中“天道有轮回”等字眼层出不穷。

1860年，英法联军冲进圆明园烧杀抢掠，大火燃烧三天三夜，这座中国有史以来最宏伟的皇家园林最终付之一炬。

诚然，圆明园被毁是我国历史上不可抹去的耻辱，给国人带来难以抚平的伤痛。

但是，将这段历史放到今天来看，与巴黎圣母院并无可比性。

圆明园被毁是野蛮战争的历史伤痕，而巴黎圣母院失火却是和平时期的安全____。

两者都是人类文明与智慧的结晶，而伟大的人类历史文明的落幕，对于全人类都是一种巨大损失。

雨果曾经________地痛斥英法联军的恶行，今天，我们又怎能借着消防安全问题口不择言地发泄仇恨？现代社会文明应不断进步，但不少人的认知水平确实不如百年前的雨果。

余秋雨曾说过:“文明可能产生于野蛮，但绝不喜欢野蛮。

我们能熬过苦难，却绝不赞美苦难。

我们不害怕迫害，却绝不肯定迫害。

”圆明园被焚毁和巴黎圣母院的大火的联系，仅仅在于它们都是人类文明的结晶，都是承载文化艺术的____，都是人类历史中________的一部分。

铭记历史并不等于延续仇恨，而是为了更好前行。

正是为了让我们铭记历史、重蹈覆辙，因而不能用圆明园发生的悲剧去恶意攻击今天的巴黎圣母院，历史从来无意教给我们用仇恨包裹文明。

（1）下列在文中括号内补写的语句，最恰当的一项是（）A . 作为建筑史上的经典杰作，作为雨果同名名著的故事舞台，巴黎圣母院无疑是无价的世界文化遗产，其中收藏着众多珍贵艺术品。

B . 作为雨果同名名著的故事舞台，作为建筑史上的经典杰作，巴黎圣母院无疑是无价的世界文化遗产，其中收藏着众多珍贵艺术品。

山西省应县第一中学2018-2019学年高二数学上学期期中试题文

山西省应县第一中学2018-2019学年高二数学上学期期中试题文时间：120分钟满分：150分一．选择题（共12题，每题5分）1．点（﹣2，3）到直线l：3x+4y+3=0的距离是（）A．2 B． C． D．2．直线2x﹣y+k=0与4x﹣2y+1=0的位置关系是（）A．平行 B．不平行C．平行或重合 D．既不平行也不重合3．直线x+y=5与直线x﹣y=1交点坐标是（）A．（1，2） B．（2，3） C．（3，2） D．（2，1）4．圆（x﹣2）2+（y+3）2=2的圆心和半径分别是（）A．（﹣2，3），1 B．（2，﹣3），3 C．（﹣2，3）， D．（2，﹣3），5．下列命题正确的是( )①平行于同一平面的两直线平行；②垂直于同一平面的两直线平行；③平行于同一直线的两平面平行；④垂直于同一直线的两平面平行．A．①② B．③④ C．①③ D．②④6．某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为（）A．2 B．2 C．3 D．27．已知圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为（）A．12π B．12π C．8πD．10π8．下列命题中正确的是（）A．经过点P0（x0，y0）的直线都可以用方程y﹣y0=k（x﹣x0）表示B．经过定点A（0，b）的直线都可以用方程y=kx+b表示C．经过任意两个不同点P1（x1，y1），P2（x2，y2）的直线都可用方程（x2﹣x1）（y﹣y1）=（y2﹣y1）（x﹣x1）表示D．不经过原点的直线都可以用方程表示9．已知A（5，2），B（﹣1，4），则AB的垂直平分线方程为（）A．x﹣3y+7=0 B．3x﹣y﹣3=0 C．3x+y﹣7=0 D．3x﹣y﹣7=010．若直线y=﹣2x+3k+14与直线x﹣4y=﹣3k﹣2的交点位于第四象限，则实数k的取值范围是（）A．﹣6＜k＜﹣2 B．﹣5＜k＜﹣3 C．k＜﹣6 D．k＞﹣211．已知直线l：kx﹣y+2﹣k=0过定点M，点P（x，y）在直线2x+y﹣1=0上，则|MP|的最小值是（）A． B． C． D．312．在三棱锥S﹣ABC中，三侧面两两互相垂直，侧面△SAB，△SAC的面积分别为1，，3，则此三棱锥的外接球的表面积为（）A．14πB．12π C．10π D．8π二．填空题（共4题，每题5分）13．直线x+ky=0，2x+3y+8=0和x﹣y﹣1=0三条直线交于一点，则k= ．14．无论m为何值，直线l：（m+1）x﹣y﹣7m﹣4=0恒过一定点P，则点P的坐标为．15．已知A（2，3）、B（1，0），动点P在y轴上，当|PA|+|PB|取最小值时，则点P的坐标为．16.如图，点P在正方形ABCD所在的平面外，PD⊥ABCD，PD=AD，则PA与BD所成角的度数为..三．解答题（共6题，第17题为10分，其余各题每题为12分）17．已知两直线l1：x+8y+7=0和l2：2x+y﹣1=0．（1）求l1与l2交点坐标；（2）求过l1与l2交点且与直线x+y+1=0平行的直线方程．18．求过三点O（0，0），A（1，1），B（4，2）的圆的方程，并求这个圆的半径和圆心坐标．19．已知平行四边形ABCD的三个顶点坐标为A（﹣1，2），B（0，﹣1），C（4，1）．（Ⅰ）求顶点D的坐标；（Ⅱ）求四边形ABCD的面积．20．(本小题满分12分)如图，在正方体ABCD－A1B1C1D1中，O是AC的中点．(1)求证：AD1∥平面DOC1；(2)求异面直线AD1和DC1所成角的大小．21. 已0知四棱锥P －ABCD ，底面ABCD 是菱形，∠DAB＝60°，PD⊥平面ABCD ，PD ＝AD ，点E 为AB 中点，点F 为PD 中点．（1）证明：平面PED⊥平面PAB ；（2）求二面角P －AB －F 的平面角的余弦值．22．已知三点A （1，3），B （﹣1，﹣1），C （2，1），直线l 平行于BC ，分别交AB 、AC 于点P 、Q ，若△APQ 的面积是△ABC 面积的，求直线l 的方程．P A C高二期中文数答案2018.1013. ﹣． 14.（7，3） 15.（0，1） 16. 60°17．解：（1）联立两条直线的方程可得：解得x=1，y=﹣1 , 所以l1与l2交点坐标是（1，﹣1）．（2）设与直线x+y+1=0平行的直线l方程为x+y+c=0因为直线l过l1与l2交点（1，﹣1） , 所以c=0 , 所以直线l的方程为x+y=0．18．解：设圆的方程为：x2+y2+Dx+Ey+F=0，则，解得D=﹣4，E=3，F=0，∴圆的方程为x2+y2﹣8x+6y=0，化为（x﹣4）2+（y+3）2=25，可得：圆心是（4，﹣3）、半径r=5．19．解：（Ⅰ）如图，设AC∩BD=M，因为四边形ABCD为平行四边形，所以对角线互相平分，又A（﹣1，2），C（4，1）．∴M，又B（0，﹣1），所以顶点D的坐标为（3，4）．（Ⅱ）依题意可得k BC==，故直线BC的方程为y=x﹣1，即x﹣2y﹣2=0，又|BC|==2，点A到直线BC的距离d==．所以四边形ABCD的面积S=|BC|•d=2=14．20．【解】(1)证明：如图，连接D1C交DC1于点O1，连接OO1，∵O、O1分别是AC和D1C的中点，∴OO1∥AD1.又OO1⊂平面DOC1，AD1⊄平面DOC1，∴AD1∥平面DOC1.(2)由OO 1∥AD 1知，AD 1和DC 1所成角等于OO 1和DC 1所成的锐角或直角．设正方体的棱长为1.在△OO 1D 中，DO 1＝22，DO ＝22，OO 1＝12AD 1＝22， ∴△OO 1D 是等边三角形．∴异面直线AD 1与DC 1所成的角为60°.21. （1）证明：连BD ．∵AB＝AD ，∠DAB＝60°，∴△ADB 为等边三角形，∴E 是AB 中点．∴AB⊥DE ，∵PD⊥面ABCD ，AB ⊂面ABCD ，∴AB⊥PD． ∵DE ⊂面PED ，PD ⊂面PED ，DE∩PD＝D ，∴AB⊥面PED ，∵AB ⊂面PAB ．∴面PED⊥面PAB ．（2）解：∵AB⊥平面PED ，PE ⊂面PED ，∴AB⊥PE．连结EF ，∵ EF ⊂面PED ，∴AB⊥EF． ∴ ∠PEF 为二面角P －AB －F 的平面角．设AD ＝2，那么PF ＝FD ＝1，DE ＝3．在△PEF 中，PE ＝7，EF ＝2，PF ＝1 ∴cos∠PEF＝147572212)7(22=⨯-+ 即二面角P －AB －F 的平面角的余弦值为1475． 22．解：过A 点作BC 边的高AE ，交PQ 于点F ，因为l ∥BC ，所以， ∵，∴．由于直线BC 的方程为2x ﹣3y ﹣1=0，所以|AE|=，所以|A F|=，所以|EF|=|AE|﹣|AF|= 设直线l 的方程为y=x+b ，即2x ﹣3y+3b=0，因为两条平行线间的距离为，∴，解得b=或b=（舍去），所以直线l 的方程是y=x+，即6x ﹣9y+13=0．。

山西省朔州市应县一中高二数学上学期期中试题文新人

高二上学期期中考试数学（文）试题时间：120分钟满分：150分一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符号题目要求的。

)1. 点(a,b)关于直线x+y=0对称的点是 ( )A 、 (－a,－b)B 、 (a,－b)C 、 (b,a)D 、 (－b,－a) 2. 若直线与直线垂直，则的值是（）A.或B.或C.或D.或1 3. 三个球半径的比为123∶∶，那么最大的球的体积是剩下两个球的体积和的（）A.1倍B.2倍C.3倍D.4倍4. 已知两点A(-1，3)，B(3，1)，点C 在坐标轴上，若∠ACB=600，则点C 有( ) A.1个 B.2个 C.3个 D.4个5. 若直线2=-y x 被圆4)(22=+-y a x 所截得的弦长为22,则实数a 的值为（）A ．0或4B ．1或3C ．-2或6D ．-1或36. 直线2(1)10x a y +++=的倾斜角的取值范围是（） A ．[0,]4π B ．3,4ππ⎡⎫⎪⎢⎣⎭C ．[0,](,)42πππUD ．3,,424ππππ⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭U 7. 下列说法不正确的．．．．是（） A. 空间中，一组对边平行且相等的四边形是一定是平行四边形； B ．同一平面的两条垂线一定共面；C. 过直线上一点可以作无数条直线与这条直线垂直，且这些直线都在同一个平面内；D. 过一条直线有且只有一个平面与已知平面垂直.8. 直线kx －y=k －1与ky －x=2k 的交点位于第二象限，那么k 的取值范围是( )1320mx y m +-=(34)10m x y -++=m 1-13113-1-13-A.k ＞1B.0＜k ＜21 C.k ＜21D.21＜k ＜19. 如图，某几何体的正视图和俯视图都是矩形，侧视图是平行四边形，则该几何体的体积为( )A ．36 B ．39C ．312D ．31810. 直线032=--y x 与圆9)3()2(22=++-y x 交于E 、F 两点，则EOF ∆（O 为原点）的面积为（）A ．32 B ．34C ．655 D ．35511. 某几何体的三视图如图所示，当a b +取最大值时，这个几何体的体积为( )A.16 B.13C.23 D.1212. 如果直线与圆交于相异两点222x y +=0x y m ++=是坐标原点，,那么实数的取值范围是（）二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)三、解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤) 17. (本小题满分10分）直线l 过点(1,2)和第一、二、四象限,若l 的两截距之和为6，求直线l的方程。

高二数学上学期期中试题文_2 7

应县第一中学2021-2021学年高二数学上学期期中试题文时间是：120分钟满分是：150分一、选择题：〔本大题一一共12小题，每一小题5分，一共60分，每一小题四个选项，只有一项是哪一项正确的。

〕10y ++=的倾斜角为〔〕A. 150°B. 60°C. 120°D. 30°()0,1-且与直线210x y +-=平行的直线方程是〔〕A.210x y ++=B.210x y +-=C.220x y ++=D.220x y +-= 2130x my m -+-=，当m 变动时，所有直线都通过定点( )A.〔21-，3〕B.1(,3)2C.1(,3)2-D.1(,3)2-- (1,)(0)a a >到直线:20l x y +-=的间隔为1，那么a 的值是〔〕A B.2-C 1 D 15.直线1:330l ax y ++=和直线2:(2)10l x a y +-+=平行，那么实数a 的值是( )A.3B.-1C.326.以下命题正确的选项是 ( )①一个平面内有两条直线都与另外一个平面平行，那么这两个平面平行；②一个平面内有无数条直线都与另外一个平面平行，那么这两个平面平行；③一个平面内任何直线都与另外一个平面平行，那么这两个平面平行；④一个平面内有两条相交直线都与另外一个平面平行，那么这两个平面平行．A ．①③B ．②④C ．②③④D ．③④7.某三棱锥的三视图如下图，那么该三棱锥的外表积为( )A ．827+B ．1027+C ．433D ．4223+ 8.过点(3,1)且与直线230x y --=垂直的直线方程是( )A ．270x y +-=B ．250x y +-=C ．210x y --=D ．250x y --=9.如图,正棱柱1111ABCD A B C D -中, 12AA AB =,那么异面直线1A B 与1AD 所成角的余弦值为( )A. 15B. 25C. 35D. 4510.假设直线1l :(4)y k x =-与直线2l 关于点(2,1)对称,那么直线2l 恒过定点( )A.(0,4)B.(0,2)C.(-2,4)D.(4,-2)11.在四面体中,棱的长为,其余各棱长都为,那么二面角的余弦值为( ) A. B. C. D.12..如图，点N 为正方形ABCD 的中心，ECD △为正三角形，平面ECD ⊥平面,ABCD M 是线段ED 的中点，那么( )A ．BM EN =，且直线BM EN 、是相交直线B ．BM EN ≠，且直线,BM EN 是相交直线C ．BM EN =，且直线BM EN 、是异面直线D ．BM EN ≠，且直线,BM EN 是异面直线二、填空题〔一共4小题，每一小题5分，一共20分〕13.直线()23y k x =-+必过定点,该定点坐标是__________.14.直线()()2130a x a y ++--=与直线()()22320a x a y ++++=不相交,那么a =______.15.在平面直角坐标系中，定义1212(,)||||d P Q x x y y =-+-为两点1122(,),(,)P x y Q x y 之间的“折线间隔〞. 假设点(1,3)A -，O 为坐标原点,那么(,)d A O =____________;O 与直线20x y +-=上一点的“折线间隔〞的最小值是__________；P ABCD －中，PD AC AB ⊥⊥，平面PAD ，底面ABCD 为正方形，且3CD PD ＋＝，假设四棱锥P ABCD －的每个顶点都在球O 的球面上，那么球O 的外表积的最小值为三、解答题〔一共6题，一共70分〕17.〔满分是10分〕求经过点2()5,A -，且在x 轴上的截距等于在y 轴上的截距的2倍的直线方程．18.〔满分是12分〕两条直线1l :260,:(2)320x my l m x y m ++=-++=,求当m 为何值时,1l 与2l 相交、平行、重合.19.〔满分是12分〕如图,四棱锥P ABCD -的底面是正方形,侧棱PA ⊥底面ABCD ,E 是PA 的中点〔1〕求证: PC 平面BDE ;〔2〕证明: BD CE ⊥20.〔满分是12分〕直线12:20l x y -+=与224:0l x y +-=，点()1,P m ．〔1〕假设点P 到直线12,l l 的间隔相等，务实数m 的值；〔2〕当1m =时，直线l 经过点P 且分别与12,l l 相交于,A B 两点，假设P 恰好平分线段AB ，求,A B 两点的坐标及直线l 的方程．21.〔满分是12分〕四棱锥E ABCD -的底面为菱形,且60ABC ∠=,2,AB EC ==2AE BE ==, O 为AB 的中点〔1〕求证: EO ⊥平面ABCD〔2〕求点D 到面AEC 的间隔22.〔满分是12分〕如图,是圆的直径,垂直圆所在的平面,是圆上的点.〔1〕求证:平面平面;〔2〕假设,求二面角的余弦值.1—5 CCDDB 6—10 DBADB 11-12 CB二、填空题 13.()2,3 14.2-或者23-15. 16.6π 三、解答题17.解析：当横截距、纵截距均为零时，设所求的直线方程为y kx =，将(5,2)-代入y kx =中，得25k =-，此时直线方程为25y x =-，即250x y +=. 当横截距、纵截距都不是零时，设所求直线方程为12x y a a+=，将(5,2)-代入所设方程，解得12a =-，此时直线方程为210x y ++=. 综上所述，所求直线方程为210x y ++=或者250x y +=.18.解析：将两直线的方程联立,得方程组60,{(2)320,x my m x y m ++=-++= 当0m =或者2m =时, 1l 与2l 相交;当0m ≠且2m ≠时,1122A B A B =, 由1122A B A B =,得123m m =-,解得1m =-或者3m =. 由1122A C A C =,得1622m m=-,解得3m =. ∴(1)当1m ≠且3m ≠时,1122A B A B ≠,方程组(*)有唯一解, 1l 与2l 相交. (2)当1m =-时,111222A B C A B C =≠,方程组(*)无解,此时, 1l 与2l 平行. (3)当3m =时, 111222A B C A B C ==,方程组(*)有无数组解, 1l 与2l 重合.19.解析：〔1〕证明:连结AC 交BD 于O ,连结OE ,因为四边形ABCD 是正方形,所以O 为AC 中点.又因为E 是PA 的中点,所以PC OE ,因为PC ⊄平面BDE ,OE ⊂平面BDE ,所以PC 平面BDE(2)证明:因为四边形ABCD 是正方形,所以BD AC ⊥.因为PA ⊥底面ABCD ,且BD ⊂平面ABCD ,所以PA BD ⊥.又AC PA A ⋂=,AC ⊂平面PAC ,PA ⊂平面PAC ,所以BD ⊥平面PAC 又CE ⊂平面PAC ,所以BD CE ⊥解析：20.解析：〔142355m m --=解得1m =-或者73m =. 〔2〕设(,22),(42,)A a a B b b +-,那么(42)2{(22)2a b a b +-=++=, 解得25a =-,45b =. ∴26124(,),(,)5555A B -,∴16115271()5k -==---, ∴1:1(1)7l y x -=--,即780x y +-=.21.解析：〔1〕证明:连接2,c =,∵2,2AE EB AB ===∴AEB ∆为等腰直角三角形∵O 为AB 的中点∴,1EO AB EO ⊥=又∵,60AB BC ABC =∠=︒,∴ACB ∆是等边三角形∴3,CO =又2EC =∴222EC EO CO =+,即∴EO CO ⊥∴EO ⊥平面ABCD〔2〕设点D 到面AEC 的间隔为h ∵2,2AE AC EC ===∴72AEC S ∆= ∵3,ADC S E ∆=到面ACB 的间隔 1EO =,∵D AEC E ADC V V --=,ABC ADC S h S EO ∆∆⋅=⋅∴2217h =∴点D 到面AEC 的间隔为221722.解析：〔1〕由是圆的直径,得, 由平面,平面,得. 又,平面, 平面, 所以平面. 因为平面,所以平面平面〔2〕如图,过作于, 因为平面, 平面, 所以.又因为,且平面,平面所以平面.过作于,连接, 由三垂线定理得, 所以为二面角的平面角.在中,由,得. 在中,由,得.因为,所以,所以所以在中,,所以,所以故二面角的余弦值为励志赠言经典语录精选句；挥动**，放飞梦想。

山西省朔州市应县第一中学2019-2020学年高二期中考试数学(文)试卷

数学试题（文）时间：120分钟满分：150分一、选择题（本大题共12个小题,每小题5分,共60分.）1．已知集合{}04A x Z x =∈<<，()(){}120B x x x =+-<，则A B =（） A ．()0,2 B ．()1,2- C ．{}0,1 D ．{}12．已知复数112i z =-，121z z ⋅=，则复数2z 的虚部为（）A ．25B ．25-C ．15D ．15-3．已知函数1,2()(3),2x x f x f x x ⎧+≥⎪=⎨+<⎪⎩，则(1)(9)f f -=（） A.1- B.2- C.6 D.74．下表是x 和Y x 0 1 2 3Y 1 3 5 7则Y 关于x A ．(2,2) B ．(1.5,0) C ．(1,2) D ．(1.5,4)5．函数()ln f x x x =的大致图象是（）A ．B ．C ．D ．6. 已知函数()f x 是定义在R 上的奇函数，当0x <时，()2x f x =，那么()2log 3f 的值为（）A ．13 B ．-3 C ．3 D ．13-7．函数()()log 43a f x ax =-在[]1,3是增函数，则a 的取值范围是（）A ．4,19⎛⎫ ⎪⎝⎭B ．9,4⎛⎫+∞ ⎪⎝⎭ C ．40,9⎛⎫ ⎪⎝⎭ D ．91,4⎛⎫ ⎪⎝⎭ 8. 命题“对任意x ∈R ，都有221x x +<”的否定是（）A ．对任意x ∈R ，都有221x x +>B ．对任意x ∈R ，都有221x x +≥C ．存在x ∈R ，使得221x x +>D ．存在x ∈R ，使得221x x +≥9. 若0.5log 0.2a ＝，5log 2b ＝，0.20.5c ＝，则a ，b ，c 的大小关系为（）A ．a c b >>B ．a b c >>C ．b a c >>D ．c b a >>10. 观察下列各式：2318-=，27148-=，2111120-=，2151224-=，据此规律.所得的结果都是8的倍数.由此推测可得（）A ．其中包含等式：2103110608-=B ．其中包含等式：28517224-=C ．其中包含等式：25312808-=D ．其中包含等式：23311088-= 11. 已知关于x 的方程21x m -=有两个不等实根，则实数m 的取值范围是（）A ．(,1]-∞-B ．(),1-∞-C ．[1,)+∞D ．()1,+∞12. 定义在R 上的函数()f x 满足'()()2(x f x f x e e -<为自然对数的底数），其中'()f x 为()f x 的导函数，若2(2)4f e =，则()2x f x xe >的解集为（） A.(),1-∞ B.()1,+∞ C.(),2-∞ D.()2,+∞二、填空题13．函数2()1log (1)f x x =--的定义域为_____________. 14．计算：13021lg8lg 25327e -⎛⎫-++= ⎪⎝⎭__________．15. 若函数21()ln 2xf x x x e =++，则曲线y=f(x)在点(1，f(1))处的切线的方程为__ _ ________.16. 已知函数2()ln f x x ax x =++有两个不同的零点，则实数a 的取值范围是_____.三、解答题17．已知直线的参数方程为(为参数)，曲线C 的参数方程为(为参数)．(1)将曲线C 的参数方程化为普通方程；(2)若直线与曲线交于两点，求线段的长．18．解不等式1054≥++-x x19．已知定义在R 上的函数()f x 是奇函数，且0x >时，()23xx f x =-．（1）求()0f ．（2）求()f x 的解析式．20．已知0()(>=a a x f x 且a ≠1)的图象经过点P(2,4).（1）求a 的值；（2）已知f(2x)-3f(x)-4=0，求x.21. 设()log (1)log (3)(0,1)a a f x x x a a =++->≠，且(1)=2f .(1)求a 的值；(2)求()f x 在区间30,2⎡⎤⎢⎥⎣⎦上的最大值.22．已知函数2()ln f x a x x =+．（1）当2a =-时，求函数()f x 的单调区间；（2）若函数2()()x g f x x=+在[1,)+∞上是单调函数，求实数a 的取值范围．文数答案1D 2B 3A 4D 5C 6D 7C 8D 9A 10A 11D 12C13、(]1,3 14、4 15、3(2)2y e x =+- 16、(1,0)-17、(1)由曲线C ：得x 2＋y 2＝16，所以曲线C 的普通方程为x 2＋y 2＝16.……3分(2)将直线的参数方程代入x 2＋y 2＝16，整理，得t 2＋3t －9＝0.……5分设A ，B 对应的参数为t 1，t 2，则t 1＋t 2＝－3，t 1t 2＝－9.…………7分|AB|＝|t 1－t 2|＝…………10分 18、，……4分 ①当时，；……7分 ②当时，，；……10分综上①②，不等式解集为.………12分 19、(1)由()f x 是定义在R 上的奇函数可知()()f x f x =--,令0x =则()(00)f f =-,故()00f =……4分(2)当0x <时0x ->,故()()(2)233x x x x f x f x ---=--=--=+,……9分又()00f =,故()2,030,02,03x x x x f x x x x -⎧->⎪⎪==⎨⎪⎪+<⎩．………12分20、解：（1）由经过点得，又解得…………6分（2）由（1）得，由得解得（舍去由解得…………12分21解：(1)∵(1)=2f ，∴(1)log 2log 2log 42a a a f =+==， ∴2a =；……4分(2)由1030x x +>⎧⎨->⎩得(1,3)x ∈-，∴函数()f x 的定义域为(1,3)-，……5分 22222()log (1)log (3)log (1)(3)]log [[(1)4]f x x x x x x =++-=+---+=，……8分 ∴当(0,1)x ∈时，()f x 是增函数；当3(1,)2x ∈时，()f x 是减函数，……10分 ∴函数()f x 在30,2⎡⎤⎢⎥⎣⎦上的最大值是2(1)log 42f ==．……12分 22解：（1）函数()f x 的定义域是0x >，2a =-时，22(1)(1)'()2x x f x x x x -+=-=，当01x <<时，'()0f x <，()f x 递减，当1x >时，'()0f x >，()f x 递增．∴()f x 的增区间是(1,)+∞，减区间是(0,1)；……4分（2）22()ln g x x a x x =++，22'()2a g x x x x=+-，由题意当1x ≥时，'()0g x ≥恒成立，或'()0g x ≤恒成立．……5分若22()20a g'x x x x =+-≥，2222(1)(1)2x x x a x x x-++≥-=-，当1x ≥时，22(1)(1)0x x x x-++-≤，∴0a ≥；……8分若22()20a g'x x x x =+-≤，2222(1)(1)2x x x a x x x-++≤-=-，当1x ≥时，22(1)(1)0x x x x-++-≤无最小值，∴'()0g x ≤不可能恒成立；……11分综上0a ≥．………12分。

(优辅资源)山西省应县一中高二上学期期中考试数文试卷Word版含答案

山西省应县高二上学期语文期中考试试卷

2018-2019学年山西省朔州市应县一中高二(上)期中数学试卷(文科)(附答案详解)

高二上学期期中试题_3 34(共23页)

山西省朔州市应县第一中学高二上学期期中考试语文试题.doc

山西省应县第一中学2018-2019学年高二数学上学期期中试题 文

高二数学上学期期中试题 文_1 10

山西省朔州市应县一中高二上学期期中考试语文试题.pdf

山西省应县一中2021-2022学年高二上学期期中考试英语试卷 Word版含答案

山西省应县高二上学期语文期中考试试卷

山西省应县第一中学2018-2019学年高二数学上学期期中试题 文

山西省朔州市应县一中高二数学上学期期中试题 文 新人

高二数学上学期期中试题 文_2 7

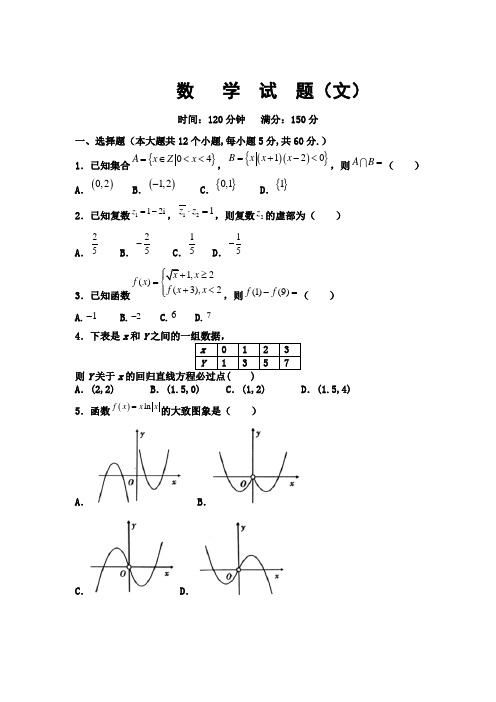
山西省朔州市应县第一中学2019-2020学年高二期中考试数学(文)试卷

山西省应县第一中学2018-2019学年高二数学上学期期中试题文

高二数学上学期期中试题文_1 10

山西省应县第一中学2018-2019学年高二数学上学期期中试题文

山西省朔州市应县一中高二数学上学期期中试题文新人

高二数学上学期期中试题文_2 7