全等变换---翻折答案

合集下载

【中考数学专题】10 与翻折或轴对称作图有关的几何证明题解析-

专题十：与翻折或轴对称作图有关的几何证明题解析专题导例如图，M、N是正方形ABCD的边CD上的两个动点，满足AM＝BN，连接AC交BN于点E，连接DE交AM于点F，连接CF，若正方形的边长为6，则线段CF的最小值是．【分析】：先判断出Rt△ADM≌Rt△BCN（HL），得出∠DAM＝∠CBN，进而判断出△DCE≌△BCE （SAS），得出∠CDE＝∠CBE，即可判断出∠AFD＝90°，根据直角三角形斜边上的中线等于斜边的一半可得OF＝AD＝3，利用勾股定理列式求出OC，然后根据三角形的三边关系可知当O、F、C 三点共线时，CF的长度最小．方法剖析轴对称的性质（1）对应线段相等，对应角相等；对称点的连线被对称轴垂直平分；（2）轴对称图形变换的特征是不改变图形的形状和大小，只改变图形的位置，新旧图形具有对称性；（3）轴对称的两个图形，它们对应线段或延长线相交，交点在对称轴上.轴对称（折叠）的思考层次全等变换：对应边相等，对应角相等；对称轴性质：对应点所连线段被对称轴（折痕）垂直平分，对称轴（折痕）上的点到对应点的距离相等；指出：（1）在翻折下，前后的图形关于折痕成轴对称，注意前后的图形成镜面对称，即前后的图形的左右位置互换；（2）翻折或对称中建构勾股方程来求取线段长及对最值类问题进行探究；（3）轴对称常见的结构，折叠会产生垂直平分，等腰三形.导例答案：解：如图，在正方形ABC D中，AD＝BC＝CD，∠ADC＝∠BCD，∠DCE＝∠BCE，在Rt△ADM和Rt△BCN中，，∴Rt△ADM≌Rt△BCN（HL），∴∠DAM＝∠CBN，在△DCE和△BCE中，，∴△DCE≌△BCE（SAS），∴∠CDE＝∠CBE∴∠DAM＝∠CDE，∵∠ADF+∠CDE＝∠ADC＝90°，∴∠DAM+∠ADF＝90°，∴∠AFD＝180°﹣90°＝90°，取AD的中点O，连接OF、OC，则OF＝DO ＝AD＝3，在Rt△OD C中，OC ＝＝3根据三角形的三边关系，OF+CF＞OC，∴当O、F、C三点共线时，CF的长度最小，最小值＝OC﹣OF＝3﹣3．故答案为：3﹣3．典型例题类型一：利用已知直线作对称图形进行证明例1、在等边△AB C中，点D在BC边上，点E在AC的延长线上，DE＝DA（如图1）．（1）求证：∠BAD＝∠EDC；（2）点E关于直线BC的对称点为M，连接DM，AM．①依题意将图2补全；②证明：在点D运动的过程中，始终有DA＝AM．【分析】（1）先判断出∠BAD+∠CAD＝60°，进而得出∠BAD+∠E＝60°，即可得出结论；（2）①由对称性即可补全图形；②由对称性判断出DM＝DE，∠MDC＝∠EDC，再用三角形的外角的性质，判断出∠ADC＝∠B+∠BAD＝∠B+∠MDC，进而判断出△ADM是等边三角形，即可得出结论．类型二：对已知图形进行翻折进行证明例2．如图，矩形ABC D中，AB＝4，AD＝3，把矩形沿直线AC折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△DEC≌△EDA；（2）求DF的值；（3）在线段AB上找一点P，连结FP使FP⊥AC，连结PC，试判定四边形APCF的形状，并说明理由，直接写出此时线段PF的大小．【分析】（1）根据矩形的性质、轴对称的性质可得到AD＝EC，AE＝DC，即可证到△DEC≌△EDA （SSS）；（2）易证AF＝CF，设DF＝x，则有AF＝4﹣x，然后在Rt△ADF中运用勾股定理就可求出DF的长．（3）根据三角形的内角和定理求得∠APF＝∠AFP根据等角对等边得出AF＝AP进而得出FC＝AP，从而证得四边形APCF是平行四边形，又因为FP⊥AC证得四边形APCF为菱形，然后根据菱形的面积S菱形＝PF•AC＝AP•AD，即可求得．专项突破1.如图，在Rt△AB C中，∠C＝90°，点D、E分别是BC、AB上一个动点，连接DE．将点B沿直线DE折叠，点B的对应点为F，若AC＝3，BC＝4，当点F落在AC的三等分点上时，BD的长为．2．如图，正方形ABC D中，点E是BC延长线上一点，连接DE，过点B作BF⊥DE于点F，连接F C．（1）求证：∠FBC＝∠CDF；（2）作点C关于直线DE的对称点G，连接CG，FG，猜想线段DF，BF，CG之间的数量关系，并证明你的结论．3.已知矩形ABCD，其中AD＞AB，依题意先画出图形，然后解答问题．（1）F为DC边上一点，把△ADF沿AF折叠，使点D恰好落在BC上的点E处．在图1中先画出点E，再画出点F，若AB＝8，AD＝10，直接写出EF的长为；（2）把△ADC沿对角线AC折叠，点D落在点E处，在图2先画出点E，AE交CB于点F，连接BE．求证：△BEF是等腰三角形．4.如图，Rt△AB C中，∠ACB=90°，AC=BC，点D为AB边上的一个动点（不与点A，B及A B中点重合），连接CD，点A关于直线CD的对称点为点E，直线BE，CD交于点F．（1）如图1，当∠ACD=15°时，根据题意将图形补充完整，并直接写出∠BFC的度数；（2）如图2，当45°＜∠ACD＜90°时，用等式表示线段AC，EF，BF之间的数量关系，并加以证明．5．在Rt△AB C中，∠ACB＝90°，CA＝C B．点D为线段BC上一个动点（点D不与点B，C重合），连接AD，点E在射线AB上，连接DE，使得DE＝D A．作点E关于直线BC的对称点F，连接BF，DF．（1）依题意补全图形；（2）求证：∠CAD＝∠BDF；（3）用等式表示线段AB，BD，BF之间的数量关系，并证明．6．如图①，在等腰三角形AB C中，AB＝AC＝8，BC＝14．如图②，在底边BC上取一点D，连结AD，使得∠DAC＝∠AC D．如图③，将△ACD沿着AD所在直线折叠，使得点C落在点E处，连结BE，得到四边形ABE D．则BE的长是．7．在等边三角形ABC外侧作射线AP，∠BAP=α，点B关于射线AP的对称点为点D，连接CD交AP于点E.（1）依据题意补全图形；（2）当α=20°时，∠ADC= ；∠AEC= ；（3）连接BE，求证：∠AEC=∠BEC；（4）当0°<α<60°时，用等式表示线段AE，CD，DE之间的数量关系，并证明．8.在等边△ABC外侧作直线AP，点B关于直线AP的对称点为D，连结BD，CD，其中CD交直线AP与点E．（1）如图1，若∠P AB＝30°，则∠ACE＝；（2）如图2，若60°＜∠P AB＜120°，请补全图形，判断由线段AB，CE，ED可以构成一个含有多少度角的三角形，并说明理由．9．如图1，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F.(1)求证：△BDF是等腰三角形；(2)如图2，过点D作DG∥BE，交BC于点G，连结FG交BD于点O.①判断四边形BFDG的形状，并说明理由；②若AB＝6，AD＝8，求FG的长．10.【问题情境】如图①，在Rt△AB C中，∠ACB＝90°，AC＝BC，点D为A B中点，连结CD，点E为CB上一点，过点E且垂直于DE的直线交AC于点F．易知：BE＝CF．（不需要证明）【探索发现】如图②，在Rt△AB C中，∠ACB＝90°，AC＝BC，点D为A B中点，连结CD，点E为CB的延长线上一点，过点E且垂直于DE的直线交AC的延长线于点F．【问题情境】中的结论还成立吗？请说明理由．【类比迁移】如图③，在等边△AB C中，AB＝4，点D是A B中点，点E是射线AC上一点（不与点A、C重合），将射线DE绕点D逆时针旋转60°交BC于点F．当CF＝2CE时，CE＝．11．在△AB C中，∠ACB＝90°，AC＜BC，点D在AC的延长线上，点E在BC边上，且BE＝AD，（1）如图1，连接AE，DE，当∠AEB＝110°时，求∠DAE的度数；（2）在图2中，点D是AC延长线上的一个动点，点E在BC边上（不与点C重合），且BE＝AD，连接AE，DE，将线段AE绕点E顺时针旋转90°得到线段EF，连接BF，DE．①依题意补全图形；②求证：BF＝DE．专题十：与翻折或轴对称作图有关的几何证明题解析例1．解：（1）∵△ABC是等边三角形，∴∠BAC＝∠ACB＝60°，∴∠BAD+∠CAD＝60°，∵DE＝DA，∴∠CAD＝∠E，∴∠BAD+∠E＝60°，∵∠EDC+∠E＝∠ACB＝60°，∴∠BAD＝∠EDC；（2）①补全图形如图2所示；②∵△ABC是等边三角形，∴∠B＝60°，由对称性得，∠EDC＝∠MDC，由（1）知，∠EDC＝∠BAD，∴∠MDC＝∠BAD，∵∠ADC＝∠B+∠BAD＝∠B+∠MD C．∴∠ADM＝∠B＝60°，由对称性得，DM＝DE，∵DE＝DA，∴DA＝DM，∴△ADM是等边三角形，∴DA＝DM，即：在点D运动的过程中，始终有DA＝AM．例2．（1）证明：∵四边形ABCD是矩形，∴AD＝BC，AB＝CD，AB∥CD，∴∠ACD＝∠CAB，∵△AEC由△ABC翻折得到，∴AB＝AE，BC＝EC，∠CAE＝∠CAB，∴AD＝CE，DC＝EA，∠ACD＝∠CAE，在△ADE与△CE D中，，∴△DEC≌△EDA（SSS）；（2）解：如图1，∵∠ACD＝∠CAE，∴AF＝CF，设DF＝x，则AF＝CF＝4﹣x，在RT△ADF中，AD2+DF2＝AF2，即32+x2＝（4﹣x）2，解得；x＝，即DF＝．（3）解：四边形APCF为菱形，设AC、FP相较于点O∵FP⊥AC∴∠AOF＝∠AOP又∵∠CAE＝∠CAB，∴∠APF＝∠AFP∴AF＝AP∴FC＝AP又∵AB∥CD∴四边形APCF是平行四边形又∵FP⊥AC∴四边形APCF为菱形，在矩形ABC D中，AB＝4，AD＝3，∴AC＝5，∵S菱形＝PF•AC＝AP•AD，∵AP＝AF＝4﹣＝∴PF＝＝．专项突破1.解：∵折叠∴BD＝DF，∵点F落在AC的三等分点上∴CF＝1或CF＝2，若CF＝1时，在Rt△CDF中，DF2＝CD2+CF2，∴BD2＝（4﹣BD）2+1∴BD＝当CF＝2时，在Rt△CDF中，DF2＝CD2+CF2，∴BD2＝（4﹣BD）2+4∴BD＝故答案为：或2．解：（1）∵ABCD为正方形，∴∠DCE＝90°．∴∠CDF+∠E＝90°，又∵BF⊥DE，∴∠FBC+∠E＝90°，∴∠FBC＝∠CDF（2）如图所示：在线段FB上截取FM，使得FM＝F D．∵∠BDC＝∠MDF＝45°，∴∠BDM＝∠CDF，∵＝＝，∴△BDM∽△CDF，∴＝＝，∠DBM＝∠DCF，∴BM＝CF，∴∠CFE＝∠FCD+∠CDF＝∠DBM+∠BDM＝∠DMF＝45°，∴∠EFG＝∠EFC＝45°，∴∠CFG＝90°，∵CF＝FG，∴CG＝CF，∴BM＝CG，∴BF＝BM+FM＝CG+DF．补充方法：连接GM，证明四边形BMGC是平行四边形即可．3.解：（1）如图1，在BC上截取AE＝AD得点E，作AF垂直DE交CD于点F（或作∠AED的平分线AF交CD于点F，或作EF垂直AE交CD于点F等等），∵四边形ABCD是矩形，∴AB＝CD＝8，AD＝BC＝10，∠B＝∠C＝90°，在Rt△ABE中，BE＝＝6，∴EC＝10﹣6＝4，设EF＝DF＝x，在Rt△EF C中，则有x2＝（8﹣x）2+42，解得x＝5，∴EF＝5．故答案为：5；（2）证明：如图2，作DH垂直AC于点H，延长DH至点E，使HE＝DH．方法1：∵△ADC≌△AEC，∴AD＝AE＝BC，AB＝DC＝EC，在△ABE与△CE B中，，∴△ABE≌△CEB（SSS），∴∠AEB＝∠CBE，∴BF＝EF，∴△BEF是等腰三角形．方法2：∵△ADC≌△AEC，∴AD＝AE＝BC，∠DAC＝∠EAC，又∴AD∥BC，∴∠DAC＝∠ACB，∴∠EAC＝∠ACB，∴F A＝FC，∴FE＝FB，∴△BEF是等腰三角形．4.（1）如图1中，连接E C．∵A，E关于CD对称，∴∠DCA=∠DCE=15°，CA=CE=C B．∵∠ACB=90°，∴∠ECB=60°，∴△ECB是等边三角形，∴∠CEB=60°，∵∠CEB=∠BFC+∠DCE，∴∠BFC=60°-15°=45°．（2）结论：EF2+BF2=2AC2．理由：如图2，连接CE，AF，延长AC交FE的延长线于点G．∵A，E关于CD对称，∴AC=CE，AF=EF，又∵CF=CF，∴△ACF≌△ECF（SSS），∴∠CAF=∠1，∵AC=BC，∴BC=CE，∴∠1=∠2，∴∠CAF=∠2，∵∠ACB=90°，∴∠G+∠2=90°，∴∠CAF+∠G=90°，∴∠AFG=90°，在Rt△AF B中，AB2=AF2+BF2，在Rt△AB C中，AB2=AC2+BC2=2AC2，∴BF2+AF2=2AC2，∴BF2+EF2=2AC2．5．（1）如图所示：（2）∵∠ACB＝90°，CA＝CB，∴∠BAC＝∠CBA＝45°，∴∠CAD+∠DAB＝45°，∵DA＝DE，∴∠DAE＝∠DEB，∵∠DBA是△DBE的一个外角，∴∠EDB+∠DEB＝∠DBA＝45°，∴∠EDB＝∠CAD，∵点E关于直线BC的对称点F，∴∠EDB＝∠FDB，∴∠CAD＝∠FDB；（3）线段AB，BD，BF之间的数量关系是AB﹣BF=√2BD，证明：过点D作AC的平行线交AB于M点，∴∠C＝∠MDB＝90°，∠CAB＝∠DMB＝45°，∴∠DMB＝∠DBM，∴DM＝DB，∴MB=√2BD，∵点E关于直线BC的对称点F，∴DE＝DF，∵AD＝DE，∴AD＝DF，∵AC∥MD，∴∠CAD＝∠ADM，∵∠CAD＝∠FDB，∴∠ADM＝∠FDB，∴△ADM≌△FDB（SAS），∴AM＝BF，∴AB﹣BF＝AB﹣AM＝MB，又∵MB=√2BD，∴AB﹣BF=√2B D．6.解：∵AB＝AC，∴∠ABC＝∠C，∵∠DAC＝∠ACD，∴∠DAC＝∠ABC，∵∠C＝∠C，∴△CAD∽△CBA，∴＝，∴＝，∴CD＝，BD＝BC﹣CD＝，∵∠DAM＝∠DAC＝∠DBA，∠ADM＝∠ADB，∴△ADM∽△BDA，∴＝，即＝，∴DM＝，MB＝BD﹣DM＝，∵∠ABM＝∠C＝∠MED，∴A、B、E、D四点共圆，∴∠ADB＝∠BEM，∠EBM＝∠EAD＝∠ABD，∴△ABD∽△MBE，∴＝，∴BE ＝＝＝．故答案为：．7．（1）如图；EDP（2）40°；60 °；（3）证明：∵点B关于射线AP的对称点为点D，∴△BAE≌△DAE．∴∠BAE=∠DAE=α．∵AD=AB=AC，∴∠ADC=()1806022α︒-︒+=60°－α．∴∠AEC=60°．∵∠ACB=60°，∠ACD=∠ADC=60°－α，∴∠BCE=α．∵∠ABC=60°，∠ABE=∠ADC=60°－α，∴∠BEC=60°．（4）证明：法一：在CD上截取AF=AE．F EDAB C P∵∠AEF =60°，∴△AEF 是等边三角形．∴∠AFC =∠AED =120°．∵∠ACD =∠ADC =60°－α，∴△ADE ≌△ACF ．∴DE =CF ．∴CD =2DE +EF ．∵AE =EF ，∴CD =2DE +AE ．法二：在CD 上截取BG =BE ．GEDAB C P∵∠BEC =60°，∴△BEG 是等边三角形．∴∠BGC =∠AED =120°．∵∠BCE =∠DAE =α，∴△BCG ≌△DAE ．∴AE =CG ．∵EG =BE =DE ，∴CD =2DE +CG ．∴CD =2DE +AE ．8.解：（1）连接AD ，如图1．∵点D 与点B 关于直线AP 对称，∴AD ＝AB ，∠DAP ＝∠BAP ＝30°，∵AB ＝AC ，∠BAC ＝60°，∴AD ＝AC ，∠DAC ＝120°，∴2∠ACE +60°+60°＝180°，∴∠ACE ＝30°，故答案为：30°；（3）线段AB ，CE ，ED 可以构成一个含有60°角的三角形．证明：连接AD ，EB ，如图2．∵点D 与点B 关于直线AP 对称，∴AD ＝AB ，DE ＝BE ，∴∠EDA ＝∠EBA ，∵AB ＝AC ，AB ＝AD ，∴AD ＝AC ，∴∠ADE ＝∠ACE ，∴∠ABE ＝∠ACE ．设AC ，BE 交于点F ，又∵∠AFB ＝∠CFE ，∴∠BAC ＝∠BEC ＝60°，∴线段AB ，CE ，ED 可以构成一个含有60°角的三角形．9．(1)根据折叠，∠DBC ＝∠DBE ，又AD ∥BC ，∴∠DBC ＝∠ADB ，∴∠DBE ＝∠ADB ，∴DF ＝BF ，∴△BDF 是等腰三角形(2)①菱形，理由：∵四边形ABCD 是矩形，∴AD ∥BC ，∴FD ∥BG ，又∵FD ∥BG ，∴四边形BFDG 是平行四边形，∵DF ＝BF ，∴四边形BFDG 是菱形②∵AB ＝6，AD ＝8，∴BD ＝10.∴OB ＝12BD ＝5.设DF ＝BF ＝x ，∴AF ＝AD －DF ＝8－x .∴在Rt △ABF 中，AB 2＋AF 2＝BF 2，即62＋(8－x )2＝x 2，解得x ＝254，即BF ＝254，∴FO ＝BF 2－OB 2＝（254）2－52＝154，∴FG ＝2FO ＝152 10.解：【问题情境】证明：∵在Rt △AB C 中，∠ACB ＝90°，AC ＝BC ，点D 为A B 中点， ∴CD ⊥AB ，CD ＝BD ＝AD ＝AB ，∠BCD ＝∠B ＝45°，∴∠BDC ＝90°，∵∠EDF ＝90°，∴∠CDF＝∠BDE，在△BDE与△CDF中，，∴△BDE≌△CDF（ASA），∴BE＝CF；【探索发现】成立，理由：∵在Rt△AB C中，D为A B中点，∴CD＝BD，又∵AC＝BC，∴DC⊥AB，∴∠DBC＝∠DCB＝45°，∵DE⊥DF，∴∠EDF＝90°，∴∠EDB+∠BDF＝∠CDF+∠BDF＝90°，∴∠CDF＝∠BDE，∴∠ADF＝∠CDE，∴AF＝CE，∴CF＝BE；【类比迁移】∵△ABC是等边三角形，∴∠A＝∠B＝60°，∵∠FDE＝60°，∴∠BDF＝120°﹣∠ADE，∠AED＝120°﹣∠ADE，∴∠BDF＝∠AED，∴△ADE∽△BDF，∴，∵点D为A B中点，AB＝4，∴AD＝BD＝2，AC＝BC＝4，∵CF＝2CE，∴设CE＝x，则CF＝2x，当点E在线段AC上时，∴AE＝4﹣x，BF＝4﹣2x，∴＝，解得：x＝3﹣，x＝3+（不合题意，舍去），∴CE＝3﹣，如图④，当点E在AC的延长线上时，∵AE＝4+x，BF＝4﹣2x，∴＝，解得：x＝﹣1+，（负值舍去），∴CE＝﹣1+．综上所述，CE＝3﹣或﹣1+，故答案为：3﹣或﹣1+．11.解：（1）∵∠AEB＝110°，∠ACB＝90°，∴∠DAE＝∠AEB﹣∠ACB＝20°；（2）①补全图形，如图所示．②证明：由题意可知∠AEF＝90°，EF＝AE．∵∠ACB＝90°，∴∠AEC+∠BEF＝∠AEC+∠DAE＝90°．∴∠BEF＝∠DAE．∵在△EBF和△ADE中，，∴△EBF≌△ADE（SAS）．∴DE＝BF．。

中考数学点对点-几何折叠翻折类问题(解析版)

专题33 中考几何折叠翻折类问题专题知识点概述1.轴对称（折痕）的性质：（1）成轴对称的两个图形全等。

（2）对称轴与连结“对应点的线段”垂直。

（3）对应点到对称轴的距离相等。

（4）对应点的连线互相平行。

也就是不管是轴对称图形还是两个图形关于某条直线对称，对称轴都是任何一对对应点所连线段的垂直平分线.对称的图形都全等.2.折叠或者翻折试题解决哪些问题（1）求角度大小；（2）求线段长度；（3）求面积；（4）其他综合问题。

3.解决折叠问题的思维方法（1）折叠后能够重合的线段相等，能够重合的角相等，能够重合的三角形全等，折叠前后的图形关于折痕对称，对应点到折痕的距离相等。

（2）折叠类问题中，如果翻折的直角，那么可以构造三垂直模型，利用三角形相似解决问题。

（3）折叠类问题中，如果有平行线，那么翻折后就可能有等腰三角形，或者角平分线。

这对解决问题有很大帮助。

（4）折叠类问题中，如果有新的直角三角形出现，可以设未知数，利用勾股定理构造方程解决。

（5）折叠类问题中，如果折痕经过某一个定点，往往用辅助圆解决问题。

一般试题考查点圆最值问题。

（6）折叠后的图形不明确，要分析可能出现的情况，一次分析验证可以利用纸片模型分析。

例题解析与对点练习【例题1】（2020•哈尔滨）如图，在Rt△ABC中，∠BAC＝90°，∠B＝50°，AD⊥BC，垂足为D，△ADB与△ADB'关于直线AD对称，点B的对称点是点B'，则∠CAB'的度数为（）A．10°B．20°C．30°D．40°【答案】A【解析】由余角的性质可求∠C＝40°，由轴对称的性质可得∠AB'B＝∠B＝50°，由外角性质可求解．∵∠BAC＝90°，∠B＝50°，∴∠C＝40°，∵△ADB与△ADB'关于直线AD对称，点B的对称点是点B'，∴∠AB'B＝∠B＝50°，∴∠CAB'＝∠AB'B﹣∠C＝10°。

备考2023年中考数学二轮复习-图形的变换_轴对称变换_翻折变换(折叠问题)

备考2023年中考数学二轮复习-图形的变换_轴对称变换_翻折变换（折叠问题）翻折变换（折叠问题）专训单选题：1、(2017长安.中考模拟) 如图，对△ABC纸片进行如下操作：第1次操作：将△ABC沿着过AB中点D1的直线折叠，使点A落在BC边上的A1处，折痕D1E1到BC的距离记作h1，然后还原纸片；第2次操作：将△AD1E1沿着过AD1中点D2的直线折叠，使点A落在D1E1边上的A1处，折痕D1E1到BC的距离记作h2，然后还原纸片；…按上述方法不断操作下去…，经过第n次操作后得到的折痕Dn En到BC的距离记作hn ，若h=1，则hn的值不可能是（）A .B .C .D .2、(2019吴兴.中考模拟) 如图，将长BC=8cm，宽AB=4cm的矩形纸片ABCD折叠，使点C与点A重合，则折痕EF的长为（）A . 4cmB . cmC . cmD . c3、(2017长清.中考模拟) 如图，在矩形ABCD中，AB=3，BC=5，在CD上任取一点E，连接BE，将△BCE沿BE折叠，使点C恰好落在AD边上的点F处，则CE的长为（）A . 2B .C . 1D .4、(2017武汉.中考模拟) 如图，折叠矩形纸片ABCD的一边AD，使点D落在BC边上的点F处，若AB=8，BC=10，则△CEF的周长为（）A . 12B . 16C . 18D . 245、(2013百色.中考真卷) 如图，在矩形纸片ABCD中，AB=4，AD=3，折叠纸片使DA 与对角线DB重合，点A落在点A′处，折痕为DE，则A′E的长是（）A . 1B .C .D . 26、(2015.中考真卷) 如图，在矩形OABC中，OA=8，OC=4，沿对角线OB折叠后，点A与点D重合，OD与BC交于点E，则点D的坐标是（）A . （4，8）B . （5，8）C . （，）D . （，）7、(2012遵义.中考真卷) 如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于F点，若CF=1，FD=2，则BC的长为（）A . 3B . 2C . 2D . 28、(2020南岸.中考模拟) △ABC中，∠ACB=45°，D为AC上一点，AD=5 ，连接BD，将△ABD沿BD翻折至△EBD，点A的对应点E点恰好落在边BC上.延长BC至点F，连接DF，若CF=2，tan∠ABD= ，则DF长为（）A .B .C . 5D . 79、(2020鄞州.中考模拟) 三角形纸片ABC中，∠C=90°，甲折叠纸片使点A与点B 重合，压平得到的折痕长记为m；乙折叠纸片使得CA与CB所在的直线重合，压平得到的折痕长记为n，则m，n的大小关系是（）A . m≤nB . m<nC . m≥nD . m>n10、(2020沙河.中考模拟) 欧几里得在《几何原本》中，记载了用图解法解方程的方法，类似地可以用折纸的方法求方程的一个正根。

备战中考--第39讲几何图形折叠问题--(附解析答案)

备战2019 中考初中数学导练学案50 讲第39 讲几何图形折叠问题【疑难点拨】1. 折叠（翻折）问题常常出现在三角形、四边形、圆等平面几何问题中，其实质是轴对称性质的应用．解题的关键利用轴对称的性质找到折叠前后不变量与变量，运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系．2. 折叠（翻折）意味着轴对称，会生成相等的线段和角，这样便于将条件集中．如果题目中有直角，则通常将条件集中于较小的直角三角形，利用勾股定理求解．3. 矩形中的一次折叠通常利用折叠性质和平行线性质求角的度数，或者利用折叠性质以及勾股定理求线段长度．矩形中的两次或多次折叠通常出现“一线三直角” 的模型（如图），从而构造相似三角形，利用相似三角形求边或者角的度数．4. 凡是在几何图形中出现“折叠”这个字眼时，第一反应即存在一组全等图形，其次找出与要求几何量相关的条件量．1. 常见的轴对称图形：等腰三角形、矩形、菱形、正方形、圆. 2. 折叠的性质：折叠的实质是轴对称，折叠前后的两图形全等，对应边和对应角相等．【基础篇】一、选择题：1. . （2018?四川凉州?3 分）如图将矩形ABCD沿对角线BD折叠，使C落在C′处，BC′交AD 于点E，则下到结论不一定成立的是（）A．AD=BC′ B．∠EBD=∠EDB C．△ABE∽△CBD D．sin ∠ABE=2. （2017 山东烟台）如图1，将一圆形纸片向右、向上两次对折后得到如图 2 所示的扇形AOB．已知OA=6，取OA的中点C，过点C作CD⊥OA交于点D，点F 是上一点．若将扇形BOD沿OD翻折，点B恰好与点F 重合，用剪刀沿着线段BD，DF，FA依次剪下，则剪下的纸片（形状同阴影图形）面积之和为（）．A．36π -108 B ．108-32 π C．2π D．π3. （2017浙江衢州）如图，矩形纸片ABCD中，AB=4，BC=6，将△ ABC沿AC折叠，使点B 落在点E处，CE交AD于点F，则DF的长等于（）4. （2018·山东青岛· 3分）如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点．沿过点E的直线折叠，使点B与点A重合，折痕现交于点F．已知EF= ，则BC的长是（）A．B．3 2 C． 3 D．3 3D．5. （2017乌鲁木齐）如图，在矩形 ABCD 中，点 F 在 AD 上，点 E 在 BC 上，把这个矩形沿 EF 折叠后，使点 D 恰好落在 BC 边上的 G 点处，若矩形面积为 4 且∠AFG=60°， GE=2BG ，则折痕 EF 的长为（）A ．1B ．C ． 2D ．、填空题：6. （2018·辽宁省盘锦市）如图，已知 Rt △ABC 中，∠ B=90°，∠ A=60°， AC=2 +4，点 M 、N 分别在线段 AC.AB 上，将△ANM 沿直线 MN 折叠，使点 A 的对应点 D 恰好落在线段 BC 上，当△ DCM 为直角三角形时，折痕 MN 的长为．7. （2018·山东威海· 8 分）如图，将矩形 ABCD （纸片）折叠，使点 B 与 AD 边上的点 K 重合，EG 为折痕；点C 与AD 边上的点 K 重合， FH 为折痕．已知∠ 1=67.5°， ∠2=75°， EF=+1，则 BC 的长．处，点 C 落在点 H 处，已知∠ DGH=3°0，连接8. （2018·湖南省常德 ·3 分）如图，将矩形ABCD 沿 EF 折叠，使点 B 落在 AD 边上的点 GBG ，则∠ AGB=三、解答与计算题：9. （2018·广东· 7 分）如图，矩形ABCD中，AB>AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ ADE≌△ CED；（2）求证：△ DEF是等腰三角形．10. （2018?山东枣庄?10 分）如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．（1）求证：四边形EFDG是菱形；（2）探究线段EG、GF、AF之间的数量关系，并说明理由；（3）若AG=6，EG=2 ，求BE的长．能力篇】、选择题：11. （ 2018·辽宁省阜新市）如图，将等腰直角三角形落在 BC 边的中点 A 1处， BC=8，那么线段 AE 的长度为（）12. （ 2018·四川省攀枝花·3 分）如图，在矩形 ABCD 中， E 是 AB 边的中点，沿 EC 对折矩形 ABCD ，使 B 点落在点 P 处，折痕为 EC ，连结 AP 并延长 AP 交 CD 于 F 点，连结 CP 并延长 CP 交 AD 于 Q 点．给出以下结论：① 四边形 AECF 为平行四边形；② ∠PBA=∠APQ ；③ △FPC 为等腰三角形；④ △APB ≌△EPC ．其中正确结论的个数为（ABC （∠ B=90°）沿 EF 折叠，使点 AD ．7A ．1B ． 2C ．3D ．413.2018·湖北省武汉 3 分）如图，在⊙ O 中，点 C 在优弧上，将弧沿 BC 折叠后刚好经过AB 的中点D．若⊙ O的半径为，AB=4，则BC的长是（）C．、填空题：14. （2018 ·辽宁省葫芦岛市）如图，在矩形ABCD中，点E是CD的中点，将△ BCE沿BE折叠后得到△ BEF、将BF 延长交AD 于点G ．若=，则且点 F 在矩形ABCD的内部，15. （2018·四川宜宾· 3分）如图，在矩形ABCD中，AB=3，CB=2，点E为线段AB上的动点，将△ CBE沿CE折叠，使点B 落在矩形内点F处，下列结论正确的是①②③ （写出所有正确结论的序号）①当E 为线段AB中点时，AF∥CE；②当E 为线段AB中点时，AF=9；5③当A、F、C三点共线时，AE=④当A、F、C三点共线时，△ CEF≌△．三、解答与计算题：16.（2018·湖北省宜昌·11 分）在矩形ABCD中，AB=12，P是边AB上一点，把△PBC 沿直线PC折叠，顶点B的对应点是点G，过点B作BE⊥CG，垂足为E且在AD 上，BE交PC于点F．（1）如图1，若点E是AD 的中点，求证：△AEB≌△DEC；（2）如图2，① 求证：BP=BF；② 当AD=25，且AE< DE 时，求cos∠ PCB的值；③ 当BP=9 时，求BE?EF的值．17. （2018·广东·7 分）如图，矩形ABCD中，AB>AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ ADE≌△ CED；（2）求证：△ DEF是等腰三角形．18. （2018?江苏盐城? 10 分）如图，在以线段为直径的上取一点，连接、. 将沿翻折后得到.（1）试说明点在上；（2）在线段的延长线上取一点，使. 求证：为的切线；（3）在（2）的条件下，分别延长线段、相交于点，若，，求线段的长.探究篇】19. （2018 年江苏省泰州市?12 分）对给定的一张矩形纸片ABCD进行如下操作：先沿CE 折叠，使点B 落在CD边上（如图①），再沿CH折叠，这时发现点E 恰好与点D重合（如图②）1）根据以上操作和发现，求的值；2）将该矩形纸片展开．①如图③，折叠该矩形纸片，使点C与点H 重合，折痕与AB相交于点P，再将该矩形纸片展开．求证：∠ HPC=9°0 ；②不借助工具，利用图④探索一种新的折叠方法，找出与图③中位置相同的P 点，要求只有一条折痕，且点P 在折痕上，请简要说明折叠方法．（不需说明理由）20. （2018 年江苏省宿迁）如图，在边长为 1 的正方形ABCD中，动点E、F 分别在边AB、CD上，将正方形ABCD沿直线EF折叠，使点B 的对应点M始终落在边AD上（点M不与点A、D重合），点C落在点N处，MN与CD交于点P，设BE=x，1）当AM= 时，求x 的值；2）随着点M 在边AD上位置的变化，△ PDM的周长是否发生变化？如变化，请说明理由；如不变，请求出该定值；3）设四边形BEFC的面积为S，求S与x 之间的函数表达式，并求出S的最小值.第39 讲几何图形折叠问题疑难点拨】1. 折叠（翻折）问题常常出现在三角形、四边形、圆等平面几何问题中，其实质是轴对称性质的应用．解题的关键利用轴对称的性质找到折叠前后不变量与变量，运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系．2. 折叠（翻折）意味着轴对称，会生成相等的线段和角，这样便于将条件集中．如果题目中有直角，则通常将条件集中于较小的直角三角形，利用勾股定理求解．3. 矩形中的一次折叠通常利用折叠性质和平行线性质求角的度数，或者利用折叠性质以及勾股定理求线段长度．矩形中的两次或多次折叠通常出现“一线三直角” 的模型（如图），从而构造相似三角形，利用相似三角形求边或者角的度数．4. 凡是在几何图形中出现“折叠”这个字眼时，第一反应即存在一组全等图形，其次找出与要求几何量相关的条件量．1. 常见的轴对称图形：等腰三角形、矩形、菱形、正方形、圆. 2. 折叠的性质：折叠的实质是轴对称，折叠前后的两图形全等，对应边和对应角相等．【基础篇】一、选择题：1. . （2018?四川凉州?3 分）如图将矩形ABCD沿对角线BD折叠，使C落在C′处，BC′交AD于点E，则下到结论不一定成立的是（）A．AD=BC′ B．∠ EBD=∠EDB C．△ABE∽△CBD D．sin ∠ABE=【分析】主要根据折叠前后角和边相等找到相等的边之间的关系，即可选出正确答案．【解答】解：A、BC=BC′，AD=BC，∴ AD=BC′，所以正确．B、∠CBD=∠EDB，∠CBD=∠EBD，∴∠ EBD=∠EDB 正确．∴∠EBD=∠EDB∴BE=DE ∴sin ∠ABE= ．故选： C ．点评】本题主要用排除法，证明 A ，B ，D 都正确，所以不正确的就是 C ，排除法也是数学中一种常用的解题方法．2. （2017 山东烟台）如图 1，将一圆形纸片向右、向上两次对折后得到如图 2 所示的扇形 AOB ．已知 OA=6，取 OA 的中点 C ，过点 C 作 CD ⊥OA 交于点 D ，点 F 是上一点．若将扇形 BOD 沿 OD 翻折，点 B 恰好与点 F 重合，用剪刀沿着线段 BD ，DF ，FA 依次剪下，则剪下的纸片（形状同阴影图形）面积之和为（）．A ．36π -108B ． 108-32 πC ．2πD ．π【考点】 MO ：扇形面积的计算； P9：剪纸问题．【分析】先求出∠ ODC ∠= BOD=3°0 ，作 DE ⊥OB 可得 DE= OD=3，先根据 S 弓形 BD =S 扇形BOD ﹣ S △ BOD 求得弓形的面积，再利用折叠的性质求得所有阴影部分面积．解答】解：如图，∵ CD ⊥ OA ，∴∠ DCO=∠AOB=9°0 ，D 、∵ sin ∠ABE= ，∴∠ ODC=∠BOD=3°0 ，作 DE ⊥ OB 于点 E ，则 DE= OD=3，则剪下的纸片面积之和为 12×（ 3π﹣ 9）=36π﹣ 108，故答案为： 36π﹣ 108．故选 A3. （2017浙江衢州）如图，矩形纸片 ABCD 中， AB=4，BC=6，将△ ABC 沿 AC 折叠，使点 B 落在点 E 处， CE 交 AD 于点 F ，则 DF 的长等于（）A ．B ．C ．D ．考点】 PB ：翻折变换（折叠问题）； LB ：矩形的性质．【分析】根据折叠的性质得到 AE=AB ，∠E=∠B=90°，易证 Rt △AEF ≌Rt △ CDF ，即可得到结论 EF=DF ；易得 FC=FA ，设 FA=x ，则 FC=x ，FD=6﹣ x ，在 Rt △CDF中利用勾股定理得到关于∴S 弓形 BD =S 扇形 BOD ﹣ S △ BOD =×6×3=3π 9，∵OA=OD=OB=，6OC= OA= OD ，x 的方程x2=42+（6﹣x）2，解方程求出x．【解答】解：∵矩形ABCD沿对角线AC对折，使△ ABC落在△ ACE的位置，∴AE=AB，∠ E=∠B=90°，又∵四边形ABCD为矩形，∴AB=CD，∴AE=DC，而∠ AFE=∠DFC，∵在△ AEF与△ CDF中，，∴△ AEF≌△ CDF（AAS），∴EF=DF；∵四边形ABCD为矩形，∴AD=BC=6，CD=AB=，4∵Rt △AEF≌Rt△CDF，∴FC=FA，设FA=x，则FC=x，FD=6﹣x，在Rt△CDF中，CF2=CD2+DF2，即x2=42+（6﹣x）则FD=6﹣x=实用文档20故选：B ．4. （2018·山东青岛· 3分）如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点．沿过点E的直线折叠，使点B与点A重合，折痕现交于点F．已知EF= ，则BC的长是（）分析】由折叠的性质可知∠ B=∠EAF=45°，所以可求出∠ AFB=90°，再直角三角形的性质解答】解：∵沿过点E的直线折叠，使点B与点A 重合，∴∠ B=∠EAF=45°，∴∠AFB=90°，∵点E 为AB中点，∴EF= 1 AB，EF= 3，22∵∠BAC=90°，AB，所以AB=AC的长可求，再利用勾股定理即可求出BC的长．D． 3 3可知EF∴AB=AC=3，故选：B．【点评】本题考查了折叠的性质、等腰直角三角形的判断和性质以及勾股定理的运用，求出∠AFB=90°是解题的关键．5. （2017乌鲁木齐）如图，在矩形ABCD中，点F在AD上，点E在BC上，把这个矩形沿EF折叠后，使点D恰好落在BC边上的G点处，若矩形面积为4 且∠AFG=60°，GE=2BG，则折痕EF 的长为（）A．1 B．C．2 D．【考点】PB：翻折变换（折叠问题）；LB：矩形的性质．【分析】由折叠的性质可知，DF=GF、HE=CE、GH=DC、∠ DFE=∠ GFE，结合∠ AFG=60°即可得出∠ GFE=60°，进而可得出△ GEF为等边三角形，在Rt △GHE中，通过解含30 度角的直角三角形及勾股定理即可得出GE=2EC、DC= EC，再由GE=2BG结合矩形面积为4 ，即可求出EC的长度，根据EF=GE=2EC即可求出结论．解答】解：由折叠的性质可知，DF=GF，HE=CE，GH=DC，∠ DFE=∠GFE．∵∠ GFE+∠DFE=180°﹣∠ AFG=12°0 ，∴∠GFE=60°．∵AF∥ GE，∠ AFG=60°，∴∠ FGE=∠AFG=60°，∴△ GEF为等边三角形，∴EF=GE．∵∠ FGE=60°，∠ FGE+∠HGE=9°0 ，∴∠ HGE=3°0 ．在Rt△GHE中，∠HGE=3°0 ，∴GE=2HE=C，E∴GH= = HE= CE．∵GE=2BG，∴BC=BG+GE+EC=4．EC∵矩形ABCD的面积为4 ，∴4EC? EC=4 ，∴EC=1，EF=GE=2．故选C．二、填空题：6. （2018·辽宁省盘锦市）如图，已知Rt△ABC中，∠ B=90°，∠ A=60°，AC=2 +4，点M、N分别在线段AC.AB上，将△ANM沿直线MN折叠，使点A 的对应点D恰好落在线段BC 上，当△ DCM为直角三角形时，折痕MN的长为．解答】解：分两种情况：①如图，当∠ CDM=9°0 时， △CDM 是直角三角形，∵在 Rt△ABC 中，∠ B=90°，∠ A=60°，AC=2 +4 ，∴∠ C=30°，AB= AC= 叠可得：∠ MDN= ∠ A=60°，∴∠ BDN=3°0 ，∴ BN= DN= AN ，∴ BN= AB=，∴∠ ANM= ∠ DNM=6°0 ，∴∠ AMN=6°0 ，∴ AN=MN=DN= AN ， BD\1AB= ，∴ AN=2 ，BN= ，过 N 作 NH ⊥AM 于 H ，则∠ ANH=30° ，∴AH=AN=1 ， HN= ，由折叠可得：∠ AMN= ∠DMN=45° ，∴△ MNH 是等腰直角三角形，∴HM=HN= ，∴ MN= ．，由折 ∵∠ DNB=6°0 AN=2BN= ②如图，当∠ CMD=9°0 时， △CDM 是直角三角形，由题可得： ∠CDM=6°0 ，∠ A= ∠ MDN=6°0 ，∴∠ BDN=6°0 ，∠BND=3°0 ，∴BD= BN故答案为：或．7. （2018·山东威海· 8 分）如图，将矩形ABCD（纸片）折叠，使点B 与AD边上的点K 重合，EG为折痕；点C与AD边上的点K重合，FH为折痕．已知∠ 1=67.5°，∠2=75°，EF= +1，求BC的长．【分析】由题意知∠ 3=180°﹣2∠1=45°、∠ 4=180°﹣2∠2=30°、BE=KE、KF=FC，作KM⊥BC，设KM=x，知EM=x、MF= x，根据EF的长求得x=1，再进一步求解可得．解答】解：由题意，得：∠3=180°﹣2∠1=45°，∠4=180°﹣2∠2=30°，BE=KE、KF=FC，如图，过点K 作KM⊥BC于点M，设KM=x，则EM=x、MF= x，∴ x+ x= +1，解得：x=1，∴EK= 、KF=2，∴BC=BE+EF+FC=EK+EF+KF=3+ + ，∴BC的长为3+ + ．点评】本题主要考查翻折变换，解题的关键是掌握翻折变换的性质：折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．8. （2018·湖南省常德·3 分）如图，将矩形ABCD沿EF折叠，使点B落在AD边上的点G 处，点C落在点H处，已知∠ DGH=3°0 ，连接BG，则∠ AGB= 75° ．【分析】由折叠的性质可知：GE=BE，∠ EGH=∠ABC=90°，从而可证明∠ EBG=∠EGB．，然后再根据∠ EGH﹣∠ EGB=∠ EBC﹣∠ EBG，即：∠GBC=∠BGH，由平行线的性质可知∠AGB=∠GBC，从而易证∠ AGB=∠ BGH，据此可得答案．【解答】解：由折叠的性质可知：GE=BE，∠ EGH=∠ABC=90°，∴∠ EBG=∠EGB．∴∠ EGH﹣∠ EGB=∠EBC﹣∠ EBG，即：∠ GBC=∠BGH．又∵ AD∥ BC，∴∠ AGB=∠GBC．∴∠ AGB=∠BGH．∵∠DGH=3°0 ，∴∠ AGH=15°0 ，∴∠ AGB= ∠AGH=7°5 ，故答案为：75【点评】本题主要考查翻折变换，解题的关键是熟练掌握翻折变换的性质：折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．三、解答与计算题：9. （2018·广东· 7 分）如图，矩形ABCD中，AB>AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ ADE≌△ CED；（2）求证：△ DEF是等腰三角形．【分析】（1）根据矩形的性质可得出AD=BC、AB=CD，结合折叠的性质可得出AD=CE、AE=CD，进而即可证出△ ADE≌△ CED（SSS）；（2）根据全等三角形的性质可得出∠ DEF=∠ EDF，利用等边对等角可得出EF=DF，由此即可证出△ DEF是等腰三角形．【解答】证明：（1）∵四边形ABCD是矩形，∴AD=BC，AB=CD．由折叠的性质可得：BC=CE，AB=AE，∴AD=CE，AE=CD．在△ ADE和△ CED中，，∴△ ADE≌△ CED（SSS）．∴∠ DEA=∠EDC ，即∠ DEF=∠EDF ，∴EF=DF ，∴△ DEF 是等腰三角形．点评】本题考查了全等三角形的判定与性质、翻折变换以及矩形的性质，解题的关键是： 1）根据矩形的性质结合折叠的性质找出 AD=CE 、 AE=CD ；（ 2）利用全等三角形的性质找出 ∠DEF=∠EDF ．10. （2018?山东枣庄 ?10 分）如图，将矩形 ABCD 沿 AF 折叠，使点 D 落在 BC 边的点 E 处，过点 E 作 EG ∥CD 交 AF 于点 G ，连接 DG ．（1）求证：四边形 EFDG 是菱形；（2）探究线段 EG 、GF 、 AF 之间的数量关系，并说明理由；（3）若 AG=6， EG=2 ，求 BE 的长．【分析】（ 1）先依据翻折的性质和平行线的性质证明∠ DGF=∠DFG ，从而得到 GD=DF ，接下来依据翻折的性质可证明 DG=GE=DF=E ；F（2）由（ 1）得△ ADE ≌△（2）连接DE，交AF 于点O．由菱形的性质可知GF⊥DE，OG=OF= GF，接下来，证明△ DOF ∽△ ADF，由相似三角形的性质可证明DF2=FO?AF，于是可得到GE、AF、FG的数量关系；（3）过点G作GH⊥DC，垂足为H．利用（2）的结论可求得FG=4，然后再△ ADF中依据勾股定理可求得AD的长，然后再证明△ FGH∽△ FAD，利用相似三角形的性质可求得GH的长，最后依据BE=AD﹣GH求解即可．【解答】解：（1）证明：∵ GE∥DF，∴∠ EGF=∠DFG．∵由翻折的性质可知：GD=G，E DF=EF，∠ DGF=∠EGF，∴∠ DGF=∠DFG．∴GD=DF．∴DG=GE=DF=E．F∴四边形EFDG为菱形．（2）EG2= GF?AF．理由：如图1 所示：连接DE，交AF 于点O．∵四边形EFDG为菱形，∴GF⊥ DE，OG=OF= GF．∵∠ DOF=∠ADF=90°，∠ OFD=∠ DFA，∴△ DOF∽△ ADF．，即DF2=FO?AF．∵FO= GF，DF=EG，∴EG2= GF?AF．3）如图2 所示：过点G作GH⊥ DC，垂足为H．∵EG2= GF?AF，AG=6，EG=2 ，∴20= FG（FG+6），整理得：FG2+6FG﹣40=0．解得：FG=4，FG=﹣10（舍去）∵DF=GE=2 ，AF=10，∴AD= =4 ．∵GH⊥ DC，AD⊥ DC，∴GH∥ AD．∴△ FGH∽△ FAD．∴GH=∴BE=AD ﹣ GH=4 ﹣ =【点评】本题主要考查的是四边形与三角形的综合应用，解答本题主要应用了矩形的性质、菱形的判定和性质、相似三角形的性质和判定、勾股定理的应用，利用相似三角形的性质得到DF 2=FO?AF 是解题答问题（ 2）的关键，依据相似三角形的性质求得 GH 的长是解答问题（3）的关键．能力篇】、选择题：11. （ 2018·辽宁省阜新市）如图，将等腰直角三角形 ABC （∠ B=90°）沿 EF 折叠，使点 A落在 BC 边的中点 A 1处， BC=8，那么线段 AE 的长度为（）．解答】解：由折叠的性质可得 AE=A 1E ．∵△ ABC 为等腰直角三角形， BC=8，∴ AB=8．2∵A 1为 BC 的中点， ∴A 1B=4，设 AE=A 1E=x ，则 BE=8﹣ x ．在 Rt △A 1BE 中，由勾股定理可得 42+（8﹣ x ） 2=x 2，解得 x=5．故答案为： 5．故选 BA ．4B ． 5C ． 6D ．7∴ ，即 = ．12. （2018·四川省攀枝花·3 分）如图，在矩形ABCD中，E 是AB 边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连结AP并延长AP交CD于F 点，连结CP并延长CP交AD于Q点．给出以下结论：①四边形AECF为平行四边形；②∠PBA=∠APQ；③△FPC为等腰三角形；④△APB≌△EPC．其中正确结论的个数为（）A．1 B．2 C．3 D．4解：①如图，EC，BP交于点G；∵点P是点B关于直线EC的对称点，∴ EC 垂直平分BP，∴ EP=EB，∴∠ EBP=∠EPB．∵点E为AB中点，∴ AE=EB，∴ AE=EP，∴∠ PAB=∠PBA．∵∠PAB+∠PBA+∠APB=180°，即∠ PAB+∠PBA+∠APE+∠BPE=2（∠PAB+∠PBA）=180°，∴∠PAB+∠PBA=90°，∴ AP⊥BP，∴AF∥EC；∵AE∥CF，∴四边形AECF是平行四边形，故①正确；∵四边形 ABCD 是正方形，∴∠ ABC=∠ABP+∠PBC=90°，∴∠ ABP=∠APQ ，故②正确；③∵AF ∥EC ，∴∠ FPC=∠PCE=∠BCE ．∵∠PFC 是钝角，当△BPC 是等边三角形，即∠BCE=30°时，才有∠ FPC=∠FCP ，如右图，△PCF 不一定是等腰三角形，故③不正确；④∵AF=EC ， AD=BC=P ，C ∠ADF=∠EPC=90°，∴ Rt △EPC ≌△FDA （ HL ）．∵∠ADF=∠APB=90°，∠ FAD=∠AB P ，当 BP=AD 或△BPC 是等边三角形时，△ APB ≌△ FDA ， ∴△APB ≌△EPC ，故④不正确；其中正确结论有①②， 2 个．故选 B ．13. （2018·湖北省武汉 ·3 分）如图，在⊙ O 中，点 C 在优弧上，将弧沿 BC 折叠后刚好经过 AB 的中点 D ．若⊙ O 的半径为， AB=4，则 BC 的长是（）②∵∠ APB=90°，∴∠ APQ+∠BPC=90°，由折叠得： BC=PC ，∴∠ BPC=∠PBC ．【分析】连接OD、AC、DC、OB、OC，作CE⊥AB于E，OF⊥ CE于F，如图，利用垂径定理得到OD⊥ AB，则AD=BD= AB=2，于是根据勾股定理可计算出OD=1，再利用折叠的性质可判断弧AC和弧CD 所在的圆为等圆，则根据圆周角定理得到= ，所以AC=DC，利用等腰三角形的性质得AE=DE=1，接着证明四边形ODEF为正方形得到OF=EF=1，然后计算出CF后得到CE=BE=3，于是得到BC=3 2 ．【解答】解：连接OD、AC、DC、OB、OC，作CE⊥ AB于E，OF⊥CE于F，如图，∵D 为AB的中点，∴OD⊥ AB，∴AD=BD= AB=2，在Rt△OBD中，OD= ( 5)2 22=1，∵将弧沿BC折叠后刚好经过AB的中点D．∴弧AC和弧CD所在的圆为等圆，∴=，∴AC=DC，∴AE=DE=1，易得四边形ODEF为正方形，∴OF=EF=1，∴CE=CF+EF=2+1=，3而 BE=BD+DE=2+1=，3∴BC=3 ．故选： B ．【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了圆周角定理和垂径定理．二、填空题：∵点 E 是 CD 的中点，∴ EC=DE∵将△BCE 沿BE 折叠后得到 △BEF 、且点 F 在矩形 ABCD 的内部， ∴EF=DE ，∠ BFE=90° ．在14. （2018 ·辽宁省葫芦岛市）如图，在矩形折叠后得到△BEF 、且点 F 在矩形 ABCD 的内将 BF 延长交 AD 于点 G ．若 = ，则在Rt △OCF 中，CF= ( 5)2 12 =2，ABCD 中，点 E 是 CD 的中点，将△ BCE 沿BE解答】解：连接GE ．，∴Rt △EDG ≌Rt △EFG （HL ），∴FG=DG ．∵ = ，∴设 DG=FG=a ，则 AG=7a ，故 AD=BC=8a ，则 BG=BF+FG=9a ，∴ AB=15. （2018·四川宜宾· 3分）如图，在矩形 ABCD 中， AB=3，CB=2，点 E 为线段 AB 上的动点，将△ CBE 沿 CE 折叠，使点 B 落在矩形内点 F 处，下列结论正确的是 ①②③ （写出所有正确结论的序号） ①当 E 为线段 AB 中点时， AF ∥CE ；②当E 为线段 AB 中点时， AF=9；5③当 A 、 F 、C 三点共线时， AE=④当 A 、 F 、 C 三点共线时，△ CEF ≌△ AEF ．=4 a ，故故答案为：考点】PB：翻折变换（折叠问题）；KB：全等三角形的判定；LB：矩形的性质．分析】分两种情形分别求解即可解决问题；解答】解：如图1 中，当AE=EB时，∵AE=EB=EF，∴∠ EAF=∠EFA，∵∠ CEF=∠CEB，∠ BEF=∠ EAF+∠EFA，∴∠ BEC=∠EAF，∴AF∥EC，故①正确，作EM⊥ AF，则AM=FM，在Rt△ECB中，EC= = ，∵∠ AME=∠B=90°，∠ EAM=∠ CEB，∴△ CEB∽△ EAM，=，∴AM= ，9∴AF=2AM= ，故②正确，5如图2 中，当A、F、C 共线时，设AE=x．则EB=EF=3﹣x，AF= 13 ﹣2，在Rt △ AEF中，∵ AE2=AF2+EF2，∴x =（﹣2）+（3﹣x）∴x=∴AE= ，故③正确，如果，△ CEF≌△ AEF，则∠ EAF=∠ECF=∠ECB=30°，显然不符合题意，故④错误，故答案为①②③．【点评】本题考查翻折变换、全等三角形的性质、勾股定理、矩形的性质、相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考填空题中的压轴题．16.（2018·湖北省宜昌 ·11 分）在矩形 ABCD 中，AB=12，P 是边 AB 上一点，把△PBC沿直线 PC 折叠，顶点 B 的对应点是点 G ，过点 B 作 BE ⊥CG ，垂足为 E 且在 AD 上，BE 交 PC 于点 F ．（1）如图 1，若点 E 是 AD 的中点，求证： △AEB ≌△DEC ；（2）如图 2，① 求证： BP=BF ；② 当 AD=25，且 AE < DE 时，求 cos ∠ PCB 的值；【分析】（1）先判断出 ∠ A=∠D=90°，AB=DC 再判断出 AE=DE ，即可得出结论；（2） ① 利用折叠的性质，得出 ∠PGC=∠PBC=9°0，∠BPC=∠GPC ，进而判断出 ∠GPF=∠PFB 即可得出结论；② 判断出 △ABE ∽ △DEC ，得出比例式建立方程求解即可得出 AE=9， DE=16，再判断出 △ECF ∽△GCP ，进而求出 PC ，即可得出结论； ③ 判断出 △GEF ∽ △EAB ，即可得出结论．【解答】解：（1）在矩形 ABCD 中， ∠A=∠D=90°，AB=DC ， ∵E 是 AD 中点，∴AE=DE ，在△ABE 和△DCE 中，三、解答与计算题：③ 当 BP=9 时，求 BE?EF 的值．∴△ABE≌△DCE（SAS）；（2）① 在矩形ABCD，∠ABC=9°0，∵△BPC沿PC折叠得到△GPC，∴∠PGC=∠PBC=90，°∠BPC=∠GPC，∵BE⊥CG，∴BE∥PG，∴∠GPF=∠PFB，∴∠BPF=∠BFP，∴BP=BF；② 当AD=25 时，∵∠BEC=90，°∴∠AEB+∠CED=90，°∵∠AEB+∠ABE=90，°∴∠CED=∠ABE，∵∠A=∠D=90 ，° ∴△ABE∽△DEC，∴，∴，设AE=x，∴ DE=25﹣x，∴，∴，∴x=9 或x=16，∵AE<DE，∴AE=9，DE=16，∴CE=20，BE=15，由折叠得，BP=PG，∴BP=BF=PG，∵BE∥PG，∴△ECF∽△GCP，设BP=BF=PG=，y∴，∴y=在Rt△PBC中，PC= ，cos∠PCB= = ；③ 如图，连接FG，∵∠GEF=∠BAE=90，∵BF∥PG，BF=PG，∴?BPGF是菱形，∴BP∥GF，∴∠GFE=∠ABE，∴△GEF∽△EAB，∴ BE?EF=AB?GF=12 × 9．=108【点评】此题是四边形综合题，主要考查了矩形的性质，全等三角形的判定和性质，相似三角形的判定和性质，折叠的性质，利用方程的思想解决问题是解本题的关键．17. （2018·广东·7 分）如图，矩形ABCD中，AB>AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ ADE≌△ CED；（2）求证：△ DEF是等腰三角形．分析】（1）根据矩形的性质可得出AD=BC、AB=CD，结合折叠的性质可得出AD=CE、AE=CD，进而即可证出△ ADE≌△ CED（SSS）；2）根据全等三角形的性质可得出∠DEF=∠ EDF，利用等边对等角可得出EF=DF，由此即可证出△ DEF是等腰三角形．解答】证明：（1）∵四边形ABCD是矩形，∴AD=BC，AB=CD．由折叠的性质可得：BC=CE，AB=AE，∴AD=CE，AE=CD．在△ ADE和△ CED中，，∴△ ADE≌△ CED（SSS）．2）由（1）得△ ADE≌△ CED，∴EF=DF ，∴△ DEF 是等腰三角形．【点评】本题考查了全等三角形的判定与性质、翻折变换以及矩形的性质，解题的关键是：（1）根据矩形的性质结合折叠的性质找出 AD=CE 、 AE=CD ；（ 2）利用全等三角形的性质找出 ∠DEF=∠EDF ．18. （2018?江苏盐城? 10 分）如图，在以线段为直径的上取一点，连接、. 将沿翻折后得到 .（1）试说明点在上；（2）在线段的延长线上取一点，使 . 求证：为的切线；（3）在（ 2）的条件下，分别延长线段、相交于点，若，，求线段的长 . 【答案】（ 1）解：连接 OC ，OD，∴∠ DEA=∠EDC ，即∠ DEF=∠EDF ，由翻折可得OD=OC，∵OC是⊙ O的半径，∴点D在⊙ O上。

2023年中考数学【选择题】讲练必考重点03 几何变换之翻折问题

【选择题】必考重点03 几何变换之翻折问题几何变换中的折叠问题，是江苏各地中考中常考的题型，难度多为一般或者较难。

几何的翻折问题，本质上考查的是轴对称的性质，常和矩形相结合。

在解题时，首先要明确折叠前后的图形全等，折叠前后的对应边、对应角相等，对称轴垂直平分对应点之间的连线，在结合矩形、菱形、三角形等的性质，运用勾股定理，列出方程，求出相应的线段长度。

【2022·江苏连云港·中考母题】如图，将矩形ABCD 沿着GE 、EC 、GF 翻折，使得点A 、B 、D 恰好都落在点O 处，且点G 、O 、C 在同一条直线上，同时点E 、O 、F 在另一条直线上．小炜同学得出以下结论：①GF ∥EC ；②AB ；③GE DF ；④OC ；⑤△COF ∽△CEG ．其中正确的是（）A ．①②③B ．①③④C ．①④⑤D ．②③④【考点分析】本题主要考查了折叠问题，解题时，我们常常设要求的线段长为x ，然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．【思路分析】由折叠的性质知∠FGE =90°，∠GEC =90°，点G 为AD 的中点，点E 为AB 的中点，设AD =BC =2a ，AB =CD =2b ，在Rt △CDG 中，由勾股定理求得b ，然后利用勾股定理再求得DF =FO =【2021·江苏苏州·中考母题】如图，在平行四边形ABCD 中，将ABC 沿着AC 所在的直线翻折得到AB C '，B C '交AD 于点E ，连接B D '，若60B ∠=︒，45ACB ∠=︒，AC =B D '的长是（）A．1BC D 【考点分析】本题考查翻折变换、等腰三角形的性质、勾股定理、平行四边形的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．【思路分析】利用平行四边形的性质、翻折不变性可得△AEC 为等腰直角三角形，根据已知条件可得CE 得长，进而得出ED 的长，再根据勾股定理可得出B D '；1．（2022·江苏苏州·二模）如图把一张矩形纸片ABCD 沿对角线AC 翻折，点B 的对应点为B ′，AB ′与DC 相交于点E ，则下列结论一定正确的是（）A ．BC ＝12ACB ．AE ＝CEC ．AD ＝DE D ．∠DAE ＝∠CAB2．（2022·江苏南京·二模）如图，矩形ABCO ，点A 、C 在坐标轴上，点B 的坐标为()2,4-．将△ABC 沿AC 翻折，得到△ADC ，则点D 的坐标是（）A．612,55⎛⎫⎪⎝⎭B．65,52⎛⎫⎪⎝⎭C．312,25⎛⎫⎪⎝⎭D．35,22⎛⎫⎪⎝⎭3．（2022·江苏泰州·一模）如图，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平后再次折叠，使点A落在EF上的点A′处，得到折痕BM，BM与EF相交于点N．若直线BA′交直线CD于点O，BC＝11，EN＝2，则FO的长为（）A B C D4．（2022·江苏宿迁·三模）已知长方形纸条ABCD，点E、G在AD边上，点F、H在BC边上．将纸条分别沿着EF、GH折叠，如图，当DC恰好落在EA'上时，1∠与2∠的数量关系是（）A．12135∠+∠=︒B．2115∠-∠=︒C．1290∠+∠=︒D．22190∠-∠=︒5．（2022·江苏苏州·二模）如图①，②，③，④，两次折叠等腰三角形纸片ABC，先使AB与AC重合，折痕为AD，展平纸片：再使点A与点C重合，折痕为EF，展平纸片，AD、EF交于点G．若5cmAB AC==，6cmBC，则DG的长为（）A．3cm4B．7cm8C．1cm D．7cm66．（2022·江苏·苏州中学二模）如图，菱形ABCD中，点E在AD上，将△ABE沿着BE翻折，点A恰好落在CD上的点F处．若∠A=65°，则∠DFE的度数为（）A．85︒B．82.5︒C．65︒D．50︒7．（2022·江苏扬州·二模）如图，在矩形ABCD中，2AB=，BC=E是BC的中点，将ABE△沿直线AE翻折，点B落在点F处，连结CF，则tan ECF∠的值为（）A B C．23D8．（2022·江苏苏州·模拟）如图，在矩形ABCD中，点E在DC上，将矩形沿AE折叠，使点D落在BC 边上的点F处，若3AB=，5BC=，则tan FEC∠的值为（）．A．12B．35C．34D．459．（2022·江苏苏州·一模）如图，在平面直角坐标系中，O为坐标原点，平行四边形ABCD的边AB在x轴上，顶点D在y轴的正半轴上，点C在第一象限，将△AOD沿y轴翻折，使点A落在x轴上的点E处、点B恰好为OE的中点．DE与BC交于点F．若y＝kx（k≠0）图象经过点C．且S△BEF＝1，则k的值为（）A．18B．20C．24D．2810．（2022·江苏·江阴市第一初级中学一模）如图，把三角形纸片ABC沿DE折叠，当点A落在四边形BCDE外部时，则∠A与∠1、∠2之间的数量关系是（）A．2∠A=∠1-∠2B．3∠A=2（∠1-∠2）C．3∠A=2∠1-∠2D．∠A=∠1-∠211．（2022·江苏·无锡市天一实验学校二模）已知：如图，在Rt△ABC中，∠A=90°，AB=8，tan∠ABC=32，点N是边AC的中点，点M是射线BC上的一动点（不与B，C重合），连接MN，将△CMN沿MN 翻折得△EMN，连接BE，CE，当线段BE的长取最大值时，sin∠NCE的值为（）A B C D12．（2022·江苏省南菁高级中学实验学校九年级）如图，在ABC 中，点D 是线段AB 上的一点，过点D 作DE ∥AC 交BC 于点E ，将BDE 沿DE 翻折，得到B DE '，若点C 恰好在线段B D '上，若90BCD ∠=︒，DC ：3CB '=：2，AB =CE 的长度为（）A．B C ．D 13．（2022·江苏·九年级专题练习）如图，在△ABC 中，90ACB ∠=，点D 是AB 的中点，将△ACD 沿CD 对折得△A ′CD ．连接BA '，连接AA ′交CD 于点E ，若14cm AB =，4cm BA '=，则CE 的长为（）A ．4cmB ．5cmC ．6cmD ．7cm14．（2022·江苏·宜兴市树人中学九年级）如图，在△ABC 中，点D 是线段AB 上的一点，过点D 作DE ∥AC 交BC 于点E ，将△BDE 沿翻折，得到△B 'DE ，若点C 恰好在线段B 'D 上，若∠BCD ＝90°，DC ：CB '＝3：2，AB ＝CE 的长度为（）A．B ．4C ．D ．615．（2022·江苏·九年级专题练习）如图①，AB ＝5，射线AM ∥BN ，点C 在射线BN 上，将△ABC 沿AC 所在直线翻折，点B 的对应点D 落在射线BN 上，点P ，Q 分别在射线AM 、BN 上，PQ ∥AB ．设AP ＝x ，QD ＝y ．若y 关于x 的函数图象（如图②）经过点E (9，2)，则cos B 的值等于（）A．25B．12C．35D．71016．（2022·江苏·苏州市吴江区铜罗中学九年级期中）如图，在△ABC中，D是AC边上的中点，连接BD，把△BDC沿BD翻折，得到△BDC′，DC'与AB交于点E，连接AC′，若AD＝AC′＝2，BD＝3，则点D到BC的距离为（）A B C D17．（2022·江苏南通·九年级）如图，AB为⊙O的一条弦，C为⊙O上一点，OC∥AB．将劣弧AB沿弦AB 翻折，交翻折后的弧AB交AC于点D．若D为翻折后弧AB的中点，则∠ABC＝（）A．110°B．112.5°C．115°D．117.5°18．（2022·江苏南京·九年级专题练习）如图，在矩形纸片ABCD中，点E、F分别在矩形的边AB、AD 上，将矩形纸片沿CE、CF折叠，点B落在H处，点D落在G处，点C、H、G恰好在同一直线上，若AB＝6，AD＝4，BE＝2，则DF的长是（）A ．2B ．74C D ．319．（2022·江苏·宿迁青华中学九年级期末）如图，四边形ABCD 内接于O ，AB AD =，3BC =．劣弧BC 沿弦BC 翻折，刚好经过圆心O ．当对角线BD 最大时，则弦AB 的长为（）A B ．C ．32D ．【选择题】必考重点03 几何变换之翻折问题几何变换中的折叠问题，是江苏各地中考中常考的题型，难度多为一般或者较难。

八年级初二数学图形的对称-翻折变换(折叠问题) 含答案

图形的对称-翻折变换（折叠问题）一．选择题（共30小题）1．将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=6，则BC的长为（）A．1 B．2 C．2D．122．如图，直角三角形纸片的两直角边长分别为6、8，按如图那样折叠，使点A 与点B重合，折痕为DE，则S△BCE：S△BDE等于（）A．2：5 B．14：25 C．16：25 D．4：213．如图①，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形．如图②，将四边形ACBD折叠，使D与C重合，EF为折痕，则∠ACE的正弦值为（）A．B．C．D．4．图1为一张三角形ABC纸片，点P在BC上，将A折至P时，出现折痕BD，其中点D在AC上，如图2所示，若△ABC的面积为80，△ABD的面积为30，则AB与PC的长度之比为（）A．3：2 B．5：3 C．8：5 D．13：85．按如图所示的方法折纸，下面结论正确的个数（）①∠2=90°；②∠1=∠AEC；③△ABE∽△ECF；④∠BAE=∠3．A．1个B．2个C．3个D．4个6．如图，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠AED′=40°，则∠EFB等于（）A．70°B．65°C．80°D．35°7．如图，把矩形ABCD沿EF折叠，使点C落在点A处，点D落在点G处，若∠CFE=60°，且DE=1，则边BC的长（）A．3 B．4 C．3.5 D．68．如图，四边形ABCD是矩形，AB=4，AD=3，把矩形沿直线AC折叠，点B 落在点E处，AE交CD于点F．连接DE，则DF的长是（）A．B．C．D．9．张萌和小平两人打算各用一张正方形的纸片ABCD折出一个等边三角形，两人作法如下：张萌：如图1，将纸片对折得到折痕EF，沿点B翻折纸片，使点A落在EF上的点M处，连接CM，△BCM即为所求；小平：如图2，将纸片对折得到折痕EF，沿点B翻折纸片，使点C落在EF上的点M处，连接BM，△BCM 即为所求，对于两人的作法，下列判断正确的是（）A．小平的作法正确，张萌的作法不正确B．两人的作法都不正确C．张萌的作法正确，小平的作法不正确D．两人的作法都正确10．如图，折叠矩形纸片ABCD的一边AD，使点D落在BC边上的点F处，若AB=8，BC=10，则△CEF的周长为（）A．12 B．16 C．18 D．2411．如图，在矩形ABCD中，AB=3，BC=5，点E在边CD上，连接BE，将△BCE 沿BE折叠，若点C恰好落在AD边上的点F处，则CE的长为（）A．B．C．D．12．如图，在△ABC中，∠C=90°，AB=5cm，AC=4cm，点D在AC上，将△BCD 沿着BD所在直线翻折，使点C落在斜边AB上的点E处，则DC的长为（）A．cm B．cm C．2cm D．cm13．如图，在平面直角坐标系中，点A（0，4）、B（3，0），连接AB，将△AOB 沿过点B的直线折叠，使点A落在x轴上的点A′处，折痕所在的直线交y轴正半轴于点C，则直线BC的解析式为（）A．y=﹣B．y=﹣x+C．y=﹣D．y=﹣2x+14．如图，四边形OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，点O落在BC边上的点E处．则直线DE的解析式为（）A．y=x+5 B．y=x+5 C．y=x+5 D．y=x+515．如图，将三角形纸片ABC沿DE折叠，使点A落在BC边上的点F处，且DE∥BC，当DE=2时，BC的长为（）A．3 B．4 C．5 D．616．如图，将平行四边形ABCD沿对角线AC折叠，点B的对应点落在点E处，且点B、A、E在同一条直线上，CE交AD于点F，连接ED．下列结论中错误的是（）A．AF=B．四边形ACDE是矩形C．图中与△ABC全等的三角形有4个D．图中有4个等腰三角形17．如图，有一张直角三角形纸片ABC，边AB=6，AC=10，∠ABC=90°，将该直角三角形纸片沿DE折叠，使点C与点B重合，则四边形ABDE的周长为（）A．16 B．17 C．18 D．1918．如图，梯形ABCD中，AD∥BC，AB=DC，∠DBC=45°，点E在BC上，点F在AB上，将梯形ABCD沿直线EF翻折，使得点B与点D重合．如果，那么的值是（）A．B．C．D．19．如图，在边长为12的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交BC于点G．则BG的长为（）A．5 B．4 C．3 D．220．如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（﹣1，0），B（﹣2，3），C（﹣3，1）．将△ABC沿y轴翻折得到△A′B′C′，则点B′的坐标为（）A．（2，1）B．（2，3）C．（4，1）D．（0，2）21．如图，△ABC周长为36cm，把其边AC对折，使点C、A重合，折痕交BC 边于点D，交AC边于点E，连结AD，若AE=6cm，则△ABD的周长是（）A．24cm B．26cm C．28cm D．30cm22．如图，矩形ABCD中，AB=8，把矩形沿直线AC折叠，点B落在点E处，AE交CD于点F，若AF=，则AD的长为（）A．3 B．4 C．5 D．623．如图的实线部分是由Rt△ABC经过两次折叠得到的，首先将Rt△ABC沿BD折叠，使点C落在斜边上的点C′处，再沿DE折叠使点A落在DC′延长线上的点A′处，若图中，∠A=30°，BC=5cm，则折痕DE的长为（）A．B．2C．2D．24．如图一直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（）A．2cm B．3cm C．4cm D．5cm25．如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为（）A．6 B．8 C．10 D．1226．如图，矩形ABCD中，AB=3，AD=9，将此矩形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（）A．6 B．8 C．10 D．1227．如图所示，有一块直角三角形纸片，∠C=90°，AC=2，BC=，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为（）A．B．C．1 D．28．如图所示，折叠平行四边形的一边AD，使点A落在DC边上的点E处，已知AB=6，BC=4，则EC的长为（）A．1 B．2 C．3 D．1.529．如图，正方形ABCD中，AB=12，点E在边BC上，BE=EC，将△DCE沿DE对折至△DFE，延长EF交边AB于点G，连接DG、BF，给出以下结论：①△DAG≌△DFG；②BG=2AG；③S△DGF=120；④S△BEF=．其中所有正确结论的个数是（）A．4 B．3 C．2 D．130．如图，将矩形纸片ABCD沿EF折叠，使D点与BC边的中点D重合，若BC=8，CD=6，则CF的长为（）A．B．C．2 D．1图形的对称-翻折变换（折叠问题）参考答案与试题解析一．选择题（共30小题）1．将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=6，则BC的长为（）A．1 B．2C．2D．12【考点】翻折变换（折叠问题）；勾股定理的应用；菱形的性质；矩形的性质．【分析】根据菱形AECF，得∠FCO=∠ECO，再利用∠ECO=∠ECB，可通过折叠的性质，结合直角三角形勾股定理求解．【解答】解：∵菱形AECF，AB=6，∴假设BE=x，∴AE=6﹣x，∴CE=6﹣x，∵四边形AECF是菱形，∴∠FCO=∠ECO，∵∠ECO=∠ECB，∴∠ECO=∠ECB=∠FCO=30°，2BE=CE，∴CE=2x，∴2x=6﹣x，解得：x=2，∴CE=4，利用勾股定理得出：BC2+BE2=EC2，BC===2，故选：C．【点评】此题主要考查了折叠问题以及勾股定理等知识，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．2．如图，直角三角形纸片的两直角边长分别为6、8，按如图那样折叠，使点A 与点B重合，折痕为DE，则S△BCE：S△BDE等于（）A．2：5 B．14：25 C．16：25 D．4：21【考点】翻折变换（折叠问题）．【分析】在Rt△BEC中利用勾股定理计算出AB=10，根据折叠的性质得到AD=BD=5，EA=EB，设AE=x，则BE=x，EC=8﹣x，在Rt△BEC中根据勾股定理计算出x=，则EC=8﹣=，利用三角形面积公式计算出S△BCE=BC•CE=×6×=，在Rt△BED中利用勾股定理计算出ED==，利用三角形面积公式计算出S△BDE=BD•DE=×5×=，然后求出两面积的比．【解答】解：在Rt△BAC中，BC=6，AC=8，∴AB==10，∵把△ABC沿DE使A与B重合，∴AD=BD，EA=EB，∴BD=AB=5，设AE=x，则BE=x，EC=8﹣x，在Rt△BEC中，∵BE2=EC2+BC2，即x2=（8﹣x）2+62，∴x=，∴EC=8﹣x=8﹣=，∴S△BCE=BC•CE=×6×=，在Rt△BED中，∵BE2=ED2+BD2，∴ED==，∴S△BDE=BD•DE=×5×=，∴S△BCE：S△BDE=：=14：25．故选B．【点评】本题考查了折叠问题：折叠前后两图形全等，即对应线段相等，对应角相等．也考查了勾股定理．3．如图①，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形．如图②，将四边形ACBD折叠，使D与C重合，EF为折痕，则∠ACE的正弦值为（）A．B．C．D．【考点】翻折变换（折叠问题）．【分析】在Rt△ABC中，设AB=2a，已知∠ACB=90°，∠CAB=30°，即可求得AB、AC的值，由折叠的性质知：DE=CE，可设出DE、CE的长，然后表示出AE的长，进而可在Rt△AEC中，由勾股定理求得AE、CE的值，即可求∠ACE 的正弦值．【解答】解：∵△ABC中，∠ACB=90°，∠BAC=30°，设AB=2a，∴AC=a，BC=a；∵△ABD是等边三角形，∴AD=AB=2a；设DE=EC=x，则AE=2a﹣x；在Rt△AEC中，由勾股定理，得：（2a﹣x）2+3a2=x2，解得x=；∴AE=，EC=，∴sin∠ACE==．故选：B．【点评】本题考查的是翻折变换，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解答此题的关键．4．图1为一张三角形ABC纸片，点P在BC上，将A折至P时，出现折痕BD，其中点D在AC上，如图2所示，若△ABC的面积为80，△ABD的面积为30，则AB与PC的长度之比为（）A．3：2 B．5：3 C．8：5 D．13：8【考点】翻折变换（折叠问题）．【分析】如图，作辅助线；首先求出△BDP的面积，进而求出△DPC的面积；借助三角形的面积公式求出的值；由旋转变换的性质得到AB=PB，即可解决问题．【解答】解：如图，过点D作DE⊥BC于点E；由题意得：S△ABD=S△PBD=30，∴S△DPC=80﹣30﹣30=20，∴=，由题意得：AB=BP，∴AB：PC=3：2，故选A．【点评】该题主要考查了翻折变换的性质及其应用问题；解题的方法是作高线，表示出三角形的面积；解题的关键是灵活运用翻折变换的性质来分析、判断、推理或解答．5．按如图所示的方法折纸，下面结论正确的个数（）①∠2=90°；②∠1=∠AEC；③△ABE∽△ECF；④∠BAE=∠3．A．1个B．2个C．3个D．4个【考点】翻折变换（折叠问题）；相似三角形的判定与性质．【分析】根据翻折变换的性质、相似三角形的判定定理解答即可．【解答】解：由翻折变换的性质可知，∠AEB+∠FEC=×180°=90°，则∠AEF=90°，即∠2=90°，①正确；由图形可知，∠1＜∠AEC，②错误；∵∠2=90°，∴∠1+∠3=90°，又∠1+∠BAE=90°，∴∠BAE=∠3，④正确；∵∠BAE=∠3，∠B=∠C=90°，∴△ABE∽△ECF，③正确．故选：C．【点评】本题考查的是翻折变换的性质，翻折变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．6．如图，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠AED′=40°，则∠EFB等于（）A．70°B．65°C．80°D．35°【考点】翻折变换（折叠问题）．【分析】根据平角的知识可求出∠DED′的度数，再由折叠的性质可得出∠D′EF=∠DEF=∠DED′，从而根据平行线的性质可得出∠EFB的度数．【解答】解：∵∠AED′=40°，∴∠DED′=180°﹣40°=140°，又由折叠的性质可得，∠D′EF=∠DEF=∠DED′，∴∠DEF=70°，又∵AD∥BC，∴∠EFB=70°．故选：A．【点评】此题考查了翻折变换的知识，解答本题的关键是根据折叠的性质得出∠D′EF=∠DEF=∠DED′，难度一般．7．如图，把矩形ABCD沿EF折叠，使点C落在点A处，点D落在点G处，若∠CFE=60°，且DE=1，则边BC的长（）A．3 B．4 C．3.5 D．6【考点】翻折变换（折叠问题）．【分析】由矩形的性质得到∠1=∠CFE=60°，由折叠可得∠2=60°，从而求得∠4的度数，得到AE=EC，在Rt△CDE中利用勾股定理可求得EC的长度，即可得到答案．【解答】解：∵矩形ABCD，∴BC∥AD，∴∠1=∠CFE=60°，∵EF为折痕，∴∠2=∠1=60°，AE=EC，∴∠3=180°﹣60°﹣60°=60°，Rt△CDE中，∠4=90°﹣60°=30°，∴EC=2×DE=2×1=2，∴BC=AE+ED=EC+ED=2+1=3．故选：A．【点评】本题考查了翻折问题；由折叠得到角相等，得到AE=EC利用勾股定理求解是正确解答本题的关键．8．如图，四边形ABCD是矩形，AB=4，AD=3，把矩形沿直线AC折叠，点B 落在点E处，AE交CD于点F．连接DE，则DF的长是（）A．B．C．D．【考点】翻折变换（折叠问题）．【分析】由四边形ABCD是矩形与△AEC由△ABC翻折得到，AD=CE，∠ADF=∠CEF，由AAS证得△ADF≌△CEF，的长FA=FC，设DF=x，则FA=4﹣x，由勾股定理得：DA2+DF2=AF2，即可求出DF的长．【解答】解：∵四边形ABCD是矩形，∴AD=BC，AB=DC=4，∠ADF=90°，∵△AEC由△ABC翻折得到，∴BC=EC，∠CEF=∠ABC=90°，∴AD=CE，∠ADF=∠CEF，在△ADF与△CEF中，，∴△ADF≌△CEF（AAS），∴FA=FC，设DF=x，则FA=FC=DC﹣DF=4﹣x，在Rt△DFA中，由勾股定理得：DA2+DF2=AF2，即32+x2=（4﹣x）2，解得：x=，即DF的长是．故选C．【点评】本题主要考查了折叠的性质、矩形的性质、全等三角形的判定与性质、勾股定理等知识；熟练掌握折叠的性质，得到相等的线段与角是解决问题的关键．9．张萌和小平两人打算各用一张正方形的纸片ABCD折出一个等边三角形，两人作法如下：张萌：如图1，将纸片对折得到折痕EF，沿点B翻折纸片，使点A落在EF上的点M处，连接CM，△BCM即为所求；小平：如图2，将纸片对折得到折痕EF，沿点B翻折纸片，使点C落在EF上的点M处，连接BM，△BCM 即为所求，对于两人的作法，下列判断正确的是（）A．小平的作法正确，张萌的作法不正确B．两人的作法都不正确C．张萌的作法正确，小平的作法不正确D．两人的作法都正确【考点】翻折变换（折叠问题）．【分析】在图1中，由BM=2BF推出∠BMF=30°，所以∠MBF=60°，再根据等边三角形的判定方法即可证明．在图2中，证明方法类似．【解答】解：图1中，∵四边形ABCD是正方形，∴AB=AD=BC∵AE=ED=BF=FC，AB=BM，∴BM=2BF，∵∠MFB=90°，∴∠BMF=30°，∴∠MBF=90°﹣∠BMF=60°，∵MB=MC，∴△MBC是等边三角形，∴张萌的作法正确．在图2中，∵BM=BC=2BF，∠MFB=90°，∴∠BMF=30°，∴∠MBF=90°﹣∠BMF=60°，∵MB=MC∴△MBC是等边三角形，∴小平的作法正确．故选D．【点评】本题考查正方形的性质、翻折不变性、直角三角形的性质，解题的关键是在一个直角三角形中如果斜边是直角边的两倍那么这条直角边所对的锐角是30度．10．如图，折叠矩形纸片ABCD的一边AD，使点D落在BC边上的点F处，若AB=8，BC=10，则△CEF的周长为（）A．12 B．16 C．18 D．24【考点】翻折变换（折叠问题）．【分析】先根据矩形的性质得AD=BC=10，AB=CD=8，再根据折叠的性质得AF=AD=10，EF=DE，在Rt△ABF中，利用勾股定理计算出BF=6，则CF=BC ﹣BF=4，易得△CEF的周长．【解答】解：∵四边形ABCD为矩形，∴AD=BC=10，AB=CD=8，∵矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上的F处，∴AF=AD=10，EF=DE，在Rt△ABF中，∵BF==6，∴CF=BC﹣BF=10﹣6=4，∴△CEF的周长为：CE+EF+CF=CE+DE+CF=CD+CF=8+4=12．故选A．【点评】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了矩形的性质和勾股定理，利用勾股定理得CF的长是解答此题的关键．11．如图，在矩形ABCD中，AB=3，BC=5，点E在边CD上，连接BE，将△BCE 沿BE折叠，若点C恰好落在AD边上的点F处，则CE的长为（）A．B．C．D．【考点】翻折变换（折叠问题）．【分析】设CE=x，由矩形的性质得出AD=BC=5，CD=AB=3，∠A=∠D=90°．由折叠的性质得出BF=BC=5，EF=CE=x，DE=CD﹣CE=3﹣x．在Rt△ABF中利用勾股定理求出AF的长度，进而求出DF的长度；然后在Rt△DEF中根据勾股定理列出关于x的方程，即可解决问题．【解答】解：设CE=x．∵四边形ABCD是矩形，∴AD=BC=5，CD=AB=3，∠A=∠D=90°．∵将△BCE沿BE折叠，使点C恰好落在AD边上的点F处，∴BF=BC=5，EF=CE=x，DE=CD﹣CE=3﹣x．在Rt△ABF中，由勾股定理得：AF2=52﹣32=16，∴AF=4，DF=5﹣4=1．在Rt△DEF中，由勾股定理得：EF2=DE2+DF2，即x2=（3﹣x）2+12，解得：x=．故选B．【点评】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了勾股定理、矩形的性质、方程思想等知识，关键是熟练掌握勾股定理，找准对应边．12．如图，在△ABC中，∠C=90°，AB=5cm，AC=4cm，点D在AC上，将△BCD 沿着BD所在直线翻折，使点C落在斜边AB上的点E处，则DC的长为（）A．cm B．cm C．2cm D．cm【考点】翻折变换（折叠问题）．【分析】首先由勾股定理求出BC，由折叠的性质可得∠BED=∠C=90°，BE=BC=3cm，得出AE=AB﹣BE=2cm，设DC=xcm，则DE=xcm，AD=（4﹣x）cm，由勾股定理得出方程，解方程即可．【解答】解：∵∠C=90°，AB=5cm，AC=4cm，∴BC==3cm，∵将△BCD沿着直线BD翻折，使点C落在斜边AB上的点E处，∴△BED≌△BCD，∴∠BED=∠C=90°，BE=BC=3cm，∴AE=AB﹣BE=2cm，设DC=xcm，则DE=xcm，AD=（4﹣x）cm，由勾股定理得：AE2+DE2=AD2，即22+x2=（4﹣x）2，解得：x=．故选：B．【点评】本题主要考查翻折变换的性质，全等三角形的性质，勾股定理；熟练掌握翻折变换的性质，由勾股定理得出方程是解决问题的关键．13．如图，在平面直角坐标系中，点A（0，4）、B（3，0），连接AB，将△AOB 沿过点B的直线折叠，使点A落在x轴上的点A′处，折痕所在的直线交y轴正半轴于点C，则直线BC的解析式为（）A．y=﹣B．y=﹣x+C．y=﹣D．y=﹣2x+【考点】翻折变换（折叠问题）；待定系数法求一次函数解析式．【分析】由点A（0，4）、B（3，0），可求得AB的长，然后由折叠的性质，求得OA′的长，且△A′OC∽△AOB，再由相似三角形的性质，求得OC的长，继而利用待定系数法求得直线BC的解析式．【解答】解：∵点A（0，4）、B（3，0），∴OA=4，OB=3，∴AB==5，由折叠的性质可得：A′B=AB=5，∠OA′C=∠OAB，∴OA′=A′B﹣OB=2，∵∠A′OC=∠AOB=90°，∴△A′OC∽△AOB，∴，即，解得：OC=，∴点C的坐标为：（0，），设直线BC的解析式为：y=kx+b，则，解得：，∴直线BC的解析式为：y=﹣x+．故选C．【点评】此题考查了折叠的性质、勾股定理、相似三角形的判定与性质以及待定系数法求一次函数的解析式．注意求得点C的坐标是解此题的关键．14．如图，四边形OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，点O落在BC边上的点E处．则直线DE的解析式为（）A．y=x+5 B．y=x+5 C．y=x+5 D．y=x+5【考点】翻折变换（折叠问题）；待定系数法求一次函数解析式．【分析】首先在RT△ABE中，求出EB，再在RT△CDE中利用勾股定理即可解决问题．【解答】解：∵△ADE是由△ADO翻折，∴DE=DO，AO=AE=10，∵四边形OABC是矩形，∴OC=AB=8，AO=BC=10，∠B=∠BCO=∠BAO=90°，在RT△ABE中，∵AE=10，AB=8，∴EB===6，∴EC=4，设DO=DE=x，在RT△DCE中，∵CD2+CE2=DE2，∴（8﹣a）2+42=a2，∴a=5，∴点D（0，5），点E（4，8），设直线DE为y=kx+b，∴解得，∴直线DE为：y=+5．故选A．【点评】本题考查翻折变换、待定系数法确定一次函数的解析式，解题的关键是巧妙利用勾股定理，用方程的思想去思考问题，属于中考常考题型．15．如图，将三角形纸片ABC沿DE折叠，使点A落在BC边上的点F处，且DE∥BC，当DE=2时，BC的长为（）A．3 B．4 C．5 D．6【考点】翻折变换（折叠问题）．【分析】首先由DE∥BC与折叠的性质，可证得DE是△ABC的中位线，继而求得答案．【解答】解：∵DE∥BC，∴∠ADE=∠B，∠EDF=∠BFD，由折叠的性质可得：∠ADE=∠EDF，AD=DF，∴∠B=∠BFD，∴BD=DF，∴AD=BD，同理：AE=EC，∴DE=BC，即BC=2DE=4．故选B．【点评】此题考查了折叠的性质以及三角形中位线的性质．注意证得DE是△ABC的中位线是关键．16．如图，将平行四边形ABCD沿对角线AC折叠，点B的对应点落在点E处，且点B、A、E在同一条直线上，CE交AD于点F，连接ED．下列结论中错误的是（）A．AF=B．四边形ACDE是矩形C．图中与△ABC全等的三角形有4个D．图中有4个等腰三角形【考点】翻折变换（折叠问题）；平行四边形的性质．【分析】由四边形ABCD是平行四边形，得到AB=CD，AB∥CD，AD=BC，由折叠的性质得到AB=AE，BC=CE，等量代换得到AE=CD，AD=CE，推出四边形ACDE是平行四边形，于是得到AF=BC，四边形ACDE是矩形，故A，B 正确；根据平行四边形和矩形的性质得到△ACD≌△ACE≌△CDE≌△ADE≌△ABC，于是得到图中与△ABC全等的三角形有4个，故C正确；推出△BCE是等腰三角形，△AEF，△ACF，△CDF，△DEF是等腰三角形，于是得到图中有5个等腰三角形，故D错误．【解答】解：∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，AD=BC，由折叠的性质得到AB=AE，BC=CE，∴AE=CD，AD=CE，∵点B、A、E在同一条直线上，∴AE∥CD，∴四边形ACDE是平行四边形，∴AF=BC，四边形ACDE是矩形，故A，B正确；∵四边形ABCD是平行四边形，四边形ACDE是矩形，∴△ACD≌△ACE≌△CDE≌△ADE≌△ABC，∴图中与△ABC全等的三角形有4个，故C正确；∵BC=CE，∴△BCE是等腰三角形，∵四边形ACDE是矩形，∴AF=EF=CF=DF，∴△AEF，△ACF，△CDF，△DEF是等腰三角形，∴图中有5个等腰三角形，故D错误；故选D．【点评】本题考查了平行四边形的性质、折叠的性质以及等腰三角形的判定和性质，解题的关键是熟记等腰三角形和矩形的判定方法．17．如图，有一张直角三角形纸片ABC，边AB=6，AC=10，∠ABC=90°，将该直角三角形纸片沿DE折叠，使点C与点B重合，则四边形ABDE的周长为（）A．16 B．17 C．18 D．19【考点】翻折变换（折叠问题）．【分析】根据勾股定理得到BC=8，由折叠的性质得到BD=CD=BC=4，DE⊥BC，根据三角形的中位线的性质得到DE=AB=3，AE=AC=5，于是得到结论．【解答】解：∵AB=6，AC=10，∠ABC=90°，∴BC=8，∵将该直角三角形纸片沿DE折叠，使点C与点B重合，∴BD=CD=BC=4，DE⊥BC，∵∠ABC=90°，∴DE∥AB，∴DE=AB=3，AE=AC=5，∴四边形ABDE的周长=AB+AE+DE+BD=6+5+3+4=18，故选C．【点评】此题考查了折叠的性质，勾股定理，三角形的中位线的性质，注意掌握折叠前后图形的对应关系．18．如图，梯形ABCD中，AD∥BC，AB=DC，∠DBC=45°，点E在BC上，点F在AB上，将梯形ABCD沿直线EF翻折，使得点B与点D重合．如果，那么的值是（）A．B．C．D．【考点】翻折变换（折叠问题）．【分析】根据对称的性质得到△BFE≌△DFE，得到DE=BE．根据已知条件得到∠DEB=90°，设AD=1，BC=4，过A作AG⊥BC于G，根据矩形的性质得到GE=AD=1，根据全等三角形的性质得到BG=EC=1.5，根据勾股定理得到AB=CD==5，通过△BDC∽△DEF，得到，求出BF=，于是得到结论．【解答】解：∵EF是点B、D的对称轴，∴△BFE≌△DFE，∴DE=BE．∵在△BDE中，DE=BE，∠DBE=45°，∴∠BDE=∠DBE=45°．∴∠DEB=90°，∴DE⊥BC．在等腰梯形ABCD中，∵，∴设AD=1，BC=4，过A作AG⊥BC于G，∴四边形AGED是矩形．∴GE=AD=1，∵Rt△ABG≌Rt△DCE，∴BG=EC=1.5，∴AG=DE=BE=2.5∴AB=CD==5，∵∠ABC=∠C=∠FDE，∵∠CDE+∠C=90°，∴∠FDE+∠CDE=90°∴∠FDB+∠BDC+∠FDB=∠FDB+∠DFE=90°，∴∠BDC=∠DFE，∵∠DEF=∠DBC=45°，∴△BDC∽△DEF，∴，∴DF=，∴BF=，∴AF=AB﹣BF=，∴=．故选B．【点评】此题考查等腰梯形的性质，翻折的性质，三角形全等的判定与性质，等腰直角三角形的性质，相似三角形的判定和性质等知识，注意结合图形，作出常用辅助线解决问题．19．如图，在边长为12的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交BC于点G．则BG的长为（）A．5 B．4 C．3 D．2【考点】翻折变换（折叠问题）．【分析】利用翻折变换对应边关系得出AB=AF，∠B=∠AFG=90°，利用HL定理得出△ABG≌△AFG即可；利用勾股定理得出GE2=CG2+CE2，进而求出BG 即可；【解答】解：在正方形ABCD中，AD=AB=BC=CD，∠D=∠B=∠BCD=90°，∵将△ADE沿AE对折至△AFE，∴AD=AF，DE=EF，∠D=∠AFE=90°，∴AB=AF，∠B=∠AFG=90°，又∵AG=AG，在Rt△ABG和Rt△AFG中，，∴Rt△ABG≌Rt△AFG（HL），∴BG=GF，∵E是边CD的中点，∴DE=CE=6，设BG=x，则CG=12﹣x，GE=x+6，∵GE2=CG2+CE2∴（x+6）2=（12﹣x）2+62，解得x=4∴BG=4．故选B．【点评】此题主要考查了全等三角形的判定和性质，勾股定理的综合应用以及翻折变换的性质，根据翻折变换的性质得出对应线段相等是解题关键．20．如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（﹣1，0），B（﹣2，3），C（﹣3，1）．将△ABC沿y轴翻折得到△A′B′C′，则点B′的坐标为（）A．（2，1）B．（2，3）C．（4，1）D．（0，2）【考点】翻折变换（折叠问题）；坐标与图形性质．【分析】根据关于y轴对称的点的特点找到B'，结合直角坐标系可得出点B′的坐标．【解答】解：∵将△ABC沿y轴翻折得到△A′B′C′，∴点B与点B′关于y轴对称，∴B′（2，3），故选B．【点评】本题考查了翻折变换﹣折叠问题，坐标与图形的关系，熟记关于y轴对称的点的特点是解答本题的关键．21．如图，△ABC周长为36cm，把其边AC对折，使点C、A重合，折痕交BC 边于点D，交AC边于点E，连结AD，若AE=6cm，则△ABD的周长是（）A．24cm B．26cm C．28cm D．30cm【考点】翻折变换（折叠问题）．【分析】根据翻折变换的性质可得AE=EC，AD=CD，然后求出△ABD的周长=AB+BC，代入数据计算即可得解．【解答】解：∵△ABC的边AC对折顶点C和点A重合，∴AE=EC，AD=CD，∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC，∵AE=6cm，∴AC=AE+EC=6+6=12，∵△ABC的周长为36cm，∴AB+BC=36﹣12=24cm，∴△ABD的周长是24cm．故选A．【点评】本题考查了翻折变换的性质，熟记翻折前后的两个图形能够完全重合得到相等的边是解题的关键．22．如图，矩形ABCD中，AB=8，把矩形沿直线AC折叠，点B落在点E处，AE交CD于点F，若AF=，则AD的长为（）A．3 B．4 C．5 D．6【考点】翻折变换（折叠问题）．【分析】根据平行线的性质和翻转变换的性质得到FD=FE，FA=FC，根据勾股定理计算即可．【解答】解：∵DC∥AB，∴∠FCA=∠CAB，又∠FAC=∠CAB，∴∠FAC=∠FCA，∴FA=FC=，∴FD=FE，∵DC=AB=8，AF=，∴FD=FE=8﹣=，∴AD=BC=EC==6，故选：D．【点评】本题考查的是翻转变换的性质，翻转变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．23．如图的实线部分是由Rt△ABC经过两次折叠得到的，首先将Rt△ABC沿BD折叠，使点C落在斜边上的点C′处，再沿DE折叠使点A落在DC′延长线上的点A′处，若图中，∠A=30°，BC=5cm，则折痕DE的长为（）A．B．2C．2D．【考点】翻折变换（折叠问题）．【分析】根据直角三角形两锐角互余求出∠ABC=60°，翻折前后两个图形能够互相重合可得∠BDC=∠BDC′，∠CBD=∠ABD=30°，∠ADE=∠A′DE，然后求出∠BDE=90°，再解直角三角形求出BD，然后求出DE即可．【解答】解：∵△ABC是直角三角形，∠A=30°，∴∠ABC=90°﹣30°=60°，∵将Rt△ABC沿BD折叠，使点C落在斜边上的点C′处，∴∠BDC=∠BDC′，∠CBD=∠ABD=∠ABC=30°，∵沿DE折叠点A落在DC′的延长线上的点A′处，∴∠ADE=∠A′DE，∴∠BDE=∠ABD+∠A′DE=×180°=90°，在Rt△BCD中，BD=BC÷cos30°=5÷=cm，在Rt△BDE中，DE=BD•tan30°=×=cm．故选：D．【点评】本题考查了翻折变换的性质，解直角三角形，熟记性质并分别求出有一个角是30°角的直角三角形是解题的关键．24．如图一直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（）A．2cm B．3cm C．4cm D．5cm【考点】翻折变换（折叠问题）．【分析】首先根据题意得到：△AED≌△ACD；进而得到AE=AC=6，DE=CD；根据勾股定理求出AB=10；再次利用勾股定理列出关于线段CD的方程，问题即可解决．【解答】解：由勾股定理得：==10，由题意得：△AED≌△ACD，∴AE=AC=6，DE=CD（设为x）；∠AED=∠C=90°，∴BE=10﹣6=4，BD=8﹣x；由勾股定理得：（8﹣x）2=42+x2，解得：x=3（cm），故选B．【点评】该命题主要考查了翻折变换及其应用问题；解题的关键是借助翻折变换的性质，灵活运用勾股定理、全等三角形的性质等几何知识来分析、判断、推理或解答．25．如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为（）A．6 B．8 C．10 D．12【考点】翻折变换（折叠问题）．【分析】因为BC为AF边上的高，要求△AFC的面积，求得AF即可，求证△AFD′≌△CFB，得BF=D′F，设D′F=x，则在Rt△AFD′中，根据勾股定理求x，于是得到AF=AB﹣BF，即可得到结果．【解答】解：易证△AFD′≌△CFB，∴D′F=BF，设D′F=x，则AF=8﹣x，在Rt△AFD′中，（8﹣x）2=x2+42，解之得：x=3，∴AF=AB﹣FB=8﹣3=5，∴S△AFC=•AF•BC=10．故选C．【点评】本题考查了翻折变换﹣折叠问题，勾股定理的正确运用，本题中设D′F=x，根据直角三角形AFD′中运用勾股定理求x是解题的关键．26．如图，矩形ABCD中，AB=3，AD=9，将此矩形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（）A．6 B．8 C．10 D．12【考点】翻折变换（折叠问题）．【分析】根据折叠的条件可得：BE=DE，在直角△ABE中，利用勾股定理就可以求解．【解答】解：将此长方形折叠，使点B与点D重合，∴BE=ED．∵AD=AE+DE=AE+BE=9．∴BE=9﹣AE，根据勾股定理可知AB2+AE2=BE2．解得AE=4．∴△ABE的面积为3×4÷2=6．故选：A．【点评】本题考查了利用勾股定理解直角三角形的能力，即：直角三角形两直角边的平方和等于斜边的平方．27．如图所示，有一块直角三角形纸片，∠C=90°，AC=2，BC=，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为（）A．B．C．1 D．【考点】翻折变换（折叠问题）．【分析】由有一块直角三角形纸片，∠C=90°，AC=2，BC=，利用勾股定理即可求得AB的长，然后由折叠的性质，求得AE的长，继而求得答案．【解答】解：∵∠C=90°，AC=2，BC=，∴AB==，由折叠的性质可得：AE=AB=，∴CE=AE﹣AC=．故选A．【点评】此题考查了折叠的性质以及勾股定理．注意掌握折叠前后图形的对应关系是解此题的关键．28．如图所示，折叠平行四边形的一边AD，使点A落在DC边上的点E处，已知AB=6，BC=4，则EC的长为（）A．1 B．2 C．3 D．1.5【考点】翻折变换（折叠问题）．【分析】利用平行四边形的对边相等得到AD=BC=4，DC=AB=6，再由折叠的性质得到DE=AD，由DC﹣DE求出EC的长即可．【解答】解：由折叠及平行四边形的性质得：AE=AD=BC=4，DC=AB=6，则EC=DC﹣DE=6﹣4=2，故选B．【点评】此题考查了翻折变换（折叠问题），以及平行四边形的性质，熟练掌握折叠的性质是解本题的关键．29．如图，正方形ABCD中，AB=12，点E在边BC上，BE=EC，将△DCE沿DE对折至△DFE，延长EF交边AB于点G，连接DG、BF，给出以下结论：。

三角形全等的判定(6种题型)-2023年新八年级数学核心知识点与常见题型(浙教版)(解析版)

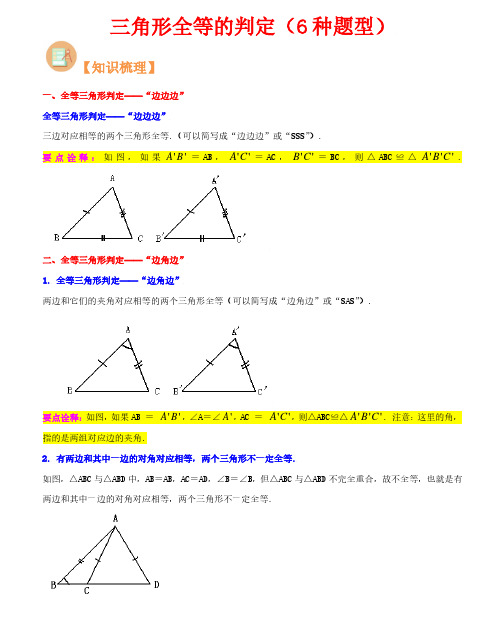
三角形全等的判定（6种题型）【知识梳理】一、全等三角形判定——“边边边”全等三角形判定——“边边边”三边对应相等的两个三角形全等.（可以简写成“边边边”或“SSS ”）.要点诠释：如图，如果''A B ＝AB ，''A C ＝AC ，''B C ＝BC ，则△ABC ≌△'''A B C .二、全等三角形判定——“边角边”1. 全等三角形判定——“边角边”两边和它们的夹角对应相等的两个三角形全等（可以简写成“边角边”或“SAS ”）.要点诠释：如图，如果AB ＝ ''A B ，∠A ＝∠'A ，AC ＝ ''A C ，则△ABC ≌△'''A B C . 注意：这里的角，指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等，两个三角形不一定全等.如图，△ABC 与△ABD 中，AB ＝AB ，AC ＝AD ，∠B ＝∠B ，但△ABC 与△ABD 不完全重合，故不全等，也就是有两边和其中一边的对角对应相等，两个三角形不一定全等.三、垂直平分线：1.定义：垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.2.性质定理：线段垂直平分线上的点到线段两端的距离相等四、全等三角形判定——“角边角”全等三角形判定——“角边角”两角和它们的夹边对应相等的两个三角形全等（可以简写成“角边角”或“ASA ”）.要点诠释：如图，如果∠A ＝∠'A ，AB ＝''A B ，∠B ＝∠'B ，则△ABC ≌△'''A B C .五、全等三角形判定——“角角边” 1.全等三角形判定——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等（可以简写成“角角边”或“AAS ”）要点诠释：由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等，也就是说，用角边角条件可以证明角角边条件，后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图，在△ABC 和△ADE 中，如果BC ，那么∠ADE ＝∠B ，∠AED ＝∠C ，又∠A ＝∠A ，但△ABC 和△ADE 不全等.这说明，三个角对应相等的两个三角形不一定全等.六、角平分线的性质定理:角平分线上的点到角两边的距离相等.【考点剖析】题型一、全等三角形的判定——“边边边”例1、已知：如图，△RPQ 中，RP ＝RQ ，M 为PQ 的中点．求证：RM 平分∠PRQ ．【思路点拨】由中点的定义得PM ＝QM ，RM 为公共边，则可由SSS 定理证明全等.【答案与解析】证明：∵M 为PQ 的中点（已知），∴PM ＝QM在△RPM 和△RQM 中，()(),,RP RQ PM QM RM RM ⎧=⎪=⎨⎪=⎩已知公共边 ∴△RPM ≌△RQM （SSS ）．∴ ∠PRM ＝∠QRM （全等三角形对应角相等）．即RM 平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到，如：公共边、公共角、对顶角等条件隐含在题目或图形之中. 用全等三角形的性质和判定.【变式】已知：如图，AD ＝BC ，AC ＝BD.试证明：∠CAD ＝∠DBC.【答案】证明：连接DC ，在△ACD 与△BDC 中()AD BC AC BDCD DC ⎧=⎪=⎨⎪=⎩公共边 ∴△ACD≌△BDC（SSS ）∴∠CAD ＝∠DBC （全等三角形对应角相等）【变式2】、如图，在△ABC 和△ADE 中，AB ＝AC ，AD ＝AE ，BD ＝CE ，求证：∠BAD ＝∠CAE.【答案与解析】证明：在△ABD 和△ACE 中，AB AC AD AE BD CE =⎧⎪=⎨⎪=⎩∴△ABD ≌△ACE （SSS ）∴∠BAD ＝∠CAE （全等三角形对应角相等）.【总结升华】把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等，综合应用全等三角形的判定和性质. 要证∠BAD ＝∠CAE ，先找出这两个角所在的三角形分别是△BDA 和△CAE ，然后证这两个三角形全等.题型二、全等三角形的判定——“边角边”例2、已知：如图，AB ＝AD ，AC ＝AE ，∠1＝∠2．求证：BC ＝DE ．【思路点拨】由条件AB ＝AD ，AC ＝AE ，需要找夹角∠BAC 与∠DAE ，夹角可由等量代换证得相等.【答案与解析】证明： ∵∠1＝∠2∴∠1＋∠CAD ＝∠2＋∠CAD ，即∠BAC ＝∠DAE在△ABC 和△ADE 中AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE （SAS ）∴BC ＝DE （全等三角形对应边相等）【总结升华】证明角等的方法之一：利用等式的性质，等量加等量，还是等量.【变式】如图，将两个一大、一小的等腰直角三角尺拼接（A 、B 、D 三点共线，AB ＝CB ，EB ＝DB ，∠ABC ＝∠EBD ＝90°），连接AE 、CD ，试确定AE 与CD 的位置与数量关系，并证明你的结论．【答案】AE ＝CD ，并且AE ⊥CD证明：延长AE 交CD 于F ，∵△ABC 和△DBE 是等腰直角三角形∴AB ＝BC ，BD ＝BE在△ABE 和△CBD 中90AB BC ABE CBD BE BD =⎧⎪∠=∠=︒⎨⎪=⎩∴△ABE ≌△CBD （SAS ）∴AE ＝CD ，∠1＝∠2又∵∠1＋∠3＝90°，∠3＝∠4（对顶角相等）∴∠2＋∠4＝90°，即∠AFC ＝90°∴AE ⊥CD例3、如图，AD 是△ABC 的中线，求证：AB ＋AC ＞2AD ．【思路点拨】延长AD 到点E ，使AD ＝DE ，连接CE ．通过证全等将AB 转化到△CEA 中，同时也构造出了2AD ．利用三角形两边之和大于第三边解决问题.【答案与解析】证明：如图，延长AD 到点E ，使AD ＝DE ，连接CE ．在△ABD 和△ECD 中，AD DE ADB EDC BD CD ⎧⎪∠∠⎨⎪⎩＝＝＝．∴△ABD ≌△ECD （SAS ）．∴AB ＝CE ．∵AC ＋CE ＞AE ，∴AC ＋AB ＞AE ＝2AD ．即AC ＋AB ＞．【总结升华】证明边的大小关系主要有两个思路：（1）两点之间线段最短；（2）三角形的两边之和大于第三边．要证明AB ＋AC ＞2AD ，如果归到一个三角形中，边的大小关系就是显然的，因此需要转移线段，构造全等三角形是转化线段的重要手段．可利用旋转变换，把△ABD 绕点D 逆时针旋转180°得到△CED ，也就把AB 转化到△CEA 中，同时也构造出了2AD ．若题目中有中线，倍长中线，利用旋转变换构造全等三角形是一种重要方法．例4、已知，如图：在△ABC 中，∠B ＝2∠C ，AD ⊥BC ，求证：AB ＝CD －BD ．【思路点拨】在DC 上取一点E ，使BD ＝DE ，则△ABD ≌△AED ，所以AB ＝AE ，只要再证出EC ＝AE 即可．【答案与解析】证明：在DC 上取一点E ，使BD ＝DE∵ AD ⊥BC ，∴∠ADB ＝∠ADE在△ABD 和△AED 中，BD DE ADB=ADE AD AD ⎧⎪⎨⎪⎩＝∠∠＝∴△ABD ≌△AED （SAS ）．∴AB ＝AE ，∠B ＝∠AED ．又∵∠B ＝2∠C ＝∠AED ＝∠C ＋∠EAC ．∴∠C ＝∠EAC ．∴AE ＝EC ．∴AB ＝AE ＝EC ＝CD —DE ＝CD —BD ．【总结升华】此题采用截长或补短方法.上升到解题思想，就是利用翻折变换，构造的全等三角形，把条件集中在基本图形里面，从而使问题加以解决．如图，要证明AB ＝CD －BD ，把CD －BD 转化为一条线段，可利用翻折变换，把△ABD 沿AD 翻折，使线段BD 运动到DC 上，从而构造出CD －BD ，并且也把∠B 转化为∠AEB ，从而拉近了与∠C 的关系.【变式】已知，如图，在四边形ABCD 中，AC 平分∠BAD ，CE ⊥AB 于E ，并且AE ＝12（AB ＋AD ），求证：∠B ＋∠D ＝180°. AE D CB【答案】证明：在线段AE 上，截取EF ＝EB ，连接FC ，∵CE ⊥AB ，∴∠CEB ＝∠CEF ＝90°在△CBE 和△CFE 中，CEB CEF EC =EC EB EF =⎧⎪∠=∠⎨⎪⎩∴△CBE 和△CFE （SAS ）∴∠B ＝∠CFE∵AE ＝12（AB ＋AD ），∴2AE ＝ AB ＋AD ∴AD ＝2AE －AB∵AE ＝AF ＋EF ，∴AD ＝2（AF ＋EF ）－AB ＝2AF ＋2EF －AB ＝AF ＋AF ＋EF ＋EB －AB ＝AF ＋AB －AB ，即AD ＝AF在△AFC 和△ADC 中(AF AD FAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义）∴△AFC ≌△ADC （SAS ）∴∠AFC ＝∠D∵∠AFC ＋∠CFE ＝180°，∠B ＝∠CFE.∴∠AFC ＋∠B ＝180°，∠B ＋∠D ＝180°.题型三、全等三角形的判定——“角边角”例5、已知：如图，E ，F 在AC 上，AD ∥CB 且AD ＝CB ，∠D ＝∠B ．求证：AE ＝CF ．【答案与解析】证明：∵AD ∥CB∴∠A ＝∠C在△ADF 与△CBE 中A C AD CB D B ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADF ≌△CBE （ASA ）∴AF ＝CE ，AF ＋EF ＝CE ＋EF故得：AE ＝CF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下：(1)找到以待证角(线段)为内角(边)的两个三角形；(2)证明这两个三角形全等；(3)由全等三角形的性质得出所要证的角(线段)相等．【变式】（2022•长安区一模）已知：点B 、E 、C 、F 在一条直线上，AB ∥DE ，AC ∥DF ，BE ＝CF ．求证：△ABC ≌△DEF ．【分析】先利用平行线的性质得到∠B＝∠DEF，∠ACB＝∠F，再证明BC＝EF，然后根据“ASA”可判断△ABC≌△DEF．【解答】证明：∵AB∥DE，∴∠B＝∠DEF，∵AC∥DF，∴∠ACB＝∠F，∵BE＝CF，∴BE+EC＝CF+EC，即BC＝EF，在△ABC和△DEF中，{∠B=∠DEF BC=EF∠ACB=∠F，∴△ABC≌△DEF（ASA）．5种判定方法是解决问题的关键．选用哪一种判定方法，取决于题目中的已知条件．例6、如图，G是线段AB上一点，AC和DG相交于点E.请先作出∠ABC的平分线BF，交AC于点F；然后证明：当AD∥BC，AD＝BC，∠ABC＝2∠ADG时，DE＝BF.【思路点拨】通过已知条件证明∠DAC＝∠C，∠CBF＝∠ADG，则可证△DAE≌△BCF【答案与解析】证明：∵AD∥BC，∴∠DAC＝∠C∵BF平分∠ABC∴∠ABC＝2∠CBF∵∠ABC＝2∠ADG∴∠CBF＝∠ADG在△DAE 与△BCF 中⎪⎩⎪⎨⎧∠=∠=∠=∠C DAC BCAD CBF ADG ∴△DAE≌△BCF（ASA ）∴DE＝BF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下：(1)找到以待证角(线段)为内角(边)的两个三角形；(2)证明这两个三角形全等；(3)由全等三角形的性质得出所要证的角(线段)相等．【变式】已知：如图，在△MPN 中，H 是高MQ 和NR 的交点，且MQ ＝NQ ．求证：HN ＝PM.【答案】证明：∵MQ 和NR 是△MPN 的高，∴∠MQN ＝∠MRN ＝90°，又∵∠1＋∠3＝∠2＋∠4＝90°，∠3＝∠4∴∠1＝∠2在△MPQ 和△NHQ 中，12MQ NQ MQP NQH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MPQ ≌△NHQ （ASA ）∴PM ＝HN题型四、全等三角形的判定——“角角边”例7.（2021秋•苏州期末）如图，在四边形ABCD 中，E 是对角线AC 上一点，AD ∥BC ，∠ADC ＝∠ACD ，∠CED +∠B ＝180°．求证：△ADE ≌△CAB ．【分析】由等角对等边可得AC＝AD，再由平行线的性质可得∠DAE＝∠ACB，由∠CED+∠B＝180°，∠CED+∠AED＝180°，得∠AED＝∠B，从而利用AAS可判定△ADE≌△CAB．【解答】证明：∵∠ADC＝∠ACD，∴AD＝AC，∵AD∥BC，∴∠DAE＝∠ACB，∵∠CED+∠B＝180°，∠CED+∠AED＝180°，∴∠AED＝∠B，在△ADE与△CAB中，{∠DAE=∠ACB ∠AED=∠BAD=AC，∴△ADE≌△CAB（AAS）．【点评】本题主要考查全等三角形的判定，解答的关键是由已知条件得出相应的角或边的关系．例8、已知：如图，AB⊥AE，AD⊥，∠E＝∠B，DE＝CB．求证：AD＝AC．【思路点拨】要证AC＝AD，就是证含有这两个线段的三角形△BAC≌△EAD.【答案与解析】证明：∵AB⊥AE，AD⊥AC，∴∠CAD＝∠BAE＝90°∴∠CAD＋∠DAB＝∠BAE＋∠DAB ，即∠BAC＝∠EAD在△BAC和△EAD中BAC EAD B E CB=DE ∠=∠⎧⎪∠=∠⎨⎪⎩∴△BAC ≌△EAD （AAS ）∴AC ＝AD【总结升华】我们要善于把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等．题型五：线段的垂直平分线例9．（2023秋·浙江杭州·八年级校考开学考试）如图所示，在ABC 中，8AC =，5BC =，AB 的垂直平分线DE 交AB 于点D ，交AC 于点E ，则BCE 的周长为（）A ．13B ．18C ．10.5D ．21【答案】A 【分析】根据线段垂直平分线的性质得到AE BE =，再将BCE 的周长转化为AC BC +的长，即可求解.【详解】解：DE 是AB 的垂直平分线，∴AE BE =，∴BCE 的周长为BE EC BC AE EC BC AC BC ++=++=+，8AC =，5BC =，∴BCE 的周长为8513AC BC +=+=，故选：A ．【点睛】本题主要考查的是线段垂直平分线的性质，掌握线段垂直平分线的性质是解题的关键．【变式1】（2022秋·浙江温州·八年级校考期中）如图，点D 是ABC 边AC 的中点，过点D 作AC 的垂线交BC 于点E ，已知6AC =，ABC 的周长为14，则ABE 的周长是（）A ．6B ．14C ．8D ．20【答案】C 【分析】由题意可知：ED 垂直平分AC ,故EA EC =，结合6AC =，ABC 的周长为14，即可得出答案．【详解】解：∵点D 是ABC 边AC 的中点， ED AC ⊥,∴ED 垂直平分AC ,∴EA EC =，∵6AC =，ABC 的周长为14，∴1468AB BC +=−=,∴8AB BC AB BE EC AB BE AE +=++=++=,∴ABE 的周长是8．故选：C ．【点睛】此题考查了垂直平分线的性质和判定，掌握垂直平分线的性质和判定是解题的关键．【答案】C 【分析】根据垂直平分线的性质可知，到A ，B ，C 表示三个居民小区距离相等的点，是AC ，BC 两边垂直平分线的交点，由此即可求解．【详解】解：如图所示，分别作AC ，BC 两边垂直平分线MN ，PQ 交于点O ，连接OA，OB，OC，∵MN，PQ是AC，BC两边垂直平分线，==，∴OA OB OC∴点O是到三个小区的距离相等的点，即点O是AC，BC两边垂直平分线的交点，故选：C．【点睛】本题主要考查垂直平分线的性质，掌握垂直平分线的性质是解题的关键．八年级专题练习）如图，在ABC中，是ABC外的一点，且【分析】根据到线段两端距离相等的点在线段的垂直平分线上，即可证明A、D都在BC的垂直平分线上，由此即可证明结论．AB AC，【详解】证明：∵=∴点A在BC的垂直平分线上，BD CD，∵=∴点D在BC的垂直平分线上，∴A、D都在BC的垂直平分线上，∴AD垂直平分BC．【点睛】本题主要考查了线段垂直平分线的判定，熟知线段垂直平分线的判定条件是解题的关键．【变式】．（2022秋·浙江·八年级专题练习）如图，点E是△ABC的边AB的延长线上一点，∠BCE＝∠A＋∠ACB，求证：点E在BC的垂直平分线上．【分析】由三角形的外角性质得到∠EBC=∠A+∠ACB，结合已知推出∠BCE=∠EBC，得到BE=CE，即可得到结论．【详解】证明：∵∠BCE=∠A+∠ACB，∠EBC=∠A+∠ACB，∴∠BCE=∠EBC，∴BE=CE，∴点E在BC的垂直平分线上．【点睛】本题考查了三角形的外角性质，线段垂直平分线的判定，用到的知识点：到线段两端点的距离相等的点在线段的垂直平分线上．题型六：角平分线【答案】A【分析】根据角平分线上的点到两边的距离相等即可解答．【详解】根据题意要使集贸市场到三条公路的距离相等即集贸市场应建在三个角的角平分线的交点．故本题选A ．【点睛】本题考查了角平分线的性质，熟记角平分线的性质是解答本题的关键．的中点，ABC ，则BED 的面积为（【答案】C【分析】作DF AC ⊥于F ，DM AB ⊥于点M ，根据角平分线的性质求出DM ，根据三角形的面积公式计算即可．【详解】解：作DF AC ⊥于F ，DM AB ⊥于点MAD 是ABC 的角平分线DF AC ⊥于F ，DM AB ⊥，112122AC DF AB DM ∴⋅+⋅=，112122AC DM AB DM ⋅+⋅=∴即：3421DM DM +=得3DM =8AB =， E 是AB 的中点，142BE AB ∴== 1143622BEDS BE DM ∴=⋅=⨯⨯= 故选：C ．【点睛】本题考查了角平分线上的点到角的两边距离相等的性质，三角形的面积，熟记性质并利用三角形的面积列出方程是解题的关键．例12．（2022秋·浙江·八年级专题练习）已知：如图，90B C ∠=∠=，M 是BC 的中点，DM 平分ADC ∠．(1)若连接AM ，则AM 是否平分BAD ∠？请你证明你的结论；(2)线段DM 与AM 有怎样的位置关系？请说明理由．【答案】(1)AM 平分BAD ∠，证明见解析(2)DM AM ⊥，理由见解析【分析】（1）过点M 作ME AD ⊥，垂足为E ，证明ME MC MB ==即可得证．（2）利用两直线平行，同旁内角互补，证明1390∠+∠=．【详解】（1）AM 平分BAD ∠，理由为：证明：过点M 作ME AD ⊥，垂足为E ，∵DM 平分ADC ∠，∴12∠=∠，∵ME AD ⊥，MC CD ⊥∴MC ME =（角平分线上的点到角两边的距离相等），又∵MC MB =，∴ME MB =，∵MB AB ⊥，ME AD ⊥，∴AM 平分BAD ∠（到角的两边距离相等的点在这个角的平分线上）．（2）DM AM ⊥，理由如下：∵90B C ∠=∠=，∴,DC CB AB CB ⊥⊥，∴DC AB ∥（垂直于同一条直线的两条直线平行），∴180DAB CDA ∠+∠=（两直线平行，同旁内角互补）又∵111,322CDA DAB ∠=∠∠=∠（角平分线定义） ∴2123180∠+∠=，∴1390∠+∠=，∴90AMD ∠=．即DM AM ⊥．【点睛】本题考查了角平分线的性质定理和判定定理，平行线的性质，熟练掌握以上的知识是解题的关键．【变式1】（2023秋·浙江台州·八年级统考期末）如图 90B C ∠=∠=︒，E 为BC 上一点，AE 平分BAD ∠，DE 平分CDA ∠．(1)求AED ∠的度数；(2)求证：E 是BC 的中点．【答案】(1)90︒(2)见解析．【分析】（1）利用已知条件可以得到180BAD CDA ∠+∠=︒，想要求AED ∠的度数，只需要根据三角形内角和定理和角平分线的性质即可得到结论．（2）过点E 做EF AD ⊥，根据角平分线上的点到角的两边距离相等即可得结论．【详解】（1）解：∵90B C ∠=∠=︒，∴DC AB ∥，∴180BAD CDA ∠+∠=︒，∵AE 平分BAD ∠，DE 平分CDA ∠， ∴12EAD BAD ∠=∠，12EDA CDA ∠=∠， ∴1()902EAD EDA BAD CDA ∠+∠=∠+∠=︒，∴180()90AED EAD EDA ∠=︒−∠+∠=︒；（2）证明：过点E 作EF AD ⊥于点F ，∵AE 平分BAD ∠，90B Ð=°，EF AD ⊥，∴EF EB =．∵DE 平分CDA ∠，90C ∠=︒，EF AD ⊥，∴EF EC =．∴EB EC =，即E 是BC 的中点．【点睛】本题考查了平行线的判定与性质，以及角平分线上的点到角两边距离相等的性质，熟记性质和定理并做出辅助线是解题的关键．【变式2】．（2022秋·浙江杭州·八年级校考期中）如图，在ABC 外作两个大小不同的等腰直角三角形，其中90DAB CAE ∠=∠=︒，AB AD =，AC AE =．连接DC 、BE 交于F 点．(1)求证：DAC BAE ≌△△； (2)直线DC 、BE 是否互相垂直，试说明理由；(3)求证：AF 平分DFE ∠．【答案】(1)见解析(2)DC BE ⊥，理由见解析(3)见解析【分析】（1）由题意可得AD AB =，AC AE =，由90DAB CAE ∠=∠=︒，可得到DAC BAE ∠=∠，从而可证DAC BAE ≌△△；（2）由（1）可得ACD AEB ∠=∠，再利用直角三角形的性质及等量代换即可得到结论；（3）作AM DC ⊥于M ，AN BE ⊥于N ，利用全等三角形的面积相等及角平分线的判定即可证得结论．【详解】（1）证明：∵90DAB CAE ∠=∠=︒，∴DAB BAC CAE BAC ∠+∠=∠+∠，即DAC BAE ∠=∠，又∵AD AB =，AC AE =，∴()SAS DAC BAE ≌△△；（2）解：DC BE ⊥，理由如下；∵DAC BAE ≌△△， ∴ACD AEB ∠=∠，∵90AEB AOE ∠+∠= ，AOE FOC ∠=∠，∴90FOC ACD ∠+∠=，∴90EFC ∠=，∴DC BE ⊥；（3）证明：作AM DC ⊥于M ，AN BE ⊥于N ，∵DAC BAE ≌△△， ∴DAC BAE S S ∆∆=，DC BE =， ∴1122DC AM BE AN ⋅=⋅，∴AM AN =，∴AF 平分DFE ∠．【点睛】本题主要考查全等三角形的判定和性质，及直角三角形的性质，角平分线的判定，熟练掌握判定和性质是解决本题的关键．【变式3】（2023春·浙江金华·八年级浙江省义乌市后宅中学校考阶段练习）已知：OP 平分MON ∠，点A ，B 分别在边OM ，ON 上，且180OAP OBP ∠∠+=︒．(1)如图1，当90OAP ∠=︒时，求证：OA OB =；(2)如图2，当90OAP ∠<︒时，作PC OM ⊥于点C ．求证：①PA PB =；②请直接写出OA ，OB ，AC 之间的数量关系．【答案】(1)见解析(2)①见解析；②2OA OB AC −=【分析】（1）证明()AAS OPA OPB ≌，即可得证；（2）①作PD ON ⊥于点D ，证明()AAS PAC PBD ≌，即可得证； ②证明()AAS OCP ODP ≌，得出OD =，根据AC BD =，即可得证．【详解】（1）证明：180OAP OBP ∠∠+=︒，且90OAP ∠=︒，90OAP OBP ∠∠∴==︒，OP 平分MON ∠，POA POB ∠∠∴=，OP OP =，()AAS OPA OPB ∴≌，OA OB ∴=；（2）证明：①如图2，作PD ON ⊥于点D ，PC OM ⊥于点C ，PC PD ∴=，90PCA PDB OCP ∠∠∠===︒，180OAP OBP ∠∠+=︒，180DBP OBP ∠∠+=︒，OAP DBP ∠∠∴=，在PAC 和PBD 中，CAP DBP PCA PDBPC PD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()AAS PAC PBD ∴≌， PA PB ∴=；②结论：2OA OB AC −=．理由：在OCP 和ODP 中，OCP ODP COP DOP OP OP ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AAS OCP ODP ∴≌，OC OD ∴=，OA AC OB BD ∴−=+，AC BD =，2OA OB AC BD AC ∴−=+=．故答案为：2OA OB AC −=．【点睛】本题考查了角平分线的性质，全等三角形的性质与判定，掌握全等三角形的性质与判定是解题的关键．【过关检测】一、单选题 1．（2022秋·浙江·八年级专题练习）如图，在ABC 中，90A ∠=︒，点D 是边AC 上一点，3DA =，若点D 到BC 的距离为3，则下列关于点D 的位置描述正确的是（）A ．点D 是AC 的中点B ．点D 是B ∠平分线与AC 的交点 C ．点D 是BC 垂直平分线与AC 的交点D ．点D 与点B 的距离为5【答案】B 【分析】作DE BC ⊥于E ，连接BD ，利用角平分线的判定定理可证明BD 是ABC ∠的角平分线，即可作答．【详解】解：如图所示：作DE BC ⊥于E ，连接BD ，∵3DA =，点D 到BC 的距离为3，∴=AD DE ，∵90A ∠=︒，∴DA BA ⊥，∵DE BC ⊥，∴BD 是ABC ∠的角平分线，即点D 是ABC ∠的角平分线与AC 的交点，故B 项正确；其余选项，利用现有条件均无法得出，故选：B ．【点睛】本题主要考查了角平分线的判定定理，作出辅助线，证明BD 是ABC ∠的角平分线，是解答本题的关键． 2．（2023·浙江·九年级专题练习）如图，已知BF DE =，AB ∥DC ，要使ABF CDE ≅△△，添加的条件可以是（）A．BE DF =B ．AF CE =C ．AB CD = D ．B D ∠=∠【答案】C 【分析】根据AB ∥DC ，可得B D ∠=∠，又BF DE =，所以添加AB CD =，根据SAS 可证ABF CDE ≅△△．【详解】解：应添加AB DC =，理由如下：AB ∥DC ，B D ∴∠=∠．在ABF △和CDE 中，AB CD B DBF DE =⎧⎪∠=∠⎨⎪=⎩，(SAS)ABF CDE ∴≅，故选：C ．【点睛】本题主要考查了平行线的性质以及全等三角形的判定，熟练掌握全等三角形的判定是解题的关键．3．（2023·浙江金华·统考二模）如图，ABC 和DEF 中，AB DE ∥，A D ∠=∠，点B ，E ，C ，F 共线，添加一个条件，不能判断ABC DEF ≌△△的是（）A ．AB DE =B ．ACB F ∠=∠C ．BE CF =D ．AC DF =【答案】B 【分析】根据AB DE ∥可得B DEF ∠=∠，加上A D ∠=∠，可知ABC 和DEF 中两组对角相等，因此一组对边相等时，即可判断ABC DEF ≌△△．【详解】解：AB DE ∥，∴B DEF ∠=∠，又A D ∠=∠，∴ABC 和DEF 中两组对角相等，当AB DE =时，根据ASA 可证ABC DEF ≌△△，故A 选项不合题意；当ACB F ∠=∠时，ABC 和DEF 中，三组对角相等，不能判断ABC DEF ≌△△，故B 选项符合题意；当BE CF =时，BC EF =，根据AAS 可证ABC DEF ≌△△，故C 选项不合题意；当AC DF =时，根据AAS 可证ABC DEF ≌△△，故D 选项不合题意；故选B ．【点睛】本题考查添加条件使三角形全等，解题的关键是熟练掌握全等三角形的各种判定方法．．ABC 的三条中线的交点．ABC 三边的垂直平分线的交点．ABC 三条角平分线的交点．ABC 三条高所在直线的交点【答案】C【分析】角平分线上的点到角的两边的距离相等，由此可解．【详解】解：要使凉亭到草坪三条边的距离相等，∴凉亭应在ABC 三条角平分线的交点处．故选C ．【点睛】本题考查了角平分线的性质，解题的关键是注意区分三角形中线的交点、高的交点、垂直平分线的交点以及角平分线的交点之间的区别． 5．（2020秋·浙江·八年级期末）如图，AD 是ABC 中BAC ∠的平分线，DE AB ⊥交AB 于点E ，DF AC ⊥交AC 于点F ，若7ABC S =△，2DE =，4AB =，则AC 的长为（）A ．3B ．4C ．5D ．6【答案】A 【分析】先根据角平分线的性质得到2DF DE ==，再利用三角形面积公式得到11242722AC ⨯⨯+⨯⨯=，然后解关于AC 的方程即可．【详解】解：∵AD 是BAC ∠的平分线，DE AB ⊥，DF AC ⊥，2DE =，∴2DF DE ==，∵7ABC S =△，4AB =，又∵ABD ACD ABC S S S +=△△△，∴111124272222AB DE DF AC AC ⋅+⋅=⨯⨯+⨯⨯=，∴3AC =．故选：A ．【点睛】本题考查角平分线的性质：角的平分线上的点到角的两边的距离相等．理解和掌握角平分线的性质是解题的关键．本题也考查了三角形的面积及等积变换．6．（2022秋·浙江·八年级专题练习）如图，用B C ∠=∠，12∠=∠，直接判定ABD ACD ≌△△的理由是（）A ．AASB ．SSSC ．ASAD ．SAS【答案】A 【分析】根据三角形全等的判定方法判定即可．【详解】解：在ABD △和ACD 中，12B CAD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴()AAS ABD ACD ≌，故A 正确．故选：A ．【点睛】本题主要考查三角形全等的判定，解题的关键是掌握证明全等三角形的几种证明方法：AAS 、ASA 、SSS 、SAS 、HL ．A ．2B ．【答案】C 【分析】由FC AB ∥，得F ADE ∠=∠,FCE A ∠=∠，即可根据全等三角形的判定定理“AAS”证明CFE ADE ≅，则4CF AD AB BD ==−=．【详解】解：FC AB ∥，F ADE ∴∠=∠，FCE A ∠=∠，在CFE 和ADE V 中，F ADE FCE AFE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AAS CFE ADE ∴≅， CF AD ∴=，5AB =，1BD =，514AD AB BD ∴=−=−=，4CF ∴=，CF ∴的长度为4．故选：C ．【点睛】此题重点考查平行线的性质、全等三角形的判定与性质等知识，正确地找到全等三角形的对应边和对应角并且证明CFE ADE ≅是解题的关键．A ．SSS【答案】B 【分析】根据已知条件两边，及两边的夹角是对顶角解答．【详解】解：在AOB 和COD △中，OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩，()AOB COD SAS ∴≌．故选：B ．【点睛】本题考查了全等三角形的应用，准确识图判断出两组对应边的夹角是对顶角是解题的关键． 9．（2022秋·浙江嘉兴·九年级校考期中）在联欢会上，有A 、B 、C 三名选手站在一个三角形的三个顶点位置上，他们在玩“抢凳子”游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放在ABC 的（）A ．三边垂直平分线的交点B ．三杂中线的交点C ．三条角平分线的交点D ．三条高所在直线的交点【答案】A【分析】根据题意可知，当木凳所在位置到A 、B 、C 三个顶点的距离相等时，游戏公平，再由线段垂直平分线的性质即可求解．【详解】解：由题意可得：当木凳所在位置到A 、B 、C 三个顶点的距离相等时，游戏公平，∵线段垂直平分线上的点到线段两端的距离相等，∴木凳应放的最适当的位置是在ABC 的三边垂直平分线的交点，故选：A ．【点睛】本题考查线段垂直平分线的性质的应用，掌握线段垂直平分线的性质是解题的关键．）可说明ABC 与△ 【答案】A 【分析】先根据垂直的定义可得90ACB ADB ∠=∠=︒，再根据角平分线的定义可得CAB DAB ∠=∠，然后根据AAS 定理即可得．【详解】解：,BC AC BD AD ⊥⊥，90ACB ADB ∴∠=∠=︒，AB 平分CAD ∠，CAB DAB ∴∠=∠，在ABC 和ABD △中，90ACB ADB CAB DABAB AB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，()AAS ABC ABD ∴≌，故选：A ．【点睛】本题主要考查了三角形全等的判定，熟练掌握三角形全等的判定方法是解题关键．二、填空题【答案】CA FD =，B E ∠=∠，A D ∠=∠，AB DE ∥等【分析】可选择CA FD =添加条件后，能用SAS 进行全等的判；也可选择B E ∠=∠添加条件后，能用ASA 进行全等的判定；也可选择A D ∠=∠添加条件后，能用AAS 进行全等的判定；也可选择AB DE ∥添加条件后，能用ASA 进行全等的判定即可；【详解】解：添加CA FD =，∵12∠=∠，BC EF =，∴()SAS ABC DEF ≌△△，故答案为：CA FD =；或者添加B E ∠=∠，∵BC EF =，12∠=∠，∴()ASA ABC DEF ≌△△，故答案为：B E ∠=∠；或者添加A D ∠=∠，∵12∠=∠，BC EF =，∴()AAS ABC DEF ≌△△，故答案为：A D ∠=∠；或者添加AB DE ∥，∵AB DE ∥，∴B E ∠=∠，∵12∠=∠，BC EF =，∴()AAS ABC DEF ≌△△，故答案为：AB DE ∥．【点睛】本题考查了全等三角形的判定，解答本题关键是掌握全等三角形的判定定理，本题答案不唯一．【答案】AB DC =【分析】添加条件AB DC =，利用SAS 证明ABC DCB △≌△即可．【详解】解：添加条件AB DC =，理由如下：在ABC 和DCB △中，AB DC ABC DCBBC CB =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS ABC DCB △≌△，故答案为：AB DC =．【点睛】本题主要考查了全等三角形的判定，熟知全等三角形的判定定理是解题的关键，全等三角形的判定定理有SSS SAS AAS ASA HL ，，，，． 13．（2023秋·浙江湖州·八年级统考期末）如图，已知AC DB =，要使得ABC DCB ≅，根据“SSS”的判定方法，需要再添加的一个条件是_______．【答案】ABDC =【分析】要使ABC DCB ≅，由于BC 是公共边，若补充一组边相等，则可用SSS 判定其全等．【详解】解：添加AB DC =．在ABC 和DCB △中AB DC BC CB AC BD =⎧⎪=⎨⎪=⎩， ∴()ABC DCB SSS ≅△△，故答案为：AB DC =．【点睛】本题考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．添加时注意：AAA 、SSA 不能判定两个三角形全等，不能添加，根据已知结合图形及判定方法选择添加的条件是正确解答本题的关键．14．（2022秋·浙江丽水·八年级统考期末）如图，在ABC 中，CD 是边AB 上的高，BE 平分ABC ∠，交CD 于点E ，6BC =，若BCE 的面积为9，则DE 的长为______．【答案】3【分析】过E 作EF BC ⊥于F ，根据角平分线性质求出EF DE =，根据三角形面积公式求出即可．【详解】解：过E 作EF BC ⊥于F ，CD 是AB 边上的高，BE 平分ABC ∠，交CD 于点E ，DE EF ∴=，192BCE S BC EF =⋅=，1692EF ∴⨯⨯=，3EF DE ∴==，故答案为：3．【点睛】本题考查了角平分线性质的应用，能根据角平分线性质求出3EF DE ==是解此题的关键，注意：在角的内部，角平分线上的点到角的两边的距离相等．八年级期末）如图，在ABC 中，【答案】4【分析】根据线段垂直平分线的性质得到2AD BD ==，则4CD AC AD =−=．【详解】解：∵AB 的垂直平分线交AB 于点E ，交AC 于点D ，∴2AD BD ==，∵6AC =，∴4CD AC AD =−=，故答案为：4．【点睛】本题主要考查了线段垂直平分线的性质，熟知线段垂直平分线上的点到线段两端的距离相等是解题的关键． 16．（2022秋·浙江温州·八年级校联考期中）如图，在ABC 中，DE 是AC 的中垂线，分别交AC ，AB 于点D ，E ．已知BCE 的周长为9，4BC =，则AB 的长为______．【答案】5【分析】先利用三角形周长得到5CE BE +=，再根据线段垂直平分线的性质得到EC EA =，然后利用等线段代换得到AB 的长．【详解】解：∵BCE 的周长为9，9CE BE BC ∴++=，又4BC =，5CE BE ∴+=，又DE 是AC 的中垂线，EC EA ∴=，5AB AE BE CE BE ∴=+=+=；故答案为：5．【点睛】本题考查了垂直平分线的性质：垂直平分线上任意一点，到线段两端点的距离相等．17．（2023秋·浙江杭州·八年级校考开学考试）如图，已知12∠=∠，要说明ABC BAD ≌，（1）若以“SAS ”为依据，则需添加一个条件是__________；（2）若以“ASA ”为依据，则需添加一个条件是__________．【答案】 BC AD = BAC ABD ∠=∠【分析】（1）根据SAS 可添加一组角相等，故可判定全等；（2）根据ASA 可添加一组角相等，故可判定全等；【详解】解：（1）已知一组角相等和一个公共边，以“SAS ”为依据，则需添加一组角，即BC AD =故答案为：BC AD =；（2）已知一组角相等，和一个公共边，以“ASA ”为依据，则需添加一组角，即BAC ABD ∠=∠．故答案为：BAC ABD ∠=∠．【点睛】本题主要考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS SAS ASA AAS HL 、、、、．添加时注意：AAA SSA 、不能判定两个三角形全等． 18．（2019秋·浙江嘉兴·八年级校考阶段练习）如图，点B 、E 、C 、F 在一条直线上，AB ∥DE ，AB=DE ，BE=CF ，AC=6，则DF=________【答案】6.【分析】根据题中条件由SAS 可得△ABC ≌△DEF ，根据全等三角形的性质可得AC=DF=6．【详解】∵AB ∥DE ，∴∠B=∠DEF∵BE=CF ，∴BC=EF ，在△ABC 和△DEF 中，AB DE B DEFBC EF =⎧⎪∠=∠⎨⎪=⎩，∴△ABC ≌△DEF （SAS ），∴AC=DF=6．考点：全等三角形的判定与性质．。

知识卡片-翻折变换(折叠问题)

翻折变换（折叠问题）能量储备● 翻折变换（折叠问题）实质上就是轴对称变换．● 折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．● 在解决实际问题时，对于折叠较为复杂的问题可以实际操作图形的折叠，这样便于找到图形间的关系．通关宝典★ 基础方法点方法点1.利用轴对称性质，解决折纸问题例1：将长方形纸片ABCD(如图①所示)按如下步骤操作：(1)以过点A 的直线为折痕折叠纸片，使点B 恰好落在AD 边上，折痕与BC 边交于点E(如图②所示)；(2)以过点E 的直线为折痕折叠纸片，使点A 落在EC 边上，折痕EF 交AD 边于点F(如图③所示)；(3)将纸片展平，那么∠AFE 的度数为( )A .60°B ．67.5°C ．72°D ．75°分析：根据轴对称的性质，可知第一次折叠后∠EAD ＝45°，∠AEC ＝135°；第二次折叠后，∠AEF ＝67.5°，∠FAE ＝45°，所以∠AFE ＝67.5°.解：B方法点2.折叠与剪纸的综合应用例1：请分析如图所示的图形，该怎样剪？设法使所剪的次数尽可能少．解：图(1)可以先折叠1次，剪出它的一半即可得到整个图形；图(2)可以折叠2次，剪出它的14即可得到整个图形．方法点3.解决矩形折叠问题的方法(1)利用折叠的性质：折叠前后的图形能够完全重合，折叠前后的图形对应边相等，对应角相等．(2)此类问题往往通过图形间的折叠找出折叠部分与原图形之间线段或角的联系，从而得到折叠部分与原图形或其他图形之间的关系．(3)尽量将数量关系利用勾股定理列方程．例1：如图所示，将矩形ABCD 沿对角线BD 折叠，点C 的对应点为点C′，BC′与AD 交于点E.若AD ＝8 cm ，AB ＝4 cm ，求△BDE 的面积．解：设DE ＝x cm ，则AE ＝(8－x)cm .由折叠的性质知△BCD 与△BC′D 全等，则∠1＝∠2.在矩形ABCD 中，∵ AD ∥BC ，∴ ∠1＝∠3，∴ ∠2＝∠3，∴ BE ＝DE ＝x.在Rt △ABE 中，由勾股定理，得BE 2＝AB 2＋AE 2，即x 2＝42＋(8－x)2，解得x ＝5.∴ △BDE 的面积为12DE·AB ＝12×5×4＝10(cm 2)． ★★ 易混易误点1.误认为折叠几次就有几条对称轴把一个图形沿一条直线折叠后，如果直线两旁的部分能够相互重合，这条直线才是这个轴对称图形的对称轴，并非是把这个图形折叠的次数当成对称轴的条数．例1：将一张正方形的纸沿对角线对折一次后得到等腰三角形，沿等腰三角形底边上的高对折一次，又得到等腰三角形，再沿着底边上的高对折一次，共对折了三次后，在中间剪去一个小圆，则展开后得到的图形至少有几条对称轴？解：4条．蓄势待发考前攻略折纸由于取材方便，又能有效地考查实践操作、归纳探索、逻辑推理、空间想象等各种能力，因而备受中考命题者的青睐，题型主要以选择题为主.完胜关卡。

全等三角形的图形全等变换

培养其合理猜想、探索、推理、论证能力。培养其独立思考、分析问题、解决问题的能力。
鼓励学生讨论、交流、探究，允许他们有不同的拼图方法和结论，培养其合作精神。
活动九
7.两个全等三角形的综合变换：
学生思考、探究解题思路和方法，小组合作交流;
师作图巡视、指导。
(1)一个长方形沿着一条对角线对折剪开,拼成如图位置的两个三角形,使点B、F、C、D在同一直线上.①求证:AB⊥DE;②若PB=BC,找出一对全等三角形,并证明出它们的正确性。
小结
学生谈感受和收获
培养学生的归纳总结能力
作业
教材P—114 （3）（5）（8）
选做题：上面活动九中的“迁移题”
分层次教学
板书
设计
略
注意渗透分类思想
活动七
5.两个全等三角形的“旋转”加“平移”变换：
学生演示，师作图指导。
特点：三角形旋转任一角度到不同位置再沿着某条直线平移到不同位置。（如图）
已知：等腰△ABC的直角顶点C放在直线a上,作AD⊥a于D,作BE⊥a于E.找出一对三角形,并证明它们是正确的结论.
结论: △ACD≌△CBE;
让学生从实践演示中探究三角形全等的结论，并迁移出其他正确结论。
活动四
2.两个全等三角形的“翻折”变换：
学生演示，师作图指导。
特点：沿着某条直线 “翻折1800”到不同位置。（如图）或沿着过某个点所在的直线“翻折”1800到不同位置。
结论：△ABC≌△ABD; △ABO≌△CDO.
迁移：连接CD,推导出CD被AB垂直平分;AB平分∠CAD。
全等三角形的图形全等变换
课题
全等三角形的图形全等变换
讲课教师
学校
时间

例谈数学翻折问题的解题方法

例谈初中数学翻折问题的解题方法翻折作为几何变换的一种,在中考试卷中愈来愈受命题人的青睐,主要原因是想通过在考査平面几何变换的基础知识点的同时也要学生学会掌握运用数学思想与方法解决问题的能力。

初中数学中的几何变换一般是指平移、对称（翻折）和旋转.《数学课程标准》在课程目标中已明确指出“经历探索物体与图形的基本性质、变换、位置关系的过程”，我们知道，图形的变换不改变图形的形状、大小，只改变图形的位置，故解题时可充分利用图形变换的特征，把图形位置进行改变，从而达到优化图形结构，进一步整合图形（题设）信息的目的，使较为复杂的问题得以创造性地解决。

要求初中阶段的学生理解基本的几何变换,通过有关数学知识的技能学习,逐步领会方程思想、函数思想、分类讨论思想等基本数学思想。

笔者下面以近几年各地中考中的翻折问题为例,简单叙述翻折问题的解答过程以及涉及到的数学思想与方法。

一、纸片中的折叠例1．如图，有一条直的宽纸带，按图折叠，则∠α的度数等于（）解：∵∠α = ∠1，∠2 = ∠1 ∴∠α = ∠2∴2∠α+∠AEB=180°，即2∠α+30°=180°，解得∠α=75°．本题考查的是平行线的性质，同位角相等，及对称的性质，折叠的角与其对应角相等，和平角为180度的性质，注意△EAB 是以折痕AB 为底的等腰三角形。

例2．如图，将一宽为2cm 的纸条，沿BC ，使∠CAB=45°，则后重合部分的面积为。

解：作CD ⊥AB ，∵CE ∥AB ，∴∠1=∠2，根据翻折不变性，∠1=∠BCA ，故∠2=∠BCA ． ∴AB=AC ．又∵∠CAB=45°，∴在Rt △ADC 中，AC = 2 2 ，AB = 2 2S △ＡＢＣ＝ 12AB ×CD = 2 2在折叠问题中，一般要注意折叠前后图形之间的联系，将图形补充完整，对于矩形（纸片）折叠，折叠后会形成“平行线+角平分线”的基本结构，即重叠部分是一个以折痕为底边的等腰三角形ABC 。

图形变换模型之翻折(折叠)模型(解析版)

图形变换模型之翻折(折叠)模型几何变换中的翻折(折叠、对称)问题是历年中考的热点问题，试题立意新颖，变幻巧妙，主要考查学生的识图能力及灵活运用数学知识解决问题的能力。

涉及翻折问题，以矩形对称最常见，变化形式多样。

无论如何变化，解题工具无非全等、相似、勾股以及三角函数，从条件出发，找到每种对称下隐藏的结论，往往是解题关键。

本专题以各类几个图形(三角形、平行四边形、菱形、矩形、正方形、圆等)为背景进行梳理及对应试题分析，方便掌握。

【知识储备】翻折和折叠问题其实质就是对称问题，翻折图形的性质就是翻折前后图形是全等的，对应的边和角都是相等的。

以这个性质为基础，结合三角形、四边形、圆的性质，三角形相似，勾股定理设方程思想来考查。

解决翻折题型的策略：1)利用翻折的性质：①翻折前后两个图形全等；②对应点连线被对称轴垂直平分；2)结合相关图形的性质(三角形，四边形等)；3)运用勾股定理或者三角形相似建立方程。

模型1.矩形中的翻折模型【模型解读】1(2023·辽宁鞍山·统考中考真题)如图，在平面直角坐标系中，矩形AOBC的边OB，OA分别在x轴、y轴正半轴上，点D在BC边上，将矩形AOBC沿AD折叠，点C恰好落在边OB上的点E处．若OA=8，OB=10，则点D的坐标是．【答案】10,3【分析】根据折叠的性质得出AE =AC =10，在Rt △AOE 中，勾股定理求得OE =6，进而得出BE =4，在Rt △DBE 中，勾股定理建立方程，求得BD 的长，即可求解．【详解】解：∵四边形AOBC 是矩形，∴AC =OB =10，∵折叠，∴AE =AC =10，在Rt △AOE 中，OE =AE 2-AO 2=102-82=6∴EB =OB -OE =10-6=4，∴设DB =m ，则CD =8-m ，∵折叠，∴DE =CD =8-m ，在Rt △DEB 中，DE 2=EB 2+BD 2，∴8-m 2=m 2+42，解得：m =3，∴DB =3，∴D 的坐标为10,3 ，故答案为：10,3 ．【点睛】本题考查矩形与折叠，勾股定理，坐标与图形，熟练掌握折叠的性质以及勾股定理是解题的关键．2(2023春·江苏泰州·八年级统考期中)如图，在矩形ABCD 中，AB =3，BC =8，E 是BC 的中点，将△ABE 沿直线AE 翻折，点落B 在点F 处，连结CF ，则CF 的长为()A.6B.325C.35D.254【答案】B【分析】连接BF 交AE 于点H ，根据三角形的面积公式求出BH ，得到BF ，根据直角三角形的判定得到∠BFC =90°，根据勾股定理求出答案．【详解】解：连接BF 交AE 于点H ，∵将△ABE 沿直线AE 翻折，点落B 在点F 处，∴点B 、F 关于AE 对称，∴BH =FH ，BF ⊥AE ，∵BC =8，点E 为BC 的中点，∴BE =4，又∵AB =3，∴AE =AB 2+BE 2=32+42=5，∴BH =3×45=125，则BF =245，∵FE =BE =EC ，∴∠BFC =90°，∴CF =BC 2-BF 2=82-245 2=325．故选：B ．【点睛】本题考查的是翻折变换的性质和矩形的性质，掌握折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解题的关键．3(2023·湖北·统考中考真题)如图，将边长为3的正方形ABCD 沿直线EF 折叠，使点B 的对应点M 落在边AD 上(点M 不与点A ,D 重合)，点C 落在点N 处，MN 与CD 交于点P ，折痕分别与边AB ，CD 交于点E ,F ，连接BM ．(1)求证：∠AMB =∠BMP ；(2)若DP =1，求MD 的长．【答案】(1)证明见解析(2)MD =125【分析】(1)由折叠和正方形的性质得到∠EMP =∠EBC =90°，EM =EB ，则∠EMB =∠EBM ，进而证明∠BMP =∠MBC ，再由平行线的性质证明∠AMB =∠MBC 即可证明∠AMB =∠BMP ；(2)如图，延长MN ,BC 交于点Q ．证明△DMP ∽△CQP 得到QC =2MD ，QP =2MP ，设MD =x ，则QC =2x ，BQ =3+2x ．由∠BMQ =∠MBQ ，得到MQ =BQ =3+2x ．则MP =13MQ =3+2x 3．由勾股定理建立方程x 2+12=3+2x 3 2，解方程即可得到MD =125．【详解】(1)证明：由翻折和正方形的性质可得，∠EMP =∠EBC =90°，EM =EB ．∴∠EMB =∠EBM ．∴∠EMP -∠EMB =∠EBC -∠EBM ，即∠BMP =∠MBC ，∵四边形ABCD 是正方形，∴AD ∥BC ．∴∠AMB =∠MBC ．∴∠AMB =∠BMP ．(2)解：如图，延长MN ,BC 交于点Q ．∵AD ∥BC ，∴△DMP ∽△CQP ．又∵DP =1，正方形ABCD 边长为3，∴CP =2∴MD QC =MP QP =DP CP=12，∴QC =2MD ，QP =2MP ，设MD =x ，则QC =2x ，∴BQ =3+2x ．∵∠BMP =∠MBC ，即∠BMQ =∠MBQ ，∴MQ =BQ =3+2x ．∴MP =13MQ =3+2x 3．在Rt △DMP 中，MD 2+DP 2=MP 2，∴x 2+12=3+2x 3 2．解得：x 1=0(舍)，x 2=125．∴MD =125．【点睛】本题主要考查了正方形与折叠问题，相似三角形的性质与判定，等腰三角形的性质与判定，勾股定理等等，正确作出辅助线构造相似三角形是解题的关键．4(2023春·江苏宿迁·八年级统考期末)如图，在矩形ABCD 中，AB =6，BC =8．点O 为矩形ABCD 的对称中心，点E为边AB上的动点，连接EO并延长交CD于点F．将四边形AEFD沿着EF翻折，得到四边形A EFD ，边A E交边BC于点G，连接OG、OC，则△OGC的面积的最小值为()A.18-3B.92+37 C.12-372D.6+372【答案】D【分析】在EA上截取EM=EG，连接OM，证明△MOE≌△GOE，所以OM=OG，即可得OM最短时，OG也就最短，而当OM⊥AB时，OM最短，且OM=4=OG，再过点O作OH⊥BC，得OH=3，又因为OC=5，就可以根据勾股定理计算GH、HC的长，从而计算出最小面积．【详解】解：在EA上截取EM=EG，连接OM，由折叠得：∠MEO=∠GEO，又∵EO=EO，∴△MOE≌△GOE SAS，∴OM=OG，∴OM最短时，OG也就最短，而当OM⊥AB时，OM最短，此时，∵点O为矩形ABCD的对称中心，∴OM=12BC=4=OG，即OG的最小值是4，在△OGC中，∵点O为矩形ABCD的对称中心，∴OC长度是矩形对角线长度的一半，即是5，定值，∠BCO度数也不变，是定值，∴当OG=4最小值时，ΔOGC面积最小．过点O作OH⊥BC，∵点O为矩形ABCD的对称中心， ∴OH=12AB=3，∴Rt△OGH中，GH=OG2-OH2=42-32=7，Rt△OHC中，HC=OC2-OH2=52-32=4，∴GC=GH+HC=7+4，∴△OGC面积的最小值是12×GC×OH=12×(7+4)×3=327+6．故选：D．【点睛】本题考查矩形的性质、全等三角形的判定与性质及垂线段最短等知识，解题关键是找到OG最小值．5(2023春·辽宁抚顺·八年级校联考期中)如图，矩形纸片ABCD中，AB=6，BC=10，点E、G分别在BC、AB上，将△DCE、△BEG分别沿DE、EG翻折，翻折后点C与点F重合，点B与点P重合．当A、P、F、E四点在同一直线上时，线段GP长为()A.832 B.83C.53D.532【答案】B【分析】据矩形的性质得到CD=AB=6，AD=BC=10，∠B=∠C=90°，据折叠的性质得到DF=CD =6，EF=CE，∠DFE=∠C=∠DFA=90°，根据勾股定理得到AF=8，设EF=CE=x，由勾股定理列方程得到AE=10，BE=8，由折叠的性质得到PG=BG，∠APG=∠EPG=∠B=90°，PE=BE=8，求得AP=AE-PE=2，设PG=BG=y，则AG=6-y，据勾股定理列方程即可得到结论．【详解】解：在矩形纸片ABCD中，AB=6，BC=10，∴CD=AB=6，AD=BC=10，∠B=∠C=90°，∵将△DCE沿DE翻折，翻折后点C与点F重合，∴DF=CD=6，EF=CE，∠DFE=∠C=∠DFA=90°，∴AF=AD2-DF2=102-62=8，设EF=CE=x，∴BE=10-x，AE=8+x，∵AB2+BE2=AE2，∴62+(10-x)2=(8+x)2，解得：x=2，∴AE=10，BE=8，∵将△BEG沿EG翻折，翻折后点B与点P重合，∴PG=BG，∠APG=∠EPG=∠B=90°，PE=BE=8，∴AP=AE-PE=2，设PG=BG=y，则AG=6-y，∵AG2=AP2+PG2，∴(6-y)2=22+y2，∴y=83，∴线段GP长为83，故选：B．【点睛】本题考查翻折变换(折叠问题)，矩形的性质，勾股定理，根据勾股定理列方程是解题关键．6(2023·江苏盐城·统考中考真题)综合与实践【问题情境】如图1，小华将矩形纸片ABCD先沿对角线BD折叠，展开后再折叠，使点B落在对角线BD 上，点B的对应点记为B ，折痕与边AD，BC分别交于点E，F.【活动猜想】(1)如图2，当点B 与点D重合时，四边形BEDF是哪种特殊的四边形？答：.【问题解决】(2)如图3，当AB=4，AD=8，BF=3时，求证：点A ，B ，C在同一条直线上.【深入探究】(3)如图4，当AB与BC满足什么关系时，始终有A B 与对角线AC平行？请说明理由. (4)在(3)的情形下，设AC与BD，EF分别交于点O，P，试探究三条线段AP，B D，EF之间满足的等量关系，并说明理由.【答案】(1)菱形；(2)证明见解答；(3)BC=3AB，证明见解析；(4)3EF=2(AP+B D)，理由见解析【分析】(1)由折叠可得：EF⊥BD，OB=OD，再证得△BFO≌△DEO(ASA)，可得OE=OF，利用菱形的判定定理即可得出答案；(2)设EF 与BD 交于点M ，过点B 作B K ⊥BC 于K ，利用勾股定理可得BD=45，再证明△BFM ∽△BDC ，可求得BM =655，进而可得BB =1255，再由△BB K ∽△BDC ，可求得B K =125，BK =245，CK =BC -BK =8-245=165，运用勾股定理可得B C =4，运用勾股定理逆定理可得∠CB F =90°，进而可得∠A B F +∠CB F =90°+90°=180°，即可证得结论；(3)设∠OAB =∠OBA =α，则∠OBC =90°-α，利用折叠的性质和平行线性质可得：∠AB ′B =∠AOB =α，再运用三角形内角和定理即可求得α=60°，利用解直角三角形即可求得答案；(4)过点E 作EG ⊥BC 于G ，设EF 交BD 于H ，设AE =m ，EF =n ，利用解直角三角形可得B D =BD-BB =3n -3m +12n =32n -3m ，AP =2AE ⋅cos30°=3m ，即可得出结论．【详解】解：(1)当点B 与点D 重合时，四边形BEDF 是菱形．理由：设EF 与BD 交于点O ，如图，由折叠得：EF ⊥BD ，OB =OD ，∴∠BOF =∠DOE =90°，∵四边形ABCD 是矩形，∴AD ∥BC ，∴∠OBF =∠ODE ，∴△BFO ≌△DEO (ASA )，∴OE =OF ，∴四边形BEDF 是菱形．故答案为：菱形．(2)证明：∵四边形ABCD 是矩形，AB =4，AD =8，BF =3，∴BC =AD =8，CD =AB =4，∠BCD =90°，∴CF =BC -BF =8-3=5，∴BD =BC 2+CD 2=82+42=45，如图，设EF 与BD 交于点M ，过点B ′作B K ⊥BC 于K ，由折叠得：∠A B F =∠ABF =∠BMF =∠B MF =90°，B F =BF =3，BB =2BM ，∴∠BMF =∠BCD ，∵∠FBM =∠DBC ，∴△BFM ∽△BDC ，∴BM BC =BF BD ，即BM 8=345，∴BM =655，∴BB =1255，∵∠BKB =∠BCD ，∠B BK =∠DBC ，∴△BB K ∽△BDC ，∴B K CD =BK BC=BB BD ，即B K 4=BK 8=125545，∴B K =125，BK =245，∴CK =BC -BK =8-245=165，∴B C =B K 2+CK 2=125 2+165 2=4，∵B F 2+B C 2=32+42=25，CF 2=52=25，∴B F 2+B C 2=CF 2，∴∠CB F =90°，∴∠A B F +∠CB F =90°+90°=180°，∴点A ′，B ′，C 在同一条直线上．(3)当BC =3AB 时，始终有A B 与对角线AC 平行．理由：如图，设AC 、BD 交于点O ，∵四边形ABCD是矩形，∴OA=OB，∠OBA+∠OBC=90°，∴∠OAB=∠OBA，设∠OAB=∠OBA=α，则∠OBC=90°-α，由折叠得：∠A B F=∠ABC=90°，B F=BF，∴∠BB F+∠A B B=90°，∠BB F=∠OBC=90°-α，∴∠AB B=∠OBA=α，∵A B∥AC，∴∠AB′B=∠AOB=α，∵∠OAB+∠OBA+∠AOB=180°，∴α+α+α=180°，即3α=180°，∴α=60°，∴∠BAC=60°，∴BCAB=tan∠BAC=tan60°=3，∴BC= 3AB；(4)3EF=2(AP+B′D)，理由如下：如图，过点E作EG⊥BC于G，设EF交BD于H，由折叠得：EF⊥BD，B F=BF，∠BFE=∠B FE，设AE=m，EF=n，由(3)得：∠BAC=60°=∠ABD，∴∠BB F=∠DBC=30°，∴∠BFE=∠B FE=60°，∴EG=EF⋅sin60°=32n，FG=EF⋅cos60°=12n，∵∠EAB=∠ABG=∠BGE=90°，∴四边形ABGE是矩形，∴AB=EG=32n，BG=AE=m，AD∥BC，∴BF=B F=m+12n，∴BH=BF⋅cos30°=32m+12n，∴BB =2BH=3m+12n，∵BD=2AB=3n，∴B D=BD-BB =3n-3m+12n=32n-3m，∵AD∥BC，∴∠DEF=∠EFG=60°，∴∠APE=∠DEF-∠DAC=60°-30°=30°=∠DAC，∴AP=2AE⋅cos30°=3m，∴AP+B D=3m+32n-3m=32n，∴AP+B D=32EF，即3EF=2(AP+B D)．【点睛】本题是四边形综合题，考查了矩形的性质和判定，菱形的判定，勾股定理，直角三角形性质，等腰三角形性质，平行线性质，全等三角形的判定和性质，相似三角形的判定和性质，解直角三角形等，涉及知识点多，综合性强，难度较大．模型2.正方形中的翻折模型【模型解读】7(2023·河南洛阳·统考二模)如图，正方形ABCD的边长为4，点F为CD边的中点，点P是AD边上不与端点重合的一动点，连接BP．将△ABP沿BP翻折，点A的对应点为点E，则线段EF长的最小值为()A.27B.25-4C.34D.37-2【答案】B【分析】先确定线段EF的最小值的临界点，然后结合正方形的性质，折叠的性质，以及勾股定理，即可求出答案．【详解】连接BF，则EF≥BF-BE，当点B、E、F在同一条直线上时，EF的长度有最小值，如图由翻折的性质，BE=AB=4，在正方形ABCD中，BC=CD=4，∠C=90°，∵点F为CD边的中点，∴CF=2，∴BF=42+22=25，∴EF=BF-BE=25-4；故选：B．【点睛】本题考查了正方形的性质，折叠的性质，勾股定理，最短路径问题，解题的关键掌握所学的知识，正确找出线段最小值的临界点，从而进行解题．8(2023·广西玉林·统考模拟预测)如图，在正方形ABCD的边AB上取一点E，连接CE，将△BCE沿CE 翻折，点B恰好与对角线AC上的点F重合，连接DF，若BE=2，则△CDF的面积是()A.1+324B.32+4 C.62+8 D.322【答案】B【分析】由折叠可得EF=BE=2，∠CFE=∠B=90°，且∠FAE=45°可得AF=2，AE=22，即可求对角线BD的长，则可求△CDF面积.【详解】如图连接BD交AC于O，∵ABCD为正方形，∴∠ABC=90°，AB=BC，AC⊥BD，DO=BO，∠BAC=45°，∵△BCE沿CE翻折，∴BE=EF=2，BC=CF，∠EFC=90°，∵∠BAC=45°，∠EFC=90°，∴∠EAF=∠AEF=45°，∴AF=EF=2，∴AE=22，∴AB=22+2=BC=CF，∴BD=2AB=4+22，∴OD=2+2，∵S△CDF=12×CF×DO=32+4，故选B．【点睛】本题考查翻折变换、正方形的性质、勾股定理、等腰三角形的判定和性质等知识，解题的关键是熟练应用所学知识解决问题．9(2023·广东九年级课时练习)如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF，则下列结论：①△ABG≌△AFG；②∠AGB+∠AED=135°③GF=3；④AG⎳CF；其中正确的有(填序号)．【答案】①②③④【分析】根据折叠，得到AD=AF，∠D=∠AFE=90°，推出AB=AF，∠AFG=∠B=90°，可证明Rt△ABG≌Rt△AFG，即可判断①正确；根据∠DAE=∠EAF,∠BAG=∠FAG，进而可得∠GAE=45°，根据三角形内角和定理即可得∠AEF+∠ADF=135°，得到∠AGB+∠AED=135°，进而判断②正确；设BG=GF=x，则CG=6-x，EG=x+2，CE=4，在Rt△EGC中，根据勾股定理建立方程(x+2)2= (6-x)2+42，解方程可得GF=3，即可判断③正确；根据BG=FG=3，得到CG=BC-BG=6-3=3，得到CG=FG，推出∠GCF=∠GFC，根据∠AGB=∠AGF，得到∠BGF=2∠AGF=2∠GFC，得到∠AGF=∠GFC，推出AG∥CF，即可判断④正确【详解】∵四边形ABCD是正方形，∴∠D=∠ABC=∠DAB=∠BCD=90°，AB=BC=CD=AD=6，∵CD=3DE，∴DE=2，∴CE=4，∵将△ADE沿AE对折至△AFE，∴∠AFE=∠ADE=90°，AF=AD，EF=DE=2，∴∠AFG=∠ABG=90°，AF=AB，在Rt△ABG和Rt△AFG中，AB=AF AG=AG，∴Rt△ABG≌Rt△AFG(HL)，∴①正确；∵将△ADE沿AE对折至△AFE，∴∠DAE=∠EAF，∵Rt△ABG≌Rt△AFG，∴∠BAG=∠FAG，∵∠DAE+∠EAF+∠BAG+∠FAG=∠DAB=90°，∴∠EAG=∠EAF+∠FAG=12∠DAB=45°，∴∠AEF+∠ADF=135°，∴∠AGB+∠AED=135°，∴②正确；设BG=GF=x，则CG=6-x，EG=x+2，∵CE=4，∴(x+2)2=(6-x)2+42，解得x=3，∴BG=GF=3，∴③正确；∵BG=FG=3,∴CG=BC-BG=6-3=3，∴CG=FG，∴∠GCF=∠GFC，∵∠AGB=∠AGF，∴∠BGF=2∠AGF=2∠GFC，∴∠AGF=∠GFC，∴AG∥CF∴④正确；故答案为：①②③④．【点睛】本题考查了正方形性质，折叠图形全等的性质，三角形全等的判断和性质，三角形内角和定理，勾股定理，熟练掌握以上知识是解题的关键．10(2023·江苏扬州·统考中考真题)如图，已知正方形ABCD的边长为1，点E、F分别在边AD、BC上，将正方形沿着EF翻折，点B恰好落在CD边上的点B 处，如果四边形ABFE与四边形EFCD的面积比为3∶5，那么线段FC的长为．【答案】3 8【分析】连接BB ，过点F作FH⊥AD于点H，设CF=x，则DH=x，则BF=1-x，根据已知条件，分别表示出AE,EH,HD，证明△EHF≌△B CB ASA，得出EH=B C=54-2x，在Rt△B FC中，B F2=BC2+CF2，勾股定理建立方程，解方程即可求解．【详解】解：如图所示，连接BB ，过点F作FH⊥AD于点H，∵正方形ABCD的边长为1，四边形ABFE与四边形EFCD的面积比为3∶5，∴S四边形ABFE =38×1=38，设CF=x，则DH=x，则BF=1-x∴S四边形ABFE =12AE+BF×AB=38即12AE+1-x×1=38∴AE=x-14∴DE=1-AE=54-x，∴EH=ED-HD=54-x-x=54-2x，∵折叠，∴BB ⊥EF，∴∠1+∠2=∠BGF=90°，∵∠2+∠3=90°，∴∠1=∠3，又FH=BC=1,∠EHF=∠C∴△EHF≌△B CB ASA，∴EH=B C=54-2x在Rt△B FC中，B F2=B C2+CF2即1-x2=x2+54-2x2解得：x=38，故答案为：38．【点睛】本题考查了正方形的性质，折叠的性质，勾股定理，全等三角形的性质与判定，熟练掌握以上知识是解题的关键．11(2023·江苏·统考中考真题)综合与实践定义：将宽与长的比值为22n+1-12n(n为正整数)的矩形称为n阶奇妙矩形．(1)概念理解：当n=1时，这个矩形为1阶奇妙矩形，如图(1)，这就是我们学习过的黄金矩形，它的宽(AD)与长CD的比值是．(2)操作验证：用正方形纸片ABCD进行如下操作(如图(2))：第一步：对折正方形纸片，展开，折痕为EF，连接CE；第二步：折叠纸片使CD落在CE上，点D的对应点为点H，展开，折痕为CG；第三步：过点G 折叠纸片，使得点A 、B 分别落在边AD 、BC 上，展开，折痕为GK ．试说明：矩形GDCK 是1阶奇妙矩形．(3)方法迁移：用正方形纸片ABCD 折叠出一个2阶奇妙矩形．要求：在图(3)中画出折叠示意图并作简要标注．(4)探究发现：小明操作发现任一个n 阶奇妙矩形都可以通过折纸得到．他还发现：如图(4)，点E 为正方形ABCD 边AB 上(不与端点重合)任意一点，连接CE ，继续(2)中操作的第二步、第三步，四边形AGHE 的周长与矩形GDCK 的周长比值总是定值．请写出这个定值，并说明理由．【答案】(1)5-12；(2)见解析；(3)12，理由见解析【分析】(1)将n =1代入22n +1-12n，即可求解．(2)设正方形的边长为2，根据折叠的性质，可得AE =EB =1，设DG =x ，则AG =2-x ，在Rt △AEG ,Rt △GHE 中，勾股定理建立方程，解方程，即可求解；(3)仿照(2)的方法得出2阶奇妙矩形．(4)根据(2)的方法，分别求得四边形AGHE 的周长与矩形GDCK 的周长，即可求解．【详解】解：(1)当n =1时，22n +1-12n=5-12，故答案为：5-12．(2)如图(2)，连接EG ，设正方形的边长为2，根据折叠的性质，可得AE =EB =1设DG =x ，则AG =2-x 根据折叠，可得GH =GD =x ，CH =CD =2，在Rt △BEC 中，EC =EB 2+BC 2=12+22=5，∴EH =5-2，在Rt △AEG ,Rt △GHE 中，AG 2+AE 2=GE 2,GH 2+EH 2=GE 2∴2-x 2+12=5-2 2+x 2解得：x =5-1∴GD DC=5-12∴矩形GDCK 是1阶奇妙矩形．(3)用正方形纸片ABCD 进行如下操作(如图)：第一步：对折正方形纸片，展开，折痕为MN ，再对折，折痕为EF ，连接CE ；第二步：折叠纸片使CD 落在CE 上，点D 的对应点为点H ，展开，折痕为CG ；第三步：过点G 折叠纸片，使得点A 、B 分别落在边AD 、BC 上，展开，折痕为GK ．矩形GDCK 是2阶奇妙矩形，理由如下，连接GE ，设正方形的边长为4，根据折叠可得EB =1，则AE =4-1=3，设DG =x ，则AG =4-x 根据折叠，可得GH =GD =x ，CH =CD =4，在Rt △BEC 中，EC =EB 2+BC 2=12+42=17，∴EH =17-4，在Rt △AEG ,Rt △GHE 中，AG 2+AE 2=GE 2,GH 2+EH 2=GE 2∴4-x 2+32=17-4 2+x 2解得：x =17-1∴GD DC=17-14当n =2时，22n +1-12n=17-14∴矩形GDCK 是2阶奇妙矩形．(4)如图(4)，连接诶GE ，设正方形的边长为1，设EB =m ，则AE =1-m ，设DG =x ，则AG =1-x 根据折叠，可得GH =GD =x ，CH =CD =1，在Rt △BEC 中，EC =EB 2+BC 2=1+m 2，∴EH =1+m 2-1，在Rt △AEG ,Rt △GHE 中，AG 2+AE 2=GE 2,GH 2+EH 2=GE 2∴1-x 2+1-m 2=1+m 2-1 2+x 2整理得，x =m 2+1-m ∴四边形AGHE 的边长为1-x +x +1+m 2-1+1-m =1+m 2-m +1=x +1矩形GDCK 的周长为2GD +DC =2x +1 ，∴四边形AGHE 的周长与矩形GDCK 的周长比值总是定值12【点睛】本题考查了正方形的折叠问题，勾股定理，熟练掌握折叠的性质是解题的关键．模型3.菱形中的翻折模型【模型解读】12(2023·四川成都·模拟预测)如图，在菱形ABCD中，∠ABC=120°，将菱形折叠，使点A恰好落在对角线BD上的点G处(不与B、D重合)，折痕为EF，若DG=2，BG=6，则BE的长为．【答案】2.8【分析】作EH⊥BD于H，根据折叠的性质得到EG=EA，根据菱形的性质、等边三角形的判定定理得到△ABD为等边三角形，得到AB=BD，根据勾股定理列出方程，解方程即可．【详解】解：作EH⊥BD于H，由折叠的性质可知，EG=EA，由题意得，BD=DG+BG=8，∠ABC=60°，∵四边形ABCD是菱形，∴AD=AB，∠ABD=∠CBD=12∴△ABD为等边三角形，∴AB=BD=8，设BE=x，则EG=AE=8-x，在Rt△EHB中，BH=12x，EH=32x，在Rt△EHG中，EG2=EH2+GH2，即(8-x)2=32x2+6-12x2，解得，x=2.8，即BE=2.8，故答案为：2.8．【点睛】本题考查的是翻转变换的性质、菱形的性质、勾股定理、解直角三角形，掌握翻转变换是一种对称变换，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解题的关键．13(2023·安徽·统考一模)如图，在边长为2的菱形ABCD中，∠A=60°，点M是AD边的中点，点N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A'MN，连结A'C，则A'C长度的最小值是( ).A.7B.7-1C.3D.2【答案】B【分析】根据题意，在N的运动过程中A′在以M为圆心、AD为直径的圆上的弧AD上运动，当A′C取最小值时，由两点之间线段最短知此时M、A′、C三点共线，得出A′的位置，进而利用锐角三角函数关系求出A′C的长即可．【详解】如图所示：∵MA′是定值，A′C长度取最小值时，即A′在MC上时，过点M作MF⊥DC于点F，∵在边长为2的菱形ABCD中，∠A=60°，M为AD中点，∴2MD=AD=CD=2，∠FDM=60°，∴∠FMD=30°，∴FD=12MD=12，∴FM=DM×cos30°=32，∴MC=FM2+CF2=7，∴A′C=MC-MA′=7-1．故选B．14(2023·山东枣庄·九年级校考阶段练习)如图，在菱形纸片ABCD中，AB=4，∠A=60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F，G分别在边AB，AD上，则EF的长为()A.72B.12C.74D.23【答案】A【分析】连接BE、BD，根据菱形的性质可知ΔBCD是等边三角形，由E是CD中点，可求得DE，BE，又因为CD∥AB，可得∠ABE=∠CEB=90°，利用勾股定理即可求解．【详解】解：连接BE、BD，∵四边形ABCD为菱形，∠A=60°，∴AB=4=BC=CD，∠A=60°=∠C，∴ΔBCD是等边三角形，∵E是CD中点，∴DE=2=CE，BE⊥CD，∠EBC=30°，∴BE=3CE=23，∵CD∥AB，∴∠ABE=∠CEB=90°，由折叠可得AF=EF，∵EF2=BE2+BF2，∴EF2=12+(4-EF)2，∴EF=72．故选：A．【点睛】本题主要考查了菱形的性质，等边三角形的性质，勾股定理等知识点，解题的关键是根据题意作出辅助线得到等边三角形再由勾股定理求解．15(2023春·湖北十堰·八年级校联考期中)如图，在菱形纸片ABCD中，∠ABC=60°，E是CD边的中点，将菱形纸片沿过点A的直线折叠，使点B落在直线AE上的点G处，折痕为AF，FG与CD交于点H，有如下结论：①∠CFH=30°；②DE=33AE；③CH=GH；④S△ABF：S四边形AFCD=3：5，上述结论中，所有正确结论的序号是()A.①②④B.①②③C.①③④D.①②③④【答案】B【分析】连接AC，得到△ACD是等边三角形，根据三线合一的性质得到AG⊥CD，由折叠得∠G=∠B= 60°，求出∠C,∠CHF的度数即可判断①；利用30度角的性质求出DE，勾股定理求出AE，即可判断②；连接CG，由折叠得AG=AB=AC，根据等边对等角求出∠ACG=∠AGC，得到∠HCG=∠HGC，即可判断③；过点F作FM⊥AB于点M，先求出∠BAG=90°，由折叠得∠BAF=∠GAF=45°，MF=3BM，设BM=x，则AM=MF=3x，求出S△ABF，再得到AD=CD=AB=1+3x，根据S菱形ABCD-S△ABF 求出四边形AFCD的面积，即可判断④．【详解】解：连接AC，∵四边形ABCD是菱形，∴AD=CD，∠D=∠ABC=60°，∴△ACD是等边三角形，∵E是CD边的中点，∴AG⊥CD，∴∠AED=∠GEH=90°，由折叠得∠G=∠B=60°，∴∠CHF=∠EHG=30°，∵∠C=180°-∠B=120°，∴∠CFH=30°，故①正确；∵∠DAE=90°-∠D=30°，∴AD=2DE，∴AE=AD2-DE2=3DE，∴DE AE =DE3DE=33，即DE=33AE，故②正确；连接CG，由折叠得AG=AB=AC，∴∠ACG=∠AGC，∵∠ACD=∠AGF=60°，∴∠HCG=∠HGC，∴CH=GH，故③正确；过点F作FM⊥AB于点M，∵∠BAD=180°-∠B=120°,∠DAE=30°，∴∠BAG=90°，由折叠得∠BAF=∠GAF=45°，∴∠AFM=45°=∠BAF，∴AM=FM，∵∠BFM=90°-∠B=30°，∴MF=3BM，设BM=x，则AM=MF=3x，∴AB=1+3x，S△ABF=12×1+3x⋅3x=3+32x2，∵AD=CD=AB=1+3x，∴AE=3 21+3x=3+32x，∴S菱形ABCD=CD⋅AE=1+3x⋅3+32x=3+23x2，∴四边形AFCD的面积=S菱形ABCD -S△ABF=3+23x2-3+32x2=3+332x2，∴S△ABF：S四边形AFCD =3+32x2:3+332x2=33≠35，故④错误；故选：B．【点睛】此题考查了菱形的性质，勾股定理，直角三角形30度角的性质，三线合一的性质，等边三角形的判定和性质，熟练掌握各知识点并综合应用是解题的关键．16(2023·浙江·九年级期末)对角线长分别为6和8的菱形ABCD如图所示，点O为对角线的交点，过点O 折叠菱形，使B，B 两点重合，MN是折痕．若B M=1，则CN的长为．【答案】4【分析】连接AC、BD，如图，利用菱形的性质得OC=12AC=3，OD=12BD=4，∠COD=90°，再利用勾股定理计算出CD =5，接着证明ΔOBM ≅ΔODN 得到DN =BM ，然后根据折叠的性质得BM =B M =1，从而有DN =1，于是计算CD -DN 即可．【详解】解：连接AC 、BD ，如图，∵点O 为菱形ABCD 的对角线的交点，∴OC =12AC =3，OD =12BD =4，∠COD =90°，在Rt ΔCOD 中，CD =32+42=5，∵AB ⎳CD ，∴∠MBO =∠NDO ，在ΔOBM 和ΔODN 中∠MBO =∠NDOOB =OD ∠BOM =∠DON，∴ΔOBM ≅ΔODN ，∴DN =BM ，∵过点O 折叠菱形，使B ，B ′两点重合，MN 是折痕，∴BM =B M =1，∴DN =1，∴CN =CD -DN =5-1=4，故答案为：4．【点睛】本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了菱形的性质．17(2023秋·重庆·九年级专题练习)如图，在菱形ABCD 中，BC =4，∠B =120°，点E 是AD 的中点，点F 是AB 上一点，以EF 为对称轴将△EAF 折叠得到△EGF ，以CE 为对称轴将△CDE 折叠得到△CHE ，使得点H落到EG 上，连接AG ．下列结论错误的是()A.∠CEF =90°B.CE ∥AGC.FG =1.6D.CF AB=145【答案】D【分析】A .由折叠的性质可以知道EF 和CE 分别是∠AEG 和∠DEG 的平分线，同时∠AED 是平角，所以可知∠CEF =90°，故选项A 正确；B .由题意和折叠的性质可以知道EF ⊥AG 、EF ⊥CE ，就可以得到CE ∥AG ，选项B 正确；C 和D .过点C 作CM ⊥AB 于点M ，∠CBA =120°，可得BM =2，CM =23．设BF =a ，可以得到FG =AF =4-a ，FM =BF +BM =a +2．根据折叠的性质可得CG =CD=4，根据勾股定理，求得a =2.4，即可得到FG =1.6，CF =5.6，所以CF AB=5.64=75．故选项C 正确，选项D 错误．【详解】解：A .由折叠可知EF 和CE 分别是∠AEG 和∠DEG 的平分线．又∵∠AED =180°，∴∠CEF =∠CEG +∠FEG =12∠AED =12×180°=90°，故选项A 正确．B .又∵点A 与点G 关于EF 对称，∴EF ⊥AG ，又∵EF ⊥CE ，∴CE ∥AG ，故选项B 正确．C 和D .如答图，过点C 作CM ⊥AB 于点M ．∵∠CBA =120°，∴∠CBM =60°，∵BC =4，∴易知BM =2，CM =23，设BF =a ，∴FG =AF =4-a ，FM =BF +BM =a +2，∵点E 是AD 的中点，折叠后点H 落到EG 上，∴点G 与点H 重合，CG =CD =4．易知点C ,G ,F 共线，∴CF =FG +CG =4-a +4=8-a ．∵FM 2+CM 2=CF 2，∴a +2 2+23 2=8-a 2，解得a =2.4．∴FG =4-2.4=1.6，CF =8-a =8-2.4=5.6，∴CF AB=5.64=75，故选项C 正确，选项D 错误．综上，故选：D ．【点睛】本题考查翻折变换(折叠问题)、菱形的性质、勾股定理，熟练掌握翻折的性质是解答本题的关键．模型4.三角形中的翻折模型【模型解读】18(2023·内江九年级期中)如图，在Rt △ABC 的纸片中，∠C =90°，AC =7，AB =25．点D 在边BC 上，以AD 为折痕将△ADB 折叠得到△ADB ，AB 与边BC 交于点E ．若△DEB 为直角三角形，则BD 的长是．【答案】17或【分析】由勾股定理可以求出的长，由折叠可知对应边相等，对应角相等，当为直角三角形时，可以分为两种情况进行考虑，分别利用勾股定理可求出的长．【详解】解：在中，，(1)当时，如图1，过点作，交的延长线于点，由折叠得：，，设，则，，在中，由勾股定理得：，即：，解得：(舍去)，，因此，．(2)当时，如图2，此时点与点C重合，由折叠得：，则，设，则，，在△中，由勾股定理得：，解得：，因此．故答案为：17或．【点睛】本题考查了翻折变换，直角三角形的性质，勾股定理等知识，解题的关键是：分类讨论思想的应用注意分类的原则是不遗漏、不重复．19(2023年四川省成都市数学中考真题)如图，在Rt△ABC中，∠ABC=90°，CD平分∠ACB交AB于点D，过D作DE∥BC交AC于点E，将△DEC沿DE折叠得到△DEF，DF交AC于点G．若AGGE =73，则tan A=．【答案】377【分析】过点G 作GM ⊥DE 于M ，证明△DGE ∽△CGD ，得出DG 2=GE ×GC ，根据AD ∥GM ，得AGGE=73=DMME，设GE =3,AG =7，EM =3n ，则DM =7n ，则EC =DE =10n ，在Rt △DGM 中，GM 2=DG 2-DM 2，在Rt △GME 中，GM 2=GE 2-EM 2，则DG 2-DM 2=GE 2-EM 2，解方程求得n =34，则EM=94，GE =3，勾股定理求得GM ，根据正切的定义，即可求解．【详解】解：如图所示，过点G 作GM ⊥DE 于M ，∵CD 平分∠ACB 交AB 于点D ，DE ∥BC ∴∠1=∠2,∠2=∠3∴∠1=∠3∴ED =EC∵折叠，∴∠3=∠4，∴∠1=∠4,又∵∠DGE =∠CGD ∴△DGE ∽△CGD ∴DG CG =GEDG∴DG 2=GE ×GC∵∠ABC =90°，DE ∥BC ，则AD ⊥DE ，∴AD ∥GM ∴AG GE=DMME ，∠MGE =∠A ，∵AG GE=73=DM ME 设GE =3,AG =7，EM =3n ，则DM =7n ，则EC =DE =10n ，∵DG 2=GE ×GC ∴DG 2=3×3+10n =9+30n 在Rt △DGM 中，GM 2=DG 2-DM 2在Rt △GME 中，GM 2=GE 2-EM 2∴DG 2-DM 2=GE 2-EM 2即9+30n -7n 2=32-3n 2解得：n =34∴EM =94，GE =3则GM =GE 2-ME 2=32-942=374∴tan A =tan ∠EGM =ME MG=94374=377故答案为：377．【点睛】本题考查了求正切，折叠的性质，勾股定理，平行线分线段成比例，相似三角形的性质与判定，熟练掌握以上知识是解题的关键．20(2023·湖北襄阳·统考中考真题)如图，在△ABC 中，AB =AC ，点D 是AC 的中点，将BCD 沿BD 折叠得到△BED ，连接AE .若DE ⊥AB 于点F ，BC =10，则AF 的长为．【答案】210【分析】取BC 中点H ，连接AH ，取CH 中点G ，连接DG ，作DM ⊥BE 于点M ．设EF =a ，由折叠可知AD =CD =DE =x 则DF =x -a ，得到cos ∠ABC =cos ∠BED ，从而推导出a =25x，由三角形中位线定理得到BG =152，从而推导出△EMD ≌△CGD AAS ，得到四边形MBGD 是正方形，DG =152，AH =15，最后利用勾股定理解答即可．【详解】解：取BC 中点H ，连接AH ，取CH 中点G ，连接DG ，作DM ⊥BE 于点M ．∵AB =AC ，H 为BC 的中点，∴AH ⊥BC，AD =CD ，BH =HC =5．∵点D 是AC 的中点，∴DG 是△AHC 的中位线，∴DG ∥AH ，则DG ⊥BC 于点G ，设EF =a ，由折叠可知AD =CD =DE =x 则DF =x -a ，∵AB =AC ，∴AB =2x ，∠ABC =∠ACB ，又由折叠得∠ACB =∠BED ，BE =BC =10，∴∠ABC =∠BED ，∴cos ∠ABC =cos ∠BED ，即BH AB=EF EB ，∴52x =a 10，解得：a =25x ，∴DF =x -a =x -25x ，∵DG 是△AHC 的中位线，∴CG =12CH =52，AH =2DG ，∴BG =152，由折叠知∠DEM =∠DCG ，ED =CD ，在△EMD 和△CGD 中，∠DEM =∠DCG∠DME =∠DGC ED =CD，∴△EMD ≌△CGD AAS ，∴DG =MD ．∵DE ⊥AB ，∴∠EFB =90°，∴∠DEB +∠EBF =90°．又∵∠CAH +∠ACB =90°，且∠ACB =∠DEB ，∴∠EBF =∠CAH ，∴∠EBF +∠ABC =90°，∴∠DMB =∠MBG =∠BGD =90°，∴四边形MBGD 是正方形，∴DG =BG =152，∴AH =2DG =15．在Rt △AHC 中，AH 2+HC 2=AC 2，∴152+52=2x 2，解得：x =5102，∴a =10，x -a =3102，即AD =5102，DF =3102，在Rt △AFD 中，AF =AD 2-DF 2=210．故答案为：210．【点睛】本题考查了折叠的性质，等腰三角形的性质，勾股定理，解直角三角形，正方形的判定及性质等，解答本题的关键是设边长，根据勾股定理列方程求解．21(2023·湖北武汉·统考中考真题)如图，DE 平分等边△ABC 的面积，折叠△BDE 得到△FDE ,AC 分别与DF ,EF 相交于G ,H 两点．若DG =m ,EH =n ，用含m ,n 的式子表示GH 的长是．【答案】m 2+n 2【分析】先根据折叠的性质可得S △BDE =S △FDE ，∠F =∠B =60°，从而可得S △FHG =S △ADG +S △CHE ，再根据相似三角形的判定可证△ADG ∽△FHG ,△CHE ∽△FHG ，根据相似三角形的性质可得S △ADG S △FHG =DG GH2=m 2GH 2，S △CHE S △FHG=EH GH 2=n 2GH 2，然后将两个等式相加即可得．【详解】解：∵△ABC 是等边三角形，∴∠A =∠B =∠C =60°，∵折叠△BDE 得到△FDE ，∴△BDE ≌△FDE ，∴S △BDE =S △FDE ，∠F =∠B =60°=∠A =∠C ，∵DE 平分等边△ABC 的面积，∴S 梯形ACED =S △BDE =S △FDE ，∴S △FHG =S △ADG +S △CHE ，又∵∠AGD =∠FGH ,∠CHE =∠FHG ，∴△ADG ∽△FHG ,△CHE ∽△FHG ，∴S △ADG S △FHG =DG GH 2=m 2GH 2，S △CHE S △FHG =EH GH 2=n 2GH 2，∴S △ADG S △FHG +S △CHE S △FHG =m 2+n 2GH 2=S △ADG +S △CHE S △FHG =1，∴GH 2=m 2+n 2，解得GH =m 2+n 2或GH =-m 2+n 2(不符合题意，舍去)，故答案为：m 2+n 2．【点睛】本题考查了等边三角形的性质、折叠的性质、相似三角形的判定与性质等知识点，熟练掌握相似三角形的判定与性质是解题关键．模型5.圆中的翻折模型(弧翻折必出等腰)如图，以圆O 的一条弦BC 为对称轴将弧BC 折叠后与弦AB 交于点D ，则CD =CA特别的，若将弧BC 折叠后过圆心，则CD =CA ，∠CAB =60°22(2022秋·浙江宁波·九年级校考期末)如图，⊙O 是△ABC 的外接圆，AB =BC =4，把弧AB 沿弦AB 向下折叠交BC 于点D ，若点D 为BC 中点，则AC 长为()A.1B.2C.22D.6【答案】C【分析】由等腰三角形的性质可得∠ACB =∠BAC ，由折叠的性质和圆周角定理可得∠ACB =∠ABD +∠BAD 可得∠ABD =∠CAD ，可证△ACD ∽△BCA ，可得CD AC=ACBC ，即可求解．【详解】解：如图，连接AD ，∵AB =BC =4，∴∠ACB =∠BAC ，∵点D 为BC 中点，∴BD =CD =2，∵弧AB 沿弦AB 向下折叠交BC 于点D ，∴AB=ADB，∴∠ACB =∠ABD +∠BAD ，∵∠BAC =∠BAD +∠CAD ，∴∠ABD =∠CAD ，又∵∠ACB =∠ACD ，∴△ACD ∽△BCA ，∴CD AC =AC BC ，∴2AC=AC 4，∴AC =8=22(负值舍去)，故选：C ．【点睛】本题考查了三角形外接圆与外心，等腰三角形的性质，折叠的性质，相似三角形的判定和性质，证明三角形相似是解题的关键．23(2023·广东广州·统考一模)如图，AB 为⊙O 的直径，点C 为圆上一点，∠BAC =20°，将劣弧AC 沿弦AC 所在的直线翻折，交AB 于点D ，则∠ACD 的度数等于( )．。

专题01 翻折问题(解析版)

专题01 翻折问题一、解答题1．（2020·江苏南京·统考模拟预测）如图，在△ABC中，∠BAC=45°，AD⊥BC于点D，BD=6，DC=4，求AD的长．小明同学利用翻折，巧妙地解答了此题，按小明的思路探究并解答下列问题：（1）分别以AB，AC所在直线为对称轴，画出△ABD和△ACD的对称图形，点D的对称点分别为点E，F，延长EB和FC相交于点G，求证：四边形AEGF是正方形；（2）设AD=x，建立关于x的方程模型，求出AD的长．【答案】（1）证明见解析；（2）12．【分析】（1）先根据△ABD≌△ABE，△ACD≌△ACF，得出∠EAF＝90°；再根据对称的性质得到AE＝AF，从而说明四边形AEGF是正方形；（2）利用勾股定理，建立关于x的方程模型（x−6）2＋（x−4）2＝102，求出AD＝x＝12．【详解】（1）证明：由题意可得：△ABD≌△ABE，△ACD≌△ACF，∴∠DAB=∠EAB，∠DAC=∠FAC，又∠BAC=45°，∴∠EAF=90°．又∵AD⊥BC，∴∠E=∠ADB=90°，∠F=∠ADC=90°，∴四边形AEGF是矩形，又∵AE=AD，AF=AD，∴AE=AF，∴矩形AEGF是正方形；（2）解：设AD=x，则AE=EG=GF=x．∵BD=6，DC=4，∴BE=6，CF=4，∴BG=x﹣6，CG=x﹣4，在Rt△BGC中，BG2+CG2=BC2，∴（x﹣6）2+（x﹣4）2=102．化简得：x2﹣10x﹣24=0解得：x1=12，x2=﹣2（舍去）所以AD=x=12．2．（2019秋·江苏盐城·九年级校考期中）在初二的数学学习中，我们已经了解了直角三角形斜边上的中线等于斜边的一半．张老师在课堂上又提出了这样的问题：如图1，在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，那么BC与AB有怎样的数量关系？（1）经过小组合作交流后，小明代表小组发言，他们发现了AB＝2BC，证明方法如下：证明：如图2，把△ABC沿着AC翻折，得到△ADC∴∠ACD＝∠ACB＝90°，∴∠BCD＝∠ACD＋∠ACB＝90°＋90°＝180°，∴点B、C、D三点共线．又∵∠DAC＝∠BAC＝30°，∴∠BAD＝60°，（请在下面补全小明的证明过程）（2）受到小明“翻折”方法的启发，另一组代表小刚发言：如图3，在△ABC中，如果把条件“∠ACB＝90°”改为“∠ACB＝135°”，保持“∠BAC＝30°”不变，若BC＝1，求AB的长．【答案】（1）AB=2BC；补全证明过程见解析；（2）【分析】（1）根据翻折的性质可得AB=AD，BC=BD，即可证明△ABD是等边三角形，可得AB=BD，即可AB；证明BC=12（2）如图，把△ABC沿着AC翻折，得到△ADC，连接BD，根据翻折的性质可得∠DAC=∠BAC=30°，∠ACD=∠ACB=135°，AB=AD，CD=BC=1，可得∠BAD=60°，∠BCD=90°，即可证明△ABD是等边三角形，可得AB=BD，根据勾股定理可得，即可得答案．【详解】（1）∵把△ABC沿着AC翻折，得到△ADC，∴AB=AD，BC=BD，∴△ABD是等边三角形，∴AB=BD=2BC．（2）如图，把△ABC沿着AC翻折，得到△ADC，连接BD，∵∠ACB＝135°，∠BAC＝30°，BC＝1，∴∠DAC=∠BAC=30°，∠ACD=∠ACB=135°，AB=AD，CD=BC=1，∴∠BCD=360°-135°-135°=90°，∠BAD=60°，∴△ABD是等边三角形，=∴．3．（2021秋·江苏南京·九年级统考期中）问题：如图1，在等边三角形△ABC中，点E在AB上，点D在CB的延长线上，ED＝EC，回答下列问题：（1）与AE相等的线段是．（2）请证明（1）中得到的结论，证明思路如下：①小聪思路：如图2，过E作EF//BC，交AC于点F，请你完成剩下解答过程；②小明思路：如图3，把△EBD沿BE翻折得到△EBF，连接CF，请你完成剩下解答过程．【答案】（1）BD；（2）①见解析；②见解析【分析】（1）思路见（2）（2）①过E作EF//BC，证明△AEF为等边三角形，再证明△DBE≌△EFC，即可得到BD=EF=AE；②把△EBD沿BE翻折得到△EBF，连接CF，得到△EBD≌△EBF，再证明△ACE≌△BCF，即可得到AE＝BF＝BD；【详解】（1）BD（2）①小聪思路：过点E作EF//BC，交AC于F∵△ABC是等边三角形∴∠ABC ＝∠ACB ＝∠A ＝60°，AB ＝BC ＝AC∵EF //BC ∴∠AEF ＝∠ABC ＝60°，∠AFE ＝∠ACB ＝60°，∠FEC ＝∠ECB∵又∠A ＝60° ∴△AEF 是等边三角形∴AE ＝AF ＝EF ，∠EFC ＝∠DBE ＝120°，∴CF ＝BE∵ED ＝EC∴∠D ＝∠ECB∴∠D ＝∠FEC∴∠FCE ＝∠BED在△DBE 和△EFC 中，CF BE FCE BEDCE DE =ìïÐ=Ðíï=î∴△DBE ≌△EFC （SAS ）∴BD ＝EF∴BD ＝AE②小明思路：∵DE ＝EC ∴∠ECB ＝∠D∵∠ABC ＝∠DEB +∠D ，∠ACB ＝∠ACE +∠ECB∴∠DEB ＝∠ACE∵△EBD 翻折到△EBF∴△EBD ≌△EBF ∴∠DEB ＝∠FEB ，DE ＝EF∴∠DEB ＝∠ACE ＝∠FEB∵∠CEB ＝∠CEF +∠FEB ＝∠A +∠ACE ∴∠CEF ＝∠A ＝60°∵DE ＝EF ＝CE ∴△ECF 为等边三角形∴CE ＝CF ，∠ECF ＝60°∴∠ACE +∠ECB ＝∠ECB +∠BCF∴∠ACE ＝∠BCF ，在△ACE 和△BCF 中CF BE BCF ACEAC BC =ìïÐ=Ðíï=î∴△ACE ≌△BCF （SAS ）∴AE ＝BF ＝BD4．（2022·江苏南京·统考一模）阅读下面的问题及解决途径．结合阅读内容，完成下面的问题．(1)填写下面的表格．(2)将函数y ＝－2x 2＋3x ＋1的图像沿y 轴翻折，所得到的图像对应的函数表达式为．(3)将函数y ＝ax 2＋bx ＋c (a ，b ，c 是常数，a ≠0)的图像先向左平移1个单位长度，再沿y 轴翻折，最后绕原点旋转180°，求所得到的图像对应的函数表达式．【答案】(1)1x +，y ，61y x =+(2)2323y x x -=-+(3)2(2)y ax a b x a b c=--+---【分析】（1）阅读题干材料，弄清题中材料中图形平移的规律，“左加右减”进行求解即可；（2）根据二次函数图像与几何变换，将x 换成x -，整理后即可得出翻折后的解析式，根据二次函数的性质即可求得结论；（3）利用图像向左平移、关于,x y 轴翻折、绕坐标原点旋转的规律进行解答．【详解】（1）解：设平移后新的函数图像上任意点P 的坐标为(,)x y ，将点P 向右平移1个单位长度得点(1,)P x y ¢+平移后的图像对应的函数表达式为：61y x =+，故答案为：1x +，y ，61y x =+；（2）解：将二次函数2231y x x =-++的图像沿着y 轴翻折，所得到的图像对应的函数表达式是22()3()1y x x +=--×-+，即2323y x x -=-+，故答案为：2323y x x -=-+；（3）解：将2y ax bx c =++(a ，b ，c 是常数，a ≠0)的图像先向左平移1个单位长度，得2(1)(1)y a x b x c =++++，再沿y 轴翻折，得2(1)(1)y a x b x c =-++-++，即2(21)(1)y a x x b x c =-++-+，最后绕原点旋转180°，得2(21)(1)y a x x b x c -=+++++，整理得：2(2)y ax a b x a b c =--+---，故答案为：2(2)y ax a b x a b c =--+---．答：所得到的图像对应的函数表达式2(2)y ax a b x a b c =--+---．5．（2022秋·江苏无锡·九年级统考期中）在数学活动《折纸与证明》中，有这样的一段活动材料：①如图①，把正方形ABCD 对折后再展开，折痕为EF ；②如图②，将点A 翻折到EF 上点A ¢处，且使折痕过点B ；③如图③，沿A C ¢折叠，得A BC ¢V （如图④）．回答下列问题：(1)判断：A BC ¢V 的形状为______________；并说明你的理由；(2)若正方形纸片的边长为2，则线段A F ¢的平方的值为______________．【答案】(1)等边三角形，理由见解析(2)3【分析】（1）由折叠的性质可知EF 垂直平分BC ，结合正方形的性质可知A C A B AB BC ¢¢===，可判断A BC ¢V 是等边三角形．（2）利用勾股定理解直角A FB ¢D 可得222A F A B FB ¢¢=-．【详解】（1）解：等边三角形．理由如下：∵如图②，把正方形纸片ABCD 对折，折痕为EF ，∴EF 垂直平分BC ．∵将点A 翻折，折痕过点B ，且使点A 落在EF 的点A ¢处，∴A C A B AB BC ¢¢===．∴A BC ¢V 是等边三角形．（2）解：∵正方形纸片的边长为2，EF 垂直平分BC ，∴2A B AB ¢==，112122FB BC ==´=，90A FB ¢Ð=°，∴2222213A F A B FB ¢¢=-=-=，线段A F ¢的平方的值为3．6．（2022秋·江苏扬州·九年级统考期中）【问题背景】小明遇到这样一个问题：如图1，在Rt ABC V 中，9060A CB ，A Ð=°Ð=°，CD 平分ACB Ð，试判断BC 和AC AD 、之间的数量关系．【初步探索】小明发现，将ACD V 沿CD 翻折，使点A 落在BC 边上的E 处，展开后连接DE ，则得到一对全等的三角形，从而将问题解决（如图2）（1）写出图2中全等的三角形____________________；（2）直接写出BC 和AC AD 、之间的数量关系__________________；【类比运用】（3）如图3，在ABC V 中，2C B Ð=Ð，AD 平分32CA B ，A B ，A D Ð==，求ACD V 的周长．小明的思路：借鉴上述方法，将ACD V 沿AD 翻折，使点C 落在AB 边上的E 处，展开后连接DE ，这样可以将问题解决（如图4）；请帮小明写出解答过程：【实践拓展】（4）如图5，在一块形状为四边形ABCD 的空地上，养殖场丁师傅想把这块地用栅栏围成两个小型的养殖场，即图5中的ABC V 和ACD V ，若AC 平分10m 17m 9m BAD BC CD AC AD Ð====，，，．请你帮丁师傅算一下需要买多长的栅栏．【答案】（1）A C D E C D @V V ；（2）BC AC AD =+；（3）ACD V 的周长为5；（4）需要买67m 长的栅栏【分析】（1）将ACD V 沿CD 翻折得到ECD V ，则A CD E C D @V V ，即可得答案；（2）由90,60ACB A Ð=°Ð=°，得30B Ð=°，由翻折得,E C A C E D A D ==，60CED A Ð=Ð=°，得30EDB B Ð=Ð=°，所以E D E B A D ==，于是B C E C E B A C A D =+=+；（3）将ACD V 沿AD 翻折，使点C 落在AB 边上的点E 处，展开后连接DE ，则,A C A E CD E D ==，2AED C B Ð=Ð=Ð，于是得2B E D B B Ð=Ð+Ð，则B EDB Ð=Ð，得EB ED CD ==，所以3A C C D A B +==，即可得答案；（4）将ACD V 沿AC 翻折，使点C 落在AB 边上的点E 处，连接CE ，作CF AB ^于F ，设m EF BF c ==，则()9A F x m =+，可得方程()222217910x x -+=-，解得：6x =，即可求得6m EF BF ==，()21m AB =，则()91010211767m AD BC CD AB AC ++++=++++=，可得答案．【详解】解：（1）如图2，ACD QV 沿CD 翻折得到ECDV A C D E C D \@V V ；（2）BC AC AD =+，理由：90,60ACB A Ð=°Ð=°Q ，30B \Ð=°，由翻折得,E C A C E D A D ==，60CED A Ð=Ð=°，603030E D B C E D B \Ð=Ð-Ð=°-°=°，EDB B \Ð=Ð，ED EB \=，EB AD \=，B C E C E B A C A D \=+=+；（3）如图4，将ACD V 沿AD 翻折，使点C 落在AB 边上的点E 处，展开后连接DE ，由翻折得,A C A E CD E D ==，2AED C B Ð=Ð=Ð，A E D E D B B Ð=Ð+ÐQ ，2B E D B B \Ð=Ð+Ð，B EDB \Ð=Ð，EB ED \=，CD EB \=，3A C C D A E E B A B \+=+==，325A C C D A D \++=+=，ACD V 的周长为5；（4）如下图5，将ACD V 沿AC 翻折，使点C 落在AB 边上的点E 处，连接CE ，作CF AB ^于F ，10m,17m,9m BC CD CA AD ====Q ，9m,10m AE AD CE CD \====，10m BC CE \==，CF AB ^Q ，\90,A FC B FC E F B F Ð=Ð=°=，设m EF BF c ==，则()9m AF x =+，22222A C A F B C B F C F -=-=Q ，()222217910x x \-+=-，解得：6x =，6m EF BF ==Q ，()96621m AB AE EF BF \=++=++=，()91010211767m AD BC CD AB AC \++++=++++=，\需要买67m 长的栅栏．7．（2022秋·江苏盐城·九年级校联考阶段练习）如图，在边长为1的小正方形组成的网格中有一个ABC V ，按要求回答下列问题：(1)ABC V 的面积为；(2)画出将ABC V 向右平移6格，再向上平移3格后的111A B C △；(3)画出ABC V 绕点B 顺时针旋转90°后的图形22A BC V ；(4)画出ABC V 沿直线EF 翻折后的图形33A B C △．【答案】(1)3(2)见解析(3)见解析(4)见解析【分析】（1）直接利用三角形面积求法得出答案；（2）利用平移的性质得出对应点位置，进而得出111A B C △；（3）直接利用旋转的性质得出对应点位置，进而得出22A BC V ；（4）直接利用翻折变换的性质得出对应点位置，进而得出33A B C △．【详解】（1）ABC V 的面积为：13232´´=；故答案为：3；（2）如图所示：111A B C △即为所求；（3）如图所示：22A BC V 即为所求；（4）如图所示：33A B C △即为所求；8．（2020·江苏无锡·统考一模）阅读材料：等腰三角形具有性质“等边对等角”．事实上，不等边三角形也具有类似性质“大边对大角”：如图1．在△ABC 中，如果AB ＞AC ，那么∠ACB ＞∠ABC ．证明如下：将AB 沿△ABC 的角平分线AD 翻折（如图2），因为AB ＞AC ，所以点B 落在AC 的延长线上的点B '处．于是，由∠ACB ＞∠B '，∠ABC =∠B '，可得∠ACB ＞∠ABC ．（1）灵活运用：从上面的证法可以看出，折纸常常能为证明一个命题提供思路和方法．由此小明想到可用类似方法证明“大角对大边”：如图3．在△ABC 中，如果∠ACB ＞∠ABC ，那么AB ＞AC ．小明的思路是：沿BC 的垂直平分线翻折……请你帮助小明完成后面的证明过程．（2）拓展延伸：请运用上述方法或结论解决如下问题：如图4，已知M 为正方形ABCD 的边CD 上一点（不含端点），连接AM 并延长，交BC 的延长线于点N ．求证：AM ＋AN ＞2BD ．【答案】（1）证明见解析；（2）证明见解析．【分析】（1）设BC的中垂线交BC于点E，交AB于点D，连接DC，结合中垂线的性质定理与三角形三边长的关系，即可得到结论；（2）延长DC到点E，使得CE=CN，连接AE交BC于点F．易证△ACE≌△CAN，得AE=AN．过点C作PQ⊥AC，分别交AN、AE于点P、Q，结合“三角形中，大角对大边”，得AP＋AQ＞2AC，QE＞CQ，PC＞PM，进而得QE＞PM，即AM＋AN＞AP＋AQ，然后即可得到结论．【详解】（1）设BC的中垂线交BC于点E，交AB于点D，连接DC．将∠B沿BC的中垂线DE翻折（如图3），使点B落在点C处．∵∠ACB＞∠ABC，∴CD在△ABC的内部，∵DE为BC的中垂线，∴DB=DC．∵在△ADC中，AD＋DC＞AC，∴AD＋DB＞AC．即AB＞AC；（2）如图4，延长DC到点E，使得CE=CN，连接AE交BC于点F．∵∠ACE=∠ACN=135°，CE=CN，AC=AC，∴△ACE≌△ACN（SAS），∴AE=AN．过点C作PQ⊥AC，分别交AN、AE于点P、Q．∵∠ACP=∠ACQ=90°，∴AP＞AC，AQ＞AC，∴AP＋AQ＞2AC．∵∠ACD＞∠E，∠ACD=45°，∠QCE=135°-90°=45°，∴∠QCE＞∠E，∴QE＞CQ．同理可得：PC＞PM．∵△ACE≌△ACN，∴∠CAN=∠CAE，又∵AC=AC，∠ACP=∠ACQ=90°，∴△ACP≌△ACQ（ASA），∴PC=CQ，∴QE＞PM，∴AM＋AN=AM＋AE=AM＋AQ＋QE＞AM＋AQ＋PM=AP＋AQ．又∵AP＋AQ＞2AC，∴AM＋AN＞2AC．∵正方形ABCD中，AC=BD，∴AM＋AN＞2BD．9．（2022秋·江苏·九年级期末）折纸，常常能为证明一个命题提供思路和方法．例如，在△ABC中，AB＞AC（如图1），怎样证明∠C＞∠B呢？把AC沿∠A的平分线AD翻折，因为AB＞AC，所以点C落在AB上的点C′处（如图2）．于是，由∠AC′D ＝∠C，∠AC′D＞∠B，可得∠C＞∠B．利用上述方法（或者思路）解决下列问题：（1）如图2，上述阅读材料中，若∠B＝45°，∠C＝60°，则∠C′DB＝_______°．（2）如图3，△ABC中，∠ACB＝90°，AD平分∠BAC，交BC于点D．若CD＝2，AB＝6．求△ABD的面积．（3）如图4，△ABC中，已知AD⊥BC于点D，且CD＝AB＋BD．若∠C＝24°，求∠CAB的度数．【答案】（1）15；（2）△ABD的面积为6；（3）∠CAB＝108°．【分析】（1）利用折叠的性质和三角形的外角性质，即可求出答案；（2）把AC沿角平分线AD翻折，点C落在AB上的点C＇处，得DC＇=CD=2，即可求出△ABD的面积；（3）把AB沿AD翻折，点B落在BC上的点B＇处，则BD＝DB＇，求得AB＇＝B＇C，然后得到∠B＇AC＝∠C ＝24°，从而得到∠B＝∠AB＇B＝48°，即可求出答案．【详解】解：（1）由折叠的性质，则∠AC′D=∠C=60°，∵∠B=45°，∴∠C′DB＝60°-45°=15°；故答案为：15°．（2）如图，把AC沿角平分线AD翻折，点C落在AB上的点C＇处，∵AD是角平分线，∠ACB＝90°，∴DC＇＝DC＝2，∠AC＇D＝∠ACD＝90°，∵DC＇是高，∴△ABD的面积为6．（3）如图，把AB沿AD翻折，点B落在BC上的点B＇处，则BD＝DB＇，∴AB＇＝AB=B＇C，∴∠B＇AC＝∠C ＝24°∴∠B＝∠AB＇B＝48°，∴∠CAB＝108°．10．（2021春·江苏无锡·九年级江苏省锡山高级中学实验学校校考期中）问题背景如图1，矩形ABCD中，AB=AB AD<，M、N分别是AB、CD的中点，折叠矩形ABCD，使点A落在MN上的点K处，折痕为BP．（1）用直尺和圆规在图1中的AD 边上作出点P （不写作法，保留作图痕迹）；（2）连接AK ，判断ABK V 的形状；（3）如图2，若点E 是直线MN 上的一个动点．连接EB ，在EB 左侧作等边三角形BEF ；连接MF ，则MF 的最小值是______；（4）如图3，若点E 是射线KM 上的一个动点将BEK △沿BE 翻折，得BET △，BT 所在直线交直线MN 于点Q ，当TQE △是直角三角形时，KE 的长为多少？请直接写出答案．【答案】（1）见详解；（2）ABK V 是等边三角形，理由见详解；（3（4）4或12【分析】（1）作∠ABK 的平分线交AD 于P ，点P 即为所求；（2）先求出∠BKM ＝30°；根据对称性可得∠AKB =60°，进而即可得到答案；（3）由△FBA ≌△EBK ，因为FM 、EH 分别是AB 、BK 上的中线，推出FM ＝EH ，根据垂线段最短可知，当HE ⊥MN 时，EH 的值最小，进而即可求解；（4）分四种情形分别画出图形，求解即可；【详解】解：（1）如图①中，点P 即为所求：（2）连接AK ，在Rt △BKM 中，∵sin ∠BKM ＝BM BK ＝12，∴∠BKM ＝30°．∵M 、N 分别是AB 、CD 的中点，∴MN 是矩形ABCD 的对称轴，∴∠AKM =∠BKM ＝30°，AK =BK ，∴∠AKB =60°，∴ABK V 是等边三角形；（3）如图②中，连接AF ，取BK 的中点H ，连接EH ．∵等边三角形BEF中，∴∠FBE＝∠ABK＝90°-∠BKM=90°-30°=60°，又∵BF＝BE，BA＝BK，∴∠FBA＝∠EBK，∴△FBA≌△EBK（SAS），∵FM、EH分别是AB、BK上的中线，∴FM＝EH，根据垂线段最短可知，当HE⊥MN时，EH的值最小，最小值EH＝12∴FMAB MKB=30°，（4）∵MB=12∴MK=6，如图，当∠TEQ＝90°时，则TE∥MB，∴∠MBQ=∠T=∠MKB=30°，∴MQ=，设EK=ET=x，则QE，x+x+2=6，解得：x EK如图，当∠TQE＝90°时，此时点Q与点M重合，QE=2=，∴EK=6-2=4；如图当∠TEQ＝90°时，则∠BEM=45°，∴EM=BM∴EK如图：当∠TQE＝90°时，此时点Q与点M重合，∵∠TEM=90°-∠T=60°，×60°=30°，∴∠KEB=12∴∠EKB=∠KEB=30°，∴ME=MK=6，∴EK=12．综上所述，满足条件的EK的值为4或12．11．（2022春·江苏扬州·九年级校联考期中）问题情境：如图，在正方形ABCD中，CE⊥DF．易证：CE＝DF．（不需要写出证明过程）问题探究：在“问题情境”的基础上请研究．(1)如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．判断线段AE与MN之间的数量关系，并说明理由．(2)如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，CQ（图中未连），判断线段EQ与CQ之间的数量关系，并说明理由．(3)在（2）的条件下延长EQ交边AD于点F．则∠AEF= °；(4)拓展提高：如图3，若该正方形ABCD边长为8，将正方形沿着直线MN翻折，使得BC的对应边B′C′恰好经过点A，过点A作AG⊥MN，垂足分别为G，若AG＝5，请直接写出AC′的长．【答案】(1)AE＝MN，理由见解析；(2)EQ＝CQ，理由见解析；(3)45；(4)2.【分析】（1）过点B作BF//MN交CD于点F，则四边形M BFN为平行四边形，得出MN =BF，BF⊥AE，由ASA证得△ABE≌△BCF，得出AE= BF，即可得出结论；（2）在图2中，连接AQ、CQ，易证△ABQ≌△CBQ，所以AQ＝CQ，再根据垂直平分线的性质得到AQ＝EQ，所以可得EQ＝CQ（3）连接AQ，过点Q作HI// AB，分别交AD，BC于点H、I，则四边形ABIH为矩形，得出HI⊥AD，HI ⊥BC，HI = AB= AD，证△DHQ是等腰直角三角形，得HD= HQ，AH = QI，由H L证得Rt△AHQ≌Rt△QIE，得∠AQH =∠QEI，证∠AQE=90°，得△AQE是等腰直角三角形，即可得出结果；(4)延长AG交BC于E，则EG = AG= 5，得AE=10，由勾股定理得：BE，则CE= BC-BE，由折叠的性质即可得出结果．（1）（1）证明：∵四边形ABCD是正方形，∴∠ABE＝∠BCD＝90°，AB＝BC，AB∥CD，过点B作BF∥MN交CD于点F，如图1所示：∴四边形MBFN为平行四边形，∴MN＝BF，BF⊥AE，∴∠ABF+∠BAE＝90°，∵∠ABF+∠CBF＝90°，∴∠BAE＝∠CBF，在△ABE和△BCF中，{BAE CBF AB BC ABE BCFÐ=Ð=Ð=Ð，∴△ABE≌△BCF（ASA），∴AE＝BF，∴AE＝MN；（2）解：在图2中，连接AQ、CQ，在△ABQ和△CBQ中，{AB CB ABQ CBQ BQ BQ=Ð=Ð=，∴△ABQ≌△CBQ，∴AQ＝CQ，∵MN⊥AE于F，F为AE中点，∴AQ＝EQ，∴EQ＝CQ（3）解：连接AQ，过点Q作HI// AB，分别交AD．BC于点H、I，如图3所示：∵四边形ABCD是正方形，∴四边形ABIH为矩形，∴HI⊥AD，HI⊥．BC，HI= AB= AD，∵BD是正方形ABCD的对角线，∴∠BDA = 45°，∴△DHQ是等腰直角三角形，∴HD=HQ，AH=QI，∵MN是AE的垂直平分线，AQ= QE，在Rt△AHQ和Rt△QIE中，∵AQ= QE，AH= QI，∴Rt△AHQ≌Rt△QIE(HL)，∴∠AQH =∠QEI，∠AQH＋∠EQI = 90°，△AQ E是等腰直角三角形，∠EAQ=∠AEQ=45°，即∠AEF= 45°故答案为：∠AEF=45°；（4）解：拓展提高：由(3)延长AG交BC于E，如图4所示：则EG =AG =5，∴AE = 10，在Rt △ABE 中，BE 6==CE = BC - BE = 8-6=2，由折叠的性质得： AC '=CE =2，故答案为： AC ′=2.12．（2022·江苏盐城·校联考一模）（1）背景问题：如图①，已知矩形ABCD ，E 是边CD 上一点，将△BCE 沿BE 翻折，使得C 落在AD 上的点F 处，求证：△ABF ∽△DFE ．（1）尝试应用：如图②，已知四边形ABCD 中，∠A =∠D =90°，点E 在AD 上，∠BEC =90°，2∠BCE +∠ECD =180°，过点E 作EF ⊥BC 垂足为F ，若EF =2，BC =5，求AE 的长．（2）拓展创新：如图③，已知矩形ABCD ，AB =9，BC =12，E 是边CD 上一动点，将△BCE 沿BE 翻折至△BPE ，连接AP 在上取点T ，使得PT =2AT ，连接DT ，求出DT 长度的最小值．【答案】（1）见解析；（2（3）4【分析】（1）由矩形的性质和翻折得到∠BFE ＝∠A ＝∠D ＝∠C ＝90°，由同角的余角相等可推得∠DEF ＝∠AFB ，证得△EDF ∽△FAB ；（2）证明△ECF ∽△BEF ，得CF =1，BF =4 ，由△ABF ∽△DFE ，2∠BCE +∠ECD =180°，构造矩形ABGD ，由BG =AD 建立方程，解方程求解即可；(3)在AB 边上取Q ，使得BO =2AQ ，连接TQ ，则ATQ APB V V ∽求得4TQ =，可得T 在以Q 为圆心4为半径的圆上，根据点圆关系求最值即可．【详解】（1）证明：如图1，在矩形ABCD 中，∠A ＝∠D ＝∠C ＝90°，由翻折得∠EFB ＝∠C ＝90°．∵∠DEF ＋∠DFE ＝90°，∠AFB ＋∠DFE ＝180°−90°＝90°，∴∠DEF＝∠AFB，∴△ABF∽△DFE．（1）尝试应用：如图2，过点B作BG⊥CD，交DC的延长线于点G，设DE＝m，CD＝x．∵EF⊥BC，∴∠EFC＝∠BFE＝90°，∵∠BEC＝90°，∴∠ECF＝90°−∠CEF＝∠FEB，∴△ECF∽△BEF，EF CFBF EF\=\EF2=CF·BF25EF BC==，Q()225CF CF\=-解得CF=1，或4（舍去）\CF=1，BF=4\EC==EB==∵△ABF∽△DFE∴12 CD DE CE AE AB BC===设CD=x，则AE=2x∵2∠BCE+∠ECD=180°∴D、C、G共线，在矩形ABGD中则DG x AB==由BG=AD得2x=∴AE=（2）拓展创新：在AB边上取Q，使得BQ=2AQ，连接TQQ PT =2AT ，PAB TAQÐ=Ð\ATQ APBV V ∽\13TQ AQ AT PB AB AP ===143TQ PB \==\T 在以Q 为圆心4为半径的圆上，当点T 落在DQ 上，即DT ＝DQ−4时，DT 的值最小，9AB DC ==Q \133AQ AB ==Q 90CB =°DQ \==∴DTmin =413．（2023·江苏·九年级专题练习）如图，在矩形ABCD 中，BD 是对角线，AB ＝6cm ，BC ＝8cm 点E 从点D 出发，沿DA 方向匀速运动，速度是2cm/s ；点F 从点B 出发，沿BD 方向匀速运动，速度是1cm/s ，MN 是过点F 的直线，分别交AB 、BC 于点M 、N ，且在运动过程中始终保持MN ⊥BD ．连接EM 、EN 、EF ，两点同时出发，设运动时间为t （s ）（0<t <3.6），请回答下列问题：(1)求当t 为何值时，△EFD ∽△ABD ?(2)求当t 为何值时，△EFD 为等腰三角形；(3)将△EMN 沿直线MN 进行翻折，形成的四边形能否是菱形?若存在，求出t 的值；若不存在，请说明理由．【答案】(1)当t 的值为207时，△EFD ∽△ABD(2)当t 的值为5021或103时△EFD 为等腰三角形(3)不存在，理由见解析【分析】（1）当△EFD ∽△ABD 时，得到相似比DE DF DA DB=，解得207t =即可；（2）根据题意，等腰三角形分三种情况：EF ＝DE 时；EF ＝DF 时；DE ＝DF 时；作出相应图形，结合条件求解即可；（3）假设存在这样的菱形，当EM EN =时，过点E 作EQ ⊥BC 于点Q ，利用勾股定理求出两条线段长，根据相等关系列方程求解即可确定结论存在与否．【详解】（1）解：如图所示：在矩形ABCD 中，AD ＝BC ＝8cm ，∠A ＝∠ABC ＝90°，在Rt △ABD 中由勾股定理得10BD ===（cm ），由题意得：DE ＝2t cm ，BF ＝t cm ，∴()10DF BD BF t =-=-cm ，∵△EFD ∽△ABD ，∴DE DF DA DB =，∴210810t t -=，解得207t =∴当t 的值为207时，△EFD ∽△ABD ；（2）解：△EFD 为等腰三角形有三种情况：①EF ＝DE 时，点E 在DF 的垂直平分线上，过点E 作EG ⊥DF 于点G ，如图所示：则11022t DG DF -==cm ，在Rt △DEG 中，4cos 15DG DE Ð==，∴5DG ＝4DE ，∴105422t t -´=´，解得：5021t =；②EF ＝DF 时，点F 在DE 的垂直平分线上，过点F 作FH ⊥AD 于点H ，如图所示：则12DH DE t ==cm ，在Rt △DHF 中，4cos 15DH DF Ð==，∴5DH ＝4DF ，∴()5410t t =-，解得409t =，∵40 3.69>，∴不合题意舍去；③DE ＝DF 时，则2t ＝10－t ，解得：103t =；综上：当t 的值为5021或103时，△EFD 为等腰三角形；（3）解：不存在．假设△EMN 沿直线MN 翻折后点E 落在点E ¢处，由折叠得：EM E M ¢=，EN E N ¢=，当翻折后的四边形为菱形时，EM E M E N E N ¢¢¢===，∴EM ＝EN ，∴22EM EN =，过点E 作EQ ⊥BC 于点Q ，如图所示：则四边形EQCD 为矩形，∴EQ ＝CD ＝6cm ，CQ ＝DE ＝2t cm ，∴51382844NQ BC CQ BN t t t æö=--=--=-ç÷èø，∴222222131696852100416EN EQ NQ t t t æö=+=+-=-+ç÷èø，∵563AM AB BM t æö=-=-ç÷èøcm ，()82AE t =-cm ，∴()2222225616825210039ME AM AE t t t t æö=+=-+-=-+ç÷èø，∴22611695210052100916t t t t -+=-+，此方程无解，∴不存在这样的菱形．14．（2022秋·江苏·九年级期中）(1)【原题呈现】在课本中，安排有这样一个思考问题：“如图1，在Rt △ABC 中，∠ACB =90°，∠BAC =30°，那么BC 和AB 有怎样的数量关系？试证明你的结论”老师在课堂中提出这样的问题，并展示了小明的部分解答小明：AB =2B C ．证明：把△ABC 沿着AC 翻折，得到△AD C ．∴∠ACD =∠ACB =90°，∴∠BCD =∠ACD +∠ACB =90°+90°=180°，即：点B 、C 、D 在一条直线上．（请在下面补全小华后面的证明过程）(2)【变式拓展】如图2，在△ABC 中，把（1）中条件“∠ACB =90°”改为“∠ACB =135°”，保持“∠BAC =30°”不变，则2AB = 2BC ．(3)【能力迁移】我们发现，翻折可以探索图形性质，请利用翻折解决下面问题．如图3，点D 是△ABC 内一点，AD =AC ，∠BAD =∠CAD =20°，∠ADB +∠ACB =210°，探求AD 、DB 、BC 三者之间的数量关系，并说明理由．【答案】(1)见解析(2)2(3)222BD BC AD +=，理由见解析【分析】（1）根据翻折的性质得出点B 、C 、D 共线，再由等边三角形的判定和性质即可证明；（2）把∆ABC 沿着AC 翻折，得到∆ADC ，根据翻折的性质得出∆ABD 为等边三角形，由题意确定∠BCD =90°，运用勾股定理即可得出结论；（3）把△ABD延AB边翻折得到△AEB，连接ED，EC，由翻折及各角之间的关系得出△AEC为等边三角形，再由勾股定理及等量代换即可得出结论．【详解】（1）证明：把△ABC沿着AC翻折，得到△ADC．∴∠ACD=∠ACB=90°，∴∠BCD=∠ACD+∠ACB=90°+90°=180°，即：点B、C、D共线，∴AB=AD，∵∠BAC=30°，∴∠ABC=60°，∴△ABD为等边三角形，∴AB=BD=2BC；（2）如图所示，把∆ABC沿着AC翻折，得到∆ADC，由翻折得：AD=AB，∠CAD=∠CAB=30°，BC=CD，∴∠BAD=60°，∴∆ABD为等边三角形，∴AB=BD，∵∠ACB=∠ACD=135°，∴∠BCD=90°，2222\=+=，BD BC CD BC2即22AB BC=；2（3）222+=；BD BC AD理由：把△ABD延AB边翻折得到△AEB，连接ED，EC，∵∠BAD=∠CAD=20°，∴∠EAB=20°，∴∠EAC=60°，∵∠ACB +∠ADB =210°，∠AEB =∠ADB ，∴∠ACB =∠AEB =210°，∴∠EBC =360°-210°-60°=90°，∵AD =AC ，AE =AD ，∴AE =AC ，∴△AEC 为等边三角形，∴EC =AE =AD ，在Rt △EBC 中，222BE BC EC +=，∵BC =BD ，EC =AD ，∴222BD BC AD +=．15．（2022秋·江苏盐城·九年级校联考阶段练习）问题情境：如图1，P 是O e 外的一点，直线PO 分别交O e 于点A ，B ．(1)探究证明：如图2，在O e 上任取一点C (不与点A ，B 重合)，连接PC ，求证：<AP PC ；(2)直接应用：如图3，在Rt ABC △中，=90ACB Ð°，3AB AC ==，以BC 为直径的半圆O 交AB 于D ，P 是弧CD 上的一个动点，则AP 的最小值是．(3)构造运用：如图4，在边长为2的菱形ABCD 中，=60A Ð°，M 是AD 的中点，N 是AB 边上一动点，将AMN V 沿MN 所在的直线翻折得到A MN ¢V ，连接A B ¢，则A B ¢长度的最小值为．(4)综合应用：如图5，平面直角坐标系中，分别以点()2,3A -，点()4,5B ，分别以1，2为半径作A e 、B e ，M ，N 分别是A e ，B e 上的动点，直接写出PM PN +的最小值为．【答案】(1)见解析321-(4)7【分析】(1)在POC △中，根据“三角形两边之差小于第三边”可求证；(2)连接OA 交O e 于点P ，根据勾股定理求得OA ，进而求得AP ；(3)A ¢的轨迹是以M 为圆心，半径是1的圆，故连接BM ，求得BM ，进而求得A B ¢的最小值；(4)作点A 关于x 轴的对称点C ，连接CB 交x 轴于点P ，求出BC 的长，进而求得PM PN +的最小值．（1）证明：如图1，<PO OC PC -Q ，()<AP OA OC PC \+-，OA OC =Q ，<AP PC \；（2）解：如图2，连接OA ，交半O e 于点P ，13==22CO BC \，在Rt AOC V 中，OA ===∴32AP OA OP =-=，\AP 32，32；（3）解：如图3，连接BM 、BD ，交M ⊙于点1A ，∵四边形ABCD 是菱形，AB AD \=，=60BAM Ð°Q ，ABD \V 是等边三角形，∵M 是AD 的中点，A ¢的轨迹是以M 为圆心，半径是1的圆，=90AMB \Ð°，1112AM A M AD ===，BM \==，∴111A B BM A M =-=，A B \¢1-，1；（4）解：如图4，作点A 关于x 轴的对称点C ，连接BC ，交x 轴于点P ，交B e 于点N ，连接PA 交A e 于M ，PA PC \=，PA PB PC PB BC \+=+=，∵点()2,3A -，点()4,5B ，∴点(2,3)C --，10BC \==，∵分别以1，2为半径作A e 、B e ，=1AM \，2BN =，PM PN \+PA PB AM BN =+-- 1012=--=7，故答案是：7．16．（2022秋·江苏盐城·九年级校考阶段练习）函数图象是研究函数的重要工具，类比一次函数的学习，对函数32y x =-的图象与性质进行探究．下表是探究过程中的部分信息：x …2-1-012 (32)y x =-…4a2-14…请按要求完成下列各小题：(1)a 的值为______；(2)在图中画出该函数的图象；(3)结合函数的图象，解决下列问题：①下列说法正确的是：______．（填所有正确选项）A ．函数图像关于x 轴对称B ．当0x =时，函数有最小值，最小值为2-C ．当0x >时，y 随x 的增大而增大②直接写出不等式1324x <-<的解集为______．(4)将该函数图像在直线1y =上方的部分保持不变，下方的部分图像沿直线1y =进行翻折，得到新函数图像，若经过点()2,0-的一次函数y kx b =+图像与新函数图像W 只有1个交点时，请直接写出k 满足的条件______．【答案】(1)1(2)见解析(3)①BC ；②2<<1x --或12x <<(4)3k ³或3k <-或13k =【分析】（1）把=1x -代入32y x =-即可求出a 的值；（2）先描点再连线画出函数图像即可；（3）①根据函数图象可以看出函数图像关于y 轴对称，关于x 轴不对称，即可判断A 错误；根据函数图象可判断当0x =时，函数有最小值，最小值为2-，得出B 正确；根据函数图象可判断当0x >时，y 随x 的增大而增大，得出C 正确；②根据函数图象写出不等式的解集即可；（4）根据题意画出翻折后的图像，然后数形结合求出k 的范围即可．【详解】（1）解：把=1x -代入32y x =-得：3121y =´--=，即1a =，故答案为：1．（2）解：该函数的图象，如图所示：（3）解：①A ．函数图像关于y 轴对称，故A 错误；B ．当0x =时，函数有最小值，最小值为2-，故B 正确；C ．当0x >时，y 随x 的增大而增大，故C 正确；故答案为：BC ；②根据函数图象可知，当2<<1x --或12x <<时，1324x <-<；故答案为：2<<1x --或12x <<；（4）解：如图所示：设点()2,4A ，()1,1B ，()0,4C ，()11D -,，()2,4E -，设AB 的解析式为11y k x b =+，把()2,4A ，()1,1B 代入得：1111241k b k b +=ìí+=î，解得：1132k b =ìí=-î，AB 的解析式为：()321y x x =->，设CD 的解析式为22y k x b =+，把()0,4C ，()11D -,代入得：22141b k b =ìí-+=î，解得：2234k b =ìí=î，CD 的解析式为：()3410y x x =+-<<，设DE 的解析式为33y k x b =+，把()11D -,，()2,4E -代入得：3333241k b k b -+=ìí-+=î，解得：3332k b =-ìí=-î，DE 的解析式为：()341y x x =--<-，根据图像可知，当直线y kx b =+经过()2,0-和点()1,1B 时，直线y kx b =+与图像W 只有一个交点，把()2,0-，()1,1B 代入得：201k b k b -+=ìí+=î，解得：13k =；∵123k k ==，∴AB CD ∥，根据图像可知，当直线y kx b =+与AB 平行时，直线y kx b =+与图像W 只有一个交点，且此时直线y kx b =+绕点()2,0-继续逆时针旋转，直到与DE 平行之前，直线y kx b =+与图像W 只有一个交点，∴当3k ³或3k <-时，直线y kx b =+与图像W 只有一个交点；综上分析可知，当3k ³或3k <-或13k =时直线y kx b =+与图像W 只有一个交点．故答案为：3k ³或3k <-或13k =．17．（2017江苏省宿迁市，第25题，10分）如图，在平面直角坐标系xOy 中，抛物线2=23y x x --交x 轴于A ，B 两点（点A 在点B 的左侧），将该抛物线位于x 轴上方曲线记作M ，将该抛物线位于x 轴下方部分沿x 轴翻折，翻折后所得曲线记作N ，曲线N 交y 轴于点C ，连接AC 、BC ．（1）求曲线N 所在抛物线相应的函数表达式；（2）求△ABC 外接圆的半径；（3）点P 为曲线M 或曲线N 上的一动点，点Q 为x 轴上的一个动点，若以点B ，C ，P ，Q 为顶点的四边形是平行四边形，求点Q 的坐标．【答案】（1）223y x x =-++；（2（3）Q （0）或（4，0）或（5，0）或（0）或（2，0）或（1，0）．【详解】试题分析：（1）由已知抛物线可求得A 、B 坐标及顶点坐标，利用对称性可求得C 的坐标，利用待定系数法可求得曲线N 的解析式；（2）由外接圆的定义可知圆心即为线段BC 与AB 的垂直平分线的交点，即直线y =x 与抛物线对称轴的交点，可求得外接圆的圆心，再利用勾股定理可求得半径的长；（3）设Q （x ，0），当BC 为平行四边形的边时，则有BQ ∥PC 且BQ =PC ，从而可用x 表示出P 点的坐标，代入抛物线解析式可得到x 的方程，可求得Q 点坐标，当BC 为平行四边形的对角线时，由B 、C 的坐标可求得平行四边形的对称中心的坐标，从而可表示出P 点坐标，代入抛物线解析式可得到关于x 的方程，可求得P 点坐标．试题解析：（1）在2=23y x x --中，令y =0可得x 2﹣2x ﹣3=0，解得x =﹣1或x =3，∴A （﹣1，0），B （3，0），令x =0可得y =﹣3，又抛物线位于x 轴下方部分沿x 轴翻折后得到曲线N ，∴C （0，3），设曲线N 的解析式为2y ax bx c =++，把A 、B 、C 的坐标代入可得：09303a b c a b c c -+=ìï++=íï=î，解得：123a b c =-ìï=íï=î，∴曲线N 所在抛物线相应的函数表达式为223y x x =-++；（2）设△ABC 外接圆的圆心为M ，则点M 为线段BC 、线段AB 垂直平分线的交点，∵B （3，0），C （0，3），∴线段BC 的垂直平分线的解析式为y =x ，又线段AB 的解析式为曲线N 的对称轴，即x =1，∴M （1，1），∴MB△ABC（3）设Q （t ，0），则BQ =|t ﹣3|．①当BC 为平行四边形的边时，如图1，则有BQ ∥PC ，∴P 点纵坐标为3，即过C 点与x 轴平行的直线与曲线M 和曲线N 的交点即为点P ，x 轴上对应的即为点Q ，当点P 在曲线M 上时，在2=23y x x --中，令y =3可解得x或x =1，∴PCPC﹣1．。

全等变换(平移、旋转、翻折)

中考全国100份试卷分类汇编全等变换（平移、旋转、翻折）1、（2013•天津）如图，在△ABC 中，AC=BC ，点D 、E 分别是边AB 、AC 的中点，将△ADE 绕点E 旋转180°得△CFE ，则四边形ADCF 一定是（）A ．矩形B ．菱形C ．正方形D ．梯形考点：旋转的性质；矩形的判定．分析：根据旋转的性质可得AE=CE ，DE=EF ，再根据对角线互相平分的四边形是平行四边形判断出四边形ADCF 是平行四边形，然后利用等腰三角形三线合一的性质求出∠ADC=90°，再利用有一个角是直角的平行四边形是矩形解答．解答：解：∵△ADE 绕点E 旋转180°得△CFE ， ∴AE=CE ，DE=EF ，∴四边形ADCF 是平行四边形， ∵AC=BC ，点D 是边AB 的中点， ∴∠ADC=90°，∴四边形ADCF 矩形．故选A ．点评：本题考查了旋转的性质，矩形的判定，主要利用了对角线互相平分的四边形是平行四边形，有一个角是直角是平行四边形是矩形的判定方法，熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键．2、(2013年黄石)把一副三角板如图甲放置，其中90ACB DEC ∠=∠=，45A ∠=，30D ∠=，斜边6AB =，7DC =，把三角板DCE 绕着点C 顺时针旋转15得到△11D CE （如图乙），此时AB 与1CD 交于点O ，则线段1AD 的长度为A.32B. 5DCAEB AD 1OE 1BC图甲图乙C. 4D.31答案：B解析：如图所示，∠3=15°，∠E1=90°，∴∠1=∠2=75°，又∵∠B=45°，∴∠OFE 1=∠B+∠1=45°+75°=120°。

∵∠OFE1=120°，∴∠D1FO=60°，∵∠CD1E1=30°，∴∠4=90°，又∵AC=BC，AB=6，∴OA=OB=3，∵∠ACB=90°，∴，又∵CD1=7，∴OD1=CD1-OC=7-3=4，在Rt△AD1O中，。

初中的几何变换——翻折

初中数学几何变换之轴对称一、知识梳理1、轴对称基本要素：对称轴。

2、基本性质：（1）对应线段、对应角相等（2）对应点所连线段被对称轴垂直平分（3）对称轴上的点到对应点的距离相等（4）对称轴两侧的几何图形全等 3、应用翻折问题、最值问题等二、常考题型类型一：轴对称性质1、如图，在平行四边形ABCD 中，13=AB ，4=AD ，将平行四边形ABCD 沿AE 翻折后，点B 恰好与点C 重合，则折痕AE 的长为__________.第1题第2题第3题2、如图，矩形中，AB =8，BC =6，P 为AD 上一点，将△ABP 沿BP 翻折至△EBP ， PE与CD 相交于点O ，且OE =OD ，则AP 的长为__________.3、如图，在△ABC 中，AB =AC ，BC =24，tanC =2，如果将△ABC 沿直线l 翻折后，点B 落在边AC 的中点E 处，直线l 与边BC 交于点D ，那么BD 的长为。

4、如图，菱形纸片ABCD中，∠A=600，将纸片折叠，点A、D分别落在A’、D’处，且A’的值为。

D’经过B，EF为折痕，当D’F CD时，CFFD5、如图，在△ABC中，∠C＝90°，将△ABC沿直线MN翻折后，顶点C恰好落在AB边上的点D处，已知MN∥AB，MC＝6，NC＝，则四边形MABN的面积是。

第4题第5题第6题6、如图，已知边长为5的等边三角形ABC纸片，点E在AC边上，点F在AB边上，沿着EF 折叠，使点A落在BC边上的点D的位置，且，则CE的长是。

折叠两次：第一次折叠纸片使点A与点E重合，如图2，折痕为MN，连接ME、NE；第二次折叠纸片使点N与点E重合，如图3，点B落在B′处，折痕为HG，连接HE，则tan∠EHG图2 图38、如图，在边长为6的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长交BC于点G，连接AG.（1）求证：△ABG≌△AFG；（2）求BG的长.类型二：轴对称应用1、菱形ABCD在平面直角坐标系中的位置如图所示，顶点B（2，0），∠DOB=60°，点P是对角线OC上一个动点，E（0，﹣1），当EP+BP最短时，点P的坐标为．2、如图，∠AOB=30°，点M、N分别是射线OA、OB上的动点，OP平分∠AOB，且OP=6，当△PMN的周长取最小值时，四边形PMON的面积为．3、如图,在锐角△ABC中,AB=6,∠BAC=60°,∠BAC的平分线交BC于点D,点M,N分别是AD 和AB上的动点,则BM+MN的最小值为。

专题十六全等变换

全等变换分类
全等变换包括平移变换、旋转变换、翻折变换（轴对称）等多种类型。
全等图形与对应元素
全等图形
能够完全重合的两个图形叫做全等图形。
对应元素
在全等图形中，互相重合的点、线段、角等几何元素称为对应元素。
全等变换基本性质
全等变换保持图形的形状和大小不变。
在全等变换下，图形的面积、周长等几何量也保持不变。
利用平行线、同位角、内错角等性质，结合全等变换来证明线段或角相等。
通过构造全等三角形来证明线段或角相等，如倍长中线法、截长补短法等。
证明图形重合或对称
利用全等变换的性质，通过旋转、翻折等变换来证明两个图形重合或对称。
利用中心对称或轴对称的性质，结合全等变换来证明图形重合或对称。
通过证明两个图形完全重合来得出它们对称的结论。
VS
性质
旋转中心、旋转方向、旋转角度为旋转的三要素。旋转只改变图形的位置，不改变图形的形状和大小。经过旋转，图形上的每一点都绕旋转中心沿相同方向转动了相同的角度，任意一对对应点与旋转中心的连线所成的角都是旋转角，对应点到旋转中心的距离相等。
翻折变换概念及性质
概念
翻折变换是指把一个图形沿着某一条直线折叠过来，直线两旁的部分能够相互重合，这个图形叫做轴对称图形，这条直线就是它的对称轴。
通过全等变换，将方程或不等式转换为更容易解的形式，从而快速找到解。
常见的全等变换包括移项、合并同类项、去括号等，以及利用等式的性质进行变换。
在解决方程或不等式问题时，需要注意保持解的范围和精度，避免出现错误解或无解的情况。
利用全等变换进行代数式证明
通过全等变换，将待证明的代数式转换为已知成立的形式，从而完成证明。

(精心整理)初中数学几何模型大全+经典题型(含答案)

初中数学几何模型大全+经典题型（含答案）全等变换平移：平行等线段（平行四边形）对称：角平分线或垂直或半角旋转：相邻等线段绕公共顶点旋转对称全等模型说明：以角平分线为轴在角两边进行截长补短或者作边的垂线，形成对称全等。

两边进行边或者角的等量代换，产生联系。

垂直也可以做为轴进行对称全等。

对称半角模型说明：上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称（翻折），翻折成正方形或者等腰直角三角形、等边三角形、对称全等。

旋转全等模型半角：有一个角含1/2角及相邻线段自旋转：有一对相邻等线段，需要构造旋转全等共旋转：有两对相邻等线段，直接寻找旋转全等中点旋转：倍长中点相关线段转换成旋转全等问题旋转半角模型说明：旋转半角的特征是相邻等线段所成角含一个二分之一角，通过旋转将另外两个和为二分之一的角拼接在一起，成对称全等。

自旋转模型构造方法：遇60度旋60度，造等边三角形遇90度旋90度，造等腰直角遇等腰旋顶点，造旋转全等遇中点旋180度，造中心对称共旋转模型说明：旋转中所成的全等三角形，第三边所成的角是一个经常考察的内容。

通过“8”字模型可以证明。

模型变形说明：模型变形主要是两个正多边形或者等腰三角形的夹角的变化，另外是等腰直角三角形与正方形的混用。

当遇到复杂图形找不到旋转全等时，先找两个正多边形或者等腰三角形的公共顶点，围绕公共顶点找到两组相邻等线段，分组组成三角形证全等。

中点旋转：说明：两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点，证明另外两个顶点与中点所成图形为等腰直角三角形。

证明方法是倍长所要证等腰直角三角形的一直角边，转化成要证明的等腰直角三角形和已知的等腰直角三角形（或者正方形）公旋转顶点，通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。

几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明：通过对称进行等量代换，转换成两点间距离及点到直线距离。

初中数学专题复习(翻折变换问题)

初中数学专题复习（翻折变换问题）1．（2020•衢州）如图，把一张矩形纸片ABCD按所示方法进行两次折叠，得到等腰直角三角形BEF，若BC＝1，则AB的长度为（）A．B．C．D．解：由折叠补全图形如图所示，∵四边形ABCD是矩形，∴∠ADA'＝∠B＝∠C＝∠A＝90°，AD＝BC＝1，CD＝AB，由第一次折叠得：∠DA'E＝∠A＝90°，∠ADE＝∠ADC＝45°，∴∠AED＝∠ADE＝45°，∴AE＝AD＝1，在Rt△ADE中，根据勾股定理得，DE＝AD＝，由第二次折叠知，CD＝DE＝，∴AB＝．故选：A．2．（2020•西宁）如图，在矩形ABCD中，AB＝5，BC＝6，点M，N分别在AD，BC上，且AM＝BN，AD＝3AM，E为BC边上一动点，连接DE，将△DCE沿DE所在直线折叠得到△DC′E，当C′点恰好落在线段MN上时，CE的长为（）A．或2B．C．或2D．解：设CE＝x，则C′E＝x，∵矩形ABCD中，AB＝5，∴CD＝AB＝5，AD＝BC＝6，AD∥BC，∵点M，N分别在AD，BC上，且3AM＝AD，BN＝AM，∴DM＝CN＝4，∴四边形CDMN为平行四边形，∵∠NCD＝90°，∴四边形MNCD是矩形，∴∠DMN＝∠MNC＝90°，MN＝CD＝5由折叠知，C′D＝CD＝5，∴MC′＝＝＝3，∴C′N＝5﹣3＝2，∵EN＝CN﹣CE＝4﹣x，∴C′E2﹣NE2＝C′E2，∴x2﹣（4﹣x）2＝22，解得，x＝，即CE＝．故选：B．3．（2020•黔南州）如图，将矩形纸条ABCD折叠，折痕为EF，折叠后点C，D分别落在点C′，D′处，D′E 与BF交于点G．已知∠BGD′＝30°，则∠α的度数是（）A．30°B．45°C．74°D．75°解：∵矩形纸条ABCD中，AD∥BC，∴∠AEG＝∠BGD'＝30°，∴∠DEG＝180°﹣30°＝150°，由折叠可得，∠α＝∠DEG＝×150°＝75°，故选：D．4．（2020•呼和浩特）如图，把某矩形纸片ABCD沿EF，GH折叠（点E、H在AD边上，点F，G在BC边上），＝8，使点B和点C落在AD边上同一点P处，A点的对称点为A'、D点的对称点为D'，若∠FPG＝90°，S△A′EPS△D′PH＝2，则矩形ABCD的长为（）A．6+10B．6+5C．3+10D．3+5解：∵四边形ABCD是矩形，∴AB＝CD，AD＝BC，设AB＝CD＝x，由翻折可知：PA′＝AB＝x，PD′＝CD＝x，∵△A′EP的面积为8，△D′PH的面积为2，又∵，∠A′PF＝∠D′PG＝90°，∴∠A′PD′＝90°，则∠A′PE+∠D′PH＝90°，∴∠A′PE＝∠D′HP，∴△A′EP∽△D′PH，∴A′P2：D′H2＝8：2，∴A′P：D′H＝2：1，∵A′P＝x，∴D′H＝x，∵S△D′PH＝D′P•D′H，即，∴x＝（负根舍弃），∴AB＝CD＝，D′H＝DH＝，D′P＝A′P＝CD＝，A′E＝2D′P＝，∴PE＝，PH＝，∴AD＝＝，即矩形ABCD的长为，故选：D．5．（2020•内江）如图，矩形ABCD中，BD为对角线，将矩形ABCD沿BE、BF所在直线折叠，使点A落在BD 上的点M处，点C落在BD上的点N处，连接EF．已知AB＝3，BC＝4，则EF的长为（）A．3B．5C．D．解：∵四边形ABCD是矩形，∴AB＝CD＝3，AD＝BC＝4，∠A＝∠C＝∠EDF＝90°，∴BD＝＝＝5，∵将矩形ABCD沿BE所在直线折叠，使点A落在BD上的点M处，∴AE＝EM，∠A＝∠BME＝90°，∴∠EMD＝90°，∵∠EDM＝∠ADB，∴△EDM∽△BDA，∴，设DE＝x，则AE＝EM＝4﹣x，∴，解得x＝，∴DE＝，同理△DNF∽△DCB，∴，设DF＝y，则CF＝NF＝3﹣y，∴，解得y＝．∴DF＝．∴EF＝＝＝．故选：C．6．（2020•青岛）如图，将矩形ABCD折叠，使点C和点A重合，折痕为EF，EF与AC交于点O．若AE＝5，BF＝3，则AO的长为（）A．B．C．2D．4解：∵矩形ABCD，∴AD∥BC，AD＝BC，AB＝CD，∴∠EFC＝∠AEF，由折叠得，∠EFC＝∠AFE，∴∠AFE＝∠AEF，∴AE＝AF＝5，由折叠得，FC＝AF，OA＝OC，∴BC＝3+5＝8，在Rt△ABF中，AB＝＝4，在Rt△ABC中，AC＝＝4，∴OA＝OC＝2，故选：C．7．（2020•滨州）如图，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平后再次折叠，使点A 落在EF上的点A′处，得到折痕BM，BM与EF相交于点N．若直线BA′交直线CD于点O，BC＝5，EN＝1，则OD的长为（）A．B．C．D．解一：∵EN＝1，∴由中位线定理得AM＝2，由折叠的性质可得A′M＝2，∵AD∥EF，∴∠AMB＝∠A′NM，∵∠AMB＝∠A′MB，∴∠A′NM＝∠A′MB，∴A′N＝2，∴A′E＝3，A′F＝2过M点作MG⊥EF于G，∴NG＝EN＝1，∴A′G＝1，由勾股定理得MG＝＝，∴BE＝DF＝MG＝，∴OF：BE＝2：3，解得OF＝，∴OD＝﹣＝．故选：B．解二：连接AA'．∵EN＝1，∴由中位线定理得AM＝2，∵对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，∴A'A＝A'B，∵把纸片展平后再次折叠，使点A落在EF上的点A′处，得到折痕BM，∴A'B＝AB，∠ABM＝∠A'BM，∴△ABA'为等边三角形，∴∠ABA′＝∠BA′A＝∠A′AB＝60°，又∵∠ABC＝∠BAM＝90°，∴∠ABM＝∠A'BM＝∠A'BC＝30°，∴BM＝2AM＝4，AB＝AM＝2＝CD．在直角△OBC中，∵∠C＝90°，∠OBC＝30°，∴OC＝BC•tan∠OBC＝5×＝，∴OD＝CD﹣OC＝2﹣＝．故选：B．8．（2020•重庆）如图，在△ABC中，AC＝2，∠ABC＝45°，∠BAC＝15°，将△ACB沿直线AC翻折至△ABC所在的平面内，得△ACD．过点A作AE，使∠DAE＝∠DAC，与CD的延长线交于点E，连接BE，则线段BE的长为（）A．B．3C．2D．4解：如图，延长BC交AE于H，∵∠ABC＝45°，∠BAC＝15°，∴∠ACB＝120°，∵将△ACB沿直线AC翻折，∴∠DAC＝∠BAC＝15°，∠ADC＝∠ABC＝45°，∠ACB＝∠ACD＝120°，∵∠DAE＝∠DAC，∴∠DAE＝∠DAC＝15°，∴∠CAE＝30°，∵∠ADC＝∠DAE+∠AED，∴∠AED＝45°﹣15°＝30°，∴∠AED＝∠EAC，∴AC＝EC，又∵∠BCE＝360°﹣∠ACB﹣∠ACE＝120°＝∠ACB，BC＝BC，∴△ABC≌△EBC（SAS），∴AB＝BE，∠ABC＝∠EBC＝45°，∴∠ABE＝90°，∵AB＝BE，∠ABC＝∠EBC，∴AH＝EH，BH⊥AE，∵∠CAE＝30°，∴CH＝AC＝，AH＝CH＝，∴AE＝2，∵AB＝BE，∠ABE＝90°，∴BE＝＝2，故选：C．9．（2020•重庆）如图，三角形纸片ABC，点D是BC边上一点，连接AD，把△ABD沿着AD翻折，得到△AED，DE与AC交于点G，连接BE交AD于点F．若DG＝GE，AF＝3，BF＝2，△ADG的面积为2，则点F到BC 的距离为（）A．B．C．D．解：∵DG＝GE，＝S△AEG＝2，∴S△ADG∴S△ADE＝4，由翻折可知，△ADB≌△ADE，BE⊥AD，＝S△ADE＝4，∠BFD＝90°，∴S△ABD∴•（AF+DF）•BF＝4，∴•（3+DF）•2＝4，∴DF＝1，∴DB＝＝＝，设点F到BD的距离为h，则有•BD•h＝•BF•DF，∴h＝，故选：B．10．（2020•济南）如图，在矩形纸片ABCD中，AD＝10，AB＝8，将AB沿AE翻折，使点B落在B'处，AE为折痕；再将EC沿EF翻折，使点C恰好落在线段EB'上的点C'处，EF为折痕，连接AC'．若CF＝3，则tan∠B'AC′＝．解：连接AF，设CE＝x，则C′E＝CE＝x，BE＝B′E＝10﹣x，∵四边形ABCD是矩形，∴AB＝CD＝8，AD＝BC＝10，∠B＝∠C＝∠D＝90°，∴AE2＝AB2+BE2＝82+（10﹣x）2＝164﹣20x+x2，EF2＝CE2+CF2＝x2+32＝x2+9，由折叠知，∠AEB＝∠AEB′，∠CEF＝∠C′EF，∵∠AEB+∠AEB′+∠CEF+∠C′EF＝180°，∴∠AEF＝∠AEB′+∠C′EF＝90°，∴AF2＝AE2+EF2＝164﹣20x+x2+x2+9＝2x2﹣20x+173，∵AF2＝AD2+DF2＝102+（8﹣3）2＝125，∴2x2﹣20x+173＝125，解得，x＝4或6，当x＝6时，EC＝EC′＝6，BE＝B′E＝10﹣6＝4，EC′＞B′E，不合题意，应舍去，∴CE＝C′E＝4，∴B′C′＝B′E﹣C′E＝（10﹣4）﹣4＝2，∵∠B′＝∠B＝90°，AB′＝AB＝8，∴tan∠B'AC′＝．故答案为：．另一解法：由折叠知，∠AEB＝∠AEB′，∠CEF＝∠C′EF，∵∠AEB+∠AEB′+∠CEF+∠C′EF＝180°，∴∠AEF＝∠AEB′+∠C′EF＝90°，∴∠AEB+∠CEF＝90°，∵四边形ABCD是矩形，∴∠B＝∠C＝90°，BC＝AD＝10，∴∠BAE+∠AEB＝90°，∴∠BAE＝∠CEF，∴△ABE∽△ECF，∴，设BE＝x，则BE＝B'E＝x，C'E＝CE＝10﹣x，∴，解得，x＝4或6，∴BE＝B'E＝4，CE＝C'E＝6，或BE＝B'E＝6，CE＝C'E＝4，∵B'E＞C'E，∴BE＝B'E＝6，CE＝C'E＝4，∴B'C'＝B'E﹣C'E＝6﹣4＝2，由折叠知，AB'＝AB＝8，∠B'＝∠B＝90°，∴tan∠B'AC′＝．解法三：设BE＝a，EC＝b，则a+b＝10．由于△AB'E～△EC'F，所以AB'：EC'＝EB'：C'F，即8：a＝b：3，ab＝24．B'C'＝a﹣b，因为（a﹣b）2＝（a+b）2﹣4ab＝100﹣96＝4．所以B'C′＝2．所以tan∠B'AC′＝．故答案为．11．（2020•淄博）如图，矩形纸片ABCD，AB＝6cm，BC＝8cm，E为边CD上一点．将△BCE沿BE所在的直线折叠，点C恰好落在AD边上的点F处，过点F作FM⊥BE，垂足为点M，取AF的中点N，连接MN，则MN＝5cm．解：连接AC，MC．由翻折的性质可知，BE垂直平分线段CF，∵FM⊥BE，∴F．M，C共线，FM＝MC，∵AN＝FN，∴MN＝AC，∵四边形ABCD是矩形，∴∠ABC＝90°，∴AC＝＝＝10（cm），∴MN＝AC＝5（cm），故答案为5．12．（2020•威海）如图，四边形ABCD是一张正方形纸片，其面积为25cm2．分别在边AB，BC，CD，DA上顺次截取AE＝BF＝CG＝DH＝acm（AE＞BE），连接EF，FG，GH，HE．分别以EF，FG，GH，HE为轴将纸片向内翻折，得到四边形A1B1C1D1．若四边形A1B1C1D1的面积为9cm2，则a＝4．解：∵四边形ABCD是一张正方形纸片，其面积为25cm2，∴正方形纸片的边长为5cm，∵AE＝BF＝CG＝DH＝acm，∴BE＝AH＝（5﹣a）cm，又∠A＝∠B＝90°，∴△AHE≌△BEF（SAS），同理可得△AHE≌△BEF≌△DGH≌CFG，由折叠的性质可知，图中的八个小三角形全等．∵四边形A1B1C1D1的面积为9cm2，∴三角形AEH的面积为（25﹣9）÷8＝2（cm2），a（5﹣a）＝2，解得a1＝1（舍去），a2＝4．故答案为：4．13．（2020•牡丹江）如图，在Rt△ABC中，∠C＝90°，点E在AC边上．将∠A沿直线BE翻折，点A落在点A'处，连接A'B，交AC于点F．若A'E⊥AE，cos A＝，则＝．解：∵∠C＝90°，cos A＝，∴，设AC＝4x，AB＝5x，则BC＝3x，∵AE⊥AE′，∴∠AEA′＝90°，A′E∥BC，由于折叠，∴∠A′EB＝∠AEB＝（360﹣90）÷2＝135°，∵∠A′EF＝∠C＝90°，∠EFA′＝∠BFC，∴△A′EF∽△BCF，∴∠BEC＝45°，即△BCE为等腰直角三角形，∴EC＝3x，∴AE＝AC﹣EC＝x＝A′E，∴，故答案为：．14．（2020•南通）矩形ABCD中，AB＝8，AD＝12．将矩形折叠，使点A落在点P处，折痕为DE．（1）如图①，若点P恰好在边BC上，连接AP，求的值；（2）如图②，若E是AB的中点，EP的延长线交BC于点F，求BF的长．解：（1）如图①中，取DE的中点M，连接PM．∵四边形ABCD是矩形，∴∠BAD＝∠C＝90°，由翻折可知，AO＝OP，AP⊥DE，∠2＝∠3，∠DAE＝∠DPE＝90°，在Rt△EPD中，∵EM＝MD，∴PM＝EM＝DM，∴∠3＝∠MPD，∴∠1＝∠3+∠MPD＝2∠3，∵∠ADP＝2∠3，∴∠1＝∠ADP，∵AD∥BC，∴∠ADP＝∠DPC，∴∠1＝∠DPC，∵∠MOP＝∠C＝90°，∴△POM∽△DCP，∴＝＝＝，∴＝＝．解法二：证明△ABP和△DAE相似，＝＝．（2）如图②中，过点P作GH∥BC交AB于G，交CD于H．则四边形AGHD是矩形，设EG＝x，则BG＝4﹣x∵∠A＝∠EPD＝90°，∠EGP＝∠DHP＝90°，∴∠EPG+∠DPH＝90°，∠DPH+∠PDH＝90°，∴∠EPG＝∠PDH，∴△EGP∽△PHD，∴＝＝＝＝，∴PH＝3EG＝3x，DH＝AG＝4+x，在Rt△PHD中，∵PH2+DH2＝PD2，∴（3x）2+（4+x）2＝122，解得x＝（负值已经舍弃），∴BG＝4﹣＝，在Rt△EGP中，GP＝＝，∵GH∥BC，∴△EGP∽△EBF，∴＝，∴＝，∴BF＝3．15．（2020•无锡）如图，在矩形ABCD中，AB＝2，AD＝1，点E为边CD上的一点（与C、D不重合），四边形ABCE关于直线AE的对称图形为四边形ANME，延长ME交AB于点P，记四边形PADE的面积为S．（1）若DE＝，求S的值；（2）设DE＝x，求S关于x的函数表达式．解：（1）∵在矩形ABCD中，∠D＝90°，AD＝1，DE＝，∴AE＝＝，∴tan∠AED＝＝，∴∠AED＝60°，∵AB∥CD，∴∠BAE＝60°，∵四边形ABCE关于直线AE的对称图形为四边形ANME，∴∠AEC＝∠AEM，∵∠PEC＝∠DEM，∴∠AEP＝∠AED＝60°，∴△APE为等边三角形，∴S＝（+）×1＝；（2）过E作EF⊥AB于F，由（1）可知，∠AEP＝∠AED＝∠PAE，∴AP＝PE，设AP＝PE＝a，AF＝ED＝x，则PF＝a﹣x，EF＝AD＝1，在Rt△PEF中，（a﹣x）2+1＝a2，解得：a＝，∴S＝＝．。

八年级数学翻折变换(折叠问题)参考答案与试题解析

八年级数学翻折变换(折叠问题)参考答案与试题解析work Information Technology Company.2020YEAR八年级数学翻折变换（折叠问题）参考答案与试题解析一．选择题（共12小题）1．如图，矩形纸片ABCD，长AD＝9m，宽AB＝3cm，将其折叠，使点D与点B重合，那么折叠后DE的长为（）A．7cm B．6cm C．5.5cm D．5cm【分析】由矩形的性质和折叠的性质以及勾股定理得出方程，解方程即可．【解答】解：由折叠的性质得：BE＝DE，设DE长为xcm，则AE＝（9﹣x）cm，BE＝xcm，∵四边形ABCD是矩形，∴∠A＝90°，根据勾股定理得：AE2+AB2＝BE2，即（9﹣x）2+32＝x2，解得：x＝5，即DE长为5cm，故选：D．【点评】本题考查了矩形的性质、翻折变换、勾股定理等知识；熟练掌握矩形和翻折变换的性质，运用勾股定理进行计算是解决问题的关键．2．如图，在等边三角形ABC中，点D、E分别是边AC、BC上两点．将△ABC沿DE翻折，点C正好落在线段AB上的点F处，使得AF：BF＝2：3．若BE＝16，则点F到BC边的距离是（）A．8B．12C．D．【分析】作EM⊥AB于M，由等边三角形的性质和直角三角形的性质求出BM＝BE＝8，ME＝BM＝8，由折叠的性质得出FE＝CE，设FE＝CE＝x，则AB＝BC＝16+x，得出BF＝（16+x），求出FM＝BF﹣BM＝（16+x）﹣8＝+x，在Rt△EFM中，由勾股定理得出方程，解方程求出BF＝21．作FN⊥BC于N，则∠BFN＝30°，由直角三角形的性质得出BN＝BF＝，得出FN＝BN＝即可．【解答】解：作EM⊥AB于M，如图所示：∵△ABC是等边三角形，∴BC＝AB，∠B＝60°，∵EM⊥AB，∴∠BEM＝30°，∴BM＝BE＝8，ME＝BM＝8，由折叠的性质得：FE＝CE，设FE＝CE＝x，则AB＝BC＝16+x，∵AF：BF＝2：3，∴BF＝（16+x），∴FM＝BF﹣BM＝（16+x）﹣8＝+x，在Rt△EFM中，由勾股定理得：（8）2+（+x）2＝x2，解得：x＝19，或x＝﹣16（舍去），∴BF＝（16+19）＝21，作FN⊥BC于N，则∠BFN＝30°，∴BN＝BF＝，∴FN＝BN＝，即点F到BC边的距离是，故选：D．【点评】本题考查了翻折变换的性质、等边三角形的性质、直角三角形的性质、勾股定理等知识；熟练掌握翻折变换和等边三角形的性质，由勾股定理得出方程是解题的关键．3．如图，在等腰Rt△ABC中∠C＝90°，AC＝BC＝2．点D和点E分别是BC边和AB 边上两点，连接DE．将△BDE沿DE折叠，得到△B′DE，点B恰好落在AC的中点处设DE与BB交于点F，则EF＝（）A．B．C．D．【分析】根据等腰直角三角形的性质得到AB＝AC＝4，∠A＝∠B＝45°，过B′作B′H⊥AB与H，得到AH＝B′H＝AB′，求得AH＝B′H＝1，根据勾股定理得到BB′＝＝＝，由折叠的性质得到BF＝BB′＝，DE ⊥BB′，根据相似三角形即可得到结论．【解答】解：∵在等腰Rt△ABC中∠C＝90°，AC＝BC＝2，∴AB＝AC＝4，∠A＝∠B＝45°，过B′作B′H⊥AB与H，∴△AHB′是等腰直角三角形，∴AH＝B′H＝AB′，∵AB′＝AC＝，∴AH＝B′H＝1，∴BH＝3，∴BB′＝＝＝，∵将△BDE沿DE折叠，得到△B′DE，∴BF＝BB′＝，DE⊥BB′，∴∠BHB′＝∠BFE＝90°，∵∠EBF＝∠B′BH，∴△BFE∽△BHB′，∴＝，∴＝，∴EF＝，故答案为：．故选：C．【点评】本题考查了翻折变换（折叠问题），等腰直角三角形的判定和性质，勾股定理，相似三角形的判定和性质，正确的作出辅助线是解题的关键．4．如图，在△ABC中，AB＝AC＝2，∠BAC＝30°，将△ABC沿AC翻折得到△ACD，延长AD交BC的延长线于点E，则△ABE的面积为（）A．B．C．3D．【分析】由折叠的性质可知∠CAD＝30°＝∠CAB，AD＝AB＝2．由等腰三角形的性质得出∠BCA＝∠ACD＝∠ADC＝75°．求出∠ECD＝30°．由三角形的外角性质得出∠E＝75°﹣30°＝45°，过点C作CH⊥AE于H，过B作BM⊥AE于M，由直角三角形的性质得出CH＝AC＝1，AH＝CH＝．得出HD＝AD﹣AH＝2﹣．求出EH ＝CH＝1．得出DE＝EH﹣HD＝﹣1，AE＝AD+DE＝1+，由直角三角形的性质得出AM＝AB＝1，BM＝AM＝．由三角形面积公式即可得出答案．【解答】解：由折叠的性质可知：∠CAD＝30°＝∠CAB，AD＝AB＝2．∴∠BCA＝∠ACD＝∠ADC＝75°．∴∠ECD＝180°﹣2×75°＝30°．∴∠E＝75°﹣30°＝45°．过点C作CH⊥AE于H，过B作BM⊥AE于M，如图所示：在Rt△ACH中，CH＝AC＝1，AH＝CH＝．∴HD＝AD﹣AH＝2﹣．在Rt△CHE中，∵∠E＝45°，∴△CEH是等腰直角三角形，∴EH＝CH＝1．∴DE＝EH﹣HD＝1﹣（2﹣）＝﹣1，∴AE＝AD+DE＝1+，∵BM⊥AE，∠BAE＝∠BAC+∠CAD＝60°，∴∠ABM＝30°，∴AM＝AB＝1，BM＝AM＝．∴△ABE的面积＝AE×BM＝×（1+）×＝；故选：B．【点评】本题考查了翻折变换的性质、等腰三角形的性质、含30°角的直角三角形的性质、等腰直角三角形的判定与性质、三角形面积等知识；熟练掌握翻折变换和等腰三角形的性质是解题的关键．5．如图，点F是长方形ABCD中BC边上一点将△ABF沿AF折叠为△AEF，点E落在边CD上，若AB＝5，BC＝4，则BF的长为（）A．B．C．D．【分析】根据矩形的性质得到CD＝AB＝5，AD＝BC＝4，∠B＝∠D＝∠C＝90°，根据折叠的性质得到AE＝AB＝5，EF＝BF，根据勾股定理得到DE＝＝＝3，求得CE＝2，设BF＝EF＝x，则CF＝4﹣x，根据勾股定理列方程即可得到结论．【解答】解：∵四边形ABCD是矩形，∴CD＝AB＝5，AD＝BC＝4，∠B＝∠D＝∠C＝90°，∵将△ABF沿AF折叠为△AEF，∴AE＝AB＝5，EF＝BF，∴DE＝＝＝3，∴CE＝2，设BF＝EF＝x，则CF＝4﹣x，∵EF2＝CF2+CE2，∴x2＝（4﹣x）2+22，解得：x＝，故选：B．【点评】本题考查了翻折变换（折叠问题），矩形的矩形，勾股定理，熟练掌握折叠的性质是解题的关键．6．如图，在矩形纸片ABCD中，CB＝12，CD＝5，折叠纸片使AD与对角线BD重合，与点A重合的点为N，折痕为DM，则△MNB的面积为（）A．B．C．D．26【分析】由勾股定理得出BD＝＝13，由折叠的性质可得ND＝AD＝12，∠MND＝∠A＝90°，NM＝AM，得出∠EA′B＝90°，BN＝BD﹣ND＝1，设AM＝NM ＝x，则BM＝AB﹣AM＝5﹣x，在Rt△BMN中，由勾股定理得出方程，解方程得出NM ＝AM＝，即可得出答案．【解答】解：∵四边形ABCD是矩形，∴∠A＝90°，AD＝BC＝12，AB＝CD＝5，∴BD＝＝＝13，由折叠的性质可得：ND＝AD＝12，∠MND＝∠A＝90°，NM＝AM，∴∠EA′B＝90°，BN＝BD﹣ND＝13﹣12＝1，设AM＝NM＝x，则BM＝AB﹣AM＝5﹣x，在Rt△BMN中，NM2+BN2＝BM2，∴x2+12＝（5﹣x）2，解得：x＝，∴NM＝AM＝，∴△MNB的面积＝BN×NM＝×1×＝；故选：A．【点评】此题考查了折叠的性质、勾股定理以及矩形的性质．熟练掌握折叠的性质和矩形的性质，由勾股定理得出方程是解题的关键．7．如图，在△ABC中∠ACB＝90°、∠CAB＝30°，△ABD是等边三角形、将四边形ACBD折叠，使点D与点C重合，HK为折痕，则sin∠ACH的是（）A．B．C．D．【分析】在Rt△ABC中，设BC＝a，则AB＝2BC＝2a，AD＝AB＝2a．设AH＝x，则HC＝HD＝AD﹣AH＝2a﹣x．在Rt△ABC中，由勾股定理得AC2＝3a2，在Rt△ACH 中，由勾股定理得AH2+AC2＝HC2，即x2+3a2＝（2a﹣x）2．解得x＝a，即AH＝a．求得HC的值后，利用sin∠ACH＝AH：HC求值．【解答】解：∵△ABD是等边三角形，∴∠BAD＝60°，AB＝AD，∵∠CAB＝30°，∴∠CAH＝90°．在Rt△ABC中，∠CAB＝30°，设BC＝a，则AB＝2BC＝2a．∴AD＝AB＝2a．设AH＝x，则HC＝HD＝AD﹣AH＝2a﹣x，在Rt△ABC中，AC2＝（2a）2﹣a2＝3a2，在Rt△ACH中，AH2+AC2＝HC2，即x2+3a2＝（2a﹣x）2，解得x＝a，即AH＝a．∴HC＝2a﹣x＝2a﹣a＝a．∴sin∠ACH＝＝，故选：C．【点评】本题考查了折叠的性质，锐角三角函数值，勾股定理的应用，熟练掌握折叠的性质和解直角三角形是解题的关键．8．如图，在矩形ABCD中，AB＝1，在BC上取一点E，连接AE、ED，将△ABE沿AE翻折，使点B落在B'处，线段EB'交AD于点F，将△ECD沿DE翻折，使点C的对应点C'落在线段EB'上，若点C'恰好为EB'的中点，则线段EF的长为（）A．B．C．D．【分析】由折叠的性质可得AB＝AB'＝CD＝C'D＝1，∠B＝∠B'＝90°＝∠C＝∠DC'E，BE＝B'E，CE＝C'E，由中点性质可得B'E＝2C'E，可得BC＝AD＝3EC，由勾股定理可求可求CE的长，由“AAS”可证△AB'F≌△DC'F，可得C'F＝B'F＝，即可求解．【解答】解：∵四边形ABCD是矩形，∴AB＝CD＝1，AD＝BC，∠B＝∠C＝90°由折叠的性质可得：AB＝AB'＝CD＝C'D＝1，∠B＝∠B'＝90°＝∠C＝∠DC'E，BE＝B'E，CE＝C'E，∵点C'恰好为EB'的中点，∴B'E＝2C'E，∴BE＝2CE，∴BC＝AD＝3EC，∵AE2＝AB2+BE2，DE2＝DC2+CE2，AD2＝AE2+DE2，∴1+4CE2+1+CE2＝9CE2，解得：CE＝，∴B'E＝BE＝，BC＝AD＝，C'E＝，∴B'C'＝，在△AB'F和△DC'F中，∴△AB'F≌△DC'F（AAS），∴C'F＝B'F＝，∴EF＝C'E+C'F＝，故选：D．【点评】本题考查了翻折变换，矩形的性质，全等三角形的性质，勾股定理，求出CE 的长是本题的关键．9．如图，▱ABCD中，AB＝6，∠B＝75°，将△ABC沿AC边折叠得到△AB′C，B′C交AD于E，∠B′AE＝45°，则点A到BC的距离为（）A．2B．3C．D．【分析】过B′作B′H⊥AD于H，根据等腰直角三角形的性质得到AH＝B′H＝AB′，根据折叠的性质得到AB′＝AB＝6，∠AB′E＝∠B＝75°，求得∠AEB′＝60°，解直角三角形得到HE＝B′H＝，B′E＝2，根据平行线的性质得到∠DAC＝∠ACB，推出AE＝CE，根据全等三角形的性质得到DE＝B′E＝2，求得AD＝AE+DE＝3+3，过A作AG⊥BC于G，根据直角三角形的性质即可得到结论．【解答】解：过B′作B′H⊥AD于H，∵∠B′AE＝45°，∴△AB′H是等腰直角三角形，∴AH＝B′H＝AB′，∵将△ABC沿AC边折叠得到△AB′C，∴AB′＝AB＝6，∠AB′E＝∠B＝75°，∴∠AEB′＝60°，∴AH＝B′H＝×6＝3，∴HE＝B′H＝，B′E＝2，∵▱ABCD中，AD∥BC，∴∠DAC＝∠ACB，∵∠ACB＝∠ACB′，∴∠EAC＝∠ACE，∴AE＝CE，∵∠AB′E＝∠B＝∠D，∠AEB′＝∠CED，∴△AB′E≌△CDE（AAS），∴DE＝B′E＝2，∴AD＝AE+DE＝3+3，∵∠AEB′＝∠EAC+∠ACE＝60°，∴∠ACE＝∠CAE＝30°，∴∠BAC＝75°，∴AC＝AD＝BC，∠ACB＝30°，过A作AG⊥BC于G，∴AG＝AC＝，故选：C．【点评】本题考查了翻折变换（折叠问题），全等三角形的判定和性质，解直角三角形，正确的作出辅助线是解题的关键．10．如图1，在△ABC中，∠ACB＝90°，∠CAB＝30°，△ABD是等边三角形，E是AB 的中点，连结CE并延长交AD于F，如图2，现将四边形ACBD折叠，使D与C重合，HK为折痕，则sin∠ACH的值为（）A．B．C．D．【分析】在Rt△ABC中，设BC＝a，则AB＝2BC＝2a，AD＝AB＝2a．设AH＝x，则HC＝HD＝AD﹣AH＝2a﹣x．在Rt△ABC中，由勾股定理得AC2＝3a2，在Rt△ACH 中，由勾股定理得AH2+AC2＝HC2，即x2+3a2＝（2a﹣x）2．解得x＝a，即AH＝a．求得HC的值后，利用sin∠ACH＝AH：HC求值．【解答】解：∵∠BAD＝60°，∠CAB＝30°，∴∠CAH＝90°．在Rt△ABC中，∠CAB＝30°，设BC＝a，∴AB＝2BC＝2a．∴AD＝AB＝2a．设AH＝x，则HC＝HD＝AD﹣AH＝2a﹣x，在Rt△ABC中，AC2＝（2a）2﹣a2＝3a2，在Rt△ACH中，AH2+AC2＝HC2，即x2+3a2＝（2a﹣x）2，解得x＝a，即AH＝a．∴HC＝2a﹣x＝2a﹣a＝a．∴sin∠ACH＝＝，故选：B．【点评】本题考查了折叠的性质，锐角三角函数值，勾股定理的应用，注意：折叠的性质：折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．11．如图，在△ABC中，D是AC边上的中点，连结BD，把△BDC沿BD翻折，得到△BDC'，DC′与AB交于点E，连结AC'，若AD＝AC′＝2，BD＝3，则点D到BC′的距离为（）A．B．C．D．【分析】连接CC'，交BD于点M，过点D作DH⊥BC'于点H，由翻折知，△BDC≌△BDC'，BD垂直平分CC'，证△ADC'为等边三角形，利用解直角三角形求出DM＝1，C'M＝DM＝，BM＝2，在Rt△BMC'中，利用勾股定理求出BC'的长，在△BDC'中利用面积法求出DH的长．【解答】解：如图，连接CC'，交BD于点M，过点D作DH⊥BC'于点H，∵AD＝AC′＝2，D是AC边上的中点，∴DC＝AD＝2，由翻折知，△BDC≌△BDC'，BD垂直平分CC'，∴DC＝DC'＝2，BC＝BC'，CM＝C'M，∴AD＝AC′＝DC'＝2，∴△ADC'为等边三角形，∴∠ADC'＝∠AC'D＝∠C'AC＝60°，∵DC＝DC'，∴∠DCC'＝∠DC'C＝×60°＝30°，在Rt△C'DM中，∠DC'C＝30°，DC'＝2，∴DM＝1，C'M＝DM＝，∴BM＝BD﹣DM＝3﹣1＝2，在Rt△BMC'中，BC'＝＝＝，∵S△BDC'＝BC'•DH＝BD•CM，∴DH＝3×，∴DH＝，故选：B．【点评】本题考查了轴对称的性质，解直角三角形，勾股定理等，解题关键是会通过面积法求线段的长度．12．如图，在△ABC中，∠ABC＝45°，AB＝3，AD⊥BC于点D，BE⊥AC于点E，AE＝1．连接DE，将△AED沿直线AE翻折至△ABC所在的平面内，得△AEF，连接DF．过点D作DG⊥DE交BE于点G．则四边形DFEG的周长为（）A．8B．4C．2+4D．3+2【分析】先证△BDG≌△ADE，得出AE＝BG＝1，再证△DGE与△EDF是等腰直角三角形，在直角△AEB中利用勾股定理求出BE的长，进一步求出GE的长，可通过解直角三角形分别求出GD，DE，EF，DF的长，即可求出四边形DFEG的周长．【解答】解：∵∠ABC＝45°，AD⊥BC于点D，∴∠BAD＝90°﹣∠ABC＝45°，∴△ABD是等腰直角三角形，∴AD＝BD，∵BE⊥AC，∴∠GBD+∠C＝90°，∵∠EAD+∠C＝90°，∴∠GBD＝∠EAD，∵∠ADB＝∠EDG＝90°，∴∠ADB﹣∠ADG＝∠EDG﹣∠ADG，即∠BDG＝∠ADE，∴△BDG≌△ADE（ASA），∴BG＝AE＝1，DG＝DE，∵∠EDG＝90°，∴△EDG为等腰直角三角形，∴∠AED＝∠AEB+∠DEG＝90°+45°＝135°，∵△AED沿直线AE翻折得△AEF，∴△AED≌△AEF，∴∠AED＝∠AEF＝135°，ED＝EF，∴∠DEF＝360°﹣∠AED﹣∠AEF＝90°，∴△DEF为等腰直角三角形，∴EF＝DE＝DG，在Rt△AEB中，BE＝＝＝2，∴GE＝BE﹣BG＝2﹣1，在Rt△DGE中，DG＝GE＝2﹣，∴EF＝DE＝2﹣，在Rt△DEF中，DF＝DE＝2﹣1，∴四边形DFEG的周长为：GD+EF+GE+DF＝2（2﹣）+2（2﹣1）＝3+2，故选：D．【点评】本题考查了等腰直角三角形的判定与性质，全等三角形的判定与性质，勾股定理，解直角三角形等，解题关键是能够灵活运用等腰直角三角形的判定与性质．二．填空题（共7小题）13．如图，把三角形纸片折叠，使点B、点C都与点A重合，折痕分别为DE、FG，得到∠AGE＝30°，若AE＝EG＝2厘米，则△ABC的边BC的长为（6+4）厘米．【分析】根据折叠的性质和含30°的直角三角形的性质解答即可．【解答】解：∵把三角形纸片折叠，使点B、点C都与点A重合，折痕分别为DE，FG，∴BE＝AE，AG＝GC，∵∠AGE＝30°，AE＝EG＝2厘米，∴AG＝6厘米，∴BE＝AE＝2厘米，GC＝AG＝6厘米，∴BC＝BE+EG+GC＝（6+4）厘米，故答案为：（6+4），【点评】此题考查翻折问题，关键是根据折叠的性质和含30°的直角三角形的性质解答．14．如图，在Rt△ABC中，∠ACB＝90°，BC＝6，CD是斜边AB上的中线，将△BCD沿直线CD翻折至△ECD的位置，连接AE．若DE∥AC，计算AE的长度等于．【分析】根据题意、解直角三角形、菱形的性质、翻折变化可以求得AE的长．【解答】解：由题意可得，DE＝DB＝CD＝AB，∴∠DEC＝∠DCE＝∠DCB，∵DE∥AC，∠DCE＝∠DCB，∠ACB＝90°，∴∠DEC＝∠ACE，∴∠DCE＝∠ACE＝∠DCB＝30°，∴∠ACD＝60°，∠CAD＝60°，∴△ACD是等边三角形，∴AC＝CD，∴AC＝DE，∵AC∥DE，AC＝CD，∴四边形ACDE是菱形，∵在Rt△ABC中，∠ACB＝90°，BC＝6，∠B＝30°，∴AC＝，∴AE＝．【点评】本题考查翻折变化、平行线的性质、直角三角形斜边上的中线，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．15．已知Rt△ABC中，∠ACB＝90°，AC＝8，BC＝4，D为斜边AB上的中点，E是直角边AC上的一点，连接DE，将△ADE沿DE折叠至△A′DE，A′E交BD于点F，若△DEF的面积是△ADE面积的一半，则CE＝2．【分析】根据等高的两个三角形的面积比等于边长比可得AD＝2DF，A'F＝EF，通过勾股定理可得AB的长度，可可求AD，DF，BF的长度，可得BF＝DF，可证BEDA'是平行四边形，可得BE＝A'D＝2，根据勾股定理可得CE的长度【解答】解：如图连接BE∵∠ACB＝90°，AC＝8，BC＝4∴AB＝4∵D是AB中点∴BD＝AD＝2∵折叠∴AD＝A'D＝2，S△ADE＝S△A'DE∵S△DEF＝S△ADE∴AD＝2DF，S△DEF＝S△A'DE∴DF＝，A'F＝EF∴BF＝DF＝，且A'F＝EF∴四边形BEDA'是平行四边形∴A'D＝BE＝∴根据勾股定理得：CE＝2故答案为2【点评】本题考查了折叠问题，直角三角形斜边上的中线等于斜边的一半，关键是用面积法解决问题．16．如图，在△ABC中，AB＝AC＝5，tan A＝，BC＝，点D是AB边上一点，连接CD，将△BCD沿着CD翻折得△B1CD，DB1⊥AC且交于点E，则DE＝．【分析】作BF⊥AC于F，证明△B1EC≌△CFB（AAS），得出B1E＝CF＝1，设DE＝3a，则AD＝5a，得出BD＝B1D＝3a+1，得出方程，解方程即可．【解答】解：作BF⊥AC于F，如图所示：则∠AFB＝∠CFB＝90°，在Rt△ABF中，tan A＝＝，AB＝5，∴AF＝4，BF＝3，sin A＝＝，∴CF＝AC﹣AF＝1，由折叠的性质得：B1C＝BC＝，∠CB1E＝∠ABC，B1D＝BD，∵AB＝AC，∴∠ABC＝∠BCF，∴∠CB1E＝∠BCF，∵DB1⊥AC，∴∠B1EC＝90°＝∠CFB，在△B1EC和△CBF中，，∴△B1EC≌△CFB（AAS），∴B1E＝CF＝1，设DE＝3a，则AD＝5a，∴BD＝B1D＝3a+1，∵AD+BD＝AB，∴3a+1+5a＝5，∴a＝，∴DE＝；故答案为：【点评】本题考查了翻折的性质、等腰三角形的性质、全等三角形的判定与性质、解直角三角形以及方程的解题思想，熟练掌握翻折变换的性质，证明三角形全等是解题的关键．17．如图，在Rt△ABC中，∠ABC＝90°，把△ABC沿斜边AC折叠，使点B落在B’，点D，点E分别为BC和AB′上的点，连接DE交AC于点F，把四边形ABDE沿DE 折叠，使点B与点C重合，点A落在A′，连接AA′交B′C于点H，交DE于点G．若AB＝3，BC＝4，则GE的长为．【分析】设HC＝HA＝x，在Rt△CA′H中，可得x2＝32+（4﹣x）2，解得x＝，由△CA′H∽△AGE，可得＝，由此即可解决问题．【解答】解：由题意四边形ABCA′是矩形，BD＝CD＝2，AG＝GA′＝2，∵BC∥AA′，∴∠BCA＝∠CAA′，∵∠ACB＝∠ACB′，∴∠HCA＝∠HAC，∴HC＝HA，设HC＝HA＝x，在Rt△CA′H中，x2＝32+（4﹣x）2，∴x＝，∴A′H＝4﹣＝，由△CA′H∽△AGE，可得：＝，∴＝，∴EG＝．【点评】本题考查翻折变换，解直角三角形，勾股定理，相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．18．如图，在平行四边形ABCD中，∠B＝30°，且BC＝CA，将△ABC沿AC翻折至△AB′C，AB′交CD于点E，连接B′D．若AB＝3，则B′D的长度为6．【分析】作CM⊥AB于M，由折叠的性质得：B'C＝BC＝AC，∠AB'C＝∠B＝∠CAB'＝30°，AB'＝AB＝CD，由平行四边形的性质得出AD＝CB，AB＝CD，∠ADC＝∠B＝30°，求出AD＝AC，AM＝BM＝AB＝，∠BAC＝∠B＝30°，由等腰三角形的性质得出∠ACD＝∠ADC＝30°，由直角三角形的性质得出CM＝，证出AD＝BC＝2CM＝3，再由勾股定理即可得出结果．【解答】解：作CM⊥AB于M，如图所示：由折叠的性质得：B'C＝BC＝AC，∠AB'C＝∠B＝∠CAB'＝30°，AB'＝AB＝CD，∵四边形ABCD是平行四边形，∴AD＝CB，AB＝CD，∠ADC＝∠B＝30°，∠BAD＝∠BCD＝180°﹣∠B＝150°，∴∠B'AD＝150°﹣30°﹣30°＝90°，∵BC＝AC，∴AM＝BM＝AB＝，∠BAC＝∠B＝30°，∴CM＝，∴AD＝BC＝2CM＝3，在Rt△AB'D中，由勾股定理得：B'D＝＝＝6；故答案为：6．【点评】本题考查了翻折变换的性质、平行四边形的性质、等腰三角形的性质以及勾股定理等知识；熟练掌握翻折变换的性质和平行四边形的性质，求出∠B'AD＝90°是解题关键．19．如图，点E是矩形ABCD的边CD上一点，把△ADE沿AE对折，使点D恰好落在BC 边上的F点处．已知折痕AE＝10，且CE：CF＝4：3，那么该矩形的周长为96．【分析】由CE：CF＝4：3，可以假设CE＝4k，CF＝3k推出EF＝DE＝5k，AB＝CD＝9k，利用相似三角形的性质求出BF，再在Rt△ADE中，利用勾股定理构建方程即可解决问题．【解答】解：∵四边形ABCD是矩形，∴AB＝CD，AD＝BC，∠B＝∠C＝∠D＝90°，∵CE：CF＝4：3，∴可以假设CE＝4k，CF＝3k∴EF＝DE＝5k，AB＝CD＝9k，∵∠AFE＝∠D＝90°，∴∠AFB+∠EFC＝90°，∠EFC+∠FEC＝90°，∴∠AFB＝∠CEF，∴△ABF∽△FCE，∴∴∴BF＝12k∴AD＝BC＝15k，在Rt△AED中，∵AE2＝AD2+DE2，∴1000＝225k2+25k2，∴k＝2或﹣2（舍弃），∴矩形的周长＝48k＝96，故答案为：96【点评】本题考查翻折变换，矩形的性质，相似三角形的判定和性质等知识，解题的关键是学会利用参数构建方程解决问题．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

每日一题《全等变换---翻折》
10月21日
已知：E是正方形ABCD内一点，且∠ECD=∠EDC=15°，求证：△ABE是等边三角形，小萍同学灵活运用全等变换，将△ECD进行旋转与翻折，使△ECD≌△FAD，巧妙地解答了此题．请按照小萍的思路，探究并解答下列问题：
（1）证明：△DEF是等边三角形；
（2）证明：△ECD≌△FAE；
（3）证明：△ABE是等边三角形．
证明：（1）∵∠ECD=∠EDC=15°，将△ECD进行旋转与翻折，使△ECD≌△FAD，
∴∠FDA=15°，DE=DF，
∴∠FDE=90°-∠FDA-∠EDC=60°，
∴△DEF是等边三角形（有一个角是60°的等腰三角形是等边三角形）；
已知正方形ABCD，点P、Q分别是边AD、BC上的两动点，将四边形ABQP沿PQ翻折得到四边形EFQP，点E在线段CD上，EF交BC于G，连接AE．
求证：
（1）EA平分∠DEF；
（2）EC+EG+GC=2AB．
证明：（1）∵四边形ABCD是正方形
∴DC∥AB，∠BAD=90°，
∴∠DEA=∠1，
又由折叠知，PA=PE，∠PEF=∠PAB=90°
∴∠2=∠3，则∠PEF-∠3=∠PAB-∠2，
即∠1=∠4
∴∠DEA=∠4，
即EA平分∠DEF；
已知，等边△ABC中，D为BC上一点，DE∥AC交AB于C，M是AE上任意一点（M不与A、E重合），连DM，作DN平分∠MDC交AC于N．若BD=DC，求证：EM+NC=DM
已知在矩形ABCD中，AD＞AB，O为对角线的交点，过O作一直线分别交BC、AD于M、N （1）求证：S梯形ABMN=S梯形CDNM；
（2）当M、N满足什么条件时，将矩形ABCD以MN为折痕翻折后能使C点恰好与A点重合（只写出满足的条件，不要求证明）；
（3）在（2）的条件下，若翻折后不重叠部分的面积是重叠部分面积的1
2
，求
BM
MC
的值．、
（2010•张家口一模）已知点P是矩形ABCD边AB上的任意一点（与点A、B不重合）
（1）如图①，现将△PBC沿PC翻折得到△PEC；再在AD上取一点F，将△PAF沿PF翻折得到△PGF，并使得射线PE、PG重合，试问FG与CE的位置关系如何，请说明理由；
（2）在（1）中，如图②，连接FC，取FC的中点H，连接GH、EH，请你探索线段GH和线段EH 的大小关系，并说明你的理由．
注：矩形即长方形（对边相等，四个角都是90°）
探究：如图①，在正方形ABCD中，E、F、G分别是边AD、BC、CD上的点，BG⊥EF，垂足为H．求证：EF=BG．
应用：如图②，将正方形ABCD翻折，使点B落在边CD上的点B′处，折痕为EF．若AE=2，BF=6，则B′C=。