相似三角形难题集锦.docx
(完整版)相似三角形难题集锦(含答案),推荐文档

2.如图,在△ABCABC,动点P以2m/s的速度从移动.同时,动点Q以1m/s的中,ACB90°,平分CDB点到达B点时,Q点随之的速度移动.如果P、Q同时出发,用<t<6)。
中,点A的坐标为(2,1),的图象与线段OA的夹角是45°,在△ABCAB=,为边在C建议收藏下载本文,以便随时学习!我去人也就有人!为UR扼腕入站内信不存在向你偶同意调剖沙,∠ACB=90°,点M是AC上的一轴上,.那么D点的坐标为()A. B.C. D.10..已知,如图,直线y=﹣2x+——A、X字型上一点,AD=AC,BC边上的AE交CD于F求证:求证:中,AB∥CD,AB=b,CD=a,E为边上的任意一点,EF∥AB,且EF交BC于点F,某同学在研究这一问题时,发现如下事实:(1)当时,EF=;当时,;(3)当时,EF=.当时,参照上述研究结论,请你猜已知:如图,在△ABC中,M是AC的中点,E、建议收藏下载本文,以便随时学习!我去人也就有人!为UR扼腕入站内信不存在向你偶同意调剖沙离等于该顶点对边上中线长的.)角平分线定理:三角形一个AB于点E、F.求证:.O,过O作EF//AB求证:.的四个顶点分别在△ABC 求证:.长为a.求证:.,点在平行延长线于点Q,S,交于点.求证:)如图2,图,当点在平行四边形ABCD的对角线或的延长线上时,是否仍然成立?若成立,试给出证明;若不成立,试说明理由(要求仅以图2为例进行证明或说明)建议收藏下载本文,以便随时学习!我去人也就有人!为UR扼腕入站内信不存在向你偶同意调剖沙建议收藏下载本文,以便随时学习!、G、H.求证:为直角.求证:求证:的延长线交于点E.))求证:.是BC的中点,连接、CG,AE与CG相交于点证:.分别是△ABC的两边上的高,过D作BA的延长线于F、H。
;(2)BG·CG=GF·GH交于点M,EF与AC交于点旋转,使得DE与BA三角形并证明你的结论.)请写出图中各对相似三角形(相似比为1除外)建议收藏下载本文,以便随时学习!我去人也就有人!为UR扼腕入站内信不存在向你偶同意调剖沙中,AD⊥BC 于D 。
(word完整版)初中数学相似三角形经典练习难题易错题(附详解)
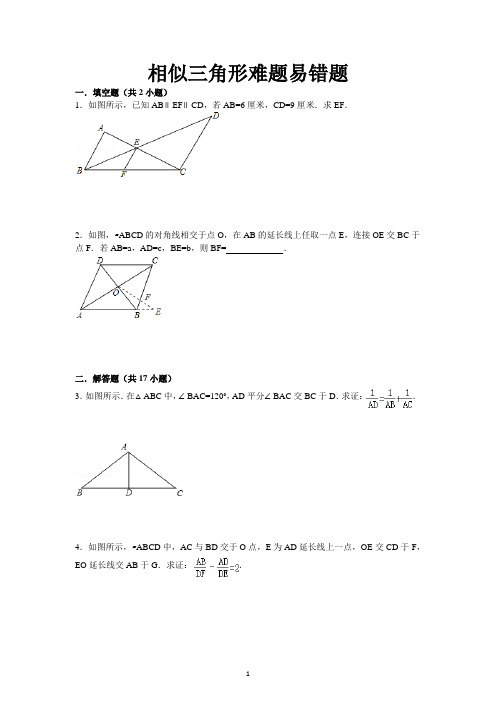
相似三角形难题易错题一.填空题(共2小题)1.如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.2.如图,▱ABCD的对角线相交于点O,在AB的延长线上任取一点E,连接OE交BC于点F.若AB=a,AD=c,BE=b,则BF=_________.二.解答题(共17小题)3.如图所示.在△ABC中,∠BAC=120°,AD平分∠BAC交BC于D.求证:.4.如图所示,▱ABCD中,AC与BD交于O点,E为AD延长线上一点,OE交CD于F,EO延长线交AB于G.求证:.5.一条直线截△ABC的边BC、CA、AB(或它们的延长线)于点D、E、F.求证:.6.如图所示.P为△ABC内一点,过P点作线段DE,FG,HI分别平行于AB,BC和CA,且DE=FG=HI=d,AB=510,BC=450,CA=425.求d.7.如图所示.梯形ABCD中,AD∥BC,BD,AC交于O点,过O的直线分别交AB,CD 于E,F,且EF∥BC.AD=12厘米,BC=20厘米.求EF.8.已知:P为▱ABCD边BC上任意一点,DP交AB的延长线于Q点,求证:.9.如图所示,梯形ABCD中,AD∥BC,MN∥BC,且MN与对角线BD交于O.若AD=DO=a,BC=BO=b,求MN.10.P为△ABC内一点,过P点作DE,FG,IH分别平行于AB,BC,CA(如图所示).求证:.11.如图所示.在梯形ABCD中,AB∥CD,AB<CD.一条直线交BA延长线于E,交DC 延长线于J,交AD于F,交BD于G,交AC于H,交BC于I.已知EF=FG=GH=HI=IJ,求DC:AB.12.已知P为△ABC内任意一点,连AP,BP,CP并延长分别交对边于D,E,F.求证:(1)(2)三者中,至少有一个不大于2,也至少有一个不少于2.13.如图所示.在△ABC中,AM是BC边上的中线,AE平分∠BAC,BD⊥AE的延长线于D,且交AM延长线于F.求证:EF∥AB.14.如图所示.P,Q分别是正方形ABCD的边AB,BC上的点,且BP=BQ,BH⊥PC于H.求证:QH⊥DH.15.已知M是Rt△ABC中斜边BC的中点,P、Q分别在AB、AC上,且PM⊥QM.求证:PQ2=PB2+QC2.16.如图所示.在△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB,CF平分∠BCD.求证:EF∥BC.17.如图所示.在△ABC内有一点P,满足∠APB=∠BPC=∠CPA.若2∠B=∠A+∠C,求证:PB2=PA•PC.(提示:设法证明△PAB∽△PBC.)18.已知:如图,△ABC为等腰直角三角形,D是直角边BC的中点,E在AB上,且AE:EB=2:1.求证:CE⊥AD.19.如图所示,△ABC中,M、N是边BC的三等分点,BE是AC边上的中线,连接AM、AN,分别交BE于F、G,求BF:FG:GE的值.20.在△ABC中,∠A∶∠B∶∠C=1∶2∶4.求证1AB +1AC=1BC提示:要证明如1a +1b=1c几何题的常用方法:①比例法:将原等式变为a+bab=1c或a+ba=bc,故构造成以a+b、b为边且与a、c所在三角形相似的三角形。
(完整word版)相似三角形题型归纳

图1 图2三角形题型归纳一、线段比例问题(构造平行)1、下图中,E 为平行四边形 ABCD 勺对角线AC 上一点,AE : EC=1: 3, BE 的延长线交 CD 的 延长线于 G,交AD 于F ,求证:BF : FG=1: 2.2、已知:如图,在直角三角形 ABC 中,/ BAC= 90° AB= AC, D 为BC 的中点,E 为AC 上 一点,点G 在BE 上,连结DG 并延长交 AE 于F ,若/ FGE=45°, (1)求证:BD- BC=BG- BE (2)求证:AGL BE ( 3)若E 为AC 的中点,求 EF : FD 的值。
3、如图1,在Rt △ ABC 中,/ BAC=90 , AD L BC 于点D,点O 是AC 边上一点,连接 BO 交—AD 于F , OEL OB 交BC 边于点E. (1)求证:△ ABF ^A COE (2)当O 为AC 的中点,:丨 时,OFAC_ 0?如图2,求「的值;(3)当O 为AC 边中点,’时,请直接写出⑴的值.AF £B4、如图,四边形 ABCD 和四边形 ACED 都是平行四边形,点 R 为DE 的中点,BR 分别 交AC , CD 于点P , Q . (1)请写出图中各对相似三角形(相似比为1除外);(2)求BP:PQ:QR .2、过厶ABC 的顶点C 任作一直线,与边AB 及中线AD 分别交于点F 和E,求证:AE : ED=2AF FB.3、如果四边形 ABCD 勺对角线交于 0,过O 作直线 0G/ AB 交BC 于E ,交AD于F ,交CD 的延长线于 G,求证:0G=GE ・ GF.B 1二、相似比乘积处理方法(逆向和正向分析找解题思路)1、如下图,已知在厶ABC 中,AD 平分/ BAC,EM 是AD 的中垂线,交D E=BE ・ CE. BC 延长线于E.求证:4、已知如图,CD 是Rt △ ABC 斜边AB 上的高,E 为BC 的中点,ED 的延长线交 CA 于F 。
相似三角形难题集锦(含答_案)

一、相似三角形中的动点问题1.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC 方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;(2)当△DEG与△ACB相似时,求t的值.3.如图1,在Rt△ABC 中,ACB=90°,AC=6,BC=8,点D在边AB上运动,DE 平分CDB交边BC于点E,EM⊥BD,垂足为M,EN⊥CD,垂足为N.(1)当AD=CD时,求证:DE∥AC;(2)探究:AD为何值时,△BME与△CNE相似?5.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2cm/s的速度移动;点Q沿DA 边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0<t<6)。
(1)当t为何值时,△QAP为等腰直角三角形?(2)当t为何值时,以点Q、A、P为顶点的三角形与△ABC 相似?二、构造相似辅助线——双垂直模型7.在△ABC中,AB=,AC=4,BC=2,以AB为边在C点的异侧作△ABD,使△ABD为等腰直角三角形,求线段CD的长.8.在△ABC中,AC=BC,∠ACB=90°,点M是AC上的一点,点N是BC上的一点,沿着直线MN折叠,使得点C恰好落在边AB上的P点.求证:MC:NC=AP:PB.9.如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折B点落在D点的位置,且AD交y 轴于点E.那么D点的坐标为()A. B.C. D.10..已知,如图,直线y=﹣2x+2与坐标轴交于A、B 两点.以AB为短边在第一象限做一个矩形ABCD,使得矩形的两边之比为1﹕2。
相似三角形难题集锦(含答_案)

一、相似三角形中的动点问题1.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC 方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;(2)当△DEG与△ACB相似时,求t的值.2.如图,在△ABC 中,ABC=90°,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向点C移动.同时,动点Q以1m/s的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.(1)①当t=2.5s时,求△CPQ的面积;②求△CPQ的面积S(平方米)关于时间t(秒)的函数解析式;(2)在P,Q移动的过程中,当△CPQ为等腰三角形时,求出t的值.3.如图1,在Rt△ABC 中,ACB=90°,AC=6,BC=8,点D在边AB上运动,DE 平分CDB交边BC于点E,EM⊥BD,垂足为M,EN⊥CD,垂足为N.(1)当AD=CD时,求证:DE∥AC;(2)探究:AD为何值时,△BME与△CNE相似?4.如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,当P点到达B点时,Q点随之停止运动.设运动的时间为x.(1)当x为何值时,PQ∥BC?(2)△APQ与△CQB能否相似?若能,求出AP的长;若不能说明理由.5.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P 沿AB边从A开始向点B以2cm/s的速度移动;点Q 沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0<t <6)。
(完整word版)相似三角形题型归纳

三角形题型归纳一、线段比例问题(构造平行)1、下图中,E为平行四边形ABCD的对角线AC上一点,AE∶EC=1∶3,BE的延长线交CD的延长线于G,交AD于F,求证:BF∶FG=1∶2.2、已知:如图,在直角三角形ABC中,∠BAC= 90°,AB= AC,D为BC的中点,E为AC上一点,点G在BE上,连结DG并延长交AE于F,若∠FGE= 45°,(1)求证:BD·BC= BG·BE;(2)求证:AG⊥BE;(3)若E为AC的中点,求EF∶FD的值。
3、如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E.(1)求证:△ABF∽△COE;(2)当O为AC的中点,时,如图2,求的值;(3)当O为AC边中点,时,请直接写出的值.4、如图,四边形ABCD 和四边形ACED 都是平行四边形,点R 为DE 的中点,BR 分别交AC CD ,于点P Q ,.(1)请写出图中各对相似三角形(相似比为1除外);(2)求::BP PQ QR .二、相似比乘积处理方法(逆向和正向分析找解题思路)1、如下图,已知在△ABC 中,AD 平分∠BAC,EM 是AD 的中垂线,交BC 延长线于E.求证:DE 2=BE·CE.2、过△ABC 的顶点C 任作一直线,与边AB 及中线AD 分别交于点F 和E ,求证:AE∶ED=2AF∶FB.3、如果四边形ABCD 的对角线交于O ,过O 作直线OG∥AB 交BC 于E ,交AD 于F ,交CD 的延长线于G ,求证:OG 2=GE·GF.A BCD EPO R4、已知如图,CD是Rt△ABC斜边AB上的高,E为BC的中点,ED的延长线交CA于F。
求证:5、如图,在Rt△ABC中,CD是斜边AB上的高,点M在CD上,DH⊥BM且与AC的延长线交于点E.求证:(1)△AED∽△CBM;(2)6、如图,BD、CE分别是△ABC的两边上的高,过D作DG⊥BC于G,分别交CE及BA的延长线于F、H。
相似三角形难题集锦(含答案解析)

一、相似三角形中的动点问题1.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC 方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH ⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;(2)当△DEG与△ACB相似时,求t的值.2.如图,在△ABC 中,ABC=90°,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向点C移动.同时,动点Q以1m/s的速度从C点出发,沿CB向点B 移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.(1)①当t=2.5s时,求△CPQ的面积;②求△CPQ的面积S(平方米)关于时间t(秒)的函数解析式;(2)在P,Q移动的过程中,当△CPQ为等腰三角形时,求出t的值.3.如图1,在Rt△ABC 中,ACB=90°,AC=6,BC=8,点D在边AB上运动,DE 平分CDB交边BC于点E,EM⊥BD,垂足为M,EN⊥CD,垂足为N.(1)当AD=CD时,求证:DE∥AC;(2)探究:AD为何值时,△BME与△CNE相似?4.如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,当P点到达B点时,Q点随之停止运动.设运动的时间为x.(1)当x为何值时,PQ∥BC?(2)△APQ与△CQB能否相似?若能,求出AP的长;若不能说明理由.5.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0<t<6)。
相似三角形难题集锦(含答_案)

一、相似三角形中的动点问题4.如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点1.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每运动;同时点Q从C点出发,沿CA以每秒3cm的速秒5个单位的速度运动,同时动点E从点C沿射线AC方度向A点运动,当P点到达B点时,Q点随之停止运向以每秒3个单位的速度运动.过点D作DH⊥AB于H,动.设运动的时间为x.过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设(1)当x为何值时,PQ∥BC?点D运动的时间为t秒.(2)△APQ与△CQB能否相似?若能,求出AP的长;(1)当t为何值时,AD=AB,并求出此时DE的长度;若不能说明理由.(2)当△DEG与△ACB相似时,求t的值.5.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P 2.如图,在△ABC中,ABC=90°,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向点C移动.同沿AB边从A开始向点B以2cm/s的速度移动;点Q 时,动点Q以1m/s的速度从C点出发,沿CB向点B移沿DA边从点D开始向点A以1cm/s的速度移动.如动.当其中有一点到达终点时,它们都停止移动.设移果P、Q同时出发,用t(s)表示移动的时间(0< t 动的时间为t秒.<6)。
(1)①当t=2.5s时,求△CPQ的面积;(1)当t为何值时,△QAP为等腰直角三角形?②求△CPQ的面积S(平方米)关于时间t(秒)的函数解(2)当t为何值时,以点Q、A、P为顶点的三角形析式;与△ABC相似?(2)在P,Q移动的过程中,当△CPQ为等腰三角形时,求出t的值.二、构造相似辅助线——双垂直模型3.如图1,在Rt△ABC中,ACB=90°,AC=6,BC=8, 6.在平面直角坐标系xOy中,点A的坐标为(2,1),点D在边AB上运动,DE平分CDB交边BC于点E,正比例函数y=kx的图象与线段EM⊥BD,垂足为M,EN⊥CD,垂足为N.OA的夹角是45°,求这个正比(1)当AD=CD时,求证:DE∥AC;例函数的表达式.(2)探究:AD为何值时,△BME与△CNE相似?5.在△ABC中,AB=,AC=4,BC=2,以AB为边在C点三、构造相似辅助线——A、X字型4.如图:△ABC中,D是AB上一点,AD=AC,BC边上的异侧作△ABD,使△ABD为等腰直角三角形,求线段CD的中线AE交CD于F。
相似三角形难题集锦(含答案)

一、相似三角形中的动点问题1.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB 于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;(2)当△DEG与△ACB相似时,求t的值.2.如图,在△ABC中,ABC=90°,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向点C移动.同时,动点Q以1m/s的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.(1)①当t=2.5s时,求△CPQ的面积;②求△CPQ的面积S(平方米)关于时间t(秒)的函数解析式;(2)在P,Q移动的过程中,当△CPQ为等腰三角形时,求出t的值.3.如图1,在Rt△ABC 中,ACB=90°,AC=6,BC=8,点D在边AB上运动,DE 平分CDB交边BC于点E,EM ⊥BD,垂足为M,EN⊥CD,垂足为N.(1)当AD=CD时,求证:DE∥AC;(2)探究:AD为何值时,△BME与△CNE相似?4.如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,当P点到达B点时,Q点随之停止运动.设运动的时间为x.(1)当x为何值时,PQ∥BC?(2)△APQ与△CQB能否相似?若能,求出AP的长;若不能说明理由.5.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0<t <6)。
相似三角形难题集锦(含答_案)

一、相似三角形中的动点问题1.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC 方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;(2)当△DEG与△ACB相似时,求t的值.2.如图,在△ABC 中,ABC=90°,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向点C移动.同时,动点Q以1m/s的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.(1)①当t=2.5s时,求△CPQ的面积;②求△CPQ的面积S(平方米)关于时间t(秒)的函数解析式;(2)在P,Q移动的过程中,当△CPQ为等腰三角形时,求出t的值.3.如图1,在Rt△ABC 中,ACB=90°,AC=6,BC=8,点D在边AB上运动,DE 平分CDB交边BC于点E,EM⊥BD,垂足为M,EN⊥CD,垂足为N.(1)当AD=CD时,求证:DE∥AC;(2)探究:AD为何值时,△BME与△CNE相似?4.如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,当P点到达B点时,Q点随之停止运动.设运动的时间为x.(1)当x为何值时,PQ∥BC?(2)△APQ与△CQB能否相似?若能,求出AP的长;若不能说明理由.5.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P 沿AB边从A开始向点B以2cm/s的速度移动;点Q 沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0<t <6)。
相似三角形难题集锦(含答_案)

一、相似三角形中的动点问题1.如图,在Rt △ABC 中,∠ACB=90°,AC=3,BC=4,过点B 作射线BB1∥AC .动点D 从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E 从点C 沿射线AC 方向以每秒3个单位的速度运动.过点D 作DH ⊥AB 于H ,过点E 作EF ⊥AC 交射线BB1于F ,G 是EF 中点,连接DG .设点D 运动的时间为t 秒.(1)当t 为何值时,AD=AB ,并求出此时DE 的长度;(2)当△DEG 与△ACB 相似时,求t 的值.2.如图,在△ABC 中,ABC =90°,AB=6m ,BC=8m ,动点P 以2m/s 的速度从A 点出发,沿AC 向点C 移动.同时,动点Q 以1m/s 的速度从C 点出发,沿CB 向点B 移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t 秒.(1)①当t=2.5s 时,求△CPQ 的面积;②求△CPQ 的面积S (平方米)关于时间t (秒)的函数解析式;(2)在P ,Q 移动的过程中,当△CPQ 为等腰三角形时,求出t 的值.3.如图1,在Rt △ABC 中,ACB =90°,AC =6,BC =8,点D 在边AB 上运动,DE 平分CDB 交边BC 于点E ,EM ⊥BD ,垂足为M ,EN ⊥CD ,垂足为N .(1)当AD =CD 时,求证:DE ∥AC ;(2)探究:AD 为何值时,△BME 与△CNE 相似?4.如图所示,在△ABC 中,BA =BC =20cm ,AC =30cm ,点P 从A 点出发,沿着AB 以每秒4cm 的速度向B 点运动;同时点Q 从C 点出发,沿CA 以每秒3cm 的速度向A 点运动,当P 点到达B 点时,Q 点随之停止运动.设运动的时间为x .(1)当x 为何值时,PQ ∥BC ?(2)△APQ 与△CQB 能否相似?若能,求出AP 的长;若不能说明理由.5.如图,在矩形ABCD 中,AB=12cm ,BC=6cm ,点P 沿AB 边从A 开始向点B 以2cm/s 的速度移动;点Q 沿DA 边从点D 开始向点A 以1cm/s 的速度移动.如果P 、Q 同时出发,用t (s )表示移动的时间(0<t <6)。
(完整word版)相似三角形经典题(含答案)

相似三角形经典习题例1 从下面这些三角形中,选出相似的三角形.例2 已知:如图,ABCD 中,2:1:=EB AE ,求AEF ∆与CDF ∆的周长的比,如果2cm 6=∆AEF S ,求CDF S ∆.例3 如图,已知ABD ∆∽ACE ∆,求证:ABC ∆∽ADE ∆.例4 下列命题中哪些是正确的,哪些是错误的?(1)所有的直角三角形都相似. (2)所有的等腰三角形都相似. (3)所有的等腰直角三角形都相似. (4)所有的等边三角形都相似.例5 如图,D 点是ABC ∆的边AC 上的一点,过D 点画线段DE ,使点E 在ABC ∆的边上,并且点D 、点E 和ABC ∆的一个顶点组成的小三角形与ABC ∆相似.尽可能多地画出满足条件的图形,并说明线段DE 的画法.例6 如图,一人拿着一支刻有厘米分画的小尺,站在距电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上约12个分画恰好遮住电线杆,已知手臂长约60厘米,求电线杆的高.例7 如图,小明为了测量一高楼MN 的高,在离N 点20m 的A 处放了一个平面镜,小明沿NA 后退到C 点,正好从镜中看到楼顶M 点,若5.1=AC m ,小明的眼睛离地面的高度为1.6m ,请你帮助小明计算一下楼房的高度(精确到0.1m ).例8 格点图中的两个三角形是否是相似三角形,说明理由.例9 根据下列各组条件,判定ABC ∆和C B A '''∆是否相似,并说明理由:(1),cm 4,cm 5.2,cm 5.3===CA BC AB cm 28,cm 5.17,cm 5.24=''=''=''A C C B B A . (2)︒='∠︒='∠︒=∠︒=∠35,44,104,35A C B A .(3)︒='∠=''=''︒=∠==48,3.1,5.1,48,6.2,3B C B B A B BC AB .例10 如图,下列每个图形中,存不存在相似的三角形,如果存在,把它们用字母表示出来,并简要说明识别的根据.例11 已知:如图,在ABC ∆中,BD A AC AB ,36,︒=∠=是角平分线,试利用三角形相似的关系说明AC DC AD ⋅=2.例12 已知ABC ∆的三边长分别为5、12、13,与其相似的C B A '''∆的最大边长为26,求C B A '''∆的面积S .例13 在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C 处(如图),然后沿BC 方向走到D 处,这时目测旗杆顶部A 与竹竿顶部E 恰好在同一直线上,又测得C 、D 两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.例14.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A ,再在河的这一边选点B 和C ,使BC AB ⊥,然后再选点E ,使BC EC ⊥,确定BC 与AE 的交点为D ,测得120=BD 米,60=DC 米,50=EC 米,你能求出两岸之间AB 的大致距离吗?例15.如图,为了求出海岛上的山峰AB 的高度,在D 和F 处树立标杆DC 和FE ,标杆的高都是3丈,相隔1000步(1步等于5尺),并且AB 、CD 和EF 在同一平面内,从标杆DC 退后123步的G 处,可看到山峰A 和标杆顶端C 在一直线上,从标杆FE 退后127步的H 处,可看到山峰A 和标杆顶端E 在一直线上.求山峰的高度AB 及它和标杆CD 的水平距离BD 各是多少?(古代问题)例16 如图,已知△ABC 的边AB =32,AC =2,BC 边上的高AD =3.(1)求BC 的长;(2)如果有一个正方形的边在AB 上,另外两个顶点分别在AC ,BC 上,求这个正方形的面积.相似三角形经典习题答案例1. 解 ①、⑤、⑥相似,②、⑦相似,③、④、⑧相似例2. 解 ABCD Θ是平行四边形,∴CD AB CD AB =,//,∴AEF ∆∽CDF ∆,又2:1:=EB AE ,∴3:1:=CD AE ,∴AEF ∆与CDF ∆的周长的比是1:3. 又)cm (6,)31(22==∆∆∆AEF CDF AEF S S S ,∴)cm (542=∆CDF S . 例3 分析 由于ABD ∆∽ACE ∆,则CAE BAD ∠=∠,因此DAE BAC ∠=∠,如果再进一步证明AECAAD BA =,则问题得证.证明 ∵ABD ∆∽ACE ∆,∴CAE BAD ∠=∠.又DAC BAD BAC ∠+∠=∠Θ,∴CAE DAC DAE ∠+∠=∠, ∴DAE BAC ∠=∠. ∵ABD ∆∽ACE ∆,∴AEACAD AB =. 在ABC ∆和ADE ∆中,∵AEACAD AB ADE BAC =∠=∠,,∴ABC ∆∽ADE ∆ 例4.分析 (1)不正确,因为在直角三角形中,两个锐角的大小不确定,因此直角三角形的形状不同.(2)也不正确,等腰三角形的顶角大小不确定,因此等腰三角形的形状也不同. (3)正确.设有等腰直角三角形ABC 和C B A ''',其中︒='∠=∠90C C ,则︒='∠=∠︒='∠=∠45,45B B A A ,设ABC ∆的三边为a 、b 、c ,C B A '''∆的边为c b a '''、、, 则a c b a a c b a '=''='==2,,2,,∴a ac c b b a a '=''=',,∴ABC ∆∽C B A '''∆. (4)也正确,如ABC ∆与C B A '''∆都是等边三角形,对应角相等,对应边都成比例,因此ABC ∆∽C B A '''∆.答:(1)、(2)不正确.(3)、(4)正确. 例5.解:画法略.例6.分析 本题所叙述的内容可以画出如下图那样的几何图形,即60=DF 厘米6.0=米,12=GF 厘米12.0=米,30=CE 米,求BC .由于ADF ∆∽ACAF EC DF AEC =∆,,又ACF ∆∽ABC ∆,∴BC GFEC DF =,从而可以求出BC 的长. 解 EC DF EC AE //,⊥Θ,∴EAC DAF AEC ADF ∠=∠∠=∠,,∴ADF ∆∽AEC ∆.∴ACAFEC DF =. 又EC BC EC GF ⊥⊥,,∴ABC AGF ACB AFG BC GF ∠=∠∠=∠,,//, ∴AGF ∆∽ABC ∆,∴BC GF AC AF =,∴BCGFEC DF =.又60=DF 厘米6.0=米,12=GF 厘米12.0=米,30=EC 米,∴6=BC 米.即电线杆的高为6米. 例7.分析 根据物理学定律:光线的入射角等于反射角,这样,BCA ∆与MNA ∆的相似关系就明确了.解 因为MAN BAC AN MN CA BC ∠=∠⊥⊥,,,所以BCA ∆∽MNA ∆.所以AC AN BC MN ::=,即5.1:206.1:=MN .所以3.215.1206.1≈÷⨯=MN (m ). 说明 这是一个实际应用问题,方法看似简单,其实很巧妙,省却了使用仪器测量的麻烦.例8.分析 这两个图如果不是画在格点中,那是无法判断的.实际上格点无形中给图形增添了条件——长度和角度.解 在格点中BC AB EF DE ⊥⊥,,所以︒=∠=∠90B E , 又4,2,2,1====AB BC DE EF .所以21==BC EF AB DE .所以DEF ∆∽ABC ∆. 说明 遇到格点的题目一定要充分发现其中的各种条件,勿使遗漏.例9.解 (1)因为7128cm 4cm ,7117.5cm 2.5cm ,7124.5cm 3.5cm ==''==''==''A C CA C B BC B A AB ,所以ABC ∆∽C B A '''∆; (2)因为︒=∠-∠-︒=∠41180B A C ,两个三角形中只有A A '∠=∠,另外两个角都不相等,所以ABC ∆与C B A '''∆不相似;(3)因为12,=''='''∠=∠C B BC B A AB B B ,所以ABC ∆相似于C B A '''∆.例10.解 (1)ADE ∆∽ABC ∆ 两角相等; (2)ADE ∆∽ACB ∆ 两角相等;(3)CDE ∆∽CAB ∆ 两角相等; (4)EAB ∆∽ECD ∆ 两边成比例夹角相等; (5)ABD ∆∽ACB ∆ 两边成比例夹角相等; (6)ABD ∆∽ACB ∆ 两边成比例夹角相等.例11.分析 有一个角是65°的等腰三角形,它的底角是72°,而BD 是底角的平分线,∴︒=∠36CBD ,则可推出ABC ∆∽BCD ∆,进而由相似三角形对应边成比例推出线段之间的比例关系.证明 AC AB A =︒=∠,36Θ,∴︒=∠=∠72C ABC . 又BD Θ平分ABC ∠,∴︒=∠=∠36CBD ABD .∴BC BD AD ==,且ABC ∆∽BCD ∆,∴BC CD AB BC ::=,∴CD AB BC ⋅=2,∴CD AC AD ⋅=2. 说明 (1)有两个角对应相等,那么这两个三角形相似,这是判断两个三角形相似最常用的方法,并且根据相等的角的位置,可以确定哪些边是对应边.(2)要说明线段的乘积式cd ab =,或平方式bc a =2,一般都是证明比例式,b dc a =,或caa b =,再根据比例的基本性质推出乘积式或平方式.例12分析 由ABC ∆的三边长可以判断出ABC ∆为直角三角形,又因为ABC ∆∽C B A '''∆,所以C B A '''∆也是直角三角形,那么由C B A '''∆的最大边长为26,可以求出相似比,从而求出C B A '''∆的两条直角边长,再求得C B A '''∆的面积.解 设ABC ∆的三边依次为,13,12,5===AB AC BC ,则222AC BC AB +=Θ,∴︒=∠90C .又∵ABC ∆∽C B A '''∆,∴︒=∠='∠90C C .212613==''=''=''B A AB C A AC C B BC , 又12,5==AC BC ,∴24,10=''=''C A C B . ∴12010242121=⨯⨯=''⨯''=C B C A S .例13.分析 判断方法是否可行,应考虑利用这种方法加之我们现有的知识能否求出旗杆的高.按这种测量方法,过F作AB FG ⊥于G ,交CE 于H ,可知AGF ∆∽EHF ∆,且GF 、HF 、EH 可求,这样可求得AG ,故旗杆AB 可求.解 这种测量方法可行.理由如下:设旗杆高x AB =.过F 作AB FG ⊥于G ,交CE 于H (如图).所以AGF ∆∽EHF ∆.因为3,30327,5.1==+==HF GF FD ,所以5.1,25.15.3-==-=x AG EH .由AGF ∆∽EHF ∆,得HF GF EH AG =,即33025.1=-x ,所以205.1=-x ,解得5.21=x (米) 所以旗杆的高为21.5米.说明 在具体测量时,方法要现实、切实可行. 例14. 解:︒=∠=∠∠=∠90,ECD ABC EDC ADB Θ,∴ABD ∆∽ECD ∆,1006050120,=⨯=⨯==CD EC BD AB CD BD EC AB (米),答:两岸间AB 大致相距100米. 例15. 答案:1506=AB 米,30750=BD 步,(注意:AK FEFHKE AK CD DG KC ⋅=⋅=,.) 例16. 分析:要求BC 的长,需画图来解,因AB 、AC 都大于高AD ,那么有两种情况存在,即点D 在BC 上或点D 在BC 的延长线上,所以求BC 的长时要分两种情况讨论.求正方形的面积,关键是求正方形的边长. 解:(1)如上图,由AD ⊥BC ,由勾股定理得BD =3,DC =1,所以BC =BD +DC =3+1=4. 如下图,同理可求BD =3,DC =1,所以BC =BD -CD =3-1=2.(2)如下图,由题目中的图知BC =4,且162)32(2222=+=+AC AB ,162=BC ,∴222BC AC AB =+.所以△ABC 是直角三角形.由AE G F 是正方形,设G F =x ,则FC =2-x , ∵G F ∥AB ,∴AC FCAB GF =,即2232x x -=. ∴33-=x ,∴3612)33(2-=-=AEGF S 正方形. 如下图,当BC =2,AC =2,△ABC 是等腰三角形,作CP ⊥AB 于P ,∴AP =321=AB ,在Rt △APC 中,由勾股定理得CP =1, ∵GH ∥AB ,∴△C GH ∽△CBA ,∵x x x -=132,32132+=x ∴121348156)32132(2-=+=GFEH S 正方形 因此,正方形的面积为3612-或121348156-.。
相似三角形难题集锦(含答-案)

一、相似三角形中的动点问题1.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC 方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;(2)当△DEG与△ACB相似时,求t的值.2.如图,在△ABC 中,ABC=90°,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向点C移动.同时,动点Q以1m/s的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.(1)①当t=2.5s时,求△CPQ的面积;②求△CPQ的面积S(平方米)关于时间t(秒)的函数解析式;(2)在P,Q移动的过程中,当△CPQ为等腰三角形时,求出t的值.3.如图1,在Rt△ABC 中,ACB=90°,AC=6,BC=8,点D在边AB上运动,DE 平分CDB交边BC于点E,EM⊥BD,垂足为M,EN⊥CD,垂足为N.(1)当AD=CD时,求证:DE∥AC;(2)探究:AD为何值时,△BME与△CNE相似?4.如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,当P点到达B点时,Q点随之停止运动.设运动的时间为x.(1)当x为何值时,PQ∥BC?(2)△APQ与△CQB能否相似?若能,求出AP的长;若不能说明理由.5.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P 沿AB边从A开始向点B以2cm/s的速度移动;点Q 沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0<t <6)。
相似三角形难题集锦(含答案)汇编

学习-----好资料一、相似三角形中的动点问题1.如图,在 Rt △ABC 中,/ ACB=90 , AC=3 BC=4 过点 B 作射线 BB1 // AC 动点D 从点A 出发沿射线AC 方向以每秒5个单位的 P 点到达B 点时,Q 点随之停止运动.设运动的时间 为x .(1) 当x 为何值时,PQ// BC ? (2) ^ APQ M^ CQB 能否相似?若能,求出 AP 的长; 若不能说明理由.速度运动,同时动点E 从点C 沿射线AC 方向以每秒3个 单位的速度运动.过点 D 作DH L AB 于H,过点E 作EF 丄 AC 交射线BB1于F , G 是EF 中点,连接 DG 设点D 运动 的时间为t 秒.(1)当t 为何值时,AD=AB 并求出此时 DE 的长度;2. 如图,在△ ABC 中,/ ABC= 90°, AB=6m BC=8m 动 点P 以2m/s 的速度从A 点出发,沿 AC 向点C 移动.同 时,动点Q 以1m/s 的速度从C 点出发,沿 CB 向点B 移 动•当其中有一点到达终点时,它们都停止移动•设移 动的时间为t 秒.(1) ①当t=2.5s 时,求△ CPQ 勺面积;②求△ CPQ 的面积S (平方米)关于时间 t (秒)的函数 解析式;(2) 在P , Q 移动的过程中,当△ CPQ 为等腰三角形时, 求出t 的值.沿AB 边从A 开始向点B 以2cm/s 的速度移动;点 Q 沿DA 边从点D 开始向点A 以1cm/s 的速度移动.如 果P 、Q 同时出发,用t (s )表示移动的时间(0v t v 6)。
(1) 当t 为何值时,△ QAP 为等腰直角三角形?(2) 当t 为何值时,以点 Q A 、P 为顶点的三角形 与厶ABC 相似?二、构造相似辅助线一一双垂直模型6.在平面直角坐标系 xOy 中,点A 的坐标为(2 , 1), 正比例函数y=kx 的图象与线段 OA 的夹角是45°,求 这个正比例函数的表达式.3. 如图 1,在 Rt △ ABC 中,—ACB= 90°, AC = 6, BC = 8, 点D 在边AB 上运动,DE 平分—CDB 交边BC 于点E , EM 丄BD,垂足为M , EN L CD 垂足为N. (1) 当 AD= CD 时,求证:DE// AC;(2) 探究:AD 为何值时,△ BME W^ CNE 相似?4. 如图所示,在△ ABC 中,BA= BC= 20cm, AC = 30cm,点 P 从 A点出发,沿着 AB 以每秒4cm 的速度向B 点运动;同时点 Q 从C 点出发,沿CA 以每秒3cm 的速度向A点运动,当(2)当厶DEG 与厶ACB 相似时, 求t 的值.7.在厶 ABC 中, AB= ■ ,AC=4, BC=2以AB 为边在C 点的异侧 作厶ABD 使厶ABD 为等腰直角 三角形,求线段 CD 的长.12.四边形ABCD中, AC为AB AD的比例中项,且AC 平分/ DAB8.在厶ABC中,AC=BC /ACB=90,点M 是AC 上的一点,点N是BC上的一点,沿着直线MN折叠,使得点C恰好落在边AB 上的P点.求证:MC NC=AP PB.求证:BE _ BC2ci-CD513.在梯形ABCD中, AB// CD AB= b, CD= a, E为AD 边上的任意一点,EF/ AB,且EF交BC于点F,某同学在研究这一问题时,空=1(1)当― 时,发现如下事实:a+b厂EF=9.如图,在直角坐标系中,矩形ABCO勺边OA在x轴上,边OC在y轴上,点B的坐标为(1, 3),将矩形沿对角线AC翻折B点落在D点的位置,且AD交y轴于点E.那么D 点的坐标为()EF= _ ;⑶当一站DEEF= .当一一时,参照上述研究结论,请你猜想用一般结论,并给出证明.B. D.2色汀丿3 12^10..已知,如图,直线y= - 2x + 2与坐标轴交于A、B两点.以AB为短边在第一象限做一个矩形ABCD使得矩形的两边之比为1 : 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似二角形1. 如图,在Rt △ ABC中,∠ ACB=90 , AC=3 BC=4过点B作射线BB1" AC-动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E 从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥ AC交射线BB1于F,G是EF中点,连接DG设点D运动的时间为t秒.(1) 当t为何值时,AD=AB并求出此时DE的长度;(2)当厶DEG与^ ACB相似时,求t的值.2. 如图,在△ ABC中,/ ABC= 90°,AB=6m BC=8m动点P以2m∕s的速度从A点出发,沿AC向点C移动.同时,动点Q以1m∕s的速度从C点岀发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.(2)在P, Q移动的过程中,当△ CPC为等腰三角形时,求出t的值.3.如图1 ,在Rt△ ABC中,_ ACB= 90°AC= 6,BC= 8,点D在边AB上运动,DE平分/ CDB交边BC于点E,EM⊥BD,垂足为M EN⊥CD,垂足为N.(1)当AD= CD时,求证:DE// AC ( 2)探究:AD为何值时,△ BME与^ CNE相似?4.如图所示, 在厶ABC中,BA= BC= 20cm, AC= 30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,当P点到达B点时,Q点随之停止运动.设运动的时间为X .(1)当X为何值时,PQ// BC?(2)^ APQ与^ CQB能否相似?若能,求出AP的长;若不能说明理由.5.如图,在矩形ABCD中, AB=12cm BC=6cm点P沿AB边从A开始向点B以2cm∕s的速度移动;点Q沿DA边从点D开始向点A以1cm∕s的速度移动•如果P、Q同时出发,用t (S)表示移动的时间(O V t V 6)。
(1) 当t为何值时,△ QAP为等腰直角三角形?(2) 当t为何值时,以点Q A、P为顶点的三角形与△ ABC相似?6.在平面直角坐标系XOy中,点A的坐标为(2 , 1),正比例函数y=kx的图象与线段OA的夹角是45°,求这个正比例函数的表达式.(1)①当t=2.5s时,求△ CPQ的面积;②求△ CPQ的面积S (平方米)关于时间t (秒)的函数解析式;210..已知,如图,直线 y= - 2x + 2与坐标轴交于 A B 两点•以AB 为短边在第一象限做一个矩形 矩形的两边之比为1 : 2。
求C 、D 两点的坐标。
11. 如图:△ ABC 中,D 是AB 上一点,AD=AC BC 边上的中线 AE 交CD 于 FAB __CF_求证:…_ *12. 四边形ABCD 中, AC 为AB AD 的比例中项,且 BE BC 27.在厶ABC 中,AB=Xi , AC=4, BC=2以AB 为边在C 点的异侧作△ ABD,使厶ABD 为等腰直角三角形,求线段 CD 的长.8.在厶ABC 中,AC=BC ∠ ACB=90 ,点M 是AC 上的一点,点 N 是BC 上的一点,沿着直线 MN 折叠,使得点 C 恰好落在边 AB 上的P 点.求证:MC NC=AP PB.9.如图,在直角坐标系中,矩形 ABCO 勺边OA 在X 轴上,边OC 在y 轴上,点B 的坐标为(1,3),将矩形沿对角线AC 翻折B 点落在D 点的位置,且 AD 交y 轴于点E .那么D 点的坐标为()312、ABCD 使得y i\qOAC 平分∠ DAB17. 已知:如图,梯形 ABCc 中, AB//DC ,对角线 AC BD 交于0,过O 作EF//AB 分别交AD BC 于B F1 1 1- + - = i -13. 在梯形ABCD K AB// CD, AB = b , CD= a , E 为AD 边上的任意一点,EF// AB,且EF 交BC 于点F ,某同学在研究这一问题时,发现如下事实:DEa+bD 思Λ + Ξ⅛ ~ I*__ — 2---------⑴当时,EF= _; (2)当一二 时,EF= _;DEm+3⅛ QE—■ = J-------- —=⅛⑶当卫“ 时,EF=•当「一时,参照上述研究结论,请你猜想用a 、b 和k 表示EF 的一般结论,并给出证明.14.已知:如图,在△ ABC中,M 是AC 的中点,E 、F 是BC 上的两点,且 BE = EF = FCO求 BN NQ QM15.证明:(1)重心定理:三角形顶点到重心的距离等于该顶点对边上中线长的 三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例.2二•(注:重心是三角形三条中线的交点)(2)角平分线定理:16.如图,在等边厶ABC 中, M N 分别是边AB, AC 的中点,D 为MN 上任意一点,BD CD的延长线分别交 1 1 3+ --- — -求证:「三 =F 一上.AC AB 于点 E 、F .20. ( 1)如图1 ,点「在平行四边形ABCD的对角线BD上,一直线过点P分别交BA BC的延长线于点Q, S,交-1.于点二.求证:PQ-PR = PSPT(2)如图2,图3 ,当点「在平行四边形ABCD的对角线—或_1的延长线上时,:-_-「•-^ -「是否仍然成立?若成立,试给出证明;若不成立,试说明理由(要求仅以图2为例进行证明或说明);21. 如图,在平行四边形ABCD中,过点A作AEI BC垂足为E,连接DE F为线段DE上一点,且∠ AFE=∠ B. ⑴求证:△ ADF^△ DEC(2) 若AB= 4,AD = 3 < 3 ,AE = 3,求AF 的长.22. 如图,已知等腰三角形ABC中,AD, BF分别为BC AC边上的高,过D作AB的垂线交AB于E,交BF于G交AC 延长线于HO求证:D E=E(?EH18. 如图,在△ ABC中,已知CD为边AB上的高,正方形EFGH勺四个顶点分别在厶ABC上1 1 1-- + --- = ---求证:•J_19.已知,在△ ABC中作内接菱形CDEF设菱形的边长为a •求证:4CPC 一(U•门23. 已知如图,P为平行四边形ABCD的对角线AC上一点,过P的直线与AD BC CD的延长线、PE PH求证:VG24. 已知,如图,锐角△ ABC中, AD丄BC于D,H为垂心(三角形三条高线的交点)25.已知如图,CD是Rt△ ABC斜边AB上的高,E为BC的中点,ED的延长线交CA于F 求证:丄26如图,在Rt △ ABC中,CD是斜边AB上的高,点M在CD上,DHL BM且与AC的延长线交于点E.求证:(1 )△ AED^△ CBM ( 2) ALCM^AC-CDEDB27.如图,△ ABC是直角三角形,∠ ACB=90,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.(1)求证:Fl^ = FBF C.(2)若G是BC的中点,连接GD GD与EF垂直吗?并说明理由.CGB28.如图,四边形ABCD DEFG都是正方形,连接AB CG,AE与CG相交于点M, CG与AD相交于点N.求证:DAB的延长线分别相交于点E、F 、G H.;在AD上有一点P,且∠ BPC为直角.求证:PD= AD∙ DH。
29.如图,BD CE分别是△ ABa的两边上的高,过D作DGL BC于G分别交CE及BA的延长线于F、HO2求证:(1) DG= BG∙ CG ( 2) BG∙ CG= GF∙ GH30. △ ABC^n△ DEF是两个等腰直角三角形,∠ A=∠ D=90°,A DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交于点M EF与AC交于点N,求证:△ BEM h^ CNE(2)如图2,将厶DEF绕点E旋转,使得DE与BA的延长线交于点M EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.31. 如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交Aa CD于点P、Q.(1)请写出图中各对相似三角形(相似比为1除外);(2)求BP PQ QRAE__AC32. 如图,在△ ABC中,AD丄BC于D, DEX AB于E, DF L AC于F。
求证:二二33.如图,Rt^ AB C ■是由Rt△ ABC绕点A顺时针旋转得到的,连结CC '交斜边于点E, CC '的延长线交BB '于点F∙(1)证明:△ ACE^△ FBE(2)设∠ ABC〉,∠ CAC = 一:,试探索:■满足什么关系时,△ ACE与^ FBE是全等三角形,并说明理由.B'C A34.在直角梯形OABCK CB// OA ∠ C(A= 90o, CB= 3, OA= 6, BA= 3{5.分别以OA OC边所在直线为X轴、y轴建立如图1所示的平面直角坐标系.(1) 求点B的坐标;(2) 已知D E分别为线段OC OB上的点,OD= 5, OE= 2E B,直线DE交X轴于点F.求直线DE的解析式;(3) 点M是 ( 2)中直线DE ±的一个动点,在X轴上方的平面内是否存在另一个点N使以OD M N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.36.如图,在正方形ABCt≠, E是BC上的一点,连结AE作BF⊥AE垂足为H交CD于F,作CQ AE交BF于G37. 刘卫同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中,∠ B=90°, ∠ A=30°, BC=6cm 图②中,∠ D=90°, ∠ E=45°,35.在图15-1至图15-3中,直线MN⅛线段AB相交于点O,∠ 1 = ∠ 2 = 45°.(1)如图15-1 ,若AO = OB请写出AO与BD的数量关系和位置关系;(2)将图15-1中的MN绕点O顺时针旋转得到图15-2 ,其中AO = OB求证:AC(3)将图15-2中的OB拉长为AO的k倍得到图15-3 ,求BD的值.ACBD(1)求证CGBH ⑵ FC=BF∙ GF ⑶FC2 GFAB2 GBDE=4cm.图③是刘卫同学所做的一个实验:他将△ DEF 的直角边DE 与厶ABC 的斜边AC 重合在一起,并将△ DEF 沿AC 方向移动.在移动过程中,D E 两点始终在AC 边上(移动开始时点D 与点A 重合).(1) 在厶DEF 沿AC 方向移动的过程中,刘卫同学发现: F 、C 两点间的距离逐渐 ▲. ( 填“不变”、“变大”或“变小”)(2) 刘卫同学经过进一步地研究,编制了如下问题:问题①:当△ DEF 移动至什么位置,即 AD 的长为多少时,F 、C 的连线与AB 平行?问题②:当△ DEF 移动至什么位置,即 AD 的长为多少时,以线段 AD FC BC 的长度为三边长的三角形是直角三角形 ? 问题③:在△ DEF 的移动过程中,是否存在某个位置,使得∠ FCD=15 ?如果存在,求出AD 的长度;如果不存在,请说明理由. 请你分别完成上述三个问题的解答过程.38. 已知△ ABC 中,AB= 2 . 5,AC= 4 5,BC = 6(1) 如图1点M 为AB 的中点,在线段 AC 上取点 汕使厶AMN 与^ABC 相似,求线段 MN 的长;(2) 如图2,是由100个边长为1的小正方形组成的10×10正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形,①请你在所给的网 格中画出格点△ ABCl ,使得△ A l BC 与厶ABC 全等(画出一个即可,不需证明)②试直接写出在所给的网格中与△ ABC 相似且面积最大的格点三角形的个数,并画出其中的一个(不需证明)39. 已知直角坐标系中菱形 ABC 的位置如图,C, D 两点的坐标分别为(4,0),(0,3).现有两动点P ,Q 分别从A , C 同时出发,点P 沿线段AD 向终点D 运动,点Q 沿折线CBA 向终点A 运动,设运动时间为t 秒. (1) 填空:菱形ABC 的边长是 ____ 、面积是 _____ 、高BE 的长是 _____ ; (2) 探究下列问题: ① 若点P 的速度为每秒1个单位,点Q 的速度为每秒2个单位.当点Q 在线段BA 上时,求△ APQ 勺面积S 关于t 的函数关系式,以及 S 的最大值。
