2015-2016学年小学二年级数学上册第三次月考试卷
湖北省黄冈市二年级上学期数学第三次月考试卷

湖北省黄冈市二年级上学期数学第三次月考试卷姓名:________ 班级:________ 成绩:________亲爱的小朋友们,这一段时间的学习,你们收获怎么样呢?今天就让我们来检验一下吧!一、轻松填一填。
(共32分) (共8题;共32分)1. (6分) (2019二上·台安期末) 把口诀补充完整。
四四________ 五________ 四十________ 八十一________ 四十八2. (5分)(2019二上·苏州期末) ________个________相加。
乘法算式:________×________或________×________3. (3分) (2019四上·景县期中) 数一数,下图中有________个锐角,________个直角,________个钝角。
4. (3分)下面的照片是谁照的?________________________________5. (6分)填上适当的运算符号.(按从上到下,从左到右顺序填)________________6. (6分)先把乘法口诀补充完整,再根据口诀写出两道乘法算式。
三________十五________ ________7. (1分)一个数是47与19的差,这个数是________。
8. (2分) 47+46=________46+29=________二、公正判一判。
(5分) (共5题;共5分)9. (1分)一本字典大约厚3平方厘米。
(判断对错)10. (1分)由两个正方形搭成的立体图形,从有的方向看只能看到一个正方形,而从有的方向看能看到两个正方形。
11. (1分)判断6×8读作8乘612. (1分) (2019三上·东莞期中) 一个数的3倍是24,这个数的5倍是40。
13. (1分) (2019二上·温岭期末) 计算3×4和2×6用同一句口决。
五年级上册数学试题-第三次月考试卷 最新人教版(含解析)

2019-2020学年五年级上学期数学第三次月考试卷一、动脑思考,正确填写。
(共24分)1.12个0.55相加的和是________;20.4是________的3倍。
2.根据15×68=1020,直接写出下面各题的得数。
1.5×68=________ 0.15×6.8=________102÷0.68=________ 0.102÷0.15=________3.在括号里填上含有字母的式子。
(1)一堆石子有b吨,运走了9.2吨,还剩下________吨。
(2)袋鼠的奔跑速度是65干米/时,t小时奔跑________千米。
(3)妈妈买了xkg大米,每干克3元,付给售货员50元,售货员应找回________元钱。
4.张阿姨昨天卖出75串糖葫芦,今天比昨天多卖出y串糖葫芦。
(1)今天卖出________串糖葫芦。
(2)当y=15时,今天卖出________串糖葫芦。
5.①8x=9.6,②1.8+a,③b+100=102,④4.6-2.4=2.2,⑤4.8+y>0.2上面的式子中________是等式,________是方程。
6.在横线上填上“>”“<”或“=”。
(1)当x=3.5时,4x-7.5________7,4x+7.5________20. 5。
(2)4.25×0.5________4.25÷0.5,16.8÷8________ 6.3÷37.盒子里有两种卡片,一种是动物卡片,一种是风景卡片。
晶晶每次从中摸出一张卡片后再放回去摇匀,重复30次,摸卡片的情况如下表。
(1)根据表中数据推测,盒子里________卡片可能多,________卡片可能少。
(2)如果晶晶从盒子里再摸出一张,摸出________卡片的可能性小。
8.在教室里,小刚坐在第6列、第4行,用数对(6,4)表示。
小红坐在第1列、第3行,用数对________表示;乐乐与小刚在同一列,与小红在同一行。
人教版四年级上册数学第三次月考试卷含参考答案

人教版四年级上册数学第三次月考试卷含参考答案小学四年级数学第三次月考测评试卷一、填空(20分,每空1分)1、五个数字2、3、4、7、5组成最大的数是(),组成最小的数是()。
2、路程=(时间)×(速度),单价=(总价)÷(数量)。
3、过一点能画出(无限)条直线,过两点能画出(一条)线段。
4、猜猜卡片最大能填几?39.429≈40万5.5000≈58万5、括号里面最大能填几?600×(8)<4900.50×(4)<185(3)×61<4457、(500)÷25=20 (15)8、在○里填上“>、<或=”。
<.<.20×68<34×409、三位数除以两位数,商最多是(2)位数,最少是(1)位数。
10、算式里有括号,要先算(括号)里面的。
二、当回裁判员。
(对的在括号里打“√”,错的打“×”)(10分)1、用3倍的放大镜看一个15的角。
这个角被放大成45.(×)2、最小的自然数是0,最大的自然数是9千亿。
(×)3、两条直线相交于一点,这点叫做垂足。
(√)4、因为17÷4=4……1,所以170÷40=40……10.(√)5、要使□45÷45的商是两位数,□里最大能填3.(√)三、选择题(10分)1、北京到天津的公路长120千米,货车要行2小时,货车的速度是(60千米/时)。
2、要使8418≈8万,里不能填(3)。
3、两数相除商为60,如果被除数和除数都乘100,那么商是(6000)。
4、一本书定价21元,___带了180元,他最多能买多少本?(8本)5、16×750,积的末尾有(2)个。
四、神机妙算显身手(32分)(10+12+4+6)1、口算400×70=320÷40=815×60=900640÷80=815×40=6001600÷80=20360÷90=4120×8=9602、竖式计算。
二年级数学上册第三次月考试卷

二年级数学上册第三次月考试卷姓名_______分数_______一、口算(20分)9×6= 7×8= 9×5= 8×4= 6×3= 6×6= 7×6= 3×8= 8×6= 7×4= 6×5= 9×4= 9×2= 8×5= 7×1= 2×6= 7+7+7+7= 9×5+5= 8×7―20= 6×9+9= 二、填一填(29分) 1.按要求补充算式7×( )=42 9×( )=63 ( )×5=35 8×( )=48 3×( )=27 ( )×6=30 2.在○里填上“>”“<”或“=”8×5○8+5 6×6○4×9 7×7○14 7×1○7+1 3.看谁填得对七( )五十六 三( )二十四 ( )九十八 五( )三十五 八( )六十四 六( )五十四 4.7×8=( ),可以表示求( )个( )连加的和是( )。
计算7×8和8×7时,都可以用 这句口诀来求积。
5.3的9倍是( ),8的6倍是( )。
6.( )里面最大能填几?7×( )<38 45>8×( ) 3×( )<25 52>9×( )7.请你写2个积是24的乘法算式三、辨一辨。
(下列图形中,是对称图形的请在□里打“√”)(5分)四1、按照对称轴画出另一半(3分)2、下面这些图分别是谁看到的?连一连。
(2分)五、画一画。
(画出下面对称图形的对称轴)(8分)2六、照镜子(4分)1.下图是镜子里面的女孩,那么照镜子的女孩是( )手拿书。
2.哪个是镜中的图像请在( )里面画√。
四年级下数学月考试题-综合考练(27)|15-16人教新课标

2015-2016学年新人教版四年级(下)月考数学试卷(4月份)(1)一、我会填.(42分每空1分)1.一个小数由、和三部分组成.2.把3.6的小数点向左移动一位是,把3.14的小数点向左移动两位是,把0.03扩大到它的倍是30,把42缩小倍是0.042,把1.2缩小是0.012.3.小数2.05读作,2表示,5表示.4.3个1,5个0.1和1个0.01写成小数是.5.8.02的计数单位是,它有个这样的计数单位.0.256的计数单位是,它有个这样的计数单位.6.大于8而小于9的一位小数有个.7.把168000改写成用“万”作单位的数是;省略万位后面的尾数是;把995000000元改写成以“亿元”为单位的数是,保留一位小数是.8.小数点向右移动一位,原数就,向左移两位,原数就.9.把1.5扩大倍是15,缩小倍是0.015.把0.73缩小为原数的十分之一是,扩大10倍是.10.13厘米=米,86克=千克.11.在横线里填上“>”、“<”或“=”.0.180.179 0.500.5 0.10.09994.954 4.96 6.8公顷6公顷8平方米108厘米10.1分米12.一个三角形有条高;一个平行四边形有条高.13.如果直角三角形的一个锐角是20°,那么另一个角一定是度.14.自行车三脚架,就是利用了三角形的特性.15.所有的等边三角形都是三角形.16.长方形的内角和是,三角形的内角和是.二、我来当法官.17.0.27吨等于27千克.(判断对错)18.5.05和5.049保留一位小数都是5.0.(判断对错)19.32.36中的两个“3”表示的意义相同.(判断对错)20.近似数是6.25的三位小数不止一个.(判断对错)21.一个大三角形和一个小三角形的三个内角和是不相等的.(判断对错)22.一个钝角三角形里最多有两个钝角.(判断对错)23.等边三角形也是锐角三角形.(判断对错)24.在三角形中,一个角是直角,另两外角一定是45度.(判断对错)三、单位换算.25.单位换算2.1元=元分3.08千米=米8米6厘米=厘米0.4平方米=平方厘米.四、比较下面每组数的大小.26.从小到大排列.0.8 0.801 0.81 0.811 0.799<<<<.五、画一画:27.画一个腰长为4厘米的等腰三角形,并画出三角形的一条高.六、28.把下面各数改写成以“万”作单位的数,再保留一位小数.7365003982008845702903200.七、解决问题.(共29分1题8分2、3、4每题7分)29.用5,0,6,4,0这五个数字完成下面各题.(各小题中每个数字只用一次)①只读一个0的最大的三位小数.②只读2个0的最小三位小数.③近似数为51的三位小数.④大于500的两位小数.30.1千克芝麻可以榨出芝麻油0.45千克,100千克芝麻可以榨出芝麻油多少千克?31.一个等腰三角形的顶角是96°,每个底角是多少度?32.在一个直角三角形中,∠1=20度,锐角∠2等于多少度?2015-2016学年新人教版四年级(下)月考数学试卷(4月份)(1)参考答案与试题解析一、我会填.(42分每空1分)1.一个小数由整数部分、小数点和小数部分三部分组成.【考点】小数的读写、意义及分类.【分析】根据小数的组成可知:一个小数是由整数部分、小数部分和小数部分三部分组成.【解答】解:一个小数是由整数部分、小数部分和小数部分三部分组成.故答案为:整数部分,小数部分,小数部分.2.把3.6的小数点向左移动一位是0.36,把3.14的小数点向左移动两位是0.0314,把0.03扩大到它的1000倍是30,把42缩小1000倍是0.042,把1.2缩小100倍是0.012.【考点】小数点位置的移动与小数大小的变化规律.【分析】根据小数点位置移动引起数的大小变化规律可知:把3.6的小数点向左移动一位是0.36,把3.14的小数点向左移动两位是0.0314,把0.03扩大到它的1000倍是30,把42缩小1000倍是0.042,把1.2缩小100倍是0.012;据此解答即可.【解答】解:把3.6的小数点向左移动一位是0.36,把3.14的小数点向左移动两位是0.0314,把0.03扩大到它的1000倍是30,把42缩小1000倍是0.042,把1.2缩小100倍是0.012.故答案为:0.36,0.0314,1000,1000,100倍.3.小数2.05读作二点零五,2表示2个一,5表示5个0.01.【考点】小数的读写、意义及分类.【分析】(1)小数的读法:整数部分按照整数的读法来读,小数点读作“点”,小数部分依次读出每一位上的数字据此读出此数即可;(2)2在个位上,表示2个一.【解答】解:(1)小数2.05读作二点零五;(2)2在个位上,表示2个一;5在百分位上,表示5个0.01.故答案为:二点零五,2个一,5个0.01.4.3个1,5个0.1和1个0.01写成小数是 3.51.【考点】小数的读写、意义及分类.【分析】3个1即个位上是3,5个0.1即十分位上是5,1个0.01即百分位上是1,据此写出.【解答】解:3个1,5个0.1和1个0.01写成小数是 3.51.故答案为:3.51.5.8.02的计数单位是0.01,它有802个这样的计数单位.0.256的计数单位是0.001,它有256个这样的计数单位.【考点】小数的读写、意义及分类.【分析】根据小数的意义可知:一位小数表示十分之几,计数单位是十分之一(0.1),两位小数表示百分之几,计数单位是百分之一(0.01),三位小数表示千分之几,计数单位是千分之一;据此解答即可.【解答】解:8.02的计数单位是0.01,它有802个这样的计数单位.0.256的计数单位是0.001,它有256个这样的计数单位;故答案为:0.01,802,0.001,256.6.大于8而小于9的一位小数有9个.【考点】小数大小的比较.【分析】由题意知题干中限制了小数的位数,所以大于8而小于9的一位小数有8.1,8.2,8.3,8.4,8.5,8.6,8.7,8.8,8.9;共有9个.【解答】解:大于8而小于9的一位小数有8.1,8.2,8.38.4,8.5,8.6,8.7,8.8,8.9;共有9个;故答案为:9.7.把168000改写成用“万”作单位的数是16.8万;省略万位后面的尾数是17万;把995000000元改写成以“亿元”为单位的数是9.95亿,保留一位小数是10.0亿.【考点】整数的读法和写法;整数的改写和近似数;近似数及其求法.【分析】把一个整数改成用“万”作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字;省略“万”后面的尾数求它的近似数,要把万位的下一位千位上的数进行四舍五入,再在数的后面带上“万”字;改写成用“亿”作单位的数,就是在亿位数的右下角点上小数点,然后把小数末尾的0去掉,在数的后面带上“亿”字;改写成用亿作单位的数,要想保留一位小数,就是要把百分位下的数进行四舍五入.【解答】解:168000=16.8万;168000≈17万;995000000=9.95亿;9.95亿≈10.0亿;故答案为:16.8万,17万,9.95亿,10.0亿.8.小数点向右移动一位,原数就扩大10倍,向左移两位,原数就缩小100倍.【考点】小数点位置的移动与小数大小的变化规律.【分析】根据小数点位置移动引起数的大小变化规律可知:小数点向右移动一位,原数就扩大10倍,向左移两位,原数就缩小100倍;据此解答.【解答】解:小数点向右移动一位,原数就扩大10倍,向左移两位,原数就缩小100倍;故答案为:扩大10倍,缩小100倍.9.把1.5扩大10倍是15,缩小100倍是0.015.把0.73缩小为原数的十分之一是0.073,扩大10倍是7.3.【考点】小数点位置的移动与小数大小的变化规律.【分析】根据小数点位置移动引起数的大小变化规律可知:1.5变成15,是小数点向右移动1位,则扩大10倍;1.5变成0.015,是小数点向左移动2位,则缩小100倍;把0.73缩小为原数的十分之一是0.073,扩大10倍是7.3;据此解答即可.【解答】解:把1.5扩大10倍是15,缩小100倍是0.015.把0.73缩小为原数的十分之一是0.073,扩大10倍是7.3.故答案为:10,100,0.073,7.3.10.13厘米=0.13米,86克=0.086千克.【考点】长度的单位换算;质量的单位换算.【分析】把13厘米换算为米数,用13除以进率100;把86克换算为千克,用86除以进率1000.【解答】解:13厘米=0.13米,86克=0.086千克;故答案为:0.13,0.086.11.在横线里填上“>”、“<”或“=”.0.18>0.179 0.50=0.5 0.1>0.09994.954< 4.96 6.8公顷>6公顷8平方米108厘米>10.1分米【考点】小数大小的比较.【分析】比较两个小数的大小,先看它们的整数部分,整数大的那个数就大;如果整数部分相同,十分位大的那个数就大.如果十分位上的那个数也相同,百分位上的数大的那个数就大,依此类推;【解答】解:0.18>0.179;0.50=0.5;0.1>0.0999;4.954<4.96;6.8公顷=6公顷8000平方米>6公顷8平方米;108厘米=10.8分米>10.1分米.故答案为:>;=;>;<;>;>.12.一个三角形有三条高;一个平行四边形有无数条高.【考点】平行四边形的特征及性质;三角形的特性.【分析】(1)因为三角形的高是指过顶点与对边垂直的线段,任意三角形都有三个顶点,所以一定有三个高;据此解答即可.(2)根据平行四边形高的含义:平行四边形的高是指对边之间的距离,那么,两组对边之间都可以画无数条垂直线段,所以,有无数条高.【解答】解:由分析知:(1)任何一个三角形都有三条高;(2)平行四边形有无数条高;故答案为:三、无数.13.如果直角三角形的一个锐角是20°,那么另一个角一定是70度.【考点】三角形的内角和.【分析】根据直角三角形两个锐角的和为90°,用90°减去已知锐角的度数,即可得另一个锐角度数.【解答】解:90°﹣20°=70°;答:那么另一个锐角是70°.故答案为:70.14.自行车三脚架,就是利用了三角形的稳定特性.【考点】三角形的特性.【分析】根据三角形的特性:三角形具有稳定性.进行填空即可.【解答】解:因为三角形具有稳定性,自行车三脚架是利用了三角形稳定性的特性;故答案为:稳定性.15.所有的等边三角形都是锐角三角形.【考点】三角形的分类.【分析】等边三角形的三个角都相等,都是60°,由此根据三角形按角分类的方法即可进行解答.【解答】解:等边三角形的三个角都是60°,都是锐角,所以所有的等边三角形都是锐角三角形.故答案为:锐角.16.长方形的内角和是360°,三角形的内角和是180°.【考点】三角形的内角和;长方形的特征及性质.【分析】因为三角形的内角和是180度,长方形有4个直角,所以长方形的内角和是90°×4=360°.据此解答.【解答】解:三角形的内角和是180°,长方形的内角和是:90°×4=360°.故答案为:360°;180°.二、我来当法官.17.0.27吨等于27千克.×(判断对错)【考点】质量的单位换算.【分析】把0.27吨换算成千克数,用0.27乘进率1000得270千克.【解答】解:0.27吨=270千克所以题干的说法是错误的.故答案为:×.18.5.05和5.049保留一位小数都是5.0.×(判断对错)【考点】近似数及其求法.【分析】运用“四舍五入”法取近似值:要看精确到哪一位,从它的下一位运用“四舍五入”取值.【解答】解:5.05≈5.1,5.049≈5.0;所以5.05和5.049保留一位小数都是5.0,说法错误;故答案为:×.19.32.36中的两个“3”表示的意义相同.×(判断对错)【考点】小数的读写、意义及分类.【分析】首先搞清这个数字在小数的什么数位上和这个数位的计数单位,它就表示有几个这样的计数单位;据此判断.【解答】解:32.36中左边的“3”在十位上,表示3个十,右边“3”在十分位上表示3个十分之一,所以32.36中的两个“3”表示的意义不相同;故答案为:×.20.近似数是6.25的三位小数不止一个.√(判断对错)【考点】近似数及其求法.【分析】6.25是一个三位小数的近似数,有两种情况:“四舍”得到的6.25比原数小,“五入”得到的6.25比原数大,由此即可判断解答问题.【解答】解:“五入”得到的6.25最小三位小数是6.245,因此这个数必须大于或等于6.245;“四舍”得到的6.25最大是6.254,所以近似数是6.25的三位小数不止一个,即本题说法正确;故答案为:√.21.一个大三角形和一个小三角形的三个内角和是不相等的.×(判断对错)【考点】三角形的内角和.【分析】依据三角形的内角和是180度,即可进行解答.【解答】解:一个三角形不论大小其内角和都是180度;所以一个大三角形和一个小三角形的三个内角和是相等的.故答案为:×.22.一个钝角三角形里最多有两个钝角.×(判断对错)【考点】三角形的分类;三角形的内角和.【分析】根据三角形内角和是180度,如果一个钝角三角形里有两个钝角,则三角形内角和大于180度,所以一个钝角三角形里不可能有两个钝角.【解答】解:根据三角形内角和是180度,一个钝角三角形里最多有一个钝角,不可能有两个钝角;故答案为:×.23.等边三角形也是锐角三角形正确.(判断对错)【考点】三角形的分类.【分析】根据等边三角形的特征:三条边都相等,三个角都是60度;因为三个角都是锐角,根据锐角三角形的含义得出结论.【解答】解:由分析知:等边三角形,三个角都是60度,即三个角都是锐角,所以是锐角三角形;故答案为:正确.24.在三角形中,一个角是直角,另两外角一定是45度.×(判断对错)【考点】三角形的内角和.【分析】根据三角形的内角和等于180度,另两个内角的和等于180﹣90=90度,另两个内角相加等于90度即可,解答判断即可.【解答】解:180﹣90=90(度)所以另两个内角可能是:10°和80°.30°和60°,45°和45°…故答案为:×.三、单位换算.25.单位换算2.1元=2元10分3.08千米=3080米8米6厘米=806厘米0.4平方米=4000平方厘米.【考点】货币、人民币的单位换算;长度的单位换算.【分析】(1)把2.1元换算成复名数,整数部分就是2元,把小数部分0.1元换算成分,用0.1乘进率100得10分.(2)把3.08千米换算成米数,用3.08乘进率1000即可.(3)6厘米单位一致不用化,8米=800厘米,再相加即可;(4)平方米和厘米之间的进率为10000,用0.4乘进率10000即可.【解答】解:2.1元=2元10分3.08千米=3080米8米6厘米=806厘米0.4平方米=4000平方厘米故答案为:2,10,3080,806,4000.四、比较下面每组数的大小.26.从小到大排列.0.8 0.801 0.81 0.811 0.7990.799<0.8<0.801<0.81<0.811.【考点】小数大小的比较.【分析】小数大小的比较,先看小数的整数部分,整数部分大的这个数就大,整数部分相同的就看十分位,十分位大的这个数就大,十分位相同的,再看百分位,百分位大的这个数就大…据此解答.【解答】解:根据小数大小的比较方法知:0.799<0.8<0.801<0.81<0.811,故答案为:0.799,0.8,0.801,0.81,0.811.五、画一画:27.画一个腰长为4厘米的等腰三角形,并画出三角形的一条高.【考点】作三角形的高.【分析】根据等腰三角形的定义,有两条边相等的三角形是等腰三角形,据此即可画出腰长为4厘米的等腰三角形;经过等腰三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是等腰三角形底边上的高,用三角板的直角即可画出.【解答】解:六、28.把下面各数改写成以“万”作单位的数,再保留一位小数.7365003982008845702903200.【考点】近似数及其求法.【分析】改写成以万为单位的数,就是从右边起数到万的下一位千位,在前面点上小数点,去掉末尾的0,加上单位“万”即可;据此改写;再保留一位小数就是把改写后的数求它的近似数,要把百分位上的数字进行四舍五入,据此求出.【解答】解:736500=73.65万≈73.7万398200=39.82万≈39.8万884570=88.457万≈88.5万2903200=290.32万≈290.3万七、解决问题.(共29分1题8分2、3、4每题7分)29.用5,0,6,4,0这五个数字完成下面各题.(各小题中每个数字只用一次)①只读一个0的最大的三位小数.②只读2个0的最小三位小数.③近似数为51的三位小数.④大于500的两位小数.【考点】小数的读写、意义及分类.【分析】(1)写出只读一个“零”的最大三位小数,即一个0在个级末尾,另一个0在千分位上,然后把数字按照从大到小的顺序,从十位依次写出即可;(2)只读2个0的最小三位小数,只要把两个0一个放在十分位,一个放在百分位,然后把另外三个数按照从小到大的顺序从十位向右依次写出;(3)近似数为51的三位小数,即整数部分是50,小数部分是640,即这个数是50.640;(4)大于500的两位小数,只要整数部分是500,小数部分可以是46,据此写出.【解答】解:①只读一个0的最大的三位小数:60.540;②只读2个0的最小三位小数:45.006;③近似数为51的三位小数:50.640;④大于500的两位小数:500.46.30.1千克芝麻可以榨出芝麻油0.45千克,100千克芝麻可以榨出芝麻油多少千克?【考点】整数的乘法及应用.【分析】1千克芝麻可以出芝麻油0.45千克,根据乘法的意义可知,100千克芝麻可以出芝麻油0.45×100=45(千克).【解答】解:0.45×100=45(千克).答:100千克芝麻可以出芝麻油45千克.31.一个等腰三角形的顶角是96°,每个底角是多少度?【考点】三角形的内角和;等腰三角形与等边三角形.【分析】因为三角形的内角和是180度,又因为等腰三角形的两个底角相等,用“180°﹣120°=60°”求出两个底角的度数,再用“60°÷2=30°”即可求出每个底角的度数;列式解答即可.【解答】解:÷2=84°÷2=42°答:每个底角是42度.32.在一个直角三角形中,∠1=20度,锐角∠2等于多少度?【考点】三角形的内角和.【分析】因为三角形的内角和是180°,用180°﹣90°﹣∠1,即可求出∠2的度数,解答即可.【解答】解:180﹣90﹣20=90﹣20=70(度)答:∠2等于70度.2016年7月16日。
高中高一数学上学期第三次月考试卷(含解析)-人教版高一全册数学试题

2015-2016学年某某省某某市航天高中高一(上)第三次月考数学试卷一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符是合题目要求的.)1.设集合A={x|x﹣1>0},B={x|2x>0},则A∩B=()A.{x|x>1} B.{x|x>0} C.{x|x<﹣1} D.{x|x<﹣1或x>1}2.若,且α是第二象限角,则cosα的值等于()A. B. C.D.3.为了得到函数的图象,只需把函数y=sinx的图象上所有的点()A.向右平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向左平移个单位长度4.下列四个函数中,既是(0,)上的增函数,又是以π为周期的偶函数的是()A.y=tanx B.y=|sinx| C.y=cosx D.y=|cosx|5.幂函数y=x m(m∈Z)的图象如图所示,则m的值可以为()A.1 B.﹣1 C.﹣2 D.26.函数y=ax2+bx+3在(﹣∞,﹣1]上是增函数,在[﹣1,+∞)上是减函数,则()A.b>0且a<0 B.b=2a<0C.b=2a>0 D.a,b的符号不确定7.根据表格内的数据,可以断定方程e x﹣x﹣2=0的一个根所在的区间是()x ﹣1 0 1 2 3e x0.37 1 2.72 7.39 20.08x+2 1 2 3 4 5A.(﹣1,0)B.(0,1)C.(1,2)D.(2,3)8.将下列各式按大小顺序排列,其中正确的是()A.cos0<cos<cos1<cos30°B.cos0<cos<cos30°<cos1C.cos0>cos>cos1>cos30°D.cos0>cos>cos30°>cos19.若lgx﹣lgy=a,则=()A.3a B.C.a D.10.若sinα,cosα是关于x的方程4x2+2x+3m=0的两根,则m的值为()A.B. C.D.11.设函数f(x)=,若方程f(x)=m有三个不同的实数解,则m的取值X围是()A.m>0或m<﹣1 B.m>﹣1 C.﹣1<m<0 D.m<012.已知a是实数,则函数f(x)=1+asinax的图象不可能是()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.)13.已知角α的终边经过点P(﹣4,3),则cosα=.14.已知扇形的周长等于它所在圆的周长的一半,则这个扇形的圆心角是.15.函数,则=.16.当x>0时,不等式(a2﹣3)x>(2a)x恒成立,则实数a的取值X围是.三、解答题(本大题共6小题,共70分,解答应写出必要的文字说明、证明过程及演算步骤.)17.已知(1)求tanα的值;(2)求的值.18.设,(1)在下列直角坐标系中画出f(x)的图象;(2)若f(t)=3,求t值.19.已知x∈[﹣,],(1)求函数y=cosx的值域;(2)求函数y=﹣3(1﹣cos2x)﹣4cosx+4的值域.20.函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=π时,y有最大值3;当x=6π时,y有最小值﹣3.(1)求此函数的解析式;(2)求此函数的单调区间.21.已知二次函数f(x)=x2﹣16x+q+3(1)若函数在区间[﹣1,1]上存在零点,某某数q的取值X围;(2)问:是否存在常数q(0<q<10),使得当x∈[q,10]时,f(x)的最小值为﹣51?若存在,求出q的值,若不存在,说明理由.22.已知函数.(1)当a=1时,求函数f(x)在(﹣∞,0)上的值域;(2)若对任意x∈[0,+∞),总有f(x)<3成立,某某数a的取值X围.2015-2016学年某某省某某市航天高中高一(上)第三次月考数学试卷参考答案与试题解析一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符是合题目要求的.)1.设集合A={x|x﹣1>0},B={x|2x>0},则A∩B=()A.{x|x>1} B.{x|x>0} C.{x|x<﹣1} D.{x|x<﹣1或x>1}【考点】交集及其运算.【专题】计算题;集合思想;定义法;集合.【分析】求出A与B中不等式的解集确定出A与B,找出两集合的交集即可.【解答】解:由A中不等式解得:x>1,即A={x|x>1},由B中不等式变形得:2x>0,得到B=R,∴A∩B={x|x>1},故选:A.【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2.若,且α是第二象限角,则cosα的值等于()A. B. C.D.【考点】同角三角函数间的基本关系.【专题】计算题;三角函数的求值.【分析】由sinα的值,以及α的X围,利用同角三角函数间的基本关系求出cosα的值即可.【解答】解:∵sinα=,α是第二象限角,∴cosα=﹣=﹣.故选C【点评】此题考查了同角三角函数间的基本关系,熟练掌握基本关系是解本题的关键.3.为了得到函数的图象,只需把函数y=sinx的图象上所有的点()A.向右平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向左平移个单位长度【考点】函数y=Asin(ωx+φ)的图象变换.【专题】三角函数的图像与性质.【分析】直接利用函数图象的平移法则逐一核对四个选项得答案.【解答】解:∵由y=sinx到y=sin(x﹣),只是横坐标由x变为x﹣,∴要得到函数y=sin(x﹣)的图象,只需把函数y=sinx的图象上所有的点向右平行移动个单位长度.故选:A.【点评】本题主要考查三角函数的平移.三角函数的平移原则为左加右减上加下减.是基础题.4.下列四个函数中,既是(0,)上的增函数,又是以π为周期的偶函数的是()A.y=tanx B.y=|sinx| C.y=cosx D.y=|cosx|【考点】正弦函数的图象;余弦函数的图象.【专题】三角函数的图像与性质.【分析】根据函数单调性,周期性和奇偶性分别进行判断即可得到结论.【解答】解:A.函数y=tanx为奇函数,不满足条件.B.函数y=|sinx|满足既是(0,)上的增函数,又是以π为周期的偶函数.C.y=cosx的周期为2π,不满足条件.D.y=|cosx|在(0,)上是减函数,不满足条件.故选:B.【点评】本题主要考查三角函数的图象和性质,要求熟练掌握三角函数的周期性,奇偶性和单调性.5.幂函数y=x m(m∈Z)的图象如图所示,则m的值可以为()A.1 B.﹣1 C.﹣2 D.2【考点】幂函数的性质.【专题】应用题;函数思想;定义法;函数的性质及应用.【分析】由给出的幂函数的图象,得到幂指数小于0,且幂函数为偶函数,即可判断答案.【解答】解:根据幂函数的图象可知函数在第一象限内单调递减,且为偶函数.则m<0且为偶数,故选:C.【点评】本题主要考查幂函数的图象和性质,要求熟练掌握幂函数的性质的应用.6.函数y=ax2+bx+3在(﹣∞,﹣1]上是增函数,在[﹣1,+∞)上是减函数,则()A.b>0且a<0 B.b=2a<0C.b=2a>0 D.a,b的符号不确定【考点】二次函数的性质.【专题】计算题.【分析】利用对称轴的公式求出对称轴,根据二次函数的单调区间得到,得到选项.【解答】解:∵函数y=ax2+bx+3的对称轴为∵函数y=ax2+bx+3在(﹣∞,﹣1]上是增函数,在[﹣1,+∞)上是减函数∴∴b=2a<0故选B【点评】解决与二次函数有关的单调性问题,一般要考虑二次函数的开口方向、对称轴.7.根据表格内的数据,可以断定方程e x﹣x﹣2=0的一个根所在的区间是()x ﹣1 0 1 2 3e x0.37 1 2.72 7.39 20.08x+2 1 2 3 4 5A.(﹣1,0)B.(0,1)C.(1,2)D.(2,3)【考点】二分法求方程的近似解.【专题】计算题;函数的性质及应用.【分析】令f(x)=e x﹣x﹣2,求出选项中的端点函数值,从而由根的存在性定理判断根的位置.【解答】解:由上表可知,令f(x)=e x﹣x﹣2,则f(﹣1)≈0.37+1﹣2<0,f(0)=1﹣0﹣2=﹣1<0,f(1)≈2.72﹣1﹣2<0,f(2)≈7.39﹣2﹣2>0,f(3)≈20.09﹣3﹣2>0.故f(1)f(2)<0,故选:C.【点评】考查了二分法求方程近似解的步骤,属于基础题.8.将下列各式按大小顺序排列,其中正确的是()A.cos0<cos<cos1<cos30°B.cos0<cos<cos30°<cos1C.cos0>cos>cos1>cos30°D.cos0>cos>cos30°>cos1【考点】余弦函数的单调性.【专题】三角函数的图像与性质.【分析】先将1和化为角度,再根据余弦函数的单调性,判断出四个余弦值的大小关系.【解答】解:∵1≈57.30°,∴≈28.56°,则0<<30°<1,∵y=cosx在(0°,180°)上是减函数,∴cos0>cos>cos30°>cos1,故选D.【点评】本题主要考查余弦函数的单调性,以及弧度与角度之间的转化,属于基础题.9.若lgx﹣lgy=a,则=()A.3a B.C.a D.【考点】对数的运算性质.【专题】计算题.【分析】直接利用对数的性质化简表达式,然后把lgx﹣lgy2a代入即可.【解答】解: =3(lgx﹣lg2)﹣3(lgy﹣lg2)=3(lgx﹣lgy)=3a故选A.【点评】本题考查对数的运算性质,考查计算能力,是基础题.10.若sinα,cosα是关于x的方程4x2+2x+3m=0的两根,则m的值为()A.B. C.D.【考点】同角三角函数基本关系的运用.【专题】转化思想;综合法;三角函数的求值.【分析】由条件利用韦达定理求得sinα+cosα=﹣,sinα•cosα=,再利用同角三角函数的基本关系求得sinα•cosα=﹣,从而求得 m的值.【解答】解:∵sinα,cosα是关于x的方程4x2+2x+3m=0的两根,∴sinα+cosα=﹣,sinα•cosα=,再根据1+2sinαcosα=,∴sinα•cosα=﹣,∴m=﹣,故选:D.【点评】本题主要考查韦达定理、同角三角函数的基本关系,属于基础题.11.设函数f(x)=,若方程f(x)=m有三个不同的实数解,则m的取值X围是()A.m>0或m<﹣1 B.m>﹣1 C.﹣1<m<0 D.m<0【考点】根的存在性及根的个数判断.【专题】函数的性质及应用.【分析】由题意可得函数y=f(x)和直线y=m有3个不同的交点,数形结合可得m的取值X 围.【解答】解:由题意可得函数y=f(x)和直线y=m有3个不同的交点,如图所示:当﹣1<m<0时,函数y=f(x)和直线y=m有3个不同的交点,故选C.【点评】本题主要考查方程的根的存在性及个数判断,体现了数形结合的数学思想,属于中档题.12.已知a是实数,则函数f(x)=1+asinax的图象不可能是()A.B.C.D.【考点】正弦函数的图象.【专题】三角函数的图像与性质.【分析】函数f(x)=1+asinax的图象是一个正弦曲线型的图,其振幅为|a|,周期为,周期与振幅成反比,从这个方向观察四个图象.【解答】解:对于振幅大于1时,三角函数的周期为:,∵|a|>1,∴T<2π,而D不符合要求,它的振幅大于1,但周期反而大于了2π.对于选项A,a<1,T>2π,满足函数与图象的对应关系,故选D.【点评】由于函数的解析式中只含有一个参数,这个参数影响振幅和周期,故振幅与周期相互制约,这是本题的关键.二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.)13.已知角α的终边经过点P(﹣4,3),则cosα=.【考点】任意角的三角函数的定义.【专题】计算题.【分析】先求出角α的终边上的点P(﹣4,3)到原点的距离为 r,再利用任意角的三角函数的定义cosα=求出结果.【解答】解:角α的终边上的点P(﹣4,3)到原点的距离为 r=5,由任意角的三角函数的定义得cosα==.故答案为:.【点评】本题考查任意角的三角函数的定义,两点间的距离公式的应用,考查计算能力.14.已知扇形的周长等于它所在圆的周长的一半,则这个扇形的圆心角是(π﹣2)rad .【考点】弧长公式.【专题】计算题.【分析】由题意,本题中的等量关系是扇形的周长等于弧所在的圆的半周长,可令圆心角为θ,半径为r,弧长为l,建立方程,求得弧长与半径的关系,再求扇形的圆心角.【解答】解:令圆心角为θ,半径为r,弧长为l由题意得2r+l=πr∴l=(π﹣2)r∴θ==π﹣2故答案为:(π﹣2)rad.【点评】本题考查弧长公式,解题的关键是熟练掌握弧长公式,且能利用公式建立方程进行运算,本题考查对公式的准确记忆能力15.函数,则= ﹣.【考点】三角函数的化简求值.【专题】计算题;转化思想;综合法;三角函数的求值.【分析】利用诱导公式先求出f(x)=,再把cos=代入,能求出结果.【解答】解:∵===,∵cos=,∴==.故答案为:﹣.【点评】本题考查三角函数值的求法,是基础题,解题时要认真审题,注意诱导公式的合理运用.16.当x>0时,不等式(a2﹣3)x>(2a)x恒成立,则实数a的取值X围是a>3 .【考点】函数恒成立问题.【专题】计算题;函数思想;综合法;函数的性质及应用.【分析】由题意结合幂函数的单调性列关于a的不等式组得答案.【解答】解:∵x>0时,不等式(a2﹣3)x>(2a)x恒成立,∴,解得:a>3.故答案为:a>3.【点评】本题考查函数恒成立问题,应用了幂函数的单调性,同时注意指数式的底数大于0且不等于1,是中档题.三、解答题(本大题共6小题,共70分,解答应写出必要的文字说明、证明过程及演算步骤.)17.已知(1)求tanα的值;(2)求的值.【考点】同角三角函数基本关系的运用.【专题】综合题;方程思想;综合法;三角函数的求值.【分析】(1)直接弦化切,即可求tanα的值;(2)法一:求出sinα,cosα,分类讨论求的值.法二:原式分子分母同除以cos2α,弦化切,即可求的值.【解答】解:(1)∵,∴tanα=﹣tanα+1(2)法一:由(1)知:,∴或当,时,原式=当,时,原式=综上:原式=法二:原式分子分母同除以cos2α得:原式==【点评】本题考查同角三角函数关系,考查学生的转化能力,属于中档题.18.设,(1)在下列直角坐标系中画出f(x)的图象;(2)若f(t)=3,求t值.【考点】分段函数的解析式求法及其图象的作法.【专题】计算题;作图题.【分析】由分段函数,按照基本函数作图,第一段一次函数,第二次二次函数,第三次为一次函数,要注意每段的定义域.【解答】解:(1)如图(2)由函数的图象可得:f(t)=3即t2=3且﹣1<t<2.∴t=【点评】本题主要考查分段函数的作图和用数形结合解决问题的能力,分段函数知识点容量大且灵活,是高考的热点,在解决中要注意部分与整体的关系.19.已知x∈[﹣,],(1)求函数y=cosx的值域;(2)求函数y=﹣3(1﹣cos2x)﹣4cosx+4的值域.【考点】余弦函数的图象.【专题】转化思想;综合法;三角函数的图像与性质.【分析】(1)由条件利用余弦函数的定义域和值域,求得函数y=cosx的值域.(2)把函数y的解析式化为y=3(cosx﹣)2﹣,结合cosx∈[﹣,1],利用二次函数的性质求得y的值域.【解答】解:(1)∵y=cosx在[﹣,0]上为增函数,在[0,]上为减函数,∴当x=0时,y取最大值1;x=时,y取最小值﹣,∴y=cosx的值域为[﹣,1].(2)原函数化为:y=3cos2x﹣4cosx+1,即y=3(cosx﹣)2﹣,由(1)知,cosx∈[﹣,1],故y的值域为[﹣,].【点评】本题主要考查余弦函数的值域,二次函数的性质,属于基础题.20.函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=π时,y有最大值3;当x=6π时,y有最小值﹣3.(1)求此函数的解析式;(2)求此函数的单调区间.【考点】函数y=Asin(ωx+φ)的图象变换;由y=Asin(ωx+φ)的部分图象确定其解析式.【专题】三角函数的图像与性质.【分析】(1)由题意得到A和周期,代入周期公式求ω,在由点(π,3)在此函数图象上结合φ的X围求得φ,则函数解析式可求;(2)直接由复合函数的单调性求函数的单调区间.【解答】解:(1)由题意可知:A=3,,∴T=10π,则,∴y=3sin(φ),∵点(π,3)在此函数图象上,∴,.φ=.∵|φ|<,∴φ=.∴y=3sin();(2)当,即﹣4π+10kπ≤x≤π+10kπ,k∈Z时,函数y=3sin()单调递增,∴函数的单调增区间为[﹣4π+10kπ,π+10kπ](k∈Z);当,即π+10kπ≤x≤6π+10kπ,k∈Z时,函数单调递减,∴函数的单调减区间为[π+10kπ,6π+10kπ](k∈Z).【点评】本题考查y=Asin(ωx+φ)型函数图象的求法,考查了复合函数的单调性的求法,复合函数的单调性满足“同增异减”的原则,是中档题.21.已知二次函数f(x)=x2﹣16x+q+3(1)若函数在区间[﹣1,1]上存在零点,某某数q的取值X围;(2)问:是否存在常数q(0<q<10),使得当x∈[q,10]时,f(x)的最小值为﹣51?若存在,求出q的值,若不存在,说明理由.【考点】二次函数的性质.【专题】存在型;分类讨论;转化思想;分类法;函数的性质及应用.【分析】(1)若函数在区间[﹣1,1]上存在零点,则,即,解得实数q的取值X围;(2)假定存在满足条件的q值,结合二次函数的图象和性质,对q进行分类讨论,最后综合讨论结果,可得答案.【解答】解:(1)若二次函数f(x)=x2﹣16x+q+3的图象是开口朝上,且以直线x=8为对称轴的抛物线,故函数在区间[﹣1,1]上为减函数,若函数在区间[﹣1,1]上存在零点,则,即,解得:q∈[﹣20,12];(2)若存在常数q(0<q<10),使得当x∈[q,10]时,f(x)的最小值为﹣51,当0<q≤8时,f(8)=q﹣61=﹣51,解得:q=10(舍去),当8<q<10时,f(q)=q2﹣15q+3=﹣51,解得:q=9,或q=6(舍去),综上所述,存在q=9,使得当x∈[q,10]时,f(x)的最小值为﹣51.【点评】本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.22.已知函数.(1)当a=1时,求函数f(x)在(﹣∞,0)上的值域;(2)若对任意x∈[0,+∞),总有f(x)<3成立,某某数a的取值X围.【考点】函数恒成立问题.【专题】综合题;函数思想;综合法;函数的性质及应用.【分析】(1)法一、把a=1代入函数解析式,由指数函数的单调性求得f(x)在(﹣∞,0)上的值域;法二、令换元,由x的X围求出t的X围,转化为二次函数求值域;(2)由f(x)<3,即,分离参数a,然后利用换元法求函数的最小值得答案.【解答】解:(1)法一、当a=1时,,由指数函数单调性知f(x)在(﹣∞,0)上为减函数,∴f(x)>f(0)=3,即f(x)在(﹣∞,1)的值域为(3,+∞);法二、令,由x∈(﹣∞,0)知:t∈(1,+∞),∴y=g(t)=t2+t+1(t>1),其对称轴为直线,∴函数g(t)在区间(1,+∞)上为增函数,∴g(t)>g(1)=3,∴函数f(x)在(﹣∞,1)的值域为(3,+∞);(2)由题意知,f(x)<3,即,由于,在[0,+∞)上恒成立.若令2x=t,,则:t≥1且a≤h min(t).由函数h(t)在[1,+∞)上为增函数,故φmin(t)=φ(1)=1.∴实数a的取值X围是(﹣∞,1].【点评】本题考查函数恒成立问题,考查了指数函数的单调性,训练了分离变量法,是中档题.。
第1-4单元月考检测(月考)-2024-2025学年二年级上册数学苏教版

○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________○…………内…………○…………装…………○…………订…………○…………线…………○…………第一至四单元期中测试一、选择题1.下面哪道算式可以用口诀“二六十二”算出得数( )。
A .6×2B .6+2C .6÷22.口算“8÷2”要用的口诀是( )。
A .二八十六 B .二九十八C .二四得八3.左图有( )个平行四边形。
A .2B .3C .44.4个西瓜与12个菠萝一样重,1个西瓜与( )个菠萝一样重。
A .4B .3C .25.3个6相加,下面算式错误的是( )。
A .3×6B .6+6+6C .3+66.每棵树上有3只鸟,现在有五棵树,请问一共有多少只鸟?( ) A .14B .15C .167.一共有多少个笑脸,可以用算式( )来表示。
A .3×4×2B .3×4+2C .4×4-28.式子“5+5+5+5+5+6”可以改写成下面哪一道算式?( ) A .5×5+1B .5×6+1C .5×6-19.下面哪个平行四边形是由边框内的三个图形拼成的?( )A .B .C .10.任意一个四边形,沿直线剪一刀,不可能被分成( )。
A .两个三角形B .一个三角形和一个四边形C .一个四边形和一个五边形二、填空题11.30÷5=6读作( ),其中被除数是( ),除数是( ),商是( )。
12.一个乘数是6,另一个乘数是5,积是( )。
13.根据“二六十二”这句乘法口诀写出两道乘法算式。
、14.小明拍皮球,第一次拍了15下,第二次拍了27下,第三次拍的下数比第一次多,比第二次少。
2015-2016学年第一学期月考考成绩表 (空白) - 副本
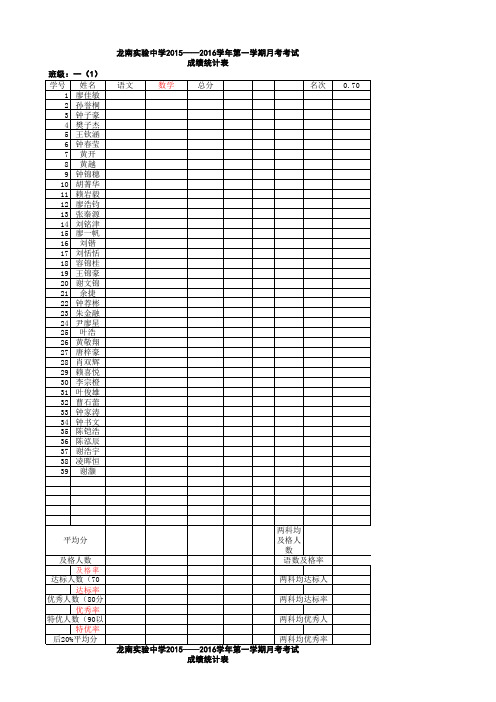
四(2)
学号 姓名
1 陈涵
2 钟铭淦
3 肖文杰
4
刘卓熙
5 赖允祺
6 曾少羿
7 吴雨舒
8 黄雪涵
9 叶柳妃
10 赖诗涵
11 欧阳金
12 刘槿雯
13 林煌东
14 蔡丰泽
15 叶晶晴
16 肖烨
17 曾馨缘
18 刘莹钦
19 钟其宏
20 黄文涛
21 叶静茹
22 刘薇
23 林瑶
24 刘议联
达标率 优秀人数(80分
优秀率 特优人数(90以
特优率 后20%平均分
五(2) 学号 姓名
1 叶芸萱 2 叶灵 3 叶智鹏 4 刘龙建 5 黄朦瑶 6 蔡惠 7 黄明强 8 曾文杰 9 廖宁锋 10 李晋成 11 钟榕 12 李位杰 13 刘帅 14 杨子韬 15 吴一雄 16 肖舒彤 17 徐智超 18 钟菊 19 钟培 20 刘钰烁 21 钟治语 22 邱庆松 23 赖鸿涛 24 邱泽豪 25 刘俊伟 26 李美靓 27 钟宇林 28 廖胤宇 29 廖鑫源 30 刘宏曜 31 唐文昱 32 刘楠 33 叶怡成 34 李芳萍 35 李家建 36 钟日城 37 刘煌晖 38 谢冰 39 黄建翀
龙南实验中学2015——2016学年第一学期月考考试 成绩统计表
语文
数学
总分
名次
0.70
平均分
及格人数 及格率
达标人数(70 达标率
优秀人数(80分 优秀率
特优人数(90以 特优率
后20%平均分
两科均 及格人
数 语数及格率
两科均达标人
两科均达标率
两科均优秀人
两科均优秀率 龙南实验中学2015——2016学年第一学期月考考试
苏教版数学二年级上学期摸底混合第三次月考(三套)

苏教版数学二年级上学期摸底混合第三次月考(三套)目录:苏教版数学二年级上学期摸底混合第三次月考一苏教版数学二年级上学期摸底混合第二次月考二苏教版数学二年级上学期摸底混合第四次月考三苏教版数学二年级上学期摸底混合第三次月考一(时间:90分钟)班级:__________ 姓名:__________一、填空题。
(每小题1分共10分)1. 在横线上填“>”“<"或“=”5米______50分米 7分米______70毫米 1时______100分 689______698 2. 如图的五边形中有个______锐角,______个直角______个钝角。
3. 小康买文具盒用去3元7角,还剩5元,他原来有______。
4. 把48、39、73、32、50按从小到大排列在横线上。
______<______<______<______<______。
其中双数有______,单数有______,最接近30的数是______。
5. 算盘上一个下珠表示______,一个上珠表示______。
6. 六千零五十写作______,4078读作______.7. 比73少30的数是______,______比25大30,74比______大40。
8. 4000克=______千克 2米=______厘米9. 在10. 等腰三角形的一个底角是40°,它的顶角是______度;等腰三角形的一个顶角是40°,它的底角是______度。
二、判断题。
(共10分)1. 火眼金睛辨对错.数位顺序表中,亿位在右起第9位.2. 判断正误.一万里面有100个百.3. 判断对错.一个八位数,它的最高位是千万位.4. 小红家在学校的正南方,学校就在小红家的正北方。
()5. 两个数相乘的积一定大于两个数相加的和.()6. □÷5=☆……▲,▲最大能填6。
()7. 比1000小1的数是999。
2022-2023学年江苏省连云港市海头高二年级上册学期第三次月考数学试题【含答案】

2022-2023学年江苏省连云港市海头高级中学高二上学期第三次月考数学试题一、单选题1.过两点()2,4-和()41-,的直线在y 轴上的截距为( ) A .145B .145-C .73D .73-【答案】C【分析】求出直线方程,令x =0,即可求出纵截距. 【详解】由题可知直线方程为:()()411424y x --+=⋅---,即()5416y x =---, 令x =0,则73y =,故直线在y 轴上的截距为73.故选:C.2.某厂去年的产值记为1,计划在今后五年内每年的产值比上年增长10%,则从今年起到第五年,这个厂的总产值为 A .41.1 B .51.1C .610(1.11)⨯-D .511(1.11)⨯-【答案】D【分析】利用等比数列的求和公式即得.【详解】依题意可得,从今年起到第五年这个厂的总产值为;52551(110%)[1(110%)]1(110%)1(110%)1(110%)11(1.11)1(110%)⋅+-+⋅++⋅+++⋅+==⨯--+.故选:D3.若双曲线经过点(),且它的两条渐近线方程是3y x =±,则双曲线的方程是( ).A .2219y x -=B .2219x y -=C .221273y x -=D .221273x y -=【答案】A【分析】由渐近线方程可设双曲线为229y x m -=且0m ≠,再由点在双曲线上,将点代入求参数m ,即可得双曲线方程.【详解】由题设,可设双曲线为229y x m -=且0m ≠,又()在双曲线上,所以36319m =-=-,则双曲线的方程是2219y x -=. 故选:A4.过圆x 2+y 2=5上一点M (1,﹣2)作圆的切线l ,则l 的方程是( ) A .x +2y ﹣3=0 B .x ﹣2y ﹣5=0 C .2x ﹣y ﹣5=0 D .2x +y ﹣5=0【答案】B【分析】本题先根据圆的切线的几何意义建立方程求切线的斜率,再求切线方程即可. 【详解】解:由题意:点M (1,﹣2)为切点,则1OM l k k ⋅=-,20210OM k --==--, 解得:12l k =, ∴l 的方程:1(2)(1)2y x --=-,整理得:250x y --=, 故选:B.【点睛】本题考查圆的切线的几何意义,点斜式直线方程,两线垂直其斜率相乘等于1-,是基础题. 5.已知函数()2ln af x x x x=-+在定义域内单调递减,则实数a 的取值范围是( )A .(],1-∞B .(),1∞-C .()1,+∞D .[)1,+∞【答案】D【分析】由题意转化为()0f x '≤,0x >恒成立,参变分离后转化为()2max2a x x≥-+,求函数()()22,0g x x x x =-+>的最大值,即可求解.【详解】函数的定义域是()0,∞+, ()222221a x x af x x x x-+-'=--=, 若函数()f x 在定义域内单调递减,即220x x a -+-≤在()0,∞+恒成立,所以22a x x ≥-+,0x >恒成立,即()2max2a x x≥-+设()()22211g x x x x =-+=--+,0x >, 当1x =时,函数()g x 取得最大值1,所以1a ≥. 故选:D6.《九章算术》中的“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积是( ) A .6766升 B .176升 C .10933升 D .1336升【答案】A【分析】设此等差数列为{}n a ,利用方程思想求出1a 和d ,再利用通项公式进行求解. 【详解】根据题意得该竹子自上而下各节的容积形成等差数列{}n a , 设其首项为1a ,公差为d ,由题意可得123478934a a a a a a a +++=⎧⎨++=⎩,所以114633214a d a d +=⎧⎨+=⎩,解得113=227=66a d ⎧⎪⎪⎨⎪⎪⎩,所以511376744226666a a d =+=+⨯=, 即第5节竹子的容积为6766升. 故选:A .7.在平面直角坐标系xOy 中,线段AB 的两端点A ,B 分别在x 轴正半轴和y 轴正半轴上滑动,若圆22:(4)(3)1C x y -+-=上存在点M 是线段AB 的中点,则线段AB 长度的最小值为 ( ) A .4 B .6 C .8 D .10【答案】C【分析】首先求点M 的轨迹,将问题转化为两圆有交点,即根据两圆的位置关系,求参数t 的取值范围.【详解】设AB t =,()0t >,AB 的中点为M ,则1122OM AB t ==, 故点M 的轨迹是以原点为圆心,12t 为半径的圆,问题转化为圆:M 22214x y t +=与圆()()22:431C x y -+-=有交点,所以111122t MC t -≤≤+,5MC =,即11521152t t ⎧+≥⎪⎪⎨⎪-≤⎪⎩,解得:812t ≤≤,所以线段AB 长度的最小值为8. 故选:C8.设函数()f x 是定义在(0,)+∞上的可导函数,其导函数为()f x ',且有()2()xf x f x '>,则不等式24(2022)(2022)(2)0f x x f ---<的解集为( )A .(0,2023)B .(2022,2024)C .2022(,)+∞D .(,2023)-∞【答案】B【分析】构造函数2()()f x g x x =,根据()2()xf x f x '>得到2()()f x g x x =的单调性,在变形不等式由单调性求解即可.【详解】由题知,函数()f x 是定义在(0,)+∞上的可导函数,其导函数为()f x ',且有()2()xf x f x '>,即()2()0xf x f x '->, 设2()()f x g x x =, 所以243()2()()2()()0x f x xf x xf x f x g x x x ''--'==>,所以()g x 在(0,)+∞上单调递增, 因为24(2022)(2022)(2)0f x x f ---<, 所以22(2022)(2)(2022)2f x f x -<-,所以2022020222x x ->⎧⎨-<⎩,解得20222024x <<,所以不等式24(2022)(2022)(2)0f x x f ---<的解集为(2022,2024), 故选:B二、多选题9.若在1和256中间插入3个数,使这5个数成等比数列,则公比q 为( ) A .2 B .-2C .4D .-4【答案】CD【分析】由等比数列的性质,即可求解.【详解】由条件可知,11a =,5256a =,所以4256q =,解得:4q =±. 故选:CD10.若直线l 经过点0(3,1)P -,且被圆2282120x y x y +--+=截得的弦长为4,则l 的方程可能是( ) A .3x = B .3y =C .34130x y --=D .43150x y --=【答案】AC【分析】由弦长公式得出圆心到直线距离,考虑直线斜率不存在和存在两种情况,根据距离公式得出所求方程.【详解】圆的标准方程为:()()22415x y -+-=,由题意圆心到直线l的距离1d == ①当直线的斜率不存在时,直线方程为3x =,圆心到直线的距离1d =,符合题意, ②当直线的斜率存在时,设直线的方程为()13y k x +=-,即130kx y k ---=,圆心到直线的距离为1d ==,解得34k =,则直线方程为34130x y --=, 综上,直线 l 的方程为3x =或34130x y --=. 故选:AC .11.已知数列{}n a 是等比数列,则下列结论中正确的是( )A .数列{}2n a 是等比数列B .若32a =,732a =,则58a =±C .若123a a a <<,则数列{}n a 是递增数列D .若数列{}n a 的前n 和13n n S r -=+,则 1r =- 【答案】AC【解析】利用等比数列的定义可判断A 选项的正误;利用等比中项的性质可判断B 选项的正误;分10a <和10a >两种情况讨论,求得对应的q 的取值范围,结合数列单调性的定义可判断C 选项的正误;求得1a 、2a 、3a ,由2213a a a =求得r 的值,可判断D 选项的正误.【详解】设等比数列{}n a 的公比为q ,则0q ≠,且1n na q a +=. 对于A 选项,222112n n n n a a q a a ++⎛⎫== ⎪⎝⎭,所以,数列{}2n a 是等比数列,A 选项正确; 对于B 选项,由等比中项的性质可得253764a a a ==,又因为2530a q a =>,则5a 与3a 同为正数,则58a =,B 选项错误;对于C 选项,若10a <,由123a a a <<可得1211a a q a q <<,可得21q q q <⎧⎨<⎩,解得01q <<,则110n n a a q -=<,11n na q a +=<,则1n n a a +>,此时,数列{}n a 为递增数列; 若10a >,由123a a a <<可得1211a a q a q <<,可得21q q q >⎧⎨>⎩,解得1q >,则110n n a a q -=>,11n na q a +=>,则1n n a a +>,此时,数列{}n a 为递增数列. 综上所述,C 选项正确;对于D 选项,111a S r ==+,()()221312a S S r r =-=+-+=,()()332936a S S r r =-=+-+=, 由于数列{}n a 是等比数列,则2213a a a =,即()2612r +=,解得13r =-,D 选项错误.故选:AC.【点睛】本题考查等比数列的定义、等比中项的性质以及等比求和相关命题正误的判断,考查计算能力与推理能力,属于中等题. 12.已知函数()2ln f x x x=+,则下列判断正确的是( ) A .存在()0x ∈+∞,,使得()0f x < B .函数()y f x x =-有且只有一个零点 C .存在正数k ,使得()0f x kx ->恒成立D .对任意两个正实数12,x x ,且21x x >,若()()12f x f x =,则124x x +> 【答案】BD【分析】先对函数求导,结合导数与单调性关系分析函数的单调性及最值可检验选项A ; 求得()y f x x =-的导数可得单调性, 计算1,2x x ==的函数值,可判断选项B ;由参数分离和构造函数求得导数判断单调性,可判断选项C ;构造函数()(2)(2)g t f t f t =+--,结合导数分析()g t 的性质,结合已知可分析12x x +的范围即可判断选项D. 【详解】22122()x f x x x x-'=-=,易得, 当02x << 时,()0f x '<,函数单调递减, 当 2x > 时,()0f x '>,函数单调递增,故函数在2x =处取得极小值也是最小值(2)1ln 20f =+>, 不存在,()0x ∈+∞,使得()0f x <, 故选项A 错误;()y f x x =-的导数为22222191222410x x x y x x x x ⎛⎫-+ ⎪--⎝⎭'=--==-<恒成立, 所以 ()y f x x =-递减,且(1)110f -=>,(2)21ln 22ln 210f -=+-=-<,可得 ()y f x x =- 有且只有一个零点,介于(1,2), 故选项B 正确;()f x kx > 等价为 2ln 0x kx x+-> ,设()2ln e h x x x =>,则()10h x x '=, 故()h x 在()2e ,+∞上为减函数,故()2lne e 2e 0h x <-=-<,故2ln e x x <>,故当22max e ,x ⎧⎫⎪⎪>⎨⎬⎝⎭⎪⎪⎩⎭,2ln 20x kx kx x +-<-<,所以()k g x <不恒成立,故选项C 错误; 设(0,2)t ∈,则2(0,2),2(2,4)t t -∈+∈, 令22242()(2)(2)ln(2)ln(2)ln 2242t t g t f t f t t t t t t t+=+--=+--+-=++---, 则 ()()222222241648()0444t t g t t t t --'=+=-<---, 故()g t 在(0,2)上单调递减,()(0)0g t g <=,不妨设12x t =-,因为()()12f x f x =,所以22x t >+, 则12224x x t t +>-++=,故选项D 正确. 故选:BD.【点睛】本题考查导数的运用,求单调性和极值、最值,以及函数的零点和不等式恒成立问题解法,考查转化思想和运算能力、推理能力,属于难题.三、填空题13.已知()tan f x x =,则=3f π⎛⎫⎪⎝⎭'______.【答案】4【详解】试题分析:因为()tan f x x =,所以2222sin cos sin 1'()(tan )'()'cos cos cos x x x f x x x x x+====,所以21'()43cos 3f ππ== 【解析】1.导数的运算;14.两条平行直线433x y ++=0与869x y +-=0的距离是________. 【答案】32【解析】将直线869x y +-=0化为94302x y +-=,再根据平行线间距离公式即可求解. 【详解】可将直线869x y +-=0化为94302x y +-=, 所以两条平行直线间的距离为229323243⎛⎫-- ⎪⎝⎭=+. 故答案为:32.【点睛】本题考查平行线间距离公式,属于基础题.15.已知圆221O x y +=:,圆()()2241M x a y a -+-+=:.若圆M 上存在点P ,过点P 作圆O 的两条切线,切点为,A B ,使得60APB ∠=︒,则实数a 的取值范围为________. 【答案】222,222⎡⎤-+⎢⎥⎣⎦【分析】由题意画出图形,利用两点间的距离关系求出OP 的距离,再由题意得到关于a 的不等式求得答案.【详解】解:如图,圆O 的半径为1,圆M 上存在点P , 过点P 作圆O 的两条切线,切点为,A B ,使得60APB ∠=︒, 则30APO ∠=︒,在Rt PAO ∆中,=2PO , 又圆M 的半径等于1,圆心坐标(),4M a a -,min 1PO MO ∴=-,max 1PO MO =+,()224MO a a =++,∴由()()222241241a a a a ++-≤≤+++,解得:222222a -≤≤+. 故答案为:222,222⎡⎤-+⎢⎥⎣⎦.【点睛】本题考查直线和圆的位置关系的应用,利用数形结合将条件进行等价转化是解决本题的关键.16.已知函数2(1)e 1,0()2,0x x x f x x x x ⎧+-≤=⎨->⎩,(e 是自然对数的底数),若函数()()10f f x a -+=有4个不同的零点,则实数a 的取值范围是__________. 【答案】()0,1【分析】利用导函数画出()f x 的图像,由图像可得当(())1f f x a -=-时,()1f x a 或1-,再利用图像求()1f x a =±有四个交点时a 的范围即可.【详解】令()(1)e 1(0)x g x x x =+-≤得()(2)e x g x x '=+, 所以()g x 在(,2)-∞-单调递减,在(2,0]-单调递增, 且当x →-∞时()1g x <-,2(2)e 11g --=--<-,(1)1g -=-, 所以()f x 图像如图所示:由图像可得令()1f t =-解得1t =或1-, 令()f x k =,由图像可得当0k >时,有一个解;当0k =时,有两个解;当10k -<<时有三个解;当1k =-时有两个解;当2e 11k ---<<-时有两个解;当2e k -=-时有一个解;当2e k -<-时,无解; 所以当()f x t a =+有四个不同的解时,(0,1)a ∈, 故答案为:()0,1四、解答题17.已知函数32()f x x ax =-,a ∈R ,且(1)3f '=.求: (1)a 的值及曲线()y f x =在点(1,(1))f 处的切线方程; (2)函数()f x 在区间[]0,2上的最大值. 【答案】(1)320x y --= (2)8【分析】(1)由题意,求出a 的值,然后根据导数的几何意义即可求解;(2)根据导数与函数单调性的关系,判断函数()f x 在区间[0,2]上的单调性,从而即可求解. 【详解】(1)由题意,2()32f x x ax '=-, 因为()13f '=,所以23123a ⨯-=,解得0a =, 所以3()f x x =,2()3f x x '=, 因为(1)1f =,(1)3f '=,所以曲线()y f x =在点(1,(1))f 处的切线方程为()131y x -=-,即320x y --=; (2)因为2()30f x x '=≥,且[0,2]x ∈, 所以()f x 在[]0,2上单调递增,所以max ()(2)8f x f ==,即函数()f x 在区间[0,2]上的最大值为8.18.在数列{}n a 中,14a =,21(1)22n n na n a n n +-+=+.(1)求证:数列n a n ⎧⎫⎨⎬⎩⎭是等差数列;(2)求数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和n S .【答案】(1)证明见解析;(2)2(1)nn +.【分析】(1)由21(1)22n n na n a n n +-+=+,两边同除以n (n +1)可得:121n n a a n n +-=+,且141a=,即可证得. (2)由(1)可得:22na n n =+,可得1111()21na n n =-+,再利用裂项求和方法即可得出. 【详解】(1)在数列{}n a 中,满足21(1)22n n na n a n n +-+=+,同时两边除以(1)n n +,得121n n a a n n +-=+,且141a =,所以数列n a n ⎧⎫⎨⎬⎩⎭是以4为首项,以2为公差的等差数列. (2)由(1)得,()4+2122n a n n n=-=+,所以222n a n n =+,故2111(1)111()222(1)21n n n a n n n n n n +-===-+++, 所以111111[(1)()()]22231n S n n =-+-+⋯+-+1111111[(1)()]223231n n =+++⋯+-++⋯++11(1)212(1)n n n =-=++. 【点睛】本题考查了数列递推关系、等差数列的定义通项公式、裂项求和方法,考查了推理能力与计算能力,属于中档题.19.已知圆F : 22(3)1x y ++=,直线:2,l x =动圆M 与直线l 相切且与圆F 外切.(1)记圆心M 的轨迹为曲线C , 求曲线C 的方程;(2)若直线260x y -+=与曲线C 相交于A ,B 两点,求AB 的长.【答案】(1)212y x =-(2)15【分析】(1)设(,)M x y ,用坐标表示题设条件化简可得;(2)设交点为11(,)A x y ,22(,)B x y ,直线方程与曲线C 方程联立消元,应用韦达定理得1212,x x x x +,然后由弦长公式求得弦长.【详解】(1)设(,)M x y ,显然点M 在直线2x =左侧,22x x -=-,12x =+-123x x =+-=-,平方整理得212y x =-,所以M 的轨迹方程是212y x =-;(2)联立方程组212260y x x y ⎧=-⎨-+=⎩,化简得,++=2x 9x 90, 设直线260x y -+=与曲线C 相交于A ,B 两点,11(,)A x y ,22(,)B x y ,则129x x +=-,129x x ⋅=,15AB .20.已知等差数列{}n a 的前n 项和为78,13,64n S a S ==.(1)求数列{}n a 的通项公式;(2)设3n n n b a =,求数列{}n b 的前n 项和n T .【答案】(1)21n a n =-(2)13(1)3n n T n +=+-⋅【分析】(1)根据等差数列的通项公式与求和公式列方程组,求解1,a d ,即可得通项公式;(2)利用错位相减法代入计算{}n b 的前n 项和n T .【详解】(1)因为数列{}n a 为等差数列,设等差数列{}n a 的公差为d ,所以1116131828642a d a a d d +==⎧⎧⇒⎨⎨+==⎩⎩,所以数列{}n a 的通项公式为()12121n a n n =+-=-; (2)由(1)得(21)3n n b n =-,∴121333(21)3n n T n =⨯+⨯++-⋅,23131333(21)3n n T n +=⨯+⨯++-⋅.∴1212132323(21)3n n n T n +-=⨯+⨯++⨯--⋅()12123333(21)3n n n +=+++---⋅162(1)3n n +=---⋅.∴13(1)3n n T n +=+-⋅21.淮北市政府响应习总书记在十九大报告中提出的“绿水青山就是金山银山”,对环境进行了大力整治,目前淮北市的空气质量位列全省前列,吸引了大量的外地游客。
2024-2025学年华东师大版(上海)八年级数学上册月考试卷885

2024-2025学年华东师大版(上海)八年级数学上册月考试卷885考试试卷考试范围:全部知识点;考试时间:120分钟学校:______ 姓名:______ 班级:______ 考号:______总分栏题号一二三四五总分得分评卷人得分一、选择题(共6题,共12分)1、下列式子中,是最简二次根式的是()A.B.C.D.2、在;;;;+中,属于分式的有()A. 2个B. 3个C. 4个D. 5个3、在平面直角坐标系xOy中,点P(-3,5)关于x轴的对称点的坐标是()A. (3,5)B. (3,-5)C. (5,-3)D. (-3,-5)4、已知(a+b)2=m,(a-b)2=n,则ab等于()A.B.C.D.5、【题文】要使有意义,则字母x应满足的条件是( ).A. x=2B. x<2C. x≤2D. x≥26、菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家.对截至2014年获奖者获奖时的年龄进行统计,整理成下面的表格.组别第一组第二组第三组第四组年龄段(岁)27<x≤3131<x≤3434<x≤3737<x≤40频数(人)8 11 17 20则这56个数据的中位数落在()A. 第一组B. 第二组C. 第三组D. 第四组评卷人得分二、填空题(共5题,共10分)7、等腰三角形有一个外角是100°,这个等腰三角形的底角是____.8、如图,▱[ABCD <]的对角线[AC <]、[BD <]相交于点[0 <],[EF <]过点[O <]与[AD <]、[BC <]分别相交于点[E <]、[F <],若[AB=5 <],[AD=8 <],[OE=3 <],那么四边形[EFCD <]的周长为 ______ .9、(2013秋•安庆期末)如图,在平面直角坐标系中,第一次将三角形OAB变换成三角形OA1B1,第二次将三角形OA1B1,变换成三角形OA2B2,第三次将三角形OA2B2变换成二角形OA3B3,已知A (-3,1),A1(-3,2),A2(-3,4),A3(-3,8);B (0,2),B1(0,4),B2(0,6),B3(0,8).(1)观察每次变换前后三角形有何变化,找出规律,按此变换规律再将三角形OA3B3变换成OA4B4,则点A4的坐标为,点B4的坐标为.(2)若按(1)题找到的规律,将三角形OAB进行n次变换,得到三角形OA n B n,则点A n的坐标是,B n的坐标是.10、在数轴上点A表示实数,点B表示实数,那么离原点较远的点是.11、【题文】.二元一次方程x+y=5的正整数解有______________.评卷人得分三、判断题(共9题,共18分)12、正数的平方根有两个,它们是互为相反数13、判断:方程=与方程5(x-2)=7x的解相同. ()14、判断:菱形的对角线互相垂直平分.()15、线段是中心对称图形,对称中心是它的中点。
四年级上数学月考试题-综合考练(26)|15-16人教新课标

2015-2016学年新人教版四年级(上)月考数学试卷(9月份)(3)一、我会填,相信聪明的你是最棒的!(每空1分,共30分)1.直线端点,线段端点,射线端点.2.千位的左边是位.右边是位.3.10个十万是,个一万是百万.4.301 2789≈万,5 3994 9800≈亿.5.在50后面添上个0是5万.6.最小的三位数和最大的两位数相差,比最小的四位数多1的数是.7.30500000=万10200000000=亿.8.你认为,过一点可以画条直线,过两点可以画条直线.9.在横线里填上“>”、“<”或“=”.78900798009996812000085万85000010000199999.10.4052631是位数,4在位上,表示个,5在位上,它的计数单位是.11.一个数是由9个十万,9个千和9个十组成的,这个数是,读作.12.横线里可以填几?99859≈99万24990000≈3亿.二、我会判.(每题2分,共10分)13.个位、十位、百位…是计数单位.(判断对错)14.线段和射线都是直线的一部分.(判断对错)15.一条射线的长度是20厘米.(判断对错)16.连接两点的线中,线段是最短的.(判断对错)17.不相交的两条直线叫平行线.(判断对错)三、选择题.(每题2分,共10分)18.小东画了两条直线都与直线AB垂直,那么这两直线()A.互相平行 B.互相垂直 C.不能确定19.直线和射线中,()长.A.直线 B.射线 C.不确定20.506780≈()A.50万B.51万C.5121.6□2567≈61万,□里填()A.1 B.0 C.822.在3后面添上几个0,这个数才是三亿?()A.8 B.9 C.10四、计算部分23.直接写出得数.24×11= 161÷7= 35﹣15×2= 125×6=100﹣17= 96﹣69= 280﹣73﹣27= 25×4=24.列竖式计算.23×416=307×42=3100×14=五、操作题.(共12分)25.过M点画已知直线L1的垂线;26.过N点画出已知直线L2的平行线27.用三角板画出60°的角.28.用量角器画一个140°的角.六、解决问题.(每小题5分,共21分)29.水果店卖出苹果256筐,是卖出梨的筐数的4倍.水果店卖出梨多少筐?30.刘叔叔带700元钱买化肥,买了16袋化肥,剩60元,每袋化肥的价钱是多少?31.儿童文学:10.00元/本问题:学校要买28本儿童文学,至少需要多少元?32.在运动会开幕式上进行大型团体表演,一共有12个方阵,每个方阵16行,每行16人,一共有多少人参加表演?2015-2016学年新人教版四年级(上)月考数学试卷(9月份)(3)参考答案与试题解析一、我会填,相信聪明的你是最棒的!(每空1分,共30分)1.直线没有端点,线段2个端点,射线1个端点.【考点】直线、线段和射线的认识.【分析】根据线段、射线和直线的特点:线段有2个端点,射线有1个端点,直线没有端点进行解答即可.【解答】解:直线没有端点,线段有2个端点,射线有1个端点;故答案为:无,2个,1个.2.千位的左边是万位.右边是百位.【考点】整数的认识.【分析】根据数位顺序表:从右向左依次分:个位、十位、百位、千位、万位、十万位、百万位、千万位、亿位、十亿位、…;可知:千位的左边是万位,右边是百位;据此解答即可.【解答】解:千位的左边是万位.右边是百位.故答案为:万,百.3.10个十万是一百万,100个一万是百万.【考点】整数的认识.【分析】根据相邻的两个计数单位间的进率是“十”,万和十万,百万和千万,都是两个相邻的计数单位,它们的进率都是“十”,千万和十万,百万和万,亿和百万都是隔一个计数单位,它们的进率都是“100”,据此解答即可.【解答】解:10个十万是一百万,100个一万是百万.故答案为:一百万,100.4.301 2789≈301万,5 3994 9800≈5亿.【考点】整数的改写和近似数.【分析】省略“万”后面的尾数就是四舍五入到万位,把万位后的千位上的数进行四舍五入,再在数的后面写上“万”字.省略“亿”后面的尾数就是四舍五入到亿位,把亿位后的千万位上的数进行四舍五入,再在数的后面写上“亿”字.【解答】解:3012789≈301万,539949800≈5亿故答案为:301,5.5.在50后面添上3个0是5万.【考点】整数的读法和写法.【分析】5万是一个五位数,要在50后面添上3个0.【解答】解:在50后面添上3个0是5万;故答案为:3.6.最小的三位数和最大的两位数相差1,比最小的四位数多1的数是1001.【考点】整数的加法和减法.【分析】求最小的三位数和最大的两位数相差多少,可先确定最小的三位数是100和最大的两位数各是99,然后用三位数减去两位数即可得出答案,最小的四位数是1000,多1,加上1.【解答】解:100﹣99=11000+1=1001答:最小的三位数和最大的两位数相差1,比最小的四位数多1的数是1001.故答案为:1,1001.7.30500000=3050万10200000000=102亿.【考点】整数的改写和近似数.【分析】改成用万作单位的数,是把万位后面的4个“0”去掉,或者在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字,据此改写;改写成用“亿”作单位的数,是把亿位后面的8个“0”去掉,或者在亿位数的右下角点上小数点,然后把小数末尾的0去掉,在数的后面带上“亿”字,据此写出.【解答】解:30500000=3050万10200000000=102亿.故答案为:3050、102.8.你认为,过一点可以画无数条直线,过两点可以画一条直线.【考点】直线、线段和射线的认识.【分析】因为直线无端点,所以过一点可以画无数条直线;两点确定一条直线,所以两点可以画一条直线;进而得出结论.【解答】解:由分析知:过一点可以画无数条直线,过两点可以画一条直线;故答案为:无数,一.9.在横线里填上“>”、“<”或“=”.78900<7980099968<12000085万=850000100001>99999.【考点】整数大小的比较.【分析】根据整数大小比较的方法,位数多的大于位数少的,位数相同的,从最高位开始比较,最高位上大的数就大,如果最高位相同,再比较次高位,依此类推.据此解答即可.【解答】解:78900<79800;99968<120000;85万=850000;100001>99999;故答案为:<;<;=;>.10.4052631是7位数,4在百万位上,表示4个百万,5在万位上,它的计数单位是万.【考点】整数的认识.【分析】只要有几个数字就是几位数,数字在什么数位上根据数位顺序表就可以知道,几在什么数位上就表示有几个计数单位;据此解答.【解答】解:4052631是7位数,4在百万位上,表示4个百万,5在万位上,它的计数单位是万;故答案为:7,百万,4,百万,万,万.11.一个数是由9个十万,9个千和9个十组成的,这个数是909090,读作九十万九千零九十.【考点】整数的读法和写法.【分析】这是一个六位数,最高位十万位、千位和十位上都是9,写这个数时,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0;读这个数时,从高位到低位,一级一级地读,每一级末尾的0都不读出来,其余数位一个零或连续几个0都只读一个零.【解答】解:这个数写作:909090;909090读作:九十万九千零九十;故答案为:909090,九十万九千零九十.12.横线里可以填几?990、1、2、3、4859≈99万25、6、7、8、94990000≈3亿.【考点】整数的改写和近似数.【分析】根据近似数的求法,要精确到某一位,就要看这一位的下一位数,然后根据四舍五入的方法来求出近似数.【解答】解:99﹣﹣859≈99万,显然是“四舍法”,故可以填0、1、2、3、4;2﹣﹣4990000≈3亿,亿位上是“2”,所以是“五入法”,故填5、6、7、8、9故答案为为:.0、1、2、3、4;5、6、7、8、9.二、我会判.(每题2分,共10分)13.个位、十位、百位…是计数单位×.(判断对错)【考点】整数的认识.【分析】计数单位与数位形式上的区别是:数位后面带个“位”字,而计数单位后面没有“位”字.【解答】解:个位、十位、百位后面有“位”字是数位,不是计数单位.故答案为:×.14.线段和射线都是直线的一部分.√(判断对错)【考点】直线、线段和射线的认识.【分析】在直线上画两点,两点之间的部分就是一条线段,在直线上画一点,这点把直线分成两部分,这两部分就是两个相反方向的射线.所以线段和射线都是直线的一部分.【解答】解:由分析知:线段和射线都是直线的一部分,说法正确;故答案为:√.15.一条射线的长度是20厘米.×(判断对错)【考点】直线、线段和射线的认识.【分析】根据射线的含义:射线有一个端点,无限长;进行判断即可.【解答】解:一条射线的长度是20厘米,说法错误;因为射线无限长;故答案为:×.16.连接两点的线中,线段是最短的.√(判断对错)【考点】直线、线段和射线的认识.【分析】根据线段的性质:两点之间,线段最短;两点之间的距离:连接两点间的线段的长度叫两点间的距离可得答案.【解答】解:连接两点的线中,线段是最短的,说法正确;故答案为:√.17.不相交的两条直线叫平行线.×(判断对错)【考点】垂直与平行的特征及性质.【分析】根据平行线的定义,在同一平面内,不相交的两条直线是平行线.所以说法错误.【解答】解:在同一平面内不相交的两条直线叫做平行线,所以本题成立的前提是:在同一平面内,所以原题说法错误.故答案为:×.三、选择题.(每题2分,共10分)18.小东画了两条直线都与直线AB垂直,那么这两直线()A.互相平行 B.互相垂直 C.不能确定【考点】垂直与平行的特征及性质.【分析】根据垂直的性质:在同一平面内,垂直于同一条直线的两条直线平行;进行解答即可.【解答】解:根据垂直和平行的特征:在同一平面内,垂直于同一条直线的两条直线平行;而题干中缺少了“在同一平面内”这个条件,所以无法确定这两条直线的关系.故选:C.19.直线和射线中,()长.A.直线 B.射线 C.不确定【考点】直线、线段和射线的认识.【分析】直线没有端点,它向两方无限延伸,无法量得其长度;射线只有一个端点,它向一方无限延伸,也无法量得其长度;据此判断.【解答】解:由分析可知:射线和直线都无限长,所以无法比较其长度;故选:C.20.506780≈()A.50万B.51万C.51【考点】整数的改写和近似数.【分析】省略万位后面的尾数求近似数,根据千位上数字的大小确定用“四舍”法、还是用“五入”法.千位上是4或比4小的数,直接把尾数省略;千位上是5或比5大的数,省略尾数并向万位进一.由此解答.【解答】解:506780≈51万.故选:B.21.6□2567≈61万,□里填()A.1 B.0 C.8【考点】整数的改写和近似数.【分析】根据题意是将整数省略万后面的尾数求近似数得出的61万,千位上是2,所以需要舍去尾数,所以万位上是1.【解答】解:“6□2567≈61万”,□里填1.故选:A.22.在3后面添上几个0,这个数才是三亿?()A.8 B.9 C.10【考点】整数的读法和写法.【分析】三亿是一个九位数,因此,要在3后添加上8个0才是三亿.【解答】解:在3后面添上8个0,这个数才是三亿:300000000.故选:A.四、计算部分23.直接写出得数.24×11= 161÷7= 35﹣15×2= 125×6=100﹣17= 96﹣69= 280﹣73﹣27= 25×4=【考点】整数的乘法及应用;整数四则混合运算.【分析】根据整数乘法、除法、减法的计算方法进行计算即可.【解答】解:24×11=264 161÷7=23 35﹣15×2=5 125×6=750100﹣17=83 96﹣69=27 280﹣73﹣27=180 25×4=10024.列竖式计算.23×416=307×42=3100×14=【考点】整数的乘法及应用.【分析】根据整数乘法的计算方法进行计算即可.【解答】解:23×416=9568307×42=128943100×14=43400五、操作题.(共12分)25.过M点画已知直线L1的垂线;【考点】过直线上或直线外一点作直线的垂线.【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和M点重合,过M点沿三角板的直角边,向已知直线画直线即可.【解答】解:画图如下:26.过N点画出已知直线L2的平行线【考点】过直线外一点作已知直线的平行线.【分析】把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和N点重合,过N点沿三角板的直角边画直线即可.【解答】解:画图如下:27.用三角板画出60°的角.【考点】画指定度数的角.【分析】60°角用三角板直接就可画出,据此解答.【解答】解:如图所示:28.用量角器画一个140°的角.【考点】画指定度数的角.【分析】根据角的画法:(1)画一条射线,使量角器的中心与射线的端点重合,0刻度线与射线重合;(2)在量角器140度的地方点上一个点;(3)以画出的射线的端点为端点,通过刚画的点,再画出另一条射线;(4)画完后在角上标上符号,写出度数.【解答】解:如图所示:.六、解决问题.(每小题5分,共21分)29.水果店卖出苹果256筐,是卖出梨的筐数的4倍.水果店卖出梨多少筐?【考点】整数的除法及应用.【分析】用卖出的苹果的筐数除以4,就是卖出的梨的筐数,据此解即可.【解答】解:256÷4=64(筐)答:水果店卖出梨64筐.30.刘叔叔带700元钱买化肥,买了16袋化肥,剩60元,每袋化肥的价钱是多少?【考点】整数、小数复合应用题.【分析】刘叔叔带700元钱买化肥,买了16袋化肥,剩60元,根据减法的意义可知,共花了700﹣60元,根据除法的意义,每袋化肥的价钱是÷16元.【解答】解:÷16=640÷16,=40(元).答:每袋化肥40元.31.儿童文学:10.00元/本问题:学校要买28本儿童文学,至少需要多少元?【考点】整数、小数复合应用题.【分析】根据题意,购买28本儿童文学,可以先购买20本,因为20里面有5个4,所以购买20本就赠送4本,然后再购买4本即可,实际上花了24本儿童文学的钱数,根据公式:单价×数量=总价进行计算即可.【解答】解:28÷(5+1)=28÷6,≈4(本),(28﹣4)×10,=24×10,=240(元),答:至少需要240元钱.32.在运动会开幕式上进行大型团体表演,一共有12个方阵,每个方阵16行,每行16人,一共有多少人参加表演?【考点】整数、小数复合应用题.【分析】先依据乘法的意义计算出每个方阵的人数,即16×16=375(人),再乘方阵的个数12,即可得解.【解答】解:16×16×12=256×12=3072(人);答:一共有3072人参加表演.2016年7月29日。
第二次月考(试题)-2024-2025学年三年级数学上册人教版

12.秒千米/km 999 1
【分析】根据生活经验可知,50米比较短,跑50米的用时用秒作单位即可;
飞机速度很快,每小时飞行的距离用千米作单位;
1吨=1000千克,先进行单位换算,再进行计算即可解答;
1张身份证比较薄,大约有1毫米那么厚,大树的高度约是9米。
故答案为:A
7.3 5070 4 5 20
【详解】略
8.
【详解】试题分析:用直尺的“0”刻度线和线段的一个端点重合,另一个端点在直尺上的刻度,就是该线段的长度,据此测量即可.
解:
【点评】此题主要考查长度的测量,要注意题目要求的长度单位.
9.=<=>
【解析】略
13.40 3000 140 6500
【分析】
(1)1分米=10厘米,所以4分米=40厘米;
(2)5千米-2千米=3千米,1千米=1000米,所以3千米=3000米。故5千米-3000米=2千米;
(3)1分=60秒,所以2分=120秒。故2分20秒=120秒+20秒=140秒;
(4)1吨=1000千克,10吨=10000千克。10000千克-3500千克=6500千克。所以3500千克+6500千克=10吨。
(2)先算小括号里面的加法,再算括号外面的减法;
(3)先算小括号里面的减法,再算括号外面的除法。
【详解】(1)437-298+68
=139+68
=207
(2)806-(143+289)
=806-432
=374
(3)(600-565)÷5
=35÷5
=7
24.
【解析】略
25.能
【分析】用三年级的人数加上四年级的人数,求出三、四年级一共有多少人,再和电影院的座位数量进行比较即可。
2022-2023学年四年级(上)第三次月考数学试卷(含答案)

2022-2023学年四年级(上)第三次月考数学试卷一、智慧填空(37分)1.(11分)75268643000是一个位数,读作,最高位是。
5在位上,表示;8在位上,表示;3在位上,表示。
省略亿位后面的尾数约是;省略万位后面的尾数约是。
2.(1分)在3和5之间添上个0,这个数就成为三百万零五.3.(2分)10时整,时针和分针所成的角是度,是角。
4.(2分)450里面有个90;325是的25倍.5.(2分)一间卧室的面积大约是25 ;一座小学的面积大约是5 。
6.(2分)□51÷45,要使商是两位数,□里最小填;要使商是一位数,□里最大填.7.(2分)两个数相除的商是16,如果除数和被除数都同时乘4,商是;如果被除数除以4,除数不变,商是.8.(2分)在☆÷20=31……△中,△最大是,☆最大是。
9.(1分)把7公顷,7平方千米,7公顷70平方米,77000平方米按从小到大的顺序排列是。
10.(2分)76□908≈76万,□里最大填;9□8888000≈10亿,□里最小填。
11.(2分)横线上面最大能填几?42× <310530>87×12.(2分)两条平行线间可以画条垂直的线段,这些线段的长度都.13.(6分)在横线上填上“>”“<”或“=”。
5703789 5707398 109万 1090000 540×36 360×54759950 76万54公顷 5400平方米200000平方米 2平方千米二、明辨是非(对的,在括号里打“√”,错的打“×”)(6分)14.(1分)自然数都是整数..(判断对错)15.(1分)一条长方形路宽10米,长1千米,则它占地1公顷。
(判断对错)16.(1分)如果因数的末尾有0,那么积的末尾也一定有0。
(判断对错)17.(1分)每支铅笔多少钱,就是我们说的总价。
(判断对错)18.(1分)三位数除以两位数的商一定是两位数。
2021-2022学年吉林省四平市第一高二年级上册学期第三次月考数学试题【含答案】

2021-2022学年吉林省四平市第一高级中学高二上学期第三次月考数学试题一、单选题1.已知椭圆22:143x y C +=,则下列各点不在椭圆内部的是( )A .()1,1B .)1-C .D .1,12⎛⎫⎪⎝⎭【答案】C【分析】根据点和椭圆位置关系的判断方法,分别把点的坐标代入椭圆方程的左侧部分,计算其数值大于1的点即为答案.【详解】由椭圆方程为22:143x y C +=, 因为11714312+=<,所以点()1,1在椭圆内部,A 错误;因为2151436+=<,所以点)1-在椭圆内部,B 错误;因为2271436+=>,所以点在椭圆外部,C 正确;因为1119414348+=<,所以点1,12⎛⎫⎪⎝⎭在椭圆内部,D 错误.故选:C.2.抛物线26y x =的准线方程为( ) A .124y =-B .112y =-C .y =-6D .=3y -【答案】A【分析】先把抛物线化成标准方程,求出p ,即可得到准线方程.【详解】抛物线26y x =的标准方程为:216x y =,令2126x y py ==,得112p =,于是该抛物线的准线为:124y =-. 故选:A3.已知椭圆22142x y +=的左顶点为A ,上顶点为B ,则AB =( )A .B .3C .4D 【答案】D【分析】由方程得出,A B 的坐标,再由距离公式求解即可 【详解】因为椭圆22142x y +=的左顶点为A ,上顶点为B ,所以()2,0A ,(B ,所以AB =故选:D4.已知双曲线()22101x y a a a -=>+的虚轴长是实轴长的3倍,则实数a 的值为( )A .18B .14C .13D .12【答案】A【分析】根据“虚轴长是实轴长的3倍”列方程,化简求得a 的自豪.【详解】由题意有(232⨯,解得18a =.故选:A5.已知抛物线23y x =的焦点为F ,点P 为抛物线上任意一点,则PF 的最小值为( ) A .1 B .34C .43D .32【答案】B【分析】结合抛物线的定义求得正确答案.【详解】抛物线23y x =的焦点为3,04F ⎛⎫⎪⎝⎭,准线为34x =-,设点P 的坐标为()00,x y ,00x ≥,根据抛物线的定义有03344PF x =+≥,故PF 的最小值为34.故选:B6.已知方程22124x y m m+=--表示一个焦点在y 轴上的椭圆,则实数m 的取值范围为( )A .()3,4B .()2,3C .()()2,33,4D .()2,4【答案】B【分析】由椭圆的简单几何性质即可求解.【详解】解:因为方程22124x y m m+=--表示一个焦点在y 轴上的椭圆,所以有20,40,24,m m m m ->⎧⎪->⎨⎪-<-⎩,解得23m <<,所以实数m 的取值范围为23m <<, 故选:B.7.已知椭圆22122:1(0)x y C a b a b +=>>的离心率为1e ,双曲线22222:1x y C a b-=的离心率为2e ,则( )A .212e e =B .112e e +=C .22211e e =+ D .22122e e +=【答案】D【分析】根据给定的方程求出离心率1e ,2e 的表达式,再计算判断作答.【详解】因椭圆22122:1(0)x y C a b a b+=>>的离心率为1e ,则有22221221a b b e a a -==-, 因双曲线22222:1x y C a b-=的离心率为2e ,则有22222221a b b e a a +==+,所以22122e e +=. 故选:D8.直线(0)y kx k =>与双曲线22126x y -=没有交点,则k 的取值范围为( )A.⎫+∞⎪⎪⎣⎭B .(2,)+∞ C.)+∞ D.【答案】C【解析】把直线方程代入双曲线方程,方程无解即得.【详解】由22126y kx x y =⎧⎪⎨-=⎪⎩得221126k x ⎛⎫-= ⎪⎝⎭,此方程无实数解,则21026k -≤,解得k ≤k ≥又0k >,所以k ≥故选:C .9.已知双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为F ,过点F 作双曲线C 的两条渐近线的垂线,垂足分别为12,H H ,若21120H FH ∠=,则双曲线C 的离心率为( ) ABCD【答案】A【解析】转化条件为该双曲线的一条渐近线的倾斜角为30,进而可得3a b ,由离心率公式即可得解.【详解】由题意,1260H OH ∠=(O 为坐标原点),所以该双曲线的一条渐近线的倾斜角为30, 所以3tan 303b a ==,即3a b ,所以离心率22423133c b e a a ==+==. 故选:A.10.如图,已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ,P 为椭圆C 上一点,212PF F F ⊥,直线1PF 与y 轴交于点Q ,若||4bOQ =,则椭圆C 的离心率为( )A 2B 3C .12D .23【答案】B【解析】由题可得212OQ PF =,代入点P 的横坐标x c =可得2by a =,则有224b b a =,解得2a b =,即可由此求出离心率.【详解】设2F 的坐标为(,0)c ,由2//OQ PF ,可得212OQ PF =, 代入点P 的横坐标x c =,有22221c y a b+=,可得2by a =,则有224b ba =,得2ab =, 则椭圆C 的离心率为222243ca b b b e a--====故选:B.11.已知抛物线2:2(0),C y px p O =>为坐标原点,点P 为抛物线上的一点,且点P 在x 轴的上方,若线段OP 的垂直平分线过点()2,0Q p ,则直线OP 的斜率为( ) A .1 B .2C .12D .32【答案】A【分析】设出点P 的坐标,写出的线段OP 所在直线的解析式,进而求出线段OP 垂直平分线所在直线的解析式,通过线段OP 的垂直平分线过点()2,0Q p ,得到点P 的横坐标与p 的关系,即可求出直线OP 的斜率.【详解】解:由题意设(0P x,则0:OP l y x =,线段OP的中点为02x A ⎛⎝⎭∴线段OP的垂直平分线为::AQ l y =∵线段OP 的垂直平分线过点()2,0Q p∴20p =解得:02x p =∴直线OP1=故选:A.12.已知双曲线C :()222210,0x y a b a b-=>>的左、右焦点分别为1F ,2F ,过点2F 的直线与双曲线的右支相交于A ,B 两点,12224BF BF AF ==,1ABF 的周长为10,则双曲线C 的焦距为( ) A .3 BCD【答案】C【分析】由双曲线的定义和三角形的周长解得m 的值,再由余弦定理列式可得结果. 【详解】设2AF m =,22BF m =,14BF m =, 由双曲线的定义知:121222AF AF BF BF a m -=-==, ∴13AF m =,a =m ,∴有23410m m m m +++=,解得1m =,∵在12AF F 和12BF F 中,1212cos cos 0F F A F F B ∠+∠=,∴由余弦定理得224194416048c c c c +-+-+=,解得c =.故选:C.二、填空题13.椭圆222520x y +=的一个焦点与抛物线22(0)y px p =>的焦点重合,则抛物线的标准方程为__________.【答案】2y =【分析】由已知,先将椭圆方程化为标准形式,然后读取其焦点坐标,然后再根据给出的抛物线方程,写出其焦点坐标,列出等量关系,即可求解方程. 【详解】由已知,椭圆222520x y +=,可化为:221104x y +=,所以其焦点坐标为)和(), 抛物线22(0)y px p =>,其焦点坐标为02p ⎛⎫⎪⎝⎭,,因为椭圆的焦点与抛物线的焦点重合,所以2pp ==所以抛物线的标准方程为:2y =.故答案为:2y =.14.已知双曲线2214x y m +=的一条渐近线与直线6210x y --=垂直,则m 的值为__________.【答案】49-【分析】由垂直得一条渐近线的斜率,从而结合双曲线标准方程求得m 值.【详解】一条渐近线与直线6210x y --=垂直,则该渐近线的斜率为13-,双曲线的标准方程为2214x y m -=-,2a =,b =13=-,49m =-.故答案为:49-.15.已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F ,2F ,点A 在双曲线C 上,212AF F F ⊥,直线1AF 与双曲线C 交于另一点B ,114F F A B =,则双曲线C 的离心率为___________.【分析】根据题目条件设点A 和B 的坐标,带入双曲线方程即可. 【详解】由于212AF F F ⊥ ,不妨设点A 的坐标为()(),0c m m >, 点B 的坐标为(),s t ,有22221c m a b -=,解得2b m a=,又由212,b F A c a ⎛⎫= ⎪⎝⎭,()1,F B s c y =+,有()22,4,b c s c y a ⎛⎫=+ ⎪⎝⎭,解得2c s =-,24b t a=,将点B 的坐标代入双曲线方程,有22221416c b a a -=,22222241,31616c b c a a a-=+=, 解得c =,双曲线C 的离心率为ce a=.三、双空题16.已知抛物线2:4C y x =的准线为l ,点P 为抛物线上的一个动点,则点P 到准线l 和直线50x y -+=的距离之和的最小值为__________,此时点P 的坐标为__________.【答案】 ()32-【分析】根据抛物线的定义把点P 到l 的距离转化到点P 到焦点F 的距离,就是求点F 到直线50x y -+=的距离,从而能求出直线FP ,与抛物线2:4C y x =联立可求点P 的坐标.【详解】设过点P 分别向l 和50x y -+=作垂线,垂足分别为12,P P , 因为抛物线2:4C y x =的焦点()1,0F ,由抛物线的定义得:1PP PF =, 所以只需要求2PF PP +最小即可.当且仅当2,,F P P 三点共线时2PF PP +最小,且最小值为点F 到直线50x y -+=的距离,即=此时直线50x y -+=与FP 垂直,所以1FP k =-,所以直线FP 为:()1y x =--直线FP 与抛物线2:4C y x =联立得()214x x -=,即2610x x -+=,且01x <<所以32x y =-=,故点P ()32-答案为:()32-四、解答题17.求适合下列条件的双曲线的标准方程:(1)焦点坐标为12(6,0),(6,0)F F -,且经过点()5,2P ; (2)焦点在坐标轴上,经过点(22,2),(23,2)--. 【答案】(1)2215x y -=;(2)22142x y -=.【分析】(1)利用双曲线定义求出双曲线的实轴长即可计算作答. (2)设出双曲线的方程,利用待定系数法求解作答.【详解】(1)因双曲线的焦点坐标为12(6,0),(6,0)F F -,且经过点()5,2P ,令双曲线实半轴长为a , 则有2222122||||(56)2(56)23510635106a PF PF =-++-++-22(305)(305)25=+-=5a =6c =b 有2221b c a =-=,所以所求双曲线的标准方程为2215x y -=.(2)依题意,设双曲线的方程为:221(0)mx ny mn +=<,于是得8211241m n m n +=⎧⎨+=⎩,解得:11,42m n ==-,所以所求双曲线的标准方程为22142x y -=. 18.已知抛物线C :28y x =的焦点为F ,P 为抛物线C 上一动点,点Q 为线段PF 的中点.(1)求点Q 的轨迹方程;(2)求点Q 的轨迹与双曲线224x y -=的交点坐标. 【答案】(1)244y x =-(2)(4,,(4,-.【分析】(1)利用中点坐标公式与直接代入法即可求得点Q 的轨迹方程; (2)联立两曲线方程,解之即可得解. 【详解】(1)设点Q 的坐标为(),x y ,因为抛物线C :28y x =,所以点F 的坐标为()2,0, 又点Q 为线段PF 的中点,所以点P 的坐标()22,2x y -,将点P 的坐标代入抛物线C 的方程,得()24822y x =-,整理为244y x =-,故点Q 的轨迹方程为244y x =-;(2)联立方222444x y y x ⎧-=⎨=-⎩,解得4x y =⎧⎪⎨=±⎪⎩故点Q 的轨迹与双曲线224x y -=的交点坐标为(4,,(4,-.19.已知椭圆:22:12x C y +=,直线l 与椭圆C 相交于A ,B 两点,点11,2P ⎛⎫ ⎪⎝⎭为线段AB 的中点.(1)求直线l 的方程;(2)若O 为坐标原点,求OAB 的面积. 【答案】(1)2230x y +-=【分析】(1)由题意,直线l 的斜率存在,设出直线l 的方程,然后联立椭圆方程,利用韦达定理即可求出斜率k ,从而即可得答案;(2)根据弦长公式求出弦AB 的长,由点到直线的距离公式求出高,然后由三角形的面积公式即可求解.【详解】(1)解:由题意,直线l 的斜率存在,设直线l 的方程为()112y k x -=-,即12y kx k =+-,()()1122,,,A x y B x y ,由221212y kx k x y ⎧=+-⎪⎪⎨⎪+=⎪⎩得()()222242484430k x k k x k k ++-+--=, 因为点11,2P ⎛⎫ ⎪⎝⎭为线段AB 的中点,所以2122842142k k x x k -+==⨯+,解得1k =-,直线l 的方程为()()1112y x -=-⨯-,即2230x y +-=;(2)解:由(1)知122x x +=,21224435642k k x x k --==+, 所以AB === O 到直线l的距离d ==所以1122OABSAB d ===20.在平面直角坐标系xOy 中,抛物线2:2(0)C y px p =>的焦点为F ,过点F 的直线l 与抛物线C 相交于,A B 两点,且3OA OB ⋅=-. (1)求p 的值;(2)若以线段AB 为直径的圆与直线4x =相切,求直线l 的方程. 【答案】(1)2(2)22y x =-或22y x =-+.【分析】(1)设点,A B 的坐标分别为()()1122,,,x y x y ,直线l 的方程为2pmy x =-,联立抛物线方程得2220y pmy p --=,已知3OA OB ⋅=-,利用数量积的坐标运算和韦达定理,即可求出p 的值; (2)利用韦达定理求出弦长AB ,已知以线段AB 为直径的圆与直线4x =相切,求出半径列得方程求解即可算出参数m 的值,进而得到直线方程. 【详解】(1)设点,A B 的坐标分别为()()1122,,,x y x y , 由点F 的坐标为,02p ⎛⎫⎪⎝⎭,设直线l 的方程为2p my x =-,联立方程222y pxp my x ⎧=⎪⎨=-⎪⎩,消去x 后整理得2220y pmy p --=,所以122y y pm +=,212y y p =-,2221212244y y p x x p ==.又由22212123344p p OA OB x x y y p ⋅=+=-=-=-,解得2p =. 所以p 的值为2.(2)由()21212124,242y y m x x m y y m +=+=++=+,可得线段AB 中点的坐标为()221,2m m +,212244AB x x m =++=+.若以线段AB 为直径的圆与直线4x =相切, 有()221442142m m +=+-,解得12m =±. 所以直线l 的方程为112y x ±=-,即22y x =-或22y x =-+. 21.已知双曲线2222:1(0,0)x y C a b a b -=>>的一条渐近线方程为20x y +=,点()1-在双曲线C 上. (1)求双曲线C 的标准方程;(2)过定点()0,1P 的动直线l 与双曲线C 的左、右两支分别交于,A B 两点,与其两条渐近线分别交于,M N (点M 在点N 的左边)两点,证明:线段AM 与线段BN 的长度始终相等.【答案】(1)2214x y -= (2)证明见解析【分析】(1)根据已知条件求得,a b ,从而求得双曲线C 的标准方程.(2)设出直线l 的方程,并分别与双曲线的渐近线方程、双曲线方程联立,利用中点坐标公式判断出线段AB 和MN 共中点,从而证得线段AM 与线段BN 的长度始终相等.【详解】(1)由双曲线2222:1x y C a b-=可得渐近线方程为b y x a =-, 由渐近线方程20x y +=的斜率为12-,有12b a -=-,可得2a b =.将点()1-代入双曲线C 的方程,有22811a b-=. 联立方程222811a b a b =⎧⎪⎨-=⎪⎩,解得21a b =⎧⎨=⎩, 故双曲线C 的标准方程为2214x y -=. (2)设点,,,A B M N 的坐标分别为()()()()11223344,,,,,,,x y x y x y x y ,线段AB 的中点D 的坐标为()55,x y ,线段MN 的中点E 的坐标为()66,x y .依题意可知直线l 的斜率存在,设直线l 的方程为1y kx =+,12k ≠±, 联立方程112y kx y x =+⎧⎪⎨=-⎪⎩,得3221x k =-+;联立方程112y kx y x =+⎧⎪⎨=⎪⎩,得4221x k =--. 所以可得6212242212141k x k k k ⎛⎫=--=- ⎪+--⎝⎭. 联立方程22114y kx x y =+⎧⎪⎨-=⎪⎩,消去y 后整理得()2241880k x kx -++=, 由()22264324132640k k k ∆=--=->解得2222k -<<,且12k ≠±, 由于直线l 与双曲线左右两支分别相交,所以1122k -<<. 所以122841k x x k +=--,可得52441k x k =--,所以56x x =, 所以线段AB 和MN 共中点,故有AM BN =.【点睛】方法点睛:利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下: (1)设直线方程,设交点坐标为()()1122,,,x y x y ;(2)联立直线与圆锥曲线的方程,得到关于x (或y )的一元二次方程,必要时计算∆;(3)列出韦达定理;(4)将所求问题或题中的关系转化为12x x +、12x x (或12y y +、12y y )的形式;(5)代入韦达定理求解.22.如图,在平面直角坐标系xOy 中,已知椭圆1M :2213y x +=,椭圆2M :22193x y +=,点P 为椭圆1M 的上顶点,点A ,C 为椭圆1M 上关于原点对称的两个动点.斜率为1k 的直线P A 与椭圆2M 交于另一点B ,斜率为2k 的直线PC 与椭圆2M 交于另一点D(1)求12k k 的值;(2)求PA PC PB PD +的值. 【答案】(1)-3 (2)109 【分析】(1)设点A 的坐标为(),m n ,则点C 的坐标为(),m n --,且2213n m +=, 根据两点斜率公式求12k k ,,由此可得12k k 的值;(2)分别联立直线AP 与椭圆方程1M ,2M 求点A 的横坐标和点B 的横坐标,由此可求PAPB ,同理可求PC PD ,再求PA PC PB PD+的值. 【详解】(1)设点A 的坐标为(),m n ,可得点C 的坐标为(),m n --,由点A 在椭圆1M 上有2213n m +=,可得2233n m -=, 点P 的坐标为()0,3,由13n k m -=,233n n k m m --+==-, 有()()221222233333n n nm k k m m m-+--====-, 故12k k 的值为-3;(2)直线AP 的方程为13y k x =+,联立方程消去y 可得()22113230k x k x ++=,解得0x =或1123k x =A 的横坐标为1123A k x =联立方程1223,1,93y k x x y ⎧=⎪⎨+=⎪⎩消去y 可得()221131630k x k x ++=,解得0x =或1163k x =,点B 的横坐标为12163B k x = 有()122112112123331336331k PA k k PB k k k -++=+-+;同理()()()22221211222221113313127273333993333PC k k k k PD k k k k ⎛⎫⨯-+ ⎪+++⎝⎭====⎡⎤+++⎛⎫⎢⎥-+ ⎪⎢⎥⎝⎭⎣⎦, 可得()()()()()()()()22222211111122222111119327103312710301093393939393k k k PA PC k k k PB PD k k k k k ++++++++=+====+++++, 故PA PC PB PD +的值为109.。
