2013年中考初中数学知识点:平面直角坐标系【知识点拓展】 特殊位置的点的坐标的特点
(完整版)平面直角坐标系知识点归纳.doc

平面直角坐标系知识点归纳1 、 在平面内,两条互相垂直且有公共原点的数轴组成了平面直角坐标系;2 、 坐标平面上的任意一点P 的坐标,都和惟一的一对有序实数对 ( a,b )一一对应;其中, a 为横坐标, b 为纵坐标坐标;3 、 x 轴上的点,纵坐标等于 0 ; y 轴上的点,横坐标等于0 ;Y坐标轴上的点 不属于 任何象限;b P(a,b)4 、四个象限的点的坐标具有如下特征:1象限横坐标 x纵坐标 y-3-2 -1 0 1ax-1 第一象限正 正 -2 第二象限负正-3第三象限 负 负 第四象限正负小结:( 1 )点 P ( x, y )所在的象限 横、纵坐标 x 、 y 的取值的正负性;( 2 )点 P ( x, y )所在的数轴横、纵坐标 x 、 y 中必有一数为零;y 5 、在平面直角坐标系中,已知点P (a,b) ,则a点 P 到 x 轴的距离为bP ( a, b )(1 ) b ; ( 2 )点 P 到 y 轴的距离为 a ;(3 ) 点 P 到原点 O 的距离为 PO =a 2b 2b6 、平行直线上的点的坐标特征:Oaxa) 在与 x 轴平行的直线上,所有点的纵坐标相等;YA B点 A 、 B 的纵坐标都等于 m ;mXb)在与 y 轴平行的直线上,所有点的横坐标相等;YC点 C 、 D 的横坐标都等于n ;nDX7 、对称点的坐标特征:a)点 P (m, n)关于x轴的对称点为P1(m, n),即横坐标不变,纵坐标互为相反数;b)点 P (m, n)关于y轴的对称点为P2( m, n),即纵坐标不变,横坐标互为相反数;c) 点 P (m, n)关于原点的对称点为P3 ( m, n) ,即横、纵坐标都互为相反数;y y yPn P2 n P n PO mX mmm XO m X OnP1n P3关于 x 轴对称关于 y 轴对称关于原点对称8 、两条坐标轴夹角平分线上的点的坐标的特征:a) 若点 P(m,n)在第一、三象限的角平分线上,则m n ,即横、纵坐标相等;b) 若点 P(m,n)在第二、四象限的角平分线上,则m n ,即横、纵坐标互为相反数;y yn P P nO m X m O X 在第一、三象限的角平分线上在第二、四象限的角平分线上基本练习:练习 1 :在平面直角坐标系中,已知点P(m 5,m 2 )在 x 轴上,则P点坐标为练习 2 :在平面直角坐标系中,点P(m2 2, 4 )一定在象限;练习3 P a 1, a29)在 x 轴的负半轴上,则P点坐标为;:已知点(练习 4 :已知 x 轴上一点A(3,0),y轴上一点B(0,b ),且 AB=5 ,则b的值为;练习 5 :点 M (2 ,- 3 )关于 x 轴的对称点 N 的坐标为;关于y轴的对称点 P 的坐标为;关于原点的对称点Q 的坐标为。
(完整版)平面直角坐标系知识点归纳及例题

X平面直角坐标系知识点归纳1、在平面内,两条互相垂直且有公共原点的数轴组成了平面直角坐标系;2、坐标平面上的任意一点 P 的坐标,都和惟一的一对有序实数对(a,b )一一对应;其中,a 为横坐标,b 为纵坐标坐标;3、 x 轴上的点,纵坐标等于 0; y 轴上的点,横坐标等于 0; 坐标轴上的点 不属于任何象限;4、 四个象限的点的坐标具有如下特征:小结:(1 )点P ( x, y )所在的象限 —►横、纵坐标X 、y 的取值的正负性;(2 )点P ( X, y )所在的数轴 —*■横、纵坐标X 、y 中必有一数为零;5、 在平面直角坐标系中,已知点p (a,b ),则(1) 点P 到X 轴的距离为b ;( 2 )点P 到y 轴的距离为(3) 点P 到原点o 的距离为PO = .a 2 b 26、 平行直线上的点的坐标特征:a )在与x 轴平行的直线上,所有点的纵坐标相等;b )在与y 轴平行的直线上,所有点的横坐标相等;d bJ_____ P(a,b) 1____________ 1-3 -2 -1 0 -1-2 -31a X点A 、B 的纵坐标都等于m ;象限 横坐标X 纵坐标y 第一象限 正 正 第二象限 负 正 第三象限负 负 第四象限正负点C、D的横坐标都等于n ;X7、对称点的坐标特征:8、两条坐标轴夹角平分线上的点的坐标的特征:a) 若点P ( m,n )在第一、三象限的角平分线上,则 b)若点P ( m,n )在第二、四象限的角平分线上,则习题1、在平面直角坐标系中,线段 BC// x 轴,则 A.点B 与C 的横坐标相等 BC •点B 与C 的横坐标与纵坐标分别相等D 2 •若点P (x, y)的坐标满足xy 0则点P 必在A.原点 B . x 轴上 C . y 轴上 D . x 轴或y 轴上 3.点P在x 轴上,且到y 轴的距离为5,则点P 的坐标是 (A. (5,0) B . (0,5) C . (5,0)或(-5,0) D . (0,5)或(0,-5) 4.平面上的点(2,-1)通过上下平移不能与之重合的是 (A . (2,-2)B . (-2,-1)C . (2,0)D . 2,-3)5. 将△ ABC 各顶点的横坐标分别减去3,纵坐标不变,得到的厶ABC 相应顶点的坐标,则 △ A 'B 'C '可以看成厶ABCi 卜y1 y匸y n P--------- —--•P2 • __ n P _ ___ 亠n -------- * P1m ;亠 1 11 ----- T P U f imII V 1 ""O ' XHm O ------------ X 1 1 O mn __ _ ▲1Rb-n关于x 轴对称 关于y 轴对称关于原点对称点P (m,n)关于y 轴的对称点为 b) 点P (m,n)关于原点的对称点为P 3( m, n),即横、纵坐标都互为相反数; c) XP 2( m,n),即纵坐标不变,横坐标互为相反数; a)点P (m, n)关于x 轴的对称点为 R(m, n),即横坐标不变,纵坐标互为相反数;m n ,即横、纵坐标相等;m n ,即横、纵坐标互为相反数;( •点B 与C 的纵坐标相等 •点B 与C 的横坐标、纵坐标都不相等 )) ) )y在第一、三象限的角平分线上在第二、四象限的角平分线上A.向左平移3个单位长度得到B .向右平移三个单位长度得到C•向上平移3个单位长度得到 D •向下平移3个单位长度得到6•线段CD是由线段AB平移得到的,点A(-1,4)的对应点为C(4,7),则点B(-4,-1)的对应点D的坐标是A . (2,9)B . (5,3)C . (1,2)D . (-9,-4)7•在坐标系内,点P (2, -2)和点Q(2,4 )之间的距离等于______________ 单位长度,线段PQ和中点坐标是____________8. 将点M(2,-3)向左平移2个单位长度,再向下平移1个单位长度,得到的点的坐标为9. 在直角坐标系中,若点P(a 2,b 5)在y轴上,则点P的坐标为___________________10. 已知点P( 2,a),Q(b,3),且PQ// x 轴,则a ___________ ,b ____________11. 将点P( 3,y)向下平移3个单位,并向左平移2个单位后得到点Q(x, 1),则xy = _______12. 则坐标原点0( 0,0 ),A (-2,0 ) ,B(-2,3)三点围成的△ ABO勺面积为_______________13. 点P(a,b)在第四象限,则点Q(b, a)在第_________ 限14. 已知点P在第二象限两坐标轴所成角的平分线上,且到x轴的距离为3,则点P的坐标为 ____________15. 在同一坐标系中,图形a是图形b向上平移3个单位长度得到的,如果在图形a中点A的坐标为(5, 3),则图形b中与A对应的点A'的坐标为______________16. 在平面直角坐标系中,将坐标为(0,0),(2,0),(3,4),(1,4) 的点用线段依次连接起来形成一个图像,并说明该图像是什么图形。
中考数学-平面直角坐标系知识点归纳总结
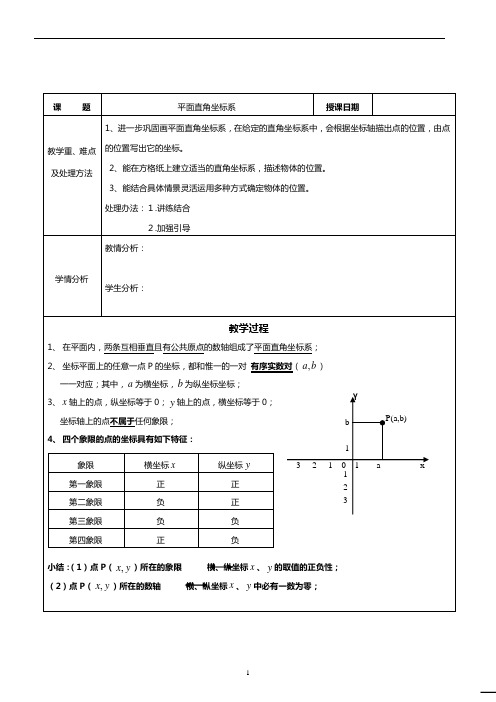
考点六——平面直角坐标系中面积的求法,图形的平移【例1】如图所示的直角坐标系中,三角形ABC的顶点坐标分别是A(0,0)、B(6,0)、C(5,5)。
求:(1)求三角形ABC的面积;(2)如果将三角形ABC向上平移3个单位长度,得三角形A1B1C1,再向右平移2个单位长度,得到三角形A2B2C2。
分别画出三角形A1B1C1和三角形A2B2C2。
并试求出A2、B2、C2的坐标?【例2】如图,正方形ABCD以(0,0)为中心,边长为4,求各顶点的坐标.【例3】三角形ABC三个顶点A、B、C的坐标分别为A(2,-1)、B(1,-3)、C(4,-3.5).把三角形A1B1C1向右平移4个单位,再向下平移3个单位,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标,并在直角坐标系中描出这些点;在平面直角坐标系中,将点M(1,0)向右平移3个单位,得到点1M,则点1M 的坐标为________ACAxyBA课后作业一、选择题1、若点P ()n m ,在第二象限,则点Q ()n m --,在( )A .第一象限B .第二象限C .第三象限D .第四象限 2、点P 的横坐标是-3,且到x 轴的距离为5,则P 点的坐标是( )A. (5,-3)或(-5,-3)B. (-3,5)或(-3,-5)C. (-3,5)D. (-3,-5) 3、如果点M 到x 轴和y 轴的距离相等,则点M 横、纵坐标的关系是 ( ) A .相等 B .互为相反数 C .互为倒数 D .相等或互为相反数4、在平面直角坐标系中,点()2,12+-m 一定在 ( )A .第一象限B .第二象限C .第三象限D .第四象限 5、如果a -b <0,且ab <0,那么点(a ,b)在 ( ) A 、第一象限 B 、第二象限 C 、第三象限, D 、第四象限.6、如上右图,小明从点O 出发,先向西走40米,再向南走30米到达点M ,如果点M 的位置用(-40,-30)表示,那么(10,20)表示的位置是 ( ) A 、点A B 、点B C 、点C D 、点D7、一个长方形在平面直角坐标系中三个顶点的坐标为(-1,- 1)、(-1,2)、(3,-1),则第四个顶点的坐标为 ( ) A .(2,2) B .(3,2) C .(3,3) D .(2,3) 8、若点P (a ,b )到x 轴的距离是2,到y 轴的距离是3,则这样的点P 有 ( )A.1个 B.2个 C.3个 D.4个9、已知点P(102-x ,x -3)在第三象限,则x 的取值范围是 ( )。
数学平面直角坐标系的知识点

数学平面直角坐标系的知识点数学平面直角坐标系的知识点汇总在日复一日的学习中,大家都没少背知识点吧?知识点就是学习的重点。
想要一份整理好的知识点吗?以下是店铺帮大家整理的数学平面直角坐标系知识点汇总,希望对大家有所帮助。
数学平面直角坐标系知识点1平面直角坐标系平面直角坐标系:在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系。
水平的数轴称为x轴或横轴,竖直的数轴称为y轴或纵轴,两坐标轴的交点为平面直角坐标系的原点。
平面直角坐标系的要素:①在同一平面②两条数轴③互相垂直④原点重合三个规定:①正方向的规定横轴取向右为正方向,纵轴取向上为正方向②单位长度的规定;一般情况,横轴、纵轴单位长度相同;实际有时也可不同,但同一数轴上必须相同。
③象限的规定:右上为第一象限、左上为第二象限、左下为第三象限、右下为第四象限。
相信上面对平面直角坐标系知识的讲解学习,同学们已经能很好的掌握了吧,希望同学们都能考试成功。
初中数学知识点:平面直角坐标系的构成对于平面直角坐标系的构成内容,下面我们一起来学习哦。
平面直角坐标系的构成在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系。
通常,两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向。
水平的数轴叫做X轴或横轴,铅直的数轴叫做Y轴或纵轴,X轴或Y轴统称为坐标轴,它们的公共原点O称为直角坐标系的原点。
通过上面对平面直角坐标系的构成知识的讲解学习,希望同学们对上面的内容都能很好的掌握,同学们认真学习吧。
初中数学知识点:点的坐标的性质下面是对数学中点的坐标的性质知识学习,同学们认真看看哦。
点的坐标的性质建立了平面直角坐标系后,对于坐标系平面内的任何一点,我们可以确定它的坐标。
反过来,对于任何一个坐标,我们可以在坐标平面内确定它所表示的一个点。
对于平面内任意一点C,过点C分别向X轴、Y轴作垂线,垂足在X轴、Y轴上的对应点a,b分别叫做点C的横坐标、纵坐标,有序实数对(a,b)叫做点C的坐标。
数学平面直角坐标系的知识点

数学平面直角坐标系的知识点在日复一日的学习中,大家都没少背知识点吧?知识点就是学习的重点。
想要一份整理好的知识点吗?以下是店铺帮大家整理的数学平面直角坐标系知识点汇总,希望对大家有所帮助。
数学平面直角坐标系知识点1平面直角坐标系平面直角坐标系:在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系。
水平的数轴称为x轴或横轴,竖直的数轴称为y轴或纵轴,两坐标轴的交点为平面直角坐标系的原点。
平面直角坐标系的要素:①在同一平面②两条数轴③互相垂直④原点重合三个规定:①正方向的规定横轴取向右为正方向,纵轴取向上为正方向②单位长度的规定;一般情况,横轴、纵轴单位长度相同;实际有时也可不同,但同一数轴上必须相同。
③象限的规定:右上为第一象限、左上为第二象限、左下为第三象限、右下为第四象限。
相信上面对平面直角坐标系知识的讲解学习,同学们已经能很好的掌握了吧,希望同学们都能考试成功。
初中数学知识点:平面直角坐标系的构成对于平面直角坐标系的构成内容,下面我们一起来学习哦。
平面直角坐标系的构成在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系。
通常,两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向。
水平的数轴叫做X轴或横轴,铅直的数轴叫做Y轴或纵轴,X轴或Y轴统称为坐标轴,它们的公共原点O称为直角坐标系的原点。
通过上面对平面直角坐标系的构成知识的讲解学习,希望同学们对上面的内容都能很好的掌握,同学们认真学习吧。
初中数学知识点:点的坐标的性质下面是对数学中点的坐标的性质知识学习,同学们认真看看哦。
点的坐标的性质建立了平面直角坐标系后,对于坐标系平面内的任何一点,我们可以确定它的坐标。
反过来,对于任何一个坐标,我们可以在坐标平面内确定它所表示的一个点。
对于平面内任意一点C,过点C分别向X轴、Y轴作垂线,垂足在X轴、Y轴上的对应点a,b分别叫做点C的横坐标、纵坐标,有序实数对(a,b)叫做点C的坐标。
九年级数学知识点归纳之平面直角坐标系

九年级数学知识点归纳之平面直角坐标系鉴于数学知识点的重要性,小编为您提供了这篇九年级数学知识点归纳之平面直角坐标系,希望对同学们的数学有所帮助。
一、平面直角坐标系1.平面直角坐标系:(1)在平面内两条有公共点并且互相垂直的数轴就构成了平面直角坐标系,通常把其中水平的一条数轴叫横轴或轴,取向右的方向为正方向;铅直的数轴叫纵轴或轴,取向上的方向为正方向;两数轴的交点叫做坐标原点。
(2)建立了直角坐标系的平面叫坐标平面.x轴和y轴把坐标平面分成四个部分,称为四个象限,按逆时针顺序依次叫第一象限、第二象限、第三象限、第四象限,如图所示.说明:两条坐标轴不属于任何一个象限。
2.点的坐标:对于平面直角坐标系内任意一点P,过点P分别向x轴和y 轴作垂线,垂足在x轴,y轴对应的数a,b分别叫做点P的横坐标,纵坐标,有序数对(a,b)叫做P的坐标。
3.点与有序实数对的关系:坐标平面内的点可以用有序实数对来表示,反过来每一个有序实数对应着坐标平面内的一个点,即坐标平面内的点和有序实数对是一一对应的关系。
常见考法(1)由点的位置确定点的坐标,由点的坐标确定点的位置;(2)求某些特殊点的坐标。
误区提醒(1)求点的坐标时,容易将横、纵坐标弄反,还容易忽略坐标符号;(2)思考问题不周,容易出现漏解。
(如点P到x轴的距离为1,这里点P的纵坐标应当是,而不是1)。
【典型例题】(2019江苏常州)点p(1,2)关于x轴的对称点p1的坐标是,点p(1,2)关于原点O的对称点P2的坐标是。
【解析】关于x轴的对称点的坐标是横坐标不变,纵坐标相反,关于原点对称的点的坐标,横、纵坐标都要乘以-1,故本题应当填(1,-2),(-1,-2)。
这篇九年级数学知识点归纳之平面直角坐标系是精品小编精心为同学们准备的,祝大家学习愉快!。
《平面直角坐标系》知识点整理

《平面直角坐标系》知识点整理一、平面直角坐标系平面直角坐标系:在平面内两条有公共点并且互相垂直的数轴就构成了平面直角坐标系,通常把其中水平的一条数轴叫横轴或轴,取向右的方向为正方向;铅直的数轴叫纵轴或轴,取向上的方向为正方向;两数轴的交点叫做坐标原点。
建立了直角坐标系的平面叫坐标平面.x轴和y轴把坐标平面分成四个部分,称为四个象限,按逆时针顺序依次叫象限、第二象限、第三象限、第四象限,如图所示.说明:两条坐标轴不属于任何一个象限。
点的坐标:对于平面直角坐标系内任意一点P,过点P分别向x轴和y轴作垂线,垂足在x轴,y轴对应的数a,b分别叫做点P的横坐标,纵坐标,有序数对叫做P的坐标。
点与有序实数对的关系:坐标平面内的点可以用有序实数对来表示,反过来每一个有序实数对应着坐标平面内的一个点,即坐标平面内的点和有序实数对是一一对应的关系。
常见考法由点的位置确定点的坐标,由点的坐标确定点的位置;求某些特殊点的坐标。
误区提醒求点的坐标时,容易将横、纵坐标弄反,还容易忽略坐标符号;思考问题不周,容易出现漏解。
【典型例题】点p关于x轴的对称点p1的坐标是,点p 关于原点o的对称点P2的坐标是。
【解析】关于x轴的对称点的坐标是横坐标不变,纵坐标相反,关于原点对称的点的坐标,横、纵坐标都要乘以-1,故本题应当填,。
一、目标与要求解有序数对的应用意义,了解平面上确定点的常用方法。
培养学生用数学的意识,激发学生的学习兴趣。
掌握坐标变化与图形平移的关系;能利用点的平移规律将平面图形进行平移;会根据图形上点的坐标的变化,来判定图形的移动过程。
发展学生的形象思维能力,和数形结合的意识。
坐标表示平移体现了平面直角坐标系在数学中的应用。
二、重点掌握坐标变化与图形平移的关系;有序数对及平面内确定点的方法。
三、难点利用坐标变化与图形平移的关系解决实际问题;利用有序数对表示平面内的点。
四、知识框架五、知识点、概念总结有序数对:用含有两个数的词表示一个确定的位置,其中各个数表示不同的含义,我们把这种有顺序的两个数a与b组成的数对,叫做有序数对,记作其中a表示横轴,b表示纵轴。
平面直角坐标系知识点归纳

平面直角坐标系知识点归纳平面直角坐标系的知识点同学们归纳过吗?如果还没有,请来小编这里瞧瞧。
下面是由小编为大家整理的“平面直角坐标系知识点归纳”,仅供参考,欢迎大家阅读。
平面直角坐标系知识点归纳一、基本概念1、有序数对:我们把这种有顺序的两个数a与b组成的数队,叫做有序数对。
2、平面直角坐标系:我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系。
水平的数轴称为x轴或横轴,习惯上取向右为正方向竖直的数轴称为y轴或纵轴,取向上方向为正方向两坐标轴的交战为平面直角坐标系的原点3、象限:坐标轴上的点不属于任何象限第一象限:x>0,y>0第二象限:x0第三象限:x0,y纵坐标轴上的点:(0,y)4、距离问题:点(x,y)距x轴的距离为y的绝对值距y轴的距离为x的绝对值坐标轴上两点间距离:点A(x1,0)点B(x2,0),则AB距离为x1-x2的绝对值点A(0,y1)点B(0,y2),则AB距离为y1-y2的绝对值5、绝对值相等的代数问题:a与b的绝对值相等,可推出1)a=b或者2)a=-b6、角平分线问题若点(x,y)在一、三象限角平分线上,则x=y若点(x,y)在二、四象限角平分线上,则x=-y7、平移:在平面直角坐标系中,将点(x,y)向右平移a个单位长度,可以得到对应点(x+a,y)向左平移a个单位长度,可以得到对应点(x-a,y)向上平移b个单位长度,可以得到对应点(x,y+b)向下平移b个单位长度,可以得到对应点(x,y-b)二、平面直角坐标特点1、平行于坐标轴的直线的点的坐标特点:平行于x轴(或横轴)的直线上的点的纵坐标相同;平行于y轴(或纵轴)的直线上的点的横坐标相同。
2、各象限的角平分线上的点的坐标特点:第一、三象限角平分线上的点的横纵坐标相同;第二、四象限角平分线上的点的横纵坐标相反。
3、与坐标轴、原点对称的点的坐标特点:关于x轴对称的点的横坐标相同,纵坐标互为相反数关于y轴对称的点的纵坐标相同,横坐标互为相反数关于原点对称的点的横坐标、纵坐标都互为相反数4、特殊位置点的特殊坐标:5、利用平面直角坐标系绘制区域内一些点分布情况平面图过程如下:建立坐标系,选择一个适当的参照点为原点,确定x轴、y轴的正方向;根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;在坐标平面内画出这些点,写出各点的坐标和各个地点的名称。
(完整word版)平面直角坐标系知识点总结

平面直角坐标系二、知识要点梳理知识点一:有序数对比如教室中座位的位置,常用“几排几列”来表示,而排数和列数的先后顺序影响座位的位置,因此用有顺序的两个数a与b组成有序数时,记作(a,b),表示一个物体的位置。
我们把这种有顺序的两个数a与b组成的数对叫做有序数对,记作: (a,b).要点诠释:对“有序”要准确理解,即两个数的位置不能随意交换,(a,b)与(b,a)顺序不同,含义就不同,表示不同位置。
知识点二:平面直角坐标系以及坐标的概念1.平面直角坐标系在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系。
水平的数轴称为x 轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方向为正方向,两坐标轴的交点为平面直角坐标系的原点(如图1)。
注:我们在画直角坐标系时,要注意两坐标轴是互相垂直的,且有公共原点,通常取向右与向上的方向分别为两坐标轴的正方向。
平面直角坐标系是由两条互相垂直且有公共原点的数轴组成的。
2.点的坐标点的坐标是在平面直角坐标系中确定点的位置的主要表示方法,是今后研究函数的基础。
在平面直角坐标系中,要想表示一个点的具体位置,就要用它的坐标来表示,要想写出一个点的坐标,应过这个点A分别向x轴和y轴作垂线,垂足M在x轴上的坐标是a,垂足N在y轴上的坐标是b,我们说点A的横坐标是a,纵坐标是b,那么有序数对(a,b)叫做点A的坐标.记作:A(a,b).用(a,b)来表示,需要注意的是必须把横坐标写在纵坐标前面,所以这是一对有序数。
注:①写点的坐标时,横坐标写在前面,纵坐标写在后面。
横、纵坐标的位置不能颠倒。
②由点的坐标的意义可知:点P(a,b)中,|a|表示点到y轴的距离;|b|表示点到x轴的距离。
知识点三:点坐标的特征l.四个象限内点坐标的特征:两条坐标轴将平面分成4个区域称为象限,按逆时针顺序分别叫做第一、二、三、四象限,如图2.这四个象限的点的坐标符号分别是(+,+),(-,+),(-,-),(+,-).2.数轴上点坐标的特征:x轴上的点的纵坐标为0,可表示为(a,0);y轴上的点的横坐标为0,可表示为(0,b).注意:x轴,y轴上的点不在任何一个象限内,对于坐标平面内任意一个点,不在这四个象限内,就在坐标轴上。
初中数学平面直角坐标系的知识点

初中数学平面直角坐标系的知识点关于数学的学习中,对平面直角坐标系知识点的内容讲解学习,盼望同学们仔细看看下面的知识。
平面直角坐标系:〔1〕在平面内两条有公共点并且相互垂直的数轴就构成了平面直角坐标系,通常把其中水平的一条数轴叫横轴或轴,取向右的方向为正方向;铅直的数轴叫纵轴或轴,取向上的方向为正方向;两数轴的交点叫做坐标原点。
〔2〕建立了直角坐标系的平面叫坐标平面.*轴和y轴把坐标平面分成四个部分,称为四个象限,按逆时针顺次依次叫第一象限、第二象限、第三象限、第四象限。
以上对平面直角坐标系知识的内容总结学习,相信同学们已经能很好的掌控了吧,盼望同学们仔细学习哦。
中学数学知识点总结:平面直角坐标系下面是对平面直角坐标系的内容学习,盼望同学们很好的掌控下面的内容。
平面直角坐标系平面直角坐标系:在平面内画两条相互垂直、原点重合的数轴,组成平面直角坐标系。
水平的数轴称为*轴或横轴,竖直的数轴称为y轴或纵轴,两坐标轴的交点为平面直角坐标系的原点。
平面直角坐标系的要素:①在同一平面②两条数轴③相互垂直④原点重合三个规定:①正方向的规定横轴取向右为正方向,纵轴取向上为正方向②单位长度的规定;一般状况,横轴、纵轴单位长度相同;实际有时也可不同,但同一数轴上需要相同。
③象限的规定:右上为第一象限、左上为第二象限、左下为第三象限、右下为第四象限。
相信上面对平面直角坐标系知识的讲解学习,同学们已经能很好的掌控了吧,盼望同学们都能考试胜利。
中学数学知识点:平面直角坐标系的构成对于平面直角坐标系的构成内容,下面我们一起来学习哦。
平面直角坐标系的构成在同一个平面上相互垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系。
通常,两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向。
水平的数轴叫做*轴或横轴,铅直的数轴叫做Y轴或纵轴,*轴或Y轴统称为坐标轴,它们的公共原点O称为直角坐标系的原点。
平面直角坐标系知识点

平面直角坐标系知识点平面直角坐标系是解析几何中非常重要的一个概念,它是二维空间中经常用到的坐标系之一。
它的出现使得在平面上的点可以用有序的数字对来表示,从而方便进行计算和表示几何图形。
下面我们将详细介绍平面直角坐标系的定义、性质和应用。
一、平面直角坐标系的定义平面直角坐标系是由两个互相垂直的坐标轴构成的。
通常情况下,我们把水平的坐标轴称为x轴,竖直的坐标轴称为y轴。
这两个轴的交点称为坐标原点O。
每个点P都可以由与x轴的距离和与y轴的距离分别表示,记作P(x, y),其中x表示点P在x轴上的坐标,y表示点P在y轴上的坐标。
二、平面直角坐标系的性质1. 坐标轴的正向和负向:平面直角坐标系中,x轴从左向右延伸,正方向为右方,负方向为左方;y轴从下向上延伸,正方向为上方,负方向为下方。
2. 坐标轴的单调性:在平面直角坐标系中,随着x坐标的增大,点的位置会向右移动;随着y坐标的增大,点的位置会向上移动。
3. 坐标轴的交点:坐标原点O是各个坐标轴的交点,它的坐标为O(0,0)。
4. 坐标轴的单位长度:在实际应用中,我们通常将单位长度在x轴和y轴上分别表示为Δx和Δy。
两个单位长度的比值称为坐标轴的比例尺。
5. 相关性:平面直角坐标系中,两个点P(x1,y1)和Q(x2,y2)之间的距离d可以用勾股定理表示:d = √[(x2-x1)² + (y2-y1)²]。
6. 坐标轴的划分:我们可以将x轴和y轴分别划分为若干个等分点,以方便表示坐标。
三、平面直角坐标系的应用平面直角坐标系广泛应用于解析几何、物理学、工程学等领域,具有重要的实际应用意义。
1. 几何图形的表示:平面直角坐标系可以方便地表示各种几何图形,如点、线段、直线、圆等。
通过坐标系可以计算图形的属性,如长度、角度、面积等。
2. 位置关系的描述:通过平面直角坐标系,我们可以方便地描述点与点、点与线、线与线之间的位置关系。
例如,通过坐标系可以判断两个点是否重合、两条线是否相交等。
七年级平面直角坐标系知识点大全

平面直角坐标系是数学中常用的一种坐标系,它由x轴和y轴组成,x轴和y轴分别代表水平和垂直方向。
在平面直角坐标系中,点的位置可以用有序数对(x,y)来表示,其中x表示点在x轴上的位置,y表示点在y轴上的位置。
以下是七年级平面直角坐标系的知识点:1.坐标系的构成:平面直角坐标系由x轴和y轴组成,它们相互垂直,并且以原点O作为坐标系的起点。
2.坐标系中的点:坐标系中的点用有序数对(x,y)来表示,其中x表示点在x轴上的位置,y表示点在y轴上的位置。
例如,点A的坐标是(3,2),表示它在x轴上的位置是3,y轴上的位置是23.坐标系中的区域:坐标系将平面分成四个象限,第一象限位于x轴和y轴的右上方,第二象限位于x轴的左上方,第三象限位于x轴和y轴的左下方,第四象限位于x轴的右下方。
4.坐标系中的距离:两个点在平面直角坐标系中的距离可以用勾股定理来计算。
设两个点的坐标分别是(x1,y1)和(x2,y2),它们之间的距离d可以用以下公式表示:d=√((x2-x1)²+(y2-y1)²)5. 坐标系中的直线:在平面直角坐标系中,直线可以由斜率和截距表示。
斜率是直线上的任意两点在x轴和y轴上的坐标差的比值,截距是直线与y轴的交点的y坐标。
直线的方程一般形式为y = mx + b,其中m为斜率,b为截距。
6.坐标系中的图形:平面直角坐标系中的图形可以用等式、不等式和方程组来表示。
例如,方程x+y=5表示平面上所有满足x+y=5的点的集合,这是一条直线。
7.坐标系中的平移:平面直角坐标系中的图形可以通过平移来改变它们的位置。
对于一个图形而言,如果它的每个点的坐标都分别增加或减少了一个固定的数,那么该图形就发生了平移。
8.坐标系中的对称:平面直角坐标系中的图形可以通过对称来改变它们的形状。
对于一个图形而言,如果它的每个点关于条直线对称,那么该图形就是关于这条直线对称的。
9.坐标系中的缩放:平面直角坐标系中的图形可以通过缩放来改变它们的大小。
平面直角坐标系知识点

平面直角坐标系知识点1.坐标轴:-x轴:水平方向的直线,与y轴垂直。
-y轴:竖直方向的直线,与x轴垂直。
-坐标原点:x轴与y轴的交点,坐标为(0,0)。
2.坐标表示:-一点的坐标表示为(x,y),其中x为该点在x轴上的坐标值,y为该点在y轴上的坐标值。
-向右移动x个单位,向上移动y个单位,可以到达坐标点(x,y)。
3.象限:-平面直角坐标系被分为四个象限,分别为第一象限、第二象限、第三象限和第四象限。
-第一象限:x轴与y轴的正方向所在的象限,x轴和y轴上的坐标值都为正数。
-第二象限:x轴的负方向与y轴的正方向所在的象限,x轴上的坐标值为负数,y轴上的坐标值为正数。
-第三象限:x轴与y轴的负方向所在的象限,x轴和y轴上的坐标值都为负数。
-第四象限:x轴的正方向与y轴的负方向所在的象限,x轴上的坐标值为正数,y轴上的坐标值为负数。
4.距离公式:-两点之间的距离可以使用勾股定理计算。
设A(x1,y1)和B(x2,y2)是两个点,在平面上划出一个三角形,其底边为x轴上的线段,高为y轴上的线段。
-这时,AB的距离d可以使用勾股定理表示:d=√((x2-x1)²+(y2-y1)²)。
5.直线和斜率:- 平面上的直线可以用方程表示,通常形式为y = kx + b,其中k 是斜率,表示直线与x轴的夹角的正切值;b是该直线与y轴交点的纵坐标。
-平行于y轴的直线的斜率为无穷大,与y轴相交的点无x坐标,方程为x=a,其中a是与y轴相交的点的横坐标。
6.对称性:-平面上的点关于x轴对称:设点A的坐标为(x,y),则点A'的坐标为(x,-y)。
-平面上的点关于y轴对称:设点A的坐标为(x,y),则点A'的坐标为(-x,y)。
-平面上的点关于原点对称:设点A的坐标为(x,y),则点A'的坐标为(-x,-y)。
7.坐标变换:-平面上的点可通过平移、旋转、缩放等方式进行坐标变换。
-平移:将点A(x,y)平移h个单位到点A'(x+h,y)。
七年级下数学第六章平面直角坐标系知识点总结

平面直角坐标系是数学中常用的一种坐标系,用来描述平面上的点的位置。
它由两条互相垂直的直线(通常称为x轴和y轴)组成。
1.坐标系的建立平面直角坐标系是由一组互相垂直的数轴组成的。
我们可以将其中一条数轴作为x轴,另一条数轴作为y轴。
两条轴的交点称为原点O,它的坐标为(0,0)。
2.坐标表示在平面直角坐标系中,每个点的位置都可以用一个有序数对表示,称为坐标。
其中第一个数表示x轴上的位置,第二个数表示y轴上的位置。
例如,点A的坐标是(2,3),表示它在x轴上距离原点2个单位,在y轴上距离原点3个单位。
3.坐标的正负在平面直角坐标系中,x轴向右延伸为正方向,向左延伸为负方向;y轴向上延伸为正方向,向下延伸为负方向。
4.坐标轴和象限平面直角坐标系由x轴和y轴组成。
x轴将平面分为上半平面和下半平面,y轴将平面分为右半平面和左半平面。
根据点的位置,可以将平面分为四个象限。
第一象限:x>0,y>0。
第二象限:x<0,y>0。
第三象限:x<0,y<0。
第四象限:x>0,y<0。
5.关于坐标原点的对称性对于任意一个点P(x,y),与原点O之间有以下关系:关于x轴对称点的坐标为P'(x,-y)。
关于y轴对称点的坐标为P'(-x,y)。
关于原点对称点的坐标为P'(-x,-y)。
6.坐标系上的线段和中点在平面直角坐标系中,可以用两点的坐标表示一条线段。
例如,线段AB的两个端点的坐标分别是A(x1,y1)和B(x2,y2)。
线段的中点的坐标可以用以下公式计算:中点的横坐标为(x1+x2)/2中点的纵坐标为(y1+y2)/27.坐标系上的距离在平面直角坐标系中,可以用两点之间的距离来度量两点的位置关系。
两点P1(x1,y1)和P2(x2,y2)之间的距离可以用以下公式计算:距离d=√((x2-x1)²+(y2-y1)²)。
8.斜率和直线的方程直线可以通过两点确定,例如,通过点A(x1,y1)和点B(x2,y2)可以确定一条直线。
初中数学知识点总结:平面直角坐标系

初中数学知识点总结:平面直角坐标系
初中数学知识点总结:平面直角坐标系
在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称直角坐标系。
以下是小编搜索整理初中数学知识点总结:平面直角坐标系,欢迎大家阅读!
平面直角坐标系:
在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系。
水平的数轴称为x轴或横轴,竖直的数轴称为y轴或纵轴,两坐标轴的交点为平面直角坐标系的原点。
平面直角坐标系的要素:
①在同一平面
②两条数轴
③互相垂直
④原点重合
三个规定:
①正方向的规定横轴取向右为正方向,纵轴取向上为正方向
②单位长度的'规定;一般情况,横轴、纵轴单位长度相同;实际有时也可不同,但同一数轴上必须相同。
③象限的规定:右上为第一象限、左上为第二象限、左下为第三象限、右下为第四象限。
相信上面对平面直角坐标系知识的讲解学习,同学们已经能很好的掌握了吧,希望同学们都能考试成功。
初中数学知识点:平面直角坐标系的构成
对于平面直角坐标系的构成内容,下面我们一起来学习哦。
平面直角坐标系的构成
在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系。
通常,两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向。
水平的数轴
叫做X轴或横轴,铅直的数轴叫做Y轴或纵轴,X轴或Y轴统称为坐标轴,它们的公共原点O称为直角坐标系的原点。
初中数学 平面直角坐标系 知识点

平面直角坐标系知识点
1.有序数对:有顺序的两个数a与b组成的数对叫做有序数对,记做(a,b)
2.平面直角坐标系:在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系。
3.横轴、纵轴、原点:水平的数轴称为x轴或横轴;竖直的数轴称为y轴或纵轴;两坐标轴的交点为平面直角坐标系的原点。
4.坐标:对于平面内任一点P,过P分别向x轴,y轴作垂线,垂足分别在x轴,y轴上,对应的数a,b分别叫点P的横坐标和纵坐标。
5.象限:两条坐标轴把平面分成四个部分,右上部分叫第一象限,按逆时针方向一次叫第二象限、第三象限、第四象限。
坐标轴上的点不在任何一个象限内。
数学平面直角坐标系知识点

数学平面直角坐标系知识点数学平面直角坐标系知识点在学习中,看到知识点,都是先收藏再说吧!知识点有时候特指教科书上或考试的知识。
相信很多人都在为知识点发愁,以下是店铺收集整理的数学平面直角坐标系知识点,欢迎阅读,希望大家能够喜欢。
数学平面直角坐标系知识点1平面直角坐标系:在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系。
水平的数轴称为x轴或横轴,竖直的数轴称为y轴或纵轴,两坐标轴的交点为平面直角坐标系的原点。
平面直角坐标系的要素:①在同一平面②两条数轴③互相垂直④原点重合三个规定:①正方向的规定横轴取向右为正方向,纵轴取向上为正方向②单位长度的规定;一般情况,横轴、纵轴单位长度相同;实际有时也可不同,但同一数轴上必须相同。
③象限的规定:右上为第一象限、左上为第二象限、左下为第三象限、右下为第四象限。
相信上面对平面直角坐标系知识的讲解学习,同学们已经能很好的掌握了吧,希望同学们都能考试成功。
数学平面直角坐标系知识点2平面直角坐标系的用用很广,可以用坐标表示地理位置,也可以用坐标表示平移。
平面直角坐标系在平面“二维”内画两条互相垂直,并且有公共原点的数轴。
简称直角坐标系。
平面直角坐标系有两个坐标轴,其中横轴为X轴(x-axis),取向右方向为正方向;纵轴为Y轴(y-axis),取向上为正方向。
坐标系所在平面叫做坐标平面,两坐标轴的公共原点叫做平面直角坐标系的原点。
X轴和Y轴把坐标平面分成四个象限(quadrant),右上面的叫做第一象限,其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限。
象限以数轴为界,横轴、纵轴上的点及原点不属于任何象限。
一般情况下,x轴和y轴取相同的单位长度。
点的坐标建立了平面直角坐标系后,对于坐标系平面内的任何一点,我们可以确定它的坐标(coordinate)。
反过来,对于任何一个坐标,我们可以在坐标平面内确定它所表示的一个点。
对于平面内任意一点C,过点C分别向X轴、Y轴作垂线,垂足在X轴、Y轴上的对应点a,b分别叫做点C的横坐标、纵坐标,有序实数对(ordered pair)(a,b)叫做点C的坐标。
数学知识点平面直角坐标系

数学知识点平面直角坐标系聪明出于勤奋,天才在于积累。
我们要振作精神,下苦功学习。
小编准备了数学知识点平面直角坐标系,希望能帮助到大家。
一、平面直角坐标系1.平面直角坐标系:(1)在平面内两条有公共点并且互相垂直的数轴就构成了平面直角坐标系,通常把其中水平的一条数轴叫横轴或轴,取向右的方向为正方向;铅直的数轴叫纵轴或轴,取向上的方向为正方向;两数轴的交点叫做坐标原点。
(2)建立了直角坐标系的平面叫坐标平面.x轴和y轴把坐标平面分成四个部分,称为四个象限,按逆时针顺序依次叫第一象限、第二象限、第三象限、第四象限,如图所示.说明:两条坐标轴不属于任何一个象限。
2.点的坐标:对于平面直角坐标系内任意一点P,过点P分别向x轴和y 轴作垂线,垂足在x轴,y轴对应的数a,b分别叫做点P的横坐标,纵坐标,有序数对(a,b)叫做P的坐标。
3.点与有序实数对的关系:坐标平面内的点可以用有序实数对来表示,反过来每一个有序实数对应着坐标平面内的一个点,即坐标平面内的点和有序实数对是一一对应的关系。
常见考法(1)由点的位置确定点的坐标,由点的坐标确定点的位置;(2)求某些特殊点的坐标。
误区提醒(1)求点的坐标时,容易将横、纵坐标弄反,还容易忽略坐标符号;(2)思考问题不周,容易出现漏解。
(如点P到x轴的距离为1,这里点P的纵坐标应当是,而不是1)。
【典型例题】(江苏常州)点p(1,2)关于x轴的对称点p1的坐标是,点p(1,2)关于原点O的对称点P2的坐标是。
【解析】关于x轴的对称点的坐标是横坐标不变,纵坐标相反,关于原点对称的点的坐标,横、纵坐标都要乘以-1,故本题应当填(1,-2),(-1,-2)。
上面就是为大家准备的数学知识点平面直角坐标系,希望同学们认真浏览,希望同学们在考试中取得优异成绩。
