【数学】江苏省泰州市第二中学2017届高三下学期第二次限时作业(1)
江苏省泰州市第二中学高一数学下学期第二次限时作业(

2015~2016学年度第二学期第二次限时作业 高一数学试卷 一、填空题:(本大题共14题,每小题5分,共70分,请将答案填入答题纸填空题的相应答题线上)1、 直线错误!未找到引用源。
的倾斜角为_____弧度2、 若直线错误!未找到引用源。
与错误!未找到引用源。
直线平行,则实数错误!未找到引用源。
的值是_____3、 当0>x 时,函数xx x y 422++=的最小值为______ 4、 在等比数列错误!未找到引用源。
中,错误!未找到引用源。
,则错误!未找到引用源。
______5、 不等式错误!未找到引用源。
的解集为______6、 若错误!未找到引用源。
,则Z=错误!未找到引用源。
的最大值为_____7、 已知,A B 两点的坐标分别为(0,4),(4,6),则以AB 为直径的圆的标准方程为8、 数列错误!未找到引用源。
的前项和为错误!未找到引用源。
,且满足错误!未找到引用源。
,则错误!未找到引用源。
______9、在等式m y x y x m y x 则的最小值为若中,65,0,0,94+>>=+的值为 ___ 10、在坐标平面内,与点A (1,2)的距离为1,且与点B (3,1)距离为2的直线有 条 11、若1)tan(,2)(tan =-=+βαβα,则=βα2cos 2s in ______ 12、若点P 在平面区域⎩⎪⎨⎪⎧2x -y +2≥0,x +y -2≤0,2y -1≥0内,点Q 在曲线x 2+(y +2)2=1上,则PQ 的最小值为_ __ 13、已知下列四个命题,其中正确的是 (填序号).(1)若210ax ax -+>在x ∈R 上恒成立,则04a <<;(2)锐角三角形ABC ∆中,3A π=,则1sin 12B <<; (3)已知直线方程为(2)(21)340m x m y m -++++=,其中m R ∈,则直线恒过定点()1,2--; (4)数列{}n a 共有5项,其中150,2a a ==,且11,1,2,3,4i i a a i +-==,则满足条件的不同数列有3个。
江苏省泰州市2017届高三数学考前模拟试卷及答案

2016~2017高三模拟考试数学试题(考试时间:120分钟 总分:160分)注意事项:所有试题的答案均填写在答题纸上,答案写在试卷上的无效.一、填空题:(本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上.) 1.已知集合2{1,1,2,3},{|,3},A B x x R x =-=∈<则A B = ▲ .2.函数()sin(4)6f x x π=+的最小正周期为 ▲ .3.复数(i)(12i)a ++是纯虚数(i 是虚数单位),则实数a = ▲ . 4.某算法的伪代码如图所示,如果输入的x 值为32,则输出的y 值 为 ▲ .5.从1,2,3,4 这四个数中一次随机取两个数,则两个数的和是偶数的概率为 ▲ .6.若双曲线22221x y a b -=的离心率2=e ,则该双曲线的渐近线方程为▲ .7.公差不为0的等差数列{}n a 的前n 项和为n S ,若2514,,a a a 成等比数列,253S a =,则10a = ▲ .8.将1个半径为1的小铁球与1个底面周长为2π,高为4的铁制圆柱重新锻造成一个大铁球,则该大铁球的表面积为 ▲ .9.若正实数,x y 满足2210x xy +-=,则2x y +的最小值为 ▲ .10.如图,在由5个边长为1,一个顶角为60的菱形组成的图形中, AB CD ⋅= ▲ .11.已知点,F A 是椭圆:C 2211612x y +=的左焦点和上顶点,若点 P 是椭圆C 上一动点,则PAF ∆周长的最大值为 ▲ .第10题图DBA第4题图Read x If 5x ≤Theny ←2xElse y ←2log x End IfPrint y12.已知函数3()1f x x x =++,若对任意的x ,都有2()()2f x a f ax ++>,则实数a 的取值范围是 ▲ .13.在ABC ∆中,若120C =,tan 3tan A B =,sin sin A B λ=,则实数λ= ▲ . 14.若函数22()(1)(0)f x ax a x a a =++->的一个零点为0x ,则0x 的最大值为 ▲ . 二、解答题:(本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤.) 15.(本题满分14分)已知向量(1,)m =a ,(2,)n =b .(1)若3m =,1n =-,且(λ⊥+)a a b ,求实数λ的值; (2)若5+=a b ,求⋅a b 的最大值. 16.(本题满分14分)如图,在四棱锥P ABCD -中,PC ⊥平面ABCD ,AB //CD ,CD AC ⊥,过CD 的平面分别与,PA PB 交于点,E F . (1)求证:CD ⊥平面PAC ; (2)求证://AB EF . 17.(本题满分14分)如图,圆O 是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中,A B 两点在O 上,,,,A B C D 恰是一个正方形的四个顶点.根据规划要求,在,,A B ,C D 四点处安装四盏照明设备,从圆心O 点出发,在地下铺设4条到,,,A B C D 四点线路,,,OA OB OC OD . (1)若正方形边长为10米,求广场的面积;(2)求铺设的4条线路,,,OA OB OC OD 总长度的最小值.18.(本题满分16分)在平面直角坐标系xOy 中,过点(0,1)P 且互相垂直的两条直线分别与 圆22:4O x y +=交于点,A B ,与圆22:(2)(1)1M x y -+-=交于点,C D .(1)若AB =CD 的长; (2)若CD 中点为E ,求ABE ∆面积的取值范围.19.(本题满分16分)已知函数2()2ln f x x x ax =+-,R a ∈.(1)若函数()y f x =在(0,)+∞上单调递增,求实数a 的取值范围; (2)若a =e ,解不等式:()2f x <;(3)求证:当4a >时,函数()y f x =只有一个零点.20.(本题满分16分)已知数列{}n a 的前n 项和为n S ,且满足22n n S a =-;数列{}n b 的前n 项和为n T ,且满足11b =,22b =,12n n n n T bT b ++=. (1)求数列{}n a 、{}n b 的通项公式; (2)是否存在正整数n ,使得11n n n n a b a b +++-恰为数列{}n b 中的一项?若存在,求所有满足要求的n b ;若不存在,说明理由.2016~2017高三模拟考试高三数学参考答案一、填空题1.{1,1}-; 2.2π; 3.2; 4.5; 5.13;6.y =; 7.19; 8.; 9; 10.4-;11.16; 12.04a <<; 13.12+ ; 141. 二、解答题15. 解:(1)当3m =,1n =-时,(1,3)=a ,又(2,1)=-b ,(1,3)(2,1)(12,3)λλλλ∴+=+-=+-a b ,若(λ⊥+)a a b ,则(0)=λ⋅+a a b ,即(12)3(3)0λλ++-=,解得10λ=. ……………7分 (2)因为(1,)m =a ,(2,)n =b ,所以(3,)m n ++a b =, 因为5+=a b ,所以2223()5m n ++=,则2()16m n +=,所以211122()216644mn m n ⋅⨯+≤++=+⨯=a b =, 故当2m n ==或2m n ==-时,⋅a b 的最大值为6. ……………14分 16. 证:(1)因为PC ⊥平面ABCD ,所以PC CD ⊥,又因为CD AC ⊥,所以CD ⊥平面PAC . ……………7分 (2)因为AB //CD ,AB ⊄平面CDEF ,CD ⊂平面CDEF , 所以//AB 平面CDEF , ……………10分 又因为平面PAB 平面CDEF EF =,AB ⊄平面CDEF ,所以//AB EF . ……………14分17. 解:(1)连接AB ,因为正方形边长为10米,所以10OA OB AB ===,则3AOB π∠=,所以103AB π=,………2分所以广场的面积为2211050(1010)101002343ππ⋅⋅-⋅+=+-2m )………6分 (2)作OG CD ⊥于G ,OK AD ⊥于K G ,记OAK α∠=,则2220sin AD DG OK α===, ………8分 由余弦定理得 2222cos OD OA AD OA AD α=+-⋅221cos 210(20sin )21020sin cos 100400200sin 22ααααα-=+-⨯⨯=+⨯-230045)1)α=-+≥, ………12分所以1)OD ≥,当且仅当22.5α=时取等号,所以201)OA OB OC OD +++≤+= 因此求4条小路的总长度的最小值为 答:(1)广场的面积为501003π+- (2)4条小路的总长度的最小值为 …………14分 18. 解:(1)直线AB 斜率显然存在,设为k ,则直线:1AB y kx =+,因为22()42AB +=,所以AB = ………3分由=215k =,22211()12CD -+-=-,CD === ………6分 (2)当直线AB 斜率不存在时,ABE ∆的面积14242S =⨯⨯=; 当直线AB 斜率存在时,设为k ,则直线:1AB y kx =+,显然0k ≠,直线1:1CD y x k =-+1<得23k >, ………8分所以(,(3,)k ∈-∞+∞.因为22()42AB+=,所以AB =E 到直线AB 的距离即M 到AB的距离,为d ==,所以ABE ∆的面积12S AB d =⋅== ………12分 令234(45)t t k +=<<,则4)S ==.综上,ABE ∆面积的取值范围4]. …………16分说明:求S =范围还可以: 令214k t +=>,S ==∈19.解:(1)函数的定义域为(0,)+∞,2()2ln f x x x ax =+-,2()2f x x a x'=+-, 由题意,对任意的0x >,都有2()20f x x a x '=+-≥,只要min 2(2)x a x+≥,由基本不等式得224x x +≥=,当且仅当1x =时取等号, 所以4a ≤,即实数a 的取值范围是(,4]-∞. ………4分(2)当a =e 时,2()2ln f x x x x =+-e ,2222()20x x f x x x x-+'=+-=>e e , 所以()f x 在(0,)+∞上单调递增,又因为2()2ln 2f =+-⋅e e e e e =,所以()2()()f x f x f <⇔<e ,因此0x <<e , 故不等式()2f x <的解集为(0,)e . ………9分(3)2222()2x ax f x x a x x-+'=+-=,(0,)x ∈+∞,令2()22g x x ax =-+,当4a >时,因为2160a ∆=->,所以2()22g x x ax =-+一定有两个零点, 设为1212,()x x x x <,又因为121x x =,所以1201x x <<<,则()f x 在区间1(0,)x 或2(,)x +∞上单调递增,在12(,)x x 上单调递减, ………12分因为2111()220g x x ax =-+=,所以22111111()2ln 2ln 2f x x x ax x x =+-=--, 因为101x <<,所以221111()2ln 22ln120f x x x x =--<--<,所以21()()0f x f x <<,又()2ln ()f x x x x a =+-,则()2ln 0f a a =>,所以()f x 在(0,)+∞上只有一个零点. ………16分 说明:事实上,对任意的R a ∈,函数()y f x =只有一个零点. 20. 解:(1) 因为22n n S a =-,所以当2n ≥时,1122n n S a --=-, 两式相减得122n n n a a a -=- ,即12n n a a -=,又1122S a =-,则12a =,所以数列{}n a 是以12a =为首项,2为公比的等比数列,故2nn a =. ………4分由12n n n n T b T b ++=得 33111122233445112,,,,,n n n n n n n n T bT b T bT b T b T b T b T b T b T b --+++=====, 以上n 个式子相乘得11212n n n T b bT b b ++=,即12n n n T b b += ①,当2n ≥时,112n n n T b b --=②, 两式相减得 112()n n n n b b b b +-=-,即112n n b b +--=(2n ≥), ………6分所以数列{}n b 的奇数项、偶数项分别成等差数列, 又1123T b T b =,所以32123b T b b ==+=,则1322b b b +=, 所以数列{}n b 是以11b =为首项,1为公差的等差数列,因此数列{}n b 的通项公式为n b n =. ………8分另法:由已知显然0n b ≠,因为12n n n n T bT b ++=,所以1112n n n n n n T T b b b b ++++=,则数列1{}n n n T b b +是常数列,所以111212n n n T T b b b b +==,即12n n n T b b +=,下同上. (2)当1n =时,11n n n n a b a b +++-无意义,设1121(2,)2(1)n n n n n n n a b n c n n a b n *+++++==∈--+N≥,显然1n c >,则111112221202(2)2(1)[2(2)][2(1)]n n n n n n n n nn n n c c n n n n +++++++++-⋅-=-=<-+-+-+⋅-+,即11n n c c +>>, 显然212(1)nnn n ++>-+,所以234731c c c =>=>>>,所以存在2n =,使得72b c =,33b c =, ………12分下面证明不存在2n c =,否则2122(1)n n nn c n ++==-+,即23(1)n n =+, 此式右边为3的倍数,而2n不可能是3的倍数,故该式不成立.综上,满足要求的n b 为37,b b . ………16分附加题参考答案21.A .证明:因为CD 为圆的切线,弧BC 所对的圆周角为BAC ∠ 所以 BCD BAC ∠=∠ (1) 又因为 AB 为半圆O 的直径所以90ACB ∠=︒,又BD ⊥CD ,所以90CDB ACB ∠=︒=∠ (2) 由(1)、(2)得ABC CBD ∆∆ 所以2AB BCBC BA BD BC BD=⇒=⋅ ……………10分 21.B . 解:因为02513MN ⎡⎤=⎢⎥⎣⎦ ,所以25,413.x y x y -=⎧⎨-=⎩所以4,3x y ==; ……………5分矩阵1243M ⎡⎤=⎢⎥⎣⎦的逆矩阵132554155M -⎡⎤-⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦. ……………10分21.C . 解:曲线C 的普通方程是2213x y +=. ……………………………2分直线l的普通方程是0x +=. ……………………………4分 设点M的直角坐标是,sin )θθ,则点M 到直线l 的距离是d=10分21.D .证明:因为2≤(a +1+b +1)(12+12)=6, ………… 8分. …………10分,即证22≤,即证116a b +++≤,即证3(1)(1)a b =+++ 由基本不等式易得。
江苏省扬州、泰州、南通、淮安、宿迁、徐州六市2017届高三二模数学考试

江苏省扬州、泰州、南通、淮安、宿迁、徐州六市2017届高三二模数学考试————————————————————————————————作者:————————————————————————————————日期:2i ←1Whil e i < 6(第3题)宿迁市2017届高三第二次调研测试 数学学科参考答案及评分建议一、填空题:本大题共14小题,每小题5分,共计70分.1. 已知集合{} 03 4 A =,,,{} 102 3 B =-,,,,则A B =I ▲ . 【答案】{}03,2. 已知复数3i1iz -=+,其中i 为虚数单位,则复数z 的模是 ▲ . 【答案】53. 根据如图所示的伪代码,可知输出的结果S 是 ▲ .【答案】174. 现有1 000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm )的数据分组及各组的频数见右上表,据此估计这1 000根中纤维长度不小于37.5 mm 的根数是 ▲ . 【答案】1805. 100张卡片上分别写有1,2,3,…,100.从中任取1张,则这张卡片上的数是6的倍数的概率是 ▲ . 【答案】425(或0.16) 6. 在平面直角坐标系xOy 中,已知抛物线24y x =上一点P 到焦点的距离为3,则点P 的横 坐标是 ▲ .【答案】2纤维长度频数 [22.5,25.5) 3 [25.5,28.5) 8 [28.5,31.5) 9 [31.5,34.5) 11 [34.5,37.5) 10 [37.5,40.5) 5 [40.5,43.5]4(第4题)7. 现有一个底面半径为3 cm ,母线长为5 cm 的圆锥状实心铁器,将其高温融化后铸成一个 实心铁球(不计损耗),则该铁球的半径是 ▲ cm . 【答案】398. 函数()2()lg 5f x x =-的定义域是 ▲ . 【答案】[]22-,9. 已知{}n a 是公差不为0的等差数列,n S 是其前n 项和.若2345a a a a =,927S =,则1a 的值是 ▲ . 【答案】5-10.在平面直角坐标系xOy 中,已知圆1C :()()22481x y -+-=,圆2C :()()22669x y -++=.若圆心在x 轴上的圆C 同时平分圆1C 和圆2C 的圆周,则圆C 的方程是 ▲ . 【答案】2281x y +=11.如图,在平面四边形ABCD 中,O 为BD 的中点,且3OA =,5OC =.若AB →·AD →=-7, 则BC →·DC →的值是 ▲ .【答案】912.在△ABC 中,已知2AB =,226AC BC -=,则tan C 的最大值是 ▲ . 【答案】25513.已知函数20()1 0x m x f x x x -+<⎧=⎨-⎩≥,,,,其中0m >.若函数()()1y f f x =-有3个不同的零点,则m 的取值范围是 ▲ . 【答案】(01),14.已知对任意的x ∈R ,()()3sin cos 2sin 2 3 a x x b x a b ++∈R ≤,恒成立,则当a b +取得最 小值时,a 的值是 ▲ . 【答案】45- BCD O(第11题)A二、解答题:本大题共6小题,共计90分. 15.(本小题满分14分)已知()2πsin 410α+=,()ππ2α∈,.求:(1)cos α的值; (2)()πsin 24α-的值.解:(1)法一:因为()ππ2α∈,,所以()π3π5π444α+∈,,又()2πsin 410α+=,所以()()()22272ππcos 1sin 1441010αα+=--+=--=-. …… 3分所以()ππcos cos 44αα⎡⎤=+-⎢⎥⎣⎦()()ππππcos cos sin sin 4444αα=+++72222102102=-⨯+⨯35=-. …… 6分 法二:由()2πsin 410α+=得,2ππsin cos cos sin 4410αα+=,即1sin cos 5αα+=. ① …… 3分又22sin cos 1αα+=. ②由①②解得3cos 5α=-或cos α=45.因为()ππ2α∈,,所以3cos 5α=-. …… 6分 (2)因为()ππ2α∈,,3cos 5α=-, 所以()2234sin 1cos 155αα=-=--=. …… 8分 所以()4324sin 22sin cos 25525ααα==⨯⨯-=-,()2237cos22cos 12525αα=-=⨯-=-. …… 12分所以()πππsin 2sin 2cos cos2sin 444ααα-=-()()22247252252=-⨯--⨯17250=-.…… 14分16.(本小题满分14分)如图,在直三棱柱111ABC A BC -中,AC BC ⊥,A 1B 与AB 1交于点D ,A 1C 与AC 1交于点E .求证:(1)DE ∥平面B 1BCC 1; (2)平面1A BC ⊥平面11A ACC . 证明:(1)在直三棱柱111ABC A BC -中,四边形A 1ACC 1为平行四边形. 又E 为A 1C 与AC 1的交点,所以E 为A 1C 的中点. …… 2分同理,D 为A 1B 的中点,所以DE ∥BC . …… 4分 又BC ⊂平面B 1BCC 1,DE ⊄平面B 1BCC 1,所以DE ∥平面B 1BCC 1. …… 7分(2)在直三棱柱111ABC A BC -中,1AA ⊥平面ABC ,又BC ⊂平面ABC ,所以1AA BC ⊥. …… 9分 又AC BC ⊥,1AC AA A =I ,1AC AA ⊂,平面11A ACC ,所以BC ⊥平面11A ACC . …… 12分 因为BC ⊂平面1A BC ,BC 1ACA 1B 1D (第16题)E所以平面1A BC ⊥平面11A ACC . …… 14分17.(本小题满分14分)如图,在平面直角坐标系xOy 中,已知椭圆2222 1 (0)y x a b a b+=>>的离心率为23,C 为椭圆上位于第一象限内的一点.(1)若点C 的坐标为()523,,求a ,b 的值;(2)设A 为椭圆的左顶点,B 为椭圆上一点,且AB →=12OC →,求直线AB 的斜率.解:(1)因为椭圆的离心率为23,所以2223a b a -=,即2259b a=.①又因为点C ()523,在椭圆上,所以2242519a b +=. ② …… 3分 由①②解得2295a b ==,. 因为0a b >>,所以35a b ==,. …… 5分 (2)法一:由①知,2259b a =,所以椭圆方程为2222915y x a a+=,即222595x y a +=.设直线OC 的方程为x my =()0m >,11()B x y ,,22()C x y ,.由222595x my x y a=⎧⎨+=⎩,得2222595m y y a +=, 所以222559a y m =+.因为20y >,所以22559a y m =+. …… 8分 因为AB →=12OC →,所以//AB OC .可设直线AB 的方程为x my a =-.由222595x my a x y a=-⎧⎨+=⎩,得22(59)100m y amy +-=, (第17题)OA B Cxy所以0y =或21059am y m =+,得121059am y m =+. …… 11分因为AB →=12OC →,所以()()11221122x a y x y +=,,,于是212y y =,即2559a m +22059am m =+()0m >,所以35m =.所以直线AB 的斜率为5313m =. …… 14分法二:由(1)可知,椭圆方程为222595x y a +=,则(0)A a -,.设11()B x y ,,22()C x y ,.由AB →=12OC →,得()()11221122x a y x y +=,,,所以1212x x a =-,1212y y =. …… 8分 因为点B ,点C 都在椭圆222595x y a +=上, 所以()()22222222225951595.22x y a y x a a ⎧+=⎪⎨-+=⎪⎩,解得24a x =,2543a y =, ……12分所以直线AB的斜率22533y k x ==. …… 14分18.(本小题满分16分)一缉私艇巡航至距领海边界线l (一条南北方向的直线)3.8海里的A 处,发现在其北偏 东30°方向相距4海里的B 处有一走私船正欲逃跑,缉私艇立即追击.已知缉私艇的最 大航速是走私船最大航速的3倍.假设缉私艇和走私船均按直线方向以最大航速航行. (1)若走私船沿正东方向逃离,试确定缉私艇的追击方向,使得用最短时间在领海内拦截成功;(参考数据:sin17°36≈,33 5.7446≈) (2)问:无论走私船沿何方向逃跑,缉私艇是否总能在领海内成功拦截?并说明理由.领B北公l解:(1)设缉私艇在C 处与走私船相遇(如图甲),依题意,3AC BC =. …… 2分 在△ABC 中,由正弦定理得,sin sin BC BAC ABC AC∠=∠sin1203=o36=.因为sin17°36≈,所以17BAC ∠=°.从而缉私艇应向北偏东47o 方向追击. …… 5分 在△ABC 中,由余弦定理得, 2224cos1208BC AC BC+-=o,解得1334BC += 1.68615≈.又B 到边界线l 的距离为3.84sin30 1.8-=o .因为1.68615 1.8<,所以能在领海上成功拦截走私船. …… 8分 (2)如图乙,以A 为原点,正北方向所在的直线为y 轴建立平面直角坐标系xOy . 则()223B ,,设缉私艇在()P x y ,处(缉私艇恰好截住走私船的位置)与走私 船相遇,则3PA PB=,即()22223(2)23x y x y +=-+-.整理得,()()229993444x y -+-=, …… 12分所以点()P x y ,的轨迹是以点()99344,为圆心,32为半径的圆. 因为圆心()99344,到领海边界线l : 3.8x =的距离为1.55,大于圆半径32,所以缉私艇能在领海内截住走私船. …… 14分 答:(1)缉私艇应向北偏东47o 方向追击;(2)缉私艇总能在领海内成功拦截走私船. …… 16分19.(本小题满分16分)AB C图甲 y 公领AB图乙6lx已知函数1()ex f x =,()ln g x x =,其中e 为自然对数的底数.(1)求函数()()y f x g x =在x =1处的切线方程;(2)若存在12x x ,()12x x ≠,使得[]1221()()()()g x g x f x f x λ-=-成立,其中λ为常数,求证:e λ>;(3)若对任意的(]01x ∈,,不等式()()(1)f x g x a x -≤恒成立,求实数a 的取值范围. 解:(1)因为ln ()()e x xy f x g x ==,所以()211e ln e ln e e x x x x x xx x y ⋅-⋅-'==,故11e x y ='=. 所以函数()()y f x g x =在x =1处的切线方程为1(1)ey x =-,即e 10x y --=. …… 2分(2)由已知等式[]1221()()()()g x g x f x f x λ-=-得1122()()()()g x f x g x f x λλ+=+.记()()()ln ex p x g x f x x λλ=+=+,则e ()e xx x p x x λ-'=. …… 4分 假设e λ≤.① 若λ≤0,则()0p x '>,所以()p x 在()0+∞,上为单调增函数. 又12()()p x p x =,所以12x x =,与12x x ≠矛盾. …… 6分 ② 若0e λ<≤,记()e x r x x λ=-,则()e x r x λ'=-.令()0r x '=,解得0ln x λ=.当0x x >时,()0r x '>,()r x 在()0x +∞,上为单调增函数; 当00x x <<时,()0r x '<,()r x 在()00x ,上为单调减函数. 所以0()()=1ln )0r x r x λλ-≥(≥,所以()0p x '≥, 所以()p x 在()0+∞,上为单调增函数. 又12()()p x p x =,所以12x x =,与12x x ≠矛盾.综合①②,假设不成立,所以e λ>. …… 9分 (3)由()()(1)f x g x a x -≤得ln e (1)x x a x --≤0.记ln e (1)x F x x a x --()=,0x <≤1, 则()211e e e x x xF x ax x a x x '-=-()=. ① 当1e a ≤时,因为211ee x x ≥,e 0x x >,所以0F x '()≥, 所以F x ()在(]0+∞,上为单调增函数,所以(1)F x F ()≤=0,故原不等式恒成立. …… 12分 ② 法一:当1ea >时,由(2)知e e x x ≥,3211e e a x F x a x x x -'-=()≤,当()13e 1a x -<<时,0F x '<(),()F x 为单调减函数, 所以(1)F x F >()=0,不合题意. 法二:当1ea >时,一方面1=1e 0F a '-<().另一方面,111e x a ∃=<,()()111121111e e e e 10F x a x x a x a a x x '-=-=->()≥.所以01(1)x x ∃∈,,使0=0F x '(),又F x '()在(0)+∞,上为单调减函数, 所以当01x x <<时,0F x '<(),故F x ()在0(1)x ,上为单调减函数, 所以(1)F x F >()=0,不合题意.综上,1ea ≤. …… 16分20.(本小题满分16分)设数列{}n a 的前n 项和为S n ()*n ∈N ,且满足:①12 a a ≠;②()()()22112n n r n p S n n a n n a +-=++--,其中r p ∈R ,,且0r ≠. (1)求p 的值;(2)数列{}n a 能否是等比数列?请说明理由; (3)求证:当r =2时,数列{}n a 是等差数列.解:(1)n =1时,211(1)220r p S a a -=-=, 因为12a a ≠,所以20S ≠,又0r ≠,所以p =1. …… 2分 (2){}n a 不是等比数列.理由如下: 假设{}n a 是等比数列,公比为q ,当n =2时,326rS a =,即211(1)6ra q q a q ++=,所以2(1)6r q q q ++=, (i ) …… 4分 当n =3时,431212+4rS a a =,即2321112(1)124ra q q q a q a +++=+,所以232(1)62r q q q q +++=+, (ii ) …… 6分由(i )(ii )得q =1,与12a a ≠矛盾,所以假设不成立.故{}n a 不是等比数列. …… 8分(3)当r =2时,易知3122a a a +=.由22112(1)()(2)n n n S n n a n n a +-=++--,得2n ≥时,11(1)(1)(2)211n n n n a n n a S n n +++-=+--, ① 112(1)(2)(1)(2)2n n n n a n n a S n n++++-+=+,② ②-①得,2112(1)(2)(1)(2)21(1)n n n n n a n n a n n a a n n n n +++++-+=-+--, …… 11分 即11121(1)(2)()(1)()2()1n n n n n a a n n a a a a n n ++++-+--=--, 211112()(2)()()11n n n a a n a a n a a n n n ++-+--=-+-, 即()2111111121n n n n a a a a n a a a a n n n n +++-----=-+- ()111(1)2212n n n n a a a a n n ----=-⨯-- =……()3121(1)3202223121n n a a a a -⨯⋅⋅⋅⨯--=-=⨯⨯⋅⋅⋅⨯--,所以11121121n n a a a a a an n ----==⋅⋅⋅=--,令21a a -=d ,则11n a a d n -=-(2)n ≥. …… 14分 所以1(1)(2)n a a n d n =+-≥. 又1n =时,也适合上式, 所以*1(1)()n a a n d n =+-∈N . 所以*1()n n a a d n +-=∈N .所以当r =2时,数列{}n a 是等差数列. …… 16分数学Ⅱ(附加题)21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作答.................... 若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. A .[选修4-1:几何证明选讲](本小题满分10分)如图,已知△ABC 内接于⊙O ,连结AO 并延长交⊙O 于点D ,ACB ADC ∠=∠. 求证:2AD BC AC CD ⋅=⋅. 证明:连结OC .因为ACB ADC ∠=∠,ABC ADC ∠=∠,所以ACB ABC ∠=∠. …… 3分 因为OC =OD ,所以OCD ADC ∠=∠. 所以ACB OCD ∠=∠.所以△ABC ∽△ODC . …… 8分 所以AC BC OC CD=,即AC CD OC BC ⋅=⋅.因为12OC AD =,所以2AD BC AC CD ⋅=⋅. …… 10分B .[选修4-2:矩阵与变换](本小题满分10分)设矩阵A 满足:A 1206⎡⎤=⎢⎥⎣⎦1203--⎡⎤⎢⎥⎣⎦,求矩阵A 的逆矩阵1-A . 解:法一:设矩阵a b c d ⎡⎤=⎢⎥⎣⎦A ,则1206a b c d ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦1203--⎡⎤⎢⎥⎣⎦,所以1a =-,262a b +=-,0c =,263c d +=. …… 4分DACB O(第21—A 题)解得0b =,12d =,所以10102-⎡⎤⎢⎥=⎢⎥⎣⎦A . …… 6分 根据逆矩阵公式得,矩阵11002--⎡⎤=⎢⎥⎣⎦A . …… 10分 法二:在A 1206⎡⎤=⎢⎥⎣⎦1203--⎡⎤⎢⎥⎣⎦两边同时左乘逆矩阵1-A 得, 1206⎡⎤=⎢⎥⎣⎦1-A 1203--⎡⎤⎢⎥⎣⎦.…… 4分设1-=A a b c d ⎡⎤⎢⎥⎣⎦,则1206⎡⎤=⎢⎥⎣⎦a b c d ⎡⎤⎢⎥⎣⎦1203--⎡⎤⎢⎥⎣⎦, 所以1a -=,232a b -+=,0c -=,236c d -+=. …… 6分 解得1a =-,0b =,0c =,2d =,从而11002--⎡⎤=⎢⎥⎣⎦A . …… 10分C .[选修4-4:坐标系与参数方程](本小题满分10分)在平面直角坐标系xOy 中,已知直线232222x l y l ⎧=-+⎪⎨⎪=⎩,(l 为参数)与曲线218x t y t⎧=⎪⎨⎪=⎩,(t 为参数)相交于A ,B 两点,求线段AB 的长.解:法一:将曲线218x t y t⎧=⎪⎨⎪=⎩,(t 为参数)化为普通方程为28y x =. …… 3分将直线232222x l y l ⎧=-+⎪⎨⎪=⎩,(l 为参数)代入28y x =得,282240l l -+=,…… 6分解得122l =,262l =.则1242l l -=,所以线段AB 的长为42. …… 10分 法二:将曲线218x t y t⎧=⎪⎨⎪=⎩,(t 为参数)化为普通方程为28y x =, …… 3分将直线232222x l y l ⎧=-+⎪⎨⎪=⎩,(l 为参数)化为普通方程为302x y -+=, …… 6分由28302y x x y ⎧=⎪⎨-+=⎪⎩,得,122x y ⎧=⎪⎨⎪=⎩,或926.x y ⎧=⎪⎨⎪=⎩, 所以AB 的长为()()2291624222-+-=. …… 10分D .[选修4-5:不等式选讲](本小题满分10分)设x y z ,,均为正实数,且1xyz =,求证:333111xy yz zx x y y z z x++++≥. 证明:因为x y z ,,均为正实数,且1xyz =,所以3122xy yz x x y +=≥,3122yz xz y y z +=≥,3122xz xy z z x +=≥. …… 8分 所以333111xy yz zx x y y z z x++++≥. …… 10分【必做题】第22、23题,每小题10分,共计20分.请在答题卡指定区域.......内作答,解答时应 写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)某乐队参加一户外音乐节,准备从3首原创新曲和5首经典歌曲中随机选择4首进行演唱. (1)求该乐队至少演唱1首原创新曲的概率;(2)假定演唱一首原创新曲观众与乐队的互动指数为a (a 为常数),演唱一首经典歌曲观 众与乐队的互动指数为2a .求观众与乐队的互动指数之和X 的概率分布及数学期望.解:(1)设“至少演唱1首原创新曲”为事件A ,则事件A 的对立事件A 为:“没有1首原创新曲被演唱”.所以()4548C 13()1114C P A P A =-=-=.答:该乐队至少演唱1首原创新曲的概率为1314. …… 4分(2)设随机变量x 表示被演唱的原创新曲的首数,则x 的所有可能值为0,1,2,3. 依题意,()24X ax a x =+-,故X 的所有可能值依次为8a ,7a ,6a ,5a .则4548C 1(8)(0)14C P X a P x =====,133548C C 3(7)(1)7C P X a P x =====,223548C C3(6)(2)7C P X a P x =====,313548C C 1(5)(3)14C P X a P x =====.从而X 的概率分布为:…… 8分 所以X 的数学期望()133191876514771414E X a a a a a =⨯+⨯+⨯+⨯=.…… 10分23.(本小题满分10分)设*2n n ∈N ≥,.有序数组()12n a a a ⋅⋅⋅,,,经m 次变换后得到数组()12m m m n b b b ⋅⋅⋅,,,,,,,其中11i i i b a a +=+,,111m i m i m i b b b --+=+,,,(i =1,2,⋅⋅⋅,n ),11n a a +=,1111m n m b b -+-=,,(2)m ≥. 例如:有序数组()123,,经1次变换后得到数组()122331+++,,,即()354,,;经第 2次变换后得到数组()897,,. (1)若 (12)i a i i n ==⋅⋅⋅,,,,求35b ,的值;X 8a 7a 6a 5aP114 37 37 114(2)求证:0C mjm i i j m j b a +==∑,,其中i =1,2,⋅⋅⋅,n .(注:当i j kn t +=+时,*k ∈N ,t =1,2,⋅⋅⋅,n ,则i j t a a +=.) 解:(1)依题意,()12345678n ⋅⋅⋅,,,,,,,,, 经1次变换为:()35791113151n ⋅⋅⋅+,,,,,,,,, 经2次变换为:()812162024284n ⋅⋅⋅+,,,,,,,, 经3次变换为:()202836445212n ⋅⋅⋅+,,,,,,, 所以3552b =,. …… 3分(2)下面用数学归纳法证明对*m ∈N ,0C mjm i i j m j b a +==∑,,其中12i n =⋅⋅⋅,,,.(i )当1m =时,11110C j i i i i j j b a a a ++==+=∑,,其中12i n =⋅⋅⋅,,,,结论成立;(ii )假设*()m k k =∈N 时,k i b =,0C kj i jk j a+=∑,其中12i n =⋅⋅⋅,,,. …… 5分则1m k =+时,11k i k i k i b b b ++=+,,,10C C kkjj i j ki j k j j a a +++===+∑∑1101C C kk j j i j ki j k j j a a +-++===+∑∑()0111C C C C kj j ki ki j k k i k k j a a a -+++==+++∑0111111C C C kj k i k i j k i k k j a a a +++++++==++∑ 110C k j i j k j a +++==∑,所以结论对1m k =+时也成立.由(i )(ii )知,*m ∈N ,0C mjm i i j m j b a +==∑,,其中12i n =⋅⋅⋅,,,. …… 10分。
江苏省泰州市第二中学高三2月质量检测——数学(数学)

江苏省泰州市第二中学2017届高三2月质量检测数 学 试 题参考公式:锥体体积公式:,其中为底面积,为高;柱体体积公式:,其中为底面积,为高;球体体积公式:,其中是R 的球的半径.样本数据的方差,其中.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上)1.已知集合A={1,2,4,6,8},B={x |x=2k ,k ∈A },则A ∩B= ▲ .2.已知a ,b ∈R ,i 是虚数单位.若a +i=2﹣bi ,则(a +bi )2= ▲ .3.已知样本数据的方差,则样本数据的方差为 ▲ .4.执行如图所示的程序框图,若输入n=1时,则输出S= ▲ .5.同时抛掷两颗质地相同的骰子(各面上分别标有1,2,3,4,5,6的正方体玩具),点数之和是5的概率是 ▲ .6.若实数x ,y 满足243700x y x y x y +⎧⎪+⎪⎨⎪⎪⎩≤,≤,≥,≥,则z =3x +2y 的最大值为 ▲ . 7.若双曲线的一个焦点到其渐近线的距离为,则该双曲线的焦距等于 ▲ .8.各项均为正数的等比数列的前项和为,若,,则_ ▲ .9.已知A ,B 分别是函数f (x )=2sinωx (ω>0)在y 轴右侧图象上的第一个最高点和第一个最低点,且∠AOB=,则该函数的最小正周期是 ▲ .10.已知圆锥底面半径与球的半径都是1cm ,如果圆锥的体积与球的体积恰好也相等,那么这个圆锥的侧面积是 ▲ .11.已知点O 为△ABC 的垂心,, 则角A= ▲ .12.设二次函数f (x )=ax 2+bx +c (a ,b ,c 为常数)的导函数为f′(x ).对任意x ∈R ,不等式f (x)≥f′(x )恒成立,则b 2a 2+c 2的最大值为 ▲ . 13.当实数x ,y 满足x 2+y 2=1时,|x +2y +a |+|3﹣x ﹣2y |的取值与x ,y 均无关,则实数a 的取范围是 ▲ .14.已知实数不全为零,正数满足,设的最大值为,则的最小值为 ▲ .二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内)15.(本小题满分14分)如图,在三棱柱中,底面,,点和分别是和的中点.(1)求证:平面;(2)求证:.16.(本小题满分14分) 设)(21cos sin 3sin )(2R x x x x x f ∈-+=. (1)求函数的最小正周期与值域;(2)设内角的对边分别为,为锐角,,若,求.17. (本小题满分14分)如图,F 1,F 2分别是椭圆C : +=1(a >b >0)的左、右焦点,且焦距为2,动弦AB 平行于x 轴,且|F 1A |+|F 1B |=4.(1)求椭圆C 的方程;(2)若点P 是椭圆C 上异于点A ,B 的任意一点,且直线PA 、PB 分别与y 轴交于点M 、N ,若MF 2、NF 2的斜率分别为k 1、k 2,求证:k 1•k 2是定值.18.(本小题满分16分)现有半径为、圆心角为的扇形材料,要裁剪出一个五边形工件,如图所示.其中分别在上,在上,且,,.记,五边形的面积为.(1)试求关于的函数关系式;(2)求的最大值.19.(本小题满分16分)已知集合M是满足下列性质的函数f(x)的全体,存在实数a、k(k≠0),对于定义域内的任意x 均有f(a+x)=kf(a﹣x)成立,称数对(a,k)为函数f(x)的“伴随数对”(1)判断f(x)=x2是否属于集合M,并说明理由;(2)若函数f(x)=sinx∈M,求满足条件的函数f(x)的所有“伴随数对”;(3)若(1,1),(2,﹣1)都是函数f(x)的“伴随数对”,当1≤x<2时,;当x=2时,f(x)=0.求当2014≤x≤2016时,函数y=f(x)的零点.20.(本小题满分16分)已知数列,满足(…).(1)若,求的值;(2)若且,则数列中第几项最小?请说明理由;(3)若(n=1,2,3,…),求证:“数列为等差数列”的充分必要条件是“数列为等差数列且(n=1,2,3,…)”.。
2017年江苏省泰州市高考数学二模试卷(解析版)

2017年江苏省泰州市高考数学二模试卷一、填空题:本大题共14小题,每小题5分,共70分).1.(5分)已知集合A={0,3,4},B={﹣1,0,2,3},则A∩B=.2.(5分)已知复数z=,其中i为虚数单位,则复数z的模是.3.(5分)根据如图所示的伪代码,可知输出的结果S为.4.(5分)现有1000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm)的数据分组及各组的频数如表,据此估计这1000根中纤维长度不小于37.5mm的根数是.5.(5分)100张卡片上分别写有1,2,3,…,100,从中任取1张,则这张卡片上的数是6的倍数的概率是.6.(5分)在平面直角坐标系xOy中,已知抛物线y2=4x上一点P到焦点的距离为3,则点P的横坐标是.7.(5分)现有一个底面半径为3cm,母线长为5cm的圆锥实心铁器,将其高温融化后铸成一个实心铁球(不计损耗),则该铁球的半径是cm.8.(5分)函数f(x)=的定义域是.9.(5分)已知{a n}是公差不为0 的等差数列,S n是其前n项和,若a2a3=a4a5,S9=1,则a1的值是.10.(5分)在平面直角坐标系xOy中,已知圆C1:(x﹣4)2+(y﹣8)2=1,圆C2:(x﹣6)2+(y+6)2=9.若圆心在x轴上的圆C同时平分圆C1和圆C2的圆周,则圆C的方程是.11.(5分)如图,在平面四边形ABCD中,O为BD的中点,且OA=3,OC=5,若•=﹣7,则•的值是.12.(5分)在△ABC中,已知AB=2,AC2﹣BC2=6,则tan C的最大值是.13.(5分)已知函数f(x)=其中m>0,若函数y=f(f(x))﹣1有3个不同的零点,则m的取值范围是.14.(5分)已知对任意的x∈R,3a(sin x+cos x)+2b sin2x≤3(a,b∈R)恒成立,则当a+b 取得最小值时,a的值是.二、解答题:本大题共6小题,共90分.解答写出文字说明、证明过程或演算过程. 15.(14分)已知sin(α+)=,α∈(,π).求:(1)cosα的值;(2)sin(2α﹣)的值.16.(14分)如图,在直三棱柱ABC﹣A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.求证:(1)DE∥平面B1BCC1;(2)平面A1BC⊥平面A1ACC1.17.(14分)如图,在平面直角坐标系xOy中,已知椭圆+=1(a>b>0)的离心率为,C为椭圆上位于第一象限内的一点.(1)若点C的坐标为(2,),求a,b的值;(2)设A为椭圆的左顶点,B为椭圆上一点,且=,求直线AB的斜率.18.(16分)一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击,已知缉私艇的最大航速是走私船最大航速的3倍,假设缉私艇和走私船均按直线方向以最大航速航行.(1)若走私船沿正东方向逃离,试确定缉私艇的追击方向,使得用最短时间在领海内拦截成功;(参考数据:sin17°≈,≈5.7446)(2)问:无论走私船沿何方向逃跑,缉私艇是否总能在领海内成功拦截?并说明理由.19.(16分)已知函数f(x)=,g(x)=lnx,其中e为自然对数的底数.(1)求函数y=f(x)g(x)在x=1处的切线方程;(2)若存在x1,x2(x1≠x2),使得g(x1)﹣g(x2)=λ[f(x2)﹣f(x1)]成立,其中λ为常数,求证:λ>e;(3)若对任意的x∈(0,1],不等式f(x)g(x)≤a(x﹣1)恒成立,求实数a的取值范围.20.(16分)设数列{a n}的前n项和为S n(n∈N*),且满足:①|a1|≠|a2|;②r(n﹣p)S n+1=(n2+n)a n+(n2﹣n﹣2)a1,其中r,p∈R,且r≠0.(1)求p的值;(2)数列{a n}能否是等比数列?请说明理由;(3)求证:当r=2时,数列{a n}是等差数列.A.[选修4-1:几何证明选讲]21.(10分)如图,已知△ABC内接于⊙O,连结AO并延长交⊙O于点D,∠ACB=∠ADC.求证:AD•BC=2AC•CD.B.[选修4-2:矩阵与变换]22.(10分)设矩阵A满足:A=,求矩阵A的逆矩阵A﹣1.C.[选修4-4:坐标系与参数方程选讲]23.在平面直角坐标系xOy中,已知直线(l为参数)与曲线(t为参数)相交于A,B两点,求线段AB的长.D.[选修4-5:不等式选讲]24.设x,y,z均为正实数,且xyz=1,求证:++≥xy+yz+zx.【必做题】每小题10分,共计20分.25.(10分)某乐队参加一户外音乐节,准备从3首原创新曲和5首经典歌曲中随机选择4首进行演唱.(1)求该乐队至少演唱1首原创新曲的概率;(2)假定演唱一首原创新曲观众与乐队的互动指数为a(a为常数),演唱一首经典歌曲观众与乐队的互动指数为2a,求观众与乐队的互动指数之和X的概率分布及数学期望.26.(10分)设n≥2,n∈N*,有序数组(a1,a2,…,a n)经m次变换后得到数组(b m,1,b m,2,…,b m,n),其中b1,i=a i+a i+1,b m,i=b m﹣1,i+b m﹣1,i+1(i=1,2,…,n),a n+1=a1,b m﹣1,n+1=b m﹣1,1(m≥2).例如:有序数组(1,2,3)经1次变换后得到数组(1+2,2+3,3+1),即(3,5,4);经第2次变换后得到数组(8,9,7).(1)若a i=i(i=1,2,…,n),求b3,5的值;(2)求证:b m,i=a i+j∁m j,其中i=1,2,…,n.(注:i+j=kn+t时,k∈N*,i=1,2,…,n,则a i+j=a1)2017年江苏省泰州市高考数学二模试卷参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共70分).1.(5分)已知集合A={0,3,4},B={﹣1,0,2,3},则A∩B={0,3}.【解答】解:集合A={0,3,4},B={﹣1,0,2,3},则A∩B={0,3};故答案为:{0,3}2.(5分)已知复数z=,其中i为虚数单位,则复数z的模是.【解答】解:∵z==,∴.故答案为:.3.(5分)根据如图所示的伪代码,可知输出的结果S为7.【解答】解:模拟执行程序,可得S=1,I=1满足条件I<8,S=3,I=4满足条件I<8,S=5,I=7满足条件I<8,S=7,I=10不满足条件I<8,退出循环,输出S的值为7.故答案为:7.4.(5分)现有1000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm)的数据分组及各组的频数如表,据此估计这1000根中纤维长度不小于37.5mm的根数是180.【解答】解:由频率分布表知:纤维长度不小于37.5mm的频率为:=0.18,∴估计这1000根中纤维长度不小于37.5mm的根数是1000×0.18=180.故答案为:180.5.(5分)100张卡片上分别写有1,2,3,…,100,从中任取1张,则这张卡片上的数是6的倍数的概率是.【解答】解:在100张卡片上分别写上1至100这100个数字,从中任取一张共有100种取法,其中所得卡片上的数字为6的倍数的数是:6,12,18,24,30,36,42,48,54,60,66,72,78,84,90,96共16个,∴所得卡片上的数字为6的倍数的数共有16个.∴所得卡片上的数字为6的倍数的概率P==,故答案为:.6.(5分)在平面直角坐标系xOy中,已知抛物线y2=4x上一点P到焦点的距离为3,则点P的横坐标是2.【解答】解:∵抛物线y2=4x=2px,∴p=2,由抛物线定义可知,抛物线上任一点到焦点的距离与到准线的距离是相等的,∴|PF|=x+1=3,∴x=2,故答案为:2.7.(5分)现有一个底面半径为3cm,母线长为5cm的圆锥实心铁器,将其高温融化后铸成一个实心铁球(不计损耗),则该铁球的半径是cm.【解答】解:设该铁球的半径为r,∵底面半径为3cm,母线长为5cm的圆锥实心铁器,∴锥体的母线、半径、高构成直角三角形,∴h==4,锥体体积V=×π×32×4=12π,圆球体积=锥体体积V==12π,解得r=.故答案为:.8.(5分)函数f(x)=的定义域是[﹣2,2].【解答】解:由lg(5﹣x2)≥0,得5﹣x2≥1,即x2≤4,解得﹣2≤x≤2.∴函数f(x)=的定义域是[﹣2,2].故答案为:[﹣2,2].9.(5分)已知{a n}是公差不为0 的等差数列,S n是其前n项和,若a2a3=a4a5,S9=1,则a1的值是.【解答】解:设等差数列{a n}的公差为d(d≠0),∵a2a3=a4a5,S9=1,∴,解得:a1=,故答案为:.10.(5分)在平面直角坐标系xOy中,已知圆C1:(x﹣4)2+(y﹣8)2=1,圆C2:(x﹣6)2+(y+6)2=9.若圆心在x轴上的圆C同时平分圆C1和圆C2的圆周,则圆C的方程是x2+y2=81.【解答】解:由题意,圆C与圆C1和圆C2的公共弦分别为圆C1和圆C2的直径,设C(x,0),则(x﹣4)2+(0﹣8)2+1=(x﹣6)2+(0+6)2+9,∴x=0,∴圆C的方程是x2+y2=81.故答案为x2+y2=81.11.(5分)如图,在平面四边形ABCD中,O为BD的中点,且OA=3,OC=5,若•=﹣7,则•的值是9.【解答】解:平面四边形ABCD中,O为BD的中点,且OA=3,OC=5,∴+=;若•=﹣7,则(+)•(+)=+•+•+•=+•(+)﹣=32﹣=﹣7;∴=16,∴||=||=4;∴•=(+)•(+)=•+•+•+=﹣+•(+)+=﹣42+0+52=9.12.(5分)在△ABC中,已知AB=2,AC2﹣BC2=6,则tan C的最大值是.【解答】解:∵AB=c=2,AC2﹣BC2=b2﹣a2=6,∴由余弦定理可得:4=a2+b2﹣2ab cos C,∴(b2﹣a2)=a2+b2﹣2ab cos C,∴()2﹣2××cos C+=0,∵△≥0,∴可得:cos C≥,∵b>c,可得C为锐角,又∵tan C在(0,)上单调递增,∴当cos C=时,tan C取最大值,∴tan C===.故答案为:.13.(5分)已知函数f(x)=其中m>0,若函数y=f(f(x))﹣1有3个不同的零点,则m的取值范围是(0,).【解答】解:1、当x<0时,f(f(x))=(﹣x+m)2﹣1,图象为开口向上的抛物线的在y 轴左侧的部分,顶点为(0,m2﹣1)2、当0≤x<1时,f(f(x))=﹣x2+1+m,图象为开口向下的抛物线在0≤x<1之间的部分,顶点为(0,m+1).根据题意m>0,所以m+1>13、当x≥1时,f(f(x))=(x2﹣1)2﹣1,图象为开口向上的抛物线在x=1右侧的部分,顶点为(1,﹣1)根据题意,函数y=f(f(x))﹣1有3个不同的零点,即f(f(x))的图象与y=1有3个不同的交点.根据以上分析的3种情况,第2及第3种情况的图象分别与y=1有不同的2个交点,所以只需要第1种情况与y=1有1个交点即可,所以只要m2﹣1<1即可,解得m<.再根据题意m>0可得m的取值范围为(0,)故答案为(0,).14.(5分)已知对任意的x∈R,3a(sin x+cos x)+2b sin2x≤3(a,b∈R)恒成立,则当a+b取得最小值时,a的值是﹣.【解答】解:由题意可令sin x+cos x=﹣,两边平方可得1+2sin x cos x=,即有sin2x=﹣,代入3a(sin x+cos x)+2b sin2x≤3,可得﹣a﹣b≤3,可得a+b≥﹣2,当a+b=﹣2时,令t=sin x+cos x=sin(x+)∈[﹣,],即有sin2x=t2﹣1,代入3a(sin x+cos x)+2b sin2x≤3,可得﹣2bt2+3(2+b)t+3+2b≥0,对t∈[﹣,]恒成立,则△=9(2+b)2+8b(3+2b)≤0,即为(5b+6)2≤0,但(5b+6)2≥0,则5b+6=0,可得b=﹣,a=﹣.而当b=﹣,a=﹣时,3a(sin x+cos x)+2b sin2x=﹣t﹣(t2﹣1)=﹣(t+)2+3≤3.所以当a+b取得最小值﹣2,此时a=﹣.另解:由a+b取得最小值,故令3(sin x+cos x)=2sin2x=λ<0,则a+b≥,即a+b的最小值为,t=sin x+cos x=sin(x+)∈[﹣,],sin2x=t2﹣1,则λ=3t=2(t2﹣1),解得t=﹣,则λ=﹣,此时﹣(a+b)≤3,解得a+b≥﹣2,即有当a+b=﹣2时,3at+2(﹣2﹣a)(t2﹣1)≤3,对t∈[﹣,]恒成立,即2(a+2)t2﹣3at﹣2a﹣1≥0对t∈[﹣,]恒成立,设f(t)=2(a+2)t2﹣3at﹣2a﹣1,由f(﹣)=0且为f(t)的最小值,所以只能把f(t)看做t为自变量的函数,则2(a+2)>0,=﹣,解得a=﹣.故答案为:﹣.二、解答题:本大题共6小题,共90分.解答写出文字说明、证明过程或演算过程. 15.(14分)已知sin(α+)=,α∈(,π).求:(1)cosα的值;(2)sin(2α﹣)的值.【解答】解:(1)sin(α+)=,即sinαcos+cosαsin=,化简:sinα+cosα=…①sin2α+cos2α=1…②.由①②解得cosα=﹣或cosα=∵α∈(,π).∴cosα=﹣(2)∵α∈(,π).cosα=﹣∴sinα=,那么:cos2α=1﹣2sin2α=,sin2α=2sinαcosα=∴sin(2α﹣)=sin2αcos﹣cos2αsin=.16.(14分)如图,在直三棱柱ABC﹣A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.求证:(1)DE∥平面B1BCC1;(2)平面A1BC⊥平面A1ACC1.【解答】证明:(1)由题意,D,E分别为A1B,A1C的中点,∴DE∥BC,∵DE⊄平面B1BCC1,BC⊂平面B1BCC1,∴DE∥平面B1BCC1;(2)∵AA1⊥平面ABC,BC⊂平面ABC,∴AA1⊥BC,∵AC⊥BC,AC∩AA1=A,∴BC⊥平面A1ACC1,∵BC⊂平面A1BC,∴平面A1BC⊥平面A1ACC1.17.(14分)如图,在平面直角坐标系xOy中,已知椭圆+=1(a>b>0)的离心率为,C为椭圆上位于第一象限内的一点.(1)若点C的坐标为(2,),求a,b的值;(2)设A为椭圆的左顶点,B为椭圆上一点,且=,求直线AB的斜率.【解答】解:(1)由题意可知:椭圆的离心率e===,则=,①由点C在椭圆上,将(2,)代入椭圆方程,,②解得:a2=9,b2=5,∴a=3,b=,(2)方法一:由(1)可知:=,则椭圆方程:5x2+9y2=5a2,设直线OC的方程为x=my(m>0),B(x1,y1),C(x2,y2),,消去x整理得:5m2y2+9y2=5a2,∴y2=,由y2>0,则y2=,由=,则AB∥OC,设直线AB的方程为x=my﹣a,则,整理得:(5m2+9)y2﹣10amy=0,由y=0,或y1=,由=,则(x1+a,y1)=(x2,y2),则y2=2y1,则=2×,(m>0),解得:m=,则直线AB的斜率=;方法二:由(1)可知:椭圆方程5x2+9y2=5a2,则A(﹣a,0),B(x1,y1),C(x2,y2),由=,则(x1+a,y1)=(x2,y2),则y2=2y1,由B,C在椭圆上,∴,解得:,则直线直线AB的斜率k==.直线AB的斜率.18.(16分)一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击,已知缉私艇的最大航速是走私船最大航速的3倍,假设缉私艇和走私船均按直线方向以最大航速航行.(1)若走私船沿正东方向逃离,试确定缉私艇的追击方向,使得用最短时间在领海内拦截成功;(参考数据:sin17°≈,≈5.7446)(2)问:无论走私船沿何方向逃跑,缉私艇是否总能在领海内成功拦截?并说明理由.【解答】解:(1)设缉私艇在C处与走私船相遇,则AC=3BC.△ABC中,由正弦定理可得sin∠BAC==,∴∠BAC=17°,∴缉私艇应向北偏东47°方向追击,△ABC中,由余弦定理可得cos120°=,∴BC≈1.68615.B到边界线l的距离为3.8﹣4sin30°=1.8,∵1.68615<1.8,∴能最短时间在领海内拦截成功;(2)以A为原点,建立如图所示的坐标系,则B(2,2),设缉私艇在P(x,y)出与走私船相遇,则P A=3PB,即x2+y2=9[(x﹣2)2+(y﹣2)2],即(x﹣)2+(y﹣)2=,∴P的轨迹是以(,)为圆心,为半径的圆,∵圆心到边界线l:x=3.8的距离为1.55,大于圆的半径,∴无论走私船沿何方向逃跑,缉私艇总能在领海内成功拦截.19.(16分)已知函数f(x)=,g(x)=lnx,其中e为自然对数的底数.(1)求函数y=f(x)g(x)在x=1处的切线方程;(2)若存在x1,x2(x1≠x2),使得g(x1)﹣g(x2)=λ[f(x2)﹣f(x1)]成立,其中λ为常数,求证:λ>e;(3)若对任意的x∈(0,1],不等式f(x)g(x)≤a(x﹣1)恒成立,求实数a的取值范围.【解答】解:(1)y=f(x)g(x)=,y′=,x=1时,y=0,y′=,故切线方程是:y=x﹣;(2)证明:由g(x1)﹣g(x2)=λ[f(x2)﹣f(x1)],得:g(x1)+λf(x1)=g(x2)+λf(x2),令h(x)=g(x)+λf(x)=lnx+,(x>0),h′(x)=,令ω(x)=e x﹣λx,则ω′(x)=e x﹣λ,由x>0,得e x>1,①λ≤1时,ω′(x)>0,ω(x)递增,故h′(x)>0,h(x)递增,不成立;②λ>1时,令ω′(x)=0,解得:x=lnλ,故ω(x)在(0,lnλ)递减,在(lnλ,+∞)递增,∴ω(x)≥ω(lnλ)=λ﹣λlnλ,令m(λ)=λ﹣λlnλ,(λ>1),则m′(λ)=﹣lnλ<0,故m(λ)递减,又m(e)=0,若λ≤e,则m(λ)≥0,ω(x)≥0,h(x)递增,不成立,若λ>e,则m(λ)<0,函数h(x)有增有减,满足题意,故λ>e;(3)由f(x)g(x)≤a(x﹣1)得lnx﹣ae x(x﹣1)≤0,令F(x)=lnx﹣ae x(x﹣1),x∈(0,1],则F′(x)=﹣axe x=xe x(﹣a),F′(1)=﹣a①a≤,因为≥,xe x>0,所以F′(x)≥0,所以F(x)在(0,+∞]上为单调增函数,所以F(x)≤F(1)=0,故原不等式恒成立.②法一:当a>,由(2)知e x≥ex,F′(x)≤﹣aex2=,当(ae)<x<1时,F′(x)<0,F(x)为单调减函数.所以F(x)>F(1)=0,不合题意.法二:当a>,一方面F′(1)=1﹣ae<0.另一方面,∃x1=<1,F(x1)≥﹣aex1=x1(﹣ae)=x1ae(ae﹣1)>0.所以∃x1∈(x1,1),使F′(x0)=0,又,F′(x)在(0,+∞)上为单调减函数,所以当x0<x<1时,使F′(x)<0,故F(x)在(x0,1)上为单调减函数.所以F(x)>F(1)=0,不合题意.综上:a≤20.(16分)设数列{a n}的前n项和为S n(n∈N*),且满足:①|a1|≠|a2|;②r(n﹣p)S n+1=(n2+n)a n+(n2﹣n﹣2)a1,其中r,p∈R,且r≠0.(1)求p的值;(2)数列{a n}能否是等比数列?请说明理由;(3)求证:当r=2时,数列{a n}是等差数列.【解答】解:(1)n=1时,r(1﹣p)(a1+a2)=2a1﹣2a1,其中r,p∈R,且r≠0.又|a1|≠|a2|.∴1﹣p=0,解得p=1.(2)设a n=ka n﹣1(k≠±1),r(n﹣1)S n+1=(n2+n)a n+(n2﹣n﹣2)a1,∴rS3=6a2,2rS4=12a3+4a1,化为:r(1+k+k2)=6k,r(1+k+k2+k3)=6k2+2.联立解得r=2,k=1(不合题意),舍去,因此数列{a n}不是等比数列.(3)证明:r=2时,2(n﹣1)S n+1=(n2+n)a n+(n2﹣n﹣2)a1,∴2S3=6a2,4S4=12a3+4a1,6S5=20a4+10a1.化为:a1+a3=2a2,a2+a4=2a3,a3+a5=2a4.假设数列{a n}的前n项成等差数列,公差为d.则2(n﹣1)=(n2+n)[a1+(n﹣1)d]+(n2﹣n﹣2)a1,化为a n+1=a1+(n+1﹣1)d,因此第n+1项也满足等差数列的通项公式,综上可得:数列{a n}成等差数列.A.[选修4-1:几何证明选讲]21.(10分)如图,已知△ABC内接于⊙O,连结AO并延长交⊙O于点D,∠ACB=∠ADC.求证:AD•BC=2AC•CD.【解答】证明:∵∠ACB=∠ADC,AD是⊙O的直径,∴AD垂直平分BC,设垂足为E,∵∠ACB=∠EDC,∠ACD=∠CED,∴△ACD∽△CED,∴,∴AD•BC=AC•CD,∴AD•BC=2AC•CD.B.[选修4-2:矩阵与变换]22.(10分)设矩阵A满足:A=,求矩阵A的逆矩阵A﹣1.【解答】解:A=,设B=,则丨B丨=6,B*=,则B﹣1=×B*=×=,A=×B﹣1==,A=,丨A丨=﹣,A*=A﹣1=×=,矩阵A的逆矩阵A﹣1=.C.[选修4-4:坐标系与参数方程选讲]23.在平面直角坐标系xOy中,已知直线(l为参数)与曲线(t为参数)相交于A,B两点,求线段AB的长.【解答】解:直线(l为参数)与曲线(t为参数)的普通方程分别为x﹣y=﹣,y2=8x,联立可得x2﹣5x+=0,∴|AB|==4.D.[选修4-5:不等式选讲]24.设x,y,z均为正实数,且xyz=1,求证:++≥xy+yz+zx.【解答】证明:∵x,y,z均为正实数,且xyz=1,∴++=++,∴由柯西不等式可得(++)(xy+yz+zx)≥(++)2=(++)2=(xy+yz+zx)2.∴++≥xy+yz+zx.【必做题】每小题10分,共计20分.25.(10分)某乐队参加一户外音乐节,准备从3首原创新曲和5首经典歌曲中随机选择4首进行演唱.(1)求该乐队至少演唱1首原创新曲的概率;(2)假定演唱一首原创新曲观众与乐队的互动指数为a(a为常数),演唱一首经典歌曲观众与乐队的互动指数为2a,求观众与乐队的互动指数之和X的概率分布及数学期望.【解答】解:(1)设“该乐队至少演唱1首原创新曲”的事件为A,则P(A)=1﹣P =1﹣=.(2)由题意可得:X=5a,6a,7a,8a.P(X=5a)===,P(X=6a)===,P(X=7a)===,P(X=8a)===.E(X)=5a×+6a×+7a×+8a×=a.26.(10分)设n≥2,n∈N*,有序数组(a1,a2,…,a n)经m次变换后得到数组(b m,1,b m,2,…,b m,n),其中b1,i=a i+a i+1,b m,i=b m﹣1,i+b m﹣1,i+1(i=1,2,…,n),a n+1=a1,b m﹣1,n+1=b m﹣1,1(m≥2).例如:有序数组(1,2,3)经1次变换后得到数组(1+2,2+3,3+1),即(3,5,4);经第2次变换后得到数组(8,9,7).(1)若a i=i(i=1,2,…,n),求b3,5的值;(2)求证:b m,i=a i+j∁m j,其中i=1,2,…,n.(注:i+j=kn+t时,k∈N*,i=1,2,…,n,则a i+j=a1)【解答】解:(1)依题意(1,2,3,4,5,6,7,8,…,n),第一次变换为(3,5,7,9,11,13,15,…,n+1),第二次变换为(8,12,16,20,24,28,…,n+4),第三次变换为(20,28,36,44,52,…,n+12),∴b3,5=52,(2)用数学归纳法证明:对m∈N*,b m,i=a i+j∁m j,其中i=1,2,…,n,(i)当m=1时,b1,i=a i+j C1j,其中i=1,2,…,n,结论成立,(ii)假设m=k时,k∈N*时,b k,i=a i+j∁k j,其中i=1,2,…,n,则m=k+1时,b k+1,i=b k,i+b k,i+1=a i+j∁k j+a i+j+1∁k j=a i+j∁k j+a i+j+1∁k j﹣1,=a i∁k0+a i+j(∁k j+∁k j﹣1)+a i+k+1∁k k,=a i C k+10+a i+j C k+1j+a i+k+1C k+1k+1,=a i+j C k+1j,所以结论对m=k+1时也成立,由(i)(ii)可知,对m∈N*,b m,i=a i+j∁m j,其中i=1,2,…,n成立。
江苏省泰州中学2017届高三上学期第二次月考数学试题 含答案bybao

江苏省泰州中学2016-2017学年度第一学期高三数学第二次质量检测2016.12一、填空题:(本大题共14小题,每小题5分,共70分)1. 已知R 为实数,集合{}(){}1,2,3,4,5,|40A B x x x ==-<,则()R AC B = 。
2. “1x >”是“()12log 20x +<"的一个条件.(在“充分不必要条件”、“必要不充分条件”、“充要”、“既不充分也不必要"选择一个填写).3。
已知等差数列{}na 的前n 项和为nS ,若132,12aS ==,则6a = 。
4。
设曲线11x y x +=-在点()3,2处的切线与直线30ax y ++=垂直,则a = .5.设实数,x y 满足条件1024x y x y x +≤⎧⎪-≤⎨⎪≥⎩,则23z x y =+的最大值是.6。
已知奇函数()f x 的图象关于直线2x =-对称,当[]0,2x ∈时,()2f x x =,那么()9f -= 。
7。
直线3y kx =+与圆()()22234x y -+-=相交于M ,N 两点,若23MN ≥实数k 的取值范围是 。
8.已知3sin 4cos 5αα+=,则tan α= 。
9.设平面向量()()(),0,,0,2,1a x b y c ===(其中0,0x y >>)若()()a c b c -⊥-,则a b +的最小值为 . 10。
已知函数()3sin 2cos2f x x x ωω=-(其中()0,1ω∈),若()f x 的图象经过点,06π⎛⎫⎪⎝⎭,则()f x 在[]0,π区间上的单调递增区间为 。
11。
已知ABC ∆中,BC=2,G 为ABC ∆的重心,且满足AG BG ⊥,则ABC ∆的面积的最大值为 .12。
已知,,x y z 均为非负实数,且2x y z ++=,则3213xy z ++的最小值为 。
13。
2017届高三第二次教学质量检测数学理试题(12页有答案)

-1012}012}01}-101}-1012} 23B.5A.4C.D.3[+高三年级第二次教学质量检测试题理科数学注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题共60分)一.选择题:本大题共12个小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={-2,,,,,B={x|-2<x≤2},则A B=A.{-1,,,B.{-1,,C.{-2,,,D.{-2,,,,2.复数2-i1+i对应的点在A.第一象限B.第二象限C.第三象限D.第四象限3.已知向量a=(2,-1),b=(3,x),若a⋅b=3,则x=A.3B.4C.5D.64.已知双曲线x2y2-a b23=1的一条渐近线方程为y=x,则此双曲线的离心率为457445.已知条件p:x-4≤6;条件q:x≤1+m,若p是q的充分不必要条件,则m的取值范围是A.(-∞,-1]B.(-∞,9]C.1,9]D.[9,∞)6.运行如图所示的程序框图,输出的结果S=A.14B.30C.62D.1268.已知α,β是两个不同的平面,l,m,n是不同的直线,下列命题不正确的是A.πA.332D.27.(x-1)n的展开式中只有第5项的二项式系数最大,则展开式中含x2项的系数是xA.56B.35C.-56D.-35...A.若l⊥m,l⊥n,m⊂α,n⊂α,则l⊥αB.若l//m,l⊂/α,m⊂α,则l//αC.若α⊥β,αβ=l,m⊂α,m⊥l,则m⊥βD.若α⊥β,m⊥α,n⊥β,,则m⊥n9.已知f(x)=sin x+3cos x(x∈R),函数y=f(x+ϕ)的图象关于直线x=0对称,则ϕ的值可以是πππB.C.D.263410.男女生共8人,从中任选3人,出现2个男生,1个女生的概率为1528,则其中女生人数是A.2人B.3人C.2人或3人D.4人11.已知抛物线y2=4x,过焦点F作直线与抛物线交于点A,B(点A在x轴下方),点A与1点A关于x轴对称,若直线AB斜率为1,则直线A B的斜率为12B.3C.12.下列结论中,正确的有①不存在实数k,使得方程x ln x-1x2+k=0有两个不等实根;2②已知△ABC中,a,b,c分别为角A,B,C的对边,且a2+b2=2c2,则角C的最大值为π6;③函数y=ln与y=ln tan x2是同一函数;④在椭圆x2y2+a2b2=1(a>b>0),左右顶点分别为A,B,若P为椭圆上任意一点(不同于A,B),则直线PA与直线PB斜率之积为定值.A.①④B.①③C.①②D.②④13.已知等比数列{a}的前n项和为S,且a+a=5n2414.已知实数x、y满足约束条件⎨y≥2,则z=2x+4y的最大值为______.⎪x+y≤6②若a∈(0,1),则a<a1+11-x是奇函数(第Ⅱ卷(非选择题共90分)本卷包括必考题和选考题两部分.第13题~21题为必考题,每个试题考生都必须做答.第22题、第23题为选考题,考生根据要求做答.二.填空题:本大题共4小题;每小题5分,共20分.5,a+a=,则S=__________.n13246⎧x≥2⎪⎩15.一个几何体的三视图如图所示,则这个几何体的外接球的半径为__________.16.下列命题正确是.(写出所有正确命题的序号)①若奇函数f(x)的周期为4,则函数f(x)的图象关于(2,0)对称;③函数f(x)=ln;三.解答题:本大题共6小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分12分)在△ABC中,角A、B、C的对边分别为a,b,c,且a=3,b=4,B=A+高三理科数学试题和答案第3页共6页π2., 20 40 60 80 ,(1)求 cos B 的值;(2)求 sin 2 A + sin C 的值.18.(本小题满分 12 分)如图,三棱柱 ABC - A B C 中,侧棱 AA ⊥ 平面 ABC , ∆ABC 为等腰直角三角形,1 1 1 1∠BAC = 90 ,且 AA = AB , E , F 分别是 C C , BC 的中点.1 1(1)求证:平面 AB F ⊥ 平面 AEF ;1(2)求二面角 B - AE - F 的余弦值.119.(本小题满分 12 分)某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0 100],样本数据分组为第一组[0, ),第二组[20, ),第 三组 [40, ),第四组 [60, ),第五组 [80 100].(1)求直方图中 x 的值;(2)如果年上缴税收不少于 60 万元的企业可申请政策优惠,若共抽取企业 1200 家,试估计有多少企业可以申请政策优惠;(3)从所抽取的企业中任选 4 家,这 4 家企业年上缴税收少于 20 万元的家数记为 X ,求 X 的分布列和数学期望.(以直方图中的频率作为概率)= 1(a > b > 0) 经过点 P (2, 2) ,离心率 e = ,直线 l 的方程为 220.(本小题满分 12 分)已知椭圆 C : x 2 y 2+ a 2 b 22 2x = 4 .(1)求椭圆 C 的方程;(2)经过椭圆右焦点 F 的任一直线(不经过点 P )与椭圆交于两点 A , B ,设直线 AB 与l 相交于点 M ,记 P A , PB , PM 的斜率分别为 k , k , k ,问:是否存在常数 λ ,使得1 2 3k + k = λ k ?若存在,求出 λ 的值,若不存在,说明理由.12321.(本小题满分 12 分)已知函数 f ( x ) = ax + ln x ,其中 a 为常数,设 e 为自然对数的底数.(1)当 a = -1 时,求 f ( x ) 的最大值;(2)若 f ( x ) 在区间 (0, e ] 上的最大值为 -3 ,求 a 的值;(3)设 g ( x ) = xf ( x ), 若 a > 0, 对于任意的两个正实数 x , x ( x ≠ x ) ,1 2 1 2证明: 2 g ( x 1 + x 2) < g ( x ) + g ( x ) .1 2请考生在第 22、23 二题中任选一题做答,如果多做,则按所做的第一题记分.做答时,用⎪⎪ 5⎩17.解:(1)∵ B = A + , ∴ A = B -, ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 1 分 ==2B 铅笔在答题卡上把所选题目对应的题号涂黑.22.(本小题满分 10 分)选修 4-4:坐标系与参数方程⎧3 x =- t + 2 在直角坐标系 xOy 中,直线 l 的参数方程为 ⎨ ( t 为参数),以原点 O 为极点, x⎪ y = 4 t ⎪5轴正半轴为极轴建立极坐标系,圆C 的极坐标方程为 ρ = a sin θ .(1)若 a = 2 ,求圆 C 的直角坐标方程与直线 l 的普通方程;(2)设直线 l 截圆 C 的弦长等于圆 C 的半径长的 3 倍,求 a 的值.23.(本小题满分 10 分)选修 4-5:不等式选讲已知函数 f ( x ) = 2x -1 + 2x + 5 ,且 f ( x ) ≥ m 恒成立.(1)求 m 的取值范围;(2)当 m 取最大值时,解关于 x 的不等式: x - 3 - 2x ≤ 2m - 8 .高三第二次质量检测理科数学答案一.ADABD CCABC CA二.13.631614.20 15. 61 16.①③ππ2 23 4 又 a = 3, b = 4 ,所以由正弦定理得 ,sin Asin B34所以, ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅3 分- cos B sin B所以 -3sin B = 4cos B ,两边平方得 9sin 2 B = 16cos 2 B ,3又 sin 2 B + cos 2 B = 1 ,所以 cos B = ± , ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 5 分5π 3而 B > ,所以 cos B = - . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 6 分2 53 4(2)∵ cos B = - ,∴ sin B = , ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 7 分5 5∴面 ABC ⊥ 面 BB C C..........2 分+ = 则 F (0,0,0) , A ( 22 2 2 2 2 1 ∵ B = A +π2,∴ 2 A = 2 B - π ,∴ sin 2 A = sin(2 B - π ) = - sin 2 B ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 8 分4 3 24= -2sin B cos B = -2 ⨯ ⨯ (- ) = ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 10 分5 5 25又 A + B + C = π ,∴ C = 3π 2- 2 B ,7 24 7 31∴ sin C = - cos 2 B = 1 - cos 2 B = .∴ sin 2 A + sin C = . (12)25 25 25 25分18.解答: (1)证明:∵ F 是等腰直角三角形 ∆ABC 斜边 BC 的中点,∴ AF ⊥ BC .又∵侧棱 AA ⊥ 平面ABC ,11 1∴ AF ⊥ 面 BB 1C 1C , AF ⊥ B 1F .…3 分设 AB = AA = 1 ,则1,EF= , .∴ B F 2 + EF 2 = B E 2 ,∴ B F ⊥ EF ........... 4 分1 11又 AF ⋂ EF = F ,∴ B F ⊥平面 AEF .…1而 B F ⊂ 面 AB F ,故:平面 AB F ⊥ 平面 AEF . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅5 分1 11(2)解:以 F 为坐标原点, FA , FB 分别为 x , y 轴建立空间直角坐标系如图,设 AB = AA = 1 ,12 2 1,0,0) , B (0, - ,1) , E (0, - , ) ,12 2 1 2 2AE = (- , - , ) , AB = (- , ,1) .… ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 6 分2 2 2 2 2由(1)知, B F ⊥平面 AEF ,取平面 AEF 的法向量:12m = FB = (0, ,1) . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 7 分14 4 256 4 4 4 644 4 64 4 4 64设平面 B AE 的法向量为 n = ( x , y , z ) ,1由取 x = 3 ,得 n = (3, -1,2 2) (10),分设二面角 B - AE - F 的大小为θ ,1则 cos θ=|cos <>|=| |= .由图可知θ 为锐角,∴所求二面角 B - AE - F 的余弦值为.… ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 12 分119.解答: 解:(I )由直方图可得: 20 ⨯ (x + 0.025 + 0.0065 + 0.003 ⨯ 2) = 1解得 x = 0.0125 .⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 2 分(II )企业缴税收不少于 60 万元的频率 = 0.003 ⨯ 2 ⨯ 20 = 0.12 , ∴1200 ⨯ 0.12 = 144 .∴1200 个企业中有144 个企业可以申请政策优惠.⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 4 分(III ) X 的可能取值为 0,1,2,3,4 .由(I )可得:某个企业缴税少于 20 万元的概率 = 0.0125 ⨯ 20 = 0.25 =分1 3 81 1 3 27P ( X = 0) = C 0 ( )0 ( )4 = P ( X = 1) = C 1 ( )1 ( )3 = 41 3 27 1 3 3P ( X = 2) = C 2 ( )2 ( )2 = P ( X = 3) = C 3 ( )3 ( )1 =4 4 14 (5)X0 1 2 3 44 4 256∴ E ( X ) = 0 ⨯ 81+ = 1 ① 又e = , 所以 = = 4, a = 8,b 1 + 2k 2 1 + 2k 2, x x = x - 2 x - 22, k = k = 2k - 2 4 - 2 2P8125627 64 27 64 3 64 1 2561 3 1P ( X = 4) = C 4 ( )4 ( )0 =4...................................... 10 分............. 11 分27 27 3 1+ 1⨯ + 2 ⨯ + 3 ⨯ + 4 ⨯= 1. ....12 分25664 64 64 25620.解:(1)由点 P (2, 2) 在椭圆上得, 4 2 2 c 2 a 2 b 2 2 a 2②由 ①②得 c 2 2 2 = 4 ,故椭圆 C 的方程为 x 2 y 2+ = 1 ……………………..4 分 8 4(2)假设存在常数 λ ,使得 k + k = λ k .1 23由题意可设 AB 的斜率为k , 则直线AB 的方程为 y = k ( x - 2) ③代入椭圆方程x 2 y 2+ = 1 并整理得 (1+ 2k 2 ) x 2 - 8k 2 x + 8k 2 - 8 = 0 8 48k 2 8k 2 - 8设 A ( x , y ), B ( x , y ) ,则有 x + x = ④ ……………6 分 1 1 2 2 1 2 1 2在方程③中,令 x = 4 得, M (4,2 k ) ,从而 k = y 1 - 2 y 2 - 21 2 1,3 2= k - .又因为 A 、F 、B 共线,则有 k = k AF = k BF ,即有y当 a = -1 时, f ( x ) = - x + ln x , f ' ( x ) = -1 + 1①若 a ≥ - ,则 f ' ( x ) ≥ 0 ,从而 f ( x ) 在 (0, e ] 上是增函数,y1=2= k ……………8 分x - 2x - 21 2所以 k + k = 1 2 y - 2 y - 2 1 + 2 x - 2 x - 21 2= y y 1 11 +2 - 2( + )x - 2 x - 2 x - 2 x - 2 1 2 1 2= 2k - 2x 1 + x 2 - 4x x - 2( x + x ) + 41 212⑤ ……………10 分将④代入⑤得 k + k = 2k - 2 1 2 8k 2- 41 + 2k2 8k 2 - 8 8k 2- 2 + 41 + 2k2 1 + 2k 2= 2k - 2 ,又 k = k - 32 2 ,所以 k + k = 2k 1 2 3 . 故存在常数 λ = 2 符合题意…………12 分21.【解答】解:(1)易知 f ( x ) 定义域为 (0, +∞) ,1 - x= ,x x令 f ' ( x ) = 0 ,得 x = 1 .当 0 < x < 1 时, f ' ( x ) > 0 ;当 x > 1 时, f ' ( x ) < 0 . (2)分∴ f ( x ) 在 (0,1) 上是增函数,在 (1,+∞) 上是减函数.f ( x )max= f (1) = -1.∴函数 f ( x ) 在 (0, +∞) 上的最大值为 -1 . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 4 分(2)∵ f '( x ) = a + 1 1 1, x ∈ (0, e ], ∈ [ , +∞) .x x e1e∴ f ( x )max= f (e ) = ae + 1 ≥ 0 ,不合题意. ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 5 分11② 若 a < - ,则由 f ' ( x ) > 0 ⇒ a +ex> 0 ,即 0 < x < -1a11由 f ' ( x ) < 0 ⇒ a +< 0 ,即 - < x ≤ e . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 6 分xa从而 f ( x ) 在 (0, - ) 上增函数,在 (- (3)法一:即证 2a ( x + x 2) + 2( 12 )ln( 222 2 x 2 x21 1a a, e ) 为减函数∴ f ( x ) max 1 1 = f (- ) = -1 + ln(- ) a a1 1令 -1 + ln(- ) = -3 ,则 ln(- ) = -2a a∴- 11= e -2 -e 2 < -a ,即 a = -e 2.∵ e ,∴ a = -e 2 为所求 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 8 分1 1 x + x x + x2 2 22 ) ≤ ax 2 + ax 2 + x ln x + x ln x 1 2 1 1 222a ( x + x ( x + x )21 2 )2 - ax 2 - ax 2 = a ⋅[ 1 21 2- x 2 - x 2 ]1 2( x - x )2= -a 1 2 2< 0 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 9 分另一方面,不妨设 x < x ,构造函数1 2k ( x ) = ( x + x )ln(1x + x12) - x ln x - x ln x ( x > x )1 1 1x + xx + x则 k ( x ) = 0 ,而 k ' ( x ) = ln 1 - ln x = ln 1 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 10 分1x + x由 0 < x < x 易知 0 < 11< 1 , 即 k ' ( x ) < 0 , k ( x ) 在 ( x , +∞) 上为单调递减且连续, 1x + x故 k ( x ) < 0 ,即 ( x + x )ln( 11) < x ln x + x ln x 1 1相加即得证⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 12 分1法二: g ' ( x ) = 2ax + 1 + ln x , g '' ( x ) = 2a + > 0.........9 分x故 g ' ( x ) 为增函数,不妨令 x > x 21令 h ( x ) = g ( x ) + g ( x ) - 2 g (1x + x12)( x > x )1h ' ( x ) = g '(x ) - g ' (x + x12) ......... 10 分易知 x > x + x x + x1 , 故h ' ( x ) = g '(x ) - g ' ( 12 2) > 0 (11)分而 h ( x ) = 0 , 知 x > x 时, h ( x ) > 0112(2)圆 C : x 2 + y - a ⎫2∴圆心 C 到直线的距离 d = 2- 8 得 a = 32 或 a = 32 ⎪ -4 x - 4, x < - 523.解 (1) f (x) = ⎨6, - 5⎩ 4 x + 4, x > 22 ≤ x ≤ ⎩3 - x - 2 x ≤4 ⎧ 3 ≤ x < 3 .所以,原不等式的解集为 ⎨⎧x x ≥ - ⎬ .故 h ( x ) > 0 , 即 2 g ( x 1 + x 2) < g ( x ) + g ( x )21 2 (12)分22.解 (1) a = 2 时,圆 C 的直角坐标方程为 x 2 + (y -1)2 = 1 ;直线 l 的普通方程为 4 x + 3 y - 8 = 0 . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 4 分⎛⎪ = ⎝ 2 ⎭a 2 4 ,直线 l : 4 x + 3 y - 8 = 0 ,∵直线 l 截圆 C 的弦长等于圆 C 的半径长的 3 倍,3a1 a5 = 2 ⨯ 2 ,11 .⎧2 ⎪1 ⎪2 ≤ x ≤ 2 ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 2 分⎪1 ⎪ ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 7 分⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 10 分当 - 5 12 时,函数有最小值 6 ,所以 m ≤ 6 . ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 5 分另解:∵ 2x -1 + 2x + 5 ≥ (2x -1) - (2x + 5) = -6 = 6 .∴ m ≤ 6 .(2)当 m 取最大值 6 时,原不等式等价于 x - 3 - 2x ≤ 4 ,⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 6 分等价于 ⎨ x ≥ 3 ⎩ x - 3 - 2x ≤ 4 ⎧ x < 3 ,或 ⎨,⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 8 分可得 x ≥ 3 或 - 11 ⎫ ⎩ 3 ⎭⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ 10 分。
2017届江苏省泰州市高三第二次模拟考试数学试卷及答案

2017~2017学年度泰州市第二次模拟考试高三数学试题(考试时间:120分钟总分:160分)命题人:朱占奎张圣官张俊龚才权丁连根审题人:丁凤桂石志群注意事项:所有试题的答案均填写在答题纸上,答案写在试卷上的无效.(参考公式:柱体体积公式为V Sh=)一、填空题:(本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上.)1.若复数(2)ia-+(i是虚数单位)是纯虚数,则实数a= ▲.2.已知集合{}=,若{1,2,3,4}1,2,4A=,{},4B a,则A B=A B=▲.3.某高中共有1200人,其中高一、高二、高三年级的人数依次成等差数列.现用分层抽样的方法从中抽取48人,那么高二年级被抽取的人数为 ▲ .4.已知双曲线2214x y m -=的渐近线方程为2y x =±,则m = ▲ .5.执行右边的伪代码后,输出的结果是 ▲ .6.若圆柱的侧面积和体积的值都是12π,则该圆柱的高为 ▲ .7.小明通过做游戏的方式来确定周末活动,他随机地往单位圆中投掷一点,若此点到圆心的距离大于21,则周末看电影;若此点到圆心的距离小于41,则周末打篮球;否则就在家看书.那么小明周末在家看书的概率是 ▲ .8.在等比数列{}n a 中,已知3754,2320a a a =--=,则7a = ▲ . 9.已知函数a x x y +-=22的定义域为R ,值域为),0[+∞,则实数a 的取值集合为▲ . 10.已知实数,x y满足40210440x y x y x y +-≤⎧⎪-+≥⎨⎪+-≥⎩,则3z x y =+-的取值范围是▲ . 11.设函数π()π)3f x x =+和π()sin(π)6g x x =-的图象在y 轴左、右两侧靠近y轴的交点分别为M、N,已知O为原点,则OM ON ⋅=▲ .12.若斜率互为相反数且相交于点(1,1)P 的两条直线被圆O :224x y +=所截得的弦长之比为2,则这两条直线的斜率之积为▲ .13. 若函数2()(2)f x x x a =--在区间[2,4]上单调递增,则实数a 的取值范围是▲ .14. 在ABC ∆中,D 为边AC 上一点,4,6AB AD AC ===,若ABC ∆的外心恰在线段BD 上,则BC = ▲ .二、解答题:(本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤.) 15.(本题满分14分)已知向量1(2=-a ,(2cos ,2sin )θθ=b ,0πθ<<. (1)若a ∥b ,求角θ的大小; (2)若+=a b b ,求sin θ的值. 16.(本题满分14分)如图,矩形ABCD 所在平面与直角三角形AE⊥,点NABE所在平面互相垂直,BEAE,的中点.M,分别是CD(1)求证:MN∥平面BCE;(2)求证:平面⊥BCE平面ADE.17.(本题满分14分)如图,某市有一条东西走向的公路l,现欲经过公路l上的O处铺设一条南北走向的公路m.在施工过程中发现在O处的正北1百米的A处有一汉代古迹.为了保护古迹,该市决定以A为圆心,1百米为半径设立一个圆形保护区.为了连通公路l、m,欲再新建一条公路PQ,点P、Q分别在公路l、m上,且要求PQ与圆A相切.(1)当P距O处2百米时,求OQ的长;(2)当公路PQ长最短时,求OQ的长.18.(本题满分16分)如图,在平面直角坐标系xOy中,椭圆:E22221(0)x ya ba b+=>>的左顶点为A,与x轴平行的直线与椭圆E交于B、C两点,过B、C两点且分别与直线AB、AC垂直的直线相交于点D.已知椭圆E右焦点到右准线的距离为5.(1)求椭圆E的标准方程;(2)证明点D在一条定直线上运动,并求出该直线的方程;(3)求BCD∆面积的最大值.19.((本题满分16分)已知}{n a ,}{n b ,}{n c 都是各项不为零的数列,且满足1122n n n n a b a b a b c S +++= ,n *∈N ,其中n S 是数列}{n a 的前n 项和, }{n c 是公差为(0)d d ≠的等差数列.(1)若数列}{n a 是常数列,2d =,23c =,求数列}{n b 的通项公式; (2)若n a n λ=(λ是不为零的常数),求证:数列}{n b 是等差数列; (3)若11a c d k ===(k 为常数,k *∈N ),n n k b c +=(2,)n n *≥∈N ,求证:对任意的2,n n *≥∈N ,数列{}nnb a 单调递减.20.(本题满分16分)己知()ln x f x a x a =--e ,其中常数0a >. (1)当a =e 时,求函数()f x 的极值; (2)若函数()y f x =有两个零点1212,(0)x x x x <<,求证:1211x x a a<<<<; (3)求证:221ln 0x x x x ----≥e e .2017~2017学年度泰州市第二次模拟考试高三数学试题(附加题)21.([选做题]请考生在A 、B 、C 、D 四小题中任选两题作答,如果多做,则按所做的前两题记分.A .(本小题满分10分,几何证明选讲)如图,CD 是圆O 的切线,切点为D ,CA 是过圆心的割线且交圆O 于B 点,过B 作O 的切线交CD 于点1,2E DE EC =. 求证:(1)3CA CB =;(2)CA =.B .(本小题满分10分,矩阵与变换)已知矩阵010A a ⎡⎤=⎢⎥⎣⎦,矩阵020B b ⎡⎤=⎢⎥⎣⎦,直线04:1=+-y x l 经矩阵A 所对应的变换得到直线2l ,直线2l 又经矩阵B所对应的变换得到直线04:3=++y x l .(1)求,a b 的值;(2)求直线2l 的方程.AC .(本小题满分10分,坐标系与参数方程选讲)已知极坐标系的极点与直角坐标系的原点重合,极轴与x 轴的正半轴重合.若直线l 的极坐标方程为sin 4ρθπ⎛⎫-= ⎪⎝⎭(1)把直线l 的极坐标方程化为直角坐标方程;(2)已知P 为椭圆221169:x y C +=上一点,求P 到直线l 的距离的最小值.D .(本小题满分10分,不等式选讲)已知不等式2|1|a b x +≤-对于满足条件1222=++c b a 的任意实数c b a ,,恒成立,求实数x 的取值范围.[必做题]第22题,第23题,每题10分,共计20分.解答时应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)某班组织的数学文化节活动中,通过抽奖产生了5名幸运之星.这5名幸运之星可获得A 、B 两种奖品中的一种,并规定:每个人通过抛掷一枚质地均匀的骰子决定自己最终获得哪一种奖品,抛掷点数小于3的获得A 奖品,抛掷点数不小于3的获得B 奖品.(1)求这5名幸运之星中获得A 奖品的人数大于获得B 奖品的人数的概率;(2)设X 、Y 分别为获得A 、B 两种奖品的人数,并记X Y ξ=-,求随机变量ξ的分布列及数学期望.23.(本小题满分10分)已知2()(1)n f x x x =++(n N *∈),()g x 是关于x 的2n 次多项式;(1)若23()()()f x g x g x =恒成立,求(1)g 和(1)g -的值;并写出一个满足条件的()g x 的表达式,无需证明.(2)求证:对于任意给定的正整数n ,都存在与x 无关的常数0a ,1a ,2a ,…,n a ,使得221222110121()(1)()()()n n n n n n n n f x a x a x x a x x a x x a x ---+-=+++++++++ .2017~2017学年度泰州市第二次模拟考试高三数学参考答案一、填空题1.2 ; 2.{4}; 3.16; 4.2; 5.28;6.3; 7.163; 8.64; 9.{1}; 10.[1,7];11.89-; 12.9-或19- ; 13. (,2][5,)-∞+∞ ; 14.. 二、解答题15. 解:(1) 因为//a b ,所以12sin 2cos 22θθ-⋅=⋅,即sin θθ-=, 所以tan θ= 又0πθ<<,所以2π3θ=. ……………7分(2)因为+=a b b ,所以22()+=a b b ,化简得220+⋅=a a b ,又1(2=-a ,(2cos ,2sin )θθ=b ,则21=a ,cos θθ⋅=-a b , 所以1cos 2θθ=--,则π1sin()064θ-=-<, ……………10分又0πθ<<,πcos()6θ-=,所以ππππππsin[()]sin()cos cos()sin 66i 66n 6s 6θθθθ-+=-+-==. ……………14分16. 证:(1)取BE 中点F ,连接,CF MF , 又M 是AE 中点,则1//,2MF AB MF AB =, 又N 是矩形ABCD 边CD 中点,所以//,MF NC MF NC =,则四边形MNCF 是平行四边形,所以//MN CF ,又MN ⊄面BCE ,CF ⊂面BCE ,所以MN ∥平面BCE .…(2)因为平面ABCD⊥平面ABE,BC AB ⊥,所以BC ⊥平面ABE ,因为AE ⊂平面ABE ,所以BC AE ⊥,又BE AE ⊥,BC BE B ⋂=,所以AE ⊥平面BCE , 而AE ⊂平面ADE,所以平面⊥BCE 平面ADE . ……………14分17. 解:以O 为原点,直线l 、m 分别为,x y 轴建立平面直角坐标系. 设PQ 与圆A 相切于点B ,连结AB ,以1百米为单位长度,则圆A 的方程为22(1)1x y +-=, (1)由题意可设直线PQ 的方程为12x yq+=,即220qx y q +-=,(2)q > ,∵PQ 与圆A1=,解得83q =, 故当P距O处2百米时,OQ的长为83百米. ……………5分 (2)设直线PQ 的方程为1x yp q+=,即0qx py pq +-= ,(1,2)p q >>, ∵PQ与圆A相切,∴1=,化简得22q p q =-,则22222qPQ p q q q =+=+-,令2()(2)2q f q q q q =+>-,∴22222(1)(31)()2(2)(2)q q q f q q q q --+'=-=-- (2)q >,当322q <<时,()0f q '<,即()f q在3(2,2上单调递减;当32q +>()0f q '>,即()f q在3()2+∞上单调递增,∴()f q在q =PQ 长最短时,OQ的长为 答:(1)当P 距O 处2百米时, OQ 的长为83百米;(2)当公路PQ 长最短时, OQ 的 长为百米. ……………14分18. 解:(1)由题意得c a =,2a c c -=,解得3,a c ==,所以4b =,所以椭圆E 的标准方程为22194x y +=.……………4分(2)设0000(,),(,)B x y C x y -,显然直线,,,AB AC BD CD 的斜率都存在,设为1234,,,k k k k ,则001200,33y y k k x x ==+-+,00340033,x x k k y y +-=-=,所以直线,BD CD 的方程为:0000000033(),()x x y x x y y x x y y y +-=--+=++, 消去y 得0000000033()()x x x x y x x y y y +---+=++,化简得3x =, 故点D在定直线3x =上运动. ……………10分(3)由(2)得点D 的纵坐标为2000000039(3)D x x y x y y y y --=++=+,又2200194x y +=,所以220994y x -=-,则200000009354(3)4D y x y x y y y y y --=++=+=-,所以点D 到直线BC 的距离h 为00005944D y y y y y -=--=,将0y y =代入22194x y +=得x =±所以BCD ∆面积0119224ABCS BC h y ∆=⋅=⨯22000112727442224y y y -+=≤⋅=,当且仅当2200144y y -=,即0y =时等号成立,故0y =时,BCD∆面积的最大值为274. ……………16分19.解:(1)因为2d =,23c =,所以21n c n =-,因为数列}{n a 是各项不为零的常数列,所以12n a a a === ,1n S na =, 则由1122n n n n S c a b a b a b =+++ 及21n c n =-得12(21)n n n b b b -=+++ , 当2n ≥时,121(1)(23)n n n b b b ---=+++ ,两式相减得43n b n =-,当1n =时,11b =,也满足43n b n =-,故43()n b n n *=-∈N . …………4分(2)因为1122n n n n a b a b a b c S +++= ,当2n ≥时,11112211n n n n S c a b a b a b ----=+++ ,两式相减得11n n n n n n S c S c a b ---=, 即111()n n n n n n n S a c S c a b ---+-=,11()n n n n n n n S c c a c a b ---+=,即1n n n S d nc nb λλ-+=, 又1(1)(1)(1)22n n n n S n λλλ-+--=-=,所以(1)2n n n n d nc nb λλλ-+=,即(1)2n n n d c b -+=, 所以当3n ≥时,11(2)2n n n d c b ---+=,两式相减得132n n b b d --=(3)n ≥, 所以数列}{n b 从第二项起是公差为32d 等差数列;又当1n =时,由1111S c a b =得11c b =, 当2n =时,由2211(21)13()222b d c d c d b d -=+=++=+得2132b b d -=, 故数列}{n b 是公差为32d 等差数列. …………15分(3)由(2)得当2n ≥时,11()n n n n n n n S c c a c a b ---+=,即1()n n n n S d a b c -=-, 因为n n k b c +=,所以n n b c kd =+,即n n b c kd -=,所以1n n S d a kd -=⋅,即1n n S ka -=, 所以1(1)n n n n S S a k a -=+=+,当3n ≥时,11(1)n n S k a --=+,两式相减得 1(1)(1)n n n a k a k a -=+-+,即11n n k a a k-+=,故从第二项起数列}{n a 是等比数列, 所以当2n ≥时,221()n n k a a k-+=, 221(1)(1)()n n k n b c c kd c n k k k n k k k n k +==+=+-+=+-+=+,另外由已知条件得1221122()a a c a b a b +=+,又22c k =,1b k =,2(2)b k k =+,所以21a =,因而21()n n k a k -+=,令n d =n nba ,则111n n n n n n d b a d a b +++=(1)()(1)n k kn k k ++=++, 因为(1)()(1)0n k k n k k n ++-++=-<,所以11n nd d +<,所以对任意的2,n n *≥∈N ,数列{}n nba 单调递减. ……………16分20. 解:函数()f x 的定义域为(0,)+∞,(1)当e a =时,()e eln e x f x x =--,e ()e x f x x'=-, 而e ()e x f x x'=-在(0,)+∞上单调递增,又(1)0f '=, 当01x <<时,()(1)0f x f ''<=,则()f x 在(0,1)上单调递减;当1x >时,()(1)0f x f ''>=,则()f x 在(1,)+∞上单调递增,所以()f x 有极小值(1)0f =,没有极大值. …………3分 (2)先证明:当()0f x ≥恒成立时,有 0a <≤e 成立. 若10ex <≤,则()(ln 1)0x f x a x =-+≥e 显然成立; 若1e x >,由()0f x ≥得e ln 1xa x ≤+,令e ()ln 1xx x ϕ=+,则21e (ln 1)()(ln 1)x x x x x ϕ+-'=+, 令11()ln 1()e g x x x x =+->,由21()10g x x '=+>得()g x 在1(,)e+∞上单调递增, 又因为(1)0g =,所以()x ϕ'在1(,1)e 上为负,在(1,)+∞上为正,因此()x ϕ在1(,1)e上递减,在(1,)+∞上递增,所以min ()(1)e x ϕϕ==,从而0e a <≤.因而函数()y f x =若有两个零点,则e a >,所以(1)e 0f a =-<,由()ln (a f a a a a a =-->e e)得()ln 2a f a a '=--e ,则111()0e ea a f a a ''=->->->e e e , 所以()ln 2a f a a '=--e 在(,)+∞e 上单调递增,所以2()()330f a f ''>=->->e e e e ,所以()ln a f a a a a =--e 在(,)+∞e 上单调递增,所以2()()22f a f >=->->e e e e e e 0,则(1)()0f f a <,所以21x a <<,由a >e 得111111()ln ln ln 0a a a a f a a a a a a a a a=--=+->+-=>e e e e e ,则 1(1)()0f f a <,所以111x a <<,综上得1211x x a a<<<<. (10)分(3)由(2)知当a =e 时,()0f x ≥恒成立,所以()ln 0x f x x =--≥e e e , 即()ln x f x x =-≥e e e , 设()(0)e x x h x x =>,则1()exxh x -'=, 当01x <<时,()0x ϕ'> ,所以()g x 在(0,1)上单调递增; 当1x >时,()0h x '<,所以()g x 在(1,)+∞上单调递增, 所以()(0)e x x h x x =>的最大值为1(1)e h =,即1x x ≤e e ,因而2x x-≤e e, 所以2()ln x x xf x x -=-≥≥e e e e,即221()ln 0x x f x x x --=--≥e e . (16)分附加题参考答案21.A .证:(1)∵CD 是圆O 的切线,∴2CD CA CB =⋅, 连结OD ,则OD CD ⊥, ∵BE 是圆O 的切线,∴BE ED =, 又12DE EC =,∴12BE EC =,∴30C ∠= ,则12OD OC =, 而OB OD =,∴CB BO OD OA ===,∴3CA CB =, …………5分 (2)将3CA CB =代入2CD CA CB =⋅得213CD CA CA =⋅,故CA =.……10分21.B . 解:(1)020120000a BA b a b ⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦设(,)P x y 是1l 上的任意一点,其在BA 作用下对应的点为(,)x y '',得1l 变换到3l 的变换公式{2x ax y by '='=,则240ax by ++=即为直线1:40l x y -+=,则得1,12a b ==-. (5)分(2)0210B ⎡⎤=-⎢⎥⎣⎦,同理可得2l 的方程为240y x -+=,即240x y --=.………10分21.C . 解:(1)直线l的极坐标方程sin 4ρθπ⎛⎫-= ⎪⎝⎭,则sin cos θθ= 即sin cos 6ρθρθ-=,所以直线l的直角坐标方程为60x y -+=;…………5分(2)P 为椭圆221169x y C +=:上一点,设(4cos 3sin )P αα,,其中[)02,α∈π,则P到直线l的距离d ==,其中4cos 5ϕ=,3sin 5ϕ=,∴当cos()1αϕ+=-时,d的最小值为21.D . 解: 因为2222()(112)()4a b a b c +≤++++=,所以2a b +≤,…………5分又|1-|22x c b a ≤++对任意实数c b a ,,恒成立, 故2max |-1|()2x a b ≥+=, 解得33≥-≤x x 或 . …………10分22. 解:这5名幸运之星中,每人获得A 奖品的概率为2163=,B 奖品的概率为4263=. (1)要获得A 奖品的人数大于获得B 奖品的人数,则A 奖品的人数可能为3,4,5,则则所求概率为33244555551212151()()()()()33333243P C C C =++=. …………4分 (2)ξ的可能取值为1,3,5,且33222355121240(1)()()()()333381P C C ξ==+=,441455121210(3)()()()()333327P C C ξ==+=,0555552111(5)()()3381P C C ξ==+=, …………8分所以ξ的分布列是:故随机变量ξ的数学期望E ξ=401381⨯+⨯10275+⨯118118581=. (10)分23.解:(1)令1x =,则(1)(1)(1)f g g =,即(1)[(1)1]0g f ⋅-=, 因为(1)1310n f -=-≠,所以(1)0g =; 令1x =-,则23(1)(1)(1)fg g ⎡⎤⎡⎤--=-⎣⎦⎣⎦,即(1)(1)(1)f g g -=-,因为(1)[(1)1]0g f -⋅-=,因为(1)1310n f -=-≠,所以(1)0g -=; 例如2()(1)()n g x x n *=-∈N . (4)分(2)当1n =时,22()1(1)f x x x x x =++=++,故存在常数01a =,11a =, 使得201()(1)f x a x a x =++.假设当n k =(k N *∈)时,都存在与x 无关的常数0a ,1a ,2a ,…,k a , 使得221222110121()(1)()()()k k k k k k k k f x a x a x x a x x a x x a x ---+-=+++++++++ ,即2221222110121(1)(1)()()()k k k k k k k k k x x a x a x x a x x a x x a x ---+-++=+++++++++ .则当1n k =+时,2122()(1)(1)(1)k k f x x x x x x x +=++=++⋅++222111011(1)(1)()()k k k k kk k x x a x a x x a x x a x --+-⎡⎤=++⋅+++++++⎣⎦11212011110()k k k k k k k k a a x a x a x a x a x a x -+---=++++++++ 212221011110()k k k k k k k k a x a x a x a x a x a x a x +++--+++++++++231232122011110()k k k k k k k k a x a x a x a x a x a x a x +++++--+++++++++ 231010*********()()()()k k k k a a a x a a a x a a a x a a a x ----=+++++++++++++ 1212112()(2)()k k k k k k k k k k k a a a x a a x a a a x ++-----++++++++++ 2122122321210100()()()k k k k a a a x a a a x a a x a x -+++++++++++ 222122010210()()()()()k k k a x x a a x x a a a x x ++=+++++++++ 21121()()(2)k k k k k k k k a a a x x a a x ++---++++++;令00'a a =,101'a a a =+,21'm m m m a a a a --=++(2m k ≤≤),11'2k k k a a a +-=+; 故存在与x 无关的常数0'a ,1'a ,2'a ,…,'k a ,1'k a +;使得222122210121()'(1)'()'()'()'k k k k k k k k f x a x a x x a x x a x x a x +++++=+++++++++ .综上所述,对于任意给定的正整数n ,都存在与x 无关的常数0a ,1a ,2a ,…,n a ,使得221222110121()(1)()()()n n n n n n n n f x a x a x x a x x a x x a x ---+-=+++++++++ . …………10分。
江苏省泰州市第二中学2016-2017学年高一数学下学期期初检测试题(无答案)

泰州二中2016-2017学年度第二学期期初检测高一数学试卷一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上.1. 已知集合{}{}220,0log 2,A x x B x x A B =-≥=<<=则____________.2. 若幂函数(,)y mx m R αα=∈的图像经过点1(8,)4,则α=____________. 3. 若一扇形的圆心角为72,半径为20cm ,则扇形的面积为_____________.4. 若1,2,+=a b a b a b ==-=则_______________.5. 函数5()log (21)f x x =+的单调增区间是____________.6. 已知1)f x =+则()f x 的解析式为__________________.7. 121(lg lg 25)1004--÷=_________________.8. 函数3sin 44y x x ππ⎛⎫=-≤≤ ⎪⎝⎭的值域为_____________. 9. 设D ,E 分别是∆ABC 的边AB ,BC 上的点,AD=12AB ,BE=23BC.若1212(,)DE AB AC λλλλ=+为实数,则12λλ+的值为_____________. 10. 函数()lg 3f x x x =+-的零点在区间(m ,m+1)(m ∈Z )内,则m=____________.11. 已知2tan()3,2cos 4πθθθ+=-则sin2的值为____________.12. 设α为锐角,若4cos(),sin(2)6512ππαα+=+则的值为_____________. 13.方程22sin lg 0x x π-=实数解的个数是 .14. 给定两个长度为1的平面向量OA 和OB ,他们的夹角为120,点C 在以O 为圆心的圆弧AB 上运动,若OC xOA yOB =+∈,其中x,y R ,则x y +的最大值为______________.二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程.15. (本小题满分14分)已知集合{()lg(1)A x f x x ==-,集合{}2,0x B y y a x ==+≤, (1)若32a =,求A B ;(2)若A B φ=,求实数a 的取值范围。
江苏省泰州市第二中学2017届高三12月月考数学试题 Word版含答案
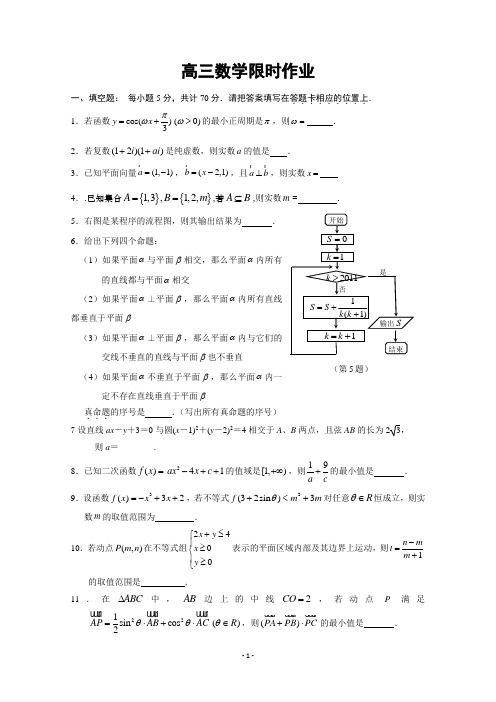
高三数学限时作业一、填空题: 每小题5分,共计70分.请把答案填写在答题卡相应的位置上.......... 1.若函数cos()3y x πω=+(0)ω>的最小正周期是π,则ω= .2.若复数(12)(1)i ai ++是纯虚数,则实数a 的值是 .3.已知平面向量(1,1)a =- ,(2,1)b x =-,且a b ⊥ ,则实数x =4..已知集合{}{}1,3,1,2,A B m ==,若A B ⊆,则实数m = . 5.右图是某程序的流程图,则其输出结果为 . 6.给出下列四个命题:(1)如果平面α与平面β相交,那么平面α内所有的直线都与平面α相交(2)如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β(3)如果平面α⊥平面β,那么平面α内与它们的交线不垂直的直线与平面β也不垂直(4)如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β真命题...的序号是 .(写出所有真命题的序号) 7设直线ax -y +3=0与圆(x -1)2+(y -2)2=4相交于A 、B 两点,且弦AB 的长为23,则a =________.8.已知二次函数()f x =241ax x c -++的值域是[1,)+∞,则19a c+的最小值是 . 9.设函数3()32f x x x =-++,若不等式2(32sin )3f m m θ+<+对任意R θ∈恒成立,则实数m 的取值范围为 .10.若动点(,)P m n 在不等式组2400x y x y +≤⎧⎪≥⎨⎪≥⎩表示的平面区域内部及其边界上运动,则1n m t m -=+的取值范围是 . 11.在ABC∆中,AB 边上的中线2CO =,若动点P 满足221sin cos 2AP AB AC θθ=⋅+⋅ ()R θ∈,则()PA PB PC +⋅ 的最小值是 .(第5题)A BC DD 1C 1B 1A 1 12.设D 是函数()y f x =定义域内的一个区间,若存在D x ∈0,使00()f x x =-,则称0x 是()f x 的一个“次不动点”,也称()f x 在区间D 上存在次不动点.若函数25()32f x ax x a =--+在区间[1,4]上存在次不动点,则实数a 的取值范围是 . 13.已知函数132s i n (4)(+-=πx x f ,给定条件p :24ππ≤≤x ,条件q :2)(2<-<-m x f ,若p 是q 的充分条件,则实数m 的取值范围为14.设等差数列{}n a 的前n 项和为n S ,若对任意的等差数列{}n a 及任意的正整数n 都有不等式22212n n S a a nλ+≥成立,则实数λ的最大值为二、解答题:15.(本小题满分14分)已知△ABC 中,∠A ,∠B ,∠C 的对边分别为,,a b c ,且2cos cos cos a B c B b C =+. (1)求角B 的大小;(2)设向量(cos ,cos2)m A A = ,(12,5)n =- ,求当m n ⋅ 取最大值时,tan()4A π-的值.16.(本小题满分14分)如图,直四棱柱1111ABCD A B C D -中,底面ABCD 是直角梯形,90BAD ADC ∠=∠=︒,2AB AD =,CD AD =.(1)求证:1B CB ∠是二面角1B AC B --的平面角; (2)在A 1B 1上是否存一点P ,使得DP 与平面BCB 1与平面ACB 1都平行?证明你的结论.A117.(本小题满分14分)如图所示:一吊灯的下圆环直径为4m ,圆心为O ,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离)(OB 即为2m ,在圆环上设置三个等分点A1,A2,A3。
江苏省泰州市第二中学2016-2017学年高一数学下学期期初检测试题(无答案)

泰州二中2016-2017学年度第二学期期初检测高一数学试卷一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上.1. 已知集合{}{}220,0log 2,A x x B x x A B =-≥=<<=则____________.2. 若幂函数(,)y mx m R αα=∈的图像经过点1(8,)4,则α=____________. 3. 若一扇形的圆心角为72,半径为20cm ,则扇形的面积为_____________.4. 若1,2,+=a b a b a b ==-=则_______________.5. 函数5()log (21)f x x =+的单调增区间是____________.6. 已知1)f x =+则()f x 的解析式为__________________.7. 121(lg lg 25)1004--÷=_________________.8. 函数3sin 44y x x ππ⎛⎫=-≤≤ ⎪⎝⎭的值域为_____________. 9. 设D ,E 分别是∆ABC 的边AB ,BC 上的点,AD=12AB ,BE=23BC.若1212(,)DE AB AC λλλλ=+为实数,则12λλ+的值为_____________. 10. 函数()lg 3f x x x =+-的零点在区间(m ,m+1)(m ∈Z )内,则m=____________.11. 已知2tan()3,2cos 4πθθθ+=-则sin2的值为____________.12. 设α为锐角,若4cos(),sin(2)6512ππαα+=+则的值为_____________. 13.方程22sin lg 0x x π-=实数解的个数是 .14. 给定两个长度为1的平面向量OA 和OB ,他们的夹角为120,点C 在以O 为圆心的圆弧AB 上运动,若OC xOA yOB =+∈,其中x,y R ,则x y +的最大值为______________.二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程.15. (本小题满分14分)已知集合{()lg(1)A x f x x ==-,集合{}2,0x B y y a x ==+≤, (1)若32a =,求A B ;(2)若A B φ=,求实数a 的取值范围。
泰州中学2017届高三下学期期初考试数学试题 含答案bybao

江苏省泰州中学2016—2017学年度第二学期期初考试数学试题2017。
2一、填空题:(本大题共14小题,每小题5分,共70分)若集合{}(){}22|1381,|log 1x A x B x x x =≤≤=->,则AB = 。
1. 已知i 是虚数单位,则32ii-+的虚部为 .3.已知函数()2log ,1,1x x f x x c x ≥⎧=⎨+<⎩,则“1c =-"是“函数在R 上单调递增”的条件.4.下图是某算法流程图,则算法运行后输出的结果是 。
5.将四个人(含甲、乙)分成两组,则甲、乙为同一组的概率为 。
6。
已知抛物线28y x =的焦点恰好是椭圆()22210x y a a +=>的右焦点,则椭圆方程为 。
7。
已知正四棱锥的底面边长为2383是 。
8.平面向量a 与b 的夹角为23π,()3,0,2a b ==则2a b +=. 9.若等比数列{}na 的公比1q ≠且满足:12376,a aa a ++++=2222123718a a a a ++++=,则1234567a a a a a a a -+-+-+的值为。
10。
点P 为直线34y x=上任一点,()()215,0,5,0F F -,则12PF PF -的取值范围为 .11.在OMN ∆中,点A 在OM 上,点B 在ON 上,且//,2AB MN OA OM =,若OP xOA yOB =+,则终点P 落在四边形ABNM 内(含边界)时,21y x x +++的取值范围为 . 12。
函数()cos2xf x π=,对任意的实数t ,记()f x 在[],1t t +上的最大值为()M t ,最小值为()m t ,则函数()()()h t M t m t =-的值域为 。
13。
已知A 是射线()00x y x +=≤上的动点,B 是x 轴正半轴上的动点,若直线AB 与圆221x y +=相切,则AB 的最小值为 .14。
【数学】江苏省泰州市第二中学2020届高三下学期第二次限时作业

江苏省泰州市第二中学2021届高三下学期第二次限时作业参考公式:样本数据x 1 ,x 2 ,… ,x n 的方差s 2=1n i =1∑n (x i --x )2 ,其中-x =1n i =1∑nx i .锥体的体积公式:V =13Sh ,其中S 为锥体的底面积 ,h 为锥体的高.一、填空题 (本大题共14小题 ,每题5分 ,计70分. 不需写出解答过程 ,请把答案写在答题纸的指定位置上 )1.集合A ={-3 ,-1 ,1 ,2} ,集合B = ,使得f (x 1 ) =g (x 2 )成立 ,那么实数a 的取值范围是 ▲ .13.如图 ,用一块形状为半椭圆(y≥0 )的铁皮截取一个以短轴BC 为底的等腰梯形ABCD ,记所得等腰梯形的面积为S ,那么的最||小值是 ▲ .14.给出定义:假设m ﹣<x≤m + (其中m 为整数 ) ,那么m叫做离实数x 最||近的整数 ,记作{x} =m .在此根底上给出以下关于函数f (x ) =|x ﹣{x}|的四个命题:①函数y =f (x )的定义域为R ,值域为;②函数y =f (x )的图象关于直线x = (k ∈Z )对称; ③函数y =f (x )是周期函数 ,最||小正周期为1;④函数y =f (x )在上是增函数.其中正确的命题的序号 ▲ .二、解答题 (本大题共6小题 ,计90分.解容许写出必要的文字说明 ,证明过程或演算步骤 ,请把答案写在答题纸的指定区域内 ) 15.(本小题总分值14分)在平面直角坐标系xOy 中 ,点,sin ,cos ),0,56()(ααP A 其中20πα<<.(1 )假设,65cos =α求证:.PO PA ⊥ (2 )。
)4sin(2的值求若πα+=,PO PA16.(本小题总分值14分)如图 ,在棱长为2的正方体1111ABCD A BC D -中 ,E 为BC 的中点 , F 为1DC 的中点.(1 )求证:1BD ∥平面1C DE ; (2 )求三棱锥A BDF -的体积.17.(本小题总分值14分)为了保护环境 ,开展低碳经济 ,某单位在国|家科研部门的支持下 ,进行技术攻关 ,采用了新工艺 ,把二氧化碳转化为一种可利用的化工产品.该单位每月的处理量最||少为400吨 ,最||多为600吨 ,月处理本钱y (元 )与月处理量x (吨 )之间的函数关系可近似的表示为:21200800002y x x =-+ ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元. (1 )该单位每月处理量为多少吨时 ,才能使每吨的平均处理本钱最||低 ?(2 )该单位每月能否获利 ?如果获利 ,求出最||大利润;如果不获利 ,那么国|家至||少需要补贴多少元才能使该单位不亏损 ?18. (本小题总分值16分)如图 ,椭圆C :22221(0)x y a b a b +=>> ,以椭圆C 的左顶点T 为圆心作圆T :222(2)(0)x y r r ++=> ,设圆T 与椭圆C 交于点M 与点N .(1 )求椭圆C 的方程;(2 )求TM TN ⋅的最||小值 ,并求此时圆T 的方程;(3 )设点P 是椭圆C 上异于M ,N 的任意一点 ,且直线,MP NP 分别与x 轴交于点,R S ,O 为坐标原点 ,求证:OR OS ⋅为定值.19.(本小题总分值16分)设等差数列{a n }的前n 项和为S n ,a 1=2 ,S 6=22. (1 )求S n ;(2 )假设从{a n }中抽取一个公比为q 的等比数列{a k n } ,其中k 1=1 , 且k 1<k 2<…<k n <… ,k n ∈N *.①当q 取最||小值时 ,求{ k n }的通项公式;②假设关于n (n ∈N *)的不等式6S n >k n +1有解 ,试求q 的值.20.(本小题总分值16分) 函数22()ln(21)2().3x f x ax x ax a R =++--∈(1 )假设x =2为()f x 的极值点 ,求实数a 的值;(2 )假设()y f x =在[)3,+∞上为增函数 ,求实数a 的取值范围;(3 )当12a =-时 ,方程3(1)(1)3x b f x x--=+有实根 ,求实数b 的最||大值 .高三数学(附加题)21.选修4-2:矩阵与变换二阶矩阵A 有特征值11λ=及对应的一个特征向量111⎡⎤=⎢⎥⎣⎦e 和特征值22λ=及对应的一个特征向量210⎡⎤=⎢⎥⎣⎦e ,试求矩阵A .22.选修4-4:坐标系与参数方程在直角坐标系xOy 中 ,曲线C 的参数方程是sin 1cos y x θθ=+⎧⎨=⎩(θ是参数 ) ,假设以O 为极点 ,x 轴的正半轴为极轴 ,取与直角坐标系中相同的单位长度 ,建立极坐标系 ,求曲线C 的极坐标方程.23.抛物线顶点在原点 ,焦点在坐标轴上 ,又知此抛物线上的一点A (m ,-3)到焦点F 的距离为5 ,求m 的值 ,并写出此抛物线的方程.24.如图 ,在正四棱锥P -ABCD 中 ,P A =AB = 2 ,点M ,N 分别在线段P A 和BD 上 ,BN =13BD .(1 )假设PM =13P A ,求证:MN ⊥AD ;(2 )假设二面角M -BD -A 的大小为π4,求线段MN 的长度.参考答案一、填空题:本大题共14小题 ,每题5分 ,计70分. 1. {1,2} 2. -3 3.23 4. 55 5. 2656. 3y x =±7.8. 2 9、 a =2或a≤1 10. 2x 2﹣2y 2 =1 11. k>0,且k 22≠12.13.14. ①②③ .二、解答题: 15. (1 ) (方法一 )由题设知).sin ,cos (),sin ,cos 56(a a PO a a PA --=--=……………………2分所以2sin ()cos )(cos 56()a a a PO PA -+--=⋅.1cos 56sin cos cos 5622+-=++-=a a a a ……………………6分 因为,65cos =a 所以.0=⋅PO PA 故.PO PA ⊥……………………7分(方法二)因为,65cos =a ,20π<<a 所以611sin =a ,故.611,65()P ………………2分因此).611,65(),611,3011(--=-=PO PA ……………………4分 因为.0)611()65(30112=-+-⨯=⋅PO PA所以.PO PA ⊥ ……………………7分(2 ),PO PA ⊥,PO PA即.sin cos sin )56cos 2222a a a a +=+-(解得.53cos =a 因为,20π<<a 所以.54sin =a 因此 .2571cos 22cos ,2524cos sin 22sin 2-=-===a a a a a 从而.50217)257(222524222cos 222sin 2242sin(=-⨯+⨯=+=+a a a )π……14分 16.解: (1 )连接1D C 与1DC 交于点F ,连接EF因为E 为BC 的中点 ,F 为1DC 的中点.所以1EF BD又 EF ⊂平面1C DE ,1BD ⊄平面1C DE所以1BD 平面1C DE - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -8分(2 )由于点F 到平面ABD 的距离为1故三棱锥A BDF -的体积111212213323A BDF F ABD ABD V V S --∆==== - - - - - - - -14分17、解: (1 )由题意可知 ,二氧化碳的每吨平均处理本钱为:1800002002y x x x=+-…………………………………………………4分200200≥= , 当且仅当1800002x x= ,即400x =时 , 才能使每吨的平均处理本钱最||低 ,最||低本钱为200元.…………………8分 (2 )设该单位每月获利为S ,那么100S x y =-…………………………………………………………………10分2211100(20080000)3008000022x x x x x =--+=-+-21(300)350002x =---因为400600x ≤≤ ,所以当400x =时 ,S 有最||大值40000-.故该单位不获利 ,需要国|家每月至||少补贴40000元 ,才能不亏损.…………14分18.此题考查椭圆的方程和几何性质、圆的方程等根底知识 ,考查运算求解能力、推理论证能力 ,考查函数与方程思想、数形结合思想解: (1 )依题意 ,得2a = ,c e a ==,1,322=-==∴c a b c ; 故椭圆C 的方程为2214x y += . …………………3分 (2 )方法一:点M 与点N 关于x 轴对称 ,设),(11y x M ,),(11y x N - , 不妨设01>y .由于点M 在椭圆C 上 ,所以412121xy -=. (* ) ……………4分由(2,0)T - ,那么),2(11y x TM += ,),2(11y x TN -+= ,21211111)2(),2(),2(y x y x y x TN TM -+=-+⋅+=⋅∴3445)41()2(1212121++=--+=x x x x 51)58(4521-+=x .………6分由于221<<-x ,故当581-=x 时 ,TM TN ⋅取得最||小值为15-.由 (* )式 ,531=y ,故83(,)55M - ,又点M 在圆T 上 ,代入圆的方程得到21325r =.故圆T 的方程为:2213(2)25x y ++=. …………………8分方法二:点M 与点N 关于x 轴对称 ,故设(2cos ,sin ),(2cos ,sin )M N θθθθ- , 不妨设sin 0θ> ,由(2,0)T - ,那么)sin ,2cos 2()sin ,2cos 2(θθθθ-+⋅+=⋅TN TM3cos 8cos 5sin )2cos 2(222++=-+=θθθθ51)54(cos 52-+=θ.……6分故当4cos 5θ=-时 ,TM TN ⋅取得最||小值为15- ,此时83(,)55M - ,又点M 在圆T 上 ,代入圆的方程得到21325r =.故圆T 的方程为:2213(2)25x y ++=. ………8分(3) 方法一:设),(00y x P ,那么直线MP 的方程为:)(010100x x x x y y y y ---=- ,令0y = ,得101001y y y x y x x R --=, 同理:101001y y y x y x x S ++= , …………10分故212021202021y y y x y x x x S R --=⋅ (** ) ………………12分又点M 与点P 在椭圆上 ,故)1(42020y x -= ,)1(42121y x -= ,……………………14分 代入 (** )式 ,得: 4)(4)1(4)1(421202120212021202021=--=----=⋅y y y y y y y y y y x x S R .所以4=⋅=⋅=⋅S R S R x x x x OS OR 为定值.……………………16分方法二:设(2cos ,sin ),(2cos ,sin )M N θθθθ- ,不妨设sin 0θ> ,)sin ,cos 2(ααP ,其中θαsin sin ±≠.那么直线MP 的方程为:)cos 2(cos 2cos 2sin sin sin αθαθαα---=-x y ,令0y = ,得θαθαθαsin sin )sin cos cos (sin 2--=R x ,同理:θαθαθαsin sin )sin cos cos (sin 2++=S x ,………………12分故4sin sin )sin (sin 4sin sin )sin cos cos (sin 42222222222=--=--=⋅θαθαθαθαθαS R x x . 所以4=⋅=⋅=⋅S R S R x x x x OS OR 为定值.…………14分19. 解: (1 )设等差数列的公差为d ,那么611665222S a d =+⋅⋅= ,解得23d = ,…2分 所以(5)3n n n S +=. …………4分 (2 )因为数列}{n a 是正项递增等差数列 ,所以数列}{n k a 的公比1>q , 假设22=k ,那么由382=a ,得3412==a a q ,此时932)34(223=⋅=k a ,由)2(32932+=n , 解得*310N n ∉= ,所以22>k ,同理32>k ; …………6分 假设42=k ,那么由44=a ,得2=q ,此时122-⋅=n k n a ,另一方面 ,2(2)3n k n a k =+ ,所以2(2)23n n k += ,即1322n n k -=⨯- , ………8分 所以对任何正整数n ,n k a 是数列}{n a 的第2231-⋅-n 项.所以最||小的公比2=q . 所以2231-⋅=-n n k . …………10分(3 )因为12423n n n k k a q -+== ,得132n n k q -=- ,而1q > , 所以当1q >且q N ∈时 ,所有的132n n k q -=-均为正整数 ,适合题意; 当2q >且q N ∉时 ,132n n k q N -=-∈不全是正整数 ,不合题意.而16n n S k +>有解 ,所以2(5)213nn n q++>有解 ,经检验 ,当2q = ,3q = ,4q =时 ,1n =都是2(5)213nn n q ++>的解 ,适合题意; ……………12分下证当5q ≥时 ,2(5)213nn n q++>无解, 设2(5)23n n n n b q ++= , 那么212[(1)(75)7]3n n nq n q n q b b q+-+-+--= , 因为57022q q-<- ,所以2()2[(1)(75)7]f n q n q n q =-+-+-在*n N ∈上递减 ,又因为(1)0f < ,所以()0f n <恒成立 ,所以10n n b b +-< ,所以1n b b ≤恒成立 , 又因为当5q ≥时 ,11b < ,所以当5q ≥时 ,16n n S k +>无解. ……………15分 综上所述 ,q 的取值为2,3,4. ………………16分20. (1)解:222[2(14)(42)]2()222121x ax a x a a f x x x a ax ax +--+'=+--=++ (1)分因为x = 2为f (x )的极值点 ,所以(2)0f '= ……2分 即22041aa a -=+ ,解得:a = 0 ……3分 又当a = 0时 ,()(2)f x x x '=- ,从而x = 2为f (x )的极值点成立. ……4分(2)解:∵f (x )在区间 ……10分(3)解:12a =-时 ,方程3(1)(1)3xb f x x --=+可化为 ,2ln (1)(1)bx x x x --+-=. 问题转化为2[ln ]b x x x x =+-在(0 , +∞)上有解 ……12分令2()ln h x x x x =+- ,那么(21)(1)1()12x x h x x x x+-'=+-=…14分 当0 < x < 1时 ,()0h x '> ,∴h (x )在(0 ,1)上为增函数 当x > 1时 ,()0h x '< ,∴h (x )在(1 , +∞)上为减函数故h (x )≤h (1) = 0 ,而x > 0 ,故()0b xh x =≤ 即实数b 的最||大值是0. ……16分21设矩阵a b A c d ⎡⎤=⎢⎥⎣⎦,这里a b c d ∈R ,,, , 因为11⎡⎤⎢⎥⎣⎦是矩阵A 的属于11λ=的特征向量 ,那么有110110a b c d --⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦① ,……4分又因为10⎡⎤⎢⎥⎣⎦是矩阵A 的属于22λ=的特征向量 ,那么有210100a b c d --⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦②…6分 根据①② ,那么有1010200a b c d a c --=⎧⎪-+-=⎪⎨-=⎪⎪-=⎩,,,, …………………………………………………8分从而2101a b c d ==-==,,,,因此2101A -⎡⎤=⎢⎥⎣⎦,………………………………10分 22C . (选修4 -4:坐标系与参数方程 )由sin 1cos y x θθ=+⎧⎨=⎩得1sin cos y x θθ-=⎧⎨=⎩ ,两式平方后相加得22(1)1x y +-= ,…………4分 ∴曲线C 是以(0,1)为圆心 ,半径等于的圆.令cos ,sin x y ρθρθ== ,代入并整理得2sin ρθ=.即曲线C 的极坐标方程是2sin ρθ=. …………10分 23证明:连接AC ,BD 交于点O ,以OA 为x 轴正方向 ,以OB 为y 轴正方向 ,OP 为z 轴建立空间直角坐标系.因为P A =AB = 2 ,那么A (1 ,0 ,0) ,B (0 ,1 ,0) ,D (0 ,-1 ,0) ,P (0 ,0 ,1). (1 )由BN →=13BD → ,得N (0 ,13 ,0) ,由PM →=13PA →,得M (13 ,0 ,23) ,所以MN →=(-13 ,13 ,-23) ,AD →=(-1 ,-1 ,0).因为MN →·AD →=0.所以MN ⊥AD . ………………………………………4分 (2 )因为M 在P A 上 ,可设PM →=λPA →,得M (λ ,0 ,1-λ). 所以BM →=(λ ,-1 ,1-λ) ,BD →=(0 ,-2 ,0). 设平面MBD 的法向量n =(x ,y ,z ) ,由⎩⎪⎨⎪⎧n ·BD →=0 n ·BM →=0得⎩⎨⎧-2y =0 λx -y +(1-λ)z =0其中一组解为x =λ-1 ,y =0 ,z =λ ,所以可取n =(λ-1 ,0 ,λ).………8分 因为平面ABD 的法向量为OP →=(0 ,0 ,1) ,所以cos π4=|n ·OP →|n ||OP →|| ,即22=λ(λ-1)2+λ2 ,解得λ=12 , 从而M (12 ,0 ,12) ,N (0 ,13,0) ,所以MN =(12-0)2+(0-13)2+(12-0)2=226. ………10分 24解 ①假设抛物线开口方向向下 ,设抛物线方程为x 2=-2py (p >0) , 这时准线方程为y =p2,由抛物线定义知p2-(-3)=5 ,解得p =4 ,∴抛物线方程为x 2=-8y ,这时将点A (m ,-3)代入方程 ,得m =±2 6.②假设抛物线开口方向向左或向右 ,可设抛物线方程为y 2=2ax (a ≠0) ,从p =|a |知准线方程可统一成x =-a 2的形式 ,于是从题设有⎩⎪⎨⎪⎧⎪⎪⎪⎪a 2+m =52am =9 ,解此方程组可得四组解⎩⎪⎨⎪⎧ a 1=1m 1=92 ,⎩⎪⎨⎪⎧ a 2=-1m 2=-92 ,⎩⎪⎨⎪⎧ a 3=9m 3=12 ,⎩⎪⎨⎪⎧a 4=-9m 4=-12. ∴y 2=2x ,m =92;y 2=-2x ,m =-92;y 2=18x ,m =12;y 2=-18x ,m =-12.综上所述:所求结果为:y 2=2x ,m =92;y 2=-2x ,m =-92;y 2=18x ,m =12;y 2=-18x ,m =-12;x 2=-8y ,m =±2 6.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
联系电话:4000-916-716江苏省泰州市第二中学2017届高三下学期第二次限时作业参考公式:样本数据x 1,x 2,…,x n 的方差s 2=1n i =1∑n (x i --x )2,其中-x =1n i =1∑n x i . 锥体的体积公式:V =13Sh ,其中S 为锥体的底面积,h 为锥体的高.一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上)1.已知集合A ={-3,-1,1,2},集合B =,使得f (x 1)=g (x 2)成立,则实数a 的取值范围是 ▲ . 13.如图,用一块形状为半椭圆(y≥0)的铁皮截取一个以短轴BC 为底的等腰梯形ABCD ,记所得等腰梯形的面积为S ,则的最小值是 ▲ .14.给出定义:若m ﹣<x≤m+(其中m 为整数),则m 叫做离实数x 最近的整数,记作{x}=m .在此基础上给出下列关于函数f (x )=|x ﹣{x}|的四个命题: ①函数y=f (x )的定义域为R ,值域为;②函数y=f (x )的图象关于直线x=(k ∈Z )对称; ③函数y=f (x )是周期函数,最小正周期为1;④函数y=f (x )在上是增函数.其中正确的命题的序号 ▲ . 联系电话:4000-916-716二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内) 15.(本小题满分14分)在平面直角坐标系xOy 中,已知点,sin ,cos ),0,56()(ααP A 其中20πα<<.(1)若,65cos =α求证:.PO PA ⊥ (2)。
)4sin(2的值求若πα+=,PO PA16.(本小题满分14分)如图,在棱长为2的正方体1111ABCD A BC D -中,E 为BC 的中点, F 为1DC 的中点.(1)求证:1BD ∥平面1C DE ; (2)求三棱锥A BDF -的体积. 联系电话:4000-916-71617.(本小题满分14分)为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本y (元)与月处理量x (吨)之间的函数关系可近似的表示为:21200800002y x x =-+,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损? 联系电话:4000-916-71618. (本小题满分16分)如图,已知椭圆C :22221(0)x y a b a b +=>>的离心率为32,以椭圆C 的左顶点T 为圆心作圆T :222(2)(0)x y r r ++=>,设圆T 与椭圆C 交于点M 与点N .(1)求椭圆C 的方程;(2)求TM TN ⋅的最小值,并求此时圆T 的方程;(3)设点P 是椭圆C 上异于M ,N 的任意一点,且直线,MP NP 分别与x 轴交于点,R S ,O 为坐标原点,求证:OR OS ⋅为定值.19.(本小题满分16分)设等差数列{a n }的前n 项和为S n ,已知a 1=2,S 6=22. (1)求S n ;(2)若从{a n }中抽取一个公比为q 的等比数列{a k n },其中k 1=1, 且k 1<k 2<…<k n <…,k n ∈N *.①当q 取最小值时,求{ k n }的通项公式;②若关于n (n ∈N *)的不等式6S n >k n +1有解,试求q 的值. 联系电话:4000-916-71620.(本小题满分16分) 已知函数22()ln(21)2().3x f x ax x ax a R =++--∈(1)若x=2为()f x 的极值点,求实数a 的值;(2)若()y f x =在[)3,+∞上为增函数,求实数a 的取值范围;(3)当12a =-时,方程3(1)(1)3x b f x x--=+有实根,求实数b 的最大值。
高三数学(附加题)21.选修4-2:矩阵与变换已知二阶矩阵A 有特征值11λ=及对应的一个特征向量111⎡⎤=⎢⎥⎣⎦e 和特征值22λ=及对应的一个特征向量210⎡⎤=⎢⎥⎣⎦e ,试求矩阵A .22.选修4-4:坐标系与参数方程在直角坐标系xOy中,已知曲线C的参数方程是sin1cosyxθθ=+⎧⎨=⎩(θ是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C 的极坐标方程.23.已知抛物线顶点在原点,焦点在坐标轴上,又知此抛物线上的一点A(m,-3)到焦点F的距离为5,求m的值,并写出此抛物线的方程.联系电话:4000-916-716 联系电话:4000-916-71624.如图,在正四棱锥P -ABCD 中,P A =AB =2,点M ,N 分别在线段P A 和BD 上,BN =13BD . (1)若PM =13P A ,求证:MN ⊥AD ;(2)若二面角M -BD -A 的大小为π4,求线段MN 的长度. 联系电话:4000-916-716参考答案一、填空题:本大题共14小题,每小题5分,计70分. 1. {1,2} 2. -3 3.23 4. 55 5. 2656. 3y x =±7.8. 2 9、 a=2或a≤1 10. 2x 2﹣2y 2=1 11. k>0,且k 22≠12. 13.14. ①②③ .二、解答题: 15.(1)(方法一)由题设知).sin ,cos (),sin ,cos 56(a a PO a a PA --=--=……………………2分所以2sin ()cos )(cos 56()a a a PO PA -+--=⋅.1cos 56sin cos cos 5622+-=++-=a a a a ……………………6分 因为,65cos =a 所以.0=⋅PO PA 故.PO PA ⊥……………………7分(方法二)因为,65cos =a ,20π<<a 所以611sin =a ,故.611,65()P ………………2分因此).611,65(),611,3011(--=-=PO PA ……………………4分因为.0)611()65(30112=-+-⨯=⋅PO PA所以.PO PA ⊥ ……………………7分(2)因为,PO PA ⊥所以,22PO PA = 联系电话:4000-916-716即.sin cos sin )56cos 2222a a a a +=+-(解得.53cos =a 因为,20π<<a 所以.54sin =a 因此 .2571cos 22cos ,2524cos sin 22sin 2-=-===a a a a a 从而.50217)257(222524222cos 222sin 2242sin(=-⨯+⨯=+=+a a a )π……14分 16.解:(1)连接1D C 与1DC 交于点F ,连接EF因为E 为BC 的中点,F 为1DC 的中点.所以1EF BD又 EF ⊂平面1C DE ,1BD ⊄平面1C DE所以1BD 平面1C DE --------------------------------------------------------8分 (2)由于点F 到平面ABD 的距离为1故三棱锥A BDF -的体积111212213323A BDF F ABD ABD V V S --∆==== --------14分 17、解:(1)由题意可知,二氧化碳的每吨平均处理成本为:1800002002y x x x=+-…………………………………………………4分 18000022002002x x≥⋅-=, 当且仅当1800002x x=,即400x =时, 才能使每吨的平均处理成本最低,最低成本为200元.…………………8分 (2)设该单位每月获利为S ,则100S x y =-…………………………………………………………………10分2211100(20080000)3008000022x x x x x =--+=-+-21(300)350002x =---因为400600x ≤≤,所以当400x =时,S 有最大值40000-. 联系电话:4000-916-716故该单位不获利,需要国家每月至少补贴40000元,才能不亏损.…………14分18.本题考查椭圆的方程和几何性质、圆的方程等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想 解:(1)依题意,得2a =,32c e a ==,1,322=-==∴c a b c ; 故椭圆C 的方程为2214x y += . …………………3分 (2)方法一:点M 与点N 关于x 轴对称,设),(11y x M ,),(11y x N -, 不妨设01>y .由于点M 在椭圆C 上,所以412121xy -=. (*) ……………4分由已知(2,0)T -,则),2(11y x TM +=,),2(11y x TN -+=,21211111)2(),2(),2(y x y x y x TN TM -+=-+⋅+=⋅∴3445)41()2(1212121++=--+=x x x x 51)58(4521-+=x .………6分由于221<<-x ,故当581-=x 时,TM TN ⋅ 取得最小值为15-.由(*)式,531=y ,故83(,)55M -,又点M 在圆T 上,代入圆的方程得到21325r =.故圆T 的方程为:2213(2)25x y ++=. …………………8分方法二:点M 与点N 关于x 轴对称,故设(2cos ,sin ),(2cos ,sin )M N θθθθ-, 不妨设sin 0θ>,由已知(2,0)T -,则)sin ,2cos 2()sin ,2cos 2(θθθθ-+⋅+=⋅TN TM 3cos 8cos 5sin )2cos 2(222++=-+=θθθθ51)54(cos 52-+=θ.……6分故当4cos 5θ=-时,TM TN ⋅ 取得最小值为15-,此时83(,)55M -,又点M 在圆T 上,代入圆的方程得到21325r =. 联系电话:4000-916-716故圆T 的方程为:2213(2)25x y ++=. ………8分 (3) 方法一:设),(00y x P ,则直线MP 的方程为:)(010100x x x x y y y y ---=-,令0y =,得101001y y y x y x x R --=, 同理:101001y y y x y x x S ++=, …………10分故212021202021y y y x y x x x S R --=⋅ (**) ………………12分又点M 与点P 在椭圆上,故)1(42020y x -=,)1(42121y x -=,……………………14分 代入(**)式,得: 4)(4)1(4)1(421202120212021202021=--=----=⋅y y y y y y y y y y x x S R .所以4=⋅=⋅=⋅S R S R x x x x OS OR 为定值.……………………16分方法二:设(2cos ,sin ),(2cos ,sin )M N θθθθ-,不妨设sin 0θ>,)sin ,cos 2(ααP ,其中θαsin sin ±≠.则直线MP 的方程为:)cos 2(cos 2cos 2sin sin sin αθαθαα---=-x y ,令0y =,得θαθαθαsin sin )sin cos cos (sin 2--=R x ,同理:θαθαθαsin sin )sin cos cos (sin 2++=S x ,………………12分故4sin sin )sin (sin 4sin sin )sin cos cos (sin 42222222222=--=--=⋅θαθαθαθαθαS R x x . 所以4=⋅=⋅=⋅S R S R x x x x OS OR 为定值.…………14分19. 解:(1)设等差数列的公差为d ,则611665222S a d =+⋅⋅=,解得23d =,…2分 所以(5)3n n n S +=. …………4分 (2)因为数列是正项递增等差数列,所以数列的公比,若,则由,得,此时,由, }{n a }{n k a 1>q 22=k 382=a 3412==a a q 932)34(223=⋅=k a )2(32932+=n 联系电话:4000-916-716解得,所以,同理; …………6分 若,则由,得,此时,另一方面,2(2)3n k n a k =+,所以2(2)23n n k +=,即1322n n k -=⨯-, ………8分 所以对任何正整数,是数列的第项.所以最小的公比. 所以. …………10分(3)因为12423n n n k k a q -+==,得132n n k q -=-,而1q >, 所以当1q >且q N ∈时,所有的132n n k q -=-均为正整数,适合题意; 当2q >且q N ∉时,132n n k q N -=-∈不全是正整数,不合题意. 而16n n S k +>有解,所以2(5)213nn n q ++>有解,经检验,当2q =,3q =,4q =时,1n =都是2(5)213nn n q++>的解,适合题意; ……………12分 下证当5q ≥时,2(5)213n n n q ++>无解, 设2(5)23nnn n b q ++=, 则212[(1)(75)7]3n n nq n q n q b b q +-+-+--=,因为57022q q-<-,所以2()2[(1)(75)7]f n q n q n q =-+-+-在*n N ∈上递减,又因为(1)0f <,所以()0f n <恒成立,所以10n n b b +-<,所以1n b b ≤恒成立, 又因为当5q ≥时,11b <,所以当5q ≥时,16n n S k +>无解. ……………15分 综上所述,q 的取值为2,3,4. ………………16分20. (1)解:222[2(14)(42)]2()222121x ax a x a a f x x x a ax ax +--+'=+--=++ (1)分*310N n ∉=22>k 32>k 42=k 44=a 2=q 122-⋅=n k n a n n k a }{n a 2231-⋅-n 2=q 2231-⋅=-n n k 联系电话:4000-916-716因为x = 2为f (x )的极值点,所以(2)0f '= ……2分 即22041aa a -=+,解得:a = 0 ……3分 又当a = 0时,()(2)f x x x '=-,从而x = 2为f (x )的极值点成立. ……4分(2)解:∵f (x )在区间 ……10分(3)解:12a =-时,方程3(1)(1)3xb f x x --=+可化为,2ln (1)(1)bx x x x --+-=. 问题转化为2[ln ]b x x x x =+-在(0,+∞)上有解 ……12分 令2()ln h x x x x =+-,则(21)(1)1()12x x h x x x x+-'=+-=…14分 当0 <x < 1时,()0h x '>,∴h (x )在(0,1)上为增函数 当x > 1时,()0h x '<,∴h (x )在(1,+∞)上为减函数故h (x )≤h (1) = 0,而x > 0,故()0b xh x =≤ 即实数b 的最大值是0. ……16分21设矩阵a b A c d ⎡⎤=⎢⎥⎣⎦,这里a b c d ∈R ,,,, 因为11⎡⎤⎢⎥⎣⎦是矩阵A 的属于11λ=的特征向量,则有110110a b c d --⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦①,……4分 又因为10⎡⎤⎢⎥⎣⎦是矩阵A 的属于22λ=的特征向量,则有210100a b c d --⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦②…6分 根据①②,则有1010200a b c d a c --=⎧⎪-+-=⎪⎨-=⎪⎪-=⎩,,,, …………………………………………………8分从而2101a b c d ==-==,,,,因此2101A -⎡⎤=⎢⎥⎣⎦,………………………………10分 22C .(选修4-4:坐标系与参数方程)由sin 1cos y x θθ=+⎧⎨=⎩得1sin cos y x θθ-=⎧⎨=⎩,两式平方后相加得22(1)1x y +-=,…………4分 ∴曲线C 是以(0,1)为圆心,半径等于的圆.令cos ,sin x y ρθρθ==,代入并整理得2sin ρθ=.即曲线C 的极坐标方程是2sin ρθ=. …………10分 联系电话:4000-916-71623证明:连接AC ,BD 交于点O ,以OA 为x 轴正方向,以OB 为y 轴正方向,OP 为z 轴建立空间直角坐标系.因为P A =AB =2,则A (1,0,0),B (0,1,0),D (0,-1,0),P (0,0,1). (1)由BN →=13BD →,得N (0,13,0),由PM →=13PA →,得M (13,0,23),所以MN →=(-13,13,-23),AD →=(-1,-1,0).因为MN →·AD →=0.所以MN ⊥AD . ………………………………………4分 (2)因为M 在P A 上,可设PM →=λPA →,得M (λ,0,1-λ). 所以BM →=(λ,-1,1-λ),BD →=(0,-2,0). 设平面MBD 的法向量n =(x ,y ,z ), 由⎩⎪⎨⎪⎧n ·BD →=0,n ·BM →=0,得⎩⎨⎧-2y =0,λx -y +(1-λ)z =0,其中一组解为x =λ-1,y =0,z =λ,所以可取n =(λ-1,0,λ).………8分 因为平面ABD 的法向量为OP →=(0,0,1),所以cos π4=|n ·OP →|n ||OP →||,即22=λ(λ-1)2+λ2,解得λ=12, 从而M (12,0,12),N (0,13,0),所以MN =(12-0)2+(0-13)2+(12-0)2=226. ………10分 24解 ①若抛物线开口方向向下,设抛物线方程为x 2=-2py (p >0), 这时准线方程为y =p2,由抛物线定义知p2-(-3)=5,解得p =4,∴抛物线方程为x 2=-8y ,这时将点A (m ,-3)代入方程,得m =±2 6.②若抛物线开口方向向左或向右,可设抛物线方程为y 2=2ax (a ≠0),从p =|a |知准线 联系电话:4000-916-716方程可统一成x =-a 2的形式,于是从题设有⎩⎪⎨⎪⎧⎪⎪⎪⎪a 2+m =52am =9,解此方程组可得四组解⎩⎪⎨⎪⎧ a 1=1m 1=92,⎩⎪⎨⎪⎧ a 2=-1m 2=-92,⎩⎪⎨⎪⎧ a 3=9m 3=12,⎩⎪⎨⎪⎧a 4=-9m 4=-12. ∴y 2=2x ,m =92;y 2=-2x ,m =-92;y 2=18x ,m =12;y 2=-18x ,m =-12.综上所述:所求结果为:y 2=2x ,m =92;y 2=-2x ,m =-92;y 2=18x ,m =12;y 2=-18x ,m =-12;x 2=-8y ,m =±2 6.。
