(人教新课标)高二数学必修5第二章 数列2-5《等比数列的前n项和》)课件(共21张PPT)
合集下载
高中数学人教A版必修5第二章2.5 等比数列的前n项和课件(共11张PPT)

Sn a1 a2 a3 an
Sn a1 a1q a1q2 a1qn2 a1qn1. ⑴
⑴×q, 得
等式两边能否同
qSn a1q a1q2 a1qn2 a1qn除1 以a(1q1n-.q)?⑵
⑴-⑵,得 1 q Sn a1 a1qn ,
当q
1时,
Sn
a(1 1-qn) 1-q
1 q
1 q
(q≠1).
2、等比数列求和公式推导的方法:错位相
减法
11
=? 465 (万元)
第一天有1万, 以后每天比前 一天多1万元, 连续一个月(30
天)
第一天返还1分, 第二天返还2分, 第三天返还4分…… 后一天返还数为
前一天的24倍.
思考:该问题是一个等比数列的求和问题, 对于知
Office组件之word2007
等比数列an 的首项为a1,公比为q, 求前n项和Sn
Office组件之word2007
n 2.5 等比数列的前 项和
难点:等比数列前n项和公式的推导
1
复习引入
1. 等比数列的定义: an q(n 2, n N , q 0) an1
2. 等比数列通项公式:
an a1 qn1(a1, q 0)
2
新课引入 小故事
Office组件之word2007
该数列首项是1,公比是2,项数是30
S30
=
1(1-230)=230 1-2
-1
S30 = 230 - 1 = 1073741823 (分)
1073(万元) >465(万元)
不会数学很可怕!!!
10
总结:
1、等比数列的前n项和公
{ 式
Sn
Sn a1 a1q a1q2 a1qn2 a1qn1. ⑴
⑴×q, 得
等式两边能否同
qSn a1q a1q2 a1qn2 a1qn除1 以a(1q1n-.q)?⑵
⑴-⑵,得 1 q Sn a1 a1qn ,
当q
1时,
Sn
a(1 1-qn) 1-q
1 q
1 q
(q≠1).
2、等比数列求和公式推导的方法:错位相
减法
11
=? 465 (万元)
第一天有1万, 以后每天比前 一天多1万元, 连续一个月(30
天)
第一天返还1分, 第二天返还2分, 第三天返还4分…… 后一天返还数为
前一天的24倍.
思考:该问题是一个等比数列的求和问题, 对于知
Office组件之word2007
等比数列an 的首项为a1,公比为q, 求前n项和Sn
Office组件之word2007
n 2.5 等比数列的前 项和
难点:等比数列前n项和公式的推导
1
复习引入
1. 等比数列的定义: an q(n 2, n N , q 0) an1
2. 等比数列通项公式:
an a1 qn1(a1, q 0)
2
新课引入 小故事
Office组件之word2007
该数列首项是1,公比是2,项数是30
S30
=
1(1-230)=230 1-2
-1
S30 = 230 - 1 = 1073741823 (分)
1073(万元) >465(万元)
不会数学很可怕!!!
10
总结:
1、等比数列的前n项和公
{ 式
Sn
高中数学人教A版必修5第二章2.5等比数列前n项的求和公式课件

意思意思,第一天给我1元,第二天给我2元,第三天给我4
元,...以后就每天给我的钱是前一天的两倍,一直给我30天,
我们就算两清了,你看100万元,..哇,发财了!猪八戒:猴哥,你可别反悔呀!
孙悟空:那我们可以签一个合同嘛!说着就起草了一份合同.猪八戒
230 = 2 + 22 + ⋯ + 229 + 230
①-②,得到 30 -230 =1-230
(1-2)30 =1-230
30 =
−
−
≈1.1× (元)
大约就是11亿元
②
•
•
•
•
•
猪八戒应还孙悟空的钱:
等比数列
2
3
29
1, 2,2 ,2 , ⋯ ,2
30 = 1 +2+22 +⋯ + 228 + 229 ①
①×2得到:
230 = 2 + 22 + ⋯ + 229 +230
②
①-②,得到 30 -230 =1-230
(1-2)30 =1-230
30 =
−
−
≈1.1× (元)
大约就是11亿元
等比数列的前 n 项和公式
当 q≠1 时, Sn =
a1 ( 1- q n )
.
1-q
正想签字,可转念一想,发现不对劲了,这猴哥本来就精明,做了
生意之后更精了,他会不会又在耍我?
孙悟空借给猪八戒的钱:100×10000×30=3× (元)
就是 3千万元
猪八戒应还孙悟空的钱:
1, 2,22 ,23 , ⋯ ,229
30 = 1 +2+22 ⋯ + 228 + 229
元,...以后就每天给我的钱是前一天的两倍,一直给我30天,
我们就算两清了,你看100万元,..哇,发财了!猪八戒:猴哥,你可别反悔呀!
孙悟空:那我们可以签一个合同嘛!说着就起草了一份合同.猪八戒
230 = 2 + 22 + ⋯ + 229 + 230
①-②,得到 30 -230 =1-230
(1-2)30 =1-230
30 =
−
−
≈1.1× (元)
大约就是11亿元
②
•
•
•
•
•
猪八戒应还孙悟空的钱:
等比数列
2
3
29
1, 2,2 ,2 , ⋯ ,2
30 = 1 +2+22 +⋯ + 228 + 229 ①
①×2得到:
230 = 2 + 22 + ⋯ + 229 +230
②
①-②,得到 30 -230 =1-230
(1-2)30 =1-230
30 =
−
−
≈1.1× (元)
大约就是11亿元
等比数列的前 n 项和公式
当 q≠1 时, Sn =
a1 ( 1- q n )
.
1-q
正想签字,可转念一想,发现不对劲了,这猴哥本来就精明,做了
生意之后更精了,他会不会又在耍我?
孙悟空借给猪八戒的钱:100×10000×30=3× (元)
就是 3千万元
猪八戒应还孙悟空的钱:
1, 2,22 ,23 , ⋯ ,229
30 = 1 +2+22 ⋯ + 228 + 229
人教A版高中数学必修5课件:2.5等比数列的前n项和(共16张PPT)

求a 9 .
解: S6 63 9 2, q 1.
S3 7
7 63
a1 (1 q 3 ) , 1 q
a1 (1 q 6 ) ,
1 q
① ②
② 得 9 1 q3,
①
则 q2,a11.
a9a1q828256.
课堂练习
练习3:
已 知 在 等 比 数 列 a n 中 , S 3 3 ,a 3 1 ,
和
知三求二
课后思考
已 知 在 等 比 数 列 a n 中 , S 3 0 1 3 S 1 0 ,
S 1 0 S 3 0 1 4 0 ,则 S 2 0 _ _ _ _ _ _ .
当一个人用工作去迎接光明,光明很快就会来照耀着他。人在身处逆境时,适应环境的能力实在惊人。人可以忍受不幸,也可以战胜不幸,因为人有着惊人的 挥它,就一定能渡过难关。倘若你想达成目标,便得在心中描绘出目标达成后的景象;那么,梦想必会成真。心等待,就可以每一个人都具有特殊能力的电路, 知道,所以无法充分利用,就好像怀重宝而不知其在;只要能发掘出这项秘藏的能力,人类的能力将会完全大改观,也能展现出超乎常人的能力我这一生不曾 和伟大的著作都来自于求助潜意识心智无穷尽的宝藏。那些最能干的人,往往是那些即使在最绝望的环境里,仍不断传送成功意念的人。他们不但鼓舞自己, 成功,誓不休止。灵感并不是在逻辑思考的延长线上产生,而是在破除逻辑或常识的地方才有灵感。真正的强者,善于从顺境中找到阴影,从逆境中找到光亮 进的目标。每一种挫折或不利的突变,是带着同样或较大的有利的种子。什么叫做失败?失败是到达较佳境地的第一步。失败是坚忍的最后考验。对于不屈不 失败这回事。一次失败,只是证明我们成功的决心还够坚强。失败也是我需要的,它和成功对我一样有价值。我们关心的,不是你是否失败了,而是你对失败 失败?失败是到达较佳境地的第一步。没有人事先了解自己到底有多大的力量,直到他试过以后才知道。对于不屈不挠的人来说,没有失败这回事。要成功不 能,只要把你能做的小事做得好就行了。成功的唯一秘诀——坚持最后一分钟。只有胜利才能生存,只有成功才有代价,只有耕耘才有收获。只有把抱怨环境 的力量,才是成功的保证。不要为已消尽之年华叹息,必须正视匆匆溜走的时光。 当许多人在一条路上徘徊不前时,他们不得不让开一条大路,让那珍惜时间 面去。 敢于浪费哪怕一个钟头时间的人,说明他还不懂得珍惜生命的全部价值。成功=艰苦劳动+正确的方法+少说空话。合理安排时间,就等于节约时间。
人教版高中数学必修5第二章数列-《2.5等比数列的前n项和》课件(2)
变式训练:如果是前n项和呢?
1 1 1 2 3 2 2 2
1 2
1 1 n 1 n 2 2
1 2
1
1 1 2 2 2
1 1 1 2 3 2 2 2
1 1 1 1 2 3 4 2 2 2 2
1 2 2 1 3 2
1 4 2
吴敬所著的《九章算法比类大全》中 载有如下这样一首“数学诗”:
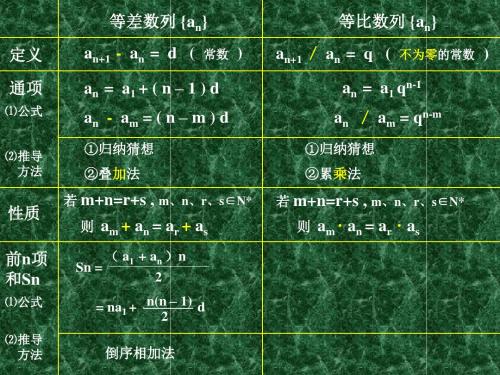
an - am = ( n – m ) d
①归纳猜想 ②叠加法 若 m+n=r+s , m、n、r、s∈N* 则 am + an = ar + as ( a1 + a n ) n Sn = 2 = na1 + n(n – 1) d 2 倒序相加法
⑵推导 方法
性质
前n项 和Sn
⑴公式 ⑵推导 方法
等比数列的前n项和
数学就像人类的一部特制的精密的大型望 远镜或显微镜一样,它大大延伸了人们洞察自 然地能力,看到了不掌握数学的人无法看到的 那个世界,能使人看到那些不懂数学的人无法 看到的东西。 ---张楚廷《数学文化》
五.小结
1.从知识方面来小结 na1 sn a1 (1 q n ) a1 an q 1 q 或 1 q
q 1
q 1
结论:若数列an 是等比数列,
则sm , s2m sm , s3m s2m,
也是等比数列
2.从数学思想方法方面来小结
1 2 2 2 2 =18446744073709551615
①归纳猜想 ②叠加法 若 m+n=r+s , m、n、r、s∈N* 则 am + an = ar + as ( a1 + a n ) n Sn = 2 = na1 + n(n – 1) d 2 倒序相加法
人教版2017高中数学(必修五)第2章《数列》2.5等比数列的前n项和 PPT课件

知识 链接
新知 探究
(一)等比数列的前n项和公式
新知 探究
(一)等比数列的前n项和公式
新知 探究
(一)等比数列的前n项和公式
问题2. 若把等比数列通项公式代入上式,你会得到什么呢?
【获取新知】 (1)等比数列前n项和公式:
新知 探究
(一)等比数列的前n项和公式
_________________________________________________.
典例 突破
(三)等比数列前n项和性质的应用
C
典例 突破
(三)等比数列前n项和性质的应用
同学们,再见!
典例 突破
(三)等比数列前n项和性质的应用
=
40
130,则 S20 的值为________. 【解析】由 S 10,S20-S10,S30-S20 成等比数列, 得 (S20-S10)2=S10(S30-S20), 即 (S20-10)2=10(130-S20), 解得S20=40或S20=-30 又 S20>0 ∴ S20=40.
(一)等比数列前n项和公式的基本运算
(1)等比数列前n项和公式的使用条件是什么?利用该公式解
题时,需要注意什么问题?
(2)在等比数列的五个基本量a1,an,n,q,Sn中,至少要
知道几个量才能求其他的量呢?
典例 突破
(一)等比数列前n项和公式的基本运算
典例 突破
(一)等比数列前n项和公式的基本运算
第二章
数列 §2.5 等比数列的前n项和
【学习目标】 1.理解并掌握等比数列前n项和公式及其推导过程;
2.能够应用前n项和公式解决等比数列的有关问题;
目标 定位
学习目标和重难点
人教A版高中数学必修五:2.5等比数列的前n项和 课件 (共25张PPT)

Office组件之word2007
八戒吸纳的资金
返还给悟空的钱数
22 33 29 S 2, 22 , 22 , , 2 T30 1 2 3 30 30 1, 2
465 (万元)
=?
以1为首项,2为公比的 等比数列的前30项之和
第一天有1万, 以后每天比前 一天多1万元, 连续一个月(30 天)
⑴-⑵,得 1 q Sn a1 a1q ,
n
探究新知
小练习:判断下列计算是否正确
Office组件之word2007
1 2 2 2 2
2 3 n
1 ( 1 2 ) n1 1 2 4 8 16 (2) 1 (2) n 1 2 n 1 (1 2 )
题号 (1) (2) (3)
a1 3 8
q 2
n 6
an
Sn
96
189
1 2
7
6
3
2
127 1 8 8 96 63
a1、q、n、an、Sn中 知三求二
例题讲解 例1.等比数列1, x, x
n
Office组件之word2007
2
, 的前n项和 Sn 为(
n 1 n 1 1 x 1 x 1 x A. B. C. D.以上均不对 1 x 1 x 1 x
2
n 2 S 3 1 ②-①可得: n
n1
n
②
3n 1 Sn 2
探究新知
Office组件之word2007
an 的首项为a1,公比为q, 如何求前n项和Sn呢? 等比数列
Sn a1 a2 a3 an 2 n 2 n1 Sn a1 a1q a1q a1q a1q .
人教版数学必修五:2.5《等比数列的前n项和》ppt课件

注意:(1)等比数列前 n 项和公式及通项公式中共有五个量 a1、q、an、n、Sn,这五个量可“知三求二”. (2)利用等比数列的前 n 项和公式求和时,要特别注意公比 q 的取值,应当按 q=1 和 q≠1 分别求解,如果其中含有参数 不能确定时,必须进行分类讨论.
第二章
2.5
第1课时
高中新课程 ·学习指导 ·人教A版 ·数学 ·必修5
第二章
2.5
第1课时
高中新课程 ·学习指导 ·人教A版 ·数学 ·必修5
即数列{an}是非常数列的等比数列的充要条件是前 n 项和 公式为 Sn=-Aqn+A,(A≠0,q≠0,且 q≠1,n∈N*) 当公比 q=1 时,因为 a1≠0,所以 Sn=na1 是 n 的正比例 函数.
第二章
2.5
第1课时Βιβλιοθήκη 1 已知 a1=27,a9=243,q<0,求这个等比数列前 5 项的和.
[ 分析] 出 S5.
[ 解析]
由 a1, a9 可求出 q, 再用等比数列前 n 项和公式求 1 243 1 1 8 ∵a1=27,a9=243,∴q = 27 =38,
1 又∵q<0,∴q=-3, 15 a11-q5 27[1--3 ] 61 ∴S5= = 1 =3. 1-q 1--3
高中新课程 ·学习指导 ·人教A版 ·数学 ·必修5
等比数列{an}的前 n 项和 Sn=2×3n+a,则 a 等于( A.3 C.0 [ 答案] B.1 D.-2
)
D
[ 解析]
数列{an}是非常数列的等比数列的充要条件是前 n
项和公式为 Sn=-Aqn+A,由此可知 a=-2.
第二章
2.5
第1课时
第1课时
第二章
2.5
第1课时
高中新课程 ·学习指导 ·人教A版 ·数学 ·必修5
第二章
2.5
第1课时
高中新课程 ·学习指导 ·人教A版 ·数学 ·必修5
即数列{an}是非常数列的等比数列的充要条件是前 n 项和 公式为 Sn=-Aqn+A,(A≠0,q≠0,且 q≠1,n∈N*) 当公比 q=1 时,因为 a1≠0,所以 Sn=na1 是 n 的正比例 函数.
第二章
2.5
第1课时Βιβλιοθήκη 1 已知 a1=27,a9=243,q<0,求这个等比数列前 5 项的和.
[ 分析] 出 S5.
[ 解析]
由 a1, a9 可求出 q, 再用等比数列前 n 项和公式求 1 243 1 1 8 ∵a1=27,a9=243,∴q = 27 =38,
1 又∵q<0,∴q=-3, 15 a11-q5 27[1--3 ] 61 ∴S5= = 1 =3. 1-q 1--3
高中新课程 ·学习指导 ·人教A版 ·数学 ·必修5
等比数列{an}的前 n 项和 Sn=2×3n+a,则 a 等于( A.3 C.0 [ 答案] B.1 D.-2
)
D
[ 解析]
数列{an}是非常数列的等比数列的充要条件是前 n
项和公式为 Sn=-Aqn+A,由此可知 a=-2.
第二章
2.5
第1课时
第1课时
高中数学人教版必修5课件:2.5等比数列的前n项和(共22张PPT)

问题7 问题8
题型1
例1
解作业布置
课本P61 A组 1,2,3,4,5
题型2
例3
解1
解2
数列的求和方法的类型 类型1 公式法
公式法常与其它方法相结合使用,单独命题并不多见
类型2 错位相减法
例4
解
类型3 裂项相消法
例5
解
类型4 并项求和法
直接把求和的项按加法结合律两两结合(或三三 结合)求和 例6
解
类型5 分组求和法
把数列的每一项分成若干部分,并分别 的把具有相同特征的部分放到一起,使 其转化为前面的类型数列求和.
2.5等比数列 的前n项和
问题预习
问题1
问题2
首项、公比、项数分别为1,2, 64
问题3
两边同乘以2,即两边同乘以公比2,使 原数列的各项相应增加1次,两式相减时,就有 许多项可以抵消.这种方法称“错位相减法”
问题4 在这个算中, 两边同乘以2,“2”在这个数列中
是一个什么角色?
问题5 问题6
高中数学人教A版必修5第二章:2.5等比数列的前n项和课件

1 4
1 2
1,n 2
8,得
Sn
1 [1 (1 )8 ] 22
1 1
255 256
2
例2
已知等比数列 an,
a1 27, a9
1 243
.
求前8项的和.
高中数学人教A版必修5第二章:2.5等 比数列 的前n 项和课 件
高中数学人教A版必修5第二章:2.5等 比数列 的前n 项和课 件
课堂练习 :
aman ar as
高中数学人教A版必修5第二章:2.5等 比数列 的前n 项和课 件
等差数列求和方法回顾:(倒序相加)
Sn a1 a2 a3 an1 an + Sn an an1 an2 a2 a1
2Sn (a1 an ) (a2 an1) (an a1)
高中数学人教A版必修5第二章:2.5等 比数列 的前n 项和课 件
高中数学人教A版必修5第二章:2.5等 比数列 的前n 项和课 件
Sn
a1
na1 (1 q
n
1 q
(q )
1) (q 1)
q 1时 :
Sn
a1 a1qn 1 q
a1 anq 1 q
注意:
1、使用公式求和时,需注意对 q 1 和 q 1 的情
n个相 同的数
Sn
n(a1 2
an )
高中数学人教A版必修5第二章:2.5等 比数列 的前n 项和课 件
高中数学人教A版必修5第二章:2.5等 比数列 的前n 项和课 件
国王赏麦的故事
1 2 22 23 263
高中数学人教A版必修5第二章:2.5等 比数列 的前n 项和课 件
高中数学人教A版必修5第二章:2.5等 比数列 的前n 项和课 件
人教A版高中数学必修5《二章 数列 2.5 等比数列的前n项和 等比数列的前n项和》示范课课件_9

【课后作业】
教材第58 页 练习 第1题
教材第61 页 习题2.5A组 第1 、2题
(2)a1=27,a9=
1 ,q 243
0
2由a1
27, a9
1 ,可得 1 =27
243
243
q8
又由q 0,可得q 1 3
于是当n
8时,S8
271
1 3
8
1
1 3
1640 81
例题与变式
变式1: 根据下列条件,求相应的等比数列an 的 S n (1)a1 3, q 2, n 6;
a1(1 qn )
当q=1时,等 比数列的前n 项和是什么?
当q≠1时,
Sn
a1(1 qn ) 1q
Sn na1
新课探究
等比数列的前n项和公式的其它形式
当q≠1时,
Sn
a1(1 qn ) 1q
a1 (1qn )a1 a1qn a1 (a1qn1 )qa1 anq
变式3:求等比数列1,x, x2, x3,的前n项和Sn
归纳小结
1、知识小结
本节课主要学习了等比数列的前n项和公式
na1,
Sn
a1
1 qn
1 q
= a1 anq 1 q
q 1 及其简单应用. q 1
2、思想方法小结
由特殊到一般 、错位相减法、分类讨论思想、 方程思想等
a1
1, 2
q 11 1, 42 2
n=8,得
高中数学第二章数列2.5等比数列的前n项和课件新人教A版必修5[1]
![高中数学第二章数列2.5等比数列的前n项和课件新人教A版必修5[1]](https://img.taocdn.com/s3/m/ae15f7fa03d8ce2f01662391.png)
题型一
题型二
题型三
题型四
等比数列前n项和性质的应用
【例2】 在等比数列{an}中,已知Sn=48,S2n=60,求S3n.
分析用求和公式(gōngshì)直接求解或用性质求解.
解法一∵S2n≠2Sn,∴q≠1.
由已知,得1 ຫໍສະໝຸດ 1- )= 48,1-
1 (1-2 )
= 60.
1-
5
①
若q≠1,则由等比数列的前n项和公式,
得 S3=
1 (1-3 )
2(1-3 )
=
=
1-
1-
6,
解得q=1(舍去)或q=-2.
此时,a3=a1q2=2×(-2)2=8.
综上所述,q=1,a3=2或q=-2,a3=8.
反思在使用(shǐyòng)等比数列的前n项和公式解题时,要注意对公比q是否
将文字语言翻译成数学语言,将数量关系用数学式子表达.
(3)将实际问题抽象为数学问题,将已知与所求的量联系起来,并根据题意列
出数学关系式.
2.价格升降、细胞繁殖(fánzhí
)、利率、税率、增长率(如本题)等问题常归
结为等比数列模型,即从实际背景中抽象出数学事实,归纳转化为数列问题去
解决.
第十五页,共18页。
2.5
等比数列(děnɡ bǐ shù liè)的前
n项和
第一页,共18页。
1.理解并掌握等比数列的前n项和公式及其推导方法(fāngfǎ).
2.能利用等比数列的前n项和公式解决有关问题.
3.掌握等比数列的前n项和的性质及应用.
第二页,共18页。
等比数列(děnɡ bǐ shù liè)的前n项和公式
求二”是常见题型,常用(chánɡ yònɡ)解方程组的方法求得,解方程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两式相减,得-Sn=2+22+23+„+2n-n· 2n+1 21-2n + = -n· 2n 1 1-2 =2n 1-2-n· 2n
+ +1
=(1-n)· 2n+1-2, ∴Sn=(n-1)· 2n+1+2.
2n-1 1 3 5 7 变式 5:求数列2,4,8,16,„, 2n 的前 n 项和.
整理,得 1+q3=9,解得 q=2. a11-q3 7 1 将 q=2 代入 =2,得 a1=2, 1-q 故 an=a1qn 1=2n 2.
- -
例3:某商场第1年销售计算机5000台,如果平均每年的销售量比
上一年增加10%,那么从第1年起,约几年内可使总销售量达到
30000台(保留到个位)?
解:a1=5000,
q=1+10%=1.1
sn=30000
5000(1 1.1n ) 于是得到 30000 1 1.1
整理后,得1.1n 1.6
两边取对数, 得n lg1.1 lg1.6
lg1.6 0.20 n 5(年) lg1.1 0.041
变式 4:在等比数列{an}中,公比 q=-2,S5=22,则 a1 的值 等于( D ) A.-2 C. 1 B.-1 D.2
① ②
2n-1 1 1 1 1 ①-②,得-Sn=-1-2(2+22+23+„+ n-1)+ 2n = 2 1 1 21-2n-1 2n-1 -1-2× 1 + 2n 1-2 2n-1 2n+3 =-1-2+ n-2+ 2n =-3+ 2n , 2 1 2n+3 ∴Sn=3- 2n .
即数列{an}是非常数列的等比数列的充要条件是前 n 项和 公式为 Sn=-Aqn+A,(A≠0,q≠0,且 q≠1,n∈N*) 当公比 q=1 时,因为 a1≠0,所以 Sn=na1 是 n 的正比例 函数.
例 2:等比数列{an}的前 n 项和 Sn=2×3n+a,则 a 等于( A.3 C.0 B.1 D.-2
注:(1)公式中涉及 a1 , q, n, an , Sn “知三求二” (方程思想)
五个量
(2)选择合适的公式,简化运算过程
a1 (1 q n ) q≠1时,已知首项和公比,用 S n 1 q 已知首项和末项,用 S a1 an q n 1 q
1 1 1 例1: 求等比数列 , , , 的前8项的和. 2 4 8
D
)
解析:数列{an}是非常数列的等比数列的充要条件是前 n 项 和公式为 Sn=-Aqn+A,由此可知 a=-2.
7 63 变式 3:在等比数列{an}中,S3= ,S6= ,求 an. 2 2
解析: ∵S6≠2S3,∴q≠1,
3 a 1 - q 7 1 =2, 1 - q 7 63 又∵S3=2,S6= 2 ,∴ 6 a11-q 63 =2, 1 - q
解析:∵S5=22,q=-2, a1[1--25] ∴ =22, 1--2 ∴a1=2.
错位相减法
例 4:求和:Sn=2+2· 22+3· 23+„+n· 2n.
解析: ∵Sn=2+2· 22+3· 23+„+n· 2n ∴2Sn=1· 22+2· 23+„+(n-1)· 2n+n· 2n+1
1 1 解: a1 , q , n 8 2 2
1 1 1 2 2 S8 1 1 2
8
255 256
变式1:已知a1=27,a9=,q<0,求这个等比数列前5项ቤተ መጻሕፍቲ ባይዱ和.
1 243 1 1 8 解析:∵a1=27,a9=243,∴q = 27 =38, 1 又∵q<0,∴q=-3, 15 a11-q5 27[1--3 ] 61 ∴S5= = =3. 1 1-q 1--3
国际象棋的棋盘上共有8 行8列,构成64个格子.国际 象棋起源于古代印度,关于 国际象棋有这样一个传说.
国际象棋与等比数列的前n项和
等比数列的前n项和 设等比数列 a1 , a2 , a3 ,, an ,
它的前n项和是
Sn a1 a2 a3 an
⑴
即 Sn a1 a1q a1q 2 a1q n2 a1q n1.
⑴×q, 得
qSn
a1q a1q a1q
2
n2
a1q
n1
a1q .
n
⑵
⑴-⑵,得
1 q Sn a1 a1qn ,
说明:这种求和方法称为错位相减法
当q≠1时, 当q=1时,
a1 1 q Sn 1 q
n
Sn na1
于是
na1 , (q 1), S n a1 (1 q n ) 1 q , (q 1).
第二章 数列
2.5 等比数列的前n项和
本节课主要学习等比数列的前 n项和公式。本课件以关于象棋的
传说提出问题,以问题引入新课,吸引学生注意力。以学生探究为
主,研究等比数列求和公式的两种方法,开阔学生的思路。强调公 式的运用方法。 用例1和变式1,2加以巩固。探究等比数列前n项和公式与函数的关 系,通过例 2和变式3,4巩固掌握有关公式,并学会运用。教学过程 有讲有练,例 3 运用等比数列的求和公式计算实际问题,增加变式 用来巩固公式。例4展示错位相减法的应用.
1 1 1 1 分析:本题中的数列是由数列 1,3,5,7,„与2,4,8,16,„ 的各项对应相乘得到的,前面的数列是等差数列,后面的数列 是等比数列,可用错位相减法求和.
2n-1 1 3 5 解析:设 Sn=2+22+23+„+ 2n , 2n-1 3 5 则 2Sn=1+2+22+„+ n-1 . 2
变式2. 根据下列条件,求相应的等比数列 an 的 S n
(1)a1 3, q 2, n 6;
1 1 ( 2) a1 8, q , an ; 2 2
等比数列前n项和公式与函数的关系
当公比 q≠1 时,我们已经知道等比数列的前 n 项和公式 a11-qn a1 n a1 a1 Sn= , 它可以变形为 Sn=- q+ , 设 A= , 1-q 1-q 1-q 1-q 上式可写成 Sn=-Aqn+A,
