人教版高中数学必修五知识点总结
高中数学必修5知识点总结归纳(人教版最全)
高中数学必修五知识点汇总第一章 解三角形 一、知识点总结 正弦定理:1．正弦定理:2sin sin sin a b cR A B C=== (R 为三角形外接圆的半径).步骤1.证明：在锐角△ABC 中，设BC=a,AC=b,AB=c 。
作CH ⊥AB 垂足为点H CH=a ·sinB CH=b ·sinA ∴a ·sinB=b ·sinA得到b ba a sin sin =同理，在△ABC 中， bbc c sin sin =步骤2.证明：2sin sin sin a b cR A B C===如图，任意三角形ABC,作ABC 的外接圆O. 作直径BD 交⊙O 于D. 连接DA.因为直径所对的圆周角是直角,所以∠DAB=90°因为同弧所对的圆周角相等,所以∠D 等于∠C.所以C RcD sin 2sin ==故2sin sin sin a b c R A B C ===2.正弦定理的一些变式：()sin sin sin i a b c A B C ::=::；()sin ,sin ,sin 22a bii A B C R R==2c R =；()2sin ,2sin ,2sin iii a R A b R B b R C ===；（4）R CB A cb a 2sin sin sin =++++ 3．两类正弦定理解三角形的问题：（1）已知两角和任意一边，求其他的两边及一角.（2）已知两边和其中一边的对角，求其他边角.（可能有一解，两解，无解） 4.在ABC ∆中，已知a,b 及A 时，解得情况： 解法一：利用正弦定理计算解法二：分析三角形解的情况，可用余弦定理做，已知a,b 和角A ，则由余弦定理得 即可得出关于c 的方程：0cos 2222=-+-a b Ac b c 分析该方程的解的情况即三角形解的情况 ①△=0,则三角形有一解 ②△>0则三角形有两解 ③△<0则三角形无解 余弦定理:1．余弦定理： 2222222222cos 2cos 2cos a b c bc A b a c ac B c b a ba C ⎧=+-⎪=+-⎨⎪=+-⎩2.推论： 222222222cos 2cos 2cos 2b c a A bc a c b B ac b a c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩.设a 、b 、c 是C ∆AB 的角A 、B 、C 的对边，则： ①若222a b c +=，则90C =； ②若222a b c +>，则90C <； ③若222a b c +<，则90C >．3.两类余弦定理解三角形的问题：（1）已知三边求三角.（2）已知两边和他们的夹角，求第三边和其他两角. 面积公式:已知三角形的三边为a,b,c,1.111sin ()222a S ah ab C r a b c ===++（其中r 为三角形内切圆半径）2.设)(21c b a p ++=,))()((c p b p a p p S ---=(海伦公式)例：已知三角形的三边为，、、c b a 设)(21c b a p ++=，求证：（1）三角形的面积))()((c p b p a p p S ---=； （2）r 为三角形的内切圆半径，则pc p b p a p r ))()((---=（3）把边BC 、CA 、AB 上的高分别记为，、、c b h h a h 则))()((2c p b p a p p ah a ---=))()((2c p b p a p p b h b ---=))()((2c p b p a p p ch c ---=证明：（1）根据余弦定理的推论：222cos 2a b c C ab+-=由同角三角函数之间的关系，sin C ==代入1sin 2S ab C =，得12S ====记1()2p a b c =++，则可得到1()2b c a p a +-=-，1()2c a b p b +-=-，1()2a b c p c +-=-代入可证得公式（2）三角形的面积S 与三角形内切圆半径r 之间有关系式122S p r pr =⨯⨯=其中1()2p a b c =++，所以S r p == 注：连接圆心和三角形三个顶点，构成三个小三角形，则大三角形的面积就是三个小三角形面积的和 故得：pr cr br ar S =++=212121（3）根据三角形面积公式12a S a h =⨯⨯所以，2a S h a =a h =同理b h c h 【三角形中的常见结论】（1）π=++C B A (2) sin()sin ,A B C +=cos()cos ,A B C +=-tan()tan ,A B C +=-2cos 2sinC B A =+,2sin 2cos CB A =+;A A A cos sin 22sin ⋅=, （3）若⇒>>C B A c b a >>⇒C B A sin sin sin >> 若C B A sin sin sin >>⇒c b a >>⇒C B A >> （大边对大角，小边对小角）（4）三角形中两边之和大于第三边，两边之差小于第三边 （5）三角形中最大角大于等于 60，最小角小于等于 60(6) 锐角三角形⇔三内角都是锐角⇔三内角的余弦值为正值⇔任两角和都是钝角⇔任意两边的平方和大于第三边的平方.钝角三角形⇔最大角是钝角⇔最大角的余弦值为负值 （7）ABC ∆中，A,B,C 成等差数列的充要条件是 60=B .(8) ABC ∆为正三角形的充要条件是A,B,C 成等差数列，且a,b,c 成等比数列. 二、题型汇总:题型1:判定三角形形状判断三角形的类型（1）利用三角形的边角关系判断三角形的形状:判定三角形形状时，可利用正余弦定理实现边角转化，统一成边的形式或角的形式.（2）在ABC ∆中，由余弦定理可知:222222222是直角ABC 是直角三角形是钝角ABC 是钝角三角形是锐角a b c A a b c A a b c A =+⇔⇔∆>+⇔⇔∆<+⇔⇔ABC 是锐角三角形∆（注意：是锐角A ⇔ABC 是锐角三角形∆） (3) 若B A 2sin 2sin =，则A=B 或2π=+B A .例1.在ABC ∆中，A b c cos 2=，且ab c b a c b a 3))((=-+++，试判断ABC ∆形状.题型2:解三角形及求面积一般地，把三角形的三个角A,B,C 和它们的对边a,b,c 叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形.例2.在ABC ∆中，1=a ，3=b ，030=∠A ，求的值例3.在ABC ∆中，内角C B A ,,对边的边长分别是c b a ,,，已知2=c ，3π=C ．（Ⅰ）若ABC ∆的面积等于3，求a ，b（Ⅱ）若A A B C 2sin 2)(sin sin =-+，求ABC ∆的面积．题型3:证明等式成立证明等式成立的方法：（1）左⇒右，（2）右⇒左，（3）左右互相推.例4.已知ABC ∆中，角C B A ,,的对边分别为c b a ,,，求证：B c C b a cos cos +=.题型4:解三角形在实际中的应用考察：（仰角、俯角、方向角、方位角、视角）例5．如图所示，货轮在海上以40km/h 的速度沿着方位角（从指北方向顺时针转到目标方向线的水平转角）为140°的方向航行，为了确定船位，船在B 点观测灯塔A 的方位角为110°，航行半小时到达C 点观测灯塔A 的方位角是65°，则货轮到达C 点时，与灯塔A 的距离是多少？三、解三角形的应用 1.坡角和坡度：坡面与水平面的锐二面角叫做坡角，坡面的垂直高度h 和水平宽度l 的比叫做坡度，用i 表示，根据定义可知：坡度是坡角的正切，即tan i α=.lhα2.俯角和仰角：如图所示，在同一铅垂面内，在目标视线与水平线所成的夹角中，目标视线在水平视线的上方时叫做仰角，目标视线在水平视线的下方时叫做俯角.3. 方位角从指北方向顺时针转到目标方向线的水平角，如B点的方位角为 .注：仰角、俯角、方位角的区别是：三者的参照不同。
高中数学人教版_必修五_不等式_知识点最完全精炼总结
2012.3.264.公式： 1.两实数大小的比较⎪⎩⎪⎨⎧<-⇔<=-⇔=>-⇔>0b a b a 0b a b a 0b a b a 一.不等式(淮上陌客）3.基 本不等式定理⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧-≤+⇒<≥+⇒>≥+⎪⎪⎩⎪⎪⎨⎧+≤+≥+⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+≤⎪⎭⎫ ⎝⎛+≤+≥+≥+2a 1a 0a 2a 1a 0ab ,a (2b aa b )b a (2b a ab 2b a 2b a ab 2b a ab )b a (21b a ab 2b a 2222222222倒数形式同号）分式形式根式形式整式形式2211222a b a b ab a b --++≤≤≤+2.不等式的性质：8条性质.3.解不等式(1)一元一次不等式(2)一元二次不等式：判别式△=b2- 4ac△>0 △=0△<0y=ax2+bx+c的图象(a>0)ax2+bx+c=0 (a>0)的根有两相异实根x1, x2 (x1<x2)有两相等实根x1=x2=没有实根ax2+bx+c>0(y>0)的解集{x|x<x1,或x>x2} {x|x≠}Rax2+bx+c<0 (y<0)的解集{x|x1< x <x2}ΦΦx1x2xyOyxO x1yxO⎪⎩⎪⎨⎧<<>>≠>)0a(abx)0a(abx)0a(baxab2-ab2-一元二次不等式的求 解流程：一化：化二次项前的系数为正数. 二判：判断对应方程的根. 三求：求对应方程的根. 四画：画出对应函数的图象.五解集：根据图象写出不等式的解集. (3)解分式不等式：高次不等式：(4)解含参数的不等式：（1）(x – 2)(ax – 2)>0（2）x 2 – (a +a 2)x +a 3>0；（3）2x 2 +ax +2 > 0；注:解形如ax 2+bx+c>0的不等式时分类讨 论的标准有：1、讨论a 与0的大小；2、讨论⊿与0的大小；3、讨论两根的大小；二、运用的数学思想：1、分类讨论的思想；2、数形结合的思想；3、等与不等的化归思想(4)含参不等式恒成立的问题：⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧≠≤⋅⇔≤>⋅⇔>0)x (g 0)x (g )x (f 0)x (g )x (f 0)x (g )x (f 0)x (g )x (f 0)())((21>---n a x a x a x⎪⎩⎪⎨⎧用图象分离参数后用最值函数、、、321例1．已知关于x 的不等式在(–2，0)上恒成立，求实数a 的取值范围． 例2．关于x 的不等式对所有实数x ∈R 都成立，求a 的取值范围.(5)一元二次方程根的分布问题：方法：依据二次函数的图像特征从：开口方向、判别式、对称轴、 函数值三个角度列出不等式组，总之都是转化为一元二次20,31xx a x x >≤++恒成立，例3.若对任意则 的取值范围.a22(3)210x a x a +-+-<)1(log 22++-=ax ax y不等式组求解. 二次方程根的分布问题的讨论：y()020f k b k a >⎧⎪⎪-<⎨⎪∆>⎪⎩1．x 1< x 2< kxOkx 1x 2xyO x 2x 1 k ()020f k b k a >⎧⎪⎪->⎨⎪∆>⎪⎩2．k < x 1< x xyO xx 1 k()0f k <3．x 1< k < x 24． k 1 < x 1 < x 2 < k 2 5． x 1 < k 1 < k 2 < x 2 1212()0()002f k f k b k k a >⎧⎪>⎪⎪⎨∆>⎪⎪<-<⎪⎩12()0()0f k f k >⎧⎨>⎩6． k 1 <x 1 < k 2 < x 2< k 3122()0()0()0f k f k f k >⎧⎪<⎨⎪>⎩ 4解线性规划问题的一般步骤：第一步：在平面直角坐标系中作出可行域； 第二步：在可行域内找到最优解所对应的点；第三步：解方程的最优解，从而求出目标函数的最大值或最小值。
人教版数学必修五知识点精要归纳整理(精编Word版)
必修五第一章解三角形一、正弦定理和余弦定理1、正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即是外接圆半径。
解三角形（三角形元素：角A、B、C，对应边a、b、c。
）已知三个元素，求出另外三个元素。
2、余弦定理：三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍。
即：（应用：已知两边与夹角，算出第三边。
）推论：，，。
二、应用举例1、、三、实习作业（略）第二章数列一、概念与简单表示法1、概念：按照一定顺序排列的一列数。
2、项、首项、有穷数列、无穷数列、递增数列、递减数列、常数列、摆动数列。
3、通项公式4、递推公式二、等差数列& 前n项和（书本P36：本利和=本金（1+利率存期））单利1、等差数列、公差d、等差中项。
，，、、、2、3、三、等比数列& 前n项和（书本P48：本利和=本金（1+利率）存期）复利1、等比数列、公比、等比中项。
，，、、、2、，；3、，。
课外补充：平方数列，，。
立方数列，，。
第三章不等式一、不等式关系与不等式（性质）1、2、，3、4、，，若5、，6、，7、，8、，二、一元二次不等式及其解法1、概念：只含有一个未知数，并且未知数的最高次数是2的不等式。
2、解法（结合图象）时△（两解，一解，无解）时与x轴的交点三、二元一次不等式（组）与简单的线性规划问题1、……与平面区域（1）解集：有序数对（x，y）构成的集合，是一个平面区域（有限的）。
（2）边界：虚线表示，实线表示。
（补充）区域判断：，下方，上方，上方，下方2、简单的线性规划问题（1）资源利用、人力调配、生产安排等。
（2）目标函数（又称线性目标函数）：最大（小）值线性规划问题可行解可行域步骤：画线——画目标函数——在可行域范围内平移——最优解。
四、基本不等式：1、对于任意实数a、b，我们有，当且仅当时，等号成立。
2、，时，。
人教版数学必修5知识点总结
高中数学 必修5知识点第一章 解三角形（一）解三角形：1、正弦定理：在C ∆AB 中，a 、b 、c 分别为角A 、B 、C 的对边，，则有2sin sin sin a b cR C===A B (R 为C ∆AB 的外接圆的半径)2、正弦定理的变形公式：①2sin a R =A ，2sin b R =B ，2sin c R C =； ②sin 2a R A =，sin 2b R B =，sin 2c C R=；③::sin :sin :sin a b c C =A B ； 3、三角形面积公式：111sin sin sin 222C S bc ab C ac ∆AB =A ==B ．4、余弦定理：在C ∆AB 中，有2222cos a b c bc =+-A ，推论：222cos 2b c a bc+-A =第二章 数列 1、数列中n a 与n S 之间的关系：11,(1),(2).n nn S n a S S n -=⎧=⎨-≥⎩注意通项能否合并。
2、等差数列： ⑴定义：如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，即n a －1-n a =d ，（n ≥2，n ∈N +），那么这个数列就叫做等差数列。
⑵等差中项：若三数a A b 、、成等差数列2a bA +⇔= ⑶通项公式：1(1)()n m a a n d a n m d =+-=+- 或(n a pn q p q =+、是常数）. ⑷前n 项和公式：()()11122n n n n n a a S na d -+=+= ⑸常用性质：①若()+∈ +=+N q p n m q p n m ,,,，则q p n m a a a a +=+； ②下标为等差数列的项() ,,,2m k m k k a a a ++，仍组成等差数列； ③数列{}b a n +λ（b ,λ为常数）仍为等差数列；④若{}n a 、{}n b 是等差数列，则{}n ka 、{}n n ka pb + (k 、p 是非零常数)、*{}(,)p nq a p q N +∈、，…也成等差数列。
高中数学必修5知识点总结归纳8篇
高中数学必修5知识点总结归纳8篇篇1一、引言高中数学必修5是整个数学学科体系中重要的一部分，它涵盖了代数、几何、三角学等多个领域的知识点。
本文将对该课程的核心知识点进行系统的总结归纳，以便学生更好地掌握数学基础知识，提高数学应用能力。
二、代数部分1. 集合与函数：集合的运算、集合的表示方法、函数的定义、函数的性质、函数的图像等。
2. 不等式：不等式的性质、一元二次不等式的解法、绝对值不等式的解法等。
3. 数列与极限：数列的定义、等差数列与等比数列、数列的极限等。
三、几何部分1. 平面解析几何：直线的方程、圆的方程、二次曲线的方程及其性质等。
2. 立体几何：空间向量、空间角、距离公式、几何体的表面积与体积等。
四、三角学部分1. 三角函数：三角函数的定义、性质、图像，三角函数的和差公式、倍角公式等。
2. 解三角形：正弦定理、余弦定理、三角形的面积公式等。
五、知识点详解1. 代数式的化简与求值：掌握代数式的运算规则，能够对方程进行化简和求值。
2. 不等式的解法：掌握一元二次不等式和绝对值不等式的解法，能够解决实际问题中的不等式问题。
3. 数列的性质与应用：了解数列的定义、性质，掌握等差数列与等比数列的通项公式和求和公式，能够应用数列知识解决实际问题。
4. 平面解析几何：掌握直线与二次曲线的方程，能够求解与几何图形相关的问题。
5. 立体几何的体积与表面积：熟悉几何体的体积与表面积公式，能够计算不规则几何体的体积与表面积。
6. 三角函数的性质与应用：掌握三角函数的性质，如周期性、奇偶性，熟悉三角函数的和差公式和倍角公式，能够应用三角函数解决实际问题。
7. 解三角形的方法：掌握正弦定理和余弦定理，能够解决与三角形相关的问题，如三角形的角度、边长等。
六、学习方法与建议1. 掌握基础知识：牢固掌握必修5中的基本概念和性质，这是解题的基础。
2. 多做练习：通过大量的练习来巩固知识点，提高解题能力。
3. 归纳总结：对学过的知识点进行总结归纳，形成知识体系和框架。
人教版高中数学必修五知识点汇总
人教版高中数学必修5知识点第一章：解三角形一、知识点总结正弦定理：1.正弦定理：2sin sin sin a b cR A B C===(R 为三角形外接圆的半径).步骤1：证明：在锐角△ABC 中，设BC=a ，AC=b ，AB=c 。
作CH ⊥AB 垂足为点H CH=a·sinB CH=b·sinA ∴a·sinB=b·sinA得到b b a a sin sin =同理，在△ABC 中，b bc c sin sin =步骤2：证明：2sin sin sin a b cR A B C===如图，任意三角形ABC ，作ABC 的外接圆O.作直径BD 交⊙O 于D.连接DA.因为直径所对的圆周角是直角，所以∠DAB=90°因为同弧所对的圆周角相等，所以∠D 等于∠C.所以C RcD sin 2sin ==故2sin sin sin a b cR A B C===2.正弦定理的一些变式：()sin sin sin i a b c A B C ::=::；()sin ,sin ,sin 22a b ii A B C R R ==2c R=；()2sin ,2sin ,2sin iii a R A b R B b R C ===；(iv )RCB A cb a 2sin sin sin =++++3.两类正弦定理解三角形的问题：(1)已知两角和任意一边，求其他的两边及一角.(2)已知两边和其中一边的对角，求其他边角.(可能有一解，两解，无解)4.在ABC ∆中，已知a ，b 及A 时，解得情况：解法一：利用正弦定理计算解法二：分析三角形解的情况，可用余弦定理做，已知a ，b 和角A ，则由余弦定理得即可得出关于c 的方程：0cos 2222=-+-a b Ac b c 分析该方程的解的情况即三角形解的情况①△=0，则三角形有一解②△>0则三角形有两解③△<0则三角形无解余弦定理：1.余弦定理：2222222222cos 2cos 2cos a b c bc A b a c ac Bc b a ba C ⎧=+-⎪=+-⎨⎪=+-⎩2.推论：222222222cos 2cos 2cos 2b c a A bc a c b B ac b a c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩.设a 、b 、c 是C ∆AB 的角A 、B 、C 的对边，则：①若222a b c +=，则90C = ；②若222a b c +>，则90C < ；③若222a b c +<，则90C > .3.两类余弦定理解三角形的问题：(1)已知三边求三角；(2)已知两边和他们的夹角，求第三边和其他两角.面积公式：已知三角形的三边为a ，b ，c ，1.111sin ()222a S ah ab C r a b c ===++(其中r 为三角形内切圆半径)2.设)(21c b a p ++=，))()((c p b p a p p S ---=(海伦公式)例：已知三角形的三边为，、、c b a 设)(21c b a p ++=，求证：(1)三角形的面积))()((c p b p a p p S ---=；(2)r 为三角形的内切圆半径，则pc p b p a p r ))()((---=(3)把边BC 、CA 、AB 上的高分别记为，、、c b h h a h 则))()((2c p b p a p p ah a ---=))()((2c p b p a p p bh b ---=))()((2c p b p a p p ch c ---=证明：(1)根据余弦定理的推论：222cos 2a b c C ab+-=由同角三角函数之间的关系，sin C =代入1sin 2S ab C =，得12S ====记1()2p a b c =++，则可得到1()2b c a p a +-=-，1()2c a b p b +-=-，1()2a b c p c +-=-代入可证得公式(2)三角形的面积S 与三角形内切圆半径r 之间有关系式122S p r pr =⨯⨯=其中1()2p a b c =++，所以S r p==注：连接圆心和三角形三个顶点，构成三个小三角形，则大三角形的面积就是三个小三角形面积的和故得：pr cr br ar S =++=212121(3)根据三角形面积公式12aS a h =⨯⨯所以，2a S h a ==a h =同理b h =c h =【三角形中的常见结论】(1)π=++C B A (2)sin()sin ,A B C +=cos()cos ,A B C +=-tan()tan ,A B C +=-2cos 2sinC B A =+，2sin 2cos C B A =+；A A A cos sin 22sin ⋅=，(3)若⇒>>C B A c b a >>⇒C B A sin sin sin >>若C B A sin sin sin >>⇒c b a >>⇒C B A >>(大边对大角，小边对小角)(4)三角形中两边之和大于第三边，两边之差小于第三边(5)三角形中最大角大于等于 60，最小角小于等于60(6)锐角三角形⇔三内角都是锐角⇔三内角的余弦值为正值⇔任两角和都是钝角⇔任意两边的平方和大于第三边的平方.钝角三角形⇔最大角是钝角⇔最大角的余弦值为负值(7)ABC ∆中，A ，B ，C 成等差数列的充要条件是 60=B .(8)ABC ∆为正三角形的充要条件是A ，B ，C 成等差数列，且a ，b ，c 成等比数列.二、题型汇总：题型1：判定三角形形状判断三角形的类型(1)利用三角形的边角关系判断三角形的形状：判定三角形形状时，可利用正余弦定理实现边角转化，统一成边的形式或角的形式。
高中数学人教版必修五不等式知识点最完全精炼总结
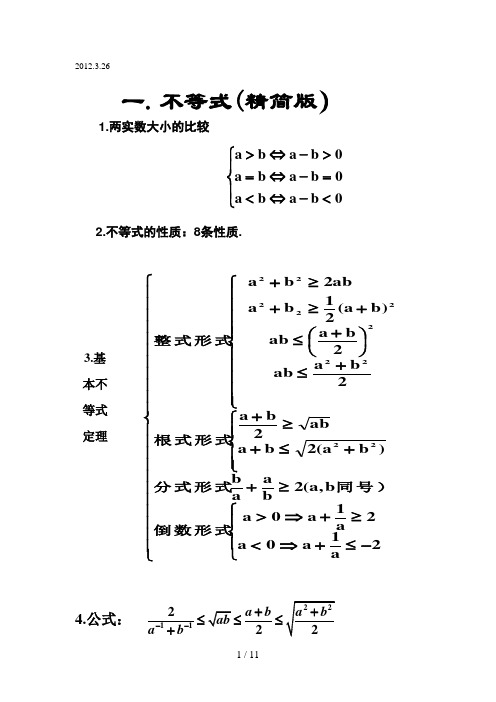
2012.3.264.公式： 1.两实数大小的比较⎪⎩⎪⎨⎧<-⇔<=-⇔=>-⇔>0b a b a 0b a b a 0b a b a 一. 不等式(精简版）3.基 本不等式定理⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧-≤+⇒<≥+⇒>≥+⎪⎪⎩⎪⎪⎨⎧+≤+≥+⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+≤⎪⎭⎫ ⎝⎛+≤+≥+≥+2a 1a 0a 2a 1a 0ab ,a (2b aa b )b a (2b a ab 2b a 2b a ab 2b a ab )b a (21b a ab 2b a 2222222222倒数形式同号）分式形式根式形式整式形式1122a b a b --+≤≤≤+2.不等式的性质：8条性质.3.解不等式(1)一元一次不等式 (2)一元二次不等式：一元二次不等式的求 解流程：一化：化二次项前的系数为正数. 二判：判断对应方程的根. 三求：求对应方程的根.⎪⎪⎨⎧<<>>≠>)0a (bx )0a (a bx )0a (b ax四画：画出对应函数的图象.五解集：根据图象写出不等式的解集. (3)解分式不等式：高次不等式：(4)解含参数的不等式：（1） (x – 2)(ax – 2)>0（2）x 2 –(a +a 2)x +a 3>0；（3）2x 2 +ax +2 > 0；注:解形如ax 2+bx+c>0的不等式时分类讨论的标准有：1、讨论a 与0的大小；2、讨论⊿与0的大小；3、讨论两根的大小；二、运用的数学思想：1、分类讨论的思想；2、数形结合的思想；3、等与不等的化归思想(4)含参不等式恒成立的问题：⎪⎩⎪⎨⎧用图象分离参数后用最值函数、、、321例1．已知关于x 的不等式在(–2，0)上恒成立，求实数a 的取值范围． 例2．关于x 的不等式22(3)210x a x a +-+-<)1(log 22++-=ax ax y ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧≠≤⋅⇔≤>⋅⇔>0)x (g 0)x (g )x (f 0)x (g )x (f 0)x (g )x (f 0)x (g )x (f 0)())((21>---n a x a x a x对所有实数x ∈R 都成立，求a 的取值范围.(5)一元二次方程根的分布问题：方法：依据二次函数的图像特征从：开口方向、判别式、对称轴、函数值三个角度列出不等式组，总之都是转化为一元二次不等式组求解. 二次方程根的分布问题的讨论：20,31xx a x x >≤++恒成立，例3.若对任意则 的取值范围.a()02f kbka>⎧⎪⎪-<⎨⎪∆>⎪⎩1．x1< x2< k()02f kbka>⎧⎪⎪->⎨⎪∆>⎪⎩2．k < x1< x()0f k<3．x1< k < x24．k1 < x1 < x2 < k25．x1 < k1 < k2 < x21212()0()002f k f k b k k a >⎧⎪>⎪⎪⎨∆>⎪⎪<-<⎪⎩12()0()0f k f k >⎧⎨>⎩6．k 1 <x 1 < k 2 < x 2< k 3122()0()0()0f k f k f k >⎧⎪<⎨⎪>⎩ 4解线性规划问题的一般步骤：第一步：在平面直角坐标系中作出可行域； 第二步：在可行域内找到最优解所对应的点；第三步：解方程的最优解，从而求出目标函数的最大值或最小值。
(完整)人教版高二数学必修5知识点归纳(最完整版),推荐文档
必修五数学知识点归纳资料.A BCsincos —22b >c , a b v c ; A > B si nA > sin B ,A >B cosA v cosB, ab 22、正弦定理与余弦定理:2b 2abcosC第一章解三角形1三角形的性质: ③.若 ABC 为锐角’则AB >2，B +C>-,A+C2①.A+B+C= ②.在ABC①.正弦定理:（2R 为 ABC 外接圆的直径）a 2Rs inA 、b 2Rsin B 、c 2Rs inC（边化角） sin A —2Rsin B 面积公式:ABC b2R 、 1 absin C 2 sin C —2R1bcs inA 2acsin B 余弦定理b 2 2bc cos Ab 22accosB.2 2 “ b c cosA2bccosBa 2 c 2b 2ac2-、cosCa 2b 2 2abc 2补充：两角和与差的正弦、余弦和正切公式：⑴co s coscos sin sin;(2) cos cos cos sin sin⑶sinsin cos cos sin;(4) sin sin cos cos sin⑸ta n tantan tan tantan1tan tan77）；3、常见的解题方法：| (边化角或者角化边) 第二章数列1、数列的定义及数列的通项公式： ①.a n f(n)，数列是定义域为N 的函数f(n)，当n 依次取1, 2， 时的一列函 数值 ②.a n 的求法：i. 归纳法 S ，n 1 ii. a nSi S n 1, n 2iv.若S n f (a n )，先求a 1，再I 构造方程组I ：'"" 得到关于a n 1和a n 的递推 S n 1 f(a n 1) 关系式S 2a 1例如：& 2an 1先求a1，再构造方程组：Si2n a1(下减上)an12a n1 2a n2. 等差数列：① 定义：a n1 a n =d (常数)，证明数列是等差数列的重要工具。
(完整版)高中数学人教版必修五不等式知识点最完全精炼总结,推荐文档
△>0
Байду номын сангаас
ax
b(a
x 0)
x
b
a b
(a (a
0) 0)
a
△=0
△<0
y=ax2+bx+c
y
的图象
(a>0)
x1 O
x2x
y
O x1
x
y x
O
ax2+bx+c=0 有两相异实根 (a>0)的根 x1, x2 (x1<x2)
有两相等实根
x1=x2=
b 2a
ax2+bx+c>0 {x|x<x1,或 x>x2} {x|x≠ b }
一.不等式知识要点
1.两实数大小的比较
a b a b 0 a b a b 0 a b a b 0
2.不等式的性质：8条性质.
3.基 本不 等式 定理
且且且且 且且且且 且且且且 且且且且
a 2 b 2 2ab
a2
b2
1 (a b)2 2
值。
z ax by z x2 y2
z y x
6
练习：1.求满足 | x | + | y | ≤4 的整点（横、纵坐标为整数）的
个数。
2.且且且且且且且f
(x)
2
log2
x
1 log2
x
(0
x
1)
34.f(x)=x+ 1 且x4且且且且且 x1
4.求函数 f ( x) ( x 1)2 4 ( x 1) 的最小值.
(5)一元二次方程根的分布问题： 方法：依据二次函数的图像特征从：开口方向、判别式、对称 轴、
高中数学必修五(人教版)知识点总结。
高中数学必修5知识点（一）解三角形1、正弦定理：在C ∆A B 中，a 、b 、c 分别为角A 、B 、C 的对边，R 为C ∆A B 的外接圆的半径，则有2sin sin sin a b c R C===AB ．正弦定理的变形公式：①2sin a R =A ，2sin b R =B ，2sin c R C =； ②sin 2a RA =，sin 2b RB =，sin 2c C R=；③::sin :sin :sin a b c C =A B ； ④sin sin sin sin sin sin a b c a b c CC ++===A +B +AB．2、三角形面积公式：111sin sin sin 222C S bc ab C ac ∆A B =A ==B ．3、余弦定理：在C ∆A B 中，有2222cos a b c bc =+-A ，2222cos b a c ac =+-B ，2222cos c a b ab C =+-．4、余弦定理的推论：222cos 2b c abc+-A =，222cos 2a c bac+-B =，222cos 2a b cC ab+-=．5、射影定理：cos cos ,cos cos ,cos cos a b C c B b a C c A c a B b A =+=+=+6、设a 、b 、c 是C ∆A B 的角A 、B 、C 的对边，则：①若222a b c +=，则90C = ； ②若222a b c +>，则90C < ；③若222a b c +<，则90C > ． (二)数列7、数列：按照一定顺序排列着的一列数． 8、数列的项：数列中的每一个数． 9、有穷数列：项数有限的数列． 10、无穷数列：项数无限的数列．11、递增数列：从第2项起，每一项都不小于它的前一项的数列．10n n a a +-> 12、递减数列：从第2项起，每一项都不大于它的前一项的数列．10n n a a +-< 13、常数列：各项相等的数列．14、摆动数列：从第2项起，有些项大于它的前一项，有些项小于它的前一项的数列． 15、数列的通项公式：表示数列{}n a 的第n 项与序号n 之间的关系的公式．16、数列的递推公式：表示任一项n a 与它的前一项1n a -（或前几项）间的关系的公式．17、如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，则这个数列称为等差数列，这个常数称为等差数列的公差．18、由三个数a ，A ，b 组成的等差数列可以看成最简单的等差数列，则A 称为a 与b 的等差中项．若2a cb +=，则称b 为a 与c 的等差中项．19、若等差数列{}n a 的首项是1a ，公差是d ，则()11n a a n d =+-． 20、通项公式的变形：①()n m a a n m d =+-；②()11n a a n d =--；③11n a a d n -=-；④11n a a n d-=+；⑤n m a a d n m-=-．21、若{}n a 是等差数列，且m n p q +=+（m 、n 、p 、*q ∈N ），则m n p q a a a a +=+；若{}n a 是等差数列，且2n p q =+（n 、p 、*q ∈N ），则2n p q a a a =+．22、等差数列的前n 项和的公式：①()12n n n a a S +=；②()112n n n S na d -=+．23、等差数列的前n 项和的性质：①若项数为()*2n n ∈N ，则()21n n n S n a a +=+，且S S nd -=偶奇，1n n S a S a +=奇偶．②若项数为()*21n n -∈N，则()2121n n Sn a -=-，且n S S a -=奇偶，1S n S n =-奇偶（其中n S na =奇，()1n S n a =-偶）．24、如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，则这个数列称为等比数列，这个常数称为等比数列的公比．25、在a 与b 中间插入一个数G ，使a ，G ，b 成等比数列，则G 称为a 与b 的等比中项．若2G ab =，则称G 为a 与b 的等比中项．注意：a 与b 的等比中项可能是G ±26、若等比数列{}n a 的首项是1a ，公比是q ，则11n n a a q -=．27、通项公式的变形：①n mn m a a q -=；②()11n n a a q--=；③11n n a qa -=；④n mn ma qa -=．28、若{}n a 是等比数列，且m n p q +=+（m 、n 、p 、*q ∈N ），则m n p q a a a a ⋅=⋅；若{}n a 是等比数列，且2n p q =+（n 、p 、*q ∈N ），则2n p q a a a =⋅．29、等比数列{}n a 的前n 项和的公式：()()()11111111n n n na q S a q a a q q qq =⎧⎪=-⎨-=≠⎪--⎩．30、等比数列的前n 项和的性质：①若项数为()*2n n ∈N ，则S q S =偶奇．②n n m n m S S q S +=+⋅．③n S ，2n n S S -，32n n S S -成等比数列（0n S ≠）． （三）不等式31、0a b a b ->⇔>；0a b a b -=⇔=；0a b a b -<⇔<．32、不等式的性质： ①a b b a >⇔<；②,a b b c a c >>⇒>；③a b a c b c >⇒+>+； ④,0a b c ac bc >>⇒>，,0a b c ac bc ><⇒<；⑤,a b c d a c b d >>⇒+>+； ⑥0,0a b c d ac bd >>>>⇒>；⑦()0,1n na b a b n n >>⇒>∈N >；⑧)0,1a b n n >>⇒>∈N >．33、一元二次不等式：只含有一个未知数，并且未知数的最高次数是2的不等式． 34、二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系：若二次项系数为负，先变为正 35、设a 、b 是两个正数，则2a b +称为正数a 、b a 、b 的几何平均数．36、均值不等式定理： 若0a >，0b >，则a b +≥，即2a b +≥．37、常用的基本不等式： ①()222,a b ab a b R +≥∈；②()22,2a b ab a b R +≤∈；③()20,02a b ab a b +⎛⎫≤>> ⎪⎝⎭；④()222,22a b a b a b R ++⎛⎫≥∈ ⎪⎝⎭．38、极值定理：设x 、y 都为正数，则有⑴若x y s +=（和为定值），则当x y =时，积xy 取得最大值24s ．⑵若xy p =（积为定值），则当x y =时，和x y +取得最小值．。
人教版高一数学必修5主要知识点整理
人教版高一数学必修5主要知识点第一章 解三角形1、三角形三角关系：A+B+C=180°；C=180°-(A+B)；2、三角形三边关系：a+b>c; a-b<c3、三角形中的基本关系：sin()sin ,A B C +=cos()cos ,A B C +=-tan()tan ,A B C +=-sincos ,cos sin ,tan cot 222222A B C A B C A B C+++=== 4、正弦定理：在C ∆AB 中，a 、b 、c 分别为角A 、B 、C 的对边，R 为C ∆AB 的外接圆的半径，则有2sin sin sin a b cR C ===A B ．5、正弦定理的变形公式：①化角为边：2sin a R =A ，2sin b R =B ，2sin c R C =；②化边为角：sin 2a R A =，sin 2b R B =，sin 2c C R=；③::sin :sin :sin a b c C =A B ；④sin sin sin sin sin sin a b c a b cC C++===A +B +A B ． 6、两类正弦定理解三角形的问题：①已知两角和任意一边，求其他的两边及一角.②已知两角和其中一边的对角，求其他边角.(对于已知两边和其中一边所对的角的题型要注意解的情况（一解、两解、三解）)7、余弦定理：在C ∆AB 中，有2222cos a b c bc =+-A ，2222cos b a c ac =+-B ，2222cos c a b ab C =+-．8、余弦定理的推论：222cos 2b c a bc +-A =，222cos 2a c b ac+-B =，222cos 2a b c C ab +-=．(余弦定理主要解决的问题：1.已知两边和夹角，求其余的量。
2.已知三边求角) 9、余弦定理主要解决的问题：①已知两边和夹角，求其余的量。
人教版数学必修五知识点总结
第一章 解三角形一、内角和定理：（1）三角形三角和为π，任意两角和与第三个角总互补，任意两半角和与第三个角的半角总互余．（2）锐角三角形⇔三内角都是锐角⇔三内角的余弦值为正值⇔任两角和都是钝角⇔任意两边的平方和大于第三边的平方．二、正弦定理：2sin sin sin a b c R A B C===（R 为三角形外接圆的半径）． C R c B R b A R a C B A c b a sin 2,sin 2,sin 2)2(;sin :sin :sin ::)1(====）（3解三角形：已知三角形的几个元素求另外几个元素的进程。
⎩⎨⎧，可求其它元素已知两边和一边的对角可求其它边和角已知两角和任意一边， 注意：已知两边一对角，求解三角形，假设用正弦定理，那么务必注意可能有两解．3、余弦定理：⎪⎩⎪⎨⎧-+=-+=-+=C ab b a c B ac c a b A bc c b a cos 2cos 2cos 2222222222（求边） 或 （求角）⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=-+=-+=ab c b a C ac b c a B bc a c b A 2cos 2cos 2cos 222222222 ⎪⎩⎪⎨⎧求其它已知两边和一边对角，已知三边求所有三个角已知两边一角求第三边（注:常用余弦定理鉴定三角形的类型）． 4、三角形面积公式：R abc B ac A bc Cab ah S a 4sin 21sin 21sin 2121=⎪⎪⎪⎩⎪⎪⎪⎨⎧==． 5、解三角形应用（1）在视线和水平线所成的角中，视线在水平线上方的角叫仰角；视线在水平线下方的角叫俯角。
（2）从正北方向顺时针转到目标方向的水平角叫方位角。
（3）坡面与水平面所成的二面角度数的正切值叫做坡度。
（4）解斜三角形应用题的一样步骤：分析→建模→求解→查验第二章 数 列1．数列的通项、数列的项数，递推公式与递推数列，数列的通项与数列的前n 项和公式的关系：{11,(1),(2)n n n S n a S S n -==-≥（必要时请分类讨论）．注意：112211()()()n n n n n a a a a a a a a ---=-+-++-+；121121n n n n n a a a a a a a a ---=⋅⋅⋅⋅． 2．等差数列{}n a 中： （1）等差数列公差的取值与等差数列的单调性．.000R d d d d d ∈⎪⎩⎪⎨⎧→<→=→>的取值为，可知数列单调递减数列为常数列数列单调递增 （2）1(1)n a a n d =+-()m a n m d =+-；p q m n p q m n a a a a +=+⇒+=+．（3）{}n n b a 21λλ+、{}n ka 也成等差数列．（4）在等差数列{}n a 中，假设.0),(,=≠==+n m n m a n m m a n a 则（5）1211,,m k k k m a a a a a a ++-++++++仍成等差数列． （6）1()2n n n a a S +=，1(1)2n n n S na d -=+，21()22n d d S n a n =+-，2121n n S a n -=-，。
人教版高二数学必修5知识点归纳(最完整版)
现在的努力就是为了实现小时候吹下的牛逼——标必修五数学知识点归纳资料第一章解三角形1、三角形的性质：①.A+B+C= , sin( A B) sin C ， cos( A B) cosCA B2 C sin A2B cos C2 2 2②.在 ABC 中 , a b ＞c , a b ＜ c ; A＞ B sin A ＞ sin B ,A＞ B cosA ＜ cosB, a ＞b A＞B③.若 ABC 为锐角，则 A B＞ ,B+C ＞,A+C ＞ ;2 2 2a2b2＞ c2， b2c2＞ a2， a2＋ c2＞ b22、正弦定理与余弦定理：a b c2R (2R 为 ABC 外接圆的直径 )①.正弦定理：sin B sin Csin Aa 2 R s i nA、b 2R sin B 、c2R sin C （边化角）sin A a、 sin B b、 sin C c （角化边）2R 2R2R面积公式： S ABC1 ab sin C 1 bc sin A 1 ac sin B2 2 2②.余弦定理： a2b2c22c b o c、s b2A a2c22ac cosB 、c2a2b22ab cosCcos A b2c2a2、 cos B a2c2b2、 cosC a2b2c2（角化边）2bc2ac2ab补充：两角和与差的正弦、余弦和正切公式：⑴ cos cos cos sin sin ；⑵ cos cos cos sin sin ；⑶ sin sin cos cos sin ；⑷ sin sin cos cos sin ；⑸ tantan tan（ tan tantan1tan tan ）；1 tan tan- 1 -现在的努力就是为了实现小时候吹下的牛逼——标⑹ tantan tan（ tan tan tan 1 tan tan ）．1 tan tan二倍角的正弦、余弦和正切公式：⑴ sin2 2sin cos． 1 sin 2 sin2cos2 2 sin cos(sin cos ) 2⑵ cos2cos2sin22cos2 1 1 2sin2升幂公式 1 cos 2 cos2,1 cos 2 sin222降幂公式 cos2cos 2 1， sin 2 1 cos2 ．2 23、常见的解题方法：（边化角或者角化边）第二章数列1、数列的定义及数列的通项公式：①.a n( ) ，数列是定义域为N的函数 f(n)，当n依次取，，时的一列函f n 1 2数值②. a n的求法：i.归纳法ii. a S1 , n 1若 S00 ，则 a n不分段；若 S00 ，则 a n分段nS n S n 1, n 2iii. 若 a n 1pa n q ，则可设 a n 1m p(a n m) 解得 m,得等比数列 a n miv. 若 S n f ( a n ) ，先求 a1，再构造方程组：S n f ( a n )得到关于 a n 1和 a n的递推S n 1 f ( an 1 )关系式例如： 2 1 先求a1，再构造方程组：Sn2an 1 （下减上）a n 1 2an 1 2a nS n a nS n12an 1 12.等差数列：①定义： a n 1 a n = d （常数） , 证明数列是等差数列的重要工具。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
必修5 第一章 解三角形
一、正弦定理
1.定理
2.sin sin sin a b c
R A B C
=== 其中a ，b ，c 为一个三角形的三边，A ，B ，C 为其对角，R 为外接圆半径.
变式：a =2R sin A ，b =2R sin B ，c =2R sin C
二、余弦定理
1.定理
a 2=
b 2+
c 2-2bc cos A 、b 2=a 2+c 2-2ac cos B 、c 2=a 2+b 2-2ab cos C 变形：222cos 2b c a A bc +-=、222cos 2a c b B ac +-=、222
cos 2a b c C ab
+-=
2.可解决的问题
①已知三边，解三角形； ②已知两边及其夹角，解三角形； ③已知两边及一边的对角，求第三边.
三、三角形面积公式
（1）111
222
a b c S ah bh ch ∆===.
其中h a ，h b ，h c 为a ，b ，c 三边对应的高.
（3）如果一个数列已给出前几项，并给出后面任一项与前面的项之间关系式，这种给出数列的方法叫做递推法，其中的关系式称为递推公式.
（4）一个重要公式：对任何数列，总有
111,
(2).
n n n a S a S S n -⎧⎪⎨
⎪⎩==-≥ 注：数列是特殊的函数，要注意数列与函数问题之间的相互转化.
二、等差数列
（1）定义：如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列.这个常数叫做数列的公差.
（2）递推公式：a n +1=a n ＋d . （3）通项公式：a n =a 1+(n -1)d . （4）求和公式：11()(1).22
n n n a a n n S na d +-==+ （5）性质：
①若m +n =p +q ，则a m +a n =a p +a q ； ②若m +n =2p ，则a m +a n =2a p ； ③a n =a m +(n -m )d . （6）等差中项：
①若m +n =p +q ，则a m a n =a p a q ； ②若m +n =2p ，则a m a n =a 2p ； ③a n =a m q n -m . （6）等比中项：
a ，
b 的等比中项G ab =±
a ，
b ，
c 成等比数列2(,,0).a b c b ac ≠⇔=
注：①a 1和q 叫做等比数列的基本元素，把S n 和a n 都用a 1和q 表示往往能使问题简化.②注意方程思想的应用，在a 1，q ，n ，S n ，a n 五个数中，知道三个可求剩下的两个.③使用求和公式时，要注意q ≠1的条件.
四、数列求和
主要求和方法有：
（1）公式法：主要用于等差数列与等比数列，这是首先应该考虑的方法.
（2）分组求和法：将数列的每一项拆分成几项，然后重新组合成几组，使每一组都能求和.如数列{n +2n }.
（3）并项求和法：将相邻几项合并，使合并后有规律，便于求和.如12－22＋32－42＋…＋(－1)n －1n 2.
（4）裂项相消法：将每项分成两项的差，并且正负能抵消.如求
111
....1223(1)
n n +++⋅⋅+ （5）错位相减法：设{a n }是等差数列，{b n }是等比数列，求S n =a 1b 1+a 2b 2+⋅⋅⋅+a n b n 时用错位相消法.做法：将上式两端乘以{b n }的公比，错一位相减，中间n －1项构成等比数列，可以求和.注意将n =1，2，3代入检验.
性质8 a >b >0，n ∈N ，1.n n n a b >⇒
二、一元二次不等式
1.一元二次不等式的标准形式 ax 2+bx +c >0(a >0) ax 2+bx +c <0(a >0) ax 2+bx +c ≥0(a >0) ax 2+bx +c ≤0(a >0)
2.一元二次不等式的解集 不等式 Δ＞0 Δ＝0 Δ＜0 ax 2+bx +c >0 (-∞ , x 1)∪(x 2 , +∞)
{x |x ≠ x 1}
R
ax 2+bx +c <0 (x 1，x 2) ∅
∅
ax 2+bx +c ≥0
(-∞ , x 1]∪[x 2 , +∞)
R
R
ax2+bx+c≤0[x1 , x2]{x1}∅
说明：①表中内容不需死记硬背，可结合二次函数图象灵活掌握.
②表中x1，x2是方程ax2+bx+c＝0的根，且x1<x2.
③当Δ＞0时，解集有口诀：大于0取两边，小于0取中间.
三、二元一次不等式和线性规划
1.直线划分平面区域
在平面直角坐标系中，二元一次不等式Ax＋By＋C >0(＜0)表示直线Ax+By＋C=0某一侧所有点组成的平面区域，把直线画成虚线，以表示区域不包括边界．不等式Ax＋By＋C
先画出直线ax+by=0作为参考直线，然后向上或下平移参考直线，使其与可行域有公共点且到达最上（或最下）的位置，此时z即取得最大或最小值.当b>0时，最上方的为最大值，最下方的最小值；当b<0时则相反.
四、基本不等式
1.基本不等式
（1）a2+b2≥2ab(a，b∈R). （2）a b ab
+≥a>0，b>0).
变式：（3）
22
(,R).
2
a b
ab a b
+
≤∈（4）
2
(,R).
2
a b
ab a b
+
⎛⎫
≤∈
⎪
⎝⎭
以上各不等式当且a=b时等号成立.
2.用基本不等式求最值。