进制转换表
二进制八进制十进制十六进制之间的进制转换

二进制八进制十进制十六进制之间的进制转换详情可参考百度百科:进制转换这个词条【主要搞懂1和2两条,其他的进制之间的转化就迎刃而解,很好懂了】1. 十进制-> 二进制:将这个十进制数连续除以2的过程,第一步除以2,得到商和余数,将商再继续除以2,得到又一个商和余数,直到商为0。
最后将所有余数倒序排列,得到的数就是转换成二进制的结果。
2. 二进制-> 十进制:二进制数第1位的权值是2的0次方,第2位的权值是2的1次方,第3位的权值是2的2次方。
(例如1258这个十进制数,实际上代表的是:1x1000+2x100+5x10+8x1=1258)那么1011这个二进制数,实际上代表的是:1x8+0x4+1x2+1x1=11(十进制数11)。
(这里的8就是2的3次方,4就是2的2次方,2就是2的1次方,1就是2的0次方)3. 十进制-> 八进制:十进制数转换成八进制的方法,和转换为二进制的方法类似,唯一变化:除数由2变成8。
4. 八进制-> 十进制和转换为二进制的方法类似,唯一变化是,底数变成8,第1位表示8的0次方,第二位表示8的一次方,第三位表示8的2次方,第四位表示8的3次方。
例如1314这个八进制数,十进制数就是1x512+3x64+1x8+4x1=716(十进制)5. 十进制-> 十六进制10进制数转换成16进制的方法,和转换为2进制的方法类似,唯一变化:除数由2变成16。
十六进制是0123456789ABCDEF这十六个字符表示。
那么单独一个A就是10,单独一个B就是11,CDEF,就分表表示12,13,14,15。
而10这个十六进制数,实际就是十进制中的16。
6. 十六进制-> 十进制和转换为二进制的方法类似,唯一变化是,底数变成16,第1位表示16的0次方,第二位表示16的一次方,第三位表示16的2次方,第四位表示16的3次方。
7. 二进制<--->八进制,之间的相互转换,更简单一些,因为8本身是2的三次方。
进制转换计算+ASCII表

一、二进制转化成其他进制1. 二进制(BINARY)——>八进制(OCTAL)例子1:将二进制数(10010)2转化成八进制数。
(10010)2=()2=(2 2)8=(22)8例子2:将二进制数(0.1010)2转化为八进制数。
(0.10101)2=(0. 101 )2=(0. 5 2)8=(0.52)8诀窍:因为每三位二进制数对应一位八进制数,所以,以小数点为界,整数位则将二进制数从右向左每3位一隔开,不足3位的在左边用0填补即可;小数位则将二进制数从左向右每3位一隔开,不足3位的在右边用0填补即可。
2. 二进制(BINARY)——>十进制(DECIMAL)例子1:将二进制数(10010)2转化成十进制数。
(10010)2=(1x24+0x23+0x22+1x21+0x20)10=(16+0+0+2+0)10=(18) 10例子2:将二进制数(0.10101)2转化为十进制数。
(0.10101)2=(0+1x2-1+0x2-2+1x2-3+0x2-4+1x2-5)10=(0+0.5+0.25+0.125+0.0625+0.03125)10=(0.96875)10诀窍:以小数点为界,整数位从最后一位(从右向左)开始算,依次列为第0、1、2、3………n,然后将第n位的数(0或1)乘以2的n-1次方,然后相加即可得到整数位的十进制数;小数位则从左向右开始算,依次列为第1、2、3……..n,然后将第n位的数(0或1)乘以2的-n次方,然后相加即可得到小数位的十进制数(按权相加法)。
3. 二进制(BINARY)——>十六进制(HEX)例子1:将二进制数(10010)2转化成十六进制数。
(10010)2=(0001 0010)2=(1 2)16=(12) 16例子2:将二进制数(0.1010)2转化为十六进制数。
(0.10101)2=(0. 1010 1000)2=(0. A 8)16=(0.A8)16诀窍:因为每四位二进制数对应一位十六进制数,所以,以小数点为界,整数位则将二进制数从右向左每4位一隔开,不足4位的在左边用0填补即可;小数位则将二进制数从左向右每4位一隔开,不足4位的在右边用0填补即可。
各进制之间的转换方法及表格

各进制之间的转换方法及表格1. 介绍在计算机科学和数学领域中,进制是表示数字的一种方式。
常见的进制包括二进制、八进制、十进制和十六进制。
不同进制之间的转换是计算机科学和数学中非常重要的基本知识点。
本文将介绍各种进制之间的转换方法,并提供一个详细的表格以便于查阅。
2. 进制介绍2.1 二进制(Binary)二进制是计算机中最基础也最常用的一种进制,它只有两个数字:0和1。
在二进制中,每一位上的数字称为一个比特(bit)。
2.2 八进制(Octal)八进制使用0到7这8个数字来表示数值。
在八进制中,每一位上的数字相当于三个二进制位。
2.3 十进制(Decimal)十进制是我们日常生活中最常用的一种数字表示方式,它使用0到9这10个数字来表示数值。
2.4 十六进制(Hexadecimal)十六进制使用0到9这10个数字以及A到F这6个字母来表示数值。
在十六进制中,每一位上的数字相当于四个二进制位。
3. 进制转换方法3.1 二进制转换为八进制和十六进制将二进制数转换为八进制和十六进制的方法非常简单。
只需要将二进制数从右往左每三(对于八进制)或四(对于十六进制)个数字分组,并将每组转换为对应的八进制或十六进制数字即可。
示例1:将二进制数10101011转换为八进制和十六进制•八进制:10101011 = (001)(010)(101) = 125•十六进制:10101011 = (0010)(1011) = 2B3.2 八进制转换为二进制和十六进制将八进制数转换为二进制和十六进制的方法也很简单。
只需要将每一位上的数字分别转换为对应的三个(对于二进制)或四个(对于十六禁止)二级禁止即可。
示例2:将八禁止数125转换为二禁止和十禁止•二禁止:125 = (001)(010)(101) = 10101011•十禁止:125 = (2B)3.3 十禁止转换为二禁止和八禁止将十禁止数转换为二禁止和八禁止的方法也很简单。
二进制十进制十六进制转换表
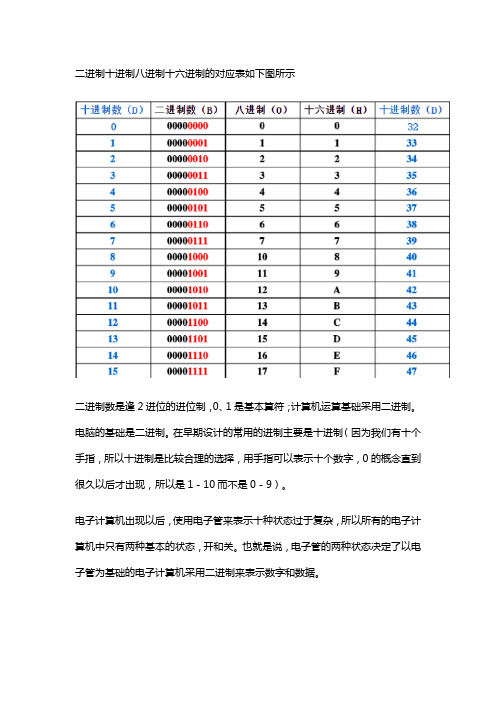
二进制十进制八进制十六进制的对应表如下图所示二进制数是逢2进位的进位制,0、1是基本算符;计算机运算基础采用二进制。
电脑的基础是二进制。
在早期设计的常用的进制主要是十进制(因为我们有十个手指,所以十进制是比较合理的选择,用手指可以表示十个数字,0的概念直到很久以后才出现,所以是1-10而不是0-9)。
电子计算机出现以后,使用电子管来表示十种状态过于复杂,所以所有的电子计算机中只有两种基本的状态,开和关。
也就是说,电子管的两种状态决定了以电子管为基础的电子计算机采用二进制来表示数字和数据。
常用的进制还有8进制和16进制,在电脑科学中,经常会用到16进制,而十进制的使用非常少,这是因为16进制和二进制有天然的联系:4个二进制位可以表示从0到15的数字,这刚好是1个16进制位可以表示的数据,也就是说,将二进制转换成16进制只要每4位进行转换就可以了。
二进制的“00101000”直接可以转换成16进制的“28”。
字节是电脑中的基本存储单位,根据计算机字长的不同,字具有不同的位数,现代电脑的字长一般是32位的,也就是说,一个字的位数是32。
字节是8位的数据单元,一个字节可以表示0-255的十进制数据。
对于32位字长的现代电脑,一个字等于4个字节,对于早期的16位的电脑,一个字等于2个字节。
扩展资料采用二进制数的原因容易表示二进制数只有“0”和“1”两个基本符号,易于用两种对立的物理状态表示。
运算简单二进制数的算术运算特别简单,加法和乘法仅各有3条运算规则(0+0=0,0+1=1,1+1=10和0×0=0,0×1=0,1×1=1 ),运算时不易出错。
此外,二进制数的“1”和“0”正好可与逻辑值“真”和“假”相对应,这样就为计算机进行逻辑运算提供了方便。
算术运算和逻辑运算是计算机的基本运算,采用二进制可以简单方便地进行这两类运算。
进制之间的转换关系表

进制之间的转换关系表进制是数学中重要的概念,用于表示数字的一种方式。
常见的进制包括十进制、二进制、八进制和十六进制。
在不同进制之间进行转换是计算机科学和信息技术领域中的基础操作之一。
本文将介绍进制之间的转换关系表,帮助读者更好地理解和应用进制转换。
在十进制系统中,我们使用的是基数为10的进制。
它是人类社会中最常用的进制,因为我们有十根手指,可以按照个位、十位、百位等顺序进行计数。
相对于十进制,其他进制系数的基数不同。
二进制是计算机内部使用的进制,它的基数是2。
在二进制中,只有两个数字,即0和1。
转换二进制到十进制的方法是每一位的数字乘以2的幂次方,然后将结果相加。
例如,二进制数1001可以转换为十进制数9,计算方式是1*2^3 + 0*2^2+ 0*2^1 + 1*2^0 = 9。
八进制是基数为8的进制系统。
八进制中使用的数字是0到7。
转换八进制到十进制的方法类似于二进制。
每一位的数字乘以8的幂次方,然后将结果相加。
例如,八进制数123可以转换为十进制数83,计算方式是1*8^2 + 2*8^1 + 3*8^0 = 83。
十六进制是基数为16的进制系统。
除了0到9的数字,十六进制还使用A到F的六个字母表示10到15的数字。
转换十六进制到十进制的方法和前面两种进制类似。
每一位的数字乘以16的幂次方,然后将结果相加。
例如,十六进制数1A可以转换为十进制数26,计算方式是1*16^1 + 10*16^0 = 26。
除了从较低的进制转换到较高的进制,我们还可以从较高的进制转换到较低的进制。
转换的方法与前面相反,即将原数除以对应基数并取余数,然后将余数从低位到高位排列。
这样可以得到新的进制表示。
在计算机科学中,进制转换是一个基础的操作。
计算机内部的运算都是使用二进制进行的,但人们更习惯于使用十进制进行计算。
因此,在数据传输和存储中,常常需要将十进制转换为二进制,然后再进行处理。
同样地,在计算机程序中,十六进制经常用于表示内存地址和数据的编码。
各进制之间的转换方法及表格

各进制之间的转换方法及表格进制之间的转换方法及表格:在计算机科学和数学领域中,进制是使用不同的基数来表示数字的一种方法。
常见的进制包括二进制、八进制、十进制和十六进制。
在这些进制之间进行转换非常重要,因为不同的进制在不同的场景中具有不同的优势和适用性。
下面我将详细介绍各种进制之间的转换方法,并提供一个表格以方便参考。
1.二进制转换为十进制:-方法:将二进制数每一位与2的幂相乘,然后求和。
2.十进制转换为二进制:-方法:使用短除法将十进制数连续除以2,直到商为0为止,然后依次取所得余数,从最后一个除数开始。
3.十进制转换为八进制:-方法:使用短除法将十进制数连续除以8,直到商为0为止,然后依次取所得余数,从最后一个除数开始。
-示例:将十进制数219转换为八进制数:219÷8=27余3,27÷8=3余3,3÷8=0余3、所以219的八进制表示为3334.八进制转换为十进制:-方法:将八进制数每一位与8的幂相乘,然后求和。
-示例:将八进制数333转换为十进制数:(3*8^2)+(3*8^1)+(3*8^0)=2195.十进制转换为十六进制:-方法:使用短除法将十进制数连续除以16,直到商为0为止,然后依次取所得余数,从最后一个除数开始。
十六进制中的10到15分别用字母A到F表示。
-示例:将十进制数255转换为十六进制数:255÷16=15余15,15÷16=0余15、所以255的十六进制表示为FF。
6.十六进制转换为十进制:-方法:将十六进制数每一位与16的幂相乘,然后求和。
十六进制中的A到F分别用数字10到15表示。
-示例:将十六进制数3FF转换为十进制数:(3*16^2)+(15*16^1)+(15*16^0)=1023下面是一个表格,展示了各种进制之间的转换方法和示例:进制转换,二进制,十进制,八进制,十六进制---------,----------,-------,-------,---------十进制转二进制,/,47,/,/十进制转八进制,/,219,333,/八进制转十进制,/,333,/,/十进制转十六进制,/,255,/,FF十六进制转十进制,/,3FF,/,/通过上述的转换方法和表格,我们可以在不同的进制之间进行转换,进而满足不同场景下对数据的需求。
二进制八进十六进制转换表

二进制八进十六进制转换表在计算机科学和电子工程领域,二进制、八进制和十六进制是常用的数制。
通过将数值转换成不同的进制,我们可以更好地理解和表示数字。
下面是一个二进制、八进制和十六进制的转换表,可作为参考使用。
1. 二进制转八进制和十六进制将二进制数转换为八进制和十六进制相对简单,只需要将二进制数按照位数分组。
- 八进制:每三个二进制位为一组,从低位向高位对应地分组,再将每组转换成相应的八进制数。
下表是常用的二进制转八进制的对应关系。
二进制八进制000 0001 1010 2011 3100 4101 5110 6111 7- 十六进制:每四个二进制位为一组,从低位向高位对应地分组,再将每组转换成相应的十六进制数。
下表是常用的二进制转十六进制的对应关系。
二进制十六进制0000 00001 10010 20011 30100 40101 50110 60111 71000 81001 91010 A1011 B1100 C1101 D1110 E2. 八进制和十六进制转二进制将八进制和十六进制数转换为二进制也很简单,只需要将八进制数每一位对应转换为对应的三个二进制位,将十六进制数每一位对应转换为对应的四个二进制位即可。
- 八进制转二进制:下表是常用的八进制转二进制的对应关系。
八进制二进制0 0001 0012 0103 0114 1005 1016 1107 111- 十六进制转二进制:下表是常用的十六进制转二进制的对应关系。
十六进制二进制0 00001 00013 00114 01005 01016 01107 01118 10009 1001A 1010B 1011C 1100D 1101E 1110F 1111通过以上转换表,我们可以方便地将不同进制的数值进行转换。
这对于计算机科学和电子工程领域的学习和应用是非常重要的。
总结:本文提供了一个二进制、八进制和十六进制的转换表,可帮助读者快速而准确地进行数值转换。
进制转换计算+ASCII表

一、二进制转化成其他进制例子1:将二进制数(10010)2转化成八进制数。
(10010)2=(010 010)2=(2 2)8=(22)8例子2:将二进制数(0.1010)2转化为八进制数。
(0.10101)2=(0. 101 010)2=(0. 5 2)8=(0.52)8诀窍:因为每三位二进制数对应一位八进制数,所以,以小数点为界,整数位则将二进制数从右向左每3位一隔开,不足3位的在左边用0填补即可;小数位则将二进制数从左向右每3位一隔开,不足3位的在右边用0填补即可。
例子1:将二进制数(10010)2转化成十进制数。
(10010)2=(1x24+0x23+0x22+1x21+0x20)10=(16+0+0+2+0)10=(18) 10例子2:将二进制数(0.10101)2转化为十进制数。
(0.10101)2=(0+1x2-1+0x2-2+1x2-3+0x2-4+1x2-5)10=(0+0.5+0.25+0.125+0.0625+0.03125)10=(0.96875)10诀窍:以小数点为界,整数位从最后一位(从右向左)开始算,依次列为第0、1、2、3………n,然后将第n位的数(0或1)乘以2的n-1次方,然后相加即可得到整数位的十进制数;小数位则从左向右开始算,依次列为第1、2、3……..n,然后将第n位的数(0或1)乘以2的-n次方,然后相加即可得到小数位的十进制数(按权相加法)。
例子1:将二进制数(10010)2转化成十六进制数。
(10010)2=(0001 0010)2=(1 2)16=(12) 16例子2:将二进制数(0.1010)2转化为十六进制数。
(0.10101)2=(0. 1010 1000)2=(0. A 8)16=(0.A8)16诀窍:因为每四位二进制数对应一位十六进制数,所以,以小数点为界,整数位则将二进制数从右向左每4位一隔开,不足4位的在左边用0填补即可;小数位则将二进制数从左向右每4位一隔开,不足4位的在右边用0填补即可。
二、八、十、十六进制对照表

二、八、十、十六进制对照表进制转换是计算机科学中的一个重要课题,并且在数字逻辑和计算中发挥着重要作用。
在一种进制转换成另一种进制时,我们常常需要借助“进制表”来辅助计算。
在本文中,我们将对比分析二进制、八进制、十进制和十六进制之间的关系,并用表格的形式来展现它们的对照表。
下面就来一起认识一下吧!首先,让我们来了解一下什么是进制。
所谓进制,就是指一个计数系统里使用的基数或底数。
当我们把一个数表示成几个数之和的形式时,每一个数就叫做一个进制。
常见的进制有二进制、八进制、十进制和十六进制,分别使用0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F这15个数来表示。
其次,让我们看一下它们之间的转换。
要从十进制转换成其它进制,我们可以采用除法取余法,先除以2,然后除以8,再除以16,我们就可以得到每一位的余数,然后以进制表中对应的数字来表示。
同样的,我们可以用乘法取商法来从其它进制转换成十进制,先把每一位的数字乘以2,8,16,再把它们相加,就可以得到转换的结果。
最后,让我们来看看它们之间的对照表:二进制|八进制|十进制|十六进制------|------|------|------0|0|0|01|1|1|110|2|2|211|3|3|3100|4|4|4101|5|5|5110|6|6|6111|7|7|71000|10|8|81001|11|9|91010|12|10|A1011|13|11|B1100|14|12|C1101|15|13|D1110|16|14|E1111|17|15|F从上面的表格中,我们可以发现它们之间的关系,当我们从十进制转换成其它进制时,我们只需要从左到右逐位除以进制的底数,然后取余数;当我们从其它进制转换成十进制时,我们只需要从右到左把每一位乘以底数的幂,然后把它们相加即可。
以上就是二、八、十、十六进制之间的对照表,希望本文能够帮助大家熟悉这几种有关进制转换的知识。
