利用CoordTool计算七参数

用七参数法实现坐标转换应用七参数...

第9章GPS测量数据处理9.1概述GPS数据处理过程大致分为GPS测量数据的基线向量解算、GPS基线向量网平差以及GPS网平差或与地面网联合平差等几个阶段。

各阶段数据处理软件可采用随机软件或经正式鉴定的软件，对于高精度的GPS网成果处理也可选用国际著名的GAMIT/GLOBK、BERNESE、GIPSY、GFZ等软件。

数据处理的基本流程如图9-1所示。

9.1.1数据传输大多数的GPS接收机（如ASHTECH，TRIMBLE等型号），采集的数据记录在接收机的内存模块上。

数据传输是用专用电缆将接收机与计算机连接，并在后处理软件的菜单中选择传输数据选项后，便将观测数据传输至计算机。

数据传输的同时进行数据分流，生成四个数据文件：载波相位和伪距观测值文件、星历参数文件、电离层参数和UTC参数文件、测站信息文件。

经数据分流后生成的四个数据文件中，除测站文件外，其余均为二进制数据文件。

为下一步预处理的方便，必须将它们解译成直接识别的文件，将数据文件标准化。

9.1.2预处理GPS 数据预处理的目的是：① 对数据进行平滑滤波检验，剔除粗差；② 统一数据文件格式并将各类数据文件加工成标准化文件（如GPS 卫星轨道方程的标准化，卫星时钟钟差标准化，观测值文件标准化等）； ③ 找出整周跳变点并修复观测值(整周跳变的修复见5.3.3)； ④ 对观测值进行各种模型改正。

GPS 卫星轨道方程的标准化数据处理中要多次进行卫星位置的计算，而GPS 广播星历每小时有一组独立的星历参数，使得计算工作十分繁杂，需要将卫星轨道方程标准化，以便计算简便，节省内存空间。

GPS 卫星轨道方程标准化一般采用以时间为变量的多项式进行拟合处理。

将已知的多组不同历元的星历参数所对应的卫星位置Pi(t)表达为时间t 的多项式形式：)19()(2210-++++=nin i i i i t a t a t a a t P利用拟合法求解多项式系数。

解出的系数ain 记入标准化星历文件，用它们来计算任一时刻的卫星位置。

土地确权登记中数据七参数坐标转换方法

土地确权登记中数据七参数坐标转换方法作者：李俊俊来源：《经营者》2016年第06期摘要农村土地承包经营权确权登记颁证工作中，涉及数据坐标转换的事项较多，对确权、颁证过程中土地信息的准确性以及承包经营权的核准均有重要影响。

本文基于上述背景，对农村土地承包经营权确权登记颁证工作中，数据坐标转换工作进行概述，并探讨数据七参数坐标转换方法，以期能为农村土地确权工作提供参考。

关键词农村土地确权颁证七参数坐标转换 ACRGIS一、开展农村土地确权颁证工作的背景在确权颁证过程中，要以第二轮土地承包合同以及相应的农村土地承包经营权权属资料为主要依据，同时要结合国土二调成果资料、林权发证资料和图件成果、农村集体土地所有权数据、基本农田划定数据、行政区域勘界资料以及相关基础地理信息资料等。

由于涉及多部门的多类资料且坐标基准和投影方式各不相同，其中包含了1980西安坐标系、1954北京坐标系，而本次确权颁证工作明确了坐标系统为2000国家大地坐标系，选择高斯-克吕格投影，采用标准三度分带。

坐标基准不统一将对数据资料的使用造成极大不便，还会引起不必要的权属纠纷和部门纠纷。

因此，对数据坐标进行转换处理在农村土地确权颁证工作中有重要意义。

以下将从实际数据出发，对数据坐标转换的特点进行简要介绍，希望能提高农村土地确权颁证的工作效率。

二、坐标转换方法确权颁证工作中大量数据需从80坐标系转换到2000国家大地坐标系，由于采用不一样的椭球基准，因此转换是不严密的转换，一般选用七参数法，即X平移，Y平移，Z平移，X旋转，Y旋转，Z旋转，尺度变化K。

当然，如果区域范围不大，最远点间的距离小于30Km （经验值），就可以使用三参数法，即X平移，Y平移，Z平移，而将X旋转，Y旋转，Z旋转，尺度变化K视为0，三参数只是七参数的一种特例，因此，本文只对七参数转换法进行介绍。

（一）七参数坐标转换原理两个空间直角坐标系，它们的原点不一致，相应的坐标轴相互不平行，两个坐标轴间除了三个平移参数，还有三个欧勒角，即三个旋转参数，又考虑到两个坐标系的尺度不尽相同，还需设一个尺度变化参数k，总计共有七个参数。

坐标转换程序：（1）四参数和七参数的计算

坐标转换程序：（1）四参数和七参数的计算
个人想分享一些在大学中编写的一些程序，在进行坐标转换的时候，我们经常涉及到四参数与七参数的计算，在文章中，采用C#语言来进行编程，方便计算。

（1）四参数的计算：
在转换范围较小内不同的平面坐标转换通常采用二维四参数模型转换，二维四参数的转换模型的公式如下：
式中的x1，y1与x2，y2是两个坐标系下的坐标点；
是平移参数，单位为米；
α是旋转参数，单位为弧度；
m是尺度参数，无单位。

（2）七参数的计算：
两个空间直角坐标系进行转换计算就需要用到七个参数，其中包括：三个平移参数，（ΔX，ΔY ，ΔZ），三个旋转角度参数（εX，εY，εZ）以及一个尺度参数dK
公式如下：
式中的X T与X是用来表示P点在图中的两个坐标系O-XYZ与O T-X T Y T Z T的坐标向量
∆X0是原点的平移向量，
R（ε）是一个旋转参数矩阵
为了便于计算，我们需要简化公式，因此假设当旋转角的值很小时，可以得到与得到公式的最终形式：
（3）四参数转换主要代码：
（4）七参数转换主要代码：。

七参数转换代码

七参数转换代码七参数转换通常用于地理坐标系之间的转换，包括三个平移参数（ΔX、ΔY、ΔZ）、三个旋转参数（Rx、Ry、Rz）和一个比例因子（S）。

以下是一个简单的Python代码示例，使用七参数进行坐标转换：```pythonimport numpy as npdef transform_coordinates(xyz, delta_x, delta_y, delta_z, rx, ry, rz, scale):"""使用七参数进行坐标转换。

参数:xyz: 输入的坐标 (N, 3) 的 numpy 数组。

delta_x: 平移参数ΔX。

delta_y: 平移参数ΔY。

delta_z: 平移参数ΔZ。

rx: 旋转参数 Rx。

ry: 旋转参数 Ry。

rz: 旋转参数 Rz。

scale: 比例因子 S。

返回:转换后的坐标 (N, 3) 的 numpy 数组。

"""定义旋转矩阵Rx = ([[1, 0, 0], [0, (rx), -(rx)], [0, (rx), (rx)]])Ry = ([[(ry), 0, (ry)], [0, 1, 0], [-(ry), 0, (ry)]])Rz = ([[(rz), -(rz), 0], [(rz), (rz), 0], [0, 0, 1]])R = (Rz, (Ry, Rx))平移和缩放T = ([[-delta_x, -delta_y, -delta_z], [0, 0, 0], [0, 0, 0]]) S = ([[scale, 0, 0], [0, scale, 0], [0, 0, scale]])总变换矩阵M = (S, (T, R))应用变换transformed_xyz = (M, ).Treturn transformed_xyz```请注意，这个代码示例假设输入和输出都是地理坐标系（例如经纬度）。

测量坐标系转换及COORD转换实例

测量坐标系转换及COORD转换实例RSS 打印复制链接大中小发布时间：2013-01-05 17:29:34坐标转换问题的详细了解对于测量很重要，那么请和我一起来讨论这个问题。

首先，我们要弄清楚几种坐标表示方法。

大致有三种坐标表示方法：大地坐标经纬度和高程(B、L、H)，空间直角坐标(X、Y、H)，高斯平面坐标和高程(X、Y、H)。

我们通常说的WGS-84坐标是大地坐标经纬度和高程这一种，北京54坐标是高斯平面坐标和高程这一种。

现在，再搞清楚转换的严密性问题，在同一个椭球里的转换都是严密的，而在不同的椭球之间的转换是不严密的。

举个例子，在WGS-84坐标系和北京54坐标系之间是不存在一套转换参数可以全国通用的，在每个地方会不一样，因为它们是两个不同的椭球基准。

那么，两个椭球间的坐标转换应该是怎样的呢？一般而言比较严密的是用七参数法，即X平移，Y平移，Z平移，X旋转，Y旋转，Z旋转，尺度变化K。

要求得七参数就需要在一个地区需要3个以上的已知点，如果区域范围不大，最远点间的距离不大于30Km(经验值)，这可以用三参数，即X平移，Y平移，Z平移，而将X旋转，Y旋转，Z旋转，尺度变化K视为0，所以三参数只是七参数的一种特例。

在本软件中提供了计算三参数、七参数的功能。

在一个椭球的不同坐标系中转换需要用到四参数转换，举个例子，在深圳既有北京54坐标又有深圳坐标，在这两种坐标之间转换就用到四参数，计算四参数需要两个已知点。

本软件提供计算四参数的功能。

现在举个例子说明：在珠江有一个测区，需要完成WGS-84坐标到珠江坐标系（54椭球）的坐标转换，整个转换过程是这样的：分析：WGS-84坐标和北京54坐标是两个不同椭球间的坐标转换，所以要求得三参数或七参数，而北京54和佛山坐标都是同一个椭球，所以他们之间的转换是地方坐标转换，需要求得地方转化四参数，因为要求得到的北京54是平面坐标所以需要设置投影参数。

：步骤：1．新建坐标转换文件，便于下次使用转换是不用重新输入，直接打开即可。

网络RTK七参数的求解方法与精度分析

网络RTK七参数的求解方法与精度分析发布时间：2021-05-10T16:28:00.353Z 来源：《建筑科技》2021年2月下作者：李辉[导读] 目前，随着各地区省级CORS系统的建立，网络RTK技术的发展逐渐代替了传统的测绘方法和常规RTK技术，大大提高了测绘的速度与效率, 降低测绘劳动强度和成本，在工程领域中得到广泛应用。

本文结合上海某线路工程地形测图探讨坐标转换中的七参数求解与精度分析。

上海新地海洋工程技术有限公司李辉 200080摘要：目前，随着各地区省级CORS系统的建立，网络RTK技术的发展逐渐代替了传统的测绘方法和常规RTK技术，大大提高了测绘的速度与效率, 降低测绘劳动强度和成本，在工程领域中得到广泛应用。

本文结合上海某线路工程地形测图探讨坐标转换中的七参数求解与精度分析。

关键词：CORS系统网络RTK技术坐标转换七参数0.前言目前GPS能够测量得到较高精度的WGS-84坐标系下的大地坐标，我们在实际测量中应用的通常是采用地方坐标系，高程为正常高。

为了把WGS-84坐标系坐标转换为地方坐标系下坐标，施工前应首先求得两种坐标系间的转换参数。

由于不同区域的转换参数不完全相同，为了提高GPS-RTK的测量精度，就必须求出适合本区域内的坐标转换参数。

[1, 2]1.网络RTK技术及应用指在一定区域内建立多个基准站,对该地区构成网状覆盖,并进行连续跟踪观测,通过这些站点组成卫星定位观测值的网络解算,获取覆盖该地区和某时间段的RTK改正参数,用于该区域内RTK用户进实时改正的定位方式。

[3] 网络RTK技术的出现省去了传统测量中控制网的建立以及常规RTK基准站的设立，并且能快速、精确地获得地形地物点坐标，节省了大量的人力、物力。

目前网络RTK技术广泛应用于地形图测绘、水下测量、地籍测量、航空摄影测量、环境监测等多个领域。

2.工程概况及控制点收集本工程位于上海市浦东新区，线路长度约4公里，红线范围19米～34米。

布尔莎七参数据快速计算工具

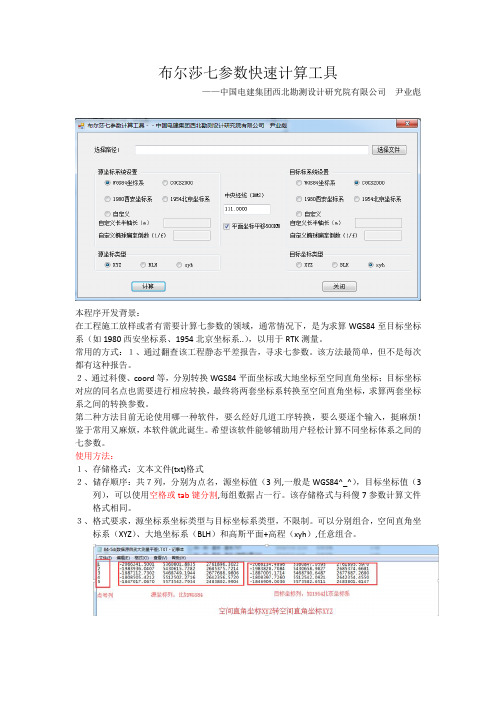
布尔莎七参数快速计算工具——中国电建集团西北勘测设计研究院有限公司尹业彪本程序开发背景：在工程施工放样或者有需要计算七参数的领域，通常情况下，是为求算WGS84至目标坐标系（如1980西安坐标系、1954北京坐标系..），以用于RTK测量。

常用的方式：１、通过翻查该工程静态平差报告，寻求七参数。

该方法最简单，但不是每次都有这种报告。

２、通过科傻、coord等，分别转换WGS84平面坐标或大地坐标至空间直角坐标；目标坐标对应的同名点也需要进行相应转换，最终将两套坐标系转换至空间直角坐标，求算两套坐标系之间的转换参数。

第二种方法目前无论使用哪一种软件，要么经好几道工序转换，要么要逐个输入，挺麻烦！鉴于常用又麻烦，本软件就此诞生。

希望该软件能够辅助用户轻松计算不同坐标体系之间的七参数。

使用方法：１、存储格式：文本文件(txt)格式２、储存顺序：共７列，分别为点名，源坐标值（3列,一般是WGS84^_^），目标坐标值（3列），可以使用空格或tab键分割,每组数据占一行。

该存储格式与科傻7参数计算文件格式相同。

３、格式要求，源坐标系坐标类型与目标坐标系类型，不限制。

可以分别组合，空间直角坐标系（XYZ）、大地坐标系（BLH）和高斯平面+高程（xyh）,任意组合。

转换本质：不同坐标系只是表现类型不同，其本质仍是在空间直角坐标系下进行七参求算。

不同类型坐标系均通过相应转换，先求算出对应坐标系下的空间直角坐标，最终计算七参数。

成果形式：成果输出到起始数据文件相同文件夹下，并以追加”_7参数计算”字样。

第一部分内容共10列，前7列与原文件内容相同，第8 /9/10 三列，分别是经七参数据计算后，转换残差，以米为单位。

残差小，说明两套系统兼容性好；反之，则兼容性不好，或者两套坐标中，有错误输入值。

第二部分为七参数部分，请注意单位！最后一行为求参单位权中误差，由第一部分后3列计算获得。

祝您使用愉快！作者于2018.07.11。

七参数坐标转换原理

七参数坐标转换原理七参数坐标转换是一种在地理坐标系中进行坐标变换的方法，通过使用七个参数来描述不同坐标系或者大地测量坐标系之间的转换关系。

该方法将源坐标系的坐标转换为目标坐标系的坐标，从而实现不同坐标系之间的坐标转换。

首先，确定转换的参考坐标是进行坐标转换的基准。

选取合适的参考坐标可以使坐标转换精度更高。

常用的参考坐标有椭球面的参数和地表控制点的坐标等。

其次，计算源坐标系与目标坐标系之间的偏移量是实现坐标转换的关键。

偏移量表示源坐标系的坐标相对于目标坐标系的坐标的平移关系。

通过测量地面控制点的坐标，可以求得源坐标系与目标坐标系之间的偏移量。

然后，计算旋转角度是为了解决源坐标系与目标坐标系之间的旋转关系。

旋转角度表示源坐标系相对于目标坐标系的旋转角度，通常通过对地面控制点进行共面平差来估计旋转角度。

最后，计算尺度因子是为了解决源坐标系与目标坐标系之间的尺度变化关系。

尺度因子表示源坐标系相对于目标坐标系的比例尺，可以通过对地面控制点进行尺度变换来估计尺度因子。

七参数坐标转换在地理信息系统、测绘工程等领域中广泛应用。

它可以用于不同坐标系之间的坐标转换，实现不同数据源之间的数据对齐和整合。

同时，七参数坐标转换还可以用于地表形变分析、地壳运动监测等研究中，实现精度更高的坐标变换。

总之，七参数坐标转换是一种在地理坐标系中进行坐标转换的方法，通过使用七个参数来描述不同坐标系或者大地测量坐标系之间的转换关系。

它通过确定参考坐标、计算偏移量、旋转角度和尺度因子等参数来实现坐标转换，广泛应用于地理信息系统和测绘工程等领域。

七参数坐标转换范文

七参数坐标转换范文
以下是七个参数的介绍：
1.三个平移参数：
平移参数用于修正两个坐标系之间的平移差异。

通常，在实际测量中
会发现两个坐标系的原点位置不同，因此需要通过平移参数对其进行修正。

2.三个旋转参数：
旋转参数用于修正两个坐标系之间的旋转差异。

通常，在不同的坐标
系中，坐标轴的方向和角度可能不同，因此通过旋转参数来修正这些差异。

3.一个尺度因子参数：
尺度因子参数用于修正两个坐标系之间的比例差异。

不同的坐标系可
能采用不同的度量单位和比例尺，因此需要通过尺度因子参数来进行转换。

1.收集需要转换的坐标数据：包括大地坐标系和平面投影坐标系的测
量数据。

2.计算坐标差异：通过比较两个坐标系之间的差异，得到需要转换的
平移、旋转和尺度变换参数的初值。

3.求解参数：使用最小二乘法或其他数学方法，求解出误差最小的最
优参数值。

4.修正坐标差异：根据计算得到的参数值，修正坐标差异，实现坐标
的转换。

5.检验转换结果：对转换后的坐标数据进行验证，确保转换结果的准
确性。

七参数坐标转换是一种经典的坐标转换方法，在地理测量和地图制图中得到广泛应用。

它可以实现不同坐标系之间的无畸变、无失真的转换，为地理数据的整合和分析提供了坚实的基础。

不过，需要注意的是，七参数坐标转换仅适用于小范围的坐标转换，对于大范围的转换可能存在较大的误差。

因此，在实际应用中，需要根据具体情况选择合适的坐标转换方法。

利用COORD进行坐标系转换教学内容

利用C O O R D进行坐标系转换利用COORD进行坐标系转换南方测绘技术部主管朱代军摘要：坐标转换在测绘工程中经常会用到，特别是在处理原始数据的时候，在这里以COORD坐标转换软件为例，谈一谈如何进行两个坐标椭球系之间的数据转换，也就是求取七参数。

关键字：坐标系七参数一．COORD软件介绍COORD 4.1坐标转换软件(其它版本可能有问题)，是一个免费的坐标转换软件,也是测绘人常备的一个工具之一。

在此感谢COORD的作者Jerry。

在下边的时间里，就给大家演示一下该软件在通过三个以上已知点计算七参数时的一些操作。

图１：软件界面1.1 参数的分类1.1.1 三参数即 X 平移， Y 平移， Z 平移只需一个已知点即可。

适用于小范围内使用，不同椭球间可以互转，转换后的坐标系方向与源坐标系方向一致，只有当源坐标系与当前坐标系的方向一致或在精度范围内才可使用。

1.1.2 四参数即 X 平移， Y 平移，坐标旋转，投影比例需两个已知点,在高程精度不高的情况下使用，因为在四参数中，没有高程改正参数，在实际的测量中，会加上三参数中的高程改正参数或利用高程拟后来得到较高精度的高程。

四参数属于同一椭球下的转换，当源坐标系与当前坐标系不一致时，如将WGS84经纬度转换到北京54坐标系，一般会利用以下的转换原理。

源坐标系： WGS84坐标系目标坐标系：北京54坐标系(地方坐标)或由于四参数中，没有高程改正，如果需要高程精度较高的用户，需再计算高程改正参数，高程改参数根据所使用已知点的数量又分为多种参数：1~2个高程已知点时，即Z平移，在使用中即为三参数中的Z平移参数；3~4个高程已知点时，采用高程拟合中的平面拟合参数；6~7个高程已知点时，采用高程拟合中的曲面拟合参数。

在一般使用过程中，高程拟合参数可根据输入已知点的个数自动或手动选择计算各参数。

1.1.3 七参数X 平移， Y 平移， Z 平移， X 旋转（WX）， Y 旋转（WY）， Z 旋转（WZ），尺度变化（DM ）。

CoordMG坐标转换

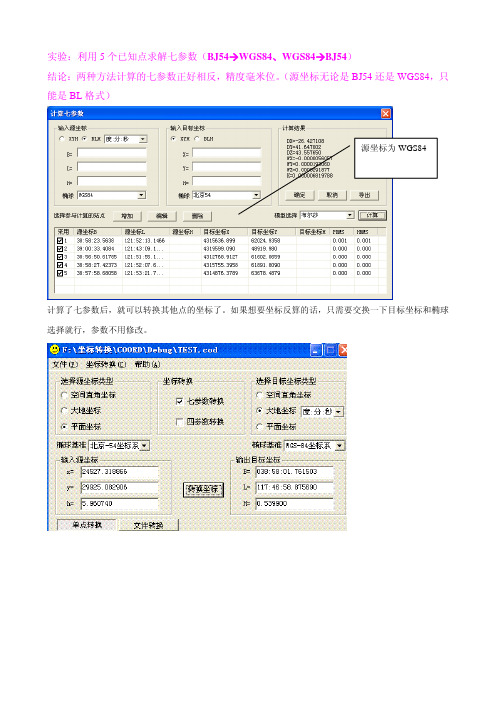
源坐标为 BJ54，输入 BL，计算出来的七参数与上边的相反
利用计算的七参数，验算已知控制点，精度在毫米位。输出目标坐标，可以是 BL、XY
源坐标，如果输入 XY ，计算的就有问题。
实验：使用一个已知点计算三参数（BJ54WGS84、WGS84BJ54）。结论：两种方法算出来的三参数符号正好相反。
源坐标为 WGS84
源坐标为 BJ54。在此只能输入 BL
Hale Waihona Puke 需要注意的是：此软件计算三参数的时候，源坐标只能输入 BL，目标坐标只能输入 XY
验算结果显示，精度可以达到毫米位
在此需要注意，源坐标只能输入 BL，否则转换错误。
第二个转换点，转换精度可达到毫米位
Caris 中定义的七参数同 coord 软件计算出的七参数正好相反
原则上在 caris 软件 datum.dat 中定义也同样可以定义一个 WGS84 带七参数的坐标系。这样 Evia 软件外业采集时使用 BJ54 坐标系，使用 caris 软件处理后，同样可以导出一个 WGS84 坐标系的数据(选择我们定义的带七参数的 84 坐标系)。有待研究
实验：利用 5 个已知点求解七参数（BJ54WGS84、WGS84BJ54）结论：两种方法计算的七参数正好相反，精度毫米位。（源坐标无论是 BJ54 还是 WGS84，只能是 BL 格式）
源坐标为 WGS84
计算了七参数后，就可以转换其他点的坐标了。如果想要坐标反算的话，只需要交换一下目标坐标和椭球选择就行，参数不用修改。

利用CoordTool计算七参数

利用CoordTool计算七参数
利用CoordTool计算七参数
【使用软件】
软件名字：CoordTool
【数据准备】
首选需要准备数据,一套为点的wgs84大地坐标,还有一份是相应点的当地坐标.并且需要把两份数据按照规定格式合并为一个数据文件，如下图所示：
或者
【软件计算七参数】
打开CoordTool软件
【设置椭球参数】
设置好相应的椭球参数，源椭球一定要选择WGS84（因为原坐标选用的是WGS84大地坐标），当地椭球按照当地坐标的坐标系进行选择。

【设置投影参数】
输入相对应的中央子午线，北向加常数，投影面高程等信息
参数设置已经设置完毕，然后确定，接着把准备好的数据用来计算七参数
【参数计算器】
实用工具-参数计算器，如下图所示：
在参数计算器界面，选择原坐标系坐标（大地坐标or空间坐标）
和地方坐标系坐标（大地坐标or空间坐标），选择好坐标参数后。

点击导入文件，选择开始我们准备好的txt。

如图所示
最后点击计算七参数，结果如下图所示。

计算好了七参数，一般情况，dx和dy一般小于2cm，dh一般小于5cm，超过这个精度的点考虑不启用，然后重新计算七参数。

七参数计算公式范文

七参数计算公式范文
地理坐标系转换是将一个地理坐标系的坐标点转换到另一个地理坐标系下的坐标点。

常见的地理坐标系包括WGS84、北京54等。

下面是七参数计算公式的详细介绍：
1.平移参数：
平移参数表示两个坐标系之间的平移关系，即在x、y、z轴方向上的平移量。

可以用一个三维向量表示，分别为∆X、∆Y、∆Z。

2.旋转参数：
旋转参数表示两个坐标系之间的旋转关系，即绕x、y、z轴旋转的角度。

可以用欧拉角表示，分别为ω、φ、κ。

其中，ω表示绕z轴旋转的角度，φ表示绕x轴旋转的角度，κ表示绕y轴旋转的角度。

3.缩放参数：
缩放参数表示两个坐标系之间的尺度关系，即坐标点的缩放比例。

可以用一个实数表示，即缩放因子s。

X2=X1+∆X+(1+s)*Y1*κ-s*Z1*φ
Y2=Y1+∆Y-(1+s)*X1*κ+s*Z1*ω
Z2=Z1+∆Z+(1+s)*X1*φ-s*Y1*ω
其中，X1、Y1、Z1表示原始地理坐标系下的坐标点，X2、Y2、Z2表示目标地理坐标系下的坐标点。

需要注意的是，七参数计算公式只是理论上的模型，实际应用时可能还需要考虑其他因素，如椭球体参数的影响等。

在实际计算中，可能还需要考虑更复杂的转换模型和精度控制方法。

总之，七参数计算公式是进行地理坐标系转换的一种方法，通过平移参数、旋转参数和缩放参数实现。

它在大地测量、航空航天等领域有着广泛的应用。

南方RTK测量如何求七参数[精选五篇]

南方RTK测量如何求七参数[精选五篇]第一篇：南方RTK测量如何求七参数演讲稿工作总结调研报告讲话稿事迹材料心得体会策划方案南方RTK测量如何求七参数通常最大距离小于10公里的测区，使用四参数就可以了，很多论文的实验结论都证明了对于小范围的测区，使用四参数坐标转换的结果优于七参数坐标转换的结果。

1.参数求解的过程基本相同，就是在测区中心位置架设好基准站，然后使用流动站新建工程，设置基本的投影的参数，如西安80坐标系，高斯投影，中央子午线，Y坐标常数500km等，2.直接使用流动站到三个及以上已知高等级控制点测量固定解状态下的坐标。

3.求解参数：依次输入已知控制点的成果坐标，并指定之前RTK 测量获得对应控制点的坐标，保存参数后应用。

4.检核：使用应用参数后的RTK流动站，测量一个已知的控制点，并检查观测坐标值与成果坐标的互差。

南方灵锐S82RTK操作步骤及使用技巧分享首次分享者：郜亚辉已被分享1次评论(0)复制链接分享转载举报一．基准站部分精心收集精心编辑精致阅读如需请下载！演讲稿工作总结调研报告讲话稿事迹材料心得体会策划方案1）基准站安装１．在基准站架设点上安置脚架，安装上基座，再将基准站主机用连接头安置于基座之上，对中整平（如架在未知点上，则大致整平即可）。

注意：基准站架设点可以架在已知点或未知点上，这两种架法都可以使用，但在校正参数时操作步骤有所差异。

2.安置发射天线和电台，将发射天线用连接头安置在另一脚架上，将电台挂在脚架的一侧，用发射天线电缆接在电台上，再用电源电缆将主机、电台和蓄电池接好，注意电源的正负极必须连接正确（红正黑负），否则保险丝将被烧断。

注意：主机和电台上的接口都是唯一的，在接线时必须红点对红点，拔出连线接头时一定要捏紧线头部位，不可直接握住连线强行拨出。

2）主机操作1．打开主机精心收集精心编辑精致阅读如需请下载！演讲稿工作总结调研报告讲话稿事迹材料心得体会策划方案主机上只有一个操作按钮（电源键），轻按电源键打开主机，主机开始自动初始化和搜索卫星，当卫星数和卫星质量达到要求后（大约１分钟），主机上的ＤＬ指示灯开始５秒钟快闪２次，表明基准站开始正常工作。

七参数四参数转化

七参数四参数转化南方RTK使用中参数的求取及分类一、控制点坐标库的应用GPS 接收机输出的数据是WGS-84 经纬度坐标，需要转化到施工测量坐标，这就需要软件进行坐标转换参数的计算和设置，控制点坐标库就是完成这一工作的主要工具。

控制点坐标库是计算四参数和高程拟合参数的工具，可以方便直观的编辑、查看、调用参与计算四参数和高程拟合参数的校正控制点。

在进行四参数的计算时，至少需要两个控制点的两套坐标系坐标参与计算才能最低限度的满足控制要求。

高程拟合时，使用三个点的高程进行计算时，控制点坐标库进行加权平均的高程拟合；使用 4 到 6 个点的高程时，控制点坐标库进行平面高程拟合；使用7 个以上的点的高程时，控制点坐标库进行曲面拟合。

控制点的选用和平面、高程拟合都有着密切而直接的关系，这些内容涉及到大量的布设经典测量控制网的知识，在这里没有办法多做介绍，建议用户查阅相关测量资料。

利用控制点坐标库的做法大致是这样的:假设我们利用A、B 这两个已知点来求取参数，那么首先要有A、B 两点的GPS 原始记录坐标和测量施工坐标。

A、B 两点的GPS原始记录坐标的获取有两种方式：一种是布设静态控制网，采用静态控制网布设时后处理软件的GPS 原始记录坐标；另一种是GPS 移动站在没有任何校正参数起作用的Fixed（固定解）状态下记录的GPS 原始坐标。

其次在操作时，先在控制点坐标库中输入 A 点的已知坐标，之后软件会提示输入A 点的原始坐标,然后再输入 B 点的已知坐标和 B 点的原始坐标,录入完毕并保存后（保存文件为*.cot 文件）控制点坐标库会自动计算出四参数和高程拟合参数。

1.1、校正参数操作：工具→ 校正向导或设置→ 求转换参数(控制点坐标库)所需已知点数：1个校正参数是工程之星软件很特别的一个设计，它是结合国内的具体测量工作而设计的。

校正参数实际上就是只用同一个公共控制点来计算两套坐标系的差异。

根据坐标转换的理论，一个公共控制点计算两个坐标系误差是比较大的，除非两套坐标系之间不存在旋转或者控制的距离特别小。

[教学]七参数求解过程

关于GPS打桩定位系统七参数求解方法引言：随着GPS水上沉桩定位系统在东海大桥工程中的成功应用，越来越多的工程使用该定位系统。

它解决了在常规方法定位的一些较难完成的工作，而且它的最大优点是定位迅速、准确而且所需测量人员较少，减轻测量人员的繁重的工作量。

在该系统中最重要的部分是七参数的设置，七参数是打桩系统中的转换参数，它随着施工地点的不同而改变，其中DX、DY、DZ为平移参数，单位：m；RX、RY、RZ为旋转参数，单位：秒；Scale为比例系数（尺比度），单位：ppm。

七参数的选择有两种坐标转换方法，（1）、WGS84-BJ54；（2）、WGS84-工程。

这两种坐标转换方法随着工程的要求而选择，两种方法的精度相差无几。

下面以曹妃甸试桩工程为例分别介绍一下这两种坐标转换方法的解算过程，重点介绍WGS84－BJ54七参数的求解过程。

（一）WGS84－BJ541.求解WGS84坐标：将野外静态测量数据通过Pinnacle静态解算软件解算出每个点的WGS84坐标（至少三个点，无约束或约束平差结果）2.定义地方坐标系统：（1）.在工具条或工具栏中点击坐标系统编辑器，如图所示：图（一）.1（2）.选择椭球面板，①.点击新建建立新的椭球参数并输入新的椭球名称：例如：BJ54，其相关参数：a=6378245,1/f=298.3,点击确定返回②.或者直接选择KRASS椭球。

如下图所示：图（一）.2（3）.选择基准面板，点击新建命令输入基准名称：CFD84-54，并选择椭球为BJ54或KRASS图（一）.3(4).选择平面坐标系统面板，点击新建命令建立平面坐标系统名称：CFD84-54点击新建命令输入如下内容：①．基准面名称：CFD84-54;②．影方式：TMERC TM投影（一个投影带）：③．单位名称：Meters;④．点击编辑投影进入下一栏：⑤．输入：中央子午线：118°30′；尺比度：1；E偏移量：500000。

基于VC++的七参数转换实现（主要代码）

基于VC++的七参数转换实现（主要代码）// CoordTra.cpp : implementation file//七参数转换。

//#include "stdafx.h"#include "GPSCoord.h"#include "CoordTra.h"#include <fstream.h>#include "Matrix.h"#include "math.h"#define PI 3.1415926535897932384626433#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif/////////////////////////////////////////////////////////////////////////////// CCoordTra dialogCCoordTra::CCoordTra(CWnd* pParent ): CDialog(CCoordTra::IDD, pParent){//{{AFX_DATA_INIT(CCoordTra)m_Py = 0;m_Px = 0;m_Pz = 0;m_Xx = 0;m_Xy = 0;m_Xz = 0;m_ChiDu = 0;m_num = 0;Count2=4;f_coord.x =0;f_coord.y =0;f_coord.z =0;n_coord.x =0;n_coord.y =0;n_coord.z =0;//}}AFX_DATA_INIT}void CCoordTra::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CCoordTra)DDX_Text(pDX, IDC_FCOORD_X, f_coord.x);DDX_Text(pDX, IDC_FCOORD_Y, f_coord.y);DDX_Text(pDX, IDC_FCOORD_Z, f_coord.z);DDX_Text(pDX, IDC_NCOORD_X, n_coord.x);DDX_Text(pDX, IDC_NCOORD_Y, n_coord.y);DDX_Text(pDX, IDC_NCOORD_Z, n_coord.z);DDX_Text(pDX, IDC_NUM, m_num);//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(CCoordTra, CDialog)//{{AFX_MSG_MAP(CCoordTra)ON_BN_CLICKED(IDC_TRANSFORM, OnTransform)ON_BN_CLICKED(IDC_READ, OnRead)//}}AFX_MSG_MAPEND_MESSAGE_MAP()/////////////////////////////////////////////////////////////////////////////// CCoordTra message handlersvoid CCoordTra::OnTransform(){// TODO: Add your control notification handler code hereUpdateData();n_coord=tracoord(f_coord);UpdateData(FALSE);}coord CCoordTra::tracoord(coord p_coord)//坐标转换函数{coord q_coord;q_coord.x=m_Px+p_coord.x*(1+m_ChiDu)+m_Xz*p_coord.y-m_Xy*p_coord.z; q_coord.y=m_Py+p_coord.y*(1+m_ChiDu)-m_Xz*p_coord.x+m_Xx*p_coord.z; q_coord.z=m_Pz+p_coord.z*(1+m_ChiDu)+m_Xy*p_coord.x-m_Xx*p_coord.y; return q_coord;}void CCoordTra::OnRead(){// TODO: Add your control notification handler code hereUpdateData();Count2=m_num;coord *result;result=new coord[Count2];date=new coord[Count2];CFileDialog fileDlg(TRUE);fileDlg.m_ofn.lpstrTitle="输⼊需要转换的点坐标";fileDlg.m_ofn.lpstrFilter="Text Files(*.txt)\0*.txt\0All Files(*.*)\0*.*\0\0";int i;if(IDOK==fileDlg.DoModal()){CString filefullname=fileDlg.GetPathName();ifstream file(filefullname);for(i=0;i<Count2;i++){file>>date[i].x;file>>date[i].y;file>>date[i].z;result[i]=tracoord(date[i]);}}//读取⽂件并计算新坐标MessageBox("转换成功，请保存！");CFileDialog fileDlg1(FALSE);fileDlg1.m_ofn.lpstrTitle="保存对话框";fileDlg1.m_ofn.lpstrFilter="Text Files(*.txt)\0*.txt\0All Files(*.*)\0*.*\0\0"; fileDlg1.m_ofn.lpstrDefExt="txt";if(IDOK==fileDlg1.DoModal()){CString filefullname=fileDlg1.GetPathName();ofstream file(filefullname);MessageBox(filefullname);int i;for(i=0;i<Count2;i++){CString str;str.Format("%.4f", result[i].x);file<<str<<" ";str.Format("%.4f", result[i].y);file<<str<<" ";str.Format("%.4f", result[i].z);file<<str<<" ";file<<"\n";}}//保存数据}// ParameterCount.cpp : implementation file//反解七参数#include "stdafx.h"#include "GPSCoord.h"#include "ParameterCount.h"//#include "PointNum.h"#include <fstream.h>#include "Matrix.h"#include "math.h"#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif/////////////////////////////////////////////////////////////////////////////// CParameterCount dialogCParameterCount::CParameterCount(CWnd* pParent ): CDialog(CParameterCount::IDD, pParent){//{{AFX_DATA_INIT(CParameterCount)m_Py = 0;m_Px = 0;m_Pz = 0;m_Xx = 0;m_Xy = 0;m_Xz = 0;m_ChiDu = 0;f_c1.x=0;f_c1.y=0;f_c1.z=0;f_c2.x=0;f_c2.y=0;f_c2.z=0;f_c3.x=0;f_c3.y=0;f_c3.z=0;n_c1.x=0;n_c1.y=0;n_c1.z=0;f_c2.x=0;n_c2.y=0;n_c2.z=0;f_c3.x=0;n_c3.y=0;n_c3.z=0;m_Px = 0;m_Pz = 0;m_Xx = 0;m_Xy = 0;m_Xz = 0;m_ChiDu = 0;m_control=false;m_num = 3;//}}AFX_DATA_INIT}void CParameterCount::DoDataExchange(CDataExchange* pDX) {CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CParameterCount)DDX_Text(pDX, IDC_FCOORD_X1, f_c1.x);DDX_Text(pDX, IDC_FCOORD_X2, f_c2.x);DDX_Text(pDX, IDC_FCOORD_X3, f_c3.x);DDX_Text(pDX, IDC_FCOORD_Y1, f_c1.y);DDX_Text(pDX, IDC_FCOORD_Y2, f_c2.y);DDX_Text(pDX, IDC_FCOORD_Y3, f_c3.y);DDX_Text(pDX, IDC_FCOORD_Z1, f_c1.z);DDX_Text(pDX, IDC_FCOORD_Z2, f_c2.z);DDX_Text(pDX, IDC_FCOORD_Z3, f_c3.z);DDX_Text(pDX, IDC_NCOORD_X1, n_c1.x);DDX_Text(pDX, IDC_NCOORD_X2, n_c2.x);DDX_Text(pDX, IDC_NCOORD_X3, n_c3.x);DDX_Text(pDX, IDC_NCOORD_Y1, n_c1.y);DDX_Text(pDX, IDC_NCOORD_Y2, n_c2.y);DDX_Text(pDX, IDC_NCOORD_Y3, n_c3.y);DDX_Text(pDX, IDC_NCOORD_Z1, n_c1.z);DDX_Text(pDX, IDC_NCOORD_Z2, n_c2.z);DDX_Text(pDX, IDC_NCOORD_Z3, n_c3.z);DDX_Text(pDX, IDC_NUM, m_num);DDV_MinMaxInt(pDX, m_num, 3, 20);//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(CParameterCount, CDialog)//{{AFX_MSG_MAP(CParameterCount)ON_BN_CLICKED(IDC_READ, OnRead)//}}AFX_MSG_MAPEND_MESSAGE_MAP()/////////////////////////////////////////////////////////////////////////////// CParameterCount message handlersvoid CParameterCount::OnOK(){// TODO: Add extra validation hereUpdateData();Count1=3;DATA=new double[Count1*6];DATA[0]=f_c1.x;DATA[1]=f_c1.y;DATA[2]=f_c1.z;DATA[3]=n_c1.x;DATA[4]=n_c1.y;DATA[5]=n_c1.z;DATA[6]=f_c2.x;DATA[7]=f_c2.y;DATA[8]=f_c2.z;DATA[9]=n_c2.x;DATA[10]=n_c2.y;DATA[11]=n_c2.z;DATA[12]=f_c3.x;DATA[13]=f_c3.y;DATA[14]=f_c3.z;DATA[15]=n_c3.x;DATA[16]=n_c3.y;DATA[17]=n_c3.z;//值传递 Calculate();m_control=true;CDialog::OnOK();}void CParameterCount::Calculate(){double *A=new double[Count1*3*7]; //系数阵double *L=new double[Count1*3]; //常数项X=new double[7]; //结果double *AT=new double[Count1*3*7]; //系数转置阵double *ATA=new double[7*7];double *ATL=new double[7];double *invATA=new double[7*7];int i;for(i=0;i<Count1;i++){double X_WGS84=DATA[0+i*6];double Y_WGS84=DATA[1+i*6];double Z_WGS84=DATA[2+i*6];double X_54=DATA[3+i*6];double Y_54=DATA[4+i*6];double Z_54=DATA[5+i*6];//系数矩阵第⼀⾏A[7*3*i]=1;A[7*3*i+1]=0;A[7*3*i+2]=0;A[7*3*i+3]=0;A[7*3*i+4]=-Z_WGS84;A[7*3*i+5]=Y_WGS84;A[7*3*i+6]=X_WGS84;//系数矩阵第⼆⾏A[7*(3*i+1)]=0;A[7*(3*i+1)+1]=1;A[7*(3*i+1)+2]=0;A[7*(3*i+1)+3]=Z_WGS84;A[7*(3*i+1)+4]=0;A[7*(3*i+1)+5]=-X_WGS84;A[7*(3*i+1)+6]=Y_WGS84;//系数矩阵第三⾏A[7*(3*i+2)]=0;A[7*(3*i+2)+1]=0;A[7*(3*i+2)+2]=1;A[7*(3*i+2)+3]=-Y_WGS84;A[7*(3*i+2)+4]=X_WGS84;A[7*(3*i+2)+5]=0;A[7*(3*i+2)+6]=Z_WGS84;//常数项L[3*i]=-(X_WGS84-X_54);L[3*i+1]=-(Y_WGS84-Y_54);L[3*i+2]=-(Z_WGS84-Z_54);}Trans(A,AT,3*Count1,7);//求转置damul(AT,A,7,3*Count1,7,ATA);//矩阵相乘damul(AT,L,7,3*Count1,1,ATL);//矩阵相乘invATA=ATA;dcinv(invATA,7);//求逆矩阵damul(invATA,ATL,7,7,1,X);//V=AX+L矩阵相乘m_Px = X[0];m_Py = X[1];m_Pz = X[2];m_Xx = X[3];m_Xy = X[4];m_Xz = X[5];m_ChiDu = X[6];}void CParameterCount::OnRead(){// TODO: Add your control notification handler code hereUpdateData();Count1=m_num;DATA=new double[Count1*6];CFileDialog fileDlg(TRUE);fileDlg.m_ofn.lpstrTitle="我的⽂件打开对话框";fileDlg.m_ofn.lpstrFilter="Text Files(*.txt)\0*.txt\0All Files(*.*)\0*.*\0\0"; int i;if(IDOK==fileDlg.DoModal()){CString filefullname=fileDlg.GetPathName(); ifstream file(filefullname);for(i=0;i<6*Count1;i++){file>>DATA[i];}}Calculate();m_control=true;CDialog::OnOK();//坐标转换}。

COORD程序使用方法

坐标转换问题坐标转换问题的详细了解对于测量很重要，那么请和我一起来讨论这个问题。

首先，我们要弄清楚几种坐标表示方法。

大致有三种坐标表示方法：经纬度和高程，空间直角坐标，平面坐标和高程。

我们通常说的WGS-84坐标是经纬度和高程这一种，北京54坐标是平面坐标和高程着一种。

现在，再搞清楚转换的严密性问题，在同一个椭球里的转换都是严密的，而在不同的椭球之间的转换是不严密的。

举个例子，在WGS-84坐标和北京54坐标之间是不存在一套转换参数可以全国通用的，在每个地方会不一样，因为它们是两个不同的椭球基准。

那么，两个椭球间的坐标转换应该是怎样的呢？一般而言比较严密的是用七参数法（包括布尔莎模型，一步法模型，海尔曼特等），即X平移，Y平移，Z平移，X旋转，Y旋转，Z旋转，尺度变化K。

要求得七参数就需要在一个地区需要3个以上的已知点，如果区域范围不大，最远点间的距离不大于30Km(经验值)，这可以用三参数（莫洛登斯基模型），即X平移，Y平移，Z平移，而将X旋转，Y旋转，Z旋转，尺度变化K视为0，所以三参数只是七参数的一种特例。

在本软件中提供了计算三参数、七参数的功能。

在一个椭球的不同坐标系中转换可能会用到平面转换，现阶段一般分为四参数和平面网格拟合两种方法，以四参数法在国内用的较多，举个例子，在深圳既有北京54坐标又有深圳坐标，在这两种坐标之间转换就用到四参数，计算四参数需要两个已知点。

更精确的可以提供网格拟合数据,本软件提供计算和应用四参数的功能,也提供了网格拟合的功能。

另外，还有高程拟合的问题，大地水准面模型在国内用户中很少会用到，但在国际上已经是标准之一，本软件提供最常用的EGM96模型和Geoid99模型。

最后，本软件提供了ITRF框架转换方法，涉及到ITRF2000和以往用过的ITRF96，ITRF93之间的换算，对于方面的需求的用户是个尝试。

现在举个例子说明：在珠江有一个测区，需要完成WGS-84坐标到珠江坐标系（54椭球）的坐标转换，整个转换过程是这样的：本软件使用说明：本软件采用坐标系统库管理，用户可以将一种转换在系统库里保存下来，下次使用时从文件菜单中选择打开库文件来调用所有已有的转换参数。

(TGO)关于七参数求法

选横轴魔卡托投影
输入中央子午线
再输入长半轴与扁率
基准转换
选七参数
分别将TGO求出的七个参数输入即可
点接受
水平平差和垂直平差选无平差，然后接受即可
再接受，参数设置完毕
点改变选择当地坐标系
确认
插入点
将三个点的WGS84和当地坐标分别输入，注意点名不能一样
输入后点插入
点“测量”-“GPS点校正”
选7参数，水平平差，垂直平差空着，然后点“点列表”
分别选取两套坐标
点确认
点计算
会出来残差，如果残差过大，可能是点输入错误或者精度不够造成的
再点报告就可以看到七参数了
旋转
-0°00'01.047243"
绕Y轴旋转
0°00'00.018181"
绕Z轴旋转
0°00'00.387181"
沿x轴转换
90.623m
沿Y轴转换
73.722m
沿Z轴转换
-14.381m
比例因子(ppm)
281.953
回到顶部
将七参数输入到手簿里面就可以了
新任务，点坐标系统
点键入参数