算法与流程图A---002+答案
算法设计与分析第二版课后习题解答

算法设计与分析第二版课后习题解答算法设计与分析基础课后练习答案习题 4.设计一个计算的算法,n是任意正整数。
除了赋值和比较运算,该算法只能用到基本的四则运算操作。
算法求//输入:一个正整数n2//输出:。
step1:a=1;step2:若a*a 5. a.用欧几里德算法求gcd。
b. 用欧几里德算法求gcd,比检查min{m,n}和gcd间连续整数的算法快多少倍?请估算一下。
a. gcd(31415, 14142) = gcd(14142, 3131) = gcd(3131, 1618) =gcd(1618, 1513) = gcd(1513,105) = gcd(1513, 105) = gcd(105, 43) =gcd(43, 19) = gcd(19, 5) = gcd(5, 4) = gcd(4, 1) = gcd(1, 0) = 1.b.有a可知计算gcd欧几里德算法做了11次除法。
连续整数检测算法在14142每次迭代过程中或者做了一次除法,或者两次除法,因此这个算法做除法的次数鉴于1·14142 和 2·14142之间,所以欧几里德算法比此算法快1·14142/11 ≈ 1300 与 2·14142/11 ≈ 2600 倍之间。
6.证明等式gcd(m,n)=gcd(n,m mod n)对每一对正整数m,n都成立. Hint:根据除法的定义不难证明:如果d整除u和v, 那么d一定能整除u±v;如果d整除u,那么d也能够整除u的任何整数倍ku.对于任意一对正整数m,n,若d能整除m和n,那么d一定能整除n和r=m mod n=m-qn;显然,若d能整除n和r,也一定能整除m=r+qn和n。
数对(m,n)和(n,r)具有相同的公约数的有限非空集,其中也包括了最大公约数。
故gcd(m,n)=gcd(n,r)7.对于第一个数小于第二个数的一对数字,欧几里得算法将会如何处理?该算法在处理这种输入的过程中,上述情况最多会发生几次? Hint:对于任何形如0 gcd(m,n)=gcd(n,m)并且这种交换处理只发生一次.对于所有1≤m,n≤10的输入, Euclid算法最少要做几次除法?(1次) b. 对于所有1≤m,n≤10的输入, Euclid算法最多要做几次除法?(5次) gcd(5,8) 习题 1.(农夫过河)P—农夫 W—狼G—山羊C—白菜 2.(过桥问题)1,2,5,10---分别代表4个人, f—手电筒4. 对于任意实系数a,b,c, 某个算法能求方程ax^2+bx+c=0的实根,写出上述算法的伪代码(可以假设sqrt(x)是求平方根的函数) 算法Quadratic(a,b,c)//求方程ax^2+bx+c=0的实根的算法 //输入:实系数a,b,c//输出:实根或者无解信息 If a≠0D←b*b-4*a*c If D>0temp←2*ax1←(-b+sqrt(D))/temp x2←(-b-sqrt(D))/temp return x1,x2else if D=0 return –b/(2*a) else return “no real roots” else //a=0if b≠0 return –c/b else //a=b=0if c=0 return “no real numbers”else return “no real roots”5. 描述将十进制整数表达为二进制整数的标准算法 a.用文字描述 b.用伪代码描述解答:a.将十进制整数转换为二进制整数的算法输入:一个正整数n输出:正整数n相应的二进制数第一步:用n除以2,余数赋给Ki(i=0,1,2...),商赋给n 第二步:如果n=0,则到第三步,否则重复第一步第三步:将Ki按照i从高到低的顺序输出 b.伪代码算法 DectoBin(n)//将十进制整数n转换为二进制整数的算法 //输入:正整数n//输出:该正整数相应的二进制数,该数存放于数组Bin[1...n]中 i=1while n!=0 do { Bin[i]=n%2; n=(int)n/2; i++; } while i!=0 do{ print Bin[i]; i--; }9.考虑下面这个算法,它求的是数组中大小相差最小的两个元素的差.(算法略) 对这个算法做尽可能多的改进. 算法 MinDistance(A[0..n-1]) //输入:数组A[0..n-1] //输出:the smallest distance d between two of its elements习题1. 考虑这样一个排序算法,该算法对于待排序的数组中的每一个元素,计算比它小的元素个数,然后利用这个信息,将各个元素放到有序数组的相应位置上去.a.应用该算法对列表”60,35,81,98,14,47”排序b.该算法稳定吗?c.该算法在位吗? 解:a. 该算法对列表”60,35,81,98,14,47”排序的过程如下所示:b.该算法不稳定.比如对列表”2,2*”排序c.该算法不在位.额外空间for S and Count 4.(古老的七桥问题) 第2章习题7.对下列断言进行证明:(如果是错误的,请举例) a. 如果t(n)∈O(g(n),则g(n)∈Ω(t(n)) b.α>0时,Θ(αg(n))= Θ(g(n)) 解:a. 这个断言是正确的。
算法设计与分析习题答案

算法设计与分析习题答案算法设计与分析是计算机科学中一个重要的领域,它涉及到算法的创建、优化以及评估。
以下是一些典型的算法设计与分析习题及其答案。
习题1:二分查找算法问题描述:给定一个已排序的整数数组,编写一个函数来查找一个目标值是否存在于数组中。
答案:二分查找算法的基本思想是将数组分成两半,比较中间元素与目标值的大小,如果目标值等于中间元素,则查找成功;如果目标值小于中间元素,则在左半部分继续查找;如果目标值大于中间元素,则在右半部分继续查找。
这个过程会不断重复,直到找到目标值或搜索范围为空。
```pythondef binary_search(arr, target):low, high = 0, len(arr) - 1while low <= high:mid = (low + high) // 2if arr[mid] == target:return Trueelif arr[mid] < target:low = mid + 1else:high = mid - 1return False```习题2:归并排序算法问题描述:给定一个无序数组,使用归并排序算法对其进行排序。
答案:归并排序是一种分治算法,它将数组分成两半,分别对这两半进行排序,然后将排序好的两半合并成一个有序数组。
```pythondef merge_sort(arr):if len(arr) > 1:mid = len(arr) // 2left_half = arr[:mid]right_half = arr[mid:]merge_sort(left_half)merge_sort(right_half)i = j = k = 0while i < len(left_half) and j < len(right_half): if left_half[i] < right_half[j]:arr[k] = left_half[i]i += 1else:arr[k] = right_half[j]j += 1k += 1while i < len(left_half):arr[k] = left_half[i]i += 1k += 1while j < len(right_half):arr[k] = right_half[j]j += 1k += 1arr = [38, 27, 43, 3, 9, 82, 10]merge_sort(arr)print("Sorted array is:", arr)```习题3:动态规划求解最长公共子序列问题问题描述:给定两个序列,找到它们的最长公共子序列。
算法与程序框图习题(含答案)
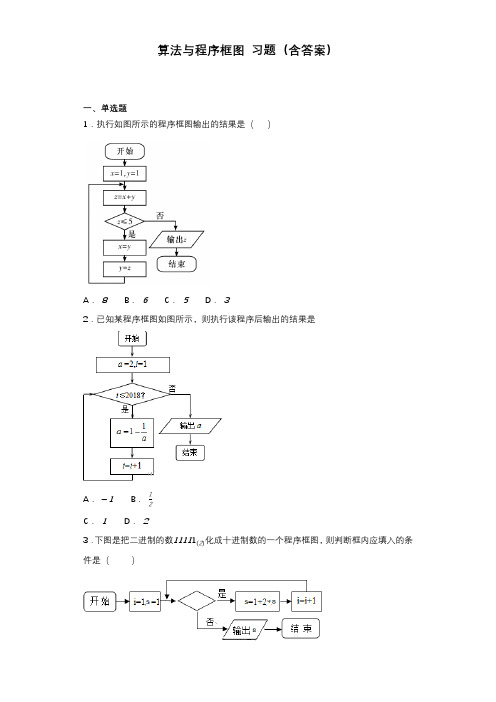
【点睛】
本题主要考查的是程序框图,考查了进位制,本题是程序框图中的循环结构,是先进行了一次判断,实则是直到型性循环,这是一道基础题.首先将二进制数化为十进制数,得到十进制数的数值,然后假设判断框中的条件不满足,执行算法步骤,待累加变量 的值为 时,算法结束,此时判断框中的条件要满足,即可得到答案.
【详解】
由题意输出的S=1+1×2+1×22+1×23+1×24,
按照程序运行:S=1,i=1;S=1+1×2,i=2;S=1+1×2+1×22,i=3;S=1+1×2+1×22+1×23,i=4;S=1+1×2+1×22+1×23+1×24,i=5,此时跳出循环输出结果,故判断框内的条件应为i≤4.
点睛:本题主要考查算法语句,意在考查学生对该基础知识的掌握水平.
12.16
【解析】
【分析】
模拟执行程序,依次写出每次循环得到的x,i的值,当i=10时不满足条件,退出循环,输出x的值为16.
【详解】
模拟程序的运行,可得
i=1,x=4
满足条件i<10,执行循环体,x=5,i=4
满足条件i<10,执行循环体,x=9,i=7
A. B. C. D.
6.在 中, , ,边 的四等分点分别为 , 靠近 ,执行下图算法后结果为( )
A.6B.7C.8D.9
7.宋元时期名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长五尺,若输入的 分别是5,2,则输出的 =( )
A. B. C. D.
8.如图所示的程序框图,输出的
A.18B.41
24.图C16所示的程序框图表示了一个什么样的算法?试用当型循环写出它的算法并画出相应的程序框图.
专题十二算法初步第三十七讲算法与程序框图的理解与应用答案

专题十二算法初步第三十七讲算法与程序框图的理解与
应用答案
1、算法与程序框图的区别是什么?
答:算法是一组完整的、解决问题的、有明确步骤的指令,而程序框
图是一种图形表示,将算法转化为可视化的步骤结构,用来表示程序的结
构和流程。
可以说算法与程序框图是相辅相成的。
2、什么是算法?
答:算法(Algorithm)是一组完整的,解决特定问题的,有明确步
骤的指令。
它们常常用来构建程序。
3、程序框图有哪些图形表示?
答:结构框图、箭头框图(流程框图)和状态框图(有穷状态机)等。
4、算法在计算机编程中的作用是什么?
答:算法是数据处理的基础,它可以解决特定的问题,让计算机能够
完成一系列有一定规律的复杂步骤。
5、程序框图是如何表示程序结构和流程的?
答:程序框图是一种图形表示,将算法转化为可视化的步骤结构,可
以用来表示程序的结构和流程,并且能够有效地指导程序的开发。
6、程序框图是如何构建的?
答:程序框图是基于一系列框来组合的,分别代表不同的程序步骤,
以及每个步骤之间的连接。
7、什么是箭头框图?
答:箭头框图(也称为流程框图)是一种图形表示,它与结构框图不同,结构框图表示程序的结构。
2012高考文科数学算法与程序框图 (答案详解)
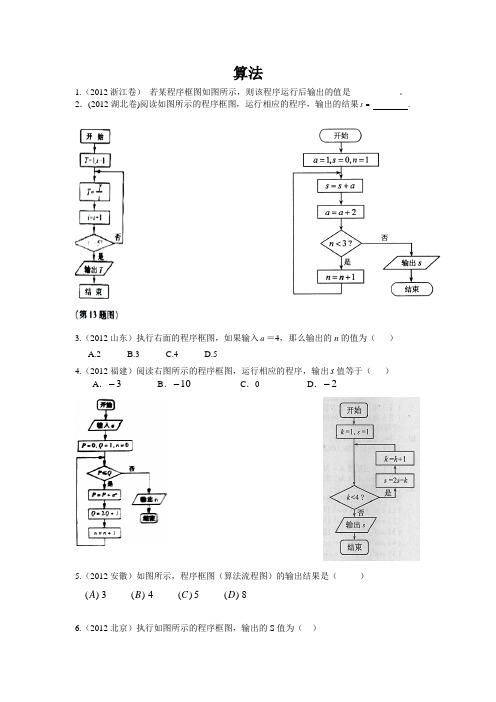
算法1.(2012浙江卷) 若某程序框图如图所示,则该程序运行后输出的值是___________。
2.(2012湖北卷)阅读如图所示的程序框图,运行相应的程序,输出的结果s = .3.(2012山东)执行右面的程序框图,如果输入a =4,那么输出的n 的值为( ) A.2 B.3 C.4 D.54.(2012福建)阅读右图所示的程序框图,运行相应的程序,输出s 值等于( )A .3-B .10-C .0D .2-5.(2012安徽)如图所示,程序框图(算法流程图)的输出结果是( ) ()A 3 ()B 4 ()C 5 ()D 86.(2012北京)执行如图所示的程序框图,输出的S 值为( )A .2B .4C .8D .167(2012广东)执行如图2所示的程序框图,若输入n 的值为6,则输出s 的值为A.105B.16C.15D.18.(2012湖南)如果执行如图3所示的程序框图,输入 4.5x =,则输出的数i = .9.(2012江西)下图是某算法的程序框图,则程序运行后输入的结果是_________。
10.(2012辽宁)执行如图所示的程序框图,则输出的S 的值是(第4题图)A. 4B.32C.23D.-111.(2012陕西)下图是计算某年级500名学生期末考试(满分为100分)及格率q 的程序框图,则图中空白框内应填入( )A .N q M =B .M q N=C .Nq M N =+D .M q M N=+12.(2012天津)阅读右边的程序框图,运行相应的程序,则输出S 的值为(A )8 (B )18 (C )26 (D )80 【解析】第一次循环2,2330==-=n S ,第二次循环3,83322==-+=n S ,第三次循环4,2633823==-+=n S ,第四次循环满足条件输出26=S ,选C. 【答案】C13.(2012新课标)如果执行右边的程序框图,输入正整数N (N ≥2)和实数1a ,2a ,…,N a ,输出A ,B ,则A .A +B 为1a ,2a ,…,N a 的和B .2A B +为1a ,2a ,…,N a 的算术平均数C .A 和B 分别为1a ,2a ,…,N a 中的最大数和最小数D .A 和B 分别为1a ,2a ,…,N a 中的最小数和最大数【命题意图】本题主要考查框图表示算法的意义,是简单题.【解析】由框图知其表示的算法是找N 个数中的最大值和最小值,A 和B 分别为1a ,2a ,…,N a 中的最大数和最小数,故选C.答案1. 【答案】1120【命题意图】本题主要考查了框图。
人教版高中数学必修5算法与程序框图教(学)案有答案
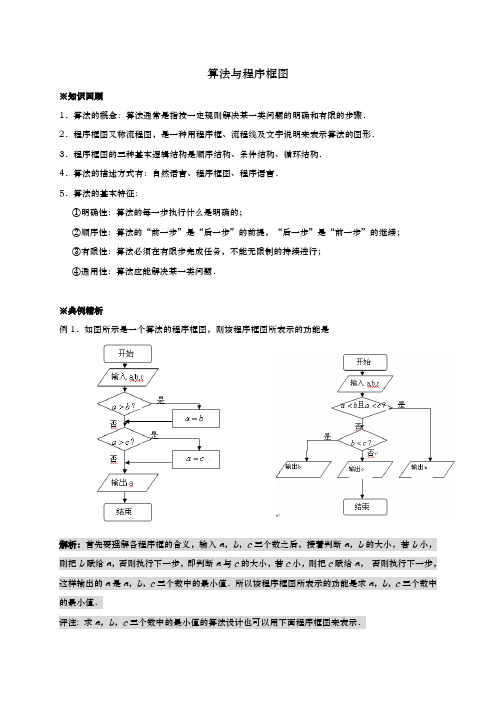
算法与程序框图※知识回顾1.算法的概念:算法通常是指按一定规则解决某一类问题的明确和有限的步骤.2.程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.3.程序框图的三种基本逻辑结构是顺序结构、条件结构、循环结构.4.算法的描述方式有:自然语言、程序框图、程序语言.5.算法的基本特征:①明确性:算法的每一步执行什么是明确的;②顺序性:算法的“前一步”是“后一步”的前提,“后一步”是“前一步”的继续;③有限性:算法必须在有限步完成任务,不能无限制的持续进行;④通用性:算法应能解决某一类问题.※典例精析例1.如图所示是一个算法的程序框图,则该程序框图所表示的功能是解析:首先要理解各程序框的含义,输入a,b,c三个数之后,接着判断a,b的大小,若b小,则把b赋给a,否则执行下一步,即判断a与c的大小,若c小,则把c赋给a,否则执行下一步,这样输出的a是a,b,c三个数中的最小值.所以该程序框图所表示的功能是求a,b,c三个数中的最小值.评注: 求a,b,c三个数中的最小值的算法设计也可以用下面程序框图来表示.例2.下列程序框图表示的算法功能是()(1)计算小于100的奇数的连乘积(2)计算从1开始的连续奇数的连乘积(3)计算从1开始的连续奇数的连乘积,当乘积大于100时,计算奇数的个数(4)计算≥1×3×5××n100成立时n的最小值解析:为了正确地理解程序框图表示的算法,可以将执行过程分解,分析每一步执行的结果.可以看出程序框图中含有当型的循环结构,故分析每一次循环的情况,列表如下:第一次:13,5S i=⨯=;第二次:135,7S i=⨯⨯=;第三次:1357,9S i=⨯⨯⨯=,此时100S<不成立,输出结果是7,程序框图表示的算法功能是求使≥1×3×5××n100成立时n的最小值.选D.评注:通过列表,我们能清楚了解程序的每一步中的各个变量是怎样变化的,这正是程序运行的本质所在.本题若要求编写求使≥1×3×5××n100成立时n的最小值的程序框图或程序时,很容易弄错输出的结果,应注意.例3.在音乐唱片超市里,每唱片售价为25元,顾客如果购买5以上(含5)唱片,则按九折收费,如果购买10以上(含10)唱片,则按八折收费,请设计算法步骤并画出程序框图,要求输入数x,输出实际收费y(元).分析:先写出y与x之间的函数关系式,有25(5)22.5(510)20(10)x xy x xx x<⎧⎪=≤<⎨⎪≥⎩,再利用条件结构画程序框图.解:算法步骤如下: 第一步,输入购买的数x,第二步,判断x是否小于5,若是,计算25y x=;27?x =否是 输出X1i i =+ 11?i >否否则,判断x是否小于10,若是,计算22.5y x =;否则,计算20y x =. 第三步,输出y . 程序框图如下:评注:凡必须先根据条件做出判断,然后再决定进行哪一个步骤的问题,在画程序框图时,必须引入判断框,采用条件结构设计算法.如果变量分三级(或以上)时,就需要用到条件结构的嵌套,不能忽视结果中“是”、“否”的书写,否则不知道执行哪一条路径.一般地,分n 段的分段函数,需要引入1n -个判断框.条件结构有以下两种基本类型.例4.画出求222111123100++++的值的程序框图. 分析:这是一个有规律的数列求和问题,每次都进行了相同的运算,故应用循环结构进行算法设计. 解:程序框图如下:(1)当型循环 (2)直到型循环评注: (1) 解题关键是选择好计数变量i 和累加变量S 的初始值,并写出用i 表示的数列的通项公式是;(2)循环结构主要用在一些有规律的重复计算的算法中,如累加求和,累乘求积等问题.在循环结构中,要注意根据条件,设计合理的计数变量、累加(积)变量以及它们的初始值等,特别要注意循环结构中条件的表述要恰当、精确,以免出现多一次或少一次循环.(3)循环结构分为两类:一类是当型循环结构,如下左图所示;另一类是直到型循环结构,如下右图所示.变式训练画出求222111147100++++的值的程序框图. 解:程序框图如下:例5.某工厂2005年的生产总值为200万元,技术改进后预计以后后每年的年生产总值都比上一年增长5%.设计一个程序框图,输出预期年生产总值超过300万元的最早年份及2005年到此年份之前(不包此年份)的年生产总值的和.分析:本例可用循环结构来实现. (1) 确定“循环体”:设a 为某年的年生产总值,n 为年份,S 为年产值的总和,则循环体为(2)初始化变量: n 的初始值为2005,a 的初始值为200,S 的初始值为0. (3)设定循环控制条件:300a > 解: 程序框图如下:评注:本问题的关健是设计好循环体,注意S S a =+与n 之间的对 应关系.本题若将S S a =+放在1n n =+之后,则输出时须重新 赋值1n n =-,否则n 的值为超过300万的年份的下一年.本题 也可用当型循环结构来表示.变式训练:设计一个程序框图,求使1235000S n =⨯⨯⨯⨯>的最小n 的值,并输出此时S 的值.解:程序框图如下:,0.05,1.S S a a a a n n =+=+=+※基础自测一、选择题1.下列说确的是()A.算法就是某个问题的解题过程;B.算法执行后可以产生不同的结果;C.解决某一个具体问题算法不同结果不同;D.算法执行步骤的次数不可以很大,否则无法实施.1.解析:选项A,算法不能等同于解法;选项B,例如:判断一个正整数是否为质数,结果为“是质数”和“不是质数”两种;选项C,解决某一个具体问题算法不同结果应该相同,否则算法构造的有问题;选项D,算法可以为很多次,但不可以无限次.选B.2、如图所示的程序框图中,则第3个输出的数是( )A.1 B.32C.2 D.52开始00S T ==,T T n =+ S S n =+2?n ≥结束是否 输出S T 、输入n1n n =- 1n n =- 3.如图给出的是求201614121+⋅⋅⋅+++的值的一个程序框图, 其中判断框应填入的条件是( )A .i >10?B .i < 10?C .i >20?D .i < 20?3.解析:通过列表,我们能清楚了解程序的每一步中的各个变量 是怎样变化的, 第一次:11,,42i S n ===, 第二次:112,,624i S n ==+=,…依此可知循环的条件是i >10?.选A 4.阅读右边的程序框图,若输入的n 是100,则输出的变量S 和T 的值依次是( )A .2550,2500B .2550,2550C .2500,2500D .2500,2550第3题图第4题图4.解析:依据框图可得1009896...22550S =++++=,999795...12500T =++++=.选A .5.2006年1月份开始实施的《个人所得税法》规定:全月总收入不超过1600元的免征个人工资、薪金所得税,超过1600元部分需征税.设全月总收入金额为x 元,前三级税率如下左表所示:当工资薪金所得不超过3600元,计算个人所得税的一个算法框图如图. 则输出①、输出②分别为( ).A .0.05;0.1x xB .0.05;0.1185x x -C . 0.0580;0.1;x x - D .0.0580;0.1185x x --开始S=0 输入G i ,F ii=1 S= S +G i ·F ii ≥5? i= i +1NY 输出S 结束5.解析: 设全月总收入金额为x 元, 所得税额为y 元,则y 与x 之间的函数关系为0(01600)(1600)5%(16002100)25(2100)10%(21003600)x y x x x x <≤⎧⎪=-<≤⎨⎪+-<≤⎩选D .二、填空题6.执行右边的程序框图,若p =0.8,则输出的n =________.6.解析:第一次循环后,10.82S =<,此时n =2;第二次循环后,110.824S =+<,此时n =3;第三次循环后,1110.8248S =++>,此时4n =,输出,故填4.7.某地区为了解7080-岁的老人的日平均睡眠时间(单位:h ),随机选择了50位老人进行调查,下表是这50位老人睡眠时间的频率分布表:在上述统计数据的分析中一部分计算见算法流程图,则输出的S 的值为________.序号i 分组 (睡眠时间)组中值(i G )频数 (人数)频率(i F )1 [4,5) 4.56 0.12 2 [5,6) 5.5 10 0.203 [6,7) 6.5 20 0.404 [7,8)7.510 0.205[8,9]8.540.08解析:由流程图1122334455S G F G F G F G F G F =++++4.50.12 5.50.20 6.50.407.50.28.50.08=⨯+⨯+⨯+⨯+⨯ 6.42=故填6.42.8.如果执行右面的程序框图,那么输出的S =________.8.解析:2461002550S =++++=三、解答题9.请阅读下面程序框图,说明此程序的功能解:程序功能是求s的值.26122 (2)s=++++,并输出s10.已知函数22(2)(0)4(0)(2)(0)x xy xx x⎧+<⎪==⎨⎪->⎩,请画出程序框图,要求输入自变量x的值,输出函数值y.10.解:11.画出一个计算151015100⨯⨯⨯⨯⨯的程序框图.11解:程序框图如下12、甲、乙两位同学为解决数列求和问题,试图编写一程序.两人各自编写的程序框图分别如图1和如图2.(Ⅰ)根据图1和图2,试判断甲、乙两位同学编写的程序框图输出的结果是否一致? 当n=20时分别求它们输出的结果;(Ⅱ)若希望通过对图2虚框中某一步(或几步)的修改来实现“求首项为2,公比为3的等比数列的前n项和”,请你给出修改后虚框部分的流程图.12、解:(Ⅰ)输出结果一致. 当n =20时,图1的结果为2+4+6+…+38+40=2×(1+2+3+…+20)=420 图2的结果为2+4+6+…+38+40=2×(1+2+3+…+20)=420 (Ⅱ)修改后虚框部分的流程图为开始输入ni =1S =0a =2S =S +aa =a+2i =i+1i>n 输出S结束是 否图2开始 输入ni =0S =0i=i+1S=S+2输出S结束 i ≤n?否是图1。
算法设计与分析2-2,答案

2-2下面的7个算法……..请给出正确性证明public class TestbinarySearch {public static int binarySearch1(int a[], int x, int n) { int left = 0;int right = n - 1;while (left <= right) {int middle = (left + right) / 2;System.out.println("left=" + left + " right" + right + " middle="+ middle);if (x == a[middle])return middle;if (x > a[middle])left = middle;elseright = middle;}return -1;}public static int binarySearch2(int a[], int x, int n) { int left = 0;int right = n - 1;while (left < (right - 1)) {int middle = (left + right) / 2;System.out.println("left=" + left + " right" + right + " middle="+ middle);if (x < a[middle])right = middle;elseright = middle;}if (x == a[left]) {return left;}return -1;}public static int binarySearch3(int a[], int x, int n) { int left = 0;int right = n - 1;int middle = (left + right) / 2;System.out.println("left=" + left + " right" + right + " middle="+ middle);if (x >= a[middle]) {left = middle;} else {right = middle;}}if (x == a[left]) {return left;}return -1;}public static int binarySearch4(int a[], int x, int n) { if (n > 0 && x >= a[0]) {int left = 0;int right = n - 1;while (left < right) {int middle = (left + right) / 2;System.out.println("left=" + left + " right" + right+ " middle=" + middle);if (x < a[middle]) {right = middle - 1;} else {left = middle;}}if (x == a[left]) {return left;}}return -1;}public static int binarySearch5(int a[], int x, int n) { if (n > 0 && x >= a[0]) {int left = 0;int right = n - 1;int middle = (left + right + 1) / 2;System.out.println("left=" + left + " right" + right+ " middle=" + middle);if (x < a[middle]) {right = middle - 1;} else {left = middle;}}if (x == a[left]) {return left;}}return -1;}public static int binarySearch6(int a[], int x, int n) { if (n > 0 && x >= a[0]) {int left = 0;int right = n - 1;while (left < right) {int middle = (left + right) / 2;System.out.println("left=" + left + " right" + right+ " middle=" + middle);if (x < a[middle]) {right = middle - 1;} else {left = middle + 1;}}if (x == a[left]) {return left;}}return -1;}public static int binarySearch7(int a[], int x, int n) { if (n > 0 && x >= a[0]) {int left = 0;int right = n - 1;while (left < right) {int middle = (left + right) / 2;System.out.println("left=" + left + " right" + right+ " middle=" + middle);if (x < a[middle]) {right = middle;} else {left = middle;}}if (x == a[left]) {return left;}}return -1;}/** 测试方法一方法一的while的循环条件出错,因为middle=(left+right)/2 而left=middle或者right=middle* 所以当left+1=right时,left<=righ一直成立所以无法返回x=5这个值* left=0,right=4.middle=2,x>a[middle],left=2;* left=2,right=4.middle=3,x>a[middle],left=3;* left=3,right=4.middle=3,x>a[middle],left=3;* left=3,right=4.middle=3,x>a[middle],left=3;出现死循环*/public static void Test1() {int a[] = new int[5];for (int i = 1; i < 6; i++) {a[i - 1] = i;}for (int i = 0; i < a.length; i++) {System.out.print(a[i] + "");}System.out.println("");for (int i = 1; i < a.length+1; i++)System.out.println("在下标为"+ binarySearch1(a, i, a.length) + "的位置");;// 当x=5无法查找到边界问题没有出处理好}/** 方法二和方法一差不多但是由于下条件left<rigth-1使下标的判断题条件出错了left=0 right4 middle=2 left=0* right2 middle=1 在下标为0的位置 left=0 right4 middle=2 left=0 right2 middle=1* 在下标为-1的位置 left=0 right4 middle=2 left=0 right2 middle=1 在下标为-1的位置 left=0* right4 middle=2 left=0 right2 middle=1 在下标为-1的位置*/public static void Test2() {int a[] = new int[5];for (int i = 1; i < 6; i++) {a[i - 1] = i;}for (int i = 0; i < a.length; i++) {System.out.print(a[i] + "");}System.out.println("");for (int i = 1; i < a.length + 1; i++)System.out.println("在下标为"+ binarySearch2(a, i, a.length) + "的位置");// 当x=5无法查找到边界问题没有出处理好}/** 方法三也是会出现边界的问题当x5时会出现死循环其它正常 left=0 right4 middle=2 left=0 right2 middle=1* 在下标为0的位置 left=0 right4 middle=2 left=0 right2 middle=1 在下标为1的位置 left=0* right4 middle=2 left=2 right4 middle=3 在下标为2的位置 left=0 right4 middle=2* left=2 right4 middle=3 在下标为3的位置当x=5时会有以下死循环 left=3 right4 middle=3* left=3 right4 middle=3 left=3 right4 middle=3 left=3 right4 middle=3 * left=3 right4 middle=3*/public static void Test3() {int a[] = new int[5];for (int i = 1; i < 6; i++) {a[i - 1] = i;}for (int i = 0; i < a.length; i++) {System.out.print(a[i] + "");}System.out.println("");for (int i = 1; i < a.length + 1; i++)System.out.println("在下标为"+ binarySearch3(a, i, a.length) + "的位置");}/** 方法四也是因为下标出现问题所以出现死循环 left=0 right1 middle=0left=0 right1 middle=0* left=0 right1 middle=0 left=0 right1 middle=0 left=0 right1 middle=0 */public static void Test4() {int a[] = new int[5];for (int i = 1; i < 6; i++) {a[i - 1] = i;}for (int i = 0; i < a.length; i++) {System.out.print(a[i] + "");}System.out.println("");for (int i = 1; i < a.length + 1; i++)System.out.println("在下标为"+ binarySearch4(a, i, a.length) + "的位置");}/** 方法五是正确的结果如下 left=0 right4 middle=2 left=0 right1 middle=1 在下标为0的位置* left=0 right4 middle=2 left=0 right1 middle=1 在下标为1的位置 left=0 right4* middle=2 left=2 right4 middle=3 在下标为2的位置 left=0 right4 middle=2 left=2* right4 middle=3 left=3 right4 middle=4 在下标为3的位置 left=0 right4 middle=2* left=2 right4 middle=3 left=3 right4 middle=4 在下标为4的位置*/public static void Test5() {int a[] = new int[5];for (int i = 1; i < 6; i++) {a[i - 1] = i;}for (int i = 0; i < a.length; i++) {System.out.print(a[i] + "");}System.out.println("");for (int i = 1; i < a.length + 1; i++)System.out.println("在下标为"+ binarySearch5(a, i, a.length) + "的位置");}/** 方法六是错误的由于下标混乱导致除了最后一个元素可以搜索到,其他元素都不可以搜索到结果如下 left=0 right4 middle=2* left=0 right1 middle=0 在下标为-1的位置 left=0 right4 middle=2 left=0 right1* middle=0 在下标为1的位置 left=0 right4 middle=2 left=3 right4 middle=3 在下标为-1的位置* left=0 right4 middle=2 left=3 right4 middle=3 在下标为-1的位置 left=0 right4* middle=2 left=3 right4 middle=3 在下标为4的位置*/public static void Test6() {int a[] = new int[5];for (int i = 1; i < 6; i++) {a[i - 1] = i;}for (int i = 0; i < a.length; i++) {System.out.print(a[i] + "");}System.out.println("");for (int i = 1; i < a.length + 1; i++)System.out.println("在下标为"+ binarySearch6(a, i, a.length) + "的位置");}/** 方法七是错误的,原因是左边的边界没有处理好导致x=1时会出现死循环所以算法是错误的结果如下 left=0 right1 middle=0* left=0 right1 middle=0 left=0 right1 middle=0 left=0 right1 middle=0 * left=0 right1 middle=0*/public static void Test7() {int a[] = new int[5];for (int i = 1; i < 6; i++) {a[i - 1] = i;}for (int i = 0; i < a.length; i++) {System.out.print(a[i] + "");}System.out.println("");for (int i = 1; i < a.length; i++)System.out.println("在下标为"+ binarySearch7(a, i, a.length) + "的位置");}public static void main(String[] args) {Test1();//死循环Test2();//只能找到左边界Test3();//只能有边界Test4();//死循环Test5();//正确Test6();//只能找到右边界Test7();//左边死循环}}。
黄宇《算法设计与分析》课后习题解析(二)精选全文

黄宇《算法设计与分析》课后习题解析(⼆)第2章:从算法的视⾓重新审视数学的概念2.1:(向下取整)题⽬:请计算满⾜下⾯两个条件的实数的区间解析:根据向下取整的含义,令,讨论a的取值范围即可解答:令,则可得:即:故的取值区间为:2.2: (取整函数)题⽬:证明:对于任意整数,(提⽰:将n划分为)。
解析:根据提⽰将n进⾏划分,根据取整函数的定义⽤k表⽰取整函数,即可证明;证明如下:因为对于任意整数,可划分为,则:① ;② ;综上:对于任意整数,, 得证;2.3: (斐波拉契数列)对于斐波拉契数列,请证明:1)题⽬:是偶数当且仅当n能被3整除解析:由斐波拉契数列的递归定义式,容易联想到数学归纳法;证明如下:(采⽤数学归纳法)i)当n = 1,2,3时,依次为1,1,2,符合命题;ii)假设当(k>=1)时命题均成⽴,则:① 当n = 3k+1时,是奇数,成⽴;② 当n = 3k+2时,是奇数,成⽴;③ 当 n = 3(k+1)时,是偶数,成⽴;综上:归纳可得为偶数当且仅当,得证;2)题⽬:x x =1+a (0<a <1)x =1+a (0<a <1)⌊x ⌋=1⇒⌊x ⌋=21⌊x ⌋=2⌊1+a +22a ⌋=1a +22a <1⇒0<a <−21⇒1<a +1<⇒21<x <2x (1,)2n ≥1⌈log (n +1)⌉=⌊logn ⌋+12≤k n ≤2−k +11n ≥12≤k n ≤2−k +11k +1=⌈log (2+k 1)⌉≤⌈log (n +1)⌉≤⌈log (2)⌉=k +1k +1=>⌈log (n +1)⌉=k +1k =⌊log (2)⌋≤k ⌊logn ⌋≤⌊log (2−k +11)⌋=k =>⌊logn ⌋=k n ≥1⌈log (n +1)⌉=k +1=⌊logn ⌋+1F n F n n ≤3k F =n F +n −1F =n −2F +3k F =3k −1>F 3k +1F =n F +3k +1F =3k >F 3k +2F =n F +3k +2F =3k +1>F 3k +3F n 3∣n F −n 2F F =n +1n −1(−1)n +1解析:同1)理,容易联想到数学归纳法证明如下:(采⽤数学归纳法)i)当n = 2时,, 易知成⽴;ii)假设当 n = k 时命题成⽴,① 若k = 2m, 则,当n = k+1 = 2m+1时,要证命题成⽴,即证: => ,代⼊递推式, 得:, 易知是恒等式,故命题成⽴;②当 k=2m+1时,同①理可证命题成⽴;综上:归纳可得,得证;2.4:(完美⼆叉树)给定⼀棵完美⼆叉树,记其节点数为,⾼度为,叶节点数为,内部节点数为1)题⽬:给定上述4个量中的任意⼀个,请推导出其他3个量解析:根据完美⼆叉树的结构特点易得解答:(仅以已知⾼度h推导其他三个量为例,其余同理)已知⾼度为h,可得:节点数:叶节点数:内部节点数:2)题⽬:请计算完美⼆叉树任意⼀层的节点个数:① 如果任意指定深度为的⼀层节点,请计算该层节点个数;② 如果任意指定⾼度为的⼀层节点,请计算该层节点个数;解析:根据完美⼆叉树的结构特点易得(注意节点深度和节点⾼度是互补的,相加为树⾼)解答:① ; ② ;2.5: (⼆叉树的性质)对于⼀棵⾮空的⼆叉树T,记其中叶节点的个数为,有1个⼦节点的节点个数为,有两个⼦节点的节点个数为1)题⽬:如果T是⼀棵2-tree,请证明。
算法设计与分析(第2版)习题答案

习题11. 图论诞生于七桥问题。
出生于瑞士的伟大数学家欧拉(Leonhard Euler ,1707—1783)提出并解决了该问题。
七桥问题是这样描述的:一个人是否能在一次步行中穿越哥尼斯堡(现在叫加里宁格勒,在波罗的海南岸)城中全部的七座桥后回到起点,且每座桥只经过一次,图 1.7是这条河以及河上的两个岛和七座桥的草图。
请将该问题的数据模型抽象出来,并判断此问题是否有解。
七桥问题属于一笔画问题。
输入:一个起点输出:相同的点1, 一次步行2, 经过七座桥,且每次只经历过一次3, 回到起点该问题无解:能一笔画的图形只有两类:一类是所有的点都是偶点。
另一类是只有二个奇点的图形。
2.在欧几里德提出的欧几里德算法中(即最初的欧几里德算法)用的不是除法而是减法。
请用伪代码描述这个版本的欧几里德算法1.r=m-n2.循环直到r=02.1 m=n2.2 n=r2.3 r=m-n3 输出m3.设计算法求数组中相差最小的两个元素(称为最接近数)的差。
要求分别给出伪代码和C ++描述。
//采用分治法//对数组先进行快速排序//在依次比较相邻的差#include <iostream>using namespace std;int partions(int b[],int low,int high) {图1.7 七桥问题int prvotkey=b[low];b[0]=b[low];while (low<high){while (low<high&&b[high]>=prvotkey)--high;b[low]=b[high];while (low<high&&b[low]<=prvotkey)++low;b[high]=b[low];}b[low]=b[0];return low;}void qsort(int l[],int low,int high){int prvotloc;if(low<high){prvotloc=partions(l,low,high); //将第一次排序的结果作为枢轴 qsort(l,low,prvotloc-1); //递归调用排序由low 到prvotloc-1qsort(l,prvotloc+1,high); //递归调用排序由 prvotloc+1到 high}}void quicksort(int l[],int n){qsort(l,1,n); //第一个作为枢轴,从第一个排到第n个}int main(){int a[11]={0,2,32,43,23,45,36,57,14,27,39};int value=0;//将最小差的值赋值给valuefor (int b=1;b<11;b++)cout<<a[b]<<' ';cout<<endl;quicksort(a,11);for(int i=0;i!=9;++i){if( (a[i+1]-a[i])<=(a[i+2]-a[i+1]) )value=a[i+1]-a[i];elsevalue=a[i+2]-a[i+1];}cout<<value<<endl;return 0;}4.设数组a[n]中的元素均不相等,设计算法找出a[n]中一个既不是最大也不是最小的元素,并说明最坏情况下的比较次数。
算法设计与分析课后答案

5..证明等式gcd(m,n)=gcd(n,m mod n)对每一对正整数m,n都成立.Hint:根据除法的定义不难证明:●如果d整除u和v, 那么d一定能整除u±v;●如果d整除u,那么d也能够整除u的任何整数倍ku.对于任意一对正整数m,n,若d能整除m和n,那么d一定能整除n和r=m mod n=m-qn;显然,若d能整除n和r,也一定能整除m=r+qn和n。
数对(m,n)和(n,r)具有相同的公约数的有限非空集,其中也包括了最大公约数。
故gcd(m,n)=gcd(n,r)6.对于第一个数小于第二个数的一对数字,欧几里得算法将会如何处理?该算法在处理这种输入的过程中,上述情况最多会发生几次?Hint:对于任何形如0<=m<n的一对数字,Euclid算法在第一次叠代时交换m和n, 即gcd(m,n)=gcd(n,m)并且这种交换处理只发生一次.7.a.对于所有1≤m,n≤10的输入, Euclid算法最少要做几次除法?(1次)b. 对于所有1≤m,n≤10的输入, Euclid算法最多要做几次除法?(5次)gcd(5,8)习题1.21.(农夫过河)P—农夫W—狼G—山羊C—白菜2.(过桥问题)1,2,5,10---分别代表4个人, f—手电筒4. 对于任意实系数a,b,c, 某个算法能求方程ax^2+bx+c=0的实根,写出上述算法的伪代码(可以假设sqrt(x)是求平方根的函数)算法Quadratic(a,b,c)//求方程ax^2+bx+c=0的实根的算法//输入:实系数a,b,c//输出:实根或者无解信息D←b*b-4*a*cIf D>0temp←2*ax1←(-b+sqrt(D))/tempx2←(-b-sqrt(D))/tempreturn x1,x2else if D=0 return –b/(2*a)else return “no real roots”else //a=0if b≠0 return –c/belse //a=b=0if c=0 return “no real numbers”else return “no real roots”5.描述将十进制整数表达为二进制整数的标准算法a.用文字描述b.用伪代码描述解答:a.将十进制整数转换为二进制整数的算法输入:一个正整数n输出:正整数n相应的二进制数第一步:用n除以2,余数赋给Ki(i=0,1,2...),商赋给n第二步:如果n=0,则到第三步,否则重复第一步第三步:将Ki按照i从高到低的顺序输出b.伪代码算法DectoBin(n)//将十进制整数n转换为二进制整数的算法//输入:正整数n//输出:该正整数相应的二进制数,该数存放于数组Bin[1...n]中i=1while n!=0 do {Bin[i]=n%2;n=(int)n/2;i++;}while i!=0 do{print Bin[i];i--;}9.考虑下面这个算法,它求的是数组中大小相差最小的两个元素的差.(算法略) 对这个算法做尽可能多的改进.算法MinDistance(A[0..n-1])//输入:数组A[0..n-1]//输出:the smallest distance d between two of its elements习题1.31.考虑这样一个排序算法,该算法对于待排序的数组中的每一个元素,计算比它小的元素个数,然后利用这个信息,将各个元素放到有序数组的相应位置上去.a.应用该算法对列表‖60,35,81,98,14,47‖排序b.该算法稳定吗?c.该算法在位吗?解:a. 该算法对列表‖60,35,81,98,14,47‖排序的过程如下所示:b.该算法不稳定.比如对列表‖2,2*‖排序c.该算法不在位.额外空间for S and Count[]4.(古老的七桥问题)习题1.41.请分别描述一下应该如何实现下列对数组的操作,使得操作时间不依赖数组的长度. a.删除数组的第i 个元素(1<=i<=n)b.删除有序数组的第i 个元素(依然有序) hints:a. Replace the i th element with the last element and decrease the array size of 1b. Replace the ith element with a special symbol that cannot be a value of the array ’s element(e.g., 0 for an array of positive numbers ) to mark the i th position is empty. (―lazy deletion ‖)第2章 习题2.17.对下列断言进行证明:(如果是错误的,请举例) a. 如果t(n )∈O(g(n),则g(n)∈Ω(t(n)) b.α>0时,Θ(αg(n))= Θ(g(n)) 解:a. 这个断言是正确的。
算法流程图(附答案)
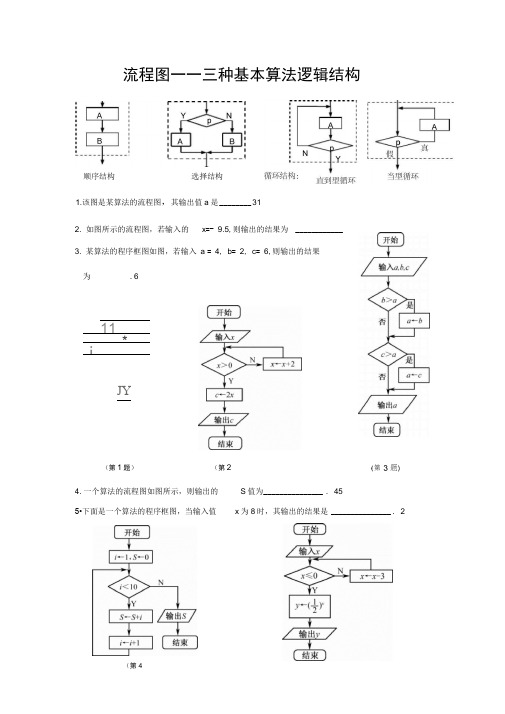
1.该图是某算法的流程图,其输出值a是________ 312. 如图所示的流程图,若输入的x=- 9.5,则输出的结果为 ____________3. 某算法的程序框图如图,若输入a = 4, b= 2, c= 6,则输出的结果为.611*iJY(第1题)4. 一个算法的流程图如图所示,则输出的5•下面是一个算法的程序框图,当输入值S值为_______________ . 45x为8时,其输出的结果是_______________ . 2流程图一一三种基本算法逻辑结构顺序结构选择结构(第2题)(第4题)6. 运行如图所示的程序框图,则输出的结果 S = ___________ . 617. 如图所示的算法流程框图中, 若输入a = 4,b = 48,则最后输出的a 的值是 ________________ .96 8. 如图,程序执行后输出的结果为 _________ 6410.阅读下面的流程图,若输入______________a = 10, b = 6,则输出的结果是 211. _____________________________________________ 右图是一个算法的流程图,则输出 S 的值是 _________________________________________________ 7500开始/输出P/ 卩/9•按如图所示的流程图运算 ,则输出的S 二 _________20 (第6题)(第7题)I —12. ___________________________________________ 右图是一个算法的流•程图,最后输出的k= _________________ . 1113•阅读右边的流程图,则输出S= ________ . 3015、图中是一个算法流程图,则输出的n= ______ 1116. 右图是一个算法的流程图,最后输出的x= ________ .-1017.执行右边的程序框图,若p =15,则输出的n二fT-li S^-0(第16题)5/输入/n=l,S=0沪針严/5丽7ZE~~TM=n+1 [结束](第15题)(第17题))如图所示,其输出结果是127开始(第14 题)结束14•程序框图(即算法流程图(第12题)(第13题)c-2cr+'l/输出口/18. 根据如图所示的算法流程图,可知输出的结果i为______________ .719. 右图是一个算法的流程图,最后输出的n = ____________ .10020. 右图是一个算法的流程图,则输出a的值是_____________. log2321. 已知某算法的流程图如图所示,若将输出的数组(x, y)依次记为(X1, y1), (X2, y2),…, (X n, y n),…,则程序运行结束时输出的最后一个数组为22. _________________________________ 如图,该程序运行后输出的结果为______________________________ 1623•执行右边的程序框图,若p= 9,则输出的s= _(第19题)(第18题)(开始〕1 rm2托(第20题)(第22 题)—• (27,—6)2.5苏州市第六中学2014数学必修三(算法)。
流程图表示算法的简单题目及答案

流程图表示算法的简单题目及答案下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!理解流程图:一种表示算法的直观工具在计算机科学和编程领域,算法是解决问题或执行任务的精确步骤序列。
高考数学模拟复习试卷试题模拟卷第01节 算法与程序框图002 5
高考模拟复习试卷试题模拟卷第01节 算法与程序框图一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选择中,只有一个是符合题目要求的.)1.【高考天津,理3】阅读右边的程序框图,运行相应的程序,则输出S 的值为( )(A )10- (B )6 (C )14 (D )18 否是开始结束输出2. 【改编题】行下图所示的程序框图,则输出的S 为( )A .10B .12C .20D .30 3. 某程序框图如右图所示,当输出y 值为8-时,则输出x 的值为( )开始4?n >否是1,0n S ==结束S输出2S S n=+1n n =+A. 64B. 32C. 16D.84.【改编题】如图所示的程序框图,输出S 的值是20161,则判断框内应填()A. 2015?n <B. 2014?n ≤C.2016?n ≤D. 2015?n ≤5. 【高考湖南卷第6题】执行如图1所示的程序框图,如果输入的]2,2[-∈t ,则输出的S 属于( )A.]2,6[--B.]1,5[--C.]5,4[-D.]6,3[-6.【改编题】执行如图所示的程序框图,输出结果是i =1209x dx ⎰.若{}01,2,3a ∈,则0a 所有可能的取值为( )A .1,2,3B .1C .2D .2,3是否 开始结束1S =1n =1n S S n =⨯+ 1n n =+输出S7.【山东高考理第11题改编】执行右面的程序框图,若输入的x的值为1,则输出的n的值为().A. 1B. 2C. 3D. 48.一个算法的程序框图如下图所示,若该程序输出的结果为56,则判断框中应填入的条件是()A.4i <B.5i <C. 5i ≥D. 6i <9. 【郑州市高中毕业年级第一次质量预测试题】执行如图的程序框图,若输出的78S =,则输入的整数P 的值为( ).A. 1B. 2C. 3D. 410. 【原创题】如图是一个算法的流程图.若输入x 的值为3,则输出y 的值是( )A.12B.12-C.32-D.3-11.【高考湖北卷第13题】设a是一个各位数字都不是0且没有重复数字的三位数.将组成a的3个数字按从小到大排成的三位数记为()I a,按从大到小排成的三位数记为()D a(例如815a=,则()158I a=,()851D a=).阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=( ).A.495B.594C.693D.81512. 【原创题】执行如图所示的程序框图,输出的a值为______.输入x112y x=-||1y x-<2x y=否是结束开始输出yA .12B .3C .2-D .13- 二、填空题(本大题共6小题,每小题5分,共30分.把答案填在题中的横线上.)13. 如图,是一程序框图,则输出结果为K =,S =.(说明,M N =是赋值语句,也可以写成M N ←,或:M N =14. 下图是一个算法的程序框图,最后输出的W =_______.开始a =3,i =1i >511a a a +=- i =i +1结束输出a是否,则输出的S的最大值为15. 【高考四川卷文第6题】执行如图1所示的程序框图,如果输入的,x y R_________16. 【高考山东卷第11题】执行右面的程序框图,若输入的x的值为1,则输出的n的值为.17. 【黄冈市重点中学第二学期高三三月月考】若下框图所给的程序运行结果为S=20,那么判断框中应填入的关于整数k 的条件是 _______________18. 【湖北八校高三第二次联考数学试题】定义某种运算⊗,b a S ⊗=的运算原理如图所示.设)3()0()(x x x x f ⊗-⊗=.则=)3(f ______;()f x 在区间[]3,3-上的最小值为______高考模拟复习试卷试题模拟卷高考模拟复习试卷试题模拟卷第03节 几何概型A 基础巩固训练1.在区间[0,π]上随机取一个数x ,则事件“sin x≥cos x”发生的概率为( ) A.14 B.12 C.34D .1 【答案】 C【解析】 ∵sin x≥cos x ,x ∈[0,π],∴π4≤x≤π, ∴事件“sin x≥cos x”发生的概率为π-π4π-0=34. 2.(·西城模拟)在区间[0,2]上任取两个实数a ,b ,则函数f(x)=x3+ax -b 在区间[-1,1]上有且只有一个零点的概率是( )A.18B.14C.34D.78【答案】D3.如图10-6-8所示,墙上挂有一边长为a 的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,a 2为半径的扇形,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是( )A .1-π4B.π4C .1-π8D.与a 的取值有关【解析】 由题意知,阴影部分的面积为a2-4×14×π⎝⎛⎭⎫a 22=⎝⎛⎭⎫1-π4a2,故概率为1-π4. 【答案】 A4. (·阜阳模拟)一艘轮船从O 点的正东方向10 km 处出发,沿直线向O 点的正北方向10 km 处的港口航行,某台风中心在点O ,距中心不超过r km 的位置都会受其影响,且r 是区间[5,10]内的一个随机数,则轮船在航行途中会遭受台风影响的概率是( ) A.2-12B.1-22C.2-1D.2- 2【答案】 D【解析】 以O 为圆心,r 为半径作圆,易知当r >52时,轮船会遭受台风影响,所以P =10-5210-5=10-525=2- 2. 5.在棱长为2的正方体ABCD -A1B1C1D1中,点O 为底面ABCD 的中心,在正方体ABCD -A1B1C1D1内随机取一点P ,则点P 到点O 的距离大于1的概率为________. 【答案】1-π12B 能力提升训练1. 【高考辽宁卷第6题】若将一个质点随机投入如图所示的长方形ABCD 中,其中AB=2,BC=1,则质点落在以AB 为直径的半圆内的概率是( ) A .2π B .4π C .6π D .8π【答案】B2. 在区间(0,1)内任取两个实数,则这两个实数的和大于13的概率为()A.1718B.79C.29D.118【答案】A3.【湖北八校高三第二次联考数学试题】记集合{}22(,)|4A x y x y=+≤和集合{}(,)|20,0,0B x y x y x y=+-≤≥≥表示的平面区域分别为1Ω和2Ω,若在区域1Ω内任取一点(,)M x y,则点M落在区域2Ω的概率为.【答案】12πBAyxO4.一只小蜜蜂在一个棱长为4的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个表面的距离均大于1,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为( )A .18B .116C .127D .2764【答案】A【解析】根据几何概型知识,概率为体积之比,即P =4-2343=18. 5. (·福建三明质量检测)已知集合M ={x|-2≤x ≤8},N ={x|x2-3x +2≤0},在集合M 中任取一个元素x ,则“x ∈(M ∩N)”的概率是( )A .110B .16C .310D .12【答案】A【解析】因为N ={x|x2-3x +2≤0}=[1,2],所以M ∩N =[1,2],所以所求的概率为2-18+2=110.C 思维扩展训练1. 【东莞市高三模拟考试一】已知(2,1)A ,(1,2)B -,31,55C ⎛⎫- ⎪⎝⎭,动点(,)P a b 满足02OP OA ≤⋅≤且02OP OB ≤⋅≤,则点P 到点C 的距离大于14的概率为( )A .5164π-B .564πC .116π- D .16π 【答案】A2. 【高考重庆卷第15题】某校早上8:00开始上课,假设该校学生小张与小王在早上7:30—7:50之间到校,且每人在该时间段的任何时刻到校是等可能的,则小张比小王至少早5分钟到校的概率为_____(用数字作答)【答案】932【解析】用x表示小张到校的时间,3050x≤≤,用y表示小王到校的时间,3050y≤≤则所有可能的结果对应直角坐标平面内的正方形区域ABCD记“小张比小王至少早到5分钟”为事件M,则M所对区域为图中的阴影部分DEF∆所以()1151592202032DEFABCDSP AS∆⨯⨯===⨯正方形,所以答案应填:932.3. (济南市高三3月考模拟考试)如图,长方体ABCD—A1B1C1D1,有一动点在此长方体内随机运动,则此动点在三棱锥A—A1BD内的概率为.【答案】164. 【北京市丰台区高三一模】设不等式组2210x yy⎧+-≤⎨≥⎩,表示的平面区域为M,不等式组201t x ty t-≤≤⎧⎪⎨≤≤-⎪⎩,表示的平面区域为N.在M内随机取一个点,这个点在N内的概率的最大值是_________.【答案】2π5. 若k∈[-3,3],则k的值使得过A(1,1)可以作两条直线与圆(x-k)2+y2=2相切的概率等于( )A .12B .13C .23D .34【答案】C【解析】点在圆外,过该点可做两条直线与圆相切.故使圆心与点A 的距离大于半径即可,即(1-k)2+1>2,解得k <0或k >2,所以所求k ∈[-3,0)∪(2,3],所求概率P =46=23.高考模拟复习试卷试题模拟卷第八章 直线与圆一.基础题组1.(重庆市巴蜀中学高三月考数学、文、1)若直线210ax y ++=与直线20x y +-=互相垂直,那么a 的值等于( )A .1B .13-C .23-D .2- 2.(文昌中学高三模拟考试、文、15)圆心在直线x -2y =0上的圆C 与y 轴的正半轴相切,圆C 截x 轴所得弦的长为23,则圆C 的标准方程为________________.3.(重庆市巴蜀中学高三月考数学、文、15)在平面直角坐标系xOy 中,以点)0,1(为圆心且与直线)(012R m m y mx ∈=---相切的所有圆中,半径最大的圆的标准方程为.4.(重庆市部分区县高三上学期入学考试、文、16)若实数c b a ,,成等差数列,点)0,1(-P 在动直线0:==+c by ax l 上的射影为M ,点)3,0(N ,则线段MN 长度的最小值是.二.能力题组1.(五校协作体高三上学期期初考试数学、文、9)曲线21y x =+在点(1,2)处的切线为l ,则直线l 上的任意点P 与圆22430x y x +++=上的任意点Q 之间的最近距离是( )A.4515- B.2515- C.51- D.2 2.(示范高中高三第一次联考、文、14)已知圆的方程为()2214x y +-=。
算法部分作业答案

首先,选择最优量度标准为收益重量比;
其次,依据收益重量比的非增次序对输入(物品)进行排序
(p0/w0,p1/w1,p2/w2,p3/w3,p4/w4,p5/w5,p6/w6)=(5,5/3,3,1,6,4.5,3)
对物品排序结果为:4,0,5,2,6,1,3
最后,进行贪心选择:
X=(4) X=(4,0)X=(4,0,5)
=2n2+2n=O(n2)
5-8三分搜索算法的做法是:它先将待查元素X与n/3处的元素比较,然后将X与2n/3处的元素比较,比较的结果或者找到X,或者将范围缩小到原来的n/3
int Search3(int a[],int left,int right,int x)/*递归算法*/
{
int l,u;
if(left<=right)
6,2,3,5,1,0,4
接着执行JS函数:
最初,解集合X为空.
if((r<0||d[x[r]]<=d[j]) && d[j]>r+1){//若条件不满足,选下一个作业
for (int i=k;i>=r+1;i--) x[i+1]=x[i];//将x[r]以后的作业后移
x[r+1]=j; k++;//将作业j插入r+1处
}
}
return k;
}
在执行JS函数之前,必须先对输入(即作业)按作业的收益非增次序排序,结果为:
正确的算法不一定的是健壮的,健壮的算法也不一定是完全正确的.正确性和健壮性是相互补充的.一个可靠的算法,要求能在正常情况下正确的工作,而在异常情况下,亦能做出适当处理.
2-9(1)设计一个C/C++程序,实现一个n*m的矩阵转置,原矩阵与其转置矩阵保存在二维数组中.
算法设计与分析-课后习题集答案

第一章3. 最大公约数为1。
快1414倍。
程序1-2的while 循环体做了10次,程序1-3的while 循环体做了14141次(14142-2循环)8.(1)画线语句的执行次数为log n ⎡⎤⎢⎥。
(log )n O 。
(2)画线语句的执行次数为111(1)(21)16jnii j k n n n ===++=∑∑∑。
3()n O 。
(3)画线语句的执行次数为。
O 。
(4)当n 为奇数时画线语句的执行次数为(1)(1)4n n +-, 当n 为偶数时画线语句的执行次数为 (2)4n n +。
2()n O 。
10.(1) 当 1n ≥ 时,225825n n n -+≤,所以,可选 5c =,01n =。
对于0n n ≥,22()5825f n n n n =-+≤,所以,22582()-+=O n n n 。
(2) 当 8n ≥ 时,2222582524n n n n n -+≥-+≥,所以,可选 4c =,08n =。
对于0n n ≥,22()5824f n n n n =-+≥,所以,22582()-+=Ωn n n 。
(3) 由(1)、(2)可知,取14c =,25c =,08n =,当0n n ≥时,有22212582c n n n c n ≤-+≤,所以22582()-+=Θn n n 。
11. (1) 当3n ≥时,3log log n n n <<,所以()20log 21f n n n n =+<,3()log 2g n n n n =+>。
可选212c =,03n =。
对于0n n ≥,()()f n cg n ≤,即()(())f n g n =O 。
(2) 当 4n ≥ 时,2log log n n n <<,所以 22()/log f n n n n =<,22()log g n n n n =≥。
可选 1c =,04n =。
算法分析教材习题答案(第2章)

第2章算法分析题2-2分析与解答:算法BinarySearch1与教材中的算法BinarySearch 相比,数组段左右游标left 和right 的调整不正确,导致陷入死循环。
算法BinarySearch2与教材中的算法BinarySearch 相比,数组段左右游标left 和right 的调整不正确,导致x=a[n-1]时返回错误。
算法BinarySearch3与正确算法BinarySearch5相比,数组段左右游标left 和right 的调整不正确,导致x=a[n-1]时返回错误。
算法BinarySearch4与正确算法BinarySearch5相比,数组段左右游标left 和right 的调整不正确,导致陷入死循环。
算法BinarySearch5正确,且当数组中有重复元素时,返回满足条件的最右元素。
算法BinarySearch6与正确算法BinarySearch5相比,数组段左右游标left 和right 的调整不正确,导致x=a[n-1]时返回错误。
算法BinarySearch7与正确算法BinarySearch5相比,数组段左右游标left 和right 的调整不正确,导致x=a[0]时陷入死循环。
算法分析题2-5分析与解答:这个问题有更一般的解。
将两个 n 位大整数u 和v 都分割为n/m 位的m 段,可以用2m-1次n/m 位整数的乘法求得uv 的值。
事实上,设x=2n/m ,可以将u 和v 及其乘积w=vu 表示为:U=u 0+u 1x+…+u m-1x m-1,v=v o +v 1x+…+v m-1x m-1W=uv=w 0+w 1x+w 2x 2+...+w 2m-2x 2m-2将u,v 和w 都看作关于变量x 的多项式,并取2m-1个不同的数x1,x2,…x2m-1,代入多项式,可得:U(x i )=u 0+u 1x+…+u m-1x m-1,V(xi)=v o +v 1x+…+v m-1x m-1W(x i )=u(x i )v(x i )= w 0+w 1x+w 2x 2+...+w 2m-2x 2m-2用矩阵形式表示为:w(x 1) 1 x 1 x 12 … x 12m-2 w 0w(x 2) = 1 x 2 x 22 … x 22m-2 w 1. .. . .... .W(x 2m-1) 1 x 2m-1 x 2m-12 ... x 2m-12m-2 w 2m-2设 B= =B -1其中,W(x i )=u(x i )v(x i )是两个n/m 位数的乘法去处,共有2m-1个乘法,其他均为加减法或数乘运算。
算法设计与分析第二版课后习题解答

算法设计与分析基础课后练习答案习题1.14.设计一个计算的算法,n是任意正整数。
除了赋值和比较运算,该算法只能用到基本的四则运算操作。
算法求//输入:一个正整数n 2//输出:。
tep1:a=1;step2:若a*a<n 转step 3,否则输出a;step3:a=a+1转step 2;5. a.用欧几里德算法求gcd(31415,14142)。
. gcd(31415, 14142) = gcd(14142, 3131) = gcd(3131, 1618) =gcd(1618, 1513) = gcd(1513, 105) = gcd(1513, 105) = gcd(105, 43) =gcd(43, 19) = gcd(19, 5) = gcd(5, 4) = gcd(4, 1) = gcd(1, 0) = 1..有a可知计算gcd(31415,14142)欧几里德算法做了11次除法。
连续整数检测算法在14142每次迭代过程中或者做了一次除法,或者两次除法,因此这个算法做除法的次数鉴于1·14142 和2·14142之间,所以欧几里德算法比此算法快1·14142/11 ≈1300 与2·14142/11 ≈2600 倍之间。
6.证明等式gcd(m,n)=gcd(n,m mod n)对每一对正整数m,n都成立.Hint:根据除法的定义不难证明:●如果d整除u和v, 那么d一定能整除u±v;●如果d整除u,那么d也能够整除u的任何整数倍ku.对于任意一对正整数m,n,若d能整除m和n,那么d一定能整除n和r=m mod n=m-qn;显然,若d能整除n和r,也一定能整除m=r+qn和n。
数对(m,n)和(n,r)具有相同的公约数的有限非空集,其中也包括了最大公约数。
故gcd(m,n)=gcd(n,r)7.对于第一个数小于第二个数的一对数字,欧几里得算法将会如何处理?该算法在处理这种输入的过程中,上述情况最多会发生几次?Hint:对于任何形如0<=m<n的一对数字,Euclid算法在第一次叠代时交换m和n, 即gcd(m,n)=gcd(n,m)并且这种交换处理只发生一次.8.a.对于所有1≤m,n≤10的输入, Euclid算法最少要做几次除法?(1次)b. 对于所有1≤m,n≤10的输入, Euclid算法最多要做几次除法?(5次)gcd(5,8)习题1.21.(农夫过河)P—农夫W—狼G—山羊C—白菜2.(过桥问题)1,2,5,10---分别代表4个人, f—手电筒4. 对于任意实系数a,b,c, 某个算法能求方程ax^2+bx+c=0的实根,写出上述算法的伪代码(可以假设sqrt(x)是求平方根的函数)算法Quadratic(a,b,c)//求方程ax^2+bx+c=0的实根的算法//输入:实系数a,b,c//输出:实根或者无解信息f a≠0D←b*b-4*a*cIf D>0temp←2*ax1←(-b+sqrt(D))/tempx2←(-b-sqrt(D))/tempreturn x1,x2else if D=0 return –b/(2*a)else return “no real roots”lse //a=0if b≠0 return –c/belse //a=b=0if c=0 return “no real numbers”else return “no real roots”5.描述将十进制整数表达为二进制整数的标准算法a.用文字描述b.用伪代码描述解答:a.将十进制整数转换为二进制整数的算法输入:一个正整数n输出:正整数n相应的二进制数第一步:用n除以2,余数赋给Ki(i=0,1,2...),商赋给n第二步:如果n=0,则到第三步,否则重复第一步第三步:将Ki按照i从高到低的顺序输出b.伪代码算法DectoBin(n)//将十进制整数n转换为二进制整数的算法//输入:正整数n//输出:该正整数相应的二进制数,该数存放于数组Bin[1...n]中i=1while n!=0 do {in[i]=n%2;=(int)n/2;++;}while i!=0 do{rint Bin[i];--;}9.考虑下面这个算法,它求的是数组中大小相差最小的两个元素的差.(算法略)对这个算法做尽可能多的改进.算法MinDistance(A[0..n-1])//输入:数组A[0..n-1]//输出:the smallest distance d between two of its elements习题1.31.考虑这样一个排序算法,该算法对于待排序的数组中的每一个元素,计算比它小的元素个数,然后利用这个信息,将各个元素放到有序数组的相应位置上去.a.应用该算法对列表”60,35,81,98,14,47”排序b.该算法稳定吗?c.该算法在位吗? 解:a. 该算法对列表”60,35,81,98,14,47”排序的过程如下所示:b.该算法不稳定.比如对列表”2,2*”排序c.该算法不在位.额外空间for S and Count[] 4.(古老的七桥问题)第2章 习题2.17.对下列断言进行证明:(如果是错误的,请举例) a. 如果t(n )∈O(g(n),则g(n)∈Ω(t(n)) b.α>0时,Θ(αg(n))= Θ(g(n)) 解:a. 这个断言是正确的。
算法导论第二章答案

第二章算法入门由于时间问题有些问题没有写的很仔细,而且估计这里会存在不少不恰当之处。
另,思考题2-3 关于霍纳规则,有些部分没有完成,故没把解答写上去,我对其 c 问题有疑问,请有解答方法者提供个意见。
给出的代码目前也仅仅为解决问题,没有做优化,请见谅,等有时间了我再好好修改。
插入排序算法伪代码INSERTION-SORT(A)1 for j ←2 to length[A]2 do key ←A[j]3 Insert A[j] into the sorted sequence A[1..j-1]4 i ←j-15 while i > 0 and A[i] > key6 do A[i+1]←A[i]7 i ←i − 18 A[i+1]←keyC#对揑入排序算法的实现:public static void InsertionSort<T>(T[] Input) where T:IComparable<T>{T key;int i;for (int j = 1; j < Input.Length; j++){key = Input[j];i = j - 1;for (; i >= 0 && Input[i].CompareTo(key)>0;i-- )Input[i + 1] = Input[i];Input[i+1]=key;}}揑入算法的设计使用的是增量(incremental)方法:在排好子数组A[1..j-1]后,将元素A[ j]揑入,形成排好序的子数组A[1..j]这里需要注意的是由于大部分编程语言的数组都是从0开始算起,这个不伪代码认为的数组的数是第1个有所丌同,一般要注意有几个关键值要比伪代码的小1.如果按照大部分计算机编程语言的思路,修改为:INSERTION-SORT(A)1 for j ← 1 to length[A]2 do key ←A[j]3 i ←j-14 while i ≥ 0 and A[i] > key5 do A[i+1]←A[i]6 i ← i − 17 A[i+1]←key循环丌变式(Loop Invariant)是证明算法正确性的一个重要工具。
流程图编程参考(答案)

RAPTOR程序设计评分标准1.从键盘输入任意整数N,当N 0时显示“Error!”,否则利用循环结构计算并显示1+3+5+…+(2×N - 1)的值。
(100分)2.设计循环结构程序输入任意10个整数,分别统计其中的奇数个数、偶数个数、所有数的累加和,然后显示结果。
(100分)3.设计循环结构程序输入任意10个数,然后求这批数的最大值、最小值、平均值,显示结果。
(100分)4.设计循环结构程序输入任意10个学生某门课程考试成绩X,如果X≥90,则显示“A”;如果75≤X<90,则显示“B”;如果60≤X<75,则显示“C”;如果X<60,则显示“D”。
(100分)5分5. 设计循环结构程序输入任意10个学生某门课程考试成绩,然后分别计算并显示成绩在80分(含80分)以上的学生人数、不及格学生人数、全班平均分。
(100分)5分6. 设计循环结构程序输入某商场10个顾客的消费金额X ,当X ≥5000元,折扣率为10%;当3000≤X <5000,折扣率为5%;当1000≤X <3000,折扣率为3%;否则,折扣率为0;计算并显示每位顾客的实际支付金额。
(100分)7. 输入任意数X ,当X=0时显示“Error!”, 否则利用循环结构计算并显示表达式1/X + 2/X + 3/X + … + 10/X 的值。
(100分)5分8.设计循环结构程序输入任意10个整数,分别统计其中的正数和、负数和以及总和,然后显示结果。
(100分)9.从键盘输入任意整数N,当N 0时显示“Error!”,否则利用循环结构计算并显示N 的阶乘值(1 × 2 × 3 ×…×N)。
(100分)10.输入任意整数N值,当N 0时显示“Error!”,否则利用循环结构计算并显示1/2+1/4+1/6+….+1/(2 ×N)的值。
(100分)11.设计循环结构程序输入任意10个圆的半径值R,当R 0时,则显示“Error!”,否则分别计算并显示这些圆的面积值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算法与流程图A---002+答案
一、选择题
1.已知直角三角形两直角边长为a ,b ,求斜边长c 的一个算法分下列三步:
①计算c a ,b 的值;
③输出斜边长c 的值。
其中正确的顺序是( D )
A.①②③
B.②③①
C.①③②
D.②①③
2.直到型循环结构为 ( D ) A 是“当型”,B 和C 啥也不是,D 是“直到型”。
3.如图,该程序运行后输出的结果为( B )
A .36
B .45
C . 55
D .66
4.当型循环结构的特征是( C )
A .先执行,后判断;当条件为真时执行之
B .先执行,后判断;当条件为假时执行之
C .先判断,后执行;当条件为真时执行之
D .先判断,后执行;当条件为假时执行之
若改为“直到型”,则选B
AA
A B
C
5. 如图,该程序运行后输出的结果P 为 ( C )
A . 36 B. 49 C. 64 D. 81 6.如图,该程序运行后输出的结果S 为(
B )
A .14
B .16
C .18
D .64
7.下左图给出的是计算
20
1
614121++++ 的值的一个框图,其中菱形判断框内应填入的条件是( D ) A .9≥i B . 9>i C .10≥i D .10i >i=S的项数加1 8.右面的程序框图输出S 的值为( B )
A .62 B.126 C .254 D.510
(第7题)
9.如果执行下面的程序框图,那么输出的S=( C ).A.2450 B.2500 C.2550 D.2652
【解析】
50(2100) 212223250255
2
S
⨯+
=⨯+⨯+⨯++⨯==0
10 如果执行下面的程序框图,那么输出的S=( C )
A.2450 B.2500 C.2550 D.5050
11.如果执行下面的程序框图,那么输出的S=( A )
A.2450 B.2500 C.2550 D.2650
12.如图给出的算法流程图中,输出的结果s = ( D )
A.19 B.25 C.23 D.21
13.如图给出的算法流程图中,输出的结果p = ( A )
A.600 B.648 C.650 D.702
第10题第11题
k←2
p←0
k<50
p←p+k k←k+2
p N
第13题
第12题
14.如图所示的程序框图输出的结果A 是 ( C )
A .
34 B .45 C .56 D .67
15.如果执行如图所示的程序框图,那么输出的S=( C )改为 100≤i ,则选B
A .1
B .101100
C .10099
D .99
98
二、填空题
16.若某程序框图如左下图所示,则该程序运行后输出的=s 69 (此时P=65,n=7 )
17.如图(上中)所示的流程图,若输出的结果是17,则判断框中的横线上可以填入的最大
整数为____64__。
18. 如上右图所示的算法流程图中,输出S 的值为 52。
