第二章 习题汇总
七年级数学上册第二章各节练习题含答案

七年级数学上册第二章:2.1有理数同步练习题一、选择题1.若向东记为正,向西记为负,那么向东走3米,再向西走﹣3米,结果是()A.回到原地B.向西走3米C.向东走6米D.向西走6米2.在,2,,3这四个数中,比小的数是A.B.2 C.D.33.如果赚120万元记作万元,那么亏100万元记作A.万元B.万元C.万元D.万元4.在0,,,3这四个数中,最小的数是A.0 B.C.D.35.下列说法正确的是( )A.一个数前面加上“-”号,这个数就是负数 B.零既是正数也是负数C.若a是正数,则-a不一定是负数D.零既不是正数也不是负数6.下列四个数中,是正整数的是()A.﹣1 B.0 C.D.17.若数轴上点A、B分别表示数2、﹣2,则A、B两点之间的距离可表示为()A. 2+(﹣2) B. 2﹣(﹣2) C. (﹣2)+2 D. (﹣2)﹣28.下列四个数中,是正整数的是()A.﹣1 B.0 C.D.1二、填空题9.用“ <” 、“ >” 或“ =” 连接:(1) 2 _____+6;(2)0 _____ 1.8;(3)_____10.有理数包含正有理数、负有理数和____________.11.A为数轴上表示﹣1的点,将点A沿数轴向右平移3个单位到点B,则点B所表示的数为______.12.在实数﹣3,0,1中,最大的数是_____.13.如果收入60元记作+60元,那么支出40元记作________ 元14.数轴上到1的距离是3的数有_________个,是______________.15.比较大小:-3__________0.(填“< ”“="”“" > ”)16.如果水位上升8米记作+8米,那么﹣5米表示_____.17.如果将“收入50元”记作“+50元”,那么“﹣20元”表示__________.18.在数轴上点A表示7,点B,C所表示的数互为相反数,且C与A间的距离为2,点B,C对应的数分别是__________.三、解答题19.所有的正数组成正数集合,所有的负数组成负数集合,所有的整数组成整数集合,所有的分数组成分数集合,请把下列各数填入相应的集合中:-2.5,3.14,-2,+72,-0.6,0.618,0,-0.101正数集合:{ …};负数集合:{ …};分数集合:{ …};非负数集合:{ …}.20.甲、乙两人同时从某地出发,如果甲向东走250 m记作+250 m,那么乙向西走150 m 怎样表示?这时甲、乙两人相距多远?21.某足球守门员练习折返跑,从守门员位置出发,向前跑记为正数,向后跑记为负数,他的练习记录如下(单位:米):+5,﹣3,+10,﹣8,﹣6,+13,﹣10.(1)守门员最后是否回到了守门员位置?(2)守门员离开守门员位置最远是多少米?(3)守门员离开守门员位置达到10米以上(包括10米)的次数是多少?22.粮库3天内进出库的粮食记录日下单位:吨进库的吨数记为正数,出库的吨数记为负数:,,,,,.经过这3天,库里的粮食是增多了还是减少了?经过这3天,仓库管理员结算发现库存粮食480吨,那么3天前库存粮食是多少吨?23.同学们都知道,|5-(-2)|表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对的两点之间的距离.试探索:(1)求|5-(-2)|=___________.(2)数轴上表示x和-1的两点之间的距离表示为___________.(3)找出所有符合条件的整数x,使|x+5|+|x-2|=7,这样的整数有___________个.(4)若x表示一个有理数,且|x-2|+|x+4|>6,则有理数x的取值范围是_________.24.体育课上,某中学对七年级女生进行仰卧起坐测试,以做28个为标准,超过的个数用正数表示,不足的个数用负数表示,其中10名女生的成绩如下:-2 +5 -1 0 +10 +3 0 +8 +1 +6(1)这10名女生有百分之几达到标准?(2)她们共做了多少个仰卧起坐?北师大新版数学七年级上册《2.2数轴》同步练习一.选择题(共9小题)1.若数a和﹣2两点之间的距离是3,那么a的值为()A.1 B.﹣5 C.﹣1或5 D.﹣5或12.小明同学将2B铅笔笔尖从原点O开始沿数轴进行连续滑动,先将笔尖沿正方向滑动1个单位长度完成第一次操作;再沿负半轴滑动2个单位长度完成第二次操作;又沿正方向滑动3个单位长度完成第三次操作,再沿负方向滑4个单位长度完成第四次操作,…,以此规律继续操作,经过第50次操作后笔尖停留在点P处,则点P对应的数是()A.0 B.﹣10 C.﹣25 D.503.数轴上表示整数的点称为整点,某数轴的单位长度为1cm,若在这个数轴上随意画出一条长2017cm的线段AB,则线段AB盖住的整点有()A.2016个B.2017个C.2016个或2017个D.2017个或2018个4.一个小虫在数轴上先向右爬3个单位,再向左爬7个单位,正好停在0的位置,则小虫的起始位置所表示的数是()A.0 B.2 C.4 D.﹣45.若数a,b在数轴上的位置如图示,则()A.a+b>0 B.ab>0 C.a﹣b>0 D.﹣a﹣b>06.下列各对数中,互为相反数的是()A.2和B.﹣0.5和C.﹣3和D.和﹣27.若2(a+3)的值与4互为相反数,则a的值为()A.﹣1 B.﹣C.﹣5 D.8.﹣a﹣b+c的相反数是()A.a﹣b+c B.﹣a+b﹣c C.a+b﹣c D.﹣a﹣b﹣c9.下列说法正确的是()A.符号相反的两个数是相反数B.任何一个负数都小于它的相反数C.任何一个负数都大于它的相反数D.0没有相反数二.填空题(共7小题)10.在数轴上,点P表示的数是a,点P′表示的数是,我们称点P′是点P的“相关点”,已知数轴上A1的相关点为A2,点A2的相关点为A3,点A3的相关点为A4…,这样依次得到点A1、A2、A3、A4,…,A n.若点A1在数轴表示的数是,则点A2016在数轴上表示的数是.11.已知数轴上点A对应的数为3,点B对应的数为﹣5,则到A、B两点距离相等的点对应的数为.12.电影《哈利•波特》中,小哈利波特穿越墙进入“站台”的镜头(如示意图的Q站台),构思奇妙,能给观众留下深刻的印象.若A、B站台分别位于﹣,处,AP=2PB,则P站台用类似电影的方法可称为“站台”.13.﹣(﹣2)=,与﹣[﹣(﹣8)]互为相反数.14.如果a、b互为相反数,那么2016a+2016b﹣100=.15.当两数时,它们的和为0.16.若a=﹣5,则﹣a=.三.解答题(共2小题)17.操作探究:已知在纸面上有一数轴(如图所示),操作一:(1)折叠纸面,使表示的1点与﹣1表示的点重合,则﹣3表示的点与表示的点重合;操作二:(2)折叠纸面,使﹣1表示的点与3表示的点重合,回答以下问题:①5表示的点与数表示的点重合;②若数轴上A、B两点之间距离为11,(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少.18.已知m是6的相反数,n比﹣m的相反数大3,求n﹣1与n﹣m的值.参考答案一.选择题1.D.2.C.3.D.4.C.5.D.6.B.7.C.8.C.9.B.二.填空题10.﹣1.11.﹣112..13.2,8.14.﹣100.15.互为相反数.16.5.三.解答题17.解:(1)∵1与﹣1重合,∴折痕点为原点,∴﹣3表示的点与3表示的点重合.故答案为:3.(2)①∵由表示﹣1的点与表示3的点重合,∴可确定折痕点是表示1的点,∴5表示的点与数﹣3表示的点重合.故答案为:﹣3.②由题意可得,A、B两点距离折痕点的距离为11÷2=5.5,∵折痕点是表示1的点,∴A、B两点表示的数分别是﹣4.5,6.5.18.解:∵m是6的相反数,n比﹣m的相反数大3,∴m=﹣6,n﹣m=3,∴n=9,∴n﹣1=8,n﹣m=3,答:n﹣1与n﹣m的值分别为8,3.北师大新版数学七年级上册《2.2数轴》同步练习一.选择题(共9小题)1.若数a和﹣2两点之间的距离是3,那么a的值为()A.1 B.﹣5 C.﹣1或5 D.﹣5或12.小明同学将2B铅笔笔尖从原点O开始沿数轴进行连续滑动,先将笔尖沿正方向滑动1个单位长度完成第一次操作;再沿负半轴滑动2个单位长度完成第二次操作;又沿正方向滑动3个单位长度完成第三次操作,再沿负方向滑4个单位长度完成第四次操作,…,以此规律继续操作,经过第50次操作后笔尖停留在点P处,则点P对应的数是()A.0 B.﹣10 C.﹣25 D.503.数轴上表示整数的点称为整点,某数轴的单位长度为1cm,若在这个数轴上随意画出一条长2017cm的线段AB,则线段AB盖住的整点有()A.2016个B.2017个C.2016个或2017个D.2017个或2018个4.一个小虫在数轴上先向右爬3个单位,再向左爬7个单位,正好停在0的位置,则小虫的起始位置所表示的数是()A.0 B.2 C.4 D.﹣45.若数a,b在数轴上的位置如图示,则()A.a+b>0 B.ab>0 C.a﹣b>0 D.﹣a﹣b>06.下列各对数中,互为相反数的是()A.2和B.﹣0.5和C.﹣3和D.和﹣27.若2(a+3)的值与4互为相反数,则a的值为()A.﹣1 B.﹣C.﹣5 D.8.﹣a﹣b+c的相反数是()A.a﹣b+c B.﹣a+b﹣c C.a+b﹣c D.﹣a﹣b﹣c9.下列说法正确的是()A.符号相反的两个数是相反数B.任何一个负数都小于它的相反数C.任何一个负数都大于它的相反数D.0没有相反数二.填空题(共7小题)10.在数轴上,点P表示的数是a,点P′表示的数是,我们称点P′是点P的“相关点”,已知数轴上A1的相关点为A2,点A2的相关点为A3,点A3的相关点为A4…,这样依次得到点A1、A2、A3、A4,…,A n.若点A1在数轴表示的数是,则点A2016在数轴上表示的数是.11.已知数轴上点A对应的数为3,点B对应的数为﹣5,则到A、B两点距离相等的点对应的数为.12.电影《哈利•波特》中,小哈利波特穿越墙进入“站台”的镜头(如示意图的Q站台),构思奇妙,能给观众留下深刻的印象.若A、B站台分别位于﹣,处,AP=2PB,则P站台用类似电影的方法可称为“站台”.13.﹣(﹣2)=,与﹣[﹣(﹣8)]互为相反数.14.如果a、b互为相反数,那么2016a+2016b﹣100=.15.当两数时,它们的和为0.16.若a=﹣5,则﹣a=.三.解答题(共2小题)17.操作探究:已知在纸面上有一数轴(如图所示),操作一:(1)折叠纸面,使表示的1点与﹣1表示的点重合,则﹣3表示的点与表示的点重合;操作二:(2)折叠纸面,使﹣1表示的点与3表示的点重合,回答以下问题:①5表示的点与数表示的点重合;②若数轴上A、B两点之间距离为11,(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少.18.已知m是6的相反数,n比﹣m的相反数大3,求n﹣1与n﹣m的值.数轴测试题时间:45分钟总分:100题号一二三四总分得分一、选择题(本大题共8小题,共32.0分)1.在数轴上到原点距离等于3的数是A. 3B.C. 3或D. 不知道2.有理数a,b在数轴的位置如图,则下面关系中正确的个数为.A. 1B. 2C. 3D. 43.若数轴上表示和3的两点分别是点A和点B,则点A和点B之间的距离是A. B. C. 2 D. 44.如图,M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且数a对应的点在M与N之间,数b对应的点在P与R之间,若,则原点是A. M或RB. N或PC. M或ND. P或R5.A,B是数轴上两点,线段AB上的点表示的数中,有互为相反数的是A. B.C. D.6.点M为数轴上表示的点,将点M沿数轴向右平移5个单位到点N,则点N表示的数是A. 3B. 5C.D. 3或7.在数轴上,与表示数的点的距离是3的点表示的数是A. 2B.C.D. 2或8.下列说法错误的有最大的负整数是;绝对值是本身的数是正数;有理数分为正有理数和负有理数;数轴上表示的点一定在原点的左边;在数轴上7与9之间的有理数是8.A. 1个B. 2个C. 3个D. 4个二、填空题(本大题共8小题,共32.0分)9.已知A,B,C是数轴上的三个点,且C在B的右侧点A,B表示的数分别是1,3,如图所示若,则点C表示的数是______ .10.在数轴上,与表示的点相距6个单位长度的点表示的数是______ .11.在数轴上,点A表示1,点C与点A间的距离为3,则点C所表示的数是______ .12.在数轴上把表示的点A沿数轴移动6个单位后得到点B,则B所表示的数为______ .13.已知数轴上的A点表示那么在数轴上与A点的距离5个长度单位的点所表示的数是______.14.如图的数轴上有两处不小心被墨水淹没了,所标注的数据是墨水部分边界与数轴相交点的数据;则被淹没的整数点有______ 个,负整数点有______ 个,被淹没的最小的负整数点所表示的数是______ .15.在数轴上与所对应的点相距4个单位长度的点表示的数是______.16.数轴上表示与之间的所有整数之和是______.三、计算题(本大题共4小题,共24.0分)17.点A、B在数轴上的位置如图所示:点A表示的数是______ ,点B表示的数是______ ;在原图中分别标出表示的点C、表示的点D;在上述条件下,B、C两点间的距离是______ ,A、C两点间的距离是______ .18.在抗洪抢险中,解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民,早晨从A地出发,晚上到达B地,约定向东记为正,向西记为负,当天的航行路程记录如下单位:千米:14,,,,,,,.请你帮忙确定B地相对于A地的位置;若冲锋舟每千米耗油升,油箱容量为28升,求冲锋舟当天救灾过程中至少还需补充多少升油?19.已知数轴上有A,B,C三个点,分别表示有理数,,10,动点P从A出发,以每秒4个单位长度的速度向终点C移动,设移动时间为t秒.用含t的代数式表示点P与A的距离:______;点P对应的数是______;动点Q从点B出发,以每秒1个单位长度的速度向终点C移动,若P、Q同时出发,求:当点P运动多少秒时,点P和点Q间的距离为8个单位长度?20.把下列各数在数轴上表示出来,并用“”把它们连接起来,3,,,0.四、解答题(本大题共2小题,共12.0分)21.已知数轴上三点A,O,B表示的数分别为6,0,,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是______;另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.22.在数轴上有A、B两点,所表示的数分别为n,,A点以每秒5个单位长度的速度向右运动,同时B点以每秒3个单位长度的速度也向右运动,设运动时间为t秒.当时,则______ ;当t为何值时,A、B两点重合;在上述运动的过程中,若P为线段AB的中点,数轴上点C所表示的数为是否存在t的值,使得线段,若存在,求t的值;若不存在,请说明理由.答案和解析【答案】1. C2. C3. D4. A5. B6. A7. D8. D9. 710. 或411. 或412. 1或13. 或214. 70;53;15. 2或16.17. ;1;;718. 解:,答:B地在A地的东边20千米;这一天走的总路程为:千米,应耗油升,故还需补充的油量为:升,答:冲锋舟当天救灾过程中至少还需补充9升油.19. 4t;20. 解:,.21. 122.【解析】1. 解:设这个数是x,则,解得或.故选:C.先设出这个数为x,再根据数轴上各点到原点的距离进行解答即可.本题考查的是数轴,熟知数轴上各点到原点的距离的定义是解答此题的关键.2. 解:由图可知:,,,,,,,所以只有、、成立.故选:C.由图可判断a、b的正负性,a、b的绝对值的大小,即可解答.此题考查了数轴的有关知识,利用数形结合思想,可以解决此类问题数轴上,原点左边的点表示的数是负数,原点右边的点表示的数是正数.3. 解:.故选:D.根据数轴上两点间的距离等于这两个数的差的绝对值列式计算即可得解.本题考查了数轴,主要利用了两点间的距离的表示,需熟记.4. 解:,,;当原点在N或P点时,,又因为,所以,原点不可能在N或P点;当原点在M、R时且时,;综上所述,此原点应是在M或R点.故选A.先利用数轴特点确定a,b的关系从而求出a,b的值,确定原点.主要考查了数轴的定义和绝对值的意义解此类题的关键是:先利用条件判断出绝对值符号里代数式的正负性,再根据绝对值的性质把绝对值符号去掉,把式子化简后根据整点的特点求解.5. 解:表示互为相反数的点,必须要满足在数轴原点0的左右两侧,从四个答案观察发现,只有B选项的线段AB符合,其余答案的线段都在原点0的同一侧,所以可以得出答案为B.故选:B数轴上互为相反数的点到原点的距离相等,通过观察线段AB上的点与原点的距离就可以做出判断.本题考查了互为相反数的概念,解题关键是要熟悉互为相反数概念,数形结合观察线段AB 上的点与原点的距离.6. 解:由M为数轴上表示的点,将点M沿数轴向右平移5个单位到点N可列:,故选A.根据在数轴上平移时,左减右加的方法计算即可求解.此题主要考查点在数轴上的移动,知道“左减右加”的方法是解题的关键.7. 解:在数轴上,与表示数的点的距离是3的点表示的数有两个:;.故选:D.此题可借助数轴用数形结合的方法求解在数轴上,与表示数的点的距离是3的点有两个,分别位于与表示数的点的左右两边.本题考查的是数轴,注意此类题应有两种情况,再根据“左减右加”的规律计算.8. 解:最大的负整数是,故正确;绝对值是它本身的数是非负数,故错误;有理数分为正有理数、0、负有理数,故错误;时,在原点的右边,故错误;在数轴上7与9之间的有理数有无数个,故错误;故选:D.根据负整数的意义,可判断;根据绝对值的意义,可判断;根据有理数的分类,可判断;根据负数的意义,可判断;根据有理数的意义,可判断.本题考查了有理数,理解概念是解题关键.9. 解:点A,B表示的数分别是1,3,,,,点C表示的数是7.故答案为7.先利用点A、B表示的数计算出AB,存在计算出BC,然后计算点C到原点的距离即可得到C点表示的数.本题考查了数轴:所有的有理数都可以用数轴上的点表示,但数轴上的点不都表示有理数一般取右方向为正方向,数轴上的点对应任意实数,包括无理数10. 解:在数轴上,与表示的点相距6个单位长度的点表示的数是或4,故答案为:,4.根据数轴上到一点距离相等的点有两个,分别位于该点的左右,可得答案.本题考查了数轴,数轴上到一点距离相等的点有两个,以防漏掉.11. 解:若点在1的左面,则点为;若点在1的右面,则点为4.故答案为:或4.此类题注意两种情况:要求的点可以在已知点的左侧或右侧.本题考查了数轴,注意:要求的点在已知点的左侧时,用减法;要求的点在已知点的右侧时,用加法.12. 解:在数轴上把表示的点A沿数轴移动6个单位后得到点B,则B所表示的数为:,或,故答案为:1或.考虑两种情况:要求的点在已知点左移或右移6个单位长度.此题考查了数轴,要求掌握数轴上的两点间距离公式的运用在数轴上求到已知点的距离为一个定值的点有两个.13. 解:若该点在A点左边,则该点为:;若该点在A点右边,则该点为:.故答案为:2或.该点可以在数轴的左边或右边,即或.本题考查了数轴,此类题一定要考虑两种情况:左减右加.14. 解:由数轴可知,和之间的整数点有:,,,,共32个;和之间的整数点有:,,,16,共38个;故被淹没的整数点有个,负整数点有个,被淹没的最小的负整数点所表示的数是.故答案为:70,53,.根据数轴的构成可知,和之间的整数点有:,,,,共32个;和之间的整数点有:,,,16,共38个;依此即可求解.本题考查了数轴,熟悉数轴的结构是解题的关键.15. 解:当该点在的右边时,由题意可知:该点所表示的数为2,当该点在的左边时,由题意可知:该点所表示的数为,故答案为:2或由于题目没有说明该点的具体位置,故要分情况讨论.本题考查数轴,涉及有理数的加减运算、分类讨论的思想.16. 解:如图所示:,数轴上表示与之间的所有整数为:,,,,0,1,2,故符合题意的所有整数之和是:.故答案为:.根据题意画出数轴,进而得出符合题意的整式,求出答案即可.此题主要考查了数轴,根据题意得出符合题意的所有整数是解题关键.17. 解:点A表示的数是,点B表示的数是1;根据题意得:;根据题意得:,.故答案为:;1;;7 根据数轴上点的位置找出A与B表示的点即可;在数轴上找出表示与的两个点C与D即可;找出B、C之间的距离,以及A,C之间的距离即可.此题考查了数轴,弄清题意是解本题的关键.18. 根据有理数的加法,可得和,再根据向东为正,和的符号,可判定方向;根据行车就耗油,可得耗油量,再根据耗油量与已有的油量,可得答案.本题考查了正数和负数,有理数的加法运算是解题关键,有理数的大小比较得出最远距离.19. 解:;点P对应的数是;故答案为:4t;;分两种情况:当点P在Q的左边:,解得:;当点P在Q的右边:,解得:,综上所述:当点P运动2秒或秒时,点P和点Q间的距离为8个单位长度.根据题意容易得出结果;需要分类讨论:当点P在Q的左边和右边列出方程解答.本题考查了数轴,一元一次方程的应用解答题,对t分类讨论是解题关键.20. 根据有理数大小比较法则先把这些数按照从小到大的顺序排列起来,再在数轴上表示出来即可.本题考查了有理数大小比较的法则以及数轴的知识,解题时牢记法则是关键,比较有理数的大小可以利用数轴,他们从左到有的顺序,即从大到小的顺序在数轴上表示的两个有理数,右边的数总比左边的数大;也可以利用数的性质比较异号两数及0的大小,利用绝对值比较两个负数的大小.21. 解:,B表示的数分别为6,,,,点P表示的数是1,故答案为:1;设点P运动x秒时,在点C处追上点R,则:,,,,解得,,点P运动5秒时,追上点R;线段MN的长度不发生变化,理由如下分两种情况:当点P在A、B之间运动时如图:.当点P运动到点B左侧时如图,;综上所述,线段MN的长度不发生变化,其长度为5.由已知条件得到,由,于是得到结论;设点P运动x秒时,在点C处追上点R,于是得到,,根据,列方程即可得到结论;线段MN的长度不发生变化,理由如下分两种情况:当点P在A、B之间运动时当点P运动到点B左侧时,求得线段MN的长度不发生变化.此题主要考查了一元一次方程的应用、数轴,以及线段的计算,解决问题的关键是根据题意正确画出图形,要考虑全面各种情况,不要漏解.22. 解:当运动时间为t秒时,点A表示的数为,点B表示的数为.当时,点A表示的数为,点B表示的数为,.故答案为:.根据题意得:,解得:.当t为3时,A、B两点重合.为线段AB的中点,点P表示的数为,,,解得:或.存在t的值,使得线段,此时t的值为或.找出运动时间为t秒时,点A、B表示的数.将代入点A、B表示的数中,再根据两点间的距离公式即可得出结论;根据点A、B重合即可得出关于t的一元一次方程,解之即可得出结论;根据点A、B表示的数结合点P为线段AB的中点即可找出点P表示的数,根据即可得出关于t的一元一次方程,解之即可得出结论.本题考查了一元一次方程的应用、两点间的距离、数轴以及列代数式,解题的关键是:找出点A、B表示的数;根据两点重合列出关于t的一元一次方程;根据PC列出关于t 的含绝对值符号的一元一次方程.参考答案一.选择题1.D.2.C.3.D.4.C.5.D.6.B.7.C.8.C.9.B.二.填空题10.﹣1.11.﹣112..13.2,8.14.﹣100.15.互为相反数.16.5.三.解答题17.解:(1)∵1与﹣1重合,∴折痕点为原点,∴﹣3表示的点与3表示的点重合.故答案为:3.(2)①∵由表示﹣1的点与表示3的点重合,∴可确定折痕点是表示1的点,∴5表示的点与数﹣3表示的点重合.故答案为:﹣3.②由题意可得,A、B两点距离折痕点的距离为11÷2=5.5,∵折痕点是表示1的点,∴A、B两点表示的数分别是﹣4.5,6.5.18.解:∵m是6的相反数,n比﹣m的相反数大3,∴m=﹣6,n﹣m=3,∴n=9,∴n﹣1=8,n﹣m=3,答:n﹣1与n﹣m的值分别为8,3.第二章有理数及其运算 2.3 绝对值同步练习题1.3的相反数是()A.-3 B.3 C.-13 D.132.如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为()A.-1 B.1 C.-2 D.23. 下列说法中不正确的是()A.正数的相反数是负数B.负数的相反数是正数C.0的相反数是0 D.0没有相反数4. 如果a与-3互为相反数,那么a等于()A .3B .-3 C.13 D .-13 5. 如果两个数的绝对值相等,则这两个数( )A .相等B .是0,1,-1C .相等或互为相反数D .都是06. |-12|的值是( )A .-12 B.12 C .-2 D .27. 实数a ,b ,c ,d 在数轴上的对应点的位置如图所示,这四个数中,绝对值最大的是( )A .aB .bC .cD .d8. 如图,数轴上有A ,B ,C ,D 四个点,其中绝对值为2的数对应的点是( )A .点A 与点CB .点A 与点DC .点B 与点CD .点B 与点D9. 检验4个工件,其中超过标准质量的克数记作正数,不足标准质量的克数记作负数.从轻重的角度看,最接近标准的工件是( ) A .-2 B .-3 C .3 D .510. 在0,-2,1,-3这四个数中,最小的是( ) A .0 B .-2 C .1 D .-311. 下列说法中:①一个数的绝对值越大,这个数越大;②一个正数的绝对值越小,这个数越小;③一个数的绝对值越小,这个数越大;④一个负数的绝对值越小,这个数越大.其中正确的有( ) A.1个 B.2个 C.3个 D.4个12. 如图,数轴的单位长度为1,若点A,B表示的数的绝对值相等,则点A表示的数是( )A.-4 B.-2 C.0 D.413.有理数a,b在数轴上的位置如图所示,那么( )A.b>a B.|a|>|b| C.-a<b D.-b>a14. 如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )A.点M B.点N C.点P D.点Q15.已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )A.|a|<1<|b| B.1<-a<b C.1<|a|<b D.-b<a<-116. 若|x|=|-3.5|,则x=;绝对值大于3但不大于5的整数有 . 17. 若a ,b ,c 在数轴上的表示如图,|a|=5,|b|=2,|c|=3,则a =____,b =____,c =____. 18. 比较下列各组数的大小: (1)-13和-14; (2)-45和-1.1 19. 计算:(1)|-12|+|-5|-|+12|;(2)|-313|÷|-114|×|-112|.20. 师傅让一名学徒工加工一些标准长度为0.5米的钢管,为了检查加工的质量,师傅随便从加工成品中抽出六根,经测量发现: (表中正数表示超过标准的长度/米,负数表示不足标准的长度/米). 问哪一根钢管加工的质量要好些?你能否用所学的绝对值的知识加以解释?。
高数(上)第二章 复习题(含参考答案)

高数上第二章 复习题1. 求下列函数的导数: (1) y =ln(1+x 2); 解 222212211)1(11xx x x x x y +=⋅+='+⋅+='.(2) y =sin 2x ;解 y '=2sin x ⋅(sin x )'=2sin x ⋅cos x =sin 2x .(3)22x a y -=;解[]22212222121222122)2()(21)()(21)(x a x x x a x a x a x a y --=-⋅-='-⋅-='-='--.(4)xx y ln 1ln 1+-=;解 22)ln 1(2)ln 1(1)ln 1()ln 1(1x x x x x x x y +-=+--+-='.(5)xx y 2sin =;解222sin 2cos 212sin 22cos xxx x x x x x y -=⋅-⋅⋅='.(6)x y arcsin =;解2222121)(11)()(11x x x x x x y -=⋅-='⋅-='.(7))ln(22x a x y ++=;解])(211[1)(12222222222'+++⋅++='++⋅++='x a xa x a x x a x x a x y2222221)]2(211[1x a x x a x a x +=++⋅++=.(8)xx y +-=11arcsin .解 )1(2)1(1)1()1()1(1111)11(11112x x x x x x xxx x x x y -+-=+--+-⋅+--='+-⋅+--='.(9)xx y -+=11arctan ;解222211)1()1()1()11(11)11()11(11x x x x xx x x x x y +=-++-⋅-++='-+⋅-++='.(10)x x x y tan ln cos 2tan ln ⋅-=; 解)(tan tan 1cos tan ln sin )2(tan 2tan 1'⋅⋅-⋅+'⋅='x x x x x x x yx x x x x x x x x tan ln sin sec tan 1cos tan ln sin 212sec 2tan 122⋅=⋅⋅-⋅+⋅⋅.(11))1ln(2x x e e y ++=;解xx x x x x x x x x x e ee e e e e e e e e y 2222221)122(11)1(11+=++⋅++='++⋅++='.2. 求下列函数的n 阶导数的一般表达式: (1) y =sin 2 x ;解y '=2sin x cos x =sin2x , )22sin(22cos 2π+==''x x y ,)222sin(2)22cos(222ππ⋅+=+='''x x y ,)232sin(2)222cos(233)4(ππ⋅+=⋅+=x x y , ⋅ ⋅ ⋅,]2)1(2sin[21)(π⋅-+=-n x y n n .(2) y =x ln x ; 解1ln +='x y ,11-==''x xy , y '''=(-1)x -2, y (4)=(-1)(-2)x -3, ⋅ ⋅ ⋅,y (n )=(-1)(-2)(-3)⋅ ⋅ ⋅(-n +2)x -n +1112)!2()1()!2()1(-----=--=n n n n xn xn . (3) y =x e x .解 y '=e x +xe x ,y ''=e x +e x +xe x =2e x +xe x , y '''=2e x +e x +xe x =3e x +xe x , ⋅ ⋅ ⋅,y (n )=ne x +xe x =e x (n +x ) .3. 求方程y =1+xe y 所确定的隐函数的二阶导数22dxyd .解 方程两边求导数得 y '=e y +x e y y ', ye y e xe e y yy y y -=--=-='2)1(11,3222)2()3()2()3()2()()2(y y e y y y e y y e y y e y y y y y --=-'-=-'---'=''.4.求参数方程⎩⎨⎧-=+=t t y t x arctan )1ln(2所确定的函数的三阶导数33dx y d :解t t t t t t t dx dy 2112111])1[ln()arctan (222=++-='+'-=, t t t t t dx y d 4112)21(2222+=+'=,3422338112)41(t t t t t t dx y d -=+'+=. 5. 注水入深8m 上顶直径8m 的正圆锥形容器中, 其速率为4m 2/min . 当水深为5m 时, 其表面上升的速度为多少?解 水深为h 时, 水面半径为h r 21=, 水面面积为π241h S =,水的体积为3212413131h h h hS V ππ=⋅==,dtdh h dt dV ⋅⋅=2312π, dtdVh dt dh ⋅=24π.已知h =5(m ),4=dtdV (m 3/min), 因此 πππ2516425442=⋅=⋅=dt dV h dt dh (m/min).6. 求下列函数的微分: (1)21arcsin x y -=;解 dx x x x dx x x dx x dx y dy 22221||)12()1(11)1(arcsin --=--⋅--='-='=.(2) y =tan 2(1+2x 2); 解dy =d tan 2(1+2x 2)=2tan(1+2x 2)d tan(1+2x 2)=2tan(1+2x 2)⋅sec 2(1+2x 2)d (1+2x2)=2tan(1+2x 2)⋅sec 2(1+2x 2)⋅4x dx =8x ⋅tan(1+2x 2)⋅sec 2(1+2x 2)dx .(3)2211arctan xx y +-=;解)11()11(1111arctan 2222222x x d x x x x d dy +-+-+=+-=dx x x dx x x x x x xx 4222222214)1()1(2)1(2)11(11+-=+--+-⋅+-+=. 7. 讨论函数⎪⎩⎪⎨⎧=≠=000 1sin )(x x xx x f 在x =0处的连续性与可导性.解 因为f (0)=0, )0(01sin lim )(lim 00f xx x f x x ===→→, 所以f (x )在x =0处连续; 因为极限xx x x x f x f x x x 1sin lim 01sin lim )0()(lim000→→→=-=-不存在, 所以f (x )在x =0处不导数.。
概率论第二章习题答案

概率论第二章习题答案习题1:离散型随机变量及其分布律设随机变量X表示掷一枚公正的六面骰子得到的点数。
求X的分布律。
解答:随机变量X的可能取值为1, 2, 3, 4, 5, 6。
由于骰子是公正的,每个面出现的概率都是1/6。
因此,X的分布律为:\[ P(X=k) = \frac{1}{6}, \quad k = 1, 2, 3, 4, 5, 6 \]习题2:连续型随机变量及其概率密度函数设随机变量Y表示从标准正态分布中抽取的数值。
求Y的概率密度函数。
解答:标准正态分布的概率密度函数为高斯函数,其形式为:\[ f(y) = \frac{1}{\sqrt{2\pi}} e^{-\frac{y^2}{2}}, \quad -\infty < y < \infty \]习题3:随机变量的期望值已知随机变量X的分布律为:\[ P(X=k) = p_k, \quad k = 1, 2, ..., n \]求X的期望值E(X)。
解答:随机变量X的期望值定义为:\[ E(X) = \sum_{k=1}^{n} k \cdot p_k \]习题4:随机变量的方差继续使用习题3中的随机变量X,求X的方差Var(X)。
解答:随机变量X的方差定义为期望值的平方与每个值乘以其概率之和的差:\[ Var(X) = E(X^2) - (E(X))^2 \]其中,\( E(X^2) = \sum_{k=1}^{n} k^2 \cdot p_k \)习题5:二项分布设随机变量X表示n次独立伯努利试验中成功的次数,每次试验成功的概率为p。
求X的分布律和期望值。
解答:X服从参数为n和p的二项分布。
其分布律为:\[ P(X=k) = \binom{n}{k} p^k (1-p)^{n-k}, \quad k = 0, 1, ..., n \]X的期望值为:\[ E(X) = np \]结束语:以上是概率论第二章的一些典型习题及其解答。
第二章 导数与微分习题汇总

第二章 导数与微分【内容提要】1.导数的概念设函数y =f (x )在x 0的某邻域(x 0-δ,x 0 + δ)(δ>0)内有定义,当自变量x 在点x 0处有改变量Δx 时,相应地,函数有改变量00()()y f x x f x ∆=+∆-.若0→∆x 时,极限xyx ∆∆→∆0lim 存在,则称函数y =f (x )在x =x 0处可导,称此极限值为f(x)在点x 0 处的导数,记为)(0x f '或)(0x y '或0|x x y ='或0|d d x x xy =或0|d d x x x f=+→∆0x 时,改变量比值的极限xyx ∆∆+→∆0lim 称f(x)在x 0处的右导数,记为)(0x f +'。
-→∆0x 时,改变量比值的极限xyx ∆∆-→∆0lim 称f(x)在x 0处的左导数,记为)(0x f -'。
2.导数的意义导数的几何意义:)(0x f '是曲线y =f (x )在点(x 0,y 0)处切线的斜率,导数的几何意义给我们提供了直观的几何背景,是微分学的几何应用的基础。
导数的物理意义:路程对时间的导数)(0t s '是瞬时速度v (t 0) 。
以此类推,速度对时间的导数)(0t v '是瞬时加速度a (t 0)。
3.可导与连续的关系定理 若函数)(x f y =在点x 0处可导,则函数在点x 0处一定连续。
此定理的逆命题不成立,即连续未必可导。
4.导数的运算定理1(代数和求导法则)若u (x )和v (x )都在点x 处可导,则v u v u '±'='±)(定理2(积的求导法则)若u (x )和v (x )都在点x 处可导,则v u v u uv '+'=')(定理3(商的求导法则)若u (x )和v (x )都在点x 处可导,且v (x )≠0,则2v v u v u v u '-'='⎪⎭⎫ ⎝⎛定理4 若函数)(x g u =在点x 处可导,且)(u f y =在其相应点u 处可导,则复合函数)]([x g f y =在x 处可导,且x u x u y y '⋅'=' 或d d d d d d y y ux u x=⋅5.基本初等函数求导公式本节中我们已求出了所有基本初等函数的导数,整理所下:0)(='C 1)(-='μμμx xa a a x x ln )(='x x e )e (='ax x a ln 1)(log ='x x 1)(ln ='x x cos )(sin =' x x sin )(cos -='x x 2sec )(tan =' x x 2csc )(cot -='x x x tan sec )(sec =' x x x cot csc )(csc -=211)(arcsin x x -=' 211)(arccos x x --='211)(arctan xx +=' 211)cot arc (x+-='这些基本导数公式必须熟记,与各种求导法则、求导方法配合,可求初等函数的导数。
经济学第二章课堂练习题答案
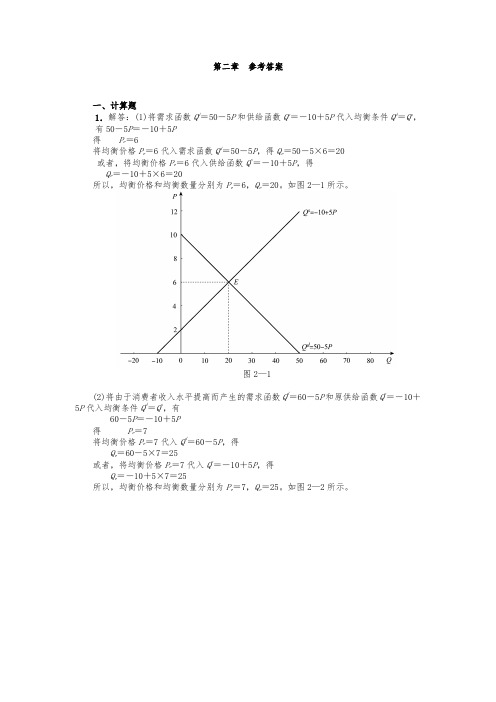
第二章参考答案一、计算题1.解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Q s=-10+5P和需求函数Q d=50-5P表示,均衡点E具有的特征是:均衡价格P e=6,且当P e=6时,有Q d=Q s=Q e=20;同时,均衡数量Q e=20,且当Q e=20时,有P d=P s=P e=6。
教材第二章部分习题参考解答Word版

教材第二章部分习题参考解答Word版教材第二章部分习题参考解答一、单选题1. B2. A3. C4. B5. D6. C二、填空题1.值指针2.(38,56,25,60,42,74)3. O(n) O(1)4. O(1) O(n)5. i-1 i+16. p->next a[p].next7. 表头8.前驱后继9.表尾表头10.HL->next==NULL HL->next==HL11. a[i].next=a[1].next; a[1].next=i;12. i=a[1].next; a[1].next=a[i].next;13. p=a[i].next; a[i].next=a[p].next; i=p;14. a[j].next=a[i].next; a[i].next=j;三、普通题第1小题1. (79, 62, 34, 57, 26, 48)2. (26, 34, 48, 57, 62, 79)3. (48, 56, 57, 62, 79, 34)4. (56, 57, 79, 34)5. (26, 34, 39, 48, 57, 62)第2小题分析:为了排版方便,假定采用以下输出格式表示单链表示意图:每个括号内的数据表示一个元素结点,其中第一个数据为元素值,第二个数据为后继结点的指针,第一个元素结点前的数值为表头指针。
1. (7(79,6), (62,5), (34,4), (57,3), (26,2), (48,0))2. (3(26,5), (34,2), (48,4), (57,6), (62,7), (79,0))3. (2(48,8), (56,4), (57,6), (62,7), (79,5), (34,0))4. (8(56,4), (57,7), (79,5), (34,0))第3小题1. ElemType DMValue(List& L)//从线性表中删除具有最小值的元素并由函数返回,空出的位置//由最后一个元素填补,若线性表为空则显示出错信息并退出运行。
初二第二章练习题及参考答案

初二第二章练习题及参考答案第一节选择题1. 答案:B。
解析:根据题意,判断一个数字是奇数还是偶数,只需要判断最后一位数字是否为偶数即可。
若为偶数,则整个数字为偶数;若为奇数,则整个数字为奇数。
故答案为B。
2. 答案:C。
解析:将小数转化为百分数,就是将小数乘以100。
故答案为C。
3. 答案:A。
解析:计算两个小数的和,保留末尾两位小数。
故答案为A。
4. 答案:D。
解析:折扣价 = 原价 - 原价 ×折扣百分比。
故答案为D。
5. 答案:B。
解析:编码密码需要根据26个字母的顺序进行移位加密。
故答案为B。
第二节填空题6. 答案:250。
解析:由百分数的定义可知,如果一个百分数的百分数部分是整数,那么这个百分数就是这个整数本身,百分数部分为100时表示完整的数值。
故答案为250。
7. 答案:11。
解析:解方程 x + 4 = 15,得 x = 11。
故答案为11。
8. 答案:32。
解析:计算 4 × 8,得 32。
故答案为32。
9. 答案:15。
解析:在等差数列中,等差数列公式为 an = a1 + (n-1)d,其中 a1 为首项,d 为公差,n 为项数,an 为第n项。
故答案为15。
10. 答案:10。
解析:利用圆的周长公式C = 2πr,其中 C 为周长,r 为半径。
故答案为10。
第三节解答题11. 解:根据题意,有 a ÷ b = 2 且 a + b = 13,求 a 和 b 的值。
解法一:利用方程组求解,将 a 和 b 分别表示为 x 和 y,则可以得出以下方程组:x ÷ y = 2x + y = 13根据第一式可得 x = 2y,将其代入第二式得到 2y + y = 13,解得 y = 4,代入第一式可得 x = 8。
故 a = 8,b = 4。
解法二:利用代入法求解,将 a = 2b 代入 a + b = 13,得 2b + b = 13,解得 b = 4,代入 a = 2b 可得 a = 8。
高等无机化学习题汇总

第二章原子结构和分子结构一、判断题3.杂化轨道中含p成分越多,原子的电负性越大。
×4.根据VSEPR理论,在SiF62-中,中心原子的价层电子总数为10个。
×5.根据VSEPR理论,氧族原子提供的电子数为6。
×6.在SO3-中,中心原子的价层电子总数为12个。
×7.SnCl2几何构型为直线型。
×8.ICl4—几何构型为四面体。
×9.NH3和NO3-的几何构型均为平面三角型。
×10.H2O和XeF2的几何构型均为平面三角型。
×11.SO32-和NO3-的几何构型均为平面三角型。
×12.下列三种离子,其极化作用顺序为:Al3+ > Mg2+ > Na+ √13.下列三种离子,其极化作用顺序为:Pb2+ > Fe2+ > Mg2+√14.Ag+的极化作用大于K+的极化作用,因此Ag+的极化率小于K+的极化率。
×15.H+的极化能力很强。
√16.极化作用愈强,激发态和基态能量差愈小,化合物的颜色就愈深。
√17.温度升高,离子间的相互极化作用增强。
√18.半径相近、电子层构型相同时,阳离子正电荷越大,极化作用越强。
√19.其它条件相同或相近时,阴离子半径越大,变形性越大。
√20.无机阴离子团的变形性通常较大。
×二、选择题3、与元素的电离能和电子亲和能有关的电负性标度是(B):(A)鲍林标度(B)密立根标度(C)阿莱-罗周标度(D)埃伦标度4、下列基团中,电负性值最大的是(A):(A)CF3- (B)CCl3- (C)CBr3- (D)CI3-5、在以下化合物中,碳原子电负性最大的是(C):(A)CH4 (B)C2H4 (C)C2H2 (D)电负性相同7、XeO3离子的几何构型为(A)(A) 三角锥 (B) 四面体 (C) V型 (D) 平面三角形8、根据VSEPR理论,多重键对成键电子对的排斥作用最大的是(A)(A) 叁重键 (B) 双重键 (C) 单重键9、根据VSEPR理论,成键电子对(BP)和孤电子对(LP)之间相互排斥作用最大的是(A)(A) LP-LP (B) LP-BP (C) BP-BP10、ClO3-离子的几何构型为(A)(A) 三角锥 (B) 四面体 (C) V型 (D) 平面三角形11、ClF3的几何构型为(C):(A)平面三角型(B)三角锥型(C)T型(D)V型12、NF3的几何构型为(B):(A)平面三角型(B)三角锥型(C)T型(D)V型13、BrF3的几何构型为(C):(A)平面三角型(B)三角锥型(C)T型(D)V型14、下列分子中键角最大的是(A):(A)NH3(B)NBr3(C)NCl3(D)NF315、下列分子中键角最大的是(A)(A) CH4 (B) NH3 (C)H2O (D)H2S16、下列分子中键角最大的是(A)(A) NH3 (B) PH3 (C) AsH3 (D)SbH317、下列分子中键角最小的是(D):(A)PI3(B)PBr3(C)PCl3(D)PF318、若阳离子电荷相同,半径相近,则最外层电子层构型为(A)电子构型的阳离子的变形性最小。
经济学第二章习题集并课后习题- 附参考答案

课后习题解答要点1、第30页计算题1提示:由生产者均衡条件MPL/PL=MPK/PK得第一个方程2K/l=PL/PK;由题目中给出的总成本函数可得第二个方程PL/PK=2;而当产量为64时,由题目中给出的生产函数可得第三个方程8=K1/4L1/2联立上述三个方程可求得K=L=162、第30页计算题2提示:市场的均衡价格和均衡产量可由题目中给出的市场的需求函数和供给函数联立求得。
而厂商的需求函数即为D=均衡价格。
3、第30页计算题3提示:用到利润最大化公式MR=MC其中MR=dTR/dQ,而TR=PQ,将题目中给出的产品需求函数代入即得。
此外,MC=dTC/dQ。
第二章习题集单选题1、生产函数中的产量,是指一定的投入要素组合所可能生产的( B )的产品数量。
A.最小B.最大C.平均D.不定2、在完全竞争条件下,企业短期均衡的条件为( A )A.P=MCB.P>MCC.P<MCD.P=AC3、规模报酬递减是在( A )情况下发生的。
A.按比例连续增加各种生产要素B.不按比例连续增加各种生产要素C.连续地投入某种生产要素而保持其他生产要素不变D.上述都正确4、不随产量变动而变动的成本称为( B )A.平均成本B.固定成本C.长期成本D.总成本5、寡头垄断厂商的产品是( C )A.同质的B.有差异的C.既可以是同质的,也可以是有差异的D.以上都不对6、生产函数表示( C )。
A.一定数量的投入,至少能生产多少产品B.生产一定数量的产品,最多要投入多少生产要素C.投入与产出的关系D.以上都对7、如果连续地增加某种生产要素,在总产量达到最大值的时候,边际产量( C )A.为正,且也是最大值B.为正,但不是最大值C.为零D.为负8、等产量曲线( A )。
A.说明为生产一个给定的产出量而可能的各种投入要素的组合B.除非得到所有要素的价格,否则不能划出该曲线C.表明投入与产出的关系D.表示无论投入数量怎样变化,产出量都是一定的9、假定两个人一天可以生产60单位产品,4个人一天可以生产100单位产品,那么( A )。
数学七年级上册第二章《有理数及其运算》同步训练 及 答案

第二章《有理数及其运算》同步训练答案一、选择题(本大题共有10个小题,每小题3分,共30分)1.【答案】C2.【答案】D3.【答案】C4.【答案】A5.【答案】C6.【答案】C7.【答案】D8.【答案】B9.【答案】A10.【答案】A二、填空题(本大题共有6个小题,每小题3分,共18分)11.【答案】>12.【答案】4−−13.【答案】314.【答案】1−15.【答案】-1016.【答案】12− 三、解答题(本大题共有6个小题,共52分)17.解:(1)正数集合:{227,2012,1.99,(6)−−,}; (2)负数集合:{-5,34−,-3.14,|12|−−}; (3)整数集合:{-5,0,2012,(6)−−,|12|−−};(4)分数集合:{ 34− ,-3.14,227,1.99,} 18.解:﹣|412|=﹣412,|﹣3|=3,﹣(﹣5)=5, 用数轴表示为:.故它们的大小关系为﹣6<﹣|412|<﹣122<﹣1<0<|﹣3|<3.5<﹣(﹣5). 19.解:(1)()()()18318315−−−=−+=−;(2)12(18)(7)151218(7)(15)30(22)8−−+−−=++−+−=+−=;20 .(1)解:()()()()111216151810+−+−++−+−30=−,∵300−<,∴仓库里的货品是减少了;(2)解:()27030300−−=(吨),答:6天前仓库里有货品300吨;(3)解:111216151810+−+−++−+−82=(吨),825410⨯=(元);答:要付410元装卸费.21.解:(1)11112 4612⎛⎫−+⨯ ⎪⎝⎭111=121212 4612⨯−⨯+⨯=321−+=2.(2)772(6) 483÷−⨯−78=447⨯+=6.22.解:(1)∵1⊙3=1×4+3=7 3⊙1=3×4+1=13 5⊙4=5×4+4=24 ,a⊙b=4a+b;故答案为4a+b;(2)若a≠b,a⊙b=4a+b,b⊙a=4b+a,∵(4a+b)﹣(4b+a),=3a﹣3b,≠0,∴a ⊙b ≠b ⊙a .故答案为≠;(3)﹣5⊙(4⊙﹣3),=﹣5⊙(4×4﹣3),=﹣5⊙13,=﹣5×4+13,=﹣20+13,=﹣7.23.解:(1)根据题意可得:到终点前,车上有1815312471051129+−+−+−+−=,即29人; 故到终点下车29人.故答案为29;(2)根据图表可知各站之间车上人数分别是: 起点A →站,车上有18人,A 站B →站,车上有1815330+−=人, B 站C →站,车上有3012438+−=人, C 站D →站,车上有3871035+−=人, D 站→终点,车上有3551129+−=人, 易知B 站和C 站之间人数最多.故答案为B ;C ;(3)根据题意可知:起点A →站,车上有18人, A 站B →站,车上有1815330+−=人, B 站C →站,车上有3012438+−=人, C 站D →站,车上有3871035+−=人, D 站→终点,车上有3551129+−=人, 则()18303835291150++++⨯=(元). 答:该车出车一次能收入150元.24.解:(1)点B 向右移动5个单位长度后,点B 表示的数为1; 三个点所表示的数中最小的数是点A ,为1−.(2)点D 到A ,C 两点的距离相等;故点D 为AC 的中点.D 表示的数为:0.5.(3)当点E 在A 、B 之间时,2=EA EB ,从图上可以看出点E 为3−, ∴点E 表示的数为3−;当点E 在点B 的左侧时,根据题意可知点B 是AE 的中点, ∴点E 表示的数是7−.综上:点E 表示的数为3−或7−.。
生物氧化习题汇总

第二章生物氧化习题汇总一、名词解释:1、生物氧化(biological oxidation):2、高能键(high-energy bond):4、呼吸链(电子传递链)(respiratory electron-transport chain):5、氧化磷酸化(oxidative phosphorylation):6. 底物水平磷酸化(substrate level phosphorylation):7. 磷氧比(P/O ratio):8.解偶联剂(uncoupling agent):9. 高能化合物(high energy compound):10. 化学渗透学说(chemiosmotic theory):二、填空题1.生物氧化中CO2生成的基本方式是:。
2.生物体内发生氧化作用的三种主要方式是:、、。
参与物质氧化的酶一般有_________、_________和_________等几类。
3.电对的标准氧化还原电势负值越大,得电子,倾向于电子;相反,正值越大,则得电子。
4.线粒体内膜上存在的典型呼吸链有_________呼吸链和_________呼吸链两种,这是根据接受代谢物脱下的氢的_________不同而区别的,其P/O值分别为_________和_________。
5.呼吸链上唯一的非蛋白组分是:,呼吸链上唯一能溶于水的传递体是:。
6.ATP合酶由、、三部分构成,其活性部位存在于亚基上,该亚基有、、三种构型,在状态下,该亚基可合成ATP。
7.体内呼吸链的调节主要通过调节,使用呼吸链抑制剂等可阻断电子传递,使用等,可使氧化过程与磷酸化过程脱节,使用等,可抑制氧化磷酸化过程。
8.线粒体外的氧化主要通过穿梭和穿梭完成,前者可将胞质中NADH转换成线粒体中的,主要发生在组织,后者可将胞质中NADH转换成线粒体中的,主要发生在组织,其P/O值分别为_________和_________。
9.高等动物线粒体呼吸链中主要含有5种细胞色素、、、、。
高等数学第二章习题.doc

第二章极限与连续第一节数列的极限一、观察下列数列{%…}的变化趋势,判断是否有极限?若有极限,写出其极限1、2、3^ x z/=lnn4、心=1 + (_1)“ 丄n二、利用数列极限的定义证明:、v 3n + l 3K lim --------- =—;n* 2/7 + 1 22.lim0.999_9=l三、设数列{x I满足lim兀=01〃T8 n 证明:lim £H—>oo2/1-12〃(-1)〃第二节函数的极限一、填空题1、当x->2吋,y“T4,问当5取_时,只要Ov|兀-2|v5,必有卜-4|<0.001.丫2_12^当兀T8时,y = —------------- 1,问当z取__________ 时,只要\x\ > z,必有|y-l| <0.01.”+3二、用函数极限的沱义证明:三、试证:函数/(兀)当JVTX。
时极限存在的充分必要条件是左极限、右极限各自存在并且相等.四、讨论:函数0(兀)二包在兀T0时的极限是否存在?第三节极限的性质填空题1、 limx —» 2— 3 x-32. v x~l lim——XT 】- 1 3、 4、 5、 limHT8(〃 + l )G +2)(〃 + 3)limx 2 sin —= “TO x / 】• COS X 6、 lim -----------XTZ x+ 厂 r .. 4x 4 - 2x 2 + x 7^ lim -------- ; ------z ) 32 + 2x8、 lim•Y T8(2兀一 3严(3兀+ 2严 二、求下列各极限2、 lim U + /?)2-x2 D h3、lim (— ------- 二)z \-x \-x 34、lim"Tv 2 + ijxlim (l + 丄 +第四节无穷大、无穷小一、填空题1、凡无穷小量皆以 _________ 为极限2、lim /(兀)=A是/(x) = A + Q _ 条件,(其中limo = 0)XT々)尤-»心3、在同一过程中,若/(兀)是无穷大,则 ____ 是无穷小.4^当XT O时,无穷小l-cosx与mx n等价,贝ij m = ____________ ,n ____ .i _L?r二、根据定义证明:当XT O时,函数丁 =匸2是无穷大,问兀应满足什么条件,x能使卜|〉104・三、证明函数y = -sin丄在区间(0,1]上无界,但当XT()+时,这个函数不是无穷大. XX四、证明:当兀->0时,兀'一1与3兀2 -兀一2是同阶无穷小第五节极限的存在准则一、填空题-…sin 2x“ sin cox 1、 lim --------- =2、.hm ----------- =go sin 3x 3、cotx lim ------------ = 4、 lim x ・ cot 3x=XT O %XT O 5、 sinx lim =6> 1 lim(l +兀)* =XT8 2X大TO 1 + x 八]r7、 lim( )2r- 8、 lim(l — —Y =XToo %28X二、 求下列各极限1 — cos2x1、 lim -------------2、 lim(tanx),an2xgo xsmx4三、利用极限存在准则证明数列V2J2+V2J2+V2+V2,……的极限存在,并求出该 极限.3、 血(斗XT® x-a 4、 lim("d"T8 n * 1 )"第六节:连续函数及其性质填空题21、 ____________________________________ 指出尸 x j 在x = l 是第 ______ 类间断点;在x = 2是第 _____________________________ 类间断点.兀2 — 3x + 2 2、 _________________________________ 指出• J 在x = 0是第 ________ 类间断点;在x = l 是第 _____________________________ 类间断点;在x|(x 2 -1) x = -1是第 类间断点 3、limln(2cos2x) = _________ .61-®二、讨论函数 /(x)=lim —— 的连续性,若有间断点,判断其类型.三、指出下列函数在指定范围内的间断点,并说明这些间断点的类型,如果是可去间断点 则补充或改变函数的定义使它连续.X2、/(%)=——在XG R 上tanx4.1、 /(兀)=四.五、六、使x<0设f(x) = < 1 , X =()已知/(%)在x = 0处连续,试确定G和b ln(b + x + x ), x>0设Q>0,b>0,证明方程x = asinx + b,至少有一个不超过a^b正根若/(%)在[d,b]上连续,a<x l<x2<-'<x n<b则在[兀],暫]上必有丁© = /(西)+ /(兀2)+ ……+ /(£)的值.复习题二一、选择题:X1、 函数/(X )= —在定义域为()1 + JT(A)有上界无下界; (B)有下界无上界; (C)有界,且 ^</(x)<^ ;(D)有界,且—25—^52 •L1 +厂2、 当XTO 时,下列函数哪一•个是其它三个的高阶无穷小() (A) x 2 ;(B) 1-cosx ;(C) x-tanx ; (D) ln(l + x)3、设认冲则当()时有卿甞:當:二篇遗(A) m > /7 ;(B) m - n ; (C) m < n ;(D) m. n 任意取4、 设 f(x)= :U 则 limgO< X< 1XTO(A)-l ; (B)l ; (C)0 ;(D)不存在5、 (A)l ;(B)-l ; (C)0; (D)不存在.二、求极限:1、v 2/ + 〃 + l lim -------------- — “T8 (i-/?y 2、1曲"-2XT 3x-33、lim(l + ;r)AXT O 4、lim x(e x -1)XT81x arctan ------四、讨论函数/(x)= --------------- 的连续性,并判断其间断点的类型.• 71sin —x2x< x>\试确定a 的值使/(x)在x = l 连续•x X5、当 xHO 吋,limcos —cos — .............. cos — ........................................................................ ;2 • 丄 x sin — 6、lim / *f 如 2 — i三、设冇函数/(x) =sin ax.五、证明奇次多项式:P(兀)=兔兀2“+1+坷兀2”+..・+夠出(勺北0)至少存在一个实根.六、若/(x)在|0,2°]上连续,/(0)=/(2G),证明在|0卫]上至少存在一点g ,使。
版第二章 坚定理想信念练习题

第二章(一)坚定理想信念练习题汇总一、单项选择题1、( C )是人的精神世界的核心,是人精神上的“钙”。
A、思想道德B、道德素质C、理想信念D、人生价值2、理想是( C )。
A、与生活愿望相结合并指向未来的想象B、缺乏客观根据的随心所欲的对未来的想象C、在实践中形成的、有实现可能性的、对未来社会和自身发展目标的向往与追求。
D、与现实有很大差距,毫无实现可能的种未来想象3、以下关于理想表述错误的是( C )A、理想带有时代的烙印,在阶级社会中,还必然带有特定阶级的烙印。
B、理想之所以能够成为一种推动人们创造美好生活的巨大力量,就在于它不仅具有现实性,而且具有预见性。
C、理想是人的主观能动性与社会发展客观趋势的一致性的反映,是人们在正确把握社会历史发展客观规律的基础上形成的,因此理想必然可以实现。
D、实践产生理想,理想指引实践,理想与实践的相互作用推动着人们立足现实、着眼未来,在奋斗中追求,在追求中奋斗。
4、现阶段我国各族人民建设中国特色的共同理想和我们建立共产主义社会的最高理想,属于人生理想中( D )的内容。
A、生活理想B、职业理想C、道德理想D、政治理想5、理想和现实的统一性表现在( C )。
A、理想就是现实。
B、有了坚定的信念,理想就能自动变为现实。
C、现实是理想的基础,理想是现实的未来。
D、理想总是美好的,而现实中既有美好的一面,也有丑陋的一面。
6、以下关于理想、幻想、空想的表述正确的是( B )。
A、理想是个人对幻想空想的改进B、理想源于实践具有实现可能是对未来的向往和追求C、理想是永恒的,幻想和空想可以随时间的变化而变化D、知识渊博的人具有崇高的理想,而空想幻想则源于无知7、一般来说, ( B )有盲目和科学之分。
盲目的就是对虚幻的世界、不切实际的观念、荒谬的理论等的和狂热崇拜,科学的则来自人们对自然界和人类社会发展规律的正确认识。
A、理想B、C、信念D、意志8、中国特色思想,明确中国特色最本质的特征是( D )。
高中第二章数学试题及答案

高中第二章数学试题及答案一、选择题(每题3分,共15分)1. 若函数f(x) = 2x^2 + 3x + 1,下列哪个选项是f(x)的对称轴?A. x = -1/4B. x = 1/4C. x = -3/2D. x = 3/22. 已知等差数列{a_n}的首项a_1 = 2,公差d = 3,求a_5的值。
A. 17B. 14C. 11D. 83. 若复数z满足|z| = 1,且z的实部为1/2,则z的虚部的值是多少?A. √3/2B. -√3/2C. √3/2iD. -√3/2i4. 已知直线l的方程为y = 2x + 3,点P(1, 2)是否在直线l上?A. 是B. 否5. 函数y = x^3 - 3x^2 + 2在区间[0, 2]上的最大值是多少?A. 0B. 1C. 2D. 3二、填空题(每题4分,共20分)6. 计算等比数列1, 2, 4, ...的前四项和S_4。
7. 已知圆的方程为(x - 2)^2 + (y + 1)^2 = 9,求该圆的半径。
8. 若函数f(x) = ax^2 + bx + c在x = 1处取得极值,且f(1) = 0,则a的值是多少?9. 计算双曲线x^2/4 - y^2/9 = 1的渐近线方程。
10. 已知向量a = (2, -1),b = (1, 3),求向量a与向量b的数量积。
三、解答题(每题10分,共50分)11. 证明:若a, b, c是等差数列,则a^2 + c^2 = 2b^2。
12. 已知函数f(x) = x^2 - 4x + m,求证:对于任意x ∈ R,都有f(x) ≥ m - 4。
13. 已知抛物线y = x^2 + 2x - 3与x轴交于点A和点B,求线段AB的长度。
14. 已知三角形ABC的顶点坐标分别为A(-1, 2),B(2, 3),C(3, -1),求三角形ABC的面积。
15. 已知函数f(x) = x^3 - 6x^2 + 9x + a,求证:对于任意x ∈ R,都有f(x) ≥ 2a + 3。
第二章化工原理习题汇总

1. 如图2-1用离心泵将20℃的水由敞口水池送到一压力为2.5atm的塔内,管径为φ108×4mm管路全长100m(包括局部阻力的当量长度,管的进、出口当量长度也包括在内)。
已知:水的流量为56.5m3·h-1,水的粘度为10-3 Pa·S,密度为1000kg·m-3,管路摩擦系数可取为0.024,计算并回答:(1)水在管内流动时的流动形态;(2) 管路所需要的压头和功率;解:已知:d = 108-2×4 = 100mm = 0.1mA=(π/4)d 2 = 3.14×(1/4)×0.12 = 0.785×10-2m l+Σl e =100m q v = 56.5m 3/h∴u = q/A = 56.5/(3600×0.785×10-2) = 2m/sμ = 1cp = 10-3 Pa ·S ρ=1000 kg.m -3, λ = 0.024 ⑴ ∵ Re = du ρ/μ=0.1×2×1000/10-3 = 2×105 > 4000 ∴水在管内流动呈湍流⑵ 以1-1面为水平基准面,在1-1与2-2面间列柏努利方程: Z 1 +(u 12/2g)+(p 1/ρg)+H =Z 2+(u 22/2g)+(p 2/ρg)+ΣHf∵Z 1=0, u 1=0, p = 0 (表压), Z 2=18m, u 2=0 p 2/ρg=2.5×9.81×104/(1000×9.81)=25m ΣHf =λ[(l+Σle )/d](u 2/2g)=0.024×(100/0.1)×[22/(2×9.81)] = 4.9m ∴H = 18+25+4.9 = 47.9mNe = Hq v ρg = 47.9×1000×9.81×56.5/3600 = 7.4kw2. 采用IS80-65-125水泵从一敞口水槽输送60℃热水。
(完整版)数学必修2第二章知识点小结及典型习题

第二章 点线面位置关系总复习1、(1)平面含义:平面是无限延展的,没有大小,厚薄之分。
另外,注意平面的表示方法。
(2)点与平面的关系:点A 在平面内,记作;点不在平面α内,记作A α∉点与直线的关系:点A 的直线l 上,记作:A ∈l ;点A 在直线l 外,记作A ∉l ;直线与平面的关系:直线l 在平面α内,记作l ⊂α;直线l 不在平面α内,记作l ⊄α。
2、四个公理与等角定理:(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内. 符号表示为A ∈LB ∈L ⇒ L α A ∈α B ∈α公理1作用:判断直线是否在平面内.(只要找到直线的两点在平面内,则直线在平面内) (2)公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α, 使A ∈α、B ∈α、C ∈α。
公理2的三个推论:(1):经过一条直线和这条直线外的一点,有且只有一个平面。
(2):经过两条相交直线,有且只有一个平面。
(3):经过两条平行直线,有且只有一个平面。
公理2作用:确定一个平面的依据。
(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
符号表示为:P ∈α∩β =>α∩β=L ,且P ∈L公理3说明:两个不重合的平面只要有公共点,那么它们必定交于一条过该公共点的直线,且线唯一。
公理3作用:判定两个平面是否相交的依据,是证明三线共点、三点共线的依据。
即:①判定两个平面相交的方法。
②说明两个平面的交线与两个平面公共点之间的关系:交线必过公共点。
③可以判断点在直线(交线)上,即证若干个点共线的重要依据。
(4)公理4:平行于同一条直线的两条直线互相平行。
a ∥bc ∥b强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。
公理4作用:判断空间两条直线平行的依据。
(表明空间中平行于一条已知直线的所有直线都互相平行)(5)等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补. 3、(1)证明共面问题:方法1是先证明由某些元素确定一个平面,在证明其余元素也在这个平面内。
高等数学第二章复习题及答案

高等数学习题集及解答第二章一、 填空题1、设()f x 在x a =可导,则0()()lim x f a x f a x x →+--=。
2、设(3)2f '=,则0______________(3)(3)lim 2h f h f h →--=。
3、设1()xf x e -=,则0_____________(2)(2)limh f h f h→--=。
4、已知00cos (),()2,(0)1sin 2x f x f x x x π'==<<-,则0_______________________()f x =。
5、已知2220x y y x +-=,则当经x =1、y =1时,_______________dydx =。
6、()x f x xe =,则_______________(ln 2)f '''=。
7、如果(0)y ax a =>是21y x =+的切线,则__________a =。
8、若()f x 为奇函数,0()1f x '=且,则0_________________()f x '-=。
9、()(1)(2)()f x x x x x n =+++,则_________________(0)f '=。
10、ln(13)x y -=+,则____________________y '=。
11、设0()1f x '=-,则0___________00lim(2)()x xf x x f x x →=---。
12、设tan x y y +=,则_________________________dy =。
13、设lny =_______________(0)y '''=。
14、设函数()y f x =由方程42ln xy x y +=所确定,则曲线()y f x =在点(1,1)处的切线方程是______________________。
生物氧化习题汇总

生物氧化习题汇总第二章生物氧化习题汇总一、名词解释:1、生物氧化(biological oxidation):2、高能键(high-energy bond):4、呼吸链(电子传递链)(respiratory electron-transport chain ):5、氧化磷酸化(oxidative phosphorylation):6. 底物水平磷酸化(substrate level phosphorylation):7. 磷氧比(P/O ratio):8.解偶联剂(uncoupling agent):9. 高能化合物(high energy compound):10. 化学渗透学说(chemiosmotic theory):二、填空题生成的基本方式1.生物氧化中CO2是:。
2.生物体内发生氧化作用的三种主要方式是:、、。
参与物质氧化的酶一般有_________、_________和_________等几类。
3.电对的标准氧化还原电势负值越大,得电子,倾向于电子;相反,正值越大,则得电子。
4.线粒体内膜上存在的典型呼吸链有_________呼吸链和_________呼吸链两种,这是根据接受代谢物脱下的氢的_________不同而区别的,其P/O值分别为_________和_________。
5.呼吸链上唯一的非蛋白组分是:,呼吸链上唯一能溶于水的传递体是:。
6.A TP合酶由、、三部分构成,其活性部位存在于亚基上,该亚基有、、三种构型,在状态下,该亚基可合成ATP。
7.体内呼吸链的调节主要通过调节,使用呼吸链抑制剂等可阻断电子传递,使用等,可使氧化过程与磷酸化过程脱节,使用等,可抑制氧化磷酸化过程。
8.线粒体外的氧化主要通过穿梭和穿梭完成,前者可将胞质中NADH转换成线粒体中的,主要发生在组织,后者可将胞质中NADH 转换成线粒体中的,主要发生在组织,其P/O值分别为_________和_________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算与论述题:
1. 求 [11 1 ] 和 [201] 两晶向所决定的晶面,并绘图 表示出来。 答:设所求的晶面指数为(h k l) 则 1 1 1 1 1 1 h:k :l : : (112) 0 1 1 2 2 0
2. MgO 具有NaCl 结构。根据O2-半径为0.140nm 和Mg2+半 径为0.072nm,计算球状离子所占据的体积分数和计算 MgO 的密度。并说明为什么其体积分数小于74.05%? 解:在MgO 晶体中,正负离子直接相邻, a=2(r++r-)=0.424(nm) 4 3 4 3 4 rMg 4 r0 3 3 体积分数K (2rMg 2r0 ) 3 4×(4π/3)×(0.143+0.0723)/0.4243=68.52%
第二章 习题
习题3: 标出具有下列密勒指数的晶面和晶向: (1)立方晶系(421),(123),[211], [311]; (2)六方晶系(2111),(1101), [2111],[1213]
4. 判断面心立方晶胞中的[110]是否位于 (111)面上,并计算[110]方向上的线密度。 5. 已知纯钛有两种同素异构体:低温稳定 的密排六方结构ɑ-Ti和高温稳定的体心立方 结构β -Ti,其同素异构转变温度为882.5℃。 计算纯钛在室温和900 ℃的晶体中(112) 和(001)的晶面间距(已知aɑ(20 ℃)=0.2951nm,c ɑ(20 ℃)=0.4679nm, a β (900 ℃)=0晶面间距
(101 0)
晶面间距
3、立方晶体中的[001]方向是 4、理想密排六方结构金属的c/a为
5、任意合金的有序结构形成温度
次对称轴?
无序结构形成温度
6、某单质金属从高温冷却到室温的过程中发生同素异构 转变时体积膨胀,则低温相的原子配位数比高温相 。
7、简单立方晶体的致密度为?原子的配位数为? 8、立方晶体中(110)和(211)面同属于 晶带。 9、已知fcc结构中原子在(111)面上的堆垛方式为 ABCABC…,则在(001)面上的堆垛方式为? 10、由A和B两种元素组成的固溶体,同类原子间的结合 能分别为EAA,EBB,而异类原子间的结合能为EAB。当 A和B原子在该固溶体中呈现无序分布(随机分布)时, 则EAA≈EBB≈EAB。如果EAB<EBB和EAA,该固溶体最易形 成为无序、有序、偏聚态固溶体?
6. Ni的晶体结构为面心立方结构,原子半 径为r=0.1243nm,试求Ni的晶格常数和密 度。 7. Cr的晶格常数a=0.2884nm,密度为 ρ =7.19g/cm3,试求此时Cr的晶体结构。 8.In具有四方结构,其相对原子质量为 114.82,原子半径r=0.1625nm,晶格常数 a=0.3252nm,c=0.4946nm,密度 ρ =7.286g/cm3,试问In的单位晶胞内有多少 个原子?In的致密度为多少?
11、晶体中的对称轴中不存在 次对称轴。 12、fcc晶体若以100面为外表面,则表面上每个 原子的最邻近原子数为 个。 13、立方晶体中含有[111]晶向的晶面为? (1 01) (110)、(101)、 14、立方晶体中(111),(112),(110)晶面 间距最大的是? 15、在四方晶体中[100]晶向是 次对称轴?
密度 4[M(Mg) M(O) ] (2rMg 2r0 )3 N A
4×(24.3+16)/[6.023×1023×(0.424×10-7)3]=3.5112(g/cm3)
MgO 体积分数小于 74.05% ,原因在 于 r+/r-=0.072/0.14=0.514>0.414 ,正负 离子紧密接触,而负离子之间不直接 接触,即正离子将负离子形成的八面 体空隙撑开了,负离子不再是紧密堆 积,所以其体积分数小于等径球体紧 密堆积的体积分数74.05%。
9. Cu-Zn和Cu-Sn组成固溶体最多可溶入多少 原子数分数的Zn或Sn?若Cu晶体中固溶入 Zn的分子数为10%,最多还能溶入多少原 子分数的Sn?(Cu基固溶体的极限电子浓 度为1.36) 10.含ω (Mn)为12.3%, ω (C)为1.34%的奥 氏体钢,点阵常数为0.3624nm,密度为 7.83g/cm3,C、Fe、Mn的相对原子质量分别 为12.01,55.85,54.94,试判断此固溶体 的类型。
12. MgO具有NaCl型结构。Mg2+的离子半径 为0.078nm,O2-的离子半径为0.132nm。 试求MgO的密度、致密度。 13. Al3+和O2-的离子半径分别为0.051nm, 0.132nm,试求Al2O3的配位数。
填空题:
1、 CsCl为有序体心立方结构,它属于 2、六方晶系中
3. 写出图示立方晶格中晶面 ABCD和晶向CE的指数; 在 右 图 的 单 胞 中 画 出 晶 面 ( 111 ) 和 该 面 上 属 于 <112>三个晶向,并标出具体指数。
4. 试从结合键的角度,分析工程材料的分类及其特点。 答: 金属材料:主要以金属键为主,大多数金属强度和硬 度较高,塑性较好。 陶瓷材料:以共价键和离子键为主,硬、脆,不易变 形,熔点高。 高分子材料:分子内部以共价键为主,分子间为分子 键和氢键为主。 复合材料:是以上三中基本材料的人工复合物,结合 键种类繁多。性能差异很大。
