北师大版黄冈密卷八年级数学(上)密卷练测(9)第五章位置的确定双基卷
北师大版八年级数学上第五章《位置的确定》单元检测(1).docx
初中数学试卷 桑水出品初二数学第五章位置的确定一、填空题(每空4分,共33分)1. 生活中,确定物体的平面位置需要_____________数据。
2. 电影院里6排4号可用(6,4)来表示,则5排1号可表示为___________,(7,3)表示的含义是__________________。
3. 对于平面内任意一点P ,过点P 分别向x 轴、y 轴做垂线,垂足分别是A,B,若P 点坐标是(6,8),则PB=_____________.4. 如图,从观测点O 观察到A 点位置,如图所示,试用两种方式表示A 点位置__________。
第4题 第5题5.写出图中各点坐标:A_________,B________,C__________.6.点A 在x 轴上,位于原点右侧,距离原点5个单位长度;点B 在y 轴上,距离原点3个点为长度,则A点的坐标是____________,B 点的坐标是_____________.7.将点P (-4,+3)沿x 轴负方向平移一个单位,得到点P ’_________, 再将点P ’沿y 轴负方向平移两个单位得到P ”_______________.8.在平面直角坐标系中,点A (3,a )在x 轴上,点B (b ,4)在y 轴上,则a=___________,b=__________,ABC S ∆=_________. 9.如图,在直角坐标系中,ABO ∆是等边三角形,若B 点坐标是(2,0),则A 点坐标是_______________. 第9题10.在直角坐标系中,点p 和p ’关于y 轴对称,点p 与点p ’’关于x 轴对称,若点p 的坐标是(3,1),那么点p ’的坐标是__________,点p ’’的坐标是__________。
11.A (-a,b)和点B(a,b)关于________成轴对称;点P(-1,2)关于原点的对称点是________;已知点Q(-8,6),它到x 轴的距离是__________,它到y 轴的距离是_________,它到原点点的距离是________;当x=0, y 是任意实数时,点A(x,y)在__________上;如果点1p (-1,3)和2p (b,-3)关于x 轴对称,则b=_______.12.已知点A 在x 轴上,且距原点的距离为4个单位长度,则A 点的坐标为__________;一 个点在y 轴上,位于原点下方,距离原点3个单位长度,这个点是__________.13.(a,b )位于x 轴上方,y 轴左侧,则a_____0,b_______0。
北师大版八年级数学上册第五章-第八章单元测试卷(含答案)

第五章 《位置的确定》一、选择题1. 点M 在x 轴的上侧,距离x 轴5个单位长度,距离y 轴3个单位长度,则M 点的坐标为………………………………………………………………( )A. (5,3)B. (-5,3)或(5,3)C. (3,5)D. (-3,5)或(3,5)2. 设点A (m ,n )在x 轴上,位于原点的左侧,则下列结论正确的是( )A. m=0,n 为一切数B. m=O ,n <0C. m 为一切数,n=0D. m <0,n=03.在已知M (3,-4),在x 轴上有一点与M 的距离为5,则该点的坐标为( )A. (6,0)B. (0,1)C. (0,-8)D. (6,0)或(0,0)4. 在坐标轴上与点M (3,-4)距离等于5的点共有…………………( )A. 2个B. 3个C.4个D. 1个5. 在直角坐标系中A (2,0)、B (-3,-4)、O (0,0),则△AOB 的面积为…………………………………………………………………………………( )A. 4B. 6C. 8D. 36. 在坐标平面内,有一点P (a ,b ),若ab=0,那么点P 的位置在…( )A. 原点B. x 轴上C. y 轴D. 坐标轴上7. 若0 xy ,则点P (x,y )的位置是……………………………………( ) A. 在数轴上 B. 在去掉原点的横轴上C. 在纵轴上D. 在去掉原点的纵轴上8. 如果直角坐标系下两个点的横坐标相同,那么过这两点的直线……( )A. 平行于x 轴B. 平行于y 轴C. 经过原点D. 以上都不对9. 直角坐标系中,一个图案上各个点的横坐标和纵坐标分别乘以正数a (a >1),那么所得的图案与原来图案相比………………………………………( )A. 形状不变,大小扩大到原来的a 2倍B. 图案向右平移了a 个单位C. 图案向上平移了a 个单位D. 图案沿纵向拉长为a 倍二、填空题1. 点A (a ,b )和B 关于x 轴对称,而点B 与点C (2,3)关于y 轴对称,那么,a= _______ , b=_______ , 点A 和C 的位置关系是________________。
北师大版-数学-八年级上册-新版《第五章 位置的确定》单元综合练习

初中-数学-打印版《第五章 位置的确定》单元练习姓名: 班别: : 座号: 评分: 一. 选择题( 本大题共8小题, 每小题3分,共24分)1. 在直角坐标系中,M(-3,4), M 到x 、y 轴的距离与M /到x 、y 轴的距离相等,则M 的坐标为( ) A .(-3,-4) B. (3,4) C. (3,-4) D. (3,0). 2. 如图, 点A 与B 的横坐标( ) A. 相同 B. 相隔3个单位长度 C. 相隔1个单位长度 D. 无法确定. 3. 在直角坐标系中, 点P(-2,3)向右平移3个单位长度 后的坐标为( )A. (3,6)B. (1,3)C. (1,6)D. (3,3) 4. 如图, 与①中的三角形相比, ②中的三角形发生的变化是( ) A. 向左平移3个单位B. 向左平移1个单位C. 向上平移3个单位D. 向下平移1个单位.5. 如图, 点M(-3,4)离原点的距离是( )单位长度. A. 3 B. 4 C. 5 D. 7. 6. 若点P 在x 轴的下方, y 轴的左方, 到每条件坐标轴的距离都是3,则点P 的坐标为( ) A. (3,3) B. (-3,3) C. (-3,-3) D. (3,-3). 7. 点M(1,2)关于x 轴对称的点坐标为( )A. (-1,2)B. (1,-2)C. (2,-1)D. (-1,-2).8. 若某四边形顶点的横坐标变为原来的相反数, 而纵坐标不变, 此时图形位置也不变,则这四边形不是( )A.矩形B. 直角梯形C. 正方形D. 菱形. 二. 填空题(本大题共8小题,每小题3分,共24分)9. 在电影票上表示座位有 个数据, 分别是 .10. 如图,用(0,0)表示O 点的位置, 用(2,3)表示M 点的 位置, 则用 表示N 点的位置. 11.如图, 在直角坐标系中, O 是原点, A 在x 轴上, B 在y 轴上, 点O 的坐标是 ,点A 的坐标是 , 点B的坐标是 .12. 点P(-4,6)关于原点对称的点坐标为 .13. 在直角坐标系内, 将点A(-2.3)向右平移3个单位到B 点, 则点B 的坐标是 . 14. 一正三角形ABC, A(0,0),B(-4,0),C(-2,23),将三角形ABC 绕原点顺时针旋转1200得到的三角形的三个顶点坐标分别是 . 15. 点P(3,a )与点q(b,2)关于y 轴对称, 则a= , b= . 16. 如图, 将图中的点A 的纵坐标保持不变, 横坐标乘以-2,y 2 •A O x -1 •B y3 1 O 1 3 x ① y31-2 O x②yM • 4 -3 O x O•M•N 4•B O 2 •A O A-2则所得的图案与原图案相比, 变化的是.三. 解答题(本大题共6小题,共52分)17. 你能用两个数据表示学校篮球场的位置吗? 试试看.(6/)19. 在如图所示的直角坐标系中, 菱形ABCD的位置如图所示, 写出四个顶点A,B,C,D的坐标, 并计算其面积.(10/)20. 建立适当的直角坐标系, 表示边长为4的正方形的各顶点的坐标.(10/)21. 在直角坐标系中, 矩形ABCD的顶点坐标为A(-4,0),B(0,0),C(0,2),D(-4,2).将矩形的边AB和BC的长分别扩大一倍, 所得矩形的四个顶点坐标是什么?(10/)-2-2 –1 0 1 2531-142初中-数学-打印版。
北师大版八年级数学试题第五章位置的确定.doc

八年级数学试题第五章位置的确定一、填空题(每空2分,共50分)1.点P (一彳卫)和B (人7)关于原点对称,贝\\a^b= ___________2. ____________________________________ 点P 仏耐,其中ab = 0,P 点的位置在 .3. __________________________________________________ 点P (2d + 1卫一 1)到兀轴的距离是3,则P 点的坐标是 ___________________________________________ .4•如果点A 、B 、C 、D 的坐标依次为人⑶2)、B (3,-2)、C (-3,-2)、D (-3,0),则四边形ABCD 的而积是 _____________ .5.若点4(7°), 〃仇2)两点关于y 轴对称,贝, b= _____________________________ ・6. _____________________________________________________ 点P 在『轴上,它到4(72)的距离为3, P 点的坐标为 _______________________________________________ .7. 正方形的四个顶点中有两个点的坐标为©°)、⑵2),那么,其他两个点坐标为8. ________________________________________________________________ 如图18・1所示,多边形ABCDEF 是正六边形,六个顶点中纵朋标相同的点有 _______________________ 对;关于x 轴对称的点有 ____________ 对,到原点距离相等的点冇 __________ 个.9. _________________________________ 如图18・2所示,2图是1图经过平移、对称得到的图形,其屮点厶与点。
北师大版八年级上册数学第五章 位置的确定练习题(带解析)

北师大版八年级上册数学第五章位置的确定练习题(带解析)北师大版八年级上册数学第五章位置的确定练习题(带解析)..... 线线线考试范围:xxx;考试时间:100分钟;命题人:xxx学校:________________________;名称:_______________。
0___ ○…___……___…_…_:…… 不,预约考试班○ 班次○_…___……___…_…__……:名字姓氏u安装…u学校○ 学习○ 外部和内部。
0○ 1在回答问题之前,请填写您的姓名、班级、考试号和其他信息。
2.请正确填写答题表分卷i分数I记录评分员的分数I.单选题(备注)1、在下列图形中既是轴对称图形又是中心对称图形的是a.角b.线段c.等腰三角形d.平行四边形2.下面的公式是ab.(>)c=d.3.如图所示,在矩形纸ABCD中,ab=6cm,BC=8cm。
现在沿着AE将其对折,使点B落在边ad上的点B1处,折痕和边BC在点E处相交,则CE的长度为[]a.6cmb.4cmc.2cmd.1cm4.如果X上的方程式x24x+M=0没有实根,则实数M的取值范围为a.M<4B。
M>4C。
M<4D。
M>45、如图,点o在直线ab上,射线oc平分∠dob.若∠cob=35°,则∠aod等于试卷第1页,共22页………线…………○…………………线…………○…………a、35°b.70°c.110°d.145°6、一个不透明的袋子中有3个红球和2个黄球,这些球除颜色外完全相同.从袋子中……○___○…___……___…_…_:……号订考…__订_…__…_…___……__:……级…○班_○_…___……___…_…__……:名…装姓_装…___…_…__…_…___……:校…○学○……………………外内……………………○○……………………随机摸出一个球,它是黄球的概率为a.b.c。
北师大版-数学-八年级上册-第五章 位置的确定 单元测试【含答案】.

北师大版八上第五章《位置的确定》单元测试一、填空题(每小题3分,共30分)1.某学校的平面示意图如图1所示,如果实验楼所在位置的坐标为(4,2 ),语音室的所在位置的坐标为(5,1),那么学生公寓所在位置的坐标为.2.如果点(mn,m+n)在第四象限,那么点(m-1,n-2)在第象限.3.已知点P在第三象限,到x轴的距离为4,到原点O的距离为5,则点P的坐标为.4.已知长方形OABC在平面直角坐标系中的位置如图2所示,点B的坐标为(-4,-3),则该长方形的面积等于.5.平面直角坐标系内,点A(n,1-n)一定不在第象限.6.“怪兽吃豆豆”是一种计算机游戏,如图3的标志表示“怪兽”先后经过的几个位置,如果用(0,0)表示“怪兽”的第一个位置,用(7,8)表示“怪兽”的第九个位置,那么用同样的方式表示“怪兽”按图中箭头所指路线经过的第三个位置是,第五个位置是.7.如图4,作△ABC关于y轴的轴对称图形,那么所得图形△A′B′C′的顶点坐标分别是.8.对于边长为4的等边三角形ABC,以BC所在直线为x轴,以边BC的垂直平分线为y 轴建立直角坐标系,那么点A的坐标是.9.杨洋将点M关于x轴的对称点误认为是关于y轴的对称点,得到点(-4,-3),则点M 关于x轴的对称点是.10.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.观察图5中每一个正方形(实线)四条边上的整点的个数,请你猜测由里向外第10个正方形(实线)四条边上的整点个数共有个.二、选择题(每小题3分,共30分)1.在平面直角坐标系中,下列各点在第四象限的是( )A .(0,3-)B .(1-,3-)C .(3,1-)D .(1-,3)2.如图6所示的象棋盘上,若士的坐标是(-2,-2),相的坐标是(3,2),则炮的坐标是( )A .(3-,1-)B .(3-,0)C .(3-,2-)D .(2-,3-)3.点M (3a -,3a +)在x 轴上,则点M 的坐标是( )A .(0,6)B .(6,0)C .(6-,0)D .(0,6-)4.设点M (m ,n )在y 轴的负半轴上,则下列结论正确的是( )A .m =0,n 为任意实数B .m <0,n <0C .m =0,n <0D .m 为任意实数,n =05.已知长方形三个顶点的坐标分别为A (0,0),B (2,0),C (0,3-),那么第四个顶点D 的坐标是( )A .(2,3)B .(2,3-)C .(2-,3-)D .(3-,2)6a ab 有意义,则直角坐标系中点M (a ,b )的位置在( ) A .第一象限 B .第二象限C .第三象限D .第四象限 7.已知点P (x ,y ),且2(1)2x y +=--P 的坐标为( )A .(1-,0)B .(1-,2)C .(0,2)D .(1,2-)8.点M 为x 轴上方的点,到x 轴的距离为5,到y 轴的距离为3,则点M 的坐标为( )A .(5,3)B .(5-,3)或(5,3)C .(3,5)D .(3-,5)或(3,5)9.在平面直角坐标系内,A 、B 、C 三点的坐标分别是(0,0)、(4,0)、(3,2),以A 、B 、C 三点为顶点画平行四边形,则第四个顶点不可能在( )A .第一象限B .第二象限C .第三象限D .第四象限10.如图7,已知点A (1-,0)和点B (1,2),在坐标轴上确定点P ,使得△ABP 为直角三角形,则满足这样条件的点共有( )A .2个B .4个C .6个D .7个三、解答题(本大题共40分)1.(本小题8分)正方形ABCD 的边长为6,请选择一种你最喜欢的方法建立平面直角坐标系,写出各个顶点的坐标.2.(本小题8分)如图8,把△ABC 沿着y 轴对称变换得到111A B C △,再沿x 轴对称变换得到222A B C △,试问顶点A 2、B 2、C 2的坐标分别是什么?3.(本小题8分)如图9,长方形ABCD 的顶点A 的坐标为(1-,0),点B 的坐标(4-,0),点C 在第三象限,若长方形的周长为14,求C 、D 两点的坐标.4.(本小题8分)在平面直角坐标系中,△ABC 的边AB 在x 轴上,且AB =3,顶点A 的坐标为(5-,0),顶点C 的坐标为(2,5).(1)画出所有符合条件的△ABC ,并写出点B 的坐标;(2)求△ABC 的面积.5.(本小题8分)已知平面直角坐标系中有6个点:A (3,3),B (1,1),C (9,1),D (5,3),E (1-,9-),F (2-,12-),请将它们按下列要求分成两类,并写出同类点具有而另一类点不具有的一个特征(将答案按下列要求写在横线上:特征不能用否定形式表述,点用字母表示).甲类含有两个点,乙类含其余四个点:(1)甲类:点 、 是同一类点,其特征是 ;(2)乙类:点 , , , 是同一类点,其特征是 .四、综合题(本大题共20分)1.(本小题10分)如图10,A 点坐标为(6,6),B 点坐标为(8,2),求△AOB 的面积.2.(本小题10分)如图11,A 点坐标为(3,3),将△ABC 先向下移4个单位得△A ′B ′C ′,再将△A ′B ′C ′绕点O 逆时针旋转180°得△A ″B ″C ″,请你画出△A ′B ′C ′和△A ″B ″C ″,并写出点A ″的坐标.参考答案:一、1.(2,3-)2.三3.(3-,4-)4.125.三6.(1,2),(3,4)7.A′(2-,3),B′(1-,0),C′(4-,0)8.(0,-0,9.(4,3)10.40二、1.C2.B3.C4.C5.B6.A7.B8.D9.C10.C三、1.略.2.A2(6,5),B2(1,6),C3(3,1).3.C(4-,4-),D(1-,4-).4.(1)B(2-,0)或(8-,0);(2)152ABCS=△.5.(1)E,F,它们都在第三象限;(2)A,B,C,D,它们都在第一象限.四、1.18.2.解:A″(3-,1-).。
北师大版八年级数学上第五章《位置的确定》单元检测(1).docx

初中数学试卷 桑水出品初二数学第五章位置的确定一、填空题(每空4分,共33分)1. 生活中,确定物体的平面位置需要_____________数据。
2. 电影院里6排4号可用(6,4)来表示,则5排1号可表示为___________,(7,3)表示的含义是__________________。
3. 对于平面内任意一点P ,过点P 分别向x 轴、y 轴做垂线,垂足分别是A,B,若P 点坐标是(6,8),则PB=_____________.4. 如图,从观测点O 观察到A 点位置,如图所示,试用两种方式表示A 点位置__________。
第4题第5题 5.写出图中各点坐标:A_________,B________,C__________.6.点A 在x 轴上,位于原点右侧,距离原点5个单位长度;点B 在y 轴上,距离原点3个点为长度,则A 点的点的坐标是_____________.7.将点P (-4,+3)沿x 轴负方向平移一再将点P ’沿y 轴负方向平移两个单位8.在平面直角坐标系中,点A (3,a )在x y 轴上, 则a=___________,b=__________,ABC S ∆=_________.9.如图,在直角坐标系中,ABO ∆是等边三角形,若B 点坐标是(2,0),则A 点坐标是_______________. 第9题10.在直角坐标系中,点p 和p ’关于y 轴对称,点p 与点p ’’关于x 轴对称,若点p 的坐标是(3,1),那么点p ’的坐标是__________,点p ’’的坐标是__________。
11.A(-a,b)和点B(a,b)关于________成轴对称;点P(-1,2)关于原点的对称点是________;已知点Q(-8,6),它到x 轴的距离是__________,它到y 轴的距离是_________,它到原点点的距离是________;当x=0, y 是任意实数时,点A(x,y)在__________上;如果点1p (-1,3)和2p (b,-3)关于x 轴对称,则b=_______.12.已知点A 在x 轴上,且距原点的距离为4个单位长度,则A 点的坐标为__________;一 个点在y 轴上,位于原点下方,距离原点3个单位长度,这个点是__________.13.(a,b )位于x 轴上方,y 轴左侧,则a_____0,b_______0。
最新北师大版八年级数学(上册)单元测试题(卷)带答案全套7全

一、选择题(每小题3分,共30分)1.下列各组线段中,能够组成直角三角形的一组是( )A.3,4,4 B.3,4,6C.3,4,7 D.3,4,52.如图,在Rt△ABC中,∠A=90°,BC=2.5cm,AC=1.5cm,则AB的长为( ) A.3.5cm B.2cm C.3cm D.4cm第2题图第3题图3.如图,Rt△ABC中,∠ACB=90°,若AB=15cm,则正方形ADEC和正方形BCFG 的面积和为( )A.150cm2 B.200cm2 C.225cm2 D.无法计算4.适合下列条件的△ABC中,直角三角形的个数为( )①a=6,b=8,c=10;②a∶b∶c=1∶2∶2;③∠A=32°,∠B=58°;④a=7,b=24,c=25.A.2个 B.3个 C.4个 D.1个5.在△ABC中,AB=12,BC=16,AC=20,则△ABC的面积为( )A.96 B.120 C.160 D.2006.若△ABC的三边长a,b,c满足(a-b)(a2+b2-c2)=0,则△ABC是( )A.等腰三角形 B.直角三角形C.等边三角形 D.等腰三角形或直角三角形7.如图是医院、公园和超市的平面示意图,超市在医院的南偏东25°的方向,且到医院的距离为300m,公园到医院的距离为400m.若公园到超市的距离为500m,则公园在医院的( )A.北偏东75°的方向上 B.北偏东65°的方向上C.北偏东55°的方向上 D.无法确定第7题图第8题图8.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )A.32B.3 C.1 D.439.图①是我国古代著名的“赵爽弦图”,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长是( )A.51 B.49 C.76 D.无法确定第9题图第10题图10.如图,长方体的高为9m,底面是边长为6m的正方形,一只蚂蚁从如图的顶点A 开始,爬向顶点B.那么它爬行的最短路程为( )A.10m B.12m C.15m D.20m二、填空题(每小题3分,共24分)11.如图,一架长为4m的梯子,一端放在离墙脚2.4m处,另一端靠墙,则梯子顶端离墙脚________m.第11题图第12题图第13题图12.如图,△ABC中,AB=5cm,BC=6cm,BC边上的中线AD=4cm,则∠ADB的度数是________.13.如图是某地的长方形广场的示意图,如果小明要从A角走到C角,那么至少要走________.14.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,以点A为圆心,AC长为半径画弧,交AB于点D,则BD=________.15.如图是一个三级台阶,每一级的长,宽和高分别是50cm,30cm,10cm,A和B 是这个台阶的两个相对的端点,若一只壁虎从A点出发沿着台阶面爬到B点,则壁虎爬行的最短路线的长是________.第14题图第15题图第17题图16.已知长方形的两邻边的差为2,对角线长为4,则长方形的面积是________.17.如图,是一种饮料的包装盒,长、宽、高分别为4cm,3cm,12cm,现有一长为16cm的吸管插入到盒的底部,则吸管露在盒外部分的长度h的取值范围为____________.18.在△ABC中,若AC=15,BC=13,AB边上的高CD=12,则△ABC的周长为________.三、解答题(共66分)19.(8分)如图,正方形网格中有△ABC,若小方格边长为1,请你根据所学的知识,判断△ABC是什么三角形,并说明理由.20.(8分)如图,在△ABC中,AD=15,AC=12,DC=9,点B是CD延长线上一点,连接AB.若AB=20,求△ABD的面积.21.(8分)如图,在Rt△ABC中,∠ABC=90°,AB=16cm,正方形BCEF的面积为144cm2,BD⊥AC于点D,求BD的长.22.(10分)如图,一座城墙高13m,墙外有一条宽为9m的护城河,那么一架长为15m的云梯能否到达墙的顶端?23.(10分)如图,铁路上A,B两点相距25km,C,D为两村庄,AD⊥AB于点A,BC⊥AB 于点B,已知AD=15km,BC=10km,现在要在铁路AB旁建一个货运站E,使得C,D两村到E站距离相等,问E站应建在离A地多远的地方?24.(10分)如图,公路MN和公路PQ在点P处交会,公路PQ上点A处有学校,点A 到公路MN的距离为80m,现有一拖拉机在公路MN上以18km/h的速度沿PN方向行驶,拖拉机行驶时周围100m以内都会受到噪音的影响,试问该校受影响的时间为多长?25.(12分)图甲是任意一个直角三角形ABC,它的两条直角边的长分别为a,b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b 的正方形内.(1)图乙、图丙中①②③都是正方形.由图可知:①是以________为边长的正方形,②是以________为边长的正方形,③是以________为边长的正方形;(2)图乙中①的面积为________,②的面积为________,图丙中③的面积为________;(3)图乙中①②面积之和为__________;(4)图乙中①②的面积之和与图丙中正方形③的面积有什么关系?为什么?由此你能得到关于直角三角形三边长的关系吗?参考答案与解析1.D 2.B 3.C 4.B 5.A 6.D 7.B 8.A9.C 解析:依题意,设“数学风车”中的四个直角三角形的斜边长为x ,则x 2=(6×2)2+52=169,所以x =13,所以“数学风车”的周长是(13+6)×4=76.10.C 解析:如图①,AB 2=62+152=261;如图②,AB 2=122+92=225.∵261>225,∴蚂蚁爬行的最短路程为15m.11.3.2 12.90° 13.100m 14.4 15.130cm 16.6 17.3cm ≤h ≤4cm18.32或42 解析:∵AC =15,BC =13,AB 边上的高CD =12,∴AD 2=AC 2-CD 2,即AD =9,BD 2=BC 2-CD 2,即BD =5.如图①,CD 在△ABC 内部时,AB =AD +BD =9+5=14,此时,△ABC 的周长为14+13+15=42;如图②,CD 在△ABC 外部时,AB =AD -BD =9-5=4,此时,△ABC 的周长为4+13+15=32.综上所述,△ABC 的周长为32或42.19.解:△ABC 是直角三角形.(3分)理由如下:∵AC 2=22+42=20,AB 2=12+22=5,BC 2=32+42=25,∴AB 2+AC 2=BC 2,(6分)∴△ABC 是直角三角形.(8分)20.解:在△ADC 中,∵AD =15,AC =12,DC =9,∴AC 2+DC 2=122+92=152=AD 2,∴△ADC 是直角三角形.(3分)在Rt △ABC 中,AC 2+BC 2=AB 2,∵AB =20,∴BC =16,∴BD =BC -DC =16-9=7,(6分)∴S △ABD =12BD ×AC =12×7×12=42.(8分)21.解:∵正方形BCEF 的面积为144cm 2,∴BC =12cm.(2分)∵∠ABC =90°,AB =16cm ,∴AC =20cm.(4分)∵BD ⊥AC ,∴S △ABC =12AB ·BC =12BD ·AC ,∴BD =485cm.(8分)22.解:不能.(4分)理由如下:设这架云梯能够到达的墙的最大高度是h ,则根据勾股定理得h 2=152-92=144,解得h =12m.(8分)∵12<13,∴这架长为15米的云梯不能够到达墙的顶端.(10分)23.解:设AE =x km ,则BE =(25-x )km.(3分)根据题意列方程,得152+x 2=(25-x )2+102,解得x =10.(8分)故E 站应建立在离A 地10km 处.(10分)24.解:设拖拉机开到C 处学校刚好开始受到影响,行驶到D 处时,结束了噪声的影响,则有CA =DA =100m.(3分)在Rt △ABC 中,CB 2=1002-802=602,∴CB =60m ,(5分)∴CD =2CB =120m.(7分)∵18km/h =5m/s ,∴该校受影响的时间为120÷5=24(s).(9分)答:该校受影响的时间为24s.(10分) 25.解:(1)a b c (3分)(2)a 2 b 2 c 2(6分)(3)a 2+b 2(7分)(4)S ①+S ②=S ③.(8分)由图乙和图丙可知大正方形的边长为a +b ,则面积为(a +b )2,图乙中把大正方形的面积分为了四部分,分别是:边长为a 的正方形,边长为b 的正方形,还有两个长为a ,宽为b 的长方形,(10分)根据面积相等得(a +b )2=a 2+b 2+2ab ,由图丙可得(a +b )2=c 2+4×12ab .所以a 2+b 2=c 2.(12分)第二章 实数 检测卷分 题号 一 二 三 总分 得分一、选择题(每小题3分,共30分) 1.9的平方根是( )A .±3 B.±13 C .3 D .-32.下列实数中是无理数的是( ) A.9 B.227 C .π D.(3)03.下列各式计算正确的是( )A.2+3= 5 B .43-33=1 C .23×33=6 3 D.27÷3=34.已知a +2+|b -1|=0,那么(a +b )2017的值为( )A .-1B .1C .32017D .-320175.若m =30-3,则m 的范围是( )A .1<m <2B .2<m <3C .3<m <4D .4<m <56.实数a ,b 在数轴上的位置如图所示,且|a |>|b |,则化简a 2-|a +b |的结果为( )A .2a +bB .-2a +bC .bD .2a -b 7.估计8×12+18的运算结果应在哪两个连续自然数之间( ) A .5和6 B .6和7 C .7和8 D .8和9 8.已知a =3+2,b =3-2,则a 2+b 2的值为( ) A .4 3 B .14 C.14 D .14+4 39.化简二次根式-a 3的正确结果是( )A .a -aB .a aC .-a -aD .-a a10.若6-13的整数部分为x ,小数部分为y ,则(2x +13)y 的值是( ) A .5-313 B .3 C .313-5 D .-3 二、填空题(每小题3分,共24分)11.-5的绝对值是________,116的算术平方根是________.12.在实数-2,0,-1,2,-2中,最小的是________.13.若代数式x -3有意义,则实数x 的取值范围是______________.14.一个长方形的长和宽分别是62cm 与2cm ,则这个长方形的面积等于________cm 2,周长等于________cm.15.若最简二次根式5m -4与2m +5可以合并,则m 的值可以为________.16.已知x ,y 都是实数,且y =x -3+3-x +4,则y x=________. 17.已知 3.456≈1.859,34.56≈5.879,则345600≈________.18.任何实数a ,可用[a ]表示不超过a 的最大整数,如[4]=4,[3]=1.现对72进行如下操作:72――→第一次[72]=8――→第二次[8]=2――→第三次[2]=1,这样对72进行3次操作后变为1,类似地,①对81进行________次操作后变为1;②进行3次操作后变为1的所有正整数中,最大的是________.三、解答题(共66分)19.(每小题3分,共6分)求下列各式中x 的值:(1)(x -2)2+1=17; (2)(x +2)3+27=0.20.(每小题3分,共12分)计算下列各题:(1)8+32-2;(2)614+30.027-31-124125;(3)(6-215)×3-612;(4)(548-627+12)÷ 3.21.(6分)一个数的算术平方根为2M-6,平方根为±(M-2),求这个数.22.(8分)如图,四边形ABCD中,AB=AD,∠BAD=90°,若AB=22,CD=43,BC=8,求四边形ABCD的面积.23.(8分)用48米长的篱笆在空地上围一个绿化场地,现有两种设计方案:一种是围成正方形场地,另一种是围成圆形场地.选用哪一种方案围成的场地的面积较大?并说明理由.24.(8分)已知a-17+217-a=b+8.(1)求a的值;(2)求a2-b2的平方根.25.(8分)已知x=1-2,y=1+2,求x2+y2-xy-2x+2y的值.26.(10分)阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+22=(1+2)2.善于思考的小明进行了以下探索:设a +b 2=(m +n 2)2(其中a ,b ,m ,n 均为整数),则有a +b 2=m 2+2n 2+2mn 2.∴a =m 2+2n 2,b =2mn .这样小明就找到了一种把类似a +b 2的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:(1)当a ,b ,m ,n 均为正整数时,若a +b 3=(m +n 3)2,用含m ,n 的式子分别表示a 、b ,得a =______________,b =________;(2)利用所探索的结论,找一组正整数a ,b ,m ,n 填空:________+________3=(________+________3)2;(3)若a +43=(m +n 3)2,且a ,m ,n 均为正整数,求a 的值.参考答案与解析第二章检测卷1.A 2.C 3.D 4.A 5.B 6.C 7.B 8.B 9.C10.B 解析:∵3<13<4,∴6-13的整数部分x =2,则小数部分y =6-13-2=4-13,则(2x +13)y =(4+13)(4-13)=16-13=3.11. 5 14 12.-2 13.x ≥314.12 14 2 15.3 16.64 17.587.918.3 255 解析:①[81]=9,[9]=3,[3]=1,故答案为3;②最大的是255,[255]=15,[15]=3,[3]=1,而[256]=16,[16]=4,[4]=2,[2]=1,即进行3次操作后变为1的所有正整数中,最大的正整数是255.19.解:(1)(x -2)2=16,x -2=±4,∴x =6或-2;(3分)(2)(x +2)3=-27,x +2=-3,x =-5.(6分)20.解:(1)原式=22+42-2=52;(3分)(2)原式=52+0.3-15=2.6;(6分)(3)原式=18-245-32=32-65-32=-65;(9分)(4)原式=(203-183+23)÷3=43÷3=4.(12分)21.解:应分两种情况:①2M -6=M -2,解得M =4,∴2M -6=8-6=2,22=4;(3分)②2M -6=-(M -2),解得M =83,∴2M -6=163-6=-23(不合题意,舍去).故这个数是4.(6分)22.解:∵AB =AD ,∠BAD =90°,AB =22,∴BD =AB 2+AD 2=4.(3分)∵BD 2+CD 2=42+(43)2=64,BC 2=64,∴BD 2+CD 2=BC 2,∴△BCD 为直角三角形.(6分)∴S 四边形ABCD=S △ABD +S △BCD =12×22×22+12×43×4=4+8 3.(8分)23.解:选用围成圆形场地的方案围成的面积较大.(2分)理由如下:设S 1,S 2分别表示围成的正方形场地、圆形场地的面积,则S 1=⎝ ⎛⎭⎪⎫4842=5764(平方米),(4分)S 2=π·⎝ ⎛⎭⎪⎫482π2=576π(平方米).(6分)∵π<4,∴1π>14,∴5764<576π,即S 1<S 2,因此围成圆形场地的面积较大.(8分)24.解:(1)由题意知a -17≥0,17-a ≥0,(2分)∴a -17=0,∴a =17;(4分)(2)由(1)可知a =17,∴b +8=0,∴b =-8.(6分)∴a 2-b 2=172-(-8)2=225,∴a 2-b 2的平方根为±a 2-b 2=±15.(8分)25.解:∵x =1-2,y =1+2,∴x -y =(1-2)-(1+2)=-22,xy =(1-2)(1+2)=-1,(4分)∴x 2+y 2-xy -2x +2y =(x -y )2-2(x -y )+xy =(-22)2-2×(-22)+(-1)=7+4 2.(8分)26.解:(1)m 2+3n 22mn (2分) (2)4 2 1 1(答案不唯一)(6分)(3)由题意,得a =m 2+3n 2,b =2mn ,∴4=2mn ,且m ,n 为正整数,(8分)∴m =2,n =1或m =1,n =2,∴a =22+3×12=7或a =12+3×22=13.(10分)第三章 位置与坐标 检测卷分题号 一 二 三 总分 得分一、选择题(每小题3分,共30分)1.如果座位表上“5列2行”记作(5,2),那么(4,3)表示( )A .3列5行B .5列3行C .4列3行D .3列4行 2.如图,在直角坐标系中卡片盖住的数可能是( )A .(2,3)B .(-2,1)C .(-2,-2.5)D .(3,-2)3.点M (2,1)关于x 轴对称的点的坐标是( )A .(1,-2)B .(-2,1)C .(2,-1)D .(-1,2) 4.点P (-m +2,m -1)在y 轴上,则点P 的坐标为( )A .(0,-2)B .(1,0)C .(0,1)D .(0,2)5.如图是中国象棋的一盘残局,如果用(2,-3)表示“帅”的位置,用(1,6)表示“将”的位置,那么“炮”的位置应表示为( )A .(6,4)B .(4,6)C .(8,7)D .(7,8)6.已知点A (-1,-4),B (-1,3),则( )A .A ,B 关于x 轴对称 B .A ,B 关于y 轴对称C .直线AB 平行于y 轴D .直线AB 垂直于y 轴 7.如果点P (a ,2)在第二象限,那么点Q (-3,a )在( )A .第一象限B .第二象限C .第三象限D .第四象限 8.从车站向东走400m ,再向北走500m 到小红家;从车站向北走500m ,再向西走200m 到小强家,若以车站为原点,以正东、正北方向为正方向建立平面直角坐标系,则小红家、小强家的坐标分别为( )A .(400,500),(500,200)B .(400,500),(200,500)C .(400,500),(-200,500)D .(500,400),(500,-200)9.如图,直线BC 经过原点O ,点A 在x 轴上,AD ⊥BC 于D ,若B (m ,2),C (n ,-3),A (2,0),则AD ·BC 的值为( )A .不能确定B .5C .10D .710.如图,在平面直角坐标系中,半径均为1个单位长度的半圆O 1,O 2,O 3…组成一条平滑的曲线,点P 从原点O 出发,沿这条曲线向右运动,速度为每秒π2个单位长度,则第2017秒时点P 的坐标是( )A .(2016,0)B .(2017,1)C .(2017,-1)D .(2018,0)二、填空题(每小题3分,共24分)11.写出平面直角坐标系中一个第三象限内点的坐标:________.12.若点P(x,y)满足xy<0,则点P在第________象限.13.如图,用(0,0)表示点O的位置,用(3,2)表示点M的位置,则点N的位置可表示为________.14.若点P在第四象限,且到x轴、y轴的距离分别为3和4,则点P的坐标为________.15.已知点P(3,-1)关于y轴的对称点Q的坐标是(a+b,1-b),则ab的值为________.16.如果将点(-b,-a)称为点(a,b)的“反称点”,那么点(a,b)也是点(-b,-a)的“反称点”,此时称点(a,b)和点(-b,-a)互为“反称点”.容易发现,互为“反称点”的两点有时是重合的,例如(0,0)的“反称点”还是(0,0).请再写出一个这样的点:____________.17.如图,正方形ABCD的边长为4,点A的坐标为(-1,1),AB平行于x轴,则点C的坐标为________.第17题图第18题图18.如图,A,B两点的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP 的面积为6,则点P的坐标为________.三、解答题(共66分)19.(8分)(1)在坐标平面内画出点P(2,3);(2)分别作出点P关于x轴、y轴的对称点P1,P2,并写出P1,P2的坐标.20.(8分)图中标明了小英家附近的一些地方,已知游乐场的坐标为(3,2).(1)在图中建立平面直角坐标系,并写出汽车站和消防站的坐标;(2)某星期日早晨,小英同学从家里出发,沿(3,2),(3,-1),(1,-1),(-1,-2),(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.21.(10分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系后△ABC的顶点均在格点上.(1)画出△ABC关于x轴对称的图形△A1B1C1;(2)分别写出△A1B1C1的顶点A1,B1,C1的坐标.22.(8分)在平面直角坐标系中,已知点A(-5,0),B(3,0),C点在y轴上,△ABC 的面积为12,试求点C的坐标.23.(10分)在平面直角坐标系中,点A关于y轴的对称点为点B,点B关于x轴的对称点为点C.(1)若A点的坐标为(1,2),请在给出的坐标系中画出△ABC,设AB与y轴的交点为D,则S△ADO∶S△ABC=________;(2)若点A的坐标为(a,b)(ab≠0),试判断△ABC的形状.24.(10分)如图,平面直角坐标系中,过点A(0,2)的直线a垂直于y轴,M(9,2)为直线a上一点.若点P从点M出发,以2cm/s的速度沿直线a向左移动;点Q从原点同时出发,以1cm/s的速度沿x轴向右移动,多久后线段PQ平行于y轴?25.(12分)在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫作整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.(1)当m=3时,求点B的坐标的所有可能值;(2)当点B的横坐标为4n(n为正整数)时,用含n的代数式表示m.参考答案与解析1.C 2.D 3.C 4.C 5.A 6.C 7.C 8.C9.C 解析:据三角形面积公式得到S △ABC =12AD ·BC ,而S △ABC =S △ABO +S △ACO =12×2×2+12×2×3=5,因此得到12AD ·BC =5,∴AD ·BC =10. 10.B 解析:当点P 从原点O 出发,沿这条曲线向右运动,运动时间为1秒时,点P 的坐标为(1,1),运动时间为2秒时,点P 的坐标为(2,0),运动时间为3秒时,点P 的坐标为(3,-1),运动时间为4秒时,点P 的坐标为(4,0).根据图象可得第n 秒时,点P 的横坐标为n ,纵坐标每4秒一个循环.∵2017÷4=504……1,∴第2017秒时,点P 的坐标是(2017,1).11.(-1,-1)(答案不唯一) 12.二或四 13.(6,3) 14.(4,-3) 15.-1016.(-2,2)(答案不唯一) 17.(3,5)18.(3,0)或(9,0) 解析:设点P 的坐标为(x ,0),根据题意得12×4×|6-x |=6,解得x =3或9,所以点P 的坐标为(3,0)或(9,0).19.解:(1)点P (2,3)如图所示;(4分)(2)点P 1,P 2如图所示,(6分)P 1(2,-3),P 2(-2,3).(8分)20.解:(1)建立平面直角坐标系如图所示;(2分)汽车站的坐标为(1,1),消防站的坐标为(2,-2);(4分)(2)家→游乐场→公园→姥姥家→宠物店→邮局→家.(8分) 21.解:(1)作图略;(4分)(2)A 1(-1,-4),B 1(-2,-2),C 1(0,-1).(10分)22.解:设C 点坐标为(0,b ),那么S △ABC =12AB ·OC .(2分)又A (-5,0),B (3,0),所以AB =8,OC =|b |.(4分)所以12×8×|b |=12,|b |=3,所以b =3或-3.(6分)故点C 的坐标为(0,3)或(0,-3).(8分)23.解:(1)图略(3分) 1∶4(5分)(2)△ABC为直角三角形.(10分)24.解:设经过t s后PQ∥y轴,则AP=9-2t,OQ=t.(3分)∵PQ∥y轴,∴点P 与点Q的横坐标相等,即AP=OQ,(6分)∴9-2t=t,解得t=3.(9分)故3s后线段PQ 平行于y轴.(10分)25.解:(1)如图①,当点B的横坐标分别为3或4时,m=3,(3分)即当m=3时,点B的坐标的所有可能值是(3,0),(4,0);(5分)(2)如图②,当点B的横坐标为4n=4时,n=1,此时m=0+1+2=3;当点B的横坐标为4n=8时,n=2,m=1+3+5=9;当点B的横坐标为4n=12时,n=3,m=2+5+8=15;…,(10分)当点B的横坐标为4n时,m=(n-1)+(2n-1)+(3n-1)=6n-3.(12分)第四章一次函数检测卷分题号一二三总分得分一、选择题(每小题3分,共30分)1.下列图象中,表示y是x的函数的个数有( )A.1个 B.2个 C.3个 D.4个2.直线y=2x-4与y轴的交点坐标是( )A.(4,0) B.(0,4) C.(-4,0) D.(0,-4)3.直线y=-2x+b与x轴的交点坐标是(2,0),则关于x的方程2x-b=0的解是( )A.x=2 B.x=4 C.x=8 D.x=104.已知点M(1,a)和点N(2,b)是一次函数y=-2x+1图象上的两点,则a与b 的大小关系是( )A.a>b B.a=b C.a<b D.以上都不对5.若直线y=kx+b经过A(0,2)和B(3,0)两点,那么这个一次函数的关系式是( )A.y=2x+3 B.y=-23x+2 C.y=3x+2 D.y=x-16.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体重量x(kg)间有如下关系(其中x≤12).下列说法不正确的是( )x 01234 5y 1010.51111.51212.5A.x与y都是变量,且是自变量B.弹簧不挂重物时的长度为10cmC.物体重量每增加1kg,弹簧长度y增加0.5cmD.所挂物体重量为7kg时,弹簧长度为14.5cm7.正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )8.为了鼓励节约用水,按以下规定收取水费:(1)每户每月用水量不超过20立方米,则每立方米水费1.8元;(2)若每户每月用水量超过20立方米,则超过部分每立方米水费3元.设某户一个月所交水费为y(元),用水量为x(立方米),则y与x的函数关系用图象表示为( )9.一家电信公司提供两种手机的月通话收费方式供用户选择,其中一种有月租费,另一种无月租费.这两种收费方式的通话费用y(元)与通话时间x(min)之间的函数关系如图所示.小红根据图象得出下列结论:①l1描述的是无月租费的收费方式;②l2描述的是有月租费的收费方式;③当每月的通话时间为500min时,选择有月租费的收费方式省钱.其中,正确结论的个数是( )A.0 B.1 C.2 D.3第9题图第10题图10.如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(m,n),且2m +n=6,则直线AB的解析式是( )A .y =-2x -3B .y =-2x -6C .y =-2x +3D .y =-2x +6二、填空题(每小题3分,共24分)11.直线y =2x +1经过点(0,a ),则a =________.12.已知一次函数y =(1-m )x +m -2,当m ________时,y 随x 的增大而增大.13.已知函数y =(k -1)x +k 2-1,当k ________时,它是一次函数,当k ________时,它是正比例函数.14.如图,射线OA ,BA 分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s ,t 分别表示行驶距离和时间,则这两人骑自行车的速度相差________km/h.第14题图 第16题图15.已知关于x 的方程ax -5=7的解为x =1,则一次函数y =ax -12与x 轴交点的坐标为________.16.甲和乙同时加工一种产品,如图所示,图①、图②分别表示甲和乙的工作量与工作时间的关系,如果甲已经加工了75kg ,则乙加工了________kg.17.过点(-1,7)的一条直线与x 轴,y 轴分别相交于点A ,B ,且与直线y =-32x+1平行.则在线段AB 上,横、纵坐标都是整数的点的坐标是______________.18.如图,已知点A 和点B 是直线y =34x 上的两点,A 点坐标是⎝ ⎛⎭⎪⎫2,32.若AB =5,则点B 的坐标是________________.三、解答题(共66分)19.(8分)某市长途电话按时分段收费,3分钟内收费1.8元,以后每超过1分钟加收0.8元.若通话t 分钟(t ≥3).(1)求需付电话费y (元)与t (分钟)之间的函数关系式; (2)画出函数图象.20.(8分)已知一次函数y =kx +b 的图象经过M (0,2),N (1,3)两点.(1)求k,b的值;(2)若一次函数y=kx+b的图象与x轴交点为A(a,0),求a的值.21.(9分)已知一次函数y=kx+b的图象经过点A(0,2)和点B(-a,3),且点B 在正比例函数y=-3x的图象上.(1)求a的值;(2)求一次函数的解析式并画出它的图象;(3)若P(m,y1),Q(m-1,y2)是这个一次函数图象上的两点,试比较y1与y2的大小.22.(9分)已知一次函数y=mx+3-m,当m为何值时,(1)y随x值的增大而减小;(2)一次函数的图象与直线y=-2x平行;(3)一次函数的图象与x轴交于点(2,0).23.(10分)某销售公司推销一种产品,设x(件)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:(1)求每种付酬方案y关于x的函数表达式;(2)当选择方案一所得报酬高于选择方案二所得报酬时,求x的取值范围.24.(10分)一次函数y=kx+b(k≠0)的图象由直线y=3x向下平移得到,且过点A (1,2).(1)求一次函数的解析式;(2)求直线y =kx +b 与x 轴的交点B 的坐标;(3)设坐标原点为O ,一条直线过点B ,且与两条坐标轴围成的三角形的面积是12,这条直线与y 轴交于点C ,求直线AC 对应的一次函数的解析式.25.(12分)甲、乙两车分别从A ,B 两地同时出发相向而行,并以各自的速度匀速行驶,甲车途经C 地时休息一小时,然后按原速度继续前进到达B 地;乙车从B 地直接到达A 地,如图是甲、乙两车和B 地的距离y (km)与甲车出发时间x (h)的函数图象.(1)直接写出a ,m ,n 的值;(2)求出甲车与B 地的距离y (km)与甲车出发时间x (h)的函数关系式(写出自变量x 的取值范围);(3)当两车相距120km 时,乙车行驶了多长时间?参考答案与解析1.B 2.D 3.A 4.A 5.B 6.D 7.B 8.D 9.D10.D 解析:原直线的k =-2,向上平移后得到了新直线,那么新直线的k =-2. ∵直线AB 经过点(m ,n ),且2m +n =6,∴直线AB 经过点(m ,6-2m ).可设新直线的解析式为y =-2x +b 1,把点(m ,6-2m )代到y =-2x +b 1中,可得b 1=6.∴直线AB 的解析式是y =-2x +6.11.1 12.<1 13.≠1 =-114.4515.(1,0) 16.360 17.(1,4),(3,1) 解析:依据与直线y =-32x +1平行设出直线AB 的解析式y=-32x +b ,代入点(-1,7)即可求得b ,然后求出与x 轴交点的横坐标,列举符合条件的x 的取值,依次代入即可.18.⎝ ⎛⎭⎪⎫6,92或⎝ ⎛⎭⎪⎫-2,-32 解析:由题意可得|A ,B 两点的纵坐标之差||A ,B 两点的横坐标之差|=34,再由AB2=|A ,B 两点的纵坐标之差|2+|A ,B 两点的横坐标之差|2,求得|A ,B 两点的横坐标之差|=4,|A ,B 两点的纵坐标之差|=3.再分两种情况讨论求解即可.19.解:(1)依题意,得y =1.8+0.8(t -3)=0.8t -0.6(t ≥3);(4分) (2)画图略.(8分)20.解:(1)将M ,N 的坐标代入一次函数y =kx +b ,得b =2,k +b =3,解得k =1,故k ,b 的值分别是1和2;(4分)(2)将k =1,b =2代入y =kx +b 中得y =x +2.(6分)∵点A (a ,0)在y =x +2的图象上,∴0=a +2,∴a =-2.(8分)21.解:(1)∵点B (-a ,3)在正比例函数y =-3x 的图象上,∴3=-3×(-a ),∴a =1;(2分)(2)由(1)可得点B 的坐标为(-1,3),将(-1,3)和(0,2)代入y =kx +b 中,得b =2,-k +b =3,解得k =-1,∴一次函数的解析式为y =-x +2.(5分)画图象略;(7分)(3)∵-1<0,∴y 随x 的增大而减小.又∵m >m -1,∴y 1<y 2.(9分) 22.解:(1)由题意,得m <0;(3分)(2)由题意,得m =-2,3-m ≠0,解得m =-2;(6分)(3)把点(2,0)代入y =mx +3-m ,得2m +3-m =0,解得m =-3.(9分)23.解:(1)设方案一的解析式为y =kx ,把(40,1600)代入解析式,可得k =40,故解析式为y =40x ;(3分)设方案二的解析式为y =ax +b ,把(40,1400)和(0,600)代入解析式,可得a =20,b =600,故解析式为y =20x +600;(6分)(2)根据两直线相交可得方程40x =20x +600,解得x =30.(8分)根据两函数图象可知,当x >30时,选择方案一所得报酬高于选择方案二所得报酬.(10分)24.解:(1)根据题意,得k =3,k +b =2,解得b =-1.∴y =3x -1;(3分)(2)在y =3x -1中,当y =0时,x =13,∴点B 的坐标为⎝ ⎛⎭⎪⎫13,0;(5分) (3)设直线AC 的解析式为y =mx +n (其中m ≠0),则点C 的坐标为(0,n ),根据题意得S △BOC =12×13|n |=12,∴|n |=3,∴n =±3.(7分)当n =3时,m +n =2,解得m =-1,∴y =-x +3;当n =-3时,m +n =2,解得m =5,∴y =5x -3.∴直线AC 的解析式为y =-x +3或y =5x -3.(10分)25.解:(1)a =90,m =1.5,n =3.5;(3分) 解析:∵甲车途经C 地时休息一小时,∴2.5-m =1,∴m =1.5.乙车的速度为a m =1202,即a1.5=60,解得a =90.甲车的速度为300n -1=300-1201.5,解得n =3.5; (2)设甲车的y 与x 的函数关系式为y =kx +b .①休息前,0≤x ≤1.5,函数图象经过点(0,300)和(1.5,120),所以b =300,1.5k +b =120,所以k =-120,所以y =-120x +300;②休息时,1.5<x <2.5,y =120;③休息后,2.5≤x ≤3.5,函数图象经过点(3.5,0),又由题意可知k=-120,故b=420,所以y=-120x+420.(6分)综上,y与x的函数关系式为y=⎩⎪⎨⎪⎧-120x+300(0≤x≤1.5),120(1.5<x<2.5),-120x+420(2.5≤x≤3.5);(7分)(3)设当两车相距120km时,乙车行驶了x h.甲车的速度为(300-120)÷1.5=120(km/h),乙车的速度为120÷2=60(km/h).(8分)①若相遇前,则120x+60x=300-120,解得x=1;②若相遇后,则120(x-1)+60x=300+120,解得x=3.(11分) 答:当两车相距120km时,乙车行驶了1h或3h.(12分)第五章二元一次方程组检测卷分题号一二三总分得分一、选择题(每小题3分,共30分)1.下列方程组中,是二元一次方程组的是( )2.若方程mx+ny=6有两个解1,1xy=-⎧⎨=-⎩2,1xy=-⎧⎨=⎩,则m,n的值为( ) A.4,2 B.2,4 C.-4,-2 D.-2,-43.用加减法解方程组下列解法错误的是( )A.①×3-②×2,消去xB.①×2-②×3,消去yC.①×(-3)+②×2,消去xD.①×2-②×(-3),消去y4.实验课上,王老师把班级里40名学生分成若干小组,每小组只能是5人或6人,则有几种分组方案( )A.4种 B.3种 C.2种 D.1种5.若方程组的解满足x+y=0,则a的取值是( )A.-1 B.1 C.0 D.不能确定6.若|a+b-1|+(a-b+3)2=0,则a b的值( )A.1 B.2 C.3 D.-17.一个两位数,十位上的数字x比个位上的数字y大1,若颠倒个位与十位数字的位置,得到的新数比原数小9,求这个两位数列出的方程组正确的是( )8.如图,以两条直线l1,l2的交点坐标为解的方程组是( )第8题图第9题图9.为增强居民的节水意识,某市自2016年实施“阶梯水价”.按照“阶梯水价”的收费标准,居民家庭每年应缴水费y(元)与用水量x(m3)的函数关系的图象如图所示.如果某个家庭2016年全年上缴水费1180元,那么该家庭2016年用水的总量是( ) A.240m3 B.236m3 C.220m3 D.200m310.若方程组有无穷多组解,则2k+b2的值为( )A.4 B.5 C.8 D.10二、填空题(每小题3分,共24分)11.方程组的解是________.12.如图,直线l1的解析式是y=2x-1,直线l2的解析式是y=x+1,则方程组的解是________.13.已知关于x,y的二元一次方程2x+□y=7中,y的系数已经模糊不清,但已知是这个方程的一个解,那么原方程是____________.14.美术馆举办的一次画展中,展出的油画作品和国画作品共有100幅,其中油画作品的数量比国画作品数量的2倍多7幅,则展出的油画作品有________幅.15.对于实数x,y,定义新运算x*y=ax+by+1,其中a,b为常数,等式右边为通常的加法和乘法运算,若3*5=14,4*7=19,则5*9=________.16.甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价20%,乙商品提价60%,调整后两种商品的单价和比原来的单价和提高了50%,则购买调价后的3件甲商品和2件乙商品共需________元.17.如图①,在边长为a的大正方形中剪去一个边长为b的小正方形,再将图中的阴影部分剪拼成一个长方形,如图②.这个拼成的长方形的长为30,宽为20.则图②中Ⅱ部分的面积是________.第17题图第18题图18.甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地后,立即按原路以相同速度匀速返回(停留时间不作考虑),直到两车相遇.若甲、乙两车之间的距离y(千米)与两车行驶的时间x(小时)之间的函数图象如图所示,则A,B两地之间的距离为________千米.三、解答题(共66分)19.(9分)解下列方程组:20.(8分)若方程组的解是求(a+b)2-(a-b)(a+b)的值.21.(8分)如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).(1)求b的值;(2)不解关于x,y的方程组请你直接写出它的解.22.(10分)根据要求,解答下列问题:(1)解下列方程组(直接写出方程组的解即可):①的解为__________;②的解为__________;③的解为__________;(2)以上每个方程组的解中,x与y的大小关系为________;(3)请你构造一个具有以上外形特征的方程组,并直接写出它的解.23.(10分)湘西自治州风景优美,物产丰富,一外地游客到某特产专营店,准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产.若购买3盒豆腐乳和2盒猕猴桃果汁共需180元,购买1盒豆腐乳和3盒猕猴桃果汁共需165元.(1)请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格;(2)该游客购买了4盒豆腐乳和2盒猕猴桃果汁,共需多少元?24.(9分)为响应国家节能减排的号召,鼓励居民节约用电,各省先后出台了居民用电“阶梯价格”制度,下表中是某省的电价标准(每月).例如:方女士家5月份用电500度,电费=180×0.6+220×二档电价+100×三档电价=352元;李先生家5月份用电460度,交费316元.请问表中二档电价、三档电价各是多少?阶梯电量电价一档0~180度0.6元/度二档181~400度二档电价三档401度及以上三档电价25.(12分)已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A 骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题:(1)A比B后出发几个小时?B的速度是多少?(2)在B出发几小时后两人相遇?。
八年级数学上册第五章位置的确定单元测试卷试题

卜人入州八九几市潮王学校北师大龙岭2021年八年级数学上册第五章位置确实定单元测试卷一、选择题〔一共8小题,每一小题3分,总分值是24分〕1、在平面直角坐标系中,点P〔﹣3,2021〕在〔〕A、第一象限B、第二象限C、第三象限D、第四象限2、如图,右边坐标系中四边形的面积是〔〕C、D、53、假设a>0,那么点P〔﹣a,2〕应在〔〕A、第﹣象限内B、第二象限内C、第三象限内D、第四象限内4、以下语句,其中正确的有〔〕①点〔3,2〕与〔2,3〕是同一个点②点〔0,﹣2〕在x轴上③点〔0,0〕是坐标原点A、0个B、1个C、2个D、3个5、如图,点M〔﹣3,4〕到原点的间隔是〔〕A、3B、4C、5D、76、如图,假设将△ABC绕点C顺时针旋转90°后得到△A′B′C′,那么A点的对应点A′的坐标是〔〕A、〔﹣3,﹣2〕B、〔2,2〕C、〔3,0〕D、〔2,1〕7、将平面直角坐标系内某个图形各个点的横坐标不变,纵坐标都乘﹣1,所得图形与原图形的关系是〔〕A、关于x轴对称B、关于y轴对称C、关于原点对称D、重合8、点A〔﹣3,2〕关于原点对称的点是B,点B关于y轴对称的点是C,那么点C的坐标是〔〕A、〔3,﹣2〕B、〔3,2〕C、〔﹣3,﹣2〕D、〔﹣3,2〕二、填空题〔一共6小题,总分值是26分〕9、如图是几个主要景点示意图,根据图中信息可确定九疑山的中心位置C点的坐标为.10、矩形ABCD中,A、B、C三点的坐标分别是〔0,0〕〔6,0〕〔6,4〕,那么D点的坐标是,D点关于x轴的对称点是.11、点A〔3a﹣1,2﹣b〕,B〔2a﹣4,2b+5〕.假设A与B关于x轴对称,那么a=,b=;假设A与B关于y轴对称,那么a=,b=;假设A与B关于原点对称,那么a=,b=.12、一束光线从y轴上点A〔0,1〕出发,经过x轴上某点C反射后经过点B〔3,3〕,光线从A点到B点经过的道路长是.13、A在B的北偏东30°的方向上,且距B处500米,那么B在小岛A的的方向上,间隔A处米.14、如图,正方形ABCO的边长是2,E是BC中点,那么E点的坐标是,直线AE的解析式是.三、解答题〔一共3小题,总分值是50分〕15、对于边长为4的正方形,在图上建立适当的直角坐标系,并写出表示的各顶点的坐标.16、作图分析题:〔1〕在如图直角坐标系中,描出点〔9,1〕〔11,6〕〔16,8〕〔11,10〕〔9,15〕〔7,10〕〔2,8〕〔7,6〕〔9,1〕,并将各点用线段顺次连接起来.〔2〕这个图形是中心对称图形吗?假设是,它的对称中心的坐标是什么?〔3〕将上面各点的横坐标不变,纵坐标缩小为原来的一半,求出各点的坐标,再将各点依次连接起来.与原图形相比,所得图形有什么变化?〔4〕假设将原图形上各点的横坐标加2、纵坐标减5,猜一猜,图形会发生怎样的变化?〔5〕假设想让变化后的图形与原图形关于原点对称,原图形各点的坐标应该如何变化?17、李明设计的广告模板草图如下列图〔单位:米〕,李明想通过征求陈伟的意见,假设你是李明,你将如何把这个图形告知陈伟呢?答案及分析:一、选择题〔一共8小题,每一小题3分,总分值是24分〕1、在平面直角坐标系中,点P〔﹣3,2021〕在〔〕A、第一象限B、第二象限C、第三象限D、第四象限考点:点的坐标。
北师大版八年级(上)数学《确定位置》同步练习1(含答案)

3.1 确定位置一、考考你。
1.当我们面对朝阳时,前面是( ),后面是( ),左面是( ),右面是( )。
2.而当我们面对地图时,上面是( ),下面是( ),左面是( ),右面是( )。
二、解决问题。
1.下图中,A、B、C、D、E、F六户人家分布在两个相邻正方形道路的顶点上。
张小辉是一个投递员,他要给这六户人家送邮件。
(1)以A户人家为观测点:①B户人家在A点的( )方向上,距离是( )米。
②C户人家在A点的( )偏( )的方向上,距离是( )米。
③F户人家在A点的( )方向上,距离是( )米。
④E户人家在A点的( )方向上,距离是( )米。
⑤D户人家在A点的( )偏( )的方向上,距离是( )米。
(2)张小辉从A户出发,最后把信送到E户或D户,规定走的路线不得重复,请你设计出张小辉行走的路线。
2.据气象卫星观测,编号为F号的热带风暴的中心已移动到漳厦市北偏西65°方向,约720千米的海面上。
请你在平面图上标出此刻热带风暴的中心位置。
3.根据下面的描述,在平面图上标出各场所的位置。
(1)实验小学在凤蝶公园的北偏东75°方向1500米处。
(2)花卉市场在凤蝶公园的东偏北75°方向500米处。
(3)圣水寺在凤蝶公园正南方向1000米处。
(4)明珠山庄在凤蝶公园东偏南15°方向2000米处。
生活拓展滨海市的逸夫中学和逸夫小学分别位于大路的同侧(如下图)。
现在要在大路上设一个公共汽车停靠站,这个站建在什么位置,可以使两所学校的学生到停靠站的距离相等。
(1)请画出示意图,并说明理由。
(2)这个站处于中学的什么方向上?处于小学的什么方向上?参考答案二、1.(2)共有8种行走路线可供选择,如A—B—C—F—E—D等。
生活拓展(1)连结中学与小学两点成一条线段,取线段中点作垂线,延长垂线相交于大路,交点就是建立停靠站的最佳点。
(2)东南方向;西南方向。
(北师大版)八年级数学上册(全册)单元检测卷汇总9

D C B A FE D C B A (北师大版)八年级数学上册(全册)单元检测卷汇总新版北师大版八年级数学上册第1章《勾股定理》单元测试试卷及答案(1)一、填空题(1. 如图,在长方形ABCD 中,已知BC=10cm ,AB=5cm ,则对角线BD= cm 。
2. 如图,在正方形ABCD 中,对角线为22,则正方形边长为 。
3. 把直角三角形的两条直角边同时扩大到原来的2倍,则其斜边扩大到原来的 。
4. 三角形中两边的平方差恰好等于第三边的平方,则这个三角形是 三角形。
5. 飞机在空中水平飞行,某一时刻刚好飞到小刚头顶正上方4000米处,过了20秒,飞机距离小刚5000米,则飞机每小时飞行 千米。
6. 在Rt △ABC 中,∠C=90°,若a:b=3:4,c=20,则a= ,b= 。
7. 已知一个直角三角形的两边长分别是3和4,则第三边长为 。
8. 如图所示,在矩形ABCD 中,AB=16,BC=8,将矩形沿AC 折叠,点D 落在点E 处,且CE 与AB 交于点F ,那么AF= 。
9. 如图,将一根长24cm 的筷子,置于底面直径为5cm ,高为12cm 的圆柱形茶杯中,设筷子露在杯子外面的长为acm (茶杯装满水),则a 的取值范围是 。
10. 如图,数轴上有两个Rt △ABC 、Rt △ABC ,OA 、OC 是斜边,且OB=1,AB=1,CD=1,OD=2,分别以O为圆心,OA、OC为半径画弧交x轴于E、F,则E、F分别对应的数是。
11. 一艘轮船以16海里/时的速度离开港口向东南方向航行,另一艘轮船在同时同地以12海里/时的速度向西南方向航行,则一个半小时后两船相距海里。
12. 所谓的勾股数就是指使等式a2+b2=c2成立的任何三个自然数。
我国清代数学家罗士林钻研出一种求勾股数的方法,即对于任意正整数m、n(m>n),取a=m2-n2,b=2mn,c=m2+n2,则a、b、c就是一组勾股数。
北师大版八年级(上)数学《确定位置》同步练习3(含答案)
3.1 确定位置
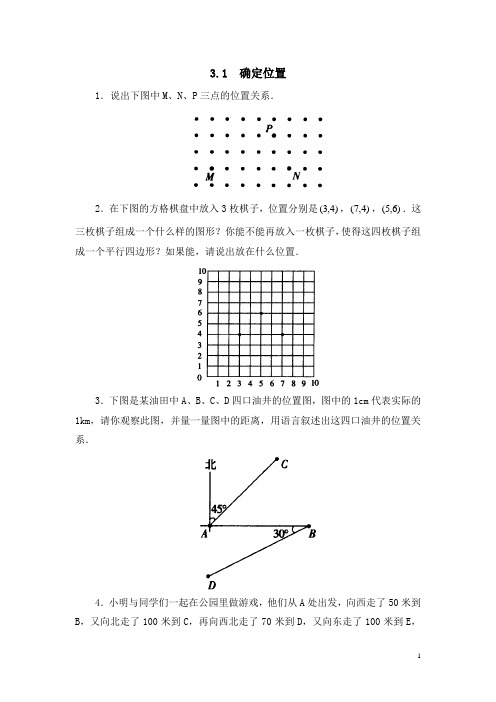
1.说出下图中M、N、P三点的位置关系.
2.在下图的方格棋盘中放入3枚棋子,位置分别是)4,3(,)4,7(,)6,5(.这三枚棋子组成一个什么样的图形?你能不能再放入一枚棋子,使得这四枚棋子组成一个平行四边形?如果能,请说出放在什么位置.
3.下图是某油田中A、B、C、D四口油井的位置图,图中的1cm代表实际的1km,请你观察此图,并量一量图中的距离,用语言叙述出这四口油井的位置关系.
4.小明与同学们一起在公园里做游戏,他们从A处出发,向西走了50米到B,又向北走了100米到C,再向西北走了70米到D,又向东走了100米到E,
再向南走了80米到F,请画出这次活动中他们所走的线路.
5.请你观察一下你家周围的环境,画出一个你家周围的地形图,图中至少应有四条路,三个地点(如家的位置,某商店,饭店,银行,某标志性建筑等).
参考答案
1.N在M的右边5个单位,M在N的左边5个单位.P在M的右边4个单位、上边2个单位的位置,M在P的下边2个单位、左边4个单位的位置.P在N的左边1个单位,上边2个单位的位置,N在P的下边2个单位,右边1个单位的位置.
2.三角形(或等腰三角形、等腰直角三角形),)6,1(或)6,9(或)2,5(.
3.C油井在A油井的东北方向2.5千米处,B油井在A油井的正东4千米处,D油井在B油井的南偏西60°,距离3千米处.
4、5画图略.。
北师大版八年级上第三章《位置的确定》单元测试题(含答案) (43)

第三章位置的确定拔高训练一、学科内综合题(每题20分,共40分)1.A、B、C、D、E各点的坐标如图所示,确定△ABE、△EBD、△ABC的面积,你是怎样做的?你发现了什么规律?2.设m是实数,那么平面上的点P(3m2-5m+2,1-m)不可能在第几象限?二、应用题(20分)3.下图是一种活动门的示意图,平时不用的时候推到一边去,•晚上用的时候拉过来锁上,节约空间,非常方便,它是由一个个菱形组成的,图中菱形的两对角线之比为2:3,请用适当的方法表示菱形的各顶点的位置.三、创新题(20分)4.矩形的两条边长分别为4、6,建立适当的直角坐标系,使它的一个顶点的坐标为(-2,-3),与同伴交流,你们的答案相同吗?四、中考题(20分)5.已知两点P1(-2,3),P2(4,-5),求P1、P2两点的距离.答案:一、1.分析:由坐标求出线段的长.(可利用勾股定理)解:A、B、C、D、E各点的坐标分别为A(0,6),B(0,3),C(6,1),D(-2,-2),E(-•8,0).△ABE的面积为12(8×6-8×3)=12.△EBD的面积为8×5-12×8×3-12×2×5-12×6•×2=17.△ABC的面积为12(6×5-2×6)=9.•规则为可以将每个三角形的面积看成边与坐标轴平行的矩形的一半.2.分析:要判断点P不经过第几象限,需讨论点P的横、纵坐标符号的可能性.解:∵3m2-5m+2=(m-1)(3m-2),∴当m≤23时,3m2-5m+2≥0.此时1-m>0,点P•在第一象限或y轴上,当23<m<1时,3m2-5m+2<0.此时1-m>0,点P在第二象限.当m≥1时,3m2-5m+2≥0,此时1-m≤0,点P在第四象限或坐标原点.综观以上结论,可知点P不可能在第三象限.点拨:象限与其中点的坐标符号的关系要记清楚,此为易考点.二、3.分析:用横、竖两线交点的方法确定点的位置.解:如图:JH=4,AI=6,∴JH:AI=2:3.这些点的位置为A (3,1),B (7,1),C (11,1),D (13,4),E (11,7),F (9,4),G (7,7),H (5,4),I (3,7),J (1,4).1312111098765432101234567J IDH G FECBA点拨:此题有多种方法. 三、4.分析:在平面直角坐标系中先找出点(-2,-3),然后选取其他的点,使其成为一个矩形,但由于只确定一个点,所以答案有无数个.解:如图,建立直角坐标系,则四个点的坐标分别为 A (-2,3),B (-2,-3),C (2,-3),D (2,3),答案有无数个.点拨:选点时,尽可能使点之间有规律,易于点的坐标的表示. 四、5.分析:如图D-5-11,欲求P 1与P 2之间的距离,就是要求线段P 1P2的长,过P 1作x 轴的垂线,过P 2作y 轴的垂线,设两条线段交于A 点,则△P 1AP 2是直角三角形.根据勾股定理,得P 1P 2解:如图所示,过P 1、P 2分别作x 轴、y 轴的垂线相交于A 点. 则A 点的坐标为A (-2,•-5),∴P 1A=│-5-3│=8,P2A=│-2-4│=6,∴P 1P 2.点拨:此题能顺利求出P1P2的长的关键是过P1、P2两点分别作x轴、y轴的垂线,构造出Rt△P1AP2,然后利用勾股定理求解.。
八年级数学上册 第五章位置的确定提高训练(无答案) 北师大版

一、确定位置适当的方式借助刻度尺、量角器等作图工具,确定出三个景点的位置.二、平面直角坐标系平面直角坐标系是沟通代数和几何的桥梁,是非常重要的数学工具.要掌握以下几点:1.坐标平面内的点和有序实数对一一对应已知点P(x,y),它的横坐标x和纵坐标y的顺序是不能任意交换的,A(3,2)和B(2,3)表示两个不同的点.对于坐标平面内的任意一点P,存在唯一的一对有序实数(x,y)和它对应;反过来,对于任意一对有序实数(x,y),在坐标平面内有唯一的P点和它对应.这里,(x,y)称为点P的坐标,x是横坐标,y是纵坐标,x写在前,y写在后.各象限内坐标的符号点P(x,y)在第一象限内,则x>0,y>0,反之亦然.点P(x,y)在第二象限内,则x<0,y>0,反之亦然.点P(x,y)在第三象限内,则x<0,y<0,反之亦然.点P(x,y)在第四象限内,则x>0,y<0,反之亦然.2.特殊点的坐标x轴上点的纵坐标为零,即(x,0),如果某点的坐标为(x,0),则它在x轴上.y轴上点的横坐标为零,即(0,y),如果某点的坐标为(0,y),则它在y轴上.第一、三象限角平分线上点的横坐标和纵坐标相等,即(x,x),如果点的坐标为(x,x),则它必定在一、三象限角平分线上.第二、四象限角平分线上点的横坐标和纵坐标互为相反数,即(x,-x),如果点的坐标为(x,-x),则它在二、四象限角平分线上.原点的坐标是(0,0),反之,坐标是(0,0)的点是原点.3.对称点关于x轴对称的两个点的横坐标相等,纵坐标互为相反数.关于y轴对称的两点的横坐标互为相反数,纵坐标相等.关于原点对称的两点的横坐标纵坐标都互为相反数.如果一个点的坐标为(a ,b ),那么这个点关于x 轴、y 轴、原点的对称点分别是(a ,-b ),(-a ,b ),(-a ,-b ).它的逆命题亦成立.4.点P (x ,y )到两坐标轴的距离点P(x ,y )到x 轴和y 轴的距离分别是|y |和|x |.点P(x ,y )到坐标原点的距离为22x y .(由勾股定理可证)读一读:有一次,小明的爸爸维修店里缺少一个如图1的零件,准备交代出差在千里之外的姑父购买,他用电话和姑父联系,可是不管爸爸怎么描述零件的形状和大小,在电话那头的姑父总是弄不明白,一直在电话里“什么形状的?再说一遍……”,急得小明的爸爸直抖脚.刚学过用坐标表示位置的小明马上量了一下各边的长度,然后建立如图的直角坐标系.爸爸把电话交给了小明,小明慢条斯理地向姑父描述道:这是一个封闭的图形,共有10个顶点,按照顺时针的顺序,各点的坐标依次是(0,0),(0,7),(4,7),(4,5),(2,5),(2,2),(6,2),(6,6),(8,6),(8,0). 在电话那头的姑父只须记下了这10点的坐标,然后再在直角坐标系中描出这些点,并按顺时针的顺序连结各点便可得到该零件的形状,这时只须再告诉他坐标单位,在点话那头的他便可知零件的大小了. 你是否体验到了应用方向角和坐标确定位置的好处了呢?1、春天来了,初一(2)班同学到人民公园春游,张明、王丽、李华三位同学和其他同学走散了,同学们已经到了中心广场,而他们仍在牡丹园赏花,他们对着景区示意图(图2)在电话中向老师告诉了他们的位置.张明:“我这里的坐标是(300,300)”. 王丽:“我这里的坐标是(200,300)”. 李华:“我在你们东北方向约420m 处”.实际上,他们所说的位置都是正确的.你知道张明 和王丽同学是如何在景区示意图上建立的坐标吗? 你理解李华同学所说的“东北方向约420m 处”吗? 用他们的方法,你能描述公园内其他景点的位置吗?O x y 1 2 3 4 5 6 7 8 7654321图22、在平面直角坐标系中,点(-2,4)所在的象限是( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限 3、若a >0,则点P (-a ,2)应在 ( )A .第—象限内B .第二象限内C .第三象限内D .第四象限内4、已知0a b <<,则点()A a b b -,在第______象限.5、已知点P (x ,y +1)在第二象限,则点Q (-x +2,2y +3)在第______象限.6、点P (1,2)关于y 轴对称点的坐标是 . 已知点A 和点B (a ,-b )关于y 轴对称,求点A 关于原点的对称点C 的坐标___________.7、已知点 A(3a -1,2-b),B(2a -4,2b+5). 若A 与B 关于x 轴对称,则a=________,b=_______; 若A 与B 关于y 轴对称,则a=________,b=_______; 若A 与B 关于原点对称,则a=________,b=_______.8、学生甲错将P 点的横坐标与纵坐标的次序颠倒,写成(m ,n ),学生乙错将Q 点的坐标写成它关于x 轴对称点的坐标,写成(-n ,-m),则P 点和Q 点的位置关系是_________.9、点P (x ,y )在第四象限内,且|x |=2,|y | =5,P 点关于原点的对称点的坐标是_______.10、若点(5-a ,a -3)在第一、三象限角平分线上,则a=______________。
3.1确定位置 同步练习题(含答案)2021-2022学年北师大版八年级数学上册

3.1确定位置同步练习题2021-2022学年北师大版八年级数学上册A组(基础题)一、填空题1.如图,若用(2,3)表示点A的位置,则点C的位置可表示成______,(7,7)表示点______的位置.2.一张足球门票上,如果将6区12排8号记为(6,12,8),那么(2,2,3)的含义是______.3.根据下列表述,能确定一点位置的是______.①东经118°,北纬40°;①宝鸡市文化东路;①北偏东60°;①奥斯卡影院1号厅3排.4.如图是一台雷达探测相关目标得到的部分结果,若图中目标A的位置表示为(2,90°),B 的位置表示为(4,210°),则C的位置表示为______.二、选择题5.点A的位置如图所示,则关于点A的位置下列说法中正确的是( )A.距点O 4 km处B.北偏东40°方向上4 km处C.在点O北偏东50°方向上4 km处D.在点O北偏东40°方向上4 km处6.某地发生了7.0级地震,以下能够准确表示这次地震震中位置的是( ) A.北纬30.3° B.东经103°C.该地西南方向D.北纬30.3°,东经103°7.某人买了一张电影票,当他进去时,发现是一座多厅多层电影院,他要找自己的位置,需要在电影票上找到相关的数据有( )A.1个B.2个C.3个D.4个8.如图是沈阳市地区简图的一部分,图中“故宫”“鼓楼”所在的区域分别是( )A.D7,E6 B.D6,E7 C.E7,D6 D.E6,D7三、解答题9.如图,对于点O来说,点A的位置是南偏东30°方向30 km处.(1)对于点O来说,点B的位置是______.(2)对于点O来说,点C的位置是______.(3)求A,D两点间的距离.B组(中档题)四、填空题10.如图,A表示三经路与一纬路的十字路口,B表示一经路与三纬路的十字路口.如果用(3,1)→(3,2)→(3,3)→(2,3)→(1,3)表示一条由A到B的路径,那么用同样的方式写出另一条由A到B的路径:(3,1)→______→(1,1)→______→(1,3).(答案不唯一)11.用一个8位数为每一个学生设计一个准考证号码.规定前两位数字表示入学年份,第3位数字表示所在的年级,第4~5位数字表示所在的班级,第6~7位数字表示座位号,末位数字用1表示男生,用2表示女生.如:06年入学八年级12班3号的一名男学生的准考证号码为06812031.那么07年入学七年级5班15号的一名女学生的准考证号码为______.12.若小明家在学校的北偏东60°的方向,距离学校3 000米,则学校在小明家的______方向______米处.13.如图,点A在观测点北偏东30°方向,且与观测点的距离为8千米,将点A的位置记作A(8,30°).用同样的方法将点B,点C的位置分别记作B(8,60°),C(4,60°),则观测点的位置应在点______1.五、解答题14.明明在一处资料中得知,在某海洋的小岛A,小岛B,小岛C的附近有一珊瑚群,如图所示.但此资料并未标出珊瑚群的确切位置,只给出一段文字:此珊瑚群距离小岛B,小岛C一样远,又在小岛A的东南方向.明明能找到珊瑚群的位置吗?他是怎样找的?C组(综合题)15.射线a绕原点O从数轴的正半轴逆时针旋转一定的角度θ(0°≤θ≤360°),射线上的一点N 与原点O的距离(ON)为n,并规定:当0°≤θ≤90°或270°≤θ ≤360°时,点N的位置记作N(θ,n);当90°<θ<270°时,点N的位置记作N(θ,-n).如图,点S,T的位置表示为S(30°,2.5),T(235°,-4).回答下列问题:(1)已知点A(70°,3),点B(250°,-4),则点A与点B的距离为7;线段AB的中点M 的位置是(______,______).(2)已知点C(120°,-5),点D(300°,6),P(0°,4),点Q从C点出发,以2个单位长度/秒的速度在线段CD上来回运动;同时射线OP以10°/秒的速度绕原点O逆时针旋转,当时间t秒(0≤t≤36)为何值时,OP①CD?并求出此时①POQ的面积.(3)直接写出位置满足(θ,5)的所有点与图中纵轴所围成的图形面积(结果保留一位小数).参考答案3.1确定位置同步练习题2021-2022学年北师大版八年级数学上册A组(基础题)一、填空题1.如图,若用(2,3)表示点A的位置,则点C的位置可表示成(6,2),(7,7)表示点E的位置.2.一张足球门票上,如果将6区12排8号记为(6,12,8),那么(2,2,3)的含义是2区2排3号.3.根据下列表述,能确定一点位置的是①.①东经118°,北纬40°;①宝鸡市文化东路;①北偏东60°;①奥斯卡影院1号厅3排.4.如图是一台雷达探测相关目标得到的部分结果,若图中目标A的位置表示为(2,90°),B 的位置表示为(4,210°),则C的位置表示为(3,150°).二、选择题5.点A的位置如图所示,则关于点A的位置下列说法中正确的是( D )A.距点O 4 km处B.北偏东40°方向上4 km处C.在点O北偏东50°方向上4 km处D.在点O北偏东40°方向上4 km处6.某地发生了7.0级地震,以下能够准确表示这次地震震中位置的是( D ) A.北纬30.3° B.东经103°C.该地西南方向D.北纬30.3°,东经103°7.某人买了一张电影票,当他进去时,发现是一座多厅多层电影院,他要找自己的位置,需要在电影票上找到相关的数据有( D )A.1个B.2个C.3个D.4个8.如图是沈阳市地区简图的一部分,图中“故宫”“鼓楼”所在的区域分别是( C )A.D7,E6 B.D6,E7 C.E7,D6 D.E6,D7三、解答题9.如图,对于点O来说,点A的位置是南偏东30°方向30 km处.(1)对于点O来说,点B的位置是北偏东45°方向40km处.(2)对于点O来说,点C的位置是北偏西30°方向35km处.(3)求A,D两点间的距离.解:连接AD.由题意,得OD=40 km,OA=30 km,①AOD=30°+60°=90°.所以①AOD是直角三角形.在Rt①AOD中,由勾股定理,得AD=302+402=50(km).答:A,D两点间的距离是50 km.B组(中档题)四、填空题10.如图,A表示三经路与一纬路的十字路口,B表示一经路与三纬路的十字路口.如果用(3,1)→(3,2)→(3,3)→(2,3)→(1,3)表示一条由A到B的路径,那么用同样的方式写出另一条由A到B的路径:(3,1)→(2,1)→(1,1)→(1,2)→(1,3).(答案不唯一)11.用一个8位数为每一个学生设计一个准考证号码.规定前两位数字表示入学年份,第3位数字表示所在的年级,第4~5位数字表示所在的班级,第6~7位数字表示座位号,末位数字用1表示男生,用2表示女生.如:06年入学八年级12班3号的一名男学生的准考证号码为06812031.那么07年入学七年级5班15号的一名女学生的准考证号码为07705152.12.若小明家在学校的北偏东60°的方向,距离学校3 000米,则学校在小明家的南偏西60°方向3__000米处.13.如图,点A在观测点北偏东30°方向,且与观测点的距离为8千米,将点A的位置记作A(8,30°).用同样的方法将点B,点C的位置分别记作B(8,60°),C(4,60°),则观测点的位置应在点O1.五、解答题14.明明在一处资料中得知,在某海洋的小岛A ,小岛B ,小岛C 的附近有一珊瑚群,如图所示.但此资料并未标出珊瑚群的确切位置,只给出一段文字:此珊瑚群距离小岛B ,小岛C 一样远,又在小岛A 的东南方向.明明能找到珊瑚群的位置吗?他是怎样找的?解:能找到珊瑚群的位置.如图,作BC 的垂直平分线,再沿小岛A 的东南方向作射线,则它们的交点P 为珊瑚群的位置.C 组(综合题)15.射线a 绕原点O 从数轴的正半轴逆时针旋转一定的角度θ(0°≤θ≤360°),射线上的一点N 与原点O 的距离(ON )为n ,并规定:当0°≤θ≤90°或270°≤θ ≤360°时,点N 的位置记作N (θ,n );当90°<θ<270°时,点N 的位置记作N (θ,-n ).如图,点S ,T 的位置表示为S (30°,2.5),T (235°,-4).回答下列问题:(1)已知点A (70°,3),点B (250°,-4),则点A 与点B 的距离为7;线段AB 的中点M 的位置是(250°,-0.5).(2)已知点C (120°,-5),点D (300°,6),P (0°,4),点Q 从C 点出发,以2个单位长度/秒的速度在线段CD 上来回运动;同时射线OP 以10°/秒的速度绕原点O 逆时针旋转,当时间t 秒(0≤t ≤36)为何值时,OP ①CD ?并求出此时①POQ 的面积.(3)直接写出位置满足(θ,5)的所有点与图中纵轴所围成的图形面积(结果保留一位小数).解:(2)①当OP 逆时针旋转30°时,OP ①CD . 此时t =3010=3.点Q 移动的长度为2×3=6. 所以OQ =1.所以S ①POQ =12 OP ·OQ =12 ×4×1=2.①当OP 逆时针旋转210°时,OP ①CD . 此时t =21010=21.点Q 移动的长度为2×21=42. 所以OQ =3.所以S ①OPQ =12 OP ·OQ =12×4×3=6.(3)由题意可知,位置满足(θ,5)的所有点与图中纵轴所围成的图形是半径为5的半圆形,其面积为12 ×π×52≈39.3.。
北师版八年级数学上册 3.1确定位置 能力提升卷

北师版八年级数学上册3.1确定位置能力提升卷一、选择题(共10小题,3*10=30)1.确定一个地点的位置,下列说法正确的是( )A.南偏东1000米B.西北方向C.距此500米D.距此南600米2.电影院里的座位按“×排×号”编排,排数与号数都按由小到大的顺序编排,小明的位置简记为(8,6),小菲的位置简记为(8,12),则以下关于小明与小菲的位置判断正确的是() A.同一排B.前后同一条直线上C.中间隔6个人D.前后隔6排3.根据下列表述,能确定位置的是()A.红星电影院2排B.北京市四环路C.北偏东30° D.东经118°,北纬40°4.点A的位置如图,则关于点A的位置下列说法正确的是()A.距点O 4 km处B.北偏东40°方向上4 km处C.在点O北偏东50°方向上4 km处D.在点O北偏东40°方向上4 km处5.钓鱼岛历来就是中国不可分割的领土,中国对钓鱼岛及其附近海域拥有无可争辩的主权,能够准确表示钓鱼岛位置的是()A.北纬25°40′~26°B.东经123°~124°34′C.福建的正东方向D.东经123°~124°34′,北纬25°40′~26°6. 如图,雷达探测器测得六个目标A,B,C,D,E,F出现,按照规定的目标表示方法,目标C,F的位置分别表示为C(6,120°),F(5,210°),按照此方法在表示目标A,B,D,E的位置时,其中表示不正确的是()A.A(5,30°) B.B(2,90°) C.D(4,240°) D.E(3,60°)7.如图是株洲市的行政区域平面图,下列说法明显错误的是()A.炎陵位于株洲市区南偏东约35°的方向上B.醴陵位于攸县的北偏东约17°的方向上C.株洲县位于茶陵的南偏东约30°的方向上D.株洲市区位于攸县的北偏西约21°的方向上8.电影院里的座位按“×排×号”编排,排数与号数都按由小到大的顺序编排,小明的位置简记为(8,6),小菲的位置简记为(8,12),则以下关于小明和小菲的位置判断正确的是() A.同一列B.前后同一条直线C.中间隔6人D.中间隔5人9.如图是某古塔周围建筑群的平面示意图,这座古塔A的位置用(5,4)来表示,小明同学由点B出发到古塔A的路径表示错误的是()A.(2,2)→(2,4)→(4,5)B.(2,2)→(2,4)→(5,4)C.(2,2)→(2,4)→(4,4)→(5,4)D.(2,2)→(2,3)→(5,3)→(5,4)10.如图,在象棋盘上“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )A.(-1,1) B.(-2,-1) C.(-3,1) D.(1,-2)二.填空题(共8小题,3*8=24)11.如果将教室里第5行、第3列的座位表示为(5,3),那么第4行、第6列的座位表示为________;(2,3)表示的是教室里第________行、第________列的座位.12. 如图,OP是一条射线,OA,OB,OC是三条线段,其中OA=a,OB=b,OC=c,并且∠BOP=30°,AO⊥BO,OC是∠AOB的角平分线.若点B可表示为(b,30°),则点A 可表示为,点C可表示为.13.有一个英文单词的字母顺序对应如图中的(2,1),(2,2),(4,2),(5,1)(列在前,行在后),则这个英文单词是________.14.如图,如果规定行号写在前面,列号写在后面,那么A点的位置用有序数对表示为()15.如图是小明所在学校的示意图,学校大门位于从左数第5条纵向网格线与从下数第1条横向网格线的交点上,它的位置表示为(5,1),则实验楼的位置表示为_____________,________的位置表示为(7,5).16.如图,A表示三经路与一纬路的十字路口,B表示一经路与三纬路的十字路口,如果用(3,1)→(3,2)→(3,3)→(2,3)→(1,3)表示由A到B的一条路径,用同样的方式写出另一条由A到B的路径:(3,1)→ _________ →_________→ _________→(1,3).17.如图是小刚在镜子中看到的自己的脸,他对妹妹说:如果我用有序数对(0,2)表示左眼,用有序数对(2,2)表示右眼,那么嘴的位置可以表示成___________.18.将正整数按如图的规律排列下去,用(n,m)表示第n排从左到右第m个数.若(4,2)表示实数9,则表示实数17的是(________,________).三.解答题(共7小题,46分)19.(6分) 下面的表格中有25个汉字,每一个汉字需要用一个大写字母和一个阿拉伯数字来表示.如D5表示“大”,如果约定的是B1,C2,A1,B4,D4,D3,B2,那么表达的意思是“我是最棒的孩子”。
