苏教版高中数学必修二课时37直线与圆的复习课2
高中数学必修2直线与圆优质课件:直线与圆的位置关系(复习课)

和直线l2之间运动才可,此时相应的m∈1,23 3.
∴m的取值范围是1,2 3 3.
[类题通法] 要注意结合图象,得出正确的答案,不能想当然.要 注意直线之间倾斜程度的比较,像在此例题中,我们要 注意比较直线 l 的斜率 k=- 33与直线 AB 的斜率 k=- 1,如果注意到它们的关系了,就不易出错.
[对点训练]
2.已知直线 l:y=- 33x+m 与圆 x2+y2=1 在第一象限内 有交点,求 m 的取值范围. 解:∵l:y=- 33x+m,圆x2+y2=1, ∴l可变形为: 3 x+3y-3m=0,圆的圆心为(0,0), 半径长r=1. 当直线和该圆相切时,应满足d=|-33+m9|=1,解得m=
又OP⊥OQ,∴KOP·KOQ=-1即x1x2+y1y2=0. ∴x1·x2+12(3-x1)·12(3-x2)=0, 整理得5x1x2-3(x1+x2)+9=0, ∴5×4m-5 27-3×(-2)+9=0. 解得m=3满足① ∴实数m的值为3.
[类题通法] 此题设出 P,Q 两点的坐标,但在求解过程中又不 能刻意地求出来,只将它作为一个转化过程中的桥梁, 这种“设而不求”的解题方法在解析几何中很常见,要注 意认真体会并掌握.
[类题通法] 过已知圆外一点求切线的方程一般有三种方法: (1)设切线斜率,用判别式法; (2)设切线斜率,用圆心到直线的距离等于半径长; (3)设切点(x0,y0),用切线公式法.
[对点训练] 1.已知圆 C:(x-2)2+(y-1)2=1.求:
(1)过 A(3,4)的圆 C 的切线方程; (2)在两坐标轴上的截距相等的圆 C 的切线方程. 解:(1)当所求直线的斜率存在时,设过 A(3,4)的直线方程为 y -4=k(x-3),即 kx-y+4-3k=0, 由|2k-11++4k-2 3k|=1,得 k=43. 所以切线方程为 y-4=43(x-3),即 4x-3y=0. 当所求直线的斜率不存在时,直线方程为 x=3,也符合题意. 故所求直线方程为 4x-3y=0 或 x=3.
2019—2020年最新苏教版高中数学必修二《直线与圆》综合考点复习及解析.docx

(新课标)2019—2020学年苏教版高中数学必修二课题:直线与圆综合复习【教学目标】1.掌握直线方程的几种形式,能判断两直线平行或垂直的位置关系,能用解方程组的方法求两条相交直线的交点坐标.理解两点间的距离公式,点到直线的距离公式,会求与此有关的距离问题.2.掌握圆的标准方程与一般方程,并能判断直线与圆的位置关系;能根据给定两个圆的方程,判断两圆的位置关系,初步了解用代数方法处理几何问题的思路. 【重点与难点】1. 掌握直线方程的几种形式;2. 掌握圆的标准方程与一般方程,并能判断直线与圆的位置关系、两圆的位置关系。
【教学过程】一、热身训练1.(2010年苏州质检)直线x +ay +3=0与直线ax +4y +6=0平行的充要条件是a =_______。
解析:由两条直线平行可知⎩⎪⎨⎪⎧4-a 2=0,6≠3a ,∴a =-2.答案:-22. (2009年高考安徽卷改编)直线l 过点(-1,2)且与直线2x -3y +4=0垂直,则l 的方程是 。
解析:由题意知,直线l 的斜率为-32,因此直线l 的方程为y -2=-32(x +1),即3x +2y -1=0.答案:3x +2y -1=03. 若圆C 的半径为1,圆心在第一象限,且与直线4x -3y =0和x 轴都相切,则该圆的标准方程是 . 解析:由题意,设圆心(x 0,1),∴|4x 0-3|42+(-3)2=1,解得x 0=2或x 0=-12(舍),∴所求圆的方程为(x -2)2+(y -1)2=1. 答案:(x -2)2+(y -1)2=14.已知圆C 1:(x +1)2+(y -1)2=1,圆C 2与圆C 1关于直线x -y -1=0对称,则圆C 2的方程为________________.解析:圆C 1:(x +1)2+(y -1)2=1的圆心为(-1,1).圆C 2的圆心设为(a ,b ),C 1与C 2关于直线x -y -1=0对称,∴⎩⎪⎨⎪⎧b -1a +1=-1,a -12-b +12-1=0,解得⎩⎪⎨⎪⎧a =2,b =-2,圆C 2的半径为1,∴圆C 2的方程为(x -2)2+(y +2)2=1.5. (2009年高考天津卷) 若圆x 2+y 2=4与圆x 2+y 2+2ay -6=0(a >0)的公共弦的长为23,则a =________.解析:两圆方程作差易知弦所在直线方程为:y =1a,如图,由已知|AC |=3,|OA |=2,有|OC |=1a=1,∴a =1.答案:1二、知识要点1.直线的倾斜角(1)在平面直角坐标系中,对于一条与x 轴相交的直线,如果把x 轴所在的直线绕着 按 方向旋转到和直线重合时所转的 记为α,那么α就叫做直线的倾斜角.(2)当直线与x 轴平行或重合时,规定直线的倾斜角 . (3)倾斜角的取值范围是 . 2.直线的斜率(1) 倾斜角不是 的直线,它的倾斜角α的 叫做这条直线的斜率,直线的斜率常用k 表示,即k = .(2)经过两点()11,P x y 和()()2212,Q x y x x ≠的直线的斜率公式为:k = . 3.直线方程的几种形式:4.平行(1)若两条直线的斜率k 1、k 2均存在,在y 轴上的截距分别为b 1、b 2,则l 1∥l 2的充要条件是 .(2)若两条直线l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0,则l 1∥l 2的充要条件为 . 5.垂直(1)若两条直线的斜率k 1,k 2均存在,则l 1⊥l 2⇔ .(2)若两条直线l 1:A 1x +B 1y +C 1=0和l 2:A 2x +B 2y +C 2=0,则l 1⊥l 2名称 方程的形式适用范围点斜式不能表示垂直于x 轴的直线 斜截式不能表示垂直于x 轴的直线两点式 不能表示垂直于x 轴和y 轴的直线截距式 不能表示垂直于x 轴和y 轴以及过原点的直线一般式 无限制,可表示任意位置的直线⇔.6.点到直线的距离点P(x0,y0)到直线Ax+By+C=0的距离为d=,特别地,两条平行直线Ax+By+C1=0,Ax+By+C2=0间的距离为d =.7.直线系方程(1)平行直线系:与直线Ax+By+C=0平行的直线可以表示为.(2)垂直直线系:与直线Ax+By+C=0垂直的直线可以表示为.(3)过两条直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0的交点的直线系为:.8.圆的方程(1)标准方程:(x-a)2+(y-b)2=r2,其中为圆心,r为半径.(2)一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0)其中圆心为,半径为 .9.直线l∶Ax+By+C=0与圆(x-a)2+(y-b)2=r2(r>0)的位置关系(1)几何方法:圆心(a,b)到直线Ax+By+C=0的距离d=,⇔直线与圆相交;⇔直线与圆相切;⇔直线与圆相离.(2)代数方法:由消元,得到一元二次方程判别式为Δ,则⇔直线与圆相交;⇔直线与圆相切;⇔直线与圆相离.10.两圆的位置关系:(设两圆的半径分别为12,r r,圆心距为d)外离外切相交内切内含三、典例精讲题型一:直线的倾斜角与斜率例1.已知直线l过点P(-1,2),且与以A(-2,-3)、B(3,0)为端点的线段相交,求直线l 的斜率的取值范围.法一:(数形结合)15,2 PA PBk k==-(-∞,12-]∪[5,+∞).法二:设直线l的斜率为k,则直线l的方程为y-2=k(x+1),即kx-y+k+2=0.∵A、B两点在直线的两侧或其中一点的直线l上,∴(-2k+3+k+2)(3k-0+k+2)≤0,即(k-5)(4k+2)≥0,∴k≥5或k≤1 2 -.即直线l的斜率k的取值范围是(-∞,12-]∪[5,+∞).题型二:直线的位置关系例2.求直线l1:2x+y-4=0关于直线l:3x+4y-1=0对称的直线l2的方程.题型三:圆的方程例3.根据下列条件求圆的方程:(1)经过坐标原点和点P (1,1),并且圆心在直线2x +3y +1=0上;(2)已知一圆过P (4,-2)、Q (-1,3)两点,且在y 轴上截得的线段长为43,求圆的方程; (3)已知圆的半径为10,圆心在直线y =2x 上,圆被直线x -y =0截得的弦长为42. (1)22(4)(3)25x y -++=(2)222120x y x +--=或2210840x y x y +--+= (3)22(2)(4)10x y -+-=或22(2)(4)10x y +++=题型四:直线与圆的位置关系例4.已知圆C :x 2+y 2-2x +2y +1=0,与圆C 相切的直线l 交x 轴、y 轴的正方向于A 、B 两点,O 为原点,OA =a ,OB =b (a >2,b >2).(1)求证:圆C 与直线l 相切的条件是(a -2)(b -2)=2; (2)求线段AB 中点的轨迹方程; (3)求△AOB 面积的最小值.解 依题意得,直线L 的方程为 xa +yb=1即bx+ay-ab=0,圆C 的方程为(x-1)2+(y-1)2=1(1) ∵直线与圆相切, ∴|a+b-ab|a 2+b 2=1,化简: (a-2)(b-2)=2 ①(2) 设AB 的中点为(,)x y ,则22a x b y=⎧⎨=⎩代人①得:1(1)(1)(1,1)2x y x y --=>>(3) 由(a-2)(b-2)=2, 得ab=2a+2b-2 ∴SΔAOB =12|ab|=a+b-1=(a-2)+(b-2)+3≥2(a-2)(b-2) +3=2 2 +3, 当且仅当a=b=2+ 2 时,面积有最小值:2 2 +3.四、走进高考(模拟)1. 在△ABC 中,BC 边上的高所在直线方程为x -2y +1=0,∠A 的平分线所在直线方程为y =0,若点B 坐标为(1,2),求点A 和C 的坐标.分析:利用高线与∠A 的平分线求得点A 坐标,然后求出直线AC 与BC 的方程,从而求出C 点坐标.解 A 点既在BC 边的高线上,又在∠A 的平分线上,由210x y y -+=⎧⎨=⎩得A(-1,0),∴k AB =1,而x 轴是角A 的平分线, ∴k AC = –1,∴AC 边所在直线方程为y =-(x +1) ①又k BC = –2, ∴BC 边所在直线方程为y –2=–2(x –1) ② 联立① ②得C 的坐标为(5,–6)点拨: 综合运用三角形和直线有关知识,寻找解题突破口,将问题转化为先求一些直线方程,再求直线的交点.这是解决这一类问题的常用办法.2. (2009年高考上海卷改编) 求点P (4,-2)与圆x 2+y 2=4上任一点连线的中点轨迹方程。
高中数学新苏教版精品教案《苏教版高中数学必修2 2.2.2 直线与圆的位置关系》2

直线与圆的位置关系【考纲要求】直线与圆、圆与圆的位置关系,B 级要求. 【学习目标】能判断直线与圆的位置关系,能用直线与圆的方程解决一些简单的问题.主要问题:(1)判断直线与圆位置关系;(2)相切时会求切线方程;(3)相交时会求弦长;(4)相离时会求有关距离最值. 【课堂活动】问题1 直线30mx y -+=与圆22:16C x y +=的位置关系是 .练习1.已知直线:5120l x y a ++=,圆22:20C x y x +-=. (1)若l 与圆C 相切,则a 的值为 ;(2)若l 与圆C 相交,则a 的取值范围为 ; (3)若l 与圆C 相离,则a 的取值范围为 ; (4)若l 被圆C 截得的弦长为1013,则a 的值为 .问题2 过点()3,1P 作圆()22:11C x y -+=的两条切线,切点分别为,A B ,以此为条件,你认为哪些问题可以研究?请你把问题编写完整,并尝试解答.问题3 如图,已知圆22:1O x y +=与x 轴相交于,A B 两点,P 是圆O 上异于,A B 的任意一点,直线,PA PB 分别交直线3x =于,M N 两点,E 为线段MN 的中点. (1)判断直线PE 与圆O 的位置关系并加以证明;(2)求证:以MN 为直径的圆总经过定点,并求出定点坐标.【课堂归纳】1.直线与圆的位置关系:如何判断?(1)相交⇔ ⇔ ; (2)相切⇔ ⇔ ; (3)相离⇔ ⇔ . 2.直线与圆相切问题:设322264120x y x y +--+=1ax by +=221x y +=(),P a b 10x y -+=22(3)1x y -+=b x y +=21y x -=b P 0843=++y x PB PA ,012222=+--+y x y x B A ,C 1,2,则四边形ABCD 的面积的最大值_________.9如图,已知圆O :22=2交轴于A ,B 两点,点P -1,1为圆O 上一点.曲线C 是以AB的椭圆,点F 为其右焦点.过原点O 作直线PF 的垂线交椭圆C 的右准线l 于点Q .1求椭圆C 的标准方程;2证明:直线PQ 与圆O 相切.3试探究:当点P 在圆O 上运动时(不与A,B 重合), 直线PQ 与圆是否保持相切的关系?2.(备用) 已知圆25)2()1(:22=-+-y x C ,直线047)1()12(:=--+++m y m x m l (m ∈R ). (1)求证:不论m 取什么值,直线l 与圆C 恒交于两点;(2)求直线l 被圆C 截得的线段的最短长度,以及此时直线l 的方程.。
苏教版高中数学必修2课件 2.2.2 直线与圆的位置关系课件

当 堂
案
双
设
计
【提示】 相切、相交和相离.
基 达
标
课
前
2.能否用代数的方法,即通过联立直线与圆的方程,依
自
课
主 导
据方程组解得个数,判定直线与圆的位置关系?
时 作
学
业
【提示】 能.
课 堂 互 动 探 究
教 师 备 课 资 源
菜单
SJ ·数学 必修2
教 学
直线 Ax+By+C=0(A2+B2≠0)与圆(x-a)2+(y-b)2= 易
教 学 教 法 分 析
教 学 方 案 设 计
课 前 自 主 导 学
课 堂 互 动 探 究
菜单
SJ ·数学 必修2
易 错 易 误 辨 析
当 堂 双 基 达 标
课 时 作 业
教 师 备 课 资 源
教 学 教 法 分 析
教 学 方 案 设 计
课 前 自 主 导 学
课 堂 互 动 探 究
菜单
SJ ·数学 必修2
SJ ·数学 必修2
教
学
易
教 法
错
《2.2.2 直线与圆的位置关系》课件
易
分
误
析
辨
析
教
学
当
方
堂
案
双
设 计
●三维目标
基 达
标
课
1.知识与技能
前
自 主
(1)理解直线与圆的三种位置关系.
课 时
导
作
学
(2)掌握用圆心到直线的距离 d 与圆的半径 r 比较,以及 业
课 堂
通过方程组解的个数判断直线与圆位置关系的方法.
高中数学新苏教版精品教案《苏教版高中数学必修2 2.2.2 直线与圆的位置关系》

直线、圆的复习
导学目标:1能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系2能用直线和圆的方程解决一些简单的问题3在学习过程中,体会用代数方法处理几何问题的思想.
教学重点和难点:直线与圆的位置关系。
圆的弦长和中点弦问题。
教学方法:设问、合作、探究
教学程序:
一、设问研习
以问题的形式梳理重点知识点。
二、合作探究
四个小题,学生板演。
2+2+4-2+5m=0表示圆时,m的取值范围为______________.
:-12+-12=1外一点=0和直线+2-3=0交于P,Q两点,且OP⊥OQ O 为坐标原点,求该圆的圆心坐标及半径.
思考:圆C:2+2-6-8+21=0和直线--4+3=0
1证明:不管取何值,直线和圆总有两个不同交点;
2求当取什么值时,直线被圆截得的弦最短,并求这条最短弦的长。
四、评价稳固
学生练习。
2+2=4与圆2+2+2a-6=0a>0的公共弦的长为2错误!,那么a=________-+3=0与圆-12+-22=4相交于A、B两点,且弦AB的长为2错误!,那么a=________
五、小结。
高中数学 第二章 2.2.2直线与圆的位置关系配套课件 苏教版必修2

第三页,共22页。
研一研·问题探究(tànjiū)、课堂更高效
2.2.2
探究点一 如何判定直线与圆的位置关系 问题 1 平面几何中,直线与圆有哪几种位置关系?
答 直线与圆有三种位置关系:相交、相切、相离.
第四页,共22页。
研一研·问题探究(tànjiū)、课堂更高效
2.2.2
问题 2 在初中,我们怎样判断直线与圆的位置关系? 答 (1)利用直线与圆的公共点个数可以判断,即有两个公 共点是相交,有一个公共点是相切,没有公共点是相离; (2)利用圆心到直线的距离 d 与圆半径的大小关系判断它们 之间的位置关系,若 d>r,直线与圆相离;若 d=r,直线 与圆相切;若 d<r,直线与圆相交.
研一研·问题探究、课堂(kètáng)更高效
2.2.2
探究点三 与直线截圆所得弦长有关的问题
例 3 求直线 x- 3y+2 3=0 被圆 x2+y2=4 截得的弦长.
解 方法一 如图,设直线 x- 3y+2 3=0
与圆 x2+y2=4 交于 A,B 两点,弦 AB 的中点
为 M,则 OM⊥AB(O 为坐标原点),
样当方程组无解时,直线与圆相离;方程组有一解时,直线
与圆相切;方程组有两解时,直线与圆相交.
第六页,共22页。
研一研·问题探究(tànjiū)、课堂更高效
2.2.2
探究点二 直线与圆的位置关系的应用 例 1 求直线 4x+3y=40 和圆 x2+y2=100 的公共点坐标,
并判断它们的位置关系.
解 直线 4x+3y=40 和圆 x2+y2=100 的公共点坐标就是方
不满足条件.
当直线 l 不垂直于 x 轴时,可设直线 l 的方程为 y-4=k(x+
高中数学 复习直线与圆的方程(2) 苏教版必修2

C 1yxNMPB A直线与圆的方程(2)1.已知直线l :(m2-2m-3)x+(2m2+m-1)y=m+5(m ∈R),其倾斜角为4π,则m 为___43_______2.不论k 为何实数,直线1+=kx y 与曲线0422222=--+-+a a ax y x 恒有交点,则实数a 的取值范围是______[]1,3-____3.已知直线的倾斜角为α,且sinα=4/5,则此直线的斜率是__43±______4.若AC<0,BC<0,那么直线Ax+By+C=0不经过第 三 象限5.已知两点P(-1,1),Q(2,2),若直线l:x+my+m=0与线段PQ 没有公共点,则m 的取值范围是6.将直线y=3x 绕原点逆时针旋转90°,再向右平移1个单位,所得到的直线为____310x y +-=__________.7.若直线l:y=kx-1与直线x+y-1=0的交点位于第一象限,则k 的范围是_____(1,)+∞_________.8.已知a >0,若平面内三点A(1,-a),B(2,a2),C(3,a3)共线,则a=____12+9.若直线l 过点P(2,3),且方向向量n=(1,43-),则直线l 的方程为_______34180x y +-=_______.10.过点P(1,2)且在坐标轴上的截距相等的直线方程为2y x =,_30x y +-=__________.11.若直线0234=--y x 与圆01242222=-++-+a y ax y x 总有两个不同的交点,则实数a的取值范围是___________(6,4)-_____________12.过点)1,1(),1,1(--B A ,且圆心在直线02=-+y x 上的圆的方程是___22(1)(1)4x y -+-=_____________13.过点)4,3(),2,1(),5,0(---C B A 的圆的方程是________2262150x y x y ++--=__________ 14已知两条直线1l :x+(m-1)y+1=0, 2l :(m-1)x+(m+1)y+2=0,当m 为何值时, 1l 与2l(1) 平行;(2)垂直;(3)相交?(1)0(2)1,-2(3)0,3m m ≠≠15.过点),4(),1,0(m B A 且与x 轴相切的圆有且仅有一个,求实数m 的值和这个圆的方程。
高中数学 直线与圆课件 苏教必修2

( 2 ) 设 切 点 分 别 为 A 、 B , 求 过 A 、 B 、 C 三 点 的 圆 的 方 程 ;
(1)4x3y80或x2 (2 )x 2y23 x3 y20 切线长为3
变(2009.镇江三调)
已知圆C:(x3)2(y4)24直线 l 1 经过
定点A(1,0).
(1)若
(2)若l
l
1
1
与与圆圆相 相切交,于求P,Ql 1两的点方,程线段PQ的中
点为M,又 l 1 与l 2 :x+2y+2=0的交点为N,判断
AMAN是否为定值?证明你的结论。
例2.已知点P(0,5)及圆C: x2y24x12y240
(1)若直线l过点P且被圆截得的线段长为 4 3 ,求直线l的方程。
1、直线与圆的位置关系小结
有两交点 d<r 两不等根 △>0 有一交点 d =r 有一实根 △=0 无公共点 d>r 无实根 △<0
2.弦心距: 直线 l:A x B y C O , 圆 C :(x a )2 (y b )2 r2,
AaBbC
则弦心距 d A2 B2
A
r
Od M B
d2 ( AB)2 r2 2
三.圆与圆的位置关系
内含,内切,相交,外切,相离(几何法判断)
6.已知圆M:x2y22mx2nym210与圆N: x2y22x2y20交于A,B两点,且这两点平 分圆N的圆周,求圆M的圆心的轨迹方程,并求其 中半径最小时圆M的方程.
圆与圆锥曲线
7.设F为椭圆x2 y2 1的右焦点,O为坐标原点,P这为 5
小结
本节课我们主要从几何法、代数法两个 角度去研究直线和圆的相切、相交、相离及 相关的问题,通过练习让大家体会到两种方 法各自的优点和局限性,希望大家在日后处 理类似问题时,要灵活的选取方法。
苏教版直线和圆知识点复习教案

苏教版直线和圆知识点复习教案直线与圆复习(一)直线的倾斜角α与斜率k求k方法:1.已知直线上两点(,)(,)(≠) 则2.已知α时,k=tanα(α≠90) k不存在(α=90)3.直线Ax+By+C=0,(A,B不全为0,)B=0时k不存在,B≠0时 k=-(二)直线方程名称已知条件方程说明斜截式斜率k纵截距by=kx+b不包括垂直于x轴的直线点斜式点P(x,y)斜率k =k()不包括垂直于x轴的直线两点式点P(x,y)和P(x,y)不包括坐标轴和平行于坐标轴的直线截距式横截距a纵坐标b不包括坐标轴,平行于坐标轴和过原点的直线一般式Ax+By+C=0 A、B不同时为0(三)位置关系判定方法:当直线不平行于坐标轴时(要特别注意这个限制条件)∶∶∶x+y+=0∶x+y+=0与组成的方程组平行=k且≠b或无解重合= k且= b有无数多解相交垂直k1≠k2有唯一解k1・k2=-1(四)点P(x0,y0)到直线Ax+By+C=0的距离是d=两平行直线Ax+By+C1=0和Ax+By+C2=0间的距离为d=.(五)直线过定点。
如直线(3m+4)x+(5-2m)y+7m-6=0,不论m取何值恒过定点(-1,2)(六)直线系方程(1)与已知直线Ax+By+C=0平行的直线的设法: Ax+By+m=0 (m≠C)( 2 ) 与已知直线Ax+By+C=0垂直的直线的设法: Bx-Ay+m=0 (3)经过直线∶x+y+=0,∶x+y+=0交点的直线设法:x+y++λ(x+y+)=0(λ为参数,不包括)(七)关于对称(1)点关于点对称(中点坐标公式)(2)线关于点对称(转化为点关于点对称,或代入法,两条直线平行)(3)点关于线对称(点和对称点的连线被线垂直平分,中点在对称轴上、kk'= -1二个方程)(4)线关于线对称(求交点,转化为点关于线对称)(八)圆的标准方程:圆心(a,b)半径r>0圆的一般方程:(>0)圆心() r=(九)点与圆的位置关系设圆C∶,点M()到圆心的距离为d,则有:(1)d>r 点M在圆外;(2)d=r 点M在圆上;(3)d<r 点M在圆内.(十)直线与圆的位置关系设圆C∶,直线l的方程Ax+By+C=0,圆心(a,b)到直线l的距离为d,判别式为△,则有:(几何特征)(1)d<r 直线与圆相交;(2)d=r 直线与圆相切;(3)d>r 直线与圆相离;弦长公式:或(代数特征)(1)△>0 直线与圆相交,圆C和直线l组成的方程组有两解;(2)△=0 直线与圆相切,圆C和直线l组成的方程组有一解;(3)△<0 直线与圆相离,圆C和直线l组成的方程组无解。
苏教版学高中数学必修二平面解析几何初步直线与圆的位置关系讲义
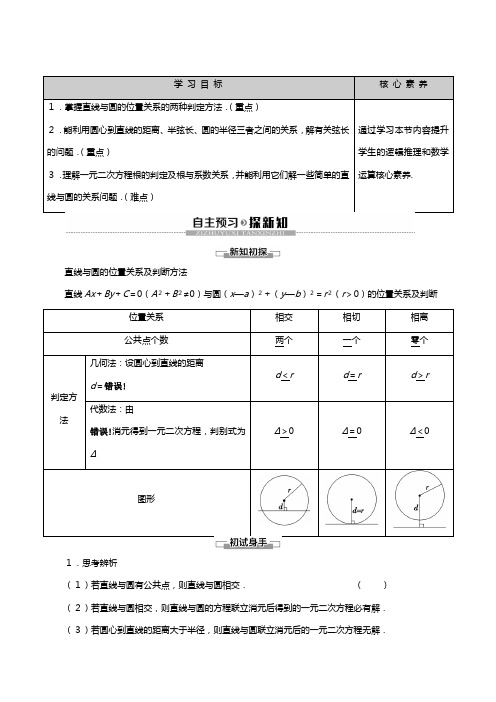
学习目标核心素养1.掌握直线与圆的位置关系的两种判定方法.(重点)2.能利用圆心到直线的距离、半弦长、圆的半径三者之间的关系,解有关弦长的问题.(重点)3.理解一元二次方程根的判定及根与系数关系,并能利用它们解一些简单的直线与圆的关系问题.(难点)通过学习本节内容提升学生的逻辑推理和数学运算核心素养.直线与圆的位置关系及判断方法直线Ax+By+C=0(A2+B2≠0)与圆(x—a)2+(y—b)2=r2(r>0)的位置关系及判断位置关系相交相切相离公共点个数两个一个零个判定方法几何法:设圆心到直线的距离d=错误!d<r d=r d>r 代数法:由错误!消元得到一元二次方程,判别式为ΔΔ>0Δ=0Δ<0图形1.思考辨析(1)若直线与圆有公共点,则直线与圆相交.()(2)若直线与圆相交,则直线与圆的方程联立消元后得到的一元二次方程必有解.(3)若圆心到直线的距离大于半径,则直线与圆联立消元后的一元二次方程无解.[答案] (1)×(2)√(3)√2.已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是________.相交[由题意知点M(a,b)在圆外,则a2+b2>1,圆心到直线的距离d=错误!<1,故直线与圆相交.]3.直线x+y+m=0与圆x2+y2=m(m>0)相切,则m的值为________.2[由直线与圆的距离d=错误!=错误!,解得m=2.]4.设直线y=x+2a与圆C:x2+y2—2ay—2=0相交于A,B两点,若|AB|=2错误!,则圆C的面积为________.4π[圆C:x2+y2—2ay—2=0化为标准方程是C:x2+(y—a)2=a2+2,所以圆心C(0,a),半径r=错误!.|AB|=2错误!,点C到直线y=x+2a即x—y+2a=0的距离d=错误!,由勾股定理得错误!错误!+错误!错误!=a2+2,解得a2=2,所以r=2,所以圆C的面积为π×22=4π.]直线与圆的位置关系的判断22思路探究:法一:利用代数法;法二:利用几何法;法三:利用直线方程(此题直线过定点(0,1)).[解] 法一:∵错误!∴5x2+4x—3=0.判别式Δ=42—4×5×(—3)=76>0.∴直线与圆相交.法二:∵x2+y2=4,∴圆心为(0,0),半径r=2.又∵y=2x+1,∴圆心到直线的距离d=错误!=错误!<2=r.∴直线与圆相交.法三:由题意知,直线过定点(0,1).而02+12=1<4.所以点(0,1)在圆内,从而直线与圆相交.直线与圆位置关系的判定方法1.已知直线方程mx—y—m—1=0,圆的方程x2+y2—4x—2y+1=0.当m为何值时,圆与直线(1)有两个公共点;(2)只有一个公共点;(3)没有公共点.[解] 法一:将直线mx—y—m—1=0代入圆的方程化简整理得,(1+m2)x2—2(m2+2m+2)x+m2+4m+4=0.∵Δ=4m(3m+4),(1)当Δ>0,即m>0或m<—错误!时,直线与圆相交,即直线与圆有两个公共点;(2)当Δ=0,即m=0或m=—错误!时,直线与圆相切,即直线与圆只有一个公共点;(3)当Δ<0,即—错误!<m<0时,直线与圆相离,即直线与圆没有公共点.法二:已知圆的方程可化为(x—2)2+(y—1)2=4,即圆心为C(2,1),半径r=2.圆心C(2,1)到直线mx—y—m—1=0的距离d=错误!=错误!.(1)当d<2,即m>0或m<—错误!时,直线与圆相交,即直线与圆有两个公共点;(2)当d=2,即m=0或m=—错误!时,直线与圆相切,即直线与圆只有一个公共点;(3)当d>2,即—错误!<m<0时,直线与圆相离,即直线与圆没有公共点.直线与圆的相交弦问题22a的值是__________.(2)已知过点(2,5)的直线l被圆C:x2+y2—2x—4y=0截得的弦长为4,则直线l的方程为__________.思路探究:(1)将圆的一般方程化为标准方程,利用弦心距、半弦长和半径构成直角三角形求解.(2)设出直线方程、利用弦心距、半弦长和半径构成的直角三角形得关于斜率的方程求解,验证斜率不存在的情况.(1)—4(2)x—2=0或4x—3y+7=0 [(1)将圆的方程化为标准方程为(x+1)2+(y—1)2=2—a,所以圆心为(—1,1),半径r=错误!,圆心到直线x+y+2=0的距离d=错误!=错误!,故r2—d2=4,即2—a—2=4,所以a=—4.(2)当直线斜率不存在时,x—2=0满足题意;当直线斜率存在时,设方程为y—5=k(x—2),即kx—y—2k+5=0.圆C:x2+y2—2x—4y=0可化为(x—1)2+(y—2)2=5,因为直线l被圆C:x2+y2—2x—4y=0截得的弦长为4,所以2错误!=4,所以k=错误!,所以直线l的方程为4x—3y+7=0.综上所述,直线l的方程为x—2=0或4x—3y+7=0.]解决与圆有关的弦长问题时,多采用几何法,即在弦心距、半弦长和半径构成的直角三角形中求解.2.过点(3,1)作圆(x—2)2+(y—2)2=4的弦,其中最短的弦长为________.2错误![最短的弦为过点(3,1)且与圆心(2,2)和点(3,1)连线的垂直的弦,弦长l=2错误!=2错误!.]圆的切线问题1.求过点P(3,4)的圆C:x2+y2=25的切线方程.[提示] ∵点P(3,4)在圆上,∴切点为P,设切线斜率为k.则k·k PC=—1,∴k=—错误!=—错误!.切线方程为y—4=—错误!(x—3),即3x+4y—25=0.2.求过点Q错误!的圆x2+y2=25的切线方程.[提示] ∵(—5)2+错误!错误!>25,∴点Q在圆外.若所求直线斜率存在,设切线斜率为k,则切线方程为y—错误!=k[x—(—5)],即kx—y+5k+错误!=0.因圆心C(0,0)到切线的距离等于半径5,所以错误!=5,∴k=错误!.故所求切线方程为错误!x—y+错误!+错误!=0,即3x—4y+25=0.若所求直线斜率不存在,则直线方程为x=—5,圆心C(0,0)到x=—5的距离为5,符合题意.综上,过点Q的切线方程为x+5=0或3x—4y+25=0.【例3】已知圆C:(x—3)2+(y—1)2=1.(1)过点A(3,2),求圆的切线方程;(2)过点B(4,—3),求圆的切线方程.思路探究:(1)直线和圆相切,则过圆心和切点的直线与切线垂直.(2)直线和圆相切,则圆心到直线的距离等于半径.[解] (1)∵(3—3)2+(2—1)2=1,∴A在圆上.由题意知圆心C(3,1),直线CA无斜率,∴切线斜率为0,∴所求切线方程为y=2.(2)∵(4—3)2+(—3—1)2=17>1,∴点B在圆外.1若所求直线的斜率存在,设切线斜率为k,则切线方程为y+3=k(x—4).因为圆心C(3,1)到切线的距离等于半径1,所以错误!=1,解得k=—错误!.所以切线方程为y+3=—错误!(x—4),即15x+8y—36=0;2若切线斜率不存在,圆心C(3,1)到直线x=4的距离也为1,这时直线与圆也相切,所以另一条切线方程是x=4.综上,所求切线方程为15x+8y—36=0或x=4.过一点的圆的切线方程的求法(1)当点在圆上时,圆心与该点的连线与切线垂直,从而求得切线的斜率,用直线的点斜式方程可求得圆的切线方程.对于填空题可以直接利用以下两个结论:(1)当点(x0,y0)在圆x2+y2=r2上时,切线方程为x0x+y0y=r2;(2)当点(x0,y0)在圆(x—a)2+(y—b)2=r2上时,切线方程为(x0—a)(x—a)+(y0—b)(y—b)=r2.(2)若点在圆外时,过这点的切线将有两条,但在设斜率来解题时可能求出的切线只有一条,这是因为有一条过这点的切线的斜率不存在.3.已知圆的方程为x2+y2=13,它与斜率为—错误!的直线相切,求该切线的方程.[解] 设切线方程为y=—错误!x+b,即2x+3y—3b=0,依题意得:错误!=错误!,解得b=±错误!.∴切线方程为2x+3y+13=0或2x+3y—13=0.1.本节课的重点是理解直线和圆的三种位置关系,会用圆心到直线的距离来判断直线与圆的位置关系,能解决直线与圆位置关系的综合问题.难点是解决直线与圆的位置关系.2.本节课要重点掌握的规律方法(1)直线与圆位置关系的判断方法.(2)求圆的切线的方法.(3)求直线与圆相交时弦长的方法.3.本节课的易错点是在解决直线与圆位置关系问题时易漏掉斜率不存在的情况.1.直线3x+4y+12=0与圆(x—1)2+(y+1)2=9的位置关系是()A.相离B.相切C.相交且过圆心D.相交但不过圆心D[圆心(1,—1)到直线的距离为错误!=错误!<3,∴直线与圆相交.又圆心(1,—1)不在直线上,故选D.]2.由点P(1,3)引圆x2+y2=9的切线的长是________.1[点P到原点O的距离为PO=错误!,∵r=3,∴切线长为错误!=1.]3.直线y=x+1与圆x2+y2+2y—3=0交于A,B两点,则|AB|=________.2错误![由题意知圆的方程为x2+(y+1)2=4,所以圆心坐标为(0,—1),半径长为2,则圆心到直线y=x+1的距离d=错误!=错误!,所以|AB|=2错误!=2错误!.]4.已知圆x2+y2=8,定点P(4,0),问过P点的直线的斜率在什么范围内取值时,这条直线与已知圆:(1)相切,(2)相交,(3)相离?[解] 设圆心到直线的距离为d,过P点的直线斜率为k,由题意,知斜率k存在,则其方程为y=k(x—4),则d=错误!=错误!.(1)d=r,即错误!=错误!,∴k2=1,∴k=±1时,直线与圆相切.(2)d<r,即错误!<错误!,∴k2<1,即—1<k<1时,直线与圆相交.(3)d>r,即错误!>错误!,∴k2>1,即k<—1或k>1时,直线与圆相离.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学学习材料(灿若寒星精心整理制作)课时37 直线与圆的复习课(2)【课标展示】1、熟练掌握用待定系数法求圆的方程;2、能应用直线与圆的相关知识解决一些综合问题。
【要点归纳】1、圆的标准方程为,圆心坐标为;半径为圆的一般方程为,圆心坐标为;半径为2、直线与圆的位置关系为判断方法有两种方法(1)代数法(2)几何法3、圆与圆有五种位置关系即其判断方法有两种:(1)代数式法(2)几何法4、经过两圆交点的圆系方程为【典例探究】例1 已知△ABC的三个项点坐标分别是A(4,1),B(6,-3),C(-3,0),求△ABC 外接圆的方程。
例2 已知与曲线C :012222=+--+y x y x 相切的直线l 交y x ,的正半轴与B A 、两点,O 为原点,OA =a ,b OB =,)2,2(>>b a . (1)求线段AB 中点的轨迹方程; (2)求ab 的最小值.例3 已知直线l :y=k(x +22)与圆O :x 2+y 2=4相交于A 、B 两点,O 是坐标原点,三角形ABO 的面积为S .(1)试将S 表示成k 的函数,并求出它的定义域; (2)求S 的最大值,并求取得最大值时k 的值【课时作业37】1.若直线y x b =+与曲线21x y =-恰有一个交点,则实数b 的取值范围是 . 2.已知点P 在xoy 平面内,点A 的坐标为(0,0,4),5PA =,则满足此条件的点P 组成的曲线是 .3.圆2244100x y x y +---=上的点到直线140x y +-=的最大距离与最小距离的差是 .4.圆心为(11),且与直线4x y +=相切的圆的方程 .5.半径为25,且与直线:260l x y +-=切于点(1,4)T 的圆的方程是 .6. 实数x,y 满足2x 4y ,01y 2x 2y x 22--=+--+则的取值范围为 . 7. 如图,直角三角形ABC 的顶点坐标(20)A -,,直角顶点(0,22)B -,顶点C 在x 轴上, (Ⅰ)求BC 边所在直线方程;(Ⅱ)M 为直角三角形ABC 外接圆的圆心,求圆M 的方程.yxPOCBA8. 设圆上的点(2,3)A 关于直线20x y +=的对称点仍在圆上,且与直线10x y -+=相交的弦长为22,求圆的方程.9.(探究创新题)已知圆心坐标为)1,3(M 的圆M 与x 轴及直线x y 3=均相切,切点分别为A 、B ,另一圆N 与圆M 、x 轴及直线x y 3=均相切,切点分别为C 、D .(1)求圆M 和圆N 的方程;(2)过点B 作直线MN 的平行线l ,求直线l 被圆N 截得的弦的长度.10.在平面直角坐标系xOy 中,记二次函数2()2f x x x b =++(x ∈R )与两坐标轴有三个交点.经过三个交点的圆记为C . (1)求实数b 的取值范围; (2)求圆C 的方程;(3)问圆C 是否经过定点(其坐标与b 的无关)?请证明你的结论.【疑点反馈】(通过本课时的学习、作业之后,还有哪些没有搞懂的知识,请记录下来)课时37 直线与圆的复习课(2)例1 分析:如果设圆的标准方程222()()x a y b r -+-=,将三个顶点坐标分别代入,即可确定出三个独立参数a ,b ,r ,写出圆的标准方程;如果注意到△ABC 外接圆的圆心是△ABC 三边垂直平分线的交点,由此可求圆心坐标和半径,也可以写出圆的标准方程。
解法一:设所求圆的方程是222()()x a y b r -+-= ①因为A (4,1),B (6,-3),C (-3,0)都在圆上, 所以它们的坐标都满足方程①,于是222222222(4)(1),(6)(3),(3)(0).a b r a b r a b r ⎧-+-=⎪-+--=⎨⎪--+-=⎩可解得21,3,25.a b r =⎧⎪=-⎨⎪=⎩ 所以△ABC 的外接圆的方程是22(1)(3)25x y -++=。
解法二:因为△ABC 外接圆的圆心既在AB 的垂直平分线上,也在BC 的垂直平分线上,所以先求AB 、BC 的垂直平分线方程,求得的交点坐标就是圆心坐标。
∵31264AB k --==--,0(3)1363BC k --==---,线段AB 的中点为(5,-1),线段BC 的中点为33(,)22-,∴AB的垂直平分线方程为11(5)2y x +=-,①BC 的垂直平分线方程333()22y x +=- ②解由①②联立的方程组可得1,3.x y =⎧⎨=-⎩∴△ABC 外接圆的圆心为E(1,-3), 半径22||(41)(13)5r AE ==-++=。
故△ABC 外接圆的方程是22(1)(3)25x y -++=.点评:解法一用的是“待定系数法”,解法二利用了圆的几何性质。
“待定系数法”是求圆的方程的常用方法.一般地,在选用圆的方程形式时,若问题涉及圆心和半径,则选用标准方程比较方便,否则选用一般方程方便些。
例 2 [解析]:(1)设AB 的中点为P(x ,y) ,圆C 的方程化简为:1),1,1(,1)1()1(22=∴-+-r C y x又直线l 的方程为:)2,2(0,1>>=-+=+b a ab ay bx bya x 即,相切与圆C l , ExyOCBA0222)(1222222222=--+⇒-+=+⇒=+-+=∴→ab b a ab b a ab b a b a b a ab b a d l C 2,2>>b a22222)2(0222--=⇒-=-⇒=--+⇒a a b a b a b a ab ①,又∵P 是AB 的中点,2,2b y a x ==∴ y b x a 2,2==⇒,代入①得)1(2212>--=x x x y ,即线段AB 中点的轨迹方程为;)1(2212>--=x x x y . (2)624)2(224)2(6)2(22222)1(222+-+-=-+-+-=--=--=a a a a a a a a a a a ab ,02>-a2424)2(2≥-+-∴a a ,246+≥∴ab .∴246+的最小值为ab 例3 [解析]:(1)22222114)122(42122,022:k k k kAB k kd k y kx l l O +-=+-=∴+=∴=+-→ 2221)1(2421k k k d AB S l O +-=⋅=∴→,定义域:01120≠<<-⇒<<→k k d l O 且.(2)设23)2)(1()1(),1(12222-+-=--=-≥=+t t t t k k t t k 则81)431(224231242324222+--=-+-=-+-⋅=∴t t t t t t S ,222124,3334,431max =⋅=±===∴S k t t 时,即当,∴S 的最大值为2,取得最大值时k=33±【课时作业37】 1、-1<b ≤1或2b =2、以(0,0,0)为圆心,3为半径的圆3、624、22(1)(1)2x y -+-=5、22(3)(2)20x y ++-=或22(5)(6)20x y -+-= 6、4[,)3+∞ 7、解:(1)222AB BC k k =-∴=从而直线BC 所在的直线方程为 240x y --=(2)由(1)得C (4,0),所以圆M 的圆心M (1,0),半径为3 所以圆M 的方程为22(1)9x y -+=8、解:设所求圆的圆心为(a ,b ),半径为r ,因为点A 关于直线20x y +=的对称点仍在圆上,所以圆心在直线20x y +=上,从而 2a b =- ① 又因(2,3)A 在圆上,所以222(2)(3)a b r -+-= ② 又因为圆与直线10x y -+=相交的弦长为22 ,所以22|1|2()2a b r -+=+ ③解①②③得26,3,52a b r ==-=或214,7,244a b r ==-=,故所求的圆方程为22(6)(3)52x y -++=或22(14)(7)244x y -++=9、解:(1)由题意得圆M 的方程为22(3)(1)1x y -+-=,圆N 的方程为22(33)(3)9x y -+-=(2)可求出33(,)22B ,又3113333MN k -==-,所以直线l 的方程为330x y -+=,从而直线l 被圆N 截得的弦的长度为3310、解:(Ⅰ)令x =0,得抛物线与y 轴交点是(0,b );令()220f x x x b =++=,由题意b ≠0 且Δ>0,解得b <1 且b ≠0.(Ⅱ)设所求圆的一般方程为2x 20y Dx Ey F ++++=令y =0 得20x Dx F ++=这与22x x b ++=0 是同一个方程,故D =2,F =b . 令x =0 得2y Ey +=0,此方程有一个根为b ,代入得出E =―b ―1. 所以圆C 的方程为222(1)0x y x b y b ++-++=. (Ⅲ)圆C 必过定点,证明如下:假设圆C 过定点0000(,)(,)x y x y b 不依赖于 ,将该点的坐标代入圆C 的方程,并变形为22000002(1)0x y x y b y ++-+-= (*)为使(*)式对所有满足1(0)b b <≠的b 都成立,必须有010y -=,结合(*)式得2200020x y x y ++-=,解得000002 11x x y y ==⎧⎧⎨⎨==⎩⎩,-,或,,经检验知,点(0,1),(2,0)-均在圆C 上,因此圆C 过定点。
