垂线(第一课时)PPT教学课件
合集下载
《垂线》课件
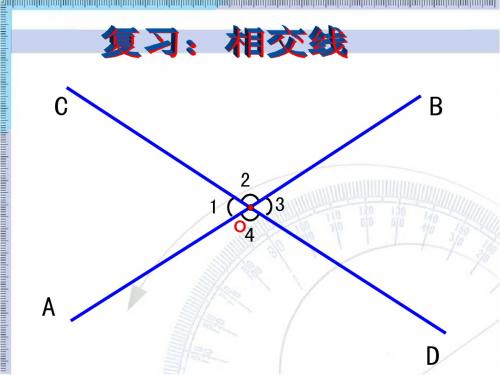
D O B
反之,若直线AB与CD垂直,垂足为O 那么, 反之,若直线AB与CD垂直,垂足为O,那么, AB 垂直 AOD=90° ∠AOD=90°。 书写形式: 已知) 书写形式: ∵ AB⊥CD (已知) ∴ ∠AOD=90° (垂直的定义) ∠AOD=90° 垂直的定义) AOD=90 应用垂直的定义: 应用垂直的定义: ∠AOC=∠BOC=∠BOD=90° AOC=∠BOC=∠BOD=90°
活动5 归纳小结、布置作业
小结 1.垂线的定义; .垂线的定义 2.经过一点有且只有一条直线与已知直线平行; .经过一点有且只有一条直线与已知直线平行 3.垂线段最短. .垂线段最短 作业: 作业: 习题5.1 第3、4、5、6、9、10、11、12 . 习题 、 、 、 、 、 、 、
张庄
B
拓 展 应 用2
如图:要把水渠中的水引到水池C中,在渠岸 如图:要把水渠中的水引到水池C 的什么地方开沟,水沟的长度才能最短? 的什么地方开沟,水沟的长度才能最短? 请画出图来,并说明理由。 请画出图来,并说明理由。
C
拓展应用3
如图,一辆汽车在直线公路 上由 上由A向 行驶 行驶, 、 如图,一辆汽车在直线公路AB上由 向B行驶,M、 N分别位于公路两侧的村庄 分别位于公路两侧的村庄 上点P的位置时 (1)设汽车行驶到公路 上点 的位置时,距离 )设汽车行驶到公路AB上点 的位置时, 村庄M最近 行驶到点Q位置时 距离村庄N最近 最近, 位置时, 最近, 村庄 最近,行驶到点 位置时,距离村庄 最近, 请在图中公路AB上分别画出点 和点Q 的位置。 上分别画出点P和点 请在图中公路 上分别画出点 和点 的位置。 出发向B行驶时 (2)当汽车从 出发向 行驶时,在公路的哪一段 )当汽车从A出发向 行驶时, 上距离M、 两村庄都越来越近 两村庄都越来越近? 上距离 、N两村庄都越来越近?在哪一段公路上 距离村庄N越来越近 而离村庄M越来越远?(用 越来越近, 越来越远?( 距离村庄 越来越近,而离村庄 越来越远?(用 文字表述你的结论) 文字表述你的结论)
四年级数学上册课件-5.1 垂线的画法(1)-人教版(共20张PPT)

(4)标出直角符号。(¬)
方法三: 用一把三角尺画相互垂直的两条直线。
①
②
③
(1)先把这把三角尺放好。(如图①)
(2)沿着三角尺的两条直角边画两条直线。 (如图②)
(3)标出直角符号。(如图③)
要 点 提 示:
这三种画法中 直角边所在的直线是互相垂直的。
人教版小学数学四年级上册第五单元
垂线的画法
1.你能画出互相垂直的两条直线吗? ①用两把三角尺来画。 ②用量角器画。 ③用一把三角尺来画。
2.过直线上一点画垂线。
3.过直线外一点画这条直线的垂线,用三角尺应该怎样画呢?
问题1:画互相垂直的两条直线的方法。
方法一: 用两把三角尺拼出一个直角来画。
(1)先放好一把三角尺,沿着三角尺的一条边画一条 直线。 (2)用另一把三角尺的一条直角边紧靠第一把三角尺的那 条边。
问题2:用三角尺过直线上一点画这条直线的垂线
(1)把三角尺的一条直角边与已知直线重合; (2)沿直线移动三角尺,使三角尺的直角顶点与直线上的 已知点重合;
(3)过已知点沿三角尺另一条直角边画一条直线; (4)在垂足处标出垂直符号。
用三角尺过直线外一点画这条直线的垂线(类推法):
•
(1)把三角尺的一条直角边与已知直线重合; (2)沿直线移动三角尺,使三角尺的另一条直角边经过直线外的已知点; (3)沿三角尺另一条直角边画一条直线;
(4)在垂足处标出垂直符号。
归纳总结:
用三角尺画已知直线的垂线,移 动三角尺时,必须保证与直线重合 的直角边要始终与直线重合,不能 错位。画好后别忘了标出垂直符号。
1.练一练:分别过直线外的A点画垂线。
A
A
2.画图。 过已知点向对边画垂线。
方法三: 用一把三角尺画相互垂直的两条直线。
①
②
③
(1)先把这把三角尺放好。(如图①)
(2)沿着三角尺的两条直角边画两条直线。 (如图②)
(3)标出直角符号。(如图③)
要 点 提 示:
这三种画法中 直角边所在的直线是互相垂直的。
人教版小学数学四年级上册第五单元
垂线的画法
1.你能画出互相垂直的两条直线吗? ①用两把三角尺来画。 ②用量角器画。 ③用一把三角尺来画。
2.过直线上一点画垂线。
3.过直线外一点画这条直线的垂线,用三角尺应该怎样画呢?
问题1:画互相垂直的两条直线的方法。
方法一: 用两把三角尺拼出一个直角来画。
(1)先放好一把三角尺,沿着三角尺的一条边画一条 直线。 (2)用另一把三角尺的一条直角边紧靠第一把三角尺的那 条边。
问题2:用三角尺过直线上一点画这条直线的垂线
(1)把三角尺的一条直角边与已知直线重合; (2)沿直线移动三角尺,使三角尺的直角顶点与直线上的 已知点重合;
(3)过已知点沿三角尺另一条直角边画一条直线; (4)在垂足处标出垂直符号。
用三角尺过直线外一点画这条直线的垂线(类推法):
•
(1)把三角尺的一条直角边与已知直线重合; (2)沿直线移动三角尺,使三角尺的另一条直角边经过直线外的已知点; (3)沿三角尺另一条直角边画一条直线;
(4)在垂足处标出垂直符号。
归纳总结:
用三角尺画已知直线的垂线,移 动三角尺时,必须保证与直线重合 的直角边要始终与直线重合,不能 错位。画好后别忘了标出垂直符号。
1.练一练:分别过直线外的A点画垂线。
A
A
2.画图。 过已知点向对边画垂线。
《垂线》课件完整版PPT初中数学1

2、直线外一点到这条直线的
的长度,叫做点到直线的距离。
D、线段BD是点B到线段CD的距离
中,长度是最短的,但是,题意
2、直线外一点到这条直线的
的长度,叫做点到直线的距离。
经历观察、操作、想像、归纳概括、交流等
没有说明 线段AD 是 线段BF 的
2、如图2,AO⊥BO,O为垂足,直线CD过点O,且∠BOD=2∠AOC,则∠BOD=________. ∴ ∠BOC=∠AOC﹣∠AOB
五、强化训练
4、画一条线段或射线的垂线,就是画它们
所在直线的垂线。如图,请你过点P画出线
段AB或射线AB的垂线。
解:如图所示
.
P·
P·
B
A
PB A
A
B
(1)
(2)
(3)
垂 线(2)
一、新课引入
(1)两点之间, 线段 最短. (2)问题:要把河中的水引到农田P处, 如何挖渠能使渠
道最短?
怎么办呢?
2、点到直线的距离:直 做线点外到一直点线到的这距条离直。线的 垂线段 的长度,叫
3、连接直线外一点与直线上各点的所有线段中,垂线段最短。简单 说成: 垂线段最短
4、垂线、垂线段与点到直线的距离的区别是 : 垂线是一条 直 线; 垂线段是一条 线段 ,是图形; 点到直线的距离是垂线段的 长度 ,是一个数量,不能说垂线段是距
二、学习目标
1 进一步发展空间观念,用几何语言准 确表达能力。
2 了解垂线段的概念,了解垂线段最短的 性质,体会点到直线的距离的意义, 并 会度量点到直线的距离.
三、研读课文
垂线段及性质 1、从直线外一点引一条直线的
垂
线,这点和 垂足 之间的
【数学课件】5.1.2《垂线》ppt课件

3 4 5 6 7 8 9 10
折一折
根据图示能折出互相垂直的直线,您不妨试 试看!
结论
垂直的表示
图中,直线AB与直线CD垂直, 记作:AB⊥CD;
n A O
C
B m D
ห้องสมุดไป่ตู้
直线 m 与直线 n 垂直,
记作:m⊥n ; 互相垂直的两条直线的交点叫做垂足. 注意:“⊥”是“垂直”的记号, 而“
” 是图形中“垂直(直角)” 的标记.
A.36° B.54° C.64°
)
D.72°
【解析】选B.因为OC⊥OD,所以 ∠COD=90°,又因为∠AOB=180°, 所以∠DOB=∠AOB-∠COD- ∠COA=180°-90°-36°=54°.
3.如图所示,直线AB⊥CD,垂足为O,射线OP在∠AOD的内
部,且∠POA=4∠POD,则∠COP︰∠BOP的值为( C A B )
∠BOP=∠BOD+∠POD=90°+18°=108°.
所以∠COP︰∠BOP=162°︰108°= 3︰2.
4.点P是直线l外一点,点A,B,C是直线l上的三点,且 PA=10,PB=8,PC=6,那么点P到直线l的距离为( A.6 C.大于6的数 B.8 D.不大于6的数 )
【解析】选D.根据“垂线段最短”,垂线段的长度一定小
角时,其他三个角也都成为直角,此时,直线AB,CD互
相垂直.
做一做 (1)你能用三角尺在白纸上画两条互相垂直的直线吗? (2)你能用量角器在白纸上画两条互相垂直的直线吗? (3)如果只有直尺,你能在方格纸上画出两条互相垂直的 直线吗?
用三角尺作两条互相垂直的直线
0 1 2
0
1
初一数学《垂线》课件

过一点作已知直线的平行线
总结词
通过给定的一个点,使用直尺和三角板,可以作出与给定直线平行的线段。
详细描述
首先确定给定的点,然后将三角板的一条边放在该点上,另一条边与给定直线 重合,沿着这条边画一条线段,即为所求的平行线。
作平行四边形的垂线
总结词
在平行四边形中,可以通过连接 对角线上的两个端点来作出垂线 。
在地球科学中,垂线被用来测量地壳的倾斜度和地震的震源深度, 对于研究地球的运动和地震预测具有重要意义。
03 垂线的作法
过一点作已知直线的垂线
总结词
通过给定的一个点,使用直角三角板 或量角器,可以作出与给定直线垂直 的线段。
详细描述
首先确定给定的点,然后将直角三角 板的一条直角边放在该点上,另一条 直角边与给定直线重合,沿着这条直 角边画一条线段,即为所求的垂线。
01
如果一条线段与另一条直线相交 形成的角为直角,则该线段垂直 于另一条直线。
02
如果一条线段与另一条直线相交 ,且经过另一条直线上的一点, 则该线段垂直于另一条直线。
垂线定理的推论
垂线的斜率互为相反数
如果一条直线的斜率为k,则其垂线的斜率为-1/k。
垂线与原直线平行
如果一条直线平行于x轴,则其垂线与x轴垂直。
题目2
已知两条直线互相垂直,其中 一条直线的方程为y=2x+1,求 另一条直线的方程。
题目3
在直角坐标系中,点A的坐标为 (1,2),点B的坐标为(3,4),求线
段AB的垂直平分线的方程。
答案及解析
01 02
题目1答案及解析
垂线是两条直线相交成直角时,所形成的线段。生活中常见的例子有窗 户的边框、墙角等。解析:此题考察垂线的定义,理解垂线的概念是解 题的关键。
5.1.2垂线ppt课件
.
25
垂线的画法:
如图,已知直线 l 和l外的一点A ,作l的垂线.
结论:过直线外
A
一点有且只有一条
直线与已知直线垂
直.
则所画直线AB是经过点A的 直线l的垂线.
l B
1放:放直尺,直尺的一边要与已知直线重合;
2靠:靠三角板,把三角板的一直角边靠在直尺上;
0 1 2 3 4 5 6 7 8 9 1 0 1 1
A 垂 线 段
C
B
D
注 意: 点A到直线CD的距离是 垂线段AB的长度,而不是垂线段AB。
.
46
拓展应用
如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能 最短? 请画出图来,并说明理由。
垂线段最短
C
.
47
三、知识应用 1、如图,点A处是一座小屋,BC是一条公路,一人在O处。
A
P
B C
.
51
三、知识应用
5 .文峰学校第六届运动会上,701班一名运动员第五跳打破了年级记录。 如图A、B为这一跳的脚印落点,起跳线为CD。请画图说明如何测量他的 成绩。
C ┓
F D
A •
E• B
解:过脚印B的后跟E作 EF⊥CD,垂足为点F。 那么垂线段EF的长度就是这名 运动员跳远的成绩。
你能再举出其他例子吗?
.
8
生活中的垂直
.
9
生活中的垂直
.
10
生活中的垂直
.
11
3.垂直的书写形式:
C
如图,当直线AB与CD相交于O点,∠AOC=90°
时,AB⊥CD,垂足为O。
A
B
O
几何语言
认识垂线课堂ppt课件

为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
图①
图②
1
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
你能说一些互相垂直的例子吗?
18
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
课间十分钟……
19
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
相垂直
三角尺有两条 边互相垂直
10
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
从点P点向已知直线画一条垂直的 线段和几条不垂直的线段。量一量 所有画出的线段的长度,你有什么 发现?
和这条直线 垂直的线段 最短。
学以致用
26
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
为您解难
27
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
28
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
图①
图②
1
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
你能说一些互相垂直的例子吗?
18
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
课间十分钟……
19
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
相垂直
三角尺有两条 边互相垂直
10
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
从点P点向已知直线画一条垂直的 线段和几条不垂直的线段。量一量 所有画出的线段的长度,你有什么 发现?
和这条直线 垂直的线段 最短。
学以致用
26
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
为您解难
27
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
28
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
《5.1垂线》(第一课时)课件(新人教版)

含义1: ∵AB⊥CD ∴∠1=90°
含义2:
符号 “⊥” ∵∠1=90° 来表示, 读作“垂 ∴AB⊥CD 直于” )
练一练
如图,CD ⊥EF, ∠1= ∠2,则 AB⊥EF.请说明理由(补全解 答过程)
A
2
F B
C 解: ∵ CD ⊥EF(已知) 1 1 ∴∠1= ____ ( 垂线的定义 ) 90° E ∵ ∠1= ∠2=____ 90° ∴ AB___EF ( 垂线的定义 ) ⊥
C
当∠BOD=α°( α≠90°)时. ∠AOD=( 180- α )° A ∠AOC=( α )° O ∠BOC=( 180- α )°
D
B
当α ≠90°时,AB与CD不垂直, 此时我们说AB与CD斜交.
两条直线相交斜交来自垂直——相交的特殊情况
┓
知识要点
垂直
当两条直线相交所成的四个角中,有一 个角是直角时,这两条直线互相垂直,其中 一条直线叫另一条直线的垂线,它们的交点 叫垂足. m
点到直线的距离
随堂练习
1. 已知:如图AB⊥CD.垂足为O,EF为过点 O的一条直线.则∠1与∠2的关系一定成立的是 ( B) A.相等 B.互余 C.互补 D.互为对顶角 1 ┓
2
2. 下面四种判定两条直线的垂直的方 法.正确的个数为( B ) ①两条直线相交所成的四个角中有一个角是直 角.则这两条直线互相垂直 ②两条直线相交.只要有一组邻补角相 等.则这两条直线互相垂直 ③两条直线相交.所成的四个角相等.这两 条直线互相垂直 ④两条直线相交.有一组对顶角互补.则这 两条直线互相垂直 A.5 B.4 C.3 D.2
┓
D B
O
画一画:
请用三角尺和量角器过点P画直线AB的垂线.
垂线(第1课时)PPT课件

l 1 a
2 b
在平面内,如果一直线垂直于两平行线中 的一条,那么这条直线必垂直于另一条.
归纳总结
在同一平面内,垂直于同一条直线的两条直线平行.
bc
几何语言: 因为 b⊥a,c⊥a (已知),
a 12
所以 b∥c (同一平面内,垂直于同一条直线的两条直线平行).
反之,在同一平面内,如果一条直线垂直于两条平行线中的一条, 那么这条直线也垂直于另一条直线.
m
BC
1
n
O
图1
O
A
图2
新知探究
如图,在同一平面内,如果a⊥l, b⊥l,那么a//b吗?
a
b
1
2
l
因为∠1=∠2=90º,它 们是同位角,所以a//b
在平面内垂直于同一条两条直线平行
新知探究
如图,设a//b,l⊥a,那么l⊥b吗? 因为l⊥a, 所以∠1=90º, 因为a//b, 所以∠2=∠1=90º, 从而l⊥b
如图,直线 CD 是 AB 的斜线,同样,直线 AB 也是 CD 的斜线,点 O 是斜足.
课堂练习
1、(1) 如图1,若直线 m、n 相交于点 O,∠1 = 90°,则 m⊥n ;
(2) 若直线 AB、CD 相交于点 O,且 AB⊥CD,那么 ∠BOD =_9_0___°;
(3) 如图2,BO⊥AO,∠BOC 与∠BOA 的度数之比为 1∶5,则∠COA = 72 °,∠BOC 的补角为 162 °.
巩固练习
4. 如图,AB⊥CD,垂足为 O,EF 为过点 O 的一条直线,则∠1 与∠2 的 关系一定成立的是( B
A
C E
1
O
B
2
F D
垂线第一课时课件

支撑结构
在桥梁、房屋等建筑中,垂线作为支撑结构的一 部分,起到重要的承重作用。
测量工具
垂线在测量工作中也常被使用,如测量高度、深 度等。
05
垂线的历史与发展
古代的垂线知识
古希腊数学家对垂线的探索
古希腊数学家通过几何学研究,发现了垂线的基本性质和定理,奠定了垂线理论的基础 。
阿拉伯数学家的贡献
阿拉伯数学家在继承和发展古希腊数学的基础上,对垂线进行了更深入的研究,丰富了 垂线的理论体系。
详细描述
首先确定给定直线和直线外一点,然 后利用圆规或直尺从该点出发,以与 给定直线垂直的方向为方向,以适当 的长度为半径,画出与给定直线相交 的直线。
利用其他几何知识作图
总结词
利用平行线、角平分线等其他几何知识辅助作图。
详细描述
首先确定给定直线和直线外一点,然后利用平行线或角平分线的性质,画出与给定直线相交的直线, 再利用垂线的性质确定垂足的位置,最后画出垂线。
化计算过程。
02
垂线的判定方法
利用定义判定
总结词
直接应用垂线的定义进行判定
详细描述
垂线是指与给定直线垂直的直线。根据定义,如果一条直线上的任意一点到另 一条直线的距离都相等且为零,则这两条直线互相垂直。因此,可以根据这个 性质来判断两条直线是否垂直。
利用性质判定
总结词
利用垂线的性质定理进行判定
详细描述
垂线的性质定理指出,过一点与给定直线垂直的直线有且仅有一条。因此,如果 已知一条直线上的一个点,可以过该点作另一条直线的垂线,且只有一条这样的 垂线。
利用其他几何知识判定
总结词
利用其他几何知识进行判定
详细描述
除了定义和性质定理外,还可以利用其他几何知识来判断两条直线是否垂直。例如,可以根据勾股定理或三角形 的性质来判断两条直线是否垂直。此外,在坐标系中,可以通过计算两条直线的斜率来判断它们是否垂直。
在桥梁、房屋等建筑中,垂线作为支撑结构的一 部分,起到重要的承重作用。
测量工具
垂线在测量工作中也常被使用,如测量高度、深 度等。
05
垂线的历史与发展
古代的垂线知识
古希腊数学家对垂线的探索
古希腊数学家通过几何学研究,发现了垂线的基本性质和定理,奠定了垂线理论的基础 。
阿拉伯数学家的贡献
阿拉伯数学家在继承和发展古希腊数学的基础上,对垂线进行了更深入的研究,丰富了 垂线的理论体系。
详细描述
首先确定给定直线和直线外一点,然 后利用圆规或直尺从该点出发,以与 给定直线垂直的方向为方向,以适当 的长度为半径,画出与给定直线相交 的直线。
利用其他几何知识作图
总结词
利用平行线、角平分线等其他几何知识辅助作图。
详细描述
首先确定给定直线和直线外一点,然后利用平行线或角平分线的性质,画出与给定直线相交的直线, 再利用垂线的性质确定垂足的位置,最后画出垂线。
化计算过程。
02
垂线的判定方法
利用定义判定
总结词
直接应用垂线的定义进行判定
详细描述
垂线是指与给定直线垂直的直线。根据定义,如果一条直线上的任意一点到另 一条直线的距离都相等且为零,则这两条直线互相垂直。因此,可以根据这个 性质来判断两条直线是否垂直。
利用性质判定
总结词
利用垂线的性质定理进行判定
详细描述
垂线的性质定理指出,过一点与给定直线垂直的直线有且仅有一条。因此,如果 已知一条直线上的一个点,可以过该点作另一条直线的垂线,且只有一条这样的 垂线。
利用其他几何知识判定
总结词
利用其他几何知识进行判定
详细描述
除了定义和性质定理外,还可以利用其他几何知识来判断两条直线是否垂直。例如,可以根据勾股定理或三角形 的性质来判断两条直线是否垂直。此外,在坐标系中,可以通过计算两条直线的斜率来判断它们是否垂直。
垂线ppt课件公开课

技巧2
使用颜色和形状来突出重 点和区分不同的内容。
技巧3
利用动画和过渡效果来增 强演示的吸引力和效果。
垂线的实战案例
案例1
某公司年度财务报告,利用垂线将各 个季度的数据进行了可视化展示。
案例2
某培训课程,利用垂线将各个知识点 进行了串联和展示。
垂线的应用难题与解决方案
问题1
如何在保证美观的同时,保证 数据的准确性和可读性?
垂线与不同工具的对比
垂线与Word
Word是一种文字处理工具,用于编辑文档和排版。相比之下,垂线更适合制作 具有丰富内容和多媒体元素的课件,如插入图片、视频、动画等。
垂线与在线教育平台
在线教育平台通常集成了教学管理、学生管理、作业管理等功能,而垂线则专注 于课件的制作与发布。相比之下,垂线更注重课件内容的展示和教学效果的优化 。
解决方案1
选择合适的图表类型和颜色, 使数据更加清晰易读。同时, 要仔细核对数据,确保准确无 误。
问题2
如何避免在复杂的数据中迷失 重点?
解决方案2
利用颜色、形状、大小等视觉 元素来突出重点和区分不同的 内容,使观众更容易理解和记
忆。
04
CATALOGUE
垂线与其他工具的对比分析
垂线与同类工具的对比
2. 对于不熟悉PPT的用户来说 ,需要一定时间适应操作界面
3. 无法直接编辑和修改原始 PPT文件,需要另存为新文件
进行编辑
05
CATALOGUE
垂线的未来发展趋势与展望
垂线的未来发展趋势
数字化发展
随着数字化技术的不断进 步,垂线行业将逐渐实现 数字化转型,提升生产效 率和产品质量。
智能化发展
垂线与PowerPoint
七年级数学《垂线(1)》课件

P
B
试一试,你能行!
如图,一辆汽车在直线形公路AB上由A向B行驶,M,N分 别是位于公路两侧的村庄,设汽车行驶到点P位置时,距 离村庄M最近, 行驶到点Q位置时,距离村庄N最近在图 中公路AB上分别画出P,Q两点位置。
课后作业:
一、P8页 5题
修改意见:增加选做题
记得下要去 复习哟!
孔课
子后
学 而
解:如图所示:可以抽象出校门口大道与 南门外大道的位置关系是垂直的。
南门外大道
垂直
校门口大道
动手作图:
一、已知一条直线AB和外一点P,作过P点垂 直于AB的直线。
二、已知一条直线AB和AB上一点P,作过P点 垂直于AB的直线。
存在性
在同一平面内,经
过直线外一点,有
且只有一条直线和 P 已知直线垂直。
AB CD
它们的交点O叫做垂足。
一、已知一条直线AB和外一点P,作过P点垂 直于AB的直线。
二、已知一条直线AB和AB上一点P,作过P点 垂直于AB的直线。
存在性
在同一平面内,经
过直线外一点,有
且只有一条直线和 P 已知直线垂直。
唯一性
A
C
B
A
在同一平面 内,经过直 线上一点,有 且只有一条直 线和已知直线 垂直。
线AB,CD互相垂直,记作: 注意垂直
AB CD
它们的交点O叫做垂足。
的记法哟!
学科引例:
下图是地理课上的方位坐标图,仔细观察图中表 示南北方向和东西方向的直线位置有什么关系?
北
西
东
南
答:两条直线是垂直的关系。
生活引例:
下图是我们学校大门口的大道与 南边车棚外大道的位置关系图,试着 说出它们的位置关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)两条直线垂直,是对两条直线而言 的,因此说到垂线一定是两条直线的位置 关系
2021/01/21
8
(3)垂线的定义有以下两层含义:
A
A
D
C
1
D
1
B
C
B
• 1、∵AB⊥CD
°(垂线的性质) •
∴AB⊥CD(垂线的判 定)
2021/01/21
9
画一画
• 画一条直线的垂线,这样的垂线能画多 少条?(无数条)
过一点有且只有一条直线与已知直线 垂直。
注意:
(1)“有且只有”中,“有”指存在,“只有”
指唯一性。
(2)“过一点”中的点,可以在已知直线上,也
可以在已知直线外。
2021/01/21
11
练习:
(1)如图1,已知 ∠ B=90度,过B点分别 作AB、BC、CA的垂线。 (2)在图2中,过B点作AC的垂线,过A 点作BC的垂线,过C点作AB的垂线。
汇报人:XXX
时间:20XX.XX.XX
2021/01/21
14
2021/01/21
无水花
A
O
C
D
B
5
生活中的垂直
2021/01/21
6
5.1.2 垂线
当∠AOD=90°时, 直线AB、CD互相垂
直。 记作AB⊥CD, 交点O叫做垂足。
垂直于 读作AB 2021/01/21
CD
7
对垂线定义的理解:
(1)在垂直的定义中,只要一个角是直 角就可以了,而不必说四个角都是直角, 因为其他三个角是直角都可以由一个角 是直角推出。
2021/01/21
1
2021/01/21
2
2021/01/21
3
1. 跳水比赛中,入水时水花的 大小直接影响跳水的成绩。那么,水 花的大小是什么原因造成的?
2. 如果用一条直线代表水面, 用另一条直线表示身体,试画出无 水花和水花大的示意图。
2021/01/21
4
水花大
A
O
C
D
B
直线AB、CD相交于 点O.
A
A
B
C
2021/01/21图1
B
C
图2
12
小结
1.垂线的意义 2.过一点作一条直线的垂线
3.垂线的第一性质
作业
1.书本P9 3、4、5(做在书上)
2.作业本 5.1.2 垂线(一)
2021/01/21
13
THANKS FOR WATCHING
谢谢大家观看
为了方便教学与学习使用,本文档内容可以在下载后随意修改,调整。欢迎下载!
• 过直线上一点作已知直线的垂线,这样 的垂线能画多少条?(一条)
• 过直线外一点作已知直线的垂线,这样 的垂线能画多少条?(一条)
画垂线的基本方法:
一贴:三角尺的一条直角边贴住已知直线
二靠: 另一条直角边靠住已知点
三画: 2021/01/21 按要求画垂线
10
根据以上的结果,你能得出什么结论?
垂线的第一性质:
2021/01/21
8
(3)垂线的定义有以下两层含义:
A
A
D
C
1
D
1
B
C
B
• 1、∵AB⊥CD
°(垂线的性质) •
∴AB⊥CD(垂线的判 定)
2021/01/21
9
画一画
• 画一条直线的垂线,这样的垂线能画多 少条?(无数条)
过一点有且只有一条直线与已知直线 垂直。
注意:
(1)“有且只有”中,“有”指存在,“只有”
指唯一性。
(2)“过一点”中的点,可以在已知直线上,也
可以在已知直线外。
2021/01/21
11
练习:
(1)如图1,已知 ∠ B=90度,过B点分别 作AB、BC、CA的垂线。 (2)在图2中,过B点作AC的垂线,过A 点作BC的垂线,过C点作AB的垂线。
汇报人:XXX
时间:20XX.XX.XX
2021/01/21
14
2021/01/21
无水花
A
O
C
D
B
5
生活中的垂直
2021/01/21
6
5.1.2 垂线
当∠AOD=90°时, 直线AB、CD互相垂
直。 记作AB⊥CD, 交点O叫做垂足。
垂直于 读作AB 2021/01/21
CD
7
对垂线定义的理解:
(1)在垂直的定义中,只要一个角是直 角就可以了,而不必说四个角都是直角, 因为其他三个角是直角都可以由一个角 是直角推出。
2021/01/21
1
2021/01/21
2
2021/01/21
3
1. 跳水比赛中,入水时水花的 大小直接影响跳水的成绩。那么,水 花的大小是什么原因造成的?
2. 如果用一条直线代表水面, 用另一条直线表示身体,试画出无 水花和水花大的示意图。
2021/01/21
4
水花大
A
O
C
D
B
直线AB、CD相交于 点O.
A
A
B
C
2021/01/21图1
B
C
图2
12
小结
1.垂线的意义 2.过一点作一条直线的垂线
3.垂线的第一性质
作业
1.书本P9 3、4、5(做在书上)
2.作业本 5.1.2 垂线(一)
2021/01/21
13
THANKS FOR WATCHING
谢谢大家观看
为了方便教学与学习使用,本文档内容可以在下载后随意修改,调整。欢迎下载!
• 过直线上一点作已知直线的垂线,这样 的垂线能画多少条?(一条)
• 过直线外一点作已知直线的垂线,这样 的垂线能画多少条?(一条)
画垂线的基本方法:
一贴:三角尺的一条直角边贴住已知直线
二靠: 另一条直角边靠住已知点
三画: 2021/01/21 按要求画垂线
10
根据以上的结果,你能得出什么结论?
垂线的第一性质:
