立体几何中的最值(教师版)2014.10.06
高中数学 立体几何中的最值解法

高中数学 立体几何中的最值问题一、考情分析立体几何中的最值问题一般涉及到距离、面积、体积、角度等四个方面,此类问题多以规则几何体为载体,涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等,题目较为综合,解决此类问题一般可从两个方面思考:一是函数法,即利用传统方法或空间向量的坐标运算,建立所求的目标函数,转化为函数的最值问题求解;二是直接法,即根据几何体的结构特征或平面几何中的相关结论,直接判断最值. 纵观近几年高考对于组合体的考查,重点放在与球相关的外接与内切问题上.要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答.从实际教学来看,这部分知识是学生掌握最为模糊,看到就头疼的题目.分析原因,除了这类题目的入手确实不易之外,主要是学生没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理.二、经验分享1.解决立体几何中的最值问题常见方法有:(1)建立函数法是一种常用的最值方法,很多情况下,我们都是把这类动态问题转化成目标函数,最终利用代数方法求目标函数的最值.解题途径很多,在函数建成后,可用一次函数的端点法;二次数的配方法、公试法; 有界函数界值法(如三角函数等)及高阶函数的拐点导数法等.(2)公理与定义法通常以公理与定义作依据,直接推理问题的最大值与最小值,一般的公理与定理有:两点之间以线段为最短,分居在两异面直线上的两点的连线段中,以它们的公垂线段为短.球面上任意两点间的连线中以过这两点与球心的平面所得圆的劣弧长为最短等.如果直接建立函数关系求之比较困难,而运用两异面直线公垂线段最短则是解决问题的捷径.(3)解不等式法是解最值问题的常用方法、在立体几何中同样可利用不等式的性质和一些变量的特殊不等关系求解:如ab b a ≥+2222ba ab +≤最小角定理所建立的不等关系等等. (4)展开体图法是求立体几何最值的一种特殊方法,也是一种常用的方法,它可将几何题表面展开,也可将几何体内部的某些满足条件的部分面展开成平面,这样能使求解问题,变得十分直观,由难化易. (5)变量分析法是我们要透过现象看本质,在几何体中的点、线、面,哪些在动,哪些不动,要分析透彻,明白它们之间的相互关系,从而转化成求某些线段或角等一些量的求解最值总题的方法.除了上述5种常用方法外,还有一些使用并不普遍的特殊方法,可以让我们达到求解最值问题的目的,这就是:列方程法、极限思想法、向量计算法等等其各法的特点与普遍性,大家可以通过实例感受其精彩内涵与思想方法所在.2.决定棱锥体积的量有两个,即底面积和高,当研究其体积的最值问题时,若其中有一个量确定,则只需另一个量的最值;若两个量都不确定,可通过设变量法,将体积表示为变量的函数解析式,利用函数思想确定其最值;将空间问题转化为平面问题是转化思想的重要体现,通过旋转到一个平面内,利用两点之间距离最短求解3.解决几何体体积最值问题的方法(1) 根据条件建立两个变量的和或积为定值,利用基本不等式求体积的最值;通过建立相关函数式,将所求的最值问题转化为函数的最值问题求解,此法应用最为广泛;由图形的特殊位置确定最值,如垂直求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.4.解题时,通常应注意分析题目中所有的条件,首先应该在充分理解题意的基础上,分析是否能用公理与定义直接解决题中问题;如果不能,再看是否可将问题条件转化为函数,若能写出确定的表意函数,则可用建立函数法求解;再不能,则要考虑其中是否存在不等关系,看是否能运用解等不式法求解;还不行则应考虑是否可将其体图展开成平面,这样依次从本文所标定的方法顺序思考,必能找到解题的途径三、题型分析(一) 距离最值问题1.空间中两点间距离的最值问题【例1】正方体1111ABCD A B C D 的棱长为1,M 、N 分别在线段11A C 与BD 上,求MN 的最小值.由正方体的棱长为1可得1PQ =.连结AC ,则11//AC AC ,所以BQC ∠为两异面直线11A C 与BD 所成角. 在正方形ABCD 中,AC BD ⊥,所以90BQC ∠=.过点M 作MH AC ⊥,垂足为H ,连结NH ,则//MH PQ ,且1MH PQ ==. 设PM m =,QN t =,则QH m =.在Rt QNH ∆中,22222HN QN QH n m =+=+, 在Rt MHN ∆中,2222221MN MH HN n m =+=++. 显然,当0m n ==时,2MN 取得最小值1,即MN 的最小值为1.【点评】空间中两点距离的最值,最基本的方法就是利用距离公式建立目标函数,根据目标函数解析式的结构特征求解最值.对于分别在两个不同对象上的点之间距离的最值,可以根据这两个元素之间的关系,借助立体几何中相关的性质、定理等判断并求解相应的最值.如【典例1】中的两点分别在两条异面直线上,显然这两点之间距离的最小值即为两异面直线的公垂线段的长度.另外注意直线和平面的距离,两平面的距离等的灵活运用.学科#网【小试牛刀】【2017甘肃省天水市第一中学上学期期末】如图所示,在空间直角坐标系中,是坐标原点,有一棱长为的正方体,和分别是体对角线和棱上的动点,则的最小值为()A. B. C. D.【答案】B2.几何体表面上的最短距离问题【例2】正三棱柱ABC —A 1B 1C 1中,各棱长均为2,M 为AA 1中点,N 为BC 的中点,则在棱柱的表面上从点M 到点N 的最短距离是多少?并求之.【分析】将正三棱柱的表面展开,即可转化为平面内两点间距离的最小值问题求解.注意两种不同的展开方式的比较.【解析】 (1)从侧面到N,如图1,沿棱柱的侧棱AA 1剪开,并展开, 则22MN AM AN =+221(21)10=++=(2)从底面到N 点,沿棱柱的AC 、BC 剪开、展开,如图2.则222cos120MN AM AN AM AN =+-⋅︒图(1)图(2)【点评】求解几何体表面上的最短距离问题,往往需要将几何体的侧面或表面展开,将问题转化为平面图形中的最值,进而利用平面几何中的相关结论判断并求解最值.如【典例2】中就是利用了平面内两点间线段最短来确定最值,但要注意几何体表面的展开方式可能有多种,求解相关最值时,需要比较才能得到正确结论.【小试牛刀】【2017甘肃省天水市第一中学上学期期末】在侧棱长为的正三棱锥中,,过作截面,交于,交于,则截面周长的最小值为__________.【答案】6【解析】将棱锥的侧面沿侧棱展开,如图,的长就是截面周长的最小值,由题意,由等腰三角形的性质得.(二) 面积的最值 1.旋转体中面积的最值【例3】一个圆锥轴截面的顶角为56π,母线为2,过顶点作圆锥的截面中,最大截面面积为 . 【分析】本题是截面问题中的常见题,应根据几何体的结构特征确定截面形状,然后求解截面的数字特征,进而确定其最值.【点评】由圆锥的性质可知,过圆锥顶点的截面一定是等腰三角形,且腰长等于圆锥的母线长,该等腰三角形的顶角的最大值为轴截面的顶角,所以截面面积的最大值取决于轴截面顶角的取值范围,不能误认为轴截面的面积就是最大值.【小试牛刀】圆柱轴截面的周长l 为定值,求圆柱侧面积的最大值. 【解析】设圆柱的底面直径为d ,高为h . 则由题意得:2()d h L +=. 所以12d h L +=. 而圆柱的侧面积为2S rh dh ππ==.由均值不等式可得2()2d h dh +≥,即216L dh ≤(当且仅当d h =时等号成立). 所以圆柱侧面积为216S dh L ππ=≤,即圆柱侧面积的最大值为216L π.2.多面体中的面积最值【例4】如图中1所示,边长AC =3,BC =4,AB =5的三角形简易遮阳棚,其A 、B 是地面上南北方向两个定点,正西方向射出的太阳光线与地面成30°角,试问:遮阳棚ABC 与地面成多大角度时,才能保证所遮影面ABD 面积最大?【分析】首先分析几何体的结构特征,明确遮影面ABD中的定值——AB,则所求最值问题转化为该边上的高中AB上的高建立联系,从而确定最值.的最值,进而根据已知——太阳光的照射角度将其与ABC【点评】求解几何体中的面积最值,首先要明确所求图形面积的表示式,区分该图形中的定值与变量,然后根据几何体的结构特征和已知条件确定变量的最值即可.如该题中抓住QD的变化,建立与已知——太阳光的照射角的关系是准确确定最值的关键所在.学¥科网【小试牛刀】在三棱锥A—BCD中,ΔABC和ΔBCD都是边长为a的正三角形,求三棱锥的全面积的最大值.(三) 体积的最值问题【例5】如图3,已知在∆ABC 中,∠=︒C 90,PA ⊥平面ABC,AE PB ⊥于E,AF PC ⊥于F,AP AB ==2,∠=AEF θ,当θ变化时,求三棱锥P AEF -体积的最大值.图3【分析】θ的变化是由AC与BC的变化引起的,要求三棱锥P-AEF 的体积,则需找到三棱锥P-AEF 的底面积和高,高为定值时,底面积最大,则体积最大.【解析】因为PA ⊥平面ABC,BC ⊂平面ABC,所以PA BC ⊥又因为BC AC PA AC A ⊥⋂=,,所以BC ⊥平面PAC,又AF ⊂平面PAC,所以BC AF ⊥,又AF PC PC BC C ⊥⋂=,,所以AF ⊥平面PBC,即AF EF ⊥.EF 是AE 在平面PBC 上的射影,因为AE PB ⊥,所以EF PB ⊥,即PE ⊥平面AEF.在三棱锥P AEF -中,AP AB AE PB ==⊥2,, 所以PE AE ==22,,AF EF V S PEP AEF AEF ===⋅=⨯⨯⋅⨯-22131312222sin ,cos sin cos θθθθ,∆=262sinθ,因为02<<θπ,所以02021<<<≤θπθ,sin因此,当θπ=4时,VP AEF-取得最大值为26. 学.科网【点评】几何体体积的最值问题的解决,要根据几何体的结构特征确定其体积的求解方式,分清定量与变量,然后根据变量的取值情况,利用函数法或平面几何的相关结论判断相应的最值.如该题中确定三棱锥底面的面积最值是关键.【小试牛刀】【2017安徽省黄山市上学期期末质量检测】在棱长为6的正方体中,是中点,点是面所在的平面内的动点,且满足,则三棱锥的体积最大值是()A. 36 B. C. 24 D.【答案】B(四) 角的最值【例6】如图,在四棱锥S -ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA =AB=BC =2,AD =1.M是棱SB的中点.(Ⅰ)求证:AM∥面SCD;(Ⅱ)求面SCD与面SAB所成二面角的余弦值;(Ⅲ)设点N是直线CD上的动点,MN与面SAB所成的角为错误!未找到引用源。
(完整版)立方体中的最值问题

(完整版)立方体中的最值问题立方体中的最值问题 (完整版)在立方体中,最值问题是指在一定的约束条件下,寻找出立方体边界上或内部的最大值或最小值。
本文将详细介绍立方体中的最值问题以及相关的数学原理和解题方法。
1. 问题描述假设给定一个立方体,其边长为$L$,我们需要在这个立方体中寻找一个点,使得该点的坐标和满足一定的约束条件,并且使得某个目标函数的值最大或最小。
2. 约束条件和目标函数在立方体问题中,通常会给出一些约束条件和一个目标函数。
约束条件可以是线性等式或不等式,用来限制点的坐标和的取值范围。
目标函数是我们希望最大化或最小化的函数,可以是线性函数、多项式函数或其他类型的函数。
3. 解决方法立方体中的最值问题可以使用各种数学方法来解决。
以下是几种常用的方法:- 拉格朗日乘数法:适用于有等式约束的问题,通过引入拉格朗日乘子来将约束条件转化为无约束问题,并使用最值定理求解。
拉格朗日乘数法:适用于有等式约束的问题,通过引入拉格朗日乘子来将约束条件转化为无约束问题,并使用最值定理求解。
- 线性规划:适用于有线性约束的问题,将目标函数和约束条件表示为线性表达式,通过线性规划模型求解。
线性规划:适用于有线性约束的问题,将目标函数和约束条件表示为线性表达式,通过线性规划模型求解。
- 梯度下降法:适用于目标函数是可导函数的问题,通过计算目标函数的梯度并迭代更新点的位置,最终找到最值点。
梯度下降法:适用于目标函数是可导函数的问题,通过计算目标函数的梯度并迭代更新点的位置,最终找到最值点。
- 动态规划:适用于问题具有最优子结构性质的情况,将问题划分为子问题,通过动态规划递推求解最值问题。
动态规划:适用于问题具有最优子结构性质的情况,将问题划分为子问题,通过动态规划递推求解最值问题。
4. 示例问题为了更好地理解立方体中的最值问题,以下是一个示例问题:问题:在一个边长为5的立方体中,寻找一个点$(x, y, z)$使得$2x + y - z$的值最大。
立体几何中的最值问题

在 △A 中 ,由余 弦定 理 ,得 AA 一 11。
于点 D ,则 PD上 BC,且 球 0 与 面 PBC 的切 点 E 在
故 截面 AADE周长 的最小 值 为 l1。
说 明 :对 于 几 何 体表 面 上 两 点距 离 的最 值 问题 ,
PD k
现 考 虑 截 面 PAD (如 图
一 … t 一 。
过 点 0作 O0 上平 面 ABC,垂 足为 0l,设 001一
z,则点 D 到 平面 ABC 的距 离为 1+ 。
所 以
1 ·
PO  ̄-
一
因为 01A一01B===01C=  ̄/16一z。,所 以 S△ABc≤
2
一 (tanz 一专)。+丢。 故当tan。 一号时, 。取得最小值为8 。
解 :当 A,B,c 三 点 固定 时 ,要 使 四 面体 ABCD
‘)
01D tan 20 一
,A D 一
的体积 最大 ,则 点 D 到平 面 ABC 的距离 应 最 大 。 由
于点 D 在 以 0 为 球心 ,1为半 径 的球 面 上运 动 ,故 当 30。D:==3cot 0。从 而 ,正 三 角 形 ABC的 边 长 为 n一 D0上平 面 ABC时 ,四面体 ABCD 的体积 最大 。
形 面 积为 最大 ,且最 大面 积 为 R。。
‘士
例 4 如 图 3,四 棱 锥
ABCD的底 面 是 平 行 四 边 形 ,过
点 A 和 侧 棱 SC 的 中 点 M 作 平
面分 别 交 侧 棱 SB,SD 于 点 P, .
T,
Q,求
的最 大值 和最 小值 。
高中数学立体几何中的最值问题

高中数学立体几何中的最值问题在高中数学的学习中,立体几何一直是一个重点和难点,而其中的最值问题更是让许多同学感到头疼。
这类问题往往需要我们综合运用空间想象力、几何知识以及数学方法来求解。
接下来,让我们一起深入探讨立体几何中的最值问题。
一、常见类型及解法1、距离最值问题(1)两点间距离最值在立体几何中,求两点间距离的最值,常常需要我们将空间中的两点转化到同一平面内。
例如,在长方体中,求异面直线上两点的最短距离,就需要通过平移将其转化为共面直线,然后利用平面几何中的知识求解。
(2)点到直线距离最值求点到直线的距离最值时,通常要找到点在直线上的投影。
如果直线是某一平面的斜线,那么可以通过作垂线找到投影,再利用勾股定理计算距离。
(3)点到平面距离最值对于点到平面的距离最值,一般可以利用空间向量法。
先求出平面的法向量,然后通过向量的数量积来计算点到平面的距离。
2、面积最值问题(1)三角形面积最值在立体几何中,涉及三角形面积的最值问题,可能需要考虑三角形的边长关系或者角度大小。
例如,已知三角形的两边及其夹角,当夹角为直角时,面积最大。
(2)四边形面积最值对于四边形,如平行四边形,其面积可以表示为底边乘以高。
当底边长度固定时,高取得最大值时面积最大;或者当四边形的对角线相互垂直时,面积等于对角线乘积的一半。
3、体积最值问题(1)柱体体积最值对于柱体,如圆柱、棱柱,其体积等于底面积乘以高。
当底面积不变时,高最大则体积最大;反之,高最小时体积最小。
(2)锥体体积最值锥体体积为三分之一底面积乘以高。
在求解锥体体积最值时,需要关注底面积和高的变化。
二、例题分析例 1:在棱长为 2 的正方体 ABCD A1B1C1D1 中,E、F 分别是棱AB、BC 的中点,求点 A1 到直线 EF 的距离。
解:连接 A1C1、C1F、EF,因为 A1C1 平行于 EF,所以点 A1 到直线 EF 的距离等于点 A1 到直线 C1F 的距离。
立体几何的最值问题

立体几何最值问题立体几何是数学中的一个重要分支,它研究的是空间图形的性质和数量关系。
在立体几何中,我们经常遇到最值问题,即寻找某个量的最大值或最小值。
本文将介绍立体几何中最值问题的几个方面:1.立体几何位置关系立体几何中的位置关系是指空间中点、线、面之间的相对位置。
解决位置关系问题需要运用空间想象和逻辑推理。
在立体几何中最值问题中,位置关系往往与距离、角度等问题交织在一起,需要综合考虑多种因素。
2.立体几何中的距离立体几何中的距离是指空间中两点之间的直线距离,或者是点与线、线与面之间的距离。
在解决最值问题时,我们需要考虑如何利用距离公式来计算最短路径、最大距离等。
3.立体几何中的体积立体几何中的体积是指空间中封闭图形的体积,或者是两个平面图形之间的距离。
计算体积需要运用体积公式,而解决最大或最小面积问题则需要考虑如何调整图形的形状和大小。
4.立体几何中的最短路径立体几何中的最短路径问题是指寻找空间中两点之间的最短距离。
解决这类问题需要运用距离公式和几何定理,有时还需要借助对称、旋转等技巧。
5.立体几何中的最大/最小面积立体几何中的最大/最小面积问题通常涉及到平面图形在空间中的展开和折叠。
解决这类问题需要运用面积公式和平面几何定理,同时要注意图形的对称性和边长之间的关系。
6.立体几何中的角度问题立体几何中的角度问题是指空间中两条直线或两个平面之间的夹角。
解决这类问题需要运用角度公式和空间向量,同时要注意图形的对称性和边长之间的关系。
7.立体几何中的轨迹问题立体几何中的轨迹问题是指一个点或一条线在空间中按照一定规律移动所形成的轨迹。
解决这类问题需要运用轨迹方程和运动学原理,同时要注意轨迹的形状和大小随时间的变化情况。
专题突破立体几何之《立体几何中的最值问题》
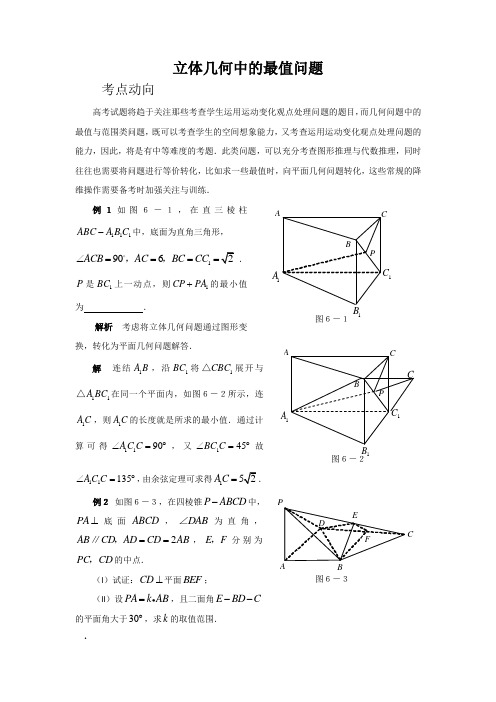
立体几何中的最值问题考点动向高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目,而几何问题中的最值与范围类问题,既可以考查学生的空间想象能力,又考查运用运动变化观点处理问题的能力,因此,将是有中等难度的考题.此类问题,可以充分考查图形推理与代数推理,同时往往也需要将问题进行等价转化,比如求一些最值时,向平面几何问题转化,这些常规的降维操作需要备考时加强关注与训练.例1如图6-1,在直三棱柱111ABC A B C -中,底面为直角三角形,1906ACB AC BC CC ∠===,,.P 是1BC 上一动点,则1CP PA +的最小值为 .解析 考虑将立体几何问题通过图形变换,转化为平面几何问题解答.解 连结1A B ,沿1BC 将1CBC △展开与11A BC △在同一个平面内,如图6-2所示,连1A C ,则1A C 的长度就是所求的最小值.通过计算可得1190A C C ∠=︒,又145BC C ∠=︒故11135A C C ∠=︒,由余弦定理可求得1AC = 例2 如图6-3,在四棱锥P ABCD -中,PA ⊥底面ABCD ,DAB ∠为直角,2AB CD AD CD AB ==,∥,E F ,分别为PC CD ,的中点.(I )试证:CD ⊥平面BEF ;(II )设PA k AB =,且二面角E BD C --的平面角大于30︒,求k 的取值范围.·A1A 11图6-1AC PB1A1C1B图6-2C BC图6-3解析 对(I ),可以借助线面垂直的判定定理,或者借助平面的法向量及直线的方向向量解答;对(II ),关键是确定出所求二面角的平面角.解法1(I )证:由已知DF AB ∥且DAB ∠为直角, 故ABFD 是矩形,从而CD BF ⊥.又PA ⊥底面ABCD ,CD AD ⊥,故由三垂线定理知CD PD ⊥. 在PDC △中,E ,F 分别为PC ,CD 的中点,故EF PD ∥,从而CD EF ⊥,由此得CD ⊥面BEF .(II )连接AC 交BF 于G ,易知G 为AC 的中点,连接EG ,则在PAC △中易知EG PA ∥.又因PA ⊥底面ABCD ,故EG ⊥底面ABCD . 在底面ABCD 中,过G 作GH BD ⊥,垂足为H ,连接EH ,由三垂线定理知EH BD ⊥,从而EHG ∠为二面角E BD C --的平面角. 设AB a =,则在PAC △中,有1122EG PA ka ==.以下计算GH ,考虑底面的平面图(如图6-5),连接GD ,因1122BD S BD GH GB DF ==△G , 故GB DFGH BD =.在ABD △中,因AB a=,2AD a =,得BD =.而1122GB FB AD a ===,DF AB =, 从而得55GB AB GH a BD a===.因此1tan 2kaEG EHG k GH ===. ~故0k >知EHG ∠是锐角,故要使30EHG >∠,必须3tan 3023>=, 解之得,k 的取值范围为15k >.BC图6-4图6-5解法2(I )如图6-6,以A 为原点,AB 所在直线为x 轴,AD 所在直线为y 轴,AP 所在直线为z 轴建立空间直角坐标系,设AB a =,则易知点A ,B ,C ,D ,F 的坐标分别为()000A ,,,()00B a ,,,()220C a a ,,,()020D a ,,,()20F a a ,,.从而(200)(020)DC a BF a ==,,,,,,0DC BF =,故DC BF ⊥. 设PA b =,则(00)P b ,,,而E 为PC 中点,故2b E a a ⎛⎫ ⎪⎝⎭,,,从而02b BE a ⎛⎫= ⎪⎝⎭,,.0DC BE =,故DC BE ⊥.由此得CD BEF ⊥面.(II )设E 在xOy 平面上的投影为G ,过G 作GH BD ⊥垂足为H ,由三垂线定理知EH BD ⊥.从而EHG ∠为二面角E BD C --的平面角.由PA k AB =得(00)P ka ,,,2ka E a a ⎛⎫ ⎪⎝⎭,,,(0)G a a ,,.设(0)H x y ,,,则(0)(20)GH x a y a BD a a =--=-,,,,,, 由0GH BD =得()2()0a x a a y a --+-=,即2x y a -=-. ①又因(0)BH x a y =-,,,且BH 与BD 的方向相同,故2x a ya a-=-, 即22x y a +=. ②由①②解得3455x a y a ==,,从而215055GH a a GH a ⎛⎫=--= ⎪⎝⎭,,,. (2tan 25kaEGEHG k GH===.由0k >知EHG ∠是锐角,由30EHG ∠>︒,得tan tan30EHG >︒,即23k >.图6-6故k的取值范围为k >. [规律小结]立体几何中的最值与范围,需要首先确定最值或范围的主体,确定题目中描述的相关变动的量,根据必要,可确定是利用几何方法解答,还是转化为代数(特别是函数)问题解答.其中的几何方法,往往是进行翻折变换,这时可以想象实际情形,认为几何体是利用硬纸等折成的,可以动手翻折的,在平时做练习时,不妨多动手试试,培养自己的空间想象能力,在考试时就可以不动手,动脑想就可以了.特别注意变动的过程,抓住变动的起始与终了等特殊环节.考点误区分析(1)这类问题容易成为难点,关键是学生的空间想象能力缺乏,或者对问题的转化方向不明确.因此,要注意常见的转化方向,如化立体几何问题为平面几何问题,或化立体几何问题为代数问题等,根据题目特征进行转化.(2)对题目所描述的情形没有清醒的认识也是造成错解的主要原因,注意产生量的变化的主要原因是什么,相关的数量和位置关系都做怎样的变化,抓住问题的关键,才能顺利解决问题.同步训练1.如图6-7,在直三棱柱111ABC A B C -中,AB BC ==12BB =, 90=∠ABC ,,E F分别为111,AA C B 的中点,沿棱柱的表面从E 到F 两点的最短路径的长度为 .》2.有两个相同的直三棱柱,高为a2,底面三角形的三边长分别为)0(5,4,3>a a a a .用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则a 的取值范围是__________.3.如图6-8,正四面体ABCD 的棱长为1,棱AB ∥平面α,则正四面体上的所有点在平面αA图6-71A 1E图6-8内的射影构成的图形面积的取值范围是 .[参考答案]1.[解析]分别将111A B C △沿11A B 折到平面11ABB A 上;将111A B C △沿11A C 折到平面11ACC A 上;将11BCC B 沿1BB 折到平面11ABB A 上;将11BCC B 沿1CC 折到平面11ACC A 上,比较其中EF 长即可.. 2.[解析]可知,全面积最小的是四棱柱面积为22428a +,全面积最小的是三棱柱面积为21248a +,解2212482428a a +>+即可.[答案]3150<<a . 3.[解析]当CD 所在的直线与平面α平行时,所求射影面积最大,为1122AB CD ⨯=;当CD 所在的直线与平面α.[答案]1]2.。
立体几何第三讲 空间几何体得最值问题

分清定量与变量,然后根据变量的取值情况,利用函数法或平面几何的相关结论判断相应的
最值.如该题中确定三棱锥底面的面积最值是关键.
【玩转跟踪】在棱长为 1 的正方体 ABCD A1B1C1D1 中,点 P1, P2 分别是线段 AB 、BD1(不
包括端点)上的动点,且线段 P1P2 平行于 平面 A1 ADD1 ,则四面体 P1P2 AB 的体积的最大值
锥 P-AEF 的底面积和高,高为定值时,底面积最大,则体积最大.
【解析】因为 PA 平面 ABC, BC 平面 ABC,所以 PABC 又因为 BCAC, PA AC A ,所以 BC 平面 PAC,又 AF 平面 PAC,所以 BCAF , 又 AFPC, PC BC C ,所以 AF 平面 PBC,即 AFEF 。EF 是 AE 在平面 PBC 上的 射影,因为 AEPB ,所以 EFPB ,即 PE 平面 AEF。在三棱锥 P AEF 中, AP AB 2, AEPB ,
5
.
5
又 P 在 BD 上运动,且当 P 运动到点 O 时,PQ 最小,等于 OQ 的长为 2 5 ,也就是异面直 5
线 BD 和 SC 的公垂线段的长.故选 B. 2.几何体表面上的最短距离问题
【例 2】正三棱柱 ABC—A1B1C1 中,各棱长均为 2,M 为 AA1 中点,N 为 BC 的中点,则 在棱柱的表面上从点 M 到点 N 的最短距离是多少?并求之.
又∵ 0<α+β<π,∴(α+β)max=π-arctan 2 ,(α+β)min=π-arctan2 2 .
【迁移运用】
1.【西藏日喀则一中高三 10 月检测】已知正三C 的距离为1,点 是线段 的中点,过点 作球 的截面,则截面面
最新3. 立体几何中的最值问题资料资料

3. 立体几何中的最值问题(一)求解立体几何的最值问题主要应用代数中的有关函数知识或不等式有关知识求解。
解题的关键是恰当地引入参变量(一元或二元),建立目标函数,然后由表达式的特点求最值;求曲面上的两点间距离或多面体中的折线的最短长度问题,可考虑展开后转化为平面上两点间的最短距离问题,然后用通常的解三角形的方法加以解决。
一、面积的最值问题1. 【湖南省怀化市2014届高三第二次模拟考试统一检测】在空间中有一棱长为a 的正四面体,其俯视图的面积的最大值为( )A .2a B .22a C .24D .24a2. (湖北省荆州市2013届高三3月质量检测(Ⅱ)数学(理)试题)在半径为R 的球内有一内接圆柱,设该圆柱底面半径为r ,当圆柱的侧面积最大时,rR 为 ( )A .14B .12C .2D3.(东北三省三校2013年3月高三第一次联合模拟)点A B C D 、、、在同一个球的球面上,AB BC ==2AC =,若四面体ABCD 体积的最大值为23,则这个球的表面积为( )A .1256π3B .8πC .254πD .2516π4 .(河北省武邑中学2013届高三第一次模拟考试数学(理)试题)如图,在三棱锥ABC P -中,PA ⊥底面ABC ,∠ACB = 90,AE ⊥PB 于E ,AF ⊥PC 于F ,若2==AB PA ,∠BPC =θ,则当AEF ∆的面积最大时,θtan 的值为( )A .2B .21 C .2 D .225.(河南省豫东、豫北十所名校2012届高三阶段性测试四理科)已知长方体ABCD -A 1B 1C 1D 1的外接球的表面积为16,则该长方体的表面积的最大值为( )A .32B .36C .48D .646. (湖南省株洲市2008届高三第二次质检)已知三棱锥P —ABC 的四个顶点均在半径为1的球面上,且满足0=⋅,0=⋅,0=⋅,则三棱锥P —ABC 的侧面积的最大值为( )A .2B .1C .21D .417. 设圆柱轴截面的对角线长为定值,为使圆柱的侧面积最大,则轴截面的对角线与底面所成的角为( )A 、6πB 、4πC 、3πD 、125πFEPCBA8. 有一个棱长为a 的正方体骨架,其内放置一气球,使其充气且尽可能地膨胀(仍保持为球的形状),则气球表面积的最大值为( )A 、2a πB 、22a πC 、23a πD 、24a π9. 已知圆锥的母线长为,l 底面半径为R ,如果过圆锥顶点的轴截面面积的最大值是221l ,则( )A 、22≤l R B 、22=l R C 、22≥l R D 、22<l R10、如果过圆锥顶点的面积最大的截面是轴截面,则圆锥的侧面展开图的圆心角的取值范围是( )A 、⎪⎪⎭⎫ ⎝⎛π220,B 、()π20,C 、⎥⎦⎤ ⎝⎛π220, D 、(]π20,11. 圆锥的轴截面为正三角形,母线长为8,圆锥的内接圆柱的高为h ,当内接圆柱的侧面积最大时,h 的值是( )A 、334 B 、4 C 、33 D 、3212. 在正三棱锥P -ABC 中,AB =8,PC =54,动点ABM PC M ∆∈,则面积的最小值为( )A 、524B 、374C 、354D 、5551613. 【2014年呼伦贝尔市高考模拟统一考试(二)】设A 、B 、C 、D 是半径为2的球面上的四点,且满足,,AB AC AD AC AB AD ⊥⊥⊥,ABC ABD ACD S S S ∆∆∆++的最大值是 _______ .14【东北三省三校2014届高三第一次联合模拟】 正四面体ABCD 的棱长为4,E 为棱BC 的中点,过E 作其外接球的截面,则截面面积的最小值为 .答案:1-12 BCCD AABB CCDD 13. 8; 14. 4π3. 立体几何中的最值问题(二)二、体积的最值问题1. (2010全国卷2理数)(9)已知正四棱锥S ABCD -中,SA =,那么当该棱锥的体积最大时,它的高为( )A .1B .C .2D .32. (2010全国卷1文理数)(12)已知在半径为2的球面上有A 、B 、C 、D 四点,若AB =CD =2,则四面体ABCD 的体积的最大值为( )A B C . D3.【湖北省稳派教育2014届高三上学期强化训练(三)数学(理)试题】在三棱锥ABC P -中,PC PB PA ,,两两垂直,且1,2,3===PC PB PA ,设M 是底面ABC ∆内一点,定义),,()(p n m M f =,其中p n m ,,分别是三棱锥PAB M -,三棱锥PBC M -,三棱锥PCA M -的体积,若),,21()(y x M f =,且81≥+y a x ,则正实数a 的最小值为( )A . 1B .2C .22D .44. 【陕西省西工大附中2014届高三第四次适应性训练】已知一个四面体有五条棱长都等于2,则该四面体的体积最大值为( )A .12B .1C .22 D .25. (北京市朝阳区2013届高三上学期期末考试数学理试题 )在棱长为1的正方体1111ABCD A B C D 中,点1P ,2P 分别是线段AB ,1BD (不包括端点)上的动点,且线段12P P 平行于平面11A ADD ,则四面体121PP AB 的体积的最大值是( ) A .124B .112 C .16D .126.(河南省十所名校2013届高三第三次联考数学(理)试题)四面体ABCD 中,AD 与BC 互相垂直,AD =2BC =4,且AB +BD =AC +CD =2,则四面体ABCD 的体积的最大值是( )A .4B .2C .5 D7.(吉林省实验中学2012届高三第六次模拟理科)已知正四棱锥S ABCD-中,SA=,那么当该棱锥的体积最大时,它的高为()A.1 B C.2 D.38.(四川省成都市新都一中高2008级12月月考)已知一个四面体有五条棱长都等于2,则该四面体的体积最大值为( )A、12B、22C、1D、29. (2009湖南师大附中第五次月考)如图,三棱柱ABC-A1B1C1的侧面A1ABB1⊥BC,且A1C与底面成 45°角,AB=BC=2,则该棱柱体积的最小值为 ()A.34B.33C.4 D. 310.【湖南省衡阳市八中2014届高三上学期第三次月考试卷数学(理)】在三棱锥D-ABC中,已知BC丄AD,BC=2 ,AD=6,AB+BD=AC+CD=10,则三棱锥D一ABC的体积的最大值是__________.11. 【山东省东营市高三4月统一质量检测】已知直角梯形ABCD,AB AD⊥,CD AD⊥,222AB AD CD===,沿AC折叠成三棱锥,当三棱锥体积最大时,三棱锥外接球的体积为.12.【2012高考真题上海理14】如图,AD与BC是四面体ABCD中互相垂直的棱,2=BC,若cAD2=,且aCDACBDAB2=+=+,其中a、c为常数,则四面体ABCD的体积的最大值是。
立体几何(教师版)空间想象力及最值问题

立体几何------空间想象力及最值问题1.(温州一模第4题)下列命题正确的是()A.垂直于同一直线的两条直线互相平行B.平行四边形在一个平面上的平行投影一定是平行四边形C. 锐角三角形在一个平面上的平行投影不可能是钝角三角形D. 平面截正方体所得的截面图形不可能是正五边形2.有如下四个命题:①平面α和平面β垂直的充要条件是平面α内至少有一条直线与平面β垂直;②平面α和平面β平行的一个必要不充分条件是α内有无数条直线与平面β平行;③直线a与平面α平行的一个充分不必要条件是平面α内有一条直线与直线a平行;④两条直线平行是这两条直线在一个平面内的射影互相平行的既不充分也不必要条件.其中正确的序号是.3.下面是空间线面位置关系中传递性的部分相关命题:①与两条平行直线中一条平行的平面必与另一条直线平行;②与两条平行直线中一条垂直的平面必与另一条直线垂直;③与两条垂直直线中一条平行的平面必与另一条直线垂直;④与两条垂直直线中一条垂直的平面必与另一条直线平行;⑤与两个平行平面中一个平行的直线必与另一个平面平行;⑥与两个平行平面中一个垂直的直线必与另一个平面垂直;⑦与两个垂直平面中一个平行的直线必与另一个平面垂直;⑧与两个垂直平面中一个垂直的直线必与另一个平面平行;其中正确命题的个数有个.4.在正方形中,过对角线的一个平面交于E,交于F,则①四边形一定是平行四边形;②四边形有可能是正方形;③四边形在底面ABCD内的投影一定是正方形;④平面有可能垂直于平面.以上结论正确的为.(写出所有正确结论的编号)5.如图,正四面体ABCD的棱长为1,平面过棱AB,且CD∥α,则正四面体上的所有点在平面α6.已知异面直线a,b所成的角为θ,P为空间任意一点,过P作直线l,若l与a,b所成的角均为,有以下命题:①若θ= 60°,= 90°,则满足条件的直线l有且仅有l条;②若θ= 60°,=30°,则满足条件的直线l有仅有l条;③若θ= 60°,= 70°,则满足条件的直线l有且仅有4条;④若θ= 60°,= 45°,则满足条件的直线l有且仅有2条;上述4个命题中真命题有()A.l个B.2个C.3个D.4个7.定点A和B都在平面α内,定点P∉α,PB⊥α,C是α内异于A和B的动点,且PC⊥AC.那么,动点C在平面α内的轨迹是()A.一条线段,但要去掉两个点B.一个圆,但要去掉两个点C.一个椭圆,但要去掉两个点D.半圆,但要去掉两个点8.如图,在正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是()C B.线段BC1A.线段BC.BB1中点与CC1中点连成的线段D.BC中点与B1C1中点连成的线段9.如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面ABCD为正方形,侧面PAD ⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD 内的轨迹为()10.如图,在正方体中,P是侧面内一动点,若P到直线BC 与直线的距离相等,则动点P的轨迹所在的曲线是()A.直线B.圆C.双曲线D.抛物线11.如图,是平面的斜线段,为斜足。
立体几何中的最值

立体几何最值问题立体几何主要研究空间中点、线、面之间的位置关系,与空间图形有关的线段、角、体积等最值问题常常在试题中出现。
下面举例说明解决这类问题的常用方法。
一、运用变量的相对性求最值例1. 在正四棱锥S-ABCD 中,SO ⊥平面ABCD 于O ,SO=2,底面边长为2,点P 、Q 分别在线段BD 、SC 上移动,则P 、Q 两点的最短距离为( )A. 55 B. 552 C. 2 D. 1二、定性分析法求最值例2. 已知平面α//平面β,AB 和CD 是夹在平面α、β之间的两条线段。
AB ⊥CD ,AB=3,直线AB 与平面α成30°角,则线段CD 的长的最小值为______。
三、展成平面求最值例3. 如图3-1,四面体A-BCD 的各面都是锐角三角形,且AB=CD=a ,AC=BD=b ,AD=BC=c 。
平面α分别截棱AB 、BC 、CD 、DA 于点P 、Q 、R 、S ,则四边形PQRS 的周长的最小值是( )A. 2aB. 2bC. 2cD. a+b+c图3-1四、利用向量求最值例4. 在棱长为1的体ABCD-EFGH 中,P 是AF 上的动点,则GP+PB 的最小值为_______。
一、线段长度最短或截面周长最小问题例1. 正三棱柱ABC —A 1B 1C 1中,各棱长均为2,M 为AA 1中点,N 为BC 的中点,则在棱柱的表面上从点M 到点N 的最短距离是多少?并求之.例2.如图,形ABCD 、ABEF 的边长都是1,而且平面ABCD 、ABEF 互相垂直。
点M 在AC 上移动,点N 在BF 上移动,若CM=BN=a ).20(<<a (1)求MN 的长;(2)当a 为何值时,MN 的长最小; (3)当MN 长最小时,求面MNA 与面MNB 所成的二面角α的大小。
例3. 如图,边长均为a 的形ABCD 、ABEF 所在的平面所成的角为)20(πθθ<<。
立体几何中的最值问题

取 BC 中点 F,∴ EF⊥BC,EF⊥AD,四面体 ABCD 的体 积的最大值,只需 EF 最大即可,
当△ABD 是等腰直角三角形时几何体的体积最大. ∵ AB + BD = AC + CD = 2a,
∴ AB = a,所以 EB = 槡a2 - c2 ,EF = 槡a2 - c2 - 1,
棱 AA1 的长的最小值为
.
解析 设 AA1 = m,AE = x,以 D 为坐标
原点建系,则 D( 0,0,0) ,E( a,0,x) ,B( a,
a,0)
所,C以1 ( E→0B,a=,m( 0)
, ,a,-
x)
,E→C1
=
(
- a,a,m - x) ,
所以 x2 - mx + a2 = 0,x∈[0,m].
点评 本题求的是动点到两个定点距离和的最值问
题,采用了补型的 技 巧,化 曲 为 直,将 折 线 的 最 值 转 化 为 直
线的最值得解,这是动点距离和中常用的技巧.
题型二 棱长最值问题
例 2 长方体 ABCD - A1 B1 C1 D1 的底
面是边长为 a 的正方形,若在侧棱 AA1 上
至少存在一点 E,使得 ∠C1 EB = 90°,则侧
解题技巧与方法
126
JIETI JIQIAO YU FANGFA
立体几何中的最值问题
◎孙岳炜 ( 山东省寿光现代中学,山东 寿光 262700)
立体几何中 的 最 值 问 题 一 般 是 指 有 关 距 离 的 最 值 、角
的最值或面积的最值的问题. 在立体几何中,计算几何体的
立体几何解析几何最值问题

立体几何解析几何最值问题立体几何和解析几何都是数学中的分支领域,它们在研究物体的形状、位置和运动等方面有着不同的方法和应用。
在解析几何中,最值问题是其中一个重要的问题类型,它涉及到找到函数在特定区域内的最大值或最小值。
在立体几何中,我们研究的是空间中的物体,比如点、线、面、体等。
解析几何则是研究平面几何与坐标系统之间的关系,通常使用坐标点来表示点、线、曲线等。
解析几何中最值问题的解决方法通常是通过求导来进行。
我们可以将问题转化为一个函数,然后求该函数的导数,找到导数为0的点,再通过比较得出最大值或最小值。
这种方法在求解平面最值问题时非常有效。
而在立体几何中,最值问题通常涉及到体积、面积或长度等量的最大化或最小化。
解决这类问题可以利用几何性质和定理来进行推导和求解。
比如,要求一个几何体的体积的最大值,我们可以通过寻找几何体的特定形状的体积公式以及几何性质来得出最优解。
具体地说,在立体几何中,最值问题的解决方法可以归纳如下:1.求解体积最大问题:对于已知形状的几何体,我们可以通过推导体积公式,并利用一些方法来求解体积的最大值。
例如,求解一个长方体在给定表面积约束条件下的最大体积,我们可以设长方体的长、宽、高分别为x、y、z,然后利用约束条件和体积公式写出等式,最后通过求解方程组可得到最优解。
2.求解表面积最小问题:类似地,我们可以通过推导表面积公式,并利用一些方法来求解表面积的最小值。
例如,求解一个包含给定体积的圆柱体的表面积最小值,我们可以设圆柱体的底面半径为r、高度为h,然后通过体积公式将h表示为r的函数,并利用表面积公式得到表面积的表达式,最后求解表面积的最小值。
3.求解长度最短问题:有时候我们需要找到连接两个点的最短路径,可以利用几何性质和定理求解。
例如,求解从一个点到直线的最短距离,我们可以利用点到直线的距离公式,并通过求导的方法求解最短距离的点。
总而言之,立体几何和解析几何最值问题的求解方法有所不同,但都可以通过推导公式、利用几何性质和定理以及求导等方法来解决。
怎样求解立体几何最值问题

立体几何中的最值问题具有较强的综合性,对同学们的空间想象能力和运算能力有较高的要求.常见的立体几何最值问题有线段最值问题、面积最值问题以及体积最值问题.下面结合实例来谈一谈这三类立体几何最值问题的解法.一、线段最值问题立体几何中的线段最值问题比较常见,通常要求某条线段的最大值或最小值.求解立体几何中的线段最值问题,需先将该线段视为平面几何图形的一条边,然后根据平面几何图形的性质,如平行四边形的性质、等腰三角形的性质、直角三角形的性质,确定该条边的最大、小值,或根据勾股定理、正余弦定理求得该线段的表达式,运用函数的性质、基本不等式求得最值.例1.如图1,在三棱锥P -ABC 中,PA ⊥底面ABC ,△ABC 为等边三角形,PA =AB =2,点N 为BC 的中点.若点M 为△ABC 内一点,且∠MPA =30°,则MN 的最小值为____.图1图2分析:由于点A 为定点,点M 为动点,且∠MPA =30°,故AM 为定值,则可推断出点M 的轨迹为一段圆弧.将求MN 的最值问题转化为圆上的点到圆心的距离问题,根据圆的性质即可求出最值.解:如图2,连接AM ,AN ,∵PA ⊥底面ABC ,∴PA ⊥AM ,∵∠MPA =30°,PA =2,∴AM =,∴点M 的轨迹在以A 为圆心,AM 为半径的圆弧,∵△ABC 为等边三角形,AB =2,点N 为BC 的中点,∴AN =3,∴MN 的最小值为3-=.将点M 视为圆弧上的一点,将MN 看作圆内的一条线段,便可将立体几何中的线段问题转化为平面内的距离问题,利用平面几何图形的性质来解题.二、面积最值问题立体几何中的面积最值问题往往和截面有关,这类问题的求解思路为:①将已知的线段、角及其关系转化到截面上;②利用勾股定理、正余弦定理,求得在截面上的各条线段、角的大小;③根据平面几何图形的面积公式求得几何图形面积的表达式;④利用函数的性质、基本不等式等求得最值.例2.某圆锥的母线长为2,底面半径为3,则过该圆锥顶点的平面截此圆锥所得截面的面积最大值为____.图3分析:首先作出截面△SMN ,如图3所示,然后对未知变量做出假设,设OP =x ,再根据三角形的面积公式求出截面的面积,利用二次函数的性质即可求得最值.解:由题意可知SB =2,设OP =x ()0≤x ≤3,在Rt△SOB 中,SO =SB 2-OB 2=1,在Rt△SOP 中,SP =SO 2+OP 2=1+x 2,连接OM ,如图3,则MN =2OM 2-OP 2=2()32-x2,故S △SMN =12MN ∙SP ×23-x 2=-()x 2-12+4,因此,当x =1时,△SMN 的面积最大,其值为2.三、体积最值问题立体几何中的体积最值问题较为复杂.要求得最值,需先根据题意确定变化的量,如动点、动直线、动平面,然后设出相应的参数,将其视为自变量,求出几何体体积的表达式,再根据函数的性质、基本不等式求得最值.还可以通过分析几何图形,找到几何体的体积取得最值时的情形,根据简单几何体的体积公式求得最值.方法集锦46思路探寻例3.如图4所示,在三棱锥P -ABC 中,BC ⊥平面PAC ,PA ⊥AB ,PA =AB =4,且E 为PB 的中点,AF ⊥PC 于F .当AC 变化时,三棱锥P -AEF 体积的最大值是_____.解:在三棱锥P -ABC 中,由BC ⊥平面PAC ,得BC ⊥AC ,∵AB =4,∴AC 2+BC 2=AB 2=16,∴V P -AEF =V E -PAF =13∙BC2∙S △PAF ,易知△PAF ~△PCA ,∴S △PAF S △PCA =PA 2PC 2=PA 2PA 2+AC 2,∵S △PAC =12AC ∙PA ,PA =4,∴S △PAF =32AC16+AC 2,∴V E -PAF =163∙AC ∙BC16+AC 2,设AC =a ,0<a <4,∴BC =16-a 2,∴V E -PAF =163∙,令m =a 2+16,易知16<m <32,∴V E -PAF =163∙,令x =1m ∈æèöø0,116,VE -PAF =163∙-512x 2+48x -1,由二次函数f ()x =-512x 2+48x -1性质可得,当x =364时,f ()x 有最大值18,∴VE -PAF 最大值为163×.由于AC 为动直线,故三棱锥P -AEF 体积也随之发生变化.需首先设出参数,根据已知条件和三棱锥的体积公式得到三棱锥P -AEF 的表达式,然后根据相似三角形的性质求出S △PAF 的表达式,再根据二次函数的性质求得最值.通过上述分析不难发现,大部分的立体几何最值问题都需借助平面几何知识来求解.因此求解立体几何最值问题时,可根据题意和几何图形的特点,将点、线、面及其关系转化到同一个平面内,然后利用平面几何知识列出关系式,再根据函数的性质、基本不等式求得最值.(作者单位:江苏省如皋市第一中学)求曲线的方程问题在圆锥曲线中比较常见.此类问题侧重于考查圆锥曲线的定义、几何性质以及一元二次方程的性质.求解曲线的方程问题的方法有很多种,如定义法、相关点法、消参法、数形结合法等.那么,如何选择合适的方法进行求解呢?下面结合实例加以说明.一、定义法运用定义法求解曲线的方程问题,主要是根据椭圆、双曲线、抛物线、圆的定义来求解.这就要求同学们熟练掌握椭圆、双曲线、抛物线、圆的定义,根据这些定义来建立关系式,求得曲线的方程.例1.已知双曲线x 2a 2-y 2b2=1()a >0,b >0的焦距为4,F 1,F 2分别是双曲线的左、右焦点,点P 是双曲线在第一象限上的点,且 PF 1∙PF 2=0,|| PF 1∙|| PF 2=6,求双曲线的方程.解:由题意可得||F 1F 2=4,c =2,∵ PF 1∙ PF 2=0,∴PF 1⊥PF 2,||PF 12+||PF 22=16,由||PF 1-||PF 2=2a 可得||PF 12+||PF 22-2||PF 1||PF 2=4a 2,∵||PF 12+||PF 22=16,|| PF 1∙|| PF 2=6,图447。
立体几何中的最值问题

如 图 5所 示 , 了 制 作 一 个 圆 为
例 2 三 棱 锥 SABC - 中 , 条棱 长为 , 余 棱 长 一 其 均 为 1 求 a为 何 值 时 ,
最 大 , 求最 大值 . 并 如图 3设 s , c—n ,
ቤተ መጻሕፍቲ ባይዱ形 灯笼 , 要 制 作 4个 全 等 的 先
形 骨架 , 总计 耗用 9 6m 铁 丝 , . 用 S I 塑 料 片制 成 圆柱 的侧 I T
1 )利 用 一 次 、 次 、 比 例 函 数 性 质 求 最 值 二 反
■r’,-
何性 质 . 比较 常用 的性 质如 :1 )两 点之 间以直 线段 最
短 ; )垂 线段 最短 等. 2
■■ _
例 3 ( 0 9 全 国卷 )已知二 面角 z 的大小 20 年
为 6 。动 点 P、 分别在 平 面 a J内 , 0, Q 、 9 P到 p的距离 为
) .
B 2; C 2 ; D 4
的侧 面绕 行 2周到 达 A 点 的最 短路线 的长 为
.
如 图 4 分别 作 Q , A一
析 a于 A , AC ̄ Z于 C PBj 口于 B , _ PD - Z于 D , l -
C B 则 AC Q、 D, Q= PDB
C
。 c
和下 底面 ( 安装 上 底 面 ) 不 .当
析
其余 棱长 均为 1 取 ,
柱 底 面 半 径 r取 何 值 时 , S取 得 最大 值?并 求 出该 最 大值 ( 果 结 图5
罐
AB 中点 H , 接 HS HC, 连 、
图 3
精 确 到 0 0 ) . 1m。 .
立体几何中的最值问题

立体几何中的最值问题1、利用垂直关系确定高的最值锥体的体积由底面面积和高决定,底面确定只要高最大即可,借助面面垂直的性质和特殊位置关系确定高的最值进而求得体积最值。
例1.表面积为60π的球面上有四点S、A、B、C,且△ABC是等边三角形,球心O到平面ABC的距离为,若平面SAB⊥平面ABC,则棱锥S﹣ABC体积的最大值为.1.如图,四棱锥P﹣ABCD中,P A⊥底面ABCD,底面ABCD是矩形,AB =2,AD=3,P A=4,E为棱CD上一点,则三棱锥E﹣P AB的体积为.2.把正方形ABCD沿对角线AC折起,当以A,B,C,D四点为顶点的三棱锥体积最大时,直线BD和平面ABC所成的角的大小为.2、利用圆锥曲线定义转化为点到面距离的最值例2.已知正方形ABCD的边长为6,空间有一点M(不在平面ABCD内)满足|MA|+|MB|=10,则三棱锥A﹣BCM的体积的最大值是()A.48B.36C.30D.243、利用侧面展开图求距离的最小值解决空间图形中表面距离最短的问题,常采用“化曲为直”的思想,把空间图形沿侧棱(或母线)展开,达到化空间几何问题为平面几何问题。
例3.如图,在正三棱柱ABC﹣A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M的最短路线长为,设这条最短路线与CC1的交点为N,求P点的位置.1、圆台的上、下底面半径分别为5cm、10cm,母线长AB=20cm,从圆台母线AB的中点M拉一条绳子绕圆台侧面转到B点(B在下底面),求:(1)绳子的最短长度;(2)在绳子最短时,上底圆周上的点到绳子的最短距离;(3)圆锥底面半径为r,母线长为4r,求从底面边缘一点A出发绕圆锥侧面一周再回到A的最短距离.2.如图,正方体ABCD﹣A1B1C1D1的棱长为a,点E为AA1的中点,在对角面BB1D1D上取一点M,使AM+ME最小,其最小值为.4、利用目标函数求体积的最值解决此类问题的两大核心思路:一是化立体问题为平面问题,结合平面几何的相关知识求解;二是建立目标函数的数学思想,选择合理的变量构建目标函数,常利用导数或利用基本不等式,求其最值。
立体几何动点最值问题

立体几何动点最值问题
立体几何动点最值问题是指在立体几何空间中,给定一些特定条件下,求一个动点的某个值的最大或最小值。
这类问题广泛应用于建筑设计、机械工程、地理测量等领域。
在解决立体几何动点最值问题时,通常需要利用几何性质和数学方法进行分析和求解。
下面以两个典型的问题为例进行拓展说明。
问题一:在一个正方体中,找到离一个定点最远的顶点。
解答:首先,我们找到这个正方体的中心点,然后根据对称性可以知道,离中心点最远的顶点就是通过连接中心点和一个面的对角线的顶点。
因此,我们可以通过计算这个对角线的长度,并找出最长的对角线来确定离定点最远的顶点。
问题二:在一个球体上,找到离球心最远的点。
解答:根据球体的几何性质,离球心最远的点是球体表面上的点。
因此,我们可以通过计算球心到球面上各点的距离,并找出最大距离的点来确定离球心最远的点。
在实际应用中,立体几何动点最值问题的解决往往需要结合具体的条件和约束条件进行分析和求解。
这些问题可能涉及到线段、面积、体积等几何量的计算,以及最优化等数学方法的运用。
因此,解决这类
问题需要理解立体几何的基本概念和性质,并熟练掌握相关的计算和求解技巧。
第22讲-几何最值(2014!!!.师.培优竞赛新方法.)

第22讲 几何最值知识纵横几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积等)的最大值或最小值。
求几何最值问题的基本方式有:1.特殊位置与极端位置法:先考虑特殊位置或极端位置,确定最值的具体数据,在进行一般情况下的推证。
2.几何定理(公理)法:应用几何中的不变量性质、定理.3.数形结合法:揭示问题中变动元素的代数关系,构造一元二次方程、二次函数等。
例题求解【例1】如图,在锐角ABC ∆中,24=AB ,45=∠BAC ,BAC ∠平分线交BC 于点D ,点M 、N 分别是AD 和AB 上的动点,则BN BM +的最小值 4 .(陕西省中考题)思路点拨 画折线为直线,综合运用轴对称、垂线段最短等知识.【例2】 如图,在ABC ∆中,AB=10,AC=8,BC=6,经过点C 且与AB 相切的动圆与CB 、CA 分别相交于点E 、F ,则线段EF 的最小值( D )。
A.24 B. 4.75 C. 5 D. 4.8 (兰州市中考题)思路点拨 设O 与AB 相切与T ,连OC 、OT,EF 为O 直径,则EF=OE+OF=OC+OT,将问题转化为求OC+OT 的最小值.【例3】 如图,正方形ABCD 的边长为4cm ,点P 是BC 边上不与点B 、C 重合的任意一点,连接AP ,过点P 作PQ ⊥AP 交DC 于点Q ,设BP 的长为x cm ,CQ 的长为y cm.(1) 求点P 在BC 上运动的过程中y 的最大值;(2) 当41=y cm 时,求x 的值. (河南省中考题)思路点拨 利用相似形建立y 与x 的函数关系式,由此导出y 的最大值例2 例1※【例4】 如图,已知平行四边形ABCD ,AB=a ,BC=b (a>b ),P 为AB 边上的一动点,直线DP 交CB 的延长线于Q ,求AP+BQ 的最小值.(永州市竞赛题)思路点拨 设AP=x ,把AP 、BQ 分别用x 的代数式表示,运用不等式ab b a 222≥+或ab b a 2≥+(当且仅当a=b 时取等号)来求最小值.【解析】在平行四边形abcd 中,ab=a,bc=b,﹙a >b ﹚.p 为ab 上一动点,直线dp 交cb 的延长线于q,则ap ﹢bq 的最小值为:设AP=x,AP+BQ=y,则∵AD ∥BC,则△ADP ∽△BQP,∴AD/BQ=AP/BQ,即:b/(y-b)=x/(a-x).化简得:xy=ab.∴AP+CQ=AP+CQ=x+y ≥2√xy=2√ab∴AP+BQ=AP+(y-CB)=x+y-b ≥2√ab-b (x=y 时取“=”号)※【例5】 如图,在四边形ABCD 中,AD=DC=1,∠DAB=∠DCB=90,BC 、AD 的延长线交于P ,求AB 〃S △PAB 的最小值.例5例3 例4设PD=x (x >1),则由勾股定理得:PC =12-x,∵∠P=∠P ,∠PCD=∠A=90°,∴Rt △PCD ∽Rt △PAB , ∴AB/CD=PA/PC ,∴AB =CD.PA/PC =112++x x ,设y=AB •S △PAB ,代入可得y =)1(2)1(2-+x x ,去分母,得x 2+2(1-y )x+1+2y=0,因为x 是实数,所以△=4(1-y )2-4(1+2y )=4y (y-4)≥0, 又因为y >0,所以y ≥4.即y 的最小值为4,故当PD=3时,AB •S △PAB 的最小值为4. 图形折叠【例6】 在等腰ABC ∆中,AB =AC =5,BC =6.动点M 、N 分别在两腰AB 、AC 上(M 不与A 、B 重合,N 不与A 、C 重合),且MN//BC ,将△AMN 沿MN 所在的直线折叠,使点A 的对应点为P.(1)当MN 为何值时,点P 恰好落在BC 上?(2)设x MN =,MNP ∆与等腰ABC ∆重叠部分的面积为y ,试写出y 与x 的函数关系式.当x 为何值时,y 的值最大,最大值是多少?.(2011年宁夏中考题)思路点拨:P 点能落在BC 上或△ABC 内或外,因此,解题的关键是分类讨论,建立不同的函数关系式. 【例7】(2013•日照)问题背景:如图(a ),点A 、B 在直线l 的同侧,要在直线l 上找一点C ,使AC 与BC 的距离之和最小,我们可以作出点B 关于l 的对称点B ′,连接AB ′与直线l 交于点C ,则点C 即为所求.(1)实践运用:如图(b ),已知,⊙O 的直径CD 为4,点A在⊙O 上,∠ACD=30°,B 为弧AD 的中点,P 为直径CD 上一动点,则BP+AP 的最小值为 .(2)知识拓展:如图(c ),在Rt △ABC 中,AB=10,∠BAC=45°,∠BAC 的平分线交BC 于点D ,E 、F 分别是线段AD 和AB 上的动点,求BE+EF 的最小值,并写出解答过程.分析与解 尽管在实践运用中改变了问题情境,在知识拓展中增加了动点个数,但解决问题的关键都是:化归为基本模式------构造对称点例6(1)作点B关于CD的对称点E,连接AE交CD于点P,此时PA+PB最小,且等于AE.作直径AC′,连接C′E.根据垂径定理得:弧BD=弧DE.∵∠ACD=30°,∴∠AOD=60°,∠DOE=30°,∴∠AOE=90°,∴∠C′AE=45°,又AC′为圆的直径,∴∠AEC′=90°,∴∠C′=∠C′AE=45°,∴C′E=AE=2/2 AC′=22,即AP+BP的最小值是22.(2)如图,在斜边AC上截取AB′=AB,连结BB′.∵AD平分∠BAC,∴∠B′AM=∠BAM,在△B′AM和△BAM中∴△B′AM≌△BAM(SAS),∴BM=B′M,∠BMA=∠B′MA=90°,∴点B与点B′关于直线AD对称.过点B′作B′F⊥AB,垂足为F,交AD于E,连结BE,则线段B′F的长即为所求.(点到直线的距离最短)在Rt△AFB′中,∵∠BAC=45°,AB′=AB=10,∴B′F=52学力训练基础夯实1.如图,菱形ABCD的两条对角线分别长为6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是5。
例谈立体几何最值问题的几种解法

思路探寻立体几何最值问题侧重于考查同学们的空间想象、逻辑推理和数学运算等能力.常见的立体几何最值问题是求立体几何图形中某条线段、某个角、体积、表面积的最值,那么如何求解呢?一、利用函数思想在大多数情况下,我们可以把与动点有关的立体几何问题看作函数问题来求解.以其中某一个量,如动点的坐标、线段的长、角的大小为变量,建立关于该变量的关系式,并将其视为函数式,即可利用一次函数、二次函数、三角函数的性质和图象求得最值.例1.如图1,正方体ABCD-A1B1C1D1的棱长为1,P为AA1的中点,M在侧面AA1B1B上,若D1M⊥CP,则ΔBCM).C.5D.2图1图2解:过M作MG⊥平面ABCD,垂足为G,作GH⊥BC于点H,连接MH,以D为坐标原点,建立如图2所示的空间直角坐标系,可得D()0,0,0,C()0,1,0,A()1,0,0,P()1,0,12,D1(0,0,1),B()1,1,0.设M()1,a,b,则D1M=()1,a,b-1,CP=()1,-1,12,∵D1M⊥CP,∴ D1M⋅ CP=12b-a+12=0,∴b=2a-1,∴CH=1-a,MG=2a-1,∴MH=()1-a2+()2a-12=5a2-6a+2,∴SΔBCM=12BC⋅MH=1=可知当a=35时,ΔBCM面积取最小值,为SΔBCM=12×=故选B.在建立空间直角坐标系后,设出点M的坐标,以a、b为变量,构建关于a的函数式SΔBCM=然后将5a2-6a+2看作二次函数式,对其配方,根据二次函数的性质即可知函数在a=35时取最小值.二、运用基本不等式在解答立体几何最值问题时,我们往往可以先根据立体几何中的性质、定义、定理求得目标式;然后将其进行合理的变形,采用拆项、凑系数、补一次项,去掉常数项等方式,配凑出两式的和或积,就可以直接运用基本不等式来求得最值.在运用基本不等式求最值时,要把握三个条件:一正、二定、三相等.例2.已知三棱锥P-ABC的4个顶点均在球心为O、直径为23的球面上,PA=2,且PA,PB,PC两两垂直.当PC+AB取最大值时,三棱锥O-PAB的体积为().A. C.6解:∵PA,PB,PC两两互相垂直,∴三棱锥P-ABC可补全为如图3所示的长方体.则长方体的外接球即为三棱锥P-ABC的外接球,∴PA2+PB2+PC2=()232=12,又PA=2,∴PB2+PC2=10,∵AB2=PA2+PB2=2+PB2,∴PC2+AB2=2+PB2+PC2=12,∴()PC+AB2-2PC⋅AB=12,又PC⋅AB≤()PC+AB22,∴12=()PC+AB2-2PC⋅AB≥()PC+AB2-2()PC+AB22=12()PC+AB2,当且仅当PC=AB时取等号,∴()PC+AB max=26,此时PC=AB=6,PB=图347思路探寻AB 2-PA 2=2,∴V O -PAB =12V C -PAB =16S △PAB ⋅PC =112PA ⋅PB⋅PC =112×2×2×6故选B.根据长方体的性质得到()PC +AB 2-2PC ⋅AB =10后,可发现该式中含有PC 、AB 的和与积,根据基本不等式a +b ≥2ab 求解,即可得到三棱锥O -PAB 的体积.三、转化法运用转化法求解立体几何最值问题有两种思路.一是将问题转化为平面几何问题.先将几何体的表面展开,或将几何体内部满足条件的某些面展开成平面;再在平面内利用平面几何知识,如正余弦定理、两点间的距离最短、三角形的两边之和大于第三边等求解,这样问题就变得十分直观,容易求解了.另一种思路是根据题意和几何图形中的点、线、面的位置关系,明确其中改变的量和不变的量及其关系,根据简单几何体的性质、表面积公式、体积公式,将问题转化为求某些线段或角的最值.再结合简单几何体的性质,几何图形中点、线、面的位置关系求得最值例3.如图4,在正三棱柱ABC -A 1B 1C 1中,AA 1=AB =2,D 在A 1C 上,E 是A 1B 的中点,则()AD +DE 2的最小值是().A.6-7 B.27 C.3+7 D.5+7图4图5解:将平面A 1BC 与平面A 1AC 翻折到同一平面上,连接AE ,如图5所示,设AE ⋂A 1C =F .由题意可知A 1A =AC =BC =2,A 1C =A 1B =22,所以AA 21+AC 2=A 1C 2,所以AA 1⊥AC ,则∠AA 1C =45°,由余弦定理可得cos∠BA 1C =A 1B 2+A 1C 2-BC 22A 1B ⋅A 1C=8+8-42×22×22=34,则sin∠BA 1C =1-cos 2∠BA 1C =故cos∠AA 1B =cos ()∠AA 1C +∠BA 1C =cos ∠AA 1C cos ∠BA 1C -sin ∠AA 1C sin ∠BA 1C =32-148.因为E 是A 1B 的中点,所以A 1E =2,由余弦定理可得AE 2=AA 21+A 1E 2-2AA 1⋅A 1E cos∠BA 1A=4+2-2×2×2×32-148=3+7.因为D 在A 1C 上,所以AD +DE ≥AE ,当A 、E 、D 三点共线时,等号成立,则()AD +DE 2≥3+7.故选C .将平面A 1BC 与平面A 1AC 翻折到同一平面上,就可以把立体几何问题转化为平面几何问题,即可根据勾股定理和余弦定理求得A 1E 以及AE 的值.分析图形可知当A 、E 、D 三点共线时,AD +DE 取得最大值,再结合余弦定理求解即可.例4.已知球O 的表面积为60π,四面体P -ABC 内接于球O ,ΔABC 是边长为6的正三角形,平面PBC ⊥平面ABC ,则四面体P -ABC 体积的最大值为().A.18B.27C.32D.81解:因为球O 的表面积为60π,所以球的半径R ==15,由题意知四面体P -ABC 底面三角形的面积为定值,要使四面体的体积最大,只须使顶点P 到底面的距离最大,又因为平面PBC ⊥平面ABC ,所以当PB =PC 时,点P 到底面的距离最大,而ΔABC 外接圆的半径r =62sin60°=23,则O 到面ABC 的距离为d =R 2-r 2=3,且O 到面PBC 的距离为h =12r =3,设点P 到平面ABC 的距离为H ,则R 2=()H -d 2+h 2,解得H =33,此时体积最大值为V max =13×12×6×6×sin60°×33=27.故选B.解答本题,首先根据球的表面积求得球的半径;再根据题意和几何体的特征明确当PB =PC 时,点P 到底面的距离最大;最后根据外接圆的性质、勾股定理求出点P 到底面的距离,即可求出最大值.除了上述三种方法外,有时还可采用定义法、构造法来求立体几何最值问题的答案.总之,同学们在解题时,要先根据题意和几何体的结构特征寻找取得最值的情形,求得目标式;然后根据目标式的特征,选用合适的方法求最值.(作者单位:贵州省江口中学)48。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何中的最值问题一、运用变量的相对性求最值例1. 在正四棱锥S-ABCD 中,SO ⊥平面ABCD 于O ,SO=2,底面边长为2,点P 、Q 分别在线段BD 、SC 上移动,则P 、Q 两点的最短距离为( )A.55 B.552 C. 2 D. 1解析:如图1,由于点P 、Q 分别在线段BD 、SC 上移动,先让点P 在BD 上固定,Q 在SC 上移动,当OQ 最小时,PQ 最小。
过O 作OQ ⊥SC ,在Rt △SOC 中,552=OQ 中。
又P 在BD 上运动,且当P 运动到点O 时,PQ 最小,等于OQ 的长为552,也就是异面直线BD 和SC 的公垂线段的长。
故选B 。
图1 图2二、定性分析法求最值例2. 已知平面α//平面β,AB 和CD 是夹在平面α、β之间的两条线段。
AB ⊥CD ,AB=3,直线AB 与平面α成30°角,则线段CD 的长的最小值为______。
解析:如图2,过点B 作平面α的垂线,垂足为O ,连结AO ,则∠BAO=30°。
过B 作BE//CD 交平面α于E ,则BE=CD 。
连结AE ,因为AB ⊥CD ,故AB ⊥BE 。
则在Rt △ABE 中,BE=AB ·tan ∠BAE ≥AB ·tan ∠BAO=3·tan30°=3。
故3≥CD 。
三、展成平面求最值例3. 如图3-1,四面体A-BCD 的各面都是锐角三角形,且AB=CD=a ,AC=BD=b ,AD=BC=c 。
平面α分别截棱AB 、BC 、CD 、DA 于点P 、Q 、R 、S ,则四边形PQRS 的周长的最小值是( )A. 2aB. 2bC. 2cD. a+b+c图3-1 图3-2解析:如图3-2,将四面体的侧面展开成平面图形。
由于四面体各侧面均为锐角三角形,且AB=CD ,AC=BD ,AD=BC ,所以,A 与A ’、D 与D ’在四面体中是同一点,且''////D A BC AD ,'//CD AB ,A 、C 、A ’共线,D 、B 、D ’共线,BD DD AA 2''==。
又四边形PQRS 在展开图中变为折线S ’PQRS ,S ’与S 在四面体中是同一点。
因而当P 、Q 、R 在S ’S 上时,RS QR PQ P S +++'最小,也就是四边形PQRS 周长最小。
又''SA A S =,所以最小值''DD SS L ==b BD 22==。
故选B 。
四、利用向量求最值例4. 在棱长为1的正方体ABCD-EFGH 中,P 是AF 上的动点,则GP+PB 的最小值为_______。
解析:以A 为坐标原点,分别以AB 、AD 、AE 所在直线为x ,y ,z 轴,建立如图4所示的空间直角坐标系,则B (1,0,0),G (1,1,1)。
根据题意设P (x ,0,x ),则)01(x x BP ,,-=→,)111(---=→x x GP ,,,那么图412234222+-++-=+x x x x PB GP222221021220)1(2⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-+-=x x 式子222221021220)1(⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-+-x x 可以看成x 轴正半轴上一点(x ,0,0)到xAy 平面上两点⎪⎪⎭⎫ ⎝⎛0221,,、⎪⎭⎫ ⎝⎛02121,,的距离之和,其最小值为221+。
所以GP+PB 的最小值为222212+=+⋅。
一、线段长度最短或截面周长最小问题例5. 正三棱柱ABC —A 1B 1C 1中,各棱长均为2,M 为AA 1中点,N 为BC 的中点,则在棱柱的表面上从点M 到点N 的最短距离是多少?并求之.解析: (1)从侧面到N ,如图1,沿棱柱的侧棱AA 1剪开,并展开,则MN =22AN AM +=22)12(1++=10(2)从底面到N 点,沿棱柱的AC 、BC 剪开、展开,如图2. 则MN =︒⋅-+120cos 222AN AM AN AM =21312)3(122⨯⨯⨯++=34+ ∵34+<10 ∴m in MN =34+.例6.如图,正方形ABCD 、ABEF 的边长都是1,而且平面ABCD 、ABEF 互相垂直。
点M 在AC 上移动,点N 在BF 上移动,若CM=BN=a ).20(<<a (1)求MN 的长;(2)当a 为何值时,MN 的长最小; (3)当MN 长最小时,求面MNA 与面MNB 所成的二面角α的大小。
解析:(1)作MP ∥AB 交BC 于点P ,NQ ∥AB 交BE 于点Q ,连接PQ ,依题意可得MP ∥NQ ,且MP=NQ ,即MNQP 是平行四边形。
∴MN=PQ,由已知,CM=BN=a,CB=AB=BE=1, ∴2==BF AC ,21,21a BQ a CP ==, 即2aBQ CP ==, ∴=+-==22)1(BQ CP PQ MN )20(21)22()2()21(222<<+-=+-a a a a(2)由(1)知: 2222==MN a 时,当,的中点时,分别移动到即BF AC N M ,, 22的长最小,最小值为MN (3)取MN 的中点G ,连接AG 、BG ,∵AM=AN,BM=BN ,∴AG ⊥MN,BG ⊥MN ,∴∠AGB 即为二面角α的平面角。
又46==BG AG ,所以由余弦定理有31464621)46()46(cos 22-=••-+=α。
故所求二面角)31arccos(-=α。
例7. 如图,边长均为a 的正方形ABCD 、ABEF 所在的平面所成的角为)20(πθθ<<。
点M 在AC 上,点N 在BF 上,若AM=FN ,(1)求证:MN//面BCE ; (2)求证:MN ⊥AB; (3)求MN 的最小值.解析:(1)如图,作MG//AB 交BC 于G, NH//AB 交BE 于H, MP//BC 交AB 于P, 连PN, GH , 易证MG//NH,且MG=NH, 故MGNH 为平行四边形,所以MN//GH , 故MN//面BCE ; (2)易证AB ⊥面MNP, 故MN ⊥AB ;(3)MPN ∠即为面ABCD 与ABEF 所成二面角的平面角,即θ=∠MPN ,设AP=x , 则BP=a -x , NP=a -x , 所以:θcos )(2)(22x a x x a x MN ---+=22)cos 1(21)2)(cos 1(2a a x θθ-+-+=,故当2ax =时,MN有最小值a )cos 1(21θ-. 例8.如图,正方形ABCD 、ABEF 的边长都是1,而且平面ABCD 、ABEF 互相垂直。
点M 在AC 上移动,点N 在BF 上移动,若CM=x ,BN=y, ).2,0(<<y x (1)求MN 的长(用x,y 表示);(2)求MN 长的最小值,该最小值是否是异面直线AC ,BF 之间的距离。
解析:在面ABCD 中作MP ⊥AB 于P ,连PN ,则MP ⊥面ABEF ,所以MP ⊥PN ,PB=1-AP=x 22在∆PBN 中,由余弦定理得:PN 2=02245cos 2)22(xy y x -++ xy y x -+=2221,在PMN Rt ∆中,MN=xy y x x PN MP -++-=+2222221)221(ABFECDPNM1222+--+=x xy y x ).2,0(<<y x ;(2)MN 1222+--+=x xy y x 31)322(43)2(22+-+-x x y ,故当322=x ,32=y 时,MN 有最小值33。
且该最小值是异面直线AC ,BF 之间的距离。
例9. 如图,在ΔABC 中,∠ACB =90°,BC =a,AC =b,D 是斜边AB 上的点,以CD 为棱把它折成直二面角A —CD —B 后,D 在怎样的位置时,AB 为最小,最小值是多少?解析: 设∠ACD =θ,则∠BCD =90°-θ,作AM ⊥CD 于M ,BN ⊥CD 于N ,于是AM =bsin θ,CN =asin θ.∴MN =|asin θ-bcos θ|,因为A —CD —B 是直二面角,AM ⊥CD ,BN ⊥CD ,∴AM 与BN 成90°的角,于是AB =22222)cos sin (cos sinθθθθb a a b -++=θ222sin ab b a -+≥ab b a -+22.∴当θ=45°即CD 是∠ACB 的平分线时,AB 有最小值,最小值为ab b a -+22.例10. 正三棱锥A-BCD ,底面边长为a ,侧棱为2a ,过点B 作与侧棱AC 、AD 相交的截面,在这样的截面三角形中,求(1)周长的最小值;(2)周长为最小时截面积的值,(3)用这周长最小时的截面截得的小三棱锥的体积与三棱锥体积之比.解析:(1)沿侧棱AB 把正三棱锥的侧面剪开展成平面图.如图1,当周长最小时,EF 在直线BB ′上,∵ΔABE ≌ΔB ′AF ,∴AE =AF ,AC =AD ,∴B ′B ∥CD ,∴∠1=∠2=∠3,∴BE =BC =a ,同理B ′F =B ′D =a.∵ΔFDB ′∽ΔADB ′,∴B D DF'=B A B D '',a DF=a a 2=21,∴DF =21a,AF =23a.又∵ΔAEF ∽ΔACD ,∴BB ′=a+43a+a =411a,∴截面三角形的周长的最小值为411a.(2)如图2,∵ΔBEF 等腰,取EF 中点G ,连BG ,则BG ⊥EF.∴BG =22EG BE -=22)83(a a -=855a ∴S ΔBEF =21·EF ·BG =21·43a ·855a =64553a 2.(3)∵V A-BCD =V B-ACD ,而三棱锥B —AEF ,三棱锥B —ACD 的两个高相同,所以它们体积之比于它们的两底面积之比,即CADB AEF B V V --=ACD AEF S S △△=22CD EF =169 评析 把曲面上的最短路线问题利用展开图转化为平面上两点间距离的问题,从而使问题得到解决,这是求曲面上最短路线的一种常用方法.本题中的四面体,其中任何一个面都可以做为底面,因而它可有四个底面和与之对应的四条高,在解决有关三棱锥体积题时,需要灵活运用这个性质.二、面积最值问题例11. 如图1所示,边长AC =3,BC =4,AB =5的三角形简易遮阳棚,其A 、B 是地面上南北方向两个定点,正西方向射出的太阳光线与地面成30°角,试问:遮阳棚ABC 与地面成多大角度时,才能保证所遮影面ABD 面积最大?解析: 易知,ΔABC 为直角三角形,由C 点引AB 的垂线,垂足为Q ,则应有DQ 为CQ 在地面上的斜射影,且AB 垂直于平面CQD ,如图2所示.因太阳光与地面成30°角,所以∠CDQ =30°,又知在ΔCQD 中,CQ =512,由正弦定理,有 ︒30sin CQ =QCD QD ∠sin 即 QD =56sin ∠QCD.为使面ABD 的面积最大,需QD 最大,这只有当∠QCD =90°时才可达到,从而∠CQD = 60°. 故当遮阳棚ABC 与地面成60°角时,才能保证所遮影面ABD 面积最大.例12. 在三棱锥A —BCD 中,ΔABC 和ΔBCD 都是边长为a 的正三角形,二面角A —BC —D =φ,问φ为何值时,三棱锥的全面积最大。
