人教版数学中考复习专项练习含答案：一次函数与二次函数图像的交点问题

合集下载

中考数学总复习《二次函数图像与坐标轴的交点问题》练习题-附带答案

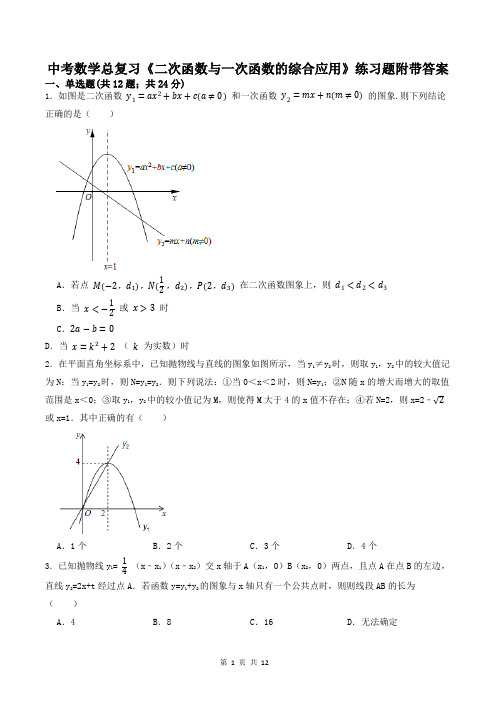
中考数学总复习《二次函数图像与坐标轴的交点问题》练习题-附带答案一、单选题(共12题；共24分)1．二次函数y=ax2+bx+c（a≠0）的部分图象如图，图象过点（-1，0），对称轴为直线x=2，下列结论：①抛物线与x轴的另一个交点是（5，0）；②4a+c＞2b；③4a+b=0；④当x＞-1时y的值随x值的增大而增大．其中正确的结论有（）A．1个B．2个C．3个D．4个2．二次函数y=a（x﹣4）2﹣4（a≠0）的图象在2＜x＜3这一段位于x轴的下方，在6＜x＜7这一段位于x轴的上方，则a的值为（）A．1B．-1C．2D．-2 3．已知二次函数y=x2−x+14m−1的图象与x轴有交点，则m的取值范围是（）A．m≤5B．m≥2C．m<5D．m>2 4．二次函数y=x2-2x-2与坐标轴的交点个数是（）A．0B．1C．2D．3 5．已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=2，与x轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论：①抛物线过原点；②4a+b+c=0；③a﹣b+c＜0；④抛物线的顶点坐标为（2，b）；⑤当x＜2时y随x增大而增大．其中结论正确的是（）A．①②③B．③④⑤C．①②④D．①④⑤6．如图，抛物线y＝ax2＋bx＋c交x轴于（-1，0），（3，0），则下列判断错误的是（）．A．图象的对称轴是直线x＝1B．当x>1时y随x的增大而减小C．一元二次方程ax2＋bx＋c＝0的两个根分别是-1和3D．当y<0时x<-17．若抛物线y=x2﹣2x+m与x轴有两个交点，则m的取值范围是（）A．m＜﹣1 B．m＜1C．m＞﹣1D．m＞1 8．二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：X﹣1013y﹣1353①ac＜0；②当x＞1时y的值随x值的增大而减小．③3是方程ax2+（b﹣1）x+c=0的一个根；④当﹣1＜x＜3时ax2+（b﹣1）x+c＞0．其中正确的个数为（）A．4个B．3个C．2个D．1个9．二次函数y=ax2+bx+c（a≠0，a，b，c为常数）的图象如图，ax2+bx+c=m有实数根的条件是（）A．m≥﹣2B．m≥2C．m≥0D．m＞4 10．如图是抛物线y＝ax2＋bx＋c(a≠0)的部分图象，其顶点坐标为(1，n)，且与x轴的一个交点在点(3，0)和(4，0)之间．则下列结论：①a－b＋c＞0；②3a＋b＝0；③b2＝4a(c－n)；④一元二次方程ax2＋bx＋c＝n－1有两个不相等的实数根．其中正确结论的个数是()A．1B．2C．3D．4 11．已知抛物线y＝ax2﹣2ax＋a﹣c（a≠0）与y轴的正半轴相交，直线AB∥x轴，且与该抛物线相交于A（x1，y1）B（x2，y2）两点，当x＝x1＋x2时函数值为p；当x＝x1+x2q.则p﹣q的值为（）2时函数值为A．a B．c C．﹣a＋c D．a﹣c 12．函数y=ax2+bx+c的图象如图所示，那么关于x的一元二次方程ax2+bx+c﹣4=0的根的情况是（）A．有两个不相等的实数根B．有两个异号的实数根C．有两个相等的实数根D．没有实数根二、填空题(共6题；共6分)13．若函数y=mx2+2x+1的图象与x轴只有一个公共点，则常数m的值是．14．如图，点A，B的坐标分别为（1，4）和（4，4），抛物线y=a（x+m）2+n的顶点在线段AB上，与x轴交于C，D两点（C在D的左侧），点C的横坐标最小值为﹣3，则点D的横坐标的最大值为．15．若抛物线y=x2与直线y=x+2的交点坐标为（﹣1，1）和（2，4），则方程x2﹣x﹣2=0的解为．16．已知二次函数y=x2－2x－3与x轴交于A、B两点，在x轴上方的抛物线上有一点C，且∥ABC的面积等于10，则C点坐标为．17．抛物线y＝（m﹣1）x2+2x+ 12m图象与坐标轴有且只有2个交点，则m＝．18．若二次函数y=kx2−4x+3的函数值恒大于0，则k取值范围是.三、综合题(共6题；共56分)19．已知二次函数y＝x2－（m＋2）x＋2m－1（1）求证：不论m取何值，该函数图象与x轴总有两个公共点；（2）若该函数的图象与y轴交于点（0，3）．①求函数图象与x轴的交点坐标；②当0＜x＜5时求y的取值范围．20．（1）解方程：x2−x+13=3(x2+1)+5x；（2）求二次函数y=2x2−5x的图象与x轴的交点坐标．21．已知二次函数y=mx2﹣5mx+1（m为常数，m＞0），设该函数的图象与y轴交于点A，该图象上的一点B与点A关于该函数图象的对称轴对称．（1）求点A，B的坐标；（2）点O为坐标原点，点M为该函数图象的对称轴上一动点，求当M运动到何处时∥MAO的周长最小．22．已知二次函数的图象以A（﹣1，4）为顶点，且过点B（2，﹣5）．（1）求该函数的关系式；（2）求该函数图象与坐标轴的交点坐标．23．已知函数y=mx2﹣6x+1（m是常数）．（1）求证：不论m为何值，该函数的图象都经过y轴上的一个定点；（2）若该函数的图象与x轴只有一个交点，求m的值．24．已知二次函数y=ax2﹣4ax+1（1）写出二次函数图象的对称轴：；（2）如图，设该函数图象交x轴于点A、B（B在A的右侧），交y轴于点C．直线y=kx+b经过点B、C．①如果k=﹣13，求a的值②设点P在抛物线对称轴上，PC+PB的最小值为√13，求点P的坐标．参考答案1．【答案】B2．【答案】A3．【答案】A4．【答案】D5．【答案】C6．【答案】D7．【答案】B8．【答案】B9．【答案】A10．【答案】C11．【答案】A12．【答案】C13．【答案】0或114．【答案】815．【答案】﹣1或216．【答案】（4，5）或（－2，5）17．【答案】﹣1或2或018．【答案】k>4 319．【答案】（1）解：令y=0，则x2−(m+2)x+2m−1=0，∴△=[−(m+2)2]−4(2m−1)=m2+4m+4−8m+4=m2−4m+8=(m−2)2+4≥4∴△＞0，∴方程总有两个不相等的实数根，即抛物线与x轴总有两个交点；（2）解：①∵函数的图象与y轴交于点（0，3）．∴2m−1=3，∴m=2，∴抛物线的解析式为：y=x2−4x+3，当x2−4x+3=0，∴(x−1)(x−3)=0，∴x1=1，x2=3，所以抛物线与x 轴的交点坐标为：(−1，0)，(−3，0). ②∵y =x 2−4x +3=(x −2)2−1，∴ 抛物线的开口向上，当x =2时函数的最小值为−1，当x =0时当x =5时∴ 当0＜x ＜5时y 的取值范围为：−1≤y ＜8.20．【答案】（1）解：将方程化为一般式，得x 2+3x −5=0．∵Δ=b 2−4ac =32−4×1×(−5)=29>0．∴x =−3±√292×1=−3±√292．解得x 1=−3+√292，x 2=−3+√292．（2）解：把y =0代入y =2x 2−5x 中得2x 2−5x =0．解得x 1=0，x 2=52．∴二次函数y =2x 2−5x 的图象与x 轴的交点坐标是(0，0)和(52，0)．21．【答案】（1）解：当x=0时y=1，则点A 的坐标为（0，1）∵抛物线对称轴为x= 5m 2m = 52∴B 点坐标为（5，1）（2）解：设直线OB 解析式为y=kx ，把B （5，1）代入可得5k=1，解得k= 15 ∴直线OB 解析式为y= 15 x由轴对称的性质可知当点M 运动到直线OB 与二次函数对称轴的交点时∥MAO 的周长最小．当x= 52时y= 12∴M 点的坐标为（ 52， 12 ）22．【答案】（1）解：由顶点A （﹣1，4），可设二次函数关系式为y=a （x+1）2+4（a≠0）．∵二次函数的图象过点B （2，﹣5） ∴点B （2，﹣5）满足二次函数关系式 ∴﹣5=a （2+1）2+4 解得a=﹣1．∴二次函数的关系式是y=﹣（x+1）2+4（2）解：令x=0，则y=﹣（0+1）2+4=3∴图像与y轴的交点坐标为（0，3）；令y=0，则0=﹣（x+1）2+4解得x1=﹣3，x2=1故图像与x轴的交点坐标是（﹣3，0）、（1，0）23．【答案】（1）解：当x=0时y=1．所以不论m为何值，函数y=mx2﹣6x+1的图象都经过y轴上一个定点（0，1）；（2）解：①当m=0时函数y=mx2﹣6x+1的图象与x轴只有一个交点；②当m≠0时若函数y=mx2﹣6x+1的图象与x轴只有一个交点，则方程mx2﹣6x+1=0有两个相等的实数根所以∥=（﹣6）2﹣4m=0，m=9．综上，若函数y=mx2﹣6x+1的图象与x轴只有一个交点，则m的值为0或9 24．【答案】（1）直线x=2（2）解：①当x=0时y=1∴点C的坐标为（0，1）．将（0，1）代入y=kx+b，得：b=1．∵k= −1 3∴y=−13x+1当y=0时有−13x+1=0解得：x=3∴点B的坐标为（3，0）．将B（3，0）代入y=ax2﹣4ax+1，得：9a﹣12a+1=0解得：a=3；②当PC+PB取最小值时点P是直线BC与直线x=2的交点，且PC+PB的最小值=BC= √13．∵OC=1∴在Rt∥OBC中OB= 2√3∴此时点B的坐标为(2√3，0)将点B的坐标代入y=kx+1得：2√3k+1=0解得：k=−√36∴此时直线BC的解析式为：y=−√36x+1∵当x=2时.∴点P的坐标为(2，3−√33)。

中考数学总复习《二次函数图像与坐标轴的交点问题》专题测试卷带答案

中考数学总复习《二次函数图像与坐标轴的交点问题》专题测试卷带答案班级：___________姓名：___________考号：___________一、单选题(共12题；共24分)1．抛物线y =x 2−2x +1与坐标轴的交点个数为（）A ．无交点B ．1个C ．2个D ．3个2．如图，已知二次函数y ＝ax 2＋bx ＋c （a≠0）的图象与x 轴交于点A （﹣1，0），与y 轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x ＝1.下列结论：①abc ＞0；②4a ＋2b ＋c ＞0；③4ac ﹣b 2＞8a ；④13<a <23； ⑤b ＞c.其中含所有正确结论的选项是（） A ．①②③B ．②③④C ．①④⑤D ．①③④⑤3．已知二次函数y=ax 2+bx+c （a≠0，a ，b ，c 为常数）的y 与x 的部分对应值如下表：x 3.23 3.24 3.25 3.26 y﹣0.06﹣0.08﹣0.030.09判断方程ax 2+bx+c=0的一个解x 的取值范围是（） A ．3＜x ＜3.23 B ．3.23＜x ＜3.24 C ．3.24＜x ＜3.25D ．3.25＜x ＜3.264．已知抛物线y =−3x 2+bx +c 与x 轴只有一个交点，且过点A(m −2，n)和B(m +4，n)，则n 的值为（） A ．-9B ．-16C ．-18D ．-275．如图，二次函数y=ax 2+bx+c （a≠0）的图象与x 轴交于点A 、B 两点，与y 轴交于点C ，对称轴为直线x=-1，点B 的坐标为（1，0），则下列结论：①AB=4；②b 2-4ac ＞0；③ab ＜0；④a 2-ab+ac ＜0，其中正确的结论有（）个．A．3B．4C．2D．16．坐标平面上某二次函敷图形的顶点为(2，-1)，此函数图形与x轴相交于P、Q两点，且PQ=6若此函数图形通过(1，a)、(3，b)、(-1，c)、(-3，d)四点，则下列结论错误的是() A．a=b B．d>c C．c>a D．d<07．二次函数y＝ax2＋bx＋c的图象如图所示，则下列判断中错误的是()A．图象的对称轴是直线x＝1；B．一元二次方程ax2＋bx＋c＝0的两个根是－1、3；C．当x＞1时，y随x的增大而减小；D．当－1＜x＜3时，y＜0.8．如图，已知抛物线l：y= 12（x-2）2-2与x轴分别交于0、A两点，将抛物线l1向上平移得到l2，过点A作AB⊥x轴交抛物线l2于点B，如果山抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16，则抛物线l2的函数表达式为（）A．y= 12（x-2）2+4B．y= 12（x-2）2+3C．y= 12（x-2）2+2D．y= 12（x-2）2+19．如图，铅球运动员掷铅球的高度y（m）与水平距离x（m）之间的函数关系式是y=﹣112x2+ 23x+ 53，则该运动员此次掷铅球的成绩是（）A．6m B．12m C．8m D．10m10．已知函数y= x2+2x-3，当x=m时，y＜0，则m的值可能是（）.A．-4B．0C．2D．311．对于二次函数y=（x+1）2+2的图象，下列说法正确的是（）A．开口向下B．对称轴是直线x=﹣1C．顶点坐标是（1，2）D．与x轴有两个交点12．已知二次函数y=ax2+bx+c（a，b，c为常数，a≠0）的图象如图所示，有下列结论：①abc＞0，②b2-4ac＜0，③a-b+c＞0，④4a-2b+c＜0，其中正确结论的个数是（）A．1B．2C．3D．4二、填空题(共6题；共6分)13．如图，抛物线y=a(x−4)(x+1)(a>0)与x轴交于A，B两点（点A在点B的左边）与y轴交于点C，连接BC，过点A作直线BC的平行线交抛物线于另一点E，交y轴于点D，则ADDE的值为.14．已知抛物线y＝2x2+bx﹣1与x轴的交点坐标分别是（﹣3，0）和（2，0），那么关于x的一元二次方程2x2+bx﹣1＝0的根是．15．抛物线y=(x+2)2+3上的点到x轴最短的距离是．16．如图，二次函数y＝ax2+bx+c的图象经过点A（﹣1，0），B（3，0）．有下列结论：①图象的对称轴为直线：x＝1；②a：b：c＝﹣1：2：3；③若0＜x＜4，则5a＜y＜﹣3a；④一元二次方程cx2+bx+a＝0的两个根分别为﹣1和13，其中正确的结论有（填序号）．17．如图，二次函数y＝ax2＋bx＋c的图象与x轴的两个交点分别为（﹣1，0），（3，0）对于下列命题：①b﹣2a＝0；②abc＜0；③a﹣2b＋4c＜0④8a＋c＜0，其中正确的有．18．如图，抛物线y=−x2+bx+c与x轴交于点A(1，0)、点B，与y轴相交于点C(0，3)，下列结论：①b=−2﹔②B点坐标为(−3，0)，③抛物线的顶点坐标为(−1，3)，④直线y=ℎ与抛物线交于点D、E，若DE<2，则h的取值范围是3<ℎ<4﹔⑤在抛物线的对称轴上存在一点Q，使△QAC的周长最小，则Q点坐标为(−1，2)．其中正确的有．三、综合题(共6题；共75分)19．已知二次函数y=x2−mx+m−2．（1）求证：不论m为何实数，此二次函数的图象与x轴都有两个不同交点；（2）若此函数y有最小值−54，求这个函数表达式．20．已知y=x2−(m+2)x+(2m−1)是关于x的抛物线解析式.（1）求证：抛物线与x轴一定有两个交点；（2）点A(−2,y1)、B(1,y2)和C(4,y3)是抛物线上的三个点，当抛物线经过原点时，判断y1、y2和y3的大小关系.21．如图，在平面直角坐标系中，抛物线y＝12（x﹣1）2﹣2与x轴交于点A和点B（点A在点B 的左侧），第一象限内的点C在该抛物线上．（1）直接写出A、B两点的坐标；（2）若△ABC的面积为12，求点C坐标；（3）在（2）问的条件下，直线y＝mx+n经过点A、C，12（x﹣1）2﹣2＞mx+n时，直接写出x的取值范围．22．如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式y=a（x-6）2+h．已知球网与O点的水平距离为9m，高度为2.43m，球场的边界距O点的水平距离为18m．（1）当h=2.6时，求y与x的关系式（不要求写出自变量x的取值范围）（2）当h=2.6时，球能否越过球网？球会不会出界？请说明理由；（3）若球一定能越过球网，又不出边界，求h的取值范围．23．如图，已知抛物线y=−x2+bx+c与x轴、y轴分别相交于点A（－1，0）和B（0，3），其顶点为D．（1）求这条抛物线的解析式；（2）若抛物线与x轴的另一个交点为E，求⊥ODE的面积；抛物线的对称轴上是否存在点P使得⊥PAB的周长最短．若存在请求出点P的坐标，若不存在说明理由．24．已知，如图，二次函数y=−x2+bx+c的图象与x轴交于A，B两点，与y轴交于点C(0, 5)，且经过点(1, 8)（1）求该抛物线的解析式；（2）求该抛物线的顶点坐标和对称轴.（3）求△ABC的面积S△ABC.参考答案1．【答案】C 2．【答案】C 3．【答案】D 4．【答案】D 5．【答案】A 6．【答案】D 7．【答案】D 8．【答案】C 9．【答案】D 10．【答案】B 11．【答案】B 12．【答案】B 13．【答案】1514．【答案】x 1＝−3，x 2＝2 15．【答案】3 16．【答案】①②④ 17．【答案】③18．【答案】①②④⑤19．【答案】（1）证明： Δ=(−m)2−4(m −2)=m 2−4m +8=(m −2)2+4 ，不论 m 为何值时，都有 Δ>0此时二次函数图象与 x 轴有两个不同交点．（2）解： ∵4ac−b 24a =4(m−2)−m 24=−54， m 2−4m +3=0 ， ∴m =1 或 m =3所求函数式为 y =x 2−x −1 或 y =x 2−3x +1 ．20．【答案】（1）证明：y=x 2﹣（m+2）x+（2m ﹣1）.∵⊥=[﹣（m+2）]2﹣4×1×（2m ﹣1）=（m －2）2+4＞0，∴抛物线与x 轴一定有两个交点（2）解：∵抛物线y=x 2﹣（m+2）x+（2m ﹣1）经过原点，∴2m ﹣1=0.解得：m =12 ，∴抛物线的解析式为y=x 2−52x.当x=﹣2时，y1=9；当x=1时，y2=－3.5；当x=4时，y3=6，∴y2＜y3＜y121．【答案】（1）解：令y=0，则12（x-1）2-2=0解得x1=−1，x2=3∴A（-1，0），B（3，0）（2）解：∵A（-1，0），B（3，0）∴AB=4∵S△ABC=12AB·yC=12∴12×4×y C=12解得y C=6∴12(x−1)2−2=6解得x1=5，x2=−3（不符题意，舍去）∴C（5，6）（3）解：由图象可知，当12(x−1)2−2>mx+n时，x的取值范围是x＜-1或x＞522．【答案】（1）解：∵h=2.6，球从O点正上方2m的A处发出∴抛物线y=a（x-6）2+h过点（0，2）∴2=a（0-6）2+2.6解得：a=- 1 60故y与x的关系式为：y=- 160（x-6）2+2.6（2）解：当x=9时，y=- 160（x-6）2+2.6=2.45＞2.43所以球能过球网；当y=0时解得：x1=6+2 √39＞18，x2=6-2 √39（舍去）故会出界；（3）解：当球正好过点（18，0）时，抛物线y=a（x-6）2+h还过点（0，2），代入解析式得：{2=36a+ℎ0=144a+ℎ解得： {a =−154ℎ=83此时二次函数解析式为：y=- 154 （x-6）2+ 83此时球若不出边界h≥ 83当球刚能过网，此时函数解析式过（9，2.43），抛物线y=a （x-6）2+h 还过点（0，2），代入解析式得：{2.43=a(9−6)2+ℎ2=a(0−6)2+ℎ解得： {a =−432700ℎ=19375此时球要过网h≥19375故若球一定能越过球网，又不出边界，h 的取值范围是：h≥ 83．23．【答案】（1）解：根据题意得{−1−b +c ＝0c ＝3 ，解得 {b ＝2c ＝3∴抛物线解析式为y=-x 2+2x+3；（2）解：当y=0时，-x 2+2x+3=0解得x 1=-1，x 2=3，则E （3，0）； y=-（x-1）2+4，则D （1，4）， ∴S ⊥ODE = 12×3×4=6；连接BE 交直线x=1于点P ，如图，则PA=PE ， ∴PA+PB=PE+PB=BE ，此时PA+PB 的值最小，易得直线BE 的解析式为 y=-x+3，当x=1时，y=-x+3=3， ∴P （1，2）．24．【答案】（1）解：∵二次函数 y =−x 2+bx +c 的图象经过点 (0, 5) 和 B(1, 8)∴{c =5−1+b +c =8 解这个方程组，得 {b =4c =5∴该二次函数的解析式是 y =−x 2+4x +5 ；（2）解： y =−x 2+4x +5=−(x −2)2+9 ∴顶点坐标是 (2, 9) ；对称轴是x=2；（3）解：∵二次函数y=−x2+4x+5的图象与x轴交于A，B两点∴−x2+4x+5=0解这个方程得：x1=−1即二次函数y=−x2+4x+5与x轴的两个交点的坐标为A(−1, 0)和B(5, 0).∴△ABC的面积S△ABC=12AB×OC=12×|5−(−1)|×5=15.。

中考数学专项复习《二次函数图像与坐标轴的交点问题》练习题附答案

中考数学专项复习《二次函数图像与坐标轴的交点问题》练习题附答案一、单选题1．若函数y=x2−2x+b的图象与x轴有两个交点，则b的取值范围是（）A．b≤1B．b＞1C．0＜b＜1D．b＜12．二次函数与y=kx2−8x+8的图象与x轴有交点，则k的取值范围是() A．k<2B．k<2且k≠0C．k≤2D．k≤2且k≠03．函数y=ax2+bx+c的图象如图所示，那么关于x的方程ax2+bx+c-3=0的根的情况是（）A．有两个不相等的实数根B．有两个异号的实数根C．有两个相等的实数根D．没有实数根4．已知二次函数y=2(x+1)(x－a)，其中a>0，若当x≤2时，y随x增大而减小，当x≥2时y随x增大而增大，则a的值是（）A．3B．5C．7D．不确定5．在平面直角坐标系中，二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论正确的（）A．ac＞0B．b2﹣4ac＜0C．4a+2b+c＜0D．b＝2a6．如图所示，二次函数y=ax2+bx+c的图象中，王刚同学观察得出了下面四条信息：（1）b2﹣4ac＞0；（2）c＞1；（3）2a﹣b＜0；（4）a+b+c＜0，其中错误的有（）A．1个B．2个C．3个D．4个7．若二次函数y＝（m﹣1）x2+2x+1的图象与x轴有两个不同的交点，则m的取值范围是（）A．m≤2B．m＜2C．m≤2且m≠1D．m＜2且m≠18．如图为抛物线y=ax2+bx+c的图象，A，B，C为抛物线与坐标轴的交点，且OA=OC=1，则下列关系中正确的是（）A．a+b=﹣1B．a﹣b=﹣1C．b＜2a D．ac＜09．已知二次函数y=ax2+bx+c（a≠0）的图象如图，在下列代数式中（1）a+b+c＞0；（2）﹣4a＜b＜﹣2a（3）abc＞0；（4）5a﹣b+2c＜0；其中正确的个数为（）A．1个B．2个C．3个D．4个10．如图是二次函数y=ax2+bx+c的图象，下列结论：①二次三项式ax2+bx+c的最大值为4；②4a+2b+c＜0；③一元二次方程ax2+bx+c=1的两根之和为﹣1；④使y≤3成立的x的取值范围是x≥0．其中正确个数有（）．A．1个B．2个C．3个D．4个11．二次函数y=kx2﹣6x+3的图象与x轴有交点，则k的取值范围是（）A．k＜3B．k＜3且k≠0C．k≤3D．k≤3且k≠012．如图，一次函数y1＝2x与二次函数y2＝ax2+bx+c图象相交于P、Q两点，则函数y＝ax2+（b﹣2）x+c的图象可能是（）A．B．C．D．二、填空题13．已知函数y= 12(m+3)x2+2x+1的图象与x轴只有一个公共点，则m的值为. 14．如图，是抛物线y=ax2+bx+c的一部分，其对称轴为直线x=1，它与x轴的一个交点为A（3，0），根据图象，可知关于x的一元二次方程ax2+bx+c=0的解是．15．如图是抛物线y=ax2+bx+c的一部分，其对称轴为直线x=1，若其与x轴一交点为B（3，0），则由图象可知，不等式ax2+bx+c＞0的解集是．16．如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=x2﹣6x﹣16，AB为半圆的直径，则这个“果圆”被y 轴截得的线段CD的长为.17．已知：y关于x的函数y=k2x2−(2k−1)x+1的图象与坐标轴只有两个不同的交点A、B，P 点坐标为(3,2)，则△PAB的面积为.18．抛物线y=ax2+bx+c的顶点为D(−1,2)，与x轴的一个交点A在点(−3,0)和(−2,0)之间，则以下结论：①b2−4ac<0；②a+b+c<0；③c−a=2；④方程ax2+bx+c−2=0有两个不相等的实数根，其中正确结论为.三、综合题19．设二次函数y1=2x2+bx+c(b，c是常数)的图象与x轴交于A，B两点．（1）若A，B两点的坐标分别为(1，0)，(2，0)，求函数y)的表达式及其图象的对称轴．（2）若函数y1的表达式可以写成心=2(x-h)2-2(h是常数)的形式，求b+c的最小值．（3）设一次函数y2=x-m(m是常数)，若函数y1的表达式还可以写成y1=2(x-m)(x-m-2)的形式，当函数y=y1-y2的图象经过点(x0，0)时，求x0-m的值．20．已知函数y＝x2-2kx＋k2+1.（1）求证：不论k取何值，函数y>0；（2）若函数图象与y轴的交点坐标为（0，10），求函数图象的顶点坐标.21．已知二次函数y=x2+2bx−3b．（1）当该二次函数的图象经过点A(1，0)时，求该二次函数的表达式；（2）在(1) 的条件下，二次函数图象与x轴的另一个交点为点B，与y轴的交点为点C，点P从点A出发在线段AB上以每秒2个单位长度的速度向点B运动，同时点Q从点B出发，在线段BC上以每秒1个单位长度的速度向点C运动，直到其中一点到达终点时，两点停止运动，求△BPQ面积的最大值；（3）若对满足x≥1的任意实数x，都使得y≥0成立，求实数b的取值范围．22．已知关于x的方程x2﹣（m+2）x+2m﹣1=0．（1）求证：此方程有两个不相等的实数根；（2）若抛物线y=x2﹣（m+2）x+2m﹣1=0与x轴有两个交点都在x轴正半轴上，求m的取值范围；（3）填空：若x2﹣（m+2）x+2m﹣1=0的两根都大于1，则m的取值范围是．23．函数y＝mx2﹣2mx﹣3m是二次函数．（1）如果该二次函数的图象与y轴的交点为（0，3），那么m＝；（2）在（1）的条件下，结合图象当0＜x＜3时，求y的取值范围．24．已知抛物线y＝ax2﹣bx＋3经过点A（1，2），B（2，3）.（1）求此抛物线的函数解析式.（2）写出该抛物线与坐标轴的交点坐标.参考答案1．【答案】D2．【答案】D3．【答案】C4．【答案】B5．【答案】C6．【答案】A7．【答案】D8．【答案】B9．【答案】A10．【答案】B11．【答案】D12．【答案】A13．【答案】m=﹣1或m=﹣314．【答案】3或﹣115．【答案】x＜﹣1或x＞316．【答案】2017．【答案】1或1218．【答案】②③19．【答案】（1）解：由题意，得y1=2(x-1)(x-2)．图象的对称轴是直线x= 3 2（2）解：由题意，得y1=2x2-4hx+2h2-2∴b+c=2h2-4h-2=2(h-1)2-4∴当h=1时，b+c的最小值是-4.（3）解：由题意，得y=y1-y2=2(x-m)(x-m-2)-(x-m)=(x-m)[2(x-m)-5]∵函数y的图象经过点(x0，0)∴(x0-m)[2(x0-m)-5]=0∴x0-m=0，或x0-m= 52.20．【答案】（1）解：y＝（x-k）2+1∵不论k取何值，（x-k）2≥0∴（x-k）2+1＞0；即不论k取何值，函数y＞0；（2）解：∵二次函数图象与y轴交于点（0，10）∴当x＝0时，y＝10∴k2+1＝10，解得k＝±3∴y＝x2±9x+10＝（x±3）2+1∴顶点坐标为（3，1）或（﹣3，1）.21．【答案】（1）解：把A(1，0)代入y=x2+2bx−3b 得：0=12+2b−3b，解得：b=1∴该二次函数的表达式为：y=x2+2x−3；（2）解：令y=0代入y=x2+2x−3得：0=x2+2x−3解得：x1=1或x2=−3令x=0代入y=x2+2x−3得：y=-3∴A(1，0)，B(-3，0)，C(0，-3)设运动时间为t，则AP=2t，BQ=t∴BP=4-2t过点M作MQ△x轴∵OB=OC=3∴△OBC=45°∴△BMQ是等腰直角三角形∴MQ= √22BQ= √22t∴△BPQ的面积= 12BP⋅MQ=12(4−2t)⋅√22t= −√22(t−1)2+√22∴当t=1时，△BPQ面积的最大值= √22；（3）解：抛物线y=x2+2bx−3b的对称轴为：直线x=-b，开口向上设y=f(x)=x2+2bx−3b∵对x≥1的任意实数x，都使得y≥0成立∴{−b≤1f(1)≥0或{−b>1f(−b)≥0∴-1≤b≤1或-3≤b＜-1∴-3≤b≤1．22．【答案】（1）证明：∵△=[﹣（m+2）]2﹣4（2m﹣1）=m2+4m+4﹣8m+4=m2﹣4m+8=（m﹣2）2+4∵（m﹣2）2≥0∴（m﹣2）2+4＞0∴无论m取何实数时，此方程都有两个不相等的实数根（2）解：设抛物线y=x2﹣（m+2）x+2m﹣1=0与x轴两个交点的横坐标是x1，x2则x1+x2=m+2，x1•x2=2m﹣1．根据题意，得{m+2>02m−1>0解得m＞1 2．即m的取值范围是m＞1 2（3）m＞223．【答案】（1）-1（2）解：由（1）可知函数的解析式为y=−x2+2x+3∵y=−x2+2x+3=−(x−1)2+4∴顶点坐标为（1，4）列表如下：x…-2-101234…y…-503430-5…描点、连线，函数图象如下：结合图象当 0<x <3 时， 0<y <3 ．24．【答案】（1）解：将点A （1，2），B （2，3）代入y ＝ax 2﹣bx ＋3得 {a −b +3=24a −2b +3=3 解得 {a =1b =2∴抛物线的函数解析式为y ＝x 2−2x ＋3 （2）解：当x=0时，y ＝x 2−2x ＋3=3 ∴抛物线与y 轴的交点坐标为（0，3）当y ＝0时，x 2−2x ＋3=0 解得x 1=3，x 2=-1∴抛物线与x 轴的交点坐标为（3，0）和（-1，0）.故抛物线与坐标轴的交点坐标为（0，3）、（3，0）、（-1，0）.。

中考数学复习《与二次函数图象相关的交点问题》专项检测卷(附带答案)

中考数学复习《与二次函数图象相关的交点问题》专项检测卷(附带答案)学校:___________班级：___________姓名：___________考号：___________1．如图1，已知二次函数图象与y 轴交点为(0,3)C ，其顶点为(1,2)D ．(1)求二次函数的表达式；(2)直线CD 与x 轴交于M ，现将线段CM 上下移动，若线段CM 与二次函数的图象有交点，求CM 向上和向下平移的最大距离；(3)若将（1）中二次函数图象平移，使其顶点与原点重合，然后将其图象绕O 点顺时针旋转90︒，得到抛物线G ，如图2所示，直线2y x =-+与G 交于A ，B 两点，P 为G 上位于直线AB 左侧一点，求ABP ∆面积最大值，及此时点P 的坐标．2．综合与探究如图，某一次函数与二次函数2y x mx n =++的图象交点为()1,0A -和()4,5B ．(1)求抛物线的解析式；(2)点C 为抛物线对称轴上一动点，当AC 与BC 的和最小时，点C 的坐标为；(3)点D 为二次函数位于线段AB 下方图象上一动点，过点D 作DE x ⊥轴，交线段AB 于点E ，求ABD 面积的最大值；(4)在（2）的条件下点M 为y 轴上一点点F 为直线AB 上一点点N 为平面直角坐标系内一点若以点C M F N 为顶点的四边形是正方形请直接写出点N 的坐标．3．综合与探究如图某一次函数与二次函数2y x mx n =++的图象交点为A （-1 0） B （4 5）．(1)求抛物线的解析式；(2)点C为抛物线对称轴上一动点当AC与BC的和最小时点C的坐标为；(3)点D为抛物线位于线段AB下方图象上一动点过点D作DE⊥x轴交线段AB于点E求线段DE 长度的最大值；(4)在（2）条件下点M为y轴上一点点F为直线AB上一点点N为平面直角坐标系内一点若以点C M F N为顶点的四边形是正方形请直接写出点N的坐标．4．如图在直角坐标系中点A（3 a）和M是一次函数y＝x－2和反比例函数y＝mx图象的交点点B是一次函数y＝x－2与y轴的交点．(1)求反比例函数与一次函数的另一个交点M 的坐标．(2)C 为线段AB 上一点作CD ⊥y 轴与反比例函数y ＝m x交于点D 求△BCD 的面积得最大值．5．如图在平面直角坐标系中已知二次函数图像222(1)2y x a x a a =-+++的顶点为P 点B 39(2,)16- 是一次函数5119216y x =+上一点．(1)当a ＝0时求顶点P 坐标；(2)若a ＞0 且一次函数2y x b =-+的图象与此抛物线没有交点请你写出一个符合条件的一次函数关系式（只需写一个不必写出过程）；(3)作直线OC：12y x=与一次函数5119216y x=+交于点C．连结OB当抛物线与⊥OBC的边有两个交点时求a的取值范围．6．如图抛物线2=++y x bx c-的对称轴为x=1 与x轴的一个交点为A(-1,0) 另一交点为B与y轴交点为C．(1)求抛物线的函数解析式；(2)若点N为抛物线上一点且BC⊥NC求点N的坐标；(3)点P是抛物线上一点点Q是一次函数3322y x=+的图像上一点是否存在四边形OAPQ为平行四边形？若存在求出点Q的坐标；若不存在说明理由．7．综合与实践如图1 某兴趣小组计划开垦一个面积为28m 的矩形地块ABCD 种植农作物地块一边靠墙另外三边用木栏围住木栏总长为m a【问题提出】小组同学提出这样一个问题：若10a = 能否围出矩形地块？【问题探究】小颖尝试从“函数图象”的角度解决这个问题：设AB 为x m BC 为y m ．由矩形地块面积为28m 得到8xy = 满足条件的(,)x y 可看成是反比例函数8y x=的图象在第一象限内点的坐标；木栏总长为10m 得到210x y += 满足条件的(,)x y 可看成一次函数210y x =-+的图象在第一象限内点的坐标同时满足这两个条件的(,)x y 就可以看成两个函数图象交点的坐标．如图2 反比例函数()80y x x=>的图象与直线1:210=-+l y x 的交点坐标为(1,8)和______ 因此木栏总长为10m 时能围出矩形地块分别为：1m =AB 8m BC =；或AB =______m BC =______m ．（1）根据小颖的分析思路完成上面的填空．【类比探究】（2）若10a = 能否围出矩形地块？请仿照小颖的方法在图2中画出一次函数图象并说明理由．【问题延伸】（3）当木栏总长为a m 时小颖建立了一次函数2y x a =-+．发现直线2y x a =-+可以看成是直线2y x =-通过平移得到的在平移过程中当直线2y x a =-+与反比例函数()80y x x=>的图象有唯一交点时求出a 的值并求出这个交点的坐标．8．如图在平面直角坐标系中点A B ，是一次函数y x =图象上两点它们的横坐标分别为,3,a a +其中0a > 过点,?A B 分别作y 轴的平行线交抛物线248y x x =-+于点C D （1）若,AD BC =求a 的值；（2）点E 是抛物线上的一点求ABE 面积的最小值．9．如图一次函数y =kx+b 的图象与x 轴交于点B （6,0）与y 轴交于点A 与二次函数y=ax 2的图象在第一象限内交于点C （3,3）．(1)求此一次函数与二次函数的表达式；(2)若点D 在线段AC 上与y 轴平行的直线DE 与二次函数图象相交于点E ⊥ADO =⊥OED 求点D 坐标．10．如图二次函数2y x ax c =++的图象与x 轴相交于A ()10B ,两点与y 轴交于点()0,3C -.（1）求二次函数的解析式；（2）将二次函数图象向右平移2个单位长度再向上平移3个单位长度得到新二次函数图象当06x ≤≤时求新二次函数的最小值.11．如图已知二次函数G 1：y ＝ax 2+bx +c （a ≠0）的图象过点（﹣1 0）和（0 3）对称轴为直线x ＝1．（1）求二次函数G 1的解析式；（2）当﹣1＜x ＜2时求函数G 1中y 的取值范围；（3）将G 1先向右平移3个单位再向下平移2个单位得到新二次函数G 2 则函数G 2的解析式是．（4）当直线y ＝n 与G 1 G 2的图象共有4个公共点时直接写出n 的取值范围．12．如图抛物线2y ax bx =+x 轴交于点A 和点()1,0B 与y 轴交于点C 连接AC 经过点A的一次函数()0y kx c k =+≠图象与抛物线的另一个交点为点D ⎛ ⎝⎭点P 是抛物线上的一动点连接AP CP ．(1)求抛物线2y ax bx =+ 并直接写出点A 的坐标；(2)点P 在点A 和点C 之间运动当APC △的面积最大时求点P 的横坐标；(3)若点P 位于y 轴左侧过点P 作PE y ∥轴交直线AD 于点E 当2PE OC =时求点P 的坐标．13．如图1 在平面直角坐标系xOy 中二次函数24y x x c =-+的图象与y 轴的交点坐标为()0,5 图象的顶点为M ．矩形ABCD 的顶点D 与原点O 重合顶点A C ，分别在x 轴 y 轴上顶点B 的坐标为()1,5．(1)求c 的值及顶点M 的坐标．(2)如图2 将矩形ABCD 沿x 轴正方向平移2个单位得到对应的矩形A B C D ''''．已知边C D A B ''''，分别与函数24y x x c =-+的图象交于点P Q ，连结PQ 过点P 作PG A B ''⊥于点G ．求PQ 的长．14．如图二次函数的图象与x 轴交于()10A -， ()50B ，两点与y 轴交于点()05C -，．(1)求二次函数的表达式；(2)当14x -≤≤时求函数最大值与最小值的差；(3)点P 的坐标为(),5n - 点Q 的坐标为()2,5n +- 若线段PQ 与二次函数图象恰有一个交点请直接写出n 的取值范围．15．如图1 平面之间坐标系中等腰直角三角形的直角边BC 在x 轴正半轴上滑动点C 的坐标为（t 0）直角边AC=4 经过O C 两点作抛物线y 1=ax （x -t ）（a 为常数 a ＞0）该抛物线与斜边AB 交于点E 直线OA ：y 2=kx （k 为常数 k ＞0）（1）填空：用含t 的代数式表示点A 的坐标及k 的值A k= ；（2）随着三角板的滑动当a=14时： ⊥请你验证：抛物线y 1=ax （x -t ）的顶点在函数y=-14x 2的图象上； ⊥当三角板滑至点E 为AB 的中点时求t 的值；（3）直线OA 与抛物线的另一个交点为点D 当t≤x≤t+4 |y 2﹣y 1|的值随x 的增大而减小当x≥t+4时 |y 2﹣y 1|的值随x 的增大而增大求a 与t 的关系式及t 的取值范围．参考答案：1．(1)223y x x =-+(2)CM 向下平移的最大距离为14向上平移的最大距离为6． (3)11,42P ⎛⎫- ⎪⎝⎭2．(1)2=23y x x --(2)()1,2 (3)758 (4)123415(1,1),(1,2),(1,4),,22N N N N ⎛⎫- ⎪⎝⎭3．(1)2=23y x x --(2)（1 2） (3)254 (4)123415(1,1),(1,2),(1,4),,22N N N N ⎛⎫- ⎪⎝⎭4．(1)M （-1 -3）(2)25．(1)（1 -1）(2)21y x =--(答案不唯一) (3)2855a -<<-或20a -<<6．(1)223y x x =-++(2)（1 4）(3)Q 的坐标是（1 3)或315,24⎛⎫⎪⎝⎭．7．（1）(4,2)；4；2；（2）不能围出（3）a 的值为8 此时交点坐标为()24，． 8．（1）1a =；（2）ABE S 的最小值为2189．（1）一次函数的表达式为6y x =-+ 二次函数的表达式为213y x =；（2）点D 的坐标为39(,)22D ． 10．（1）223y x x =+-；（2）最小值为1-11．（1）二次函数G 1的解析式为y ＝﹣x 2+2x +3；（2）0＜y ≤4；（3）y ＝﹣（x ﹣4）2+2；（4）n 的取值范围为2336＜n ＜2或n ＜2336．12．(1)抛物线解析式为2y =点A 的坐标为()3,0- (2)点P 的横坐标为32-(3)点P 的坐标为1,⎛- ⎝⎭或⎛- ⎝⎭13．(1)5c = ()2,1M14．(1)二次函数的解析式为245y x x =--；(2)函数最大值与最小值的差为9；(3)n 的取值范围为20n -≤≤或24n ≤≤．15．（1）A 的坐标是（t 4） k=4t （k ＞0）；（2）⊥见解析；⊥t=2．；（3）a=1t（t ＞0）．。

中考数学《二次函数图像与坐标轴的交点问题》专项练习题及答案

中考数学《二次函数图像与坐标轴的交点问题》专项练习题及答案一、单选题1．如图，将二次函数y=31x2-999x+892的图形画在坐标平面上，判断方程31x2-999x+892=0的两根，下列叙述何者正确（）A．两根相异，且均为正根B．两根相异，且只有一个正根C．两根相同，且为正根D．两根相同，且为负根2．已知抛物线y=ax2+bx+c(a＜0）过A（-3，0）、O（1，0）、B（-5，y1）、C（5，y2）四点，则y1与y2的大小关系是（）A．y1＞y2B．y1=y2C．y1<y2D．不能确定3．已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列结论正确的是（）A．c＜0B．a+b+c＜0C．2a﹣b=0D．b2﹣4ac=04．已知函数y=(k-1)x2-4x+4的图象与x轴只有一个交点,则k的取值范围是() A．k≤2且k≠1B．k<2且k≠1C．k=2D．k=2或15．函数y=ax+1与抛物线y=ax2+bx+1(b≠0)的图象可能是（）.A．B．C．D．6．若关于x的一元二次方程（x-2）(x-3）=m有实数根x1、x2，且x1≠x2，有下列结论：①x1=2，x2=3；②m＞；③二次函数y=（x-x1）（x-x2）+m的图象与x轴交点的坐标为（2，0）和（3，0）．其中，正确结论的个数是（）A．0B．1C．2D．37．对于每个非零自然数n，抛物线y=x2-2n+1n(n+1)x+1n(n+1)与x轴交于A n，B n两点，以A n B n表示这两点间的距离，则A1B1+A2B2+…+A2009B2009（）A．20092008B．20082009C．20102009D．200920108．二次函数y=kx2-6x+3的图象与x轴有交点，则k的取值范围是()A．k<3B．k<3，且k≠0C．k≤3D．k≤3，且k≠010．如图，抛物线y=ax2+bx+c与x轴交于点（-1，0），对称轴为x=1，则下列结论中正确的是（）A．a＞0B．当x＞1时，y随x的增大而增大C．c＜0D．x=3是一元二次方程ax2+bx+c=0的一个根11．已知抛物线y=ax2+bx+c（b＞a＞0）与x轴最多有一个交点，现有以下四个结论：①该抛物线的对称轴在y轴左侧；②关于x的方程ax2+bx+c+2=0无实数根；③a﹣b+c≥0；3．④a+b+cb−a的最小值为其中，正确结论的个数为（）A．1个B．2个C．3个D．4个12．已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=2，与x轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论：①抛物线过原点；②4a+b+c=0；③a﹣b+c＜0；④抛物线的顶点坐标为（2，b）；⑤当x＜2时，y随x增大而增大．其中结论正确的是（）A．①②③B．③④⑤C．①②④D．①④⑤二、填空题13．已知函数y=ax2−2x+1的图象与x轴只有一个公共点，则a的值是.14．经过A（4，0），B（﹣2，0），C（0，3）三点的抛物线解析式是．15．如图，P是抛物线y=2（x﹣2）2对称轴上的一个动点，直线x=t平行y轴，分别与y=x、抛物线交于点A、B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，求满足条件的t的值，则t=．16．抛物线y=x2﹣4x+c与x轴交于A、B两点，已知点A的坐标为（1，0），则线段AB的长度为．17．抛物线y= 49(x-3)2与x轴的交点为A，与y轴的交点为B，则△AOB的面积为18．已知二次函数y=﹣x2+2x+m的部分图象如图所示，则关于x的一元二次方程﹣x2+2x+m=0的解为．三、综合题19．如图，二次函数y=- 12x2+bx+c的图象经过A(2，0)、B(0，-4)两点（1）求二次函数的解析式；（2）设该二次函数的对称轴与x轴交于点C，连接BA、BC，求△ABC的面积．20．已知二次函数y=ax2+bx+8，经过点(1,9)和(6,−16).（1）求此二次函数解析式；（2）若此二次函数与x轴的交点为点A、点B，与y轴的交点为点C，求△ABC的面积. 21．在平面直角坐标系xOy中，抛物线y＝﹣x2+mx+n与x轴交于点A，B（A在B的左侧）．（1）若抛物线的对称轴为直线x＝﹣3，AB＝4．求抛物线的表达式；（2）平移（1）中的抛物线，使平移后的抛物线经过点O，且与x正半轴交于点C，记平移后的抛物线顶点为P，若△OCP是等腰直角三角形，求点P的坐标；22．已知二次函数y=（x-1）（x-m）．（1）若二次函数的对称轴是直线x=3，求m的值．（2）当m>2，0≤x≤3时，二次函数的最大值是7，求函数表达式．23．已知抛物线y=ax2－2ax－3+2a2 （a<0）．（1）求这条抛物线的对称轴；（2）若该抛物线的顶点在x轴上，求抛物线的函数解析式；24．已知抛物线顶点坐标为（1，3），且过点A（2，1）．（1）求抛物线解析式；（2）若抛物线与x轴两交点分别为点B、C，求线段BC的长度．参考答案1．【答案】A2．【答案】A3．【答案】C4．【答案】D5．【答案】C6．【答案】C7．【答案】D8．【答案】D9．【答案】C10．【答案】D11．【答案】D12．【答案】C13．【答案】0或114．【答案】y=﹣38x2+ 34x+315．【答案】5±√52或1或316．【答案】217．【答案】618．【答案】x1=4，x2=﹣219．【答案】（1）解：分别把点A(2，0)、B(0，-4)代入y=−12x2+bx+c得{−12×22+2x+c=0c=−4解得：{b=3c=−4∴这个二次函数的解析式为：y=−12x2+3x−4（2）解：由（1）中抛物线对称轴为直线∴点C的坐标为：(3，0)∴AC=3−2=1∴△ABC的面积为：12⋅OB⋅AC=12×4×1=220．【答案】（1）解：把点(1,9)和(6,−16)代入函数解析式得{9=a+b+8−16=36a+6b+8解得a=-1, b=2. 所以二次函数的解析式为y=−x2+2x+8（2）解：令y=0,得-x 2+2x+8=0, 解得x=-4或x=2 得A 、B 的坐标为（-4,0），（2,0）则AB=6令x=0, 得y=8 ∴C 点坐标为（0,8），则OC=8 ∴S △ABC =12AB ×OC =12×6×8=24 .21．【答案】（1）解：∵抛物线的对称轴为直线x ＝﹣3，AB ＝4∴A 、B 两点到对称轴的距离相等，且为2 ∴A 点坐标为（-5，0），B 点坐标为（-1，0）把A 、B 两点的坐标分别代入函数解析式中，得： {−25−5m +n =0−1−m +n =0解得： {m =−6n =−5∴y =−x 2−6x −5（2）解：∵y =−x 2−6x −5 平移后过原点∴设平移后过原点的抛物线为 y =−x 2+bx 令 y =−x 2+bx =0 ，解得：x=0 ∴C （b ，0）且b>0∵y =−x 2+bx =−(x −b 2)2+b 24∴顶点P 的坐标为 (b 2，b 24) ∵△OCP 是等腰直角三角形 ∴b 2=b 24解得：b=2∴顶点P 的坐标为 (1，1)22．【答案】（1）解：令y =0，即0=(x −1)(x −m) ，得x 1=1，x 2=m也即抛物线与x轴的交点坐标为（1，0），（m，0）∵（1，0），（m，0）关于抛物线对称轴对称，且对称轴是直线x=3∴1+m2=3，解得m=5（2）解：由（1）可知，抛物线的对称轴为直线x=1+m 2∵m>2，∴x=1+m 2>32∵a=1＞0，且0≤x≤3时，二次函数的最大值是7∴当x＝0时y max=7∴把（0，7）带入抛物线表达式得7=(0−1)(0−m)∴m=723．【答案】（1）解：∵抛物线y=ax2−2ax−3+2a2=a(x−1)2+2a2−a−3∴抛物线的对称轴为直线x=1；（2）解：由（1）可得y=a(x−1)2+2a2−a−3∵抛物线的顶点在x轴上∴2a2−a−3=0解得a1=32，a2=－1∵a<0∴a=－1∴抛物线的解析式为y=−x2+2x−1．24．【答案】（1）解：设抛物线解析式为y=a（x﹣1）2+3把A（2，1）代入得a•（2﹣1）2+3=1，解得a=﹣2所以抛物线解析式为y=﹣2（x﹣1）2+3（2）解：y=0时，﹣2（x﹣1）2+3=0解得x1=1+ √62，x2=1﹣√62所以BC=1+ √62﹣（1﹣√62）= √6。

中考数学总复习《一次函数与反比例函数交点问题》专项训练题(附带有答案)

中考数学总复习《一次函数与反比例函数交点问题》专项训练题(附带有答案）学校:___________班级：___________姓名：___________考号：___________1．如图，在平面直角坐标系中，有函数13(0)y x x=>，2(0,0)k y k x x =<>和36y kx =+．(1)若2y 与3y 相交于点(2,)A m ①求k 与m 的值；①结合图像，直接写出23y y <时x 的取值范围；(2)在x 轴上有一点(,0)P a 且0a >，过点P 作y 轴平行线，分别交1y 、2y 和3y 于点B 、C 、D ，经计算发现，不论k 取何值，BC BD -的值均为定值，请求出此定值和点B 的坐标． 2．如图所示，一次函数2y x =-的图象与反比例函数ky x=的图象相交于A 、B 两点，其中点A 的横坐标是1-．(1)求反比例函数的解析式； (2)直接写出不等式2kx x-≥的解集； (3)按照既得数据，计算AOB 的面积．3．如图，在直角坐标系中，矩形OABC 的顶点O 与坐标原点重合，顶点A ，C 分别在坐标轴上，顶点B 的坐标为（4，2）．过点D （0，3）和E （6，0）的直线分别与AB ，BC 交于点M ，N ．(1)求直线DE 的解析式和点M 的坐标； (2)若反比例函数my x=（x ＞0）的图象经过点M ，求该反比例函数的解析式，并通过计算判断点N 是否在该函数的图象上； (3)若反比例函数my x=（x ＞0）的图象与①MNB 有公共点，请直接写出m 的取值范围． 4．如图，一次函数4y x =+的图象与反比例函数ky x=（k 为常数且0k ≠）的图象交于1A a -（，），B 两点，与x 轴交于点C ．(1)求此反比例函数的表达式； (2)若点P 在x 轴的正半轴上，且4ACPBOCSS＝，求点P 的坐标．5．已知：关于x 的一元二次方程2(32)220(0)tx t x t t -+++=>． (1)求证：方程有两个不相等的实数根；(2)设方程的两个实数根分别为1x ，2x （其中12x x <）．若y 是关于t 的函数，且212y x x =-，求这个函数的解析式，并画出函数图象；(3)观察（2）中的函数图象，当2y t ≥时，写出自变量t 的取值范围． 6．如图，一次函数1y kx b =+和反比例函数2my x=的图象相交于()4,3A --和B 两点，点B 的纵坐标是2，一次函数1y kx b =+的图象与x 轴交于点C ，与y 轴交于点D ．(1)求一次函数和反比例函数的解析式； (2)根据图象直接写出当mkx b x+≥时，x 的取值范围； (3)求证：2OC OD =．7．如图，一次函数y x b =-+的图象与反比例函数ky x=的图象交于A 、B 两点，A 点坐标为(2,3)-．(1)求一次函数与反比例函数的解析式；(2)已知(),0M m ，若ABM 的面积为10，求m 的值． 8．如图，反比例函数my x=的图象与一次函数y kx b =+的图象交于A ，B 两点，点A 的坐标为(2,6)，点B 的坐标为(,1)n ．（1）求反比例函数和一次函数的解析式；（2）结合图象，直接写出不等式mkx b x<+的解集；（3）点E 为y 轴上一个动点，若5AEBS=，试求点E 的坐标．9．如图，一次函数12y x b =+的图像与x 轴交于点()2,0A -，与反比例函数()0k y x x=>的图像交于点(),2E a ，过直线AE 上的点B 作BC x ⊥轴于点C ，与反比例函数交于点(),1D m ，连接AD ，DE ．(1)求k 的值与B 点坐标； (2)求ADES；(3)若点P 是直线AB 上的动点，是否存在点P ，使得BCP 与BDE △相似？若存在，求出此时P 点的坐标；若不存在，请说明理由．10．Rt ABC 在直角坐标系内的位置如图所示，反比例函数y ＝kx（k ≠0）在第一象限内的图象与BC 边交于点D (4，1)，与AB 边交于点E (2，n )．(1)求反比例函数的解析式和n 值； (2)当12BC AC =时，求直线AB 的解析式． 11．如图，已知一次函数1122y x =-与反比例函数2my x =的图象在第一、三象限分别交于(6,1)A ，(,3)B a -两点，连接OA ，OB ．(1)求反比例函数的解析式； (2)求AOB 的面积；(3)直接写出12y y >时，x 的取值范围．12．如图，一次函数1y kx =-的图象与反比例函数my x=的图象交于A 、B 两点，其中A 点坐标为()2,1，点B 到y 轴的距离为1．(1)试确定k 、m 的值； (2)求B 点的坐标．13．如图，在平面直角坐标系xOy 中，正比例函数12y x =-的图像经过点(2,)A m -，点A 与点B 关于y 轴对称，且点B 在反比例函数(0)ky k x=≠的图像上．(1)求m 的值和反比例函数的解析式；(2)设P 是直线12y x =-上的一动点．当线段BP 最短时，求ABP 的面积．14．已知反比例函数2ky x=和一次函数y ＝2x +b ，其中一次函数的图象经过点A （﹣1，﹣3）和B （1，m ）．反比例函数图象经过点B ．(1)求反比例函数的解析式和一次函数的解析式；(2)若直线12y x =-+交x 轴于C ，交y 轴于D ，点P 为反比例函数2k y x=（x ＞0）的图象上一点，过P 作y轴的平行线交直线CD 于E ，过P 作x 轴的平行线交直线CD 于F①请问：在该反比例函数图像上是否存在点P ，使①PFE ①①OCD ？若存在，求点P 的坐标；若不存在，请说明理由．①求证：DE •CF 为定值．15．如图，一次函数y kx b =+与反比例函数(0)my x x=>的图像交于(1,3)A ，(,2)B n 两点．(1)求一次函数表达式和反比例函数表达式； (2)直接写出关于x 的不等式mkx b x+<的解集； (3)求AOB 的面积．16．如图，在平面直角坐标系中，正比例函数=y kx 的图象与反比例函数=my x的图象经过点()2,2A ． (1)分别求这两个函数的表达式；(2)将直线OA 向上平移3个单位长度后与y 轴交于点B ，与反比例函数图象在第一象限内的交点为C ，连接AB ，AC ，求点C 的坐标及①ABC 的面积；(3)在第一象限内，直接写出反比例函数的值大于直线BC 的值时，自变量x 的取值范围．参考答案：1．(1)①m 的值为2-，k 的值为4-；①02x <<(2)①若从上到下为B D C 、、时，此定值为6，点B 的坐标为(1,3)；①若从上到下为B C D 、、时，此定值为6，点B 的坐标为(1,3)；①若C 与D 重合时，此定值为0，点B 的坐标为3,a a ⎛⎫⎪⎝⎭，其中0a >且1a ≠2．(1)3y x= (2)10x -≤<或3x ≥ (3)43．(1)132y x =-+，M （2，2）(2)4y x=，在 (3)4≤ m ≤84．(1)3y x-＝ (2)403P （，）5．(1)证明略(2)2(0)y t t=>(3)当01t <≤时2y t ≥6．(1)1112y x =- 212y x= (2)40x -≤<或6x ≥(3)117．(1)一次函数解析式为：1y x =-+；反比例函数的解析式为6y x-=； (2)5m =或3-．8．（1）12y x =172y x =-+；（2）0x <或212x <<；（3）点E 的坐标为(0,6)或(0,8) 9．(1)4k = ()4,3B ； (2)4(3)存在，31,2P ⎛⎫ ⎪⎝⎭或89,55⎛⎫⎪⎝⎭．10．(1)反比例函数的解析式为y =4x ，n =2；(2)直线AB 的函数解析式为y =12x +1．11．(1)26y x= (2)8AOB S =(3)20x -<<或6x >．12．(1)1k = 2m =； (2)()1,2B --13．(1)1；2y x= (2)16514．(1)1y x=；21y x =- (2)不存在15．(1)一次函数解析式为25y x =-+，反比例函数解析式为：3y x= (2)不等式mkx b x+<的解集为：01x ＜＜或32x ＞ (3)5416．(1)=y x 4y x =(2)1,4C （） 32(3)01x <<。

数学人教版九年级上册一次函数与二次函数图像的交点个数

A O y
N
B x
C P
.M
5、如图，在平面直角坐标系中，己知点O（0，0）， A（5，0），B（4，4）．（1）求过O、B、A三点的抛物线的解析式．（2）在第一象限的抛物线上存在点M，使以O、A、B、M 为顶点的四边形面积最大，求点M的坐标．
随堂练习 3、已知函数y=|8-2x-x2|和y=kx+k（k为常数），则不论k为何值，这两个函数的图象（） A 有且只有一个交点 B 有且只有二个交点 C 有且只有三个交点 D 有且只有四个交点
(3)当k .直线y=x+k 与抛物线y=x2-2x-3没有交点；
你能根据方程组：
y＝ax2+bx+c y＝kx＋m
的解的情况，来判定函数y＝ax2+bx+c 与y＝kx＋m图象交点个数吗?请说说你的看法。
归纳：
方程组的解的个数与直线抛物线的交点个数相等！
随堂练习 1.直线 y=2x+1 与抛物线 y= x2 + 4x +3 有＿＿＿＿个交点. 2、已知函数y=-x2-2x+8和y=kx+k（k为常数），则不论k为何值，这两个函数的图象（） A 只有一个交点 B 有两个交点 C 没有交点 D交点的情况随k的值变化而变化
（1）若点P是该抛物线上位于AB 下方的一点，求△APB面积的最大值. （2）若抛物线的对称轴与直线AB相交于点D，E为直线 AB上的任意一点，过点E作 EF∥CD交抛物线于点F，则以 C，D，E，F为顶点的四边形能否为平行四边形？若能，求出点E的坐标；若不能，请说明理由.
x 1
D
A (-1,0) N (0,-3)
B
M(3,0)Pຫໍສະໝຸດ C5、如图，在平面直角坐标系中，己知点O（0，0）， A（5，0），B（4，4）．（1）求过O、B、A三点的抛物线的解析式．（2）在第一象限的抛物线上存在点M，使以O、A、B、M 为顶点的四边形面积最大，求点M的坐标．（3）作直线x=m交抛物线于点P，交线段OB于点Q，当△PQB为等腰三角形时，求m的值．

中考数学《一次函数图像与坐标轴交点问题》专项练习题及答案

中考数学《一次函数图像与坐标轴交点问题》专项练习题及答案一、单选题1．若直线y=k1x+1与y=k2x−4的交点在x轴上，那么k1k2等于(）A．4B．-4C．14D．−142．当一次函数y=2x−3的图象在第四象限时，自变量x的取值范围是（）A．0＜x＜32B．x＞0C．x＜32D．无法确定3．已知在平面直角坐标系中，C是x轴上的点，点A（0，3），B（6，5），则AC+BC的最小值是( )A．10B．8C．6D．2√104．一次函数y = kx + 4的图象与坐标轴围成的三角形的面积为4，则k的值为（）．A．2B．−2C．±2D．不存在5．一次函数y=2x+6图象与y轴的交点坐标是（）A．（-3，0）B．（3，0）C．（0，-6）D．（0，6）6．一次函数y＝﹣2x﹣3的图象和性质．叙述正确的是（）A．y随x的增大而增大B．与y轴交于点（0，﹣2）C．函数图象不经过第一象限D．与x轴交于点（﹣3，0）7．如图，在平面直角坐标系xOy中，半径为2的⊙O与x轴的正半轴交于点A，点B是⊙O上一动点，点C为弦AB的中点，直线y＝34x﹣3与x轴、y轴分别交于点D、E，则⊙CDE面积的最小值为（）A．3.5B．2.5C．2D．1.28．一次函数y=-2x+m的图象经过点P(-2,3)，且与x轴、y轴分别交于点A，B，则⊙AOB的面积是()A．B．C．4D．89．直角坐标系中已知两点A(−8，3)B(−4，5)以及动点C(0，n)D(m ，0)，当四边形ABCD 的周长最小时，求比值mn .（） A ．−23B ．-2C ．−32D ．-310．将一次函数y ＝2x ＋4的图象与坐标轴围成的三角形面积是（）A ．4B ．5C ．6D ．711．如图所示，直线 y =k(x −2)+k −1 与x 轴、y 轴分别交于B 、C 两点，且 OB OC =12。

则K 的值为（）A ．13B ．12C ．1D ．212．如图，直线y=kx+b 交坐标轴于A （﹣2，0），B （0，3）两点，则不等式kx+b ＞0的解集是A ．x ＞3B ．﹣2＜x ＜3C ．x ＜﹣2D ．x ＞﹣2二、填空题13．一次函数y =x −1的图像向上平移3个单位后与y 轴的交点是． 14．若函数y ＝2x ＋3与y ＝3x －2b 的图象交x 轴于同一点，则b 的值为．15．如图，在平面直角坐标系中，点A ，A 1，A 2，A 3…A n 都在直线1：y ＝ √32x+1上，点B ，B 1，B 2，B 3…B n 都在x 轴上，且AB 1⊙1，B 1A 1⊙x 轴，A 1B 2⊙1，B 2A 2⊙x 轴，则A n 的横坐标为（用含有n 的代数式表示）。

中考数学总复习《二次函数图像与坐标轴的交点问题》练习题(有答案)

中考数学总复习《二次函数图像与坐标轴的交点问题》练习题(有答案)班级:___________姓名：___________考号：_____________一、单选题1．如图，抛物线y=﹣112x2+ 23x+ 53与x轴交于A，B两点，与y轴交于点C．若点P是线段AC上方的抛物线上一动点，当△ACP的面积取得最大值时，点P的坐标是（）A．（4，3）B．（5，3512）D．（5，3）C．（4，3512）2．如图所示是二次函数y=ax2+bx+c图象的一部分，图象过点A(3， 0)，二次函数图象对称轴为直线x=1，给出五个结论：①bc>0；②a+b+c<0；③当x<1时，y随x的增大而增大；④方程ax2+bx+c=0的根为x1=−1，x2=3；⑤4a−2b+c>0其中正确结论是（）A．①②③B．①③④C．②③④D．③④⑤3．已知抛物线y=x2+bx+c的部分图象如图所示，若y＜0，则x的取值范围是()A．－1＜x＜4B．－1＜x＜3C．x＜－1或x＞4D．x＜－1或x＞34．二次函数y=ax2+bx+c(a≠0)的图象如图，给出下列四个结论：①abc<0；②b2−4ac>0；③a+b+c<0；④2a+b=0；其中结论正确的个数有（）A．1个B．2个C．3个D．4个5．已知二次函数y=mx2−3mx−4m(m≠0)的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，且∠ACB=90°，则m的值为（）A．±2B．±4C．±12D．±1 46．已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（﹣1，0），（3，0）．对于下列命题：①b﹣2a=0；②abc＜0；③a﹣2b+4c＜0；④8a+c＞0．其中正确的有（）A．3个B．2个C．1个D．0个7．在平面直角坐标系中，已知a≠b，设函数y=(x+a)(x+b)的图象与x轴有M个交点，函数y=(ax+1)(bx+1)的图象与x轴有N个交点，则（）A．M=N−1或M=N+1B．M=N−1或M=N+2C．M=N或M=N+1D．M=N或M=N−18．已知二次函数y=x2﹣4x+m（m为常数）的图象与x轴的一个交点为（1，0），则关于x的一元二次方程x2﹣4x+m=0的两个实数根是（）A．x1=1，x2=﹣1B．x1=﹣1，x2=2C．x1=﹣1，x2=0D．x1=1，x2=39．若函数y= x2+2x-b的图像与坐标轴有三个交点，则b的取值范围是()A．b>1且b≠0B．b<1且b≠0C．b≤1且b≠0D．b≥-1且b≠010．已知函数y=ax2-2ax-1（a≠0），下列四个结论：①当a =1时，函数图象经过点（-1，2）；②当a = -2时，函数图象与x轴没有交点；③函数图象的对称轴是x = -1；④若a＞0，则在对称轴的右侧，y 随x的增大而增大．其中正确的是（）A．①④B．②③C．①②D．③④11．对于抛物线y=x2−2x−3 ，下列判断错误的是（）A．对称轴是直线x=−1B．与x轴有两个交点C．开口向上D．与y轴在的交点在x轴下方12．已知二次函数y=x2+x+m，当x取任意实数时，都有y＞0，则m的取值范围是（）A．m ≥14B．m <14C．m ≤14D．m＞14二、填空题13．已知抛物线y=x2﹣x﹣1与x轴的一个交点为（a，0），则代数式a2﹣a+2018的值为．14．如图，是一个半圆和抛物线的一部分围成的“芒果”，已知点A、B、C、D分别是“芒果”与坐标轴的交点，AB是半圆的直径，抛物线的解析式为y= 32x2﹣32，则图中CD的长为．15．如图是二次函数y＝﹣x2+4x的图象，若关于x的一元二次方程﹣x2+4x﹣t＝0（t为实数）在1＜x ＜5的范围内有解，则t的取值范围是．16．二次函数y=x2+2x−3的图像与x轴有个交点．17．抛物线y=ax2+bx+c经过点A（-3，0），B（1，0）两点，则关于x的一元二次方程ax2+bx+c= 0的解是.18．如图，抛物线y= -12x2+ 32x+2与x轴交于点A，B(点B在点A的左侧），与y轴交于点C，连接BC，AC.（1）△ACB的度数是º；（2）若点P是AC上一动点，则OP的最小值为.三、综合题19．如果过抛物线y=ax2+bx+c(a≠0)与y的交点作y轴的垂线与该抛物线有另一个交点，并且这两点与该抛物线的顶点构成正三角形，那么我们称这个抛物线为正三角抛物线．（1）抛物线y=2x2+3√3x正三角抛物线；（填“是”或“不是”）（2）如图，已知二次函数y=−x2+2mx+3m2（m > 0）的图像是正三角抛物线，它与x轴交于A、B两点(点A在点B的左侧)，点E在y轴上，当△AEB=2△ABE时，求出点E的坐标．20．如图，利用函数y=x2−4x+3的图象，直接回答：（1）方程x2−4x+3=0的解是；（2）当x时，y随x的增大而减小；（3）当x满足时，函数值大于0；（4）当0<x<5时，y的取值范围是.21．已知二次函数y=x2﹣2x﹣8．（1）求此二次函数的图象与x轴的交点坐标．（2）将y=x2的图象经过怎样的平移，就可以得到二次函数y=x2﹣2x﹣8的图象．22．已知抛物线y=12x2+x+c与x轴有两个不同的交点．（1）求c的取值范围；（2）抛物线y=12x2+x+c与x轴两交点的距离为2，求c的值．23．已知关于x的方程kx2﹣（3k﹣1）x+2（k﹣1）=0．（1）求证：无论k为任何实数，方程总有实数根．（2）若抛物线y=kx2﹣（3k﹣1）x+2（k﹣1）与x轴交于A（x1，0），B（x2，0）两段，且线段AB=2，求k的值．24．已知抛物线y=mx2+(1−2m)x+m与x轴有两个不同的交点.（1）求m的取值范围；（2）证明该抛物线一定经过某一定点P，并求出该定点的坐标.参考答案1．【答案】B 2．【答案】B 3．【答案】B 4．【答案】B 5．【答案】C 6．【答案】B 7．【答案】C 8．【答案】D 9．【答案】B 10．【答案】A 11．【答案】A 12．【答案】D 13．【答案】2019 14．【答案】5215．【答案】﹣5＜t≤4 16．【答案】217．【答案】x 1=−3，x 2=1 18．【答案】（1）90°（2）4√5519．【答案】（1）不是（2）解：设抛物线与y 轴交于点C ，顶点为D ，过点C 作CM△y 轴交抛物线于点M.C （0，3m 2）D （m ，4m 2） M （2m ，3m 2）易知： m m2=1√3 解得 m =√3 .∴A （ −√3 ，0） B （ 3√3 ，0）.连接BE 交抛物线对称轴于点H ，连接AH ，则AH=BH ∴AE=AH.由 HG EO =2m 3m =23，设 EO =3ℎ ， GH =2ℎ ，（h > 0）由勾股定理得：(3ℎ)2+(√3)2=(2ℎ)2+(2√3)2，解得：ℎ=3√55E点的坐标为（0，9√55）或（0，−9√55）.20．【答案】（1）x1=1（2）x<2（3）x<1或x>3（4）−1≤y<821．【答案】（1）解：二次函数的解析式y=x2﹣2x﹣8令y=0，得到x2﹣2x﹣8=0解得：x1=4，x2=﹣2；则此二次函数的图象与x轴的交点坐标分别为（﹣2，0）、（4，0）.（2）解：将二次函数y=x2﹣2x﹣8化为顶点式为y=（x﹣1）2﹣9∴将y=x2的图象先向右平移1个单位，再向下平移9个单位，可得到二次函数y=x2﹣2x﹣8的图象22．【答案】（1）解：∵抛物线与x轴有两个不同的交点∴Δ>0，即1−2c>0解得c<1 2（2）解：设抛物线y=12x2+x+c与x轴的两交点的横坐标为x1，x2，∵两交点间的距离为2∴x1−x2=2由题意，得x1+x2=−2解得x1=0，x2=−2∴c=x1x2=0即c的值为023．【答案】（1）证明：k=0时，方程为x﹣2=0，方程有实数根．k≠0时，方程为一元二次方程△=（3k﹣1）2﹣8k（k﹣1）=k2+2k+1=（k+1）2∵（k+1）2≥0∴一元二次方程有实根∴无论k为任何实数，方程总有实根（2）解：解方程kx2﹣（3k﹣1）x+2（k﹣1）=0得：x= 3k−1±(k+1)2k，即x2=2，x2= k−1k．∵AB=2∴2﹣k−1k=2或k−1k﹣2=2∴k=1或k= −1 3．∴k的值为1或﹣1 324．【答案】（1）解：∵y=mx2+(1−2m)x+m是二次函数，∴m≠0. ∵抛物线与x轴相交于不同的两点∴Δ=(1−2m)2−4m2=−4m+1>0，∴m<14.∴m的取值范围是m<14且m≠0；（2）解：y=mx2+(1−2m)x+m=mx2+x−2mx+m=m(x2−2x+1)+x故只要x2−2x+1=0，那么y的值便与m的取值无关，也就是说抛物线必过定点由x2−2x+1=0，得（x-1）2=0∴x1=x2=1当x=1时，y=m+1−2m+m=1，即P(1，1)∴该抛物线一定经过点P，点P的坐标为(1，1)。

中考数学总复习《二次函数图像与坐标轴的交点问题》练习题及答案

中考数学总复习《二次函数图像与坐标轴的交点问题》练习题及答案班级:___________姓名：___________考号：_____________一、单选题1．已知二次函数y=ax2+bx+c的y与x的部分对应值如表：x−1013y−3131x<2时，函数值y随x 的增大而增大；④方程ax2+bx+c=0有一个根大于4．其中正确的结论有（）A．1个B．2个C．3个D．4个2．二次函数y=x2﹣2x﹣3的图象如图所示，下列说法中错误的是（）A．函数图象与y轴的交点坐标是（0，﹣3）B．顶点坐标是（1，﹣3）C．函数图象与x轴的交点坐标是（3，0）、（﹣1，0）D．当x＜0时，y随x的增大而减小3．已知抛物线y=ax2+bx+c(a＜0）过A（-3，0）、O（1，0）、B（-5，y1）、C（5，y2）四点，则y1与y2的大小关系是（）A．y1＞y2B．y1=y2C．y1<y2D．不能确定4．已知二次函数y=−x2+2mx−m2−m+1(m为常数)的图象与x轴有交点，且当x<−3时，y随x 的增大而增大，则m的取值范围是（）A．−3≤m<1B．−3≤m≤1C．−3<m<1D．m≤−3或m≥15．二次函数y=x2－4x+3的图象交x轴于A、B两点，交y轴于点C，△ABC的面积为() A．1B．3C．4D．66．如表是二次函数y＝ax2+bx+c的几组对应值：x 6.17 6.18 6.19 6.20y＝ax2+bx+c﹣0.03﹣0.010.020.04A．6＜x＜6.17B．6.17＜x＜6.18C．6.18＜x＜6.19D．6.19＜x＜6.207．抛物线y=x2−6x+m与x轴只有一个交点，则m的值为（）A．－6B．6C．3D．98．关于二次函数y=−4(x+6)2−5的图象，下列说法正确的是（）A．对称轴是直线x=6B．顶点坐标为(−6，5)C．图象与y轴交点的坐标是(0，−5)D．当x<−6时，y随x的增大而增大9．已知a，b是抛物线y＝（x﹣c）（x﹣c﹣d）﹣3与x轴交点的横坐标，a＜b，则|a﹣c|+|c﹣b|化简的结果是（）A．b﹣a B．a﹣b C．a+b﹣2c D．2c﹣a﹣b10．已知抛物线y＝ax2＋bx＋c如图所示，则下列结论中，正确的是（）A．a＞0B．a－b＋c＞0C．b2－4ac＜0D．2a＋b＝011．抛物线y=x2−2x+1与坐标轴的交点个数为（）A．无交点B．1个C．2个D．3个12．如图，抛物线y=2x2−52x+a与x轴正半轴交于A，B两点（点A在点B的左边），与y轴正半轴交于C，且∠OCA=∠OBC，则点B的坐标是（）A．(14，0)B．(1，0)C．(4，0)D．(3√3，0)二、填空题13．如图是二次函数y＝ax2＋bx＋c图象的一部分，图象过点A（－3，0），对称轴为直线x＝－1，给出四个结论：①b2＞4ac；②2a＋b＝0；③a＋b＋c＞0；④若点B（−52，y1），C（−12，y2）为函数图象上的两点，则y1＜y2．其中正确结论是．14．已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣2，0）、B（x1，0），且1＜x1＜2，与y轴正半轴的交点在（0，2）的上方，顶点为C．直线y=kx+m（k≠0）经过点C、B．则下列结论：①b＞a；②2a﹣b＞﹣1；③2a+c＜0；④k＞a+b；⑤k＜﹣1. 其中正确的结论有（填序号）15．已知抛物线y=x2+2x−n与x轴交于A，B两点，抛物线y=x2−2x−n与x轴交于C，D两点，其中n＞0，若AD＝2BC，则n的值为.16．已知抛物线y=x2−2kx+k2+k−2的顶点在坐标轴上，则k=．17．抛物线y=x2+3x−4与y轴的交点坐标是，与x轴的交点坐标是.18．二次函数y=ax2+bx+c（a≠0）中，自变量x与函数y的部分对应值如表：则一元二次方程ax2+bx+c=0（a≠0）的两个根x1，x2的取值范围是．x﹣1-120121322523y﹣2﹣14142741﹣14﹣219．已知二次函数y=−x2−2x+3．（1）求这个二次函数图象与y轴的交点坐标、与x轴的交点坐标．（2）画出这个二次函数图象．20．已知二次函数y＝ax2＋bx－4(a，b是常数，且a≠0)的图象过点(3，－1)．（1）判断点(2，2－2a)是否也在该函数的图象上，并说明理由．（2）若该二次函数的图象与x轴只有一个交点，求该函数的表达式．（3）已知点(x1，y1)和(x2，y2)在该函数图象上，且当x1＜x2≤23时，始终有y1＞y2，求a的取值范围．21．已知抛物线y＝x2﹣2x﹣3的图象如图所示．（1）求抛物线与x轴、y轴的交点坐标；（2）根据图象回答：当x取何值时，y＞0？当x取何值时，y＜0？22．抛物线y=﹣2x2+8x﹣6．（1）求抛物线的顶点坐标和对称轴；（2）x取何值时，y随x的增大而减小？（3）x取何值时，y=0；x取何值时，y＞0；x取何值时，y＜0．23．如图，二次函数y＝x2﹣4x+3的图象交x轴于A，B两点，交y轴于C（1）分别求A，B，C三点的坐标；（2）求△ABC的面积．24．已知：抛物线y=−x2+2x+m．（1）若抛物线过点A(3,0)，与y轴交于点B，与x轴的另一个交点是点C．①求这个抛物线的解析式，并求出点B，C的坐标；②若该抛物线有一点D(x,y)，且点D与点B不重合，若S△ABC=S△ACD，求点D的坐标．（2）若M(−1,3)，N(4,3)，抛物线y=−x2+2x+m与线段MN有两个不同交点，则m 的取值范围是．参考答案1．【答案】A2．【答案】B3．【答案】A4．【答案】B5．【答案】B6．【答案】C7．【答案】D8．【答案】D9．【答案】A10．【答案】D11．【答案】C12．【答案】B13．【答案】①④14．【答案】①⑤15．【答案】816．【答案】0或217．【答案】（0,4）；（-4,0），（1,0）18．【答案】﹣12＜x1＜0，2＜x2＜5219．【答案】（1）解：∵y=−x2−2x+3∴当x=0时∴这个二次函数图象与y轴的交点坐标是(0，3)∵令y=0，即−x2−2x+3=0解得：x1=−3，x1= 1∴图象与x轴的交点坐标为(−3，0)（2）解：正确列表x…−4−3−2−1012…y…−503430−5…20．【答案】（1）解：当x＝3，y＝－1时，有3a＋b－1＝0，所以b＝－3a＋1．把x＝2与b＝－3a＋1同时代入y＝ax2＋bx－4 得y=-2a-2≠2-2a所以点(2，2－2a)不在该函数的图象上；（2）解：因为二次函数y＝ax2＋(－3a＋1)x－4与x轴只有一个交点∴△＝0，即(－3a＋1)2＋16a＝0解得a＝－1或a＝－19所以y＝－x2＋4x－4或y＝－19x2＋43x－4；（3）解：y1－y2＝a(x1－x2)(ax1＋ax2－3a＋1)>0因为x1－x2<0，所以a(x1＋x2)－3a＋1<0因为x1＜x2≤ 23时，始终有y1＞y2，所以a>0因为抛物线的对称轴直线为x=3a−12a所以x1＋x2< 3a－1a＝3−1 a因为x1＋x2< 43，所以3−1a≤ 43即a≥ 3 5．21．【答案】（1）解：令x＝0，则y＝-3∴抛物线与y轴的交点为（0，-3）令y＝0，则x2-2x-3＝0解得：x1＝-1，x2＝3∴抛物线与x轴的交点为（-1，0）和（3，0）.（2）解：由图象以及抛物线与x轴的交点坐标可知当x＞3或x＜-1时，y＞0；当-1＜x＜3时，y＜0．22．【答案】（1）解：∵y=﹣2x2+8x﹣6=﹣2（x﹣2）2+2∴顶点坐标为（2，2），对称轴为直线x=2（2）解：∵a=﹣2＜0，抛物线开口向下，对称轴为直线x=2∴当x＞2时，y随x的增大而减小（3）解：令y=0，即﹣2x2+8x﹣6=0，解得x=1或3，抛物线开口向下∴当x=1或x=3时，y=0；当1＜x＜3时，y＞0；当x＜1或x＞3时，y＜023．【答案】（1）在y＝x2﹣4x+3中当y＝0时，x2﹣4x+3＝0解得x＝1或3则A（1，0）、B（3，0）当x＝0时，y＝3则C（0，3）（2）由（1）知，A（1，0）、B（3，0）、C（0，3）．故△ABC的面积为：12×（3﹣1）×3＝3．24．【答案】（1）解：①∵y=−x2+2x+m过点A(3,0)∴0=−9+6+m∴m=3∴y=−x2+2x+3当x=0时∴B(0,3)当y=0时∴x1=3∵A(3,0)∴C(−1,0)②∵S△ABC=S△ACD∴点D的纵坐标为3或−3当y=3时∴x2−2x=0∴x1=0∵点D与点B不重合∴D1(2,3)当y=−3时∴x2−2x−6=0∴x1=1−√7∴D2(1−√7,−3)，D3(1+√7,−3)；（2）2<m⩽6。

中考专题复习7：一次函数与二次函数相交问题

中考专题复习7：一次函数与二次函数相交问题
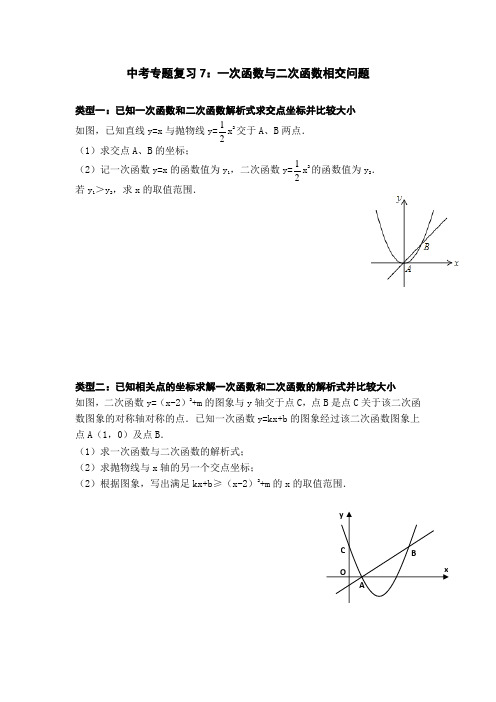
类型一：已知一次函数和二次函数解析式求交点坐标并比较大小
如图，已知直线y=x 与抛物线y=2
1x 2交于A 、B 两点．（1）求交点A 、B 的坐标；
（2）记一次函数y=x 的函数值为y 1，二次函数y=2
1x 2的函数值为y 2．若y 1＞y 2，求x 的取值范围．
类型二：已知相关点的坐标求解一次函数和二次函数的解析式并比较大小如图，二次函数y=（x-2）2+m 的图象与y 轴交于点C ，点B 是点C 关于该二次函数图象的对称轴对称的点．已知一次函数y=kx+b 的图象经过该二次函数图象上点A （1，0）及点B ．
（1）求一次函数与二次函数的解析式；
（2）求抛物线与x 轴的另一个交点坐标；
（2）根据图象，写出满足kx+b≥（x-2）2+m 的x 的取值范围．
A B C O x y
练习：在同一直角坐标系，开口向上的抛物线与坐标轴分别交于A（-1，0），B （3，0），C（0，-3），一次函数图象与二次函数图象交于B、C两点．
（1）求一次函数和二次函数的解析式．
（2）当自变量x为何值时，两函数的函数值都随x的增大而增大？
（3）当自变量x为何值时，一次函数值大于二次函数值．
（4）当自变量x为何值时，两函数的函数值的积小于0．。

2023年中考数学《二次函数的交点问题》真题及答案解析

2023中考真题抢先练·数学二次函数的交点问题1.（2023自贡11题）经过A （2-3b ，m ），B （4b +c -1，m ）两点的抛物线22122y x bx b c=-+-+（x 为自变量）与x 轴有交点，则线段AB 的长为（）A.10B.12C.13D.15【推荐区域：陕西、福建】【参考答案】B 【解析】∵抛物线22122y x bx b c =-+-+的对称轴为直线122()2b bx b a =-=-=´-，且抛物线经过A （2-3b ，m ），B （4b +c -1，m ）两点，∴23412b bc b -++-=，即1c b =-，∴原方程为221222y x bx b b =-+-+-，∵抛物线与x 轴有交点，∴240b ac D =-≥，即2214()(22)02b b b -´-´-+-≥，即2440b b -+≤，即()220b -≤，∴2b =，1211c b =-=-=，∴23264b -=-=-，418118b c +-=+-=∴()()41238412AB b c b =+---=--=.规律探索2.（2023重庆A 卷7题）用长度相同的木棍按如图所示的规律拼图案，其中第①个图案用了9根木棍，第②个图案用了14根木棍，第③个图案用了19根木棍，第④个图案用了24根木棍，…，按此规律排列下去，则第⑧个图案用的木棍根数是（）第2题图A.39B.44C.49D.54【推荐区域：云南、江西】【参考答案】B 【解析】由题图可知，第①个图案中木棍根数为4+6-1=9（根），第②个图案中木棍根数为4+6×2-2=14（根），第③个图案中木棍根数为4+6×3-3=19（根），第④个图案中木棍根数为4+6×4-4=24（根），…，由此规律可知，第⑧个图案中木棍根数为4+6×8-8=44（根）.全等三角形的判定与性质3.（2023乐山19题）如图，已知AB 与CD 相交于点O ，AC //BD ，AO =BO .求证：AC =BD .第3题图【推荐区域：云南、陕西、广西、广东】【参考答案】证明：∵//AC BD ，∴A B Ð=Ð.在AOC △和BOD △中，∵A B Ð=Ð，AO BO =，AOC BOD Ð=Ð，∴AOC △≌BOD △（ASA ），∴AC BD =.数据的统计与分析4.（2023自贡22题）某校为了解“世界读书日”主题活动开展情况，对本学期以来学生课外读书情况进行了随机抽样调查，所抽取的12名学生课外读书数量（单位：本）数据如下：2，4，5，4，3，5，3，4，1，3，2，4，第4题图（1）补全学生课外读书数量条形统计图；（2）请直接写出本次所抽取学生课外读书数量的众数、中位数和平均数；（3）该校有600名学生，请根据抽样调查的结果，估计本学期开学以来课外读书数量不少于3本的学生人数.【推荐区域：云南、陕西】【参考答案】解：（1）补全学生课外读书数量条形统计图如解图；第4题解图（2）4，72，103；【解法提示】∵本次所抽取学生课外读书数量的数据中出现次数最多的是4，∴众数是4．将本次所抽取的12名学生课外读书数量的数据，按照从小到大的顺序排列为：1，2，2，3，3，3，4，4，4，4，5，5．∵这组数据中位于中间的两位数是3，4，∴中位数是34722+=．平均数为：112233445210123x ´+´+´+´+´==．（3）34296006004501212++´=´=（名），∴该校有600名学生，估计本学期开学以来课外读书数量不少于3本的学生人数为450名．5.（2023重庆A 卷21题）为了解A 、B 两款品质相近的智能玩具飞机在一次充满电后运行的最长时间，有关人员分别随机调查了A 、B 两款智能玩具飞机各10架，记录下它们运行的最长时间（分钟），并对数据进行整理、描述和分析（运行最长时间用x 表示，共分为三组：合格60≤x ＜70，中等70≤x ＜80，优等x ≥80），下面给出了部分信息：A 款智能玩具飞机10架一次充满电后运行最长时间是：60，64，67，69，71，71，72，72，72，82．B 款智能玩具飞机10架一次充满电后运行最长时间属于中等的数据是：70，71，72，72，73．根据以上信息，解答下列问题：（1）上述图表中a＝，b＝，m＝；（2）根据以上数据，你认为哪款智能玩具飞机运行性能更好？请说明理由（写出一条理由即可）；（3）若某玩具仓库有A款智能玩具飞机200架、B款智能玩具飞机120架，估计两款智能玩具飞机运行性能在中等及以上的共有多少架？【推荐区域：云南、陕西、福建、河南、广东】【参考答案】解：（1）72，70.5，10；【解法提示】∵10架A款智能玩具飞机运行时间中72出现了3次，为最多次数，∴众数a=72；∵10架B款智能玩具飞机中性能为合格的飞机占比40%，∴飞机运行时间小于70分钟的数量为10×40%=4（架），∴排在第5，6位的数量为70，71，∴中位数b=70712+=70.5，∴B款智能玩具飞机性能为优等的数量为10-4-5=1（架），∴1%100%10m=´，解得m=10.（2）A款智能具飞机运行性能更好,理由如下(写出一条理由即可)；①A款智能玩具飞机运行最长时间的中位数71大于B款智能玩具飞机运行最长时间的中位数70.5；②A款智能玩具飞机运行最长时间的众数72大于B款智能玩具飞机运行最长时间的众数67；B 款智能玩具飞机运行性能更好，理由如下：A 、B 两款智能玩具飞机运行长时间的平均数均为70，B 款智能玩具飞机运行最长时间的方差26.6小于A 款智能玩具飞机运行最长时间的方差30.4.（3）200×610+120×(1-40%)=192(架).答：估计两款智能玩具飞机运行性能在中等及以上的共有192架.一次函数的实际应用6.（2023达州22题）某县著名传统土特产品“豆笋”、“豆干”以“浓郁豆香，绿色健康”享誉全国，深受广大消费者喜爱，已知2件豆笋和3件豆干进货价为240元，3件豆笋和4件豆干进货价为340元.（1）分别求出每件豆笋、豆干的进价；（2）某特产店计划用不超过10440元购进豆笋、豆干共200件，且豆笋的数量不低于豆干数量的32，该特产店有哪几种进货方案？（3）若该特产店每件豆笋售价为80元，每件豆干售价为55元，在（2）的条件下，怎样进货可使该特产店获得利润最大，最大利润为多少元？【推荐区域：云南、陕西、福建、河南】【参考答案】解：（1）设豆笋、豆干的进价分别是a 元/件、b 元/件，则2324034340a b a b +=ìí+=î，解得6040a b =ìí=î，∴豆笋、豆干的进价分别是60元/件，40元/件．（2）设豆干购进n 件，则豆笋购进()200n -件，由题意可得4060(200)1044032002n n n n +-£ìïí-³ïî，解得7880n ££，∴78n =时，200122n -=，即豆干购进78件，则豆笋购进122件，79n =时，200121n -=，即豆干购进79件，则豆笋购进121件，80n =时，200120n -=，即豆干购进80件，则豆笋购进120件．（3）设总利润为W 元，豆干购进n 件，则(5540)(8060)(200)W n n =-+--54000n =-+由（1）可知，7880n ££且n 为整数，∵50-<，∴当7880n ££时，W 随n 的增大而减小，∴当78n =时，W 取最大值，为57840003610W =-´+=．此时，购进豆干购进78件，则豆笋购进122件，获得最大利润为3610元．几何测量问题7.（2023泸州22题）如图，某数学兴趣小组为了测量古树DE 的高度，采用了如下的方法：先从与古树底端D 在同一水平线上的点A 出发，沿斜面坡度为i ＝2AB 前进m 到达点B ，再沿水平方向继续前进一段距离后到达点C .在点C 处测得古树DE 的顶端E 的俯角为37°，底部D 的俯角为60°，求古树DE 的高度（参考数据：sin37°≈35，cos37°≈45，tan37°≈34，计算结果用根号表示，不取近似值）.第7题图【推荐区域：陕西、河南】【参考答案】解：如解图，延长BC ，DE 交于点G ，过点B 作BF AD ^于点F ，第7题图则90AFB BFD Ð=Ð=°，∵斜面AB 的坡度为2:i =∴设2BF x =，则AF =，在Rt ABF 中，根据勾股定理得：222BF AF AB +=，即222(2))x +=，解得：20x =（负值已舍去），即()22040m BF =´=，∵BC 为水平方向，DE 为竖直方向，∴90BGD Ð=°，∵90BFD FDG BGD Ð=Ð=Ð=°，∴四边形BFDG 为矩形，∴40m DG BF ==，∵∠DCG=60°，∴在Rt DCG △中，3340340tan ==Ð=DCG DG CG ，∵37ECG Ð=°，∴在Rt ECG 中，EG =CG ·tan ∠ECG 310433340tan373340=´»°´=，∴(40DE DG EG =-=-．答：古树DE 的高度为(40-．切线的相关证明与计算8.（2023南充22题）如图，AB 与⊙O 相切于点A ，半径OC ∥AB ，BC 与⊙O 相交于点D ，连接AD .（1）求证：∠OCA ＝∠ADC .（2）若AD ＝2，tan B ＝13，求OC 的长.第8题图【推荐区域：云南、陕西、福建】【参考答案】解：（1）证明：如解图，连接OA交BC于点E.∵AB是⊙O的切线，∴∠OAB＝90°.∵OC∥AB，∴∠AOC＝∠OAB＝90°.∵OC＝OA，∴∠OCA＝45°.∵∠ADC＝12∠AOC＝45°，∴∠OCA＝∠ADC.第8题解图（2）解：如解图，过点A作AF⊥BC于点F.∵sin∠ADF＝AF AD，∴AF＝AD·sin∠ADF＝2×2在Rt △ABF 中，tan B ＝13AF BF ＝，∴BF ＝3AF ＝.∴AB =.在Rt △ABE 中，tan B ＝AE AB =13，∴AE ＝13AB ＝3.∵OC ∥AB ，∴∠OCE ＝∠B ，∴tan ∠OCE ＝OE OC ＝13.设OC ＝r ，则OE ＝OA －AE ＝r －3，∴3（r －3）＝r ，解得r OC .。

一次函数与二次函数图象的交点问题专项练习及答案

一次函数与二次函数图象的交点问题专项练习1.已知：关于x 的一元二次方程mx 2﹣（4m +1）x +3m +3=0（m ＞1）。

（1）求证：方程有两个不相等的实数根；（2）设方程的两个实数根分别为x 1，x 2（其中x 1＞x 2），若y 是关于m 的函数，且y =x 1﹣3x 2，求这个函数的解析式；（3）将（2）中所得的函数的图象在直线m =2的左侧部分沿直线m =2翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当关于m 的函数y =2m +b 的图象与此图象有两个公共点时，b 的取值范围。

2.已知抛物线2221y x mx m =-+-+与x 轴交点为A 、B （点B 在点A 右侧），与y 轴交于点C 。

（1）试用含m 的代数式表示A 、B 两点的坐标；（2）当点B 在原点的右侧，点C 在原点的下方时，若BOC △是等腰三角形，求抛物线的解析式；（3）已知一次函数y kx b =+，点P （n ，0）是x 轴上一个动点，在（2）的条件下，过点P 作垂直于x 轴的直线交这个一次函数的图象于点M ，交抛物线2221y x mx m =-+-+于点N ，若只有当14n <<时，点M 位于点N 的下方，求这个一次函数的解析式。

3.已知关于x 的方程mx 2+（3m +1）x +3=0（m ≠0）。

（1）求证：方程总有两个实数根；（2）若方程的两个实数根都是整数，求正整数m 的值；（3）在（2）的条件下，将关于x 的二次函数y =mx 2+（3m +1）x +3的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象，请结合这个新的图象回答：当直线y =x +b 与此图象有两个公共点时，b 的取值范围。

4.已知一次函数1y kx b=+（k ≠0）的图象经过(2,0)，(4,1)两点，二次函数2224y x ax =-+（其中a ＞2）。

中考数学数学总复习《二次函数图象与X轴的交点》练习题(含答案)

二次函数图象与X 轴的交点一、选择题（本大题共1小题）1.对于每个非零自然数n ，抛物线()()221111n y x x n n n n +=-+++与x 轴交于n n A B 、两点，以n n A B 表示这两点间的距离，则112220092009A B A B A B +++…的值是（） A ．20092008 B ．20082009 C ．20102009 D ．20092010二、解答题（本大题共4小题）2.已知：关于x 的方程()213210ax a x a --+-=（1）当a 取何值时，二次函数()21321y ax a x a =--+-的对称轴是2x =-；（2）求证：a 取任何实数时，方程总有实数根.3.已知二次函数2y ax bx c =++（其中a 是正整数）的图象经过点()14A -，和()21B ，，且与x 轴有两个不同的交点，求b c +的最大值．4.已知二次函数2(1)1y x m x m =-++-（1）求证：不论m 为任何实数，这个函数的图象与x 轴总有交点，（2）m 为何实数时，这两个交点间的距离最小？这个最小距离是多少？5.设二次函数()2f x ax bx c =++满足条件；()02f =，()11f =-，且其图象在x 轴上所截得的线段长012)31(2=-+--a x a ax二次函数图象与X 轴的交点答案解析一、选择题1.D二、解答题2.考查二次函数的对称轴的性质，以及函数图象与坐标轴交点的情况．(1)解：∵二次函数()21321y ax a x a =--+-的对称轴是2x =- ∴()11322a a--=- 解得1a =-经检验1a =-是原分式方程的解.所以1a =-时，二次函数()21321y ax a x a =--+-的对称轴是2x =-；（2）1）当0a =时，原方程变为10x --=，方程的解为1x =-；2）当0a ≠时，原方程为一元二次方程，，当240b ac -≥时，方程总有实数根 ∴()()2134210a a a ----≥⎡⎤⎣⎦ 整理得，2210a a -+=,()210a -≥ ∵0a ≠时 ()210a -≥总成立所以a 取任何实数时，方程总有实数根.3.由函数经过点()14A -，，()21B ，，则有 4421a b c a b c -+=⎧⎨++=⎩，解得132b a c a =--⎧⎨=-⎩．因为二次函数与x 轴有两个不同的交点，则240b ac ∆=->，即()()24320a a a a ---->，整理为()()9110a a -->，解得19a <或1a >．由于a 为正整数，所以2a ≥．又因为324b c a +=-+-≤，且当2a =、3b =-、1c =-时，满足题意，故b c +的最大值为4-．012)31(2=-+--a x a ax 012)31(2=-+--a x a ax4.（1）当0y =时，2(1)10x m x m -++-=∵222(1)4(1)25(1)440m m m m m ∆=+--=-+=-+≥>， ∴不论m 为任何实数，方程都有两个不等的实数根. ∴不论m 为任何实数，这个函数的图象与x 轴总有交点. （2）设12x x ，是方程2(1)10x m x m -++-=的两个根，∴121x x m +=+，121x x m ⋅=-，且1x ，2x 是这个函数图象与x 轴交点的横坐标， ∴这两个交点间的距离为12x x -.∵12x x -==∴当1m =时，12x x -的值最小，最小值为2.5.()242f x x x =-+，或者()2912277f x x x =--+；本题一方面学生要理解()f x 的表示，另一方面要会应用在x 轴上截取线段的应用。

人教版数学2018年中考专题复习一次函数与二次函数图像的交点问题 (共32张PPT)

解：根据对称, 抛物线C1在-2<x<-1这一段位于C2下方,相当于抛物线
C1在3<x<4这一段位于C2下方.
∵抛物线C1在1<x<3这一段位于C2上方， ∴两条抛物线的交点横坐标:x=3
∴把x=3代入y=x2-2x ∴y=3
∴抛物线C1:y=-mx2+2mx+4经过点（3,3） ∴
m 1 3 1 3 x
在平面直角坐标系xOy中，抛物线y=mx2-2mx+m+4与y轴交于点A
（0,3），与x轴交于点B，C（点B在点C左侧）. (2)抛物线的对称轴与x轴交于点D，若直线y=kx+b经过点D和点
E(-1,-2)，求直线DE的表达式；
D
E
在平面直角坐标系xOy中，抛物线y=mx2-2mx+m+4与y轴交于点
(3)已知点P(m,0)是x轴上的一个动点,过点P作垂直于x轴的直线交(2) 中的二次函数图象于点M,交一次函数y=px+q的图象于点N.若只有当 1<m<5时,点M位于点N的下方,求一次函数y=px+q 的解析式．
C
A
பைடு நூலகம்
B
(3)已知点P(m,0)是x轴上的一个动点,过点P作垂直于x轴的直线交(2) 中的二次函数图象于点M,交一次函数y=px+q的图象于点N.若只有当 1<m<5时,点M位于点N的下方,求一次函数y=px+q 的解析式．解：依题意并结合图象可知，一次函数的图
当x=-1时，m+2m-2=4，解得m=2，
∴抛物线的解析式为y=2x2-4x-2．
在平面直角坐标系xOy中，抛物线y=mx2-2mx+m+4与y轴交于点A （0,3），与x轴交于点B，C（点B在点C左侧）. (1)求该抛物线的表达式及点B，C的坐标；

中考数学总复习《二次函数与一次函数的综合应用》练习题附带答案

中考数学总复习《二次函数与一次函数的综合应用》练习题附带答案一、单选题(共12题；共24分)1．如图是二次函数 y 1=ax 2+bx +c(a ≠0) 和一次函数 y 2=mx +n(m ≠0) 的图象.则下列结论正确的是（）A ．若点 M(−2，d 1)，N(12，d 2)，P(2，d 3) 在二次函数图象上，则 d 1<d 2<d 3B ．当 x <−12或 x >3 时C ．2a −b =0D ．当 x =k 2+2 （ k 为实数）时2．在平面直角坐标系中，已知抛物线与直线的图象如图所示，当y 1≠y 2时，则取y 1，y 2中的较大值记为N ；当y 1=y 2时，则N=y 1=y 2．则下列说法：①当0＜x ＜2时，则N=y 1；②N 随x 的增大而增大的取值范围是x ＜0；③取y 1，y 2中的较小值记为M ，则使得M 大于4的x 值不存在；④若N=2，则x=2﹣√2或x=1．其中正确的有（）A ．1个B ．2个C ．3个D ．4个3．已知抛物线y 1= 14（x ﹣x 1）（x ﹣x 2）交x 轴于A （x 1，0）B （x 2，0）两点，且点A 在点B 的左边，直线y 2=2x+t 经过点A ．若函数y=y 1+y 2的图象与x 轴只有一个公共点时，则则线段AB 的长为（） A ．4B ．8C ．16D ．无法确定4．如图，抛物线y ＝ax 2+bx +c 和直线y ＝kx +b 都经过点（﹣1，0），抛物线的对称轴为x ＝1，那么下列说法正确的是（）A ．ac ＞0B ．b 2﹣4ac ＜0C ．k ＝2a +cD ．x ＝4是ax 2+（b ﹣k ）x +c ＜b 的解5．直线y=ax ﹣6与抛物线y=x 2﹣4x+3只有一个交点，则a 的值为（）A ．a=2B ．a=10C ．a=2或a=﹣10D ．a=2或a=106．如图是函数y ＝x 2+bx+c 与y ＝x 的图象，有下列结论：（1）b 2﹣4c ＞0；（2）b+c+1＝0；（3）方程x 2+（b ﹣1）x+c ＝0的解为x 1＝1，x 2＝3；（4）当1＜x ＜3时，则x 2+（b ﹣1）x+c ＜0.其中正确结论的个数为（） A ．1B ．2C ．3D ．47．在直角坐标系中，直线y=x+2和抛物线y=x 2-x+1的若干组函数值如下表所示：x … 1 1.5 2 2.5 3 … y=x+2 … 3 3.5 4 4.5 6 … y=x 2-x+1…11.7534.7513…A ．1<x<1.5B ．1.5<Xx2C ．2<x<2.5D ．2.5<x<38．割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法：随着圆内接正多边形边数的增加，它的周长和面积越来越接近圆周长和圆面积，“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”．刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率．请你也用这个方法求出二次函数 y=14(x −4)2的图象与两坐标轴所围成的图形最接近的面积是（）A ．5B ．225C ．4D ．17﹣4π9．如图，“心”形是由抛物线 y =−x 2+6和它绕着原点O ，顺时针旋转60°的图形经过取舍而成的，其中顶点C 的对应点为D ，点A ，B 是两条抛物线的两个交点，直线AB 为“心”形对称轴，点E ，F ，G 是抛物线与坐标轴的交点，则AB=（）A ．6√3B ．8C ．10D ．10√310．已知一次函数y=ax+c 与二次函数y=ax 2+bx+c ，它们在同一坐标系内的大致图象是（）A ．B ．C ．D ．11．如图，抛物线y ＝﹣x 2+4x ﹣3与x 轴交于点A 、B ，把抛物线在x 轴及其上方的部分记作C 1，将C 1向右平移得到C 2，C 2与x 轴交于B 、D 两点．若直线y ＝kx ﹣k 与C 1、C 2共有3个不同的交点，则k 的最大值是（）A ．12B ．2 √5 ﹣6C ．6+4 √2D ．6﹣4 √212．在平面直角坐标系中，已知点 A(−1,4) ， B(2,1) 直线 AB 与 x 轴和 y 轴分别交于点 M ，N 若抛物线 y =x 2−bx +2 与直线 AB 有两个不同的交点，其中一个交点在线段 AN 上（包含 A ， N 两个端点），另一个交点在线段 BM 上（包含 B ， M 两个端点），则 b 的取值范围是（）A．1≤b≤52B．b≤1或b≥52C．52≤b≤113D．b≤52或b≥113二、填空题(共6题；共6分)13．如图，抛物线y=ax2﹣2与y轴交于点A，过点A与x轴平行的直线交抛物线y=﹣12 x2于点B，C，则S△BOC= ．14．在平面直角坐标系xOy中，函数y1＝x（x＜m）的图象与函数y2＝x2（x≥m）的图象组成图形G．对于任意实数n，过点P（0，n）且与x轴平行的直线总与图形G有公共点，写出一个满足条件的实数m的值为（写出一个即可）．15．如图，抛物线y=ax2+bx+1的顶点在直线y=kx+1上，对称轴为直线x=1，以下四个结论：①ab<0；②b<13；③a=−k；④当0<x<1其中正确的是．（填序号）16．如图，抛物线y=x2﹣2x+k与x轴交于A、B两点，与y轴交于点C（0，﹣3）．若抛物线y=x2﹣2x+k上有点Q，使△BCQ是以BC为直角边的直角三角形，则点Q的坐标为．17．已知抛物线p ：y=ax 2+bx+c 的顶点为C ，与x 轴相交于A 、B 两点（点A 在点B 左侧），点C 关于x轴的对称点为C ′，我们称以A 为顶点且过点C ′，对称轴与y 轴平行的抛物线为抛物线p 的“梦之星”抛物线，直线AC ′为抛物线p 的“梦之星”直线．若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x 2+2x+1和y=2x+2，则这条抛物线的解析式为．18．如图，抛物线y=13x 2﹣4√33x+3与x 轴交于A ，B 两点，与y 轴交于点C ，点M 的坐标为（2√3，1）．以M 为圆心，2为半径作⊙M ．则下列说法正确的是（填序号）． ①tan ∠OAC=√3； ②直线AC 是⊙M 的切线； ③⊙M 过抛物线的顶点； ④点C 到⊙M 的最远距离为6；⑤连接MC ，MA ，则△AOC 与△AMC 关于直线AC 对称．三、综合题(共6题；共73分)19．在平面直角坐标系中，已知A ，B 是抛物线y=ax 2（a ＞0）上两个不同的点，其中A 在第二象限，B 在第一象限．（1）如图1所示，当直线AB 与x 轴平行，∠AOB=90°，且AB=2时，则求此抛物线的解析式和A ，B 两点的横坐标的乘积；（2）如图2所示，在（1）所求得的抛物线上，当直线AB 与x 轴不平行，∠AOB 仍为90°时，则求证：A、B两点横坐标的乘积是一个定值；（3）在（2）的条件下，如果直线AB与x轴、y轴分别交于点P、D，且点B的横坐标为1 2．那么在x轴上是否存在一点Q，使△QDP为等腰三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．20．某公司成功开发出一种产品，正式投产后，生产成本为5元/件.公司按订单生产该产品（销售量=产量），年销售量y（万件）与售价x（元/件）之间满足如图1所示的函数关系，公司规定产品售价不超过15元/件，受产能限制，年销售量不超过30万件；为了提高该产品竞争力，投入研发费用P 万元（P万元计入成本），P与x之间的函数关系式如图2所示，当10≤x≤15时可看成抛物线P= 14x2−4x+m.（1）求y与x之间的函数关系式.（2）求这种产品年利润W（万元）与售价x（元/件）满足的函数关系式.（3）当售价x为多少元时，则年利润W最大，并求出这个最大值.21．如图，抛物线y＝ax2＋32 x＋c（a≠0）与x轴交于点A，B两点，其中A(－1，0)，与y轴交于点C(0，2)．（1）求抛物线的表达式及点B坐标；（2）点E是线段BC上的任意一点（点E与B、C不重合），过点E作平行于y轴的直线交抛物线于点F，交x轴于点G．①设点E的横坐标为m，用含有m的代数式表示线段EF的长；②线段EF长的最大值是．22．已经二次函数y=ax2+bx+1 .（1）如图，其图象与x轴交于点A(−1,0)和点B，与y轴交于点C，对称轴为直线x=1 .①求二次函数解析式；②F为线段BC上一点，过F分别作x轴，y轴垂线，垂足分别为E、F，当四边形OEFG为正方形时，则求点F坐标；（2）其图象上仅有一个点的横坐标、纵坐标互为相反数，且二次函数y=ax2+bx+1函数值存在负数，求b的取值范围.23．定义符号min{a，b}的含义为：当a≥b时，则min{a，b}=b；当a＜b时，则min{a，b}=a．如：min{1，﹣2}=﹣2，min{﹣1，2}=﹣1．（1）求min{x2﹣1，﹣2}；（2）已知min{x2﹣2x+k，﹣3}=﹣3，求实数k的取值范围；（3）已知当﹣2≤x≤3时，则min{x2﹣2x﹣15，m（x+1）}=x2﹣2x﹣15．直接写出实数m的取值范围．24．某企业研发了一种新产品，已知这种产品的成本为30元/件，且年销售量y（万件）与售价x（元/件）的函数关系式为y={−2x+140，(40≤x<60)−x+80.(60≤x≤70)（1）当售价为60元/件时，则年销售量为万件；（2）当售价为多少时，则销售该产品的年利润最大？最大利润是多少？（3）若销售该产品的年利润不少于750万元，直接写出x的取值范围.参考答案1．【答案】D 2．【答案】B 3．【答案】B 4．【答案】D 5．【答案】C 6．【答案】B 7．【答案】C 8．【答案】A 9．【答案】A 10．【答案】C 11．【答案】C 12．【答案】C 13．【答案】414．【答案】1（答案不唯一） 15．【答案】①③④16．【答案】（1，﹣4）和（﹣2，5） 17．【答案】y=x 2﹣2x ﹣3 18．【答案】①②③④ 19．【答案】（1）解：如图1作BE ⊥x 轴∴△AOB 是等腰直角三角形 ∴BE=OE= 12AB=1∴A （﹣1，1），B （1，1）∴A ，B 两点的横坐标的乘积为﹣1×1=﹣1∵抛物线y=ax 2（a ＞0）过A ，B ∴a=1 ∴抛物线y=x 2 （2）解：如图2作BN ⊥x 轴，作AM ⊥x 轴 ∴∠AOB=AMO=∠BNO=90° ∴∠MAO=∠BON ∴△AMO ∽△ONB ∴AM ON =OM BN ∴AM ×BN=OM ×ON设A （x 1，y 1），B （x 2，y 2）在抛物线上 ∴AM=y 1=x 12，BN=y 2=x 22，OM=﹣x 1，ON=x 2 ∴x 12×x 22=﹣x 1×x 2 ∴x 1×x 2=﹣1∴A ，B 两点横坐标的乘积是一个定值；（3）解：由（2）得，A ，B 两点横坐标的乘积是一个定值为﹣1，∵点B 的横坐标为 12，∴点A 的横坐标为﹣2，∵A ，B 在抛物线上，∴A （﹣2，4），B （ 12 ， 14 ），∴直线AB 解析式为y=﹣ 32x+1，∴P （ 23 ，0），D （0，1）设Q （n ，0），∴DP 2= 139 ，PQ 2=（n ﹣ 23）2，DQ 2=n 2+1∵△QDP 为等腰三角形∴①DP=PQ ，∴DP 2=PQ 2，∴139 =（n ﹣ 23 ）2，∴n= 2±√133 ，∴Q 1（ 2+√133 ，0），Q 2（ 2−√133 ，0）②DP=DQ ，∴DP 2=DQ 2，∴139 =n 2+1，∴n= 23 （舍）或n=﹣ 23 ，Q 3（﹣ 23 ，0）③PQ=DQ ，∴PQ 2=DQ 2，∴（n ﹣ 23 ）2=n 2+1∴n=﹣ 512 ，∴Q4（﹣ 512 ，0），∴存在点Q 坐标为Q 1（ 2+√133 ，0），Q 2（2−√133 ，0），Q 3（﹣ 23 ，0），Q4（﹣ 512 ，0）20．【答案】（1）解：设y 与x 的函数关系式为：y=kx+b将点（5，30），（15，10）代入可得：{30=5k +b 10=15k +b解得：{b =40k =−2∴y 与x 的函数关系式为：y=-2x+40（5≤x ≤15）；（2）解：当5≤x ≤10时，则根据图像可得：P=60 ∴W=(x-5)y-P=(x-5)(-2x+40)-60=-2x 2+50x-260；当10≤x ≤15时，则P =14x 2−4x +m由图可得经过点（10，60），将其代入可得：60=14×102−4×10+m 解得：m=75∴P =14x 2−4x +75；∴W=(x-5)y-P=(x-5)(-2x+40)-(14x 2−4x +75)=−94x 2+54x −275；综上：W ={−2x 2+50x −260(5≤x ≤10)−94x 2+54x −275(10≤x ≤15)；（3）解：由（2）可得：当5≤x ≤10时W=-2x 2+50x-260=-2(x −252)2+1052∴x =252不在5≤x <10，由于开口向下在5≤x <10内随x 增大而增大在x=10时，则取得最大值为W=40；当10≤x ≤15时W=−94x 2+54x −275对称轴为x=−b2a=12 由于函数开口向下 ∴当x=12时，则W=49∴当x=12时，则W 取得最大值为49；综上可得：当售价为12元时，则年利润最大，最大为49万元.21．【答案】（1）解：将A(－1，0)、 C(0，2)代入y ＝ax 2＋ 32x ＋c （a ≠0）得：a ＝－ 12， c ＝2y ＝－ 12 x 2＋ 32x ＋2 当y ＝0时，则x 1＝－1，x 2＝4，故B(4，0)（2）解：设直线BC 的函数表达式为y ＝kx ＋b ，将B(4，0)、 C(0，2)代入得：y ＝－ x ＋2，EF ＝FG －GE ＝－ m 2＋ m ＋2－(－ m ＋2) ＝－ m 2＋2m ；2 22．【答案】（1）解：①由题： {a −b +1=0−b 2a =1 解得 {a =−13b =23∴ 二次函数解析式为： y =−13x 2+23x +1 ； ②设BC 解析式为： y =kx +b 对称轴为直线 x =1 .∵ 图象与x 轴交于点 A(−1,0) 和点B ，对称轴为直线 x =1 .∴ 点 B(3,0)将 B(3,0) ， C(0,1) 代入得： {3k +b =0b =1解得： {a =−13b =1∴BC 解析式为： y =−13x +1 设点 F(m,−13m +1) ∵ 四边形 OEFG 是正方形∴EF =GF∴m =−13m +1解得 m =34∴F(34,34) （2）解：二次函数的图象其有且只有一个点横、纵坐标之和互为相反数∴−x =ax 2+bx +1 有两相等实根，即 ax 2+(b +1)x +1=0 有两相等实根 ∴{a ≠0(b +1)2−4a =0解得： a =(b+1)24>0 ，且 b ≠−1 ∵y =ax 2+bx +1 存在负值∴b 2−4a =b 2−(b +1)2>0 ，解得 b <−12综上： b <−12且 b ≠−123．【答案】（1）解：∵x2≥0∴x2﹣1≥﹣1∴x2﹣1＞﹣2．∴min{x2﹣1，﹣2}=﹣2（2）解：∵x2﹣2x+k=（x﹣1）2+k﹣1∴（x﹣1）2+k﹣1≥k﹣1．∵min{x2﹣2x+k，﹣3}=﹣3∴k﹣1≥﹣3．∴k≥﹣2（3）解：对于y=x2﹣2x﹣15，当x=﹣2时，则y=﹣7当x=3时，则y=﹣12由题意可知抛物线y=x2﹣2x﹣15与直线y=m（x+1）的交点坐标为（﹣2，﹣7），（3，﹣12）所以m的范围是：﹣3≤m≤7．24．【答案】（1）20（2）解：设销售该产品的年利润为W万元当40≤x<60时W=(x−30)(−2x+140)=−2(x−50)2+800 .∵－2<0∴当x=50时W最大=800当60≤x≤70时W=(x−30)(−x+80)=−(x−55)2+625∵−1<0∴当x=60时W最大=600∵800>600∴当x=50时W最大=800∴当售价为50元/件时，则年销售利润最大，最大为800万元.（3）解：45≤x≤55理由如下：由题意得(x−30)(−2x+140)≥750解得45≤x≤55。

中考数学总复习《二次函数与一次函数综合》专题测试卷及答案解析

中考数学总复习《二次函数与一次函数综合》专题测试卷及答案解析班级：___________姓名：___________考号：___________ 1．过原点的抛物线212y x bx c =++与x 轴的另一个交点为A ，且抛物线的对称轴为直线2x =，顶点为B ．（1）求抛物线的解析式；（2）如图（1），点E 是直线AB 上方抛物线上一点，连接AB ，BE ，AE ，若ABE ∆的面积为4，求点E 的坐标；（3）如图（2），设直线2(0)y kx k k =-≠与抛物线交于C ，D 两点，点D 关于直线2x =的对称点为D '，直线CD '与直线2x =交于点P ，求证：BP 的长为定值．2．定义：函数2(0)y x bx c c =++≠的图象与x 轴的交点A ，B 的横坐标分别为A x 和B x ，与y 轴的交点C 的纵坐标为1y ，若A x ，B x 中至少存在一个值，且满足A C x y =（或)B C x y =则称该函数为“M 函数”，例如，函数223y x x =+-的图象与x 轴的一个交点A 为(3,0)-，与y 轴的交点C 为(0,3)-，满足A C x y =，则称223y x x =+-为“M 函数”．（1）请探究“M 函数” 2(0)y x bx c c =++≠中，b 与c 的关系．（2）如图，“M 函数” 2y x bx c =++的图象与x 轴交于A ，B 两点（点A 在点B 的左侧），且经过点(3,4)P -，现将抛物线沿射线AP 方向平移，使点P 落在点M 处，同时抛物线上的点B 落在点D 处，已知由抛物线平移前P ，B 之间的曲线部分，平移后M ，D 之间的曲线部分及线段MP ，BD 所围成的图形的面积S 为5求线段PM 的长．3．如图，已知：点P是直线:2=-上的一动点，其横坐标为(m m是常数），点M是抛物线l y x2=+-+的顶点．C y x mx m:222（1）当点P在直线l运动时抛物线C始终经过一个定点N，求点N的坐标，并判断点N是否是点M的最高位置？（2）当点P在直线l运动时点M也随之运动，此时直线l与抛物线C有两个交点A，B（A，B可以重合）A、B两点到y轴的距离之和为d．①求m的取值范围；②求d的最小值．（3）连接PM，当直线PM与抛物线C的另一个交点也在线段PM上时求m的取值范围．4．如图1，抛物线2y x bx c =-++的对称轴为直线1x =-，抛物线与x 轴相交于A 、B 两点，与y 轴交于点C ，其中点A 的坐标为(3,0)-．（1）直接写出B 点坐标；（2）求抛物线2y x bx c =-++解析式及直线AC 解析式；（3）如图2，若点P 在直线AC 上方的抛物线上一动点，过点P 作x 轴垂线垂足为N ，交直线AC 于点M ，求当线段PM 长度最大时的点P 的坐标？5．如图，在平面直角坐标系xOy 中，抛物线22:()2(0)E y x m m m =--+<的顶点P 在抛物线2:F y ax =上，直线x t =与抛物线E 、F 分别交于点A ，B ．（1）求a 的值；（2）将A ．B 的纵坐标分别记为A y 和B y ，设A B s y y =-，若s 的最大值为3，则m 的值是多少？（3）Q 是x 轴的正半轴上一点，且PQ 的中点M 恰好在抛物线F 上，试探究：此时无论m 为何负值，在y 轴的负半轴上是否存在定点G ，使PQG ∠总为直角？若存在，请求出点G 的坐标；若不存在，请说明理由．6．如图，抛物线24y ax bx =++与x 轴交于(3,0)A -，(4,0)B 两点，与y 轴交于点C ，点P 是抛物线上的一个动点，过点P 作直线PD x ⊥轴，垂足为D ，直线PD 交直线BC 于点E ，过点P 作直线PF y ⊥轴，垂足为F ，直线PF 与直线BC 的交点为G ，设点P 的横坐标为m ．（1）求抛物线的表达式；（2）若34m -<<且0m ≠，当2PE CF =时请求出点P 的坐标；（3）若04m <<，作直线AC ，在直线AC 上有一动点Q ，连接BQ ，GQ ，当45BQG ∠=︒时请直接写出满足条件的BG 的最小值以及此时点P 的坐标．7．如图1，二次函数2y x bx c=-++的图象与x轴交于A、B两点，与y轴交于C点，点B的坐标为(3,0)，点C的坐标为(0,3)，直线l经过B、C两点．（1）求该二次函数的表达式及其图象的顶点坐标；（2）点P为直线l上的一点，过点P作x轴的垂线与该二次函数的图象相交于点M，再过点M作y轴的垂线与该二次函数的图象相交于另一点N，当12PM MN=时求点P的横坐标；（3）如图2，点C关于x轴的对称点为点D，点P为线段BC上的一个动点，连接AP，点Q为线段AP上一点，且3AQ PQ=，连接DQ，当AQ DQ+的值最小时直接写出DQ的长．8．如图，抛物线24832999y x x =-++与x 轴交于A ，B 两点（点A 在点B 的左侧），顶点为D ．点P 为对称轴右侧抛物线上的一个动点，其横坐标为m ，直线AD 交y 轴于点C ，过点P 作//PF AD 交x 轴于点F ，//PE x 轴，交直线AD 于点E ，交直线DF 于点M ．（1）直接写出点A ，B ，D 的坐标；（2）当3DM MF =时求m 的值；（3）试探究点P 在运动过程中，是否存在m ，使四边形AFPE 是菱形，若存在，请直接写出点P 的坐标；若不存在，请说明理由．9．抛物线21:()2(03)C y a x b b b =-+-<<过点(2,0)H ，抛物线的顶点为点D ．（1）若1a =，求抛物线的顶点D 的坐标；（2）在（1）的条件下，抛物线与y 轴交于点E ，且y 轴上有点(0,2)F ，y 轴上是否存在点N 使得FNH EHF ∠=∠，若存在请求出点N 的坐标；若不存在，请说明理由；（3）若14a =，将抛物线1C 平移使得其顶点和原点重合，得到新抛物线2C ，过点(2,3)A -的直线交抛物线2C 于M 、Q 两点，过点(6,3)B -的直线交抛物线2C 于M 、P 两点．求证：直线PQ 过定点，并求出定点坐标．10．如图，抛物线22y ax bx=++经过点(1,0)A-和(4,0)B，交y轴于点C．（1）写出a=，b=；（2）点D为y轴右侧抛物线上一点，是否存在点D，使23ABC ABDS S∆∆=？若存在，求出点D的坐标，若不存在，请说明理由．（3）将直线BC绕点B顺时针旋转45︒，与直线AC相交于点F，求直线BF的函数表达式．11．如图所示，在平面直角坐标系中，直线3=-+交坐标轴于B、C两点，抛物线23y x=++经过y ax bxDQ CO，DQ交B、C两点，且交x轴于另一点(1,0)A-．点D为抛物线在第一象限内的一点，过点D作//BC于点P，交x轴于点Q．（1）求抛物线的解析式；（2）设点P的横坐标为m，在点D的移动过程中，存在DCP DPC∠=∠，求出m值；（3）在抛物线上取点E，在平面直角坐标系内取点F，问是否存在以C、B、E、F为顶点且以CB为边的矩形？如果存在，请求出点F的坐标；如果不存在，请说明理由．参考答案与解析1．【解答】解：（1）抛物线的对称轴为直线2x =，过原点，可得 02122c b =⎧⎪⎪⎨-=⎪⋅⎪⎩；解得：02c b =⎧⎨=-⎩；即解析式为：2122y x x =- （2）由（1）得22112(2)222y x x x =-=--，得(2,2)B -．令0y =，解得：10x =和 24x =．得：(4,0)A设AB 上方x 轴上点(,0)P p 满足4PAB S ∆=，即1(4)|2|42p -⋅-=解得：0p =即(0,0)P 与原点重合．设直线AB 解析式为：y kx b =+则有：4022k b k b +=⎧⎨+=-⎩解得：14k b =⎧⎨=-⎩∴直线AB 解析式为：4y x =-∴与直线AB 平行，且过(0,0)P 的直线为：y x =点E 在直线y x =上时4ABE PAB S S ∆∆==，满足题意． ∴2122y x x y x⎧=-⎪⎨⎪=⎩；解得：1100x y =⎧⎨=⎩或2266x y =⎧⎨=⎩；故：1(0,0)E 和2(6,6)E ．（3）C 、D 为2y kx k =-与抛物线的交点22122y kx k y x x =-⎧⎪⎨=-⎪⎩；解得：21221244x k k y k k ⎧=++⎪⎨=-+⎪⎩22222244x k k y k k ⎧=+++⎪⎨=++⎪⎩ ∴222222(24,4),(24,4)C k k k k D k k k k k ++++++-+-+ D '与D 关于直线2x =对称，得：222(24,4)D k k k k '-++-+ 设直线CD '的解析式为：y mx n =+222222(24)4(24)4k k m n k k k k m n k k k ⎧+++=++⎪⎨-++=-+⎪⎩；解得：224244m k n k ⎧=+⎪⎨=-+⎪⎩ 即直线CD '的解析式为：224244y k x k =++-+当2x =时4y =-．∴点(2,4)P -为定点，BP 为定值2．2．【解答】解：（1）当0x =时y c =．函数2y x bx c =++是“M 函数”∴当x c =时0y =，即点(,0)c 在抛物线2y x bx c =++上20c bc c ∴=++0(1)c c b ∴=++0c ≠1b c ∴+=-．答：b 与c 的关系为：1b c +=-（2）由（1）可得1c b =--，即21y x bx b =+--将(3,4)-代入21y x bx b =+--得24331b b -=+--，解得6b =-∴抛物线的解析式为265y x x =-+令2650x x -+=，解得11x = 25x =(1,0)A ∴ (5,0)B如图，连接PB ，MD 根据平移的性质可知，PB 与MD 平行且相等∴四边形MPBD 是平行四边形．易知，P ，B 之间的曲线部分，M ，D 之间的曲线部分，线段MP ，BD 所围成的图形的面积就是平行四边形MPBD 的面积．过点B 作BF PA ⊥于F(1,0)A ，(5,0)B 和(3,4)P -224(31)25PA ∴=+-4AB =4sin BE PAB PA AB ∴∠==8525BF ∴== ∴8585MPBD S PM BF =⋅==5PM ∴=．答：线段PM 的长为5．3．【解答】解：（1）抛物线C 的解析式2222222(1)y x mx m x m x =+-+=++- ∴当1x =时3y =∴抛物线C 始终经过一个定点(1,3)，即(1,3)N ；抛物线C 的解析式为222222()22y x mx m x m m m =+-+=+--+ ∴顶点M 的坐标为2(,22)m m m ---+2222(1)3m m m --+=-++，10-<．∴当1m =-时222m m --+的最大值为3M ∴的纵坐标最大值为3∴点N 是点M 的最高位置；（2）①联立22222y x y x mx m =-⎧⎨=+-+⎩得22240x mx x m +--+=直线l 与抛物线C 有两个交点A ，B （A ，B 可以重合）∴△2224(21)4(24)44150b ac m m m m =-=---+=+-244150m m +-= 解得：1253,22m m =-=∴当244150m m +-时52m -或32m ；②设A ，B 的坐标分别为1(x ，1)y 和2(x ，2)y 其中12x x <由①可知1x ，2x 是方程22240x mx x m +--+=的两根1221x x m ∴+=-+当3m =-时如图所示0A y =当532m --时10y 20y 则12|||21|d x x m =+=-+20-<∴当52m =-时d 取得最小值为52()15162-⨯-+=+= 当32m 时12()(21)21d x x m m =-+=--+=- ∴当32m =时d 取得最小值为32122⨯-=综上所述，d 取得最小值为2；（3）直线PM 与抛物线C 的另一个交点也在线段PM 上时∴点P 一定要在点M 的上方点P 是直线:2l y x =-上的一动点，其横坐标为m(,2)P m m ∴-2222m m m ∴->--+2340m m ∴+->，即(4)(1)0m m +->4m ∴<-或1m >．4．【解答】解：（1）抛物线2y x bx c =-++的对称轴为直线1x =-和(3,0)A - B ∴的横坐标为121-+=(1,0)B ∴；（2）抛物线2y x bx c =-++的对称轴为直线1x =- ∴12(1)b -=-⨯-解得：2b =-22y x x c ∴=--+(3,0)A -960c ∴-++=解得：3c =∴抛物线的解析式为：223y x x =--+(0,3)C ∴设直线AC 的解析式为3y kx =+330k ∴-+=，解得1k =∴直线AC 的解析式为3y x =+；（3）由223y x x =--+，设2(,23)P x x x --+直线3ACy x =+，PN x ⊥轴(,3)M x x ∴+222333(30)PM x x x x x x ∴=--+--=---<< 当332(1)2x -=-=-⨯-时PM 取到最大值最大值为：2339()3()224---⨯-= ∴315(,)24P -． 5．【解答】解：（1）由题意可知，抛物线22:()2(0)E y x m m m =--+<的顶点P 的坐标为2(,2)m m 点P 在抛物线2:F y ax =上222am m ∴=2a ∴=；（2）直线x t =与抛物线E ，F 分别交于点A ，B2222()22A y t m m t mt m ∴=--+=-++ 22B y t =A B s y y ∴=-22222t mt m t =-++-2232t mt m =-++22143()33t m m =--+30-<∴当13t m =时s 的最大值为243m s 的最大值为3 ∴2433m =，解得32m =±0m <32m ∴=-．（3）无论m 为何负值，在y 轴的负半轴上存在定点G ，使PQG ∠总为直角，理由如下：设点M 的横坐标为n ，则2(,2)M n n22(2,42)Q n m n m ∴--点Q 在x 轴正半轴上20n m ∴->且22420n m -=22n ∴=- 2(M ∴，2)m 和(2Q m m --，0）如图，过点Q 作x 轴的垂线KN ，分别过点P ，G 作x 轴的平行线，与KN 分别交于K ，N90K N ∴∠=∠=︒ 90QPK PQK ∠+∠=︒90PQG ∠=︒90PQK GQN ∴∠+∠=︒QPK GQN ∴∠=∠PKQ QNG ∴∆∆∽::PK QN KQ GN ∴=，即PK GN KQ QN ⋅=⋅222PK m m m m m =---=-- 22KQ m = 2GN m m =-- 2(22)(2)2m m m m m QN ∴---=⋅ 解得324QN +=． 324(0,G +∴． 6．【解答】解：（1）抛物线24y ax bx =++与x 轴交于(3,0)A -，(4,0)B 两点，代入得： 934016440a b a b -+=⎧⎨++=⎩ 解得：1313a b ⎧=-⎪⎪⎨⎪=⎪⎩∴抛物线为：211433y x x=-++（2）令0x =，则2114433y x x =-++=(0,4)C ∴设BC 为4y kx =+，把C 点坐标代入得：440k +=解得：1k =-BC ∴为4y x =-+设点P 的横坐标为m ．34m -<<且0m ≠ 则211(,4)33P m m m -++(,4)E m m ∴-+ 211(0,4)33F m m -++ ∴221114|44|||3333EP m m m m m =-+++-=-+221111|44|||3333CF m m m m =+--=-2PE CF = ∴222141122||2||||333333m m m m m m -+=-=- 当2214223333m m m m -+=-时即220m m -=解得：12m = 20m =（不符合题意舍去 ∴10(2,)3P 当22142203333m m m m -++-=时即220m m +=解得：12m =- 20m =（不符合题意，舍去）(2,2)P ∴- 综上：10(2,)3P 或(2,2)P -；（3）如图04m <<，则P 在第一象限内的抛物线上 (4,0)B ，(0,4)C 和(3,0)A -4OB OC ∴==，22345AC =+=和45OBC OCB ∠=∠=︒ 过G 作GK x ⊥轴于K ，则KG KB =，以K 为圆心，KG 为半径画圆交直线AC 于Q ，则1452BQG BKG ∠=∠=︒PD GK ∴=∴当K 与AC 相切时BG 最短，此时Q 为切点KQ AC ⊥，连接QK设211(,4)33P m m m -++ G 在BC 上 ∴2114433m m x -++=-+，即21133x m m =- ∴221111(,4)3333G m m m m --++ 211(,0)33K m m - ∴211333AK m m =-+ 而211433KQ GK m m ==-++ 由4sin 5CO QK CAO AC AK ∠=== ∴22114433115333m m m m -++=-+，即23380m m --= 解得13105m +=，23105m -=（不符合题意，舍去） ∴22111149284()3332129m m m -++=--+= ∴310528()9P +此时282229BG KG PD =． 7．【解答】解：（1）将(3,0)B ，(0,3)C 两点代入2y x bx c =-++得：9303b c c -++=⎧⎨=⎩解得：23b c =⎧⎨=⎩223y x x ∴=-++2223(1)4y x x x ∴=-++=--+∴该函数图象顶点坐标为(1,4)；（2）设直线BC 的解析式为y kx d =+，将(3,0)B ，(0,3)C 两点代入，得： 303k d d +=⎧⎨=⎩解得：13k d =-⎧⎨=⎩3y x ∴=-+设(,3)P t t -+，则2(,23)M t t t -++ 2(2,23)N t t t --++2|3|PM t t ∴=- |22|MN t =-12PM MN = ∴21|3||22|2t t t -=- 解得：12t =12t =-23t =+23t =-P ∴点横坐标为12+122323（3）过Q 点作//QG BC 交x 轴于G 点，作A 点关于GQ 的对称点A '，连接A D '、AG点C 关于x 轴的对称点为点D(0,3)D ∴-令0y =，则2230x x -++=解得：1x =-或3x =(1,0)A ∴-，(3,0)B3(1)4AB ∴=--=3AQ PQ = //QG BC ∴AQ AG AP AB = ∴344AG =3AG ∴=(2,0)G ∴3OB OC ==45OBC ∴∠=︒AQ A Q '=AQ DQ A Q DQ A D ''∴+=+A '∴、Q 、D 三点共线时AQ DQ +的值最小．45QGA CBO ∠=∠=︒ AA QG '⊥45A AG '∴∠=︒AG A G '=45AA G '∴∠=︒90AGA '∴∠=︒(2,3)A '∴设直线DA '的解析式为11y k x b =+，把A '、D 坐标代入得：111323b k b =-⎧⎨+=⎩解得：1133k b =⎧⎨=-⎩∴直线DA '的解析式为33y x =-同理可求直线QG 的解析式为2y x =-+联立方程组233y x y x =-+⎧⎨=-⎩ 解得：5434x y ⎧=⎪⎪⎨⎪=⎪⎩ ∴53(,)44Q ∴2253250510(0)(3)4416DQ =-++ 8．【解答】解：（1）24832999y x x =-++当0y =时248320999x x -++=解得12x =- 24x =．点A 在点B 的左侧(2,0)A ∴- (4,0)B ．24832999y x x =-++，即24(1)49y x =--+(1,4)D ∴．（2）如图，过点D 作DQ x ⊥轴于点Q ，交PE 于点N ．点P 的横坐标为m24832(,)999P m m m ∴-++(1,4)D2248324844()999999DN m m m m ∴=--++=-+ 24832||999NQ m m =-++//PE x 轴 ∴DN DM NQ MF =当3DM MF =时3DN DM NQ MF == 3DN NQ ∴=，即2248448323||999999m m m m -+=-++ 当2248448323()999999m m m m -+=-++时3132m =点P 在抛物线对称轴的右侧331m ∴=+；当2248448323()999999m m m m -+=--++时3162m =±点P 在抛物线对称轴的右侧3162m ∴=综上所述，3132m =或3162m =+；（3）存在，理由如下：当点P 在x 轴上方时设点24832(,)999P m m m -++，则点E 的坐标为24832(,)999x m m -++把点E 的坐标代入AD 的表达式得：248483233999x m m +=-++ 解得2122333x m m =-++故点E 的坐标为2122(333m m -++，24832)999m m -++则2122()333EP m m m =--++由直线AD 的表达式知4tan 3EAO ∠=，则3cos 5EA x x EAO AE -∠== 则255122()(2)33333E A AE x x m m =-=-+++四边形AFPE 是菱形，则AE EP = 即221225122()(2)3333333m m m m m --++=-+++解得2m =-（舍去）或238 故点P 的坐标为23(8，39)16当点P 在x 轴下方时同理可得，点P 的坐标为17(2，21)- 综上，点P 的坐标为23(8，39)16或17(2，-21）． 9．【解答】解：（1）当1a =时2()2y x b b =-+-代入(2,0)H ，得：20(2)2b b =-+-解得2b =或3b =03b <<2b ∴=当2b =时2(2)y x =-(2,0)D ∴；（2）当0x =时2(02)4y =-=(0,4)E ∴(2,0)H∴由勾股定理得222425EH =+当点N 在y 轴的负半轴时如图所示FNH EHF ∠=∠ FEH NEH ∠=∠ EFH EHN ∴∆∆∽ ∴EH EN EF EH =2EH EN EF ∴=⋅ 即2(25)2EN =⋅10EN ∴=6ON EN OE ∴=-=1(0,6)N ∴-由对称性可得2(0,6)N综上所述，存在点1(0,6)N -，2(0,6)N 使得FNH EHF ∠=∠；（3）14a =，且平移后的抛物线顶点在原点 ∴214y x = 设M 的坐标为21(,)4m m则直线AM 可表示为：212(2)34(2)m y x m -=+++和抛物线联立得：222(2)(12)2(12)12(2)m x m x m m +=-+-++ 解得：x m =或2122m x m +=-+ 设62m t m +=+则Q 的坐标为2(2,)t t -；直线BM 可表示为：212(6)34(6)m y x m -=+++和抛物线联立得：222(6)(12)6(12)12(6)m x m x m m +=-+-++ 解得：x m =或6126m x m +=-+则P 的坐标为269(,)t t-； ∴直线QP 可表示为：23()32t y x t +=--当0x = 3y =-∴直线QP 过定点(0,3)-．10．【解答】解：（1）根据题意，得： 2016420a b a b -+=⎧⎨++=⎩ 解得1232a b ⎧=-⎪⎪⎨⎪=⎪⎩ 故答案为：12-和32；（2）当0x =时2y =∴点C 的坐标为(0,2)．145AB =+= ∴33155222ABD ABC S S ∆∆==⨯=．设点D 的坐标为213(,2)22x x x -++ ①2113155(2)2222x x ⨯⨯-++=解得：11x = 22x =∴当1x =时2132322y x x =-++=；当2x =时2132322y x x =-++=． ∴点D 的坐标为(1,3)或(2,3)． ②2113155[(2)]2222x x ⨯⨯--++=解得：15x = 22x =-（舍去）．∴当5x =时2132322y x x =-++=-． ∴点D 的坐标为(5,3)-．所以存在点D 的坐标为(1,3)，(2,3)或(5,3)-；2222(3)125,2425AC BC =+=+222AC BC AB ∴+=ABC ∴∆是直角三角形BC AC ∴⊥过F 作FM x ⊥轴于点M45FBC CFB ∠=∠=︒ ∴25CF BC ==//OC FM ∴51335OA OC AC AM FM AF ==== 3AM ∴= 6FM =∴点F 的坐标为(2,6)设直线BF 的函数表达式为y kx m =+，将(2,6)F 、(4,0)B 代入得： 2640k m k m +=⎧⎨+=⎩解得：312k m =-⎧⎨=⎩所以直线BF 的函数表达式为：312y x =-+ 11．【解答】解：（1）直线3y x =-+交坐标轴与B 、C 两点 ∴点(3,0)B ，点(0,3)C抛物线23y ax bx =++经过B 、C 两点，且交x 轴于另一点(1,0)A - 933030a b a b ++=⎧⎨-+=⎩∴12a b =-⎧⎨=⎩∴抛物线解析式为：223y x x =-++；（2）解：(3,0)B (0,3)C3OB OC ∴==45OCB OBC BPQ DPC ∴∠=∠=∠=∠=︒ DCP DPC ∠=∠（已知）90DCO DCP OCB ∴∠=∠+∠=︒ 90AOC ∠=︒//CD AB ∴（内错角相等，两直线平行） ∴点D 的纵坐标与点C 的纵坐标相同，即为3 当3y =时2233x x -++= 解得2x =或0x =（舍去）则2m =；（3）存在，求解如下：设点F 的坐标为(,)F s t ①当四边形BCEF 是矩形时则CE BC ⊥ 直线BC 的解析式为3y x =-+ ∴设直线CE 的解析式为y x c =+ 把点(0,3)C 代入得：3c = ∴直线CE 的解析式为：3y x =+联立2323y x y x x =+⎧⎨=-++⎩ 解得：14x y =⎧⎨=⎩或03x y =⎧⎨=⎩（即为点C ，舍去） (1,4)E ∴四边形BCEF 是矩形，且(3,0)B ，(0,3)C 和(1,4)E ∴0312230422s t ++⎧=⎪⎪⎨++⎪=⎪⎩解得41s t =⎧⎨=⎩则此时点F 的坐标为(4,1)F ； ②当四边形BCFE 是矩形时则BE BC ⊥ 设直线BE 的解析式为y x n =+ 将点(3,0)B 代入得：30n += 解得：3n =- 则直线BE 的解析式为3y x =-联立2323y x y x x =-⎧⎨=-++⎩ 解得：25x y =-⎧⎨=-⎩或30x y =⎧⎨=⎩（即为点B ，舍去） (2,5)E ∴-- 四边形BCFE 是矩形，且(3,0)B ，(0,3)C 和(2,5)E --∴32022 05322st+-+⎧=⎪⎪⎨+-+⎪=⎪⎩解得：52 st=-⎧⎨=-⎩则此时点F的坐标为(5,2)F--综上，存在以C、B、E、F为顶点且以CB为边的矩形，此时点F的坐标为(4,1)或(5,2)--。

人教版数学中考专题复习一次函数与二次函数图像的交点问题课后练习

人教版数学中考专题复习一次函数与二次函数图像的交点问题课后练习学校:___________姓名：___________班级：___________考号：___________一、解答题1．已知：关于x的一元二次方程mx2﹣（4m+1）x+3m+3=0 （m＞1）.（1）求证：方程有两个不相等的实数根；（2）设方程的两个实数根分别为x1，x2（其中x1＞x2），若y是关于m的函数，且y=x1﹣3x2，求这个函数的解析式；（3）将（2）中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当关于m的函数y=2m+b的图象与此图象有两个公共点时，b的取值范围.2．已知抛物线y=-x2+2mx-m2+1与x轴交点为A、B（点B在点A右侧），与y轴交于点C．（1）试用含m的代数式表示A、B两点的坐标；（2）当点B在原点的右侧，点C在原点的下方时，若△BOC是等腰三角形，求抛物线的解析式；（3）已知一次函数y=kx+b，点P（n，0）是x轴上一个动点，在（2）的条件下，过点P作垂直于x轴的直线交这个一次函数的图象于点M，交抛物线y=−x2+2mx−m2+1于点N，若只有当1<n<4时，点M位于点N的下方，求这个一次函数的解析式.3．已知关于x的方程mx2+（3m+1）x+3=0（m≠0）.（1）求证：方程总有两个实数根；（2）若方程的两个实数根都是整数，求正整数m的值；（3）在（2）的条件下，将关于x 的二次函数y = mx 2+（3m +1）x +3的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象，请结合这个新的图象回答：当直线y =x +b 与此图象有两个公共点时，b 的取值范围.4．已知一次函数1y kx b =+（k ≠0）的图象经过(2,0)，(4,1)两点，二次函数2224y x ax =-+（其中a ＞2）.（1）求一次函数的表达式及二次函数图象的顶点坐标（用含a 的代数式表示）；（2）利用函数图象解决下列问题： ①若52a =，求当10y >且2y ≤0时，自变量x 的取值范围； ②如果满足10y >且2y ≤0时的自变量x 的取值范围内恰有一个整数，直接写出a 的取值范围.5．已知二次函数y 1=x 2+bx +c 的图象C 1经过(−1,0)，(0,−3)两点.（1）求C 1对应的函数表达式；（2）将C 1先向左平移1个单位，再向上平移4个单位，得到抛物线C 2，将C 2对应的函数表达式记为y 2=x 2+mx +n ，求C 2对应的函数表达式；（3）设y 3=2x +3，在（2）的条件下，如果在−2≤x ≤a 内存在．．某一个x 的值，使得y 2≤y 3成立，根据函数图象直接写出a 的取值范围.参考答案1．(1)证明见解析；（2）y=−3m ；（3）-9<b<-112【解析】试题分析：（1）本题的突破口在于利用△，化简得出(2m−1)2>0得出△＞0，从而方程有两个不相等的实数根．（2）由求根公式得出x的解，由y=x1﹣3x2，求出关于m的解析式．（3）作出函数y=−3m(m>1)的图象，并将图象在直线m=2左侧部分沿此直线翻折，所得新图形如图所示，易知点A、B的坐标分别为A(3,−3),B(2,−32)，求出直线y=2m+b过点A、B时的b的值，二者之间即为所求．（1）Δ=(4m+1)2−4m(3m+3) =(2m−1)2，∵m＞1，∴(2m−1)2>0∴方程有两个不等实根．（2）x=4m+1±√(2m−1)22m =4m+1±(2m−1)2m∴两根分别为3,1+1m．∵m＞1，∴0<1m <1，即1+1m<2．∵x1>x2，∴x1=3,x2=1+1m．∴y=3−3(1+1m ) =−3m．（3）作出函数y=−3m(m>1)的图象，并将图象在直线m=2左侧部分沿此直线翻折，所得新图形如图所示，易知点A、B的坐标分别为A(3,−3),B(2,−32)．当直线y=2m+b过点A时，b=−9；当直线y=2m+b过点B时，b=−112．∴−9<b<−112．考点：1．一次函数和反比例函数综合题；2．一元二次方程根的判别式；3．解一元二次方程；4．翻折对称的性质．2．(1)A(m−1,0)，B(m+1,0)；(2) y=−x2+4x−3；（3）一次函数的解析式为y=−x+1. 【解析】试题分析：（1）根据点在曲线上点的坐标满足方程的关系，令y=0，解出即可求得用含m 的代数式表示的A、B两点坐标.（2）根据等腰三角形的性质，OB=OC，列式求出m的值即可求得抛物线的解析式. （3）依题意并结合图象可知，一次函数的图象与二次函数的图象交点的横坐标分别为1和4，由此可得交点坐标，应用待定系数法，将交点坐标分别代入一次函数解析式即可求解. 试题解析：（1）令y=0，有−x2+2mx−m2+1=0．∴−(x−m)2+1=0．∴(x−m)2=1．∴x1=m+1，x2=m−1．∵点B在点A的右侧，∴A(m−1,0)，B(m+1,0)．（2）∵点B在原点的右侧且在点A的右侧，点C在原点的下方，抛物线开口向下，∴m−1>0．∴m>1．∴OB=m+1．令x=0，有y=−m2+1．∴OC=m2−1．∵△BOC是等腰三角形，且∠BOC =90°，∴OB=OC，即m+1=m2−1．∴m2−m−1=0，解得m1=2,m2=−1（舍去）．∴m=2．∴抛物线的解析式为y=−x2+4x−3．（3）依题意并结合图象可知，一次函数的图象与二次函数的图象交点的横坐标分别为1和4，由此可得交点坐标为(1,0)和(4,−3)．将交点坐标分别代入一次函数解析式y =kx +b 中，得{k +b =04k +b =−3 ，解得{k =−1b =1. ∴一次函数的解析式为y =−x +1．考点：1.二次函数综合题；2.动点问题；3.待定系数法的应用；4.曲线上点的坐标与方程的关系；5.等腰三角形的性质；6.数形结合思想的应用.3．（1）证明见解析；（2）1；（3）1＜b ＜3，b ＞134. 【解析】试题分析：（1）求出根的判别式总是非负数即可；（2）由求根公式求出两个解，令这两个解是整数求出m 即可；（3）先求出A 、B 的坐标，再根据图像得到b 的取值范围．试题解析：（1）证明：∵m≠0，∴mx 2+(3m+1)x+3=0是关于x 的一元二次方程.∴△=(3m+1)2－12m =(3m －1)2． ∵ (3m －1)2≥0， ∴方程总有两个实数根.（2）解：由求根公式，得x 1=－3，x 2=1m． ∵方程的两个根都是整数，且m 为正整数， ∴m=1．（3）解：∵m=1时，∴y=x 2+4x+3．∴抛物线y=x 2+4x+3与x 轴的交点为A （－3，0）、B （－1，0）．依题意翻折后的图象如图所示．当直线y=x+b 经过A 点时，可得b=3．当直线y=x+b 经过B 点时，可得b=1．∴1＜b ＜3．当直线y=x+b 与y=－x 2－4x －3的图象有唯一公共点时，可得x+b=－x 2－4x －3， ∴x 2+5x+3+b=0， ∴△=52－4(3+b) =0，∴b=134．∴b ＞134．综上所述，b 的取值范围是1＜b ＜3，b ＞134．考点：根的判别式，求根公式的应用，函数的图像.4．（1）1112y x =-；二次函数图象的顶点坐标为2(,4)a a -；（2）①2＜x ≤4.②136≤a ＜52. 【解析】（1）根据待定系数法即可求得一次函数的解析式；把y 2=x 2-2ax +4通过配方转化成顶点式即可求得顶点坐标．（2）①当a =52时，y 2=x 2-5x +4，画出函数的图象，根据图象即可求得自变量x 的取值范围； ②根据题意结合图象可知x =3，把x =3代入y 2=x 2-2ax +4≥0即可求得a 的取值；解：（1）∵ 一次函数1y kx b =+（k ≠0）的图象经过()2,0，()4,1两点，∴ 20,4 1.k b k b +=⎧⎨+=⎩ 解得1,21.k b ⎧=⎪⎨⎪=-⎩∴ 1112y x =-. ∵ ()2222244y x ax x a a =-+=-+-，∴ 二次函数图象的顶点坐标为()2,4a a-；（2）①当52a =时，2254y x x =-+，如图,因为y 1>0且y 2⩽0，由图象得2<x ⩽4.②由①可知a =52时，2<x ⩽4有两个整数， ∴a <52， ∵如果满足y 1>0且y 2⩽0时的自变量x 的取值范围内恰有一个整数，∴x =3，当x =3时,y 2=x 2−2ax +4⩽0，解得a ⩾136， ∴136⩽a <52. 点睛：本题主要考查二次函数的性质.利用二次函数的性质及与二次函数与一次函数的图象关系是解题的关键.5．（1）y 1=x 2−2x −3；（2）y 2=x 2；（3）a ≥−1.【解析】试题分析：（1）根据待定系数法，可得函数解析式；（2）根据抛物线平移的规律：向左平移加，向上平移加，可得答案；（3）根据函数与不等式的关系，可得答案．试题解析：解：（1）∵二次函数y 1=x 2+bx +c 的图象C 1经过(−1,0)，(0,−3)两点，∴{1−b +c =0c =−3 ，解得{b =−2c =−3 ，∴抛物线的函数表达式为；（2）∵y 1=x 2−2x −3=(x −1)2−4，∴抛物线的顶点为(1,−4)，∴平移后抛物线的顶点为(0,0)，它对应的函数表达式为y 2=x 2；（3）−1≤a ≤3（见图）．考点：1．二次函数与不等式（组）；2．二次函数图象与几何变换；3．待定系数法求二次函数解析式．。

人教版初三数学上册一次函数与二次函数图像的交点个数

.直线y=x+k
与抛物线y=x2-2x-3只有1个交点；
(3)当k
.直线y=x+k
与抛物线y=x2-2x-3没有交点；
y＝ax2+bx+c
你能根据方程组：
y＝kx＋m
的解的情况，来判定函数y＝ax2+bx+c 与y＝kx＋m图象交点个数吗?请说说你的看法。
归纳：
方程组的解的个数与直线抛物线的交点个数相等！
随堂练习 1.直线 y=2x+1 与抛物线 y= x2 + 4x +3
有＿＿＿＿个交点.
2、已知函数y=-x2-2x+8和y=kx+k（k为常数），则不论k为何值，这两个函数的图象（） A 只有一个交点 B 有两个交点 C 没有交点 D交点的情况随k的值变化而变化
3.已知抛物线y=x2-2x-3与直线 y=x+1交于
A O
C
NB x
.M
P
5、如图，在平面直角坐标系中，己知点O（0，0）， A（5，0），B（4，4）．（1）求过O、B、A三点的抛物线的解析式．（2）在第一象限的抛物线上存在点M，使以O、A、B、M 为顶点的四边形面积最大，求点M的坐标．
随堂练习
3、已知函数y=|8-2x-x2|和y=kx+k（k为常数），则不论k为何值，这两个函数的图象（） A 有且只有一个交点 B 有且只有二个交点 C 有且只有三个交点 D 有且只有四个交点
B
x 1
（2）若抛物线的对称轴与直线AB相交于点D，E为直线 AB上的任意一点，过点E作
EF∥CD交抛物线于点F，则以
C，D，E，F为顶点的四边形能否为平行四边形？若能，求出点E的坐标；若不能，请说明理由.

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一次函数与二次函数图象的交点问题专项练习
1. 已知：关于x 的一元二次方程mx 2﹣（4m +1）x +3m +3=0 （m ＞1）。

（1）求证：方程有两个不相等的实数根；
（2）设方程的两个实数根分别为x 1，x 2（其中x 1＞x 2），若y 是关于m 的函数，且y =x 1
﹣3x 2，求这个函数的解析式；
（3）将（2）中所得的函数的图象在直线m =2的左侧部分沿直线m =2翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当关于m 的函数y =2m +b 的图象与此图象有两个公共点时，b 的取值范围。

2. 已知抛物线22
21y x mx m =-+-+与x 轴交点为A 、B （点B 在点A 右侧），与y 轴交于点C 。

（1）试用含m 的代数式表示A 、B 两点的坐标；
（2）当点B 在原点的右侧，点C 在原点的下方时，若BOC △是等腰三角形，求抛物线的解析式；
（3）已知一次函数y kx b =+，点P （n ，0）是x 轴上一个动点，在（2）的条件下，过点P 作垂直于x 轴的直线交这个一次函数的图象于点M ，交抛物线2221y x mx m =-+-+于点N ，若只有当14n <<时，点M 位于点N 的下方，求这个一次函数的解析式。

3. 已知关于x 的方程mx 2+（3m +1）x +3=0（m ≠0）。

（1）求证：方程总有两个实数根；
（2）若方程的两个实数根都是整数，求正整数m 的值；
（3）在（2）的条件下，将关于x 的二次函数y = mx 2+（3m +1）x +3的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象，请结合这个新的图象回答：当直线y =x +b 与此图象有两个公共点时，b 的取值范围。

4. 已知一次函数1y kx b =+（k ≠0）的图象经过(2,0)，(4,1)两点，二次函数2224
y x ax =-+（其中a ＞2）。

（1）求一次函数的表达式及二次函数图象的顶点坐标（用含a 的代数式表示）；（2）利用函数图象解决下列问题： ①若2
5
=
a ，求当10y >且2y ≤0时，自变量x 的取值范围； ②如果满足10y >且2y ≤0时的自变量x 的取值范围内恰有一个整数，直接写出a 的取值范围。

5. 已知二次函数2
1y x bx c =++的图象1C 经过(1,0)-，(0,3)-两点。

（1）求1C 对应的函数表达式；
（2）将1C 先向左平移1个单位，再向上平移4个单位，得到抛物线2C ，将2C 对应的
函数表达式记为2
2y x mx n =++，求2C 对应的函数表达式；
（3）设323y x =+，在（2）的条件下，如果在2-≤x ≤a 内存在．．某一个x 的值，使得2y ≤3
y 成立，根据函数图象直接写出a 的取值范围。

一次函数与二次函数图象的交点问题专项练习
参考答案
1.（1）证明：
()()()22
=41433=21,
m m m m ∆+-+-
()2
1,=210.
m m >∴∆->
所以方程有两个不等实根；（2）解：()
()2
4121412122m m m m x m
m
+±
-+±-=
=
，
13,1+
m
∴两根分别为。

1212111,01,1 2.1
,3,1.
13331.
m m m
x x x x m
y m m >∴<
<∴+<>∴==+⎛
⎫∴=-+=- ⎪⎝⎭
（3）解：作出函数3
(1)m m
>y=-的图象，并将图象在直线2m =左侧的部分沿此直
线翻折，所得新图形如图所示，易知点,A B 的坐标分别为3
(3,3),(2,).
2A B --
当直线2y m b =+过点 A 时，可求得9b =-
过点B 时，可求得11
,2
b =-
因此，。

2. 解：（1）令0y =，有2
2
210x mx m -+-+=，
∴2()10x m --+=，∴2()1x m -=， ∴11x m =+，21x m =-，
∵点B 在点A 的右侧，
∴(1,0)A m -，(1,0)B m +；
（2）∵点B 在原点的右侧且在点A 的右侧，点C 在原点的下方，抛物线开口向下，
∴10m ->，∴1m >， ∴1OB m =+，
令0x =，有21y m =-+， ∴21OC m =-，
∵BOC △是等腰三角形，且∠BOC =90°，
∴OB OC =，即211m m +=-，
∴210m m --=，∴12m =，21m =-（舍去），∴2m =， ∴抛物线的解析式为243y x x =-+-。

（3）依题意并结合图象可知，一次函数的图象与二次函数的图象交点的横坐标分别为1和4，
由此可得交点坐标为(1,0)和(4,3)-。

将交点坐标分别代入一次函数解析式y kx b =+中，得 0 4 3.k b k b +=⎧⎨+=-⎩
，解得
1
1k b =-⎧⎨
=⎩
，．一次函数的解析式为1y x =-+。

3.（1）证明：∵m ≠0，
∴mx 2+（3m +1）x +3=0是关于x 的一元二次方程.
∴△=（3m +1）2－12m =（3m －1）2。

∵ （3m －1）2≥0，∴方程总有两个实数根；
（2）解：由求根公式，得x 1=－3，x 2=1
m
-。

∵方程的两个根都是整数，且m 为正整
数，∴m =1；
（3）解：∵m =1时，∴y =x 2+4x +3，
∴抛物线y =x 2+4x +3与x 轴的交点为A （－3，0）、B （－1，0）。

依题意翻折后的图象如图所示，
当直线y =x +b 经过A 点时，可得b =3。

当直线y =x +b 经过B 点时，可得b =1。

∴1＜b ＜3。

当直线y =x +b 与y =－x 2－4x －3 的图象有唯一公共点时，可得x +b =－x 2－4x －3，∴x 2+5x +3+b =0，
∴△=52－4（3+b ） =0，∴b =134，∴b ＞13
4
，
综上所述，b 的取值范围是1＜b ＜3，b ＞
134。

4.（1）∵ 一次函数1y kx b =+（k ≠0）的图象经过(2,0)，(4,1)两点，
∴ 20,
4 1.
k b k b +=⎧⎨
+=⎩ 解得1,21.k b ⎧
=⎪⎨⎪=-⎩
∴ 12
1
1-=
x y 。

∵ 22224)(42a a x ax x y -+-=+-=，
∴ 二次函数图象的顶点坐标为2
(,4)a a -；
（2）①当2
5
=
a 时，4522+-=x x y ，因为10y >且2y ≤0，由图象得2＜x ≤4。

②
136≤a ＜52。

5.（1）∵二次函数21y x bx c =++的图象1C 经过(1,0)-，(0,3)-两点，
∴10,3,b c c -+=⎧⎨=-⎩
解得2,3,
b c =-⎧⎨=-⎩
∴ 抛物线1C 的函数表达式为3221--=x x y ；（2）∵22123=(1)4y x x x =----， ∴ 抛物线1C 的顶点为(1,4)-，
∴ 平移后抛物线2C 的顶点为(0,0)，它对应的函数表达式为22y x =；（3）a ≥1-。