微积分2习题答案
微积分下 第二版 课后习题答案 同济大学

习题1—1解答 1. 设y x xy y x f +=),(,求),(1),,(),1,1(),,(y x f y x xy f y x f y x f -- 解yxxy y x f +=--),(;x xy y y x f y x y x xy f x y xy y x f +=+=+=222),(1;),(;1)1,1(2. 设y x y x f ln ln ),(=,证明:),(),(),(),(),(v y f u y f v x f u x f uv xy f +++=),(),(),(),(ln ln ln ln ln ln ln ln )ln )(ln ln (ln )ln()ln(),(v y f u y f v x f u x f v y u y v x u x v u y x uv xy uv xy f +++=⋅+⋅+⋅+⋅=++=⋅=3. 求下列函数的定义域,并画出定义域的图形: (1);11),(22-+-=y x y x f(2);)1ln(4),(222y x y x y x f ---=(3);1),(222222cz b y a x y x f ---=(4).1),,(222zy x z y x z y x f ---++=解(1)}1,1),{(≥≤=y x y x D (2)}{xy y x y x D 4,10),(222≤<+<=(3)⎭⎬⎫⎩⎨⎧≤++=1),(222222c z b y a x y x D(4){}1,0,0,0),,(222<++≥≥≥=z y x z y x z y x D4.求下列各极限:(1)22101limy x xy y x +-→→=11001=+- (2)2ln 01)1ln(ln(lim022)01=++=++→→e yx e x y y x(3)41)42()42)(42(lim 42lim000-=+++++-=+-→→→→xy xy xy xy xy xy y x y x(4)2)sin(lim )sin(lim202=⋅=→→→→x xy xy y xy y x y x5.证明下列极限不存在:(1);lim 00yx y x y x -+→→ (2)2222200)(lim y x y x y x y x -+→→ (1)证明 如果动点),(y x P 沿x y 2=趋向)0,0( 则322lim lim0020-=-+=-+→→=→x x xx y x y x x x y x ;如果动点),(y x P 沿y x 2=趋向)0,0(,则33lim lim 0020==-+→→=→y yy x y x y y x y所以极限不存在。
微积分复习题集带参考答案(二)

微积分习题集带参考答案综合练习题1(函数、极限与连续部分)1.填空题 (1)函数)2ln(1)(-=x x f 的定义域是 . 答案:2>x 且3≠x .(2)函数24)2ln(1)(x x x f -++=的定义域是 .答案:]2,1()1,2(-⋃--(3)函数74)2(2++=+x x x f ,则=)(x f . 答案:3)(2+=x x f(4)若函数⎪⎩⎪⎨⎧≥<+=0,0,13sin )(x k x xx x f 在0=x 处连续,则=k .答案:1=k (5)函数x x x f 2)1(2-=-,则=)(x f .答案:1)(2-=x x f(6)函数1322+--=x x x y 的间断点是 .答案:1-=x(7)=∞→xx x 1sin lim .答案:1(8)若2sin 4sin lim 0=→kxxx ,则=k .答案:2=k2.单项选择题(1)设函数2e e xx y +=-,则该函数是( ).A .奇函数B .偶函数C .非奇非偶函数D .既奇又偶函数 答案:B(2)下列函数中为奇函数是().A .x x sinB .2e e x x +- C .)1ln(2x x ++ D .2x x +答案:C(3)函数)5ln(4+++=x x xy 的定义域为( ). A .5->x B .4-≠x C .5->x 且0≠x D .5->x 且4-≠x答案:D(4)设1)1(2-=+x x f ,则=)(x f ( ) A .)1(+x x B .2xC .)2(-x xD .)1)(2(-+x x 答案:C(5)当=k ( )时,函数⎩⎨⎧=≠+=0,,2)(x k x e x f x 在0=x 处连续.A .0B .1C .2D .3 答案:D(6)当=k ( )时,函数⎩⎨⎧=≠+=0,,1)(2x k x x x f ,在0=x 处连续.A .0B .1C .2D .1- 答案:B (7)函数233)(2+--=x x x x f 的间断点是( ) A .2,1==x xB .3=xC .3,2,1===x x xD .无间断点 答案:A 3.计算题(1)423lim 222-+-→x x x x . 解:4121lim )2)(2()1)(2(lim 423lim 22222=+-=+---=-+-→→→x x x x x x x x x x x x (2)329lim 223---→x x x x解:234613lim )1)(3()3)(3(lim 329lim 33223==++=+-+-=---→→→x x x x x x x x x x x x (3)4586lim 224+-+-→x x x x x解:3212lim )1)(4()2)(4(lim 4586lim 44224=--=----=+-+-→→→x x x x x x x x x x x x x综合练习题2(导数与微分部分)1.填空题 (1)曲线1)(+=x x f 在)2,1(点的切斜率是 .答案:21 (2)曲线xx f e )(=在)1,0(点的切线方程是 . 答案:1+=x y(3)已知xx x f 3)(3+=,则)3(f '= . 答案:3ln 33)(2x x x f +=')3(f '=27()3ln 1+(4)已知x x f ln )(=,则)(x f ''= . 答案:x x f 1)(=',)(x f ''=21x- (5)若xx x f -=e )(,则='')0(f.答案:xx x x f --+-=''e e 2)(='')0(f 2-2.单项选择题 (1)若x x f xcos e)(-=,则)0(f '=( ).A. 2B. 1C. -1D. -2 因)(cos e cos )e ()cos e()('+'='='---x x x x f x x x)sin (cos e sin e cos e x x x x x x x +-=--=---所以)0(f '1)0sin 0(cos e 0-=+-=- 答案:C (2)设,则( ). A . B .C .D .答案:B(3)设)(x f y =是可微函数,则=)2(cos d x f ( ). A .x x f d )2(cos 2' B .x x x f d22sin )2(cos 'C .x x x f d 2sin )2(cos 2'D .x x x f d22sin )2(cos '- 答案:D(4)若3sin )(a x x f +=,其中a 是常数,则='')(x f ( ).A .23cos a x + B .a x 6sin + C .x sin - D .x cos 答案:C3.计算题(1)设xx y 12e =,求y '.解: )1(e e 22121xx x y xx -+=')12(e 1-=x x(2)设x x y 3cos 4sin +=,求y '.解:)sin (cos 34cos 42x x x y -+='x x x 2cos sin 34cos 4-=(3)设xy x 2e 1+=+,求y '. 解:2121(21exx y x -+='+ (4)设x x x y cos ln +=,求y '.解:)sin (cos 12321x x x y -+=' x x tan 2321-= 综合练习题3(导数应用部分)1.填空题 (1)函数的单调增加区间是 .答案:),1(+∞(2)函数1)(2+=ax x f 在区间),0(∞+内单调增加,则a 应满足 . 答案:0>a2.单项选择题(1)函数2)1(+=x y 在区间)2,2(-是( )A .单调增加B .单调减少C .先增后减D .先减后增 答案:D(2)满足方程0)(='x f 的点一定是函数)(x f y =的( ). A .极值点 B .最值点 C .驻点 D . 间断点 答案:C(3)下列结论中( )不正确. A .)(x f 在0x x =处连续,则一定在0x 处可微. B .)(x f 在0x x =处不连续,则一定在0x 处不可导. C .可导函数的极值点一定发生在其驻点上.D .函数的极值点一定发生在不可导点上. 答案: B(4)下列函数在指定区间上单调增加的是( ).A .x sinB .xe C .2x D .x -3答案:B3.应用题(以几何应用为主)(1)欲做一个底为正方形,容积为108m 3的长方体开口容器,怎样做法用料最省?解:设底边的边长为x m ,高为h m ,容器的表面积为y m 2。
微积分(二)课后题答案,复旦大学出版社__第六章

(x)
=
max{1,
x2}
=
⎪ ⎨
1
⎪ ⎩
x2
−2 ≤ x < −1 −1 ≤ x < 1 ,于是 1≤ x≤ 2
∫ ∫ ∫ ∫ 2 max{1, x2}dx = −2
−1 x2dx +
−2
1 1dx +
−1
2 1
x2dx
=
1 3
x3
−1 −2
+
x
1 −1
+
1 3
x3
2 1
=
20 3
∫ ∫ 6.
已知 f(x)连续,且 f(2)=3,求 lim x→2
a i)2
+1,
于是
∑ ∑ n
i=1
f (ξi )Δxi
=
n [(a + b − a i)2 +1] b − a
i=1
n
n
∑ =
(b
−
a)
n i=1
[a2
+
(b
−
a)2
i2 n2
+
2 a(b
−
a)
i n
+1]
1 n
= (b − a)[na2 + (b − a)2 ⋅ 1 ⋅ 1 n(n +1)(2n +1) + 2(b − a)a⋅ 1 ⋅ n(n + 1) + n]⋅ 1
x⎡ 2 ⎢⎣
2 t
f
(u)du
⎤ ⎥⎦
dt
(x − 2)2
.
解
∫ ∫ ∫ ∫ ∫ ∫ lim
x→2
x⎡ 2⎣
2019版 2微积分练习题(下) 第二章 答案

dx f (x, y)dy
1
1
x
13
33
dy f (x, y)dx dy f (x, y)dx
1
1
3
y
1y
12
练习题 7
班级
学号
姓名
1. 把下列二重积分化为累次积分.
(1) f (x, y)d ,其中 D 是由 y x ,
D
x 2 及 x 轴所围成的闭区域;
解:原式= 2 x f (x, y)dydx . 00
2. 交换下列二次积分的积分次序(要求画出积 分区域的图形):
1
y
(1) dy f (x, y)dx ;
0
y
1x
解:原式= dx f (x, y)dy . 0 x2
1x
2 2x
(3) dx f (x, y)dy + dx f (x, y)dy .
00
1
0
1 2 y
解:原式= dy f (x, y)dx .
积函数关于 x 轴、 y 轴不对称,所以该式不
成立.
2.计算二重积分:
(| x | y)dxdy , D : x y 1;
D
解:积分区域 D 关于 x 轴、 y 轴都对称, y 关于
y 是奇函数, ydxdy 0
D
1 1x
x dxdy 2 xdxdy 2 dx xdy
D
D1
0 x1
2
2
cos
原式=
2
0
f ( cos , sin )dd
2
2.利用极坐标计算下列各题:
(1) e x2 y2 dxdy , D : x 2 y 2 4 ; D
解:设 x r cos , y r sin .则
微积分课后题答案第二章习题详解

例如是其的一个第二类间断点,但即在处左极限存在,而,即在处右极限不存在.
4.求下列函数的间断点,并说明间断点的类型:
(1) f(x)= ;(2) f(x)=;
(3) f(x)= ;(4) f(x)= ;
(5) f(x)= .
解: (1)由得x=-1, x=-2
证:
,由极限的保号性知.
,使当时有,此时与同号,因为n为奇数,所以(2X)n与(-2X)n异号,于是与异号,以在上连续,由零点存在定理,至少存在一点,使,即至少有一实根.
(7)正确,见教材§2.3定理5;
(8)错误,只有非零的无穷小量的倒数才是无穷大量。零是无穷小量,但其倒数无意义。
3. 指出下列函数哪些是该极限过程中的无穷小量,哪些是该极限过程中的无穷大量.
(1) f(x)= ,x→2;(2) f(x)=lnx,x→0+,x→1,x→+∞;
(3) f(x)= ,x→0+,x→0-;(4) f(x)= -arctanx,x→+∞;
也即,所以当时,.
再证必要性:
若当时,,则,
所以==.
综上所述,当x→x0时,(x)~β(x)的充要条件是
=0.
2. 若β(x)≠0,β(x)=0且存在,证明(x)=0.
证:
即.
3. 证明: 若当x→0时,f(x)=o(xa),g(x)=o(xb),则f(x)·g(x)=o(),其中a,b都大于0,并由此判断当x→0时,tanx-sinx是x的几阶无穷小量.
解: ∵f(0)=a,
要f(x)在x=0处连续,必须.
即a=1.
6※.设f(x)= ,讨论f(x)的连续性.
微积分第二章习题参考答案

f ( 0 )
lim
x 0
(2e x
1) x
1
2,
f ( 0 )
lim
x 0
(x2
bx x
1)
1
b ,
b
2.
当 a 1,b 2时 , f ( x )在 x 0处 可 导 .
5.设 t时 刻 水 面 的 高 度 为 h , 液 面 半 径 为 r ,则 r R h , H
2.当 0时 ,函 数 在 x 0处 连 续 ,
当 0时 ,函 数 在 x 0处 不 连 续 ;
当 1时 ,函 数 在 x 0处 可 导 ,
当 1时 ,函 数 在 x 0处 不 可 导 .
五 .证 明.
设 切 点 为( x0, y0 ),
y( x0 )
a2
x
2 0
y0 x0
y
x
y y( y x ln y) . x( x y ln x)
3.解 : y ln(1 t) ln(1 t),
y(n)
(1)n1 [(1 t)n
1 (1 t)n
](n 1)!.
4.解 : f (0 0 ) lim (2e x a ) 2 a , x 0 f (0 0) lim ( x 2 bx 1) 1, x 0
,
切线方程为
:
y
y0
y0 x0
(x
x0 ),其 截 距 式 为
xy 1,
2 x0 2 y0
切线与两坐标轴构成的三角形面积
S
1 2
| 2x0
|
| 2 y0
|
2a 2为 常 数 ,与 切 点 无 关 .
§2.2求导法则(21-22)
地大《微积分(二)》在线作业二

C:arcsin2x
D:arcsin2x+c
答案:A
若∫_0^1[(2x+k)dx=2],则k=( )
A:0
B:-1
C:1
D:1/2
答案:C
当被积函数含有√(x^2-a^2 )时,可考虑令x=( )
A:asint
B:atant
C:asect
D:accost
答案:C
如果∫df(x)=∫dg(x),则必有( )。
A:f(x,y)=(√(x^2*y^2)与g(x,y)=(√xy)^2
B:f(x,y)=(√(x^2*y^2)与g(x,y)=|xy|
C:f(x,y)=ln(xy)^2与g(x,y)=2ln|xy|
D:f(x,y)=ln(xy)与g(x,y)=lnx+lny
答案:B,C
下列级数中,收敛的是( )。
A:∑1/(n^3)
地大《微积分(二)》在线作业二
设f(x+y,x-y)=x^2-y^2,则?f(x,y)/?x+?f(x,y)/?y=( )
A:2x-2y
B:2x+2y
C:x+y
D:x-y
答案:D
∫{(e^x-1)/(e^x+1)}dx =( )
A:(e^x-1)/(e^x+1)+C
B:(e^x-x)ln(e^x+1)+C
C:F(x)=ln(2+x)
D:F(x)=lnx/2
答案:D
设f(x)是连续函数,F(x)是f(x)的原函数,则( )
A:当f(x)是奇函数时,F(x)必是偶函数
B:当f(x)是偶函数时,F(x)必是奇函数
微积分2答案完整版

知识点:积分收敛性,中。
4.
答案:C
学霸解析:
可微
可微
可微
知识点:二元函数可微性,中。
5.
答案:C
学霸解析
知识点:求原函数,中。
三、计算题(共8题,每题6分,满分48分)
1.答案:
学霸解析:令
则
知识点:求定积分,中。
2.答案:
学霸解析:
3.
解:
知识点:二重积分,中。
4.
答案:
学霸解析:
二 、
1答案:A
学霸解析: 为偶函数, 为奇函数,且 有意义,则 是偶函数。
知识点:组合函数,易。
2、
答案:B
学霸解析:若函数 在 处不可导,则 在 处一定不可微。
知识点:可导和可微积,易。
3、
答案:D
学霸解析:收益与成本的情况下,获得最大利润的必要条件是 .
知识点:二重求导,中。
4、
答案:B
学霸解析:
考查知识点:敛散性
(2)答案:
学霸解析:
考查知识点:级数收敛的函数
六、
答案:480
学霸解析:
考查知识点:求导运用
七、
答案:2/15
学霸解析:
考查知识点:双边求导
八、
1.答案:
右式
=左式
2.答案:
① 在(a,b)上恒成立
由于f(x)-x在(a,b)上连续
可知
故只能有f(x)=0
② 在(a,b)上恒成立
考查知识点:间断点
3.答案:B
学霸解析:可微的定义
考查知识点:可微的定义
4.答案:D
学霸解析:R(Q)导数减去C(Q)导数为0点为题目所求点
微积分(二)课后题答案,复旦大学出版社_第十章[1]
![微积分(二)课后题答案,复旦大学出版社_第十章[1]](https://img.taocdn.com/s3/m/7d254eb9a6c30c2259019ef6.png)
第十章习题10_11.指出下列各微分方程的阶数:)3 5(y,)4-y5 x°=0;(1) 2x(y' ) -2yy,xd0; ⑵(y〃⑶Xy 2y'' χ2yq ⑷ 2 2 2 2(X -y )dx (X y )dy=0.解: (1)因为方程中未知函数y的最高阶导数的阶数为1,故该方程为一阶微分方程(2) 二阶.(3) 三阶.(4) 一阶.2. 验证下列给定函数是其对应微分方程的解:(1) y=(x C)e», y' y=e»;X X(2) Xy=C I e C2e , xy'' 2y' -Xy ^0;(3) X -cos2t Cιcos3t C2sin3t, x" 9x=5cos2t;2 2⑷X -1, Xyy" X(y' )2-yy' oC l C2解(1):y = e」_(x C) e」y y = e~ -(X C)e」(X C)e」=ey = (x c)e」是微分方程y、y =e *的解.X _X . X X、 .(2) 在方程Xy =C l e ∙ c?e 两边对X求导有y ■ x√ = C l e -^e 上方程两边对X求导有 2 y Xy =C I eX c2e」,即2 y Xy =Xy 即Xy 2 y - xy = 0所以X y = C l^ ■ c2e」所确定的函数y = y( x)是方程x^ 2 y - xy = 0的解.(3)X= -2 Sin 2t 7c1sin 3t 3c2cos 3tX = -4 cos 2t —9c1cos 3t —9c2Sin 3tX 9^=-4 cos 2t —9c1cos 3t —9c2Sin 3t■ 9 cos 2t ' 9c1cos 3t 9c2Sin 3t=5 cos 2t所以X=CoS 2t c1cos 3t ■ c2 Sin 3t 是微分方程√ 9 5 cos 2t 的解.2 2Xy(3)方程 1两边对X 求导得C1c2C 2X C I yy=O(1)(1) 式两边对X 求导得2C 2 ■ C1( y )- syy = 0 (2)(2) 式两边同乘以X 得2C 2XC 1X (y ) C I Xyy =0(3)(3) -(2)得 Xyy (K^- y y 02 2所以 —^y ^ =1是方程Xy^ X(y ) - yy ■ = 0的解. C 1 C3. 已知曲线的切线在纵轴上的截距等于切点的横坐标,求这曲线所满足的微分方程.解:设(X , y)是曲线y = f (X )上任一点,则过该点的切线方程为 Y - y = y∙(X - x),由已知X =0时,Y = x,得x -y = -xy ■即xy "-y ∙ x = 0为y = f (x)所满足得微分方程 4. 求通解为y=Ce x ∙χ的微分方程,这里 C 为任意常数.解:由y=CeX-χ得√ = C e 1 ,而由已知C^ =^X 得 y >y -x T 故通解为 ^Ce XX 的微分方程为y ■ = y 一 X 1 .习题10-21. 求下列微分方程的通解或在给定的初始条件下的特解: (2) xydx 、.一1 一 X 2 dy=0;2 2⑶(Xy x)dx (y -χ y)dy=0;2 I 2(4) Sin XCoS ydχ cos xdy=0;(6) yy'∙χe y =0, y(1)=0; ⑺ y'=e 2τ,y x ^=0 .(1) y =⑸亠d X-丄d y=0,y1 y 1 X解:(1)原方程分离变量得dy dx 1 y 1 - X(V^Z 0),两边积分得2In 1+y| = _ln 1 _x +G 即 In (1 一x)(1 + y) = G , 即 ∣(1 —x)(1 +y)∣ =e c1 , (1 — x)(1 +y) =±e c1 , 记_e c1 =c,有(1 —x)(1 ∙ y) =c(c =0),而当 y∙1=0即y = —1时,显然是方程的解,上又y = 0显然是方程的解方程的通解为 y = ce 1 * (C 为任意常数).2 y 2 X(3) ---------------------------- 分离变量得 dy = ——dx,两边积分得In(1 +y 2)=ln X^^C 1 ,即1 + y X -1In —2^^- =c 1从而 I J ry^= ±e°1 (x? -1),记 C= ±e°1有『 =c(x? -1) —1.X -1(4) 分离变量得,一S i n 2X dx ,两边积分得,tan y-— C 即 CoS y CoS XCoS Xtan y ■ SeC x = c .2 3 2 3(5) 原方程可化为:y(1 ∙ y)dy =x(1 - x)dx,两边积分得 - - - X C 2 3 23亠 11 5 、 由yχ±=1 得c=—+—=—,所以原方程满足初始条件的特解为2 3 6 23 23yy x x5 33 22即 2 (x 3 - y 3)3X 2 - y 2 )= . 52 32 362(6) 分离变量得-ye^y dy =xdx,两边积分得 y^ e C21由y(1) =0得C ,故原方程满足初始条件的特解为2.y 12(y 1)e(X 1). 21(7) 分离变量得 e y dy=e 2x dχ ,两边积分得e y =-e 2x +c,由yxτ=0 得式取C =O 时包含了 y - _1 ,故方程的解为(1 _x)(1 y) =c(C 为任意常数)(2)分离变量得21 一 X = 0, y = 0 ,两边积分得XdX dyJ 1 -x? =In y +c 1,可知1ιC,所以,原方程满足初始条件的特解为 e y (e 2x 1).2 22.物体冷却速度与该物质和周围介质的温差成正比,具有温度为 T o 的物体放在保持常温为:•的室内,求温度 T 与时间t 的关系. 解:设t 时刻物体的温度为 T,由题意有dTk(T-:.) (k 为比例系数)dt -J —p分离变量得 --------- =_kdt,两边积分得,In τ _- -kt ■ C 1 ,得 T =Ce —工,由题意有T 「: t =0时,T =T O ,代入上式得 ,C =T 0 —「・.T=(T O —:・)e*(k 为比例系数).3. 求下列微分方程的通解或在给定条件下的特解: y y⑵ y = Sin ;X X23 3、,⑶ 3χy dy = (2y -X )dχ;2 2⑷ xy'∙χy=y ,y(1)=1 ;(5) χy =y(lny-lnx),y(1) =1;(6) (y-x 2)dx =(x y 4)dy;⑺(X y)dx (3x 3y -4)dy =0.r du dxXU :=叮 U 即两边积分得 √V∏u 2 X即 u . 1 U =CX将u = 丫代入得 y X y =CXX 、V(2)令U 贝U y = uχ, y =U XU 代入原方程得X du du dχSin U 即 ------- =—dχS i ruX两边积分得I n t a-in := XnC l ,≡ta U n= =cx,u = 2 arctan CX ,22(1) ×y -y-χ2解:(1)原方程可化为1 (;)2 ,令=_yXy =U XU 代入原方程得:l n U 亠 1 U )= Xn 亠C将U='代入得y二2xX arctan CX .(3)原方程可化为找=2(Y)1X 2(一)”y du,令U ,则X U V,代入上式得dχ 3 X 3 y X dχdχ23U两边积分得ln(1 ::U 3)-_ I n X ■ C1 ,即 3x( j U )=CyU 代入得X原方程可化为du2U 「2U XdxU - 2 =GUXy(1) =1 得C »12二CXy - =(-)2,X X_u -2 Udxdu=UX , — =U X ,代入上式dxdy=I n X,两边积分得■ c1将U='代入得'-2=GXyy—2 = -Xy ,即2x2X所以原方程满足初始条件的特解为2x2 1 X(5)原方程可化为3lndx X 令UJ dyUdx• X巴,上方程可化为dxduU 亠X — =Ul n udu dXdx U(InUT) X两边积分得I n∣nu _ 1= IrX 即InU —1 =CX亦即u =e1 CX将U=Y 代入得 1 -CX^=Xe由初始条件y(i) =1得c--i故原方程满足初始条件的特解为^=Xe 1 -X(6)原方程可化为dydx X亠y亠4解方程组y —X 2=0X y 4=0 y ~ -3X=U _1,原方程化为y =V -3 dv du这是一个齐次方程,按齐次方程的解法:令' =~ ,方程可化为-^τdUdu两边积分可得,整理可得,2arctan ' ∙ In up 「2) = C 将∙=V 代入上式得UV222 arctan — In(U V)=C U将U=X 亠1,v = y 亠3代入上式得2即(3)dt =2dx ,t -2积分得 3t 2 In ∣t 「2 = 2 x C .将 t = X + y 代入上式得,x+3y+2ln x + y-2 = c∙4. 求下列微分方程的通解或在给定初始条件下的特解: (1) y'-y =Si nx;n X⑵ y - y=x e ;X⑶(x-2y)dy dx=0;(4) (1 XSiny)y '-cosy -0;yX⑸ y -(x 1)e , y(0)=1;X +1 ,1 2⑺ y - y Inx, y(1)W; X X2(8) y'N xy =(xsinx) ∙, y(0)=1;(10) y=— X y Xy(9) y =X 4 y 32Xy2 arctan— In(X 1)2 (y 3)2 =C(7)原方程可化为巴dxX 亠y 3x 3y —4 d t令 t = X ■ y ,≡ 一 =1dxdy 、,代入上方程得dxdt 2t — 4 dx3t — 4,丄2x⑹y "22xy=Cy (o )二;3二 e ^y (2 ye'dy c) _yy=e (2e (y -1) C) =2( y -1) ce~y(4)原方程可化为Xtan y = SeC y ,这是一个关于y 的一阶非齐次线性微分方程dy且 P (y) = - tan y ,Q ( y) = SeC y ,所以解:(1)这是一阶非齐次线性微分方程P(X)= _1, Q(X) =Sin X_P(x)dxP.y =e ∙( Q(x)e- (X) dx dχ +c)dx卫X=e ( Sin χe 一 dx C) =e x ( Sin X e ^dχ ■ C)XXX-Sin x e 一 一CoS x e-=e (C)X1= Ce- -(Sin x 亠 CoS x)2这是一阶非齐次线性微分方程 ,P(x) =-n ,Q(x)Xn X=Xe-P (X )dχP.y =e( Q(x)e(x)dx dx +c)dx^e Xn X_严= nln X(X e e dx c) = e ( XX_pln X ■e e dx C)nn Xnx」n X =x ( X e X dχ c) = x ( e dχ c) = x (e C)原方程可化为 竺∙χ=2y,这是一个关于y 的一阶齐次线性微分方程,且dyP(y) =1,Q(y) =2y ,所以(Q(y)e;(y)dydy +c)(y )dy=eI d y(2y e dy C)_p (y)dyP X =e ∙ ( Q(y)e ■ tan ydy_ t=e ∙( SeC ye ■1 X------- (SeC y CoS ydy ■ C) CoS y ' 1 (y ■ C)cos y(5)这是一阶非齐次线性微分方程且P(X) J,Q(x) = (X - 1)e x ,所以 X 十1------dx—dx=e x 1 ( (X 1)e x e -X 1 dx C) ・ x ・X=(X 1)( e dx C)=(X 1)(e C)故,原方程满足初始条件的特解是2X2 X ,且 P(X)2 ,Q(x)2 ,所以1 +x1 + x_ P(x)dxy =e(Q(X)e(X)dXdx +c)将初始条件 y(0) =1代入上式中得C=O-P (x)dy = e(Q(X)e(X )dχdχ +c)22x^e-x 2dx c) 2C JD (I ÷ ), =e(I X( 一 .I X22Xeln(1 ∙x 2 )dy e dχ +c) 12 ( 2x 2dx ■ C) 1 x^(-x 3 ' C) 1 X 32将初始条件y(0) =1代入上式得C=,所以原方程满足初始条件的特解是3I 32(1 ■ X )χ2)(7)这是一阶非齐次线性微分方程,且 P(X)12,Q (X) = InX 所以 X X(y )d ydy +c)tan ydydy +c)(6)这是一阶非齐次线性微分方程Xdx c) = χ3( 3dx c) = 3χ4 cx 533 43z = y 代入上式得原方程的通解为y = 3x CX .d X3 3 1 _3 2(10)原方程可化为-Xy=X y ,这是关于y 的〉=3的伯努利方程,令Z=X X , dy上述方程可化为dx X dz 33z = 3X 3 ,这是一阶非齐次线性微分方程_ P (X)dχP(x)dχy =e_( Q(x)e dx C)1 1X dX 2 - 7d×1=e ( InXe dx 亠 C)X 2 =x^ - — In XdX 亠 C)2 2 二 x(_ In X ——C) X X =2(1 In x) CX 将初始条件 y(1) =1代入上式得 C = _1 所以,原方程满足初始条件的特解是 (8)这是一阶非齐次线性微分方程 -"P(x)dxy = 2(1 In x) - X . 2,且 P(X)= 2X , Q(x) = xsin X e^ ,所以 ∣P (x)dxy =e ( Q(x)e dx C) _2XdX 」2 2xd X=e ( XSin X e e dx ■ C )2=e ( X Sin XdX - C) 2 =e (Sin X-X cos X C) 将初始条件y(0) =1 代入上式得 C =:1 ,故原方程满足初始条件的特解是 2 y =e * (Sin X- XCaS X 亠1).(9)原方程可化为* 13y y = X X 1 3 3—y =X X-2 ,这是-2的伯努利方程,方程两边同除以14』)^y3=y ,则上面方程化为P(X) --,Q(x) =3X 3,其通解为XI dX 3 -z = e x( 3x e试求y=f(χ)所满足的微分方程,并求该微分方程满足条件y(2)的特解.9解:依题意有πtπI f (x)dx t2f(t)-f(1),两边同时对t 求导有:3 π- 2f (t) 2tf (t) t f3 -(t) t 2 f (t) =3f 2(t) —2tf (t)亦即χ2y ^3y 2 —2Xy故y=f(x)所满足的微分方程是χ2y'=3y 2-2Xy ,该方程可化为y 2 y=3( ) -2(), X X这是齐次方程•可求得该齐次方程的通解为3y —X 二CXy 将初始条件 y(2)2代入上式得 c = -1 ,所以,该微分方程满足条件 92y(2) 的特解是9*6 .设某生物群体的出生率为常数 a ,由于拥挤及对食物的竞争的加剧等原因,死亡率与当时群体中的个体量成正比 (比例系数为b >0).如果t=0时生物个体总数为 X 0,求时刻t 时 的生物个体的总数(注:将生物群体中的个体量当做时间t 的连续可微变量看待).解:设时刻t 时的生物个体的总数为 X,依题意得dxdx a bx 即 dtdt bx = a解得 Jata btX =e (_eC)b又t =0时x = X 0 ,代入上式得C =X oa ,, ,故 bdz32 yz = _2 y dy这是关于y 的一阶非齐次线性微分方程 ,且P (y) =2 y,Q( y) = _2 y 3 ,其通解为:2 2.y 3 y-e( (-2y e )dy C)2 2_y / y2=e (e (1 - y2_y 2=1 一 y CeZ=e-fydy((-2y 3)e∙2 ydyIdy■ C))■ C)将 ^X-代入上式得原方程的通解为1F =1X-y 2 ce 』5. 设函数f(x)在[1, + ∞)上连续,若由曲线 平面图形绕X 轴旋转一周所成的旋转体的体积为 y=f(x),直线x=1,x=t(t > 1)与X 轴所围成的bt za bta 、 a Z a 、 btX =e (— e+ x 0 — — ) = — +(x 0 — — )ebb b b 3x7.已知 f(x) = [ f-d X + 3x4,求 f(x).I 3 .丿解:方程两边对X 求导得f (X) =3f (x) ∙ 3 即 y '3y =3这是一阶非齐次线性微分方程 ,P(x) = _3,Q(X)=3 ,其通解为--∙3dχ∙3dχ .3x 3xy =e ( 3e dχ ∙ C) =e ( 3e 一 dx ∙ C)3x_3x3 X=e ( _e ∙ m e) - 一 1 x ・ce3xt由已知f (X) = f (―)dt ∙ 3x - 3 得 f (O) - -3 ,代入上式得 e - -2 ,所以 b 3&已知某商品的成本C = C(X)随产量X 的增加而增加,其增长率为且产量为零时,固定成本 C(O) = C O > 0.求商品的生产成本函数C(x).H 1 +x + C /白 H 1解:由C (X)得CC =1 ,这是一阶非齐次线性微分方程1 +x1+X1P(X),Q(x) =1,其通解为1 +x由初始条件C(0) =C °代入上式得 C 1 =c °∙所以商品的生产成本函数C(X)=(I - X) Iln(1 X) C 0 ].9.某公司对某种电器设备的使用费用进行考察,结果发现,随该电路使用时间 X 的延长,它的保养维修费会加倍增长, 因而平均单位时间的使用费 S 也在增加,即S 为X 的函数Sgx), 其变化率为d S b b 1 S — a , d X X X其中a,b 均为正常数•若当x=×0时S = S 0,试问:使用时间为多少时,其平均单位时间的 使用费S 最高?解:原方程 竺=b s -b Ja 可化为 竺- b s = -(b 2I)a ,这是一阶非齐次线性微分方 dx X X dx X X 程,且 P(X) - -b ,Q(x) - -(b 2I)a ,其通解为,X XC '(X)=IxC=(1 x)〔In(1 x) C 1 1丄dχ1 xdx C 1)2习题10;1.求下列微分方程的通解:(1) y :::=xe X;(2) y 〃 1 ;2 ;1 X2 (3) (1 x)y''∙ 2xy'=0; ⑷y 〃 -(y)2O 23d X(5) X2 仁0;(6) yy " -(y')2 (y)3=od t解:(1)对方程两端连续积分三次得Il- Xy =(X - 1)e' C 1X V 1“y =(X - 2)e 亠c 1x 亠 C 22X L C I X y = (x -3) e C 2X C 32这就是所求的通解•(2) 对方程两端连续积分两次得y =arctan X C 1由已知X b bS =e X dX ( J b I)a ^,dXb dχ Xb _1 b =X (ax C) e X dx c^x b ( -(b 2I)aX __bχ- dx 亠 C) =-CX bX =X o 时,S = S o 代入上式得 s o x o f a,C = X o b1S 二--a r bcx X ,令S y O 得唯一驻点 x =(2)r7 ,将C bc s o x o - bΓ x o =( ) bs 0x 0 -ab X o,由问题的实际意义知,最值存在,所 b ,rC X 得a代入得是时间=( )bs 0 X 0 - abX o时,其平均单位时间的使用费 S 最高.y = arctan XdX C I X=XarCtan1 X -―In(12X)C I XC 2这就是所求的通解(3) 令y = p(x),则y =P(X),于是原方程可化为2 *(IX)P 2xp = 0分离变量得 空 2^xτdx ,积分得P 1 X再积分得 y = c 1 arctan X C 2.d⅞=dX P亦即dx X C 1| X ■ C i | ■ C 2(5)令 X=P (X ),则 X=P,原方程变为 dxdp 卄 P 1=0,即 PdP = dx 13dx.X2两边积分得P 2 -1 C1X2C i Xd X亦即兰―dtXIdx =dt . 1 ■ cx 2 积分得一..1 C 2 . 从而 1 亠c 1χ2 =(C I t 亠C 2)2 . 这就是所求的通解• (6)令y =P(y),则∙ p,代入原方程得. dy dp 2 3 yp ——-P + P =0 即 P y dy J些-P P 2dy =O若P=O,则y = 0, y = c 是方程的解.c ι p=C ,即 y(4)令 y= P(X),则 y =P ■,原方程可化为两边积分得1 -=X PC i ,即1 X C 1dy再积分得若 y d ^.p.p 3 =O ,分离变量得y.dyp — Py积分得C l yp “y(1 - P )即 P^C l y于是:dyc1y Hn J即( c 1 )dy =c 1dx.dt 1 ■ c 1yy积分得 C l (X _y)y =c 2e 2. 求下列微分方程满足初始条件的特解:3⑴ y F nx , y(1)T, y '⑴,y 〃(1)=1; 32(2) xy 〃 对=1, y(l)=0, y ' (1)=1; (3) y 〃 y 2 =1,y(0)=0, y ' (0)=1.解:(1)方程两边积分得:y " = X In X —X ∙ q ,由 y 1 =1- 得 C 1 = 0 ,于是 y " = x In x - x ,2上式两边再积分得y = — In X -∙3 X?c 2.2 43由y(1)得C 2 4由 y (1) =1 得 C 1 =1 ,于是 (In X 1),从而X3X In 2=0 ,于是 两边再积分得 由y(1) =0得I3X In 6 II 11X- — X36 C 3.36所以,原方程满足初始条件的特解为 11 3In X-——X36 11+—— 36 (2)令y ■ = p(x),则y = p :原方程化为 X 2空XP =1.即如1P dx Xdx一阶非齐次线性方微分方程1 P(X)= 一,Q(x) =X ,X-2其通解为 dx X-2(Xe1dx y X1dx c 1) = 一(In X ■ c 1)X1即 y (In X G ),X1 1 2y (In x 1)dx = j(ln X 1)d(ln X 1) (11 n x) c2• x 21由y(1) =O 得c221 2 1 1 2y (1 In x) 即y = In x In x.2 2 2(3)令y J p ,则y χ = p ■,原方程可化为d P 21 一p ,由y (0) =1 ,即X =0 时,P =1 . dxdy显然p =1是上述方程的解,即 1 ,积分得y = x ∙ c,由y(0) =0得C=O ,所以,dx原方程满足初始条件的特解为y = X .3. 已知某个二阶非齐次线性微分方程有三个特解y1=x, y2^∙e x和y3=1∙χ∙e x,求这个方程的通解.解:因为y1, y2, W是某二阶非齐次线性微分方程的三个特解,则y? - y1= e x, y3 - y? = 1是Xe某对应的齐次微分方程的特解且一=e x=常数,故e x和1是其对应的二阶齐次线性微分方1程的两个线性无关的特解,故对应齐次线性方程的通解为y = C1亠c2e x又y1 =x是这个二阶非齐次线性微分方程的特解,故这个方程的通解是y = C1亠C2e x亠X .4. 求下列齐次线性方程的通解或在给定条件下的特解:(1) y〃My' 4y=0; (2) y〃-y' -2y=0;(3) y〃5y' 6y=0, y(0)=1, y' (0) ≡6;πππ 6⑷ y" -2y' -10y=0, y( )=0, y'(—)= e .6 6解:(1)特征方程为r2 -4r ∙4 = 0 ,它有两个相等的特征根r1 = r2 = 2 ,所以,所求的通解为y = (c1■ c2x)e2x .(2) 特征方程为r —r —2 = 0 ,它有两个不相等的实特征根r1 = T,r2 = 2,故所求的通解为y = c1e ■ c2e2x.(3) 特征方程为r2 5r,6 = 0 ,它有两个不相等的实特征根r1 = -2, r2 = -3 ,故所求的通解为y =c1e I +c2e'x由y(0) =1 得G +c2=1 ,又由y(0) =6 及厂=—2c1e'x—3c2e'x得2c1 +3c2 = —6 ,解方程组c1 c2 =1 C1 = 91 2得42c1 3c2 = -6 J c2 = -8所以,原方程满足初始条件的特解为y =9e'x _8e^.(4) 特征方程为r2-2r -10 = 0,它有两个共轭复数根,1 X Oy = --e cos 3X35. 求下列非齐次线性微分方程的通解或给定初始条件下的特解:(1) y'' +3y' -10 y =144xe-2x;2⑵ y'' -6y' 8y=8x 4x-2;ππ(3) y" y=cos3x, y( )=4, y'(-)=-1;2 24x⑷ y〃-8y,16y=e , y(0)=0,y' (0) =1.2解: (1)特征方程r ∙ 3r -10 = 0有两个不相等的实数根r1 = -5, D = 2 ,故对应齐次方程的通解为Y ^C I e^X■ c2e2x因为■ - -2不是特征方程的根,故可特解为* 2 Xy =(AXB )e代入原方程可解得 A =「12, B =1.所以y =(1 -12 X) =e X .所求通解为-2 X -5 X 2 Xy = (1 —12 x)e ■ c1e ■ c2e(2)特征方程r2 - 6r= 0有两个不同的特征根r1 = 2, r2 = 4 ,故对应齐次方程的通4-2x=(-2 Ax A -2B)e 仏=1±3i ,故方程的通解为y =e x(c1CoS 3x 亠c2sin 3x),ππ- π Z由y( ) =o, y ( ) = e 得G =6 61-,C2 =0,故所求特解为3y = ( -4 AX 4B 4 Ax )e -2x2x 4 xY =c1e 亠c2e 又因为∙=O不是特征方程的根,故可设特解为* 2y =AX bx = 2Ax∙B,y =2A ,代入原方程可解得2 2=X 2x 1 =(x 1) ∙Y=G CoS X c2 Sin X为: 考察方程y y则y*l3iAe3ix3i X=e 因为w =3i不是特征方程的根,故可设特解为* 3ixy = Ae1■ -9 Ae ,代入方程y ■ y = e?",得A ,所以8* 1 3i x 1y e (cos 3x 亠i Sin 3x)8 8取y的实部,即得到方程y y = cos 3x的特解.故原方程y亠y = cos 3x的通解为由初始条件y — =4,12 J(4)特征方程r2 -8r* 1y 1 = -一cos 3x81y cos 3x c1 cos X c2 Sin X8y = 3 sin 3x - c1 Sin x 亠c2 cos X8y - =1得G =-,c^4,故所求的特解为2 81 丄5 丄y = --cos 3X 一cos X 4 sin x8 81^=0有两个相等的实根r1 = r2 = 4,故对应齐次方程的通解解为A =1,B =2,C =1,所求通解为y =(X ∙ 1)2 2x亠c1e 4x亠c?e(3)特征方程为r2 1 =0 , 它有两个共复数根r1,2=±i ,故对应齐次方程的通解为因为.=4是特征方程的重根,故可设特解为*2 4xy =AXe1将其代入方程y“—8y'16y =e 4x得A,故特解为 2所以原方程的特解为 y = 1x 5e 4x (c 1 ■ c 2 x)e 4x24x -24x4 X4x_又由 y =Xe 2x e c 2e 4c 2xe 及 y (0) = 1 ,得 C 2 =1 .1所以,所求特解为y =丄x 2e 4x xe 4x2 6. 设对一切实数X,函数f(x)连续且满足等式f '(x )=x 2 ∙ ∖ (t)dt ,且 f(0)=2,求函数f(x). f (x) = 2x 亠f (x),即y —y = 2x ,特征方程r —1=0有两个不同的实根r 1 =1,r 2 =-1,故对应齐次方程的通解为Y =C I e X ∙c 2e^因为■ =0不是特征方程的根,故可设特解为Y= Ax B,代入原方程得--2xC 1 e x ■ C 2e J又由题设得「(0) = 0 ,及 y • = -2 ■ C I e X -■ C 2得y " +ay ' +by=θe xf^c 1 +c 2 =2 解方程得C 1 =2, C 2C1 -C2 =2所以满足题设条件特解为y - -2x 2e x--2, B =0 ,故特解为y =…2 ∏,所以方程的通解为C i -C 2 = 2 .=0f(x)X--2x 2e .7.设二阶常系数非齐次线性微分方程12 4x =—X e 2解:方程两边求导得由已知 f (0) =2 得 c 1 ■ C 2 =2的一个特解为y=e2x∙(1 x)e x,试确定常数a,b「并求该微分方程的通解. 解:将已给的特解代入原方程,得(4 2a b)e2x (3 2 a b)e X (I a b)Xe X= : e x比较两端同类项的系数,有4 2a b =OIab=O3 2a b =:解得a = _3, b = 2, = _1.于是原方程为y J3y 2y 二_e x .其特征方程为r2-3r∙2=0,特征根为r1=1,r2=2 ,对齐次方程的通解为X 2 X= c1e 亠c2e又因为,=1是特征方程的单根,故设特解为y = AXe X ,代方程y'"—3y ' 2y = -e x,可解得A=1,故特解为y^xe x所以该微分方程的通解为X 丄2χ丄Xy = c1e 亠c2e 亠Xe .& 设函数(X)可微,且满足X X「(x)=e 亠I (t 一X):(t)d t,求(X) •X X X解:由:(X) = e X亠I (t —x) '(t)d t 得:(0) = 1,又:(x) = e X亠∣ t「(t)d t —x ∣(t)d t ⅛*0*0X两边求导得::(x)=e X∙χ>(x)-°:(t)dt -X :(x),即X「(X) =e x - 0 ;:(t)dt ,从而:(0) =1再求导得::(X)= ^^(X),即、、二e可求得对应齐次方程的通解为Y =C I CoSX ∙ C2 sin X ,又因为,=1不是特征方程2r 7=0的根,故可设特解为* Xy =Ae1将其代方程y'y=e x中可求得 A = 1,故方程的通解为y=c一一--1XI CoS X c2 Sin X — e ..又2 2由1(0) =1, :(0) =1 及y - -G Sin X c2 cos X e得1 1C l, C2 ,所以2 2 2y1 X. 1 X =-(C ox S S i, r即(Xe = 丁(CoS X Sin X e ).2 29∙求方程y'' -y' -2y=3e^在x=0处与直线^X相切的解.解:特征方程r 2 —r _2=0有两个实根r 1=-1,r 2=2,故对应的齐次方程的通解为Y =c 1e* ■ c 2e 2x ,又因为‘ --1是特征方程的单根,故可方程的特解为*Xy = AXe _代入原方程可解得 A=-I ,故原方程的通解为_x2x_xy = c 1e _ ■ c 2e—xe _ , (1)由已知在X =O 处与直线y =X 相切,则y(0)= 0, y (0) =1 ,又X2 XXXy = -c 1 e ^ - 2c 2e-e ^ ■ Xe 一, (2)将y(0) =0, y(0) =1分别代入(1),( 2)式中得2可解得c 1 , c 2 32 2所以,所求的解为 y--—e -Xe3 310.设函数y(x)的二阶导函数连续且 y'(0)=0,试由方程y(x)=1 1 ∙ y (t)-2y(t) 6t e 」d t3占确定此函数.1解:方程两边对X 求导得y (x) = —[ —y ∙(x) — 2 y(x)亠6xe 」],即y 亠3 y 亠2 y = 6xe 」 (1)3 它的特征方程r 2 3r ∙2 =0有两个相异的实根 r 1 =-1,r 2 =-2,故方程(1)对应的齐次方程的通解是Y ^C I e ^ ■ c 2e^x又• = -1是特征方程的单根,故方程(1)的特解可设为*-K 2y =X(AX B)e (AX Bx) =e将其代入方程(1),可解得A=3, B=—6 ,从而特解为y =(3x 2—6x)e 」,方程(1)的 通解为_V2 X2 _Vy = c 1e C 2e(3 X - 6x)e ,…⑵1由 y(x) =1— ;[ —y (t) —2y(t) 6te 丄]dt 得 y(0) =1 ,又 3 •V2 Yy2 __x^=-C I e —2c 2e (6 x —6)e—(3 X —6x)e ,… ⑶c 1 c 2 = 0 c 1 2C 2 - -2由y(0) =1,y(0) =0 及(2),(3)式可得G c 2 =1 G 亠 2c 2 - -6X2 X2Xy =8J7e 一 (3x -6x)e 一即由所给方程确定的函数为y(x^8e^ -7e-x (3χ6 _6x)e 」11. 一质点徐徐地沉入液体, 的运动规律.解:由题设条件与牛顿第二定律有习题10∙41.某公司办公用品的月平均成本 C 与公司雇员人数 X 有如下关系:C ' =C 2e^-2C6m g2 •因而有 kd 2sm —7 = mg dt -k 空 (k 为比例系数) dt 2d S k ds即 g,…⑴ dt m dt这是一个二阶线性非齐次方程,它的特征方程 kr = 0有两个不相等的实根 mk r =0, r ,它对应的齐次方程的通解m c 2 e k tm,又因∙ =0特征方程的单根,故 可设特解为S =At ,代入方程(1)可得A mg kk ,故方程(1)的通解为 c 1 c 2e m mg t. k且 s _ _kc 2e mkηm mg,又开始沉入时即kt=0 时,s = 0, ds = 0 ,将其代入上两式可解得dtC1C22m g S 厂 k2m g2kmg t.k故方程(1)的满足已知条件y(0) =1, y (0) =0 的特解为 当沉入时,液体的反作用力与下沉的速度成正比例,求质点且C(0)=1,求C(X).解:方程C ∙ = C 2e* _2C 可变形为:C 2C =e~ C=这是:• = 2的伯努利方程,令 Z -C I --C J ,方程可化为:Z •一2Z ,这是一阶非齐次线性微分方程且P(X)= -2 ,Q(x) = _e —,其通解为:= e 2x (1e~x dx m) =1e3311(为了与成本C 区别,这里的任意常数用 m 表示),于是 e 」 me 2x ,由已知C(O)=I ,可C 3其中a , b 为正的已知常数,若R o) =0, S (0) =S(购买成本),求R(t)与S (t ).解:先解一阶线性方程 S - _bS ,求出S(t),分离变量得:竺-_bdt ,积分得 ^C I e^tSS(0) = S 0 ,可得C 1 = S 0 ,所以S(t) = S 0M ,将S(t) = S 0/ 代入所给方程—e bt ,积分得:R(t) — e bt C 2,由已知条件R(0) =0得C ? SCbS3.设D=D(t)为国民债务,Y=Y(t)为国民收入,它们满足如下的关系:D' R Y +P , Y' ="Y其中:■, ^-,为正已知常数. (1)若 D(O)=D 0,Y(0)=Y °,求 D(t)和 Y(t);⑵求极限Iim D°tτ 乂 丫⑴解:(1)先解方程Y= Y,求出Y(t);分离变量得:也 =dt ,积分得Y=C 1e t ,由Y(O)=Y O 得YC l =丫0 ,所以 Y(t) =Λe t ,将 Y(t) =Y °e t 代入D 丄〉丫「中得:D =〉Y °e t 「,积分得 O(Y O Y QG Y OD -e ,-C ?,由 D(O)=D O 得 C^D O,所以Z =e^-2dx-Jdx.X ∣~i'2x .3x((-e 一)edx m) = e ( -e~ dx m) 得:m =2,从而 1=1e js 2e 2x3 C 333x1 2eX3e2.设R=R(t)为小汽车的运行成本, 3e x,所以 C(X)=FS=S(t)为小汽车的转卖价值,它满足下列方程: aR'-,S ' --bS, S由已知条件 所以R(t)=a bS。
微积分(二)课后题答案,复旦大学出版社_第十章[1]
![微积分(二)课后题答案,复旦大学出版社_第十章[1]](https://img.taocdn.com/s3/m/992ef9c06137ee06eff91822.png)
1 y 2 ec1 ( x2 1) ,记 c ec1 有 y 2 c( x 2 1) 1.
(4) 分离变量得,
1 dy sin x c dx ,两边积分得, tan y 2 2 cos x cos y c.
x 1 y 3
作变换
x u 1 ,原方程化为 y v 3
dv v u du u v
这是一个齐次方程,按齐次方程的解法: 令
v 1 du , 方程可化为 d 2 u 1 u
5
两边积分可得,整理可得, 2arctan ln u 2 (1 2 ) c 将
x y dx dy 0, y x 0 1 ; 1 y 1 x
y(1)0;
(6) yy′xey0, (7) y′e2xy,
y x 0 0 .
dy dx 1 y 1 x (1 y 0) ,两边积分得
解: (1) 原方程分离变量得
2
ln 1 y ln 1 x c1
y 2x
y
(7) 分 离 变 量 得 e dy e dx , 两 边 积 分 得 e
1 2x e c , 由 y 2
x 0
0 得
3
c
1 1 2x y ,所以,原方程满足初始条件的特解为 e (e 1) . 2 2
2. 物体冷却速度与该物质和周围介质的温差成正比,具有温度为 T0 的物体放在保持常温 为的室内,求温度 T 与时间 t 的关系. 解: 设 t 时刻物体的温度为 T,由题意有
(5) 原方程可化为: y(1 y)dy x(1 x)dx ,两边积分得 由 y
y 2 y3 x 2 x3 c 2 3 2 3
微积分(二)课后题答案,复旦大学出版社 第八章
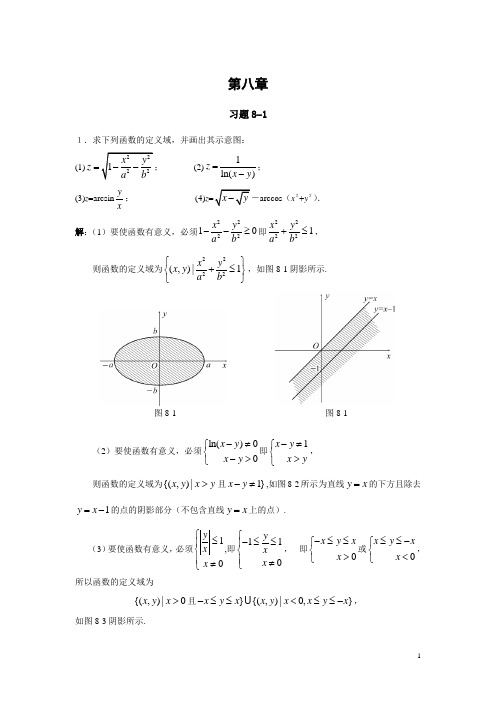
第八章习题8-1 1.求下列函数的定义域,并画出其示意图:(1)z=(2)1ln()zx y=-;(3)z=arcsin yx;(4)zarccos(x2+y2).解:(1)要使函数有意义,必须222210x ya b--≥即22221x ya b+≤,则函数的定义域为2222(,)|1x yx ya b⎧⎫+≤⎨⎬⎩⎭,如图8-1阴影所示.图8-1 图8-1(2)要使函数有意义,必须ln()0x yx y-≠⎧⎨->⎩即1x yx y-≠⎧⎨>⎩,则函数的定义域为{(,)|x y x y>且1}x y-≠,如图8-2所示为直线y x=的下方且除去1y x=-的点的阴影部分(不包含直线y x=上的点).(3)要使函数有意义,必须1yxx⎧≤⎪⎨⎪≠⎩,即11yxx⎧-≤≤⎪⎨⎪≠⎩,即x y xx-≤≤⎧⎨>⎩或x y xx≤≤-⎧⎨<⎩,所以函数的定义域为{(,)|0x y x>且}{(,)|0,}x y x x y x x y x-≤≤<≤≤-,如图8-3阴影所示.图8-3 图8-4(4)要使函数有意义,必须2200||1x y x y ⎧⎪≥⎨⎪+≤⎩即222001x y x y x y ≥⎧⎪≥⎪⎨≥⎪⎪+≤⎩, 所以函数的定义域为222{(,)|0,0,,1}x y x y x y x y ≥≥≥+≤,如图8-4阴影所示.2.设函数f (x ,y )=x 3-2xy +3y 2,求 (1) f (-2,3); (2) f 12,x y ⎛⎫⎪⎝⎭; (3)f (x +y ,x -y ). 解:(1)32(2,3)(2)2(2)33331f -=--⨯-⨯+⨯=;(2)23321211221412,23f x y x x y y x xy y ⎛⎫⎛⎫⎛⎫=-⋅⋅+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭; (3)32(,)()2()()3()f x y x y x y x y x y x y +-=+-+-+- 3222()2()3()x y x y x y =+--+-. 3.设F (x ,y )f,若当y =1时,F (x ,1)=x ,求f (x )及F (x ,y )的表达式. 解:由(,1)F x x =得1)x f =即1)1f x =-1t =则2(1)x t =+代入上式有2()(1)1(2)f t t t t =+-=+所以 ()(2)f x x x =+于是(,)1)1) 1F x y f x ===-4.指出下列集合A 的内点、边界点和聚点:(1){(,)01,0}A x y x y x =≤≤≤≤;(2){(,)31}A x y x y =+=; (3)A ={(x ,y )|x 2+y 2>0}; (4)(0,2]A =. 解:(1)内点{(,)|01,0}x y x y x <<<<边界点{(,)|01,0}{(,)|01,1}x y x y x y y x ≤≤=≤≤= {(,)|,01}x y y x x =≤≤ 聚点A (2)内点∅ 边界点A 聚点A (3)内点A边界点(0,0) 聚点A(4)内点∅ 边界点[0,2] 聚点[0,2]习题8-21.讨论下列函数在点(0,0)处的极限是否存在:(1) z =224xy x y+; (2) z =x y x y +-. 解:(1)当(,)P x y 沿曲线2x ky =趋于(0,0)时,有24244200lim (,)lim 1y y y kxky kf x y k y y k →→===++这个值随k 的不同而不同,所以函数224Z=xy x y+在(0,0)处的极限不存在. (2)当(,)P x y 沿直线(1)y kx k =≠趋于(0,0)时,有001lim (,)lim(1)1y x y kxx kx kf x y k x kx k→→=++==≠--,这个极限值随k 的不同而不同,所以函数Z=x yx y+-在(0,0)处的极限不存在. 2.求下列极限:(1) 00sin limx y xy x →→; (2)22011lim x y xyx y→→-+;(3)00x y →→ (4)22sin lim x y xy x y →∞→∞+.解:(1)0000sin sin()limlim 0x x y y xy xy y x xy →→→→=⋅=(2)222211101lim101x y xy x y →→--⨯==++(3)0000001)2x x x y y y →→→→→→=== (4)当,x y →∞→∞时,221x y+是无穷小量,而sin xy 是有界函数,所以它们的积为无穷小量,即22sin lim0x y xyx y →∞→∞=+.3.求函数z =2222y xy x+-的间断点.解:由于220y x -=时函数无定义,故在抛物线22y x =处函数间断,函数的间断点是2{(,)|2,R}x y y x x =∈.习题8-31.求下列各函数的偏导数:(1) z =(1+x )y ; (2) z =lntany x; (3) z =arctan yx; (4) u =zx y .解:(1)1(1)y zy x x-∂=+∂(1)ln(1)y zx x y∂=++∂; (2)22221sec cot sec ;tan z y y y y y yx x x x x x x∂-=⋅⋅=-∂ 22111sec cot sec ;tan z y y y yy x x x x xx∂=⋅⋅=∂ (3)22221;1zy yxx x yy x ∂--=⋅=∂+⎛⎫+ ⎪⎝⎭22211;1zx yx x y y x ∂=⋅=∂+⎛⎫+ ⎪⎝⎭(4)22ln ln ;z zx x u z z yy y y x x x∂-=⋅⋅=-⋅∂1;1ln ln .zxzz x xu z y y xu y y y y z x x-∂=∂∂=⋅⋅=⋅∂2.已知f (x ,y )=e -sin x (x +2y ),求x f '(0,1),y f '(0,1).解:sin sin sin (,)e (cos )(2)e e [cos (2)1]x x x x f x y x x y x x y ---'=⋅-++=-⋅++ s i ns i n(,)e22ex x y f x y --'=⋅= 所以sin0(0,1)e (cos0(021)1)1x f -'=-⋅+⨯+=- s i n 0(0,1)2e 2y f -'== 3.设z =x +y +(y -,求112811,x x y y z z x y====∂∂∂∂.解:1122112d (,1)d(1)1d d x x y x z f x x xx x====∂==+=∂又23211(3z x x y y y y-⎛⎫∂-=+-⋅ ⎪∂⎝⎭所以1811π11arcsin 126x y z y==∂=+=+=+∂. 4.验证z =11+ex y ⎛⎫- ⎪⎝⎭满足222z zxy z x y∂∂+=∂∂. 解:1111()()2211e ex yx y z x x x-+-+∂-=⋅-=∂ 1111()()2211e ex yx yz y y y-+-+∂-=⋅-=∂所以1111()()22222211e ex yx y z z x y x y x y x y-+-+∂∂+=⋅+⋅∂∂ 11()2e 2x yz --+==5.设函数z =2222422,00,0xy x y x y x y ⎧+≠⎪+⎨⎪+=⎩,试判断它在点(0,0)处的偏导数是否存在?解:00(0,0)(0,0)00(0,0)lim lim 0y y y f y f z y y ∆→∆→+∆--'===∆∆ 00(0,0)(0,0)00(0,0)limlim 0x x x f x f z x x∆→∆→+∆--'===∆∆ 所以函数在(0,0)处的偏导数存在且(0,0)(0,0)0x y z z ''==.6.求曲线22(),4z x y y ⎧=+⎪⎨⎪=⎩14在点(2,4,5)处的切线与x 轴正向所成的倾角. 解:因为 242z x x x ∂==∂,故曲线221()44z x y y ⎧=+⎪⎨⎪=⎩在点(2,4,5)的切线斜率是(2,4,5)1z x ∂=∂,所以切线与x 轴正向所成的倾角πarctan14α==.7.求函数z =xy 在(2,3)处,当Δx =0.1与Δy =-0.2时的全增量Δz 与全微分d z . 解:,z zy x x y ∂∂==∂∂∴ d d d z zz x y x y∂∂=+∂∂ 而()()z x x y y xy x y y x x y ∆=+∆+∆-=∆+∆+∆∆ 当0.1,0.2,2,3x y x y ∆=∆=-==时,d 30.12(0.2)0.1z =⨯+⨯-=-2(0.2)30.10.1(0.2)0.12z ∆=⨯-+⨯+⨯-=-. 8.求下列函数的全微分:(1) 设u =()zx y,求d u |(1,1,1).(2) 设z,求d z .解:(1)1121(),()z z u x u x x z z x y y y y y --∂∂-=⋅⋅=⋅⋅∂∂;()ln ,z u x xz y y∂=∂ (1,1,1)(1,1,1)1,1,u u x y∂∂∴==-∂∂ (1,1,1)0u z∂=∂,于是(1,1,1)(1,1,1)(1,1,1)(1,1,1)d d d d d d z z z ux y z x y xyz∂∂∂=++=-∂∂∂(2)z x∂==∂2zy∂==∂ ∴22d d d d d z z z x y xyx y ∂∂=+=∂∂习题8-41.求下列各函数的全导数:(1) z =e 2x +3y , x =cos t , y =t 2; (2) z =tan(3t +2x 2+y 3), x =1t,y.解:(1)d d d d d d z z x z yt x t y t∂∂=+⋅∂∂ 22323232cos 3e 2(sin )e 32=2e(3sin )2e (3sin )x y x y x yt t t tt t t t ++++=⋅⋅-+⋅⋅-=-(2)d d d d d d z f f x f y t t x t y t∂∂∂=+⋅+⋅∂∂∂223223222321sec (32)3sec (32)4 sec (32)3t x y t x y xt t x y y -=++⋅+++⋅+++⋅3223242(3(3)t t t t=-++. 2.求下列各函数的偏导数:(1) z =x 2y -xy 2, x =u cos v , y =u sin v ;(2) z =e uv , u =, v =arctany x. 解:(1)z z x z yu x u y u∂∂∂∂∂=⋅+⋅∂∂∂∂∂ 22222222222(2)cos (2)sin 2sin cos sin cos sin cos 2sin cos 3sin cos (cos sin )xy y v x xy vu v v u v v u v v u v v u v v v v =-+-=-+-=-z z x z y v x v y v∂∂∂∂∂=⋅+⋅∂∂∂∂∂ 22323333323333(2)sin (2)cos 2sin cos sin cos 2sin cos 2sin cos (sin cos )(sin cos )xy y u v x xy u vu v v u v u v u v v u v v v v u v v =--+-=-++-=-+++(2)221e e 1()uv uv z z u z v y v u y x u x v x x x∂∂∂∂∂-=⋅+⋅=⋅⋅∂∂∂∂∂+arctan2222e e()(arctanyuvxyxv yu x y x y x y x=-=-++211e e 1()uv uv z z u z vv u y y u y v yxx∂∂∂∂∂=⋅+⋅=+⋅⋅∂∂∂∂∂+2222e e()(arctanln y uvxyyv xu x x x y x y x=+=+++ 3.求下列函数的一阶偏导数,其中f 可微: (1) u =f (,x yy z); (2) z =f (x 2+y 2); (3) u =f (x , xy , xyz ). 解:(1)121110u f f f x y y ∂'''=⋅+⋅=∂12212211u x x f f f f y y z z y ∂-''''=⋅+⋅=-∂122220u y y f f f z z z∂-'''=⋅+⋅=∂ (2)令22,u x y =+则()z f u =22d ()22()d z f u f u x xf x y x u x∂∂''=⋅=⋅=+∂∂22d ()22()d z f u f u y yf x y y u y∂∂''=⋅=⋅=+∂∂ (3)令,,t x v xy w xyz ===,则(,,)u f t v w =.123123d 1d u f t f v f w f f y f yz f yf yzf x t x v x w x∂∂∂∂∂∂''''''=⋅+⋅+⋅=⋅+⋅+⋅=++∂∂∂∂∂∂ 12323d 0d u f t f v f w f f x f xz xf xzf y t y v y w y∂∂∂∂∂∂'''''=⋅+⋅+⋅=⋅+⋅+⋅=+∂∂∂∂∂∂1233d 00d u f t f v f w f f f xy xyf z t z v z w z∂∂∂∂∂∂''''=⋅+⋅+⋅=⋅+⋅+⋅=∂∂∂∂∂∂ 4.设z =xy +x 2F(u ),u =yx,F(u )可导.证明:2z zxy z x y∂∂+=∂∂. 证:222()()2()()z yy xF u x F u y xF u yF u x x∂-''=++⋅=+-∂21()()z x x F u x xF u y x∂''=+⋅=+∂22()()()z zxy xy x F u xyF u xy xyF u x y∂∂''∴==+-++∂∂ 22[()]x y x F u z=+=∂ 5.利用全微分形式不变性求全微分:(1) z =(x 2+y 2)sin(2x +y ); (2) u =222()yf x y z --,f 可微. 解:(1)令22,sin(2)u x y v x y =+=+,则vz u =122d d d d()ln d sin(2)v v z zz u v vu x y u u x y u v-∂∂=+=++⋅+∂∂122sin(2)2222(2d 2d )ln cos(2)d(2)[2(d d )ln cos(2)(2d d )]2sin(2)()(d d )cos(2)ln()(2d d )v v v x y vu x x y y u u x y x y vu x x y y u x y x y ux y x y x x y y x y x y x y x y -+=++⋅++=⋅++⋅++⎡⎤+=++++++⎢⎥+⎣⎦(2)22222222111d d d d ()d()yu y y f y f x y z x y z f f f f-'=+⋅=-----222222222222221()d (2d 2d 2d )12()d (d d d )()()yf x y z y x x y y z z f f yf x y z y x x y y z z f x y z f x y z '--=---'--=-------6.求下列隐函数的导数:(1) 设e x +y +xyz =e x ,求x z ',y z '; (2)设x z =ln z y,求,z zx y ∂∂∂∂. 解:(1)设(,,)e e 0x yx F x y z xyz +=+-=,则ee ,e ,x yx x y x y z F yz F xz F xy ++'''=+-=+=故e e e ,x x y x yy x y z F Fx yz xzz z Fz xy F xy++'--+''=-==-=-(2)设(,,)ln 0x zF x y z z y=-=,则 2221111,,x y z y z x y x F F F z z y y z z y z z--'''==-⋅==-⋅=--故21x z F z z z xF x z z z '∂=-=-='∂+--2211()y z F z z yx yF y x z z z'∂=-=-='∂+-- 7.设x +z =yf (x 2-z 2),其中f 可微,证明:z zzy x x y∂∂+=∂∂. 证:设22(,,)()F x y z x z yf x z =+--则2212()x F xyf x z ''=--2222()12()y z F f x z F yzf x z '=--''=+-故22222()112()x z F zxyf x z x F yzf x z ''∂--=-=''∂+- 2222()12()y zF z f x y y yzf x z F '∂-=-='∂+-' 从而22222222()()12()12()z z xyzf x z z yf x y z y x y yzf x z yzf x z '∂∂∂---+=+''∂∂+-+- 222222222222222()()12()2()12()[2()1]12()xyzf x z z yf x y yzf x z xyzf x z z x zyzf x z x yzf x z x yzf x z '--+-='+-'--++='+-'-+=='+-8.设x =e u cos v , y =e u sin v , z =uv ,求z x ∂∂及z y∂∂. 解法一:由e cos ,e sin u ux v y v ==得221ln(),arctan ,2yu x y v z uv x=+== 故22(cos sin )e uz z u z v xv yu v v u v x u x v x x y-∂∂∂∂∂-=+==-∂∂∂∂∂+22(sin cos )e uz z u z v yv xu v v u v y u y v y x y-∂∂∂∂∂+=+==-∂∂∂∂∂+ 解法二:设方程组e cos e sin uux vy v⎧=⎪⎨=⎪⎩确定了函数(,),(,)u u x y v v x y ==,对方程组的两个方程关于x 求偏导得1e cos e sin 0e sin e cos uu u u u v v v x xu v v v x x ∂∂⎧=-⎪⎪∂∂⎨∂∂⎪=+⎪∂∂⎩解方程组得e cos e sin u u uv xv v x --∂⎧=⎪⎪∂⎨∂⎪=-⎪∂⎩又方程组的两个方程关于y 求偏导得0e cos e sin 1e sin e cos uu u u u v v v y y u v v vy y ∂∂⎧=-⎪∂∂⎪⎨∂∂⎪=+⎪∂∂⎩解方程组得:e sin e cos uu u v y v v y--∂⎧=⎪∂⎪⎨∂⎪=⎪∂⎩ 从而e (cos sin )u z z u z vv v u v x u x v x-∂∂∂∂∂=⋅+=-∂∂∂∂∂e (s i n c o s )uz z u z v v v u v y u y v y-∂∂∂∂∂=⋅+⋅=+∂∂∂∂∂ 9.设u =f (x ,y ,z )有连续偏导数,y =y (x )和z =z (x )分别由方程0xye y -=和e z -xz =0确定,求d d ux. 解:方程e 0xyy -=两边对x 求导得d de ()0d d xyy y y x x x +-=,解得2d e d 1e 1xy xy y y y x x xy==-- 方程e 0zxz -=两边对x 求导得d de 0d d zz z z x x x--= 解得d de z z z z x x xz x==-- 从而2d d d d d d 1y z x y z x y f zf u y zf f f f x x x xy xz x''''''=++=++--习题8-51.求下列函数的二阶偏导数: (1) z =x 4+y 4-4x 2y 2; (2) z =arctany x; (3) z =y x ; (4) z =x ln(xy ).解:(1)23222248, 128;z z x xy x y x x∂∂=-=-∂∂232222248, 128;1622z z y x y y x y y zxy x y∂∂=-=-∂∂∂=-(2)22221,1()z y y y x x x y x∂-=⋅=-∂++ 22222222222222222222222222222211,1()2(2),()()22()()()2()()z x y y x x y xz y xyx x x y x y z x xyy y x y x y z x y y y y x x y x y x y ∂=⋅=∂++∂-=-⋅=∂++∂--=⋅=∂++∂+-⋅-=-=∂∂++(3)1ln , ,x x z zy y xy x y-∂∂==∂∂222222211ln , (1),1ln (1ln )x x x x x z z y y x x y x y z xy y y y x y x y y---∂∂==-∂∂∂=+⋅=+∂∂(4)1ln()1ln(),z xy x y xy x xy∂=+⋅⋅=+∂22222211,1,11.z y x xy x z x x x y xy y z xy y z x x y xy y∂=⋅=∂∂=⋅⋅=∂∂=-∂∂=⋅=∂∂2.求下列函数的二阶偏导数,其中f (u ,v )可微: (1) z =f (x 2+y 2); (2) z =f (xy ,x +2y ).解:(1)2222, 22224z zxf f xf x f x f x x∂∂'''''''==+⋅=+∂∂ 2222, 22224z zyf f yf y f y f y y ∂∂'''''''==+⋅=+∂∂2224zxf y xyf x y∂''''=⋅=∂∂(2)1212, =+2 z zyf f xf f x y∂∂''''=+∂∂ 22111221221112222(1)12zy f y f f y f y f yf f x∂''''''''''''''=⋅+⋅+⋅+⋅=++∂ 22111221*********(2)2(2)44z x f x f f x f x f xf f y∂''''''''''''''=⋅+⋅+⋅+⋅=++∂ 21111221221111222(2)2 (2)2zf y f x f f x f x y f xyf x y f f ∂'''''''''=++⋅+⋅+⋅∂∂'''''''=++++3.求由e z -xyz =0所确定的z =f (x ,y )的所有二阶偏导数. 解:设(,,)e 0zF x y z xyz =-=,则,,e z x y z F yz F xz F xy '''=-=-=-于是,e x z z F z yz zx F xy xz x∂=-==∂--e z z xz zy xy yz y∂==∂-- 从而222()(1)()z z xz x z z x zx x xxz x ∂∂--+-∂∂∂=∂-232223(1)221.(1)(1)z z z z z z z z x z x z --+---==-- 223222223()(1)(1)221.()(1)(1)z zz yz y z z y z z z z z z z y y z y yz y y z y z ∂∂--+---+∂--∂∂-===∂--- 2222233()()(1)(1).()(1)(1)(1)z z z z xz x z x z z z z z y y y y z x y xz x x z xy z xy z ∂∂---∂---∂∂-====∂∂----习题8-61.求z =x 2+y 2在点(1,2)处沿从点(1,2)到点(2,2的方向的方向导数.解:设(1,2),(2,2o p p ,则射线l的方向就是向量(1o p p =的方向,将o p p 单位化得:1(,),22||o o p p p p =于是1cos ,cos 2αβ==, 又2,2,f fx y x y ∂∂==∂∂ 于是(1,2)(1,2)2,4,f f x y∂∂==∂∂所以(1,2)124122f l∂=⨯+=+∂ 2.设u =xyz +x +y +z ,求u 在点(1,1,1)处沿该点到点(2,2,2)的方向的方向导数.解:设0(1,1,1),(2,2,2)p p ,则射线l 的方向就是向量0p p =(1,1,1)的方向,将0p p单位化得00||p p p p =⎝⎭,于是cos αβγ=== 又1,1,1f f f yz xz xy x y z ∂∂∂=+=++∂∂∂,于是(1,1,1)(1,1,1)(1,1,1)2,2,2fff xyz∂∂∂===∂∂∂,所以(1,1,1)222333f l∂=⨯+⨯+⨯=∂. 3.求函数z =x 2-xy +y 2在点M(1,1)处沿与Ox 轴的正方向所成角为α的方向l 上的方向导数.问在什么情况下,此方向导数取得最大值?最小值?等于零? 解:2,2f f x y x y x y ∂∂=-=-+∂∂, (1,1)(1,1)1,1f fx y∂∂==∂∂∴(1,1)π1c o s 1s i n 2s i n ()4f lααα∂=⋅+⋅+∂当πsin()4α+=1,时,即π4α=当πsin()14α+=-时,即5π4α=时,此方向导数有最小值当πsin()04α+=时,即3π4α=或7π4时,此方向导数为0.习题8-71.求下列函数的极值: (1) z=x 3-4x 2+2xy -y 2+3; (2) z =e 2x (x +2y +y 2); (3) z =xy (a -x -y ), a ≠0. 解:(1)由方程组:23820220xy z x x y z x y ⎧'=-+=⎪⎨'=-=⎪⎩ 得驻点(0,0),(2,2) 又68,2,2,xx xy yy z x z z ''''=-==-在点(0,0)处,2120B AC -=-<,又80A =-<,所以函数取得极大值(0,0)3;f = 在点(2,2)处,2120,B AC -=>该点不是极值点.(2)由方程组222e (2241)0e (22)0x xx y z x y y z y ⎧'=+++=⎪⎨'=+=⎪⎩ 得驻点1(,1)2-.又2222e (4484),e (44),2e xxxxx xy yy z x y y z y z ''''''=+++=+=,在点1(,1)2-处22202e 2e 4e 0,B AC -=-⋅=-<且2e 0A =>,所以函数取得极小值11(,1) e.22f -=- (3)由方程组(2)0(2)0xy z y a x y z x a y x ⎧'=--=⎪⎨'=--=⎪⎩ 得四个驻点(0,0),(0,),(,0),,.33a a a a ⎛⎫ ⎪⎝⎭又2,22,2xx xy yy z y z a x y z x ''''''=-=--=-.在点(0,0)处,220,B AC a -=>该点不是极值点. 在点(0,)a 处,220B AC a -=>,该点不是极值点. 在点(,0)a 处,220B AC a -=>,该点不是极值点.在点,33a a ⎛⎫ ⎪⎝⎭处,2203a B AC -=-<,所以函数在该点有极值,且极值为3,3327aa a f ⎛⎫= ⎪⎝⎭,由于23xx A z a ''==-故 当0a >时,(0)A <,函数有极大值327a ,当0a <时,(0)A >,函数有极小值327a .2.求函数z =x 3-4x 2+2xy -y 2在闭区域D :-1≤x ≤4,-1≤y ≤1上的最大值和最小值. [分析]由(,)f x y 在D 上连续,所以必有最大最小值,又由于(,)f x y 在D 内可导,所以(,)f x y 的最值在D 的内部驻点或在D 的边界上,由(,)f x y 在D 内部驻点上值与边界上函数比较可求出(,)f x y 的最大和最小值.解:由方程23820220xy z x x y z x y ⎧'=-+=⎪⎨'=-=⎪⎩得驻点(0,0),(2,2)(2,2)D ∈应该舍去,(0,0)0f =(可由充分条件判别知是极大值).D 的边界可分为四部分:12:1,11; :1,14;L x y L y x =--≤≤=--≤≤ 34:4,11; :1,1 4.L x y L y x =-≤≤=-≤≤在1L 上,2(1,)52(),1 1.f y y y y y ϕ-=---=-≤≤因为()2(1)0,y y ϕ'=-+≤所以()y ϕ单调递减,因而(1)4ϕ-=-最大,(1)8ϕ=-最小. 在2L 上,32(,1)421(),14f x x x x g x x -=---=-≤≤令()0g x '=得124433x x ==.而122227min{(1),(),(),(4)}()27g g x g x g g x --==,1214227m a x {(1),(),(),(4)}()27g g x g x g g x -==分别是(,)f x y 在2L 上的最小值与最大值.类似讨论可得:在3L 上(4,1)7,(4,1)9f f =-=-,分别是(,)f x y 的最大值与最小值;在4L 上(4,1)7,(1,1)f f =-=-8分别是(,)f x y 的最大值与最小值.比较(,)f x y 在内部驻点(0,0)与整个边界上函数值的情况得到(4,1)7f =是函数(,)f x y 在D 上的最大值,116.1f ⎫-=≈-⎪⎪⎝⎭. 3.求函数z =x +y 在条件111x y+= (x >0,y >0)下的条件极值. 解:构造拉格朗日函数11(,)1F x y x y x y λ⎛⎫=+++- ⎪⎝⎭解方程组221010111x y F x F y x yλλ⎧'=-=⎪⎪⎪'=-=⎨⎪⎪+=⎪⎩ 得2,2,4x y λ===,故得驻点(2,2)。
微积分第二版习题二答案

微积分第二版习题二答案微积分是数学中的一门重要学科,它研究的是变化的规律和量的计算方法。
而微积分的学习过程中,习题是非常重要的一环。
本文将为大家提供《微积分第二版》习题二的详细答案,希望能帮助大家更好地掌握微积分的知识。
第一题:计算函数 f(x) = 3x^2 - 2x + 1 在 x = 2 处的导数。
解答:首先,我们需要求函数 f(x) 的导数。
对于多项式函数,我们可以使用求导法则来计算导数。
根据求导法则,我们有:f'(x) = d/dx (3x^2) - d/dx (2x) + d/dx (1)= 6x - 2将 x = 2 代入上式,我们得到:f'(2) = 6(2) - 2= 12 - 2= 10所以,函数 f(x) 在 x = 2 处的导数为 10。
第二题:计算函数 g(x) = e^x - x 在 x = 1 处的导数。
解答:函数 g(x) 包含了指数函数和多项式函数的运算。
对于指数函数 e^x,它的导数仍然是 e^x。
而对于多项式函数 -x,它的导数是 -1。
因此,我们可以得到函数 g(x) 的导数为:g'(x) = d/dx (e^x) - d/dx (x)= e^x - 1将 x = 1 代入上式,我们得到:g'(1) = e^1 - 1= e - 1所以,函数 g(x) 在 x = 1 处的导数为 e - 1。
第三题:计算函数 h(x) = ln(x^2 + 1) 在 x = 0 处的导数。
解答:函数 h(x) 是一个复合函数,它包含了对数函数和多项式函数的运算。
对于对数函数 ln(x),它的导数是 1/x。
而对于多项式函数 x^2 + 1,它的导数是 2x。
因此,我们可以得到函数 h(x) 的导数为:h'(x) = d/dx (ln(x^2 + 1))= 1/(x^2 + 1) * d/dx (x^2 + 1)= 2x/(x^2 + 1)将 x = 0 代入上式,我们得到:h'(0) = 2(0)/(0^2 + 1)= 0所以,函数 h(x) 在 x = 0 处的导数为 0。
2019《微积分II》期末复习题一 - 参考答案

.
M
gradu
u i x
u y
j
u k z
u x
,
u y
,
u z
2 9
,
4 9
,
4 9
u
2x
x x2 y2 z2
u
2y
y x2 y2 z2
u
2z
z x2 y2 z2
gradu M
S
曲面方程, x用 x替换, 曲面边界方程不变化.
(1)被积函数f ( x, y, z)关于x是奇函数 (即f ( x, y, z) f ( x, y, z)),
则 f ( x, y, z)dS 0;
S
(2)被积函数f ( x, y, z)关于x是偶函数 (即f ( x, y, z) f ( x, y, z)),
x2 y2 1以及平面z 0围成.
法一: 积分区域为圆柱去掉圆锥的部分,
z
用先一后二法
V
:
0
z
x2 y2
Dxy : 0 x2 y2 1
I
2
d
1
rdr
r z r 2dz
0
0
0
2 1 r 3 1 z2 r dr 1 r 5dr
0 0
1 x cos 2x 1
cos 2xd 2x
0 2 0
1 1 sin 2x
2
0
1
11/24
三、设z
xn
f
微积分B2练习1+答案

微积分B2 练习卷一、 选择题 1、设有直线l 1:158121x y z --+==-与l 2:⎩⎨⎧=+=-326z y y x ,则两直线夹角( ). A .6πB .4πC .3πD .2π2、函数z =f (x ,y )在点P 0处两个偏导数存在与可微的关系是( ). A .可微不一定两个偏导数存在 B .两个偏导数存在一定可微 C .可微两个偏导数一定存在 D .两个偏导数存在一定不可微3、设(,)ln()z f x y x x y ==+,则(1,2)xx f =( ). A . 0 B . 79 C . 59 D . 1ln 33+ 4、设1,DI σ=⎰⎰222cos(),DI x y d σ=+⎰⎰2223cos(),DI x y d σ=+⎰⎰其中22{(,)|1}D x y x y =+≤,则( ).A .321I I I >>B .123I I I >>C .213I I I >>D .312I I I >> 5、设22()=+⎰⎰DI x y dxdy ,其中D 由222a y x =+所围成,则I =( ).A .2200a d a rdr πθ⎰⎰ B .2200a d r dr πθ⎰⎰ C .2300ad r dr πθ⎰⎰ D .230ad a dr πθ⎰⎰6、设曲线L 为椭圆2241x y +=,并取正向,则曲线积分224-++⎰ Lydx xdyx y=( ). A .0 B .2π C .π- D .π7、设L 为椭圆22143x y +=,其周长记为a ,则=+⎰ds y x L )43(22( ).A .-aB .0C .aD . 12a 8、微分方程sin y x '''=的通解是( ).A .21231cos 2y x C x C x C =+++B .2sin 2y x =C .21231sin 2y x C x C x C =+++ D .1cos y x C =+9、函数),(y x f ⎪⎩⎪⎨⎧=+≠+++=0,00,1sin )(22222222y x y x y x y x 在原点)0,0(处 ( ).A .偏导数不存在B .不可微C .偏导数存在且连续D .可微 10、设{(,)|0, , 1}D x y y x y x ====,则二重积分Ddxdy ⎰⎰的值为( ).A .2B .21 C .0 D .21-二、 填空题1、过点(1,0,-1)且与平面x +2y +3z +4=0平行的平面方程为 .2、设函数2xy z x e -=-,则z zx y∂∂+=∂∂ . 3、曲面z =在(1,1,2)处的切平面方程为 . 4、设{(,)|||,01}D x y x y π=≤≤≤,则(2)+=⎰⎰Dxy d σ .5、若L 是上半椭圆⎩⎨⎧==,sin ,cos t b y t a x 取顺时针方向,则L ydx xdy -⎰= .6、已知2()()+++x ay dx ydyx y 是某个二元函数的全微分,则a = . 7、判别级数11(1)10∞-=-∑n nn n的敛散性: . 8、微分方程320y y y '''++=的通解为 . 三、计算题1、设方程y z z x ln =确定函数),(y x f z =,求yz x z ∂∂∂∂,.2、将积分22200)+⎰ady x y dx (a >0)化为极坐标形式,并计算积分值.3、计算sin =⎰⎰DxI dxdy x,其中D 由直线,2==x y x y 及x =2所围的闭区域.4、计算22()(sin )=--+⎰L I x y dx x y dy , 其中L 是在圆周22x x y -=上由点(0, 0)到点(1, 1)的一段弧.5、求幂级数1(21)nn n x ∞=-∑的收敛域.6、求微分方程()22124dyx xy x dx++=的通解.四、综合题1、设曲线积分[()]sin ()cos x L f x e ydx f x ydy --⎰与路径无关,其中f (x )具有一阶连续导数,且f (0)=0,求f (x ).2、已知函数(,)z f x y =的全微分22dz xdx ydy =-,并且f (1,1)=2.求f (x ,y )在椭圆域22{(,)|1}4y D x y x =+≤上的最大和最小值.《高等数学》练习参考答案一、 选择题:1、 C ;2、C ;3、C ;4、A ;5、C ;6、D ;7、D ;8、A .9、D ;10、B 二、 填空题:1、2320x y z +++=;2、2()xy x x y e -++;3、260++-=x y z ;4、4π;5、ab π;6、2;7、收敛;8、x x e C e C y 221--+=. 三、计算题:1、解:令y z z z x z y x F ln ln ),,(+-=, 则11,,ln ln 1x y z z x F F F z z y yzz'''===--⋅+=--故)(,2z x y z F F y z z x z F F x z z y z x +=-=∂∂+=-=∂∂. 2、解:由题设积分限,222{(,)|,0,0}=+≤≥≥D x y x y a x y , 令)20,0(sin ,cos πθθθ≤≤≤≤==a r r y r x ,则222)+⎰ady x y dx =562012=⎰⎰ad r dr a ππθ.3、解:取D 为X 型区域,:,0 2.2≤≤≤≤xD y x x22002sin sin sin 2∴==⋅⎰⎰⎰⎰⎰x x D xx x x d xdy d x d y d x x x x []2200111sin cos (1cos 2)222==-=-⎰xd x x . 4、解:P =x 2-y , Q =-x -sin 2y , 0)1(1=---=∂∂-∂∂yP x Q ,由格林公式有0)(=∂∂-∂∂-=+⎰⎰⎰++dxdy yPx Q Qdy Pdx DBO AB L , 其中L 、AB 、BO 及D 如图所示. 故⎰⎰++--=+--L OB BA dy y x dx y x dy y x dx y x )sin ()()sin ()(22222sin 4167)sin 1(12102+-=++-=⎰⎰dx x dy y .5、解:11limlim 1n n n n a n a n+→∞→∞+==,故1R =.当 211x -=时,1n n ∞=∑ 发散;当 211x -=-时,1(1)n n n ∞=-∑ 发散;故该级数的收敛域为(0,1).6、解:1412222+=++x x y x x dx dy ,22222d d ()d ()d 1124e ()e d e e d 1x x x x P x xP x xx x x y Q x x C x C x --++⎛⎫⎰⎰⎛⎫⎰⎰=+=+ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎰⎰ ()()()222ln 1ln 122241ee d 4d 11x x x x C x x C x x -++⎛⎫=+=+ ⎪++⎝⎭⎰⎰⎪⎭⎫ ⎝⎛++=C x x 323411. 四、综合题:1、解:设 (,)[()]sin ,(,)()cos x P x y f x e y Q x y f x y =-=- 则由曲线积分(,)(,)L P x y dx Q x y dy +⎰与路径无关得(,)(,)P x y Q x y y x∂∂=∂∂,即()()0,x f x f x e '+-= 由一阶微分方程通解公式知:21()()(),2--⎰⎰=+=-+⎰dx dx x x x f x e e e dx C e e C又由f (0)=0知12C =-,所以()2x xe ef x --=.2、解:由22dz xdx ydy =-可知 22=-+z x y C , 再由f (1,1)=2,得C=2,故222,=-+z x y 令20,20,∂∂===-=∂∂z zx y x y解得驻点(0,0), 在椭圆2214+=y x 上,222(44)252(11)=--+=--≤≤z x x x x ,其最大值为13=±=x z ,最小值为02==-x z .。
微积分上第二章习题参考答案

微积分第二章习题参考答案
16
x e x sin e x cos 0 x 三.解: , 2 3 2 0 y
1 S | 2 x0 | | 2 y0 | 2a 2为常数,与切点无关. 2
微积分第二章习题参考答案 6
§2.2求导法则(21-22)
一.1. 2cos x sec x, 3cos x 2sec x; x e sin 2. cos e , ; 2x 1 e
2 2
x 2 x cos2 x sin2 x 1 2 3. , e ( cos3 x 3sin3 x ); 2 x 2
微积分第二章习题参考答案 26
(n)
2
n 1
2. y xe .
x x x x y e xe e ( x 1),
y e x ( x 1) e x e x ( x 2),
t2 2 t2
3. y
1 1 x
2
, y
x (1 x )
2 3 2
;
4. y ( n ) n ! 2n e 2 x 1 ;
5. y e (sin cos ) 2e sin(
4
);
微积分第二章习题参考答案
20
2 dy d y 2 2 2 2 6. 2tf ( t ) , 2 2 f ( t ) 4t f ( t ) ; dt dx
lim f (cos x )( sin x )
x 0
习题参考答案_经济数学——微积分(第2版)(微课版)_[共28页]
![习题参考答案_经济数学——微积分(第2版)(微课版)_[共28页]](https://img.taocdn.com/s3/m/c3dacd3d998fcc22bdd10dca.png)
烆0.8653狓-1158, 狓 >4200
习题12
1. (1)4π ;
(2)56π;
(3)1 2 ; (4)3π .
2.(1)犳-1(狓)=1狓+-狓1,(- ∞,-1)∪ (-1,+ ∞);
(2)犳-1(狓)=
1 3
(狓3
+5),(-
∞,+
∞ );
(3)犳-1(狓)=1-e狓+1,(- ∞,+ ∞); (4)犳-1(狓)=log3(狓-1),(1,+ ∞);
5.犳[φ(狓)]=sin32狓-sin2狓 ;φ[犳(狓)]=sin(2狓3 -2狓). 习题13
1.3045;2859.3;2659.9.
2.(1)3狓+100,100元; (2)700元,3.5元.
3.(1)犘e =80,犙e =70; (2)图略;
(3)表示此时的价格为最低销售价格,市场上供给量为0.
(2)狔=e狌,狌=arctan狏,狏=狓2 ;狓 ∈犚 ;
(3)狔=狌3,狌=1+狏,狏=狊2,狊=ln狓 ;狓 ∈ {狓 狓 >0};
(4)狔 =log2狌,狌 =
槡狏,狏=cot狊,狊=
狓 2
,狓 ∈
{狓
2犽π<狓 <
(2犽+1)π,犽∈犣}.
经济数学———微积分(第2版)(微课版)
1.(1)犳(狓)在 (- ∞,-1)∪ (-1,+ ∞)上连续,图略 ; (2)犳(狓)在 [0,2]上连续,图略. 2.(1)犪=2; (2)犪=2,犫=-1. 3.(1)狓 =2为可去间断点,令犳(2)=-4;狓 =3为无穷间断点. (2)狓 =0为可去间断点,令犳(0)=1;
( ) 狓
4.(1)1; (2)1 2 .
5.(1)e-6 ; (2)2; (3)1 ; 槡2
大一微积分二至四章课后习题答案

第二章习题解答 习 题 2—11. 用定义求函数2y x =在1x =处的导数。
解:(1)22(1)(1)(1)12()y f x f x x x ∆=+∆-=+∆-=∆+∆;(2)22()2y x x x x x∆∆+∆==+∆∆∆; (3)00limlim(2)2x x yx x ∆→∆→∆=+∆=∆.2. 已知一物体的运动方程为38s t =+ ()m ,求该物体在2()t s =时的瞬时速度。
解:(1)323(2)(2)(2)816126()()s s t s t t x t ∆=+∆-=+∆+-=∆+∆+∆;(2)230[126()()](2)lim12t s t x t v t t∆→∆∆+∆+∆===∆∆。
3. 求在抛物线22y x =+上点1x =处的切线方程与法线方程. 解:因为2(2)2y x x ''=+=,12,x y ='= 故所求的切线方程为 32(1)y x -=- 即 210x y -+-=所求的法线方程为 13(1)2y x -=--即 15022x y +-=。
4. 设0()f x '存在,试利用导数的定义求下列极限:(1)000()()limx f x x f x x ∆→-∆-∆; (2)000()()lim h f x h f x h h →+--;(3)000()(2)lim 2x f x x f x x x∆→+∆--∆∆.解:(1) 0000000()()[()]()lim lim ()x x f x x f x f x x f x f x x x∆→∆→-∆-+-∆-'=-=-∆-∆;(2)原式0000000()()()()lim lim 2()h h f x h f x f x h f x f x h h→→+---'=+=-;(3)原式0000000()()(2)()3lim lim ()222x x f x x f x f x x f x f x x x ∆→∆→+∆--∆-'=+=∆-∆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空题1.设)(x P 是x 的多项式,且26)(lim 23=-∞→x x x P x ,3)(lim 0=→xx P x ,则=)(x P 2.=-++∞→))(arcsin(lim 2x x x x6π x x x 32623++↑ 3.=⎪⎭⎫⎝⎛-∞→321lim x x x 32-e4.设A x x ax x x =-+--→14lim31,则有=a ,=A 4,-2 5.设xxx x x f sin 2sin )(+=,则=∞→)(lim x f x 26.=⋅+→232031sinsin limx x x x x 31 7.函数)2)(1(1+-+=x x xy 的间断点是 1=x8.为使函数()x x x f tan 1⋅=在点0=x 处连续,应补充定义()=0f 19.设函数⎪⎩⎪⎨⎧=≠-=00)1(3x Kx x y x 在0=x 处连续,则参数=K 3-e 10.函数⎩⎨⎧>+≤+=010)(x e x a x x f x 在点0=x 处连续,则=a 2二、单项选择题1.设0>n x ,且n n x ∞→lim 存在,则n n x ∞→lim ②①0> ②0≥ ③0= ④0< 2.极限=-→111lim x ex ③①∞ ②1 ③不存在 ④0 3.=++∞→-→xx x x xx 1sinlim )1(lim 10 ④①e ; ②1e -; ③1e +; ④11e -+4.()()213++-=x x x y 的连续区间是__________________ ②①()()()+∞----∞-,11,22, ②[)+∞,3③()()+∞--∞-,22, ④()()+∞--∞-,11,5.函数1211111+----=x x x x y 的不连续点有 ③ ①2个 ②3个 ③4个 ④4个以上6.下列函数中,.当0→x 时,与无穷小量x 相比是高阶无穷小量的是___________;是等价无穷小量的是__________________ ①,②①x cos 1- ②2x x + ③x ④x 2sin7.当+→0x 时,x sin 与||x 相比是 ② ①高阶无穷小量 ②低阶无穷小量 ③同阶但不等价的无穷小量 ④等价无穷小量8.当0→x 时,x 2cos 1-与2x 相比是 ② ①高阶无穷小量 ②同阶但不等价的无穷小量③低阶无穷小量 ④等价无穷小量9.设()⎪⎩⎪⎨⎧=≠-=00,3sin x k x xx x f 为连续函数,则k =_______________ ② ① 1 ② -3 ③ 0 ④ 310.函数()x f 在点0x 处有定义是()x f 当0x x →时极限存在的 ④ ①充分但非必要条件 ②必要但非充分条件③充分必要条件 ④既非充分又非必要条件11.当0→x 时,下列函数中比x 高阶的无穷小量是 ②①x x sin + ②x x sin - ③()x +1ln ④()x -1ln 12.当0→x 时,下列函数中为无穷小量的是 ② ①x x 1sin+ ②x x 1sin ⋅ ③x x sin 1+ ④x xsin 1⋅ 13.当∞→x 时,下列函数中为无穷小量的是 ③①x x 1sin+ ②x x 1sin ⋅ ③x x sin 1+ ④x xsin 1⋅ 14.设在某个极限过程中函数()x f 与()x g 均是无穷大量,则下列函数中哪一个也必是无穷大量 ③ ① ()()x g x f + ② ()()x g x f - ③ ()()x g x f ⋅ ④()()x g x f 15.设()a x f =0,()b x f x x =-→0lim ,()c x f x x =+→0lim ,则函数()x f 在点0x 处连续的充分必要条件是 ④ ①b a = ②c a = ③c b = ④c b a ==16.1=x 是⎪⎩⎪⎨⎧=≠--=-10111)(112x x ex x x f x 的 ④ ①连续点 ②跳跃间断点 ③可去间断点 ④无穷间断点三、求下列极限1.)1(lim 2x x x -++∞→011lim2=++=+∞→xx x2.)1(lim 2x x x -+-∞→+∞=3.)2222(lim 22+--+++∞→x x x x x22212214lim22224lim2222=+-+++=+-+++=+∞→+∞→xx x x x x x x xx x4.⎪⎭⎫⎝⎛⋅∞→x x x 1arcsinarctan lim 0=5.)111)(110()110()13()12()1(lim 2222--++++++++∞→x x x x x x x (27=)6.)21(lim 222nn nn n n n n ++++++∞→[解] 记n n nn n n n x n ++++++=22221 因为 222222n nn n n n x n n n n n n n n n n +++≤≤++++++即 11≤≤+n x n n ,由于11lim =+∞→n n n ,所以由夹逼定理,得1lim =∞→n n x7.设2006)1(lim =--∞→ββαn n n n ,求βα,[解] 原式左端⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--=∞→∞→n o n n n n n n n n 1111lim111limββαββαβββα11lim 1=⎥⎦⎤⎢⎣⎡⋅⎪⎭⎫ ⎝⎛-=-∞→n n o n n n (1-=βα)由于极限存在,故1-=βα。
20061=β ∴20061=β,200620051200611-=-=-=βα 四、分析题1.讨论极限x x x |sin |lim 0→[解] 因为1|sin |lim 0=+→x x x ,1|sin |lim 0-=-→x x x ,故原极限不存在。
2.求23122+--=x x x y 的间断点,并判别间断点的类型。
[解] 因为)2)(1(232--=+-x x x x ,而2231lim 221-=+--→x x x x ,∞=+--→231lim 222x x x x 因此有间断点:1=x 为可去间断点,2=x 为无穷间断点。
.3.求函数xx y 16+=的连续区间,若有间断点,试指出间断点的类型。
[解] 函数的连续区间为),0()0,(+∞-∞ ,点0=x 为函数的第二类无穷间断点。
4.讨论函数tx t x t t x x f -→⎪⎭⎫⎝⎛--=11lim )(的连续性。
[解] ()1)1(011lim 11lim 11lim )(--+→--=-→-→=+⎪⎭⎫⎝⎛--+=⎪⎭⎫ ⎝⎛--==x xx y yx y t tx y tx t x t tx t x t e y t t x t x x f 令 在点1=x 处没有定义,是间断点,故)(x f 的连续区间为),1()1,(+∞-∞ ,点1=x 为)(x f 的第二类无穷间断点。
5.讨论函数⎩⎨⎧<+≥=010cos )(x x x x x f 在点0=x 处的连续性。
[解] 1cos lim )(lim 0==++→→x x f x x ,1)1(lim )(lim 0=+=--→→x x f x x∴ )(x f 在点0=x 处连续性。
6.设函数()⎪⎪⎩⎪⎪⎨⎧≥+<--==02cos 0x x x x x xa a x f y (0>a )(1)当a 取何值时,点0=x 是函数()x f 的间断点?是何种间断点?(2)当a 取何值时,函数()x f 在()∞+∞-,上连续?为什么? [解](1)在点0=x 处,21)0(=f ,212cos lim )(lim 00=+=++→→x x x f x x ,ax a a x x a a x f x x x 211lim lim )(lim 000=-+=--=---→→→ 当0>a 且1≠a 时,由于)(lim )(lim 0x f x f x x -+→→≠,所以点0=x 是()x f 的跳跃间断点。
(2)当1=a 时,由于)0()(lim )(lim 0f x f x f x x ==-+→→,则()x f 在点0=x 处连续。
又因为在)0,(-∞或),0(∞+上,()x f 为初等函数,所以连续。
故当1=a 时,函数()x f 在()∞+∞-,上连续。
7.设函数()⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤<≤<+==4110011x a x x x x x f y(1)求函数()x f 的定义域;(2)讨论函数()x f 在点0=x 处的极限是否存在?为什么?(3)a 为何值时,函数()x f 在点1=x 处连续?并求函数()x f 的连续区间;(4)画出函数()x f y =的图形。
[解](1)]4,1()1,(---∞= f D(2)因为111lim )(lim 00=+=--→→x x f x x ,0lim )(lim 00==-+→→x x f x x ,所以)(lim 0x f x →不存在(3)在点1=x 处,a f =)1(,1lim )(lim 11==--→→x x f x x ,a a x f x x ==++→→11lim )(lim , 所以,当1=a 时,)1()(lim )(lim 11f x f x f x x ==-+→→,即函数()x f 在点1=x 处连续。
此时,()x f 的连续区间为:]4,1()1,(---∞ (4)略 五、证明题1.证明方程475=-x x 在区间)2,1(内至少有一个实根。
[证] 设47)(5--=x x x f ,)(x f 在]2,1[上连续,又010)1(<-=f ,014)2(>=f ,由零点定理知,在)2,1(内至少存在一点ξ,使得0)(=ξf ,即0475=--ξξ,故方程475=-x x 在区间)2,1(内至少有一个实根。
2.证明:方程k x x =-sin 2(0>k )至少有一个正根。
[证] 设),0[sin 2)(∞+∈--=C k x x x f因为0)0(<-=k f ,0)3sin(23)3(>+-=+k k f故由零点定理知,)3,0(+∈∃k ξ,使得0)(=ξf ,所以方程k x x =-sin 2至少有一正根。
3.证明方程2sin +=x a x (0>a )至少有一个正根,并且不超过2+a 。
[证] 设2sin )(--=x a x x f ,下面分两种情形来讨论:情形1 若 1)2sin(=+a ,则因为0>a ,故2+a 是方程2sin +=x a x (0>a )的正根,并且不超过2+a 。
