重庆中考第26题专题专训(教师版)
重庆数学中考26题专题训练(教师版)

重庆数学中考26题专题训练(教师版)重庆数学中考题26题专题训练0026、如图(1)Rt AOB中,A 90,AOB 60,OB 2,AOB 的平分线OC交AB于C,过O点作与OB垂直的直线ON.动点P从点B 出发沿折线BC CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.(1)求OC、BC的长;(2)设CPQ的面积为S,直接写出S与t的函数关系式;(3)当P在OC上、Q在ON上运动时,如图(2),设PQ 与OA交于点M,当t为何值时,OPM为等腰三角形?求出所有满足条件的t值.NACPNAPCQO图(1)BO图(2)B(1)在Rt AOB中,ABO 90 AOB 30 AO1OB 3 21AOB 300 2在Rt AOC中,令AC x OC 2AC 2xOC平分AOB AOC BOC (2x) x () x1 1,x2 1(舍)AC 1,OC 2。
3分COB CBO 30 BC OC 2。
4分(2)当0 t 2时,S222323t t。
6分__t t 2。
8分42当2 t 4时,SNAPQCOB(3)QO t 2,PO 4 t,POQ 60 ①OM MP时,如图MOP MPO 30 PQO 90 PO 2QO 4 t 2(t 2) t ②OM OP时,如图8。
9分31800 POMOMP OPM 7502PQO PMO POM 4510过P点作PD ON于D点,DOP 30 DO OP 2 PDPO2 DO2 (4 t) 2(4 t)2PQD 450QD PDOQ OD DQ t 2 分8 413(4 t) (4 t) t 。
__ ③OP PM时,此时POM PMO 30,而NOM 30,PM//ON,故舍。
10088 4时,OPM为等腰三角形当t 或33 326.如图1,梯形ABCD中,AD∥BC,AB AD DC 5,BC 11.一个动点P从点B出发,以每秒1个单位长度的速度沿线段BC方向运动,过点P作PQ BC,交折线段BA AD于点Q,以PQ为边向右作正方形PQMN,点N在射线BC上,当Q点到达D点时,运动结束.设点P的运动时间为t秒(t 0).(1)当正方形PQMN 的边MN恰好经过点D时,求运动时间t的值;(2)在整个运动过程中,设正方形PQMN与△BCD的重合部分面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围;(3)如图2,当点Q在线段AD上运动时,线段PQ与对角线BD交于点E,将△DEQ沿BD翻折,得到△DEF,连接PF.是否存在这样的t ,使△PEF是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.QQB2B26.解:(1)作AG BC,DH BC,垂足分别为G、H 则四边形AGHD为矩形∵梯形ABCD,AB AD DC 5 ∴△ABG≌△DCH ∴BGQ(M)1(BC AD) 3,AG 4 2B∴3秒后,正方形PQMN的边长恒为4∴当正方形PQMN的边MN恰好经过点D时,点M与点D 重合,此时MQ 4 ∴GP AQ AD DQ 1,BP BG GP 4∴t 4 即4秒时,正方形PQMN的边MN恰好经过点D 。
重庆中考,26题专练(1)
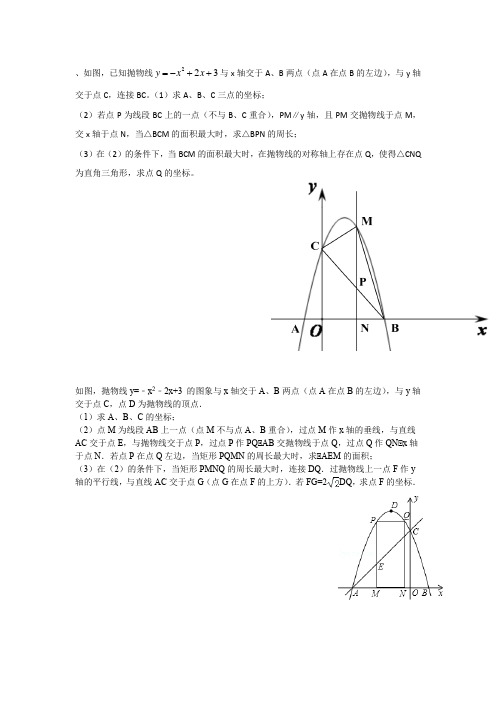
、如图,已知抛物线223y x x =-++与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,连接BC 。
(1)求A 、B 、C 三点的坐标;(2)若点P 为线段BC 上的一点(不与B 、C 重合),PM ∥y 轴,且PM 交抛物线于点M ,交x 轴于点N ,当△BCM 的面积最大时,求△BPN 的周长;(3)在(2)的条件下,当BCM 的面积最大时,在抛物线的对称轴上存在点Q ,使得△CNQ 为直角三角形,求点Q 的坐标。
如图,抛物线y=﹣x 2﹣2x+3 的图象与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,点D 为抛物线的顶点.(1)求A 、B 、C 的坐标;(2)点M 为线段AB 上一点(点M 不与点A 、B 重合),过点M 作x 轴的垂线,与直线AC 交于点E ,与抛物线交于点P ,过点P 作PQ ∥AB 交抛物线于点Q ,过点Q 作QN ⊥x 轴于点N .若点P 在点Q 左边,当矩形PQMN 的周长最大时,求△AEM 的面积;(3)在(2)的条件下,当矩形PMNQ 的周长最大时,连接DQ .过抛物线上一点F 作y 轴的平行线,与直线AC 交于点G (点G 在点F 的上方).若FG=2DQ ,求点F 的坐标.图,已知在平面直角坐标系xOy 中,直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA=AB=3抛物线c x ax y ++=492,过点A 、B ,,与x 轴的的正半轴于点E ,C ,(1)求抛物线的解析式;(2)点P 为x 轴上的一个动点,当△ACP 为等腰三角形时,求点P 的坐标;(3),过点B 作BD ⊥BC ,交OA 于点D .将∠DBC 绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F .连接EF ,设△BEF 与△BFC 的面积的差为S ,问当CF 为何值时,S 最小,并求出这个最小值。
2021年重庆市中考二轮复习数学第26题几何证明专练专题(四)

重庆市中考二轮复习数学第26题几何证明专练专题(四)1.如图(甲),在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)在如图(甲)中,若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?证明你的结论.(3)运用(1)(2)解答中积累的经验和知识,完成下题:如图(乙)四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,点E是AB上一点,且∠DCE=45°,BE=2,求DE的长.2.如图,菱形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD,连接OE.(1)求证:OE=CD;(2)探究:当∠ABC等于多少度时,四边形OCED是正方形?并证明你的结论.3.已知,在平行四边形ABCD中,AC=AD,AE⊥CD于点E,BF⊥AC分别交AC、AE于点G、点F,连接GE,若BF=BC.(1)若BE=12,求平行四边形ABCD的面积.(2)求证:GE=2AG.4,如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.5.已知,在平行四边形ABCD中,E为AD上一点,且AB=AE,连接BE交AC于点H,过点A作AF⊥BC于F,交BE于点G.(1)若∠D=50°,求∠EBC的度数.(2)若AC⊥CD,过点G作GM∥BC交AC于点M,求证:AH=MC.6.正方形ABCD中,E是BC上一点,F是CD延长线上一点,BE=DF,连接AE,AF,EF,G为EF中点,连接AG,DG.(1)如图1:若AB=3,BE=1,求DG;(2)如图2:延长GD至M,使GM=GA,过M作MN∥FD交AF的延长线于N,连接NG,若∠BAE=30°,求证:NM+NA=3NG.7.如图,在平行四边形ABCD 中,AC=BC,E 是AB 中点,G 在AD 延长线上,连接CE 、BG 相交于点F.(1)若BC=6,∠ABC=75°,求平行四边形ABCD 的面积;(2)若∠GBC=∠ECB,求证:GF=BF+2EF.8.在菱形ABCD 中,∠B=60°,E 是边CD 上一点,以CE 为边作等边△CEF .(1)如图1,当CE⊥AD,CF=32时,求菱形ABCD 的面积;(2)如图2,过点E 作∠CEF 的平分线交CF 于H,连接DH,并延长DH 与AC 的延长交于点P,若∠ECD=15°,求证:CF=26CP9.如图,平行四边形ABCD中,CG⊥AB于点G,∠ABF=45°,F在CD上,BF交CD于点E,连接AE,AE⊥AD.(1)若BG=1,BC=1O,求EF的长度;(2)求证:CE+2BE=AB.10.如图,在矩形ABCD中,点E为AD上一点,连接BE、CE∠ABE=45°.(1)如图1,若BE=32,BC=4,求DE.(2)如图2,点P是EC的中点,连接BP并延长交CD于点F,H为AD上一点,连接HF,且∠DHF=∠CBF,求证:BP=PF+FH.11.在平行四边形ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.(1)若AB=22,BC=7,求CE的长.(2)求证:BE=CG-AG.12.如图,在菱形ABCD中,∠BAD=120°,E为AB边上一点,过E作EG⊥BC于点G,交对角线BD于点F.(1)如图(1),若∠ACE=15°,BC=6,求EF的长.(2)如图(2),H为CE的中点,连接AF,求证:AF=2FH.13.已知平行四边形ABCD ,过点A 作BC 的垂线,垂足为点E ,且满足AE =EC ,过点C 作AB 的垂线,垂足为点F ,交AE 于点G ,连接BG .(1)如图1,若AC =,CD =4,求BC 的长度;(2)如图2取AC 上一点Q ,连接EQ ,在△QEC 内取一点,连接QH ,EH ,过点H 作AC 的垂线,垂足为点P ,若QH =EH ,∠QEH =45°.求证:AQ =2HP .14.如图,在平行四边形 ABCD 中, A C 为对角线,过点 D 作 DE ⊥ DC 交直线 AB 于点 E ,过点 E 作 EH ⊥ AD 于点 H ,过点 B 作 BF ⊥ AD 于点 F .(1)如图 1,若∠BAD = 60︒ , AF = 3 , AH = 2 ,求 AC 的长;( 2 )如图 2 ,若 BF = DH ,在 AC 上取一点 G , 连接 DG 、 GE ,若 ∠DGE = 75︒ ,∠CDG = 45︒ - ∠CAB ,求证: DG =26CG15.如图,正方形ABCD中,E为AB边上一点,过点D作DF⊥DE,与BC延长线交于点F,连接EF,与CD边交于点G,与对角线BD交于点H.(1)若BF=BD=2,求BE的长:(2)若∠ADE=2∠BFE,求证:FH=HE+HD。
2020重庆中考复习数学第26题专题训练六(含答案解析)

2020重庆中考复习数学第26题专题训练六 1、如图1,在△ABC中,∠BAC=90°,AC=2AB,D是线段AC中点,E是线段AD上一点,过点D作DF⊥BE交BE的延长钱于点F,连接AF,过点A作AG⊥AF于点A,交BF于点G(1)若∠ABE=∠C,BC=2,求AE的长;(2)若点E为AD中点,求证:GE﹣FE=FD;(3)如图2,连接BD,点N为BD中点,连接GN,若AD=GF,请直接写出NG、GE、EA的数量关系.4、已知△ABC中,点D为BC的中点,BD=AB,AD⊥BC.(1)如图1,求∠BAD的度数;(2)如图2,点E为BC上一点,点F为AC上一点,连接AE、BF交于点G,若∠AGF=60°,求证:BE=CF;(3)如图3,在(2)的条件下,点G为BF的中点,点H为AG上一点,延长BH交AC于点K,AK =HK,BM⊥AE交AE延长线于点M,BG=9,HM=10,求线段AG的长.5、已知△ABC中,∠B=60°,点D是AB边上的动点,过点D作DE∥BC交AC于点E,将△ADE沿DE折叠,点A对应点为F点.(1)如图1,当点F恰好落在BC边上,求证:△BDF是等边三角形;(2)如图2,当点F恰好落在△ABC内,且DF的延长线恰好经过点C,CF=EF,求∠A的大小;(3)如图3,当点F恰好落在△ABC外,DF交BC于点G,连接BF,若BF⊥AB,AB=9,求BG 的长.6、如图,在△ABC中,AB=AC,∠BAC=90°,D为BC边的中点,点E在直线BC上(不与点D重合),连接AE,过点C作直线AE的垂线,垂足为点F,交直线AD于点G,连接EG.(1)如图(1),当点E在线段BD上时,易证DE=DG,请直接写出三条线段BE,AB,EG之间的数量关系是 ;(2)如图(2),当点E在线段BC的延长线上时,请写出三条线段BE、AB、EG之间的数量关系,并证明你的结论;(3)若线段BC=2,当△AEG为等腰三角形时,请直接写出的值.7、如图,在△ABC中,∠BAC=90°,将△ABC沿AD翻折,点B恰好与点C重合,点E在AC边上,连接BE.(1)如图①,若点F是BE的中点,连接DF,且AF=5,AE=6,求DF的长;(2)如图②,若AF⊥BE于点F,并延长AF交BC于点G,当点E是AC的中点时,连接EG,求证:AG+EG=BE;(3)在(2)的条件下,连接DF,请直接写出∠DFG的度数.8、如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D、E分别在AC、BC上,BD与AE交于点O,且CD=CE,若点F是BD的中点,连接CF,交AE于点G.(1)求证:CF⊥AE;(2)如图2,过点F作FM⊥BC,交AE的延长线于点M,垂足为H,连接CM,若CG=GM.①求证:CF=CM;②求的值.9、(1)【问题发现】如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为AC的中点,过点A作BD的垂线,垂足为E,延长AE交BC于点F,求△ABF的面积.小明发现,过点C作AC的垂线,交AF的延长线于点G,构造出全等三角形,经过推理和计算,能够得到BF与CF的数量关系,从而使问题得到解决,请直接填空:= 2,△ABF的面积为 .(2)【类比探究】如图2,将(1)中的条件“点D为AC的中点”改为“点D为边AC上的一点,且满足CD=2AD”,其他条件不变,试求△ABF的面积,并写出推理过程.(3)【拓展迁移】如图3,在△ABC中,AB=AC=4,∠BAC=120°,点D为AC上一点,且满足CD =2AD,E为BD上一点,∠AEB=60°,延长AE交BC于F,请直接写出△ABF的面积.2020重庆中考复习数学第26题专题训练六参考答案 1、如图1,在△ABC中,∠BAC=90°,AC=2AB,D是线段AC中点,E是线段AD上一点,过点D作DF⊥BE交BE的延长钱于点F,连接AF,过点A作AG⊥AF于点A,交BF于点G(1)若∠ABE=∠C,BC=2,求AE的长;(2)若点E为AD中点,求证:GE﹣FE=FD;(3)如图2,连接BD,点N为BD中点,连接GN,若AD=GF,请直接写出NG、GE、EA的数量关系.解:(1)∵△ABC中,∠BAC=90°,AC=2AB,BC=2,∴由勾股定理可得AB=2,AC=4,∵∠ABE=∠C,∠BAE=∠CAB=90°,∴△BAE∽△CAB,∴AB2=AE×AC,即22=AE×4,解得AE=1,(2)证明:如图1,过A作AH⊥BF于H,则∠AHE=90°,∵DF⊥BE,∠BAC=90°,∠AEB=∠FED,∴∠ABG=∠ADF,∵AG⊥AF,∠BAC=90°,∴∠BAG=∠DAF,∵AC=2AB,D是线段AC中点,∴AB=AD,在△ABG和△ADF中,,∴△ABG≌△ADF(ASA),∴AG=AF,∴△AGF是等腰直角三角形,∴AH=GF=GH,∵点E为AD中点,∴AE=DE,在△AEH和△DEF中,,∴△AEH≌△DEF(AAS),∴EH=EF,AH=DF=GH,∵GE﹣HE=GH,∴GE﹣FE=FD;(3)NG、GE、EA的数量关系为:NG+GE=2AE.理由:如图2,连接AN,NF,由(2)可得,△AGF是等腰直角三角形,∵AB=AD,∠BAD=90°,N是BD的中点,∴∠DAN=45°=∠ADN,∴△ADN是等腰直角三角形,∵AD=GF,∴等腰Rt△AGF与等腰Rt△ADN全等,∴AG=AF=AN=ND,∵Rt△BDF中,N是BD的中点,∴NF=ND=BN,∴AN=NF=AF,即△ANF是等边三角形,∴∠NAF=∠ANF=60°,∵∠DAN=45°,△ABG≌△ADF,∴∠DAF=15°=∠BAG,∵∠ABN=∠BAN=45°,∴∠GAN=30°,∵∠AGF=45°,∴∠ABE=30°,∴Rt△ABE中,BE=2AE,∵∠ABN=45°,∴∠GBN=15°,由NF=ND=NB,可得∠FND=2∠GBN=30°,在△ANG和△NDF中,,∴△ANG≌△NDF(SAS),∴GN=FD=BG,∵BG+GE=BE=2AE,∴NG+GE=2AE.MDEFBACG解: (1)由E 为CR 中点可得AG 平分BAC ,过G 作GH AB ,则有GH=CG=1,故BG=2(2)延长FD 交AG 于点M ,易证:()BFD AMD AAS ,所以BF=AM再证:()BFC CEA AAS ,所以BF=CE=AM ,CF=AE∴CF-CE=AE-AM ,即EM=EF ∴EFM 为等腰直角三角形 ∴222EFFMDF(3)结论为:622BDEF4、(2017秋?许昌月考)已知△ABC中,点D为BC的中点,BD=AB,AD⊥BC.(1)如图1,求∠BAD的度数;(2)如图2,点E为BC上一点,点F为AC上一点,连接AE、BF交于点G,若∠AGF=60°,求证:BE=CF;(3)如图3,在(2)的条件下,点G为BF的中点,点H为AG上一点,延长BH交AC于点K,AK =HK,BM⊥AE交AE延长线于点M,BG=9,HM=10,求线段AG的长.解:(1)∵点D为BC的中点,AD⊥BC,∴AB=AC,BD=CD=BC,∵BD=AB,∴AB=BC=AC,∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BC,∴∠BAD=∠BAC=30°;(2)由(1)知,△ABC是等边三角形,∴AB=BC,∠ABC=∠C=60°,∴∠ABF+∠CBF=60°,∵∠AGF=60°,∴∠BAE+∠ABF=60°,∴∠BAE=∠CBF,在△ABE和△BCF中,,∴△ABE≌△BCF(ASA),∴BE=CF,(3)如图,过F作FN⊥AE于N,过F作FD⊥BM,交BM的延长线于D,∵AM⊥BM,∴GM∥DF,∵BG=GF,∴BM=DM,∵∠AGF=60°,∴∠BGM=60°,∵BM⊥AE,∴∠BMG=90°,∴∠GBM=30°,在Rt△BMG中,MG=BG=,BM=DM=FN=,∵AK=HK,∴∠HAK=∠AHK=∠BHM,∵∠ANF=∠HMB=90°,∴△ANF≌△HMB,∴AN=HM=10,Rt△FGN中,∠NFG=∠GBM=30°,∴GN=GF=,∴AG=AN+NG=10+=14.5.5、(2019秋?中山市期末)已知△ABC中,∠B=60°,点D是AB边上的动点,过点D作DE∥BC交AC于点E,将△ADE沿DE折叠,点A对应点为F点.(1)如图1,当点F恰好落在BC边上,求证:△BDF是等边三角形;(2)如图2,当点F恰好落在△ABC内,且DF的延长线恰好经过点C,CF=EF,求∠A的大小;(3)如图3,当点F恰好落在△ABC外,DF交BC于点G,连接BF,若BF⊥AB,AB=9,求BG 的长.(1)证明:如图1,∵∠B=60°,DE∥BC,∴∠ADE=∠B=60°,∵△ADE沿DE折叠,点A对应点为F点,∴∠ADE=∠FDE=60°,∴∠BDF=60°,∴∠DFB=60°=∠B=∠BDF,∴△BDF是等边三角形;(2)解:∵∠B=60°,DE∥BC,∴∠ADE=∠B=60°,∵△ADE沿DE折叠,点A对应点为F点,∴∠ADE=∠FDE=60°,∠A=∠DFE,∴∠ADC=120°,∵CF=EF,∴∠FEC=∠FCE,设∠FEC=∠FCE=x,则∠A=∠DFE=∠FEC+∠FCE=2x,在△ADC中,∠A+∠ACD+∠ADC=180°,即2x+x+120°=180°,解得:x=20°,∴∠A=2x=40°;(3)解:同(1)得:∠BDF=60°,△BDG是等边三角形,∠ADE=∠B=60°,∴BG=BD,由折叠的性质得:AD=FD,∵BF⊥AB,∴∠BFD=90°﹣60°=30°,∴FD=2BD,∴AD=2BD,∵AD+BD=AB,∴2BD+BD=9,∴BD=3,∴BG=BD=3.6、(2018?连山区一模)如图,在△ABC中,AB=AC,∠BAC=90°,D为BC边的中点,点E在直线BC上(不与点D重合),连接AE,过点C作直线AE的垂线,垂足为点F,交直线AD于点G,连接EG.(1)如图(1),当点E在线段BD上时,易证DE=DG,请直接写出三条线段BE,AB,EG之间的数量关系是 AB﹣EG=BE;(2)如图(2),当点E在线段BC的延长线上时,请写出三条线段BE、AB、EG之间的数量关系,并证明你的结论;(3)若线段BC=2,当△AEG为等腰三角形时,请直接写出的值.解:(1)如图1中,结论:AB﹣EG=BE理由:∵AB=AC,∠BAC=90°,BD=DC,∴AD⊥BC,∠ABC=∠ACB=45°,AD=BD=DC,∴BD=AB,∵CF⊥AE,∴∠AFG=∠CDG=90°,∵∠AGF=∠CGD,∴∠FAG=∠GCD,∵∠ADE=∠CDG,∴△ADE≌△CDG,∴DE=DG,∴DE=EG,∵BE+ED=BD,∴BE+EG=AB,∴AB﹣EG=BE.(2)如图2中,结论:AB+EG=BE.理由:同法可证:△ADE≌△CDG,∴DE=DG,∴DE=EG,∵BE﹣ED=BD,∴BE+﹣EG=AB,∴AB+EG=BE.(3)①如图2中,当GA=GE时,DG=DE=2﹣2,EG=4﹣2,此时:==﹣1.②如图3中,当GA=GE时,设BD=AD=CD=a,则AB=AC=CE=a,DG=DE=a+a,EG=a+2a,∴==1+.③当点E与点C重合时,EG=AB,可得EG:AB=1,综上所述,的值为﹣1或1+或1.7、(2018?站前区校级一模)如图,在△ABC中,∠BAC=90°,将△ABC沿AD翻折,点B恰好与点C重合,点E在AC边上,连接BE.(1)如图①,若点F是BE的中点,连接DF,且AF=5,AE=6,求DF的长;(2)如图②,若AF⊥BE于点F,并延长AF交BC于点G,当点E是AC的中点时,连接EG,求证:AG+EG=BE;(3)在(2)的条件下,连接DF,请直接写出∠DFG的度数.解:(1)∵将△ABC沿AD翻折,点B恰好与点C重合,∴AB=AC,BD=CD,∠ADB=∠ADC=90°,且∠BAC=90°,∴△ABC是等腰直角三角形,∵点F是BE的中点,AF=5,∠BAC=90°,∴BE=10,∴AB===8,∴AC=8,∴EC=2,∵BD=CD,BF=EF,∴DF=EC=1,(2)如图②,过点C作CH⊥AC交AG的延长线于点H,∵AB=AC,∠BAC=90°,BD=CD,∴∠ABC=∠BAD=∠DAC=∠ACB=45°,∵∠BEA+∠CAH=90°,∠CAH+∠H=90°,∴∠H=∠BEA,且AB=AC,∠AFB=∠ACH=90°,∴△ABE≌△CAH(AAS)∴BE=AH,AE=CH,∠CAH=∠ABE,∵AE=CE,∴CE=CH,∵∠ACH=90°,∠ACB=45°,∴∠ACB=∠GCH,且CE=CH,CG=CG,∴△CEG≌△CHG(SAS)∴EG=GH,∵BE=AH=AG+GH,∴AG+EG=BE;(3)如图②,连接NG,∵∠ABC=∠BAD=∠DAC=∠ACB=45°,∴AD=BD=CD,∵∠BAN=∠ACG=45°,AB=AC,∠ABE=∠CAH,∴△ABN≌△CAG(ASA)∴AN=CG,∴AD﹣AN=CD﹣CG,∴DN=DG,∴∠DNG=45°∵∠NDG=∠NFG=90°,∴点N,点F,点G,点D四点共圆,∴∠DFG=∠DNG=45°.8、如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D、E分别在AC、BC上,BD与AE交于点O,且CD=CE,若点F是BD的中点,连接CF,交AE于点G.(1)求证:CF⊥AE;(2)如图2,过点F作FM⊥BC,交AE的延长线于点M,垂足为H,连接CM,若CG=GM.①求证:CF=CM;②求的值.(1)证明:如图1中,∵AC=BC,∠ACE=∠BCD=90°,CE=CD,∴△ACE≌△BCD(SAS),∴∠CAE=∠CBD,∵DF=FB,∴CF=FD=FB,∴∠FCB=∠FBC,∴∠FCB=∠CAE,∵∠CAB+∠AEC=90°,∴∠AEC+∠FCB=90°,∴∠CGE=90°,∴CF⊥AE.(2)①证明:如图2中,∵FM⊥BC,∴∠FHC=∠CGE=∠MGF=90°,∴∠ECG+∠CEG=90°,∠ECG+∠CFH=90°,∴∠CEG=∠CFH,∵CG=GM,∴△CGE≌△MGF(AAS),∴CE=FM,EG=GF,∵CD=CE,∴CD=FM,∵∠FHB=∠ACB=90°,∴CD∥FM,∴四边形CDFM是平行四边形,∴CM=DF,∵CF=DF=FB,∴CM=CF.②连接EF,BM.设FG=EG=a,∵CM=BF,CM∥BF,∴FG∥BM,∴=,∵△CAE≌△CBD,∴∠CAE=∠CBD,∵∠CAB=∠CBA,∴∠OAB=∠OBA,∴OA=OB,∴=,易知OG=GF=EG=a,EF=EM=a,∴OM=2a+a,∴==.9、(2015?新乡二模)(1)【问题发现】如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为AC的中点,过点A作BD的垂线,垂足为E,延长AE交BC于点F,求△ABF的面积.小明发现,过点C作AC的垂线,交AF的延长线于点G,构造出全等三角形,经过推理和计算,能够得到BF与CF的数量关系,从而使问题得到解决,请直接填空:= 2,△ABF的面积为 .(2)【类比探究】如图2,将(1)中的条件“点D为AC的中点”改为“点D为边AC上的一点,且满足CD=2AD”,其他条件不变,试求△ABF的面积,并写出推理过程.(3)【拓展迁移】如图3,在△ABC中,AB=AC=4,∠BAC=120°,点D为AC上一点,且满足CD =2AD,E为BD上一点,∠AEB=60°,延长AE交BC于F,请直接写出△ABF的面积.解:(1)如图1,过点C作AC的垂线,交AF的延长线于点G.∵∠BAC=90°,∴∠ABD+∠ADB=90°,∵AE⊥BD,∴∠DAE+∠ADB=90°,∴∠CAG=∠ABD,在△ACG和△BAD中,,∴△ACG≌△BAD(ASA),∴CG=AD=AC=,∵BA∥CG,∴△CFG∽△BFA,∴==,即BF=BC,BF:CF=2,∴△ABF的面积=××4×4=;故答案为2,.(2)如图2,过点C作AC的垂线,交AF的延长线于点H.∵∠BAC=90°∴∠ABD+∠ADB=90°,∵AE⊥BD,∴∠DAE+∠ADB=90°,∴∠CAG=∠ABD,在△ACG和△BAD中,,∴△ACH≌△BAD(ASA),∴CH=AD=AC=AB,∵BA∥CH,∴△CFH∽△BFA,∴==,即BF=BC,∴△ABF的面积=××4×4=6;(3)如图3中,作CH⊥BC交AF的延长线于H,AK⊥BC于K.∵AB=AC,∠BAC=120°,∴∠ABC=∠ACB=30°,∵∠BCH=90°,∴∠ACH=∠BAD=120°,∵∠ABD+∠ADB=180°﹣120°=60°,∠AEB=∠EAD+∠ADE=60°,∴∠ABD=∠CAH,∴△BAD≌△ACH(ASA),∴CH=AD∵AK⊥BC,∴BK=CK,在Rt△ACK中,∵AC=4,∠ACK=30°,∴AK=AC=2,CK=BK=2,∵AK∥CH,AD=CH=,∴FK:FC=AK:CH=2:=3:2,∴BF:BC=4:5,∴S△ABF=?S△ABC=××4×2=.。
2020重庆中考复习数学第26题专题训练六(含答案解析)

2020重庆中考复习数学第26题专题训练六1、如图1,在△ABC中,∠BAC=90°,AC=2AB,D是线段AC中点,E是线段AD上一点,过点D作DF⊥BE交BE的延长钱于点F,连接AF,过点A作AG⊥AF于点A,交BF于点G(1)若∠ABE=∠C,BC=2,求AE的长;(2)若点E为AD中点,求证:GE﹣FE=FD;(3)如图2,连接BD,点N为BD中点,连接GN,若AD=GF,请直接写出NG、GE、EA的数量关系.4、已知△ABC中,点D为BC的中点,BD=AB,AD⊥BC.(1)如图1,求∠BAD的度数;(2)如图2,点E为BC上一点,点F为AC上一点,连接AE、BF交于点G,若∠AGF=60°,求证:BE=CF;(3)如图3,在(2)的条件下,点G为BF的中点,点H为AG上一点,延长BH交AC于点K,AK =HK,BM⊥AE交AE延长线于点M,BG=9,HM=10,求线段AG的长.5、已知△ABC中,∠B=60°,点D是AB边上的动点,过点D作DE∥BC交AC于点E,将△ADE沿DE折叠,点A对应点为F点.(1)如图1,当点F恰好落在BC边上,求证:△BDF是等边三角形;(2)如图2,当点F恰好落在△ABC内,且DF的延长线恰好经过点C,CF=EF,求∠A的大小;(3)如图3,当点F恰好落在△ABC外,DF交BC于点G,连接BF,若BF⊥AB,AB=9,求BG 的长.6、如图,在△ABC中,AB=AC,∠BAC=90°,D为BC边的中点,点E在直线BC上(不与点D重合),连接AE,过点C作直线AE的垂线,垂足为点F,交直线AD于点G,连接EG.(1)如图(1),当点E在线段BD上时,易证DE=DG,请直接写出三条线段BE,AB,EG之间的数量关系是 ;(2)如图(2),当点E在线段BC的延长线上时,请写出三条线段BE、AB、EG之间的数量关系,并证明你的结论;(3)若线段BC=2,当△AEG为等腰三角形时,请直接写出的值.7、如图,在△ABC中,∠BAC=90°,将△ABC沿AD翻折,点B恰好与点C重合,点E在AC边上,连接BE.(1)如图①,若点F是BE的中点,连接DF,且AF=5,AE=6,求DF的长;(2)如图②,若AF⊥BE于点F,并延长AF交BC于点G,当点E是AC的中点时,连接EG,求证:AG+EG=BE;(3)在(2)的条件下,连接DF,请直接写出∠DFG的度数.8、如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D、E分别在AC、BC上,BD与AE交于点O,且CD=CE,若点F是BD的中点,连接CF,交AE于点G.(1)求证:CF⊥AE;(2)如图2,过点F作FM⊥BC,交AE的延长线于点M,垂足为H,连接CM,若CG=GM.①求证:CF=CM;②求的值.9、(1)【问题发现】如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为AC的中点,过点A作BD的垂线,垂足为E,延长AE交BC于点F,求△ABF的面积.小明发现,过点C作AC的垂线,交AF的延长线于点G,构造出全等三角形,经过推理和计算,能够得到BF与CF的数量关系,从而使问题得到解决,请直接填空:= 2,△ABF的面积为.(2)【类比探究】如图2,将(1)中的条件“点D为AC的中点”改为“点D为边AC上的一点,且满足CD=2AD”,其他条件不变,试求△ABF的面积,并写出推理过程.(3)【拓展迁移】如图3,在△ABC中,AB=AC=4,∠BAC=120°,点D为AC上一点,且满足CD =2AD,E为BD上一点,∠AEB=60°,延长AE交BC于F,请直接写出△ABF的面积.2020重庆中考复习数学第26题专题训练六参考答案1、如图1,在△ABC中,∠BAC=90°,AC=2AB,D是线段AC中点,E是线段AD上一点,过点D作DF⊥BE交BE的延长钱于点F,连接AF,过点A作AG⊥AF于点A,交BF于点G(1)若∠ABE=∠C,BC=2,求AE的长;(2)若点E为AD中点,求证:GE﹣FE=FD;(3)如图2,连接BD,点N为BD中点,连接GN,若AD=GF,请直接写出NG、GE、EA的数量关系.解:(1)∵△ABC中,∠BAC=90°,AC=2AB,BC=2,∴由勾股定理可得AB=2,AC=4,∵∠ABE=∠C,∠BAE=∠CAB=90°,∴△BAE∽△CAB,∴AB2=AE×AC,即22=AE×4,解得AE=1,(2)证明:如图1,过A作AH⊥BF于H,则∠AHE=90°,∵DF⊥BE,∠BAC=90°,∠AEB=∠FED,∴∠ABG=∠ADF,∵AG⊥AF,∠BAC=90°,∴∠BAG=∠DAF,∵AC=2AB,D是线段AC中点,∴AB=AD,在△ABG和△ADF中,,∴△ABG≌△ADF(ASA),∴AG=AF,∴△AGF是等腰直角三角形,∴AH=GF=GH,∵点E为AD中点,∴AE=DE,在△AEH和△DEF中,,∴△AEH≌△DEF(AAS),∴EH=EF,AH=DF=GH,∵GE﹣HE=GH,∴GE﹣FE=FD;(3)NG、GE、EA的数量关系为:NG+GE=2AE.理由:如图2,连接AN,NF,由(2)可得,△AGF是等腰直角三角形,∵AB=AD,∠BAD=90°,N是BD的中点,∴∠DAN=45°=∠ADN,∴△ADN是等腰直角三角形,∵AD=GF,∴等腰Rt△AGF与等腰Rt△ADN全等,∴AG=AF=AN=ND,∵Rt△BDF中,N是BD的中点,∴NF=ND=BN,∴AN=NF=AF,即△ANF是等边三角形,∴∠NAF=∠ANF=60°,∵∠DAN=45°,△ABG≌△ADF,∴∠DAF=15°=∠BAG,∵∠ABN=∠BAN=45°,∴∠GAN=30°,∵∠AGF=45°,∴∠ABE=30°,∴Rt△ABE中,BE=2AE,∵∠ABN=45°,∴∠GBN=15°,由NF=ND=NB,可得∠FND=2∠GBN=30°, 在△ANG和△NDF中,,∴△ANG≌△NDF(SAS),∴GN=FD=BG,∵BG+GE=BE=2AE,∴NG+GE=2AE.G解:(1)由E 为CR 中点可得AG平分BAC ∠,过G 作GH AB ⊥,则有GH=CG=1,故 (2)延长FD 交AG 于点M,易证:()BFD AMD AAS ∆≅∆,所以BF=AM 再证:()BFC CEA AAS∆≅∆,所以BF=CE=AM,CF=AE ∴CF-CE=AE-AM,即EM=EF ∴EFM ∆为等腰直角三角形∴2EF FM ==(3)结论为:2BD EF +=4、(2017秋•许昌月考)已知△ABC中,点D为BC的中点,BD=AB,AD⊥BC.(1)如图1,求∠BAD的度数;(2)如图2,点E为BC上一点,点F为AC上一点,连接AE、BF交于点G,若∠AGF=60°,求证:BE=CF;(3)如图3,在(2)的条件下,点G为BF的中点,点H为AG上一点,延长BH交AC于点K,AK =HK,BM⊥AE交AE延长线于点M,BG=9,HM=10,求线段AG的长.解:(1)∵点D为BC的中点,AD⊥BC,∴AB=AC,BD=CD=BC,∵BD=AB,∴AB=BC=AC,∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BC,∴∠BAD=∠BAC=30°;(2)由(1)知,△ABC是等边三角形,∴AB=BC,∠ABC=∠C=60°,∴∠ABF+∠CBF=60°,∵∠AGF=60°,∴∠BAE+∠ABF=60°,∴∠BAE=∠CBF,在△ABE和△BCF中,,∴△ABE≌△BCF(ASA),∴BE=CF,(3)如图,过F作FN⊥AE于N,过F作FD⊥BM,交BM的延长线于D,∵AM⊥BM,∴GM∥DF,∵BG=GF,∴BM=DM,∵∠AGF=60°,∴∠BGM=60°,∵BM⊥AE,∴∠BMG=90°,∴∠GBM=30°,在Rt△BMG中,MG=BG=,BM=DM=FN=,∵AK=HK,∴∠HAK=∠AHK=∠BHM,∵∠ANF=∠HMB=90°,∴△ANF≌△HMB,∴AN=HM=10,Rt△FGN中,∠NFG=∠GBM=30°,∴GN=GF=,∴AG=AN+NG=10+=14.5.5、(2019秋•中山市期末)已知△ABC中,∠B=60°,点D是AB边上的动点,过点D作DE∥BC交AC于点E,将△ADE沿DE折叠,点A对应点为F点.(1)如图1,当点F恰好落在BC边上,求证:△BDF是等边三角形;(2)如图2,当点F恰好落在△ABC内,且DF的延长线恰好经过点C,CF=EF,求∠A的大小;(3)如图3,当点F恰好落在△ABC外,DF交BC于点G,连接BF,若BF⊥AB,AB=9,求BG 的长.(1)证明:如图1,∵∠B=60°,DE∥BC,∴∠ADE=∠B=60°,∵△ADE沿DE折叠,点A对应点为F点,∴∠ADE=∠FDE=60°,∴∠BDF=60°,∴∠DFB=60°=∠B=∠BDF,∴△BDF是等边三角形;(2)解:∵∠B=60°,DE∥BC,∴∠ADE=∠B=60°,∵△ADE沿DE折叠,点A对应点为F点,∴∠ADE=∠FDE=60°,∠A=∠DFE,∴∠ADC=120°,∵CF=EF,∴∠FEC=∠FCE,设∠FEC=∠FCE=x,则∠A=∠DFE=∠FEC+∠FCE=2x,在△ADC中,∠A+∠ACD+∠ADC=180°,即2x+x+120°=180°,解得:x=20°,∴∠A=2x=40°;(3)解:同(1)得:∠BDF=60°,△BDG是等边三角形,∠ADE=∠B=60°,∴BG=BD, 由折叠的性质得:AD=FD,∵BF⊥AB,∴∠BFD=90°﹣60°=30°,∴FD=2BD,∴AD=2BD,∵AD+BD=AB,∴2BD+BD=9,∴BD=3,∴BG=BD=3.6、(2018•连山区一模)如图,在△ABC中,AB=AC,∠BAC=90°,D为BC边的中点,点E在直线BC上(不与点D重合),连接AE,过点C作直线AE的垂线,垂足为点F,交直线AD于点G,连接EG. (1)如图(1),当点E在线段BD上时,易证DE=DG,请直接写出三条线段BE,AB,EG之间的数量关系是 AB﹣EG=BE;(2)如图(2),当点E在线段BC的延长线上时,请写出三条线段BE、AB、EG之间的数量关系,并证明你的结论;(3)若线段BC=2,当△AEG为等腰三角形时,请直接写出的值.解:(1)如图1中,结论:AB﹣EG=BE理由:∵AB=AC,∠BAC=90°,BD=DC,∴AD⊥BC,∠ABC=∠ACB=45°,AD=BD=DC,∴BD=AB,∵CF⊥AE,∴∠AFG=∠CDG=90°,∵∠AGF=∠CGD,∴∠F AG=∠GCD,∵∠ADE=∠CDG,∴△ADE≌△CDG,∴DE=DG,∴DE=EG,∵BE+ED=BD,∴BE+EG=AB,∴AB﹣EG=BE.(2)如图2中,结论:AB+EG=BE.理由:同法可证:△ADE≌△CDG,∴DE=DG,∴DE=EG,∵BE﹣ED=BD,∴BE+﹣EG=AB,∴AB+EG=BE.(3)①如图2中,当GA=GE时,DG=DE=2﹣2,EG=4﹣2,此时:==﹣1.②如图3中,当GA=GE时,设BD=AD=CD=a,则AB=AC=CE=a,DG=DE=a+a,EG=a+2a,∴==1+.③当点E与点C重合时,EG=AB,可得EG:AB=1,综上所述,的值为﹣1或1+或1.7、(2018•站前区校级一模)如图,在△ABC中,∠BAC=90°,将△ABC沿AD翻折,点B恰好与点C重合,点E在AC边上,连接BE.(1)如图①,若点F是BE的中点,连接DF,且AF=5,AE=6,求DF的长;(2)如图②,若AF⊥BE于点F,并延长AF交BC于点G,当点E是AC的中点时,连接EG,求证:AG+EG=BE;(3)在(2)的条件下,连接DF,请直接写出∠DFG的度数.解:(1)∵将△ABC沿AD翻折,点B恰好与点C重合,∴AB=AC,BD=CD,∠ADB=∠ADC=90°,且∠BAC=90°,∴△ABC是等腰直角三角形,∵点F是BE的中点,AF=5,∠BAC=90°,∴BE=10,∴AB===8,∴AC=8,∴EC=2,∵BD=CD,BF=EF,∴DF=EC=1,(2)如图②,过点C作CH⊥AC交AG的延长线于点H,∵AB=AC,∠BAC=90°,BD=CD,∴∠ABC=∠BAD=∠DAC=∠ACB=45°,∵∠BEA+∠CAH=90°,∠CAH+∠H=90°,∴∠H=∠BEA,且AB=AC,∠AFB=∠ACH=90°,∴△ABE≌△CAH(AAS)∴BE=AH,AE=CH,∠CAH=∠ABE,∵AE=CE,∴CE=CH,∵∠ACH=90°,∠ACB=45°,∴∠ACB=∠GCH,且CE=CH,CG=CG,∴△CEG≌△CHG(SAS)∴EG=GH,∵BE=AH=AG+GH,∴AG+EG=BE;(3)如图②,连接NG,∵∠ABC=∠BAD=∠DAC=∠ACB=45°,∴AD=BD=CD,∵∠BAN=∠ACG=45°,AB=AC,∠ABE=∠CAH,∴△ABN≌△CAG(ASA)∴AN=CG,∴AD﹣AN=CD﹣CG,∴DN=DG,∴∠DNG=45°∵∠NDG=∠NFG=90°,∴点N,点F,点G,点D四点共圆,∴∠DFG=∠DNG=45°.8、如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D、E分别在AC、BC上,BD与AE交于点O,且CD=CE,若点F是BD的中点,连接CF,交AE于点G.(1)求证:CF⊥AE;(2)如图2,过点F作FM⊥BC,交AE的延长线于点M,垂足为H,连接CM,若CG=GM.①求证:CF=CM;②求的值.(1)证明:如图1中,∵AC=BC,∠ACE=∠BCD=90°,CE=CD,∴△ACE≌△BCD(SAS),∴∠CAE=∠CBD,∵DF=FB,∴CF=FD=FB,∴∠FCB=∠FBC,∴∠FCB=∠CAE,∵∠CAB+∠AEC=90°,∴∠AEC+∠FCB=90°,∴∠CGE=90°,∴CF⊥AE.(2)①证明:如图2中,∵FM⊥BC,∴∠FHC=∠CGE=∠MGF=90°,∴∠ECG+∠CEG=90°,∠ECG+∠CFH=90°, ∴∠CEG=∠CFH,∵CG=GM,∴△CGE≌△MGF(AAS),∴CE=FM,EG=GF,∵CD=CE,∴CD=FM,∵∠FHB=∠ACB=90°,∴CD∥FM,∴四边形CDFM是平行四边形,∴CM=DF,∵CF=DF=FB,∴CM=CF.②连接EF,BM.设FG=EG=a,∵CM=BF,CM∥BF,∴FG∥BM,∴=,∵△CAE≌△CBD,∴∠CAE=∠CBD,∵∠CAB=∠CBA,∴∠OAB=∠OBA,∴OA=OB,∴=,易知OG=GF=EG=a,EF=EM=a,∴OM=2a+a,∴==.9、(2015•新乡二模)(1)【问题发现】如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为AC的中点,过点A作BD的垂线,垂足为E,延长AE交BC于点F,求△ABF的面积.小明发现,过点C作AC的垂线,交AF的延长线于点G,构造出全等三角形,经过推理和计算,能够得到BF与CF的数量关系,从而使问题得到解决,请直接填空:= 2,△ABF的面积为.(2)【类比探究】如图2,将(1)中的条件“点D为AC的中点”改为“点D为边AC上的一点,且满足CD=2AD”,其他条件不变,试求△ABF的面积,并写出推理过程.(3)【拓展迁移】如图3,在△ABC中,AB=AC=4,∠BAC=120°,点D为AC上一点,且满足CD =2AD,E为BD上一点,∠AEB=60°,延长AE交BC于F,请直接写出△ABF的面积.解:(1)如图1,过点C作AC的垂线,交AF的延长线于点G.∵∠BAC=90°,∴∠ABD+∠ADB=90°,∵AE⊥BD,∴∠DAE+∠ADB=90°,∴∠CAG=∠ABD,在△ACG和△BAD中,,∴△ACG≌△BAD(ASA),∴CG=AD=AC=,∵BA∥CG,∴△CFG∽△BF A,∴==,即BF=BC,BF:CF=2,∴△ABF的面积=××4×4=;故答案为2,.(2)如图2,过点C作AC的垂线,交AF的延长线于点H.∵∠BAC=90°∴∠ABD+∠ADB=90°,∵AE⊥BD,∴∠DAE+∠ADB=90°,∴∠CAG=∠ABD,在△ACG和△BAD中,,∴△ACH≌△BAD(ASA),∴CH=AD=AC=AB,∵BA∥CH,∴△CFH∽△BF A,∴==,即BF=BC,∴△ABF的面积=××4×4=6;(3)如图3中,作CH⊥BC交AF的延长线于H,AK⊥BC于K.∵AB=AC,∠BAC=120°,∴∠ABC=∠ACB=30°,∵∠BCH=90°,∴∠ACH=∠BAD=120°,∵∠ABD+∠ADB=180°﹣120°=60°,∠AEB=∠EAD+∠ADE=60°, ∴∠ABD=∠CAH,∴△BAD≌△ACH(ASA),∴CH=AD∵AK⊥BC,∴BK=CK,在Rt△ACK中,∵AC=4,∠ACK=30°,∴AK=AC=2,CK=BK=2,∵AK∥CH,AD=CH=,∴FK:FC=AK:CH=2:=3:2,∴BF:BC=4:5,∴S△ABF=•S△ABC=××4×2=.。
最新重庆中考数学第26题专题训练

N MPCBA 1.如图,抛物线y=﹣x 2﹣2x+3 的图象与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,点D 为抛物线的顶点.(1)求A 、B 、C 的坐标;(2)点M 为线段AB 上一点(点M 不与点A 、B 重合),过点M 作x 轴的垂线,与直线AC 交于点E ,与抛物线交于点P ,过点P 作PQ ∥AB 交抛物线于点Q ,过点Q 作QN ⊥x 轴于点N .若点P 在点Q 左边,当矩形PQMN 的周长最大时,求△AEM 的面积;(3)在(2)的条件下,当矩形PMNQ 的周长最大时,连接DQ .过抛物线上一点F 作y轴的平行线,与直线AC 交于点G (点G 在点F 的上方).若FG=2DQ ,求点F 的坐标.2.如图,已知抛物线223y x x =-++与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,连接BC 。
(1)求A 、B 、C 三点的坐标;(2)若点P 为线段BC 上的一点(不与B 、C 重合),PM ∥y 轴,且PM 交抛物线于点M ,交x 轴于点N ,当△BCM 的面积最大时,求△BPN 的周长;(3)在(2)的条件下,当BCM 的面积最大时,在抛物线的对称轴上存在点Q ,使得△CNQ 为直角三角形,求点Q 的坐标。
3.如图,对称轴为直线x 1=-的抛物线()2y ax bx c a 0=++≠与x 轴相交于A 、B 两点,其中A 点的坐标为(-3,0)。
(1)求点B 的坐标;(2)已知a 1=,C 为抛物线与y 轴的交点。
①若点P 在抛物线上,且POC BOC S 4S ∆∆=,求点P 的坐标;②设点Q 是线段AC 上的动点,作QD ⊥x 轴交抛物线于点D ,求线段QD 长度的最大值。
4.如图,已知抛物线y=x 2+bx+c 的图象与x 轴的一个交点为B (5,0),另一个交点为A ,且与y 轴交于点C (0,5).(1)求直线BC与抛物线的解析式;(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标.5.如图1,在平面直角坐标系中,抛物线233334y x x=-++交x轴于A,B两点(点A在点B的左侧),交y轴于点W,顶点为C,抛物线的对称轴与x轴的交点为D。
2020年重庆中考复习几何第26题专题训练二(含答案解析)

2020年重庆中考复习几何题专题训练二\1、(2018•山西模拟)综合与实践美妙的黄金矩形阅读理解在数学上称短边与长边的比是(约为0.618)的矩形叫做黄金矩形(GoldenRec tan gle),黄金矩形蕴藏着丰富的美学价值,给我们以协调、匀称的美感.(1)某校团委举办“五•四手抄报比赛”,手抄报规格统一设计成:长是40cm的黄金矩形,则宽约为cm;(精确到0.1cm)操作发现利用一张正方形纸片折叠出一个黄金矩形.第一步,如图1,折叠正方形纸片ABCD,使AB和DC重合,得到折痕EF(点E,F分别在百年AD,BC上),然后把纸片展平.第二步,如图2,折叠正方形纸片ABCD,使得BC落在BE上,点C′和点C对应,得到折痕BG(点G在CD上),再次纸片展平.第三步,如图3,沿过点G的直线折叠正方形纸片ABCD,使点A和点D分别落在AB和CD上,折痕为HG,显然四边形HBCG为矩形.(2)在上述操作中,以AB=2为例,证明矩形HBCG是黄金矩形.拓广探索(3)“希望小组”的同学通过探究发现:以黄金矩形的长边为一边,在原黄金矩形外作正方形,得到的新矩形仍然是黄金矩形.如图4,如果四边形ABCD是黄金矩形(AB>AD),四边形DCEF是正方形,那么四边形ABEF也是黄金矩形,他们的发现正确吗?请说明理由.2、(2019•周口二模)在△ABC中,∠ABC为锐角,点M为射线AB上一动点,连接CM,以点C为直角顶点,以CM为直角边在CM右侧作等腰直角三角形CMN,连接NB.(1)如图1,图2,若△ABC为等腰直角三角形,问题初现:①当点M为线段AB上不与点A重合的一个动点,则线段BN,AM之间的位置关系是,数量关系是;深入探究:②当点M在线段AB的延长线上时,判断线段BN,AM之间的位置关系和数量关系,并说明理由;类比拓展:(2)如图3,∠ACB≠90°,若当点M为线段AB上不与点A重合的一个动点,MP⊥CM交线段BN于点P,且∠CBA=45°,BC=,当BM=时,BP的最大值为.3、(2016秋•青羊区校级期中)已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:(1)如图1,若点P在线段AB上,且AC=,P A=2,则:①线段PB=;②猜想:P A2,PB2,PQ2三者之间的数量关系为;(2)如图2,若点P在AB的延长线上,求证:P A2+PB2=PQ2;(3)如图3,在平面直角坐标系中,以AC所在的直线为x轴建立平面直角坐标系,点A的坐标为(2,0),点C的坐标为(5,0),点P为线段AC外一动点,且P A=2,PM=PC,∠CPM=90°.请直接写出线段AM长的最大值及此时点P的坐标.4、(2018秋•鞍山期末)如图,在△ABC中,∠ACB=90°,AC=BC,以C为顶点作等腰直角三角形CMN.使∠CMN=90°,连接BN,射线NM交BC于点D.(1)如图1,若点A,M,N在一条直线上,①求证:BN+CM=AM;②若AM=4,BN=,求BD的长;(2)如图2,若AB=4,CN=2,将△CMN绕点C顺时针旋转一周,在旋转过程中射线NM交AB于点H,当三角形DBH是直角三角形时,请你直接写出CD的长.5、探究学习:已知:C是线段AB所在平面内任意一点,分别以AC、BC为边在AB同侧作等腰直角三角形ACD和等腰直角三角形BCE,∠ACD=∠BCE=90°,连接AE、BD.(1)如图1,当点C在线段AB上移动时,线段AE与BD的数量关系是,位置关系是.(2)如图2,当点C在直线AB外,等腰直角三角形ECB绕点C逆时针旋转至图2位置,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)如图3,在(1)基础上等腰直角三角形BCE绕顶点C逆时针旋转到图3位置,取等腰直角三角形ACD的斜边AD的中点M,连接CM交BE于点G,试探究BG、GH、HE的数量关系,并写出证明思路.6、(2018春•市南区期末)如图①,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边且在AD的上方作等腰直角三角形ADF,连接CF.(1)若AB=AC,∠BAC=90°①当点D在线段BC上时(与点B不重合),试探究CF与BD的数量关系和位置关系,并说明理由.②当点D在线段BC的延长线上时,①中的结论是否仍然成立,请在图②中画出相应图形并直接写出你的猜想.(2)如图③,若AB≠AC,∠BAC≠90°,∠BCA=45°,点D在线段BC上运动,试探究CF与BC 的位置关系,并说明理由.7、实践操作在矩形ABCD中,AB=8,AD=6,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.初步思考(1)若点P落在矩形ABCD的边AB上(如图①).①当点P与点A重合时,∠DEF=;当点E与点A重合时,∠DEF=;②当点E在AB上,点F在DC上时(如图②),求证:四边形DEPF为菱形,并直接写出当AP=7时的菱形EPFD的边长.深入探究(2)若点P落在矩形ABCD的内部(如图③),且点E、F分别在AD、DC边上,请直接写出AP的最小值.拓展延伸(3)若点F与点C重合,点E在AD上,射线BA与射线FP交于点M(如图④).在各种不同的折叠位置中,是否存在某一情况,使得线段AM与线段DE的长度相等?若存在,请直接写出线段AE的长度;若不存在,请说明理由.8、(2019•虞城县一模)特殊:(1)如图1,在等腰直角三角形ABC中,∠ACB=90°,作CM平分∠ACB交AB于点M,点D为射线CM上一点,以点C为旋转中心将线段CD逆时针旋转90°得到线段CE,连接DE交射线CB于点F,连接BD、BE.填空:①线段BD、BE的数量关系为.②线段BC、DE的位置关系为.一般:(2)如图2,在等腰三角形ABC中,∠ACB=a,作CM平分∠ACB交AB于点M,点D为△ABC外部射线CM上一点以点C为旋转中心将线段CD逆时针旋转α度得到线段CE,连接DE、BD、BE,请判断(1)中的结论是否成立,请说明理由.特殊:(3)如图3,在等边三角形ABC中,作BM平分∠ABC交AC于点M,点D为射线BM上一点,以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,连接DE交射线BA于点F,连接AD、AE.若AB=4,当△ADM与△AFD全等时,请直接写出DE的值.\ 2020年重庆中考复习几何题专题训练二答案1、(2018•山西模拟)综合与实践美妙的黄金矩形阅读理解在数学上称短边与长边的比是(约为0.618)的矩形叫做黄金矩形(GoldenRec tan gle),黄金矩形蕴藏着丰富的美学价值,给我们以协调、匀称的美感.(1)某校团委举办“五•四手抄报比赛”,手抄报规格统一设计成:长是40cm的黄金矩形,则宽约为24.7cm;(精确到0.1cm)操作发现利用一张正方形纸片折叠出一个黄金矩形.第一步,如图1,折叠正方形纸片ABCD,使AB和DC重合,得到折痕EF(点E,F分别在百年AD,BC上),然后把纸片展平.第二步,如图2,折叠正方形纸片ABCD,使得BC落在BE上,点C′和点C对应,得到折痕BG(点G在CD上),再次纸片展平.第三步,如图3,沿过点G的直线折叠正方形纸片ABCD,使点A和点D分别落在AB和CD上,折痕为HG,显然四边形HBCG为矩形.(2)在上述操作中,以AB=2为例,证明矩形HBCG是黄金矩形.拓广探索(3)“希望小组”的同学通过探究发现:以黄金矩形的长边为一边,在原黄金矩形外作正方形,得到的新矩形仍然是黄金矩形.如图4,如果四边形ABCD是黄金矩形(AB>AD),四边形DCEF是正方形,那么四边形ABEF也是黄金矩形,他们的发现正确吗?请说明理由.解:(1)宽约为40×≈40×0.681≈24.7cm.故答案为24.7.(2)如图2中,连接EG,设CG=C′G=x.∵AB=2,AE=ED=1,∴BE=,EC′=﹣2,在Rt△EGD和Rt△EGC′中,12+(2﹣x)2=x2+(﹣2)2,解得x=﹣1,∴=,∴图3中的矩形HBCG是黄金矩形;(3)如图4中,四边形ABEF是黄金矩形这个结论正确;理由:设AB=a,则AD=BC=a,∵四边形DCEF是正方形.∴DC=DF=EF=CE=a,∴AE=BE=a+a=a,∴==,∴矩形ABEF是黄金矩形.2、(2019•周口二模)在△ABC中,∠ABC为锐角,点M为射线AB上一动点,连接CM,以点C为直角顶点,以CM为直角边在CM右侧作等腰直角三角形CMN,连接NB.(1)如图1,图2,若△ABC为等腰直角三角形,问题初现:①当点M为线段AB上不与点A重合的一个动点,则线段BN,AM之间的位置关系是AM ⊥BN,数量关系是AM=BN;深入探究:②当点M在线段AB的延长线上时,判断线段BN,AM之间的位置关系和数量关系,并说明理由;类比拓展:(2)如图3,∠ACB≠90°,若当点M为线段AB上不与点A重合的一个动点,MP⊥CM交线段BN于点P,且∠CBA=45°,BC=,当BM=2时,BP的最大值为1.解:问题初现:(1)①AM与BN位置关系是AM⊥BN,数量关系是AM=BN.理由:如图1,∵△ABC,△CMN为等腰直角三角形,∴∠ACB=∠MCN=90°,AC=BC,CM=CN,∠CAB=∠CBA=45°∴∠ACM=∠BCN,且AC=BC,CM=CN,∴△ACM≌△BCN(SAS)∴∠CAM=∠CBN=45°,AM=BN.∵∠CAB=∠CBA=45°,∴∠ABN=45°+45°=90°,即AM⊥BN故答案为:AM⊥BN;AM=BN深入探究:②当点M在线段AB的延长线上时,AM与BN位置关系是AM⊥BN,数量关系是AM=BN.理由如下:如图,∵△ABC,△CMN为等腰直角三角形,∴∠ACB=∠MCN=90°,AC=BC,CM=CN,∠CAB=∠CBA=45°∴∠ACM=∠BCN,且AC=BC,CM=CN,∴△ACM≌△BCN(SAS)∴∠CAM=∠CBN=45°,AM=BN.∵∠CAB=∠CBA=45°,∴∠ABN=45°+45°=90°,即AM⊥BN类比拓展:(2)如图,过点C作CE⊥AB于点E,过点N作NF⊥CE于点F,则FN∥AB∵△MCN是等腰直角三角形∴CM=CN,∠MCN=90°∴∠ECM+∠FCN=90°,且∠ECM+∠CME=90°∴∠FCN=∠CME,且CM=CN,∠F=∠CEM=90°∴△CNF≌△CME(AAS)∴FN=EC,EM=CF∵BC=4,CE⊥AB,∠CBA=45°∴CE=BE=4,∴FN=BE=CE,且FN∥BA∴四边形FNBE是平行四边形,且∠F=90°∴四边形FNBE是矩形∴∠CEM=∠ABN=90°∴∠PMB+∠MPB=90°∵CM⊥MP∴∠CME+∠PMB=90°∴∠CME=∠MPB,且∠CEM=∠ABN=90°∴△CEM∽△MBP∴∴BP==﹣(BM﹣2)2+1∴当BM=2时,BP有最大值为1.3、(2016秋•青羊区校级期中)已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:(1)如图1,若点P在线段AB上,且AC=,P A=2,则:①线段PB=2;②猜想:P A2,PB2,PQ2三者之间的数量关系为P A2+PB2=PQ2;(2)如图2,若点P在AB的延长线上,求证:P A2+PB2=PQ2;(3)如图3,在平面直角坐标系中,以AC所在的直线为x轴建立平面直角坐标系,点A的坐标为(2,0),点C的坐标为(5,0),点P为线段AC外一动点,且P A=2,PM=PC,∠CPM=90°.请直接写出线段AM长的最大值及此时点P的坐标.解:(1)①∵△ABC是等腰直角三角形,∴AB=AC=2+2,∴PB=AB﹣AP=2,故答案为:2;②连接BQ,∵∠ACB=∠PCQ=90°,∴∠ACP=∠BCQ,在△ACP和△BCQ中,,∴△ACP≌△BCQ(SAS),∴AP=BQ,∠CBQ=∠A=45°,∴∠PBQ=90°,∴BQ2+PB2=PQ2,即P A2+PB2=PQ2;(2)由(1)②得,△ACP≌△BCQ,∴AP=BQ,∠CBQ=∠A=45°,∴∠PBQ=90°,∴BQ2+PB2=PQ2,即P A2+PB2=PQ2;(3)如图3,连接CM,将△APM绕着点P顺时针旋转90°得到△PCN,连接AN,则△APN是等腰直角三角形,∴PN=P A=2,CN=AM,∵A的坐标为(2,0),点C的坐标为(5,0),∴OA=2,OC=5,∴AC=3,∴线段AM长的最大值=线段CN长的最大值,∴当N在线段CA的延长线时,线段CN取得最大值,最大值=AC+AN,∵AN=AP=2,∴最大值为2+3;如图4,过P作PE⊥x轴于E,∵△APN是等腰直角三角形,∴PE=AE=,∴OE=CO﹣AC﹣AE=5﹣3﹣=2﹣,∴P(2﹣,).4、(2018秋•鞍山期末)如图,在△ABC中,∠ACB=90°,AC=BC,以C为顶点作等腰直角三角形CMN.使∠CMN=90°,连接BN,射线NM交BC于点D.(1)如图1,若点A,M,N在一条直线上,①求证:BN+CM=AM;②若AM=4,BN=,求BD的长;(2)如图2,若AB=4,CN=2,将△CMN绕点C顺时针旋转一周,在旋转过程中射线NM交AB于点H,当三角形DBH是直角三角形时,请你直接写出CD的长.证明:(1)①如图,过点C作CF⊥CN,交AN于点F,∵△CMN是等腰直角三角形,∴∠CNM=45°,CM=MN,∵CF⊥CN,∠ACB=90°,∴∠FCN=∠ACB,∠CFN=∠CNF=45°,∴∠ACF=∠BCN,CF=CN,且AC=BC,∴△ACF≌△BCN(SAS),∴AF=BN,∵CF=CN,CM⊥MN,∴MF=MN=CM,∴AM=AF+FM=BN+CM②∵AM=4,BN=,BN+CM=AM,∴CM=MN=,∵△ACF≌△BCN,∴∠CAF=∠CBN,∵∠CAF+∠ACF=∠CFN=45°,∠BCN+∠MCD=∠MCN=45°∴∠CAF=∠MCD,且∠CAF=∠CBN,∴∠MCD=∠CBN∴CM∥BN∴△MCD∽△NBD,∠CMD=∠BND=90°∴=∴MD=ND∵MD+ND=MN=∴ND=在Rt△DNB中,BD==(2)若∠BDH=90°,如图,此时点M与点D重合,∵△CMN是等腰直角三角形,CN=2∴CM=MN=∴CD=,若∠BHD=90°,如图,∵∠BHD=90°,∠B=45°,∴∠BDH=45°∴∠CDN=45°=∠N∴CD=CN=2.5、探究学习:已知:C是线段AB所在平面内任意一点,分别以AC、BC为边在AB同侧作等腰直角三角形ACD和等腰直角三角形BCE,∠ACD=∠BCE=90°,连接AE、BD.(1)如图1,当点C在线段AB上移动时,线段AE与BD的数量关系是AE=BD,位置关系是AE ⊥BD.(2)如图2,当点C在直线AB外,等腰直角三角形ECB绕点C逆时针旋转至图2位置,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)如图3,在(1)基础上等腰直角三角形BCE绕顶点C逆时针旋转到图3位置,取等腰直角三角形ACD的斜边AD的中点M,连接CM交BE于点G,试探究BG、GH、HE的数量关系,并写出证明思路.解:(1)如图1,延长AE交BD于F,根据等腰直角三角形ACD和等腰直角三角形BCE,可得AC=DC,∠ACE=∠DCB,EC=BC,易得△ACE≌△DCB,∴AE=DB,∠CAE=∠CDB,又∵∠ACE=90°,∠AEC=∠DEF,∴∠DFE=90°,∴AF⊥DB,即AE⊥DB,故线段AE与BD的数量关系是AE=BD,位置关系是AE⊥BD.故答案为:AE=BD,AE⊥BD.(2)结论AE=BD,AE⊥BD仍然成立.证明:∵△ACD和△BCE是等腰直角三角形,∠ACD=∠BCE=90°,∴AC=CD,CE=CB,又∵∠ACE+∠ECD=90°,∠BCD+∠ECD=90°,∴∠ACE=∠BCD,在△ACE和△DCB中,,∴△ACE≌△DCB(SAS),∴AE=BD,∠EAC=∠BDC,如图2,延长AE交BD于点F,∵∠ACD=90°,∴∠DAC+∠ADC=90°,又∵∠ADF+∠DAF+∠DF A=180°,∴∠ADC+∠BDC+∠DAF+∠DF A=180°,∴∠ADC+∠EAC+∠DAF+∠DF A=180°,∴∠ADC+∠DAC+∠DF A=180°,∴90°+∠DF A=180°,∴∠DF A=90°,∴AE⊥BD;(3)BG、GH、HE的数量关系是BG2+HE2=GH2.证明:如图3,过点C作CF⊥CG,且CF=CG,连接HF、EF.∵CF⊥CG,CE⊥CB,∴∠BCG=∠ECF,在△BCG和△ECF中,,∴△BCG≌△ECF(SAS),∴BG=EF,∠CBG=∠CEF=45°,∴∠HEF=∠HEC+∠CEF=90°,又∵△ACE≌△DCB,∴∠ACE=∠DCB,∴∠FCH=∠ACE+∠ECF=∠DCB+∠BCG=45°,∴∠GCH=∠FCH,在△GCH和△FCH中,,∴△GCH≌△FCH(SAS),∴GH=FH,∵在Rt△HEF中,EF2+HE2=FH2,∴BG2+HE2=GH2.6、(2018春•市南区期末)如图①,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边且在AD的上方作等腰直角三角形ADF,连接CF.(1)若AB=AC,∠BAC=90°①当点D在线段BC上时(与点B不重合),试探究CF与BD的数量关系和位置关系,并说明理由.②当点D在线段BC的延长线上时,①中的结论是否仍然成立,请在图②中画出相应图形并直接写出你的猜想.(2)如图③,若AB≠AC,∠BAC≠90°,∠BCA=45°,点D在线段BC上运动,试探究CF与BC 的位置关系,并说明理由.解:(1)①CF=BD,CF⊥BD,理由如下:∵∠BAC=90°,△ADF是等腰直角三角形,∴∠CAF+∠CAD=90°,∠BAD+∠CAD=90°,∴∠CAF=∠BAD,在△ACF和△ABD中,,∴△ACF≌△ABD(SAS),∴CF=BD,∠ACF=∠ABD=45°,∵∠ACB=45°,∴∠FCB=90°,∴CF⊥BD;②成立,理由如下:如图2:∵∠CAB=∠DAF=90°,∴∠CAB+∠CAD=∠DAF+∠CAD,即∠CAF=∠BAD,在△ACF和△ABD中,,∴△ACF≌△ABD(SAS),∴CF=BD,∠ACF=∠B,∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°,∴∠BCF=∠ACF+∠ACB=45°+45°=90°,∴CF⊥BD;(3)如图3,过点A作AE⊥AC交BC于E,∵∠BCA=45°,∴△ACE是等腰直角三角形,∴AC=AE,∠AED=45°,∵∠CAF+∠CAD=90°,∠EAD+∠CAD=90°,∴∠CAF=∠EAD,在△ACF和△AED中,,∴△ACF≌△AED(SAS),∴∠ACF=∠AED=45°,∴∠BCF=∠ACF+∠BCA=45°+45°=90°,∴CF⊥BD.7、实践操作7、在矩形ABCD中,AB=8,AD=6,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.初步思考(1)若点P落在矩形ABCD的边AB上(如图①).①当点P与点A重合时,∠DEF=90°;当点E与点A重合时,∠DEF=45°;②当点E在AB上,点F在DC上时(如图②),求证:四边形DEPF为菱形,并直接写出当AP=7时的菱形EPFD的边长.深入探究(2)若点P落在矩形ABCD的内部(如图③),且点E、F分别在AD、DC边上,请直接写出AP的最小值.拓展延伸(3)若点F与点C重合,点E在AD上,射线BA与射线FP交于点M(如图④).在各种不同的折叠位置中,是否存在某一情况,使得线段AM与线段DE的长度相等?若存在,请直接写出线段AE的长度;若不存在,请说明理由.解:(1)①当点P与点A重合时,如图1,∴EF是AD的中垂线,∴∠DEF=90°,当点E与点A重合时,如图2,此时∠DEF=∠DAB=45°,故答案为:90°,45°;②当点E在AB上,点F在DC上时,如图3,∵EF是PD的中垂线,∴DO=PO,EF⊥PD,∵四边形ABCD是矩形,∴DC∥AB,∴∠FDO=∠EPO,∵∠DOF=∠EOP,∴△DOF≌△POE(ASA),∴DF=PE,∵DF∥PE,∴四边形DEPF是平行四边形,∵EF⊥PD,∴▱DEPF为菱形,当AP=7时,设菱形的边长为x,则AE=7﹣x,DE=x,在Rt△ADE中,由勾股定理得:AD2+AE2=DE2,∴62+(7﹣x)2=x2,x=,∴当AP=7时,设菱形的边长为;(2)若点P落在矩形ABCD的内部,且点E、F分别在AD、DC边上,如图4,设DF=PF=x,则AF=,当A,P,F在一直线上时,AP最小,最小值为,所以当x最大取8时,AP最小值为2;(3)情况一:如图5,连接EM,∵DE=EP=AM,∴△EAM≌△MPE,设AE=x,则AM=DE=6﹣x,则BM=x+2,∵MP=EA=x,CP=CD=8,∴MC=8﹣x,∴(x+2)2+62=(8﹣x)2,解得:x=;情况二,如图6,∵DE=EP=AM,∴△GAM≌△GPE,设AE=x,则DE=6﹣x,则AM=PE=DE=6﹣x,MP=AE=x,则MC=MP+PC=x+8,BC=6,BM=14﹣x,∴(14﹣x)2+62=(x+8)2,解得:x=.8、(2019•虞城县一模)特殊:(1)如图1,在等腰直角三角形ABC中,∠ACB=90°,作CM平分∠ACB交AB于点M,点D为射线CM上一点,以点C为旋转中心将线段CD逆时针旋转90°得到线段CE,连接DE交射线CB于点F,连接BD、BE.填空:①线段BD、BE的数量关系为BD=BE.②线段BC、DE的位置关系为BC⊥DE.一般:(2)如图2,在等腰三角形ABC中,∠ACB=a,作CM平分∠ACB交AB于点M,点D为△ABC 外部射线CM上一点以点C为旋转中心将线段CD逆时针旋转α度得到线段CE,连接DE、BD、BE,请判断(1)中的结论是否成立,请说明理由.特殊:(3)如图3,在等边三角形ABC中,作BM平分∠ABC交AC于点M,点D为射线BM上一点,以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,连接DE交射线BA于点F,连接AD、AE.若AB=4,当△ADM与△AFD全等时,请直接写出DE的值.解:(1)如图1中,∵CM平分∠ACB,∠ACB=90°,∴∠ACM=∠BCM=45°,∵∠DCE=90°,∴∠BCD=∠BCE=45°,∵BC=BC,CD=CE,∴△BCD≌△BCE(SAS),∴BE=BE,∵CD=CE,∴BC垂直平分线段DE,故答案为BD=BE,BC⊥DE.(2)结论仍然成立.理由:如图2中,∵CM平分∠ACB,∠ACB=α,∴∠ACM=∠BCM=α,∵∠DCE=α,∴∠BCD=∠BCE=α,∵BC=BC,CD=CE,∴△BCD≌△BCE(SAS),∴BD=BE,∵CD=CE,∴BC垂直平分线段DE.(3)①如图3﹣1中,当点D在线段BM上时,由题意:AF=AM=CM=BF=2在Rt△BEF中,∵∠BFE=90°,EF=BF•tan30°=,∴DE=2EF=.②如图3﹣2中,当点D在线段BM的延长线上时,同法可得DE=2EF=4③如图3﹣3中,当点D在线段BM的延长线上,△ADM≌△AFD时,可得DE=4,综上所述,满足条件的DE的值为或4或4.。
2020重庆中考复习数学第26题专题训练五(含答案解析)
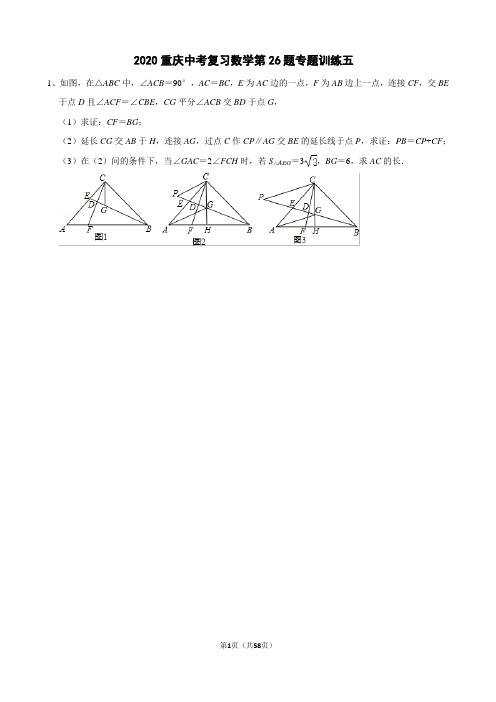
2020重庆中考复习数学第26题专题训练五1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△,可推证△CEF是三角形,从而求得∠DCE=.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.3、(2019秋•锦江区校级期末)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.4、(2019•镇平县三模)如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为;∠EFC的度数为;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.5、(2017春•西城区校级期末)如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.7、(1)如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.9、(2018•大东区一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于时,线段BC的长取得最大值,且最大值为(用含b,c的式子表示)(直接填空).模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.13、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.14、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)16、在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.17、在△ABC中,∠BAC=60°,点D、E分别在边AC、AB上,AD=AE,连接CE、BD相交于点F,且∠BEC=∠ADF,连接AF.(1)如图1,连接ED,求证:∠ABD=∠CED;(2)如图2,求证:EF+FD=AF;(3)如图3,取BC的中点G,连接AG交BD于点H,若∠GAC=3∠ABD,BH=7,求△ABH的面积.18、点D,E分别在△ABC的边AC,BD上,BD,CE交于点F,连接AF,∠F AE=∠F AD,FE=FD.(1)如图1,若∠AEF=∠ADF,求证:AE=AD;(2)如图2,若∠AEF≠∠ADF,FB平分∠ABC,求∠BAC的度数;(3)在(2)的条件下,如图3,点G在BE上,∠CFG=∠AFB若AG=6,△ABC的周长为20,求BC长.2020重庆中考复习数学第26题专题训练五参考答案1、(2019秋•天桥区期末)如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.证明:(1)如图1,∵∠ACB=90°,AC=BC,∴∠A=45°,∵CG平分∠ACB,∴∠ACG=∠BCG=45°,∴∠A=∠BCG,在△BCG和△CAF中,∵,∴△BCG≌△CAF(ASA),∴CF=BG;(2)如图2,∵PC∥AG,∴∠PCA=∠CAG,∵AC=BC,∠ACG=∠BCG,CG=CG,∴△ACG≌△BCG,∴∠CAG=∠CBE,∵∠PCG=∠PCA+∠ACG=∠CAG+45°=∠CBE+45°,∠PGC=∠GCB+∠CBE=∠CBE+45°,∴∠PCG=∠PGC,∴PC=PG,∵PB=BG+PG,BG=CF,∴PB=CF+CP;(3)解法一:如图3,过E作EM⊥AG,交AG于M,∵S△AEG=AG•EM=3,由(2)得:△ACG≌△BCG,∴BG=AG=6,∴×6×EM=3,EM=,设∠FCH=x°,则∠GAC=2x°,∴∠ACF=∠EBC=∠GAC=2x°,∵∠ACH=45°,∴2x+x=45,x=15,∴∠ACF=∠GAC=30°,在Rt△AEM中,AE=2EM=2,AM==3,∴M是AG的中点,∴AE=EG=2,∴BE=BG+EG=6+2,在Rt△ECB中,∠EBC=30°,∴CE=BE=3+,∴AC=AE+EC=2+3+=3+3.解法二:同理得:∠CAG=30°,AG=BG=6,如图4,过G作GM⊥AC于M,在Rt△AGM中,GM=3,AM===3,∵∠ACG=45°,∠MGC=90°,∴GM=CM=3,∴AC=AM+CM=3+3.2、(2019秋•淮安期末)[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△ADB,可推证△CEF是等腰直角三角形,从而求得∠DCE=135°.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.解:[问题初探]如图2,过点E作EF⊥BC交直线BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=135°,故答案为:ADB,等腰直角,135;[继续探究]如图3,过点E作EF⊥BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=45°;[拓展延伸]如图4,在△ABC中,∠ABC=90°,AB=BC=,∴∠ACB=45°当点D在射线BC上时,由[问题初探]知,∠BCM=135°,∴∠ACM=∠BCM﹣∠ACB=90°,当点D在线段CB的延长线上时,由[继续探究]知,∠BCE=45°,∴∠ACN=∠ACB+∠BCM=90°,∴点E是过点C垂直于AC的直线上的点,∴当BE⊥MN时,BE最小,∵∠BCE=45°,∴∠CBE=45°=∠BCE,∴BE=CE,∴BE最小=BC=,即:BE的最小值为.3、(2019秋•锦江区校级期末)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.证明:(1)如图1,过点D作DE⊥AB,∵BD是△ABC的角平分线,DE⊥AB,∠ACB=90°,∴DC=DE,∵∠A=30°,DE⊥AB,∴AD=2DE,∴AD=2DC;(2)如图2,过点M作ME∥BD,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵BD是△ABC的角平分线,∴∠ABD=∠DBC=30°,∵BM平分∠CBD,∴∠CBM=15°=∠DBM,∵ME∥BD,∴∠MEC=∠CBD=30°,∠EMB=∠DBM=∠MBE,∴ME=BE,∵∠MEC=30°,∠C=90°∴CE=MC=,ME=2MC=2=BE,∴BC=+2,∵∠CBD=30°,∠C=90°,∴BC=CD,∴CD=1+,∴DM=,∴△DBM的面积=××(+2)=1+;(3)若点N在CD上时,AD=DG+DN,理由如下:如图3所示:延长ED使得DW=DN,连接NW,∵∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E,∴∠ADE=∠BDE=60°,AD=BD,∵DN=DW,且∠WDN=60°∴△WDN是等边三角形,∴NW=DN,∠W=∠WND=∠BNG=∠BDN=60°,∴∠WNG=∠BND,在△WGN和△DBN中,∴△WGN≌△DBN(SAS),∴BD=WG=DG+DN,∴AD=DG+DN.(3)若点N在AD上时,AD=DG﹣DN,理由如下:如图4,延长BD至H,使得DH=DN,连接HN,由(1)得DA=DB,∠A=30°.∵DE⊥AB于点E.∴∠2=∠3=60°.∴∠4=∠5=60°.∴△NDH是等边三角形.∴NH=ND,∠H=∠6=60°.∴∠H=∠2.∵∠BNG=60°,∴∠BNG+∠7=∠6+∠7.即∠DNG=∠HNB.在△DNG和△HNB中,∴△DNG≌△HNB(ASA).∴DG=HB.∵HB=HD+DB=ND+AD,∴DG=ND+AD.∴AD=DG﹣ND.4、(2019•镇平县三模)如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为EF=CF;∠EFC的度数为120°;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.解:(1)如图1中,∵DE⊥AB,∴∠BED=90°,∵∠BCD=90°,BF=DF,∴FE=FB=FD=CF,∴∠FBE=∠FEB,∠FBC=∠FCB,∴∠EFC=∠EFD+∠CFD=∠FBE+∠FEB+∠FBC+∠FCB=2(∠FBE+∠FBC)=2∠ABC=120°,故答案为:EF=CF,120°.(2)结论成立.理由:如图2中,取AB的中点M,AD的中点N,连接MC,MF,ED,EN,FN.∵BM=MA,BF=FD,∴MF∥AD,MF=AD,∵AN=ND,∴MF=AN,MF∥AN,∴四边形MFNA是平行四边形,∴NF=AM,∠FMA=∠ANF,在Rt△ADE中,∵AN=ND,∠AED=90°,∴EN=AD=AN=ND,同理CM=AB=AM=MB,在△AEN和△ACM中,∠AEN=∠EAN,∠MCA=∠MAC,∵∠MAC=∠EAN,∴∠AMC=∠ANE,又∵∠FMA=∠ANF,∴∠ENF=∠FMC,在△MFC和△NEF中,,∴△MFC≌△NEF(SAS),∴FE=FC,∠NFE=∠MCF,∵NF∥AB,∴∠NFD=∠ABD,∵∠ACB=90°,∠BAC=30°,∴∠ABC=60°,△BMC是等边三角形,∠MCB=60°∴∠EFC=∠EFN+∠NFD+∠DFC=∠MCF+∠ABD+∠FBC+∠FCB=∠ABC+∠MCB=60°+60°=120°.(3)如图3中,作EH⊥AB于H.在Rt△ABC中,∵∠BAC=30°,BC=3,∴AB=2BC=6,在Rt△AED中,∠DAE=30°,AD=2,∴DE=AD=1,在Rt△DEH中,∵∠EDH=60°,DE=1,∴EH=ED•sin60°=,DH=ED•cos60°=,在Rt△EHG中,EG==.5、(2017春•西城区校级期末)如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.解:(1)BC=2BD,理由:如图2,连接CD,由旋转可得,CP=DP,∠CPD=60°,∴△CDP是等边三角形,∴∠CDP=60°=∠PCD,又∵P是AB的中点,AB=AC,∠A=60°,∴等边三角形ABC中,∠PCB=30°,CP⊥AB,∴∠BCD=30°,即BC平分∠PCD,∴BC垂直平分PD,∴∠BDC=∠BPC=90°,∴Rt△BCD中,BC=2BD.(2)如图3,取BC中点F,连接PF,∵∠A=90°,AB=AC,∴△ABC是等腰直角三角形,∵P是AB的中点,F是BC的中点,∴PF是△ABC的中位线,∴PF∥AC,∴∠PFB=∠ACB=45°,∠BPF=∠A=90°,∴△BPF是等腰直角三角形,∴BF=BP,BP=PF,∵∠DPC=∠BPF=90°,∴∠BPD=∠FPC,又∵PD=PC,∴△BDP≌△FCP,∴BD=CF,∵BC=BF+FC,∴BC=BD+BP.6、(2019春•碑林区校级月考)【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A 为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.【发现问题】解:延长CA到M,作∠MAC的平分线AN,在AN上截取AD=AC,连接CD,即可得到等腰直角△ACD;连接BD、CE,如图1所示:∵△ABE与△ACD都是等腰直角三角形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE,【拓展探究】解:BD=CE;理由如下:∵四边形AEFB与四边形ACGD都是正方形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;【解决问题】解:以AB为边向外作等边三角形ABE,连接CE,如图3所示:则∠BAE=60°,BE=AB=AE=8,∵AD=CD,∠ADC=60°,∴△ACD是等边三角形,∴∠CAD=60°,AC=AD,∴∠CAD+∠BAC=∠BAE+∠BAC,即∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;当C、B、E三点共线时,CE最大=BC+BE=15+8=23,∴BD的最大值为23.7、(2018春•铁西区期中)(1)如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为a+b(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.(1)解:∵点C为线段AB外一动点,且AC=b,AB=a,∴当点C位于BA的延长线上时,线段BC的长取得最大值,且最大值为AC+AB=a+b,(2)①证明:如图2中,∵△ACD与△BCE是等边三角形,∴CD=AC,CB=CE,∠ACD=∠BCE=60°,∴∠DCB=∠ACE,在△CAD与△EAB中,,∴△CAD≌△EAB(SAS),∴AE=BD.②∵线段AE长的最大值=线段BD的最大值,由(1)知,当线段BD的长取得最大值时,点D在BA的延长线上,∴最大值为AD+AB=3+10=13;(3)如图3中,连接BN,∵将△AMN绕着点M顺时针旋转90°得到△PBM,连接AP,则△APM是等腰直角三角形,∴MA=MP=2,BP=AN,∴P A=2,∵AB=6,∴线段AN长的最大值=线段BP长的最大值,∴当P在线段BA的延长线时,线段BP取得最大值最大值=AB+AP=6+2.8、(2019秋•武冈市期中)【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是∠BAE+∠F AD=∠EAF;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.解:(1)∠BAE+∠F AD=∠EAF.理由:如图1,延长FD到点G,使DG=BE,连接AG,根据SAS可判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再根据SSS可判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF.故答案为:∠BAE+∠F AD=∠EAF;(2)仍成立,理由:如图2,延长FD到点G,使DG=BE,连接AG,∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,∴∠B=∠ADG,又∵AB=AD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AE=AG,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF;(3)∠EAF=180°﹣∠DAB.证明:如图3,在DC延长线上取一点G,使得DG=BE,连接AG,∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,∴∠ADC=∠ABE,又∵AB=AD,∴△ADG≌△ABE(SAS),∴AG=AE,∠DAG=∠BAE,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠F AE=∠F AG,∵∠F AE+∠F AG+∠GAE=360°,∴2∠F AE+(∠GAB+∠BAE)=360°,∴2∠F AE+(∠GAB+∠DAG)=360°,即2∠F AE+∠DAB=360°,∴∠EAF=180°﹣∠DAB.9、(2018•大东区一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.解:(1)CP=BQ,理由:如图1,连接OQ,由旋转知,PQ=OP,∠OPQ=60°⊅∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(2)CP=BQ,理由:如图2,连接OQ,由旋转知,PQ=OP,∠OPQ=60°∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(3)如图3,在Rt△ABC中,∠A=30°,AC=,∴BC=AC•tan∠A=,过点O作OH⊥BC,∴∠OHB=90°=∠BCA,∴OH∥AB,∵O是AB中点,∴CH=BC=,OH=AC=,∵∠BPQ=45°,∠OHP=90°,∴∠BPQ=∠PQH,∴PH=OH=,∴CP=PH﹣CH=﹣=,连接BQ,同(1)的方法得,BQ=CP=.10、(2018秋•东海县期末)模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于线段BA的延长线上时,线段BC的长取得最大值,且最大值为b+c(用含b,c的式子表示)(直接填空)模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为5.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.解:当点C位于线段BA的延长线上时,线段BC的长取得最大值,最大值为b+c,故答案为:线段BA的延长线上;b+c;模型应用:(1)证明:∵△ACD、△BCE都是等边三角形,∴CD=CA=AD,CB=CE,∠ACD=60°,∠BCE=60°,∴∠DCB=∠ACE,在△DCB和△ACE中,,∴△DCB≌△ACE(SAS)∴BD=AE;(2)当点D位于线段BA的延长线上时,线段BD的长取得最大值,最大值为AB+AD=AB+AC=3+2=5,∵AE=BD,∴线段AE长的最大值为5,模型拓展:取AB的中点G,连接OG、CG,在Rt△AOB中,G为AB的中点,∴OG=AB=4,在Rt△CAG中,CG===5,当点O、G、C在同一条直线上时,OC最大,最大值为4+5=9.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.(1)证明:如图1中,∵BE⊥AD于E,∴∠AEF=∠BCF=90°,∵∠AFE=∠CFB,∴∠DAC=∠CBF,∵BC=CA,∴△BCF≌△ACD,∴BF=AD.(2)结论:BD=2CF.理由:如图2中,作EH⊥AC于H.∵∠AHE=∠ACD=∠DAE=90°,∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,∴∠DAC=∠AEH,∵AD=AE,∴△ACD≌△EHA,∴CD=AH,EH=AC=BC,∵CB=CA,∴BD=CH,∵∠EHF=∠BCF=90°,∠EFH=∠BFC,EH=BC,∴△EHF≌△BCF,∴FH=CF,∴BD=CH=2CF.(3)如图3中,同法可证BD=2CM.∵AC=3CM,设CM=a,则AC=CB=3a,BD=2a,∴==.12、(2019秋•松北区期末)已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.(1)①证明:如图1中,∵AB=AC,∠ABC=60°∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BN,∴∠ADB=90°,∵∠MBN=30°,∠BFD=60°=∠1+∠BAF=∠2+∠BAF,∴∠1=∠2②证明:如图2中,在Rt△BFD中,∵∠FBD=30°,∴BF=2DF,∵BF=2AF,∴BF=AD,∵∠BAE=∠FBC,AB=BC,∴△BFC≌△ADB,∴∠BFC=∠ADB=90°,∴BF⊥CF(2)在BF上截取BK=AF,连接AK.∵∠BFE=∠2+∠BAF,∠CFE=∠4+∠1,∴∠CFB=∠2+∠4+∠BAC,∵∠BFE=∠BAC=2∠EFC,∴∠1+∠4=∠2+∠4∴∠1=∠2,∵AB=AC,∴△ABK≌CAF,∴∠3=∠4,S△ABK=S△AFC,∵∠1+∠3=∠2+∠3=∠CFE=∠AKB,∠BAC=2∠CEF,∴∠KAF=∠1+∠3=∠AKF,∴AF=FK=BK,∴S△ABK=S△AFK,∴=2.13、(2017春•合肥期末)已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.(1)解:如图1中,在AB上取一点M,使得BM=ME,连接ME.在Rt△ABE中,∵OB=OE,∴BE=2OA=2,∵MB=ME,∴∠MBE=∠MEB=15°,∴∠AME=∠MBE+∠MEB=30°,设AE=x,则ME=BM=2x,AM=x,∵AB2+AE2=BE2,∴(2x+x)2+x2=22,∴x=(负根已经舍弃),∴AB=AC=(2+)•,∴BC=AB=+1.方法二:作EH⊥BC于H,求出BH,CH即可解决问题.(2)证明:如图2中,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.∵BE⊥AP,∴∠AHB=90°,∴∠ABH+∠BAH=90°,∵∠BAH+∠P AC=90°,∴∠ABE=∠P AC,在△ABE和△CAP中,,∴△ABE≌△CAP,∴AE=CP=CF,∠AEB=∠P,在△DCF和△DCP中,,∴△DCF≌△DCP,∴∠DFC=∠P,∴∠GFE=∠GEF,∴GE=GF,∵GM⊥EF,∴FM=ME,∵AE=CF,∴AF=CE,∴AM=CM,在△GAH和△GAM中,,∴△AGH≌△AGM,∴AH=AM=CM=AC(3)解:结论:AG=EF.理由:如图3中,作CM⊥AC交AD的延长线于M,连接PG交AC于点O.由(2)可知△ACM≌△BAE,△CDF≌△CDM,∴∠AEB=∠M=∠GEF,∠M=∠CFD=∠GFE,AE=CM=CF,∴∠GEF=∠GFE,∴GE=GF,∵△EFP是由△EFG翻折得到,∴EG=EP=GF=PF,∴四边形EGFP是菱形,∴PG⊥AC,OE=OF,∵AE=CF,∴AO=OC,∵AB∥OP,∴BP=PC,∵PF∥BE,∴EF=CF=AE,∵PB=PC,AO=OC,∴PO=OG=AB,∴AB=PG,AB∥PG,∴四边形ABPG是平行四边形,∴AG∥BC,∴∠GAO=∠ACB=45°,设EO=OF=a,则OA=OG=3a,AG=3a,∴==,∴AG=EF14、(2017春•南岗区校级月考)如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.解:(1)∵E为AC中点,作ED⊥AC交AB于D,∴AD=CD,∵∠ACB=90°,∴BC∥DE,∴AD=BD,∴CD=BD,∴AB=2CD;(2)如图2,连接CH,∵点E是AC的中点,∴AE=CE,∵DE⊥AC,∴CH=AH,∴∠ACH=∠CAH,∵∠ACB=90°,∴∠B+∠BAC=90°,∵CF⊥AB,∴∠BAC+∠ACF=90°,∴∠ACF=∠B,∴∠HCG=∠ACH+∠ACF=∠CAH+∠B,∠AHG=2∠B∴在四边形AHGF中,∠AFG+∠FGH+∠AHG+∠F AH=360°,∴∠FGH=360°﹣(∠AFG+∠AHG+∠F AH)=360°﹣(90°+2∠B+∠CAH+∠BAC)=360°﹣(90°+2∠B+∠CAH+90°﹣∠B)=360°﹣(180°+∠B+∠CAH)=180°﹣(∠B+∠CAH),∵∠CGH=180°﹣∠FGH=∠B+∠CAH=∠HCG,∴CH=GH,∵CH=AH,∴AH=GH;(3)如图3,由(1)知,DE∥BC,∴∠B=∠ADE,在△BFC和△DEA中,,∴△BFC≌△DEA,∴BC=AD,∵AD=BD=CD,∴BC=BD=CD,∴△BCD是等边三角形,∴∠B=60°,在Rt△ABC中,AC=6,∴BC=2,AB=4,∵CF⊥BD,∴DF=,CF=3,∵∠BAC=30°,∴∠ADE=60°,∵∠EDG=90°,∠FDG=30°,在Rt△DFG中,DF=,∴FG=1,DG=2,∴CG=CF﹣FG=2过点H作HN⊥CF,由(2)知,CH=GH,∴NG=CG=1,∴FN=NG+FG=2,过点H作HM⊥AB,∴∠FMH=∠NFM=∠HNF=90°,∴四边形NFMH是矩形,∴HM=FN=2,在Rt△DMH中,∠ADE=60°,HM=2,∴DH=,在Rt△HDG中,根据勾股定理得,HG==.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)(1)证明:∵AC=BC,∠ACB=90°,∴∠A=∠B=45°,∵CD⊥AB,∴∠CDB=90°,∴∠DCB=45°,∵∠ECF=∠DCB+∠1=45°+∠1,∠EFC=∠B+∠2=45°+∠2,∠1=∠2,∴∠ECF=∠EFC,∴CE=EF,∵CD⊥AB,FG⊥AB,∴∠CDE=∠EGF=90°,在△CDE和△EGF中,,∴△CDE≌△EGF(AAS);(2)证明:由(1)得:CE=EF,∠A=∠B,∵CE平分∠ACD,∴∠ACE=∠1,∵∠1=∠2,∴∠ACE=∠2,在△ACE和△BEF中,,∴△ACE≌△BEF(AAS),∴AE=BF;(3)AE=BF,作EH⊥BC与H,如图3所示:设DE=x,根据题意得:BE=DE=x,AD=BD=2x,CD=AD=2x,AE=3x,根据勾股定理得:BC=AC=2x,∵∠ABC=45°,EH⊥BC,∴BH=x,∴CH=BC﹣BH=x,∵EC=EF,∴FH=CH=x,∴BF=x﹣x=x,∴=,∴AE=.。
2021重庆中考26题专题讲义教师版

针对性演练1、(2019重庆A卷)2、(2019重庆B卷)3、(2019一中二模)26、如图1,在平面直角坐标系中,抛物线6332612++-=x x y 与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C 。
(1)点P 为线段BC 上方抛物线上(不与B 、C 重合)的一动点,连接OP 交BC 于点D ,当ODPD 取得最大值时,将P 点沿着射线CB 方向平移6个单位长度,设点P 平移后的对应点记为'P ,在线段BC 上取一点E ,当CE E P 3'32+值最小时,求此时E 点的坐标;(2)如图2,抛物线对称轴与x 轴交于点K ,与线段BC 交于点M ,在对称轴上取一点R ,使得KR =12(点R 在第一象限),连接BR 。
已知点N 为线段BR 上一动点,连接MN ,将△BMN 沿MN 翻折到△MN B '。
若'B 罗在直线BR 的右侧或直线BR 上,当△MN B '与△BMR 重叠部分(如图中的△MNQ )为直角三角形时,将此Rt △MNQ 绕点Q 顺时针旋转α(︒<≤︒1800α)得到Rt △Q N M '',直线''N M 分别与直线BR 、直线BM 交于点G 、H 。
当△BGH 是以∠GBH 为底角的等腰三角形时,请直接写出BG 的长。
4、(2019南开阶段测试(四))5、(2019育才一诊)6、(2019八中初三下入学)7、(2019万唯白卷)8、(2019万唯黑卷)9、(2019南开(融侨)九下阶段二)26.(8分)已知抛物线y=﹣x2+x+9与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.(1)如图1,点P为线段BC上方抛物线上的任意一点,当四边形PCAB面积最大时,连接OP并延长至点Q,使PQ=OP,在对称轴上有一动点E,将△ACE沿边CE翻折得到△A′CE,取BA′的中点N,求BQ+QN的最大值;(2)如图2,将△AOC绕点O顺时针旋转至△A1OC1的位置,点A,C的对应点分别为A1,C1,且点A1落在线段AC上,再将△A1OC1沿y轴平移得△A2O1C2,其中直线O1C2与x轴交于点K,点T是抛物线对称轴上的动点,连接KT,O1T,△O1KT能否成为以O1K为直角边的等腰直角三角形?若能,请直接写出所有符合条件的点T的坐标;若不能,请说明理由.26.【分析】(1)先判断出四边形ACPB面积最大时,△BPC的面积最大,进而求出点P 的坐标,再求出QB的值,由折叠得出点A'是以点C为圆心,AC为半径的圆上,利用三角形的中位线构造出图形,判断出点A',C,F在同一条直线上时,A'F最大得出QN最大,即可得出结论;(2)根据题意画出图形,分两种情况,建立方程即可得出结论.【解答】解:(1)针对于抛物线y=﹣x2+x+9,令x=0,则y=9,∴C(0,9),令y=0,∴0=﹣x2+x+9,∴x=﹣3,或x=9,∴A(﹣3,0),B(9,0),∵S四边形ABPC =S△ABC+S△BPC=×(9+3)×9+S△BPC =45+S△BPC,要四边形ABPC的面积最大,只要△BPC的面积最大,∵B(9,0),C(0,9)∴直线BC的解析式为y=﹣x+9,如图1,过点P作PD'∥y轴交BC于D',设点P(m,﹣m2+m+9)(0<m<9),∴D(m,﹣m+9),∴PD'=﹣m2+m+9﹣(﹣m+9)=﹣m2+m=﹣(m﹣)2+,=[﹣(m﹣)2+]×9=﹣(m﹣)2+∴S△BPC∴当m=时,△BPC的面积最大,即:四边形ABPC的面积最大,∴P(,),∵点Q在OP的延长线上,且PQ=OP,∴Q(9,),∵B(9,0)∴BQ⊥x轴,BQ=,如图2,延长BQ至F,使QF=BQ,连接A'F,∴BF=45,∴F(9,45),∵点N是A'B的中点,∴QN是△A'BF的中位线,∴A'F=2QN,∵BQ+QN=9+QN,最大,∴QN最大,即:A'F最大,由折叠知,点A'在以点C为圆心,AC=6为半径的圆上,∴FA'过点C时,A'F最大,∵C(0,9),F(9,45),∴直线CF的解析式为y=x+9,令y=0,∴x=﹣>3,∴点A'在x轴下方,如图3,过点C作CD⊥BF于D,在Rt△CDF中,CF==9,∴A'F=CF+A'C=9+6,最大=,∴QN最大∴(QN+QB)=+=;最大(2)在Rt△AOC中,OA=3,OC=9,∴∠OAC=60°,由旋转知,OA=OA1,∴△AOA1是等边三角形,∠A1OA=60°=∠OA1C1,∴A1C1∥x轴,∴∠OC1A1=30°,C1(9,3)∴直线OC1的解析式为y=x,∵OC1∥O1C2,∴设直线O1C2的解析式为y=x+b,∴O1(0,b),K(﹣b,0),∴OO1=|b|,OK=|b|,∵抛物线的解析式为y=﹣x2+x+9,∴此抛物线的对称轴为x=3,①当∠O1KT=90°时,b<0,OO1=﹣b,OK=﹣b,如图4,易证,△O1OK≌△KHT(AAS),∴OO1=KT,OK=HT,∴|b|+|b|=3,∴b=.∴T(3,);②当∠KO1T=90°时,当b>0时,如图5,OO1=b,OK=b,易证,△O1OK≌△O1HT(AAS),∴OO1=HT,OK=O1H,∴b=3,∴OH=O1H﹣OO1=OK﹣OO1=9﹣3,∴T(3,9﹣3);当∠KO1T=90°时,当b<0时,如图6,OO1=﹣b,OK=﹣b,易证,△O1OK≌△O1HT(AAS),∴OO1=HT,OK=O1H,∴b=﹣3,∴OH=O1H+OO1=OK+OO1=9+3,∴T(3,﹣9﹣3);即:(3,)或(3,9﹣3)或(3,﹣9﹣3).【点评】此题是二次函数综合题,主要考查了全等三角形的判定和性质,极值的确定,三角形中位线的性质,折叠的性质,正确作出辅助线是解本题的关键.10、(2019巴蜀初三上期末)26.解:(1)令06332612=++-x x , 解得32,36-==B A x x ,所以)6,0()0,36(C A ,,………………………(1分) 设直线AC 解析式为b kx y +=,⎩⎨⎧==+6036b b k ,所以直线AC 解析式为:633+-=x y .…………………………(2分) (2)如图,过P 作x PH ⊥轴交AC 于点H,PH x x PH S C A PCA 33)(21=-⋅=∆ , ∴当PH 取最大值时,PCA S ∆最大, 设)633,(),633261,(2+-++-m m H m m m P , )360(3612<<+-=m m m PH , ∴当33=m 时,PH 取最大值, 此时),(21533P ,………………………………………………………………………(4分) 由题意可得直线l 为:237=x ,)215,237(1P ∴, 设直线l 与x 轴垂直的垂足为Q ,连接A P 1,AQ P 1∆∴是直角三角形,且35,215,23511===A P Q P QA , 111tan 360PQ P AQ P AQ QA∴∠==∴∠=, , 作1P 关于直线AC 的对称点'1P ,连接'11P P ,与直线AC 、A’C’分别交于S 、T 点,A P P '11∆∴是等边三角形,111'53'(3,0)P A PA P ∴==∴, , ,'2,''30,3MN AC CC C A A MN ⊥=∠=∴……………………………………(6分)将'1P 沿MN 方向平移3个单位得到)23,233(''1P ,将直线A’C’绕点A’顺时针旋转 45得到直线1l ,过点''1P 作11''l G P ⊥于点G ,与A’C’的交点即为N 点,易知GN A TN P ',''1∆∆都为等腰直角三角形,111min ''''''(')P N T A N A T TN GN PM MN ∴===-=∴=∴+=+……………………………………………………………………………(8分)(3)),6221,2311(),6221,2311(),233,23(),221,2313(4321+-S S S S …………………………………………………………………………(12分)11、(2019全真预测一)12、(2019全真预测二)13、(2019全真预测三)14、(2019全真预测四)15、(2019南开初三下半期)16、(2019八中一模)(1)设294P m m ⎛-- ⎝5,4Q m m ⎛- ⎝∴()29222PQMN C QP NP m ⎛=+=+ ⎝矩形∵0<,开口向下,∴m =当 (P - ∵最少时间12t RK KT TB =++, ∵R -,作R 关于y 轴对称'R ⎛- ⎝ 过'R 点作直线:4l y =的垂线交于H 点'H R 即为所求. ''''t R K K T TH =++ ∴过''R 作''R H l ⊥∴min 9'2t R H ==(2)综上()()((21310,6;0,12;0,3;0,3E E E E +-17、(2018重庆A 卷)26. 如图,在平面直角坐标系中,点A 在抛物线=y x 4x -2+上,且横坐标为1,点B 与点A 关于抛物线的对称轴对称,直线AB 与y 轴交于点C ,点D 为抛物线的顶点,点E 的坐标为)11(,(1)求线段AB 的长;(2)点P 为线段AB 上方抛物线上的任意一点,过点P 作AB 的垂线交AB 于点H ,点F 为y 轴上一点,当PBE △的面积最大时,求FO 21HF PH ++的最小值;(3)在(2)中,FO 21HF PH ++取得最小值时,将CFH △绕点C 顺时针旋转︒60后得到''H CF △,过点'F 作'CF 的垂线与直线AB 交于点Q ,点R 为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S ,使得点S R Q D ,,,为顶点的四边形为菱形,若存在,请直接写出点S 的坐标,若不存在,请说明理由。
重庆中考26题专题训练

1. 已知:如图,在平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3.过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.(1)求过点E、D、C的抛物线的解析式;(2)将∠EDC绕点D按顺时针方向旋转后,角的一边与y轴的正半轴交于点F,另一边与线段OC交于点G.如果DF与(1)中的抛物线交于另一点M,点M的横坐标为65,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.2. 已知:如图,抛物线)0(22≠+-=a c ax ax y 与y 轴交于点C (0,4),与x 轴交于点A 、B ,点A 的坐标为(4,0)。
(1)求该抛物线的解析式;(2)点Q 是线段AB 上的动点,过点Q 作QE ∥AC ,交BC 于点E ,连接CQ 。
当△CQE 的面积最大时,求点Q 的坐标;(3)若平行于x 轴的动直线l 与该抛物线交于点P ,与直线AC 交于点F ,点D 的坐标为(2,0)。
问:是否存在这样的直线l ,使得△ODF 是等腰三角形?若存在,请求出点P 的坐标;若不存在,请说明理由。
Y XE C A D Q B O 28题图3.如图28-1所示,一张三角形纸片ABC ,∠ACB=90°,AC=8,BC=6.沿斜边AB 的中线CD 把这张纸片剪成11AC D ∆和22BC D ∆两个三角形(如图28-2所示).将纸片11AC D ∆沿直线2D B (AB )方向平移(点12,,,A D D B 始终在同一直线上),当点1D 于点B 重合时,停止平移.在平移过程中,11C D 与2BC 交于点E,1AC 与222C D BC 、分别交于点F 、P.(1) 当11AC D ∆平移到如图28-3所示的位置时,猜想图中的1D E 与2D F 的数量关系,并证明你的猜想; (2) 设平移距离21D D 为x ,11AC D ∆与22BC D ∆重叠部分面积为y ,请写出y 与x 的函数关系式,以及自变量的取值范围;(3) 对于(2)中的结论是否存在这样的x 的值;若不存在,请说明理由.CB D A 28-1图P E F A D 1B C 1D 2C 228-3图 C 2D 2C 1B D 1A 28-2图4.如图1,在平面直角坐标系中有一个Rt △OAC ,点A (6,8),点C (6,0),将其沿直线AC 翻折,翻折后图形为△BAC .动点P 从点O 出发,沿折线O →A →B 的方向以每秒2个单位的速度向B 运动,同时动点Q 从点B 出发,在线段BO 上以每秒1个单位的速度向点O 运动,当其中一个点到达终点时,另一点也随之停止运动.设运动的时间为t (秒).(1)设△OPQ 的面积为S ,求S 与t 之间的函数关系式,并写出自变量t 的取值范围;(2)如图2,固定△OAC ,将△ACB 绕点C 逆时针旋转,旋转后得到的三角形为△''CB A ,设''B A 与AC 交于点D ,当∠'BCB =∠CAB 时,求线段CD 的长;(3)如图3,在△ACB 绕点C 逆时针旋转的过程中,若设C A '所在直线与OA 所在直线的交点为E ,是否存在点E 使△ACE 为等腰三角形,若存在,求出点E 的坐标,若不存在,请说明理由.图1 图2 图3备用图42251015BEB'A'OCAxyx642251015DB'A'OCBAyxy42251015OCBAx422451015Q POCBAy5.如图1,抛物线24y x x c =-+交x 轴于点A 和(1,0),B -交y 轴于点C ,且抛物线的对称轴交x 轴于点D . (1)求这个抛物线的解析式;(2)若点E 在抛物线上,且位于第四象限,当四边形ADCE 面积最大时,求点E 的坐标;(3)如图2,在抛物线上是否存在这样的点P ,使PAB ∆中的内角..中有一边与x 轴所夹锐角..的正切值为12?若存在,求出点P 的坐标,若不存在,请说明理由.6. 如图1,矩形OABC 的顶点O 为原点,点E 在AB 上,把CBE ∆沿CE 折叠,使点B 落在OA 边上的点D 处,点A D 、坐标分别为(10,0)和(6,0),抛物线215y x bx c =++过点C B 、. (1)求C B 、两点的坐标及该抛物线的解析式;(2)如图2,长、宽一定的矩形PQRS 的宽1PQ =,点P 沿(1)中的抛物线滑动,在滑动过程中x PQ //轴,且RS 在PQ 的下方,当P 点横坐标为-1时,点S 距离x 轴511个单位,当矩形PQRS 在滑动过程中被x 轴分成上下..两部分的面积比为2:3时,求点P 的坐标;(3)如图3,动点M N 、同时从点O 出发,点M 以每秒3个单位长度的速度沿折线ODC 按C D O →→的路线运动,点N 以每秒8个单位长度的速度沿折线OCD 按D C O →→的路线运动,当M N 、两点相遇时,它们都停止运动.设M N 、同时从点O 出发t 秒时,OMN ∆的面积为S .①求出S 与t 的函数关系式,并写出t 的取值范围:②设0S 是①中函数S 的最大值,那么0S = .。
2018重庆中考数学第26题专题训练
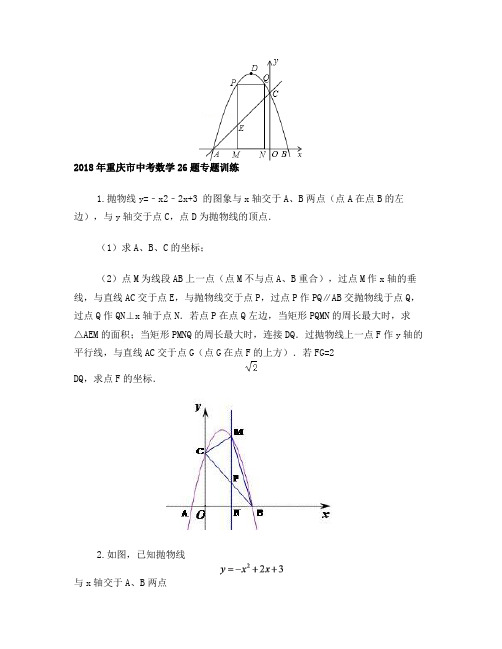
2018年重庆市中考数学26题专题训练1.抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.(1)求A、B、C的坐标;(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=2DQ,求点F的坐标.2.如图,已知抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC。
(1)求A、B、C三点的坐标;(2)若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;当△BCM的面积最大时,在抛物线的对称轴上存在点Q,使得△CNQ为直角三角形,求点Q的坐标。
3.如图,对称轴为直线的抛物线与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
(1)求点B的坐标和抛物线的解析式。
(2)已知,C为抛物线与y轴的交点。
若点P在抛物线上,且,求点P的坐标;设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
4.如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).(1)求直线BC与抛物线的解析式;(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN 的面积为S2,且S1=6S2,求点P的坐标.5.如图1,在平面直角坐标系中,抛物线交轴于A,B两点(点A在点B的左侧),交轴于点W,顶点为C,抛物线的对称轴与轴的交点为D。
2021重庆中考26题专题复习及答案2

重庆中考26题专题复习1、如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为EF=CF;∠EFC的度数为120°;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.解:(1)如图1中,∵DE⊥AB,∴∠BED=90°,∵∠BCD=90°,BF=DF,∴FE=FB=FD=CF,∴∠FBE=∠FEB,∠FBC=∠FCB,∴∠EFC=∠EFD+∠CFD=∠FBE+∠FEB+∠FBC+∠FCB=2(∠FBE+∠FBC)=2∠ABC=120°,故答案为:EF=CF,120°.(2)结论成立.理由:如图2中,取AB的中点M,AD的中点N,连接MC,MF,ED,EN,FN.∵BM=MA,BF=FD,∴MF∥AD,MF=AD,∵AN=ND,∴MF=AN,MF∥AN,∴四边形MFNA是平行四边形,∴NF=AM,∠FMA=∠ANF,在Rt△ADE中,∵AN=ND,∠AED=90°,∴EN=AD=AN=ND,同理CM=AB=AM=MB,在△AEN和△ACM中,∠AEN=∠EAN,∠MCA=∠MAC,∵∠MAC=∠EAN,∴∠AMC=∠ANE,又∵∠FMA=∠ANF,∴∠ENF=∠FMC,在△MFC和△NEF中,,∴△MFC≌△NEF(SAS),∴FE=FC,∠NFE=∠MCF,∵NF∥AB,∴∠NFD=∠ABD,∵∠ACB=90°,∠BAC=30°,∴∠ABC=60°,△BMC是等边三角形,∠MCB=60°∴∠EFC=∠EFN+∠NFD+∠DFC=∠MCF+∠ABD+∠FBC+∠FCB=∠ABC+∠MCB=60°+60°=120°.(3)如图3中,作EH⊥AB于H.在Rt△ABC中,∵∠BAC=30°,BC=3,∴AB=2BC=6,在Rt△AED中,∠DAE=30°,AD=2,∴DE=AD=1,在Rt△DEH中,∵∠EDH=60°,DE=1,∴EH=ED•sin60°=,DH=ED•cos60°=,在Rt△EHG中,EG==.2、如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.解:(1)BC=2BD,理由:如图2,连接CD,由旋转可得,CP=DP,∠CPD=60°,∴△CDP是等边三角形,∴∠CDP=60°=∠PCD,又∵P是AB的中点,AB=AC,∠A=60°,∴等边三角形ABC中,∠PCB=30°,CP⊥AB,∴∠BCD=30°,即BC平分∠PCD,∴BC垂直平分PD,∴∠BDC=∠BPC=90°,∴Rt△BCD中,BC=2BD.(2)如图3,取BC中点F,连接PF,∵∠A=90°,AB=AC,∴△ABC是等腰直角三角形,∵P是AB的中点,F是BC的中点,∴PF是△ABC的中位线,∴PF∥AC,∴∠PFB=∠ACB=45°,∠BPF=∠A=90°,∴△BPF是等腰直角三角形,∴BF=BP,BP=PF,∵∠DPC=∠BPF=90°,∴∠BPD=∠FPC,又∵PD=PC,∴△BDP≌△FCP,∴BD=CF,∵BC=BF+FC,∴BC=BD+BP.3、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.【发现问题】解:延长CA到M,作∠MAC的平分线AN,在AN上截取AD=AC,连接CD,即可得到等腰直角△ACD;连接BD、CE,如图1所示:∵△ABE与△ACD都是等腰直角三角形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE,【拓展探究】解:BD=CE;理由如下:∵四边形AEFB与四边形ACGD都是正方形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;【解决问题】解:以AB为边向外作等边三角形ABE,连接CE,如图3所示:则∠BAE=60°,BE=AB=AE=8,∵AD=CD,∠ADC=60°,∴△ACD是等边三角形,∴∠CAD=60°,AC=AD,∴∠CAD+∠BAC=∠BAE+∠BAC,即∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;当C、B、E三点共线时,CE最大=BC+BE=15+8=23,∴BD的最大值为23.。
2021重庆中考26题专题复习及答案5

重庆中考数学26题专题复习1、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC 于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;①如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.(1)解:如图1中,在AB上取一点M,使得BM=ME,连接ME.在Rt△ABE中,∵OB=OE,∴BE=2OA=2,∵MB=ME,∴∠MBE=∠MEB=15°,∴∠AME=∠MBE+∠MEB=30°,设AE=x,则ME=BM=2x,AM=x,∵AB2+AE2=BE2,∴(2x+x)2+x2=22,∴x=(负根已经舍弃),∴AB=AC=(2+)•,∴BC=AB=+1.方法二:作EH⊥BC于H,求出BH,CH即可解决问题.(2)证明:如图2中,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.∵BE⊥AP,∴∠AHB=90°,∴∠ABH+∠BAH=90°,∵∠BAH+∠P AC=90°,∴∠ABE=∠P AC,在△ABE和△CAP中,,∴△ABE≌△CAP,∴AE=CP=CF,∠AEB=∠P,在△DCF和△DCP中,,∴△DCF≌△DCP,∴∠DFC=∠P,∴∠GFE=∠GEF,∴GE=GF,∵GM⊥EF,∴FM=ME,∵AE=CF,∴AF=CE,∴AM=CM,在△GAH和△GAM中,,∴△AGH≌△AGM,∴AH=AM=CM=AC(3)解:结论:AG=EF.理由:如图3中,作CM⊥AC交AD的延长线于M,连接PG交AC于点O.由(2)可知△ACM≌△BAE,△CDF≌△CDM,∴∠AEB=∠M=∠GEF,∠M=∠CFD=∠GFE,AE=CM=CF,∴∠GEF=∠GFE,∴GE=GF,∵△EFP是由△EFG翻折得到,∴EG=EP=GF=PF,∴四边形EGFP是菱形,∴PG⊥AC,OE=OF,∵AE=CF,∴AO=OC,∵AB∥OP,∴BP=PC,∵PF∥BE,∴EF=CF=AE,∵PB=PC,AO=OC,∴PO=OG=AB,∴AB=PG,AB∥PG,∴四边形ABPG是平行四边形,∴AG∥BC,∴∠GAO=∠ACB=45°,设EO=OF=a,则OA=OG=3a,AG=3a,∴==,∴AG=EF2、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.解:(1)∵E为AC中点,作ED⊥AC交AB于D,∴AD=CD,∵∠ACB=90°,∴BC∥DE,∴AD=BD,∴CD=BD,∴AB=2CD;(2)如图2,连接CH,∵点E是AC的中点,∴AE=CE,∵DE⊥AC,∴CH=AH,∴∠ACH=∠CAH,∵∠ACB=90°,∴∠B+∠BAC=90°,∵CF⊥AB,∴∠BAC+∠ACF=90°,∴∠ACF=∠B,∴∠HCG=∠ACH+∠ACF=∠CAH+∠B,∠AHG=2∠B∴在四边形AHGF中,∠AFG+∠FGH+∠AHG+∠F AH=360°,∴∠FGH=360°﹣(∠AFG+∠AHG+∠F AH)=360°﹣(90°+2∠B+∠CAH+∠BAC)=360°﹣(90°+2∠B+∠CAH+90°﹣∠B)=360°﹣(180°+∠B+∠CAH)=180°﹣(∠B+∠CAH),∵∠CGH=180°﹣∠FGH=∠B+∠CAH=∠HCG,∴CH=GH,∵CH=AH,∴AH=GH;(3)如图3,由(1)知,DE∥BC,∴∠B=∠ADE,在△BFC和△DEA中,,∴△BFC≌△DEA,∴BC=AD,∵AD=BD=CD,∴BC=BD=CD,∴△BCD是等边三角形,∴∠B=60°,在Rt△ABC中,AC=6,∴BC=2,AB=4,∵CF⊥BD,∴DF=,CF=3,∵∠BAC=30°,∴∠ADE=60°,∵∠EDG=90°,∠FDG=30°,在Rt△DFG中,DF=,∴FG=1,DG=2,∴CG=CF﹣FG=2过点H作HN⊥CF,由(2)知,CH=GH,∴NG=CG=1,∴FN=NG+FG=2,过点H作HM⊥AB,∴∠FMH=∠NFM=∠HNF=90°,∴四边形NFMH是矩形,∴HM=FN=2,在Rt△DMH中,∠ADE=60°,HM=2,∴DH=,在Rt△HDG中,根据勾股定理得,HG==.3、一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)(1)证明:∵AC=BC,∠ACB=90°,∴∠A=∠B=45°,∵CD⊥AB,∴∠CDB=90°,∴∠DCB=45°,∵∠ECF=∠DCB+∠1=45°+∠1,∠EFC=∠B+∠2=45°+∠2,∠1=∠2,∴∠ECF=∠EFC,∴CE=EF,∵CD⊥AB,FG⊥AB,∴∠CDE=∠EGF=90°,在△CDE和△EGF中,,∴△CDE≌△EGF(AAS);(2)证明:由(1)得:CE=EF,∠A=∠B,∵CE平分∠ACD,∴∠ACE=∠1,∵∠1=∠2,∴∠ACE=∠2,在△ACE和△BEF中,,∴△ACE≌△BEF(AAS),∴AE=BF;(3)AE=BF,作EH⊥BC与H,如图3所示:设DE=x,根据题意得:BE=DE=x,AD=BD=2x,CD=AD=2x,AE=3x,根据勾股定理得:BC=AC=2x,∵∠ABC=45°,EH⊥BC,∴BH=x,∴CH=BC﹣BH=x,∵EC=EF,∴FH=CH=x,∴BF=x﹣x=x,∴=,∴AE=.。
2018年重庆中考数学第26题专题训练

(2)点P为直线x=1右方抛物线上的 一点(点P不与点B重合),记A、B、C、P四点所构成的四边形面积为 ,若 ,求点P的坐标;
(3)点Q是线段BD上的动点,将△DEQ沿边EQ翻折得到△ ,是否存在点Q使得△ 与△BEQ的重叠部分图形为直角三角形,若存在,请求出BQ的长,若不存在,请说明理由.
8.如图1,已知抛物线 与 轴交于 两点(点 在点 的左侧),与 轴交于点 ,点 是点 关于抛物线对称轴的对称点,连接 ,过点 作 轴于点 ,过点 作 交 的延长线于点 .
(1)求线段 的长度;
(2)如图2,试在线段 上找一点 ,在线段 上找一点P,且点 为直线 上方抛物线上的一点,求当 的周长最小时, 面积的最大值是多少;
设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
4.如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
1.如图,抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求Aபைடு நூலகம்B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)如图2,以AC为对角线作正方形AMCN,将正方形AMCN在平面内平移得正方形A′M′C′N′.当正方形A′M′C′N′有顶点在△ABC的边AC上(不含端点)时,正方形A′M′C′N′与△ABC重叠部分得到的多边形能否为轴对称图形,如果能,求出此时重叠部分面积S的值,或重叠部分面积S的取值范围;如果不能,请说明理由.
2021年重庆市中考二轮复习数学第26题几何证明专练专题(三)

2021年重庆市中考二轮复习数学第26题几何证明专练专题(三)1.已知在平行四边形ABCD 中,过点D 作DE ⊥BC 于点E,且AD=DE,连接AC 交DE 于点F,作DG⊥AC 于点G(1)如图1,若DF EF =21,AF=13,求DG 的长 (2)如图2,作EM⊥AC 于点M,连接DM,求证:AM-EM=2DG,2.如图,∆ABC 是等边三角形,AC 上有点,分别以BD 为边作等边∆BDE 和等 腰∆BDF,边BC 、DE 交于点H,点F 在BA 延长线上且DB=DF,连接CE,求 证(1) ∆ABD=∆CBE:(2)BC= AF+CE.3.如图,在菱形ABCD中,∠BAD=60°,M为对角线BD延长线上一点,连接AM 和CM,E为CM上一点,且满足CB=CE,连接BE,交CD于点F.(1)若∠AMB=30°,且DM=3,求BE的长:(2)证明:AM=CF+DM.4.如图,在矩形ABCD中,点E为AD上一点,连接BE、CE,∠ABE=45°(1)如图1,若BE=32,BC=4,求EC的长.(2)如图2,点P是EC的中点,连接BP并延长交CD于F,H为AD上一点,接HF,且∠DHF=∠CBF,求证:BP=PF+FH.5.(1)如图1,四边形EFGH中,FE=EH,∠EF G+∠EHG=180°,点A,B分1∠FEH,别在边FG,GH上,且∠AEB=2(1)求证:AB=AF+BH(2)如图2,四边形EFGH中,FE=EH,点M在边E上连接FM,EN平分∠FEH交FM于点N,∠ENM=a,∠FGH=180°-2a,连接GN,HN①找出图中与NH相等的线段,并加以证明;②求∠NGH的度数(用含a的式子表示).6.如图,在平行四边形ABCD中,点E在对角线BD上,AB=AE,AF⊥BD于点F, ∠ADB=45°(1)若BC=122,AB=13,求BF的长(2)延长AF交BC于点G,延长AD到点H.使得DH=BG,连接EH,求证:AE=EH.7.如图,在菱形ABCD中,∠B=120o,E、F分别是边BC、CD上的点,且满足CE=CF.连接EF.(1)若CE=1,AB=3,求AF的长;(2)取AF的中点G,连接EG、DG,求证:EG⊥DG.8.如图,在正方形ABCD中,对角线AC,BD相较于点O,以AD为边向外作等边∆MDE,连接CE,交BD于F(1)如图1,若AE=6,求DF的长;(2)如图2,点M为AB的延长线上一点,连接CM,连接FM且FM平分∠AMC.求证:CM=3MF-AM.9.如图,在平行四边形ABCD中,∠B=45°,过点C作CE⊥AD于点,连结AC,过点D作DF⊥AC于点F,交CE于点G,连结EF.(1)若DG=8,求对角线AC的长.(2)求证:AF+FG=2EF.10.如图, 平行四边形ABCD中,DF平分∠ADC交AC于点H,G为DH的中点(1)如图①,若M为AD的中点,AB⊥AC,AC=9,CF=8,CG=25,求GM.(2)如图②,M为线段AB上一点,连接MF,满足∠MCD=∠BCG,∠MFB=∠BAC,求证:MC=2CG.11.如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N.(1)若BM=4,MC=3,AC=38,求AM的长度;(2)若∠ACB=∠AFE=45°,求证AN+AF=2 EF.12.平行四边形ABCD中,点E为BC边上一点,连接DE交对角线AC于点F,点G为DE一点,AH⊥DE于H,BC=2AG且∠ACE=∠GAC,点M为AD的中点,连接MF;若∠DFC=75°.(1)求∠MFD的度数;(2)求证:GF+GH=AH.13.在平行四边形ABCD中,AD=BD,E为AB的中点,F为CD上一点,连接EF交BD于G.(1)如图1,若DF=DG=2,AB=8,求EF的长;(2)如图2,∠ADB=90°,点P为平行四边形ABCD外部一点,且AP=AD,连接BP、DP、EP,DP交EF于点Q,若BP⊥DP,EF⊥EP,求证:DQ=PQ.14.如图,□ABCD的对角线AC、BD相交于点O,AC=BC.(1)如图1,过点B作BE⊥AC于点E,若AC=8,BE=5时,求OE的长度;(2)如图2,若∠BDC=45°,过点C作CF⊥CD交BD于点F,过点B作BG⊥BC且BG=BC,连接AG、DG,求证:AG=2OF.15.如图1,在矩形ABCD中,∠ABC的平分线交AD于点E,连接CE,(1)若BE=42,CE=17,求AD的长;(2)如图2,点F是BC上一点,且EF=EC.过点C作CG⊥EF于点G,交BE于点H,求证:BH=2DEBH的值,(3)如图3,在(2)的条件下,连接DG,当BE=BC时,请直接写出DG。
[精品]重庆中考数学26题专训45.docx
![[精品]重庆中考数学26题专训45.docx](https://img.taocdn.com/s3/m/79ac17d2a5e9856a5712608d.png)
如图1,在长为44,宽为12的矩形PQRS中,将一张直角三角形纸片和一张正方形纸片QEFG如图放置,其中边力8、DE !6.在户。
上,边砂在上,边BC、DG在同一直线上,且Rt/\ABC两直角边BC=6, AB=3,正方形班FG的边长为4.从初始时刻开始,三角形纸片ABC.沿4P方向以每秒1个单位长度的速度向左平移:同时正方形纸片D时‘G,沿0?方向以每秒2个单位长度的速度向上平移,当边G尸落在S&上时,纸片立即沿RS方向以原速度向左平移,直至G点与S点集合时,两张纸片同时停止移动.设平移时间为x秒.(1)请填空:当尸2 时,CD= ▲, DO= A ,此时CD + DO A CO (请填"v”、"=”、">”);(2)如图2,当缗片p野Q沿娜方向平移甘,连接CQ、和C0 求平移过程中△C£>Q的面积S与x的函数关系式,并写出自变量x的取值范围(这里规定线段的面积为零);(3)如图3,当纸片DEFG沿战方向平移时,是否存在这样的时刻x,使以4、C、Z)为顶点的三角形图2AB Q图32.将•张矩形纸片沿对角线剪开(如图1),得到两张三角形纸片AABC、NDEF(如图2),量得他们的斜边长为6cm,较小锐角为30。
,再将这两张三角纸片摆成如图3的形状,旦点A、C、E、F在同一条直线上,点C与点E重合.NABC保持不动,OB为NABC的中线.现对KDEF纸片进行如卜操作时遇到了三个问题,请你帮助解决.(1)将图3中的沿C4向右平移,直到两个三角形完全重合为止.设平移距离CE 为x (即CE的长),求平移过程中,ADEF与^BOC重叠部分的面积S与x的函数关系式,以及自变量的取值范围;(2)平移到E与。
重合时(如图4),将绕点。
顺时针旋转,旋转过程中AQEF的斜边EF交AABC的BC边于G,求点C、。
、G构成等腰二角形时,AOCG的面积;(3)在(2)的旋转过程中,的边EF、DE分别交线段BC于点G、"(不与端点重合).求旋转角ZCOG为多少度时,线段BH、GH、CG之间满足GH- +BH- =CG2,3.如图,已知:△ABC为边长是4占的等边三角形,四边形DEFG为边长是6的正方形.现将等边AABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C (E)、F在同一条直线上,AABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设AABC的运动时间为t秒(1)在整个运动过程中,设等边AABC和正方形DEFG重叠部分的面积为S,请直接写出S与f之间的函数关系式;(2)如图2,当点A与点O重合时,作/ABE的角平分线交AE于M点,将绕点A逆时针旋转,使边AB与边AC重合,得到△ACN.在线段AG上是否存在H点,使得为等腰三角形.如果存在,请求出线段的长度;若不存在,请说明理由.(3)如图3,若四边形DEFG为边长为4也的正方形,△ABC的移动速度为每秒占个单位长度,其余条件保持不变.△ABC开始移动的同时,。
2021年重庆中考几何第26题专题训练一(含答案解析)
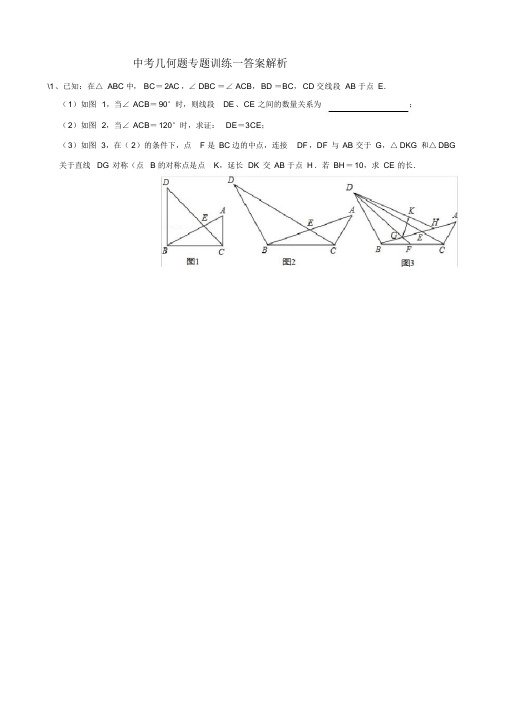
中考几何题专题训练一答案解析\1 、已知:在△ ABC 中,BC=2AC ,∠ DBC =∠ACB,BD =BC,CD 交线段AB 于点E.(1)如图1,当∠ACB=90°时,则线段DE 、CE 之间的数量关系为;(2)如图2,当∠ACB=120°时,求证:DE=3CE;(3)如图3,在(2)的条件下,点 F 是BC 边的中点,连接DF ,DF 与AB 交于G,△DKG 和△DBG 关于直线DG 对称(点 B 的对称点是点K,延长DK 交AB 于点H .若BH =10,求CE 的长.2、(2016 春?重庆校级期中)在△ABC 中,AB=AC,D 为射线BC 上一点,DB =DA,E 为射线AD 上一点,且AE=CD ,连接BE.(1)如图1,若∠ADB =120°,AC=2 ,求DE 的长;(2)如图2,若BE=2CD ,连接CE 并延长交AB 于点F,求证:CF =3EF;(3)如图3,若BE⊥AD ,垂足为点E,猜想AE,BE,BD 之间的数量关系,直接写出关系式.3、(2019 秋?江岸区校级月考)在菱形ABCD 中,∠ABC=60°(1)如图1,P 是边BD 延长线上一点,以AP 为边向右作等边△APE,连接BE、CE.①求证:CE⊥AD;② 若AB =,BE=,求AE 的长;(2)如图2,P 是边CD 上一点,点 D 关于AP 的对称点为E,连接BE 并延长交AP 的延长线于点 F ,连接DE 、DF .若BE=11,DE =5,求△ADF 的面积.4、(2016 秋?南岗区校级月考)已知:如图,在等边△ABC 中,点 D 是AC 上任意一点,点 E 在BC 延长线上,连接DB ,使得BD =DE .(1)如图1,求证:AD=CE;(2)如图2,取BD 的中点 F ,连接AE、AF .求证:∠ CAE =∠BAF;(3)如图3,在(2)的条件下,过点F 作AE 的垂线,垂足为H,若AH =.求EH 的长.5、已知,在Rt△ABC 中,∠C=90°,AC=BC,点D 在边BC 上,连接AD,作DE⊥AD ,且DE=AD ,连接BE、AE,DE 与AB 交于点H,(1)如图 1 所示,求证:∠C=∠ABE;(2)如图2,把射线AD 沿AB 折叠,分别交BE、DE 的延长线于点F、点G.若∠AEB=75°,求证:HG =2DH ;(3)在(2)的条件下,若BE=3,求DH 的长?6、如图,在△ABC 中,∠ABC=90°,AB=BC,点D 是△ABC 内部一点,连接AD,BD 和CD .(1)如图1,若∠ BDC=90°,BD=1,CD =2,求AC 的长.(2)如图2,若CD 平分∠ACB,∠BDC =90°,过点 B 作BE∥AC 交AD 的延长线于点E,求证:AD =DE .(3)如图3,若CD =CB,∠BCD =30°,取线段AC 的中点 F ,连接DF ,求证:∠AFD =45°7、(2013?洪山区模拟)如图1,直角梯形ABCD 中,BC=CD ,AB ∥CD ,∠ABC=90°,点P 为边AD上一点,BC=PB.(1)求证:∠ CBP=2∠DCP ;(2)如图2,若∠ABP 的平分线交CP 的延长线于点E,连接DE ,求证:BE+DE=CE;(3)在(2)的条件下,若AB=1,BC=2,请直接写出线段CE 的长度.8、(2016 秋?松北区期末)如图,在△ABC 中,∠ACB=60°,点 D 在射线BC 上,AB=AD .(1)如图1,求证:BC+CD =AC;( 3)如图 3,在( 2)的条件下, FG ⊥ BE 于点 G , FG = 4,EF = ,求△ ( 2)如图 2,取 AB 的中点 F ,延长 CA 至点 E ,连接 BE 、DE 、EF ,使得∠ ABE =∠ CAD ,EF =AE , 求证:∠ BEF = 2∠ABD ;AED 的面积.9、( 2016?九龙坡区校级一模)已知, Rt △ ABC 中,∠ ACB = 90°,∠ CAB = 30°,分别以 AB 、 AC 为边,向Rt△ABC 外作等边△ABD 和等边△ACE(1)如图1,连接BE、CD ,若BC=2,求BE 的长;(2)如图2,连接DE 交AB 于点F ,作BH⊥AD 于H,连接FH .求证:BH =2FH ;(3)如图3,取AB、CD 得中点M 、N,连接M 、N,试探求MN 和AE 的数量关系,并直接写出结论.10、重庆八中初2020 级九上期末11、重庆实验外国语学校初2020 级九上期末12、重庆双福育才中学初2020 级九上期末2020 年中考几何题专题训练一答案解析\1 、已知:在△ ABC 中,BC=2AC ,∠ DBC =∠ACB,BD =BC,CD 交线段AB 于点E.(1)如图1,当∠ACB=90°时,则线段DE 、CE 之间的数量关系为DE=2CE ;(2)如图2,当∠ACB=120°时,求证:DE=3CE;(3)如图3,在(2)的条件下,点 F 是BC 边的中点,连接DF ,DF 与AB 交于G,△DKG 和△DBG 关于直线DG 对称(点 B 的对称点是点K,延长DK 交AB 于点H .若BH =10,求CE 的长.(1)解:∵∠ DBC =∠ACB =90°,∴∠DBC +∠ACB =180°,∴AC ∥BD ,∴∠DBE =∠CAE又∵∠ DEB =∠AEC ,∴△DBE ∽△CAE ,∴=,又∵ BD =BC =2AC ,∴DE =2CE;故答案为:DE =2CE .(2)证明:如图2,∵∠DBC =∠ACB =120°,BD =BC,∴∠D=∠BCD =30°,∴∠ ACD =90°,过点 B 作BM ⊥DC 于M ,则DM =MC ,BM =BC ,∵AC =BC ,∴BM =AC,∵在△ BME 和△ ACE 中∴△BME ≌△ACE (AAS),∴ME =CE =CM ,∴DE =3EC;(3)解:如图,过点 B 作BM ′⊥DC 于点M ′,过点 F 作FN ⊥DB 交DB 的延长线于点N,设BF =a,∵∠DBF =120°,∴∠FBN =60°,∴FN =a,BN =a,∵DB =BC =2BF =2a,∴DN =DB +BN =a,∴DF ===a,∵AC =BC ,BF =BC,∴BF =AC ,∴△BDF ≌△BCA (SAS),∴∠ BDF =∠ CBA ,又∵∠ BFG =∠DFB ,∴△FBG ∽△FDB ,∴==,∴BF 2=FG ×FD ,∴a2=a×FG ,∴FG =a,∴DG =DF ﹣FG =a,BG==a,∵△DKG 和△DBG 关于直线DG 对称,∴∠ GDH =∠BDF ,∴∠ ABC =∠ GDH ,又∵∠ BGF =∠DGH ,∴△BGF ∽△DGH ,∴=,∴GH ==a,∵B H =BG +GH =a=10,∴a=2 ;∴BC =2a=4 ,CM ′=BC cos30°=2 ,∴DC =2CM ′=4 ,∵DE =3EC,∴EC =DC =.2、(2016 春?重庆校级期中)在△ABC 中,AB=AC,D 为射线BC 上一点,DB =DA,E 为射线AD 上一点,且AE=CD ,连接BE.(1)如图1,若∠ADB =120°,AC=2 ,求DE 的长;(2)如图2,若BE=2CD ,连接CE 并延长交AB 于点F,求证:CF =3EF;(3)如图3,若BE⊥AD ,垂足为点E,猜想AE,BE,BD 之间的数量关系,直接写出关系式.(1)解:∵DA =DB ,∠ADB =120°,∴∠ABC =∠BAD =30°,∵AB =AC ,∴∠ABC =∠C=30°,∴∠CAD =90°,在RtACD 中,tan30 °=,∴A D =2 ×=2,AE =CD =2AD =4 ∴DE =AE ﹣AD =CD ﹣AD =4﹣2=2;(2)证明:如图,过 A 作AG∥B C ,∵DB =DA ,AB =AC ,∴∠BAD =∠ABC ,∠ ABC =∠ACB ,∴∠BAD =∠ACB ,∵AE =CD ,在△ ABE 和△ CAD 中∴△ABE ≌△CAD (SAS),∴BE =AD ,∵BE =2CD,∴AD =2CD =2AE ,∴AE =DE ,∵AG ∥BC ,∴∠ G=∠DCE ,∠ GAE =∠CDE ,在△ AGE 和△ DCE 中∴△AGE ≌△DCE (AAS ),∴GE =CE ,AG=CD =AE ,∴△ AGE 为等腰三角形,∴∠GAF =∠ABC =∠ BAD ,∴F 为GE 的中点,∴CE =EG =2EF ,∴CF =3EF ;(3)如图3,取BE 中点M ,延长AM 至N,使MN =AM ,连接BN ,EN ,∴四边形ABNE 是平行四边形,∴AE ∥BN ,∴∠NBC =∠D,BN =AE =CD,∵AB =AC ,DB =DA ,∴∠ABC =∠ACB =∠ BAD ,∴∠BAC =∠D=∠NBC ,∵∠ABN =∠NBC +∠ABC ,∠ACD =∠BAC +∠ABC ,∴∠ ABN =∠ ACD ,在△ ABN 和△ ACD 中∴△ABN ≌△ACD (SAS),∴BD =AD =AN =2AM ,∵BE ⊥AD ,∴AE 2+ME 2=AM 2,∴AE 2+(BE )2=(AN )2,∴AE 2+ BE 2=BD 2.3、(2019 秋?江岸区校级月考)在菱形ABCD 中,∠ABC=60°(1)如图1,P 是边BD 延长线上一点,以AP 为边向右作等边△APE,连接BE、CE.①求证:CE⊥AD;② 若AB =,BE=,求AE 的长;(2)如图2,P 是边CD 上一点,点 D 关于AP 的对称点为E,连接BE 并延长交AP 的延长线于点 F ,连接DE 、DF .若BE=11,DE =5,求△ADF 的面积.(1)①证明:在菱形ABCD 中,∠ABC =60°,∴∠ ADC =60°,且AB =BC=DA =DC ,∴△ ADC 和△ ABC 是等边三角形,∴AB =AC ,∠ BAC =∠CAD =60°,又∵△ APE 是等边三角形,∴AE =AP,∠EAP =60°,∴∠ BAC +∠CAP =∠PAE +∠CAP,即∠ BAP =∠CAE ,∴△BAP ≌△CAE (SAS),∴∠ACE =∠ABP =∠ABC =30°,∵∠CAD =60°,∴∠ACE +∠CAD =90°,∴CE ⊥AD ;② 解:如图1,设AC 与BD 交于点O,由① 知,∠ ACE =30°,且∠ ACB =60°,∴∠ACE +∠ACB =∠BCE =90°,∵在Rt △BCE 中,BC =AB =,BE =,∴CE ==4,由① 知,△ BAP ≌△ CAE ,∴BP =CE=4,在Rt △BOC 中,∠ ACB =60°,∴BO =BC=,CO=AO=BC =,∴OP=BP﹣BO=,∴在Rt △AOP 中,AP ===,∴A E =AP=;(2)解:如图2,连接AE ,过点 A 作AH ⊥BF 于点H ,∵点 D 关于AP 的对称点为E,∴AP 垂直平分DE ,∴AD =AE ,FD =FE ,∴∠EAF =∠DAF =∠EAD ,∠DFA =∠EFA =∠DFE ,又∵在菱形ABCD 中,AB =AD ,∴AB =AE ,∴AH 垂直平分BE ,∴EH =BH =BE =,∠BAH =∠EAH =∠B AE ,∴∠HAF =∠EAH +∠EAF =∠BAD ,∵∠ABC =60°,∴∠BAD =180°﹣∠ABC =120°,∴∠HAF =60°,∴∠AFH =90°﹣∠ HAF =30°,∴∠DFE =60°,∴△ DEF 为等边三角形,∴EF =DE =5,∴HF =HE +EF =+5=,在Rt △AHF 中,∠ AFH =30°,∴AH =HF =,∴S△AEF =EF ?AH =×5×=,∵AD =AE ,FD =FE ,AF =AF ,∴△ADF ≌△AEF (S S S),∴△ADF 的面积为.4、(2016 秋?南岗区校级月考)已知:如图,在等边△ABC 中,点 D 是AC 上任意一点,点 E 在BC 延长线上,连接DB ,使得BD =DE .(1)如图1,求证:AD=CE;(2)如图2,取BD 的中点 F ,连接AE、AF .求证:∠ CAE =∠BAF;(3)如图3,在(2)的条件下,过点 F 作AE 的垂线,垂足为H,若AH =.求EH 的长.解:( 1)如图 1,作 DF ∥ AB ,,过点 B 作 BG ∥ AC 交 AF 的延长线于 G ,∴∠ G =∠ DAF ,∠ CBG =∠ ACB = 60°,∴∠ ABG =∠ ABC +∠ CBG = 120°=∠ ACE ,∵ DF ∥ AB , ∴ , ∵ AC = BC , ∴ CF = CD , ∴ BF = AD , ∵ DF ∥ AB , ∴∠ DFC = 60°, ∴∠ BFD = 120°, ∵ BD =DE , ∴∠ E =∠ DBE ,在△ BDF 和△ EDC 中,∴△ BDF ≌△ EDC ,( AAS ) ∴ BF = CE , ∴ AD = CE , ( 2)如图 2,∵点 F 是BD 中点,∴BF =DF ,在△BFG 和△DFA 中,,∴△BFG ≌△DFA ,∴BG =AD ,由(1)知,AD =CE ,∴BG =CE ,在△ABG 和△ACE 中,,∴△ABG ≌△ACE ,∴∠BAF =CAE ;(3)由(2)知,∠ BAF =∠CAE ,∴∠FAE =∠FAC +∠CAE =∠FAC +∠BAF =∠BAC =60°,∵F H ⊥AE ,∴∠AHF =90°,∴∠AFH =90°﹣∠FAE =30°,在Rt △AFH 中,AH =,∴AF =2 ,由(2)知,△ BFG ≌△ DFA ,∴GF =AF =2 ,由(2)知,△ ABG ≌△ ACE ,∴AE =AG =2AF =4 ,∴EH =AE ﹣AH =4 ﹣=3 .5、已知,在Rt△ABC 中,∠C=90°,AC=BC,点D 在边BC 上,连接AD,作DE⊥AD ,且DE=AD ,连接BE、AE,DE 与AB 交于点H,(1)如图 1 所示,求证:∠C=∠ABE;(2)如图2,把射线AD 沿AB 折叠,分别交BE、DE 的延长线于点F、点G.若∠AEB=75°,求证:HG =2DH ;(3)在(2)的条件下,若BE=3,求DH 的长?证明:(1)如图1,过点 E 作EM ⊥BC 于M ,∵∠ACB =90°,AD ⊥DE∴∠ACB =∠ADE =90°∵∠ADB =∠ACB +∠DAC =∠ADE +∠EDB∴∠ DAC =∠EDB ,且∠ ACD =∠ EMD =90°,AD=DE ∴△ACD ≌△DME (AAS )∴AC =DM ,CD =EM∵AC =BC ,∴BC =DM∴CD =BM∴BM =EM ,且EM ⊥BM∴∠EBM =45°∵∠C=90°,AC=BC∴∠ABC =∠BAC =45°∴∠ABE =180°﹣∠ABC ﹣∠EBM =90°∴∠ C=∠ABE(2)如图2,过点 E 作EM ⊥BC 于M ,∵∠C=90°,AC=BC ,∠ADE =90°,AD =DE∴∠ CAB =∠DAE =∠AED =45°由(1)可知∠ EBM =45°,∴∠CBE =135°,∵∠ DAE +∠AEB +∠DBE + ∠ADB =360°,且∠ AEB =75°,∴∠ADB =105°∴∠ACD +∠CAD =∠ADB =105°∴∠CAD =15°∴∠DAB =30°∵把射线AD 沿AB 折叠,分别交BE 、DE 的延长线于点 F 、点G.∴∠DAB =∠BAG =30°∴∠ DAG =60°,且∠ ADE =90°∴∠G=30°=∠BAG∴AH =HG∵∠ADE =90°,∠ DAH =30°∴AH =2DH∴HG =2DH(3)作EN 平分∠ DEB 交BC 于点N ,∵EM =BM ,∠EMB =90°∴BE =EM ,且BE =3,∴E M =∵∠AEB =75°,∠ AED =45°∴∠DEN =30°∵EN 平分∠ DEB∴∠DEN =15°∵∠ EDM =∠C AD =15°∴∠DEN =∠EDB =15°,∴DN =EN ,∠ ENM =30°,且EM ⊥BM∴NE =2EM =3 ,NM =EM =在Rt △DEM 中,DE ==3 +3=AD∵∠DAH =30°,∠ ADH =90°∴AD =DH =3 +3∴ DH =3+6、如图,在△ABC 中,∠ABC=90°,AB=BC,点D 是△ABC 内部一点,连接AD,BD 和CD .(1)如图1,若∠ BDC=90°,BD=1,CD =2,求AC 的长.(2)如图2,若CD 平分∠ACB,∠BDC =90°,过点 B 作BE∥AC 交AD 的延长线于点E,求证:AD =DE .(3)如图3,若CD =CB,∠BCD =30°,取线段AC 的中点 F ,连接DF ,求证:∠AFD =45°解:(1)如图1,∵∠ BDC =90°,BD =1,CD =2,∴BC ===,∵AB =BC =,由勾股定理得:AC ===;(2)如图2,延长BD 交AC 于P,∵DC 平分∠ ACB ,∴∠BCD =∠ACD ,∵∠BDC =90°,∴∠BDC =∠PDC=90°,∵CD =CD ,∴△BDC ≌△PDC,∴BD =PD ,∵BE ∥AC ,∴∠E=∠EAC ,∠EBD =∠ DPA,∴△BDE ≌△PDA ,∴AD =DE ;(3)如图3,以BD 为边作等边三角形BDE ,连接BF 、CE,∴BD =DE =BE ,∵AB =BC ,F 是AC 的中点,∴BF ⊥AC ,∴∠AFB =90°,∵∠ABC =90°,∴BF =AF ,∵CD =BC ,∠BCD =30°,∴∠CBD =∠CDB =75°,∵CE =CE ,∴△CEB ≌△CED ,∴∠BCE =∠DCE =15°,∵∠CBD =75°,∠ DBE =60°,∴∠CBE =75°﹣60°=15°,∵∠ABC =90°,∴∠ABD =90°﹣75°=15°,∴∠ABD =∠CBE ,∴△ABD ≌△CBE ,∴∠BAD =∠BCE =15°,∴∠ABD =∠BAD =15°,∴AD =BD ,∵D F =DF ,∴△ADF ≌△BDF ,∴∠ AFD =∠B FD =∠AFB =×90°=45°.7、(2013?洪山区模拟)如图1,直角梯形ABCD 中,BC=CD ,AB ∥CD ,∠ABC=90°,点P 为边AD上一点,BC=PB.(1)求证:∠ CBP=2∠DCP ;(2)如图2,若∠ABP 的平分线交CP 的延长线于点E,连接DE ,求证:BE+DE=CE;(3)在(2)的条件下,若AB=1,BC=2,请直接写出线段CE 的长度.解:(1)取CP 的中点F,连接BF ,如图1,∵BC =BP,BF 是底边上的中点,∴∠CBF =∠PBF =∠CBP,BF ⊥PC,∴∠CBF +∠BCF =90°,∵∠BCF +∠DCP =90°,∴∠DCP =∠CBF ,∴∠CBP =2∠DCP ;(2)过得 C 作CG ⊥CE 交EB 的延长线于点G,连接BD ,如图2,∵BC =CD ,∠BCD =90°,∴∠CBD =45°,∵∠EBF =∠EBP +∠PBF =∠ABP + ∠CBP =45°,∴∠BEF =180°﹣∠EBF ﹣∠BFE =45°,∴△ CEG 是等腰直角三角形,∴EG =CE,CG =CE ,∵∠ECG =90°=∠ BCD ,∴∠ BCG =∠DCE ,在△ CBD 和△ CDE 中∴△CBD ≌△CDE (SAS),∴BG =DE ,∴DE +BE =BG+BE =EG =CE;(3)CE=,理由如下;取CD 的中点M ,连接MF ,设MF 的延长线交直线AB 与B ′,如图2,∵F 是PC 的中点,∴FM ∥AD ,∵AB ∥CD ,∴四边形AB ′MD 是平行四边形,∴AB ′=DM =1=AB ,∴B′与 B 重合,即B、F、M 在一条直线上,∴BM ⊥CE ,∵∠CBF =∠MBC ,∴△BFC ∽△BCM ,∴=,即=,∴BF =2CF ,∵∠BEF =45°,∠ BFE =90°,∴EF =BF =2CF ,∵CF =PF ,∴CF =PF =PE,CE=3CF ,∵S△BCM =CF ?BM =BC?CM ,∴CF ===,∴CE =3CF =.8、(2016 秋?松北区期末)如图,在△ABC 中,∠ACB=60°,点 D 在射线BC 上,AB=AD .(1)如图1,求证:BC+CD =AC;(2)如图2,取AB 的中点F,延长CA 至点E,连接BE、DE、EF ,使得∠ ABE=∠CAD ,EF =AE,求证:∠ BEF =2∠ABD ;(3)如图3,在(2)的条件下,FG ⊥BE 于点G,FG =4,EF =,求△AED 的面积.(1)证明:延长DB 至E ,使BE =CD ,连接AE ,∵AB =AD ,∴∠ABD =∠ADB ,∵∠ABE +∠ABD =180°,∠ADC +∠ADB =180°,∴∠ ABE =∠ ADC ,在△ ABE 和△ ADC 中,,∴△ABE ≌△ADC ,∴∠C=∠ E=60°,∴△ AEC 为等边三角形,∴AC =CE ,∵BC +BE =CE ,∴BC +CD =AC ;(2)证明:∵ AB =AD ,∴∠ABD =∠ADB ,∵∠CAD +∠ADB =∠ACB =60°,∠ CAD =∠ABE ,∴∠ABE +∠ABD =∠CAD +∠ADB =60°,∴△ BEC 为等边三角形,过点 A 作AN ∥BC 交EB 于N,∴△ENA 为等边三角形,∠NAB =∠ABD ,∴AN =AE ,∴BN =AC ,∴∠ NAB =∠ ADC ,在△ BNA 和△ ACD 中,,∴△BNA ≌△ACD ,∴AN =CD ,∴CD =AE ,延长EF 至M 使得EF =FM ,连接BM ,∴△ AEF ≌△BMF ,∴AE =BM ,AE ∥BM ,∴BM =CD ,∠MBC =∠ECB =60°,∴∠ EBM =∠EBC +∠MBC =120°,又∵∠ ECD =∠EBM =120°,∴△ BEM ≌△C ED ,∴∠BEF =∠CED ,∵EF =AE ,∴∠EFA =∠EAF ,∴∠BEF +∠EBF =∠ACB +∠ABD ,∴∠BEF +60 °﹣∠ ABD =∠ABD +60°,∴∠BEF =2∠ABD ∠CED =2∠ABD ;(3)解:由(2)得,△ EMD 是等边三角形,∴,过点 A 作AP ⊥DE 于P,由(2)可证△ EFG ≌△ EAP ,∴AP =FG =4,∴S△AED=DE ×AP =××4=37.9、(2016?九龙坡区校级一模)已知,Rt△ABC 中,∠ACB=90°,∠CAB=30°,分别以AB、AC 为边,向Rt△ABC 外作等边△ABD 和等边△ACE(1)如图1,连接BE、CD ,若BC=2,求BE 的长;(2)如图2,连接DE 交AB 于点F ,作BH⊥AD 于H,连接FH .求证:BH =2FH ;(3)如图3,取AB、CD 得中点M 、N,连接M 、N,试探求MN 和AE 的数量关系,并直接写出结论.解:(1)如图1,Rt △ABC 中,∠ CAB =30°,BC =2,∴AB =4,AC=2 ,∵△ ACE 是等边三角形,∴AE =AC =2 ,∠EAC =60°,∴∠EAB =60°+30°=90°,在Rt △EAB 中,EB ===2 ;(2)如图2,过 E 作EG ∥BD ,交BA 的延长线于G,∴∠EGA =∠ABD ,∵△ ABD 是等边三角形,∴∠ABD =60°,∴∠EGA =60°,Rt △AEG 中,设AG=x,∴EG =2x,AE =x,∴AC =AE =BH =x ,∵∠BDH =60°,∴BD =2x,∴EG =BD =2x ,∵∠EFG =∠BFD ,∴△EFG ≌△DFB ,∴EF =DF ,等边△ ABD 中,∵ BH ⊥AD ,∴AH =DH ,∴FH 是△ AED 的中位线,∴FH =AE =BH ,∴BH =2FH ;(3)如图3,连接BN ,并延长交AD 于H ,∵∠CBA =60°=∠ BAD ,∴BC ∥AD ,∴∠BCN =∠NDH ,∵CN =ND ,∠CNB =∠ DNH ,∴△CNB ≌△DNH ,∴BN =NH ,BC=DH ,∵M 是AB 的中点,∴MN 是△ ABH 的中位线,∴MN =AH ,设BC=x,则DH =x,AB =AD =2x,∴AH =x,∴MN =x,Rt △ACB 中,AC =2 x ,∴AE =2 x ,∴==,∴AE =4 MN .10、重庆八中初2020 级九上期末11、重庆实验外国语学校初2020 级九上期末12、重庆双福育才中学初2020 级九上期末。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆中考数学第26题专题专训1.如图1,在平面直角坐标系中,抛物线y=﹣x2﹣x﹣2与x轴交于A,B两点(点A 在点B的左侧),交y轴于点C.(1)求直线AC的解析式;(2)点P是直线AC上方抛物线上的一动点,过点P作PD⊥AC,垂足为D,当线段PD的长度最大时,点Q从点P出发,先以每秒1个单位的速度沿适当的路径运动到y轴上的点M处,再沿MC以每秒3个单位的速度运动到点C停止,当点Q在整个运动中所用时间t最少时,求点M的坐标;(3)如图2,将△BOC沿直线BC平移,平移后B,O,C三点的对应点分别是B′,O′,C′,点S是坐标平面内一点,若以A,C,O′,S为顶点的四边形是菱形,请直接写出所有符合条件的点S的坐标.解:(1)当y=0时,﹣x2﹣x﹣2=0,解这个方程,得:x1=﹣6,x2=﹣1,∴点A(﹣6,0),B(﹣1,0),当x=0时,y=﹣2,∴C(0,﹣2),设直线AC的解析式为:y=ax+b(a≠0),将点A(﹣6,0),C(0,﹣2)代入得:,∴,∴直线AC的解析式为:y=﹣x﹣2;(3分)(2)如图1,过点P作PE∥y轴交直线AC于点E,设P(a,﹣),则点E(a,﹣﹣2),∴PE=(﹣)﹣(﹣﹣2)=﹣﹣2a,∵AO=6,OC=2,∴AC===2,∵∠PDE=∠AOC=90°,∠PED=∠ACO,∴△PDE∽△AOC,∴=,∴PD=PE==﹣﹣,对称轴是:a=﹣3,∵﹣,∴当a=﹣3时,PD的长度最大,此时点P的坐标为(﹣3,2),如图1所示,在x轴上取点F(1,0),连接CF并延长,∴CF===3,∴sin∠OCF==,点M是y轴上一点,过点M作MH⊥CF于点H,由△CHM∽△COF,可知:=,∵t==PM+MH,如图2,当P、M、H在同一直线上时,t的值最小,此时,过P作PK⊥y轴于K,由△PKM∽△COF,可知:=2,∴KM=,∴M(0,),(7分)(3)如图3,当四边形ACSO'是菱形时,过S作SG⊥y轴于G,延长O'C'交x轴于H,∵四边形ACSO'是菱形,∴AO'=AC=SC,AO'∥SC,∴∠AMC=∠BCS,∴∠AO'H+∠MC'O'=∠BCO+∠OCS,∵∠MC'O'=∠BCO,∴∠AO'H=∠OCS,∵∠AHO'=∠CGS,∴△O'AH≌△CSG,∴AH=SG,O'H=CG,Rt△OCB中,sin∠OCB==,∴sin∠BC'H==,设BH=x,则BC'=3x,∴C'H=2x,∴AH=SG=5﹣x,∵O'C'=OC=2,∴C'H=OG=2x,由勾股定理得:AC2=O'A2,∴AO2+OC2=O'H2+AH2,∴=(5﹣x)2+(2+2x)2,解得:x=,当x=时,SG=5﹣x=,OG=2x=,当x=<0时,不符合题意,舍去,SG=5﹣x=,OG=2x=,此时S的坐标为:或;②如图4,过S作SH⊥AO于H,延长O'B'到y轴交于G,∵SE∥CF,EC∥SF,∴四边形SECF是平行四边形,∴∠ESF=∠ECF,∵四边形ASO'C是菱形,∴∠ASO'=∠ACO',∴∠ASH=∠O'CG,同理得:△ASH≌△O'CG,∴AH=O'G,SH=CG,sin∠GCB'==,设GB'=x,则CB'=3x,CG=2x,∴O'G=1+x,由勾股定理得:AC2=O'C2,∴62+(2)2=(2x)2+(x+1)2解得:x=,当x=时,SH=CG=2x=,OH=6﹣AH=6﹣O'G=5﹣x=,当x=<0时,不符合题意,舍去,此时,点S的坐标为:(,);③如图5,AC为对角线时,同理可得S(,)④如图6,过S作SE⊥x轴于E,延长B'O'交y轴于H,延长O'C'交x轴于G,设GB'=x,则CB'=3x,CG=2x,∴O'G=O'H=1+x,∵∠HO'D=∠O'DA=∠EAS,易得△SEA≌△CHO',同理可得S(,);⑤如图7,过S作SH⊥x轴于H,过O'作O'E⊥SH于E,延长C'O'交x轴于G,设OG=x,则BG=1+x,∵O'B'∥BG,∴,∴,∴C'G=2(1+x),∴O'G=C'G﹣C'O'=2x,∴AG=1+x,同理得:62+(2)2=(1+x)2+(2x)2,解得:x1=,x2=(舍),可得S;综上所述,S的坐标为:或或(,)或(,)或(,).(12分)2.在平面直角坐标系中,已知抛物线322+--=x x y 的图象交x 轴于A 、B 两点(点A 在点B 左侧),交y 轴于点C .(1)求直线AC 的解析式;(2)抛物线的对称轴交直线AC 于点E ,直线AC 上方的抛物线上有一动点P ,当△PEC 面积最大时,线段CE 在直线AC 上平移,记线段CE 平移 后为E C '',求E C P ''∆的周长最小值;(3)抛物线的顶点为D ,连接AD ,将线段AD 沿直线AC 平移,记线段AD 平移后为D A '',过点D '作x 轴的垂线交x 轴于点G ,当G D A ''∆ 为等腰三角形时,求A A '的长度.解:(1)抛物线y=﹣x 2﹣2x+3,∴A (﹣3,0),B (1,0),C (0,3),∴直线AC 的解析式 y=x+3; (2)∵对称轴为x=﹣1,∴E (﹣1,2),设P (m ,﹣m 2﹣2m+3), ∴S △PEC =﹣m 2﹣m=﹣(m+)2+,∴当m=﹣时,S △PEC 的有最大值, 即:P (﹣,),将线段PC 平移,使得C 与E 重合,得到线段P'E , ∴P'(﹣,),P''(﹣,),∴△PC'E'的周长的最小值为PP''+CE=+(3)∵抛物线y=﹣x 2﹣2x+3, ∴D (﹣1,4),设A'(﹣3+n ,n ),D'(﹣1+n ,4+n ),则G (﹣1+n ,0), ∴AA'=|n|, ∴A'D'2=20,A'G 2=n 2+4,D'G 2=n 2+8n+16,∵△A ′D ′G 为等腰三角形,①当A'D'=A'G时,∴20=n2+4,∴n=±4,∴AA'=4②当A'D'=D'G时,∴20=n2+8n+16,∴n=±2﹣4,∴AA'=2±4③当D'G=A'G时,∴n2+4=n2+8n+16,∴n=﹣,∴AA'=,即:AA′的长度为4或2或.3.如图,在平面直角坐标系中,抛物线y=﹣x2+x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD∥BC交y轴于点D.(1)求平行线AD、BC之间的距离;(2)如图1,点P为线段BC上方抛物线上的一动点,当△PCB的面积最大时,Q从点P出发,先沿适当的路径运动到直线BC上点M处,再沿垂直于直线BC的方向运动到直线AD上的点N处,最后沿适当的路径运动到点B处停止.当点Q的运动路径最短时,求点M的坐标及点Q经过的最短路径的长;(3)如图2,将抛物线以每秒个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作A′、C′,当△A′C′B是以C′B为底边的等腰三角形时,将等腰△A′C′B 绕点D逆时针旋转一周,记旋转中的△A′C′B为△A″C″B′,若直线A″C″与y轴交于点K,直线A″C″与直线AD交于点I,当△DKI是以KI为底边的等腰三角形时,求出DK2的值.解:(1)如图1中,作AH⊥BC于H.对于抛物线y=﹣x2+x+3,令y=0,得到﹣x2+x+3=0,解得x=﹣或3,∴A(﹣,0),B(3,0),令x=0,得到y=3,∴C(0,3),∴OA=,OB=3,AB=4,OC=3,BC==3,∵S△ABC=•AB•CO=•BC•AH,∴AH==,∵AD∥BC,∴AD与BC之间的距离为.(2)如图2中,设P(m,﹣m2+m+3),S△PBC =S△POB+S△PCO﹣S△BOC=×3×(﹣m2+m+3)+×3×m﹣×3×3=﹣(m﹣)2+,∵﹣<0,∴m=时,△PBC的面积最大,此时P(,),作B关于直线AD的对称点B′交AD于K,连接PK交BC于M,作MN⊥AD于N,连接BN,则PM+MN+BN 的值最小.∵直线BC的解析式为y=﹣x+3,AD∥BC,∴直线AD的解析式为y=﹣x﹣1,∵BB′⊥BC,∴直线BB′的解析式为y=x﹣6,由,解得,∴K(,﹣),∴直线PK的解析式为y=﹣x+,由,解得,∴M(,),∴点Q经过的最短路径的长=PM+MN+BN=MN+(PM+MK)=MN+PK,∵MN=,PK==,∴点Q经过的最短路径的长为+.4. 抛物线y=﹣x2﹣x+与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D 是该抛物线的顶点.(1)如图1,连接CD,求线段CD的长;(2)如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;(3)如图3,点H是线段AB的中点,连接CH,将△OBC沿直线CH翻折至△O2B2C的位置,再将△O 2B2C绕点B2旋转一周,在旋转过程中,点O2,C的对应点分别是点O3,C1,直线O3C1分别与直线AC,x轴交于点M,N.那么,在△O2B2C的整个旋转过程中,是否存在恰当的位置,使△AMN是以MN为腰的等腰三角形?若存在,请直接写出所有符合条件的线段O2M的长;若不存在,请说明理由.解:(1)如图1,过点D作DK⊥y轴于K,当x=0时,y=,∴C(0,),y=﹣x2﹣x+=﹣(x+)2+,∴D(﹣,),∴DK=,CK=﹣=,∴CD===;(4分)(2)在y=﹣x2﹣x+中,令y=0,则﹣x2﹣x+=0,解得:x1=﹣3,x2=,∴A(﹣3,0),B(,0),∵C(0,),易得直线AC的解析式为:y=,设E(x,),P(x,﹣x2﹣x+),∴PF=﹣x2﹣x+,EF=,Rt△ACO中,AO=3,OC=,∴AC=2,∴∠CAO=30°,∴AE=2EF=,∴PE+EC=(﹣x2﹣x+)﹣(x+)+(AC﹣AE),=﹣﹣x+[2﹣()],=﹣﹣x﹣x,=﹣(x+2)2+,(5分)∴当PE+EC的值最大时,x=﹣2,此时P(﹣2,),(6分)∴PC=2,∵O1B1=OB=,∴要使四边形PO1B1C周长的最小,即PO1+B1C的值最小,如图2,将点P向右平移个单位长度得点P1(﹣,),连接P1B1,则PO1=P1B1,再作点P1关于x轴的对称点P2(﹣,﹣),则P1B1=P2B1,∴PO1+B1C=P2B1+B1C,∴连接P2C与x轴的交点即为使PO1+B1C的值最小时的点B1,∴B 1(﹣,0),将B 1向左平移个单位长度即得点O 1,此时PO 1+B 1C=P 2C==,对应的点O 1的坐标为(﹣,0),(7分)∴四边形PO 1B 1C 周长的最小值为+3;(8分) (3)O 2M 的长度为或或2+或2.(12分)理由是:如图3,∵H 是AB 的中点,∴OH=,∵OC=,∴CH=BC=2,∴∠HCO=∠BCO=30°,∵∠ACO=60°,∴将CO 沿CH 对折后落在直线AC 上,即O2在AC 上, ∴∠B 2CA=∠CAB=30°, ∴B 2C ∥AB , ∴B 2(﹣2,),①如图4,AN=MN ,∴∠MAN=∠AMN=30°=∠O 2B 2O 3,由旋转得:∠CB 2C 1=∠O 2B 2O 3=30°,B 2C=B 2C 1, ∴∠B 2CC 1=∠B 2C 1C=75°,过C 1作C 1E ⊥B 2C 于E , ∵B 2C=B 2C 1=2,∴=B 2O 2,B 2E=,∵∠O 2MB 2=∠B 2MO 3=75°=∠B 2CC 1, ∠B 2O 2M=∠C 1EC=90°, ∴△C 1EC ≌△B 2O 2M , ∴O 2M=CE=B 2C ﹣B 2E=2﹣;②如图5,AM=MN ,此时M 与C 重合,O 2M=O 2C=,③如图6,AM=MN ,∵B 2C=B 2C 1=2=B 2H ,即N 和H 、C 1重合,∴∠CAO=∠AHM=∠MHO 2=30°,∴O 2M=AO 2=;④如图7,AN=MN ,过C 1作C 1E ⊥AC 于E , ∴∠NMA=∠NAM=30°,∵∠O 3C 1B 2=30°=∠O 3MA ,∴C 1B 2∥AC ,∴∠C 1B 2O 2=∠AO 2B 2=90°, ∵∠C 1EC=90°, ∴四边形C 1EO 2B 2是矩形, ∴EO 2=C 1B 2=2,,∴EM=,∴O 2M=EO 2+EM=2+, 综上所述,O 2M 的长是或或2+或2.5. 如图,在平面直角坐标系中,点A 在抛物线y=﹣x 2+4x 上,且横坐标为1,点B 与点A 关于抛物线的对称轴对称,直线AB 与y 轴交于点C ,点D 为抛物线的顶点,点E 的坐标为(1,1). (1)求线段AB 的长;(2)点P 为线段AB 上方抛物线上的任意一点,过点P 作AB 的垂线交AB 于点H ,点F 为y 轴上一点,当△PBE 的面积最大时,求PH+HF+FO 的最小值;(3)在(2)中,PH+HF+FO 取得最小值时,将△CFH 绕点C 顺时针旋转60°后得到△CF′H′,过点F'作CF′的垂线与直线AB 交于点Q ,点R 为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S ,使以点D ,Q ,R ,S 为顶点的四边形为菱形,若存在,请直接写出点S 的坐标,若不存在,请说明理由.解:(1)由题意A (1,3),B (3,3), ∴AB=2.(2)如图1中,设P (m ,﹣m 2+4m ),作PN ∥y 轴J 交BE 于N .∵直线BE 的解析式为y=x , ∴N (m ,m ), ∴S △PEB =×2×(﹣m 2+3m )=﹣m 2+3m , ∴当m=时,△PEB 的面积最大,此时P (,),H (,3),∴PH=﹣3=,作直线OG 交AB 于G ,使得∠COG=30°,作HK ⊥OG 于K 交OC 于F , ∵FK=OF ,∴PH+HF+FO=PH+FH+FK=PH+HK ,此时PH+HF+OF 的值最小, ∵•HG•OC=•OG•HK,∴HK==+, ∴PH+HF+OF 的最小值为+. (3)如图2中,由题意CH=,CF=,QF=,CQ=1,∴Q (﹣1,3),D (2,4),DQ=,①当DQ 为菱形的边时,S 1(﹣1,3﹣),S 2(﹣1,3+),②当DQ 为对角线时,可得S 3(﹣1,8), ③当DR 为对角线时,可得S 4(5,3) 综上所述,满足条件的点S 坐标为(﹣1,3﹣)或(﹣1,3+)或(﹣1,8)或(5,3).6.如图1,在平面直角坐标系中,抛物线y=与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,抛物线的顶点为点D ,过点B 作BC 的垂线,交对称轴于点E .(1)求证:点E 与点D 关于x 轴对称;(2)点P 为第四象限内的抛物线上的一动点,当△PAE 的面积最大时,在对称轴上找一点M ,在y 轴上找一点N ,使得OM+MN+NP 最小,求此时点M 的坐标及OM+MN+NP 的最小值;(3)如图2,平移抛物线,使抛物线的顶点D 在射线AD 上移动,点D 平移后的对应点为D′,点A 的对应点A′,设抛物线的对称轴与x 轴交于点F ,将△FBC 沿BC 翻折,使点F 落在点F′处,在平面内找一点G ,若以F′、G 、D′、A′为顶点的四边形为菱形,求平移的距离.(1)证明:如图1中,令y=0,得到x2﹣x﹣3=0,解得x=﹣或3,∴A(﹣,0),B(3,0),令x=0,可得y=﹣3,∴C(0,﹣3),∵y=x2﹣x﹣3=(x﹣)2﹣4,∴顶点D(,﹣4),设对称轴与x轴交于F,则BF=2,∵△EFB∽△BOC,∴=,∴=,∴EF=4,∴E(,4),∴E、D关于x轴对称.(2)过点P作PQ∥y轴,交直线AE于点Q.∵yAE=x+2,∴设P(a,a2﹣a﹣3),Q(a,a+2),(0<a<3),7.如图1,在平面直角坐标系中,抛物线2y x x=-与x轴交于A、B两点(点A在点B 的左侧),与y轴交于点C.(1)求直线AC的解析式;(2)如图2,点E(a,b)是对称轴右侧抛物线上一点,过点E垂直于y轴的直线与AC交于点D(m,n).点P是x轴上的一点,点Q是该抛物线对称轴上的一点,当a m+最大时,求点E的坐标,并直接写出23EQ PQ PB++的最小值;(3)如图3,在(2)的条件下,连结OD,将△AOD沿x轴翻折得到△AOM,再将△AOM沿射线CB 的方向以每秒3个单位的速度沿平移,记平移后的△AOM为△A O M''',同时抛物线以每秒1个单位的速度沿x 轴正方向平移,点B 的对应点为B '.△A B M '''能否为等腰三角形?若能,请求出所有符合条件的点M '的坐标;若不能,请说明理由.8.如图1,在平面直角坐标系中,抛物线423412++-=x x y 与x 轴交于A 、B 两点(点A 在点B左侧),与y 轴交于点C .(1)求抛物线的对称轴及△ABC 的周长;(2)点D 是线段AC 的中点,过点D 作BC 的平行线,分别与x 轴、抛物线交于点E 、F ,点P 为直线BC 上方抛物线上的一动点,连接PD 交线段BC 于点G ,当四边形PGEF 面积最大时,点Q 从点P 出发沿适当的路径运动到x 轴上的点M 处,再沿射线DF 方向运动5个单位到点N 处,最后回到直线BC 上的点H 处停止,当点Q 的运动路径最短时,求点Q 的最短运动路径长及点H 的坐标;(3)如图2,将△AOC 绕点O 顺时针旋转至△A 1OC 1的位置,点A 、C 的对应点分别为点A 1、C 1,且点A 1落在线段AC 上,再将△A 1OC 1沿y 轴平移得△A 2O 1C 2,其中直线O 1C 2与x 轴交于点K ,点T 是抛物线对称轴上的动点,连接KT 、O 1T ,△O 1KT 能否成为以O 1K 为直角边的等腰直角三角形?若能,请直接写出所有符合条件的点T 的坐标;若不能,请说明理由.9.如图,在平面直角坐标系中,抛物线y=-x 2-3x+4交x 轴于A 、D 两点(点A 在点B 的左例), 交y 轴于点C,顶点为点D,连接BC,作直线AC.(1)求点D 的坐标和直线BC 的解析式;(2)若点P 为BC 上方抛物线上的一个动点,连接PC 、PB,过P 作PE ⊥y 轴于点E,当△PBC 面积最大时,将△PEC 绕平面内一点逆时针方向旋转90°后得到△111C E P .点P 、E 、C 的对应点分别是点1P 、1E 、1C ,当点C 1C 落在线段AC 上时,连接PP 1,求A C C P PP 111122++的最小值,并求出此时点1C 的坐标;(3)在(2)的条件下,将△111C E P 沿射线AC 以每秒2个单位长度的速度平移,记平移后的△111C E P 为△222C E P 点1P 、1E 、1C 的对应点分别是点2P 、2E ,C 2,设平移时间为秒,当△CD P2为等腰三角形时,求t 的值.10.如图,在平面直角坐标系中,抛物线)0≠(++=2a c bx ax y 交x 轴于A 、B 两点,交y 轴于点C ,AO=CO=4,BO=6,点D 是第四象限抛物线上一点,且点F 的纵坐标为-4.(1)求抛物线的解析式和直线CF 的解析式; (2)如图1,点P 是直线CF 上方抛物线上一点,点E 在直线CF 上,点E 的横坐标为3,当△PCF 的面积最大时,在y 轴有一动点M ,在x 轴有一动点N ,当PM+MN+NE 的值最小时,求出PM+MN+NE 的最小值.(3)如图2,点D 为线段BO 的中点,连接CD ,将C D O∆绕着点D 顺时针旋转α度得到对应''C DO ∆()0180α︒<<︒.设直线'C D 和直线''C O 分别与直线BC 交于H 、G 两点,当三角形C ′HG 是等腰三角形11.如图1,在平面直角坐标系中,抛物线c bx x y ++-=2的图像与x 轴交于点A 和点B (5,0),与y 轴交于点C ,点D (1,8)是抛物线上一点.(1)求抛物线和直线AD 的解析式;(2)点Q 是抛物线一象限内一动点,过点Q 作QN ∥AD 交BC 于N ,QG ⊥AB 交BC 与点M ,交AB 于点G (如图1),当QNM ∆的周长最大时,求QNM ∆周长的最大值;此时,在直线BC 上有两动点P 、H ,且PH=22(P 在H 的右边),K (2,0),当HK PQ -最大时求点P 的坐标(3)直线AD 与y 轴交于点F ,点E 是点C 关于对称轴的对称点,点P 是线段AE 上的一动点,将AFP ∆沿着FP 所在的直线翻折得到FP A '∆(点A 的对应点为点A ')(如图2),当FP A '∆与AED ∆重叠部分为直角三角形时,求AP 的长.(第26题1) (第26题2) (第26题备用图)13.如图1,在平面直角坐标系中,抛物线y=﹣x2﹣x﹣2与x轴交于A,B两点(点A 在点B的左侧),交y轴于点C.(1)求直线AC的解析式;(2)点P是直线AC上方抛物线上的一动点,过点P作PD⊥AC,垂足为D,当线段PD的长度最大时,点Q从点P出发,先以每秒1个单位的速度沿适当的路径运动到y轴上的点M处,再沿MC以每秒3个单位的速度运动到点C停止,当点Q在整个运动中所用时间t最少时,求点M的坐标;(3)如图2,将△BOC沿直线BC平移,平移后B,O,C三点的对应点分别是B′,O′,C′,点S是坐标平面内一点,若以A,C,O′,S为顶点的四边形是菱形,请直接写出所有符合条件的点S的坐标.解:(1)当y=0时,﹣x 2﹣x ﹣2=0,解这个方程,得:x 1=﹣6,x 2=﹣1, ∴点A (﹣6,0),B (﹣1,0), 当x=0时,y=﹣2,∴C (0,﹣2),设直线AC 的解析式为:y=ax+b (a ≠0), 将点A (﹣6,0),C (0,﹣2)代入得:, ∴,∴直线AC 的解析式为:y=﹣x ﹣2;(3分)(2)如图1,过点P 作PE ∥y 轴交直线AC 于点E , 设P (a ,﹣),则点E (a ,﹣﹣2), ∴PE=(﹣)﹣(﹣﹣2)=﹣﹣2a ,∵AO=6,OC=2, ∴AC===2,∵∠PDE=∠AOC=90°,∠PED=∠ACO , ∴△PDE ∽△AOC ,∴=, ∴PD=PE==﹣﹣,对称轴是:a=﹣3, ∵﹣,∴当a=﹣3时,PD 的长度最大,此时点P 的坐标为(﹣3,2),如图1所示,在x 轴上取点F (1,0),连接CF 并延长, ∴CF===3,∴sin ∠OCF==,点M 是y 轴上一点,过点M 作MH ⊥CF 于点H , 由△CHM ∽△COF ,可知:=,∵t==PM+MH,如图2,当P、M、H在同一直线上时,t的值最小,此时,过P作PK⊥y轴于K,由△PKM∽△COF,可知:=2,∴KM=,∴M(0,),(7分)(3)如图3,当四边形ACSO'是菱形时,过S作SG⊥y轴于G,延长O'C'交x轴于H,∵四边形ACSO'是菱形,∴AO'=AC=SC,AO'∥SC,∴∠AMC=∠BCS,∴∠AO'H+∠MC'O'=∠BCO+∠OCS,∵∠MC'O'=∠BCO,∴∠AO'H=∠OCS,∵∠AHO'=∠CGS,∴△O'AH≌△CSG,∴AH=SG,O'H=CG,Rt△OCB中,sin∠OCB==,∴sin∠BC'H==,设BH=x,则BC'=3x,∴C'H=2x,∴AH=SG=5﹣x,∵O'C'=OC=2,∴C'H=OG=2x,由勾股定理得:AC2=O'A2,∴AO2+OC2=O'H2+AH2,∴=(5﹣x)2+(2+2x)2,解得:x=,当x=时,SG=5﹣x=,OG=2x=,当x=<0时,不符合题意,舍去,SG=5﹣x=,OG=2x=,此时S的坐标为:或;②如图4,过S作SH⊥AO于H,延长O'B'到y轴交于G,∵SE∥CF,EC∥SF,∴四边形SECF是平行四边形,∴∠ESF=∠ECF,∵四边形ASO'C是菱形,∴∠ASO'=∠ACO',∴∠ASH=∠O'CG,同理得:△ASH≌△O'CG,∴AH=O'G,SH=CG,sin∠GCB'==,设GB'=x,则CB'=3x,CG=2x,∴O'G=1+x,由勾股定理得:AC2=O'C2,∴62+(2)2=(2x)2+(x+1)2解得:x=,当x=时,SH=CG=2x=,OH=6﹣AH=6﹣O'G=5﹣x=,当x=<0时,不符合题意,舍去,此时,点S的坐标为:(,);③如图5,AC为对角线时,同理可得S(,)④如图6,过S作SE⊥x轴于E,延长B'O'交y轴于H,延长O'C'交x轴于G,设GB'=x,则CB'=3x,CG=2x,∴O'G=O'H=1+x,∵∠HO'D=∠O'DA=∠EAS,易得△SEA≌△CHO',同理可得S(,);⑤如图7,过S作SH⊥x轴于H,过O'作O'E⊥SH于E,延长C'O'交x轴于G,设OG=x,则BG=1+x,∵O'B'∥BG,∴, ∴,∴C'G=2(1+x ),∴O'G=C'G ﹣C'O'=2x , ∴AG=1+x ,同理得:62+(2)2=(1+x )2+(2x )2, 解得:x 1=,x 2=(舍), 可得S ;综上所述,S 的坐标为:或或(,)或(,)或(,).(12分)。
