找规律试题几道经典题目(含答案)
初中数学找规律练习题(有答案)

精心整理一、简答题1、已知a、b互为相反数,c、d互为倒数,m的倒数等于它本身,则的值是多少?(4分)2、先阅读,再解题:因为,?,?……所以.参照上述解法计算:3、目前市场上有一种数码照相机,售价为3800元/架,预计今后几年内平均每年比上一年降价4%.3年后这种数码相机的售价估计为每架多少元(精确到1元)?4、已知a、b互为相反数,m、n互为倒数,x绝对值为2,求的值5、如果规定符号“﹡”的意义是﹡=,求2﹡﹡4的值。
6、某商店营业员每月的基本工资为300元,奖金制度是:每月完成规定指标10000元营业额的,发奖金300元;若营业额超过规定指标,另奖超额部分营业额的5%,该商店的一名营业员九月份完成营业额13200元,问他九月份的收入为多少元?7、王叔叔家的装修工程接近尾声,油漆工程结束了,经统计,油漆工共做50工时,用了150升油漆,已知油漆每升128元,共粉刷120平方米,在结算工钱时,有以下几种结算方案:(1)按工时算,每6工时300元。
(2)按油漆费用来算,油漆费用的15%为工钱;(3)按粉刷面积来算,每6平方米132元。
请你帮王叔叔算一下,用哪种方案最省钱?8、定义一种新的运算:观察下列式子1⊙3=1×4+3=7;3⊙(-1)=3×4+(-1)=11;5⊙4=5×4+4=24;4⊙(-3)=4×4+(-3)=13.⑴请你想一想:a⊙b=??????????;⑵请你判断a⊙b??????b⊙a(填入“=”或“≠”)???⑶若a=-2,b=-4,求(2a-b)⊙(a-2b)的值.9、阅读下列材料:1×2=(1×2×3-0×1×2),2×3=(2×3×4-1×2×3),3×4=(3×4×5-2×3×4),由以上三个等式相加,可得1×2+2×3+3×4=×3×4×5=20.读完以上材料,请你计算下列各题:(1)1×2+2×3+3×4+…+10×11(写出过程);(2)1×2+2×3+3×4+…+n×(n+1)=________;(3)1×2×3+2×3×4+3×4×5=________.10、从2004年8月1日起,浙江省城乡居民生活用电执行新的电价政策:安装“一户一表”的居民用户,按所抄见电量(每家用户电表所表示的用电量)实行阶梯式累进加价,收费标准如下:月用电量不超过50千瓦时的部分超过50千瓦时不超过200千瓦时的部分超过200千瓦时的部分收费标准(元/千瓦时)0.53 0.56 0.63 ????例:若某户月用电300千瓦时,需交电费为????(元)(1)若10月份许老师家用电量为130千瓦时,则10月份许老师家应付电费多少元??(2)已知许老师家10月份的用电量为千瓦时,请完成下列填空(用代数式表示):①若千瓦时,则10月份许老师家应付电费为?????????????元;②若千瓦时,则10月份许老师家应付电费为???????元;③若千瓦时,则10月份许老师家应付电费为??????????元。
找规律练习题及答案

找规律练习题及答案找规律练习题一.数字排列规律题1. 4、10、16、22、28……,求第n位数( )。
2. 2、3、5、9,17增幅为1、2、4、8. 第n位数( )3. 观察下列各式数:0,3,8,15,24,……。
试按此规律写出的第100个数是----,第n个数是---------。
4. 1,9,25,49,(),(),的第n项为(),5: 2、9、28、65.....:第n位数()6:2、4、8、16...... 第n位数. ()7:2、5、10、17、26……,第n位数. ()8 : 4,16,36,64,?,144,196,…?第一百个数()9、观察下面两行数2,4,8,16,32,64,...(1)5,7,11,19,35,67...(2)根据你发现的规律,取每行第十个数,求得他们的和。
10、白黑白黑黑白黑黑黑白黑黑黑黑白黑黑黑黑黑排列的珠子,前2002个中有几个是黑的?11. =8 =16 =24 ……用含有N的代数式表示规律()12. 12,20,30,42,( )127,112,97,82,( )3,4,7,12,( ),2813 . 1,2,3,5,( ),1314. 0,1,1,2,4,7,13,( )15 .5,3,2,1,1,( )16. 1,4,9,16,25,( ),4917. 66,83,102,123,( ) ,18. 1,8,27,( ),12519。
3,10,29,( ),12720, 0,1,2,9,( )21; ( )。
则第n项代数式为:()22 , 2/3 1/2 2/5 1/3 ( )。
则第n项代数式为()23 , 1,3,3,9,5,15,7,( )24. 2,6,12,20,( )25. 11,17,23,( ),35。
26. 2,3,10,15,26,( )。
27. : 1,8,27,64,( )28. :0,7,26,63 ,( )29. -2,-8,0,64,( )30. 1,32,81,64,25,( )31. 1,1,2,3,5,( )。
找规律填数练习(含解析)

找规律填数练习1.找出下面数列的规律,并根据规律在横线上填上合适的数.(1)14,17,20,23,26,,(2)86,75,64,53,,(3)2,6,11,17,,(4)1,3,9,27,,2.先找出规律,再在括号里填上合适的数。
(1)18,3,15,4,12,5,,(2)1,15,3,13,5,11,,(3)1,2,3,2,4,6,3,8,9,,,3.在1、4、9、16、()36、49这个数列中,括号里应填的数是()A.30B.25C.324.先找出下列数列的排列规律,再在括号里填上合适的数。
(1)2,5,14,41,,(2)252,124,60,28,,5.下面括号里的两个数是按一定的规律组合的,在□里填适当的数。
(1)(1,24),(2,12),(3,8),(4,)(2)(64,62),(48,46),(29,27),(15,)6.找规律,填一填找规律填数-解析1.找出下面数列的规律,并根据规律在横线上填上合适的数.(1)14,17,20,23,26,,(2)86,75,64,53,,(3)2,6,11,17,,(4)1,3,9,27,,【分析】(1)17﹣14=3,20﹣17=3,23﹣20=3,26﹣23=3,依次加3即可。
(2)86﹣75=11、75﹣64=11、64﹣53=11,…,相邻两个数之间相差11,从第一个数开始,依次减11就是它后面的数。
(3)在这一组数列中每相邻两个数的差依次是4,5,6,由此可以推算出下一个加7,加8。
(4)前一个数乘3等于后一个数。
【解答】(1)26+3=29,29+3=32;(2)86,75,64,53,42,31;(3)17+7=24,24+8=32;(4)27×3=81,81×3=243;2.先找出规律,再在括号里填上合适的数。
(1)18,3,15,4,12,5,,(2)1,15,3,13,5,11,,(3)1,2,3,2,4,6,3,8,9,,,【分析】(1)观察这组数可得,每两个数为一组,其中第一个数依次减3,第二个数依次加1,据此填空即可;(2),观察这组数可得,每两个数为一组,其中第一个数依次加2,第二个数依次减2,据此填空即可;(3),观察这组数可得,每三个数为一组,其中第一个数依次加1,第二个数依次乘2,第三个数依次加3,据此填空即可。
找规律奥数试题及答案

找规律奥数试题及答案
找规律奥数试题及答案
1.找规律:根据规律填数
(1)2、4、6、8、()、
(2)1、4、7、()、
(3)30、25、20、()、
2.找规律:根据规律填数
(1)30、28、26、()、()……
(2)1、3、6、()……
(3)15、20、25、()……
3.题目:观察列的前面几项,找出规律,写出该数列的第100项来?
12345,23451,34512,45123,……
1.找规律答案:
(1)在这数列中,后一个比前一个数多2,根据这个规律,括号里里应该填10、12;
(2)在这个数列里,后一个比前一个数多3,根据这个规律,括号里里应该填10、13;
(3)在这个数列里,前一个数比后一个数多5,根据这个规律,括号里应填15、10。
2.找规律答案:
(1)在这数列中,前一个比后一个数多2,根据这个规律,括号里里应该填24、22、20;
(2)在这个数列里,第一个数加2是第二个数,第三个数加3是第三个数,依次规律,括号里应填10和15
(3)在这个数列里,前一个数比后一个数少5,根据这个规律,括号里应填30、35。
3.找规律答案:
为了寻找规律,再多写出几项出来:
12345,23451,34512,45123,51234,12345,23451,34512,45123,51234,12345,23451……
仔细观察,可发现该数列的.第6项同第1项,第7项同第2项,第8项同第3项……也就是说该数列各项的出现具有周期性,他们是循环出现的,一个循环节包含5项。
100÷5=20
可见第100项与第5项、第10项一样(项数都能被5整除),即第100项是51234。
找规律练习题及答案

找规律练习题一.数字排列规律题1. 4、10、16、22、28……,求第n位数( )。
2. 2、3、5、9,17增幅为1、2、4、8. 第n位数( )3. 观察下列各式数:0,3,8,15,24,……。
试按此规律写出的第100个数是----,第n个数是---------。
4. 1,9,25,49,(),(),的第n项为(),5: 2、9、28、65.....:第n位数()6:2、4、8、16...... 第n位数. ()7:2、5、10、17、26……,第n位数. ()8 : 4,16,36,64,,144,196,…第一百个数()9、观察下面两行数2,4,8,16,32,64,...(1)5,7,11,19,35,67...(2)根据你发现的规律,取每行第十个数,求得他们的和。
10、白黑白黑黑白黑黑黑白黑黑黑黑白黑黑黑黑黑排列的珠子,前2002个中有几个是黑的11. =8=16=24 ……用含有N的代数式表示规律()12. 12,20,30,42,( )127,112,97,82,( )3,4,7,12,( ),2813 . 1,2,3,5,( ),1314. 0,1,1,2,4,7,13,( )15 .5,3,2,1,1,( )16. 1,4,9,16,25,( ),4917. 66,83,102,123,( ) ,18. 1,8,27,( ),12519。
3,10,29,( ),12720, 0,1,2,9,( )21;( )。
则第n项代数式为:()22 , 2/3 1/2 2/5 1/3 ( )。
则第n项代数式为()23 , 1,3,3,9,5,15,7,( )24. 2,6,12,20,( )25. 11,17,23,( ),35。
26. 2,3,10,15,26,( )。
27. : 1,8,27,64,( )28. :0,7,26,63 ,( )29. -2,-8,0,64,( )30. 1,32,81,64,25,( )31. 1,1,2,3,5,( )。
奥数 找规律(30道选择题、20道解答题)试题及解析

找规律一、选择题(共30小题)1.一个数串219⋯,从第4个数字开始,每个数字都是前面3个数字和的个位数.下面有4个四位数:1113,2226,2125,2215,其中共有( )个不出现在该数串中.A.1B.2C.3D.42.有一种数,是以法国数学家梅森的名字命名的,它们就是形如21(n n -为质数)的梅森数,当梅森数是质数时就叫梅森质数,是合数时就叫梅森合数.例如2213-=就是第一个梅森质数,第一个梅森合数是( )A.4B.15C.127D.20473.一些小球按下面的方式堆放,第7堆小球有( )个.A.19B.20C.21D.22 4.如图由“”复制组合成的,探索复制组合100次后的阴影部分占整个组合图的几分之几问题,解决的最优策略是( )A.猜想与尝试B.特例找规律C.画图D.列表5.如图,一张桌子可以坐4人,两张桌子拼起来可以坐6人,三张桌子拼起来可以坐8人.像这样( )张桌子拼起来可以坐40人.A.17B.18C.19D.206.先找出规律,然后在括号里填上适当的数:23,4,20,6,17,8,14,10,( ),()( )A.12,13B.13,12C.11,12D.12,147.如图,有一排间距相同但高度不等的小树,树根成一条直线,树顶也成一条直线,这两条直线成45度角,最高的小树高2.8米,最低的小树高峰1.4米,那么从左向右数第4棵树的高度是( )米.A.2.6B.2.4C.2.2D.2.08.在下面的两个图形中发现其中四个数的关系,进而在第三个图形中的空白三角形中填入适当的数( ),使该图中四个数也符合上述关系.A.9B.12C.10D.119.如图,第(1)个多边形由正三角形“扩展”而来,边数记为3a ,第(2)个多边形由正方形“扩展”而来,边数记为4a ,⋯,依此类推,由正n 边形“扩展”而来的多边形的边数记为(3n a n … ),则345111120146051n a a a a +++⋯+=,那么(n = )A.2014B.2015C.2016D.201710.观察下列图形,“?”位置对应的图形是( )A. B. C. D.11.把足够大的一张厚度为0.1mm纸连续对折,要使对折后的整叠纸总厚度超过12mm,至少要对折()A.6次B.7次C.8次D.9次12.有一组式子:2a,32a-,43a,54a-⋯从左往右数的第10个式子是下面算式的第()个.A.1110aB.1110a- C.1011a- D.1111a-13.找出规律,将你认为合适的数填入(),2、4、3、9、4、16、5、()、()、36、7、⋯那么正确的数是()A.18、6B.22、6C.25、6D.2514.有一列数,开头四个是2,0,1,3;从第5个数开始,每个数是前面四个数的和除以4所得的余数,那么这列数中的第2013个数是()A.0B.1C.2D.315.有一列数,第1个数是22,第2个数是12,从第3个数开始,每个数是它前面两个数的平均数,这列数的第10个数的整数部分是()A.17B.14C.15D.1616.杰克和吉莉每人各有一只水壶,其中都装有1升水.第一天,杰克把他壶中的1毫升水倒入吉莉的壶中,第二天吉莉把她的壶中的3毫升水倒入杰克的壶中,第三天杰克把他壶中的5毫升水倒入吉莉的壶中,这样继续做下去,其中每个人倒出的水比前一天从对方得到的水多2毫升.那么第101天结束后,杰克壶中有()毫升水?(1升1000=毫升)A.799B.899C.900D.100017.下列图形,第10个图中△比〇多()个A.44B.60C.56D.4518.根据1()1A,1()8B,1()27C,1()64D,(E)⋯⋯中数的变化规律,E中的数是()A.165B.181C.1125D.121619.一本童话书,每两页之间有3页插图,也就是说3页插图前后各有1页文字.那么第36页是()A.插图B.文字20.下面空白的椭圆内应填入的数是()A.1730B.1750C.1780D.179021.观察下面图形我们发现:第一个图中有1个正方形,第2个图中共有5个正方形,第3个图中共有14个正方形,按照这种规律下去的第6个图形中正方形的个数是()A.80B.81C.90D.9122.下列一列数中:5、8、11、14⋯,第()个数为2009.A.667B.668C.669D.70023.小王利用计算机设计了一个计算程序,输入和输出的数据如下表:输入⋯12345⋯输出⋯1225310417526⋯那么,当输入数据是8时,输出的数据是()A.861B.863C.865D.86724.动物园里猩猩比狒狒多,猴子比猩猩多.一天,饲养员拿了十箱香蕉分给它们.每只猩猩比每只狒狒多分一根,每只猴子比每只猩猩多分一根.分完后,只剩下2根香蕉.如果每箱香蕉数量相同,都是40多个,而且猴子比狒狒多6只,猩猩有16只.那么,动物.园里有( )只猴子.A.18B.19C.20D.1725.数列1,2,4,5,10,11,22,23,46,47⋯,它形成的规律:第2项等于第1项加1的和,第3项等于第2项的2倍,第4项等于第3项加1的和,第5项等于第4项的2倍,⋯,如此继续下去,得到上面的数列.那么,这个数列的第100项的个位数字是( )A.2B.5C.7D.826.盒中原有7个小球,魔术师从中取出若干个球,把每个球都变成7个小球,将其放回盒中;他又由其中取出若干个球,把每个球都变成7个小球,再将其放回盒中;⋯,如此进行到某一时刻,当魔术师停止变魔术时,盒中球的总数可能是()A.2003个B.2004个C.2005个D.2006个27.在一个没有余数的除法算式里,如果被除数扩大6倍,除数缩小2倍,那么商的变化是()A.扩大12倍B.缩小2l倍C.扩大3倍D.缩小3倍28.按照如图所示的规律,图6中小三角形共有()个.A.53B.51C.49D.4729.给出一列11,21,12,31,22,13,L,1k,12k-,L,1k.在这列数中,第40个值等于1的项是这列数中第()项.A.3120B.3121C.3200D.320130.观察图1至图5中小黑点的摆放规律,并按照这样的规律继续摆放,那么第10个图形中的小黑点个数是( )个.A.100B.90C.91D.101二、解答题(共20小题)31.以下一串密码代表一句话,数字代表拼音字母顺序,其中(28,20)代表“我”,那么这串密码代表的这句话是什么?(28,20)(6,14)(19,14)(31,13,20,19,12)(12,26,20)32.小强编了一个程序:从a 开始,交错地做加法或乘法(第一次可以是加法,也可以是乘法).每次做加法时,将上次运算的结果加2或加(3)-;每次做乘法时,将上次运算的结果乘以2或乘以3.例如:24a 可以这样得到3a ⨯−−→2232322332646112212124224a a a a a a a a +⨯-⨯-⨯+−−→+−−→+−−→+−−→+−−→-−−→-−−→请你用此程序得到8a ,写出过程.33.有12个位置,每个位置放一个自然数.若第二个数与第一个数相等,从第三个数开始,每个数恰好是它前边所有数的总和,则我们称这样的12个数为“好串数”.请问含1992这个数的好串数共 个.34.称分母是分子的3倍少1的分数为“可儿”,例如25就是“可儿”,将分数320写成两个“可儿”之积,这两个“可儿”是 .35.2017位同学排成一列依次报数.若某位同学报的是一位数,后面的同学就报这个数的2倍;若某位同学报的是两位数,后面的同学就报其个位数字与5的和.已知一位同学报1,到了第100位同学,他却把前面那位同学报的数加上了另一个一位自然数,其他人都没有注意到,仍然按以前的规则继续报数,直到最后一位同学报的数是5.那么第100位同学所报的数是把前一位同学报的数加上了多少?36.有一列数2,9,8,2,6,⋯从第3个数起,每个数都是前面两个数乘积的个位数字.例如第四个数就是第二、第三两数乘积9872⨯=的个位数字是2.问这一列数第2003个数是几?37.2017位同学从左到右排成一行,然后按如下规律从左向右报数:先让第一位同学报4,第二位同学报9,然后从第三位同学开始,每位同学都把自己前面两位同学所报的数相乘,再报出乘积的个位来.试问,最后一位同学报的是几?38.(1)今天是3月1日,小明买了一些橙子,他如果每天吃3个,十多天能吃完,最后一天只吃2个;如果小明每天吃4个,不到十天就吃完了,最后一天吃了3个,那么,这些橙子原来有多少个?(2)小明好奇地看了看这一年3月份的日历,发现3月份有四个星期日,却有五个星期六,那么今天(3月1日)是星期几?39.黑板上先写下一串数:1,2,3,⋯,100,如果每次都擦去最前面的6个,并在这串数的最后再写上擦去的6个数的和,得到新的一串数,再做同样的操作,直到黑板上剩下的数不足6个.问:(1)最后黑板上剩下的这些数的和是多少?(2)最后所写的那个数是多少?40.例2.根据下表中数的排列规律,在空格里填上适当的数.(1)13207917859(2)247536126141641.按照下面的规律在黑板上写整数,:一开始写1,然后每一次操作在它后面写上比它大1的数.例如,一开始的时候,黑板上的数是1.第一次操作:比1大1的数是2,就在它后面写上2,现在黑板上的数是12;第二次操作:比黑板上的12大1的数是13,就在它后面连写上13,现在黑板上的数就是1213;以此类推⋯(1)请求出第三次操作后黑板上的数是多少?(2)当黑板上第一次出现“321”时,是在第几次操作之后?(3)请求出从左数第2016位数字是多少?42.某年,端午节距离儿童节和父亲节的天数相同,在月历中与六月最后一天同列,父亲节是六月的第三个星期日,则该年的父亲节是六月日.(如图是某个月的月历示意图)43.将自然数1,2,3,4,从小到大无间隔地排列起来,得到:1234567891011121314,这串数码中,当偶数数码首次连续出现5个时,其中的第一个(偶)数码所在位置从左数是第多少位?44.等边三角形的边长3厘米,现将三角形ABC沿一条直线翻滚30次,如图:求A点经过的路程的长是多少厘米?(π取3.14).45.一棵生命力极强的树苗,第一周在树干上长出2条树枝(如图1),第二周在原先长出的每条树枝上又长出2条新的树枝(如图2),第三周又在第二周新长出的每条树枝上再长出2条新枝(如图3),这棵树苗按此规律生长,到第十周新的树枝长出来后,共有条树枝.46.1,1,3,2,5,4,7,8,9,16, , ,13,64.47.一列数,其前七项依次为1,1,3,4,5,9,7,第8项是什么?说明理由.48.在棋盘上滚动骰子,使骰子的一面和棋盘格的大小相等,然后将骰子以棱为轴,滚动到邻近的棋盘格,每滚动一次,骰子朝上一面的数字就会变化.如果骰子的初始位置如图1,当骰子滚动六次到达对角顶点时(如图2),那么,第一步、第四步、第六步朝上的面分别是几点?(说明:骰子的相对两个面的点数之和为7)49.在平面上用长度为5cm 的火柴棒摆正方形,摆出1个边长为5cm 的正方形需要4根火柴,摆出2015个这样的正方形最少需要多少根火柴?说明你的摆法(不必画图).50.如图所示,圆周上的两个点1A 、2A 将圆等分成2份,在这两个点处写上14;圆周上的两个点1A 、2A 再将两段半圆弧等分,在点3A 、4A 处分别写上相邻2个数之和;如此继续这样操作,问能否出现圆周上所有数字之和2015?若可能,请求出经过了多少次操作?若不能,请说明理由.参考答案与试题解析一、选择题(共30小题)1.一个数串219⋯,从第4个数字开始,每个数字都是前面3个数字和的个位数.下面有4个四位数:1113,2226,2125,2215,其中共有( )个不出现在该数串中.A.1B.2C.3D.4【答案解析】枚举法219的数字和是12,接下来就是2192数字和是12,接下来就是2922的数字和是13,接下来就是3223的数字和为7,接下来就是7237的数字和为12,接下来的数2以此类推数字为:2192237221584790651281102⋯规律总结数字和的尾数呈现两奇数两个偶数的周期规律.故选:C .2.有一种数,是以法国数学家梅森的名字命名的,它们就是形如21(n n -为质数)的梅森数,当梅森数是质数时就叫梅森质数,是合数时就叫梅森合数.例如2213-=就是第一个梅森质数,第一个梅森合数是( )A.4B.15C.127D.2047【答案解析】选项:214n A -=,n 无整数解;选项:2115n B -=,n 为4,但n 不是质数,故舍去;选项:21127n C -=,n 为7,127不是合数,故舍去;选项:212047n D -=,n 为11,n 为质数,且20472389=⨯,是合数,满足条件. 故选:D .3.一些小球按下面的方式堆放,第7堆小球有( )个.A.19B.20C.21D.22【答案解析】5813+=第7堆小球有:13821+=;故选:C.4.如图由“”复制组合成的,探索复制组合100次后的阴影部分占整个组合图的几分之几问题,解决的最优策略是()A.猜想与尝试B.特例找规律C.画图D.列表【答案解析】如图由“”复制组合成的,探索复制组合100次后的阴影部分占整个组合图的几分之几问题,解决的最优策略是特例找规律;故选:B.5.如图,一张桌子可以坐4人,两张桌子拼起来可以坐6人,三张桌子拼起来可以坐8人.像这样()张桌子拼起来可以坐40人.A.17B.18C.19D.20【答案解析】第一张桌子可以坐4人;拼2张桌子可以坐4216+⨯=人;拼3张桌子可以坐4228+⨯=人;故n张桌子拼在一起可以坐42(1)22+-=+.n n当2240n=,n+=时,19答:像这样19张桌子拼起来可以坐40人.故选:C.6.先找出规律,然后在括号里填上适当的数:23,4,20,6,17,8,14,10,(),()()A.12,13B.13,12C.11,12D.12,14【答案解析】根据上面的分析,第9个数应该是14311+=,-=,第10个数应该是10212故选:C.7.如图,有一排间距相同但高度不等的小树,树根成一条直线,树顶也成一条直线,这两条直线成45度角,最高的小树高2.8米,最低的小树高峰1.4米,那么从左向右数第4棵树的高度是()米.A.2.6B.2.4C.2.2D.2.0【答案解析】因为:树根成一条直线,树顶也成一条直线,45∠=︒,最高的小树高 2.8米,最低的小树高峰A1.4米,所以 2.8BC AC AB=-=米,AC=米, 1.4AB=米, 1.4又因为:这排树的间距相同,所以:÷=(米)1.470.2⨯+0.24 1.4=+0.8 1.4=(米)2.2答:那么从左向右数第4棵树的高度是2.2米.故选:C.8.在下面的两个图形中发现其中四个数的关系,进而在第三个图形中的空白三角形中填入适当的数(),使该图中四个数也符合上述关系.A.9B.12C.10D.11【答案解析】54210⨯÷=所以,第三个图形中的空白三角形中填入的数是10.故选:C.9.如图,第(1)个多边形由正三角形“扩展”而来,边数记为a,第(2)个多边形由正方3形“扩展”而来,边数记为a,⋯,依此类推,由正n边形“扩展”而来的多边形的边4数记为(3na n…),则345111120146051na a a a+++⋯+=,那么(n=)A.2014B.2015C.2016D.2017【答案解析】33(22)34a=+=⨯,44(23)45a=+=⨯,55(24)56a=+=⨯,⋯(1)na n n=+,∴11112014344556(1)6051n n+++⋯+=⨯⨯⨯+,∴11111111201434455616051n n-+-+-+⋯+-=+,∴112014316051n-=+,12017n∴+=,2016n∴=.10.观察下列图形,“?”位置对应的图形是()A. B. C. D.【答案解析】再逆时针旋转90︒是.故选:C .11.把足够大的一张厚度为0.1mm 纸连续对折,要使对折后的整叠纸总厚度超过12mm ,至少要对折( ) A.6次B.7次C.8次D.9次【答案解析】设对折n 次,由此可得, 0.1212n ⨯> 2120n = 72128= 6264= 64120128<<所以,7n = 答:至少要对折7次. 故选:B .12.有一组式子:2a ,32a -,43a ,54a -⋯从左往右数的第10个式子是下面算式的第( )个.A.1110a B.1110a -C.1011a -D.1111a -【答案解析】由题意,奇数项为正,偶数项为负,分母是正整数,分子是1n a +,所以从左往右数的第10个式子是1110a -,故选:B .13.找出规律,将你认为合适的数填入( ),2、4、3、9、4、16、5、( )、( )、36、7、⋯那么正确的数是( ) A.18、6B.22、6C.25、6D.25【答案解析】注意到:4是2的平方,9是3的平方,16是4的平方,25是5的平方,36是6的平方,⋯根据这个规律,可知中间两个括号分别应填25和6.故选:C.14.有一列数,开头四个是2,0,1,3;从第5个数开始,每个数是前面四个数的和除以4所得的余数,那么这列数中的第2013个数是()A.0B.1C.2D.3【答案解析】(2013)4+++÷64=÷=⋯12所以第5个数是2;(0132)4+++÷=÷64=⋯12第6个数是2;+++÷(1322)4=÷8420=⋯第7个数是0;+++÷(3220)4=÷74=⋯13(2203)4+++÷=÷74=⋯13第9个数是3;+++÷(2033)4 =÷8420=⋯第10个数是0;+++÷(0330)4 =÷64=⋯12第11个数是2;(3302)4+++÷=÷84=⋯20第12个数是0;+++÷(3020)4 =÷5411=⋯第13个数是1;+++÷(0201)4 =÷34=⋯03此时这些数是:2,1,0,3,2,2,0,3,3,0,2,0,1,3再向下计算又会是2,2,0,3,3,0,2,0,1,3⋯看以看出这些数是以“2,1,0,3,2,2,0,3,3,0”为一个循环不断循环出现这个循环节中有10个数字;2013102013÷=⋯余数是3,所以第2013个数第202个循环中的第3个数字,是0.故选:A.15.有一列数,第1个数是22,第2个数是12,从第3个数开始,每个数是它前面两个数的平均数,这列数的第10个数的整数部分是()A.17B.14C.15D.16【答案解析】第三个数:(2212)217+÷=第四个数:(1217)214.5+÷=第五个数:(1714.5)215.75+÷=第六个数:(14.515.75)215.125+÷=第七个数:(15.7515.125)215.4375+÷=⋯再向下计算由于两个数都不大于15.5,所以它们的平均数的整数部分只能是15.答:这列数的第10个数的整数部分是15.故选:C.16.杰克和吉莉每人各有一只水壶,其中都装有1升水.第一天,杰克把他壶中的1毫升水倒入吉莉的壶中,第二天吉莉把她的壶中的3毫升水倒入杰克的壶中,第三天杰克把他壶中的5毫升水倒入吉莉的壶中,这样继续做下去,其中每个人倒出的水比前一天从对方得到的水多2毫升.那么第101天结束后,杰克壶中有()毫升水?(1升1000=毫升)A.799B.899C.900D.1000【答案解析】-=(毫升)312752-=(毫升)⋯1012501÷=⋯(天)前100天杰克的壶中增加250100⨯=(毫升)第101天杰克倒出(1011)21201-⨯+=(毫升)201100101-=(毫升)1升1000=(毫升)1000101899-=(毫升)故选:B.17.下列图形,第10个图中△比〇多()个A.44B.60C.56D.45【答案解析】第10图中△的个数1010100⨯=(个)〇的个数4(102)444⨯+-=(个)1004456-=(个)故选:C.18.根据1()1A,1()8B,1()27C,1()64D,(E)⋯⋯中数的变化规律,E中的数是()A.165B.181C.1125D.1216【答案解析】35125=所以,这个分数是1 125.故选:C.19.一本童话书,每两页之间有3页插图,也就是说3页插图前后各有1页文字.那么第36页是()A.插图B.文字【答案解析】3649÷=(组),所以第36页和第四页相同,应该是插图;故选:A.20.下面空白的椭圆内应填入的数是()A.1730B.1750C.1780D.1790【答案解析】1700501750+=故选:B.21.观察下面图形我们发现:第一个图中有1个正方形,第2个图中共有5个正方形,第3个图中共有14个正方形,按照这种规律下去的第6个图形中正方形的个数是()A.80B.81C.90D.91【答案解析】第一个图形有1个正方形,第二个图形有22512=+个正方形,第三个图形有22214123=++个正方形,⋯第六个图形有14916253691+++++=个正方形.故选:D.22.下列一列数中:5、8、11、14⋯,第()个数为2009.A.667B.668C.669D.700【答案解析】这是一个首项是5,公差是3的等差数列由5(1)32009n+-⨯=,可得669n=.故选:C.23.小王利用计算机设计了一个计算程序,输入和输出的数据如下表:输入⋯12345⋯输出⋯1225310417526⋯那么,当输入数据是8时,输出的数据是()A.861B.863C.865D.867【答案解析】28165+=,所以输出的数是8 65.故选:C.24.动物园里猩猩比狒狒多,猴子比猩猩多.一天,饲养员拿了十箱香蕉分给它们.每只猩猩比每只狒狒多分一根,每只猴子比每只猩猩多分一根.分完后,只剩下2根香蕉.如果每箱香蕉数量相同,都是40多个,而且猴子比狒狒多6只,猩猩有16只.那么,动物.园里有( )只猴子.A.18B.19C.20D.17【答案解析】动物园里有x只猴子,则狒狒6x-只,猩猩有16只,狒狒分y根香蕉,猩猩1y+根,猴子2y+根,(2)(6)16(1)400x y y x y++-++>,261616xy x xy y y++-++,2(1)1016x y y=+++,假设19x=,383810164854400y y y+++=+>,48346y>,7.2y>,设:8y=,4854438y+=. 符合题意.故选:B.25.数列1,2,4,5,10,11,22,23,46,47⋯,它形成的规律:第2项等于第1项加1的和,第3项等于第2项的2倍,第4项等于第3项加1的和,第5项等于第4项的2倍,⋯,如此继续下去,得到上面的数列.那么,这个数列的第100项的个位数字是( )A.2B.5C.7D.8【答案解析】(991)248-÷=,48412÷=,没有余数,个位数就是4,它的下一项(第100项)的个位数就是:故选:B.26.盒中原有7个小球,魔术师从中取出若干个球,把每个球都变成7个小球,将其放回盒中;他又由其中取出若干个球,把每个球都变成7个小球,再将其放回盒中;⋯,如此进行到某一时刻,当魔术师停止变魔术时,盒中球的总数可能是()A.2003个B.2004个C.2005个D.2006个【答案解析】根据以上分析知:-÷=⋯,2003减7的差不是6的倍数,(20037)63324-÷=⋯,2004减7的差不是6的倍数,(20047)63325-÷=,2005减7的差是6的倍数,(20057)6333-÷=⋯,2006减7的差不是6的倍数,(20067)63331所以盒中球的总数可能是2005个.故选:C.27.在一个没有余数的除法算式里,如果被除数扩大6倍,除数缩小2倍,那么商的变化是()A.扩大12倍B.缩小2l倍C.扩大3倍D.缩小3倍【答案解析】例如80108÷=,被除数扩大6倍,由80变成480,除数缩小2倍,由10变成5,则商变为:480596÷=,商由8变成96,是商扩大了12倍;据此可知:被除数扩大6倍,除数缩小2倍,那么商扩大6212⨯=倍.故选:A.28.按照如图所示的规律,图6中小三角形共有()个.A.53B.51C.49D.47【答案解析】根据分析可得,2++(16)453=(个)答:图6中小三角形共有53个.故选:A.29.给出一列11,21,12,31,22,13,L,1k,12k-,L,1k.在这列数中,第40个值等于1的项是这列数中第()项.A.3120B.3121C.3200D.3201【答案解析】分子分母和为2的有1个,分子分母和为3的有2个,分子分母和为4的有3个,⋯,分子分母和为79的数有78个,123783081+++⋯+=(项),第40个值等于1的项分子分母和为80且为4040是这一数列中的第40项,3081403121+=(项).故选:B.30.观察图1至图5中小黑点的摆放规律,并按照这样的规律继续摆放,那么第10个图形中的小黑点个数是()个.A.100B.90C.91D.101【答案解析】根据图形分析可知:(用s表示图中小黑点的个数)1n=时,1s=;2n=时,3211s==⨯+;3n=时,7321s==⨯+;4n=时,13431s==⨯+;5n=时,21541s==⨯+;⋯;第n个图中小黑点的个数为(1)1n n-+.第10个图形中的小黑点个数是10(101)191⨯-+=.故选:C .二、解答题(共20小题)31.以下一串密码代表一句话,数字代表拼音字母顺序,其中(28,20)代表“我”,那么这串密码代表的这句话是什么?(28,20)(6,14)(19,14)(31,13,20,19,12)(12,26,20)【答案解析】28代表w ,20代表o ,根据这个规律可以确定:(6,14)代表ai(19,14)代表ni(31,13,20,19,12)代表zhong(12,26,20)guo这些拼音对应的中文是“我爱你中国”.答:这串密码代表的这句话是“我爱你中国”.32.小强编了一个程序:从a 开始,交错地做加法或乘法(第一次可以是加法,也可以是乘法).每次做加法时,将上次运算的结果加2或加(3)-;每次做乘法时,将上次运算的结果乘以2或乘以3.例如:24a 可以这样得到3a ⨯−−→2232322332646112212124224a a a a a a a a +⨯-⨯-⨯+−−→+−−→+−−→+−−→+−−→-−−→-−−→请你用此程序得到8a ,写出过程.【答案解析】利用其程序运算如下:2232322224214241828a a a a a a a a +⨯-⨯-⨯+−−→+−−→+−−→+−−→+−−→-−−→-−−→.33.有12个位置,每个位置放一个自然数.若第二个数与第一个数相等,从第三个数开始,每个数恰好是它前边所有数的总和,则我们称这样的12个数为“好串数”.请问含1992这个数的好串数共 4 个.【答案解析】通过以上分析得出含1992这个数的好串数共.4个:249 249 498 996 1992 3984498⋯ 498 996 1992 3984 7968996⋯ 996 1992 3984 7968159361992⋯ 1992 3984 7968 15936 31872⋯34.称分母是分子的3倍少1的分数为“可儿”,例如25就是“可儿”,将分数320写成两个“可儿”之积,这两个“可儿”是25、38.【答案解析】362323 20405858⨯===⨯⨯即,这两个“可儿”是25、38.故答案为:25、38.35.2017位同学排成一列依次报数.若某位同学报的是一位数,后面的同学就报这个数的2倍;若某位同学报的是两位数,后面的同学就报其个位数字与5的和.已知一位同学报1,到了第100位同学,他却把前面那位同学报的数加上了另一个一位自然数,其他人都没有注意到,仍然按以前的规则继续报数,直到最后一位同学报的数是5.那么第100位同学所报的数是把前一位同学报的数加上了多少?【答案解析】按照规则将前面几位同学所报数写出:1,2,4,8,16,11,6,12,7,14,9,18,13,8,16⋯可以发现从第3位同学开始,每10位同学为一个周期,所以第99位同学报的数为7;由于最后一位同学报的数是5,往前倒推,应该是5、10、5、10⋯可知,第100位同学报的数只能为倒数第偶数个,应该是10,所以第100位同学报的数是把前一位同学报的数加上了3.36.有一列数2,9,8,2,6,⋯从第3个数起,每个数都是前面两个数乘积的个位数字.例如第四个数就是第二、第三两数乘积9872⨯=的个位数字是2.问这一列数第2003个数是几?【答案解析】(20032)63333-÷=⋯,可以知道这一列数第2003个数为第333组后面的第3个数是“6”.答:这一列数第2003个数是6.故答案为:637.2017位同学从左到右排成一行,然后按如下规律从左向右报数:先让第一位同学报4,第二位同学报9,然后从第三位同学开始,每位同学都把自己前面两位同学所报的数相乘,再报出乘积的个位来.试问,最后一位同学报的是几?【答案解析】从第三个同学开始,他们依次报出的数为6、4、4、6、4、4、6⋯(20172)36712-÷=⋯即循环周中的第2个数是4.答:最后一位同学报的是4.38.(1)今天是3月1日,小明买了一些橙子,他如果每天吃3个,十多天能吃完,最后一天只吃2个;如果小明每天吃4个,不到十天就吃完了,最后一天吃了3个,那么,这些橙子原来有多少个?(2)小明好奇地看了看这一年3月份的日历,发现3月份有四个星期日,却有五个星期六,那么今天(3月1日)是星期几?【答案解析】(1)【3,4】12=,12336-=(个)⨯=,36135答:这些橙子原来有35个.(2)31473-⨯=3月3日是星期六,那么3月2日是星期五,3月1日是星期四答:今天(3月1日)是星期四.39.黑板上先写下一串数:1,2,3,⋯,100,如果每次都擦去最前面的6个,并在这串数的最后再写上擦去的6个数的和,得到新的一串数,再做同样的操作,直到黑板上剩下的数不足6个.问:(1)最后黑板上剩下的这些数的和是多少?(2)最后所写的那个数是多少?【答案解析】依题意可知:(1)擦去1,2,3,4,5,6但是写上了21数字和没有变化.最后的数字和是123100+++⋯+的数字和为5050.(2)第一次擦下去的数字是1,2,3,4,5,6写上去的是21,第二次擦去的是7,8,9,10,11,12写上的数字是57.那么21与57的数字差为36.÷=⋯.说明擦去96个数字填上了16 个数字,这16个数字是以21位首项公差为100616436的等差数列.后来共20个数字.这20个数字为:97,98,99,100,21,57,93,129,165,201,237,273,309,345,381,417,453,489,525,561.然后20632÷=⋯.说明最后两个数字剩下了,新添加了3个数字,那么最后写的数字就是309,345,381,417,453,489的数字和为2394.答:(1)最后黑板上剩下的这些数的和是5050.(2)最后所写的那个数是2394.40.例2.根据下表中数的排列规律,在空格里填上适当的数.(1)13207917859(2)2475361261416【答案解析】(1)5914+=(2)(1416)260+⨯=故填14和60.41.按照下面的规律在黑板上写整数,:一开始写1,然后每一次操作在它后面写上比它大1的数.例如,一开始的时候,黑板上的数是1.第一次操作:比1大1的数是2,就在它后面写上2,现在黑板上的数是12;第二次操作:比黑板上的12大1的数是13,就在它后面连写上13,现在黑板上的数就是1213;以此类推⋯(1)请求出第三次操作后黑板上的数是多少?(2)当黑板上第一次出现“321”时,是在第几次操作之后?(3)请求出从左数第2016位数字是多少?【答案解析】(1)第二次操作:比黑板上的1213大1的数是1214,就是在它的后面写上1214,则需在黑板的数就是12131214答:第三次操作后黑板上的数是12131214.(2)黑板上的数是12,末位是12;第二次操作后,黑板上的数是1213,末两位是13;第三次操作后,黑板上的数是12131214,末两位14;⋯第n次操作后,黑板上的数的末两位是11n+,要想黑板出现“321”,须在末两位是32,与开头的1连起来才可以,第21。
找规律练习题及答案

找规律练习题一.数字排列规律题1. 4、10、16、22、28……,求第n位数( )。
2. 2、3、5、9,17增幅为1、2、4、8. 第n位数( )3. 观察下列各式数:0,3,8,15,24,……。
试按此规律写出的第100个数是----,第n个数是---------。
4. 1,9,25,49,(),(),的第n项为(),5: 2、9、28、65.....:第n位数()6:2、4、8、16...... 第n位数. ()7:2、5、10、17、26……,第n位数. ()8 : 4,16,36,64,?,144,196,…?第一百个数()9、观察下面两行数2,4,8,16,32,64,...(1)5,7,11,19,35,67...(2)根据你发现的规律,取每行第十个数,求得他们的和。
10、白黑白黑黑白黑黑黑白黑黑黑黑白黑黑黑黑黑排列的珠子,前2002个中有几个是黑的?11. =8=16=24 ……用含有N的代数式表示规律()12. 12,20,30,42,( )127,112,97,82,( )3,4,7,12,( ),2813 . 1,2,3,5,( ),1314. 0,1,1,2,4,7,13,( )15 .5,3,2,1,1,( )16. 1,4,9,16,25,( ),4917. 66,83,102,123,( ) ,18. 1,8,27,( ),12519。
3,10,29,( ),12720, 0,1,2,9,( )21;( )。
则第n项代数式为:()22 , 2/3 1/2 2/5 1/3 ( )。
则第n项代数式为()23 , 1,3,3,9,5,15,7,( )24. 2,6,12,20,( )25. 11,17,23,( ),35。
26. 2,3,10,15,26,( )。
27. : 1,8,27,64,( )28. :0,7,26,63 ,( )29. -2,-8,0,64,( )30. 1,32,81,64,25,( )31. 1,1,2,3,5,( )。
找规律试题几道经典题目(含答案)

1、如图所示,观察小圆圈的摆放规律,第一个图中有5个小圆圈,第二个图中有8个小圆圈,第100个图中有__________个小圆圈.(1) (2) (3)2、 找规律.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有 个菱形,第n 幅图中有 个菱形.3、用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子 枚(用含n 的代数式表示).4、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a 、b 、c 的值分别为______________.5、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个22⨯的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个33⨯的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个44⨯的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个1010⨯的正方形图案, 则其中完整的圆共有 个.6、 如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n 个图案需要用白色棋子 枚(用含有n 的代数式表示,并写成最简形式).○ ○ ○ ○ ○ ○ ○ ○ ○○ ○ ○ ○ ● ● ○ ○ ● ● ● ○○ ● ○ ○ ● ● ○ ○ ● ● ● ○○ ○ ○ ○ ○ ○ ○ ○ ● ● ● ○1 2 3n … … 第1个图第2个图第3个图 …○ ○ ○ ○ ○7、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形需 根火柴棒。
8、将正整数按如图5所示的规律排列下去,若有序实数对(n ,m )表示第n 排,从左到右第m 个数,如(4,2)表示实数9,则表示实数17的有序实数对是 .9、如图 2 ,用n 表示等边三角形边上的小圆圈,f(n)表示这个三角形中小圆圈的总数,那么f(n)和n 的关系是10、观察图4的三角形数阵,则第50行的最后一个数是 ( )1-2 3-4 5 -67 -8 9 -10。
找规律练习题及答案

找规律练习题一.数字排列规律题1.4、10、16、22、28……,求第n位数()。
2.2、3、5、9,17增幅为1、2、4、8.第n位数()3.观察下列各式数:0,3,8,15,24,……。
试按此规律写出的第100个数是----,第n个数是---------。
4.1,9,25,49,(),(),的第n项为(),5:2、9、28、65.....:第n位数()6:2、4、8、16......第n位数.()7:2、5、10、17、26……,第n位数.()8:4,16,36,64,?,144,196,…?第一百个数()9、观察下面两行数2,4,8,16,32,64,...(1)5,7,11,19,35,67...(2)根据你发现的规律,取每行第十个数,求得他们的和。
10、白黑白黑黑白黑黑黑白黑黑黑黑白黑黑黑黑黑排列的珠子,前2002个中有几个是黑的?11.=8=16=24……用含有N的代数式表示规律()12.12,20,30,42,()127,112,97,82,()3,4,7,12,(),2813.1,2,3,5,(),1314.0,1,1,2,4,7,13,()15.5,3,2,1,1,()16.1,4,9,16,25,(),4917.66,83,102,123,(),18.1,8,27,(),12519。
3,10,29,(),12720,0,1,2,9,()21;()。
则第n项代数式为:()22,2/31/22/51/3()。
则第n项代数式为()23,1,3,3,9,5,15,7,()24.2,6,12,20,()25.11,17,23,(),35。
26.2,3,10,15,26,()。
27.:1,8,27,64,()28.:0,7,26,63,()29.-2,-8,0,64,()30.1,32,81,64,25,()31.1,1,2,3,5,()。
32.4,5,(),14,23,3733.6,3,3,(),3,-334.1,2,2,4,8,32,()35。
找规律填数 含答案

找规律填数小朋友们,在学习和生活中,我们经常会遇到许多按一定顺序排列起来的数。
在数学上,我们把这样的一组数叫做“数列”。
找规律填数,就是先通过对数列的观察,再经过严密的逻辑推理,然后发现数列中数的排列规律,并依据这个规律把所缺的数填写出来,从而达到解决问题的目的。
这一讲,就让我们一起来探讨数列中的奥秘吧!例1.找出下面各数的排列规律,在括号里填上合适的数。
〈1〉1,2,3,4,(),()〈2〉2,4,6,8,(),()〈3〉45,40,35,(),()点拨:〈1〉在这个数列中,通过观察可以发现,这一列数越来越大,而且后一个数都比前一个数多1,也就是说相邻两个数的差都是1,因此,括号里应按顺序填上5,6.〈2〉根据上题的方法,依次求出相邻两数的差,可以发现这列数的排列规律是:从第二个数起,后一个数都比前一个数多2,因此,括号里应按顺序填上10,12.〈3〉也可以用下面的计算过程来推算45 40 35 30 (25) (20)-5 -5 -5 -5 -5例2.找规律填数.〈1〉1,2,4,7,11,(),()〈2〉1,3,7,13.21,(),()〈3〉1,2,4,8,16,(),()点拨:〈1〉通过观察和计算我们发现,在这一列数中,数也在逐渐增加,但每次增加的数并不相同,具体变化如下:第一个数加1得到第二个数,第二个数加2得到第三个数,第三个数加3得到第四个数,第四个数加4得到第五个数,依次推算,第五个数应该加5得到第六个数是16,第六个数加6得到第七个数是22,也就是说,每次增加的数都比上次增加的数多1,也可以用下面的计算过程来推算:1 2 4 7 11 (16)(22)+1 +2 +3 +4 +5 +6〈2〉这一列数每次增加的数都比上次增加的数多2.1 3 7 13 21 (31) (43)+2 +4 +6 +8 +10 +12〈3〉这一列数每次增加的数都是它本身,第一个数是1,再加上1得到第二个数,第二个数是2,再加上2得到第三个数,第三个数是4,再加上4得到第四个数,第四个数是8,再加上8得到第五个数,依次推算,第五数是16,也应该加上16得到第六个数是32,第六个数是32,也应该加上32得到第七个数是64.可以用下面的计算过程来推算:1 2 4 8 16 (32)(64)+1 +2 +4 +8 +16 +32例3.寻找下面一列数的规律,在()填上合适的数.〈1〉1,3,1,5,1,7,(),()〈2〉17,2,14,2,11,2,(),()〈3〉25,6,20,7,15,8,(),()点拨:〈1〉通过观察可以发现,这一列数是间隔着变化的。
找规律练习习题及答案

找规律练习习题及答案欢迎共阅找规律练习题⼀.数字排列规律题1.4、10、16、22、28……,求第n位数()。
2.2、3、5、9,17增幅为1、2、4、8.第n位数()3.观察下列各式数:0,3,8,15,24,……。
试按此规律写出的第100个数是----,第n个数是---------。
4.1,9,25,49,(),(),的第n项为(),5:2、9、28、65.....:第n 位数()6:2、47:2、58:4,1692,4,85,7,111011.=1612.12,127,1123,4,713.1,214.0,115.5,316.1,417.66,18.1,819。
3,20,0,121;()22,2/31/22/51/3()。
则第n项代数式为()23,1,3,3,9,5,15,7,()24.2,6,12,20,()25.11,17,23,(),35。
26.2,3,10,15,26,()。
27.:1,8,27,64,()28.:0,7,26,63,()29.-2,-8,0,64,()30.1,32,81,64,25,()31.1,1,2,3,5,()。
32.4,5,(),14,23,3733.6,3,3,(),3,-334.1,2,2,4,8,32,()35。
2,12,36,80,()36.3/2,2/3,3/4,1/3,3/8()37.观察下列各算式:1+3=4=2的平⽅,1+3+5=9=3的平⽅,1+3+5+7=16=4的平⽅…按此规律(1)试猜想:1+3+5+7+…+2005+2007的值?(2)推⼴:1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少?38、下⾯数列后两位应该填上什么数字呢?23581217____39.40100 4142个数A.143、10010044从第14546.(2005n表⽰),设计如图a所⽰的图形。
(1)请你利⽤这个⼏何图形求的值为。
(2)请你利⽤图b,再设计⼀个能求的值的⼏何图形。
图形找规律练习60题有答案
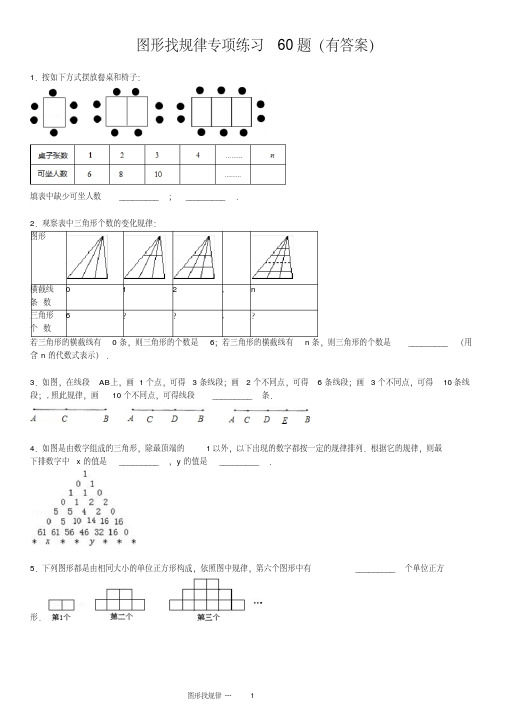
横截线 0
1
2
条数
三角形 6
?
?
个数
若三角形的横截线有 0 条,则三角形的个数是
含 n 的代数式表示) .
,
n
,
?
6;若三角形的横截线有
n 条,则三角形的个数是
_________ (用
3.如图,在线段 AB上,画 1 个点,可得 3 条线段;画 2 个不同点,可得 6 条线段;画 3 个不同点,可得 10 条线 段; , 照此规律,画 10 个不同点,可得线段 _________ 条.
11.如图,用围棋子按下面的规律摆图形,则摆第
n 个图形需要围棋子的枚数为
_________ .
图形找规律 --- 2
8.观察下列图案:
它们是按照一定规律排列的,依照此规律,第
6 个图案中共有 _________ 个三角形.
9.如图,依次连接一个边长为 1 的正方形各边的中点,得到第二个正方形,再依次连接第二个正方形各边的中点,
得到第三个正方形,按此方法继续下去,则第二个正方形的面积是
_________ ;第六个正方形的面积是
1
6.如图,用相同的火柴棒拼三角形,依此拼图规律,第
7 个图形中共有 _________ 根火柴
棒.
7.图 1 是一个正方形,分别连接这个正方形的对边中点,得到图 得到图 3;再分别连接图 3 中右下角的小正方形对边中点,得到图 个数是 _________ 个.
2;分别连接图 2 中右下角的小正方形对边中点, 4;按此方法继续下去,第 n 个图的所有正方形
如图依次连接一个边长为的正方形各边的中点得到第二个正方形再依次连接第二个正方形各边的中点得到第三个正方形按此方法继续下去则第二个正方形的面积是个图形有10个小正方形按照这样的规律则第10个图形有个小正方形
(完整版)找规律(含答案)

练习一:先找出下列各列数的排列规律,然后在括号里填上适当的数。
年级:日期:(1)2,6,10,14,(),22,26找规律(2)3,6,9,12,(),18,21专题简介:(3)33,28,23,(), 13,(),3 观察是解决问题的根据。
通过观察,得以揭示出事物的发展和变化规(4)55,49,43,(), 31,(),19律,在一般情况下,我们可以从以下几个方面来找规律:(5)3,6,12,(),48,(),192 1.根据每组相邻两个数之间的关系,找出规律,推断出所要填的数;(6)2,6,18,(),162,()2.根据相隔的每两个数的关系,找出规律,推断出所要填的数;(7)128,64,32,(),8,(),23.要善于从整体上把握数据之间的联系,从而很快找出规律;(8)19,3,17,3,15,3,(),(),11,34.数之间的联系往往可以从不同的角度来理解,只要言之有理,所例 2:先找出下列数排列的规律,然后在括号里填上适当的数。
得出的规律都可以认为是正确的。
1,2,4,7,(),16,22例 1:先找出下列数排列的规律,并根据规律在括号里填上适当的数。
分析:在这列数中,前 4 个数每相邻的两个数的差依次是1,2,3。
1 ,,,,(),,19由此可以推算 7 比括号里的数少4,括号里应填: 7+4=11。
4 7 10 16分析:在这列数中,相邻的两个数的差都是 3,即每一个数加上 3 都经验证,所填的数是正确的。
等于后面的数。
根据这一规律,括号里应填的数为:应填的数为: 7+4=11 或 16-5=11 10+3=13 或 16-3=13 练习二:先找出下列数排列的规律,然后在括号里填上适当的数。
像上面按照一定的顺序排列的一串数叫做数列。
(1)10,11,13,16,20,(),31(2)1,4,9,16,25,(),49,64(3)3,2,5,2,7,2,(),(),11,2(4)53,44,36,29,(),18,(),11,9,8(5)81,64,49,36,(),16,(),4,1,0(6)28,1,26,1,24,1,(),(),20,1(7)30,2,26,2,22,2,(),(),14,2(8)1,6,4,8,7,10,(),(),13,14例 3:先找出规律,然后在括号里填上适当的数。
(完整版)七年级找规律经典题汇总带答案

一、数字排列规律题1、观察下列各算式: 1+3=4=22,1+3+5=9=23,1+3+5+7=16=24… 按此规律(1)试猜想:1+3+5+7+…+2005+2007的值 ?(2)推广: 1+3+5+7+9+…+(2n—1)+(2n+1)的和是多少 ?2、下面数列后两位应该填上什么数字呢? 2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 1 2 3 5 8 ____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个( )二、几何图形变化规律题1、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球 个.2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是 (填图形名称).三、数、式计算规律题1、已知下列等式:① 13=12; ② 13+23=32; ③ 13+23+33=62; ④ 13+23+33+43=102 ;……由此规律知,第⑤个等式是 . 2、观察下面的几个算式:1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,…根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…+3+2+1=____. 3、,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+=+⨯=+b a aba b 则符合前面式子的规律,,若 (21010)规律发现专题训练1.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地砖4块;那么第(n )个图案中有白色..地砖 块。
找规律试题几道经典题目含答案

数学试题分类汇编一一找规律1、如图所示,观察小圆圈的摆放规律,第一个图中有5个小圆圈,第二个图中有 8个小圆圈,第100个图中有 ___________ 个小圆圈.(1) (2) (3)2、找规律.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有 _______ 个菱形,第n 幅图中有 个菱形.C.::> <沐〉<3:«「> …二•…123n3、用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子 ________ 枚(用含n 的代数式表示)4、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a 、b 、c 的值分别为 ________________•••••第2个图 第3个图L3 42 4 6 苦3 6 9 1343 12 Id---1821 C71第1个图5、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个 2 2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3 3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4 4的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个1 0 10的正方形图案,则其中完整的圆共有个--:l6、如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子______________ 枚(用含有n的代数式表示,并写成最简形式).0^0 O • • O O • • • O O O OO O O OO • • • OO O O O O7、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第 334个图形需 ______ 根火柴棒。
run fuxq 厂ajb? ic )8将正整数按如图5所示的规律排列下去,若有序实数对(n ,m )表示第n 排, 从左到右第m 个数,如(4 ,2)表示实数9,则表示实数17的有序实数对是O OO-2 3 -4 5 -6 7 -8 9 -1011、下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,一 4101 3□ 2 5 9 口 8第一排 第二排 第三排 第四排9、如图 2,用n 表示等边三角形边上的小圆圈,f (n )表示这个三角形中小圆圈的总数,那么 f (n )和n 的关系是10、观察图4的三角形数阵, 则第 50行的最后一个数是( )第n 个图案中白色正方形的个数为12、观察下列各式:13=1213 23 = 32 13 23 32 = 6213 23 33 4亠102猜想:13 23 33 ||II|| 103 二 _____________ .答案解析:1解析:n=1时,m=5 n 再每增加一个数时,m 就增加3个数.解答:根据所给的具体数据,发现:8=5+3, 1仁5+3X 2, 14=5+3X 3,….以此类推,第 n 个圈中,m=5+3( n-1 ) =3n+2.2解析:分析可得:第1幅图中有1X2-1=1个,第2幅图中有2X 2-1=3个,第3幅图中有3X2-1=5个,…, 故第n 幅图中共有2n-1个3解析:在4的基础上,依次多3个,得到第n 个图中共有的棋子数.观察图形,发现:在4的基础上,依次多3个.即第n 个图中有4+3 (n-1) =3n+1 .当n=6时,即原 式=19 .故第6个图形需棋子19枚4解析:此题只要找出截取表一的那部分,并找出其规律即可解. 解答:解:表二截取的是其中的一列:上下两个数字的差相等,所以a=15+3=18 .表三截取的是两行两列的相邻的四个数字:右边一列数字的差应比左边一列数字的差大 1,所b=24+25-20+1=30 .表四中截取的是两行三列中的 6个数字:18是3的6倍,则c 应是4的7倍,即28. 故选D.第一个认真观察表格,熟知各个数字之间的关系:第一列是 1 , 2, 3,…;第二列是对应第一列的2倍;等三列是对应第一列的3倍5解析:据给出的四个图形的规律可以知道,组成大正方形的每个小正方形上有一个完整的圆,因此圆的数目是大正方形边长的平方,每四个小正方形组成一个完整的圆,从而可得这样的圆是大正方形边长减1的平方,从而可得若这样铺成一个10X10的正方形图案,则其中完整的圆共有102+ (10-1 )2=181 个.解答:解:分析可得完整的圆是大正方形的边长减1的平方,从而可知铺成一个10X10的正方形图案中,完整的圆共有102+ (10-1)2=181个.点评:本题难度中等,考查探究图形的规律.本题也只可以直接根据给出的四个图形中计数出的圆的个数,找出数字之间的规律得出答案.6解析:解:第1个正方形图案有棋子共32=9枚,其中黑色棋子有12=1枚,白色棋子有(32-12)枚; 第2个正方形图案有棋子共42=16枚,其中黑色棋子有22=4枚,白色棋子有(42-22)枚;…由此可推出想第n个图案的白色棋子数为(n+2)2-n2=4 (n+1).故第n个图案的白色棋子数为(n+2)2-n2=4 (n+1).点评:根据图形提供的信息探索规律,是近几年较流行的一种探索规律型问题.解决这类问题首先要从简单图形入手,抓住随着编号”或序号”曾加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论7解析:根据题意分析可得:搭第1个图形需12根火柴;搭第2个图形需12+6X1=18根;搭第3个图形需12+6X2=24根;搭第n个图形需12+6 (n-1)=6n+6根.解答:解:搭第334个图形需6X334+6=2010根火柴棒8解析:寻找规律,然后解答.每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.解答:解:观察图表可知:每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.实数15=1+2+3+4+5,则17在第6 排,第5个位置,即其坐标为(6,5).故答案填:(6,5).对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.一 1 29解析:根据题意分析可得:第n行有n个小圆圈.故f (n)和n的关系是?(n)= -(n +n).(n —l)xn10解析:根据题意可得:第n 行有n 个数;且第n 行第一个数的绝对值为-—+1,最后一个数的(n —1)X71绝对值为 —2— +n ;奇数为正,偶数为负;故第50行的最后一个数是1275 .奇数为正,偶数为负, 第50行的最后一个数是1275第一个图中白色正方形的个数为 3X 3-1 ; 第二个图中白色正方形的个数为 3X5-2 第三个图中白色正方形的个数为 3X 7-3 ;当其为第n 个时,白色正方形的个数为 3 (2n+1) -n=5n+312解析:根据所给的等式,可以发现右边的底数是前边的底数的和,指数是平方,则最后的底数是 1+2+3+..+10=5 X 11=55,则原式=552.解答:解:根据分析最后的底数是1+2+3+..+10=5 X 11=55,则原 式=552. 故答案552解答:解:第n 行第一个数的绝对值为 (n —ljxn""2+1 , 最后一个数的绝对值为(n —ljxn3 +n ,。
完整)初中数学找规律专项练习题(有答案)

完整)初中数学找规律专项练习题(有答案)1、观察规律:1=1;1+3=4;1+3+5=9;1+3+5+7=16;…,则2+6+10+14+…+2014的值是多少?2、用四舍五入法对取近似数,并精确到千位,用科学计数法表示为多少?3、观察下面的一列数:-1,2,-3,4,-5,6…请找出其中排列的规律,并按此规律填空。
(1)第10个数是多少?第21个数是多少?(2)-40是第几个数?26是第几个数?4、一组按规律排列的数:1,3,6,10,15…请推断第9个数是多少?5、计算:(-100)+(-101)=多少?(-2)+(-2)=多少?6、若。
则等于多少?7、大肠杆菌每过20分钟便由1个分裂成2个,经过3小时后这种大肠杆菌由1个分裂成多少个?8、猜数字游戏中,XXX写出如下一组数:1,3,5,7,9…n个数是…,XXX猜想出第六个数字是多少?根据此规律,第9、10个数字分别是多少?9、若。
与|b+5|的值互为相反数,则等于多少?10、在计数制中,通常我们使用的是“十进位制”,即“逢十进一”.而计数制方法很多,如60进位制:60秒化为1分,60分化为1小时;24进位制:24小时化为1天;7进位制:7天化为1周等…而二进位制是计算机处理数据的依据.已知二进位制与十进位制的比较如下表:十进位制二进制 1 1 2 10 3 11 4 100 5 101 6 110 …… 请将二进位制xxxxxxxx(二)写成十进位制数为多少?11、为求。
值,可令S=。
则2S=。
因此所以。
仿照以上推理计算出的值是多少?二、选择题13、的值是多少?【】A.-2 B.-1 C.0 D.114、已知8.62=73.96,若x=0.7396,则x的值等于()A.86.2B.862C.±0.862D.±86215、计算:(-2)+(-2)的值是多少?A.2B.-1C.-2D.-416、计算等于多少?A. B. C. D.17、已知a、b互为相反数,c、d互为倒数,m的绝对值为1,p是数轴到原点距离为1的数,那么的值是多少?A.3 B.2 C.1 D.018、若。
中考数学找规律练习题(20道-后附答案)

中考数学找规律练习题(20道,后附答案)一:数式问题1.已知22223322333388+=⨯+=⨯,,244441515+=⨯,……,若288a ab b+=⨯(a 、b 为正整数)则a b +=.2.有一列数a 1,a 2,a 3,a 4,a 5,…,a n ,其中a 1=5×2+1,a 2=5×3+2,a 3=5×4+3,a 4=5×5+4,a 5=5×6+5,…,当a n =2009时,n 的值等于()A.2010B.2009C.401D.3343.有一组单项式:a 2,-a 32,a 43,-a 54,….观察它们构成规律,用你发现的规律写出第10个单项式为.4.有一列数1234251017--,,,…,那么第7个数是.5.观察下列等式:111122⨯=-,222233⨯=-,333344⨯=-,……(1)猜想并写出第n 个等式;(2)证明你写出的等式的正确性.6.将正整数依次按下表规律排成四列,则根据表中的排列规律,数2009应排的位置是第行第列.第1列第2列第3列第4列第1行123第2行654第3行789第4行121110……7.将正整数1,2,3,…从小到大按下面规律排列.若第4行第2列的数为32,则①n=;②第i行第j列的数为(用i,j表示).第1列第2列第3列…第n列第1行123…n第2行1+n2+n3+n…n2第3行12+n22+n32+n…n3………………二:定义运算问题8、有一列数1a,2a,3a, ,n a,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差,若12a=,则2007a为()A.2007B.2C.12D.1-三:剪纸问题9.如图(9),把一个正方形三次对折后沿虚线剪下则得到的图形是()10题图四:数形结合问题10、已知,A、B、C、D、E 是反比例函数16y x=(x>0)图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图5所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是(用含π的代数式表示)11、阅读材料:设一元二次方程ax 2+bx +c =0(a ≠0)的两根为x 1,x 2,则两根与方程系数之间有如下关系:x 1+x 2=-b a ,x 1·x 2=c a.根据该材料填空:已知x 1、x 2是方程x 2+6x +3=0的两实数根,则21x x +12x x 的值为.12、如图,在x 轴的正半轴上依次截取112233445OA A A A A A A A A ====,过点12345A A A A A 、、、、分别作x 轴的垂线与反比例函数()20y x x=≠的图象相交于点12345P P P P P 、、、、,得直角三角形1112233344455OP A A P A A P A A P A A P A 2、、、、,并设其面积分别为12345S S S S S 、、、、,则5S 的值为.四:图形问题13.如图所示,已知:点(00)A ,,3B ,,(01)C ,在ABC △内依次作yxO P 1P 2P 3P4P 5A 1A 2A 3A 4A 5(第12题图)2y x=第14题图C 2D 2C 1D 1CD AB等边三角形,使一边在x 轴上,另一个顶点在BC 边上,作出的等边三角形分别是第1个11AA B △,第2个122B A B △,第3个233B A B △,…,则第n 个等边三角形的边长等于()14.如图,边长为1的菱形ABCD 中,︒=∠60DAB .连结对角线AC ,以AC 为边作第二个菱形11D ACC ,使︒=∠601AC D ;连结1AC ,再以1AC 为边作第三个菱形221D C AC ,使︒=∠6012AC D ;……,按此规律所作的第n 个菱形的边长为.15.如图,已知Rt ABC △,1D 是斜边AB 的中点,过1D 作11D E AC ⊥于E 1,连结1BE 交1CD 于2D ;过2D 作22D E AC ⊥于2E ,连结2BE 交1CD 于3D ;过3D 作33D E AC ⊥于3E ,…,如此继续,可以依次得到点45D D ,,…,n D ,分别记112233BD E BD E BD E △,△,△,…,n n BD E △的面积为123S S S ,,,…n S .则n S =________ABC S △(用含n 的代数式表示).16.用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个图案多一个正六边形和两个正三角O yx(A )A 1C112B A 2A 3B 3B 2B 1第13题图BCAE 1E 2E 3D 4D 1D 2D 3(第15题)(第16题)形,则第n个图案中正三角形的个数为(用含n 的代数式表示).17.如图,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第100个图案需棋子枚.18.观察下列图形(每幅图中最小..的三角形都是全等的),请写出第n 个图中最小..的三角形的个数有个.19.观察下列图形:它们是按一定规律排列的,依照此规律,第16个图形共有个★.五:对称问题20.在平面直角坐标系中,已知3个点的坐标分别为1(11)A ,、2(02)A ,、3(11)A ,.一只电子蛙位于坐标原点处,第1次电子蛙由原点第1个图第2个图第3个图第4个图(第18题图)第17题图图案1图案2图案3……跳到以A为对称中心的对称点1P,第2次电子蛙由1P点跳到以2A为对1称中心的对称点P,第3次电子蛙由2P点跳到以3A为对称中心的对称2点P,…,按此规律,电子蛙分别以1A、2A、3A为对称中心继续跳下3去.问当电子蛙跳了2009次后,电子蛙落点的坐标是P(_______,2009_______).参考答案1、8+63=712、D3、-a11104、-7505、(1)n×=n-;(2)证明见解析.【解析】试题分析:(1)等号左边第一个因数为整数,与第二个因数的分子相同,第二个因数的分母比分子多1;等号右边为等号左边的第一个数式-第二个因数,即n×=n-;(2)把左边进行整式乘法,右边进行通分.试题解析:(1)猜想:n×=n-;(2)证:右边==左边,即n×=n-考点:规律型:数字的变化类.6、670,第三列7、1010(i-1)+j8、D 9、C 10、13π-2611、1012、1/513、14、15、16、2n+217、30218、19、4920、(2,2)。
找规律小学奥数题100道及答案(完整版)

找规律小学奥数题100道及答案(完整版)题目1:1,3,5,7,9,()答案:11(相邻两个数的差为2,依次递增)题目2:2,4,6,8,10,()答案:12(相邻两个数的差为2,依次递增)题目3:5,10,15,20,25,()答案:30(相邻两个数的差为5,依次递增)题目4:1,4,9,16,25,()答案:36(分别是1、2、3、4、5 的平方,下一个是 6 的平方)题目5:3,6,9,12,15,()答案:18(相邻两个数的差为3,依次递增)题目6:1,2,4,8,16,()答案:32(后一个数是前一个数的2 倍)题目7:2,6,12,20,30,()答案:42(相邻两个数的差依次为4、6、8、10、12)题目8:1,1,2,3,5,8,()答案:13(前两个数相加等于后一个数)题目9:3,4,7,11,18,()答案:29(前两个数相加等于后一个数)题目10:1,3,7,13,21,()答案:31(相邻两个数的差依次为2、4、6、8、10)题目11:2,5,10,17,26,()答案:37(相邻两个数的差依次为3、5、7、9、11)题目12:9,16,25,36,()答案:49(分别是3、4、5、6 的平方,下一个是7 的平方)题目13:1,8,27,64,()答案:125(分别是1、2、3、4 的立方,下一个是5 的立方)题目14:5,12,19,26,33,()答案:40(相邻两个数的差为7,依次递增)题目15:3,8,15,24,()答案:35(相邻两个数的差依次为5、7、9、11)题目16:2,3,5,8,13,()答案:21(前两个数相加等于后一个数)题目17:1,4,10,22,46,()答案:94(相邻两个数的差依次为3、6、12、24、48)题目18:1,5,14,30,55,()答案:91(相邻两个数的差依次为4、9、16、25、36)题目19:2,6,18,54,()答案:162(后一个数是前一个数的3 倍)题目20:7,14,28,56,()答案:112(后一个数是前一个数的2 倍)题目21:1,2,6,24,120,()答案:720(后一个数依次是前一个数乘2、3、4、5、6)题目22:3,5,9,17,33,()答案:65(相邻两个数的差依次为2、4、8、16、32)题目23:1,3,8,19,42,()答案:89(相邻两个数的差依次为2、5、11、23、47,这些差依次增加3、6、12、24)题目24:2,4,10,28,82,()答案:244(相邻两个数的差依次为2、6、18、54、162,后一个差是前一个差的 3 倍)题目25:5,9,17,33,65,()答案:129(相邻两个数的差依次为4、8、16、32、64)题目26:1,4,27,256,()答案:3125(分别是1、2、3、4 的1、2、3、4 次方,下一个是5 的 5 次方)题目27:1,6,21,66,201,()答案:606(相邻两个数的差依次为5、15、45、135、405,后一个差是前一个差的3 倍)题目28:3,8,15,24,35,()答案:48(相邻两个数的差依次为5、7、9、11、13)题目29:2,3,7,18,47,()答案:123(7 = 3×2 + 1,18 = 7×2 + 4,47 = 18×2 + 11,下一个数应为47×2 + 16 = 123)题目30:1,2,5,14,41,()答案:122(相邻两个数的差依次为1、3、9、27、81,后一个差是前一个差的3 倍)题目31:2,5,11,23,47,()答案:95(相邻两个数的差依次为3、6、12、24、48)题目32:4,9,16,25,36,()答案:49(分别是2、3、4、5、6 的平方,下一个是7 的平方)题目33:6,12,20,30,42,()答案:56(相邻两个数的差依次为6、8、10、12、14)题目34:1,3,7,15,31,()答案:63(相邻两个数的差依次为2、4、8、16、32)题目35:3,9,27,81,()答案:243(后一个数是前一个数的3 倍)题目36:5,13,25,41,()答案:61(相邻两个数的差依次为8、12、16、20)题目37:2,8,32,128,()答案:512(后一个数是前一个数的4 倍)题目38:7,16,29,46,()答案:67(相邻两个数的差依次为9、13、17、21)题目39:1,5,13,25,()答案:41(相邻两个数的差依次为4、8、12、16)题目40:6,18,54,162,()答案:486(后一个数是前一个数的3 倍)题目41:8,18,32,50,()答案:72(相邻两个数的差依次为10、14、18、22)题目42:1,4,13,40,()答案:121(相邻两个数的差依次为3、9、27、81)题目43:3,10,21,36,()答案:55(相邻两个数的差依次为7、11、15、19)题目44:5,15,45,135,()答案:405(后一个数是前一个数的3 倍)题目45:2,6,14,30,()答案:62(相邻两个数的差依次为4、8、16、32)题目46:9,25,49,81,()答案:121(分别是3、5、7、9 的平方,下一个是11 的平方)题目47:7,19,37,61,()答案:91(相邻两个数的差依次为12、18、24、30)题目48:4,12,36,108,()答案:324(后一个数是前一个数的3 倍)题目49:1,6,15,28,()答案:45(相邻两个数的差依次为5、9、13、17)题目50:8,20,36,56,()答案:80(相邻两个数的差依次为12、16、20、24)题目51:3,11,23,39,()答案:59(相邻两个数的差依次为8、12、16、20)题目52:6,15,35,77,()答案:143(相邻两个数的差依次为9、20、42、66,差依次增加11、22、24)题目53:2,9,28,65,()答案:126(分别是1、2、3、4 的立方加1,下一个是5 的立方加1)题目54:1,7,19,37,()答案:61(相邻两个数的差依次为6、12、18、24)题目55:5,16,29,46,()答案:67(相邻两个数的差依次为11、13、17、21)题目56:3,12,27,48,()答案:75(相邻两个数的差依次为9、15、21、27)题目57:7,18,33,52,()答案:77(相邻两个数的差依次为11、15、19、25)题目58:2,10,30,68,()答案:130(相邻两个数的差依次为8、20、38、62,差依次增加12、18、24)题目59:4,15,32,55,()答案:84(相邻两个数的差依次为11、17、23、29)题目60:6,21,42,72,()答案:106(相邻两个数的差依次为15、21、30、34)题目61:1,9,25,49,()答案:81(分别是1、3、5、7 的平方,下一个是9 的平方)题目62:8,24,48,80,()答案:120(相邻两个数的差依次为16、24、32、40)题目63:3,13,31,57,()答案:91(相邻两个数的差依次为10、18、26、34)题目64:5,19,41,71,()答案:105(相邻两个数的差依次为14、22、30、34)题目65:2,11,26,47,()答案:76(相邻两个数的差依次为9、15、21、29)题目66:9,27,51,81,()答案:117(相邻两个数的差依次为18、24、30、36)题目67:7,17,33,55,()答案:83(相邻两个数的差依次为10、16、22、28)题目68:4,14,30,52,()答案:78(相邻两个数的差依次为10、16、22、26)题目69:6,18,36,60,()答案:90(相邻两个数的差依次为12、18、24、30)题目70:1,11,27,51,()答案:81(相邻两个数的差依次为10、16、24、30)题目71:5,17,33,53,()答案:77(相邻两个数的差依次为12、16、20、24)题目72:3,14,31,58,()答案:91(相邻两个数的差依次为11、17、27、33)题目73:8,22,42,70,()答案:106(相邻两个数的差依次为14、20、28、36)题目74:2,13,30,53,()答案:84(相邻两个数的差依次为11、17、23、31)题目75:9,29,55,91,()答案:133(相邻两个数的差依次为20、26、36、42)题目76:7,20,39,64,()答案:95(相邻两个数的差依次为13、19、25、31)题目77:4,16,36,64,()答案:100(分别是2、4、6、8 的平方,下一个是10 的平方)题目78:3,15,33,57,()答案:87(相邻两个数的差依次为12、18、24、30)题目79:6,22,44,74,()答案:110(相邻两个数的差依次为16、22、30、36)题目80:1,13,29,53,()答案:89(相邻两个数的差依次为12、16、24、36)题目81:5,21,41,67,()答案:99(相邻两个数的差依次为16、20、26、32)题目82:8,26,50,82,()答案:118(相邻两个数的差依次为18、24、32、36)题目83:3,17,37,67,()答案:107(相邻两个数的差依次为14、20、30、40)题目84:7,23,45,73,()答案:107(相邻两个数的差依次为16、22、28、34)题目85:2,14,32,56,()答案:88(相邻两个数的差依次为12、18、24、32)题目86:9,31,59,95,()答案:139(相邻两个数的差依次为22、28、36、44)题目87:6,24,48,84,()答案:126(相邻两个数的差依次为18、24、36、42)题目88:1,15,33,57,()答案:87(相邻两个数的差依次为14、18、24、30)题目89:5,23,47,77,()答案:113(相邻两个数的差依次为18、24、30、36)题目90:8,28,52,82,()答案:118(相邻两个数的差依次为20、24、30、36)题目91:3,19,41,69,()答案:105(相邻两个数的差依次为16、22、28、36)题目92:7,27,51,81,()答案:117(相邻两个数的差依次为20、24、30、36)题目93:4,18,38,66,()答案:100(相邻两个数的差依次为14、20、28、34)题目94:6,26,50,80,()答案:116(相邻两个数的差依次为20、24、30、36)题目95:2,16,36,60,()答案:90(相邻两个数的差依次为14、20、24、30)题目96:9,33,63,99,()答案:141(相邻两个数的差依次为24、30、36、42)题目97:8,28,56,92,()答案:136(相邻两个数的差依次为20、28、36、44)题目98:5,21,43,71,()答案:105(相邻两个数的差依次为16、22、28、34)题目99:3,17,37,67,()答案:107(相邻两个数的差依次为14、20、30、40)题目100:7,25,49,79,()答案:115(相邻两个数的差依次为18、24、30、36)。
找规律试题几道经典题目(含答案)
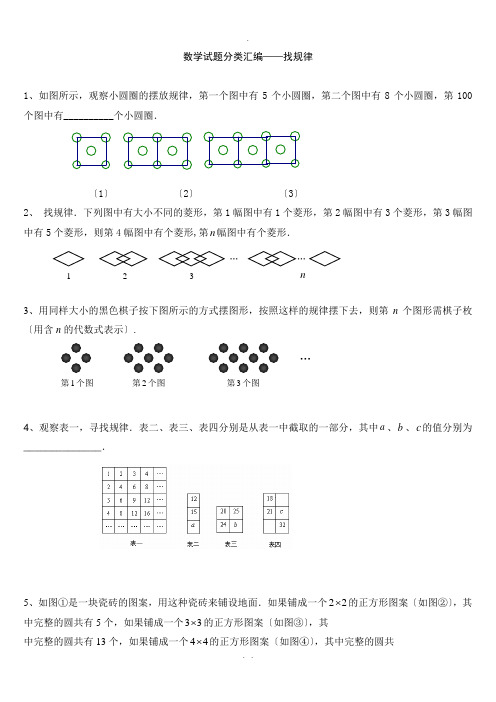
数学试题分类汇编——找规律1、如图所示,观察小圆圈的摆放规律,第一个图中有5个小圆圈,第二个图中有8个小圆圈,第100个图中有__________个小圆圈.〔1〕 〔2〕 〔3〕2、 找规律.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有个菱形,第n 幅图中有个菱形.3、用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子枚〔用含n 的代数式表示〕.4、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a 、b 、c 的值分别为______________.5、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个22⨯的正方形图案〔如图②〕,其中完整的圆共有5个,如果铺成一个33⨯的正方形图案〔如图③〕,其中完整的圆共有13个,如果铺成一个44⨯的正方形图案〔如图④〕,其中完整的圆共1 2 3n … … 第1个图 第2个图 第3个图…有25个.若这样铺成一个1010 的正方形图案, 则其中完整的圆共有个.6、 如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n 个图案需要用白色棋子枚〔用含有n 的代数式表示,并写成最简形式〕.○○○○○○○○○○○○○●●○○●●●○○●○○●●○○●●●○○○○○○○○○●●●○○○○○○7、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形需根火柴棒。
8、将正整数按如图5所示的规律排列下去,若有序实数对〔n ,m 〕表示第n 排,从左到右第m 个数,如〔4,2〕表示实数9,则表示实数17的有序实数对是. 9、如图 2 ,用n 表示等边三角形边上的小圆圈,f(n)表示这个三角形中小圆圈的总数,那么f(n)和n 的关系是10、观察图4的三角形数阵,则第50行的最后一个数是 〔 〕1第一排 第二排 第三排 第四排 6 ┅┅ 10 9 87 32 15 4-2 3-4 5 -67 -8 9 -10。
小学奥数---简单数列中的规律专项练习30题(有答案)

小学奥数---简单数列中的规律专项练习30题(有答案)1.在数列1×2、2×3、3×4、4×5、…、99×100中,要求找到第6个数是多少。
答案:B。
562.给定数列1、3、5、…、9,要求找到第8组的三个数的和是多少。
答案:213.给定数列3、5、7、X、Y、Z,要求填出X、Y、Z应该是多少,同时找到这个数列的规律。
答案:X=9,Y=11,Z=13,规律为每个数加2.4.根据规律填数或者划出适当的图形。
1) 3,20;5,40;7,80;9,…2) 4,6,10,16,26,42,…3) 16,25,36,49,64,…4) □○△→△□○→○△□→□○△5.给定数列100,81,64,49,36,要求填出下面的两个数是多少。
答案:25,166.按规律在括号里填上适当的数。
1) 1、15、3、13、5、11、7、92) 198、297、396、495、5943) 21、4、18、5、15、6、14、77.根据规律填数。
①30,28,26,24,22,20;②1,3,6,10,15;③15,20,25,30,35,40.8.给定数列1,4,9,16,要求找到下面两个数是多少。
答案:25,369.找规律填后面的数。
1,4,9,16,25,36,49,64,81;2,3,5,8,13,21,34,55,89.10.给定数列:1) 1,4,9,16,25,36,49;2)4565456777要求填出缺少的数。
答案:1) 642)7898889911.给定数列xxxxxxxx,要求填出下一个数是多少。
答案:512.按规律填空。
1) 1,5,9,13,17,21,25,292) 2,4,6,10,16,26,42,…3) 1,3,6,10,15,21,28,…1.缺少一组数字,无法判断规律。
2.缺少两个数字,无法判断规律。
3.数列中每一项都是前一项的两倍再加1,所以下一个数是191.14.数列中第n个数组内的三个数分别是n^2.4n。
