广东省广州市天河区普通高中18届高考数学一轮复习模拟试题031801160215
广州市天河区毕业班2018届高考数学一轮复习模拟试题(6)--有答案

第8题一轮复习数学模拟试题06第Ⅰ卷 选择题(共60分)一.选择题:(本大题共12小题,每小题5分.在每小题给出的四个选项中.只有一项是符合题目要求的.)1.已知集合{}{}22log (2),,A x y x x x R B x y x R ==-++∈==∈,则A B ⋂=( )()[]()(].1,21,2A -- B. C.-1,1 D.-1,12.已知等比数列}{n a 的公比为正数,且23952a a a =,21a =,则1a = ( )A.21B. 22C. 2D.23.已知圆C 与直线0x y -=及40x y --=都相切,圆心在直线0x y +=上,则圆C 的方程为( )A .22(1)(1)2x y ++-=B .22(1)(1)2x y -++=C .22(1)(1)2x y -+-= D .22(1)(1)2x y +++=4.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是( )B .12π33 5.函数()sin()(0,0)f x A x A ωϕω=+>>的图像如图所示, 则(1)(2)(3)(2011)f f f f ++++的值等于( )..1A B.2 C.2+2 2 D.2+26.某班班会准备从甲、乙等7名学生中选派4名学生发言,要求甲、乙两人至少有一人参加。
当甲、乙同时参加时,他们两人的发言不能相邻,那么不同的发言顺序的种数为( ) ..360A B.520 C.600 D.7207.定义方程'()()f x f x =的实数根0x 叫做函数()f x 的“新驻点”。
若函数3(),()ln(1),()1g x x h x x x x ϕ==+=-的新驻点分别为,,αβγ,则,,αβγ的大小关系是( )..A αβγβαγγαββγα>>>>>>>> B. C. D.8.右图给出的是计算111124620++++的值的一个程序框图, 其中判断框内应填入的条件是( )A . 10i >B .10i < C. 20i > D.20i <0 y x 2 2 6-2 正视图 俯视图侧视图9.已知ABC ∆中,():():()1:2:3,AB BC BC CA CA AB ∙∙∙=则ABC ∆的形状为( ) A .钝角三角形 B 等边三角形 C 直角三角形 D 非等腰锐角三角形 10.已知函数()f x 与()g x 满足: (2)(2),f x f x +=-(1)(1),g x g x +=-且()f x 在区间[)2,+∞上为减函数,令()()()h x f x g x =∙,则下列不等式正确的是( ) ..(2)(4)(2)(4)(0)(4)(0)(4)A h h h h h h h h -≥-≤>< B. C. D.11.已知圆的方程224x y +=,若抛物线过定点(0,1),(0,1)A B -且以圆的切线为准线,则抛物线焦点的轨迹方程是( )22222222..1(0)1(0)1(0)1(0)34433443x y x y x y x y A y y x x +=≠+=≠+=≠+=≠ B. C. D.12.若点O 和点(2,0)F -分别为双曲线2221(0)x y a a-=>的中心和焦点,点P 为双曲线右支上的任意一点,则OP FP ∙的取值范围是( )A.)3⎡-+∞⎣ B.)323,⎡++∞⎣ C.7,4⎡⎫-+∞⎪⎢⎣⎭ D.7,4⎡⎫+∞⎪⎢⎣⎭第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.13.若命题:p “存在实数x,使2(1)10x a x +-+<”是假命题,则实数a 的取值范围是.14.已知{}n a 是由非负整数组成的数列,满足*1220,3,2,(,3)n n a a a a n N n -===+∈≥,则数列{}n a 的通项公式为15.已知21(0)()1(0)x x f x x ⎧+≤=⎨>⎩ ,则满足不等式2(1)(2)f x f x -<的x 的取值范围是16.在平面直角坐标系中,点集{}22(,)1,A x y x y =+≤{(,)4,0,B x y x y =≤≥}340x y -≥,则点集{}12121122(,),,(,),(,)Q x y x x x y y y x y A x y B ==+=+∈∈所表示的区域的面积是三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)已知复数12cos (),(2)cos 4z b C a c i z a c B i =++=-+,且12z z =,其中,,A B C 是ABC ∆的内角,,,a b c 是角,,A B C 所对的边。
广州市天河区毕业班2018届高考数学一轮复习模拟试题(6)--有答案

一轮复习数学模拟试题06第Ⅰ卷 选择题(共60分)一.选择题:(本大题共12小题,每小题5分.在每小题给出的四个选项中.只有一项是符合题目要求的.)1.已知集合{}{}22log (2),,A x y x x x R B x y x R ==-++∈==∈,则A B ⋂=( )()[]()(].1,21,2A -- B. C.-1,1 D.-1,12.已知等比数列}{n a 的公比为正数,且23952a a a =,21a =,则1a = ( )A.21B. 22C. 2D.23.已知圆C 与直线0x y -=及40x y --=都相切,圆心在直线0x y +=上,则圆C 的方程为( )A .22(1)(1)2x y ++-=B .22(1)(1)2x y -++=C .22(1)(1)2x y -+-= D .22(1)(1)2x y +++=4.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是( )A .3 B .12π C . 3 D. 65.函数()sin()(0,0)f x A x A ωϕω=+>>则(1)(2)(3)(2011)f f f f ++++的值等于( )..1A + B.2 C.2+2 2 D.2+26.某班班会准备从甲、乙等7名学生中选派4..360A B.520 C.600 D.7207.定义方程'()()f x f x =的实数根0x 叫做若函数3(),()ln(1),()1g x x h x x x x ϕ==+=-的新驻点分别为,α..A αβγβαγγαββγα>>>>>>>> B. C. D.8.右图给出的是计算111124620++++的值的一个程序框图, 其中判断框内应填入的条件是( )A . 10i >B .10i < C. 20i > D.20i <6正视图 侧视图9.已知ABC ∆中,():():()1:2:3,AB BC BC CA CA AB ∙∙∙=则ABC ∆的形状为( ) A .钝角三角形 B 等边三角形 C 直角三角形 D 非等腰锐角三角形 10.已知函数()f x 与()g x 满足: (2)(2),f x f x +=-(1)(1),g x g x +=-且()f x 在区间[)2,+∞上为减函数,令()()()h x f x g x =∙,则下列不等式正确的是( )..(2)(4)(2)(4)(0)(4)(0)(4)A h h h h h h h h -≥-≤>< B. C. D.11.已知圆的方程224x y +=,若抛物线过定点(0,1),(0,1)A B -且以圆的切线为准线,则抛物线焦点的轨迹方程是( )22222222..1(0)1(0)1(0)1(0)34433443x y x y x y x y A y y x x +=≠+=≠+=≠+=≠ B. C. D.12.若点O 和点(2,0)F -分别为双曲线2221(0)x y a a-=>的中心和焦点,点P 为双曲线右支上的任意一点,则OP FP ∙的取值范围是( )A.)3⎡-+∞⎣B.)3⎡++∞⎣ C.7,4⎡⎫-+∞⎪⎢⎣⎭ D.7,4⎡⎫+∞⎪⎢⎣⎭第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.13.若命题:p “存在实数x,使2(1)10x a x +-+<”是假命题,则实数a 的取值范围是.14.已知{}n a 是由非负整数组成的数列,满足*1220,3,2,(,3)n n a a a a n N n -===+∈≥,则数列{}n a 的通项公式为15.已知21(0)()1(0)x x f x x ⎧+≤=⎨>⎩ ,则满足不等式2(1)(2)f x f x -<的x 的取值范围是16.在平面直角坐标系中,点集{}22(,)1,A x y x y =+≤{(,)4,0,B x y x y =≤≥}340x y -≥,则点集{}12121122(,),,(,),(,)Q x y x x x y y y x y A x y B ==+=+∈∈所表示的区域的面积是三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)已知复数12cos (),(2)cos 4z b C a c i z a c B i =++=-+,且12z z =,其中,,A B C 是ABC ∆的内角,,,a b c 是角,,A B C 所对的边。
广东广州市天河区普通高中毕业班2018届高考数学一轮复习模拟试题 11 含答案 精品

一轮复习数学模拟试题11第Ⅰ卷 选择题(共60分)一.选择题:(本大题共12小题,每小题5分.在每小题给出的四个选项中.只有一项是符合题目要求的.)1.若函数()f x A ,函数()lg(1)g x x =-,[2,11]x ∈的值域为B ,则A B 为A (,1]-∞B (,1)-∞C [0,1]D [0,1)2.已知等比数列}{n a 的公比为正数,且23952a a a =,21a =,则1a =() A.21 B. 22 C. 2 D.23.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形, 俯视图是半径为1的半圆,则该几何体的体积是( )B 12π 4.将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数依次为( )A .26,16,8B .25,17,8C .25,16,9D .24,17,95函数()cos 22sin f x x x =+的最小值和最大值分别为( )A 3,1-B 2,2-C 33,2- D 32,2-6已知12,F F 是椭圆221169x y +=的两个焦点,经过点2F 的直线交椭圆于点,A B ,若||5AB =,则11||||AF BF +等于( )A 11B 10C 9D 16 7 设02x π<<,则“2sin 1x x <”是“sin 1x x <”的( )A 充分不必要条件B 必要不充分条件正视图俯视图侧视图第8题C 充要条件D 既不充分也不必要条件8 右图给出的是计算111124620++++的值的一个程序框图,其中判断框内应填入的条件是( )A 10i >B 10i <C 20i >D 20i <9.对于复数,,,a b c d ,若集合{,,,}S a b c d =具有性质“对任意,x y S ∈,必有xy S ∈”,则当2211a b c b =⎧⎪=⎨⎪=⎩时,b c d ++等于( )A .1B .-1C .0D .i10已知向量(,),(1,2),(,)a m n b c k t ===,且//,,||10a b b c a c ⊥+=,则mt 的取值范围是( )A (,1]-∞B (0,1]C [1,1]-D (1,1)- 11.已知函数()()x f x y x R e=∈满足'()()f x f x >,则(1)f 与(0)ef 大小关系是( ) A (1)(0)f ef < B (1)(0)f ef > C (1)(0)f ef = D 不能确定 12.已知函数()y f x =是定义在R 上的增函数,函数(1)y f x =-的图像关于点(1,0)对称。
广东省普通高中2018届高考数学一轮复习模拟试题(含答案)02

一轮复习数学模拟试题02满分150分,考试用时120分钟. 第一部分 选择题(共40分)一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若全集U=R ,集合}01x 3x |x {N },4x |x {M 2<+-=>=,则)N C (M U ⋂等于( ) A. }2x |x {-< B . }3x 2x |x {≥-<或 C. }3x |x {≥ D. }3x 2|x {<≤-2.与函数)1lg(10-=x y 的图象相同的函数是 ( )A. 1-=x yB. 1-=x yC.112+-=x x y D. 211⎪⎪⎭⎫ ⎝⎛--=x x y3.若a ∈R ,则2a =是()()120a a --=的( ).A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分又不必要条件4.在下列图象中,二次函数y =ax 2+bx 与指数函数y =(ab )x的图象只可能是( )5.对于定义在R 上的函数)(x f y =,若),,(0)()(b a R b a b f a f <∈<∙且,则函数)(x f y =在区间),(b a 内( )A .只有一个零点B .至少有一个零点C .无零点D .无法判断6.二次函数()x f 满足()()22+-=+x f x f ,又()30=f ,()12=f ,若在[0,m ]上有最大值3,最小值1,则m 的取值范围是( )A. ()+∞,0B. [)+∞,2C. (]2,0D. [2,4]7.设奇函数f (x )的定义域为R , 且)()(x f x f =+4, 当x ] ,[64∈时f (x)=12+x, 则f (x )在区间] ,[02-上的表达式为( ) A .12+=xx f )( B .124--=+-x x f )( C .124+=+-x x f )( D .12+=-x x f )(8. 正实数12,x x 及函数()f x 满足)(1)(14x f x f x-+=,且12()()1f x f x +=,则12()f x x +的最小值为 ( ) A . 4B . 2C . 54 D .41 第二部分 非选择题(共110分)二、填空题:本大题共6小题,每小题5分,满分30分.9.已知命题P: “对任何2,220x R x x ∈++>”的否定是_____________________ 10.函数2()lg(31)f x x =+的定义域是____________11.设,0.(),0.x e x g x lnx x ⎧≤=⎨>⎩则1(())2g g =__________.12.下列命题:(1)梯形的对角线相等;(2)有些实数是无限不循环小数;(3)有一个实数x ,使0322=++x x ;(4)y x y x ≠⇔≠22或y x -≠;(5)命题“b a 、都是偶数,则ba +是偶数”的逆否命题“若b a +不是偶数,则b a 、都不是偶数”;(6)若p 或q ”为假命题,则“非p 且非q ”是真命题;(7)已知c b a 、、是实数,关于x 的不等式02≤++c bx ax 的解集是空集,必有0>a 且0≤∆。
广东广州市天河中学2018届高三数学一轮复习模拟试题精

数列一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.数列{}n a 的通项公式为n n a n 2832-=,则数列{}n a 各项中最小项是( )A . 第4项B . 第5项C . 第6项D . 第7项【答案】B2.已知两个等差数列{}n a 和{}n b 的前n 项和分别A n 和B n ,且3457++=n n B A n n ,则使得nn b a为整数的正整数n 的值是( ) A .1,3,5,8,11 B .所有正整数 C .1,2,3,4,5 D .1,2,3,5,11【答案】D 3.等差数列{}n a 的前n 项和为n S ,若17S 为一确定常数,则下列各式也为确定常数的是( )A .215a a + B .215a a ⋅C .2916a a a ++ D .2916a a a ⋅⋅【答案】C4.设等比数列{n a }的公比q=2,前n 项和为S 。
,则43S a 的值为( ) A .154B .152C .74 D .72【答案】A5.利用数学归纳法证明 “*),12(312)()2)(1(N n n n n n n n∈-⨯⋅⋅⋅⨯⨯⨯=+⋅⋅⋅++ ”时,从“k n =”变到“1+=k n ”时,左边应增乘的因式是( )A . 12+kB .112++k k C .1)22)(12(+++k k k D . 132++k k【答案】C6.已知等差数列5724,743…,则使得n S 取得最大值的n 值是( ) A .15 B .7C .8和9D . 7和8【答案】D7.已知等比数列}{n a 中,各项都是正数,且2312,21,a a a 成等差,则87109a a a a ++=( ) A .21+ B .21- C .223+ D .223-【答案】C8.在等差数列{a n }中,若a 4+a 6+a 8+a 10+a 12=120,则2 a 10-a 12的值为( )A .20B .22C .24D .28【答案】C9.在等差数列中,有,则此数列的前13项之和为( ) A .24 B .39 C .52 D .104【答案】C10.一个正项等比数列{}n a 中,225)()(1088977=+++a a a a a a ,则=+97a a ( )A .20B .15C .10D .5【答案】B11.已知等比数列}{n a 的公比为正数,且3a ·9a =225a ,2a =1,则1a =( )A .12B .C .D . 2【答案】B12.若数列{}n a 的通项公式为),n a n N *=∈若前n 项和为10,则项数为( ) A . 11 B .99 C .120 D .121【答案】C二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.已知数列{}n a (*n N ∈),其前n 项和为n S ,给出下列四个命题: ①若{}n a 是等差数列,则三点10(10,)10S 、100(100,)100S 、110(110,)110S共线; ②若{}n a 是等差数列,且111a =-,376a a +=-,则1S 、2S 、…、n S 这n 个数中必然存在一个最大者;③若{}n a 是等比数列,则m S 、2m m S S -、32m m S S -(*m N ∈)也是等比数列;④若11n n S a qS +=+(其中常数10a q ≠),则{}n a 是等比数列.其中正确命题的序号是 .(将你认为的正确命题的序号..都填上) 【答案】①④14.设为等差数列的前项和,若,,则当取得最大值时,的值为 。
广东广州市天河中学2018届高三数学一轮复习模拟试题精选:导数及应用 Word版含答案

导数及其应用一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.曲线y P x y 处的切线与在点)12,1(113+=轴交点的纵坐标是( )A .-9B .-3C . 9D .15【答案】C2.曲线3sin (0)2y x x π=≤≤与两坐标轴所围成图形的面积为( ) A . 1B . 2C . 52D . 3【答案】A3.设a ∈R ,函数f(x)=e x +a ·e -x的导函数f ′(x),且f ′(x)是奇函数.若曲线y =f(x)的一条切线的斜率是32,则切点的横坐标为( )A .- ln22B .-ln2C .ln22 D .ln2【答案】D4.由曲线3,y x y x ==围成的封闭图形面积为( )A .112 B .14C .13D .712【答案】A5.设()f x 在[]a b ,上连续,则()f x 在[]a b ,上的平均值是( )A .()()2f a f b + B .()baf x dx ⎰C .1()2baf x dx ⎰ D .1()baf x dx b a -⎰【答案】C6.已知函数()f x 的定义域为(2,2),-导函数为(0)0()2cos ,f f x x ='=+且,则满足2(1)()0f x f x x ++->的实数x 的取值范围为( )A . (1,1)-B .(11)-+,C .(1 D .(1,1+【答案】C7.由抛物线x y 22=与直线4-=x y 所围成的图形的面积是( )A .18B .38/3C .16/3D .16【答案】A8.设函数)(x f 在区间],[b a 上连续,用分点b x x x x x a n i i =<<<<<=- 110,把区间],[b a 等分成n 个小区间,在每个小区间],[1i i x x -上任取一点),,2,1(n i i =ξ,作和式∑=∆=n i i nxf S 1)(ξ(其中x ∆为小区间的长度),那么n S 的大小( )A .与)(x f 和区间],[b a 有关,与分点的个数n 和i ξ的取法无关B . 与)(x f 和区间],[b a 和分点的个数n 有关,与i ξ的取法无关C . 与)(x f 和区间],[b a 和分点的个数n,i ξ的取法都有关。
广东省广州市天河区普通高中18届高考数学一轮复习模拟试题041801160216

一轮复习数学模拟试题04一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设全集R ,若集合}1|12|{},3|2||{>-=≤-=x x B x x A ,则)(B A C R 为 ( ) A .}51|{≤<x x B .}51|{>-≤x x x 或C .}51|{>≤x x x 或D .}51|{≤≤-x x(2)复数ii z -+=1)2(2(i 是虚数单位)在复平面上对应的点位于 ( )A .第一象限B .第二象限C .第三象限D .第四象限(3)在长为10㎝的线段AB 上任取一点P ,并以线段AP 为边作正方形,这个正方形的面积介于25cm 2与49 cm 2之间的概率为 ( )A .51B .52 C .54 D .103 (4)设等比数列{}n a 的公比为q ,前n 项和为n S ,若1n S +,n S ,2n S +成等差数列,则公 比q 为 ( ) A .2-=qB .1=qC .12=-=q q 或D .12-==q q 或(5)已知i 与j 为互相垂直的单位向量,2a i j =- ,b i j λ=+ 且a 与b的夹角为锐角,则实数λ的取值范围是( )A .1(,)2-∞B .1(,)2+∞C .22(2,)(,)33-+∞D .1(,2)(2,)2-∞--(6)设f (x )是R 上的奇函数, 且在(0, +∞)上递增, 若f (21)=0, f (log 4x )>0, 那么x 的 取值范围是( ) A.21<x <1 B.x >2 C. x >2或21<x <1 D.21<x <1或1<x <2 (7)一起,则不同的站法有( )A .240种B .192种C .96种D .48 (8)如果执行下面的程序框图,那么输出的S = ( ). A.2450 B.2500 C.2550 D.2652(9)球面上有三个点A 、B 、C. A 和B ,A 和C 间的球面距离等于大圆周长的16. B 和C 间的球面距离等于大圆周长的14.如果球的半径是R ,那么球心到截面ABC 的距离等于( ) A.12RR D. 13R(10)已知x ,y 满足⎪⎩⎪⎨⎧≤++≤+≥041c by ax y x x , 且目标函数y x z +=2的最大值为7,最小值为1,则=++acb a ( ) A.1 B.1- C.2D. 2-(11)下列命题:①若)(x f 是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,)2,4(ππθ∈,则 ).(cos )(sin θθf f > ②若锐角α、.2,sin cos πβαβαβ<+>则满足③若.)()(,12cos2)(2恒成立对则R x x f x f xx f ∈=+-=π④要得到函数.42sin ,)42sin(个单位的图象向右平移只需将的图象ππx y x y =-= 其中真命题的个数有( )A .1B .2C .3D .4(12)设函数xbax x g x x f +==)(,ln )(,它们的图象在x 轴上的公共点处有公切线,则当1>x 时,)(x f 与)(x g 的大小关系是 ( )A.)()(x g x f >B.)()(x g x f <C.)()(x g x f =D.)(x f 与)(x g 的大小不确定 二、填空题:本大题共4小题,每小题5分。
广东广州市天河区普通高中2018届高考数学一轮复习精选试题:算法初步与框图(解答题) Word版含答案 (5)

推理与证明02解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)1.已知1,1≤≤y x ,用分析法证明:xy y x +≤+1.【答案】要证xy y x +≤+1,即证()()221xy y x +≤+,即证22221y x y x +≤+,即证()()01122≤--y x , 因为1,1≤≤y x ,所以01,0122≥-≤-y x ,所以()()01122≤--y x ,不等式得证.2.求证:2222,2,2y ax bx c y bx cx a y cx ax b =++=++=++(,,a b c 是互不相等的实数),三条抛物线至少有一条与x 轴有两个交点.【答案】假设这三条抛物线全部与x 轴只有一个交点或没有交点,则有 ⎪⎩⎪⎨⎧≤-=≤-=≤-=044044044232221bc a Δab c Δac b Δ 三式相加,得a 2+b 2+c 2-ab -ac -bc ≤0⇒(a -b )2+(b -c )2+(c -a )2≤0.∴a=b=c 与已知a ,b ,c 是互不相等的实数矛盾,∴这三条抛物线至少有一条与x 轴有两个交点.3.祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家、祖冲之的儿子祖暅首先提出来的. 祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等. 可以用诗句“两个胖子一般高,平行地面刀刀切,刀刀切出等面积,两人必然同样胖”形象表示其内涵. 利用祖暅原理可以推导几何体的体积公式,关键是要构造一个参照体.试用祖暅原理推导球的体积公式.【答案】我们先推导半球的体积. 为了计算半径为R 的半球的体积,我们先观察V 圆锥、V 半球、V 圆柱这三个量(等底等高)之间的不等关系,可以发现V 圆锥<V 半球<V 圆柱,即3313R V R ππ<<半球,根据这一不等关系,我们可以猜测323V R π=半球,并且由猜测可发现V V V =-半球圆柱圆锥. 下面进一步验证了猜想的可靠性. 关键是要构造一个参照体,这样的参照体我们可以用圆柱内挖去一个圆锥构造出,如右图所示. 下面利用祖暅原理证明猜想.证明:用平行于平面α的任意一个平面去截这两个几何体,截面分别为圆面和圆环面. 如果截平面与平面α的距离为l ,那么圆面半径r =半径为R ,小圆半径为r.因此222()S r R l ππ==-圆,2222()S R l R l πππ=-=-环, ∴ S S =圆环. 根据祖暅原理,这两个几何体的体积相等,即2231233V R R R R R πππ=-=半球, 所以343V R π=球.4<0>,0>,故只需证明22<.只需证1020+<5.只需证2125<. 因为2125<显然成立,<5.已知函数)1(,12)(>+-+=a x x a x f x ,用反证法证明:方程0)(=x f 没有负实数根.【答案】假设存在x 0<0(x 0≠-1),满足f(x 0)=0,则0x a =-0021x x -+,且0<0x a <1, 所以0<-0021x x -+<1,即12<x 0<2. 与假设x 0<0矛盾,故方程f(x)=0没有负数根.6.用适当方法证明:如果,0,0>>b a 那么b a ab b a +≥+。
广东省广州市天河区普通高中2018届高考数学一轮复习模拟试题07

一轮复习数学模拟试题07一、选择题:本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}5,4,3,2,1=A ,⎭⎬⎫⎩⎨⎧∈-==A x x y y B ,1212,则B A ⋂= A. {1} B. {2} C. {1,2} D. {2,4} 2.若复数z 满足i i z +=⋅1,那么=zA 、i +1B 、i -1C 、i -2D 、i +2 3.“p ∨q 是假命题”是“⌝p 为真命题”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件4.甲、乙两人独立地解决同一问题,甲解决这个问题的概率是31,乙解决这个问题的概率是41,那么其中至少有一人解决这个问题的概率是 A .121 B .21 C .127 D . 12115.已知n S 是等差数列}{n a 的前n 项和,若4151183=++-a a a a ,则515S S -的值是A 、5B 、8C 、16D 、206.函数⎪⎭⎫⎝⎛<<+=20)2sin(πϕϕx y 图象的一条对称轴在⎪⎭⎫⎝⎛3,6ππ内,则满足此条件的一个ϕ值为A .12π B. 6π C. 3πD. 65π 7. 设m 、n 是两条不同的直线,βα,是两个不同的平面,则下列命题中正确的是A .若m ∥n ,m ⊂α,则n ∥α;B .若α⊥β,m ∥α,则m ⊥β;C .若α⊥β,m ⊥β,则m ∥α ;D .若m ⊥n ,m ⊥α,n ⊥β,则α⊥β.8. 从抛物线y x 22=上任意一点M 向圆1)2(:22=-+y x C 作切线MT ,则切线长MT 的最小值为A 、21B 、1C 、2D 、3 9. 如图,目标函数y ax z +=的可行域为四边形OABC (含边界),若)74,32(是该目标函数y ax z +=的最优解,则实数a 的取值范围是 A .⎪⎭⎫ ⎝⎛--149,712 B .⎪⎭⎫ ⎝⎛-149,712 C .⎥⎦⎤⎢⎣⎡--149,712 D .⎥⎦⎤⎢⎣⎡-149,71210.已知B A ,是椭圆长轴的两个端点,N M ,是椭圆上关于x 轴对称的两点,直线BN AM ,的斜率分别为21,k k ,且021≠k k 。
广东广州市天河区普通高中毕业班2018届高考数学一轮复习模拟试题 02 含答案 精品

一轮复习数学模拟试题02一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.设1z i =-(i 是虚数单位),则22z z+的虚部为 ( )A .-iB .1-iC . -1D .-1-i2. 下列各数集及对应法则,不能构成映射的是 ( ) A. {}Z n n x ∈∈|2,{}Z n n y ∈+∈|12,1:-=→x y x f B. Z x ∈,{}Z n n y ∈∈|2,x y x f 4:=→ C. N x ∈,Q y ∈,xx y x f 1:+=→ D. ⎥⎦⎤⎢⎣⎡∈43,4ππx ,[]2,0∈y ,x y x f sin :=→ 3.已知三条不重合的直线,,m n l 和两个不重合的平面α、β,有下列命题 ①若//,,//;m n n m αα⊂则 ②βαβα⊥⊥⊥⊥则且若m l m l ,③m l n m n l //,,则若⊥⊥ ④αββαβα⊥⊥⊂=⊥n m n n m 则若,,,,其中正确命题的个数为 ( )A .4B .3C .2D .14.已知函数错误!未找到引用源。
,其中错误!未找到引用源。
为实数,若错误!未找到引用源。
对错误!未找到引用源。
恒成立, 且 错误!未找到引用源。
,则错误!未找到引用源。
的单调递增区间是 ( )(A ) )(],6,3[Z k k k ∈+-ππππ错误!未找到引用源。
(B ))(],2,[Z k k k ∈+πππ错误!未找到引用源。
(C )错误!未找到引用源。
)(],32,6[Z k k k ∈++ππππ (D ))(],,2[Z k k k ∈-πππ错误!未找到引用源。
5.设函数f (x )=sin θ3x 3+3cos θ2x 2+tan θ,其中θ∈⎣⎢⎡⎦⎥⎤0,5π12,则导数f ′(1)的取值范围是 ( ) A .[-2,2] B .[2,3] C .[3,2] D .[2,2]第6 题图6.某医院安排三名男医生,两名女医生到三所乡医院工作,每所医院至少安排一名医生且女医生不安排在同一所乡医院工作,则不同分配方法总数为 ( ) A.78 B.114 C.108 D.1207.已知函数(),(),x a x x f x a x ---≤⎧=⎨>⎩63377,若数列{}n a 满足()n a f n =(n N *∈),且{}n a 是递增数列,则实数a 的取值范围是 ( )A 、,⎡⎤⎢⎥⎣⎦934B 、,⎛⎫ ⎪⎝⎭934 C 、(2,3) D 、(1,3)8.输入ln 0.8a =,12b e =,2ec -=,经过下列程序程度运算后, 输出a ,b 的值分别是 ( ) A .2e a -=,ln 0.8b = B .ln 0.8a =,2e b -=C .12a e =, 2eb -= D .12a e =, ln 0.8b = 9.已知)(x f 为定义在R 上的可导函数,且)()('x f x f < 对任意R x ∈恒成立,则 ( ))0()2012(),0()2(.20122f e f f e f A >>)0()2012(),0()2(.20122f e f f ef B ><)0()2012(),0()2(.20122f e f f ef C <> )0()2012(),0()2(.20122f e f f e f D <<10.定义:数列{}n a ,满足d a a a a nn n n =-+++112()*N n ∈d 为常数,我们称{}n a 为等差比数列,已知在等差比数列{}n a 中,2,1321===a a a ,则20062009a a 的个位数 ( ) A ,3 B ,4 C ,6 D ,811.已知椭圆2222:1(0)x y C a b a b+=>>,F 1,F 2为其左、右焦点,P 为椭圆C 上任一点,12F PF ∆的重心为G ,内心I ,且有12IG F F λ=(其中λ为实数),椭圆C 的离心率e=( )A .12B .13C .23D.212.若对任意长方体A ,都存在一个与A 等高的长方体B ,使得B 与A 的侧面积之比和体积 之比都等于常数K ,则K 的取值范围是 ( )(]1,0.A ⎥⎦⎤ ⎝⎛21,0.B [)+∞,1.C ⎪⎭⎫⎢⎣⎡+∞,21.D二、填空题:本大题共4小题,每小题5分,共20分,将答案填在答题卷相应位置上。
广州市天河区毕业班2018届高考数学一轮复习模拟试题(3)--有答案

一轮复习数学模拟试题03一、选择题(满分60分,每题5分,共12小题)1、已知复数,,则对应点位于复平面的( )i z 341+-=i z 212-=21z z z ⋅=A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限2、等差数列的前项和为,若,则( ){}n a n n S 58215a a a -=+=9S A 、18B 、36C 、45D 、603、已知与的夹角为,,,则( )a b o1203=a 13=b a =b A 、5 B 、4 C 、3 D 、14、如果一个几何体的三视图如图所示,则该几何体的表面积为( )A 、 B 、C 、96D 、8021680+21664+5、已知函数,若,则实数的取值范围( )()⎩⎨⎧<-≥+=0,40,422x x x x x x x f ()()a f a f >-22a A 、 B 、 C 、 D 、()()+∞⋃-∞-,21,()2,1-()1,2-()()+∞⋃-∞-,12,6、已知命题:抛物线的准线方程为;命题:平面内两条直线的斜率相等是两条直线平p 22x y =21-=y q 行的充分不必要条件;则下列命题是真命题的是( )A 、B 、C 、D 、q p ∧()q p ⌝∧()()q p ⌝∧⌝qp ∨7、定义行列式运算:,将向左平移个单位,所得32414321a a a a a a a a -=()xxx f cos 1sin 3----=()0>m m 图象对应的函数为偶函数,则的最小值为( )m A 、 B 、 C 、 D 、8π3π32π65π8、球面上有三点A ,B ,C ,其中OA ,OB ,OC 两两互相垂直(O 为球心),且过A 、B 、C 三点的截面圆的面积为,则球的表面积( )π4A 、 B 、 C 、 D 、π24π18π36π209、下图是一个算法的程序框图,该算法输出的结果是( )A 、B 、C 、D 、2132435444正视图侧视图俯视图10、以双曲线的离心率为半径,右焦点为圆心的圆与双曲线的渐近线相切,则的值为(1422=-my x m )A 、B 、C 、D 、2334455611、在研究函数的单调区间时,可用如下作法:设得到()x f 在()xax f 1=()1>a ()()xx f x g a 1log ==,上是减函数,类比上述作法,研究的单调性,则其单调增区间为()()0,∞-()+∞,0x x y =()0>x A 、 B 、 C 、D 、()1,0()+∞,1⎪⎭⎫ ⎝⎛+∞,1e⎪⎭⎫ ⎝⎛e 1,012、若关于的方程有四个不相等的实根,则实数的取值范围是( )x ()k x x ++=1ln 2122k A 、 B 、 C 、 D 、⎪⎭⎫ ⎝⎛-∞-2ln 21,()+∞,0⎥⎦⎤ ⎝⎛-0,2ln 21⎪⎭⎫⎝⎛-0,2ln 21二、填空题(满分20分,每题5分,共4小题,将答案写在横线上)13、展开式中含的奇次项的系数和为 。
广州市天河区毕业班2018届高考数学一轮复习模拟试题(9)--有答案

2 3
n
3i
.(1)求
OAn
及
OBn
的坐标;
20090520
(2)若四边形 An Bn Bn1An1 的面积是 an ,求 an n N* 的表达式;
A
B
位向量分别
足下 列两个
OB1 3i 且
(3)对于(Ⅱ)中的 an ,是否存在最小的自然数 M,对一切 n N* 都有 an < M 成立?若存在,求 M;若
SACD
SBAD
168 ,∴ SABD
5
SBCD
3. 2
18 解:(Ⅰ)先后 2 次抛掷一枚骰子,将得到的点数分别记为 a, b ,事件总数为 6 6 36 .
∵函数 F (x) 有且只有一个零点函数 f (x) x a 与函数 g(x) x b 有且只有一个交点 所以 b a ,
一轮复习数学模拟试题 09
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只有一项是符合题目 要求的,) 1.对于集合 M、N 定义: M N { x | x M且x N }, M N (M N ) ( N M ) ,
设 M { y | y x 2 3x, x R}, N { y | y 2 x , x R} ,则 M N ( )
∴函数 F (x) 有且只有一个零点的概率是 15 5 36 12
(Ⅱ)先后 2 次抛掷一枚骰子,将得到的点数分别记为 a, b ,事件总数为 6 6 36 .
∵三角形的一边长为 5 ∴当 a 1时, b 5 , (1,5,5) , 1种 ; 当 a 2 时, b 5 , (2,5,5) , 1 种; 当
广东广州市天河区普通高中毕业班2018届高考数学一轮复习模拟试题: 09 Word版含答案

一轮复习数学模拟试题09一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,)1.对于集合NM、定义:)()(},|{M MNNMNMNxMxxN-⋃-=+∉∈=-且,设},2|{},,3|{2RxyyNRxxxyyM x∈-==∈-==,则=+NM( )A.(-49,0) B.[-49,0) C.(-∞,-49)∪[0,+∞) D.(-∞,-49]∪(0,+∞)2,已知:αβαββαtan)tan(,0cos5)2cos(3+=++则的值为( )A.±4B.4C.-4D.13.关于for循环说法错误的是()A.在for循环中,循环表达式也称为循环体B.在for循环中,步长为1,可以省略不写,若为其它值,则不可省略C.使用for循环时必须知道终值才可以进行D.for循环中end控制结束一次循环,开始一次新循环,4.如图,样本数为9的四组数据,它们的平均数都是5,频率条形图如下,则标准差最大的一组是第一组第二组第三组第四组A.B.C.D.5.已知*,2)(,2),2()2(,)(Nnxfxxfxfxf x∈=≤≤--=+若时当且为偶函数,==2007),(anfa n则()A.2007 B.21C.2 D.-26.在△OAB中,ODbOBaOA,,==是AB边上的高,若ABADλ=,则实数λ等于A.()2baaba--⋅B.()2babaa--∙C.()baaba--∙D.()babaa--∙7.已知aba,0,0>>、b的等差中项是βαβα++=+=则且,1,1,21bbaa的最小值是 ( ) A.3 B.4 C.5 D.68.从抛物线x y 42=上一点P 引抛物线准线的垂线,垂足为M ,且|PM|=5,设抛物线的焦点为F ,则△MPF 的面积为 ( )A .5B .10C .20D .159.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形。
广东广州市天河区普通高中毕业班2018届高考数学一轮复习模拟试题: 01 Word版含答案
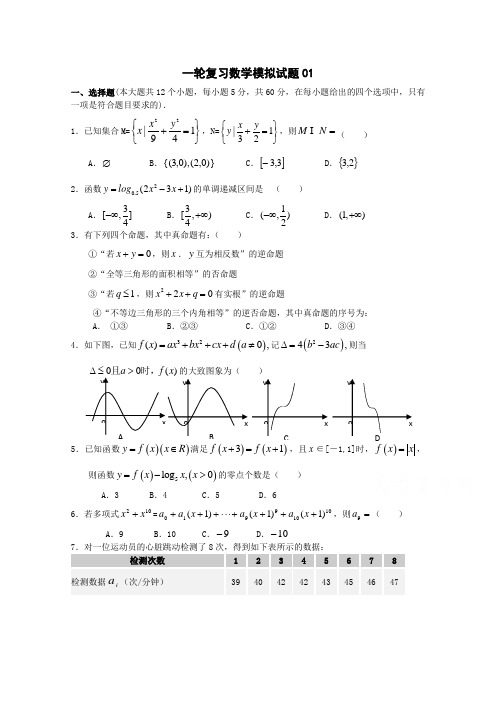
一轮复习数学模拟试题01一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的).1.已知集合M=⎭⎬⎫⎩⎨⎧=+149|22y x x ,N=⎭⎬⎫⎩⎨⎧=+123|y x y ,则=N M ( )A .∅B .)}0,2(),0,3{(C .[]3,3-D .{}2,32.函数20.5(231)y log x x =-+的单调递减区间是 ( )A .3[,]4-∞B .3[,)4+∞C .1(,)2-∞D .(1,)+∞3.有下列四个命题,其中真命题有:( )①“若0x y +=,则x .y 互为相反数”的逆命题 ②“全等三角形的面积相等”的否命题 ③“若1q ≤,则220x x q ++=有实根”的逆命题 ④“不等边三角形的三个内角相等”的逆否命题,其中真命题的序号为:A . ①③B .②③C .①②D .③④4.如下图,已知()32()0,f x ax bx cx d a =+++≠记()243,b ac ∆=-则当5则函数()()5log ,0y f x x x =->的零点个数是( )A .3B .4C .5D .66.若多项式102x x +=10109910)1()1()1(++++⋅⋅⋅+++x a x a x a a ,则=9a ( )A .9B .10C .9-D .10-7.对一位运动员的心脏跳动检测了8次,得到如下表所示的数据:检测次数 1 2 3 4 5 6 7 8 检测数据i a (次/分钟) 3940424243454647上述数据的统计分析中,一部分计算见如右图所示的程序框图(其中a 是这 8个数据的平均数),则输出的的值是( ) A .6 B .7 C .8 D .568.设A={}5,4,3,2,1,B={}8,7,6,从集合A 到集合B 的映射中,满足)5()4()3()2()1(f f f f f ≤≤≤≤的映射有( )A .27个B .9个C .21个D .12个9.设不等式组 110330530x y x y x y 9+-≥⎧⎪-+≥⎨⎪-+≤⎩表示的平面区域为D ,若指数函数y=xa 的图像上存在区域D 上的点,则a 的取值范围是 ( )A .(]3,1B .[]3,2C .(]2,1D .[)+∞,310.设][x 表示不超过x 的最大整数(如2]2[=,1]45[=),对于给定的*N n ∈,定义)1][()1()1][()1(+--+--=x x x x x n n n C x n ,),1[+∞∈x ,则当)3,23[∈x 时,函数xC 8的值域是( )]28,316.[A )56,316.[B )56,28[)328,4.(⋃C ]28,328(]316,4.(⋃D11.由曲线2y x =和直线()20,1,,0,1x x y t t ===∈所围成的图形(阴影部分)的面积的最小值为( ) A .23 B .13 C .12 D .1412.已知函数),2[)(+∞-的定义域为x f ,且1)2()4(=-=f f , )()(x f x f 为'的导函数,函数)(x f y '=的图象如图所示.则平面区域⎪⎩⎪⎨⎧<+≥≥1)2(00b a f b a 所围成的面积是( ) A. 2 B.4 C.5 D.8二、填空题:(本大题共4小题,每小题5分,共20分.)13.已知随机变量ξ服从正态分布)1(,8413.0)3(),,2(2≤=≤ξξδP p N 则= 。
广州市天河区毕业班2018届高考数学一轮复习模拟试题(4)--有答案

(14) 6
(15) (1,
2 3) 3
A
2 2 .即 0 x 3 3 3 AC BC BC ∴ AC sin B 4sin x sin B sin A sin A 1 2 2 y AB AC sin A 4 3 sin x sin( x) (0 x ) ……………… 6 分 2 3 3 2 3 1 (Ⅱ) y 4 3 sin x sin( x) 4 3 sin x( cos x sin x) 3 2 2 7 6sin x cos x 2 3 sin 2 x 2 3 sin(2 x ) 3, ( 2 x ) 6 6 6 6
D.
1 <x<1 2
1 <x<1 2
1 <x<1 或 1<x<2 2
(7)有七名同学站成一排照毕业纪念照,其中甲必须站在正中间,并且乙、丙两位同学要站在一起,则不同的 开始 站法有( ) A.240 种 B.192 种 C.96 种 D.48 种 (8)如果执行下面的程序框图,那么输出的 S ( A.2450 C.2550 B.2500 D.2652 ) .
1 侧侧侧
1 侧侧侧
(20) (本小题满分 12 分) 已知点 R(- 3,0) ,点 P 在 y 轴上,点 Q 在 x 轴的正半轴上,点 M 在直线 PQ 上 ,且满足 2 PM 3MQ 0 , RFra bibliotek PM 0 .
(Ⅰ)当点 P 在 y 轴上移动时,求点 M 的轨迹 C 的方程; (Ⅱ)设 A( x1 , y1 ) 、B ( x2 , y2 ) 为轨迹 C 上两点,且 x1 1, y1 0 , N(1,0),求实数 ,使 AB AN , 16 且 AB . 3
广东广州市天河中学2018届高三数学一轮复习模拟试题精选:数列 Word版含答案

高考专题---数列一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.数列{}n a 的通项公式为n n a n2832-=,则数列{}n a 各项中最小项是( )A . 第4项B . 第5项C . 第6项D . 第7项【答案】B2.已知两个等差数列{}n a 和{}n b 的前n 项和分别A n 和B n ,且3457++=n n B A n n ,则使得nn b a为整数的正整数n 的值是( ) A .1,3,5,8,11 B .所有正整数 C .1,2,3,4,5 D .1,2,3,5,11【答案】D 3.等差数列{}n a 的前n 项和为n S ,若17S 为一确定常数,则下列各式也为确定常数的是( )A .215a a + B .215a a ⋅C .2916a a a ++ D .2916a a a ⋅⋅【答案】C4.设等比数列{n a }的公比q=2,前n 项和为S 。
,则43S a 的值为( ) A .154B .152C .74 D .72【答案】A5.利用数学归纳法证明 “*),12(312)()2)(1(N n n n n n n n∈-⨯⋅⋅⋅⨯⨯⨯=+⋅⋅⋅++ ”时,从“k n =”变到“1+=k n ”时,左边应增乘的因式是( )A . 12+kB .112++k k C .1)22)(12(+++k k k D . 132++k k【答案】C6.已知等差数列5724,743…,则使得n S 取得最大值的n 值是( ) A .15 B .7C .8和9D . 7和8【答案】D7.已知等比数列}{n a 中,各项都是正数,且2312,21,a a a 成等差,则87109a a a a ++=( ) A .21+ B .21- C .223+ D .223-【答案】C8.在等差数列{a n }中,若a 4+a 6+a 8+a 10+a 12=120,则2 a 10-a 12的值为( )A .20B .22C .24D .28【答案】C9.在等差数列中,有,则此数列的前13项之和为( ) A .24 B .39 C .52 D .104【答案】C10.一个正项等比数列{}n a 中,225)()(1088977=+++a a a a a a ,则=+97a a ( )A .20B .15C .10D .5【答案】B11.已知等比数列}{n a 的公比为正数,且3a ·9a =225a ,2a =1,则1a =( )A .12B .C .D . 2【答案】B12.若数列{}n a 的通项公式为),n a n N *=∈若前n 项和为10,则项数为( ) A . 11 B .99 C .120 D .121【答案】C二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.已知数列{}n a (*n N ∈),其前n 项和为n S ,给出下列四个命题: ①若{}n a 是等差数列,则三点10(10,)10S 、100(100,)100S 、110(110,)110S共线; ②若{}n a 是等差数列,且111a =-,376a a +=-,则1S 、2S 、…、n S 这n 个数中必然存在一个最大者;③若{}n a 是等比数列,则m S 、2m m S S -、32m m S S -(*m N ∈)也是等比数列;④若11n n S a qS +=+(其中常数10a q ≠),则{}n a 是等比数列.其中正确命题的序号是 .(将你认为的正确命题的序号..都填上) 【答案】①④14.设为等差数列的前项和,若,,则当取得最大值时,的值为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一轮复习数学模拟试题03一、选择题(满分60分,每题5分,共12小题)1、已知复数i z 341+-=,i z 212-=,则21z z z ⋅=对应点位于复平面的( ) A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限2、等差数列{}n a 的前n 项和为n S ,若58215a a a -=+,则=9S ( ) A 、18 B 、36 C 、45 D 、603、已知a 与b 的夹角为o1203=13=+=( ) A 、5 B 、4 C 、3 D 、14、如果一个几何体的三视图如图所示,则该几何体的表面积为( ) A 、21680+ B 、21664+ C 、96 D 、805、已知函数()⎩⎨⎧<-≥+=0,40,422x x x x x x x f ,若()()a f a f >-22,则实数a 的取值范围( ) A 、()()+∞⋃-∞-,21, B 、()2,1- C 、()1,2- D 、()()+∞⋃-∞-,12,6、已知命题p :抛物线22x y =的准线方程为21-=y ;命题q :平面内两条直线的斜率相等是两条直线平行的充分不必要条件;则下列命题是真命题的是( ) A 、q p ∧ B 、()q p ⌝∧ C 、()()q p ⌝∧⌝ D 、q p ∨7、定义行列式运算:32414321a a a a a a a a -=,将()xx x f cos 1sin 3----=向左平移()0>m m 个单位,所得图象对应的函数为偶函数,则m 的最小值为( ) A 、8π B 、3π C 、32π D 、65π8、球面上有三点A ,B ,C ,其中OA ,OB ,OC 两两互相垂直(O 为球心),且过A 、B 、C 三点正视图侧视图 俯视图的截面圆的面积为π4,则球的表面积( ) A 、π24 B 、π18 C 、π36 D 、π209、下图是一个算法的程序框图,该算法输出的结果是( ) A 、21 B 、32 C 、43 D 、5410、以双曲线1422=-my x 的离心率为半径,右焦点为圆心的圆与双曲线的渐近线相切,则m 的值为( ) A 、23 B 、34 C 、45 D 、5611、在研究函数()xax f 1=()1>a 的单调区间时,可用如下作法:设()()xx f x g a 1log ==得到()x f 在()0,∞-,()+∞,0上是减函数,类比上述作法,研究xx y =()0>x 的单调性,则其单调增区间为( )A 、()1,0B 、()+∞,1C 、⎪⎭⎫ ⎝⎛+∞,1eD 、⎪⎭⎫ ⎝⎛e 1,0 12、若关于x 的方程()k x x ++=1ln 2122有四个不相等的实根,则实数k 的取值范围是( ) A 、⎪⎭⎫ ⎝⎛-∞-2ln 21, B 、()+∞,0 C 、⎥⎦⎤ ⎝⎛-0,2ln 21 D 、⎪⎭⎫ ⎝⎛-0,2ln 21二、填空题(满分20分,每题5分,共4小题,将答案写在横线上) 13、()131x -展开式中含x 的奇次项的系数和为 。
14、设变量y x ,满足约束条件⎪⎩⎪⎨⎧≤-+≥+-≤+-07401201y x y x y x ,线性目标函数y ax z +=的最大值为3+a ,则实数a 的取值范围是 。
15、已知椭圆方程15922=+y x ,点()0,21F ,A ()1,1,P 为椭圆上任意一点,则1PF PA +的取值范围是 。
16、设[]x 表示不超过x 的最大整数。
例如[]25.2=、[]41.3-=-,当1-<m 时,有[][]1443222+++≥--m m m x x 恒成立,则x的取值范围是 。
三、解答题(满分70分,共6小题,解答应写出文字说明,证时过程或演算步骤) 17、(本小题满分12分)某班从6名班干部中(男生4人,女生2人)选3人参加学校义务劳动;(1)求男生甲或女生乙被选中的概率;(2)在男生甲被选中的情况下,求女生乙也被选中的概率; (3)设所选3人中女生人数为ξ,求ξ的分布列及数学期望。
18、(本小题满分12分)已知O 为坐标原点,向量()1,sin α=OA ,()0,cos α=OB ,()2,sin α-=OC 点P 是直线AB 上一点,且BP AB =;(1)设函数()f ⋅=α, ⎪⎭⎫⎝⎛-∈2,8ππα,讨论()αf 的单调性,并求其值域; (2)若点O 、P 、C +的值。
19、(本小题满分12分)在三棱锥ABC S -中,ABC ∆是边长为4的正三角形,52=SB ,32==SC SA ,M 、N 分别是AB 、SB 的中点;(1)证明:平面SAC ⊥平面ABC ;(2)求直线MN 与平面SBC 所成角的正弦值。
·SN C20、(本小题满分12分)设圆C :()3222=+-y x ,此圆与抛物线px y =2()0>p 有四个不同的交点,若在x 轴上方的两交点分别为A ,B ,坐标原点为O ,AOB ∆的面积为s 。
(1)求实数p 的取值范围;(2)求s 关于p 的函数()p f 的表达式及s 的取值范围。
21、(本小题满分12分)已知函数()x x f ln =,()()0212≠+=a bx ax x g (1)若2-=a 时,()()()x g x f x h -=在其定义域内单调递增,求b 的取值范围; (2)设函数()x f 的图象1C 与函数()x g 的图象2C 交于P ,Q 两点,过线段PQ 的中点R 作x 轴的垂线分别交1C 、2C 于点M ,N ,问是否存在点R ,使1C 在M 处的切线与2C 在N处的切线平行?若存在,求R 的横坐标,若不存在,请说明理由。
(请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分) 22、(本小题满分10分)选修4-1:几何证明选讲已知:如图,ABC ∆中,oB 60=∠,AD ,CE 是角平分线。
求证:AC CD AE =+。
23、(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xoy 中,直线l :⎪⎪⎩⎪⎪⎨⎧+=-=t y t x 225223(t 为参数),在极坐标系中(以原点为极点,CABED以x 轴正半轴为极轴),圆C 的方程:θρsin 52= (1)求圆C 的直角坐标方程;(2)设圆C 与直线l 交于A ,B 两点,点P 的坐标()5,3,求PB PA + 24、(本小题满分10分)选修4-5:不等式选讲若关于x 的不等式20102<+-++a x a x 的解集为非空集合,求实数a 的取值范围。
答案一、选择题:ACBAC CDACB CD二、填空题:13、-4096 14、[]4,2- 15、[]106,106+- 16、()[)+∞⋃∞-,30, 三、解答题17、解:(1)543614222412=+=C C C C C p ……………………………………………………………4分(2)522514==C C p (8)分(3)()1=ξE ………………………………………………………………… ………..12分18、解:(1)()1,cos sin αα-= ,()1,sin 2-=α,所以()⎪⎭⎫⎝⎛+-=42sin 2πααf ….2分所以()αf 在⎪⎭⎫ ⎝⎛-8,8ππ上单调递减,在⎪⎭⎫⎝⎛2,8ππ上单调递增……………… ………..4分 又45420ππα<+<,得到()αf 的值域为[)1,2-………………………… ………..6分(2)()1,sin cos --=ααAB ,()y x BP ,cos α-=得到()1,sin cos 2--ααP (8)分所以()1,sin cos 2--=ααOP ,()2,sin α-=OC ,又因为O ,P ,C 三点共线, 所以得到αααs i n2c o s 4s i n -=,所以34tan =α………………………… ………..10分 所以25242sin =α,5742sin 2=+=+α……………… …… ………..12分 19、解:(1)取AC 中点D ,连SD ,BD ,得到22=SD ,32=BD得到⇒⎭⎬⎫⊂⊥⇒⎭⎬⎫⊥⊥S ASD ABC SD AC SD BD SD 面面ABC SAC 面面⊥……………… ………..6分(2)以D 为原点,DA 为x 轴,DB 为y 轴,DS 为z 轴建立空间直角坐标系有, ()0,0,2A ,()0,0,2-C ,()0,32,0B ,()22,0,0S ,()0,3,1M ,()2,3,0N 得到()2,0,1-=MN ,()22,0,2=CS ,()0,32,2=CB 设平面SCB 的法向量为()z y x ,,=,则有⎩⎨⎧=+=+03220222y x z x ,令1=x得到⎪⎪⎭⎫⎝⎛--=22,33,1………………………………………………………….……..8分 设直线MN与平面SBC所成角为θ,则11222sin ==θ…… ………..12分 20、解:(1)()⎩⎨⎧==+-px y y x 22232得到()0142=+-+x p x ,又因为()⎩⎨⎧>->--040442p p 解得20<<p ............ ............ ... ......... ...... ...... ...... ......... ......... ... .. (4)分(2)设()11,y x A ,()22,y x B 可得p x x -=+421,121=x x ,p y y =21()212221x x p y y +=+得到2216p p y y -=+……… … … …… … … … ……. .6分212121y y px x y y k AB +=--=,所以AB l :()1211x x y y p y y -+=-整理得到062=+--p y p p px ... ... ......... ...... ...... ...... ...... ... ......... ... .. (8)分()[]()[]py y y y x x x x AB 612442122121221-=-++-+=,所以6pd =…..10分 ()21221≤-=p p s ,所以⎥⎦⎤⎝⎛∈21,0s … …… …… …… …… … ……… ………..12分21、解:(1)()bx x x x h -+=2ln ,()021'≥-+=b x x x h 得到x x b 21+≤在()+∞∈,0x 上恒成 立,因为2221≥+x x,所以22≤b ………… …… …… … ……… … ………..4分(2)设()11,y x P ,()22,y x Q ,则有221x x x x x N M R +===,令210x x << ()b ax x g +=',假设R 点存在,则()212122x x b x x a +=++… …… … … … ……. . 6分又因为121121ln bx ax x +=,222221ln bx ax x +=,得到 ()21212121221ln ln x x b x x a x x x x +=++=--,即⎪⎪⎪⎪⎭⎫⎝⎛+-=112ln 212121x x x x x x …… … ……. .8分令21x x t =,设()()112ln +--=t t t t h ,()1,0∈t ,()()()01122'>+-=t t t h ,得到 ()t h 在()1,0内单调递增,()()01=<h t h ,假设不成立,所以点R 不存在。
