机械原理 西工大第八版第4章 平面机构的力分析
西工大教材-机械原理各章习题及答案
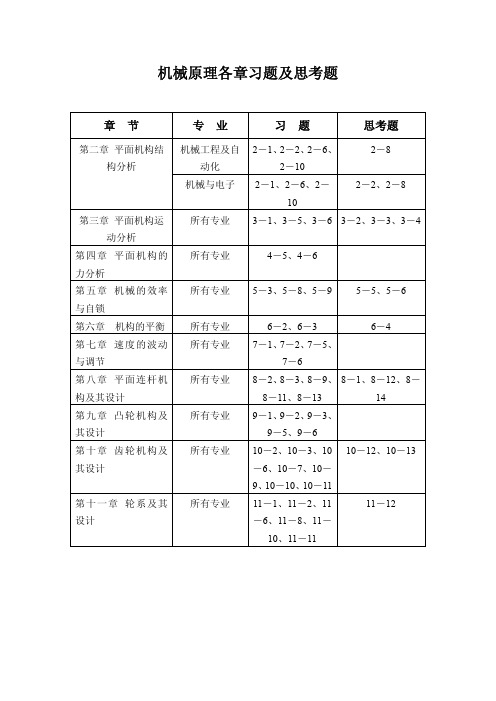
电动机所需的功率为
p = ρ • v /η = 5500 ×1.2 ×10−3 / 0.822 = 8.029(KW )
5-8 在图示斜面机构中,设已知摩擦面间的摩擦系数 f=0.2。求在 G 力作用下(反行程),此斜面 机构的临界自锁条件和在此条件下正行程(在 F 力作用下)的效率。 解 1)反行程的自锁条件 在外行程(图 a),根据滑块的平衡条件:
解 1 ) 取 比 例 尺 μ 1 = 1mm/mm 绘 制 机 构 运 动 简 图 ( 图 b )
(a)
2 )计算该机构的自由度
n=7
pι=9
ph=2(算齿轮副,因为凸轮与齿轮为一体) p’=
F’= F=3n-2pe-ph
=3x7-2x8-2 =1
G7
D 64 C
EF
3
9
B
2
8
A
ω1
b)
2-6 试计算如图所示各机构的自由度。图 a、d 为齿轮一连杆组合机构;图 b 为凸轮一连杆组合 机构(图中在 D 处为铰连在一起的两个滑块);图 c 为一精压机机构。并问在图 d 所示机构中, 齿轮 3 与 5 和齿条 7 与齿轮 5 的啮合高副所提供的约束数目是否相同?为什么?
C3 重合点继续求解。
解 1)速度分析(图 b)取重合点 B2 与 B3,有
方向 大小 ?
v vv vB3 = vB2 + vB3B2 ⊥ BD ⊥ AB // CD ω1lAB ?
D
C
3 d3
ω3
4
ω3 90°
2
B(B1、B2、B3)
ω1
A1 ϕ = 90°
西北工业大学机械原理课后答案第4章

第四章 平面机构的力分析题4-7机械效益Δ是衡量机构力放大程度的一个重要指标,其定义为在不考虑摩擦的条件下机构的输出力(力矩)与输入力(力矩)之比值,即Δ=d r d r F F M M //=。
试求图示各机构在图示位置时的机械效益。
图a 所示为一铆钉机,图b 为一小型压力机,图c 为一剪刀。
计算所需各尺寸从图中量取。
(a ) (b) (c)解:(a)作铆钉机的机构运动简图及受力 见下图(a )由构件3的力平衡条件有:02343=++R R rF F F由构件1的力平衡条件有:04121=++d R R按上面两式作力的多边形见图(b )得θcot ==∆d r F F(b )作压力机的机构运动简图及受力图见(c )由滑块5的力平衡条件有:04565=++R R F F G由构件2的力平衡条件有:0123242=++R R R 其中 5442R R =按上面两式作力的多边形见图(d ),得tF G =∆(c) 对A 点取矩时有 b F a F d r ⋅=⋅ab =∆其中a 、b 为F r 、F d 两力距离A 点的力臂。
tF G =∆(d)(a)(b)drR41F R43F dG题4-8在图示的曲柄滑块机构中,设已知l AB=0.1m,l BC=0.33m,n1=1500r/min(为常数),活塞及其附件的重量G3=21N,连杆质量G2=25N,J S2=0.0425kg·m2,连杆质心S2至曲柄销B的距离l BS2=l BC/3。
试确定在图示位置时活塞的惯性力以及连杆的总惯性力。
解:1) 选定比例尺, mmml005.0=μ绘制机构运动简图。
(图(a) )2)运动分析:以比例尺vμ作速度多边形,如图(b)以比例尺aμ作加速度多边形如图4-1 (c)244.23smcpaaC=''=μ2222100smspaaS=''=μ22215150sBCcnlalaBCtBC=''==μμα3) 确定惯性力活塞3:)(37673333NagGamFCSI=-=-=方向与cp''相反。
机械原理平面机构的力分析

机械原理平面机构的力分析机械原理平面机构的力分析是对平面机构进行力学分析和力学设计的过程。
平面机构是平面运动副的组合,由多个刚体构成,通过运动副连接起来的,因此需要进行力学分析来了解各个部件之间的力的传递和影响。
平面机构力分析的目的是确定各个部件之间的相对运动和受力情况,从而确定设计参数和优化设计。
首先,进行平面机构的力分析需要了解机构的运动副类型和特点。
平面机构包括直线副、转动副和滑动副等,而不同类型的运动副对应不同的受力情况。
例如,直线副的受力主要是拉力和压力,转动副的受力主要是转轴上的扭矩和轴承力,滑动副的受力主要是摩擦力和压力等。
其次,需要确定机构的约束和自由度,以及受力分析的基准点和坐标系。
约束是机构中连接各部件的运动约束,包括固定约束和运动约束;自由度是机构允许的运动自由度,通过自由度的分析可以了解机构的运动特性。
基准点和坐标系的选择是为了方便受力分析和结果的表示。
接下来,通过自由度分析和约束条件,可以得到机构中各个部件之间的受力关系。
根据受力分析的原理,可以采用静平衡条件、动力学方程或功率分析等方法来计算各个部件的受力情况。
静平衡条件可以用来计算处于平衡状态时的受力情况,动力学方程可以用来计算部件在运动过程中的受力情况,功率分析可以用来计算部件之间的能量传递和能量转换情况。
最后,通过力分析的结果可以进行力学设计和性能评估。
根据受力情况,可以确定各个部件的尺寸、材料和结构形式,以满足所要求的工作条件。
同时,还可以通过分析得到的各个部件的受力情况,来评估机构的运动稳定性和工作性能,从而进行优化设计和改进。
总的来说,机械原理平面机构的力分析是对平面机构进行力学分析和力学设计的过程。
通过力分析可以了解机构中各个部件之间的力的传递和影响,为机构的设计和优化提供基础。
力分析需要了解机构的运动副类型和特点,确定约束和自由度,选择基准点和坐标系,采用适当的方法进行受力分析,最后进行力学设计和性能评估。
机械原理,孙恒,西北工业大学版第4章平面机构的力分析

§4-1 作用在机械上的力和力分析的方法
1、作用在机械上的力: 驱动力----驱动机械运动的力 阻抗力----阻止机械运动的力 有效阻力(工作阻力)----有效功,(输出功) 有害阻力(摩擦力、介质阻力),----损失功 2、分析的目的和方法 目的:①确定运动副中的反力(大小和性质) ②确定机械上的平衡力(或平衡力偶),(即确定驱动力) 步骤:①求出各构件的惯性力和力偶,视为外加的力 ②根据静定条件将机构分解为若干构件组和平衡力系 (从最远的构件组,即外力全部已知的构件组开始) ③逐步推算到平衡力作用的构件
M f = f v ⋅ G ⋅ r = FR21.ρ
其中:
ρ = f v .r
称为摩擦圆半径
摩擦圆的概念: 1)以轴颈中心O 为圆心,以ρ为半径的圆。 2)在转动副中,只要发生相对转动,总反力 就总是切于摩擦圆,即轴承对轴颈的总反力 FR21始终相切于摩擦圆。 3)FR21对铰联中心所形成的摩擦力矩的方向 总是与相对角速度的方向相反。的确切方向 须从该构件的其它力平衡条件中得到。
3、什么是静力分析和动态静力分析: 静力分析----不计惯性力对机械进行力分析 动态静力分析----计入惯性力,利用达朗伯 原理(动静法)作力分析 方法: 图解法 解析法:矢量方程式法 直角坐标法(矩阵法) 复数法
§4-2 构件惯性力的确定
FIi-----i构件质心上的惯心力 FIi’--- i构件偏离质心某一点上的惯心力 mi -----各构件的质量 Jsi-----绕过质心轴的转动惯量 asi-----质心Si的加速度 αi-----角加速度
需水平驱动力F,:F,=G tan (α - φ)
图4-5----矩形螺纹:
等速拧紧螺母所需力矩: M = Fd2 / 2 = Gd2 tan(α + ϕ) / 2 等速放松螺母所需力矩: M ′ = Gd tan(α −ϕ) / 2 2
机械原理之平面机构的力分析

机械原理之平面机构的力分析1. 引言在机械设计中,平面机构是一种常用的力传递装置。
它由多个固定的连杆构成,通过铰链连接点连接。
平面机构广泛应用于各种机械设备中,如发动机、传动装置等。
为了正确设计和优化平面机构,了解力的分析是很重要的。
本文将介绍平面机构的力分析方法,包括静力学方法和动力学方法。
2. 静力学方法静力学方法可以帮助我们计算平面机构的力。
它主要根据平衡条件和力的平衡方程来进行计算。
2.1 平衡条件平面机构的平衡条件是指在任何时刻,机构中的各个连杆受力之和为零。
这可以表示为以下公式:$$ \\sum F_x = 0 $$$$ \\sum F_y = 0 $$其中F x和F y分别表示平衡方程的水平和垂直分量。
2.2 力的平衡方程力的平衡方程可以通过使用力向量的加法和减法来得到。
在平面机构中,力的平衡方程可以表示为以下公式:$$ \\sum F_x = \\sum F_{xi} \\cos(\\theta_i) - \\sum F_{xj}\\cos(\\theta_j) = 0 $$$$ \\sum F_y = \\sum F_{yi} \\sin(\\theta_i) - \\sum F_{yj}\\sin(\\theta_j) = 0 $$其中F xi和F yi是作用在连杆上的水平和垂直分力,$\\theta_i$是作用力的夹角,$\\sum F_{xj}$和$\\sum F_{yj}$是作用在铰链上的水平和垂直反力,$\\theta_j$是反力的夹角。
2.3 举例说明假设我们有一个简单的平面机构,由两个连杆和一个铰链组成。
其中,连杆1的长度为l1,连杆2的长度为l2。
连杆1和连杆2之间的夹角为$\\theta$,铰链受到的水平反力和垂直反力分别为F xj和F yj。
现在我们需要计算连杆1和连杆2受力的大小和方向。
根据力的平衡方程,我们可以得到以下公式:$$ F_{x1} - F_{x2} \\cos(\\theta) = 0 $$$$ F_{y1} + F_{yj} - F_{y2} \\sin(\\theta) = 0 $$通过解这些方程,我们可以得到连杆1和连杆2受力的大小和方向。
机械原理 第四章 平面机构的力分析

P
1
P
Q
α- φ α
Q 2
HIGH EDUCATION PRESS
HIGH EDUCATION PRESS
第四章 平面机构的力分析
二、机构力分析的目的
1. 根据机构所受的已知外力确定各运动副中的 反力。 反力。 2. 根据作用在机构上已知的外力及给定的原动 件运动规律, 件运动规律,确定需要加在机构上的平衡力或平 衡力矩。 衡力矩。
HIGH EDUCATION PRESS
∑F =0,∑F =0,∑M =0
x y
F41x + F21x − m1 a s1x = 0 F41 y + F21 y − m1 a s1 y = 0 M 1 − F21x L1 sin ϕ 1 + F21 y L1 cos ϕ 1 − (− m1 a s1x ) r1 sin ϕ 1 + (− m1 a s1 y )r1 cos ϕ 1 + (− J s1α 1 ) = 0
B
M2 s
s2
G2
F 2 = −m as2 I 2 Ms2 = −JS2α2
《机械原理》课件_第4章_平面机构的力分析(
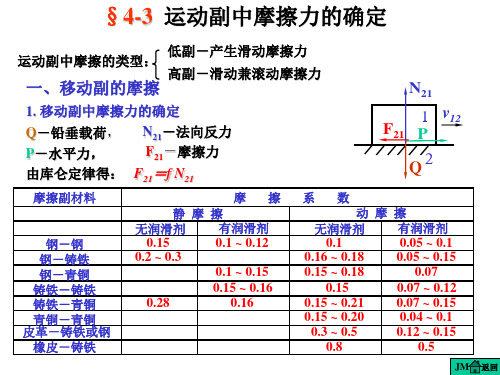
对于三角带:θ =18°
fv=3.24 f
θ
2.移动副中总反力的确定 总反力为法向反力与摩擦力的合成:
θ R21 N21 1 v12 P Q 2
φ
F21
R21=N21+F21
tgφ= F21 / N21 = fN21 / N21 =f
φ-摩擦角,
方向:∠R21V12 =(90°+φ)
阻碍相对运动
JM
Q
△N
△N
β
Q
β △N ∑△N=Q
矩形螺纹――忽略升角影响时,△N近似垂直向上,
――∑△N△cosβ=Q, β-牙形半角 ∑△N△=∑△N /cosβ fv = f / cosβ φv= arctg fv
d2 拧松: M ' Qtg ( v ) 2
JM
返回
比较可得:∑△N△cosβ=Q=∑△N 引入当量摩擦系数: 当量摩擦角:
R r
f
JM
返回
§4-4 不考虑摩擦的平面机构力分析
一、构件组的静定条件 假设已对机构作过运动分析,得出 了惯性力,因为运动副中的反力对整个 机构是内力,因此必须把机构拆成若干 构件组分析,所拆得的杆组必须是静定 的才可解。
对构件列出的独立的平衡方程数目等于所有力 的未知要素数目。显然构件组的静定特性与构 件的数目、运动副的类型和数目有关。 ①转动副:反力大小和方向未知,作用点已知,两个未知数
槽面接触: N’21 +N”21= -Q
柱面接触:
N’21 = N”21 = Q / (2sinθ) F21=f N’21 + f N”21 = ( f / sinθ)• Q = fv Q
Q N”21 θ N’21 θ θ N’21 N”21 1
4 《机械原理》平面机构的力分析

C ε
FI′
FI
ε
可以用总惯性力FI’来代替FI和MI ,FI’ = FI,作用线由质心
S 偏移 lh
MI lh = F I
在确定构件惯性力时,如用一般的力学方法, 在确定构件惯性力时 , 如用一般的力学方法 , 就需先求出 构件质心的加速度和角加速度,如对一系列位置分析非常繁琐, 构件质心的加速度和角加速度,如对一系列位置分析非常繁琐, 为简化,可采用质量代换法。 为简化,可采用质量代换法。
ƒv ------当量擦系数 当量擦系数
5)槽面接触效应 所以在其它条件相同的情况下 槽面、 其它条件相同的情况下,槽面 因为 f v > f ,所以在其它条件相同的情况下 槽面、圆柱 面的摩擦力大于平面摩擦力。 面的摩擦力大于平面摩擦力
2. 移动副中总反力方向的确定
1)总反力和摩擦角 总反力FR21 :法向反力 N21和摩擦力 f21的合力。 法向反力F 和摩擦力F 的合力。 总反力 总反力和法向反力之间的夹角。 摩擦角ϕ :总反力和法向反力之间的夹角。
绕质心的转动惯量 用一个力简化之
v FI
v FIlhS源自εv MIv aS v v FI = − ma S v J Sε MI v lh = F = ma I S
2. 作平面移动的构件
v v 等速运动: 等速运动: FI = 0; M I = 0 v v v 变速运动: 变速运动: FI = − m a S ; M I = 0
mB + mK = m mBb = mkk mBb2 + mKk2 = Js
优点:代换精确。 优点:代换精确。
S B
b c
C
S B
m
B
机械原理-平面机构的力分析

传动条件
曲柄摇杆机构、齿轮传动机构
存储条件
转动机构、滑动机构
力的基本概念
1 力的作用点
力作用的位置或接触点。
2 力的方向
力作用的方向或施力线。
3 力的大小
力作用的大小或强弱。
平面机构的受力分析
1
受力分析
2
根据力的分解结果,分析各构件的受力情况。
3
力的分解
将力分解为平行于连接构件的分力和垂直于 连接构件的分力。
交叉槽的弯曲影响
交叉槽是指曲柄和滑块之间存在的交叉形状,它会导致机构的弯曲失效和运 动不稳定。
非正交曲柄机构的分析
1 自由度分析
根据曲柄滑块机构的结构,确定其自由度以及运动学约束。
2 力分析
通过力的平衡分析,确定机构各处的力大小和方向。
3 运动模拟
使用模拟软件或物理实验,验证机构设计的正确性和稳定性。
摆线和椭圆曲柄机构的分析
摆线曲柄机构
利用摆线曲线的特性,实现更平稳的运动传动。
椭圆曲柄机构
利用椭圆曲线的特性,实现更精确的运动传动。
内嵌框架的应用
机构设计
通过内嵌框架的布局,实现机构零 件的紧凑排列和高效传动。
机器人技术
内嵌框架在机器人领域的应用,提 高了机器人的稳定性和工作效率。
汽车工程
通过内嵌框架的结构布局,实现汽 车发动机和悬挂系统的高性能和节 能效果。
力的平衡
通过分析和计算,判断平面机构是否处于力 的平衡状态。
计算机构的自由度
自由度是指机构中独立变量的个数,它决定了机构的运动和约束情况。
平面机构的结构形式
齿轮传动
通过齿轮的啮合来实现转动传动功 能。
机械原理(第4章 平面机构的力分析)

一、作用在机构上的力: 作用在机构上的力:
6.附加动压力:在运动副反力中,由惯性力引起的部分, 6.附加动压力:在运动副反力中,由惯性力引起的部分,称为 附加动压力 附加动压力。对于高速机械来讲,其值比较大。 附加动压力。对于高速机械来讲,其值比较大。 而机械在静态时对应的是静态附加动压力。 而机械在静态时对应的是静态附加动压力。 1、小型低速机械可以不考虑重力、惯性力的影响; 、小型低速机械可以不考虑重力、惯性力的影响; 注意 2、一般在进行力分析时,可以不考虑摩擦力,但对 、一般在进行力分析时,可以不考虑摩擦力, 于摩擦力影响比较大, 于摩擦力影响比较大,特别是依靠摩擦力来作功时 则必须考虑; 则必须考虑; 3、高速、重载的情况下由于惯性力远大于重力,可 、高速、重载的情况下由于惯性力远大于重力, 以不考虑重力。 以不考虑重力。 总的来说作用在机械上的力可以归并为两大类: 总的来说作用在机械上的力可以归并为两大类: 驱动力和阻抗力。 驱动力和阻抗力。
质点的达郎伯原理—当非自由质点运动时, 质点的达郎伯原理 当非自由质点运动时,作用于 当非自由质点运动时 质点的所有力和惯性力在形式上形成一平衡力系。 质点的所有力和惯性力在形式上形成一平衡力系。
机构的力分析法具体包括图解法和解析法,本章采用图解法。 机构的力分析法具体包括图解法和解析法,本章采用图解法。
Northwest A&F University
第四章 平面机构的力分析
一、作用在机构上的力: 作用在机构上的力:
摩擦力和介质阻力在某些情况下也可能是有效阻力, 摩擦力和介质阻力在某些情况下也可能是有效阻力, 有效阻力 注意 甚至为驱动力 比如磨床砂轮受到工件给与的摩擦力, 驱动力。 甚至为驱动力。比如磨床砂轮受到工件给与的摩擦力, 搅拌机叶轮所受到的被搅拌物质的阻力等等均为有效 阻力。 阻力。 3.重力:地心对构件的引力。 3.重力:地心对构件的引力。 重力 其特征是机构的重心向下运动时重力为驱动力, 其特征是机构的重心向下运动时重力为驱动力,重力所作 是机构的重心向下运动时重力为驱动力 的功是正功;机构的重心向上运动时重力为阻抗 的功是正功;机构的重心向上运动时重力为阻抗 正功 力,重力所作的功是负功; 重力所作的功是负功; 负功 重力在物体的一个运动循环过程中所做的功的总和为零。 重力在物体的一个运动循环过程中所做的功的总和为零。
西工大机械原理第八版(免费版)

免费版 平面机构的结构分析1、如图a 所示为一简易冲床的初拟设计方案,设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析其是否能实现设计意图?并提出修改方案。
解 1)取比例尺l μ绘制其机构运动简图(图b )。
2)分析其是否能实现设计意图。
图 a ) 由图b 可知,3=n ,4=l p ,1=h p ,0='p ,0='F 故:00)0142(33)2(3=--+⨯-⨯='-'-+-=F p p p n F h l因此,此简单冲床根本不能运动(即由构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架),故需要增加机构的自由度。
图 b )3)提出修改方案(图c )。
为了使此机构能运动,应增加机构的自由度(其方法是:可以在机构的适当位置增加一个活动构件和一个低副,或者用一个高副去代替一个低副,其修改方案很多,图c 给出了其中两种方案)。
图 c1) 图 c2)2、试画出图示平面机构的运动简图,并计算其自由度。
图a )解:3=n ,4=l p ,0=h p ,123=--=h l p p n F图 b )解:4=n ,5=l p ,1=h p ,123=--=h l p p n F3、计算图示平面机构的自由度。
将其中的高副化为低副。
机构中的原动件用圆弧箭头表示。
3-1解3-1:7=n ,10=l p ,0=h p ,123=--=h l p p n F ,C 、E 复合铰链。
3-2解3-2:8=n ,11=l p ,1=h p ,123=--=h l p p n F ,局部自由度3-3 解3-3:9=n ,12=l p ,2=h p ,123=--=h l p p n F4、试计算图示精压机的自由度解:10=n ,15=l p ,0=h p 解:11=n ,17=l p ,0=h p13305232=⨯-+⨯='-'+'='n p p p h l 26310232=⨯-⨯='-'+'='n p p p h l0='F 0='FF p p p n F h l '-'-+-=)2(3 F p p p n F h l '-'-+-=)2(310)10152(103=--+⨯-⨯= 10)20172(113=--+⨯-⨯=(其中E 、D 及H 均为复合铰链) (其中C 、F 、K 均为复合铰链)5、图示为一内燃机的机构简图,试计算其自由度,并分析组成此机构的基本杆组。
机械原理第4章 平面机构的力分析

Fig.4-7 Friction in a journal bearing(径向轴承中的摩擦)
2) 推力轴承的摩擦。 图4-8a为推力轴承示意图,G为轴向载荷。未经跑合时,接 触面压强p为常数,p=c。经过跑合时,压强与半径的乘积为 常数,pρ=c。
Fig.4-8 Friction in a thrust bearing(推力轴承的摩擦)
例4-4 图4-12a所示的摆动从动件盘形凸轮机构中,已知凸轮机构的尺 寸、轴径尺寸、运动副处的摩擦因数f以及作用在从动件F点的阻力Fr, 在不计构件质量和惯性力时,求各运动副处的反作用力及作用在凸轮上 的平衡力矩Mb。
2.计入摩擦力的力分析
例4-3 图4-11所示的曲柄滑块机构中,已知各构件尺寸和曲柄的位置和 作用在滑块4上的阻力Fr以及各运动副中的摩擦因数f,忽略各构件质量和 惯性力。在图4-11上标注出各运动副的反力以及加在曲柄上的平衡力矩Mb。
Fig.4-11 Force analysis considering the friction in a slider-crank linkage (考虑摩擦的曲柄滑块机构力分析)
Байду номын сангаас
(3)螺旋副中的摩擦 根据螺纹牙型可将螺纹分为矩形螺纹 和三角形螺纹。 图4-9a所示为一矩形螺纹,将螺母2简化为图4-9b所示的滑 块,承受轴向载荷[WTBX]G,由于螺纹可以看成是斜面缠 绕在圆柱体上形成的,故将矩形螺纹沿螺纹中径[WTBX]d展 开,该螺纹成为图4-9b所示的斜面,斜面底长为螺纹中径 处圆周长,高度为螺纹的导程l。驱动力F等于拧紧力矩M除 以螺纹半径d/2,方向一般垂直于螺纹轴线。
3) 槽面摩擦。如果将图4-6a所示滑块作成图4-6b所示夹角为 2θ的楔形滑块,并置于相应的槽面中,楔形滑块1在外力F 的作用下沿槽面等速运动。设两侧法向反力分别为N21 , 铅直载荷为G,总摩擦力为Ff。
西工大机械原理第八版答案版

免费版平面机构的结构分析1、如图a 所示为一简易冲床的初拟设计方案,设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析其是否能实现设计意图?并提出修改方案。
解 1)取比例尺l μ绘制其机构运动简图(图b )。
2)分析其是否能实现设计意图。
图 a ) 由图b 可知,3=n ,4=l p ,1=h p ,0='p ,0='F 故:00)0142(33)2(3=--+⨯-⨯='-'-+-=F p p p n F h l因此,此简单冲床根本不能运动(即由构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架),故需要增加机构的自由度。
图 b )3)提出修改方案(图c )。
为了使此机构能运动,应增加机构的自由度(其方法是:可以在机构的适当位置增加一个活动构件和一个低副,或者用一个高副去代替一个低副,其修改方案很多,图c 给出了其中两种方案)。
图 c1) 图 c2)2、试画出图示平面机构的运动简图,并计算其自由度。
图a )解:3=n ,4=l p ,0=h p ,123=--=h l p p n F图 b )解:4=n ,5=l p ,1=h p ,123=--=h l p p n F3、计算图示平面机构的自由度。
将其中的高副化为低副。
机构中的原动件用圆弧箭头表示。
3-1解3-1:7=n ,10=l p ,0=h p ,123=--=h l p p n F ,C 、E 复合铰链。
3-2解3-2:8=n ,11=l p ,1=h p ,123=--=h l p p n F ,局部自由度3-3 解3-3:9=n ,12=l p ,2=h p ,123=--=h l p p n F4、试计算图示精压机的自由度解:10=n ,15=l p ,0=h p 解:11=n ,17=l p ,0=h p13305232=⨯-+⨯='-'+'='n p p p h l 26310232=⨯-⨯='-'+'='n p p p h l0='F 0='FF p p p n F h l '-'-+-=)2(3 F p p p n F h l '-'-+-=)2(310)10152(103=--+⨯-⨯= 10)20172(113=--+⨯-⨯=(其中E 、D 及H 均为复合铰链) (其中C 、F 、K 均为复合铰链)5、图示为一内燃机的机构简图,试计算其自由度,并分析组成此机构的基本杆组。
机械原理第八版第四章

2
2r 2R
轴端接触面
取环形微面积 ds = 2πρdρ, 设 ds 上的压强p为常数,则其正压 力dFN = pds ,摩擦力dFf = fdFN = fρds, 故其摩擦力矩 dMf为
dMf = ρdFf = ρfpds
运动副中摩擦力的确定(7/8)
总摩擦力矩Mf为 R Mf =∫r ρ fpds = 2π f ∫r pρR2dρ 1)新轴端 对于新制成的轴端和轴承,或很少相对运动的 各接触面压强处处相等, 即 p=G/[π (R2-r2)] = 常数, 轴端和轴承, ,则 2 Mf = fG(R3-r3)/(R2-r2) 3 2)跑合轴端 轴端经过一定时间的工作后,称为跑合轴端。 此时轴端和轴承接触面各处的压强已不能再假定为处处相等。而 较符合实际的假设是轴端与轴承接触面间处处等磨损,即近似符 合 pρ=常数的规律。则 Mf = 2πf∫r (R pρ) ρdρ
其功为正功, 称为驱动功或输入功。 (2)阻抗力 阻止机械运动的力。 其特征: 与其作用点的速度方向相反或成钝角; 其功为负功,称为阻抗功。 1)有效阻力 (工作阻力) 其功称为有效功或输出功; 2)有害阻力 (非生产阻力) 其功称为损失功。
§4-3 运动副中摩擦力的确定
1.移动副中摩擦力的确定 (1)摩擦力的确定 移动副中滑块在力F 的作用下右移时, 所受的摩擦力为 Ff21 = f FN21 FN21 1
FR21
φ
FN21
Ff21
1 2
v12 F
运动副中摩擦力的确定(5/8)
二、转动副总反力的确定 1)根据力的平衡条件,确定不计摩擦时总反力的方向; 2)计摩擦时的总反力应与摩擦圆相切; ρ = fv r 3)总反力FR21 对轴心之矩的方向必与轴颈1相对轴承2的相对 角速度的方向相反。 G
机械原理平面机构的力分析新

S2
?2
2
a
t
CB
3
C
? 58? 5 ? 290m/ s2
?2
?
aCt B lBC
?
c??c?? a
BC ? l
p
? 48 .6 ? 5 ? 103 .4rad / s 2
2.35
c c?
p?
a
t CB
aS2
b
s2?
c?? b?
第十二页,编辑于星期二:一点 二十三分。
3 求惯性力和惯性力矩
(1)活塞 3 的惯性力
第十九页,编辑于星期二:一点 二十三分。
例2 在图示的曲柄滑块机构中,设已知曲柄长度 l AB ? 0.1m, 连
杆长度 lBC ? 0.33m, 曲柄的转速 n1 ? 1500r / min,活塞及其附
件的重量 Q3 ? 21N , 连杆重量 Q2 ? 25N , 连杆对其重心的
转动惯量 J S2 ? 0.0425 kg. m2 ,连杆重心 S2 至曲柄销的 B
M I 3 ? ? J 3?3
? ? 0.2 ? 231
? ?46N ?m
p (b3 )
A
4
C p?
?
1
1a? B32源自?B3 MI3
?3
第十一页,编辑于星期二:一点 二十三分。
例3 在图示发动机曲柄滑块机构中,已知曲柄长度 lAB ? 0.35m,
连杆长度 lBC ? 2.35m,连杆重心 S2 至曲柄销轴 B的距离
?
25 ?
9.8
0.151
0.151 ? 0.11
? 1.476 kg
mK
?
m2
?
mB
机械原理第八版答案解析和解析
机械原理 第八版 西北工业大学 平面机构的结构分析1、如图a 所示为一简易冲床的初拟设计方案,设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析其是否能实现设计意图?并提出修改方案。
解 1)取比例尺l μ绘制其机构运动简图(图b )。
2)分析其是否能实现设计意图。
图 a ) 由图b 可知,3=n ,4=l p ,1=h p ,0='p ,0='F 故:00)0142(33)2(3=--+⨯-⨯='-'-+-=F p p p n F h l因此,此简单冲床根本不能运动(即由构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架),故需要增加机构的自由度。
图b)3)提出修改方案(图c)。
为了使此机构能运动,应增加机构的自由度(其方法是:可以在机构的适当位置增加一个活动构件和一个低副,或者用一个高副去代替一个低副,其修改方案很多,图c 给出了其中两种方案)。
图c1)图c2)2、试画出图示平面机构的运动简图,并计算其自由度。
图a )解:3=n ,4=l p ,0=h p ,123=--=h l p p n F图 b )解:4=n ,5=l p ,1=h p ,123=--=h l p p n F3、计算图示平面机构的自由度。
将其中的高副化为低副。
机构中的原动件用圆弧箭头表示。
3-1解3-1:7=n ,10=l p ,0=h p ,123=--=h l p p n F ,C 、E 复合铰链。
3-2解3-2:8=n ,11=l p ,1=h p ,123=--=h l p p n F ,局部自由度3-3 解3-3:9=n ,12=l p ,2=h p ,123=--=h l p p n F4、试计算图示精压机的自由度解:10=n ,15=l p ,0=h p 解:11=n ,17=l p ,0=h p13305232=⨯-+⨯='-'+'='n p p p h l 26310232=⨯-⨯='-'+'='n p p p h l0='F 0='FF p p p n F h l '-'-+-=)2(3 F p p p n F h l '-'-+-=)2(310)10152(103=--+⨯-⨯= 10)20172(113=--+⨯-⨯=(其中E 、D 及H 均为复合铰链) (其中C 、F 、K 均为复合铰链)5、图示为一内燃机的机构简图,试计算其自由度,并分析组成此机构的基本杆组。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结论 只要轴颈相对轴承运动,
运动副中摩擦力的确定(5/8)
(2)总反力方向的确定 1)根据力的平衡条件,确定不计摩擦时总反力的方向; 2)计摩擦时的总反力应与摩擦圆相切; 3)总反力FR21 对轴心之矩的方向必与轴颈1相对轴承2的相对 角速度的方向相反。 举例: 例4-3 铰链四杆机构考虑摩擦时的受力分析 例4-4 曲柄滑块机构考虑摩擦时的受力分析
阻抗力
有效阻力
有害阻力 驱动力―驱使机械运动的力。驱动力与其作用点的速度 方向相同或成锐角,其所作的功为正功。
阻抗力―阻止机械运动的力。阻抗力与其作用点的速度方向
相反或成钝角,其所作的功为负功。
驱动力 1 阻抗力
F
F
V12
<90
2
1
V12
2
>90
阻抗力又可分为
有效阻力―即工作阻力,它是机械在生产过程中为了改变
(2)总反力方向的确定 FR21 运动副中的总反力=法向反力+摩擦力 总反力与法向力之间的夹角φ, 称 为摩擦角,即 φ = arctan f φ 1 FN21
v12 F
Ff21
总反力方向的确定方法: 2 1)FR21偏斜于法向反力一摩擦角φ ; 2) FR21偏斜的方向应与相对速度v12的方向相反。 G
1
C
mK= m2b/(b+k) 动代换: 优点:代换后构件惯性力及惯性力偶矩不改变。 缺点:代换点及位置不能随意选择,给工程计算带来不便。
构件惯性力பைடு நூலகம்确定(5/5)
(3)质量静代换 只满足前两个条件的质量代换称为静代换。
如连杆BC的分布质量可用B、C两点集中质量mB、mC 代换,则 B mB mB=m2c/(b+c) S2 C m2 mC=m2b/(b+c) B mC 2 m2 1 S 3 1 A C S2 S3
B
A 3 C B α2 1 S1 m1 JS 1 ′ FI2
4 (1)作平面复合运动的构件(如连杆2) FI2=-m2aS2 MI2=-JS2α2 ′ 可简化为总惯性力FI2 lh2=MI2/FI2 ′ )与α2方向相反。 MS2(FI2
2
lh2
FI2 MI2
aS2
S2 m2 JS2 3 C S3 m3
例1:
反行程 F′=Gtan(α-φ) 正行程 F = Gtan(α+φ)
arctan 0.15 10.750
例2 螺旋机构
拧紧和防松螺母所需要的力
图a 所示为矩形螺旋,设其螺母上承受一轴向载荷Fr,根据螺纹形成 原理,可将其沿中径d2展开成一升角为 的斜面,如图b所示。
当以力矩Md拧紧螺母时,相当于滑块在驱动力Fd作用下克服阻力Fr沿斜 面等速上升,如图a所示。Fd为作用在螺母中径d2上的圆周力,设此时斜面对 滑块的全反力为FR21, 则根据滑块的力平衡方程可得 Fd + Fr + FR21 = 0
构件惯性力的确定(3/5)
2.质量代换法 质量代换法 是指设想把构件的质量按一定条件集中于构件上 某几个选定点上的假想集中质量来代替的方法。 这样便只需求各 集中质量的惯性力,而无需求惯性力偶矩, 从而使构件惯性力的 确定简化。 假想的集中质量称为代换质量; 代换质量所在的位置称为代换点。 (1)质量代换的参数条件 代换前后构件的质量不变; 代换前后构件的质心位置不变; 代换前后构件对质心轴的转动惯量不变。 (2)质量动代换 同时满足上述三个条件的质量代换称为动代换。
运动副中摩擦力的确定(6/8)
2.2 轴端的摩擦 轴用以承受轴向力的部分称为轴端。 当轴端1在止推轴承2上 旋转时,接触面间也将产生摩擦力。 G ω dρ ds 2 d ω M 1 r M
f
2
2r 2R
轴端接触面
设微圆环 ds 上的压强p为常数, 则其正压 力dFN = pds , 摩擦力dF = fdF = fpds, 故其摩擦力矩 dMf为 f N
作力多边形(如图b所示), 由图可得
Fd Fr tan( )
M d Fd d2 2
三角形螺纹的当量摩擦角 v arctan f v arctan
f cos
运动副中摩擦力的确定(4/8)
2.转动副中摩擦力的确定 2.1 轴颈的摩擦 (1)摩擦力
Ff21 = fv G
FN21 2
G
FN21 2
运动副中摩擦力的确定(2/8)
3)半圆柱面接触: FN21= k G,(k = 1~π/2) Ff21 = f FN21 = kfG = fvG 其中, fv 称为当量摩擦系数
G
说明 引入当量摩擦系数之后, 使不同接触形状的移动副中 的摩擦力计算和大小比较大为简化。
因而这也是工程中简化处理问题的一种重要方法。
平衡力
驱动力―根据机构的阻力大小选择适当的驱动力来平衡 生产阻力―根据机构的驱动力大小选择适当的阻力来平衡
平衡力即可以是驱动力又可以是阻力
机构力分析的目的
1) 为现有机械工作性能的评价、鉴定提供参数;
2) 为新机械的强度计算、结构设计提供重要依据。
机构力分析的方法
图解法 解析法
驱动力
作用在机械上的力
r
R
Rr fG 2
根据 pρ =常数的关系知,在轴端中心部分的压强非常大, 极 易压溃,故轴端常做成空心的。
运动副中摩擦力的确定(8/8)
3.平面副中摩擦力的确定 平面高副两元素之间的相对运动通常是滚动兼滑动,故有滚 动摩擦力和滑动摩擦力;因滚 Mf t 动摩擦力一般较小,机构力分 FR21 析时通常只考虑滑动摩擦力。 n Ff21 φ ω12 FN21 平面高副中摩擦力的确定, 通常是将摩擦力和法向反力合 1 成一总反力来研究。 V12 n 2 其总反力方向的确定为: t 1)总反力FR21的方向与 法向反力偏斜一摩擦角; 2)偏斜方向应与构件1相对构件2的相对速度v12的方向相反。
构件惯性力的确定(4/5)
如连杆BC的分布质量可用集中在B、K两点的集中质量mB、 mK来代换。 mB + mK= m2 mB b= mK k mB b2+mK k2=JS 2 在工程中,一般选定 代换点B的位置,则 k= JS 2 /(m2b) mB= m2k/(b+k) A B B mB S2 m2 2 S1 S2 m2 mk K 3 S3 C
静代换: 优缺点:构件的惯性力偶会产生一定的误差,但一般工程是 可接受的。
§4-3 运动副中摩擦力的确定
1.移动副中摩擦力的确定 (1)摩擦力的确定 移动副中滑块在力F 的作用下右移时, 所受的摩擦力为 Ff21 = f FN21 FN21
v12
F
式中 f 为 摩擦系数。 G FN21 的大小与摩擦面的几何形状有关: 1)平面接触: FN2 = G , 2)槽面接触: FN21= G / sinθ θ θ FN21 1 G 2
工件的外形、位置或状态时所受到的阻力,克服这些阻
力就完成了工作。如机床中作用在刀具上的切削阻力, 起重机提升重物的重力等都是有效阻力。
有害阻力―为非工作阻力,克服这些阻力所做的功纯粹
是一种浪费,故称为损失功。摩擦力、介质阻力等 一般为有害阻力。
§4-2 构件惯性力的确定
1.一般力学方法 以曲柄滑块机构为例 B 2 1 A
第四章
平面机构的力分析
§4-1 机构力分析的任务和方法
§4-2 构件惯性力的确定
§4-3 运动副中摩擦力的确定
§4-4 不考虑摩擦时机构的力分析 §4-5 考虑摩擦时机构的力分析
返回
§4—1机构力分析的任务、目的和方法
机构力分析的任务 1)确定运动副中的反力 运动副反力指运动副处作用的正压力和摩擦力的合力 2)确定机械中的平衡力 平衡力是指机械在已知外力的作用下,为了使该机械能按 给定运动规律运动,还须加于机械上的未知外力
C
构件惯性力的确定(2/5)
(2)作平面移动的构件(如滑块3) 作变速移动时,则 FI3 =-m3aS3 (3)绕定轴转动的构件(如曲柄1) 若曲柄轴线不通过质心,则 FI1=-m1aS1 aS3 3 C FI3
MI1=-JS1α1
若其轴线通过质心,则 MI1=-JS1α1 A
FI1 α1
1
B S1 MI1 aS1
摩擦力矩
G
ω12
Md
fv=(1~π/2)
O
ρ ρ
FR21 Mf FN21 Ff21
Mf = Ff21r = fv G r
总反力 FR21 = - G ,
故 Mf = fv G r =FR21ρ
式中 ρ = fv r , 为摩擦圆半径。
一个具体轴颈 ρ 为定值, 故可作摩擦圆,ρ 称
轴承对轴颈的总反力FR21将始 终切于摩擦圆,且与 G 大小相等,方向相反。
dMf = ρdFf = ρfpds
ds 2 d
总摩擦力矩Mf为
M f fpds
r
R
1)新轴端 各接触面压强处处相等 Mf = 2 fG(R3-r3)/(R2-r2) 3
2)跑合轴端 轴端与轴承接触面间处处等磨损,即近似符合 pρ=常
数的规律。
M f 2 f ( p) d
小结: 1、移动副中摩擦力的确定 FN21 = f NN21 = fvG 2、转动副中摩擦力的确定
(1)轴颈
Ff21 = fv G
摩擦圆半径 ρ = fv r
Mf = Ff21r = fv G r
(2)轴端 摩擦力矩
M f fpds
r
R
