第三届(2009)全品高考有奖猜题活动

合集下载

【精品课件】2009届高考数学研讨会解题思路资料(答题相约)

答题相约
（1）猜字破题解字圆说
考场应试，靠“答”得分，靠“猜”破题，而“解”只是对猜和答的圆说！况且，一半以上的答案是“不要解”的！
只要不考记忆复述，则必然是考探究。而探究从猜想开始。
猜想是解题时的一种期待，没有期待就没有目标，没有目标就没有行动。思维的启动是从猜想开始的。
高考出题经常考虑“两性结合”：（1）理论的“一般性” ，（2）载体的“特殊性” 。 “一般特殊思想” 是 “猜想解题”最常见、最适用的方法。
– 7 y – 4 = 0，原点在等腰三角形的底边上，则底边所在直线的斜率为
（）
A．3
B．2
C．
1 3
D．
1 2
【图解】截距法直线作图，如右所示.
y
底边
【初看】一眼就看清： C、D 不可能.
3
【细看】斜率3 看好，斜率2 偏小 .
2
【工具】眼睛不对光，可用圆规量！【答案】(A) 3.
O
1
2
4
x
x – 7y – 4 = 0
【分析】命题人为实现“会想少算”，突出考查数学思想，客观题中的数据一般选取得较特殊。你看：
（1）抛物线的焦参数选为 p=2，使得焦点坐标特殊F（1，0）；（2）线段AB中点M（2，2）也特殊，在直线 y = x 上。
【猜想】线段AB的两个端点分别为（0，0）和（4，4）！
一验：y2=4x ，果然不错！
【拙解】原不等式等价于不等式组：
x 1 0
(Ⅰ)
x
2
4
0
或(Ⅱ)
x 1 0
x
2
4
0
【评说】 “ 拙解”可练基本功，平时训练可把选择题当解答题来练.

【语文】2015全品高考猜题最有可能考的20题[简易版]

……
4.很久以前，森林里的鸟类没有国王，各类鸟都为了争夺食物和地盘吵个不停。森林女神见后十分担心，于是她把所有的鸟都召集起来，开会商议选举国王的事。女神说：“为了大家能够和睦相处，我们选一位最漂亮的鸟做国王，你们觉得怎么样？”鸟儿们听了，都叽叽喳喳地叫个不停，都觉得自己最漂亮，可以当国王。有一只乌鸦知道自己又黑又丑，只好躲到河边去叹气。刚到河边，乌鸦就听到天鹅说：“我们把身上洗干净，然后去竞选国王吧！”这时，所以的鸟都跑到河里来洗澡，乌鸦也混在里
…… 【名人言论】 1.不忘初心，方得始终。——《华严经》 2.每个人的心灵深处都有着只有他自己理解的东西。——列夫•托尔斯泰 3.人生在世的时间非常短，如果你总是不敢做想做的事情，那么一生过去了，你留下来的只有悔恨，只有懊恼。——李开复 4.我们要以全心来绽放，以花的姿态证明自己的存在。——林清玄 5.无论你能做什么，或梦想去做什么，就放手去做吧！勇气蕴含着天赋、才能和魅力。 ——歌德 6.我可以让自己过得很好。——汤唯 7.真正有血性的人，绝不曲意求得别人重视，也不怕别人忽视。──乔治·戈登·拜伦 8.当我回顾所有的烦恼时，想起一位老人的故事，他临终前说：“一生中烦恼太多，但大部分担忧的事情却从来没有发生过。”——温斯顿·丘吉尔 9.上帝等待着人类在智慧中获得新的童年。——泰戈尔 10.有志者，事竟成，破釜沉舟，百二秦关终属楚；苦心人，天不负；卧薪尝胆，三千越甲可吞吴。— —蒲松龄【最新素材】 1．比尔·盖茨在访问北京师范大学附属实验中学时，一位高中生问他：“你的理想是什么？”盖茨说： “我从小的梦想就是把计算机做成一个完美的工具，这也是我毕生的追求，现在，我已经走完了一半的路程，我希望，我最终结束工作的时候能完全实现这样的一个梦想。” 2.陈士骏是华裔美籍企业家，为网络影音分享网站 YouTube 的创办人之一。目前是美国杂志 Business 2.0 公布的全球排名第 28 最具影响力的企业人物。正是在他创业取得圆满成功并需要再次规划未来的转折点上，陈士骏知道了一个不亚于晴天霹雳的坏消息——他得了脑瘤。在个人自传《20 个月赚 130 亿： YouTube 创始人陈士骏自传》中他这样写道：“有什么东西，有可能是永恒的？我还没有博学到可以回答这个问题，但病痛和休养让我从混沌到清醒。我意识到得为自己的心活着，因为反正我们都逃不脱死亡；我得为最爱的事情活着，因为反正我们都逃不脱死亡。而在那一天到来之前，我们得抓紧时间…… 如果大公司不是我的最爱，那么我就离职，如果我最爱的还是创业，那么就在硅谷租一间办公室重新开始。既然你所拥有的一切都有可能戛然而止，那么，在此之前，为什么不选择你最中意的生活，干吗要让自己后悔？” 3.“你的时间是非常有限的，所以千万不要重复他人的生活，不要为此而浪费时间，不要失掉思考的自由，因为那就等于你躺在别人的思想上生活。聆听自己内心真实的声音，不要被别人的观点所左右。最重要的一点是，你要勇敢面对自己的直觉和内心的真实想法，因为它们最清楚你想成为什么样的人，其他的一切与此相比，都是微不足道的。”——乔布斯 2005 年在斯坦福大学毕业典礼上的演讲。 4.尼泊尔的柯伊蕾拉本是一名英语教师，偶然间知道有许多尼泊尔女童被诱拐到印度，受尽凌辱磨难之后便被丢弃。作为一名虔诚的印度教徒，知道这样的事情如果不去帮助，这将会让她余生在自我惭怍中度过。于是，为了解救这些可怜的女孩儿们，她辞职并且变卖所有财产，创立了“尼泊尔母亲之家”，对那些得到解救的心灵受创的女童给予帮助。她与犯罪分子殊死搏斗，与警察一同在边境巡逻，无论是怎样的危险她都不在乎，只求能告慰自己那颗慈爱的心。她如今苍老却孑然一身，但她使 9800 多个孩子得到解救。 5.李昆仑，目前任全国贫困县冠县定远寨人民法院法庭庭长。这个人民法院地处盐碱地，工作条件非常艰苦，水资源一直非常紧缺。然而李昆仑丝毫没有抱怨过，她说：“我在哪都能干，只要好好干，在哪都是一样的。”李昆仑不是没有调离的机会，但是她从来没有主动向领导提出过，因为她明白这里的百姓需要她，这里的领导信赖她，这里的同事舍不得她。而且她说：“我发现这里的条件也越来越好，

2009年高考临近：数学猜题卷陕西特级教师安振平

2009年高考临近：数学猜题卷陕西咸阳师范学院基础教育课程研究中心安振平 712000本试卷分为第I 卷（选择题）和第II 卷（非选择题）两部分.满分150分.考试时间120分钟.第I 卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（理科）复数411i ⎛⎫-- ⎪⎝⎭的值是（）A ．4iB ．－4iC ．4D ．－4（文科）设全集U ={|x x 是不大于9的正整数}，A ={1，2，3 }，B =｛3，4，5，6｝则图中阴影部分所表示的集合为（） A.｛1，2，3，4，5，6｝ B. ｛7，8｝C.｛7，8，9｝D. ｛1，2，4，5，6，7，8，9｝2．满足方程2(3,1)(2,1)(8,6)0x x +-+--=的实数x 为（）A ． 2-B ． 3-C ．３D ．433．函数2sin sin 3y x x =-+的最大值是（）A. 2B. 3C. 4D. 54．已知F 1、F 2是双曲线)0,0(12222>>=-b a by a x 的两焦点，以线段F 1F 2为边作正三角形，若双曲线恰好平分正三角形的另两边，则双曲线的离心率是（）A ．324+B ．13-C ．213+ D ．13+5．山坡水平面成30 角，坡面上有一条与山底坡脚的水平线成30 角的直线小路，某人沿小路上坡走了一段400米的路后，升高了100米，则此人升高了（）A ．50米B ．100米C ．200米D ．3200米 6．图中一组函数图像，它们分别与其后所列的一个现实情境相匹配：情境ａ：一份30分钟前从冰箱里取出来，然后被放到微波炉里加热，最后放到餐桌上的食物的温度（将0时刻确定为食物从冰箱里被取出来的那一刻）；情境ｂ：一个1970年生产的留声机从它刚开始的售价到现在的价值（它被一个爱好者收藏，并且被保存得很好）；情境ｃ：从你刚开始放水洗澡，到你洗完后把它排掉这段时间浴缸里水的高度；情境ｄ：根据乘客人数，每辆公交车一趟营运的利润；其中情境ａ、ｂ、ｃ、ｄ分别对应的图象是（） A ．①、③、④、② B ．①、③、②、④、C ．②、③、④、①D ．②、④、③、① 7．(理科)已知等比数列｛a n ｝的公比为q （q 为实数），前n 项和为S n ,且S 3、S 9、S 6成等差数列，则q 3等于（）A ．1B ．－21C ．－1或21 D ．1或－21 （文科）若数列{}n a 满足关系111n na a +=+，且83421a =，则3a =（）A.32B.53 C. 85 D.1388．已知22ππθ-<<，且sin cos ,aθθ+=其中()0,1a ∈，则关于tan θ的值，在以下四个答案中，可能正确的是（）A ．3-B ．3 或13C ．13-D ．3-或13-9．李先生忘记了自己电脑的开机密码，但记得密码是由两个3，一个6，一个9组成的四位数，于是，他用这四个数字随意排成一个四位数输入电脑尝试. 那么他打开电脑最多尝试的次数为（）A ．64B ．18C ．12D ．610．若对(],1x ∈-∞-时，不等式()21212xx m m ⎛⎫--< ⎪⎝⎭恒成立，则实数m 的取值范围是A ． ()2,3-B ． ()3,3-C ．()2,2-D ．()3,4-11．如果,x y R ∈，且)1yx =，那么（）A ．x y =B. x y >C ．x y <D. x y ≤12．（理科）若实数,x y 满足0xy >，则1122x y y x+++的最小值是（）A ．B ．C ．D ．2（文科）若实数,,x y z 满足3222233,5,4,x y y z z x +=+=+=则xy yz zx ++的最小值是（）A BCD第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题5分，共20分．将答案填在题中的横线上. 13．点P 是抛物线214y x =上一个动点，则点P 到点)1,0(-A 的距离与点P 到直线1-=x 的距离和的最小值是．14．（理科）函数55()(1)(1)f x x x =++-的单调减区间为．（文科）如果5(1)mx -的展开式中3x 的系数为80，那么实数m 的值应当是___________．15．已知x ，y ∈R ，且1,1,y y x ≤⎧⎪⎨≥-⎪⎩则x+2y 的最大值是______．16．下列四个命题：①圆4)1()2(22=+++y x 与直线02=-y x 相交，所得弦长为2；②直线kxy =与圆1)sin ()cos (22=-+-θθy x 恒有公共点；③若棱长为3的正方体的顶点都在同一球面上，则该球的表面积为108π；④若棱长为2的正四面体的顶点都在同一球面上，则该球的体积为.23π其中，正确命题的序号为．写出所有正确命的序号）三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．17．（本小题满分10分）已知向量552),sin ,(cos ),sin ,(cos ===ββαα．（Ⅰ）求的值)cos(βα-；（Ⅱ）若202παβπ<<<<-，且αβsin ,135sin 求-=的值． 18．（本小题满分12分）（理科）有A ，B ，C ，D 四个城市，它们都有一个著名的旅游点，依此记为a ，b ，c ，d.把ABCD 和a ，b ，c ，d 分别写成左、右两列，现在一名旅游爱好者随机用4条线把左右两边的字母全部连接起来，构成“一一对应”，已知每连对一个得2分，连错得0分．（Ⅰ）求该爱好者得分的分布列；（Ⅱ）求该爱好者得分的数期望．（文科）西安万国家具城进行促销活动，促销方案是：顾客每消费1000元，便可以获得奖券一张，每张奖券中奖的概率为51，若中奖，则家具城返还顾客现金200元. 某顾客购买一张价格为3400元的餐桌，得到3张奖券.（I ）求家具城恰好返还该顾客现金200元的概率；（II ）求家具城至少返还该顾客现金200元的概率．19．（本小题满分12分）如图，已知△ABC 是正三角形，EA 、CD 都垂直于平面ABC ，且EA=AB=2a ，DC=a ，F 是BE 的中点．求证：（I ）FD ∥平面ABC ；（II ）AF ⊥平面EDB ．20．（本小题满分12分）（理科）已知函数75()1x f x x +=+，数列{}n a 满足：11220n n n n a a a a ++-+=且0n a ≠.数列{}n b 中,1(0)b f =且(1)n n b f a =- (I) 求证:数列1{}na 是等差数列； (II) 求数列{||}nb 的前n 项和n T ；(III) 是否存在自然数n ，使得（2）中的(480,510)n T ∈.若存在,求出所有的n ;若不存在,请说明理由.（文科）已知函数432()41f x x x ax =-+-在区间[0，1]上单调递增，在区间[1，2]上递减．（I ）求a 的值；（II ）设2()1g x bx =-，若方程()()f x g x =的解集恰有3个元素，求b 的取值范围．21．（本小题满分12分）已知椭圆方程为22128x y +=，射线2(0)y x x =≤与椭圆的交点为,M 过M 作倾斜角互补的两条直线，分别与椭圆交于B A 、两点（异于M ）．（I ）求证: 直线AB 的斜率2AB k =；（II ）求△AMB 面积的最大值．22．（本小题满分12分）（理科）定义在（0，+∞）上的函数)1,()(1>∈-=p Q p x px x f p且. （Ⅰ）求函数)(x f 的最大值；（Ⅱ）对于任意正实数a 、b ，设.:,111qb p a ab q p qp +≥=+证明（文科）已知数列{a n }中，a 1＝2，前n 项和为S n ，对于任意n ≥2，3S n －4，a n ，1322n S -- 总成等差数列．（I ）求数列{}n a 通项公式a n（II ）若数列{}n b 满足3n n b S =，求数列{}n b 的前n 项和n T ．参考答案一、选择题１．（理科）C ．44241(1)(1)(2)4i i i i---=-=--=. （文科）C ．图中阴影部分所表示的集合为()U AB u ð,∵{1,2,3,4,5,6,7,8,9}U =，{1,2,3,4,5,6}A B =，(){7,8,9}U AB ∴=u ð． 2． A ．注意(),a b 是向量的坐标表示，将2x =-代入知道，方程成立．3．D. 将函数关系变形为2sin sin 3(sin 1)(sin 2)55y x x x x =-+=+-+≤．显然，当sin 1x =-时，max 5.y =4． D ．设F 2 (c , 0)，M (0 ,3c)，依照MF 2中点N (2c 3,2c )在双曲线上，得2222b4c 3a 4c -=1，即)a c (4c 3a 4c 22222--=1)1e (4e34e 222--⇒=1．注意到e >1，解得e =3+1．5． B ．如图，30,30ACD ADB ∠=∠=，而400AC =．在Rt ADB ∆中，2200AD AB ==．在Rt ADC ∆中，24400AC AD AB ===，所以 100AB =．6．A ．依照实际体验，不难作出判断与正确的选择．7．(理科) B ．若q=1, 则S 3、S 9、S 6 不成等差数列,即 1.q ≠由题意知()9362111111q q q qq q---=+---, 解得q 3=－21. （文科）A ．由873411,21a a ==+得762111,13a a ==+ 类似有651311,8a a ==+54811,5a a ==+43511,3a a ==+从而332a =．8．C ．由题意知02πθ-<<，从而tan 0θ<.此时有cos sin sin 0cos sin ,a θθθθθ=->->⇒>-即有 1tan 0.θ-<< 对照选择支．9．C ．4个密码的位置里先选2个位置，用6和9排，有24A 种排法；再在剩余的2个位置里填上3就可以了．显然总数是2412A =．10．A ．由已知不等式，得2214x x m m +-<．设12xt ⎛⎫= ⎪⎝⎭，由于(],1x ∈-∞-，则2t ≥，于是有D222111()6424x xt t t +=+=+-≥．便得26m m -<，解得23m -<<． 11．A ．当x y =时，等式)1yx =显然成立．再取特殊值，可以否定B ，C ，D ． 12．（理科）C ．由２元均值不等式，得1122x y y x +++≥=≥=（文科） C ．解已知中关于322,,x y z 的三元一次方程，得3221,2,3x y z ===，于是有四组解：1,23x y =，1,x y z ===，1,x y z ===，1,x y z ===1,x y z ==时，代数式则xy yz zx ++的最小值二、填空题13．2．由于x y 42=的准线是1-=x ，所以点p 到1-=x 的距离等于P 到焦点F 的距离，故点P 到点)1,0(-A 的距离与P 到x =1-的距离之和的最小值是2=FA ．14．（理科）(),0-∞．对函数求导数，得 /442()5(1)5(1)20(1)f x x x x x =+--=+．由/2()20(1)0,f x x x =+<得0x <．（文科）2．因为555155()(1)(1)r r r r r rr r T C mx m C x ---+=⋅-=-⋅⋅⋅，所以由35=-r ，得 2=r ．由33580m C ⋅=，得2m =．15．利用线性规划求最值. 可行域为三角形，其顶点为 ()()()0,1,1,0,2,1，当x+2y 过()2,1 时最大，其最大值为4．16．②④．直线恒过定点()0,0始终在圆上，即直线与圆恒有公共点；或由圆心)sin ,(cos θθ 到0=-y kx 的距离111|sin cos |222++≤+-k k k k θθ=1=r ，故直线与圆恒有公共点，②正确；棱长为a的正四面体的外接球半径R =∴=⨯=∴,23246,46R a V 球=π23，所以④正确．三、解答题17．（Ⅰ）1=1=，)s i n s i n c o s (c o s 2222βαβα+-+⋅-=b b a a )cos(211βα--+=．545522=⎪⎪⎭⎫⎝⎛= ， 53)cos(54)cos(22=-=--∴βαβα得（Ⅱ）0,022ππβααπ-<<<<∴<<．由 53)cos(=-βα，得54)sin(=-βα．由 135sin -=β 得1312sin =β[]ββαββαββααs i n )c o s (c o s )s i n ()(s i n s i n-+-=+-=∴ 6533)135(53131254=-⨯+⨯=18．（理科）（I ）设答对题的个数为y ，得分为ξ,y=0，1，2，4；所以ξ=0，2，4，8．2499)0(44===A P ξ， 312481)2(4424==⨯==A C P ξ， 412461)4(4424==⨯==A C P ξ， 2411)8(44===A P ξ，则ξ（II ）E ξ=0×249+2×31+4×41+8×241=2．答：该人得分的期望为2分．（文科）（I ）家具城恰好返还给该顾客现金200元，即该顾客的三张奖券有且只有一张中奖．12548)54()51(213=⋅=C p ．（II ）设家具城至少返还给该顾客现金200元为事件A ，这位顾客的三张奖券有且只有一张中奖为事件1A ，这位顾客有且只有两张中奖为事件2A ，这位顾客有且只有三张中奖为事件 3A ，则123A A A A =++，1A 、2A 、3A 是互斥事件．123()()()()P A P A P A P A =++333223213)51()54()51()54()51(c c c +⋅+⋅=12511251212548++= 12561=．19．(I)取AB 的中点M ，连FM 、MC ．∵ F 、M 分别是BE 、BA 的中点， ∴ FM ∥EA, FM=12EA ． ∵ EA 、CD 都垂直于平面ABC ，∴ CD ∥EA ， ∴ CD ∥FM ．又 DC=a ，∴ FM=DC ，∴四边形FMCD 是平行四边形．∴ FD ∥MC ，FD ∥平面ABC ．（II ）因为M 是AB 的中点，△ABC 是正三角形，所以CM ⊥AB ．又因为CM ⊥AE,所以CM ⊥面EAB, CM ⊥AF, FD ⊥AF ．因为F 是BE 的中点，EA=AB ，所以AF ⊥EB ． 20．（理科）（I ）由11220n n n n a a a a ++-+=得11112n n a a +-=, 所以,数列1{}na 是等差数列.(II)而1(0)5b f ==,所以117(1)5511a a -+=-+,11725a a -=,所以11a =,111(1)2n n a =+-, 所以 21n a n =+. 727(1)6n n na b n n a -==-+=-. 当6n ≤时,(11)(56)22n n n n T n -=+-=, 当7n ≥时,26116015(16)22n n n n T n --+=++-=. 所以，2(11),6;21160,7.2n n n n T n n n -⎧≤⎪⎪=⎨-+⎪≥⎪⎩（III ）不存在这样的自然数．如果存在必定7n >,而在7n >时n T 是递增的,而36n =时,480n T =, 37n =时, 511n T =,所以不存在这样的自然数.（文科）（I ）求导数，得32'()4122f x x x ax =-+．由题设可知1x =是'()0f x =的根，4a =．（II ）由22()()(44)0f x g x x x x b =⇒-+-=有三个相异实根，故方程2440x x b -+-=有两个相异实根，所以，164(4)0,40,b b ∆=-->⎧⎨-≠⎩04b b ⇒>≠且．故b 的取值范围是(0,4)(4,)+∞．21．（I ）∵ 斜率 k 存在，不妨设k ＞0，求出 M （1-， 2-）；直线 MA 方程为)1(2+=+x k y ，直线 MB 方程 )1(2+-=+x k y ．分别与椭圆方程联立，可解出22444A k k x k --=+，22444B k k x k +-=+，∴ 2)2(=-++=--BA B A B A B A x x x x k x x y y ， ∴ 2=AB k ．（II ）设直线AB 方程为m x y +=2，与2422=+y x 联立，消去y ，得 mx x 482+0)8(2=-+m ．由∆>得-4＜ m ＜4，且 m ≠0，点到 AB 的距离为5||m d =．222m -162528-m -)2m (5AB ==．设△MAB 的面积为S ，所以4)216(161)16(161||41222222=≤-==⋅m m d AB S ．当22±=m 时，得2max =S ．22．（理科）（Ⅰ）.1)(11-='-p x x f,011<-p∴由)(x f '=0，得x=1．当x 变化时，)(x f '、)(x f 的变化如下表：又)(),1()(,1)1(x f f x f p f 即所以≤-=的最大值为p －1. （Ⅱ）由（Ⅰ）得.011≤+--p x px p 设,0111,01,≤+-⋅-≤+--⋅=p b a p ba pb a b a p b a x q p p q q p p q q p 即则∴,,11,1111q b p a ab q b a p b a q p b a p b aqp q p q q p q p q p q p +≤+⋅≤=-≤⋅--即所以将.,111qb p a ab q p qp +≤=+得代入（文科）（I ）∵n ≥2时，3S n －4，a n ，2－132n S -总成等差数列， ∴1323422n n n a S S -=-+-13333()222222n n n n n S S S a S -=-+-=+-，即 34n n S a =+， ∴ 1134n n S a ++=+．113n n n a a a ++=-，211-=+n n a a ． ∴a 2，a 3，…a n ，…成等比数列．∵a 1=2 当n =2时，a 2= 1-，∴a 1，a 2，a 3，…a n ，…成等比数列，∴a n =211()2n --．（II ）由（I ）得 34n n n b S a ==+，∴ 12n n T b b b =+++12(4)(4)(4)n a a a =++++++ 4n S n =+．∵ 14214()3323n n n a S -+==-+， ∴ 1214()4323n n T n -=-++．。

2009年山东高考作文题目竞猜活动启事

年山东高考作文题目竞猜活动启事2009距离高考越来越近了，看看谁能猜中山东卷高考作文题目？如果你有好的作文创意，请传至“作文指要”栏目，高考后加以评比。

要求：话题作文、命题作文及新材料作文均可。

要简要评点你拟定的作文题目。

附录范例：、请以“情趣”为话题，写一篇文章。

1，如生活很有情趣；这首，如他和他的学生情趣相投；也可以指“情调趣味”现代汉语词典：情趣，可以指“性情志趣” 诗写得很有情趣。

要求：文体不限，题目自拟，立意自定，不得少于字，不得套作，不得宿构，不得抄袭。

800 ：]写作导引[ 本话题写作领域较为宽泛，可写的方面较广；但要写好该话题，就要做到宽题“窄”写，以小见大。

应该注意以下三点：首先，选择最适合的文体。

虽然本话题要求文体不限，但行文必须注意突出文体特征。

从“情趣”话题的内涵来看，写，成一篇记叙文或者散文当为佳。

对于高中学生来说，应该写出一篇关涉“情趣”的复杂的记叙文或者散文，杜绝“低幼化”才更加符合本话题的立意要求。

无论写成复杂的记叙文，还是写作叙事或抒情散文，都应该运用各种记叙、描写方式凸显“情趣”主旨，或环境描写渲氛围，或细节描绘凸形象，或对话描写彰性格，或心态刻画显深刻，或场面描写揭背景，或正面描写显力度，或侧面刻画变角度；不一而足。

其次，写真事，抒真情，凸显主体色彩。

虽然本话题要求立意自定，但题材的选择必须注意遵循“最熟悉”的原则，即开掘自己的生活资源，叙写一些自己最为熟悉的人与事件。

学生应该围绕着“情趣”话题搜索筛选让自己感动的写作素材，开阔写作思路：或写自己与情趣相投朋友交往的几件有意义的事，或写一些轻松惬意的假日生活片段，或写一些旅游途中的“探“我”的感悟及“我”的思考。

“我”的气息、险”经历，或写一段刻骨铭心的读书生活……行文中要彰显出“我”的色彩、“情趣”；“情趣”话题写成复杂记叙文，最忌讳的是诠释生活，失去生活的“本真”再次，要写出一点值得回味的意味来。

、，成为一盘散沙。

09年高考模拟试题2009年高考模拟试题(新课程)(五)

09年高考模拟试题2009年高考模拟试题(新课程)(五)测试题 2019.91,一、选择题2008年12月26日中午，福州仓山下渡派出所民警在连江南路拓福超市路口执勤时，发现一男子驾驶燃油助动车违规上路。

民警随即上前盘查，并意外地从助动车的后备箱和座位下方，搜出9万余元面值百元的假钞。

警方发现这些假币有多种不同编号，其中以“HD90”开头的有6.98万元。

警方透露，犯罪嫌疑人郑某供称，这些假币是他在福州火车站附近，以每张6.5元的价格从假币贩子手中买来的。

回答1-4题。

1、上述材料中郑某的做法①违背了公民的权利与义务统一的原则②是一般的违法行为③没有把个人利益与国家利益相结合④违背了公民在法律面前一律平等的原则A．①③ B．②④ C．②③ D．①③④2,2、对待郑某的行为，福州警方A．要公正司法，严格审判 B．依法行政，坚决打击C．加强普法宣传，让公民知法、懂法、用法 D．完善法律监督体3,3、HD90编号开头百元假钞由南向北、自东向西，严重地冲击着我国的金融秩序，影响着我国经济发展和居民生活。

这体现了A．联系的绝对性 B．联系的普遍性和客观性C．认识的无限性和反复性 D．意识活动的主动创造性4,4、HD90编号开头百元假钞的蔓延造成的影响可能是：①人民币的实际购买力上升②人民币贬值，物价上涨③人民币汇率不稳定④使周边国家获益增加A．①③ B．②④ C．①④ D．②③5,2008年11月15日，二十国集团领导人金融市场和世界经济峰会在美国华盛顿举行。

按照惯例，国际货币基金组织与世界银行列席该组织的会议。

回答5--6题。

5、二十国集团领导人金融市场和世界经济峰会成功举办的政治学依据是：A.国家性质决定国际关系B.共同利益是各国合作的基础C.经济全球化已经形成D.国际政治旧秩序的存在6、从经济常识角度看，二十国集团领导人金融市场和世界经济峰会成功举办体现了①世界经济国际化、一体化趋势加强②区域集团化趋势加强③和平与发展是当今世界的两大主题④有利于区域经济和世界经济的发展A.①②③B.①②④C.②③④D.①②③④6,2008年9月8日，襄汾县新塔矿业有限公司尾矿库发生特别重大溃坝事故，泄流量26.8万立方米，过泥面积30.2万平方米，波及下游500米左右的矿区办公楼及集贸市场、部分民宅，造成建筑物毁坏、人员伤亡。

2009考年高考校模拟考试试题征集评比通知试

2009年高考校模拟考试试题征集评选通知一、命题学科和试题征集对象高考模拟试题涉及高考中十二个学科，即语文、理科数学、文科数学、英语、理科基础、文科基础、物理、化学、生物、政治、历史、地理。

十二套试题的征集面向本校所有高中教师。

以自愿为原则，任何高中教师都可以向本科组试题评定小组提供试题。

经试题评定小组选定后，该试题方可被录用。

二、征集试题评定小组由学科组长、学术委员会成员、一名高三备课组长组成“征集试题评定小组”。

由学科组长任组长。

文、理科基础学科试题评定小组由高三备课组长（任组长）组成六人小组。

征集试题评定小组负责评定、录用试题，核准获奖试题、获奖教师和奖励金额。

三、试题录用的基本要求：1试题属于原创，不能出现抄袭现象。

2命题的依据是本学科课程标准和2008年广东省高考考试大纲。

题目要紧扣本学科的主干知识与核心概念，在考查基本知识的同时还应考查基本能力和技能。

试题特别应尽可能体现2008年我省高考的命题要求，反映新课程高考的特征。

3试题精巧干练，蕴涵知识、能力的要求较为丰富。

4试题不超出高考大纲，不出现科学性错误。

5、每道试题后附参考答案。

试题录用、组卷时，应在试卷旁注明命题教师和命题时间。

四、征集试题和组卷时间09届试题征集分为两期：即共组织命出两套高考模拟试卷。

1月10日前，各学科征集试题评审小组在教师们提供大量试题的基础上，经过评定、筛选，录用质量较高试题组成“深圳高级中学2009年第一套高考模拟试卷”。

5月21日前，各学科征集试题评审小组在教师们提供大量试题的基础上，经过评审、筛选，录用质量较高试题组成“深圳高级中学2009年第二套高考模拟试卷”。

五、奖励1、试题录用奖励如教师所命试题被试题评定小组选定录用，学校将按该试题的分数乘以10元，给予该教师奖励。

2、市一模后奖励如教师所命试题与“市一模”中的试题有60%以上相同，学校将按该试题的分数乘以30—50元，给予该教师奖励。

3、高考后奖励如教师所命试题与高考试卷中的试题有60%以上相同，学校将按该试题的分数乘以300—500元，给予该教师奖励。

关于开展2009年新课程高考模拟试题征集评选活动的通知

关于开展2009年新课程高考模拟试题征集评选活动的通知为了加强高三教师对2009年高考内容的研究，2009年区教育局继续开展番禺区新课程高考模拟试题征集评选活动，现将活动的有关事宜通知如下：一、活动目的以试题的命制、改编、组合、选择为研究的切入点，促进广大高中教师加强对新课标和新考纲的研究，加强对新课程高考考试内容的研究，提高备考复习内容的针对性，提高命题和组卷水平，从而提高复习效率。

二、征集范围全区高三任课教师，欢迎高二、高一教师参加。

三、征稿要求1、本次活动征集模拟试题欢迎个人或集体踊跃参与,但要求每所高中学校必须对每个高考科目（语文、理数/文数、英语、物理、化学、生物、地理、政治、历史、理基/文基）提供1～2套模拟试题，其中至少有一套是科组集体研究的成果。

即先由科组教师供题，然后集中讨论，提出修改意见，最后定稿，并将定稿试题在本校学生中使用，使用后再作适当修改后形成模拟试题。

2、试题题型、结构、难度，按2009年广东省高考大纲和考试说明的要求。

命题依据各学科课程标准和2009年广东省高考考试大纲和考试说明。

题目要紧扣本学科的主干知识与核心概念，在考查基本知识的同时还应考查基本能力和技能。

试题特别应尽可能体现2009年我省高考的命题要求，反映新课程高考的特征。

3、应有一定比例的原创题或改编题，若是改编题，要附上原题和出处；若是现题，要标明出处。

4、每套试题后附详细的参考答案。

5、每套试题后要有一个命题说明。

至少包括如下内容：●每道试题的作者和来龙去脉，是原创、改编还是现题？若是改编题，要附上原题和出处；若是现题，要标明出处。

●每道试题的考查目的。

例如题目考查什么知识点（或考点），侧重考查哪些能力。

这些考点和能力在新课标和07年考纲中是怎样具体要求的，题目是如何体现的，预测在2009年新课程的高考中将会有怎样的地位，变化趋势等。

●试题的预计难度。

例如使用试题进行测试，本校的难度是多少？估计全省的难度是多少？尽量按各学科考试说明规定的难度设计。

全品高考网2009年高考有奖猜题活动

7
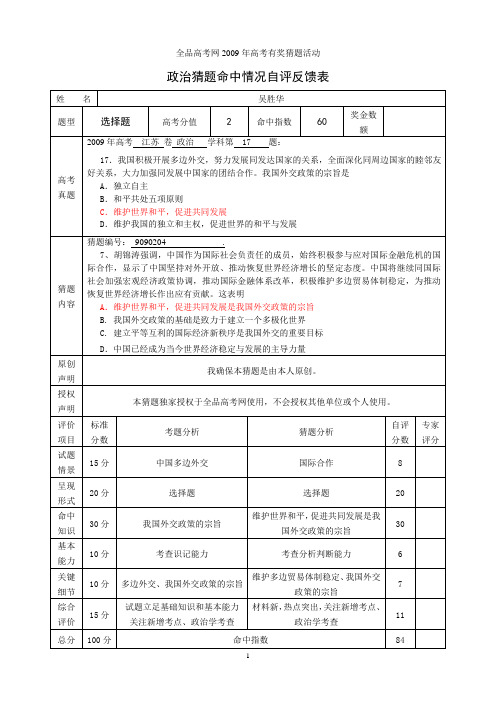
综合评价
15分
试题立足基础知识和基本能力
关注新增考点、政治学考查
材料新，热点突出，关注新增考点、政治学考查
11
总分
100分
命中指数
84
A．维护世界和平，促进共同发展是我国外交政策的宗旨
B.我国外交政策的基础是致力于建立一个多极化世界
C.建立平等互利的国际经济新秩序是我国外交的重要目标
D．中国已经成为当今世界经济稳定与发展的主导力量
原创声明
我确保本猜题是由本人原创。
授权声明
本猜题独家授权于全品高考网使用，不会授权其他单位或个人使用。
B．和平共处五项原则
C．维护世界和平，促进共同发展
D．维护我国的独立和主权，促进世界的和平与发展
猜题内容
猜题编号：9090204 .
7、胡锦涛强调，中国作为国际社会负责任的成员，始终积极参与应对国际金融危机的国际合作，显示了中国坚持对外开放、推动恢复世界经济增长的坚定态度。中国将继续同国际社会加强宏观经济政策协调，推动国际金融体系改革，积极维护多边贸易体制稳定，为推动恢复世界经济增长作出应有贡献。这表明
评价
项目
标准分数
考题分析
猜题分析
自评分数
专家评分
试题情景
15分
中国多边外交
国际合作
8
呈现形式
20分
选择题
选择题
20
命中知识
30分
我国外交政策的宗旨
维护世界和平，促进共同发展是我国外交政策的宗旨
30
基本能力
10分
考查识记能力
考查分析判断能力
6
关键细节
10分
多边外交、我国外交政策的宗旨
维护多边贸易体制稳定、我国外交政策的宗旨

09年高考模拟试题2009高考模拟试题(4)

09年高考模拟试题2009高考模拟试题(4) 测试题2019.91,29．材料一：2008年9月10日三鹿奶粉事件发现以来，胡锦涛总书记、温家宝总理等中央领导同志连续作出指示批示，中央政治局常委会和国务院多次召开会议，对事件处置工作进行研究部署，国务院启动了重大食品安全事故（Ｉ级）应急响应。

各地区和有关部门认真贯彻党中央、国务院决策部署，本着对人民群众生命健康高度负责的精神，全力救治患儿，全面清查问题奶粉，深入调查事件原因和责任，并及时向社会公开发布了信息。

材料二：三鹿问题奶粉事件发生后，根据《食品卫生法》的规定，国家标准委正在加紧组织制订食品中三聚氰胺检测方法国家标准，改进食品检测手段，确保新产品的质量合格。

材料三：有关专家建议：“在现有国情下，我国食品标准体系和检验手段绝不能仅仅满足与国际接轨，必须在此基础上根据我们国情和食品安全监管实践进一步改善食品标准体系、改进食品检测手段，才能有效防范重大食品安全事件的发生。

”回答（1）结合材料一说明党中央和国务院对三鹿奶粉事件处置工作进行研究部署体现了哪些政治学道理？（4分）（2）结合三鹿奶粉事件，运用商品的有关知识谈谈企业为什么要注重产品质量？（6分）（3）结合材料三从唯物论角度说明有关专家建议的哲学依据是什么？（4分）2,一.单项选择题：1.党的"十七大"报告中指出：要繁荣发展哲学社会科学，推进学科体系、学术观点、科研方法创新，鼓励哲学社会科学界为党和人民事业发挥思想库的作用，推动我国哲学社会科学优秀成果和优秀人才走向世界。

这是因为①哲学是世界观和方法论的统一②真正的哲学可以指导人们正确地认识世界和改造世界③真正的哲学是"科学之科学" ④真正的哲学能推动时代前进的步伐，指导社会变革A.①②B.②④C.②③④D.①②③④3,2.右图漫画中公鸡的观点与下列选项中哪种说法的哲学思想一致A.人不能两次踏入同一条河流B.谋事在人、成事在天C.存在就是被感知D.天不变道亦不变4, "人生易老天难老，岁岁重阳，今又重阳，战地黄花分外香。

2015年第九届全品高考猜题公告

第九届(2015)全品高考网有奖猜题活动启动公告全品高考网高考猜题活动历经八个春秋，得到了广大高中教师的积极响应和支持，其最终作品《最有可能考的50（20）题》不但成为全品高考网的金牌产品，更成为高考猜题行业中的领导品牌。

随着2015年高考的临近，第九届（2015）全品高考网有奖猜题活动于2015年1月6日正式拉开序幕，奖励更多，奖金更高，到位更快，欢迎大家踊跃参与！一、参与对象全国各地高中各学科教师、省市县教研机构教研员以及其他高考命题研究人员。

二、猜题依据本次猜题以《2015年普通高等学校招生全国统一考试大纲》和各自主命题省份颁布的《考试说明》（新课标）为唯一依据，题型参照《考试大纲》（或《考试说明》）中的“题型示例”。

三、征稿时间2015年1月6日—2015年5月15日。

四、具体要求1. 猜题以“道”为单位高考猜题一律以“道”为单位，不要完整的套题，但同一作者可以猜多道题，猜题的题型、题量和所赋分值与高考试卷保持一致。

2。

上传路径点击上传/UserUpload_caiti.aspx“高考猜题”栏目下的子目录为新课标版，每道题必须传至全品高考网所属学科“高考猜题”栏目相应子目录下，如果上传的猜题内容在本学科子目录中未涉及到，请传至“综合资源”子目录下。

英语、语文猜题只猜写作题，其他类型试题不列入本届猜题和评奖范围。

3．试题要求（1）必须为全新原创，非原创试题一票否决所有参赛稿件不符合“全新原创要求”的按非参赛稿件处理，不符合“稿件格式要求”的按非参赛稿件处理。

凡是参赛稿件一律视为作者同意全品高考网拥有独家著作使用权。

一稿多投一经核实即取消参赛资格。

同一作者可以投多份内容不同的稿件。

2014年7月1日以前在本网站或其他网站发布的原创试题不得参与本届大赛，一经核实即取消参赛资格。

（2）试题背景材料的设计应以2015年最新的社会生活为载体，高度关注主流媒体出现的高频关键词和社会各界广泛关注的重大事件，突出鲜活的时代气息。

湖北高考最后猜题押题卷六

湖北省2009届高考最后猜题、押题卷㈥语文命题、审题：黄冈中学高三语文备课组孙淑莲2009．5本试卷共150分，考试用时150分钟。

注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

非选择题用黑色墨水的签字笔或钢笔直接答在答题卡上。

答在试题卷上无效。

3．考试结束，监考人员将本试题和答题卡一并收回。

第Ⅰ卷（选择题部分，共36分）一、基础知识部分（本大题共5题，每小题3分，共15分）在每小题给出的四个备选项中只有一项是符合题目要求的，请将其选出。

未选、错选或多选均不得分。

1．下列各组加点字的读音正确的一组是A．峥嵘（zhēng）蛩音（qióng）鲫鱼（jí）央浼（měi）B．青荇（xìng）竹篙（gāo）分娩（wǎn）夹带（jiā）C．漫溯（sù）倾圮（pǐ）伛偻（yǔlǚ）太监（jiàn）D．发酵（jiào）踟蹰（zhízhú）似的（shì）搽粉（chá）2．下列各句中没有错别字的一句是A．沟通协奏曲批沙拣金颠扑不破B．陷阱必须品欲盖弥彰滔滔不绝C．荟萃哈蜜瓜集腋成裘茹毛饮血D．记账豆腐渣杀一儆百蓦然回首3．下列各句中，加点的成语使用不恰当的一句是A．在宁夏银川贺兰山东麓，有两座苍凉而雄壮的城堡，这就是镇北堡，在这里你可以闻到“十八里红酒”的香味，也可以听到荡气回肠．．．．、率真可爱的“颠轿歌”。

B．自去年7月次贷危机爆发以来，美国已采取了多种措施，以避免经济陷入衰退，然而这些举措的效果大多如昙花一现．．．．，股市往往是小幅上扬，随即再度低迷。

C．中央电视台“同一首歌”栏目组来到了山东莱芜，在晚会上，当年参加抗日战争的老英雄们又一次听到了那些耳熟能详．．．．的抗战歌曲。

2009年高考猜题讲解(数学)重点

2009年高考猜题讲解（数学）选择题部分一、选择题常考考点⒈ 设全集为R ,集合{|||2}M x x =>，1{|0}1x N x x-=≥+，则有A ．R C M N N ⋂=B ．}11|{≤≤-=⋂x x N M C.}2112|{<<-<<-=⋂x x x N M 或 D ．}11|{≤<-=⋂x x M NC R 【标准答案】A解答：{}{|22},11,{|22},.或R R M x x x N x x C M x x C M N N =<->=-<≤∴=-≤≤∴⋂= 2．若R,1xx x ∈+那么是正数的充要条件是（） A ．0>x B ．1-<x C ．01<<-xD ．10-<>x x 或【标准答案】D 解答：0(1)00 1.1xx x x x x >⇔+>⇔><-+或 3．在等差数列｛a n ｝中，已知a 1=2,a 2+a 3=13，则a 4+a 5+a 6等于（） A ．40B ．42C ．43D ．45【标准答案】B在等差数列{}n a 中，已知1232,13,a a a =+=得d=3，a 5=14，456a a a ++=3a 5=42.4．若A 、B 、C 为三个集合，C B B A ⋂=⋃，则一定有（）A ．C A ⊆B ．AC ⊆ C ．C A ≠D ．φ=A 【标准答案】A解答：因为A A B C B C ⊆⊆且，A B C B =由题意得A C ⊆所以选A 5．定义运算()()x x y xy y x y ⎧=⎨⎩≥＜，则函数()(sin )(cos )f x x x =的值域为（）A ．11[,]22-B ．[1,1]-C ．[D ．[- 【标准答案】C解答：在同一坐标系中作出)(x f =⎩⎨⎧x x cos sin x x x x cos sin cos sin <≥图，知选C. 6．已知函数)(1x fy -=的图象过点)0,1(，则(21)y f x =-的反函数的图象一定过点（） A 1)2 B 1,1)2 C 1)2D 1(,0)2【标准答案】A.解答：依题意知函数()y f x =的图象过点(0,1),由210x -=得1,2x =则函数(21)y f x =-的图象过点1(,1)2,故函数(21)y f x =-的反函数图象过点(1,12).7．函数x x f ωsin )(=+)6cos(πω+x 的图象相邻两条对称轴间的距离是32π，则ω的一个值是（）A ．32B ．34C ．23 D ．43 【标准答案】C解答：由已知.23,342,34),3sin()(=∴=∴=+=ωπωπππωT x x f8．m 、R n ∈，、、是共起点的向量，、不共线，n m +=，则、、的终点共线的充分必要条件是（）A ．1-=+n mB ．0=+n mC ．1=-n mD ．1=+n m【标准答案】D ．解答：设、、的终点分别为A 、B 、C ，而A 、B 、C 三点共线的充要条件是存在非零常数λ，使得AB BCλ=，即()(1b a c b b a n b m aλλλ-=-⇔-=-+，于是有(1) 1.n m n m λλ-=-⇒+=9．定义在（-∞，0）⋃（0，+∞）上的奇函数f x ()，在（0，+∞）上为增函数，当x>0时，f x ()图像如图所示，则不等式x f x f x [()()]--<0的解集为（） A ．()()-⋃3003，， C ．()()-∞-⋃+∞，，33 B ．()()-∞-⋃，，303 D ．()()-⋃+∞303，，【标准答案】A解答：因为)]()([x f x f x --,0<所以x ·f （x ）0<，即⎩⎨⎧<>0)(0x f x 或,0)(0⎩⎨⎧><x f x 由图知－30<<x 或0.3<<x10 已知 {}()(){}032:;4:>--<-=x x x q a x x A p ，且非p 是非q 的充分条件，则a 的取值范围为（）A. -1<a<6B. 61≤≤-aC. 61>-<a a 或D. 61≥-≤a a 或【标准答案】 B解法1特殊值法验证，取a=-1，(][)+∞⋃-∞-=,35,A ,(][)+∞⋃∞-=,32,B ，非p 是非q 的充分条件成立，排除A ，C ；取a=7，(][)+∞⋃∞-=,113,A , (][)+∞⋃∞-=,32,B ，非p 是非q 的充分条件不成立，排除D ，选B ；解法2集合观念认识充分条件化归子集关系构建不等式组求解，解不等式切入，()()61,3424,,3,2,4,4__≤≤-∴⎩⎨⎧≥+≤-∴⊆=+-=a a a B A B a a A ，选B ；解法3用等价命题构建不等式组求解，非p 是非q 的充分条件等价命题为q 是p 的充分条件，集合观念认识充分条件化归子集关系构建不等式组求解，解不等式切入，)3,2(),4,4(=+-=B a a A ，由q 是p 的充分条件知11 计算复数(1－i)2－ii 2124-+等于（）A.0B.2C. 4iD. －4i【标准答案】解法一：(1－i)2－i i 2124-+=－2i －)21)(21()21)(24(i i i i +-++=－2i －54284-++i i=－2i －2i=－4i .解法二：(1－i)2－ii 2124-+=－2i －i ii 21422--=－2i －ii i 21)21(2--=－2i －2i=－4i .故选D.，故61≤≤-a ，选B 。

山东省2009届高三高考猜题语文试题

山东省2009届高三高考猜题语文试题选择题部分一、字音1．下列词语中，加点汉字的读音，有误的两组是（）（3分）①卑鄙（bǐ）麻痹（bì）瓦窑堡（bǔ）咸与维新（yù）②簸箕（bǒ）贿赂（lù）哺乳类（bǔ）奴颜婢膝（bì）③商埠（bù）重创（chuāng）差不多（chà）从容不迫（cóng）④豆豉（chǐ）捧场（chǎng）应届生（yìng）乳臭未干（xiù）A①② B①③ C②③ D②④【答案及解析】选D。

簸箕（bò）应届生（yīng），考查方言误读和多音字误读。

瓦窑堡（bǔ）、咸与维新（yù）、重创（chuāng）差不多（chà）、捧场（chǎng）、瓦窑堡（bǔ）、应届生（yìng）、乳臭未干（xiù）属多音字，读音正确；豆豉（chǐ）、奴颜婢膝（bì）要防止方言干扰。

2．下列词语中，没有错别字且加点字注音正确的一组是A．贷款迫不急待忧心忡忡(zhǒng) 雄赳赳，气昂昂B．掂量叱咤风云(zhà) 长年累月言必信，行必果C．媲美(bì) 以德报怨殚精竭虑钉是钉，铆是铆D．耗废因噎废食(yī) 偃旗息鼓胜不骄，败不馁【答案及解析】选B。

A项错误的应改为：迫不及待、忡(chōng)，C项错误的应改为：媲(pì)、丁是丁，卯是卯，钉是钉铆是铆也对D项错误的应改为：耗费，噎(yē)3．下列词语中加点的字，每对的读音全不相同的一组是A. 垃圾/汲水惩罚/驰骋着火/不着边际B. 粘连/占星簇拥/箭镞薜荔/穷乡僻壤C. 道行/行头范蠡/妯娌擂台/危若累卵D. 框架/诓骗杂烩/教诲打颤/颤颤巍巍【答案及解析】A.垃圾（jī）/汲水（jí）惩罚（chéng）/驰骋（chěng）着火（zháo）/不着边际（zhuó）B“粘（zhān）连/占（zhān）星”相同，簇（cù）拥/箭镞（zú），薜（bì）荔/穷乡僻壤（pì）C“范蠡（lǐ）/妯娌（lǐ）”相同，道行（héng）/行（xíng）头，擂台（lèi）/危若累（lěi）卵D“杂烩（huì）/教诲（huì）”相同，框（kuàng）架/诓（kuāng）骗，打颤（zhàn）/颤（chàn）颤巍巍4．下列各组中没有错别字且读音全都正确的一组是A．北京东四奥林匹克社区公园已变成了欢乐的海洋，在飞舞的空竹里，在嗡嗡的旋律中，人们把对北京的热爱，把对2008奥运会的期盼与憧(chōng)憬(jǐng)表达得淋漓尽致。

2009年苏州市高考数学有奖竞猜题(第二稿)

2009年苏州市高考数学有奖竞猜40题（内部资料请勿外传）一、填空题1. 正方体1111ABCD A B C D -的俯视图如图，则其左视图的面积为．（江苏省木渎高级中学吴亭改编）答案：2．提示：正方体的放置如图：则左视图为对角面11AB C D ，所以面积为211122A B B C a a a ⨯=⨯． 2. 三边长分别为6,8,10的直角ABC ∆的斜边BC 的两端点分别在两坐标轴上滑动．记ABC ∆ 的外接圆圆心为M ，某区域D 内的动点P 满足||1PM ≤，则区域D 内的整点（横坐标和纵坐标都是整数的点）个数是_____________．（吴中区苏苑中学杨品方原创）答案：68提示：圆心M 到原点的距离为斜边的一半，即5，则M 点轨迹是圆心在原点半径为5的圆，点P 到点M 的距离不超过1，则P 的活动范围即区域D 是一个圆环，圆心在原点，半径分别为4和6的两个圆所组成的圆环．画出图形，第一象限内，圆环内的整点有14个，分别为(1,4),(1,5),(2,4),(2,5),(3,3),(3,4),(3,5),(4,1),(4,2),(4,3),(4,4),(5,1),(5,2),,3)，对称到其它三个象限，共56个；还有坐标轴上的点，如x 轴正半轴上的点(4,0),(5,0),(6,0)，共12个．所有满足条件的点的个数是68．3. ABC ∆中，A 、B 分别对应复数21,z z ，3221=-z z ，点C 位于以A 、B 为焦点，长轴长是4的椭圆上，且0=⋅，点P 对应的复数为z 且满足1z z -=2z z -，则=⋅AB CP ________．（新区一中吕有杰改编）答案：24±解：由已知得ABC ∆为直角三角形，||||4CA CB +=12=+，2222-=+=或2222+=-=．点P 在线段AB 的垂直平分线（即y 轴）上，设原点为O ，则=⋅AB CP AB CO AB OP CO ⋅=⋅+)(=)()(21-⋅+=)(2122-=24±．4. 已知a 、b 是平面内两个单位向量，若向量c 满足()()0a c b c -⋅-=，则c 的最大值是．（新区一中顾日新改编）解：不妨设(cos ,sin ),(cos ,sin )(02),a OA b OB ααβββαπ====≤≤<(,)c OC x y == 则点C 的轨迹是以线段AB 为直径的圆，其圆心M 的坐标为cos cos sin sin (,),22αβαβ++则原点到圆心的距离：OM = =cos 2αβ-．半径r =sin2αβ-．所以 c ≤OM r +=cossin22αβαβ--+．若0αβπ≤-≤，则c ≤sin()24αβπ-+≤2παβ-=时取“=”，此时a ⊥b ；若2παβπ<-<，则c ≤sin()24αβπ--≤32παβ-=时取“=”，此时a ⊥b ．故c的最大值是 5. 已知函数1)(2+=x ax x f ，x x x g 44cos sin )(-=，若对于任意的R x ∈1，都存在R x ∈2使得)()(12x f x g =，则实数a 的范围为．（吴县中学潘九洲原创）答案：22a -≤≤解：因为]1,1[2cos cos sin )(44-∈-=x x x x g ＝－． 22()[,]1122a a ax xf x a x x ==⋅∈-++，对于任意的R x ∈1，都存在R x ∈2使得)()(12x f x g =，)(x g 的值域包含)(x f 的值域，则22,12≤≤-≤a a ．6. △ABC 内接于以O 为圆心半径为1的圆，且3450OA OB OC ++=，则△ABC 的面积S = ．(苏大附中徐开改编) 答案：65解：如图，34,OA OB OD +=则5OD OC =-．易得OA OB ⊥，且34sin ,sin 55BOC AOC ∠=∠=，所以113146225255ABC OAB OBC OAC S S S S =++=+⋅+⋅=．7. 某同学在计算123n ++++的值时，发现了可用如下的方法：1121222+⨯=-1222322+⨯=- 1323422+⨯=-┅┅12)1(22+⨯=-+n n n将以上各式分别相加得：n n n +++++⨯=-+)321(21)1(22（1）ODCBA即：2)1(321+=++++n n n 他欲类比上述求法，试图求出2222321n ++++ 的值，在类比求解的过程中，（1）式可以类比得到：__________________．（相城实验中学万福昌原创题）答案：332222(1)13(123)3(123)n n n n +-=+++++⨯+++++解： 3322131311-=⨯+⨯+3323232321-=⨯+⨯+ 3324333331-=⨯+⨯+┅┅332(1)331n n n n +-=++（1）式可以类比得到：332222(1)13(123)3(123)n n n n +-=+++++⨯+++++．8. 用电脑浏览网页时，经常会跳出移动着的广告，当鼠标点在广告的区域中时，就会打开广告，如使用的电脑屏幕的大小是15英寸，(电脑屏幕的大小是指屏幕的对角线的长度，其长与宽的比值满足标准黄金分割为16：9；１英寸＝2.54cm )，若广告是10cm ×7.5cm 的矩形，则在浏览网页时，点开广告的概率是______________．(结果保留一位小数)(吴江市高级中学陆颖原创) 答案：0.1解：由题意得电脑屏幕的长：宽=16：9，分别设为16t ，9t )0(>t ，屏幕对角线的长度为15英寸=15×2．54=38．1cm ，所以2221.38)9()16(=+t t 解得1.2≈t ，屏幕长为33.6，宽为18.9，所求的概率是1.09.186.335.710≈⨯⨯=P ．9. 在平面直角坐标系xOy 中，已知曲线C ：)0(22>=p py x 的准线与y 轴交于点A ，以点A 为圆心，焦准距大2为半径做圆，交曲线C 于点B ，若曲线C 与圆A 在点B 处的切线互相垂直，则=p __________． (吴江市高级中学韩保席改编)DCBAC 3D 3A 3B 3B 2A 2D 2C 2C 1D 1A 1B 1答案：2+解：由题意得：圆A 方程为222)2()2(+=++p p y x ，曲线C ：221x p y =，x p y 1'=，设点B （00,y x ），则⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+=+=++00002022020122)2()2(x p x p y py x p py x ，解之得222+=p ．10. 如图1，在等腰直角∆ABC 中，2AC BC ==，点M ，N 分别是AB 、BC 的中点，P 点是∆ABC （包括边界）内任一点，则AN MP ⋅的取值范围是． (吴江市高级中学韩保席原创 )答案：[]3,3-解：如图2所示，建立平面直角坐标系，设(,)P x y ，则0,0,2x y x y ≥≥+≤，由(2,0),(0,2),(1,1),(0,A B MN易求得：(2,1)AN =-，(1,1)MP x y =--，所以21AN MP x y ⋅=-++，令21t x y =-++，即求t 的取值范围．由线性规划知识可知当21y x t =+-过B 时t 最大，当21y x t =+-过A 时t最小．于是[]3,3t ∈-，即[]3,3AN MP ⋅∈-． 11. 如图，正方形ABCD 的边长为1，分别作边B 图1图2DA CD BC AB ,,,上的三等分点1111,,,D C B A ，得正方形1111D C B A ，再分别取11111111,,,A D D C C B B A 上的三等分点2222,,,D C B A ，得正方形2222D C B A ，如此继续下去，得正方形3333D C B A ……，记正方形n n n n D C B A 的面积为n a ，则数列}{n a 的前n 项的和=n S ．（吴江市松陵高级中学金晔改编）答案：])95(1[45n -12. 已知A (-2，0)，B (2，0)，P 是直线x =－1上一动点，则以A 、B 为焦点，且过点P 的双曲线的离心率的取值范围是． (昆山中学薛国清原创) 答案：e ∈[)+∞,2．解：∵ A 、O 关于直线x=-1对称，∴ e =a c =a c22=PA PB -4=POPB -4，∵△POB 中，PO PB -≤OB =2 ，∴e ∈[)+∞,2．13. 古希腊大数学家欧几里得借助下图证明了勾股定理，即在Rt △ABC （∠C =90°）边 AB 、BC 和 AC 之上分别画上三个正方形 ABGF 、BCIH 和 ACDE ，若△ABC 的面积为定值S ，则多边形DEFGHI 的面积的最小值是．(昆山中学薛国清原创) 答案：12S解：∵S △AEF = S △BGH =S △CID =S △ABC ，∴S DEFGHI =4S +a 2+b 2+c 2=4S +2(a 2+b 2)≥4S +4ab =12S14. 双曲线22221x y a b-=的左右焦点分别为12,F F ，P 为左支上一点，M 点在右准线上，且满足1PM FO =,11(),(0)OF OM OP OF OMλλ=+≠，则该双曲线的离心率为．（昆山中学顾美花原创）答案：e ＝2F G H解：由已知条件，四边形1PFOM 为菱形，所以1PF c =，由椭圆的定义知，22PF a c =+，由椭圆的第二定义得，22PF a ce PM c+==，解得e=2（e=-1舍去）． 15. 已知全集{(,)|,}U x y x R y R =∈∈，集合{(,)|cos sin 2cos ,}P x y x y R θθθθ=+=+∈，则集合U C P 所表示的平面区域面积为．（震川高级中学李小峰原创）答案：4π 解答：集合P 中的方程可整理成直线:l (1)cos sin 20x y θθ-+-=，则定点(1,0)到直线l 的距离为定值2，所以直线l 为定圆22(1)4x y -+=的所有切线，如图所示，则集合P 表示圆的外部及边界，所以集合P 的补集为圆的内部(不含边界)，故所求面积为4π．16. 若不等式22log 12xx a x -+≥在1,22x ⎛⎫∈ ⎪⎝⎭上恒成立，则a的取值范围为．（江苏省常熟中学周文英原创）答案：1a ≥．解：不等式即为2log 12xa x x ≥--+在1,22x ⎛⎫∈ ⎪⎝⎭恒成立而函数2log 1()2xf x x x=--+的图像如右图：所以()f x 在1,22x ⎛⎫∈⎪⎝⎭上的最大值为1，所以1a ≥． 17. 已知函数()f x 的定义域是(2,)-+∞，且(4)(2)1f f =-=，()f x '为()f x 的导数，且()y f x '=的图像如图所示，则平面区域00(2)1x y f x y ≥⎧⎪≥⎨⎪+<⎩所围成的面积是____________．（常熟市中学夏国良改编）-2yxO答案：418. 若函数()3213f x x a x =-满足对于任意的[]12,0,1x x ∈都有()()12||1f x f x -≤恒成立，则a 的取值范围是．（常熟市中学夏国良改编）答案：⎡⎢⎣⎦． 19. 已知公差d （d >1）的等差数列{}n a 和公比为q （1q >）的等比数列{}n b ．若集合{}{}{}345345,,,,1,2,3,4,5a a a b b b ⋃=则345345a a a b b b +++++=_____．（常熟市练塘中学朱文军原创）答案：16．20. 已知3()3f x x x =-≤≤，(-1x 1)则满足条件()()0()()0f x f y f x f y +≥⎧⎨-≤⎩的点(,)x y 所形成区域的面积为_______．（常熟市练塘中学朱文军原创）答案：1．21. 已知函数)3||(log )(31+-=x x f 定义域是],[b a ),(z b a ∈，值域是]0,1[-，则满足条件的整数对),(b a 有对．（江苏省苏州市第十中学吴锷原创）答案： 5解：函数()f x 中，令||30x -+>，定义域为[,]a b (,)a b Z ∈，又(0)1,(2)(2)0f f f =--==，∴),(b a 为：（－2，0），（－2，1），（－2，2），（－1，2），（0，2），共有5对． 22. 设n S 为等差数列{}n a 的前n 项和，已知15160,0S S ><，记(12,15)nn nS b n a ==，则使n b 取得最大值的自然数n ＝．（江苏省苏州市第十中学吴锷原创）答案：8解：由15160,0S S ><，可知11515815()1502a a S a +==>，116168916()8()02a a S a a +==+<，∴890,0a a ><，且0d <，∴8a 是最小的正数项，8S 是前n 项和n S 的最大值，以此n n n Sb a =取得最大值时的自然数n ＝8．23. 2009年江苏省学业水平测试规定：考生一门科目得A ，则可加1分，若四门科目均得A ，则可加5分．考生甲、乙参加四门科目考试每门得A 的概率均为21，则考生甲比考生乙多得2分加分的概率为．（江苏省苏州市第十中学王岳原创)答案：13128解：有三种情况： ① 甲得2A ，乙没有A ，422241212121⎪⎭⎫⎝⎛⋅⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=C P ； ② 甲得3A ，乙得1A ，3141334221212121⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=C C P ； ③ 甲得4A ，乙得3A ，131443212121⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛=C P ；则甲比考生乙多得2分加分的概率为.12813321=++=P P P P 24. 已知函数()f x 和()g x 的定义域都是实数集R ，()f x 是奇函数，()g x 是偶函数，且当0x <时，'()()()'()0f x g x f x g x +>，0)1(=-f ，则不等式()()0f x g x >的解集是（江苏省苏州市第十中学徐青改编) 答案：),1()0,1(+∞- 25. 已知数列：2233344441213214321,,,,,,,,,,1121231234依它的前10项规律，此数列第2009项2009a ＝________．(张家港市暨阳高级中学罗建宇原创)答案：6385626. 已知ABC ∆中，,,A B C ∠∠∠的对边分别为,,a b c ，三角形的重心为G ，若有2aGA bGB cGC ++=0，则A ∠＝______． (张家港市暨阳高级中学罗建宇原创) 答案：4π简析：2a b c ==27. 已知圆4)3(:22=+-y x C 上两点B A ,,若)(23为原点O CO CA CB -=，这=AB ________（苏州三中雷虎珍改编题）答案：3152 28. 设函数)(,13)(3R x x x x f ∈++=，若20πθ≤≤时，不等式2)1()s i n (>-+m f m f θ，则实数m 的取值范围是．（张家港外国语学校戈永石改编）答案：1<m解：设1)()(-=x f x g ，则)(x g 为R 上的奇函数，且恒单调递增，则原不等式可化为0)1()sin (>-+m g m g θ，即：)1()sin (->m g m g θ，所以1)sin 1(<-θm 恒成立，当2πθ=时，R m ∈，当20πθ<≤时，θsin 11-<m 恒成立．所以min )sin 11(θ-<m ，而1)sin 11(min =-θ，所以1<m ． 29. 一束光线从平面直角坐标系中的(1,0)点沿与x 轴垂直的方向发出，经过直线(1)()n y x n n N =+-⋅∈反射后在这些直线上分别得到一系列的投射点，设这些点的坐标为(,)n n a b ，则当这束光线经过第20次反射后，得到的投射点的坐标是__ ．（江苏省苏州市第十中学朱嘉隽改编）答案：（191，172）解：{}2121n n a a +--是以1为首项，4为公差的等差数列．30. 设函数()|cos ||cos 2|f x x x =+，若[0,]2x π∀∈，不等式()f x ≥124a a+，恒成立，则正数a 的取值集合为___________．（苏州市田家炳中学秦月新）答案： 2⎪⎪⎩⎭ 二、解答题31. 设函数()22sin cos 63f x x x ππ⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭ ，x R ∈．（1）求()f x 的最小正周期和单调递增区间；（2）设A 为锐角三角形ABC 的一个内角，()5750f A =，BC =2，求△ABC 面积的最大值．（吴中区苏苑中学艾建生改编）解：()2211cos cos 22f x x x x x ⎫⎛⎫=-++⎪ ⎪⎪ ⎪⎝⎭⎝⎭=2231sin cos 22x x +=1cos 212x -+．（1）()f x 的最小正周期22T ππ==，()f x 的单调递增区间：,2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦；（2）()157cos 21250f A A =-+=，7cos 225A =-，02A π<<， 43sin ,cos 55A A ∴==．又2226442cos 255BC b c bc A bc bc bc ==+-≥-=，5bc ∴≤（当且仅当b =c 时取等号）．12sin 225S bc A bc ∴==≤．故△ABC 面积的最大值为2．32. 已知函数1()||(,)nm i i f x x x i m N +==∑-∈，211()()2n g x x x d -=---，{}(1,2,i x i =…)n 是公差为0d >的等差数列．（1）设0,0a b ≥≥，比较222a b +与2()2a b +，以及332a b +与3()2a b +的大小，并依据合情推理给出一个一般性的结论（不必证明）．（2）问是否存在实数M ，使方程()()f x g x M =+存在唯一的实数根0x ，若存在求出M 和0x 的值，若不存在说明理由．（吴中区苏苑中学张国棣原创）解：（1）易得222a b +≥2()2a b +，332a b +≥3()2a b +．一般性的结论2m m a b +≥()2ma b +（0.0,a b m N *≥≥∈）当且仅当a b =时取“=”．（可用数学归纳法证明，略）（2）当n 为奇数时，设21()n k k N +=-∈，∵(,0,)22nn n a b a b a b n N +++⎛⎫≥>∈ ⎪⎝⎭，且a b =时取“=” ，∴121121||||||||22mm m k k x x x x x x x x ---+-⎛⎫-+-≥ ⎪⎝⎭，当且仅当1212k x x x -+=取“=”号．又121211||||2(1)k k x x x x x x k d ---+-≥-=-，当且仅当121[,]k x x x -∈时取“=”号，且121121[,]2k k x x x x --+∈． ∴()121||||21mmmmk x x x x dk --+-≥-，当1212k x x x -+=时取“=”号．同理： ()222||||22m m m mk x x x x d k --+-≥-，当222=2k x x x -+时取“=”号．……11||||2m m m k k x x x x d -+-+-≥，当112k k x x x -++=时取“=”号．又∵||0k x x -≥，当k x x =时取“=”号，且12122222k k x x x x --++== (112)k k k x xx -++== ∴当112k n x x x d -==+时，()f x 有最小值2[12m m m d ++…(1)]m k +-．当n 为偶数时，设2n k =，1212||||||||22mmm kk x x x x x x x x -+-⎛⎫-+-≥⎪⎝⎭，当且仅当122kx x x +=取“=”号．又1221||||(21)k k x x x x x x k d -+-≥-=-，当且仅当12[,]k x x x ∈时取“=”号，且1212[,]2kk x x x x +∈． ∴1221||||22mm m m k k x x x x d -⎛⎫-+-≥ ⎪⎝⎭，当122k x x x +=时取“=”号．同理：22123||||22mmmmk k x x x x d --⎛⎫-+-≥ ⎪⎝⎭，当2212k x x x -+=时取“=”号． ……11||||2()2m m m m k k x x x x d +-+-≥，当12kk x x x ++=时取“=”号．又∵1222122k k x x x x -++==…11(21)22k k x x k d x ++-==+， ∴当1121122k n x x d x d --=+=+时，()f x 有最小值132[22m m m d ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭…21]2mk -⎛⎫+ ⎪⎝⎭．又211()()2n g x x x d -=---，∴当112n x x d -=+时，()g x 有最大值0，∴若使方程()()f x g x M =+存在唯一的实数根0x ，则M 为()f x 的最小值． ∴当n 为奇数时，2[12mmmM d =++…1()]2m n -+，0112n x x d -=+；当n 为偶数时，M =132[22m m md ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭…1]2mn -⎛⎫+ ⎪⎝⎭，0112n x x d -=+． 33. 已知S n 是数列}{n a 的前n 项和，且.2),2(211=≥+=-a n S a n n 数列{}n b 满足1n n a b +=．（1）求数列}{n a 和{}n b 的通项公式；（2）设圆222:()()n n n n C x a y b r -+-=，若圆n C 与圆1n C +外切，{}n r 是各项都是正数的等比数列，设n T n 是前个圆的面积之和，求n T ．（江苏省木渎高级中学吴亭改编）解：（1）由已知21+=-n n S a ①得 21+=+n n S a ②②－①，得 )2(11≥-=--+n S S a a n n n n ∴2)2(211=≥=+a n a a n n 又∴112242a a a ==+=，∴)3,2,1(21 ==+n a a n n ∴数列 }{n a 是一个以2为首项，2为公比的等比数列∴n n n a 2221=⋅=-，则12n n b =-．（2）由题意：222111()()()n n n n n n r r a a b b ++++=-+-1212(22)(1212)n n n n ++=-+--+2222222n n n =+=⨯．∴12n n n r r ++，则1212n n n r r ++++=，∴{}n r 的公比2q =．由1211123r r r r r +=+==13r =． ∴2222242(1)121()(1)n n n T r r r r q q q ππ-=+++=++++8148(41)91427n n ππ--=⨯⨯=-．34. 已知点)(),,(+∈N n y n B n n 是某直线l 上的点，以n B 为圆心作圆．所作的圆与x 轴交于n A 和1n A +两点，记n A 、1n A +的横坐标分别为n x 、1n x +．其中1(01)x a a =<≤ （1）证明n n x x -+2是常数，并求数列}{n x 的通项公式；（2）若l 的方程为)(,121411++∈∆+=N n A B A x y n n n 试问在中是否存在直角三角形，若存在，求出a 的值；若不存在，请说明理由．(新区一中盛邦南改编)解：（1）因),(1n n n n n y n B A B A 构成以+∆这顶点的等腰三角形，)(2,211+++∈=+=+∴N n n x x n x x n n n n 即（1）从而122(1) (2)n n x x n +++=+由（2）—（1）得，.,22为常数=-+n n x x显然 ,,,,,,,,264212531n n x x x x x x x x 及-分别成等差数列．,1)12(2)1(112-+-=⨯-+=∴-a n n x x n)(22)1()2(2)1(112+-∈-=⨯-+-=⨯-+=N n a n n a n x x n⎩⎨⎧--+=∴为偶数为奇偶数n n n a n x n ,1,1（2）当n 为奇数时，)0,1(),0,1(1a n A a n A n n -+-++，)1(2||1a A A n n -=∴+ 当n 为偶数时，1(,0),(,0)n n A n a A n a +-+，a A A n n 2||1=∴+．作x C B n n ⊥轴于,),(,上在直线由于点l y n B C n n n.12141||,12141+=+=∴n C B n y n n n 即要使|,|2||11n n n n n n n C B A A A B A =∆++为直角三角形当且仅当,31112)12141(2)1(2,n a n a n -=+=-∴即有为奇数时当（※）当5,61,3,32,1≥====n a n a n 当时当时时，方程（※）无解．当n 为偶数时，有127,1312=+=a n a 同时求得．综上所述，当1276132===a a a 或或时，存在直角三角形．35. 如图所示,已知圆22:(1)4E x y +-=交x 轴分别于A ,B 两点, 交y 轴的负半轴于点M ,过点M 作圆E 的弦MN ．（1）若弦MN 所在直线的斜率为2,求弦MN 的长；（2）若弦MN 的中点恰好落在x 轴上,求弦MN 所在直线的方程；（3）设弦MN 上一点P (不含端点)满足,,PA PO PB 成等比数列(其中O 为坐标原点),试探求PA PB ⋅的取值范围．（苏州外国语学校张锦成原创）解：（1）在圆E 的方程中令x =0,得M (0,－1),又2MN K =,所以弦MN 所在直线的方程为12y x +=,即210x y --=．∵圆心到直线MN的距离为d =且2r =,∴MN ==．（2）因为0M N y y +=,所以1N y =,代入圆E 的方程中得(2,1)N ±．由M (0,－1), (2,1)N ±得直线MN 的方程为10x y --=或10x y ++=．易得(A B ,设(,)P x y ,则由2PA PB PO ⋅=,22x y =+, 化简得2232x y =+① 由题意知点P 在圆E 内,所以22(1)4x y +-<,结合①,得24430y y --<,解得1322y -<<．从而PA PB ⋅=2223332,322x y y ⎡⎫+-=-∈-⎪⎢⎣⎭．36. 设椭圆)22(18:222>=+a y ax M 焦点坐标为F 1（-c ,0）, F 2（c ,0）,点Q 是椭圆短轴上的顶点，且满足122c QF QF +=．（1）求椭圆M 的方程；（2）设A ,B 是圆与()12:22=-+y x N 与y 轴的交点，P 是椭圆M 上的任一点，求PA PB ⋅的最大值．（3）设P 0是椭圆M 上的一个顶点，EF 为圆()12:22=-+y x N 的任一条直径，求证00P E P F ⋅为定值． (园区二中耿道永原创)解:（1）122c QO=c QF QF +=⇒⇒故a 2=8+8=16,故椭圆方程为：221168x y +=．（2）令x =0,得y =3或y =1．故A （0，3）,B （0，1）．设P （x ,y ）,则PA PB ⋅=（-x ,3-y ）·(-x ,1-y )=x 2+(3-y )(1-y )= x 2+y 2-4y +3．又221168x y +=，故x 2=16-2 y 2．所以PA PB ⋅=16-2 y 2+y 2-4y +3=-2（y +1）2+21．又y ≤y =-1时，PA PB ⋅取最大值21．（3）方法一：()()0000P E P F NE NP NF NP ⋅=-⋅-()()()22200001NF NP NF NP NP NF NP =--⋅-=--=-．故00P E P F ⋅为定值．方法二：设P （x 0,y 0）, E （x 1,y 1）,F （x 2,y 2）,∵N （0，2）,EF 为直径，∴x 1 +x 2=0,y 1+y 2=4，0010102020(,)(,)P E P F x x y y x x y y ⋅=--⋅--=x 1x 2-(x 1+x 2)x +x 02+y 1y 2-(y 1+y 2)y 0+y 02= x 1x 2+y 1y 2+x 02 +y 02-4y 0．设A 是（2）中圆与y 轴的交点，即A （0，3），则AE AF ⋅=0，即（x 1,y 1-3）·（x 2,y 2-3）=0,即x 1x 2+y 1y 2-3(y 1+y 2)+9=0,x 1x 2+y 1y 2=3．故00P E P F ⋅= x 02 +y 02-4y 0+3为定值． 37. 设函数2()t a n 4t a n 3f x x xππ=-在[)1,n n -内的所有零点之和为*()n a n N ∈．(1)求1a 、2a 的值，并求数列{}n a 的通项公式； (2)设数列{}n b 满足条件：112,n n b b b a +=≥，求证：当2n ≥时，231112222n b b b +++≤--- （苏大附中葛桂华改编）解：令2()t a n 4t a n30f x x x ππ=-+=得tan 3x π=或tan x π=，故6x k πππ=+或()3x k k Z πππ=+∈（1）当1n =时，[)0,1x ∈，则[)0,x ππ∈，∴6x ππ=或3x ππ=，得16x =或13x =，故1111632a =+=；当2n =时，[)1,2x ∈，则[),2x πππ∈，∴76x ππ=或43x ππ=，得76x =或43x =，故1745632a =+=；当[)1,x n n ∈-时，[)(1),x n n πππ∈-，∴(1)6x n πππ=+-或(1)3x n πππ=+-，得1(1)6x n =+-或1(1)3x n =+-，故113(1)2632n a n n n =+-++=-．（2）由（1）得1322n n b n b a b +≥=-∴211133332()2()2()2222n n n n b b b b +--≥-≥-≥≥- ∵12b =，∴11322n n b -+-≥，即11322n n b -+≥+由题意知n b 是正整数，故122(2)n n b n -≥+≥，∴当2n ≥时，1220n n b --≥>故2223111111122222222n n n b b b --+++≤+++=-≤---．38. 已知：())1,0(ln 2212<>+-=a x x x ax x f 在区间)31,0(上是增函数，求函数()x f 的减区间．（吴江市青云中学陈敬国原创）解：()xx ax xax x f 12122/+-=+-=)1,0(<>a x因为：())1,0(ln 2212<>+-=a x x x ax x f 在区间)31,0(上是增函数所以()012122/≥+-=+-=x x ax xax x f 在区间)31,0(上恒成立，因为0>x所以0122≥+-x ax 恒成立．即212x x a -≥在区间)31,0(上恒成立．令()212xx x g -=，则()()()2/43221221x x x x g x x x --⋅-==，因为)31,0(∈x 所以()0/>x g 恒成立，所以()max 133g x g ⎛⎫==- ⎪⎝⎭，所以13<≤-a ．（1）当0=a 时，()x x xx f1212/+-=+-=此时函数()x f 的减区间为),21(+∞．（2）当01a <<时，044>-=∆a ，此时函数()x f 的减区间为)11,11(aaa a -+--．当03<≤-a 时，044>-=∆a ，此时函数()x f 的减区间为,)+∞．39. 过点2(,)(*,)2n t P t n N t R n∈∈作⊙C ：()()12222=-++y x 的两条切线n n n n B P A P ,，n A ，n B 分别为切点，n n n B A P ∆的外接圆⊙M被y 轴截得的弦记为n n F E ，n n F E 的最小值为n a ．（1）求数列{}n a 的通项公式；（2）求证：2143ni ii E F i =>+∑（吴江市青云中学陈敬国原创）解：（1）由平面几何知识可知：的n CA ⊥n n A P ，n CB ⊥n n B P ，n n n B A P ∆的外接圆也就是四边形n n n B A CP 的外接圆，所以线段n CP 就是⊙M 的直径，设2,2n t P t n ⎛⎫⎪⎝⎭，∵()2,2-C ，∴⊙M 的方程为： ()()()22202t x x y y t n ⎛⎫+-+--= ⎪⎝⎭ ，令0=x 时，得y 的方程为：()22220t y t y t n-++-=．∴12n n E F y y =-==当42442nt n n n-=-=++⋅时，n n E F 取得最小，且n n E F 的最小值为44+n ，即44+=n a n ．（2）因为221633(3)(4)i i n E F a i i i i ≥=++++，则213ni ii E F i =≥+∑1161116()4(3)(4)44ni i i n ==->+++∑．40. 如图，椭圆22221y x a b+=(a >b >0)的左、右焦点分别为F 1、F 2，M 、N 是椭圆右准线上的两个动点，且120F M F N ⋅=．（1）求证∠MON 为锐角；（2）设椭圆的离心率为12，MN的最小值为椭圆方程．（常熟市练塘中学朱文军原创）解：（1）设椭圆22221yx a b+=的焦距为2c (c >0)，则其右准线方程为x ＝2a c，且F 1(－c , 0), F 2(c , 0)．设M ()()2212,,a a y N y c c ，，则1F M ＝()()22122,,a a c y F N c y c c +=-，，()()2212,,a a OM y ON y c c ==，．因为120F M F N ⋅=，所以()()22120a a c c y y c c +-+=，即()22212a y y c c+=．于是()222120a OM ON y y c c⋅=+=>，故∠MON 为锐角．（2）因为椭圆的离心率为12，所以a =2c ，于是M ()()124,4,c y N c y ，，且()22221215.ay y c c c=-=-MN 2＝(y 1－y 2)2＝y 12+y 22－2y 1y 22221212122460y y y y y y c =++=≥．当且仅当 y 1＝－y 2或y 2＝－y 1时取“=”号，所以(MN )min = 215c ＝215，于是c =1, 从而a ＝2，b ＝3，故所求的椭圆方程是22143y x +=． 41. 已知函数)(21)(xax x f +=是在()∞+，1上的增函数，函数ax x x g -=ln )(是在()∞+，1上的减函数．（1）求实数a 的值；（2）求证：对任意的[]m x ，11∈ ()1>m ，总存在[]m x ，12∈使得0)()(12=+x f x g ．（江苏省沙溪高级中学建新改编）解：（1）0)(21)('2≥+=xax x f 在()∞+，1上恒成立，即2x a ≤在()∞+，1上恒成立 ∵12≥x ∴1≤a ，又01)('≤-=a x x g 在()∞+，1上恒成立，即xa 1≥在()∞+，1上恒成立∴1≥a ∴1=a（2）要证原命题成立，即证)(x f -的值域A 是)(x g 的值域B 的子集)1(21)(x x x f +-=-在[]m ,1上是减函数 ∴⎥⎦⎤⎢⎣⎡-+-=1),1(21m m A∵x x x g -=ln )( 在[]m ,1上为减函数 ∴[]1,ln --=m m B要使B A ⊆ 即证m m mm -≥+-ln )1(21 )1(>m ----* 即证0ln 2)1(≥-+m mm 令m m m m h ln 2)1()(-+=则由2221221'()10m m h m m m m --=--== 得1m =+，且)(m h 在(1,1+上为间减函数，在(1)++∞上为增函数,∴()(12ln(12ln 0h m h e >=+>> ． ∴ *式成立 ∴原命题成立． 42. 设点C 为曲线)0(2>=x xy 上任一点，以点C 为圆心的圆与x 轴交于点A E 、，与轴交于点E 、B ．（1）证明：多边形EACB 的面积是定值，并求这个定值；（2）设直线42+-=x y 与圆C 交于点N M ,，若||||EN EM =，求圆C 的方程．（江苏省苏州市第十中学吴锷原创）解: （1）点)0)(2,(>t tt C ,因为以点C 为圆心的圆与x 轴交于点A E 、，与y 轴交于点E 、B ．所以,点E 是直角坐标系原点,即)0,0(E ．于是圆C 的方程是22224)2()(tt t y t x +=-+-．则)4,0(),0,2(t B t A ．由CE CA CB ==知,圆心C 在AEB Rt ∆斜边AB 上,于是多边形EACB 为AEB Rt ∆,其面积1142422S EA EB t t=⋅=⋅⋅=．所以多边形EACB 的面积是定值，这个定值是4．(2) 若||||EN EM =,则E 在MN 的垂直平分线上,即EC 是MN 的垂直平分线，222EC t k t t==,2MN k =-．所以由1EC MN k k ⋅=-得2=t , 所以圆C 的方程是22(2)(1)5x y -+-=．43. 已知()()0,3,0,3C B -，动点A 与B ，C 两点的距离之和为10，过点A 作线段BC 的垂线,垂足为D ,设AD y =，AB x =．（1）求)(x f y =的函数表达式及函数的定义域；（2）设43d x y =+，试求d 的取值范围．（江苏省苏州市第十中学王岳原创)解:（1）由椭圆的定义知,动点A 的轨迹是以B ，C 为焦点,长轴长为10的椭圆,点A 的轨迹方程为2212516x y +=．设()00,A x y ,则220012516x y += 又 0||y AD y ==,…………①0355xx AB ==+()0553x x ∴=-,……………② 代入椭圆方程得: 22(5)1916x y -+=,由0y >,()y f x ∴==．()[]0555,5,283x x x =-∈-∴≤≤．∴)(x f y =的定义域为[2,8]．（2）434d x y x =+=+ []28,53,3,x x ≤≤∴-∈-令[]53cos ,0,x ααπ-=∈,则()453cos 12sin 12cos 12sin 20204d πααααα⎛⎫=++=++=++ ⎪⎝⎭,[]50,,,,sin 4444ππππαπαα⎤⎡⎤⎛⎫∈∴+∈∴+∈⎥ ⎪⎢⎥⎣⎦⎝⎭⎣⎦, 32,220d ⎡⎤∈⎣⎦．说明:本题第（2）小问也可以利用导数求解． 44. 如果无穷数列{}n a 对于*n N ∀∈，都有11111nk k k n na a a a =++=∑，求证{}n a 为等差数列．（苏州市第一中学倪红改编) 解:11111nk k k n n a a a a =++=∑，111121112111111n nk k n n k k k k n n n na a a a a a a a a a +==+++++++∴=-=-∑∑，即：12121111n n n n n na a a a a a +++++=-，121(1)n n n a na a ++∴+-=，231(2)(1)n n n a n a a ++∴+-+=，1223(1)(2)(1)n n n n n a na n a n a ++++∴+-=+-+， 132(1)()2(1)n n n n a a n a +++∴++=+1223n n n n a a a a ++++∴-=-， 121(2,*)n n n n a a a a n n N +++∴-=-≥∈;又由11111223131112nk k k n na a a a a a a a a a =++=⇒+=∑，2132a a a a ∴-=-， 121(*)n n n n a a a a n N +++∴-=-∈，∴{}n a 为等差数列．45. 已知2,3ABC AB BC AC ∆===中，．（１）求AB AC ⋅的值；（２）设点O ABC AO p AB q AC ∆=+是的外心，当时，求实数,p q 的值．（张家港高级中学赵松原创）解：（1）413221094cos =⨯⨯-+=A 1234AB AC ∴⋅=⨯⨯（2）过O 作AC OF ⊥于F ，AB OE ⊥于EO 为ABC ∆外心 ∴E F ,分别为AB AC ,中点12EO AO AE p AB q AC ⎛⎫∴=-=-+ ⎪⎝⎭，12FO AO AF p AB q AC ⎛⎫=-=+- ⎪⎝⎭，又由0OE AB ⋅=且0OF AC ⋅=，得94,31==q p 46. 如图,正方形ABCD 边长为2,内切圆为O ⊙,点P 是O ⊙上任意一点． (1) 求PA PB PC PD +++的值；(2) 求证: ()()PA PB PC PD +⊥+．（苏州中学王思俭原创）(1)解:设正方形内切圆半径为r ，则r =1． ∵PA PB PC PD OA OP OB OP OC OP OD OP+++=-+-+-+-=4OA OB OC OD OP +++-，又,OA OB OC OD O OP r +++==,∴44PA PB PC PD r +++==． (2)证明建立如图的直角坐标系， ∴()()()()1,1,1,1,1,1,1,1,A B C D ----()22,,1P x y x y +=且．∴ ()()1,1,1,1PA x y PB x y =--=---,()()1,1,1,1PC x y PD x y =----=---,∴()()2,22,2,22PA PB x y PC PD x y +=--+=---, ∴()()224440PA PBPC PD xy ++=+-=．∴()()PA PB PC PD +⊥+．47. 某人去参加抽奖游戏，主持人将三个箱子放在他面前，其中一个里面装有1000元奖金，主持人是知道哪个箱子有奖金的．现在让他选一个箱子，主持人打开另外2个箱子中的一个空箱子，给那个抽奖的人看，然后问他，是不是要更改她的选择．（1）试用数学方法说明那个参加抽奖的人是该更改选择呢？DCBA（2）如果该抽奖人已经得奖，主持人提出2种方案：一、就此结束游戏，得到1000元奖金；二、继续游戏，抛掷一枚硬币，正面向上则奖金翻倍，反面向上则奖金减半．该抽奖人是否继续游戏，用数学方法说明理由．（昆山中学秦春勇原创）解：（1）不更改而中奖的概率为31;更改而中奖的概率即为第一次没选到有奖金箱子的概率，为32 （2）不继续游戏获奖金的数学期望为1000元；继续下去获奖金的数学期望为：12505.020005.0500=⨯+⨯元．所以应该继续游戏． 48. 已知函数()ln()f x ax b =+在1x =处的切线方程为11ln 222y x =-+．（1）证明：方程()0f x x -=有且只有一个实根；（2）若,(0,),s t t ∈+∞<且s ，试证明：(1)(1)(1)(1)f t f s ee s t --+>+；（3）求证：当2,*n n N ≥∈时，有121113(1)32nn i i i i ==+->∑∑．（江苏省常熟中学陈志江原创）解：（1）()a f x ax b '=+，由条件得1(1)2(1)ln()ln 2a f ab f a b ⎧'==⎪+⎨⎪=+=⎩，解得 1a b ==，即()ln(1)f x x =+，所以方程即为ln(1)0x x +-=．设1()ln(1),()1001g x x x g x x x '=+-=-==+则由得，且当(1,0)x ∈-时，()0g x '>，故()g x 在(1,0)-上单调递增；当(0,)x ∈+∞时，()0g x '<，故()g x 在(0,)+∞上单调递减，所以当0x =时，有max ()(0)0g x g ==，即()0,0()0g x x g x ≤==当且仅当时有．故方程()0f x x -=有且只有一个实根0x =．（2）由（１）知(1)ln (1)ln(11)ln ,f t t f t t t ee t --=+-=∴==，故(1)f s e s -=．E ABD C1A 1B 1D 1C 不等式即为(1)(1)t ss t +>+，由0s t <<，将不等式两边取对数，只要证ln(1)ln(1)t s s t +>+，即证ln(1)ln(1)s t s t++>（＊）．构造函数ln(1)()(0)x h x x x+=>，则2(1)ln(1)()(1)x x x h x x x -++'=+，显然2(1)0x x +>，设()(1)ln(1),0()ln(1)0I x x x x x I x x '=-++>=-+<则当有，故()[0I x +∞在，）上为减函数，所以0()(0)0x I x I ><=当时，．从而()0h x '<，所以()(0,)h x +∞在上为单调递减函数，因为0s t <<，所以()()h s h t >，即（＊）式成立，结论得证．（3）由（2）知当,(0,),s t t ∈+∞<且s 时，有(1)(1)tss t +>+．令12,(1,2,3,,)t s i n i===，则有102i<<，所以121(13(1,2,3,,)i i n i +>=．当1i =时，有21(11)31+-=，即21(11)31+=+ ①当2i =时，有122191(13242+-=>，即12211(1322+>+ ②当3,4,,i n =时，有121(13i i+> ③由①②③得当2,*n n N ≥∈时，有121113(1)32nn i i i i ==+>+∑∑，即121113(1)32n ni i i i ==+->∑∑．49. 如图，在正方体ABCD －A 1B 1C 1D 1中，棱长为a ，E 为棱CC 1上的的动点．（1）求证：A 1E ⊥BD ；（2）当E 恰为棱CC 1的中点时，求证：平面A 1BD ⊥平面EBD ； (3)在（2）的条件下，求1_A BDE V ．证明：（1）连AC ，A 1C 1．正方体AC 1中，AA 1⊥平面ABCD ， ∴AA 1⊥BD ．正方形ABCD ， AC ⊥BD 且AC AA 1=A ．∴BD ⊥平面ACC 1A 1 且E ∈CC 1．∴A 1E ⊂平面ACC 1A 1．∴BD ⊥A 1E ．（2）设AC BD =O ，则O 为BD 的中点，连A 1O ，EO ．由（1）得BD ⊥平面A 1ACC 1 ，∴BD ⊥A 1O ,BD ⊥EO ． EO A 1∠∴即为二面角A 1-BD -E 的平面角． AB =a ，E 为CC 1中点，∴A 1O =a 26，A 1E =a 23，EO =a 23． ∴A 1O 2+OE 2=A 1E 2．∴A 1O ⊥OE ．0190=∠∴OE A ． ∴平面A 1BD ⊥平面BDE ． (3)由（2）得A 1O ⊥平面BDE 且A 1O =a 26，又246a S BDE =∆， ∴V =34131a Sh = ﹒ 50. 如图1，等腰梯形ABCD 中，AD BC ，AB AD a ==，∠060ABC =，E 是BC 的中点，如图2，将三角形ABE 沿AE 折起，使平面BAE ⊥平面AECD ，F 、P 分别是CD 和BC 的中点．（1）求证：AE BD ⊥．(2)点M 在四边形AECD 的内部及边界运动，且始终保持BM 平面PEF ，求M 点所经过的路径的长度．(3)判断DE 能否垂直于平面ABC ，并说明理由．（相城实验中学冯志强改编）图 2图 1AE解答：（1）证明：取AE 的中点H ，连BH ，DH ，则∆ABE 为正三角形，四边形ADCE 为边长为a 的菱形且060DCB ∠=．∴在图2中有BH AE ⊥，容易得ADE ∆为正三角形，∴AE HD ⊥，又∵HDBH H =，∴AE ⊥平面BHD ，∴AE BD ⊥．（2）∵12DF CD =，12HE AE =，CD AE =，又HE DF ，∴四边形HEFD 为平行四边形，∴HD EF ，∴HD 平面PEF ，又∵P 为BC 的中点，F 为DC 的中点，∴PFBD ，∴BD 平面PEF ，又HD BD D =，∴平面BHD 平面PEF ，∴M ∈平面PHD ，又M ∈平面AECD ，∴M HD ∈，故点M 在平面AECD 内部及边界运行的路径为线段HD ，在RT ADH ∆中，容易得出路径的长度为2HD a =．（3）DE 不能平行于平面ABC ．证明如下：（反证法）假设DE 平行于平面ABC ，则DE BA ⊥．又平面BAE ⊥平面AECD ，交线为AE ，而BH AE ⊥，∴BH ⊥平面AECD ，∴BH DE ⊥，又BH BA B =，∴DE ⊥平面BAE ，∴DE AE ⊥，而DE AC ⊥，这与平面内过直线外一点有且只有一条直线与已知直线垂直相矛盾，故假设不成立，即：DE 不能平行于平面ABC ．51. 某校有一贫困学生因病需手术治疗．校团委计划在全校开展爱心募捐活动，为了增加活动的趣味性吸引更多学生参与，特举办“摇奖100%中奖”活动．凡捐款10元便可享受一次摇奖机会，如图是摇奖机的示意图，摇奖机的旋转盘是均匀的，扇形区域A ，B ，C ，D ，E 所对应的圆心角的比值分别为1:2:3:4:5．相应区域分别设立一、二、三、四、五等奖，奖品分别为价值5元、4元、3元、2元、1元的学习用品．摇奖时，转动圆盘片刻，待停止后，固定指针指向哪个区域（边线忽略不计）即可获得相应价值的学习用品（如图指针指向区域，可获得价值3元的学习用品）．如果学生甲捐款10元，获得了一次摇奖机会，求（1）他获得价值2元学习用品的概率；（2）他获得价值不小于3元学习用品的概率．（苏大附中徐开改编）解：（1）1415P =;（2）225P =． 52. 已知函数11()1x f x x +=-．（1）过函数图象对称中心的直线l 交()y f x =图象于点A 、B 两点，若定点1,0)P 对线段AB 的张角为锐角，求直线l 斜率的取值范围；（2）数列{}n a 满足1()n n a f a +=，*n N ∈，若1001909ii a==∑，求10011i i i a a +=∑的值．（张家港市梁丰高级中学黄耀平原创）解：（1）1112()111x f x x x +==+--，故函数图象对称中心为(1,1)，设直线l 方程为1(1)y k x -=-，由(1)111y kx k x y x =--⎧⎪+⎨=⎪-⎩得：22120kx kx k -+-=，设交点1122(,),(,)A x y B x y ，则4800k k ∆=>⇒>，且1212212x x k x x k +=⎧⎪⎨-⋅=⎪⎩，∴1212[(1)][(1)]121y y kx k kx k k ⋅=--⋅--=-+，∵定点1,0)P 对线段AB 的张角为锐角，∴0PA PB ⋅>，即11221212(1,)(1,)(1)(1)0x y x y x x y y -⋅--=-⋅-+⋅>， ∵0k >，可化简得：234122512043k k k -+<⇒<<，故所求直线l 斜率的取值范围为34(,)43．（2）由已知11112111n n n n a a a a ++==+--得：1(1)(1)12n n a a +--=，当2n ≥时，1(1)(1)12n n a a ---=，∴1111n n a a +--=-，即：11n n a a +-=， ∴数列{}n a 是以2为周期的周期数列，13101a a a ===，又由1111n n n a a a ++=-得：1111n n n n a a a a ++⋅=++， ∴10011223100101112231001011001(11)(11)(11)110022009.i i i i i a aa a a a a a a a a a a a a +===+++=+++++++++=+=∑∑。

全品高考网2009年高考有奖猜题活动

评价
项目
标准分数
考题分析
猜题分析
自评分数
专家评分
题干
情景
10分
日照长短对鸟类繁殖活动的调节
哺乳动物生命活动的调节
10
9
设问
问题
15分
（1）动物生命活动调节的方式、下丘脑的功能
（2）性激素稳态反馈调节中各器官的作用
（3）实验验证促性腺激素的作用
（1）体温平衡中甲状腺激素合成的调节过程
（2）缺碘对生物的影响
②分别测量甲、乙两组鼠的体温，并做好记录；
③；
④把甲、乙两组鼠置于可人工控制的温室中，将室内温度调为0℃，在相对安静的条件下观察24小时，每隔4小时分别测量一次体温，并做好记录。
预期结果与结论：
①；
②。
【标准解答】
(1)①→②→③→④(2分)
(2)促甲状腺激素(2分)
甲状腺(2分)
(3)①→⑥→④(2分)
(4)下丘脑是调节体温的主要中枢(2分)
用一定的方法破坏甲组鼠的下丘脑，乙组鼠不做处理作为对照(3分)
若实验前后甲组鼠体温发生明显改变、乙组鼠体温保持相对恒定，则假设成立(3分)
若实验前后甲、乙两鼠体温均保持相对恒定，则假设不成立(3分)
原创声明
我确保本猜题是由本人原创。
授权声明
本猜题独家授权于全品高考网使用，不会授权其他单位或个人使用。
10
10
方法
侧重
20分
以图表形式综合考查理解能力、实验与探究能力、综合应用能力
以图表形式综合考查理解能力、实验与探究能力、综合应用能力
20
20
关键
细节
10分
反馈调节过程的深刻认识和综合应用是解题的关键

第二届(2008)全品高考有奖猜题活动

第二届（2008）全品高考有奖猜题活动命中高考真题分析报告·语文全品高考网2008年高考预测报告特约专家语文评审组在全品网络总部的领导和策划下，历时两个多月，全品高考网高考预测活动圆满结束！此次全品高考网语文猜题是第二次猜题活动，语文猜题报告是在去年的基础上写作的，由于有去年的经验，我们的猜题报告更全面；同时由于吸取了去年的教训，我们的猜题报告更完美。

总体来说，我们的语文高考猜题预测报告体现了以下特点：准确性强、时效性强、编写阵容强大、影响面广等。

一、准确性强。

黑猫白猫，捉住老鼠才是好猫；说一千道一万，猜中才是硬道理。

我们的语文猜题报告体现了猜题的准确性，不论是分值在3至4分的小题，还是占到60至70分的作文题，我们的猜题报告都有猜中的内容；不论是课本上的内容还是课外拓展的内容，我们的老师都能猜中。

这里边体现了老师的心血和才智，这里边有我们对千千万万读者朋友的责任。

我们将继续努力，以期来年取得更大的成绩。

（一）【2008·福建卷】阅读下面这首唐诗，按要求答题。

（6分）绝句漫兴九首（其三）杜甫熟知茅斋绝低小，江上燕子故来频。

衔死点污琴书内，更接飞虫打着人。

[注]这首诗写于杜甫寓居成都草堂的第二年（公元761年）。

请从表现手法的角度，对这首诗作简要赏析。

【答案】这首诗景中含情。

诗人从燕子落笔，细腻逼真地描写了它们频频飞人草堂书斋，“点污琴书”、“打着人”等活动。

这些描写既凸现了燕子的可爱之态，又生动传神地表现出燕子对草堂书斋的喜爱，以及对诗人的亲昵。

全诗洋溢着浓厚的生活气息，给人自然、亲切之感，同时也透露出诗人在草堂安定生活的喜悦和悠久闲之情。

也可以理解为诗人通过对燕子频频飞入草堂书斋扰人情景的生动描写，借燕子引出禽鸟也好像欺负人的感慨，表现出诗人远客孤居的诸多烦恼和心绪不宁的神情。

负人的感慨，表现出诗人远客孤居的诸多烦恼和心绪不宁的神情。

（言之成理即可）【预测报告：诗歌预测题三】猜题编号：8010239越调·平湖乐王恽采菱人语隔秋烟，波静如横练①。

09年高考试题精选江西省大余中学2009届高考猜题试卷930

09年高考试题精选江西省大余中学2009届高考猜题试卷测试题 2019.91,已知函数上的最小值为－2，则的取值范围是（）A ．B ．C ．D ．2,正四棱锥的五个顶点在同一个球面上,若其底面边长为4,侧棱长为,则此球的表面积为（A ）（B ）（C ）（D ）3,对于使成立的所有常数中，我们把的最小值叫做的上确界，若，则的上确界为()－3 () ()－ ()4,已知O 是平面上的一个定点，A ，B ，C ，是平面上不共线三个点，动点P 满足，则动点P 的轨迹一定通过△ABC 的（） A ．重心 B ．垂心 C ．外心 D ．内心5,设函数，且，，则（） A.2 B.1 C.0 D.6,的各项系数之和大于,小于,则展开式中系数最大的项是（A ）（B ）（C ）（D ）或 7,地面上有四个科研机构在接收嫦娥卫星发回的某类信息,它]4,3[sin 2)(ππω-=在区间x x f ω[)+∞⎥⎦⎤ ⎝⎛-∞-,629, ⎪⎭⎫⎢⎣⎡+∞⎥⎦⎤ ⎝⎛-∞-,2329, (][)+∞-∞-,62, (]⎪⎭⎫⎢⎣⎡+∞-∞-,232, ABCD V -62π18π36π72π922x x M -+≤M M 122x x -+,,1a b R a b +∈+=且122a b --A B 4-C 41D 92-),0(cos ||cos ||(+∞∈++=λλCAC BAB 1463)(23+++=x x x x f 1)(=a f 19)(=b f =+b a 2-nxx )1(3+83236x x 464x x x 464x x D C B A ,,,们两两之间可以互相接发信息,由于功率限制,卫星只能随机地向其中一个科研机构发送信息,每个科研机构都不能同时向两个或两个以上的科研机构发送信息,某日四个机构之间发送了三次信息后,都获得了卫星发回的同一条信息,那么是接收到该信息后互相联系的方式共有（A ） 16种（B ）17种（C ） 34种（D ） 48种8,已知,,,数列满足,,.证明:.9,已知从“神七”飞船带回的某种植物种子每粒成功发芽的概率都为，某植物研究所进行该种子的发芽实验，每次实验种一料种子，每次实验结果相互独立。

第三届(2009)全品高考有奖猜题活动

【精品课件】2009届高考数学研讨会解题思路资料(答题相约)

【语文】2015全品高考猜题最有可能考的20题[简易版]

2009年高考临近：数学猜题卷陕西特级教师 安振平

2009年山东高考作文题目竞猜活动启事

09年高考模拟试题2009年高考模拟试题(新课程)(五)

2009考年高考校模拟考试试题征集评比通知试

关于开展2009年新课程高考模拟试题征集评选活动的通知

全品高考网2009年高考有奖猜题活动

09年高考模拟试题2009高考模拟试题(4)

2015年第九届全品高考猜题公告

湖北高考最后猜题押题卷六

2009年高考猜题讲解(数 学)重点

山东省2009届高三高考猜题语文试题

2009年苏州市高考数学有奖竞猜题(第二稿)

全品高考网2009年高考有奖猜题活动

第二届(2008)全品高考有奖猜题活动

09年高考试题精选江西省大余中学2009届高考猜题试卷930

2009年高考临近：数学猜题卷陕西特级教师安振平

2009年高考猜题讲解(数学)重点