数学必修4人教A全册教案2.5《平面向量应用举例》
人教A版高中数学必修四-2.5《平面向量应用举例》教案复习过程

人教A版高中数学必修四-2.5《平面向量应用举例》教案2.5平面向量应用举例一、教材分析向量概念有明确的物理背景和几何背景,物理背景是力、速度、加速度等,几何背景是有向线段,可以说向量概念是从物理背景、几何背景中抽象而来的,正因为如此,运用向量可以解决一些物理和几何问题,例如利用向量计算力沿某方向所做的功,利用向量解决平面内两条直线平行、垂直位置关系的判定等问题。
二、教学目标1.通过应用举例,让学生会用平面向量知识解决几何问题的两种方法-----向量法和坐标法,可以用向量知识研究物理中的相关问题的“四环节”和生活中的实际问题2.通过本节的学习,让学生体验向量在解决几何和物理问题中的工具作用,增强学生的积极主动的探究意识,培养创新精神。
三、教学重点难点重点:理解并能灵活运用向量加减法与向量数量积的法则解决几何和物理问题.难点:选择适当的方法,将几何问题或者物理问题转化为向量问题加以解决.四、学情分析在平面几何中,平行四边形是学生熟悉的重要的几何图形,而在物理中,受力分析则是其中最基本的基础知识,那么在本节的学习中,借助这些对于学生来说,非常熟悉的内容来讲解向量在几何与物理问题中的应用。
五、教学方法1.例题教学,要让学生体会思路的形成过程,体会数学思想方法的应用。
2.学案导学:见后面的学案3.新授课教学基本环节:预习检查、总结疑惑→情境导入、展示目标→合作探究、精讲点拨→反思总结、当堂检测→发导学案、布置预习六、课前准备1.学生的学习准备:预习本节课本上的基本内容,初步理解向量在平面几何和物理中的应用2.教师的教学准备:课前预习学案,课内探究学案,课后延伸拓展学案。
七、课时安排:1课时八、教学过程(一)预习检查、总结疑惑检查落实了学生的预习情况并了解了学生的疑惑,使教学具有了针对性。
(二)情景导入、展示目标教师首先提问:(1)若O 为ABC ∆重心,则OA u u u r +OB u u u r +OC u u u r =0r(2)水渠横断面是四边形ABCD ,DC u u u r =12AB u u u v ,且|AD u u u v |=|BC u u u v |,则这个四边形 为等腰梯形.类比几何元素之间的关系,你会想到向量运算之间都有什么关系?(3) 两个人提一个旅行包,夹角越大越费力.为什么?教师:本节主要研究了用向量知识解决平面几何和物理问题;掌握向量法和坐标法,以及用向量解决平面几何和物理问题的步骤,已经布置学生们课前预习了这部分,检查学生预习情况并让学生把预习过程中的疑惑说出来。
高中数学人教A版必修4教案-2.5_平面向量应用举例_教学设计_教案

教学准备
1. 教学目标
向量的应用
2. 教学重点/难点
向量的应用
3. 教学用具
4. 标签
教学过程
一. 内容归纳
1. 知识精讲: 掌握向量的概念、坐标表示、运算性质,做到融会贯通,能应用向量的有关性质解决诸如平面几何、解析几何等的问题.
2. 重点难点: 向量的性质及相关知识的综合应用.
3. 思维方式: 能换一个角度看问题,善于应用向量的有关性质解题.
4. 特别注意: 向量性质的应用要准确无误,不能想当然.
思维点拔]正确熟练地应用向量的运算性质,同时要善于运用其他数学知识解题.
例5.一条河的两岸平行,河的宽度为,一艘船从A处出发航行到河
的正对岸B处,船的航行
[思维点拔] 理解物理意义,用向量的知识解决.。
人教A版高中数学必修4《二章 平面向量 2.5 平面向量应用举例 2.5.2 向量在物理中的应用举例》优质课教案_6

学生:在练习本上画出图形
老师:检查练习情况,了解学生对物理概念的掌握情况
(2)两个学生公共提一个包,改变手臂的夹角,有何感觉?
让学生体验物理现象,感受过程,提高学生学习的兴趣
学生:学生代表每两个提一个包,改变夹角,体验用力情况。
老师:指导学生感受过程。
(3)两个同学分别做ቤተ መጻሕፍቲ ባይዱ体向上,改变手臂的夹角,有何感受?
老师:小结数学模型
(6)p124探究: 为何值时, 最小,最小是多大?同学们相互讨论。
培养学生提壶问题,提高探究能力,大胆猜测,自由发挥
学生1:……
学生2:……
学生3:……
(7) 能等于 吗?为什么?
培养学生的向量运算能力,培养发散思维
学生1:……
学生2:……
老师:点评
(8)对本节课的探究有不同的意见吗?
让学生亲自体验拉力与夹角有关
学生:各自说说自己的感受。
学生:说说为什么
老师:点评理由
(4)例3中 ?
掌握向量加法的平行四边形法则及三角函数的定义
学生:作出两个力的合力
学生:作出直角三角形
老师:点评学生结论
(5)当 逐渐变大时, 如何变化?
考察学生三角函数的单调性情况,尝试构建数学模型
学生:回答问题,构建数学模型
(2)讲物理问题转化为向量问题;
(3)通过向量运算解决物理问题。
2.过程与方法
(1)体验物理现象;
(2)合作研究,构建数学模型。
3.情感态度与价值观
(1)通过学生个人体验、合作交流。感受物理现象,培养学生勇于探索、善于法现、不畏艰辛的创新品质,增强学习的成功心理,激发学习数学的兴趣。
高中数学教案 必修4教案 第二章 平面向量 2.5平面向量应用举例

第一课时 2.5.1 平面几何中的向量方法教学要求:理解向量加减法与向量数量积的运算法则;会用向量知识解决几何问题;能通过向量运算研究几何问题中点、线段、夹角之间的关系.教学重点:理解并能灵活运用向量加减法与向量数量积的法则.教学难点:理解并能灵活运用向量加减法与向量数量积的意义和性质.教学过程:一、复习准备:1.提问:向量的加减运算和数量积运算是怎样的?2.讨论:① 若o 为ABC ∆的重心,则OA +OB +OC =0②水渠横断面是四边形ABCD ,DC =12AB ,且|AD |=|BC |,则这个四边形为等腰梯形.类比几何元素之间的关系,你会想到向量运算之间都有什么关系?二、讲授新课:1.教学平面几何的向量:① 平移、全等、相似、长度、夹角等几何性质可以由向量线性运算及数量积表示出来例如,向量数量积对应着几何中的长度.如图: 平行四边行ABCD 中,设AB=a ,AD =b ,则AC AB BC a b =+=+(平移),DB AB AD a b =-=-,222||AD b AD ==(长度).向量AD ,AB 的夹角为DAB ∠ ② 讨论:(1)向量运算与几何中的结论"若a b =,则||||a b =,且,a b 所在直线平行或重合"相类比,你有什么体会?(2)由学生举出几个具有线性运算的几何实例.③ 用向量方法解平面几何问题的步骤(一般步骤)(1) 建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量.(2) 通过向量运算研究几何运算之间的关系,如距离、夹角等.(3) 把运算结果"翻译"成几何关系.2.教学例题:① 出示例1:求证:平行四边形两条对角线的平方和等于四条边的平方和.分析:由向量的数量积的性质,线段的长的平方可看做相应向量自身的内积.练习:已知平行四边形ABCD ,AB =a ,BC =b ,且||||a b =,试用向量a b ,表示BD 、AC ,并计算BD .AC ,判断BD 与AC 的位置关系.② 出示例2:如图,在OBCA 中,OA a =,OB b =,||||a b a b +=-,求证四边形OBCA为矩形分析:要证四边形OBCA 为矩形,只需证一角为直角.③ 练习:AC 为O 的一条直径,ABC ∠为圆周角,求证90ABC ∠=︒④ 出示例3:在ABC 中,M 是BC 的中点,点N 在边AC 上,且2AN NC =,AM BN与相交于点P ,如图,求:AP PM 的值.⑤ 练习:求证平行四边形对角线互相平分.3. 小结:向量加减法与向量数量积的运算法则;向量加减法与向量数量积的意义和性质.三、巩固练习:1. 已知平行四边形ABCD ,E F 、在对角线BD 上,并且BE=FD ,求证AECF 是平行四边形.2. 求证:两条对角线互相垂直平分的四边形是菱形.3. 在平行四边形ABCD 中,已知AD=1,AB=2,对角线BD=2,求对角线AC 的长.4. 作业:书P125 2.第二课时:2.5.2 向量在物理中的应用举例教学要求:理解向量线性运算及数量积运算,会用向量知识解决物理问题.教学重点:理解并能灵活应用向量线性运算及数量积的意义和性质.教学难点:理解并能灵活应用向量线性运算及数量积的意义和性质.教学过程:一、复习准备:1. 讨论: ①两个人提一个旅行包,夹角越大越费力.②在单杠上做引体向上运动,两臂夹角越小越省力.2. 提问: 类比物理元素之间的关系,你会想到向量运算之间有什么关系?二、讲授新课:1. 教学物理中的向量:①物理中有许多量,比如力、速度、加速度、位移都具有大小和方向,因而它们都是向量.②力、速度、加速度、位移的合成就是向量的加法,因而它们也符合向量加法的三角形法则和平行四边形法则. 力、速度、加速度、位移的分解也就是向量的分解,运动的叠加也用到了向量的加法.③动量mv是数乘向量.④力所做的功就是作用力F与物体在力F的作用下所产生的位移s的数量积.⑤用向量研究物理问题的方法:首先把物理问题转化成数学问题,即将物理量之间的关系抽象成数学模型,然后利用建立起来的数学模型解释和回答相关的物理现象.⑥探究:学生举出几个关于力、速度、加速度、位移的例子.2 .教学例题:①出示例1:某人在静水中游泳,速度为(1)如果他径直游向河对岸,水流速度为4km/h,那么他实际上沿什么方向前进?速度大小为多少?(2)他必须朝哪个方向游才能沿与水流垂直的方向前进?实际前进的速度大小为多少? (分析:解决此类行船问题的关键在于"水速+船速=船实际速度”,注意到速度是一个向量,既有大小,又有方向.)②练习:某人在无风天气行走,速度为4km/h,如果他沿正北方向行走,东风的风速为4km/h,那么他实际沿什么方向前进?速度大小为多少?和的绳子将100N的物体吊在水平屋顶②出示例2:如图,用两根分别长10m上,平衡后G点距屋顶的距离恰好为5m,求A处受力的大小.(分析:解决此类问题要先依题意将物理向量用有向线段来表示,利用向量加法的平行四边形法则,将物理问题转化为数学中向量加法,然后由已知条件进行计算.)④练习:用两条成120 角的等长的绳子挂一个灯具,已知灯具的重量10N,则,每根绳子的拉力大小是多少?.3. 小结:物理中的向量;用向量研究物理问题的方法.三、巩固练习:1. 静水中船的速度是每分钟40m,水水流的速度是每分钟20m,如果船沿着垂直水流的方向到达对岸,那么船行进的方向与河岸的夹角为_________.2. 甲飞机从A城市向北飞行了,然后向东飞行300km;乙飞机从B城市向东飞行了300km,然后向北飞行,那么甲、乙两飞机飞行的位移相等吗?为什么?。
高一数学 人教A版必修四教案:2.5 平面向量的应用 Word版含答案

2.5 平面向量应用举例(一)导入新课思路 1.(直接导入)向量的概念和运算都有着明确的物理背景和几何背景,当向量和平面坐标系结合后,向量的运算就完全可以转化为代数运算.这就为我们解决物理问题和几何研究带来了极大的方便.本节专门研究平面几何中的向量方法.思路2.(情境导入)由于向量的线性运算和数量积运算具有鲜明的几何背景,平面几何图形的许多性质,如平移、全等、相似、长度、夹角等都可以由向量的线性运算及数量积表示出来,因此,可用向量方法解决平面几何中的一些问题.下面通过几个具体实例,说明向量方法在平面几何中的运用.(二)推进新课、新知探究、提出问题图1①平行四边形是表示向量加法和减法的几何模型,如图1,你能观察、发现并猜想出平行四边形对角线的长度与两邻边长度之间有什么关系吗?②你能利用所学知识证明你的猜想吗?能利用所学的向量方法证明吗?试一试可用哪些方法?③你能总结一下利用平面向量解决平面几何问题的基本思路吗?活动:①教师引导学生猜想平行四边形对角线的长度与两邻边长度之间有什么关系.利用类比的思想方法,猜想平行四边形有没有相似关系.指导学生猜想出结论:平行四边形两条对角线的平方和等于四条边的平方和.②教师引导学生探究证明方法,并点拨学生对各种方法分析比较,平行四边形是学生熟悉的重要的几何图形,在平面几何的学习中,学生得到了它的许多性质,有些性质的得出比较麻烦,有些性质的得出比较简单.让学生体会研究几何可以采取不同的方法,这些方法包括综合方法、解析方法、向量方法.图2证明:方法一:如图2.作CE⊥AB于E,DF⊥AB于F,则Rt△ADF≌Rt△BCE.∴AD=BC,AF=BE.由于ACAE2+CE2=(AB+BE)2+CE2=AB2+2AB·BE+BE2+CE2=AB2+2AB·BE+BC2.BD2=BF2+DF2=(AB-AF)2+DF2=AB2-2AB·AF+AF2+DF2=AB2-2AB·AF+AD2=AB2-2AB·BE+BC2.∴AC2+BD2=2(AB2+BC2).图3方法二:如图3.以AB所在直线为x轴,A为坐标原点建立直角坐标系.设B(a,0),D(b,c),则C(a+b,c).∴|AC|2=(a+b)2+c2=a2+2ab+b2+c2,|BD|2=(a-b)2+(-c)2=a2-2ab+b2+c2.∴|AC|2+|BD|2=2a2+2(b2+c2)= 2(|AB|2+|AD|2).用向量方法推导了平行四边形的两条对角线与两条邻边之间的关系.在用向量方法解决涉及长度、夹角的问题时,常常考虑用向量的数量积.通过以下推导学生可以发现,由于向量能够运算,因此它在解决某些几何问题时具有优越性,它把一个思辨过程变成了一个算法过程,学生可按一定的程序进行运算操作,从而降低了思考问题的难度,同时也为计算机技术的运用提供了方便.教学时应引导学生体会向量带来的优越性.因为平行四边形对角线平行且相等,考虑到向量关系=-,AC=+,教师可点拨学生设=a,=b,其他线段对应向量用它们表示,涉及长度问题常常考虑向量的数量积,为此,我们计算||2与||2.因此有了方法三.方法三:设=a,=b,则AC=a+b,=a-b,||2=|a|2,||2=|b|2.∴||2=·=(a+b)·(a+b)=a·a+a·b+b·a+b·b=|a|2+2a·b+|b|2.①同理||2=|a|2-2a·b+|b|2.②观察①②两式的特点,我们发现,①+②得||2+||2=2(|a|2+|b|2)=2(||2+||2),即平行四边形两条对角线的平方和等于两条邻边平方和的两倍.③至此,为解决重点问题所作的铺垫已经完成,向前发展可以说水到渠成.教师充分让学生对以上各种方法进行分析比较,讨论认清向量方法的优越性,适时引导学生归纳用向量方法处理平面几何问题的一般步骤.由于平面几何经常涉及距离(线段长度)、夹角问题,而平面向量的运算,特别是数量积主要涉及向量的模以及向量之间的夹角,因此我们可以用向量方法解决部分几何问题.解决几何问题时,先用向量表示相应的点、线段、夹角等几何元素.然后通过向量的运算,特别是数量积来研究点、线段等元素之间的关系.最后再把运算结果“翻译”成几何关系,得到几何问题的结论.这就是用向量方法解决平面几何问题的“三步曲”,即(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;(3)把运算结果“翻译”成几何关系.讨论结果:①能.②能想出至少三种证明方法.③略.(三)应用示例图4例1 如图4,ABCD 中,点E 、F 分别是AD 、DC 边的中点,BE 、BF 分别与AC 交于R 、T 两点,你能发现AR 、RT 、TC 之间的关系吗?活动:为了培养学生的观察、发现、猜想能力,让学生能动态地发现图形中AR 、RT 、TC 之间的相等关系,教学中可以充分利用多媒体,作出上述图形,测量AR 、RT 、TC 的长度,让学生发现AR=RT=TC,拖动平行四边形的顶点,动态观察发现,AR=RT=TC 这个规律不变,因此猜想AR=RT=TC.事实上,由于R 、T 是对角线AC 上的两点,要判断AR 、RT 、TC 之间的关系,只需分别判断AR 、RT 、TC 与AC 的关系即可.又因为AR 、RT 、TC 、AC 共线,所以只需判断、、AT 、与之间的关系即可.探究过程对照用向量方法解决平面几何问题的“三步曲”很容易地可得到结论.第一步,建立平面几何与向量的联系,用向量表示问题中的几何元素,将平面几何问题转化为向量问题;第二步,通过向量运算,研究几何元素之间的关系;第三步,把运算结果“翻译”成几何关系:AR=RT=TC.解:如图4,设=a ,=b ,=r ,AT =t ,则AC =a +b . 由于与共线,所以我们设r =n(a +b ),n ∈R . 又因为EB =AB -AE =a -21b , ER 与EB 共线,所以我们设=m =m(a -21b ). 因为+=,所以r =21b +m(a -21b ). 因此n(a +b )=21b +m(a -b ),即(n-m)a +(n+21-m )b =0.由于向量a 、b 不共线,要使上式为0,必须⎪⎩⎪⎨⎧=-+=-.021,0m n m n 解得n=m=31. 所以=31,同理=31.于是=31. 所以AR=RT=TC.点评:教材中本例重在说明是如何利用向量的办法找出这个相等关系的,因此在书写时可简化一些程序.指导学生在今后的训练中,不必列出三个步骤. 变式训练图5如图5,AD 、BE 、CF 是△ABC 的三条高.求证:AD 、BE 、CF 相交于一点. 证明:设BE 、CF 相交于H,并设=b ,=c ,=h , 则BH =h -b ,=h -c ,=c -b .因为BH ⊥AC ,CH ⊥AB , 所以(h -b )·c =0,(h -c )·b =0, 即(h -b )·c =(h -c )·b . 化简得h ·(c -b )=0. 所以AH ⊥BC .所以AH 与AD 共线,即AD 、BE 、CF 相交于一点H.图6例2 如图6,已知在等腰△ABC 中,BB′、CC′是两腰上的中线,且BB′⊥CC′,求顶角A 的余弦值. 活动:教师可引导学生思考探究,上例利用向量的几何法简捷地解决了平面几何问题.可否利用向量的坐标运算呢?这需要建立平面直角坐标系,找出所需点的坐标.如果能比较方便地建立起平面直角坐标系,如本例中图形,很方便建立平面直角坐标系,且图形中的各个点的坐标也容易写出,是否利用向量的坐标运算能更快捷地解决问题呢?教师引导学生建系、找点的坐标,然后让学生独立完成.解:建立如图6所示的平面直角坐标系,取A(0,a),C(c,0),则B(-c,0),OA =(0,a),=(c,a),=(c,0),=(2c,0).因为BB′、CC′都是中线,所以BB =21(BC +)=21[(2c,0)+(c,a)]=(2,23a c ), 同理CC =(2,23ac -).因为BB′⊥CC′,所以22449a c +-=0,a 2=9c 2.所以54299||||2222222=+-=+-=c c c c ca c a AC AB . 点评:比较是最好的学习方法.本例利用的方法与例题1有所不同,但其本质是一致的,教学中引导学生仔细体会这一点,比较两例的异同,找出其内在的联系,以达融会贯通,灵活运用之功效.变式训练图7(2004湖北高考) 如图7,在Rt △ABC 中,已知BC=a.若长为2a 的线段PQ 以点A 为中点,问:BC PQ 与的夹角θ取何值时,CQ BP ∙的值最大?并求出这个最大值. 解:方法一,如图7.∵⊥,∴·=0.∵AC AQ CQ AB AP BP AQ AP -=-=-=,,, ∴)()(-∙-=∙ =∙+∙-∙-∙ =-a 2-AC +·=-a 2+·(-AC ) =-a 2+21·=-a 2+a 2cosθ. 故当cosθ=1,即θ=0,PQ 与BC 的方向相同时,CQ BP ∙最大,其最大值为0.图8方法二:如图8.以直角顶点A为坐标原点,两直角边所在的直线为坐标轴,建立如图所示的平面直角坐标系.设|AB|=c,|AC|=b,则A(0,0),B(c,0),C(0,b),且|PQ|=2a,|BC|=a.设点P的坐标为(x,y),则Q(-x,-y).∴=(x-c,y),=(-x,-y-b),=(-c,b),=(-2x,-2y).∴∙=(x-c)(-x)+y(-y-b)=-(x2+y2)+cx-by.∵2||||a bycxBCPQ -=∴cx-by=a2cosθ.∴∙=-a2+a2cosθ.故当cosθ=1,即θ=0,与的方向相同时, ∙最大,其最大值为0. (四)知能训练图91.如图9,已知AC为⊙O的一条直径,∠ABC是圆周角.求证:∠ABC=90°.证明:如图9.设AO=a,OB=b,则AB=a+b,OC=a,BC=a-b,|a|=|b|.因为·BC=(a+b)·(a-b)=|a|2-|b|2=0,所以⊥.由此,得∠ABC=90°.点评:充分利用圆的特性,设出向量.2.D 、E 、F 分别是△ABC 的三条边AB 、BC 、CA 上的动点,且它们在初始时刻分别从A 、B 、C 出发,各以一定速度沿各边向B 、C 、A 移动.当t=1时,分别到达B 、C 、A.求证:在0≤t≤1的任一时刻t 1,△DEF 的重心不变.图10证明:如图10.建立如图所示的平面直角坐标系,设A 、B 、C 坐标分别为(0,0),(a,0),(m,n).在任一时刻t 1∈(0,1),因速度一定,其距离之比等于时间之比,有111||||||||||||t t FA CF EC BE DB AD -====λ,由定比分点的坐标公式可得D 、E 、F 的坐标分别为(at 1,0),(a+(m-a)t 1,nt 1),(m-mt 1,n-nt 1).由重心坐标公式可得△DEF 的重心坐标为(3,3mm a +).当t=0或t=1时,△ABC 的重心也为(3,3mm a +),故对任一t 1∈[0,1],△DEF 的重心不变. 点评:主要考查定比分点公式及建立平面直角坐标系,只要证△ABC 的重心和时刻t 1的△DEF 的重心相同即可.(五)课堂小结1.由学生归纳总结本节学习的数学知识有哪些:平行四边形向量加、减法的几何模型,用向量方法解决平面几何问题的步骤,即“三步曲”.特别是这“三步曲”,要提醒学生理解领悟它的实质,达到熟练掌握的程度.2.本节都学习了哪些数学方法:向量法,向量法与几何法、解析法的比较,将平面几何问题转化为向量问题的化归的思想方法,深切体会向量的工具性这一特点.(六)作业。
高中数学必修4《平面向量应用举例》教案

高中数学必修4《平面向量应用举例》教案高中数学必修4《平面向量应用举例》教案
教学准备
教学目标
1.通过平行四边形这个几何模型,归纳总结出用向量方法解决平面几何的问题的三步曲;
2.明确平面几何图形中的有关性质,如平移、全等、相似、长度、夹角等可以由向量的线性运算及数量积表示.;
3.让学生深刻理解向量在处理平面几何问题中的优越性.
教学重难点
教学重点:用向量方法解决实际问题的基本方法:向量法解决几何问题的三步曲.
教学难点:如何将几何等实际问题化归为向量问题.
教学过程
由于向量的线性运算和数量积运算具有鲜明的几何背景,平面几何图形的许多性质,如平移、全等、相似、长度、夹角等都可以由向量的线性运算及数量积表示出来,因此,可用向量方法解决平面几何中的一些问题,下面我们通过几个具体实例,说明向量方法在平面几何中的运用。
例1、平行四边形是表示向量加法与减法的几何模型。
如图,你能发现平行四边形对角线的长度与两条邻边长度之间的关系吗?
思考:
运用向量方法解决平面几何问题可以分哪几个步骤?
运用向量方法解决平面几何问题可以分哪几个步骤?
三步曲:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果翻译成几何关系.。
数学人教A版必修4示范教案:第二章第五节平面向量应用

第二章第五节平面向量应用举例第二课时整体设计教学分析向量与物理学天然相联.向量概念的原型就是物理中的力、速度、位移以及几何中的有向线段等概念,向量是既有大小、又有方向的量,它与物理学中的力学、运动学等有着天然的联系,将向量这一工具应用到物理中,可以使物理题解答更简捷、更清晰.并且向量知识不仅是解决物理许多问题的有利工具,而且用数学的思想方法去审视相关物理现象,研究相关物理问题,可使我们对物理问题的认识更深刻.物理中有许多量,比如力、速度、加速度、位移等都是向量,这些物理现象都可以用向量来研究.用向量研究物理问题的相关知识.(1)力、速度、加速度、位移等既然都是向量,那么它们的合成与分解就是向量的加、减法,运动的叠加亦用到向量的合成;(2)动量是数乘向量;(3)功即是力与所产生位移的数量积.用向量知识研究物理问题的基本思路和方法.(1)通过抽象、概括,把物理现象转化为与之相关的向量问题;(2)认真分析物理现象,深刻把握物理量之间的相互关系;(3)利用向量知识解决这个向量问题,并获得这个向量的解;(4)利用这个结果,对原物理现象作出合理解释,即用向量知识圆满解决物理问题.教学中要善于引导学生通过对现实原型的观察、分析和比较,得出抽象的数学模型.例如,物理中力的合成与分解是向量的加法运算与向量分解的原型.同时,注重向量模型的运用,引导解决现实中的一些物理和几何问题.这样可以充分发挥现实原型对抽象的数学概念的支撑作用.三维目标1.通过力的合成与分解的物理模型,速度的合成与分解的物理模型,掌握利用向量方法研究物理中相关问题的步骤,明了向量在物理中应用的基本题型,进一步加深对所学向量的概念和向量运算的认识.2.通过对具体问题的探究解决,进一步培养学生的数学应用意识,提高应用数学的能力.体会数学在现实生活中的重要作用.养成善于发现生活中的数学,善于发现物理及其他科目中的数学及思考领悟各学科之间的内在联系的良好习惯.重点难点教学重点:1.运用向量的有关知识对物理中力的作用、速度的分解进行相关分析和计算.2.归纳利用向量方法解决物理问题的基本方法.教学难点:将物理中有关矢量的问题转化为数学中向量的问题.课时安排1课时教学过程导入新课思路1.(章头图引入)章头图中,道路、路标体现了向量与位移、速度、力等物理量之间的密切联系.章引言说明了向量的研究对象及研究方法.那么向量究竟是怎样应用于物理的呢?它就像章头图中的高速公路一样,是一条解决物理问题的高速公路.在学生渴望了解的企盼中,教师展示物理模型,由此展开新课.思路2.(问题引入)你能举出物理中的哪些向量?比如力、位移、速度、加速度等,既有大小又有方向,都是向量,学生很容易就举出来.进一步,你能举出应用向量来分析和解决物理问题的例子吗?你是怎样解决的?教师由此引导:向量是有广泛应用的数学工具,对向量在物理中的研究,有助于进一步加深对这方面问题的认识.我们可以通过对下面若干问题的研究,体会向量在物理中的重要作用.由此自然地引入新课.应用示例例1在日常生活中,你是否有这样的经验:两个人共提一个旅行包,夹角越大越费力;在单杠上做引体向上运动,两臂的夹角越小越省力.你能从数学的角度解释这种现象吗?活动:这个日常生活问题可以抽象为如图1所示的数学模型,引导学生由向量的平行四边形法则,力的平衡及解直角三角形等知识来思考探究这个数学问题.这样物理中力的现象就转化为数学中的向量问题.只要分析清楚F、G、θ三者之间的关系(其中F为F1、F2的合力),就得到了问题的数学解释.图1在教学中要尽可能地采用多媒体,在信息技术的帮助下让学生来动态地观察|F|、|G |、θ之间在变化过程中所产生的相互影响.由学生独立完成本例后,与学生共同探究归纳出向量在物理中的应用的解题步骤,也可以由学生自己完成,还可以用信息技术来验证.用向量解决物理问题的一般步骤是:①问题的转化,即把物理问题转化为数学问题;②模型的建立,即建立以向量为主体的数学模型;③参数的获得,即求出数学模型的有关解——理论参数值;④问题的答案,即回到问题的初始状态,解释相关的物理现象.解:不妨设|F 1|=|F 2|,由向量的平行四边形法则、力的平衡以及直角三角形的知识,可以知道cos θ2=12|G||F 1|⇒|F 1|=|G |2cos θ2. 通过上面的式子,我们发现:当θ由0°到180°逐渐变大时,θ2由0°到90°逐渐变大,cos θ2的值由大逐渐变小,因此|F 1|由小逐渐变大,即F 1,F 2之间的夹角越大越费力,夹角越小越省力.点评:本例是日常生活中经常遇到的问题,学生也会有两人共提一个旅行包以及在单杠上做引体向上运动的经验.本例的关键是作出简单的受力分析图,启发学生将物理现象转化成模型,从数学角度进行解释,这就是本例活动中所完成的事情.教学中要充分利用好这个模型,为解决其他物理问题打下基础.得到模型后就可以发现,这是一个很简单的向量问题,这也是向量工具优越性的具体体现.图2 ,实际风速为v .端,子弹击中砂箱后,陷入箱内,使砂箱摆至某一高度h .设子弹和砂箱的质量分别为m 和M ,求子弹的速度v 的大小.图3解:设v 0为子弹和砂箱相对静止后开始一起运动的速度,由于水平方向上动量守恒,所以m |v |=(M +m )|v 0|. ①由于机械能守恒,所以12(M +m )v 20=(M +m )gh . ② 联立①②解得|v |=M +m m2gh . 又因为m 相对于M 很小,所以|v |≈M m2gh , 即子弹的速度大小约为M m2gh . 知能训练1.一艘船以4 km/h 的速度沿着与水流方向成120°的方向航行,已知河水流速为2 km/h ,则经过3小时,该船实际航程为( )A .215 kmB .6 kmC.84 km D .8 km答案:B点评:由于学生还没有学习正弦定理和余弦定理,所以要通过作高来求.2.如图4,已知两个力的大小和方向,则合力的大小为________ N ;若在图示坐标系中,用坐标表示合力F ,则F =________.图4 答案:41 (5,4)3.一艘船以5 km/h 的速度向垂直于对岸的方向行驶,而该船实际航行的方向与水流方向成30°角,求水流速度与船的实际速度.答案:如图5所示,设OA →表示水流速度,OB →表示船垂直于对岸的速度,OC →表示船的实际速度,∠AOC =30°,|OB →|=5 km/h.图5因为OACB 为矩形,所以|OA →|=|AC →|·cot30°=|OB →|·cot30°=53≈8.66 km/h ,|OC →|=|OA →|cos30°=5332=10 km/h. 答:水流速度为8.66 km/h ,船的实际速度为10 km/h.点评:转化为数学模型,画出向量图,在直角三角形中解出.课堂小结1.与学生共同归纳总结利用向量解决物理问题的步骤.①问题的转化,即把物理问题转化为数学问题;②模型的建立,即建立以向量为主体的数学模型;③参数的获得,即求出数学模型的有关解——理论参数值;④问题的答案,即回到问题的初始状态,解释相关的物理现象.2.与学生共同归纳总结向量在物理中应用的基本题型.①力、速度、加速度、位移都是向量;②力、速度、加速度、位移的合成与分解对应相应向量的加减;③)动量m v 是数乘向量,冲量Δt F 也是数乘向量;④功是力F 与位移s 的数量积,即W =F·s .作业1.课本习题2.5 A 组3、4,B 组1、2.2.归纳总结物理学中哪些地方可用向量.设计感想1.本教案设计的指导思想是:由于本节重在解决两个问题,一是如何把物理问题转化成数学问题,也就是将物理量之间的关系抽象成数学模型;二是如何用建立起来的数学模型解释和回答相关的物理现象.因此本教案设计的重点也就放在怎样让学生探究解决这两个问题上.而把这个探究的重点又放在这两个中的第一个上,也就是引导学生认真分析物理现象、准确把握物理量之间的相互关系.通过抽象、概括,把物理现象转化为与之相关的向量问题,然后利用向量知识解决这个向量问题.2.经历是最好的老师.充分让学生经历分析、探究并解决实际问题的过程,这也是学习数学,领悟思想方法的最好载体.学生这种经历的实践活动越多,解决实际问题的方法就越恰当而简捷.教科书中对本节的两个例题的处理方法,都不是先给出解法,而是先进行分析,探索出解题思路,再给出解法,就足以说明这一点.3.突出数形结合的思想.教科书例题都是先画图进行分析的,本教案的设计中也突出了这一点.让学生在活动的时候就先想到画图,并在这个活动中,体会数形结合的应用,体会数学具有广泛的应用,体会向量这个工具的优越性.备课资料一、向量与重心问题假如有两个质点M 1,M 2,它们的质量分别是m 1,m 2,由物理学知识,这两个质点的重心M 在线段M 1M 2上,并且分此线段为与质量成反比例的两部分,即M 1M MM 2=m 2m 1,或m 1M 1M →=m 2MM 2→. 现设点M 1、M 2、M ,对应的向量分别是r 1、r 2、r ,则上式可以写成m 1(r -r 1)=m 2(r 2-r ).所以r =m 1r 1+m 2r 2m 1+m 2,点M 处的质量为m 1+m 2. 现求三个质点的重心问题.三个质点M 1、M 2、M 3的质量分别是m 1、m 2、m 3,所对应的向量分别是r 1、r 2、r 3,我们可设M 1,M 2的重心在点D 处,该处对应的向量为r D =m 1r 1+m 2r 2m 1+m 2,该点的质量为m 1+m 2,然后求点D 与点M 3的重心M 所对应的向量r ,易得r =m 1r 1+m 2r 2+m 3r 3m 1+m 2+m 3. 二、备用习题1.作用于同一点的两个力F 1和F 2,|F 1|=5,|F 2|=3,夹角为60°,则F 1+F 2的大小为________.答案:72.一条渔船距对岸为4 km ,现正以2 km/h 的速度向垂直于对岸的方向划去,到达对岸时,船的实际航程为8 km ,求河水的流速.答案:解:如图7所示,设AB →表示船垂直于对岸的速度,则AB →+BC →=AC →,图7 知AC →就是渔船实际航行的速度.因为航行的时间为4÷2=2(h),所以在Rt △ABC 中,|A B →|=2 km/h ,|AC →|=8÷2=4 km/h ,则|B C →|=2 3 km/h.答:河水的流速为2 3 km/h.3.在半径为15 cm 的均匀铁板上,挖出一个圆洞,已知圆洞的圆心和铁板中心相距8 cm ,圆洞的半径是5 cm ,求挖去圆洞后所剩下铁板的重心.答案:解:如图8所示,建立平面直角坐标系,两圆的圆心分别为O 1(0,0),O 2(8,0),圆O 2是挖去的圆,不妨设铁板的密度为ρ=1,则小圆的质量m 1=25π,挖去圆洞后,铁板的质量为m 2=(225-25)π=200π,设所求的重心为O 3.图8 根据物理学知识,知O 3在直线O 1O 2上,即可设O 3(x 3,0),且满足O 3O 1→=λO 1O 2→,其中λ=m 1m 2=25200=18.由定比分点坐标公式知0=x 3+18×81+18,解得x 3=-1, 即O 3(-1,0)为挖去圆洞后所剩下铁板的重心.4.如图6所示,重力为G 的均匀小球放在倾角为α的斜面上,球被与斜面夹角为θ的木板挡住,球面、木板均光滑,若使球对木板的压力最小,求木板与斜面间夹角θ的大小.图6答案:解:对小球的受力分析如图6所示,重力为G ,斜面弹力为N 2(垂直于斜面向上),木板弹力N 1(垂直于木板),其中N 1与N 2的合力的大小恒为|G ′|,方向向上,N 2的方向始终不变,随着木板的转动,N 1的方向始终垂直于木板,N 1的大小在变化,且满足|N 1|sin α=|G ′|sin θ,又|G ′|=|G |,∴|N 1|=|G |sin αsin θ.∴当sin θ取最大值1时,|N 1|min =|G |sin α,此时θ=π2.。
最新-高中数学《平面向量应用举例》教案5 新人教A版必
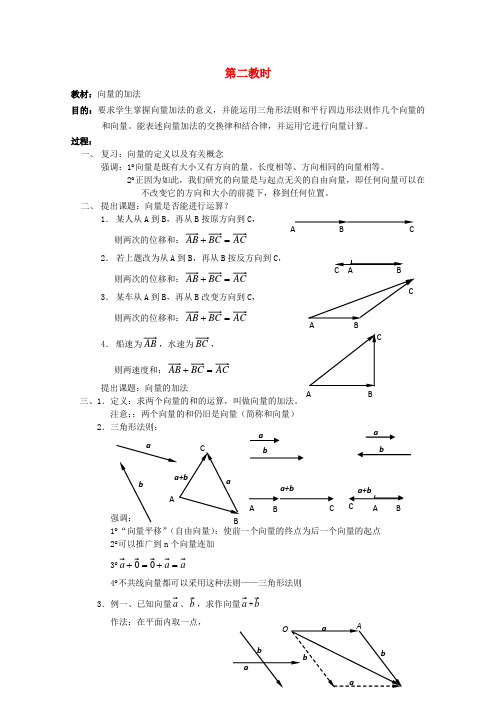
第二教时教材:向量的加法目的:要求学生掌握向量加法的意义,并能运用三角形法则和平行四边形法则作几个向量的和向量。
能表述向量加法的交换律和结合律,并运用它进行向量计算。
过程: 一、 复习:向量的定义以及有关概念强调:1︒向量是既有大小又有方向的量。
长度相等、方向相同的向量相等。
2︒正因为如此,我们研究的向量是与起点无关的自由向量,即任何向量可以在不改变它的方向和大小的前提下,移到任何位置。
二、 提出课题:向量是否能进行运算?1. 某人从A 到B ,再从B 按原方向到C ,则两次的位移和:=+2. 若上题改为从A 到B ,再从B 按反方向到C , 则两次的位移和:=+ 3. 某车从A 到B ,再从B 改变方向到C , 则两次的位移和:=+ 4. 船速为,水速为, 则两速度和:=+提出课题:向量的加法三、1.定义:求两个向量的和的运算,叫做向量的加法。
注意:;两个向量的和仍旧是向量(简称和向量) 2.三角形法则:强调: 1︒“向量平移”(自由向量):使前一个向量的终点为后一个向量的起点 2︒可以推广到n 个向量连加 3︒=+=+4︒不共线向量都可以采用这种法则——三角形法则 3.例一、已知向量、,求作向量+ 作法:在平面内取一点,A B CA BCA BCAA AB B BC C OAaaabb ba +b a +b aa b b b a a作a OA = b AB = 则+=4.加法的交换律和平行四边形法则上题中b +a 的结果与a +b 是否相同 验证结果相同 从而得到:1︒向量加法的平行四边形法则 2︒向量加法的交换律:a +b =b +a 5. 向量加法的结合律:(a +b ) +c =a + (b +c )证:如图:使=, =, =则(+) +==+ + (+) ==+ ∴(a +b ) +c =a + (b +c )从而,多个向量的加法运算可以按照任意的次序、任意的组合来进行。
四、例二(P98—99)略五、小结:1︒向量加法的几何法则 2︒交换律和结合律3︒注意:|+| > || + ||不一定成立,因为共线向量不然。
高一数学人教A版必修四教案:平面向量的应用

2.5 平面向量應用舉例一、教學分析1.本節的目的是讓學生加深對向量的認識,更好地體會向量這個工具的優越性.對於向量方法,就思路而言,幾何中的向量方法完全與幾何中的代數方法一致,不同的只是用“向量和向量運算”來代替“數和數的運算”.這就是把點、線、面等幾何要素直接歸結為向量,對這些向量借助於它們之間的運算進行討論,然後把這些計算結果翻譯成關於點、線、面的相應結果.代數方法的流程圖可以簡單地表述為:則向量方法的流程圖可以簡單地表述為:這就是本節給出的用向量方法解決幾何問題的“三步曲”,也是本節的重點.2.研究幾何可以採取不同的方法,這些方法包括:綜合方法——不使用其他工具,對幾何元素及其關係直接進行討論;解析方法——以數(代數式)和數(代數式)的運算為工具,對幾何元素及其關係進行討論;向量方法——以向量和向量的運算為工具,對幾何元素及其關係進行討論;分析方法——以微積分為工具,對幾何元素及其關係進行討論,等等.前三種方法都是中學數學中出現的內容.有些平面幾何問題,利用向量方法求解比較容易.使用向量方法要點在於用向量表示線段或點,根據點與線之間的關係,建立向量等式,再根據向量的線性相關與無關的性質,得出向量的係數應滿足的方程組,求出方程組的解,從而解決問題.使用向量方法時,要注意向量起點的選取,選取得當可使計算過程大大簡化.二、教學目標1.知識與技能:通過平行四邊形這個幾何模型,歸納總結出用向量方法解決平面幾何問題的“三步曲”.2.過程與方法:明瞭平面幾何圖形中的有關性質,如平移、全等、相似、長度、夾角等可以由向量的線性運算及數量積表示.3.情感態度與價值觀:通過本節學習,讓學生深刻理解向量在處理有關平面幾何問題中的優越性,活躍學生的思維,發展學生的創新意識,激發學生的學習積極性,並體會向量在幾何和現實生活中的意義.教學中要求儘量引導學生使用資訊技術這個現代化手段.三、重點難點教學重點:用向量方法解決實際問題的基本方法;向量法解決幾何問題的“三步曲”.教學難點:如何將幾何等實際問題化歸為向量問題.四、教學設想(一)導入新課思路 1.(直接導入)向量的概念和運算都有著明確的物理背景和幾何背景,當向量和平面坐標系結合後,向量的運算就完全可以轉化為代數運算.這就為我們解決物理問題和幾何研究帶來了極大的方便.本節專門研究平面幾何中的向量方法.思路2.(情境導入)由於向量的線性運算和數量積運算具有鮮明的幾何背景,平面幾何圖形的許多性質,如平移、全等、相似、長度、夾角等都可以由向量的線性運算及數量積表示出來,因此,可用向量方法解決平面幾何中的一些問題.下麵通過幾個具體實例,說明向量方法在平面幾何中的運用.(二)推進新課、新知探究、提出問題圖1①平行四邊形是表示向量加法和減法的幾何模型,如圖1,你能觀察、發現並猜想出平行四邊形對角線的長度與兩鄰邊長度之間有什麼關係嗎?②你能利用所學知識證明你的猜想嗎?能利用所學的向量方法證明嗎?試一試可用哪些方法?③你能總結一下利用平面向量解決平面幾何問題的基本思路嗎?活動:①教師引導學生猜想平行四邊形對角線的長度與兩鄰邊長度之間有什麼關係.利用類比的思想方法,猜想平行四邊形有沒有相似關係.指導學生猜想出結論:平行四邊形兩條對角線的平方和等於四條邊的平方和.②教師引導學生探究證明方法,並點撥學生對各種方法分析比較,平行四邊形是學生熟悉的重要的幾何圖形,在平面幾何的學習中,學生得到了它的許多性質,有些性質的得出比較麻煩,有些性質的得出比較簡單.讓學生體會研究幾何可以採取不同的方法,這些方法包括綜合方法、解析方法、向量方法.圖2證明:方法一:如圖2.作CE⊥AB於E,DF⊥AB於F,則Rt△ADF≌Rt△BCE.∴AD=BC,AF=BE.由於ACAE2+CE2=(AB+BE)2+CE2=AB2+2AB·BE+BE2+CE2=AB2+2AB·BE+BC2.BD2=BF2+DF2=(AB-AF)2+DF2=AB2-2AB·AF+AF2+DF2=AB2-2AB·AF+AD2=AB2-2AB·BE+BC2.∴AC2+BD2=2(AB2+BC2).圖3方法二:如圖3.以AB所在直線為x軸,A為座標原點建立直角坐標系.設B(a,0),D(b,c),則C(a+b,c).∴|AC|2=(a+b)2+c2=a2+2ab+b2+c2,|BD|2=(a-b)2+(-c)2=a2-2ab+b2+c2.∴|AC|2+|BD|2=2a2+2(b2+c2)= 2(|AB|2+|AD|2).用向量方法推導了平行四邊形的兩條對角線與兩條鄰邊之間的關係.在用向量方法解決涉及長度、夾角的問題時,常常考慮用向量的數量積.通過以下推導學生可以發現,由於向量能夠運算,因此它在解決某些幾何問題時具有優越性,它把一個思辨過程變成了一個演算法過程,學生可按一定的程式進行運算操作,從而降低了思考問題的難度,同時也為電腦技術的運用提供了方便.教學時應引導學生體會向量帶來的優越性.因為平行四邊形對角線平行且相等,考慮到向量關係DB =AB -AD ,AC =AB +AD ,教師可點撥學生設AB =a ,AD =b ,其他線段對應向量用它們表示,涉及長度問題常常考慮向量的數量積,為此,我們計算|AC |2與|DB |2.因此有了方法三.方法三:設AB =a ,AD =b ,則AC =a +b ,DB =a -b ,|AB |2=|a |2,|AD |2=|b |2.∴|AC |2=AC ·AC =(a +b )·(a +b )=a ·a +a ·b +b ·a +b ·b =|a |2+2a ·b +|b |2.① 同理|DB |2=|a |2-2a ·b +|b |2.② 觀察①②兩式的特點,我們發現,①+②得|AC |2+|DB |2=2(|a |2+|b |2)=2(|AB |2+|AD |2),即平行四邊形兩條對角線的平方和等於兩條鄰邊平方和的兩倍.③至此,為解決重點問題所作的鋪墊已經完成,向前發展可以說水到渠成.教師充分讓學生對以上各種方法進行分析比較,討論認清向量方法的優越性,適時引導學生歸納用向量方法處理平面幾何問題的一般步驟.由於平面幾何經常涉及距離(線段長度)、夾角問題,而平面向量的運算,特別是數量積主要涉及向量的模以及向量之間的夾角,因此我們可以用向量方法解決部分幾何問題.解決幾何問題時,先用向量表示相應的點、線段、夾角等幾何元素.然後通過向量的運算,特別是數量積來研究點、線段等元素之間的關係.最後再把運算結果“翻譯”成幾何關係,得到幾何問題的結論.這就是用向量方法解決平面幾何問題的“三步曲”,即(1)建立平面幾何與向量的聯繫,用向量表示問題中涉及的幾何元素,將平面幾何問題轉化為向量問題;(2)通過向量運算,研究幾何元素之間的關係,如距離、夾角等問題; (3)把運算結果“翻譯”成幾何關係. 討論結果:①能.②能想出至少三種證明方法. ③略.(三)應用示例圖4例1 如圖4,ABCD 中,點E 、F 分別是AD 、DC 邊的中點,BE 、BF 分別與AC 交於R 、T 兩點,你能發現AR 、RT 、TC 之間的關係嗎?活動:為了培養學生的觀察、發現、猜想能力,讓學生能動態地發現圖形中AR 、RT 、TC 之間的相等關係,教學中可以充分利用多媒體,作出上述圖形,測量AR 、RT 、TC 的長度,讓學生發現AR=RT=TC,拖動平行四邊形的頂點,動態觀察發現,AR=RT=TC 這個規律不變,因此猜想AR=RT=TC.事實上,由於R 、T 是對角線AC 上的兩點,要判斷AR 、RT 、TC 之間的關係,只需分別判斷AR 、RT 、TC 與AC 的關係即可.又因為AR 、RT 、TC 、AC 共線,所以只需判斷、、AT AR 、AD與AC 之間的關係即可.探究過程對照用向量方法解決平面幾何問題的“三步曲”很容易地可得到結論.第一步,建立平面幾何與向量的聯繫,用向量表示問題中的幾何元素,將平面幾何問題轉化為向量問題;第二步,通過向量運算,研究幾何元素之間的關係;第三步,把運算結果“翻譯”成幾何關係:AR=RT=TC.解:如圖4,設AB =a ,AD =b ,AR =r ,AT =t ,則AC =a +b . 由於AR 與AC 共線,所以我們設r =n(a +b ),n ∈R . 又因為EB =AB -AE =a -21b , ER 與EB 共線,所以我們設ER =m EB =m(a -21b ). 因為ER AE AR +=,所以r =21b +m(a -21b ). 因此n(a +b )=21b +m(a -b ),即(n-m)a +(n+21-m )b =0.由於向量a 、b 不共線,要使上式為0,必須⎪⎩⎪⎨⎧=-+=-.021,0m n m n 解得n=m=31. 所以AR =31AC ,同理TC =31AC .於是RT =31AC .所以AR=RT=TC.點評:教材中本例重在說明是如何利用向量的辦法找出這個相等關係的,因此在書寫時可簡化一些程式.指導學生在今後的訓練中,不必列出三個步驟. 變式訓練圖5如圖5,AD 、BE 、CF 是△ABC 的三條高.求證:AD 、BE 、CF 相交於一點. 證明:設BE 、CF 相交於H,並設AB =b ,AC =c ,AH =h , 則BH =h -b ,CH =h -c ,BC =c -b .因為BH ⊥AC ,CH ⊥AB , 所以(h -b )·c =0,(h -c )·b =0, 即(h -b )·c =(h -c )·b . 化簡得h ·(c -b )=0. 所以AH ⊥BC .所以AH 與AD 共線,即AD 、BE 、CF 相交於一點H.圖6例2 如圖6,已知在等腰△ABC 中,BB′、CC′是兩腰上的中線,且BB′⊥CC′,求頂角A 的余弦值. 活動:教師可引導學生思考探究,上例利用向量的幾何法簡捷地解決了平面幾何問題.可否利用向量的座標運算呢?這需要建立平面直角坐標系,找出所需點的座標.如果能比較方便地建立起平面直角坐標系,如本例中圖形,很方便建立平面直角坐標系,且圖形中的各個點的座標也容易寫出,是否利用向量的座標運算能更快捷地解決問題呢?教師引導學生建系、找點的座標,然後讓學生獨立完成.解:建立如圖6所示的平面直角坐標系,取A(0,a),C(c,0),則B(-c,0),OA =(0,a),BA =(c,a),OC =(c,0),BC =(2c,0).因為BB′、CC′都是中線,所以'BB =21(BC +BA )=21[(2c,0)+(c,a)]=(2,23a c ), 同理'CC =(2,23ac ).因為BB′⊥CC′,所以22449a c +-=0,a 2=9c 2.所以cosA=54299||||2222222=+-=+-=•c c c c ca c a AC AB ACAB . 點評:比較是最好的學習方法.本例利用的方法與例題1有所不同,但其本質是一致的,教學中引導學生仔細體會這一點,比較兩例的異同,找出其內在的聯繫,以達融會貫通,靈活運用之功效.變式訓練圖7(2004湖北高考) 如圖7,在Rt △ABC 中,已知BC=a.若長為2a 的線段PQ 以點A 為中點,問:BC PQ 与的夾角θ取何值時,CQ BP •的值最大?並求出這個最大值. 解:方法一,如圖7.∵AB ⊥AC ,∴AB ·AC =0.∵AC AQ CQ AB AP BP AQ AP -=-=-=,,, ∴)()(AC AQ AB AP CQ BP -•-=• =AC AB AQ AB AC AP AQ AP •+•-•-• =-a 2-AP AC +AB ·AP =-a 2+AP ·(AB -AC ) =-a 2+21PQ ·BC =-a 2+a 2cosθ. 故當cosθ=1,即θ=0,PQ 與BC 的方向相同時,CQ BP •最大,其最大值為0.圖8方法二:如圖8.以直角頂點A 為座標原點,兩直角邊所在的直線為坐標軸,建立如圖所示的平面直角坐標系.設|AB|=c,|AC|=b,則A(0,0),B(c,0),C(0,b),且|PQ|=2a,|BC|=a.設點P 的座標為(x,y), 則Q(-x,-y).∴BP =(x-c,y),CQ =(-x,-y-b),BC =(-c,b),PQ =(-2x,-2y). ∴CQ BP •=(x-c)(-x)+y(-y-b)=-(x 2+y 2)+cx-by. ∵cosθ=2||||abycx BC PQ BC PQ -=• ∴cx-by=a 2cosθ. ∴CQ BP •=-a 2+a 2cosθ.故當cosθ=1,即θ=0,PQ 與BC 的方向相同時, CQ BP •最大,其最大值為0.(四)知能訓練圖91.如圖9,已知AC 為⊙O 的一條直徑,∠ABC 是圓周角. 求證:∠ABC=90°.證明:如圖9.設AO =a ,OB =b ,則AB =a +b ,OC =a ,BC =a -b ,|a |=|b |. 因為AB ·BC =(a +b )·(a -b )=|a |2-|b |2=0, 所以AB ⊥BC .由此,得∠ABC=90°.點評:充分利用圓的特性,設出向量.2.D 、E 、F 分別是△ABC 的三條邊AB 、BC 、CA 上的動點,且它們在初始時刻分別從A 、B 、C 出發,各以一定速度沿各邊向B 、C 、A 移動.當t=1時,分別到達B 、C 、A.求證:在0≤t≤1的任一時刻t 1,△DEF 的重心不變.圖10證明:如圖10.建立如圖所示的平面直角坐標系,設A 、B 、C 座標分別為(0,0),(a,0),(m,n).在任一時刻t 1∈(0,1),因速度一定,其距離之比等於時間之比,有111||||||||||||t t FA CF EC BE DB AD -====λ,由定比分點的座標公式可得D 、E 、F 的座標分別為(at 1,0),(a+(m-a)t 1,nt 1),(m-mt 1,n-nt 1).由重心座標公式可得△DEF 的重心座標為(3,3mm a +).當t=0或t=1時,△ABC 的重心也為(3,3mm a +),故對任一t 1∈[0,1],△DEF 的重心不變. 點評:主要考查定比分點公式及建立平面直角坐標系,只要證△ABC 的重心和時刻t 1的△DEF 的重心相同即可.(五)課堂小結1.由學生歸納總結本節學習的數學知識有哪些:平行四邊形向量加、減法的幾何模型,用向量方法解決平面幾何問題的步驟,即“三步曲”.特別是這“三步曲”,要提醒學生理解領悟它的實質,達到熟練掌握的程度.2.本節都學習了哪些數學方法:向量法,向量法與幾何法、解析法的比較,將平面幾何問題轉化為向量問題的化歸的思想方法,深切體會向量的工具性這一特點.(六)作業。
《平面向量应用举例》教案4(新人教A版必修4)

第五章 平面向量第一教时教材:向量目的:要求学生掌握向量的意义、表示方法以及有关概念,并能作一个向量与已知向量相等,根据图形判定向量是否平行、共线、相等。
过程:一、开场白:课本P93(略)实例:老鼠由A 向西北逃窜,猫在B 处向东追去,问:猫能否追到老鼠?(画图)结论:猫的速度再快也没用,因为方向错了。
二、 提出课题:平面向量1. 意义:既有大小又有方向的量叫向量。
例:力、速度、加速度、冲量等注意:1?数量与向量的区别:数量只有大小,是一个代数量,可以进行代数运算、比较大小; 向量有方向,大小,双重性,不能比较大小。
2?从19世纪末到20世纪初,向量就成为一套优良通性的数学体系,用以研究空间性质。
2. 向量的表示方法: 1?几何表示法:点—射线 有向线段——具有一定方向的线段 有向线段的三要素:起点、方向、长度记作(注意起讫)2?字母表示法:AB 可表示为a (印刷时用黑体字) P95 例 用1cm 表示5n mail (海里)3. 模的概念:向量AB 记作:|AB | 模是可以比较大小的4. 两个特殊的向量:1?零向量——长度(模)为0的向量,记作0。
0的方向是任意的。
注意0与0的区别2?单位向量——长度(模)为1个单位长度的向量叫做单位向量。
例:温度有零上零下之分,“温度”是否向量?答:不是。
因为零上零下也只是大小之分。
例:AB 与BA 是否同一向量?答:不是同一向量。
A BA(起点)B (终点) a例:有几个单位向量?单位向量的大小是否相等?单位向量是否都相等? 答:有无数个单位向量,单位向量大小相等,单位向量不一定相等。
三、 向量间的关系:1. 平行向量:方向相同或相反的非零向量叫做平行向量。
记作:a ∥b ∥c规定:与任一向量平行2. 相等向量:长度相等且方向相同的向量叫做相等向量。
记作:a =b规定:=任两相等的非零向量都可用一有向线段表示,与起点无关。
3. 共线向量:任一组平行向量都可移到同一条直线上 ,所以平行向量也叫共线向量。
人教版高中数学高一A版必修4学案 平面向量应用举例
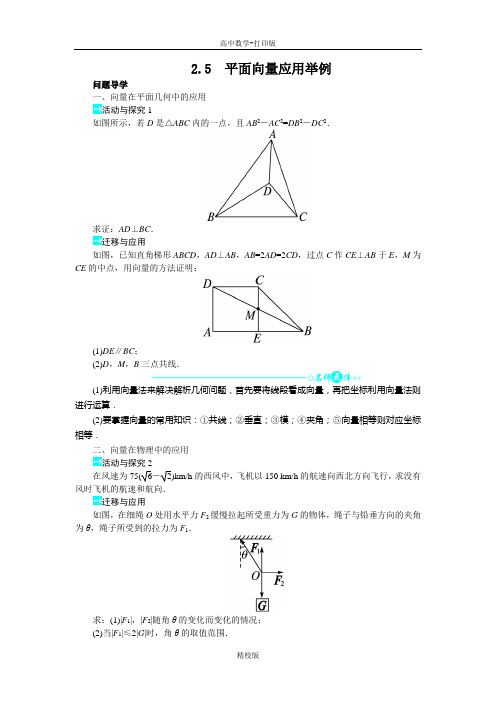
2.5 平面向量应用举例问题导学一、向量在平面几何中的应用活动与探究1如图所示,若D是△ABC内的一点,且AB2-AC2=DB2-DC2.求证:AD⊥BC.迁移与应用如图,已知直角梯形ABCD,AD⊥AB,AB=2AD=2CD,过点C作CE⊥AB于E,M为CE的中点,用向量的方法证明:(1)DE∥BC;(2)D,M,B三点共线.(1)利用向量法来解决解析几何问题,首先要将线段看成向量,再把坐标利用向量法则进行运算.(2)要掌握向量的常用知识:①共线;②垂直;③模;④夹角;⑤向量相等则对应坐标相等.二、向量在物理中的应用活动与探究2在风速为75(6-2)km/h的西风中,飞机以150 km/h的航速向西北方向飞行,求没有风时飞机的航速和航向.迁移与应用如图,在细绳O处用水平力F2缓慢拉起所受重力为G的物体,绳子与铅垂方向的夹角为θ,绳子所受到的拉力为F1.求:(1)|F1|,|F2|随角θ的变化而变化的情况;(2)当|F1|≤2|G|时,角θ的取值范围.向量在物理学中的应用一般涉及力或速度的合成与分解,充分借助向量平行四边形法则把物理问题抽象转化为数学问题.同时该类题目往往涉及三角形问题,能够正确作图是解决问题的关键.当堂检测1.若向量1OF =(2,2),2OF =(-2,3)分别表示两个力F 1,F 2,则|F 1+F 2|为( ) A .(0,5) B .(4,-1) C .2 2 D .52.在四边形ABCD 中,若AB +CD =0,AC ·BD =0,则四边形为( ) A .平行四边形 B .矩形 C .等腰梯形 D .菱形3.坐标平面内一只小蚂蚁以速度ν=(1,2)从点A (4,6)处移动到点B (7,12)处,其所用时间长短为( )A .2B .3C .4D .84.在△ABC 中,若∠C =90°,AC =BC =4,则BA ·BC =__________. 5.已知力F =(2,3)作用于一物体,使物体从A (2,0)移动到B (-2,3),则力F 对物体所做的功为________.答案:课前预习导学 【预习导引】 1.向量 2.加3.向量 向量问题 数量积预习交流 提示:所选择基向量的长度和夹角应该是已知的. 课堂合作探究 【问题导学】活动与探究1 思路分析:解答本题可先表示出图中线段对应的向量,找出所给等式所蕴含的等量关系,再利用它计算所需向量的数量积.证明:设AB =a ,AC =b ,AD =e ,DB =c ,DC =d ,则a =e +c ,b =e +d . ∴a 2-b 2=(e +c )2-(e +d )2=c 2+2e ·c -2e ·d -d 2. 由已知a 2-b 2=c 2-d 2,∴c 2+2e ·c -2e ·d -d 2=c 2-d 2,即e ·(c -d )=0. ∵BC =BD +DC =d -c ,∴AD·BC=e·(d-c)=0.∴AD⊥BC,即AD⊥BC.迁移与应用证明:以E为原点,AB所在直线为x轴,EC所在直线为y轴建立直角坐标系.令|AD|=1,则|DC|=1,|AB|=2.∵CE⊥AB,而AD=DC,∴四边形AECD为正方形.∴可求得各点坐标分别为:E(0,0),B(1,0),C(0,1),D(-1,1),A(-1,0).(1)∵ED=(-1,1)-(0,0)=(-1,1),BC=(0,1)-(1,0)=(-1,1),∴ED=BC,∴ED∥BC,即DE∥BC.(2)连接MB,MD,∵M为EC的中点,∴M1 0,2⎛⎫ ⎪⎝⎭,∴MD=(-1,1)-10,2⎛⎫⎪⎝⎭=11,2⎛⎫- ⎪⎝⎭,MB=(1,0)-10,2⎛⎫⎪⎝⎭=11,2⎛⎫-⎪⎝⎭.∴MD=-MB,∴MD∥MB.又MD与MB有公共点M,∴D,M,B三点共线.活动与探究2思路分析:解本题首先根据题意作图,再把物理问题转化为向量的有关运算求解.解:设ω=风速,v a=有风时飞机的航行速度,νb=无风时飞机的航行速度,νb=νa-ω.如图所示.设|AB |=|νa |,|CB |=|ω|,|AC |=|νb |, 作AD ∥BC ,CD ⊥AD 于D ,BE ⊥AD 于E , 则∠BAD =45°.设|AB |=150,则|CB |=2)-.∴|CD |=|BE |=|EA |=|DA |=从而|AC |=CAD =30°.∴|νb |=km/h ,方向为北偏西60°.迁移与应用 解:(1)由力的平衡及向量加法的平行四边形法则得G =F 1+F 2,|F 1|=cos θG,|F 2|=|G |tan θ,当θ从0°趋向于90°时,|F 1|,|F 2|都逐渐增大.(2)令|F 1|=cos θG ,由|F 1|≤2|G |得 cos θ≥12. 又因为0°≤θ<90°,所以0°≤θ≤60°.【当堂检测】1.D 解析:|F 1+F 2|=|1OF +2OF | =|(2,2)+(-2,3)|=|(0,5)|=5.2.D 解析:∵AB ∥CD ,|AB |=|CD |,且AC ⊥BD , 故四边形为菱形. 3.B 解析:|ν|=12+22=5,又|AB |=(7-4)2+(12-6)2=45,∴时间t =455=3. 4.16 解析:由∠C =90°,AC =BC =4,知△ABC 是等腰直角三角形, ∴BA =42,∠ABC =45°,∴BA ·BC =42×4×cos 45°=16.5.1 解析:W =F·s =F ·AB =(2,3)·(-4,3)=。
高中数学必修4(人教A版)教案—2.5平面向量应用举例

2. 5平面向量应用举例一、教材分析向量概念有明确的物理背景和几何背景,物理背景是力、速度、加速度等,几何背景是有向线段,可以说向量概念是从物理背景、几何背景中抽象而来的,正因为如此,运用向量可以解决一些物理和几何问题,例如利用向量计算力沿某方向所做的功,利用向量解决平面内两条直线平行、垂直位置关系的判定等问题。
二、教学目标1.通过应用举例,让学生会用平面向量知识解决几何问题的两种方法-----向量法和坐 标法,可以用向量知识研究物理中的相关问题的“四环节” 和生活中的实际问题2.通过本节的学习,让学生体验向量在解决几何和物理问题中的工具作用,增强学生的 积极主动的探究意识,培养创新精神。
三、教学重点难点重点:理解并能灵活运用向量加减法与向量数量积的法则解决几何和物理问题. 难点:选择适当的方法,将几何问题或者物理问题转化为向量问题加以解决. 四、学情分析在平面几何中,平行四边形是学生熟悉的重要的几何图形,而在物理中,受力分析则是其中最基本的基础知识,那么在本节的学习中,借助这些对于学生来说,非常熟悉的内容来讲解向量在几何与物理问题中的应用。
五、教学方法1.例题教学,要让学生体会思路的形成过程,体会数学思想方法的应用。
2.学案导学:见后面的学案3.新授课教学基本环节:预习检查、总结疑惑→情境导入、展示目标→合作探究、精讲点拨→反思总结、当堂检测→发导学案、布置预习六、课前准备1.学生的学习准备:预习本节课本上的基本内容,初步理解向量在平面几何和物理中的 应用2.教师的教学准备:课前预习学案,课内探究学案,课后延伸拓展学案。
七、课时安排:1课时 八、教学过程(一)预习检查、总结疑惑检查落实了学生的预习情况并了解了学生的疑惑,使教学具有了针对性。
(二)情景导入、展示目标教师首先提问:(1)若O 为ABC ∆重心,则OA u u u r +OB u u u r +OC u u u r =0r(2)水渠横断面是四边形ABCD ,DC u u u r =12AB u u u v,且|AD u u u v |=|BC u u u v |,则这个四边形为等腰梯形.类比几何元素之间的关系,你会想到向量运算之间都有什么关系?(3) 两个人提一个旅行包,夹角越大越费力.为什么?教师:本节主要研究了用向量知识解决平面几何和物理问题;掌握向量法和坐标法,以及用向量解决平面几何和物理问题的步骤,已经布置学生们课前预习了这部分,检查学生预习情况并让学生把预习过程中的疑惑说出来。
高中数学必修四教学方案:《平面向量应用举例》

高中数学必修四教学方案:《平面向量应用举例》
在人类历史发展和社会生活中,数学发挥着不可替代的作用,同时也是学习和研究现代科学技术必不可少的基本工具。
下面跟着一起来看看吧。
高中数学必修4《平面向量应用举例》教案
教学准备
教学目标
1.通过平行四边形这个几何模型,归纳总结出用向量方法解决平面几何的问题的”三步曲”;
2.明确平面几何图形中的有关性质,如平移、全等、相似、长度、夹角等可以由向量的线性运算及数量积表示.;
3.让学生深刻理解向量在处理平面几何问题中的优越性.
教学重难点
教学重点:用向量方法解决实际问题的基本方法:向量法解决几何问题的“三步曲”.
教学难点:如何将几何等实际问题化归为向量问题.
教学过程
由于向量的线性运算和数量积运算具有鲜明的几何背景,平面几何图形的许多性质,如平移、全等、相似、长度、夹角等都可以由向量的线性运算及数量积
表示出来,因此,可用向量方法解决平面几何中的一些问题,下面我们通过几个具体实例,说明向量方法在平面几何中的运用。
例1、平行四边形是表示向量加法与减法的几何模型。
如图,你能发现平行四边形对角线的长度与两条邻边长度之间的关系吗?
思考:
运用向量方法解决平面几何问题可以分哪几个步骤?
运用向量方法解决平面几何问题可以分哪几个步骤?
“三步曲”:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3)把运算结果“翻译”成几何关系.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2. 5平面向量应用举例一、教材分析向量概念有明确的物理背景和几何背景,物理背景是力、速度、加速度等,几何背景是有向线段,可以说向量概念是从物理背景、几何背景中抽象而来的,正因为如此,运用向量可以解决一些物理和几何问题,例如利用向量计算力沿某方向所做的功,利用向量解决平面内两条直线平行、垂直位置关系的判定等问题。
二、教学目标1.通过应用举例,让学生会用平面向量知识解决几何问题的两种方法-----向量法和坐 标法,可以用向量知识研究物理中的相关问题的“四环节” 和生活中的实际问题2.通过本节的学习,让学生体验向量在解决几何和物理问题中的工具作用,增强学生的 积极主动的探究意识,培养创新精神。
三、教学重点难点重点:理解并能灵活运用向量加减法与向量数量积的法则解决几何和物理问题. 难点:选择适当的方法,将几何问题或者物理问题转化为向量问题加以解决. 四、学情分析在平面几何中,平行四边形是学生熟悉的重要的几何图形,而在物理中,受力分析则是其中最基本的基础知识,那么在本节的学习中,借助这些对于学生来说,非常熟悉的内容来讲解向量在几何与物理问题中的应用。
五、教学方法1.例题教学,要让学生体会思路的形成过程,体会数学思想方法的应用。
2.学案导学:见后面的学案3.新授课教学基本环节:预习检查、总结疑惑→情境导入、展示目标→合作探究、精讲点拨→反思总结、当堂检测→发导学案、布置预习六、课前准备1.学生的学习准备:预习本节课本上的基本内容,初步理解向量在平面几何和物理中的 应用2.教师的教学准备:课前预习学案,课内探究学案,课后延伸拓展学案。
七、课时安排:1课时 八、教学过程(一)预习检查、总结疑惑检查落实了学生的预习情况并了解了学生的疑惑,使教学具有了针对性。
(二)情景导入、展示目标 教师首先提问:(1)若O 为ABC ∆重心,则OA +OB +OC =0(2)水渠横断面是四边形ABCD ,DC =12AB ,且|AD |=|BC |,则这个四边形为等腰梯形.类比几何元素之间的关系,你会想到向量运算之间都有什么关系?(3) 两个人提一个旅行包,夹角越大越费力.为什么?教师:本节主要研究了用向量知识解决平面几何和物理问题;掌握向量法和坐标法,以及用向量解决平面几何和物理问题的步骤,已经布置学生们课前预习了这部分,检查学生预习情况并让学生把预习过程中的疑惑说出来。
(设计意图:步步导入,吸引学生的注意力,明确学习目标。
) (三)合作探究、精讲点拨。
探究一:(1)向量运算与几何中的结论"若a b =,则||||a b =,且,a b 所在直线平行或重合"相类比,你有什么体会?(2)由学生举出几个具有线性运算的几何实例.教师:平移、全等、相似、长度、夹角等几何性质可以由向量线性运算及数量积表示出来: 例如,向量数量积对应着几何中的长度.如图: 平行四边行ABCD 中,设AB =a ,AD =b ,则AC AB BC a b =+=+(平移),DB AB AD a b =-=-,222||AD b AD ==(长度).向量AD ,AB 的夹角为DAB ∠.因此,可用向量方法解决平面几何中的一些问题。
通过向量运算研究几何运算之间的关系,如距离、夹角等.把运算结果"翻译"成几何关系.本节课,我们就通过几个具体实例,来说明向量方法在平面几何中的运用例1.证明:平行四边形两条对角线的平方和等于四条边的平方和.已知:平行四边形ABCD .求证:222222AC BD AB BC CD DA +=+++. 分析:用向量方法解决涉及长度、夹角的问题时,我们常常要考虑向量的数量积.注意到AC AB AD =+, DB AB AD =-,我们计算2||AC 和2||BD .证明:不妨设AB =a ,AD =b ,则AC =a +b ,DB =a -b ,2||AB =|a |2,2||AD =|b |2.得 2||AC AC AC =⋅=( a +b )·( a +b )= a ·a+ a ·b +b ·a+b ·b = |a |2+2a ·b +|b |2. ①同理 2||DB =|a |2-2a ·b +|b |2. ② ①+②得 2||AC +2||DB =2(|a |2+|b |2)=2(2||AB +2||AD ). 所以,平行四边形两条对角线的平方和等于四条边的平方和.师:你能用几何方法解决这个问题吗?让学生体会几何方法与向量方法的区别与难易情况。
师:由于向量能够运算,因此它在解决某些几何问题时具有优越性,他把一个思辨过程变成了一个算法过程,可以按照一定的程序进行运算操作,从而降低了思考问题的难度.用向量方法解决平面几何问题,主要是下面三个步骤,⑴建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;⑵通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;⑶把运算结果“翻译”成几何关系.变式训练:ABC ∆中,D 、E 、F 分别是AB 、BC 、CA 的中点,BF 与CD 交于点O ,设,.AB a AC b ==(1)证明A 、O 、E 三点共线;(2)用,a b 表示向量AO 。
例2,如图,平行四边形ABCD 中,点E 、F 分别是AD 、DC 边的中点,BE 、BF 分别与AC 交于R 、T 两点,你能发现AR 、RT 、TC 之间的关系吗?分析:由于R 、T 是对角线AC 上两点,所以要判断AR 、RT 、TC 之间的关系,只需要分别判断AR 、RT 、TC 与AC 之间的关系即可.解:设AB =a ,AD =b ,则AC =a +b .由 AR 与AC 共线,因此。
存在实数m ,使得 AR =m (a +b ). 又 由BR 与BE 共线因此 存在实数n ,使得 BR =n BE = n (12b - a ). 由AR AB BR =+=AB + n BE ,得m (a +b )= a + n (12b - a ). 整理得 (1)m n +-a +1()2m n -b =0. 由于向量a 、b 不共线,所以有 10102m n m n +-=⎧⎪⎨-=⎪⎩,解得1323m n ⎧=⎪⎪⎨⎪=⎪⎩. 所以 13AR AC =. 同理 13TC AC =.于是 13RT AC =.所以 AR =RT =TC .说明:本例通过向量之间的关系阐述了平面几何中的方法,待定系数法使用向量方法证明平面几何问题的常用方法.探究二:(1)两个人提一个旅行包,夹角越大越费力.(2)在单杠上做引体向上运动,两臂夹角越小越省力. 这些问题是为什么?师:向量在物理中的应用,实际上就是把物理问题转化为向量问题,然后通过向量运算解决向量问题,最后再用所获得的结果解释物理现象.例3.在日常生活中,你是否有这样的经验:两个人共提一个旅行包,夹角越大越费力;在单杠上作引体向上运动,两臂的夹角越小越省力.你能从数学的角度解释这种现象吗?分析:上面的问题可以抽象为如右图所示的数学模型.只要分析清楚F 、G 、θ三者之间的关系(其中F 为F 1、F 2的合力),就得到了问题的数学解释.解:不妨设|F 1|=|F 2|, 由向量加法的平行四边形法则,理的平衡原理以及直角三角形的指示,可以得到|F 1|=||2cos2G θ.通过上面的式子我们发现,当θ由0~180逐渐变大时,2θ由0~90逐渐变大,cos2θ的值由大逐渐变小,因此,|F 1|有小逐渐变大,即F 1、F 2之间的夹角越大越费力,夹角越小越省力.师:请同学们结合刚才这个问题,思考下面的问题: ⑴θ为何值时,|F 1|最小,最小值是多少? ⑵|F 1|能等于|G |吗?为什么?例4如图,一条河的两岸平行,河的宽度500d =m ,一艘船从A 处出发到河对岸.已知船的速度|v 1|=10km/h ,水流的速度|v 2|=2km/h ,问行驶航程最短时,所用的时间是多少(精确到0.1min)?分析:如果水是静止的,则船只要取垂直于对岸的方向行驶,就能使行驶航程最短,所用时间最短.考虑到水的流速,要使船的行驶航程最短,那么船的速度与水流速度的合速度v 必须垂直于对岸.(用《几何画板》演示水流速度对船的实际航行的影响)解:||v 96=(km/h), 所以, 60 3.1||96d t v ==≈(min). 答:行驶航程最短时,所用的时间是3.1 min .本例关键在于对“行驶最短航程”的意义的解释,即“分析”中给出的穿必须垂直于河岸行驶,这是船的速度与水流速度的合速度应当垂直于河岸,分析清楚这种关系侯,本例就容易解决了。
变式训练:两个粒子A 、B 从同一源发射出来,在某一时刻,它们的位移分别为(4,3),(2,10)A B s s ==,(1)写出此时粒子B 相对粒子A 的位移s;(2)计算s 在A s 方向上的投影。
九、板书设计§2.5 平面向量应用举例例⒈ 用向量法解平面几何 例2 变式训练 问题的“三步曲”例3. 例4 变式训练 十、教学反思本小节主要是例题教学,要让学生体会思路的形成过程,体会数学思想方法的应用。
教学中,教师创设问题情境,引导学生发现解题方法,展示思路的形成过程,总结解题规律。
指导学生搞好解题后的反思,从而提高学生综合应用知识分析和解决问题的能力.十一、学案设计(见下页)2.5平面向量应用举例课前预习学案一、预习目标预习《平面向量应用举例》,体会向量是一种处理几何问题、物理问题等的工具,建立实际问题与向量的联系。
二、预习内容阅读课本内容,整理例题,结合向量的运算,解决实际的几何问题、物理问题。
另外,在思考一下几个问题:1. 例1如果不用向量的方法,还有其他证明方法吗?2. 利用向量方法解决平面几何问题的“三步曲”是什么?3. 例3中,⑴θ为何值时,|F 1|最小,最小值是多少?⑵|F 1|能等于|G |吗?为什么? 三、提出疑惑同学们,通过你的自主学习,你还有哪些疑惑,请把它填在下面的表格中课内探究学案一、学习内容1.运用向量的有关知识(向量加减法与向量数量积的运算法则等)解决平面几何和解析 几何中直线或线段的平行、垂直、相等、夹角和距离等问题.2.运用向量的有关知识解决简单的物理问题. 二、学习过程探究一:(1)向量运算与几何中的结论"若a b =,则||||a b =,且,a b 所在直线平行或重合"相类比,你有什么体会?(2)举出几个具有线性运算的几何实例.例1.证明:平行四边形两条对角线的平方和等于四条边的平方和. 已知:平行四边形ABCD .求证:222222AC BD AB BC CD DA +=+++.试用几何方法解决这个问题利用向量的方法解决平面几何问题的“三步曲”?(1)建立平面几何与向量的联系,(2)通过向量运算,研究几何元素之间的关系,(3)把运算结果“翻译”成几何关系。
