机械设计转动惯量计算公式-参考模板
转动惯量公式表
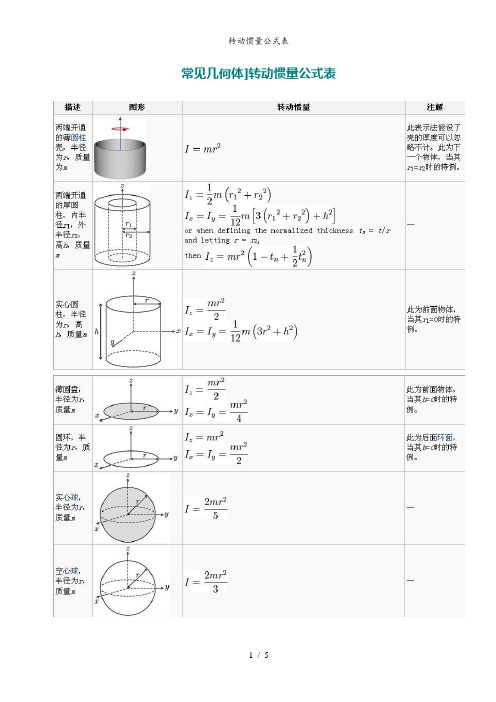
常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12 其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3 其中m是杆的质量,L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回转轴为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外力矩,β为角加速度。
可以看出这个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v 只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
转动惯量计算折算公式

转动惯量计算折算公式
转动惯量(即转动惯性矩)是描述物体对转动运动的惯性的物理量,
它可以用公式I=mr^2来计算,其中I是转动惯量,m是物体的质量,r是
物体的转动半径。
然而,在实际问题中,物体的形状往往是复杂的,不可能直接通过上
述公式来计算转动惯量。
为了解决这个问题,我们可以通过一些折算公式
来将复杂物体的转动惯量转换为一些简单形状的转动惯量之和。
以下是一些常见的折算公式:
1.对于长方体:
-绕通过质心垂直于一条边的转动轴转动:I=(1/12)*m*(a^2+b^2),
其中m是质量,a和b是长方体的两个边长。
-绕通过质心垂直于两条平行边的转动轴转动:I=(1/3)*m*(a^2+b^2),其中m是质量,a和b是长方体的两个边长。
2.对于球体:
-绕通过质心的任意轴转动:I=(2/5)*m*r^2,其中m是质量,r是球
体的半径。
3.对于圆环:
-绕通过圆环中心的垂直于其平面的转动轴转动:I=m*r^2,其中m是
质量,r是圆环的半径。
4.对于圆盘:
-绕通过圆盘中心的垂直于其平面的转动轴转动:I=(1/2)*m*r^2,其中m是质量,r是圆盘的半径。
5.对于薄杆(在转动轴与薄杆所在直线垂直的情况下):
-绕通过薄杆中心的转动轴转动:I=(1/12)*m*L^2,其中m是质量,L 是薄杆的长度。
这些折算公式可以帮助我们将复杂物体的转动惯量转换为一些简单形状的转动惯量之和,从而简化计算过程。
在实际应用中,我们可以根据物体的形状选择合适的折算公式来计算转动惯量,从而更好地描述物体的转动运动。
机械设计转动惯量计算公式讲解学习

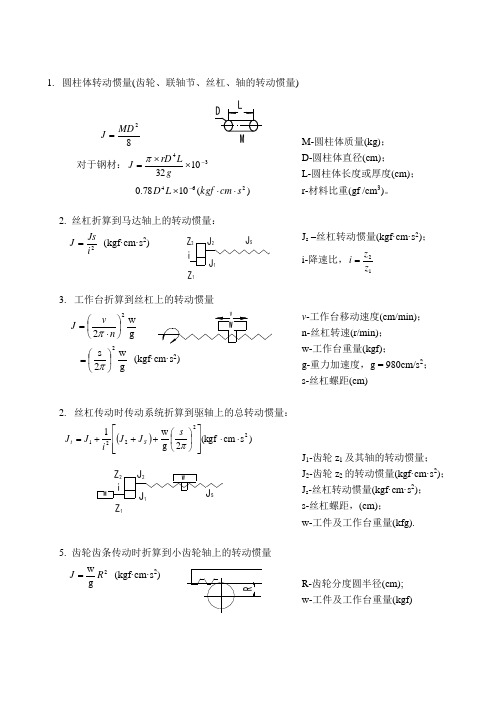
机械设计转动惯量计算公式1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯- M-圆柱体质量(kg);D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2i Js J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π (kgf·cm·s 2)v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J JiJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2);J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm);w-工件及工作台重量(kgf)。
机械设计常用计算公式 集(一)

运动学篇一、直线运动:基本公式:(距离、速度、加速度和时间之间的关系)1)路程=初速度x时间+加速度x时间^2/22)平均速度=路程/时间;3)末速度-初速度=2x加速度x路程;4)加速度=(末速度-初速度)/时间5)中间时刻速度=(初速度+末速度)/26)力与运动之间的联系:牛顿第二定律:F=ma,[合外力(N)=物体质量(kg)x加速度(m/s^2)] (注:重力加速度g=9.8m/s^2或g=9.8N/kg)二、旋转运动:(旋转运动与直线运动类似,注:弧度是没有单位的)单位对比:圆的弧长计算公式:弧长s=rθ=圆弧的半径x圆弧角度(角位移)周长=C=2πr=πd,即:圆的周长=2x3.14x圆弧的半径=3.14x圆弧的直径旋转运动中角位移、弧度(rad)和公转(r)之间的关系。
1)1r(公转)=2π(弧度)=360°(角位移)2)1rad=360°/(2π)=57.3°3)1°=2π/360°=0.01745rad4)1rad=0.16r5)1°=0.003r6)1r/min=1x2x3.14=6.28rad/min7)1r/min=1x360°=360°/min三、旋转运动与直线运动的联系:1)弧长计算公式(s=rθ):弧长=圆弧的半径x圆心角(圆弧角度或角位移)2)角速度(角速度是角度(角位移)的时间变化率)(ω=θ/t):角速度=圆弧角度/时间注:结合上式可推倒出角速度与圆周速度(即:s/t也称切线速度)之间的关系。
S3)圆周速度=角速度x半径,(即:v=ωr)注:角度度ω的单位一般为rad/s,实际应用中,旋转速度的单位大多表示为r/min (每分钟多少转)。
可通过下式换算:1rad/s=1x60/(2x3.14)r/min例如:电机的转速为100rad/s的速度运行,我们将角速度ω=100rad/s换算成r/min 单位,则为:ω=100rad/s=100x60/(2π)=955r/min4)rad/s和r/min的联系公式:转速n(r/min)= ω(rad/s)x60/(2π),即:转速(r/min)=角速度(rad/s)x60/(2π);5)角速度ω与转速n之间的关系(使用时须注意单位统一):ω=2πn,(即:带单位时为角速度(rad/s)=2x3.14x转速(r/min)/60)6)直线(切线)速度、转速和2πr(圆的周长)之间的关系(使用时需注意单位):圆周速度v=2πrn=(πd)n注:线速度=圆周速度=切线速度四、转矩计算公式:(1)普通转矩:T=Fr即:普通转矩(N*m)=力(N)x半径(m);(2)加速转矩:T=Jα即:加速转矩(N*m)=角加速度α(rad/s^2)x转动惯量J(kg*m^2)单位换算:转动惯量J(kg*cm^2):1kg*cm^2=10^-6kg*m^2;角加速度α(rad/s^2):1r/s^2=1x2xπrad/s^2;单位转换过程推导:(注:kgf*m(千克力*米),1kgf*m=9.8N*m,g=9.8N/kg=9.8m/s^2)假设转动惯量J =10kg*m^2,角加速度α=10rad/s^2,推导出转矩T的单位过程如下:T=J x α=10x(kg*m^2)x10(rad/s^2)=100(kgf*m/s^2)=()()()=100N*m两个简化单位换算公式:(注:单位换算其物理含义也不同,下式仅用于单位换算过程中应用。
转动惯量公式

nema标准中的计算是如下(转化公式):J=A×0.055613×(Pn^0.95)÷(n/1000)^2.4-0.004474×(Pn^1.5)÷(n/1000)^1.8A小于等于1800rpm时取24,A大于1800rpm时取27 Pn为功率(kw) n 为同步转速高压电动机在设计时,要求计算出转子的转动惯量。
下面对计算方法做一分析。
转动惯量是物体在转动时惯性的度量,它不仅与物体质量的大小有关,还与物体质量分体情况有关。
机械工程师手册给出了一些简单形状物体的转动惯量。
1、圆柱体沿轴线转动惯量:Kg•m2 (1)式中:M —圆柱体质量KgR —圆柱体外径半径 m2、空心圆柱体沿轴线转动惯量:Kg•m2 (2)式中: M —空心圆柱体质量KgR —空心圆柱体外半径 mr —空心圆柱体内半径m3、薄板沿对称线转动惯量:Kg•m2 (3)式中:M —薄板质量Kga —薄板垂直于轴线方向的宽度m物体的转动惯量除了用J表示外,在工程上有的用物体的重量G和物体的回转直径D的平方的乘积GD2来表示,也称为物体的飞轮力矩或惯量矩,单位N•m2或Kg f m2。
物体的飞轮力矩GD2和转动惯量J之间的关系,用下式表示:N•m2 (4)式中:g —重力加速度 g=9.81 m/s2将重力单位N化为习惯上的重力单位Kgf ,则(4)变为:Kg f m2 (5)由以上公式,可以对鼠笼型高压电机的转动惯量进行计算。
计算时,将高压电机转子分解为转子铁心(包括导条和端环)、幅铁、转轴三部分,分别算出各部分的Jn,各部分的转动惯量相加即得电机的转动惯量J。
如需要,按(5)式换算成飞轮力矩GD2。
一般产品样本中要求给定的是转动惯量J,兰州引进的电磁设计程序计算出的是飞轮力矩GD2。
计算程序如下:1、转子铁心的转动惯量,按空心圆柱公式(2)进行计算,考虑导条端环度大小的因素,以系数c进行修正。
转动惯量基本公式

转动惯量基本公式
常用转动惯量表达式:I=mr2。
其中m是其质量,r是质点和转轴的垂直距离。
转动惯量是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度。
1、对于细杆:
当回转轴过杆的中点(质心)并旋转轴杆时i=ml2/i2;其中m就是杆的'质量,l就是
杆的长度。
当回转轴过杆的端点并旋转轴杆时i=ml2/3;其中m就是杆的质量,l就是杆
的长度。
2、对于圆柱体:
当回转轴就是圆柱体轴线时i=mr2/2;其中m就是圆柱体的质量,r就是圆柱体的半径。
3、对于细圆环:
当回转轴通过环心且与环面横向时,i=mr2;当回转轴通过环路边缘且与环面横向时,i=2mr2;i=mr2/2沿环的某一直径;r为其半径。
4、对于立方体:
当回转轴为其中心轴时,i=ml2/6;当回转轴为其棱边时i=2ml2/3;当回转轴为其体
对角线时,i=3ml2/16;l为立方体边长。
5、对于实心球体:
当回转轴为球体的中心轴时,i=2mr2/5;当回转轴为球体的切线时,i=7mr2/5;r为
球体半径。
转动惯量计算折算公式

1.圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)之蔡仲巾千创作82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg);D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-资料比重(gf /cm 3)。
2.丝杠折算到马达轴上的转动惯量:2iJsJ =(kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π(kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf); g-重力加速度,g=980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm);w-工件及工作台重量(kgf)。
转动惯量计算公式-转动惯量公式

创作编号:GB8878185555334563BT9125XW创作者: 凤呜大王*1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg); D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2i Js J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2);J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J iJ J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm);w-工件及工作台重量(kgf)。
转动惯量计算折算公式
1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg); D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2iJs J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
机械设计常用计算公式 集(一)

运动学篇一、直线运动:基本公式:(距离、速度、加速度和时间之间的关系)1)路程=初速度x时间+加速度x时间^2/22)平均速度=路程/时间;3)末速度-初速度=2x加速度x路程;4)加速度=(末速度-初速度)/时间5)中间时刻速度=(初速度+末速度)/26)力与运动之间的联系:牛顿第二定律:F=ma,[合外力(N)=物体质量(kg)x加速度(m/s^2)] (注:重力加速度g=9.8m/s^2或g=9.8N/kg)二、旋转运动:(旋转运动与直线运动类似,注:弧度是没有单位的)单位对比:圆的弧长计算公式:弧长s=rθ=圆弧的半径x圆弧角度(角位移)周长=C=2πr=πd,即:圆的周长=2x3.14x圆弧的半径=3.14x圆弧的直径旋转运动中角位移、弧度(rad)和公转(r)之间的关系。
1)1r(公转)=2π(弧度)=360°(角位移)2)1rad=360°/(2π)=57.3°3)1°=2π/360°=0.01745rad4)1rad=0.16r5)1°=0.003r6)1r/min=1x2x3.14=6.28rad/min7)1r/min=1x360°=360°/min三、旋转运动与直线运动的联系:1)弧长计算公式(s=rθ):弧长=圆弧的半径x圆心角(圆弧角度或角位移)2)角速度(角速度是角度(角位移)的时间变化率)(ω=θ/t):角速度=圆弧角度/时间注:结合上式可推倒出角速度与圆周速度(即:s/t也称切线速度)之间的关系。
S3)圆周速度=角速度x半径,(即:v=ωr)注:角度度ω的单位一般为rad/s,实际应用中,旋转速度的单位大多表示为r/min (每分钟多少转)。
可通过下式换算:1rad/s=1x60/(2x3.14)r/min例如:电机的转速为100rad/s的速度运行,我们将角速度ω=100rad/s换算成r/min 单位,则为:ω=100rad/s=100x60/(2π)=955r/min4)rad/s和r/min的联系公式:转速n(r/min)= ω(rad/s)x60/(2π),即:转速(r/min)=角速度(rad/s)x60/(2π);5)角速度ω与转速n之间的关系(使用时须注意单位统一):ω=2πn,(即:带单位时为角速度(rad/s)=2x3.14x转速(r/min)/60)6)直线(切线)速度、转速和2πr(圆的周长)之间的关系(使用时需注意单位):圆周速度v=2πrn=(πd)n注:线速度=圆周速度=切线速度四、转矩计算公式:(1)普通转矩:T=Fr即:普通转矩(N*m)=力(N)x半径(m);(2)加速转矩:T=Jα即:加速转矩(N*m)=角加速度α(rad/s^2)x转动惯量J(kg*m^2)单位换算:转动惯量J(kg*cm^2):1kg*cm^2=10^-6kg*m^2;角加速度α(rad/s^2):1r/s^2=1x2xπrad/s^2;单位转换过程推导:(注:kgf*m(千克力*米),1kgf*m=9.8N*m,g=9.8N/kg=9.8m/s^2)假设转动惯量J =10kg*m^2,角加速度α=10rad/s^2,推导出转矩T的单位过程如下:T=J x α=10x(kg*m^2)x10(rad/s^2)=100(kgf*m/s^2)=()()()=100N*m两个简化单位换算公式:(注:单位换算其物理含义也不同,下式仅用于单位换算过程中应用。
机械设计转动惯量计算公式

机械设计转动惯量计算公式
机械设计中,转动惯量是描述物体对于转动运动的惯性特性的物理量。
转动惯量的大小与物体的质量分布和物体的形状有关,计算转动惯量的公
式也与不同形状的物体有关。
以下将介绍几种常见的物体形状对应的转动惯量计算公式。
1.球体:
对于球体,其转动惯量计算公式为I=2/5*m*r^2,其中,I表示转动
惯量,m为球体的质量,r为球体的半径。
2.长直柱体:
对于长度为L、半径为r的长直柱体,其转动惯量计算公式为
I=1/12*m*L^2,其中,I表示转动惯量,m为长直柱体的质量,L为直柱
体的长度。
3.长直线杆:
对于长度为L的直线杆,其转动惯量计算公式为I=1/3*m*L^2,其中,I表示转动惯量,m为直线杆的质量,L为直线杆的长度。
4.圆盘/圆环:
对于半径为R,质量为m的圆盘/圆环,其转动惯量计算公式为
I=1/2*m*R^2,其中,I表示转动惯量,m为圆盘/圆环的质量,R为圆盘/
圆环的半径。
5.长方体:
对于边长为a、b、c的长方体,其转动惯量计算公式为
I=1/12*m*(a^2+b^2),其中,I表示转动惯量,m为长方体的质量,a、b
分别为长方体的两个相邻边的长度。
需要注意的是,上述公式中的质量单位为千克(kg),长度单位为米(m)。
同时,以上公式仅适用于转轴经过物体质心的情况,若转轴位于
其他位置,则需要使用平行轴定理对转动惯量进行修正计算。
总结起来,机械设计中常用的转动惯量计算公式包括球体、长直柱体、长直线杆、圆盘/圆环、长方体等形状对应的公式。
通过合理运用这些公式,可以方便地计算出物体在转动运动中的惯性特性。
转动惯量计算公式转动惯量公式

转动惯量计算公式转动惯量公式The Standardization Office was revised on the afternoon of December 13, 20201. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯- M-圆柱体质量(kg);D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2i Js J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π (kgf·cm·s 2)v -工作台移动速度(cm/min); n-丝杠转速(r/min);w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2);J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm);w-工件及工作台重量(kgf)。
转动惯量计算折算公式
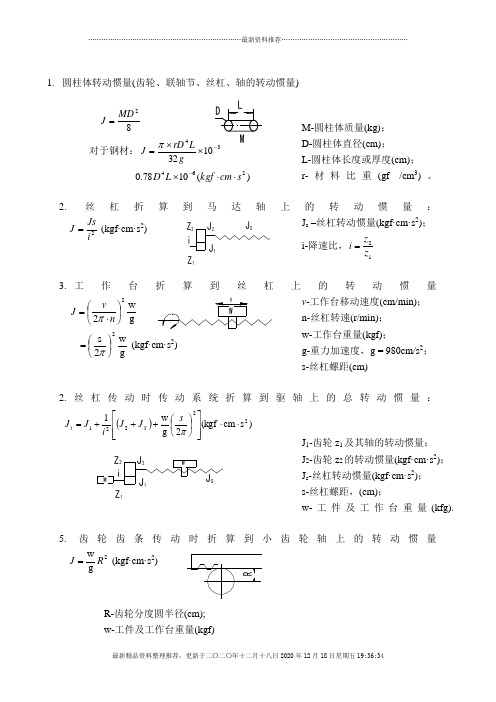
1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:432⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg); D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2.丝杠折算到马达轴上的转动惯量:2i Js J = (kgf·cm·s 2) J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2;s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J i J J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm);w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
转动惯量计算公式-转动惯量公式

1.圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)之马矢奏春创作82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg);D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-资料比重(gf /cm 3)。
2.丝杠折算到马达轴上的转动惯量:2iJsJ =(kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π(kgf·cm·s 2)v -工作台移动速度(cm/min);n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g=980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J i J J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm);w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2g wR J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴, Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2); R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
转动惯量公式表
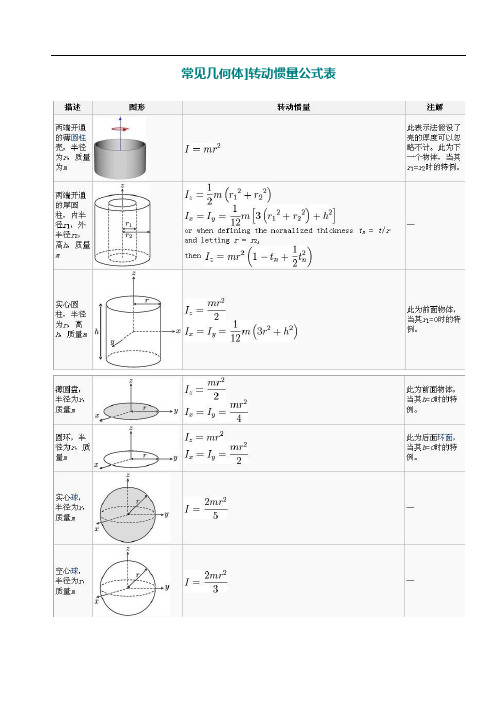
常见几何体]转动惯量公式表对于细杆当回转轴过杆的中点并垂直于杆时;J=m(L^2)/12 其中m是杆的质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时:J=m(L^2)/3 其中m是杆的质量,L是杆的长度。
对于圆柱体当回转轴是圆柱体轴线时;J=m(r^2)/2其中m是圆柱体的质量,r是圆柱体的半径。
对于细圆环当回转轴通过中心与环面垂直时,J=mR^2;当回转轴通过边缘与环面垂直时,J=2mR^2;R为其半径对于薄圆盘当回转轴通过中心与盘面垂直时,J=﹙1/2﹚mR^2;当回转轴通过边缘与盘面垂直时,J=﹙3/2﹚mR^2;R为其半径对于空心圆柱当回转轴为对称轴时,J=﹙1/2﹚m[(R1)^2+(R2)^2];R1和R2分别为其内外半径。
对于球壳当回转轴为中心轴时,J=﹙2/3﹚mR^2;当回转轴为球壳的切线时,J=﹙5/3﹚mR^2;R为球壳半径。
对于实心球体当回转轴为球体的中心轴时,J=﹙2/5﹚mR^2;当回转轴为球体的切线时,J=﹙7/5﹚mR^2;R为球体半径对于立方体当回转轴为其中心轴时,J=﹙1/6﹚mL^2;当回转轴为其棱边时,J=﹙2/3﹚mL^2;当回转轴为其体对角线时,J=(3/16)mL^2;L为立方体边长。
只知道转动惯量的计算方式而不能使用是没有意义的。
下面给出一些(绕定轴转动时)的刚体动力学公式。
角加速度与合外力矩的关系:角加速度与合外力矩式中M为合外力矩,β为角加速度。
可以看出这个式子与牛顿第二定律是对应的。
角动量:角动量刚体的定轴转动动能:转动动能注意这只是刚体绕定轴的转动动能,其总动能应该再加上质心动能。
只用E=(1/2)mv^2不好分析转动刚体的问题,是因为其中不包含刚体的任何转动信息,里面的速度v 只代表刚体的质心运动情况。
由这一公式,可以从能量的角度分析刚体动力学的问题。
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
机械设计转速公式

机械设计转速公式
转动惯量篇:
常用单位介绍:
密度一般为 g/ 或 kg/(1g/=1000kg/);g=9.8m/;转动惯
量 J 的单位一般为 kg*;力矩的单位为 N*m;角加速度α的单位为 r/
皮带重力惯量计算公式:
皮带传送系统的总惯量为:
J 总=J 电机转动惯量+J 电机侧滚轮转动惯量+J 对于电机轴而言的负载侧滚轮的转动惯量+J 对于电机轴而言的传送带转动惯量+J 对于电机轴而言负载转动惯量
(1)J 对于电机轴而言:负载转动惯量=
(2)J 对于电机轴而言的传送带转动惯量
(3)J 对于电机轴而言的负载侧滚轮的转动惯量
(4)传动比
式中:
WB 一传送带所受的重力;
i 一传动比;
DPL 一负载侧滚轮直径;
DPM 一电机侧滚轮直径;
e 一机械效率;
伺服电机驱动滚珠丝杠:
电机输出转矩=匀速运动时的驱动转矩+预压引起的摩擦转矩+加速运动时
的加速转矩;
(1)匀速动时的驱动转矩:
匀速运动时的驱动转矩(N*cm)=匀速运动时的外部载荷(N)x 丝杆导程(cm)/
(2x 丝杆效率 x3.14);
注:丝杆效率一般取 0.9;
(2)预压引起的摩擦转矩:
预压引起的摩擦转矩(N*cm)=内部摩擦系数 x 预压载荷(N)x 丝杆导程(cm)
/(2x3.14);
注:无预压时,载荷为 0;预压载荷大小查相关产品手册;
(3)加速运动时的加速转矩:
加速转矩(N*m)=总惯量(kg*m^2)x 电动机轴角加速度(rad/s^2);
加速度(rad/s)=转速(r/min)x60/(2x3.14);。
常用转动惯量公式

常用转动惯量公式
常用转动惯量表达式:I=mr2。
其中m是其质量,r是质点和转轴的垂直距离。
转动惯量是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度。
扩展资料
转动惯量计算公式
1、对于细杆:
当回转轴过杆的中点(质心)并垂直于杆时I=mL2/I2;其中m是杆的'质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时I=mL2/3;其中m是杆的质量,L是杆的长度。
2、对于圆柱体:
当回转轴是圆柱体轴线时I=mr2/2;其中m是圆柱体的质量,r 是圆柱体的半径。
3、对于细圆环:
当回转轴通过环心且与环面垂直时,I=mR2;当回转轴通过环边缘且与环面垂直时,I=2mR2;I=mR2/2沿环的某一直径;R为其半径。
4、对于立方体:
当回转轴为其中心轴时,I=mL2/6;当回转轴为其棱边时I=2mL2/3;当回转轴为其体对角线时,I=3mL2/16;L为立方体边长。
5、对于实心球体:
当回转轴为球体的中心轴时,I=2mR2/5;当回转轴为球体的切线时,I=7mR2/5;R为球体半径。
转动惯量计算折算公式
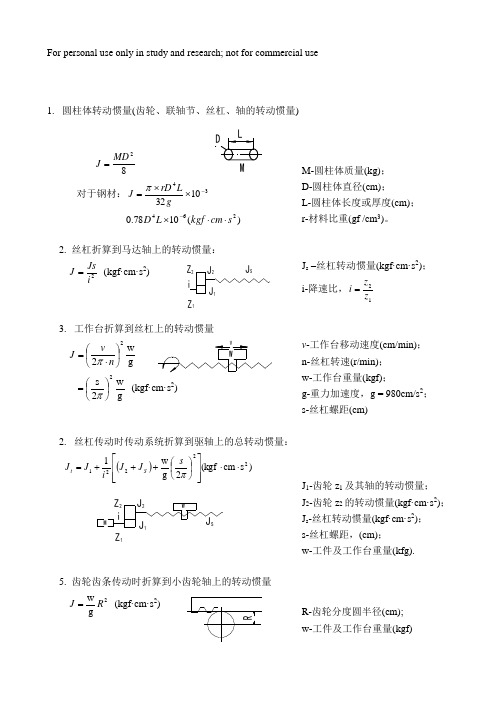
For personal use only in study and research; not for commercial use1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材:341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg); D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:2iJs J = (kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1,J 2-分别为Ⅰ轴,Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
常用转动惯量公式

常用转动惯量公式
常用转动惯量表达式:I=mr2。
其中m是其质量,r是质点和转轴的垂直距离。
转动惯量是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度。
扩展资料
转动惯量计算公式
1、对于细杆:
当回转轴过杆的中点(质心)并垂直于杆时I=mL2/I2;其中m是杆的'质量,L是杆的长度。
当回转轴过杆的端点并垂直于杆时I=mL2/3;其中m是杆的质量,L是杆的长度。
2、对于圆柱体:
当回转轴是圆柱体轴线时I=mr2/2;其中m是圆柱体的质量,r 是圆柱体的半径。
3、对于细圆环:
当回转轴通过环心且与环面垂直时,I=mR2;当回转轴通过环边缘且与环面垂直时,I=2mR2;I=mR2/2沿环的某一直径;R为其半径。
4、对于立方体:
当回转轴为其中心轴时,I=mL2/6;当回转轴为其棱边时I=2mL2/3;当回转轴为其体对角线时,I=3mL2/16;L为立方体边长。
5、对于实心球体:
当回转轴为球体的中心轴时,I=2mR2/5;当回转轴为球体的切线时,I=7mR2/5;R为球体半径。
向你推荐的相关文章
相关文章列表
微信扫码分享。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)
8
2
MD J =
对于钢材:3
410
32-⨯⨯=g
L
rD J π
)
(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg); D-圆柱体直径(cm); L-圆柱体长度或厚度(cm); r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量:
2i Js J = (kgf·cm·s 2) J s –丝杠转动惯量(kgf·cm·s 2); i-降速比,1
2
z z i =
3. 工作台折算到丝杠上的转动惯量
g
w
22⎪
⎭⎫ ⎝⎛⋅
=n v J π g w
2s 2
⎪
⎭⎫ ⎝⎛=π (kgf·cm·s 2) v -工作台移动速度(cm/min); n-丝杠转速(r/min); w-工作台重量(kgf);
g-重力加速度,g = 980cm/s 2; s-丝杠螺距(cm)
2. 丝杠传动时传动系统折算到驱轴上的总转动惯量:
())
s
cm (kgf 2g w 122
221⋅⋅⎥
⎥⎦⎤
⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs
J J i J J S t
J 1-齿轮z 1及其轴的转动惯量; J 2-齿轮z 2的转动惯量(kgf·cm·s 2); J s -丝杠转动惯量(kgf·cm·s 2); s-丝杠螺距,(cm); w-工件及工作台重量(kfg).
5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量
2
g
w R J =
(kgf·cm·s 2)
R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)
6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量
⎪⎪⎭⎫
⎝⎛++=2221g w 1R J i J J t
J 1,J 2-分别为Ⅰ轴,
Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2);
R-齿轮z 分度圆半径(cm); w-工件及工作台重量(kgf)。
马达力矩计算
(1) 快速空载时所需力矩:
0f amax M M M M ++= (2) 最大切削负载时所需力矩: t 0f t a M M M M M +++=
(3) 快速进给时所需力矩:
0f M M M +=
式中M amax —空载启动时折算到马达轴上的加速力矩(kgf·m);
M f —折算到马达轴上的摩擦力矩(kgf·m);
M 0—由于丝杠预紧引起的折算到马达轴上的附加摩擦力矩(kgf·m);
M at —切削时折算到马达轴上的加速力矩(kgf·m); M t —折算到马达轴上的切削负载力矩(kgf·m)。
在采用滚动丝杠螺母传动时,M a 、M f 、M 0、M t 的计算公式如下: (4) 加速力矩: 2a 106.9M -⨯=
T
n
J r (kgf·m) s T 17
1=
J r —折算到马达轴上的总惯量; T —系统时间常数(s); n —马达转速( r/min ); 当 n = n max 时,计算M amax n = n t 时,计算M at
n t —切削时的转速( r / min )
(5) 摩擦力矩:
20f 10i
2s
F M -⨯⋅⋅⋅=
ηπ(kgf·m)
F 0—导轨摩擦力(kgf); s —丝杠螺距(cm); i —齿轮降速比;
η—传动链总效率;一般η=0.7~0.85。
(6) 附加摩擦力矩:
()
22
0001012M -⨯-⋅=
ηπηi
s P (kgf·m) P 0—滚珠丝杠预加载荷(kg·f);
s —丝杠螺距(cm);
η—传动链总效率; i —齿轮降速比;
η0—滚珠丝杠未预紧式的效率,计算公式 见本手册第2测第425页,一般η0≥0.9。
(7) 切削力矩: 2t 102M -⨯⋅=
i
s
P t πη(kgf·m) P t —进给方向的最大切削力(kg· f); s —丝杠螺距(cm);
η—传动链总效率;
i —齿轮降速比。
---精心整理,希望对您有所帮助。
