河北省中考数学总复习 第一编 教材知识梳理篇 第6章 图形的变化 第1节 图形的对称与择叠中考真题及
中考数学 第一编 教材知识梳理篇 第六章 图形的变化

中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
2017年中考数学命题研究(河北专版)
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
2017年中考数学命题研究(河北专版)
河北8年中考真题及模拟
中考考点清单
中考重难点突破
中考备考方略
河北省中考数学总复习 第一编 教材知识梳理篇 第6章 图形的变化 第3节 视图与投影(精讲)试题
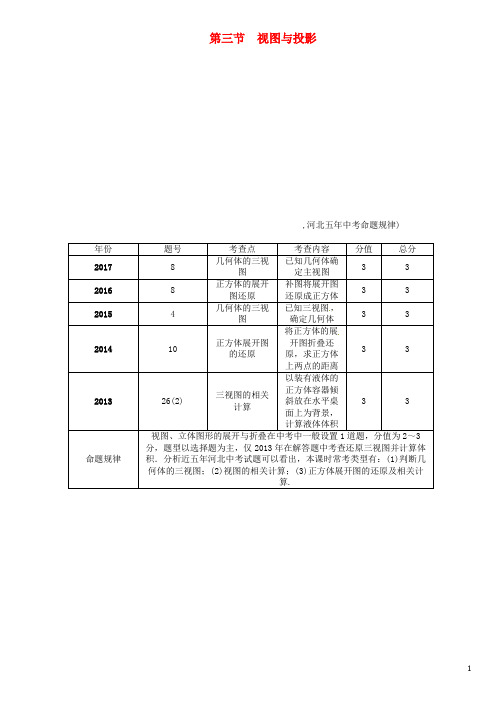
第三节视图与投影,河北五年中考命题规律)年份题号考查点考查内容分值总分20178 几何体的三视图已知几何体确定主视图3 320168 正方体的展开图还原补图将展开图还原成正方体3 32015 4 几何体的三视图已知三视图,确定几何体3 3201410 正方体展开图的还原将正方体的展开图折叠还原,求正方体上两点的距离3 3201326(2) 三视图的相关计算以装有液体的正方体容器倾斜放在水平桌面上为背景,计算液体体积3 3命题规律视图、立体图形的展开与折叠在中考中一般设置1道题,分值为2~3分,题型以选择题为主,仅2013年在解答题中考查还原三视图并计算体积.分析近五年河北中考试题可以看出,本课时常考类型有:(1)判断几何体的三视图;(2)视图的相关计算;(3)正方体展开图的还原及相关计算.,河北五年中考真题及模拟)视图的识别与相关计算1.(2017河北中考)如图是由相同的小正方体木块粘在一起的几何体,它的主视图是( A ),A) ,B),C) ,D) 2.(2016沧州一模)如图中的三视图所对应的几何体是( B ),A) ,B),C) ,D) 3.(2014张家口二模)图中几何体的主视图是( A ),A),B),C) ,D)正方体展开图的还原及相关计算4.(2016河北中考)图①和图②中所有的正方形都全等,将图①的正方形放在图②中的①②③④某一位置,所组成的图形不能围成正方体的位置是( A )A.①B.②C.③ D.④5.(2015保定中考模拟)将图①围成图②的正方体,则图①中的红心“”标志所在的正方形是正方体中的( A ) A.面CDHE B.面BCEFC.面ABFG D.面ADHG6.(2014河北中考)图①是边长为1的六个小正方形组成的图形,它可以围成图②的正方体,则图①中小正方形顶点A,B在围成的正方体上的距离是( B )A.0 B.1 C. 2 D. 37.(2014保定中考模拟)图①是一个小正方体的侧面展开图,小正方体从图②所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是( D )A.和 B.谐 C.社 D.会投影8.(2017沧州一模)如图,晚上小亮在路灯下散步,在小亮由A处走到B处这一过程中,他在地上的影子( C)A.逐渐变短B.逐渐变长C.先变短后变长D.先变长后变短9.(2017邯郸中考模拟)小华拿着一块正方形木板在阳光下做投影实验,这块正方形木板在地面上形成的投影不可能是( A),A) ,B),C) ,D),中考考点清单)投影平行投影由平行光线照射在物体上所形成的投影,叫做平行投影正投影投影线垂直照射在投影面上的物体的投影叫做正投影中心投影由一点射出的光线照射在物体上所形成的投影,叫做中心投影几何体的三视图1.一个几何体的正投影,又叫做这个几何体的视图.从正面得到的视图叫做主视图,从上面得到的视图叫做俯视图,从左面得到的视图叫做左视图.2.三种视图的关系(1)主视图可反映出物体的长和高,俯视图可反映出物体的长和宽,左视图可反映出物体的高和宽.(2)在画三视图时,主、俯视图要长对正,主、左视图要高平齐,俯、左视图要宽相等,看得见的轮廓线要画成实线,看不见的轮廓线要画成虚线.34.名称几何体体积表面积正方体__a3__ 6a2长方体abc__2(ab+bc+ac)__三棱柱h·S底面2S底面+h·C底长圆锥13πr2hπr2+πlr(l为母线长)圆柱πr2h2πr2+2πrh球43πR34πR21.由三视图确定出实物的形状和结构.2.由部分特殊图确定出实物的形状和结构.立体图形的展开与折叠5常见几何体展开图图示(选其一种)6.续表【易错警示】由上面几个展开图可以看出,不会出现两种形式的图形即“凹”字型和“田”字型.如下面2个图形:图①与图②两种形式不是正方体的表面展开图.7.立体图形的折叠一个几何体能展开成一个平面图形,这个平面图形就可以折叠成相应的几何体,展开与折叠是一个互逆的过程.,中考重难点突破)几何体的三视图【例1】(2017烟台中考)如图所示的工件,其俯视图是( D),A) ,B),C) ,D) 【解析】俯视图是从上往下看的,有两个圆面,但小圆面的线条应该是虚线.【答案】B1.(2017武汉中考)某物体的主视图如图所示,则该物体可能为( A ),A) ,B),C) ,D) 2.(宜昌中考)将一根圆柱形的空心钢管任意放置,它的主视图不可能是( A ),A) ,B),C) ,D) 3.(2017绵阳中考)如图所示的几何体的主视图正确的是( D),A) ,B),C) ,D) 4.(2017常德中考)如图是一个几何体的三视图,则这个几何体是( B),A) ,B),C) ,D)5.(山西中考)如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置上小正方体的个数,则该几何体的左视图是( A),A) ,B),C) ,D) 6.(2017绍兴中考)如图是一个正方体,则它的表面展开图可以是( B),A),B),C),D)7.(2017通辽中考)下列四个几何体的俯视图中与众不同的是( B),A),B),C) ,D) 8.(枣庄中考)有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( C)A.白B.红C.黄D.黑9.(2017齐齐哈尔中考)一个几何体的主视图和俯视图如图所示,若这个几何体最多有a个小正方体组成,最少有b个小正方体组成,则a+b等于( C)A.10 B.11 C.12 D.13立体图形的有关计算【例2】(扬州中考)如图,这是一个长方体的主视图和俯视图,由图示数据(单位:cm)可以得出该长方体的体积是____cm3.【解析】观察其视图知:该几何体为长方体,且长方体的长为3,宽为2,高为3,故其体积为:3×3×2=18.【答案】1810.(2017荆州中考)如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( D)A.800π+1 200 B.160π+1 700C.3 200π+1 200 D.800π+3 00011.(2017湖州中考)如图是按1∶10的比例画出的一个几何体的三视图,则该几何体的侧面积是( D) A.200 cm2B.600 cm2C.100πcm2D.200πcm212.(2017呼和浩特中考)如图是某几何体的三视图,根据图中数据,求得该几何体的表面积为__(225+252)π__.(第12题图)(第13题图)13.(2017滨州中考)如图,一个几何体的三视图分别是两个矩形.一个扇形,则这个几何体表面积的大小为__15π+12__.。
(河北专版)2019年中考数学一轮复习第六章图形的变换6.1图形的相似(讲解部分)素材(pdf)

(3) 在 әBCA 与 әACD 中, øB + øC = 90ʎ , øDAC + øC = AC DC = , BC AC
BD AB = ,即 AB 2 = BD㊃BC. AB BC
(1) AD 2 = BD㊃DC. (2) AB 2 = BD㊃BC. (3) AC 2 = CD㊃BC. 证明㊀ (1) 在әBAD 与әACD 中,øB +øC = 90ʎ ,øDAC + øC = 90ʎ ,ʑ øB = øDAC,
㊀ ㊀ 变式训练 1㊀ 如图, 小正方形的边长均为 1, 则下列图中的 三角形( 阴影部分) 与әABC 相似的是 (㊀ ㊀ )
ȵ әABC 是等腰直角三角形,ʑ AB = AC = 3a, ʑ AP = AB - BP = 2a,AQ = CQ - AC = ʑ P,Q 两点间的距离 PQ = 3 a, 2
㊀ ㊀ ㊀ ㊀
角形余料 ABC,它的边 BC = 120 mm, 高 AD = 正方形零件,使正方形的一边在 BC 上, 其余两个 顶点分别在 AB, AC 上. 问加工成的正方形零件的 边长为多少 mm? 80 mm. 要把它加 工成
如 图, 有 一 块 三
AE 2x 80- x 240 480 = ,ʑ ,解得 x = ,ʑ PN = 2x = mm. AD 120 80 7 7 ʑ 这个矩形零件的两条邻边长分别为 ʑ (2) 设 PQ = y mm,易得әAPNʐәABC,
ʑ S 矩形 = y 120-
PN AE PN 80- y 3 = ,ʑ = ,解得 PN = 120- y mm, BC AD 120 80 2
(
)
(
两个并排放置的正方形所组成的, 如图 ①, 此时, 这个矩形零件 的两条邻边长又分别为多少 mm? 请你计算; 样,此矩形零件的两条邻边长就不能确定, 但这个矩形面积有最 大值,求达到最大值时矩形零件的两条邻边长.
河北省2018年中考数学总复习 第一编 教材知识梳理篇 第6章 图形的变化 第1节 图形的对称与折叠(精讲)试题
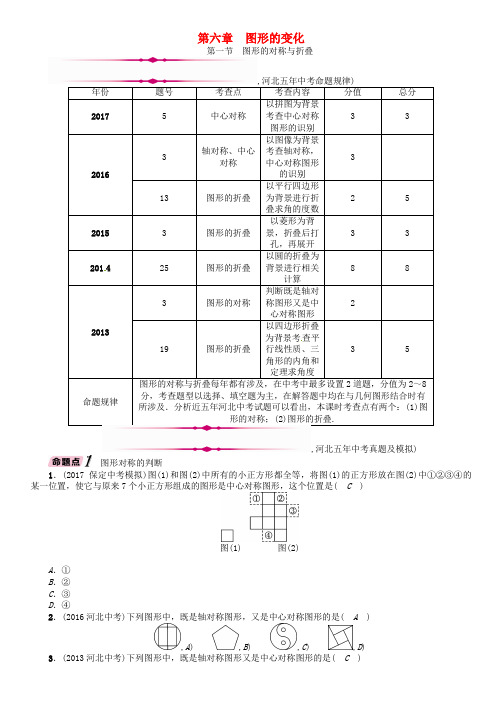
第六章 图形的变化第一节 图形的对称与折叠4为背景考查平形的对称;(2)图形的折叠,河北五年中考真题及模拟)图形对称的判断1.(2017保定中考模拟)图(1)和图(2)中所有的小正方形都全等,将图(1)的正方形放在图(2)中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是( C )图(1) 图(2)A .①B .②C .③D .④2.(2016河北中考)下列图形中,既是轴对称图形,又是中心对称图形的是( A ) ,A ) ,B ) ,C ) ,D )3.(2013河北中考)下列图形中,既是轴对称图形又是中心对称图形的是( C ),A),B),C),D)4.(2015石家庄四十一中一模)下列四个艺术字中,不是轴对称的是( C),A),B),C),D)5.(2013保定中考模拟)如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有__3__种.,(第5题图)),(第6题图))图形折叠及相关计算6.(2016河北中考)如图,将▱ABCD沿对角线AC折叠,使点B落在点B′处,若∠1=∠2=44°,则∠B为( C)A.66° B.104°C.114°D.124°7.(2016邯郸一模)如图,在▱ABCD中,∠A=70°,将▱ABCD折叠,使点D, C分别落在点F,E处(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于( B)A.70° B.40° C.30° D.20°,(第7题图)),(第8题图)) 8.(2016保定中考模拟)如图,在△ABC中,∠C=90°,BC=6,D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在A′处,若A′为CE的中点,则折痕DE的长为 ( B )A.12B.2 C.3 D.49.(2013河北中考)如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B=__95°__.,中考考点清单)轴对称图形与轴对称2.折叠的性质:折叠的实质是轴对称,折叠前后的两图形全等,对应边和对应角相等.【方法技巧】凡是在几何图形中出现“折叠”这个字眼时,第一反应即存在一组全等图形,其次找出与要求几何量相关的条件量.1.与三角形结合:(1)若涉及直角,则优先考虑直角三角形的性质(勾股定理及斜边上的中线等于斜边的一半),若为含特殊角的直角三角形,则应利用其边角关系计算;(2)若涉及两边(角)相等,则利用等腰三角形的相关性质计算,若存在60°角,则利用等边三角形性质进行相关计算,一般会作出高线构造特殊角的直角三角形进行求解;(3)若含有中位线,则需利用中位线的位置及数量关系进行量的代换. 2.与四边形结合:(1)与平行四边形、矩形、菱形、正方形结合,往往会利用其特殊性质求解; (2)若为一般的四边形,则可通过构造特殊的三角形或四边形求解.C ′续表把成中,中考重难点突破)轴对称与中心对称图形的识别【例1】(2017庆阳中考)下面四个手机应用图标中,属于中心对称图形的是( D ),A),B),C),D)【解析】中心对称是属于特殊的图形旋转不变性质,要旋转180°. 【答案】B1.(浙江中考)下列四个图形分别是四届国际数学大会的会标:其中属于中心对称图形的有( B ) A .1个 B .2个 C .3个 D .4个2.(2017盐城中考)下列图形中,是轴对称图形的是( D ),A) ,B) ,C) ,D)图形折叠应用【例2】(2017嘉兴中考)一张矩形纸片ABCD ,已知AB =3,AD =2,小明按所给图步骤折叠纸片,则线段DG 长为( A )A. 2 B .2 2 C .1 D .2【解析】先据折叠的性质求出DA ′,CA ′和DC ′的长,进而求线段DG 长. 【答案】A3.(宁夏中考)如图,在矩形ABCD 中,AB =3,BC =5,在CD 上取一点E ,连接BE ,将△BCE 沿BE 折叠,使点C 恰好落在AD 边上的点F 处,则CE 的长为__53__.。
河北中考数学一轮复习图形的变化

段最短.
作任意一定点关于直
线l的对称点,然后连
接对称点与另一定点, 根据两点之间线段最
短,得出PA+PB的最小 值.
微专项11 线段最值问题
常见模型
结构示例
应用的原理
处理方法
轴对称最 值模型
如图,点P是∠AOB内部的一定点,在OA上 找一点M,在OB上找一点N,使△PMN的周 长最小.
微专项11 线段最值问题
常见模型
结构示例
应用的原理
处理方法
折叠求最 值模型
如图,点N为定点,点M为动点,折
叠图形后.
①求A'B的最小值; ②求点A'到BC距离的最小值.
①平面内的 点与圆上距 离最大和最 小的点均在 该点与圆心 连线所在的 直线上;②垂 线段最短.
以点N为圆心、AN的 长为半径作圆.①连 接BN交☉N于一点,当 点A'与该交点重合时 ,A'B取最小值;②过 点N作BC的垂线,交 ☉N于一点,当点A'与 该交点重合时,点A' 到BC的距离最小.
命题角度 与图形的折叠相关的计算
的问题时,常利用中线或中位线的知识解决问题.当折叠背景为平行四边形时,要考 虑平行四边形的性质,常利用角平分线和平行线构造等腰三角形解决问题.当折叠 和圆或扇形结合时,根据设置的问题选择解题方法,若问题与角度有关,要根据对应 点确定折叠前后的等弧,以此来构造等弧、等角、等弦,将问题转化为直线形的问 题解决;若问题与位置关系有关,要根据轴对称的性质找到圆心的对应点,利用圆心 连线被对称轴垂直平分转化问题,再利用相关知识解决问题.
(2)作射线O'A;
作一个角等 (3)以点③ O'
