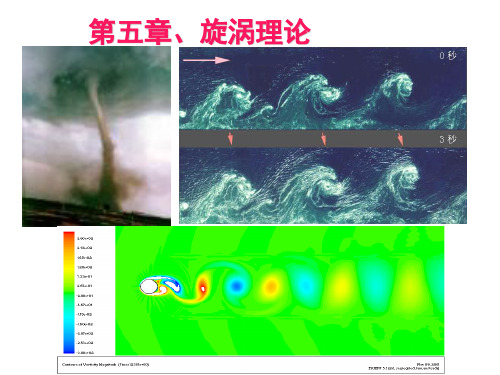
第五章 漩涡理论
第五章漩涡理论基础

第五章不可压缩流体的二维流动引言:在前面几章主要讨论了理想流体和黏性流体一维流动,为解决工程实际中存在的一维流动问题打下了良好的基础。
本章讨论理想不可压流体的二维有势流动以及二维黏性流体绕物体流动的基本概念。
第一节有旋流动和无旋流动刚体的运动可分解为移动和转动两种运动形式,流体具有移动和转动两种运动形式。
另外,由于流体具有流动性,它还具有与刚体不同的另外一种运动形式,即变形运动(deformationmotion)。
本节只介绍流体旋转运动即有旋流动(rotation—alflow)和无旋流动(irrotational flow)。
一、有旋流动和无旋流动的定义流体的流动是有旋还是无旋,是由流体微团本身是否旋转来决定的。
流体在流动中,如果流场中有若干处流体微团具有绕通过其自身轴线的旋转运动,则称为有旋流动,如果在整个流场中各处的流体微团均不绕自身轴线的旋转运动,则称为无旋流动。
强调“判断流体流动是有旋流动还是无旋流动,仅仅由流体微团本身是否绕自身轴线的旋转运动来决定,而与流体微团的运动轨迹无关。
”举例虽然流体微团运动轨迹是圆形,但由于微团本身不旋转,故它是无旋流动;在图5—1(b)中,虽然流体微团运动轨迹是直线,但微团绕自身轴线旋转,故它是有旋流动。
在日常生活中也有类似的例子,例如儿童玩的活动转椅,当转轮绕水平轴旋转时,每个儿童坐的椅子都绕水平轴作圆周运动,但是每个儿童始终是头向上,脸朝着一个方向,即儿童对地来说没有旋转。
二、旋转角速度(rotationalangularvelocity)为了简化讨论,先分析流体微团的平面运动。
如图5—2所示有一矩形流体微团ABCD在XOY平面内,经丛时间后沿一条流线运动到另一位置,微团变形成A,B,C,D。
流体微团在Z周的旋转角速度定义为流体微团在XOY平面上的旋转角速度的平均值速度环量是一个标量,但具有正负号。
速度环量的正负号与速度方向和积分时所取的绕行方向有关。
流体力学--漩涡理论 ppt课件

2 有限平面
C 2 n d 2 J
(单连通区域)
单连通区域: C 所包围的区域σ 内全部是流
体,没有固体或空洞。
3 任面
PPT课件
C
18
复连通域(多连通域):
C的内部有空洞或者包 含其他的物体。 双连通域的斯托克斯定理
ABDB ' A' EA AB C BA L
该处的速度
v vx i v y j vz k
流速与流线相切
dx dy dz vx ( x, y, z, t ) vy ( x, y, z, t ) vz ( x, y, z, t )
v
ds
PPT课件
ds
8
涡管vortex tube
流管
元流 截面积为无限小的涡束 截面积为无限小的流束 称为元流 称为涡索(涡丝)。 PPT课件 9
AB Vx dx Vy dy Vz dz dx dy dz x y z AB AB
B
d B A
A
V
Vs
B
对于有旋场:
AB V ds Vx dx Vy dy Vz dz
AB AB
PPT课件
Bˊ Aˊ B A
σ
C
L
E
AB BA
C L 2 n d
C
区域在走向的左侧
PPT课件 19
漩涡理论
推论一 单连域内的无旋运动,流场中处处 为零,则沿任意封闭周线的速度环量为 零
c 2 n d 2 0d 0
沿某闭周线的速度环量为零,不一定无旋。
vx ( )dxdy x y vy
流体力学5-漩涡理论说课材料

(vy vx )dxdy x y
y
d
vx
vx y
dy
c
而
(vy x
vx y
)
2z
微矩形面积ds上的环量:
v y dy
av x
0
dx
vy
vy x
dx
b x
d 2zd S 2n d S 2 d J
漩涡理论
2 有限平面
C 2nd2J (单连通区域)
单连通区域: C 所包围的区域σ内全部是流
ds
A BV d sV xd x V yd y V zd z
A B
A B
A
漩涡理论
2. 若已知速度场,求沿一条闭曲线的速度环量
对于无旋场:
c cVxdx Vydy Vzdz
c x dx y dy z dz c d 0
对于有旋场:
V
α Vs
ds C
c cVsds2nd
————斯托克斯定理
即涡管永远由相同的流体质点所组成。 但涡管的形状和位置可能随时间变化。
涡管
涡管
漩涡理论
海姆霍兹第三定理 ——涡管旋涡强度不随时间而变
正压、理想流体在有势质量力作用下,涡管 的旋涡强度不随时间而变。
2 J (斯 托 克 斯 定 理 )
不 随 时 间 变 化 ( 汤 姆 逊 定 理 )
J不 随 时 间 变 化
定义 AB ABVsds
速度环量是标量,速度方向与
积分AB曲线方向相同时(成锐 角)为正,反之为负。
ΓAB=-ΓBA
A
V
Vs
B
ds
漩涡理论
速度环量的其他表示形式:
AB V ds
第五章 涡旋理论

7-7已知有旋流动的速度场为。
试求旋转角速度,角变形速度和涡线方程。
[]1.1) 21212121c y z c x z yz xz z y x =-=-=====ωωω2))垂直,故涡量为零,,(与平面的法线212121)1,1,1(1=-==+-ωn z y x 3)s m z /105.024.-⨯=ω2.yz xz z y x =====212121ωωω3.2点对1点的诱导速度:21140x v u πΓ== 1点对2点的诱导速度:12240x v u πΓ== 涡对1,2的涡旋惯性中心:121211=Γ+ΓΓ-Γ=y x 涡对相互作用引起的自身运动是涡旋惯性中心的旋转运动,且旋转角速度:20211012x x x v πωΓ+Γ=-=直线涡1Γ的运动轨道:20212220212021210210221)2()2(2)()(x y x x x x x x x y x x Γ+ΓΓ=+Γ+ΓΓ-Γ+ΓΓ=--=+-直线涡2Γ的运动轨道:20211220212021110210221)2()2(2)()(x y x x x x x x x y x x Γ+ΓΓ=+Γ+ΓΓ-Γ+ΓΓ=++=+-4.kz y x 10===ωωω运用stokes 定理:kS k A J z ππω1812222=⋅⋅⋅===Γ 或0sin sin =+-=-=-=θθθθθy x r y x V con V V rkcon V V V在圆周上径向速度为常数,⎰==Γkdl V r π18例5.4 已知速度场22x y v x y -=+,22y xv x y=+,求绕圆心的速度环量。
解 由极坐标 cos x r θ= s i ny r θ= 有 sin cos x y v rv rθθ⎧=-⎪⎪⎨⎪=⎪⎩在r =R 上sin cos dx R d dy R d θθθθ=-⎧⎨=⎩ 所以 S x y r Rr Rvd s v dx v dy ==Γ==+⎰⎰222222022sin cos ()2R R d d R R ππθθθθπ+==⎰⎰15. 已知流线为同心圆族,其速度分别为15(5)15x y v y r v x ⎧=-⎪⎪≤⎨⎪=⎪⎩22225(5)5x y y v x y r x v x y -⎧=⎪+⎪⎨⎪=⎪+⎩试求:沿圆周222x y R +=的速度环量。
第05章__漩涡理论

海姆霍兹第一定理既适用于理想流体又适用于 粘性流体。
海姆霍兹第二、三定理只适用于理想流体。
因为流体的粘性将导致剪切、速度等 参数脉动以及能量耗散,旋涡强度将随时 间衰减。
40
§5-4 毕奥一沙伐尔定理
问题 已知速度场可由式(3-39)和(3-40)
求偏导来确定旋涡场。
已知旋涡场,能否确定速度场?这是本节 要讨论的问题.
诱导速度场
涡丝(线)
旋涡强度
诱导速度场 dV
42
电磁场与诱导速度场的类比
dH
i
ds sin r2
场点 43
电磁学中,电流强度为i的导线,微元导
线ds对场点P所产生的磁场强度由毕奥——沙
伐尔公式得:
dH i ds sin
式中:
r2
r: ds离场点P的矢径
θ: 是ds与r的夹角
dH的方向:
垂直于ds和r所在的平面,按右手法则确定。
15
旋涡运动理论广泛地应用于工程实际: 机翼、 螺旋桨理论等。旋涡与船体的阻力、振动、噪 声等问题密切相关。
旋涡的产生: 与压力差、质量力和粘性力等
因素有关。
流体流过固体壁面时,除壁面附近粘性影响严 重的一薄层外,其余区域的流动可视为理想流体 的无旋运动。
16
旋涡场的几个基本概念:
一、涡线,涡管,旋涡强度 涡线(vortex line):
向相同时(成锐角)为正,反之为负。
线积分方向相反的速度环量相差一负号,即
ΓAB=-ΓBA
(5-5)
速度环量的其他表示形式:
AB V ds V cos(V , ds)ds Vxdx Vydy Vzdz
AB
AB
AB
2010-第五章旋涡理论 流体力学

∂ω x ∂ω y ∂ω z + + =0 ∂x ∂y ∂z
∂a x ∂a y ∂a z + + =0 ∂x ∂y ∂z
1 ∂a z ∂a y − vx = ∂z 2 ∂y 1 ∂a x ∂a z v = − y ∂x 2 ∂z 1 ∂a y ∂a x v = z 2 ∂x − ∂y
∫
B
A
ϕ ϕB − ϕ A d=
Γ AB = ∫ V ⋅ ds =
AB
对于有旋场: 由公式
AB
∫ V dx + V dy + V dz
x y
计算 z
2. 若已知速度场,求沿一条闭曲线的速度环量
对于无旋场:
Γc
∂ϕ ∂ϕ ∂ϕ = z dz ∫ c Vx dx + Vy dy + V ∫ c ∂x dx + ∂y dy + ∂z dz dϕ ∫=
n n
1 2
结论: 涡管不能在流体中以尖端形式终止或开始, 否则dσ→0时有ω→∞。 涡管存在的形式:要么终止于流体边界或固 体边界,要么自行封闭形成涡环。 不可能 的情况
由该定理得到: 涡管(涡线)本身首尾相接,形成一封闭的涡环或涡圈; 涡管(涡线)两端可以终止于所研究流体的边壁上(固体 壁面或自由面)。
例5.1 已知速度分布,求涡线方程。
ω=const
方法(详见p146):
例5.2 已知漩涡强度, 求速度环量。
例5.4 已知速度向量,求绕圆心的速度环量。
方法(详见p146): 由速度环量定义,式(5-1-9),直接积分求得。
旋涡运动基本定理
流体力学漩涡理论(课堂PPT)

汤姆逊定理: 沿流体质点组成的任一封闭流体 周线的速度环量不随时间而变.
即 d 0
dt .
漩涡理论
22
汤姆逊定理和斯托克斯定理说明:
1) 推论: 2) 流场中原来没有旋涡和速度环量的, 就永远
无旋涡和速度环量。 原来有旋涡和速度环量的,永远有旋涡并保 持环量不变
2)在理想流体中,速度环量和旋涡不生不灭。 因为不存在切向应力,不能传递旋转运动。
第五章:旋涡理论(vortex theory) 1.旋涡场的基本概念(涡线,涡管,旋涡强
度和速度环量) 2.司托克斯定理 3.汤姆逊定理 4.海姆霍兹定理 5.毕奥-沙伐尔定理 6.兰金组合涡
.
1
§5-1 旋涡运动的基本概念
旋涡场: 存在旋涡运动的流场 有旋运动: ωx,ωy,ωz在流场中不全为零的流动
ABABVxdxVydyVzdzABxdxydryzdzA BdBAVFra bibliotekVsB
对于有旋场:
A B V rd s rV x d x V y d y V zd z
A B
A B
A
d sr
.
漩涡理论
14
2. 若已知速度场,求沿一条闭曲线的速度环量
对于无旋场:
Ñ c cVxdx Vydy Vzdz
流管
涡丝vortex filament 元流
截面积为无限小的涡束 截面积为无限小的流束
称为涡索(涡丝)。
称为元流
.
9
旋涡强度
J表征流场中旋涡强 弱和分布面积大小
dJ=ωndσ
J nd
如果 是涡管的截面
则J为涡管强度
n
r
流量
QdQud
d
流体力学漩涡理论ppt课件

路径的线积分。
定义 AB ABVsds
速度环量是标量,速度方向与
积分AB曲线方向相同时(成锐 角)为正,反之为负。
Γ AB=-Γ BA
A
V Vs
B
ds
漩涡理论
11
速度环量的其他表示形式:
AB V ds
AB
V cos(V , ds)ds
C L 2 nd
n 0 Γ c+Γ L=0
Γ c=-Γ L
Bˊ Aˊ BA
L
E
C
Γc=ΓL (与积分路径方向一致时)
漩涡理论
21
§5-2 汤姆逊定理
假设:
(1)理想流体;
(2)质量力有势; (3)正压流体(流体密度仅为压力的函数)
汤姆逊定理: 沿流体质点组成的任一封闭流体 周线的速度环量不随时间而变.
第五章:旋涡理论(vortex theory) 1.旋涡场的基本概念(涡线,涡管,旋涡强 度和速度环量) 2.司托克斯定理 3.汤姆逊定理 4.海姆霍兹定理 5.毕奥-沙伐尔定理 6.兰金组合涡
1
§5-1 旋涡运动的基本概念
旋涡场: 存在旋涡运动的流场 有旋运动: ω x,ω y,ω z在流场中不全为零的流动
流场,非有势力。
漩涡理论
23
§5-3 海姆霍兹定理
海姆霍兹第一定理
(同一涡管各截面上的旋涡强度都相同)
abdbaea 2 nd
涡a面bdb上aea n0 0
ab ba 0
ab ba
流线微分方程:
取流线上一段微弧长
ds dxi dyj dzk
该处的速度
第五章漩涡理论基础

p
p0
1 2
v2
v02
1 2
v2
1 2
v02
p
1 2
v2
2v02
当 r 0 p pc ,vc 0
故
pc p
p p0
p0
1 2
v02
1 2
v02
p pc
p0 p0
1
2
v02
B vx+(∂vx/∂x)dx
均值。
o
x
注意:v与L垂直时, 0
d
ABCD
1 2
vx
vx
vx x
dx
dx
1 2
vy
vy x
dx
vy
vx x
dx
vy y
dy
dy
1 2
L 2J 2ndA
A
若:周线上各点速度均与周线垂直,则:
L 0
1)、 无限小矩形面积的斯托克斯定理。
在流场中,xoy坐标平面上,取矩形微元周线 ABCD,边长dx,dy,dA=dxdy,如图。 。
A点的速度分量为vx,vy,则B,C,D各点速 度分量如图示(忽略二阶微量),沿微元周
r v
称为涡量
第一节 涡线,涡管,涡束, 旋涡强度
1. 涡线:
在瞬时,涡量场中所作一条空间曲线,该瞬时,
各点的ω均与该线相切,该曲线称为涡线。
涡线为所有质点的转动轴线。注意:涡线是瞬
第五章漩涡理论基础

2、涡管、涡束 、涡管、
在瞬时,过任意封闭曲线(非涡线) 在瞬时,过任意封闭曲线(非涡线)上各点作 涡线形成涡管 充满质点的涡管称涡束。 涡管, 的涡管称涡束 涡线形成涡管,充满质点的涡管称涡束。 特点:随涡束长度变化。但微小涡束, 特点:随涡束长度变化。但微小涡束,即涡线 上,ω相同。注意涡束与流束定义不同。 相同。注意涡束与流束定义不同。 相同
第五章 旋涡理论基础
由第三章速度分解知 :
1 ∂vz ∂vy 1 ∂vx ∂vz ω x= − − ,ωy = 2 ∂y ∂z 2 ∂z ∂x 1 ∂vy ∂vx ωz = − 2 ∂x ∂y
r 1 r 1 即: ω = ∇× v = rot v 2 2 r r v v 称为涡量 在场论中, 在场论中,Ω= 2ω = ∇× v = rot v 称为涡量 v
∂v y ∂vx = + dxdy = 2ω z dA ∂x ∂y
即:
d Γ ABCD = 2dJ
2)、有限面积单连通域的斯托克斯定理 ) 所谓单连通域和复连通域, 所谓单连通域和复连通域 , 即 : 如果周线区 域内所做的任意一条周线, 域内所做的任意一条周线 , 都可连续收缩至 一点而不越出边界, 单连通域, 否则为复 一点而不越出边界 , 称 单连通域 , 否则为 复 连通域。 连通域。 对于周线 所围面积, 周线L所围面积 对于周线 所围面积,用两组互相垂直的直线 将面积划分为无限多个单元矩形, 将面积划分为无限多个单元矩形 , 对任意矩 形都有: 形都有:
A A
速度环量, 第二节 速度环量,斯托克斯定理
第五章 旋涡

该定理说明:涡管或涡束既不能在流体中开始,也不能 在流体中终止,它必须呈现为闭合环形,或者从流体边 界(容器壁面或自由面)上开始或终止,如图5-3所示。例 如抽烟者喷的烟圈成圆形烟环,自然界中的龙卷风开始 和终止于水面和云层等边界面。
图5-3
第三节 流体运动的一些基本概念
迹线与流线
迹线是流场中其一质点运动的轨迹。 例如在流动的水面上撤一片木屑,木屑随水流漂流的途径就是某一水点的 运动轨迹,也就是迹线。流场中所有的流体质点都有自己的迹线,迹线是流 体运动的一种几何表示,可以用它来直观形象地分析流体的运动,清楚地看 出质点的运动情况。迹线的研究是属于拉格朗日法的内容,迹线农示同一流 体质点在个同时刻所形成的曲线。 流线是某一瞬时在流场中所作的一条曲线,在这条曲线上的各流体质点的速 度方向都与该曲线相切,因此流线是同一时刻不问流体质点所组成的曲线。 流线可以形象地给出流场的流动状态。通过流 线,可以清楚地看出某时刻流场中各点的速度 方向,由流线的密集程度,也可以判定出速度 的大小。流线的引入是欧拉法的研究特点。例 如在流动水面上同时撤一大片木屑,这时可看 到这些木屑将连成若干条曲线,每一条曲线表 示在同一瞬时各水点的流动方向线,就是流线。
2 n dA
A
第三节 汤姆生定理和亥姆霍兹定理 一、汤姆生定理 汤姆孙(W.Thomson)定理:正压性的理想流体在有势的质量力作用下沿任 何由流体质点所组成的封闭周线的速度环量不随时间而变化。
根据斯托克斯定理和汤姆孙定理可知:旋涡强度直接由速度环 量所度量。在理想流体中始终由某一些流体质点所组成的任意 封闭曲线的速度环量既然保持为常数,与时间无关,也就是它 的旋涡强度保持为常数,且与时间无关。这样流体在运动过程 中本来是无旋流动就不可能变为有旋流动;或者相反,本来具 有旋涡就不能消失。当然这是因为将流体看作为理想的,不考 虑粘性影响的缘故。事实上在真实流体中旋涡将会产生也会消 失。但是在较短时间内,粘性力影响较小时,可以近似地认为 满足汤姆孙定理的条件,而用它来阐明某些现象。
旋涡理论ppt课件

C 2nd 2 0d 0
反之,若沿任意封闭周线的速度环量等于零,可得处处为 零的结论。
但沿某闭周线的速度环量为零,并不一定无旋(可能包围强
度相同转向相反的旋涡)。
推论二
对于包含一个翼截面在内的双连通区域,如果流动是无旋的,
旋涡运动理论广泛地应用于工程实际: 机 翼、螺旋桨理论等。旋涡与船体的阻力、振动、 噪声等问题密切相关。
旋涡的产生: 与压力差、质量力和粘性力等
因素有关。
流体流过固体壁面时,除壁面附近粘性影响严 重的一薄层外,其余区域的流动可视为理想流体 的无旋运动。
4
旋涡运动基本概念
流场
涡场
流速v
涡量 Ω
流量Q
Thomson定理和Lagrange 定理适用条件为: 1. 理想流体
2. 正压流体 ( p)
3. 在有势质量力作用下
旋涡起因: (1) 粘性:均匀流体经过物体边界层时运动变为有旋; (2) 非正压流场:大气和海洋中的密度分层形成旋涡; (3) 非有势力场:地球哥氏力使气流生成旋涡(旋风); (4) 流场的间断(非连续):曲面激波后形成有旋流动。 19
亥姆霍兹(Helmholtz)定理 (1)亥姆霍兹第一定理:
——涡管强度空间守恒
在同一瞬间涡管各截面上 的旋涡强度都相同
由斯托克斯定理 abdbaea 2 nd
因为内ωn=0所以 0
由斯托克斯定理上式写成:
nd nd
1
2
20
结论: 涡管不能在流体中以尖端形式终止或开始, 否则dσ→0时有ω→∞。
15
旋涡理论ppt课件

d s sin
r2
S
dv
P dH
如要研究空间有限长涡丝在P点的诱导速度,则将上式积分得:
v
4
sin ds
s
r2
直涡丝MN
25
dv
4
ds sin
r2
直涡丝MN
诱导速度方向指向纸外。 直线涡丝段对P点所产生的诱导速度为:
v
4R
2 sind
1
电流面密度δ H δ v Ω
涡量 Ω
电流强度 i
i H dl δ nds
l
S
速度环量 Γ
v dl Ω nds
24
l
S
Biot-Savart 定理:
电流诱导磁场强度
d
H
i
d
s
sin r2
i ds
Γ
r
旋涡诱导流体速度
dv
29
5-6、二维旋涡的速度和压强分布
如图5-17所示,涡束内的流动为有旋流动,称为涡核 区;涡束外的流动区域为无旋流动,称为环流区。
一、速度分布
1)旋涡内部:
涡束内部的速度分布为:
vr 0, v r
(r R)
2)旋涡外部: 在环流区内,速度分布为:
vr 0,
v
2r
R 2
亥姆霍兹(Helmholtz)定理 (1)亥姆霍兹第一定理:
——涡管强度空间守恒
在同一瞬间涡管各截面上 的旋涡强度都相同
由斯托克斯定理 abdbaea 2 nd
因为内ωn=0所以 0
第五章:旋涡理论

5.兰金组合涡
兰金组合涡:半径为 R 的无限长圆柱形涡,在 R 内,流体象刚一样能轴线旋转,角速度为 ωG 。
速度分布: vθ = ωr
vr = 0
vθ
=
Γ 2π r
vr = 0
压力分布:
p
−
p0
=
1 2
ρ vθ 2
−
ρ vR 2
p − p0 = −ρvR2
( r < R ) 有旋 (r > R ) 无旋
涡线:同流线定义相似,即同一瞬时涡线上每一流体质点的旋转角速度矢量与涡线相切。 涡线微分方程:
dx = dy = dz ωx ωy ωz
可组成一常微分方程组
用右手法则确定旋转角速度的方向,由涡线定义,说明流体质点在该瞬时绕其旋转
速度轴旋转。
涡管:与流管类似,流管的管壁为流线,涡管的管壁为涡线,这些涡线处处与涡管的
1 (∂vz 2 ∂y
−
∂vy ) ∂z
=0
JK 所以:ω =
c
KK (z j − yk)
y2 + z2
2)由涡线微分方程 dx = dy = dz , ωx ωy ωz
有 积分得
dy = − dz zy y2 + z2 = c1
R3
R2
Γ
Γ
R1
Γ
x = c2
5.试求图 5-2 所示的马蹄涡对流场中任意一点 处的诱导速度。 解:设流场中任意一点 A,分别距三条涡线的垂
A)定常不可压缩无旋流场
B)静止,不可压缩理想流场
C)不可压缩有旋流场
D)不可压缩非定常流场
JK
v∫ ∫∫ 2.斯托克斯定理 Γ = c vsds = 2 wndσ ,若 Γ =0,而ω 不一定为零,这是因为( )。 σ
旋涡理论 PPT课件
此式称为斯托克斯定理
斯托克斯(Stokes)定理:在涡量场中,沿任意封闭周线的速度 环量等于通过该周线所包围曲面面积的旋涡强度的两倍,即:
C 2J
C vsds 2nd
速度环量与旋 转角速度关系
推广到有限大平面
给出了通过速度环量计算旋涡强度的方法
3、复连通区域的修正
dv
4
ds • sin
r2
直涡丝MN
诱导速度方向指向纸外。 直线涡丝段对P点所产生的诱导速度为:
v
4R
2 sind
1
4R
c
os1
c
os2
v
4 R
cos 1
cos2
M
半无限长直涡线( 1 90 , 2
180 ):V
4R
R
无限长直涡线( 1 = 0 , 2=
180 ) :
V
2R
v
平面点涡诱导速度场:
ABB'A'EA 2 nd
ABDB'A'EA AB C BA L
ΓC:沿外边界逆时针的环量 ΓL :沿内边界顺时针的环量
AB BA
C L 2 nd
双连通区域的斯托克斯定理
推论一
单连通区域内的无旋运动,流体 中的旋度处处为零,则沿任意封 闭周线的速度环量为零,即:
C 2nd 2 0d 0
由于涡束内部为有旋流动,伯努利积分常数随流线变化,故其
压强分布可由欧拉运动微分方程导出。对于平面定常流动,欧拉
运动微分方程为:
vx
v x x
vy
v x y
1
p x
vx
v y x
vy
第五章 漩涡理论

第五章 漩涡理论内容1. 基本概念。
2. 漩涡随空间,时间的变化规律。
3. 漩涡对周围流场的影响。
4. 二元漩涡的特性。
5.1.1涡量和平均旋转角速度。
涡量场:Ω =▽V ⨯▽V ⨯=VzVyVxz y x k j i ∂∂∂∂∂∂令 ωx =⎪⎪⎭⎫⎝⎛∂∂-∂∂z Vy yVz 21 ⎪⎭⎫ ⎝⎛∂∂-∂∂=x Vz zVxy 21ω ω2=Ω∴ ⎪⎪⎭⎫⎝⎛∂∂-∂∂=y Vx xVy z 21ω其中ω称为平均旋转角速度。
ωωωzyx,, 的物理意义。
设M 点的速度Vx,Vy A 点()dx xVx x VV xA∂∂+=()dx xVy y VV yA∂∂+=()()[]()[]11_sin 0,11dtx dtx dtx dt dtx dxy A A MA d V V V VV VV AA y dt x y xAyA⎪⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂=+-='+==→θ dt xd V y∂∂≈∴θ1 即xV dtd y∂∂=θ1Ω是否为0判断有旋无旋例:1)r V∙=ωθ=ω常sin sin cos 0012xy z xyyxzr yrcso xV V V V VV V yx θθθωθωθωθωωωωω=-=-=-======⎛⎫⎪=-= ⎪⎝⎭∂∂∂∂有旋2)rV πθ2Γ=无旋02100222222=⎪⎪⎪⎭⎫⎝⎛-===∴=+Γ=+Γ-=∴∂∂∂∂yV x V VyxV yxVxyzyx zyxx yωωωππ5.1.2涡线,涡面和涡管涡线:是一条曲线,在同一瞬时曲线上所有点旋转角速度Ω与该线相切。
1. 瞬时性2. 流动速度与旋转速度相垂直。
涡线方程()()()z y x dzz y x dyz y x dxz y x ,,,,,,ΩΩΩ==涡线涡管速度场 涡量场 Ω=⨯∇v 流线:zyxv dz v dy v dx == 涡线:zyxdz dy dx Ω=Ω=Ω流管: 涡管:流量:⎰=sn ds v Q 涡量:⎰⎰⎰==Γ=sn CC s ndsl d v dsJ ωω25.1.3涡通量和涡管强度⎰⎰=∙=ssnds ds n J ωω又称涡管强度流量⎰⎰=∙=ssnds ds n v Q v5.2速度环流和斯托克斯定理1)速度环流:定义:速度在曲线切线上的分量沿该曲线的线积分⎰Γ=BAABl d V定义:某瞬时AB 线上所有质点沿AB 运动的趋势。
船舶流体力学第5章(打印)

第五章旋涡理论本章主要研究:旋涡运动,不涉及力,属于运动学范畴。
由于旋涡场的特性不同于一般流场,在这里我们专门对其进行分析研究。
旋涡与船体的阻力、振动、噪声等问题密切相关。
旋涡运动理论广泛地应用于工程实际,比如机翼、螺旋桨理论等。
旋涡的产生:与压力差、质量力和粘性力等因素有关。
根据边界层理论,流体流过固体壁面时,除壁面附近粘性影响严重的一薄层外,其余区域的流动可视为理想流体的无旋运动。
图片:§5.1 旋涡运动的基本概念流体微团:由大量流体质点所组成的,具有线性尺度效应的微小流体团。
刚体的运动是由于平移和绕某瞬时轴的转动两部分组成。
流体微团的运动一般除了平移和绕某瞬时轴的转动之外,还有线变形运动和角变形运动。
一.速度分解定理:设t时刻流场中任一流体微团中某点A(x,y,z)的速度为V x、V y、V z,则与点A相邻的点M(x+dx,y+dy,z+dz)的速度为:dz zv dy y v dx x v v v xx x x mx∂∂+∂∂+∂∂+= dz z v dy y v dx x v v v y y y y my ∂∂+∂∂+∂∂+= dz zvdy y v dx x v v v z z z z mz ∂∂+∂∂+∂∂+= dy y v x v dz x v z v dz x v z v dy x v y v dx x v v v x y z x z x y x x x mx⎪⎪⎭⎫⎝⎛∂∂-∂∂-⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂+∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂+=∴21212121引入符号: x v x x ∂∂=ε y v y y ∂∂=ε zv z z ∂∂=ε⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=z v y v y z x 21γ ⎪⎭⎫ ⎝⎛∂∂+∂∂=x v z v z x y 21γ ⎪⎪⎭⎫⎝⎛∂∂+∂∂=y v x v x y z 21γ ⎪⎪⎭⎫⎝⎛∂∂-∂∂=z v y v y zx 21ω ⎪⎭⎫⎝⎛∂∂-∂∂=x v z v z x y 21ω ⎪⎪⎭⎫⎝⎛∂∂-∂∂=y v x v x y z 21ω dy dz dz dy dx v v z y y z x x mx ωωγγε-++++=∴同理:dz dx dx dz dy v v x z z x y y my ωωγγε-++++=dx dy dy dx dz v v y x x y z z mz ωωγγε-++++=上式称为海姆霍茨(Helmholtz )速度分解定理。
旋涡理论

(r
a2 r
)
2
vr
r
V0
cos (1
a2 r2
)
v
1 r
V0 sin (1
a2 r2
)
2
r
柱面上(r = a):
v
vr 0
2V0 sin
2 a
v 0
sin 4 aV0
6.1.4 点涡 (vortex)
流场中坐标原点处有一根无穷长的直涡线,方向垂直
于图平面,则该涡线与图平面的交点即为一个点涡。
位于(0,0)点涡:
vr
0,
v
2 r
vr dr
v rd
2
v dr
vr rd
2
ln
r
v
Γ顺时针方向,若逆时针,上式加负号。
第5章 旋涡理论
内容:介绍描述旋涡运动的基本方法和旋涡运动的
基本定理。
包括:(1)旋涡运动的基本概念。
(2)旋涡运动的基本定理。 汤姆逊(Thomson)定理 拉格朗日(Lagrange)定理 亥姆霍兹(Helmholtz)定理 毕奥沙伐(Biot——Savart)定理
4
1、涡线:流场中的一条曲线。 其上所有流体
d
J:表征流场中旋涡的强弱和分布面积大小的物理量。
4 、旋速度环量:
C C vsds C v cosds C v ds
阿甘本|不应该把主体设想为实体,而应该设想为流动中的漩涡。

阿甘本|不应该把主体设想为实体,而应该设想为流动中的漩涡。
文|阿甘本译|蓝江第五章漩涡最典型的水的运动是螺旋形的。
当河流中的水流遇到障碍物时,无论是树枝还是桥墩,都会在这一点上产生螺旋运动,如果它被稳定下来,就会呈现出漩涡和连贯性。
如果两股具有不同温度或速度的水流相遇,也会发生同样的情况:即使在这种情况下,我们也会看到漩涡的形成,它们似乎在波浪或水流中保持不动。
但是,在波峰上形成的线圈本身就是一个漩涡,由于重力的作用,它被打成泡沫。
漩涡有它的节奏,这好比行星围绕太阳的运动。
它的内部运动速度高于其外部边缘,就像行星根据其与太阳的距离而旋转得更快或更慢。
在旋转中,漩涡向下延伸,然后以一种脉动向上移动。
此外,如果我们在漩涡中放下一个物体——例如,一小块针状的木头——它将在不断旋转中指向同一个方向,表明一个点,可以说是漩涡的北方。
然而,漩涡不断旋转的中心是一个黑色的太阳,其中有无限的吸力在发挥作用。
根据科学家的说法,这可以通过以下方式来表达:在半径等于零的旋涡点上,压力等于“无限小”。
让我们思考一下,漩涡定义具有何种特殊地位:它是一个从水流中分离出来的形状,而它过去和现在仍然是水流的一部分;一个封闭在自己身上的自主性区域里,遵循着自己的规律。
然而,它与它所在整体有着密切联系,是由与它周围的液体不断物质交换而构成的。
它是一个独立的存在物,但没有任何一滴是单独属于它自己的,它的同一性是绝对非物质性的。
众所周知,本雅明将起源比作一个漩涡:起源(Ursprung)作为一个漩涡处在不断生成的流中,并将所有出现的材料(Entstehung)拼凑成它自己的节奏…… 一方面,作为原初之物希望被恢复和重建,但另一方面,也正是因为如此,作为不完整和未完成的东西。
在每一个原初现象中,都有一个确定的形象,在这个形象中,一个思想将不断面对历史世界,直到它在历史的整体中被揭示出来,得到满足。
因此,起源不是通过对实际发现的检验来发现的,而是与它们的前史和后史有关……因此,起源的范畴并不像科恩(Cohen)所说的那样是一个纯粹的逻辑范畴,而是一个历史范畴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 漩涡理论内容1. 基本概念。
2. 漩涡随空间,时间的变化规律。
3. 漩涡对周围流场的影响。
4. 二元漩涡的特性。
5.1.1涡量和平均旋转角速度。
涡量场:Ω =▽V ⨯▽V ⨯=VzVyVxz y x k j i ∂∂∂∂∂∂令 ωx =⎪⎪⎭⎫⎝⎛∂∂-∂∂z Vy yVz 21 ⎪⎭⎫ ⎝⎛∂∂-∂∂=x Vz zVxy 21ω ω2=Ω∴ ⎪⎪⎭⎫⎝⎛∂∂-∂∂=y Vx xVy z 21ω其中ω称为平均旋转角速度。
ωωωzyx,, 的物理意义。
设M 点的速度Vx,Vy A 点()dx xVx x VV xA∂∂+=()dx xVy y VV yA∂∂+=()()[]()[]11_sin 0,11dtx dtx dtx dt dtx dxy A A MA d V V V VV VV AA y dt x y xAyA⎪⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂=+-='+==→θ dt xd V y∂∂≈∴θ1 即xV dtd y∂∂=θ1Ω是否为0判断有旋无旋例:1)r V∙=ωθ=ω常sin sin cos 0012xy z xyyxzr yrcso xV V V V VV V yx θθθωθωθωθωωωωω=-=-=-======⎛⎫⎪=-= ⎪⎝⎭∂∂∂∂有旋2)rV πθ2Γ=无旋02100222222=⎪⎪⎪⎭⎫⎝⎛-===∴=+Γ=+Γ-=∴∂∂∂∂yV x V VyxV yxVxyzyx zyxx yωωωππ5.1.2涡线,涡面和涡管涡线:是一条曲线,在同一瞬时曲线上所有点旋转角速度Ω与该线相切。
1. 瞬时性2. 流动速度与旋转速度相垂直。
涡线方程()()()z y x dzz y x dyz y x dxz y x ,,,,,,ΩΩΩ==涡线涡管速度场 涡量场 Ω=⨯∇v 流线:zyxv dz v dy v dx == 涡线:zyxdz dy dx Ω=Ω=Ω流管: 涡管:流量:⎰=sn ds v Q 涡量:⎰⎰⎰==Γ=sn CC s ndsl d v dsJ ωω25.1.3涡通量和涡管强度⎰⎰=∙=ssnds ds n J ωω又称涡管强度流量⎰⎰=∙=ssnds ds n v Q v5.2速度环流和斯托克斯定理1)速度环流:定义:速度在曲线切线上的分量沿该曲线的线积分⎰Γ=BAABl d V定义:某瞬时AB 线上所有质点沿AB 运动的趋势。
符号:锐角“+” 钝角“-”2)斯托克斯定理速度环流等于涡通量的两倍AB⎰⎰Γ∙==s d l d V Cω2证明:abcd 微元整形 ()V V yx a ,222yxx yxyzsd d x d x d y d y d xd yV y V xd x d yd x d y d sJxy V V VV V V yxωω⎛⎫⎛⎫ ⎪Γ=++-+- ⎪⎪ ⎪⎝⎭⎝⎭⎛⎫∂∂=-=== ⎪∂∂⎝⎭∂∂∂∂⎰对任意曲线C 所包围的面积sssJds sn C1222-===⎰Γω5.3汤姆逊定理1)速度环量的全微分等于加速度环量l d Dtv D l d v DtD CC∙=⎰⎰证明:⎰⎰⎰∙+=Dt l d v l d Dtv D l d v DtD CC()()()022121212lim=⎪⎪⎭⎫ ⎝⎛===-'=+=-+=-+=-+='⎰⎰⎰→v v v Dt lD v v dtl d l d l DtD dtv l dtl dt dt l ddl l CCt vvvv r rδδδδδδδδδδδ于是又5.3.1汤姆逊定理1)速度环流的全微分l Dt v D l d v DtD CCδ⎰⎰=022=⎪⎪⎭⎫ ⎝⎛⎰Cv δ 2)汤姆逊定理理想流体的Euler 方程p F Dt vD ∇-=ρ1质量力有势: U F ∇=正压流体∇℘=∇p ρ1()0CCD v l U dl D tδ=∇-℘=⎰⎰0=ΓDtD理想正压流体,质量力有势,则沿任一封闭曲线的速度环流,在运动过程中不随时间改变。
初始时刻 无旋 则永远无旋 有旋 有旋 漩涡不生不灭定理()起动涡附着涡附着涡起动涡Γ-=Γ∴=Γ+Γ=-=Γ=Γ=Γ⎰000120L v v ld v 5.5海姆霍兹定理第一定理:同一瞬时沿涡管长度涡的强度保持不变Sv 1起动涡''220C n sC C n s dsdss ωωδ'Γ=Γ=Γ+→⎰⎰又∞→ω不可能即漩涡不能在流体内部终止或开始(a)涡环 (b)终止于流体界面上的涡管 (c)非旋转固壁上的涡管第二定理:理想正压流体,质量力有势构成涡管的流体质量在任何瞬时也构成涡管。
涡管表面:0 0C D D tΓΓ==0=Γ'第三定理:理想正压流体,质量力有势涡管强度不随时间改变。
漩涡运动学性质:随空间不变(沿涡管)动力学性质:理想,正压流体,质量力有势随时间⎪⎩⎪⎨⎧涡管强度涡管环量 不变漩涡具有保持性5.6漩涡的诱导速度5.6.2诱导速度公式水电比拟方法 电磁场电流感应的磁场强度23sin 44rL d i r r L d i H d αππ=⨯= 漩涡诱导速度23sin 44rL d r r L d v d αππΓ=⨯Γ= 直线涡索长度L ,距离涡索为R 的M 点的诱导速度为:αsin R r =()12212cos cos 4cos 4sin 4sin 4sin 4sin sin 4sin 412ααπαααπααπααπααπαααπαπαα-Γ=Γ-=Γ==Γ=Γ=⋅Γ=Γ=⎰⎰RRd Rv d v d R R d rr rd rL d v d L半无限长涡索 02=α R v πα4901Γ=⇒=无限长涡索 02=α Rv πα21801Γ=⇒=一对平行直涡线的互相作用()()R rR v v a B A 24=Γ==π 作等速直线向下运动 Rv v y x π40Γ==()θπv Rv v b B A=Γ==4 绕原点作半径为R 的等速圆周运动(a) xy(b)y5.6.1点涡斯托克斯定理2022 20ACrv ndA vdl v Rd v R R v πθθθωθππΓ⎧=⎪Γ====⎨⎪=⎩⎰⎰⎰无旋点涡周围速度场是无旋的 公转角速度 212RR v πωθΓ==自转角速度 222Rdrdv πωθΓ-==021=+=ωωω势涡5.7兰金涡(二元漩涡)半径为R 角速度ω 环量Γ 求漩涡内外速度分布 涡核内兰金涡速度分布涡核外: ()R r rv ≥Γ=πθ25.7.2压力分布圆柱坐标系运动方程()rpf rv v v t v r r r∂∂-=-∇∙+∂∂ρθ1220 01r r v f v prrθρ==∂=∂压力分布当R r ≥时 122421C rR p +-=ωρ()R r r v r rv r ≤===Γωωππθθ222当∞→r 时 ∞∞=⇒=p C p p 1()R r r R p p ≥-=∞22421ωρ当R r ≤时 22221C r p +=ωρ 当R r =时 222ωρR p C -=∞ ⎪⎪⎭⎫⎝⎛--=∞2222r R p p ρω。
