线性分析记录表
数学辅导记录表10篇

数学辅导记录表10篇
一、线性代数辅导记录
1. 学生姓名:张某
2. 辅导时间:2018年4月10日
3. 辅导内容:线性代数的基本概念、矩阵的运算、线性方程组的解法
4. 辅导效果:学生对线性代数的基本概念有了比较深入的理解,对矩阵的运算和线性方程组的解法有了基本掌握。
二、概率论辅导记录
1. 学生姓名:李某
2. 辅导时间:2018年5月2日
3. 辅导内容:概率论的基本概念、随机变量的分布、独立性、条件概率
4. 辅导效果:学生对概率论的基本概念有了比较深入的理解,对随机变量的分布、独立性和条件概率有了基本掌握。
三、微积分辅导记录
1. 学生姓名:王某
2. 辅导时间:2018年6月15日
3. 辅导内容:微积分的基本概念、极限、微分、积分
4. 辅导效果:学生对微积分的基本概念有了比较深入的理解,对极限、微分和积分有了基本掌握。
四、几何辅导记录
1. 学生姓名:赵某
2. 辅导时间:2018年7月20日
3. 辅导内容:几何的基本概念、直线的性质、圆的性质、平面图形的面积
4. 辅导效果:学生对几何的基本概念有了比较深入的理解,对直线的性质、圆的性质和平面图形的面积有了基本掌握。
五、统计学辅导记录
1. 学生姓名:钱某
2. 辅导时间:2018年8月。
excel求解线性规划和灵敏度分析实训过程记录及学习收获

excel求解线性规划和灵敏度分析实训过程记录及学习收获线性规划是一种数学优化模型,用于对一组线性限制条件下的线性目标函数进行优化。
Excel 能够进行线性规划问题的求解和灵敏度分析,以下是实习过程的记录和收获总结:1. 实训任务我们的实训任务是一个有饲料限制的生产计划问题,其中需要决定生产哪些种类的产品、购买何种原材料、以及在何时生产这些产品,以使得利润最大化。
任务中给定了各种产品需要的原材料数量,各种原材料的数量与价格,及一些限制条件,例如生产时间,最小生产量等。
2. Excel求解线性规划问题Excel中求解线性规划问题的函数是“Solver”,首先需要打开Excel中的“数据”选项卡,然后在“分析”工具中找到“Solver”。
进入“Solver参数”对话框后,需要输入目标函数和限制条件,并且设置决策变量的可变性、约束条件的类型和数量。
最后根据需要设置求解的约束条件和目标函数的目标方向,点击“求解”即可。
在我们的实训任务中,我们首先需要设置约束条件,限制了各种产品需要的原材料数量,并且确保生产时间在规定范围内。
然后我们需要设置各个决策变量的可变性,例如选择生产哪些产品,购买何种原材料以及在何时生产这些产品等。
最后将目标函数设置为生产的利润最大化,并且设置约束条件为“>=0”,以确保决策变量的可行性。
点击“求解”即可得出最优解。
3. Excel灵敏度分析Excel的灵敏度分析功能可以帮助我们了解线性规划问题的各个变量对于目标函数的影响程度。
Excel中灵敏度分析的函数是“规划求解器的报告”,在对话框中选择“接受解决方案”,然后勾选“制作规划求解器报告”选项,即可生成报告。
在报告中,我们可以看到各个决策变量的最优解以及目标函数的最优值。
同时,报告中还包括影响目标函数的变量的“系数范围”和“变化量”,我们可以通过调整这些参数来预测目标函数的变化情况。
4. 学习收获通过这次实训,我学会了如何使用Excel求解线性规划问题以及如何进行灵敏度分析。
跟我学一步步学Minitab的使用 (2)进行量具的线性研究

大家好!今天我们谈谈:“如何进行量具的线性研究”。这是计量型量具所必须进行的测量系统分析
线性
在量具预期的工作范围内,偏移值之间的差值
就是偏移在不同量程是 不同的,这些不同的偏 移之间的差别就是量具 的线性
线性
如何获得一个量具的线性?
一般先获得不同量程的偏移,然后比较这些偏移量的差别来获得线性的值
这是截距b
这里P值为 0.315 , 大 于 0.05;可以判定 偏移是可以接受 的
线性分析步骤 步骤7:对分析获得的数据进行解释
斜率指的是:线 于 0.05;可以判定 线性是可以接受 的
y=-0.00167x+0.04
线性分析步骤 步骤7:对分析获得的数据进行解释
采取的例子如下。测量后的基准值填入表格中
线性分析步骤
步骤3:让经常使用该量具的操作者测量每个零件m≥ 10次
按照如下表格记录以整理测量结果
必须随机地选择零件 ,从而减少评价人对 测量中偏倚的“记忆 ”
线性分析步骤 步骤4:利用Minitab软件进行分析 在Minitab工作表中,按照如下方式整理好数据
拟合的回归线 在 95% 置 信 区 间内(红色 线),说明线 性是可以接受 的
y=-0.00167x+0.04
对斜率的解释:斜率为 -0.00167;表示量程每增 加1mm,偏移会减少 0.00167mm
今天就谈到这,欢迎大家交流!
线性分析步骤
步骤5:选择分析方法:量具线性和偏倚研究 在Minitab菜单中,统计>质量工具>量具研究>量具线性和偏倚研 究
线性分析步骤 步骤6:在弹出的选项中,按如下方式进行选择
_事件统计分析记录表

培训效果差作业人员没有掌握( )
设计缺陷( ) 建设原因( )
其他 :
最高管理层的意见
回顾的形式
会议学习( )张贴告知( ) 纳入培训教材( )
调查记录档案号
填表说明:
1、“事故列表”填写需知:
当提前统计的年度范围时,应将该范围段发生的事故与事件全部列入分析范围;
事故统计分析
索引号:JL-年号记录人:
会议召开时间
参与部门
参加人员姓名
参加人员专业
分析负责人姓名
负责人职务
事故列表
统计分析的范围为:年至年所有发生的事故。分别为:
发生时间规律分析伤亡人员年龄构分析伤亡人员工作年限分析
统计事故主要原因分析
伤害率分析
费用分析
安全标准化系统缺陷分析
讨论所采取的事故主要防范措施
第八章测量系统分析-1

第八章测量系统分析(Measurement Systems Analysis,MSA)一、有关术语及定义1、测量系统——一套组装的并适用于特定量在规定区间内给出测得值信息的一台或多台测量仪器,通常还包括其他装置,诸如试剂和电源。
1)一个测量系统可以仅包括一台测量仪器。
注:测量系统——是用来获得测量结果的整个过程。
▲2、测量仪器(计量器具)——单独或与一个或多个辅助设备组合,用于进行测量的装置。
1)一台可单独使用的测量仪器是一个测量系统。
2)测量仪器可以是指示式测量仪器,也可以是实物量具。
3、测量设备——为实现测量过程所必需的测量仪器、软件、测量标准、标准物质、辅助设备或其组合。
4、示值——由测量仪器或测量系统给出的量值。
5、示值误差——测量仪器示值与对应输入量的参考量值之差。
6、分辨力——引起相应示值产生可察觉到变化的被测量的最小变化。
7、显示装置的分辨力——能有效辨别的显示示值间的最小差值。
8、仪器偏移——重复测量示值的平均值减去参考量值。
9、测量仪器的稳定性——测量仪器保持其计量特性随时间恒定的能力。
简称稳定性。
稳定性可用几种方式量化:1)用计量特性变化到某个规定的量所经过的时间间隔表示。
2)用计量特性在规定时间间隔内发生的变化表示。
10、仪器漂移——由于测量仪器计量特性的变化引起的示值在一段时间内的连续或增量变化。
1)仪器漂移既与被测量的变化无关,也与任何认识到的影响量的变化无关。
11、影响量引起的变差——当影响量依次呈现两个不同的量值时,给定被测量的示值差或实物量具提供的量值差。
1)对实物量具,影响量引起的变差是影响量呈现两个不同值时其提供量值间的差值。
12、影响量——在直接测量中不影响实际被测的量,但会影响示值与测量结果之间关系的量。
例:1)用安培计直接测量交流电流恒定幅度时的频率。
2)测量某杆长度时测微计(千分尺)的温度。
13、测量重复性——在一组重复性测量条件下的测量精密度。
简称重复性。
MSA分析报告

XXX 公司计量型MSA 分析报告日 期:实 施 人: 评 价 人:仪器名称: 仪器编号: 分析结论: 合格 不合格 审 核:批 准:2017年2月23日陈秋凤、雷丽花、欧阳丽敏 X 志超数显卡尺(中间检验) XXX计量型MSA分析报告目录稳定性 (1)偏倚 (4)线性 (7)重复性和 (9)再现性备注: 对于有条件接收的项目应阐述接受原因.第一节稳定性分析1.1 稳定性概述在经过一段长时间下,用相同的测量系统对同一基准或零件的同一特性进行测量所获得的总变差,即稳定性是整个时间的偏倚变化。
1.2试验方案2017年02月份,随机抽取一常见印制板样品,让中间检验员工每天的早上与晚上分别使用数显卡尺对样品外形尺寸测量5次/组,共测量25组数据,并将每次测量的数据记录在表1。
1.3数据收集表1 稳定性分析数据收集记录表1.4 测量系统稳定性可接受判定标准1.4.1 不允许有超出控制限的点;1.4.2 连续7点位于中心线同一侧;1.4.3 连续6点上升或下降;1.4.4 连续14点交替上下变化;1.4.5 连续3点有2点距中心的距离大于两个标准差;1.4.6 连续5点中有4点距离中心线的距离大于一个标准差;1.4.7 连续15点排列在中心线的一个标准差X围内;1.4.8 连续8点距中心线的距离大于一个标准差。
1.5数据分析图1中间检验_数显卡尺Xbar-R控制图从图1 Minitab生成Xbar-R控制图可知,没有控制点超出稳定性可接受判定标准,表明该测量系统稳定性可接受。
1.6测量系统稳定性分析结果判定对中间检验_数显卡尺进行稳定性分析,分析结果表明该测量系统稳定性可接受。
第二节偏倚分析2.1 偏倚分析概述对相同零件上同一特性的观测值与真值(参考值)的差异。
2.2 试样方案2.2.1选择一个被测样品,确定样品的外形尺寸基准值x,样品外形尺寸基准值通过__铣边工序所使用的泛用型尺寸测量机重复测量10次取测量均值获得。
MSA分析报告(精编文档).doc

【最新整理,下载后即可编辑】XXX 公司 计量型MSA 分析报告日 期:实 施 人: 评 价 人:仪器名称: 仪器编号:分析结论: 合格不合格 审 核:批 准:2017年2月23日陈秋凤、雷丽花、欧阳丽敏张志超数显卡尺(中间检验)XXX计量型MSA分析报告目录稳定性………………………………………………………………………………………1偏倚………………………………………………………………………………………4线性………………………………………………………………………………………7重复性和再现性………………………………………………………………………………………9备注: 对于有条件接收的项目应阐述接受原因.第一节稳定性分析1.1 稳定性概述在经过一段长时间下,用相同的测量系统对同一基准或零件的同一特性进行测量所获得的总变差,即稳定性是整个时间的偏倚变化。
1.2 试验方案2017 年02 月份,随机抽取一常见印制板样品,让中间检验员工每天的早上及晚上分别使用数显卡尺对样品外形尺寸测量5次/组,共测量25组数据,并将每次测量的数据记录在表1。
1.3 数据收集表1 稳定性分析数据收集记录表1.4 测量系统稳定性可接受判定标准1.4.1 不允许有超出控制限的点;1.4.2 连续7点位于中心线同一侧;1.4.3 连续6点上升或下降;1.4.4 连续14点交替上下变化;1.4.5 连续3点有2点距中心的距离大于两个标准差;1.4.6 连续5点中有4点距离中心线的距离大于一个标准差;1.4.7 连续15点排列在中心线的一个标准差范围内;1.4.8 连续8点距中心线的距离大于一个标准差。
1.5 数据分析图1 中间检验_数显卡尺Xbar-R控制图从图1 Minitab生成Xbar-R控制图可知,没有控制点超出稳定性可接受判定标准,表明该测量系统稳定性可接受。
1.6 测量系统稳定性分析结果判定对中间检验_数显卡尺进行稳定性分析,分析结果表明该测量系统稳定性可接受。
线性和偏倚分析

量具线性和偏倚研究概述使用量具线性和偏倚研究可评估测量设备操作范围内的精确度。
选择覆盖量具操作范围的部件。
每个部件必须有一个参考值。
例如,一名工程师要评估量具的线性和偏倚。
该工程师选择5 个表示测量预期极差的部件。
每个选中的部件均通过布局检查进行测量以确定其主要测量值。
一个操作员使用量具随机测量每个部件12 次。
在何处可找到此分析要执行量具线性和偏倚研究,请选择统计 > 质量工具 > 量具研究 > 量具线性和偏倚研究。
何时使用备择分析●要在具有交叉数据的情况下完整分析测量系统,请使用交叉量具R&R 研究。
●要在具有嵌套数据的情况下完整分析测量系统,请使用嵌套量具R&R 研究。
量具线性和偏倚研究的数据注意事项要确保结果有效,请在收集数据、执行分析和解释结果时注意以下准则。
每个参考部件必须具有已知测量值参考值是参考部件的已知标准测量值。
在测量系统分析过程中,将参考值用作主值进行比较。
例如,您使用已知重为0.025 g 的参考部件校准天平。
应按随机顺序收集数据如果不随机收集数据,分析结果可能会有误导性。
选择表示测量实际或预期极差的部件。
跨测量实际或预期极差选择部件,可以评估您的量具是否对量具测量的所有部件大小具有相同准确度。
一个操作员应执行所有测量单个操作员应测量所有部件和所有仿行,这样来自不同操作员的量具变异才不会成为因子。
量具线性和偏倚研究示例一位工程师想要评估用于测量轴承内径的测量量具的线性和偏倚。
该工程师选择了五个表示测量预期极差的部件。
按布局检查测量每个部件以确定其主测量值,然后由一位操作员随机测量每个部件12 次。
该工程师之前使用方差分析法执行了交叉量具R&R 研究,确定该总研究变异是16.5368。
1.打开样本数据,轴承直径.MTW.轴承直径.MTW2.选择统计 > 质量工具 > 量具研究 > 量具线性和偏倚研究。
3.在部件号中,输入部件。
;2运用EXCEL、SPSS进行相关分析和线性、非线性回归分析

《计量地理学》实验指导§2 运用EXCEL、SPSS进行相关分析和线性、非线性回归分析回归分析是处理两个及两个以上变量间线性依存关系的统计方法。
可以通过软件EXCEL 和SPSS实现。
一、利用EXCEL软件实现回归分析以第4章习题2为例,运用EXCEL进行回归分析。
首先在菜单中选择工具==>加载宏,把“分析工具库”和“规划求解”加载上。
然后在“工具”菜单中将出现“数据分析”选项。
点击“数据分析”中的“回归”,将出现对话框如下图1所示。
图1 回归界面【输入】用以选择进行回归分析的自变量和因变量。
在“Y值输入区域”内输入B7:B11,在“X值输入区域”输入A7:A11,如果是多元线性回归,则X值的输入区就是除Y变量以外的全部解释变量“标志”;置信度水平为95%,输出结果选择在一张新的工作表中;“残差分析”,并绘制回归拟合图,点击“确定”即得到残差表。
【输出选项】用于指定输出结果要显示的内容,包括是否需要残差表及图,参差的正态分布图等。
输出结果解释图 2 回归结果显示回归结果分为三部分:(1)回归统计:包括R^2 及调整后的R^2、标准误差和观测值个数(2)方差分析:包括回归平方和、残差平方和总离差平方和以及它们的自由度、均方差和F通机量(3)回归方程的截距、自变量的系数以及它们的t统计值、95%的上下限值图3 残差与子变量之间的散点图图4 预测值与实际值散点图同样,如果在“数据分析”中点击“相关系数”,可以对多个变量进行相关系数的计算。
二、.利用SPSS软件实现回归分析在SPSS软件中,同样可以简单的实现回归分析,因为回归分析包含了线性回归与曲线拟合两部分内容,首先来看线性回归分析过程(LINEAR)(一)线性回归分析过程(LINEAR)例如,课本中数据,把降水量(P)看作因变量,把纬度(Y)看作自变量,在平面直角坐标系中作出散点图,发现它们之间呈线性相关关系,因此,可以用一元线性回归方程近似地描述它们之间的数量关系。
SPSS多元线性回归结果分析

SPSS多元线性回归结果分析输出下⾯三张表第⼀张R⽅是拟合优度对总回归⽅程进⾏F检验。
显著性是sig。
结果的统计学意义,是结果真实程度(能够代表总体)的⼀种估计⽅法。
专业上,p 值为结果可信程度的⼀个递减指标,p 值越⼤,我们越不能认为样本中变量的关联是总体中各变量关联的可靠指标。
p 值是将观察结果认为有效即具有总体代表性的犯错概率。
如 p=0.05 提⽰样本中变量关联有 5% 的可能是由于偶然性造成的。
即假设总体中任意变量间均⽆关联,我们重复类似实验,会发现约 20 个实验中有⼀个实验,我们所研究的变量关联将等于或强于我们的实验结果。
(这并不是说如变量间存在关联,我们可得到 5% 或 95% 次数的相同结果,当总体中的变量存在关联,重复研究和发现关联的可能性与设计的统计学效⼒有关。
)在许多研究领域,0.05 的 p 值通常被认为是可接受错误的边界⽔平。
F检验:对于多元线性回归模型,在对每个回归系数进⾏显著性检验之前,应该对回归模型的整体做显著性检验。
这就是F检验。
当检验被解释变量y t与⼀组解释变量x1, x2 , ... , x k -1是否存在回归关系时,给出的零假设与备择假设分别是H0:b1 = b2 = ... = b k-1 = 0 ,H1:b i, i = 1, ..., k -1不全为零。
⾸先要构造F统计量。
由(3.36)式知总平⽅和(SST)可分解为回归平⽅和(SSR)与残差平⽅和(SSE)两部分。
与这种分解相对应,相应⾃由度也可以被分解为两部分。
SST具有T - 1个⾃由度。
这是因为在T个变差 ( y t -), t = 1, ..., T,中存在⼀个约束条件,即 = 0。
由于回归函数中含有k个参数,⽽这k个参数受⼀个约束条件制约,所以SSR具有k -1个⾃由度。
因为SSE中含有T个残差,= y t -, t = 1, 2, ..., T,这些残差值被k个参数所约束,所以SSE具有T - k个⾃由度。
数据结构线性表实验报告
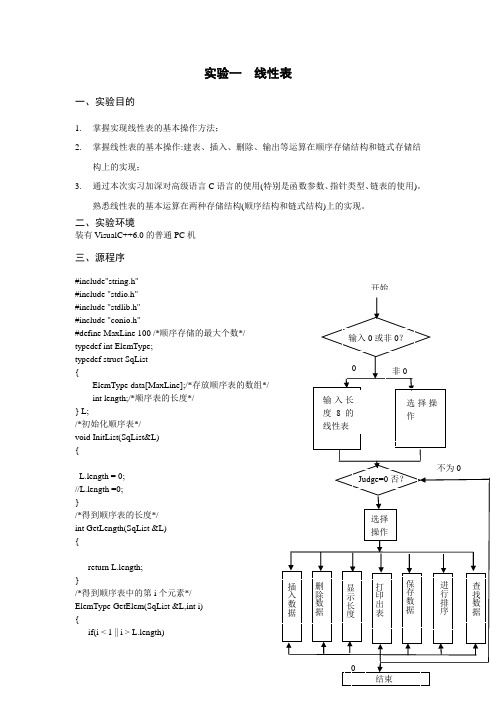
实验一线性表一、实验目的1.掌握实现线性表的基本操作方法;2.掌握线性表的基本操作:建表、插入、删除、输出等运算在顺序存储结构和链式存储结构上的实现;3.通过本次实习加深对高级语言C语言的使用(特别是函数参数、指针类型、链表的使用)。
熟悉线性表的基本运算在两种存储结构(顺序结构和链式结构)上的实现。
二、实验环境装有VisualC++6.0的普通PC机三、源程序#include"string.h"#include "stdio.h"#include "stdlib.h"#include "conio.h"#define MaxLine 100 /*顺序存储的最大个数*/ typedef int ElemType;typedef struct SqList{ElemType data[MaxLine];/*存放顺序表的数组*/ int length;/*顺序表的长度*/} L;/*初始化顺序表*/void InitList(SqList&L){L.length = 0;//L.length =0;}/*得到顺序表的长度*/int GetLength(SqList &L){return L.length;}/*得到顺序表中的第i个元素*/ElemType GetElem(SqList &L,int i){if(i < 1 || i > L.length) 开始{printf("error");exit(1);}return L.data[i-1];}void ListInsert(SqList &L,int i,ElemType x)/*添加线性表中第i个位置上的元素,i从1开始*/{int j;if(i < 1 || i > L.length+1) /*检查添加位置的合法性*/{printf("error");exit(1);}if(L.length >= MaxLine){printf("overflow!");exit(1);}j = L.length;while(j>=i)/*此处语句相对参考语句有较大改变*/{L.data[j]=L.data[j-1];j--;}L.data[i-1] = x;L.length++;}void ListDelete(SqList &L,int i) /* 删除线性表中第i个位置上的元素*/ {int j;if(i<1 || i>L.length) /* 检查空表及删除位置的合法性*/ {printf ("不存在第i个元素");exit(0);}for(j=i;j<=L.length-1;j++)L.data[j-1]=L.data[j]; /* 向前移动元素*/L.length--;}int main(){FILE *fp;struct SqList A;InitList(A);/*初始化顺序表*/int Judge2=0;printf(" ***线性表操作实验***\n \n\n请输入0对长度为8的线性表输入数据或者其他任意数进行其他操作^_^\n");scanf("%d",&Judge2);if(Judge2==0){int t = 1,d=1;for(t=1;t<=8;t++)/*此处为顺序表首先输入8个元素*/{printf("请输入第%d个线性表元素:",t);scanf("%d",&d);ListInsert(A,t,d);}}int Judge=0;printf("输入0结束程序或者输入其他任意数继续对该表进行操作^_^\n");scanf("%d",&Judge);while(Judge)/*判断是结束程序还是要继续操作该顺序表*/{int a=0;int pos=0;int c=0;int Judge1=0;int P;/*给出顺序表操作选择菜单分别为输入,删除,显示长度,打印顺序表*/printf(" ***************\n *输入1进行插入*\n");printf(" *输入2进行删除*\n");printf(" *输入3显示长度*\n");printf(" *输入4打印该表*\n");printf(" *输入5保存数据*\n");printf(" *输入6进行排序*\n");printf(" *输入7查找数据*\n ***************\n");printf("请选择:");/*选择要进行的操作*/scanf("%d",&P);if(P==0)return 0;else if(P>=1&&P<=7)switch(P){case 1:printf("请输入想进行插入操作的位置:");/*选择待插入位置*/scanf("%d",&pos);int PP;printf("请输入待插入的元素:\n");/*输入要插入的元素*/scanf("%d",&PP);ListInsert(A,pos,PP);c=GetLength(A);printf("该线性表的长度为:%d!\n",c);/*此处选择是重新选择操作还是按顺序进行下一项操作*/printf("请输入0结束操作或者其他任意数继续其他操作^_^\n");scanf("%d",&Judge1);if(Judge1==1)continue;else break;case 2:printf("输入要删除元素的位置:");/*选择要删除的元素位置*/scanf("%d",&a);ListDelete(A,a);c=GetLength(A);printf("该线性表的长度为:%d!\n",c);/*此处选择是重新选择操作还是按顺序进行下一项操作*/printf("请输入0结束操作或者其他任意数继续进行其他操作^_^\n");scanf("%d",&Judge1);if(Judge1==1)continue;else break;case 3:c=GetLength(A);printf("该线性表的长度为:%d!\n",c);printf("请输入0结束操作或者其他任意数继续进行其他操作^_^\n");scanf("%d",&Judge1);if(Judge1==1)continue;else break;case 4:{c=GetLength(A);int d=0;printf("%s"," 该线性表数据记录如下\n");printf("%s","*****************************************************\n");for(int aa=0;aa<c;aa++){printf(" ");printf("%d \t",A.data[aa]); d++;/*打印该线性表*/if( d%4 ==0) printf("\n");}printf("\n");printf("%s","*****************************************************\n");printf("请输入0结束操作或者其他任意数继续进行其他操作^_^\n");scanf("%d",&Judge1);if(Judge1==1)continue;else break;}case 5:{fp=fopen("Test.txt","wt+");int i=0,j=0;fprintf(fp,"%s"," 文件Test数据记录\n");fprintf(fp,"%s","_________________________\n");for(i=0;i<GetLength(A);){fprintf(fp,"%d",A.data[i]);i++;fputc('\t',fp);j++;if(j%4==0) fputc(10,fp);} ;fprintf(fp,"%s","\n_________________________");fclose(fp);printf("相关数据已经存入文件Test.txt中^_^\n");printf("请输入0结束操作或者其他任意数继续进行其他操作^_^\n");scanf("%d",&Judge1);if(Judge1==1)continue;else break;}case 6:{int i,j,temp;for(i=0;i<GetLength(A)-1;i++)for(j=i+1;j<GetLength(A);j++) /*注意循环的上下限*/{if(A.data[i]>A.data[j]){temp=A.data[i];A.data[i]=A.data[j];A.data[j]=temp;}}c=GetLength(A);int d=0;printf("%s","排序后该线性表数据记录如下\n");printf("%s","**************************\n");for(int aa=0;aa<c;aa++){printf("%d \t",A.data[aa]); d++;/*打印该线性表*/if( d%4 ==0) printf("\n");}printf("\n");printf("%s","**************************\n");printf("请输入0结束操作或者其他任意数继续进行其他操作^_^\n");scanf("%d",&Judge1);if(Judge1==1)continue;else break;}case 7:{int value;printf("请输入待查找的数据:\n");scanf("%d",&value);for(int i=0;i<GetLength(A);){if(A.data[i] == value)printf("待查找的是表中第%d个数据%d^_^\n",i+1,value);else if(i>=(GetLength(A)-1)) printf("待查找的数据不存在+_+\n");i++;}printf("请输入0结束操作或者其他任意数继续进行其他操作^_^\n");scanf("%d",&Judge1);if(Judge1==1)continue;else break;}}printf("请输入0 结束程序或者输入其他任意数继续进行操作^_^\n");scanf("%d",&Judge);}return 0;}四、实验数据记录1,生成长度为8的线性表2,选择插入数据3,删除数据4,打印表5,保存数据6,排序7,查找数据五、实验总结实验在编写源程序是由于参考给的参考程序较多,但是参考程序存在一定的问题且相当不完善,走了弯路。
偏移及线性分析数据记录表

線性方程式 Y=ax+b 計算平方和 S(xy)= S(xx)= S(yy)= #DIV/0! 0 #DIV/0!
製程變異=公差= 計算a,b a= a'= x= y= #DIV/0! #DIV/0! 0.0000 #DIV/0! #DIV/0! #DIV/0! #DIV/0!
線性= %線性=
#DIV/0! #DIV/0! %
2
Y
2
0.000 #DIV/0! 0.000 #DIV/0! 0.000 #DIV/0! 0.000 #DIV/0! 0.000 #DIV/0! 0.00 #DIV/0!
0.00
#DIV/0!
0.00 #DIV/0! 0.00 #DIV/0! 0.00 0.00 0.00 #DIV/0! #DIV/0! #DIV/0!
b=Y-ax= R2 = R2'=
0.0050 0.0040 0.0030 0.0020 0.0010 0.0000 -0.0010 -0.0020 -0.0030 -0.0040 -0.0050
0 0
0.0000 #DIV/0! #DIV/0!
0.0000 #DIV/0! #DIV/0!
線性圖 0.0000
執行人: 日期:
*在量具全作業範圍內選取5個樣本,並已求得各樣本之真值
制表:
審核:
JQAD-4-0050-A1(保存期限為1年以上)
偏移及線性分析數據記錄表
計算 樣本編號 1 2 3 4 5 合計 X Y X*Y #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! X
偏移及線性分析數據記錄表
量具名稱: 量具編號:
分別為 每一個樣本再由一作業者量測10次 量具數據總表 樣本 真值(X) 1 2 3 量 測 次 數 4 5 6 7 8 9 10 平均值X 偏移 全距R %偏移 #DIV/0! #DIV/0! 0.0000 #DIV/0! #DIV/0! #DIV/0! 0.0000 #DIV/0! #DIV/0! #DIV/0! 0.0000 #DIV/0! #DIV/0! #DIV/0! 0.0000 #DIV/0! #DIV/0! #DIV/0! 0.0000 #DIV/0! 1 2 3 4 5
本特利振动探头的动态校验(线性度)

甲醇合成器压缩机振动探头校验记录表1、确认探头、前置器编号:探头S/N:前置器S/N:注:探头和前置器是相互匹配的,若与其他的探头和前置器相互更换,需重新拉线性。
校验装置:TK-3e2、万用表接线:(-24)、(Com---万用表笔的负)、(Out ---万用表笔的正)3、参数记录(手操校验台就地做):1)校验装置(TK-3e)通电,固定探头,安装间隙电压在-8VDC至-12VDC之间。
2)万用表打至交流电压档测前置器Com、Out信号电压,测得对应振动的电压变化数值(万用表测得为有效值)。
3)校验装置(TK-3e)按下开关按钮至i位,通电,转盘旋转,通过调节探头固定支架的前后左右位置,使振动示值变化。
探头针对转盘中心振动值最小,向转盘外缘移动,振动值逐渐增大,向中心移动逐渐减小。
甲醇合成器压缩机5103X 振动探头校验记录表 安装间隙电压: -9.71VDC,灵敏度:7.87V/mm DCS 画面示值μm 24 49 76 102 测量电压mv(AC) 60 129 203 272 验证电压mv(AC)67128212284甲醇合成器压缩机5103X振动探头校验记录表50100150200250300244976102画面示值(μm)电压(m V )测量电压验证电压甲醇合成器压缩机5103Y 振动探头校验记录表 安装间隙电压: -10.58VDC, 灵敏度:7.87V/mm DCS 画面示值μm 24 49 74 101 测量电压mv(AC) 59 128 199 271 验证电压mv(AC)67128206281甲醇合成器压缩机5103Y振动探头校验记录表50100150200250300244974101画面示值(μm)电压(m V )测量电压验证电压甲醇合成器压缩机5104X 振动探头校验记录表 安装间隙电压: -9.86VDC, 灵敏度:7.87V/mm DCS 画面示值μm 25 49 75 99 测量电压mv(AC) 56 122 192 258 验证电压mv(AC)70136208275甲醇合成器压缩机5104X振动探头校验记录表5010015020025030025497599画面示值(μm)电压(V )测量电压mv(AC)验证电压mv(AC)甲醇合成器压缩机5103Y 振动探头校验记录表 安装间隙电压: -10.32VDC, 灵敏度:7.87V/mmDCS 画面示值μm 26 50 74 99 测量电压mv(AC) 67 132 197 265 验证电压mv(AC)72139206276甲醇合成器压缩机5103Y振动探头校验记录表5010015020025030026507499画面示值(μm)电压(m V )测量电压验证电压注:DCS 画面显示的振动值为峰-峰值(设为A ),万用表测前置器Com 、Out 信号电压为交流电压有效值(设为U),探头灵敏度设为k;函数关系为:U= KA/22;K=7.87V/mm;例如: 5103X 振动探头校验记录表,DCS 画面示值49μm ,计算对应信号电压有效值。
免疫室定量项目方法性能验证标准操作程序

免疫室定量项目方法性能验证标准操作程序1 目的对免疫室检测项目进行性能验证,以保证所采用的相关试剂盒的分析性能能满足临床检测的要求和实验室检测结果的准确性。
2范围适应于免疫室开展的所有检测项目。
3 操作程序3.1 验证前准备3.1.1 仪器设备的准备:根据免疫室仪器设备的维护保养程序, 验证前,实验人员或请仪器厂家工程师对验证过程中需要用到的仪器设备进行全面的维护保养,以确保所涉及的仪器设备在最佳运行状态。
3.1.2 试剂的准备3.1.2.1 试剂盒的准备:验证前,确保足够用于验证的同批号试剂盒,如可能,可以再适当准备一些另一批号的试剂。
3.1.2.2 室内质控品的准备:按照《免疫室定量项目室内质控管理程序》规定的室内质控品购买和制备方法进行准备。
3.2 免疫室定量项目的验证方法3.2.1 拟验证参数的确定根据试剂盒说明书或行业内(如CLIA´88)要求制定拟验证的性能参数。
免疫室定量项目需要验证的参数包括:精密度(批内、批间精密度)、正确度、线性范围、临床可报告范围、生物参考区间、干扰、不同方法和仪器间的比对等。
要求检测过程中采取质量控制措施,尽可能保证检测系统处于一个稳定状态。
3.2.2 批内精密度实验3.2.2.1 标本来源:浓度分别处于正常和病理水平的混合的新鲜临床标本。
3.2.2.2 步骤:按照临床标本相同的检测方法,同批次内检测相同的20份混合的新鲜临床标本。
记录结果并计算均值、标准差和批内变异系数CV(%):表1:批内精密度检测结果记录项目:3.2.3 批间精密度实验3.2.3.1 标本来源:浓度分别处于正常和病理水平的室内质控标本。
3.2.3.2 步骤:按照临床标本相同的检测方法,将室内质控标本连续检测20天。
记录结果,计算均值、标准差和批间精密度CV(%):表2:批间精密度检测结果记录表项目:3.2.4 正确度验证实验免疫室对参加卫生部临检中心室间质评涵盖的项目进行正确度验证,以卫生部临床检验中心室间质评结果为依据,成绩在80%以上者即为验证通过。
MSA

HOW?
1.偏倚分析
准备2个数据比较接近的样品 对2个样品进行编号 确定其中1个样品的参考值 对2个样品进行测量,测量人不清楚被测量样品的编号 测量人连续测量15-25次 数据导入MINITAB,数据由3列组成,分别为测量人,零件编号和参考值 选择统计\质量工具\量具研究\量具线性和偏倚研究 选择对应的数据,在过程变异中输入公差带或过程变差 在选项中选择以极差或标准差 在量具信息中填写量具相关信息 观察P值,P值在0.05以上时,测量系统的偏倚符合系统要求 观察偏倚的百分比,10%以下可以接受 偏倚不符合要求时,进行改进
Minth Group Quality Center
WHY?
以下几种情况下,评价结果又会如何呢?
1.参考值为5,公差为+/-1? 2.参考值为5.3,公差为+/-1?
根据分析结果说明:张三 和李四的测量存在明显差 异,这种差异会不会对测 量结果造成很大的风险?
Minth Group Quality Center
WHY?
例1.对测量数据的评价
张三和李四分别对同一零件的尺寸用游标卡尺进行24次测量,测量数据如下: 张三测量的数据 李四测量的数据
5.1 5.27 5.05 5.24 5.29 5.17
5.2 5.28 5.14 5.19 5.06 5.07
5.28 5.16 5.08 5.29 5.04 5.04
Measurement System Analysis 测量系统分析
Minth Group Quality Center
目
• 为什么要进行MSA? • 什么是MSA? • 如何进行MSA?
偏倚-线性-稳定性(测量系统分析)

v=
7.7
t=偏倚/σ b= #DIV/0! ● 给定α =0.05,算出偏倚值的1-α 置信区间: 95%置信区间上限:偏倚+d2×σ b×(tv,1-α /2)/d2*= 95%置信区间下限:偏倚-d2×σ b×(tv,1-α /2)/d2 = 4、数据分析: 上限值 下限值 偏 倚 0 0 0 0 0 0.00 0 0 0.00 0 0 0.00 0 0 0.00 0 0 0.00 0 0 0.00 0 0 0.00 0 0 0.00
*
d2= 0 0
3.07751
d2*=
3.17905
0 0 0.00
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 1 2 3 4 5 6 7 8 9 10
上限值
下限值 偏 倚
5、结 论:
通过
分 析 者:
分析时间:
审
核:
注:表格中蓝色区域为数据填充区,请将测量数据添入。
量具编号: 零件名称: 高精度量具(编)型号: 主要设备更换
操作者: 测量参数: 操作者: 新 设 备
4
10
3、数据处理: ● 计算10个读数的平均值: ● 计算可重复性标准偏差: ● 确定偏倚的t统计量: σ X均=
重复性=
0 0 0 0
tv,1-α/2=
1.8595
偏倚=X均 - 基准值= σ b= σ r/√n=
1将测量数据填入下列蓝色区域中试验记基准值x线性442t检验可能是指样本均值的自由度分布的算法針對重要特性其線性度5一般特性其線性度10線性度10以上者判為不合格此平均值y斜率a截距b拟合度r10div0
测量系统分析评定报告(偏倚分析)
文件编号: QR4-02--T26--
minitab之MSA篇

偏倚分析的做法
決定要分析的測量系統 抽取樣本,取值參考值 請現場測量人員測量15次
保留记录 各项的线性分析的记录要保存下来, 可以和PPAP档案存放在一起,以有 效证明公司的测量仪器其测量能力是 足够的。
輸入數據到EXCEL表格中
計算t值,並判定
是否合格,是否要加補正值
保留記錄
偏差练习
基准值=6.0
取至少5个样本,样本测量值要 覆盖测量仪器一定的量程范围。 确定每个样本的基准值
测量样本大于等于10次,取均 值作为“基准值”
绘制线性图
画出“偏倚=0”并判定
輸入數據到minitab表格中
計算t值,並判定
是否合格,是否要加補正值
保留記錄
偏倚分析的做法
決定要分析的測量系統 抽取樣本,取值參考值 請現場測量人員測量15次 輸入數據到EXCEL表格中
計算t值,並判定 是否合格,是否要加補正值
计算t值,并加以判定 t值的计算法:利用(平均值-标准值) /平均值的标准差。
計算控制界限,並用圖判定是否穩定
後續持續點圖,判圖
保留記錄
稳定性分析的做法
決定要分析的測量系統
選取一標准樣本,取值參考值 請現場測量人員連續測量 25組數據每次測量2~5次
輸入數據到EXCEL,Xbar-R表格中
計算控制界限,並用圖判定是否穩定
後續持續點圖,判圖
计算控制界限 平均值图:Xbarbar+-A2Rbar, Xbarbar R值图:D4Rbar, Rbar, D3Rbar
偏倚
1
5.8
-0.2
2
5.7
-0.3
3
5.9
-0.1
4
5.9
ZL05-1测量系统线性分析作业指导书

1.目的通过对控制计划中提出的测量系统进行线性分析,以了解测量系统的偏倚差值,更好的满足测量的要求。
2.适用范围适用于控制计划中提出的测量系统或部份新购、修史及提交PPAP的测量系统。
3.内容3.1选取一种可追溯标准的基准样本5个零件。
如果不能得到,则选取所代表测量器具的实际测量范围的产品零件,(或采用能全覆盖量具工作范围的基准量块),指定其作为基准样本进行线性分析。
3.2在质量部,由专人对零件编号并用高精度检测仪器/设备将每个基准零件精密测量10次,把10次的平均测量值作为每个零件的“基准值”。
3.3让一位评价人(检验员、计量员)用正被分析的量具或检测设备测量每个零件至少10次,记录其数据。
3.4计算出每个零件的测量均值及其偏倚和极差,填写《测量系统线性分析数据表》。
3.5按照以下公式计算线性和拟合优度:假设偏倚与基准值之间的交点标绘成一直线:y=b+ax式中X=基准值y=偏倚a=斜率ΣXy一(∑χ(∑y)/n)a= ------------------------------------------------ΣX2-(ΣX)2/nb=Σ(y/n)-a×Σ(x/n)(∑xy-EX(∑y)/n)2R2= ________________________________________(Σx2-(∑x)2/n)×(∑y2-(∑y)2/n)偏倚=b+ax线性=I斜率X过程变差%线性=100(线性/过程变差)3.6依据计算结果绘制线性图。
3.7线性判定是根据最佳似合直线斜率决定的,斜率越小,量具线性越好,相反斜率越大,量具线性越差。
4.形成记录和引用文件4.1形成记录《测量系统线性分析数据表》4.2引用文件《测量系统分析手册》。
