数理经济学 (4)
数理经济学茹少峰课后题及答案

第四章 习题答案1.求下列函数的极值。
(1)by ax y xy x y 3322--++= (2)xxy 212-=(3)()1613+-=x y (4)()1ln >=x xxy 解:(1)根据二元函数极值的必要条件,可得032=-+=a y x f x ,032=-+=b y x f y解得,)2,2(),(a b b a y x --=为可能的极值点。
根据充分条件,函数),(y x f 的二阶导师组成的Hessian 矩阵为03>=H ,因此)2,2(a b b a --为),(y x f 的严格极小值点,极值为22353b ab a ---。
(2)根据一元函数极值的必要条件,可得因此该函数在其定义域内为单调递增函数,极值不存在。
(3)根据一元函数极值的必要条件,可得 求得极值点为1=x 。
由充分条件知66''-=x y 。
当1=x 时0''=y ,所以该函数极值不存在。
(4)根据一元函数极值的必要条件,可得 求的极值点为e x =。
由充分条件知4''3ln 2xxx x y -=。
当e x =时,013''<-=ey ,因此该函数存在极大值为e 1。
2. 讨论函数()()122-+=y x xy y x f ,的极值。
解:根据二元函数极值的必要条件,可得)21,21(),(),21,21(),(),21,21(),(),21,21(),(),0,0(),(--=-=-===y x y x y x y x y x 为可能的极值点。
根据充分条件,函数),(y x f 的二阶导师组成的Hessian 矩阵为)0,0(),(=y x 时,01<-=H ,因此函数在该点无极值;)21,21(),(=y x 时,0223212123>==H ,海赛矩阵为正定矩阵,因此函数在该点有严格极小值为81-;)21,21(),(--=y x 时,0223212123>==H ,海赛矩阵为正定矩阵,因此函数在该点有严格极小值为81-;)21,21(),(-=y x 时,0223212123>=--=H ,0)1(,0)1(221>->-A A ,则海赛矩阵为负定矩阵,因此函数在该点有严格极大值为81;)21,21(),(-=y x 时,0223212123>=--=H ,0)1(,0)1(221>->-A A ,则海赛矩阵为负定矩阵,因此函数在该点有严格极大值为813. 试说明对于任意的0>βα,,生产函数βαL AK x f =)(是凹函数。
数理经济学的基本方法

数理经济学是一门研究经济问题的综合性学科,它结合了数学、经济学和计算机科学的方法,以及其他社会科学的理论和技术,旨在分析、研究和解决经济问题。
下面介绍数理经济学的基本方法。
一、数理经济学的抽象模型数理经济学采用抽象模型来描述经济系统的运作,这些模型可以帮助我们理解经济系统的运作机制,从而更好地解决实际的经济问题。
抽象模型的基本构成是经济变量、经济关系和经济机制。
经济变量是指经济系统中的可测量变量,如价格、收入、利润等;经济关系是指经济变量之间的关系,如供求关系、收入和消费之间的关系等;经济机制是指经济变量之间的相互作用,如市场竞争机制、政府干预机制等。
抽象模型可以采用数学方法来表达,如线性规划、动态规划等,也可以采用计算机模拟的方法来表达,如智能体模型、混合模型等。
通过这些模型,可以更清晰地描述经济系统的运作机制,从而解决实际经济问题。
二、数理经济学的实证分析实证分析是数理经济学的重要方法,它是通过实证研究,利用实际观测数据,建立经济模型,以及对模型进行验证和检验,以探索经济现象的规律,从而解决实际的经济问题。
实证分析的基本步骤包括:首先,确定研究的目的和研究的对象;其次,收集有关的观测数据;然后,建立实证模型;最后,对模型进行验证和检验,以探索经济现象的规律。
实证分析的方法可以分为统计分析和计量分析两大类。
统计分析是指利用统计方法,如回归分析、卡方检验、协方差分析等,来探索经济现象的规律;而计量分析是指利用计量经济学的方法,如模型拟合、概率分析等,来探索经济现象的规律。
三、数理经济学的模拟分析模拟分析是数理经济学的另一种重要方法,它是通过模拟经济系统的运作机制,以及模拟经济系统中的各种经济变量,来探索经济现象的规律,从而解决实际的经济问题。
模拟分析的基本步骤包括:首先,确定研究的目的和研究的对象;其次,建立模拟模型;然后,模拟经济系统的运作机制;最后,模拟经济系统中的各种经济变量,以探索经济现象的规律。
经济学分支介绍数理经济学

经济学分支介绍数理经济学经济学是一门研究人类社会生产、分配、交换和消费等方面的学科,随着科技的发展和社会需求的提高,经济学逐渐形成了许多分支,其中数理经济学是其中一种非常重要的分支之一。
数理经济学是将数学和统计学的思想、理论和方法应用于经济学研究的一种学科,主要使用数理模型来分析经济现象、解决经济问题。
数理经济学的研究对象包括但不限于个人、家庭、企业、市场、行业、国家和国际经济等方面。
数理经济学主要依赖于数学模型和统计模型来解释和预测经济现象和经济行为,因此,其理论和方法非常精密和准确。
下面我们将介绍数理经济学的几个重要分支。
1. 数理规划数理规划是一种将最优化方法应用于经济决策问题的学科,其主要目的是优化资源利用、提高效率、降低成本并实现最大回报。
数理规划主要使用的方法包括线性规划、非线性规划、整数规划等。
2. 博弈论博弈论是一种通过对多人决策的分析来描述和研究人类行为的学科,其中多人之间的互动和竞争是非常重要的研究对象。
博弈论主要通过建立博弈模型来分析和研究人类行为,其主要方法包括纳什均衡理论、信息博弈、演化博弈等。
3. 经济计量学经济计量学是一种将数理统计学方法应用于经济问题研究的学科,其主要目的是确定经济理论的有效性并为经济预测提供预测模型。
经济计量学主要使用的方法包括时间序列分析、回归分析、协整分析等。
4. 资源与环境经济学资源与环境经济学是一种研究人类活动对自然资源和环境的影响及其管理和政策解决方案的学科。
该领域主要研究环境污染、自然资源管理、可持续发展和生态经济等问题。
其主要方法包括环境评估、成本效益分析、环境税和贸易政策等。
5. 金融工程学金融工程学是将数学、计算机科学和金融理论结合起来研究金融市场和金融工具的学科。
其重点研究金融工具的设计、建模和风险管理等问题,其主要应用包括金融衍生品、风险管理、资产定价等。
综上所述,数理经济学是一种非常重要的经济学分支,其方法和理论在实际经济决策和管理中发挥着重要的作用。
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第10章 指数函数与对数函数)【圣才
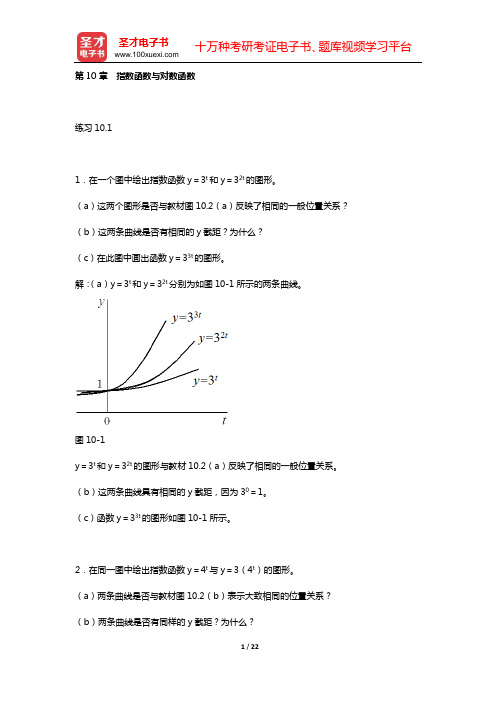
第10章指数函数与对数函数练习10.11.在一个图中绘出指数函数y=3t和y=32t的图形。
(a)这两个图形是否与教材图10.2(a)反映了相同的一般位置关系?(b)这两条曲线是否有相同的y截距?为什么?(c)在此图中画出函数y=33t的图形。
解:(a)y=3t和y=32t分别为如图10-1所示的两条曲线。
图10-1y=3t和y=32t的图形与教材10.2(a)反映了相同的一般位置关系。
(b)这两条曲线具有相同的y截距,因为30=1。
(c)函数y=33t的图形如图10-1所示。
2.在同一图中绘出指数函数y=4t与y=3(4t)的图形。
(a)两条曲线是否与教材图10.2(b)表示大致相同的位置关系?(b)两条曲线是否有同样的y截距?为什么?(c)在同一图中绘出函数y=3(4t)/2的图形。
解:(a)y=4t和y=3(4t)曲线为如图10-2所示的两条曲线。
y=4t和y=3(4t)的曲线与教材10.2(b)中的曲线有大致相同的位置关系。
图10-2(b)两条曲线不具有同样的y截距,因为40=1,3×40=3。
(c)函数y=3(4t)/2的图形如图10-2所示。
3.认可e t的导数为其自身,运用链式法则求下列函数的dy/dt:(a)y=e5t;(b)y=4e3t;(c)y=6e-2t。
解:(a)dy/dt=[dy/d(5t)][d(5t)/dt]=5e5t。
(b)dy/dt=[dy/d(3t)][d(3t)/dt]=12e3t。
(c)dy/dt=[dy/d(-2t)][d(-2t)/dt]=-12e-2t。
4.根据我们对(10.1)的讨论,你能预期函数y=e t是以递增速率单调地递增吗?通过确定此函数的一阶和二阶导数的符号验证你的答案。
在验证答案时,记住此函数的定义域为全体实数的集合,即区间(-∞,+∞)。
解:y′=e t>0,y″=e t>0。
所以,函数是以递增速率单调地递增。
5.在(10.2)中,若a与c被赋予负值,则教材图10.2中的曲线图形便不再适用。
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第9章 最优化:一类特殊的均衡分析)

第9章最优化:一类特殊的均衡分析练习9.21.假设定义域为全部实数的集合,求下列函数的稳定值,并检验其为相对极大值、极小值还是拐点:(a)y=-2x2+8x+7;(b)y=5x2+x;(c)y=3x2+3;(d)y=3x2-6x+2。
解:(a)令y′=-4x+8=0,解得x=2。
当x<2时,y′>0;当x>2时,y′<0。
所以,稳定值y=-2×22+8×2+7=15是函数的极大值。
(b)令y′=10x+1=0,解得x=-1/10。
当x<-1/10时,y′<0;当x>-1/10时,y′>0。
所以,稳定值y=5×(-1/10)2-1/10=-1/20是函数的极小值。
(c)令y′=6x=0,解得x=0。
当x<0时,y′<0;当x>0时,y′>0。
所以,稳定值y =3是函数的极小值。
(d)令y′=6x-6=0,解得x=1。
当x<1时,y′<0;当x>1时,y′>0。
所以,稳定值y=3×1-6×1+2=-1是函数的极小值。
2.假设定义域为区间[0,∞),求下列函数的稳定值,并检验其为相对极小值、极大值,还是拐点:(a)y=x3-3x+5;(b)y=x3/3-x2+x+10;(c)y=-x3+4.5x2-6x+6。
解:(a)令y′=3x2-3=0,解得x=1。
当0≤x<1时,y′<0;当x>1时,y′>0。
所以,稳定值y=1-3+5=3是函数的极小值。
(b)令y′=x2-2x+1=0,解得x=1。
当0≤x<1时,y′>0;当x>1时,y′>0。
所以,稳定值y=1/3-1+1+10=31/3是函数的拐点。
(c)令y′=-3x2+9x-6=0,解得x1=1,x2=2。
当0≤x<1时,y′<0;当1<x<2时,y′>0;当x>2时,y′<0。
所以,稳定值y=-1+4.5-6+6=3.5是函数的极小值,稳定值y=-23+4.5×22-6×2+6=4是函数的极大值。
数理经济学

数理经济学
数理经济学(Mathematical Economics):有狭 义、中义、广义三种定义。狭义的数理经济学指的 是一般均衡理论,广义的数理经济学指的是运用数 学符号、公式、图标和方法来研究和表述经济现象 及其规律数理经济学也着重研究经济的定量方面, 但是它不注重经济变量的随机特征,它仅是用数学 形式表达经济理论,并不关心经济理论的可测性, 且模型所反映的经济变量之间的关系是确定的。而 计量经济学的主要兴趣在于利用数理经济学提出的 数学方程及实际数据来验证经济理论,模型所反映 的经济变量之间的关系是非确定性的、随机的相关 关系。数理经济学为计量经济学提供建模基础。
数理经济学

2011-4-30
IV.12.2
GuoSipei@CCNUMATH
求稳定值
• 拉格朗日乘数法
其实质是将约束极值问题转化为另一种等价形式, 从而使得自由极值问题的一阶条件仍然可以应用. 问题:给定U=x1x2+2x1,约束条件4x1+2x2=60, 求U的极大值.
先写出拉格朗日函数,它是容纳了约束条件的目标函数的 变形:Z=x1x2+2x1+λ(60-4x1-2x2) 如果约束条件得到满足(上式括号中的部分等于0),则无 论λ(拉格朗日乘数)取何值Z=U,于是,问题转化为加入变 量λ后的,Z的自由极值问题
第四篇 最优化问题
• 第12章 具有约束方程的最优化
约束的影响 求稳定值 二阶条件 拟凹性和拟凸性 效用最大化与消费需求 齐次函数 投入的最小成本组合
2011-4-30
IV.12.1
GuoSipei@CCNUMATH
约束的影响
• 约束
一个约束确立了两个变量在充当选择变量时的关系, 但这种关系与其他类型的将两个变量联系在一起的 关系是不同的. 施加约束的基本目的是对在所讨论的最优化问题中 存在的某些限制因素给出合理的认识 生产配额问题是典型的约束最优化问题 约束的作用在于缩小定义域,从而缩小目标函数的 值域
2011-4-30
IV.12.15
GuoSipei@CCNUMATH
2011-4-30
IV.12.16
GuoSipei@CCNUMATH
• 代数定义
三个相关定理:
2011-4-30
IV.12.17
GuoSipei@CCNUMATH
有用的说明:
两个拟凹函数的和不一定是拟凹函数 检验拟凹性和拟凸性的简便方法:
数理经济学茹少峰第4章课后题及标准答案

第四章 习题答案1.求下列函数的极值。
(1)by ax y xy x y 3322--++= (2)x xy 212-=(3)()1613+-=x y (4)()1ln >=x xx y 解:(1)根据二元函数极值的必要条件,可得032=-+=a y x f x ,032=-+=b y x f y解得,)2,2(),(a b b a y x --=为可能的极值点。
根据充分条件,函数),(y x f 的二阶导师组成的Hessian 矩阵为⎪⎪⎭⎫⎝⎛=2112)(x H03>=H ,因此)2,2(a b b a --为),(y x f 的严格极小值点,极值为22353b ab a ---。
(2)根据一元函数极值的必要条件,可得0)21(22'>-=x y因此该函数在其定义域内为单调递增函数,极值不存在。
(3)根据一元函数极值的必要条件,可得03632'=+-=x x y求得极值点为1=x 。
由充分条件知66''-=x y 。
当1=x 时0''=y ,所以该函数极值不存在。
(4)根据一元函数极值的必要条件,可得0ln 12'=-=xxy 求的极值点为e x =。
由充分条件知4''3ln 2xxx x y -=。
当e x =时,013''<-=ey ,因此该函数存在极大值为e 1。
2. 讨论函数()()122-+=y x xy y x f ,的极值。
解:根据二元函数极值的必要条件,可得03,032332=-+==-+=x x y x f y y y x f y x)21,21(),(),21,21(),(),21,21(),(),21,21(),(),0,0(),(--=-=-===y x y x y x y x y x 为可能的极值点。
根据充分条件,函数),(y x f 的二阶导师组成的Hessian 矩阵为⎪⎪⎭⎫ ⎝⎛-+-+=yx y x y x xy x H 61331336)(2222 )0,0(),(=y x 时,01<-=H ,因此函数在该点无极值;)21,21(),(=y x 时,0223212123>==H ,海赛矩阵为正定矩阵,因此函数在该点有严格极小值为81-;)21,21(),(--=y x 时,0223212123>==H ,海赛矩阵为正定矩阵,因此函数在该点有严格极小值为81-;)21,21(),(-=y x 时,0223212123>=--=H ,0)1(,0)1(221>->-A A ,则海赛矩阵为负定矩阵,因此函数在该点有严格极大值为81;)21,21(),(-=y x 时,0223212123>=--=H ,0)1(,0)1(221>->-A A ,则海赛矩阵为负定矩阵,因此函数在该点有严格极大值为813. 试说明对于任意的0>βα,,生产函数βαL AK x f =)(是凹函数。
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第12章 具有约束方程的最优化)【圣

第12章具有约束方程的最优化练习12.21.运用拉格朗日乘数法求z的稳定值:(a)z=xy,满足约束x+2y=2;(b)z=x(y+4),满足约束x+y=8;(c)z=x-3y-xy,满足约束x+y=6;(d)z=7-y+x2,满足约束x+y=0。
解:(a)拉格朗日函数为:Z=xy+λ(2-x-2y),稳定值的必要条件为:Zλ=2-x-2y=0Z x=y-λ=0Z y=x-2λ=0解得:λ*=1/2,x*=1,y*=1/2,故z的稳定值为z*=1/2。
(b)拉格朗日函数为:Z=xy+4x+λ(8-x-y),稳定值的必要条件为:Zλ=8-x-y=0Z x=y+4-λ=0Z y=x-λ=0解得:λ*=6,x*=6,y*=2,故z的稳定值为z*=36。
(c)拉格朗日函数为:Z=x-3y-xy+λ(6-x-y),稳定值的必要条件为:Zλ=6-x-y=0Z x=1-y-λ=0y解得λ*=-4,x*=1,y*=5,故z的稳定值为z*=-19。
(d)拉格朗日函数为:Z=7-y+x2+λ(-x-y),稳定值的必要条件为:Zλ=-x-y=0Z x=2x-λ=0Z y=-1-λ=0解得λ*=-1,x*=-1/2,y*=1/2,故z的稳定值为z*=27/4。
2.在上题中,约束条件略微放松是增加还是降低了z的最优值,增加或降低的速率是多少?解:(a)增加,增加的速率为:dz*/dc=λ*=1/2。
(b)增加,增加的速率为:dz*/dc=λ*=6。
(c)降低,降低的速率为:dz*/dc=λ*=-4。
(d)降低,降低的速率为:dz*/dc=λ*=-1。
3.写出下列函数的拉格朗日函数和稳定值的一阶条件(不必解方程):(a)z=x+2y+3w+xy-yw,满足约束x+y+2w=10;(b)z=x2+2xy+yw2,满足约束2x+y+w2=24和x+w=8。
解:(a)拉格朗日函数为:Z=x+2y+3w+xy-yw+λ(10-x-y-2w)稳定值的一阶条件为:Zλ=10-x-y-2w=0Z x=1+y-λ=0y Z w =3-y -2λ=0 (b )拉格朗日函数为:Z =x 2+2xy +yw 2+λ(24-2x -y -w 2)+v (8-x -w ) 稳定值的一阶条件为: Z λ=24-2x -y -w 2=0 Z v =8-x -w =0 Z x =2x +2y -2λ-v =0 Z y =2x +w 2-λ=0 Z w =2yw -2λw -v =04.若将约束条件写成G (x ,y )=0,而不是写成g (x ,y )=c 的形式,那么,拉格朗日函数和一阶条件应如何修正? 解:拉格朗日函数应修正为:一阶条件应修正为: Z λ=-G (x ,y )=0 Z x =f x -λG x =0 Z y =f y -λG y =05.在讨论全微分法时,我们曾指出已知约束条件g (x ,y )=c ,可以推导出dg =0。
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第8章 一般函数模型的比较静态分析)

5.上题中两个偏弹性如何随 P 和 R 的变化而变化?若 P 和 R 为正,变化是严格单调的吗? 解:∂εQP/∂P=4bP(a+R1/2)/(a+bP2+R1/2)2,∂εQP/∂R=-bP2R-1/2/(a+bP2+R1/2) 2<0。 所以,供给的价格弹性随 R 增大而减小;如果 a+R1/2>0,则随 P 的增大而增大,如果 a +R1/2<0,则随 P 的增大而减小,如果 a+R1/2=0,则不随 P 变化。但是供给的价格弹性 关于 R 和 P 的变化都是单调的。
4.某商品的供给函数为: Q=a+bP2+R1/2(a<0,b>0)[R:降雨量] 求供给的价格弹性 εQP,供给的降雨量弹性 εQR。 解:供给的价格弹性为:εQP=(∂Q/∂P)/(Q/P)=2bP/[(a+bP2+R1/2)/P]=2bP2/ (a+bP2+R1/2)。 供给的降雨量弹性为:εQR=(∂Q/∂R)/(Q/R)=(R-1/2/2)/[(a+bP2+R1/2)/R]= R1/2/8.2
1.以梯度向量▽U 表示全微分 dU。
dx1
dx2
解:▽U 为行向量(U1,U2,…,Un),而 dx 为列向量 dxn
那么全微分
dU U1,U2 ,
dx1
,U
蒋中一《数理经济学的基本方法》(第4版)课后习题详细分析和解答(第4章 线性模型与矩阵代数)【圣才出

4 30
CB 也有定义:
CB
7 6
2 2
2 3
3 3
7 6
0 0
2 8 3 8
20
21
16 24
BC=CB 不成立。
3.在例 9 给出的矩阵的基础上,判断 BA 是否有定义?若有,计算其积。在此例中,我们 是否有 AB=BA?
4 / 27
圣才电子书
1 4
1 2
5.在例 7 中,如果我们将数量和价格写成列向量而非行向量,Q·P 有定义吗?我们能否将 总采购成本表示为 Q·P?或 Q′·P?或 Q·P′? 答:Q·P 有定义。两个元素个数相同的向量的内积是对应元素的积的和,两个行向量、两个 列向量、一个行向量和一个列向量、一个列向量和一个行向量的内积均有定义。所以能将采 购成本表示为 Q·P 或 Q′·P 或 Q·P′。
1 / 27
圣才电子书 十万种考研考证电子书、题库视频学习平台
Qd1 Qs1 Qd1
Qs1
0
a1P1 a2 P2 a0
b1P1 b2 P2 b0
Qd 2 Qs2
0
Qd 2
1P1 2 P2 0
Qs2 1P1 2 P2 0
则系数矩阵为
1 1 0 0 0 0
Qd-Qs=0
Qd+bP=a
Qs-dP=-c
1 1 0
0
1 0
b
a
如果系数矩阵为 0 1 d ,则常数向量为 c 。
2.变量按下列顺序排列:Qd1,Qs1,Qd2,Qs2,P1,P2。按(4.1)方式改写方程组(3.12)。 写出系数矩阵、变量向量和常数向量。 解:将方程组(3.12)改写为:
,常数向量为
推荐下载-数理经济学课程教学大纲精品

推荐下载-数理经济学课程教学大纲精品《数理经济学》课程教学大纲一、课程的基本信息课程编号:09040060课程中文名称:数理经济学课程英文名称:Mathematical Economics课程性质:专业主干课考核方式:考查开课专业:金融学、经济学开课学期: 4总学时:40(其中理论32学时,上机8学时)总学分: 2.5二、课程目的和任务数理经济学是经济学专业的重要课程之一,是一门融合了线性代数、数理统计和经济学的综合课程,它强调运用数学方法,主要是线性代数、数理统计方法来解决经济学中的一些原理问题。
通过数理经济学课程的学习,使学生能够运用多元经济分析方法,分析解决经济学中的基础原理问题,并具备基本的分析和解决实际经济问题的能力。
三、教学基本要求(含素质教育与创新能力培养的要求)1、对数理经济学的基本概念和核心思想的认识。
2、掌握简单的多元分析方法。
3、能够分析简单的多元消费者和生产者均衡问题。
4、了解动态分析方法。
5、掌握博弈论的基础知识。
6、能够运用简单的博弈论模型分析问题。
7、掌握一般均衡理论。
8、能够运用SPSS等统计分析软件解决实际经济问题四、教学内容与学时分配第一章绪论(2学时)数理经济学的概念、数理经济学的起源和发展、数理经济学的研究对象、研究方法。
第二章效用函数(6学时)效用函数的表达式、效用函数的假设条件、效用最大化模型;直接效用函数和间接效用函数的表达式及其特点;支出最小化模型;效用函数应用举例。
第三章需求函数(8学时)需求函数的计算方法、需求函数与效用函数的关系;希克斯需求函数、补偿需求函数;几种常见的效用函数和需求函数;价格变化对需求的影响,收入变化对需求的影响;斯拉茨基方程,需求函数的性质、需求弹性;需求函数应用举例;根据实际数据建立需求函数模型(上机)。
第四章生产函数(10学时)一种生产要素可变情况下的生产函数、若干种生产要素可变情况下的生产函数;生产要素的最佳组合,利润最大化模型、成本最小化模型;影子价格;产量变化对均衡的影响、。
北京市考研经济学专业数理经济学重点概念解析

北京市考研经济学专业数理经济学重点概念解析数理经济学是经济学与数理科学相结合的跨学科领域,它运用数学和统计方法来研究经济学中的理论与现象。
在考研经济学专业中,数理经济学是非常重要的一门课程,它涉及到许多关键概念和理论。
本文将对数理经济学的重点概念进行解析,帮助考生更好地掌握相关知识。
1. 边际概念在经济学中,边际是指增量或减量的变化,边际理论主要用来解释资源分配和个体决策。
其中,边际效用、边际成本和边际产品是数理经济学中的重要概念。
边际效用指的是消费者每多消费一单位商品所增加的满足程度,边际成本则是生产者每多生产一单位产品所增加的成本,边际产品是指生产者每多生产一单位产品所增加的产量。
2. 弹性概念弹性是指经济变量对于其他相关经济变量变化的敏感程度。
常见的弹性概念有价格弹性、收入弹性和交叉弹性。
价格弹性衡量了消费者对产品价格变化的敏感程度,收入弹性衡量了消费者对产品收入变化的敏感程度,交叉弹性衡量了两个不同产品之间相互替代或互补程度的变化。
3. 均衡概念均衡是指市场供求关系达到一种相对稳定的状态。
数理经济学中的均衡概念包括了需求与供给的均衡、市场的均衡以及一般均衡。
需求与供给的均衡是指市场上商品数量需求等于商品数量供给的状态,市场的均衡是指市场上商品价格和数量达到相对稳定的状态,一般均衡是指所有市场达到均衡的状态。
4. 最优化概念最优化是指在给定的限制条件下追求某种目标的最佳决策。
在数理经济学中,最优化问题涉及到最大化或最小化一个目标函数,同时满足一系列限制条件。
最优化方法在经济学和管理学中有广泛的应用,它可以帮助研究者找到一个问题的最佳解决方案。
5. 博弈论概念博弈论是研究决策者在互动中进行决策的数学理论。
博弈论模型分析了不同决策者之间的策略选择和结果预测。
博弈论中的重要概念包括纳什均衡、囚徒困境和博弈树等。
纳什均衡是指在每个决策者都选择了最优策略的情况下,无法通过改变策略来获得更好结果的状态。
数理经济学本ppt课件

Walras(瓦尔拉斯)---列写多种产品静态供求平衡方 程的方法,创立了非线性一般均衡理论。
Arrow(阿罗),Debreu(德布鲁)(1955左右)---在一般 情况下证明了供求平衡解的存在性和惟一性。
Scarf(斯卡夫)等人给出了求解供求平衡点的具体算 法。创建了可计算一般均衡(CGE)理论。
《数理经济学》, Longman, London and • New York, 1978。 • 3. Akira Takayama, Mathematical Economics,
Cambridge University Press, 1985。 • 4. 见教材后附国内外文献。
4
内容提要
第1章 效用函数与需求函数 1.1 效用函数的数学表达式及其特性 1.2 效用最大法则与需求函数 1.3 考虑多个时期的消费者最优选择
28
本学期的主要内容:
* 掌握瓦尔拉斯,列昂惕夫一般均衡理论,初步了解一般
均衡理论基本知识。
* 掌握效用函数丶需求函数的各种数学表达式, 以及在实 际中的具体应用。
* 掌握生产函数、供给函数、要素需求函数的各种数学表 达式, 以及在实际中的具体应用。
* 掌握瓦尔拉斯一般均衡构模基本方法。
* 掌握列昂惕夫(Leontief)线性多部门模型建模技术与基本 应用。
第2 步:解方程并讨论解的5个基本问题: 解的
存在性、稳定性、合理性、能控性、一定时间内
到达合理轨道的能达性。
12
数理经济学与微观经济学、宏观经济学、国际贸 易经济学、福利经济学、计量经济学和经济控制论之 间的关系。
微观经济学: 主要讨论产品市场、要素市场( 如 资本市场、资源市场、劳动市场等) 的供求描述。
数理经济学数学模型基本要素

数理经济学数学模型基本要素数理经济学是经济学的一个分支领域,它通过运用数学和统计学的方法来研究和解释经济现象。
数理经济学的核心是数学模型,它是通过数学语言来描述和分析经济活动的工具。
一个完整的数理经济学数学模型包含以下基本要素。
1. 决策者:决策者是指在经济活动中做出决策的个体、企业或政府等。
决策者的行为和决策将影响到整个经济系统的运行。
2. 决策变量:决策变量是决策者可以选择的变量,它们可以是生产数量、价格、投资规模、消费水平等。
决策变量的选择将直接影响到经济系统的效果。
3. 目标函数:目标函数是决策者根据自身利益所追求的目标,它可以是利润最大化、效用最大化等。
决策者的决策将会根据目标函数来进行优化。
4. 约束条件:约束条件是限制决策者决策的条件,它可以是资源约束、市场需求约束、技术约束等。
决策者的决策必须在约束条件下进行。
5. 假设:数理经济学模型中通常会做出一些假设,以简化模型的复杂度。
这些假设可以是市场完全竞争、决策者理性、信息完全等。
假设的合理性将直接影响到模型的准确性和适用性。
6. 方程:数理经济学模型中的方程是描述经济关系的数学表达式。
方程可以是需求方程、供给方程、成本方程等。
通过建立和求解方程,可以得到模型的解析解或数值解。
7. 均衡:数理经济学模型中的均衡是指经济系统在特定条件下达到的一种稳定状态。
常见的均衡包括市场均衡、社会均衡等。
通过分析和求解模型,可以得到经济系统的均衡状态。
8. 分析方法:数理经济学模型的分析方法通常包括静态分析和动态分析。
静态分析是在特定时间点上对经济系统进行分析,而动态分析则是考虑时间因素对经济系统进行分析。
9. 参数估计:数理经济学模型中的参数是用来描述经济关系的重要指标,通过对观测数据的估计,可以得到模型中的参数值。
参数估计的准确性将直接影响到模型的预测和应用。
10. 策略分析:数理经济学模型可以用于分析不同策略对经济系统的影响。
通过对模型进行模拟和实验,可以评估不同策略的效果,并为决策者提供决策支持。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.学时安排:周学时3,总学时54
5.学分分配:3学分
(二)开设目的
数理经济学是一门融合了线性代数、数理统计和经济学的综合课程,它强调运用数学方法,主要是线性代数、数理统计方法来解决经济学中的一些原理问题。
(三)基本要求
通过本课程的学习,使学生能够运用多元经济分析方法,分析解决经济学中的基础原理问题,并具备基本的分析和解决实际经济问题的能力。
基本要求
理解数理经济学的产生和发展,掌握数理经济学的研究方法、经济模型的构成要素。
第二章矩阵论基础
教学目的
通过本章的学习使学生掌握矩阵论的基本方面,如矩阵乘法、逆与分块、矩阵特征值和矩阵函数等,这些是数理经济学方法的理论基础。
教学内容
第一节矩阵乘法、逆及其经济学应用
第二节矩阵的初等变换及其应用
第三节矩阵特征值与矩阵函数
第五章比较静态分析3学时
第六章无约束最优化问题4学时
第七章具有约束方程的最优化4学时
第八章积分计算方法及其经济学应用5学时
第九章常微分方程模型10学时
第十章联立常微分方程模型10学时
第十一章差分方程模型8学时
(二)考核要求
1.成绩评定
平时成绩(含作业,测验,考勤作为参考)占30%,期末(卷面)占70%.
第二节边际、弹性与增长率
第三节成本函数及相关的概念基 Nhomakorabea要求理解边际、弹性、增长率以及成本函数的概念,掌握边际、弹性、增长率与导数的关系。
第五章比较静态分析
教学目的
通过本章的学习,使学生隐函数求导在经济学中的应用有比较好的理解,会利用隐函数求导解决一些实际问题。
教学内容
第一节Jacobi矩阵和Jacobi行列式
2.命题说明
通过多样化的题型来测试学生各种能力,设计适当的开放性问题。基本题(
主要考查学生对数理经济学基本概念、理论与方法的一般掌握和理解)、计算题(主要考查学生对数理经济学的基本方法的具体、灵活应用)、应用题(主要考查学生对数理经济学基本理论、基本方法的综合运用能力)各占约1/3。难易比例控制在20%难、50%适中、30%易之间。涉及教材章的100%,节的85%,内容70%左右,试卷末设置能反映学生综合能力且有较大难度和较高要求的附加题。试卷采用A、B卷。
第二节收入决定模型
第三节IS-LM模型
基本要求
理解均衡分析方法在经济中的应用,掌握商品市场均衡模型、收入决定模型和IS-LM模型。
第四章边际与弹性分析
教学目的
通过本章的学习,使学生边际、弹性与增长率的概念有深刻认识,明白微分学中的全微分概念与边际、弹性等经济学概念的关系。
教学内容
第一节全微分与全导数
深圳大学数学与计算科学学院
课程教学大纲
(2006年10月重印版)
课程编号22123066C
课程名称数理经济学
课程类别综合选修
教材名称数理经济学导论
制订人蒋春福
审核人胡鹏彦
2005年4月修订
一、课程设计的指导思想
(一)课程性质
1.课程类别:综合选修课
2.适应专业:数学与应用数学专业(金融数学方向)
3.开设学期:第四学期
[3]张齐林.博弈论.天津:南开大学出版社,2003.
二、教学内容
第一章数理经济学概述
教学目的
通过本章的学习,使学生了解数理经济学的产生和发展、研究方法与基本问题以及经济模型的构成要素。
教学内容
第一节数理经济学的产生和发展
第二节数理经济学的研究方法和基本问题
第三节与宏微观经济学等经济学分支的比较
第四节经济模型的构成要素
第十章联立常积分方程模型
教学目的
学习微分方程及其解法,并能够掌握一些微分方程的经济应用模型。
教学内容
第一节一阶微分方程组
第二节变系数线性微分方程组
第三节常系数线性微分方程组
第四节稳定性与定性理论
第五节经济学应用
基本要求
理解动力学体系、自治系统和非自治系统、极限环等概念,掌握微分方程的解法及稳定性理论,了解Walras一般均衡的稳定性分析、物价的微分方程模型、广告的微分方程模型等。
(四)主要内容
首先,从均衡系统出发,介绍了比较静态分析方法和极大化分析方法,并应用这些方法对消费者的行为、生产者的行为进行了局部均衡分析,在此基础上介绍了瓦尔拉斯一般均衡理论,从而形成了数理经济分析的基本框架;其次,介绍了投入产出分析的基本理论;再次,介绍了积分计算方法、常微分方程模型、差分方程模型等动态分析方法在经济学的应用。
注:根据各课程的具体情况编写,但必须写明各章教学目的、要求、内容提要。
三、课时分配及其它
(一)课时分配
课程总教学时数为54学时,安排在第四学期,每周3学时,上课18周,共54学时,其中包括4个实验学时。
第一章数理经济学概述1学时
第二章矩阵论基础4学时
第三章市场均衡模型3学时
第四章边际与弹性分析2学时
教学内容
第一节不定积分的计算
第二节定积分的计算
第三节二重积分的计算
第四节积分的经济应用
第五节Domar模型
基本要求
掌握基本积分公式、换元积分法、分部积分法和某些特殊函数的积分法,了解积分在经济学的应用。
第九章常微分方程模型
教学目的
通过学习本章内容,能够求解一阶常微分方程和高阶常系数线性微分方程,掌握一些经济学微分方程模型。
第二节隐函数求导
第三节比较静态导数的应用
基本要求
理解比较静态分析的原理和意义,掌握利用隐函数求导方法对经济学模型进行比较静态分析。
第六章无约束最优化问题
教学目的
通过本章的学习,使学生能够运用微分学的知识解决经济学中的极值问题。
教学内容
第一节一元函数的极值
第二节多元函数的极值
第三节凸分析概要
第四节经济与管理中的应用
(五)先修课程
微观经济学、宏观经济学、高等数学等
(六)后继课程
计量经济学、数学建模、金融数学等
(七)考核方式
闭卷考试
(八)使用教材
伍超标.数理经济学导论.北京:中国统计出版社,2002.
(九)参考书目
[1]张金水.数理经济学:理论与应用.北京:清华大学出版社,1999.
[2]谢胜智.数理经济学.成都:西南财经大学出版社,2004.
第十一章差分方程模型
教学目的
学习差分方程及其解法,并能够掌握一些差分方程的经济应用模型。
教学内容
第一节一阶差分方程
第二节一阶差分方程的经济应用
第三节高阶差分方程的解法
第四节高阶差分方程的经济应用
第五节联立差分系统及其经济学应用
基本要求
掌握求解差分方程的待定系数法、特征根法以及解的收敛性定理,了解乘数动力学模型、蛛网模型、具有存货的市场模型、Harrod经济增长模型、Samuelson乘数加速模型、Hicks经济周期模型、Goodwin期望价格模型、Phillips模型、Smith模型等。
教学内容
第一节一阶常微分方程的解法
第二节一阶常微分方程的经济应用
第三节高阶常系数线性微分方程的解法
第四节高阶常系数线性微分方程的经济应用
基本要求
掌握一阶常微分方程的解法和高阶常系数线性微分方程的解法,并会由点弹性确定需求函数,对供需需求进行定性分析,了解蛛网模型、Solow新古典经济增长模型、具有价格预期的市场模型、封闭经济的Phillips模型。
第六节生产函数与技术进步
基本要求
理解函数极值、凸凹性和凸集、替代率和规模报酬的概念,掌握生产函数定义和的基本性质,技术进步及其偏倚。
第七章具有约束方程的最优化
教学目的
通过本章的学习,使学生掌握具有约束方程的最优化问题,并应用到效用最大化、成本最小化、利润最大化、产出最大化等经济问题。
教学内容
第一节Lagrange乘数法
第二节凸分析概要:拟凸性
第三节效用最大化与需求函数
第四节成本函数
第五节利润最大化的经济优化问题与市场均衡
第六节比较静态分析
基本要求
理解函数拟凸性的定义,理解效用函数、成本函数和需求函数的概念与性质,掌握效用最大化、成本最小化、利润最大化等经济优化问题。
第八章积分计算方法及其经济学应用
教学目的
通过学习本章内容,使学生掌握不定积分和定积分的计算方法,了解积分在经济学的应用。
第四节实二次型
基本要求
理解矩阵特征值、Jordan标准型和矩阵函数的概念,掌握矩阵初等变换、Hamilton-Cayley定理与最小多项式。
第三章市场均衡模型
教学目的
通过本章的学习,使学生领会“供给、需求、均衡”是经济学中最核心的概念,并通过一些简单的经济均衡模型的学习掌握均衡分析方法。
教学内容
第一节商品市场均衡
