湖南职高对口高考数学仿真试题

合集下载

中职数学 2024年湖南省对口招生高考数学模拟试卷

2024年湖南省对口招生高考数学模拟试卷一、选择题（本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）A ．∅B ．{d }C ．{a ,c }D ．{b ,e }1．（4分）已知全集U ={a ,b ,c ,d ,e }，集合N ={b ,d ,e }，M ={a ,c ,d }，则∁U （M ∪N ）=（）A ．{x |x <1}B ．{x |x >4}C ．{x |1<x <4}D ．{x |x <1或x >4}2．（4分）不等式-x 2+5x -4>0的解集是（）A ．6B ．-4C ．4或-6D ．6或-43．（4分）已知点P （a ,2）到直线4x -3y +2=0的距离等于4，则a =（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．（4分）已知直线m 、n 和平面α，且n ⊆α，则“m ⊥α”是“m ⊥n ”的（）A ．4B ．4+4C ．4D ．4+45．（4分）设正四棱锥的底面边长和侧棱长都是2，则该四棱锥的表面积为（）M 3M 3M 5M 5A ．2B ．-2C ．1D ．-16．（4分）已知向量a =（-2，1），b =（4，3），c =（-1，λ）．若（a +b ）∥c ，则λ的值为（）→→→→→→A ．（0，]B ．[0，]C ．（-∞，]D ．[，+∞）7．（4分）已知函数f （x ）=log a x （a >0且a ≠1）满足f （2）=-1，则不等式f （x ）≥3的解集是（）18181818二、填空题（本大题共5个小题，每小题4分，共20分）A ．10B ．9C ．8D ．78．（4分）从某小学随机抽取100名学生，将他们的身高数据绘制成频率分布直方图如图所示，若要从身高在[120，130）、[130，140）、[140，150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从身高在[120，130）内的学生中选取的人数应为（）A ．f （-π）>f （-2）>-f （3）B ．-f （3）>f （-π）>f （-2）C ．f （-2）>-f （3）>f （-π）D ．f （-π）>-f （3）>f （-2）9．（4分）已知f （x ）是R 上的奇函数，且在区间[0，+∞）上是减函数，则f （-2），f （-π），-f （3）的大小关系是（A ．函数y =sin 2x 的周期为πB ．函数y =sinx 在区间（，）内是减函数C ．函数y =sinx +cosx 的值域是[-2，2]D ．函数y =sin 2x 的图像可由y =sin （2x -）的图像向左平移个单位得到10．（4分）下列命题中错误的是（）3π45π4π5π1011．（4分）已知sin （π+α）=-，α∈（，π），则sin 2α= ．45π212．（4分）不等式|x -a |<2的解集为{x |-1<x <3}，则实数a = ．13．（4分）从7名运动员中选出4人参加校运会的4×100米接力赛，则甲、乙两人都不跑中间两棒的方法有种．14．（4分）过点P （2，-1）作圆C ：（x -1）2+（y -2）2=2的切线，切点为A 、B ．则|PA |= ．15．（4分）已知等差数列{a n }中a 1=13，且S 3=S 11，则S n 的最大值为．三、解答题（本大题共7个小题，其中第21、22小题为选做题．满分50分．解答应写出文字说明、证明过程或演算步选做题：请考生在第21、22题中选择一题作答．若两题都做，则按所做的第21题计分．作答时，请写清题号．老师建科类做第21题，服务类做22题.16．（10分）已知点（4，2）在函数f （x ）=的图象上．（1）求a 的值，并画出函数f （x ）的图象；（2）求不等式f （x ）<1的解集．{x +4，x ≤0x ,x ＞0log a 17．（10分）我校学生心理咨询中心服务电话的接通率为．21机2班的3名同学分别就某一问题在某天咨询该服务中心，只拨打一次电话，设X 表示他们中成功咨询的人数．求：（1）恰有2人成功咨询的概率；（2）随机变量X 的概率分布和数学期望、方差．3418．（10分）已知数列{a n }的前n 项和为S n ，且S n =2a n -3n （n ∈N +）．（1）求a 1，a 2，a 3的值；（2）设b n =a n +3，证明数列{b n }为等比数列，并求通项公式a n ．19．（10分）如图四棱锥P -ABCD 的底面是边长为2的菱形，且∠ABC =60°，PA =PC =2，PB =PD ．（1）若O 是AC 与BD 的交点，证明：PO ⊥平面ABCD ．（2）若点M 是PD 的中点，求异面直线AD 与CM 所成角的余弦值．20．（10分）已知椭圆C 的中心在坐标原点O ，焦点在x 轴上，离心率为，椭圆上一点P 到椭圆左右两焦点的距离之和为（1）求椭圆C 的标准方程；（2）已知直线l ：y =x +m 与椭圆C 交于A 、B 两个不同的点，且弦AB 的中点恰好在圆+=上，求直线l 的方程．M 32x 2y 2172521．（10分）在平面四边形ABCD中，∠ADC=90°，∠A=45°，AB=2，BD=5．（1）求cos∠ADB；（2）若DC=2，求BC．M222．某公司计划在今年内同时出售变频空调机和智能洗衣机．由于这两种产品的市场需求量非常大，有多少就能销售多少，该公司要根据实际情况（如资金、劳动力）确定产品的月供应量，以使得总利润达到最大．已知对这两种产品有直接限制的是资金和劳动力．通过调查，得到关于这两种产品的有关数据如表：资金（表中单位：百元）单位产品所需资金月资金供应量空调机洗衣机成本3020300劳动力：工资510110单位利润6试问：怎样确定两种货物的月供应量，才能使总利润达到最大，最大利润是多少？。

湖南省职高对口高考模拟试题六

湖南省职高对口高考模拟试题六（命题人：陈民福考试范围：教育学与设计学考试时间：90分钟满分：205分） QQ ：一．单项选择题（每题2分，共40分）1.提出活教育理论的儿童教育家是（）A ．蒙台梭利B ．福禄培尔C ．陈鹤琴D ．陶行知2．促进幼儿全面发展的首要条件是( )。

A ．良好的智力品质B ．良好的道德素质C ．良好的身体素质D ．良好的个性品质3．下列行为中不属于婴儿喂养的要求是（）班级：姓名：A．母乳与乳类食物结合喂养B．及时添加辅食C．营养搭配合理，并做细、软、烂D．单独烹调，做到色、香、味俱全4、幼儿体育活动的内容不包括（）A．体育游戏B．基本动作练习C．基本体操D．体育技巧训练5、教师是幼儿学习的（）A.照料者B.支持者C.监督者D.中介者6．下列课程评价观中，正确的是（）A．教师既是被评价者，又是评价者B．评价中要对幼儿进行相互比较，这样才能体现个体差异C．幼儿缺乏自我评价的能力，所以评价中不能接纳幼儿的看法D．评价的主要目的就是为小学选拔优秀的学生7．“在生活情境中对事物进行分类、排序、感知集合、数数、比较数的大小”这一内容属于A．语言领域内容B．科学领域内容C．健康领域内容D．艺术领域内容A．体育游戏B．音乐游戏C．智力游戏 D．积木游戏8．下列游戏类别中不属于创造性游戏的是（）A．角色游戏 B．结构游戏 C．表演游戏 D．体育游戏9．不属于幼儿园教育与小学教育的差别的是（）A．幼儿园主导活动是游戏，而小学生主导活动是上课B．幼儿园的生活节奏与管理宽松，小学生的生活则快速而紧张C．幼儿园师生关系关系密切，而小学师生关系较为淡薄D．社会及成人对幼儿的要求相对具体和严格，而对小学生的要求较为宽松10．下列关于家长学校的教育作用，错误的是（）A．传授科学教育知识，帮助家长提高育儿的水平；B．帮助家长理解和接受主流的学前教育价值观；C．帮助家长对不合理、片面的学前教育能作出独立而正确的评价，并以主动回避或反对；D．帮助幼儿园提前教授小学的教学内容，以适应未来的小学教育。

湖南职高对口升学数学复习模拟试题14(含答案)

2014届湖南职高对口升学数学复习模拟试题14（含答案）19．（12分）已知函数(),12f x x x R π⎛⎫=-∈ ⎪⎝⎭.(1) 求3f π⎛⎫⎪⎝⎭的值；(2) 若33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭.20．（12分）为进行科学实验，观测小球A 、B 在两条相交成60︒角的直线型轨道上运动的情况，如图（乙）所示，运动开始前，A 和B 分别距O 点3m 和1m ，后来它们同时以每分钟4m 的速度各沿轨道l l 12、按箭头的方向运动。

问：（1）运动开始前，A 、B 的距离是多少米？（结果保留三位有效数字）。

（2）几分钟后，两个小球的距离最小？图（乙）21．（12分）如图,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲.乙两位游客从A 处下山,甲沿AC 匀速步行,速度为min /50m .在甲出发min 2后,乙从A 乘缆车到B ,在B 处停留min 1后,再从匀速步行到C .假设缆车匀速直线运动的速度为min /130m ,山路AC 长为m 1260,经测量,1312cos =A ,53cos =C . (1)求索道AB 的长;(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?22．（14分）如图,在等腰直角三角形OPQ ∆中,90OPQ ∠=,22OP =,点M 在线段PQ上. (1)若3OM =,求PM 的长;(2)若点N 在线段MQ 上,且30MON ∠=,问:当POM ∠取何值时,OMN ∆的面积最小?并求出面积的最小值..参考答案19．解：(1)22133124f ππππ⎛⎫⎛⎫⎛⎫=-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ (2)33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,24sin 1cos 5θθ=--=-,1=22cos cos sin sin 64445f ππππθθθθ⎛⎫⎛⎫⎫∴--=+=- ⎪ ⎪⎪⎝⎭⎝⎭⎭.20．解：（1）小球开始运动前的距离为：AB m =+-⨯⨯⨯︒=≈3123160726522cos .（）（2）设t 分钟后，小球A 、B 分别运动到A’、B’处，则AA t BB t ''.==44，当034≤≤t 时，()()()()()A B t t t t t t ''cos 22223414234146048247=-++-⋅-⋅+⋅︒=-+ CBA当t >34时，()()()()()A B t t t t t t ''cos 222243142431412048247=-++-⋅-⋅+⋅︒=-+ 故 ()A B t t t ''22482470=-+≥（） ()A B t t ''22481440=-⎛⎝ ⎫⎭⎪+≥（）∴当t =14，()()A B m ''min =2 故14分钟后两个小球的距离最小。

职高对口高考模拟数学试卷

#### 一、填空题（每空2分，共20分）1. 若函数 \( f(x) = ax^2 + bx + c \) 在 \( x = 1 \) 处取得极值，则 \( a + b + c = \) ________。

2. 在等差数列 \(\{a_n\}\) 中，若 \( a_1 = 3 \)，公差 \( d = 2 \)，则\( a_5 = \) ________。

3. 已知圆的方程为 \( x^2 + y^2 - 4x - 6y + 9 = 0 \)，则该圆的半径为________。

4. 若 \( \cos \alpha = \frac{1}{3} \)，则 \( \sin \alpha \) 的值为________。

5. 函数 \( y = \frac{1}{x} \) 的图像关于 ________ 对称。

6. 若 \( \sqrt{a^2 + b^2} = 5 \)，\( a = 3 \)，则 \( b \) 的值为________。

7. 三个数的和为 12，其中两个数分别为 3 和 5，则第三个数为 ________。

8. 若 \( \triangle ABC \) 中，\( a = 5 \)，\( b = 6 \)，\( c = 7 \)，则\( \cos A \) 的值为 ________。

9. 下列不等式中，正确的是 ________（选项：A. \( 2x > 4 \)；B. \( 3x \leq 9 \)；C. \( x^2 \geq 4 \)；D. \( \frac{1}{x} < 1 \)）10. 已知 \( \log_2 8 = 3 \)，则 \( \log_2 32 = \) ________。

#### 二、选择题（每题3分，共30分）1. 函数 \( y = x^3 - 3x \) 的图像在 \( x = 0 \) 处的切线斜率为：A. 0；B. -3；C. 3；D. 不存在。

湖南职高对口升学数学复习基础训练题04(含答案)

2014届湖南职高对口升学数学复习基础训练题04（含答案）三、解答题(本大题共6小题，共75分.解答时应写出必要的文字说明、证明过程或演算步骤)16．(12分)求下列关于x的函数的定义域和值域：(1) y=(2)y=log2(-x2+2x);(3)18.(12分)(2012·长沙模拟)已知函数f(x)=1xlnx ax-+.(1)当a=1时，求f(x)的最小值；(2)若函数g(x)=f(x)-xa在区间(1，2)上不单调，求a的取值范围.19.(13分)为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C(单位：万元)与隔热层厚度x(单位：cm)满足关系：C(x)=k3x5+(0≤x≤10)，若不建隔热层，每年能源消耗费用为8万元．设f(x)为隔热层建造费用与20年的能源消耗费用之和．(1)求k的值及f(x)的表达式；(2)隔热层修建多厚时，总费用f(x)达到最小，并求最小值．20.(13分)(2012·湘潭模拟)已知f(x)是定义在[-e,e]上的奇函数，当x∈(0,e]时f(x)=ax+2lnx,(a∈R).(1)求f(x)的解析式；(2)是否存在实数a，使得当x∈[-e,0)时，f(x)的最小值是4？如果存在，求出a的值；如果不存在，请说明理由.21.(12分)已知二次函数g(x)对任意x∈R都满足g(x-1)+g(1-x)=x2-2x-1且g(1)=-1，设函数f(x)=g(x+12)+mlnx+98(m∈R，x>0)．(1)求g(x)的表达式；(2)若存在x∈(0，+∞)，使f(x)≤0成立，求实数m的取值范围；(3)设1<m≤e，H(x)=f(x)-(m+1)x，求证：对于任意x1,x2∈［1,m］，恒有|H(x1)-H(x2)|<1.16．【解析】(1)要使函数有意义，则1x0, x0-≥⎧⎨≥⎩∴0≤x≤1,函数的定义域为［0，1］.∵函数y=为减函数，∴函数的值域为［-1，1］.(2)要使函数有意义，则-x2+2x>0,∴0<x<2.∴函数的定义域为(0，2).又∵当x∈(0,2)时，-x2+2x∈(0,1］,∴log2(-x2+2x)∈(-∞,0］.即函数的值域为(-∞,0］.(3)函数的定义域为{0，1，2，3，4，5}，函数的值域为{2，3，4，5，6，7}.17．【解析】(1)Δ=(a-3)2-4a<0,解得1<a<9,故a的取值范围为a∈(1,9).(2)由题意得x2+(a-3)x+a>0对x∈(-1,2)恒成立,即a(x+1)>3x-x2.又x∈(-1,2),故x+1∈(0,3),∴a>()()22x15x143x xx1x1-+++--=++=-(x+1)-4x1++5.∵x+1∈(0,3)时，x+1+4x1+的最小值为4(当且仅当x=1时取得)，∴a>1为所求.18．【解析】(1)当a=1时，f(x)=1x+lnx-1, ()()2211x 1f x x 0x x x-'=-+=>, 令f ′(x)=0得x=1;f ′(x)<0得0<x<1;f ′(x)>0得x>1, ∴f(x)在(0，1)上单调递减，在(1，+∞)上单调递增，故f min (x)=f(1)=0. (2)g(x)=()x 1x xf x lnx a ax a--=+-, ()222111x ax 1g x .ax x a ax -+'=-+-=-∵g(x)在(1，2)上不单调，∴x 2-ax+1=0在(1，2)上有根且无重根，即方程a=x+1x 在(1，2)上有根，且无重根，∴2<a<52.19．【解析】(1)由题意建筑物每年的能源消耗费用为C(x)=k3x 5+(0≤x ≤10)，再由C(0)=8得k=40, 故C(x)=403x 5+(0≤x ≤10);又x 厘米厚的隔热层建造费用为6x,所以由题意()40800f x 206x 6x(0x 10)3x 53x 5=⨯+=+≤≤++. (2)方法一：()()()()222554(x )x 52 4003f x 6,3x 53x 5+-'=-=++ 令f ′(x)=0得x=5,x=-253(舍去)，当x ∈(0,5)时，f ′(x)<0,当x ∈(5,10)时，f ′(x)>0，故x=5时f(x)取得最小值，且最小值f(5)=6×5+800155+=70. 因此当隔热层修建5cm 厚时，总费用达到最小，且最小值为70万元. 方法二：∵f(x)=8003x 5++6x=8003x 5++(6x+10)-10≥当且仅当8003x 5+=6x+10，即x=5∈［0,10］时取等号)∴x=5时，f(x)取得最小值，且最小值f(5)=6×5+800155+=70. 因此当隔热层修建5cm 厚时，总费用达到最小，且最小值为70万元. 20．【解析】(1)设x ∈[-e,0)，则-x ∈(0,e], ∴f(-x)=-ax+2ln(-x). ∵f(x)是奇函数， ∴f(x)=-f(-x)=ax-2ln(-x).又f(0)=0,故函数f(x)的解析式为：()()[)(]ax 2ln x , x e,0f x 0 x 0.ax 2lnx, x 0,e⎧--∈-⎪==⎨⎪+∈⎩，(2)假设存在实数a,使得当x ∈[-e,0)时， f(x)=ax-2ln(-x)有最小值是4. ∵()2ax 2f x a .x x-'=-= ①当a ≥0或2e,a a 0⎧≤-⎪⎨⎪<⎩即a ≥2e -时，由于x ∈[-e,0),则f ′(x)≥0.故函数f(x)=ax-2ln(-x)是[-e,0)上的增函数. ∴所以f(x)min=f(-e)=-ae-2=4,解得62ae e=-<-(舍去).②当2e,aa0⎧>-⎪⎨⎪<⎩即a<-2e时，则x (-e,2a) (2a,0) f′(x) - +f(x)∴f(x)min=f(a )=2-2ln(-a)=4,解得a=-2e.综上所知，存在实数a=-2e,使得当x∈[-e,0)时，f(x)最小值是4.21.【解析】(1)设g(x)=ax2+bx+c(a≠0)，于是g(x-1)+g(1-x)=2a(x-1)2+2c=(x-1)2-2，所以1 a.2 c1⎧=⎪⎨⎪=-⎩又g(1)=-1，则1b2=-．所以g(x)=211x x1.22--(2)f(x)=g(x+12)+mlnx+98=12x2+mlnx(m∈R,x>0).当m>0时，由对数函数的性质知，f(x)的值域为R；当m=0时，f(x)=2x2，对任意x>0，f(x)>0恒成立；当m<0时，由f′(x)=x+mx=0得x m=-，列表：这时f(x)min 2-+ 由f(x)min ≤0得m2m 0⎧-+≤⎪⎨⎪<⎩，所以m ≤-e,综上，存在x>0使f(x)≤0成立，实数m 的取值范围是(-∞,-e ］∪(0,+∞)． (3)由题知H(x)=12x 2-(m+1)x+mlnx, ()()()x 1x m H x .x --'=因为对任意x ∈［1,m ］，()()()x 1x m H x 0,x--'=≤所以H(x)在［1,m ］内单调递减.于是|H(x 1)-H(x 2)|≤H(1)-H(m)=12m 2-mlnm-12. 要使|H(x 1)-H(x 2)|<1恒成立，则需12m 2-mlnm-12<1成立，即12m-lnm-32m<0.记()13h m m lnm (1m e)22m =--<≤，则 ()221133111h m ()0,2m 2m 2m 33'=-+=-+>所以函数h(m)=12m-lnm-32m在(1,e ］上是单调增函数，所以h(m)≤h(e)=e 2-1-32e=()()e 3e 12e -+<0，故命题成立.。

2024年湖南对口高考数学试卷(含参考答案)

湖南省2024年普通高等学校对口招生考试数学本试题卷包括选择题、填空题和解答题三部分，共5页。

时量120分钟，满分120分。

一、选择题(本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.已知集合M={1,3,5},N={3,4,5,6},则=N MA.{3,5}B.{4,6}C.{1,4,6}D.{1,3,4,5,6 } 2.已知数列{a n }的通项公式为32+=n a n ,*∈N n ,若37=m a ,则=mA.15B.17C.20D.34 3.函数xx y 1+=的图像 A.关于原点对称 B.关于x 轴对称 C.关于y 轴对称 D.关于直线y=x 对称4.从7名学生中选派2名学生分别到甲、乙两地参加社会实践活动，则不同的选派方法共有A.14种B.21种C.42种D.49种 5.已知2log ,2,3.03.03.02===c b a ,则A.c b a <<B.a b c <<C.b c a <<D.b a c << 6.下列命题中，正确的是A.平行于同一个平面的两条直线必平行B.平行于同一个平面的两个平面必平行C.过平面外一点只可以作一条直线与这个平面平行D.过直线外一点只可以作一个平面与这条直线平行 7.“()()042=+-x x ”是“2=x ”的A.充分必要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件 8.函数x x y cos sin 3+=取最大值时，x 的值可以为A.6π B.4π C.3π D.2π9.光线从点M(-3,3)射到点P(1,0)后被x 轴反射，则反射光线必经过的点是A.(3,5)B.(4,2)C.(4,4)D.(5,3)10.已知函数()x f y =在)[∞+，0上单调递增，且()()x f x f =-,则不等式()()31f x f <-的解集为A.()42，- B.()4，∞- C.()∞，4 D.()()∞+∞-，，42二、填空题(本大题共5小题，每小题4分，共20分)11.某学校为了解一年级120名男生和80名女生的身高情况，计划用分层抽样的方法抽取20名学生进行测量，则抽取的男生人数为 .12.已知向量()m a ,1=,()1,2=b ,且()b b a ⊥+,则实数=m .13.已知角α的顶点在坐标原点，始边与x 轴的非负半轴重合，终边上一点的坐标为⎪⎪⎭⎫⎝⎛-21,23,则α2sin . 14.已知函数()x x f ln =,若0>>b a ,且()()b f a f =,则=ab .15.已知点P 在圆01022=-+y y x 上运动，则点P 到直线0543=-+y x 的距离的最大值为 .三、解答题(本大题共7小题，其中第21,22小题为选做题。

中职对口高考湖南数学复习单元卷(全册)含答案

(这是边文，请据需要手工删加)第一章集合与不等式测试卷(时间：120分钟总分：120分)一、选择题(每小题4分，共40分)1．下列各组集合中，表示同一集合的是( )A ．M ＝{(3，2)}，N ＝{(2，3)}B ．M ＝{3，2}，N ＝{2，3}C ．M ＝{(x ，y )|x ＋y ＝1}，N ＝{y |x ＋y ＝1}D ．M ＝{1，2}，N ＝{(1，2)}2．已知全集U ＝{1，2，3，4，5}．集合M ＝{1，2}，N ＝{1，4，5}，则集合{1，3，4，5}是( )A ．(∁U M )∩NB ．M ∩(∁U N )C ．(∁U M )∪ND ．M ∪(∁U N )3．若全集U ＝Z ，M ＝{x |x ＝2k ，k ∈Z }，N ＝{x |x ＝2k ＋1，k ∈Z }，则下列关系式成立的是( )A ．M ＝NB ．M ∪N ＝UC ．M ND ．M N4．不等式x 2＋3x ＋2＞0的解集是( )A ．(1，2)B ．(－∞，1)∪(2，＋∞)C ．(－2，－1)D ．(－∞，－2)∪(－1，＋∞)5．不等式－|x －5|＞－15的解集是( )A ．{x |x ＜20}B ．{x |－10＜x ＜20}C ．{x |x ＞－10}D ．{x |x ＜－10或x ＞20}6．不等式|x －3|＜－1的解集是( )A ．B ．{x |x ＜3}C ．{x |x ＞3}D ．R7．“x ＞1”是“x 2(x －1)＞0”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件8．若x 2－ax －b ＜0的解集是{x |2＜x ＜3}，则bx 2－ax －1＞0的解集为( )A ．{x |－12≤x ≤13}B ．{x |－12＜x ＜13} C ．{x |－12＜x ＜－13} D ．{x |－12≤x ≤－13} 9．不等式3≤|5－2x |＜9的解集是( )A ．(－∞，－2)∪(7，＋∞)B ．[1，4]C ．[－2，1]∪[4，7]D ．(－2，1]∪[4，7)10．不等式x －12－x＞0的解集是( ) A ．(－∞，1)∪(2，＋∞) B ．[1，2]C ．(2，＋∞)D ．(1，2)二、填空题(每小题4分，共20分)11．已知集合A ＝{(x ，y )|2x ＋y ＝1}，集合B ＝{(x ，y )|x ＋2y ＝5}，则A ∩B ＝________________．12．已知全集U ＝R ，集合A ＝{x |x 2＜5}，集合B ＝{x |x 2－5x －6≥0}．则A ∩B ＝________________，A ∪B ＝________________，∁U A ∪B ＝________________．13．设全集U ＝R ，集合A ＝{x |x ≥3}，集合B ＝{x |x ＜0}，则集合(∁U A )∪(∁U B )＝________________________________________________________________________.14．设mn <0，若m <0，则n ________________．15．比较大小(x －1)(x ＋3)________________(x ＋1)2.三、解答题(共60分)16．(10分)已知集合M＝{x2，x＋1，－3}，N＝{x－3，x2＋1，2x－1}，若M∩N＝{－3}，求实数x的值．17．(10分)已知集合A＝{x|x2－3x－10≤0}，B＝{x|m＋1≤x≤2m－1}，若A∪B＝A，求实数m的取值范围．18.(10分)已知集合A＝{a，b，2}，B＝{2a，b2，2}，且满足A＝B，求a，b的值．19．(10分)已知集合A＝{x|x2－5x＋p＝0}，集合B＝{x|2x2－qx＋1＝0}，且A∩B＝{1}，求A∪B.20.(10分)解不等式：x 2－x －6x －1＞0.21．(10分)已知不等式(m 2－2m －3)x 2－(m －3)x －1＜0的解集为R ，求实数的m 取值范围．(这是边文，请据需要手工删加)第二章函数测试卷(时间：120分钟总分：120分)一、选择题(每小题4分，共40分)1．函数y ＝（x ＋1）0|x |－x的定义域为( ) A ．{x |x ＞0} B ．{x |x ＜0}C ．{x |x ≠0且x ≠－1}D ．{x |x ＜0且x ≠－1}2．设函数f (x )＝m x＋m (x ≠0)，且f (1)＝2，则f (2)＝( ) A ．0 B ．1 C.32D ．2 3．函数y ＝x 2－2x ＋5的值域是( )A ．[4，＋∞)B ．(4，＋∞)C ．(－∞，4]D ．(－∞，4)4．若x ∈(－∞，＋∞)，下列函数中为奇函数的是( )A ．f (x )＝log 2xB ．f (x )＝3xC ．f (x )＝x 3＋x ＋1D ．f (x )＝－x |x |5．下列各式不成立的是( )A ．3x ·2x ＝6xB ．2a ＋b ＝2a ＋2b C.22＝234 D ．(15)a －b ＝5b 5a 6．设函数f (x 2＋34)＝log 3(8x 2＋7)，则f (1)＝( ) A ．2 B ．log 339 C ．1 D ．log 3157．函数y ＝lg （x 2－2x －2）的定义域是( )A ．{x |x ＜3}B ．{x |x ＞－1}C ．{x |－1＜x ＜3}D ．{x |x ≤－1或x ≥3}8．若102x ＝25，则10－x ＝( )A.15 B ．－15 C.1625 D.1509．函数f (x )＝3x ＋1＋5的值域是( )A ．(0，＋∞)B ．(5，＋∞)C ．(6，＋∞)D ．(－∞，＋∞)10．已知函数f (x )的定义域是(0，1)，则f (2－x )的定义域为( )A ．(0，1)B ．(1，2)C ．(12，1) D ．(0，＋∞) 二、填空题(每小题4分，共20分)11．设x 38＝334，则x ＝________________．12．设log 155＝m ，则log 153＝________________．13．已知23x －5＞4x ，则x 的取值范围是________________．14．5a ＝2，25b ＝9，则52a －b ＝________________．15．函数y ＝log 13(0.5x －1)的定义域是________________．三、解答题(共60分)16．(10分)计算3－2＋(－35)0－(338)－23.1 2x(x－2)≥log123.17．(10分)解不等式：log18.(10分)求函数y＝2x＋12－3x的定义域．19．(10分)已知函数y＝f(x)，且lg(lg y)＝lg(2x)＋lg(2－x)．(1)求函数f(x)的解析式及其定域；(2)求函数f(x)的单调区间．20.(10分)某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不低于51元．(1)当一次订购量为多少个时，零件的实际出厂价恰好降为51元？(2)设一次订购量为x 个，零件的实际出厂单价为P 元，写出函数P ＝f (x )的表达式．21．(10分)设y ＝(34a ＋1)x 与y ＝log (a ＋2)x 在区间(0，＋∞)上都是减函数，求a 的取值范围．(这是边文，请据需要手工删加)第三章三角函数测试卷(时间：120分钟总分：120分)一、选择题(每小题4分，共40分)1．若cos α(sin α＋4)＝0则α等于( )A ．0B ．±π2C ．k πD ．k π＋π2(k ∈Z ) 2．下列各式中与sin A 相等的是( )A ．sin(90°－A )B ．cos(90°＋A )C ．cos(270°＋A )D ．sin(180°＋A )3．若α＝17π3，则下列判断正确的是( ) A ．sin α>0，cos α<0 B ．sin α<0，cos α>0C ．sin α>0，cos α>0D ．sin α<0，cos α<04．下列不等式成立的是( )A ．sin π8＜sin 5π8B ．tan π8＜tan 5π8C ．cos π8<cos 13π8D ．tan π8<tan 13π85．函数y ＝sin 2x 2的最小正周期是( ) A.π2B ．πC ．2πD ．4π 6．下列函数是奇函数的是( )A ．y ＝sin(π2－x ) B ．y ＝cos(π－x ) C ．y ＝tan(π＋x ) D ．y ＝cos(2π－x ) 7．已知cos(π＋α)＝－12，3π2<α<2π，则sin(2π－α)的值是( ) A.12 B ．±32 C.32 D ．－328．函数y ＝3sin 12x －cos 12x 的值域为( ) A ．[－2，2] B ．(－2，2) C ．[－3，3] D ．(－1，1)9．x ∈R ，y ＝5－sin x 2的最大值是( ) A ．3 B ．4 C ．5 D ．610．要得到函数y ＝cos(2x －π4)的图象，只须将函数y ＝sin 2x 的图象( ) A ．向左平移π8个单位 B ．向右平移π8个单位 C ．向左平移π4个单位 D ．向右平移π4个单位二、填空题(每小题4分，共20分)11．已知sin α＝5－12，则sin 2(α－π4)＝________________． 12．在△ABC 中，a 、b 分别是角A 和角B 所对的边，若a ＝3，b ＝1，B 为30°，则角A 的值是________．13．函数y ＝sin 2x ＋2cos x (π3≤x ≤2π3)的最小值是________________． 14．若扇形的周长为8，面积为23，则其中心角的弧度数是________________．15．函数y ＝sin x －3cos x 2的定义域是________________．三、解答题(共60分)16．(10分)化简：sin （α－2π）tan （π＋α）cos （π－α）cos （2π－α）tan （2π＋α）.17．(10分)已知tan α＝2，求sin α＋cos αsin α－cos α的值．18.(10分)已知：cos α＝－35，α∈(π，3π2)，求sin(α－π3)，sin 4α，cos α2的值．19．(10分)已知sin α＝35，α∈(π2，π)，tan(π－β)＝12，求tan(α－2β)．20.(10分)已知函数y ＝12cos 2x ＋32sin x cos x ＋1. (1)当x 为何值时，y 取最大值； (2)上述函数图象怎样由函数y ＝sin x 图象变换所得． 21．(10分)已知0<α<π2，0<β<π2，且cos α＝17，cos(α＋β)＝－1114，求β的值．(这是边文，请据需要手工删加)第四章数列测试卷(时间：120分钟总分：120分)一、选择题(每小题4分，共40分)1．已知数列{a n }中，a 1＝1且a n ＝a n －1＋1(n ≥2)，则a 15等于( )A ．31B ．29C ．17D ．152．数列{a n }的通项公式为a n ＝2n 2－n ，那么下列各数为数列中某一项的是( )A ．66B ．50C ．54D ．683．已知x ，2x ＋2，3x ＋3是一个等比数列的前3项，则该数列的第4项等于( )A ．－27B ．－272C ．27 D.2724．等差数列{a n }的公差为－2，若a 1＋a 3＋a 5＋…＋a 99＝50，则a 2＋a 4＋a 6＋…＋a 100等于( )A ．－30B ．－50C ．50D ．605．等比数列{a n }中，若a 3a 4a 6a 7＝81，则a 1a 9等于( )A ．3B ．±3C ．9D ．±96．等差数列{a n }中，S 3＋S 4＝S 5且S 7＝49，则公差d 等于( )A ．1B ．2C ．－1D ．－27．数列{a n }中，如果a n ＋1＝12a n ，且a 1＝2，则数列的前5项之和等于( ) A.318 B ．－318 C.3132 D ．－31328．在1与16之间插入三个正数a 、b 、c ，使1、a 、b 、c 、16成等比数列，那么b 等于( )A ．2B ．4C ．8 D.1729．等比数列{a n }的前n 项和为S n ，已知S 3＝3，S 6＝12，则S 9＝( )A ．27B ．30C ．36D ．3910．{a n }为等比数列，且a n ＜0，a 2a 4＋2a 3a 5＋a 4a 6＝25，则a 3＋a 5＝( )A ．－5B ．－10C ．5D ．10二、填空题(每小题4分，共20分)11．在等比数列{a n }中，已知a 1＋a 2＋a 3＝30，a 4＋a 5＋a 6＝60，那么a 10＋a 11＋a 12＝____________．12．已知公差不为零的等差数列{a n }中，a 5＝10，且a 5，a 7，a 11成等比数列，那么a 14＝____________．13．已知数列{a n }，a n ＝－2n ＋25，当S n 达到最大值时，n 为________________．14．log 64与log 69的等差中项为________________．15．在等比数列{a n }中，已知S n ＝3n ＋b ，则b 的值为________________．三、解答题(共60分)16．(10分)在等比数列{a n }中，从第1项到第3项的和为1，从第1项到第6项的和为9，求首项a 1，公比q ，以及前5项的和S 5.17．(10分)在等差数列{a n}中，已知a n＝16，S n＝49，d＝3，求a1和n的值．18.(10分)已知三个数组成公比大于1的等比数列，其和为21，若将此三个数分别加上1，5，6后，则所得三个数成等差数列，求原来的三个数？19．(10分)已知等比数列{a n}的各项均为正数，a1＝2，前3项的和为14.(1)求数列{a n}的通项公式；(2)设b n＝3n－log2a n，求数列{b n}的前n项和S n.20.(10分)已知等比数列{a n}的前n项和S n，且S1，S3，S2成等差数列．(1)求数列{a n}的公比q；(2)若a1－a3＝3，求S n.21．(10分)在等差数列{a n}中，a7＝4，a19＝2a9.(1)求数列{a n}的通项公式；(2)设b n＝1na n，求数列{b n}的前n项和S n.(这是边文，请据需要手工删加)第五章平面向量测试卷(时间：120分钟总分：120分)一、选择题(每小题4分，共40分)1．若a ＝λb ，则下列说法不正确的是( )A ．a 、b 方向相同B ．|a |－|λb |＝0C ．a ∥bD ．a －λb ＝02．下列各式中仍是向量的为( )A ．a ·bB ．a 2C ．|b |cos θD ．(a·b )c3．若a 与b 的夹角为θ，且a·b ≥0，下列各式中成立是( )A ．θ＝0°B ．0°≤θ＜90°C ．90°≤θ＜180°D ．0°≤θ≤90°4．下列各式中正确的是( )A ．λa 的模是a 的模的λ倍B ．λa 的模是a 的模的|λ|倍C ．λa >aD ．－3a <a5．下列各式中不正确的个数是( )①a ·b ＝b·a ②(λa )(μb )＝λμ(a·b ) ③(a·b )2＝a 2·b 2 ④(a·b )·c ＝a ·(b·c )A ．1B ．2C ．3D ．46．已知a ＝(－1，3)，b ＝(x ，－1)，若a ∥b ，则x 等于( )A ．3B ．－13 C.13D ．－3 7．已知向量a 与b 的夹角θ＝60°，且|a |＝8，|b |＝5，则a·b ＝( )A ．20B ．30C ．20 3D ．408．一质点受到平面上的三个力F 1，F 2，F 3(单位：N)的作用而处于平衡状态．已知F 1，F 2成60°角，且F 1，F 2的大小分别为2和4，则F 3的大小为( )A ．6B ．2C ．2 5D ．279．设P 是△ABC 所在平面内的一点，BC →＋BA →＝2BP →，则( )A.P A →＋PB →＝0B.PC →＋P A →＝0C.PB →＋PC →＝0D.P A →＋PB →＋PC →＝010．设A (2，3)，B (3，4)，向量a ＝(－5，－5)，则下列命题不正确的是( )A ．向量AB →是单位向量 B.AB →∥aC.AB →与a 的夹角是π D ．|a |＝5|AB →|二、填空题(每小题4分，共20分)11．已知|a |＝1，|b |＝2，如果a ∥b ，则a·b ＝________________．12．点A (2，1)与点B (5，1)之间的距离|AB |＝________________．13．已知向量a ＝(4，3)，e 是与a 垂直的单位向量，则e ＝________________．14．线段MN 的中点坐标为P (－3，－1)，点M (3，2)，则N 的坐标是________________．15．已知a ＝(3，1)、b ＝(3，0)，则a 与b 的夹角θ＝________________．三、解答题(共60分)16．(10分)已知向量a ＝(1，2)，b ＝(3，－4)，求：(1)a ＋b ；(2)a －b ；(3)2a ＋b .17．(10分)已知向量a＝i－j，b＝－2i＋2j，试判断向量a与b是否共线．18.(10分)已知a ＝(－2，5)，|b |＝2|a |，若b 与a 反向，求b 的坐标．19．(10分)已知ABCD 是梯形，AB ∥CD ，且AB ＝2CD ，M 、N 分别是DC 和AB 的中点，已知AB →＝a ，AD →＝b ，试用a 、b 表示MN →.20.(10分)已知|a |＝3，|b |＝4，a 与b 的夹角为3π4，求：(a ＋2b )·(3a －2b )． 21．(10分)已知|a |＝2，|b |＝4，且向量a ＋k b 与向量a －k b 垂直，求k 的值．(这是边文，请据需要手工删加)第六章直线与圆的方程测试卷(时间：120分钟总分：120分)一、选择题(每小题4分，共40分)1．直线l 的斜率为－3，则直线l 的倾斜角为( )A ．30°B ．60°C ．150°D ．120°2．直线经过两点P (－2，m 2)，Q (m ，4)，且斜率是1，则m 的值等于( )A ．1或－2B ．－1或2C ．1D ．－23．如果直线ax ＋2y ＋2＝0与3x －y －2＝0互相平行，则a 的值是( )A ．－3B ．－6C ．－32 D.234．直线ax ＋(1－a )y ＝3与直线(a －1)x ＋(2a ＋3)y ＝2垂直，则a 的值为( ) A ．－32或0 B ．－3或1 C ．－3 D ．1 5．过点(0，1)且与直线y ＝2x ＋3平行的直线方程为( )A ．x ＋2y －2＝0B ．x －2y ＋2＝0C ．2x －y ＋1＝0D ．2x －y －1＝06．已知点A (－3，4)，M (1，－3)，则点A 关于点M 的中心对称点的坐标是( ) A ．(－12，12) B ．(－3，52) C ．(－5，10) D ．(5，10) 7．已知直线方程是2x －3y ＋6＝0，则直线在x 轴上、y 轴上的截距分别是( )A ．3、2B ．－3、2C ．－3、－2D ．3、－28．坐标原点到直线x sin x ＋y cos x ＝1的距离为( )A ．0B ．1C ．2 D.129．过点A (3，－2)且在两坐标轴上截距相等的直线方程是( )A ．x ＋y ＋1＝0B ．x ＋y －1＝0或2x ＋3y ＝0C.x 2＋y 2＝1D.x 2＋y 2＝－1 10．点P (1－22，22)与圆x 2＋y 2＝1的位置关系是( ) A ．P 在圆内 B ．P 在圆外 C ．P 在圆上 D ．P 在圆心二、填空题(每小题4分，共20分)11．经过点(2，5)，且和x 轴平行的直线方程为________________；经过点(3，－2)且与y 轴平行的直线方程为________________．12．已知点A (a ，6)到直线3x －4y －2＝0的距离等于4，则a 为________________．13．已知直线经过点(1，2)，倾斜角是135°，则直线方程为________________．14．过点A (－5，1)，且垂直于直线y ＝3x ＋2的直线方程为________________．15．两平行线2x ＋3y －8＝0与4x ＋6y －1＝0的距离是________________．三、解答题(共60分)16．(10分)已知直线ax ＋4y －2＝0与2x －5y ＋c ＝0垂直且相交于点(1，m )，求a 、c 、m 的值．17．(10分)已知直线l在y轴上的截距式－3，且它与两坐标轴围成的三角形的面积为6，求直线l的方程．18.(10分)已知△ABC的三个顶点A(0，0)，B(1，1)，C(4，2)，求△ABC的外接圆的方程．19．(10分)已知圆C：x2＋y2－2x－2y＋1＝0，求过点P(3，2)且与圆C相切的直线方程．20.(10分)求经过点P(2，－1)，圆心在y＝－2x上，并且与直线x－y－1＝0相切的圆的方程．21．(10分)直线l经过点A(1，3)，B(2，2)解答下列问题：(1)求直线l的方程；(2)求直线l与坐标轴围成的三角形的面积；(3)画出直线l的图形．(这是边文，请据需要手工删加)第七章二次曲线测试卷(时间：120分钟总分：120分)一、选择题(每小题4分，共40分)1．已知双曲线方程x 220－y 25＝1，那么它的焦距是( ) A ．10 B ．5 C.15 D ．2152．顶点在原点，准线方程为y ＝4的抛物线的标准方程为( )A ．y 2＝16xB ．y 2＝－16xC ．x 2＝16yD ．x 2＝－16y3．过椭圆x 29＋y 281＝1的一个焦点F 1的直线与椭圆交于A 、B 两点，且A 、B 与椭圆的另一个焦点F 2构成的△ABF 2的周长为( )A ．36B ．18C ．6D ．94．以椭圆9x 2＋25y 2＝225的焦点为焦点，且离心率为e ＝2的双曲线方程为( ) A.x 212－y 24＝1 B.x 24－y 212＝1 C.x 220－y 24＝1 D.x 220－y 220＝1 5．如果方程x 2＋ky 2＝2表示焦点在y 轴上的椭圆，那么实数k 的取值范围是( )A ．(0，＋∞)B ．(0，2)C ．(1，＋∞)D ．(0，1)6．已知直线y ＝kx －2与抛物线y 2＝8x 交于A 、B 两点，且AB 中点的横坐标为2，则k 的值为( )A ．－1或2B ．－1C ．2D ．1±37．抛物线x 2－5y ＝0的准线方程是( )A ．x ＝－54B ．x ＝52C ．y ＝54D ．y ＝－548．双曲线x 216－y 29＝1的焦点坐标是( ) A ．(0，－5)和(0，5) B ．(－5，0)和(5，0)C ．(0，－7)和(0，7)D ．(－7，0)和(7，0)9．已知双曲线的实轴长为8，焦点坐标为F 1(0，－25)和F 2(0，25)，则双曲线方程是( )A.x 216－y 24＝1B.x 24－y 216＝1 C ．4x 2－y 2＋16＝0 D ．4y 2－x 2－16＝010．顶点在原点，对称轴是y 轴，顶点与焦点的距离等于2的抛物线方程是( )A ．x 2＝±4yB ．y 2＝±4xC ．x 2＝±8yD ．y 2＝±8x二、填空题(每小题4分，共20分)11．抛物线y 2＋8x ＝0的焦点坐标是__________________，离心率是________________，准线方程是________________，开口方向________________．12．已知两点F 1(－5，0)，F 2(5，0)，求与它们的距离的差的绝对值是6的点P 的轨迹方程为________________．13．双曲线的标准方程是x 25－y 24＝1，其中a ＝__________，b ＝__________，c ＝__________，焦点坐标是________________．14．经过抛物线y 2＝2px 的焦点F 作一条直线垂直于它的对称轴，与抛物线交于P 1，P 2两点，线段P 1P 2称为抛物线的通径，通径P 1P 2的长是________________．15．已知点P (3，2)，抛物线y 2＝2x 的焦点为F ，P 为该抛物线上的一个动点，若|P A |＋|PF |取最小值，则P 的坐标是________________．三、解答题(共60分)16．(10分)求离心率e ＝12，焦距＝42，焦点在y 轴上的椭圆的标准方程．17．(10分)已知抛物线方程x 2＝2py 上有一点M ，它的纵坐标为3，它到焦点距离为5，求抛物线方程、焦点坐标、准线方程及M 点坐标．18.(10分)椭圆与双曲线的中心在原点，对称轴为坐标轴，它们有相同的焦点(±5，0)，并且它们的离心率e都可以使方程2x2＋4(2e－1)x＋4e2－1＝0有相等的实根，求椭圆和双曲线的方程．19．(10分)求双曲线5x2－4y2＝20的实半轴、虚半轴、焦点坐标、离心率和渐近线方程．20.(10分)已知直线y＝x－2与抛物线y2＝x交于A、B两点，求弦AB的长．21．(10分)已知F1，F2是椭圆的两个焦点，现有椭圆上一点M到两焦点距离之和为20，且|MF1|、|F1F2|、|MF2|成等差数列，试求该椭圆的标准方程．(这是边文，请据需要手工删加)第八章立体几何测试卷(时间：120分钟总分：120分)一、选择题(每小题4分，共40分)1．直线a ∥b 成立的条件可以是( )A ．a ⊥α b ⊥αB ．a ⊥c b ⊥cC ．a ⊥α b ⊥βD ．a 、b 与α成等角2．过平面外一点( )A ．只有一条直线和这个平面平行B ．存在无数个平面和这个平面平行C ．存在无数条直线和这个平面垂直D ．存在无数个平面和这个平面垂直3．下列命题中正确的是( )A ．和两条异面直线都垂直的直线叫这两条异面直线的公垂线B ．直线l ∥平面α，则l 平行于α内任一直线C ．如果平面内无数条直线都平行于另一个平面，那么这两个平面平行D ．如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面4．下列命题中真命题是( )A ．等长的斜线段在同一平面上的射影长相等B ．平面外的直线上有两个点到该平面距离相等，则这直线与该平面平行C ．直线l 在平面α上射影为l ′，A ∈l ，A 在α上的射影为A ′，则A ′∈l ′D ．垂直于同一条直线的两条直线平行5．若两条直线m ，n 分别在平面α，β内，且α∥β，则m ，n 的关系一定是( )A ．平行B ．相交C ．异面D ．平行或异面6．已知P A ⊥平面ABC ，∠ABC ＝90°，则下列垂直关系不成立的是( )A ．平面P AC ⊥平面ABCB ．平面P AB ⊥平面ABCC ．平面PBC ⊥平面P ACD ．平面P AC ⊥平面P AD7．在正三棱柱ABC －A 1B 1C 1中，若AB ＝2BB 1，则AB 1与C 1B 所成的角的大小为( )A ．60°B ．90°C ．105°D ．75°8．如果等边圆柱(底面直径与母线相等)的体积是16π cm 3，那么它的底半径等于( ) A ．432 cm B ．4 cm C ．232 cm D ．2 cm9．一个圆锥的侧面积是其底面积的2倍，则该圆锥的母线与底面所成的角为( )A ．30°B ．45°C ．60°D ．75°10．设正六棱锥的底面边长为1，侧棱长为5，那么它的体积为( )A ．6 3B ．2 3 C. 3 D ．2二、填空题(每小题4分，共20分)11．在棱长为1的正方体ABCD －A 1B 1C 1D 1中，M ，N 分别为A 1B 1和BB 1的中点，则直线AM 与CN 所成角的余弦值为________________．12．侧棱长为3 cm ，底面边长为4 cm 的正四棱锥的体积为________________cm 3.13．在三棱锥的四个面中，直角三角形最多可以有________________个．14．过平面α外一点P 的斜线段是过这点垂线段的233倍，则斜线与平面α所成的角为________________________________________________________________________．15．若P A 是过平面α外一点P 向平面引出的所有线段中最短的一条，则P A 与平面α内的直线BC 的关系是________________．三、解答题(共60分)16．(10分)如图所示，长方体ABCD－A1B1C1D1中，AB＝1，BC＝2，C1C＝3，求(1)A1B与C1D1所成的角的度数．(2)BC1与平面CC1D1D所成的角的正切值．17．(10分)已知三棱锥D－ABC的三个侧面与底面全等，且AB＝AC＝3，BC＝2，求以BC为棱，以面BCD与面BCA为面的二面角的大小．矩形ABCD在平面α上，AK⊥α，已知KB＝6，KC＝9，KD＝7(1)求证：∠KBC＝∠KDC＝90°；(2)求AK之长．19．(10分)已知E，F分别为正方体ABCD－A1B1C1D1的棱BC，C1D1的中点，求证：EF∥平面BB1D1D.四面体A－BCD被一平面所截，截面EFGH是一个矩形，若∠ADC＝90°.(1)求证：CD∥平面EFGH；(2)求证：CD⊥平面ABD.21．(10分)一个山坡面与水平面成60°的二面角，坡脚的水平线(即二面角的棱)为AB，甲沿山坡自P朝垂直于AB的方向走30 m，同时乙沿水平面自Q朝垂直于AB的方向走30 m，P、Q都是AB上的点，若PQ＝10 m，这时甲、乙2个人之间的距离为多少？(这是边文，请据需要手工删加)第九章排列组合与二项式定理测试卷(时间：120分钟总分：120分)一、选择题(每小题4分，共40分)1．从3名女同学和2名男同学中选1人主持主题班会，则不同的选法种数为( )A ．6B ．5C ．3D ．22．设x ，y ∈N 且x ＋y ≤3，则直角坐标系中满足条件的点M (x ，y )有( )A ．3个B ．4个C ．5个D ．10个3．由0，1，2，3这四个数字组成的四位数中，有重复数字的四位数共有( )A ．238个B ．232个C ．174个D ．168个4．从集合{1，2，3，…，10}中任意选出三个不同的数，使这三个数成等比数列，这样的等比数列的个数为( )A ．3B ．4C ．6D ．85．用0，1，…，9十个数字，可以组成有重复数字的三位数的个数为( )A ．243B ．252C ．261D ．2796．把3封信投到4个信箱，所有可能的投法共有( )A ．A 34种B ．C 34种 C ．43种D ．34种7．有四个舞蹈节目和四个独唱节目，要排一个节目单，要求舞蹈节目和独唱节目间隔出场，则不同的排法种数为( )A ．2P 44P 44B ．P 44P 44C ．P 44＋P 44D ．2(P 44＋P 44)8．二项式(x ＋3x )50的展开式中的有理项共有( )A ．6项B ．7项C ．8项D ．9项9．若(x －1)4＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋a 4x 4，则a 0＋a 2＋a 4的值为( )A ．9B ．8C ．7D ．610．(1＋2x )5的展开式中，x 2的系数等于( )A ．80B ．40C ．20D ．10二、填空题(每小题4分，共20分)11．若k ∈{1，2，3，4}，b ∈{3，4，5}，则函数表示不同的直线共有________________条．12．将标号为1，2，3，…，10的10个球放入标号为1，2，3，…，10的10个盒子内，每个盒子内放一球，则恰好有3个球的标号与所在盒子的标号不一致的放法有________________种．13．若将两名医生和四名护士分成两个体验小组，每个小组一名医生和两名护士，则不同的分组方法有________________种．14．若将6个人排成一排，则其中甲不站在两端并且甲、乙两人必须相邻的排法共有____________种．15．(2x －1x 2)9的展开式中含1x的项是________________．三、解答题(共60分)16．(10分)六名女同学和两名男同学站成两排进行合唱表演，每排四人．(1)两名男同学必须站在一起，有多少种站法？(2)两名男同学间恰有一名女同学，有多少种站法？17．(10分)某医院有内科医生12名，外科医生8名，现选派5名参加赈灾医疗队，其中(1)某内科医生甲与某外科医生乙必须参加，共有多少种不同选法？(2)甲、乙均不能参加，有多少种选法？(3)甲、乙两人至少有一人参加，有多少种选法？(4)队中至少有一名内科医生和一名外科医生，有几种选法？18.(10分)给图中五个区域涂色，要求同一区域相同色、相邻区域不同色，现有4种可选颜色，则不同的着色方法有多少种？19．(10分)4个不同的球，4个不同的盒子，把球全部放入盒内．(1)恰有1个盒不放球，共有几种放法？(2)恰有1个盒内有2个球，共有几种放法？20.(10分)(1)3人坐在有八个座位的一排上，若每人的左右两边都要有空位，则不同坐法的种数有几种？(2)有5个人并排站成一排，若甲必须在乙的右边，则不同的排法有多少种？(3)现有10个保送上大学的名额，分配给7所学校，每校至少1个名额，问名额分配的方法共有多少种？21．(10分)用数字0，1，2，3，4，5组成没有重复数字的数．(1)能组成多少个自然数？(2)能组成多少个能被3整除的四位数？(这是边文，请据需要手工删加)第十章概率与统计初步测试卷(时间：120分钟总分：120分)一、选择题(每小题4分，共40分)1．从装有5个红球和3个白球的口袋内任取3个球，那么互斥而不对立的事件是( )A ．至少有一个红球与都是红球B ．至少有一个红球与都是白球C ．至少有一个红球与至少有一个白球D ．恰有一个红球与恰有二个红球2．某射手在一次射击中，射中10环，9环，8环的概率分别是0.20，0.30，0.10，则此射手在一次射击中不够8环的概率为( )A ．0.40B ．0.30C ．0.60D ．0.903．甲、乙两人下棋，甲获胜的概率是0.3，甲不输的概率为0.8，则甲、乙两人下成和棋的概率为( )A ．0.6B ．0.3C ．0.1D ．0.5A ．0.35B ．0.45C ．0.55D ．0.655．甲、乙两人下棋，和棋的概率为12，乙获胜的概率为13，则下列说法正确的是( ) A ．甲获胜的概率是16 B ．甲不输的概率是12C ．乙输了的概率是23D ．乙不输的概率是126．集合A ＝{2，3}，B ＝{1，2，3}，从A ，B 中各任意取一个数，则这两数之和等于4的概率是( )A.23B.12C.13D.167．某单位有职工52人，现将所有职工随机编号，用系统抽样的方法抽取一个容量为4的样本，已知6号，32号，45号职工在样本中，则样本中另外一个职工的编号是( )A ．19B ．20C ．18D ．218．某校选修乒乓球课程的学生中，高一年级有30名，高二年级有40名．现用分层抽样的方法在这70名学生中抽取一个样本，已知在高一年级的学生中抽取了6名，则在高二年级的学生中应抽取的人数为( )A ．6B ．8C ．10D ．129．某工厂生产A ，B ，C 三种不同型号的产品，产品的数量之比依次为3∶4∶7，现用分层抽样的方法抽出容量为n 的样本，样本中A 型产品有15件，那么样本容量n 为( )A ．50B ．60C ．70D ．8010．某工厂对一批产品进行了抽样检测，图是根据抽样检测后的产品净重(单位：克)数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98)，[98，100)，[100，102)，[102，104)，[104，106]，已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是()A．90 B．75C．60 D．4二、填空题(每小题4分，共20分)11．6位同学参加百米赛跑初赛，赛场共有6条跑道，其中甲同学恰好被排在第一道，乙同学恰好被排在第二道的概率为________________．12．在一次数学考试时出了10个选择题，每道选择题均有4个可供选择的答案，其中只有1个答案是正确的，其余3个答案是错误的，某学生只知道5个题的正确答案，对其它5个题全靠猜回答，那么这个学生卷面上正确答案不少于7个题的概率是________________．13．从{1，2，3，4，5}中随机选取一个数为a，从{1，2，3}中随机选取一个数为b，则a<b的概率为________________．14．若甲、乙、丙三人随机地站成一排，则甲、乙两人相邻而站的概率为________________．15．从3男3女共6名同学中任选2名(每名同学被选中的机会均等)，这2名都是女同学的概率等于________________．三、解答题(共60分)16．(10分)某学校共有教职工900人，分成三个批次进行继续教育培训，在三个批次中男、女教职工人数如下表所示．已知在全体教职工中随机抽取1名，抽到第二批次中女教职工的概率是0.16.(1)求x(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查，问应在第三批次中抽取教职工多少名？17．(10分)在人寿保险业中，要重视某一年龄的投保人的死亡率，经过随机抽样统计，得到某城市一个投保人能活到75岁的概率为0.60，试求：(1)3个投保人都能活到75岁的概率；(2)3个投保人中只有1人能活到75岁的概率；(3)3个投保人中至少有1人能活到75岁的概率(结果精确到0.01)．18.(10分)甲、乙两人分别对同一目标射击1次，甲射中的概率为0.8，乙射中的概率为0.9，求：(1)两人都射中的概率？(2)两人中有1人射中的概率？(3)两人中至少有1人射中的概率？(4)两人中至多有1人射中的概率？19．(10分)甲、乙两台机床相互没有影响地生产某种产品，甲机床产品的正品率是0.9，乙机床产品的正品率是0.95.(1)从甲机床生产的产品中任取3件，求其中恰有2件正品的概率；(2)从甲、乙两台机床生产的产品中各任取1件，求其中至少有1件正品的概率．20.(10分)袋中有12个除颜色外其余均相同的小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率为14，得到黑球或黄球的概率是512，得到黄球或绿球的概率是12，试求得到黑球、黄球、绿球的概率各是多少？21．(10分)学校文娱队的每位队员唱歌、跳舞至少会一项，其中会唱歌的有2人，会跳舞的有5人，现从中选2人．设ξ为选出的人中既会唱歌又会跳舞的人数，且P (ξ>0)＝710. (1)求文娱队的人数；(2)写出ξ的概率分布．。

湖南省职高对口数学模拟试题(1)

职高二数学月考试题班次_______ 姓名_______一、选择题（40分）1、下列关系正确的是（）A 、b a b a >>则若,B 、bc ac b a >>则若,C 、b a c b c a >+>+，则若D 、b a ba <<则若,1 2、）的定义域是函数(log 3x y =A 、10≤≤xB 、10<<xC 、10≤<xD 、1≥x3、已知等差数列—5，—9，—13，┈，则—397是这个数列的（）A 、第97项B 、第98项C 、第99项D 、第100项4、在====∆B ,2,245A 则角，中，已知b a ABC （）A 、 45B 、030C 、 13545或D 、 15030或5、（工科）复数411⎪⎭⎫ ⎝⎛+i 的值是（） A 、i 4 B 、i 4- C 、4 D 、—4（旅游、会计）两数组的内积是（）A 、一个数组B 、一个数C 、将对应元素相乘D 、以上都不对6、的值为没有公共点，则与直线直线m y x y x m 5420322=+=++（）A 、1±B 、2±C 、22± D 、0 7、的准线方程为抛物线y x 42-=（）A 、1=yB 、1-=yC 、161-=xD 、161=x 8、从1,2,3,4,5,6,7,8,9这9个数字中，任取两个作为对数的底数和真数，可得到不同的对数的个数是（）A 、52B 、53C 、54D 、559、下列命题正确的是（）A 、平行于同一条直线的两个平面平行B 、空间两条不相交的直线一定平行C 、若一直线垂直于一平面，则该直线垂直于平面内所有的直线D 、若一直线与一平面平行，则该直线与平面内任何一条直线平行10、一个容量为n 的样本分成若干个小组，若其中一组的頻数和频率分别是40和0.25，则n=（）A 、10B 、40C 、100D 、160二、填空题（20分）11、 75sin 15sin 75sin 15sin 022++=_______12、以C （-2,3）为圆心且与y 轴相切的圆的方程是______________13、设()()=⊥-=-=x b a m b a 则若向量,,6,,3,4_______14、甲、乙两人各自参加对口升学考试，考上本科的概率分别为0.6和0.7，则甲、乙两人有且只有一人考上本科的概率_______15、===++k a c y k x ，则且已知椭圆21,19822_______三、解答题（60分）16、已知53cos ,20=<<x x π，求： ① 的值x 2sin ； ② 若()的值。

湖南中职对口升学高考数学冲刺模拟试题：选择题02

对口升学高考数学冲刺模拟试题选择题：本大题共12小题，每小题5分，共60分。

1．己知全集U=R ，集合{|2},{|05},()U A x x B x x C A B =≥=≤<⋂=则集合A ．{|02}x x <<B ．{|02}x x <≤C ．{|02}x x ≤<D ．{|02}x x ≤≤2．函数12()ln 1x f x x x =+-的定义域为 A ．（0，+∞）B ．（1，+∞）C ．（0，1）D ．（0，1）（1，+∞） 3．经过曲线2()(2)1(1,(1))f x x x f =-+上点处的切线方程为A ．x+2y 一1=0B ．2x+y 一1=0C ．x —y+1=0D ．x+y 一1=04．设条件p ：2()21(0,)x f x e x mx =++++∞在上单调递增，条件:50,q m +≥则p 是q 的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不允分也不必要条件 5．已0.6143log 2,2,log 3,,,a b c a b c ===则的大小关系为A ．b<c<aB ．c<b<aC ．c<a<b O ．a<c<b6．已知函数y=log 2x 的反函数是y=f 一1（x ），则函数Y=f 一1（1一x ）的图象是7．函数22211()()2x mx m f x -+--=的单调增区间与值域相同，则实数聊的取值为 A ．一2 B ．2C ．一1D ．1 8．已知函数22,1(),1x ax x f x ax x x ⎧+≤⎪=⎨+>⎪⎩在R 上单调递减，则实数口的取值范围是 A ．a>一2 B ．一2<a<一1 C ．a ≤一2 D ．a ≤一129．设P 为曲线C ：y=x 2+2X+3上的点，且曲线C 在点P 处切线倾斜角的取值范围为[0，4π]，则点P 横坐标的取值范围为A ．[一1，一12]B ．[—1,0]C ．【0，1】D ．1[,1]210．已知e 为自然对数的底数，设函数()(1)(1)(1,2)x k f x e x k =--=，则A ．当k=l 时，f （x ）在x=1处取得极小值B ．当k=1时，f （x ）在x=1处取得极大值C ．当k=2时，f （x ）在x=1处取得极小值D ．当k=2时，f （x ）在x=1处取得极大值11．函数f （x ）是定义域为R ，且21,0(),(1),0x x f x f x x -⎧-≤=⎨->⎩若方程()f x x a =+有两个不同实根，则a 的取值范围为 A ．（一∞，1） B ．（一∞，1] C ．（0，1） D ．（一∞，+∞）12．设函数()f x 是定义在R 上的奇函数，且f '（x ）=0，当x>0时，有 ()()xf x f x '<恒成立，则不等式2()0x f x >的解集是A ．（-2，0）（2，+∞）B ．（-2，O ）（0，2）C ．（-∞，-2）（2，+∞）D ．（-∞，-2）（0，2）。

湖南对口高考数学模拟试卷(二)

错误！未找到引用源。

湖南对口高考数学模拟试卷（二）时量120分钟，满分120分一. 选择题（本大题共10小题，每小题4分，共40分。

在每小题给的4个选项中，只有一项是符合题目要求的）1.设合集U {}5,4,3,2,1==N M ，N C M u U ={}4,2 ，则N =( )A .｛1,2,3｝B .｛1,3,5｝C .｛1,4,5｝D .｛2,3,4｝2. 解不等式的解集为( ) A . (1,0)(1,)-+∞ B .C . (1,0)(0,1)-D . 3.设函数 f (x )= ,则f ( f ( f (2) ) ) =( )1 (x ﹤1)A. 0B. 1C. 2D. 24.若a,b 为实数，则“0﹤ab ﹤1”是“b ﹤ ”的（）A. 充分而不必要条件B. 必要而不充分条件C. 充分而必要条件D. 既不充分也不必要条件5. 在△ABC 中，若 a =2、b =3、c =3+1，则△ABC 是( )A. 锐角三角形B. 直角三角形C. 钝角三角形D. 无法确定6.直线 1l : x +ay +6=0 与 2l : (a -2)x +3y +a =0平行，则a 的值为( )A . -1或3B . 1或3C . -3D . -17.若直线3x +y +a =0过圆04222=-++y x y x 的圆心，则a 的值为( ) (,1)(0,1)-∞- (,1)(1,)-∞-+∞ 221x x +>+1a 1)1(x x -≥A . -1B . 1C . 3D . -38.已知等比数列公比为，且a 1+a 3+a 5…+a 99=60，则a 1+a 2+a 3…+a 100 等于( )。

A . 30B . 90C . 100D . 120 9. =( ) A . -1 B . - C . D . 110.某班有50名学生，其中正副班长各1名，现选派10名学生参加劳动，班长和副班长中至少一人在内的选法种数有( )。

湖南省职高对口升学高考数学冲刺模拟试题七(含答案)

数学试题一、选择题：本题共12小题，每小题5分，共60分。

1．已知全集U=R ，集合A={x|x ≥2}，B={x|0≤x<5），则集合么A BA ．{|02}x x <≤B ．{|05}x x <<C ．{|05}x x ≤<D ．{|2}x x ≤2．若a ，b 是空间两条不同的直线，,αβ是空间的两个不同的平面，则a α⊥的一个充分不必要条件是A ．//,a βαβ⊥B ．,a βαβ⊂⊥C ．,//a b b α⊥D ．,//a βαβ⊥3．设{n a }是公差为一2的等差数列，如果147691250,a a a a a a ++=++=则A ．40B ．30C ．20D ．104． 61)x 的展开式中常数项等于A ．1 5B ．一l 5C ．20D ．一20 5．已知函数()y f x =的定义域是[一1，2]，则函数y=f （log 2 x ）的定义域是A ．（0，+∞）B ．（0，1）C ．[1，2]D ．[1,42] 6．已知12(1)3123log log 0,01,,,a ax x a x x x +==><<则的大小关系是A ．321x x x <<B ．213x x x <<C ．132x x x <<D ．231x x x << 7．若△ABC 的内角A 满足sin2A=23，则sinA+cosA=A ．3B ．一3C ．53D ．－538．已知函数f(x)为（一∞，+∞）上的奇函数，且f(x)的图象关于x=1对称，当x ∈【0，1】时，()21,(2014)x f x =-则f 的值为A ．一2B ．一1C ．0D ．19．若双曲线的焦点到渐近线的距离等于实轴长，则该双曲线的离心率e 等于A B C D 10．己知a ，b 是非零向量且满足（a-2b ）⊥a ，（b-2a ）⊥b ，则a 与b 的夹角是A ．6πB ．3πC ．23πD ．56π 11．正四棱柱ABCD-A 1B 1C 1D 1中，对角线BD 1=8，BD 1与侧面BC 1所成的角为30°，则平面BC 1D 1和平面ABB 1A 1所成的角正弦值为A ．12B 3C 3D 612．设抛物线2(0)y ax a =>与直线(0)y kx b k =+≠有两个交点，其横坐标分别是x 1,x 2，而直线(0)y kx b k =+≠与x 轴交点的横坐标是x 3，那么x 1，x 2，x 3的关系是A ．321111x x x =+B ．312x x x =+C ．132111x x x =+D ．123x x x =+二、填空题：本题共4小题，每小题5分，共20分。

职高高考模拟数学试卷答案

一、选择题（每题5分，共50分）1. 下列各数中，有理数是（）A. √2B. πC. √9D. 无理数答案：C2. 已知 a < b，下列不等式中正确的是（）A. a - b < 0B. a + b > 0C. a - b > 0D. a + b < 0答案：A3. 下列函数中，定义域为全体实数的是（）A. y = √(x - 1)B. y = 1/xC. y = x^2D. y = log2x答案：C4. 已知等差数列 {an} 的前n项和为 Sn，若 S5 = 25，S10 = 75，则 a1 = （）A. 1B. 2C. 3D. 4答案：A5. 下列命题中，正确的是（）A. 若 a > b，则 a^2 > b^2B. 若 a > b，则 a - b > 0C. 若 a > b，则 ac > bcD. 若 a > b，则 a/c > b/c答案：B6. 已知等比数列 {an} 的前三项为 a1, a2, a3，若 a1 + a2 + a3 = 12，a1 a2 a3 = 64，则 a1 = （）A. 1B. 2C. 4D. 8答案：C7. 已知函数 y = ax^2 + bx + c，若 a ≠ 0，且函数图象开口向上，则（）A. a > 0, b > 0, c > 0B. a > 0, b < 0, c > 0C. a < 0, b > 0, c >0 D. a < 0, b < 0, c > 0答案：B8. 已知正方形的对角线长为2√2，则其面积是（）A. 4B. 6C. 8D. 10答案：A9. 下列各数中，绝对值最小的是（）A. -1/2B. -1C. 1/2D. 1答案：C10. 已知函数 y = x^3 - 3x，求该函数的极值点。

湖南职高对口升学数学复习模拟试题12(含答案)

2014届湖南职高对口升学数学复习模拟试题12（含答案）19．（12分）在如图所示的平面直角坐标系中，已知点(1,0)A 和点(1,0)B -，||1OC =，且AOC x ∠=，其中O 为坐标原点.（Ⅰ）若34x π=，设点D 为线段OA 上的动点，求||OC OD +的最小值; （Ⅱ）若[0,]2x π∈，向量m BC =，(1cos ,sin 2cos )n x x x =--，求m n ⋅的最小值及对应的x 值.20．（12分）已知ABC ∆，)23sin , 23(cosx x AB -=，)2sin , 2(cos xx AC =，其中)2, 0(π∈x ．（Ⅰ）求| |BC 和ABC ∆的边BC 上的高h ；（Ⅱ）若函数h BC x f ⋅+=λ2| |)(的最大值是5，求常数λ的值．21．（14分）已知两定点1(2,0),F -2(2,0),F 满足条件212PF PF -=的点P 的轨迹是曲线E ，直线ｙ＝kx －1与曲线E 交于A 、B 两点。

（Ⅰ）求ｋ的取值范围；（Ⅱ）如果63,AB =且曲线E 上存在点C ，使,OA OB mOC +=求m ABC ∆的值和的面积S 。

22．（14分）如图,三定点A(2,1),B(0,－1),C(－2,1); 三动点D,E,M 满足AD →=tAB →, BE → = t BC →, DM →=t DE →, t ∈[0,1]. (Ⅰ) 求动直线DE 斜率的变化范围; (Ⅱ)求动点M 的轨迹方程.参考答案19．解：（Ⅰ）设(,0)D t （01t ≤≤），又(,22C -，所以(,22OC OD t +=-+，所以 22211||122OC OD t t +=++=+21()(01)22t t =-+≤≤，所以当2t =时，||OC OD +最小值为2，（Ⅱ）由题意得(cos ,sin)C x x ,(cos 1,sin )m BC x x ==+，则221cos sin 2sin cos 1cos 2sin 2m n x x x x x x ⋅=-+-=--1)4x π=+ ，因为[0,]2x π∈,所以52444x πππ≤+≤，所以当242x ππ+=，即8x π=时，sin(2)4x π+取得最大值1，所以8x π=时，12)4m n x π⋅=-+取得最小值1-所以m n ⋅的最小值为1，此时8x π=。

湖南省普通高等学校对口招生考试全真数学模拟试卷1

湖南省普通高等学校对口招生考试数学模拟试卷(一)一、选择题：在每小题给出的四个选项中，只有一个选项是正确的，请把你认为正确的选项填入题后的括号内，多选不给分，本大题共10小题，每小题5分，共50分。

1、设集合M={x|x 2<9}，N={x|log 2x<1}，则M ⋂N=( )A){x|-3<x<3} B){x|x<2} C){x|0<x<2} D){x|x>-3}2、若a<b<0，则下列不等式不正确的是( ) A) a 1>b1 B)b a -1>a1 C) |a|>|b| D)a 2>b2 3、已知定义在R 上的偶函数f(x)在[0，+∞)上地增函数，且f(31)=0，则不等式f(x)<0的解集为( ) A) (31,1)⋃(2+ ∞) B) (0, 31) C) (0, 31)⋃(3,+ ∞) D) (-31,31) 4、已知数列a 1＝1，a 2＝2，a 3＝2，a 4＝22为等比数列，则a 2＋a 4＋a 6＋…+ a m 2=( )A)212-m -2 B)1-212-m C) 2⨯2m -2 D)1-2m5、已知向量m =(a ，b )，向量n ⊥m ，且|n |=|m |，则n 的坐标可能是( )A) (a ，b ) B) (－a ，b ) C) (b ，－a ) D) (－b ，－a )6、已知点P(sin2α，cos α)是第四象限的点，则α-π是( )的角。

A) 第一象限 B) 第二象限 C) 第三象限 D) 第四象限7、抛物线2y x =-上的点到直线4380x y +-=距离的最小值是( ) A)43 B)54 C)85D)3 8、下列命题中正确的命题的个数为( )(1)如果一条直线与一平面平行，那么这条直线与平面内的任意一条直线平行。

(2)如果一条直线与一个平面相交，那么这个平面内有无数条直线与这条直线垂直。

湖南省对口高考数学模拟试题

2020年湖南省对口高考数学模拟试题考试时间：120 分钟总分：120 一,单项选择题（本大题共10小题，每小题4分，共40分） 1已知集合A={x |x 2−mx +15=0},B={3,4},若A ∩B ={3},则m =( ) A.-11 B.-8 C.8 D.11 2.在∆ABC 中,“A =B”是“sin A =sin B ”的（） A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 3.函数y =√3+2x −x 2的值域为（） A.(-1,3) B.[-1,3] C.(−∞,4] D.[0.2] 4.已知直线ax −y +2a =0与(2a −1)x +ay +a =0垂直，则a 的值是（）A.0B.-1C.0或-1D.0或1 5.在∆ABC 中，若sin 2A =14，则sin A +cos A =( ) A. 54 B. ±√52 C. √52 D. −√526.若函数y =f (x )是周期为4的奇函数，且f (−5)=1，则（）A. f (5)=1B. f (−3)=1C. f (−1)=−1D. f (1)=−17.如果椭圆的短轴长，焦距，长轴长依次成等差数列，则这个椭圆的离心率为（）A. 35B. 45C. 34 D 238.PA 垂直矩形ABCD 所在的平面，且AB=3,AD=4,PA=12,则点P 到点C 的距离是（）A. 5B. 6C. 8D. 139.已知等比数列{a n }的公比为12，且a 1+a 3+a 5+⋯+a 99=60，则a 1+a 2+a 3+⋯+a 100=( )A. 30B. 90C. 100D. 12010.已知点M 的坐标为(1,1),点F 为抛物线y 2=4x 的焦点，点P 在抛物线上移动，当|PM |+|PF |的值最小时，点P 的坐标为（）A.（0，0）B.（14，1））C.（1，1）D.（2，2） ------------------------------------------------------装-----------------------------------------------订----------------------------------------线----------------------------------------------------姓名：班级：准考证号：二.填空题（本大题共5小题，每小题4分，共20分。

湖南职高对口升学数学复习模拟试题10(含答案)

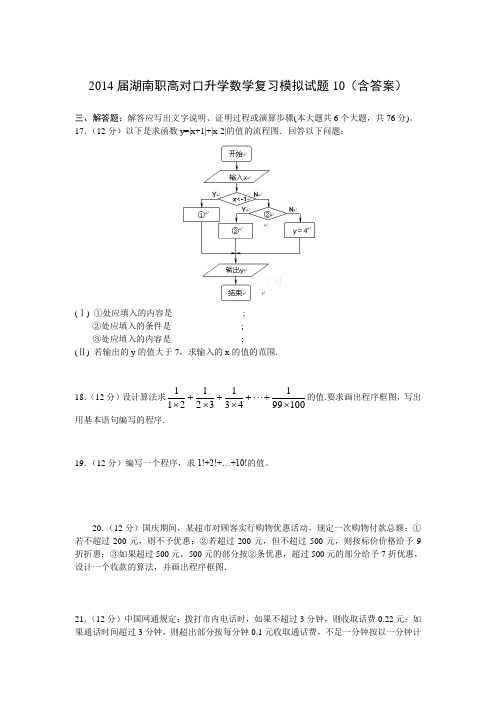
2014届湖南职高对口升学数学复习模拟试题10（含答案）三、解答题：解答应写出文字说明、证明过程或演算步骤(本大题共6个大题，共76分)。

17．（12分）以下是求函数y=|x+1|+|x-2|的值的流程图．回答以下问题：(Ⅰ) ①处应填入的内容是________________;②处应填入的条件是________________;③处应填入的内容是________________;(Ⅱ) 若输出的y 的值大于7，求输入的x 的值的范围.18．（12分）设计算法求100991431321211⨯+⋅⋅⋅+⨯+⨯+⨯的值.要求画出程序框图，写出用基本语句编写的程序.19．（12分）编写一个程序，求1!+2!+…+10!的值。

20．（12分）国庆期间，某超市对顾客实行购物优惠活动，规定一次购物付款总额：①若不超过200元，则不予优惠；②若超过200元，但不超过500元，则按标价价格给予9折折惠；③如果超过500元，500元的部分按②条优惠，超过500元的部分给予7折优惠，设计一个收款的算法，并画出程序框图．21．（12分）中国网通规定：拨打市内电话时，如果不超过3分钟，则收取话费0.22元；如果通话时间超过3分钟，则超出部分按每分钟0.1元收取通话费，不足一分钟按以一分钟计算。

设通话时间为t （分钟），通话费用y （元），如何设计一个程序，计算通话的费用。

22．（14分）已知数列{}n a 的各项均为正数，观察下面程序框图，（1）分别写出当2k =；3k =时，S 的表达式。

（2）当输入11,5,a k ==时，有115=S ，求数列{}n a 的通项公式n a ；（3）在（2）的条件下，若令2n a n b =，求123m b b b b ++++的值。

第18题程序框图 S=0K=1Dos=s+1/k(k+1)k=k+1LOOP UNTIL k>99 PRINT sEND(第18题程序)参考答案一、选择题1．C ；2． B ；3．C ；4．B ；5．B ；6．A ；7．B ；8．C ；9．C ；10．C ；11．C ；12．A ；二、填空题13．7；14．计算并输出使1×3×5×7…× >10 000成立的最小整数；15．5；16．2。

中职数学 2024年湖南省高考数学全真模拟试卷

2024年湖南省高考数学全真模拟试卷一、选择题（本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）A ．M ∩N =∅B ．M ∩N =MC ．M ∪N =MD ．M ∪N =R 1．（4分）设集合M ={x |x （x -1）<0}，N ={x |x 2<4}，则（）A ．{x |x >-4或x <3}B ．{x |x <-3或x >4}C ．{x |-3<x <4}D ．{x |-3＜x ＜}2．（4分）不等式＞1的解集为（）2x -1x +312A ．y =x 3B ．y =|x |+1C ．y =-x 2+1D ．y =2-|x |3．（4分）下列函数中既是偶函数又在（0，+∞）上是增函数的是（）A ．-3B ．3C ．-1D ．14．（4分）已知等比数列{a n }的前n 项和为=+a ,n ∈，则实数a 的值是（）S n 3n +1N *A ．6B ．C ．2D ．不确定5．（4分）过点A （4，a ）与B （5，b ）的直线与直线y =x +m 平行，则|AB |=（）M 2A ．[2kπ，2kπ+]，k ∈Z B ．[2kπ+，2kπ+π]，k ∈ZC ．[2kπ-π，2kπ-]，k ∈ZD ．[2kπ-，2kπ]，k ∈Z 6．（4分）满足函数y =sinx 和y =cosx 都是增函数的区间是（）π2π2π2π2二、填空题（本大题共5小题，每小题4分，共20分）A ．24πcm 2，12πcm 3B ．15πcm 2，12πcm 3C ．24πcm 2，36πcm 3D ．以上都不正确7．（4分）如图，有一个几何体的三视图及其尺寸（单位：cm ）则该几何体的表面积和体积分别为（）A ．①，②B ．②，③C ．②，④D ．③，④8．（4分）已知下列命题（其中a ,b 为直线，α为平面）：①若一条直线垂直于一个平面内无数条直线，则这条直线与这个平面垂直；②若一条直线平行于一个平面，则垂直于这条直线的直线必垂直于这个平面；③若a ∥α，b ⊥α，则a ⊥b ；④若a ⊥b ,则过b 有唯一一个平面α与a 垂直．上述四个命题中，真命题是（）A ．90种B ．180种C ．270种D ．540种9．（4分）3名医生和6名护士被分配到3所学校为学生体检，每校分配1名医生和2名护士，不同的分配方法共有（）A ．B ．C ．2D ．1010．（4分）设x ,y ∈R ，向量a =（x ,1），b =（1，y ），c =（2，4），且a ⊥c ，b ∥c ，则|a +b |=（）→→→→→→→→→M 5M 10M 511．（4分）设sinα+cosα=，则sin 2α= ．35三、解答题（本大题共5小题，其中第21，22小题为选做题.满分50分.解答应写出文字说明、证明过程或演算步骤）12．（4分）已知函数y =f （x ）（x ∈[-1，5]）的图象如图所示，则f （x ）的单调递减区间为．13．（4分）从某部门参加职业技能测试的2000名员工中抽取100名员工，将其成绩（满分100分）按照[20，40），[40，60），[60，80），[80，100]分成4组，得到如图所示的频率分布直方图，估计该部门参加测试员工的平均成绩为．14．（4分）已知直线x -y =1与圆x 2+y 2-2ay +1=0（a >0）没有公共交点，则a 的取值范围是．（用区间表示）15．（4分）在等差数列{a n }中，若S 4=1，S 8=4，则a 17+a 18+a 19+a 20的值为．16．（10分）已知函数f （x ）=log a x （a >0，且a ≠1），且f （3）=1．（Ⅰ）求a 的值，并写出函数f （x ）的定义域；（Ⅱ）设函数g （x ）=f （1+x ）-f （1-x ），试判断g （x ）的奇偶性，并说明理由．17．（10分）已知数列{a n }满足+++…+=+2n ．（Ⅰ）求数列{a n }的通项公式；（Ⅱ）设数列{}的前n 项和为S n ，求S n ．a 1a 23a 35a n2n -1n 21a n18．（10分）在一块耕地上种植一种作物，每季种植成本为1000元，此作物的市场价格和这块地上的产量具有随机性，且互响，其具体情况如下表：作物产量（kg ）300500概率0.50.5选做题：请考生在第21，22题中选择一题作答．如果两题都做，则按所做的第21题计分．作答时，↩请写清题号．作物市场价格（元/kg ）610概率0.40.6（Ⅰ）设X 表示在这块地上种植1季此作物的利润，求x 的分布列；（Ⅱ）若在这块地上连续3季种植此作物，求这3季中至少有2季的利润不少于2000元的概率．19．（10分）如图，在三棱柱ABC -A 1B 1C 1中，点D 是AB 的中点．（Ⅰ）求证：AC 1∥平面CDB 1；（Ⅱ）若CC 1⊥平面ABC ，CC 1=6，AC =3，BC =4，∠ACB =120°，求三棱柱ABC -A 1B 1C 1的体积．20．（10分）点A 、B 分别是椭圆+=1长轴的左、右端点，点F 是椭圆的右焦点．点P 在椭圆上，且位于x 轴的上方，PF ．（Ⅰ）求点P 的坐标；（Ⅱ）设M 是椭圆长轴AB 上的一点，M 到直线AP 的距离等于|MB |，求椭圆上的点到M 的距离d 的最小值．x 236y 22021．（10分）设a ,b ,c 分别是△ABC 的三个内角A 、B 、C 所对的边，S 是△ABC 的面积，已知a =4，b =5，S =5．（1）求角C ；（2）求c 边的长度．M 3。