2010-2011学年度第二学期北京市各区高三模拟试题汇编---《生活与哲学》

合集下载

北京市东城区2011届高三综合练习(二)(理综)

北京市东城区2010—2011学年第二学期高三综合练习（二）理科综合能力测试本试卷分选择题和非选择题两部分，共300分。

考试时长150分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将答题卡交回。

以下数据可供解题时参考：可能用到的相对原子质量：H 1 C 12 N 14 O 16选择题共120分选择题共20小题，每小题6分，共120分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1．下列关于细胞内化合物的叙述不正确．．．的是（）A．由葡萄糖合成的糖原作为储能物质存在于动物细胞中B．由氨基酸缩合形成的蛋白质是细胞和生物体功能的重要体现者C．含有三个高能磷酸键的ATP分子可直接为细胞的生命活动一共能D．多种无机盐离子对维持细胞和生物体的生命活动有重要作用2．下列关于高等动物体内细胞的生命历程的叙述不正确．．．的是（）A．细胞增殖包括物质准备和细胞分裂整个连续的过程B．细胞的分化有利于提高生物体各种生理功能的效率C．细胞在癌变的过程中发生了基因突变和基因重组D，细胞的衰老与凋亡并不能说明动物个体已经衰老3．图—1为人体内基因对性状的控制过程，分析可知（）A．基因l和基因2一般不会出现在人体内的同一个细胞中B．图中①过程需RNA聚合酶的催化，②过程需tRNA的协助C．④⑤过程的结果存在差异的根本原因是血红蛋白结构的不同D．过程①②③表明基因通过控制酶的合成来控制生物体的所有性状4．某种昆虫对经常使用的一种杀虫剂产生了抗药性，下列叙述正确的是（）A．杀虫剂诱发种群中特定个体产生了可遗传的抗药性变异B．在使用杀虫剂之前昆虫种群基因库中就存在抗药性基因C．种群抗药性基因频率在使用此杀虫剂过程中保持不变D．已经具有了抗药性的昆虫种群属于一个新的物种5．血糖平衡对机体生命活动具有重要作用。

图—2为人体部分血糖调控模式图，相关叙述正确的是（）A．通过图中②和⑤过程可同时促进肝糖原的合成和脂肪转化成葡萄糖B．低血糖状态时，除图中途径外还可通过肌糖原的分解使血糖恢复正常C．高血糖状态时，④过程可使胰岛A细胞分泌的胰岛素增多进而使血糖恢复正常D．在血糖调控过程中，胰岛素的作用结果可以通过反馈影响胰岛素的分泌6．下列说法不正确．．．的是（）A．淀粉可以制得葡萄糖和酒精B．铝合金的熔点和硬度均高于纯铝C．玻璃、塑料、金属、纸类均是可回收的物品D．硬化油不易被空气氧化而便于储存和运输7．下列做法正确的是（）A．用无色试剂瓶盛放新制氯水B．用10 mL量筒量取3.24 mL稀硫酸C．用蒸馏水鉴别溴蒸气和二氧化氮气体D．用氨水清洗做过银镜反应的试管内壁8．下叙述正确的是（）A．NH4C1只含共价键，所以它是共价化合物B．Al（OH）3是两性氢氧化物，所以它能溶解于盐酸或氨水中C．硅胶多孔，吸附水份能力强，所以常用作袋装食品的干燥剂D．元素周期表中氢原子半径最小，所以氢是最活泼的非金属元素9．下列各组物质不能．．按“→”所示关系实现转化的是（“→”表示反应一步完成）（）10．加热聚丙烯废塑料可以得到碳、氢气、甲烷、乙烯、丙烯、苯和甲苯。

北京市西城区2010-2011学年第二学期高三综合练习(二)(数学理)

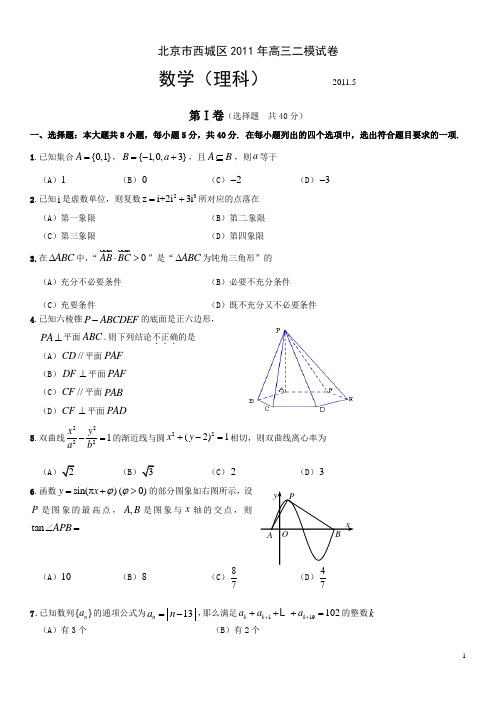
北京市西城区2011年高三二模试卷数学（理科） 2011.5第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分. 在每小题列出的四个选项中，选出符合题目要求的一项. 1.已知集合{0,1}A =，{1,0,3}B a =-+，且A B ⊆，则a 等于（A ）1（B ）0（C ）2- （D ）3-2.已知i 是虚数单位，则复数23z i+2i 3i =+所对应的点落在（A ）第一象限（B ）第二象限（C ）第三象限（D ）第四象限3.在ABC ∆中，“0AB BC ⋅>”是“ABC ∆为钝角三角形”的（A ）充分不必要条件（B ）必要不充分条件（C ）充要条件（D ）既不充分又不必要条件4.已知六棱锥P ABCDEF -的底面是正六边形，PA ⊥平面ABC .则下列结论不正确．．．的是（A ）//CD 平面PAF （B ）DF ⊥平面PAF （C ）//CF 平面PAB （D ）CF ⊥平面PAD5.双曲线22221x y a b-=的渐近线与圆22(2)1x y +-=相切，则双曲线离心率为（A（B（C ）2（D ）3 6.函数sin()(0)y x ϕϕ=π+>的部分图象如右图所示，设P 是图象的最高点，,A B 是图象与x 轴的交点，则tan APB ∠=（A ）10 （B ）8 （C ）87（D ）77．已知数列{}n a 的通项公式为13n a n =-，那么满足119102k k k a a a +++++= 的整数k （A ）有3个（B ）有2个（C ）有1个（D ）不存在8．设点(1,0)A ，(2,1)B ，如果直线1ax by +=与线段AB 有一个公共点，那么22a b +（A ）最小值为15 （B）最小值为5 （C ）最大值为15（D第Ⅱ卷（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分. 9．在ABC ∆中，若2B A =，:a b =A =_____. 10.在521()x x+的展开式中，2x 的系数是_____. 11．如图，AB 是圆O 的直径，P 在AB 的延长线上，PD切圆O 于点C .已知圆O2OP =，则PC =______；ACD ∠的大小为______.12.在极坐标系中，点(2,)2A π关于直线:cos 1l ρθ=的对称点的一个极坐标为_____.13．定义某种运算⊗，a b ⊗的运算原理如右图所示.设()(0)(2)f x x x x =⊗-⊗. 则(2)f =______；()f x 在区间[2,2]-上的最小值为______.14.数列{}n a 满足11a =，11n n n a a n λ+-=+，其中λ∈R ， 12n = ，，．①当0λ=时，20a =_____；②若存在正整数m ，当n m >时总有0n a <，则λ的取值范围是_____.三、解答题：本大题共6小题，共80分. 解答应写出必要的文字说明、证明过程或演算步骤. 15.（本小题满分13分）已知函数cos 2()sin()4x f x x π=+.（Ⅰ）求函数()f x 的定义域；（Ⅱ）若4()3f x =，求s i n 2x 的值.16.（本小题满分13分）如图，已知菱形ABCD 的边长为6，60BAD ∠=,AC BD O = .将菱形ABCD 沿对角线AC折起，使BD =B ACD -.（Ⅰ）若点M 是棱BC 的中点，求证://OM 平面ABD ；（Ⅱ）求二面角A B D O --的余弦值；（Ⅲ）设点N 是线段BD 上一个动点，试确定N点的位置，使得CN =.17.（本小题满分13分）甲班有2名男乒乓球选手和3名女乒乓球选手，乙班有3名男乒乓球选手和1名女乒乓球选手，学校计划从甲乙两班各选2名选手参加体育交流活动.（Ⅰ）求选出的4名选手均为男选手的概率.（Ⅱ）记X 为选出的4名选手中女选手的人数，求X 的分布列和期望.18.（本小题满分14分）已知函数()(1)e (0)xa f x x x=->，其中e 为自然对数的底数.（Ⅰ）当2a =时，求曲线()y f x =在(1,(1))f 处的切线与坐标轴围成的面积；（Ⅱ）若函数()f x 存在一个极大值点和一个极小值点，且极大值与极小值的积为5e ，求a 的值.19.（本小题满分14分）已知椭圆2222:1x y M a b +=(0)a b >>的离心率为3，且椭圆上一点与椭圆的两个焦点构成的三角形周长为246+．（Ⅰ）求椭圆M 的方程；M（Ⅱ）设直线l 与椭圆M 交于,A B 两点，且以AB 为直径的圆过椭圆的右顶点C ，求ABC ∆面积的最大值．20.（本小题满分13分）若m A A A ,,,21 为集合2}(,,2,1{≥=n n A 且)n ∈*N 的子集，且满足两个条件： ①12m A A A A = ；②对任意的A y x ⊆},{，至少存在一个},,3,2,1{m i ∈，使}{},{x y x A i = 或}{y . 则称集合组m A A A ,,,21 具有性质P .如图，作n 行m 列数表，定义数表中的第k 行第l 列的数为⎩⎨⎧∉∈=)(0)(1l l kl A k A k a .（Ⅰ）当4n =时，判断下列两个集合组是否具有性质P ，如果是请画出所对应的表格，如果不是请说明理由；集合组1：123{1,3},{2,3},{4}A A A ===；集合组2：123{2,3,4},{2,3},{1,4}A A A ===. （Ⅱ）当7n =时，若集合组123,,A A A 具有性质P ，请先画出所对应的7行3列的一个数表，再依此表格分别写出集合123,,A A A ；（Ⅲ）当100n =时，集合组12,,,t A A A 是具有性质P 且所含集合个数最小的集合组，求t 的值及12||||||t A A A ++ 的最小值.（其中||i A 表示集合i A 所含元素的个数）北京市西城区2011年高三二模试卷参考答案及评分标准数学（理科） 2011.5一、选择题：本大题共8小题，每小题5分，共40分.二、填空题：本大题共6小题，每小题5分，共30分.9. 30 10. 5 11.1；7512.)4π（或其它等价写法） 13.2-；6- 14.120；(21,2),k k k -∈*N . 注：11、13、14题第一问2分，第二问3分.三、解答题：本大题共6小题，共80分.若考生的解法与本解答不同，正确者可参照评分标准给分. 15.（本小题满分13分）解：（Ⅰ）由题意，sin()04x π+≠， ………………2分所以()4x k k π+≠π∈Z ， ………………3分所以()4x k k π≠π-∈Z ， ………………4分函数()f x 的定义域为{x x ≠,4k k ππ-∈Z }.………………5分（Ⅱ）c o s 2co s 2()sin()sin cos cos sin444x x f x x x x ==πππ++ ………………7分 2sincos xx x=+ ………………8分22sin )sin )sin cos x x x x x x-==-+. ………………10分因为4()3f x =，所以cos sin x x -=. ………………11分所以，2sin 21(cos sin )x x x =-- ………………12分81199=-= . ………………13分16.（本小题满分13分）（Ⅰ）证明：因为点O 是菱形ABCD 的对角线的交点，所以O 是AC 的中点.又点M 是棱BC 的中点，所以OM 是ABC ∆的中位线，//OM AB . ………………1分因为OM ⊄平面ABD ,AB ⊂平面ABD ,所以//OM 平面ABD . ………………3分（Ⅱ）解：由题意，3OB OD ==，因为BD =所以90BOD ∠=，OB OD ⊥. ………………4分又因为菱形ABCD ，所以OB AC ⊥，OD AC ⊥. 建立空间直角坐标系O xyz -，如图所示.(0,3,0),A D (0,0,3)B .所以((AB AD =-=-………………6分设平面ABD 的法向量为n =(,,)x y z ，则有0,0AB AD ⎧⋅=⎪⎨⋅=⎪⎩n n即：30,30z y ⎧-+=⎪⎨-+=⎪⎩令1x =，则y z ==n=(1. ………………7分因为,AC OB AC OD ⊥⊥,所以AC ⊥平面BOD . 平面BOD 的法向量与AC 平行，所以平面BOD 的法向量为0(1,0,0)=n . ………………8分000cos ,7⋅〈〉===n n n n n n ，因为二面角A B D O --是锐角，所以二面角A B D O --的余弦值为. ……………9分（Ⅲ）解：因为N 是线段BD 上一个动点，设111(,,)N x y z ，BN BD λ=，则111(,,3)(0,3,3)x y z λ-=-，所以1110,3,33x y z λλ===-， ……………10分则(0,3,33)N λλ-，,33)CN λλ=-，由CN ==，即29920λλ-+=，…………11分解得13λ=或3λ=， ……………12分所以N 点的坐标为(0,2,1)或(0,1,2). ……………13分（也可以答是线段BD 的三等分点，2BN ND = 或2BN ND =）17.（本小题满分13分）解：（Ⅰ）事件A 表示“选出的4名选手均为男选手”.由题意知232254()C P A C C = ………………3分11110220=⨯=. ………………5分（Ⅱ）X 的可能取值为0,1,2,3. ………………6分23225431(0)10620C P X C C ====⨯， ………………7分11212333225423337(1)10620C C C C P X C C +⨯⨯+====⨯， ………………9分 21332254333(3)10620C C P X C C ⨯====⨯， ………………10分 (2)1(0)(1)(3)P X P X P X P X ==-=-=-=920=. ………………11分 X………………12分179317()01232020202010E X =⨯+⨯+⨯+⨯=. ………………13分18、（本小题满分14分）解：（Ⅰ）22()e xx ax a f x x-+'=， ………………3分当2a =时，2222()e xx x f x x -+'=， 12122(1)e e 1f -+'=⨯=，(1)e f =-，所以曲线()y f x =在(1,(1))f 处的切线方程为e 2e y x =-， ………………5分切线与x 轴、y 轴的交点坐标分别为(2,0)，(0,2e)-， ………………6分所以，所求面积为122e 2e 2⨯⨯-=. ………………7分（Ⅱ）因为函数()f x 存在一个极大值点和一个极小值点，所以，方程20x ax a -+=在(0,)+∞内存在两个不等实根， ………………8分则240,0.a a a ⎧∆=->⎨>⎩ ………………9分所以4a >. ………………10分设12,x x 为函数()f x 的极大值点和极小值点，则12x x a +=，12x x a =， ………………11分因为，512()()e f x f x =，所以，1251212e e e x x x a x a x x --⨯=， ………………12分即1225121212()e e x x x x a x x a x x +-++=，225e e a a a a a -+=，5e e a =，解得，5a =，此时()f x 有两个极值点，所以5a =. ………………14分19.（本小题满分14分）解：（Ⅰ）因为椭圆M 上一点和它的两个焦点构成的三角形周长为246+，所以24622+=+c a ， ……………1分又椭圆的离心率为3，即3c a =，所以3c a =， ………………2分所以3a =，c =………………4分所以1b =，椭圆M 的方程为1922=+y x . ………………5分（Ⅱ）方法一：不妨设BC 的方程(3),(0)y n x n =->，则AC 的方程为)3(1--=x ny . 由22(3),19y n x x y =-⎧⎪⎨+=⎪⎩得0196)91(2222=-+-+n x n x n ， ………………6分设),(11y x A ，),(22y x B ，因为222819391n x n -=+，所以19327222+-=n n x ， ………………7分同理可得2219327nn x +-=， ………………8分所以1961||22++=n n BC ，222961||nn n n AC ++=， ………………10分 964)1()1(2||||212+++==∆n n n n AC BC S ABC ， ………………12分设21≥+=n n t ，则22236464899t S t t t==≤++， ………………13分当且仅当38=t 时取等号，所以ABC ∆面积的最大值为83. ………………14分方法二：不妨设直线AB 的方程x ky m =+.由22,1,9x ky m x y =+⎧⎪⎨+=⎪⎩ 消去x 得222(9)290k y kmy m +++-=， ………………6分设),(11y x A ，),(22y x B ，则有12229km y y k +=-+，212299m y y k -=+. ① ………………7分因为以AB 为直径的圆过点C ，所以 0CA CB ⋅=.由 1122(3,),(3,)CA x y CB x y =-=-，得 1212(3)(3)0x x y y --+=. ………………8分将1122,x ky m x ky m =+=+代入上式，得 221212(1)(3)()(3)0k y y k m y y m ++-++-=.将 ① 代入上式，解得 125m =或3m =（舍）. ………………10分所以125m =（此时直线AB 经过定点12(,0)5D ，与椭圆有两个交点），所以121||||2ABC S DC y y ∆=-12==……………12分设211,099t t k =<≤+，则ABC S ∆=所以当251(0,]2889t =∈时，ABC S ∆取得最大值83. ……………14分20.（本小题满分13分）（Ⅰ）解：集合组1具有性质P . ………………1分所对应的数表为：………………3分集合组2不具有性质P . ………………4分1 1 0 0 00 1 1 0 0 1因为存在{{2,3}1,2,3,4}⊆，有123{2,3}{2,3},{2,3}{2,3},{2,3}A A A ===∅ ，与对任意的A y x ⊆},{，都至少存在一个{1,2,3}i ∈，有}{},{x y x A i = 或}{y 矛盾，所以集合组123{2,3,4},{2,3},{1,4}A A A ===不具有性质P . ………………5分（Ⅱ）……………7分123{3,4,5,7},{2,4,6,7},{1,5,6,7}A A A ===. ………………8分（注：表格中的7行可以交换得到不同的表格，它们所对应的集合组也不同）（Ⅲ）设12,,,t A A A 所对应的数表为数表M ，因为集合组12,,,t A A A 为具有性质P 的集合组，所以集合组12,,,t A A A 满足条件①和②，由条件①：12t A A A A = ，可得对任意x A ∈，都存在{1,2,3,,}i t ∈ 有i A x ∈，所以1=xi a ，即第x 行不全为0，所以由条件①可知数表M 中任意一行不全为0. ………………9分由条件②知，对任意的A y x ⊆},{，都至少存在一个{1,2,3,,}i t ∈ ，使}{},{x y x A i = 或}{y ，所以yi xi a a ,一定是一个1一个0，即第x 行与第y 行的第i 列的两个数一定不同.所以由条件②可得数表M 中任意两行不完全相同. ………………10分因为由0,1所构成的t 元有序数组共有2t个，去掉全是0的t 元有序数组，共有21t-个，又因数表M 中任意两行都不完全相同，所以10021t≤-，所以7t ≥.又7t =时，由0,1所构成的7元有序数组共有128个，去掉全是0的数组，共127个，选择其中的100个数组构造100行7列数表，则数表对应的集合组满足条件①②，即具有性质P .所以7t =. ………………12分因为12||||||t A A A +++ 等于表格中数字1的个数，所以，要使12||||||t A A A +++ 取得最小值，只需使表中1的个数尽可能少，而7t =时，在数表M 中，1的个数为1的行最多7行；1的个数为2的行最多2721C =行；1的个数为3的行最多3735C =行； 1的个数为4的行最多4735C =行；1 1 1 1 1 11 1 1 1 1 1 0 0 0 0 0 0 0 0 011 因为上述共有98行，所以还有2行各有5个1，所以此时表格中最少有722133543552304+⨯+⨯+⨯+⨯=个1.所以12||||||t A A A +++ 的最小值为304. ………………14分。

历年北京高中政治合格性考试汇编：生活与哲学(学生版)

历年北京高中政治合格性考试汇编：生活与哲学一．选择题（共25小题）1．（2020•北京学业考试）马克思主义哲学的产生，实现了哲学史上的伟大变革，标志着哲学发展进入一个崭新时代。

之所以作出这样的判断，是因为马克思主义哲学（）①全盘照搬德国古典哲学，将哲学发展推向更高阶段②第一次实现了唯物主义与辩证法的有机结合③第一次实现了唯物辩证的自然观与历史观的统一④第一次实现了实践基础上科学性和革命性的统一A．①②③B．①②④C．①③④D．②③④2．（2020•北京学业考试）下面漫画《方向比速度重要》启示我们（）A．注重加快发展速度，促成事物质变B．发挥意识能动作用，明确正确方向C．坚信前途是光明的，保持乐观精神D．价值判断因人而异，没有统一标准3．（2020•北京学业考试）宋代画家郭熙在山水取景构图上创立了“三远”法，“山有三远：自山下而仰山巅，谓之高远；自山前而窥山后，谓之深远；自近山而望远山，谓之平远。

……高远之势突兀，深远之意重叠，平远之意冲融而缥缥渺渺。

”同样都是“远”，意境却不同，这其中蕴含的哲理是（）A．共性与个性相统一B．外因对内因起决定作用C．真理与谬误无界限D．想象可以直接变为现实4．（2020•北京学业考试）海绵城市体现新一代城市雨洪管理理念。

城市可以像海绵一样，下雨时吸水、蓄水、渗水、清水，需要时将蓄存的水“开释”并加以使用，提高城市生态系统功用和削减城市洪涝灾害的发生。

从哲学角度看，建设海绵城市（）A．可改变水循环规律更好造福人类B．需抛弃以往城市建设的所有做法C．能更好地促进人与自然和谐发展D．要把人的主观需要作为根本出发点5．（2020•北京学业考试）生活中我们可能有这样的体验，指示方向的路标牌并没有错，但跟着它还是容易走晕：如果加上全景图，并特别标注出“您的位置”，感觉就会不同。

这种体验表明（）①作为整体的全景图发挥着重要作用，主导着行程的方向②立足整体统筹全局，利用全景图能更好地规划行程③未标注全景图的路标牌，不能单独发挥关键部分的导向作用④明确自己在全局中的位置，有利于顺利抵达目的地A．①③B．①④C．②③D．②④6．（2020•北京学业考试）在科普作品《一颗原子的时空之旅》中有这样的话，“你身体里的每一个原子都来自一颗爆炸了的恒星，形成你左手的原子可能和形成你右手的来自不同的恒星。

北京市东城区10-11下学期高三数学(理科)一模考试试卷

北京市东城区2010-2011学年第二学期高三综合练习(一)数学(理科)本试卷分为第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷（选择题共40分）一、本大题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1．“x ＞2”是“x 2＞4”的（A ）充分不必要条件（B ）必要不充分条件（C ）充要条件（D ）既不充分也不必要条件2．已知数列{a n }为等差数列，且a 1=2，a 2+a 3=13，则a 4+a 5+a 6等于（A ）40 （B ）42 （C ）43 （D ）45 3．已知函数f (x )对任意的x ∈R 有f (x )+f (―x )=0，且当x ＞0时，f (x )=ln(x +1)，则函数f (x )的图象大致为4．已知平面上不重合的四点P ，A ，B ，C 满足PA PB PC ++=0，且AB AC m A P +=，那么实数m 的值为（A ）2 （B ）3（C ）4（D ）55．若右边的程序框图输出的S 是126，则条件①可为（A ）n ≤5 （B ）n ≤6（C ）n ≤7 （D ）n ≤86．已知(,)2παπ∈，1tan()47πα+=，那么sin α+cos α的值为（A ）15-（B ）75 （C ）75-（D ）347．已知函数131()()2xf x x =-，那么在下列区间中含有函数f (x )零点的是（A ）1(0,)3（B ）11(,)32（C ）12(,)23（D ）2(,1)38．空间点到平面的距离定义如下：过空间一点作平面的垂线，这点和垂足之间的距离叫做这个点到这个平面的距离。

已知平面α，β，γ两两互相垂直，点A ∈α，点A 到平面β，γ的距离都是3，点P 是α上的动点，且满足P 到β的距离是P 到点A 距离的2倍，则点P 到平面γ的距离的最大值是（A ）3（B（C ）3（D ）6第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分。

2011年北京各城区高三一模二模语文真题-分类汇编之作文

_________高考题库，荣誉出品_________ ●-------------------------密--------------封--------------线--------------内--------------请--------------不--------------要--------------答--------------题-------------------------●2011年北京各城区高三一模二模语文真题-分类汇编之作文题库出品，必是精品题号一总分得分△注意事项：1.本系列试题包含2011年-2013年北京市各城区一模二模真题。

2.本系列文档有相关的试题分类汇编，具体见封面。

3.本系列文档为高考题库精心校对版本4.本系列试题涵盖北京高考所有学科,并有纸质版讲义出版。

一、作文题（本大题共11小题，共0分） 1.（2011北京西城区高三一模语文）作文。

阅读下面文字，按要求作文。

“思悟网”论坛，主题：关于“未知”。

甲：这个世界，有着太多的未知——未知的人、领域，未知的前程、命运……它们陌生神秘，莫测难解。

明天，永远是未知的。

乙：昨天，有些东西也同样“未知”啊。

“未知”，不等于“无知”，也不等于“不可知”。

丙：是的，“未知”二字，总令人充满好奇与期待。

丁：我恐惧“未知”。

戊：让我们将“未知”变为“已知”！己：所有东西，一定要“知道”才有意思吗？ ……你对“未知”有着怎样的体验与感悟？请以此为内容，写一篇文章。

要求：角度自选，立意自定，标题自拟，文体自选（除诗歌外），不少于800字。

2.（2011北京西城区高三二模语文）作文。

请以 “耐力”作为题目，写一篇不少于800字的文章。

除诗歌外，文体不限。

_________高考题库，荣誉出品_________ ●-------------------------密--------------封--------------线--------------内--------------请--------------不--------------要--------------答--------------题-------------------------●3.（2011北京朝阳区高三二模语文）作文（60分）课堂上，老师给同学们展示了下面这两幅图,让大家比较两幅图中间的圆的大小。

2010~2011学年度高三年级第二学期检测试卷答案3

2010~2011学年度高三年级第二学期政治检测试卷参考答案（三）高三政治试卷1-5BABDB 6-11BBDCCA12．（24分）(1) （12分）①大力发展生产力，实现国民经济又好又快的发展。

（2分）②坚持和完善以公有制为主体、多种所有制经济共同发展的基本经济制度；让各种所有制经济在市场竞争中相互促进，共同发展。

（2分）③坚持按劳分配为主、多种分配方式并存的分配制度，继续完善按生产要素分配的原则。

（2分）④保证居民收入在国民收入分配中占合理比重，劳动报酬在初次分配中占合理的比重。

（2分）⑤再分配更加注重公平，调节过高收入，保障过低收入，扩大中等收入者比重。

（2分）⑥加强政府对收入分配的调节，完善社会保障制度，防止出现两极分化。

（2分）⑦坚持落实科学发展观，以人为本。

（2分）（只要回答出六点即可得满分，每点2分，共12分，不超过12分）12.（2）(12分)①矛盾即对立统一，具有普遍性，要求我们坚持一分为二的观点看问题。

政府要正确分析我国现阶段的经济和社会发展取得的成绩，也要看到存在的问题。

(3分)②矛盾具有特殊性，事物在不同方发展阶段上有不同的特点。

要正确分析我国现阶段的经济和社会问题的特殊性，制定解决相应的措施。

(3分)③主要矛盾在事物发展中居主导地位，起决定作用。

要集中精力解决主要矛盾，抓好经济发展。

次要矛盾的解决也会影响主要矛盾的解决，恰当解决好次要矛盾，促进主要矛盾的解决。

(3分)④矛盾的普遍性和特殊性是相互连接，不可分割的，普遍性寓于特殊性之中。

世界各国在经济发展上都会遇到同样的社会问题，因此我们要加强国际交流与合作，借鉴别国经验。

(3分)13．（21分）(1)（9分）①发展低碳经济利于贯彻全面协调可持续的科学发展观的要求，体现以人为本。

（3分）②发展低碳经济有利于增强我国自主创新能力，加快转变经济发展方式，推动产业结构优化升级；有利于能源资源节约和环境保护。

（3分）③发展低碳经济有利于转变人们的消费观念，倡导人们形成节能环保的消费行为。

生活与哲学样卷及答案

北京市普通高中课程改革实验模块考试思想政治必修4《生活与哲学》参考样卷本试卷共6页，考试时间60分钟，满分100分。

一、在下列各题的四个选项中，只有一个是最符合题意的。

请把答案填在答案格内。

（每小题《列子·天瑞》记载：“杞国有人忧天地崩坠，身亡所寄，废寝食者。

”因为害怕天地崩坠而不吃不睡固然可笑，但是每一个正常的人从童年时代起，往往会自觉或不自觉地进行着类似的追问和思考。

追问和思考这样的问题，实际上已经不自觉地与哲学发生了联系。

回答1、2题。

1．之所以得出上述的结论，原因在于①哲学并不神秘，人人都有哲学②哲学研究的对象是广阔的自然界③哲学的本义是爱智慧和追求智慧④哲学源于对实践的追问和对世界的思考A.①②B.①④C.②③D.③④2．下列关于哲学的说法中，正确的是①哲学是关于世界观的学问②哲学是系统化理论化的世界观③哲学是科学的世界观和方法论④哲学是对自然、社会和思维知识的概括和总结A.①②③B.①②④C.①③④D.②③④在人类追索智慧的过程中，出现了各种各样的哲学派别。

它们在相互辩难中发展，在湍急的思想河流中曲折前进。

回答3～5题。

3．有人说哲学应该研究宇宙中的大问题，有人说哲学应该研究人生问题，也有人说哲学应该研究人类的认识问题。

哲学研究的问题有许多，但______的关系问题是哲学的基本问题。

A.世界观和方法论B.唯物主义和唯心主义C.思维和存在D.辩证法和形而上学4. 我们的思想能不能认识现实世界？我们能不能在我们关于现实世界的表象和概念中正确地反映现实？用哲学的语言来说，这个问题叫做A.思维和存在的同一性问题B.思维和存在何为本原的问题C.物质是否依赖意识的问题D.物质和意识是否均是本原的问题5．唯物主义和唯心主义是哲学上的两大阵营。

划分唯物主义和唯心主义的标准是A.物质和意识的关系问题B.重视物质生活还是重视精神生活C.对物质和意识哪个是世界本原的不同回答D.承认物质的决定作用，又承认意识的能动作用马克思主义的哲学诞生，实现了哲学史上的伟大变革，标志着哲学发展进入了一个崭新时代。

北京市东城区2011届高三综合练习(二)(文综)有答案

北京市东城区2010—2011学年第二学期高三综合练习（二）文科综合能力测试本试卷300分钟。

考试时长150分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共35小题，每小题4分，共140分。

在每小题列出的四个选项中，选出最符合题目要求的一项。

读表l，完成1、2题。

1．影响该地天气变化的天气系统是（）A．暖锋B．冷锋C．高压D．低压2．表中所示期间（）A．天安门广场升旗时间越来越晚B．伦敦正午太阳高度变小C．南极附近极夜范围扩大D．地球公转速度变快近年来，台湾省已成为大陆游客的旅游热点地区。

读图l，完成3—6题。

3．游客出发前观察图1，判断图示地区的河流流向特点是（）A．多数从西流向东B．从中部流向四周C．多数从南流向北D．从四周流向中部4．游客从M走到N，其所经地区地势起伏与图2所示剖面线对应的是（）A．①B．②C．③D．④中国是世界上农业的发祥地之一。

回答12、13题。

12．从表2你能获得的相关信息有（）表2战国时期生产工具出土情况表②生产力水平提高④铁器使用的区域广阔A．①②B．②④C．②③④D．①②④13．纵观中国古代历史，尽管“农夫早出暮入，耕稼树艺”，“妇女夙兴夜寐，纺绩积红”，但温饱问题长期得不到解决。

造成这种现象的原因是（）A．天灾战乱连年不断B．重农抑商政策的推行C．农民赋役负担沉重D．耕作技术始终停滞不前14．2010年我国的两部中医药古籍成功入选《世界记忆亚太地区名录》，一部奠定了中医学理论的基础，另一部被誉为“东方药物巨典”。

这两部著作是（）A．《黄帝内经》、《本草纲目》B．《伤寒杂病论》、《本草纲目》C．《齐民要术》、《农政全书》D．《本草纲目》、《农政全书》15．从1918年1月起，《新青年》全部刊登白话文，仅1919年一年，中国就出现了400种以上的白话报，1920年3月，教育部要求小学各年级一律废除文言教科书。

北京市东城区2010-2011示范校第二学期高三综合练习二(理综)

2010－2011学年度北京东城区示范校综合练习理科综合试题 2011年3月命题：物理北京景山学校化学北京市第五中学生物 166中学审查：东城区(北区)教研中心本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分300分。

考试时间150分钟。

第Ⅰ卷（选择题共120分）本卷共20小题，每小题6分，共120分。

在每小题列出的四个选项中，选出符合题目要求的一项。

以下数据可供解题时参考：可能用到的相对原子质量：H-1 C-12 N-14 O-16 S-32 Fe-56 Cu-641．图Ⅰ表示细胞分裂和受精过程中核DNA 和染色体含量的变化，图Ⅱ表示二倍体生物细胞分裂过程中染色体的行为。

据图分析，下列说法正确的是（）A ．Ⅰ中染色体数目加倍发生在①、④、⑧和⑨4个时期B ．Ⅰ中只有③、⑥、⑦和⑨时期的染色体数目与DNA 数目相等C ．Ⅱ中与Ⅰ中a 段对应的细胞是B 和B ＇，与Ⅰ中b 段对应的是C 和C ＇D ．Ⅱ中含有两个染色体组的细胞有A ＇、B ＇、C 、C ＇、D2．某株植物的基因型为AaBb ，则下列有关叙述中错误的选项有（）①如果该植物自交，后代有两种表现型，说明该植物的等位基因（A 和a ）的遗传不遵循孟德尔的基因分离定律 ②如果两对等位基因遵循自由组合定律，让该植物接受aabb 植株的花粉，形成的子代的基因型有4种③如果该植物自交，且遵循自由组合定律后代有三种表现型，则子代中表现型不同于亲本的个体所占比例可能为7/16④如果该植物的性别决定方式属于XY 型，且A 和a 位于性染色体上，则不能确定该株植物一定是雌性个体。

A ．1项B ．两项C ．三项D ．四项3．现有一种含催产素的新药，它能使人们对陌生人产生信赖感。

这一新药可能有助于治疗时间ⅠABC DA ＇B ＇C ＇D ＇Ⅱ孤独症等疾病。

催产素是由下丘脑合成、垂体后叶释放的一种九肽荷尔蒙。

下列有关叙述正确的是( )A．催产素一定含有C、H、O、N四种元素，含有9个肽键B．孤独症患者直接口服适量催产素可以有效地缓解症状C．下丘脑中有些细胞不仅能够分泌激素，而且能传导兴奋D．催产素参与的调节过程具有作用范围比较局限、作用时间比较长等特点4．右图示根尖的结构及细胞分裂和分化的情况。

北京市东城区10—11下学期高三语文一模考试试卷

北京市东城区2010-2011学年第二学期高三综合练习(一)语文本试卷共7页，150分。

考试时长150分钟。

考生务必将答案写在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（27分）一、本大题共5小题，每小题3分，共15分。

1．下列词语中，字形和加点的字的读音全都正确的一项是A．精粹挥豪泼墨编纂．（cuán）斐．（fěi）然成章B．防犯家长里短苍劲．（jìn）乳臭．（xiù）未干C．袒护明察暗访湖泊．（pō）奴颜婢．（bì）膝D．费时精减节约绮．（yǐ）丽返璞．（pú）归真2．下列句子中，加点的词语使用不恰当．．．的一句是A．在校级篮球赛中，两支球队原定予月底进行比赛，因场地问题无法按时进行，最终这场比赛无疾而终．．．．。

B．一时间，许多国人把健康类图书中的某些观点视为金科玉律．．．．，大有不按照此法去做就有被健康抛弃的危险。

C．国家人力资源和社会保障部表示，规范旅游培训市场势在必行，行业龙头企业主抓社会培训工作责无旁贷．．．．。

D．当今一些人或唯物质利益马首是瞻．．．．，或把实用主义奉为准则，或以及时行乐为目标，丧失了人生应有的境界。

3．下列句子中，没有语病的一句是A．部分省市普遍遭遇的用工荒，根本的原因是工人的工资和付出不成正比，导致工人不愿到生活成本高的城市务工而造成的。

B．针对当今社会上频发的拐卖儿童现象，全国妇联发表声明，呼吁广大群众增强反拐意识并积极提供被拐卖儿童的有关线索。

C．在地震发生后，日本反核游行已举行数次，3月20日的涩谷游行参加人数接近2000人，日本警视厅出动上百名警察维持。

D．圆明园遗址不是一般意义的旅游景点，它是严肃神圣的地方，是人们接受教育和熏陶，瞻仰历史，感受人类智慧和文明的场所。

4．对下面文学常识的判断不正确的一项是A．《孟子》是由战国时期思想家孟轲及其弟子编成的，它具有浓厚的雄辩色彩，善于用典型事例、比喻和寓言说理。

高考政治《生活与哲学》试题新人教版必修4

2011年高考《生活与哲学》试题一、选择题（本大题共25小题，每题2分，共50分。

请选出每题中一个最符合题意的正确选项。

）2010年11月5日，第七届“全国马克思主义论坛”在武汉举行。

与会者认为，应该认真贯彻中央精神，用好哲学社会科学人才并充分发挥他们的作用，切实把哲学社会科学工作摆在重要位置。

回答1-2题。

1、之所以要切实把哲学社会科学工作摆在重要位置，是因为A、哲学是人们对整个世界的根本看法B、哲学是人们认识世界和改造世界的重要工具C、哲学是人类社会发展的根本动力D、哲学发展水平是社会文明程度的唯一标志2、我国哲学领域越来越以时代的目光和世界的视野聚焦于建设中国特色社会主义最为重大的理论问题和现实问题。

“问题”是当代哲学研究的“最实际的呼声”。

这表明①哲学与我们的生活、与我们置身其中的社会密切相关②中国特色社会主义建设的实践是我国哲学研究的重要基础③哲学为具体科学提供世界观和方法论的指导④当代中国的哲学就是中国特色社会主义理论A、①②B、②③C、①③D、②④3、下列表述，符合马克思主义哲学对哲学基本问题第一个方面回答的是A、理无常是，事无常非B、物我一体，心物一体C、仓廪实而知礼节，衣食足而知荣辱D、尽人事，听天命4、英国哲学家休谟认为，世界上存在的只有心理的知觉、感觉，此外是否有真实的存在，那是不可能知道的。

休谟的观点属于①客观唯心主义②主观唯心主义③可知论④不可知论A、①③B、②④C、①④D、②③2010年10月1日，我国“嫦娥二号”月球探测卫星升空，我国绕月探测工程又迈出重要一步。

回答5-8题。

5、右图为我国月球探测工程标志。

设计师用意味十足的书法线条和带有一定象形意味的脚丫，组合成篆书“月”字，暗寓龙的传人登月的梦想。

从哲学上看，这一标志A、源于设计师的独特创意B、是对月球的逼真反映C、是意识活动主动创造性的充分体现D、对探月工程有重要的指导作用6、我们的先人曾对月亮充满无限遐想，有着独特的情怀，从苏东坡的“把酒问月”到今天的“嫦娥探月”，以及未来的“载人登月”，月亮将在我们面前进一步揭开她的神秘面纱。

北京市东城区10-11下学期高三数学(文科)一模考试试卷

北京市东城区2010-2011学年第二学期高三综合练习(一)数学(文科)本试卷分为第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷（选择题共40分）一、本大题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1．已知复数z 满足(1―i)z =2，则z 等于（A ）1+i （B ）1―i （C ）―1+i （D ）―1―i2．命题“0x ∃∈R ，20log 0x ≤”的否定为（A ）0x ∃∈R ，20log 0x > （B ）0x ∃∈R ，20log 0x ≥ （C ）x ∀∈R ，2log 0x ≥（D ）x ∀∈R ，2log 0x >3．已知函数f (x )是定义在R 上的偶函数，且当x ＞0时，f (x )=ln(x +1)，则函数f (x )的图象大致为4．给定下列四个命题：①若一个平面内的两条直线与另外一个平面都平行，则这两个平面互相平行； ②若两个平面都垂直于同一条直线，则这两个平面互相平行；③若两个平面互相垂直，则在其中一个平面内的直线垂直另外一个平面； ④若两个平面互相平行，则在其中一个平面内的直线平行另外一个平面. 其中为真命题的是（A ）①和② （B ）②和③ （C ）③和④ （D ）②和④5．已知函数sin()y x ωϕ=+(0,0)2πωϕ><≤的部分图如图所示，则点(,)P ωϕ的坐标为（A ）(2,)3π（B ）(2,)6π（C ）1(,)23π（D ）1(,)26π6．若右边的程序框图输出的S 是126，则条件①可为（A ）n ≤5 （B ）n ≤6 （C ）n ≤7 （D ）n ≤87．已知函数131()()2xf x x =-，那么在下列区间中含有函数f (x)零点的是（A ）1(0,)3（B ）11(,)32（C ）1(,1)2（D ）（1，2）8．空间点到平面的距离定义如下：过空间一点作平面的垂线，这点和垂足之间的距离叫做这个点到这个平面的距离.平面α，β，γ两两互相垂直，点A ∈α，点A 到平面β，γ的距离都是3，点P 是α上的动点，且满足P 到β的距离是P 到A 距离的2倍，则点P 到平面γ的距离的最小值为（A（B ）3（C ）6（D ）3第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分。

2011北京各区模拟考试试题分类(生活与哲学)

2020年春季三年级数学期末试卷(苏教版)（满分：120分时间：90分钟）姓名：电话：得分：一、填空题。

（每空1分；共30分）1.0.28是由（）个0.1和（）个0.01组成的。

2.今年是2016年；是（）年；共（）天；今年的二、三、四月一共有（）天。

3. 58是（）个18；（）个14是34。

4.在（）里填上合适的单位。

水杯高12（）教室的占地面积是80（）跑道长100( ) 一枚邮票的大小是4（）小李的身高是141（）数学书的封面大约是320( )5.25×40的积的末尾有( )个0 ；438÷5的商是( )位数。

6.某年的1月8日是星期三；该年的1月25日是星期（）。

7.比3.2少0.9的数（）；（）比1.7多2.3。

8.在○里填上“＞”、“＜”或“＝”。

5平方分米○50000平方分米 6平方分米○6000平方厘米90×15○30×45 390÷6○493÷64角○0.39元 7.8分米○8分米9.□46÷5；如果商是三位数；□里最小可以填（）；如果商是两位数；□里最大可以填（）。

10.用一根铁丝围成一个长8厘米；宽6厘米的长方形（无剩余）；如果用这根铁丝围成一个最大的正方形；那么正方形的面积是（）平方厘米。

11.从1、2、3中任选一个数作为分子；从5；6；7中任选一个数作为分母；一共可以组成（）个分数。

12.甲数除以乙数；商是12；那么甲数是乙数的（）倍。

甲、乙两数的和是乙数的（）倍。

二、选择题。

（每题2分；共12分）1. 要使45×2□的积是一个四位数；□里最小应填（）。

A.3B.4C.5D.22. 红红晚上9时睡觉；第二天早上7时起床；她一共睡了（）时。

A.7B.8C.9D.103.一个长方形的长增加1米；宽不变；它的周长将（）。

A.增加1米B.增加200厘米C.4厘米D.不变4.体育课上同学们站成一排；老师让他们按1、2、3、4、5循环报数；最后一个报的数是2；这一排的人数可能是（）A.30人B.31人C.32人D.33人5. 多多跑100米需要18.2秒；乐乐跑100米需要17.8秒个；欢欢跑100米需要18.6秒；莉莉跑100米需要19.1秒。

2010-2011年年北京各地高考模拟试题精析数学(理)2

崇文区2009－2010学年度第二学期统一练习（一）高三数学（理科） 2010．4本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分．考试时间120分钟．考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷（选择题共40分）注意事项：1．考生务必将答案答在答题卡上，在试卷上作答无效．2．答题前考生务必用黑色字迹的签字笔在答题卡上填写姓名、准考证号，然后再用2B 铅笔将与准考证号对应的信息点涂黑．3．答题卡上第Ⅰ卷必须用2B 铅笔作答，将选中项涂满涂黑，黑度以遮住框内字母为准，修改时用橡皮擦除干净．第Ⅱ卷必须用黑色字迹的签字笔按照题号顺序在各题目的答题区域内作答，未在对应的答题区域内作答或超出答题区域作答的均不得分．一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．（崇文·理·题1）1．已知全集U =R ，集合{}|12A x x =->，{}2|680B x x x =-+<，则集合()U A B =ð（）A ．{}|14x x -≤≤B ．{}|14x x -<<C ．{}|23x x <≤D ． {}|23x x <≤ 【解析】 D ；容易解得{3A x x x =>或者}0x <，{}26B x x =<<．于是()U A B =ð{}23x x <≤．（崇文·理·题2）2．一个单位共有职工200人，其中不超过45岁的有120人，超过45岁的有80人．为了调查职工的健康状况，用分层抽样的方法从全体职工中抽出一个容量为25的样本，应抽取不超过45岁的职工人数为 ( )A ． 5B ． 10C ．15D ．50 【解析】 C ；容易知道样本中不超过45岁的人与超过45岁的人数之比为1203802=．于是抽取不超过45岁的职工人数为325155⋅=人．（崇文·理·题3）3．已知PA 是O 的切线，切点为A ，2PA =，AC 是O 的直径，PC 交O 于点B ，30PAB ∠=，则O 的半径为（）A ．1B ．2 CD．【解析】 C ；30,2tan30PAPCAPAB CA ∠=∠===（崇文·理·题4）4．已知等比数列{}n a 为递增数列，且373a a +=，282a a ⋅=，则117a a = （） A ．2 B ． 43 C ． 32 D ．12【解析】 A ；不妨设等比数列的公比为q ．由2375213a a a q q ⎛⎫+=+=⎪⎝⎭知50a >．于是228552a a a a ⋅==⇒=2q =或者2q =．而数列单调增，于是2q =42q =．（崇文·理·题5）5．已知,m n 是两条不同直线，,,αβγ是三个不同平面，下列命题中正确的为 ( ) A ．若,,αγβγ⊥⊥则αβ∥ B ．若,,m n αα⊥⊥则m n ∥ C ．若,m n αα∥∥，则m n ∥ D ．若,,m m αβ∥∥则αβ∥ 【解析】 B ；A 中,αβ可以是任意关系；B 正确；C 中,m n 平行于同一平面，其位置关系可以为任意．D 中平行于同一直线的平面可以相交或者平行．（崇文·理·题6）6．设33,,2x yx y M N P ++===0x y <<），则,,M N P 大小关系为 ( )A ．M N P <<B ．N P M <<C ．P M N <<D ．P N M << 【解析】D ；由0x y <<，有2x y+．由指数函数的单调性，有23x y x y P N ++=<==；PA23332x yx y M N ++=>==．（崇文·理·题7）7．2位男生和3位女生共5位同学站成一排．若男生甲不站两端，3位女生中有且只有两位女生相邻，则不同排法的种数为（）A ．36B ．42C ． 48D ．60 【解析】 C ；不妨将5个位置从左到右编号为1，2，3，4，5．于是甲只能位于2，3，4号位． ①当甲位于2号位时，3位女生必须分别位于1，3，4位或者1，4，5位．于是相应的排法总数为33212A =； ②当甲位于3号位时，3位女生必须分别位于1，2，4位或者1，2，5位或者1，4，5或者2，4，5位．于是相应的排法总数为33424A =． ③当甲位于4号位时，情形与①相同．排法总数为33212A =．综上，知本题所有的排法数为12+24+12=48．（崇文·理·题8）8．设定义在R 上的函数1,(1),1()1,(1)x x f x x ⎧≠⎪-=⎨⎪=⎩．若关于x 的方程2()()0f x bf x c ++=有3个不同的实数解1x ，2x ，3x ，则123x x x ++等于（）A ． 3B ．2C ．1b --D ．c 【解析】 A ；易知()f x 的图像关于直线1x =对称．2()()0f x bf x c ++=的解必有一根使()1f x =．不妨设为1x ．23,x x 关于直线1x =对称．于是1233x x x ++=．崇文区2009－2010学年度第二学期统一练习（一）高三数学（理科） 2010．4第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分．（崇文·理·题9）9．如果复数()()2i 1i m m ++（其中i 是虚数单位）是实数，则实数m =___________．【解析】 1-；()()()()223i 1i 1mm m m i m ++=-++．于是有3101m m +=⇒=-．（崇文·理·题10）10．若12a x ⎫⎪⎭的展开式中的常数项为220-，则实数a =___________．【解析】 1-；由二项式定理4124311212CC rrr rr r r a T a x x --+⎛⎫== ⎪⎝⎭．令44033r r -=⇒=．于是有3312C 2201a a =-⇒=-．（崇文·理·题11）11．将参数方程12cos ,2sin ,x y θθ=+⎧⎨=⎩（θ为参数）化成普通方程为．【解析】 ()2214x y -+=；由12cos ,2sin x y θθ-==知()2214x y -+=．（崇文·理·题12）12．某程序框图如图所示，该程序运行后输出,M N 的值分别为．【解析】 13，21；依据程序框图画出运行n 次后,,M N i 的4次运行后43i =>，于是有13,21M N ==．（崇文·理·题13）13．若数列{}n a 的前n 项和为n S ，则11,(1),,(2)n nn S n a S S n -=⎧=⎨-⎩．≥若数列{}n b 的前n 项积为n T ，类比上述结果，则n b =_________；此时，若2()n T n n *=∈N ，则n b =___________．【解析】 11,2;, 1.nT n T T n ⎧⎪⎨⎪=⎩≥，()221,1;, 2.1n n n n =⎧⎪⎨⎪-⎩≥；由12....n n T b b b =，知()1211...n n n n n T b b b b T b --==．（崇文·理·题14）14．定义在R 上的函数满足1(0)0,()(1)1,()()52x f f x f x f f x =+-==，且当1201x x <≤≤时，12()()f x f x ≤，则12010f ⎛⎫= ⎪⎝⎭_________________．【解析】 132；容易知道()11,f =于是()1111522f f ⎛⎫== ⎪⎝⎭．而1111112222f f f ⎛⎫⎛⎫⎛⎫+-=⇒= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．又由()f x 单调增，知()1,2f x =当1152x ≤≤时．而441111155201052⋅⋅≤≤，4411111522232f f ⎛⎫⎛⎫⎛⎫⋅== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．于是11201032f ⎛⎫= ⎪⎝⎭．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．（崇文·理·题15）15．在ABC ∆中，角,,A B C 所对的边分别为,,a b c，满足sin 2A =ABC ∆的面积为2． ⑴求bc 的值；⑵若6b c +=，求a 的值．【解析】 ⑴∵sin2A =0πA <<．∴cos 2A =． ∴4sin 2sin cos 225A A A ==．∵1sin 22ABC S bc A ∆==，∴5bc =． --------------------6分⑵∵sin 2A =∴23cos 12sin 25A A =-=．∵5bc =，6b c +=，∴2222cos a b c bc A =+-2()2(1cos )b c bc A =+-+20=∴a = -----------12分（崇文·理·题16）16．为了调查某厂2000名工人生产某种产品的能力，随机抽查了m 位工人某天生产该产品的数量，产品数量的分组区间为[)10,15，[)15,20，[)20,25，[)25,30，[30,35]，频率分布直方图如图所示．已知生产的产品数量在[)20,25之间的工人有6位． ⑴求m ；10 15 20 25 30 35产品数量⑵工厂规定从各组中任选1人进行再培训，则选取5人不在同一组的概率是多少？【解析】 ⑴根据直方图可知产品件数在[)20,25内的人数为50.066m ⨯⨯=，则20m =（位）．---------------- 6分 ⑵根据直方图可知产品件数在[)10,15，[)15,20，[)20,25，[)25,30，[30,35]，组内的人数分别为2，4，6， 5，3．设选取这5人不在同组为B 事件，则5202465315()C 323P B ⨯⨯⨯⨯==．答：选取这5人不在同组的概率为15323．（崇文·理·题17）17．三棱柱111C B A ABC -中，侧棱与底面垂直，90=∠ABC ，12AB BC BB ===， ,M N 分别是AB ，1A C 的中点． ⑴求证：MN ∥平面11B BCC ； ⑵求证：⊥MN 平面C B A 11； ⑶求二面角11A C B M --的余弦值．C 1B 1A 1NCBM A【解析】 ⑴连结1BC ，1AC ．在1ABC ∆中，∵,M N 是AB ，1A C 的中点，∴MN ∥1BC ．又∵MN ⊄平面11BCC B ，∴MN ∥平面11BCC B ． --------------------4分 ⑵如图，以1B 为原点建立空间直角坐标系1B xyz -．则1(0,0,0)B ，(0,2,2)C ，1(2,0,0)A -，(1,0,2)M -，(1,1,1)N - 1B C =(0,2,2)，11(2,0,0)A B =，(0,1,1)NM =-．设平面11A B C 的法向量为(,,)x y z =n ． 111000B C x y z A B ⎧⋅==⎧⎪⇒⎨⎨=-⋅=⎩⎪⎩n n 令1z =，则0,1x y ==-，∴ (0,1,1)=-n ．∴NM n =． ∴MN ⊥平面11A B C ． --------------------9分 ⑶设平面1MB C 的法向量为000(,,)x y z =m ,1(1,0,2)B M =-．001001200x z B C y z B M ⎧=⋅=⎧⎪⇒⎨⎨=-⋅=⎩⎪⎩m m 令01z =，则002,1x y ==- ∴(2,1,1)=-m ．∴cos,||||⋅<>===⋅n mn mn m所求二面角11M B C A--．--------------------14分（崇文·理·题18）18．已知322()69f x x ax a x=-+（a∈R）．⑴求函数()f x的单调递减区间；⑵当0a>时，若对[]0,3x∀∈有()4f x≤恒成立，求实数a的取值范围．【解析】⑴22'()31293()(3)0f x x ax a x a x a=-+=--<ⅰⅰ)当3a a=，即0a=时，2'()30f x x=>，不成立．ⅱⅱ)当3a a>，即0a<时，单调减区间为(3,)a a．ⅲⅲ)当3a a<，即0a>时，单调减区间为(,3)a a．-------------------5分⑵22'()31293()(3)f x x ax a x a x a=-+=--，()f x在(0,)a上递增，在(,3)a a上递减，在(3,)a+∞上递增．ⅰⅰ)当3a≥时，函数()f x在[0,3]上递增，所以函数()f x在[0,3]上的最大值是(3)f，若对[]0,3x∀∈有()4f x≤恒成立，需要有(3)4,3,fa⎧⎨⎩≤≥解得a∈∅．ⅱⅱ)当13a<≤时，有33a a<≤，此时函数()f x在[0,]a上递增，在[,3]a上递减，所以函数()f x在[0,3]上的最大值是()f a，若对[]0,3x∀∈有()4f x≤恒成立，需要有()4,13,f aa⎧⎨<⎩≤≤解得1a=．⑶当1a<时，有33a>，此时函数()f x在[,3]a a上递减，在[3,3]a上递增，所以函数()f x在[0,3]上的最大值是()f a或者是(3)f．由2()(3)(3)(43)f a f a a-=--，①34a<≤时，()(3)f a f≤，若对[]0,3x∀∈有()4f x≤恒成立，需要有(3)4,30,4fa⎧⎪⎨<⎪⎩≤≤解得3[1]4a∈．②314a<<时，()(3)f a f>，若对[]0,3x∀∈有()4f x≤恒成立，需要有()4,31,4f aa⎧⎪⎨<<⎪⎩≤解得3(,1)4a∈．综上所述，[11]a∈．-------------14分（崇文·理·题19）19．已知抛物线24y x =，点(1,0)M 关于y 轴的对称点为N ，直线l 过点M 交抛物线于,A B 两点． ⑴证明：直线,NA NB 的斜率互为相反数； ⑵求ANB ∆面积的最小值；⑶当点M 的坐标为(,0)(0m m >，且1)m ≠．根据⑴⑵推测并回答下列问题（不必说明理由）： ① 直线,NA NB 的斜率是否互为相反数？ ② ANB ∆面积的最小值是多少？【解析】 ⑴设直线l 的方程为()1(0)y k x k =-≠．由()21,4,y k x y x ⎧=-⎪⎨=⎪⎩ 可得 ()2222240k x k x k -++=．设()()1122,,,A x y B x y ，则21212224,1k x x x x k ++==．∴124y y =-∴()1,0N - 1212221212441144NA NB y y y yk k x x y y +=+=+++++ ()()()()()()2212212112222212124444(4444)04444y y y y y y y y yy yy ⎡⎤+++-+-+⎣⎦===++++．又当l 垂直于x 轴时，点,A B 关于x 轴，显然0,NA NB NA NB k k k k +==-．综上，0,NA NB NA NB k k k k +==-． ---------------- 5分 ⑵12NAB S y y ∆=-==4>．当l 垂直于x 轴时，4NAB S ∆=．∴ANB ∆面积的最小值等于4． ----------------10分 ⑶推测：①NA NB k k =-；②ANB ∆面积的最小值为4 ---------------- 14分（崇文·理·题20）20．已知数列{}n a 中，11a =，21(0a a a =-≠且1)a ≠，其前n 项和为n S ，且当2n ≥时，1111n n n S a a +=-． ⑴求证：数列{}n S 是等比数列； ⑵求数列{}n a 的通项公式；⑶若4a =，令19(3)(3)nn n n a b a a +=++，记数列{}n b 的前n 项和为n T ．设λ是整数，问是否存在正整数n ，使等式13758n n T a λ++=成立？若存在，求出n 和相应的λ值；若不存在，请说明理由．【解析】 ⑴当2n ≥时，11+111111n n n n n n nS a a S S S S +-=-=---，化简得211(2)n n n S S S n -+=≥，又由1210,0S S a =≠=≠，可推知对一切正整数n 均有0n S ≠， ∴数列{}n S 是等比数列． ---------------- 4分 ⑵由⑴知等比数列{}n S 的首项为1，公比为a ， ∴1n n S a -=．当2n ≥时，21(1)n n n n a S S a a --=-=-，又111a S ==， ∴21,(1),(1),(2).n n n a a a n -=⎧=⎨-⎩≥ ----------8分 ⑶当4,2a n =≥时，234n n a -=⨯，此时 22119934(3)(3)(343)(343)n n n n n n n a b a a ---+⨯⨯==++⨯+⨯+ 221213411(41)(41)4141n n n n n -----⨯==-++++，又111293(3)(3)8a b a a ==++，∴213,(1)811,(2)4141n n n n b n --⎧=⎪⎪=⎨⎪-⎪⎩++≥1138T b ==，当2n ≥时，1222212131111()()841414141n n n n T b b b ----=+++=+-++-++++171841n -=-+．若1n =，则等式13758n n T a λ++=为37858λ+=，52λ=不是整数，不符合题意．若2n ≥，则等式13758n n T a λ++=为11717841548n n λ---+=+⨯，15541n λ-=-+ λ是整数，∴141n -+是5的因数．∴当且仅当2n =时，1541n -+是整数， ∴4λ=综上所述，当且仅当4λ=时，存在正整数2n =，使等式13758n n T a λ++=成立．。

2010-2011年年北京各地高考模拟试题精析数学(理)3

北京市丰台区2010年高三年级第二学期统一练习（一）数学试题（理）注意事项：1．答题前，考生务必先将答题卡上的学校、年级、班级、姓名、准考证号用黑色字迹签字笔填写清楚，并认真核对条形码上的准考证号、姓名，在答题卡的“条形码粘贴区”贴好条形码．2．本次考试所有答题均在答题卡上完成．选择题必须使用2B 铅笔以正确填涂方式将各小题对应选项涂黑，如需改动，用橡皮擦除干净后再选涂其它选项．非选择题必须使用标准黑色字迹签字笔书写，要求字体工整、字迹清楚．作图题用2B 铅笔作图，要求线条、图形清晰．3．请严格按照答题卡上题号在相应答题区内作答，超出答题区域书写的答案无效，在试题、草稿纸上答题无效．4．请保持答题卡卡面清洁，不要装订、不要折叠、不要破损．（丰台·理科·题1）一、本大题共8小题，每小题5分共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．如果1i1ia z a -=+为纯虚数，则实数a 等于（）A ．0B ．1-C ．1D ．1-或1 【解析】 D ；设i z x =，0x ≠则1ii 1i a x a -=+()1i 0ax a x ⇔+-+=100ax a x +=⎧⇔⎨+=⎩11a x =⎧⇔⎨=-⎩或11a x =-⎧⎨=⎩．（丰台·理科·题2）2．设集合[)1{|(),0,}2x M y y x ==∈+∞，(]2{|log ,0,1}N y y x x ==∈，则集合M N 是（）A ．[)(,0)1,-∞+∞B ．[)0,+∞C ．(],1-∞D ．(,0)(0,1)-∞ 【解析】 C ；(]0,1M =，(],0N =-∞，因此(],1MN =-∞．（丰台·理科·题3）3．若2012(12)n n n x a a x a x a x -=++++，则2a 的值是（） A ．84 B ．84- C ．280 D ．280- 【解析】 A ；()222C 2na =-()212a n n ⇔=-，四个选项中只有8442762==⨯满足．（丰台·理科·题4）4．奇函数()f x 在(),0-∞上单调递增，若(1)0,f -=则不等式()0f x <的解集是（） A ．(,1)(0,1)-∞- B ．(,1)(1,)-∞-+∞C ．(1,0)(0,1)-D ．(1,0)(1,)-+∞【解析】 A ；如图，根据()f x 所具有的性质可以画出()f x 的草图，因此()01f x x <⇔<-或01x <<．（丰台·理科·题5）5．从0,2,4中取一个数字，从1,3,5中取两个数字，组成无重复数字的三位数，则所有不同的三位数的个数是（）A ．36B ．48C ．52D ．54 【解析】 B ；从0,2,4中取一个数字，从1,3,5中取两个数字进行排列，然后在得到的排列中去掉首数字为0的即满足题意，因此12323333C C A A -336648=⨯⨯-=为所求．（丰台·理科·题6）6．在ABC ∆中，“AB AC BA BC ⋅=⋅”是“||||AC BC =”的（） A ．充分而不必要条件 B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【解析】 C ；AB AC BA BC ⋅=⋅0AB AC BA BC ⇔⋅-⋅=()0AB AC BC ⇔⋅+=即AB 与AB 边上的中线相互垂直也即ABC △为等腰三角形，且AC BC =，因此||||AB AC BA BC AC BC ⋅=⋅⇔=．（丰台·理科·题7）7．设0,0,24a b a b ab >>++=，则（） A ．a b +有最大值8 B ．a b +有最小值8 C ．ab 有最大值8 D ．ab 有最小值8 【解析】 B ；∵24241aa b ab b a-++=⇒=+∴()2242425128111a a a b a a a a a -++=+==++-+++≥；而()24252611611a ab a a a a -⎡⎤=⋅=-++⎢⎥++⎣⎦≤．（丰台·理科·题8） 8．已知整数以按如下规律排成一列：()1,1、()1,2、()2,1、()1,3、()2,2，()3,1，()1,4，()2,3，()3,2，()4,1，……，则第60个数对是（）A ．()10,1B ．()2,10C ． ()5,7D ．()7,5【解析】 C ；根据题中规律，有()1,1为第1项，()1,2为第2项，()1,3为第4项，…，()1,11为第56项，因此第60项为()5,7．二、填空题：本大题共6小题，每小题5分，共30分．把答案填在题中横线上．（丰台·理科·题9）9．在平行四边形ABCD 中，点E 是边AB 的中点，DE 与AC 交于点F ，若AEF ∆的面积是12cm ，则CDF ∆的面积是 2cm ．【解析】 4；取CD 的中点G ，连结BG 交AC 于H ，则∵BE DG ∥且1122BE AB CD DG ===，∴四边形BEDG 为平行四边形 ∴AF FH HC == ∴44DFC AEFS S ==△△（丰台·理科·题10）10．若一个正三棱柱的三视图及其尺寸如下图所示（单位：cm），则该几何体的体积是3cm ．【解析】； 223V S h h =⋅⋅=⋅=⎝⎭（丰台·理科·题11）11．样本容量为1000的频率分布直方图如图所示．根据样本的频率分布直方图计算，x 的值为，样本数据落在[)6,14内的频数为．【解析】 0.09，680；10.020.0820.034x +++⨯=0.09x ⇒=；10EB侧视图俯视图主视图样本数据落在[)6,14内的频数为()0.080.0941000680+⨯⨯=．（丰台·理科·题12）12．在平面直角坐标系xOy 中，直线l 的参数方程为11x y t =⎧⎨=+⎩（参数t ∈R ），圆C 的参数方程为cos 1sin x y θθ=+⎧⎨=⎩（参数[)0,2πθ∈），则圆心到直线l 的距离是．；直线方程为1y x =+，圆的方程为()2211x y -+=．于是圆心()1,0到直线10x y -+=的距（丰台·理科·题13）13．在右边的程序框图中，若输出i 的值是4，则输入x 的取值范围是．【解析】 (]2,4；∵328228x x ->⇔>，322810x x ->⇔>，32104x x ->⇔>，3242x x ->⇔>∴要使得刚好进行4次运算后输出的82x > ，则有24x <≤．（丰台·理科·题14）14．函数21(01)y x x =+≤≤图象上点P 处的切线与直线0,0,1y x x ===围成的梯形面积等于S ，则S 的最大值等于，此时点P 的坐标是．【解析】 54，15,24⎛⎫⎪⎝⎭；函数()2101y x x =+≤≤在P ()200,1x x +点处的切线方程为()()200012y x x x x -+=⋅-，即20021y x x x =⋅-+它与y 轴的交点为201x -，与1x =的交点为20021x x -+．于是题中梯形的面积()()222000001121112S x x x x x ⎡⎤=-+-+⋅=-++⎣⎦201524x ⎛⎫=--+ ⎪⎝⎭ 当012x =时，S 取得最大值为54，此时P 点坐标为211,122⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭即15,24⎛⎫⎪⎝⎭．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．（丰台·理科·题15）15．（12分）已知函数()sin cos f x a x b x =+的图象经过点π,06⎛⎫ ⎪⎝⎭，π,13⎛⎫⎪⎝⎭．（I ）求实数a 、b 的值；（II ）若π0,2x ⎡⎤∈⎢⎥⎣⎦，求函数()f x 的最大值及此时x 的值．【解析】（I ）∵函数()sin cos f x a x b x =+的图象经过点π,06⎛⎫ ⎪⎝⎭，π,13⎛⎫⎪⎝⎭，∴102112a b ⎧+=⎪⎪+=解得：,1a b ==（II ）由（I）知：π()cos 2sin 6f x x x x ⎛⎫=-=- ⎪⎝⎭∵π0,2x ⎡⎤∈⎢⎥⎣⎦，∴πππ,663x ⎡⎤-∈-⎢⎥⎣⎦∴当ππ63x -=，即π2x =时，()f x（丰台·理科·题16） 16．（13分）如图，在底面是正方形的四棱锥P ABCD -中，PA ⊥面ABCD ，BD 交AC 于点E ，F 是PC 中点，G 为AC 上一点．（I ）求证：BD FG ⊥；（II ）确定点G 在线段AC 上的位置，使FG //平面PBD ，并说明理由．（III ）当二面角B PC D --的大小为2π3时，求PC 与底面ABCD 所成角的正切值．PGFE DCBA【解析】（I ）∵PA ⊥面ABCD ，四边形ABCD 是正方形，其对角线BD ，AC 交于点E ，∴PA BD ⊥，AC BD ⊥． ∴BD ⊥平面APC ，∵FG ⊂平面PAC ，∴BD FG ⊥（II ）当G 为EC 中点，即34AG AC =时，FG ∥平面PBD ，理由如下：连结PE ，由F 为PC 中点，G 为EC 中点，知FG PE ∥，而FG ⊄平面PBD ，PB ⊂平面PBD ，故FG ∥平面PBD ．（III ）作BH PC ⊥于H ，连结DH ， ∵PA ⊥面ABCD ，四边形ABCD 是正方形， ∴PB PD =，又∵BC DC =，PC PC =，∴PCB PCD △≌△， ∴DH PC ⊥，且DH BH ⊥，∴BHD ∠是二面角B PC D --的平面角，即2π3BHD ∠=，∵PA ⊥面ABCD ，∴PCA ∠就是PC 与底面ABCD 所成的角连结EH ，则EH BD ⊥，π3BHE ∠=，EH PC ⊥∴tan BEBHE EH∠=BE EC =∴ECEH=∴sin EH PCA EC ∠=∴tan PCA ∠=∴PC 与底面ABCD．另解：以A 为原点，AB 、AD 、PA 所在的直线分别为x 、y 、z 轴建立空间直角坐标系如图所示，设正方形ABCD 的边长为1，则()0,0,0A ，()1,0,0B ，()1,1,0C ，()0,1,0D ，()0,0,P a ()0a >，11,,022E ⎛⎫ ⎪⎝⎭，11,,222a F ⎛⎫⎪⎝⎭，(),,0G mm (0m <．（I ）()1,1,0BD =-，11,,222a FG m m ⎛⎫=--- ⎪⎝⎭，110022BD FG m m ⋅=++-+=∴BD FG ⊥（II ）要使FG ∥平面PBD ，只需F G E P ∥，而11,,22EP a ⎛⎫=- ⎪⎝⎭，由FG EP λ=可得11222m a a λλ⎧-=⎪⎪⎨⎪-=-⎪⎩，解得1λ=，34m =，∴33,,044G ⎛⎫⎪⎝⎭，∴34AG AC =故当34AG AC =时，FG ∥平面PBD设平面PBC 的一个法向量为(),,u x y z =，则00u PC u BC ⎧⋅=⎪⎨⋅=⎪⎩，而PC =()1,1,a -，()0,1,0BC =，∴00x y az y +-=⎧⎨=⎩，取1z =，得(),0,1u a =，同理可得平面PBC 的一个法向量()0,,1v a = 设,u v 所成的角为0，则2π1|cos |cos 32θ==，即||12||||u v u v ⋅=，12=，∴1a = ∵PA ⊥面ABCD ，∴PCA ∠就是PC 与底面ABCD 所成的角，∴tanPA PCA AC ∠===．（丰台·理科·题17） 17．（14分）某工厂师徒二人各加工相同型号的零件2个，是否加工出精品均互不影响．已知师父加工一个零件是精品的概率为23，师徒二人各加工2个零件都是精品的概率为1.9（I ）求徒弟加工2个零件都是精品的概率；（II ）求徒弟加工该零件的精品数多于师父的概率；（III ）设师徒二人加工出的4个零件中精品个数为ξ，求ξ的分布列与均值E ξ．【解析】（I ）设徒弟加工1个零件是精品的概率为1p ，则21221339p ⨯=，得2114p =，所以徒弟加工2个零件都是精品的概率是14（II ）设徒弟加工零件的精品数多于师父的概率为p ，由（I ）知，11p =，师父加工两个零件中，精品个数的分布列如下：所以294949436p =⨯+⨯+⨯=ξ的期望为470123436363636363⨯+⨯+⨯+⨯+⨯=．（丰台·理科·题18）18．（13分）已知函数()ln a f x x x=+．（I ）当0a <时，求函数()f x 的单调区间；（II ）若函数()f x 在[]1,e 上的最小值是3,2求a 的值．【解析】函数()ln a f x x x =+的定义域为()0,+∞，221'()a x af x x x x-=-=（1）∵0a <，∴()0f x '>故函数在其定义域()0,+∞上是单调递增的．（II ）在[]1,e 上，发如下情况讨论：①当1a <时，()0f x '>，函数()f x 单调递增，其最小值为(1)1f a =<，这与函数在[]1,e 上的最小值是32相矛盾；②当1a =时，函数()f x 在(]1,e 单调递增，其最小值为(1)1f =，同样与最小值是32相矛盾；③当1e a <<时，函数()f x 在[)1,a 上有()0f x '<，单调递减，在(],e a 上有'()0f x '>，单调递增，所以函数()f x 满足最小值为()ln 1f a a =+由3ln 12a +=，得a ④当e a =时，函数()f x 在[)1,e 上有()0f x '<，单调递减，其最小值为()2f e =，还与最小值是32相矛盾； ⑤当e a >时，显然函数()f x 在[]1,e 上单调递减，其最小值为()12af e e=+>，仍与最小值是32相矛盾；综上所述，a（丰台·理科·题19）19．（13分）在直角坐标系xOy 中，点M到点()1,0F，)2,0F 的距离之和是4，点M 的轨迹是C 与x 轴的负半轴交于点A ，不过点A 的直线:l y kx b =+与轨迹C 交于不同的两点P 和Q ．（I ）求轨迹C 的方程；（II ）当0AP AQ ⋅=时，求k 与b 的关系，并证明直线l 过定点．【解析】（1）∵点M到(),0，),0的距离之和是4，∴M 的轨迹C 是长轴为4，焦点在x轴上焦中为其方程为2214x y +=．（2）将y kx b =+，代入曲线C的方程，整理得22(14)40k x +++=因为直线l 与曲线C 交于不同的两点P 和Q ，所以222222644(14)(44)16(41)0k b k b k b ∆=-+-=-+> ① 设()11,P x y ，()22,Q x y，则12x x +=，122414x x k =+ ② 且2212121212()()()()y y kx b kx b k x x kb x x b ⋅=++=+++显然，曲线C 与x 轴的负半轴交于点()2,0A -，所以()112,AP x y =+，()222,AQ x y =+．由0AP AQ ⋅=，得1212(2)(2)0x x y y +++=．将②、③代入上式，整理得22121650k kb b -+=．所以(2)(65)0k b k b -⋅-=，即2b k =或65b k =．经检验，都符合条件①当2b k =时，直线l 的方程为2y kx k =+．显然，此时直线l 经过定点()2,0-点．即直线l 经过点A ，与题意不符．当65b k =时，直线l 的方程为6556y kx k k x ⎛⎫=+=+ ⎪⎝⎭．显然，此时直线l 经过定点6,05⎛⎫- ⎪⎝⎭点，且不过点A ．综上，k 与b 的关系是：65b k =，且直线l 经过定点6,05⎛⎫- ⎪⎝⎭点．（丰台·理科·题20） 20．（14分）设集合W 由满足下列两个条件的数列{}n a 构成： ①212n n n a a a +++<；②存在实数M ，使n a M ≤．（n 为正整数）（I ）在只有5项的有限数列{}n a ，{}n b 中，其中123451,2,3,4,5a a a a a =====； 123451,4,5,4,1b b b b b =====；试判断数列{},{}n n a b 是否为集合W 的元素；（II ）设{}n c 是各项为正的等比数列，n S 是其前n 项和，314c =，374S =，证明数列{}n S W ∈；并写出M 的取值范围；（III ）设数列{},n d W ∈且对满足条件的M 的最小值0M ，都有()*n n d M n ≠∈N ．求证：数列{}n d 单调递增．【解析】（I ）对于数列{}n a ，取13222a a a +==，显然不满足集合W 的条件，① 故{}n a 不是集合W 中的元素，对于数列{}n b ，当{1,2,3,4,5}n ∈时，不仅有13232b b b +=<，24342b bb +=<，33432b b b +=<，而且有5n b ≤，显然满足集合W 的条件①②，故{}n b 是集合W 中的元素．（II ）∵{}n c 是各项为正数的等比数列，n S 是其前n 项和，3317,,44c S == 设其公比为0q >，∴333274c c c q q ++=，整理得2610q q --=． ∴12q =，∴1111,2n n c c -==，1122n n S -=-对于*n ∀∈N ，有222111222222n n n n n n S S S ++++=--<-=，且2n S <，故{}n S W ∈，且[)2,M ∈+∞（III ）证明：（反证）若数列{}n d 非单调递增，则一定存在正整数k ，使1k k d d +≥，易证于任意的n k ≥，都有1k k d d +≥，证明如下：假设()n m m k =≥时，1k k d d +≥当1n m =+时，由212m m m d d d +++<，212m m m d d d ++<-．而12111(2)0m m m m m m m d d d d d d d +++++->--=-≥ 所以12,m m d d ++>所以对于任意的n k ≥，都有1m m d d +≥．显然12,,,k d d d 这k 项中有一定存在一个最大值，不妨记为0n d ；所以0*()n n d d n ∈N ≥，从而00n d M =与这题矛盾．所以假设不成立，故命题得证．。

2010-2011学年度第二学期北京市各区高三模拟试题汇编---《生活与哲学》

北京市东城区2011届高三综合练习(二)(理综)

北京市西城区2010-2011学年第二学期高三综合练习(二)(数学理)

历年北京高中政治合格性考试汇编：生活与哲学(学生版)

北京市东城区10-11下学期高三数学(理科)一模考试试卷

2011年北京各城区高三一模二模语文真题-分类汇编之作文

2010~2011学年度高三年级第二学期检测试卷答案3

生活与哲学样卷及答案

北京市东城区2011届高三综合练习(二)(文综)有答案

北京市东城区2010-2011示范校第二学期高三综合练习二(理综)

北京市东城区10—11下学期高三语文一模考试试卷

高考政治 《生活与哲学》试题 新人教版必修4

北京市东城区10-11下学期高三数学(文科)一模考试试卷

2011北京各区模拟考试试题分类(生活与哲学)

2010-2011年年北京各地高考模拟试题精析数学(理)2

2010-2011年年北京各地高考模拟试题精析数学(理)3

高考政治《生活与哲学》试题新人教版必修4