与圆有关的位置关系复习

合集下载

九年级数学专题复习圆的有关概念、性质与圆有关的位置关系

总复习圆的有关概念、性质与圆有关的位置关系【考纲要求】1. 圆的基本性质和位置关系是中考考查的重点，但圆中复杂证明及两圆位置关系中证明会有下降趋势，不会有太复杂的大题出现；2.中考试题中将更侧重于具体问题中考查圆的定义及点与圆的位置关系，对应用、创新、开放探究型题目，会根据当前的政治形势、新闻背景和实际生活去命题，进一步体现数学来源于生活，又应用于生活．【知识网络】【考点梳理】考点一、圆的有关概念及性质 1．圆的有关概念圆、圆心、半径、等圆；弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧；三角形的外接圆、三角形的内切圆、三角形的外心、三角形的内心、圆心角、圆周角．要点进阶：等弧：在同圆或等圆中，能够互相重合的弧叫做等弧． 2．圆的对称性圆是轴对称图形，任何一条直径所在直线都是它的对称轴，圆有无数条对称轴；圆是以圆心为对称中心的中心对称图形；圆具有旋转不变性． 3．圆的确定不在同一直线上的三个点确定一个圆．要点进阶：圆心确定圆的位置，半径确定圆的大小． 4．垂直于弦的直径垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．推论平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧．要点进阶：在图中(1)直径CD ，(2)CD ⊥AB ，(3)AM ＝MB ，(4)C C A B =，(5)AD BD =．若上述5个条件有2个成立，则另外3个也成立．因此，垂径定理也称“五二三定理”．即知二推三．注意：(1)(3)作条件时，应限制AB不能为直径．5．圆心角、弧、弦之间的关系定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量也相等．6．圆周角圆周角定理在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论1 在同圆或等圆中，相等的圆周角所对的弧也相等．推论2 半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径．要点进阶：圆周角性质的前提是在同圆或等圆中．7.圆内接四边形（1）定义: 圆内接四边形：顶点都在圆上的四边形，叫圆内接四边形．（2）性质：圆内接四边形对角互补，外角等于内对角（即它的一个外角等于它相邻内角的对角）．考点二、与圆有关的位置关系1．点和圆的位置关系设⊙O的半径为r，点P到圆心的距离OP＝d，则有：点P在圆外⇔d＞r；点P在圆上⇔d＝r；点P在圆内⇔d＜r．要点进阶：圆的确定：①过一点的圆有无数个，如图所示．②过两点A、B的圆有无数个，如图所示．③经过在同一直线上的三点不能作圆．④不在同一直线上的三点确定一个圆．如图所示．2．直线和圆的位置关系（1）切线的判定切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线．(会过圆上一点画圆的切线)（2）切线的性质切线的性质定理圆的切线垂直于过切点的半径．（3）切线长和切线长定理切线长经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长．切线长定理从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角．要点进阶：直线l是⊙O的切线，必须符合两个条件：①直线l经过⊙O上的一点A；②OA⊥l．（4）三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆.（5）三角形的内心：三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心. 三角形的内心到三边的距离都相等.要点进阶：(1) 任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形；(2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积的一半，即(S为三角形的面积，P为三角形的周长，r为内切圆的半径).(3) 三角形的外心与内心的区别：名称确定方法图形性质外心(三角形外接圆的圆心) 三角形三边中垂线的交点(1)到三角形三个顶点的距离相等，即OA=OB=OC；(2)外心不一定在三角形内部内心(三角形内切圆的圆心) 三角形三条角平分线的交点(1)到三角形三边距离相等；(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB； (3)内心在三角形内部.3．圆和圆的位置关系(1)基本概念两圆相离、相切、外离、外切、相交、内切、内含的定义．(2)请看下表：要点进阶：①相切包括内切和外切，相离包括外离和内含．其中相切和相交是重点．②同心圆是内含的特殊情况．③圆与圆的位置关系可以从两个圆的相对运动来理解．④“R-r”时，要特别注意，R＞r．考点三、与圆有关的规律探究1．和圆有关的最长线段和最短线段了解和圆有关的最长线段与最短线段，对有关圆的性质的了解极为重要，下面对有关问题进行简单论述．(1)圆中最长的弦是直径．如图①，AB是⊙O的直径，CD为非直径的弦，则AB＞CD，即直径AB是最长的弦．过圆内一点最短的弦，是与过该点的直径垂直的弦，如图②，P是⊙O内任意一点，过点P作⊙O的直径AB，过P作弦CD⊥AB于P，则CD是过点P的最短的弦．(2)圆外一点与圆上一点的连线中，最长的线段与最短的线段都在过圆心的直线上．如图所示，P在⊙O外，连接PO交⊙O于A，延长PO交⊙O于B，则在点P与⊙O上各点连接的线段中，PB最长，PA最短．(3)圆内一点与圆上一点的连线中，最长的线段与最短的线段也都在过圆心的直线上．如图所示，P为⊙O内一点，直径过点P，交⊙O于A、B两点，则PB最长、PA最短．2．与三角形内心有关的角(1)如图所示，I是△ABC的内心，则∠BIC1902A =+∠°．(2)如图所示，E是△ABC的两外角平分线的交点，1902BEC A ∠=-∠°．(3)如图所示，E是△ABC内角与外角的平分线的交点，12E A ∠=∠．(4)如图所示，⊙O是△ABC的内切圆，D、E、F分别为切点，则∠DOE＝180°－∠A．(5)如图所示，⊙O是△ABC的内切圆，D、E、F为切点，1902DFE A ∠=-∠°．(6)如图所示，⊙O是△ABC的内切圆，D、E、F为切点，P为DE上一点，则1902 DPE A ∠=+∠°．【典型例题】类型一、圆的性质及垂径定理的应用例1．已知：如图所示，⊙O中，半径OA＝4，弦BC经过半径OA的中点P，∠OPC＝60°，求弦BC的长．例2．如图所示，在⊙O 中，弦AB 与CD 相交于点M ，AD BC =，连接AC ． (1)求证：△MAC 是等腰三角形；(2)若AC 为⊙O 直径，求证：AC 2＝2AM ·AB ．举一反三：【变式】如图所示，在⊙O 中，AB ＝2CD ，则( )A ．2AB CD > B ．2AB CD <C ．2AB CD = D ．AB 与2CD 的大小关系无法确定例3．已知：如图所示，△ABC 内接于⊙O ，BD ⊥半径AO 于D ．(1)求证：∠C ＝∠ABD ；(2)若BD ＝4.8，sinC ＝45，求⊙O 的半径．类型二、圆的切线判定与性质的应用例4．如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB 的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE．（1）求证：AC平分∠DAB；（2）求证：△PCF是等腰三角形；（3）若AC=8，BC=6，求线段BE的长．举一反三：【变式】如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，AC=FC．（1）求证：AC是⊙O的切线；（2）已知圆的半径R=5，EF=3，求DF的长．类型三、切线的性质与等腰三角形、勾股定理综合运用例5．如图所示，⊙O是Rt△ABC的外接圆，AB为直径，∠ABC＝30°，CD是⊙O的切线，ED⊥AB于F．(1)判断△DCE的形状；(2)设⊙O的半径为1，且312OF-=，求证△DCE≌△OCB．举一反三：【变式】如图所示，PQ＝3，以PQ为直径的圆与一个以5为半径的圆相切于点P，正方形ABCD的顶点A、B在大圆上，小圆在正方形的外部且与CD切于点Q，则AB＝________．例6．如图所示，⊙O的直径AB＝4，点P是AB延长线上的一点，PC切⊙O于点C，连接AC．PM平分∠APC交AC于M．(1)若∠CPA＝30°，求CP的长及∠CMP的度数；(2)若点P在AB的延长线上运动，你认为∠CMP的大小是否发生变化？若变化，说明理由；若不变化，请求出∠CMP的度数；(3)若点P在直径BA的延长线上，PC切⊙O于点C，那么∠CMP的大小是否变化？请直接写出你的结论．举一反三：A的中点，CD⊥AB于D，CD与AE相交于F．【变式】如图所示，AB是⊙O的直径，C是E(1)求证：AC2＝AF·AE；(2)求证：AF＝CF．【巩固练习】一、选择题1. 在△ABC中，，∠C=45°，AB=8，以点B为圆心4为半径的⊙B与以点C为圆心的⊙C相离，则⊙C的半径不可能为（）A．5 B．6 C．7 D．152．如图，AB为⊙ O 的直径，CD 为弦，AB⊥CD，如果∠BOC=70°，那么∠A的度数为（）A. 70°B.35°C. 30°D. 20°3．已知AB是⊙O的直径，点P是AB延长线上的一个动点，过P作⊙O的切线，切点为C，∠APC的平分线交AC于点D，则∠CDP等于（）A.30°B.60°C.45°D.50°第2题第3题第4题第5题4．如图，⊙O的半径为5，弦AB的长为8，M是弦AB 上的动点,则线段OM长的最小值为（）A. 5B. 4C. 3D. 25．如图所示，四边形ABCD中，DC∥AB，BC=1，AB=AC=AD=2．则BD的长为（）A. 14B. 15C. 32D. 236. 如图，O 为原点，点A 的坐标为（3，0），点B 的坐标为（0，4），⊙D 过A 、B 、O 三点，点C 为0AB 上一点（不与O 、A 两点重合），则cosC 的值为（）A ．34B ．35 C ．43D ．45二、填空题7．已知⊙O 的半径为1，圆心O 到直线l 的距离为2，过l 上任一点A 作⊙O 的切线，切点为B ，则线段AB 长度的最小值为 .8．如图，AD ，AC 分别是⊙O 的直径和弦．且∠CAD=30°．O B⊥AD，交AC 于点B ．若OB=5，则BC 的长等于 .9．如图所示，已知⊙O 中，直径MN ＝10，正方形ABCD 的四个顶点分别在半径OM 、OP 以及⊙O 上，并且∠POM ＝45°，则AB 的长为________．第8题第9题第10 题10．如图所示，在边长为3 cm 的正方形ABCD 中，1O 与2O 相外切，且1O 分别与,DA DC 边相切，2O 分别与,BA BC 边相切，则圆心距12O O = cm ．11．如图所示，,EB EC 是O 的两条切线，,B C 是切点，,A D 是O 上两点，如果∠E=46°，∠DCF=32°那么∠A 的度数是 .12．如图，在⊙O 中，AB 是直径，点D 是⊙O 上一点，点C 是的中点，CE⊥AB 于点E ，过点D 的切线交EC 的延长线于点G ，连接AD ，分别交CE 、CB 于点P 、Q ，连接AC ，关于下列结论：①∠BAD=∠ABC；②GP=GD；③点P 是∠ACQ 的外心，其中正确结论是（只需填写序号）．三、解答题13．如图所示，AC 为⊙O 的直径且PA⊥AC，BC 是⊙O 的一条弦，直线PB 交直线AC 于点D ，DB DC 2DP DO 3==．（1）求证：直线PB 是⊙O 的切线；（2）求cos∠BCA 的值．14．如图所示，点A、B在直线MN上，AB＝11厘米，⊙A、⊙B的半径均为1厘米．⊙A以每秒2厘米的速度自左向右运动，与此同时，⊙B的半径也不断增大，其半径r(厘米)与时间t(秒)之间的关系式为r ＝1+t(t≥0)．(1)试写出点A、B之间的距离d(厘米)与时间t(秒)之间的函数关系式；(2)问点A出发后多少秒两圆相切?15.已知⊙O的直径AB=10，弦BC=6，点D在⊙O上（与点C在AB两侧），过D作⊙O的切线PD．（1）如图①，PD与AB的延长线交于点P，连接PC，若PC与⊙O相切，求弦AD的长；（2）如图②，若PD∥AB，①求证：CD平分∠ACB；②求弦AD的长．16. 如图1至图4中，两平行线AB、CD间的距离均为6，点M为AB上一定点．思考如图1，圆心为0的半圆形纸片在AB，CD之间（包括AB，CD），其直径MN在AB上，MN=8，点P 为半圆上一点，设∠MOP=α．当α=度时，点P到CD的距离最小，最小值为．探究一在图1的基础上，以点M为旋转中心，在AB，CD 之间顺时针旋转该半圆形纸片，直到不能再转动为止，如图2，得到最大旋转角∠BMO=度，此时点N到CD的距离是．探究二将如图1中的扇形纸片NOP按下面对α的要求剪掉，使扇形纸片MOP绕点M在AB，CD之间顺时针旋转．（1）如图3，当α=60°时，求在旋转过程中，点P到CD的最小距离，并请指出旋转角∠BMO的最大值；（2）如图4，在扇形纸片MOP旋转过程中，要保证点P能落在直线CD上，请确定α的取值范围．（参考数椐：sin49°=34，cos41°=34，tan37°=34．）。

圆复习课(与圆有关的位置关系)

3、两圆相切,圆心距为10cm, 其中一个圆的半径为6cm,则
4cm或16cm 另一个圆的半径为____________.
A
B
（第2题图）
1、两圆的半径分别为3和5，圆心距为7，则两圆的位置关系是（ B ）
A.内切
B.相交
C.外切
D.外离
2、已知两圆的半径R、r分别为方程 x 2 5x 6 0 的两根，两圆的圆心距为1，两圆的位置关系是（ B ）
2、已知直线与⊙O相切，若圆心O到直线的 6 ．距离是6，则⊙O的半径是
3、⊙O的半径为5，圆心O到直线n的距离为3，则直线n与
⊙O的位置关系是（
A ）
B.相切 D.无法确定
A.相交 C.相离
4、在平面直角坐标系中，以点（-3,4）为圆心，4为半径的圆（ C ）
A.与x轴相交，与y轴相切 C.与X轴相切，与y轴相交 B.与X轴相离，与y轴相交 D.与X轴相切，与y轴相离
O1
d
O2
O1
d
O2
O1
dO1
外切
d=R+r
O1
相交
R-r<d<R+r
dO
2
dO
2
内切
d=R-r
内含
d<R-r
数形结合：位置关系
数量关系
对比小结
外离相离内含圆和圆的位置关系相交 R-r<d<R+r 外切相切 d=R+r 1个交点 2个交点 d<R-r d>R+r 0个交点
7、已知圆 O 与圆 O 的半径分别为
1 2
12和2,圆心 O1 的坐标为(0,8),圆心

中考数学复习之与圆有关的位置关系,考点过关与基础练习题

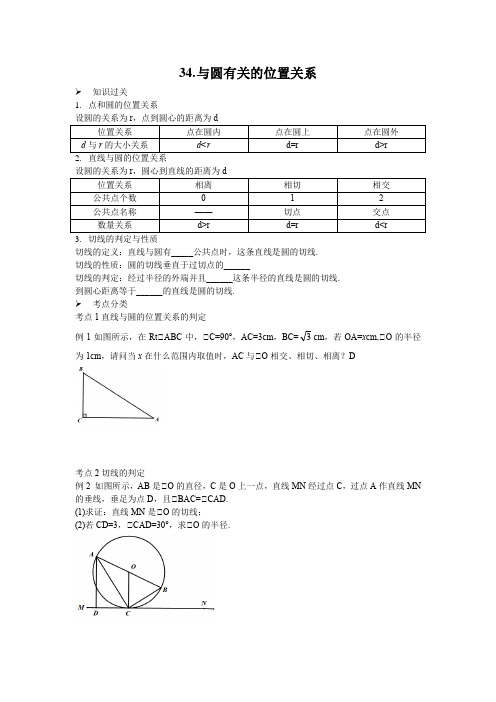
34.与圆有关的位置关系➢知识过关1.点和圆的位置关系2.直线与圆的位置关系3.切线的判定与性质切线的定义：直线与圆有_____公共点时，这条直线是圆的切线.切线的性质：圆的切线垂直于过切点的______切线的判定：经过半径的外端并且______这条半径的直线是圆的切线.到圆心距离等于______的直线是圆的切线.➢考点分类考点1直线与圆的位置关系的判定例1如图所示，在Rt△ABC中，△C=90°，AC=3cm，BC=3cm，若OA=x cm,△O的半径为1cm，请问当x在什么范围内取值时，AC与△O相交、相切、相离？D考点2切线的判定例2 如图所示，AB是△O的直径，C是O上一点，直线MN经过点C，过点A作直线MN 的垂线，垂足为点D，且△BAC=△CAD.(1)求证：直线MN是△O的切线；(2)若CD=3，△CAD=30°，求△O的半径.考点3 切线的性质例3 如图所示，在△O 中，点C 是直径AB 延长线上一点，过点C 作△O 的切线，切点为D ，连接BD.(1)求证：△A=△BDC(2)若CM 平分△ACD ，且分别交AD 、BD 于点M 、N ，当DM=1时，求MN 的长.➢ 真题演练1.如图，A 、P 、B 、C 是⊙O 上的四点，∠APC ＝∠BPC ＝60°，P A ＝2，PC ＝4，则△ABC 的面积为（）A ．43√3B ．32√3C ．2√3D ．3√32．如图，四边形ABCD 是⊙O 的内接四边形，∠B ＝90°，∠BCD ＝120°，AB ＝4，BC ＝2，则AD 的长为（）A ．2√3B ．4−√3C ．√3+1D ．2+√33．如图，P A 、PB 、CE 分别与⊙O 相切于点A 、B 、D 点，若圆O 的半径为6，OP ＝10，则△PCE 的周长为（）A ．10B ．12C ．16D ．204．如图所示，点P 是⊙O 的半径OC 延长线上的一点，过点P 作⊙O 的切线，切点为A ，AB 是⊙O 的弦，连接AC ，BC ，若∠P AB ＝70°，则∠ACB 的大小为（）A ．70°B ．110°C ．120°D ．140°5．如图，在△ABC 中，∠A ＝60°，BC ＝12，若⊙O 与△ABC 的三边分别相切于点D ，E ，F ，且△ABC 的周长为32，则DF 的长为（）A ．2B ．3C ．4D ．66．如图，已知DC 是⊙O 的直径，点B 为CD 延长线上一点，AB 是⊙O 的切线，点A 为切点，且∠BAD ＝35°，则∠ADC ＝（）A ．75°B ．65°C ．55°D ．50°7．如图，PC 、PB 是⊙O 的切线，AB 是⊙O 的直径，延长PC ，与BA 的延长线交于点E ，过C 点作弦CD ，且CD ∥AB ，连接DO 并延长与圆交于点F ，连接CF ，若AE ＝2，CE ＝4，则CD 的长度为（）A ．3B ．4C ．185D ．2458．如图，四边形ABCD 内接于⊙O ，AE ⊥CB ，交CB 的延长线于点E ．若BA 平分∠DBE ，AD ＝7，CE =√13，则AE 的长度为．9．如图，四边形ABCD 内接于⊙O ，AB 为直径，AD ＝CD ，过点D 作DE ⊥AB 于点E ，连接AC 交DE 于点F ．若sin ∠CAB =35，DF ＝5，则AB 的长为．10．如图，P A、PB分别与⊙O相切于A、B两点，C为⊙O上一点连接AC、BC，若∠C＝55°，则∠P的度数是°．11.如图，AB为圆O直径，∠DAB＝∠ABC＝90°，CD与圆O相切于点E，EF⊥AB于点F，EF交BD于点G，若AD＝2，BC＝6．（1）求CD的长度．（2）求EG的长度．（3）求FB的长度．12．如图，P A、PB、CD是⊙O的切线，点A、B、E为切点．（1）如果△PCD的周长为10，求P A的长；（2）如果∠P＝40°，①求∠COD；②连AE，BE，求∠AEB．13．如图，P A、PB分别与⊙O相切于点A、B，PO的延长线交⊙O于点C，连接BC，OA．（1）求证：∠POA＝2∠PCB；（2）若OA＝3，P A＝4，求tan∠PCB的值．➢ 课后练习1．如图，P A ，PB 是⊙O 的两条切线，A ，B 是切点，过半径OB 的中点C 作CD ⊥OB 交P A 于点D ，若PD ＝3，AD ＝5，则⊙O 的半径长为（）A ．2√7B ．4√2C ．3√3D ．2√52．如图，等边三角形ABC 的边长为4，⊙C 的半径为√3，P 为AB 边上一动点，过点P 作⊙C 的切线PQ ，切点为Q ，则PQ 的最小值为（）A ．12B ．√3C ．2√3D ．33．如图，点O 是矩形ABCD 对角线BD 上的一点，⊙O 经过点C ，且与AB 边相切于点E ，若AB ＝4，BC ＝5，则⊙O 的半径长为（）A ．165B ．258C ．5√419D ．44．如图，在△ABC 中，∠ACB ＝90°，AC ＝BC =√2，点D 是AB 边上一个动点，以点D 为圆心r 为半径作⊙D ，直线BC 与⊙D 切于点E ，若点E 关于CD 的对称点F 恰好落在AB 边上，则r 的值是（）A ．√2−1B ．1C ．√2D ．√2+15．如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，如果∠D＝30°，AB＝4，那么线段CD的长是．6．如图，△ABD内接于⊙O，AD为直径，CD为⊙O的切线，连接BC，若CD＝AD，AB ＝2，BC=2√13，则BD＝．7．已知菱形ABCD的边长为4，∠BAD＝60°，M是线段AD的中点，点P是对角线AC 上的动点，连接PM，以P为圆心，PM长为半径作⊙P，当⊙P与菱形ABCD的边相切时，AP的长为．8．如图，已知△ABC，以AB为直径的⊙O交AC于点E，交BC于点D，且BD＝CD，DF ⊥AC于点F．给出以下四个结论：̂=DÊ；④∠A＝2∠FDC．①DF是⊙O的切线；②CF＝EF；③AE其中正确结论的序号是．9．如图，在Rt△ABC中，AC＝BC＝6，点O为边BC上一动点，连接OA．以O为圆心，OB为半径作圆，交OA于D，过D作⊙O的切线，交AC于点E．当⊙O与边AC相切时，CE的长为．10．如图，在Rt△ABC中，∠C＝90°，以AC为直径的⊙O交AB于点D，点Q为CA延长线上一点，延长QD交BC于点P，连接OD，∠ADQ=12∠DOQ．若AQ＝AC，AD＝4时，写出BP的长为．11．如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆交于点D．（1）如图1，连接DB，求证：DB＝DE；（2）如图2，若∠BAC＝60°，求证：AB+AC=√3AD．12．如图，△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F．（1）若∠ABC＝50°，∠ACB＝75°，求∠BOC的度数；（2）若AB＝13，BC＝11，AC＝10，求AF的长．➢冲击A+。

中考数学考点系统复习第六章圆第二节与圆有关的位置关系

点 C，过点 A 作 AD∥OB 交⊙O 于点 D，连接 CD.若∠B＝50°，则∠OCD
为
( B)
A．15°
B．20°
C．25°
D．30°
5．(2021·贺州)如图，在 Rt△ABC 中，∠C＝90°，AB＝5，点 O 在 AB
上，OB＝2，以 OB 为半径的⊙O 与 AC 相切于点 D，交 BC 于点 E，CE 的长
∴CE＝DH＝2 5，∠DEC＝90°， ∴OD⊥BC， ∴BC＝2CE＝4 5，
BC 5 ∵sin∠BAC＝AB＝ 3 ， ∴AB＝12，即半圆的直径为 12.
12．(2020·宜宾)如图，已知 AB 是⊙O 的直径，点 C 是圆上异于 A，B 的一点，连接 BC 并延长至点 D，使 CD＝BC，连接 AD 交⊙O 于点 E，连接 BE. (1)求证：△ABD 是等腰三角形； (2)连接 OC 并延长，与以 B 为切点的切线交于点 F，若 AB＝4，CF＝1，求 DE 的长．
为
( B)
A.12
2 B.3
2 C. 2
D．1
6．(2021·泰安)如图，在△ABC 中，AB＝6，以点 A 为圆心，3 为半径的
圆与边 BC 相切于点 D，与 AC，AB 分别交于点 E 和点 G，F 是优弧 GE 上一
点，∠CDE＝18°，则∠GFE 的度数是
( B)
A．50°
B．48°
C．45°
连接 EM，过点 M 作 MH⊥EF 于 H，则 EF＝2EH，
在 Rt△EHM 中，EM＝4，MH＝3，根据勾股定理得 EH＝ EM2－MH2＝ 42－32＝ 7， ∴弦长 n＝EF＝2EH＝2 7.
形内一点，连接 CF，DF，且∠ADF＝∠DCF，点 E 是 AD 边上一动点，连接 EB，EF，则 EB＋EF 长度的最小值为_33－133－3 .

考点20 与圆有关的位置关系及计算(精讲)(解析版)

考点20.与圆有关的位置关系及计算（精讲）【命题趋势】与圆相关的位置关系也是各地中考数学中的必考考点之一，主要内容包括点、直线与圆的位置关系、切线的性质和判定、三角形的内切圆和外接圆三块，在解答题中想必还会考查切线的性质和判定，和直角三角形结合的求线段长的问题和三角函数结合的求角度的问题等知识点综合，考查形式多样，多以动点、动图的形式给出，难度较大。

关键是掌握基础知识、基本方法，力争拿到全分。

【知识清单】1：点、直线与圆的位置关系类（☆☆）1）点和圆的位置关系：已知⊙O的半径为r，点P到圆心O的距离为d，则：图1图2(1)d<r⇔点在⊙O内，如图1；(2)d=r⇔点在⊙O上，如图2；(3)d>r⇔点在⊙O外，如图3．解题技巧：掌握已知点的位置，可以确定该点到圆心的距离与半径的关系，反过来已知点到圆心的距离与半径的关系，可以确定该点与圆的位置关系。

2）直线和圆的位置关系：设⊙O的半径为r，圆心到直线l的距离为d，则直线和圆的位置关系如下：图1图2图3(1)d>r⇔相离，如图1；(2)d=r⇔相切，如图2；(3)d<r⇔相交，如图3。

2：切线的性质与判定（☆☆☆）1）切线的性质：（1）切线与圆只有一个公共点；（2）切线到圆心的距离等于圆的半径；（3）切线垂直于经过切点的半径。

解题技巧：利用切线的性质解决问题时，通常连过切点的半径，利用直角三角形的性质来解决问题。

2）切线的判定（1）与圆只有一个公共点的直线是圆的切线（定义法）；（2）到圆心的距离等于半径的直线是圆的切线（数量关系法）；（3）经过半径外端点并且垂直于这条半径的直线是圆的切线（判定定理法）。

切线判定常用的证明方法：①知道直线和圆有公共点时，连半径，证垂直；②不知道直线与圆有没有公共点时，作垂直，证垂线段等于半径。

3）切线长定理定义：在经过圆外一点的圆的切线上，这点和切点之间的线段的长，叫做这点到圆的切线长。

定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

与圆有关的位置关系

A：2cmB：3cmC：5cmD：2cm或5cm
例3.(1)已知在△ ABC中，AC=5 ，BC =12，AB=13 ．则△ABC的外接圆的半径_________
(2)如图，已知⊙O是△ABC的外接圆，连接AO，若∠B=40 ，则∠OAC =____________ ．
练3.1.若一个三角形的外心在它的一条边上，那么这个三角形一定是（）
以2.5cm为半径画圆，则⊙C与直线AB的关系是.
分析：根据勾股定理可知：AB=5cm,作CD AB于D点，则CD的长表示
圆心C到AB的距离，由，得CD=2.4cm
， ⊙C与直线AB相交.
例4.（1）在Rt△ABC中，∠C = 90 ，AC = 3，BC = 4，以点C为圆心，2为半径的圆与AB的位置关系是（）
练4.2.设⊙O的半径为3，点O到直线l的距离为d，若直线l与⊙O至少有一个公共点，则d应满足的条件是（）
A：d= 3B：d≤3C：d<3D：d>3
【知识点三】切线的性质
切线的性质定理：
圆的切线垂直于过切点的半径.
几何语言：直线⊙C是的切线，点A为切点， OA .
注意：当题目出现圆的切线时，常连接过切点的半径，得切线垂直半径.
①锐角三角形，外接圆圆心，在它的内部.
②直角三角形，外接圆圆心，在斜边中点.
③钝角三角形，外接圆圆心，在它的处型.
例1.（1）⊙O的半径为5cm，点A到圆心O的距离OA = 3cm，则点A与⊙O的位置关系为（）
A：点A在圆上B：点A在圆内
C：点A在圆外D：无法确定
(2)在平面直角坐标系中，M (2, 0)，圆M半径为4，那么点P (−2, 3)与圆M的位置关系是（）
A：等腰三角形B：直角三角形C：等边三角形D：钝角三角形

直线与圆的位置关系(复习课)

B
10
O
C
如图， ⊙O的半径为 cm，正三角形的边长为 10 cm， 3 圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动，设运动时间为 t（s）问：（1）在移动过程中， ⊙O与△ABC 的三条边相切几次？（2） t为何值时， ⊙O与 AC相切？ A
B
O
C 10
如图， ⊙O的半径为 cm，正三角形的边长为 10 cm， 3 圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动，设运动时间为 t（s）问：（1）在移动过程中， ⊙O与△ABC 的三条边相切几次？（2） t为何值时， ⊙O与 AC相切？
P 4cm l A
P 4cm A l
2．如图，A，B是⊙O的两点，AC是 ⊙O的切线，∠B＝65°则∠BAC=( B ) A、35° B、25°C、50° D、65°
O B A C
3、已知:PA为⊙O的切线，A为切点， OB交⊙O于点B ，PB＝2，PA ３＝4.⊙O的半径r=
O
r
r
B２
４
P
A
B
C 10
如图， ⊙O的半径为 cm，正三角形的边长为 10 cm， 3 圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动，设运动时间为 t（s）问：（1）在移动过程中， ⊙O与△ABC 的三条边相切几次？（2） t为何值时， ⊙O与 AC相切？ A
O
B
C 10
如图， ⊙O的半径为 cm，正三角形的边长为 10 cm， 3 圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动，设运动时间为 t（s）问：（1）在移动过程中， ⊙O与△ABC 的三条边相切几次？（2） t为何值时， ⊙O与 AC相切？ A

中考数学复习《与圆有关的位置关系》专题训练含答案

中考复习专题训练与圆有关的位置关系一、选择题1.⊙O1的半径为1cm，⊙O2的半径为4cm，圆心距O1O2=3cm，这两圆的位置关系是( )A. 相交B. 内切C. 外切D. 内含2.⊙O的半径为4，线段OP=4，则点P与⊙O的位置关系是（）A. 点P在⊙O外B. 点P在⊙O内C. 点P在⊙O上D. 不能确定3.两圆外离，作它们的两条内公切线，四个切点构成的四边形是（）A. 矩形B. 等腰梯形C. 矩形或等腰梯形D. 菱形4. 已知线段AB=7cm，现以点A为圆心，2cm为半径画⊙A；再以点B为圆心，3cm为半径画⊙B，则⊙A 和⊙B的位置关系（）A. 内含B. 相交C. 外切D. 外离5.下列四个命题中，真命题是( )A. 相等的圆心角所对的两条弦相等；B. 圆既是中心对称图形也是轴对称图形；C. 平分弦的直径一定垂直于这条弦；D. 相切两圆的圆心距等于这两圆的半径之和.6.在△ABC中，cosB=，∠C=45°，AB=8，以点B为圆心4为半径的⊙B与以点C为圆心的⊙C相离，则⊙C的半径不可能为（）A. 15B. 5C. 6D. 77. 如图，已知⊙O的半径为4，点D是直径AB延长线上一点，DC切⊙O于点C，连接AC，若∠CAB=30°，则BD的长为（）A. 4B. 8C. 4D. 28.下列说法正确的是（）A. 任意三点可以确定一个圆B. 平分弦的直径垂直于弦，并且平分该弦所对的弧C. 同一平面内，点P到⊙O上一点的最小距离为2，最大距离为8，则该圆的半径为5D. 同一平面内，点P到圆心O的距离为5，且圆的半径为10，则过点P且长度为整数的弦共有5条9.如图，AB为⊙O的直径，P为AB延长线上一点，PT切⊙O于T，若PT=6，PB=2，则⊙O的直径为（）A. 8B. 10C. 16D. 1810.如图，在等腰三角形△ABC中，O为底边BC的中点，以O为圆心作半圆与AB，AC相切，切点分别为D，E．过半圆上一点F作半圆的切线，分别交AB，AC于M，N．那么的值等于（）A. B. C. D. 111.如图，⊙O的半径为2，点O到直线L的距离为3，点O是直线L上的一个动点，PQ切⊙O于点Q，则PQ的最小值为（）A. B. C. 3 D. 512.已知如图，PA、PB切⊙O于A、B，MN切⊙O于C，交PB于N；若PA=7.5cm，则△PMN的周长是（）A. 7.5cmB. 10cmC. 15cmD. 12.5cm二、填空题13.已知⊙P在直角坐标平面内，它的半径是5，圆心P（﹣3，4），则坐标原点O与⊙P的位置关系是________14.已知点P在半径为5的⊙O外，如果设OP=x，那么x的取值范围是________．15.如图，已知扇形AOB的半径为6，圆心角为90°，E是半径OA上一点，F是上一点．将扇形AOB沿EF对折，使得折叠后的圆弧恰好与半径OB相切于点G．若OE=4，则O到折痕EF的距离为________．16.如图，在Rt△ABC中，∠C=90°，AC≠BC，点M是边AC上的动点．过点M作MN∥AB交BC于N，现将△MNC沿MN折叠，得到△MNP．若点P在AB上．则以MN为直径的圆与直线AB的位置关系是________．17.如图，在⊙O中，OB为半径，AB是⊙O的切线，OA与⊙O相交于点C，∠A=30°，OA=8，则阴影部分的面积是________．18. 如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是的中点，CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE、CB于点P、Q，连接AC，关于下列结论：①∠BAD=∠ABC；②GP=GD；③点P是∠ACQ的外心，其中正确结论是________ （只需填写序号）．19.如图，AE、AD、BC分别切⊙O于E、D、F，若AD=20，则△ABC的周长为 ________20.如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=4 ．若动点D在线段AC上（不与点A、C重合），过点D作DE⊥AC交AB边于点E．点A关于点D的对称点为点F，以FC为半径作⊙C，当DE=________时，⊙C与直线AB相切．21.如图，在△ABC中，BC=4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于点E，交AC于点F，点P是⊙A上的一点，且∠EPF=45°，则图中阴影部分的面积为________．三、解答题22.如图，已知PA、PB是⊙O的切线，A、B为切点，∠OAB＝30°．（1）求∠APB的度数；（2）当OA＝3时，求AP的长．23.如图所示，在梯形ABCD中，AD∥BC，AB⊥BC，以AB为直径的⊙O与DC相切于E．已知AB=8，边BC 比AD大6．（1）求边AD、BC的长；（2）在直径AB上是否存在一动点P，使以A、D、P为顶点的三角形与△BCP相似？若存在，求出AP的长；若不存在，请说明理由．24.在⊙O中，AB为直径，C为⊙O上一点．（Ⅰ）如图①，过点C作⊙O的切线，与AB的延长线相交于点P，若∠CAB=32°，求∠P的大小；（Ⅱ）如图②，D为优弧ADC上一点，且DO的延长线经过AC的中点E，连接DC与AB相交于点P，若∠CAB=16°，求∠DPA的大小．25.解答题（1）如图1，已知⊙O的半径是4，△ABC内接于⊙O，AC=4 ．①求∠ABC的度数；②已知AP是⊙O的切线，且AP=4，连接PC．判断直线PC与⊙O的位置关系，并说明理由；（2）如图2，已知▱ABCD的顶点A、B、D在⊙O上，顶点C在⊙O内，延长BC交⊙O于点E，连接DE．求证：DE=DC．参考答案一、选择题B C C D B D C D C B B C二、填空题13.点O在⊙P上14.x＞515.216.相交17.8 ﹣π18.②③19.4020.或21.4﹣π三、解答题22.解：（1）∵在△ABO中，OA=OB，∠OAB=30°，∴∠AOB=180°-2×30°=120°，∵PA、PB是⊙O的切线，∴OA⊥PA，OB⊥PB，即∠OAP=∠OBP=90°，∴在四边形OAPB中，∠APB=360°-120°-90°-90°=60°．（2）如图，连接OP；∵PA、PB是⊙O的切线，∴PO平分∠APB，即∠APO=∠APB=30°，又∵在Rt△OAP中，OA=3，∠APO=30°，∴AP=.23.解：（1）方法1：过D作DF⊥BC于F，在Rt△DFC中，DF=AB=8，FC=BC﹣AD=6，∴DC2=62+82=100，即DC=10．设AD=x，则DE=AD=x，EC=BC=x+6，∴x+（x+6）=10．∴x=2．∴AD=2，BC=2+6=8．方法2：连OD、OE、OC，由切线长定理可知∠DOC=90°，AD=DE，CB=CE，设AD=x，则BC=x+6，由射影定理可得：OE2=DE•EC．即：x（x+6）=16，解得x1=2，x2=﹣8，（舍去）∴AD=2，BC=2+6=8．（2）存在符合条件的P点．设AP=y，则BP=8﹣y，△ADP与△BCP相似，有两种情况：①△ADP∽△BCP时，有即∴y=；②△ADP∽△BPC时，有即∴y=4．故存在符合条件的点P，此时AP=或4．24.解：（Ⅰ）连接OC，如图①，∵PC为切线，∴OC⊥PC，∴∠OCP=90°，∵OA=OC，∴∠OCA=∠CAB=32°，∴∠POC=∠OCA+∠CAB=64°，∴∠P=90°﹣∠POC=90°﹣64°=26°；（Ⅱ）如图②，∵点E为AC的中点，∴OD⊥AC，∴∠OEA=90°，∴∠AOD=∠CAB+∠OEA=16°+90°=106°，∴∠C= ∠AOD=53°，∴∠DPA=∠BAC+∠C=16°+53°=69°25.（1）解：①连结OA、OC，如图1，∵OA=OC=4，AC=4 ，∴OA2+OC2=AC2，∴△OCA为等腰直角三角形，∠AOC=90°，∴∠ABC= ∠AOC=45°；②直线PC与⊙O相切．理由如下：∵AP是⊙O的切线，∴∠OAP=90°，而∠AOC=90°，∴AP∥OC，而AP=OC=4，∴四边形APCO为平行四边形，∵∠AOC=90°，∴四边形AOCP为矩形，∴∠PCO=90°，∴PC⊥OC，∴PC为⊙O的切线（2）证明：∵四边形ABCD为平行四边形，∴AB∥CD，AD∥BC，∴∠B+∠A=180°，∠DCE=∠B，∵∠E+∠A=180°，∴∠E=∠B，∴∠DCE=∠E，∴DC=DE．。

2025年甘肃中考数学一轮复习中考命题探究第6章圆第24讲与圆有关的位置关系

∵OB 是⊙O 的半径，∴BE 是⊙O 的切线．
(2)当⊙O的半径为2，BC＝3时，求tan∠AEB的值．
解：∵OB＝2，
∴AB＝2OB＝4，
∴AC＝ AB 2－BC2＝ 42－32＝ 7，
AC
7
∴tan∠AEB＝tan∠ABC＝＝ .
BC 3
2．[2023省卷25题]如图，△ABC内接于⊙O，AB是⊙O的直径，D是⊙O上的一点，CO
2025年甘肃中考数学一轮复习中考命题探究
第24讲
与圆有关的位置关系
(省卷：5年5考；兰州：3年3考)
1 考点梳理
2 重难点突破
3 甘肃5年中考真题及拓展
考点梳理
2022年版课标重要变化
探索切线与过切点的半径的关系，会用三角尺过圆上一点画圆的切
线．(删除)
考点 1
点、直线与圆的位置关系
点与圆的位置关系
考点 41
三角形的外接圆与内切圆
三角形的外接圆
圆心
垂直平分线
外心：三角形三条边的⑧____________
内心：三角形三条
的交点
描述经过三角形的三个顶点的圆
图示
三角形的内切圆
角平分线
⑨_________的交点
与三角形三边都相切的圆
性质
三角形的外心到三个顶点的
三角形的内心到三角形三边的
距离相等，即OA＝OB＝OC 距离相等，即OD＝OE＝OF
3
(2)当⊙O的半径为5，sinB＝ 5 时，求CE的长．
解：∵AB 是⊙O 的直径，∴∠ACB＝90°.
AC 3
∵sin B＝＝，AB＝10，∴AC＝6.
AB 5
∵∠OCE＝∠ACB＝90°，∴∠ACE＝∠OCB＝∠B，

高二数学复习考点知识与题型专题讲解13---圆与圆的位置关系

高二数学复习考点知识与题型专题讲解2.5.2 圆与圆的位置关系【考点梳理】考点一：两圆的位置关系及其判定(1)几何法：若两圆的半径分别为r 1，r 2，两圆连心线的长为d ，则两圆的位置关系如下：位置关系外离外切相交内切内含图示d 与r 1，r 2的关系 d >r 1＋r 2 d ＝r 1＋r 2|r 1－r 2|< d <r 1＋r 2d ＝|r 1－r 2|d <|r 1－r 2|(2)代数法：设两圆的一般方程为C 1：x 2＋y 2＋D 1x ＋E 1y ＋F 1＝0(D 21＋E 21－4F 1>0)，C 2：x 2＋y 2＋D 2x ＋E 2y ＋F 2＝0(D 22＋E 22－4F 2>0)，联立方程得⎩⎨⎧x 2＋y 2＋D 1x ＋E 1y ＋F 1＝0，x 2＋y 2＋D 2x ＋E 2y ＋F 2＝0，则方程组解的个数与两圆的位置关系如下：方程组解的个数 2组 1组 0组两圆的公共点个2个1个0个【题型归纳】题型一：判断圆与圆的位置关系1．（2022·全国·高二课时练习）已知圆221:210()C x y x my m +-++=∈R 的面积被直线210x y ++=平分，圆222:(2)(3)25C x y ++-=，则圆1C 与圆2C 的位置关系是（）A ．外离B ．相交C ．内切D ．外切2．（2022·江苏·高二课时练习）已知圆221:()()4C x a y b -+-=（a ，b 为常数）与222:20C x y x +-=．若圆心1C 与圆心2C 关于直线0x y -=对称，则圆1C 与2C 的位置关系是（）A ．内含B ．相交C ．内切D ．相离3．（2022·天津市第九十五中学益中学校高二期末）圆222830x y x y +++-=与圆()()22225x y -+-=的位置关系为（）A ．外切B ．内切C ．相交D ．相离题型二：求圆的交点坐标4．（2021·全国·高二课时练习）圆心在直线x ﹣y ﹣4＝0上，且经过两圆x 2+y 2﹣4x ﹣3＝0，x 2+y 2﹣4y ﹣3＝0的交点的圆的方程为（） A ．x 2+y 2﹣6x +2y ﹣3＝0B ．x 2+y 2+6x +2y ﹣3＝0C ．x 2+y 2﹣6x ﹣2y ﹣3＝0D ．x 2+y 2+6x ﹣2y ﹣3＝05．（2021·江苏·高二专题练习）若圆C 的圆心在直线40x y --=上，且经过两圆22460x y x +--=和22460x y y +--=的交点，则圆C 的圆心到直线3450x y ++=的距离为（） A ．0B ．85C ．2D ．1856．（2022·山西·运城市景胜中学高二阶段练习（文））设点(1,0)A ，(4,0)B ，动点P 满足2||||PA PB =，设点P 的轨迹为1C ，圆2C ：22((3)4x y +-=，1C 与2C 交于点,M N ，Q 为直线2OC 上一点（O 为坐标原点），则MN MQ ⋅=（）A ．4B ．C ．2D题型三：圆与圆的位置关系求参数范围7．（2022·全国·高二课时练习）已知圆()()()22:140C x y m m ++-=>和两点()2,0A -，()10B ,，若圆C 上存在点P ，使得2PA PB =，则m 的取值范围是（）A ．[8，64]B ．[9，64]C ．[8，49]D ．[9，49]8．（2022·全国·高二课时练习）若圆()()2221:10C x y r r +-=>上存在点P ，且点P 关于直线y ＝x 的对称点Q 在圆()()222:211C x y -+-=上，则r 的取值范围是（）A ．1⎤⎦B ．C ．⎡⎣D ．(]0,19．（2022·江苏·高二课时练习）已知圆1O ：2216x y +=和圆2O ：22268240x y mx my m +--+=有且仅有4条公切线，则实数m 的取值范围是（）A ．()(),11,-∞-⋃+∞B ．()1,1-C ．()(),23,-∞-⋃+∞D ．()2,3- 题型四：圆与圆的位置求圆的方程10．（2022·全国·高二单元测试）若圆22210x y ax y +-++=与圆221x y +=关于直线1y x =-对称，过点(,)C a a -的圆P 与y 轴相切，则圆心P 的轨迹方程是（）A ．24480y x y -++=B ．22220y x y +-+=C ．24480y x y +-+=D ．2210y x y ---=11．（2022·全国·高二课时练习）已知圆221:64120C x y x y +-++=与圆222:1420C x y x y a +--+=，若圆1C 与圆2C 有且仅有一个公共点，则实数a 等于A ．14B ．34C ．14或45D ．34或1412．（2019·安徽马鞍山·高二期中）已知半径为1的动圆与圆C ：()()225316x y +++=相切，则动圆圆心的轨迹方程是（）A ．()()225325x y +++=B ．()()225325x y -+-=或()()22539x y -+-= C ．()()22539x y -+-=D ．()()225325x y +++=或()()22539x y +++=题型五：圆的公共弦长问题（参数、弦长问题）13．（2022·全国·高二专题练习）已知圆221:420C x y x y +-+=与圆222:240C x y y +--=相交于A ､B 两点，则圆()()22:331C x y ++-=上的动点P 到直线AB 距离的最大值为（）A1B ．1C ．12+D 1 14．（2022·四川资阳·高二期末（理））已知圆221:20C x y x ++=，圆222:60C x y y +-=相交于P ，Q 两点，其中1C ，2C 分别为圆1C 和圆2C 的圆心.则四边形12PC QC 的面积为（）A ．3B ．4C ．6D ．15．（2021·广东·人大附中深圳学校高二期中）若圆221:4C x y +=与圆()222:2600C x y ay a ++-=>的公共弦长为=a （）A ．1B ．1.5C ．2D ．2.5题型六：圆的共切线问题16．（2022·全国·高二专题练习）已知圆()()22:211M x y -+-=，圆()()22:211N x y +++=，则下列不是M ，N 两圆公切线的直线方程为（） A ．0y =B ．430x y -=C ．20x y -=D ．20x y +17．（2022·江苏·高二课时练习）若直线l 与圆()221:11C x y ++=，圆()222:14C x y -+=都相切，切点分别为A 、B ，则AB =（）A ．1B．18．（2022·江苏·高二课时练习）在平面直角坐标系xOy 中，圆1C ：222660x y x y ++-+=与圆2C ：224240x y x y +-++=，则两圆的公切线的条数是（） A ．4条B ．3条C ．2条D ．1条题型七：圆与圆位置关系的综合类问题19．（2022·陕西·武功县普集高级中学高二阶段练习（理））已知圆C ：22240x y x y m +--+=．(1)若圆C 与圆D ：22(2)(2)1x y +++=有三条外公切线，求m 的值；(2)若圆C 与直线20x y +-=交于两点M ，N ，且OM ON ⊥（O 为坐标原点），求m 的值．20．（2022·全国·高二单元测试）已知圆1C ：²²4230x y x y +---=，圆2:?²20C x y x m +-+=，其中51m -<<.（1）若1m =-，判断圆1C 与2C 的位置关系，并求两圆公切线方程（2）设圆1C 与圆2C 的公共弦所在直线为l ，且圆2C 的圆心到直线l 的距离为2，求直线l 的方程以及公共弦长21．（2021·江苏·高二专题练习）已知圆221:(1)1C x y -+=与圆222:80C x y x m +-+=．（1）若圆1C 与圆2C 恰有3条公切线，求实数m 的值；（2）在（1）的条件下，若直线0x n +=被圆2C 所截得的弦长为2，求实数n 的值．【双基达标】一、单选题22．（2021·黑龙江·勃利县高级中学高二期中）两圆224210x y x y +-++=与224410x y x y ++--=的公切线有（）A ．1条B ．2条C ．3条D ．4条23．（2019·江西省大余县新城中学高二阶段练习）圆221:430C x y x +-+=与圆222:(1)(4)C x y a ++-=恰有三条公切线，则实数a 的值是（）A ．4B ．6C ．16D ．3624．（2022·全国·高二课时练习）圆1O 的方程为()()22231x y ++-=，圆2O 的圆心为()21,7O ．(1)若圆2O 与圆1O 外切，求圆2O 的方程；(2)若圆2O 与圆1O 交于A 、B 两点，且AB =2O 的方程．25．（2022·全国·）已知圆1C 与y 轴相切于点(03)，，圆心在经过点(21)，与点(23)--，的直线l 上． (1)求圆1C 的方程；(2)若圆1C 与圆222:6350C x y x y +--+=相交于M ，N 两点，求两圆的公共弦长．【高分突破】一：单选题26．（2021·黑龙江·双鸭山一中高二阶段练习）以下四个命表述正确的是（）个①若点()1,2A ，圆的一般方程为222410x y x y ++-+=，则点A 在圆外 ②圆C ：2228130+--+=x y x y 的圆心到直线4330x y -+=的距离为2 ③圆1C ：2220x y x ++=与圆2C ：224840x y x y +--+=恰有三条公切线④两圆22440x y x y ++-=与222120x y x ++-=的公共弦所在的线方程为：260x y ++= A ．1B ．2C ．3D ．427．（2021·江苏·高二专题练习）已知圆()221:24C x a y ++=与圆()22:1C x y b +-=有且仅有1条公切线，则2211a b +的最小值为（） A ．6B ．7C ．8D ．928．（2017·江西南昌·高二阶段练习（文））与圆222212:26260,:4240C x y x y C x y x y ++--=+-++=都相切的直线有A ．1条B ．2条C ．3条D ．4条29．（2022·全国·高二课时练习）已知Rt PAB 的直角顶点P 在圆(()22:11C x y +-=上，若点(),0A t -，()(),00B t t >，则t 的取值范围为（） A ．(]0,2B ．[]1,2C ．[]2,3D ．[]1,330．（2022·全国·高二）已知半径为1的动圆与圆()()225716x y -++=相切，则动圆圆心的轨迹方程是（） A ．()()225725x y -++=B ．()()225717x y -+-=或()()225715x y -++=C ．()()22579x y -+-=D ．()()225725x y -++=或()()22579x y -++=二、多选题31．（2022·江苏·南京市中华中学高二开学考试）已知圆()()221:1311C x y -+-=与圆2222:2230C x y x my m ++-+-=，则下列说法正确的是（）A ．若圆2C 与x 轴相切，则2m =B ．若3m =-，则圆C 1与圆C 2相离C ．若圆C 1与圆C 2有公共弦，则公共弦所在的直线方程为()246220x m y m +-++=D ．直线210kx y k --+=与圆C 1始终有两个交点32．（2022·全国·高二专题练习）圆221:20+-=Q x y x 和圆222:240++-=Q x y x y 的交点为A ，B ，则（）A ．公共弦AB 所在直线的方程为0x y -= B ．线段AB 中垂线方程为10x y +-=C ．公共弦AB 的长为2D ．P 为圆1Q 上一动点，则P 到直线AB 1+ 33．（2022·江苏·高二单元测试）设有一组圆()()()22:4R k C x k y k k -+-=∈，下列命题正确的是（）A ．不论k 如何变化，圆心k C 始终在一条直线上B ．存在圆kC 经过点（3，0） C ．存在定直线始终与圆k C 相切D ．若圆k C 上总存在两点到原点的距离为1，则k ⎛∈⋃ ⎝⎭⎝⎭34．（2022·重庆市实验中学高二期末）已知直线l ：10kx y k --+=与圆C ：()()222216x y -++=相交于A ，B 两点，O 为坐标原点，下列说法正确的是（）A ．AB 的最小值为．若圆C 关于直线l 对称，则3k =C ．若2ACB CAB ∠=∠，则1k =或17k =-D ．若A ，B ，C ，O 四点共圆，则13k =-35．（2022·江苏南通·高二期末）已知圆1O ：225x y +=和圆2O ：22(4)13x y -+=相交于A ，B 两点，且点A 在x 轴上方，则（） A ．||4AB =B ．过2O 作圆1O 的切线，切线长为C ．过点A 且与圆2O 相切的直线方程为3210x y -+=D ．圆1O 的弦AC 交圆2O 于点D ，D 为AC 的中点，则AC 的斜率为7236．（2022·广东·高二阶段练习）已知点(),P x y 是圆()22:14C x y -+=上的任意一点，直线()):1130l m x y m ++-=，则下列结论正确的是（） A ．直线l 与圆C 的位置关系只有相交和相切两种 B ．圆C 的圆心到直线l C ．点P 到直线43160++=x y 距离的最小值为2D ．点P 可能在圆221x y +=上37．（2022·河北石家庄·高二期末）设m R ∈，直线310mx y m --+=与直线310x my m +--=相交于点(,)P x y ，线段AB 是圆22:(2)(1)9C x y +++=的一条动弦，Q 为弦AB 的中点，||AB = ）A ．点P 在定圆22(2)(2)8x y -+-=上B ．点P 在圆C 外C ．线段PQ 长的最大值为6D ．PA PB ⋅的最小值为15-38．（2022·浙江省杭州学军中学高二期中）过点(A 作圆221:4C x y +=的切线l ，P是圆222:40C x y x +-=上的动点，则下列说法中正确的是（）A ．切线l 40y -+=B ．圆1C 与圆2C 的公共弦所在直线方程为1x = C ．点P 到直线l 的距离的最小值为1D ．点O 为坐标原点，则AO OP ⋅的最大值为4 三、填空题39．（2022·江苏·徐州华顿学校高二阶段练习）设两圆22110C x y +-=：与圆222240C x y x y +-+=：的公共弦所在的直线方程为_______40．（2022·全国·高二课时练习）已知两圆O ：224x y +=，C ：22224510x ax y ay a -+-+-=，当两圆相交时，实数a 的取值范围是______.41．（2022·江苏·高二课时练习）已知圆221:(1)(2)4C x y -+-=和圆222:(2)(1)2C x y -+-=交于,A B 两点，直线l 与直线AB 平行，且与圆2C 相切，与圆1C 交于点,M N ，则MN =__________．42．（2022·全国·高二课时练习）已知圆1C 的标准方程是()()224425x y -+-=，圆222:430C x y x my +-++=关于直线10x +=对称，则圆1C 与圆2C 的位置关系为______．43．（2022·北京房山·高二期末）心脏线，也称心形线，是一个圆上的固定一点在该圆绕着与其相切且半径相同的另外一个圆周滚动时所形成的轨迹，因其形状像心形而得名.心脏线的平面直角坐标方程可以表示为22x y ay ++=0a >，则关于这条曲线的下列说法： ①曲线关于x 轴对称；②当1a =时，曲线上有4个整点（横纵坐标均为整数的点）； ③a 越大，曲线围成的封闭图形的面积越大； ④与圆()222x a y a ++=始终有两个交点. 其中，所有正确结论的序号是___________.四、解答题44．（2022·全国·高二单元测试）已知圆()222:0O x y r r +=>，直线:40l kx y k --=，当k =l 与圆O 恰好相切． (1)求圆O 的方程；(2)若直线l 上存在距离为2的两点M ，N ，在圆O 上存在一点P ，使得0PM PN ⋅=，求实数k 的取值范围．45．（2022·江苏·高二阶段练习）已知圆22:(1)4C x y -+=. (1)若直线l 经过点(1,3)A -，且与圆C 相切，求直线l 的方程；(2)若圆2221:2280C x y mx y m +--+-=与圆C 相切，求实数m 的值.46．（2022·上海市行知中学高二期中）已知圆()()22:10C x y a a ++=>，定点()(),0,0,A m B n ，其中,m n 为正实数，(1)当9a =时，若对于圆C 上任意一点P 均有PA PO λ=成立（O 为坐标原点），求实数,m λ的值；(2)当2,4m n ==时，对于线段AB 上的任意一点P ，若在圆C 上都存在不同的两点,M N ，使得点M 是线段PN 的中点，求实数a 的取值范围47．（2022·江苏·高二课时练习）若圆221:C x y m +=与圆222:68160C x y x y +--+=相外切．(1)求m 的值；(2)若圆1C 与x 轴的正半轴交于点A ，与y 轴的正半轴交于点B ，P 为第三象限内一点且在圆1C 上，直线PA 与y 轴交于点M ，直线PB 与x 轴交于点N ，求证：四边形ABNM 的面积为定值．48．（2022·江苏·高二单元测试）已知圆()22:24M x y -+=，点()()1,R P t t -∈.(1)若1t =，半径为1的圆N 过点P ，且与圆M 相外切，求圆N 的方程；(2)若过点P 的两条直线被圆M 截得的弦长均为且与y 轴分别交于点S 、T ，34ST =，求t .49．（2022·广东揭阳·高二期末）过点()3,1P 作圆()22:11C x y -+=的两条切线，切点分别为A ，B ；(1)求直线AB 的方程；(2)若M 为圆上的一点，求MAB △面积的最大值．【答案详解】1．B【分析】由圆1C 的面积被直线210x y ++=平分，可得圆心在直线上，求出m ，进而利用圆心距与半径和以及半径差的关系可得圆1C 与圆2C 的位置关系．【详解】因为圆1C 的面积被直线210x y ++=平分，所以圆1C 的圆心1,2m ⎛⎫- ⎪⎝⎭在直线210x y ++=上，所以12102m ⎛⎫+⨯-+= ⎪⎝⎭，解得2m =，所以圆1C 的圆心为(1,1)-，半径为1．因为圆2C 的圆心为(2,3)-，半径为5，所以125C C ==，故125151C C -<<+，所以圆1C 与圆2C 的位置关系是相交．故选：B ． 2．B【分析】由对称求出,a b ，再由圆心距与半径关系得圆与圆的位置关系．【详解】222:(1)1C x y -+=，2(1,0)C ，半径为1r =，2(1,0)C 关于直线0x y -=的对称点为(0,1)，即(,)1C 01，所以0,1a b ==，圆1C 半径为2R =，12C C =13R r R r -=<<=+，所以两圆相交．故选：B ． 3．A【分析】根据两圆半径和、差、圆心距之间的大小关系进行判断即可. 【详解】由22222830(1)(4)20x y x y x y +++-=⇒+++=，该圆的圆心为(1,4)--，半径为圆()()22225x y -+-=的圆心为(2,2)= 所以两圆的半径和等于两圆的圆心距，因此两圆相外切，故选：A 4．A【分析】求出两个圆的交点，再求出中垂线方程，然后求出圆心坐标，求出半径，即可得到圆的方程．【详解】由2222430,430x y x x y y +--=+--=解得两圆交点为M ⎝⎭与N ⎝⎭因为1MN k =，所以线段MN 的垂直平分线斜率21k =-；MN 中点P 坐标为（1，1）所以垂直平分线为y ＝﹣x +2 由240y x x y =-+⎧⎨--=⎩解得x ＝3，y ＝﹣1，所以圆心O 点坐标为（3，﹣1）所以r 所以所求圆的方程为（x ﹣3）2+（y +1）2＝13即：x 2+y 2﹣6x +2y ﹣3＝0 故选：A 5．C【解析】求出过AB 两点的垂直平分线方程，再联立直线40x y --=，求得圆心，结合点到直线距离公式即可求解【详解】设两圆交点为,A B ，联立2222460460x y x x y y ⎧+--=⎨+--=⎩得1111x y =-⎧⎨=-⎩或2233x y =⎧⎨=⎩，1AB k =，则AB 中点为()1,1，过AB 两点的垂直平分线方程为()112y x x =--+=-+，联立240y x x y =-+⎧⎨--=⎩得31x y =⎧⎨=-⎩，故圆心为()3,1-，由点到直线距离公式得334525d ⨯-+==故选：C【点睛】本题考查线段垂直平分线方程的求解，点到直线距离公式的应用，属于中档题 6．C【分析】由题意先求动点P 的轨迹1C 的方程,联立1C 和2C 求出M,N 的坐标,如图由平面几何知识和向量数量积的运算规则可求得MN MQ ⋅.【详解】设点P(,x y ),由()()A 1,0,B 4,0,2PA PB =可得()()2222214x y x y -+-+化简得动点P 的轨迹1C 的方程为:224x y +=,联立(()22224334x y x y ⎧+=⎪⎨+-=⎪⎩解得:()()M 3,1,N 0,2-,如图所示,有平面几何知识可得:()1cos 2MQ QMN MN ∠=,向量数量积的运算规则可得:()1cos 2MN MQ MN MQ QMN MN MN ⋅=⋅∠=⋅()(()22211021222MN ⎡⎤==+-=⎢⎥⎣⎦. 故选:C.【点睛】本题考查了由已知条件求动点轨迹的问题,考查了求两圆交点坐标的运算,借助于平面几何知识求向量的数量积的问题,考查了综合运算能力,属于中档题. 7．D【分析】设P 的坐标为(),x y ，由2PA PB =可得P 的轨迹为()2224x y -+=，又因为点P在圆C 上，所以两圆有公共点，从而求解即可.【详解】解：设P 的坐标为(),x y ，因为2PA PB =，()2,0A -，()10B ,，=()2224x y -+=，又因为点P 在圆()()()22:140C x y m m ++-=>上，所以圆()2224x y -+=与圆C 有公共点，22≤且0m >，解得949m ≤≤，故选：D ． 8．A【分析】利用对称圆，把问题转化为两圆的位置关系问题进行处理.【详解】根据题意，圆1C 的圆心坐标为（0，1），半径为r ，其关于直线y ＝x 的对称圆3C 的方程为()2221x y r -+=，根据题意，圆3C 与圆2C 有交点，既可以是外切，也可以是相交，也可以是内切．又圆()()222:211C x y -+-=，所以圆3C 与圆2C 的圆心距为23||C C =以只需11r r -+，解得1r ⎤∈⎦．故B ，C ，D 错误.故选：A. 9．A【分析】根据题意圆1O 、2O 相离，则1212O O r r >+，分别求圆心和半径代入计算．【详解】圆1O ：2216x y +=的圆心()10,0O ，半径14r =，圆2O ：22268240x y mx my m +--+=的圆心()23,4O m m ，半径1r m =根据题意可得，圆1O 、2O 相离，则1212O O r r >+，即54m m >+ ∴,11,m故选：A ． 10．C【分析】由圆与圆的对称性可得a ，再利用几何关系，求点P 的轨迹方程.【详解】由圆22210x y ax y +-++=与圆221x y +=关于直线1y x =-对称，可知两圆半径相等且两圆圆心连线的中点在直线1y x =-上，可得2a =，即点C 的坐标为(2,2)-，所以圆P 的圆心的轨迹方程为222(2)(2)x y x ++-=，整理得24480y x y +-+=. 故选：C. 11．D【分析】先将两个圆的方程化为圆的标准方程，写出两个圆的圆心坐标和半径，然后计算两个圆的圆心之间的距离，圆心距等于两个圆的半径差的绝对值、和，得到关于a 的方程，即可解得a 的值.【详解】设圆1C ､圆2C 的半径分别为1r ､2r .圆1C 的方程可化为22(3)(2)1x y -++=，圆2C 的方程可化为22(7)(1)50x y a -+-=-. 由两圆相切得，1212C C r r =+或1212C C r r =-，∵125C C =，∴215r +=或22154r r -=⇒=或26=r 或24r =-(舍去). 因此，5016a -= 解得a =34 或5036a -= 解得14a = 故选:D.【点睛】本题考查了利用两个圆相切求解参数值的问题，属于中档题目，解题时需要准确将圆的一般方程化为圆的标准方程，利用圆心距与半径的关系建立关于参数的方程. 12．D【分析】根据动圆与圆C 相内切、相外切分类讨论进行求解即可.【详解】设动圆圆心为O ，圆C ：()()225316x y +++=的圆心坐标为：(5,3)C --，半径为4.动圆与圆C 相内切时，413OC =-=，所以动圆圆心的轨迹方程()()22539x y +++=；动圆与圆C 相外切时，415OC =+=，所以动圆圆心的轨迹方程()()225325x y +++=. 故选：D【点睛】本题考查了圆与圆的相切关系，考查了圆的定义，考查了圆的标准方程，属于基础题. 13．A【分析】判断圆1C 与2C 的位置并求出直线AB 方程，再求圆心C 到直线AB 距离即可计算作答.【详解】圆221:(2)(1)5C x y -++=的圆心1(2,1)C -，半径1r =222:(1)5C x y +-=的圆心2(0,1)C ，半径2r =，12||C C =121212||||||r r C C r r -<<+，即圆1C 与2C 相交，直线AB 方程为：10x y --=，圆()()22:331C x y ++-=的圆心(3,3)C -，半径1r =，点C 到直线AB 距离的距离2d ==，所以圆C 上的动点P 到直线AB 1. 故选：A 14．A【分析】求得12,C C PQ ，由此求得四边形12PC QC 的面积. 【详解】圆1C 的圆心为()1,0-，半径11r =；圆2C 的圆心为()0,3，所以12C C =由2220x y x ++=、2260x y y +-=两式相减并化简得30x y +=，即直线PQ 的方程为30x y +=，()1,0-到直线PQ，所以PQ ==，所以四边形12PC QC 的面积为1211322C C PQ ⨯⨯==. 故选：A15．A【分析】先求得公共弦所在直线方程，代入224x y +=，运算即得解【详解】由题意，圆221:4C x y +=的圆心11(0,0),2C r =；圆()222222:2600()6C x y ay a x y a a ++-=>⇔++=+，圆心22(0,),C a r -设圆心距为12C C d ，故12C C d a =由于两圆相交，故122112C C r r d r r -<<+2a <，解得12a >两圆方程作差得公共弦所在直线方程为1y a =，代入224x y +=，解得x == 解得1a =（负根舍去），满足12a > 故选：A 16．D【分析】计算两圆的圆心和半径，可得两圆相离，有四条公切线，两圆心坐标关于原点O 对称，则有两条切线过原点O ，另两条切线与直线MN 平行且相距为1，数形结合可计算四条切线方程，结合选项，即得解【详解】由题意，圆()()22:211M x y -+-=的圆心坐标为()2,1M ，半径为11r =圆()()22:211N x y +++=的圆心坐标为()2,1N --，半径为21r =如图所示，两圆相离，有四条公切线.两圆心坐标关于原点O 对称，则有两条切线过原点O ，设切线:l y kx =22111k k -=+，解得0k =或43k =，另两条切线与直线MN 平行且相距为1，又由1:2MN l y x =，设切线1:2l y x b =+1114b=+，解得5b = 结合选项，可得D 不正确. 故选：D 17．C【分析】设直线l 交x 轴于点M ，推导出1C 为2MC 的中点，A 为BM 的中点，利用勾股定理可求得AB .【详解】如下图所示，设直线l 交x 轴于点M ，由于直线l 与圆()221:11C x y ++=，圆()222:14C x y -+=都相切，切点分别为A 、B ，则1AC l ⊥，2BC l ⊥，12//AC BC ∴，2122BC AC ==，1C ∴为2MC 的中点，A ∴为BM 的中点，1122MC C C ∴==，由勾股定理可得22113AB MA MC AC ==-故选：C.【点睛】关键点点睛：求解本题的关键在于推导出A 为M B 的中点，并利用勾股定理进行计算，此外，在直线与圆相切的问题时，要注意利用圆心与切点的连线与切线垂直这一几何性质. 18．A【分析】根据给定条件，求出两圆圆心距，再判断两圆位置关系即可作答. 【详解】圆1C ：22(1)(3)4x y ++-=的圆心1(1,3)C -，半径12r =，圆2C ：22(2)(1)1x y -++=的圆心2(2,1)C -，半径21r =，2212||(12)[3(1)]5C C =--+--，显然1212||C C r r >+，即圆1C 与圆2C 外离，所以两圆的公切线的条数是4. 故选：A19．(1)11m =- (2)2m =【分析】（1）两圆有三条公切线，说明两圆外切，根据两圆外切可以求出参数的值（2）设()11,M x y ，()22,N x y ，则OM ON ⊥等价于12120x x y y +=，直线与圆联立方程，根据韦达定理，得到关于m 的等式，即可求解m 的值 (1)由2222240(1)(2)5x y x y m x y m +--+=⇒-+-=-，知圆C 的圆心(1,2)C由圆D ：22(2)(2)1x y +++=，有圆心()2,2D --，半径为1，依题意有圆C 与圆D 相外切，故||1511CD m ==⇒=-； (2)设()11,M x y ，()22,N x y ，有112x y =-，222x y =-，由OM ON ⊥，有()()121212120220x x y y y y y y +=⇒--+=，整理得12122y y y y +=+………①由2222402602x y x y m y y m x y⎧+--+=⇒-+=⎨=-⎩，3680m ∆=->得：92m <，易知1y ，2y 是方程的根，故有123y y +=，122m y y =代入①，得3222mm =+⇒=，满足要求，故2m =20．（1）两圆内切，10x y ++=；（2）直线l 的方程为0x y +=【分析】（1）由1m =-，分别得到圆1C 和圆2C 的圆心，半径，然后利用圆圆的位置关系判断，再由两圆方程相减得到公切线；（2）先得到两圆公共弦所在直线l 的方程，再利用弦长公式求解. 【详解】（1）当1m =-时，圆1C 的圆心()12,1C ，半径1r =圆2C 的圆心()21,0C ，半径2r圆心距1212C C r r ==-，所以两圆内切；因为两圆内切，所以公切线只有一条，两圆的公切线方程可由两圆方程相减得到：10x y ++=；（2）两圆公共弦所在直线l 的方程为：2230x y m +++=，圆2C 的圆心()21,0C 到直线l 2=，于是52m +=，3m =-或7(-舍)，所以直线l 的方程为0x y +=；因为圆2C 半径22r =，弦心距d ==21．（1）12m =；（2）1n =-或7n =-．【分析】（1）由公切线条数知两圆外切，从而可得m 值；（2）求出圆2C 圆心坐标和半径，求得圆心到直线的距离，用勾股定理求得圆心到直线的距离从而得参数值．【详解】解：（1）圆221:(1)1C x y -+=，圆心1(1,0)C ，半径11r =；圆222:(4)16C x y m -+=-，圆心2(4,0)C ，半径2r因为圆1C 与圆2C 有3条公切线，所以圆1C 与圆2C 相外切，所以1212C C r r =+，即31=12m =．（2）由（1）可知，圆222:(4)4C x y -+=，圆心2(4,0)C ，半径22r =．因为直线0x n +=与圆2C 相交，弦长是2，所以圆心2C 到直线0x n ++=的距离d ===，解得1n =-或7n =-．【点睛】结论点睛：本题实质考查圆与圆的位置关系，圆与圆的位置关系与公切线条数：两圆圆心距离为d ，半径分别为,r R ，则相离d R r ⇔>+，公切线有4条；外切d R r ⇔=+，公切线有3条；相交R r d R r ⇔-<<+，公切线有2条；内切d R r ⇔=-，公切线有1条；内含d R r ⇔<-，无公切线． 22．C【详解】由题意，得两圆的标准方程分别为22(2)(1)4x y -++=和22(2)(2)9x y ++-=，则两圆的圆心距523d =+，即两圆外切，所以两圆有3条公切线；故选C ．【点睛】本题考查圆与圆的位置关系和两圆公切线的判定；在处理两圆的公切线条数时，要把问题转化为两圆位置关系的判定：当两圆相离时，两圆有四条公切线；当两圆外切时，两圆有三条公切线；当两圆相交时，两圆有两条公切线；当两圆内切时，两圆有一条公切线；当两圆内含时，两圆没有公切线. 23．C【分析】两圆外切时，有三条公切线．【详解】圆1C 标准方程为22(2)1x y -+=， ∵两圆有三条公切线，∴两圆外切，116a =．故选C ．【点睛】本题考查圆与圆的位置关系，考查直线与圆的位置关系．两圆的公切线条数：两圆外离时，有4条公切线，两圆外切时，有3条公切线，两圆相交时，有2条公切线，两圆内切时，有1条公切线，两圆内含时，无无公切线． 24．(1)()()221716x y -+-=(2)()()221725x y -+-=或()()221727x y -+-=．【分析】（1）根据圆与圆的位置关系，求出圆2O 的半径即可写出圆2O 的方程；（2）由两圆的圆心距确定圆心到公共弦的的距离公式，从而求出圆2O 的半径即可求解. （1）圆1O 的方程为()()22231x y ++-=，则圆心坐标为()2,3-，半径为1．圆2O 的圆心()21,7O ，5=．由圆2O 与圆1O 外切，则所求圆2O 的半径为4，所以圆2O 的方程()()221716x y -+-=．（2）圆2O 与圆1O 交于A 、B 两点，且AB =所以圆1O 到AB 110=.5=，当圆2O 到AB 的距离为14951010-=时，2O 5=，所以圆2O 的方程为()()221725x y -+-=．当圆2O 到AB 的距离为15151010+=时，圆2O = 所以圆2O 的方程为()()221727x y -+-=．综上所述，圆2O 的方程为()()221725x y -+-=或()()221727x y -+-=． 25．(1)()()224316x y -+-=(2)【分析】(1)利用两点求出直线方程l ，利用圆心在l 上又在3y =求出圆心坐标，进而求出圆的半径求出圆1C 的方程；(2)利用两圆的方程相减得到公共弦所在直线方程，求出圆心1C 到公共弦的距离，利用勾股定理求出两圆的公共弦长．（1）经过点(21)，与点(23)--，的直线l 的方程为123122y x --=----，即1y x =-，因为圆1C 与y 轴相切于点(03)，，所以圆心在直线3y =上，联立31y y x =⎧⎨=-⎩解得43x y =⎧⎨=⎩可得圆心坐标为(43)，，又因为圆1C 与y 轴相切于点(03)，，故圆1C 的半径为4，故圆1C 的方程为()()224316x y -+-=．（2）圆1C 的方程为()()224316x y -+-=，即228690x y x y +--+=，圆222:6350C x y x y +--+=，两式作差可得两圆公共弦所在的直线方程为2340x y +-=，圆1C 的圆心(43)，到直线2340x y +-=的距离d ==所以两圆的公共弦长为= 26．A【分析】①将点()1,2A 代入圆可判断；②将圆化为标准方程，得出圆心，利用点到直线距离公式可得；③求出两圆圆心和半径，判断位置关系可得；④两圆方程相减即可求出. 【详解】①点()1,2A 代入圆可得2212214210++⨯-⨯+=，所以点A 在圆上，故①错误； ②由2228130+--+=x y x y 可得()()22144x y -+-=，则圆心为()1,4，由点到直线的距离公式可得圆心到线4330x y -+=1=，故②错误；③圆1C 化为()2211x y ++=，圆心为()11,0C -，半径11r =，圆2C 化为()()222416x y -+-=，圆心为()22,4C ，半径24r =，则圆心距12125C C r r ==+，故两圆外切，公切线有3条，故③正确；④两圆方程相减可得260x y -+=，故公共弦所在方程为260x y -+=，故④错误，综上，正确的有1个. 故选：A. 27．D【解析】由题意可知，圆2C 内切于圆1C ，由题意可得出2241a b +=，然后将代数式2211a b +与224a b +相乘，展开后利用基本不等式可求得2211a b +的最小值. 【详解】圆()221:24C x a y ++=的圆心为()12,0C a -，半径为12r =，圆()22:1C x y b +-=的圆心为()20,C b ，半径为21r =，由于两圆有且仅有1条公切线，则圆2C 内切于圆1C ，所以12121C C r r =-=，可得2241a b +=，()2222222222111144559b a a b a b a b a b ⎛⎫+=++=∴++≥+= ⎪⎝⎭，当且仅当222b a =时，等号成立，因此，2211a b +的最小值为9. 故选：D.【点睛】结论点睛：圆与圆的位置关系：设圆1C 与圆2C 的半径长分别为1r 和2r . （1）若1212C C r r <-，则圆1C 与圆2C 内含；（2）若1212C C r r =-，则圆1C 与圆2C 内切；（3）若121212r r C C r r -<<+，则圆1C 与圆2C 相交；（4）若1212C C r r =+，则圆1C 与圆2C 外切；（5）若1212C C r r >+，则圆1C 与圆2C 外离.【分析】根据两圆的位置关系判断.【详解】解：圆1C 的标准方程：22(1)(3)36x y ++-=，圆心()11,3C -，半径16r =，圆2C 的标准方程：22(2)(1)1x y -++=，圆心()22,1C -，21r =，因为圆心距12125C C r r ===-，所以两圆内切，所以与两圆都相切的直线有1条. 故选：A 29．D【分析】求出P 的轨迹方程，结合点P 为两圆交点且2CM，列出不等式，求出t 的取值范围.【详解】由题意得P 在以AB 为直径的圆222:M x y t +=上（去掉A ，B 两点）．又因为点P 在圆(()22:11C x y +-=上，所以圆C 与圆M 有交点，因为2CM ，所以121t t -≤≤+，所以13t ≤≤．故选：D ． 30．D【分析】设动圆圆心为(),x y ，两半径相加，内切两半径相减，即可求解【详解】设动圆圆心为(),x y 41=+，∴()()225725x y -++=；41=-，∴()()22579x y -++=．31．BD【分析】对A ，圆心到x 轴的距离等于半径判断即可；对B ，根据圆心间的距离与半径之和的关系判断即可；对C ，根据两圆有公共弦，两圆的方程相减可得公共弦所在直线方程求解即可；对D ，根据直线210kx y k --+=过定点()2,1以及()2,1在圆C 1内判断即可.【详解】因为221:(1)(3)11C x y -+-=，222:(1)()4C x y m ++-=，对A ，故若圆2C 与x 轴相切，则有||2m =，故A 错误；对B ，当3m =-时，1262C C =>>B 正确；对C ，由两圆有公共弦，两圆的方程相减可得公共弦所在直线方程24(62)20x m y m +-+-=，故C 错误；对D ，直线210kx y k --+=过定点()2,1，而22(21)(13)511-+-=<，故点()2,1在圆221:(1)(3)11C x y -+-=内部，所以直线210kx y k --+=与圆1C 始终有两个交点，故D 正确.故选：BD 32．ABD【分析】两圆方程作差后可得公共弦方程，从而可判断A 的正误，求出圆1Q 的圆心坐标后求出垂直平分线的方程后可判断B 的正误，利用垂径定理计算弦长后可判断C 的正误，求出1Q 到直线的距离后可求动点到直线距离的最大值，从而可判断D 的正误.【详解】对于A ，因为圆221:20+-=Q x y x ，222:240++-=Q x y x y ，两式作差可得公共弦AB 所在直线的方程为440x y -=，即0x y -=，故A 正确；对于B ，圆221:20+-=Q x y x 的圆心为（1，0），1AB k =，则线段AB 中垂线的斜率为1-，即线段AB 中垂线方程为()011y x -=-⨯-，整理可得10x y +-=，故B 正确；对于C ，圆心()11,0Q 到0x y -=的距离为2d ==又圆1Q 的半径1r =，所以AB =C 不正确；对于D ，P 为圆1Q 上一动点，圆心()11,0Q 到0x y -=的距离为d =又圆1Q 的半径1r =，所以P 到直线AB 1，故D 正确.故选：ABD. 33．ACD【分析】对于A ，考查圆心k C 的横纵坐标关系即可判断；对于B ，把3x =，0y =代入圆k C 方程，由关于k 的方程根的情况作出判断；对于C ，判断圆心k C 到直线0x y -±=距离与半径的关系即可；对于D ，圆k C 与以原点为圆心的单位圆相交即可判断作答．【详解】解：根据题意，圆22:()()4(R)k C x k y k k -+-=∈，其圆心为(,)k k ，半径为2，依次分析选项：对于A ，圆心为(,)k k ，其圆心在直线y x =上，A 正确；对于B ，圆22:()()4k C x k y k -+-=，将(3,0)代入圆的方程可得22(3)(0)4k k -+-=，化简得22650k k -+=，364040∆=-=-<，方程无解，所以不存在圆k C 经过点()3,0，B 错误；对于C ，存在直线y x =±，即0x y -+=或0x y --=，圆心(,)k k 到直线0x y -+=或0x y --=的距离2d =，这两条直线始终与圆k C 相切，C 正确，对于D ，若圆k C 上总存在两点到原点的距离为1，问题转化为圆221x y +=与圆k C 有两个交点，，则有1|3k <<，解可得：k <k <，D 正确．故选：ACD ． 34．ACD【分析】判断出直线l 过定点()1,1D ，结合勾股定理、圆的对称性、点到直线的距离公式、四点共圆等知识对选项进行分析，从而确定正确答案. 【详解】直线():11l y k x =-+过点()1,1D ，圆()()22:2216C x y -++=，即224480x y x y +-+-=①，圆心为()2,2C -，半径为4r =，由于()()22121216-++<，所以D 在圆C 内.CD =所以min AB =AB CD ⊥，所以A 选项正确.若圆C 关于直线l 对称，则直线l 过,C D 两点，斜率为21321--=--，所以B 选项错误. 设22ACB CAB θ∠=∠=，则π2π,4θθθθ++==，此时三角形ABC 是等腰直角三角形，C 到直线AB 的距离为42==解得1k =或17k =-，所以C 选项正确.对于D 选项，若,,,A B C O 四点共圆，设此圆为圆E ，圆E 的圆心为(),E a b ，,O C 的中点为()1,1-，1OC k =-，所以OC 的垂直平分线为:11,2l y x y x +=-=-，则2b a =-②，圆E 的方程为()()2222x a y b a b -+-=+，整理得22220x y ax by +--=③，直线AB 是圆C 和圆E 的交线，由①-③并整理得()():422480AB a x b y --++=，将()1,1D 代入上式得()()422480a b --++=，40a b +-=④，由②④解得3,1a b ==，所以直线AB 即直线l 的斜率为42212463a b --==-+，D 选项正确. 故选：ACD【点睛】求解直线和圆位置关系有关题目，首先要注意的是圆和直线的位置，是相交、相切还是相离.可通过点到直线的距离来判断，也可以通过直线所过定点来进行判断. 35．ACD【分析】根据给定条件，求出点A ，B 的坐标，再结合圆的性质逐项分析、计算判断作答.【详解】依题意，由22225(4)13x y x y ⎧+=⎨-+=⎩解得12x y =⎧⎨=±⎩，则(1,2),(1,2)A B -，圆1O 的圆心1(0,0)O ，半径1r =2O 的圆心2(4,0)O ，半径2r||4AB =，A 正确；。

(中考考点梳理)圆的性质及与圆有关的位置关系-中考数学一遍过

考点18 圆的性质及与圆有关的位置关系一、圆的有关概念1．与圆有关的概念和性质（1）圆：平面上到定点的距离等于定长的所有点组成的图形．（2）弦与直径：连接圆上任意两点的线段叫做弦，过圆心的弦叫做直径，直径是圆内最长的弦．（3）弧：圆上任意两点间的部分叫做弧，小于半圆的弧叫做劣弧，大于半圆的弧叫做优弧．（4）圆心角：顶点在圆心的角叫做圆心角．（5）圆周角：顶点在圆上，并且两边都与圆还有一个交点的角叫做圆周角．（6）弦心距：圆心到弦的距离．2．注意（1）经过圆心的直线是该圆的对称轴，故圆的对称轴有无数条；（2）3点确定一个圆，经过1点或2点的圆有无数个．学-科网（3）任意三角形的三个顶点确定一个圆，即该三角形的外接圆．二、垂径定理及其推论1．垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．关于垂径定理的计算常与勾股定理相结合，解题时往往需要添加辅助线，一般过圆心作弦的垂线，构造直角三角形．2．推论（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧．三、圆心角、弧、弦的关系1．定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等．圆心角、弧和弦之间的等量关系必须在同圆等式中才成立．2．推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．四、圆周角定理及其推论1．定理一条弧所对的圆周角等于它所对的圆心角的一半．2．推论（1）在同圆或等圆中，同弧或等弧所对的圆周角相等．（2）直径所对的圆周角是直角．圆内接四边形的对角互补．在圆中求角度时，通常需要通过一些圆的性质进行转化．比如圆心角与圆周角间的转化；同弧或等弧的圆周角间的转化；连直径，得到直角三角形，通过两锐角互余进行转化等．五、与圆有关的位置关系1．点与圆的位置关系设点到圆心的距离为d．(1)d<r⇔点在⊙O内；(2)d=r⇔点在⊙O上；(3)d>r⇔点在⊙O外．判断点与圆之间的位置关系，将该点的圆心距与半径作比较即可．2．直线和圆的位置关系位置关系相离相切相交图形公共点个数0个1个2个数量关系d>r d=r d<r 由于圆是轴对称和中心对称图形，所以关于圆的位置或计算题中常常出现分类讨论多解的情况．六、切线的性质与判定1．切线的性质（1）切线与圆只有一个公共点．（2）切线到圆心的距离等于圆的半径．（3）切线垂直于经过切点的半径．利用切线的性质解决问题时，通常连过切点的半径，利用直角三角形的性质来解决问题．2．切线的判定（1）与圆只有一个公共点的直线是圆的切线（定义法）．（2）到圆心的距离等于半径的直线是圆的切线．（3）经过半径外端点并且垂直于这条半径的直线是圆的切线．切线判定常用的证明方法：①知道直线和圆有公共点时，连半径，证垂直；②不知道直线与圆有没有公共点时，作垂直，证垂线段等于半径．七、三角形与圆1．三角形的外接圆相关概念经过三角形各顶点的圆叫做三角形的外接圆，外接圆的圆心叫做三角形的外心，这个三角形叫做圆的内接三角形．外心是三角形三条垂直平分线的交点，它到三角形的三个顶点的距离相等．2．三角形的内切圆与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．内心是三角形三条角平分线的交点，它到三角形的三条边的距离相等．考向一圆的基本认识1．在一个圆中可以画出无数条弦和直径．2．直径是弦，但弦不一定是直径．3．在同一个圆中，直径是最长的弦．4．半圆是弧，但弧不一定是半圆．弧有长度和度数，规定半圆的度数为180°，劣弧的度数小于180°，优弧的度数大于180°．5．在同圆或等圆中能够互相重合的弧是等弧，度数或长度相等的弧不一定是等弧．典例1下列命题中正确的有①弦是圆上任意两点之间的部分；②半径是弦；③直径是最长的弦；④弧是半圆，半圆是弧．A．1个B．2个C．3个D．4个【答案】A【解析】①弦是圆上任意两点之间所连线段，所以①错误；②半径不是弦，所以②错误；③直径是最长的弦，正确；④只有180°的弧才是半圆，所以④错误，故选A．1．把圆的半径缩小到原来的14，那么圆的面积缩小到原来的A．12B．14C．18D．1162．半径为5的圆的一条弦长不可能是A．3 B．5 C．10 D．12考向二垂径定理1．垂径定理中的“弦”为直径时，结论仍然成立．2．垂径定理是证明线段相等、弧相等的重要依据，同时也为圆的计算和作图问题提供了理论依据．典例2把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=16 cm，则球的半径为A．cm B．10 cmC．cm D．cm【答案】B【点睛】解本题的关键是作辅助线弦心距，构造直角三角形，这个直角三角形的斜边是半径，另两条边分别为弦心距和弦的一半，再根据解直角三角形解题．典例3 如图，将半径为2 cm 的圆形纸片折叠后，圆弧恰好经过圆心O ，则折痕AB 的长为A ．2 cmB cmCD 【答案】C【解析】在图中构建直角三角形，先根据勾股定理得AD 的长，再根据垂径定理得AB 的长．作OD ⊥AB 于D ，连接OA ．根据题意得OD =12OA =1cm ，再根据勾股定理得：AD cm ，根据垂径定理得AB ．故选C ．3．如图，⊙O 的直径为10，圆心O 到弦AB 的距离OM 的长为4，则弦AB 的长是A ．3B ．6C．4 D．84．如图，某菜农在蔬菜基地搭建了一个横截面为圆弧形的蔬菜大棚，大棚的跨度弦AB 大棚顶点C离地面的高度为2．3米．（1）求该圆弧形所在圆的半径；（2）若该菜农的身高为1．70米，则他在不弯腰的情况下，横向活动的范围有几米？考向三弧、弦、圆心角、圆周角1．圆心角的度数等于它所对弧的度数，把顶点在圆心的周角等分成360份，每一份的圆心角是1°的角，1°的圆心角对着1°的弧．2．圆周角要具备两个特征：①顶点在圆上；②角的两边都和圆相交，二者缺一不可．典例4如图，AB和CD是⊙O的两条直径，弦DE∥AB，若弧DE为40°的弧，则∠BOC=A．110° B．80°C．40° D．70°【答案】A【解析】连接OE，如图所示：∵弧DE 为40°的弧，∴∠DOE =40°．∵OD =OE ，∴∠ODE =180402︒-︒=70°． ∵弦DE ∥AB ，∴∠AOC =∠ODE =70°，∴∠BOC =180°–∠AOC =180°–70°=110°．故选A ．【点睛】本题考查的是圆心角、弧、弦的关系，根据题意作出辅助线，构造出等腰三角形是解答此题的关键．典例5　如图，在⊙O 中，圆心角∠AOB =120°，P 为弧AB 上一点，则∠APB 度数是A ．100°B ．110°C ．120°D ．130°【答案】C【解析】如图，在优弧AB 上取点C ，连接AC 、BC ，由圆周角定理得由圆内接四边形的性质得到，180120APB ACB ∠=︒-∠=︒，故选C ．【点睛】在同圆或等圆中，同弧所对的圆周角等于圆心角的一半．5．如图，AB 为⊙O 的直径，点C 在⊙O 上，若∠OCA =50°，AB =4，则 BC的长为A ．103π B ．109π C ．59π D ．518π 6．如图，AB 是⊙O 的直径， =BCCD DE =，∠COD =38°，则∠AEO 的度数是A．52° B．57° C．66° D．78°考向四点、直线与圆的位置关系1．点和圆的位置关系：①在圆上；②在圆内；③在圆外．2．直线和圆的位置关系：相交、相切、相离．典例6　已知⊙O的半径是5，点A到圆心O的距离是7，则点A与⊙O的位置关系是A．点A在⊙O上B．点A在⊙O内C．点A在⊙O外D．点A与圆心O重合【答案】C【解析】∵O的半径是5，点A到圆心O的距离是7，即点A到圆心O的距离大于圆的半径，∴点A在⊙O外．故选C．【点睛】直接根据点与圆的位置关系的判定方法进行判断．典例7　在△ABC中，AB=AC=2，∠A=150°，那么半径长为1的⊙B和直线AC的位置关系是A．相离B．相切C．相交D．无法确定【答案】B【解析】过B作BD⊥AC交CA的延长线于D，∵∠BAC=150，∴∠DAB=30°，∴BD=11222AB=⨯=1，即B到直线AC的距离等于⊙B的半径，∴半径长为1的⊙B和直线AC的位置关系是相切，故选B．【点睛】本题考查了直线与圆的位置关系的应用，过B作BD⊥AC交CA的延长线于D，求出BD和⊙B的半径比较即可，主要考查学生的推理能力．7．如图，⊙O的半径为5cm，直线l到点O的距离OM=3cm，点A在l上，AM=3．8cm，则点A与⊙O的位置关系是A．在⊙O内B．在⊙O上C．在⊙O外D．以上都有可能8．如图，⊙O的半径OC=5cm，直线l⊥OC，垂足为H，且l交⊙O于A、B两点，AB=8cm，则l沿OC所在直线向下平移__________cm时与⊙O相切．学_科网考向五切线的性质与判定有圆的切线时，常常连接圆心和切点得切线垂直半径，这是圆中作辅助线的一种方法．典例8　如图，已知BC是⊙O的直径，AB是⊙O的弦，切线AD交BC的延长线于D，若∠D=40°，则∠B 的度数是A．40° B．50°C．25° D．115°【答案】C【解析】连接OA，根据切线的性质得到OA⊥AD，由三角形的内角和得到∠AOC=50°，根据等腰三角形的性质得到∠B=∠OAB，根据圆周角定理可得到结论．连接OA，∵AD是⊙O的切线，∴OA⊥AD，∴∠D=40°，∴∠AOC=50°，∵BO=OA，∴∠B=∠BAO，∴∠B+∠BAO=∠AOC=50°，∴∠B=∠BAO=12∠AOC=25°．故选C．【点睛】本题考查了切线的性质，三角形内角和，圆周角定理，正确的作出辅助线是解题的关键．典例9　如图，Rt△ABC中，∠C＝90°，AB＝5，AC＝3，点E在中线AD上，以E为圆心的⊙E分别与AB、BC相切，则⊙E的半径为A．78B．67C．56D．1【答案】B9．已知四边形ABCD是梯形，且AD∥BC，AD<BC，又⊙O与AB、AD、CD分别相切于点E、F、G，圆心O在BC上，则AB+CD与BC的大小关系是A．大于B．等于C．小于D．不能确定10．如图，以等腰△ABC的腰AB为⊙O的直径交底边BC于D，DE AC于E．；（2）DE为⊙O的切线．求证：（1）DB DC1．下列关于圆的叙述正确的有①圆内接四边形的对角互补；②相等的圆周角所对的弧相等；③正多边形内切圆的半径与正多边形的半径相等；④同圆中的平行弦所夹的弧相等．A．1个B．2个C．3个D．4个2．如图所示，△ABC的三个顶点在⊙O上，D是 AB上的点，E是 AC上的点，若∠BAC=50°，则∠D+∠E=A．220° B．230°C．240° D．250°3．如图，半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD，已知DE=6，∠BAC＋∠EAD =180°，则弦BC 的长等于A BC ．8D ．64．如图，在平面直角坐标系中，过格点A ，B ，C 作一圆弧，则圆心坐标是A ．点（1，0）B ．点（2，1）C ．点（2，0）D ．点(2．5，1)5．如图，点O 是△ABC 的内心，∠A =62°，则∠BOC =A ．59°B ．31°C ．124°D ．121°6．如图，一圆内切四边形ABCD ，且BC =10，AD =7，则四边形的周长为A ．32B ．34C ．36D ．387．已知在⊙O 中，AB =BC ，且 34AB AMC ∶∶，则∠AOC =__________．8．如图，A 、B 、C 、D 都在⊙O 上，∠B =130°，则∠AOC 的度数是__________．9．如图，PA 、PB 分别切⊙O 于A 、B ，并与圆O 的切线DC 分别相交于D 、C ．已知△PCD 的周长等于14cm ，则PA =__________cm ．10．如图，在⊙O 的内接四边形ABCD 中，AB AD =，120C ∠=︒，点E 在弧AD 上．若AE 恰好为⊙O 的内接正十边形的一边， DE的度数为__________．11．如图，在圆内接四边形ABCD 中，若∠A ，∠B ，∠C 的度数之比为4∶3∶5，则∠D 的度数是__________°．12．如图，AB 为⊙O 的直径，C 、F 为⊙O 上两点，且点C 为弧BF 的中点，过点C 作AF 的垂线，交AF的延长线于点E，交AB的延长线于点D．（1）求证：DE是⊙O的切线；学_科网（2）如果半径的长为3，tan D=34，求AE的长．13．如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．（1）判断直线DE与⊙O的位置关系，并说明理由；（2）若AC=6，BC=8，OA=2，求线段DE的长．14．如图，⊙O是△ABC的外接圆，BC为⊙O的直径，点E为△ABC的内心，连接AE并延长交⊙O于D 点，连接BD并延长至F，使得BD=DF，连接CF、BE．（1）求证：DB=DE；（2）求证：直线CF为⊙O的切线．1．（2018•张家界）如图，AB是⊙O的直径，弦CD⊥AB于点E，OC=5cm，CD=8cm，则AE=A．8cm B．5cmC．3cm D．2cm2．（2018•甘孜州）如图，在⊙O中，直径CD⊥弦AB，则下列结论中正确的是A．AC=AB B．∠C=12∠BODC．∠C=∠B D．∠A=∠BOD3．（2018•乐山）《九章算术》是我国古代第一部自成体系的数学专著，代表了东方数学的最高成就．它的算法体系至今仍在推动着计算机的发展和应用．书中记载：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深1寸（ED=1寸），锯道长1尺（AB=1尺=10寸）”，问这块圆柱形木材的直径是多少？”如图所示，请根据所学知识计算：圆柱形木材的直径AC是A．13寸B．20寸C．26寸D．28寸4．（2018•日照）如图，边长为1的小正方形构成的网格中，半径为1的⊙O的圆心O在格点上，则∠BED 的正切值等于A BC．2 D．1 25．（2018•常州）某数学研究性学习小组制作了如下的三角函数计算图尺：在半径为1的半圆形量角器中，画一个直径为1的圆，把刻度尺CA的0刻度固定在半圆的圆心O处，刻度尺可以绕点O旋转．从图中所示的图尺可读出sin∠AOB的值是A．58B．78C．710D．456．（2018•襄阳）如图，点A，B，C，D都在半径为2的⊙O上，若OA⊥BC，∠CDA=30°，则弦BC的长为A．4 B．C D ．7．（2018•邵阳）如图所示，四边形ABCD 为⊙O 的内接四边形，∠BCD =120°，则∠BOD 的大小是A ．80°B ．120°C ．100°D ．90°8．（2018•宜宾）在△ABC 中，若O 为BC 边的中点，则必有：AB 2+AC 2=2AO 2+2BO 2成立．依据以上结论，解决如下问题：如图，在矩形DEFG 中，已知DE =4，EF =3，点P 在以DE 为直径的半圆上运动，则PF 2+PG 2的最小值为A B ．192C ．34D ．109．（2018•牡丹江）如图，△ABC 内接于⊙O ，若sin ∠BAC =13，BC ，则⊙O 的半径为A ．B ．C ．D ．10．（2018•湘西州）已知⊙O 的半径为5cm ，圆心O 到直线l 的距离为5cm ，则直线l 与⊙O 的位置关系为 A ．相交 B ．相切 C ．相离D ．无法确定11．（2018•常州）如图，AB 是⊙O 的直径，MN 是⊙O 的切线，切点为N ，如果∠MNB =52°，则∠NOA 的度数为A．76° B．56°C．54° D．52°12．（2018•广元）如图是一块测环形玉片的残片，作外圆的弦AB与内圆相切于点C，量得AB=8cm、点C 与 AB的中点D的距离CD=2cm．则此圆环形士片的外圆半径为__________cm．13．（2018•毕节市）如图，AB是⊙O的直径，C、D为半圆的三等分点，CE⊥AB于点E，∠ACE的度数为__________．14．（2018•牡丹江）如图，在⊙O中， AB=2 AC，AD⊥OC于D．求证：AB=2AD．15．（2018•湖北）如图，在⊙O中，AB为直径，AC为弦．过BC延长线上一点G，作GD⊥AO于点D，交AC于点E，交⊙O于点F，M是GE的中点，连接CF，CM．（1）判断CM与⊙O的位置关系，并说明理由；（2）若∠ECF=2∠A，CM=6，CF=4，求MF的长．16．（2018•黄石）如图，已知A、B、C、D、E是⊙O上五点，⊙O的直径BE，∠BCD=120°，A为 BE的中点，延长BA到点P，使BA=AP，连接PE．（1）求线段BD的长；（2）求证：直线PE是⊙O的切线．17．（2018•贺州）如图，AB是⊙O的弦，过AB的中点E作EC⊥OA，垂足为C，过点B作直线BD交CE 的延长线于点D，使得DB=DE．（1）求证：BD是⊙O的切线；（2）若AB=12，DB=5，求△AOB的面积．1．【答案】D【解析】设原来的圆的半径为r ，则面积S 1=πr 2，∴半径缩小到原来的14后所得新圆的面积22211ππ416S r r ⎛⎫== ⎪⎝⎭，∴22211π116π16rS S r ==.故选D ． 2．【答案】D【解析】∵圆的半径为5，∴圆的直径为10，又∵直径是圆中最长的弦，∴圆中任意一条弦的长度10l ≤.故选D ． 3．【答案】B【解析】如图，连接OA ，∵O 的直径为10，5OA ∴=， ∵圆心O 到弦AB 的距离OM 的长为4，由垂径定理知，点M 是AB 的中点，12AM AB =，由勾股定理可得，3AM =，所以6AB =．故选B ．4．【解析】（1）如图所示：CO ⊥AB 于点D ，设圆弧形所在圆的半径为xm，根据题意可得：DO2+BD2=BO2，则（x–2．3）2+12）2=x2，解得x=3．答：圆弧形所在圆的半径为3米；（2）如图所示：当MN=1.7米，则过点N作NF⊥CO于点F，可得：DF=1.7米，则FO=2.4米，NO=3米，故FN=1.8（米），故该菜农身高1.70米，则他在不弯腰的情况下，横向活动的范围有3．6米．5．【答案】B【解析】根据题意可知：∠OAC=∠OCA=50°，则∠BOC=2∠OAC=100°，则弧BC的长度为故选B．7．【答案】A【解析】如图，连接OA，则在直角△OMA中，根据勾股定理得到OA5=<．∴点A与⊙O的位置关系是：点A在⊙O内．故选A．8．【答案】2【解析】连接OA．∵直线和圆相切时，OH=5，又∵在直角三角形OHA中，HA=AB÷2=4，OA=5，∴OH=3．∴需要平移5–3=2（cm）．故答案是：2．【点睛】本题考查垂径定理及直线和圆的位置关系．注意：直线和圆相切，应满足d=R．9．【答案】B【解析】如图，连接OF，OA，OE，作AH⊥BC于H．∵AD是切线，∴OF⊥AD，易证四边形AHOF是矩形，∴AH=OF=OE，∵S△AOB=12•OB•AH=12•AB•OE，∴OB=AB，同理可证：CD=CO，∴AB+CD=BC，故选B．【点睛】本题考查了切线的性质，切线垂直于过切点的半径，正确作出辅助线是关键． 10．【解析】（1）如图，连AD ，∵AB 是直径，∴90ADB ∠=︒，AD BC ⊥，又AB AC =，∴D 为BC 中点，DB DC =；（2）连OD ，∵D 为BC 中点，OA OB =， ∴OD 为ABC △中位线，OD AC ∥，又DE AC ⊥于,E ∴90ODE DEC ∠=∠=︒， ∴DE 为⊙O 的切线．学科_网1．【答案】B【解析】①圆内接四边形的对角互补；正确；②相等的圆周角所对的弧相等；错误；③正多边形内切圆的半径与正多边形的半径相等；错误；④同圆中的平行弦所夹的弧相等；正确；正确的有2个，故选B ． 2．【答案】B【解析】如图，连接OA 、OB 、OC ，由圆心角、弧、弦的关系定理得出∠BOC =100°，得出∠AOB +∠AOC =260°，由圆周角定理得出∠D =12（∠BOC +∠AOC ），∠E =12（∠BOC +∠AOB ），即可得出∠D+∠E=12（∠BOC+∠AOC+∠BOC+∠AOB）=12（260°+100°+100°）=230°．故选B．3．【答案】C【解析】如图，延长CA，交⊙A于点F，∵∠BAC+∠BAF=180°，∠BAC+∠EAD=180°，∴∠BAF=∠DAE，∴BF=DE=6，∵CF是直径，∴∠ABF=90°，CF=2×5=10，∴BC8=．故选C．4．【答案】C【解析】根据勾股定理可知A、B、C点到（2，0，然后可知圆心为（2，0）或者通过AB、BC的垂直平分线求解也可以．故选C．5．【答案】D【解析】∵∠BAC=62°，∴∠ABC+∠ACB=180°–62°=118°，∵点O是△ABC的内心，∴∠OBC=12∠ABC，∠OCB=12∠ACB，∴∠OBC+∠OCB=12（∠ABC+∠ACB）=12×118°=59°，∴∠BOC=180°–59°=121°．故选D．6．【答案】B【解析】由题意可得圆外切四边形的两组对边和相等，所以四边形的周长=2×（7+10）=34．故选B．7．【答案】144°【解析】根据AB =BC 可得：弧AB 的度数和弧BC 的度数相等，则弧AMC 的度数为：(360°÷10)×4=144°，则∠AOC =144°． 8．【答案】100°【解析】∵∠B =130°，∴∠D =180°－130°=50°，∴∠AOC =2∠D =100°．故答案为100°． 9．【答案】7【解析】如图，设DC 与⊙O 的切点为E ；∵PA 、PB 分别是⊙O 的切线，且切点为A 、B ，∴PA =PB ；同理，可得：DE =DA ，CE =CB ；则△PCD 的周长=PD +DE +CE +PC =PD +DA +PC +CB =PA +PB =14（cm ）； ∴PA =PB =7cm ，故答案是：7． 10．【答案】84︒【解析】如图，连接BD ，OA ，OE ，OD ，∵四边形ABCD 是圆的内接四边形，∴180BAD C ∠+∠=︒， ∵120C ∠=︒，∴60BAD ∠=︒，∵AB AD =，∴ABD △是正三角形，∴60ABD ∠=︒，2120AOD ABD ∠=∠=︒， ∵AE 恰好是⊙的内接正十边形的一边，∴3603610AOE ︒∠==︒， ∴1203684DOE ∠=︒-︒=︒，∴ DE的度数为84°．故答案为：84°．11．【答案】120【解析】∵∠A ，∠B ，∠C 的度数之比为4∶3∶5， ∴设∠A =4x ，则∠B =3x ，∠C =5x ．∵四边形ABCD是圆内接四边形，∴∠A+∠C=180°，即4x+5x=180°，解得x=20°，∴∠B=3x=60°，∴∠D=180°–60°=120°．故答案为：120．13．【解析】（1）直线DE与⊙O相切，理由如下：如图，连接OD，∵OD=OA，∴∠A=∠ODA，∵EF是BD的垂直平分线，∴EB=ED，∴∠B=∠EDB，∵∠C=90°，∴∠A+∠B=90°，∴∠ODA+∠EDB=90°，∴∠ODE=180°–90°=90°，∴直线DE与⊙O相切；（2）连接OE，设DE=x，则EB=ED=x，CE=8–x，∵∠C=∠ODE=90°，∴OC2+CE2=OE2=OD2+DE2，∴42+（8–x）2=22+x2，解得：x=4.75，则DE=4.75．14．【解析】（1）∵E是△ABC的内心，∴∠BAE=∠CAE，∠EBA=∠EBC，∵∠BED=∠BAE+∠EBA，∠DBE=∠EBC+∠DBC，∠DBC=∠EAC，∴∠DBE=∠DEB，∴DB=DE．（2）如图，连接CD．∵AD平分∠BAC，∴∠DAB=∠DAC，∴ BD= CD，∴BD=CD，∵BD=DF，∴CD=DB=DF，∴∠BCF=90°，∴BC⊥CF，∴CF是⊙O的切线．1．【答案】A【解析】∵弦CD⊥AB于点E，CD=8cm，∴CE=12CD=4cm．在Rt△OCE中，OC=5cm，CE=4cm，∴OE=3cm，∴AE=AO+OE=5+3=8cm．故选A．2．【答案】B【解析】A、根据垂径定理不能推出AC=AB，故A选项错误；B、∵直径CD⊥弦AB，∴ AD= BD，∵ AD对的圆周角是∠C， BD对的圆心角是∠BOD，∴∠BOD=2∠C，故B选项正确；C、不能推出∠C=∠B，故C选项错误；D、不能推出∠A=∠BOD，故D选项错误；故选B．3．【答案】C【解析】设⊙O的半径为r．在Rt△ADO中，AD=5，OD=r–1，OA=r，则有r2=52+（r–1）2，解得r=13，∴⊙O的直径为26寸，故选C．4．【答案】D【解析】∵∠DAB=∠DEB，∴tan∠DAB=tan∠DEB=12．故选D．5．【答案】D【解析】如图，连接AD．∵OD是直径，∴∠OAD=90°，∵∠AOB+∠AOD=90°，∠AOD+∠ADO=90°，∴∠AOB=∠ADO，∴sin∠AOB=sin∠ADO=810=45，故选D．6．【答案】D【解析】如图，∵OA⊥BC，∴CH=BH， AC= AB，∴∠AOB=2∠CDA=60°，∴BH=OB•sin∠AOB BC=2BH D．7．【答案】B【解析】∵四边形ABCD为⊙O的内接四边形，∴∠A=180°–∠BCD=60°，由圆周角定理得，∠BOD=2∠A=120°，故选B．8．【答案】D【解析】如图，设点M为DE的中点，点N为FG的中点，连接MN交半圆于点P，此时PN取最小值．∵DE=4，四边形DEFG为矩形，∴GF=DE，MN=EF，∴MP=FN=12DE=2，∴NP=MN–MP=EF–MP=1，∴PF2+PG2=2PN2+2FN2=2×12+2×22=10．故选D．9．【答案】A【解析】如图：连接OB ，O C ．作OD ⊥BC 于D∵OB =OC ，OD ⊥BC ，∴CD =12BC ，∠COD =12∠BOC ，又∵∠BOC =2∠A ，BC ，∴∠COD =∠A ，CD ，∵sin ∠BAC =13，∴sin ∠COD =CD OC =13，∴OC ，故选A ． 10．【答案】B【解析】∵圆心到直线的距离5cm=5cm ，∴直线和圆相切．故选B ． 11．【答案】A【解析】∵MN 是⊙O 的切线，∴ON ⊥NM ，∴∠ONM =90°，∴∠ONB =90°–∠MNB =90°–52°=38°，∵ON =OB ，∴∠B =∠ONB =38°，∴∠NOA =2∠B =76°．故选A ． 12．【答案】5【解析】如图，连接OA ，∵CD =2cm ，AB =8cm ， ∵CD ⊥AB ，∴OD ⊥AB ，∴AC =12AB =4cm ，∴设半径为r ，则OD =r –2，根据题意得：r 2=（r –2）2+42，解得：r =5． ∴这个玉片的外圆半径长为5cm ．故答案为：5．13．【答案】30°【解析】如图，连接OC ．∵AB是直径， AC= CD= BD，∴∠AOC=∠COD=∠DOB=60°，∵OA=OC，∴△AOC是等边三角形，∴∠A=60°，∵CE⊥OA，∴∠AEC=90°，∴∠ACE=90°–60°=30°．故答案为30°．14．【解析】如图，延长AD交⊙O于E，∵OC⊥AD，∴ AE=2 AC，AE=2AD，∵ AB=2 AC，∴ AE= AB，∴AB=AE，∴AB=2AD．15．【解析】（1）CM与⊙O相切．理由如下：连接OC，如图，∵GD⊥AO于点D，∴∠G+∠GBD=90°，∵AB为直径，∴∠ACB=90°，∵M点为GE的中点，∴MC=MG=ME，∴∠G=∠1，∵OB=OC，∴∠B=∠2，∴∠1+∠2=90°，∴∠OCM=90°，∴OC⊥CM，∴CM为⊙O的切线；16．【解析】（1）连接DE，如图，∵∠BCD+∠DEB=180°，∴∠DEB=180°–120°=60°，∵BE为直径，∴∠BDE=90°，在Rt △BDE 中，DE =12BE =12×，BD DE ；（2）连接EA ，如图， ∵BE 为直径，∴∠BAE =90°，∵A 为 BE的中点，∴∠ABE =45°， ∵BA =AP ，而EA ⊥BA ， ∴△BEP 为等腰直角三角形， ∴∠PEB =90°，∴PE ⊥BE ， ∴直线PE 是⊙O 的切线．17．【解析】（1）∵OA =OB ，DB =DE ，∴∠A =∠OBA ，∠DEB =∠DBE ，∵EC ⊥OA ，∠DEB =∠AEC ，∴∠A +∠DEB =90°， ∴∠OBA +∠DBE =90°，∴∠OBD =90°， ∵OB 是圆的半径，∴BD 是⊙O 的切线；（2）如图，过点D 作DF ⊥AB 于点F ，连接OE ， ∵点E 是AB 的中点，AB =12， ∴AE =EB =6，OE ⊥AB ，又∵DE =DB ，DF ⊥BE ，DB =5，DB =DE ，∴EF =BF =3，∴DF =4， ∵∠AEC =∠DEF ，∴∠A =∠EDF ，∵OE ⊥AB ，DF ⊥AB ，∴∠AEO =∠DFE =90°，∴△AEO ∽△DFE ，∴EO AE FE DF =，即634EO =，得EO =4.5， ∴△AOB 的面积是：12 4.522AB OE ⋅⨯==27．。

第27讲与圆有关的位置关系(课件)中考数学一轮复习(全国通用)

【说明】掌Байду номын сангаас已知点的位置，可以确定该点到圆心的距离与
1. 点和圆的位置关系
已知⊙O的半径为r，点P到圆心O的距离为d，则：
位置关系
图形
半径的关系，反过来已知点到圆心的距离与半径的关系，可
以确定该点与圆的位置关系．
定义
性质及判定
点在圆的外部
d > r 点P在圆外
点在圆周上
d = r 点P在圆上
点在圆的内部
内切
内含
O2
d
性质及判定
无
> + ⇔两圆外离
1个切点
= + ⇔两圆外切
两个交点
− < < + ⇔两圆相交
1个切点
= − ⇔两圆内切
R
r
O1
O2
d
r
相交
公共点个数
O1
R
d
O2
rd R
O1 O2
R
r d
O1 O2
无
0 ≤ < − ⇔两圆内含
∴圆A与圆C外切，圆B与圆C相交，圆A与圆B外离，
故选：D．
）
考点二切线的性质与判定
1.切线的性质与判定
定义
线和圆只有一个公共点时，这条直线叫圆的切线，这个公共点叫做切点．
圆的切线垂直于过切点的半径．（实际上过切点的半径也可理解为过切点的直径或经过切点与圆心的直线．）
解题方法：当题目已知一条直线切圆于某一点时，通常作的辅助线是连接切点与圆心（这是圆中作辅助线的一
∴不能判定BC是⊙A切线；
故选：D．
）
考点二切线的性质与判定
题型02 利用切线的性质求线段长

最新中考数学-一轮复习：与圆有关的位置关系

与圆有关的位置关系基础知识知识点一、点与圆的位置关系1. 点和直线有三种位置关系：①点在圆外，即这个点到圆心的距离大于半径；②点在圆上，即这个点到圆心的距离等于半径；③点在圆内，即这个点到圆心的距离小于半径．2. 用数量关系表示位置关系：⊙O的半径为r，点P到圆心的距离OP＝d，则有①点P在⊙O外d＞r；②点P在⊙O上d＝r；③点P在⊙O内d＜r．知识点二、直线和圆的位置关系1．直线和圆的三种位置关系：（1）相离：直线和圆没有公共点，这时我们说这条直线和圆相离．（2）相切：直线和圆只有一个公共点，这时我们说这条直线和圆相切，这条直线叫做圆的切线，这个点叫做切点．（3）相交：直线和圆有两个公共点，这时我们说这条直线和圆相交．2、直线和圆的位置关系的性质与判断：设圆的半径为r，圆心到直线的距离为d，则：①直线和圆相离 d < r②直线和圆相切 d = r③直线和圆相交 d > r．知识点三、切线的判定定理1.切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．在应用定理时，必须先弄清两个条件：一是经过半径的外端；二是垂直于这条半径，两者缺一不可．2. 切线的判定方法有以下几种：①可以直接应用定义：直线与圆有一个公共点时，直线是圆的切线．②圆心到直线的距离等于半径的直线是圆的切线.③切线的判定定理．当已知条件中没有指出圆与直线的公共点时，常运用方法②进行判定；当已知条件中明确指出圆与直线有公共点时，常运用判定定理进行判定.证题方法“有点连半径，无点作垂线”.知识点四、切线的性质定理与切线长定理1. 切线的性质定理：圆的切线垂直于过切点的半径．当已知圆的切线时，常常连接过切点的半径，得两线垂直关系. 2.切线长定理（1）切线长的定义：过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长．（2）切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等．知识点五、三角形的外接圆与外心1. 三角形的外接圆：经过三角形的三个顶点的圆叫做三角形的外接圆．2. 三角形的外心：三角形外接圆的圆心，是三角形三条边垂直平分线的交点.这个点叫做三角形的外心．3. 三角形外心的性质：①三角形的外心是外接圆的圆心，它到三角形各顶点的距离相等；②三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的；但一个圆的内接三角形却有无数个，这些三角形的外心重合．知识点六、三角形的内切圆与内心1.三角形的内切圆是指与三角形各边都相切的圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．任意一个三角形都有且只有一个内切圆．但一个圆的外切三角形有无数个．2. 三角形的内心：三角形内切圆的圆心，是三角形三条角平分线的交点，到三角形三边的距离相等. 常见结论：（1）Rt △ABC 的三条边分别为：a 、b 、c （c 为斜边），则它的内切圆的半径2ab cr ；（2）△ABC 的周长为l ，面积为S ，其内切圆的半径为r ，则12S lr ．知识点七、正多边形与圆的关系1. 正多边形的概念：各边相等，各角也相等的多边形叫做正多边形．2. 正多边形与圆的关系可以这样表述：把圆分成n （n≥3）等份，依次连接各分点所得的多边形就是这个圆的内接正n 边形.利用这一关系可以判定一个多边形是否是正多边形或作出一个正多边形．这个圆是这个正多边形的外接圆.正多边形的外接圆的圆心叫做这个正多边形的中心．外接圆的半径叫做这个正多边形的半径．正多边形每一边所对的圆心角叫做正多边形的中心角．3. 对称性：①正多边形的轴对称性：正多边形都是轴对称图形，一个正n 边形共有n 条对称轴，每条对称轴都通过正n 边形的中心．②正多边形的中心对称性：边数为偶数的正多边形是中心对称图形，它的中心是对称中心． ③正多边形的旋转对称性：正多边形都是旋转对称图形，最小的旋转角等于中心角．典型例题解析例1. 已知点P到⊙O上的点的最短距离为3cm，最长距离为5cm，则⊙O的半径为cm．例2. 已知⊙O的半径长为2cm，如果直线l上有一点P满足PO=2cm，那么直线l与⊙O的位置关系是（）A．相切B．相交C．相离或相切D．相切或相交例3. Rt△ABC中，∠C=90°，AC=5，BC=12，如果以点C为圆心，r为半径，且⊙C与斜边AB仅有一个公共点，那么半径r的取值范围是.例4. （朝阳）如图，△MBC中，∠B=90°，∠C=60°，MB=23，点A在MB上，以AB为直径作⊙O与MC相切于点D，则CD的长为（）A．2B．3C．2 D．3例5. （葫芦岛）如图，边长为a的正六边形内有一边长为a的正三角形，则SS阴影空白（）A．3 B．4 C．5 D．6例6. 如图：⊙I是Rt△ABC的内切圆，∠C=90°，AC=6，BC=8，则⊙I的半径是.例7. （锦州）已知，⊙O为∆ABC的外接圆，BC为直径，点E在AB上，过点E作EF⊥BC，点G在FE 的延长线上，且GA=GE．（1）求证：AG与⊙O相切．（2）若AC=6，AB=8，BE=3，求线段OE的长．（2）过点O作OH⊥AB，垂足为H，例8. （来宾）如图，AB为⊙O的直径，BF切⊙O于点B，AF交⊙O于点D，点C在DF上，BC交⊙O 于点E,且∠BAF=2∠CBF,CG⊥BF于点G.连接AE.(1) 直接写出AE与BC的位置关系；(2) 求证：△BCG∽△ACE ；(3) 若∠F=60°，GF=1，求⊙O得半径.巩固训练1. （青岛）直线l与半径为r的⊙O相交，且点O到直线l的距离为6，则r的取值范围是（）A．r＜6 B．r=6 C．r＞6 D．r≥62. 在⊙O中，圆心O在坐标原点上，半径为210，点P的坐标为（4，5），那么点P与⊙O的位置关系是（）A．点P在⊙O外B．点P在⊙O上C．点P在⊙O内D．不能确定3. 已知正三角形外接圆半径为3，这个正三角形的边长是（）A．2 B．3 C．4 D．54. （天津）如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心．若∠B=25°，则∠C的大小等于（）A．20°B．25°C．40°D．50°△放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上，用一个圆面5. 如下图，将ABC△，能够完全覆盖这个三角形的最小圆面的半径是________．去覆盖ABC6. （曲靖）如图,正六边形ABCDEF的边长为2，则对角线AE的长是.7. （莱芜）如图，正五边形ABCDE中，连接AC、AD、CE,CE交AD于点F，连接BF,下列说法不正确的是（）A. △CDF的周长等于AD＋CDB. FC平分∠BFDC. AC2＋BF2＝4CD2D. DE2＝EF·CE8. （广安）如图，矩形ABCD的长为6，宽为3，点O1为矩形的中心，⊙O2的半径为1，O1O2⊥AB于点P，O1O2＝6，若⊙O2绕点P按顺时针方向旋转360°，在旋转过程中，⊙O2与矩形的边只有一个公共点的情况一共出现（）A．3次B．4次C．5次D．6次9. （日照）如图，在Rt△OAB中，OA=4，AB=5，点C在OA上，AC=1，⊙P的圆心P在线段BC上，且⊙P与边AB，AO都相切.若反比例函数kyx（k≠0）的图象经过圆心P，则k= ．10. （德州）如图，⊙O的直径AB为10cm，弦BC为6cm，D、E分别是∠ACB的平分线与⊙O，AB的交点，P为AB延长线上一点，且PC＝PE.（1）求AC，AD的长；（2）试判断直线PC与⊙O的位置关系，并说明理由.11. （河南）如图，CD是⊙O的直径，且CD=2cm，点P为CD的延长线上一点，过点P作⊙O的切线P A、PB，切点分别为点A、B.（1）连接AC，若∠APO=30°，试证明△ACP是等腰三角形；（2）填空：①当DP= cm时，四边形AOBD是菱形；②当DP=cm时，四边形AOBP是正方形.12. （抚州）如图，在平面直角坐标系中，⊙P经过x轴上一点C，与y轴分别相交于A，B两点，连接AP 并延长分别交⊙P、x轴于点D、点E，连接DC并延长交y轴于点F，若点F的坐标为(0，1)，点D的坐标为(6，－1).(1)求证：DC＝FC.(2)判断⊙P与x轴的位置关系，并说明理由.(3)求直线AD的解析式.中考预测1. 在直角坐标平面内，点A的坐标为（1，0），点B的坐标为（a，0），圆A的半径为2．下列说法中不正确的是（）A．当a=-1时，点B在圆A上B．当a＜1时，点B在圆A内C．当a＜-1时，点B在圆A外D．当-1＜a＜3时，点B在圆A内2. 如图，△ABC的边AC与⊙O相交于C，D两点，且经过圆心O，边AB与⊙O相切，切点为B．已知∠A ＝30°，则∠C的大小是( )A．30°B．45°C．60°D．40°3. 如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为(－3, 0)，将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为（）A．1 B．1或5 C．3 D．54. 如图，P为⊙O的直径BA延长线上一点，PC与⊙O相切，切点为C，点D是⊙O上一点，连接PD. 已知PC=PD=BC. 下列结论：（1）PD与⊙O相切；（2）四边形PCBD是菱形；（3）PO=AB；（4）∠PDB=120°. 其中正确的个数为（）A. 4个B. 3个C. 2个D. 1个5. ⊙O的半径为R，点O到直线l的距离为d，R，d是方程x2－4x+m=0的两根，当直线l与⊙O相切时，m的值为．6. 直角三角形的两边长分别为16和12，则此三角形的外接圆半径是．7. 已知∠BAC=45°，一动点O在射线AB上运动（点O与点A不重合），设OA=x，如果半径为1的⊙O与射线AC只有一个公共点，那么x的取值范围是．8. 如图，两圆圆心相同，大圆的弦AB与小圆相切，AB＝8，则图中阴影部分的面积是__________．(结果保留π)9. 如图，正方形ABCD的边长为2，⊙O的直径为AD，将正方形沿EC折叠，点B落在圆上的F点，则BE的长为．10. 如图，Rt△ABC中，∠ABC=90°.以AB的中点O为圆心、OA长为半径作半圆，交AC于点D.点E为BC的中点，连接DE.（1）求证：DE是该半圆的切线；（2）若∠BAC=30°，DE=2，求AD的长.11．如图，已知等腰三角形ABC的底角为30°，以BC为直径的⊙O与底边AB交于点D，过D作DE AC，垂足为E.（1）证明：DE为⊙O的切线；（2）连接OE，若BC=4，求△OEC的面积.12. 如图，AB 是⊙O 的直径，点C 在⊙O 上，与⊙O 相切， BD ∥AC ． (1)图中∠OCD ＝_______°，理由是_____________________； (2)⊙O 的半径为3，AC ＝4，求OD 的长．13. 阅读材料：已知，如图(1)，在面积为S 的△ABC 中， BC ＝a ，AC ＝b ， AB ＝c ，内切圆O 的半径为r.连接OA 、OB 、OC ，△ABC 被划分为三个小三角形． ∵r c b a r AB r AC r BC S S S S OAB OAC OBC )(21212121++=⋅+⋅+⋅=++=△△△.. ∴cb a Sr ++=2．(1)类比推理：若面积为S 的四边形ABCD 存在内切圆(与各边都相切的圆)，如图(2)，各边长分别为AB ＝a ，BC ＝b ，CD ＝c ，AD ＝d ，求四边形的内切圆半径r ；(2)理解应用：如图(3)，在等腰梯形ABCD 中，AB ∥DC ，AB ＝21，CD ＝11，AD ＝13，⊙O 1与⊙O 2分别为△ABD 与△BCD 的内切圆，设它们的半径分别为r 1和r 2，求21r r 的值.参考答案：巩固训练∵∠ODE=∠DEA=90°，∴OD∥AC,∴11313222 OCES CE DE∆=⨯⨯=⨯=.13. 【解析】 (1)连接OA 、OB 、OC 、OD. ∵AOD COD BOC AOB S S S S S △△△△+++=dr cr br ar 21212121+++=r d c b a )(21+++=。

中考数学专题特训第二十四讲：与圆有关的位置关系(含详细参考答案)

中考数学专题复习第二十四讲与圆有关的位置关系【基础知识回顾】一、点与圆的位置关系：1、点与圆的位置关系有种，若圆的半径为r点P到圆心的距离为d则：点P在圆内<＝> 点P在圆上<＝>点P在圆外<＝>2、过三点的圆：⑴过同一直线上三点作用，过三点，有且只有一个圆⑵三角形的外接圆：经过三角形各顶点的圆叫做三角形的外接圆的圆心叫做三角形的这个三角形叫做这个圆的⑶三角形外心的形成：三角形的交点，外心的性质：到相等【赵老师提醒：1、锐角三角形外心在三角形直角三角形的外心是锐角三角形的外心在三角形】一、直线与圆的位置关系：1、直线与圆的位置关系有种：当直线和圆有两个公共点时，叫做直线和圆直线叫圆的线，这的直线叫做圆的直线和圆没有公共点时，叫做直线和圆2、设Qo的半径为r，圆心o到直线l的距离为d，则：直线l与Qo相交<＝>d r,直线l与Qo相切<＝>d r直线l与Qo相离<＝>d r3、切线的性质和判定：⑴性质定理：圆的切线垂直于经过切点的【赵老师提醒：根据这一定理，在圆中遇到切线时，常用连接圆心和切点，即可的垂直关系】⑵判定定理：经过半径的且这条半径的直线式圆的切线【赵老师提醒：在切线的判定中，当直线和圆的公共点标出时，用判定定理证明。

当公共点未标出时，一般可证圆心到直线的距离d=r来判定相切】4、切线长定理：⑴切线长定义：在经过圆外一点的圆的切线上，这点和切点之间的长叫做这点到圆的切线长。

⑵切线长定理：从圆外一点到圆的两条切线，它们的相等，并且圆心和这一点的连线平分的夹角5、三角形的内切圆：⑴与三角形各边都的圆，叫做三角形的内切圆，内切圆的圆心叫做三角形的⑵三角形内心的形成：是三角形的交点内心的性质：到三角形各的距离相等，内心与每一个顶点的连接线平分【赵老师提醒：三类三角形内心都在三角形若△ABC三边为a、b、c面积为s，内切圆半径为r，则s= ，若△ABC为直角三角形，则r= 】二、圆和圆的位置关系：圆和圆的位置关系有种，若Qo1半径为R，Qo2半径为r，圆心距外，则Qo1 与Qo2 外距<＝> Qo1 与Qo2 外切<＝>两圆相交<＝> 两圆内切<＝>两圆内含<＝>【赵老师提醒：两圆相离无公共点包含和两种情况，两圆相切有唯一公共点包含和两种情况，注意题目中两种情况的考虑圆心同是两圆此时d= 】三、反证法：假设命题的结论，由此经过推理得出由矛盾判定所作的假设从而得到原命题成立，这种证明命题的方法叫反证法【赵老师提醒：反证法正题的关键是提出即假设所证结论的反面成立，择推理论证得出的矛盾可以与相矛盾，也可以与相矛盾，从而肯定原命题成立】【典型例题解析】考点一：切线的性质线，证明：AB=4PD．考点：切线的性质；等边三角形的判定与性质；含30度角的直角三角形；圆心角、弧、弦的关系；圆周角定理．专题：几何综合题．分析：（1）PO与BC的位置关系是平行；（2）（1）中的结论成立，理由为：由折叠可知三角形APO与三角形CPO全等，根据全等三角形的对应角相等可得出∠APO=∠CPO，再由OA=OP，利用等边对等角得到∠A=∠APO，等量代换可得出∠A=∠CPO，又根据同弧所对的圆周角相等得到∠A=∠PCB，再等量代换可得出∠COP=∠ACB，利用内错角相等两直线平行，可得出PO与BC平行；（3）由CD为圆O的切线，利用切线的性质得到OC垂直于CD，又AD垂直于CD，利用平面内垂直于同一条直线的两直线平行得到OC与AD平行，根据两直线平行内错角相等得到∠APO=∠COP，再利用折叠的性质得到∠AOP=∠COP，等量代换可得出∠APO=∠AOP，再由OA=OP，利用等边对等角可得出一对角相等，等量代换可得出三角形AOP三内角相等，确定出三角形AOP为等边三角形，根据等边三角形的内角为60°得到∠AOP为60°，由OP 平行于BC，利用两直线平行同位角相等可得出∠OBC=∠AOP=60°，再由OB=OC，得到三角形OBC为等边三角形，可得出∠COB为60°，利用平角的定义得到∠POC也为60°，再加上OP=OC，可得出三角形POC为等边三角形，得到内角∠OCP为60°，可求出∠PCD为30°，在直角三角形PCD中，利用30°所对的直角边等于斜边的一半可得出PD为PC的一半，而PC等于圆的半径OP等于直径AB的一半，可得出PD为AB的四分之一，即AB=4PD，得证．解答：解：（1）PO与BC的位置关系是PO∥BC；（2）（1）中的结论PO∥BC成立，理由为：由折叠可知：△APO≌△CPO，∴∠APO=∠CPO，又∵OA=OP，∴∠A=∠APO，∴∠A=∠CPO，又∵∠A与∠PCB都为PB所对的圆周角，∴∠A=∠PCB，∴∠CPO=∠PCB，对应训练1．（2012•玉林）如图，已知点O为Rt△ABC斜边AC上一点，以点O为圆心，OA长为半径的⊙O与BC相切于点E，与AC相交于点D，连接AE．（1）求证：AE平分∠CAB；（2）探求图中∠1与∠C的数量关系，并求当AE=EC时，tanC的值．考点：切线的性质；特殊角的三角函数值．专题：探究型．分析：（1）连接OE，则OE⊥BC，由于AB⊥BC，故可得出AB∥OE，进而可得出∠2=∠AEO，由于OA=OE，故∠1=∠AEO，进而可得出∠1=∠2；（2）由三角形外角的性质可知∠1+∠AEO=∠EOC，，因为∠1=∠AEO，∠OEC=90°，所以2∠1+∠C=90°；当AE=CE时，∠1=∠C，再根据2∠1+∠C=90°即可得出∠C的度数，由特殊角的三角函数值得出tanC即可．解答：（1）证明：连接OE，∵⊙O与BC相切于点E，∴OE⊥BC，∴∠OBP+∠ABP=90°，∠ACP+∠APC=90°，∵OP=OB，∴∠OBP=∠OPB，∵∠OPB=∠APC，∴∠ACP=∠ABC，∴AB=AC；（2）延长AP交⊙O于D，连接BD，∵设圆半径为r，则OP=OB=r，PA=5-r，∴AB2=OA2-OB2=52-r2，AC2=PC2-PA2=(25)2-（5-r）2，∴52-r2=(25)2-（5-r）2，解得：r=3，∴AB=AC=4，∵PD是直径，∴∠PBD=90°=∠PAC，∵∠DPB=∠CPA，∴△DPB∽△CPA，∴CP AP PD BP=，∴2553 33BP-=+，解得：PB=655．考点二：切线的判定（2）解：作BG⊥CD，垂足是G，在Rt△ABD中∵AB=10，sin∠DAB=35，又∵sin∠DAB=BD AB，∴BD=6∵C是弧AB的中点，∴∠ADC=∠CDB=45°，∴BG=DG=BDsin45°=6×22=32，∵∠DAB=∠DCB∴tan∠DCB=BGCG=34，∴CG=42，∴CD=CG+DG=42+32=72，∴S△CBD=12CD•BG=7232212⨯=．点评：本题考查的是切线的判定定理，涉及到圆周角定理、解直角三角形及三角形的面积公式，根据题意作出辅助线，构造出直角三角形是解答此题的关键．对应训练考点三：三角形的外接圆和内切圆例4 （2012•阜新）如图，在△ABC中，BC=3cm，∠BAC=60°，那么△ABC能被半径至少为cm的圆形纸片所覆盖．考点：三角形的外接圆与外心；圆周角定理；锐角三角函数的定义．专题：计算题．分析：作圆O的直径CD，连接BD，根据圆周角定理求出∠D=60°，根据锐角三角函数的定义得出sin∠D= BCCD，代入求出CD即可．解答：解：作圆O的直径CD，连接BD，∵弧BC对的圆周角有∠A、∠D，∴∠D=∠A=60°，∵直径CD，A．r B．2r C．2r D．2r考点：三角形的内切圆与内心；矩形的判定；正方形的判定；切线长定理．专题：计算题．分析：连接OD、OE，求出∠ODB=∠DBE=∠OEB=90°，推出四边形ODBE是正方形，得出BD=BE=OD=OE=r，根据切线长定理得出MP=DM，NP=NE，代入MB+NB+MN得出BD+BE，求出即可．解答：解：连接OD、OE，∵⊙O是Rt△ABC的内切圆，∴OD⊥AB，OE⊥BC，∵∠ABC=90°，∴∠ODB=∠DBE=∠OEB=90°，∴四边形ODBE是矩形，∵OD=OE，∴矩形ODBE是正方形，∴BD=BE=OD=OE=r，∵⊙O切AB于D，切BC于E，切MN于P，∴MP=DM，NP=NE，∴Rt△MBN的周长为：MB+NB+MN=MB+BN+NE+DM=BD+BE=r+r=2r，故选C．点评：本题考查的知识点是矩形的判定、正方形的判定、三角形的内切圆和内心、切线长定理等，主要考查运用这些性质进行推理和计算的能力，题目比较好，难度也适中．对应训练4．（2012•台州）已知，如图1，△ABC中，BA=BC，D是平面内不与A、B、C重合的任意一点，∠ABC=∠DBE，BD=BE．（1）求证：△ABD≌△CBE；∴sin∠D=BCCD=45，∴CD=25 4，答：三角形ABC外接圆的直径是254．（2）解：连接IC、BI，且延长BI交AC于F，过I作IE⊥AB于E，∵AB=BC=5，I为△ABC内心，∴BF⊥AC，AF=CF，∵sin∠A=45=BFAB，∴BF=4，在Rt△ABF中，由勾股定理得：AF=CF=3，AC=2AF=6，∵I是△ABC内心，IE⊥AB，IF⊥AC，IG⊥BC，∴IE=IF=IG，设IE=IF=IG=R，∵△ABI、△ACI、△BCI的面积之和等于△ABC的面积，∴12AB×R+12BC×R+12AC×R=12AC×BF，即5×R+5×R+6×R=6×4，∴R=32，在△AIF中，AF=3，IF=32，由勾股定理得：AI=352．答：AI的长是352．点评：本题考查了三角形的面积公式，三角形的内切圆和内心，勾股定理，等腰三角形的性质，圆周角定理等知识点的应用，主要考查学生运用性质进行推理和计算的能力，题目综合性比较强，有一定的难度．考点三：圆与圆的位置关系例6（2012•毕节地区）第三十奥运会将于2012年7月27日在英国伦敦开幕，奥运会旗图案有五个圆环组成，如图也是一幅五环图案，在这个五个圆中，不存在的位置关系是（）A．外离B．内切C．外切D．相交考点：圆与圆的位置关系．分析：根据两圆的位置关系易得到它们的位置关系有外切、外离、相交．解答：解：观察图形，五个等圆不可能内切，也不可能内含，并且有的两个圆只有一个公共点，即外切；有的两个圆没有公共点，即外离；有的两个圆有两个公共点，即相交．故选B．点评：本题考查了圆与圆的位置关系：若两圆的半径分别为R，r，圆心距为d，若d＞R+r，两圆外离；若d=R+r，两圆外切；若R-r＜d＜R+r（R≥r），两圆相交；若d=R-r（R＞r），两圆内切；若0≤d＜R-r（R＞r），两圆内含．对应训练6．（2012•德阳）在平面直角坐标系xOy中，已知点A（0，2），⊙A的半径是2，⊙P的半径是1，满足与⊙A及x轴都相切的⊙P有个．6．4考点：圆与圆的位置关系；坐标与图形性质；直线与圆的位置关系．分析：分两圆内切和两圆外切两种情况讨论即可得到⊙P的个数．解答：解：如图，满足条件的⊙P有4个，故答案为4．点评：本题考查了圆与圆的位置关系、坐标与图形的性质及直线与圆的知识，能充分考虑到分内切和外切是解决本题的关键．【聚焦山东中考】1．（2012•济南）已知⊙O1和⊙O2的半径是一元二次方程x2-5x+6=0的两根，若圆心距O1O2=5，则⊙O1和⊙O2的位置关系是（）A．外离B．外切C．相交D．内切考点：圆与圆的位置关系．分析：先根据一元二次方程根与系数的关系，可知圆心距=两圆半径之和，再根据圆与圆的位置关系即可判断．解答：解：∵⊙O1和⊙O2的半径是一元二次方程x2-5x+6=0的两根，∴两根之和=5=两圆半径之和，又∵圆心距O1O2=5，∴两圆外切．故选B．点评：此题综合考查一元二次方程根与系数的关系及两圆的位置关系的判断．圆和圆的位置与两圆的圆心距、半径的数量之间的关系：①两圆外离⇔d＞R+r；②两圆外切⇔d=R+r；③两圆相交⇔R-r＜d＜R+r（R≥r）；④两圆内切⇔d=R-r（R＞r）；⑤两圆内含⇔d＜R-r（R＞r）．2．（2012•青岛）已知，⊙O1与⊙O2的半径分别是4和6，O1O2=2，则⊙O1与⊙O2的位置关系是（）A．内切B．相交C．外切D．外离考点：圆与圆的位置关系．分析：由⊙O1与⊙O2的半径分别是4和6，O1O2=2，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可得出两圆位置关系．解答：解：∵⊙O1与⊙O2的半径分别是4和6，O1O2=2，∴O1O2=6-4=2，∴⊙O1与⊙O2的位置关系是内切．故选A．点评：此题考查了圆与圆的位置关系．此题比较简单，注意掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系是解此题的关键．3．（2012•泰安）如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC，若∠ABC=120°，OC=3，则BC的长为（）A．π B．2πC．3π D．5π考点：切线的性质；弧长的计算．分析：连接OB，由于AB是切线，那么∠ABO=90°，而∠ABC=120°，易求∠OBC，而OB=OC，那么∠OBC=∠OCB，进而求出∠BOC的度数，在利用弧长公式即可求出BC的长．解答：解：连接OB，∵AB与⊙O相切于点B，∴∠ABO=90°，∵∠ABC=120°，∴∠OBC=30°，∵OB=OC，∴∠OCB=30°，∴∠BOC=120°，∴ BC 的长为nπr 180 =120×π×3 180 =2π，故选B．点评：本题考查了切线的性质、弧长公式，解题的关键是连接OB，构造直角三角形．4．（2012•潍坊）已知两圆半径r1、r2分别是方程x2-7x+10=0的两根，两圆的圆心距为7，则两圆的位置关系是（）A．相交B．内切C．外切D．外离考点：圆与圆的位置关系；解一元二次方程-因式分解法．分析：首先解方程x2-7x+10=0，求得两圆半径r1、r2的值，又由两圆的圆心距为7，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可得出两圆位置关系．解答：解：∵x2-7x+10=0，∴（x-2）（x-5）=0，∴x1=2，x2=5，即两圆半径r1、r2分别是2，5，∵2+5=7，两圆的圆心距为7，∴两圆的位置关系是外切．故选C．点评：此题考查了圆与圆的位置关系与一元二次方程的解法．此题比较简单，注意掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系是解此题的关键．5．（2012•济南）如图，在Rt△ABC中，∠B=90°，AB=6，BC=8，以其三边为直径向三角形外作三个半圆，矩形EFGH的各边分别与半圆相切且平行于AB或BC，则矩形EFGH的周长是．5．4848考点：切线的性质；勾股定理；矩形的性质．分析：首先取AC的中点O，过点O作MN∥EF，PQ∥EH，由题意可得PQ⊥EF，PQ⊥GH，MN⊥EH，MN⊥FG，PL，KN，OM，OQ分别是各半圆的半径，OL，OK是△ABC的中位线，又由在Rt△ABC中，∠B=90°，AB=6，BC=8，即可求得个线段长，继而求得答案．解答：解：取AC的中点O，过点O作MN∥EF，PQ∥EH，∵四边形EFGH是矩形，∴EH∥PQ∥FG，EF∥MN∥GH，∠E=∠H=90°，∴PQ⊥EF，PQ⊥GH，MN⊥EH，MN⊥FG，∵AB∥EF，BC∥FG，∴AB∥MN∥GH，BC∥PQ∥FG，∴AL=BL，BK=CK，∴OL=12BC=12×8=4，OK=12AB=12×6=3，∵矩形EFGH的各边分别与半圆相切，∴PL=12AB=12×6=3，KN=12BC=12×8=4，在Rt△ABC中，AC= ，∴OM=OQ=12AC=5，∴EH=FG=PQ=PL+OL+OQ=3+4+5=12，EF=GH=MN=OM+OK+NK=5+3+4=12，∴矩形EFGH的周长是：EF+FG+GH+EH=12+12+12+12=48．故答案为：48．点评：此题考查了切线的性质、矩形的性质，三角形中位线的性质以及勾股定理等知识．此题难度较大，解题的关键是掌握辅助线的作法，注意数形结合思想的应用．6．（2012•菏泽）如图，PA，PB是⊙O是切线，A，B为切点，AC是⊙O的直径，若∠P=46°，则∠BAC= 度．6．23考点：切线的性质．专题：计算题．分析：由PA、PB是圆O的切线，根据切线长定理得到PA=PB，即三角形APB为等腰三角形，由顶角的度数，利用三角形的内角和定理求出底角的度数，再由AP为圆O的切线，得到OA与AP垂直，根据垂直的定义得到∠OAP为直角，再由∠OAP-∠PAB即可求出∠BAC 的度数．解答：解：∵PA，PB是⊙O是切线，∴PA=PB，又∠P=46°，∴∠PAB=∠PBA=180-462=67°，又PA是⊙O是切线，AO为半径，∴OA⊥AP，∴∠OAP=90°，∴∠BAC=∠OAP-∠PAB=90°-67°=23°．故答案为：23。

与圆有关的位置关系-2022年中考数学一轮复习满分突破精讲精练(全国通用) (解析版)

2.19 与圆有关的位置关系一、点与圆的位置关系1、设圆的半径为r，点到圆心的距离为d，则（1）点在圆内⇔d r<；（2）点在圆上⇔d r=；（3）点在圆外⇔d r>；2、不在同一条直线上的三个点确定一个圆.3、经过三角形的三个顶点可以作一个圆，这个圆叫做三角形的外接圆. 外接圆的圆心是三角形三条边的垂直平分线的交点，叫做这个三角形的外心.二、直线与圆的位置关系1、设圆的半径为r，圆心到直线的距离为d，则（1）直线与圆相交（图1）⇔d r<⇔有两个交点；（2）直线与圆相切（图2）⇔d r=⇔有一个交点；（3）直线与圆相离（图3）⇔d r>⇔无交点；2、相关概念：（1）直线和圆有两个公共点，这时我们说这条直线和圆相交，这条直线叫做圆的割线.（2）直线和圆有一个公共点，这时我们说这条直线和圆相切，这条直线叫做圆的切线，这个点叫做切点.（3）直线和圆没有公共点，这时我们说这条直线和圆相离，（4）切线长：经过圆外一点的圆切线上，这点和圆的切点之间的线段的长，叫做这点到圆的切线长.（5）与三角形三边都相切的圆叫做三角形的内切圆，内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心.3、相关定理：知识回顾（1）切线的判定定理：经过半径外端且垂直于半径的直线是圆的切线. （2）切线的性质定理：圆的切线垂直于过切点的半径；推论1：过圆心垂直于切线的直线必过切点；推论2：过切点垂直于切线的直线必过圆心.以上三个定理及推论也称二推一定理：即：①过圆心；②过切点；③垂直切线，三个条件中知道其中两个条件就能推出最后一个.（3）切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.三、圆和圆的位置关系1、设两圆的半径分别为R 、r （R >r ），圆心距为d ，则（1）两圆外离（图1）⇔d R r >+⇒无交点；（2）两圆外切（图2）⇔d R r =+⇒有一个交点；（3）两圆相交（图3）⇔d R r R r -<<+⇔有两个交点；（4）两圆内切（图4）⇔d R r =-⇒ 有一个交点；（5）两圆内含（图5）⇔d R r <-⇒无交点；2、相关概念：（1）如果两个圆没有公共点，那么这两个圆相离，分为外离（图1）和内含（图5）两种情况；（2）如果两个圆只有一个公共点，那么这两个圆相切，分为外切（图2）和内切（图4）两种情况；（3）如果两个圆有两个公共点，那么这两个圆相交.考点一：点与圆的位置关系考点精讲O的半径为5cm，点P到圆心O的距离OP=6cm，则点P（）A.在⊙O外B.在⊙O上C.在⊙O内D.不能确定【答案】A【解析】解：∵OP=6cm＞5cm，∴点P在⊙O外．故选A．【点评】利用点与圆的位置关系的判断方法求解．变式跟进1如图，△ABC中，∠C=90°，AB=5，AC=4，且点D，E分别是AC，AB的中点，若作半径为3的⊙C，则下列选项中的点在⊙C外的是（）A.点BB.点DC.点ED.点A【答案】D【解析】解：∵∠C=90°，AB=5，AC=4，∴BC=3，∵且点D，E分别是AC，AB的中点，∴CD=2，CE= 52，∴点B在⊙C上，∴点E在⊙C内，∵BC=3，∴点D在⊙C内，∴点A在⊙C外，故选：D．【点评】分别求出AC、CE、BC、CD的长，根据点与圆的位置关系的判断方法进行判断即可．考点二：确定圆的条件AB的垂直平分线交弧AB于点C，交弦AB于点D．已知：A B=24cm，CD=8cm．例1例2（1）求作此残片所在的圆（不写作法，保留作图痕迹）；（2）求（1）中所作圆的半径．【答案】答案见解析【解析】（1）解：作弦AC的垂直平分线与弦AB的垂直平分线交于O点，以O为圆心OA 长为半径作圆O就是此残片所在的圆，如图．（2）解：连接OA，设OA=x，AD=12cm，OD=（x﹣8）cm，则根据勾股定理列方程：x2=122+（x﹣8）2，解得：x=13．答：圆的半径为13cm．【点评】（1）根据垂径定理作图即可。

圆与圆的位置关系复习课

圆与圆的位置关系复习课
1．圆与圆的位置关系：设两圆的半径为R 和r，圆心距d，则（1）两圆外离，等价于d>R＋r，此时有四条公切线；（2）两圆外切，等价于d＝R ＋r，此时有三条公切线；（3）两圆相交，等价于∣R－r ∣<d<R+r，此时有
两条公切线；（4）两圆内切，等价于d＝∣R－r ∣，此时有一条公切线；（5）两圆内含，等价于0≤d<∣R－r ∣，此时无公切线．
圆与圆的位置关系
2．两圆连心线的性质：（1）相交两圆的连心线垂直平分公共弦；（2）相切的两圆的连心线经过切点，并且垂直于过
切点的切线．
3．两圆外公切线长和内公切线长的计算公式：设两圆的半径为R 和r，圆心距为d，则
两圆外公切线长L＝两圆内公切线长L＝
1、已知⊙O1 与⊙O2 的半径分别为5cm 和3cm，圆心距O1O2=7cm，则⊙O1 与⊙O2 的位置关系为。

2、如图，PT 是外切两圆的公切线，
T 为切点，PAB，PCD 分别为这两
圆的割线，若PA=3，AB=3，PC=2，
则PD= 。

3、相切两圆的圆心距为6，
其中一圆的半径为4，
则另一圆的半径为。

相交92 或104、已知相交两圆的半径分别为5 和4，公共弦长是6，。

圆与圆的位置关系

O
. .
5 R
解：设⊙P的半径为R
P
(1)若⊙O与⊙P外切，则 R =op-5=8-5 则 R =8-5 R=3 cm (2)若⊙O与⊙P内切，则 R=OP+5=8， R=13 cm 综上⊙P的半径为3cm或13cm
5
O
. .
R
P
练习3.两圆的半径之比为5:3，当两圆相切时，圆心距为8cm，求两圆的半径？
外离
外切
相交
O1O2>R+r
R r
O1O2=R+r
R
R-r<O1O2<R+r
R
r
O1 O2
O1 O2
r
O1O2
内切
内含
同心圆 (一种特殊的内含)
O1O2=R-r
0≤O1O2<R-r
O1O2=0
歌诀：
计算差与和，两圆相切了
大于和，各管各
（相切）
（相离）
小于差，中间落
大差小和双手握相切两圆的性质
（内含）
O2
d
O1 A
d
B
精彩源于发现
外离
o1 R d
r o2
d>R+r
外切
o1
T
o2
R d
r
d=R+r
内切
o2 o1
T
r R
d
d=R-r (R>r)
相交
R-r<d<R+r
(R>r)
o1
R
d
r
o2
o1
o2
o1
o2
o1 o 2
d=R+r

与圆有关的位置关系重难点研习

与圆有关的位置关系重难点研习研习点1点与圆的位置关系1.点与圆的位置关系⑴如图,设⊙O的半径为r,①若点A在⊙O内,则OA＜r;反过来,若OA＜r,则点A在⊙O内.②若点B在⊙O上,则OB=r;反过来,则OB=r,则点B在⊙O上. ③若点C在⊙O外,则OC＞r; 反过来,若OC＞r,则点C在⊙O外.⑵其关系列表如下:其中:r为圆的半径,d为点到圆心的距离.[类比·扩展]⑴点与圆的位置关系,与初一学习的点与角的位置关系一样,也有三种情况.⑵如果一个几何图形是封闭图形,点与该封闭图形的位置关系一般都有三种情况:点在此封闭图形内;点在此封闭图形上;点在此封闭图形外.⑶圆心只是用来确定圆的位置, 圆心不是圆的一个部分, 圆心在圆内.2.我们知道:两点确定一条直线,那么至少需要多少个点可以确定一个圆呢?[归纳·总结]⑴过一点A 可以画无数个圆,圆心是除点A 外任意一点．⑵过两点A 、B 可以画无数个圆,这些圆的圆心在AB 的垂直平分线上．⑶不在同一直线上的三个点确定一个圆．如上图示，过三点Ａ、Ｂ、Ｃ所作的圆Ｏ的圆心在线段ＡＢ、ＢＣ的垂直平分线的交点处。

如果A 、B 、C 三点在一条直线上,不能画出经过这三点的圆．因为AB 、BC 的垂直平分线互相平行,没有交点,所以过同一直线上的三点不能画圆 3.三角形与圆经过三角形三个顶点的圆叫做三角形的外接圆．三角形外接圆的圆心叫做这个三角形的外心．这个三角形叫做这个圆的内接三角形．三角形的外心就是三角形三条边的垂直平分线的交点, [梳理·总结]⑴任何一个三角形都有一个外接圆,而一个圆有无数个内接三角形.⑵锐角三角形的外心在锐角三角形的内部;直角三角形的外心在斜边的中点;钝角三角形的外心在钝角三角形的外部. 反之亦然.⑶三角形的外心到三角形三个顶点的距离相等.典例1:如图,已知 ⊙O 的半径为r ＝10 ,圆心O 到直线l 的距离OD ＝6 ,在直线l 上有A 、B 、C 三点,且AD ＝6 ,BD ＝8 ,CD ＝53 ．问A 、B 、C 三点对于⊙O 的位置关系各是怎样?【研析】只要计算出这些点到圆心的距离,看其是大于、等于还是小于圆的半径,就可以相应得出点在圆外、圆上、圆内的位置关系来．解:连结OA,在Rt △AOD 中,72=6+6=+=2222AD OD OA ＜10,即OA ＜r,则点A 在⊙O 内;同理,108622=+=OB ,即O B =r,则点B 在⊙O 上;111=)35(+5=22OC ＞10, 即OC ＞r,则点C 在 ⊙O 外．研习点2 直线与圆的位置关系 1.直线与圆的位置关系直线与圆的位置关系有三种:⑴如果一条直线与一个圆没有公共点,那么就说这条直线与这个圆相离.⑵如果一条直线与一个圆只有一个公共点,那么就说这条直线与这个圆相切,此时这条直线叫做圆的切线,这个公共点叫做切点.⑶如果一条直线与一个圆有两个公共点,那么就说这条直线与这个圆相交,此时这条直线叫做圆的割线,这两个公共点叫做交点. 2.直线与圆的位置关系的特征与识别典例2:在平面直角坐标系中,以A (1,2)为圆心的圆的半径满足下列条件时,分别求出其半径的取值范围:⑴与坐标轴只有唯一交点;⑵与坐标轴只有两个交点;⑶与坐标轴只有三个交点;⑷与坐标轴有四个交点.【研析】因为点A 到x 轴的距离是2,到y 轴的距离是1,所以与坐标轴只有唯一交点,就是与y 轴相切而与x 轴相离;与坐标轴只有两个交点,就是与y 轴相交而与x 轴相离;与坐标轴只有三个交点,就是与y 轴相交而与x 轴相切;与坐标轴有四个交点,就是与x 轴、y 轴都相交.解:⑴r ＝1;⑵1＜r ＜2;⑶r ＝2;⑷r ＞2 . 研习点3、切线 1.切线的判定和性质切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线. 切线的性质定理:圆的切线垂直于经过切点的半径注意:要识别直线是否为圆的切线,常用以下两种方法:①到圆心的距离等于圆的半径的直线是圆的切线。