[名校联盟]浙江省泰顺县新城学校九年级数学《圆的轴对称性》课件
合集下载
圆的轴对称性PPT教学课件

(2)代表人物——转化中的资产阶级的新型知 识分子
王韬 薛福成 郑观应 ……
(3)主张:
改革制度 —— 君主立宪制 发展工商业 —— 商战救国 (4)评价:
积极:反映了资产阶级阶级的利益和要求,为 康梁维新思想的形成奠定了思想基础。
局限:没有形成完整的理论,更没有付诸行动。
2、甲午中日战争后19世纪90年代的维 新思想
复习
• 如图,如AB=CD则(
⌒⌒
AB=CD
则(
如∠AOB= ∠COD则(
) O
)如 )
D
C
A
B
想一想
圆的对称性
• 圆是轴对称图形吗? 它的对称轴是什么?你能找到多少条对称轴? 你是用什么方法解决上述问题的?
●O
圆的对称性
• 圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线(直径所 在的直线),它有无数条对称轴. 可利用折叠的方法即可解决上述问题.
结局:中日甲午战争的失败,标志洋务运 动的破产。
实践:洋务运动(19世纪60—90年代)
军事工业
民用(辅助军 事工业)
曾国藩
安庆军械所
(最早)
李鸿章
江南制造总局 (最大)
天津开平煤矿、 上海轮船招商 局(最早)
左宗棠
福州船政局
崇厚
天津机器制造局
张之洞
汉阳铁厂
同文馆等洋务学堂在学习内容上与中国 古代学校有什么区别?
?
代表阶级利益:地主阶级
要
宣传手段:前者著书,后者实践办厂;
实践效果 结果 作用
洋务运动的影响
1、引进西方先进科技和工具 2、培养科技人员和技术工人 3、刺激民族资本主义发展 4、一定程度抵制外国经济扩张 5、在改革封建教育制度上打开了缺口
王韬 薛福成 郑观应 ……
(3)主张:
改革制度 —— 君主立宪制 发展工商业 —— 商战救国 (4)评价:
积极:反映了资产阶级阶级的利益和要求,为 康梁维新思想的形成奠定了思想基础。
局限:没有形成完整的理论,更没有付诸行动。
2、甲午中日战争后19世纪90年代的维 新思想
复习
• 如图,如AB=CD则(
⌒⌒
AB=CD
则(
如∠AOB= ∠COD则(
) O
)如 )
D
C
A
B
想一想
圆的对称性
• 圆是轴对称图形吗? 它的对称轴是什么?你能找到多少条对称轴? 你是用什么方法解决上述问题的?
●O
圆的对称性
• 圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线(直径所 在的直线),它有无数条对称轴. 可利用折叠的方法即可解决上述问题.
结局:中日甲午战争的失败,标志洋务运 动的破产。
实践:洋务运动(19世纪60—90年代)
军事工业
民用(辅助军 事工业)
曾国藩
安庆军械所
(最早)
李鸿章
江南制造总局 (最大)
天津开平煤矿、 上海轮船招商 局(最早)
左宗棠
福州船政局
崇厚
天津机器制造局
张之洞
汉阳铁厂
同文馆等洋务学堂在学习内容上与中国 古代学校有什么区别?
?
代表阶级利益:地主阶级
要
宣传手段:前者著书,后者实践办厂;
实践效果 结果 作用
洋务运动的影响
1、引进西方先进科技和工具 2、培养科技人员和技术工人 3、刺激民族资本主义发展 4、一定程度抵制外国经济扩张 5、在改革封建教育制度上打开了缺口
2.2 第2课时 圆的轴对称性-2020秋苏科版九年级数学上册课件(共19张PPT)
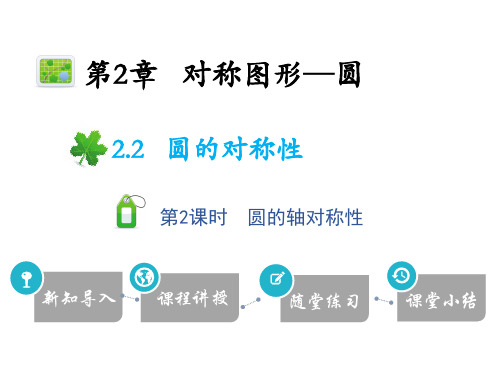
A.13寸
B.20寸
C.26寸
D.28寸
随堂练习
4.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象
限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的
半径为13,则点P的坐标为__(3_,_2_)___.
随堂练习
5.如图,⊙O的直径为10,弦AB长为8,点P在AB上运动, 则OP的最小值是____3____.
第2章 对称图形—圆
2.2 圆的对称性
第2课时 圆的轴对称性
新知导入 课程讲授
随堂练习 课堂小结
知识要点
1.圆的轴对称性 2.垂径定理
新知导入
看一看:观察下图中图形的变化,试着发现它们的规律。
新知导入
看一看:观察下图中图形的变化,试着发现它们的规律。
课程讲授
1 圆的轴对称性
问题1:剪一个圆形纸片,沿着它的任意一条直径对折, 重复几次,你发现了什么?由此你能得出什么结论?你 能证明你的结论吗?
) ) ) )
课程讲授
2 垂径定理
证明 如图,AB是⊙O的直径,CD是⊙O上
的弦,AB⊥CD,垂足为CD中,
∵OC=OD,OP⊥CD
∴PC=PD,∠BOC=∠BOD ∴∠AOC=∠AOD BC BD,AC AD.
A
O
P
D
B
课程讲授
2 垂径定理
从上面的证明过程中我们可以知道:
课程讲授
1 圆的轴对称性
O
O
O
归纳:圆是轴对称图形,任何一条直径所在的直线都 是圆的对称轴.
课程讲授
2 垂径定理
问题1 请大家在纸上画一个圆O,再任意画一条非直径的 弦CD,作一直径AB与CD垂直,交点为P(如图).在所 画图中有哪些相等的线段、相等的弧?
圆的轴对称性PPT课件

C
CC
C C
A A
A
CC C D D C
O
O
OO
A
AA
B BB
O O
B B
O O
O
A A
O O B
AA
①
D DD
DD D
② ②
③
B B B
④
① ①
③ ③
⑤ ⑤
探索规律
• AB是⊙O的一条弦. 作直径CD,使CD⊥AB,垂足为M.
下图是轴对称图形吗?如果是,其对称轴是什么?
C
A
• 你能发现图中有哪些等量关系?与同伴说 说你的想法和理由.
A O
B D
2.在半径为5cm的⊙ O中,弦AB∥CD,且 AB=6cm,CD=8cm,求AB,CD之间的距离 3.如图,∠C=90°,⊙C与 AB交于点D,AC=5,CB=12, 求AD的长
A C B D
一、圆是轴对称图形,其对称轴是 任意一 条过圆心的直线(或直径所在直线.) 并且平分弦所对的弧. 三、垂径定理和勾股定理相结合,构造 直角三角形,可解决计算弦长、半 径、圆心到弦的距离等问题.
●
O
如何确定圆形纸片的圆心?说 说你的想法。
将圆纸片对折,确定出圆的一条直径; 用同样的方法,再确定出圆的另一条直 径.两条直径的交点即为圆形纸片的圆 心.
(1)判断下列图形是否具有对称性? 如果一个对称图形与圆具有相同 如果是中心对称图形,指出它的对称 的对称中心或对称轴,那么它和 中心,如果是轴对称图形,指出它的 对称轴。 圆组成的新图形也是对称图形.
O
解:过O点作OE⊥AB, 垂径定理和勾股定理相结合,构
造直角三角形,把圆的问题化归 并延长OE交⊙O于F,连接 为直线形问题解决。
CC
C C
A A
A
CC C D D C
O
O
OO
A
AA
B BB
O O
B B
O O
O
A A
O O B
AA
①
D DD
DD D
② ②
③
B B B
④
① ①
③ ③
⑤ ⑤
探索规律
• AB是⊙O的一条弦. 作直径CD,使CD⊥AB,垂足为M.
下图是轴对称图形吗?如果是,其对称轴是什么?
C
A
• 你能发现图中有哪些等量关系?与同伴说 说你的想法和理由.
A O
B D
2.在半径为5cm的⊙ O中,弦AB∥CD,且 AB=6cm,CD=8cm,求AB,CD之间的距离 3.如图,∠C=90°,⊙C与 AB交于点D,AC=5,CB=12, 求AD的长
A C B D
一、圆是轴对称图形,其对称轴是 任意一 条过圆心的直线(或直径所在直线.) 并且平分弦所对的弧. 三、垂径定理和勾股定理相结合,构造 直角三角形,可解决计算弦长、半 径、圆心到弦的距离等问题.
●
O
如何确定圆形纸片的圆心?说 说你的想法。
将圆纸片对折,确定出圆的一条直径; 用同样的方法,再确定出圆的另一条直 径.两条直径的交点即为圆形纸片的圆 心.
(1)判断下列图形是否具有对称性? 如果一个对称图形与圆具有相同 如果是中心对称图形,指出它的对称 的对称中心或对称轴,那么它和 中心,如果是轴对称图形,指出它的 对称轴。 圆组成的新图形也是对称图形.
O
解:过O点作OE⊥AB, 垂径定理和勾股定理相结合,构
造直角三角形,把圆的问题化归 并延长OE交⊙O于F,连接 为直线形问题解决。
3.2.1圆的对称性(垂径定理)PPT课件
.
45
课堂小结:
本节课探索发现了垂径定理的推论1和推
论2,并且运用推论1等分弧。
●要分清推论1的题设和结论,即已知什么条 件,可推出什么结论. 这是正确理解应用推论1 的关键;
●例3是基本几何作图,会通过作弧所夹弦
的垂直平分线来等分弧.能够体会转化思想
在这里的运用.
.
46
圆的相关概念
A⌒mB
圆上任意两点间的部分叫做圆弧,简称弧(arc).
H 弧长 FE = 3.84 cm
G
E
F
A
.
C
6
看一看
C
.O
A E B D
AE≠BE
C
.O
A
E
B
D
AE=BE
.
7
垂径定理
A⌒mB
AB是⊙O的一条弦.
作直径CD,使CD⊥AB,垂足为M.
下图是轴对称图形吗?如果是,其对称轴是什么?
C
A M└
你能发现图中有哪些等量关系? B 与同伴说说你的想法和理由.
D
A
B
E
A
O
O
CE
O
A
E
B
B
C
A
C D
O
E
C
D
A E.
B
D
O
BA
E
B
12
C
练习
如图,已知在⊙O中, 弦AB的Байду номын сангаас为8厘米,圆心 A
O到AB的距离为3厘米,
求⊙O的半径。
E
B
.
O
解:连结OA. 过O作OE⊥AB,垂足为E,
则OE=3厘米,AE=BE。
圆的轴对称性PPT课件

在RtAOE中,根据勾股定理有OA=5厘米 ∴⊙O的半径为5厘米。
2020年10月2日
11
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
汇报人:XXX 汇报日期:20XX年10月10日
12
.
圆是轴对称图形,经过圆
心的每一条直线都是它们
的对称轴。
2020年10月2日
2
看一看
C
.O
A E B D
AE≠BE
2020年10月2日
C
.O
A
E
B
D
AE=BE
3
动动脑筋
1、 已知:在⊙O中,CD是直径, AABE是=B弦E,,CA⌒DC⊥=AB⌒BC,,垂A⌒足D=为B⌒ED。。求证:
证明:连结OA、OB,则OA=OB。 A 因为垂直于弦AB的直径CD所在的 直线既是等腰三角形OAB的对称轴 又是⊙ O的对称轴。所以,当把圆 沿着直径CD折叠时,CD两侧的两 个和B⌒D半B重E圆重合重合。合,因⌒,A此AC点、⌒和ADB分点别重和合⌒B,CA、E AE=BE,A⌒C=B⌒C,A⌒D=B⌒D
A 可用圆的轴对称性来说明。
推论:
.O
E
B
D
如果圆的一条直径平分一条弧,那么这条直径垂直平分这条
弧所对的弦。
用图式概括:直径平分弧
{直径平分弧所对的弦 直径垂直于弧所对的弦
圆的轴对称性第一课时课件

在数学中,许多函数的图像是圆或圆弧,这些图像具有轴对 称性。利用这种对称性,可以更好地理解和分析函数的性质 和特征。
几何证明
在几何证明中,圆的轴对称性常常被用来证明某些几何定理 和性质。例如,利用圆的对称性证明圆周角定理等重要的几 何定理。
05
课堂互动与讨论
问题一:如何理解圆的轴对称性?
总结词:直观理解 总结词:数学定义 总结词:几何特性
的直线对称。
详细描述:对于矩形,可以通过连接 对角线,证明矩形关于对角线所在的 直线对称。
总结词:菱形
总结词:矩形
详细描述:对于菱形,可以通过连接 对角线,证明菱形关于其中垂线所在 的直线对称。
THANKS
感谢观看
03
圆的轴对称性证明
证明方法一:几何证明
总结词:直观明了
详细描述:通过观察圆在平面上的形状,可以直观地看出圆具有轴对称性。当一 个圆沿一条直线对折时,两侧的图形完全重合,证明了圆的轴对称性。
证明方法二:代数证明
总结词:严谨推导
详细描述:利用代数公式和定理,通过严谨的推导证明圆的轴对称性。具体来说,设圆心为$O$,任 意一点$P$在圆上,当点$P$关于直线$l$对称时,有$OP = OP'$且$angle P'OP = angle P'PO = angle PLO$,从而证明了圆的轴对称性。
问题二:圆的轴对称性有哪些应用场景?
在此添加您的文本17字
总结词:几何证明
在此添加您的文本16字
详细描述:在建筑设计中,圆的轴对称性被广泛应用于穹 顶、拱门、桥梁等结构的设计,以实现力量的均匀分布和 视觉的美感。
在此添加您的文本16字
详细描述:在几何证明中,圆的轴对称性常常用于证明与 圆相关的定理和性质,如垂径定理、切线长定理等。
几何证明
在几何证明中,圆的轴对称性常常被用来证明某些几何定理 和性质。例如,利用圆的对称性证明圆周角定理等重要的几 何定理。
05
课堂互动与讨论
问题一:如何理解圆的轴对称性?
总结词:直观理解 总结词:数学定义 总结词:几何特性
的直线对称。
详细描述:对于矩形,可以通过连接 对角线,证明矩形关于对角线所在的 直线对称。
总结词:菱形
总结词:矩形
详细描述:对于菱形,可以通过连接 对角线,证明菱形关于其中垂线所在 的直线对称。
THANKS
感谢观看
03
圆的轴对称性证明
证明方法一:几何证明
总结词:直观明了
详细描述:通过观察圆在平面上的形状,可以直观地看出圆具有轴对称性。当一 个圆沿一条直线对折时,两侧的图形完全重合,证明了圆的轴对称性。
证明方法二:代数证明
总结词:严谨推导
详细描述:利用代数公式和定理,通过严谨的推导证明圆的轴对称性。具体来说,设圆心为$O$,任 意一点$P$在圆上,当点$P$关于直线$l$对称时,有$OP = OP'$且$angle P'OP = angle P'PO = angle PLO$,从而证明了圆的轴对称性。
问题二:圆的轴对称性有哪些应用场景?
在此添加您的文本17字
总结词:几何证明
在此添加您的文本16字
详细描述:在建筑设计中,圆的轴对称性被广泛应用于穹 顶、拱门、桥梁等结构的设计,以实现力量的均匀分布和 视觉的美感。
在此添加您的文本16字
详细描述:在几何证明中,圆的轴对称性常常用于证明与 圆相关的定理和性质,如垂径定理、切线长定理等。
3.2圆的轴对称性(第2课时)课件ppt浙教版九年级上(精品课件在线)

●O
由 CD是直径
可推得
AM=BM
D
课件分享
CD⊥AB,
A⌒C=B⌒C,
A⌒D=B⌒D.
4
思考:
平分弧的直径会垂直平分弧所对的弦吗?
• A⌒B是⊙O的一条弧,且A⌒C=⌒BC.
下图是轴对称图形吗?如果是,其对称轴是什么?
• 你能发现图中有哪些等量关系?与同伴说
C
说你的想法和理由.
A
●
M
B 小明发现图中有:
结论 CD平分弧ACB
CD⊥AB
课件C分D享平分弧ADB
3
探索规律
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
• AB是⊙O的一条弦,且AM=BM.
过点M作直径CD.
下图是轴对称图形吗?如果是,其对称轴是什么?
• 你能发现图中有哪些等量关系?与同伴说
C
说你的想法和理由.
A
●
M
B 小明发现图中有:
经过圆心O作弦AB的垂线OD,D为垂足,与 AB 相交于点C.根
据 由垂题径设定得理A,BD是 A7.B2的,C中D点,2C.是4, HANB的中1点M,CND就1.是5.拱高.
1
1
2
AD AB 7.2 3.6,
2
2
OD OC DC R 2.4.
在Rt△OAD中,由勾股定理,得
OA2 AD2 OD 2 ,
CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一
点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.
C
解:连接OC.
老师提示:
E设弯路的半径为 Rm,则OF (R 90)m.
注意闪烁的 三角形的特 点.
圆的轴对称性课件(浙教版)

探索规律
▪ AB是⊙O的一条弦,且AM=BM, 过点M作直径CD.
▪ 逆命题1:平分弦的直径垂直于弦。成立吗?
CD⊥AB,
C
CD是直径 可推得
A⌒C=B⌒C,
A
┗●
BF AM=BM
A⌒D=B⌒D.
M
●O
定理1.平分弦(不是直径 )的
E
直径垂直于弦,并且平 分弦所对
D
的两条弧.
探索规律
▪ AB是⊙O的一条弦,点C为弧AB的中点.
∴AE-CE=BE-DE 即AC=BD
D
B
O
2.已知圆O的半径为5cm,AB∥CD,AB=6cm,CD=8cm, 则AB与CD距离是__________cm
可能1: 两条弦在圆心的两侧 则EF=OE+OF=7
可能2: 两条弦在圆心的同侧 EF=OE-OF=1
C
4
F
4
5
●O3
D
4
5
A
3E 3
B
C
5
4
▪ ⑶经过弦的中点的直径一定垂直于弦.( )
▪ ⑷圆的两条弦所夹的弧相等,则这两条弦平行. () ▪ ⑸弦的垂直平分线一定平分这条弦所对的弧. (√ )
九年级数学(下)第三章 圆
圆的对称性(2)
复习
定理:垂直于弦的直径平分弦,并且平分弦
所对的弧
条件 CD为直径 CD⊥AB CD平分弦AB 结论 CD平分弧ACB CD平分弧ADB
C
A
B
M└
●O
D
想一想
垂径定理的逆命题是什么?
垂直于弦的直径平分弦,并且平分弦所对的弧.
条件
结论1
结论2
圆的轴对称性浙教版课件

VS
解析
利用点到直线的距离公式和三角函数的性 质,求出最小值。通过计算,得到最小值 为$frac{9sqrt{2}}{10}$。
THANKS
感谢观看
05
圆的对称性的习题解析
基础题解析
题目1
给定圆心为$O(0,0)$,半径为$r$的 圆,求圆上点$P(3,4)$关于$x$轴的对 称点的坐标。
解析
点$P(3,4)$关于$x$轴的对称点,其横 坐标不变,纵坐标变为相反数。因此 ,对称点的坐标为$(3,-4)$。
提高题解析
题目2
圆$x^2 + y^2 = 1$关于直线$y = 2x + 1$对称的圆的方程是什么?
圆心和对称轴之间的关系是相 互依存的,圆心在直线上,直 线就是对称轴,反之亦然。
03
圆的对称性的应用
在几何作图中的应用
利用圆的对称性进行作图
在几何作图中,我们可以利用圆的对称性来简化作图过程。例如,当我们需要 绘制一个圆形时,我们可以先绘制半个圆,然后利用圆的对称性来画出完整的 圆。
利用圆的对称性检查作图准确性
圆的轴对称性
圆关于任何经过其圆 心的直线都具有轴对 称性。
圆关于任何经过其圆 心的直线都可以被分 割成两个对称的部分 。
圆心是圆关于任何经 过其圆心的直线的对 称中心。
圆心与对称轴的关系
圆心是圆的对称中心,任何经 过圆心的直线都可以作为圆的 对称轴。
圆心决定了圆的对称轴,圆心 位置的变化会导致对称轴的变 化。
利用圆的对称性简化解析几何计算
在解决解析几何问题时,我们有时需要计算一些复杂的表达式。利用圆的对称性 ,我们可以简化这些计算。例如,当我们需要计算一个圆上两点之间的距离时, 我们可以利用圆的对称性来找到这两点的中点,从而简化计算过程。
九年级数学《3-2 圆的对称性》课件

B
E
·
C
O
D
A
例2 如图,AB是⊙O 的直径, BC=CD=DE, ∠COD=35°,求∠AOE 的度数.
ED
C
A
· O
B
例3 如图,在⊙O中, A⌒B=A⌒C ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
A
O·
B
C
4.如图,已知AB、CD为⊙O的两条弦,AD BC
求证:AB=CD.
第三章 圆
3.2 圆的对称性
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.掌握圆是轴对称图形及圆的中心对称性和旋 转不变性.
2.探索圆心角、弧、弦之间关系定理并利用其 解决相关问题.(重点)
3.理解圆心角、弧、弦之间关系定理中的“在 同圆或等圆”条件的意义.(难点)
圆的对称性
自主学习
圆的对称性: 圆是轴对称图形,其对称轴是任意一条过圆心的直线.
在 同 圆 或 等 圆 中
当堂练习
1.如果两个圆心角相等,那么 ( D ) A.这两个圆心角所对的弦相等 B.这两个圆心角所对的弧相等 C.这两个圆心角所对的弦的弦心距相等 D.以上说法都不对
2.弦长等于半径的弦所对的圆心角等于 60 °.
3.在同圆中,圆心角∠AOB=2∠COD,则A⌒B与C⌒D
弦AB与弦CD有怎样的数量关系?
C B
D
归纳 由圆的旋转不变性,我们发现:
·
在⊙O中,如果∠AOB= ∠COD
O
A
那么,AB CD ,弦AB=弦CD
在等圆中探究
如图,在等圆中,如果∠AOB=∠CO ′ D,你发现的等量关
系是否依然成立?为什么?
圆的轴对称性 PPT

探索规律
• 如图,连接OA,OB则, OA=OB. 在Rt△OAM和Rt△OBM中, ∵OA=OB,OM=OM, ∴Rt△OAM≌Rt△OBM.
在同圆中能 够重合的弧 叫等弧
C
A M└ ●O
D
∴AM=BM. ∴点A和点B关于CD对称. B ∵⊙O关于CD对称, ∴点当B重圆合沿⌒ A,C着和B直⌒C重径合C, D⌒ A对D和折B⌒D时重,合点. A与 ∴A⌒C =B⌒C, A⌒D =B⌒D.
复习
• 如图,如AB=CD则(
⌒⌒
AB=CD
则(
如∠AOB= ∠COD则(
) O
)如 )
D
C
A
B
想一想
圆的对称性
• 圆是轴对称图形吗? 它的对称轴是什么?你能找到多少条对称轴? 你是用什么方法解决上述问题的?
●O
特权福利
特权说明
VIP用户有效期内可使用VIP专享文档下载特权下载或阅读完成VIP专享文档(部分VIP专享文档由于上传者设置不可下载只能 阅读全文),每下载/读完一篇VIP专享文档消耗一个VIP专享文档下载特权。
=8 ㎝ ,DC=2㎝,直径
CE⊥AB于D,求半径OC的
O
长。
D
A
B
练习2:在圆O中,直径 CE⊥AB于D,OD=4 ㎝, 弦AC= 10 ㎝ ,求圆O的半 径。
A
C E
O D
B
C
挑战自我画一画
• 如图,M为⊙O内的一点,利用尺规作一条弦AB, 使AB过点M.并且AM=BM.
A
●M B
●O
1条.如平图行,弦A,BA,⌒CCD与是B⌒⊙D相O的等两吗? CA
如图∵ CD是⊙O的直径( ⊙O中,CD经 C 过点O), CD⊥弦AB,
九年级数学3.2圆的对称性优秀课件
3.2 圆的对称性
O
自主学习
1.圆是轴对称图形吗?如果是,它的对称轴是什么? 你能找到多少条对称轴?你用什么方法解决? 2.圆是中心对称图形吗?如果是,它的对称中心是什么? 3.在同圆或等圆中,两个圆心角、对应的两条弦、两条
弧、两条弦心距,这四组量之间有什么相等关系?
想一想:
圆是轴对称图形吗? 如果是,它的对称轴是什么?你能找到几条对
随堂练习 ︵
1.已知 A、B 是⊙O 上的两点,∠AOB=120°,C 是 AB的中点。
试确定四边形 OACB 的形状,并说明理由。
A
C
B O
知识技能
2.如图,A、B、C、D是⊙O上的四点,AB=DC,△ABC与 △DCB全等吗?为什么?
B
C
A
O D
课堂小结: 本节课你有什么收获?
:如图,点P在⊙O上,点O在∠EPF的平分线上, ∠ EPF的两边交⊙O于点A和B。
点拨归纳 〔一〕圆的对称性
〔1〕圆是轴对称图形,其对称轴是任意一 条过圆心的直线.
〔2〕圆是中心对称图形,对称中心为圆心.
〔3〕圆具有旋转不变性。即圆绕圆心旋转 任意角度α,都能够与原来的图形重合.
几个概念
圆心角、等圆、等弧、弦心距
〔1〕顶点在圆心的角叫圆心角 ,即∠AOB
〔2〕能够重合的两个圆 叫做等圆 〔同圆或 等圆的半径相等 〕
称轴?你是用什么方法解决上述问题的?
圆是轴对称图形,对称轴是任意一条经过 圆心的直线,它有无数条对称轴. 利用折叠的方法 可以解决上述问题.
想一想:
圆是中心对称图形吗? 如果是,它的对称中心是什么?
圆是中心对称图形,其对称中心就 是圆心. 思考:圆绕着圆心旋转任意角度,那么旋
O
自主学习
1.圆是轴对称图形吗?如果是,它的对称轴是什么? 你能找到多少条对称轴?你用什么方法解决? 2.圆是中心对称图形吗?如果是,它的对称中心是什么? 3.在同圆或等圆中,两个圆心角、对应的两条弦、两条
弧、两条弦心距,这四组量之间有什么相等关系?
想一想:
圆是轴对称图形吗? 如果是,它的对称轴是什么?你能找到几条对
随堂练习 ︵
1.已知 A、B 是⊙O 上的两点,∠AOB=120°,C 是 AB的中点。
试确定四边形 OACB 的形状,并说明理由。
A
C
B O
知识技能
2.如图,A、B、C、D是⊙O上的四点,AB=DC,△ABC与 △DCB全等吗?为什么?
B
C
A
O D
课堂小结: 本节课你有什么收获?
:如图,点P在⊙O上,点O在∠EPF的平分线上, ∠ EPF的两边交⊙O于点A和B。
点拨归纳 〔一〕圆的对称性
〔1〕圆是轴对称图形,其对称轴是任意一 条过圆心的直线.
〔2〕圆是中心对称图形,对称中心为圆心.
〔3〕圆具有旋转不变性。即圆绕圆心旋转 任意角度α,都能够与原来的图形重合.
几个概念
圆心角、等圆、等弧、弦心距
〔1〕顶点在圆心的角叫圆心角 ,即∠AOB
〔2〕能够重合的两个圆 叫做等圆 〔同圆或 等圆的半径相等 〕
称轴?你是用什么方法解决上述问题的?
圆是轴对称图形,对称轴是任意一条经过 圆心的直线,它有无数条对称轴. 利用折叠的方法 可以解决上述问题.
想一想:
圆是中心对称图形吗? 如果是,它的对称中心是什么?
圆是中心对称图形,其对称中心就 是圆心. 思考:圆绕着圆心旋转任意角度,那么旋
圆的轴对称性PPT课件

×
(4)平分弦的直径垂直于弦,并且平分弦所对的 两条弧………………………………………( )
× (5)圆内两条非直径的弦不能互相平分( √ )
讲解
例1 如图,已知在⊙O中, 弦AB的长为8厘米,圆心O到 AB的距离为3厘米,求⊙O的 半径。 A E
. O
B
解:连结OA。过O作OE⊥AB,垂足为E, 则OE=3厘米,AE=BE。∵AB=8厘米 ∴AE=4厘米 在RtAOE中,根据勾股定理有OA=5厘米 ∴⊙O的半径为5厘米。
复习提问:
1、什么是轴对称图形?我们在平面图形中学过 哪些轴对称图形? 如果一个图形沿一条直线对折,直线两旁的部分能 够互相重合,那么这个图形叫轴对称图形。如线段、 角、等腰三角形、矩形、菱形、等腰梯形、正方形。 2、我们所学的圆是不是 轴对称图形呢? 圆是轴对称图形,经过圆 心的每一条直线都是它们 的对称轴。
A
. O
B
小结:
解决有关弦的问题,经常是过圆心作弦 的垂线,或作垂直于弦的直径,连结半 径等辅助线,为应用垂径定理创造条件。
想一想:
{
为什么定理中强调“不是直径”呢?
C
练习:
CO是直径,且D点是AB的中点, 能不能证到CD ⊥AB。
可用圆的轴对称性来说明。
⌒
.
A
O E B
D
推论:
如果圆的一条直径平分一条弧,那么这条直径垂直平分这条 弧所对的弦。
直径平分弧 用图式概括:
{
直径平分弧所对的弦 直径垂直于弧所对的弦
记忆
垂径定理
.
看一看
C C
.
A
O E A B
.
O
E B
D
D
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B 13
A
D 5
.
C
间有什么关系? 答:在同一个圆中, 弦心距越长,所对应的弦就越短;
O
弦心距越短,所对应的弦就越长.
小结:
1.作弦心距和半径是圆中 常见的辅助线; 2 .半径(r)、半弦、弦心 距(d)组成的直角三角形是研 究与圆有关问题的主要思路, 它们之间的关系:
d A
O
.
C
r
B
弦长AB 2 r 2 d 2 .
学· 网 科·
A
B
作法:
1.连结AB; 2.作AB的垂直平分线CD,交AB与点E;
⌒
⌒ ∴点E就是所求AB的中点.
变式: 求弧AB的四等分点.
学· 网 科·
C
m
F
E G
n
B
D
例2:一条排水管的截面如图所示。已知排水管的半
径OB=10,水面宽AB=16。求截面圆心O到水面的距离。
想一想:排水管中水最深多少? 解:作OC⊥AB于C, 由垂径定理得: AC=BC=1/2AB=0.5×16=8 由勾股定理得:
OC OB BC 10 8 6
2 2 2 2
8
C
10 8
答:截面圆心O到水面的距离为6. 圆心到圆的一条弦的距离叫做弦心距.
例如,上图中,OC的长就是弦AB的弦心距.
D
1、已知⊙O的半径为13cm,一条弦的弦心距为5cm, 求
这条弦的长. 想一想:在同一个圆中,两条弦 的长短与它们所对应的弦心距之
A
C 1 3D O
3
B
4、已知:如图在⊙O中,弦AB//CD。 ⌒ ⌒ 求证:AC=BD
O A C B D
说能出你这节课的收获和体验让大家
与你分享吗?
总结回顾
师生共同总结:
1.本节课主要内容:(1)圆的轴对称性;(2)垂径定理. 2.垂径定理的应用:(1)作图;(2)计算和证明.
3.解题的主要方法:
M B
.
O
N C
学· 网 科·
A
垂径定理的几何语言叙述:
C
E B CD平分弦AB 条件 CD为直径 结论 CD平分弧A B CD平分弧ADB
O
D
CD⊥AB
分一条弧成相等的两条弧的点,叫做这条弧的中点.
⌒ 例1:已知AB如图,用直尺和圆规求作这条弧 E 的中点。 ⌒ 分析:要平分AB,只要画垂直
于弦AB的直径.而这条直径 应在弦AB的垂直平分线上. 因此画AB的垂直平分线就能 ⌒ 把AB平分.
C
E
O
D
根据圆的轴轴对称性,可得射线EA与EB重合, B ∴点A与点B重合,弧AC和弧BC重合,弧AD和弧BD重合. ⌒ ⌒ ⌒ ⌒ ∴ EA=EB, AC= BC, AD=BD.
思考:你能利用等腰三角形的性质,说明OC平分AB吗?
结论2: 垂径定理:垂直于弦的直径平分这条弦, 并且平分弦所对的弧.
在白纸上任意作一个圆和这个圆的任意一条直径CD, 然后沿着直径所在的直线把纸折叠,你发现了什么?
学· 网 科·
C
O
D
结论1:
圆是轴对称图形,每一条直径所在的直线都是对称轴。 强调:
(1)圆的对称轴是直线,不能说每一条直径都是圆的对称轴; (2)圆的对称轴有无数条.
判断:任意一条直径都是圆的对称轴(
(1)画弦心距和半径是圆中常见的辅助线; (2)半径(r)、半弦、弦心距(d)组成的直角三角形 是研究与圆有关问题的主要思路,它们之间的关系:
弦长AB 2 r 2 d 2 .
五、目标训练
5. 已知⊙O的半径为10,弦AB∥CD,AB=12, CD=16,则AB和CD的距离为 2或14 . 6.如图,已知AB、AC为弦,OM⊥AB于点M, A ON⊥AC于点N ,BC=4,求MN的长. 思路:由垂径定理可得M、N分别是 1 AB、AC的中点,所以MN= BC=2. 2
2、已知⊙O的半径为10cm,点P是⊙O内一点,且
OP=8,则过点P的所有弦中,最短的弦是( D )
(A)6cm (B)8cm (C)10cm (D)12cm
O
8
10 6
P
• 3、已知:如图,⊙O 中, AB为 弦,OC ⊥AB OC交AB 于D ,AB = 6cm ,CD = 1cm. 求⊙O 的半径.
X)
在刚才操作的基础上,再作一条和直径CD垂直的弦AB,AB 与CD相交于点E,然后沿着直径CD所在的直线把纸折叠,你 发现哪些点、线互相重合? 如果把能够重合的圆弧叫做 相等的圆弧,那么在下图中,哪些圆弧相等? 请用命题的 形式表述你的结论. A
学· 网 科·
得出结论:⌒
⌒ ⌒ ⌒ ② ①EA=EB; AC=BC,AD=BD. 理由如下:∵∠OEA=∠OEB=Rt∠,
A
D 5
.
C
间有什么关系? 答:在同一个圆中, 弦心距越长,所对应的弦就越短;
O
弦心距越短,所对应的弦就越长.
小结:
1.作弦心距和半径是圆中 常见的辅助线; 2 .半径(r)、半弦、弦心 距(d)组成的直角三角形是研 究与圆有关问题的主要思路, 它们之间的关系:
d A
O
.
C
r
B
弦长AB 2 r 2 d 2 .
学· 网 科·
A
B
作法:
1.连结AB; 2.作AB的垂直平分线CD,交AB与点E;
⌒
⌒ ∴点E就是所求AB的中点.
变式: 求弧AB的四等分点.
学· 网 科·
C
m
F
E G
n
B
D
例2:一条排水管的截面如图所示。已知排水管的半
径OB=10,水面宽AB=16。求截面圆心O到水面的距离。
想一想:排水管中水最深多少? 解:作OC⊥AB于C, 由垂径定理得: AC=BC=1/2AB=0.5×16=8 由勾股定理得:
OC OB BC 10 8 6
2 2 2 2
8
C
10 8
答:截面圆心O到水面的距离为6. 圆心到圆的一条弦的距离叫做弦心距.
例如,上图中,OC的长就是弦AB的弦心距.
D
1、已知⊙O的半径为13cm,一条弦的弦心距为5cm, 求
这条弦的长. 想一想:在同一个圆中,两条弦 的长短与它们所对应的弦心距之
A
C 1 3D O
3
B
4、已知:如图在⊙O中,弦AB//CD。 ⌒ ⌒ 求证:AC=BD
O A C B D
说能出你这节课的收获和体验让大家
与你分享吗?
总结回顾
师生共同总结:
1.本节课主要内容:(1)圆的轴对称性;(2)垂径定理. 2.垂径定理的应用:(1)作图;(2)计算和证明.
3.解题的主要方法:
M B
.
O
N C
学· 网 科·
A
垂径定理的几何语言叙述:
C
E B CD平分弦AB 条件 CD为直径 结论 CD平分弧A B CD平分弧ADB
O
D
CD⊥AB
分一条弧成相等的两条弧的点,叫做这条弧的中点.
⌒ 例1:已知AB如图,用直尺和圆规求作这条弧 E 的中点。 ⌒ 分析:要平分AB,只要画垂直
于弦AB的直径.而这条直径 应在弦AB的垂直平分线上. 因此画AB的垂直平分线就能 ⌒ 把AB平分.
C
E
O
D
根据圆的轴轴对称性,可得射线EA与EB重合, B ∴点A与点B重合,弧AC和弧BC重合,弧AD和弧BD重合. ⌒ ⌒ ⌒ ⌒ ∴ EA=EB, AC= BC, AD=BD.
思考:你能利用等腰三角形的性质,说明OC平分AB吗?
结论2: 垂径定理:垂直于弦的直径平分这条弦, 并且平分弦所对的弧.
在白纸上任意作一个圆和这个圆的任意一条直径CD, 然后沿着直径所在的直线把纸折叠,你发现了什么?
学· 网 科·
C
O
D
结论1:
圆是轴对称图形,每一条直径所在的直线都是对称轴。 强调:
(1)圆的对称轴是直线,不能说每一条直径都是圆的对称轴; (2)圆的对称轴有无数条.
判断:任意一条直径都是圆的对称轴(
(1)画弦心距和半径是圆中常见的辅助线; (2)半径(r)、半弦、弦心距(d)组成的直角三角形 是研究与圆有关问题的主要思路,它们之间的关系:
弦长AB 2 r 2 d 2 .
五、目标训练
5. 已知⊙O的半径为10,弦AB∥CD,AB=12, CD=16,则AB和CD的距离为 2或14 . 6.如图,已知AB、AC为弦,OM⊥AB于点M, A ON⊥AC于点N ,BC=4,求MN的长. 思路:由垂径定理可得M、N分别是 1 AB、AC的中点,所以MN= BC=2. 2
2、已知⊙O的半径为10cm,点P是⊙O内一点,且
OP=8,则过点P的所有弦中,最短的弦是( D )
(A)6cm (B)8cm (C)10cm (D)12cm
O
8
10 6
P
• 3、已知:如图,⊙O 中, AB为 弦,OC ⊥AB OC交AB 于D ,AB = 6cm ,CD = 1cm. 求⊙O 的半径.
X)
在刚才操作的基础上,再作一条和直径CD垂直的弦AB,AB 与CD相交于点E,然后沿着直径CD所在的直线把纸折叠,你 发现哪些点、线互相重合? 如果把能够重合的圆弧叫做 相等的圆弧,那么在下图中,哪些圆弧相等? 请用命题的 形式表述你的结论. A
学· 网 科·
得出结论:⌒
⌒ ⌒ ⌒ ② ①EA=EB; AC=BC,AD=BD. 理由如下:∵∠OEA=∠OEB=Rt∠,
