立体体积和侧面积计算中的微元法

合集下载

如何利用微元法计算旋转体的体积

如何利用微元法计算旋转体的体积在考研数学中，定积分有着举足轻重的地位，其几何意义是曲边梯形面积的代数和，该思想方法为微元法，具体概括为以下四步：1分割、2近似、3求和、4取极限。

该思想方法同样适用于定积分的应用----平面图形的面积、旋转体的体积、平面曲线的弧长（数学一、二）、旋转曲面的侧面积（数学一、二）等。

由于篇幅有限，不可能一一列举每种题型计算方法，我们就其中一个应用----旋转体的体积相关考情进行分析。

该部分知识点是历年考研数学试卷的高频考点，多以解答题形式出现，比如，16、15、14、13等年份，对于个别年份，该部分考点也会以填空题的形式出现，比如，11、10年份。

有关计算旋转体体积的题目，大多需要考生自己列出相应积分式，因此务必熟记以下3个公式：（1）由连续曲线)(x f y =，直线a x =，b x =及x 轴所围曲边梯形绕x 轴旋转一周而成的立体。

该立体的体积公式为dx x f V ba ⎰=)(2π。

推广：若该曲边梯形绕0y y =旋转一周而成的立体的体积公式为dx y x f V b a ⎰-=20])([π。

（2）由连续曲线)(y x ϕ=，直线a y =，b y =及y 轴所围曲边梯形绕y 轴旋转一周而成的立体。

该立体的体积公式为dy y V ba ⎰=)(2ϕπ。

推广：若该曲边梯形绕0x x =轴旋转一周而成的立体的体积公式为dy x y V ba ⎰-=20])([ϕπ。

（3）由连续曲线)(x f y =，直线a x =，b x =及x 轴所围曲边梯形绕y 轴旋转一周而成的立体。

该立体的体积公式为dx x xf V ba ⎰=)(2π。

推广：若该曲边梯形绕0x x =轴旋转一周而成的立体的体积公式为dx x f x x V ba ⎰-=)(||20π。

注：（2）、（3）均为绕y 轴旋转体的计算方法，但是（2）适用于)(y x ϕ=的情况，即能够找到x 关于y 的解析式，（3）适用范围是找不到)(y x ϕ=的关系式，那么我们可以根据)(x f y =来列相应的体积公式。

球体被平面截下的体积-概述说明以及解释

球体被平面截下的体积-概述说明以及解释1.引言1.1 概述概述球体被平面截下的体积是一个有趣而又实用的几何问题。

我们常常可以在生活中看到球体被平面截下的例子，比如切割水果或者切开一个球形蛋糕等等。

研究球体被平面截下的体积不仅涉及到基本的几何知识，还涉及到数学、物理等多个学科的知识。

这个问题既有理论上的求解方法，也有实际应用上的价值。

在本文中，我们将介绍球体的基本性质，探讨平面截下球体的体积计算方法，并探讨这个问题在实际应用中的意义。

首先，我们将回顾一些基本的几何概念和公式，以便更好地理解后续的内容。

然后，我们将详细介绍球体被平面截下的体积的计算方法，包括几何推导和解析几何方法。

最后，我们将探讨这个几何问题在现实生活中的应用，比如在建筑设计、工程计算以及科学研究中的应用。

本文的目的是帮助读者全面理解球体被平面截下的体积这个复杂的几何问题，并能够运用所学知识解决实际的问题。

通过学习本文，读者将能够掌握求解球体被平面截下的体积的计算方法，了解这个问题在实际应用中的意义，以及对未来研究的展望。

在下面的章节中，我们将一步步地介绍球体被平面截下的体积的计算方法，并提供实际应用中的例子来帮助读者更好地理解和应用所学知识。

希望本文能对读者在几何学和应用数学的学习中起到积极的促进作用。

1.2文章结构文章结构部分的内容如下：1.2 文章结构本文主要分为三个部分：引言、正文和结论。

在引言中，将对本文的研究主题进行概述，介绍球体被平面截下的体积的基本背景和相关问题。

同时，还将介绍本文的目的，即通过研究球体被平面截下的体积计算方法，探讨其实际应用与意义。

在正文部分，首先会介绍球体的基本性质，包括球体的定义、特点以及基本公式。

然后，将详细说明平面截下球体的体积计算方法，包括具体的数学推导和计算过程。

此外，还会探讨不同情况下的特殊情况和计算方法，提供更全面的研究结果。

最后，在结论部分，将对本文的研究进行总结，回顾讨论的主要内容和研究成果。

第七章微元法

二、用定积分表示量U的基本步骤:
(1)根据问题的具体情况,选取一个变量
例如x为积分变量,并确定其变化区间[a,b];
[ (2) 在区间[a,b]内任取一个小区间 x , x dx] ,
求出相应于这个小区间的部分量 U的近似值. 如果 U 能近似地表示为[a,b]上的一个连续函数在
x 处的值 f ( x ) 与 dx 的乘积,
0
a 2 2 [2 1 4 ln(2 1 4 )] 2
微元法求体积
一、平行截面面积为已知的立体的体积如果一个立体不是旋转体，但却知道该立体上垂直于一定轴的各个截面面积，那么，这个立体的体积也可用定积分来计算.
o
a
b
x
设立体介于x=a,x=b之间, A( x ) 表示过点
图形的面积.
解
两曲线的交点 (0,0) (1,1) 选 x 为积分变量 x [0,1] 面积元素dA ( x x )dx
2
x y2
y x2
2 3 x 1 A 0 ( x x )dx x 2 . 3 0 3 3
1
3
1
2
例 2 计算由曲线 y 2 2 x 和直线 y x 4 所围成的图形的面积.
a
b
x 且垂直于 x 轴
A 的截面面积， ( x ) 为x 的已知连续函数取x为积分变量,其变化范围为[a,b].
[ x , x dx]
立体体积
体微元 dV A( x )dx,
x
V

b
a
A( x )dx.
例 7 一平面经过半径为 R 的圆柱体的底圆中心，并与底面交成角，计算这平面截圆柱体所得立体的体积.

立体体积和侧面积计算中的微元法

维普资讯
第７卷
第２朝
株洲师范高等专科学校学报
Ｊ０ＵＲＮＡＩＯＦＨＵＺＨＯｚＴＥＡＣＨＥＲｓＯＩＬＥＧＥＣ
ＶｏＮ０２【．
２００２年４月
立体体积和侧面积计算中的微元法
将区间［阳上连续的曲线一，ｚ绕ｚ轴旋Ｎ－ＮＮ￣Ｎ体．旋转体体积为一ｎ，（）－该
一占
Ｉ，（）ｘ体积微元ｄ＝ｆ（）：即把分割后的ｚｄ，Ｖ￣ｚｄ，ｌｒ小立体近似看成圆柱体把小圆柱，
体积视体积体为微元，体侧面旋转积为Ａ，ｚｄ面微元ｄ＝，）ｄ表一２Ｉ（），积ｓＡ（（示ｄｔａｏａｓｌｓｄｖｄｄｉｔｏｅｍｉｒｅｅｎｓｗｈｎｄｆｎｔｎｅｒｌｓａｐｅ，ｔａｂｔｓａａｙｅｈｔｈｗｏｉｉｉｉｅｏｓｍｃｏｌｍｅｔｅｅｉｉｉｔｇａｐ￣ｄｄｎｅｉ
ｔａｃｌｔｎｓｖｌｍｅｏｃｌｕａｉｇｉｏｕ．Ｔｈｅｓｎｒｌｏｇｖｎｗｈｈｕｄｖｄｄｓｌｓａｅｒｓｅｔｖｌａｅｓｃ１ｔｅｒａｏｓａｅａｓｉｅｙｔｅｓｂｉｉｅｉｒｅｐｃｉｅｙｔｋｎａｖ一ｏｄ［ｄｒａｄｃｒｕａｒｓｕｗｈｎｔｅｖｌｍｅｏｈＭｅａｅｆａｂｄｆｒｖｌｔｎｉｃｌｕａｅｎｅｎｉｃｌｒｆｕｔｍｅｈｏｕｒｔｅｓｒ８ｏｏｙｏｅｏｕｉａｃｌｔｏｓｄＫｅｏｄ：ｄｆｉｅｉｔｇａ￣ＭｉｒｅｅｎｔｏｙｒｓｅｉｔｅｒｌｎｎｅｏｌｍｅｔＭｅｈｄ；ｃｌｕａｉｎｏｕａｃｌｔ；ｖｌｍｅｉｅａｅｏ：ｓｄｒａ

微元法_精品文档

微元法1. 引言微元法是一种数学和物理学中常用的计算方法，用于求解曲线、曲面以及体积、质量、密度等相关问题。

它基于将一个复杂的形状或区域分割为无数个微小的元素，再对每个微元进行分析和计算的原理。

通过将微元的贡献累加起来，最终可以得到整体的属性或解答。

本文将介绍微元法的基本原理、应用领域以及常见的数学公式和计算方法。

2. 基本原理微元法基于微积分的概念，将一个复杂的形状或区域分割为许多无穷小的微元。

这些微元可以是线段、面积元或体积元，具体取决于问题的性质。

每个微元都具有一定的属性，如长度、面积或体积。

通过将微元的贡献进行累加，可以得到整体的属性或解答。

这是因为微元法假设微元足够小，可以近似地视为一条直线、一个平面或一个体积。

在微元法中，常用的方法包括求和、积分、微分等。

3. 应用领域微元法在各个领域中都有广泛的应用。

以下是几个常见的应用领域：3.1 物理学在物理学中，微元法常用于求解各种物理量。

例如，在力学中，可以使用微元法计算质点的质量、速度、加速度等。

在电磁学中，微元法可以用于计算电场、磁场的强度以及电势和磁势。

3.2 工程学微元法在工程学中也有广泛的应用。

例如，在结构力学中，可以使用微元法计算杆件或板件的应力、应变以及变形。

在流体力学中，微元法可以用于计算流体的速度、压力以及流量等。

3.3 经济学在经济学中，微元法被用于计算经济指标以及分析经济现象。

例如，在微观经济学中，微元法可以用于计算市场的需求曲线、供应曲线以及均衡价格和数量。

在宏观经济学中，微元法可以用于计算国民经济的总产出、总投资以及总消费等。

4. 常见公式和计算方法在微元法中，有一些常见的公式和计算方法可以用于求解问题。

下面是几个例子：4.1 长度的微元在计算曲线的长度时，可以使用以下公式：∆s = √(∆x^2 + ∆y^2 + ∆z^2)其中，∆s 表示曲线的微小长度，∆x、∆y 和∆z 分别表示曲线在 x、y 和 z 方向上的微小切线。

微元法求体积

微元法求体积
微元法：任取x,x+dx小段，绕y轴旋转，得一个空心圆柱体，沿平行于y轴剪开，得一个长方体：厚为dx,宽为f(x),长2πx(圆的周长），故dV=2πxf(x)dx。

旋转而得的立体是一个中间圆台形镂空、以x＝2为旋转轴的立体，所谓在[0,1]上取小区间[x,x+dx]，实际上是在x处取了一个厚为dx、环绕直线x＝2的圆环，该圆环的周长是2π(2-x)，高是上半圆周对应的函数减去直线对应的函数，厚度是dx，周长×高×厚度就是微元dV
最常见的换“元”技巧有如下几种
（1）“时间元”与“空间元”间的相互代换（表现时、空关系的运动问题中最为常见）；
（2）“体元”、“面元”与“线元”间的相互代换（实质上是降“维”）；（3）“线元”与“角元”间的相互代换（“元”的表现形式的转换）；（4）“孤立元”与“组合元”间的相互代换（充分利用“对称”特征）。

推导过程立体几何体积的计算方法

推导过程立体几何体积的计算方法在立体几何中，求解各种形状物体的体积是一个基本的数学问题。

本文将介绍一些常见几何体的体积计算方法，包括球体、圆柱体和长方体。

1. 球体体积的计算方法球体是一种具有无限个半径相等的点所组成的几何体，其体积的计算方法如下：首先，我们知道球体的体积公式为V = (4/3) * π * r^3，其中V表示体积，r表示球的半径。

2. 圆柱体体积的计算方法圆柱体是由两个平行且相等的圆底面和一个连接两个底面圆心的圆柱面组成的几何体，其体积的计算方法如下：首先，我们需要计算出圆柱底面的面积，即A = π * r^2，其中A表示底面面积，r表示底面圆的半径。

然后，我们需要计算出圆柱体的高度h。

最后，圆柱体的体积V = A * h，即V = π * r^2 * h。

3. 长方体体积的计算方法长方体是一种具有三对互相平行的矩形面的几何体，其体积的计算方法如下：首先，我们需要计算出长方体的三个相邻面的面积，分别是底面积A，侧面积B和前后面积C。

然后，将这三个面积相加，即可得到长方体的体积V = A + B + C。

通过以上的推导过程，我们获得了计算球体、圆柱体和长方体体积的公式。

但是，在实际的问题中，可能会遇到其他更复杂的几何体，这时我们需要根据具体情况，寻找相应的公式来计算体积。

总结：本文介绍了求解球体、圆柱体和长方体体积的计算方法，通过推导过程，我们得到了相应的公式。

这些公式在解决几何体体积问题时非常有用。

然而，稍微复杂一些的几何体可能需要更复杂的计算方法，需要根据具体情况寻找相应的公式。

最后，通过运用这些公式，我们可以准确地计算出各种形状物体的体积。

立体几何的计算总结

立体几何的计算总结立体几何是数学的一个重要分支，涉及到三维空间中的图形、体积、表面积等计算问题。

在学习立体几何的过程中，我们需要掌握一些计算方法和公式，以便解决各种几何问题。

本文将对立体几何的常见计算方法进行总结和归纳。

一、长方体的计算长方体是最简单的立体图形之一，其计算公式如下：1. 长方体的体积计算公式：长方体的体积（V）等于长（L）乘以宽（W）乘以高（H），即V = L * W * H。

其中，长、宽、高的单位需保持一致。

2. 长方体的表面积计算公式：长方体的表面积（A）等于长方体的底面积（A底）加上长方体的四个侧面积（A侧）。

A = A底 + A侧，其中 A底 = L * W，A侧 = 2 * (L * H + W * H)。

二、正方体和立方体的计算正方体和立方体是特殊的长方体，其计算公式如下：1. 正方体和立方体的体积计算公式：正方体和立方体的体积（V）等于边长（a）的立方，即V = a^3。

2. 正方体和立方体的表面积计算公式：正方体和立方体的表面积（A）等于正方体或立方体的一个面积（A面）乘以6个，即 A = A面 * 6。

A面 = a * a，其中 a为边长。

三、圆柱体的计算圆柱体是由一个矩形和两个平行圆面组成的立体图形，其计算公式如下：1. 圆柱体的体积计算公式：圆柱体的体积（V）等于底面积（A底）乘以高（H），即 V = A 底 * H。

A底= πr^2，其中 r为底面圆的半径。

2. 圆柱体的表面积计算公式：圆柱体的表面积（A）等于底面积（A底）加上两个底面和侧面的面积和（A侧）。

A = A底+ 2πrh，其中 A底= πr^2，A侧= 2πrh，r为底面圆的半径，h为圆柱体的高。

四、圆锥体的计算圆锥体是由一个圆锥面和一个底面组成的立体图形，其计算公式如下：1. 圆锥体的体积计算公式：圆锥体的体积（V）等于底面积（A底）乘以高（H）再除以3，即 V = (A底 * H) / 3。

立体图形体积的计算方法

立体图形体积的计算方法
立体图形体积的计算方法
三维图形的体积是指图形中实际存在的立体空间，计算三维体积有多种方法，其中主要有以下几种：
一种是采用体积公式法，即利用三维图形的体积公式来求解，通常比较复杂的图形对应的体积公式将会更复杂，因此需要计算时需要谨慎考虑；
另一种是采用积分法，即利用积分定理来求解，其原理是将原有的三维图形分解成多个梯形的集合，然后再求出每一个梯形的面积乘上高度之和，从而得出最终的结果；
最后还有一种是采用分块法，即将三维图形分成数个小体积块，通过求出每一块体积之后相加，计算出最终的体积。

总之，计算三维图形体积是一门有趣又有挑战性的数学领域，我们可以根据自己的能力选择不同的方法来求解，只要我们善于专注、认真计算，就一定能得出满意的结果。

利用扁圆台求旋转体的体积元素与侧面积元素

第29卷第5期高师理科学刊 Vol. 29 No.5 2009年 9 月 Journal of Science of Teachers′College and University Sep. 2009文章编号：1007-9831（2009）05-0020-02利用扁圆台求旋转体的体积元素与侧面积元素田巍（齐齐哈尔大学理学院，黑龙江齐齐哈尔 161006）摘要：利用扁圆台求旋转体的体积元素与侧面积元素，并且得出利用扁圆柱体求侧面积元素产生错误的原因．关键词：旋转体；体积元素；面积元素；圆台中图分类号：O172.2 文献标识码：A1 引言及预备知识在微积分学中，可以用元素法计算旋转体的体积及其侧面积[1-5]．应用元素法计算旋转体的体积时，为确定体积元素，将“分割”后的小旋转体用扁圆柱体“近似代替”，而计算同一旋转体的侧面积时，则将“分割”后的小旋转体用扁圆台“近似代替”．同是一个旋转体，我们注意到，计算旋转体体积时用扁圆柱体代替小旋转体则体积元素的表达式正确，而计算旋转体侧面积时用扁圆柱体代替小旋转体，导致面积元素的表达式是错误的．本文利用扁圆台求旋转体的体积元素与侧面积元素，使旋转体的体积元素与侧面积元素在选取时将“近似代替”统一起来，并给出利用扁圆柱体求侧面积元素产生错误的原因．在文献[1-5]中，元素法如下：一般地，如果某一实际问题中所求量U 符合下列条件：（1）U 是与一个变量x 的变化区间] ,[b a 有关的量；（2）U 对于区间] ,[b a 具有可加性，就是说，如果把区间] ,[b a 分成许多部分区间，则U 相应地分成许多部分量，而U 等于所有部分量之和；（3）部分量i U Δ的近似值可表示为i i x f Δ)(ξ，那么就可以考虑用定积分来表达这个量U ．通常写出这个量U 的积分表达式的步骤是：（1）根据问题的具体情况，选取一个变量如x 为积分变量，并确定它的变化区间] ,[b a ；（2）设想把区间] ,[b a 分成n 个小区间，取其中任一小区间并记作]d ,[x x x +，求出相应于这个小区间的部分量U Δ的近似值．如果U Δ能近似地表示为] ,[b a 上的一个连续函数在x 处的值)(x f 与x d 的乘积，且U Δ与x x f d )(相差一个比x d 高阶的无穷小，就把x x f d )(称为量U 的元素且记作U d ，即x x f U d )(d =；（3）以所求量U 的元素x x f d )(为被积表达式，在区间] ,[b a 上做定积分，得∫=ba x x f U d )(，这就是所求量U 的积分表达式．这个方法通常叫做元素法．2 主要结果2.1 利用扁圆台求旋转体体积元素v d以连续曲线0)(≥=x f y 、直线a x =，b x =及x 轴所围成的曲边梯形绕x 轴旋转一周而成的立体为例，我们寻求这种旋转体的体积元素v d ．如图1所示，取横坐标x 为积分变量，它的变化区间为] ,[b a ，相应于] ,[b a 上的任一小区间] ,[x x x Δ+的窄曲边梯形绕x 轴旋转而成的薄片收稿日期：2009-03-12基金项目：黑龙江省教育厅科学技术研究项目（11531426）作者简介：田巍（1971-），女，黑龙江齐齐哈尔人，副教授，硕士，从事微分方程研究．E-mail：qqhrmy@第5期田巍：利用扁圆台求旋转体的体积元素与侧面积元素 21 的体积近似于以)(x f 为上底半径，)(x x f Δ+为下底半径，x Δ为高的扁圆台的体积，从而体积的改变量为x x x f x x f x f x f v ΔΔ++Δ++=Δ))()()()((π3122，选取体积元素x x f x f x f x f v )d )()()()(π(31d 22+⋅+=，即体积元素x x f v d ))(π(d 2=，因为()0)(2)()()(lim 3πd d lim 2200=−Δ++Δ+=−Δ→Δ→Δx f x x f x x f x f x v v x x ，即)d (d x v v ο=−Δ，所以，由元素法可知，利用扁圆台求得的旋转体体积元素是正确的．此时得到的旋转体体积体积公式与用圆柱体“近似代替” 小旋转体得到的旋转体体积公式相同．2.2 利用扁圆台求旋转体侧面积元素S d图1中，设0)(≥=x f y 是] ,[b a 上一条光滑曲线．相应于] ,[b a 上的任一小区间] ,[x x x Δ+对应的曲线为弧PQ ，其中：点))( ,(x f x P =；点))( ,(x x f x x Q Δ+Δ+=．窄曲边梯形绕x 轴旋转而成的小旋转体的侧面积近似等于以)(x f 为上底半径，)(x x f Δ+为下底半径，x Δ为高，母线为直线2))((1x f PQ ′+=的扁圆台的侧面积，从而小旋转体侧面积的改变量为 x x f x x f x f S Δ′+Δ++=Δ2))((1))()((π，选取旋转体侧面积元素x x f x f S d ))((1)(π2d 2′+=，因为0))()((lim ))((1πd lim 020=−Δ+′+=Δ−Δ→Δ→Δx f x x f x f xS S x x ，即)(d x S S Δ=−Δο，所以，由元素法的思想可知，利用扁圆台求得的旋转体侧面积元素是正确的．如果用扁圆柱体代替小旋转体，可以类似证明，相应的S S d ,Δ不满足)(d x S S Δ=−Δο，导致面积元素的表达式错误．3 结束语由结果的分析可知，在求同一个旋转体的体积元素和侧面积元素时，如果利用扁圆台，完全可以将“近似代替”统一起来，即：无论求旋转体体积或是求旋转体侧面积，都将分割后的小旋转体近似看作扁圆台，这样，同样一种“分割”方法，对“分割”后的小旋转体同样一种“近似代替”，使得在利用元素法求旋转体的体积和侧面积时的方式不再产生差异．而利用扁圆柱体计算旋转体的体积元素和旋转体侧面积元素时，导致体积元素的表达式正确而面积元素的表达式错误的原因是：用扁圆柱体替代小旋转体时的体积元素v d 是v Δ的线性主部，而用圆柱体替代小旋转体时的旋转体侧面积元素S d 并非是S Δ的线性主部．参考文献：[1] 四川大学数学系高等数学教研室．高等数学[M]．北京：高等教育出版社，1995：340-348．[2] 田巍．应用微元法求旋转体体积的一般公式[J]．克山师范专科学校学报，2003（3）：28-29．[3] Wilfred K ．Advanced Calculus[M]．New York ：Addison-Wesley Punlishing Company ，1984：217-247．[4] Michael S P ．Calculus[M]．New York ：W.A.Benjamin Inc.，1967：214-216.[5] 同济大学应用数学系．高等数学[M]．北京：高等教育出版社，2002：273-275.Searching the differential of volume for body of rotation and the area forsurface of revolution by using the frustum of coneTIAN Wei（School of Science ，Qiqihar University ，Qiqihar 161006，China ）Abstract ：Researched the differential of volume for body of rotation and the differential of area for surface of revolution by using the frustum of a cone ，and pointed out the faith reason by using the cylinder to do the same thing. Key words ：rotation ；differential of volume ；differential of area ；frustum of a cone。

初中数学知识归纳立体几何的体积和表面积的计算方法

初中数学知识归纳立体几何的体积和表面积的计算方法初中数学知识归纳：立体几何的体积和表面积的计算方法在初中数学学习中，立体几何是一个重要的内容，涉及到体积和表面积的计算方法。

本文将综合归纳立体几何中常见的几何体的体积和表面积计算方法，以帮助同学们更好地掌握这一知识点。

1. 立方体立方体是一种几何体，具有六个相等的正方形面。

计算立方体的体积和表面积十分简单。

体积的计算方法：立方体的体积等于边长的立方，即体积 = 边长 x 边长 x 边长。

表面积的计算方法：立方体的表面积等于六个面的面积之和，即表面积 = 6 x 面积。

2. 正方体正方体是一种特殊的立方体，其六个面都是正方形。

体积的计算方法：正方体的体积与立方体相同，体积 = 边长 x 边长x 边长。

表面积的计算方法：正方体的表面积也与立方体相同，表面积 = 6 x 面积。

3. 长方体长方体是一种具有六个面的几何体，分别为矩形。

体积的计算方法：长方体的体积等于底面积乘以高，即体积 = 底面积 x 高。

表面积的计算方法：长方体的表面积等于两个底面积和四个侧面积之和，即表面积 = 2 x 底面积 + 4 x 侧面积。

4. 圆柱体圆柱体由一个圆形底面和一个平行于底面的圆形顶面连接而成。

体积的计算方法：圆柱体的体积等于底面积乘以高，即体积 = 底面积 x 高。

其中，底面积为圆的面积，可以使用πr²来表示（π取3.14或近似值），r为圆的半径。

表面积的计算方法：圆柱体的表面积等于两个底面积和一个侧面的面积之和，即表面积 = 2 x 底面积 + 侧面积。

其中，侧面积可以看作一条长方形的面积，长度为圆周长，宽度为圆柱体的高。

因此，侧面积 = 圆周长 x 高= 2πr x 高。

5. 锥体锥体由一个圆形底面和一个尖顶连接而成。

体积的计算方法：锥体的体积等于底面积乘以高再除以3，即体积= (底面积 x 高) / 3。

其中，底面积为圆的面积，可以使用πr²来表示（π取3.14或近似值），r为圆的半径。

空间几何体的体积认识空间几何体的体积计算方法

空间几何体的体积认识空间几何体的体积计算方法空间几何体的体积认识与计算方法在数学中，空间几何体的体积是指三维物体所占据的空间大小。

体积的计算是几何学中的重要概念，对于建筑、制造业、地理学等领域具有重要意义。

本文将介绍空间几何体的体积认识和计算方法。

一、立方体的体积计算方法立方体是一种拥有六个相等正方形面的空间几何体。

其体积可以使用以下公式进行计算：V = a³其中，V表示立方体的体积，a表示立方体的边长。

通过计算边长的立方，我们可以得到立方体的体积。

二、长方体的体积计算方法长方体是一种拥有六个矩形面的空间几何体。

其体积可以使用以下公式进行计算：V = lwh其中，V表示长方体的体积，l表示长方体的长度，w表示长方体的宽度，h表示长方体的高度。

通过计算长度、宽度和高度的乘积，我们可以得到长方体的体积。

三、圆柱体的体积计算方法圆柱体是一种拥有两个圆形底面和一个侧面的空间几何体。

其体积可以使用以下公式进行计算：V = πr²h其中，V表示圆柱体的体积，π表示圆周率（取近似值3.14），r表示圆柱体底面的半径，h表示圆柱体的高度。

通过计算底面半径的平方乘以高度再乘以π，我们可以得到圆柱体的体积。

四、球体的体积计算方法球体是一种拥有无边界几何形状的空间几何体。

其体积可以使用以下公式进行计算：V = (4/3)πr³其中，V表示球体的体积，π表示圆周率（取近似值3.14），r表示球体的半径。

通过计算半径的立方乘以4再除以3再乘以π，我们可以得到球体的体积。

五、锥体的体积计算方法锥体是一种拥有一个圆形底面和一个尖顶的空间几何体。

其体积可以使用以下公式进行计算：V = (1/3)πr²h其中，V表示锥体的体积，π表示圆周率（取近似值3.14），r表示底面半径，h表示锥体的高度。

通过计算底面半径的平方乘以高度再乘以1/3再乘以π，我们可以得到锥体的体积。

综上所述，通过不同几何体的特点和计算公式，我们可以准确计算出空间几何体的体积。

初中数学知识归纳立体形的表面积与体积

初中数学知识归纳立体形的表面积与体积初中数学知识归纳—立体形的表面积与体积在初中数学中，立体形的表面积与体积是我们学习的基础知识之一。

理解和掌握这些概念对我们解决与三维图形相关的问题至关重要。

本文将对立体形的表面积和体积进行归纳总结，并分享一些解决问题的方法和技巧。

一、立体形的表面积立体形的表面积是指该立体形所拥有的所有表面的总面积。

不同的立体形具有不同的计算方法，下面将对几种常见的立体形进行介绍。

1. 立方体：立方体是由六个相等的正方形组成的立体形，它的表面积可以通过公式 6a^2 来计算，其中 a 表示正方形的边长。

2. 正方体：正方体是特殊的立方体，它的六个面都是相等的正方形。

它的表面积计算方法与立方体相同，也是 6a^2。

3. 圆柱体：圆柱体由两个相等的圆面和一个侧面组成。

它的表面积可以通过计算圆的面积并加上侧面的矩形面积来求得。

具体计算公式为2πr^2+2πrh，其中 r 表示圆的半径，h 表示圆柱体的高。

4. 圆锥体：圆锥体由一个圆锥面和一个底面组成。

它的表面积也可以通过计算圆的面积并加上锥面的三角形面积来求得。

计算公式为πr^2+πrl，其中r 表示底面圆的半径，l 表示斜高。

5. 球体：球体是由无数个等距离于球心的点组成的。

它的表面积计算公式为4πr^2，其中 r 表示球体的半径。

通过以上的介绍，我们可以了解到不同立体形的表面积计算方法。

掌握这些方法，我们就能够准确计算出各种立体形的表面积。

二、立体形的体积立体形的体积是指该立体形所包含的空间容积。

与表面积不同，立体形的体积需要考虑到形状的三维特性。

下面我们将介绍几种常见立体形的体积计算方法。

1. 立方体：立方体的体积计算非常简单，只需要将正方形的边长 a 直接相乘即可，公式为 V=a^3。

2. 正方体：正方体与立方体类似，它的体积也可以通过边长a 的乘积计算得到，公式为 V=a^3。

3. 圆柱体：圆柱体的体积计算需要考虑到圆柱体的高度 h。

立体体积和侧面积计算中的微元法

论应用 , * 来作 !* 的近似值 $ 而若用 !# 来作 !* 的近似值，则所求侧面积的误差不一定是比 !# 更高阶的无穷小量 $
-
实例分析
求底半径为 , ，高为 + 的圆锥体的体积和侧面积（如图
#） $ 先求体积，体积微元用圆柱体近似代替，有 +） ,! ! # !# $ 求小圆台体积的实际 +! 值，判断 , ! 是否为 !! 的线性主要部分 $
’
曲线弧长的近似计算
设曲线 ( " （，［ # ，" ］（如图 %）（ % &） &" % &）
为连续可微函数，令曲线弧段 )* 长为 !+ ，用弧长
’ 微分近似代替 !+ $ 弧长微分 # + " # % $ %,（ &） # &这个公式告诉我们，弧长微分实为 & 处的切线在［ &，
第%卷第#期 #$$# 年 ! 月
株洲师范高等专科学校学报
Q’RS-(T ’U BGRBG’R DV(EGVSW E’TTV.V
P=F & % -=& # (8: & #$$#
立体体积和侧面积计算中的微元法
王名学 !
（株洲师范高等专科学校数学系，湖南株洲 !"#$$%）
摘要：分析了在定积分的应用中如何确定所求量的微元 & 讨论了求旋转体体积和侧面积时，把
! 是体积 ! 在 # 的微分，也恰是矩形区域上式表明 ""（ #） !# 是 !! 的线性主要部分，
在计算旋转体体积时，分割后的微元可用圆柱 &’() 绕 # 轴旋转所成的圆柱体体积 $ 因此，体近似代替 $

微元法应用误区浅析

微元法应用误ቤተ መጻሕፍቲ ባይዱ浅析
张民珍
!
（运城学院应用数学系，山西运城 )""))) ） # # 摘# 要：微元法是高等数学和数学分析课程中经常使用的一种解决问题的方法。此方法的关键是寻找微元的近似值，而人们往往忽视了近似代替量所需满足的条件，即误差应为 !! 的高阶无穷小。关键词：微元法；误差；高阶无穷小中图分类号： >?"@# 文献标识码： < # # 文章编号： ?))A B A))A （ !))* ） )! B )))A B )! ?、微元法的基本思想微元法是用定积分解决实际问题的一种重要方法，因为有太多的求总量的问题都可以用微元法来解决。［ !， ! # !!］上的分量 !" 近微元法解决问题的基本思想是：将可分解为若干段上分量之和的所求量 " 在任意微小区间似为 $" % （ & !）然后再积分求和，所求量 " % !!， & !） $!。因此，使用微元法时，所求量 " 应满足以下两个条件： .（
所以 !. $ "+ $ -+ !
! ! ｛［! $ - +! ］（ " - !"）］ )（ ! $ - +! " ）｝ !
图%
! ! $ "+ ! $ - +［ ! "!" -（ !"）］ ! ! $ ! "+ ! $ - +! " ! " - " + ! $ - +（ !"）
（! ）
于是
. !"+"’" $ "+,

立体图形的体积表面积侧面积几何重心与转动惯量计算公式

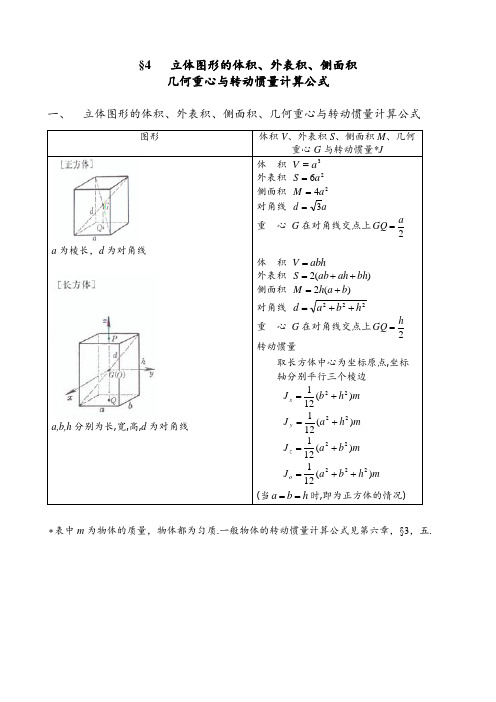
§4立体图形的体积、外表积、侧面积几何重心与转动惯量计算公式一、立体图形的体积、外表积、侧面积、几何重心与转动惯量计算公式图形体积V、外表积S、侧面积M、几何重心G与转动惯量*Ja为棱长，d为对角线a,b,h分别为长,宽,高,d为对角线体积3aV=外表积26aS=侧面积24aM=对角线ad3=重心G在对角线交点上2aGQ=体积abhV=外表积)(2bhahabS++=侧面积)(2bahM+=对角线222hbad++=重心G在对角线交点上2hGQ=转动惯量取长方体中心为坐标原点,坐标轴分别平行三个棱边mhbJx)(12122+=mhaJy)(12122+=mbaJz)(12122+=mhbaJo)(121222++=(当hba==时,即为正方体的情况)*表中m为物体的质量，物体都为匀质.一般物体的转动惯量计算公式见第六章，§3，五.图形体积V、外表积S、侧面积M、几何重心G与转动惯量Ja,b,c为边长,h为高a为底边长,h为高,d为对角线n为棱数,a为底边长,h为高,g为斜高体积FhV=外表积MFS+=2侧面积hcbaM)(++=式中F为底面积重心2hGQ=(P、Q分别为上下底重心)转动惯量对于正三棱柱(a=b=c)取G为坐标原点,z轴与棱平行mahaJz1248324==体积hahaV225981.2233≈=外表积ahaahaS61962.563322+≈+=侧面积ahM6=对角线224ahd+=重心2hGQ=(P、Q分别为上下底重心)转动惯量取G为坐标原点,z轴与棱平行mahaJz12583524==体积FhV31=外表积FMS+=侧面积agnnFM2'==式中F为底面积,'F为一侧三角形面积重心 4hGQ =(Q 为底面的重心)图形体积V 、外表积S 、侧面积M 、几何重心G 与转动惯量Ja,b,c,p,q,r 为棱长h 为高体积011111010101028812222222222222c b a c p qb p r a q r V = 重心 PQ GQ 41=(P 为顶点,Q 为底面的重心)体积 )''(3FF F F hV ++=式中F F ,'分别为上下底面积重心 '''3'24FF F F F FF F PQ GQ ++++=(P ,Q 分别为上下底重心)a’,a 分别为上下底边长,n 为棱数,h 为高,g 为斜高体积 ⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛++=2''13a a a a hF V 外表积 F F M S ++='侧面积 g a a nM )'(2+= 式中F F ,'分别为上下底面积重心 2222'''3'24a a a a a a a a h GQ ++++=(P 、Q 分别为上下底重心)图形体积V 、外表积S 、侧面积M 、几何重心G 与转动惯量J两底为矩形,a’,b’,a,b 分别为上下底边长,h 为高,1a 为截头棱长体积]'')')('([6b a b b a a ab hV ++++='''1b b ab b a a --=重心 ''2''2''3''2b a b a ab ab b a b a ab ab PQ GQ ++++++=(P ,Q 分别为上下底重心)hb底为矩形,a,b为其边长,h为高,a’为上棱长r为半径重心'2'2aaaaPQGQ++=(P为上棱中点,Q为下底面重心) 体积33352360.0634ddrV≈==ππ外表积24rSπ=重心G与球心O重合转动惯量取球心O为坐标原点mrJJJzyx252===mrJo253=图形体积V、外表积S、侧面积M、几何重心G与转动惯量J[半球体]r为半径,O为球心r为球半径,a为弓形底圆半径,h为拱高,α为锥角(弧度)r为球半径,a为拱底圆半径,h为拱高体积331232drVππ==外表积23rSπ=侧面积22rMπ=重心rGO83=转动惯量取球心O为坐标原点,z轴与GO重合mrJJJzyx252===mrJo253=体积hrhrV220944.232≈=π外表积)2(ahrS+=π侧面积(锥面部分) rMπα=重心)2(83hrGO-=转动惯量z轴与GO重合⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛-=2sin2cos2cos1215225αααπrJz⎪⎭⎫⎝⎛+-=2cos2cos32533ααhmr体积)3(3)3(6222hrhhahV-=+=ππ外表积)2()2(222aharhS+=+=ππ侧面积(球面部分))(222harhM+==ππ重心)3()2(432hrhrGO--=图形体积V、外表积S、侧面积M、几何重心G与转动惯量J[球台]r为球半径,a',a分别为上下底圆的半径,h为高R为中心半径,D为中心直径,r为圆截面半径,d 为圆截面直径体积)'33(6222haahV++=π外表积)'2(22aarhS++=π侧面积rhMπ2=2222222'⎪⎪⎭⎫⎝⎛--+=hhaaar重心22244'33'23haaaahGO++-=222222'33'422haahaahGQ++++=(Q为下底圆心)体积222242DdRrVππ==外表积DdRrS224ππ==重心G在圆环的中心上转动惯量取圆环的中心为坐标原点,z轴垂直于圆环所在平面mRrJJyx⎪⎪⎭⎫⎝⎛+==28522mRrJz⎪⎭⎫⎝⎛+=2243图形体积V、外表积S、侧面积M、几何重心G与转动惯量J[圆柱体]r为底面半径,h为高R为外半径,r为内半径,h为高r为底圆半径,h,H分别为最小,最大高度,α为截角,D为截头椭圆轴体积hrV2π=外表积)(2hrrS+=π侧面积rhMπ2=重心2hGQ=(P,Q分别为上下底圆心)转动惯量取重心G为坐标原点,z轴垂直底面mhrJJyx⎪⎪⎭⎫⎝⎛+==34122mrJz22=体积thRrRhVππ2)(22=-=外表积)(222rRMS-+=π侧面积RhrRhMππ4)(2=+=式中t为管壁厚,R为平均半径重心2hGQ=转动惯量取z轴与GQ重合mrRJz2)(22+=体积)(22hHrV+=π外表积⎪⎭⎫⎝⎛++=απcos112rMS⎪⎭⎫⎝⎛+++=2DhHrrπ侧面积)(hHrM+=π截头椭圆轴22)(4hHrD-+=重心)(4tan422hHrhHGQ+++=α)(2tan 2h H r GK +=α (GQ 为重心到底面距离,GK 为重心到轴线O O '的距离)图形体积V 、外表积S 、侧面积M 、几何重心G 与转动惯量Jh 为截段最大高度,b 为底面拱高,2a 为底面弦长,r 为底面半径,α2为弧所对圆心角(弧度)体积])(3)3([3222a r b r a r a b hV -+-=⎪⎭⎫⎝⎛--=αααcos sin 31sin 33a b hr侧面积(柱面部分) ])[(2a r b brhM +-=α体积 abc abc V 1888.434≈=π重心 G 在椭球中心O 上转动惯量取椭球中心为坐标原点,z 轴与c 轴重合m c b J x )(5122+=m a c J y )(5122+=m b a J z )(5122+=a,b,c 为半轴图形体积V 、外表积S 、侧面积M 、几何重心G 与转动惯量J 体积 h r V 23π=外表积 )(l r r S +=π 侧面积 rl M π=母线 22h r l +=重心 4hGQ =(Q 为底圆中心,O 为圆锥顶r为底圆半径,h为高,l为母线r,R分别为上,下底圆半径,h为高,l为母线上下底平行,F',F分别为上,下底面积,F为中截面面积,h为高取圆锥顶点为坐标原点,z轴与GQ 重合mhrJJyx⎪⎪⎭⎫⎝⎛+==22453mrJz2103=体积)(322RrrRhV++=π外表积)(22rRMS++=π侧面积)(rRlM+=π母线22)(hrRl+-=圆锥高(母线交点到底圆的距离)rRhrhH-+=重心2222324rRrRrRrRhGQ++++=(P,Q分别为上下底圆心)体积)4'(60FFFhV++≈[注] 棱台、圆台、球台、圆锥、棱柱、圆柱等都是拟棱台的特例图形体积V、外表积S、侧面积M、几何重心G与转动惯量Jd为上,下底圆直径,D 为中截面直径,h为高母线为圆弧时:体积)2(26180.0)2(122222dDhdDhV+≈+=π2)2(08727.0dDh+≈母线为抛物线时:体积⎪⎭⎫⎝⎛++=2243215dDdDhVπ)348(05236.022dDdDh++≈重心2hGQ=(P,Q分别为上下底圆心)二、多面体[正四面体] [正八面体] [正十二面体] [正二十面体] 图形面数f 4 8 12 20棱数k 6 12 30 30顶点数e 4 6 20 12 体积V31179.0a34714.0a36631.7a31817.2a外表积S27321.1a24641.3a26457.20a26603.8a 表中a为棱长.[欧拉公式] 一个多面体的面数为f，棱数为k，顶点数为e,它们之间满足2=+-fke。

几何体的体积和表面积计算方法

几何体的体积和表面积计算方法知乎专栏标题：几何体的体积和表面积计算方法摘要：本文将介绍几何体的体积和表面积计算方法，并通过简洁明了的解释和举例，帮助读者全面理解这些计算方法的原理和应用。

从基础的三维几何体开始，逐步深入，为读者提供全面的知识体验。

1. 三维几何体的体积和表面积计算方法在几何学中，我们经常需要计算三维几何体的体积和表面积。

这些计算方法不仅在数学领域有重要意义，也广泛应用于物理学、工程学和建筑学等领域。

下面，我们将介绍一些常见几何体的计算方法。

1.1 立方体的体积和表面积计算方法立方体是最简单的三维几何体，它的所有面都是正方形，所有边长相等。

计算立方体的体积非常简单，只需将边长相乘即可，即体积V = 边长^3。

而表面积的计算，则需要将所有的面积相加，即表面积S = 6 * 边长^2。

1.2 圆柱体的体积和表面积计算方法圆柱体由一个圆形底面和一个平行于底面的侧面组成。

计算圆柱体的体积需要使用到底面的面积和高度，即体积V = 底面面积 * 高度。

而表面积则需要将底面和侧面的面积相加，即表面积S = 底面面积 + 侧面面积。

1.3 球体的体积和表面积计算方法球体是一个完全由曲面构成的三维几何体。

计算球体的体积需要使用到半径，即体积V = (4/3) * π * 半径^3。

而表面积的计算则需要使用到半径，即表面积S = 4 * π * 半径^2。

2. 深入理解几何体的体积和表面积计算除了上述常见几何体之外，还有许多其他形状的几何体，如圆锥、棱柱和多面体等。

这些几何体的体积和表面积计算方法可能稍微复杂一些，但其核心原理仍然是基于相应面积和长度的计算。

深入理解这些计算方法的原理，有助于我们更好地应用它们解决实际问题。

在工程学中，我们经常需要计算建筑物或零件的体积，以便进行材料和成本的评估。

而在物理学中，理解物体的表面积和体积有助于我们研究物体的性质和行为。

3. 本文的观点和理解几何体的体积和表面积计算是数学中的基本概念之一，对我们的学习和生活有着重要意义。

微元法——精选推荐

微元法方法简介微元法是分析、解决物理问题中的常用方法，也是从部分到整体的思维方法。

用该方法可以使一些复杂的物理过程用我们熟悉的物理规律迅速地加以解决，使所求的问题简单化。

在使用微元法处理问题时，需将其分解为众多微小的“元过程”，而且每个“元过程”所遵循的规律是相同的，这样，我们只需分析这些“元过程”，然后再将“元过程”进行必要的数学方法或物理思想处理，进而使问题求解。

使用此方法会加强我们对已知规律的再思考，从而引起巩固知识、加深认识和提高能力的作用。

赛题精讲例1：如图3—1所示，一个身高为h 的人在灯以悟空速度v 沿水平直线行走。

设灯距地面高为H ，求证人影的顶端C 点是做匀速直线运动。

解析：该题不能用速度分解求解，考虑采用“微元法”。

设某一时间人经过AB 处，再经过一微小过程Δt（Δt→0），则人由AB 到达A′B′，人影顶端C 点到达C′点，由于ΔS AA ′= v Δt 则人影顶端的移动速度：v C =CC t 0S lim t '∆→∆∆=AA t 0H S H h lim t '∆→∆-∆=H H h -v 可见v c 与所取时间Δt 的长短无关，所以人影的顶端C 点做匀速直线运动。

例2：如图3—2所示，一个半径为R 的四分之一光滑球面放在水平桌面上，球面上放置一光滑均匀铁链，其A 端固定在球面的顶点，B 端恰与桌面不接触，铁链单位长度的质量为ρ 。

试求铁链A 端受的拉力T 。

解析：以铁链为研究对象，由由于整条铁链的长度不能忽略不计，所以整条铁链不能看成质点，要分析铁链的受力情况，须考虑将铁链分割，使每一小段铁链可以看成质点，分析每一小段铁边的受力，根据物体的平衡条件得出整条铁链的受力情况。

在铁链上任取长为ΔL 的一小段（微元）为研究对象，其受力分析如图3—2—甲所示。

由于该元处于静止状态，所以受力平衡，在切线方向上应满足：T θ + ΔT θ = ΔGcosθ + T θ ，ΔT θ = ΔGcosθ = ρgΔLcosθ由于每段铁链沿切线向上的拉力比沿切线向下的拉力大ΔT θ ，所以整个铁链对A 端的拉力是各段上ΔT θ的和，即：T = ΣΔT θ = ΣρgΔLcosθ = ρgΣΔLcosθ观察ΔLcosθ的意义，见图3—2—乙，由于Δθ很小，所以CD ⊥OC ，∠OCE = θΔLcosθ表示ΔL 在竖直方向上的投影ΔR ，所以ΣΔLcosθ = R ，可得铁链A 端受的拉力：T = ρgΣΔLcosθ = ρgR例3：某行星围绕太阳C 沿圆弧轨道运行，它的近日点A 离太阳的距离为a ，行星经过近日点A 时的速度为v A ，行星的远日点B 离开太阳的距离为b ，如图3—3所示，求它经过远日点B 时的速度v B 的大小。

立体形的计算

立体形的计算在数学中，立体形是指具有三个维度的物体，例如立方体、圆柱体、球体等。

计算立体形的体积、表面积和其他相关参数是数学中的基本技能之一。

本文将介绍一些常见立体形的计算方法，并提供实际应用的例子。

一、立方体的计算立方体是最简单的立体形之一，它的六个面都是正方形。

计算立方体的体积和表面积非常简单。

1. 体积的计算公式：V = a³，其中a为立方体的边长。

例如，一个边长为5cm的立方体的体积为V = 5³ = 125cm³。

2. 表面积的计算公式：S = 6a²，其中a为立方体的边长。

例如，一个边长为5cm的立方体的表面积为S = 6 × 5² = 150cm²。

二、圆柱体的计算圆柱体是一个底部为圆形的立体形，上下底面平行且相等。

计算圆柱体的体积和表面积需要涉及底面半径和高度。

1. 体积的计算公式：V = πr²h，其中r为底面圆的半径，h为圆柱体的高度，π取近似值3.14。

例如，一个半径为4cm、高度为8cm的圆柱体的体积为V = 3.14 × 4² × 8 = 402.56cm³。

2. 表面积的计算公式：S = 2πrh + 2πr²，其中r为底面圆的半径，h为圆柱体的高度，π取近似值3.14。

例如，一个半径为4cm、高度为8cm的圆柱体的表面积为S = 2 × 3.14 × 4 × 8 + 2 × 3.14 × 4² = 267.52cm²。

三、球体的计算球体是一个所有点到中心的距离都相等的立体形。

计算球体的体积和表面积需要涉及半径。

1. 体积的计算公式：V = (4/3)πr³，其中r为球体的半径，π取近似值3.14。

例如，一个半径为6cm的球体的体积为V = (4/3) × 3.14 × 6³ = 904.32cm³。

立体体积和侧面积计算中的微元法

如何利用微元法计算旋转体的体积

球体被平面截下的体积-概述说明以及解释

第七章 微元法

立体体积和侧面积计算中的微元法

微元法_精品文档

微元法求体积

推导过程立体几何体积的计算方法

立体几何的计算总结

立体图形体积的计算方法

利用扁圆台求旋转体的体积元素与侧面积元素

初中数学知识归纳立体几何的体积和表面积的计算方法

空间几何体的体积认识空间几何体的体积计算方法

初中数学知识归纳立体形的表面积与体积

立体体积和侧面积计算中的微元法

微元法应用误区浅析

立体图形的体积表面积侧面积几何重心与转动惯量计算公式

几何体的体积和表面积计算方法

微元法——精选推荐

立体形的计算

第七章微元法