中考数学考前冲刺几何总复习系列训练(知识点总结、典型例题、强化训练、答案) 第24讲圆与圆(一)

合集下载

中考数学三轮冲刺-真题集训：知识点47 几何最值(pdf版,含答案)

一、选择题1．（2019·长沙）如图，△ABC 中，AB =AC =10，tanA =2，BE ⊥AC 于点E ，D 是线段BE 上的一个动点，则CD +5的最小值是【】A．．．D ．10【答案】B二、填空题1．（2019·黄冈）如图，AC ，BD 在AB 的同侧，AC ＝2，BD ＝8，AB ＝8.点M 为AB 的中点.若∠CMD ＝120°，则CD 的最大值是（）【解析】将△CAM 沿CM 翻折到△CA ′M ，将△DBM 沿DM 翻折至△DB ′M ，则A ′M ＝B ′M ，∠AMC ＝∠A ′MC ，∠DMB ＝∠DMB ′， ∵∠CMD ＝120°，∴∠AMC +∠DMB ＝∠A ′MC +∠DMB ′＝60°，∴∠A ′MB ′＝180°-（∠AMC +∠DMB +∠A ′MC +∠DMB ′）＝60°， ∴△A ′MB ′是等边三角形，又∵AC ＝2，BD ＝8，AB ＝8.点M 为AB 的中点，知识点47——几何最值∴A ′B ′＝A ′M ＝B ′M ＝AM ＝12AB ＝4，CA ′＝AC ＝2，DB ′＝DB ＝8，又CD ≤CA ′+A ′B ′+DB ′＝2+4+8＝14.三、解答题1．（2019山东威海，24，12分）如图，在正方形ABCD 中，AB ＝10cm ，E 为对角线BD 上一动点，连接AE ，CE ，过E 点作EF ⊥AE ，交直线BC 于点F ．E 点从B 点出发，沿着BD 方向以每秒2cm 的速度运动，当点E 与点D 重合时，运动停止，设△BEF 的面积为ycm 2，E 点的运动时间为x 秒．（1）求证：CE ＝EF ；（2）求y 与x 之间关系的函数表达式，并写出自变量x 的取值范围；（3）求△BEF 面积的最大值．【解析】（1）证明：过E 作MN ∥AB ，交AD 于M ，交BC 于N ， ∵四边形ABCD 是正方形，∴AD ∥BC ，AB ⊥AD ，∴MN ⊥AD ，MN ⊥BC ，∴∠AME ＝∠FNE ＝90°＝∠NFE ＋∠FEN ， ∵AE ⊥EF ，∴∠AEF ＝∠AEM ＋∠FEN ＝90°，∴∠AEM ＝∠NFE ， ∵∠DBC ＝45°，∠BNE ＝90°，∴BN ＝EN ＝AM .， ∴△AEM ≌△EFN （AAS ），∴AE ＝EF .∵四边形ABCD 是正方形，∴AD ＝CD ，∠ADE ＝∠CDE ， ∵DE ＝DE ，∴△ADE ≌△CDE （SAS ），∴AE ＝CE ＝EF .（2）在Rt △BCD 中，由勾股定理得：BD， ∴0≤x ≤.由题意，得BE ＝2x ，∴BN ＝EN x .由（1）知：△AEM≌△EFN，∴ME＝FN，∵AB＝MN＝10，∴ME＝FN＝10x，如图（1），当0≤x∴BF＝FN－BN＝10x x＝10－x. ∴y＝12BF·EN＝1(102−＝－2x2＋（0≤x；如图（2）x≤∴BF＝BN－FN x－（10x）＝x－10，∴y＝12BF·EN＝12−＝2x2－x≤.∴222(02x xyx x−+≤≤=−<≤（1）（2）（3）y＝－2x2＋5x＝－2（x2＋254，∵－2＜0，∴当x y有最大值是；即△BEF面积的最大值是；x≤y＝2x2－＝22(x－254，此时2＞0，开口向上，对称轴为直线x∵对称轴右侧，y 随x 的增大而增大， ∴当x＝y 最大值＝50.∴当x＝BEF 面积的最大值是50.25．（2019山东省威海市，题号25，分值12）（1）方法选择如图①，四边形ABCD 是OO 的内接四边形，连接AC ，BD .AB ＝BC ＝AC ，求证：BD ＝AD ＋CD . 小颖认为可用截长法证明：在DB 上截取DM ＝AD ，连接AM ..…… 小军认为可用补短法证明：延长CD 至点N ，使得DN ＝AD …… 请你选择一种方法证明.（2）类比探究【探究1】如图②，四边形ABCD 是⊙O 的内接四边形，连接AC ，BD .BC 是⊙O 的直径，AB ＝AC .试用等式表示线段AD ，BD ，CD 之间的数量关系，并证明你的结论.【探究2】如图③，四边形ABCD 是⊙O 的内接四边形，连接AC ，BD .若BC 是⊙O 的直径，∠ABC ＝30°，则线段AD ，BD ，CD 之间的等量关系式是.图①图②B图③B图④B（3）拓展猜想如图④，四边形ABCD 是⊙O 的内接四边形，连接AC ，BD .若BC 是O 0的直径，BC ：AC ：AB ＝a ：b ：c ，则线段AD ，BD ，CD 之间的等量关系式是.【思路分析】（1）选小颖的截长法，如图①，在DB 上截取DM ＝AD ，连接AM ，由旋转全等得BM ＝CD ，∴BD ＝MD ＋BM ＝AD ＋CD（2）【探究1】数量关系为：BDAD ＋CD如图②，在DB 上截取AD ＝AN ，连接AN ，可得△AND 为等腰直角三角形，∴ND，由旋转全等得BN ＝CD ，∴BD ＝ND ＋BNAD ＋CD【探究2】数量关系为：BD ＝2ADCD如图③，在DB 上截取2AD ＝PD ，连接AP ，可得△APD 为30°的直角三角形，由旋转相似得BP，∴BD ＝PD ＋BP ＝2ADCD （3）拓展猜想数量关系为：BD ＝abAD ＋c b CD如图④，过A 作AQ ⊥AD 交BD 于Q ，连接AQ ，由旋转相似得=BQ AB c CD AC b =，=DQ BC aAD AC b=， ∴BQ ＝cb CD ，BQ ＝a b AD ，∴BD ＝PD ＋BP ＝abAD ＋c b CD【解析】（1）选小颖的截长法，如图①，在DB 上截取DM ＝AD ，连接AM ，可得△AMD 为等边三角形，可证△BAM ≌△CAD （SAS ）得BM ＝CD ，∴BD ＝MD ＋BM ＝AD ＋CD（2）【探究1】数量关系为：BDAD ＋CD如图②，在DB 上截取AD ＝AN ，连接AN ，可得△AND 为等腰直角三角形，∴NDAD ，∠BAN ＝答案图①答案图②B∠CAD ，可证△BAN ≌△CAD （SAS ）得BN ＝CD ，∴BD ＝ND ＋BNAD ＋CD【探究2】数量关系为：BD ＝2ADCD如图③，在DB 上截取2AD ＝PD ，连接AP ，可得△APD 为30°的直角三角形，∴=tan 30AP ABAD AC=°，∠BAP ＝∠CAD ，可证△BAP ∽△CAD 得BPCD ，∴BD ＝PD ＋BP ＝2AD（3）拓展猜想数量关系为：BD ＝a b AD ＋c bCD 如图④，过A 作AQ ⊥AD 交BD 于Q ，连接AQ ，可得∠BAQ ＝∠CAD ，∠ABQ ＝∠ACD ，∠ADQ ＝∠ACB ，∠BAC ＝∠QAD ∴△BAP ∽△CAD ，△ADQ ∽△ACB ∴=BQ AB c CD AC b =，=DQ BC aAD AC b=， ∴BQ ＝cb CD ，BQ ＝a b AD ，∴BD ＝PD ＋BP ＝a b AD ＋c bCD 2．（2019·益阳）如图，在半面直角坐标系x O y 中，矩形ABCD 的边AB =4，BC =6.若不改变矩形ABCD 的形状和大小，当形顶点A 在x 轴的正半轴上左右移动时，矩形的另一个顶点D 始终在y 轴的正半上随之上下移动.(1)当∠O AD =30°时，求点C 的坐标；(2)设AD 的中点为M ，连接O M 、MC ，当四边形 O MCD 的面积为221时，求O A 的长； (3)当点A 移动到某一位置时，点C 到点O 的距离有最大值，请直接写出最大值，并求此时c os ∠O AD 的值.答案图③B答案图④B第2题图第2题备用图第2题答图1 第2题答图2【解析】（1）如图1，过点C 作CE ⊥y 轴，垂足为E .∵矩形ABCD 中，CD ⊥AD ，∴∠CDE +∠AD O=90°，又∵∠O AD +∠AD O=90°，∴∠CDE =∠O AD =30°.在R t △CED 中，CE =21CD =2，∴DE =32242222=−=−CE CD ; 在R t △O AD 中，∠O AD =30°，∴O D =21AD =3.∴点C 的坐标为(2，323+).(2)∵M 为AD 的中点，∴DM =3，6=DCM S △. 又∵221=OMCD S 四边形，∴29=ODM S △，∴9=OAD S △.设O A =x ，O D =y ，则 ==+9213622xy y x ，∴xy y x 222=+，即0)(2=−y x ，∴x =y .将x =y 代入3622=+y x 得182=x ，解得23=x (23−不合题意，舍去)，∴O A 的长为23.（3）O C 的最大值为8.理由如下：如图2，∵M 为AD 的中点，∴O M =3，522=+=DMCD CM .∴O C ≤O M +CM =8,当O 、M 、C 三点在同一直线时，O C 有最大值8. 连接O C ，则此时O C 与AD 的交点为M ，过点O 作O N ⊥AD ，垂足为N . ∵∠CDM =∠O NM =90°，∠CMD =∠O MN ，∴△CMD ∽△O MN ，∴OMCMMN DM ON CD ==，即3534==MN ON ，解得59=MN ，512=ON ，∴56=−=MN AM AN . 在R t △O AN 中，∵55622=+=AN ON OA ，∴55cos ==∠OA OAD AN .3．（2019·衡阳）如图，在等边△ABC 中，AB ＝6cm ，动点P 从点A 出发以cm /s 的速度沿AB 匀速运动．动点Q 同时从点C 出发以同样的速度沿BC 延长线方向匀速运动．当点P 到达点B 时，点P 、Q 同时停止运动．设运动时间为t （s ）．过点P 作PE ⊥AC 于E ，连接PQ 交AC 边于D ．以CQ 、CE 为边作平行四边形CQFE ．（1）当t 为何值时，△BPQ 为直角三角形；（2）是否存在某一时刻t ，使点F 在∠ABC 的平分线上？若存在，求出t 的值，若不存在，请说明理由；（3）求DE 的长；（4）取线段BC 的中点M ，连接PM ，将△BPM 沿直线PM 翻折，得△B ′PM ，连接AB ′当t 为何值时，AB ′的值最小？并求出最小值．【解析】：（1）∵△ABC 为等边三角形，∴∠B ＝60°，∵BP ⊥PQ ，∴2BP ＝BQ 即2（6－t ）＝6＋t ，解得t ＝2．∴当t 为2时，△BPQ 为直角三角形；（2）存在．作射线BF ，∵PE ⊥AC ，∴AE ＝0.5t ．∵四边形CQFE 是平行四边形，∴FQ ＝EC ＝6－0.5t ，∵BF 平分∠ABC ，∴∠FBQ ＋∠BQF ＝90°．∵BQ ＝2FQ ，BQ ＝6＋t ，∴6＋t ＝2（6－0.5t ），解得t ＝3．（3）过点P 作PG ∥CQ 交AC 于点G ，则△APG 是等边三角形．∵BP ⊥PQ ，∴EG ＝12AG ．∵PG ∥CQ ，∴∠PGD ＝∠QCD ，∵∠PDG ＝∠QDC ，PG ＝PA ＝CG ＝t ，∴△PGD ≌△QCD ．∴GD ＝12GC ．∴DE＝12AC＝3．（4）连接AM，∵△ABC为等边三角形，点M是BC的中点，∴BM＝3．由勾股定理，得AM＝．由折叠，得BM′＝3．当A 、B′、M在同一直线上时，AB′的值最小，此时AB′＝3.过点B′作B′H⊥AP于点H，则c os30°＝AHAB′,，解得t＝9－．∴t为9－时，AB′的值最小，最小值为－3．4.（2019·重庆A卷）如图，在平面在角坐标系中，抛物线y＝x2－2x－3与x轴交与点A，B（点A 在点B的左侧）交y轴于点C，点D为抛物线的顶点，对称轴与x轴交于点E．（1）连结BD，点M是线段BD上一动点（点M不与端点B，D重合），过点M作MN⊥BD交抛物线于点N（点N在对称轴的右侧），过点N作NH⊥x轴，垂足为H，交BD于点F，点P是线段OC上一动点，当MN取得最大值时，求HF＋FP＋13PC的最小值；（2）在（1）中，当MN取得最大值，HF＋FP＋13PC取得小值时，把点P单位得到点Q，连结AQ，把△AOQ绕点O顺时针旋转一定的角度α（0°<α<360°），得到△A OQ′′，其中边A Q′′交坐标轴于点G，在旋转过程中，是否存在一点G，使得OGQQ''∠=∠？若存在，请直接写出所有满足条件的点Q′的坐标；若不存在，请说明理由．【解析】（1）由题意得A(－1，0)，B(3，0)，C(0，－3)，D(1，－4)，直线BD：y＝2x－6．如答图1，连接DN、BN，则S△BDN＝12BD•MN，而BD为定值，故当MN最大时，S△BDN取最大值．此Q时由S △BDN ＝S △DFN ＋S △BFN ＝12EH •FN ＋12BH •FN ＝12BE •FN ＝FN ，从而S △BDN 取最大值时，即为FN 有最大值．令N (m ，m 2－2m －3)，则F (m ，2m －6)，从而FN ＝(2m －6)－(m 2－2m －3)＝－m 2＋4m －3＝－(m －2)2＋1，此时，当且仅当m ＝2，FN 有最大值为1，于是N (2，－3)，F (2，－2)，H (2，0)．在直角三角形中，设最小的直角边为a ，斜边为3a ，较长直角边为3，即可求出a x 轴上取点K (，0)，连接KC ，易求直线KC ：y ＝－x －3．如答图1，过点F 作FR ⊥CK 于点R ，交OC 于点P ，作FT ⊥OC ，交CK 于点T ，则∠OCK ＝∠TFR ，于是，由△PCR ∽△ACO ∽△TFR ，得133PR OK a PC KC a ===，从而PR ＝13PC ，因此由FH 为定值，再由定点F 到直线的垂直线最短，可知MN 取得最大值时，HF ＋FP ＋13PC 最小值＝HF ＋FR ．在y ＝－x －3中，当y ＝－2，x ，于是FT ＝2．在R t △FTR 中，由FR FT =，得FR FT (2)＝13，故HF ＋FP ＋13PC 最小值＝2＋13．（2）(，(，，．5.（2019·重庆B 卷）在平面直角坐标系中，抛物线242y ++与x 轴交于A ，B 两点（点A 在点B 左侧），与y 轴交于点C ，顶点为D ，对称轴与x 轴交于点Q .（1）如图1，连接AC ，BC ．若点P 为直线BC 上方抛物线上一动点，过点P 作PE ∥y 轴交BC 于点E ，作PF ⊥BC 于点F ，过点B 作BG ∥AC 交y 轴于点G ．点H ，K 分别在对称轴和y 轴上运动，连接PH ，HK ．当△PEF 的周长最大时，求PH +HK 的最小值及点H 的坐标．（2）如图2，将抛物线沿射线AC 方向平移，当抛物线经过原点O 时停止平移，此时抛物线顶点记作D ’，N 为直线DQ 上一点，连接点D ’，C ，N ，△D’CN 能否构成等腰三角形？若能，直接写出满足条件的点N 的坐标；若不能，请说明理由．【解析】（1）∵2y x ++与x 轴交于A ，B 两点，∴当y =0时，即20+，∴122,4x x =−=，即A （－2，0），B （4，0），设直线BC 的解析式为y =kx +b ，∵C （0，），B （4，0），∴40b k b =+=，∴b k = = ，∴直线BC的解析式为y +设点2(,4),P m m ++<< ∵PE ∥y 轴且点E 在直线BC上，∴(,E m +∠PEF =∠OCE ，∴2(04),PE m +<< ∵PF ⊥BC ，∴∠PFE =∠COB =90°，∴△PEF ∽△BCO ，设△PEF 的周长为1l ，△BCO 的周长为2l ，则12l PEl BC=，∵B （4，0），C （0，），∴BC=24l =+，∴21)(04),l m +<< ∴当m=2时，1l此时点P 的坐标为（2，）， ∵A （－2，0），C （0，），∴∠ACO =30°，∠CAO =60°，备用图图1图2∵BG∥AC，∴.∠BGD=30°，∠OBG=60°，∴G（0，−，直线B G解析式为y=−PM解析式为y=，过点G作GN⊥BG，过点P作PM⊥GN于点M，如图1，此时，点H为PM与对称轴的交点，K为PM与y轴的交点，点K与点O重合，则KM=OMKG，PH+HKKG的最小值为线段PM的长.（此问题是胡不归问题）.解法一：（作一线三直角利用相似求解）如图2，过点P作PQ∥x轴交对称轴于点T，过点M作MQ⊥y轴交PT于点Q，过点G作GJ⊥MQ交MQ于点J.设点Q（n，），∴J（n，−，∴PQ=2－n，M2－n），∵GJ=－n，∴MJ=，∴MQ+MJ=CG=(−−，2－n）+()=，∴n=-3，∴Q（－3，），∴PQ=5，∴PM=2PQ=10，∴PH+HKKG的最小值为10，∵∠OGM=60°，∠PHT=30°，∠HPT=60°，∴PT=1，∴HTH（1.图1 N解法二：由上面的解法可知MG ⊥BG ，直线MG的解析式为：y x −如图3，过点P 作PR ⊥x 轴交MG 于点R ，∴R （2，），由第一种解法可知∠PRG =60°，∴PMPR（）=10， ∴PH +HKKG 的最小值为10，同理可求H （1.（2）这样的N 点存在.当△'CD N 为等腰三角形时，这样的N有：1N,2N，3N,4N,5N .【提示】由（1）可知∠AC O=30°，∠O AC =60°,图2NN又∵221)y x x ++−+D （1，∵抛物线按射线AC 的方向平移，设平移后顶点'(D a ++，平移后的抛物线解析式为21)y x a =−−++该抛物线经过原点，则201)a =−−+∴2280a a −−=，∴a =4或a =－2（舍去），即D .设点N （1，b ）'CD ==CN =，'ND 如图4，当△'CD N 为等腰三角形时，分三种情况：①当'CD CN =，可得1N ,2N ；②当''CD D N =3N ,4N ,③当'CN D N =可得5N ,∴当△'CD N 为等腰三角形时，这样的N 有：1N ,2N ，3N ,4N ,5N .6.（2019·天津）已知抛物线y =x 2-bx +c (b ,c 为常数，b >0)经过点A （-1,0），点M (m ,0)是x 轴正半轴上的动点，（1）当b =2时，求抛物线的顶点坐标；（2）点D (b ,y D )在抛物线上，当AM =AD ,m =5时，求b 的值；（3）点Q(1,2b +y Q)2QM +b 的值. 【解析】(1)∵抛物线y =x 2-bx +c 经过点A （-1,0），∴1+b +c =0，∴c =-1-b 当b =2时，c =-3，∴抛物线的解析式为y =x 2-2x -3，∴顶点坐标为（1，-4）（2）由(1)知，c =-1-b ，∵点D (b ,y D )在抛物线上，∴y D =-b -1， ∵b >0,∴b 02b >>，-b -1<0,∴D (b ,-b -1)在第四象限，且在抛物线对称轴2bx =的右侧.如图，过点D 作DE ⊥x 轴于E ，则E （b ，0），∴AE =b +1=DE ,所以AD 1)b +，∵m =5，∴AM =5-（-1）=6，∴1)b +，∴b =（3）∵点Q(1b ,2+y Q )在抛物线上，∴y Q=2113)()12224b b b b b +−+−−=−−（， ∴点Q （1b ,2+3-24b −）在第四象限，且在直线x =b 的右侧，2QM +，A (-1，0)，∴取点N (0，1)，如图，过点Q 作Q H ⊥x 轴于H ，作QG ⊥AN 于G,QG 与x 轴交于点M ，则H （1b ,2+0），∠G AM =45°，∴G M AM ， ∵M （m ,0),∴AM =m +1,MH =1b 2m +−,Q H =324b +,∵MH =Q H ,∴1b 2m +−=324b +，∴m =1-24b ，∴AM =13-12424b b +=+，Q M 3)24b +（2QM +33)))24244（b ++b +b =4.7.（2019·自贡）如图，已知直线AB 与抛物线：y =ax 2+2x +c 相交于点A （-1，0）和点B （2，3）两点.（1）求抛物线C 函数解析式；（2）若点M 是位于直线AB 上方抛物线上的一动点，以MA 、MB 为相邻的两边作平行四边形MANB ，当平行四边形MANB 的面积最大时，求此时平行四边形MANB 的面积S 及点M 的坐标；（3）在抛物线C 的对称轴上是否存在顶点F ，使抛物线C 上任意一点P 到F 的距离等于到直线y =174的距离，若存在，求出定点F 的坐标；若不存在，请说明理由.【解析】（1）将A（-1，0）和B（2，3）代入抛物线解析式得�aa−2+cc=04aa+4+cc=3解得，�aa=−1cc=3∴抛物线解析式为y=-x2+2x+3.（2）过M作MH∥y轴，交AB于H，设直线AB为y=kx+b，将A，B坐标代入得，�−kk+bb=02kk+bb=3解得，�kk=1bb=1.∴直线AB的解析式为y=x+1.设M为（m，-m2+2m+3）,则H（m，m+1）∴MH=y M-Y H=(-m2+2m+3)-( m+1)=-m2+m+2.∴S△ABM=S△AMH+S△BMH=12·MH·（x B-x A）=12·(-m2+m+2)·(2+1)=-32(m2-m)+3=-32(m-12)2+278. ∵四边形MANB是以MA、MB为相邻的两边的平行四边形，∴△ABM≌△BAN.∴S四边形MANB=2 S△ABM=-3(m-12)2+274，∵a=-3＜0且开口向下，∴当m=12时，S四边形MANB的最大值为274.此时，M坐标为（12，154）. （3）存在，理由如下：过P作直线y=174的垂线，垂足为T，∵抛物线为y=-x2+2x+3=-(x-1)2+4.∴抛物线的对称轴为直线x=1，顶点坐标为（1,4）.当P为顶点，即P（1.4）时，设F点坐标为（1，t），此时PF=4-t，PT=174-4=14.∵P到F的距离等于到直线y=174的距离，∴4-t=14，即t=154.∴F为（1，154）设P点为（a，-a2+2a+3）,由勾股定理，PF2=(a-1)2+(-a2+2a+3-154)2=a4-4a3+132a2-5a+2516.又∵PT2=[174-(-a2+2a+3)]2= a4-4a3+132a2-5a+2516.∴PF2=PT2，即PF=PT.∴当F为（1，154）时，抛物线C上任意一点P到F的距离等于到直线y=174的距离. 8．（2019·淮安）如图①，在△ABC中，AB=AC=3，∠BAC=100°，D是BC的中点.小明对图①进行了如下探究：在线段AD上任取一点P，连接PB.将线段PB绕点P按逆时针方向旋转80°，点B的对应点是点E，连接BE，得到△BPE.小明发现，随着点P在线段AD上位置的变化，点E的位置也在变化，点E可能在直线AD的左侧，也可能在直线AD上，还可能在直线AD的右侧.请你帮助小明继续探究，并解答下列问题：(1)当点E在直线AD上时，如图②所示.①∠BEP= ；②连接CE，直线CE与直线AB的位置关系是.(2)请在图③中画出△BPE，使点E在直线AD的右侧，连接CE.试判断直线CE与直线AB的位置关系，并说明理由.(3)当点P在线段AD上运动时，求AE的最小值.【解析】（1）①由题意得，PE =PB ，∠BPE =80°，∴∠BEP =°=°−°50280180； ②如图所示，∵AB =AC ，D 是BC 的中点，∠BAC =100°，∴∠ABC =°=°−°402100180，∵∠BEP =50°，∴∠BCE =∠CBE =40°，∴∠ABC =∠BCE ，∴CE ∥AB . 答案：①50°；②平行（2）在DA 延长线上取点F ，使∠BF A =∠CF A =40°，总有△BPE ∽△BFC . 又∵△BPF ∽△BEC ，∴∠BCE =∠BFP =40°，∴∠BCE =∠ABC =40°，∴CE ∥AB .当点P 在线段AD 上运动时，由题意得PB =PE =PC ， ∴点B 、E 、C 在以P 为圆心、PB 为半径的圆上，如图所示：∴AE 的最小值为AC =3.9.（2019·凉山州）如图，抛物线y = ax 2+bx +c 的图象过点A （-1，0）、B （3,0）、C （0,3）.（1）求抛物线的解析式；（2）在抛物线的对称轴上是否存在一点P ，使得△P AC 的周长最小，若存在，请求出点 P 的坐标及△P AC 的周长；若不存在，请说明理由；（3）在（2）的条件下，在x 轴上方的抛物线上是否存在点M （不与C 点重合），使得 S △P AM =S △P AC ，若存在，请求出点M 的坐标；若不存在，请说明理由.【解析】（1）由题知 ==++=+−30390c c b a c b a ，解得==−=321c b a ，∴抛物线的解析式为y = -x 2+2x +3；（2）存在.连接BC 交抛物线对称轴于点P ，此时△P AC 的周长最小.设BC :y =kx +3，则3k +3=0，解得k =-1，∴BC :y =-x +3.由抛物线的轴对称性可得其对称轴为直线x =1，当x =1时，y =-x +3=2，∴P （1,2）.在Rt △OAC 中，AC =2231+=10；在Rt △OBC 中，BC =2233+=32.∵点P 在线段AB 的垂直平分线上，∴P A =PB ，∴△P AC 的周长=AC +PC +P A = AC +PC +PB =AC +BC =10+32.综上，存在符合条件的点P ，其坐标为（1,2），此时△P AC 的周长为10+32；（3）存在.由题知AB =4，∴S △P AC =S △ABC -S △P AB =21×4×3-21×4×2=2.设：AP :y =mx +n ，则=+=+−20n m n m ，解得==11n m ，∴AP :y =x +1.①过点C 作AP 的平行线交x 轴上方的抛物线于M ，易得CM :y =x +3，由++−=+=3232x x y x y 解得 ==3011y x ，==4122y x ，∴M （1,4）； ②设抛物线对称轴交x 轴于点E （1,0）,则S △P AC =21×2×2=2=S △P AC .过点E 作AP 的平行线交x 轴上方的抛物线于M ，设EM :y =x +t ，则1+t =0,∴t =-1，∴EM :y =x -1. 由 ++−=−=3212x x y x y 解得−−=−=2171217111y x （舍），+−=+=2171217122y x ，∴M （2171+,2171+−）. 综上，存在符合条件的点M ，其坐标为（1,4）或（2171+,2171+−）. 10．（2019·苏州，26，10）已知矩形ABCD 中，AB ＝5cm ，点P 为对角线AC 上的一点，且AP ＝cm ．如图①，动点M 从点A 出发，在矩形边上沿着A →B →C 的方向匀速运动（不包含点C ）．设动点M 的运动时间为t （s ），△APM 的面积为S （cm 2），S 与t 的函数关系如图②所示．（1）直接写出动点M 的运动速度为cm /s ，BC 的长度为cm；（2）如图③，动点M 重新从点A 出发，在矩形边上按原来的速度和方向匀速运动，同时，另一个动点N 从点D 出发，在矩形边上沿着D →C →B 的方向匀速运动，设动点N 的运动速度为v （cm /s ）．已知两动点M ，N 经过时间x （s ）在线段BC 上相遇（不包含点C ），动点M ，N 相遇后立即同时停止运动，记此时△APM 与△DPN 的面积分别为S 1（cm 2），S 2（cm 2） ①求动点N 运动速度v （cm /s ）的取值范围； ②试探究S 1•S 2是否存在最大值，若存在，求出S 1•S 2的最大值并确定运动时间x 的值；若不存在，请说明理由．图① 图② 图③ 第27题答图【解析】（1）∵t ＝2.5s 时，函数图象发生改变，∴t ＝2.5s 时，M 运动到点B 处，∴动点M 的运动速度为52.5=2cm /s ，∵t ＝7.5s 时，S ＝0，∴t ＝7.5s 时，M 运动到点C 处，∴BC ＝（7.5﹣2.5）×2＝10（cm ），故答案为2，10；（2）①∵两动点M ，N 在线段BC 上相遇（不包含点C ），∴当在点C 相遇时，v527.53=（cm /s ），当在点B 相遇时，v 5102.5+=6（cm /s ），∴动点N 运动速度v （cm /s ）的取值范围为23cm /s ＜v ≤6cm /s ； AB ，交CD EF ∥BC ，EF ＝BC ＝10，∴AF APAB AC=，∵AC∴5AF =解得AF ＝2，∴DE ＝AF ＝2，CE ＝BF ＝3，PF 4，∴EP ＝EF ﹣PF ＝6，∴S 1＝S △APM ＝S △APF +S 梯形PFBM ﹣S △ABM 12=×4×212+（4+2x ﹣5）×312−×5×（2x ﹣5）＝﹣2x +15，S 2＝S △DPM ＝S △DEP +S 梯形EPMC ﹣S △DCM 12=×2×612+（6+15﹣2x ）×312−×5×（15﹣2x ）＝2x ，∴S 1•S 2＝（﹣2x +15）×2x ＝﹣4x 2+30x ＝﹣4（x 154−）22254+，∵2.5154＜＜7.5，在BC 边上可取，∴当x 154=时，S 1•S 2的最大值为2254．11.(2019·巴中)如图,抛物线y ＝ax 2+bx －5(a ≠0)经过x 轴上的点A (1,0)和点B 及y 轴上的点C ,经过B ,C 两点的直线为y ＝x +n .①求抛物线的解析式;②点P 从A 出发,在线段AB 上以每秒1个单位的速度向B 运动,同时点E 从B 出发,在线段BC 上以每秒2个单位的速度向C 运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t 描,求t 为何值时,△PBE 的面积最大,并求出最大值.③过点A 作AM ⊥BC 与点M ,过抛物线上一动点N (不与点B ,C 重合)作直线AM 的平行线交直线BC 于点Q,若点A ,M ,N ,Q 为顶点的四边形是平行四边形.求点N 的横坐标.分析:①由点A 和直线y ＝x +n 可得方程组,解出系数,求得二次函数的解析式;②根据题意表示出三角形面积,利用二次函数最值进行求解;③分析得到AM 平行且等于N Q,设出坐标,利用坐标关系列方程进行求解,并检验.【解析】①因为点B ,C 在y ＝x +n 上,所以B (－n ,0),C (0,n ),因为点A (1,0)在抛物线上,所以250505a b an bn n ì+-=ïï--=íï=-ïî,解得,a ＝－1,b ＝6,所以抛物线的解析式为:y ＝－x 2+6x －5.②由题意得:PB ＝4－t ,，BE ＝2t ，由①可知:∠O BC ＝45°,点P 到BC 上的高h ＝BP s in 45(4－t),所以S △PBE ＝12BE h 鬃＝)22t --+当t ＝2时,S 取得最大值为③因为l BC :y ＝x －5,所以B (5,0), 因为A (1,0),所以AB ＝4,在R t △ABM 中,∠ABM ＝45°,AM AB ＝M (3,－3)，过点N 作x 轴的垂线交直线BC 于点P 交x 轴于点H , 设N (m ,－m 2+6m －5),则H (m ,0),P (m ,m －5),易证△P Q N 为等腰直角三角形,即N Q ＝P Q ＝所以PN ＝4.当NH +HP ＝4时,即－m 2+6m －5－(m －5)＝4,解之得,m 1＝1,m 2＝4. 当m 1＝1时,点N 与点A 重合,故舍去;当NH +HP ＝4时,即m －5－(－m 2+6m －5)＝4,解得,m 1,m 2因为m >5,所以m当NH －HP ＝4,即－(－m 2+6m －5)－[－(m －5)]＝4,解得,m 1,m 2因为m <0,所以m综上所述,要使点A ,M ,N ,Q 为顶点的四边形是平行四边形,点N 的横坐标为:412.（2019·淄博）顶点为M 的抛物线y ＝ax 2＋bx ＋3与x 轴交于A (3，0)，B (－1，0)两点，与y 轴交于点C ．(1)求这条抛物线对应的函数表达式；(2)问在y 轴上是否存在点P ，使得△P AM 为直角三角形？若存在，求出点P 的坐标；若不存在，说明理由．(3)若在第一象限的抛物线下方有一动点D ，满足DA ＝OA ，过D 作DG ⊥x 轴于点G ，设△ADG 的内心为I ，试求CI 的最小值．【解析】(1)将A、B两点坐标代入抛物线表达式,得933030a ba b++=−+=,解得12ab=−=.∴y＝－x2＋2x＋3.(2)假设存在点P，使△P AM是直角三角形.当点M为直角顶点，过M作CD⊥y轴，过A作AD⊥x轴，交CD于D，CD交y轴于C，∵∠AMP＝90°，∴∠CMP＋∠AMD＝90，∴∠CMP＝∠MAD，又∵∠DM＝∠PCM，∴△CPM∽△DMA,∴CMAD＝PCMD，∴14＝2PC，∴PC＝12，∴P1(0,72);当点A为直角顶点，过A作CD⊥x轴，过M作MD⊥y轴交AD于D，过P作PC⊥y轴交CD于C，同上△CP A∽△DAM，∴PCAD＝ACMD，∴34＝2AC，∴AC＝32，∴P2(0,－32);当点P为直角顶点，过M作CM⊥y轴于C，∴△CPM∽△OAP，∴PCAO＝CMPO，∴3PC＝14-PC，∴PC＝1或3，∴P3(0,3)，P4(0,1).综上所述，使△P AM是直角三角形的点P的是P1(0,72)，P2(0,－32)，P3(0,3)，P4(0,1).（方法1）由(1)得DA ＝OA ＝3，设D (x ,y )，△ADG 的内切圆半径为r ，则△ADG 的内心I 为(x ＋r ,r ), ∴DG ＝y ,AG ＝3－x由两点距离公式可得()2222339DA x y =−+==①由等面积法得r ＝()33+22y x DG AG DA +−−−==2y x−② ∴()()2223CI x r r =++−③由①②③得222312CI x y =−+−+2CI在312x y =−−最小，此时CI 也最小，min 32CI =（方法2）简解：如图，由内心易知：∠DIA ＝135°，∠DAI ＝∠OAI ，△DAI ≌△OAI （SAS ），∴∠DIA ＝∠OIA ＝135°，则I 在圆周角∠OIA ＝135°⊙T的圆周上运动，且半径R T 为(32,32)，∴CI 在△CIA 中，CI ≥CT－IT＝32，当C 、I 、T三点一线时，min 3=2CI .13.(2019·枣庄)已知抛物线y ＝ax 2+32x +4的对称轴是直线x ＝3，与x 轴相交于A 、B 两点(点B 在点A 的右侧)，与y 轴交于点C .(1)求抛物线的解析式和A 、B 两点的坐标；(2)如图1，若点P 是抛物线上B 、C 两点之间的一个动点(不与B 、C 重合)，是否存在点P ，使四边形DIGxy O1241234PB O C 的面积最大？若存在，求点P 的坐标及四边形PB O C 面积的最大值；若不存在，请说明理由. (3)如图2，若点M 是抛物线上任意一点，过点M 作y 轴的平行线，交直线BC 于点N ，当MN ＝3时，求点M 的坐标.解：(1)抛物线y ＝ax 2+32x +4的对称轴为:x ＝332224b a a a−=−=−＝3,∴a ＝14−,∴抛物线的解析式为:y ＝14−x 2+32x +4,令y ＝0,得14−x 2+32x +4＝0,解之,得,x 1＝－2,x 2＝8,∵点B 在点A 的右侧,∴A (－2,0),B (8,0);(2)连接BC ,在抛物线y ＝14−x 2+32x +4中,令x ＝0,得y ＝4,∴C (0,4),∴O C ＝4,O B ＝8,∴S △O BC ＝16,∵B (8,0),C (0,4),设l BC ：y ＝kx +b ，得0＝8k +b ，4＝b ，∴k ＝12−,b ＝4,l BC ：y ＝12−x +4,∴过点P 作PD ∥y轴交BC 于点D ,过点C 作CE 垂直PD 于点E ,过点B 作BF ⊥PD 于点F ,则S △PBC ＝S △PCD +S △PBD ＝12PD×CE +12PD ×BF ＝12PD ×(CE +BF )＝12PD ×(x B －x C )＝12PD ×8＝4PD ,∵点P 在抛物线上,设点P (x ,14−x 2+32x +4),∵PD ∥y 轴,点D 在直线BC 上,∴D (x ,12−x +4),∵点P 在B ,C 间的抛物线上运动,∴PD ＝y P－y D ＝14−x 2+32x +4－(12−x +4)＝14−x 2+2x ,S △PBC ＝4PD ＝4(14−x 2+2x )＝－x 2+8x ＝－(x －4)2+16，当x ＝4时，S △PBC 最大16，∴S 四边形O BPC ＝S △O BC +S △PBC ＝32;∵MN ∥y 轴,∴设M ,N 的横坐标为m ,∵点M 在抛物线上,设点M (m ,n ),其中n ＝14−m 2+32m +4,点N 在直线BC 上,∴N (m ,12−m +4),∵点M 是抛物线上任意一点,∴点M 和点N 的上下位置关系不确定,∴MN ＝|14−m 2+32m +4－(12−m +4)|＝|14−x 2+2x |,∵MN ＝3,∴|14−x 2+2x |＝3,即14−x 2+2x ＝3或14−x 2+2x ＝－3,解这两个方程,得m 1＝2, m 2＝6, m 3＝4+m 4＝4－∴n 1＝6, n 2＝4, n 31, n 41,∴M 1(2,6), M 2(6,4), M 3(4+1), M 4(4－－1).14.(2019·聊城)如图,在平面直角坐标系中,抛物线y ＝ax 2+bx +c 与x 轴交于点A (－2,0),点B (4,0),与y 轴交于点C (0,8),连接BC ,又已知位于y 轴右侧且垂直于x 轴的动直线l ,沿x 轴正方向从O 运动到B (不含O 点和B 点),且分别交抛物线,线段BC 以及x 轴于点P ,D ,E .(1)求抛物线的表达式;(2)连接AC ,AP ,当直线l 运动时,求使得△PEA 和△A O C 相似的点P 的坐标;(3)作PF ⊥BC ,垂足为F ,当直线l 运动时,求R t △PFD 面积的最大值.解：(1)由已知,将C (0,8)代入y ＝ax 2+bx +c ,∴c ＝8,将点A (－2,0)和B (4,0)代人y ＝ax 2+bx +8,得428016480a b a b −+= ++= ,解得12a b =−= ,∴抛物线的表达式为y ＝－x 2+2x +8; (2)∵A (－2,0),C (0,8),∴O A ＝2,O C ＝8,∵l ⊥x 轴,∠PEA ＝∠A O C ＝90°,∵∠P AE ≠∠CA O,只有当∠P AE ＝∠AC O 时,△PEA ∽△A O C .此时AE PECO AO=,∴AE ＝4PE .设点P 的纵坐标为k ,则PE ＝k ,AE ＝4k ,∴O E ＝4k －2,P 点的坐标为(4k －2,k ),将P (4k －2,k )代入y ＝－x 2+2x +8,得－(4k －2)2+2(4k －2)+8＝k ,解得k 1＝0(舍去),k 2＝2316,当k ＝2316时,4k －2＝154,∴P 点的坐标为(154,2316). (3)在R t △PFD 中,∠PFD ＝∠C O B ＝90°,∵l ∥y 轴,∴∠PDF ＝∠O CB ,∴R t △PFD ∽R t △B O C ,∴2PFD=S PDS BC△△BOC,∴S △PFD ＝2PD S BC ⋅△BOC ,由B (4,0)知O B ＝4,又∵O C ＝8,∴BC ＝又S △B O C ＝12OB OC ⋅＝16,∴S △PFD ＝215PD ,∴当PD 最大时,S △PFD 最大.由B (4,0),C (0,8)可解得BC 所在直线的表达式为y ＝－2x +8,设P (m ,－m 2+2m +8),则D (m ,－2m +8),∴PD ＝－(m －2)2+4,当m ＝2时,PD 取得最大值4,∴当PD ＝4时,S △PFD ＝165,为最大值.15.（2019·滨州）如图①，抛物线y ＝－x 2+x +4与y 轴交于点A ，与x 轴交于点B ，C ，将直线AB 绕点A 逆时针旋转90°，所得直线与x 轴交于点D ．（1）求直线AD 的函数解析式；（2）如图②，若点P 是直线AD 上方抛物线上的一个动点①当点P 到直线AD 的距离最大时，求点P 的坐标和最大距离；②当点P 到直线AD 的距离为时，求s in ∠P AD 的值．解：（1）当x ＝0时，y ＝4，则点A 的坐标为（0，4），当y ＝0时，0＝－x 2+x +4，解得x 1＝－4，x 2＝8，则点B 的坐标为（－4，0），点C 的坐标为（8，0）， ∴OA ＝OB ＝4，∴∠OBA ＝∠OAB ＝45°． ∵将直线AB 绕点A 逆时针旋转90°得到直线AD ，∴∠BAD＝90°，∴OAD＝45°，∴∠ODA＝45°，∴OA＝OD，∴点D的坐标为（4，0）．设直线AD的函数解析式为y＝kx+b，，得，即直线AD的函数解析式为y＝－x+4（2）作PN⊥x轴交直线AD于点N，如右图①所示，设点P的坐标为（t，－t2+t+4），则点N的坐标为（t，－t+4），∴PN＝（－t2+t+4）－（－t+4）＝－t2+t∴PN⊥x轴，∴PN∥y轴，∴∠OAD＝∠PNH＝45°．作PH⊥AD于点H，则∠PHN＝90°，∴PH＝＝（－t2+t）＝t＝－（t－6）2+，∴当t＝6时，PH取得最大值，此时点P的坐标为（6，）即当点P到直线AD的距离最大时，点P的坐标是（6，），最大距离是②当点P到直线AD的距离为时，如右图②所示，则t＝，解得t1＝2，t2＝10，则P1的坐标为（2，），P2的坐标为（10，－）．当P1的坐标为（2，），则P1A＝＝，∴s in∠P1AD＝＝当P2的坐标为（10，－），则P2A＝＝，∴s in∠P2AD＝＝；由上可得，s in∠P AD的值是或。

中考数学复习 29个考点强化训练考点16-20

内容考点强化练16等腰三角形考点强化练17直角三角形与锐角三角函数考点强化练18多边形与平行四边形考点强化练19矩形、菱形、正方形考点强化练20圆的有关概念及性质考点强化练16等腰三角形夯实基础一、选择题1.若等腰三角形的顶角为80°,则它的底角度数为( )A.80°B.50°C.40°D.20°2.已知2是关于x的方程x2-2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,则△ABC的周长为( )A.10B.14C.10或14D.8或103.如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,已知∠ADE=40°,则∠DBC的度数为( )A.15°B.20°C.25°D.30°4.等腰三角形补充下列条件后,仍不一定成为等边三角形的是( )A.有一个内角是60°B.有一个外角是120°C.有两个角相等D.腰与底边相等二、填空题5.边长为2的正三角形的面积是.6.如图,一张三角形纸片ABC,AB=AC=5,折叠该纸片使点A落在边BC的中点上,折痕经过AC上的点E,则线段AE的长为.三、解答题7.如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.8.如图,在等边△ABC中,AC=8,点O在AC上,且AO=3,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.当点D恰好落在BC上时,AP的长是多少?综合提高一、选择题1.如图,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )A.(4,0)B.(1,0)C.(-2,0)D.(2,0)2.已知:如图,AB∥CD,BE平分∠ABC,∠CDE=150°,则∠C= ( )A.120°B.60°C.150°D.30°3.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )A.6B.7C.8D.94.(预测题)如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )A.1对B.2对C.3对D.4对第1题第2题第3题第4题二、填空题5.如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则S n=.(用含n的式子表示)6.下面给出几种三角形,其中是等边三角形的有.(填写序号)①有两个内角为60°的三角形;②外角都相等的三角形;③一边上的高也是这边上中线的三角形;④有一个角是60°的三角形.三、解答题7.如图,在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.(1)写出点O到△ABC的三个顶点A,B,C距离之间的关系;(2)如果点M,N分别在线段AB,AC上移动,移动中保持AN=BM,请判断△OMN的形状,并证明你的结论.8.已知∠ABC=90°,D是直线AB上的点,AD=BC.(1)如图①,过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF,判断△CDF的形状并证明;(2)如图②,E是直线BC上的一点,且CE=BD,直线AE,CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数,若不是,请说明理由.图①图②考点强化练17直角三角形与锐角三角函数夯实基础一、选择题1.将一副直角三角尺如图放置,若∠AOD=20°,则∠BOC的大小为( )A.140°B.160°C.170°D.150°2.如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )A.6米B.9米C.12米D.15米3.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠BAC的正弦值是( )A. B. C. D.4.如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB交BC于点D,E为AB上一点,连接DE,则下列说法错误的是( )A.∠CAD=30°B.AD=BDC.BD=2CDD.CD=ED第1题第2题第3题第4题二、填空题5.如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC=.6.一个正方体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=米时,有DC2=AE2+BC2.第5题第6题三、解答题7.“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:≈1.41,≈1.73)综合提高一、选择题1.如图,在△ABC中,∠A=60°,BE⊥AC,垂足为E,CF⊥AB,垂足为F,BE,CF交于点M.如果CM=4,FM=5,则BE等于( )A.9B.12C.13D.142.如图,在△ABC中,∠C=45°,点D在AB上,点E在BC上.若AD=DB=DE,AE=1,则AC的长为( )A. B.2 C. D.3.如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC的点F处.若AE=5,BF=3,则CD的长是( )A.7B.8C.9D.10第1题第2题第3题二、填空题4.如图,△ABC中,AB=AC,∠BAC=120°,BC=9 cm,D为BC上一点,DE⊥AB于E,DF⊥CA交CA的延长线于F,则DE+DF=.三、解答题5.如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向向内旋转35°到达ON位置,此时,点A,C的对应位置分别是点B,D.测量出∠ODB为25°,点D到点O的距离为30 cm.(1)求B点到OP的距离;(2)求滑动支架的长.(结果精确到1 cm.参考数据:sin 25°≈0.42,cos 25°≈0.91,tan25°≈0.47,sin 55°≈0.82,cos 55°≈0.57,tan 55°≈1.43)考点强化练18多边形与平行四边形夯实基础一、选择题1.如图,在▱ABCD中,AC与BD相交于点O,则下列结论不一定．．．成立的是( )A.BO=DOB.CD=ABC.∠BAD=∠BCDD.AC=BD2.已知▱ABCD中,∠A+∠C=200°,则∠B的度数是( )A.100°B.160°C.80°D.60°3.当多边形每增加一条边时,它的( )A.外角和与内角和都增加180°B.外角和与内角和都增加360°C.外角和增大180°,内角和不变D.外角和不变,内角和增大180°4.如图,在▱ABCD中,BE⊥AB,且交对角线AC于点E,若∠1=20°,则∠2的度数是( )A.90°B.100°C.110°D.160°5.如图所示,小华从A点出发,沿直线前进10 m后左转24°,再沿直线前进10 m,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )A.140 mB.150 mC.160 mD.240 m第1题第4题第5题二、填空题6.下面是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=.7.如图,平行四边形ABCD的对角线相交于点O,且AB=5,△OCD的周长为23,则平行四边形ABCD的两条对角线长度的和是.第6题第4题三、解答题8.如图,C为AB的中点,四边形ACDE为平行四边形,BE与CD相交于点F.求证:EF=BF.9.如图,在▱ABCD中,BD是一条对角线,过A,C两点作AE⊥BD,CF⊥BD,垂足分别为E,F,延长AE,CF分别交CD,AB于点M,N.(1)求证:四边形CMAN是平行四边形.(2)已知DE=4,FN=3,求BN的长.综合提高一、选择题1.顺次连接任意一个四边形的四边中点所得的四边形一定是( )A.平行四边形B.矩形C.菱形D.正方形2.如图,将▱ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )A.66°B.104°C.114°D.124°3.一个多边形截取一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )A.5B.5或6C.5或7D.5或6或74.如图,过▱ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的▱AEMG的面积S1与▱HCFM的面积S2的大小关系是( )A.S1>S2B.S1<S2C.S1=S2D.2S1=S25.如图,在▱ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB,AD于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )A.AG平分∠DABB.AD=DHC.DH=BCD.CH=DH第2题第4题第5题二、填空题6.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E,若△CDE的周长为10,则平行四边形ABCD的周长为.7.在▱ABCD中,BC边上的高为4,AB=5,AC=2,则▱ABCD的周长等于.三、解答题8.如图,AC是▱ABCD的对角线,∠BAC=∠DAC.(1)求证:AB=BC;(2)若AB=2,AC=2,求▱ABCD的面积.9.如图1,▱ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD 分别相交于点G,H,连接EG,FG,FH,EH.(1)求证:四边形EGFH是平行四边形;(2)如图2,若EF∥AB,GH∥BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).考点强化练19矩形、菱形、正方形夯实基础一、选择题1.下列命题中是真命题的是( )A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直平分的四边形是正方形D中的条件只能推出四边形是菱形,因此也是假命题.2.如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是( )A.25B.20C.15D.103.将一张长方形纸片折叠成如图所示的形状,则∠ABC=( )A.73°B.56°C.68°D.146°4.如图,矩形ABCD的顶点A,C分别在直线a,b上,且a∥b,∠1=60°,则∠2的度数为( )A.30°B.45°C.60°D.75°5.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )A.2.5B.C.D.2第2题第3题第4题第5题二、填空题6.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为E,若∠EAC=2∠CAD,则∠BAE=度.第6题第7题7.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为E,则OE=.三、解答题8.如图所示,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)求证:D是BC的中点;(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.9.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?综合提高一、选择题1.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )A.1B.2C.3D.42.如图,在Rt△ABC中,∠C=90°,AC=BC=6 cm,点P从点A出发,沿AB方向以每秒 cm的速度向终点B 运动;同时,动点Q从点B出发沿BC方向以每秒1 cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P'.设Q点运动的时间为t秒,若四边形QPCP'为菱形,则t的值为( )A. B.2 C.2 D.33.如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( )A.4B.3C.2D.第1题第2题第3题第4题4.如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=2.以上结论中,你认为正确的有( )个.A.1B.2C.3D.45.如图,在给定的一张平行四边形纸片上作一个菱形,甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.根据两人的作法可判断( )A.甲正确,乙错误B.乙正确,甲错误C.甲、乙均正确D.甲、乙均错误二、填空题6.如图,已知正方形ABCD的边长为1,连接AC,BD,CE平分∠ACD交BD于点E,则DE=.7.(预测题)在矩形ABCD中,AD=5,AB=4,点E,F在直线AD上,且四边形BCFE为菱形.若线段EF的中点为点M,则线段AM的长为.答案5.5或0.5三、解答题8.如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.(1)求证:四边形EGFH是矩形;(2)小明在完成(1)的证明后继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请补全他的证明思路.9.如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE.连接FG,FC.(1)请判断:FG与CE的数量关系是,位置关系是;(2)如图2,若点E,F分别是CB,BA延长线上的点,其他条件不变,(1)中结论是否仍然成立?请判断并予以证明;(3)如图3,若点E,F分别是BC,AB延长线上的点,其他条件不变,(1)中结论是否仍然成立?请直接写出你的判断.考点强化练20圆的有关概念及性质夯实基础一、选择题1.如图,☉O是△ABC的外接圆,已知∠ABO=50°,则∠ACB的大小为( )A.40°B.30°C.45°D.50°2.如图,AB是☉O的直径,点C,D在☉O上,∠BOC=110°,AD∥OC,则∠AOD的度数为( )A.70°B.60°C.50°D.40°第1题第2题第3题第4题3.如图,已知BD是☉O的直径,☉O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )A.30°B.40°C.50°D.60°4.如图,☉O是正方形ABCD的外接圆,点P在☉O上,则∠APB等于( )A.30°B.45°C.55°D.60°5.一条排水管的截面如图所示.已知排水管的截面圆半径OB=10,截面圆圆心O到水面的距离OC是6,则水面宽AB是( )A.16B.10C.8D.66.如图,已知圆心角∠BOC=78°,则圆周角∠BAC的度数是( )A.39°B.49°C.59°D.78°7.有下列四个命题:①直径是弦;②圆上任意两点间的部分叫弦;③直径都等于半径的2倍;④半径相等的两个圆是等圆.其中正确的有( )A.4个B.3个C.2个D.1个第5题第6题第8题第9题8.如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )A.25°B.40°C.50°D.65°9.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )A.点PB.点QC.点RD.点M二、填空题10.如图,☉O的直径AB过弦CD的中点E,若∠C=25°,则∠D=.11.如图,A,D是☉O上的两个点,BC是直径.若∠D=32°,则∠OAC=.12.如图,在半径为1的☉O中,∠AOB=45°,则sin C的值为.第10题第11题第12题三、解答题13.“今有圆材,埋在壁中,不知大小,以锯锯之,深1寸,锯道长一尺,问径几何?”这是《九章算术》中的问题,用现在的数学语言可以表述为:如图,CD为☉O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,求直径CD的长.14.如图,已知☉O的半径为12 cm,弦AB=16 cm.(1)求圆心到弦AB的距离;(2)若弦AB的两个端点在圆周上滑动,那么,弦AB的中点形成什么样的图形?综合提高一、选择题1.《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )A.3步B.5步C.6步D.8步2.如图,AB为☉O的直径,AB=6,AB⊥弦CD,垂足为G,EF切☉O于点B,∠A=30°,连接AD,OC,BC,下列结论不正确的是( )A.EF∥CDB.△COB是等边三角形C.CG=BGD.的长为π第1题第2题第3题二、填空题3.如图,点A,B,C,D为☉O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为.三、解答题4.如图,有一座拱桥是圆弧形的,它的跨度为60 m,拱高18 m,当洪水泛滥到跨度只有30 m时,要采取紧急措施.若拱顶离水面只有4 m,即PN=4 m时是否要采取紧急措施?5.如图,AB是☉O的直径,弦CD⊥AB于点E,点P在☉O上,∠1=∠C.(1)求证:CB∥PD;(2)若BC=3,sin∠P=,求☉O的直径.答案及解析考点强化练16等腰三角形夯实基础一、选择题1.答案B解析底角度数为(180°-80°)=50°.2.答案B解析将x=2代入方程x2-2mx+3m=0,得4-4m+3m=0,即m=4.将m=4代入原方程,得x2-8x+12=0,解得x1=2,x2=6.∵6+6>2,∴等腰三角形ABC的三边长可以是2,6,6,此时△ABC的周长为2+6+6=14;∵2+2<6,∴等腰三角形ABC的三边长不可以是2,2,6.故选B.3.答案A解析∵DE垂直平分AB,∴∠AED=90°,且AD=DB.∵∠AED=90°,∴∠A=90°-∠ADE=50°.∵AB=AC,∴∠ABC=°-°=65°.∵AD=DB,∴∠DBA=∠A=50°.∴∠DBC=15°.4.答案C解析由定义判定,三条边都相等的三角形是等边三角形.判定定理:三个角都相等的三角形是等边三角形.判定定理:有一个角是60°的等腰三角形是等边三角形.二、填空题5.答案解析如图,过点A作AD⊥BC,∵AB=AC=BC=2,∴BD=CD=BC=1.在Rt△ACD中,根据勾股定理得AD=--,则S△ABC=BC·AD=.6.答案2.5解析如图所示,∵D为BC的中点,AB=AC,∴AD⊥BC.∵折叠该纸片使点A落在边BC的中点D上,∴折痕EF垂直平分AD,∴E是AC的中点.∵AC=5,∴AE=2.5.三、解答题7.证明方法一:∵AB=AC,∴△ABC是等腰三角形,∵AD是BC边上的中线,∴AD⊥BC,∠BAD=∠CAD,∴∠CAD+∠C=90°,∵BE⊥AC, ∴∠CBE+∠C=90°,∴∠CBE=∠CAD,∴∠CBE=∠BAD.方法二:∵AB=AC,∴∠ABC=∠C,∵AD是BC边上的中线,∴AD⊥BC,∴∠BAD+∠ABC=90°,∵BE⊥AC,∴∠CBE+∠C=90°,∴∠CBE=∠BAD.8.解根据题意,得OP=OD,∠POD=60°,∵△ABC是等边三角形,∴∠A=∠B=∠C=60°.又∵∠AOP+∠APO=120°,∠AOP+∠COD=120°,∴∠APO=∠COD.在△APO和△COD中,,, ,∴△APO≌△COD,∴AP=CO.又∵AO=3,AC=8,∴CO=5,∴AP=5.综合提高一、选择题1.答案B2.答案A解析先根据平行线及角平分线的性质求出∠CDB=∠CBD,再根据平角的性质求出∠CDB的度数,再根据平行线的性质求出∠C的度数.3.答案D解析由∠ABC,∠ACB的平分线相交于点E,得∠MBE=∠EBC,∠ECN=∠ECB,利用两直线平行,内错角相等,等量代换可得∠MBE=∠MEB,∠NEC=∠ECN,∴BM=ME,EN=CN.∴MN=ME+EN,即MN=BM+CN.∵BM+CN=9,∴MN=9.4.答案D解析根据AD垂直平分线段BC,可得三对全等三角形,根据OE垂直平分线段AC,可得一对全等三角形,所以共有四对全等三角形.故选D.二、填空题5.答案解析∵等边三角形ABC 的边长为2,AB 1⊥BC,∴BB 1=1,AB=2,根据勾股定理得AB 1= . ∴S 1=×( )2=. ∵等边三角形AB 1C 1的边长为 2⊥B 1C 1,∴B 1B 2=.根据勾股定理得AB 2=,∴S 2=; 依此类推,S n =. 6.答案①②解析①一个三角形有两个角为60°,利用三角形内角和定理得到第三个角也为60°,可得出此三角形三内角相等,利用等角对等边得到三条边相等,故此三角形为等边三角形;②外角都相等,利用外角与相邻的内角互补,得到三内角相等,进而确定出三角形为等边三角形;③等腰三角形底边上的高为这边的中线,但不一定为等边三角形;④有一个角为60°的三角形不一定为等边三角形,比如Rt △ABC 中,∠A=90°,∠B=60°,∠C=30°. 三、解答题7.解(1)∵在Rt △ABC 中,∠BAC=90°,O 为BC 的中点,∴OA=BC=OB=OC,即OA=OB=OC. (2)△OMN 是等腰直角三角形.理由如下: 如图,连接AO, ∵AC=AB,OC=OB,∴OA=OB,∠NAO=∠B=45°.在△AON 与△BOM 中, ,, ,∴△AON ≌△BOM. ∴ON=OM,∠NOA=∠MOB. ∴∠NOA+∠AOM=∠MOB+∠AOM. ∴∠NOM=∠AOB=90°. ∴△OMN 是等腰直角三角形.8.解(1)△CDF是等腰直角三角形.证明:∵∠ABC=90°,AF⊥AB,∴∠FAD=∠DBC.∵AD=BC,AF=BD,∴△FAD≌△DBC.∴FD=DC,∠1=∠2.∵∠1+∠3=90°,∴∠2+∠3=90°,即∠CDF=90°.∴△CDF是等腰直角三角形.(2)过点A作AF⊥AB,并截取AF=BD,连接DF,CF.∵∠ABC=90°,AF⊥AB,∴AF∥CE.又∵BD=CE,AF=BD,∴AF=CE.∴四边形AFCE是平行四边形.∴FC∥AE,∴∠APD=∠FCD,由(1)知,∠APD=45°.考点强化练17直角三角形与锐角三角函数夯实基础一、选择题1.答案B解析∵将一副直角三角尺如图放置,∠AOD=20°,∴∠COA=90°-20°=70°,∴∠BOC=90°+70°=160°.此题主要考查了直角三角形的性质,得出∠COA的度数是解题关键.故选B.答案B解析根据“30°角所对的直角边等于斜边的一半”求出折断部分的长度,再加上离地面的距离就是折断前树的高度.3.答案A解析延长AC交格点于E,连接BE,由勾股定理得AE=2,BE=,AB=5,所以AE2+BE2=AB2,△ABE为直角三角形.故sin∠BAC=sin∠BAE=.4.答案D解析∵在△ABC中,∠C=90°,∠B=30°,∴∠CAB=60°.∵AD平分∠CAB,∴∠CAD=∠BAD=30°,∴∠CAD=∠BAD=∠B,∴AD=BD,AD=2CD,∴BD=2CD,根据已知不能推出CD=DE.二、填空题5.答案+1解析∵∠ADC=2∠B,∠ADC=∠B+∠BAD,∴∠B=∠BAD,∴DB=DA=.在Rt△ADC中,DC=-(-=1,∴BC=+1.6.答案解析在Rt△ABC中,∵BC=6米,∠A=30°,∴AC=2BC=12米.过点E作EG⊥AB于G,设EG=x米,则AE=2x米,EC=12-2x(米).连接DC,在Rt△DEC中,由勾股定理,得DC2=DE2+EC2=22+(12-2x)2.又∵DC2=AE2+BC2,∴22+(12-2x)2=(2x)2+62.解得x=.∴AE=2x=.三、解答题7.解此车没有超速.理由:如图,过C作CH⊥MN,∵∠CBN=60°,BC=200米,∴CH=BC·sin60°=200×=100米),BH=BC·cos60°=100(米),∵∠CAN=45°,∴AH=CH=100(米),∴AB=100-100≈73(米).∵60千米/时=米/秒,∴=14.6(米/秒)<≈16.7(米/秒),∴此车没有超速.综合提高一、选择题1.答案B解析∠EBA=∠FCA=30°,BM=2FM=10,EM=CM=2,EB=BM+EM=12.2.答案D解析利用AD=DB=DE,求出∠AEB=∠AEC=90°,在等腰直角三角形AEC中求出AC的长.3.答案C解析∵△DEF由△DEA翻折而成,∴EF=AE=5.在Rt△BEF中,∵EF=5,BF=3,∴BE=--=4.∴AB=AE+BE=5+4=9.∵四边形ABCD是矩形,∴CD=AB=9.故选C.二、填空题4.答案4.5 cm解析根据三角形内角和定理和等腰三角形的性质得到∠B=∠C=30°.在Rt△BED和Rt△CFD中,利用“30°角所对的直角边等于斜边的一半”分别求得ED=BD,DF=DC,所以DE+DF=BC=4.5cm.三、解答题5. 25°≈0.47,sin 55°≈0.82,cos 55°≈0.57,tan 55°≈1.43),解(1)在Rt△BOE中,OE=°在Rt△BDE中,DE=,°=30,解得BE≈11. 则°°故点B到OP的距离大约为11cm.≈25cm.(2)在Rt△BDE中,BD=°答:滑动支架的长为25cm.考点强化练18多边形与平行四边形夯实基础一、选择题1.答案D解析根据平行四边形的对角线互相平分,知BO=DO,选项A正确;根据平行四边形的对边相等,AB=CD,选项B正确;根据平行四边形的对角相等,∠BAD=∠BCD,选项C正确;而选项D中“AC=BD”说明对角线相等,平行四边形没有这一性质,因此选项D错误,故选D.2.答案C解析∵∠A+∠C=200°,∠A=∠C,∴∠A=100°,又∵AD∥BC,∴∠A+∠B=180°,∴∠B=80°,故选C.3.答案D解析根据多边形内角和公式可以得到多边形每增加一条边,其内角和增加[(n+1)-2]·180°-(n-2)·180°=180°,而其外角和均为360°,故选D.4答案C解析由平行四边形的性质可得AB∥CD,所以∠1=∠3=20°.根据三角形外角的性质可得∠2=∠3+∠ABE=20°+90°=110°.5.答案B解析∵多边形的外角和为360°,而每一个外角为24°,∴多边形的边数为360°÷24°=15.∴小华一共走了15×10=150m.故选B.二、填空题6.答案360°7.答案36解析平行四边形ABCD中,CD=AB=5,因为△OCD的周长为23,所以OC+OD=18,而平行四边形的对角线互相平分,所以AC+BD=36.三、解答题8.证法一在▱ACDE中,∵AC DE,∴∠D=∠BCF,∠B=∠DEF.∵AC=BC,∴ED=BC,∴△FED≌△FBC(ASA),∴EF=BF.证法二连接EC,DB,在▱ACDE中,∵AC DE,AC=BC,∴DE BC,∴四边形BDEC是平行四边形,∴EF=BF.9.(1)证明∵AE⊥BD,CF⊥BD,∴AE∥CF.又四边形ABCD是平行四边形,∴AB∥CD.∴四边形CMAN是平行四边形.(2)解由(1)知四边形CMAN是平行四边形,∴CM=AN.又四边形ABCD是平行四边形,∴AB=CD,∠MDE=∠NBF.∴AB-AN=CD-CM,即DM=BN.在△MDE和△NBF中,∠MDE=∠NBF,∠DEM=∠BFN=90°,DM=BN,∴△MDE≌△NBF.∴DE=BF=4.由勾股定理得BN==5.故BN的长为5.综合提高一、选择题1.答案A解析如右图所示,EF,GH分别为△ABD,△BCD的中位线,所以EF∥BD,GH∥BD,且EF=GH=BD,则四边形EFGH为平行四边形,故选A.2.答案C解析因为AB∥CD,所以∠1=∠B'AB.结合折叠的性质可知∠BAC=∠B'AC=22°,在△ABC中,∠B=180°-∠ACB-∠CAB=114°.3.答案D解析根据多边形的内角和公式可得(n-2)·180°=720°,于是n=6,可知后来的多边形是六边形.原来的多边形是多少边形呢?因为截取方式有三种可能性,分别如下图中的图1、图2、图3,若截法如图1,则原来是五边形,若截法如图2,则原来是六边形,若截法如图3,则原来是七边形.4.答案C解析∵四边形ABCD是平行四边形,∴AB=CD,AD=CB,∴△ABD≌△CDB,∴S△ABD=S△CDB.又∵EF,GH分别平行两边,∴四边形EBHM,GMFD均为平行四边形,∴S△EBM=S△BHM,S△GMD=S△MFD,∴S△ABD-S△BEM-S△GMD=S△CDB-S△BHM-S△DMF,即S1=S2.故选C.5.答案D解析由角平分线的作法及题意可知AG平分∠DAB,A正确;∠DAH=∠BAH,又AB∥DC,所以∠BAH=∠AHD,所以∠DAH=∠AHD.所以AD=DH.又AD=BC,所以DH=BC,B,C正确.故选D.二、填空题6.答案20解析∵四边形ABCD是平行四边形,∴O是BD的中点,∵OE⊥BD,∴DE=BE.∵△CDE的周长为10,∴CD+DE+CE=10,即CD+CE+BE=CD+BC=10,∴四边形ABCD的周长=2(CD+BC)=2×10=20.7答案12或20解析如图1所示,∵在▱ABCD中,BC边上的高AE=4,AB=5,AC=2,∴EC=-=2,AB=CD=5,BE=-=3,∴AD=BC=5,∴▱ABCD的周长为20.如图2所示,∵在▱ABCD中,BC边上的高为4,AB=5,AC=2,∴EC=-=2,AB=CD=5,BE=-=3,∴BC=3-2=1,∴▱ABCD的周长等于1+1+5+5=12.综上所述,▱ABCD的周长等于12或20.三、解答题8.(1)证明∵四边形ABCD是平行四边形,∴AD∥BC.∴∠DAC=∠BCA.∵∠BAC=∠DAC,∴∠BAC=∠BCA.∴AB=BC.(2)解连接BD交AC于点O,如图所示:∵四边形ABCD是平行四边形,AB=BC,∴四边形ABCD是菱形.∴AC⊥BD,OA=OC=AC=,OB=OD=BD.∴OB=--()=1.∴BD=2OB=2.∴▱ABCD的面积=AC·BD=×2×2=2.9.(1)证明∵四边形ABCD是平行四边形,∴AD∥BC.∴∠EAO=∠FCO.在△OAE与△OCF中,,, ,∴△OAE≌△OCF.∴OE=OF.同理OG=OH.∴四边形EGFH是平行四边形.(2)解与四边形AGHD面积相等的所有平行四边形有▱GBCH,▱ABFE,▱EFCD,▱EGFH;∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD.∵EF∥AB,GH∥BC,∴四边形GBCH,ABFE,EFCD,EGFH为平行四边形.∵EF过点O,GH过点O,∵OE=OF,OG=OH,∴▱GBCH,▱ABFE,▱EFCD,▱EGFH,▱AGHD的面积均等于▱ABCD的面积.∴与四边形AGHD面积相等的所有平行四边形有▱GBCH,▱ABFE,▱EFCD,▱EGFH.考点强化练19矩形、菱形、正方形夯实基础一、选择题1.答案C解析满足选项A或选项B中的条件时,不能推出四边形是平行四边形,因此它们都是假命题.由选项D中的条件只能推出四边形是菱形,因此也是假命题.只有选项C中的命题是真命题.故选C.2.B.20 C.15 D.10答案B解析∵AC是菱形ABCD的对角线,∠BAD=120°,∴∠BAC=60°.∵AB=BC,∴△ABC是等边三角形.∵△ABC的周长是15,∴边长AB=5.∴菱形ABCD的周长为5×4=20.故选B.3.答案A解析如图所示,折叠后,∠1=∠2=(180°-34°)÷2=73°,故选A.4.答案C解析过点D作DE∥a,∵四边形ABCD是矩形,∴∠BAD=∠ADC=90°.∴∠3=90°-∠1=90°-60°=30°.∵a∥b,∴DE∥a∥b.∴∠4=∠3=30°,∠2=∠5,∴∠2=90°-30°=60°.故选C.5.答案B解析如图,连接AC,CF,∵正方形ABCD和正方形CEFG中,BC=1,CE=3,∴AC=,CF=3,∠ACD=∠GCF=45°,∴∠ACF=90°.由勾股定理得AF==(()=2.∵H是AF的中点,∴CH=AF=×2.故选B.二、填空题6.答案22.5解析∵四边形ABCD是矩形,∴AC=BD,OA=OC,OB=OD.∴OA=OB=OC.∴∠OAD=∠ODA,∠OAB=∠OBA.∴∠AOE=∠OAD+∠ODA=2∠OAD.∵∠EAC=2∠CAD,∴∠EAO=∠AOE.∵AE⊥BD,∴∠AEO=90°.∴∠AOE=45°.∴∠OAB=∠OBA=°-°=67.5°.∴∠BAE=∠OAB-∠OAE=22.5°.7.答案解析∵菱形的对角线互相垂直平分,∴OB=3,OC=4,∠BOC=90°.∴BC==5.∵S△OBC=OB·OC,又S△OBC=BC·OE,∴OB·OC=BC·OE,即3×4=5OE.∴OE=.三、解答题8.(1)证明∵点E是AD的中点,∴AE=DE.∵AF∥BC,∴∠AFE=∠DCE,∠FAE=∠CDE.∴△EAF≌△EDC.∴AF=DC.∵AF=BD,∴BD=DC,即D是BC的中点.(2)解四边形AFBD是矩形.证明如下:∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形.∵AB=AC,又由(1)可知D是BC的中点,∴AD⊥BC.∴▱AFBD是矩形.9.(1)证明在正方形ABCD中,∵BC=CD,∠B=∠CDF,BE=DF,∴△CBE≌△CDF.∴CE=CF.(2)解GE=BE+GD成立.理由是:∵由(1)得△CBE≌△CDF,∴∠BCE=∠DCF,∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∵∠GCE=45°,∴∠GCF=∠GCE=45°.∵CE=CF,∠GCE=∠GCF,GC=GC,∴△ECG≌△FCG.∴GE=GF.∴GE=DF+GD=BE+GD.综合提高一、选择题1.答案C解析作点F关于BD的对称点F',则PF=PF',连接EF'交BD于点P.则EP+FP=EP+F'P.由两点之间线段最短可知:当E,P,F'三点在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F'P=EF'.∵四边形ABCD为菱形,且其周长为12,∴AB=BC=CD=DA=3,AB∥CD,∵AF=2,AE=1,∴DF=AE=1.∴四边形AEF'D是平行四边形.∴EF'=AD=3.∴EP+FP的最小值为3.2.答案B解析连接PP',交BC于N点,过P作PM⊥AC,垂足为M,若运动t秒时四边形QPCP'为菱形,则PQ=PC,PN⊥BC,四边形PMCN为矩形,BQ=t,AP=t,PM=NC=t,∴QC=2t,∴BC=BQ+QC=t+2t=3t=6cm,∴t=2,故选B.3.答案B解析∵四边形ABCD是菱形,∴BC=CD,∠B=∠D=60°.∵AE⊥BC,AF⊥CD,∴BC×AE=CD×AF,∠BAE=∠DAF=30°.∴AE=AF.∵∠B=60°,∴∠BAD=120°.∴∠EAF=120°-30°-30°=60°.∴△AEF是等边三角形.∴AE=EF,∠AEF=60°.∵AB=4,∴AE=2,∴EF=AE=2.过A作AM⊥EF,∴AM=AE·sin60°=3.∴△AEF的面积是EF·AM=×2×3=3.故选B.4.答案C解析∵FH与CG,EH与CF都是矩形ABCD的对边AD,BC的一部分,∴FH∥CG,EH∥CF,∴四边形CFHE是平行四边形.由翻折的性质,得CF=FH,∴四边形CFHE是菱形,故①正确;∴∠BCH=∠ECH,∴只有∠DCE=30°时EC平分∠DCH,故②错误;点H与点A重合时,设BF=x,则AF=FC=8-x,在Rt△ABF中,AB2+BF2=AF2,即42+x2=(8-x)2,解得x=3,点G与点D重合时,CF=CD=4,∴BF=4,∴线段BF的取值范围为3≤BF≤4,故③正确;过点F作FM⊥AD于M,则ME=(8-3)-3=2,由勾股定理,得EF==2,故④正确.综上所述,结论正确的有①③④共3个.故选C.5.答案C解析甲的作法:∵MN是AC的垂直平分线,∴AM=CM,OA=OC.∵四边形ABCD是平行四边形,∴AM∥CN,∴∠MAO=∠NCO,∠AMO=∠CNO,∴△AMO≌△CNO,∴AM=CN,∴四边形ANCM是平行四边形,∴▱ANCM是菱形.乙的作法:∵四边形ABCD是平行四边形,∴AF∥BE,∴∠AFB=∠EBF,∠FAE=∠BEA,∵∠ABF=∠EBF,∠BAE=∠FAE,∴∠ABF=∠AFB,∠BAE=∠BEA,∴AB=AF,AB=EB,∴AF=BE,∴四边形ABEF是平行四边形,∴▱ABEF是菱形.故选C.二、填空题6.答案-1解析过点E作EF⊥CD于点F,设对角线交点为O, ∵四边形ABCD是正方形,且边长为1,∴OD=BD=,OD⊥OC,∠ODC=45°.∵EF⊥CD,CE平分∠ACD,∴∠DEF=45°,EF=EO,∴EO=EF=FD.设OE=x,则DE=-x,EF=DF=x,∴x2+x2=-,解得x=1-,∴DE=-x=--1.7.答案5.5或0.5解析分两种情况:①如图1所示:∵四边形ABCD是矩形,∴CD=AB=4,BC=AD=5,∠ADC=∠CDF=90°.∵四边形BCFE为菱形,∴CF=EF=BE=BC=5.∴DF=--=3.∴AF=AD+DF=8,∵M是EF的中点,∴MF=EF=2.5.∴AM=AF-MF=8-2.5=5.5.②如图2所示:同①得:AE=3,∵M是EF的中点,∴ME=2.5,∴AM=AE-ME=0.5.综上所述:线段AM的长为5.5或0.5.三、解答题8.(1)证明∵EH平分∠BEF,FH平分∠DFE,∴∠FEH=∠BEF,∠EFH=∠DFE.∵AB∥CD,∴∠BEF+∠DFE=180°.∴∠FEH+∠EFH=(∠BEF+∠DFE)=×180°=90°.∵∠FEH+∠EFH+∠EHF=180°,∴∠EHF=180°-(∠FEH+∠EFH)=180°-90°=90°.同理可得:∠EGF=90°.∵EG平分∠AEF,EH平分∠BEF,∴∠GEF=∠AEF,∠FEH=∠BEF.∵点A,E,B在同一条直线上,∴∠AEB=180°,即∠AEF+∠BEF=180°.∴∠FEG+∠FEH=(∠AEF+∠BEF)=×180°=90°,即∠GEH=90°.∴四边形EGFH是矩形.(2)解答案不唯一:由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形,要证平行四边形MNQP是菱形,只要证MN=NQ,由已知条件FG平分∠CFE,MN∥EF,故只要证GM=FQ,即证△MGE≌△QFH,易证GE=FH,∠GME=∠FQH.故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,∠GEF=∠EFH,即可得证.9.解(1)FG=CE(相等),FG∥CE(平行).(2)仍然成立.证明:设CF与DE相交于点M,∵四边形ABCD是正方形,∴BC=CD,∠FBC=∠ECD=90°.∵BF=CE,∴△BCF≌△CDE.∴FC=ED,∠DEC=∠BFC.∵∠BFC+∠FCE=90°,∴∠DEC+∠FCE=90°.∴∠EMC=90°,即FC⊥DE.∵GE⊥DE,∴GE∥FC.∵EG=DE,∴EG=FC,∴四边形GECF是平行四边形.∴FG=CE,FG∥CE.(3)成立.。

中考几何知识点归纳总结

中考几何知识点归纳总结几何学是数学的一个分支，研究空间内点、线、面等几何对象的性质和相互关系的一门学科。

在中考数学考试中，几何是一个重要的知识点，涉及到平面几何和立体几何两个方面。

在几何学中，我们会学到很多与图形、空间有关的知识，今天我们就来对中考几何知识点进行归纳总结。

一、平面几何1. 点、线、面的位置关系在平面几何中，我们首先学习的是点、线、面的位置关系。

在几何中，点是没有大小的，线是由无数个点连在一起形成的，面是由无数条线组成的。

点、线、面的位置关系非常重要，它们决定了图形的形状和特征。

2. 角的概念和性质角是两条射线的夹角，我们知道角的大小是由它的两条边确定的。

在角的概念中，我们要学习角的度量、角的分类、角的性质等内容。

在中考中，有可能会考察同位角、内错角、共顶点角等角的性质，考生们要注意掌握。

3. 三角形的性质三角形是平面几何中的基本图形，它是一个有三条边和三个角的图形。

在中考中，我们会学习三角形的周长、面积、角的性质、边的关系等知识点。

重点掌握等边三角形、等腰三角形和直角三角形的性质。

4. 四边形的性质四边形是平面几何中的另一个基本图形，它是一个有四条边和四个角的图形。

在中考中，我们要学习四边形的边和角的关系、对角线的性质、平行四边形、菱形和矩形的性质等内容。

5. 圆的性质圆是一个没有边界的几何图形，它由圆心和半径确定。

在中考中，我们会学习圆的周长、面积、圆心角和弧的关系、相交圆的性质等内容。

掌握圆的性质对解题非常有帮助。

6. 相似三角形相似三角形是指对应角相等，对应边成比例的两个三角形。

在中考中，我们会学习相似三角形的判定、相似三角形的性质、相似三角形的性质应用等知识点。

7. 同比例线段同比例线段是指存在一个比值k，两条线段在同一条直线上，且它们的比等于k。

在中考中，我们要学习同比例线段的判定、同比例线段的性质、平行线和比例线段的关系等内容。

8. 平行线和垂直线平行线是指在同一平面内，不相交的两条直线，它们的方向相同。

中考数学几何题总结知识点

中考数学几何题总结知识点在中考数学中，几何题是考查学生对几何知识的掌握和运用能力的重要部分。

几何题的考查内容涉及到诸多知识点和技巧，对于学生来说是一个挑战，但也是一个机会。

下面将对中考数学中常见的几何题知识点进行总结，希望对同学们的复习有所帮助。

常见几何题型在中考数学中，几何题型可以分为以下几类：直线与角、三角形、四边形、平行线与相交线、折线与封闭线段以及空间几何等。

这些题型分别涉及到相应的知识点和技巧。

直线与角直线的分类平行线和垂直线是直线中的两种重要分类，平行线是指在同一个平面内永远不相交的两条直线，而垂直线是指两条直线的夹角为90度。

学生需要对平行线和垂直线的特点有清晰的认识，包括平行线的性质、平行线与垂直线之间的关系等。

角的性质角是几何中的一个重要概念，对角的性质的掌握是解题的基础。

对于同学们来说，需要熟练掌握各种夹角之间的关系，包括对顶角、邻补角、余补角等的理解和应用。

三角形三角形的分类在三角形中，根据边的长短和角的大小，可以分为等腰三角形、等边三角形、直角三角形、锐角三角形和钝角三角形等。

同学们需要对不同类型的三角形有清晰的认识，包括它们的性质以及相互之间的关系。

三角形的面积计算三角形的面积是几何题中常见的一种题型，同学们需要掌握计算三角形面积的方法，例如通过底和高、两边和夹角等不同的方法来计算三角形的面积。

四边形四边形的分类四边形是由四条边围成的几何图形，根据其边的性质和角的性质可以分为平行四边形、矩形、正方形、菱形、梯形等。

同学们需要对这些四边形的特点有清晰的认识，包括它们的性质和特殊的关系。

四边形的面积同样地，计算四边形的面积也是几何题中常见的一种题型，同学们需要根据四边形的类型来选择合适的计算方法，例如通过底和高、对角线和夹角等不同的方法来计算四边形的面积。

平行线与相交线平行线与交线在解决与平行线和垂直线有关的问题时，同学们需要掌握利用平行线和垂直线的性质来解题，例如通过平行线的性质来求解各角之间的关系，通过垂直线的性质来求解各边之间的关系等。

考前冲刺数学几何题型解题技巧总结

考前冲刺数学几何题型解题技巧总结数学几何作为高中数学的重要组成部分，在考试中占据着较大的比重。

考前冲刺阶段，学生们应该对数学几何的各种题型进行总结和复习，提高解题的技巧和效率。

本文将总结一些数学几何题型解题的有效方法，帮助考生在考试中取得更好的成绩。

一、平面几何题型解题技巧1. 直线与角度关系直线与角度的关系是数学几何中的基本概念，也是解题的重要出发点。

当遇到直线与角度相关的问题时，可以根据以下技巧进行解题：a) 垂直角与邻补角：垂直角的度数相等，邻补角的度数之和为90度。

利用这一性质，可以快速推导出一些新的等式，简化解题过程。

b) 同旁内角与对顶角：同旁内角的度数之和等于180度，对顶角的度数相等。

通过利用这些角度关系，可以迅速得出一些重要的定理，进一步解决问题。

2. 三角形的性质和关系三角形作为几何中最基本的图形之一，有着许多重要的性质和关系。

解决三角形相关问题时，可以运用以下技巧：a) 三角形的内角和：任意三角形的内角和为180度。

当已知部分角度或边长时，可以通过计算和已知条件的差值来求解未知角度或边长。

b) 三角形的等腰性质：等腰三角形的底边两边相等，顶角相等。

当遇到等腰三角形的问题时，可以利用这一性质快速得出结论。

c) 三角形的相似性质：两个三角形如果对应角度相等，则它们是相似三角形。

相似三角形有着一些特殊的比例关系，可以通过利用这些比例关系解决问题。

3. 圆的性质和关系圆是数学几何中的一个重要概念，解决与圆相关的问题时，可以运用以下技巧：a) 圆的周长和面积：圆的周长可以通过公式C=2πr来计算，其中r 为半径。

圆的面积可以通过公式S=πr^2来计算。

b) 切线和切点：切线与圆相切于切点，切线在切点处垂直于半径。

利用这一性质，可以解决一些与切线和切点有关的几何问题。

c) 弧长和扇形面积：弧长可以通过圆心角和半径计算，扇形面积可以通过圆心角和半径计算。

根据已知条件，可以通过这些公式求解问题。

2020年九年级数学三轮冲刺复习培优练习：《几何相似综合压轴》(二)

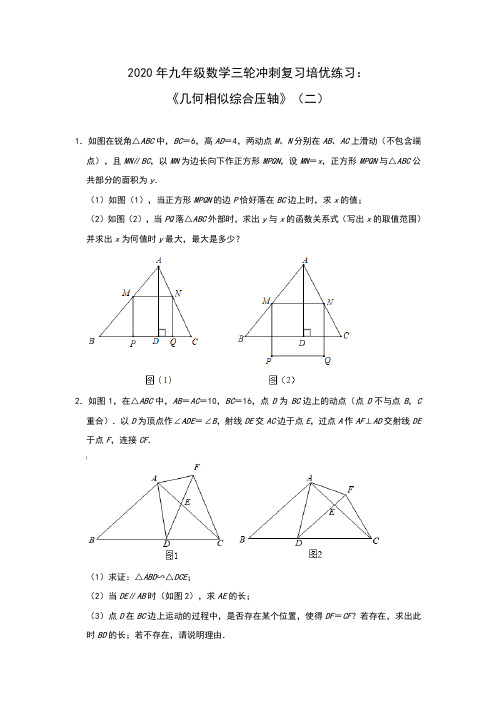
2020年九年级数学三轮冲刺复习培优练习：《几何相似综合压轴》（二）1．如图在锐角△ABC中，BC＝6，高AD＝4，两动点M、N分别在AB、AC上滑动（不包含端点），且MN∥BC，以MN为边长向下作正方形MPQN，设MN＝x，正方形MPQN与△ABC公共部分的面积为y．（1）如图（1），当正方形MPQN的边P恰好落在BC边上时，求x的值；（2）如图（2），当PQ落△ABC外部时，求出y与x的函数关系式（写出x的取值范围）并求出x为何值时y最大，最大是多少？2．如图1，在△ABC中，AB＝AC＝10，BC＝16，点D为BC边上的动点（点D不与点B，C 重合）．以D为顶点作∠ADE＝∠B，射线DE交AC边于点E，过点A作AF⊥AD交射线DE 于点F，连接CF．（1）求证：△ABD∽△DCE；（2）当DE∥AB时（如图2），求AE的长；（3）点D在BC边上运动的过程中，是否存在某个位置，使得DF＝CF？若存在，求出此时BD的长；若不存在，请说明理由．3．如图：在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，O是AB上一点，且AO＝2．（1）求点O到直线AC的距离OH的长；（2）若P是边AC上一个动点，作PQ⊥OP交线段BC于Q（不与B、C重合），设AP＝x，CQ＝y，试求y关于x的函数解析式，并写出定义域；（3）在（2）的条件下，当AP为多少时能使△OPQ与△CPQ相似．4．定义：我们知道，四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似（不全等），我们就把这条对角线叫做这个四边形的“相似对角线”．理解：（1）如图1，已知Rt△ABC在正方形网格中，请你只用无刻度的直尺在网格中找到一点D，使四边形ABCD是以AC为“相似对角线”的四边形（保留画图痕迹）；（2）如图2，在四边形ABCD中，∠ABC＝70°，∠ADC＝145°，对角线BD平分∠ABC．求证：BD是四边形ABCD的“相似对角线”；（3）如图3，已知FH是四边形EFGH的“相似对角线”，∠EFH＝∠HFG＝30°，连接EG，若△EFG的面积为2，求FH的长．5．在△ABC中，∠ABC＝90°，（1）如图1，分别过A，C两点作经过点B的直线的垂线，垂足分别为M、N，求证：△ABM～△BCN；（2）如图2，P是边BC上一点，∠BAP＝∠C，PM⊥PA交AC于点M，＝，求的值；（3）如图3，D是边CA延长线上一点，AE＝AB，∠DEB＝90°，AD：BC：AC＝2：3：5，求的长．6．已知△ABC，过△ABC的顶点B作直线MN∥AC，D为BC边上一点，连结AD，作∠ADE＝∠BAC交直线MN于点E，DE交AB于点F．（1）如图1，请找出图中与∠BED相等的角（直接写出，不必证明）；（2）如图2，当△ABC是等边三角形时，请探究出线段AD，DE之间的数量关系，并证明；（3）如图3，当AB＝AC＞BC时，（2）中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由．（4）当AB＝kAC时，请直接写出此时AD，DE之间的数量关系．（用含k的式子表示）7．在△ABC中，∠ABC＝90°，如图1，分别过A、C两点作经过点B的直线的垂线，垂足分别为M、N，则△ABM～△BCN；（1）如图2，P是边BC上一点，∠BAP＝∠C，tan∠PAC＝，求tan C的值；（2）如图3，D是边CA延长线上一点，AE＝AB，∠DEB＝90°，sin∠BAC＝，，直接写出tan∠CEB的值．8．某数学课外兴趣小组成员在研究下面三个有联系的问题，请你帮助他们解决：（1）如图1，矩形ABCD中，AB＝a，BC＝b，点E，F分别在AB，DC上，点G，H分别在AD，BC上且EF⊥GH，求的值．（2）如图2，矩形ABCD中，AB＝4，BC＝3，将矩形对折，使得B、D重叠，折痕为EF，求EF的长．（3）如图3，四边形ABCD中，∠ABC＝90°，AB＝AD＝8，BC＝CD＝4，AM⊥DN，点M，N分别在边BC，AB上，求的值．9．如图1，M为线段AB的中点，AE与BD交于点C，∠DME＝∠A＝∠B＝α，且DM交AC于F，ME交BC于G．（1）求证：△AMF∽△BGM；（2）若AM＝2，AF＝3，求BG的长；（3）如图2，连接FG，在（2）条件下，若α＝45°，求△EFG的面积．10．如图1，在矩形ABCD中，AB＝6cm，BC＝8cm，如果点E由点B出发沿BC方向向点C匀速运动，同时点F由点D出发沿DA方向向点A匀速运动，它们的速度分别为每秒2cm和1cm，FQ⊥BC，分别交AC、BC于点P和Q，设运动时间为t秒（0＜t＜4）．（1）连接EF，若运动时间t＝秒时，求证：△EQF是等腰直角三角形；（2）连接EP，当△EPC的面积为3cm2时，求t的值；（3）在运动过程中，当t取何值时，△EPQ与△ADC相似．参考答案1．解：（1）当PQ恰好落在边BC上时，∵MN∥BC，∴△AMN∽△ABC．∴＝，即＝，∴x＝．（2）设BC分别交MP，NQ于E，F，则四边形MEFN为矩形．设ME＝NF＝h，AD交MN于G（如图2）GD＝NF＝h，AG＝4﹣h．∵MN∥BC，∴△AMN∽△ABC．∴＝，即＝，∴h＝﹣x+4．∴y＝MN•NF＝x（﹣x+4）＝﹣x2+4x（2.4＜x＜6），配方得：y＝﹣（x﹣3）2+6．∴当x＝3时，y有最大值，最大值是6．2．（1）证明：∵AB＝AC，∴∠B＝∠ACB，∵∠ADE+∠CDE＝∠B+∠BAD，∠ADE＝∠B，∴∠BAD＝∠CDE，又∠B＝∠ACB，∴△BAD∽△DCE．（2）解：∵DE∥AB，∴△CDE∽△CBA，∵△CDE∽△ABD，∴△ABD∽△CBA，∴＝，即＝，解得，BD＝，∵DE∥AB，∴＝，即＝，解得，AE＝；（3）点D在BC边上运动的过程中，存在某个位置，使得DF＝CF．理由如下：如图3，作FH⊥BC于H，AM⊥BC于M，AN⊥FH于N．则四边形AMHN为矩形，∴∠MAN＝90°，MH＝AN，∵AB＝AC，AM⊥BC，∴BM＝CM＝BC＝8，在Rt△ABM中，由勾股定理，得AM＝＝＝6，∴tan B＝＝，∵∠ADE＝∠B，∴tan∠ADE＝＝，∵AN⊥FH，AM⊥BC，∴∠ANF＝90°＝∠AMD，∵∠DAF＝90°＝∠MAN，∴∠NAF＝∠MAD，∴△AFN∽△ADM，∴═＝，即＝，解得，AN＝，∴MH＝AN＝，∴CH＝CM﹣MH＝，∵FD＝FC，FH⊥CD，∴CD＝2CH＝7，∴BD＝BC﹣CD＝9．3．解：（1）如图1，过点O作OH⊥AC，∵∠C＝90°，AC＝4，BC＝3，∴AB＝＝＝5，∵∠A＝∠A，∠ACB＝∠AHO＝90°，∴△AOH∽△ABC，∴，即，∴OH＝；（2）如图2，过点O作OD⊥AC，由（1）可得OD＝，∵∠BCA＝∠ODA＝90°，∠A＝∠A，∴△AOD∽△ABC，∴，∴，∴AD＝，∴PD＝x﹣，∵PQ⊥OP，∴∠OPD+∠CPQ＝90°，又∵∠PQC+∠CPQ＝90°，∴∠OPD＝∠PQC，且∠ACB＝∠PDO＝90°，∴△POD∽△QPC，∴，∴∴y＝﹣x2+x﹣（＜x＜4）（3）如图3，当OQ∥AC时，△OPQ∽△CPQ，∵OQ∥AC，∴△QOB∽△CAB，∴，∴＝，∴CQ＝，∴＝﹣x2+x﹣，∴x＝，∴AP＝；如图4，作PE⊥OQ于点E，当PQ平分∠CQO时，△OPQ∽△CPQ，∵∠CQP＝∠PQE，PC⊥BC，PE⊥OQ，∴PC＝PE，∵∠POQ＝∠CPQ，∠DOP＝∠CPQ，∴∠POQ＝∠DOP，又∵PD⊥OD，PE⊥OE，∴PD＝PE，∴PC＝PD，即点P为CD的中点，由AP﹣AD＝AC﹣AP，∴2AP＝AC+AD＝4+，∴AP＝，综上所述：当△OPQ与△CPQ相似时，AP为．4．（1）解：如图1所示：由勾股定理得：AB＝＝，BC＝＝2，∠ABC＝90°，AC＝5，∵四边形ABCD是以AC为“相似对角线”的四边形，①当∠ACD＝90°时，△ACD∽△ABC或△ACD∽△CBA，∴＝＝，或＝＝2，∴CD＝10，或CD＝2.5②当∠CAD＝90°时，同理：AD＝2.5或AD＝10；（2）证明：∵∠ABC＝70°，BD平分∠ABC，∴∠ABD＝∠DBC＝35°，∴∠A+∠ADB＝145°∵∠ADC＝145°，∴∠BDC+∠ADB＝145°，∴∠A＝∠BDC，∴△ABD∽△DBC，∴BD是四边形ABCD的“相似对角线”；（3）解：∵FH是四边形EFGH的“相似对角线”，∴△EFH与△HFG相似，∵∠EFH＝∠HFG，∴△FEH∽△FHG，∴＝，∴FH2＝FE•FG，过点E作EQ⊥FG于Q，如图3所示：∴EQ＝FE•sin60°＝FE，∵FG×EQ＝2，∴FG×FE＝2，∴FG•FE＝8，∴FH2＝FE•FG＝8，∴FH＝2．5．（1）证明：∵AM⊥MN，∴∠MAB+∠MBA＝90°，∵∠ABC＝90°，∴∠CBN+∠MBA＝90°，∴∠MAB＝∠NBC，又∠AMB＝∠BNC＝90°，∴△ABM～△BCN；（2）解：过点P作PD⊥AM于D．∴∠BAP+∠APB＝∠CPM+∠APB＝90°，∴∠BAP＝∠CPM＝∠C，∴MP＝MC，∵PM⊥PA，PD⊥AM，∴△PDM∽△APM，∵＝＝＝，设DM＝2a，则DP＝a，由勾股定理得，PM＝＝3a，∴CD＝DM+CM＝DM+PM＝5a，则＝，∵∠CDP＝∠CBA＝90°，∠C＝∠C，∴△CDP∽△CBA，∴＝＝；（3）解：过点A作AG⊥BE于G，过点C作CH⊥BE交EB的延长线于H，∵∠DEB＝90°，∴CH∥AG∥DE，∴＝＝，∵BC：AC＝3：5，∴BC：AB＝3：4，由（1）可知，△ABG∽△BCH，∴＝＝＝，设BG＝4m，CH＝3m，AG＝4n，BH＝3n，∵AB＝AE，AG⊥BE，∴EG＝BG＝4m，∴GH＝BG+BH＝4m+3n，∵＝，∴＝，解得，n＝2m，AG＝4n＝8m，BH＝3n＝6m，由勾股定理得，BC＝＝3m，BE＝2BG＝8m，∴＝．6．解：（1）∠BAD＝∠BED，理由为：如图1，记DE与AB的交点为F，证明：∵MN∥AC，∴∠EBA＝∠BAC，∵∠BAC＝∠ADE，∴∠EBA＝∠ADE，又∵∠AFD＝∠EFB，∴△EBF∽△ADF，∴∠BED＝∠BAD；（2）AD＝DE，理由：如图2，在BA上取一点Q，使DB＝DQ，∴∠ABC＝∠DQB，∴∠BDQ＝180°﹣2∠ABC，∵AB＝AC，∴∠ABC＝∠C，∴∠BAC＝180°﹣2∠ABC，∴∠BDQ＝∠BAC，∵∠ADE＝∠BAC，∴∠BDQ＝∠ADE，∴∠BDE＝∠QDA，在△BED和△QAD中，，∴△BED≌△QAD（AAS），∴AD＝DE；（3）（2）中的结论仍然成立，即：AD＝DE，理由：如图3，在BA上取一点Q，使DB＝DQ，∴∠ABC＝∠DQB，∴∠BDQ＝180°﹣2∠ABC，∵AB＝AC，∴∠ABC＝∠C，∴∠BAC＝180°﹣2∠ABC，∴∠BDQ＝∠BAC，∵∠ADE＝∠BAC，∴∠BDQ＝∠ADE，∴∠BDE＝∠QDA，在△BED和△QAD中，，∴△BED≌△QAD（AAS），∴AD＝DE；（4）作∠BDQ＝∠ADE，交AB于点Q，如图4所示，∴∠BDQ﹣∠EDQ＝∠ADE﹣∠EDQ，即∠BDE＝∠ADQ，∵∠BED＝∠BAD，∴△BED∽△QAD，∴＝，∵∠ABC＝∠QBD，∠BDQ＝∠ADE＝∠BAC，∴△BDQ∽△BAC，∴＝＝k，∴＝k，即DE＝kAD．7．解：（1）∵AM⊥MN，CN⊥MN，∴∠AMB＝∠BNC＝90°，∴∠BAM+∠ABM＝90°，∵∠ABC＝90°，∴∠ABM+∠CBN＝90°，∴∠BAM＝∠CBN，∵∠AMB＝∠NBC，∴△ABM∽△BCN；（2）如图2，过点P作PM⊥AP交AC于M，PN⊥AM于N．∴∠BAP+∠1＝∠CPM+∠1＝90°，∴∠BAP＝∠CPM＝∠C，∴MP＝MC∵tan∠PAC＝＝＝＝，设MN＝2m，PN＝m，根据勾股定理得，PM＝＝3m＝CM，∴tan C＝＝；（3）在Rt△ABC中，sin∠BAC＝＝，过点A作AG⊥BE于G，过点C作CH⊥BE交EB的延长线于H，∵∠DEB＝90°，∴CH∥AG∥DE，∴＝同（1）的方法得，△ABG∽△BCH∴＝＝＝，设BG＝4m，CH＝3m，AG＝4n，BH＝3n，∵AB＝AE，AG⊥BE，∴EG＝BG＝4m，∴GH＝BG+BH＝4m+3n，∴＝，∴n＝2m，∴EH＝EG+GH＝4m+4m+3n＝8m+3n＝8m+6m＝14m，在Rt△CEH中，tan∠BEC＝＝．8．解：（1）如图1，过点G作GM⊥CB于M，过点E作EN⊥CD于点N，∵四边形ABCD是矩形，∴∠A＝∠B＝∠C＝∠D＝90°，AB＝CD，AD＝BC，且GM⊥BC，EN⊥CD，∴四边形DCMG是矩形，四边形ABMG是矩形，四边形AEND是矩形，四边形BCNE是矩形，∴GM＝CD＝AB，EN＝AD＝BC，∵EF⊥GH，∠BCD＝90°，∴∠EFC+∠GHC＝180°，且∠DFE+∠EFC＝180°，∴∠EFN＝∠GHC，且∠ENF＝∠GMH＝90°，∴△EFN∽△GHM，∴；（2）如图2，连接BD交EF于点O，DE，BF，∵将矩形对折，使得B、D重叠，∴BE＝DE，∠DEF＝∠BEF，∵AB∥CD，∴∠DFE＝∠BEF，∴∠DFE＝∠DEF，∴DF＝DE，且BE＝DE，∴BE＝DF，且AB∥CD，∴四边形DFBE是平行四边形，且DF＝DE，∴四边形DFBE是菱形，∴BO＝DO，EO＝FO，BD⊥EF，∵DE2＝AE2+AD2，∴DE2＝9+（4﹣DE）2，∴DE＝，∵BD＝＝＝5，∴DO＝BO＝，∴OE＝＝＝，∴EF＝2OE＝；（3）如图3，过点D作EF⊥BC，交BC的延长线于F，过点A作AE⊥EF，连接AC，∵∠ABC＝90°，AE⊥EF，EF⊥BC，∴四边形ABFE是矩形，∴∠E＝∠F＝90°，AE＝BF，EF＝AB＝8，∵AD＝AB，BC＝CD，AC＝AC，∴△ACD≌△ACB（SSS）∴∠ADC＝∠ABC＝90°，∴∠ADE+∠CDF＝90°，且∠ADE+∠EAD＝90°，∴∠EAD＝∠CDF，且∠E＝∠F＝90°，∴△ADE∽△DCF，∴，∴AE＝2DF，DE＝2CF，∵DC2＝CF2+DF2，∴16＝CF2+（8﹣2CF）2，∴CF＝4（不合题意舍去），CF＝，∴BF＝BC+CF＝＝AE，由（1）可知：＝＝．9．证明：（1）∵∠AMD＝∠B+∠D，∠BGM＝∠DMG+∠D，又∠B＝∠A＝∠DME＝α，∴∠AMF＝∠BGM，∴△AMF∽△BGM；（2）解：∵M为AB的中点，∴AM＝BM＝2，∵△AMF∽△BGM，∴＝，∴BG＝＝＝；（3）如图2，过点M作MH⊥AE于H，∵∠A＝∠B＝45°，∴∠ACB＝90°，AC＝BC，且AB＝2AM＝4，∴AC＝BC＝4，且AF＝3，BG＝，∴CF＝1，CG＝，∵∠A＝45°，MH⊥AC，AM＝2，∴AH＝HM＝2，∴CH＝2，∵∠ACB＝∠AHM＝90°，∴HM∥CB，∴△ECG∽△EHM，∴，∴＝∴CE＝4，∴EF＝CE+CF＝5，∴S＝EF×CG＝×5×＝．△EFG10．（1）证明：若运动时间t＝秒，则BE＝2×＝（cm），DF＝（cm），∵四边形ABCD是矩形∴AD＝BC＝8（cm），AB＝DC＝6（cm），∠D＝∠BCD＝90°∵∠D＝∠FQC＝∠QCD＝90°，∴四边形CDFQ也是矩形，∴CQ＝DF，CD＝QF＝6（cm），∴EQ＝BC﹣BE﹣CQ＝8﹣﹣＝6（cm），∴EQ＝QF＝6（cm），又∵FQ⊥BC，∴△EQF是等腰直角三角形；（2）解：由（1）知，CE＝8﹣2t，CQ＝t，在Rt△ABC中，tan∠ACB＝＝，在Rt△CPQ中，tan∠ACB＝＝＝，∴PQ＝t，∵△EPC的面积为3cm2，＝CE×PQ＝×（8﹣2t）×t＝3，∴S△EPC∴t＝2秒，即：t的值为2秒；（3）解：分两种情况：Ⅰ．如图1中，点E在Q的左侧．①∠PEQ＝∠CAD时，△EQP∽△ADC，∵四边形ABCD是矩形，∴AD∥BC，∴∠CAD＝∠ACB，∵△EQP∽△ADC，∴∠CAD＝∠QEP，∴∠ACB＝∠QEP，∴EQ＝CQ，∴CE＝2CQ，由（1）知，CQ＝t，CE＝8﹣2t，∴8﹣2t＝2t，∴t＝2秒；②∠PEQ＝∠ACD时，△EPQ∽△CAD，∴＝，∵FQ⊥BC，∴FQ∥AB，∴△CPQ∽△CAB，∴＝，即＝，解得：PQ＝t，∴＝，解得：t＝；Ⅱ．如图2中，点E在Q的右侧．∵0＜t＜4，∴点E不能与点C重合，∴只存在△EPQ∽△CAD可得＝，即＝，解得t＝，综上所述，t的值为2秒或秒或秒时，△EPQ与△ADC相似．。

2022年中考数学复习专题几何压轴题题型分类整理

专题训练一平移问题基本模型经过平移，对应线段平行（或共线）且相等，对应角相等，对应点所连接的线段平行（或共线）且相等，因此可以通过平移构造平行四边形，转移线段和角.（基本模型图1）（基本模型图2）如图1，将线段CD 进行平移可得到线段EA ，连接EC ，AD. 根据平移的性质，得CD ∥EA.∴四边形CDAE 是平行四边形.∴EC ∥AD.同理，四边形CDFA 、四边形CDBG 和四边形CDHB 均为平行四边形. 如图2，平移线段AB ，即可得到▱ABCP 、▱ABDM 、▱ABND 和▱ABQC. 典型题在Rt △BAC 中，∠A=90°，D,E 分别为AB ，AC 上的点.（1）如图1，CE=AB ，BD=AE ，过点C 作CF ∥EB ，且CF=EB ，连接DF 交EB 于点G ，连接BF ，求EBDC 的值; （2）如图2,若CE=kAB ，BD=kAE ，EB DC =12，求k 的值.（典型题图1）（典型题图2）拓展题1.如图，在四边形ABCD中，AD∥BC，∠BAC=90°－1∠CAD，AC与BD相交于点E，且∠BEC=60°,若AD=5，2BD=15，求AC的长.（1题图）2.如图,在△ABC中，点D在AB的延长线上，点E在BC上，AC=BC=AD=DE，BE=BD，求∠BAC的度数.（2题图）3.阅读下面材料:数学课上，老师出示了下列问题:（1）如图1，过点B作AB的垂线BD，延长AB到点C,使AC=BD，延长BD到点E，使ED=CB，连接AE，CD，且CD的延长线交AE于点F，求∠AFC的度数;（2）如图2,在△ABC中,AB=AC=5m，D是边BC上一点，连接AD，延长CB到点E，使BE=kAD，过点E作EF，求EF的长.(用含m，k的式子表示)⊥AD，交AD的延长线于点F.若AF=kCD,tanC= 34（3题图1）（3题图2）同学们经过思考后，交流了自己的想法:小明:“通过观察和度量，发现∠AFC的度数等于45°”小伟:“通过平移线段AC，BD，ED，BC中的一条线段，可以构造两个全等三角形，进而可以获得等腰直角三角形,那么∠AFC的度数等于45°这一结论也就显而易见了.”……老师:“只要类比小伟平移线段构造全等三角形的思路与方法，那么（2）的问题就能迎刃而解.”请你根据上面的材料，完成上面的两个问题的解答过程.4.如图，在四边形ABCD中，AD∥BC，AD+BC=BD,AC与BD 相交于点F。

中考几何知识点总结

中考几何知识点总结几何是数学的一个重要分支，它研究空间形状、大小和位置的关系，是人们日常生活和实际工作中都会接触到的数学分支。

而中考几何知识点是应用数学的重要组成部分，其中包括平面图形的性质、空间图形的性质、相似三角形的性质、圆的性质、三角形的性质等等。

下面我们就来总结一下中考几何知识点的要点。

一、平面图形的性质1、平行四边形和矩形平行四边形是指四边形的对边是平行的四边形，平行四边形的特点是对边相等、对角相等、相邻边互补。

矩形是指四边形的对边是平行且对角相等的四边形，矩形的特点是对边相等、对角相等、相邻边垂直。

2、菱形和正方形菱形是指四边形的对边相等的四边形，菱形的特点是对边相等、对角相等、对角互补。

正方形是指四边形的对边相等且对角相等的四边形，正方形的特点是对边相等、对角相等、对角互补、对边垂直。

3、三角形的性质三角形是平面图形中的基本图形之一，三角形的性质有很多，例如三角形的内角和为180°，三角形的外角和为360°，等腰三角形的两条边相等，等边三角形的三条边相等等等。

二、空间图形的性质1、立体图形的性质立体图形是指具有三维形状的图形，如长方体、圆柱体、球体等，立体图形的性质包括表面积、体积等概念。

2、直角棱柱和直角锥直角棱柱是指底面为矩形且母线垂直于底面的棱柱，直角锥是指底面为矩形且母线垂直于底面的锥体，直角棱柱和直角锥的特点是底面积相等，高相等。

3、棱台和棱锥棱台是指底面为多边形且母线与底面平行的棱台，棱锥是指底面为多边形且母线与底面平行的锥体，棱台和棱锥的特点是底面积相等、母线平行。

三、相似三角形的性质相似三角形是指三角形的对应角相等且对应边成比例的三角形，相似三角形的性质包括对应角相等、对应边成比例、相似三角形的高、中线、角平分线比例等。

四、圆的性质1、圆的相关概念圆是平面图形中一个特殊的图形，它是平面内所有到一个固定点距离相等的点的集合，圆的性质包括圆心、半径、直径、圆周、弧、圆心角等概念。

数学冲刺班中考试题及答案

数学冲刺班中考试题及答案中考临近，许多学生都在寻找有效的复习方法和资料。

数学冲刺班就是其中一种帮助学生快速提高成绩的方式。

以下是一份数学冲刺班中考试题及答案，供同学们参考和练习。

一、选择题1. 下列哪个数是无理数？A. 2.5B. 3.14C. πD. √2答案：C2. 如果一个三角形的两边长分别为3和4，且这两边夹角为90°，那么第三边的长度是多少？A. 5B. 6C. 7D. 8答案：A二、填空题1. 已知一个圆的半径为5，那么这个圆的面积是_________（答案：25π）。

2. 如果一个多项式f(x) = x^2 - 5x + 6，那么f(2)的值是_________（答案：0）。

三、解答题1. 解不等式：2x + 5 > 3x - 2。

首先，将不等式中的项进行整理，得到2x - 3x > -2 - 5，即-x > -7。

解得x < 7。

2. 已知一个直角三角形的两个直角边分别为6和8，求斜边的长度。

根据勾股定理，斜边的长度为√(6^2 + 8^2) = √(36 + 64) =√100 = 10。

四、证明题1. 证明：对于任意一个直角三角形，其斜边的平方等于两个直角边的平方和。

设直角三角形的两个直角边分别为a和b，斜边为c。

根据勾股定理，我们有c^2 = a^2 + b^2。

这就是需要证明的结论。

五、应用题1. 一个农场主想要围成一个矩形的鸡舍，他有120米的围栏。

如果鸡舍的长是宽的两倍，那么鸡舍的长和宽各是多少？设鸡舍的宽为x米，那么长为2x米。

根据题意，我们有2(x + 2x) = 120，解得x = 15，所以宽为15米，长为30米。

结束语通过以上的数学冲刺班中考试题及答案，同学们可以检验自己的数学知识掌握情况，同时也能够对中考的题型有一个大致的了解。

希望同学们能够通过不断的练习，提高自己的数学解题能力，为中考做好充分的准备。

祝所有考生中考顺利，取得优异的成绩！。

北师大版数学[中考冲刺：几何综合问题--知识点整理及重点题型梳理](提高)

北师大版数学中考总复习重难点突破知识点梳理及重点题型巩固练习中考冲刺：几何综合问题—知识讲解（提高）【中考展望】几何综合题是中考试卷中常见的题型，大致可分为几何计算型综合题与几何论证型综合题，它主要考查学生综合运用几何知识的能力.这类题型在近几年全国各地中考试卷中占有相当的分量，不仅有选择题、填空题、几何推理计算题以及代数与几何的综合计算题,还有更注重考查学生分析问题和解决问题能力的探究性的问题、方案设计的问题等等.主要特点是图形较复杂，覆盖面广、涉及的知识点较多，题设和结论之间的关系较隐蔽，常常需要添加辅助线来解答.几何综合题的呈现形式多样，如折叠类型、探究型、开放型、运动型、情景型等，背景鲜活，具有实用性和创造性，考查方式偏重于考查考生分析问题、探究问题、综合应用数学知识解决实际问题的能力.以几何为主的综合题常常在一定的图形背景下研究以下几个方面的问题：1、证明线段、角的数量关系（包括相等、和、差、倍、分及比例关系等）；2、证明图形的位置关系（如点与线、线与线、线与圆、圆与圆的位置关系等）；3、几何计算问题；4、动态几何问题等.【方法点拨】一、几何计算型综合问题，常常涉及到以下各部分的知识：1、与三角形有关的知识；2、等腰三角形，等腰梯形的性质；3、直角三角形的性质与三角函数；4、平行四边形的性质；5、全等三角形，相似三角形的性质；6、垂径定理，切线的性质，与正多边形有关的计算；7、弧长公式与扇形面积公式.二、几何论证型综合题的解答过程，要注意以下几个方面：1、注意图形的直观提示，注意观察、分析图形，把复杂的图形分解成几个基本图形，通过添加辅助线补全或构造基本图形；2、注意分析挖掘题目的隐含条件、发展条件，为解题创造条件打好基础，要由已知联想经验，由未知联想需要，不断转化条件和结论来探求思路，找到解决问题的突破点；3、要运用转化的思想解决几何证明问题，运用方程的思想解决几何计算问题，还要灵活运用数学思想方法如数形结合、分类讨论、转化、方程等思想来解决问题.【典型例题】类型一、动态几何型问题1．（2016•太原校级自主招生）如图1，在正方形ABCD中，点E、F分别是边BC、AB上的点，且CE=BF，连接DE，过点E作EG⊥DE，使EG=DE，连接FG，FC．（1）请判断：FG与CE的数量关系和位置关系；（不要求证明）（2）如图2，若点E、F分别是CB、BA延长线上的点，其它条件不变，（1）中结论是否仍然成立？请出判断判断予以证明；（3）如图3，若点E、F分别是BC、AB延长线上的点，其它条件不变，（1）中结论是否仍然成立？请直接写出你的判断．【思路点拨】（1）结论：FG=CE，FG∥CE．如图1中，设DE与CF交于点M，首先证明△CBF≌△DCE，推出DE⊥CF，再证明四边形EGFC是平行四边形即可．（2）结论仍然成立．如图2中，设DE与CF交于点M，首先证明△CBF≌△DCE，推出DE⊥CF，再证明四边形EGFC是平行四边形即可．（3）结论仍然成立．如图3中，设DE与FC的延长线交于点M，证明方法类似．【答案与解析】解：（1）结论：FG=CE，FG∥CE．理由：如图1中，设DE与CF交于点M．∵四边形ABCD是正方形，∴BC=CD，∠ABC=∠DCE=90°，在△CBF和△DCE中，，∴△CBF≌△DCE，∴∠BCF=∠CDE，CF=DE，∵∠BCF+∠DCM=90°，∴∠CDE+∠DCM=90°，∴∠CMD=90°，∴CF⊥DE，∵GE⊥DE，∴EG∥CF，∵EG=DE，CF=DE，∴EG=CF，∴四边形EGFC是平行四边形．∴GF=EC，∴GF=EC，GF∥EC．（2）结论仍然成立．理由：如图2中，设DE与CF交于点M．∵四边形ABCD是正方形，∴BC=CD，∠ABC=∠DCE=90°，在△CBF和△DCE中，，∴△CBF≌△DCE，∴∠BCF=∠CDE，CF=DE，∵∠BCF+∠DCM=90°，∴∠CDE+∠DCM=90°，∴∠CMD=90°，∴CF⊥DE，∵GE⊥DE，∴EG∥CF，∵EG=DE，CF=DE，∴EG=CF，∴四边形EGFC是平行四边形．∴GF=EC，∴GF=EC，GF∥EC．（3）结论仍然成立．理由：如图3中，设DE与FC的延长线交于点M．∵四边形ABCD是正方形，∴BC=CD，∠ABC=∠DCE=90°，∴∠CBF=∠DCE=90°在△CBF和△DCE中，，∴△CBF≌△DCE，∴∠BCF=∠CDE，CF=DE∵∠BCF+∠DCM=90°，∴∠CDE+∠DCM=90°，∴∠CMD=90°，∴CF⊥DE，∵GE⊥DE，∴EG∥CF，∵EG=DE，CF=DE，∴EG=CF，∴四边形EGFC是平行四边形．∴GF=EC，∴GF=EC，GF∥EC．【总结升华】本题考查四边形综合题、正方形的性质、平行四边形的判定和性质、全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形，注意这类题目的解题规律，图形变了，条件不变，证明的方法思路完全一样，属于中考常考题型．举一反三：AM射线BN，AB是它们的公垂线，点D、C分别在AM、BN 【变式】已知：如图（1），射线//上运动（点D 与点A 不重合、点C 与点B 不重合），E 是AB 边上的动点（点E 与A 、B 不重合），在运动过程中始终保持EC DE ⊥，且a AB DE AD ==+．（1）求证：ADE ∆∽BEC ∆；（2）如图（2），当点E 为AB 边的中点时，求证：CD BC AD =+；（3）设m AE =，请探究：BEC ∆的周长是否与m 值有关？若有关，请用含有m 的代数式表示 BEC ∆的周长；若无关，请说明理由．【答案】（1）证明：∵EC DE ⊥，∴︒=∠90DEC ．∴︒=∠+∠90BEC AED ．又∵︒=∠=∠90B A ，∴︒=∠+∠90EDA AED ．∴EDA BEC ∠=∠．∴ADE ∆∽BEC ∆．（2）证明：如图，过点E 作EF BC //，交CD 于点F ，∵E 是AB 的中点，容易证明)(21BC AD EF +=．在DEC Rt ∆中，∵ CF DF =，∴ CD EF 21=． ∴ )(21BC AD +CD 21=． ∴ CD BC AD =+．（3）解：AED ∆的周长DE AD AE ++=m a +=，m a BE -=．设x AD =，则x a DE -=．∵ ︒=∠90A ，∴ 222AD AE DE +=．即22222x m x ax a +=+-．∴ am a x 222-=．由（1）知ADE ∆∽BEC ∆，∴ 的周长的周长BEC ∆∆ADE BE AD =m a a m a --=222am a 2+=． ∴ BEC ∆的周长⋅+=ma a 2ADE ∆的周长a 2=． ∴ BEC ∆的周长与m 值无关．2．在△ABC 中，∠ACB=45º．点D （与点B 、C 不重合）为射线BC 上一动点，连接AD ，以AD 为一边且在AD 的右侧作正方形ADEF ．（1）如果AB=AC ．如图①，且点D 在线段BC 上运动．试判断线段CF 与BD 之间的位置关系，并证明你的结论．（2）如果AB ≠AC ，如图②，且点D 在线段BC 上运动．（1）中结论是否成立，为什么？（3）若正方形ADEF 的边DE 所在直线与线段CF 所在直线相交于点P ，设AC＝3=BC ，CD=x ，求线段CP 的长．（用含x 的式子表示）【思路点拨】(1)由题干可以发现，正方形中四条边的垂直关系是不动的，于是利用角度的互余关系进行传递，就可以得解.(2)是典型的从特殊到一般的问法，那么思路很简单，就是从一般中构筑一个特殊的条件就行，和上题一样找AC 的垂线，就可以变成第一问的条件，然后一样求解.(3)D 在BC 之间运动和它在BC 延长线上运动时的位置是不一样的，所以已给的线段长度就需要分情况去考虑到底是4+X 还是4-X.分类讨论之后利用相似三角形的比例关系即可求出CP.【答案与解析】（1）结论：CF ⊥BD ；证明如下： AB=AC ，∠ACB =45º，∴∠ABC=45º．由正方形ADEF 得 AD=AF ，∵∠DAF=∠BAC =90º，∴∠DAB=∠FAC ，∴△DAB ≌△FAC ， ∴∠ACF=∠ABD ．∴∠BCF=∠ACB+∠ACF= 90º．即 CF ⊥BD ．（2）CF ⊥BD ．(1)中结论仍成立．理由是：过点A 作AG ⊥AC 交BC 于点G ，∴AC=AG可证：△GAD ≌△CAF ∴∠ACF=∠AGD=45º∠BCF=∠ACB+∠ACF= 90º．即CF ⊥BD（3）过点A 作AQ ⊥BC 交CB 的延长线于点Q ，①点D 在线段BC 上运动时，∵∠BCA=45º，可求出AQ= CQ=4．∴DQ=4-x ，易证△AQD ∽△DCP ，∴CP CD DQ AQ= ，∴44CP x x =-， 24x CP x ∴=-+．②点D 在线段BC 延长线上运动时，∵∠BCA=45°，∴AQ=CQ=4，∴DQ=4+x ．过A 作AQ ⊥BC ，24x CP x ∴=+．【总结升华】此题综合性强，需要综合运用全等、相似、正方形等知识点，属能力拔高性的题目．3．（2015•河南模拟）如图，正方形ABCD 的边长为6，点E 是射线BC 上的一个动点，连接AE 并延长，交射线DC 于点F ，将△ABE 沿直线AE 翻折，点B 坐在点B ′处．自主探究：（1）当=1时，如图1，延长AB ′，交CD 于点M ．①CF 的长为；②判断AM与FM的数量关系，并证明你的结论．（2）当点B′恰好落在对角线AC上时，如图2，此时CF的长为，=．拓展运用：（3）当=2时，求sin∠DAB′的值．【思路点拨】（1）①利用相似三角形的判定与性质得出FC=AB即可得出答案；②利用翻折变换的性质得出∠BAF=∠MAF，进而得出AM=FM；（2）根据翻折变换的性质得出∠BAE=∠MAF，进而得出AM=MF，利用△ABE∽FCE得出答案即可；（3）根据①如图1，当点E在线段BC上时，延长AB′交DC边于点M，②如图3，当点E在线段BC 的延长线上时，延长AD交B′E于点N，分别利用勾股定理求出即可．【答案与解析】解：（1）①当=1时，∵AB∥FC，∴△ABE∽FCE，∴==1，∴FC=AB=6，②AM=FM，理由如下：∵四边形ABCD是正方形，∴AB∥DC，∴∠BAF=∠AFC，∵△ABE沿直线AE翻折得到△AB′E，∴∠BAF=∠MAF，∴∠MAF=∠AFC，∴AM=FM；（2）如图2，∵当点B′恰好落在对角线AC上时，∴∠1=∠2，∵AB∥FC，∴∠1=∠F，∴∠2=∠F，∴AC=FC，∵AB=BC=6，∴AC=FC=6，∵AB∥FC，∴△ABE∽FCE，∴===，（3）①如图1，当点E在线段BC上时，延长AB′交DC边于点M，∵AB∥CF，∴△ABE∽△FCE，∴==2，∵AB=6，∴CF=3，∴DF=CD+CF=9，由（1）知：AM=FM，∴AM=FM=9﹣DM，在Rt△ADM中，由勾股定理得：DM′2=（9﹣DM）2﹣62，解得：DM=，则MA=，∴sin ∠DAB ′==， ②如图3，当点E 在线段BC 的延长线上时，延长AD 交B ′E 于点N ，由（1）知：AN=EN ，又BE=B ′E=12，∴NA=NE=12﹣B ′N ，在Rt △AB ′N 中，由勾股定理得：B ′N 2=（12﹣B ′N ）2﹣62，解得：B ′N=， AN=，∴sin ∠DAB ′==．故答案为：6；6，．【总结升华】此题主要考查了翻折变换的性质以及相似三角形的判定与性质和勾股定理等知识，熟练利用相关性质和进行分类讨论得出是解题关键．类型二、几何计算型问题4．已知如图，在梯形ABCD 中，24AD BC AD BC ==∥，，，点M 是AD 的中点，MBC △是等边三角形．（1）求证：梯形ABCD 是等腰梯形；（2）动点P 、Q 分别在线段BC 和MC 上运动，且60MPQ =︒∠保持不变．设PC x MQ y ==，，求y 与x 的函数关系式；（3）在（2）中，当y 取最小值时，判断PQC △的形状，并说明理由．【思路点拨】（1）属于纯静态问题，只要证两边的三角形全等就可以了.(2)是双动点问题，所以就需要研究在P,Q 运动过程中什么东西是不变的.题目给定∠MPQ=60°，其实就是将静态的那个等边三角形与动态条件联系了起来.因为最终求两条线段的关系,所以很自然想到要通过相似三角形找比例关系.(3)条件又回归了当动点静止时的问题，由第二问所得的二次函数，很轻易就可以求出当x 取对称轴的值时y 有最小值，接下来就变成了“给定PC=2，求△PQC 形状”的问题了，由已知的BC=4，自然看出P 是中点，于是问题轻松求解.【答案与解析】（1）证明：∵MBC △是等边三角形∴60MB MC MBC MCB ===︒，∠∠∵M 是AD 中点∴AM MD =∵AD BC ∥∴60AMB MBC ==︒∠∠，60DMC MCB ==︒∠∠∴AMB DMC △≌△∴AB DC =∴梯形ABCD 是等腰梯形．（2）解：在等边MBC △中，4MB MC BC ===，60MBC MCB ==︒∠∠，60MPQ =︒∠ ∴120BMP BPM BPM QPC +=+=︒∠∠∠∠ ∴BMP QPC =∠∠∴BMP CQP △∽△ ∴PC CQ BM BP= ∵PC x MQ y ==， ∴44BP x QC y =-=-， ∴444x y x -=- ∴2144y x x =-+（3）解：PQC △为直角三角形， ∵()21234y x =-+ ∴当y 取最小值时，2x PC ==∴P 是BC 的中点，MP BC ⊥，而60MPQ =︒∠，∴30CPQ =︒∠，∴90PQC =︒∠∴PQC △为直角三角形.【总结升华】以上题目是动点问题，这一类问题的关键就在于当动点移动中出现特殊条件，例如某边相等，某角固定时，将动态问题化为静态问题去求解.如果没有特殊条件，那么就需要研究在动点移动中哪些条件是保持不变的.举一反三：【变式】已知：如图，N、M是以O为圆心，1为半径的圆上的两点，B是MN上一动点（B不与点M、N重合），∠MON=90°，BA⊥OM于点A，BC⊥ON于点C，点D、E、F、G分别是线段OA、AB、BC、CO 的中点，GF与CE相交于点P，DE与AG相交于点Q．（1）四边形EPGQ （填“是”或者“不是”）平行四边形；（2）若四边形EPGQ是矩形，求OA的值.【答案】（1）是．证明：连接OB，如图①，∵BA⊥OM，BC⊥ON，∴∠BAO=∠BCO=90°，∵∠AOC=90°，∴四边形OABC是矩形．∴AB∥OC，AB=OC，∵E、G分别是AB、CO的中点，∴AE∥GC，AE=GC，∴四边形AECG为平行四边形．∴CE∥AG，∵点D、E、F、G分别是线段OA、AB、BC、CO的中点，∴GF∥OB，DE∥OB，∴PG∥EQ，∴四边形EPGQ是平行四边形；（2）解：如图②，5．在ABCD中，过点C作CE⊥CD交AD于点E,将线段EC绕点E逆时针旋转90得到线段EF (如图1)（1）在图1中画图探究：①当P为射线CD上任意一点（P1不与C重合）时，连结EP1绕点E逆时针旋转90得到线段EC1.判断直线FC1与直线CD的位置关系，并加以证明；②当P2为线段DC的延长线上任意一点时，连结EP2,将线段EP2绕点E 逆时针旋转90得到线段EC2.判断直线C1C2与直线CD的位置关系，画出图形并直接写出你的结论.（2）若AD=6,tanB=43,AE=1,在①的条件下，设CP1=x，S11P FC=y，求y与x之间的函数关系式，并写出自变量x的取值范围.图1 备用图【思路点拨】(1)本题在于如何把握这个旋转90°的条件.旋转90°自然就是垂直关系，于是出现了一系列直角三角形，于是证角、证线就手到擒来了.(2)是利用平行关系建立函数式，但是不要忘记分类讨论.【答案与解析】（1）①直线1FG 与直线CD 的位置关系为互相垂直．证明：如图1，设直线1FG 与直线CD 的交点为H ．∵线段1EC EP 、分别绕点E 逆时针旋转90°依次得到线段1EF EG 、，∴111190PEG CEF EG EP EF EC ∠=∠===°，，．∵1190G EF PEF ∠=-∠°，1190PEC PEF ∠=-∠°， ∴11G EF PEC ∠=∠． ∴11G EF PEC △≌△． ∴11G FE PCE ∠=∠． ∵EC CD ⊥，∴190PCE ∠=°， ∴190G FE ∠=°．∴90EFH ∠=°．∴90FHC ∠=°． FDC BAE 图1 G 2 G 1P 1 H P 2∴1FG CD ⊥．②按题目要求所画图形见图1，直线12G G 与直线CD 的位置关系为互相垂直．（2）∵四边形ABCD 是平行四边形，∴B ADC ∠=∠． ∵461tan 3AD AE B ===，，， ∴45tan tan 3DE EBC B =∠==，．可得4CE =．由（1）可得四边形EFCH 为正方形．∴4CH CE ==． ①如图2，当1P 点在线段CH 的延长线上时，∵1114FG CP x PH x ===-，， ∴11111(4)22P FG x x S FG PH -=⨯⨯=△． ∴212(4)2y x x x =->． ②如图3，当1P 点在线段CH 上（不与C H 、两点重合）时，∵1114FG CP x PH x ===-，， ∴11111(4)22P FG x x S FG PH -=⨯=△．∴212(04)2y x x x =-+<<． ③当1P 点与H 点重合时，即4x =时，11PFG △不存在．综上所述，y 与x 之间的函数关系式及自变量x 的取值范围是212(4)2y x x x =->或212(04)2y x x x =-+<<．【总结升华】本题着重考查了二次函数的解析式、图形的旋转变换、三角形全等、探究垂直的构成情况等重要知识点，综合性强，能力要求较高．考查学生分类讨论，数形结合的数学思想方法．举一反三：【变式】已知，点P 是∠MON 的平分线上的一动点，射线PA 交射线OM 于点A ，将射线PA 绕点P 逆时针旋转交射线ON 于点B ，且使∠APB+∠MON=180°．（1）利用图1，求证：PA=PB ；（2）如图2，若点C 是AB 与OP 的交点，当S △POB =3S △PCB 时，求PB 与PC 的比值；（3）若∠MON=60°，OB=2，射线AP 交ON 于点D ，且满足且∠PBD=∠ABO ，请借助图3补全图形，并求OP 的长．【答案】（1）作PE ⊥OM ，PF ⊥ON ，垂足为E 、F∵四边形OEPF 中，∠OEP=∠OFP=90°，∴∠EPF+∠MON=180°，已知∠APB+∠MON=180°，∴∠EPF=∠APB ，即∠EPA+∠APF=∠APF+∠FPB ，∴∠EPA=∠FPB ，由角平分线的性质，得PE=PF ，∴△EPA ≌△FPB ，即PA=PB ；。

中考数学总复习《几何压轴题》专项提升练习题(附答案)

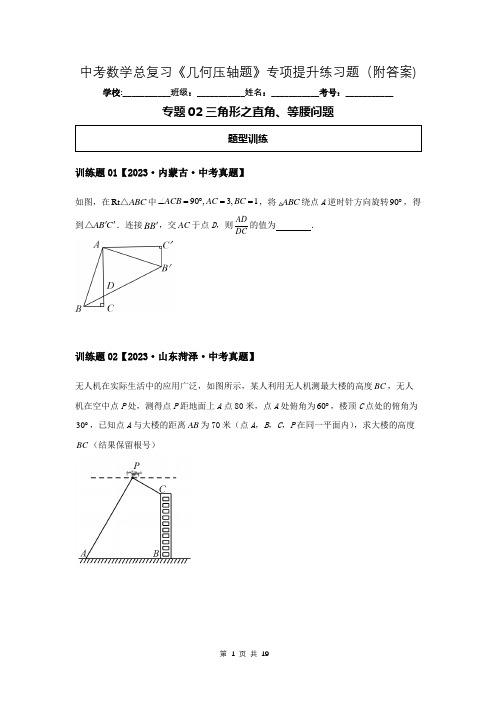
中考数学总复习《几何压轴题》专项提升练习题（附答案)学校:___________班级：___________姓名：___________考号：___________专题02三角形之直角、等腰问题题型训练训练题01【2023·内蒙古·中考真题】如图，在Rt ABC △中90,3,1ACB AC BC ∠=︒==，将ABC 绕点A 逆时针方向旋转90︒，得到AB C ''△．连接BB '，交AC 于点D ，则AD DC 的值为．训练题02【2023·山东菏泽·中考真题】无人机在实际生活中的应用广泛，如图所示，某人利用无人机测最大楼的高度BC ，无人机在空中点P 处，测得点P 距地面上A 点80米，点A 处俯角为60︒，楼顶C 点处的俯角为30︒，已知点A 与大楼的距离AB 为70米（点A ，B ，C ，P 在同一平面内），求大楼的高度BC （结果保留根号）训练题03【2023·广东·中考真题】2023年5月30日，神舟十六号载人飞船发射取得圆满成功，3名航天员顺利进驻中国空间站，如图中的照片展示了中国空间站上机械臂的一种工作状态，当两臂10m AC BC ==，两臂夹角100ACB ∠=︒时，求A ，B 两点间的距离．(结果精确到0.1m ，参考数据sin500.766︒≈ cos500.643︒≈ tan50 1.192︒≈)训练题04【2023·湖北黄冈·中考真题】综合实践课上，航模小组用航拍无人机进行测高实践．如图，无人机从地面CD 的中点A 处竖直上升30米到达B 处，测得博雅楼顶部E 的俯角为45︒，尚美楼顶部F 的俯角为30︒，已知博雅楼高度CE 为15米，则尚美楼高度DF 为米．（结果保留根号）训练题05【2023·河北沧州·模拟预测】如图1，嘉淇在量角器的圆心O 处下挂一铅锤，制作了一个简易测角仪．将此测角仪拿到眼前，使视线沿着仪器的直径刚好到达树的最高点M ．(1)在图1中，过点A 画出水平线，并标记观测M 的仰角α．若铅垂线在量角器上的读数为53︒，求α的值；(2)如图2，已知嘉淇眼睛离地1.5米，站在B 处观测M 的仰角为（1）中的α，向前走1.25米到达D 处，此时观测点M 的仰角为45︒，求树MN 的高度．（注：3tan 374︒≈ 3sin 375︒≈ 4cos375≈︒）训练题06【2023·四川成都·八年级期末联考】如图在等腰Rt EDF 中 90EDF ∠=︒ 2DE DF == DG EF ⊥于点G 点M N 分别是DE DG 上的动点且DN EM = 则FM FN +的最小值为．训练题07【2022·陕西西安·滨河期末】如图直线y ＝x ﹣3分别交x 轴 y 轴于B A 两点点C （0 1）在y 轴上点P 在x 轴上运动则2PC ＋PB 的最小值为．训练题08【2021·四川甘孜·中考真题】如图腰长为22+2的等腰ABC 中顶角∠A ＝45° D 为腰AB 上的一个动点将ACD 沿CD 折叠点A 落在点E 处当CE 与ABC 的某一条腰垂直时 BD 的长为．训练题09【2022·福建泉州·九年级联考】如图 ABC 和AGF 是等腰直角三角形 90BAC G ∠=∠=︒ AGF 的边AF AG 交边BC 于点D E ．若4=AD 3AE = 则BEDC 的值是．训练题10【2021·宁夏固元·联考一模】如图在直角△BAD中延长斜边BD到点C 使得BD=2DC 连接AC 如果则的值是（）A．B．C．D．答案&解析5 tanB3=tan CAD∠3 3351315训练题01【2023·内蒙古·中考真题】【答案】5【简证】因为tan 311tan 4522ABC CD ABD α∠=⎧⇒=⇒=⎨∠=︒⎩ 故5AD DC =【常规法】解：过点D 作DF AB ⊥于点F∵90ACB ∠=︒ 3AC = 1BC =∴223110AB =+=∵将ABC 绕点A 逆时针方向旋转90︒得到AB C ''△∴==10AB AB ' 90BAB '∠=︒∴ABB '是等腰直角三角形∴45ABB '∠=︒又∵DF AB ⊥∴45FDB ∠=︒∴DFB △是等腰直角三角形∴DF BF =∵1122ADB S BC AD DF AB =⨯⨯=⨯⨯ 即=10AD DF ∵ 90C AFD ∠=∠=︒ CAB FAD ∠=∠∴AFDACB ∴DF AF BC AC= 即3AF DF = 又∵=10AF DF -45°α∴10=4 DF∴105=10=42AD⨯51=3=22CD-∴52==512ADCD故答案为：5．训练题02【2023·山东菏泽·中考真题】【答案】大楼的高度BC 为303m ．【分析】如图过P 作PH AB ⊥于H 过C 作CQ PH ⊥于Q 而CB AB ⊥ 则四边形CQHB 是矩形可得QH BC = BH CQ = 求解3sin 60804032PH AP =︒=⨯= cos6040AH AP =︒= 可得704030CQ BH ==-= tan 30103PQ CQ =︒= 可得403103303BC QH ==-=．【详解】解：如图过P 作PH AB ⊥于H 过C 作CQ PH ⊥于Q 而CB AB ⊥则四边形CQHB 是矩形 ∴QH BC = BH CQ =由题意可得：80AP = 60PAH ∠=︒ 30PCQ ∠=︒ 70AB = ∴3sin 60804032PH AP =︒=⨯= cos6040AH AP =︒= ∴704030CQ BH ==-= ∴tan 30103PQ CQ =︒=∴403103303BC QH ==-= ∴大楼的高度BC 为303m ．训练题03【2023·广东·中考真题】【答案】15.3m【分析】连接AB 作作CD AB ⊥于D 由等腰三角形“三线合一”性质可知2AB AD = 1502ACD ACB ∠=∠=︒ 在Rt ACD △中利用sin AD ACD AC∠=求出AD 继而求出AB 即可．【详解】解：连接AB 作CD AB ⊥于D∵AC BC = CD AB ⊥∴CD 是边AB 边上的中线也是ACB ∠的角平分线∴2AB AD = 1502ACD ACB ∠=∠=︒ 在Rt ACD △中 10m AC = 50ACD ∠=︒ sin AD ACD AC ∠= ∴sin 5010AD ︒= ∴10sin50100.7667.66AD =︒≈⨯=∴()227.6615.3215.3m AB AD =≈⨯=≈答：A B 两点间的距离为15.3m ．训练题04【2023·湖北黄冈·中考真题】【答案】3053-/5330-+【分析】过点E 作EM AB ⊥于点M 过点F 作FN AB ⊥于点N 首先证明出四边形ECAM 是矩形得到15AM CE == 然后根据等腰直角三角形的性质得到15AC EM BM === 进而得到15==AD AC 然后利用30︒角直角三角形的性质和勾股定理求出53BN = 即可求解．【详解】如图所示过点E 作EM AB ⊥于点M 过点F 作FN AB ⊥于点N由题意可得四边形ECAM 是矩形 ∴15AM CE == ∵30AB = ∴15BM AB AM =-= ∵博雅楼顶部E 的俯角为45︒ ∴45EBM ∠=︒ ∴45BEM ∠=︒ ∴15AC EM BM ===∵点A 是CD 的中点 ∴15==AD AC 由题意可得四边形AMFN 是矩形 ∴15NF AD == ∵尚美楼顶部F 的俯角为30︒ ∴60NBF ∠=︒ ∴30BFN ∠=︒ ∴2BF BN =∴在Rt BNF △中 222BNNF BF += ∴()222152BN BN +=∴解得53BN =∴3053FD AN AB BN ==-=-．故答案为：3053-．训练题05【2023·河北沧州·模拟预测】【答案】(1)37︒(2)树MN 的高度为5.25米【分析】(1)根据互余的性质计算即可．(2) 过点A 作AP MN ⊥ 垂足为P 则 1.5PN AB ==米．设MN x =米．解直角三角形求解即可．【详解】（1）如图1；905337α=︒-︒=︒；（2）如图过点A 作AP MN ⊥ 垂足为P 则 1.5PN AB ==米．设MN x =米．在Rt APM △中 4( 1.5)tan 373MP AP x ==-︒（米）在Rt MCP 中 1.5CP MP x ==-（米） 4( 1.5)( 1.5) 1.253AC AP CP x x ∴=-=---=（米）解得 5.25x =．答：树MN 的高度为5.25米．训练题06【2023·四川成都·八年级期末联考】【答案】23【分析】过点E 作AE EF ⊥ 使得2AE DF == 证得AEM FDN ≅ 利用全等三角形的性质证得FN AM = 求FM FN +的最小值即求FM AM +的最小值此时只有A M F 在一条直线上时 FM AM +的最小即为AF 的长在Rt AEF 中利用勾股定理即可求解．【详解】解：过点E 作AE EF ⊥ 使得2AE DF == 如图所示∵等腰Rt EDF 中 90EDF ∠=︒ 2DE DF ==∴45DEF ∠=︒ 222222EF =+=∴9045AEM DEF ∠=︒-∠=︒∵等腰Rt EDF 中 90EDF ∠=︒ 2DE DF == DG EF ⊥∴45FDN ∠=︒∴FDN AEM ∠=∠在AEM △和FDN 中AE DF AEM FDN EM DN =⎧⎪∠=∠⎨⎪=⎩∴AEM FDN≅()SAS ∴FN AM =∴求FM FN +的最小值即求FM AM +的最小值此时只有A M F 在一条直线上时 FM AM +的最小即为AF 的长∴在Rt AEF 中()222222223AF AE EF =+=+=的最小值为23即FM FN故答案为：23训练题07【2022·陕西西安·滨河期末】【答案】4【分析】过P作PD⊥AB于D依据△AOB是等腰直角三角形可得∠BAO＝∠ABO＝45°＝∠BPD进而得到△BDP是等腰直角三角形故PD22=PB当C P D在同一直线上时CD⊥AB PC+PD的最小值等于垂线段CD的长求得CD的长即可得出结论．【详解】如图所示过P作PD⊥AB于D∵直线y＝x﹣3分别交x轴y轴于B A两点令x＝0 则y＝﹣3；令y＝0 则x＝3∴A（0 ﹣3）B（3 0）∴AO＝BO＝3又∵∠AOB＝90°∴△AOB是等腰直角三角形∴∠BAO＝∠ABO＝45°＝∠BPD∴△BDP是等腰直角三角形∴PD22=PB∴2PC+PB2=（PC22+PB）2=（PC+PD）当C P D在同一直线上即CD⊥AB时PC+PD的值最小最小值等于垂线段CD 的长此时△ACD是等腰直角三角形又∵点C（0 1）在y轴上∴AC＝1+3＝4∴CD22=AC＝22即PC+PD的最小值为22∴2PC+PB的最小值为222⨯=4 故答案为：4．训练题08【2021·四川甘孜·中考真题】【答案】2或22【分析】分两种情况：当CE ⊥AB 时设垂足为M 在Rt △AMC 中 ∠A ＝45° 由折叠得：∠ACD ＝∠DCE ＝22.5° 证明△BCM ≌△DCM 得到BM ＝DM 证明△MDE 是等腰直角三角形即可得解；当CE ⊥AC 时根据折叠的性质等腰直角三角形的判定与性质计算即可；【详解】当CE ⊥AB 时如图设垂足为M 在Rt △AMC 中 ∠A ＝45°由折叠得：∠ACD ＝∠DCE ＝22.5°∵等腰△ABC 中顶角∠A ＝45°∴∠B ＝∠ACB ＝67.5°∴∠BCM ＝22.5°∴∠BCM ＝∠DCM在△BCM 和△DCM 中90BMC DMC CM CM BCM DCM ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴△BCM ≌△DCM （ASA ）∴BM ＝DM由折叠得：∠E ＝∠A ＝45° AD ＝DE∴△MDE 是等腰直角三角形∴DM ＝EM设DM ＝x 则BM ＝x DE 2=x∴AD 2=x ．∵AB＝22+2∴2x2x＝22+2 解得：x2=∴BD＝2x＝22；当CE⊥AC时如图∴∠ACE＝90°由折叠得：∠ACD＝∠DCE＝45°∵等腰△ABC中顶角∠A＝45°∴∠E＝∠A＝45°AD＝DE∴∠ADC＝∠EDC＝90°即点D E都在直线AB上且△ADC△DEC△ACE都是等腰直角三角形∵AB＝AC＝＝22+2∴AD22=AC＝22BD＝AB﹣AD＝（22+2）﹣（22）2=综上BD的长为2或22．故答案为：2或22．训练题09【2022·福建泉州·九年级联考】【答案】916【分析】利用等腰直角三角形的性质先证明AED BEA ∽ 可得34BE AE AB AD ==,设3BE x = 则4AB x AC ==,再证明ADE CDA △∽△ 可得34AC AE CD AD == 可得163CD x = 从而可得结论．【详解】解：∵ABC 和AGF 是等腰直角三角形 ∴45,B F FAG AB AC ∠=∠=∠=︒=∵AEB AED ∠=∠∴AED BEA ∽∴AD AE DE AB BE AE ==,而4=AD 3AE = ∴34BE AE AB AD == 设3BE x = 则4AB x AC ==同理可得：ADE CDA △∽△∴AD AE DE CD AC AD == ∴34AC AE CD AD == ∴BE AC AB CD = ∴344x x x CD =,即163CD x = ∴3916163BE x CD x ==.训练题10【2021·宁夏固元·联考一模】【答案】D【详解】解：如图延长AD 过点C 作CE ⊥AD 垂足为E∵ 即∴设AD ＝5x 则AB ＝3x∵∠CDE ＝∠BDA ∠CED ＝∠BAD∴△CDE ∽△BDA∴∴CE ＝ DE ＝∴AE ＝ ∴tan ∠CAD ＝．5tanB 3=53AD AB =12CE DE CD AB AD BD ===32x 52x 152x 15CE AE =。

中考数学冲刺班复习资料几何分第一章线段、角、相交线、平行线试题

几何局部制卷人：歐陽文化、歐陽理複；制卷時間：二O 二二年二月七日第一章：线段、角、相交线、平行线知识点：一、直线：直线是几何中不加定义的根本概念，直线的两大特征是“直〞和“向两方无限延伸〞。

二、直线的性质：经过两点有一条直线，并且只有一条直线，直线的这条性质是以公理的形式给出的，可简述为：过两点有且只有一条直线，两直线相交，只有一个交点。

三、射线：1、射线的定义：直线上一点和它们的一旁的局部叫做射线。

2．射线的特征：“向一方无限延伸，它有一个端点。

〞四、线段：1、线段的定义：直线上两点和它之间的局部叫做线段，这两点叫做线段的端点。

2、线段的性质〔公理〕：所有连接两点的线中，线段最短。

五、线段的中点：1、定义如图1一1中，点B 把线段AC 分成两条相等的线段，点B 叫做线段图1－1AC 的中点。

2、表示法：∵AB ＝BC∴点 B 为 AC 的中点或者∵ AB ＝ 21MAC∴点 B 为AC 的中点，或者∵AC ＝2AB ，∴点B 为AC 的中点反之也成立∵点 B 为AC 的中点，∴AB ＝BC或者∵点B 为AC 的中点， ∴AB= 21AC 或者∵点B 为AC 的中点， ∴AC=2BC六、角1、角的两种定义：一种是有公一共端点的两条射线所组成的图形叫做角。

要弄清定义中的两个重点①角是由两条射线组成的图形；②这两条射线必须有一个公一共端点。

另一种是一条射线绕着端点从一个位置旋转到另一个位置所形成的图形。

可以看出在起始位置的射线与终止位置的射线就形成了一个角。

2．角的平分线定义：一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线。

表示法有三种：如图1—2〔1〕∠AOC ＝∠BOC〔2〕∠AOB ＝2∠AOC ＝ 2∠COB〔3〕∠AOC ＝∠COB=21∠AOB 七、角的度量：度量角的大小，可用“度〞作为度量单位。

把一个圆周分成360等份，每一份叫做一度的角。

1度=60分；1分=60秒。

八、角的分类：〔1〕锐角：小于直角的角叫做锐角〔2〕直角：平角的一半叫做直角〔3〕钝角：大于直角而小于平角的角〔4〕平角：把一条射线，绕着它的端点顺着一个方向旋转，当终止位置和起始位置成一直线时，所成的角叫做平角。

中考冲刺几何综合问题—知识讲解及典型例题解析

；；中考冲刺：几何综合问题—知识讲解及典型例题解析【中考展望】几何综合题是中考试卷中常见的题型，大致可分为几何计算型综合题与几何论证型综合题，它主要考查学生综合运用几何知识的能力.这类题型在近几年全国各地中考试卷中占有相当的分量，不仅有选择题、填空题、几何推理计算题以及代数与几何的综合计算题 ,还有更注重考查学生分析问题和解决问题能力的探究性的问题、方案设计的问题等等.主要特点是图形较复杂，覆盖面广、涉及的知识点较多，题设和结论之间的关系较隐蔽，常常需要添加辅助线来解答.几何综合题的呈现形式多样，如折叠类型、探究型、开放型、运动型、情景型等，背景鲜活，具有实用性和创造性，考查方式偏重于考查考生分析问题、探究问题、综合应用数学知识解决实际问题的能力.以几何为主的综合题常常在一定的图形背景下研究以下几个方面的问题：1、证明线段、角的数量关系（包括相等、和、差、倍、分及比例关系等）2、证明图形的位置关系（如点与线、线与线、线与圆、圆与圆的位置关系等）3、几何计算问题；4、动态几何问题等.【方法点拨】一、几何计算型综合问题，常常涉及到以下各部分的知识：1、与三角形有关的知识；2、等腰三角形，等腰梯形的性质；3、直角三角形的性质与三角函数；4、平行四边形的性质；5、全等三角形，相似三角形的性质；6、垂径定理，切线的性质，与正多边形有关的计算；7、弧长公式与扇形面积公式.二、几何论证型综合题的解答过程，要注意以下几个方面：1、注意图形的直观提示，注意观察、分析图形，把复杂的图形分解成几个基本图形，通过添加辅助线补全或构造基本图形；2、注意分析挖掘题目的隐含条件、发展条件，为解题创造条件打好基础，要由已知联想经验，由未知联想需要，不断转化条件和结论来探求思路，找到解决问题的突破点；3、要运用转化的思想解决几何证明问题，运用方程的思想解决几何计算问题，还要灵活运用数学思想方法如数形结合、分类讨论、转化、方程等思想来解决问题.【典型例题】类型一、动态几何型问题1．如图 1，在正方形 ABCD 中，点 E 、F 分别是边 BC 、AB 上的点，且 CE=BF ，连接 DE ，过点 E 作 EG ⊥DE，使 EG=DE ，连接 FG ，FC ．（1）请判断：FG 与 CE 的数量关系和位置关系；（不要求证明）（2）如图 2，若点 E 、F 分别是 CB 、BA 延长线上的点，其它条件不变，（1）中结论是否仍然成立？请出判断判断予以证明；（3）如图 3，若点 E 、F 分别是 BC 、AB 延长线上的点，其它条件不变，（1）中结论是否仍然成立？请直接写出你的判断．【思路点拨】（1）结论：FG=CE，FG∥CE．如图1中，设DE与CF交于点M，首先证明△CBF≌△DCE，推出DE⊥CF，再证明四边形EGFC是平行四边形即可．（2）结论仍然成立．如图2中，设DE与CF交于点M，首先证明△CBF≌△DCE，推出DE⊥CF，再证明四边形EGFC是平行四边形即可．（3）结论仍然成立．如图3中，设DE与FC的延长线交于点M，证明方法类似．【答案与解析】解：（1）结论：FG=CE，FG∥CE．理由：如图1中，设DE与CF交于点M．∵四边形ABCD是正方形，∴BC=CD，∠ABC=∠DCE=90°，在△CBF和△DCE中，，∴△CBF≌△DCE，∴∠BCF=∠CDE，CF=DE，∵∠BCF+∠DCM=90°，∴∠CDE+∠DCM=90°，∴∠CMD=90°，∴CF⊥DE，∵GE⊥DE，∴EG∥CF，∵EG=DE，CF=DE，∴EG=CF，∴四边形EGFC是平行四边形．∴GF=EC，∴GF=EC，GF∥EC．（2）结论仍然成立．理由：如图2中，设DE与CF交于点M．∵四边形ABCD是正方形，∴BC=CD，∠ABC=∠DCE=90°，在△CBF和△DCE中，，∴△CBF≌△DCE，∴∠BCF=∠CDE，CF=DE，∵∠BCF+∠DCM=90°，∴∠CDE+∠DCM=90°，∴∠CMD=90°，∴CF⊥DE，∵GE⊥DE，∴EG∥CF，∵EG=DE，CF=DE，∴EG=CF，∴四边形EGFC是平行四边形．∴GF=EC，∴GF=EC，GF∥EC．（3）结论仍然成立．理由：如图3中，设DE与FC的延长线交于点M．∵四边形ABCD是正方形，∴BC=CD，∠ABC=∠DCE=90°，∴∠CBF=∠DCE=90°在△CBF和△DCE中，，∴△CBF≌△DCE，∴∠BCF=∠CDE，CF=DE∵∠BCF+∠DCM=90°，∴∠CDE+∠DCM=90°，∴∠CMD=90°，∴CF⊥DE，∵GE⊥DE，∴EG∥CF，∵EG=DE，CF=DE，∴EG=CF，∴四边形EGFC是平行四边形．∴GF=EC，∴GF=EC，GF∥EC．【总结升华】本题考查四边形综合题、正方形的性质、平行四边形的判定和性质、全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形，注意这类题目的解题规律，图形变了，条件不变，证明的方法思路完全一样，属于中考常考题型．举一反三：【变式】已知：如图（1），射线AM//射线BN，AB是它们的公垂线，点D、C分别在AM、BN上运动（点D与点A不重合、点C与点B不重合），E是AB边上的动点（点E与A、B不重合），在运动过程中始终保持DE⊥EC，且AD+DE=AB=a．（1）求证：∆ADE∽∆BEC；（2）如图（2），当点E为AB边的中点时，求证：AD+BC=CD；（3）设AE=m，请探究：∆BEC的周长是否与m值有关？若有关，请用含有m的代数式表示∴1∆BEC的周长；若无关，请说明理由．【答案】（1）证明：∵DE⊥EC，∴∠DEC=90︒．∴∠AED+∠BEC=90︒．又∵∠A=∠B=90︒，∴∠AED+∠EDA=90︒．∴∠BEC=∠EDA．∴∆ADE∽∆BEC．（2）证明：如图，过点E作EF//BC，交CD于点F，∵E是AB的中点，容易证明EF=1(AD+BC)．2在Rt∆DEC中，∵DF=CF，∴EF=12 CD．1(A D+BC)=CD．22∴AD+BC=CD．（3）解：∆AED的周长=AE+AD+DE=a+m，BE=a-m．设AD=x，则DE=a-x．∵∠A=90︒，∴DE2=AE2+AD2．即a2-2ax+x2=m2+x2．a2-m2∴x=．2a由（1）知∆ADE∽∆BEC，∆ADE的周长AD a+m2a=∴a2-m2==∆BEC的周长BE a-m2a．∴∆BEC的周长=2a⋅∆ADE的周长=2a．a+m∴∆BEC的周长与m值无关．2．在△ABC中，∠ACB=45º．点D（与点B、C不重合）为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．（1）如果AB=AC．如图①，且点D在线段BC上运动．试判断线段CF与BD之间的位置关系，并证明你的结论．（2）如果AB≠AC，如图②，且点D在线段BC上运动．（1）中结论是否成立，为什么？（3）若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P，设AC＝42，BC=3，CD=x，求线段CP的长．（用含x的式子表示）【思路点拨】(1)由题干可以发现，正方形中四条边的垂直关系是不动的，于是利用角度的互余关系进行传递，就可以得解.(2)是典型的从特殊到一般的问法，那么思路很简单，就是从一般中构筑一个特殊的条件就行，和上题一样找AC的垂线，就可以变成第一问的条件，然后一样求解.(3)D在BC之间运动和它在BC延长线上运动时的位置是不一样的，所以已给的线段长度就需要分情况去考虑到底是4+X还是4-X.分类讨论之后利用相似三角形的比例关系即可求出CP.【答案与解析】（1）结论：CF⊥BD；证明如下：ΘAB=AC，∠ACB=45º，∴∠ABC=45º．由正方形ADEF得AD=AF，∵∠DAF=∠BAC=90º，∴∠DAB=∠FAC，∴△DAB≌△FAC，∴∠ACF=∠ABD．∴∠BCF=∠ACB+∠ACF=90º．即CF⊥BD．（2）CF⊥BD．(1)中结论仍成立．理由是：过点A作AG⊥AC交BC于点G，∴AC=AG可证：GAD≌CAF∴∠ACF=∠AGD=45º∠BCF=∠ACB+∠ACF=90º．即CF⊥BD（3）过点A作AQ⊥BC交CB的延长线于点Q，易证△AQD∽△DCP，∴ CP = CD ，∴ = ， ∴CP = - + x ． ∴ CP = CD , ∴ = , ∴CP = + x ． ①点 D 在线段 BC 上运动时，∵∠BCA=45º，可求出 AQ= CQ=4．∴DQ=4-x ，CP x DQ AQ4 - x 4 x 2 4②点 D 在线段 BC 延长线上运动时，∵∠BCA=45°，∴AQ=CQ=4，∴DQ=4+x．过 A 作 AQ⊥BC，∴∠Q=∠FQC=90°，∠ADQ=∠AFC，则△AQD∽△ACF．∴CF⊥BD，∴△AQD∽△DCP，CP x DQ AQ4+x 4x 2 4【总结升华】此题综合性强，需要综合运用全等、相似、正方形等知识点，属能力拔高性的题目．3．如图，正方形ABCD 的边长为 6，点 E 是射线 BC 上的一个动点，连接 AE 并延长，交射线 DC 于点 F △，将 ABE 沿直线 AE 翻折，点 B 坐在点 B ′处．自主探究：（1）当=1 时，如图 1，延长 AB ′，交 CD 于点 M ．①CF 的长为； ②判断 AM 与 FM 的数量关系，并证明你的结论．（2）当点 B ′恰好落在对角线 AC 上时，如图 2，此时 CF 的长为，拓展运用：（3）当=2 时，求 sin ∠DAB ′的值．= ．（【思路点拨】1）①利用相似三角形的判定与性质得出FC=AB即可得出答案；②利用翻折变换的性质得出∠BAF=∠MAF，进而得出AM=FM；（2）根据翻折变换的性质得出∠BAE=∠MAF，进而得出AM=MF，利用△ABE∽FCE得出答案即可；（3）根据①如图1，当点E在线段BC上时，延长AB′交DC边于点M，②如图3，当点E在线段BC 的延长线上时，延长AD交B′E于点N，分别利用勾股定理求出即可．【答案与解析】解：（1）①当=1时，∵AB∥FC，∴△ABE∽FCE，∴==1，∴FC=AB=6，②AM=FM，理由如下：∵四边形ABCD是正方形，∴AB∥DC，∴∠BAF=∠AFC，∵△ABE沿直线AE翻折得到△AB′E，∴∠BAF=∠MAF，∴∠MAF=∠AFC，∴AM=FM；（2）如图2，∵当点B′恰好落在对角线AC上时，∴∠1=∠2，∵AB∥FC，∴∠1=∠F，∴∠2=∠F，∴AC=FC，∵AB=BC=6，∴AC=FC=6，∵AB∥FC，∴△ABE∽FCE，∴===，（3）①如图1，当点E在线段BC上时，延长AB′交DC边于点M，∵AB∥CF，∴△ABE∽△FCE，∴==2，∵AB=6，∴CF=3，∴DF=CD+CF=9，由（1）知：AM=FM，∴AM=FM=9﹣DM，在△Rt ADM中，由勾股定理得：DM′2=（9﹣DM）2﹣62，解得：DM=，则MA=，∴sin∠DAB′==，②如图3，当点E在线段BC的延长线上时，延长AD交B′E于点N，由（1）知：AN=EN，又BE=B′E=12，点∴NA=NE=12﹣B′N，在△Rt AB′N中，由勾股定理得：B′N2=（12﹣B′N）2﹣62，解得：B′N=，AN=，∴sin∠DAB′=故答案为：6；6=．，．【总结升华】此题主要考查了翻折变换的性质以及相似三角形的判定与性质和勾股定理等知识，熟练利用相关性质和进行分类讨论得出是解题关键．类型二、几何计算型问题4．已知如图，在梯形ABCD中，AD∥BC，AD=2，BC=4，M是AD的中点，△MBC是等边三角形．（1）求证：梯形ABCD是等腰梯形；（2）动点P、Q分别在线段BC和MC上运动，且∠MPQ=60︒保持不变．设PC=x，MQ=y，求y与x的函数关系式；（3）在（2）中，当y取最小值时，判断△PQC的形状，并说明理由．【思路点拨】（1）属于纯静态问题，只要证两边的三角形全等就可以了.(2)是双动点问题，所以就需要研究在P,Q运动过程中什么东西是不变的.题目给定∠MPQ=60°，其实就是将静态的那个等边三角形与动态条件联系了起来.因为最终求两条线段的关系,所以很自然想到要通过相似三角形找比例关系.(3)条件又回归了当动点静止时的问题，由第二问所得的二次函数，很轻易就可以求出当x取对称轴的值时y有最小值，接下来就变成了“给定PC=2，求△PQC形状”的问题了，由已知的BC=4，自然看出P 是中点，于是问题轻松求解.【答案与解析】（1）证明：∵△MBC是等边三角形∴MB=MC，∠MBC=∠MCB=60︒∵M是AD中点∴AM=MD∵AD∥BC∴∠AMB=∠MBC=60︒，∠DMC=∠MCB=60︒∴△AMB≌△DMC∴AB=DC∴梯形ABCD是等腰梯形．∴ PC ∴ x 而（2）解：在等边 △MBC 中， MB = MC = BC = 4，∠MBC = ∠MCB = 60︒，∠MPQ = 60︒∴∠BMP + ∠BPM = ∠BPM + ∠QPC = 120︒∴∠BMP = ∠QPC∴ △BMP ∽△CQPCQ = BM BP∵ PC = x ，MQ = y ∴ BP = 4 - x ，QC = 4 - y4 - y 1 = ∴ y = x 2 - x + 4 4 4 - x4（3）解： △PQC 为直角三角形，∵ y = 1(x - 2)2 + 34 ∴当 y 取最小值时， x = PC = 2∴ P 是 BC 的中点， MP ⊥ BC ， ∠MPQ = 60︒，∴∠CPQ = 30︒，∴∠PQC = 90︒∴ △PQC 为直角三角形.【总结升华】以上题目是动点问题，这一类问题的关键就在于当动点移动中出现特殊条件，例如某边相等，某角固定时，将动态问题化为静态问题去求解 .如果没有特殊条件，那么就需要研究在动点移动中哪些条件是保持不变的.举一反三：【变式】已知：如图，N 、M 是以 O 为圆心，1 为半径的圆上的两点，B 是 MN 上一动点（B 不与点 M 、N 重合），∠MON=90°，BA⊥OM 于点 A ，BC⊥ON 于点 C ，点 D 、E 、F 、G 分别是线段 OA 、AB 、BC 、CO的中点，GF 与 CE 相交于点 P ，DE 与 AG 相交于点 Q ．（1）四边形 EPGQ（填“是”或者“不是”）平行四边形；（2）若四边形 EPGQ 是矩形，求 OA 的值.【答案】（1）是．证明：连接OB，如图①，∵BA⊥OM，BC⊥ON，∴∠BAO=∠BCO=90°，∵∠AOC=90°，∴四边形OABC是矩形．∴AB∥OC，AB=OC，∵E、G分别是AB、CO的中点，∴AE∥GC，AE=GC，∴四边形AECG为平行四边形．∴CE∥AG，∵点D、E、F、G分别是线段OA、AB、BC、CO的中点，∴GF∥OB，DE∥OB，∴PG∥EQ，∴四边形EPGQ是平行四边形；（2）解：如图②，∴ AD ,AE=1,在①的条件下，设 CP 1= x ，S VP FC = y ，求 y 与 x 之间的函数关系式， 3 ∵口 EPGQ 是矩形．∴∠AED+∠CEB=90°．又∵∠DAE=∠EBC=90°，∴∠AED=∠BCE．∴△AED∽△BCE，AE= ， BEBC x y y : = : x 设 OA=x ，AB=y ，则 2 2 2得 y 2=2x 2，又∵OA 2+AB 2=OB 2，即 x 2+y 2=12．∴x 2+2x 2=1，解得：x=3 ． 3即当四边形 EPGQ 是矩形时，OA 的长度为3 3 ．5．在 Y ABCD 中，过点 C 作 CE⊥CD 交 AD 于点 E,将线段 EC 绕点 E 逆时针旋转 90o 得到线段 EF(如图 1)（1）在图 1 中画图探究：①当 P 为射线 CD 上任意一点（P 1 不与 C 重合）时，连结EP 1 绕点 E 逆时针旋转 90o 得到线段 EC 1.判断直线 FC 1 与直线 CD 的位置关系，并加以证明； ②当 P 2 为线段 DC 的延长线上任意一点时，连结 EP 2,将线段 EP 2 绕点 E 逆时针旋转 90o 得到线段 EC 2.判断直线 C 1C 2 与直线 CD 的位置关系，画出图形并直接写出你的结论.4 （2）若 AD=6,tanB=1 1 并写出自变量 x 的取值范围.图1 备用图【思路点拨】(1)本题在于如何把握这个旋转 90°的条件.旋转 90°自然就是垂直关系，于是出现了一系列直角三角形，于是证角、证线就手到擒来了.(2)是利用平行关系建立函数式，但是不要忘记分类讨论.【答案与解析】（1）①直线 FG 与直线 CD 的位置关系为互相垂直． 112，- - ．，，证明：如图 1，设直线 FG 与直线 CD 的交点为 H ．1 G 1AE F G 2 P H 1 DBCP 2图 1∵线段 EC 、EP 分别绕点 E 逆时针旋转 90°依次得到线段 EF 、EG ， 1 1∴ ∠PEG = ∠CEF = 90° EG = EP ，EF = EC ． 1 1 1 1∵ ∠G EF = 90° ∠PEF ， ∠PEC = 90° ∠PEF ，1 1 1 1∴ ∠G EF = ∠PEC ．1 1∴ △G EF ≌△PEC ．1 1∴ ∠G FE = ∠PCE ．1 1∵ EC ⊥ C D ，∴ ∠PCE = 90°， 1∴ ∠G FE = 90° 1∴ ∠EFH = 90°．∴ ∠FHC = 90°．∴ FG ⊥ CD ． 1②按题目要求所画图形见图 1，直线 G G 与直线 CD 的位置关系为互相垂直．1 2（2）∵四边形 ABCD 是平行四边形，∴ ∠B = ∠ADC ．∵ AD = 6，AE = 1 tan B = 4 3 ， ∴ DE = 5 tan ∠EBC = tan B = 4 3．可得 CE = 4 ．由（1）可得四边形 EFCH 为正方形．∴ CH = CE = 4 ．P 1 2 2 2 2 1 ①如图 2，当 P 点在线段 CH 的延长线上时，1 G 1A EFD H BC 图 2∵ FG = CP = x ，PH = x - 4 ，1 1 1 ∴ S△P FG 1 1 1 x( x - 4) = ⨯ FG ⨯ PH = 1 1 ． ∴ y = 1 2x 2 - 2 x ( x > 4) ． ②如图 3，当 P 点在线段 CH 上（不与 C 、H 两点重合）时， 1G 1 FB A ECD P 1 H图 3∵ FG = CP = x ，PH = x - 4 ，1 1 1 ∴ S △P FG 1 = 1 x(4 - x) FG ⨯ PH = 1 1 ． 1 ∴ y = - x2 + 2 x (0 < x < 4) ． 2③当 P 点与 H 点重合时，即 x = 4 时， △PFG 不存在． 1 1 1综上所述， y 与 x 之间的函数关系式及自变量 x 的取值范围是 y =1 2 x 2 - 2 x ( x > 4) 或 1 y = - x 2 + 2 x (0 < x < 4) ． 2【总结升华】本题着重考查了二次函数的解析式、图形的旋转变换、三角形全等、探究垂直的构成情况等重要知识点，综合性强，能力要求较高．考查学生分类讨论，数形结合的数学思想方法．举一反三：【变式】已知，点 P 是∠MON 的平分线上的一动点，射线 PA 交射线 OM 于点 A ，将射线 PA 绕点 P 逆时针旋转交射线 ON 于点 B ，且使∠APB+∠MON=180°．（1）利用图 1，求证：PA=PB ；（2）如图2，若点C是AB与OP的交点，当△SPOB=3S△PCB时，求PB与PC的比值；（3）若∠MON=60°，OB=2，射线AP交ON于点D，且满足且∠PBD=∠ABO，请借助图3补全图形，并求OP的长．【答案】（1）作PE⊥OM，PF⊥ON，垂足为E、F∵四边形OEPF中，∠OEP=∠OFP=90°，∴∠EPF+∠MON=180°，已知∠APB+∠MON=180°，∴∠EPF=∠APB，即∠EPA+∠APF=∠APF+∠FPB，∴∠EPA=∠FPB，由角平分线的性质，得PE=PF，∴△EPA≌△FPB，即PA=PB；（2）∵S△POB=3S△PCB，∴PO=3PC，由（1）可知△PAB为等腰三角形，则∠PBC=又∵∠BPC=∠OPB（公共角），∴△PBC∽△POB，11（180°-∠APB）=∠MON=∠BOP，22∴PB PC=PO PB，即PB2=PO•PC=3PC2，∴PB=3PC（3）作BH⊥OT，垂足为H，当∠MON=60°时，∠APB=120°，由PA=PB，得∠PBA=∠PAB=12（180°-∠APB）=30°，又∵∠PBD=∠ABO，∠PBD+∠PBA+∠ABO=180°，∴∠ABO=12（180°-30°）=75°，则∠OBP=∠ABO+∠ABP=105°，在△OBP中，∵∠BOP=30°，∴∠BPO=45°，在Rt△OBH中，BH=1OB=1，OH=3，2在Rt△PBH中，PH=BH=1，∴OP=OH+PH=3+1．。

中考数学总结复习冲刺练几何计算专题

一、中考要求证明与计算，是几何命题的两大中心内容。

几何计算题，往常需要借助几何中的观点、定义、定理、公义等知识，求解有关几何元素的数值。

在解题时，要求能正确灵巧地采纳有关知识，采纳各样数学方法（既能够是几何方法，也能够是代数方法），加以求解。

为了能在有限的时间内，快速正确地解题，就需要在平常练习中，加强基础题，多采纳一题多解、优化方案等训练方法，累积经验，达到勤能补拙的成效。

二、知识网络图如图 1 所示：线与角计算题三角形计算题几几四边形计算题何何相似形计算题综计解直角三角形计算题合圆的有关计算题图 1三、基础知识整理几何计算题的要点比较分别，从知识点自己来说，解直角三角形的知识拥有计算题得天独厚的优势，所以波及解直角三角形的试题大多数是计算题。

可是，在实质命题时，更多的是圆的有关计算题和四边形的计算题，它们与其余几何知识都有亲密的联系，能在主要考察一个知识点的同时，考察其余知识点。

就题型而言，各样题型中都能见到几何计算题的身影，比方线与角计算题、三角形计算题、相像形计算题等等，综合性计算题则更多出此刻中档解答题和压轴题中。

需要说明的是，依据中考命题改革的大趋向，几何计算题的难度比从前有所降落，更突出在题目的内容、形式、解法上有所创新，所以，我们不用把要点放到一些繁难的计算题上，而应扎实学好基础知识，多剖析解题使用到的数学思想方法，比方方程与函数、分类议论、转变结构等数学思想方法，重视数学知识的实质应用。

四、考点剖析（所选例题均为2004 年中考试题）1、线与角计算题所用知识主要有线段的中点、角均分线、线段或角的和差倍分、余角、补角的基本观点的定义，以及角的计量、对顶角性质、平行线性质等。

难度不大，可直接利用上述定义、定理解题。

例1（黑龙江）如图1，将一副三角板叠放在一同，使直角的极点重合于O，则∠ AOC+∠DOB=____________.图 1剖析：∠ AOC+∠ DOB=( ∠ AOD+∠ DOB+∠COB)+∠DOB=( ∠ AOD+∠ DOB)+(∠ COB+∠ DOB)=∠AOB + ∠ COD=900+90 0=180 0.2、三角形计算题三角形的内角和定理、三边关系定理及其推论，等腰三角形的性质、全等三角形的性质、特别三角形（比方等边三角形、含有300的直角三角形）的性质、勾股定理、边长、周长及面积的计算等都是三角形计算题的常用知识。

中考数学总复习《几何综合问题(一次函数的实际综合应用)》专项提升训练(带答案)

中考数学总复习《几何综合问题（一次函数的实际综合应用）》专项提升训练（带答案)学校:___________班级：___________姓名：___________考号：___________1．点P 是平面直角坐标系中的一点且不在坐标轴上，过点P 向x 轴，y 轴作垂线段，若垂线段的长度的和为2，则点P 叫做“好垂点”．例如：如图中的()11P ，是“好垂点”．(1)在点()1，2A ，()133522B C ⎛⎫-- ⎪⎝⎭，，，中，是“好垂点”的点为； (2)求函数21y x =-+的图象上的“好垂点”的坐标．(3)若二次函数223y x bx =+-的图象上存在4个“好垂点”，求b 的取值范围．(4)已知T 的圆心T 的坐标为()10-，，半径为r ．若T 上存在“好垂点”，则r 的取值范围是．2．如图，在平面直角坐标系中，直线2y x =+与x 轴、y 轴分别交于A 、B 两点，点()2,C m 为直线2y x =+上一点，直线y x b =-+过点C ．(1)求m 和b 的值；(2)直线y x b =-+与x 轴交于点D ，动点P 从点D 开始以每秒1个单位的速度向x 轴负方向运动（点P 不与点D ，点A 重合）．若点P 在线段DA 上，设点P 的运动时间为t 秒． ①若ACP △的面积为10，求t 的值；②是否存在t 的值，使ACP △是以AP 为腰的等腰三角形？若存在，求出t 的值；若不存在，请说明理由．为顶点的三角形与BCO相似？若存在，求、C分别在>．AB BC为顶点的三角形与OAC相似？两点，点(2C，(1)求m 和b 的值；(2)直线12y x b =-+与x 轴交于点D ，动点P 从点D 开始以每秒1个单位的速度向x 轴负方向运动．设点P 的运动时间为t 秒．①若点P 在线段DA 上，且ACP △的面积为10，求t 的值；②是否存在t 的值，使ACP △为等腰三角形？若存在，直接写出t 的值；若不存在请说明理由． 6．如图，在平面直角坐标系中，正方形ABCD 的顶点A 为()2,0，顶点D 为()0,4．(1)直接写出直线BC 的解析式：____________；(2)点M 与点A 关于y 轴对称，点N 为正方形边上一点，且45DMN ∠=，直接写出点N 的坐标：____________；(3)将正方形沿y 轴向下平移(0)t t >个单位，直至点D 落在x 轴上．设正方形在x 轴下方的部分面积为S ，求S 关于t 的函数关系式，并写出相应自变量t 的取值范围．7．如图，在平面直角坐标系中，直线24y x =-+与x 轴交于点A ，与y 轴交于点B ，过点B 的直线交x 轴于C （点C 在A 左侧），且ABC 面积为10．(1)求点C的坐标及直线BC的解析式；(2)如图1，设点F为线段AB中点，点G为y轴上一动点，连接FG，以FG为边向FG左侧作等腰直角FGQ，其中90∠=︒，在G点的运动过程中，当顶点Q落在直线BC上时，求点G的坐FGQ标；(3)如图2，若M为线段BC上一点，且满足AMB AOB=S S△△，点E为直线AM上一动点，在x轴上是否存在点D，使以点D，E，B，C为顶点的四边形为平行四边形？若存在，请求出点D的坐标；若不存在，请说明理由．8．在同一平面直角坐标系中，我们规定点的两种移动方式：从点(,)x y移动到点(2,1)++称为x y一次甲方式移动；从点(,)x y移动到点(1,3)x y++称为一次乙方式移动．(1)若原点O经过两次甲方式移动，得到点M；原点O经过两次乙方式移动，得到点N．设过点M，N的直线为1l，求直线1l的解析式；(2)若原点O连续移动10次（每次按甲方式或乙方式移动），最终移动到点Q．试说明：无论每次按甲方式还是乙方式移动，最终点Q都落在一条确定的直线上；设这条直线为2l，请求出直线2l的解析式；(3)将（2）中的直线2l向下平移30个单位得到直线3l．分别在上述直线1l2l3l上取点AB C设点A B C的横坐标分别为a b c且a b试探究：当A B C三点共线时a b c之间有何数量关系？说明理由．9．【问题提出】△的面积为3 则ABC的面积（1）如图①点D为ABC的边AC的中点连接BD若ABD为_______；【问题探究】（2）如图②在平面直角坐标系中点A在第一象限连接OA作AB x⊥轴于点B若2AB OB = 25OA = 过点B 的直线l 将OAB 分成面积相等的两部分求直线l 的函数表达式；【问题解决】（3）如图③ 在平面直角坐标系中四边形OABC 是某市将要筹建的高新技术开发区用地示意图其中O 为坐标原点 ()()()24,728,425,0A B C ，，为了方便驻区单位计划过点O 修一条笔直的道路1l （路宽不计）并且使直线1l 将四边形OABC 分成面积相等的两部分记直线1l 与AB 所在直线的交点为D 再过点A 修一条笔直的道路2l （路宽不计）并且使直线2l 将OAD △分成面积相等的两部分你认为直线1l 和2l 是否存在？若存在请求出直线1l 和2l 的函数表达式；若不存在请说明理由．10．如图在矩形ABCD 中 4AD = 6AB = 动点P Q 均以每秒1个单位长度的速度分别从点D 点C 同时出发其中点P 沿折线D A B →→方向运动点Q 沿折线C B A →→方向运动当两者相遇时停止运动．运动时间为t 秒 PQD 的面积为y ．(1)请直接写出y 关于t 的函数表达式并注明自变量t 的取值范围；(2)在给定的直角坐标系中画出这个函数的图象并写出该函数的一条性质； (3)结合函数图象直接写出PQD 的面积大于4时t 的取值范围．11．如图在平面直角坐标系中直线AB 交x 轴 y 轴于(,0)A a 和(0,)B b 两点其中a 和b 是方程212320x x -+=的两个实数根且b a >．使PBC的面积最大？若存在PBC面积的最大值．若没有13．如图点()4,C t在第四象限段OB上．连接于点E交折线段(1)求点A B的坐标；(2)设点E F的纵坐标分别为1y2y当04≤≤时12m-为定值求t的值；y y(3)在（2）的条件下分别过点E F作EG FH垂直于y轴垂足分别为点G H当06≤≤时求长方形EGHF周长的最大值．m14．已知四边形OABC是边长为4的正方形分别以OA OC、所在的直线为x轴y轴建立如图所示的平面直角坐标系直线l经过A C、两点．(1)求直线l的函数表达式；(2)如下图若点D是OC的中点E是直线l上的一个动点求使OE DE+取得最小值时点E的坐标．(3)如下图过点O作AC的垂线垂足为点M点P是直线l上的一个点点Q是y轴上的一个点以,,O P Q为顶点的三角形与OMP全等请直接写出所有符合条件的点P的坐标．15．如图1 在平面直角坐标系xoy中等腰直角AOB的斜边OB在x轴上顶点A的坐标为()2,2与AOB重叠部分为轴对称图形时轴交于点(4,0)A-使得QAB为等腰直角三角形？若存在参考答案：5b<(4)2-或8423．(1)1 (2)4 (3)352+或352或32或3132+或3132-+4．(1)()4,8- (2)16y x=- (3)存在 ()()()()0,2,0,4,0,6,0,12---5．(1)4m = 5b = (2)①7 ②存在 4t =秒或()1242-秒或()1242+秒或8秒6．(1)214=-+y x (2)：10877，⎛⎫ ⎪⎝⎭或401877⎛⎫⎪⎝⎭， (3)当02t <≤时 254S t =；当24t <≤时 55S t =-7．(1)443y x =+ ()3,0C -； (2)1230,7G ⎛⎫ ⎪⎝⎭或()20,1G -； (3)19,03⎛⎫- ⎪⎝⎭或1,03⎛⎫ ⎪⎝⎭或31,03⎛⎫ ⎪⎝⎭． 8．(1)210y x =-+ (2)250y x =-+ (3)43b c a =-9．（1）6；（2）24y x =-+；（3）存在直线1l 的函数表达式为17y x = 直线2l 的函数表达式为152y x =- 10．(1)()()30442847t t y t t ⎧<≤⎪=⎨-+<<⎪⎩ (2)当04x <≤时 y 随x 的增大而增大当47x <≤时 y 随x 的增大而减小 (3)463t <<解题过程：（1）解：依题意 44614AD BC AB ++=++=则相遇时间为14711=+； DP CQ t ==当04t <≤时点P 在AD 上 Q 在BC 上 ∴1632y t t =⨯=当47t <≤时 142PQ t =-∴()11414222y PQ AD t =⨯=⨯⨯-428t =-+4∴4a = 8b =∴224845AB =+=；（2）设OBD ∠的度数为m ︒ 而90BOE ∠=︒ ∴90BEO m ∠=︒-︒∴90FED BEO m ∠=∠=︒-︒∵DE 的垂直平分线交x 轴负半轴于点F∴FE FD =∴90FED FDE m ∠=∠=︒-︒∴()1802902DFE m m ∠=︒-︒-︒=︒；（3）如图过B 作BQ DF ⊥于Q 过D 作DT BO ⊥于T由（2）得90FDE FED m ∠=∠=︒-︒∵BF BD =∴90BFD BDF m ∠=∠=︒-︒∴()1802902FBD m m ∠=︒-︒-︒=︒∵BF BD = BQ DF ⊥∴FBQ DBQ DBT m ∠=∠=∠=︒而DT BO ⊥ DQ BQ ⊥∴FQ DQ DT == 设FQ DQ DT x === OT y =FOD BOD S S = DFE BOE S S =2OE xy = 解得4xy OE =FOD BOD S S =可得：24xy y x ⎛⎫+ ⎪28320y +-=解得：434y =-12．(1)223y x x =--+(2)存在()1,2Q -使得QAC △的周长最小(3)存在31524P ⎛⎫- ⎪⎝⎭，使得PBC 面积最大最大为278 解题过程：（1）解：将1,0A ()3,0B -代入2y x bx c =-++中得10930b c b c -++=⎧⎨--+=⎩ ∴23b c =-⎧⎨=⎩． ∴抛物线解析式为：223y x x =--+；（2）解：∵抛物线解析式为()222314y x x x =--+=-++ ∴抛物线的对称轴为直线=1x -连接BQ由对称性可知BQ AQ =∴AQC 的周长CA AC AQ AC CQ BQ =++=++ ∵A C 为定点∴AC 为定值∴当CQ BQ +最小时 AQC 的周长最小∴当B C Q 三点共线时 CQ BQ +最小即AQC 的周长最小在223y x x =--+中当0x =时 2233y x x =--+=C ∴的坐标为()0,3设直线BC 解析式为y kx b '=+∴303k b b ''-+=⎧⎨=⎩∴13k b =⎧⎨='⎩3yx 3y x 中当时 1y =-+()1,2-∴存在()1,2Q -使得QAC 的周长最小；）解：设()PBPC S S =△∴当S 四边形BPCO S ∴四边形12BE =⋅∴点P 坐标为31524⎛⎫- ⎪⎝⎭，∴存在31524P ⎛⎫- ⎪⎝⎭，使得PBC 面积最大最大为278．13．(1)()0,9A ()6,0B(2)6-(3)26解题过程：（1）解：∵直线392y x =-+交y 轴于点A 交x 轴于点B∴当0y =时得：3902x -+= 解得：6x =当0x =时得：9y =∴()0,9A ()6,0B ；（2）设OC 的解析式为y kx = 过点()4,C t ∴4t k =∴4tk =∴OC 的解析式为()04ty x t =<∵点(),0P m 在线段OB 上过点P 作x 轴的垂线交边AB 于点E 交折线段OCB 于点F 且点EF 的纵坐标分别为1y 2y 04m ≤≤∴1392y m =-+ 24ty m =∴1233992424t t y y m m m ⎛⎫-=-+-=-+ ⎪⎝⎭∵12y y -为定值即3924t m ⎛⎫-+ ⎪⎝⎭为定值∴3024t+=解得：6t =-；（3）①当04m ≤≤时129EF y y =-=（定长）在点P 运动到图中点P ' 此时直线经过点C 即4m =∴044k b b=+⎧⎨=⎩ 解得14k b =-⎧⎨=⎩ 直线l 的函数表达式4y x =-+；（2）解：如图所示连接BE BD ，由正方形的性质可得OA BA BC OC ===又∵AC AC =∴()SSS OAC BAC △≌△∴OAE BAE ∠=∠又∵AE AE =∴()SAS OAE BAE △≌△∴OE BE =∴DE OE DE BE +=+∴当B D E 、、三点共线时 DE BE +最小即此时OE DE +取得最小值设DB 所在直线为()1110y k x b k =+≠∵点D 是OC 的中点 ()04C ，∴()02D ，又∵()44B ，∴111442k b b =+⎧⎨=⎩∴11122k b ⎧=⎪⎨⎪=⎩ ∴直线DB 为122y x =+33⎝⎭∴()224x x +=∴422x =-在4y x =-+中当422x =-时 22y =∴P 点坐标为()42222-，；如图所示当POM OPQ △≌△时同理可得PQ CQ OM CM === 24OC OM == ∴22PQ CQ OM CM ====∴422OQ =+∴P 点坐标为()22422-+，；如图所示当OMP PQO ≌△△时∴PM OQ OM PQ ==，同理可得2222OM CM OC === 设OQ PM x == 则4CQ PQ x ==- 242222CP CQ x CM MP x ==-=+=+ 解得422x =-直线AOB COP S S S ∆∆=-1122AM OB OP PC =⋅-⋅2111424222m m m =⨯⨯-⋅=-．当24m <<时如图②．COB AOP S S S ∆∆=-1122PC OB OP AM =⋅-⋅114222m m m =⨯⨯-⨯=．当4m >时如图③COP AOB S S ∆∆=-1122PC OP OB AM =-2111424222m m m =-⨯⨯=-．与AOB重叠部分为轴对称图形无重叠部分(3)Q 的坐标为(3,7)-或(7,4)-或7(2-7)2 解题过程：（1）在94y x =中令2x =得92y =9(2,)2C ∴；设直线1l 的解析式为y kx b =+ 把(4,0)A - 9(2,)2C 代入得： 40922k b k b -+=⎧⎪⎨+=⎪⎩解得343k b ⎧=⎪⎨⎪=⎩ ∴直线1l 的解析式为334y x =+；（2）如图：设(,0)M m 则3(,3)4D m m + 9(,)4E m m 2DE =39|3|244m m ∴+-= 3322m ∴-=或3322m -=- 解得23m =或103m = M ∴的坐标为2(3 0)或10(3 0)；（3）在334y x =+中令0x =得3y =(0,3)B ∴①当B 为直角顶点时过B 作BH y ⊥轴于H 如图：QAB 为等腰直角三角形 AB QB ∴= 90QBA ∠=︒ 90ABO QBH BQH ∴∠=︒-∠=∠ 90AOB QHB ∠=︒=∠ (AAS)ABO BQH ∴≌ 4OA BH ∴== 3OB QH == 7OH OB BH ∴=+= Q ∴的坐标为(3,7)-； ②当A 为直角顶点时，过Q 作QT x ⊥轴于T ，如图：同理可得(AAS)AQT BAO ≌ 3AT OB ∴== 4QT OA == 7OT OA AT ∴=+= Q ∴的坐标为(7,4)-； ③当Q 为直角顶点时，过Q 作WG y ⊥轴于G 过A 作AW WG ⊥于W ，如图：同理可得(AAS)AQW QBG ≌ AW QG ∴= QW BG = 设(,)Q p q ∴(4)3q p p q =-⎧⎨--=-⎩ 解得7272p q ⎧=-⎪⎪⎨⎪=⎪⎩Q ∴的坐标为7(2-， 7)2；综上所述 Q 的坐标为(3,7)-或(7,4)-或7722⎛⎫- ⎪⎝⎭，。

数学中考几何复习冲刺专题

3 1.73
图），在以航标 C 为圆心，120m 为半径的圆形区域内有浅滩，如果这条船继续前进，是否有被浅滩阻碍的危险？
4:（本题满分 7 分）如图 6，梯形 ABCD 是拦水坝的横断面图，（图中 i 1 : 3 是指坡面的铅直高度 DE 与水平宽度 CE 的比），∠B=60° ，AB=6，AD=4，求拦水坝的横断面 ABCD 的面积．（结果保留三位有效数字.参考 A D 数据： 3 ≈1.732， 2 ≈1.414） B i=1: 3 E 图6 C
5 3 5 3 5 3 2 2 3 cm 2 B cm 2 C cm 2 D cm 2 2 4 4 2
【题型四】证明题型：
（一）三角形全等
【判定方法 1：SAS】例 1 如图，AC 是菱形 ABCD 的对角线，点 E、F 分别在边 AB、AD 上，且
1
AE=AF。求证：△ACE≌△ACF A E B 例2 在正方形 ABCD 中，AC 为对角线，E 为 AC 上一点，连接 EB、ED．（1）求证：△BEC≌△DEC；（2）延长 BE 交 AD 于 F，当∠BED=120°时，求∠EFD 的度数．
。
例 5 如图 4.矩形纸片 ABCD 的边长 AB=4，AD=2．将矩形纸片沿 EF 折叠，使点 A 与点 C 重合，折叠后在其一面着色（图），则着色部分的面积为（ A． 8 B．
A P D
）
11 2
C． 4
D．
5 2G D Fຫໍສະໝຸດ CBEC
A 图6
E
B
图4
图5
【题型三】涉及计算题型：常见的有应用勾股定理求线段长度，求弧长，扇形面积及圆锥体积，侧面积，三角函数计算等。例 6 如图 3，P 为⊙O 外一点，PA 切⊙O 于 A，AB 是⊙O 的直径，PB 交⊙O 于 C， PA＝2cm，PC＝1cm,则图中阴影部分的面积 S 是（ A. ）图3