沪科版习题库之相似三角形的判定1
沪科版九年级上册数学 22.2 相似三角形判定

沪科版九年级上册数学相似三角形相似三角形要点提示1、相似三角形的定义三边对应成_________,三个角对应________的两个三角形叫做相似三角形. 2、相似三角形的判定方法1. 若DE ∥BC (A 型和X 型)则___________.2. 两个角对应相等的两个三角形__________.3. 两边对应成_________且夹角相等的两个三角形相似.4. 三边对应成比例的两个三角形___________.性质:⎪⎪⎩⎪⎪⎨⎧比的平方、对应面积比等于相似比、对应周长比等于相似、对应边成比例、对应角相等4321判定:⎪⎪⎩⎪⎪⎨⎧+两边对应成比例、直角三角形、三边对应成比例夹角相等、两边对应成比例,且、两角对应相等4321(1)相似比:相似三角形对应边的比叫做相似比。
当相似比等于1时,这两个三角形不仅形状相同,而且大小也相同,这样的三角形我们就称为全等三角形.全等三角形是相似三角形的特例.(2)相似三角形的判定:①两角对应相等,两三角形相似.②两边对应成比例,且夹角相等,两三角形相似. ③三边对应成比例,两三角形相似.EA DCBCBA④如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边一条直角边对应成比例,那么这两个三角形相似(3)相似三角形的性质:①相似三角形的对应角相等.②相似三角形的对应线段(边、高、中线、角平分线)成比例.③相似三角形的周长比等于相似比,面积比等于相似比的平方.典例分析1.△ABC 的三条边的长分别为3、4、5,与△ABC 相似的△A′B′C′的最长边为15.求△ A′B′C′最短边的长.2.如图,小正方形的边长均为l ,则下列图中的三角形(阴影部分)与△ABC 相似的是( )3.如图,D 是△ABC 的边AB 上的点,请你添加一个条件,使△ACD 与△ABC 相似.你添加 的条件是_________4.在△ABC 中,AB=12,AC=10,BC=9,AD 是BC 边上的高.将△ABC 按如图所示的方式折叠,使点A 与点D 重合,折痕为EF ,则△DEF 的周长为( )BCAD第3题A .9.5B .10.5C .11D .15.5基础强化1.如图,DE ∥BC ,在下列比例式中,不能成立的是( )A.DB AD =EC AE B.BC DE =EC AE C.AD AB =AE AC D.EC DB =ACAB2.下列判断中,正确的是( )A.各有一个角是67°的两个等腰三角形相似B.邻边之比都为2︰1的两个等腰三角形相似C.各有一个角是45°的两个等腰三角形相似D.邻边之比都为2︰3的两个等腰三角形相似3.如图,在Rt △ABC 中,CD 是斜边AB 上的高,则图中的相似三角形共有( )A.1对B.2对C.3对D.4对4.已知:如图,∠ADE =∠ACD =∠ABC ,图中相似三角形共有( ) A.1对 B.2对 C.3对 D.4对5.如图,□ABCD 中,E 是AD 延长线上一点,BE 交AC 于点F ,交DC 于点G ,则下列结论中错误的是( )A.△ABE ∽△DGEB.△CGB ∽△DGEC.△BCF ∽△EAFD.△ACD ∽△GCF6.如图,△ABC 中,D 、E 分别是AB 、AC 的中点,BC=6,则DE=__________;△ADE 与△ABC 的面积之比为:__________.7.如果两个相似三角形对应边的比是3:4,那么它们的对应高的比是__________ A. 9:16B. 3:2C. 3:4D. 3:78.若两个相似多边形面积比为9:4,则它们的周长比是 9.如图,已知DE ∥BC ,AD = 1,DB = DE =2, 则 BC =ABCD10.如图,已知四边形ABCD 是平行四边形,FC = 5.4cm ,CE = 2.7 cm ,BE = 3.2 cm ,求DC 的长;能力提高1.如图,在△ABC 中,D 为AC 边上一点,∠DBC =∠A ,BC =6,AC =3,则CD 的长为( )A.1B.23 C.2 D.252.如图,在Rt △ABC 中,∠C =90°,CD ⊥AB 于D ,且AD ︰BD =9︰4,则 AC ︰BC 的值为( )A.9︰4B.9︰2C.3︰4D.3︰2ABC DEF3.如图,在△ABC中,∠BAC=90°,D是BC中点,AE⊥AD交CB延长线于点E,则△BAE相似于______.4.如图,在矩形ABCD中,E是BC中点,且DE⊥AC,则CD︰AD=__________.5.一块直角三角形形状的铁皮材料,两直角边长分别为30 cm、40 cm,现要把它加工成一个面积最大的正方形,两种加工方法如图①、②,请你用学过的知识说明哪种加工方法符合要求?真题演练1.如图,在△ABC 中,DE ∥BC ,DE 分别交边AB 、AC 于D 、E 两点,若AD ∶AB =1∶3,则△ADE 与△ABC 的面积比为________.2.如图,在矩形ABCD 中,AB =4,BC =5,AF 平分∠DAE ,EF ⊥AE ,则CF 等于( )A. B.1 C. D.23.如图,△ABC 中,点D 、E 分别为AB 、AC 的中点,连接DE ,线段BE 、CD 相交于点2332O.若OD=2,则OC=________.4.如图,D是△ABC的边AB上一点,连接CD,若AD=2,BD=4,∠ACD=∠B,求AC 的长.。
练6_相似三角形的判定(沪科版)(解析版)

练习6 相似三角形的判定一.选择题1.下列条件中,不能判断ABC ∆与DEF ∆相似的是( )A .A D ∠=∠,B F ∠=∠B .BC AC EF DF =且BD ∠=∠ C .AB BC AC DE EF DF == D .AB AC DE DF =且A D ∠=∠ 【解答】解:A 、A D ∠=∠,B F ∠=∠,可以得出ABC DFE ∆∆∽,故此选项不合题意; B 、BC AC EF DF =且B D ∠=∠,不是两边成比例且夹角相等,故此选项符合题意; C 、AB BC AC DE EF DF==,可以得出ABC DEF ∆∆∽,故此选项不合题意; D 、AB AC DE DF =且A D ∠=∠,可以得出ABC DEF ∆∆∽,故此选项不合题意; 故选:B .2.如图,在正方形ABCD 中,点E 为边AD 上的一个动点(与点A 、D 不重合),45EBM ∠=︒,BE 交对角线AC 于点F ,BM 交对角线AC 于点G ,交边CD 于点M ,那么下列结论中,错误的是( )A .AEF CBF ∆∆∽B .CMG BFG ∆∆∽C .ABG CFB ∆∆∽D .ABF CBG ∆∆∽【解答】解:四边形ABCD 是正方形,//AB CD ∴,//AD BC ,45DCA ACB DAC CAB EBM ∠=∠=∠=∠=∠=︒, AEF CBF ∴∆∆∽,故选项A 不合题意;EBM DCA ∠=∠,MGC BGF ∠=∠,CMG BFG ∴∆∆∽,故选项B 不合题意;CMG CFB ∴∠=∠,//CD AB ,CMG ABG ∴∠=∠,CFB ABG ∴∠=∠,又45CAB BCF ∠=∠=︒,BCF GAB ∴∆∆∽,故选项C 不合题意;45CAB ACB FBG ∠=∠=∠=︒,45ABF CBG ∴∠+∠=︒,ABF CBG ∴∠≠∠,ABF ∴∆与CBG ∆不相似,故选项D 符合题意;故选:D .3.如图所示,给出下列哪个条件单独能够判定ABC ACD ∆∆∽的是( )A .B BCD ∠=∠ B .AC AB CD BC = C .2AC AD AB = D .AD CD AC BC= 【解答】解:A 、B BCD ∠=∠,不能判定的两个三角形相似,不符合题意; B 、A ∠不是已知的比例线段的夹角,不正确,不符合题意,C 、可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定,符合题意;D 、A ∠不是已知的比例线段的夹角,不正确,不符合题意;故选:C .二.填空题4.如图所示,在AOB ∆中,90AOB ∠=︒,12OA cm =,65AB cm =,点P 从O 开始沿OA 边向点A 以2/cm s 的速度移动;点Q 从B 开始沿BO 边向点O 以1/cm s 的速度移动,如果P ,Q 同时出发,用()x s 表示时间(06)x ,那么当x = s 时,以P ,O ,Q 为顶点的三角形与AOB ∆相似?【解答】解:POQ BOA ∠=∠,∴当OPQ OAB ∆∆∽时,OP OQ OA OB =,即26126x x -=, 解得3x =秒;当OPQ OBA ∆∆∽,OP OQ OB OA=,即26612x x -=, 解得65x =秒. 综上所述,当3x =秒或65秒时,以P 、O 、Q 为顶点的三角形与AOB ∆相似. 故答案为:65或3. 5.如图,等边ABC ∆的边长为6,点D 在AC 上且2DC =,点E 在BC 上,连接AE 交BD 于点F ,且60AFD ∠=︒,若点M 是射线BC 上一点,当以B 、D 、M 为顶点的三角形与ABF ∆相似时,则BM 的长为 .【解答】解:ABC ∆是等边三角形,6AB BC ∴==,60ABC AFD ∠=︒=∠,ABD DBC ABD BAE ∴∠+∠=∠+∠,BAE DBC ∴∠=∠,如图,当点M 在BC 上时,作BDM ABD ∠=∠,ABF BDM ∴∆∆∽,BDM ABD ∠=∠,60DMC DBC BDM ABD DBC ABC ∴∠=∠+∠=∠+∠=∠=︒,60DMC DCM ∴∠=∠=︒,DMC ∴∆是等边三角形,2DC DM CM ∴===,4BM ∴=,当点M '在BC 的延长线上时,作CDM BAE '∠=∠,60ACB CDM M ''∠=∠+∠=︒,60AFD ABD BAE ∠=∠+∠=︒,M ABD '∴∠=∠,ABF ∴∆∽△BM D ',CDM CBD '∠=∠,BDM M '∠=∠,BDM ∴∆∽△DM C ', ∴BM DM CD CM =', ∴422CM=', 1CM '∴=,7BM '∴=,综上所述:4BM =或7,故答案为:4或7.6.如图,ABC ∆中,AB AC >,D 、E 分别是边AC 、AB 上的点,且DE 与BC 不平行.不再添加其它字母和线段,请你填上一个合适的条件,使ADE ABC ∆∆∽,你填的条件是 .【解答】解:DAE CAB ∠=∠,∴当ADE B ∠=∠或AED C ∠=∠或AD AE AC AB=,时,ADE ACB ∆∆∽. 故答案是:ADE B ∠=∠或AED C ∠=∠或AD AE AC AB =. 三.解答题7.如图,在ABC ∆中,90B ∠=︒,点P 从点A 开始沿边AB 向点B 以1/cm s 的速度移动,与此同时,点Q从点B 开始沿边BC 向点C 以2cm 每秒的速度移动.如果P 、Q 分别从A 、B 同时出发,经过几秒,PBQ ∆与ABC ∆相似?(6,8)AB cm BC cm ==【解答】解:设经过y 秒后,以P 、Q 、B 三点为顶点的三角形与ABC ∆相似: 则AP y =cm ,2BQ y =cm ,(6)BP AB AP y cm ∴=-=-,①若PBQ ABC ∆∆∽,则有AB BC PB BQ =,即6862y y=-, 解得:125y =; ②若QBP ABC ∆∆∽,则有AB BC BQ BP =,即6826y y =-, 解得:1811y =. 答:经过125或1811秒后,以P 、Q 、B 三点为顶点的三角形与ABC ∆相似. 8.如图,在Rt ABC ∆中,90BAC ∠=︒,AD BC ⊥于点D .(1)求证:BAD CAD ∆∆∽;(2)若点O 是AC 边上一点,连接BO 交AD 于E ,OF OB ⊥交BC 边于点F ,求证:ABE COF ∆∆∽.【解答】(1)证明:AD BC ⊥,90ADB ∴∠=︒,90BAC ∠=︒,BAC ADB ∴∠=∠,ABD CBA ∠=∠,BAD CAD ∴∆∆∽;(2)证明:AD BC ⊥,90DAC C ∴∠+∠=︒,90BAC ∠=︒,90DAC BAE ∴∠+∠=︒,BAE C ∴∠=∠,OF OB ⊥,90BOA COF ∴∠+∠=︒,90BOA ABE ∠+∠=︒,ABE COF ∴∠=∠,ABE COF ∴∆∆∽.9.如图,在矩形ABCD 中,E 是AD 边上的一点,BE AC ⊥,垂足为点F .求证:AEF CAB ∆∆∽.【解答】证明:四边形ABCD 是矩形,//AD BC ∴,90ABC ∠=︒,AD BC =,BE AC ⊥于点F ,EAC ACB ∴∠=∠,90ABC AFE ∠=∠=︒,AEF CAB ∴∆∆∽.1.如图,在ABC ∆中,//DE BC ,:1:2AD DB =,2DE =,则下列叙述正确的是( )①4BC=;②12AEEC=;③14ADEABCSS∆∆=;④ADE ABC∆∆∽.A.①②③④B.①②③C.①②④D.②④【解答】解://DE BC,ADE ABC∴∆∆∽,∴13AD DE AEAB BC AC===,21()9ADEABCS DES BC∆∆==,∴12AEEC=,2DE=,6BC∴=,∴②④正确,故选:D.2.如图,ABC∆中,90C∠=︒,30B∠=︒,2AC=,点P是边AB上一点,将ABC∆沿经过点P的直线折叠,使得点A落在边BC上的A'处,若PBA∆'恰好和ABC∆相似,则此时AP的长为.【解答】解:①如图1中,当90PA B C∠'=∠=︒时,设PA PA x='=.在Rt ABC∆中,90C∠=︒,2AC=,30B∠=︒,24AB AC ∴==,323BC AC ==, B B ∠=∠,90BA P C ∠'=∠=︒, BPA BAC ∴∆'∆∽,∴PB PA BA AC '=, ∴442x x -=, 43x ∴=.②如图2中,当90PBC ∠=︒时,BPA BCA ∆'∆∽,∴BP PA BC AC'=, ∴223x =, 232x ∴=-,综上所述,满足条件的AP 的值为43或232-. 3.如图,AB BD ⊥,CD BD ⊥,9AB =,1CD =,6BD =,点E 在BD 上移动,当以E ,C ,D 为顶点的三角形与ABE ∆相似时,求DE 的长.【解答】解:设DE x =,则6BE BD x x =-=-, AB BD ⊥于B ,CD BD ⊥于D , 90B D ∴∠=∠=︒,∴当AB BE CD DE =时,ABP CDP ∆∆∽,即961x x-=, 解得35x =, 当AB BE DE DC =时,ABP PDC ∆∆∽,即961x x -=, 整理得2690x x -+=,解得13x =,23x =-(不合题意,舍去),∴当DE 为35或3时,以C 、D 、P 为顶点的三角形与以P 、B 、A 为顶点的三角形相似. 4.如图,在ABC ∆中,90ACB ∠=︒,AD 平分CAB ∠交BC 于点E ,过点D 作BD AD ⊥,垂足为点D .(1)若2AE BD =,求证:CA CB =;(2)在(1)的条件下,过点C 作CF AE ⊥,垂足为点F ,写出图中所有与BDE ∆相似的三角形.【解答】(1)证明:延长BD 交AC 的延长线于F .AD BD ⊥,90DB ADF ∴∠=∠=︒,AD AD =,DAB DAF ∠=∠, ADB ADF ∴∆≅∆,DB DF ∴=,2AE BD =,AE BF ∴=,90ACE BCF BDE ∠=∠=∠=︒, 又AEC BED ∠=∠, CAE CBF ∴∠=∠, ACE BCF ∴∆≅∆, AC BC ∴=.(2)如图2中,CF AD ⊥,BD AD ⊥, //CF BD ∴,BDE CFE ∴∆∆∽,90ACE ∠=︒,CF AE ⊥, ECF EAC CAF ∴∆∆∆∽∽, ∴与BDE ∆相似的三角形有ECF ∆,ACE ∆,ACF ∆.。
2相似三角形的判定定理1PPT课件(沪科版)

∴△ADE≌△A'B'C' D
E
∴△A'B'C'∽△ABC B
C B'
C'
练习
1、如果两个三角形全等,则它们必类似。 √
2、若两个三角形类似,且类似比为1,则它们
必全等。
√
3似、,如则果这两两个个三三角角形形与必第类三似个。等腰直角三角√形类
4、类似的两个三角形一定大小不等。
×
例1 已知:等腰△ABC 有AB=AC 和 △A'B'C' 有 A'B'=A'C', 并且∠A =∠A ',
求证:△ABC ∽△A'B'C'
证明:∵ △ABC中AB=AC,∠B =∠C A
∴ 2∠B =180°-∠A
B 90 1 A 2
B
C
同理 △A'B'C'中A'B'=A'C',∠B' =∠C'
∴ 2∠B' =180°-∠A'
A'
B ' 90 1 A' 2
又 ∠A=∠A' ∵ ∠B=∠B',
B'
C'
∵ △ABC∽△A'B'C'
例2. 如图,Rt△ABC中,CD是斜边上的高,
△ACD和△CBD都和△ABC类似吗?证明你的结
论.
C
证明:
12
∵∠ACB=∠ADC=90°
又∠ A = ∠ A=90°
A
D
B
∴ △ACD∽△ABC
∵∠CDB=∠ACB=90°
沪科版九年级上册相似三角形的判定定理1课件(共16张)

B
A
A'
B'
C'
C
新知讲授
例1、已知:ΔABC和ΔDEF中, ∠A=400,∠B=800, ∠E=800, ∠F=600,
求证:ΔABC∽ΔDEF 。
A
D
400
证明:∵ 在ΔABC中,∠A=400,∠B=800,
∴ ∠C=1800-∠A -∠B =1800-400 -800 =600, B
800
∴ ∠B=∠E=80°,∠C=∠F=60°,
思 考 ?如果两个三角形仅有一对角是对应相等的,那么它们是否一 定类似?
新知讲授
它们是类似三角形吗?为什么?
A
A′
5
82° 3
82°
B 47°
66
C
10
6
51°
B′
12C′新ຫໍສະໝຸດ 讲授类似三角形的判定定理1
用数学符号表示:
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
(两角对应相等,两三角形类似)
从直观上看,这两个三角形类似吗?
新知讲授
动手操作: 画一个三角形,使三个角分别为60°,45°, 75° 。 ①用刻度尺量出这个三角形三边的长度; ②看看与同桌的三角形的对应边是否成比例.
即:如果一个三角形的三个角分别与另一个三角形的三个角对应相
等,那么这两个三角形_类__似____.
一定需三个角吗?
随堂练习
3.如图,在△ABC 中, D是AB上的点,且 ∠ACD=∠B, 试说明: (1)△ABC与△ADE类似; (2)AD=4,AC=6,求AB的长.
解:∵ ∠A= ∠A,∠ABD=∠C , ∴ △ABD ∽△ACB , ∴ AB∶AC=AD∶AB,∴ AB2 = AD·AC. ∵ AD=2,AC=8,∴ AB =4.
沪科版22.2.2相似三角形的判定(角角)

A
A'
B
C B'
C'
小试牛刀 1、下列图形中两个三角形是否相似?说明原因 (1)
A A' B
C
(2)
A
B
C B'
C'
D
A
(3)
A
E
A'
(4)
D E
B
C B'
C'
B
C
2、判断题:
基础演练
( ) × ( ) √
⑴ 所有的直角三角形都相似 . ⑵ 所有的等边三角形都相似. ⑶ 所有的等腰直角三角形都相似. ⑷ 有一个角相等的两等腰三角形相似 .
2013-10-23
∴ AB =4
A
A
D B C B
0
D
C
3、如图:在Rt △ ABC中, ∠ABC=90 ,BD⊥AC于D
问:图中有几个直角三角形?它们相似吗?为什么? 解: 图中有三个直角三角形,分别是:
△ ABC、 △ ADB、 △ BDC
△ ABC ∽ △ ADB ∽ △ BDC
2013-10-23
√ ( )
(
×)
顶角相 等
2013-10-23
底角相 等
顶角与底角 相等
1、已知如图直线BE、DC交于A , ∠E= ∠C 求证:DA· AC=AB· AE
E
A
D A E B B C
将△DAE绕A点旋转
D
C
证明:∵ ∠E=∠C ∠DAE=∠BAC
∴ △ABC ∽ △ADE
∴ AC :AE=AB :AD
(2)条件
∠A=36° AB=AC BD平分∠ABC
沪科版数学九年级上册 22.2 相似三角形的判定 同步练习(带解析)

相似三角形的判定一、选择题1.如图,在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是( )A.5 B.8.2C.6.4 D.1.82.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )3.如图,在平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和点F,过点E作EG∥BC,交AB于G,则图中相似的三角形有( )A.4对B.5对C.6对D.7对4.有下列判断:①顶角相等的两个等腰三角形相似;②有一个角相等的两个等腰三角形相似;③直角三角形都相似;④若一个三角形的两边长分别为2、6,夹角为32°,另一个三角形的两边长分别为3、9,夹角为32°,则这两个三角形相似.其中判断正确的有( )A.1个B.2个C.3个D.4个5.有下列说法:①有一个角为50°的两个等腰三角形相似;②有一个角为100°的两个等腰三角形相似;③有一个锐角相等的两个直角三角形相似;④两个等边三角形相似。
其中正确的有( )A.1个B.2个C.3个D.4个二、填空题6.如图,有下列条件:①∠B=∠C;②∠ADB=∠AEC;③AD AEAC AB=;④AD AEAB AC=;⑤PE BPPD CP=.其中不需要添加其他条件就能使△BPE∽△CPD的条件有____个,它们分别是____(填序号) .7.在△ABC和△DEF中,如果AB=4,BC=3,AC=6;DE=2.4,EF=1.2,FD=1.6,那么这两个三角形能否相似的结论是____________,理由是__________________.8.如图所示,△ABC的高AD,BE交于点F,则图中的相似三角形共有______对.9.如图所示,□ABCD中,G是BC延长线上的一点,AG与BD交于点E,与DC交于点F,此图中的相似三角形共有______对.三、解答题10.已知两直角三角形ABC 与ACD ,∠ACB=∠ADC=90°,6AC =,AD=2.问当AB 的长为多少时,这两个直角三角形相似.11.根据下列各组条件,判断ABC ∆和A B C '''∆是否相似,并说明理由.(1)AB=3.5,BC=2.5,CA=4,24.5A B ''=,17.5B C ''=,28C A ''=;(2)∠A=35°,∠B=104°,∠C=44°,35A '∠=︒;(3)AB=3,BC=2.6,∠B=48°, 1.5A B ''=, 1.3B C ''=,48B '∠=︒.12.已知线段0A 丄0B ,点C 为OB 的中点,点D 为AO 上一点,连接AC ,BD 交于点P.(1)如图①,当OA=OB 且点D 为AO 的中点时,求AP PC的值; (2)如图②,当OA=OB 且14AD AO =时,求AP AC 的值.13.如图,在ABC ∆和DEF ∆中,∠A=∠D=70°,∠B=50°,∠E=30°,分别过两个三角形的一个顶点画直线1,m ,使直线l 将ABC ∆分成两个小三角形,直线m 将DEF ∆分成两个小三角形,并使ABC ∆分成的两个小三角形分别与DEF ∆分成的两个小三角形相似,并标出每个小三角形各个内角的度数.(画图工具不限,不要求写作法,只需画出一种分法即可)参考答案1.D.2.A.3.B 解析:图中相似的三角形有△ABC∽△CDA,△AGE∽△ABC,△AFE∽△CBE,△BGE∽△BAF,△AGE∽△CDA,共5对.4.B解析:①④正确.5.C解析:②③④正确.6.4 ①②④⑤7.△ABC ∽△DFE .因为这两个三角形中,三组对应边的比相等.8.6对.9.6对.10.分析:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.在Rt △ABC 和Rt △ACD 中,直角边的对应需分情况讨论.解: ∵ AD=2,∴CD =.要使 Rt △ABC 与 Rt △ACD 相似,有两种情况:(1)当 Rt △ABC ∽Rt △ACD 时,有AC AB AD AC=, ∴23AC AB AD==, (2)当 Rt △ACB ∽Rt △CDA 时,有AC AB CD AC=,∴AB=2AC CD=故当AB 的长为3或时,这两个直角三角形相似.点拨:本题考査相似三角形的判定.判定两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.11. 分析:(1)题中的条件全部是边长,因此验证三边是否成比例;(2)题中的条件全部是角,因此验证是否有两对对应角相等;(3)题中的条件既有边也有角,验证两边是否成比例且夹角相等.解:(1)因为3.51 2.5141,,''24.57''17.57''287AB BC CA A B B C C A ======, 所以''''''AB BC CA A B B C C A ==,所以△ABC ∽△A 'B 'C '. 理由:三组对应边成比例的两个三角形相似.(2) 在△ABC 中,因为∠A=35°, ∠B=104°,所以 ∠C=180°-∠A-∠B=180°-35°-104°=41°在△A 'B 'C '中,因为∠C '=44°, ∠A '=35°,所以∠B '= 180°-∠A '-∠C ' = 180°-35°-44°=101°.因为对应角不相等,所以△ABC 与△A 'B 'C '不相似.(3) 在 △ABC 与 △A 'B 'C '中∠B=∠B '= 48°,且''AB A B = 2,''BC B C = 2,所以''''AB BC A B B C =,所以 △ABC ∽△A 'B 'C '. 理由:对应边成比例且夹角相等的两个三角形相似.12. 解:(1)过点C 作CE//OA 交BD 于点E,则 △ABC ∽△BOD,. 得 CE= 12OD= 12AD. 再由△ECP ∽△DAP ,得23AP AD PC EC ==. (2)过点C 作CE//OA 交BD 于点E ,设AD=x ,则 AO=OB=4x ,OD=3x.由 △BCE ∽△BOD ,得 CE=12OD=32x , 再由△ECP ∽△DAP ,得23AP AD PC EC ==,则25AP AC =. 13.解:如图(答案不唯一).则直线l ,m 即为所求作的直线.点拨:解答本题是从构造相等的角这一角度考虑的,当然也可以从构造比例线段出发,不过从这一角度考虑相对比较困难.。
沪科版九年级数学上22.2相似三角形判定课时练习含解析

九年级上学期数学课时练习题22.2 相像三角形的判断一、精心选一选1﹒以下说法中,不正确的选项是()A . 直角边长分别是6、4 和、3 的两个直角三角形相像B . 底角为 40°的两个等腰三角形相像C. 一个锐角为30°的两个直角三角形相像D . 有个角为30°的两个等腰三角形相像2﹒如图,点P 是平行四边形ABCD边AB 上的一点,射线CP交DA的延伸线于点E,则图中相像的三角形有()A . 0 对B . 1 对 C. 2 对 D. 3对第 2 题图第 3 题图第 5 题图第 6 题图3﹒如图,在△ ABC △ ABC∽△ ADE 中,点的是(D、 E 分别在边)AB、 AC上,且DE不可以于BC,则以下条件中不可以判断A .∠AED =∠B B .∠ ADE=∠C C.AD=AED.AD=AC AB AC AE AB4﹒如图,在以下两个三角形是(4×4 的正方形(每个小正方形的边长都为)1)网格中均有一个三角形,能相像的A .①和②①②B. ②和③③C. ①和③④D. ②和④5﹒如图,在△ABC中, DE ∥ BC,AD=1,DE = 4,则BC的长为()DB2A . 12 B. 11 C. 10 D. 86﹒如图,在平行四边形ABCD中,点 E 是边AD上一点,且AE= 2ED , EC交对角线BD于点F,则EF等于()FC1123A . B. C. D.3232 7﹒如图,在平行四边形ABCD中, EF ∥ AB 交AD于点E,交BD于点F , DE: EA=3: 4, EF = 3,则CD的长为()A . 4 B. 7 C. 3 D. 12第 7 题图第 8 题图第 9 题图第 10 题图8﹒如图,在等腰梯形ABCD中, AD∥ BC,过点 C 作CE∥ AB, P 是梯形ABCD内一点,连结BP 并延伸交CD于点F,交CE 于点E,再连结PC.已知BP= PC,则以下结论错误的选项是()A .∠1=∠ 2 B. ∠ 2=∠ E C. △PFC∽△ PCE D.△EFC ∽△ ECB9﹒如图,在△ ABC DEFG 是正方形中, AB =AC,点. 若 DE= 2cm,则D、 E 分别是AC 的长为(AB、 AC)的中点,点G、 F 在BC边上,四边形A . 3 3 cmB . 4cm C. 2 3 cm D. 2 5 cm10.如图,四边形 ABCD 中, AC 均分∠ DAB,∠ ADC =∠ ACB= 90°,点 E 为 AB 的中点,给出以下结论:① CE∥ AD ;② AC 2= AB AD ;③△ CDF ∽△ BCE;④ AC: AF= DE :DF ,此中正确的有()A . ①② B. ①②③ C. ①②④ D. ①②③④二、仔细填一填11. 如图,有以下条件:①∠B=∠ C;②∠ ADB =∠ AEC;③ADAE ;④ AD AE ;AC AB AB AC⑤ PE BP,此中一个条件就能使△BPE∽△ CPD 的条件有 ___________ 个,它们分别是PD PC__________________. (只填写序号)第 11 题图第12题图第13题图12.如图,在边长为 1 的正方形网格中有点 P、 A、 B、 C,则图中所形成的三角形中,相像的三角形是 ______________________.13.如图,已知△ ABC 中, AB= 5, AC= 3,点 D 在边 AB 上,且∠ ACD=∠ B,则线段 AD 的长为__________ .14.如图,点 D 为△ ABC 外一点, AD 与 BC 边的交点为 E,AE =3, DE= 5,BE= 4,要使△BDE ∽△ ACE ,且点 B, D 的对应点为A, C,那么线段CE 的长应等于 ________.第 14 题图第15题图第16题图15.如图,正方形 ABCD 中, E 为 AB 的中点, AF ⊥ DE 于点 O,则AO等于 __________.DO16.如图,在矩形 ABCD 中, AB=6, BC= 8,沿直线 MN 对折,使 A, C 重合,直线 MN 交 AC 于点 O,则线段 OM = ________.三、解答题17. 已知:如图,△ ABC 中,∠合),∠ ADE= 45°. 求证:△BAC= 90°, AB= AC,点ABD∽△ DCE.D是 BC边上的一个动点(不与B,C重18. 在平行四边形ABCD 中, E 为 BC 边上的一点,连结AE.(1)若 AB= AE,求证:∠ DAE =∠ D;(2)若点 E 为 BC 的中点,连结 BD ,交 AE 于 F ,求 EF :FA 的值 .19.如图,在△ ABC 中, D 、E 分别是边 AB、 AC 的中点, F 为 CA 延伸线上一点,∠F =∠ C.(1)若 BC=8,求 FD 的长;(2)若 AB= AC,求证:△ ADE ∽△ DFE .20.如图,在△ ABC 中, AB =AC,点 P、 D 分别是 BC、 AC 边上的点,且∠ APD =∠ B.(1)求证: AC CD =CP BP;(2)若 AB= 10, BC= 12,当 PD∥ AB 时,求 BP 的长 .21.已知:如图, E 是矩形 ABCD 的边 BC 上一点, EF ⊥ AE, EF 分别交 AC、 CD 于点M、F , BG⊥ AC,垂足为 G, BG 交 AE 于点 H.(1)求证:△ ABE∽△ ECF ;(2)找出与△ ABH 相像的三角形,并加以证明;(3)若 E 是 BC 的中点, BC= 2AB, AB= 2,求 EM 的长 .22. 如图,正方形ABCD 中, M 为 BC 上一点, F 是 AM 的中点, EF⊥ AM ,垂足为 F,交 AD 的延伸线于点 E,交 DC 于点 N.(1)求证:△ ABM∽△ EFA ;(2)若 AB= 12, BM = 5,求 DE 的长 .23.如图,在△ ABC 中, AB =8cm, BC= 16cm,点 P 从点 A 开始沿 AB 向点 B 以 2cm/s 的速度运动,点Q 从点 B 开始沿 BC 向点 C 以 4cm/s 的速度运动 . 假如 P、 Q 分别从 A、 B 同时出发, 4 秒后停止运动,则在开始运动后第几秒,△BPQ 与△ BAC 相像?《相像三角形的判断》课时练习题参照答案一、精心选一选题号12345678910答案D D C B A A B D D C1﹒以下说法中,不正确的选项是(A . 直角边长分别是6、4 和)、3 的两个直角三角形相像B . C.底角为 40°的两个等腰三角形相像一个锐角为30°的两个直角三角形相像D . 有个角为30°的两个等腰三角形相像解答: A. 直角边长分别是6、 4 和、 3 的两个直角三角形相像,由于两边对应成比率,且夹角相等,因此这两个直角三角形相像,故 A 正确;B. 底角为40°的两个等腰三角形相像,由于有两角对应相等,因此这两个等腰三角形相像,故 B 正确;C. 一个锐角为30°的两个直角三角形相像,由于有两角对应相等,因此这两个等腰三角形相像,故C正确;D.有个角为 30°的两个等腰三角形相像,由于可能一个角为极点,另一个为底角,因此这两个等腰三角形不相像,故 D 错误,应选: D.2﹒如图,点P 是平行四边形ABCD边AB 上的一点,射线CP交DA的延伸线于点E,则图中相像的三角形有()A . 0 对B . 1 对 C. 2 对 D. 3对解答:∵四边形ABCD是平行四边形,∴AB∥DC, AD∥ BC,∴△ EAP ∽△ EDC,△ EAP∽△ CPB,∴△ EDC ∽△ CBP,故有 3 对相像三角形.应选: D.3﹒如图,在△ ABC 中,点 D、 E 分别在边AB、 AC 上,且 DE 不可以于 BC,则以下条件中不可以判断△ ABC∽△ ADE的是()A .∠AED =∠B B .∠ADE =∠C C.AD=AED.AD=AC AB AC AE AB解答:∵∠ DAE=∠ CAB,∴当∠ AED =∠ B 或∠ ADE =∠ C 时,△ ABC ∽△ ADE ,当AD=AC时,△ ABC∽△ ADE,AE AB应选: C.4﹒如图,在以下两个三角形是(4×4 的正方形(每个小正方形的边长都为)1)网格中均有一个三角形,能相像的①② ③④A . ①与②B . ①与③C. ②与③D . ②与④解答: 由勾股定理可求出图①中三角形的各边长分别为 2, 2 ,10 ,图③中三角形的各边长分别为2 2 , 2, 25 ,∵2 = 2 = 210 , 2225∴图①中三角形与图③中三角形相像,应选: B.5﹒如图,在△ ABC 中, DE ∥ BC ,AD= 1,DE = 4,则 BC 的长为()DB 2A . 12B . 11C. 10D . 8解答: ∵AD= 1, AD+DB = AB ,DB 2∴AD=1,AB 3∵ DE ∥BC ,∴△ ADE ∽△ ABC ,∴DE=AD ,即 4 = 1,BCABBC 3解得: BC = 12.应选: A.6﹒在平行四边形ABCD 中,点 E 是边 AD 上一点,且AE = 2ED ,EC 交对角线 BD 于点 F ,则EF等于()FC1 1 C.2 3 A . B .3D .322解答: ∵四边形 ABCD 是平行四边形,∴ ED ∥BC , BC = AD , ∴△ DEF ∽△ BCF ,∴EF DE , CF CB 设 ED = k ,则 AE = 2k , BC = 3k ,∴EFk1 ,CF3k3应选: A.7﹒如图,在平行四边形ABCD 中, EF ∥ AB 交 ADF , DE : EA =3: 4, EF = 3,则 CD 的长为(于点)E ,交BD于点A . 4 B. 7 C. 3 D . 12解答:∵ DE: EA= 3: 4,∴DE :DA =3:7,∵ EF ∥AB,∴DE EF ,DA AB∵EF =3,∴3 3,7 AB解得: AB= 7,∵四边形ABCD 是平行四边形,∴ CD= AB= 7,应选: B.8﹒如图,在等腰梯形ABCD 中, AD∥ BC,过点 C 作 CE∥ AB, P 是梯形 ABCD 内一点,连结BP 并延伸交CD 于点 F,交 CE 于点 E,再连结 PC. 已知 BP= PC,则以下结论错误的选项是()A . ∠1=∠ 2 B. ∠ 2=∠ E C. △ PFC ∽△ PCE D . △EFC ∽△ ECB解答:∵四边形ABCD 是等腰梯形,∴∠ ABC =∠ DCB ,∵ PB=PC,∴∠ PBC =∠ PCB,∴∠ ABC -∠ PBC=∠ DCB -∠ PCB,∴∠ 1=∠ 2,故 A 正确,∵CE∥AB,∴∠ 1=∠ E,∴∠ 2=∠ E,故 B 正确;∵∠ CPF =∠ EPC,∴△ PFC ∽△ PCE,故 C 正确;由已知条件不可以证明△EFC ∽△ ECB,应选: D.9﹒如图,在△ ABC 中, AB =AC,点 D、 E 分别是 AB、 AC 的中点,点 G、 F 在 BC 边上,四边形DEFG 是正方形 . 若 DE= 2cm,则 AC 的长为()A . 3 3 cm B. 4cm C. 2 3 cm D. 2 5 cm解答:∵ E 是 AAC 的中点,∴AE1 ,AC2∵四边形 DEFG 是正方形,∴ DE ∥ BC,∴ DE AE ,∴ 2 1 ,BC ACBC2∴BC=4cm,∵ AB=AC,且四边形DEFG 是正方形,∴FC =1( 4-2) = 1cm,2由勾股定理得:EC=EF 2FC 2= 5 cm,∴ AC =2EC = 2 5 cm ,应选 D .10. 如图,四边形 ABCD 中, AC 均分∠ DAB ,∠ ADC =∠ ACB = 90°,点 E 为 AB 的中点,给出以下结论:① CE ∥ AD ;② AC 2= AB AD ;③△ CDF ∽△ BCE ;④ AC : AF = DE :DF ,此中正确的 有( ) A . ①② B . ①②③C. ①②④D. ①②③④解答: ∵∠ ACB = 90°,点 E 为 AB 的中点,∴ AE =CE =BE ,∴∠ ACE =∠ BAC , ∵∠ DAC =∠ BAC , ∴∠ ACE =∠ DAC ,∴ CE ∥AD ,故①正确;∵∠ ADC =∠ ACB = 90°,∠ DAC =∠ BAC , ∴△ ADC ∽△ ACB ,∴AC AD,即 AC 2= AB AD ,故②正确;AB AC∵ CE ∥AD , ∴ FC EF ,∴ FC AF EF DF ,AF DFAFDF∴AC DE,故④正确,AF DF∵△ CDF 与△ BCE 不具备相像的条件,∴③不正确, 应选: C.二、仔细填一填11. 4,①②④⑤;12. △APB ∽△ CPA ;13. 9 ;514. 15 ;15. 1 ;16. 15 ;42411. 如图,有以下条件:①∠B =∠C ;②∠ ADB =∠ AEC ;③ADAE ;④ ADAE ;AC ABABAC⑤ PEBP,此中一个条件就能使△ BPE ∽△ CPD 的条件有 ___________ 个,它们分别是PD PC__________________. (只填写序号) 解答: 使△ BPE ∽△ CPD 的条件有 4 个,∵∠ CPD =∠ BPE ,∠ B =∠ C ,∴△ BPE ∽△ CPD ,故①切合; ∵∠ ADB =∠ AEC ,∴∠ CDP =∠ BEP ,∵∠ CPD =∠ BPE ,∴△ BPE ∽△ CPD ,故②切合 ∵∠ A =∠ A ,ADAE ,ABAC∴△ ACE ∽△ ABD ,∴∠ ADB =∠ AEC ,∴∠ CDP =∠ BEP ,∵∠ CPD =∠ BPE ,∴△ BPE ∽△ CPD ,故④切合;∵∠ CPD =∠ BPE , PE BP,PDPC∴△ BPE ∽△ CPD ,故⑤切合,故答案为: 4,①②④⑤.12. 如图,在边长为 1 的正方形网格中有点 P 、 A 、 B 、 C ,则图中所形成的三角形中,相像的三角形是 ______________________.解答: ∵ AP = 5 , PB = 1, PC = 5,∴ AP 5 , PB1 5 , PC5AP55∵∠ APB =∠ CPA , ∴△ APB ∽△ CPA ,故答案为:△ APB ∽△ CPA.13. 如图,已知△ ABC 中, AB = 5, AC = 3,点 D 在边 AB 上,且∠ ACD =∠ B ,则线段 AD 的长为__________ .解答: ∵∠ A =∠ A ,∠ ACD =∠ B ,∴△ ABC ∽△ ACD ,∴AB AC ,AC AD∵ AB =5, AC = 3, ∴53 ,∴ AD = 9,3 AD 5故答案为:9.514. 如图,点 D 为△ ABC 外一点, AD 与 BC 边的交点为 E ,AE =3, DE = 5,BE = 4,要使△BDE ∽△ ACE ,且点 B , D 的对应点为 A , C ,那么线段 CE 的长应等于 ________. 解答: ∵∠ AEC =∠ BED ,∴当 BE DE 时,△ BDE ∽△ ACE ,AE CE即4 5,3 CE∴ CE =15,4故答案为:15.415. 如图,正方形 ABCD 中, E 为 AB 的中点, AF ⊥ DE 于点 O ,则 AO等于 __________.DO解答: ∵∠ ADO =∠ ADO ,∠ DOA =∠ DAE =90°, ∴△ AOD ∽△ EAD ,∴AO AE 1 , DOAD 2故答案为:1.216. 如图,在矩形 ABCD 中, AB =6, BC = 8,沿直线 MN 对折,使 A , C 重合,直线 MN 交 AC 于点 O ,则线段 OM = ________. 解答: 在 Rt △ABC 中, AB = 6, BC = 8, ∴ AC =10,∴ OC = 5,∵ A 与 C 对于直线 MN 对称, ∴ AC ⊥MN ,∴∠ COM = 90°,∵在矩形 ABCD 中,∠ B =90°,∴∠ COM =∠ B = 90°, 又∵∠ MCO =∠ ACB ,∴△ COM ∽△ CBA ,∴OC OM , BC AB∴ OM =15,4故答案为: 15.4三、解答题17. 已知:如图,△ ABC 中,∠ BAC = 90°, AB = AC ,点 合),∠ ADE = 45°. 求证:△ ABD ∽△ DCE. 解答: ∵∠ BAC = 90°, AB = AC , ∴∠ B =∠ C = 45° ,∴∠ 1+ ∠ 2= 180° -∠ B = 135°,∵∠ 2+ ∠ ADE+∠ 3= 180°,∠ ADE =45°,∴∠ 2+ ∠ 3= 180° -∠ ADE = 135°,D 是 BC边上的一个动点(不与B ,C重∴∠ 1=∠ 3,∴△ ABD ∽△ DCE .18. 在平行四边形 ABCD 中, E 为 BC 边上的一点,连结 AE.( 1)若 AB = AE ,求证:∠ DAE =∠ D ;( 2)若点 E 为 BC 的中点,连结 BD ,交 AE 于 F ,求 EF :FA 的值 . 解答: ( 1)在平行四边形 ABCD 中, AD ∥ BC , ∴∠ AEB =∠ DAE ,∵ AE =AB ,∴∠ B =∠ AEB , ∴∠ B =∠ DAE , ∵∠ B =∠ D , ∴∠ DAE =∠ D ;( 2)∵四边形 ABCD 是平行四边形,∴ AD ∥BC , AD = BC , ∴△ BEF ∽△ AFD ,∴EF BE ,FA AD∵ E 为 BC 的中点,∴ BE = 1 BC = 1AD ,即BE1 ,2 2AD2∴EF :FA =1: 2.19.如图,在△ ABC 中, D 、E 分别是边 AB、 AC 的中点, F 为 CA 延伸线上一点,∠F =∠ C.(1)若 BC=8,求 FD 的长;(2)若 AB= AC,求证:△ ADE ∽△ DFE .解答:( 1)∵ D 、E 分别是边AB、 AC 的中点,∴DE =1BC= 4, DE∥ BC.2∴∠ AED =∠ C.∵∠ F =∠ C,∴∠ AED =∠ F ,∴FD =DE = 4;(2)∵ AB= AC, DE ∥ BC.∴∠ B=∠ C=∠ AED =∠ ADE,∵∠ AED =∠ F ,∴∠ ADE =∠ F ,又∵∠ AED =∠ AED ,∴△ ADE ∽△ DFE .20.如图,在△ ABC 中, AB =AC,点 P、 D 分别是 BC、 AC 边上的点,且∠ APD =∠ B.(1)求证: AC CD =CP BP;(2)若 AB= 10, BC= 12,当 PD∥ AB 时,求 BP 的长 .解答:( 1)∵ AB= AC,∴∠ B=∠ C,∵∠ APD =∠ B,∴∠ APD =∠ B=∠ C,∵∠ APC =∠ BAP+∠ B,∠ APC=∠ APD +∠ DPC ,∴∠ BAP =∠ DPC,∴△ ABP ∽△ PCD,∴BP AB ,CD CP∴AB CD = CP BP ,∵ AB=AC,∴AC CD= CP BP;(2)∵ PD ∥ AB,∴∠ APD =∠ BAP.∵∠ APD =∠ C,∴∠ BAP=∠C.∵∠ B=∠ B,∴△ BAP ∽△ BCA,∴BA BP .BC BA∵ AB=10, BC= 12,∴10BP,12 10∴ BP=25 .321.已知:如图, E 是矩形 ABCD 的边 BC 上一点, EF⊥ AE, EF 分别交 AC、CD 于点M 、F , BG⊥ AC,垂足为 G, BG 交 AE 于点 H.(1)求证:△ ABE∽△ ECF ;(2)找出与△ ABH 相像的三角形,并加以证明;( 3)若 E 是 BC 的中点, BC = 2AB , AB = 2,求 EM 的长 . 解答: ( 1)∵四边形 ABCD 是矩形, ∴∠ ABE =∠ ECF = 90°,∵ EF ⊥AE ,∴∠ AEB+∠FEC = 90°, ∵∠ AEB +∠ BAE =90°,∴∠ BAE =∠ FEC , ∴△ ABE ∽△ ECF ; ( 2)△ ABH ∽△ ECM , ∵ BG ⊥AC ,∠ ABC =90°,∴∠ ABH +∠BAG = 90°,∠ ECM +∠ BAG = 90° , ∴∠ ABH =∠ ECM , 又∠ BAH =∠ CEM , ∴△ ABH ∽△ ECM ; ( 3)作 MN ⊥ BC 于点 N , ∵ AB =BE =EC =2, MN ∥AB ,∴ABMN1,∠ AEB =45°,BC NC2∴∠ MEN = 45°, NC = 2MN , ∴ MN = EN = 1NC ,2∵ NC+EN = EC = 2,∴ MN = EN = 2× 1 = 2, 3 3∴ EM 2= MN 2+EN 2= ( 2)2+( 2)2 ,33∴ EM =2 2.322. 如图,正方形 ABCD 中, M 为 BC 上一点, F 是 AM 的中点, EF ⊥ AM ,垂足为 F ,交 AD 的延伸线于点 E ,交 DC 于点 N.( 1)求证:△ ABM ∽△ EFA ;( 2)若 AB = 12, BM = 5,求 DE 的长 . 解答: ( 1)证明:∵四边形 ABCD 是正方形,∴ AB =AD ,∠ B = 90°, AD ∥ BC , ∴∠ AMB =∠ EAF ,又∵ EF ⊥ AM , ∴∠ AFE = 90°, ∴∠ B =∠ AFE , ∴△ ABM ∽△ EFA ;( 2)解:∵∠ B = 90°,AB =12, BM =5,∴ AM = 122 52 =13, AD =12,∵ F 是 AM 的中点,∴ AF = 1AM =,2 ∵△ ABM ∽△ EFA ,∴BMAM,即 5 13 ,AFAEAE∴AE=,∴DE =AE- AD=.23.如图,在△ ABC 中, AB =8cm, BC= 16cm,点 P 从点 A 开始沿点 Q 从点 B 开始沿 BC 向点 C 以 4cm/s 的速度运动 . 假如 P、 Q停止运动,则在开始运动后第几秒,△BPQ 与△ BAC 相像?解答:设在开始运动后第 x 秒,△ BPQ 与△ BAC 相像,由题意得: AP= 2xcm,PB =( 8﹣ 2x)cm,BQ= 4x,分两种状况考虑:当∠ BPQ =∠ C,∠ B=∠ B 时,△ PBQ ∽△ CBA,AB 向点 B 以 2cm/s 的速度运动,分别从 A、 B 同时出发, 4 秒后∴ BP BQ ,即 8 2 x 4 x ,BC AB168解得: x=,当x= 0.8 秒时,△ BPQ 与△ BAC 相像;当∠ BPQ =∠ A,∠ B=∠ B 时,△ BPQ ∽△ BAC,∴ BP BQ ,即 82x4x ,BA BC816解得: x= 2,当 x= 2 秒时,△ BPQ 与△ BAC 相像.综上,当x=0.8 秒或 2 秒时,△ BPQ 与△ BAC 相像.。
相似三角形的判定-沪科版

24.2 相似三角形的判定[知识点1]相似三角形:1、两个三角形,如果各边对应成比例,各角对应相等,则这两个三角形相似。
2、各边对应成比例,各角对应相等是指三组对应角分别相等,三组对应边分别成比例。
3、△ABC与△A′B′C′相似记作“△ABC∽△A′B′C′”,书写时同三角形全等一样,要注意对应字母放在对应位置4、相似三角形的定义揭示了相似三角形的本质特性,即如果两个三角形相似,则各边对应成比例,各角对应相等,∴相似三角形的定义即是性质,又是判定。
5、全等三角形是相似比为1的相似三角形。
[知识点2]相似三角形判定方法:相似三角形的判定方法按照全等三角形的判定方法可记为“AA”、“SAS”、“SSS”和“HL”,只是这里对边要求是对应成比例,对角的要求是对应角相等。
1、“AA”:如果一个三角形的两个角分别与另一个三角形的两个角对应相等;那么这两个三角形相似。
可简单的说成:两角对应相等的两个三角形相似。
2、“SAS”:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似,可简单的说成:两边对应成比例且夹角相等的两个三角形相似。
3、“SSS”:如果一个三角形的三条边为另一个三角形的三条边对应成比例,那么这两个三角形相似,可以简单的说成:三边对应成比例的两个三角形相似。
4、“HL”:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三外形相似。
典型例题点拨例1、已知:如图,ΔABC中,AD=DB,∠1=∠2,求证:ΔABC∽ΔEAD。
例2、已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,ΔADQ与ΔQCP是否相似?为什么?例3、如图,点C、D在线段AB上,△PCD是等边三角形。
(1)当AC、CD、DB满足怎样的关系时,△ACP∽△PDB?(2)当△ACP∽△PDB时,求∠APB的度数。
沪科版 相似三角形的判定习题(1)
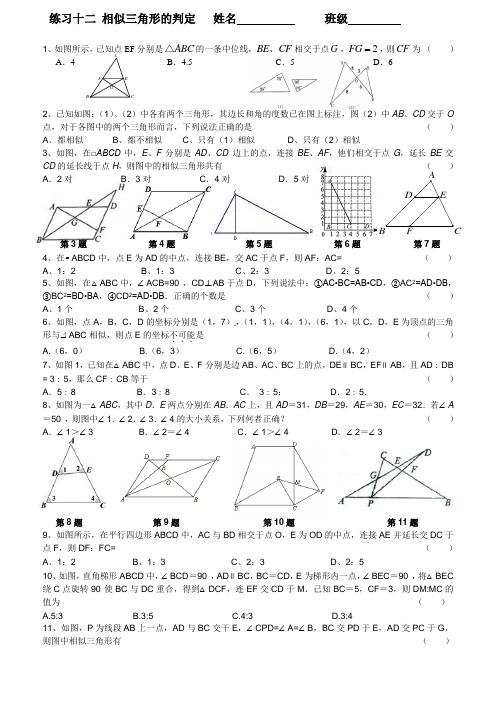
F EAB CDAF ECBG1、如图所示,已知点EF分别是ABC△的一条中位线,BE CF、相交于点G,2FG ,则CF为()A.4 B.4.5 C.5 D.62、已知如图:(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB、CD交于O 点,对于各图中的两个三角形而言,下列说法正确的是()A、都相似B、都不相似C、只有(1)相似D、只有(2)相似3、如图,在□ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,他们相交于点G,延长BE交CD的延长线于点H,则图中的相似三角形共有()A.2对B.3对C.4对D.5对第3题第4题第5题第6题第7题4、在▱ABCD中,点E为AD的中点,连接BE,交AC于点F,则AF:AC= ()A、1:2B、1:3C、2:3D、2:55、如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,下列说法中:①AC•BC=AB•CD,②AC2=AD•DB,③BC2=BD•BA,④CD2=AD•DB.正确的个数是()A、1个B、2个C、3个D、4个6、如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与⊿ABC相似,则点E的坐标不可能...是()A.(6,0)B.(6,3)C.(6,5)D.(4,2)7、如图1,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD∶DB = 3∶5,那么CF∶CB等于()A.5∶8 B.3∶8 C.3∶5;D.2∶5.8、如图为一△ABC,其中D.E两点分别在AB.AC上,且AD=31,DB=29,AE=30,EC=32.若∠A =50°,则图中∠1.∠2.∠3.∠4的大小关系,下列何者正确?()A.∠1>∠3 B.∠2=∠4 C.∠1>∠4 D.∠2=∠3第8题第9题第10题第11题9、如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC= ()A、1:2B、1:3C、2:3D、2:510、如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,∠BEC=90°,将△BEC 绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为()A.5:3B.3:5C.4:3D.3:411、如图,P为线段AB上一点,AD与BC交干E,∠CPD=∠A=∠B ,BC交PD于E,AD交PC于G,则图中相似三角形有()练习十二相似三角形的判定姓名班级A 、1对B 、2对C 、3对D 、4对12、将一副三角尺如图所示叠放在一起,则BEEC 的值是 .第12题 第13题 第14题13、如上图,在△ABC 中,D 为AC 边上的中点,AE ∥PC,,ED 交AB 于G ,交BC 延长线于F ,若BG :GA=3:1,BC=1 0,则AE 的长为 .14、在△ABC 中,P 是AB 上的动点(P 异于A ,B ),过点P 的一条直线截△ABC ,使截得的三角形与△ABC 相似,我们不妨称这种直线为过点P 的△ABC 的相似线.如图,∠A =36°,AB =AC ,当点P 在AC 的垂直平分线上时,过点P 的△ABC 的相似线最多有 条.15、如图,四边形ABCD 中,AC 平分∠DAB ,∠ADC=∠ACB=90°,E 为AB 的中点,(1)求证:AC 2=AB•AD ;(2)求证:CE ∥AD ;(3)若AD=4,AB=6,求的值.16、如图是夹文件用的铁(塑料)夹子在常态下的侧面示意图.AC BC ,表示铁夹的两个面,O 点是轴,OD AC ⊥于D .已知15mm AD =,24mm DC =,10mm OD =.已知文件夹是轴对称图形,试利用图(2),求图(1)中A B ,两点的距离(26=576)17、如图,四边形ABCD 和ACED 都是平行四边形,点R 为DE 的中点,BR 分别交AC CD ,于点P Q ,.(1)请写出图中各对相似三角形(相似比为1除外);(2)求::BP PQ QR .A BC D E P Q R。
沪科版-数学-九年级上册-23.2相似三角形的判定 判定三角形相似的方法

判定三角形相似的方法判定三角形相似的方法有五种:一、由定义判定:三个角对应相等,三边对应成比例的两三角形相似. 二、三角形相似的基本判定方法1、判定定理:平行于三角形的一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似.推理形式:如图1所示,∵DE ∥BC ,∴△ADE ∽△ABC. 2、涉及的基本图形(如图1所示).说明:⑴在运用基本方法判定两个三角形相似时,只需DE ∥BC 这一条件就能确定△ADE ∽△ABC ,不必再用定义进行判定;⑵上面的图形是判定方法所涉及的几种基本类型,在应用时要善于从图中抽象出这些基本模型.例1:(06南通)如图2,DE 与△ABC 的边AB ,AC 分别相交于D ,E 两点,且DE ∥BC .若DE =2㎝,BC =3㎝,EC =32㎝,则AC =________㎝.解析:由DE ∥BC 可知△ADE ∽△ABC,由相似三角形的对应边的比相等,有,BCDEAC AE =从而,BC DEAC EC AC =-把DE =2㎝,BC =3㎝,EC =32㎝代入得,3232=-AC AC 求AC=2, 故添2.三、由三边的比判定三角形相似1、判定定理:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.简单地说三边对应成比例的两个三角形相似.2、推理形式:如图3所示,在△ABC 和△C B A '''中,如果A C CAC B BC B A AB '=''='',那么△ABC ∽△C B A '''.类比拓展:由三边的比判定三角形相似的方法与判定三角形全等的“SSS ”方法类似,只是把三边对应相等,改为三组对应边成比例即可.“A ”型“A ”型 “X ”型 图1' 图3例2:(05山东菏泽)如图4,小正方形的边长均为1,则下图中的三角形(阴影部分)与△ABC 相似的为( )解析:由于正方形边长均为1,在△ABC 中,AC=2,BC=2,AB=10;图A 中三角形三边长为1,,22,5而与△ABC 三边的比分别为,521022,25,21=显然它们不相等;图B 中三角形三边长为1,,5,2与△ABC 的三边的比分别为,22105,22,2221==故对应边的比相等;同样的道理可以得出在图C 和图D 中的两个三角形三边分别与△ABC 三边的比不相等.故选B.四、由两边和夹角判定三角形相似1、判定方法:如果两个三角形的两组对应边的比相等,且夹角相等,那么这两个三角形形似.简单说成,两边对应成比例且夹角相等的两个三角形相似.2、推理形式:如图3,在△ABC 和△C B A '''中,如果,,A A A C CAB A AB '∠=∠'=''那么△ABC ∽△C B A '''.例3:(06云南双柏)如图5,在4×4的正方格中,△ABC 和△DEF 的顶点都在边长为1的小正方形的顶点上. ⑴填空:∠ABC=_____,BC=_____;⑵判断△ABC 与△DEF 是否相似,并证明你的结论.解析:⑴利用正方形对角线平分一组对角的性质可得∠ABC=00013545180=-,由勾股定理得BC=222222=+;⑵△DEF 中,∠DEF=0135,分别计算△ABC 的边AB 、BC 和△DEF 的边DE 、EF ,AB=2,BC=22;EF=2,DE=2.∵,2222,222====EF BC DE AB ∴ EFBC DE AB =且∠ABC=∠DEF=0135,∴△ABC ∽△DEF. 技巧点拨:本题是网格中的形似问题,首先要用正方形的性质和勾股定理求出相等的角和边长.再利用两组对边的比相等,夹角相等的两个三角形相似来判断,本题的另一种方法就是利用三边的比对应相等的两个三角形相似来判断,本题的易错点是不少同学认为:因为,,2222,122DE BCEF AB DE BC EF AB ≠====,故这两个三角形不相似.网格中的数学问题是图5A 图4 C D近几年中考的热点题型,预计这类问题在今后的中考中有所加强. 五、由两角判定三角形相似1、判定方法:如果一个三角形的两个角与另一三角形的两个角对应相等,那么这两个三角形相似,简单地说:两角对应相等,两个三角形相似。
沪科版22.2.3相似三角形的判定(边角边)

1.在Δ ABC中,D为边AB上一点,过P 点的直线截得的三角形与Δ ABC相似,则这样 的直线共有 条,并在图中画出这样的直 线。
A D B
A E E
D B E E C
C
1.如图,在RtΔ ABC中,∠C=90°,P 为斜边AB上一点,过P点的直线截得的三角形与 Δ ABC相似,则这样的直线共有 条,并在 图中画出这样的直线。
AB2 A1B1
AB : A1B1 AC : A1C1 A1B1 AB2 , A1C1 AC2
A A1
AC2 A1C1
AB2C2 A1B1C1 (S. A.S.)
AB : AB2 AC : AC2 B2C2 // BC AB2C2 ∽ ABC ABC ∽ A1B1C1
Aபைடு நூலகம்
P
C
B
练习:D是△ABC边AB上一点,
⑴若AC2=AD· , AB △ABC与△CAD相似吗?为什么?
D B C
⑵若△BCD∽△BAC,需补充什么条件?
练一练
1.如下图所示,在△ABC中,D﹑E分别在AC﹑AB上, 且AD:AB=AE:AC=1:2,BC=5,则DE=________
A
E D B
B
● ●
复习回顾 1.三角形相似判定方法?A
☆相似三角形的定义: ∵ AD AE DE AB AC BC
∴△ADE∽△ABC
A
A A, ADE B, AED C
A
B
C
B
D
A
C
E
C
☆预备定理: D 平行于三角形一边的直线 B 和其他两边(或两边的延长线) 相交,截得的三角形与原三角形相似.
《相似三角形的判定(1沪科版解读

2
D E
∵DF∥AC ∴△BDF∽△BAC
B F DF ∴B C AC
6 3
B F
6 2
C
3 6 ∴ 3 2 AC
∴ AC=10 ∴AE=AC-CE=10-6=4
你还有其他 方法吗?
2、如图,在 平行四边形ABCD中,E是 边BC上的一点,且BE:EC=3:2,连接AE、 BD交于____ 3:5
一、知识回顾
1、亲爱的同学们,我们刚刚学过相似多边形,你 还记得相似多边形的定义吗? 大胆说一说
满足
(1)对应角相等
(2)对应边成比例
1、相似三角形的定义: 对应角相等,对应边成比例的两个三角形叫做 相似三角形.它们对应边的比叫做相似比. 2、相似三角形的表示: 两三角形相似用“∽” 表示,读作:“相似于”.
C B′
C′
AB K, / / / / / 3、若△ABC∽ △A B C ,则相似比为 A B / / AB 1 / / / 那么△A B C ∽△ABC,则相似比为 AB K.
4、相似三角形与全等三角形有什么内在的联系呢? 当两个三角形的相似比为 1 时,它们是全等的 ,全等是相似的一种特殊情况。
AD AE FC AD , . AB AC BC AB
D
E
∵四边形DFCE是平行四边形,
DE AD DE FC , . BC AB
AD AE DE , AB AC BC
B
F
C
又∵∠A=∠A,∠B=∠ADE,∠C=∠AED, ∴ △ADE ∽ △ABC.
若点D是AB或BA延长线上的一点 ,过点D作DE∥BC,与AC或CA的延长 线交于点E,△ADE与△ABC相似吗? ∵ DE∥BC ∴△ADE ∽ △ABC B
沪科版习题库之相似三角形的判定1

1一、选择题1. 如图,下列条件中不能判定ACD ABC △∽△的是(的是( )(A)AB ADBC CD=(B)ADC ACB Ð=Ð(C)ACD B Ð=Ð(D)2AC AD AB =2. 下列四组图形中不一定相似的是下列四组图形中不一定相似的是 .A.有一个角等于40 的两个等腰三角形的两个等腰三角形 B.有一个角为50 的两个直角三角形的两个直角三角形C.直角三角形被斜边上的高分成的两个直角三角形C.直角三角形被斜边上的高分成的两个直角三角形 D.有一个角是60 的两个等腰三角形的两个等腰三角形3. 能判定ABC △与A B C ¢¢¢△相似的条件是相似的条件是 .A.AB ACA B A C =¢¢¢¢ B.AB A B AC A C ¢¢=¢¢,且A C ¢Ð=Ð C.AB BCA B A C =¢¢¢¢且B A ¢Ð=Ð D.AB AC A B A C =¢¢¢¢,且B B ¢Ð=Ð4. 如图,D 为ABC △的边BC 上的一点,连接AD ,要使ABD CBA △∽△,应具备下列条件中的( )A.AC ABCD BD =B.2AB BD BC =C.AB BC CD AD=D.2AC CD CB =5. 如图,若∠1=∠2=∠3,则图中相似的三角形有(,则图中相似的三角形有( ) A .1对 B .2对 C .3对 D .4对6. 如图,AB ∥CD ,AE ∥FD ,则图中的相似三角形共有(,则图中的相似三角形共有( ) A .2对 B .4对 C .6对 D .8对A CDBABDC1 A BD CE 2 3 27. Rt △ABC 中,∠ACB =90°,CD ⊥AB ,DE ⊥AC ,D ,E 为垂足,那么,和△ABC 相似的三角形共有( ) A .1个 B .2个 C .3个 D .4个8. 如图,矩形ABCD 中,DE AC E ⊥,为垂足,图中相似三角形共有(全等除外)( ) A.3对 B.4对 C.5对 D.6对9. 如图,ABC △中,90BAC Ð=,AD 是BC 边上的高线,图中相似三角形共有(边上的高线,图中相似三角形共有( )A.2对 B.3对 C.4对 D.1对10. 下列两个三角形相似的是( ) A.两个等腰三角形A.两个等腰三角形 B.两个直角三角形B.两个直角三角形 C.两个等腰直角三角形C.两个等腰直角三角形 D.两个锐角三角形D.两个锐角三角形11. 如图,12l l ∥,则图中相似三角形有(,则图中相似三角形有( )A.1对 B.2对 C.3对 D.4对ABCDEABDCOCBADE F1l2l312. 如图,在大小为4×4的正方形网格中,是相似三角形的是(的正方形网格中,是相似三角形的是( )).① ②② ③③ ④④ A .①和②.①和② B B B.②和③.②和③.②和③ C C C.①和③.①和③.①和③ D D D.②和④.②和④.②和④13. 在矩形ABCD 中,中,E E 、F 分别是CD CD、、BC 上的点,若∠上的点,若∠AEF AEF AEF==9090°,则一定有(°,则一定有(°,则一定有( )).A.ΔADE ADE∽∽ΔAEFB.ΔECF ECF∽∽ΔAEFC.ΔADE ADE∽∽ΔECFD.ΔAEF AEF∽∽ΔABF二、填空题14. 如图,在ABC △中,点D E 、分别在边AC AB 、上,且23AE AD AC AB ==,若4DE =cm ,则BC = cm .15. 在ABC △和A B C ¢¢¢△中,326cm10cm 32A AB A B A ¢¢¢Ð===Ð= ,,,,3cm AC =,5cm A C ¢¢=,则ABC △与A B C ¢¢¢△是否相似?是否相似? (填“是”或“不是”).16. 如图,线段AC BD ,相交于点O ,要使AOB DOC △∽△,已具备条件 ,还需要补充的条件是,还需要补充的条件是 ,或,或 或 .17. 在△ABC 和△C B A ¢¢¢中,C A ACB A AB¢¢=¢¢,还需要∠,还需要∠=∠ ,才能判定△ABC ∽△C B A ¢¢¢.18. △ABC 与△DEF 中,AB =3,BC =2,DE =6,EF =4,还需要∠,还需要∠ =∠ ,则△ABC ∽△∽△ .AEBCDCA DOB4ABCEDF19. 如图,平行四边形ABCD 中,E 是BA 延长线上一点,EC 交AD 于F ,交BD 于G ,则△EAF ∽△∽△ 或△或△ ,△FGD ∽△∽△ .20. 如图,点D 、E 在等边△ABC 的边AB 、BC 上,且AD =BE ,AE 、CD 相交于点F ,则△BCD ∽△∽△ ∽△∽△ .21. 如图,ABBCACAD DE AE ==,则∠BAD =∠ =∠ .22. 如图,△ABC 中,∠A =90°,∠C =30°,N 是AB 的中点,MN ⊥BC 于M ,则可识别△BMN ∽△∽△,相似比为,相似比为 .23. 如图,已知DE BC ∥,可得Ð =Ð .又A A Ð=Ð,所以△ ∽△ .24. 如图,已知EAC DAB Ð=Ð,补充条件 (写一个即可),可使ADE ABC △∽△.E ABCGFDA B C EDA B C N M AD E C BADBCE525. 如图,DE BC ∥,ACD B Ð=Ð,则图中共有,则图中共有 对相似三角形,分别是似三角形,分别是 .26. CD 是ABC Rt Rt△△斜边AB 上的高,13cm 12cm AB BC ==,,则BD = .27. 如图,ABC △中D ,E 分别是AB ,AC 上的点,在下列条件中,①AED B Ð=Ð,②A D A E A C AB =,③D E A DB C A C=,能够判断ADE △与ACB △相似的是相似的是.(填序号)(填序号)28. 已知:如图,DE ∥BC ,EF ∥AB ,下列判断正确的是(,下列判断正确的是( ))A .AD DEDB BC =B .AC BCEC FC =C .EF DE AB BC=D .AB CE AD CA=三、应用题29. 29. 如图如图如图,,在ABC 中,AD=DB,,AD=DB,∠∠1=1=∠∠2,2,试说明△试说明△试说明△ABC ABC ABC∽△∽△∽△EAD. EAD.30. 如图如图,,已知△已知△ABC ABC 中,点F 是BC 的中点,的中点,DE//BC DE//BC DE//BC,,则DG 和GE 有怎样的关系?请你说明理由系?请你说明理由. .AECB DADE CB一、选择题1. (A) 2. A3. C4. B5. D 6.C7. D 8. C 9. B10. C11. C12. C13. C二、填空题14. 6 15. 是6716. BOOA AOB DOC B C A D OCODÐ=ÐÐ=ÐÐ=Ð=,,,17. ∠A =∠A ¢18. ∠B =∠E ,DEF . 19. CDF ,,EBC ,CGB20. CAE ,FCE21. CAE ,CBE22. BAC ,1∶4 23. B ADE ABC ADE24. E C Ð=Ð或B D Ð=Ð或AD AEAB AC=25. 4 ADE ABC ADE ACD BCD CDE △∽△,△∽△,△∽△,BCA △∽CDA △26. 144cm 1327. ①②①②28. B三、应用题29. 29. 因为因为AD=DB,AD=DB,所以∠所以∠所以∠B=B=B=∠∠BAD,又因为∠又因为∠AED=AED=AED=∠∠B+B+∠∠2,2,∠∠BAC=BAC=∠∠BAD+BAD+∠∠1,1,∠∠1=1=∠∠2,2,所以∠所以∠所以∠AED=AED=AED=∠∠BAC, 所以△所以△ABC ABC ABC∽△∽△∽△EAD.. EAD..30. DG=GE.。
沪科版 22.2 相似三角形的判定1

相似三角形的判定(1课时)一、授课目的与考点分析:相似三角形的判定二、授课内容:(一)相似三角形1、定义:对应角相等,对应边成比例的两个三角形,叫做相似三角形.强调:①当一个三角形的三个角与另一个(或几个)三角形的三个角对应相等,且三条对应边的比相等时,这两个(或几个)三角形叫做相似三角形,即定义中的两个条件,缺一不可;②相似三角形的特征:形状一样,但大小不一定相等;③相似三角形的定义,可得相似三角形的基本性质:对应角相等,对应边成比例.2、相似三角形对应边的比叫做相似比.强调:①全等三角形一定是相似三角形,其相似比k=1.所以全等三角形是相似三角形的特例.其区别在于全等要求对应边相等,而相似要求对应边成比例.②相似比具有顺序性.例如△ABC∽△A′B′C′的对应边的比,即相似比为k,则△A′B′C′∽△ABC的相似比,当它们全等时,才有k=k′=1.③相似比是一个重要概念,后继学习时出现的频率较高,其实质它是将一个图形放大或缩小的倍数,这一点借助相似三角形可观察得出.3、如果两个边数相同的多边形的对应角相等,对应边成比例,那么这两个多边形叫做相似多边形.4、相似三角形的预备定理:平行于三角形的一条边直线,截其它两边所在的直线,截得的三角形与原三角形相似.强调:①定理的基本图形有三种情况,如图其符号语言:∵DE∥BC,∴△ABC∽△ADE;(双A型)②这个定理是用相似三角形定义推导出来的三角形相似的判定定理.它不但本身有着广泛的应用,同时也是证明相似三角形三个判定定理的基础,故把它称为“预备定理”;③有了预备定理后,在解题时不但要想到“见平行,想比例”,还要想到“见平行,想相似”.(二)相似三角形的判定1、相似三角形的判定:判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
可简单说成:两角对应相等,两三角形相似。
例1、已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.例2、如图,E、F分别是△ABC的边BC上的点,DE∥AB,DF∥AC ,求证:△ABC∽△DEF.判定定理2:如果三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
沪教版九年级数学同步练习:第二十四章相似三角形第三节相似三角形的判定

相似三角形相似三角形的判定(1)一、选择题1.下列语句不正确的是( )A .两个等边三角形是相似三角形B .有一个角为40°的两个等腰三角形相似C .有一个角为100°的两个等腰三角形相似D .两个等腰直角三角形是相似三角形2.下列条件不能判定ABC ∆∽'''C B A ∆的是( )A .︒=∠30A ,︒=∠50B ,︒=∠30'A ,∠C=100°B .B A ∠=∠,''C B ∠=∠,'A C ∠=∠C .'A A ∠=∠,''C B C B -∠∠=∠-∠D .'A A ∠=∠,''C B C B +∠∠=∠+∠3.如图1,已知:点D 在ABC ∆的边AB 上,且B ACD ∠=∠,则下列各式中一定成立的是( )A .AB AD AC ⋅=2 B .AC CD AB AD = C .BC CD DB AD = D .BC AC AC CD = 二、填空题1.如图2,已知:BC AD 、相交于点O ,C A ∠=∠,若4=AO ,6=OB ,8=OC ,则OD =_______.2.如图3,已知:BE AD 、是ABC ∆的两条高,BE AD 、相较于点O ,则图中共有______对相似三角形.3.如图4,已知:CD 是ABC Rt ∆斜边上的高,则_________==CDAD . 4.如图5,已知:点D 在ABC ∆的边AB 上,B ACD ∠=∠,6=AC ,4=AD ,BD =_______.5.如图6,已知:点D 在ABC ∆的边上,2=AD ,9=AB ,6=AC .过点D 的直线交AC 于点E ,使以点A 、D 、E 为顶点的三角形与ABC ∆相似,则AE =________.三、简答题1.求证:顶角对应相等的两个等腰三角形相似.2.如图,已知:等腰三角形ABC 中,点D 在BC 边上,B EDF ∠=∠,求证:BD DC FC BE ⋅=⋅.3.如图,已知:21∠=∠,ABC ADE ∠=∠,求证:AE AB AC AD ⋅=⋅.4.如图,已知:等腰ABC ∆中,AC AB =,︒=∠108BAC ,AB BD =,求:BCBD 的值. 5.如图,已知:ABC ∆中,点E 是AB 上一点,AC CE =,点D 在BC 上,DB DE =,DE 的延长线与CA 的延长线相交于点F ,连接CE ,求证:DF DE CD ⋅=2.相似三角形的判定(2)一、选择题1.如图,已知:点E D 、分别在ABC ∆的边AC AB 、上,若AC AE AB AD ⋅=⋅,则下列各式中不能成立的是( )A .ADE ∆∽ACB ∆ B .B AED ∠=∠C .AB AE BC DE =D .ABAD BC DE = 2. ABC ∆与'''C B A ∆中,由下列条件能推出ABC ∆∽'''C B A ∆的是( )A .''''C A ACB A AB =,'B B ∠=∠ B .''''C A AC B A AB =,'A A ∠=∠ C .AC AB =,''''C A B A =,'B B ∠=∠ D .AC AB =,''''C A B A =,'C C ∠=∠3.如图,已知:在ABC ∆中,CD 是高,由下列条件不一定能得出ABC ∆是直角三角形的是( )A .CD AD BC AC =B .B ACD ∠=∠C .BCBD AB BC = D .AB AD AC ⋅=2 二、填空题1.如图1,已知ABC Rt ∆中,︒=∠90C ,3=AC ,4=BC ,点D 为AB 的中点,当BE =______时,AB DE ⊥.2.如图2,已知:BD 平分ABC ∠,2=AB ,6=BC ,当BD =________时,ABD ∆∽BDC ∆.3.如图3,添加一个条件___________,则以点E D A 、、为顶点的三角形与ABC ∆相似.4. ABC ∆与'''C B A ∆中,若''''B A BC C A AB =,又∠_____=∠______时,能推出ABC ∆与'''C B A ∆. 三、简答题1.如图,已知OD BO OC AO ⋅=⋅,求证:AE DE EB CE ⋅=⋅.2.已知ABC ∆与'''C B A ∆中,AC AB =,''''C A B A =,'B B ∠=∠,求证:ABC ∆∽'''C B A ∆.3.如图,已知4=AD ,5=DC ,6=AB ,求证:ADB ABC ∠=∠.4.如图,在ABC ∆中,点E D 、在BC 边上,ADE ∆是等边三角形,EC BD DE ⋅=2,求证:︒=∠120BAC .5.如图,正方形ABCD 中,点F E 、分别在BC DC 、上,EC DE 21=,2:7:=FC BF , 求证:︒=∠90AEF . 6.如图,在ABC ∆中,AE BD 、分别是BC AC 、上的高,AE BD 、相交于点O ,连接DE ,求证(1)CDE ∆∽CBA ∆,(2)DOE ∆∽AOB ∆.7.如图,已知:在ABC ∆中,AE 是BC 上的高,CD BD ⊥,AE 的延长线交BD 于F ,BD BF AB ⋅=2,求证: ︒=∠90BAC .相似三角形的判定(3)一、选择题1.下列四组条件中,不能判定ABC ∆∽DEF ∆的是( )A. 2=AB ,22=BC ,4=AC ,3=DE ,33=EF ,6=DFB. ︒=∠36A ,︒=∠64B ,︒=∠36E ,︒=∠80FC. ED AC EF AB ::=,且E A ∠=∠D. ︒=∠=∠60E A ,AC BC =,FD DE =2.给出四个命题:①三边对应成比例的两个三角形相似②一个锐角对应相等的两个直角三角形相似③两边对应成比例,且有一个角对应相等的两个三角形相似④有一个角对应相等的两个等腰三角形相似其中不正确的有( )A. 1个B. 2个C. 3个D. 4个3.已知ABC ∆的三边长为2、3、4,DEF ∆的一边长为6,若ABC ∆∽DEF ∆,则DEF ∆的另两边不可能是下列( )组A. 12,9B.29,3 C. 8,4 D. 18,24 二、填空题1.ABC ∆与DEF ∆中,6=AB ,8=BC ,12=AC ,6=EF ,9=DE ,DF =_______时,ABC ∆∽DEF ∆.2.ABC ∆中,6=AB ,8=BC ,7=CA ,延长CA 至点P ,使PBC ∆∽PAB ∆,则AP = ____.3.已知两个三角形三边长分别为32、6、34与6,33,3时,这两个三角形_____相似三角形(填“是”或“不是”).4. ABC ∆与DEF ∆中,AC AB =,DF DE =,添加一个条件:_______________________时,ABC ∆∽DEF ∆.三、简答题1.如图,已知ACAE BC DE AB AD ==,求证:ADB ∆∽AEC ∆. 2.求证:腰及腰上中线对应成比例的两个等腰三角形相似.3.如图,画一个与ABC ∆相似的三角形,并证明.4.如图,已知:正方形ABCD 中,点E 是AD 的中点,点F 在DC 上,且DF CF 3=,BF EG ⊥,垂足为G ,求证:BF BG BE ⋅=2.5.如图,已知:ABC ∆与'''C B A ∆中,︒=∠=∠90'''C A B BAC ,AD 、''D A 分别是BC 、''C B 上的中线,''''B A AB D A AD =,求证:ABC ∆∽'''C B A ∆. 相似三角形的判定(4)一、选择题1. ABC Rt ∆和MNP Rt ∆中,︒=∠=∠90P B ,依据下列各组条件不能判定这两个三角形相似的是( )A .︒=∠46A ,︒=∠44MB .9,6,6,4====PN MP BC ABC .9,6,6,4====MN PN AC ABD .9,6,6,4====MN MP BC AB2. ABC ∆中,︒=∠90C ,CD 是斜边上的高,下列结论不一定成立的是( ) A.222111CDBC AC =+ B. AD BC DB AC ⋅=⋅ C.BD AD BCAC =22 D. AD BC CD AC ⋅=⋅ 3. ABC ∆中,CD 是AB 上的高,由下列条件不一定能推出︒=∠90ACB 的是( )A. ︒=∠+∠90ACD BB. DB AD CD ⋅=2C. DBCD BC AC = D. DCB A ∠=∠ 二、填空题1.如题1,已知:ABC Rt ∆中,︒=∠90ACB ,CD 是AB 上的高,∥MN AB 且与CD 相交于点O ,则图中与ABC ∆相似的三角形有________个.2.如图2,已知: ABC Rt ∆中,︒=∠90ACB ,AD ⊥AC ,则图中与ABC ∆相似的三角形是_______________________.3.如图3,已知:矩形ABCD 中,点P 是BC 上不与B 、C 重合的点,2=AB ,8=BC ,BP =____时,PD AP ⊥.三、简答题1.如图,已知:四边形ABCD 中,︒=∠90A ,DC BD ⊥,4=AD ,6=BD ,9=BC ,求证:AD ∥BC .2.如图,已知:ABC ∆与'''C B A ∆中,AC AB =,''''C A B A =,BD 、''D B 分别是AC 、''C A 上的高,''''D B BD C A AC =求证:ABC ∆∽'''C B A ∆. 3.如图,已知:ABC Rt ∆中,︒=∠90ACB ,点D 是AB 上一点,CD AE ⊥,CE AB AC ⋅=2,求证:点D 是AB 的中点.4.如图,已知:梯形ABCD 中,AD ∥BC ,点E 是CD 的中点,DC AD ⊥,BC DE BE AE =,求证:AE 平分BAD ∠.5.如图,已知:在平面直角坐标系中,点A (0,4)、B (0,3-)在x 轴上找点P ,使以点P 、O 、A 为顶点组成的三角形与ABO ∆相似,求点P 的坐标.相似三角形的判定(5)一、选择题1.如图,已知:ABC ∆中,BE 平分ABC ∠、∠BAD =∠C ,则下列结论不一定成立的是( )A.△AFE ∽△ACEB.△ABD ∽△CBAC.△ABF ∽△BECD.△ABE ∽△BFD2. ABC ∆与'''C B A ∆中,43''''==C B BC B A AB ,添加下列条件仍不一定能得到ABC ∆∽'''C B A ∆的是( )A. 43''=C A AC B.A A ∠=∠' C. 'B B ∠=∠ D.︒=∠=∠90'D D 3. ABC ∆中,直线DE 分别与AC AB 、相交于点E D 、,下列条件不能推出ABC ∆与ADE ∆相似的是( ) A. EC AE BD AD = B. ∠ADE =∠ACB C. AD AB AC AE ⋅=⋅ D. BCDE AB AD = 二、填空题1. ABC ∆中,E D 、分别是AC AB 、上的点,如果2=AD ,3=DB ,4=EC ,则AE =___时,ADE ∆与ABC ∆相似.2. ABC Rt ∆中,︒=∠90C ,3=AC ,4=BC ,DEF ∆中,∠D =90°,DEF ∆∽ABC ∆,且6=DE ,则EF =________.3.如图1,已知:∠A =∠E ,∠C =∠D ,则△_____∽△______,其中对应边成比例的比例式为______=______=________.4. ABC Rt ∆中,点D 是斜边AB 上一点,过点D 作直线DE ,交三角形的另一边于点E ,使截得的三角形与原三角形相似,则满足这样条件的直线有_______条.5.如图2,已知ABC Rt ∆中,∠C =90°,矩形CDEF 内接于ABC ∆,3=AC ,4=BC ,设DE =x ,则矩形CDEF 的周长y =________,x 的取值范围_________________.三、简答题1.如图,已知: ABC ∆中,21∠=∠=∠B ,求证:EBD ∆∽DAC ∆.2.如图,已知:四边形ABCD 中,对角线AC 、BD 交于点O ,21∠=∠.求证:△AOD ∽△BOC .3.如图,已知:等腰梯形ABCD 中,AD ∥BC ,AB=CD ,点E 在BC 上,∠AEF =∠B .(1)求证:△ABE ∽△ECF ;(2)当点E 在BC 上的什么位置时,△ABE 与△AEF 相似,并证明.4.如图,已知:等边△ABC 中,D 、E 分别是AB 、BC 延长线上的点,且BD=CE ,直线CD 与AE 相交于点F ,求证:△DCA ∽△DAF .。
沪科版-数学-九年级上册-- 22.2 相似三角形的判定第1课时

相似三角形的判定第1课时 相似三角形的判定定理11.△ABC ∽△A ′B ′C ′,相似比为k 1,△A ′B ′C ′∽△ABC ,相似比为k 2,则k 1k 2=1.三角形全等是三角形相似的特例.2.定理:平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.3.定理1:如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似(可简单说成:两角对应相等的两个三角形相似).4.如图,在△ABC 中,D 、E 分别是AB 、AC 边的中点,若BC =6,则DE 等于( ).A .5B .4C .3D .2 答案:C5. 如图,Rt △ABC 中,∠C=90°,DE ⊥AB 于E ,试说明△ABC 和△ADE 的关系?解:△ABC 和△A DE 相似.∵∠A=∠A ,∠C=∠AED=90°, ∴△ABC ∽△ADE.1.利用定理:“平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似”判定三角形相似【例1】 如图,在△ABC 中,D 、E 分别是AB 、AC 上的点,且AD =13AB ,AE =12EC .求证:△ADE ∽△ABC .分析:根据条件证明DE ∥BC 即可.证明:∵AE =12EC ,∴AE AC =13. 又∵AD =13AB ,即AD AB =13,∴AE AC =ADAB .∴DE ∥BC . ∴△ADE ∽△ABC .当一个三角形在另一个三角形的内部并且有一个公共角时,通常要看公共角的对边是否平行.针对性训练见当堂检测·基础达标栏目第1题2.利用定理1判定三角形相似【例2】 如图,已知△ABC ,则下列4个选项中的三角形与△ABC 相似的是( ).解析:由题中图形知△ABC 是底角为75°的等腰三角形,所以它应和顶角为30°的等腰三角形相似,根据是“两角对应相等,两三角形相似”判定. 答案:C在相似三角形的判定方法中,特别应注意的是“对应”两字,而在等腰三角形中,应是顶角和顶角对应,底角和底角对应.针对性训练见当堂检测·基础达标栏目第4题1. 如图,在△ABC 中,如果DE ∥BC ,DF ∥AC ,则相似的三角形有( ).A .0对B .1对C .2对D .3对答案:D2.如图,在△ABC 中,若DE ∥BC ,AD DB =12,DE =4 cm ,则BC 的长为( ).A .8 cmB .12 cmC .11 cmD .10 cm解析:∵DE ∥BC , ∴△ADE ∽△ABC . ∴AD AB =DE BC . 又∵AD BD =12,∴AD AB =13. ∴DE BC =13. ∴BC =3D E =12 cm. 答案:B3. 如图,在Rt △ABC 中,∠ACB=90°,BC=3,AC=4,AB 的垂直平分线DE 交BC 的延长线于点E ,则CE 的长为( ).A .32B .76C .256D .2解析:∵DE 垂直平分AB ,∴BD =12AB =2.5.∵∠B =∠B ,∠BCA =∠BDE =90°, ∴△BCA ∽△BDE . ∴BD BC =BE BA . ∴2.53=BE 5.∴BE =256.∴CE =BE -BC =256-3=76.答案:B4.已知△ABC 和△DEF 中,点A 、B 、C 分别与点D 、E 、F 相对应,且∠A =70°,∠B =34°,∠D =70°,则当∠F =__________时,△ABC ∽△DEF .解析:由已知可知∠A 和∠D 对应,∠B 和∠E 对应,∠C 和∠F 对应,所以∠F =∠C =180°-∠A -∠B =76°.答案:76°5.如图,平行四边形ABCD 中,E 是边BC 上的点,AE 交BD 于点F ,如果BE BC =23,那么BFFD=__________.解析:平行四边形ABCD 中, ∵BE BC =23, 又∵AD =BC , ∴BE AD =23. ∵AD ∥BC , ∴BE AD =BF FD . ∴BF FD =23. 答案:23。
沪科版九年级数学习题-相似三角形的判定(第1课时)
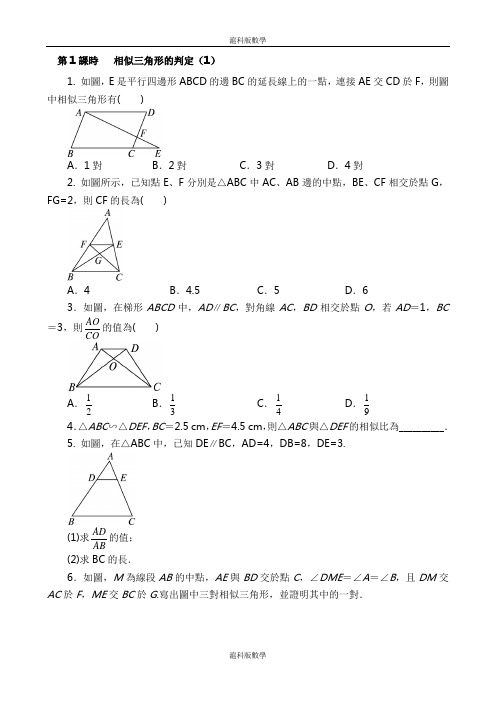
第1課時 相似三角形的判定(1)1. 如圖,E 是平行四邊形ABCD 的邊BC 的延長線上的一點,連接AE 交CD 於F ,則圖中相似三角形有( )A .1對B .2對C .3對D .4對2. 如圖所示,已知點E 、F 分別是△ABC 中AC 、AB 邊的中點,BE 、CF 相交於點G ,FG=2,則CF 的長為( )A .4B .4.5C .5D .63.如圖,在梯形ABCD 中,AD ∥BC ,對角線AC ,BD 相交於點O ,若AD =1,BC=3,則AO CO的值為( )A .12B .13C .14D .19 4.△ABC ∽△DEF ,BC =2.5 cm ,EF =4.5 cm ,則△ABC 與△DEF 的相似比為__________.5. 如圖,在△ABC 中,已知DE ∥BC ,AD=4,DB=8,DE=3.(1)求AD AB的值; (2)求BC 的長. 6.如圖,M 為線段AB 的中點,AE 與BD 交於點C ,∠DME =∠A =∠B ,且DM 交AC 於F ,ME 交BC 於G .寫出圖中三對相似三角形,並證明其中的一對.7.(1)如圖①,AB ⊥BD ,CD ⊥BD ,垂足分別為B 、D ,AD 、BC 相交於E ,過E 作EF⊥BD ,問等式111AB CD EF+=成立嗎?請說明理由. (2)若將圖①中的垂直改為斜交,如圖②,AB ∥CD ,AD 、BC 相交於E ,過E 作EF ∥AB交BD 於F ,試問111AB CD EF +=還成立嗎?8.(創新應用)如下圖,在水準桌面上的兩個“E ”,當點P 1、P 2、O 在一條直線上時,在點O 處用①號“E ”測得的視力與用②號“E ”測得的視力相同.(1)圖中b 1、b 2、l 1、l 2滿足怎樣的關係式?(2)若b 1=3.2 cm ,b 2=2 cm ,①號“E ”的測試距離l 1=8 cm ,要使測得的視力相同,則②號“E ”的測試距離l 2應為多少?參考答案1解析:由平行線可得△ADF∽△ECF,△ECF∽△EBA,所以△ADF∽△EBA,共3對.答案:C2解析:∵點E、F分別是△ABC中AC、AB邊的中點,∴EF∥BC且EF=12 BC.∴△EFG∽△BCG.∴FG∶CG=EF∶BC=1∶2.由FG=2,得CG=4,∴CF=CG+FG=6.答案:D3解析:根據梯形的性質容易證明△AOD∽△COB,然後利用相似三角形的性質,即可得到13AO ADCO BC==.答案:B4答案:595解:(1)因為AD=4,DB=8,所以AB=AD+DB=4+8=12.所以41123ADAB==.(2)因為DE∥BC,所以△ADE∽△ABC.所以DE ADBC AB=.因為DE=3,所以313BC=.所以BC=9.6解:△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM(寫出兩對即可).以下證明△AMF∽△BGM.∵∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B,∴△AMF∽△BGM.7解:(1)成立.理由:∵AB⊥BD,EF⊥BD,∴AB∥EF.∴△DEF∽△DAB.∴EF DFAB DB=.又∵CD ⊥BD ,EF ⊥BD , ∴CD ∥EF .∴△BEF ∽△BCD . ∴EF BFCD DB =. ∴EF EF DF BF DBAB CD DB DB DB +=+==1. ∴111AB CD EF +=.(2)成立.證明過程類似(1),略. 8解:(1)∵P 1D 1∥P 2D 2, ∴△P 1D 1O ∽△P 2D 2O . ∴111222PD D OP D D O =, 即1122b l b l =.(2)∵1122b l b l =且b 1=3.2 cm ,b 2=2 cm ,l 1=8 cm ,23.282l =, ∴l 2=5(cm).答:(1)圖中b 1,b 2,l 1,l 2滿足關係式1122b l b l =;(2)②號“E ”的測試距離l 2為5 cm.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
判定1
一、选择题
1. 如图,下列条件中不能判定A C D A B C △∽△的是( ) (A)
A B A D B C
C D
=
(B)A D C A C B ∠=∠
(C)A C D B ∠=∠ (D)
2
AC AD AB =
2. 下列四组图形中不一定相似的是
. A.有一个角等于40
的两个等腰三角形
B.有一个角为50
的两个直角三角形
C.直角三角形被斜边上的高分成的两个直角三角形 D.有一个角是60 的两个等腰三角形
3. 能判定A B C △与A B C '''△相似的条件是 . A.
A B A C A B A C ='''' B.A B A B A C
A C ''=
'',且A C '∠=∠
C.
A B B C
A B A C =
''
''且B A '∠=∠
D.
A B A C
A B A C =
''''
,且B B '∠=∠
4. 如上图,D 为A B C △的边B C 上的一点,连接A D ,要使A B D C B A △∽△,应具备下列条件中的( ) A.
A C A
B
C D
B D
=
B.2
AB BD BC = C.
A B B C C D
A D
=
D.2
AC
CD CB =
5. 如图,若∠1=∠2=∠3,则图中相似的三角形有( ) A .1对 B .2对 C .3对 D .4对
6. 如图,AB ∥CD ,AE ∥FD ,则图中的相似三角形共有( )
A .2对
B .4对
C .6对
D .8对
7. Rt △ABC 中,∠ACB =90︒,CD ⊥AB ,DE ⊥AC ,D ,E 为垂足,那么,和△ABC 相似的三角形共有( ) A .1个 B .2个 C .3个 D .4个
8. 如图,矩形A B C D 中,D E A C E ⊥,为垂足,图中相似三角形共
有(全等除外)( ) A.3对 B.4对 C.5对 D.6对 9. 如图,A B C △中,90BAC ∠=
,A D 是B C 边上的高线,图中相似三角形 共有( ) A.2对 B.3对 C.4对 D.1对
10. 下列两个三角形相似的是( ) A.两个等腰三角形 B.两个直角三角形
C.两个等腰直角三角形 D.两个锐角三角形
12. 如图,在大小为4×4的正方形网格中,是相似三角形的是( ).
① ② ③ ④
A .①和②
B .②和③
C .①和③
D .②和④
13. 在矩形ABCD 中,E 、F 分别是CD 、BC 上的点,若∠AEF =90°, 则一定有( ).
A.ΔADE ∽ΔAEF
B.ΔECF ∽ΔAEF
C.ΔADE ∽ΔECF
D.ΔAEF ∽ΔABF 二、填空题
14. 如图,在A B C △中,点D E 、分别在边A C A B 、上,且
2
3
A E A D A C
A B =
=,若4D E =cm ,则B C = cm . 15.
在
A B C
△和
A B C '''
△中
,
326c m A A B A B A '''∠===∠=
,,,, 3cm A C =,5cm A C ''=,则A B C △与A B C '''△是否相似?
(填“是”或“不是”).
16. 如图,线段
A C
B D ,相交于点O ,要使
A O
B D O △∽△
,已具备条件 ,还需要补充的条件
是 ,或 或 .
18. △ABC 与△DEF 中,AB =3,BC =2,DE =6,EF =4,还需要∠ =∠ ,则△ABC ∽△ .
A
C
D
B
A
B
D
C
1 A B D C
E 2
3
A
B
C
D E
D
C
A
E
B C
D C
A
D
O
B
2
A
B C E
D F 19. 如图,平行四边形ABCD 中,
E 是BA 延长线上一点,EC 交AD 于
F , 交BD 于
G ,则△EAF ∽△ 或△ ,△FGD ∽△ .
20. 如图,点D 、E 在等边△ABC 的边AB 、BC 上,且AD =BE ,AE 、CD 相交于点F ,则△BCD ∽△ ∽△ . 21. 如图,
A B B C A C A D
D E
A E
=
=
,则∠BAD =∠ =∠ .
22. 如图,△ABC 中,∠A =90°,∠C =30°,N 是AB 的中点,MN ⊥BC 于M ,则可识别△BMN ∽△ ,相似比为 .
三、应用题
29. 如图,在ABC 中,AD=DB,∠1=∠2,试说明△ABC ∽△EAD.
30. 如图,已知△ABC 中,点F 是BC 的中点,
DE//BC
,则DG
和GE 有怎样的关系?请你说明理由.
E A B
C G F
D A B C
E D。
