2019年高考考试大纲总纲文科数学
2019年文数高考考试大纲

2019年文数高考考试大纲I.考核目标与要求根据普通高等学校对新生思想道德素质和科学文化素质的要求,依据中华人民共和国教育部2003年颁布的《普通高中课程方案(实验)》和《普通高中数学课程标准(实验)》的必修课程、选修课程系列1和系列4的内容,确定文史类高考数学科考试内容。
一、知识要求知识是指《普通高中数学课程标准(实验)》(以下简称《课程标准》)中所规定的必修课程、选修课程系列1和系列4中的数学概念、性质、法则、公式、公理、定理以及由其内容反映的数学思想方法,还包括按照一定程序与步骤进行运算、处理数据、绘制图表等基本技能。
各部分知识的整体要求及其定位参照《课程标准》相应模块的有关说明。
对知识的要求依次是了解、理解、掌握三个层次。
1。
了解:要求对所列知识的含义有初步的、感性的认识,知道这一知识内容是什么,按照一定的程序和步骤照样模仿,并能(或会)在有关的问题中识别和认识它。
这一层次所涉及的主要行为动词有:了解,知道、识别,模仿,会求、会解等。
2。
理解:要求对所列知识内容有较深刻的理性认识,知道知识间的逻辑关系,能够对所列知识做正确的描述说明并用数学语言表达,能够利用所学的知识内容对有关问题进行比较、判别、讨论,具备利用所学知识解决简单问题的能力。
这一层次所涉及的主要行为动词有:描述,说明,表达,推测、想象,比较、判别,初步应用等。
3。
掌握:要求能够对所列的知识内容进行推导证明,能够利用所学知识对问题进行分析、研究、讨论,并且加以解决。
这一层次所涉及的主要行为动词有:掌握、导出、分析,推导、证明,研究、讨论、运用、解决问题等。
二、能力要求能力是指空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识。
1.空间想象能力:能根据条件作出正确的图形,根据图形想象出直观形象;能正确地分析出图形中的基本元素及其相互关系;能对图形进行分解、组合;会运用图形与图表等手段形象地揭示问题的本质。
抢先看!2019年高考《考试大纲》数学学科详解读!

立德树人鲜明导向数学素养综合考查近日,教育部考试中心颁布了《2019年普通高等学校招生全国统一考试大纲》(以下简称《考试大纲》),从考核目标与要求、考试范围与要求等方面进行了详细阐述。
2019年山东高考数学卷将第二次使用全国新课标I卷,也是最后一年进行传统高考,2020年将全面实施新高考。
作为具有历史意义的关键性过渡年,研读《考试大纲》对教学和备考有着非常重要的意义。
一、考纲解读2019年《考试大纲》是依据普通高等学校对新生思想道德素质、科学文化素质的要求以及《普通高中课程标准》制定,较2018年文化素质的要求有所提升。
《考试大纲》在延续2018年指导思想、考核要求及考试范围方面要求的基础上,增加了对学生德智体美劳全面发展的考查。
仔细研读《考试大纲》,主要体现四个注重:(一)注重高考宗旨和功能全面贯彻党的教育方针,落实构建德智体美劳培养教育体系的要求,以立德树人为鲜明导向,以促进素质教育发展为基本遵循,科学构建基于德智体美劳全面发展要求的高考评价体系。
继续坚持“一核四层四翼”高考评价体系,继续明确“立德树人、服务选才、引导教学”这一高考核心功能;通过明确“必备知识、关键能力、学科素养、核心价值”四层考查内容以及“基础性、综合性、应用性、创新性”四个方面考查要求,回答了高考“考什么”和“怎么考”的问题。
(二)注重考查数学基础知识全面而又突出重点地对数学基础知识考查,增加支撑学科知识体系的重点内容,注重学科内在联系和知识综合性,深度考查知识网络的交汇点。
(三)注重考查数学学科的关键能力强调能力立意,注重知识的理解和应用,考查考生将知识迁移到不同情境中的能力。
强调综合性、应用性的同时,切合考生实际,并展现数学科学价值和人文价值,重视试题间的层次性,合理调控综合程度,坚持多角度、多层次的考查,促进学生德智体美劳全面发展。
(四)注重考查数学学科核心素养和数学思想新《课程标准》明确提出数学学科素养,2018年高考试题处处体现学科核心素养。
2019年高考数学考纲解读及二轮备考策略

1. 2019 年理科考试大纲
(1)考核目标与要求 ①知识要求;②能力要求;③个性品质要求;④考查要求 (2)考试范围与要求 ①集合;②指对幂函数;③立体几何;④平面解析几何;⑤算法初步;⑥ 统计;⑦概率;⑧三角函数及恒等变换;⑨平面向量;⑩解三角形;⑾不 等式;⑿常用逻辑用语;⒀圆锥曲线与方程;⒁空间向量与立体几何;⒂ 导数及其应用;⒃推理与证明;⒄数系扩充与复数的引入;⒅计数原理; ⒆坐标系与参数方程;⒇不等式选讲。
(3)易错题:来源于以往的作业和考试,突出纠错;
(4)模拟题:从各地模拟题中筛选。
2、编题:以新为主。适应、迁移、运用、指导
(1)改编题:用课本题、高考题、模拟题改编;
(2)原创题:如用“定义法”原创;
3、组题:以真为主。仿真、训练
(仿高考卷,难度设计上根据实际设计)
课
两大课型:专题复习课;试卷讲评课。
B(2, b) ,且 cos 2
1 A. 5
B.
2 ,则 | a b | 3
C.
5 5
2 5 5
D. 1
2 x , x 0, 例 3. [2018·全国卷Ⅰ文 12]设函数 f ( x ) 则满足 f ( x 1) f (2 x) 的 x 的取值范围是 1, x 0,
1.专题复习课:
(1)课堂容量问题;(2)讲练比例问题; (3)学生主体问题;(4)信息反馈问题。
2.试卷讲评课:
(1)对答案式讲评:别让“假象”蒙蔽眼睛! (2)一言堂式讲评:别因“封口”扼杀灵性! (3)就题论题式讲评:别因“时间紧”放弃变式! (4)缺乏提炼式讲评:别因“散打”寻不到规律! 策略:(1)讲评前要独立研做试卷; (2)通过调研制定讲评策略; (3)以学生的思维误区为基点分类讲评。
2019年高考大纲(总纲理数文数物理)仅总纲为原版

摘自教育部考试中心(中国教育考试网)总 纲普通高等学校招生全国统一考试(以下简称“高考”)是合格的高中毕业生和具有同等学力的考生参加的选拔性考试。
高等学校根据考生成绩,按照招生章程和计划,德智体美劳全面衡量,择优录取。
高考应具有较高的信度、效度,必要的区分度和适当的难度。
《普通高等学校招生全国统一考试大纲》(以下简称《考试大纲》)是高考命题的规范性文件和标准,是考试评价、复习备考的依据。
《考试大纲》明确了高考的性质和功能,规定了考试内容与形式,对实施高考内容改革、规范高考命题具有重要意义。
《考试大纲》依据普通高等学校对新生思想道德素质、科学文化素质的要求及《普通高中课程标准》制定。
《国务院关于深化考试招生制度改革的实施意见》明确提出深化高考考试内容改革,依据高校人才选拔要求和国家课程标准,科学设计命题内容,增强基础性、综合性,着重考查学生独立思考和运用所学知识分析问题、解决问题的能力。
高考考试内容改革全面贯彻党的教育方针,落实构建德智体美劳全面培养教育体系的要求,以立德树人为鲜明导向,以促进素质教育发展为基本遵循,科学构建基于德智体美劳全面发展要求的高考评价体系。
高考评价体系由“一核 四层 四翼”组成,包括考查目的、考查内容和考查要求。
“一核”为考查目的,即“立德树人、服务选才、引导教学”,是对素质教育中高考核心功能的概括,回答“为什么考”的问题;“四层”为考查内容,即“必备知识、关键能力、学科素养、核心价值”,是素质教育目标在高考中的提炼,回答高考“考什么”的问题;“四翼”为考查要求,即“基础性、综合性、应用性、创新性”,是素质教育评价维度在高考中的体现,回答高考“怎么考”的问题。
《考试大纲》是高考评价体系的具体实现,体现高考考试内容改革的方向和阶段性成果。
《考试大纲》是制定《考试说明》的依据。
各分省命题省份在《考试大纲》的基础上,可以结合本地高考方案和教学实际制订适用的《考试说明》。
《考试大纲》的解释权归 教育部考试中心。
2019年高考考试大纲及历届真题考点分布汇编(文数)可编辑
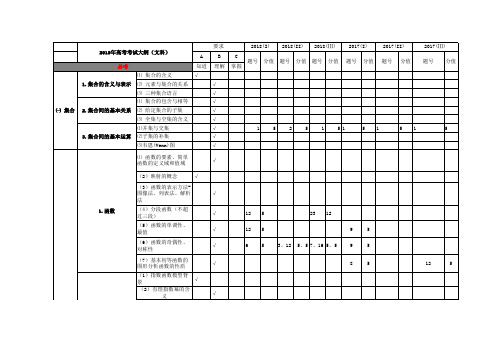
2018(I) 题号 分值
2018(II) 题号 分值
2018(Ⅲ) 题号 分值
2017(I) 题号 分值
2017(II) 题号 分值
2017(Ⅲ) 题号 分值
1
5
2
5
1
51
5
1
5
1
5
√ √ √ √
12 12 6
5 5 5 3、12
23
12 9 5 5 5 12 5
5、5 7、16 5、5
9 8
(二) 函数概念 与基本初 等函数Ⅰ
√
19(2)
6
18
12
√ √
√ 18 12
19(1)
6
1.事件与概率
5 √ √ 5 5
5
(七)概 率
2.古典概型
11
5
3.随机数与几何概型
√ 4 5
1.任意函 数Ⅱ(三 角函数)
2.三角函数
(3)画出三角函数的 图像 (4)三角函数的周期 性 (5)正弦、余弦函数 在[0,2π ]上的性质 (如单调性、最大值和 最小值、图像与x轴的 交点) (6)正切函数在区间 内的单调性 (7)同角三角函数的 基本关系式 (8)函数y=Asin(ω x +φ )的物理意义 (9)函数y=Asin(ω x +φ )的图形、性质 (10)参数A、ω 、φ 对函数图形变化的影响 (11)用三角函数解决 一些简单实际问题 (12)三角函数是描述 周期变化现象的重要函 数模型
3.空间直角坐标系
√ 1.算法的含义、程序框 (2)算法的思想 (3)程序框图的三种 图 (五)算 基本逻辑结构-顺序、 法初步 条件、循环 几种基本算法语句-输 2.基本算法语句 入、输出、赋值、条件 √ 、循环语句 (1)随机抽样的必要 性和重要性 1.随机抽样 (2)用简单随机抽样 方法从总体中抽取样本 (3)分层抽样和系统 抽样 √
高考新课标大纲及解读:数学(文)

2019年高考新课标大纲及解读:数学(文)2019年高考考试说明(课程标准实验版)数学(文)I.考试性质普通高等学校招生全国统一考试是合格的高中毕业生和具有同等学力的考生参加的选拔性考试.高等学校根据考生成绩.按己确定的招生计划。
德、智、体全面衡量.择优录取.因此.高考应具有较高的信度,效度,必要的区分度和适当的难度.Ⅱ.考试内容根据普通高等学校对新生文化素质的要求,依据中华人民共和国教育部2019年颁布的《普通搞好总课程方案(实验)》和《普通高中数学课程标准(实验)》的必修课程、选修课程系列1和系列4的内容,确定文史类高考数学科考试内容。
数学科考试,要发挥数学作为主要基础学科的作用,要考察考生对中学的基础知、基本技能的掌握程度,要考查考生对数学思想方法和数学本质的理解水平,要考察考生进入高等学校继续学习的潜能。
一、考核目标与要求1.知识要求知识是指《普通高中数学课程标准(实脸)》(以下简称《课程标准》)中所规定的必修课程、选修课程系列1和系列4中的数学概念、性质、法期、公式、公理、定理以及由其内容反映的数学思想方法,还包括按照一定程序与步孩进行运其。
处理数据、绘制图表等基本技能.各部分知识的整体要求及其定位参照《课程标准》相应模块的有关说明对知识的要求依次是了解、理解、掌握三个层次。
(1)了解:要求对所列知识的含义有初步的、感性的认识.知道这一知识内容是什么,按照一定的程序和步骤照样模仿,并能(或会)在有关的问题中识别和认识它.这一层次所涉及的主要行为动词有:了解,知道、识别,模仿,会求、会解等.(2)理解:要求对所列知识内容有较深刻的理性认识.知道知知识间的逻辑关系,能够对所列知识做正确的描述说明并用数学语言表达,能够利用所学的知识内容对有关问题进行比较、判别、讨论,具备利用所学知识解决简单问题的能力。
这一层次所涉及的主要行为动词有:描述,说明,表达,推测、想象。
比较、判断,初步应用等。
(3)掌握:要求能够对所列的知识内容进行推导证明,能够利用所学知识对问题进行分析、研究、讨论,并且加以解决。
高考大纲,2019高考大纲要求

高考大纲,2019高考大纲要求各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢2019年普通高等学校招生全国统一考试大纲:语文2019年普通高等学校招生全国统一考试大纲:文科数学2019年普通高等学校招生全国统一考试大纲正式公布:理科数学2019年普通高等学校招生全国统一考试大纲:英语英语考核目标与要求一、语言知识要求考生掌握并能运用英语语音、词汇、语法基础知识以及所学功能意念和话题,要求词汇量为3500左右。
二、语言运用1.听力要求考生能听懂所熟悉话题的简短独白和对话。
考生应能:理解主旨要义;获取具体的事实性信息;对所听内容做出推断;理解说话者的意图、观点和态度。
2.阅读要求考生能读懂书、报、杂志中关于一般性话题的简短文段以及公告、说明、广告等,并能从中获取相关信息。
考生应能:理解主旨要义;理解文中具体信息;根据上下文推断单词和短语的含义;做出判断和推理;理解文章的基本结构;理解作者的意图、观点和态度。
3.写作要求考生根据提示进行书面表达。
考生应能:清楚、连贯地传递信息,表达意思;有效运用所学语言知识。
4.口语要求考生根据提示进行口头表达。
考生应能:询问或传递事实性信息,表达意思和想法;做到语音、语调自然;做到语言运用得体;使用有效的交际策略。
附录1 语音项目表1. 基本读音(1) 26个字母的读音(2) 元音字母在重读音节中的读音(3) 元音字母在轻读音节中的读音(4) 元音字母组合在重读音节中的读音(5) 常见的元音字母组合在轻读音节中的读音(6) 辅音字母组合的读音(7) 辅音连缀的读音(8) 成节音的读音2. 重音(1) 单词重音(2) 句子重音3. 读音的变化(1) 连读(2) 失去爆破(3) 弱读(4) 同化4. 语调与节奏(1) 意群与停顿(2) 语调(3) 节奏5. 语音、语调、重音、节奏等在口语交流中的运用6. 朗诵和演讲中的语音技巧. 主要英语国家的英语语音差异附录2 语法项目表1. 名词(1) 可数名词及其单复数(2) 不可数名词(4) 名词所有格2. 代词(1) 人称代词(2) 物主代词(3) 反身代词(4) 指示代词(5) 不定代词(6) 疑问代词3. 数词(1) 基数词(2) 序数词4. 介词和介词短语5. 连词6. 形容词(比较级和最高级) . 副词(比较级和最高级)8. 冠词9. 动词(1) 动词的基本形式(2) 系动词(3) 及物动词和不及物动词(4) 助动词10. 时态(1) 一般现在时(2) 一般过去时(3) 一般将来时(4) 现在进行时(5) 过去进行时(6) 过去将来时(7) 将来进行时(8) 现在完成时(9) 过去完成时(10) 现在完成进行时11. 被动语态12. 非谓语动词(1) 动词不定式(2) 动词的-ing形式(3) 动词的-ed形式13. 构词法(1) 合成法(2) 派生法(3) 转化法(4) 缩写和简写14. 句子种类(1) 陈述句(2) 疑问句(3) 祈使句(4) 感叹句15. 句子成分(1) 主语(2) 谓语(3) 表语(4) 宾语(5) 定语(6) 状语(7) 补语16. 简单句的基本句型17. 主谓一致18. 并列复合句19. 主从复合句(1) 宾语从句(2) 状语从句(3) 定语从句(4) 主语从句(5) 表语从句20. 间接引语21. 省略22. 倒装23. 强调24. 虚拟语气附录3 功能意念项目表1. 社会交往(Social Communications)(1) 问候(Greetings)(2) 介绍(Introduction)(3) 告别(Farewells )(4) 感谢(Thanks )(5) 道歉(Apologies)(6) 邀请(Invitation)(7) 请求允许(Asking for permission)(8) 祝愿和祝贺(Expressing wishes and congratulations)(9) 提供帮助(Offering help)(10) 接受和拒绝(Acceptance and refusal)(11) 约会(Making appointments)(12) 打电话(Making telephone calls)(13) 就餐(Having meals)(14) 就医(Seeing the doctor)(15) 购物(Shopping)(16) 问路(Asking the way)(17) 谈论天气(Talking about weather)(18) 语言交际困难(Language difficulties in communication)(19) 提醒注意(Reminding)(20) 警告和禁止(Warning and prohibition)(21) 劝告(Advice)(22) 建议(Suggestions)2. 态度(Attitudes)(23) 同意和不同意(Agreement and disagreement)(24) 喜欢和不喜欢(Likes and dislikes)(25) 肯定和不肯定(Certainty and uncertainty)(26) 可能和不可能(Possibility and impossibility)(27) 能够和不能够(Ability and inability)(28) 偏爱和优先选择(Preference)(29) 意愿和打算(Intentions and plans)(30) 希望和愿望(Hopes and wishes)(31) 表扬和鼓励(Praise and encouragement)(32) 责备和抱怨(Blame and complaint)(33) 冷淡(Indifference)(34) 判断与评价(Judgement and evaluation)3. 情感(Emotions)(35) 高兴(Happiness)(36) 惊奇(Surprise)(37) 忧虑(Worries)(38) 安慰(Reassurance)(39) 满意(Satisfaction)(40) 遗憾(Regret)(41) 同情(Sympathy)(42) 恐惧(Fear)(43) 愤怒(Anger)4. 时间(Time)(44) 时刻(Point of time)(45) 时段(Duration)(46) 频度(Frequency)(47) 时序(Sequence)5. 空间(Space)(48) 位置(Position)(49) 方向(Direction)(50) 距离(Distance)6. 存在(Existence)(51) 存在与不存在(Existence and Non-existence). 特征(Features)(52) 形状(Shape)(53) 颜色(Colour)(54) 材料(Material)(55) 价格(Price)(56) 规格(Size)(57) 年龄(Age)8. 计量(Measurement)(58) 长度(Length)(59) 宽度(Width)(60) 高度(Height)(61) 数量(Number)9. 比较(Comparison)(62) 同级比较(Equal comparison)(63) 差别比较(Comparative and superlative)(64) 相似和差别(Similarity and difference)10. 逻辑关系(Logical relations)(65) 原因和结果(Cause and effect)(66) 目的(Purpose)11. 职业(Occupations)(67) 工作(Jobs)(68) 单位(Employer)10附录4 话题项目表1. 个人情况(Personal information)2. 家庭、朋友与周围的人(Family,friends and people around)3. 周围的环境(Personal environments)4. 日常活动(Daily routines)5. 学校生活(School life)6. 兴趣与爱好(Interests and hobbies). 个人感情(Emotions)8. 人际关系(Interpersonal relationships)9. 计划与愿望(Plans and intentions)10. 节假日活动(Festivals, holidays and celebrations)11. 购物(Shopping)12. 饮食(Food and drink)13. 健康(Health)14. 天气(Weather)15. 文娱与体育(Entertainment and sports)16. 旅游和交通(Travel and transport)17. 语言学习(Language learning)18. 自然(Nature)19. 世界与环境(The world and the environment)20. 科普知识与现代技术(Popular science and modern technology)21. 热点话题(Topical issues)22. 历史与地理(History and geography)23. 社会(Society)24. 文学与艺术(Literature and art)附录5 词汇表Aa(an) artabandon vability nable aabnormal aaboard prepabolish vabortion nabout ad & prepabove prep,a & ad abroad adabrupt a absence n absent a absolute a absorb v abstract a & n absurd a abundant a abuse v academic a & n academy n accelerate v accent naccept vaccess n & v accessible a accident n accommodation n accompany v accomplish vaccountant n accumulate v accuracy n accurate a accuse v accustomed a ache v & n achieve v achievement n acid a acknowledge v acquaintance n acquire v acquisition n acre nacross prep act n & v action n active a activity n actor nactual aacute aAD abbrad=advertisement n adapt v adaptation nadd vaddicted a addition n address n adequate aadjust v adjustment n administration n admirable a admire v admission nadmit v adolescence n adolescent a & n adopt vadult nadvance v & n advantage n adventure n advertise v advertisement n advice nadvise vadvocate vaffair naffect vaffection nafford vafraid aAfrica nAfrican a & nafter ad,prep & conj afternoon n afterward(s) ad again adagainst prepage n agency n agenda n agent n aggressive a ago ad agree v agreement n agricultural a agriculture n ahead adaid n & v AIDS naim n & v air naircraft n airline n airmail n airplane n airport n airspace n alarm n & valbum n alcohol n alcoholic a & n algebra nalike adalive aall ad,a & pron allergic aalley n allocate v allow v allowance n almost ad alone aalong ad & prep alongside ad aloud ad alphabet n already adalso ad alternative a although conjaltogether ad aluminium(Am aluminum) n always adam v(be)/am,/AM abbr amateur a amaze v amazing a ambassador n ambassadress n ambiguous a ambition n ambulance n America n among prep amount n & v ample aamuse v amusement n analyse vancestor n anchor v & n ancient aand conj anecdote n anger nangle nangry aanimal nankle n anniversary n announce v annoy vannual a another a & pron answer n & v ant nAntarctic a antique n anxiety n anxious aany pron & a anybody pron anyhow ad anyone pron anything pron anyway ad anywhere ad apart ad & a apartment n apologize v apology n apparent a appeal v & n appear v appearance n appendix n appetite n applaud v & n apple n applicant n application n apply vappoint v appointment n appreciate v appreciation n approach n & v appropriate a approval n approve v approximately ad apron narbitrary aarch narchitect n architecture n Arctic aare v(be)area nargue vargument narise(arose,arisen) v arithmetic narm n & varmchair narmy naround ad & prep arrange v arrangement n arrest varrival narrive varrow nart narticle n artificial aartist nas ad,conj & prep ash nashamed aAsia nAsian a & n aside adask vasleep aaspect nassess v assessment n assist v assistance n assistant n associate v association n assume v assumption n astonish v astronaut n astronomer n astronomy n at prep athlete n athletic a Atlantic a atmosphere n atom n attach v attack v & n attain vattempt v & nattend vattention nattitude nattract vattraction nattractive aaudience naunt nauthentic aauthor nauthority nautomatic aautonomous aautumn navailable aavenue naverage a & navoid vawake(awoke,awoken) v & a award naware aaway adawesome aawful aawkward a2019年普通高等学校招生全国统一考试大纲:物理2019年普通高等学校招生全国统一考试大纲:化学2019年普通高等学校招生全国统一考试大纲:地理Ⅰ. 考核目标与要求根据普通高等学校对新生思想道德素质和科学文化素质的要求,依据中华人民共和国教育部2003年颁布的《普通高中课程方案(实验)》和《普通高中地理课程标准(实验)》,确定高考地理科考核目标与要求。
普通高等学校招生全国统一考试数学(文)大纲

2019年普通高等学校招生全国统一考试数学(文)大纲2019年普通高等学校招生全国统一考试大纲数学(文)ⅰ.考试性质(略)ⅱ.考试要求(略)ⅲ.考试内容1.平面向量考试内容:向量.向量的加法与减法.实数与向量的积.平面向量的坐标表示.线段的定比分点.平面向量的数量积.平面两点间的距离、平移.考试要求:(1)理解向量的概念,掌握向量的几何表示,了解共线向量的概念.(2)掌握向量的加法和减法.(3)掌握实数与向量的积,理解两个向量共线的充要条件.(4)了解平面向量的基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算.(5)掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件.(6)掌握平面两点间的距离公式,以及线段的定比分点和中点坐标公式,并且能熟练运用.掌握平移公式.2.集合、简易逻辑考试内容:集合、子集、补集、交集、并集.逻辑联结词.四种命题.充分条件和必要条件.考试要求:(1)理解集合、子集、补订、交集、交集的概念.了解空集和全集的意义.了解属于、包含、相等关系的意义.掌握有关的术语和符号,并会用它们正确表示一些简单的集合.(2)理解逻辑联结词"或"、"且"、"非"的含义.理解四种命题及其相互关系.掌握充分条件、必要条件及充要条件的意义.3.函数考试内容:映射、函数、函数的单调性、奇偶性.反函数.互为反函数的函数图像间的关系.指数概念的扩充.有理指数幂的运算性质.指数函数.对数.对数的运算性质.对数函数.函数的应用.考试要求:(1)了解映射的概念,理解函数的概念.(2)了解函数的单调性、奇偶性的概念,掌握判断一些简单函数的单调性、奇偶性的方法.(3)了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数.(4)理解分数指数幂的概念,掌握有理指数幂的运算性质.掌握指数函数的概念、图像和性质.(5)理解对数的概念,掌握对数的运算性质.掌握对数函数的概念、图像和性质.(6)能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题.4.不等式不等式.不等式的基本性质.不等式的证明.不等式的解法.含绝对值的不等式.考试要求:(1)理解不等式的性质及其证明.(2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用.(3)掌握分析法、综合法、比较法证明简单的不等式.(4)掌握简单不等式的解法.(5)理解不等式|a|-|b|≤|a+b|≤|a|+|b|.5.三角函数考试内容:角的概念的推广.弧度制.任意角的三角函数.单位圆中的三角函数线.同角三角函数的基本关系式.正弦、余弦的诱导公式.两角和与差的正弦、余弦、正切.二倍角的正弦、余弦、正切.正弦函数、余弦函数的图像和性质.周期函数.函数y=asin(ωx+φ)的图像.正切函数的图像和性质.已知三角函数值求角.正弦定理.余弦定理.斜三角形解法.考试要求:(1)理解任意角的概念、弧度的意义.能正确地进行弧度与角度的换算.(2)掌握任意角的正弦、余弦、正切的定义.了解余切、正割、余割的定义.掌握同角三角函数的基本关系式sin2α+cos2α=1sinα/cosα=tanαtanαcotα=1.掌握正弦、余弦的诱导公式.了解周期函数与最小正周期的意义.(3)掌握两角和与两角差的正弦、余弦、正切公式.掌握二倍角的正弦、余弦、正切公式.(4)能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明.(5)了解正弦函数、余弦函数、正切函数的图像和性质,会用"五点法"画正弦函数、余弦函数和函数y=asin(ωx+φ)的简图,理解a,ω,φ的物理意义.(6)会由已知三角函数值求角,并会用符号arcsinx、arccosx、arctanx 表示.(7)掌握正弦定理、余弦定理,并能初步运用它们解斜三角形.6.数列考试内容:数列.等差数列及其通项公式.等差数列前n项和公式.等比数列及其通项公式.等比数列前n项和公式.考试要求:(1)理解数列的概念,了解数列通项公式的意义,了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项.(2)理解等差数列的概念,掌握等差数列的通项公式与前n项和公式,并能解决简单的实际问题.(3)理解等比数列的概念,掌握等比数列的通项公式与前n项和公式,并能解决简单的实际问题.7.直线和圆的方程考试内容:直线的倾斜角和斜率,直线方程的点斜式和两点式.直线方程的一般式.两条直线平行与垂直的条件.两条直线的交角.点到直线的距离.用二元一次不等式表示平面区域.简单的线性规划问题.曲线与方程的概念.由已知条件列出曲线方程.圆的标准方程和一般方程.圆的参数方程.考试要求:(1)理解直线的倾斜角和斜率的概念,掌握过两点的直线的斜率公式.掌握直线方程的点斜式、两点式、一般式,并能根据条件熟练地求出直线方程.(2)掌握两条直线平行与垂直的条件,两条直线所成的角和点到直线的距离公式.能够根据直线的方程判断两条直线的位置关系.(3)了解二元一次不等式表示平面区域.(4)了解线性规划的意义,并会简单的应用.(5)了解解析几何的基本思想,了解坐标法.(6)掌握圆的标准方程和一般方程,理解圆的参数方程.8.圆锥曲线方程考试内容:椭圆及其标准方程.椭圆的简单几何性质.椭圆的参数方程.双曲线及其标准方程.双曲线的简单几何性质.抛物线及其标准方程.抛物线的简单几何性质.考试要求:(1)掌握椭圆的定义、标准方程和椭圆的简单几何性质,理解椭圆的参数方程.(2)掌握双曲线的定义、标准方程和双曲线的简单几何性质.(3)掌握抛物线的定义、标准方程和抛物线的简单几何性质.(4)了解圆锥曲线的初步应用.9(a).①直线、平面、简单几何体平面及其基本性质.平面图形直观图的画法.平行直线.对应边分别平行的角.异面直线所成的角.异面直线的公垂线.异面直线的距离.直线和平面平行的判定与性质.直线和平面垂直的判定与性质.点到平面的距离.斜线在平面上的射影.直线和平面所成的角.三垂线定理及其逆定理.平行平面的判定与性质.平行平面间的距离.二面角及其平面角.两个平面垂直的判定与性质.多面体.正多面体.棱柱.棱锥.球.考试要求①考生可在9(a)和9(b)中任选其一.(1)掌握平面的基本性质,会用斜二测的画法画水平放置的平面图形的直观图.能够画出空间两条直线、直线和平面的各种位置关系的图形.能够根据图形想像它们的位置关系.(2)掌握两条直线平行与垂直的判定定理和性质定量.掌握两条直线所成的角和距离的概念,对于异面直线的距离,只要求会计算已给出公垂线时的距离.(3)掌握直线和平面平行的判定定理和性质定理.掌握直线和平面垂直的判定定理和性质定理.掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念.掌握三垂线定理及其逆定理.(4)掌握两个平面平行的判定定理和性质定理.掌握二面角、二面角的平面角、两个平行平面间的距离的概念.掌握两个平面垂直的判定定理和性质定理.(5)会用反证法证明简单的问题.(6)了解多面体、凸多面体的概念,了解正多面体的概念.(7)了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图.(8)了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图.(9)了解球的概念,掌握球的性质,掌握球的表面积、体积公式.9(b).直线、平面、简单几何体考试内容:平面及其基本性质.平面图形直观图的画法.平行直线.直线和平面平行的判定与性质.直线和平面垂直的判定.三垂线定理及其逆定理.两个平面的位置关系.空间向量及其加法、减法与数乘.空间向量的坐标表示.空间向量的数量积.直线的方向向量.异面直线所成的角.异面直线的公垂线.异面直线的距离.直线和平面垂直的性质.平面的法向量.点到平面的距离.直线和平面所成的角.向量在平面内的射影.平行平面的判定和性质.平行平面间的距离.二面角及其平面角.两个平面垂直的判定和性质.多面体.正多面体.棱柱.棱锥.球.考试要求:(1)掌握平面的基本性质,会用斜二测的画法画水平放置的平面图形的直观图;能够画出空间两条直线、直线和平面的各种位置关系的图形,能够根据图形想象它们的位置关系.(2)掌握直线和平面平行的判定定理和性质定理;掌握直线和平面垂直的判定定理;掌握三垂线定理及其逆定理.(3)理解空间向量的概念,掌握空间向量的加法、减法和数乘.(4)了解空间向量的基本定理;理解空间向量坐标的概念,掌握空间向量的坐标运算.(5)掌握空间向量的数量积的定义及其性质;掌握用直角坐标计算空间向量数量积的公式;掌握空间两点间距离公式.(6)理解直线的方向向量、平面的法向量、向量在平面内的射影等概念.(7)掌握直线和直线、直线和平面、平面和平面所成的角、距离的概念.对于异面直线的距离,只要求会计算已给出公垂线或在坐标表示下的距离.掌握直线和平面垂直的性质定理.掌握两个平面平行、垂直的判定定理和性质定理.(8)了解多面体、凸多面体的概念,了解正多面体的概念.(9)了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图.(10)了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图.(11)了解球的概念,掌握球的性质,掌握球的表面积、体积公式.10.排列、组合、二项式定理考试内容:分类计数原理与分步计数原理.排列.排列数公式.组合.组合数公式.组合数的两个性质.二项式定理.二项展开式的性质.考试要求:(1)掌握分类计数原理与分步计数原理,并能用它们分析睡解决一些简单的应用问题.(2)理解排列的意义,掌握排列数计算公式,并能用它解决一些简单的应用问题.(3)理解组合的意义,掌握排列数计算公式和组合数的性质,并能用它们解决一些简单的应用问题.(4)掌握二项式定理和二项展开式的性质,并能用它们计算和证明一些简单的问题.11.概率考试内容:随机事件的概率.等可能性事件的概率.互斥事件有一个发生的概率.相互独立事件同时发生的概率.独立重复试验.考试要求:(1)了解随机事件的发生存在着规律性和随机事件概率的意义.(2)了解等可能性事件的概率的意义,会用排列组合的基本公式计算一些等可能性事件的概率.(3)了解互斥事件与相互独立事件的意义,会用互斥事件的概率加法公式与相互独立事件的概率乘法公式计算一些事件的概率.(4)会计算事件在n次独立重复试验中恰好发生k次的概率.12.统计考试内容:抽样方法.总体分布的估计.总体期望值和方差的估计.考试要求:(1)了解随机抽样,了解分层抽样的意义,会用它们对简单实际问题进行抽样.(2)会用样本频率分布估计总体分布.(3)会用样本估计总体期望值和方差.13.导数考试内容:导数的背影.导数的概念.多项式函数的导数.利用导数研究函数的单调性和极值.函数的最大值和最小值.考试要求:(1)了解导数概念的实际背景.(2)理解导数的几何意义.(3)掌握函数的导数公式,会求多项式函数的导数.(4)理解极大值、极小值、最大值、最小值的概念,并会用导数求多项式函数的单调区间、极大值、极小值及闭区间上的最大值和最小值.(5)会利用导数求某些简单实际问题的最大值和最小值.ⅳ.考试表式与试卷结构考试采用闭卷、笔试形式.全卷满分为150分,考试时间为120分钟.要练说,得练听。
2019年全国高考大纲版数学(文)试卷及答案【精校版】

2019年普通高等学校统一考试(大纲)文科一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1) 设集合M={1,2,4,6,8},N={2,3,5,6,7},则MN 中元素的个数为( )A. 2B. 3C. 5D. 7 【答案】B(2)已知角α的终边经过点(-4,3),则cos α=( ) A.45 B. 35 C. -35 D. -45【答案】D (3)不等式组(2)01x x x +>⎧⎨<⎩的解集为( )A. {21}x x -<<-B. {10}x x -<<C. {01}x x <<D. {1}x x > 【答案】C(4)已知正四面体ABCD 中,E 是AB 的中点,则异面直线CE 与BD 所成角的余弦值为( )A.16 C. 13【答案】B(5)函数1)(x>-1)的反函数是( )A. 3(1)(1)x y e x =->- B. 3(1)(1)xy e x =->- C. 3(1)()x y e x R =-∈ D. 3(1)()xy e x R =-∈. 【答案】D(6)已知a 、b 为单位向量,其夹角为60︒,则(2a -b )·b =( )A. -1B. 0C. 1D.2 【答案】B(7)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )A. 60种B. 70种C. 75种D. 150种 【答案】C(8)设等比数列{a n }的前n 项和为S n ,若S 2=3,S 4=15,则S 6=( )A. 31B. 32C. 63D. 64 【答案】C(9)已知椭圆C :22221(0)x y a b a b+=>>的左右焦点为F 1,F 2离心率为3,过F 2的直线l 交C 与A 、B 两点,若△AF 1B 的周长为C 的方程为( )A.22132x y += B. 2213x y += C. 221128x y += D. 221124x y += 【答案】A(10)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积是( )A.814πB. 16πC. 9πD. 274π【答案】A(11)双曲线C:22221(0,0)x y a b a b-=>>的离心率为2C 的焦距等于( )A. 2B.【答案】C(12)奇函数f (x )的定义域为R ,若f(x+2)为偶函数,则f(1)=1,则f(8)+f(9)= ( )A. -2B.-1C. 0D. 1 【答案】D二、填空题:本大题共4个小题,每个小题5分。
2019年《高等数学》考试大纲.doc

《高等数学》考试大纲一、考试题型:单项选择题选题 8小题,每题4分,共32分填空题 6小题,每题4分,共24分解答题(包括证明题) 9小题,共94分二、考试内容:微积分学约60%微分方程与无穷级数约30%向量代数与空间解析几何约10%(一)函数、极限、连续考试内容:集合及其运算确界存在定理函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限和右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则:(单调有界准则和夹逼准)两个重要极限函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求:1.了解集合的上、下确界,理解确界存在定理,理解函数的概念,掌握函数的表示法,会建立应用问题的函数关系。
2.了解函数的有界性、单调性、周期性和奇偶性。
3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念。
4.掌握基本初等函数的性质及其图形,了解初等函数的概念。
5.了解数列极限和函数极限(包括左极限与右极限)的概念。
6.了解极限的性质与极限存在的两个准则,掌握极限的四则运算法则,掌握利用两个重要极限求极限的方法。
7.理解无穷小的概念和基本性质,掌握无穷小量的比较方法,了解无穷大量的概念及其与无穷小量的关系。
8.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型。
9.了解连续函数的性质和初等函数的连续性,了解函数的一致连续性理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理、一致连续),并会应用这些性质。
(二)一元函数微分学考试内容:导数和微分的概念导数的几何意义和经济意义函数的可导性与连续性之间的关系平面曲线的切线与法线导数和微分的四则运算基本初等函数的导数复合函数.反函数和隐函数的微分法高阶导数一阶微分形式的不变性 微分中值定理 洛必达(L'Hospital )法则 函数单调性的判别 函数的极值 函数图形的凹凸性、拐点及渐近线 函数图形的描绘 函数的最大值与最小值考试要求:1.理解导数的概念及可导性与连续性之间的关系,了解导数的几何意义与经济意义(含边际与弹性的概念),会求平面曲线的切线方程和法线方程。
2019年高考试题-文科数学(全国卷大纲版)解析版1

2019年高考试题-文科数学(全国卷大纲版)解析版1注意事项:认真阅读理解,结合历年的真题,总结经验,查找不足!重在审题,多思考,多理解!无论是单选、多选还是论述题,最重要的就是看清题意。
在论述题中,问题大多具有委婉性,尤其是历年真题部分,在给考生较大发挥空间的同时也大大增加了考试难度。
考生要认真阅读题目中提供的有限材料,明确考察要点,最大限度的挖掘材料中的有效信息,建议考生答题时用笔将重点勾画出来,方便反复细读。
只有经过仔细推敲,揣摩命题老师的意图,积极联想知识点,分析答题角度,才能够将考点锁定,明确题意。
数学〔文科〕【一】选择题:本大题共12小题,每题5分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的.〔1〕设集合{}{}1,2,3,4,5,1,2,u U A A ===集合则ð〔A 〕{}1,2〔B 〕{}3,4,5〔C 〕{}1,2,3,4,5〔D 〕∅〔2〕a 是第二象限角,5sin ,cos 13a a ==则 〔A 〕1213-〔B 〕513-〔C 〕513〔D 〕1213〔3〕向量()()()()1,1,2,2,,=m n m n m n λλλ=+=++⊥-若则〔A 〕4-〔B 〕3-〔C 〕-2〔D 〕-1〔4〕不等式222x -<的解集是〔A 〕()-1,1〔B 〕()-2,2〔C 〕()()-1,00,1〔D 〕()()-2,00,2〔5〕()862x x +的展开式中的系数是〔A 〕28〔B 〕56〔C 〕112〔D 〕224〔6〕函数()()()-121log 10=f x x f x x ⎛⎫=+> ⎪⎝⎭的反函数 〔A 〕()1021x x >-〔B 〕()1021xx ≠-〔C 〕()21x x R -∈〔D 〕()210xx ->〔7〕数列{}n a 满足{}12430,,103n n n a a a a ++==-则的前项和等于〔A 〕()-10-61-3〔B 〕()-1011-39〔C 〕()-1031-3〔D 〕()-1031+3〔8〕()()1221,0,1,0,F F C F x -是椭圆的两个焦点过且垂直于轴的直线交于 A B 、两点,且3AB =,那么C 的方程为(A )2212x y +=〔B 〕22132x y +=〔C 〕22143x y +=〔D 〕22154x y +=〔9〕假设函数()()sin 0=y x ωϕωω=+>的部分图像如图,则 〔A 〕5〔B 〕4〔C 〕3〔D 〕2〔10〕曲线()421-128=y x ax a a =+++在点,处切线的斜率为,〔A 〕9〔B 〕6〔C 〕-9〔D 〕-6〔11〕正四棱锥1111112,ABCD A B C D AA AB CD BDC -=中,则与平面所成角的正弦值等于〔A 〕23〔B 〕3〔C 〕3〔D 〕13〔12〕抛物线()2:82,2,C C y x M k C =-与点过的焦点,且斜率为的直线与交于,0,A B MA MB k ==两点,若则(A )12〔B 〕2〔C 〔D 〕2【二】填空题:本大题共4小题,每题5分.〔13〕设()[)()21,3=f x x f x ∈是以为周期的函数,且当时,.(14)从进入决赛的6名选手中决出1名一等奖,2名二等奖,3名三等奖,那么可能的决赛结果共有种.〔用数字作答〕〔15〕假设x y 、满足约束条件0,34,34,x x y x y ≥⎧⎪+≥⎨⎪+≤⎩那么z x y =-+的最小值为.(16)圆O 和圆K 是球O 的大圆和小圆,其公共弦长等于球O 的半径,3602OK O K =,且圆与圆所在的平面所成角为,那么球O 的表面积等于.【三】解答题:解答应写出文字说明、证明过程或演算步骤.17、〔本小题总分值10分〕等差数列{}n a 中,71994,2,a a a ==〔I 〕求{}n a 的通项公式;〔II 〕设{}1,.n n n nb b n S na =求数列的前项和18、〔本小题总分值12分〕设()(),,,,,.ABC A B C a b c a b c a b c ac ∆++-+=的内角的对边分别为 〔I 〕求;B〔II 〕假设sin sin C.A C =求19、〔本小题总分值12分〕如图,四棱锥902,P ABCD ABC BAD BC AD PAB PAD -∠=∠==∆∆中,,与都是边长为2的等边三角形.〔I 〕证明:;PB CD ⊥〔II 〕求点.A PCD 到平面的距离20、〔本小题总分值12分〕甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率均为1,2各局比赛的结果都相互独立,第1局甲当裁判.〔I〕求第4局甲当裁判的概率;〔II〕求前4局中乙恰好当1次裁判概率.21、〔本小题总分值12分〕函数()32=33 1.f x x ax x +++〔I 〕求()f ;a x =的单调性;〔II 〕假设[)()2,0,.x f x a ∈+∞≥时,求的取值范围22、〔本小题总分值12分〕双曲线()221222:10,0x y C a b F F a b-=>>的左、右焦点分别为,,离心率为3,直线2y C =与〔I 〕求,;a b ;〔II 〕2F l C A B 设过的直线与的左、右两支分别相交于、两点,且 11,AF BF -证明:22.AF AB BF 、、成等比数列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
文科数学Ⅰ.考核目标与要求根据普通高等学校对新生思想道德素质和科学文化素质的要求,依据中华人民共和国教育部2003年颁布的《普通高中课程方案(实验)》和《普通高中数学课程标准(实验)》的必修课程、选修课程系列1和系列4的内容,确定文史类高考数学科考试内容.一、知识要求知识是指《普通高中数学课程标准(实验)》(以下简称《课程标准》)中所规定的必修课程、选修课程系列1和系列4中的数学概念、性质、法则、公式、公理、定理以及由其内容反映的数学思想方法,还包括按照一定程序与步骤进行运算、处理数据、绘制图表等基本技能.各部分知识的整体要求及其定位参照《课程标准》相应模块的有关说明.对知识的要求依次是了解、理解、掌握三个层次.1.了解:要求对所列知识的含义有初步的、感性的认识,知道这一知识内容是什么,按照一定的程序和步骤照样模仿,并能(或会)在有关的问题中识别和认识它.这一层次所涉及的主要行为动词有:了解,知道、识别,模仿,会求、会解等.2.理解:要求对所列知识内容有较深刻的理性认识,知道知识间的逻辑关系,能够对所列知识做正确的描述说明并用数学语言表达,能够利用所学的知识内容对有关问题进行比较、判别、讨论,具备利用所学知识解决简单问题的能力.这一层次所涉及的主要行为动词有:描述,说明,表达,推测、想象,比较、判别,初步应用等.3.掌握:要求能够对所列的知识内容进行推导证明,能够利用所学知识对问题进行分析、研究、讨论,并且加以解决.这一层次所涉及的主要行为动词有:掌握、导出、分析,推导、证明,研究、讨论、运用、解决问题等.二、能力要求能力是指空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识.1.空间想象能力:能根据条件作出正确的图形,根据图形想象出直观形象;能正确地分析出图形中的基本元素及其相互关系;能对图形进行分解、组合;会运用图形与图表等手段形象地揭示问题的本质.空间想象能力是对空间形式的观察、分析、抽象的能力,主要表现为识图、画图和对图形的想象能力.识图是指观察研究所给图形中几何元素之间的相互关系;画图是指将文字语言和符号语言转化为图形语言以及对图形添加辅助图形或对图形进行各种变换;对图形的想象主要包括有图想图和无图想图两种,是空间想象能力高层次的标志.2.抽象概括能力:抽象是指舍弃事物非本质的属性,揭示其本质的属性;概括是指把仅仅属于某一类对象的共同属性区分出来的思维过程.抽象和概括是相互联系的,没有抽象就不可能有概括,而概括必须在抽象的基础上得出某种观点或某个结论.抽象概括能力是对具体的、生动的实例,经过分析提炼,发现研究对象的本质;从给定的大量信息材料中概括出一些结论,并能将其应用于解决问题或做出新的判断.3.推理论证能力:推理是思维的基本形式之一,它由前提和结论两部分组成;论证是由已有的正确的前提到被论证的结论的一连串的推理过程.推理既包括演绎推理,也包括合情推理;论证方法既包括按形式划分的演绎法和归纳法,也包括按思考方法划分的直接证法和间接证法.一般运用合情推理进行猜想,再运用演绎推理进行证明.中学数学的推理论证能力是根据已知的事实和已获得的正确数学命题,论证某一数学命题真实性的初步的推理能力.4.运算求解能力:会根据法则、公式进行正确运算、变形和数据处理,能根据问题的条件寻找与设计合理、简捷的运算途径,能根据要求对数据进行估计和近似计算.运算求解能力是思维能力和运算技能的结合.运算包括对数字的计算、估值和近似计算,对式子的组合变形与分解变形,对几何图形各几何量的计算求解等.运算能力包括分析运算条件、探究运算方向、选择运算公式、确定运算程序等一系列过程中的思维能力,也包括在实施运算过程中遇到障碍而调整运算的能力.5.数据处理能力:会收集、整理、分析数据,能从大量数据中抽取对研究问题有用的信息,并做出判断.数据处理能力主要是指针对研究对象的特殊性,选择合理的收集数据的方法,根据问题的具体情况,选择合适的统计方法整理数据,并构建模型对数据进行分析、推断,获得结论.6.应用意识:能综合应用所学数学知识、思想和方法解决问题,包括解决相关学科、生产、生活中简单的数学问题;能理解对问题陈述的材料,并对所提供的信息资料进行归纳、整理和分类,将实际问题抽象为数学问题;能应用相关的数学方法解决问题进而加以验证,并能用数学语言正确地表达和说明.应用的主要过程是依据现实的生活背景,提炼相关的数量关系,将现实问题转化为数学问题,构造数学模型,并加以解决.7.创新意识:能发现问题、提出问题,综合与灵活地应用所学的数学知识、思想方法,选择有效的方法和手段分析信息,进行独立的思考、探索和研究,提出解决问题的思路,创造性地解决问题.创新意识是理性思维的高层次表现.对数学问题的“观察、猜测、抽象、概括、证明”,是发现问题和解决问题的重要途径,对数学知识的迁移、组合、融会的程度越高,显示出的创新意识也就越强.三、个性品质要求个性品质是指考生个体的情感、态度和价值观.要求考生具有一定的数学视野,认识数学的科学价值和人文价值,崇尚数学的理性精神,形成审慎的思维习惯,体会数学的美学意义.要求考生克服紧张情绪,以平和的心态参加考试,合理支配考试时间,以实事求是的科学态度解答试题,树立战胜困难的信心,体现锲而不舍的精神.四、考查要求数学学科的系统性和严密性决定了数学知识之间深刻的内在联系,包括各部分知识的纵向联系和横向联系,要善于从本质上抓住这些联系,进而通过分类、梳理、综合,构建数学试卷的框架结构.1.对数学基础知识的考查,既要全面又要突出重点.对于支撑学科知识体系的重点内容,要占有较大的比例,构成数学试卷的主体.注重学科的内在联系和知识的综合性,不刻意追求知识的覆盖面.从学科的整体高度和思维价值的高度考虑问题,在知识网络的交汇点处设计试题,使对数学基础知识的考查达到必要的深度.2.对数学思想方法的考查是对数学知识在更高层次上的抽象和概括的考查,考查时必须要与数学知识相结合,通过对数学知识的考查,反映考生对数学思想方法的掌握程度.3.对数学能力的考查,强调“以能力立意”,就是以数学知识为载体,从问题入手,把握学科的整体意义,用统一的数学观点组织材料,侧重体现对知识的理解和应用,尤其是综合和灵活的应用,以此来检测考生将知识迁移到不同情境中去的能力,从而检测出考生个体理性思维的广度和深度以及进一步学习的潜能.对能力的考查要全面,强调综合性、应用性,并要切合考生实际.对推理论证能力和抽象概括能力的考查贯穿于全卷,是考查的重点,强调其科学性、严谨性、抽象性;对空间想象能力的考查主要体现在对文字语言、符号语言及图形语言的互相转化上;对运算求解能力的考查主要是对算法和推理的考查,考查以代数运算为主;对数据处理能力的考查主要是考查运用概率统计的基本方法和思想解决实际问题的能力.4.对应用意识的考查主要采用解决应用问题的形式.命题时要坚持“贴近生活,背景公平,控制难度”的原则,试题设计要切合中学数学教学的实际和考生的年龄特点,并结合实践经验,使数学应用问题的难度符合考生的水平.5.对创新意识的考查是对高层次理性思维的考查.在考试中创设新颖的问题情境,构造有一定深度和广度的数学问题时,要注重问题的多样化,体现思维的发散性;精心设计考查数学主体内容,体现数学素质的试题;也要有反映数、形运动变化的试题以及研究型、探索型、开放型等类型的试题.数学科的命题,在考查基础知识的基础上,注重对数学思想方法的考查,注重对数学能力的考查,展现数学的科学价值和人文价值,同时兼顾试题的基础性、综合性和应用性,重视试题间的层次性,合理调控综合程度,坚持多角度、多层次的考查,努力实现全面考查综合数学素养的要求,促进学生德智体美劳全面发展.Ⅱ.考试范围与要求本部分包括必考内容和选考内容两部分.必考内容为《课程标准》的必修内容和选修系列1的内容;选考内容为《课程标准》的选修系列4的“坐标系与参数方程”、“不等式选讲”等2个专题.必考内容(一)集合1.集合的含义与表示(1)了解集合的含义、元素与集合的属于关系.(2)能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.2.集合间的基本关系(1)理解集合之间包含与相等的含义,能识别给定集合的子集.(2)在具体情境中,了解全集与空集的含义.3.集合的基本运算(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集.(3)能使用韦恩(Venn)图表达集合的关系及运算.(二)函数概念与基本初等函数Ⅰ(指数函数、对数函数、幂函数)1.函数(1)了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念.(2)在实际情境中,会根据不同的需要选择恰当的方法(如图像法、列表法、解析法)表示函数.(3)了解简单的分段函数,并能简单应用.(4)理解函数的单调性、最大值、最小值及其几何意义;结合具体函数,了解函数奇偶性的含义.(5)会运用函数图像理解和研究函数的性质.2.指数函数(1)了解指数函数模型的实际背景.(2)理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.(3)理解指数函数的概念,理解指数函数的单调性,掌握指数函数图像通过的特殊点.(4)知道指数函数是一类重要的函数模型.3.对数函数(1)理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用.(2)理解对数函数的概念,理解对数函数的单调性,掌握对数函数图像通过的特殊点.(3)知道对数函数是一类重要的函数模型.(4)了解指数函数x y a =与对数函数log a y x =互为反函数(0a >,且1a ≠).4.幂函数(1)了解幂函数的概念.(2)结合函数y x =,2y x =,3y x =,1y x=,12y x =的图像,了解它们的变化情况. 5.函数与方程 (1) 结合二次函数的图像,了解函数的零点与方程根的联系,判断一元二次方程根的存在性及根的个数.(2)根据具体函数的图像,能够用二分法求相应方程的近似解.6.函数模型及其应用(1)了解指数函数、对数函数以及幂函数的增长特征,知道直线上升、指数增长、对数增长等不同函数类型增长的含义.(2)了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.(三) 立体几何初步1.空间几何体(1)认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.(2)能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述三视图所表示的立体模型,会用斜二侧法画出它们的直观图.(3)会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.(4)会画某些建筑物的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不做严格要求).(5)了解球、棱柱、棱锥、台的表面积和体积的计算公式.2.点、直线、平面之间的位置关系(1)理解空间直线、平面位置关系的定义,并了解如下可以作为推理依据的公理和定理. • 公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内. • 公理2:过不在同一条直线上的三点,有且只有一个平面.• 公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.• 公理4:平行于同一条直线的两条直线互相平行.• 定理:空间中如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.(2)以立体几何的上述定义、公理和定理为出发点,认识和理解空间中线面平行、垂直的有关性质与判定定理.理解以下判定定理.• 如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.• 如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行.• 如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.• 如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直.理解以下性质定理,并能够证明.• 如果一条直线与一个平面平行,那么经过该直线的任一个平面与此平面的交线和该直线平行.• 如果两个平行平面同时和第三个平面相交,那么它们的交线相互平行.• 垂直于同一个平面的两条直线平行.• 如果两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直.(3)能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题.(四)平面解析几何初步1.直线与方程(1)在平面直角坐标系中,结合具体图形,确定直线位置的几何要素.(2)理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式.(3)能根据两条直线的斜率判定这两条直线平行或垂直.(4)掌握确定直线位置的几何要素,掌握直线方程的几种形式(点斜式、两点式及一般式),了解斜截式与一次函数的关系.(5)能用解方程组的方法求两条相交直线的交点坐标.(6)掌握两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离.2.圆与方程(1)掌握确定圆的几何要素,掌握圆的标准方程与一般方程.(2)能根据给定直线、圆的方程判断直线与圆的位置关系;能根据给定两个圆的方程判断两圆的位置关系.(3)能用直线和圆的方程解决一些简单的问题.(4)初步了解用代数方法处理几何问题的思想.3.空间直角坐标系(1)了解空间直角坐标系,会用空间直角坐标表示点的位置.(2)会推导空间两点间的距离公式.(五)算法初步1.算法的含义、程序框图(1)了解算法的含义,了解算法的思想.(2)理解程序框图的三种基本逻辑结构:顺序、条件分支、循环.2.基本算法语句理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.(六) 统计1.随机抽样(1)理解随机抽样的必要性和重要性.(2)会用简单随机抽样方法从总体中抽取样本;了解分层抽样和系统抽样方法.2.用样本估计总体(1)了解分布的意义和作用,会列频率分布表,会画频率分布直方图、频率折线图、茎叶图,理解它们各自的特点.(2)理解样本数据标准差的意义和作用,会计算数据标准差.(3)能从样本数据中提取基本的数字特征(如平均数、标准差),并给出合理的解释.(4)会用样本的频率分布估计总体分布,会用样本的基本数字特征估计总体的基本数字特征,理解用样本估计总体的思想.(5)会用随机抽样的基本方法和样本估计总体的思想解决一些简单的实际问题.3.变量的相关性(1)会作两个有关联变量的数据的散点图,会利用散点图认识变量间的相关关系.(2)了解最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程.(七) 概率1.事件与概率(1)了解随机事件发生的不确定性和频率的稳定性,了解概率的意义,了解频率与概率的区别.(2)了解两个互斥事件的概率加法公式.2.古典概型(1)理解古典概型及其概率计算公式.(2)会用列举法计算一些随机事件所含的基本事件数及事件发生的概率.3.随机数与几何概型(1)了解随机数的意义,能运用模拟方法估计概率.(2)了解几何概型的意义.(八) 基本初等函数Ⅱ(三角函数)1.任意角的概念、弧度制(1)了解任意角的概念.(2)了解弧度制的概念,能进行弧度与角度的互化.2.三角函数(1)理解任意角三角函数(正弦、余弦、正切)的定义.(2)能利用单位圆中的三角函数线推导出π2α±,πα±的正弦、余弦、正切的诱导公式,能画出sin y x =,cos y x =,tan y x =的图像,了解三角函数的周期性.(3)理解正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最小值以及与x 轴的交点等),理解正切函数在区间ππ,22⎛⎫- ⎪⎝⎭内的单调性. (4)理解同角三角函数的基本关系式:22sin cos 1x x +=,sin tan cos x x x=.(5)了解函数sin()y A x ωϕ=+的物理意义;能画出sin()y A x ωϕ=+的图像,了解参数A ,ω,ϕ对函数图像变化的影响.(6)了解三角函数是描述周期变化现象的重要函数模型,会用三角函数解决一些简单实际问题.(九) 平面向量1.平面向量的实际背景及基本概念(1)了解向量的实际背景.(2)理解平面向量的概念,理解两个向量相等的含义.(3)理解向量的几何表示.2.向量的线性运算(1)掌握向量加法、减法的运算,并理解其几何意义.(2)掌握向量数乘的运算及其几何意义,理解两个向量共线的含义.(3)了解向量线性运算的性质及其几何意义.3.平面向量的基本定理及坐标表示(1)了解平面向量的基本定理及其意义.(2)掌握平面向量的正交分解及其坐标表示.(3)会用坐标表示平面向量的加法、减法与数乘运算.(4)理解用坐标表示的平面向量共线的条件.4.平面向量的数量积(1)理解平面向量数量积的含义及其物理意义.(2)了解平面向量的数量积与向量投影的关系.(3)掌握数量积的坐标表达式,会进行平面向量数量积的运算.(4)能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.5.向量的应用(1)会用向量方法解决某些简单的平面几何问题.(2)会用向量方法解决简单的力学问题与其他一些实际问题.(十) 三角恒等变换1.和与差的三角函数公式(1)会用向量的数量积推导出两角差的余弦公式.(2)能利用两角差的余弦公式导出两角差的正弦、正切公式.(3)能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式,导出二倍角的正弦、余弦、正切公式,了解它们的内在联系.2.简单的三角恒等变换能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但对这三组公式不要求记忆).(十一)解三角形1.正弦定理和余弦定理掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.2.应用能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.(十二)数列1.数列的概念和简单表示法(1)了解数列的概念和几种简单的表示方法(列表、图像、通项公式).(2)了解数列是自变量为正整数的一类函数.2.等差数列、等比数列(1)理解等差数列、等比数列的概念.(2)掌握等差数列、等比数列的通项公式与前n 项和公式.(3)能在具体的问题情境中识别数列的等差关系或等比关系,并能用有关知识解决相应的问题.(4)了解等差数列与一次函数、等比数列与指数函数的关系.(十三)不等式1.不等关系了解现实世界和日常生活中的不等关系,了解不等式(组)的实际背景.2.一元二次不等式(1)会从实际情境中抽象出一元二次不等式模型.(2)通过函数图像了解一元二次不等式与相应的二次函数、一元二次方程的联系.(3)会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.3.二元一次不等式组与简单线性规划问题(1)会从实际情境中抽象出二元一次不等式组.(2)了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组.(3)会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.4.基本不等式:2a b (0,0)a b ≥≥ (1)了解基本不等式的证明过程.(2)会用基本不等式解决简单的最大(小)值问题.(十四)常用逻辑用语1.命题及其关系(1)理解命题的概念.(2)了解“若p ,则q ”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系.(3)理解必要条件、充分条件与充要条件的意义.2.简单的逻辑联结词了解逻辑联结词“或”、“且”、“非”的含义.3.全称量词与存在量词(1)理解全称量词与存在量词的意义.(2)能正确地对含有一个量词的命题进行否定.(十五)圆锥曲线与方程(1)了解圆锥曲线的实际背景,了解圆锥曲线在刻画现实世界和解决实际问题中的作用.(2)掌握椭圆的定义、几何图形、标准方程及简单几何性质.(3)了解双曲线、抛物线的定义、几何图形和标准方程,知道它们的简单几何性质.(4)理解数形结合的思想.(5)了解圆锥曲线的简单应用.(十六)导数及其应用1.导数概念及其几何意义(1)了解导数概念的实际背景.(2)理解导数的几何意义.2.导数的运算(1)能根据导数定义求函数y C = (C 为常数), y x =,2y x =,1y x =的导数. (2)能利用下面给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数.• 常见基本初等函数的导数公式:()0C '= (C 为常数); 1()n n x nx -'=,n +∈N ;(sin )cos x x '=;(cos )sin x x '=-;(e )e x x '=;()ln x x a a a '= (0a >,且1a ≠);1(ln )x x '=;1(log )log e a a x x'= (0a >,且1a ≠). • 常用的导数运算法则:法则1: [()()]()()u x v x u x v x '''±=±.法则2: [()()]()()()()u x v x u x v x u x v x '''=+.法则3: 2()()()()()()()u x u x v x u x v x v x v x '''⎡⎤-=⎢⎥⎣⎦(()0v x ≠). 3.导数在研究函数中的应用(1)了解函数单调性和导数的关系;能利用导数研究函数的单调性,会求函数的单调区间(其中多项式函数一般不超过三次).(2)了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值(其中多项式函数一般不超过三次);会求闭区间上函数的最大值、最小值(其中多项式函数一般不超过三次).4.生活中的优化问题.会利用导数解决某些实际问题.(十七)统计案例了解下列一些常见的统计方法,并能应用这些方法解决一些实际问题.1.独立性检验了解独立性检验(只要求2×2列联表)的基本思想、方法及其简单应用.2.回归分析了解回归分析的基本思想、方法及其简单应用.(十八)推理与证明1.合情推理与演绎推理(1)了解合情推理的含义,能利用归纳和类比等进行简单的推理,了解合情推理在数学发现中的作用.(2)了解演绎推理的重要性,掌握演绎推理的基本模式,并能运用它们进行一些简单推理.(3)了解合情推理和演绎推理之间的联系和差异.2.直接证明与间接证明(1)了解直接证明的两种基本方法——分析法和综合法;了解分析法和综合法的思考过程、特点.(2)了解间接证明的一种基本方法——反证法;了解反证法的思考过程、特点.。
