山东省高三数学 各地市最新模拟试题精品分类汇编 专题13 概率统计 理(教师版)
山东省各大市 高三数学 1、3月模拟题分类汇编 专题 集合-经典通用宝藏文档

山东省各大市2013届高三1、3月模拟题数学(理)分类汇编专题 集合2013.04.06(济南市2013届高三3月一模 理科)1.已知全集R U =,集合{}21x A x =>,{}2340B x x x =-->,则A B ⋂=A .{}0x x >B .{}10x x x <->或C .{}4x x >D .{}14x x -≤≤(文登市2013届高三3月一模 理科)2.已知集合11,2A ⎧⎫=-⎨⎬⎩⎭,{}01=-=mx x B ,若B B A = ,则一切实数m 组成的集合是A .{}0,1,2-B .1,0,12⎧⎫-⎨⎬⎩⎭ C .{}1,2- D . 11,0,2⎧⎫-⎨⎬⎩⎭ A (淄博市2013届高三3月一模 理科)(2)(理)已知集合{}250M x x x =-<,{}6N x p x =<< ,且{}2MN x x q =<<,则p q += (A ) 6 (B ) 7 (C ) 8 (D )9(淄博市2013届高三期末 理科)1.全集U=R ,集合{}02|2≥+=x x x A ,则[U A=A .[]0,2-B .()0,2-C .(][)+∞⋃-∞-,02,D .[]2,0 【答案】B【 解析】{}2|20{02}A x x x x x x =+≥=><-或,所以{20}U A x x =-<<,所以选B.(青岛市2013届高三期末 理科)2.设全集,}6,5,4,3,2,1{=U 集合=⋂==)(}5,4,3{},4,3,2,1{Q C P Q P U ,则,A.{1,2,3,4,6}B.{1,2,3,4,5}C.{1,2,5}D.{1,2}【答案】D【 解析】{1,2,6}U Q =,所以(){1,2}U P C Q ⋂==,所以选D.(德州市2013届高三期末 理科)1.已知全集U={l ,2,3,4,5,6},集合A={l ,2.4:6},集合B={l ,3,5},则U A B ( )A .{l,2,3,4,5,6}B .{1,2,4,6}C .{2,4,6}D .{2,3,4,5,6} 【答案】B【 解析】{2,4,6}U B =,所以{1,2,4,6}U A B =,选B.(威海市2013届高三期末 理科)2.已知R 为全集,{|(1)(2)0}A x x x =-+≤,则R C A =(A ){|21}x x x <->或 (B ){|21}x x x ≤-≥或(C ){|21}x x -<< (D ){|21}x x -≤≤【答案】C由于{|(1)(2)0}A x x x =-+≤,所以{|(1)(2)0}{(1)(2)0}{21}R A x x x x x x x x =-+>=-+<=-<<,选C.(烟台市2013届高三期末 理科)1.设集合}{}{{}20,1,2,3,4,5,1,2,540,U A B x Z x x ===∈-+<则()U C A B ⋃A.{0,1,2,3,}B.{5}C.{1,2,4}D.{0,4,5} 【答案】D【 解析】}2{540{14}{2,3}B x Z x x x Z x =∈-+=∈<<=<,所以{1,2,3}AB =,所以(){0,4,5}U A B =,选D.成都七中实验学校 2015-2016学年(上期)第一学月考试八年级语文考生留意:1.开考之前请考生将本人的考室号、座号等信息精确的填写在指定的地位,一切答案都写在答题卷上,对错误填写的考生成绩以0分计算。
山东届高三数学一模试题分类汇编——统计与概率(理)下载地址

山东省 2009 届高三数学一模试卷分类汇编 —— 统计与概率(理)珠海市第四中学( 519015)邱金龙一、选择题、填空题1、( 20009 滨州一模) 在样本的频次散布直方图中,共有11 个小长方形,若中间一个小长方形的面积等于其余 10 个小长方形的面积和的1,且样本容量为160,则中间一组的频数4为A .32B. . 40D .A2、( 20009 聊城一模) 给出以下四个命题,此中正确的一个是( )A .在线性回归模型中,有关指数 R 2,说明预告变量对解说变量的贡献率是80%B .在独立性查验时,两个变量的2× 2 列表中对角线上数据的乘积相差越大,说明这两个变量没有关系建立的可能性就越大C .有关指数 R 2 用来刻画回归成效, R 2 越小,则残差平方和越大,模型的拟合成效越好D .随机偏差 e 是权衡预告精准度的一个量,它知足E (e ) =0D3、( 20009 临沂一模) 甲、乙、丙三位棉农,统计连续五年的单位面积产量(千克 / 亩)如下表:则产量较稳固的是棉农。
甲 67 70 73 69 71 乙 69 71 71 69 70 丙6872717069乙4、( 20009 青岛一模) 学校为了检查学生在课外读物方面的支出状况,抽出了一个容量为n 的样本,其频次散布直方图如频次[50,60) 元的同学有 30 人,则 n 的值为组距图所示,此中支出在A . 100 B. 1000C . 90 D. 900A元5、( 20009 泰安一模) 将长度为 1M 的铁丝随机剪成三段,则 20 30 40 50 60这三段能拼成三角形 (三段的端点相接 ) 的概率等于1 1 1 1(A) (B)(c)(D)8432B二、解答题1、( 20009 滨州一模) 某辆载有 5 位乘客的公共汽车在抵达终点前还有 3 个停靠点(包含终点站).若车上每位乘客在所剩的每一个停靠点下车的概率均为1,用表示这 5 位乘客中3( I )随机变量 的散布列;( II )随机变量的数学希望。
山东省高三数学 各地市最新模拟试题精品分类汇编 专题02 常用逻辑用语 理(教师版)

山东省2013届高三数学 各地市最新模拟理数试题精品分类汇编 专题02 常用逻辑用语 理(教师版)一、选择题1. (山东省济南市2013年1月高三上学期期末理10)非零向量,a b r r 使得||||||a b a b +=-r r r r成立的一个充分非必要条件是A. //a b r rB. 20a b +=r r rC. ||||a ba b =r rr r D. a b =r r2.(山东省德州市2013年1月高三上学期期末校际联考理3)设,,,,a b R ∈则“1a ≥且1b ≥”是“2a b +≥”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件3.(山东省淄博市2013届高三上学期期末理5) “1-=m ”是“直线02)12(=+-+y m mx 与直线033=++my x 垂直”的 A .充分而不必要条件 B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】A【解析】当210m -=,即12m =时,两直线方程为4x =-和13302x y ++=,此时两直线不垂直。
当0m =时,两直线方程为2y =和1x =-,此时两直线垂直。
当0m ≠且12m ≠时,两直线方程为21212m y x m m =+--和33y x m m =--,两直线的斜率为3,12m m m --,要使两直线垂直,则有3()112m m m⨯-=--,解得1-=m ,所以直线02)12(=+-+y m mx 与直线033=++my x 垂直”则有1-=m 或0m =,所以1-=m 是两直线垂直的充分而不必要条件,选A.4.(山东省诸城市2013届高三12月月考理)“22a b >”是22log log a b >”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.(山东省枣庄三中2013年1月高三上学期阶段测试理)已知,a b R +∈,那么 “122<+b a ” 是“1ab a b +>+”的A.充要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件6.(山东省潍坊市四县一区2013届高三11月联考理)下列命题中的假命题是 A.02,1>∈∀-x R x B.1lg ,<∈∃x R xC.0,2>∈∀x R x D.2tan ,=∈∃x R x7.(山东省潍坊市四县一区2013届高三11月联考理)已知条件1:≤x p ,条件11:<xq ,则p 是q ⌝成立的A.充分不必要条件B.必要不充分条件C.充要条件D.既非充分也非必要条件8.(山东省泰安市2013届高三上学期期中考试理)命题“所有实数的平方都是正数”的否定为A.所有实数的平方都不是正数B.有的实数的平方是正数C.至少有一个实数的平方是正数D.至少有一个实数的平方不是正数9.(山东省实验中学2013届高三第三次诊断性测试理)设}{}2,1{2a N M ==,,则”“1=a 是”“M N ⊆的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件10.(山东省实验中学2013届高三第三次诊断性测试理)设命题p :曲线xe y -=在点),(e 1-处的切线方程是:ex y -=;命题q :b a ,是任意实数,若b a >,则1111+<+b a ,则( )A.“p 或q ”为真B.“p 且q ”为真C.p 假q 真D.p ,q 均为假命题11.(山东省实验中学2013届高三第一次诊断性测试理)如果命题 “⌝(p 或q)”为假命题,则A .p ,q 均为真命题B .p ,q 均为假命题C .p ,q 中至少有一个为真命题D . p, q 中至多有一个为真命题12.(山东省实验中学2013届高三第二次诊断性测试理)若)(x f 是R 上的增函数,且2)2(,4)1(=-=-f f ,设{}31)(|<++=t x f x P ,{}4)(|-<=x f x Q ,若“P x ∈”是“Q x ∈的充分不必要条件,则实数t 的取值范围是A.1-≤tB.1->tC.3≥tD.3>t13.(山东省聊城市东阿一中2013届高三上学期期初考试)“3πθ≠”是“21cos ≠θ”的( ) A .充分不必要条件 B.必要不充分条件C .充要条件D. 既不充分也不必要条件14.(山东省临沂市2013届高三上学期期中考试理)已知命题:,30xp x ∀∈>R ,则 A .0:,30xp x ⌝∃∈≤R B .:,30xp x ⌝∀∈≤RC .0:,30xp x ⌝∃∈<RD .:,30xp x ⌝∀∈<R15.(山东省青岛市2013届高三上学期期中考试理)在ABC ∆中,“A B >”是“tan tan A B >”的A 充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件16.(山东省青岛市2013届高三上学期期中考试理)给出下列三个结论:(1)若命题p 为真命题,命题q ⌝为真命题,则命题“p q ∧”为真命题;(2)命题“若0xy =,则0x =或0y =”的否命题为“若0xy ≠,则0x ≠或0y ≠”;(3)命题“,20xx ∀∈>R ”的否定是“ ,20xx ∃∈≤R ”.则以上结论正确的个数为 A .3个 B .2个 C .1个 D .0个17.(山东省济南外国语学校2013届高三上学期期中考试理)"1""||1"x x >>是的( ) A .充分不必要条件 B.必要不充分条件C .充分必要条件 D .既不充分又不必要条件18.(山东省德州市乐陵一中2013届高三10月月考理)下列有关命题的说法正确的是 A .命题“若0xy =,则0x =”的否命题为:“若0xy =,则0x ≠” B .“若0=+y x ,则x ,y 互为相反数”的逆命题为真命题C .命题“R ∈∃x ,使得2210x -<”的否定是:“R ∈∀x ,均有2210x -<” D .命题“若cos cos x y =,则x y =”的逆否命题为真命题二、填空题:19.(山东省诸城市2013届高三12月月考理)已知命题P :x ∀∈[0,l],xa e ≥,命题q :“x ∃∈R ,x 2+4x+a=0”,若命题“p∧q”是真命题,则实数a 的取值范围是 ;三、解答题:20.(山东省德州市乐陵一中2013届高三10月月考理)(本小题满分12分)设命题p :实数x 满足03422<+-a ax x ,其中0<a ;命题q :实数x 满足2280,x x +->且p q ⌝⌝是的必要不充分条件,求实数a 的取值范围.21.(山东省泰安市2013届高三上学期期中考试理)(本小题满分12分)已知集合A 为函数()()()lg 1lg 1f x x x =+--的定义域,集合{}22120B x a ax x =---≥.(I )若112A B xx ⎧⎫⋂=≤<⎨⎬⎩⎭,求a 的值; (II )求证2a ≥是A B φ⋂=的充分不必要条件. 【解析】22.(山东省烟台市莱州一中20l3届高三第二次质量检测理)已知全集U=R ,非空集合{23x A xx -=-<}0,{()()22B x x a x a =---<}0. (1)当12a =时,求()U C B A ⋂;(2)命题:p x A ∈,命题:q x B ∈,若q 是p 的必要条件,求实数a 的取值范围. 【解析】23.(山东省烟台市莱州一中2013届高三10月月考理)(12分)已知{}{}m x x S x x x P ≤-=≤--=1,02082(1)若P S P ⊆⋃,求实数m 的取值范围;(2)是否存在实数m ,使得“P x ∈”是“S x ∈”的充要条件,若存在,求出m 的取值范围;若不存在,请说明理由. 【解析】。
2023年高三数学模拟题概率统计小题汇编(一)

2023年高三数学模拟题概率统计小题汇编(一)1.【山东青岛一模6】甲乙两选手进行象棋比赛,已知每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4,若采用三局二胜制,则甲最终获胜的概率为()A.0.36B.0.352C.0.288D.0.6481.D【详解】由题意可得甲最终获胜有两种情况:一是前两局甲获胜,则获胜的概率为0.60.60.36⨯=二是前两局甲胜一局,第三局甲获胜,则获胜的概率为120.60.40.60.288C⨯⨯=,而这两种情况是互斥的,所以甲最终获胜的概率为0.360.2880.648+=,2.【多选·山东青岛一模9】某市为了更好的支持小微企业的发展,对全市小微企业的年税收进行适当的减免,为了解该地小微企业年收入的变化情况,对该地小微企业减免前和减免后的年收入进行了抽样调查,将调查数据整理,得到如下所示的频率分布直方图,则下列结论正确的是()A.推行减免政策后,某市小微企业的年收入都有了明显的提高B.推行减免政策后,某市小微企业的平均年收入有了明显的提高C.推行减免政策后,某市小微企业的年收入更加均衡D.推行减免政策后,某市小微企业的年收入没有变化2.BC【详解】对于A,从图中无法确定推行减免政策后,某市小微企业的年收入是否都有了明显的提高,故A错误;对于B,从图中可以看出,减免前占比最多的平均年收入为45~50万元,其次是40~45万元及50~55万元,减免后占比最多的为50~55万元,其次是55~60万元及45~50万元,明显增多,所以平均年收入也有明显提高,所以B 正确;对C ,从图中看出,推行减免政策后,年收入的中位数是52.5,而减免前年收入的中位数是47.5,所以减免后年收入更加均衡,所以C 错误;对于 D,从图中看出,某市小微企业的年收入有明显变化,所以D 错误.3.【广东深圳一模7】假定生男孩和生女孩是等可能的,现考虑有3个小孩的家庭,随机选择一个家庭,则下列说法正确的是( )A .事件“该家庭3个小孩中至少有1个女孩”和事件“该家庭3个小孩中至少有1个男孩”是互斥事件B .事件“该家庭3个孩子都是男孩”和事件“该家庭3个孩子都是女孩”是对立事件C .该家庭3个小孩中只有1个男孩的概率为18D .当已知该家庭3个小孩中有男孩的条件下,3个小孩中至少有2个男孩的概率为473.D 【详解】A :假设事件A :该家庭3个小孩至少有1个女孩,则包含(女,男,男)的可能,事件B :该家庭3个小孩至少有一个男孩,则包含(女,女,男)的可能,所以A B ⋂≠∅,故A 错误; B :事件“3个孩子都是男孩”与事件“3个孩子都是女孩”不可能同时发生,是互斥但不对立事件,故B 错误;C :3个小孩可能发生的事件如下:男男男、男男女、男女女、男女男、女女女、女女男、D :设M ={至少一个有男孩},N ={至少有2个男孩},由选项C 可知,()4()7n MN n M ==,,4.【多选·广东深圳一模10】某人工智能公司近5年的利润情况如下表所示:已知变量y 与x 之间具有线性相关关系,设用最小二乘法建立的回归直线方程为 1.2y x a =+,则下列说法正确的是( )A .ˆ0.6a= B .变量y 与x 之间的线性相关系数0r <C .预测该人工智能公司第6年的利润约为7.8亿元D .该人工智能公司这5年的利润的方差小于2 4.AC 【详解】则回归直线方程为 1.20.6y x =+,则x 与y 成正相关,即相关系数0r >,故B 错误, 当6x =时 1.260.67.8y =⨯+=,即该人工智能公司第6年的利润约为7.8亿元,故C 正确, 该人工智能公司这5年的利润的方差为5.【广东深圳二模4】深圳是一座志愿者之城、爱心之城.深圳市卫健委为了解防疫期间志愿者的服务时长(单位:小时),对参加过防疫的志愿者随机抽样调查,将样本中个体的服务时长进行整理,得到如图所示的频率分布直方图.据此估计,7.2万名参加过防疫的志愿者中服务时长超过32小时的约有( )A .3.3万人B .3.4万人C .3.8万人D .3.9万人5.A 【详解】解:依题意样本中服务时长超过32小时的个体频率为()140.0050.040.090.46-⨯++=; 由样本估计总体,可得总体中服务时长超过32小时的个体数为7.30.46 3.312 3.3⨯=≈(万人);6.【多选·广东深圳二模10】已知随机变量X 服从正态分布(0,1)N ,密度函数()()f x P X x =≤,若0x >,则( ) A .()1()f x f x -=-B .(2)2()f x f x =C .()f x 在(0,)+∞上是增函数D .(||)2()1P X x f x ≤=-6.ACD 【详解】随机变量X 服从正态分布(0,1)N ,∴正态曲线关于直线0x =对称,()f x 在(0,)+∞上是增函数,选项C 正确;()()()0f x P X x x =≤>,∴根据正态曲线的对称性可得()()()1f x P X x f x -=>=-,选项A 正确;()()(2)(2),22f x P X x f x P X x =≤=≤,选项B 错误;()()()(||)121212()1P X x P x X x f x f x f x ≤=-≤≤=--=--=-⎡⎤⎣⎦,选项D 正确.7.【辽宁沈阳一模】夏季里,每天甲、乙两地下雨的概率分别为13和14,且两地同时下雨的概率为16,则夏季的一天里,在乙地下雨的条件下,甲地也下雨的概率为( )A .112B .12C .23D .347.C 【详解】8.【多选·辽宁沈阳一模9】某团队共有20人,他们的年龄分布如下表所示,有关这20人年龄的众数、极差、百分位数说法正确的有( ) A .众数是32B .众数是5C .极差是17D .25%分位数是308.ACD【详解】年龄为32的有5人,故众数是32,A正确,B错误;45-28=17,极差为17,C正确;8.【辽宁沈阳一模15】某次社会实践活动中,甲、乙两个班的同学共同在一社区进行民意调查.参加活动的甲、乙两班的人数之比为5:3,其中甲班中女生占35,乙班中女生占13.则该社区居民遇到一位进行民意调查的同学恰好是女生的概率是______.【详解】如果用A1,A2分别表示居民所遇到的一位同学是甲班的与乙班的事件,B表示是女生的事件,则Ω=A1∪A2,且A1,A2互斥,B∪Ω,9.【多选·辽宁沈阳二模10】甲、乙两人进行飞镖游戏,甲的10次成绩分别为8,6,7,7,8,10,10,9,7,8,乙的10次成绩的平均数为8,方差为0.4,则()A.甲的10次成绩的极差为4B.甲的10次成绩的75%分位数为8C.甲和乙的20次成绩的平均数为8D.甲和乙的20次成绩的方差为19.ACD【详解】甲的10次成绩中,最大值为10,最小值为6,极差等于4,故A正确,因为1075%7.5⨯=,所以将甲的10次成绩从小到大排列后,第8个数为75%分位数,即75%分位数等于9,故B不正确,经计算,甲的10次成绩的平均数等于8,又已知乙的10次成绩的平均数等于8,则甲和乙的20次成绩的平均数为8,故C正确,故选:ACD10.【辽宁沈阳二模14】已知随机变量()2~1,N ξσ,且()()13P P a ξξ≤=≥-,则()190x a x a x+<<-的最小值为______. 10.4 【详解】由随机变量()2~1,N ξσ,则正态分布的曲线的对称轴为1ξ=,又因为()()13P P a ξξ≤=≥-,所以()132a +-=,所以4a = 当04x <<时,。
2024届山东省联合模拟考试数学试题(解析版)

2024年全国普通高考模拟考试数学试题2024.5注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.3.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.4.考试结束后,将本试卷和答题卡一并交回.一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.1.样本数据2,3,4,5,6,8,9的第30百分位数是()A.3B.3.5C.4D.5【答案】C 【解析】【分析】利用百分位数的求法计算即可.【详解】易知730% 2.1⨯=,则该组数据的第三个数4为第30百分位数.故选:C2.已知集合{}|12024A x x =-≤≤,{}|1B x a x a =+≤≤()0a >,若A B ⋂≠∅,则a 的取值范围是()A.()0,2024 B.(]0,2024 C.()0,2023 D.(]0,2023【答案】B 【解析】【分析】由A B ⋂≠∅,则集合B 中最小元素a 应在集合A 中,即可得到a 的取值范围.【详解】由题意A B ⋂≠∅,再由0a >,所以集合B 中最小元素a 应在集合A 中,所以02024a <≤,即a 的取值范围是(]0,2024.故选:B.3.已知抛物线2:4C x y =的焦点为F ,点P 在C 上,若P 到直线=3y -的距离为5,则PF =()A.5B.4C.3D.2【答案】C【解析】【分析】利用抛物线的定义先确定准线及焦点,计算即可.【详解】由题意可知()0,1F ,抛物线的准线为1y =-,而PF 与P 到准线的距离相等,所以()()5133PF =----=.故选:C4.某所学校的3名同学和2名老师站成一排合影,若两名老师之间至少有一名同学,则不同的站法种数为()A.120B.72C.64D.48【答案】B 【解析】【分析】根据给定条件,利用不相邻的排列问题列式计算即得.【详解】依题意,两名老师不相邻,所以不同的站法种数为2334A 62A 127=⨯=.故选:B5.已知5a = ,4b = ,若a 在b 上的投影向量为58b - ,则a 与b 的夹角为()A.60° B.120°C.135°D.150°【答案】B 【解析】【分析】利用投影向量的定义计算即可.【详解】易知a 在b上的投影向量为cos ,55cos ,88a b a b a b a b b b ⋅=-⇒=- ,而51cos ,82b a b a =-⋅=-,所以a 与b 的夹角为120 .故选:B6.已知圆()22:200M x y ay a ++=>的圆心到直线322x y +=M 与圆()()22:221N x y -++=的位置关系是()A.相离B.相交C.内切D.内含【答案】D 【解析】【分析】根据点到直线的距离公式求a 的值,再利用几何法判断两圆的位置关系.【详解】圆M :2220x y ay ++=⇒()222x y a a ++=,所以圆心()0,M a -,半径为a .==,且0a >,所以112a =.又圆N 的圆心()2,2N -,半径为:1.所以2MN ==,912a -=.由922<,所以两圆内含.故选:D7.已知等差数列{}n a 满足22144a a +=,则23a a +可能取的值是()A.2-B.3- C.4D.6【答案】A 【解析】【分析】根据题意,令12cos a θ=,42sin a θ=,由等差数列的下标和性质结合三角函数的性质求解即可.【详解】设12cos a θ=,42sin a θ=,则1243π)4a a a a θ=+++=,所以23[a a ∈+-,故选:A.8.已知函数()1cos 4221f x x x ππ⎛⎫=-+ ⎪-⎝⎭,则21y x =-与()f x 图象的所有交点的横坐标之和为()A.12B.2C.32D.3【答案】D 【解析】【分析】先用诱导公式化简函数,然后变形成一致的结构,再换元,转化成新元方程根的横坐标之和,分别画图,找出交点横坐标的关系,再和即可.【详解】由题意化简()11cos 4sin(4)22121f x x x x x πππ⎛⎫=-+=+ ⎪--⎝⎭11sin(42)sin 2(21)2121x x x x πππ=-+=-+--,21y x =-与()f x 图象有交点,则1sin 2(21)2121x x x π-+=--有实根,令21t x =-,则12t x +=,则化为1sin 2t t t π+=,即1sin 2t t tπ=-的所有实根之和,即()sin 2g t t π=与1()h t t t =-所有交点横坐标之和,显然()g t 是周期为1的奇函数,()h t 为奇函数且在(0,)+∞上为增函数,图像如图所示,显然,一共有6个交点123456,,,,,t t t t t t ,它们的和为0,则12345612345616322t t t t t tx x x x x x ++++++++++=⨯+=,故选:D .二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知1z ,2z 为复数,则()A.1212z z z z +=+ B.若12z z =,则2121z z z =C.若11z =,则12z -的最小值为2 D.若120z z ⋅=,则10z =或20z =【答案】BD 【解析】【分析】通过列举特殊复数验证A ;设()1i,,R z a b a b =+∈,则()2i,,R z a b a b =-∈,通过复数计算即可判断B ;设()1i,,R z a b a b =+∈,由复数的几何意义计算模长判断C ;由120z z ⋅=得120z z =,即可判断D.【详解】对于A ,若121i,1i =+=-z z ,则121i 1i 2z z +=++-=,121i 1i z z +=++-=1212z z z z +≠+,故A 错误;对于B ,设()1i,,R z a b a b =+∈,则()2i,,R z a b a b =-∈,所以()()2212i i z z a b a b a b =+-=+,而2221z a b =+,所以2121z z z =,故B 正确;对于C ,设()1i,,R z a b a b =+∈,因为11z =,所以221a b +=,所以()1i 22a b z =-+===-,因为11a -≤≤,所以1549a ≤-≤,所以12z -的最小值为1,故C 错误;对于D ,若120z z ⋅=,所以120z z ⋅=,所以120z z =,所以10z =或20z =,所以12,z z 至少有一个为0,故D 正确.故选:BD10.袋子中有6个相同的球,分别标有数字1,2,3,4,5,6,从中随机取出两个球,设事件A =“取出的球的数字之积为奇数”,事件B =“取出的球的数字之积为偶数”,事件C =“取出的球的数字之和为偶数”,则()A.()15P A =B.()1|3P B C =C.事件A 与B 是互斥事件D.事件B 与C 相互独立【答案】AC 【解析】【分析】分别求出事件,,A B C 的概率,再根据互斥事件和相互独立事件的概率进行判断.【详解】因为“取出的求的数字之积为奇数”,就是“取出的两个数都是奇数”,所以()2326C 31C 155P A ===;故A 正确;“取出的球的数字之积为偶数”就是“取出的两个数不能都是奇数”,所以()2326C 3411C 155P B =-=-=;“取出的两个数之和为偶数”就是“取出的两个数都是奇数或都是偶数”,所以()2326C 22C 5P C =⨯=;A B +表示“取出的两个数的积可以是奇数,也可以是偶数”,所以()1P A B +=;BC 表示“取出的两个数的积与和都是偶数”,就是“取出的两个数都是偶数”,所以()2326C 1C 5P BC ==.因为()()()|P BC P B C P C =12=,故B 错误;因为()()()P A B P A P B +=+,所以,A B 互斥,故C 正确;因为()()()P BC P B P C ≠⋅,所以,B C 不独立,故D 错误.故选:AC11.已知双曲线()222:10x C y a a-=>的渐近线方程为12y x =±,过C 的右焦点2F 的直线交双曲线右支于A ,B 两点,1F AB 的内切圆分别切直线1F A ,1F B ,AB 于点P ,Q ,M ,内切圆的圆心为I,半径为,则()A.CB.切点M 与右焦点2F 重合C.11F BI F AI ABI S S S +-=△△△D.17cos 9AF B ∠=【答案】ABD 【解析】【分析】A 选项,根据渐近线方程求出2a =,得到离心率;B 选项,由双曲线定义和切线长定理得到22AP BQ AM BM AF BF -=-=-,得到切点M 与右焦点2F 重合;C 选项,根据双曲线定义和1F AB 的内切圆的半径得到11F BI F AI ABI S S S +-=△△△;D 选项,作出辅助线,得到112tan 4PI AF I PF ∠==,利用万能公式得到答案.【详解】A 选项,由题意得112a =,解得2a =,故离心率c e a ===A 正确;B 选项,11,,AP AM F P FQ QB BM ===,由双曲线定义可得1224AF AF a -==,1224BF BF a -==,两式相减得1122AF BF AF BF -=-,即22AP BQ AM BM AF BF -=-=-,故切点M 与右焦点2F 重合,B 正确;C 选项,1F AB 的内切圆的半径为2r =故()111111111122222F BI F AI ABI S S S F A r F B r AB r F A F B AB +-=+-=+- ()11112424222F A AM F B BM a =-+-=⨯=C 错误;D 选项,连接1F I ,则1F I 平分1AF B ∠,其中111224F P AF AP AF AF a =-=-==,故112tan 4PI AF I PF ∠==,所以2221111212112c i os cos co s s c s n s s in o in AF I AF IAF I AF I AF I AF IAF B ∠-∠∠-=∠=+∠∠∠2212212141tan 71tan 9214AF I AF I ⎛⎫-⎪-∠⎝⎭===+∠⎛⎫+ ⎪⎝⎭.故选:ABD【点睛】关键点点睛:利用双曲线定义和切线长定理推出切点M 与右焦点2F 重合,从而推理得到四个选项的正误.三、填空题:本题共3小题,每小题5分,共15分.12.二项式5a x x ⎛⎫+ ⎪⎝⎭的展开式中,3x 的系数为10,则=a ___________.【答案】2【解析】【分析】利用二项式展开式的通项计算即可.【详解】易知二项式5a x x ⎛⎫+ ⎪⎝⎭的展开式通项公式为()5152155C C rr rr rr r T x a x a x ---+=⋅=⋅,显然1r =时,115C 102a a =⇒=.故答案为:213.若函数()()πcos sin 3f x x x ϕ⎛⎫=-++ ⎪⎝⎭的最大值为2,则常数ϕ的一个取值为___________.【答案】π6(答案不唯一,满足πZ π2,6k k ϕ=+∈即可)【解析】【分析】利用和(差)角公式化简,再判断1sin 02ϕ+≠,利用辅助角公式化简,再结合函数的最大值,求出ϕ.【详解】因为()()πcos sin 3f x x x ϕ⎛⎫=-++⎪⎝⎭ππcos cos sin sin sin coscos sin 33x x x x ϕϕ=+++1cos cos sin sin 22x x ϕϕ⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭,若1sin 02ϕ+=,则cos 2ϕ=±,所以()0f x =或()f x x =,显然不满足()f x 的最大值为2,所以1sin 02ϕ+≠,则()()f x x θ=+,(其中3cos 2tan 1sin 2ϕθϕ+=+),依题意可得2213sin cos 422ϕϕ⎛⎛⎫+++= ⎪ ⎝⎭⎝⎭,即sin 2ϕϕ+=,所以πsin 13ϕ⎛⎫+= ⎪⎝⎭,所以ππ2π,Z 32k k ϕ+=+∈,解得πZ π2,6k k ϕ=+∈.故答案为:π6(答案不唯一,满足πZ π2,6k k ϕ=+∈即可)14.如图,正方形ABCD 和矩形ABEF 所在的平面互相垂直,点P 在正方形ABCD 及其内部运动,点Q 在矩形ABEF 及其内部运动.设2AB =,AF =,若PA PE ⊥,当四面体PAQE 体积最大时,则该四面体的内切球半径为___________.【答案】222-或84352362+-【解析】【分析】先确定P 点的轨迹,确定四面体P AQE -体积最大时,P ,Q 点的位置,再利用体积法求内切球半径.【详解】如图:因为平面ABCD ⊥平面ABEF ,平面ABCD ⋂平面ABEF AB =,BE ⊂平面ABEF ,且BE AB ⊥,所以BE ⊥平面ABCD .AP ⊂平面ABCD ,所以BE AP ⊥,又⊥PE AP ,,PE BE ⊂平面PBE ,所以AP ⊥平面PBE ,PB ⊂平面PBE ,所以AP PB ⊥.又P 在正方形ABCD 及其内部,所以P 点轨迹是如图所示的以AB 为直径的半圆,作PH AB ⊥于H ,则PH 是三棱锥P AQE -的高.所以当AQE 的面积和PH 都取得最大值时,四面体PAQE 的体积最大.此时Q 点应该与B 或F 重合,P 为正方形ABCD 的中心.如图:当Q 点与B 重合,P 为正方形ABCD 的中心时:13P AQE AQE V S PH -=⋅ 1213=23=,2AQE S = 1PEQ S = ,1PAQ S = ,APE V 中,因为AP PE ⊥,2AP =,2PE =,所以2APE S = .设内切球半径为r ,由()13P AQE AQE APE APB PQE V S S S S r -=+++⋅ 得:2222222r ==+.如图:当Q 点与F 重合,P 为正方形ABCD 的中心时:13P AQE AQE V S PH -=⋅ 1213=23=,2AQE S = 3PEQ S = ,1PAQ S = ,2APE S = .设内切球半径为r ,由()13P AQE AQE APE APB PQE V S S S S r -=+++⋅ 得:22231r =++84352362+--=.综上可知,当四面体PAQE 的体积最大时,其内切球半径为:222-或84352362+-.故答案为:222或84352362+-【点睛】关键点点睛:根据PA PE ⊥得到P 点在以AE 为直径的球面上,又P 点在正方形ABCD 及其内部,所以P 点轨迹就是球面与平面ABCD 的交线上,即以AB 为直径的半圆上.明确P 点轨迹是解决问题的关键.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知函数()()1ln f x x kx =-.(1)若曲线()f x 在e x =处的切线与直线y x =垂直,求k 的值;(2)讨论()f x 的单调性.【答案】(1)1k =(2)答案见解析【解析】【分析】(1)对函数求导,结合题意有,()()e ln e 1f k ='-=-,即可求解k 值;(2)对函数求导,分0k >和0k <两种情况讨论,根据导数的正负判断原函数的单调性.【小问1详解】因为()()1ln f x x kx =-,0k ≠,所以()()ln f x kx =-',曲线()f x 在e x =处的切线与y x =垂直,所以()()e ln e 1f k ='-=-,得1k =;【小问2详解】由()()1ln f x x kx =-得()()ln f x kx =-',当0k >时,()f x 的定义域为()0,∞+,令()0f x '=得1x k=,当10,x k ⎛⎫∈ ⎪⎝⎭时,()0f x '>,当1,x k ∞⎛⎫∈+ ⎪⎝⎭时,()0f x '<所以()f x 在10,k ⎛⎫ ⎪⎝⎭上单调递增,在1,k ∞⎛⎫+ ⎪⎝⎭上单调递减;当0k <时,()f x 的定义域为(),0∞-,令()0f x '=得1x k=当1,x k ∞⎛⎫∈- ⎪⎝⎭时,()0f x '<,当1,0x k ⎛⎫∈ ⎪⎝⎭时,()0f x '>所以()f x 在1,k ∞⎛⎫- ⎪⎝⎭上单调递减,在1,0k ⎛⎫ ⎪⎝⎭上单调递增.综上所述:当0k >时,()f x 在10,k ⎛⎫ ⎪⎝⎭上单调递增,在1,k ∞⎛⎫+ ⎪⎝⎭上单调递减;当0k <时,()f x 在1,k ∞⎛⎫- ⎪⎝⎭上单调递减,在1,0k ⎛⎫ ⎪⎝⎭上单调递增.16.如图,在四棱台1111ABCD A B C D -中,底面ABCD 为正方形,1ABC 为等边三角形,E 为AB 的中点.(1)证明:111C D B E ⊥;(2)若1124BC B C ==,1B E =,求直线1BC 与平面11CDD C 所成角的余弦值.【答案】(1)证明见解析(2)3【解析】【分析】(1)连接1EC ,可得1AB C E ⊥,由已知得11AB B C ⊥,所以得AB ⊥平面11B C E ,可得11C D ⊥平面11B C E ,则可得111C D B E ⊥;(2)以点E 为坐标原点,建立如图所示的空间直角坐标系,求出1BC的坐标及平面11CDD C 的一个法向量n的坐标,由1BC 和n夹角的余弦值的绝对值即为直线1BC 与平面11CDD C 所成角正弦值,由向量夹角的余弦公式算出,再算出直线1BC 与平面11CDD C 所成角的余弦值.【小问1详解】连接1EC ,因为1ABC 为等边三角形,所以1AB C E ⊥,因为ABCD 为正方形,所以AB BC⊥在四棱台1111ABCD A B C D -中,11//BC B C ,所以11AB B C ⊥,又1111111,,B C C E C B C C E ⋂=⊂平面11B C E ,所以AB ⊥平面11B C E ,因为11//AB C D ,所以11C D ⊥平面11B C E ,因为1B E ⊂平面11B C E ,所以111C D B E ⊥;.【小问2详解】因为底面ABCD 为正方形,1ABC 为等边三角形,所以4AB BC ==,所以1C E =因为1B E =,112B C =,所以2221111C B B E C E +=,所以111B E B C ⊥,又由(1)111C D B E ⊥,且11111C D B C C = ,1111,C D B C ⊂平面1111D C B A ,所以1B E ⊥平面1111D C B A ,即1B E ⊥平面ABCD ,取CD 的中点F ,连接EF ,以点E 为坐标原点,以EB ,EF,1EB 分别为x ,y ,z 轴的正方向,建立如图所示的空间直角坐标系,()2,0,0B ,()2,4,0C,(10,2,C ,()2,4,0D -,所以(12,2,BC =-,(12,2,CC =-- ,()4,0,0CD =-,设(),,n x y z = 是平面11CDD C 的一个法向量,所以100n CC n CD ⎧⋅=⎪⎨⋅=⎪⎩,即22040x y x ⎧-+-+=⎪⎨=⎪⎩,得()n = ,直线1BC 与平面11CDD C所成角正弦值为113BC n BC n⋅==⋅,则直线1BC 与平面11CDD C3=.17.已知数列{}n a 满足12a =,1nn n a a d q +-=⋅,*n ∈N .(1)若1q =,{}n a 为递增数列,且2,5a ,73a +成等比数列,求d ;(2)若1d =,12q =,且{}21n a -是递增数列,{}2n a 是递减数列,求数列{}n a 的通项公式.【答案】(1)12d =(2)()1171332nnn a --=+⋅【解析】【分析】(1)利用数列{}n a 为单调递增数列,得到1n n a a d +-=,再根据2,5a ,73a +成等比数列,得到28230d d +-=,即可求出的值.(2)由数列{}21n a -是递增数列得出21210n n a a +-->,可得()()2122210n n n n a a a a +--+->,但2211122n n -<,可得212221n n n n a a a a +--<-.可得()221221211122nn n n n a a ----⎛⎫-==⎪⎝⎭;由数列{}2n a 是递减数列得出2120n n a a +-<,可得()1112n n n naa ++--=,再利用累加法可求出数列{}n a 的通项公式.【小问1详解】因为12a =,且{}n a 为递增数列,所以1n n a a d +-=,所以{}n a 为等差数列,因为2,5a ,73a +成等比数列,所以()()2114263a d a d +=++,整理得28230d d +-=,得12d =,34d =-,因为{}n a 为递增数列,所以12d =.【小问2详解】由于{}21n a -是递增数列,因而21210n n a a +-->,于是()()2122210n n n n a a a a +--+->①但2211122n n -<,所以212221n n n n a a a a +--<-.②又①,②知,2210n n a a -->,因此()221221211122nn n n n a a ----⎛⎫-==⎪⎝⎭③因为{}2n a 是递减数列,同理可得2120n n a a +-<,故()21221221122n nn n n a a ++-⎛⎫-=-=⎪⎝⎭,④由③,④即知,()1112n n n na a ++--=,于是()()()121321nn n a a a a a a a a -=+-+-++- ()1211111112221222212n nn --⎛⎫-- ⎪-⎝⎭=+-++=++ ()1171332nn --=+⋅,故数列{}n a 的通项公式为()1171332nnn a --=+⋅.【点睛】思路点睛:本题可从以下方面解题.(1)数列{}n a 为等差数列,利用等差数列的性质即可;(2)根据数列{}21n a -是递增数列得,21210n n a a +-->,数列{}2n a 是递减数列得,2120n n a a +-<,综合数列{}21n a -和{}2n a 即可得()1112n n n naa ++--=,最后利用累加法可求出数列{}n a 的通项公式.18.已知椭圆C :()222210x y a b a b+=>>的上顶点为A ,左焦点为F ,点4,3b B ⎛⎫- ⎪⎝⎭为C 上一点,且以AB为直径的圆经过点F .(1)求C 的方程;(2)过点()5,0G -的直线l 交C 于D ,E 两点,线段DE 上存在点M 满足DM GE DG EM ⋅=⋅,过G与l 垂直的直线交y 轴于点N ,求GMN 面积的最小值.【答案】(1)221189x y +=(2)7【解析】【分析】(1)根据已知条件和椭圆中,,a b c 的关系,求出,,a b c 的值,可得椭圆的标准方程.(2)设直线l :()5y k x =+,再设()11,D x y ,()22,E x y ,()00,M x y ,把直线方程代入椭圆方程,消去y ,得到关于x 的一元二次方程,根据一元二次方程根与系数的关系,表示出12x x +,12x x ,并用,,120x x x 表示条件DM GE DG EM ⋅=⋅,整理得0x 为定值;再结合弦长公式表示出GM ,利用两点间的距离公式求GN ,表示出GMN 的面积,利用基本(均值)不等式求最值.【小问1详解】由题意知()0,A b ,(),0F c -,因为点4,3b B ⎛⎫- ⎪⎝⎭在椭圆C 上,所以2221619b a b+=⇒218a =,由以AB 为直径的圆经过点F ,知0FA FB ⋅= ,得22403b c c -+=①,又222b c a +=②,由①②得3c =,3b =,所以C 的方程为:221189x y +=.【小问2详解】如图:由题意,直线l 斜率存在且不为0,设直线l 的方程为()5y k x =+,且()11,D x y ,()22,E x y ,()00,M x y ,将()5y k x =+代入221189x y +=,整理可得()2222122050180kxk x k +++-=,()()()2222Δ2041250180kk k =-+->,解得77k -<<,由根与系数的关系可得21222012k x x k +=-+,2122501812k x x k -=+,根据DM GE DG EM = ,得01120255x x x x x x -+=-+,解得()22221212021225018202525121218201051012k k x x x x k k x k x x k ⎛⎫-+-⎪++++⎝⎭===-++-++,设与直线l 垂直的直线方程为()15y x k=-+,令0x =,则5y k =-,即50,N k ⎛⎫- ⎪⎝⎭,故GN ==,()1855GM =--=,记GMN 面积为S ,则12S GM GN =⨯==7272==,当且仅当1k =±时取等号,所以GMN 面积的最小值为7.【点睛】方法点睛:圆锥曲线求取值范围的问题,常见的解决方法有:(1)转化为二次函数,利用二次函数在给定区间上的值域求范围;(2)转化为不等式,利用基本(均值)不等式求最值;(3)转化为三角函数,利用三角函数的有界性求取值范围;(4)转化为其它函数的值域问题,通过分析函数的单调性求值域.19.设点集(){}{}23*1,,,,|0,1,1,n n i M a a a a a i n i =∈≤≤∈N L,从集合n M 中任取两个不同的点()123,,,,n A a a a a ,()123,,,,n B b b b b ,定义A ,B 两点间的距离()1,ni i i d A B a b ==-∑.(1)求3M 中(),2d A B =的点对的个数;(2)从集合n M 中任取两个不同的点A ,B ,用随机变量X 表示他们之间的距离(),d A B ,①求X 的分布列与期望;②证明:当n 足够大时,()24D X n <.(注:当n 足够大时,20n -≈)【答案】(1)12对(2)①分布列见解析,()()212n nE X -=-;②证明见解析【解析】【分析】(1)根据题意分析可知:A ,B 有两个位置的坐标不相等,另一个相等,进而可得结果;(2)①分析可知X k =的随机变量,在坐标()123,,,,n a a a a 与()123,,,,n b b b b 中有k 个坐标值不同,即i i a b ≠,剩下n k -个坐标值满足i i a b =,进而可求分布列,结合组合数性质可求期望;②根据方差公式()()21nk kk D X P X E X =⎡⎤=⋅-⎣⎦∑整理可得()()2121C C C 214n n n n n n D X ⎡⎤<+++⎢⎥-⎣⎦L ,结合组合数性质分析证明.【小问1详解】当3n =时,若(),2d A B =,可知A ,B 有两个位置的坐标不相等,另一个位置的坐标相等,所以共有122322C A A 12=对.【小问2详解】①由题意可知,n M 中元素的个数为2n 个,对于X k =的随机变量,在坐标()123,,,,n a a a a 与()123,,,,n b b b b 中有k 个坐标值不同,即i i a b ≠,剩下n k -个坐标值满足i i a b =,此时所对应情况数为12C 2C 22k k n k k n nn --⋅=⋅种.所以()122C 2C C 21n k n k n n n P X k -⋅===-,故X 的分布列为:X12⋅⋅⋅nP1C 21n n-2C 21n n-⋅⋅⋅C 21n nn-数学期望()1212C C C C C C 12120212121212121n nn n n n nn n n n n n n E X n n =⨯+⨯++⨯=⨯⨯+⨯+------L L ,当2k n ≤≤时,则()()()()()2!!C 2C 2!!2!2!k n k n nn n k n k k n k k n k n k k -++-+=⨯+-+⨯--+-()()()()()()()!!!111!!1!2!1!1!n n n n k k k n k n k k n k k =+=-++----+--+-()()1!C 1!1!k n n n n n k k -⋅==-+-,且1C 0C C nn n n n n n +==⋅=⋅,则()()11C C C 011212121n n n nn n n n E X n n -=+⨯+-⨯++⨯---L ,两式相加得()()01222C C C C 2121n nn n n n n n n n E X ⋅=++++=--L ,所以()()212n nE X -=-;②当n 足够大时,()2n E X ≈,由方差定义()()21nk k k D X P X E X =⎡⎤=⋅-⎣⎦∑22212C C C 12212212212n n n n n n n n n n n ⎛⎫⎛⎫⎛⎫=-+-++- ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭L222121C 1C 2C 21222n n n n n n n n n ⎡⎤⎛⎫⎛⎫⎛⎫=⋅-+⋅-++⋅-⎢⎥ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦L 222121C 1C 2C 21222n n n n n n n n n ⎡⎤⎛⎫⎛⎫⎛⎫=⋅-+⋅-++-⎢⎥ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦L ()()()21212221C C C C 1C 22214n n n n n n n n n n ⎧=+++-+-+⎨-⎩ ()()()()}23212C 33C 11C n n n n n n n n n n n n -⎡⎤-++---⋅+-⋅⎣⎦因为k n ≤,则()()()20n k n k n k k n ---⋅=-≤,当且仅当0k =或k n =时,等号成立,则()()()2221211C C C 212142144n n n n n n n n n n D X ⎡⎤⎡⎤<+++=-=⎢⎥⎢⎥--⎣⎦⎣⎦L ,所以()24D X n <.【点睛】关键点点睛:(2)①利用倒序相加法结合()21C 2C C kn k k n nn k n k n -+-+-+=分析求解;②根据方差公式结合()()20n k n k n ---⋅≤分析证明.。
山东省实验中学2023届高三第一次模拟考试数学试题

一、单选题二、多选题1. 在中,,,,则的面积为( )A.B.C.D.2.已知数列满足,则“数列是等差数列”的充要条件可以是( )A.B.C.D.3. 已知函数,则下列说法正确的是( )A .为奇函数B .为偶函数C .为奇函数D .为偶函数4. 已知,则( )A.B.C.D.5. 若复数是纯虚数,则实数( )A.B.C.D.6. 如图所示,平面向量,的夹角为60°,,点关于点的对称点,点关于点的对称点为点,则为()A.B.C .4D .无法确定7. 已知,则在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限8. 设是定义在上的奇函数,对任意,满足,则的值等于( )A .2022B .2021C .4040D .40429. 函数在上有定义,若对任意的,,有则称在上具有性质,则下列说法正确的是( )A .在上具有性质;B.在其定义域上具有性质;C .在上单调递增;D.对任意,,,,有10.已知为圆锥底面圆的直径,点是圆上异于,的一点,为的中点,,圆锥的侧面积为,则下列说法正确的是( )A.圆上存在点使平面山东省实验中学2023届高三第一次模拟考试数学试题山东省实验中学2023届高三第一次模拟考试数学试题三、填空题四、解答题B.圆上存在点使平面C .圆锥的外接球表面积为D.棱长为的正四面体在圆锥内可以任意转动11. 泊松分布适合于描述单位时间(或空间)内随机事件发生的次数.如某一服务设施在一定时间内到达的人数,显微镜下单位分区内的细菌分布数等等.其概率函数为,参数是单位时间(或单位面积)内随机事件的平均发生次数.现采用某种紫外线照射大肠杆菌,大肠杆菌的基因组平均产生3个嘧啶二体.设大肠杆菌的基因组产生的嘧啶二体个数为Y,表示经该种紫外线照射后产生k 个嘧啶二体的概率.已知Y服从泊松分布,记为,当产生的嘧啶二体个数不小于1时,大肠杆菌就会死亡,下列说法正确的有( )(参考数据:,恒等式)A .大肠杆菌a 经该种紫外线照射后,存活的概率约为5%B.设,则C .如果,那么,X的标准差D .大肠杆菌a 经该种紫外线照射后,其基因组产生的嘧啶二体个数的数学期望为312. “阿基米德多面体”又称“半正多面体”,与正多面体类似,它们也都是凸多面体,每个面都是正多边形,并且所有棱长也都相等,但不同之处在于阿基米德多面体的每个面的形状不全相同.有几种阿基米德多面体可由正多面体进行“截角”得到如图,正八面体的棱长为3,取各条棱的三等分点,截去六个角后得到一种阿基米德多面体,则该阿基米德多面体()A .共有18个顶点B .共有36条棱C.表面积为D.体积为13.若曲线,且经过这三点中的两点,则曲线的离心率可能为___________.(写出一个即可).14.在中,所对的三边分别为,且,则的取值范围是______.15. 已知平面向量,满足,,,则______.16.已知正项数列的前n项积为,且,.证明:(1)数列为等差数列,并求数列的通项公式;(2).17. 已知函数().若是的极值点.(1)求,并求在上的最小值;(2)若不等式对任意都成立,其中为整数,为的导函数,求的最大值.18. 已知,设函数,是的导函数.(1)若,求曲线在点处的切线方程;(2)若在区间上存在两个不同的零点().①求实数a的取值范围;②证明:.19.已知是焦距为的双曲线上一点,过的一条直线与双曲线的两条渐近线分别交于,,且,过作垂直的两条直线和,与轴分别交于,两点,其中与轴交点的横坐标是.(1)求的值;(2)求的最大值,并求此时双曲线的方程;(3)判断以为直径的圆是否过定点,如果是,求出所有定点;如果不是,说明理由.20. 已知椭圆的中心在坐标原点,焦点在轴上,左、右焦点分别为、,离心率,短轴长为2,.(1)求椭圆的标准方程;(2)设过且斜率不为零的直线与椭圆交于、两点,过作直线的垂线,垂足为,证明:直线恒过一定点,并求出该定点的坐标;(3)过点作另一直线,与椭圆分别交于、两点,求的取值范围.21. 为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中,从男生中随机抽取了人,从女生中随机抽取了人,男生中喜欢数学课程的占,女生中喜欢数学课程的占,得到如下列联表.喜欢数学课程不喜欢数学课程合计男生女生合计(1)请将列联表补充完整;试判断能否有的把握认为喜欢数学课程与否与性别有关;(2)从不喜欢数学课程的学生中采用分层抽样的方法,随机抽取人,现从人中随机抽取人,若所选名学生中的女生人数为,求的分布列及数学期望.附:,其中.0.1500.1000.0500.0250.0100.0050.0012,072 2.706 3.841 5.024 6.6357.87910.828。
山东省高三数学 最新模拟试题精选分类汇编9 概率 理

山东省2013届高三最新理科模拟试题精选(17套)分类汇编9:概率一、选择题1 .(山东省文登市2013届高三3月二轮模拟考试数学(理))已知随机变量ξ服从正态分布2(2,)N σ,且(4)0.9P ξ<=,则(02)P ξ<<=( )A .0.2B .0.3C .0.4D .0.6【答案】C 2 .(山东省泰安市2013届高三第二次模拟考试数学(理)试题)某艺校在一天的5节课中随机安排语文、数学、外语三门文化课和其他两门艺术课各1节,则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为 ( )A .45B .35C .25D .15【答案】A 3 .(山东省菏泽市2013届高三第二次模拟考试数学(理)试题)从四棱锥S —ABCD 的八条棱中任取两条,其中抽到两条棱成异面直线的概率为 ( )A .17B .12C .27D .47【答案】C 4 .(山东省德州市2013届高三第二次模拟考试数学(理)试题)在长为12cm 的线段AB上任取一点C,以A C .BC 的长为邻边作一个矩形,则该矩形的面积小于32cm 2的概率为 ( )A .45B .23C .13D .16【答案】B 二、填空题 5 .(山东省枣庄市2013届高三4月(二模)模拟考试数学(理)试题)如图所示,墙上挂有一块边长为2的正方形木板,它的四个角的空白总分都是以正方形的顶点为圆心,半径为1的扇形,某人向此木板投镖,假设每次击中木板,且击中木板上每一个点处的可能性都一样,则击中阴影总分的概率为_________.【答案】14π-6 .(山东省夏津一中2013届高三4月月考数学(理)试题)已知Ω= {(x,y)|x+y ≤6,x≥0,y≥0},A={(x,y)|x≤4,y>0,x -y 2≥0},若向区域Ω上随机投一点P,则点P 落入区域A 的概率是________. 【答案】2787 .(山东省文登市2013届高三3月二轮模拟考试数学(理))设不等式组0102x y ≤≤⎧⎨≤≤⎩表示的平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于的概率是_________. 【答案】18π-8 .(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))随机变量ξ服从正态分布N (40, 2σ),若P (ξ<30)=0.2,则P (30<ξ<50)= _______. 【答案】【答案】0.6【解析】2.0)50()30(=>=<ξξP P ,所以6.0)50()30(1)5030(=>-<-=<<ξξξP P P三、解答题 9 .(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)袋中有8个大小相同的小球,其中1个黑球,3个白球,4个红球. (I)若从袋中一次摸出2个小球,求恰为异色球的概率;(II)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,记此时红球的个数为ξ,求ξ的分布列及数学期望E ξ.【答案】解: (Ⅰ)摸出的2个小球为异色球的种数为11C 11173419C C C +=从8个球中摸出2个小球的种数为2828C = 故所求概率为1928P =4 分 (Ⅱ)符合条件的摸法包括以下三种: 一种是有1个红球,1个黑球,1个白球,共有11C 114312C C =种一种是有2个红球,1个其它颜色球,共有214424C C =种,一种是所摸得的3小球均为红球,共有344C =种不同摸法,故符合条件的不同摸法共有40种由题意知,随机变量ξ的取值为1,2,3.其分布列为:3319123105105E ξ=⨯+⨯+⨯= 10.(山东省枣庄市2013届高三4月(二模)模拟考试数学(理)试题)甲、乙、丙三位同学一起参加某高校组织的自主招生考试,考试分笔试和面试两部分,笔试和面试均合ξ1 2 3P310 35 110格者将成为该校的预录取生(可在高考中加分录取),两次考试过程相互独立.根据甲、乙、丙三位同学的平时成绩分析,甲、乙、丙三位同学能通过笔试的概率分别是0.6,0.5,0.4,能通过面试的概率分别是0.5,0.6,0.75.(1)求甲、乙、丙三位同学中至少有两位同学通过笔试的概率;(2)设经过两次考试后,能被该高校预录取的人数为X,求随机变量X的分布列和数学E X.期望()【答案】11.(山东省夏津一中2013届高三4月月考数学(理)试题)一次考试中,五名学生的数学、物理成绩如下表所示:学生A1 A2 A3 A4 A5数学(x分) 89 91 93 95 97物理(y分) 87 89[ 89 92 93(2)要从4名数学成绩在90分以上的同学中选2人参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X 的分布列及数学期望E(X)的值.【答案】解:(1)x =59795939189++++=93,y =59392898987++++=90,,4042 0)2()4()(22222512=+++-+-=-∑=i ix x303422)1(0)1()2()3()4())((51=⨯+⨯+-⨯+-⨯-+-⨯-=--∑=i i iy y x x,300.7540b ==,69.75bx =,20.25a y bx =-= 故这些数据的回归方程是:ˆ0.7520.25yx =+ (2)随机变量X 的可能取值为0,1,222241(0)=6C P X C ==;1122242(1)=3C C P X C ==;22241(2)=6C P X C ==故X 的分布列为:()E X ∴=610⨯+321⨯+612⨯=112.(山东省潍坊市2013届高三第二次模拟考试数学理试题(word 版))甲、乙两人玩猜数字游戏,规则如下:①连续竞猜3次,每次相互独立;②每次竟猜时,先由甲写出一个数字,记为a,再由乙猜甲写的数字,记为b,已知{},0,1,2,3,4,5a b ∈,若1a b -≤,则本次竞猜成功;③在3次竞猜中,至少有2次竞猜成功,则两人获奖 (I )求甲乙两人玩此游戏获奖的概率;(Ⅱ)现从6人组成的代表队中选4人参加此游戏,这6人中有且仅有2对双胞胎 记选出的4人中含有双胞胎的对数为X,求X 的分布列和期望【答案】X 0 1 2 p61 32 6113.(山东省泰安市2013届高三第二次模拟考试数学(理)试题)(本小题满分12分) 某次考试中,从甲、乙两个班级各随机抽取10名学生的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于60分为及格.(I)从甲、乙两班的10名学生中各抽取一人,已知有人及格,求乙班学生不及格的概率;(II)从甲班10人中取1人,乙班10人中取2人,三人中及格人数记为ξ,求ξ的分布列及期望.【答案】14.(山东省莱芜五中2013届高三4月模拟数学(理)试题)2012年10月莫言获得诺贝尔文学奖后,其家乡山东高密政府准备投资6.7亿元打造旅游带,包括莫言旧居周围的莫言文化体验区,红高粱文化休闲区,爱国主义教育基地等;为此某文化旅游公司向社会公开征集旅游带建设方案,在收到的方案中甲、乙、丙三个方案引起了专家评委的注意,现已知甲、乙、丙三个方案能被选中的概率分别为231,,543,且假设各自能否被选中是无关的.(1)求甲、乙、丙三个方案只有两个被选中的概率;(2)记甲、乙、丙三个方案被选中的个数为ξ,试求ξ的期望.【答案】解:记甲、乙、丙三个方案被选中的事件分别为,,A B C,则231(),(),()543P A P B P C ===.(1)“只有两个方案被选中”可分为三种情形:①甲未被选中,乙、丙被选中,概率为3313()()()()54320P A B C P A P B P C ⋅⋅=⋅⋅=⨯⨯=②乙未被选中,甲、丙被选中,概率为2111()()()()54330P A B C P A P B P C ⋅⋅=⋅⋅=⨯⨯=③丙未被选中,甲、乙被选中,概率为2321()()()()5435P A B C P A P B P C ⋅⋅=⋅⋅=⨯⨯= 以上三种情况是互斥的. 因此只有两个方案被选中的概率为:311232030560P =++=(2)由题意可知ξ的可能取值为0,1,2,33121(0)()()()()54310P P A B C P A P B P C ξ==⋅⋅=⋅⋅=⨯⨯=;(1)()()()P P A B C P A B C P A B C ξ==⋅⋅+⋅⋅+⋅⋅()()()()()()()()()P A P B P C P A P B P C P A P B P C =⋅⋅+⋅⋅+⋅⋅2123323112554354354360=⨯⨯+⨯⨯+⨯⨯=; 由(1)知23(2)60P ξ==;2311(3)()()()()54310P P A B C P A P B P C ξ==⋅⋅=⋅⋅=⨯⨯=故1252318901231060601060E ξ=⨯+⨯+⨯+⨯=15.(山东省莱芜市莱芜四中2013届高三4月月考数学试题)为了宣传“低碳生活”,来自五个不同生活小区的5名志愿者利用周末休息时间到这五个小区进行演讲.每个志愿者随机地选择去一个生活小区,且每个生活小区只去一个人. (1)求甲恰好去自己生活小区宣传的概率;(2)求甲、乙都没有去自己生活小区宣传的概率;(3)记五人中恰好去自己生活小区宣传的人数为X,求随机变量X 的分布列和数学期望E(X).【答案】解:(1)记事件A 为“甲恰好去自己生活小区宣传”,P(A)=51. (2)五个人分到五小区共有55A =120种排法.甲、乙都没有去自己生活小区的排法共有55A -244A +33A =78种, P=12078=6039.(3)离散型随机变量X 的可能取值为0,1,2,3,5,P(X=1)=5515A 9C ⨯=83,P(X=2)=5525A 2C ⨯=61, P(X=3)=5535A 1C ⨯=121,P(X=5)=55A 1=1201,P(X=0)=1-83-61-121-1201=3011.∴离散型随机变量X 的分布列为 X 0 1235P301183 61 121 1201数学期望E(X)=83+62+123+1205=1.16.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)实验中学的三名学生甲、乙、丙参加某大学自主招生考核测试,在本次考核中只有合格和优秀两个等次,若考核为合格,则授予10分降分资格;考核优秀,授予20分降分资格.假设甲乙丙考核为优秀的概率分别为23、23、12,他们考核所得的等次相互独立. (Ⅰ)求在这次考核中,甲乙丙三名同学中至少有一名考核为优秀的概率.(Ⅱ)记在这次考核中甲乙丙三名同学所得降分之和为随机变量ξ,求随机变量ξ的分布列和数学期望E ξ.【答案】解:(Ⅰ) 记“甲考核为优秀”为事件A ,“乙考核为优秀”为事件B ,“丙考核为优秀”为事件C ,“甲、乙、丙至少有一名考核为优秀”为事件E.则事件A 、B 、C 是相互独立事件,事件C B A 与事件E 是对立事件,于是18172131311)(1)(=⨯⨯-=-=C B A P E P(Ⅱ)ξ的所有可能取值为60,50,40,30.()181)(30===C B A P P ξ, ()185)()()(40=++==C B A P C B A P C B A P P ξ, ()188)()()(50=++==BC A P C B A P C AB P P ξ,()184)(60===ABC P P ξ所以ξ的分布列为ξ30 40 50 60P181 185 188 184 314518460188501854018130=⨯+⨯+⨯+⨯=ξE 17.(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)春节期间,某商场决定从3种服装、2种家电、3种日用品中,选出3种商品进行促销活动. ⑴)试求选出的3种商品中至少有一种是家电的概率;⑵商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高100元,规定购买该商品的顾客有3次抽奖的机会:若中一次奖,则获得数额为m 元的奖金;若中两次奖,则共获得数额为m 3元的奖金;若中3次奖,则共获得数额为m 6元的奖金.假设顾客每次抽奖中获的概率都是31,请问:商场将奖金数额m 最高定为多少元,才能使促销方案对商场有利?【答案】解:⑴设选出的3种商品中至少有一种是家电为事件A,从3种服装、2种家电、3种日用品中,选出3种商品,一共有38C 种不同的选法 , 选出的3种商品中,没有家电的选法有36C 种所以,选出的3种商品中至少有一种是家电的概率为1491)(3836=-=C C A P⑵设顾客三次抽奖所获得的奖金总额为随机变量ξ,其所有可能的取值为0,m ,m 3,m 6.(单元:元)0ξ=表示顾客在三次抽奖都没有获奖,所以278)311()0(3=-==ξP同理,9431)311()(213=⨯-⨯==C m P ξ92)31()311()3(2123=⨯-⨯==C m P ξ271)31()6(333=⨯==C m P ξ顾客在三次抽奖中所获得的奖金总额的期望值是m m m m E 342716923942780)(=⨯+⨯+⨯+⨯=ξ 2由10034≤m ,解得75≤m 所以故m 最高定为75元,才能使促销方案对商场有利 .18.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )现有长分别为1m 、2m 、3m的钢管各3根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取n 根(假设各钢管被抽取的可能性是均等的,19n ≤≤),再将抽取的钢管相接焊成笔直的一根. (Ⅰ)当3n =时,记事件A ={抽取的3根钢管中恰有2根长度相等},求()P A ; (Ⅱ)当2n =时,若用ξ表示新焊成的钢管的长度(焊接误差不计),①求ξ的分布列; ②令21ηλξλ=-++,()1E η>,求实数λ的取值范围.【答案】解:(Ⅰ)事件A 为随机事件,121336399()14C C C P A C == (Ⅱ)①ξ可能的取值为2,3,4,5,623291(2)12C P C ξ=== 1133291(3)4C C P C ξ===211333291(4)3C C C P C ξ+===1133291(5)4C C P C ξ===23291(6)12C P C ξ===∴ξ的分布列为:②11111()2345641243412E ξ=⨯+⨯+⨯+⨯+⨯=21ηλξλ=-++Q ,2()()1E E ηλξλ∴=-++241λλ=-++()1E η>Q ,2141104λλλ∴-++>⇒<<19.(山东省济宁市2013届高三4月联考理科数学)某产品按行业生产标准分成6个等级,等级系数ξ依次为1,2,3,4,5,6,按行业规定产品的等级系数5ξ≥的为一等品,35ξ≤<的为二等品,3ξ<的为三等品.若某工厂生产的产品均符合行业标准,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下;(1)以此30件产品的样本来估计该厂产品的总体情况,试分别求出该厂生产原一等品、二等品和三等品的概率;(2)该厂生产一件产品的利润y (单位:元)与产品的等级系数ξ的关系式为1,32,354,5y ξξξ<⎧⎪=≤<⎨⎪≥⎩,若从该厂大量产品中任取两件,其利润记为Z,求Z 的分布列和数学期望.【答案】20.(山东省济南市2013届高三4月巩固性训练数学(理)试题)某企业计划投资A ,B 两个项目, 根据市场分析,A ,B 两个项目的利润率分别为随机变量X 1和X 2,X 1和X 2的分布列分别为:X 1 5% 10% P0.80.2(1)若在A ,B 两个项目上各投资1000万元,Y 1和Y 2分别表示投资项目A 和B 所获得的利润,求利润的期望()()12,E Y E Y 和方差()()12,D Y D Y ;(2)由于资金限制,企业只能将x (0≤x ≤1000)万元投资A 项目,1000-x 万元投资B 项目,f (x )表示投资A 项目所得利润的方差与投资B 项目所得利润的方差的和.求f (x )的最小值,并指出x 为何值时,f (x )取到最小值.X22% 8% 12% P 0.20.50.3【答案】解: (1)由题设可知Y 1和Y 2的分布列为Y150 100 P 0.80.2E (Y 1)=50×0.8+100×0.2=60,D (Y 1)=(50-60)2×0.8+(100-60)2×0.2=400,E (Y 2)=20×0.2+80×0.5+120×0.3=80,D (Y 2)=(20-80)2×0.2+(80-80)2×0.5+(120-80)2×0.3=1200(2) ()()()()22121261000110001000100010x x f x D Y D Y x D Y x D Y -⎛⎫⎛⎫⎡⎤=+=+- ⎪ ⎪⎣⎦⎝⎭⎝⎭=4410 [x 2+3(1000-x )2]=4410(4x 2-6000x +3×106) 当600075024x ==⨯时,f (x )=300为最小值21.(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))一次考试共有12道选择题,每道选择题都有4个选项,其中有且只有一个是正确的.评分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定有8道题的答案是正确的,其余题中:有两道题都可判断两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.请求出该考生: (1) 得60分的概率;(2) 所得分数ξ的分布列和数学期望. 【答案】【答案】解:(1) 设“可判断两个选项是错误的”两道题之一选对的为事件A ,“有一道题可判断一个选项是错误”选对的为事件B ,“有一道题不理解题意”选对的为事件C ,∴P(A)=12,P(B)=13,P(C)=14,∴得60分的概率为p =11111223448⨯⨯⨯= (2) ξ可能的取值为40,45,50,55,60P (ξ=40)=1123122348⨯⨯⨯=;P (ξ=45)=121123111311211722342234223448C ⨯⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=P (ξ=50)=1122⨯2334⨯⨯+1212C ⨯1123⨯⨯34⨯12C +12⨯⨯1223⨯Y220 80 120 P 0.20.50.311111174223448⨯+⨯⨯⨯=; P (ξ=55)=12C ⨯111223⨯⨯⨯14+1122⨯⨯2134⨯+12⨯12⨯13⨯34748=P (ξ=60)=1111111111223448223448⨯⨯⨯==⨯⨯⨯=ξ 4045505560P(ξ)18 1748 1748 748 148(3) E ξ=40×648+(45+50)×1748+55×748+60×148=5751222.(山东省菏泽市2013届高三第二次模拟考试数学(理)试题)某种家用电器每台的销售利润与该电器的无故障时间T(单位:年)有关,若T ≤1,则销售利润为0元;若1<T ≤3,则销售利润为100元,若T>3,则销售利润为200元.设每台该种电器的无故障使用时间T ≤1,1<T ≤3,T>3这三种情况发生的概率分别为123,,P P P ,又知12,P P 为方程25x 2-15x+a=0的两根,且23P P =. (Ⅰ)求123,,P P P 的值;(Ⅱ)记ξ表示销售两台这种家用电器的销售利润总和,求ξ的分布列及数学期望.【答案】解:(Ⅰ)由已知得1231223135P P P P P P P ++=⎧⎪⎪+=⎨⎪=⎪⎩解得::=,=,=.(Ⅱ)ξ的可能取值为0,100,200,300,400.P(ξ=0)=51⨯51=251 P(ξ=100)= 2⨯51⨯52=254P(ξ=200)= 2⨯51⨯52+52⨯52=258P(ξ=300)= 2⨯52⨯52=258 P(ξ=400)= 52⨯52=254随机变量ξ的分布列为ξ100 200300 400p251 254 258 258 254 所求的数学期望为E ξ=0⨯25+100⨯25+200⨯25+300⨯258+400⨯254=240(元)所以随机变量ξ的数学期望为240元.23.(山东省凤城高中2013届高三4月模拟检测数学理试题 )从装有大小相同的2个红球和6个白球的袋子中,每摸出2个球为一次试验,直到摸出的球中有红球(不放回),则试验结束.(Ⅰ)求第一次试验恰摸到一个红球和一个白球概率;(Ⅱ)记试验次数为X ,求X 的分布列及数学期望()E X .【答案】解:(I)设“第一次试验恰摸到一个红球和一个白球”为设计A,则1126283()7C C P A C == (II)1122622813(1)28C C C P X C +===; 2112642222869(2)28C C C C P X C C +==⋅=; 22112642222228645(3)28C C C C C P X C C C +==⋅⋅=; 2226422228641(4)28C C C P X C C C ==⋅⋅=; X X 1 2 3 4P1328 928 528 1281395125()12342828282814E X =⨯+⨯+⨯+⨯=24.(山东省德州市2013届高三第二次模拟考试数学(理)试题)某公司组织员工活动,有这样一个游戏项目:甲箱里装有3个白球,2个黑球,乙箱里装有1个白球,2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出一个白球记3分,一个黑球记1分,规定得分不低于8分则获奖(每次游戏结束后将球放回原箱). (I)求在1次游戏中,(1)得6分的概率;(2)获奖的概率; (Ⅱ)求在2次游戏中获奖次数X 的分布列及数学期望.【答案】解:(1)依题意“在一次游戏中得6分”的事件包括两种情况; ①甲箱中摸出1个白球1个黑球,乙箱中摸出2个黑球,其概率:X的数学期望。
山东各省市2013年高三1-3月数学模拟分类汇编:专题 抽样、概率(理科).pdf

山东各省市2013年高三1-3月模拟题数学(理)分类汇编 专题 抽样、概率 2013.04.06 (济南市2013届高三3月一模 理科)3.某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,用茎叶图表示上述两组数据,对两块地抽取树苗的高度的平均数和中位数进行比较,下面结论正确的是 A. B. C. D. 3B(淄博市2013届高三3月一模 理科)(5)(理科)某校有名学生,各年级男、女生人数如表,已知在全校学生中随机抽取一名“献爱心”志愿者,抽到高一男生的概率是,现用分层抽样的方法在全校抽取名奥运志愿者,则在高二抽取的学生人数为. (A) (B) (C) (D)0 (青岛市2013届高三期末 理科)4.为了从甲乙两人中选一人参加数学竞赛,老师将二人最近6次数学测试的分数进行统计,甲乙两人的平均成绩分别是,则下列说法正确的是 A.,乙比甲成绩稳定,应选乙参加比赛 B.,甲比乙成绩稳定,应选甲参加比赛 C.,甲比乙成绩稳定,应选甲参加比赛 D.,乙比甲成绩稳定,应选乙参加比赛 【答案】D 【 解析】由茎叶图可知,乙的数据集中在88左右,所以乙比甲成绩稳定,应选乙参加比赛,所以选D. (文登市2013届高三3月一模 理科)4.已知随机变量服从正态分布,且,则 A. B. C. D. C (德州市2013届高三期末 理科)13.某市居民用户12月份燃气用量(单位:m3)的频率分布直方图如图所示,现抽取了500户进行调查,则用气量在[26,36)的户数为 。
【 解析】用气量在[26,36),所以用气量在[26,36)的户数。
(威海市2013届高三期末 理科)4.有一个容量为的样本,其频率分布直方图如图所示,据图估计,样本数据在内的频数为 (A) (B) (C) (D) 【答案】C 样本数据在之外的频率为,所以样本数据在内的频率为,所以样本数据在的频数为,选C. (淄博市2013届高三期末 理科)11.某班同学准备参加学校在寒假里组织的“社区服务”、“进敬老院”、“参观工厂”、“民俗调查”、“环保宣传”五个项目的社会实践活动,每天只安排一项活动,并要求在周一至周五内完成.其中“参观工厂”与“环保宣讲”两项活动必须安排在相邻两天,“民俗调查”活动不能安排在周一.则不同安排方法的种数是 A.48B.24C.36D.64 【答案】C 【 解析】把“参观工厂”与“环保宣讲”当做一个整体,共有种,把“民俗调查”安排在周一,有,所以满足条件的不同安排方法的种数为,选C. (威海市2013届高三期末 理科)11.从,六个数字中任取两个奇数和两个偶数,组成没有重复数字的四位奇数,有多少种取法 (A) (B) (C) (D) 【答案】B 若不选0,则有,若选0,则有,所以共有种,所以选B. (青岛市2013届高三期末 理科)11.把5张座位编号为1,2,3,4,5的电影票发给3个人,每人至少1张,最多分2张,且这两张票具有连续的编号,那么不同的分法种数是A.360B.60C.54D.18 【答案】D 【 解析】5张电影票分3份,两张连续,则有1-23-45;12-3-45;12-34-5三种分发,然后发给三个人,有种,所以不同的分法有。
山东省高三数学 各地市最新模拟试题精品分类汇编 专题03 函数 理(教师版)

一、选择题:1. (山东省济南市2013年1月高三上学期期末理3)设0.30.33,log 3,log a b c e π===则,,a b c 的大小关系是A .a b c <<B .c b a <<C .b a c <<D .c a b <<2. (山东省济南市2013年1月高三上学期期末理5)已知函数1()()2x xf x e e -=-,则()f x 的图象A. 关于原点对称 B .关于y 轴对称 C .关于x 轴对称 D. 关于直线y x =对称3. (山东省济南市2013年1月高三上学期期末理11)设函数()2xf x =,则如图所示的函数图象对应的函数是A. ()||y f x =B. ()||y f x =-C. ()||y f x =--D. ()||y f x =-4. (山东省济南市2013年1月高三上学期期末理12)已知定义在R 上的函数()f x ,对任意x R ∈,都有()()()63f x f x f +=+成立,若函数()1y f x =+的图象关于直线1x =-对称,则()2013f =A.0B.2013C.3D.2013-5.(山东省德州市2013年1月高三上学期期末校际联考理4)已知函数1,0(),3,0gx x f x x x >⎧=⎨+≤⎩则()(1)0f a f +=,则实数a 的值等于( ) A .-3B .-l 或3C .1D .-3或l6.(山东省德州市2013年1月高三上学期期末校际联考理5)已知a>0,b>0,且1ab =,则函数()xf x a = 与函数()1bg x og x =的图象可能是( )7.(山东省淄博市2013届高三上学期期末理7)函数x x y sin =在[]ππ,-上的图象是8.(山东省淄博市2013届高三上学期期末理12)已知函数⎩⎨⎧>≤+=0,10,2)(x nx x kx x f ()k R ∈,若函数()y f x k =+有三个零点,则实数k 的取值范围是A .2k ≤B .10k -<<C .21k -≤<-D .2k ≤-9. (山东省烟台市2013年1月高三上学期期末理2)设()338xf x x =+-,用二分法求方程3380xx +-=在(1,2)x ∈内近似解的过程中得(1)0,(1.5)0,(1.25)0f f f <><,则方程的根落在区间 A.(1,1.25)B.(1.25,1.5)C.(1. 5,2)D.不能确定10. (山东省烟台市2013年1月高三上学期期末理9)已知()f x 是定义在R 上的奇函数,当0x ≥时()3x f x m =+(m 为常数),则f(-1og 35)的值为 A.4B.-4C.6D.-611. (山东省烟台市2013年1月高三上学期期末理12)方程1169x x y y+=-的曲线即为函数()y f x =的图像,对于函数()y f x =,有如下结论:①()f x 在R 上单调递减;②函数()4()3F x f x x =+不存在零点;③函数()y f x =的值域是R ;④若函数()g x 和()f x 的图像关于原点对称,则函数()y g x =的图像就是方程1169y y x x +=确定的曲线。
高三数学:专题13 复数与推理证明 文(教师版)

山东省2013届高三数学 各地市最新模拟理数试题精品分类汇编 专题13 复数与推理证明 文(教师版)一、选择题:1.(山东省济南市2013年1月高三上学期期末文1)复数31i i+=+A .i 21+B .i 21-C .i +2D .i -22.(山东省德州市2013届高三上学期期末校际联考文2)已知复数z 1,z 2在复平面上对应的点分别为A (l ,2),B (-1,3),则21z z =:A .1+iB .iC .1-iD .一i3.(山东省青岛即墨市2013届高三上学期期末考试文1)已知),(2R b a i b ii a ∈+=+,其中i 为虚数单位,则=-a bA.-1B.1C.2D.34.(山东省青岛一中2013届高三1月调研考试文)2013i 的值为( )A .1B .iC .-1D .i -5.(山东省师大附中2013届高三第四次模拟测试1月文)设()2112i iz +++=,则z =A .2 B .1 C .2 D .36.(山东省潍坊市四县一区2013届高三11月联考文)已知{}n a 中n n a )31(=,把数列{}n a 的各项排列成如下的三角形状,记),n m A (表示第m 行的第n 个数,则)(12,10A =A.9331)( B.9231)( C.9431)( D.11231)(7.(山东省济南外国语学校2013届高三上学期期中考试文) 复数512i i-=( )A.2i -B.12i -C.2i -+D.12i -+8.(山东省聊城市东阿一中2013届高三上学期期初考试)是虚数单位i ,复数ii +1=( )A.i -1B.i +1C.i +-1D.i9.(山东省师大附中2013届高三12月第三次模拟检测文)复数12()1i z i i-=-为虚数单位在复平面上对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限10.(山东省兖州市2013届高三9月入学诊断检测文)复数122i i+=-( )A.i -B.iC.5iD.45i +二、填空题:11. (山东省泰安市2013届高三上学期期末文14)下面图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第n 个图形中小正方形的个数是___________.【答案】(1)2n n +【解析】12341,3,6,10a a a a ====,所以2132432,3,4a a a a a a -=-=-=,1n n a a n --=,等式两边同时累加得123n a a n-=+++ ,即(1)122n n n a n +=+++=,所以第n 个图形中小正方形的个数是(1)2n n +12. (山东省青岛即墨市2013届高三上学期期末考试文16)研究问题:“已知关于x 的不等式02>+-c bx ax 的解集为(1,2),解关于x 的不等式02>+-a bx cx ”,有如下解法:由0)1()1(022>+-⇒>+-xc xb ac bx ax ,令xy 1=,则)1,21(∈y ,所以不等式02>+-a bx cx 的解集为),(121。
概率论与数理统计模拟试题5套带答案

06-07-1《概率论与数理统计》试题A一、填空题(每题3分,共15分)1. 设A ,B 相互独立,且2.0)(,8.0)(==A P B A P ,则=)(B P __________.2. 已知),2(~2σN X,且3.0}42{=<<X P ,则=<}0{X P __________.3. 设X 与Y 相互独立,且2)(=X E ,()3E Y =,()()1D X D Y ==,则=-])[(2Y X E ___4.设12,,,n X X X 是取自总体),(2σμN 的样本,则统计量2211()n i i X μσ=-∑服从__________分布.5. 设),3(~),,2(~p B Y p B X,且95}1{=≥X P ,则=≥}1{Y P __________. 二、选择题(每题3分,共15分)1. 一盒产品中有a 只正品,b 只次品,有放回地任取两次,第二次取到正品的概率为 【 】 (A)11a a b -+-;(B) (1)()(1)a a a b a b -++-;(C) a a b +;(D) 2a ab ⎛⎫ ⎪+⎝⎭.2. 设随机变量X 的概率密度为()130, 其他c x p x <<⎧=⎨⎩则方差D(X)= 【 】(A) 2; (B)12; (C) 3; (D)13.3. 设A 、B 为两个互不相容的随机事件,且()0>B P ,则下列选项必然正确的是【 】()A ()()B P A P -=1;()B ()0=B A P ;()C ()1=B A P ;()D ()0=AB P .4. 设()x x f sin =是某个连续型随机变量X 的概率密度函数,则X 的取值范围是【 】()A ⎥⎦⎤⎢⎣⎡2,0π;()B []π,0; ()C ⎥⎦⎤⎢⎣⎡-2,2ππ;()D ⎥⎦⎤⎢⎣⎡23,ππ. 5. 设()2,~σμN X ,b aX Y -=,其中a 、b 为常数,且0≠a ,则~Y 【 】()A ()222,b a b a N +-σμ; ()B ()222,b a b a N -+σμ;()C ()22,σμa b a N +; ()D ()22,σμa b a N -.三、(本题满分8分) 甲乙两人独立地对同一目标射击一次,其命中率分别为0.5和0.4,现已知目标被命中,求它是乙命中的概率.四、(本题满分12分)设随机变量X 的密度函数为xx ee Ax f -+=)(,求: (1)常数A ; (2)}3ln 210{<<X P ; (3)分布函数)(x F .五、(本题满分10分)设随机变量X 的概率密度为()⎩⎨⎧<<-=其他,010),1(6x x x x f 求12+=X Y的概率密度.六、(本题满分10分)将一枚硬币连掷三次,X 表示三次中出现正面的次数,Y 表示三次中出现正面次数与出现反面次数之差的绝对值,求:(1)(X ,Y )的联合概率分布;(2){}X Y P>.七、(本题满分10分)二维随机变量(X ,Y )的概率密度为⎩⎨⎧>>=+-其他,00,0,),()2(y x Ae y x f y x求:(1)系数A ;(2)X ,Y 的边缘密度函数;(3)问X ,Y 是否独立。
山东省高三数学 各地市最新模拟试题精品分类汇编 专题

山东省2013届高三数学 各地市最新模拟理数试题精品分类汇编 专题12 概率统计 文(教师版)一、选择题:1.(山东省潍坊市2013年1月高三上学期期末考试A 卷文11)已知集合{}⎭⎬⎫⎩⎨⎧+-==<--=311|,032|2x x g y x B x x x A ,在区间()3,3-上任取一实数x ,则“B A x ⋂∈”的概率为(A )41(B )81 (C )31 (D )1212. (山东省青岛即墨市2013届高三上学期期末考试文4)为了从甲乙两人中选一人参加数学竞赛,老师将二人最近6次数学测试的分数进行统计,甲乙两人的平均成绩分别是乙甲、x x ,则下列说法正确的是A.乙甲x x >,乙比甲成绩稳定,应选乙参加比赛B.乙甲x x >,甲比乙成绩稳定,应选甲参加比赛C.乙甲x x <,甲比乙成绩稳定,应选甲参加比赛D.乙甲x x <,乙比甲成绩稳定,应选乙参加比赛3.(山东省济南外国语学校2013届高三上学期期中考试文)某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名。
现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )A. 6B. 7C. 8D.9二、填空题:4.(山东省济南市2013年1月高三上学期期末文13)某单位青年、中年、老年职员的人数之比为11:8:6,从中抽取200名职员作为样本,则应抽取青年职员的人数为____________.5.(山东省青岛一中2013届高三1月调研考试文)某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编号1—50号,并分组,第一组1—5号,第二组6—10号,……,第十组46—50号,若在第三组中抽得号码为12的学生,则在第八组中抽得号码为___的学生.6.(山东省师大附中2013届高三第四次模拟测试1月文)有4个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为 .三、解答题:7. (山东省济南市2013年1月高三上学期期末文20) (本小题满分12分)某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[]17,18,下图是按上述分组方法得到的频率分布直方图.(1)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;(2)若从第一、五组中随机取出两个成绩,求这两个频率/组距0.240.28 0.36成绩的差的绝对值大于1的概率. 【解析】(1)由频率分布直方图知, 成绩在[14,16)内的人数为:500.28500.3632⨯+⨯=(人)… 3分所以该班成绩良好的人数为32人.……………………… 5分(2)由频率分布直方图知,成绩在[13,14)的人数为500.042⨯=人,设为x 、y ; … 6分成绩在[17,18) 的人数为500.084⨯=人,设为A 、B 、C 、D … 7分 若,[13,14)m n ∈时,有xy 1种情况; …………………… 8分 若,[17,18)m n ∈时,有,,,,,AB AC AD BC BD CD 6种情况; ………… 9分 若,m n 分别在[13,14)和[17,18)内时,A B C D x xA xB xC xD yyA yB yC yD共有8种情况. …………………… 10分所以基本事件总数为15种,事件“||1m n ->”所包含的基本事件个数有8种. ∴P (||1m n ->)158=. …………………… 12分 8.(山东省青岛即墨市2013届高三上学期期末考试文19)(本小题满分12分)有六张纸牌,上面分别写有1,2,3,4,5,6六个数字,甲、乙两人玩一种游戏:甲先取一张牌,记下点数,放回后乙再取一张牌,记下点数。
山东省高三数学 各地市最新模拟试题精品分类汇编 专题

山东省2013届高三数学 各地市最新模拟理数试题精品分类汇编 专题01 集合 文(教师版)一、选择题1.(山东省济南市2013年1月高三上学期期末文2)已知集合{}320A x x =+>,()(){}130B x x x =+->,则A B I =A .(),1-∞- B. 21,3⎛⎫-- ⎪⎝⎭ C. 2,33⎛⎫- ⎪⎝⎭D .()3,+∞2.(山东省德州市2013届高三上学期期末校际联考文1)已知全集U={l ,2,3,4,5,6},集合A={l ,2.4:6},集合B={l ,3,5},则U A B U ð( )A .{l,2,3,4,5,6}B .{1,2,4,6}C .{2,4,6}D .{2,3,4,5,6}3. (山东省济宁市2013届高三1月份期末测试文1)设全集U R =,集合{}{}220,1A x x x B x x =-<=>,则集合()U A C B ⋂=A.{}01x x <<B.{}01x x <≤C.{}02x x <<D.{}1x x ≤4. (山东省烟台市2013届高三上学期期末文1)已知{1,2}A =-,{22}B x x =-≤<,则A B I 等于A.{12}x x -≤≤B.{2}C.{1}-D.{1,2}-【答案】D【解析】因为{1,2}A =-,{22}B x x =-≤<,所以{1,2}A B =-I ,选D.5.(山东省潍坊市2013年1月高三上学期期末考试A 卷文1)全集U=R ,集合{}02|2≥+=x x x A ,则[U A=(A )[]0,2- (B )()0,2-(C )(][)+∞⋃-∞-,02,(D )[]2,06. (山东省泰安市2013届高三上学期期末文1)已知集合{}{}1,0,1,0,1,2M N =-=,则如图所示韦恩图中的阴影部分所表示的集合为A.{}0,1B. {}1,0,1-C. {}1,2-D.{}1,0,1,2-7.(山东省青岛即墨市2013届高三上学期期末考试文2)设全集,}6,5,4,3,2,1{=U 集合=⋂==)(}5,4,3{},4,3,2,1{Q C P Q P U ,则,A.{1,2,3,4,6}B.{1,2,3,4,5}C.{1,2,5}D.{1,2}8.(山东省师大附中2013届高三第四次模拟测试1月文)若全集为实数集R ,集合12{|log (21)0},R A x x C A =->则=A .1(,)2+∞B .(1,)+∞C .1[0,][1,)2+∞UD .1(,][1,)2-∞+∞U【答案】D【解析】121 {|log(21)0}{0211}{1}2A x x x x x x=->=<-<=<<,所以1{1}2RA x x=⨯≥≤或ð,即1(,][1,)2-∞+∞U,选D.9.(山东省潍坊一中2013届高三12月月考测试文)已知集合{}(){}1,2,3,4,5,,,,A B x y x A y A x y A==挝-?,则B中所含元素的个数为A.3B.6C.8D.1010.(山东省烟台市莱州一中2013届高三10月月考文)已知集合{}(){}x2M y y2,x0,N x y lg2x x,M N====-⋂>为A.()1,2 B.()1,+∞ C.[)2,+∞ D.[)1,+∞11.(山东省烟台市2013届高三上学期期中考试文)设集合A=2{|11},{|log0}x x x B x x<->=>或,则A B=IA. |1}x x>{ B . }0|>xx{ C. }1|-<xx{ D. }11|>-<xxx或{12.(山东省烟台市2013届高三上学期期中考试文)若非空集合2{|11},{|log0}x x x B x x<->=>或,且若a S∈,则必有6a S-∈,则所有满足上述条件的集合S共有A.6个B.7个C.8个D.9个【答案】B【解析】由题意知,集合S中包含的元素可以是3,1和5,2和4中的一组、两组、三组即S={3},{1,5},{2,4},{3,1,5},{3,2,4},{1,5,2,4},{3,1,5,2,4},故选B.13.(山东省潍坊市四县一区2013届高三11月联考文)设集合}31|{},23|{≤<-∈=<<-∈=n N n B m Z m A ,则=⋂B AA.{0,1}B.{-1,0,1}C.{0,1,2}D.{-1,0,1,2}14.(山东省师大附中2013届高三上学期期中考试文)设集合{}{}()2,1,0,1,2,1,2,{212},U U A B A C B =--==--⋃,,则等于A.{}1B.{}1,2C.{}2D.{}0,1,215.(山东省实验中学2013届高三第二次诊断性测试文)设全集{}{}{}3,2,1,0,2,1,0,3,2,1,0,1,2==--=N M U ,则N M C U I )(=A.{}2,1,0B.{}3,12--,C.{}3,0D.{}316.(山东省青岛市2013届高三上学期期中考试数学文)设全集{1,2,3,4}U =,集合{1,2}A =,{2,4}B =,则()U A B =U ðA.{2}B. {1,4}C.{1,2,4}D. {3}17.(山东省师大附中2013届高三12月第三次模拟检测文)已知=>==<==B A x y y B x x y y A x I 则},1,)21(|{},1,log |{2A .φB .(0,∞-)C .)21,0( D .(21,∞-)18.(山东省临沂市2013届高三上学期期中考试 文)设集合2{3,log },{,},{0},P a Q a b P Q ===I U 若则P Q 是A .{3,0}B .{3,2,0}C .{3,1,0}D .{3,2,1,0}-19.(山东省聊城市东阿一中2013届高三上学期期初考试)已知集合m A B A mx x B A 则且,},1|{},1,1{===-=Y 的值为 ( ) A .1或-1或0 B .-1 C .1或-1 D .020.(山东省聊城市东阿一中2013届高三上学期期初考试)设集合P={1,2,3,4},集合M={3,4,5}全集U=R ,则集合P ⋂∁UM= ( )A .{1,2}B .{3,4}C .{1}D .{-2,-1,0,1,2}21.(山东省济南外国语学校2013届高三上学期期中考试文)设集合U={1,2,3,4,5},A={1,3,5},B={2,5},则A ∩(C U B)等于( )A.{2}B.{2,3}C.{3}D.{1,3}【答案】D【解析】{134}U B =,,ð,所以{134}{1,3,5}={1,3}U A B =I I (),,ð,选D.22.(山东省德州市乐陵一中2013届高三10月月考文)已知全集R U =,集合11{20},{2}4x A x x B x -=-≤<=<,则)()(=⋂B A C RA.),1[)2,(+∞-⋃--∞B.),1(]2,(+∞-⋃--∞C.),(+∞-∞D. ),2(+∞-二、填空题:23.(山东省青岛一中2013届高三1月调研考试文)已知11{|2}82x A x -=<<,2{|log (2)1}B x x =-<,则A B =U ________________.24.(山东省兖州市2013届高三9月入学诊断检测文)已知集合{}{}22160,430,____A x x B x x x A B =-<=-+>⋃=则三、解答题:25.(山东省实验中学2013届高三第二次诊断性测试数学文18)(本小题满分12分)函数132)(++-=x x x f 的定义域为集合A ,函数[])2)(1(lg )(x a a x x g ---=的定义域为集合B ,若A B ⊆,求实数a 的取值范围。
山东省高三3月模拟数学理试题分类汇编:概率与统计
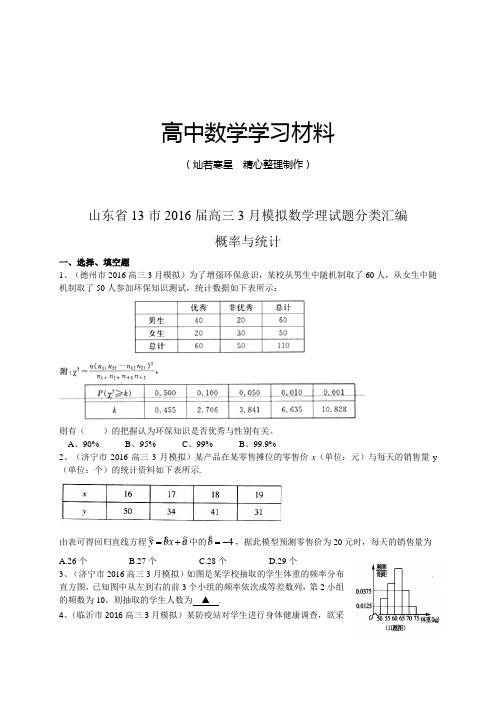
高中数学学习材料 (灿若寒星 精心整理制作)山东省13市2016届高三3月模拟数学理试题分类汇编概率与统计一、选择、填空题1、(德州市2016高三3月模拟)为了增强环保意识,某校从男生中随机制取了60人,从女生中随机制取了50人参加环保知识测试,统计数据如下表所示:则有( )的把握认为环保知识是否优秀与性别有关。
A 、90% B 、95% C 、99% B 、99.9%2、(济宁市2016高三3月模拟)某产品在某零售摊位的零售价x (单位:元)与每天的销售量y (单位:个)的统计资料如下表所示.由表可得回归直线方程y bx a =+$$$中的4b =-$,据此模型预测零售价为20元时,每天的销售量为 A.26个 B.27个 C.28个 D.29个3、(济宁市2016高三3月模拟)如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率依次成等差数列,第2小组的频数为10,则抽取的学生人数为 ▲ .4、(临沂市2016高三3月模拟)某防疫站对学生进行身体健康调查,欲采用分层抽样的办法抽取样本.某中学生共有学生2000名,抽取了一个容量为200的样本,样本中男生103人,则该中学生共有女生A. 1030人B. 97人C. 950人D.970人5、(青岛市2016高三3月模拟)已知数据12350,,,,,500x x x x ⋅⋅⋅(单位:公斤),其中12350,,,,,x x x x ⋅⋅⋅是某班50个学生的体重,设这50个学生体重的平均数为x ,中位数为y ,则12350,,,,,500x x x x ⋅⋅⋅这51个数据的平均数、中位数分别与x y 、比较,下列说法正确的是 A.平均数增大,中位数一定变大 B.平均数增大,中位数可能不变 C.平均数可能不变,中位数可能不变 D.平均数可能不变,中位数可能变小6、(泰安市2016高三3月模拟)随机抽取100名年龄在[)[)10,20,20,30…,[)50,60年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于30岁的人中按年龄段分层抽样的方法随机抽取22人,则在[)50,60年龄段抽取的人数为 ▲ . 7、(潍坊市2016高三3月模拟)如图所示,在边长为1的正方形OABC 中任取一点M ,则点M 恰好取自阴影部分的概率为__________.8、(烟台市2016高三3月模拟)已知100名学生某月零用钱消费支出情况的频率分布直方图如右图所示,则这100名学生中,该月零用钱消费支出超过150元的人数是9、(济南市2016高三3月模拟)某校高一、高二、高三年级学生人数分别是400,320,280.采用分层抽样的方法抽取50人,参加学校举行的社会主义核心价值观知识竞赛,则样本中高三年级的人数是( ) A.20 B.16 C.15 D.14参考答案:1、C2、D3、404、D5、B6、27、138、30 9、【答案】D【解析】考查分层抽样。
山东省高三数学 各地市最新模拟试题精品分类汇编 专题

山东省2013届高三数学 各地市最新模拟理数试题精品分类汇编 专题11 圆锥曲线 理(教师版)一、选择题:1. (山东省济南市2013年1月高三上学期期末理7)已知椭圆方程22143x y +=,双曲线22221(0,0)x y a b a b -=>>的焦点是椭圆的顶点, 顶点是椭圆的焦点,则双曲线的离心率为A.2B.3C. 2D. 32.(山东省德州市2013年1月高三上学期期末校际联考理10)双曲线22221(0,0)x y a b a b -=>> 的左、右焦点分别为F 1,F 2,渐近线分别为12,l l ,点P 在第 一象限内且在1l 上,若2l ⊥PF 1,2l //PF 2,则双曲线的离心率是 ( ) A 5B .2C 3D 2【答案】B【解析】双曲线的左焦点1(,0)F c -,右焦点2(,0)F c ,渐近线1:b l y x a =,2:b l y x a=-,因为点P 在第一象限内且在1l 上,所以设000(,),0P x y x >,因为2l ⊥PF 1,2l //PF 2,所以12PF PF ⊥,即1212OP F F c ==,即22200x y c +=,又00by x a=,代入得22200()b x x c a +=,解得00,x a y b ==,即(,)P a b 。
所以1PF bk a c=+,2l 的斜率为b a -,因为2l ⊥PF1,所以()1b ba c a ⨯-=-+,即2222()b a a c a ac c a =+=+=-,所以2220c ac a --=,所以220e e --=,解得2e =,所以双曲线的离心率2e =,所以选B.3.(山东省淄博市2013届高三上学期期末理8)已知双曲线()0,012222>>=-b a by a x 的一条渐近线的斜率为2,且右焦点与抛物线x y 342=的焦点重合,则该双曲线的离心率等于A .2B .3C .2D .234. (山东省济宁市2013届高三1月份期末测试理)抛物线24y x =上的一点M 到焦点的距离为1,则点M 的纵坐标是 A.78B.1516C.34D.05.(山东省枣庄三中2013届高三上学期1月阶段测试理)抛物线212y x =-的准线与双曲线22193x y -=的两渐近线围成的三角形的面积为 3 B. 233【答案】D【解析】抛物线212y x =-的准线为3x =,双曲线22193x y -=的两渐近线为33y x =和33y x =-,令3x =,分别解得123,3y y ==-,所以三角形的低为3(3)23--=,高为3,所以三角形的面积为1233332⨯⨯=,选D.6.(山东省青岛一中2013届高三1月调研理)过抛物线x y 42=的焦点作一条直线与抛物线相交于B A ,两点,它们到直线2-=x 的距离之和等于5,则这样的直线 A .有且仅有一条 B .有且仅有两条 C .有无穷多条D .不存在7.(山东省实验中学2013届高三第一次诊断性测试理)已知双曲线22221(0,0)x y a b a b-=>>的两条渐近线均与22:650C x y x +-+=相切,则该双曲线离心率等于A .355 B .62C .32D .558.(山东省实验中学2013届高三第三次诊断性测试理)已知椭圆)0(12222>>=+b a by a x 的左、右焦点分别为)0,(),0,21c F c F -(,若椭圆上存在点P 使1221sin sin F PF cF PF a ∠=∠,则该椭圆的离心率的取值范围为( )A.(0,)12-B.(122,) C.(0,22) D.(12-,1)9.(山东省聊城市东阿一中2013届高三上学期期初考试)过椭圆22221x y a b+=(0a b >>)的左焦点1F 作x 轴的垂线交椭圆于点P ,2F 为右焦点,若1260F PF ∠=o,则椭圆的离心率为 ( ) A .22 B .33 C .12 D .13二、填空题:10. (山东省济南市2013年1月高三上学期期末理15)若圆C 以抛物线24y x =的焦点为圆心,截此抛物线的准线所得弦长为6,则该圆的标准方程是 ;11. (山东省烟台市2013年1月高三上学期期末理15)设F 是抛物线C 1:24y x =的焦点,点A 是抛物线与双曲线C 2:22221(0,0)x y a b a b-=>>的一条渐近线的一个公共点,且AF x⊥轴,则双曲线的离心率为 【答案】5【解析】抛物线的焦点为(1,0)F .双曲线的渐近线为b y x a =±,不妨取by x a=,因为AF x ⊥,所以1A x =,所以2A y =±,不妨取(1,2)A ,又因为点(1,2)A 也在by x a=上,所以2b a=,即2b a =,所以22224b a c a ==-,即225c a =,所以25e =,即5e =,所以双曲线的离心率为5。
高三数学最新模拟试题精选分类汇编10统计理

山东省 高三最新理科模拟试题精选(17套)分类汇编10:统计一、选择题 1 .(山东省枣庄市 高三4月(二模)模拟考试数学(理)试题)一名篮球运动员在5场竞赛中的得分为14,16,21,24,25,则这组数据的平均数与标准不同离为 ( )A .18,B .20,18.8C .20,18.8D .18,18.8【答案】C 2 .(山东省夏津一中 高三4月月考数学(理)试题)某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了解该单位职工的健康情形,用分层抽样的方式从中抽取样本,若样本中的青年职工为7人,则样本容量为 ( ) A .35 B .25 C .15 D .7 【答案】C 3 .(山东省文登市 高三3月二轮模拟考试数学(理))一个样本容量为20的样本数据,它们组成一个公差不为0的等差数列{}n a ,若38a =且前4项和428S =,则此样本的平均数和中位数别离是 ( ) A .22,23 B .23,22 C .23,23 D .23,24【答案】C4 .(山东省泰安市 高三第二次模拟考试数学(理)试题)设某高中的女生体重y (单位:kg )与身高x (单位:cm )具有线性相关关系,依照一组样本数据()(),1,2,,i i x y i n =⋅⋅⋅,用最小二乘法成立的回归方程为0.8585.71y x =-,则下列结论不正确...的是 ( )A .y x 与具有正的线性相关关系B .回归直线过样本点的中心(),x yC .若该高中某女生身高增加1cm,则其体重约增加0.85kgD .若该高中某女生身高为170cm,则可判定其体重必为58.79kg 【答案】D 5 .(山东省济南市 高三4月巩固性训练数学(理)试题)为了解疾病A 是不是与性别有关,在一医院随机的对入院50 患疾病A 不患疾病A 合计 男 20 5 25 女 10 15 25 合计30 20 50请计算出统计量,你有多大的把握以为疾病A 与性别有关 下面的临界值表供参考:)(2k P ≥χkA .95%B .99%C .99.5%D .99.9%【答案】B 6 .x ,y ,测得一组数据如下表:x2 4 5 6 8 y2040607080根据上表,利用最小二乘法得它们的回归直线方程为ˆˆ10.5yx a =+,据此模型来预测当x = 20时,y 的估量值为 ( ) A .210 B .210.5 C . D .【答案】C 7 .(山东省德州市 高三第二次模拟考试数学(理)试题)某车间为了规定工时定额,需要确信加工零件所花费的时刻,为此进行了5次实验,依照搜集到的数据(如下表),由最小二乘法求得回归直线方程0.6854.6y x =+表中有一个数据模糊不清,请你推断出该数据的值为 ( ) A .68 B .68.2 C .69 D .75 【答案】A 二、填空题 8 .(山东省潍坊市 高三第二次模拟考试数学理试题(word 版))某市为增强市民的节约粮食意识,面向全市征召务宣传志愿者现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],取得的频率散布直方图如图所示若用分层抽样的方式从第3,4,5组中共抽取了12名志愿者参加l0月16日的“世界粮食日”宣传活动,则从第4组中抽取的人数为________.【答案】4 9 .(山东省泰安市 高三第二次模拟考试数学(理)试题)为了了解“预防禽流感疫苗”的利用情形,某市卫生部门对本地域9月份至11月份注射疫苗的所有养鸡场进行了调查,依照下图提供的信息,能够得出这三个月本地域每一个月注射了疫苗的鸡的数量平均为____万只.【答案】9010.(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))下列四种说法中正确的是___________.① “若2am <2bm ,则a <b ”的逆命题为真;② 线性回归方程对应的直线y b x a ∧∧∧=+必然通过其样本数据点 11(),x y -22()x y -,,(,)n n x y 中的一个点;③ 若实数x,y∈[],则知足:22x y +>1的概率为π4;④ 用数学归纳法证明(n +1)(n +2)(n +n )= 2n13(2n -1)(n ∈N*)时,从“k ”到“k +1”的证明,左侧需增添的一个因式是2(2k +1).【答案】【答案】④【解析】“若2am <2bm ,则a <b ”的逆命题为“若a <b ,则2am <2bm ”为假命题,当0=m 不成立.线性回归方程对应的直线y b x a ∧∧∧=+必然过),(y x ,不必然过样本点.在第一象限内圆122=+y x 的面积为4π,因此22x y +>1的概率为41π-,因此正确的命题是④.11.(山东省菏泽市 高三第二次模拟考试数学(理)试题)某单位200名职工的年龄散布情形如图,现要从中抽取40名职工作样本,用系统抽样法,将全部职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,196-200号).若第5组抽出的号码为22,则第8组抽出的号码应是_____.若用分层抽样方式,则40岁以下年龄段应抽取______人.【答案】20,37。
山东省高三数学 最新模拟试题精选(含一、二模)分类汇

山东省2013届高三最新文科模拟试题精选(26套含一、二模)分类汇编10:概率一、选择题1 .(山东省淄博市2013届高三3月第一次模拟考试数学文试题)在区间]5,1[和]6,2[内分别取一个数,记为a 和b ,则方程)(12222b a by a x <=-表示离心率小于5的双曲线的概率为( )A .21B .3215 C .3217 D .3231 【答案】B2 .(山东省凤城高中2013届高三4月模拟检测数学文试题 )ABC ∆中,8,6,10AB AC BC ===,顶点A B C 、、处分别有一枚半径为1的硬币(顶点A B C 、、分别与硬币的中心重合).向ABC ∆内部投一点,那么该点落在阴影部分的概率为( )A .124π-B .148π-C .24πD .48π【答案】A3 .(山东省淄博市2013届高三复习阶段性检测(二模)数学(文)试题)设[]0,5p 在上随机地取值,则关于x 的方程210x px ++=有实数根的概率为 ( )A .15B .25C .35 D .45【答案】C4 .(山东省泰安市2013届高三第一轮复习质量检测数学(文)试题)从{}1,2,3,4,5中随机选取一个数为a 从{}2,3,4中随机选取一个数b,则b a >的概率是 ( )A .45B .35C .25 D .15【答案】【答案】C 从两个集合中各选1个数有15种,满足b a >的数有,(1,2),(1,3),(2,3),(1,4),(2,4),(3,4)共有6个,所以b a >的概率是62155=,选 C .二、填空题 5 .(山东省菏泽市2013届高三第二次模拟考试数学(文)试题)沙糖桔是柑桔类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植沙糖桔,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(4045,,⎤⎦(((455050555560,,,,,⎤⎤⎤⎦⎦⎦进行分组,得到频率分布直方图如图 3.已知样本中产量在区间(4550,⎤⎦上的果树株数是产量在区间(5060,⎤⎦上的果树株数的43倍. (1)求a ,b 的值;(2)从样本中产量在区间(5060,⎤⎦上的果树随机抽取两株,求产量在区间(5560,⎤⎦上的果树至少有一株被抽中的概率.O4055图3a0.06b 0.02频率组距产量/kg605045【答案】(本小题主要考查频率分布直方图、概率等知识,考查数据处理、推理论证、运算求解能力和应用意识,以及或然与必然的数学思想)(1)解:样本中产量在区间(4550,⎤⎦上的果树有520100a a ⨯⨯=(株), 样本中产量在区间(5060,⎤⎦上的果树有()()002520100002b b ..+⨯⨯=+(株), 依题意,有()41001000023a b .=⨯+,即()40023a b .=+.① 根据频率分布直方图可知()00200651b a ..+++⨯=, ② 解①②得:008004a b .,.==(2)解:样本中产量在区间(5055,⎤⎦上的果树有0045204.⨯⨯=株,分别记为123A A A ,,,4A ,产量在区间(5560,⎤⎦上的果树有0025202.⨯⨯=株,分别记为12B B ,从这6株果树中随机抽取两株共有15种情况:()()1213A A A A ,,,,()14A A ,()()()()()()111223242122A B A B A A A A A B A B ,,,,,,,,,,,,()34A A ,,()31A B ,,()32A B ,,()()4142A B A B ,,,,()12B B ,其中产量在(5560,⎤⎦上的果树至少有一株共有9种情况:()()1112A B A B ,,,,PABCD()()()()21223132A B A B A B A B ,,,,,,,,()()4142A B A B ,,,,()12B B ,记“从样本中产量在区间(5060,⎤⎦上的果树随机抽取两株,产量在区间(5560,⎤⎦上的 果树至少有一株被抽中”为事件M ,则()93155P M ==6 .(山东省临沂市2013届高三3月教学质量检测考试(一模)数学(文)试题)已知向量a=(1,-2),b=(x ,y ),若x ,y ∈[1,4],则满足0a b ⋅>r r的概率为_____.【答案】19 因为0a b ⋅>r r ,所以20x y ->,又1414x y ≤≤⎧⎨≤≤⎩.做出可行域如图,当1y =时,2,2x y ==,即(2,0)B .当4x =时,4222x y ===,即(4,2)D ,所以2,1BC CD ==,即三角形BCD 的面积为11212⨯⨯=.所以由几何概型可知满足0a b ⋅>r r 的概率为11339=⨯. 7 .(山东省潍坊市2013届高三3月第一次模拟考试数学(文)试题)在区间[]0,4内随机取两个数a 、b, 则使得函数22()f x x ax b =++有零点的概率 为___________.【答案】【答案】14函数有零点,则2240a b ∆=-≥,即(2)(2)0a b a b -+≥.又0404a b ≤≤⎧⎨≤≤⎩,做出对应的平面区域为,当4a =时,2b =,即三角形OBC 的面积为14242⨯⨯=,所以由几何概型可知函数22()f x x ax b =++有零点的概率为41444=⨯. 三、解答题 8 .(山东省日照市2013届高三第一次模拟考试数学(文)试题)海曲市教育系统为了贯彻党的教育方针,促进学生全面发展,积极组织开展了丰富多样的社团活动,根据调查,某中学在传统民族文化的继承方面开设了“泥塑”、“剪纸”、“曲艺”三个社团,三个社团参加的人数如表所示:为调查社团开展情况,学校社团管理部采用分层抽样的方法从中抽取一个容量为n 的样本,已知从“剪纸”社团抽取的同学比从“泥塑”社团抽取的同学少2人. (I)求三个社团分别抽取了多少同学;(II)若从“剪纸”社团抽取的同学中选出2人担任该社团活动监督的职务,已知“剪纸”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率.【答案】解:(Ⅰ)设抽样比为x ,则由分层抽样可知,“泥塑”、“剪纸”、“曲艺”三个社团抽取的人数分别为x x x 200,240,320. 则由题意得2240320=-x x ,解得401=x . 故“泥塑”、“剪纸”、“曲艺”三个社团抽取的人数分别为⨯3208401=,6401240=⨯,5401200=⨯. 4分(Ⅱ)由(Ⅰ)知,从“剪纸”社团抽取的同学为6人,其中2位女生记为A,B,4位男生记为C,D,E,F.则从这6位同学中任选2人,不同的结果有 {A,B},{A,C},{A,D},{A,E},{A,F}, {B,C},{B,D},{B,E},{B,F}, {C,D},{C,E},{C,F}, {D,E},{D,F}, {E,F},共15种. 7分 其中含有1名女生的选法为 {A,C},{A,D},{A,E},{A,F}, {B,C},{B,D},{B,E},{B,F}, 共8种;含有2名女生的选法只有{A,B}1种 故至少有1名女同学被选中的概率为1591518=+=539.(山东省潍坊市2013届高三3月第一次模拟考试数学(文)试题)为了解社会对学校办学质量的满意程度,某学校决定用分层抽样的方法从高中三个年级的家长委员会中共抽取6人进行问卷调查,已知高一、高二、高三的家长委员会分别有54人、1 8人、36人. (I)求从三个年级的家长委员会中分别应抽的家长人数;(Ⅱ)若从抽得的6人中随机抽取2人进行训查结果的对比,求这2人中至少有一人是高三学生家长的慨率.【答案】解:(Ⅰ)家长委员会人员总数为54+18+36=108,样本容量与总体中的个体数的比为6110818=,故从三个年级的家长委员会中分别抽取的人数为3,1,2人(Ⅱ)设123,,A A A 为从高一抽得的3个家长,1B 为从高二抽得的1个家长,12,C C 为从高三抽得的2个家长. 则抽取的全部结果有:(12,A A ),(13,A A ),(11,A B ),(11,A C ),(12,A C ),(23,A A ),(21,A B ),(21,A C ),(22,A C ),(31,A B ),(31,A C ),(32,A C ),(11,B C ),(12,B C ),(12,C C )共15种,令X =“至少有一人是高三学生家长”,结果有(11,A C ),(12,A C ),(21,A C ),(22,A C ),(31,A C ),(32,A C ),(11,B C ),(12,B C ),(12,C C )共9种所以这2人中至少有1人是高三学生家长的概率是93().155P X == 10.(山东省枣庄市2013届高三3月模拟考试 数学(文)试题)有编号为A 1,A 2,A 3,,A 6的6位同学,进行100米赛跑,得到下面的成绩:其中成绩在13秒内的同学记为优秀.(l)从上述6名同学中,随机抽取一名,求这名同学成绩优秀的概率;(2)从成绩优秀的同学中,随机抽取2名,用同学的编号列出所有可能的抽取结果,并求这2名同学的成绩都在12.3秒内的概率.【答案】11.(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(文)试题)一个均匀的正四面体上分别有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为b ,c . (1)记z =(b -3)2+(c -3)2,求z =4的概率;(2)若方程x 2-bx -c =0至少有一根x ∈{1,2,3,4},就称该方程为“漂亮方程”,求方程为“漂亮方程”的概率.【答案】解:正四面体投掷两次,基本事件(b ,c )共有4×4=16个. (1)当z =4时,(b ,c )的所有取值为(1,3),(3,1).所以P (z =4)=216=18.(2)①若方程一根为x =1,则1-b -c =0,即b +c =1,不成立. ②若方程一根为x =2,则4-2b -c =0,即2b +c =4,所以⎩⎪⎨⎪⎧ b =1,c =2.③若方程一根为x =3,则9-3b -c =0,即3b +c =9.所以⎩⎪⎨⎪⎧b =2,c =3.④若方程一根为x =4, 则16-4b -c =0,即4b +c =16,所以⎩⎪⎨⎪⎧b =3,c =4.综合①②③④知,(b ,c )的所有可能取值为(1,2),(2,3),(3,4),所以,“漂亮方程”共有3个,方程为“漂亮方程”的概率为P =316.12.(山东省泰安市2013届高三第二次模拟考试数学(文)试题 )学校游园活动有一个游戏项目:箱子里装有3个红球,2个白球,这些球除颜色外完全相同.每次游戏从箱子里摸出3个球,若摸出的是3个红球为优秀;若摸出的2个红球1个白球为良好;否则为合格. (I)求在1次游戏中获得优秀的概率;(II)求在1次游戏中获得良好及以上的概率【答案】13.(山东省滨州市2013届高三第一次(3月)模拟考试数学(文)试题)甲、乙两名考生在填报志愿时都选中了A 、B 、C 、D 四所需要面试的院校,这四所院校的面试安排在同一时间.因此甲、乙都只能在这四所院校中选择一所做志愿,假设每位同学选择各个院校是等可能的,试求:(Ⅰ)甲、乙选择同一所院校的概率;(Ⅱ)院校A、B至少有一所被选择的概率.【答案】14.(山东省德州市2013届高三第二次模拟考试数学(文)试题)某种零件按质量标准分为1,2,3,4,5五个等级,现从一批该零件中随机抽取20个,对其等级进行统计分析,得到频率分布表如下:[来Array(I)在抽取的20个零件中,等级为5的恰有2个,求m,n;(Ⅱ)在(I)的条件下,从等级为3和5的所有零件中,任意抽取2个,求抽取的2个零件等级恰好相同的概率.【答案】解:(1)由抽取的20个零件中,等级为5的恰有2个15.(山东省济南市2013届高三3月高考模拟文科数学)以下茎叶图记录了甲组3名同学寒假假期中去图书馆A 学习的次数和乙组4名同学寒假假期中去图书馆B 学习的次数. 乙组记录中有一个数据模糊,无法确认,在图中以x 表示.(1)如果x =7,求乙组同学去图书馆学习次数的平均数和方差; (2)如果x =9,从学习次数大于8的学生中选两名同学,求选出的两名同学恰好分别在两个图书馆学习且学习的次数和大于20的概率.【答案】解(1)当x =7时,由茎叶图可知,乙组同学去图书馆学习次数是:7,8,9,12,所以平均数为;9412987=+++=x方差为.27])912()99()98()97[(4122222=-+-+-+-=s(2)记甲组3名同学为A 1,A 2,A 3,他们去图书馆学习次数依次为9,12,11;乙组4名同学为B 1,B 2,B 3,B 4,他们去图书馆学习次数依次为9,8,9,12;从学习次数大于8的学生中人选两名学生,所有可能的结果有15个,它们是:A 1A 2,A 1A 3,A 1B 1,A 1B 3,A 1B 4,A 2A 3,A 2B 1,A 2B 3,A 2B 4,A 3B 1,A 3B 3,A 3B 4, B 1 B 3,B 1B 4,B 3B 4用C 表示:“选出的两名同学恰好在两个图书馆学习且学习的次数和大于20”这一事件,则C 中的结果有5个,它们是:A 1B 4,A 2B 4,A 2B 3,A 2B 1,A 3B 4,故选出的两名同学恰好分别在两个图书馆学习且学习的次数和大于20概率为.31155)(==C P 12分 16.(山东省文登市2013届高三3月质量检测数学(文)试题)高三某班有两个数学课外兴趣小组,第一组有2名男生,2名女生,第二组有3名男生,2名女生.现在班主任老师要从第一组选出2人,从第二组选出1人,请他们在班会上和全班同学分享学习心得.甲组0 1x 8 29 21 9 乙组 第18题图(Ⅰ)求选出的3人均是男生的概率;(Ⅱ)求选出的3人中有男生也有女生的概率.【答案】(Ⅰ)记第一组的4人分别为1212,,,A A a a ;第二组的5人分别为12312,,,,B B B b b设“从第一组选出2人,从第二组选出1人”组成的基本事件空间为Ω,则12112212312112211111211311111212112212312112221121221321{(,,),(,,),(,,),(,,),(,,),(,,),(,,)(,,)(,,)(,,)(,,),(,,),(,,),(,,),(,,),(,,)(,,)(,,)(,A A B A A B A A B A A b A A b A a B A a B A a B A a b A a b A a B A a B A a B A a b A a b A a B A a B A a B A a Ω=1212221222223221222121122,)(,,),(,,)(,,)(,,)(,,)(,,),(,,)(,,)b A a b A a B A a B A a B A a b A a b a a B a a B123121122(,,)(,,)(,,)}a a B a a b a a b 共有30种设“选出的3人均是男生”为事件A ,则121122123{(,,),(,,),(,,)}A A A B A A B A A B =,共3种31()3010P A ∴==,所以选出的3人均是男生的概率为110(Ⅱ)设“选出的3人中有男生也有女生”为事件B ,设“都是女生”为事件C ,则12112221{(,,)(,,)},()3015C a a b a a b P C ===115()1()()110156P B P A P C ∴=--=--=所以选出的3人中有男生也有女生的概率为5617.(山东省莱芜五中2013届高三4月模拟数学(文)试题)中国共产党第十八次全国代表大会期间,某报刊媒体要选择两名记者去进行专题采访,现有记者编号分别为1,2,3,4,5的五个男记者和编号分别为6,7,8,9的四个女记者.要从这九名记者中一次随机选出取两名,每名记者被选到的概率是相等的,用符号(,)x y 表示事件“抽到的两名记者的编号分别为x 、y ,且x y <”. (1)共有多少个基本事件?并列举出来;(2)求所抽取的两记者的编号之和小于17但不小于11或都是男记者的概率.【答案】解:(1)共有36个基本事件,列举如下:)2,1(,)3,1(,)4,1(,)5,1(,)6,1(,)7,1(,)8,1(,)9,1(,)3,2(,)4,2(,)5,2(,)6,2(,)7,2(,)8,2(,)9,2(,)4,3(,)5,3(,)6,3(,)7,3(,)8,3(,)9,3(,)5,4(,)6,4(,)7,4(,)8,4(,)9,4(,)6,5(,)7,5(,)8,5(,)9,5(,)7,6(,)8,6(,)9,6(,)8,7(,)9,7(,)9,8(,共36个.(2)记事件“所抽取的记者的编号之和小于17但不小于11”为事件A ,即事件A 为“{},1,2,3,4,5,6,7,8,9x y ∈,且1117x y ≤+<,其中y x <”,由(1)可知事件A 共含有15个基本事件,列举如下:)9,2(,)8,3(,)9,3(,)7,4(,)8,4(,)9,4(,)6,5(,)7,5(,)8,5(,)9,5(,)7,6(,)8,6(,)9,6(,)8,7(,)9,7( 共15个;其中“都是男记者”记作事件B,则事件B 为“5x <且5y <,y x <”,包含:)2,1(,)3,1(,)4,1(,)5,1(,)3,2(,)4,2(,)5,2(,)4,3(,)5,3(,)5,4(,共10个;故151025()()363636P A P B +=+=. 18.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(文)试题)一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.(I)从袋中随机抽取一个球,将其编号记为a ,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为b .求关于x 的一元二次方程2220x ax b ++=有实根的概率;(II)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n.若以(,)m n 作为点P 的坐标,求点P 落在区域⎩⎨⎧<-+≥-050y x y x 内的概率.【答案】解:(1)基本事件(a,b)有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12种.∵2220x ax b ++=有实根, ∴△=4a 2-4b 2≥0,即a 2≥b 2.记“2220x ax b ++=有实根”为事件A,则A 包含的事件有:(2,1),(3,1),(3,2),(4,1),(4,2),(4,3) 共6种. ∴PA.=21126= (2)基本事件(m,n)有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2), (3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共16种. 记“点P 落在区域050x y x y -≥⎧⎨+-<⎩内”为事件B,则B 包含的事件有:(1,1),(2,1),(2,2),(3,1) 共4种.∴P B.=41164= 19.(山东省凤城高中2013届高三4月模拟检测数学文试题 )(本小题满分12分 ) 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30 .第6小组的频数是7.(Ⅰ)求这次铅球测试成绩合格的人数;(Ⅱ)若由直方图来估计这组数据的中位数,指出它在第几组内,并说明理由;(Ⅲ)若参加此次测试的学生中,有9人的成绩为优秀,现在要从成绩优秀的学生中,随机选出2人参加“毕业运动会”,已知a 、b 的成绩均为优秀,求两人至少有1人入选的概率. 【答案】解:(Ⅰ)第6小组的频率为1-(0.04+0.10+0.14+0.28+0.30)=0.14, ∴此次测试总人数为7500.14=(人). ∴第4、5、6组成绩均合格,人数为(0.28+0.30+0.14)×50=36(人)(Ⅱ)直方图中中位数两侧的面积相等,即频率相等.前三组的频率和为0.28,前四组的频率和为0.56,∴中位数位于第4组内(Ⅲ)设成绩优秀的9人分别为,,,,,,,,,a b c d e f g h k则选出的2人所有可能的情况为:,,,,,,,;ab ac ad ae af ag ah ak,,,,,,;bc bd be bf bg bh bk,,,,,;cd ce cf cg ch ck,,,,;de df dg dh dk,,,;ef eg eh ek,,;fg fh fk,;gh gk hk.共36种,其中a、b到少有1人入选的情况有15种,∴a、b两人至少有1人入选的概率为155.3612P==11。
山东各地2019高考数学最新联考试题分类汇编(13)概率

山东各地2019高考数学最新联考试题分类汇编(13)概率〔12〕(山东省淄博市2018届高三3月第一次模拟文理)在区间15,⎡⎤⎣⎦和[]6,2内分别取一个数,记为a 和b ,那么方程)(12222b a b y a x <=-表示离心率小于5的双曲线的概率为〔A 〕12〔C 〕1732〔D 〕3132【二】填空题:14、(山东省临沂市2018年3月高三教学质量检测文科)向量a=(1,-2),b=(x ,y ),假设x ,y ∈[1,4],那么满足0a b ⋅>的概率为、【答案】19【解析】因为0a b ⋅>,所以20x y ->,又1414x y ≤≤⎧⎨≤≤⎩。
做出可行域如图,当1y =时,2,2x y ==,即(2,0)B 。
当4x =时,4222x y ===,即(4,2)D ,所以2,1BC CD ==,即三角形BCD 的面积为11212⨯⨯=。
所以由几何概型可知满足0a b ⋅>的概率为11339=⨯。
【三】解答题:18、(山东省潍坊市2018年3月高三第一次模拟理)〔本小题总分值12分〕某电视台举办有奖竞答活动,活动规那么如下:①每人最多答4个小题;②答题过程中,假设答对那么继续答题,答错那么停止答题;③答对每个小题可得10分,答错得0分、甲、乙两人参加了此次竞答活动,且相互之间没有影响、甲答对每个题的概率为13,乙答对每个题的概为23、(I)设甲的最后得分为X ,求X 的分布列和数学期望; (Ⅱ)求甲、乙最后得分之和为20分的概率、 18.〔本小题总分值12分〕 解:〔I 〕X 的取值可为:0,10,20,30,40.………………………………………………1分12(0)133P X ==-=, 112(10)1339P X 骣÷ç==?=÷ç÷ç桫,2112(20)13327P X 骣骣鼢珑==-=鼢珑鼢珑桫桫,3112(30)13381P X 骣骣鼢珑==?=鼢珑鼢珑桫桫, 411(40)381P X 骣÷ç===÷ç÷ç桫. X \的分布列如下:数学期望222214000102030403927818181EX =?????.……………………7分18、(山东省潍坊市2018年3月高三第一次模拟文)〔本小题总分值12分〕为了解社会对学校办学质量的满意程度,某学校决定用分层抽样的方法从高中三个年级的家长委员会中共抽取6人进行问卷调查,高【一】高【二】高三的家长委员会分别有54人、18人、36人、(I)求从三个年级的家长委员会中分别应抽的家长人数;(Ⅱ)假设从抽得的6人中随机抽取2人进行训查结果的对比,求这2人中至少有一人是高三学生家长的慨率、 18.〔本小题总分值12分〕 解:〔Ⅰ〕家长委员会人员总数为54+18+36=108,样本容量与总体中的个体数的比为6110818,故从三个年级的家长委员会中分别抽取的人数为3,1,2……………………………………5分人.……………………………………4分〔Ⅱ〕设123,,A A A 为从高一抽得的3个家长,1B 为从高二抽得的1个家长,12,C C 为从高三抽得的2个家长.………………………………5分那么抽取的全部结果有:〔12,A A 〕,〔13,A A 〕,〔11,A B 〕,〔11,A C 〕,〔12,A C 〕,〔23,A A 〕,〔21,A B 〕,〔21,A C 〕,〔22,A C 〕,〔31,A B 〕,〔31,A C 〕,〔32,A C 〕,〔11,B C 〕,〔12,B C 〕,〔12,C C 〕共15种,……………………………………………………………………………………………8分令X =“至少有一人是高三学生家长”,结果有〔11,A C 〕,〔12,A C 〕,〔21,A C 〕,〔22,A C 〕,〔31,A C 〕,〔32,A C 〕,〔11,B C 〕,〔12,B C 〕,〔12,C C 〕共9种.…………………………10分所以这2人中至少有1人是高三学生家长的概率是93().155P X ==……………………12分 18.(山东省日照市2018年3月高三第一次模拟理)〔本小题总分值12分〕某工厂生产甲,乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如下:〔I 〕试分别估计芯片甲,芯片乙为合格品的概率;〔II 〕生产一件芯片甲,假设是合格品可盈利40元,假设是次品那么亏损5元;生产一件芯片乙,假设是合格品可盈利50元,假设是次品那么亏损10元.在〔I 〕的前提下,〔i 〕记X 为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X 的分布列和数学期望;〔ii 〕求生产5件芯片乙所获得的利润不少于140元的概率. (18)解析:〔Ⅰ〕芯片甲为合格品的概率约为4032841005++=,芯片乙为合格品的概率约为4029631004++=、………………3分 〔Ⅱ〕〔ⅰ〕随机变量X 的所有取值为90,45,30,15-、433(90)545P X ==⨯=;133(45)5420P X ==⨯=; 411(30)545P X ==⨯=;111(15)5420P X =-=⨯=、所以,随机变量的分布列为:3311904530(15)66520520EX =⨯+⨯+⨯+-⨯=、………………8分 〔ⅱ〕设生产的5件芯片乙中合格品有n 件,那么次品有5n -件. 依题意,得5010(5)140n n --≥,解得196n ≥、所以4n =,或5n =、设“生产5件芯片乙所获得的利润不少于140元”为事件A , 那么445531381()C ()()444128P A =⨯+=、………………12分18.(山东省日照市2018年3月高三第一次模拟文)〔本小题总分值12分〕 海曲市教育系统为了贯彻党的教育方针,促进学生全面发展,积极组织开展了丰富多样的社团活动,根据调查,某中学在传统民族文化的继承方面开设了“泥塑”、“剪纸”、“曲艺”三个社团,三个社团参加的人数如表所示:为调查社团开展情况,学校社团管理部采用分层抽样的方法从中抽取一个容量为n 的样本,从“剪纸”社团抽取的同学比从“泥塑”社团抽取的同学少2人.〔I 〕求三个社团分别抽取了多少同学;〔II 〕假设从“剪纸”社团抽取的同学中选出2人担任该社团活动监督的职务,“剪纸”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率.{A ,C},{A ,D},{A ,E},{A ,F},{B ,C},{B ,D},{B ,E},{B ,F}, 共8种;含有2名女生的选法只有{A ,B}1种、…………10分故至少有1名女同学被选中的概率为1591518=+=53、……………12分 18、(山东省青岛市2018年3月高三第一次模拟文)〔本小题总分值12分〕从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm 和195cm 之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,第一组与第八组人数相同,第六组的人数为4人、〔Ⅰ〕求第七组的频率;〔Ⅱ〕估计该校的800名男生的身高的中位数以及身高在180cm 以上〔含180cm 〕的人数;〔Ⅲ〕假设从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为,x y ,事件=E {5x y -≤},事件F ={15->x y },求()P EF 、18、〔本小题总分值12分〕 〔Ⅰ〕第六组的频率为40.0850=,所以第七组的频率为10.085(0.00820.0160.0420.06)0.06--⨯⨯++⨯+=;……………………………4分〔Ⅲ〕第六组[180,185)的人数为4人,设为,,,a b c d ,第八组[190,195]的人数为2人,设为,A B ,那么有,,,,,,ab ac ad bc bd cd ,,,,,,,,aA bA cA dA aB bB cB dB AB 共15种情况,因事件=E {5x y -≤}发生当且仅当随机抽取的两名男生在同一组,所以事件E 包含的基本事件为,,,,,,ab ac ad bc bd cd AB 共7种情况,故7()15P E =、……………………10分由于max 19518015x y -=-=,所以事件F ={15->x y }是不可能事件,()0P F =由于事件E 和事件F 是互斥事件,所以7()()()15P EF P E P F =+=………12分〔20〕(山东省淄博市2018届高三3月第一次模拟文)〔本小题总分值12分〕 某校举行环保知识竞赛,为了了解本次竞赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩〔得分均为整数,总分值100分〕,进行统计,请根据频率分布表中所提供的数据,解答以下问题:〔Ⅰ〕求a b 、的值;〔Ⅱ〕假设从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加社区志愿者活动,并从中选出2人做负责人,求2人中至少有1人是第四组的概率、 解:〔I 〕35,0.30a b ==……………………………………………………………12分所以其中第4组的2位同学至少有一位同学入选的概率为53159=…………12分 〔20〕(山东省淄博市2018届高三3月第一次模拟理)〔本小题总分值12分〕在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,假设是红球记1分,白球记2分,黄球记3分、现从这个盒子中,有放回地先后摸出两球,所得分数分别记为x 、y ,设O 为坐标原点,点P 的坐标为(2,)x x y --,记2OPξ=、 〔I 〕求随机变量ξ的最大值,并求事件“ξ取得最大值”的概率; 〔Ⅱ〕求随机变量ξ的分布列和数学期望、那么随机变量ξ的分布列为:……………10分因此,数学期望1422012529999E ξ=⨯+⨯+⨯+⨯=…………………12分。
山东省13市2017届高三最新考试数学文试题分类汇编_统计与概率 全国通用 Word版含答案

山东省13市2017届高三最新考试数学文试题分类汇编统计与概率2017.03一、选择、填空题1、(滨州市2017届高三上期末)在区间62ππ⎡⎤-⎢⎥⎣⎦,上随机地取一个数,则事件“1sin 2x ≥”发生的概率为 .2、(德州市2017届高三第一次模拟考试)如表是降耗技术改造后生产某产品过程中记录的产量(吨)与相应的生产能耗(吨标准煤)的几组对应数据,根据表中提供的数据,求出y 关于的线性回归方程ˆˆ0.70.3yx =+,那么表中m 的值为 .3、(菏泽市2017年高考一模)在一次化学测试中,高一某班50名学生成绩的平均分为82分,方差为8.2,则下列四个数中不可能是该班化学成绩的是( ) A .60 B .70 C .80 D .1004、(济宁市2017届高三第一次模拟(3月))在区间[]0,π上随机地取一个数,则事件“1tan x -≤≤ ) A .712B .23C .13D .145、(聊城市2017届高三上期末)某市教育局随机调查了300名高中学生周末的学习时间(单位:小时),制成了如图所示的频率分布直方图,其中学习时间的范围是[0,30],样本数据分组为,[0,5)[5,10)[10,15)[15,20)[20,25)[25,30],,,,,,根据直方图,这300名高中生周末的学习时间是15小时的人数是( )A .27B .33C .135D .1656、(临沂市2017届高三2月份教学质量检测(一模))传承传统文化再掀热潮,在刚刚过去的新春假期中,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏,下面的茎叶图是两位选手在个人追逐赛中的比赛得分,则下列说法正确的是 (A)甲的平均数大于乙的平均数 (B)甲的中位数大于乙的中位数(C)甲的方差大于乙的方差 (D)甲的平均数等于乙的中位数7、(青岛市2017年高三统一质量检测)已知变量,y 具有线性相关关系,它们之间的一组数据如下表所示,若y 关于的线性回归方程为ˆ 1.31yx =-,则m = ;8、(日照市2017届高三下学期第一次模拟)在[]2,2-上随机地取两个实数,a b ,则事件“直线1x y +=与圆()()222x a y b -+-=相交”发生的概率为 (A )1116(B )916(C )34(D )149、(泰安市2017届高三第一轮复习质量检测(一模))在区间-1,1]上随机取一个数k ,使直线y =k (x +3)与圆x 2+y 2=1相交的概率为 A .12 B .13C .3D .410、(烟台市2017届高三3月高考诊断性测试(一模))某十字路口的信号灯为红灯和绿灯交替出现,红灯持续的时间为60秒,小明放学回家途经该路口遇到红灯,则小明至少要等15秒才能出现绿灯的概率为( ) A .23 B .13 C .34 D .1411、(烟台市2017届高三3月高考诊断性测试(一模))用0,1,2,…,299给300名高三学生编号,并用系统抽样的方法从中抽取15名学生的数学成绩进行质量分析,若第一组抽取的学生的编号为8,则第四组抽取的学生编号为 . 12、(枣庄市2017届高三下学期第一次模拟考试)为了解本市居民的生活成本,甲、乙、内三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),甲、乙、丙所调查数据的标准差分别为321,,x x x ,则它们的大小关系为A .321s s s >>B .231s s s >>C .123s s s >>D .213s s s >>13、(淄博市2017届高三3月模拟考试)在区间[0,]2π上随机地取一个数,则事件“1sin 22x ≤≤”发生的概率为 ( ). A .12 B .13 C. 14 D .1614、(滨州市2017届高三上期末)如图,茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员的平均成绩相同,则成绩较为稳定的运动员成绩的方差为 .15、(淄博市2017届高三3月模拟考试)从某高校在校大学生中随机选取5名女大学生,由她们身高和体重的数据得到的回归直线方程为ˆ0.7973.56yx =-,数据列表是:则其中的数据a = .二、解答题1、(滨州市2017届高三上期末)今年我国许多省市雾霾频发,为增强市民的环境保护意识,某市面向全市学校征召100名教师做义务宣传志愿者,成立环境保护宣传组,现把该组的成员按年龄分成5组:第一组[)2025,,第2组[)2530,,第3组[)3035,,第4组[)3540,,第5组[)4045,,得到的频率分布直方图如图所示.(Ⅰ)若从第3,4,5组中用分层抽样的方法选出6名志愿者参加某社区的宣传活动,应从第3,4,5组各选出多少名志愿者?(Ⅱ)在(Ⅰ)的条件下,该组织决定在这6名志愿者中随机选2名志愿者介绍宣传经验,求第4组至少有1名志愿者被选中的概率.2、(德州市2017届高三第一次模拟考试)某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取100人做调查,得到如下22⨯列联表:已知在这100人中随机抽取一人抽到喜欢游泳的学生的概率为5.(Ⅰ)请将上述列联表补充完整,并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;(Ⅱ)针对问卷调查的100名学生,学校决定从喜欢游泳的人中按分层抽样的方法随机抽取6人成立游泳科普知识宣传组,并在这6人中任选两人作为宣传组的组长,求这两人中至少有一名女生的概率.参考公式:22112212211212()n n n n nn n n nχ++++-=,其中11122122n n n n n=+++.参考数据:3、(菏泽市2017年高考一模)某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:频率分布表(1)写出a,b,x,y的值;(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动.(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率;(ⅱ)求所抽取的2名同学来自同一组的概率.4、(济宁市2017届高三第一次模拟(3月))某中学组织了一次高二文科学生数学学业水平模拟测试,学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析,分别制成了如图所示的男生和女生数学成绩的频率分布直方图.(Ⅰ)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?(Ⅱ)在(Ⅰ)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意选取2人,求至少有一名男生的概率.5、(聊城市2017届高三上期末)元旦前夕,某校高三某班举行庆祝晚会,人人准备了才艺,由于时间限制不能全部展示,于是找四张红色纸片和四张绿色纸片上分别写1,2,3,4,确定由谁展示才艺的规则如下:①每个人先分别抽取红色纸片和绿色纸片各一次,并将上面的数字相加的和记为X ; ②当3X ≤或6X ≥时,即有资格展现才艺;当36X <<时,即被迫放弃展示.(1)请你写出红绿纸片所有可能的组合(例如2332()()红,绿,红,绿);(2)求甲同学能取得展示才艺资格的概率.6、(临沂市2017届高三2月份教学质量检测(一模))某校对高二年级选学生物的学生的某次测试成绩进行了统计,随机抽取了m 名学生的成绩作为样本,根据此数据作出了频率分布统计表和频率分布直方图如下:(I)求表中n ,p 的值和频率分布直方图中a 的值;(II)如果用分层抽样的方法,从样本成绩在60,70]和90,100]的学生中共抽取5人,再从5人中选2人,求这2人成绩在60,70]的概率. 7、(青岛市2017年高三统一质量检测)某滑雪场开业当天共有500人滑雪,滑雪服务中心根据他们的年龄分成[10,20),[20,30),[30,40),[40,50),[50,60]五个组,现按照分层抽样的方法选取20人参加有奖活动,这些人的样本数据的频率分布直方图如下图所示,从左往右分别为一组、二组、三组、四组、五组.(Ⅰ)求开业当天所有滑雪的人年龄在[20,30)有多少人?(Ⅱ)在选取的这20人样本中,从年龄不低于30岁的人中任选两人参加抽奖活动,求这两个人来自同一组的概率.8、(日照市2017届高三下学期第一次模拟)某中学高三年级有学生500人,其中男生300人,女生200人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省2013届高三数学 各地市最新模拟理数试题精品分类汇编 专题13 概率统计 理(教师版)一、选择题:1.(山东省青岛一中2013届高三1月调研理)投掷两颗骰子,其向上的点数分别为m 和n ,则复数2()m ni +为纯虚数的概率为( )A .13B .14C .16D .1122.(山东省青岛一中2013届高三1月调研理)某学生四次模拟考试时,其英语作文的减分情况如下表: 考试次数x 1 2 3 4 所减分数y4.5432.5A .25.57.0+=x yB .25.56.0+-=x yC .25.67.0+-=x yD .25.57.0+-=x y3. (山东省青岛即墨市2013届高三上学期期末考试理4)为了从甲乙两人中选一人参加数学竞赛,老师将二人最近6次数学测试的分数进行统计,甲乙两人的平均成绩分别是乙甲、x x ,则下列说法正确的是A.乙甲x x >,乙比甲成绩稳定,应选乙参加比赛B.乙甲x x >,甲比乙成绩稳定,应选甲参加比赛C.乙甲x x <,甲比乙成绩稳定,应选甲参加比赛D.乙甲x x <,乙比甲成绩稳定,应选乙参加比赛二、填空题:4.(山东省德州市2013年1月高三上学期期末校际联考理13)某市居民用户12月份燃气用量(单位:m 3)的频率分布直方图如图所示,现抽取了500户进行调查,则用气量在[26,36)的户数为 。
三、解答题:5.(山东省青岛一中2013届高三1月调研理)(本小题满分12分) 英语老师要求学生从星期一到星期四每天学习3个英语单词;每周五对一周内所学单词随机抽取若干个进行检测(一周所学的单词每个被抽到的可能性相同)(Ⅰ)英语老师随机抽了4个单词进行检测,求至少有3个是后两天学习过的单词的概率; (Ⅱ)某学生对后两天所学过的单词每个能默写对的概率为45,对前两天所学过的单词每个能默写对的概率为35.若老师从后三天所学单词中各抽取一个进行检测,求该学生能默写对的单词的个数ξ的分布列和期望.(Ⅱ)由题意可得ξ可取0,1,2,3,则有P (ξ=0)2122()55125=⨯=………6分P (ξ=1)1224121319C ()55555125=⨯⨯⨯+⨯=, P (ξ=2) 2124241356()+C 55555125=⨯⨯⨯⨯=,…………………………………9分 P (ξ=3) 24348()55125=⨯= …………………………………………………10分所以ξ的分布列为:…11分故E ξ=0×2125+1×19125+2×56125+3×48125=115……………………………12分 6.(山东省济南外国语学校2013届高三上学期期中考试理)(本小题满分12分) 以下茎叶图记录了甲、乙两组个四名同学的植树棵树。
乙组记录中有一个数据模糊,无法确认,在图中以X 表示。
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数;(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树Y 的分布列和数学期望.(Ⅱ)当X=9时,由茎叶图可知,甲组同学的植树棵树是:9,9,11,11;乙组同学的植树棵数是:9,8,9,10。
分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能的结果,这两名同学植树总棵数Y 的可能取值为17,18,19,20,21事件“Y=17”等价于“甲组选出的同学植树9棵,乙组选出的同学植树8棵”所以该事ξ 0123P2125 19125 56125 48125件有2种可能的结果,因此P (Y=17)=.81162= 同理可得;41)18(==Y P ;41)19(==Y P .81)21(;41)20(====Y P Y P所以随机变量Y 的分布列为:Y 1718192021P81 41 41 41 81 EY=17×P (Y=17)+18×P (Y=18)+19×P (Y=19)+20×P (Y=20)+21×P (Y=21)=17×81+18×41+19×41+20×41+21×81=19…………………………………….12分 7.(山东省青岛即墨市2013届高三上学期期末考试理19)(本小题满分12分)若盒中装有同一型号的灯泡共10只,其中有8只合格品,2只次品。
(1)某工人师傅有放回地连续从该盒中取灯泡3次,每次取一只灯泡,求2次取到次品的概率;(2)某工人师傅有该盒中的灯泡去更换会议室的一只已坏灯泡,每次从中取一灯泡,若是正品则用它更换已坏灯泡,若是次品则将其报废(不再放回原盒中),求成功更换会议室的已坏灯泡所用灯泡只数x 的分布列和数学期望。
(2)依据知X 的可能取值为1.2.3………5 且541081===)(x P ………6 458822210=⨯==A x P )(………7 451321022===A A x P )( (8)则X 的分布列如下表: X123p54 458 451 ……10分911455545345164536==++=EX ………12分 【好题回顾】1.(山东省临沂市2012年高三第二次模拟试题理10)已知{}()0101x y x y Ω=≤≤≤≤,,,A 是由直线0y =,(01)x a a =<≤和曲线3y x =围成的曲边三角形区域,若向区域Ω上随机投一点,点落在区域A 内的概率为164,则a 的值是 (A )164(B )18 (C )14 (D )122. (2012年山东省泰安一模理科8)下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程x y53ˆ-=,变量x 增加一个单位时,y 平均增加5个单位; ③线性回归方程a x b yˆˆˆ+=必过()y x ,; ④在一个22⨯列联表中,由计算得K 2=13.079,则有99%的把握确认这两个变量间有关系;其中错误..的个数是 A.0 B.1 C.2 D.3 ()kK P ≥20.5 0.40 0.25 0.15 0.10 0.05 0.25 0.10 0.005 0.001 k0.4550.7081.3232.0722.7063.8415.0246.5357.87910.828【答案】B【解析】①③④正确,②回归方程x y53ˆ-=,当变量x 增加一个单位时,y 平均减少5个单位,所以错误,所以错误的个数有1个,答案选B.3. (2012年山东省泰安一模理科11)已知(){}1,1,≤≤=Ωy x y x ,A 是曲线2x y =与21x y =围成的区域,若向区域Ω上随机投一点P ,则点P 落入区域A 的概率为A.31 B.41 C.81 D.121 【答案】D【解析】本题为几何概率.区域Ω的面积为422=⨯.区域A 的面积为313132)3132()(1032310221=-=-=-⎰x x dx x x ,所以点P 落入区域A 的概率为121431==P ,选D.4. (山东实验中学2012届高三第一次诊断性考试理15)已知函数,若a,b 都是在区间内任取一个数,则的概率为_______5. (山东省2012年济南市二模理科13)随机变量ξ服从正态分布N (40, 2σ),若P (ξ<30)=0.2,则P (30<ξ<50)= .6.(山东省临沂市2012年高三第二次模拟试题理13)为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数位12,则抽取的学生人数是__________。
7. (山东省威海市2012年高三第二次模拟试题理科13)某商场调查旅游鞋的销售情况,随机抽取了部分顾客的购鞋尺寸,整理得如下频率分布直方图,其中直方图从左至右的前339.5,43.5内的顾客所占百分比为______. 个小矩形的面积之比为1:2:3,则购鞋尺寸在[)8. (山东实验中学2012届高三第一次诊断性考试理18) (本小题满分12分)我校开设甲、乙、丙三门校本选修课程,学生是否选修哪门课互不影响.己知某学生选修甲而不选修乙和丙的概率为0.08,选修甲和乙而不选修丙的概率是0.12,至少选修一门的概率是0. 88.(2) 求学生李华选甲校本课程的概率;(3) 用表示该学生选修的校本课程门数和没有选修的校本课程门数的乘积,求的分布列和数学期望.9. (山东省2012年济南市二模理科20)(本小题满分12分)一次考试共有12道选择题,每道选择题都有4个选项,其中有且只有一个是正确的.评分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定有8道题的答案是正确的,其余题中:有两道题都可判断两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.请求出该考生:(1)得60分的概率;(2)所得分数ξ的分布列和数学期望.【解析】(1)设“可判断两个选项是错误的”两道题之一选对的为事件A,“有一道题可判断一个选项是错误”选对的为事件B,“有一道题不理解题意”选对的为事件C,∴P(A)= 12,P(B)=13,P(C)=14,∴得60分的概率为p=11111223448⨯⨯⨯=.………………………………………………4分(2)ξ可能的取值为40,45,50,55,60………………………………5分P(ξ=40)=1123122348⨯⨯⨯=;……………………………………6分P (ξ=45)=121123111311211722342234223448C ⨯⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=…………………………………………………………………………7分P (ξ=50)=1122⨯2334⨯⨯+1212C ⨯1123⨯⨯34⨯12C +12⨯⨯1223⨯ 11111174223448⨯+⨯⨯⨯=;…………………………………………8分 P (ξ=55)=12C ⨯111223⨯⨯⨯14+1122⨯⨯2134⨯+12⨯12⨯13⨯34748=……9分 P (ξ=60)=1111111111223448223448⨯⨯⨯==⨯⨯⨯=ξ 4045505560P(ξ)18 1748 1748 748 14810分 (3) E ξ=40×648+(45+50)×1748+55×748+60×148=57512………12分 10.(山东省青岛市2012年高三第二次模拟试题理科19)(本小题满分12分)甲居住在城镇的A 处,准备开车到单位B 处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如,A →C →D 算作两个路段:路段AC 发生堵车事件的概率为101,路段CD 发生堵车事件的概率为151,且甲在每个路段只能按箭头指的方向前进).(Ⅰ)请你为其选择一条由A 到B 的路线,使得途中发生堵车事件的概率最小;(Ⅱ)若记路线A →C →F →B 中遇到堵车次数为随机变量ξ,求ξ的分布列及E ξ. 【解析】(Ⅰ)记路段AC 发生堵车事件为AC ,各路段发生堵车事件的记法与此类同.因为各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,所以路线A →C →D →B 中遇到堵车的概率为()()()()111P P AC CD DB P AC P CD P DB =-⋅⋅=-()()()1111P AC P CD P DB =----⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦9145311015610=-⋅⋅= ……………………………………………………………………2分 A BC DEF151611011211512032011 同理:路线A →C →F →B 中遇到堵车的概率为2P =1-P (AC ·CF ·FB )=800239(小于310) ………………………………………………………………………4分 路线A →E →F →B 中遇到堵车的概率为3P =()911300P AE EF FB -⋅⋅=(大于310) 显然要使得由A 到B 的路线途中发生堵车事件的概率最小,只可能在以上三条路线中选择.因此选择路线A →C →F →B ,可使得途中发生堵车事件的概率最小 …………6分。
