95093_常用图形计算器
学生专用计算器使用说明书

目录取下和装上计算器保护壳 (1)安全注意事项 (2)使用注意事项 (3)双行显示屏 (7)使用前的准备 (7)k模式kkkkk多语句kkk基本计算kkkk度分秒计算 (15)kMODEIX, SCI, RND (15)记忆器计算 (16)k答案记忆器 (16)k连续计算 (17)k独立记忆器 (17)k变量 (18)科学函数计算 (18)k三角函数/反三角函数 (18)Ch。
6k双曲线函数/反双曲线函数 (19)k常用及自然对数/反对数 (19)kkkkkk统计计算标准偏差回归计算技术数据kkk运算的顺序 (35)k堆栈 (36)k输入范围 (37)电源(仅限 MODEx。
95MS) (39)规格(仅限 MODEx。
95MS) (40)双行显示屏双行显示屏可同时显示计算公式及其计算结果。
? 上行显示计算公式。
? 下行显示计算结果。
当尾数的整数部分多于三数字时﹐每隔三位便会有一个分隔符。
使用前的准备模式?MODEx。
按阐述。
?范例﹕注意﹗? 要返回计算模式并将计算器设置为下示初始默认值时﹐请依顺序按计算模式﹕ COMP角度单位﹕ Deg指数显示格式﹕ Norm 1分数显示格式﹕ ab/c小数点字符﹕ Dot模式指示符会出现在显示屏的上部。
? 在开始进行计算之前﹐必须检查目前的计算模式(SD﹑REG﹑COMP)及角度单位设定(Deg﹑Rad﹑Gra)。
用于储存计算输入的记忆区可储存 79“步”。
每当您按下数字键或算术运算键一步键的操作不占用一步。
例如﹐输入只占用一步。
您可为一个单独计算输入最多79计算的第”以表示记忆容量快用完了。
若您需要的输入多于步﹐请将按有关使用键的详细说明请参阅一节。
用? 按? 按键可将光标变为插入光标入光标时输入的字符将会被插入到光标目前的位置。
? 按键或键可将光标从插入光标返回至普通光标。
重现功能每当您执行计算时﹐重现功能会将计算式及其计算结果保存在重现记忆器中。
按键能重新显示上次进行的计算的公式及结果。
可视化几何计算器

可视化几何计算器
2.计算功能:计算器应该能够进行几何计算,如计算两点之间的距离、计算线的长度、计算多边形的面积等。
用户可以通过选择已绘制的图形,
并输入相关参数,计算器会自动进行计算,并显示结果。
3.几何变换:计算器应该能够进行几何变换,如平移、旋转、缩放等
操作。
用户可以选择已绘制的图形,并输入相关变换参数,计算器会自动
进行几何变换,并更新图形的显示。
4.解题辅助:计算器应该能够辅助用户解决几何问题。
用户可以输入
几何问题的条件,计算器会根据条件自动绘制图形,并提供解题提示。
5.保存和加载:计算器应该支持将绘制的图形保存为文件,并能够加
载已保存的图形。
用户可以随时保存和加载绘制的图形,方便后续的修改
和分析。
在实现时,应该首先设计好图形的数据结构,如点的坐标、线的起始
点和终止点等。
然后根据用户的操作来更新图形的数据,并重新绘制到画
布上。
同时,还需要实现各种几何计算的算法,如点到点的距离计算、线
的长度计算等。
这些算法可以参考相关的数学几何知识。
总之,可视化几何计算器是一种很有意义的工具,它能够帮助学生更
好地理解几何概念,并提高他们的几何计算能力。
这种计算器的设计和实
现需要合适的编程语言和图形库,并需要实现基本功能和可能的高级功能。
通过不断的开发和完善,可以使可视化几何计算器成为一个实用而强大的
工具。
TI图形计算器介绍下

备注:1. 配套教材《用图形计算器学数学》上海高中数学拓展型教材本套教材以《上海市中小学数学课程标准》提出的高中阶段学习内容与要求为根据,紧密结合新编高中数学课本,对其中适合运用TI手持图形技术进行教学的内容进行全面梳理,能和新编数学课本同步使用,是一套充分而有效运用TI图形计算器进行教学的特色教材。
2.培训TI公司全力支持教师在教学中运用TI手持教育技术。
公司不仅仅提供图形计算器作为基本教学工具,更提供全方位的技术培训,支持教研和教学实践活动及提供各种教学配套资料。
每年在市级和区级范围都定期举行相关的培训,旨在推广普及TI手持教育技术,让更多的数学老师掌握技术,让技术积极地为教育服务。
3.交流研讨TI公司大力支持教研部门组织教学研讨、交流以及定期开展各项教学评优活动,为教师提供一个交流、探讨的平台,从而提高图形计算器在课堂教学应用的质量。
TI-83 Plus 和TI-84 Plus图形计算器常用功能简介一、基本代数功能(一)MATH运算访问MATH(数学)菜单,可按 。
菜单中有四个子菜单,它们分别是:MATH (数学)、NUM(数值)、CPX(复数)以及PRB(概率)。
(二)角度和关系运算访问ANGLE(角度)菜单,可按ψ [ANGLE]。
ANGLE菜单显示与角度有关的指令。
但要注意的是:Radian/Degree方式设置会影响计算器对指令的解释。
访问TEST(关系)菜单,可按ψ [TEST]。
TEST菜单有两个子菜单:TEST(关系)和LOGIC(布尔)。
1.ANGLE菜单介绍0。
二、函数作图功能【例】用边长为60cm的正方形铁皮在四角各剪去一个小正方形做成一个无盖水箱,问水箱底面边长取多少时,才能使所得的水箱容量最大,并求出最大容量。
1.设置函数Func 按ζ(图1)图1 图2 图32.建立体积y与x的关系:在ο编缉器中输入函数解析式:y=(60-2x)(60-2x)x(图2)3.设置窗口变量:考虑到x的变化范围为0<x<30,估计y的范围是0<y<19000。
北师大版小学4年级数学上册第三单元(神奇的计算工具+有趣的算式)PPT教学课件

提示:注意运算的顺序。
2.括号内可以填几?先估计,再用计算器检验,找到合适的答案。
课件PPT
3.读一读,算一算。
课件PPT
4.数学游戏。 用1,2,3,4,5这五个数字,任意组成一个两位数和一个三位数,用计算器求出它们的积,积大者获胜。
课件PPT
5.自选一张报纸,估计其中一版的字数,用文字、 图或算式来说明估计的过程与方法。
同伴互相出几道计算题,两人一起用计算器算一算。
用计算器算一算。
1.用计算器计算。
课件PPT
87654+68954=
解题思路:
摁下数字键87654,然后摁+键,再摁68954,最后摁=。
1.用计算器计算。
课件PPT
87654+68954=
156608
2.用计算器计算。
课件PPT
3483610÷5486=
两千多年前,中国人用算筹计算。
课件PPT
一千多年前,中国人开始广泛使用算盘,使计算的速度快多了。
课件PPT
1822年,第一台能按一定程序自动控制的计算机诞生了。
课件PPT
课件PPT
开机
关机
清除
课件PPT
计算器是生活中常用的计算工具。关于计算器你已经知道了什么?
课件PPT
课件PPT
课件PPT
课堂小结
2. 用计算器计算时,要注意不要恩错键,摁错了可以摁清除键。
1.计算大数时,用计算器计算比较简单。
大家有什么收获?
课件PPT
谢谢
四年级 数学 上册
北师大版
课件PPT
第3单元 乘法
4 有趣的算式
课件PPT
学习目标
图形计算器:不可替代的“数学工具”?

图形计算器:不可替代的“数学工具”?一、图形计算器是什么?图形计算器(Graphing Calculator,缩写为GC),是一种手持的数学工具,是一种专门用于中学与大学数学教与学的手持技术。
不少人认为,它已经成为现代学校最重要的数学学习工具之一。
GC问世于上世纪80年代,其外形与大小类似科学计算器,但功能更为强大。
它兼具绘图(函数图像,甚至几何作图)、数表处理与统计计算等功能。
有的还能做代数符号演算,解决多项式、线性代数与微积分(甚至偏微分方程)中的计算问题,或称为计算机代数系统(CAS)。
有的GC不仅可与其他GC或计算机对接(通过红外或USB接口),而且能与各种传感器连接,而带有数据流的新一代GC(如hp39s等),则能很方便地用于采集处理来自现实世界的数据。
于是,这种手持技术的组合使用,又构成可移动的、便携的“数字化实验室”,使学生能很方便地进行数学与科学探究。
二、令人关注的发展作为一种常用的数学工具,GC早已经广泛应用于许多国家的大中学的数学课堂。
某些国家或地区明确要求在数学考试(包括大学入学考试)中使用GC。
其中,最令人关注的是新加坡教育部明确要求在高中数学课程中全面使用GC的规定。
他们将其看作为学生学习数学的一种不可替代的工具,将对数学课程,甚至其他学科的教学产生积极而深远的影响。
自1995年以来,我国的数学教师对在教学中尝试应用GC表现出极大的热情,积累了许多教学的案例。
个别地区已经考虑允许在考试中使用GC。
尽管如此,对GC应用的价值,人们还未形成普遍的共识。
且不谈没有接触过GC的人士,即使那些曾经用过的教师,对GC的潜在应用价值也未见得有充分的认识。
与“豪华”的计算机实验室与各种“超级”软件相比,GC显得小得可怜。
在与GC有过一段“亲密的接触”后,他们会发现GC的演示效果好像并不如几何画板、Z+Z平台以及不断更新的其他软件。
有的教师把GC的应用局限于浅层的数学直观或数学实验,不能支持更高、更复杂的数学思考。
图形计算器的作用

图形计算器的作用——观《优秀课例》有感我看了《利用导数研究不等式恒成立问题》一课,对图形计算器的使用及其作用产生了些许想法。
这节课体现出来的图形计算器的作用尤为突出,学生一旦掌握了图形计算器的使用方法,就可以利用图形计算器来研究一些有关函数图像的问题。
尤其是那些学生自己动手画函数图像较困难的问题,而使用了图形计算器后,函数图像由图形计算器自动生成,为学生从形的角度研究函数提供了便利的条件,直观、具体、形象。
这对学生学习函数有很大的帮助作用。
总所周知,函数是中学数学极为重要的内容,贯穿高中数学的始终.数、式、方程、不等式、数列、极限、导数与微分等内容都是以函数为中心,同时渗透到三角、立体几何、解析几何,更有内容丰富的函数实际应用性问题,跨学科的综合应用是函数的鲜明特征.所以,学好函数知识是学好整个高中数学的关键.但由于函数是学生所接触到的第一个研究变数之间关系的数学基本概念,从而学生无法很好的基于自身的知识背景来建构这一抽象的概念,并得到深刻的理解.函数图象是函数关系的一种直观、形象的表示,函数图象对函数的概念与性质的理解起着至关重要的作用,但由于作图很麻烦、不方便,甚至不可能作出,从而学生很难达到对函数知识的深刻理解.图形计算器的出现可以很好地学习函数知识.一、利用图形计算器有利于加深对函数知识的理解,挖掘函数知识蕴含的重要思想方法,领悟数学的本质教材的编写有其严密的逻辑体系.函数知识的编写遵循着由简单到复杂,由特殊到一般再到特殊的认知规律.在传统教学中限于技术手段,往往不能很好地呈现函数知识的形成过程,展现函数知识的内涵,挖掘函数知识蕴含的重要思想方法,领悟数学的本质,虽然学生通过一段时间的学习能解决一些问题,但对函数知识的认识往往是一知半解、残缺不全.现在利用图形计算器等信息技术手段,由“静”到“动”,“微观”到“宏观”地展现知识的形成过程,有利于学生构建完整的知识体系.如指数函数的学习中,只用“描点法”作出y=2x,两个图象,然后直接给出指数函数y=a x的性质.这有些“强加于人”的感觉,例如,学生对为什么要把底数a分为0<a<1和a>1两种情况加以讨论不一定理解,学习过程比较被动.而引导学生用图形计算器完成函数y=2x的对应值表,作出图象,并在信息技术环境下动态观察图象,形成对指数函数性质的感性认识,再让学生自由选择a的值,并用图形计算器在同一坐标系内作图象.在此过程中,学生可清楚地看到底数a如何影响并决定着函数y=ax的性质.由于函数的图象随着0<a<1和a>1自然聚集(如图1),学生可以清楚地看到a=1这条分界线,而函数的定义域、值域、单调性、特殊点(0,1)等更是一目了然.然后再通过a的连续变化来演示函数图象的变化规律,从而让学生更直观、更清楚地“看到”函数y = a x的性质.这样呈现内容,对学生发现和认识“为什么以a=1为分界点”“过点(0,1)为什么要作为性质之一”“为什么不讨论a=0和a<0的情形”(如图2,图3)等,都营造了很好的环境,使教学的开放性、探索式学习等成为可能.显然,如果没有信息技术,上述过程很难实现.利用信息技术构建的高中数学教学改变传统教学中学生围着老师转的教学模式,学生从以往的听众变成了积极的参与者,真正成为课堂的主体.把原来的数学学习过程转变成为自己学习数学的过程,使学生体会到知识产生的过程,从而对数学有更深刻的认识,产生更深刻的求知欲,也进一步激发了学生学习数学的积极性.二、利用图形计算器有利于掌握函数知识的重点,突破函数知识的难点,构建完整的函数知识体系函数的概念、函数的性质、基本初等函数是函数知识的重点,是函数知识的支撑,这些内容的理解掌握,对函数知识的学习至关重要.函数的概念、反函数、复合函数是函数知识的难点,对难点知识的突破,有利于构建完整的知识体系.在传统教学中,对重点知识的教学往往不直观、不具体,不是水到渠成,总有强加于人的感觉,揭示不深刻,不利于知识的理解掌握;对难点知识的教学往往说不清道不明,蜻蜓点水,浅尝辄止,不能有效突破.利用图形计算器可以直观、形象地揭示知识间的联系,有利于掌握重点突破难点.以往研究复合函数的性质,特别是复合函数单调性的判断,总是直接给出结论“同则增,异则减”,学生只知其然,而不知其所以然,往往疑惑不解.现在利用图形计算器研究复合函数,设,,在图形计算器上同时显示三个坐标系(如图4),画出(x,t)、(t,y)、(x,y)的对应点,认清这三组变量的对应关系.教师指定或由学生自选简单的复合函数进行作图和研究.例如:y =cos[sin(x)],设t=sin(x),y = cos(t),则如图5.学生可以研究:y =cos[sin(x)]的1.定义域、值域;2.单调性、奇偶性;3.最大、最小值等等.还可以用图形计算器直接作出图像进行检验(如图6).使复合函数问题变得直观、易懂.对复合函数的有关知识从疑惑不解到理解洞悉,由不确定到确定,由含糊到明确.利用信息技术构建的高中数学为学生营造了一个“探索数学”,“体验数学”的环境,大家可以做实验,互相讨论,积极思维,互相协作,大胆猜想,踊跃发表自己的观点,参与感比较强,在实验中学习,数学课也不枯燥了.信息技术给我们带来了生动形象的数学,以其图像的快捷性和直观性为进一步探索数学提供了必要的条件.有利于逐步培养学生科学研究的态度和意识.三、利用图形计算器有利于解决函数型实际应用问题,逐步培养科学研究的态度和意识利用数学知识来解决实际问题的一般方法,是把实际问题加以抽象概括,得出关于实际问题的数学描述,建立相应的数学模型,利用这些模型来研究实际问题.其基本步骤是:实际应用问题的解决关键在于数学模型的建立,函数模型的建立步骤是:确定变量,收集数据;根据收集的数据画出散点图;根据散点图选择恰当的函数;建立函数关系式.也就是对变量进行回归分析,得出回归方程,并进行相关性检验.这一过程需要大量的运算,甚至无法用纸和笔来解决,使我们对问题的解决变得厌倦甚至放弃.而利用图形计算器的函数拟合功能,使得对一些采集的实验数据进行分析,建立适当的数学模型变得轻松、容易.如:以下是某地区不同身高的未成年男性的体重平均值表:(1)根据上表中各组对应的数据,能否找到一种函数,使它比较近似的反应该地区未成年男性体重y关于身高x的函数关系,试写出这个函数关系式.(2)若体重超过相同身高男性平均值的1.2倍为偏胖,低于0.8为偏瘦,那么该地区某校一男生身高175cm,体重78kg,他的体重是否正常?这个问题的解决,只要在图形计算器中输入数据画出散点图,根据散点图引导学生用学过的函数y=ax+b, y=alnx+b, y=a b x进行拟合,学生发现用y=a b x拟合较好(如图7,图8).追问:为什么不可以用y=ax2+bx+c来拟合呢?这些点的走向趋势也很符合二次函数图像的走势啊?老师和同学们一起共同进行研究,用y=ax2+bx+c来拟合,利用图形计算器算得a =0.0037 ,b=-0.4310,c=19.6973,所以,该地区未成年男性体重关于身高的函数关系式可以选为y2(x) = 0.0037x 2– 0.4310x + 19.6973.作出y1(x)和y2(x)的图像(如图9),从拟合的图像上看,两者都拟合得较好,但究竟哪一种函数要更接近实际一些呢?图9师生、生生展开热烈的讨论,最后认为,可以利用y1(x)和y2(x)的函数值与实际值C2的差的绝对值来比较两者接近程度,利用图形计算器可以方便地算出|y1(c1)-c2|的对应数值(C3列的值) ,|y2(c1)-c2|的对应数值(C4列的值)(如图10)图10显然,C3列的误差比C4列的误差要小,由此可见,函数y1(x)的拟合效果要好,所以,函数解析式为y1(x) = 2.004 1.020x,能较好地反映该地区未成年男性体重与身高的关系.利用所得函数关系式容易判断问题(2)中的男生体型偏胖.传统应用题由于受信息技术条件的约束,背景不丰富,远离时代,和学生的实际结合得不紧密,大量数据需要人为加工,题目还常常有明显的解题途径的暗示(如上例的教材解法),所以学生难以通过解这些题,提高自己数学建模的能力,领会问题解决的思想.由于有图形计算器和计算机这些信息技术工具,就使得运算繁杂、作图困难、数据处理难度大的问题,特别是一些具有真实背景的实际问题的解决成为可能.借助图形计算器,将实验、尝试、模拟、猜想、检验、调控、运算、推理、证明等作为数学学习的重要方式,更加重视学生的亲身实践活动,促进高层次数学思维,提高数学思考力度.让学生“看到”他们以往只能想象的数学,“做”他们以往不可能做的数学,使学生感受到实实在在的数学.总之,图形计算器是数学学习的有力工具,恰当地使用图形计算器,可以有效地学习函数知识,进而学好高中数学知识.。
TI-nspire CAS 图形计算器说明书

图形计算器使用手册该使用手册适用于TI-Nspire™软件(版本1.7)。
想要获得该文档的最新版本,请访问:/guides重要信息Except as otherwise expressly stated in the License that accompanies a program, Texas Instruments makes no warranty, either express or implied, including but not limited to any implied warranties of merchantability and fitness for a particular purpose, regarding any programs or book materials and makes such materials available solely on an "as-is" basis. In no event shall Texas Instruments be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the purchase or use of these materials, and the sole and exclusive liability of Texas Instruments, regardless of the form of action, shall not exceed the amount set forth in the license for the program. Moreover, Texas Instruments shall not be liable for any claim of any kind whatsoever against the use of these materials by any other party.除非在程序所附带的许可文件中有明确表述,否则对于任何程序和书本材料,Texas Instruments(德州仪器公司)将不提供明示或默示保证,包括但不限于对特定使用之可销售性或适合性作出任何保证,并且此类材料均以“按样货”方式提供。
常用图形计算器
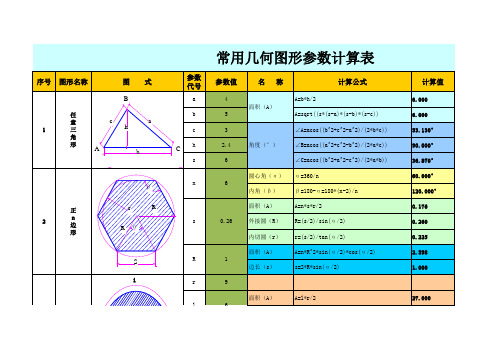
l
r
15 面积(A) A=(l*r-c*(r-h))/2 l=2*r*asin(c/(2*r)) c=2*sqrt(h*(2*r-h)) A=(l*r-c*(r-h))/2 l=2*r*asin(c/(2*r)) h=r-sqrt(r^2-c^2/4) 36.788 19.305 18.000 20.382 15.708 2.010
已知圆心角α,求面积A与弧长l
r为扇形半径。
已知矢高h,求面积A、弧长l、弦长c。
已知弦长c,求面积A、弧长l、矢高h。
已知半径R,弧心角α,求角缘面积A。
长轴 a
短轴 b
长轴 a
短轴 b
b 为抛物线半开口宽。
多边形边数n,台体高度h。
已知上、下边长a1、a2,求As、V。
已知上.下面积A1.A2,求As、V
628.319 904.779 452.389 12.000 904.779 452.389 904.779 376.991 1256.637 628.319
r
6
表面积(A) 直径(D) 体积(V)
r
11 球
D
D
12 表面积(A)
r 球 冠 r
c a h
10 6
体积(V) 侧面积(As) 体积(V)
c
1
h
a
c
A
b
C
h s
2
正 n 边 形
r α
S
l
R
1 边长(s)
r
9 面积(A) A=l*r/2 27.000
l
6
3
扇 形
l
6 圆心角(α) 面积(A) α=l/r A=0.008727*α*r^2 l=0.01745*α*r 38.197° 95.426 21.206
黑莓953095009000地图下载【乐图】官方 攻略教程

乐图官方攻略闲言碎语不要讲,直接开始!蓝色字体为链接到相应网站的链接,可按住您电脑键盘上的[Ctrl]键的同时用鼠标左键点击,可以为您打开相应的站点。
第一部分准备工作一、下载乐图软件点我〈图 1〉这里的3.2缓存版,可以事先将地图下载到手机里,提供软件使用。
3.2网络版本为在线版本,其地图(sogou地图、卫星地图、地形图、mapabc地图等)需要通过GPRS网络实时下载,比较耗费流量,但能节省几百兆的手机存储空间。
二、注册您的乐图账号点我〈图 2〉填写上面内容的时候手别抖,填完以后,点[注册],然后您的乐图账号就注册好了。
〈图 3〉这个时候页面自动跳走,请记住您的乐图号码,有助于增强身体免疫力哦~~~!乐图号或密码忘记可以通过两种方式找回:1.手机找回;进入乐图后,点击开始-->会员-->登录-->菜单-->找回账号,稍后会收到短信回复。
此服务是免费的哟2网站找回点我三、下载地图导入工具点我3.0版本的地图一定要用的。
页面底部的[请查看安装指南]是链接到论坛的,您可以在那里了解最新的乐图咨询、乐图软件的发展史、GPS技术的基础理论、并将您的心得与大家交流。
另外,论坛需要另外注册发贴,请勿在论坛或其他公开场合透露您乐图账号的密码,以免出现不必要的麻烦。
四、下载地图点我您可以在这个页面下载您所需要的地图。
〈图 4〉全国概要图一定要下载的,反正不要钱啦。
然后省市地图您可以选择您需要的下载,登陆后,您可以通过支付宝对您的帐号充值,并进行购买(下载)地图的操作。
经常出差的朋友,推荐购买VIP,30元/年,一年免费无限量下载哦,少抽两包烟,少买一个粉饼的事情啦,而且比一个个付钱便宜多了。
好啦,准备工作到此结束!现在开始拿起你的黑莓,我们开始安装乐图啦!第二部分安装一、安装乐图1.您需要一个黑莓的桌面管理器软件打开桌面管理器,点选[应用程序加载器][开始]等找到你下载的乐图3的文件夹中的gpsmaps.alx文件,点[打开]按钮。
T I 图 形 计 算 器 基 本 操 作

44
44 44
voyage 200 方式设置介绍 ---- MODE键 (1)
方式设置
第1页 第2页 第3页
作图方式 ..... 当前文件夹.... 数据位显示.... 角度单位...... 指数格式...... 复数格式...... 向量格式...... 精致显示......
回车确认 ESC取消
例三、绘制极坐标 r8sin 2.5()函数的图象。
1、方式设置:按 键,显示图象方式设置菜单,将其中的Graph(作图) 设定为 POLAR(极坐标),Angle(角度)设定为RADIAN (弧度制)
2、输入函数:按 (Thick)
键,显示Y=编辑器,输入函数图象Style(样式)为粗线
3、设置窗口:按 设置窗口变量,
方式的设置 (Mode)
进入函数编辑器 (Y= Editor)
进行窗口设置 (Windows)
作图功能 (Graph)
方法一: 选中3:Windows 方法二: +3
方法三:按 +E
方法一: 选中 2:Y=Editor
方法一: +2
方法三:按 +W
方法一: 选中 4:Graph
方法二: +4
方法三:按 +R
voyage 200 (CAS)计算机代数系统简介
按 开机 按 关机 CAS或称Home(主屏)为开机后
系统默认状态
菜单栏 表达式与结 果及显示栏 输入栏 状态栏
voyage 200 (CAS)计算机代数系统简介
F1
1. 打开 2. 保存 3. 新建 4. 剪切 5. 复制
6. 贴帖 7. 删除 8. 清屏 9. 格式 A. 关于
2、计算 arctan3e4 1 15
Sharp EL-9900图形计算器基本键盘活动指南说明书

Sharp EL-9900Graphing CalculatorBasic Keypad DRAW FORMAT CALCWINDOW ZOOM TRACE789()456x ..––+3210(–)ENTERMATHSTAT PRGM SimpSTO DEL BS int CL x 2x x –1,a b A .xxx a b ca b c b c a b INS RCL VARS SET UP QUITA a %B C D E F G H I J K L M N O {}PQ R S T CATALOG SPACE ENTRY ANSUV W x p XY ..Z1.Turn the calculator on and press Y= .2.Press CL to remove an old Y1 expression.3.Enter the linear equation ( y = 3x + 1 ) for Y1 by pressing 3 x + 1 .4.Enter the viewing window range by pressing ZOOM A (ZOOM)5 (Default). This establishes the default viewing ranges for graphing equations. These ranges are -10 < x < 10 and -10 < y < 10. The scale for the x and y axes are 1.5.To graph another equation, press Y= CL to access and clear the Y1= prompt.6.Enter the next equation, and press GRAPH to view the graph.7.If the line does not appear in the default viewing window, press ZOOM 4 (OUT)to enlarge the viewing window.GRAPHING LINEAR EQUATIONS1.Graph the equation y = 1x by pressing Y= CL to remove an old Y1 expression, and press x to enter the equation.2.Press ZOOM A (ZOOM)5(Default)to view the graph.3.Changing the slope to 2 will result in the equation y = 2x .Enter this equation for Y2 by pressing Y= ▼ 2 x .4.To view both the graphs on the same coordinate axes, press GRAPH . The graph y = 2x has a greater slope than y =x.5.Changing the slope to will result in the equation y = x . Enter this equation for Y2 by pressing Y= ▼CL 1 a/b 2 x .6.To view both the graphs on the same coordinate axes, press GRAPH . The graph y =x has less slope than y =x.7.Changing the slope to -1 will result in the equation y =-x .Enter this equation for Y2 by pressing Y= ▼CL (-)x .8.To view both the graphs on the same coordinate axes, press GRAPH . The graph y =-x has the opposite slope of y =x.CHARACTERISTICS OF SLOPE1212▼121.Graph the equation y =x by pressing Y= CL to remove an old Y1 expression, and press x to enter the equation.2.Press ENTER CL to clear Y2 or additional prompts.e the default viewing range, and press ZOOM A (ZOOM)5(Default)to view the graph.4.Adding 2 will result in the equation y =x + 2. Enter this equation for Y2 bypressing Y= ▼x + 2 .5.To view both the graphs on the same coordinate axes, press GRAPH .The graph y =x + 2 has shifted up from the graph of y =x . The y -intercept is now y =2.6.Subtracting 2 will result in the equation y =x – 2. Enter this equation for Y2 by pressing Y= ▼CL x – 2 .7.To view both the graphs on the same coordinate axes, press GRAPH . The graph y =x – 2 has shifted down from the graph of y =x . The y -intercept is now y =-2.CHARATERISTICS OF THE y-INTERCEPT1.Enter the equations Y1 = 3X + 1 and Y2 = 3X + 2 by pressing Y= CL 3 x + 1 ENTER CL 3 x + 2 .2.Press ZOOM A (ZOOM) 5 (Default)to view the graphs.3.These lines are called parallel since they have an equal slope but different y -intercepts. These lines will not intersect.4.Enter the equations Y1 = 3X - 1 and Y2 = -1/3 X + 1 by pressing Y= CL3 x – 1 ENTER CL (-) 1 a/b 3 x+ 1 .5.Press ZOOM A 7 to view the graphs.6.These line are called perpendicular since they have slopes that are negative reciprocals of each other (m 1= -1/m 2). Notice, these intersecting lines form four equal angles.7.Graph two lines with unequal slopes (not negative reciprocals). What do you see? Are the lines parallel, perpendicular or neither?PARALLEL AND PERPENDICULAR LINES▼Graphing and translations of quadratic equations1.Turn the calculator on and press Y= . Press CL to remove an old Y1 expression. Press ENTER CL to remove an old Y2 expression.2.To enter the quadratic equation ( y =x 2) for Y1, press x x 2.Enter the viewing window range by pressing ZOOM A (Zoom)7 (Dec).3.When 2 is added to x 2, the resulting equation is y =x 2+ 2. Enter this function for Y2 by pressing Y=▼x x 2+ 2 . Press GRAPH .What does the addition of 2 do?4.When -2 is added to x 2, the resulting equation is y =x 2– 2. To change Y2 for this expression, press Y= ▼CL x x 2– 2 ENTER GRAPH .What does the addition of -2 do?QUADRATIC EQUATIONSEVALUATING A FUNCTION1. For example, to evaluate f(x)=x2-2x + 3 for x=3, you will enter the functionfor Y1 by pressing Y= CL x x2 – 2 x + 3 . Be sureto clear any other expressions.2. Press 2ndF QUIT CL to return to and clear the calculation screen.3. To evaluate the function at x = 3, first store 3 into the X variable by pressing3 STO x ENTER .4. Evaluate the function stored in Y1 at 3 by pressing 2ndF V ARS A 1ENTER .5. Another way to evaluate a function for several values is using the Sharp’stable feature. Press TABLE to view a table of values.6. You can customize the table by pressing 2ndF TBLSET . You can setthe table’s minimum x value (TBLStrt)to another value than zero, and youcan change the table’s increment value (TBLStep)from 1 to another value.1.Press Y= and clear old expressions.2. Enter the functions for Y1 and Y2. For example, enter f(x)=2x + 1 for Y1 andg(x)=x 2for Y2 by moving the cursor to Y1 and pressing 2 x + 1 ,press ▼to move the cursor to Y2, and press x x 2 .3. Press 2ndF QUIT CL to return to and clear the calculation screen.4. To evaluate (f+g)(4), first store 4 into the X variable by pressing 4 STO x ENTER .5. Evaluate (f+g)(4) by pressing 2ndF V ARS A 1 (Y1) +2ndF V ARS2 (Y2)ENTER . This can be repeated for (f-g)(x), (fg)(x), and(f/g)(x).6. Another way to conduct an operation on functions and evaluate it for a value is to use Y3. Press Y= and enter the operation (f-g)(x) into Y3 by pressing 2ndF V ARS 1 (Y1) – 2ndF V ARS 2 (Y2). Press 2ndF QUIT CL to return to and clear the calculation screen. Press 2ndF V ARS 3 Y3 ( 4 )ENTER .OPERATIONS ON FUNCTIONS1.Press Y= and clear old expressions.2. Enter the two functions to be composed for Y1 and Y2. For example, enter y=x 2–1 for Y1 by pressing x x 2– 1 ENTER and y=x+1 for Y2 bypressing x + 1 ENTER .3. Enter the composition of Y2 into Y1 for Y3 by pressing 2ndF V ARS A1 (Y1) (2ndF V ARS2 (Y2) )ENTER .4. Keep Y1 and Y2 graphs from appearing by deselecting Y1 and Y2. Do this by pressing ENTER ENTER .5. Press ZOOM A 7 (Dec) to view the composition of Y2 into Y1 in the decimal window.6. Change the Y3 composition to Y1 in Y2 by pressing Y=CL 2ndF V ARS 2 (Y2) (2ndF V ARS 1 (Y1) ).7. Press ZOOM A 7 (Decimal) to view the composition of Y1 into Y2 in the decimal window.COMPOSITION OF FUNCTIONS▼▼▼▼▼▼▼1.Press 2ndF QUIT CL to return to and clear the calculation screen.2. To evaluate the formula for the area of a trapezoid (Area=(h/2)(a+b), where‘h’ is the height between the two bases (‘a’ and ‘b’) for different values, you must first type in the formula. For example, to enter the area formula for atrapezoid, press (ALPHA H ÷ 2 )(ALPHA A +ALPHA B )ENTER .3. Now, store the values for ‘h,’ ‘a,’ and ‘b’ into the calculator. Use h=1, a=2,and b=3. Store these by pressing 1STO ALPHA H ENTER 2 STO ALPHA A ENTER 3 STO ALPHAB ENTER .4. Clear the screen by pressing CL . Recall the formula by pressing 2ndFENTRY four times. Press ENTER to evaluate the formula for the stored values.5. Change the height to 4 by pressing 4 STO ALPHA HENTER . Recall the formula by pressing 2ndFENTRY two times and pressENTER to re-evaluate the formula for the new value.FORMULAS1. PressY= and clear old expressions. Press ZOOMA 7to view a clear viewing window.2. To graph the circle in the form (x–h)2+ (y–k)2= r 2, you will use the circle drawing feature. For example, in the circle (x–3)2+ (y–2)2= 12, h=3, k=2 and r=1. Press 2ndF DRAWA 9 (Circle). Move the cursor right to an ‘h’ of x=3 by pressing repeatedly until x=3. Move the cursor up to a ‘k’ of y=2 by pressing repeatedly until y=2. Press ENTER to set the center point.3. Move the cursor the length of the radius in one direction away from the center. In the example use the arrow key. Move the cursor 1 unit away from the center and press ENTER . The circle will be drawn with the cursor appearing at the point in the circle to which you moved.4. If the circle will not completely appear in the viewing window, zoom out on the decimal window to a larger window, because any other windows may distort the circle. Draw the circle again in the larger window.GRAPHING CIRCLES▼▼1.Turn the calculator on and press Y=. Y prompts will appear on the viewing window. Press CL to remove old Y expressions. Setup the calculator with rectangular coordinates and the equation editor mode by pressing 2ndF SET UP E (COORD)1(Rect)G (EDITOR)and 1 (Equation). Press CL to exit the menu and return to the Y prompts.2.To enter the polynomial y = –3x 2+x + 1, press (–)3x x 2+x+ 1 .3.Press ZOOM A (Zoom)7(Dec)to establish the decimal viewing window and view the graph. Press TRACE to engage the trace feature. Press to move the cursor near the left-hand root. 4.Press ZOOM A (ZOOM)3(In)to zoom in on the left- hand root. Press TRACE and move the tracer to approximate the root.5.Press ZOOM G (RCL)2(PreWin)to return to the decimal viewing window. Press TRACE and move the tracer to find the right-hand root.6.Press ZOOM A (ZOOM)3(In)to zoom in. Press TRACE and move the tracer to approximate the root.ZOOMING TO FIND ROOTS▼1.Press Y= CL to return to and clear the Y1 prompt.2.To enter the polynomial y = –5x 2–3x + 1, press (–)5x x 2– 3x + 1 .3.View the graph in the decimal viewing window by pressing ZOOM A (ZOOM)7 (Dec).4.Press TRACE and move cursor to the left of the left-hand root. Press 2ndF CALC to view the calculate menu.5.Press 5 (X_Incpt)to find the left-hand root.6.Press 2ndF CALC 5 (X_Incpt)to find the next root.JUMPING TO FIND ROOTS1.To solve 3(4 – 2x)≥5 – x, rewrite it as 3(4 – 2x) – 5 + x≥0 and determine thevalues of x where the function y= 3(4 – 2x) – 5 + x is on or above the x-axis.2.To do this, press Y= CL and enter 3(4 – 2x) – 5 + X in the Y1 location.3.Set the viewing window of the graph by pressing ZOOM A (ZOOM)5 (Default). You should be able to clearly view the x-intercept.4.Locate the x-intercept at the point (1.4, 0) by pressing 2ndF CALC and5 (X_Incpt).5.Since the graph is above the x-axis, to the left of the x-intercept, the solutionto the inequality 3(4 – 2x) – 5 + x≥0 is all values of x such that x≤1.4.1.To solve the inequality 3(4 – 2x )≥5 – x , press Y= CL , enter 3(4 – 2X) forY1 and 5 – X for Y2.2.Set the viewing window by pressing ZOOM A (ZOOM)5(Default).3.Next, shade the set of points that make the inequality true by pressing 2ndFDRAW G (SHADE)1(Set)to access the “Set Shade” screen. Since the inequality you are solving is Y1 ≥Y2 the solution is where the graph of Y1 is “on the top” and Y2 is "on the bottom." Do this by pressing 2ndF V ARS A ENTER 2 2ndF V ARS ENTER 1 . Press GRAPH to view theshaded region.4.Press 2ndF CALC 2 (Intsct)to find where the graphs intersect.5.Since the shaded region is to the left of x = 1.4, the solution to the inequality3(4 – 2x )≥5 – x is all values of x such that x ≤1.4.6.Turn off the shading by pressing 2ndF DRAW G (SHADE) 2 (INITIAL).▼1.The inequality -1≤2x – 5 ≤7 is commonly referred to as a “double” inequality.2.Clear any previously entered functions by pressing Y= CL .3.Enter Y1 = -1, Y2 = 2X – 5, and Y3 = 7.4.Press ZOOM A (ZOOM)5(Default)to view the line y = 2x – 5 between the lines y = -1 and y = 7.5.Press 2ndF CALC 2 (Intsct)to find the point of intersection of the lines y = 2x – 5 and y =-1 at (2, -1). Press ▲to move the tracer to the y = 7 line.Press 2ndF CALC 2 (Intsct)to find y = 2x – 5 and y = 7 at (6, 7).6.The solution to the “double” inequality -1≤2x – 5 ≤7 consists of all values of x in between, and including, 2 and 6 (i.e., x ≥2 and x ≤6). The solution is 2≤x ≤6.DOUBLE INEQUALITIESGraphing a system of equations and using the calculate feature to find the solutions1.Turn the calculator on and press Y= .2.Press CL to clear an old Y1 expression. Press ENTER CL to clear additional Y prompts.3.To enter the system of equations:y =x 2– 1y = 2x press x x 2– 1 ENTER 2 x . View the graphs by pressing ZOOM A (Zoom)5(Default).4.Press 2ndF CALC to access the calculate feature. Press 2(Intsct).The left-hand intersection will appear on the screen.5.Press 2ndF CALC to access the calculate feature again. Press 2 (Intsct). The right-hand intersection will appear on the screen.SOLVING A SYSTEM OF EQUATIONS。
Hp和TI图形计算器大集合

Hewlett Packard 图形计算器( HP48G+ / HP48GX / HP49G )精测教育2009-07-05HP-48G+HP-48GXHP-49GHP-48G+/48GX 是美国Hewlett Packard 惠普公司推出的图像计算机。
它们是上一代HP-48S/48SX 的改良版本,秉承HP 一贯传统,使用HP 独有的RPN ( Reverse Polish Notation ) 输入模式。
它们拥有128KB ( 48G+/48GX ) 记忆、符号代数( Symbolic Algebra )、程式编写、二维及三维图像、矩阵等功能,亦可像TI 的图像计算机一样直接进行複数( Complex Numbers ) 的函数( Function ) 计算。
配合HP PC Connectivity Kit 连接线( 需另外购买),更可以连接个人电脑交换资料,不过售价就真的稍高( HP-48G+ 售约$1180,比TI-89 还要贵约$100,HP-48GX 就要再多数百元)。
HP-49G 是美国惠普( Hewlett-Packard ) 推出的图像计算机,它和Texas Instruments 的TI-89 计算机可算是当时世界上功能最强大的计算机。
它亦秉承HP 一贯传统,使用HP 独有的RPN ( ReversePolish Notation ) 输入模式。
它有符号代数 ( Symbolic Algebra )、程式编写、二维及三维图像、矩阵等功能,亦可像 TI 的图像计算机一样直接进行複数 ( Complex Numbers ) 的函数 ( Function ) 计算,当然亦可配合 HP PC Connectivity Kit 连接线连接个人电脑交换资料。
但美中不足的是售价偏高 ( 比 TI-89 贵大约 $800,其实美国公司的计算机向来价钱都较高 ),而且按键的感觉不太好,要较用力按键,较长时间使用手指容易疲劳。
常用图形计算器

序号 图形 名称
正 方 形
图
式
参数代号
a
参数值
4
名称
面积A 对角线d 边长a A=a2 d=21/2*a a=d/21/2 A=a*b d=(a2+b2)1/2 b=A/a
计算公式
计算值
16 5.656854249 0 6,求面积 求对角线 已知对角线,求边a 已知边a、b,求面积 求对角线 a、b换算
S=4π r2
0
求表面积
r 14 圆 锥 l h r1 截 头 圆 锥
侧表面积M 侧表面积M 体积V
M=π rl M=π r(r2+h2)1/2 V=π r2h/3
0 0 0
求侧面积 求侧面积
侧表面积M M=π l(r1+r2) r2
0
求侧面积
15
15
截 头 圆 锥
l 体积V h V=π h(r12+r22+r1*r2)/3 0
求体积
a
表面积S
S=5.1962a2+6ah
0
求表面积
h
体积V
V=2.5981a2h
0
求体积
a 正 方 角 锥 台 表面积S b h1(斜边 高) h 表面积S 13 球 体 r 体积V V=4π r3/3 0
求体积
S=a2+b2+2(a+b)h1
0
求表面积
12
体积V
V=(a2+b2+ab)h/3
0
求体积
1
d a a 2 3 6 4
面积A 对角线d 边长b
2
长 方 形
b A
常用图形计算器

1、录入的分数需参与计算,即表示为数值,录入方法:先输入“0”,然后输入空格,再输入分数如“1/5”。 2、如果作为文本录入:a.批量录入,选定需录入区域,右键选择“设置单元格格式”--文本,再录入。 b.少量录入,加入英文状态下的"'"号,如'1/5. 3、如果一又九分之七,你需要组织成(1空格7/9)形式再写入excel 4、平方可以写成^2,开平方可以用^0.5 5、平方根可以是POWER(x,0.5),也可以用^0.5 6、平方可以是POWER(x,2),也可以写成^2,
EXCEL计算器 EXCEL计算器
1 平 方 结果b 结果b 0 0 2 立 方 结果b 结果b 0 0 3 n次方 结果b 结果b 0 三角函数sin 8 三角函数sin 结果b 结果b 0 三角函数tan 10 三角函数tan 结果b 结果b 0 12 对数函数 结果b 结果b = = = = = = = = an n 1 三角函数cos 9 三角函数cos 7 n/m次方根 a3 6 n次方根 5 立方根 a2 4 平方根 结果b 结果b 0 结果b 结果b 0 结果b 结果b 0 结果b 结果b 0 结果b 结果b 1 三角函数cot 11 三角函数cot 结果b 结果b 1 13 对数函数 结果b 结果b = = = = = = = = = = = = =
sin( = sin(a) a为度数 = tan( = tan(a) a为度数 = = 0 ln(a)
0 14 常用数据
=
1
0
=
112=121,122=144,132=169,142=196,152=255,162=256,172=289,182=324,192=361,63=
15
卡西欧图形计算器fx-CG10——统计功能详解

卡西欧图形计算器fx-CG10——统计功能详解大数据热潮的掀起,让人们重新认识到统计学的独特魅力。
统计专业化、可视化也成为了统计人员的必备素养。
卡西欧fx-CG10图形计算器拥有的专业统计功能,支持计算基本图形、正态曲线、矩形框图等单变量统计,支持一~四次回归、对数指数回归、逻辑回归等双变量统计。
还能够进行Z、t、X2GOF等测试以及使用正态分布、泊松分布和其他分布形状。
其专业性能和友好的操作界面得到了众多专业人士的赞赏。
1.进行统计计算前的参数设置在开始统计前,你可以在图形菜单中为指定图形的绘制或非绘制状态,图形类型以及一般性的图形设置。
(1)图形状态按下F1(绘图)+F4(选择),显示图形开/关屏幕;然后选择要更改的图形,按下相关键更改状态;完成后按EXIT返回图形菜单。
(2)图形类型卡西欧fx-CG10图形计算器提供了散点图、折线图、NP图、饼状图、直方图、Med框图、条形图、正态图、一次~四次回归图、对数、指数、逻辑、XList等图形。
(3)一般性图形设置进入图形设置菜单,可以图形类型(Graph Type)、列表(XList、YList)、频率(Frequency)、标记类型(Mark Type)、颜色连接、图形颜色等进行设置。
2.计算与绘制单变量数据单变量数据是只带有单个变量的数据,单变量统计包括分布计算与求和计算。
而下列图形可用于单变量统计。
(1)正态概率图该图将数据累积比与正态分布累积比进行对比。
XList指定输入数据的列表,Make Type用于绘制标记。
完成编辑后可按下AC或者EXIT返回列表编辑器。
(2)饼状图图形数据项目的最大数量为20,图形标记为A、B、C等分别对应数据列表的行1、2、3等。
(3)直方图为1。
(4)Med-矩形框图形通过此类图形,你可以了解大量数据项如何在特定范围内分组。
一个矩形框包含了从第一位四分位数(Q1)到第三位四分位数(Q3)区域中的所有数据,在中位值(Med)处绘制了一条直线。
用计算器求立方根

用计算器求立方根计算立方根是一种常见的数学运算,它可以帮助我们找到一个数的立方根。
在本文中,我们将介绍如何使用计算器来进行立方根的计算。
简介立方根是指一个数的立方等于给定数的运算,即 n^3 = x,其中 x 为给定数。
计算立方根可以帮助我们解决很多实际问题,例如在几何学中计算体积,或者在工程学中进行三维尺寸的估算。
计算器求立方根的方法在现代科技发达的时代,智能手机和计算器已经成为我们生活中必备的工具之一,计算立方根也可以通过计算器来快速完成。
下面是一些使用计算器求立方根的方法:1. 普通计算器大多数普通计算器都具有立方根功能。
要使用此功能,您只需要按下相应的按键,然后输入要计算的数值即可。
通常,立方根键的标识为“∛”,您可以在计算器的说明书中查找到正确的键位和使用方法。
2. 科学计算器科学计算器通常比普通计算器更复杂,提供了更多的功能和运算符。
要使用科学计算器来计算立方根,您需要按下立方根键(通常标识为“∛”或“^(1/3)”),然后输入要计算的数值。
在某些科学计算器中,您还可以使用表示立方根的函数,例如“cbrt(x)” 或“sqrt(x, 3)”。
3. 在线计算器除了手机和手持计算器外,互联网上还提供了许多在线计算器,您可以通过浏览器来使用这些在线计算器。
在搜索引擎中输入“在线立方根计算器”或类似的关键词,您将找到许多可供使用的计算器。
在这些在线计算器中,您只需输入要计算的数值,然后按下计算按钮即可求得立方根。
解决实际问题中的立方根求解立方根计算不仅仅是一个独立的数学问题,它在实际生活和工程中也具有重要的应用。
1. 几何学问题在几何学中,我们经常需要计算三维对象的体积。
例如,计算正方体或长方体的体积,我们可以通过立方根计算来找到边长对应的体积大小。
使用计算器可以快速计算出正确的结果,从而帮助我们在几何学问题中更好地应用立方根。
2. 工程学问题在工程学中,立方根计算可以帮助我们进行三维尺寸的估算。
Hp39gs操作入门.ppt

Hp39gs操作入门
作者:向友彬
2020/11/16
• 图形计算器的历史 • 图形计算器操作入门
2020/11/16
一:图形计算器历史
2020/11/16
1.什么是图形计算器?
• 画三角函数 F(x)=sin(x) 的图像
2020/11/16
用APLET中的Function探究二次函数性质
画出如下二次函数的图像,并总结规律: F₁(x)=x²+1 F₂(x)=2x²-1 F₃(x)=-X²+1 F₄(x)=-2x²-1
2020/11/16
探究两个函数的交点
• 输入函数F₁(x)=x²
• 按Aplet选Statistics,选择统计功能 • 输入数据0 Enter;20 Enter;35 Enter…. • 按LVAR,设置为二元变量的统计;按Shift,Plot;
设置窗口范围 • 按Plot现实函数图像 • 按Shift Symb设定拟合曲线,按Choos选Linear
(用直线拟合) • 按Plot Menu Fit画出图像 • 按Symb,选FITI,按Show,显示关系式为
2020/11/16
3.图形计算器在国外学校中的运用
• 在国外许多高中数学老师允许甚至鼓励他 们的学生在课堂上使用图形计算器。欧美 学生中图形计算器几乎是人手一台,是很 普及的理科学习工具,在某些课程(例如 微积分中)甚至是必需的。国外中学到大 学的大部分考试都是允许带图形计算器的, 在中国北京的高中数学应用竞赛的复赛 (笔试)中,图形计算器和科学计算器是 被允许带进考场的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A=2(ab+ah+bh)
0
求表面积
V=abh
0
求体积
r 9 圆 柱 体 h
侧表面积M
M=2π rh
0
求侧面积
体积V
V=π r2h
0
求体积
h1 斜 底 截 圆 柱 侧表面积M h M=π r(h1+h) 0
求侧面积
10
10
斜 底 截 圆 柱
r
体积V
V=π r2(h1+h)/2
0
求体积
11
正 六 角 柱
a
表面积S
S=5.1962a2+6ah
0
求表面积
h
体积V
V=2.5981a2h
0
求体积
a 正 方 角 锥 台 表面积S b h1(斜边 高) h 表面积S 13 球 体 r 体积V V=4π r3/3 0
求体积
S=a2+b2+2(a+b)h1
0
求表面积
12
体积V
V=(a2+b2+ab)h/3
0
求体积
2
பைடு நூலகம்求面积
0
5
圆 形
l A R
弧长l 半径r
l=2π r,l=π d r=(A/π )1/2
0 0
求弧长 已知面积,求半径
面积A 6 圆 环 r
A=π (R2-r2)
0
求面积
s
圆环S
s=R-r
0
求圆环宽度
7
正 方 体
表面积A a 体积V a
A=6a2
0
求表面积
V=a3
0
求体积
8
长 方 体
表面积A b h 体积V
1
d a a 2 3 6 4
面积A 对角线d 边长b
2
长 方 形
b A
3
平 行 四 边 形
b h A a b h A r
面积A 5 高度h
A=bh
20
求面积
h=A/b
0
已知面积、边b,求高 度
4
梯 形
面积A
A=(a+b)h/2
0
求面积
高度h
h=2A/(a+b) A=π r2
#DIV/0! 0
求高度
面积A 5 圆 形 d A=π d /4
常用几何图形参数计算表
序号 图形 名称
正 方 形
图
式
参数代号
a
参数值
4
名称
面积A 对角线d 边长a A=a2 d=21/2*a a=d/21/2 A=a*b d=(a2+b2)1/2 b=A/a
计算公式
计算值
16 5.656854249 0 6 3.605551275 3
备
注
已知边a,求面积 求对角线 已知对角线,求边a 已知边a、b,求面积 求对角线 a、b换算
求体积
S=4π r2
0
求表面积
r 14 圆 锥 l h r1 截 头 圆 锥
侧表面积M 侧表面积M 体积V
M=π rl M=π r(r2+h2)1/2 V=π r2h/3
0 0 0
求侧面积 求侧面积
侧表面积M M=π l(r1+r2) r2
0
求侧面积
15
15
截 头 圆 锥
l 体积V h V=π h(r12+r22+r1*r2)/3 0
