习题7及其解答第二版
梁前德《统计学》(第二版)学习指导与习题训练答案:07第七章 假设检验与方差分析 习题答案

旗开得胜1第七章 假设检验与方差分析 习题答案一、名词解释用规范性的语言解释统计学中的名词。
1. 假设检验:对总体分布或参数做出某种假设,然后再依据抽取的样本信息,对假设是否正确做出统计判断,即是否拒绝这种假设。
2. 原假设:又叫零假设或无效假设,是待检验的假设,表示为 H 0,总是含有等号。
3. 备择假设:是零假设的对立,表示为 H 1,总是含有不等号。
4. 单侧检验:备择假设符号为大于或小于时的假设检验。
5. 显著性水平:原假设为真时,拒绝原假设的概率。
6. 方差分析:是检验多个总体均值是否相等的一种统计分析方法。
二、填空题根据下面提示的内容,将适宜的名词、词组或短语填入相应的空格之中。
1. u ,nx σμ0-,标准正态; ),(),(2/2/+∞--∞nz nz σσααY2. 参数检验,非参数检验3. 弃真,存伪4. 方差旗开得胜25. 卡方, F6. 方差分析7. t ,u8. nsx 0μ-,不拒绝9. 单侧,双侧10.新产品的废品率为5% ,0.01 11.相关,总变异,组间变异,组内变异12.总变差平方和=组间变差平方和+组内变差平方和 13.连续,离散 14.总体均值 15.因子,水平 16.组间,组内 17.r-1,n-r18. 正态,独立,方差齐三、单项选择从各题给出的四个备选答案中,选择一个最佳答案,填入相应的括号中。
1.B 2.B 3. B 4.A 5.C 6.B 7.C 8.A 9.D 10.A 11.D 12.C四、多项选择从各题给出的四个备选答案中,选择一个或多个正确的答案,填入相应的括号中。
1.AC 2.A 3.B 4.BD 5. AD五、判断改错对下列命题进行判断,在正确命题的括号内打“√”;在错误命题的括号内打“×”,并在错误的地方下划一横线,将改正后的内容写入题下空白处。
1. 在任何情况下,假设检验中的两类错误都不可能同时降低。
( ×)样本量一定时2. 对于两样本的均值检验问题,若方差均未知,则方差分析和t检验均可使用,且两者检验结果一致。
电路与模拟电子技术(第二版)第7章习题解答
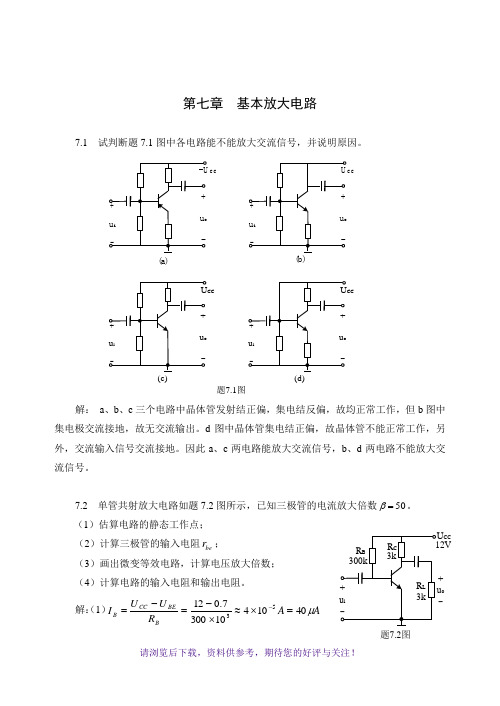
第七章 基本放大电路7.1 试判断题7.1图中各电路能不能放大交流信号,并说明原因。
解: a 、b 、c 三个电路中晶体管发射结正偏,集电结反偏,故均正常工作,但b 图中集电极交流接地,故无交流输出。
d 图中晶体管集电结正偏,故晶体管不能正常工作,另外,交流输入信号交流接地。
因此a 、c 两电路能放大交流信号,b 、d 两电路不能放大交流信号。
7.2 单管共射放大电路如题7.2图所示,已知三极管的电流放大倍数50=β。
(1)估算电路的静态工作点; (2)计算三极管的输入电阻be r ;(3)画出微变等效电路,计算电压放大倍数; (4)计算电路的输入电阻和输出电阻。
解:(1)A A R U U I B BE CC B μ40104103007.01253=⨯≈⨯-=-=-CC +o -题7.2图C CC (a)题7.1图mA A I I B C 210210405036=⨯=⨯⨯==--βV I R U U C C CC CE 61021031233=⨯⨯⨯-=-=-(2)Ω=+=+=9502265030026300C Cbe I r β (3)放大电路的微变等效电路如图所示 电压放大倍数7995.03||350||-=-=-=be L C u r R R A β(4)输入电阻:Ω≈⨯==950950||10300||3be B i r R r输出电阻 Ω==k R r C 307.3 单管共射放大电路如题7.3图所示。
已知100=β (1)估算电路的静态工作点;(2)计算电路的电压放大倍数、输入电阻和输出电阻 (3)估算最大不失真输出电压的幅值;(4)当i u 足够大时,输出电压首先出现何种失真,如何调节R B 消除失真?解:电路的直流通路如图所示,CC BQ E BEQ BQ B U I R U I R =+++)1(βAmA R R U U I EB BEQ CC BQ μβ435.010130015)1(=⨯+≈++-≈由此定出静态工作点Q 为 mA I I BQ CQ 3.4==β,V R R I U U E C C CC CEQ 3.4)5.02(3.415)(≈+⨯-=+-=(2)Ω=⨯+=9053.426100300be r 由于R E 被交流傍路,因此16690.05.1100||-=⨯-=-=be L C u r R R A βΩ≈==k r R r be B i 9.0905.0||300||+u o -CC +u o -题7.3图CCRΩ==k R R C O 2(3)由于U CEQ =4.3V ,故最大不饱和失真输出电压为 V U U CEQ 6.37.03.47.00=-=-=' 最大不截止失真输出电压近似为V R I U L CQ 4.65.13.40=⨯='⋅='' 因此,最大不失真输出电压的幅值为3.6V 。
新编基础物理学第二版第七章习题解答

习题七7-1 氧气瓶的容积为32L ,瓶内充满氧气时的压强为130atm 。
若每小时需用1atm 氧气体积为400L 。
设使用过程中保持温度不变,问当瓶内压强降到10atm 时,使用了几个小时?解 已知123130atm,10atm,1atm;p p p === 1232L,V V V ===3400L V =。
质量分别为1m ,2m ,3m ,由题意可得:11m pV RT M = 22mp V RT M =233mp V RT M=所以一瓶氧气能用小时数为: ()121233313010329.6(1.0400m m pV p V n m p V -⨯--====⨯h) 7-2 一氦氖气体激光管,工作时管内温度是 27C ︒。
压强是2.4mmHg ,氦气与氖气的压强比是7:1.求管内氦气和氖气的分子数密度.解:依题意, n n n =+氦氖, 52.41.01310Pa 760p p p =+=⨯⨯氦氖;:7:1p p =氦氖 所以552.10.31.01310Pa, 1.01310Pa 760760p p =⨯⨯=⨯⨯氦氖, 根据 p nkT =,得()5223232.1760 1.01310 6.7610(m )1.3810300p n kT --⨯⨯===⨯⨯⨯氦氦 2139.6610(m )P n kT-==⨯氖氖7-3 氢分子的质量为243.310-⨯g 。
如果每秒有2310个氢分子沿着与墙面的法线成︒45角的方向以5110cm s -⋅的速率撞击在面积为22.0cm 的墙面上,如果撞击是完全弹性的,试求这些氢分子作用在墙面上的压强.解:单位时间内作用在墙面上的平均作用力为:2cos 45F N m =︒v所以氢分子作用在墙面上的压强为27522342 3.3101010102cos 4522330(Pa)210F m N p S S---⨯⨯⨯⨯⨯︒====⨯v7-4 一个能量为1210eV 的宇宙射线粒子,射入一氖管中,氖管中含有氦气0.10mol,如果宇宙射线粒子的能量全部被氖气分子所吸收而变为热运动能量,问氖气的温度升高了多少?解: 依题意可得:23121930.1 6.0210 10 1.6102k T -⨯⨯⨯∆=⨯⨯ 氖气的温度升高了771.610 1.2810(K)0.1 6.02 1.5 1.38T --⨯∆==⨯⨯⨯⨯ 7-5 容器内储有1mol 某种气体。
新标准大学英语综合教程(第二版)UNIT 7 A篇练习答案+课文翻译

Text
Hiroshima – the “liveliest” city in Japan
Text
Hiroshima – the “liveliest” city in Japan
1
The introductions were made. Most of the guests were Japanese,
6 “Seldom
has a city gained such world renown, and I am proud and happy to welcome you to Hiroshima, a town known throughout the
world for its – oysters.”
Warming Up
Shortly after Pearl Harbor, imperial forces attacked American bases in the Philippines. And within days Japan captured the American island of Guam. Japanese troops landed in Thailand. They marched into Malaya, and they seized Hong Kong. The Japanese also moved into Indonesia and Burma. The turning point came in June 1942 in the central Pacific in the great battle of Midway Island. Japanese Admiral Isoroku Yamamoto launched the battle. He wanted to meet and destroy the remaining ships in the American fleet before the United States could recover from the destruction at Pearl Harbor. The fighting between the two sides was fierce. But when it ended, the Americans had won a great victory. Admiral Yamamoto was forced to call off his attack and sail home. For the first time, the Japanese navy hadroshima, as you know, is a city familiar to everyone,” continued
普通物理学第二版第七章课后习题答案备课讲稿

普通物理学第二版第七章课后习题答案第七章 刚体力学7.1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s?估算地球赤道上一点因地球自转具有的线速度和向心加速度.估算地心因公转而具有的线速度和向心加速度(自己搜集所需数据).[解 答]7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.(1)假设转动是匀加速转动,求角加速度.(2)在此时间内,发动机转了多少转?[解 答](1)22(30001200)1/601.57(rad /s )t 12ωπβ⨯-⨯===V V(2)222220()(30001200)302639(rad)2215.7πωωθβ--===⨯所以 转数=2639420()2π=转7.1.3 某发动机飞轮在时间间隔t 内的角位移为球t 时刻的角速度和角加速度.[解 答]7.1.4 半径为0.1m 的圆盘在铅直平面内转动,在圆盘平面内建立O-xy 坐标系,原点在轴上.x 和y 轴沿水平和铅直向上的方向.边缘上一点A 当t=0时恰好在x 轴上,该点的角坐标满足21.2t t (:rad,t :s).θθ=+求(1)t=0时,(2)自t=0开始转45o 时,(3)转过90o时,A 点的速度和加速度在x 和y 轴上的投影.[解 答](1) A ˆˆt 0,1.2,R j 0.12j(m/s).0,0.12(m/s)x y ωνωνν====∴==v(2)45θ=o时,由2A 1.2t t ,t 0.47(s)42.14(rad /s)v Rπθωω=+==∴==⨯v v v得(3)当90θ=o 时,由7.1.5 钢制炉门由两个各长1.5m 的平行臂AB 和CD 支承,以角速度10rad/s ω=逆时针转动,求臂与铅直45o时门中心G 的速度和加速度.[解 答]因炉门在铅直面内作平动,门中心G 的速度、加速度与B 或D 点相同。
《现代机械制图(第2版)》习题答案--第7章

第7章零件图7.3 根据轴测图,在白纸或坐标纸上徒手画零件草图,并标注尺寸。
H T 150技术要求 未注明圆角R 2Z A l S i 7M g材料材料 踏架 阀盖 名称 名称 1. 2.7.5 极限与配合的标注。
1.解释配合代号的含义(填空)。
(1)轴套与孔:轴套与孔属于基孔制过盈配合;H表示基准孔的基本偏差代号,s表示配合轴的基本偏差代号;轴套为IT 6 级,孔为IT 7 级。
(2)轴与孔:Φ20表示轴与孔的基本尺寸为Φ20;轴与孔属于基孔制间隙配合;H表示基准孔的基本偏差代号,f表示配合轴的基本偏差代号;轴为IT 7 级,孔为IT8 级。
2.根据题7.5.1所示装配图中的配合代号查表,分别在相应的零件图上注出基本尺寸和极限偏差值。
7.6 根据已知条件,标注形位公差。
1.(1)B面对基准面A的垂直度公差值为0.015。
(2)C面对基准面A的平行度公差值为0.012。
2.(1)φ100h6对φ45p7的径向圆跳动公差值为0.015。
(2)φ100h6的圆度公差值为0.004。
(3)右端面对左端面的平行度公差值为0.01。
7.7 解释图中形位公差标注的含义。
7.8 零件测绘。
φ20k6的圆度公差值为0.006。
φ20k6的圆柱表面的直线度公差值为0.008。
φ18h7对φ10h7的同轴度公差值为0.02。
φ18h7、φ14h6、φ10h7对φ10h7的径向圆跳动公差值为0.012。
7.10 看懂托架零件图:(1)标注该零件在长、宽、高三个方向的主要尺寸基准;(2)画出左视图。
高度方向的主要尺寸基准长度方向的主要尺寸基准宽度方向的主要尺寸基准技术要求1.未注圆角R3~ R52.铸件不得有砂眼、裂纹。
理论力学第二版习题答案

理论力学第二版习题答案理论力学是物理学中研究物体运动规律的基础学科,它包括经典力学、相对论力学和量子力学等。
在经典力学中,牛顿运动定律是核心内容,而理论力学则进一步发展了这些定律,提供了更深入的分析和理解。
第二版的理论力学教材通常会包含更丰富的习题和更详尽的解答,以帮助学生更好地掌握力学的基本概念和方法。
习题1:牛顿运动定律的应用题目:一个质量为m的物体在水平面上受到一个恒定的力F作用,求物体的加速度。
解答:根据牛顿第二定律,力F等于物体质量m与加速度a的乘积,即F=ma。
因此,物体的加速度a等于力F除以质量m,即a=F/m。
习题2:动能和势能的计算题目:一个质量为m的物体从高度h自由落体,求落地时的动能。
解答:物体在自由落体过程中,重力势能转化为动能。
落地时的动能E_k等于重力势能的减少量,即E_k=mgh。
习题3:圆周运动的动力学分析题目:一个质量为m的物体以角速度ω在半径为R的圆周上做匀速圆周运动,求物体所受的向心力。
解答:匀速圆周运动的向心力F_c由公式F_c=mω^2R给出,其中m是物体的质量,ω是角速度,R是圆周的半径。
习题4:简谐振动的周期计算题目:一个质量为m的弹簧振子,弹簧的劲度系数为k,求其振动周期。
解答:简谐振动的周期T可以通过公式T=2π√(m/k)计算,其中m是振子的质量,k是弹簧的劲度系数。
习题5:刚体转动的动力学分析题目:一个均匀分布质量的刚体,其转动惯量为I,角速度为ω,求其转动动能。
解答:刚体的转动动能E_r可以通过公式E_r=0.5Iω^2计算,其中I是转动惯量,ω是角速度。
习题6:相对论效应的讨论题目:一个质量为m的物体以接近光速的速度v运动,求其相对论质量。
解答:在相对论中,物体的相对论质量m_r可以通过洛伦兹变换公式m_r=m/√(1-v^2/c^2)计算,其中m是静止质量,v是物体速度,c是光速。
习题7:量子力学的初步介绍题目:简述量子力学与经典力学的主要区别。
单片机原理及接口技术(C51编程)(第2版)-习题答案 - 第7章习题解答

第7章思考题及习题7参考答案一、填空1.如果采用晶振的频率为3MHz,定时器/计数器T x(x=0,1)工作在方式0、1、2下,其方式0的最大定时时间为,方式1的最大定时时间为,方式2的最大定时时间为。
答:32.768ms,262.144ms,1024µs2.定时器/计数器用作计数器模式时,外部输入的计数脉冲的最高频率为系统时钟频率的。
答:1/243.定时器/计数器用作定时器模式时,其计数脉冲由提供,定时时间与有关。
答:系统时钟信号12分频后,定时器初值4.定时器/计数器T1测量某正单脉冲的宽度,采用方式可得到最大量程?若时钟频率为6MHz,求允许测量的最大脉冲宽度为。
答:方式1定时,131.072ms。
5. 定时器T2 有3种工作方式:、和,可通过对寄存器中的相关位进行软件设置来选择。
答:捕捉,重新装载(增计数或减计数),波特率发生器,T2CON6. AT89S52单片机的晶振为6MHz,若利用定时器T1的方式1定时2ms,则(TH1)= ,(TL1)= 。
答:FCH,18H。
二、单选1.定时器T0工作在方式3时,定时器T1有种工作方式。
A.1种B.2种 C.3种D.4种答:C2. 定时器T0、T1工作于方式1时,其计数器为位。
A.8位B.16位C.14位D.13位答:B3. 定时器T0、T1的GATE x=1时,其计数器是否计数的条件。
A. 仅取决于TR x状态B. 仅取决于GATE位状态C. 是由TR x和INT x两个条件来共同控制D. 仅取决于INT x的状态答:C4. 定时器T2工作在自动重装载方式时,其计数器为位。
A.8位B. 13位C.14位D. 16位答:D5. 要想测量INT0引脚上的正单脉冲的宽度,特殊功能寄存器TMOD的内容应为。
A.87HB. 09HC.80HD. 00H答:B三、判断对错1.下列关于T0、T1的哪些说法是正确的。
A.特殊功能寄存器SCON,与定时器/计数器的控制无关。
新概念英语第二册课后练习答案lesson7

新概念英语第二册课后练习答案lesson7第一篇:新概念英语第二册课后练习答案lesson7新概念英语第二册课后习题答案详解Lesson 7 练习答案Key to written exercises 1.关键句型练习答案A detectives were waiting(1.1);They were expecting(1.2);detectives were waiting(1.5);others were waiting(1.6);two detectives were keeping guard(11.7-8)B 1 When the plane arrived, some of the detectives were waiting inside the main building while others were waiting on the airfield.2 When two of the detectives opened the parcel, two others were keeping guard at the door.C(sample answers)1 I was getting into my bath when you telephoned me.2 I was reading Hamlet when you saw me in the library this morning.3 I was saying that you must see the new film when you interruped me.D 1 wa s leaving…arrived 2 worked/ was working…was sitting/ sat3 was walking…met was reading…heard was preparing…set/ was setting 6 dropped…spoke 2.难点练习答案He gave all his books away.2 She woke the children up early this morning.4 They cut the king's head off.5 Put your hat and coat on.7 Help me to lift this table up.8 T ake your shoes off and put your slippers on.11 They have pulled the old building down.12 Make your mind up.14 She threw all those old newspapers away.3.多项选择题答案1.b根据课文第3-4行someone had told the police that thieves would try to stealthe diamond 和第8-9行While two detectives were keeping guard at thedoor…可以判断出b.to prevent a robbery 是正确答案,其他3个都不对。
基础化学第二版李保山沉淀溶解平衡习题解答

7 沉淀-溶解平衡习题 (p180-182)参考解答1.解答:(1) 1.4×10-16; (2) 1.4×10-112.解答:(1) 8.2×10-5 mol/L ; (2) 2.0×10-8 mol/L3.解答:1.0×10-10 mol/L4.解答:(1) 1.2×10-3 mol/L ; (2) 1.4×10-4 mol/L ; (3)7.0×10-9 mol/L5.解答:(1) 3.5×10-3 mol/L ; (2) 0.051 mol/L ; (3) 4.3×10-7mol/L6.解答:6.3×10-11 mol/L7.解答:5.5×10-4 mol/L8.解答:5.1×10-4mg9.解答:1.6×10-5 mol/L10.解答:1.1×10-611.解答:0.067 mol/L12.解答: [Ba 2+]=6.3×10-3mol ⋅L -1 [F -]=2s=1.3×10-2 mol ⋅L -113.解答: J =[Mg 2+][OH -]2= 3.2×10-15<K θsp =1.8×10-11. 无Mg(OH)2沉淀生成14.解答:溶解0.20molMnS 需1.0L HAc 的浓度为0.42mol ⋅L -115.解答: s= 4.8×10-3 mol ⋅L -116.解答: [Ag +]=1.8×10-10 mol ⋅L -1, [Cl -]=0.020 mol ⋅L -1[Ba 2+]=0.010 mol ⋅L -1, [SO 42-]=1.1×10-8 mol ⋅L -117.解答:(1) 4.4×10-3 mol ⋅L -1(2) K θsp (SrCO 3)= 1.9×10-5(3) CO 2不能完全溢出回收,所以测定值小于实际值。
《金融学(第二版)》讲义大纲及课后习题答案详解 第七章

《金融学〔第二版〕》讲义大纲及课后习题答案详解第七章CHAPTER 7PRINCIPLES OF ASSET VALUATIONObjectives? Understand why asset valuation is important in finance.? Explain the Law of One Price as the principle underlying all asset-valuation procedures. ? Explain the meaning and role of valuation models.? Explain how information gets reflected in security prices.Outline7.1 The Relation Between an Asset’s Value and Its Price 7.2 Value Maximization and Financial Decisions 7.3 The Law of One Price and Arbitrage7.4 Arbitrage and the Prices of Financial Assets 7.5 Exchange Rates and Triangular Arbitrage 7.6 Interest Rates and the Law of One Price 7.7 Valuation Using Comparables 7.8 Valuation Models7.9 Accounting Measures of Value7.10 How Information Gets Reflected in Security Prices 7.11 The Efficient Markets HypothesisSummary? In finance the measure of an asset’s value is the price it would fetch if it were sold in a competitive market. Theability to accurately value assets is at the heart of the discipline of finance because many personal and corporate financial decisions can be made by selecting the alternative that maximizes value.? The Law of One Price states that in a competitive market, if two assets are equivalent they will tend to have thesame price. The law is enforced by a process called arbitrage, the purchase and immediate sale of equivalent assets in order to earn a sure profit from a difference in their prices.? Even if arbitrage cannot be carried out in practice to enforce the Law of One Price, unknown asset values canstill be inferred from the prices of comparable assets whose prices are known.? The quantitative method used to infer an asset’s value from information about the prices of comparable assets iscalled a valuation model. The best valuation model to employ varies with the information available and the intended use of the estimated value. ? The book value of an asset or a liability as reported in a firm’s financial statements often differs from its currentmarket value.? In making most financial decisions, it is a good idea to start by assuming that for assets that are bought and soldin competitive markets, price is a pretty accurate reflection of fundamental value. This assumption is generally warranted precisely because there are many well-informed professionals looking for mispriced assets who profit by eliminating discrepancies between the market prices and the fundamental values of assets. The proposition that an asset’s current price fully reflects all publicly-available information about future economic fundamentals affecting the asset’s value is known as the Efficient Markets Hypothesis.? The prices of traded assets reflect information about the fundamental economic determinants of their value.Analysts are constantly searching for assets whose prices are different from their fundamental value in order to buy/sell these “bargains.〞 In deciding the best strategy for the purchase/sale of a “bargain,〞 theanalyst has to evaluate the accuracy of her information. The market price of an asset reflects the weighted average of all analysts opinions with heavier weights for analysts who control large amounts of money and for those analysts who have better than average information.Instructor’s ManualChapter 7 Page 106Solutions to Problems at End of ChapterLaw of One Price and Arbitrage1. IBX stock is trading for $35 on the NYSE and $33 on the Tokyo Stock Exchange. Assume that the costs of buying and selling the stock are negligible. a. How could you make an arbitrage profit?b. Over time what would you expect to happen to the stock prices in New York and Tokyo?c. Now assume that the cost of buying or selling shares of IBX is 1% per transaction. How does this affectyour answer?SOLUTION:a. Buy IBX stock in Tokyo and simultaneously sell them in NY. Your arbitrage profit is $2 per share.b. The prices would converge.c. Instead of the prices becoming exactly equal, there can remain a 2% discrepancy between them, roughly $.70 inthis case.2. Suppose you live in the state of Taxachusetts which has a 16% sales tax on liquor. A neighboring state called Taxfree has no tax on liquor. The price of a case of beer is $25 in Taxfree and it is $29 in Taxachusetts.a. Is this a violation of the Law of One Price?b. Are liquor stores in Taxachusetts near the border with Taxfree going to prosper?SOLUTION:a. This is not a violation of the Law of One Price because it is due to a tax imposed in one state but not in the other.Illegal arbitrage will probably occur, with lawbreakers buying large quantities of liquor in Taxfree and selling it in Taxachusetts without paying the tax.b. It is likely that liquor stores will locate in Taxfree near the border with Taxachusetts. Residents of both stateswill buy their liquor in the stores located in Taxfree, and liquor stores in Taxachusetts will go out of business.Triangular Arbitrage3. Suppose the price of gold is 155 marks per ounce.a. If the dollar price of gold is $100 per ounce, what should you expect the dollar price of a mark to be?b. If it actually only costs $0.60 to purchase one mark, how could one make arbitrage profits?SOLUTION:a. $100 buys the same amount of gold (1 ounce) as 155 DM, so 1 DM should cost 100/155 or $.645.b. The marks are “cheaper〞 than they should be, so the arbitrage transaction requires you to buy marks at thecheap price, use them to purchase gold, and sell the gold for dollars. Example:1. Start with $1 million, which you borrow for only enough time to carry out the arbitrage transaction.2. Use the million dollars to buy 1,666,667 marks (1,000,000 / 0.60)3. Buy 10,752.69 ounces of gold (1,666,667 / 155)4. Sell the gold for $1,075,269 (10752.69 x 100)Your risk-free arbitrage profit is $75,269.4. You observe that the dollar price of the Italian lira is $0.0006 and the dollar price of the yen is $0.01. What must be the exchange rate between lira and yen for there to be no arbitrage opportunity?SOLUTION:.0006$/lira?.06Yen/lira.01$/YenInstructor’s ManualChapter 7 Page 1075. Fill in the missing exchange rates in the following table: US dollar British pound German mark Yen US dollar $1 $1.50 $.5 $.01 British pound £0.67 German mark DM2.0 Japanese ¥100 Yen SOLUTION: US dollar British pound German mark Japanese Yen US dollar $1 $1.50 $.5 $.01 British pound £0.67 1 = .67 / 2 = .67 / 100 German mark DM2.0 = 2 / .67 1 = 2 / 100 Japanese ¥100 = 100 / .67 = 100 / 2 1 Yen US dollar British pound German mark Japanese Yen US dollar $1 $1.50 $.5 $.01 British pound £0.67 £1 £.33 £.0067 German mark DM2.0 DM3.0 DM1.0 DM.02 Japanese ¥100 ¥150 ¥50 ¥1 Yen Valuation Using Comparables6. Suppose you own a home that you purchased four years ago for $475,000. The tax assessor’s office has just informed you that they are increasing the taxable value of your home to $525,000. a. How might you gather information to help you appeal the new assessment?b. Suppose the house next door is comparable to yours except that it has one fewer bedroom. It just sold for$490,000. How might you use that information to argue your case? What inference must you make about the value of an additional bedroom?SOLUTION:a. You should retrieve as much information as you can about recent sales of comparable homes. If you canconvince the assessor’s office that your home is comparable (and the market value of the recent sales is less than $525,000) you should have a good case. You can gather the information about home sales from a real estate broker.b. The difference between your house’s assessed value and the actual market value of the home next door is$35,000 ($525,000 - $490,000). If you can convince the tax assessor’s office that the value of a bedroom is less than $35,000, then the assessor must agree that your home is worth less than $525,000. For example, if comparable sales figures show that one additional bedroom (all else reasonably equivalent) is worth only $10,000, then you should be able to argue that your home is worth $500,000 rather than $525,000.7. The P/E ratio of ITT Corporation is currently 6 while the P/E ratio of the S&P 500 is 10. What might account for the difference? SOLUTION: There are several possible reasons:? ITT may be riskier than the S&P500 either because it is in a relatively risky industry or has a relatively higherdebt ratio.? ITT’s reported earnings may be higher than they are expected to be in the future, or they may be inflated due tospecial accounting methods used by ITT.Instructor’s ManualChapter 7 Page 1088. Suppose you are chief financial officer of a private toy company. The chief executive officer has asked you to come up with an estimate for the company’s price per share. Your company’s earnings per share were $2.00 in the year just ended. You know that you should look at public company comparables, however, they seem to fall into two camps. Those with P/E ratios of 8x earnings and those with P/E ratios of 14x earnings. You are perplexed at the difference until you notice that on average, the lower P/E companies have higher leverage than the higher P/E group. The 8x P/E group has a debt/equity ratio of 2:1. The 14x P/E group has a debt/equityratio of 1:1. If your toy company has a debt/equity ratio of 1.5:1, what might you tell the CEO about your company’s equity value per share? SOLUTION:It would be reasonable to apply a P/E of 11x earnings (= (8 + 14) / 2) because your leverage is midway between the two groups. Hence, your company’s price per share would be: 11x $2.00 = $22.00 per share.9. Assume that you have operated your business for 15 years. Sales for the most recent fiscal year were $12,000,000. Net income for the most recent fiscal year was $1,000,000. Your book value is $10,500,000. A similar company recently sold for the following statistics: Multiple of Sales: 0.8x Multiple of Net Income 12x Multiple of Book Value 0.9xa. What is an appropriate range of value for your company?b. If you know that your company has future investment opportunities that are far more profitable than thecompany above, what does that say about your company’s likely valuation? SOLUTION:a. Multiple of Sales: .8x = $12 million x .8 Multiple of Net Income 12x = $1 million x 12 Multiple of Book Value .9x = $10.5 million x .9 An appropriate range might be 9 to 12 millionb. Higher end of the range = $9.6 million = $12 million = $9.45 millionEfficient Markets Hypothesis10. The price of Fuddy Co. stock recently jumped when the sudden unexpected death of its CEO was announced. What might account for such a market reaction?SOLUTION:Investors may believe that the company’s future prospects look better(i.e., either higher earnings or less risky) without the deceased CEO.11. Your analysis leads you to believe that the price of Outel’s stock should be $25 per share. Its current market price is $30.a. If you do not believe that you have access to special information about the company, what do you do?b. If you are an analyst with much better than average information, what do you do?SOLUTION:a. If you believe that the market for Outel stock is an informationally efficient one then the $30 market price(which is a weighted average of the valuations of all analysts) is the best estimate of the stock’s true value. You should question whether your own analysis is correct.b. You sell the stock because you think you have superior information. Real Interest Rate Parity12. Assume that the world-wide risk-free real rate of interest is 3% per year. Inflation in Switzerland is 2% per year and in the United States it is 5% per year. Assuming there is no uncertainty about inflation, what are the implied nominal interest rates denominated in Swiss francs and in US dollars?SOLUTION: Switzerland: (1.03 x 1.02) =1.0506 hence nominal interest rate = 5.06% US: (1.03 x 1.05) = 1 .0815 hence nominal interest rate = 8.15%Instructor’s ManualChapter 7 Page 109Integrative Problem13. Suppose an aunt has passed away and bequeathed to you and your siblings (one brother, one sister) a variety of assets. The original cost of these assets follows:ITEM COST WHEN PURCHASEDJewelry $500 by Grandmother 75 years ago House 1,200,000 10 years ago Stocks and Bonds 1,000,000 3 years ago Vintage (used) Car 200,000 2 months ago Furniture 15,000 various dates during last 40 yearsBecause you are taking a course in finance, your siblings put you in charge of dividing the assets fairly among the three of you. Before you start, your brother approaches you and says: “I’d really like the car for myself, so when you divide up the assets, just give me the car and deduct the $200,000 from my share.〞Hearing that, your sister says: “That sounds fair, because I really like the jewelry and you can assign that to me and deduct the $500 from my share.〞You have always loved your aunt’s house and its furnishings, so you would like to keep the house and the furniture.a. How do you respond to your brother and sister’s requests? Justify your responses.b. How would you go about determining appropriate values for each asset?SOLUTION:a. Because the market price of the car is close to the what your brother is willing to give up for it, your brother’srequest is reasonable. It is, however, quite possible (even likely), that the antique jewelry is worth much more today than what your relative’s grandmother paid for it in the past. Assigning only its acquisition cost to your sister’s share is quite likely a gross miscalculation. If she wants the jewelry, she should be “charged〞 an amount equal to today’s market value. It does not matter that your sister does not want to sell the jewelry for a profit, because the jewelry has VALUE even if you do not sell it. Fairness is all about equal VALUE.b. You would probably have to hire a professional appraiser for the furniture and the jewelry. You can look up thevalue of the stocks and bonds in a financial newspaper. You can estimate the value of the house by inquiring for how much similar houses in the same neighborhood have recently been sold. The car was purchased only twomonths ago, so it is probably reasonable to assume that the current market price is very close to what your distant relative paid for the car. Instructor’s ManualChapter 7 Page 110。
概率论与数理统计(茆诗松)第二版课后第七章习题参考答案

第七章 假设检验习题7.11. 设X 1 , …, X n 是来自N (µ , 1) 的样本,考虑如下假设检验问题H 0:µ = 2 vs H 1:µ = 3,若检验由拒绝域为}6.2{≥=x W 确定. (1)当n = 20时求检验犯两类错误的概率;(2)如果要使得检验犯第二类错误的概率β ≤ 0.01,n 最小应取多少? (3)证明:当n → ∞ 时,α → 0,β → 0. 解:(1)犯第一类错误的概率为0037.0)68.2(168.220126.21}2|6.2{}|{0=Φ−=⎭⎬⎫⎩⎨⎧=−≥−==≥=∈=n X P X P H W X P µµα,犯第二类错误的概率为0367.0)79.1(79.120136.21}3|6.2{}|{1=−Φ=⎭⎬⎫⎩⎨⎧−=−<−==<=∉=n X P X P H W X P µµβ;(2)因01.0)4.0(4.0136.21}3|6.2{≤−Φ=⎭⎬⎫⎩⎨⎧−=−<−==<=n n n n X P X P µµβ,则99.0)4.0(≥Φn ,33.24.0≥n ,n ≥ 33.93,故n 至少为34;(3))(0)6.0(16.0126.21}2|6.2{∞→→Φ−=⎭⎬⎫⎩⎨⎧=−≥−==≥=n n n n n X P X P µµα,)(0)4.0(4.0136.21}3|6.2{∞→→−Φ=⎭⎬⎫⎩⎨⎧−=−<−==<=n n n n n X P X P µµβ. 2. 设X 1 , …, X 10是来自0-1总体b (1, p ) 的样本,考虑如下检验问题H 0:p = 0.2 vs H 1:p = 0.4,取拒绝域为}5.0{≥=x W ,求该检验犯两类错误的概率. 解:因X ~ b(1, p ),有),10(~10101p b X X i i =∑=,则0328.08.02.0}2.0|510{}2.0|5.0{}|{10510100=⋅⋅==≥==≥=∈=∑=−k k k kC p X P p X P H W X P α,6331.06.04.0}4.0|510{}4.0|5.0{}|{410101=⋅⋅==<==<=∉=∑=−k k k kC p X P p X P H W X P β.3. 设X 1 , …, X 16是来自正态总体N (µ , 4) 的样本,考虑检验问题H 0:µ = 6 vs H 1:µ ≠ 6,拒绝域取为}|6{|c x W ≥−=,试求c 使得检验的显著性水平为0.05,并求该检验在µ = 6.5处犯第二类错误的概率.解:因05.0)]2(1[22162162}6||6{|}|{0=Φ−=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=≥−==≥−=∈=c c c X P c X P H W X P µµα,则Φ (2c ) = 0.975,2c = 1.96,故c = 0.98;故}5.6|48.05.648.1{}5.6|98.0|6{|}|{1=<−<−==<−=∉=µµβX P X P H W X P83.0)96.2()96.0(96.01625.696.2=−Φ−Φ=⎭⎬⎫⎩⎨⎧<−<−=X P .4. 设总体为均匀分布U (0, θ ),X 1 , …, X n 是样本,考虑检验问题H 0:θ ≥ 3 vs H 1:θ < 3,拒绝域取为}5.2{)(≤=n x W ,求检验犯第一类错误的最大值α ,若要使得该最大值α 不超过0.05,n 至少应取多大?解:因均匀分布最大顺序统计量X (n ) 的密度函数为θθ<<−Ι=x nn n nx x p 01)(,则nn n n nn n n x dx nx X P H W X P ⎟⎠⎞⎜⎝⎛=====≤=∈=∫−6535.233}3|5.2{}|{5.205.201)(0θα, 要使得α ≤ 0.05,即05.065≤⎟⎠⎞⎜⎝⎛n,43.16)6/5ln(05.0ln =≥n ,故n 至少为17.5. 在假设检验问题中,若检验结果是接受原假设,则检验可能犯哪一类错误?若检验结果是拒绝原假设,则又有可能犯哪一类错误?答:若检验结果是接受原假设,当原假设为真时,是正确的决策,未犯错误;当原假设不真时,则犯了第二类错误.若检验结果是拒绝原假设,当原假设为真时,则犯了第一类错误;当原假设不真时,是正确的决策,未犯错误.6. 设X 1 , …, X 20是来自0-1总体b (1, p ) 的样本,考虑如下检验问题H 0:p = 0.2 vs H 1:p ≠ 0.2,取拒绝域为⎭⎬⎫⎩⎨⎧≤≥=∑∑==17201201i i i i x x W 或,(1)求p = 0, 0.1, 0.2, …, 0.9, 1的势并由此画出势函数的图;(2)求在p = 0.05时犯第二类错误的概率.解:(1)因X ~ b(1, p ),有),20(~201p b X i i ∑=,势函数∑∑=−=−⎟⎟⎠⎞⎜⎜⎝⎛−=⎭⎬⎫⎩⎨⎧∈=6220201)1(201)(k kk i i p p k p WX P p g , 故110201)0(6220=××⎟⎟⎠⎞⎜⎜⎝⎛−=∑=−k k k k g ,3941.09.01.0201)1.0(6220=××⎟⎟⎠⎞⎜⎜⎝⎛−=∑=−k kk k g , 1559.08.02.0201)2.0(6220=××⎟⎟⎠⎞⎜⎜⎝⎛−=∑=−k k k k g ,3996.07.03.0201)3.0(6220=××⎟⎟⎠⎞⎜⎜⎝⎛−=∑=−k k kk g ,7505.06.04.0201)4.0(6220=××⎟⎟⎠⎞⎜⎜⎝⎛−=∑=−k k kk g ,9424.05.05.0201)5.0(6220=××⎟⎟⎠⎞⎜⎜⎝⎛−=∑=−k k k k g , 9935.04.06.0201)6.0(6220=××⎟⎟⎠⎞⎜⎜⎝⎛−=∑=−k k k k g ,9997.03.07.0201)7.0(6220=××⎟⎟⎠⎞⎜⎜⎝⎛−=∑=−k k kk g , 999998.02.08.0201)8.0(6220=××⎟⎟⎠⎞⎜⎜⎝⎛−=∑=−k k kk g11.09.0201)9.0(6220≈××⎟⎟⎠⎞⎜⎜⎝⎛−=∑=−k k kk g , 101201)1(6220=××⎟⎟⎠⎞⎜⎜⎝⎛−=∑=−k kk k g ; (2)在p = 0.05时犯第二类错误的概率2641.095.005.02005.0|6220201=××⎟⎟⎠⎞⎜⎜⎝⎛=⎭⎬⎫⎩⎨⎧=∉=∑∑=−=k kk i i k p W X P β. 7. 设一个单一观测的样本取自密度函数为p (x )的总体,对p (x )考虑统计假设: H 0:p 0(x ) = I 0 < x < 1 vs H 1:p 1(x ) = 2x I 0 < x < 1.若其拒绝域的形式为W = {x : x ≥ c },试确定一个c ,使得犯第一类,第二类错误的概率满足α + 2β 为最小,并求其最小值.解:当0 < c < 1时,α = P {X ∈ W | H 0} = P {X ≥ c | X ~ p 0(x )} = 1 − c ,且20112)}(~|{}H |{c xdx x p X c X P W X P c==<=∉=∫β,则2224128721161287212⎟⎠⎞⎜⎝⎛−+=⎟⎠⎞⎜⎝⎛+−+=+−=+c c c c c βα,故当41=c 时,α + 2β 为最小,其最小值为87. 8. 设X 1, X 2, …, X 30为取自柏松分布P (λ)的随机样本.(1)试给出单侧假设检验问题H 0:λ ≤ 0.1 vs H 1:λ > 0.1的显著水平α = 0.05的检验; (2)求此检验的势函数β (λ)在λ = 0.05, 0.2, 0.3, …, 0.9时的值,并据此画出β (λ)的图像.解:(1)因)30(~3021λP X X X X n +++=L ,假设H 0:λ ≤ 0.1 vs H 1:λ > 0.1, 统计量)30(~λP X n ,当H 0成立时,设)3(~P X n ,其p 分位数)3(p P 满足∑∑=−−=−≤<)3(031)3(03e !3e !3p p P k k P k k k p k 显著水平α = 0.05,可得P 1−α (3) = P 0.95 (3) = 6,右侧拒绝域}7{≥=x n W ;(2)因∑=−−=≥=∈=630e!)30(1}|7{}|{)(k k k X n P W X n P λλλλλβ, g故0001.0e !5.11)05.0(605.1=−=∑=−k k k β,3937.0e !61)2.0(606=−=∑=−k k k β,7932.0e !91)3.0(609=−=∑=−k k k β,9542.0e !121)4.0(6012=−=∑=−k k k β,9924.0e !151)5.0(6015=−=∑=−k k k β,9990.0e !181)6.0(6018=−=∑=−k k k β,9999.0e !211)7.0(6021=−=∑=−k kk β, 1e !241)8.0(6024≈−=∑=−k k k β,1e !271)9.0(6027≈−=∑=−k k k β.习题7.2说明:本节习题均采用拒绝域的形式完成,在可以计算检验的p 值时要求计算出p 值. 1. 有一批枪弹,出厂时,其初速率v ~ N (950, 1000)(单位:m /s ).经过较长时间储存,取9发进行测试,得样本值(单位:m /s )如下:914 920 910 934 953 945 912 924 940.据经验,枪弹经储存后其初速率仍服从正态分布,且标准差保持不变,问是否可认为这批枪弹的初速率有显著降低(α = 0.05)?解:设枪弹经储存后其初速率X ~ N (µ , 1000),假设H 0:µ = 950 vs H 1:µ < 950,已知σ 2,选取统计量)1,0(~N nX U σµ−=, 显著性水平α = 0.05,u 1 − α = u 0.95 = 1.645,左侧拒绝域W = {u ≤ −1.645}, 因928=x ,µ = 950,σ = 10,n = 9, 则W u ∈−=−=6.6910950928,并且检验的p 值p = P {U ≤ −6.6} = 2.0558 × 10−11 < α = 0.05,故拒绝H 0,接受H 1,即可以认为这批枪弹的初速率有显著降低. 2. 已知某炼铁厂铁水含碳量服从正态分布N (4.55, 0.1082 ).现在测定了9炉铁水,其平均含碳量为4.484,如果铁水含碳量的方差没有变化,可否认为现在生产的铁水平均含碳量仍为4.55(α = 0.05)? 解:设现在生产的铁水含碳量X ~ N (µ , 0.1082 ),假设H 0:µ = 4.55 vs H 1:µ ≠ 4.55,已知σ 2,选取统计量)1,0(~N nX U σµ−=, 显著性水平α = 0.05,u 1 − α /2 = u 0.975 = 1.96,双侧拒绝域W = {| u | ≥ 1.96}, 因484.4=x ,µ = 4.55,σ = 0.108,n = 9, 则W u ∉−=−=8333.19108.055.4484.4,并且检验的p 值p = 2P {U ≤ −1.8333} = 0.0668 > α = 0.05,β (故接受H 0,拒绝H 1,即可以认为现在生产的铁水平均含碳量仍为4.55. 3. 由经验知某零件质量X ~ N (15, 0.05 2 ) (单位:g ),技术革新后,抽出6个零件,测得质量为14.7 15.1 14.8 15.0 15.2 14.6.已知方差不变,问平均质量是否仍为15 g (取α = 0.05)?解:设技术革新后零件质量X ~ N (µ , 0.05 2 ),假设H 0:µ = 15 vs H 1:µ ≠ 15,已知σ 2,选取统计量)1,0(~N nX U σµ−=, 显著性水平α = 0.05,u 1 − α /2 = u 0.975 = 1.96,双侧拒绝域W = {| u | ≥ 1.96}, 因9.14=x ,µ = 15,σ = 0.05,n = 6, 则W u ∈−=−=8990.4605.0159.14,并且检验的p 值p = 2P {U ≤ −4.8990} = 9.6326 × 10−7 < α = 0.05,故拒绝H 0,接受H 1,即不能认为平均质量仍为15 g . 4. 化肥厂用自动包装机包装化肥,每包的质量服从正态分布,其平均质量为100 kg ,标准差为1.2 kg .某日开工后,为了确定这天包装机工作是否正常,随机抽取9袋化肥,称得质量如下:99.3 98.7 100.5 101.2 98.3 99.7 99.5 102.1 100.5.设方差稳定不变,问这一天包装机的工作是否正常(取α = 0.05)? 解:设这天包装机包装的化肥每包的质量X ~ N (µ , 1.22 ),假设H 0:µ = 100 vs H 1:µ ≠ 100,已知σ 2,选取统计量)1,0(~N nX U σµ−=, 显著性水平α = 0.05,u 1 − α /2 = u 0.975 = 1.96,双侧拒绝域W = {| u | ≥ 1.96}, 因9778.99=x ,µ = 100,σ = 1.2,n = 9, 则W u ∉−=−=0556.092.11009778.99,并且检验的p 值p = 2P {U ≤ −0.0556} = 0.9557 > α = 0.05,故接受H 0,拒绝H 1,即可以认为这一天包装机的工作正常. 5. 设需要对某正态总体的均值进行假设检验H 0:µ = 15, H 1:µ < 15.已知σ 2 = 2.5,取α = 0.05,若要求当H 1中的µ ≤ 13时犯第二类错误的概率不超过0.05,求所需的样本容量.解:设该总体X ~ N (µ , 2.5 ),假设H 0:µ = 15 vs H 1:µ < 15,已知σ 2,选取统计量)1,0(~N nX U σµ−=, 显著性水平α = 0.05,u 1 − α = u 0.95 = 1.645,左侧拒绝域W = {u ≤ −1.645}, 因µ = 15,σ 2 = 2.5,有nx u 5.215−=,当µ ≤ 13时犯第二类错误的概率为⎭⎬⎫⎩⎨⎧≤−+−>−=⎭⎬⎫⎩⎨⎧≤−>−=13|5.21565.15.213|65.15.215µµµµβn n X P n X P 05.0)2649.165.1(15.2131565.15.2≤+−Φ−=⎭⎬⎫⎩⎨⎧−+−>−≤n n nX P µ,则95.0)2649.165.1(≥+−Φn ,即65.12649.165.1≥+−n ,6089.2≥n ,n ≥ 6.8064, 故样本容量n 至少为7.6. 从一批钢管抽取10根,测得其内径(单位:mm )为:100.36 100.31 99.99 100.11 100.64 100.85 99.42 99.91 99.35 100.10.设这批钢管内直径服从正态分布N (µ , σ 2),试分别在下列条件下检验假设(α = 0.05).H 0:µ = 100 vs H 1:µ > 100.(1)已知σ = 0.5; (2)σ 未知.解:设这批钢管内直径X ~ N (µ , σ 2),假设H 0:µ = 100 vs H 1:µ > 100,(1)已知σ 2,选取统计量)1,0(~N nX U σµ−=, 显著性水平α = 0.05,u 1 − α = u 0.95 = 1.645,右侧拒绝域W = {u ≥ 1.645}, 因104.100=x ,µ = 100,σ = 0.5,n = 10, 则W u ∉=−=6578.0105.0100104.100,并且检验的p 值p = P {U ≥ 0.6578} = 0.2553 > α = 0.05,故接受H 0,拒绝H 1,即不能认为µ > 100. (2)未知σ 2,选取统计量)1(~−−=n t nS X T µ, 显著性水平α = 0.05,t 1 − α (n − 1) = t 0.95 (9) = 1.8331,右侧拒绝域W = {t ≥ 1.8331}, 因104.100=x ,µ = 100,s = 0.4760,n = 10, 则W t ∉=−=6910.0104760.0100104.100,并且检验的p 值p = P {T ≥ 0.6910} = 0.2535 > α = 0.05,故接受H 0,拒绝H 1,即不能认为µ > 100.7. 假定考生成绩服从正态分布,在某地一次数学统考中,随机抽取了36位考生的成绩,算得平均成绩为66.5分,标准差为15分,问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70分?解:设这次考试考生的成绩X ~ N (µ , σ 2 ),假设H 0:µ = 70 vs H 1:µ ≠ 70,未知σ 2,选取统计量)1(~−−=n t nS X T µ, 显著性水平α = 0.05,t 1 − α /2 (n − 1) = t 0.975 (35) = 2.0301,双侧拒绝域W = {| t | ≥ 2.0301}, 因5.66=x ,µ = 70,s = 15,n = 36, 则W t ∉−=−=4.13615705.66,并且检验的p 值p = 2P {T ≤ −1.4} = 0.1703 > α = 0.05,故接受H 0,拒绝H 1,即可以认为这次考试全体考生的平均成绩为70分. 8. 一个小学校长在报纸上看到这样的报道:“这一城市的初中学生平均每周看8 h 电视.”她认为她所在学校的学生看电视的时间明显小于该数字.为此她在该校随机调查了100个学生,得知平均每周看电视的时间5.6=x h ,样本标准差为s = 2 h .问是否可以认为这位校长的看法是对的(取α = 0.05)? 解:设学生看电视的时间X ~ N (µ , σ 2 ),假设H 0:µ = 8 vs H 1:µ < 8,未知σ 2,选取统计量)1(~−−=n t nS X T µ,n = 100,大样本,有)1,0(~N n S X T &µ−=,显著性水平α = 0.05,t 1 − α (n − 1) = t 0.95 (99) ≈ u 0.95 = 1.645,左侧拒绝域W ≈ {t ≤ −1.645},因5.6=x ,µ = 8,s = 2,n = 100, 则W t ∈−=−=5.7100285.6,并且检验的p 值p = P {T ≤ −7.5} = 3.1909 × 10−14 < α = 0.05,故拒绝H 0,接受H 1,即可以认为这位校长的看法是对的.9. 设在木材中抽出100根,测其小头直径,得到样本平均数2.11=x cm ,样本标准差为s = 2.6 cm ,问该批木材小头的平均直径能否认为不低于12 cm (取α = 0.05)? 解:设该批木材小头的直径X ~ N (µ , σ 2 ),假设H 0:µ = 12 vs H 1:µ < 12,未知σ 2,选取统计量)1(~−−=n t n S X T µ,n = 100,大样本,有)1,0(~N nS X T &µ−=, 显著性水平α = 0.05,t 1 − α (n − 1) = t 0.95 (99) ≈ u 0.95 = 1.645,左侧拒绝域W ≈ {t ≤ −1.645},因2.11=x ,µ = 12,s = 2.6,n = 100, 则W t ∈−=−=0769.31006.2122.11,并且检验的p 值p = P {T ≤ −3.0769} = 0.0010 < α = 0.05,故拒绝H 0,接受H 1,即不能认为这批木材小头的平均直径不低于12 cm .10.考察一鱼塘中鱼的含汞量,随机地取10条鱼测得各条鱼的含汞量(单位:mg )为:0.8 1.6 0.9 0.8 1.2 0.4 0.7 1.0 1.2 1.1.设鱼的含汞量服从正态分布N (µ , σ 2),试检验假设H 0:µ = 1.2 vs H 1:µ > 1.2(取α = 0.10). 解:设鱼的含汞量X ~ N (µ , σ 2 ),假设H 0:µ = 1.2 vs H 1:µ > 1.2,未知σ 2,选取统计量)1(~−−=n t nSX T µ,显著性水平α = 0.1,t 1 − α (n − 1) = t 0.9 (9) = 1.3830,右侧拒绝域W = {t ≥ 1.3830}, 因97.0=x ,µ = 1.2,s = 0.3302,n = 10, 则W t ∉−=−=2030.2103302.02.197.0,并且检验的p 值p = P {T ≥ −2.2030} = 0.9725 > α = 0.10,故接受H 0,拒绝H 1,即不能认为µ > 1.2 . 11.如果一个矩形的宽度w 与长度l 的比618.0)15(21≈−=l w ,这样的矩形称为黄金矩形.下面列出某工艺品工厂随机取的20个矩形宽度与长度的比值.0.693 0.749 0.654 0.670 0.662 0.672 0.615 0.606 0.690 0.628 0.668 0.611 0.606 0.609 0.553 0.570 0.844 0.576 0.933 0.630.设这一工厂生产的矩形的宽度与长度的比值总体服从正态分布,其均值为µ ,试检验假设(取α = 0.05)H 0:µ = 0.618 vs H 1:µ ≠ 0.618.解:设这一工厂生产的矩形的宽度与长度的比值X ~ N (µ , σ 2 ),假设H 0:µ = 0.618 vs H 1:µ ≠ 0.618,未知σ 2,选取统计量)1(~−−=n t nS X T µ, 显著性水平α = 0.05,t 1 − α /2 (n − 1) = t 0.975 (19) = 2.0930,双侧拒绝域W = {| t | ≥ 2.0930},因6620.0=x ,µ = 0.618,s = 0.0918,n = 20, 则W t ∈=−=1422.2200918.0618.06620.0,并且检验的p 值p = 2P {T ≥ 2.1422} = 0.0453 < α = 0.05,故拒绝H 0,接受H 1,即不能认为µ = 0.618.12.下面给出两种型号的计算器充电以后所能使用的时间(h )的观测值型号A 5.5 5.6 6.3 4.6 5.3 5.0 6.2 5.8 5.1 5.2 5.9;型号B 3.8 4.3 4.2 4.0 4.9 4.5 5.2 4.8 4.5 3.9 3.7 4.6.设两样本独立且数据所属的两总体的密度函数至多差一个平移量.试问能否认为型号A 的计算器平均使用时间明显比型号B 来得长(取α = 0.01)?解:设两种型号的计算器充电以后所能使用的时间分别为),(~211σµN X ,),(~222σµN Y ,且2221σσ=,假设H 0:µ 1 = µ 2 vs H 1:µ 1 > µ 2,未知2221,σσ,但2221σσ=,选取统计量)2(~112121−++−=n n t n n S YX T w ,显著性水平α = 0.01,t 1 − α (n 1 + n 2 − 2) = t 0.99 (21) = 2.5176,右侧拒绝域W = {t ≥ 2.5176}, 因5.5=x ,3667.4=y ,s x = 0.5235,s y = 0.4677,n 1 = 11,n 2 = 12,4951.0214677.0115235.0102)1()1(22212221=×+×=−+−+−=n n s n s n s yx w ,则W t ∈=+×−=4844.51211114951.03667.45.5,并且检验的p 值p = P {T ≥ 5.4844} = 9.6391 × 10 −6 < α = 0.01,故拒绝H 0,接受H 1,即可以认为型号A 的计算器平均使用时间明显比型号B 来得长.13.从某锌矿的东、西两支矿脉中,各抽取样本容量分别为9与8的样本进行测试,得样本含锌平均数及样本方差如下:东支:1337.0,230.0211==s x ;西支:1736.0,269.0222==s x .若东、西两支矿脉的含锌量都服从正态分布且方差相同,问东、西两支矿脉含锌量的平均值是否可以看作一样(取α = 0.05)?解:设东、西两支矿脉的含锌量分别为),(~211σµN X ,),(~222σµN Y ,且2221σσ=,假设H 0:µ 1 = µ 2 vs H 1:µ 1 ≠ µ 2,未知2221,σσ,但2221σσ=,选取统计量)2(~11212121−++−=n n t n n S X X T w,显著性水平α = 0.05,t 1 − α /2 (n 1 + n 2 − 2) = t 0.975 (15) = 2.1314,双侧拒绝域W = {| t | ≥ 2.1314},因1736.0,269.0,1337.0,230.0222211====s x s x ,n 1 = 9,n 2 = 8,3903.0151736.071337.082)1()1(21222211=×+×=−+−+−=n n s n s n s w ,则W t ∉−=+×−=2056.081913903.0269.0230.0,并且检验的p 值p = 2P {T ≤ −0.2056} = 0.8399 > α = 0.05, 故接受H 0,拒绝H 1,即可以认为东、西两支矿脉含锌量的平均值是一样的.14.在针织品漂白工艺过程中,要考察温度对针织品断裂强力(主要质量指标)的影响.为了比较70°C与80°C 的影响有无差别,在这两个温度下,分别重复做了8次试验,得数据如下(单位:N ):70°C 时的强力:20.5 18.8 19.8 20.9 21.5 19.5 21.0 21.2, 80°C 时的强力:17.7 20.3 20.0 18.8 19.0 20.1 20.0 19.1.根据经验,温度对针织品断裂强力的波动没有影响.问在70°C 时的平均断裂强力与80°C 时的平均断裂强力间是否有显著差别?(假设断裂强力服从正态分布,α = 0.05)解:设在70°C 和80°C 时的断裂强力分别为),(~211σµN X ,),(~222σµN Y ,且2221σσ=,假设H 0:µ 1 = µ 2 vs H 1:µ 1 ≠ µ 2,未知2221,σσ,但2221σσ=,选取统计量)2(~112121−++−=n n t n n S Y X T w,显著性水平α = 0.05,t 1 − α /2 (n 1 + n 2 − 2) = t 0.975 (14) = 2.1448,双侧拒绝域W = {| t | ≥ 2.1448}, 因4.20=x ,375.19=y ,s x = 0.9411,s y = 0.8876,n 1 = 8,n 2 = 8,9148.0148876.079411.072)1()1(22212221=×+×=−+−+−=n n s n s n s yx w ,则W t ∈=+×−=2410.281819148.0375.194.20,并且检验的p 值p = 2P {T ≥ 2.2410} = 0.0418 < α = 0.05, 故拒绝H 0,接受H 1,即可以认为70°C 时的平均断裂强力与80°C 时的平均断裂强力间有显著差别. 15.一药厂生产一种新的止痛片,厂方希望验证服用新药片后至开始起作用的时间间隔较原有止痛片至少缩短一半,因此厂方提出需检验假设H 0:µ 1 = 2µ 2 vs H 1:µ 1 > 2µ 2.此处µ 1 , µ 2分别是服用原有止痛片和服用新止痛片后至开始起作用的时间间隔的总体的均值.设两总体均为正态分布且方差分别为已知值2221,σσ,现分别在两总体中取一样本X 1 , …, X n 和Y 1 , …, Y m ,设两个样本独立.试给出上述假设检验问题的检验统计量及拒绝域.解:设服用原有止痛片和新止痛片后至开始起作用的时间间隔分别为),(~211σµN X ,),(~222σµN Y ,因X 1 , …, X n 和Y 1 , …, Y m 分别X 和Y 为来自的样本,且两个样本独立,则),(~211n N X σµ,,(~222mN Y σµ,且X 与Y 独立,有4,2(~2222121m n N Y X σσµµ+−−, 标准化,得)1,0(~4)2()2(222121N mnY X σσµµ+−−−,假设H 0:µ 1 = 2µ 2 vs H 1:µ 1 > 2µ 2,已知2221,σσ,选取统计量)1,0(~422221N mnYX U σσ+−=,显著性水平α ,右侧拒绝域W = {u ≥ u 1 − α}.16.对冷却到−0.72°C 的样品用A 、B 两种测量方法测量其融化到0°C 时的潜热,数据如下:方法A :79.98 80.04 80.02 80.04 80.03 80.03 80.04 79.97 80.05 80.03 80.02 80.0080.02,方法B :80.02 79.94 79.98 79.97 80.03 79.95 79.97 79.97.假设它们服从正态分布,方差相等,试检验:两种测量方法的平均性能是否相等?(取α = 0.05).解:设用A 、B 两种测量方法测量的潜热分别为),(~211σµN X ,),(~222σµN Y ,且2221σσ=,假设H 0:µ1 = µ2 vs H 1:µ1 ≠ µ2,未知2221,σσ,但2221σσ=,选取统计量)2(~112121−++−=n n t n n S YX T w ,显著性水平α = 0.05,t 1−α /2 (n 1 + n 2 − 2) = t 0.975 (19) = 2.0930,双侧拒绝域W = {| t | ≥ 2.0930}, 因0208.80=x ,9787.79=y ,s x = 0.0240,s y = 0.0.314,n 1 = 8,n 2 = 8,0269.0190314.070240.0122)1()1(22212221=×+×=−+−+−=n n s n s n s yx w ,则W t ∈=+×−=4722.3811310269.09787.790208.80,并且检验的p 值p = 2P {T ≥ 3.4722} = 0.0026 < α = 0.05,故拒绝H 0,接受H 1,可以认为两种测量方法的平均性能不相等.17.为了比较测定活水中氯气含量的两种方法,特在各种场合收集到8个污水样本,每个水样均用这两种方法测定氯气含量(单位:mg /l ),具体数据如下:水样号 方法一(x ) 方法二(y ) 差(d = x − y ) 1 0.36 0.39 −0.03 2 1.35 0.84 0.51 3 2.56 1.76 0.80 4 3.92 3.35 0.57 5 5.35 4.69 0.66 6 8.33 7.70 0.63 7 10.70 10.52 0.18 8 10.91 10.92 −0.01设总体为正态分布,试比较两种测定方法是否有显著差异.请写出检验的p 值和结论(取α = 0.05).解:设用这两种测定方法测定的氯气含量之差为),(~2d d N Y X D σµ−=,成对数据检验,假设H 0:µ d = 0 vs H 1:µ d ≠ 0,未知2d σ,选取统计量)1(~−=n t nS D T d,显著水平α = 0.05,t 1−α /2 (n − 1) = t 0.975 (7) = 2.3646,双侧拒绝域W = {| t | ≥ 2.3646}, 因4138.0=d ,s d = 0.3210,n = 8, 则W t ∈==6461.383210.04138.0,并且检验的p 值p = 2P {T ≥ 3.6461} = 0.0082 < α = 0.05,故拒绝H 0,接受H 1,可以认为两种测定方法有显著差异.18.一工厂的;两个化验室每天同时从工厂的冷却水取样,测量水中的含气量(10−6)一次,下面是7天的记录:室甲:1.15 1.86 0.75 1.82 1.14 1.65 1.90, 室乙:1.00 1.90 0.90 1.80 1.20 1.70 1.95.设每对数据的差d i = x i − y i (i = 1, 2, …, 7)来自正态总体,问两化验室测定结果之间有无显著差异?(α = 0.01)解:设两个化验室测定的含气量数据之差为),(~2d d N Y X D σµ−=,成对数据检验,假设H 0:µ d = 0 vs H 1:µ d ≠ 0,未知2d σ,选取统计量)1(~−=n t nS D T d,显著水平α = 0.01,t 1−α /2 (n − 1) = t 0.995 (6) = 3.7074,双侧拒绝域W = {| t | ≥ 3.7074}, 因0257.0−=d ,s d = 0.0922,n = 7, 则W t ∉−=−=7375.070922.00257.0,并且检验的p 值p = 2P {T ≤ −0.7375} = 0.4886 > α = 0.05,故接受H 0,拒绝H 1,可以认为两化验室测定结果之间没有显著差异.19.为比较正常成年男女所含红血球的差异,对某地区156名成年男性进行测量,其红血球的样本均值为465.13(104/mm 3),样本方差为54.802;对该地区74名成年女性进行测量,其红血球的样本均值为422.16,样本方差为49.202.试检验:该地区正常成年男女所含红血球的平均值是否有差异?(取α = 0.05)解:设该地区正常成年男女所含红血球分别为),(~211σµN X ,),(~222σµN Y ,假设H 0:µ1 = µ2 vs H 1:µ1 ≠ µ2,未知2221,σσ,大样本场合,选取统计量)1,0(~2212N n S n SY X U yx&+−=,显著水平α = 0.05,u 1−α /2 = u 0.975 = 1.96,双侧拒绝域W = {| t | ≥ 1.96},因222220.49,16.422,80.54,13.465====y x s y s x ,n 1 = 156,n 2 = 74,则W u ∈=+−=9611.57420.4915680.5416.42213.46522,并且检验的p 值p = 2P {U ≥ 5.9611} = 2.5055 × 10−9 < α = 0.05,故拒绝H 0,接受H 1,可以认为该地区正常成年男女所含红血球的平均值有差异.20.为比较不同季节出生的女婴体重的方差,从去年12月和6月出生的女婴中分别随机地抽取6名及10名,测其体重如下(单位:g ):12月:3520 2960 2560 2960 3260 3960,6月:3220 3220 3760 3000 2920 3740 3060 3080 2940 3060.假定新生女婴体重服从正态分布,问新生女婴体重的方差是否是冬季的比夏季的小(取α = 0.05)?解:设12月和6月出生的女婴体重分别为),(~211σµN X ,),(~222σµN Y ,假设H 0:2221σσ= vs H 1:2221σσ<,选取统计量)1,1(~2122−−=n n F S S F yx,显著水平α = 0.05,21.077.41)5,9(1)9,5()1,1(95.005.021====−−F F n n F α,左侧拒绝域W = { f ≤ 0.21},因225960.491=x s ,225217.306=y s ,则W f ∉==5721.25217.3065960.49122,并且检验的p 值p = P {F ≤ 2.5721} = 0.8967 > α = 0.05,故接受H 0,拒绝H 1,新生女婴体重的方差冬季的不比夏季的小.21.已知维尼纶纤度在正常条件下服从正态分布,且标准差为0.048.从某天产品中抽取5根纤维,测得其纤度为1.32 1.55 1.36 1.40 1.44问这一天纤度的总体标准差是否正常(取α = 0.05)?解:设这一天维尼纶纤度X ~ N (µ , σ 2),假设H 0:σ 2 = 0.0482 vs H 1:σ 2 ≠ 0.0482,选取统计量)1(~)1(2222−−=n S n χσχ,显著性水平α = 0.05,4844.0)4()1(2025.022/==−χχαn ,1433.11)4()1(2975.022/1==−−χχαn ,双侧拒绝域W = {χ 2 ≤ 0.4844或χ 2 ≥ 11.1433}, 因σ 2 = 0.0482,s 2 = 0.08822,n = 5,则W ∈=×=5069.13048.00882.04222χ,并且检验的p 值p = 2P {χ 2 ≥ 13.5069} = 0.0181 < α = 0.05, 故拒绝H 0,接受H 1,即可以认为这一天纤度的总体方差不正常.22.某电工器材厂生产一种保险丝.测量其熔化时间,依通常情况方差为400,今从某天产品中抽取容量为25的样本,测量其熔化时间并计算得24.62=x ,s 2 = 404.77,问这天保险丝熔化时间分散度与通常有无显著差异(取α = 0.05,假定熔化时间服从正态分布)? 解:设这天保险丝熔化时间分散度X ~ N (µ , σ 2),假设H 0:σ 2 = 400 vs H 1:σ 2 ≠ 400,选取统计量)1(~)1(2222−−=n S n χσχ,显著性水平α = 0.05,4012.12)24()1(2025.022/==−χχαn ,3641.39)24()1(2975.022/1==−−χχαn ,双侧拒绝域W = {χ 2 ≤ 12.4012或χ 2 ≥ 39.3641}, 因σ 2 = 400,s 2 = 404.77,n = 25,则W ∉=×=2862.2440077.404242χ,并且检验的p 值p = 2P {χ 2 ≥ 24.2862} = 0.8907 > α = 0.05,故接受H 0,拒绝H 1,即可以认为这天保险丝熔化时间分散度与通常没有显著差异. 23.某种导线的质量标准要求其电阻的标准差不得超过0.005(Ω).今在一批导线中随机抽取样品9根,测得样本标准差s = 0.007(Ω),设总体为正态分布.问在显著水平α = 0.05下,能否认为这批导线的标准差显著地偏大?解:设这批导线的电阻X ~ N (µ , σ 2),假设H 0:σ 2 = 0.005 2 vs H 1:σ 2 > 0.005 2,选取统计量)1(~)1(2222−−=n S n χσχ,显著性水平α = 0.05,5073.15)8()1(295.021==−−χχαn ,右侧拒绝域W = {χ 2 ≥ 15.5073},因σ 2 = 0.005 2,s 2 = 0.007 2,n = 9,则W ∈=×=68.15005.0007.08222χ,并且检验的p 值p = P {χ 2 ≥ 15.68} = 0.0472 < α = 0.05, 故拒绝H 0,接受H 1,即可以认为这批导线的标准差显著地偏大.24.两台车床生产同一种滚珠,滚珠直径服从正态分布.从中分别抽取8个和9个产品,测得其直径为甲车床:15.0 14.5 15.2 15.5 14.8 15.1 15.2 14.8;乙车床:15.2 15.0 14.8 15.2 15.0 15.0 14.8 15.1 14.8.比较两台车床生产的滚珠直径的方差是否有明显差异(取α = 0.05).解:设两台车床生产的滚珠直径分别为),(~211σµN X ,),(~222σµN Y ,假设H 0:2221σσ= vs H 1:2221σσ≠,选取统计量)1,1(~2122−−=n n F S S F yx,显著性水平α = 0.05,2041.09.41)7,8(1)8,7()1,1(975.0025.0212/====−−F F n n F α,F 1 − α /2 (n 1 − 1, n 2 − 1) = F 0.975 (7, 8) = 4.53,双侧拒绝域W = {F ≤ 0.2041或F ≥ 4.53},因223091.0=x s ,221616.0=y s ,则W F ∉==6591.31616.03091.022,并且检验的p 值p = 2P {F ≥ 3.6591} = 0.0892 > α = 0.05,故接受H 0,拒绝H 1,即可以认为两台车床生产的滚珠直径的方差没有明显差异. 25.有两台机器生产金属部件,分别在两台机器所生产的部件中各取一容量为m = 14和n = 12的样本,测得部件质量的样本方差分别为46.1521=s ,66.922=s ,设两样本相互独立,试在显著性水平α = 0.05下检验假设H 0:2221σσ= vs H 1:2221σσ>.解:设两台机器生产金属部件质量分别为),(~211σµN X ,),(~222σµN Y ,假设H 0:2221σσ= vs H 1:2221σσ>,选取统计量)1,1(~2221−−=n m F S S F ,显著性水平α = 0.05,F 1 − α (m − 1, n − 1) = F 0.95 (13, 11) = 2.7614,右侧拒绝域W = {F ≥ 2.7614},因46.1521=s ,66.922=s ,则W F ∉==6004.166.946.15,并且检验的p 值p = P {F ≥ 1.6004} = 0.2206 > α = 0.05, 故接受H 0,拒绝H 1,即可以认为2221σσ=.26.测得两批电子器件的样品的电阻(单位:Ω)为A 批(x ) 0.140 0.138 0.143 0.142 0.144 0.137;B 批(y ) 0.135 0.140 0.142 0.136 0.138 0.140.设这两批器材的电阻值分别服从),(211σµN ,),(222σµN ,且两样本独立.(1)试检验两个总体的方差是否相等(取α = 0.05)? (2)试检验两个总体的均值是否相等(取α = 0.05)?解:设两批电子器件样品的电阻分别为),(~211σµN X ,),(~222σµN Y ,(1)假设H 0:2221σσ= vs H 1:2221σσ≠,选取统计量)1,1(~2122−−=n n F S S F yx,显著性水平α = 0.05,1399.015.71)5,5(1)5,5()1,1(975.0025.0212/====−−F F n n F α,F 1 − α /2 (n 1 − 1, n 2 − 1) = F 0.975 (5, 5) = 7.15,双侧拒绝域W = {F ≤ 0.1399或F ≥ 7.15},因22002805.0=x s ,22002665.0=y s ,则W F ∉==1080.1002665.0002805.022,并且检验的p 值p = 2P {F ≥ 1.1080} = 0.9131 > α = 0.05, 故接受H 0,拒绝H 1,即可以认为两个总体的方差相等; (2)假设H 0:µ 1 = µ 2 vs H 1:µ 1 ≠ µ 2,未知2221,σσ,但2221σσ=,选取统计量)2(~112121−++−=n n t n n S YX T w ,显著性水平α = 0.05,t 1 − α /2 (n 1 + n 2 − 2) = t 0.975 (10) = 2.2281,双侧拒绝域W = {| t | ≥ 2.2281}, 因1407.0=x ,1385.0=y ,s x = 0.002805,s y = 0.002665,n 1 = 6,n 2 = 6,002736.010002665.05002805.052)1()1(22212221=×+×=−+−+−=n n s n s n s yx w ,则W t ∉=+×−=3718.16161002736.01385.01407.0,并且检验的p 值p = 2P {T ≥ 1.3718} = 0.2001 > α = 0.05, 故接受H 0,拒绝H 1,即可以认为两个总体的均值相等.27.某厂使用两种不同的原料生产同一类型产品,随机选取使用原料A 生产的样品22件,测得平均质量为2.36(kg ),样本标准差为0.57(kg ).取使用原料B 生产的样品24件,测得平均质量为2.55(kg ),样本标准差为0.48(kg ).设产品质量服从正态分布,两个样本独立.问能否认为使用原料B 生产的产品质量较使用原料A 显著大(取α = 0.05)?解:设两种原料生产的产品质量分别为),(~211σµN X ,),(~222σµN Y ,假设H 0:µ 1 = µ 2 vs H 1:µ 1 < µ 2 ,未知2221,σσ,大样本,选取统计量)1,0(~2212N n S n SY X U yx&+−=,显著性水平α = 0.05,u 1 − α = u 0.95 = 1.645,左侧拒绝域W ≈ {u ≤ −1.645}, 因36.2=x ,55.2=y ,s x = 0.57,s y = 0.48,n 1 = 22,n 2 = 24, 有W u ∉−=+−=2171.12448.02257.055.236.222,并且检验的p 值p = P {U ≤ −1.2171} = 0.1118 > α = 0.05,故接受H 0,拒绝H 1,即可以认为使用原料B 生产的产品质量较使用原料A 不是显著大.习题7.31. 从一批服从指数分布的产品中抽取10个进行寿命测试,观测值如下(单位:h ): 1643 1629 426 132 1522 432 1759 1074 528 283根据这批数据能否认为其平均寿命不低于1100 h (取α = 0.05)? 解:设这批产品的寿命X ~ Exp (1/θ ),假设H 0:θ = 1100 vs H 1:θ < 1100,选取统计量)2(~222n Xn χθχ=,显著性水平α = 0.05,8508.10)20()2(205.02==χχαn ,左侧拒绝域W = {χ 2 ≤ 10.8508},因8.942=x ,n = 10,θ = 1100,则W ∉=××=1418.1711008.9421022χ,并且检验的p 值p = P {χ 2 ≤ 17.1418} = 0.3563 > α = 0.05,故接受H 0,拒绝H 1,即可以认为其平均寿命不低于1100 h .2. 某厂一种元件平均使用寿命为1200 h ,偏低,现厂里进行技术革新,革新后任选8个元件进行寿命试验,测得寿命数据如下:2686 2001 2082 792 1660 4105 1416 2089假定元件寿命服从指数分布,取α = 0.05,问革新后元件的平均寿命是否有明显提高? 解:设革新后元件的寿命X ~ Exp (1/θ ),假设H 0:θ = 1200 vs H 1:θ > 1200,选取统计量)2(~222n Xn χθχ=,显著性水平α = 0.05,2962.26)16()2(295.021==−χχαn ,右侧拒绝域W = {χ 2 ≥ 26.2962},因875.2103=x ,n = 8,θ = 1200,则W ∈=××=0517.281200875.2103822χ,并且检验的p 值p = P {χ 2 ≥ 28.0517} = 0.0312 < α = 0.05,故拒绝H 0,接受H 1,即可以认为革新后元件的平均寿命有明显提高.3. 有人称某地成年人中大学毕业生比例不低于30%,为检验之,随机调查该地15名成年人,发现有3名大学毕业生,取α = 0.05,问该人看法是否成立?并给出检验的p 值.解:设该地n 名成年人中大学毕业生人数为∑==ni i X X n 1,有),(~p n b X n ,假设H 0:p = 0.3 vs H 1:p < 0.3, 选取统计量),(~p n b X n ,显著性水平α = 0.05,n = 15,p = 0.3, 有1268.07.03.005.00353.07.03.021515101515=⋅⋅<<=⋅⋅∑∑=−=−k k k kk kkkC C ,左侧拒绝域}1{≤=x n W ,因W x n ∉=3,并且检验的p 值2969.07.03.0}3{31515=⋅⋅=≤=∑=−k k k kC X n P p ,故接受H 0,拒绝H 1,即可以认为该人看法成立.4. 某大学随机调查120名男同学,发现有50人非常喜欢看武侠小说,而随机调查的85名女同学中有23人喜欢,用大样本检验方法在α = 0.05下确认:男女同学在喜爱武侠小说方面有无显著差异?并给出检验的p 值. 解:设n 1名男同学中有∑==111n i i X X n 人喜欢看武侠小说,n 2名女同学中有∑==212n j j Y Y n 人喜欢看武侠小说,有),(~111p n B X n ,),(~222p n B Y n ,大样本,有⎟⎟⎠⎞⎜⎜⎝⎛−1111)1(,~n p p p N X &,⎟⎟⎠⎞⎜⎜⎝⎛−2222)1(,~n p p p N Y &, 则⎟⎟⎠⎞⎜⎜⎝⎛−+−−−22211121)1()1(,~n p p n p p p p N Y X &,即)1,0(~)1()1()()(22211121N n p p n p p p p Y X &−+−−−−,当p 1 = p 2 = p 但未知时,此时用总频率2121ˆn n Yn X n p++=作为p 的点估计替换p ,在大样本场合,有)1,0(~11)ˆ1(ˆ21N n n p pY X U &+−−=,假设H 0:p 1 = p 2 vs H 1:p 1 ≠ p 2, 大样本,选取统计量)1,0(~11)ˆ1(ˆ21N n n p pY X U &+−−=,显著性水平α = 0.05,u 1 − α /2 = u 0.975 = 1.96,双侧拒绝域W = {| u | ≥ 1.96},因n 1 = 120,n 2 = 85,501=x n ,232=y n ,有3561.0851202350ˆ2121=++=++=n n y n x n p,则W u ∈=+−×−=1519.28511201)3561.01(3561.0852312050,并且检验的p 值p = 2P {U ≥ 2.1519} = 0.0314 < α = 0.05,故拒绝H 0,接受H 1,可以认为男女同学在喜爱武侠小说方面有显著差异.5. 假定电话总机在单位时间内接到的呼叫次数服从泊松分布,现观测了40个单位时间,接到的呼叫次数如下:0 2 3 2 3 2 1 0 2 2 1 2 2 1 3 1 1 4 1 1 5 1 2 2 3 3 1 3 1 3 4 0 6 1 1 1 4 0 1 3.在显著性水平0.05下能否认为单位时间内平均呼叫次数不低于2.5次?并给出检验的p 值. 解:设电话总机在单位时间内接到的呼叫次数X ~ P(λ),有)(~1λn P X X n ni i ∑==,大样本,有)1,0(~N nX n n X n &λλλλ−=−,假设H 0:λ = 2.5 vs H 1:λ < 2.5, 大样本,选取统计量)1,0(~N nX U &λλ−=, 显著性水平α = 0.05,u 1 − α = u 0.95 = 1.645,左侧拒绝域W = {u ≤ −1.645}, 因975.1=x ,n = 40,λ = 2.5, 则W u ∈−=−=1.2405.25.2975.1,并且检验的p 值p = P {U ≤ −2.1} = 0.0179 < α = 0.05,故拒绝H 0,接受H 1,不能认为单位时间内平均呼叫次数不低于2.5次;6. 通常每平方米某种布上的疵点数服从泊松分布,现观测该种布100 m 2,发现有126个疵点,在显著性水平0.05下能否认为该种布每平方米上平均疵点数不超过1个?并给出检验的p 值. 解:设每平方米该种布上的疵点数X ~ P(λ),有)(~1λn P X X n ni i ∑==,大样本,有)1,0(~N nX n n X n &λλλλ−=−,假设H 0:λ = 1 vs H 1:λ > 1, 大样本,选取统计量)1,0(~N nX U &λλ−=,显著性水平α = 0.05,u 1 − α = u 0.95 = 1.645,右侧拒绝域W = {u ≥ 1.645},因26.1=x ,n = 100,λ = 1, 则W u ∈=−=6.21001126.1,并且检验的p 值p = P {U ≥ 2.6} = 0.0047 < α = 0.05, 故拒绝H 0,接受H 1,不能认为该种布每平方米上平均疵点数不超过1个; 7. 某厂的一批电子产品,其寿命T 服从指数分布,其密度函数为p (t ; θ ) = θ −1exp{− t /θ } I t > 0,从以往生产情况知平均寿命θ = 2000 h .为检验当日生产是否稳定,任取10件产品进行寿命试验,到全部失效时停止.试验得失效寿命数据之和为30200.试在显著性水平α = 0.05下检验假设H 0:θ = 2000 vs H 1:θ ≠ 2000.解:假设H 0:θ = 2000 vs H 1:θ ≠ 2000,选取统计量)2(~222n Xn χθχ=,显著性水平α = 0.05,5908.9)20()2(2025.022/==χχαn ,1696.34)20()2(2975.022/1==−χχαn ,双侧拒绝域W = {χ 2 ≤ 9.5908或χ 2 ≥ 34.1696},因30201030200==x ,n = 10,θ = 2000, 则W ∉=××=20.30200030201022χ,并且检验的p 值p = P {χ 2 ≥ 30.20} = 0.0667 > α = 0.05,故接受H 0,拒绝H 1,即可以认为其平均寿命等于2000 h . 8. 设X 1, X 2, …, X n 为取自两点分布b (1, p )的随机样本.(1)试求单侧假设检验问题H 0:p ≤ 0.01 vs H 1:p > 0.01的显著水平α = 0.05的检验; (2)若要这个检验在p = 0.08时犯第二类错误的概率不超过0.10,样本容量n 应为多大? 解:(1)假设H 0:p = 0.01 vs H 1:p > 0.01,若为小样本,选取统计量),(~1p n b X X n ni i ∑==,显著性水平α = 0.05,p = 0.01,取⎭⎬⎫⎩⎨⎧≥⋅⋅=⎭⎬⎫⎩⎨⎧≤⋅⋅=∑∑−=−=−95.099.001.0min 05.099.001.0min 102c k k n k k n n c k kn k k n C C c ,当n ≤ 5时,c 2 = 1;当6 ≤ n ≤ 35时,c 2 = 2;当36 ≤ n ≤ 82时,c 2 = 3;当83 ≤ n ≤ 137时,c 2 = 4; 右侧拒绝域}{2c x n W ≥=, 根据x n ,作出决策; 若为大样本,选取统计量)1,0(~)1(N np p pX U &−−=,显著性水平α = 0.05,u 1 − α = u 0.95 = 1.645,右侧拒绝域W = {u ≥ 1.645}, 计算u ,作出决策;(2)在p = 0.08时,)08.0,(~1n b X X n ni i ∑==,则犯第二类错误的概率10.092.008.0}08.0|{}08.0|{1022≤⋅⋅==<==∉=∑−=−c k k n k kn C p c X n P p W X n P β,当n ≤ 5时,c 2 = 1,β = 0.92n ≥ 0.6591;当6 ≤ n ≤ 35时,c 2 = 2,2184.092.008.01≥⋅⋅=∑=−k k n k kn C β;当36 ≤ n ≤ 82时,c 2 = 3, 若n = 64,1050.092.008.02=⋅⋅=∑=−k kn kknC β;若n = 65,0991.092.008.02=⋅⋅=∑=−k k n k kn C β;故n ≥ 65.9. 有一批电子产品共50台,产销双方协商同意找出一个检验方案,使得当次品率p ≤ p 0 = 0.04时拒绝的概率不超过0.05,而当p > p 1 = 0.30时,接受的概率不超过0.1,请你帮助找出适当的检验方案. 解:设这批电子产品中的次品数为∑==ni i X X n 1,有),(~p n b X n ,假设H 0:p = 0.04 vs H 1:p > 0.04, 小样本,选取统计量),(~p n b X n , 显著性水平α = 0.05,p = 0.04,。
量子力学周世勋第二版课后习题解答第7章

7.1.证明:i z y x =σσσˆˆˆ 证:由对易关系z x y y x i σσσσσˆ2ˆˆˆˆ=- 及 反对易关系0ˆˆˆˆ=+x y y x σσσσ, 得 z y x i σσσˆˆˆ= 上式两边乘z σˆ,得 2ˆˆˆˆz z y x i σσσσ= ∵ 1ˆ2=z σ ∴ i z y x =σσσˆˆˆ 7.2 求在自旋态)(21z S χ中,xS ˆ和y S ˆ的测不准关系: ?)()(22=y x S S ∆∆解:在z S ˆ表象中)(21z S χ、xS ˆ、y S ˆ的矩阵表示分别为 ⎪⎪⎭⎫ ⎝⎛=01)(21z S χ ⎪⎪⎭⎫ ⎝⎛=01102ˆ x S ⎪⎪⎭⎫ ⎝⎛-=002ˆi i S y ∴ 在)(21z S χ态中00101102)0 1(2121=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛==+ χχx x S S 4010110201102)0 1(ˆ2222121 =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==+χχx x S S4)(2222=-=∆xxx S S S 001002)0 1(ˆ2121=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-==+i i S S y y χχ 401002002)0 1(ˆ2222121 =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-==+i i i i S S y y χχ4)(2222=-=∆yyy S S S 16)()(422=∆∆y x S S讨论:由xS ˆ、y S ˆ的对易关系[x S ˆ,y S ˆ]z S i ˆ = 要求4)()(2222zy x S S S ≥∆∆ 在)(21z S χ态中,2=z S ∴ 16)()(422≥y x S S ∆∆可见①式符合上式的要求。
16)()(422=∆∆y x S S7.3.求⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛=002ˆ01102ˆi i S S y x 及的本征值和所属的本征函数。
机械原理习题册第二版(教材第七版)

题入2机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度,如图2-1(d )所示。
题2-2 图a 所示为一小型压力机。
图上,齿轮1和偏心轮1’为同一构件,绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C 轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
试绘制其机构运动简图,并计算自由度。
解:分析机构的组成:此机构由偏心轮1’(和齿轮1固结)、连杆2、滑杆3、摆杆4、齿轮5、滚子6、滑块7、冲头8和机架9组成。
偏心轮1’和机架9、连杆2和滑杆3、滑杆3和摆杆4、摆杆4和滚子6、齿轮5和机架9、滑块7和冲头8均组成转动副,滑杆3和机架9、摆杆4和滑块7、冲头8和机架9均组成移动副,齿轮1和齿轮5、凸轮(槽)5和滚子6组成高副。
故解法一:7=n 9=l p 2=h p12927323=-⨯-⨯=--=h l p p n F解法二:8=n 10=l p 2=h p 局部自由度1='F11210283)2(3=--⨯-⨯='-'-+-=F p p p n F h l题2-3如图a 所示为一新型偏心轮滑阀式真空泵。
其偏心轮1绕固定轴A 转动,和外环2固连在一起的滑阀3在可绕固定轴心C 转动的圆柱4中滑动。
当偏题2-4心轮1按图示方向连续转动时,可将设备中的空气按图示空气流动方向从阀5中排出,从而形成真空。
由于外环2和泵腔6有一小间隙,故可抽含有微小尘埃的气体。
试绘制其机构的运动简图,并计算其自由度。
解:1)取比例尺,绘制机构运动简图。
(如图题2-3所示)ABC1234题2-32) 3=n 4=l p 0=h p10423323=-⨯-⨯=--=h l p p n F题2-4 使绘制图a 所示仿人手型机械手的食指机构的机构运动简图(以手指8作为相对固定的机架),并计算其自由度。
现代大学英语第二版精读2 unit7 答案

• 3 Explain the sentences in your own words. (5%) • b) In the past Millet would have been willing to sell it for the amount of money by which he could get to buy a pork chop. • c) The sentence implies that the picture was worth far more than eighty thousand francs now. • d) 3.1 am glad that Millet is still alive. He was the only talented artist who has not died of hunger. This implies many talented artists have died of hunger simply because they weren't able to sell their works.
II. Word-Formation (10%) 1. qualifications 2. intelligence 3. fact-finding 4. historic 5. inseparable 6 breadwinner 7 superhighway 8 takeoff 9 delivering 10, hardware, software
• 8. Still, there was nothing very special in any of it, except death, which, while always special, does not necessarily bring the nation to tears or to attention. • 9. That somebody actually did so is part of the reason this particular tragedy sticks in the mind. • 10. So, when it was time to return to our home outside of Philadelphia, I insisted that we take a different route.
全新版大学英语(第二版)unit7课后答案

unit 7课后习题参考答案Unit 7 TextAVocabulary: 第210页1. divined2. nerves3. solidarity4. sacred; mourn5. coated6. perish7. hijack 8. grief 9. farewell10. take revenge on 11. revolves 12. denounced2) 第211页1. drop… off2. applied for3. went off4. are gaining on5. bring down6. blotted out7. think back on 8. picking at第212页1. brought down the American housing market in 20082. what will happen after his son steps into his shoes?3. not in the mood to go out4. long before the market began to show signs of weakness5. mourn the loss of the tranquil life we had in the countryside4) 1. in the aftermath of; to blot our; the tragic2. armed; at dust; accomplices; explosives3. in the space of; no illusion第213页II. Collocation:1. a little of2. a few; most of // many of3. much4. few5. many6. many of7. much of8. little9. few of10. Someage: 第215页1. As the boy grew older2. she sings as beautifully as a nightingale // sings like a nightingale3. they don’t see themselves as servants of the people4. As she had left her key in the office5. Just do as you are told6. Areas once regarded as rural7. as they do in China8. As he was brave and loyal as wellComprehensive Exercises:I. Cloze 第216页1) Text-related1. mood2. tragic3. in the (immediate) aftermath of4. chaos5. toppling6. solidarity7. take revenge on8. thinking back on9. mourning10. perished2) Theme-related 第217页1. crashed2. horrible3. harsh4. protect5. remove6. utterly7. truly8. justify9. rewarded10.devastatingII. Translation1)1. Some high-ranking officers of the armed forces started a coup, toppling the government and throwing the country into chaos.2. The falling market shattered the illusion about getting rich quickly3. Thinking back on the history of World War II, we can see that the formation of the Allies was the natural product of the development of political and military circumstances then.4. Paul felt stung when Jim called him a religious fanatic. But as he was in no mood for q quarrel//not in a quarreling mood, he simply pretended not to hear it.5. People say that time heals all wounds. But for those who have lost their loved ones in the event, will time fill up the void in their hearts?2) 第218页Today, long after the earthquake shook // hit my tome-town, I can still recall, in crystal detail, what I saw as I ran out of my home with my parents. The building just across the street toppled right before our eyes, debris flew everywhere and a cloud of choking dust blotted out the sun. Horror-stricken people ran in all directions, crying and screaming.Now, many years after that tragic event, a new town has risen on the wreckage of the old one. In the town square, a memorial has been build to remember those killed in the disaster. Itseems the wounds in people’s hearts have healed, but the memory will linger。
金融英语_刘文国第二版课后练习Exercises07

金融英语_刘文国第二版课后练习Exercises07Answers for Chapter sevenⅠ Answer the following questions in English:1.What is mean about debt financing?Debt financing means borrowing money that is to be repaid over a period of time, usually with interest. Debt financing can be either short-term (full repayment due in less than one year) or long-term (repayment over more than one year).2.What is equity financing?Equity financing describes an exchange of money for a share of business ownership. This form of financing allows you to obtain funds without incurring debt; in other words, without having to repay a specific amount of money at any particular time.3.Why does a company’s organizational form influence people who willbe to invest company’s business?The specific types of equity financing available to a company, to some extent, determined by the organizational form of the company because business forms involve a wide spectrum of other important issues such as the need to attract good business managers, tax considerations and the degree of personal risk.4.How many advantages for a partnership?There are three advantages for a partnership as the following: Inexpensive and simple to form and maintainFavorable tax treatmentSharing of expertise and risk5.How many disadvantages for a partnership?There are three advantages for a partnership as the following: Personal liabilityLimited transferability of ownershipLimited financing options6.What is the major disadvantage to equity financing?The major disadvantage to equity financing is the dilution of your ownership interests and the possible loss of control that mayaccompany a sharing of ownership with additional investors.7.Why does some one say debt financing is attractive?Debt financing is attractive because you do not have to sacrifice any ownership interests in your business, interest on the loan is deductible, and the financing cost is a relatively fixed expense. 8.What are the disadvantages of an LLC?The disadvantages of an LLC are the statutory formalities that must be followed and the expenses that accompany compliance with thoseformalities, as well as several unresolved legal and tax issues (e.g., multi-state transactions, whether single-member LLC are allowed, and conflicts between state LLC laws).Ⅱ Fill in the each blank with an appropriate word or expression:1.Equity financing describes an exchange of money for a share ofbusiness ownership. This form of financing allows you to obtain funds without incurring debt; in other words, without having to repay a specific amount of money at any particular time.2.Financing is categorized into two fundamental types: debt financingand equity financing.3.The effect of selling a large percentage of the ownership interestin your business may mean that your own investment will be short-term, unless you retain a majority interest in the business and control over future sale of the business.4.The business enters into a kind of contract with the state (called acorporate charter) in which the business agrees to abide by thegoverning state regulations, in return for the state's agreeing to treat the business as a separate legal entity for legal liability and tax purposes.5. A limited partnership is a partnership that requires only onepartner to assume personal liability for the business's liabilities (the general partner).6.The business must have at least one general partner who isresponsible for overseeing operations and for making daily management decisions.Ⅲ Translate the following sentences and passage into English:1.企业融资是指企业在发展扩张中筹集所需资金的行为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(d) 一旦声明虚继承,基类的性质就改变了,不能再定义新的派生类
7.2 阅读下列程序,写出执行结果
1.#include <iostream.h>
class Base
{ public:
void get( int i,int j,int k,int l )
(c) 在基类定义的静态成员在私有继承的派生类中可见
(d) 访问声明可以在公有继承派生类中把基类的public成员声明为private成员
8.在c++中,可以被派生类继承的函数是(a)。
(a) 成员函数(b)构造函数(c) 析构函数(d)友员函数
9.在创建派生类对象时,构造函数的执行顺序是(d)。
(a) 对象成员构造函数、基类构造函数、派生类本身的构造函数
第
习题7
7.1 选择题
1.在c++中,类之间的继承关系具有( c )。
(a) 自反性 (b) 对称性 (c) 传递性 (d) 反对称性
2.下列关于类的继承描述中,(d)是正确的。
(a) 派生类公有继承基类时,可以访问基类的所有数据成员,调用所有成员函数
(b) 派生类也是基类,所以它们是等价的
(c) 派生类对象不会建立基类的私有数据成员,所以不能访问基类的私有数据成员
class Base1
{ public:
Base1( int i ) { cout << "调用基类Base1的构造函数:" << i << endl ; }
};
class Base2
{ public:
Base2( int j ) { cout << "调用基类Base2的构造函数:" << j << endl ; }
u = a + b + obj3.a ; v = y - x + obj3.b;
}
void print()
{ cout << "a = " << a << '\t' << "b = " << b << '\t'
<< "x = " << x << '\t' << "y = " << y << endl;
};
class A: public Base1, public Base2
{ public:
A( int a, int b, int c, int d ) : Base2(b), Base1(c), b2(a), b1(d)
{ cout << "调用派生类A的构造函数:" << a+b+c+d << endl; }
{ a = i; b = j; x = k; y = l; }
void print()
{ cout << "a = "<< a << '\t' << "b = " << b << '\t'
<< "x = " << x << '\t' << "y = " << y << endl;
}
int a,b;
protected:
(a) public 成员(b)private成员
(c) protected成员(d)public 成员和protected成员
7.下面描述中,错误的是(d)。
(a) 在基类定义的public成员在公有继承的派生类中可见,也能在类外被访问
(b) 在基类定义的protected成员在私有继承的派生类中可见
private:
Base1 b1;
Base2 b2;
} ;
void main()
{ A obj( 1, 2, 3, 4 ); }
【答案】
调用基类BASE1的构造函数:3
调用基类BASE2的构造函数:2
调用基类BASE1的构造函数:4
调用基类BASE2构造函数:1
调用派生类A的构造函数:10
3. #include <iostream.h>
(b) 派生类本身的构造函数、基类构造函数、对象成员构造函数
(c) 基类构造函数、派生类本身的构造函数、对象成员构造函数
(d) 基类构造函数、对象成员构造函数、派生类本身的构造函数
10.当不同的类具有相同的间接基类时,有特点(c)。
(a) 各派生类对无法按继承路线产生自己的基类版本
(b) 为了建立惟一的间接基类版本,应该声明间接基类为虚类
cout << "u = " << u << '\t' << "v = " << v << endl;
}
private:
int u, v ;
};
void main()
{ Base obj1;
A obj2;
obj1.get( 10, 20, 30, 40 );
obj2.get( 30, 40, 50, 60 );
(a) public.当一个派生类保护继承一个基类时,基类中的所有公有成员和保护成员成为派生类的(c)。
(a) public成员(b)private成员(c) protected成员(d)友员
6.不论派生类以何种方式继承基类,都不能直接使用基类的(b)。
obj1.print();
obj2.print();
}
【答案】
a = 50 b = 60 x = 70 y = 80
a = 10 b = 20 x = 30 y = 40
a = 30 b = 40 x = 50 y = 60
u = 120 v = 70
2. #include <iostream.h>
int x, y;
};
class A: public Base
{ public:
void get( int i, int j, int k, int l )
{ Base obj3;
obj3.get( 50, 60, 70, 80 );
obj3.print();
a = i; b = j; x = k; y = l;
(d) 一个基类可以有多个派生类,一个派生类可以有多个基类
3.当一个派生类公有继承一个基类时,基类中的所有公有成员成为派生类的(a)。
(a) public成员(b)private成员(c) protected成员(d)友员
4.当一个派生类私有继承一个基类时,基类中的所有公有成员和保护成员成为派生类的(b)。
class A
{ public:
A(int i, int j) {a=i; b=j ;}
void Add(int x, int y) { a+=x; b+=y;}
