常用分数小数转化表
小数百分数分数必背转化

5
0.6 3
50Βιβλιοθήκη 8 450.2 1
5
小数 分数
分数 百分数
1 4
=25%
1
2 =50%
3
4 =75%
1 =12.5%
8 5
8 =62.5%
7
8 =87.5%
3.14 2 3.14 4 3.14 6 3.148
3.14 3 3.14 5 3.14 7 3.14 9
路程=速度×时间
时间= 路程÷速度 速度= 路程÷时间
三小时走了六千米,一小时走多少?
照这样走下去,五小时走多少千米?走一千米需要多少小时?
45 一辆汽车每小时走 2 千米,4小时行驶了路 程的一半,全程多少千米?
工作总量=工作效率×工作时间
工作时间= 工作总量÷工作效率 工作效率= 工作总量÷工作时间
磨面机4小时磨面8吨,每小时磨面多少吨?
磨1吨需要多长时间?
磨面机 5 小时磨面 45 吨,每小时磨面多少吨?
2
2
磨1吨需要多长时间?
正方体和长方体的表面积相同,体积相同吗? 正方体和长方体的体积相同,表面积相同吗?
常用分数小数互化表快速记忆

常用分数小数互化的快速记忆方法:
1.分数化小数:分子除以分母。
例如,要将分数2/3转化为小数,可
以执行2÷3=0.667。
2.小数化分数:首先确定小数的小数点位置,然后将小数点两边的
数字进行四舍五入得到最接近的整数,最后将整数作为分母并执行相应的除法运算。
例如,要将小数0.42转化为分数,可以确定小数点后两位为42,然后四舍五入得到40,最后执行40÷100=1/25。
3.特殊值记忆:例如,1/2=0.5,1/3≈0.333,2/3≈0.667,1/4=0.25,
3/4=0.75,1/5=0.2,2/5=0.4,3/5=0.6,4/5=0.8,1/6≈0.167,5/6≈0.833,等等。
4.分数和小数比较大小:需要将分数和小数都转化为同一类型的数
据形式进行比较。
例如,要将分数a/b和小数c进行比较,可以先将分数a/b转化为小数形式,然后再与小数c进行比较。
常用分数、小数互化表

常用分数、小数互化表在数学的学习和应用中,分数和小数的互化是一项非常基础且重要的技能。
无论是在日常生活中的购物计算、工程建设中的数据测量,还是在学术研究中的数据分析,都离不开分数和小数的相互转换。
为了帮助大家更好地掌握这一技能,下面为大家整理了一份常用分数、小数互化表。
一、常见分数化为小数1、 1/2 = 05把一个整体平均分成两份,其中的一份就是 1/2,也就是 05。
2、 1/4 = 025将一个整体平均分成四份,每份就是 1/4,化为小数为 025。
3、 3/4 = 075三份占四份的比例就是 3/4,转化为小数是 075。
4、 1/5 = 02把一个整体平均分成五份,一份就是 1/5,等于 02。
5、 2/5 = 04两份占五份的比例是 2/5,化为小数为 04。
三份占五份的比例是 3/5,等于 06。
7、 4/5 = 08四份占五份的比例是 4/5,转化为小数是 08。
8、 1/8 = 0125平均分成八份,一份就是 1/8,小数表示为 0125。
9、 3/8 = 0375三份占八份的比例是 3/8,等于 0375。
10、 5/8 = 0625五份占八份的比例是 5/8,转化为小数是 0625。
11、 7/8 = 0875七份占八份的比例是 7/8,小数表示为 0875。
二、常见小数化为分数1、 025 = 1/4025 可以理解为 25 个 001,也就是 25/100,约分后得到 1/4。
2、 05 = 1/205 表示一半,即 1/2。
075 可以写成 75/100,约分后为 3/4。
4、 02 = 1/502 相当于 2/10,约分得到 1/5。
5、 04 = 2/504 可以写成 4/10,约分后是 2/5。
6、 06 = 3/506 就是 6/10,约分得到 3/5。
7、 08 = 4/508 等于 8/10,约分后为 4/5。
8、 0125 = 1/80125 是 125/1000,约分可得 1/8。
常用分数、小数、百分数之间的互化
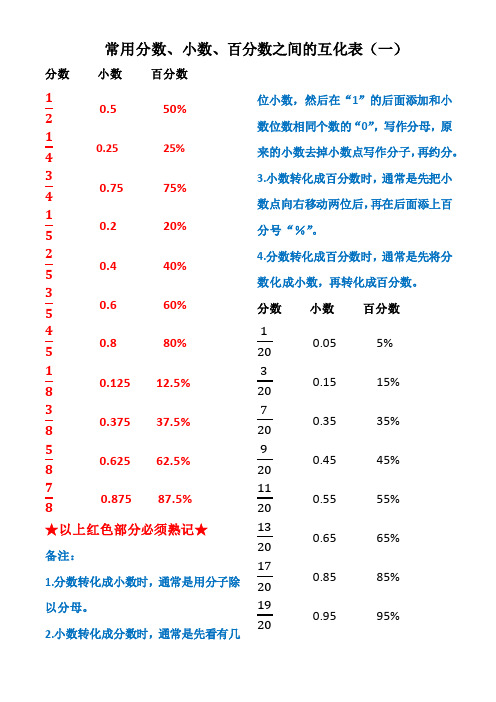
分数小数百分数120.5 50%140.25 25%340.75 75%150.2 20%250.4 40%350.6 60%450.8 80%180.125 12.5%380.375 37.5%580.625 62.5%780.875 87.5%★以上红色部分必须熟记★备注:1.分数转化成小数时,通常是用分子除以分母。
2.小数转化成分数时,通常是先看有几位小数,然后在“1”的后面添加和小数位数相同个数的“0”,写作分母,原来的小数去掉小数点写作分子,再约分。
3.小数转化成百分数时,通常是先把小数点向右移动两位后,再在后面添上百分号“%”。
4.分数转化成百分数时,通常是先将分数化成小数,再转化成百分数。
分数小数百分数1200.05 5%3200.15 15%7200.35 35%9200.45 45%11200.55 55%13200.65 65%17200.85 85%19200.95 95%分数小数百分数分数小数百分数1250.04 4%2250.08 8%3250.12 12%4250.16 16%6250.24 24%7250.28 28%8250.32 32%9250.36 36%11250.44 44%12 250.48 48%13250.52 52%14250.56 56%16250.64 64%17250.68 68%18250.72 72%19250.76 76%21250.84 84%22250.88 88%23250.92 92%24250.96 96%备注:1. 分母为20的分数转化成小数,先用分子乘以“5”,再把所得的积的小数点向左移动两位即可。
2. 分母为25的分数转化成小数,先用分子乘以“4”,再把所得的积的小数点向左移动两位即可。
常用小数分数互化表

常用小数分数互化表小数和分数是数学中常见的表示数值的方式,它们之间的转化是数学中的基本操作。
为了方便学生学习和记忆,我们可以整理出一张常用小数分数互化表,方便大家查阅和使用。
一、小数转分数小数转分数的方法主要有两种,一种是根据小数的位数进行转化,另一种是根据小数的循环部分进行转化。
1. 根据小数的位数转化当小数只有一位小数位时,可以将小数位上的数字作为分子,分母为10,即可得到对应的分数。
例如:0.3可以转化为3/10。
当小数有两位小数位时,可以将小数位上的数字作为分子,分母为100,即可得到对应的分数。
例如:0.25可以转化为25/100,进一步化简为1/4。
依此类推,可得到其他小数对应的分数。
2. 根据小数的循环部分转化当小数有循环部分时,可以利用无穷等差数列的求和公式进行转化。
例如:0.3333...可以表示为0.3+(0.03/10)+(0.003/100)+...,通过求和可以得到1/3。
二、分数转小数分数转小数的方法主要有两种,一种是进行长除法运算,另一种是利用分数的性质和小数的定义进行转化。
1. 长除法运算将分子除以分母,得到的商即为对应的小数。
例如:2/5可以通过长除法运算得到0.4。
2. 分数的性质和小数的定义分数可以表示为分子除以分母的形式,而小数可以表示为有限小数和无限循环小数的形式。
根据小数的定义,有限小数可以通过除法得到有限小数,而无限循环小数可以通过除法得到无限循环小数。
例如:1/2可以通过除法运算得到0.5,而1/3可以通过除法运算得到0.3333...。
三、常用小数分数互化表下面是一个常用小数分数互化表,方便大家查阅和使用:小数分数0.1 1/100.2 1/50.25 1/40.3 3/100.4 2/50.5 1/20.6 3/50.75 3/40.8 4/50.9 9/10通过这张小数分数互化表,我们可以快速准确地进行小数和分数之间的转化,提高我们的计算效率和准确性。
常见分数小数互化必背表

常见分数小数互化必背表(原创版)目录1.分数与小数的关系2.常见分数小数互化表的作用3.如何记忆和应用常见分数小数互化表正文一、分数与小数的关系分数和小数是数学中常见的两种数制表示方式。
它们有着密切的关系,可以相互转化。
分数的分子相当于小数的整数部分,分母相当于小数的小数点后的位数。
例如,分数 1/2 可以转化为小数 0.5,分数 3/4 可以转化为小数 0.75。
二、常见分数小数互化表的作用为了方便人们快速地进行分数与小数的互化,有人整理了一份常见分数小数互化表。
这份表以分数的形式列出了 1 到 100 的所有数字,同时也以小数的形式呈现了它们。
这样,当我们需要将一个分数转化为小数时,只需查找对应的分数,就可以直接得到小数结果。
同样地,当我们需要将一个小数转化为分数时,也可以通过查找对应的小数得到分数结果。
三、如何记忆和应用常见分数小数互化表要熟练地运用常见分数小数互化表,首先需要记住表中的数字。
以下是一些建议,可以帮助你更好地记忆:1.观察规律:仔细观察表格,你会发现,分母为 10 的分数对应的小数是一位数,分母为 100 的分数对应的小数是两位数。
这样的规律还有许多,你可以尝试找出更多的规律,以帮助你记忆。
2.制作卡片:将表格中的数据制作成卡片,一面写分数,另一面写小数。
通过不断地翻阅和记忆,可以提高对表格的熟悉度。
3.实际应用:在日常生活和学习中,尽量使用分数和小数互化的知识。
例如,在做数学题时,可以尝试用不同的方法将分数转化为小数,或者将小数转化为分数。
这样可以加深对知识的理解,提高运用能力。
总之,掌握常见分数小数互化表对我们的学习和生活都有很大帮助。
小数化分数表

小数化分数表小数化和分数的转换规律如下:小数点后有几位数字,就在1后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分。
例如,将0.2转化为分数,因为小数点后有1位数字,所以将分子2乘以10的1次方,得到2/10,即0.2转化为分数为1/5。
用分子去除分母,能除尽的就化成有限小数,有的不能除尽,不能化成有限小数的,一般保留三位小数。
例如,将0.3转化为分数,因为0.3可以表示为3/10,所以0.3可以转化为分数3/10。
一个最简分数,如果分母中除了2和5以外,不含有其他的质因数,这个分数就能化成有限小数;如果分母中含有2和5以外的质因数,这个分数就不能化成有限小数。
例如,将1/6转化为小数时,因为分母中含有质因数3,所以不能化成有限小数。
小数点向右移动两位,同时在后面添上百分号。
例如,将0.5转化为百分数时,可以将0.5的小数点向右移动两位得到50,然后添上百分号得到50%,即0.5转化为百分数为50%。
百分数化成小数时,只要把百分号去掉,同时把小数点向左移动两位。
例如,将50%转化为小数时,将百分号去掉得到50,然后将小数点向左移动两位得到0.5,即50%转化为小数为0.5。
分数化成百分数时,通常先把分数化成小数(除不尽时,通常保留三位小数),再把小数化成百分数。
例如,将1/4转化为百分数时,先将1/4转化为小数0.25,然后将小数点向右移动两位并添上百分号得到25%,即1/4转化为百分数为25%。
百分数化成分数时,先把百分数改写成分数形式(能约分的要约成最简分数)。
例如,将25%转化为分数时,先将25%改写成分数形式为1/4,然后进行约分得到最简分数1/4。
将小数或分数转换为十进制数时,应使用基数10或100(或更高)来乘以相应的幂。
例如,将0.7转化为十进制数时,可以将0.7乘以10得到7,即0.7转化为十进制数为0.7。
将二进制数转换为十进制数时,可以使用权值法来计算每一位的值,然后将它们相加得到最终的十进制数。
