带电粒子在磁场中的运动习题含答案
高中物理带电粒子在磁场中的运动试题(有答案和解析)及解析

高中物理带电粒子在磁场中的运动试题(有答案和解析)及解析一、带电粒子在磁场中的运动专项训练1.如图所示,在平面直角坐标系xOy 的第二、第三象限内有一垂直纸面向里、磁感应强度为B 的匀强磁场区域△ABC ,A 点坐标为(0,3a ),C 点坐标为(0,﹣3a ),B 点坐标为(23a -,-3a ).在直角坐标系xOy 的第一象限内,加上方向沿y 轴正方向、场强大小为E=Bv 0的匀强电场,在x=3a 处垂直于x 轴放置一平面荧光屏,其与x 轴的交点为Q .粒子束以相同的速度v 0由O 、C 间的各位置垂直y 轴射入,已知从y 轴上y =﹣2a 的点射入磁场的粒子在磁场中的轨迹恰好经过O 点.忽略粒子间的相互作用,不计粒子的重力. (1)求粒子的比荷;(2)求粒子束射入电场的纵坐标范围;(3)从什么位置射入磁场的粒子打到荧光屏上距Q 点最远?求出最远距离.【答案】(1)0v Ba(2)0≤y≤2a (3)78y a =,94a【解析】 【详解】(1)由题意可知, 粒子在磁场中的轨迹半径为r =a 由牛顿第二定律得Bqv 0=m 2v r故粒子的比荷v q m Ba= (2)能进入电场中且离O 点上方最远的粒子在磁场中的运动轨迹恰好与AB 边相切,设粒子运动轨迹的圆心为O ′点,如图所示.由几何关系知O ′A =r ·ABBC=2a 则OO ′=OA -O ′A =a即粒子离开磁场进入电场时,离O 点上方最远距离为OD =y m =2a所以粒子束从y 轴射入电场的范围为0≤y ≤2a (3)假设粒子没有射出电场就打到荧光屏上,有3a =v 0·t 02019222qE y t a a m ==>, 所以,粒子应射出电场后打到荧光屏上粒子在电场中做类平抛运动,设粒子在电场中的运动时间为t ,竖直方向位移为y ,水平方向位移为x ,则 水平方向有x =v 0·t竖直方向有212qE y t m=代入数据得x设粒子最终打在荧光屏上的点距Q 点为H ,粒子射出电场时与x 轴的夹角为θ,则00tan y x qE x v m v v v θ⋅===有H =(3a -x )·tan θ=当=y =98a 时,H 有最大值 由于98a <2a ,所以H 的最大值H max =94a ,粒子射入磁场的位置为y =98a -2a =-78a2.如图所示,一匀强磁场磁感应强度为B ;方向向里,其边界是半径为R 的圆,AB 为圆的一直径.在A 点有一粒子源向圆平面内的各个方向发射质量m 、电量-q 的粒子,粒子重力不计.(1)有一带电粒子以的速度垂直磁场进入圆形区域,恰从B点射出.求此粒子在磁场中运动的时间.(2)若磁场的边界是绝缘弹性边界(粒子与边界碰撞后将以原速率反弹),某粒子沿半径方向射入磁场,经过2次碰撞后回到A点,则该粒子的速度为多大?(3)若R=3cm、B=0.2T,在A点的粒子源向圆平面内的各个方向发射速度均为3×105m/s、比荷为108C/kg的粒子.试用阴影图画出粒子在磁场中能到达的区域,并求出该区域的面积(结果保留2位有效数字).【答案】(1)(2)(3)【解析】【分析】(1)根据洛伦兹力提供向心力,求出粒子的半径,通过几何关系得出圆弧所对应的圆心角,根据周期公式,结合t=T求出粒子在磁场中运动的时间.(2)粒子径向射入磁场,必定径向反弹,作出粒子的轨迹图,通过几何关系求出粒子的半径,从而通过半径公式求出粒子的速度.(3)根据粒子的半径公式求出粒子的轨道半径,作出粒子轨迹所能到达的部分,根据几何关系求出面积.【详解】(1)由得r1=2R粒子的运动轨迹如图所示,则α=因为周期.运动时间.(2)粒子运动情况如图所示,β=. r 2=R tanβ=R 由得(3)粒子的轨道半径r 3==1.5cm粒子到达的区域为图中的阴影部分区域面积为S=πr 32+2×π(2r 3)2−r 32=9.0×10-4m 2【点睛】本题考查了带电粒子在磁场中的运动问题,需掌握粒子的半径公式和周期公式,并能画出粒子运动的轨迹图,结合几何关系求解.该题对数学几何能力要求较高,需加强这方面的训练.3.如图所示,在两块长为3L 、间距为L 、水平固定的平行金属板之间,存在方向垂直纸面向外的匀强磁场.现将下板接地,让质量为m 、电荷量为q 的带正电粒子流从两板左端连线的中点O 以初速度v 0水平向右射入板间,粒子恰好打到下板的中点.若撤去平行板间的磁场,使上板的电势φ随时间t 的变化规律如图所示,则t=0时刻,从O 点射人的粒子P 经时间t 0(未知量)恰好从下板右边缘射出.设粒子打到板上均被板吸收,粒子的重力及粒子间的作用力均不计.(1)求两板间磁场的磁感应强度大小B .(2)若两板右侧存在一定宽度的、方向垂直纸面向里的匀强磁场,为了使t=0时刻射入的粒子P 经过右侧磁场偏转后在电场变化的第一个周期内能够回到O 点,求右侧磁场的宽度d 应满足的条件和电场周期T 的最小值T min . 【答案】(1)0mv B qL = (2)223cos d R a R L ≥+= ;min 0(632)3L T v π= 【解析】 【分析】【详解】(1)如图,设粒子在两板间做匀速圆周运动的半径为R 1,则012qv B m v R =由几何关系:222113()()2L L R R =+- 解得0mv B qL=(2)粒子P 从O 003L v t =01122y L v t = 解得03y v =设合速度为v ,与竖直方向的夹角为α,则:0tan 3yv v α== 则=3πα0023sin v v α== 粒子P 在两板的右侧匀强磁场中做匀速圆周运动,设做圆周运动的半径为R 2,则212sin L R α=, 解得23L R =右侧磁场沿初速度方向的宽度应该满足的条件为223cos d R R L α≥+=; 由于粒子P 从O 点运动到下极板右侧边缘的过程与从上板右边缘运动到O 点的过程,运动轨迹是关于两板间的中心线是上下对称的,这两个过程经历的时间相等,则:2min 0(22)2R T t vπα--=解得() min6323L Tvπ+=【点睛】带电粒子在电场或磁场中的运动问题,关键是分析粒子的受力情况和运动特征,画出粒子的运动轨迹图,结合几何关系求解相关量,并搞清临界状态.4.如图,圆心为O、半径为r 的圆形区域外存在匀强磁场,磁场方向垂直于纸面向外,磁感应强度大小为B。
带电粒子在匀强磁场中的运动练习题及答案解析

1.电子在匀强磁场中做匀速圆周运动.下列说法正确的是( ) A .速率越大,周期越大 B .速率越小,周期越大 C .速度方向与磁场方向平行 D .速度方向与磁场方向垂直解析:选D.由带电粒子在匀强磁场中做匀速圆周运动的周期公式T =2πmqB可知T 与v 无关,故A 、B 均错;当v 与B 平行时,粒子不受洛伦兹力作用,故粒子不可能做圆周运动,只有v ⊥B 时,粒子才受到与v 和B 都垂直的洛伦兹力,故C 错、D 对.2.(2011年厦门高二检测)1998年发射的“月球勘探者号”空间探测器,运用最新科技手段对月球进行近距离勘探,在研究月球磁场分布方面取得了新的成果.月球上的磁场极其微弱,探测器通过测量电子在月球磁场中的轨迹来推算磁场强弱的分布,图3-6-19中是探测器通过月球A 、B 、C 、D 四个位置时,电子运动的轨迹照片.设电子速率相同,且与磁场方向垂直,其中磁场最强的位置是( )图3-6-19解析:选A.由粒子轨道半径公式r =mvqB可知,磁场越强的地方,电子运动的轨道半径越小. 3.图3-6-20如图3-6-20所示,a 和b 带电荷量相同,以相同动能从A 点射入磁场,在匀强磁场中做圆周运动的半径r a =2r b ,则可知(重力不计)( ) A .两粒子都带正电,质量比m a /m b =4 B .两粒子都带负电,质量比m a /m b =4 C .两粒子都带正电,质量比m a /m b =1/4D.两粒子都带负电,质量比m a/m b=1/4解析:选B.由于q a=q b、E k a=E k b,动能E k=12mv2和粒子旋转半径r=mvqB,可得m=r2q2B22E k,可见m与半径r的平方成正比,故m a∶m b=4∶1,再根据左手定则判知粒子应带负电,故B 正确.4.(2009年高考广东单科卷)图3-6-21是质谱议的工作原理示意图.带电粒子被加速电场加速后,进入速度选择器.速度选择器内相互正交的匀强磁场和匀强电场的强度分别为B和E.平板S上有可让粒子通过的狭缝P和记录粒子位置的胶片A1A2.平板S下方有强度为B0的匀强磁场.下列表述正确的是( )图3-6-21A.质谱仪是分析同位素的重要工具B.速度选择器中的磁场方向垂直纸面向外C.能通过狭缝P的带电粒子的速率等于E/BD.粒子打在胶片上的位置越靠近狭缝P,粒子的荷质比越小解析:选ABC.因同位素原子的化学性质完全相同,无法用化学方法进行分析,故质谱仪就成为同位素分析的重要工具,A正确.在速度选择器中,带电粒子所受电场力和洛伦兹力在粒子沿直线运动时应等大反向,结合左手定则可知B正确.再由qE=qvB有v=E/B,C正确.在匀强磁场B0中R=mvqB,所以qm=vBR,D错误.5.图3-6-22如图3-6-22所示,在x轴上方有匀强电场,场强为E,在x轴下方有匀强磁场,磁感应强度为B,方向如图所示.在x轴上有一点M,离O点距离为L,现有一带电荷量为+q、质量为m 的粒子,从静止开始释放后能经过M 点,如果此粒子放在y 轴上,其坐标应满足什么关系(重力不计) 解析:由于此粒子从静止开始释放,又不计重力,要能经过M 点,其起始位置只能在匀强电场区域,其具体过程如下:先在电场中由y 轴向下做加速运动,进入匀强磁场中运动半个圆周再进入电场做减速运动,速度为零后又回头进入磁场,其轨迹如图所示(没有画出电场和磁场方向),故有:L =2nR (n =1,2,3,…)①又因在电场中,粒子进入磁场时的速度为v , 则有:qE ·y =12mv 2②在磁场中,又有:Bqv =mv 2R③由①②③得y =B 2qL 28n 2mE(n =1,2,3……).答案:见解析一、选择题1.(2011年杭州十四中高二检测)一个带电粒子以初速度v 0垂直于电场方向向右射入匀强电场区域,穿出电场后接着又进入匀强磁场区域.设电场和磁场区域有明确的分界线,且分界线与电场强度方向平行,如图3-6-23中的虚线所示.在下图所示的几种情况中,可能出现的是( )图3-6-23解析:选、C 选项中粒子在电场中向下偏转,所以粒子带正电,再进入磁场后,A 图中粒子应逆时针转,正确;C 图中粒子应顺时针转,错误.同理可以判断B 错、D 对. 2.如图3-6-24所示,一电子以与磁场方向垂图3-6-24直的速度v 从P 处沿PQ 方向进入长为d 、宽为h 的匀强磁场区域,从N 处离开磁场,若电子质量为m ,带电荷量为e ,磁感应强度为B ,则( ) A .电子在磁场中运动的时间t =d /v B .电子在磁场中运动的时间t =h /v C .洛伦兹力对电子做的功为Bevh D .电子在N 处的速度大小也是v解析:选D.洛伦兹力不做功,所以电子在N 处速度大小也为v ,D 正确、C 错,电子在磁场中的运动时间t =弧长v ≠d v ≠hv,A 、B 均错.3.图3-6-25在图3-6-25中,水平导线中有电流I 通过,导线正下方的电子初速度的方向与电流I 的方向相同,则电子将( ) A .沿路径a 运动,轨迹是圆 B .沿路径a 运动,轨迹半径越来越大 C .沿路径a 运动,轨迹半径越来越小 D .沿路径b 运动,轨迹半径越来越小解析:选B.电流下方的磁场方向垂直纸面向外,且越向下B 越小,由左手定则知电子沿a 路径运动,由r =mvqB知,轨迹半径越来越大.4.图3-6-26一个带电粒子沿垂直于磁场的方向射入一匀强磁场.粒子的一段径迹如图3-6-26所示.径迹上的每一小段都可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(带电量不变).从图中情况可以确定( ) A .粒子从a 到b ,带正电 B .粒子从a 到b ,带负电 C .粒子从b 到a ,带正电 D .粒子从b 到a ,带负电解析:选C.垂直于磁场方向射入匀强磁场的带电粒子受洛伦兹力作用,使粒子做匀速圆周运动,半径R =mv /qB .由于带电粒子使沿途的空气电离,粒子的能量减小,磁感应强度B 、带电荷量不变.又据E k =12mv 2知,v 在减小,故R 减小,可判定粒子从b 向a 运动;另据左手定则,可判定粒子带正电,C 选项正确. 5.如图3-6-27是图3-6-27某离子速度选择器的原理示意图,在一半径R =10 cm 的圆柱形筒内有B =1×10-4T 的匀强磁场,方向平行于轴线.在圆柱形筒上某一直径两端开有小孔a 、b 分别作为入射孔和出射孔.现有一束比荷为qm=2×1011C/kg 的正离子,以不同角度α入射,最后有不同速度的离子束射出.其中入射角α=30°,且不经碰撞而直接从出射孔射出的离子的速度v 大小是( )A .4×105m/s B .2×105m/s C .4×106 m/s D .2×106m/s答案:C 6.图3-6-28如图3-6-28所示,有界匀强磁场边界线SP ∥MN ,速率不同的同种带电粒子从S 点沿SP方向同时射入磁场.其中穿过a点的粒子速度v1与MN垂直;穿过b点的粒子速度v2与MN成60°角,设二粒子从S到a、b所需时间分别为t1和t2,则t1∶t2为(重力不计)( ) A.1∶3 B.4∶3C.1∶1 D.3∶2解析:选D.如图所示,可求出从a点射出的粒子对应的圆心角为90°.从b点射出的粒子对应的圆心角为60°.由t=α2πT,可得:t1∶t2=90°∶60°=3∶2,故D正确.7.图3-6-29目前世界上正研究的一种新型发电机叫磁流体发电机,如图3-6-29表示它的发电原理:将一束等离子体(即高温下电离的气体,含有大量带正电和带负电的微粒,而从整体来说呈中性)沿图所示方向喷射入磁场,磁场中有两块金属板A、B,这时金属板上就聚集了电荷.在磁极配置如图中所示的情况下,下列说法正确的是( )A.A板带正电B.有电流从b经用电器流向aC.金属板A、B间的电场方向向下D.等离子体发生偏转的原因是离子所受洛伦兹力大于所受静电力解析:选BD.等离子体射入磁场后,由左手定则知正离子受到向下的洛伦兹力向B板偏转,故B板带正电,B板电势高,电流方向从b流向a,电场的方向由B板指向A板,A、C错误,B正确;当Bvq>Eq时离子发生偏转,故D正确.8.带正电粒子(不计重力)以水平向右的初速度v0,先通过匀强电场E,后通过匀强磁场B,如图3-6-30甲所示,电场和磁场对该粒子做功为W1.若把该电场和磁场正交叠加,如图乙所示,再让该带电粒子仍以水平向右的初速度v0(v0<EB)穿过叠加场区,在这个过程中电场和磁场对粒子做功为W 2,则( )图3-6-30A .W 1<W 2B .W 1=W 2C .W 1>W 2D .无法判断解析:选C.电场力做的功W =Eqy ,其中y 为粒子沿电场方向偏转的位移,因图乙中洛伦兹力方向向上,故图乙中粒子向下偏转的位移y 较小,W 1>W 2,故C 正确.9.(2011年洛阳高二检测)MN 板两侧都是磁感强度为B 的匀强磁场,方向如图3-6-31所示,带电粒子从a 位置以垂直磁场方向的速度开始运动,依次通过小孔b 、c 、d ,已知ab =bc =cd ,粒子从a 运动到d 的时间为t ,则粒子的比荷为( )图3-6-31解析:选A.粒子从a 运动到d 依次经过小孔b 、c 、d ,经历的时间t 为3个T 2,由t =3×T2和T =2πmBq.可得:q m =3πtB,故A 正确.二、计算题10.回旋加速器D 形盒中央为质子流,D 形盒的交流电压为U ,静止质子经电场加速后,进入D 形盒,其最大轨道半径为R ,磁场的磁感应强度为B ,质子质量为m .求: (1)质子最初进入D 形盒的动能多大 (2)质子经回旋加速器最后得到的动能多大 (3)交流电源的频率是什么解析:(1)粒子在电场中加速,由动能定理得:eU =E k -0,解得E k =eU .(2)粒子在回旋加速器的磁场中绕行的最大半径为R ,由牛顿第二定律得:evB =m v 2R①质子的最大动能:E km =12mv 2②解①②式得:E km =e 2B 2R 22m.(3)f =1T =eB 2πm.答案:(1)eU (2)e 2B 2R 22m (3)eB2πm11.(2011年长春市高二检测)质量为m 、电荷量为q 的带负电粒子自静止开始释放,经M 、N 板间的电场加速后,从A 点垂直于磁场边界射入宽度为d 的匀强磁场中,该粒子离开磁场时的位置P 偏离入射方向的距离为L ,如图3-6-32所示.已知M 、N 两板间的电压为U ,粒子的重力不计.求:匀强磁场的磁感应强度B .图3-6-32解析:作粒子经电场和磁场中的轨迹图,如图所示.设粒子在M 、N 两板间经电场加速后获得的速度为v ,由动能定理得:qU =12mv 2①粒子进入磁场后做匀速圆周运动,设其半径为r ,则:qvB =m v 2r②由几何关系得:r 2=(r -L )2+d 2③ 联立求解①②③式得:磁感应强度B =2L L 2+d 22mUq.答案:2L L 2+d 22mUq12.图3-6-33如图3-6-33所示,有界匀强磁场的磁感应强度B =2×10-3T ;磁场右边是宽度L = m 、场强E =40 V/m 、方向向左的匀强电场.一带电粒子电荷量q =-×10-19C ,质量m =×10-27kg ,以v =4×104m/s 的速度沿OO ′垂直射入磁场,在磁场中偏转后进入右侧的电场,最后从电场右边界射出.(不计重力)求: (1)大致画出带电粒子的运动轨迹; (2)带电粒子在磁场中运动的轨道半径; (3)带电粒子飞出电场时的动能E k . 解析:(1)轨迹如图(2)带电粒子在磁场中运动时,由牛顿运动定律,有qvB =m v 2RR =mv qB=错误! m = m(3)E k =EqL +12mv 2=40××10-19× J+12××10-27×(4×104)2 J =×10-18J.答案:(1)轨迹见解析图 (2) m (3)×10-18J。
物理带电粒子在磁场中的运动题20套(带答案)

物理带电粒子在磁场中的运动题20套(带答案)一、带电粒子在磁场中的运动专项训练1.科学家设想在宇宙中可能存在完全由反粒子构成的反物质.例如:正电子就是电子的反粒子,它跟电子相比较,质量相等、电量相等但电性相反.如图是反物质探测卫星的探测器截面示意图.MN 上方区域的平行长金属板AB 间电压大小可调,平行长金属板AB 间距为d ,匀强磁场的磁感应强度大小为B ,方向垂直纸面向里.MN 下方区域I 、II 为两相邻的方向相反的匀强磁场区,宽度均为3d ,磁感应强度均为B ,ef 是两磁场区的分界线,PQ 是粒子收集板,可以记录粒子打在收集板的位置.通过调节平行金属板AB 间电压,经过较长时间探测器能接收到沿平行金属板射入的各种带电粒子.已知电子、正电子的比荷是b ,不考虑相对论效应、粒子间的相互作用及电磁场的边缘效应.(1)要使速度为v 的正电子匀速通过平行长金属极板AB ,求此时金属板AB 间所加电压U ;(2)通过调节电压U 可以改变正电子通过匀强磁场区域I 和II 的运动时间,求沿平行长金属板方向进入MN 下方磁场区的正电子在匀强磁场区域I 和II 运动的最长时间t m ; (3)假如有一定速度范围的大量电子、正电子沿平行长金属板方向匀速进入MN 下方磁场区,它们既能被收集板接收又不重叠,求金属板AB 间所加电压U 的范围.【答案】(1)Bvd (2)Bb(3)3B 2d 2b <U <221458B d b【解析】 【详解】(1)正电子匀速直线通过平行金属极板AB ,需满足 Bev=Ee因为正电子的比荷是b ,有 E=U d联立解得:u Bvd =(2)当正电子越过分界线ef 时恰好与分界线ef 相切,正电子在匀强磁场区域I 、II 运动的时间最长。
4T t =m t =2t2111v ev B m R =T =122R mv Be=ππ 联立解得:t Bbπ=(3)临界态1:正电子恰好越过分界线ef ,需满足 轨迹半径R 1=3d1ev B =m 211v R11U ev B ed=⑪ 联立解得:2213U d B b =临界态2:沿A 极板射入的正电子和沿B 极板射入的电子恰好射到收集板同一点 设正电子在磁场中运动的轨迹半径为R 1 有(R 2﹣14d )2+9d 2=22R 2Bev =m 222v RBe 2v =2U e d 联立解得:2221458B d bU =解得:U 的范围是:3B 2d 2b <U <221458B d b2.如图所示,在长度足够长、宽度d=5cm 的区域MNPQ 内,有垂直纸面向里的水平匀强磁场,磁感应强度B=0.33T .水平边界MN 上方存在范围足够大的竖直向上的匀强电场,电场强度E=200N/C .现有大量质量m=6.6×10﹣27kg 、电荷量q=3.2×10﹣19C 的带负电的粒子,同时从边界PQ 上的O 点沿纸面向各个方向射入磁场,射入时的速度大小均为V=1.6×106m/s ,不计粒子的重力和粒子间的相互作用.求:(1)求带电粒子在磁场中运动的半径r ;(2)求与x 轴负方向成60°角射入的粒子在电场中运动的时间t ;(3)当从MN 边界上最左边射出的粒子离开磁场时,求仍在磁场中的粒子的初速度方向与x 轴正方向的夹角范围,并写出此时这些粒子所在位置构成的图形的曲线方程. 【答案】(1)r=0.1m (2)43.310t s -=⨯ (3)3060~ 曲线方程为222x y R +=(30.10.1R m x m =≤≤) 【解析】 【分析】 【详解】(1)洛伦兹力充当向心力,根据牛顿第二定律可得2v qvB m r=,解得0.1r m =(2)粒子的运动轨迹如图甲所示,由几何关系可知,在磁场中运动的圆心角为30°,粒子平行于场强方向进入电场,粒子在电场中运动的加速度qE a m= 粒子在电场中运动的时间2v t a= 解得43.310t s -=⨯(3)如图乙所示,由几何关系可知,从MN 边界上最左边射出的粒子在磁场中运动的圆心角为60°,圆心角小于60°的粒子已经从磁场中射出,此时刻仍在磁场中的粒子运动轨迹的圆心角均为60°,则仍在磁场中的粒子的初速度方向与x 轴正方向的夹角范围为30°~60° 所有粒子此时分别在以O 点为圆心,弦长0.1m 为半径的圆周上,曲线方程为22x y R += 30.1,0.120R m m x m ⎛⎫=≤≤ ⎪ ⎪⎝⎭【点睛】带电粒子在组合场中的运动问题,首先要运用动力学方法分析清楚粒子的运动情况,再选择合适方法处理.对于匀变速曲线运动,常常运用运动的分解法,将其分解为两个直线的合成,由牛顿第二定律和运动学公式结合求解;对于磁场中圆周运动,要正确画出轨迹,由几何知识求解半径3.如图所示,坐标原点O 左侧2m 处有一粒子源,粒子源中,有带正电的粒子(比荷为qm=1.0×1010C/kg)由静止进人电压U= 800V 的加速电场,经加速后沿x 轴正方向运动,O 点右侧有以O 1点为圆心、r=0.20m 为半径的圆形区域,内部存在方向垂直纸面向里,磁感应强度大小为B=1.0×10-3T 的匀强磁场(图中未画出)圆的左端跟y 轴相切于直角坐标系原点O ,右端与一个足够大的荧光屏MN 相切于x 轴上的A 点,粒子重力不计。
高考物理带电粒子在磁场中的运动题20套(带答案)含解析

高考物理带电粒子在磁场中的运动题20套(带答案)含解析一、带电粒子在磁场中的运动专项训练1.如图所示,xOy 平面处于匀强磁场中,磁感应强度大小为B ,方向垂直纸面向外.点3,0P L ⎛⎫ ⎪ ⎪⎝⎭处有一粒子源,可向各个方向发射速率不同、电荷量为q 、质量为m 的带负电粒子.不考虑粒子的重力.(1)若粒子1经过第一、二、三象限后,恰好沿x 轴正向通过点Q (0,-L ),求其速率v 1;(2)若撤去第一象限的磁场,在其中加沿y 轴正向的匀强电场,粒子2经过第一、二、三象限后,也以速率v 1沿x 轴正向通过点Q ,求匀强电场的电场强度E 以及粒子2的发射速率v 2;(3)若在xOy 平面内加沿y 轴正向的匀强电场E o ,粒子3以速率v 3沿y 轴正向发射,求在运动过程中其最小速率v.某同学查阅资料后,得到一种处理相关问题的思路:带电粒子在正交的匀强磁场和匀强电场中运动,若所受洛伦兹力与电场力不平衡而做复杂的曲线运动时,可将带电粒子的初速度进行分解,将带电粒子的运动等效为沿某一方向的匀速直线运动和沿某一时针方向的匀速圆周运动的合运动. 请尝试用该思路求解. 【答案】(1)23BLq m (2221BLq32230B E E v B +⎛⎫ ⎪⎝⎭【解析】 【详解】(1)粒子1在一、二、三做匀速圆周运动,则2111v qv B m r =由几何憨可知:()2221133r L r L ⎛⎫=-+ ⎪ ⎪⎝⎭得到:123BLqv m=(2)粒子2在第一象限中类斜劈运动,有:133L v t=,212qE h t m = 在第二、三象限中原圆周运动,由几何关系:12L h r +=,得到289qLB E m=又22212v v Eh =+,得到:2221BLqv =(3)如图所示,将3v 分解成水平向右和v '和斜向的v '',则0qv B qE '=,即0E v B'= 而'223v v v ''=+ 所以,运动过程中粒子的最小速率为v v v =''-'即:22003E E v v B B ⎛⎫=+- ⎪⎝⎭2.欧洲大型强子对撞机是现在世界上最大、能量最高的粒子加速器,是一种将质子加速对撞的高能物理设备,其原理可简化如下:两束横截面积极小,长度为l -0质子束以初速度v 0同时从左、右两侧入口射入加速电场,出来后经过相同的一段距离射入垂直纸面的圆形匀强磁场区域并被偏转,最后两质子束发生相碰。
高考物理带电粒子在磁场中的运动基础练习题及解析

高考物理带电粒子在磁场中的运动基础练习题及解析一、带电粒子在磁场中的运动专项训练1.如图所示,xOy 平面处于匀强磁场中,磁感应强度大小为B ,方向垂直纸面向外.点3,03P L ⎛⎫ ⎪ ⎪⎝⎭处有一粒子源,可向各个方向发射速率不同、电荷量为q 、质量为m 的带负电粒子.不考虑粒子的重力.(1)若粒子1经过第一、二、三象限后,恰好沿x 轴正向通过点Q (0,-L ),求其速率v 1;(2)若撤去第一象限的磁场,在其中加沿y 轴正向的匀强电场,粒子2经过第一、二、三象限后,也以速率v 1沿x 轴正向通过点Q ,求匀强电场的电场强度E 以及粒子2的发射速率v 2;(3)若在xOy 平面内加沿y 轴正向的匀强电场E o ,粒子3以速率v 3沿y 轴正向发射,求在运动过程中其最小速率v.某同学查阅资料后,得到一种处理相关问题的思路:带电粒子在正交的匀强磁场和匀强电场中运动,若所受洛伦兹力与电场力不平衡而做复杂的曲线运动时,可将带电粒子的初速度进行分解,将带电粒子的运动等效为沿某一方向的匀速直线运动和沿某一时针方向的匀速圆周运动的合运动. 请尝试用该思路求解. 【答案】(1)23BLq m (2221BLq32230B E E v B +⎛⎫ ⎪⎝⎭【解析】 【详解】(1)粒子1在一、二、三做匀速圆周运动,则2111v qv B m r =由几何憨可知:()2221133r L r L ⎛⎫=-+ ⎪ ⎪⎝⎭得到:123BLqv m=(2)粒子2在第一象限中类斜劈运动,有:133L v t=,212qE h t m = 在第二、三象限中原圆周运动,由几何关系:12L h r +=,得到289qLB E m=又22212v v Eh =+,得到:22219BLqv m=(3)如图所示,将3v 分解成水平向右和v '和斜向的v '',则0qv B qE '=,即0E v B'= 而'223v v v ''=+ 所以,运动过程中粒子的最小速率为v v v =''-'即:22003E E v v B B ⎛⎫=+- ⎪⎝⎭2.如图,光滑水平桌面上有一个矩形区域abcd ,bc 长度为2L ,cd 长度为1.5L ,e 、f 分别为ad 、bc 的中点.efcd 区域存在竖直向下的匀强磁场,磁感应强度为B ;质量为m 、电荷量为+q 的绝缘小球A 静止在磁场中f 点.abfe 区域存在沿bf 方向的匀强电场,电场强度为26qB Lm;质量为km 的不带电绝缘小球P ,以大小为qBL m 的初速度沿bf 方向运动.P 与A发生弹性正碰,A 的电量保持不变,P 、A 均可视为质点.(1)求碰撞后A 球的速度大小;(2)若A 从ed 边离开磁场,求k 的最大值;(3)若A 从ed 边中点离开磁场,求k 的可能值和A 在磁场中运动的最长时间.【答案】(1)A 21k qBL v k m =⋅+(2)1(3)57k =或13k =;32m t qB π=【解析】 【分析】 【详解】(1)设P 、A 碰后的速度分别为v P 和v A ,P 碰前的速度为qBLv m= 由动量守恒定律:P A kmv kmv mv =+ 由机械能守恒定律:222P A 111222kmv kmv mv =+ 解得:A 21k qBL v k m=⋅+(2)设A 在磁场中运动轨迹半径为R , 由牛顿第二定律得: 2A A mv qvB R= 解得:21kR L k =+ 由公式可得R 越大,k 值越大如图1,当A 的轨迹与cd 相切时,R 为最大值,R L = 求得k 的最大值为1k =(3)令z 点为ed 边的中点,分类讨论如下:(I )A 球在磁场中偏转一次从z 点就离开磁场,如图2有222()(1.5)2LR L R =+-解得:56L R = 由21k R L k =+可得:57k =(II )由图可知A 球能从z 点离开磁场要满足2LR ≥,则A 球在磁场中还可能经历一次半圆运动后回到电场,再被电场加速后又进入磁场,最终从z 点离开.如图3和如图4,由几何关系有:2223()(3)22L R R L =+-解得:58L R =或2LR = 由21k R L k =+可得:511k =或13k = 球A 在电场中克服电场力做功的最大值为2226m q B L W m=当511k =时,A 58qBL v m =,由于2222222A 12521286qB L q B L mv m m ⋅=>当13k =时,A 2qBL v m =,由于2222222A 1286qB L q B L mv m m⋅=<综合(I )、(II )可得A 球能从z 点离开的k 的可能值为:57k =或13k = A 球在磁场中运动周期为2mT qBπ= 当13k =时,如图4,A 球在磁场中运动的最长时间34t T = 即32mt qBπ=3.在如图所示的平面直角坐标系中,存在一个半径R =0.2m 的圆形匀强磁场区域,磁感应强度B =1.0T ,方向垂直纸面向外,该磁场区域的右边缘与y 坐标轴相切于原点O 点。
磁场及带电粒子在磁场中的运动典型题目(含答案)

.第 9 讲磁场及带电粒子在磁场中的运动2(2018·山东省历城高三下学期模拟 )如图所示,用绝缘细线悬挂一一、选择题 (本题共 8 小题,其中 1~ 4 题为单选, 5~8 题为多选 )个导线框,导线框是由两同心半圆弧导线和在同一条水平直线上的1. (2018·山东省潍坊市高三下学期一模 ) 如图所示,导体棒ab 用直导线 EF、 GH 连接而成的闭合回路,导线框中通有图示方向的电绝缘细线水平悬挂,通有由 a 到 b 的电流。
ab 正下方放一圆形线流,处于静止状态。
在半圆弧导线的圆心处沿垂直于导线框平面的圈,线圈通过导线,开关与直流电源连接。
开关闭合瞬间,导体棒方向放置一根长直导线 O。
当 O 中通以垂直纸面方向向里的电流时ab 将 ( B )( D )A.向外摆动A.长直导线 O 产生的磁场方向沿着电流方向看为逆时针方向B.向里摆动B.半圆弧导线 ECH 受安培力大于半圆弧导线 FDG 受安培力C.保持静止,细线上张力变大C. EF所受的安培力方向垂直纸面向外D.保持静止,细线上张力变小D.从上往下看,导线框将顺时针转动[解析 ] 开关闭合瞬间,圆形线圈的电流顺时针方向,根据右手螺旋定则可知导体棒 ab 的磁场方向竖直向下,根据左手定则可知导体棒ab 将向里摆动,[解析 ] 当直导线 O 中通以垂直纸面方向向里的电流时,由安培定则可判断出故 B 正确, ACD 错误;故选 B。
O 产生的磁场方向为顺时针方向,选项 A 错误;磁感线是以 O 为长直导线圆心的同心圆,半圆弧导线与磁感线平行不受安培力,选项 B 错误;由左手定则可判断出直导线EF 所受的安培力方向垂直纸面向里,选项 C 错误;GH 所受的安培力方向垂直纸面向外,从上往下看,导线框将顺时针转动,选项 D 正确;故选D。
3 (2018·河南省郑州市高三下学期模拟 )如图所示,在边长为L 的正方形 ABCD 阴影区域内存在垂直纸面的匀强磁场,一质量为m、电荷量为 q(q<0) 的带电粒子以大小为v0的速度沿纸面垂直AB 边射入正方形,若粒子从AB 边上任意点垂直射入,都只能从 C 点射出磁场,不计粒子的重力影响。
高中物理 第三章 磁场 6 带电粒子在匀强磁场中的运动练习(含解析)新人教版选修3-1-新人教版高中

带电粒子在匀强磁场中的运动根底夯实一、选择题(1~3题为单项选择题,4~6题为多项选择题)1.有三束粒子,分别是质子(p )、氚核(31H)和α粒子(氦核)束,如果它们以一样的速度沿垂直于磁场方向射入匀强磁场(方向垂直于纸面向里),在如下图中,哪个图能正确地表示出了这三束粒子的偏转轨迹( C )解析:由Bqv =m v 2R 可知:R =mv Bq; 半径与荷质比成反比;因三束离子中质子的荷质比最大,氚核的最小,故质子的半径最小,氚核的半径最大,故C 正确。
2.1930年劳伦斯制成了世界上第一台盘旋加速器,其原理如下列图,这台加速器由两个铜质D 形盒D 1、D 2构成,其间留有空隙,如下说法不正确的答案是( B )A .带电粒子由加速器的中心附近进入加速器B .带电粒子由加速器的边缘进入加速器C .电场使带电粒子加速,磁场使带电粒子旋转D .离子从D 形盒射出时的动能与加速电场的电压无关解析:根据盘旋加速器的加速原理,被加速离子只能由加速器的中心附近进入加速器,从边缘离开加速器,故A 正确,B 错误;在磁场中洛伦兹力不做功,离子是从电场中获得能量,故C 正确;当离子离开盘旋加速器时,半径最大,动能最大,E m =12mv 2=B 2q 2r 22m,与加速的电压无关,故D 正确。
此题选不正确的,应当选B 。
3.如图,MN 为铝质薄平板,铝板上方和下方分别有垂直于图平面的匀强磁场(未画出)。
一带电粒子从紧贴铝板上外表的P 点垂直于铝板向上射出,从Q 点穿越铝板后到达PQ 的中点O 。
粒子穿越铝板时,其动能损失一半,速度方向和电荷量不变,不计重力。
铝板上方和下方的磁感应强度大小之比为( D )A .2B . 2C .1D .22解析:由E K =12mv 2可知当动能为原来的一半时,速度是原来的22。
由R =mv qB将R 1=2R 2代入可得B 1︰B 2=22,D 正确。
4.设空间存在竖直向下的匀强电场和垂直纸面向里的匀强磁场,如下列图,一粒子在电场力和洛伦兹力的作用下,从静止开始自A 点沿曲线ACB 运动,到达B 点时速度为零,C 点是运动的最低点,忽略重力,以下说法正确的答案是( ABC )A .粒子必带正电荷B .A 点和B 点位于同一高度C .粒子在C 点时速度最大D .粒子到达B 点后,将沿原曲线返回A 点解析:平行板间电场方向向下,粒子由A 点静止释放后在电场力的作用下向下运动,所以粒子必带正电荷,A 正确。
高考物理带电粒子在磁场中的运动的技巧及练习题及练习题(含答案)

高考物理带电粒子在磁场中的运动的技巧及练习题及练习题(含答案)一、带电粒子在磁场中的运动专项训练1.如图所示,一质量为m 、电荷量为+q 的粒子从竖直虚线上的P 点以初速度v 0水平向左射出,在下列不同情形下,粒子经过一段时间后均恰好经过虚线右侧的A 点.巳知P 、A 两点连线长度为l ,连线与虚线的夹角为α=37°,不计粒子的重力,(sin 37°=0.6,cos 37°=0.8).(1)若在虚线左侧存在垂直纸面向外的匀强磁场,求磁感应强度的大小B 1;(2)若在虚线上某点固定一个负点电荷,粒子恰能绕该负点电荷做圆周运动,求该负点电荷的电荷量Q (已知静电力常量为是);(3)若虚线的左侧空间存在垂直纸面向外的匀强磁场,右侧空间存在竖直向上的匀强电场,粒子从P 点到A 点的过程中在磁场、电场中的运动时间恰好相等,求磁场的磁感应强度的大小B 2和匀强电场的电场强度大小E .【答案】(1)0152mv B ql = (2)2058mv l Q kq = (3)0253mv B ql π= 220(23)9mv E qlππ-=【解析】 【分析】 【详解】(1)粒子从P 到A 的轨迹如图所示:粒子在磁场中做匀速圆周运动,设半径为r 1 由几何关系得112cos 25r l l α== 由洛伦兹力提供向心力可得2011v qv B m r =解得:0 152mv Bql=(2)粒子从P到A的轨迹如图所示:粒子绕负点电荷Q做匀速圆周运动,设半径为r2由几何关系得252cos8lr lα==由库仑力提供向心力得2222vQqk mr r=解得:258mv lQkq=(3)粒子从P到A的轨迹如图所示:粒子在磁场中做匀速圆周运动,在电场中做类平抛运动粒子在电场中的运动时间00sin35l ltv vα==根据题意得,粒子在磁场中运动时间也为t,则2Tt=又22mTqBπ=解得0253mvBqlπ=设粒子在磁场中做圆周运动的半径为r,则0v t rπ=解得:3 5 lrπ=粒子在电场中沿虚线方向做匀变速直线运动,21cos22qEl r tmα-=⋅解得:220(23)9mvEqlππ-=2.核聚变是能源的圣杯,但需要在极高温度下才能实现,最大难题是没有任何容器能够承受如此高温。
高考物理带电粒子在磁场中的运动解题技巧及练习题及解析
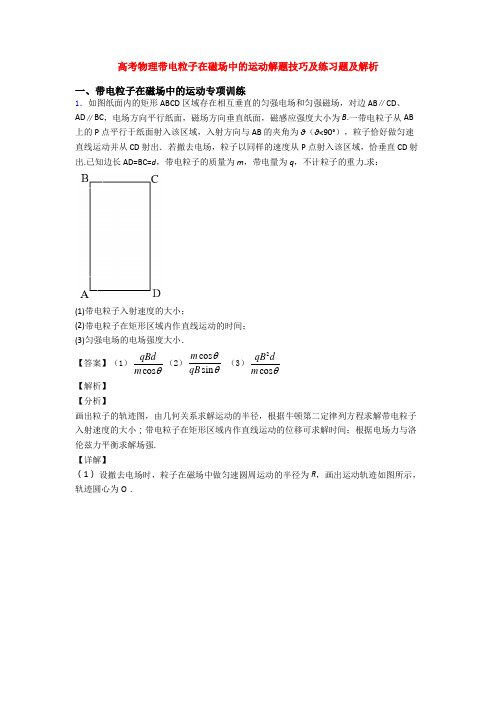
高考物理带电粒子在磁场中的运动解题技巧及练习题及解析一、带电粒子在磁场中的运动专项训练1.如图纸面内的矩形 ABCD 区域存在相互垂直的匀强电场和匀强磁场,对边 AB ∥CD 、AD ∥BC ,电场方向平行纸面,磁场方向垂直纸面,磁感应强度大小为 B .一带电粒子从AB 上的 P 点平行于纸面射入该区域,入射方向与 AB 的夹角为 θ(θ<90°),粒子恰好做匀速直线运动并从 CD 射出.若撤去电场,粒子以同样的速度从P 点射入该区域,恰垂直 CD 射出.已知边长 AD=BC=d ,带电粒子的质量为 m ,带电量为 q ,不计粒子的重力.求:(1)带电粒子入射速度的大小;(2)带电粒子在矩形区域内作直线运动的时间; (3)匀强电场的电场强度大小.【答案】(1)cos qBd m θ(2)cos sin m qB θθ (3)2cos qB dm θ【解析】 【分析】画出粒子的轨迹图,由几何关系求解运动的半径,根据牛顿第二定律列方程求解带电粒子入射速度的大小;带电粒子在矩形区域内作直线运动的位移可求解时间;根据电场力与洛伦兹力平衡求解场强. 【详解】(1) 设撤去电场时,粒子在磁场中做匀速圆周运动的半径为R ,画出运动轨迹如图所示,轨迹圆心为O .由几何关系可知:cos d Rθ=洛伦兹力做向心力:200v qv B m R= 解得0cos qBdv m θ=(2)设带电粒子在矩形区域内作直线运动的位移为x ,有sin d xθ= 粒子作匀速运动:x=v 0t 联立解得cos sin m t qB θθ=(3)带电粒子在矩形区域内作直线运动时,电场力与洛伦兹力平衡:Eq=qv 0B解得2qB dE mcos θ=【点睛】此题关键是能根据粒子的运动情况画出粒子运动的轨迹图,结合几何关系求解半径等物理量;知道粒子作直线运动的条件是洛伦兹力等于电场力.2.空间中存在方向垂直于纸面向里的匀强磁场,磁感应强度为B ,一带电量为+q 、质量为m 的粒子,在P 点以某一初速开始运动,初速方向在图中纸面内如图中P 点箭头所示.该粒子运动到图中Q 点时速度方向与P 点时速度方向垂直,如图中Q 点箭头所示.已知P 、Q 间的距离为L .若保持粒子在P 点时的速度不变,而将匀强磁场换成匀强电场,电场方向与纸面平行且与粒子在P 点时速度方向垂直,在此电场作用下粒子也由P 点运动到Q 点.不计重力.求:(1)电场强度的大小.(2)两种情况中粒子由P 运动到Q 点所经历的时间之比.【答案】22B qLE m=;2B E t t π= 【解析】 【分析】 【详解】(1)粒子在磁场中做匀速圆周运动,以v 0表示粒子在P 点的初速度,R 表示圆周的半径,则有20v qv B m R= 由于粒子在Q 点的速度垂直它在p 点时的速度,可知粒子由P 点到Q 点的轨迹为14圆周,故有2R =以E 表示电场强度的大小,a 表示粒子在电场中加速度的大小,t E 表示粒子在电场中由p 点运动到Q 点经过的时间,则有qE ma = 水平方向上:212E R at =竖直方向上:0E R v t =由以上各式,得 22B qL E m=且E mt qB = (2)因粒子在磁场中由P 点运动到Q 点的轨迹为14圆周,即142B t T m qB π==所以2B E t t π=3.电子扩束装置由电子加速器、偏转电场和偏转磁场组成.偏转电场的极板由相距为d 的两块水平平行放置的导体板组成,如图甲所示.大量电子由静止开始,经加速电场加速后,连续不断地沿平行板的方向从两板正中间OO ’射入偏转电场.当两板不带电时,这些电子通过两板之间的时间为2t 0;:当在两板间加最大值为U 0、周期为2t 0的电压(如图乙所示)时,所有电子均能从两板间通过,然后进入竖直宽度足够大的匀强酸场中,最后打在竖直放置的荧光屏上.已知磁场的水平宽度为L ,电子的质量为m 、电荷量为e ,其重力不计.(1)求电子离开偏转电场时的位置到OO ’的最远位置和最近位置之间的距离 (2)要使所有电子都能垂直打在荧光屏上, ①求匀强磁场的磁感应强度B②求垂直打在荧光屏上的电子束的宽度△y 【答案】(1)2010U e y t dm ∆= (2)①00U t B dL =②2010U e y y t dm∆=∆= 【解析】 【详解】(1)由题意可知,从0、2t 0、4t 0、……等时刻进入偏转电场的电子离开偏转电场时的位置到OO ′的距离最大,在这种情况下,电子的最大距离为:2222000max 00000311222y U e U e U e y at v t t t t dm dm dm=+=+= 从t 0、3t 0、……等时刻进入偏转电场的电子离开偏转电场时的位置到OO ′的距离最小,在这种情况下,电子的最小距离为:220min 001122U e y at t dm== 最远位置和最近位置之间的距离:1max min y y y ∆=-,2010U e y t dm∆=(2)①设电子从偏转电场中射出时的偏向角为θ,由于电子要垂直打在荧光屏上,所以电子在磁场中运动半径应为:sin L R θ=设电子离开偏转电场时的速度为v 1,垂直偏转极板的速度为v y ,则电子离开偏转电场时的偏向角为θ,1sin y v v θ=,式中00y U ev t dm = 又:1mv R Be=解得:00U t B dL=②由于各个时刻从偏转电场中射出的电子的速度大小相等,方向相同,因此电子进入磁场后做圆周运动的半径也相同,都能垂直打在荧光屏上.由第(1)问知电子离开偏转电场时的位置到OO ′的最大距离和最小距离的差值为△y 1, 所以垂直打在荧光屏上的电子束的宽度为:2010U e y y t dm∆=∆=4.如图所示,荧光屏MN 与x 轴垂直放置,与x 轴相交于Q 点,Q 点的横坐标06x cm =,在第一象限y 轴和MN 之间有沿y 轴负方向的匀强电场,电场强度51.610/E N C =⨯,在第二象限有半径5R cm =的圆形磁场,磁感应强度0.8B T =,方向垂直xOy 平面向外.磁场的边界和x 轴相切于P 点.在P 点有一个粒子源,可以向x 轴上方180°范围内的各个方向发射比荷为81.010/qC kg m=⨯的带正电的粒子,已知粒子的发射速率60 4.010/v m s =⨯.不考虑粒子的重力、粒子间的相互作用.求:(1)带电粒子在磁场中运动的轨迹半径; (2)粒子从y 轴正半轴上射入电场的纵坐标范围; (3)带电粒子打到荧光屏上的位置与Q 点间的最远距离. 【答案】(1)5cm (2)010y cm ≤≤ (3)9cm 【解析】 【详解】(1)带电粒子进入磁场受到洛伦兹力的作用做圆周运动20v qv B m r=解得:05mv r cm qB== (2)由(1)问中可知r R =,取任意方向进入磁场的粒子,画出粒子的运动轨迹如图所示,由几何关系可知四边形1PO FO '为菱形,所以1//FO O P ',又O P '垂直于x 轴,粒子出射的速度方向与轨迹半径1FO 垂直,则所有粒子离开磁场时的方向均与x 轴平行,所以粒子从y 轴正半轴上射入电场的纵坐标范围为010y cm ≤≤.(3)假设粒子没有射出电场就打到荧光屏上,有000x v t =2012h at =qE a m=解得:18210h cm R cm =>=,说明粒子离开电场后才打到荧光屏上.设从纵坐标为y 的点进入电场的粒子在电场中沿x 轴方向的位移为x ,则0x v t =212y at =代入数据解得2x y =设粒子最终到达荧光屏的位置与Q 点的最远距离为H ,粒子射出的电场时速度方向与x 轴正方向间的夹角为θ,000tan 2y qE x v m v yv v θ===g所以()(00tan 22H x x x y y θ=-=g 由数学知识可知,当(022x y y = 4.5y cm =时H 有最大值,所以max 9H cm =5.如图所示,在竖直平面内建立直角坐标系,y 轴沿竖直方向.在x = L 到x =2L 之间存在竖直向上的匀强电场和垂直坐标平面向里的匀强磁场,一个比荷(qm)为k 的带电微粒从坐标原点以一定初速度沿+x 方向抛出,进入电场和磁场后恰好在竖直平面内做匀速圆周运动,离开电场和磁场后,带电微粒恰好沿+x 方向通过x 轴上x =3L 的位置,已知匀强磁场的磁感应强度为B ,重力加速度为g .求:(1)电场强度的大小; (2)带电微粒的初速度;(3)带电微粒做圆周运动的圆心坐标.【答案】(1)g k (2)2gkB(3)2222232(,)28g k B L L k B g -【解析】 【分析】 【详解】(1)由于粒子在复合场中做匀速圆周运动,则:mg =qE ,又=qk m解得g E k=(2)由几何关系:2R cos θ=L ,粒子做圆周运动的向心力等于洛伦兹力:2v qvB m r= ;由cos y v vθ=在进入复合场之前做平抛运动:y gt =v0L v t =解得02g v kB=(3)由212h gt =其中2kBL t g = ,则带电微粒做圆周运动的圆心坐标:'32O x L =; 222'222sin 8O g k B L y h R k B g θ=-+=-6.如图所示,虚线OL与y轴的夹角θ=450,在OL上侧有平行于OL向下的匀强电场,在OL下侧有垂直纸面向外的匀强磁场,一质量为m、电荷量为q(q>0)的粒子以速率v0从y轴上的M(OM=d)点垂直于y轴射入匀强电场,该粒子恰好能够垂直于OL进入匀强磁场,不计粒子重力。
高考物理带电粒子在磁场中的运动专题训练答案及解析
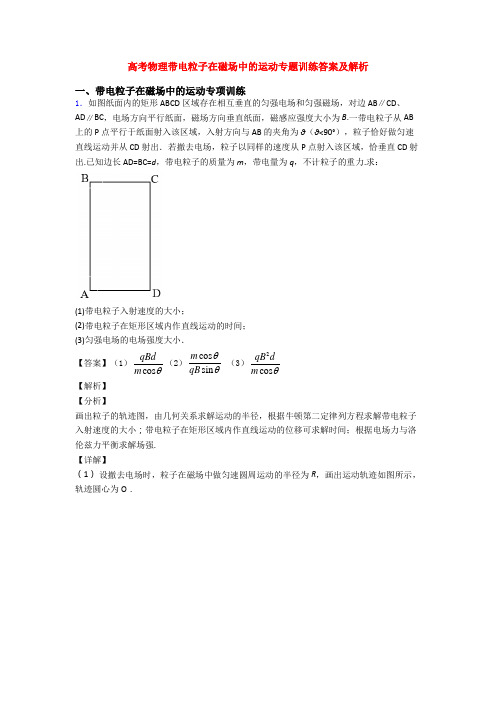
高考物理带电粒子在磁场中的运动专题训练答案及解析一、带电粒子在磁场中的运动专项训练1.如图纸面内的矩形 ABCD 区域存在相互垂直的匀强电场和匀强磁场,对边 AB ∥CD 、AD ∥BC ,电场方向平行纸面,磁场方向垂直纸面,磁感应强度大小为 B .一带电粒子从AB 上的 P 点平行于纸面射入该区域,入射方向与 AB 的夹角为 θ(θ<90°),粒子恰好做匀速直线运动并从 CD 射出.若撤去电场,粒子以同样的速度从P 点射入该区域,恰垂直 CD 射出.已知边长 AD=BC=d ,带电粒子的质量为 m ,带电量为 q ,不计粒子的重力.求:(1)带电粒子入射速度的大小;(2)带电粒子在矩形区域内作直线运动的时间; (3)匀强电场的电场强度大小.【答案】(1)cos qBd m θ(2)cos sin m qB θθ (3)2cos qB dm θ【解析】 【分析】画出粒子的轨迹图,由几何关系求解运动的半径,根据牛顿第二定律列方程求解带电粒子入射速度的大小;带电粒子在矩形区域内作直线运动的位移可求解时间;根据电场力与洛伦兹力平衡求解场强. 【详解】(1) 设撤去电场时,粒子在磁场中做匀速圆周运动的半径为R ,画出运动轨迹如图所示,轨迹圆心为O .由几何关系可知:cos d Rθ=洛伦兹力做向心力:200v qv B m R= 解得0cos qBdv m θ=(2)设带电粒子在矩形区域内作直线运动的位移为x ,有sin d xθ= 粒子作匀速运动:x=v 0t 联立解得cos sin m t qB θθ=(3)带电粒子在矩形区域内作直线运动时,电场力与洛伦兹力平衡:Eq=qv 0B解得2qB dE mcos θ=【点睛】此题关键是能根据粒子的运动情况画出粒子运动的轨迹图,结合几何关系求解半径等物理量;知道粒子作直线运动的条件是洛伦兹力等于电场力.2.如图所示,在竖直面内半径为R 的圆形区域内存在垂直于面向里的匀强磁场,其磁感应强度大小为B ,在圆形磁场区域内水平直径上有一点P ,P 到圆心O 的距离为2R,在P 点处有一个发射正离子的装置,能连续不断地向竖直平面内的各方向均匀地发射出速率不同的正离子. 已知离子的质量均为m ,电荷量均为q ,不计离子重力及离子间相互作用力,求:(1)若所有离子均不能射出圆形磁场区域,求离子的速率取值范围; (2)若离子速率大小02BqRv m=,则离子可以经过的磁场的区域的最高点与最低点的高度差是多少。
高中物理带电粒子在磁场中的运动试题(有答案和解析)及解析

O、O′在质子束的入射方向上,其连线与质子入射方向垂直且距离为 H= 7 R;整个装置处 2
于真空中,忽略粒子间的相互作用及相对论效应。
(1)试求质子束经过加速电场加速后(未进入磁场)的速度 ν 和磁场磁感应强度 B;
圆半径方向射出磁场;从
x
轴射出点的横坐标: xC
xA
R tan 53
xC 0.1425m .
由几何关系,过 A 点的粒子经 x 轴后进入磁场由 B 点沿 x 轴正向运动.
综上所述,粒子经过磁场后第二次打在 x 轴上的范围为: x 0.1425m
5.如图,平面直角坐标系中,在,y>0 及 y<- 3 L 区域存在场强大小相同,方向相反均平 2
(1)求第 I 象限内磁场的磁感应强度 B1;
(2)计算说明速率为 5v、9v 的粒子能否到达接收器;
(3)若在第Ⅱ象限内加上垂直于坐标平面的匀强磁场,使所有粒子均到达接收器,求所加磁
场的磁感应强度 B2 的大小和方向.
【答案】(1)
B1
mv qL
(2)故速率为 v
的粒子被吸收,速率为 9v
的粒子不能被吸收
速度偏转角的正切值均为: tan vy 37 v0
cos 37 v0 v
v 1106 m/s
即:所有的粒子射出极板时速度的大小和方向均相同.
qvB m v2 R
R r 0.03m
由分析得,如图所示,所有粒子在磁场中运动后发生磁聚焦由磁场中的一点 B 离开磁场.
由几何关系,恰好经 N 板右边缘的粒子经 x 轴后沿磁场圆半径方向射入磁场,一定沿磁场
第六节 带电粒子在磁场中的运动练习题 (答案详解)

第六节 带电粒子在磁场中的运动练习题一、多选择题1.如图所示,在 、 的长方形区域有垂直于xOy 平面向外的匀强磁场,磁感应强度大小为B ,坐标原点O 处有一粒子源,在某时刻发射大量质量为m 、电荷量为q 的带正电粒子 重力不计 ,其速度方向均在xOy 平面内的第一象限,且与y 轴正方向的夹角分布在~ 范围内,速度大小不同,且满足,若粒子在磁场中做圆周运动的周期为T ,最先从磁场上边界飞出的粒子经历的时间为 ,最后从磁场中飞出的粒子经历的时间为 ,则下列判断正确的是A .B .C .D .【答案】BC【解析】带电粒子在磁场中做匀速圆周运动,根据洛伦兹力提供向心力:,可得半径:,又因为,可得粒子半径满足: ,而带电粒子做匀速圆周运动的周期为:。
分析可知最先从磁场上边界飞出的粒子运动轨迹如图所示:此时粒子半径 , 为圆心,此时粒子转过圆心角 ,根据几何关系可知,,所以可知 ,故最先从磁场上边界飞出的粒子经历的时间为:,故A 错误,B 正确;设磁场区域为OACB ,根据周期公式可知粒子在磁场中运动的周期相同,分析可知最后从磁场中飞出的粒子轨迹如图所示:此时粒子半径 ,恰好在C 点离开磁场,延长CB 至 使 , 即为圆心,连接 ,根据几何关系可知,此时粒子转过圆心角 最大为 ,所以最后从磁场中飞出的粒子经历的时间为:,故C 正确,D 错误。
所以BC 正确,AD 错误。
2.如图所示,虚线框MNQP 内存在匀强磁场,磁场方向垂直纸面向里。
a 、b 、c 是三个质量和电荷量都相等的带电粒子,它们从PQ 边上的中点沿垂直于磁场的方向射入磁场,图中画出了它们在磁场中的运动轨迹。
若不计粒子所受重力,则A . 粒子 a 带负电,粒子 b 、c 带正电B . 粒子 c 在磁场中运动的时间最长C . 粒子 c 在磁场中的动能最大D . 粒子 c 在磁场中的加速度最小 【答案】BD【解析】根据左手定则知粒子a 带正电,粒子b 、c 带负电,故A 错误;粒子在磁场中做圆周运动的周期:相同,粒子在磁场中的运动时间:,由于m 、q 、B 都相同,粒子c 转过的圆心角 最大,则射入磁场时c 的运动时间最大,故B 正确;粒子在磁场中做匀速圆周运动时,由洛伦兹力提供向心力,由牛顿第二定律得:,解得:,粒子的动能,由于:q 、B 、m 都相同,因此r 越大,粒子动能越大,由图示可知,b 的轨道半径r 最大,则b 粒子动能最大,故C 错误;由牛顿第二定律得: ,解得加速度:,三粒子q 、B 、m 都相等,c 在磁场中运动的半径最小,c 的加速度最小,故D 正确。
带电粒子在磁场中的运动(答案)

×××××× × × × × × × × × × Oxy v5.(2009山东威海一中3).如图所示,实线表示在竖直平面内的电场线,电场线与水平方向成α角,水平方向的匀强磁场与电场正交,有一带电液滴沿斜向上的虚线L 做直线运动,L 与水平方向成β角,且α>β,则下列说法中错误的是 ( D ) A.液滴一定做匀速直线运动 B.液滴一定带正电 C.电场线方向一定斜向上 D.液滴有可能做匀变速直线运动3. (2009北京西城区) 如图,空间存在水平向左的匀强电场和垂直纸面向里的匀强磁场,电场和磁场相互垂直。
在电磁场区域中,有一个竖直放置的光滑绝缘圆环,环上套有一个带正电的小球。
O 点为圆环的圆心,a 、b 、c 为圆环上的三个点,a 点为最高点,c 点为最低点,Ob 沿水平方向。
已知小球所受电场力与重力大小相等。
现将小球从环的顶端a 点由静止释放。
下列判断正确的是( D )A .当小球运动的弧长为圆周长的1/4时,洛仑兹力最大B .当小球运动的弧长为圆周长的1/2时,洛仑兹力最大C .小球从a 点到b 点,重力势能减小,电势能增大D .小球从b 点运动到c 点,电势能增大,动能先增大后减小12.(07天津理综)19.如图所示,在x 轴上方存在着垂直于纸面向里、磁感应强度为B 的匀强磁场。
一个不计重力的带电粒子从坐标原点O 处以速度v 进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x 轴正方向成120°角,若粒子穿过y 轴正半轴后在磁场中到x 轴的最大距离为a ,则该粒子的比荷和所带电荷的正负是(C)A .32vaB 正电荷 B .2v aB 正电荷C .32v aB 负电荷D .2v aB负电荷9.(09年宁夏卷)16. 医生做某些特殊手术时,利用电磁血流计来监测通过动脉的血流速度。
高中物理带电粒子在磁场中的运动题20套(带答案)含解析

高中物理带电粒子在磁场中的运动题20套(带答案)含解析一、带电粒子在磁场中的运动专项训练1.如图所示为电子发射器原理图,M 处是电子出射口,它是宽度为d 的狭缝.D 为绝缘外壳,整个装置处于真空中,半径为a 的金属圆柱A 可沿半径向外均匀发射速率为v 的电子;与A 同轴放置的金属网C 的半径为2a.不考虑A 、C 的静电感应电荷对电子的作用和电子之间的相互作用,忽略电子所受重力和相对论效应,已知电子质量为m ,电荷量为e.(1)若A 、C 间加速电压为U ,求电子通过金属网C 发射出来的速度大小v C ;(2)若在A 、C 间不加磁场和电场时,检测到电子从M 射出形成的电流为I ,求圆柱体A 在t 时间内发射电子的数量N.(忽略C 、D 间的距离以及电子碰撞到C 、D 上的反射效应和金属网对电子的吸收)(3)若A 、C 间不加电压,要使由A 发射的电子不从金属网C 射出,可在金属网内环形区域加垂直于圆平面向里的匀强磁场,求所加磁场磁感应强度B 的最小值. 【答案】(1)22e eUv v m=+4alt N ed π=(3) 43mv B ae = 【解析】 【分析】(1)根据动能定理求解求电子通过金属网C 发射出来的速度大小;(2)根据=neI t求解圆柱体A 在时间t 内发射电子的数量N ;(3)使由A 发射的电子不从金属网C 射出,则电子在 CA 间磁场中做圆周运动时,其轨迹圆与金属网相切,由几何关系求解半径,从而求解B. 【详解】(1)对电子经 CA 间的电场加速时,由动能定理得221122e e U mv mv =- 解得:22e eUv v m=+(2)设时间t 从A 中发射的电子数为N ,由M 口射出的电子数为n , 则 =ne I t224d dNn N a aππ==⨯解得4altN edπ=(3)电子在 CA 间磁场中做圆周运动时,其轨迹圆与金属网相切时,对应的磁感应强度为B .设此轨迹圆的半径为 r ,则222(2)a r r a -=+2v Bev m r=解得:43mvB ae=2.“太空粒子探测器”是由加速、偏转和收集三部分组成,其原理可简化如下:如图1所示,辐射状的加速电场区域边界为两个同心平行半圆弧面,圆心为O ,外圆弧面AB 的电势为2L()o ϕ>,内圆弧面CD 的电势为φ,足够长的收集板MN 平行边界ACDB ,ACDB 与MN 板的距离为L .假设太空中漂浮着质量为m ,电量为q 的带正电粒子,它们能均匀地吸附到AB 圆弧面上,并被加速电场从静止开始加速,不计粒子间的相互作用和其它星球对粒子的影响,不考虑过边界ACDB 的粒子再次返回.(1)求粒子到达O 点时速度的大小;(2)如图2所示,在PQ (与ACDB 重合且足够长)和收集板MN 之间区域加一个匀强磁场,方向垂直纸面向内,则发现均匀吸附到AB 圆弧面的粒子经O 点进入磁场后最多有23能打到MN 板上,求所加磁感应强度的大小;(3)如图3所示,在PQ (与ACDB 重合且足够长)和收集板MN 之间区域加一个垂直MN 的匀强电场,电场强度的方向如图所示,大小4E Lφ=,若从AB 圆弧面收集到的某粒子经O 点进入电场后到达收集板MN 离O 点最远,求该粒子到达O 点的速度的方向和它在PQ 与MN 间运动的时间. 【答案】(1)2q v mϕ=;(2)12m B L q ϕ=;(3)060α∴= ;22m L q ϕ【解析】 【分析】 【详解】试题分析:解:(1)带电粒子在电场中加速时,电场力做功,得:2102qU mv =-2U ϕϕϕ=-=2q v mϕ=(2)从AB 圆弧面收集到的粒子有23能打到MN 板上,则上端刚好能打到MN 上的粒子与MN 相切,则入射的方向与OA 之间的夹角是60︒,在磁场中运动的轨迹如图甲,轨迹圆心角060θ=.根据几何关系,粒子圆周运动的半径:2R L =由洛伦兹力提供向心力得:2v qBv m R=联合解得:12m B L qϕ=(3)如图粒子在电场中运动的轨迹与MN 相切时,切点到O 点的距离最远, 这是一个类平抛运动的逆过程. 建立如图坐标.212qE L t m= 222mL mt L qE q ϕ== 22x Eq qEL q v t m m m ϕ===若速度与x 轴方向的夹角为α角 cos x v v α=1cos 2α=060α∴=3.如图甲所示,在直角坐标系中的0≤x≤L 区域内有沿y 轴正方向的匀强电场,右侧有以点(2L ,0)为圆心、半径为L 的圆形区域,与x 轴的交点分别为M 、N ,在xOy 平面内,从电离室产生的质量为m 、带电荷量为e 的电子以几乎为零的初速度从P 点飘入电势差为U 的加速电场中,加速后经过右侧极板上的小孔Q 点沿x 轴正方向进入匀强电场,已知O 、Q 两点之间的距离为2L,飞出电场后从M 点进入圆形区域,不考虑电子所受的重力。
带电粒子在匀强磁场中的运动计算题含答案

带电粒子在匀强磁场中的运动计算题1.如图,空间存在方向垂直于纸面(xOy平面)向里的磁场。
在x≥0区域,磁感应强度的大小为B0;x<0区域,磁感应强度的大小为λB0(常数λ>1)。
一质量为m、电荷量为q(q>0)的带电粒子以速度v0从坐标原点O沿x轴正向射入磁场,此时开始计时,当粒子的速度方向再次沿x轴正向时,求(不计重力)(1)粒子运动的时间;(2)粒子与O点间的距离。
2.平面直角坐标系xOy中,第Ⅰ象限存在垂直于平面向里的匀强磁场,第Ⅲ象限存在沿y轴负方向的匀强电场,如图所示。
一带负电的粒子从电场中的Q点以速度v0沿x轴正方向开始运动,Q点到y轴的距离为到x轴距离的2倍。
粒子从坐标原点O离开电场进入磁场,最终从x轴上的P点射出磁场,P点到y轴距离与Q点到y轴距离相等。
不计粒子重力,求:(1)粒子到达O点时速度的大小和方向;(2)电场强度和磁感应强度的大小之比。
3.如图,在y>0的区域存在方向沿y轴负方向的匀强电场,场强大小为E,在y<0的区域存在方向垂直于xOy 平面向外的匀强磁场。
一个氕核11H和一个氘核12H先后从y轴上y=h点以相同的动能射出,速度方向沿x 轴正方向。
已知11H进入磁场时,速度方向与x轴正方向的夹角为60°,并从坐标原点O处第一次射出磁场。
1H的质量为m,电荷量为q,不计重力。
求1(1)11H第一次进入磁场的位置到原点O的距离;(2)磁场的磁感应强度大小;(3)12H第一次离开磁场的位置到原点O的距离。
4.如图甲,空间存在﹣范围足够大的垂直于xOy平面向外的匀强磁场,磁感应强度大小为B.让质量为m,电量为q(q>0)的粒子从坐标原点O沿xOy平面以不同的初速度大小和方向入射到该磁场中。
不计重力和粒子间的影响。
(1)若粒子以初速度v1沿y轴正向入射,恰好能经过x轴上的A(a,0)点,求v1的大小;(2)已知一粒子的初速度大小为v(v>v1),为使该粒子能经过A(a,0)点,其入射角θ(粒子初速度与x 轴正向的夹角)有几个?并求出对应的sinθ值;(3)如图乙,若在此空间再加入沿y轴正向、大小为E的匀强电场,一粒子从O点以初速度v0沿y轴正向发射。
带电粒子在磁场中的圆周运动---经典练习题(含答案详解)

电粒子在磁场中的圆周运动1.处于匀强磁场中的一个带电粒子,仅在磁场力作用下做匀速圆周运动.将该粒子的运动等效为环形电流,那么此电流值( ) A .与粒子电荷量成正比 B .与粒子速率成正比 C .与粒子质量成正比 D .与磁感应强度成正比答案 D解析 假设带电粒子的电荷量为q ,在磁场中做圆周运动的周期为T =2πm qB ,则等效电流i =q T =q 2B2πm ,故答案选D.带电粒子在有界磁场中的运动2.如图377所示,在第Ⅰ象限内有垂直纸面向里的匀强磁场,一对正、负电子分别以相同速率沿与x 轴成30°角的方向从原点射入磁场,则正、负电子在磁场中运动的时间之比为( )图377A .1∶2B .2∶1C .1∶ 3D .1∶1答案 B解析 正、负电子在磁场中运动轨迹如图所示,正电子做匀速圆周运动在磁场中的部分对应圆心角为120°,负电子圆周部分所对应圆心角为60°,故时间之比为2∶1.回旋加速器问题图3783.回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个D 形金属盒,两盒间的狭缝中形成的周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D 形金属盒处于垂直于盒底面的匀强磁场中,如图378所示,要增大带电粒子射出时的动能,下列说法中正确的是( ) A .增加交流电的电压 B .增大磁感应强度 C .改变磁场方向 D .增大加速器半径答案 BD解析 当带电粒子的速度最大时,其运动半径也最大,由牛顿第二定律q v B =m v 2r ,得v =qBrm .若D 形盒的半径为R ,则R =r 时,带电粒子的最终动能E km =12m v 2=q 2B 2R 22m .所以要提高加速粒子射出的动能,应尽可能增大磁感应强度B 和加速器的半径R .(时间:60分钟)题组一 带电粒子在磁场中的圆周运动图3791.如图379所示,ab 是一弯管,其中心线是半径为R 的一段圆弧,将它置于一给定的匀强磁场中,方向垂直纸面向里.有一束粒子对准a 端射入弯管,粒子的质量、速度不同,但都是一价负粒子,则下列说法正确的是( )A .只有速度大小一定的粒子可以沿中心线通过弯管B .只有质量大小一定的粒子可以沿中心线通过弯管C .只有质量和速度乘积大小一定的粒子可以沿中心线通过弯管D .只有动能大小一定的粒子可以沿中心线通过弯管 答案 C解析 由R =m vqB 可知,在相同的磁场,相同的电荷量的情况下,粒子做圆周运动的半径决定于粒子的质量和速度的乘积.图37102.如图3710所示,水平导线中有电流I 通过,导线正下方的电子初速度的方向与电流I 的方向相同,则电子将( )A .沿路径a 运动,轨迹是圆B .沿路径a 运动,轨迹半径越来越大C .沿路径a 运动,轨迹半径越来越小D .沿路径b 运动,轨迹半径越来越小 答案 B解析 由左手定则可判断电子运动轨迹向下弯曲.又由r =m vqB 知,B 减小,r 越来越大,故电子的径迹是a .故选B.3.一电子在匀强磁场中,以一正电荷为圆心在一圆轨道上运行.磁场方向垂直于它的运动平面,电场力恰好是磁场作用在电子上的磁场力的3倍,电子电荷量为e ,质量为m ,磁感应强度为B ,那么电子运动的角速度可能为( )A .4Be mB .3Be mC .2Be m D.Be m答案 AC解析 向心力可能是F 电+F B 或F 电-F B ,即4eB v 1=m v 21R =mω21R 或2eB v 2=m v 22R =mω22R ,所以角速度为ω1=4Be m 或ω2=2Be m.故A 、C 正确.4.在匀强磁场中,一个带电粒子做匀速圆周运动,如果又顺利垂直进入另一磁感应强度是原来磁感应强度2倍的匀强磁场中做匀速圆周运动,则( ) A .粒子的速率加倍,周期减半 B .粒子的速率不变,轨道半径减半 C .粒子的速率减半,轨道半径变为原来的14D .粒子的速率不变,周期减半 答案 BD解析 由R =m v qB 可知,磁场加倍半径减半,洛伦兹力不做功,速率不变,由T =2πmBq 可知,周期减半,故B 、D 选项正确.图37115.如图3711所示,一带电粒子(重力不计)在匀强磁场中沿图中轨道运动,中央是一薄绝缘板,粒子在穿过绝缘板时有动能损失,由图可知( ) A .粒子的运动方向是abcde B .粒子带正电C .粒子的运动方向是edcbaD .粒子在下半周期比上半周期所用时间长 答案 BC题组二 带电粒子在有界磁场中运动图37126.空间存在方向垂直于纸面向里的匀强磁场,图3712中的正方形为其边界.一细束由两种粒子组成的粒子流沿垂直于磁场的方向从O 点入射.这两种粒子带同种电荷,它们的电荷量、质量均不同,但其比荷相同,且都包含不同速率的粒子.不计重力.下列说法正确的是( ) A .入射速度不同的粒子在磁场中的运动时间一定不同 B .入射速度相同的粒子在磁场中的运动轨迹一定相同 C .在磁场中运动时间相同的粒子,其运动轨迹一定相同D .在磁场中运动时间越长的粒子,其轨迹所对的圆心角一定越大 答案 BD解析 由于粒子比荷相同,由R =m vqB 可知速度相同的粒子轨迹半径相同,运动轨迹也必相同,B 正确.对于入射速度不同的粒子在磁场中可能的运动轨迹如图所示,由图可知,粒子的轨迹直径不超过磁场边界一半时转过的圆心角都相同,运动时间都为半个周期,而由T =2πmqB 知所有粒子在磁场运动周期都相同,A 、C 皆错误.再由t =θ2πT =θmqB可知D 正确,故选BD.图37137.如图3713所示,有界匀强磁场边界线SP ∥MN ,速率不同的同种带电粒子从S 点沿SP 方向同时射入磁场.其中穿过a 点的粒子速度v 1与MN 垂直;穿过b 点的粒子速度v 2与MN 成60°角,设粒子从S 到a 、b 所需时间分别为t 1和t 2,则t 1∶t 2为(重力不计)( ) A .1∶3 B .4∶3 C .1∶1 D .3∶2答案 D解析 如图所示,可求出从a 点射出的粒子对应的圆心角为90°.从b 点射出的粒子对应的圆心角为60°.由t =α2πT ,可得:t 1∶t 2=3∶2,故选D.图37148.如图3714所示,直角三角形ABC 中存在一匀强磁场,比荷相同的两个粒子沿AB 方向射入磁场,分别从AC 边上的P 、Q 两点射出,则( ) A .从P 射出的粒子速度大 B .从Q 射出的粒子速度大C .从P 射出的粒子,在磁场中运动的时间长D .两粒子在磁场中运动的时间一样长 答案 BD解析 作出各自的轨迹如图所示,根据圆周运动特点知,分别从P 、Q 点射出时,与AC 边夹角相同,故可判定从P 、Q 点射出时,半径R 1<R 2,所以,从Q 点射出的粒子速度大,B 正确;根据图示,可知两个圆心角相等,所以,从P 、Q 点射出时,两粒子在磁场中的运动时间相等.正确选项应是B 、D. 题组三 质谱仪和回旋加速器图37159.如图3715是质谱仪的工作原理示意图.带电粒子被加速电场加速后,进入速度选择器.速度选择器内相互正交的匀强磁场和匀强电场的强度分别为B 和E .平板S 上有可让粒子通过的狭缝P 和记录粒子位置的胶片A 1A 2.平板S 下方有磁感应强度为B 0的匀强磁场.下列表述正确的是( ) A .质谱仪是分析同位素的重要工具 B .速度选择器中的磁场方向垂直纸面向外 C .能通过狭缝P 的带电粒子的速率等于EBD .粒子打在胶片上的位置越靠近狭缝P ,粒子的比荷越小答案 ABC解析 质谱仪是测量带电粒子的质量和分析同位素的重 要工具,故A 选项正确;速度选择器中电场力和洛伦兹力是一对平衡力,即:q v B =qE ,故v =EB ,根据左手定则可以确定,速度选择器中的磁场方向垂直纸面向外,故B 、C 选项正确.粒子在匀强磁场中运动的半径r =m v qB 0,即粒子的比荷qm =v B 0r ,由此看出粒子的运动半径越小,粒子打在胶片上的位置越靠近狭缝P ,粒子的比荷越大,故D 选项错误. 10.用回旋加速器分别加速α粒子和质子时,若磁场相同,则加在两个D 形盒间的交变电压的频率应不同,其频率之比为( )A .1∶1B .1∶2C .2∶1D .1∶3 答案 B图371611.(2014·高新区高二检测)一个用于加速质子的回旋加速器,其核心部分如图3716所示,D 形盒半径为R ,垂直D 形盒底面的匀强磁场的磁感应强度为B ,两盒分别与交流电源相连.下列说法正确的是( ) A .质子被加速后的最大速度随B 、R 的增大而增大 B .质子被加速后的最大速度随加速电压的增大而增大 C .只要R 足够大,质子的速度可以被加速到任意值 D .不需要改变任何量,这个装置也能用于加速α粒子 答案 A解析 由r =m v qB 知,当r =R 时,质子有最大速度v m =qBRm ,即B 、R 越大,v m 越大,v m 与加速电压无关,A 对、B 错.随着质子速度v 的增大、质量m 会发生变化,据T =2πmqB 知质子做圆周运动的周期也变化,所加交流电与其运动不再同步,即质子不可能一直被加速下去,C 错.由上面周期公式知α粒子与质子做圆周运动的周期不同,故此装置不能用于加速α粒子,D 错. 题组四 综合应用图371712.带电粒子的质量m =1.7×10-27kg ,电荷量q =1.6×10-19C ,以速度v =3.2×106 m/s 沿垂直于磁场同时又垂直于磁场边界的方向进入匀强磁场中,磁场的磁感应强度为B =0.17 T ,磁场的宽度L =10 cm ,如图3717所示.(1)带电粒子离开磁场时的速度多大? (2)带电粒子在磁场中运动多长时间?(3)带电粒子在离开磁场时偏离入射方向的距离d 为多大?(g 取10 m/s 2) 答案 见解析解析 粒子所受的洛伦兹力F 洛=q v B ≈8.7×10-14 N ,远大于粒子所受的重力G =mg =1.7×10-26 N ,故重力可忽略不计.(1)由于洛伦兹力不做功,所以带电粒子离开磁场时速度仍为3.2×106 m/s.(2)由q v B =m v 2r 得轨道半径r =m v qB =1.7×10-27×3.2×1061.6×10-19×0.17m =0.2 m .由题图可知偏转角θ满足:sin θ=Lr =0.1 m 0.2 m =0.5,所以θ=30°=π6,带电粒子在磁场中运动的周期T =2πm qB,可见带电粒子在磁场中运动的时间t =θ2π·T =112T ,所以t =πm 6qB = 3.14×1.7×10-276×1.6×10-19×0.17 s ≈3.3×10-8 s. (3)带电粒子在离开磁场时偏离入射方向的距离d =r (1-cos θ)=0.2×(1-32)m ≈2.7×10-2 m.图371813.如图3718所示,两个板间存在垂直纸面向里的匀强磁场,一带正电的质子以速度v 0从O 点垂直射入.已知两板之间距离为d .板长为d ,O 点是NP 板的正中点,为使粒子能从两板之间射出,试求磁感应强度B 应满足的条件(已知质子带电荷量为q ,质量为m ). 答案4m v 05dq ≤B ≤4m v 0dq解析 如图所示,由于质子在O 点的速度垂直于板NP ,所以粒子在磁场中做圆周运动的圆心O ′一定位于NP 所在的直线上.如果直径小于ON ,则轨迹将是圆心位于ON 之间的一段半圆弧. (1)如果质子恰好从N 点射出,R 1=d 4,q v 0B 1=m v 20R 1.所以B 1=4m v 0dq.(2)如果质子恰好从M 点射出R 22-d 2=⎝⎛⎭⎫R 2-d 22,q v 0B 2=m v 20R 2,得B 2=4m v 05dq.所以B 应满足4m v 05dq ≤B ≤4m v 0dq.图371914.如图3719,一个质量为m ,电荷量为-q ,不计重力的带电粒子从x 轴上的P (a,0)点以速度v ,沿与x 轴正方向成60°的方向射入第一象限内的匀强磁场中,并恰好垂直于y 轴射出第一象限,求: (1)匀强磁场的磁感应强度B ; (2)穿过第一象限的时间. 答案 (1)3m v 2qa (2)43πa 9v解析 (1)作出带电粒子做圆周运动的圆心和轨迹,由图中几何关系知: R cos 30°=a ,得:R =23a3Bq v =m v 2R 得:B =m v qR =3m v2qa .(2)运动时间:t =120°360°·2πm qB =43πa9v.。
高中物理(新人教版)选择性必修二课后习题:带电粒子在匀强磁场中的运动(课后习题)【含答案及解析】

第一章安培力与洛伦兹力带电粒子在匀强磁场中的运动课后篇素养形成必备知识基础练1.如图所示,MN为铝质薄平板,铝板上方和下方分别有垂直于纸面的匀强磁场(未画出)。
一带电粒子从紧贴铝板上表面的P点垂直于铝板向上射出,从Q点穿越铝板后到达PQ的中点O。
已知粒子穿越铝板时,其动能损失一半,速度方向和电荷量不变。
不计重力。
铝板上方和下方的磁感应强度大小之比为()A.2B.√2C.1D.√22P点时初速度为v1,从Q点穿过铝板后速度为v2,则E k1=12m v12,E k2=12m v22;由题意可知E k1=2E k2,即12m v12=m v22,则v1v2=√21。
由洛伦兹力提供向心力,即qvB=mv2r,得r=mvqB,由题意可知r1r2=21,所以B1B2=v1r2v2r1=√22,故选项D正确。
2.(多选)空间存在方向垂直于纸面向里的匀强磁场,如图所示的正方形虚线为其边界。
一细束由两种粒子组成的粒子流沿垂直于磁场的方向从O点入射。
这两种粒子带同种电荷,它们的电荷量、质量均不同,但其比荷相同,且都包含不同速率的粒子。
不计重力。
下列说法正确的是()A.入射速度不同的粒子在磁场中的运动时间一定不同B.入射速度相同的粒子在磁场中的运动轨迹一定相同C.在磁场中运动时间相同的粒子,其运动轨迹一定相同D.在磁场中运动时间越长的粒子,其轨迹所对的圆心角一定越大由于粒子比荷相同,由r=mvqB可知入射速度相同的粒子运动半径相同,运动轨迹也必相同,B正确;对于入射速度不同的粒子在磁场中可能的运动轨迹如图所示,由图可知,粒子的轨迹直径不超过磁场边界一半时转过的圆心角都相同,运动时间都为半个周期,而由T=2πmqB知所有粒子在磁场中运动周期都相同,A、C错误;再由t=θ2πT=θmqB可知D正确。
故选B、D。
3.(多选)如图所示,a、b、c、d为4个正离子,电荷量均为q,同时沿图示方向进入速度选择器后,a粒子射向P1板,b粒子射向P2板,c、d两粒子通过速度选择器后,进入另一磁感应强度为B2的磁场,分别打在A1和A2两点,A1和A2两点相距Δx。
专题57 带电粒子在磁场中的运动(解析版)

2023届高三物理一轮复习多维度导学与分层专练专题57 带电粒子在磁场中的运动导练目标 导练内容目标1 洛伦兹力的大小方向 目标2 带电粒子在有界磁场中的运动 目标3带电粒子在磁场中运动的多解问题一、洛伦兹力的大小方向 1.洛伦兹力的大小和周期(1)大小:qvB F =(v B ⊥);(2)向心力公式:rmv qvB 2=;(3)周期:22r m T v qB ππ== 2.洛伦兹力的特点(1)利用左手定则判断洛伦兹力的方向,注意区分正、负电荷。
(2)当电荷运动方向发生变化时,洛伦兹力的方向也随之变化。
(3)运动电荷在磁场中不一定受洛伦兹力作用。
(4)洛伦兹力永不做功。
3.洛伦兹力的方向 (1)判断方法:左手定则(2)方向特点:洛伦兹力的方向一定与粒子速度方向和磁感应强度方向所决定的平面垂直(B 与v 可以有任意夹角)。
注意:由左手定则判断洛伦兹力方向时,四指指向正电荷运动的方向或负电荷运动的反方向。
【例1】如图所示,光滑的水平桌面处于匀强磁场中,磁场方向竖直向下,磁感应强度大小为B ;在桌面上放有内壁光滑、长为L 的试管,底部有质量为m 、带电量为q 的小球,试管在水平向右的拉力作用下以速度v 向右做匀速直线运动(拉力与试管壁始终垂直),带电小球能从试管口处飞出,关于带电小球及其在离开试管前的运动,下列说法中正确的是( )A .小球带负电,且轨迹为抛物线B .小球运动到试管中点时,水平拉力的大小应增大至qvBLqBmC .洛伦兹力对小球做正功D .对小球在管中运动全过程,拉力对试管做正功,大小为qvBL 【答案】BD【详解】A .小球能从试管口处飞出,说明小球受到指向试管口的洛伦兹力,根据左手定则判断,小球带正电;小球沿试管方向受到洛伦兹力的分力y F qvB =恒定,小球运动的轨迹是一条抛物线,故A 错误;B .由于小球相对试管做匀加速直线运动,会受到与试管垂直且向左的洛,则拉力应增大伦兹力的分力x y F qv B =小球运动到中点时沿管速度为22y qvB L v m =⨯qvBL F m=持匀速运动,故B 正确;C .沿管与垂直于管洛伦兹力的分力合成得到的实际洛伦兹力总是与速度方向垂直,不做功,故C 错误;D .对试管、小球组成的系统,拉力做功的效果就是增加小球的动能,由功能关系F k W E qvBL =∆=故D 正确;故选BD 。
高考物理带电粒子在磁场中的运动题20套(带答案)含解析

高考物理带电粒子在磁场中的运动题20套(带答案)含解析一、带电粒子在磁场中的运动专项训练1.如图所示,两条竖直长虚线所夹的区域被线段MN 分为上、下两部分,上部分的电场方向竖直向上,下部分的电场方向竖直向下,两电场均为匀强电场且电场强度大小相同。
挡板PQ 垂直MN 放置,挡板的中点置于N 点。
在挡板的右侧区域存在垂直纸面向外的匀强磁场。
在左侧虚线上紧靠M 的上方取点A,一比荷qm=5×105C/kg 的带正电粒子,从A 点以v 0=2×103m/s 的速度沿平行MN 方向射入电场,该粒子恰好从P 点离开电场,经过磁场的作用后恰好从Q 点回到电场。
已知MN 、PQ 的长度均为L=0.5m ,不考虑重力对带电粒子的影响,不考虑相对论效应。
(1)求电场强度E 的大小; (2)求磁感应强度B 的大小;(3)在左侧虚线上M 点的下方取一点C ,且CM=0.5m ,带负电的粒子从C 点沿平行MN 方向射入电场,该带负电粒子与上述带正电粒子除电性相反外其他都相同。
若两带电粒子经过磁场后同时分别运动到Q 点和P 点,求两带电粒子在A 、C 两点射入电场的时间差。
【答案】(1) 16/N C (2) 21.610T -⨯ (3) 43.910s -⨯ 【解析】 【详解】(1)带正电的粒子在电场中做类平抛运动,有:L=v 0t2122L qE t m = 解得E=16N/C(2)设带正电的粒子从P 点射出电场时与虚线的夹角为θ,则:0tan v qE t mθ=可得θ=450粒子射入磁场时的速度大小为2v 0粒子在磁场中做匀速圆周运动:2v qvB m r=由几何关系可知2r L = 解得B=1.6×10-2T(3)两带电粒子在电场中都做类平抛运动,运动时间相同;两带电粒子在磁场中都做匀速圆周运动,带正电的粒子转过的圆心角为32π,带负电的粒子转过的圆心角为2π;两带电粒子在AC 两点进入电场的时间差就是两粒子在磁场中的时间差; 若带电粒子能在匀强磁场中做完整的圆周运动,则其运动一周的时间22r mT v qBππ==; 带正电的粒子在磁场中运动的时间为:4135.910s 4t T -==⨯; 带负电的粒子在磁场中运动的时间为:4212.010s 4t T -==⨯ 带电粒子在AC 两点射入电场的时间差为412 3.910t t t s -∆=-=⨯2.如图纸面内的矩形 ABCD 区域存在相互垂直的匀强电场和匀强磁场,对边 AB ∥CD 、AD ∥BC ,电场方向平行纸面,磁场方向垂直纸面,磁感应强度大小为 B .一带电粒子从AB 上的 P 点平行于纸面射入该区域,入射方向与 AB 的夹角为 θ(θ<90°),粒子恰好做匀速直线运动并从 CD 射出.若撤去电场,粒子以同样的速度从P 点射入该区域,恰垂直 CD 射出.已知边长 AD=BC=d ,带电粒子的质量为 m ,带电量为 q ,不计粒子的重力.求:(1)带电粒子入射速度的大小;(2)带电粒子在矩形区域内作直线运动的时间; (3)匀强电场的电场强度大小.【答案】(1)cos qBd m θ(2)cos sin m qB θθ (3)2cos qB dm θ【解析】【分析】画出粒子的轨迹图,由几何关系求解运动的半径,根据牛顿第二定律列方程求解带电粒子入射速度的大小;带电粒子在矩形区域内作直线运动的位移可求解时间;根据电场力与洛伦兹力平衡求解场强. 【详解】(1) 设撤去电场时,粒子在磁场中做匀速圆周运动的半径为R ,画出运动轨迹如图所示,轨迹圆心为O .由几何关系可知:cos d Rθ=洛伦兹力做向心力:200v qv B m R= 解得0cos qBdv m θ=(2)设带电粒子在矩形区域内作直线运动的位移为x ,有sin d xθ= 粒子作匀速运动:x=v 0t 联立解得cos sin m t qB θθ=(3)带电粒子在矩形区域内作直线运动时,电场力与洛伦兹力平衡:Eq=qv 0B解得2qB dE mcos θ=【点睛】此题关键是能根据粒子的运动情况画出粒子运动的轨迹图,结合几何关系求解半径等物理量;知道粒子作直线运动的条件是洛伦兹力等于电场力.3.科学家设想在宇宙中可能存在完全由反粒子构成的反物质.例如:正电子就是电子的反粒子,它跟电子相比较,质量相等、电量相等但电性相反.如图是反物质探测卫星的探测器截面示意图.MN 上方区域的平行长金属板AB 间电压大小可调,平行长金属板AB 间距为d ,匀强磁场的磁感应强度大小为B ,方向垂直纸面向里.MN 下方区域I 、II 为两相邻的方向相反的匀强磁场区,宽度均为3d ,磁感应强度均为B ,ef 是两磁场区的分界线,PQ 是粒子收集板,可以记录粒子打在收集板的位置.通过调节平行金属板AB 间电压,经过较长时间探测器能接收到沿平行金属板射入的各种带电粒子.已知电子、正电子的比荷是b ,不考虑相对论效应、粒子间的相互作用及电磁场的边缘效应.(1)要使速度为v 的正电子匀速通过平行长金属极板AB ,求此时金属板AB 间所加电压U ;(2)通过调节电压U 可以改变正电子通过匀强磁场区域I 和II 的运动时间,求沿平行长金属板方向进入MN 下方磁场区的正电子在匀强磁场区域I 和II 运动的最长时间t m ; (3)假如有一定速度范围的大量电子、正电子沿平行长金属板方向匀速进入MN 下方磁场区,它们既能被收集板接收又不重叠,求金属板AB 间所加电压U 的范围.【答案】(1)Bvd (2)Bb π(3)3B 2d 2b <U <221458B d b【解析】 【详解】(1)正电子匀速直线通过平行金属极板AB ,需满足 Bev=Ee因为正电子的比荷是b ,有 E=U d联立解得:u Bvd =(2)当正电子越过分界线ef 时恰好与分界线ef 相切,正电子在匀强磁场区域I 、II 运动的时间最长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
带电粒子在磁场中的运动练习题 2016.11.231. 如图所示,一个带正电荷的物块m由静止开始从斜面上A点下滑,滑到水平面上的D点停下来.已知物块与斜面及水平面间的动摩擦因数相同,且不计物块经过B处时的机械能损失.先在所在空间加竖直向下的匀强电场,第二次让物块m从A点由静止开始下滑,结果物块在水平面上的D′点停下来.后又撤去电场,在所在空间加水平向里的匀强磁场,再次让物块m从A点由静止开始下滑,结果物块沿斜面滑下并在水平面上的D″点停下来.则以下说法中正确的是( )A.D′点一定在D点左侧B.D′点一定与D点重合C.D″点一定在D点右侧D.D″点一定与D点重合2. 一个质量为m、带电荷量为的圆环,可在水平放置的足够长的粗糙细杆上滑动,细杆处于磁感应强度为B的匀强磁场中.现给圆环向右初速度v0,在以后的运动过程中,圆环运动的速度图象可能是()A.B.C.D.3. 如图所示,在长方形区域内有正交的电磁场,2,一带电粒子从的中点垂直于电场和磁场方向射入,恰沿直线从边的中点P射出,若撤去磁场,则粒子从c点射出;若撤去电场,则粒子将(重力不计)( )A .从b 点射出B .从b 、P 间某点射出C .从a 点射出D .从a 、b 间某点射出4. 如图所示,在真空中匀强电场的方向竖直向下,匀强磁场的方向垂直纸面向里,三个油滴a 、b 、c 带有等量同种电荷,其中a 静止,b 向右做匀速运动,c 向左匀速运动,比较它们的重力、、的大小关系,正确的是( ) A .最大 B .最大 C .最大 D .最小5. 如图所示,圆形区域内有垂直于纸面向里的匀强磁场,一个带电粒子以速度v 从A 点沿直径方向射入磁场,经过Δt 时间从C 点射出磁场,与成60°角。
现将带电粒子的速度变为3,仍从A 点射入磁场,不计重力,则粒子在磁场中的运动时间变为 ( )A.t ∆21 B. t ∆2 C. t ∆31 D. t ∆36. 如图所示,在平面内存在着磁感应强度大小为B 的匀强磁场,第一、二、四象限内的磁场方向垂直纸面向里,第三象限内的磁场方向垂直纸面向外.P (-L 2,0)、Q (0,-L 2)为坐标轴上的两个点.现有一电子从P 点沿方向射出,不计电子的重力,则. ( )A .若电子从P 点出发恰好经原点O 第一次射出磁场分界线,则电子运动的路程一定为2L πB .若电子从P 点出发经原点O 到达Q 点,则电子运动的路程一定为L πC .若电子从P 点出发经原点O 到达Q 点,则电子运动的路程可能为2L πD .若电子从P 点出发经原点O 到达Q 点,则n L π(n 为任意正整数)都有可能是电子运动的路程7. 如图,一束电子(电量为e )以速度v0垂直射入磁感应强度为B ,宽为d 的匀强磁场中,穿出磁场的速度方向与电子原来的入射方向的夹角为30°,求: (1)电子的质量是多少? (2)穿过磁场的时间是多少?(3)若改变初速度,使电子刚好不能从A 边射出,则此时速度v 是多少?8. 点S为电子源,它只在下图所示的纸面上360°范围内发射速率相同、质量为m、电荷量为e的电子,是一块足够大的竖直挡板,与S的水平距离。
挡板左侧有垂直纸面向里的匀强磁场,磁感应强度为B,求:(1)要使S发射的电子能够到达挡板,则发射电子的速度至少为多大?(2)若电子发射的速度为,则挡板被击中的范围有多大?9. 空间分布着有理想边界的匀强电场和匀强磁场。
左侧匀强电场的场强大小为E、方向水平向右,电场宽度为L;中间区域匀强磁场的磁感应强度大小为B,方向垂直纸面向外。
一个质量为m、电量为q、不计重力的带正电的粒子从电场的左边缘的O点由静止开始运动,穿过中间磁场区域进入右侧磁场区域后,又回到O点,然后重复上述运动过程.求:(1)中间磁场区域的宽度d;(2)带电粒子从O点开始运动到第一次回到O点所用时间t。
10. 在平面内y>0的区域中存在垂直于纸面向外的匀强磁场,磁感应强度大小为B0,在y<0的区域也存在垂直于纸面向外的匀强磁场(图中未画出),一带正电的粒子从y轴上的P点垂直于磁场入射,速度方向与y轴正向成45°。
粒子第一次进入y<0的区域时速度方向与x轴正向成135°,再次在y>0的区域运动时轨迹恰与y轴相切。
已知的距离为a2,粒子的重力不计。
求:(1)y<0的区域内磁场的磁感应强度大小;(2)粒子第2n(n∈N*)次通过x轴时离O点的距离。
(本问只需写出结果)11. 图中左边有一对平行金属板,两板相距为d,电压为V;两板之间有匀强磁场,磁感应强度大小为B0,方向平行于板面并垂直于纸面朝里,图中右边有一边长为a的正三角形区域(边与金属板垂直),在此区域内及其边界上也有匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里,假设一系列电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射人金属板之间,沿同一方向射出金属板之间的区域,并经边中点H射入磁场区域,不计重力。
(1)已知这些离子中的离子甲到达磁场边界后,从边界穿出磁场,求离子甲的质量;(2)已知这些离子中的离子乙从边上的I点(图中未画出)穿出磁场,且长为3/4a,求离子乙的质量;(3)若这些离子中的最轻离子的质量等于离子甲质量的一半,而离子乙的质量是最大的,问磁场边界上什么区域内可能有离子到达。
12. 如图所示,在边长为L的等边三角形区域内,存在磁感应强度为B、方向垂直纸面向外的匀强磁场。
现有一束质量为m、电荷量为的带电粒子,以某一速度从边中点P、平行于边垂直磁场射入,粒子的重力可忽略不计。
(1)若粒子进入磁场时的速度大小为v0,求粒子在磁场中运动的轨道半径;(2)若粒子能从边飞出磁场,求粒子在磁场中运动的时间;(3)为使粒子能边飞出磁场,粒子进入磁场时的速度大小应满足什么条件?13. 如图所示,在半径为qBmv R 0的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度B ,圆形区域右侧有一竖直感光板,从圆弧顶点P 以速率v0的带正电粒子平行于纸面进入磁场,已知粒子的质量为m ,电量为q ,粒子重力不计.(1)若粒子对准圆心射入,求它在磁场中运动的时间;(2)若粒子对准圆心射入,且速率为03v ,求它打到感光板上时速度的垂直分量; (3)若粒子以速度v 0从P 点以任意角入射,试证明它离开磁场后均垂直打在感光板上.带电粒子在磁场中的运动 练习题 2016.11.23参考答案:1. 【答案】 【解析】仅在重力场中时,物块由A 点至D 点的过程中,由动能定理得-μ1 α-μ2=0,即h -μs1 α-μs2=0,由题意知A 点距水平面的高度h 、物块与斜面及水平面间的动摩擦因数μ、斜面倾角α、斜面长度s1为定值,所以s2与重力的大小无关,而在所在空间加竖直向下的匀强电场后,相当于把重力增大了,s2不变,D′点一定与D 点重合,B 项正确;在所在空间加水平向里的匀强磁场后,洛伦兹力垂直于接触面向上,正压力变小,摩擦力变小,重力做的功不变,所以D″点一定在D 点右侧,C 项正确.2. 【答案】.【解析】由左手定则可知圆环所受洛伦兹力F 洛的方向竖直向上,细杆对圆环的支持力,圆环所受滑动摩擦力μ,圆环所受重力方向竖直向下,当时,0,故0,故圆环做匀速直线运动,故A正确.当<时,细杆对圆环的支持力方向竖直向上,,故f>0,物体作减速运动,随速度v的减小逐渐增大,故滑动摩擦力f逐渐增大,故物体的加速度逐渐增大,即物体作加速度逐渐增大的变减速运动,故C正确,而B 错误.当>时,细杆对圆环的支持力方向竖直向下,,故f>0,物体作减速运动,随速度v的减小逐渐减小,故滑动摩擦力f逐渐减小,故物体的加速度逐渐减小,即物体作加速度逐渐减小的变减速运动,当时,0,故0,故圆环做匀速直线运动,故D正确.3. 设粒子的质量为m,带电量为q,粒子射入电磁场时的速度为v0,则粒子沿直线通过场区时:0…①撤去磁场后,在电场力的作用下,从c点射出场区,所以粒子应带正电荷;在此过程中,粒子做类平抛运动,设粒子的加速度a,穿越电场所用时间为t,则有:…②(1/2)2…③0t …④撤去电场后,在洛仑兹力的作用下,粒子做圆周运动,洛仑兹力提供向心力:rvmBqv2…⑤由以上各式解得: /2粒子做圆运动的轨迹如图,粒子将从a点射出.故选:C.4. 【答案】【解析】 a球受力平衡,有①重力和电场力等值、反向、共线,故电场力向上,由于电场强度向下,故球带负电;b球受力平衡,有②c球受力平衡,有③解得>>故选.5. 【解析】:设有界圆磁场的半径为R,带电粒子的做匀速圆周运动的半径为r,与成600角,所以∠1C60°,带电粒子做匀速圆周运动,从C点穿出,画出轨迹,找到圆心O1,中,即,带电粒子在磁场中飞行时间,现将带电粒子的速度变为3,则带电粒子的运动半径,设带电粒子的圆心角为,则,故,运动时间,所以,选项B正确。
6. 【解析】:若电子从P点出发恰好经原点O第一次射出磁场分界线,则有运动轨迹如图所示,由几何关系知:半径R=L,则微粒运动的路程为圆周的1/4,即为2L,A正确;若电子从P点出发经原点O到达Q点,运动轨迹可能如图所示,因此则微粒运动的路程可能为πL,也可能为2πL,错误C正确;7. 【解析】:(1)设电子在磁场中运动轨道半径为r,电子的质量是m,由几何关系得:30° =2d ①电子在磁场中运动0=,②由①②得:(2)电子运动轨迹圆心角θ=30°周期穿过磁场的时间(3)电子刚好不能从A边射出电子轨道半径为r'由,得:8. 【解析】:(1)从S发射电子速度方向竖直向上,并且轨道半径恰好等于时,是能够达到挡板的最小发射速度。
如图,(2)如图,,所以击中挡板上边界的电子,发射角应为与水平成30°角斜向上,电子在磁场中恰好运动半圆周到达挡板上边界。
若要击中挡板下边界,电子发射方向正对挡板O点,电子在磁场中才能恰好运动1/4圆周到达挡板下边界9. 【解析】:(1)带电粒子在电场中加速,由动能定理,可得:带电粒子在磁场中偏转,由牛顿第二定律,可得:由以上两式,可得。
可见在两磁场区粒子运动半径相同,如图所示,三段圆弧的圆心组成的三角形△O1O2O3是等边三角形,其边长为2R。
所以中间磁场区域的宽度为。
2(2)在电场中运动时间在中间磁场中运动时间在右侧磁场中运动时间则粒子第一次回到O点的所用时间为。
[答案] (1)(2)10. 【解析】:(1)当粒子通过y轴时速度方向沿y轴负向时,粒子运动的轨迹如图(a)所示设粒子第一次、第二次通过x轴上的点分别为Q、M,粒子在y>0和y<0区域做圆周运动的半径分别为R0和R1,通过y轴上的点为N,y<0区域的磁感应强度大小为B1 .连接,由题意知:2R0又由几何关系可得:2a.解得:R0 过M、N两点分别作该点速度方向的垂线,两垂线相交于O1点,O1即为粒子在y>0区域做圆周运动的圆心.由几何关系可得:粒子在y<0区域内做圆周运动的弦长粒子在y<0区域内做圆周运动的半径带电粒子在磁场中做圆岗运动的半径公式解得当粒子通过y轴时速度方向沿y轴正向时,粒子运动的轨迹如图(b)所示设粒子第一次、第二次通过x轴上的点分别为T、S,粒子在y<0区域做圆周运动的半径为R2,y<0区域的磁感应强度大小为B2由几何关系可以求得解得(2)设粒子在两种情况下,第2n 次通过x轴时离O点的距离分别为S1、S2,当粒子通过y轴时速度方向沿y轴负向时,由几何关系可推算出:当粒子通过y轴时速度方向沿y轴正向时,由几何关系可推算出:11. 【解析】:(1)由题意知,所有离子在平行金属板之间做匀速直线运动,它所受到的向上的磁场力和向下的电场力平衡,有00 ①式中,v0是离子运动的速度,E0是平行金属板之间的匀强电场的强度,有②由①②式得③在正三角形磁场区域,离子甲做匀速圆周运动设离子甲质量为m,由洛伦兹力公式和牛顿第二定律有④式中,r是离子甲做圆周运动的半径,离子甲在磁场中的运动轨迹为半圆,圆心为O;这半圆刚好与边相切于K点,与边交于I'点。
