2012全国大学数学建模竞赛题目汇总(ABCD)1
2012年全国大学生数学建模竞赛A题国一

摘要
在问题一中,首先根据 T 检验、方差显著性检验和 Wilcoxon 秩和检验对两组评酒 员给葡萄酒的评价结果的差异的显著性检验。在大多数评酒员评分可靠的假设下,分别 利用评分方差比较模型,说明第二组结果可靠。在此基础上引入了评酒员“失误度”概 念来衡量每位评酒员与所有评酒员总体评价的差异, 对各组失误度求和得到第二组结果 更可靠。为了进一步优化评酒员评分,利用根据失误度对评酒员排序,跨组选取失误度 最小的 10 位评酒员组成新的评分组,其平均值认为比第二组更可靠,作为整个文章中 评价葡萄酒质量的标准指标。 在问题二中,由于红、白葡萄的理化指标有较大差异,分开考虑红白两种葡萄酒: 对于红葡萄酒,对应问题一得出的葡萄酒质量指标,从三个角度,即外观分析(又分为 由大分子因子决定的澄清度和基于 LAB 色彩模型的色调考虑到指标间存在的竞争关系 采用非线性回归分析和逐步回归分析) 、香气分析(Fisher 线性判别分析)和口感分析 (主成分分析和因子分析) ,后进行异常点检验,逐一剔除异常点来求解酿酒葡萄的量 化指标。对于白葡萄酒的三个指标采用 Fisher 判别分析求解。最后将三个方面得分加权 平均得到酿酒葡萄量化的总分,进行聚类分析,根据聚类分析结果将红葡萄和白葡萄各 分为四级。 在问题三中,为研究酿酒葡萄与葡萄酒的理化指标之间的联系,将葡萄酒的理化指 标用酿酒葡萄的理化指标来表示。根据指标间的相关性,剔除部分相关性不强的指标, 选择部分相关性较好的酿酒葡萄的指标作为自变量, 对不同的葡萄酒指标分别进行多元 线性回归、逐步回归和回归检验。根据指标本身的特点及 AIC 信息统计量,剔除不显著 的自变量,而达到用尽量少的葡萄的理化指标来表示葡萄酒的理化指标的目的。在求解 过程中,建立典型相关分析模型来分析红葡萄酒色泽指标间的关系,利用主成分分析将 白葡萄的多个指标综合为少数几个主成分,再进行回归分析。模型求解结果显示,葡萄 酒的每个指标都能用部分葡萄的指标来线性表示,且具有较好的拟合效果。 在问题四中,为了分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,结合问 题一、二、三的结果以及理化指标和芳香物质的化学意义,综合评估各个广义上的理化 指标(附件二和附件三) ,针对红葡萄酒和白葡萄酒的区别分别在酿酒葡萄和葡萄酒的 理化指标中选取对葡萄酒质量影响较大的指标, 通过线性回归分析将理化指标和葡萄酒 质量进行拟合,从而得出酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响。为进一步 论证结果,首先,对模型进行残差分析以及拟合情况分析;其次,用分组样本检验方法, 将白葡萄酒的 28 个样本数据分成两组,采用用一组进行拟合,另一组进行结果回带分 析的方式,进一步论证用葡萄和葡萄酒的理化指标来评价葡萄酒的质量的可靠性。通过 论证分析得出结论:葡萄和葡萄酒的理化指标可以用来评价葡萄酒的质量,但也有其不 足之处,如当从葡萄酒食用性方便角度考虑,用评酒员评价方法就更直接。 关键词:葡萄酒质量 识别聚类 失误度 非线性回归 逐步回归 Fisher 判别分析 主成 分分析 因子分析 显著性检验 残差分析 异常点检测
2012高教社杯全国大学生数学建模竞赛A题

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):20122125所属学校(请填写完整的全名):参赛队员(打印并签名):1.2.3.指导教师或指导教师组负责人(打印并签名):教练组日期:2012年9月10日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):葡萄酒的评价摘要本文要研究的是酿酒葡萄和葡萄酒理化指标与葡萄酒质量之间的关系。
对于问题一:首先从外观分析、香气分析、口感分析、平衡/整体评价以及各类指标总得分五个方面进行方差分析得到有显著性差异,然后进行T检验验证出第二组品酒员的结果更可信。
对于问题二:首先分析附件2中一级指标的数据,运用主成份分析法得出综合评价值,然后用聚类分析法得到葡萄样本的冰柱图,再综合第二组的评分进行酿酒葡萄的分级(升级排序),等级1样本:27,11,26,25,10等级1样本:18,12,25,28,27,24等级2样本:19,14,16,13,4,20等级2样本:3,26,10,15,5,7等级3样本:22,24,7,5,18,8,15等级3样本:9,23,20,2,14,6等级4样本:21,6,23,17,12等级4样本:13,19,21,4,11等级5样本:1,2,9,3等级5样本:17,16,1,8,22酿酒红葡萄酿酒白葡萄对于问题三:首先运用主成分分析法得到各主成分的贡献率,取贡献率最高的主成分列出关系式进行分析,进而筛选出重要理化指标,然后再进行典型相关分析,运用matlab进行编程,求得反应酿酒葡萄与葡萄酒的理化指标之间联系的典型相关系数,再进行典型相关系数的显著性检验,得到两者有显著性关系。
2012高教社杯全国大学生数学建模竞赛全国一等奖A题

2011高教社杯全国大学生数学建模竞赛城市表层土壤重金属污染分析摘要本文主要研究重金属对城市表层土壤污染的问题,我们根据题目所给定的一些数据和信息分析并建立了扩散传播模型、权重分配模型、对比模型和转换模型解决问题。
首先,我们利用Matlab 软件拟出该城区地势图(图1),根据所给数据绘出该地区的三维地势及采样点在其上的综合空间分布图。
之后将8种重金属的浓度等高线投影到该地区三维地形图曲面上,接着分别计算8种重金属在五个区域的平均值,立体图和平面图(图1附件)相结合便可得出8种重金属元素在该城区的空间分布。
其次,在确定该城区内不同区域重金属的污染程度时,我们运用两种方法进行解答。
先假设各重金属毒性及其它性质相同,运用公式ijij P C P ='求出各区域各金属相对于背景平均值的比值作为金属污染程度,再运用1ji ij j C C ==∑求出各区域重金属污染程度,并将各区进行比较。
之后,我们加上各重金属的毒性,对各重金属求出权数,再结合国标重金属污染等级和已知的各组数据来确定金属的污染程度。
由上述两种方法的对比,更准确地得出重金属对各区的影响程度。
即: 工业区>交通区>生活区>公园绿地区>山区 并根据第一个模型的数据来说明重金属污染的主要原因。
再次,对重金属污染物的传播特征进行了分析,判断出重金属污染物主要是通过大气、土壤和水流进行传播。
在分析之中,我们得出这三种状态的传播并不是孤立存在的,而是可以相互影响和叠加的,因此,我们分别建立三个传播模型,再对这三个传播模型进行了时间和空间上的拟合,得出重金属浓度最高的区域图,并结合各重金属的分布图(图6)来确定各污染源的位置。
最后,本题中只给出了重金属对土壤的污染,对于研究城市地质环境的演变模式,还需要搜集一些信息(图7)。
根据每种因素对地质环境的影响程度进行由定性到定量的转化。
建立同一地质时期地质环境中各因素的正影响和负影响的权重分配模型,再对这些权重进行验算和修正。
2012高教社杯全国大学生数学建模竞赛题目

2012高教社杯全国大学生数学建模竞赛题目
佚名
【期刊名称】《数学建模及其应用》
【年(卷),期】2012(001)004
【摘要】A题:葡萄酒的评价确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。
酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。
附件1给出了某一年份一些葡萄酒的评价结果,附件2和附件3分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据。
请尝试建立数学模型讨论下列问题:
【总页数】2页(P55-56)
【正文语种】中文
【相关文献】
1.雨量预报方法的模糊评价模型--2005高教社杯全国大学生数学建模竞赛题目之
一 [J], 杨金山;耿玉菊;马小女
2.2016年“高教社杯”全国大学生数学建模竞赛题目 [J],
3.NBA赛程的分析和评价——2008高教社杯全国大学生数学建模竞赛题目 [J], 马明远
4.2012高教社杯全国大学生数学建模竞赛题目 [J], ;
5.2016年“高教社杯”全国大学生数学建模竞赛题目 [J],
因版权原因,仅展示原文概要,查看原文内容请购买。
全国大学数学建模竞赛题目汇总(ABCD)

2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”)A题葡萄酒地评价确定葡萄酒质量时一般是通过聘请一批有资质地评酒员进行品评.每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒地质量.酿酒葡萄地好坏与所酿葡萄酒地质量有直接地关系,葡萄酒和酿酒葡萄检测地理化指标会在一定程度上反映葡萄酒和葡萄地质量.附件1给出了某一年份一些葡萄酒地评价结果,附件2和附件3分别给出了该年份这些葡萄酒地和酿酒葡萄地成分数据.请尝试建立数学模型讨论下列问题:1. 分析附件1中两组评酒员地评价结果有无显著性差异,哪一组结果更可信?2. 根据酿酒葡萄地理化指标和葡萄酒地质量对这些酿酒葡萄进行分级.3. 分析酿酒葡萄与葡萄酒地理化指标之间地联系.4.分析酿酒葡萄和葡萄酒地理化指标对葡萄酒质量地影响,并论证能否用葡萄和葡萄酒地理化指标来评价葡萄酒地质量?附件1:葡萄酒品尝评分表<含4个表格)附件2:葡萄和葡萄酒地理化指标<含2个表格)附件3:葡萄和葡萄酒地芳香物质<含4个表格)2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”)B题太阳能小屋地设计在设计太阳能小屋时,需在建筑物外表面<屋顶及外墙)铺设光伏电池,光伏电池组件所产生地直流电需要经过逆变器转换成220V交流电才能供家庭使用,并将剩余电量输入电网.不同种类地光伏电池每峰瓦地价格差别很大,且每峰瓦地实际发电效率或发电量还受诸多因素地影响,如太阳辐射强度、光线入射角、环境、建筑物所处地地理纬度、地区地气候与气象条件、安装部位及方式<贴附或架空)等.因此,在太阳能小屋地设计中,研究光伏电池在小屋外表面地优化铺设是很重要地问题.附件1-7提供了相关信息.请参考附件提供地数据,对下列三个问题,分别给出小屋外表面光伏电池地铺设方案,使小屋地全年太阳能光伏发电总量尽可能大,而单位发电量地费用尽可能小,并计算出小屋光伏电池35年寿命期内地发电总量、经济效益<当前民用电价按0.5元/kWh计算)及投资地回收年限.在求解每个问题时,都要求配有图示,给出小屋各外表面电池组件铺设分组阵列图形及组件连接方式<串、并联)示意图,也要给出电池组件分组阵列容量及选配逆变器规格列表.在同一表面采用两种或两种以上类型地光伏电池组件时,同一型号地电池板可串联,而不同型号地电池板不可串联.在不同表面上,即使是相同型号地电池也不能进行串、并联连接.应注意分组连接方式及逆变器地选配.问题1:请根据山西省大同市地气象数据,仅考虑贴附安装方式,选定光伏电池组件,对小屋<见附件2)地部分外表面进行铺设,并根据电池组件分组数量和容量,选配相应地逆变器地容量和数量.问题2:电池板地朝向与倾角均会影响到光伏电池地工作效率,请选择架空方式安装光伏电池,重新考虑问题1.问题3:根据附件7给出地小屋建筑要求,请为大同市重新设计一个小屋,要求画出小屋地外形图,并对所设计小屋地外表面优化铺设光伏电池,给出铺设及分组连接方式,选配逆变器,计算相应结果.附件1:光伏电池组件地分组及逆变器选择地要求附件2:给定小屋地外观尺寸图附件3:三种类型地光伏电池<A单晶硅、B多晶硅、C非晶硅薄膜)组件设计参数和市场价格附件4:大同典型气象年气象数据.特别注意:数据库中标注地时间为实际时间减1小时,即数据库中地11:00即为实际时间地12:00附件5:逆变器地参数及价格附件6:可参考地相关概念附件7:小屋地建筑要求2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”)C题脑卒中发病环境因素分析及干预脑卒中<俗称脑中风)是目前威胁人类生命地严重疾病之一,它地发生是一个漫长地过程,一旦得病就很难逆转.这种疾病地诱发已经被证实与环境因素,包括气温和湿度之间存在密切地关系.对脑卒中地发病环境因素进行分析,其目地是为了进行疾病地风险评估,对脑卒中高危人群能够及时采取干预措施,也让尚未得病地健康人,或者亚健康人了解自己得脑卒中风险程度,进行自我保护.同时,通过数据模型地建立,掌握疾病发病率地规律,对于卫生行政部门和医疗机构合理调配医务力量、改善就诊治疗环境、配置床位和医疗药物等都具有实际地指导意义.数据<见Appendix-C1)来源于中国某城市各家医院2007年1月至2018年12月地脑卒中发病病例信息以及相应期间当地地逐日气象资料<Appendix-C2).请你们根据题目提供地数据,回答以下问题:1.根据病人基本信息,对发病人群进行统计描述.2.建立数学模型研究脑卒中发病率与气温、气压、相对湿度间地关系.3.查阅和搜集文献中有关脑卒中高危人群地重要特征和关键指标,结合1、2中所得结论,对高危人群提出预警和干预地建议方案.2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”)D题机器人避障问题图1是一个800×800地平面场景图,在原点O(0,0>点处有一个机器人,它只能在该平面场景范围内活动.图中有12个不同形状地区域是机器人不能与之发生碰撞点与障碍物地距离至少超过10个单位).规定机器人地行走路径由直线段和圆弧组成,其中圆弧是机器人转弯路径.机器人不能折线转弯,转弯路径由与直线路径相切地一段圆弧组成,也可以由两个或多个相切地圆弧路径组成,但每个圆弧地半径最小为10个单位.为了不与障碍物发生碰撞,同时要求机器人行走线路与障碍物间地最近距离为10个单位,否则将发生碰撞,若碰撞发生,则机器人无法完成行走.机器人直线行走地最大速度为50=v 个单位/秒.机器人转弯时,最大转弯速度为21.0100e1)(ρρ-+==v v v ,其中ρ是转弯半径.如果超过该速度,机器人将发生侧翻,无法完成行走.请建立机器人从区域中一点到达另一点地避障最短路径和最短时间路径地数学模型.对场景图中4个点O(0,0>,A(300,300>,B(100,700>,C(700,640>,具体计算:(1> 机器人从O(0,0>出发,O→A 、O→B 、O→C 和O→A→B→C→O 地最短路径.(2> 机器人从O (0,0>出发,到达A 地最短时间路径.注:要给出路径中每段直线段或圆弧地起点和终点坐标、圆弧地圆心坐标以及机器人行走地总距离和总时间.图1800×800平面场景图。
2012高教社杯全国大学生数学建模竞赛 C题

其中, 2.对标准化阵Z求相关系数矩阵
,得标准化阵Z。
R [rij ] p
ZTZ xp n 1
kj
其中, rij
z
z kj
n 1
, i, j 1,2...p
3.解样本相关矩阵R的特征方程 R I p 0 得p个特征根,确定主成分
按
m j 1 p
j
j 1 j
四.问题分析
问题的重要性:
脑卒中俗称“中风”,是由向大脑输送血液的血管疾病引起的一种急 性疾病。脑卒中或脑血管意外( CVA )会对大脑组织造成突发性损坏,通常 发生在向大脑输送氧气和其它营养物的血管爆裂之时,或发生在血管被血 凝块或其它颗粒物质阻塞之时。如果神经细胞缺乏足够的氧气供给,几分 钟内就会死亡。接着,受这些神经细胞控制的身体机能也会随之失去作用。 由于死亡的大脑细胞无法替换,因此脑卒中造成的后果通常是永久的。患 有大血管急性缺血性发作的患者,每小时损失 1 亿 2 千万神经细胞、 8300 亿神经键、 和 714 千米有髓纤维。 每分钟有 190 万神经细胞、 140 亿神经键、 12 千米有髓纤维受损。与因大脑老化而产生的神经细胞的正常死亡速率相 比,缺血性大脑如果不接受治疗,则每小时老化 3.6 年。 专家指出:全国每年新发脑卒中患者达 200 万人,因此我们应该引起 关注,到底有哪些因素导致脑卒中患者逐年增加?接下来我们就对导致脑 卒中发病率的因素进行分析。
我们参赛选择的题号是(从 A/B/C/D 中选择一项填写) : 我们的参赛报名号为(如果赛区设置报名号的话) : 所属学校(请填写完整的全名) : 参赛队员 (打印并签名) :1. 2. 3. 指导教师或指导教师组负责人 (打印并签名): 日期: 2012 年 9
2012数学建模题目3篇

2012数学建模题目一、题目描述近年来,随着互联网技术的不断进步,移动互联网已经成为人们生活中不可或缺的一部分,而移动互联网产业的发展也越来越成熟。
然而,随着移动互联网用户数量的不断增长,如何提高移动互联网用户的使用体验成为了重要的问题。
本题要求通过对用户行为分析,建立数学模型,预测用户在移动互联网上的行为,并通过模型优化提高用户使用体验。
二、问题分析基于移动互联网用户的行为特征,我们可以将用户的使用过程分为以下几个阶段:1. 需求获取阶段:用户首先会通过各种渠道获取使用移动互联网的需求信息,例如通过搜索引擎、社交媒体等方式获取信息。
在这个阶段,用户主要进行信息搜索和筛选,并逐渐形成清晰的需求。
2. 功能使用阶段:在用户确定了需求之后,用户会选择相应的应用程序进行使用。
在这个阶段,用户主要进行应用程序的功能使用。
3. 反馈阶段:用户使用应用程序的过程中会对应用程序的界面、功能、速度等方面进行评价,并可能会向软件开发者反馈问题。
通过对这三个阶段的分析,我们可以发现用户行为具有以下特征:1. 多样性:用户的需求各不相同,对应用程序的评价也因人而异。
2. 实时性:用户使用移动互联网的过程中可能会随时变化,需要及时调整模型。
3. 复杂性:用户使用移动互联网的过程中涉及到多种维度的信息,需要通过数学模型进行分析和预测。
基于以上特征,我们需要建立合适的数学模型进行分析和预测。
三、模型建立为了建立数学模型,我们需要对用户行为数据进行采集、处理和分析。
具体地,我们需要考虑以下几个问题:1. 数据采集:我们需要通过各种手段进行数据的采集,例如使用爬虫技术对用户行为数据进行抓取。
2. 数据处理:在获取了足够的用户行为数据之后,我们需要对数据进行清洗、转换和统计,以便于进行数学模型的分析。
3. 数据分析:我们需要对数据进行统计分析,了解用户的行为特征和规律,并构建对应的数学模型进行预测。
基于以上思路,我们可以建立以下数学模型:1. 需求获取模型在需求获取阶段,用户通过搜索引擎、社交媒体等方式进行信息获取。
2012全国大学生数学建模比赛作品

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):02011所属学校(请填写完整的全名):重庆邮电大学参赛队员(打印并签名) :1. 汪榕2. 田睿3. 韩旺指导教师或指导教师组负责人(打印并签名):王长有日期: 2012 年 9 月 10 日赛区评阅编号(由赛区组委会评阅前进行编号):.....编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):A题葡萄酒的评价摘要本文研究的是关于葡萄酒的评价问题,通过分析题目所给出的数据建立了样本错误!未找到引用源。
检验模型、可靠性分析模型、主成份综合评价模型、变量相关分析模型以及回归分析模型,利用SPSS软件和MATLAB软件对上述模型进行了逐一求解,分别回答了题目提出的所有问题。
针对问题一,首先利用SPSS软件判断出样品酒的评分服从正态分布,再对葡萄酒外观、香气、口感等指标分别利用F和t检验进行显著性分析,最终得出结果为:两组评酒师对红葡萄酒的所有指标的评分都有显著性差异;对白葡萄酒外观的评分数据有显著性差异,而对白葡萄酒的其余指标的评分均无显著性差异。
2012年数学建模竞赛A题答案参考

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):A题:葡萄酒的评价一、摘要确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。
酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。
附件1给出了某一年份一些葡萄酒的评价结果,附件2和附件3分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据。
请尝试建立数学模型讨论下列问题:1. 分析附件1中两组评酒员的评价结果有无显著性差异,哪一组结果更可信?2. 根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。
3. 分析酿酒葡萄与葡萄酒的理化指标之间的联系。
2012高教社杯全国大学生数学建模竞赛题目

2012高教社杯全国大学生数学建模竞赛题目2012年高教社杯全国大学生数学建模竞赛题目回顾随着科技的不断进步和人们对数学建模能力的要求日益增加,数学建模竞赛成为评价大学生综合素质和解决实际问题能力的重要途径之一。
在2012年的高教社杯全国大学生数学建模竞赛中,围绕现实生活中的一系列问题,参赛选手们展示了他们的数学建模技巧和创造力。
本文将回顾该竞赛的题目,并总结其中的亮点和困难。
本次竞赛的题目涉及多个领域,包括生态学、经济学和物理学等。
在题目设计上,高教社杯组委会精心挑选了一系列实际问题,并要求参赛选手运用数学方法进行建模分析。
这不仅考验了选手们的数学能力,也促使他们在解决问题中思维更为开阔和灵活。
首先是生态学方面的题目,题目描述了一个湖泊中的藻类生长和鱼类捕食之间的关系。
选手需要通过深入研究藻类和鱼类之间的相互作用,分析其影响因素,并提出改善水域生态环境的措施。
这个题目要求选手对生态学有一定的了解,同时需要运用微分方程等数学工具,解决鱼类和藻类数量变化的模型问题。
通过这个题目,选手们能够更深入地了解生态系统的运作机制和相互关系。
其次是经济学方面的题目,该题目考察了决策分析的能力。
以某企业生产和销售的某种商品为研究对象,选手需要通过对市场需求和成本等数据的分析,制定出最佳的定价策略,并在此基础上预测该商品的市场份额。
这个题目要求选手们综合运用微积分、概率统计和优化等数学方法,对市场进行全面的分析和预测。
这个题目挑战性较大,对选手的经济学知识和数学建模技巧都提出了较高要求。
最后是物理学方面的题目,该题目涉及了粒子在复杂电场中的运动规律。
选手需要根据给定的电场分布情况,建立适当的数学模型,分析粒子的运动轨迹和速度变化。
这个题目对于选手的物理学知识和对微分方程求解的能力都提出了挑战,同时也对选手的数学建模思维进行了锻炼。
综上所述,2012年高教社杯全国大学生数学建模竞赛的题目设计多样且具有挑战性,既考察了选手们的数学知识和建模技巧,又让他们运用所学的数学工具解决实际问题。
2012大学生数学建模试题

2012年大学生数学建模竞赛赛题注意:1. 本处列了3个题目,各队可以从中任选一个完成,也可以从2012年数学建模夏令营题目中选取一个完成。
因这些题目均有一定难度,因此交卷时间推迟一周,就是到5月15日交卷。
纸质稿提交理学院团委,电子版发送zbjianmo@2. 选择数学建模夏令营题目的队请到数学系登记一下,便于跟老师交流。
全国数学建模组委会2012年夏令营赛题/苏北地区2012年建模竞赛试题/3. 所有参赛同学不要有畏难情绪,尽量完成,做到什么程度算什么程度,对于难度大的题目,不一定要完成全部问题。
无论做到什么程度,都要按时提交。
A题原油开采与输送问题某炼油厂有四口自备油井,为了满足炼油厂的需要,炼油厂一方面计划再打一些油井,另一方面从外部购买部分原油。
该炼油厂现有的四口油井经过多年使用后,年产油量也在逐渐减少,在表1中给出它们在近9年来的产油量粗略统计数字。
表1 现有各油井在近几年的产油量(万吨)根据专家研究和预测,拟计划打的8口油井基本情况如下:表2 打井费用(万元)和当年产油量(万吨)每口油井的年产油量还会以平均每年10%左右的速率减少炼油厂与附近一个油田的输油管道距离20公里,铺设管道的费用为L.0(万元),QP51.066其中Q表示每年的可供油量(万吨/年),L表示管道长度(公里)。
铺设管道从开工到完成需要三年时间,且每年投资铺设管道的费用为万元的整数倍。
要求完成之后,每年能够通过管道至少提供100万吨油。
炼油厂从2010年开始,连续三年,每年最多可提供60万元用于打井和铺设管道,为了保证从2012至2016年这五年间每年分别能至少获得150、160、170、180、190万吨油,请作出一个从2010年起三年的打井和铺设管道计划,以使整个计划的总开支尽量节省。
B稀土资源的开发与储备问题囤积中国廉价稀土。
目前美国90%以上稀土由中国进口,美国政府为保护本土的稀土资源采取了严厉的强制措施,不但完全停止出口,还封存矿山。
2012高教社杯全国大学生数学建模竞赛A题

2012高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):CXXY参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期: 2012年 09 月 10 日赛区评阅编号(由赛区组委会评阅前进行编号):2012高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):A题葡萄酒的评价摘要问题一:针对两组评酒员的评价结果需要进行多个平均数间的差异显著性检验,首先应该对数据进行正态分布检验,结论是每一个葡萄酒样品的评价得分都服从正态分布,之后利用SPSS软件进行两独立样本T检验模型进行显著性检验得出两组评酒员的评价结果有显著性差异,结合方差分析得出第二组评分更可信。
问题二:根据酿酒葡萄的理化指标采用聚类分析和主成分分析的方法模型对酿酒葡萄评价,再结合问题一中葡萄酒的质量评价,利用正态分布将两者标准化到统一的评分尺度中,对两者赋予不同的权重系数求总得分,进而对这些酿酒葡萄划分成5个等级。
2012全国数学建模竞赛A题附件2指标总表
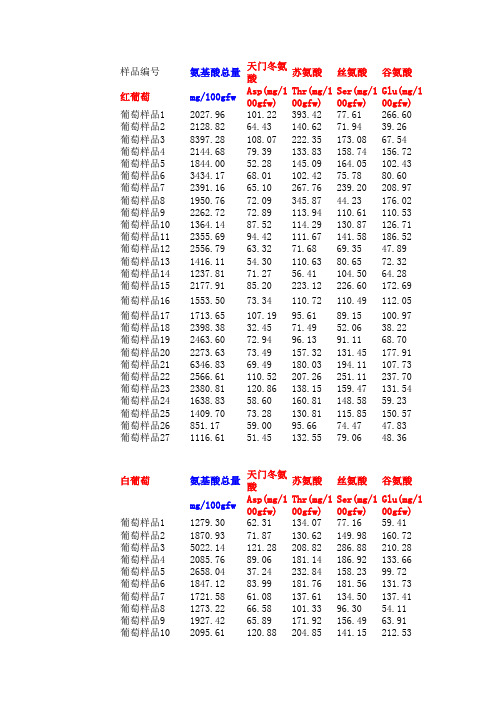
样品编号氨基酸总量天门冬氨酸苏氨酸丝氨酸谷氨酸Glu(mg/100gSer(mg/100gThr(mg/100g红葡萄mg/100gfw Asp(mg/100g葡萄样品12027.96101.22393.4277.61266.60葡萄样品22128.8264.43140.6271.9439.26葡萄样品38397.28108.07222.35173.0867.54葡萄样品42144.6879.39133.83158.74156.72葡萄样品51844.0052.28145.09164.05102.43葡萄样品63434.1768.01102.4275.7880.60葡萄样品72391.1665.10267.76239.20208.97葡萄样品81950.7672.09345.8744.23176.02葡萄样品92262.7272.89113.94110.61110.53葡萄样品101364.1487.52114.29130.87126.71葡萄样品112355.6994.42111.67141.58186.52葡萄样品122556.7963.3271.6869.3547.89葡萄样品131416.1154.30110.6380.6572.32葡萄样品141237.8171.2756.41104.5064.28葡萄样品152177.9185.20223.12226.60172.69葡萄样品161553.5073.34110.72110.49112.05葡萄样品171713.65107.1995.6189.15100.97葡萄样品182398.3832.4571.4952.0638.22葡萄样品192463.6072.9496.1391.1168.70葡萄样品202273.6373.49157.32131.45177.91葡萄样品216346.8369.49180.03194.11107.73葡萄样品222566.61110.52207.26251.11237.70葡萄样品232380.81120.86138.15159.47131.54葡萄样品241638.8358.60160.81148.5859.23葡萄样品251409.7073.28130.81115.85150.57葡萄样品26851.1759.0095.6674.4747.83葡萄样品271116.6151.45132.5579.0648.36白葡萄氨基酸总量天门冬氨酸苏氨酸丝氨酸谷氨酸Glu(mg/100gSer(mg/100gmg/100gfw Asp(mg/100gThr(mg/100g葡萄样品11279.3062.31134.0777.1659.41葡萄样品21870.9371.87130.62149.98160.72葡萄样品35022.14121.28208.82286.88210.28葡萄样品42085.7689.06181.14186.92133.66葡萄样品52658.0437.24232.84158.2399.72葡萄样品61847.1283.99181.76181.56131.73葡萄样品71721.5861.08137.61134.50137.41葡萄样品81273.2266.58101.3396.3054.11葡萄样品91927.4265.89171.92156.4963.91葡萄样品102095.61120.88204.85141.15212.53葡萄样品111566.9751.4090.5084.3566.55葡萄样品121724.1697.1797.0183.8964.37葡萄样品13664.9657.6196.7632.9829.91葡萄样品141542.1773.92146.12140.7370.85葡萄样品152669.2254.43157.9797.8051.62葡萄样品16991.9248.13139.2959.7644.14葡萄样品171167.2974.69108.03124.6476.21葡萄样品181289.9362.9676.6784.2296.05葡萄样品19817.8157.09126.2258.8851.03葡萄样品202045.2475.08160.63161.0484.96葡萄样品211554.0284.50130.07133.52112.67葡萄样品221457.6767.78122.97161.6168.22葡萄样品231522.5268.04114.82153.2776.21葡萄样品243068.34129.69167.09274.40395.73葡萄样品252350.7953.17264.29162.64109.02葡萄样品262073.3362.26143.85176.2062.54葡萄样品272475.2198.35194.81186.03181.41葡萄样品283785.5796.41158.71403.13273.55表中:蓝色为一级指标,红色为二级指标;一个项目下有几列数据,表脯氨酸甘氨酸丙氨酸胱氨酸缬氨酸蛋氨酸异亮氨酸亮氨酸Ile(mg/100gLeumg/100gfVal(mg/100gMet(mg/100gCyr(mg/100gGly(mg/100gPro(mg/100gAla(mg/100g723.88177.3789.2824.8315.7417.14 6.5810.86 1560.9732.3811.1324.1120.69 4.609.4222.82 7472.2855.7975.3413.1819.607.847.8218.17 1182.2393.2389.3646.7021.94 6.5515.7920.75816.0886.8369.5418.6433.6716.4630.4821.69 2932.7618.0119.3923.1712.63 2.6510.527.901096.2874.0689.5618.1946.9811.3618.0333.84962.01150.7342.63 6.4320.849.8016.2219.38 1334.1995.1842.807.0733.4915.1524.8226.61477.5088.1460.50 5.7525.31 4.0010.5620.05 1150.09158.3683.1633.2123.937.1713.4418.07 2127.9136.8413.9817.0619.04 3.9616.0514.60621.2541.2528.3916.7637.6715.1121.5036.36677.7839.0951.4322.2315.73 1.7012.6711.66817.5796.02100.8634.2235.0810.7223.9141.26679.2546.9540.0827.0823.88 3.9714.3119.17806.5662.4244.8526.3832.11 5.4920.1428.52 2097.6124.3110.0111.4210.85 1.59 4.62 4.441438.08165.6668.0532.0741.57 4.448.7630.10754.899.89100.7012.6242.0417.1729.9644.74 5144.8162.2216.3653.6441.4613.6616.1234.28863.99197.3270.8643.7758.8011.8666.9366.98 1341.12106.7178.8735.5142.2711.4018.6135.54797.5588.5679.4034.0730.32 6.1911.228.60479.1788.0357.0241.9726.15 4.3815.9420.85147.7022.8128.7214.9419.49 4.3018.4223.33418.0129.2528.589.9628.74 5.4010.4732.75脯氨酸甘氨酸丙氨酸胱氨酸缬氨酸蛋氨酸异亮氨酸亮氨酸Met(mg/100gLeumg/100gfVal(mg/100gIle(mg/100gCyr(mg/100gGly(mg/100gPro(mg/100gAla(mg/100g589.1950.5415.20 5.2227.070.1510.9520.74742.05150.7470.1030.7444.79 2.8112.0019.06 3217.96143.1676.4816.7254.36 6.0620.1740.11678.0177.1159.589.3948.17 6.5723.2640.73 1559.1762.79110.2013.2651.49 5.6222.8832.78687.2674.9683.8031.4046.79 6.5726.7640.95701.8043.3349.2717.5730.29 2.538.3324.44399.4340.5742.1912.3846.00 4.8320.4735.36800.5959.5393.288.7339.03 6.6415.8025.52823.18106.4975.2916.0120.57 6.3825.609.79702.8826.2656.07 3.9935.23 4.1417.0225.44600.1438.0932.6511.9032.85 4.2515.7327.09238.50 6.8757.6511.3312.04 2.69 5.869.39586.7158.5971.7134.8331.05 3.6215.8930.651767.2742.2551.4138.6530.05 2.5617.1228.75380.3632.5617.44 6.3223.01 2.609.6213.17387.6545.4429.2810.5938.748.3920.5332.04551.6433.8335.4516.7516.05 2.147.8615.28287.2321.259.119.2122.88 2.5512.3525.10995.1256.5394.4316.9634.84 6.7925.8443.19638.2052.6877.927.5735.67 5.0714.6117.81538.1545.8635.1720.5237.51 3.6622.5232.01702.9460.3131.1227.1433.84 2.9113.8219.03812.46214.87263.1127.9062.80 4.5230.3663.881020.1864.5058.4832.0862.27 4.7421.5032.761259.7648.1546.0517.6843.13 4.1523.2435.01891.09127.74170.907.2169.498.5324.7859.432006.25152.42120.2016.5460.04 4.4815.9837.34一个项目下有几列数据,表示该项目测试几次。
2012全国大学生数学建模竞赛A题(葡萄酒评价)

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):重庆交通大学参赛队员(打印并签名) :1. 孟壮2. 瞿琦3. 朱超指导教师或指导教师组负责人(打印并签名):谭远顺10 日期: 2012 年 9 月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):葡萄酒的评价摘要本文主要用数学建模的方法解决关于葡萄酒评价的一些问题。
结合题目所给信息以及查阅大量资料,对题目所提问题做了相应解答,并验证了相关模型建立及求解的合理性。
针对问题一:首先,我们运用E xcel数据分析和SP SS软件数据分析工具,分别建立了配对样本T检验模型和单因素方差分析模型,分析了两组评酒员的评价结果是否具有显著性差异。
两种方法得出的结果一致:两组评酒员的评价结果有显著性差异。
然后,通过建立权重模型,分别对评酒员与评酒员群体评价之间的“分值偏差”和“排序偏差”两方面考察,得出第二组结果可信。
全国大学生数学建模大赛2012C题

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C我们的参赛报名号为(如果赛区设置报名号的话):139C05所属学校(请填写完整的全名):浙江工贸职业技术学院参赛队员(打印并签名) :1. 郑济明2. 王庆松3. 朱松祥指导教师或指导教师组负责人(打印并签名):数模组日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):脑卒中发病环境因素分析及干预摘要关键词:一、问题重述21世纪人类倡导人与自然和谐发展,环境因素成为影响健康的重要因素。
脑卒中(俗称脑中风)就是与环境因素紧密相关且威胁人类生命的疾病之一。
这种疾病的诱发已经被证实与环境因素有关,其中与气温和湿度存在着密切的关系。
对脑卒中的发病环境因素进行分析,其目的是为了进行疾病的风险评估,对脑卒中高危人群能够及时采取干预措施,也让尚未得病的健康人,或者亚健康人了解自己得脑卒中风险程度,进行自我保护。
同时,通过数据模型的建立,掌握疾病发病率的规律,对于卫生行政部门和医疗机构合理调配医务力量、改善就诊治疗环境、配置床位和医疗药物等都具有实际的指导意义。
现从中国某城市各家医院2007年1月至2010年12月的脑卒中发病病例信息以及相应期间当地的逐日气象资料(Appendix-C2)和数据(见Appendix-C1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
A题葡萄酒的评价
确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。
每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。
酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。
附件1给出了某一年份一些葡萄酒的评价结果,附件2和附件3分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据。
请尝试建立数学模型讨论下列问题:
1. 分析附件1中两组评酒员的评价结果有无显著性差异,哪一组结果更可信?
2. 根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。
3. 分析酿酒葡萄与葡萄酒的理化指标之间的联系。
4.分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,并论证能否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量?
附件1:葡萄酒品尝评分表(含4个表格)
附件2:葡萄和葡萄酒的理化指标(含2个表格)
附件3:葡萄和葡萄酒的芳香物质(含4个表格)
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
B题太阳能小屋的设计
在设计太阳能小屋时,需在建筑物外表面(屋顶及外墙)铺设光伏电池,光伏电池组件所产生的直流电需要经过逆变器转换成220V交流电才能供家庭使用,并将剩余电量输入电网。
不同种类的光伏电池每峰瓦的价格差别很大,且每峰瓦的实际发电效率或发电量还受诸多因素的影响,如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度、地区的气候与气象条件、安装部位及方式(贴附或架空)等。
因此,在太阳能小屋的设计中,研究光伏电池在小屋外表面的优化铺设是很重要的问题。
附件1-7提供了相关信息。
请参考附件提供的数据,对下列三个问题,分别给出小屋外表面光伏电池的铺设方案,使小屋的全年太阳能光伏发电总量尽可能大,而单位发电量的费用尽可能小,并计算出小屋光伏电池35年寿命期内的发电总量、经济效益(当前民用电价按0.5元/kWh计算)及投资的回收年限。
在求解每个问题时,都要求配有图示,给出小屋各外表面电池组件铺设分组阵列图形及组件连接方式(串、并联)示意图,也要给出电池组件分组阵列容量及选配逆变器规格列表。
在同一表面采用两种或两种以上类型的光伏电池组件时,同一型号的电池板可串联,而不同型号的电池板不可串联。
在不同表面上,即使是相同型号的电池也不能进行串、并联连接。
应注意分组连接方式及逆变器的选配。
问题1:请根据山西省大同市的气象数据,仅考虑贴附安装方式,选定光伏电池组件,对小屋(见附件2)的部分外表面进行铺设,并根据电池组件分组数量和容量,选配相应的逆变器的容量和数量。
问题2:电池板的朝向与倾角均会影响到光伏电池的工作效率,请选择架空方式安装光伏电池,重新考虑问题1。
问题3:根据附件7给出的小屋建筑要求,请为大同市重新设计一个小屋,要求画出小屋的外形图,并对所设计小屋的外表面优化铺设光伏电池,给出铺设及分组连接方式,选配逆变器,计算相应结果。
附件1:光伏电池组件的分组及逆变器选择的要求
附件2:给定小屋的外观尺寸图
附件3:三种类型的光伏电池(A单晶硅、B多晶硅、C非晶硅薄膜)组件设计参数和市场价格
附件4:大同典型气象年气象数据。
特别注意:数据库中标注的时间为实际时间减1小时,即数据库中的11:00即为实际时间的12:00
附件5:逆变器的参数及价格
附件6:可参考的相关概念
附件7:小屋的建筑要求
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
C题脑卒中发病环境因素分析及干预
脑卒中(俗称脑中风)是目前威胁人类生命的严重疾病之一,它的发生是一个漫长的过程,一旦得病就很难逆转。
这种疾病的诱发已经被证实与环境因素,包括气温和湿度之间存在密切的关系。
对脑卒中的发病环境因素进行分析,其目的是为了进行疾病的风险评估,对脑卒中高危人群能够及时采取干预措施,也让尚未得病的健康人,或者亚健康人了解自己得脑卒中风险程度,进行自我保护。
同时,通过数据模型的建立,掌握疾病发病率的规律,对于卫生行政部门和医疗机构合理调配医务力量、改善就诊治疗环境、配置床位和医疗药物等都具有实际的指导意义。
数据(见Appendix-C1)来源于中国某城市各家医院2007年1月至2010年12月的脑卒中发病病例信息以及相应期间当地的逐日气象资料(Appendix-C2)。
请你们根据题目提供的数据,回答以下问题:
1.根据病人基本信息,对发病人群进行统计描述。
2.建立数学模型研究脑卒中发病率与气温、气压、相对湿度间的关系。
3.查阅和搜集文献中有关脑卒中高危人群的重要特征和关键指标,结合1、2中所得结论,对高危人群提出预警和干预的建议方案。
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
D 题 机器人避障问题
图1是一个800×800的平面场景图,在原点O(0, 0)点处有一个机器人,它只能在该平面场景范围内活动。
图中有12个不同形状的区域是机器人不能与之发生碰
标点与障碍物的距离至少超过10个单位)。
规定机器人的行走路径由直线段和圆弧组成,其中圆弧是机器人转弯路径。
机器人不能折线转弯,转弯路径由与直线路径相切的一段圆弧组成,也可以由两个或多个相切的圆弧路径组成,但每个圆弧的半径最小为10个单位。
为了不与障碍物发生碰撞,同时要求机器人行走线路与障碍物间的最近距离为10个单位,否则将发生碰撞,若碰撞发生,则机器人无法完成行走。
机器人直线行走的最大速度为50=v 个单位/秒。
机器人转弯时,最大转弯速度为21.0100e
1)(ρρ-+==v v v ,其中ρ是转弯半径。
如果超过该速度,机器人将发生侧 翻,无法完成行走。
请建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型。
对场景图中4个点O(0, 0),A(300, 300),B(100, 700),C(700, 640),具体计算:
(1) 机器人从O(0, 0)出发,O→A 、O→B 、O→C 和O→A→B→C→O 的最短路径。
(2) 机器人从O (0, 0)出发,到达A 的最短时间路径。
注:要给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标以及机器人行走的总距离和总时间。
图1 800×800平面场景图。
