往复荷载下预应力混凝土结构的数值模拟
预制钢筋混凝土结构在地震荷载下的往复荷载分析

周期 、 耗能性 能 非常 敏感 , 因此 结构 刚度 的 降低 将
影 响 到整个 结构 的抗 震性 能.
本 研究 对前 面模 拟 的数 值 模 型 进 行 修 改 , 选
用 合适 的滞 回变 形 模 型 , 单 层 预制 钢筋 混 凝 土 对
精度, S 为 AP模 型 用 于 分 析 结 构 的 地 震 响 应 提 供 了依 据 .
关 键 词 : 筋 混 凝 土 工 业 结 构 ; A 2 0 ; 复 载 荷 分 析 ; 震 响 应 钢 S P 00往 地
中 图 法 分 类 号 : 1 . P3 5 9 DOI 1 . 9 3 jis . 0 62 2 . 0 1 O . 1 :0 3 6 /.sn 1 0 — 8 3 2 1 . 1 0 3
第 3 卷 第 1期 5 21 0 1年 2月
武汉 理工 大学学 报 ( 通科 学 与工程 版 ) 交
J u n l fW u a ie st fTe h oo y r a o o h n Un v riy o c n l g
( a s o tt n S in e & En ie r g Tr n p rai ce c o gn ei ) n
根据 现有 规 范设 计 的钢 筋混 凝 土结 构 , 地 在 震 作 用下会 有 较大 的变 形 , 至 是 消 耗大 量 能 量 甚 的塑性 滞 回变形 . 塑性 变 形 只 集 中 发生 在 结 构 受 力和 变形显 著 的部位 , 即结 构 的关键 区域 . 为研 究 结 构在 静态 往复 荷 载 下 的非 线 性 反 应 , 集 中研 需
出来 , 5I. 高 在模 型中 , n 有两跨 长 8r n的梁 和一跨 长 8r n的屋 面板 , 施加 的地震荷 载方 向与屋面板平 行 , 图 1模 型的俯 视 图和地震荷载方 向见 图 2 见 . .
预应力混凝土连续梁桥应力验算数值模拟分析

预应力混凝土连续梁桥应力验算数值模拟分析摘要:利用桥梁结构分析软件对跨度为40m+70m+40m的三跨预应力混凝土连续箱梁桥进行数值模拟分析,分别对施工阶段法向压应力、受拉区预应力钢筋的拉应力、使用阶段抗裂、使用阶段抗压进行验算,其验算结果均符合规范规定。
关键词:预应力;混凝土;梁桥;验算;数值;阶段抗裂;阶段抗压;规范0 前言预应力混凝土连续箱梁桥是预应力桥梁中的一种,它具有整体性能好、抗震性能好,结构刚度大、变形小,特别是主梁变形挠曲线平缓,桥面伸缩缝少,行车舒适等优点。
加上这种桥型的设计施工均较成熟,施工质量和施工工期能得到控制,成桥后养护工作量小,在公路、城市和铁路桥梁工程中得到广泛采用。
本文以40m+70m+40m的三跨预应力混凝土连续箱梁桥为例,其施工方法为悬臂浇筑法,通过分析对施工阶段法向压应力、预应力钢筋拉应力、使用阶段抗裂、使用阶段抗压进行验算,其计算结果仅供参考。
1 模型的建立主梁为变截面的混凝土空心箱梁,桥墩为圆形墩,桥墩之间用连系梁将两桥墩连接在一起,均采用C50混凝土;桥墩顶部与主梁的边界条件采用弹性连接中的刚性连接;桥墩底部边界条件采用一般支承,6个方向均被约束;桥台采用一般支承模拟,约束Dx、Dy及Rx三个方向;主梁两端与桥台采用弹性连接中的刚性连接。
截面的建立采用PSC截面设计,利用CAD软件将各梁截面转化为dxf文件,并将其导入到midas civil的截面特性值计算器中进行截面特性计算,并生成sec文件,再将其导入到midas civil进行相应的结构计算。
全桥模型如图1所示:图1全桥模型2 结构计算分析结构分析时考虑的荷载类型包含梁体自重、二期恒载(60kN/m)、汽车车道荷载(双车道)、温度荷载(温度梯度,按《公路桥涵设计通用规范》100mm沥青混凝土铺装层(14℃/5.5℃))、挂蓝荷载(按500kN集中力,偏心距离2.8m计算)、支座沉降(5mm)及预应力荷载。
混凝土受力性能的数值模拟研究

混凝土受力性能的数值模拟研究一、研究背景混凝土是建筑工程中常用的材料之一,其力学性能直接影响到工程的安全可靠性。
数值模拟技术是目前研究混凝土受力性能的重要手段之一。
通过数值模拟可以对混凝土受力过程进行分析和预测,为工程设计和施工提供科学依据。
二、数值模拟方法目前常用的混凝土数值模拟方法有有限元方法、离散元方法和边界元方法等。
其中有限元方法是比较常用的一种方法,其优点在于适用范围广、计算精确度高、计算速度快等。
在进行混凝土数值模拟时,需要先建立混凝土的数学模型,模型的准确性和合理性直接影响到数值模拟结果的准确性和可靠性。
三、混凝土数学模型建立混凝土数学模型需要考虑混凝土的物理性质及其受力过程。
混凝土是一种非均质材料,其内部包含大量的孔隙和裂缝,因此需要考虑其非线性性。
常用的混凝土数学模型有弹性模型、弹塑性模型和本构模型等。
其中弹塑性模型是比较常用的一种模型,其可以考虑混凝土的弹性和塑性变形,并且可以考虑混凝土的蠕变性和损伤性。
四、混凝土数值模拟应用混凝土数值模拟应用广泛,主要应用于混凝土构件的设计和分析、混凝土的损伤分析和评估、混凝土的耐久性研究等。
其中混凝土构件的设计和分析是数值模拟的主要应用之一,可以通过数值模拟对混凝土构件在极限状态和耐久状态下的受力性能进行分析和预测。
五、数值模拟结果分析数值模拟结果分析是混凝土数值模拟研究中的重要环节。
通过对数值模拟结果进行分析可以得出混凝土受力过程中的各种参数和性能指标,如应力、应变、位移、破坏模式等。
同时也可以对混凝土的受力性能进行评估和优化,为工程实际应用提供科学依据。
六、数值模拟存在的问题及解决方案混凝土数值模拟研究中存在的问题主要包括数学模型准确性、计算精度和计算效率等方面。
为了解决这些问题,可以采用多种方法,如优化数学模型、提高计算精度和优化计算算法等。
同时需要结合实际工程情况和实验数据对模拟结果进行验证和修正。
七、结论混凝土数值模拟是目前研究混凝土受力性能的重要手段之一。
混凝土结构在往复荷载下的塑性损伤模型

宫婷,清华大学土木工程系
模型的优点是刚度退化最初就被耦合到本构关系中, 并且可以从线性方程式的塑 性变形中解耦。 但是正如其他基于连续损伤力学的模型一样,用实验数据来校准 表征屈服面演化的参数是十分困难的,因为大多数实验数据是基于应力的。 在 Lubliner 和 coauthors(Lubliner 等 1989) 提出的模型中 ( 本文中指的是 Barcelona 模型),一个基于断裂能的标量损伤变量描述了所有的损伤类型。除了 损伤变量之外, 模型还分别引入了一个弹性和塑性的退化变量来模拟弹性刚度的 退化。在本构关系中,刚度退化和塑性变形耦合在一起,使得用实验结果校核参 数变得较为方便。但是,耦合的关系给出了一个较为复杂和不稳定的数值算法, 使得在迭代计算时引起了伪塑性卸载(Lee 和 Fenves 1994)。 因为类准脆性材料在循环荷载作用下要经受多个损伤状态,例如受拉开裂、 受压压溃和刚度退化, 所以采用一个单一的损伤变量是不够的。可以采用多重硬 化(损伤)变量(Murray 等 1979; Mazars 1986; Ohtani and Chen 1988; Mazars and Pijaudier-Cabot 1989) 来解释不同 的损伤响 应。各向同 性连续损 伤力学模型 (Mazars 1986; Mazars and Pijaudier-Cabot 1989)采用多个损伤变量也不能描述损 伤在拉伸和压缩作用下的不同结果, 因为损伤变量会使得两种作用最终有同样的 损伤演化。 当循环荷载在拉、压之间变化时,可以在拉区向压区逐渐转化的过程中观察 到退化的刚度重新恢复(Reinhardt 1984)。刚度的恢复是裂缝闭合的结果。基于各 向同性和各向异性这两种损伤模型的研究, 一些用于模拟刚度恢复的模型也已经 被提出(Ortiz 1985; Ju 1989; Cervera e 等. 1995; Hansen and Schreyer 1995).。 本文使用基于断裂能损伤的概念建立了一个在循环荷载作用下的塑性损伤 模型,这个模型类似于 Barcelona 模型。分别采用考虑拉、压损伤的两个损伤变 量来解释不同的损伤状态。使用多重损伤(或硬化)变量对由 Lubliner 等人提出 的屈服函数进行了修改。 单轴强度函数被分解为与有效应力和弹性刚度退化两部 分,本文中将后者称为退化损伤。弹塑性响应的本构关系与退化损伤响应解耦。 有效应力的强度函数被用来控制本构模型屈服面的演化, 这使得用实验结果进行 校核变得简单易行。 最后, 引入一个简单的并满足热力学一致性的刚度恢复模型 来模拟裂缝的扩展和闭合。在现有的方法中,尽管弹性损伤仍然是各向同性的, 但塑性损伤模型已提供了拉力和压力各自单独的演化, 并且通过塑性应变诱导方 向性的损伤。 通过混凝土结构的数值算例与试验结果的对比分析可知, 本文建立的塑性损 伤方法的适用性。 目前模型的开发还局限于适用于混凝土材料微小变形理论。文 中 x 和 xl 分别代表了矩阵 x 特征值矩阵和第 i 个特征值。
往复荷载下钢筋混凝土柱受力性能的数值模拟

0
量,均按文献[5]计算。
σ
变; s、s1、s2 为控制参数,按文献[4]计算。其中,
I e 0 = 0.08
Emin
σ c 0 = σ c 0 (1 + 2.4 I e 0 0 1.2 ε c 0 = ε c 0 (1 + 35 I e 0 )
Key words: fiber model; cyclic load; concrete column; hysteretic relation; numerical analysis
钢筋混凝土柱作为混凝土框架结构及桥梁结 构的主要承重构件,在地震作用下受到反复水平地 震力作用,并表现为显著的弹塑性受力特性 。准 确预测地震作用下钢筋混凝土柱的受力性能及其 震后残余变形,对评估结构的震害程度和安全性具 有重要意义。由于材料和结构受力的复杂性,目前 对于反复荷载下钢筋混凝土柱的受力性能和残余 变形的数值模拟还存在欠缺,主要表现在混凝土和 钢筋的滞回本构关系不能全面准确的反映其复杂 的受力行为。 对于长细比较大的杆系结构(例如框架梁柱或 桥柱) , 可以采用基于杆系结构力学方法 和一维材 料本构的纤维模型进行数值模拟。所谓纤维模型,
0 0
0.7
)
(2)
σf
ft
Emin
式中,σ c 0 、ε c 0 分别为无约束混凝土 (素混凝土) 受压峰值应力和峰值应变; I e 0 为混凝土受压应变 等于峰值应变 ε c 0 时的有效约束指标,是一个与纵
ε c0 ε z ε unε re ε z − ε tz
图 2 混凝土应力-应变曲线 Fig.2 Stress-strain curve of concrete
往复荷载下圆钢管混凝土柱的数值模拟

计算模型 , 并对其进行往 复荷载作用下有限元分析, 得到 了桥墩 的滞 回曲线、 骨架 曲线. 计算结果 与试验 结果进 将 行对 比, 现计算得 到的钢 管混凝土柱滞 回曲线和骨架 曲线与试验结果 吻合 较好 , 发 因此提 出一些有 关重要参 数选 取 的建议 , 可供 相似 问题 的钢 管混凝土有 限元分析参考.
mo l d wi dee t ANS o wa e a d t o —c ce r v r e o dig tsswee n n—l a l i lt d h YS s f r n he lw t y l e e s d l a n e t r o i ry smua e .Th y tr ne e h se — e i ur e , k l tn c r e r bti e Th a c lt d h se ei u e n k lt n c r e r o r s o di tc c v s s ee o u v swe e o a n d. e c lu ae y tr tc c r sa d s e eo u v s we e c re p n ng v welwih e p rme tlr s l . o u g sin bo tc o sn a tra e g v n. l t x e i n a e u t S me s g e to s a u h o i g fc o r ie s
预应力混凝土框架模型的循环载荷试验本科学位论文

XXXXXXX学院毕业设计题目电参数测试仪设计与制作姓名学号专业班级分院指导教师20XX年XX月XX日预应力混凝土框架模型的循环载荷试验W.L.MO and R. H. Han摘要预应力混凝土框架结构通常被用在桥梁设计中。
但是,它们在反复循环荷载尤其是在遭受严重地震作用下的性能很少被了解。
并且大多是桥梁规范中没有提供所需的设计准则。
其结论来自对八个小规模的预应力混凝土框架模型分析,模拟加入地震力测试并记录不同的荷载。
这个实验的的主要曲线(水平力与位移关系)与理论结果比较,并且试验滞后的循环与按武田法则计算来的相比较。
混凝土强度约为40兆帕,预应力钢筋极限强度的有效应力在36%与51%之间。
结果发现有效应力减少延性与耗能增加。
反复循环荷载的的影响也是有作用的。
关键字:预应力混凝土框架;桥梁设计;循环荷载试验1.简介刚构桥是世界上最广泛使用的一种高速公路桥梁。
工程师把基础看做是一个单元通过用支柱构建一个连续预应力混凝土刚框架。
这种结构类型不需要混凝土桥墩和支撑面的支持,从而给予了更经济的结构。
一般来说,这种桥型,可减少主梁的高度和减少上部结构的材料。
在地震地区的调查,预应力混凝土框架桥梁对循环荷载反应是非常重要并且非常有意义。
不幸的是,过去大部分对预应力混凝土桥梁研究工作专注于非弹性静态作用下。
另一方面,人们普遍知道,预应力混凝土表现出比钢筋混凝土更加的脆。
为了在抗耐结构中使用并且通过预应力使结构更加经济,最重要的是了解各种结构部件表现出韧性的方式。
对在不同一个部分的应力状态,混凝土可能也需要表现出大的延性和耗能性。
从几个实验研究结果已经报告处理过受反复荷载的钢筋混凝土结构。
但预应力混凝土结构的数据测试很有限,尤其是在反复循环荷载作用下的记录。
由于地震的能量通过非弹性受弯构件耗散较好,在严重的地震带中,多数情况下,铰接的梁或柱更被期待使用。
因此为了防止脆性结构失效梁或柱的关键部位应当适当的详细。
要应用反复加载预应力混凝土框架结构的实用抗震设计测试数据,有必要研究各种循环载荷作用下影响。
反复荷载下钢管混凝土柱力学性能的有限元模拟

d 一1 一 — / ( 1b
t
) ・E +
雨
计算结果和实测结果吻合 良好 , 从而验证 了本文 有限元模 型 的适 用性和精确性 。
1 6
福建建设科技
21. o 6 0 1 N .
一 建筑 结构
回
∞
枷
蜘
接边界条件
[] 3 韩林海 .钢管混凝土结构一理论与 实践 ( 第二 版) M] [ .北京 : 科
和 e一 分别 为等效拉 、 压塑性应变 。 此外 , 还定义 了拉 、 刚度恢 复 系数 和 叫 来 描述 混 压
凝土 由压转拉 的刚度恢复 和由拉转压 的“ 裂面效应” 。这样 由
损伤系数 d、c d 和刚度恢 复系数 W 、 c W 就可 以定 义混 凝土在 反复荷载作用下 的加载 、 卸载和 再加载 的应力 一应变 关系 演
其 中 和 分别 为拉 、 压应 力 ; 和 d 分别为拉 、 压损 伤系数 和 e 分别 为拉 、 压应 变 ; 0为混凝 土 弹性 模量 ; E
~
本文计算的钢管混凝 土构件 的边界条 件为 ; 件 的两 端 构 施加“ 铰接 ( i e ) 的边界 条件 , 过刚性 盖板在 构件 顶端 Pn d ” n 通 施加恒定轴 压力 , 同时 在构 件 中部 施加 反 复位 移 ( slc— Di ae p met 。模 型的边 界条件如图 4所示 。 n) 3有 限元模 型的验证 采用上述有限元模型计算 了文献[ 中报道的 3根在恒定 3
Ab ta t src :Thsp p rd v lp o l e rf i lme t d l g ( M )t i lt o cee fl d se l u er if re o cee i a e e eo san ni a i t ee n n n e mo ei n FE O smuaecn rt - i e te b eno c dc n rt l t c lmn wihs u r e t nu d rc ci o dn .I h EM ,tec m ua ied ma eo o ceeu d rrv r ela ig o l e r ou t q a esci n e y l la ig nt eF o c h u lt a g fc n rt n e e es o dn ,n n i a v n g o ti b h vo ,b n ig si ewe n se lb r rse ltb n o ceea ec n ie e . Go d a re n s o tie e e merc e a ir o dn - l b t e te aso te u ea d c n rt r o sd r d p o g e me ti b an d b — t e h x e i n a eut n h rdcin ae i t eFE . we nt ee p rme tlrs lsa dt ep e it sb sdOl h M o K ywo d :c n r t- f ldsan esse l u e ii lme tmeh d;h seei u v ,d ma e e rs o cee ie tils te b ;f t ee n to l t n e y trtcc r e a g
预应力混凝土箱梁结构数值模拟与施工控制
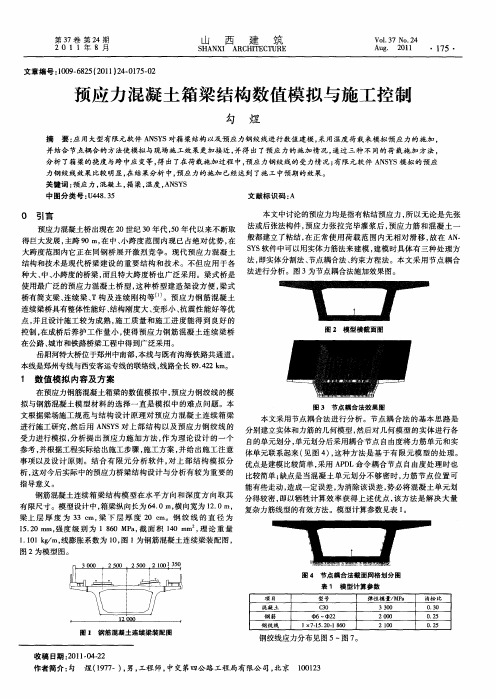
图 2 模型横截面图
岳 阳河特大桥位 于郑州 中南部 , 线与既有 沟海 铁路共通道 。 本
本线是郑州专线 与西安客运专线 的联络线 , 线路全长 8 .2 m。 9 42k
1 数值 模 拟 内容及 方 案
在预应力钢筋混凝土箱梁 的数值模 拟中 , 预应力钢 绞线 的模
使用最广泛 的预 应力 混凝 土桥 型 , 种桥 型建造 架设 方便 , 式 这 梁 桥 有简支梁 、 连续 梁、 T构 及 连续 刚构 等… 。预 应力 钢筋 混凝 土 连续 梁桥具有整体性能好 、 结构刚度 大 、 变形 小 、 震性 能好等 优 抗 点, 并且设计施工 较为 成熟 , 施工 质量 和施 工进度 能得 到 良好 的 控制 , 在成桥后养 护工作 量 小 , 得预 应力钢 筋混 凝 土连续 梁桥 使
拟 与钢筋混凝土 模型 材料 的选择 一直 是模 拟 中的难点 问题 。本 文根据 梁场施工规 范与结 构设 计原 理对 预应 力混凝 土连续 箱 梁
图 3 节点耦合法效果图
本文采 用节 点耦合 法进行 分 析。节 点耦 合法 的基 本 思路 是 进行施工研 究 , 然后 用 A S S对 上部 结构 以及 预 应力 钢绞 线 的 分别建立实体和力筋 的几何模 型 , NY 然后对 几何模 型的实体 进行各
力钢 绞线效果比较明显 , 结果分析 中, 力的施加 已经达到 了施 工中预期 的效果。 在 预应
关键词 : 应 力, 凝土 , 梁, 度 ,N Y 预 混 箱 温 A SS
中图分类号 :4 8 3 U 4 .5
文献标识码 : A
O 引 言
本文中讨 论的预应力均是指有粘 结预应力 , 以无论是 先张 所
预应力混凝土受弯构件的细观数值模拟

预应力混凝土受弯构件的细观数值模拟随着经济和科技的快速发展,建筑工程在数量和质量上都有了显著的提升。
现代建筑工程不仅要求外观美观,而且要求结构强度、耐久性等各方面指标都达到高标准。
在建筑工程中,钢筋混凝土结构得到了广泛应用。
普通混凝土结构在负载作用下的变形和开裂较大,影响结构的承载能力以及使用寿命。
为了解决这个问题,预应力混凝土 (prestressed concrete) 结构的技术被引入,它能更好地抵御外界荷载的影响,提高结构的稳定性和耐用性。
预应力混凝土结构的核心实现技术是预应力技术,它将钢筋(或钢绞线)在混凝土未拌合前就施加预定张力,使混凝土的提前压应力由张紧构件承担,降低了混凝土结构内部的应力并提高了抗弯和抗拉的能力。
而预应力混凝土受弯构件则是预应力混凝土结构的重要构件之一,主要承担建筑物的水平荷载作用。
预应力混凝土受弯构件因承担的作用不同,分为内力臂不同时的梁和板两种类型。
为了保证预应力混凝土受弯构件的安全性、强度和稳定性,必须对其进行详细的力学分析和设计。
现代工程领域中,越来越多的工程通过数值模拟来实现设计、认证和性能检测。
而预应力混凝土受弯构件的分析和设计过程,也无法摆脱细观数值模拟的应用。
细观数值模拟是一种基于离散单元法的计算力学方法,它将连续体划分为一些离散的小单元,通过求解这些小单元之间的相互作用关系,来描绘整个系统的力学行为。
作为一种近代的科学计算和分析方法,细观数值模拟具有一定的优点:效率高、计算精度高、对复杂问题有较好的应对能力等。
同时,它也有一些不足,如计算误差较大、计算成本较高等。
但是,在工程设计和安全评估领域中,细观数值模拟必定会起到非常重要的作用。
对于预应力混凝土受弯构件的细观数值模拟,需要考虑到各种因素:材料特点、外界荷载、构件尺寸和形状、筋杆数量和布置方式等,这些因素会直接影响到模拟的结果。
其中,模拟中如何准确表达材料的力学特性是一个难点问题。
在数值模拟中,混凝土和钢筋都被看作是弹性-塑性材料。
混凝土结构中预应力损失的数值模拟研究

混凝土结构中预应力损失的数值模拟研究一、引言混凝土结构中的预应力技术已经得到广泛应用,它能够提高混凝土结构的承载能力和抗震性能,但是预应力损失是影响混凝土结构性能的主要因素之一。
因此,对预应力损失进行数值模拟研究,可以更加准确地预测混凝土结构的变形和应力分布,为混凝土结构设计和施工提供支持。
二、预应力损失的分类预应力损失可以分为四类:弹性损失、瞬时损失、长期损失和不可预测损失。
其中,弹性损失是由于钢束和混凝土之间的相对滑动导致的,瞬时损失是由于混凝土收缩和钢束膨胀引起的,长期损失是由于混凝土的徐变和材料老化引起的,不可预测损失则是由于混凝土结构的外部环境和荷载变化引起的。
三、预应力损失的数值模拟方法预应力损失的数值模拟方法包括有限元法、解析法和试验法等。
其中,有限元法在预应力损失的数值模拟中应用最为广泛,它可以模拟结构的变形和应力分布,提高混凝土结构的设计和施工效率。
有限元法分为线性有限元法和非线性有限元法,线性有限元法适用于预应力损失较小的情况,非线性有限元法适用于预应力损失较大的情况。
四、预应力损失的影响因素预应力损失的影响因素包括混凝土强度、钢束间距、预应力水平、混凝土龄期、环境温度和湿度等。
其中,混凝土强度是影响预应力损失的最重要因素之一,它直接影响混凝土的徐变和材料老化,从而影响预应力损失的大小。
钢束间距也是影响预应力损失的重要因素,它影响钢束与混凝土之间的摩擦力,从而影响预应力损失的大小。
五、预应力损失的数值模拟研究案例以一座多层建筑为例,通过有限元法进行预应力损失的数值模拟研究。
首先,建立混凝土结构的三维有限元模型,确定预应力水平和钢束间距等参数。
然后,进行预应力损失的数值模拟,通过分析模拟结果,得出混凝土结构的变形和应力分布情况,评估预应力损失对混凝土结构性能的影响。
最后,根据模拟结果,提出优化混凝土结构设计和施工的建议,以减小预应力损失的影响。
六、结论预应力损失是影响混凝土结构性能的主要因素之一,对预应力损失进行数值模拟研究,可以更加准确地预测混凝土结构的变形和应力分布,为混凝土结构设计和施工提供支持。
混凝土结构应力分析的数值模拟研究

混凝土结构应力分析的数值模拟研究一、研究背景混凝土结构是目前建筑中最为常见的一种结构形式,广泛应用于桥梁、高层建筑、水利工程等领域。
在使用过程中,混凝土结构常会受到各种复杂的荷载作用,如地震、风载、温度变化等。
因此,混凝土结构的应力分析研究显得尤为重要。
传统的混凝土结构应力分析方法主要基于经验公式和实验数据,存在着计算精度低、耗时、费力等不足。
而数值模拟技术的发展为混凝土结构应力分析提供了一种全新的方法。
数值模拟技术可以通过建立混凝土结构的三维有限元模型,较为准确地模拟结构受到外界荷载作用时的应力响应情况,为工程实践提供了可靠的理论支持。
二、研究目的本研究旨在通过数值模拟技术,对混凝土结构在不同荷载作用下的应力分布情况进行研究,为混凝土结构的设计、施工和使用提供科学的理论依据。
三、研究方法本研究采用ANSYS有限元分析软件,建立混凝土结构的三维有限元模型,并进行荷载作用下的应力分析。
具体步骤如下:1.建立混凝土结构的三维有限元模型首先,根据混凝土结构的实际情况,采用ANSYS软件进行建模。
建模时需要考虑混凝土的物理性质、结构形式、构件尺寸等因素。
2.设置荷载和边界条件按照混凝土结构的实际使用情况,设置相应的荷载和边界条件。
荷载包括静载荷、动载荷、温度荷载等,边界条件包括约束条件和加载条件。
3.分析应力响应情况在模型建立和荷载设置完成后,进行数值模拟分析,分析混凝土结构在荷载作用下的应力响应情况。
分析结果包括应力云图、应力分布曲线、应力集中系数等。
四、研究结果通过数值模拟分析,得到了混凝土结构在不同荷载作用下的应力响应情况。
具体结果如下:1.静载荷作用下的应力分析静载荷是混凝土结构使用过程中最为常见的荷载形式。
通过数值模拟分析,得出了混凝土结构在静载荷作用下的应力分布情况。
结果表明,混凝土结构在静载荷作用下,应力分布较为均匀,但在某些关键位置会出现应力集中现象。
2.动载荷作用下的应力分析动载荷是混凝土结构使用过程中另一个常见的荷载形式。
混凝土结构中预应力损失的数值模拟研究

混凝土结构中预应力损失的数值模拟研究一、研究背景混凝土结构是现代建筑中使用最广泛的一种结构形式,其中预应力混凝土结构在大跨度桥梁、高层建筑、核电站等工程中得到了广泛应用。
预应力混凝土结构通过在混凝土中预先施加拉应力,能够使混凝土的承载性能明显提高,从而达到减小跨度、减轻自重、增加抗震性等目的。
然而,在预应力混凝土结构中,预应力损失是一个重要的问题,它会导致结构的变形和承载能力下降,直接影响结构的安全性和使用寿命。
因此,对预应力损失进行数值模拟研究,能够更好地理解和掌握预应力混凝土结构的变形和破坏规律,为工程实践提供理论依据和技术支持。
二、预应力损失的定义和分类预应力损失是指由于混凝土自身的变形、材料的蠕变、锚固系统的松弛等原因,导致预应力钢束或钢筋预应力的降低。
预应力损失可以分为以下几类:1. 初始损失:在施加预应力后,由于混凝土的收缩和钢筋的弹性变形,预应力损失的一部分被视为初始损失。
2. 短期损失:当混凝土在初始阶段进行蠕变,或者锚固系统存在松弛时,预应力损失的一部分被视为短期损失。
3. 长期损失:混凝土在长期使用中会发生徐变,同时锚固系统也会存在松弛,这些因素都会导致预应力损失的增加,被视为长期损失。
4. 不良施工造成的损失:如果在预应力混凝土结构的施工过程中存在缺陷或不合理的操作,也会导致预应力损失的增加。
三、预应力损失的数值模拟方法预应力损失的数值模拟方法主要包括以下几种:1. 基于理论模型的数值模拟:根据预应力损失的机理和影响因素,建立数学模型进行计算分析,这种方法适用于简单的结构和较小的预应力损失。
2. 基于试验数据的数值模拟:通过试验获取预应力损失的数据,并建立数学模型进行计算分析,这种方法适用于复杂的结构和大量的试验数据。
3. 基于有限元方法的数值模拟:通过有限元方法对结构进行模拟,考虑预应力钢束或钢筋的力学性能和混凝土的材料性能,进行预应力损失的计算,这种方法适用于各种类型的结构和各种复杂的预应力损失情况。
数值模拟法在预应力箱梁底板受力分析中的应用

数值模拟法在预应力箱梁底板受力分析中的应用摘要:以某混凝土箱梁合龙段为研究对象,采用数值模拟的方法对箱梁施工过程中的底板受力和变形进行分析,着重分析了相关因素对箱梁底板横向受力的影响,结果表明:箱梁跨中底板厚度小,跨中底板布设的预应力钢筋较多,导致箱梁合龙段底板处拉应力和变形较大,是箱梁的薄弱位置,在外界长期荷载作用下易产生纵向裂缝破坏;梁体自重增大为1.1倍和1.2倍时对应的底板最大横向拉应力值分别增大了10.9%和 23.4%,说明箱梁自重的增加会导致箱梁底板最大拉应力大幅增大;不同纵向预应力值下距离底板边缘左右两侧1m 处底板横向应力最大,在一定条件下通过降低底板纵向预应力值可以有效减小箱梁底板拉应力值;在混凝土达到设计28d强度的90%,即在龄期7d左右时进行张拉施工,可以实现在保证施工安全的前提下降低底板应力。
关键词箱梁;合龙段;数值模拟;参数预应力箱梁受力特点复杂,尤其在箱梁合龙段,钢绞线分布密集,梁高较低且底板厚度小,是施工的薄弱点[1-4],研究预应力混凝土连续箱梁合龙段受力特点及相关参数影响具有重要的意义。
近年来,国内学者对此进行了一些研究,主要有:孟磊[5]通过建立有限元桥梁模型,对不同合龙方案下的主梁应力、挠度变化规律进行对比分析,研究结果可为桥梁的合龙设计提供参考。
邱豪侠等[6]通过对桥梁建设全过程模拟,研究了拆桥施工桥跨结构的受力特性,并建议施工过程中要注意检查并及时加固梁墩的临时支撑。
赵永鹏[7]和欧从庆[8]以连续梁桥为研究对象,研究了混凝土连续梁桥的施工工艺,提出了施工关键控制方案。
本文以某混凝土箱梁合龙段为研究对象,采用数值模拟的方法对箱梁施工过程中的底板受力和变形进行分析,重点分析了箱梁自重、纵向预应力和张拉时机等因素对箱梁底板横向受力的影响。
1工程概况某高速公路起止桩号为K155+638~K162+881,全长7.243km,由大桥、互通匝道和路基组成。
互通匝道为混凝土箱梁,设计速度为60km/h。
往复荷载下圆钢管混凝土柱的数值模拟_刘文渊

析时参数设置比较合理,采用 ANSYS 模拟可以很好地达到我们期望的效果.
3 结论
通过以上分析与讨论,利用 ANSYS 大型有限元分析程序计算得到的钢管混凝土柱滞回曲线和骨架曲 线,同试验结果有较好的吻合. 因此,利用 ANSYS 大型有限元分析程序进行钢管混凝土结构构件空间有限元 分析是可行的,并具有一定的可靠性. 其中,钢管采用双线性随动强化( BKIN) 理性弹塑性材料模型,混凝土
大应变( large strain) . 结合程序内置的材料强化模型,还可模拟金属的鲍辛格效应( Bauchinger effect) .
混凝土采用 Solid 65 单元. Solid 65 单元每个节点具有 3 个平动自由度. 同时该单元具有塑性变形能力,
能够在 3 个正交方向上开裂以及压碎,能形象地描述混凝土带裂缝工作性能,与实际情况较接近. 结合混凝
图 6 P - △骨架曲线( n = 0. 385)
2. 2 ANSYS 模拟
由文献[1]中提及的简化原则,将其简化长度 0. 6m 的悬臂柱进行分析. 建立如图 4 所示的 ANSYS 有限
元模型,柱底采用完全约束. 由文献[1]核心区混凝土本构关系可确定核心混凝土曲线. William Warnke 五参
复合砼结构界面应力数值分析一种新方法

复合砼结构界面应力数值分析一种新方法甘贤军重庆交通学院桥梁结构工程系 400074复合砼结构界面应力数值分析一种新方法甘贤军重庆交通学院桥梁结构工程系 400074摘要:本文依据断裂力学的概念以及叠加原理,并利用有限元方法得到复合结构在开裂瞬间界面应力分布规律,避开了有限元程序难以模拟裂纹从萌生到发展这一过程,为了解界面应力分布规律提供了一条新方法。
关键词:断裂力学叠加原理界面应力规律新方法Abstract:according to the concept from mechanics of fracture and stacking principle,Applying the method of finite element,the paper get the distribution law of stress of interface between concrete and stickup layer,avoid the process of crack producing and developping which can not be simulated by FEA, provide a new way to find out the distribution law of stress of interface between concrete and stickup layer.Keywords: mechanics of fracture, stacking principle,stress of interface,law, new way1、引言钢筋混凝土结构用于结构工程已一百多年,是现今应用最广泛的结构形式之一,涉及的工程领域包括工业及民用建筑工程、桥梁工程、水利工程、地下工程等等。
尽管如此,混凝土这种材料仍然存在很多方面的不足:从微观上来看,混凝土本身存在很多微小缺陷和损伤,因此宏观上必然表现为各向异性的特点。
预应力混凝土结构施加预应力的Ansys模拟

工程设计GO N GC H E N GS H E J I付永强,等:预应力混凝土结构施加预应力的Ansys 模拟784 《工程与建设》 2008年第22卷第6期收稿日期:2008209209;修改日期:2008209224作者简介:付永强(1982-),男,山东滨州人,合肥工业大学硕士生,助理工程师;胡 成(1965-),男,安徽休宁人,博士,合肥工业大学副教授.预应力混凝土结构施加预应力的Ansys 模拟付永强1, 张小水2, 胡 成1(1.合肥工业大学土木与水利工程学院,安徽合肥 230009;2.山东省滨州市建筑设计研究院,山东滨州 256613)摘 要:文章介绍了在Ansys 中进行预应力混凝土结构分析时的两种建模方法,如何实现对预应力结构施加预应力以及如何处理计算过程中的预应力损失;通过算例说明了曲线预应力筋定位和初始应变扩大系数K 的确定方法。
关键词:Ansys 预应力;初始应变扩大系数K ;生死单元;预应力损失中图分类号:TU378.1 文献标识码:A 文章编号:167325781(2008)06207842030 引 言当今,预应力混凝土结构应用十分广泛,预应力的施加使得其力学性能更加复杂。
Ansys 是进行结构有限元分析的有效工具,它有着大量的单元可供选择,并具有非常完备强大的前处理和后处理功能,可用于预应力混凝土结构的计算分析。
当用Ansys 对预应力结构进行分析时,如何施加预应力以及如何考虑预应力的损失就显得特别重要[1]。
1 两种建模方法在有限元分析中,预应力混凝土结构有两种分析方法:等效荷载法和实体力筋法。
(1)等效荷载法。
该方法用一组“等效荷载”替代预应力筋的作用施加到结构上,因此进行结构分析时对单元基本上没有限制。
等效荷载法的优点是建模简单,不必考虑预应力筋的具体位置,网格划分简单。
(2)实体力筋法。
该方法对预应力混凝土结构的应力分析能够更为精确地模拟,在力学模型上有3种分析方法:实体切分法、节点耦合法和约束方程法。
循环荷载下混凝土本构模型

D.0.1
不锈钢管内核心混凝土单调受拉应力(σ)-应变(ε)关系宜按下列公式确定:
1.2x − 0.2x6
y
=
x
0.31
2 p
(
x
) −1 1.7
+
x
(x 1) (x 1)
(D.0.1-1)
x = ec ep
(D.0.1-2)
y = c p
(D.0.1-3)
D2
=
0.2σ o 0.2ε1 + εB
卸载至应力为零时的残余应变(με);
再加载过程中 C 点应力(N/mm2);
卸载过程中 D 点应力(N/mm2);
卸载过程中 C 点应力(N/mm2)。
(D.0.2-1) (D.0.2-2)
(D.0.2-3) (D.0.2-4) (D.0.2-5) (D.0.2-6)
p=0.26(1.25 fc' )2/3
式中:ep
p
f
' c
—— —— ——
ep=43.1p 峰值拉应力时的应变(με); 峰值拉应力(N/mm2); 混凝土圆柱体抗压强度(N/mm2),按本规程表 C.0.2 换算。
(D.0.1-4) (D.0.1-5)
D.0.2 不锈钢管内核心混凝土在反复荷载作用下的应力-应变关系(图 D.0.2)与受压卸载、再加载路 径宜按下列公式确定:
(eH e 0)
σ
=
σ con
(1 −
ε ε0
)
+
2ε ε0 +
ε
σo
σ
=
σ con
(1
−
ε εA
)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D c 06 e .2 o
[ 章 编 号 】 10.4 220 160 2.5 文 0281 10 60 . 50 0
往 复荷载 下预应 力混凝土结构 的数值模 拟
汪训 流 , 列 平 , 叶 陆新 征 ( 华大学土木工程系, 清 北京 1 0 ) 0 8 04
[ 摘 要] 现 阶段 , 预应力技术得 到广 泛应用 , 深入研究预应力混凝土结构 或构件 的抗 震性能有着 重要 的工 程意义 。在往复 荷载下 。 预应力混凝土结构或构件 的材 料和力学行为复杂 , 要借助数值模 型加 以准确模拟 。本文 基于杆 件结构 纤维模 型程 需 序, 编制了预应力混凝土杆系结构及构 件的数值分析模型 。利用该模 型 , 本文对 往 复荷载下 的一榀 有粘 结预应力 混凝 土框架 试件和一榀无粘结 预应 力混 凝土框架试件 , 以及一根 无粘结 预应力混 凝 土柱试 件进 行 了数 值模 拟。计 算结 果与试 验结 果 的
对 比表 明 , 由于采用 了合理而 准确 的材 料滞 回模型并合理考虑 了预应力的影响 , 本文 开发 的杆系有 限元 数值分析 模型能 够准
确预测往复荷 载下预应力混 凝土杆系结构或构件 的滞 回特性 , 以用 于预应力 混凝 土 实际结构 的计 算 分析 及其受 力机 理的 可
探讨 。
维普资讯
Байду номын сангаас
第2 8卷第 6期 20 06年 l 2月
工 程 抗 震 与 加 圈 改 造
V0 . 8. 12 No.6
Eat q a e Re itn gn e ig a d Rer f t g rh u k ssa tEn ie rn n to ti i n
la s,te p cs i lt n o tu trs o mhe ̄ un e y l o d a O d pe d o u rc lmo 1 I ti a e a n me c l od h r ie smuai fPC s cu e r me e o r l d r c ci l a s h st e n n n me a de . n hs p p r, u r a c i i a lss mo lfrt e smuain o mb rsr cursi v lp d o h a i fa f r mo e r ga .A rme。a b d d P nay i de o h i lto fPC me e tu t e sde eo e n te b ss o be d lp rm i o PC fa n un on e C
smuain n tss n c ts h t fr t e e f O o sn rto a h se ei mae a mo e a d x cl c n ie n te n le c o i lt sa d e t idiae ta , o h r l U f u ig ain l y trtc o S tr l i d l n e a t y o sd r g h ifu n e f i
Lo d as
W n nl a gXu —i Y i p n u, eLe ig,L - u —h n ( e r etfCv ni en ze g Dp t n il gn r g,Ti h aU irt,B i 00 4 C i ) am o iE e i s g u n e i n v sy ei 10 8 ,hn j g n a
f me a d a n o d d P ou n e y l o d r i ltd w t e d v l e r ga .T e c mp r o ft e r sl ew e r n n u b n e c c l mn u d r c ci la s a e s a c muae i t e eo d p o r m hh p h o a s n o h u t b t e n i e s
[ 键词] 纤维模型 ; 关 往复荷载 ; 预应力混凝土 ; 分析方法 【 中圈分 类号】 T 38 1 U 7. [ 文献标识码 ] A
Nu rc lS mu a in f r t e Hy t r ss Be a i r o e t e s d Co r t t u t r s u de ci me ia i l to o h se e i h v o fPr sr se n e e S r c u e n r Cy l c
pet se o cee( C)s cu sh srmakbesgicn ei n ier gp at e ea s ftecmpiae e air fmae a a d rs esdc nrt P r t tr a u r e e ra l inf ac ne gn e n rci .B c ueo h o l tdb h vo tr l n i i c c o i
p s e s g h u r a a a ssmo e a e n f e d l d v lp d i i su y C c u aey pe itte h s rt rp r e fP e r n r t si ,te n me c l n l i i y d lb sd o b rmo es e eo e t s t d a a c rtl rd c h y t ei p e t so C i nh n e c o i
Ab t a t Du o p o r siey u ig i r cia o sr cin o rsr se o c ee sr t rs, te es ac e o es tc p rom a e o sr c : e t r g e sv l sn n p a tc lc n tu t fpe te s d c n r t tucu o e h r e r h s fr s imai e r nc f f
