北师大版七年级下册数学《整式的除法》整式的乘除(第1)精品PPT教学课件 (2)

合集下载

北师大版七年级下册数学(第1章整式的乘除)全章单元教学课件

同底数幂相乘，底数不变，指数相加 . 运算形式（同底、乘法），运算方法（底不变、指相加）
知1－讲
当三个或三个以上同底数幂相乘时，是否也具有这一性质呢？怎样用公式表示？
或 am·an·a =(am· an ) ·ap p =am+n· ap =am+n +p
am· an· ap =(a·a· … ·a)(a·a· … ·a)(a·a· … ·a) m个 a =am+n+p n个a p个a
知1－练
1 计算： (1)52×57； (3) －x2 •x3； (2)7×73×72； (4)(－c)3 •(－c)m .
(1)52×57＝52＋7＝59. 解：
(2)7×73×72＝71＋3＋2＝76.
(3)－x2· x3＝－x2＋3＝－x5. (4)(－c)3· (－c)m＝(－c)3＋m.
4 计算(a＋b)3· (a＋b)2m· (a＋b)n的结果为(B
A．(a＋b)6m＋n C．(a＋b)2mn＋3 D．(a＋b)6mn
)
B．(a＋b)2m＋n＋3
知2－练
5 x3m＋3可以写成(D
)
A．3xm＋1
C．x3· xm＋1 A．－22 018 C．－22 019
B．x3m＋x3
D．x3m· x3 ) B．22 018 D．22 019
(2)x2· x4＋(x2)3；
(3)[(x－y)n]2· [(x－y)3]n＋(x－y)5n. 导引：按有理数混合运算的运算顺序计算．
解：(1)a4· (－a3)2＝a4· a6＝a10；
(2)x2· x4＋(x2)3＝x6＋x6＝2x6； (3)[(x－y)n]2· [(x－y)3]n＋(x－y)5n ＝(x－y)2n· (x－y)3n＋(x－y)5n ＝(x－y)5n＋(x－y)5n

北师大初中数学七下《1.0第一章整式的乘除》PPT课件 (1)

本章知识结构：一、知识结构
（一）整式的乘法
1、同底数的幂相乘 3、积的乘方 5、单项式乘以单项式 7、多项式乘以多项式 9、完全平方公式
2、幂的乘方 4、同底数的幂相除 6、单项式乘以多项式 8、平方差公式
（二）整式的除法
1、单项式除以单项式 2、多项式除以单项式
知你识回
忆起了吗？就这些
3、积的乘方
法则：积的乘方，先把积中各因式分别乘方，再把所得的幂相乘。（即等于积中各因式乘方的积。）符号表示：
(ab)n anbn , (其中n为正整数), (abc)n anbncn (其中n为正整数)
练习：计算下列各式。
(2xyz)4 , ( 1 a2b)3, (2xy2 )3, (a3b2 )3 2
5、单项式乘以单项式
法则：单项式乘以单项式，把它们的系数、相同字母的幂分别相乘，其余的字母则连同它的指数不变，作为积的一个因式。
练习：计算下列各式。
(1)(5x3) (2x2 y),(2)(3ab)2 (4b3)
(3)(am )2b (a3b2n ),
(4)( 2 a2bc3) ( 3 c5) (1 ab2c)
2、幂的乘方
法则：幂的乘方，底数不变，指数相乘。
数学符号表示： (a m )n a mn
（其中m、n为正整数）
[(a m )n ] p a mnp （其中m、n、P为正整数）
练习：判断下列各式是否正确。
(a4)4 a44 a8,[(b2)3]4 b234 b24
(x2)2n1 x4n2,(a4)m (am)4 (a2m)2
切别记注
练习：1、判断下列式子是否正确，
！意哟

北师大版七年级数学下册《整式的乘法》整式的乘除PPT优质课件

所以2n-2-n＝1且3m＋1＋m-6=3.
已知求的值.
所以m、n的值分别是m=1，n=2.
解：
所以2m+2＝4且3m＋2n＋2=9.
故 m=1, n＝2
ZYT
例2 有一块长为xm，宽为ym的长方形空地，现在要在这块地中规划一块长 xm，宽 ym的长方形空地用于绿化，求绿化的面积和剩下的面积．
3a3 ·2a2=6a5
3x2 ·4x2=12x4
5y3·3y5=15y8
×
×
×
ZYT
计算：(1) 5x3·2x2y ； (2) －3ab·(－4b2) ；(3) 3ab·2a； (4) yz·2y2z2；
(1)5x3·2x2y＝(5×2)·(x3·x2)·y＝10x5y.(2)－3ab·(－4b2)＝[(－3)×(－4)]·a·(b·b2)＝12ab3.(3)3ab·2a＝(3×2)·(a·a)·b＝6a2b.(4)yz·2y2z2＝2·(y·y2)·(z·z2)＝2y3z3.
解：
ZYT
5.若长方形的宽是a2，长是宽的2倍，则长方形的面积为 _____.【解析】长方形的长是2a2，所以长方形的面积为a2·2a2=2a4.
2a4
6.一个三角形的一边长为a，这条边上的高的长度是它的那么这个三角形的面积是_____.【解析】因为三角形的高为，所以这个三角形的面积是
＝6a3－12a2＋9a－6a3－8a2
＝－20a2＋9a.
原式＝－20×4－9×2＝－98.
方法总结：在做乘法计算时，一定要注意单项式的符号和多项式中每一项的符号，不要搞错．
ZYT
先化简再求值:
解：原式=x4-x3+x2-x4+x3-x2+5x

北师大版七年级数学下册1.7 整式的除法(第1课时) (共18张PPT)

单项式乘以单项式如何计算？
单项式乘以单项式，把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式。
刘雪今年刚刚5岁，是幼儿园里最聪明的孩子，
李老师教她做算术，告诉她5 6 30后，她马
上就知道 30 5 6，你知道她是怎样计算的
呢？
计算下列各题，并说说你的理由
A. 8x2 B. 6x2 C. 8x3 D. 6x3
计算 4x2 y2z 3xy2 的结果是( C)
A. 3 xyz
4
C. 4 xz
3
B. 3 x2z
4
D. 3 xz
4
若 2xy 16x3 y,2则( )内应填的单项式是( D)
A. 4x2 y
B. 8x3 y2 C. 4x2 y2 D. 8x2 y
拓展
已知 12x3 ym 18xn y2 2 y，2 求
3
解： 12x3 ym 18xn y2
2 x3n ym2 3
2 y2 3
3m 2的n值。
所以 3 n 0, m 2 2，解得 m 4, n ，3所以
3m 2n 3 4 2 3 18
对比学习
单项式相乘
第一步
系数相乘
单项式相除
系数相除
第二步同底数幂相乘
同底数幂相除
第三步
其余字母不变连同其指数作为积的因式
只在被除式里含有的字母连同其指数一起作为商的因式
典型例题
例1 计算
3 x2 y3 3x2 y 5
10a4b3c2 5a3bc
2x2 y
3

7 xy 2
56x7 y5 14x4 y3 4x3 y2

(新)北师大版七年级数学下册第1章《整式的乘除》课件(全章,297张PPT)

Listen attentively
课前小测
4．（2016•江岸区模拟）如果等式x3•xm=x6成立，那么m=（ B） A．2 B．3 C．4 D．5 5．（2016春•沛县期末）若am=2，an=3，则 am+n的值为（） B A．5 B．6 C．8 D．9 5 3 2 x 6．（2016•南通）计算：x •x = ． a2 ． 7．（2015•柳州）计算：a×a= 8．（2016春•张家港市期末）已知：xa=4，xb=2，则xa+b=8 ．
Listen attentively
课后作业
（5）a3m•a2m﹣1（m是正整数）；（6）（﹣x2）•x3•（﹣x）2；（7）（）4×（）3×（）2；（8）3×33﹣3×9. （4）原式=（﹣x）6+13=（﹣x）19；（5）原式=a3m+2m﹣1=a5m﹣1；（6）原式=﹣x2•x3•x2=﹣x7；（7）原式=（）4+3+2=（）9．（8）原式=3×27﹣27=54．
目录 contents
课堂精讲
Listen attentively
课堂精讲
知识点1 同底数幂的乘法【例1】计算：﹣（﹣a）•（﹣a）2•（﹣a）．解：原式=﹣a4．
【类比精练】 1.计算：﹣x5•x2•x10．解：原式=﹣x17．
Listen attentively
课堂精讲
知识点2 同底数幂的乘法公式的逆用【例2】已知2a=5，2b=3，求2a+b+3的值．
谢谢观看！
第一章整式的乘除
第2课时幂的乘方与积的乘方（1 ）
目录 contents
课前小测
课堂精讲
课后作业

北师大版七年级数学下册 (整式的除法)整式的乘除教学课件(第1课时)

D．4a4
2.（毕节市）已知a≠0，下列运算中正确的是（ B ） A．3a+2a2＝5a3 B．6a3÷2a2＝3a C．（3a3）2＝6a6 D．3a3÷2a2＝5a5
ZYT
课堂检测
基础巩固题
1.下列运算中，正确的是( D )
A.4a-a=3 B.a2+a3=a5 C.(-2a)3=-6a3 D.ab2÷a=b2
= - 4 x3 y2；
算乘方，再算乘除．
ZYT
巩固练习
下列计算错在哪里？怎样改正？同数底不数变幂，的指除数法相，减底
（1）4a8 ÷2a 2= 2a 4 ( × ) 2a6
（2）10a3 ÷5a2=5a ( × ) 2a
系数相除
（3）(-9x5) ÷(-3x) =-3x4 ( × ) 3x4
×
（4）12a3b ÷4a2=3a (
2.二个相除：把各个单项式中的系数、同底数幂分别相除.
3.三个检验：单项式除以单项式的结果是否正确，可从以下三
个方面来检验：(1)结果仍是单项式；(2)结果中的字母少于或
等于被除式中的字母；(3)结果的次数等于被除式与除式的次数
之差.
ZYT
ZYT
第一章整式的乘除
整式的除法
第2课时
知识回顾
1.用字母表示幂的运算性质：
相同的，问小明下山用了多长时间？
解：(
1 2
vt2+vt1)÷4v=
11
8t2+ 4 vt1
答：小明下山所用时间为
1 8
t2+
1 4
t1
随堂演练
1.下列计算正确的是( C ) A.(x3+x4)÷x3=x4 B.(-7x3-8x2+x)÷x=-7x2-8x C.(2x2+x6)÷x2=2+x4 D.(ab2-4a3b4)÷2ab=b-2a2b3

整式的除法(第1课时)(课件)七年级数学下册(北师大版)

式子，再与等式右边的式子进行比较求解．
3 n 2
3 n 2
12 9
解：因为 (-3 x y ) ( x y ) ( 27 x y ) ( x y )
2
2
4
3 3
＝18x12－ny7，
所以18x12－ny7＝mx8y7.因此m＝18，12－n＝8.
所以n＝4，所以n－m＝4－18＝－14.
(2) (8m2n2) ÷(2m2n) ;
(3) (a4b2c)÷(3a2b) .
可以用类似于
分数约分的方法
来计算.
探究新知
解：(1) (x5y)÷x2
5
= 2

∙∙∙∙∙
=
∙
= x·x·x·y
=x3y
把除法式子写成分数形式
把幂写成乘积形式
约分
探究新知
被除式
除式
(x5y) ÷ x2
探究新知
例3：月球距离地球大约 3.84×105千米, 一架飞机的速度约为
8×102 千米/时. 如果乘坐此飞机飞行这么远的距离, 大约需要多
少时间 ?
解：3.84×105 ÷( 8×102 )
= 0.48×103
=480(小时) =20(天) .
答：如果乘坐此飞机飞行这么远的距离, 大约需要20天时间.
5
(2) 10a 4 b 3 c 2 5a 3 bc
(3) (2 x y ) ( 7 xy ) 14 x y
2
3
2
4
3
(4) (2a b)4 (2a b)2
分析：（1）（2）直接运用单项式除法的运算法则；
（3）要注意运算顺序：先乘方，再乘除；
（4）鼓励学生悟出：将（2a+b）视为一个整体来进行

北师大版七年级数学下册第一章整式的乘除PPT课件全套

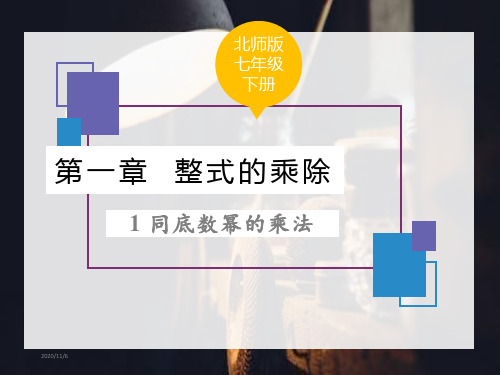
(3) (am)2 =am·am =am+m =a2m ;
n 个am
(4) (am)n =am·am·… ·am n 个m
(a m )n a mn
=am+m+ … +m =amn
2020/11/6
幂的乘方法则 (am)n=amn (m,n都是正整数) 幂的乘方，底数不变，指数相乘 .
2020/11/6
落实基础
例1 计算：
（1）(102)3 ;
(2) (b5)5 ;
（2）(an)3;
(4) －(x2)m ;
(5) (y2)3 ·y ; (6) 2(a2)6 － (a3)4 .
同底数幂相乘,底数不变,指数相加.
2020/11/6
情景导入
正方体的体积之比= 边长比的立方
乙正方体的棱长是 2 cm, 则乙正方体的体积 V乙= 8 cm3
甲正方体的棱长是乙正方体的 5 倍，则甲正方体的体积 V甲= 1000 cm3
可以看出，V甲是 V乙的 125 倍即 53 倍
2020/11/6
析出错的原因吗？试试看！
2020/11/6
例2 光在真空中的速度约为3×108m/s，太阳光照射到地球大约需要5×102s. 地球距离太阳大约有多远？
解： 3×108×5×102 =15×1010 =1.5×1011(m)
地球距离太阳大约有1.5×1011m.
2020/11/6
课堂练习
1.计算：（1）52×57; （3）-x2·x3；
北师版七年级下册
第一章整式的乘除
2 幂的乘方与积的乘方（第1课时）
2020/11/6
幂的意义:
复习旧知

北师大版初中七年级下册数学课件《整式的除法》整式的乘除PPT(第1课时)

（ ab）33 （．（ab）1＝）_a2_b_2 ___．
（（25a）2m3若bn4），（3则amm2b5）÷＝n 53＝a4b_2 _____． 3
（3）若n为正整数，且a2n＝3，则（3a3n）
1
2÷（27a4n）的值
为______．
随堂练习
4.计算： (1)－x5y13÷(－xy8)；
(2)－48a6b5c÷(24ab4)·(－5a5b2)． 6
(3) 10ab3 (5ab)
分析：
((14))可直21接x2运y4用单(3项x式2 y除3 ) 以单项式的运算法则进行计算；
(2)运算顺序与有理数的运算顺序相同．
随堂练习
4.解：
(1)－x5y13÷(－xy8) ＝x5－1·y13－8 ＝x4y5
(2)－48a6b5c÷(24ab4)·(－5a5b2) ＝[(－48)÷24×(－)5]a6－16＋5·b5－4＋2·c
第一章整式的乘除整式的除法第1课时
学习目标
1.会进行简单的单项式除以单项式的运算（结果是整式）； 2.经历探索单项式除以单项式法则的过程，理解单项式除
以单项式的算理； 3.在探索中体会类比方法的作用，发展有条理的思考与表
达能力和运算能力．
复习回顾
1．单项式与单项式相乘法则：一般地，单项式与单项式相乘，把它们的系数、同底数幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式． 2．同底数幂的除法法则：同底数幂相除，底数不变，指数相减．即：（a≠0，m，n都是正整数，并且m≥n）．那么单项式与单项式如果相除呢？
典型例题
(1) 3 x2 y3 3x2 y 5
3 5
3
xห้องสมุดไป่ตู้

北师大新版七下数学PPT课件 1.7.1 整式的除法(一)

习题1.13知识技能 1，2，5
学习了今天的知识，我们就能解决这个问题了！
你能计算下列各题吗？如果能，说说你的理由。
方法1：利用乘除法的互逆
方法2：利用类似分数约分的方法
约分时，先约系数，再约同底数幂，分子中单独存在的字母及其指数直接作为商的因式。
单项式与单项式相除的法则单项式相除，把系数，同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同它的指数一起作为商的因式。
单项式相乘第一步第二步系数相乘
单项式相除系数相除
同底数幂相乘
同底数幂相除
第三步
只在被除式里含有的字其余字母不变连同其指母连同其指数一起作为数作为积的因式商的因式
例1 计算：
解：
注意运算顺序：先乘方，再乘除，最后算加减
可以把 2a b 看成一个整体
如图所示，三个大小相同的球恰好放在一个圆柱形盒子里，三个球的体积占整个盒子容积的几分之几？
北师大新版七下
第一章 1.7.1 整式的乘除
整式的除法（一）
1.同底数幂的除法同底数幂相除，底数不变，指数相减。 2.单项式乘单项式法则单项式与单项式相乘，把它们的系数，相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式。
下雨时，常常是“先见闪电、后闻雷鸣”，这是因为光速比声速快的缘故。已知光在空气中的传播速度为3.0×108米/秒而声音在空气中的传播速度约 300米/秒，你知道光速是声速的多少倍吗？
Байду номын сангаас本随堂练习
答案
下雨时，常常是“先见闪电、后闻雷鸣”，这是因为光速比声速快的缘故。已知光在空气中的传播速度为3.0×108米/秒，而声音在空气中的传播速度约 300米/秒，你知道光速是声速的多少倍吗？解：

非常好的北师大版七年级数学下册：整式的乘除复习课(共44张PPT)名师公开课获奖课件百校联赛一等奖课

5.
（1） (1－3y )( 1+3y )( 1+9y2）
（2） ( ab+1)2－ ( ab－1)2
5.(a-3b+2c)(a+3b-2c)=(_____)2-(____)2. 【解析】(a-3b+2c)(a+3b-2c) =［a-(3b-2c)］［a+(3b-2c)］ =a2-(3b-2c)2. 答案：a 3b-2c
达为( )
(A)2.01×10-6公斤
(B)0.201×10-5公斤
(C)20.1×10-7公斤
(D)2.01×10-7公斤
【解析】选A.0.000 002 01=2.01×0.000 001=2.01×10-6.
4.计算a3b2÷ab2=____.
【解析】a3b2÷ab2=(a3÷a)(b2÷b2)=a2.
4.同底数幂旳除法旳运算性质. 同底数幂相除，底数不变，指数相减.即 am÷an＝am－n (a≠0,m，n都是正整数，m＞n). (1)底数必须相同.(2)合用于两个或两个以上旳同底数幂相除. 5.零指数幂. 因为am÷am＝1，又因为am÷am＝am－m＝a0,所以a0＝1.其中a≠0. 即：任何不等于0旳数旳零次幂都等于1. 对于a0：(1)a≠0.(2)a0＝1.
5.整式旳除法.
注：(1)单项式除以单项式漏掉某个同底数幂或只在被除式中出现旳字母. (2)多项式除以单项式时漏项造成错误.
幂旳运算【有关链接】
幂旳运算涉及同底数幂旳乘法、除法、幂旳乘方、积旳乘方及零指数幂和负整指数幂旳运算,它是整式运算旳基础，如单项式乘单项式旳实质就是同底数幂旳乘法.幂旳运算是中考命题热点之一，常以选择题、填空题旳形式出现.