高斯列主元素消去法
高斯列主元消去法

高斯列主元消去法2.3高斯列主元消去法解线性方程组一:问题的提出我们都知道,高斯列主元素消去法是计算机上常用来求解线性方程组的一种直接的方法。
就是在不考虑舍入误差的情况下,经过有限步的四则运算可以得到线性方程组的准确解的一类方法。
实际运算的时候因为只能有限小数去计算,因此只能得到近似值。
在实际运算的时候,我们很多时候也常用高斯消去法。
但是高斯消去法在计算机中运算的时候常会碰到两个问题。
1.一旦遇到一些主元等于0,消元过程便无法进行下去。
2.在长期使用中还发现,即使消元过程能进行下去,但是当一些主元的绝对值很小时,求解出的结果与真实结果相差甚远。
为了避免高斯消去法消元过程中出现的上述两个问题,一般采用所谓的选择主元法。
其中又可以分为列选主元和全面选主元两种方法。
目前计算机上常用的按列选主元的方法。
因此我在这里做的也是列选主元高斯消去法。
二、算法的基本思想大家知道,如果一个线性方程组的系数矩阵是上三角矩阵时,即这种方程组我们称之为上三角方程组,它是很容易求解的。
我们只要把方程组的最下面的一个方程求解出来,在把求得的解带入倒数第二个方程,求出第二个解,依次往上回代求解。
然而,现实中大多数线性方程组都不是上面所说的上三角方程组,所以我们有可以把不是上三角的方程通过一定的算法化成上三角方程组,由此我们可以很方便地求出方程组的解。
高斯消元法的目的就是把一般线性方程组简化成上三角方程组。
于是高斯消元法的基本思想是:通过逐次消元将所给的线性方程组化为上三角形方程组,继而通过回代过程求解线性方程组。
三、算法的描述1、设有n元线性方程组如下:=2、第一步:如果a11!=0,令li1= ai1/a11, I= 2,3,……,n用(-li1)乘第一个方程加到第i个方程上,得同解方程组:a(1)11a(1)12...a(1)1nx1b(1)1a(1)21a(1)22...a(1)2nx2b(1)2 .......=.a(1)n-11 a(1)n-12 . .a(1)n-1nxn-1b(1)n-1a(1)n1a(1)n2. . . a(1)nnxnb(1)n简记为:A(2)x=b(2)其中a(2)ij = a(1)ij – li1 a(1)1j ,I ,j = 2,3,..,nb(2)I = b(1)I – li1 b(1)1 ,I = 2,3,...,n第二步:如果a(2)22!=0,令li2= a(2)i2/a(2)22, I= 3,……,n依据同样的原理,对矩阵进行化间(省略),依次下去,直到完成!最后,得到上三角方程组:a(1)11a(1)12...a(1)1nx1b(1)1a(1)22 ...a(1)2nx2b(1)2 .......=.. .a(n-1)n-1nxn-1b(n-1)n-1. . . a(n)nnxnb(n)n简记为:A(n)x=b(n)最后从方程组的最后一个方程进行回代求解为:n = b(n) / a(n)nni = ( b(k)k - a(k)kjxj ) / a(k)kk以上为高斯消去法的基本过程。
(7) 列主元高斯消去法的实现

列主元高斯消去法是一种用于解线性方程组的经典算法,其实现过程包括主元选取、互换行、消元和回代等步骤。
本文将从理论基础、算法描述、实现步骤和代码示例等方面介绍列主元高斯消去法的实现方法,希望可以帮助读者更好地理解和掌握这一算法。
一、理论基础列主元高斯消去法是求解线性方程组的一种经典方法,其基本思想是通过逐步消去未知数,最终得到方程组的解。
在实际应用中,通常将线性方程组表示为增广矩阵的形式,然后通过主元选取、互换行、消元和回代等操作,逐步将增广矩阵转化为阶梯形矩阵或行阶梯形矩阵,最终获得方程组的解。
列主元高斯消去法的关键在于主元的选取,通过选取适当的主元可以避免出现数值不稳定的情况,从而提高求解的准确性和稳定性。
二、算法描述列主元高斯消去法的基本算法描述如下:1. 将线性方程组表示为增广矩阵的形式2. 从第一行开始,选择当前列中绝对值最大的元素作为主元,并将其所在行与当前行交换3. 通过第一个主元,将当前列下方的元素消为零,得到一个新的增广矩阵4. 重复以上步骤,直到得到一个阶梯形矩阵或行阶梯形矩阵5. 利用回代的方法,求解得到线性方程组的解三、实现步骤基于上述算法描述,可以将列主元高斯消去法的实现步骤总结如下:1. 主元选取:对于当前列,在所有未处理的元素中选择绝对值最大的元素作为主元,并将其所在行与当前行交换2. 互换行:如果选取的主元为零,则需要考虑互换行的操作,以避免出现除零错误3. 消元:利用当前列的主元将下方的元素消为零4. 回代:通过阶梯形矩阵或行阶梯形矩阵进行回代,求解得到线性方程组的解在实现列主元高斯消去法时,需要注意处理数值计算中可能出现的特殊情况,如零主元和除零错误等,并进行合理的异常处理。
四、代码示例下面是列主元高斯消去法的简单实现代码示例,该示例使用Python 语言编写:```pythonimport numpy as npdef gauss_elimination(A, b):n = len(b)for i in range(n):pivot = ifor j in range(i+1, n):if abs(A[j, i]) > abs(A[pivot, i]):pivot = jA[[i, pivot]] = A[[pivot, i]]b[[i, pivot]] = b[[pivot, i]]for j in range(i+1, n):factor = A[j, i] / A[i, i]b[j] -= factor * b[i]A[j] -= factor * A[i]x = np.zeros(n)for i in range(n-1, -1, -1):x[i] = (b[i] - np.dot(A[i, i+1:], x[i+1:])) / A[i, i]return x```以上代码示例实现了列主元高斯消去法的求解过程,通过调用该函数可以求解给定的线性方程组。
高斯列主元消去法

如果在高斯顺序消去法消去过程进行到第i 步时,现选取ri a )(n r i ≤≤中绝对值最大的元素,设为第j 行的元素ji a ,把矩阵的第i 行和第j 行互换,这时ii a 变为ji a ,然后将第i+1行至第n 行中的每一行减去第i 行乘以ii ki a a (k 代表行号),依次进行消元。
Gauss 列主元消去法的算法步骤如下:将方程组写成以下的增广矩阵的形式:⎪⎩⎪⎪⎨⎧43212423222114131211............n n n n a a a a a a a a a a a a对k=1,2,3,...,n-1,令∑==nks sk pk a a max ;交换增广矩阵的第k 行与第p 行;对j=k+1,k+2,...,n,计算kk jkkm jm jm a a a a a ⋅-=(m=看,k+1,...,n )kk jkk j j a a b b b ⋅-=算法结束。
三角分解法程序如下:建立相应的M 文件,其函数名为LU,程序如下:function y=LU(A,B);n=length(A);A=[A B];for k=1:n-1;for i=k:n;if (abs(A(i,k))==max(abs(A(k:n,k)))) P(k)=i;temp=A(k,:);A(k,:)=A(i,:);A(i,:)=temp;endendfor j=k+1:n;A(j,k)=A(j,k)/A(k,k);A(j,k+1:n+1)=A(j,k+1:n+1)-A(j,k)*A(k,k+1:n+1);endendP(n)=n;L(1,1)=1;L(2:n,1)=A(2:n,1);L(1,2:n)=0;U(1,1)=A(1,1);U(2:n,1)=0;U(1,2:n)=A(1,2:n);for i=2:n;L(i,1:i-1)=A(i,1:i-1);L(i,i)=1;L(i,i+1:n)=0;U(i,1:i-1)=0;U(i,i:n)=A(i,i:n);endx(n) = A(n,n+1)/U(n,n);for k = n-1:-1:1x(k)=A(k,n+1);for p=n:-1:k+1;x(k) = x(k)-U(k,p)*x(p); endx(k)=x(k)/U(k,k);endxLUPend在程序命令行输入:a=[0.101 2.304 1.5355;-1.347 3.712 4.623;-2.835 1.072 5.643];b=[1.183,2.137,3.035]';LU(a,b)运行结果为:x =3.1160 -1.1960 2.3305 L =1.0000 0 00.4751 1.0000 0-0.0356 0.7313 1.0000 U =-2.8350 1.0720 5.64300 3.2027 1.94180 0 0.3359 P =3 2 3。
列主元素Gauss消去法Jacobi迭代法原理及计算方法

一、 列主元素Gauss 消去法、Jacobi 迭代法原理及计算方法1. 列主元素Gauss 消去法:1.1 Gauss 消去法基本原理设有方程组Ax b =,设A 是可逆矩阵。
高斯消去法的基本思想就是将矩阵的初等行变换作用于方程组的增广矩阵[]B A b = ,将其中的A 变换成一个上三角矩阵,然后求解这个三角形方程组。
1.2 列主元Gauss 消去法计算步骤将方程组用增广矩阵[]()(1)ijn n B A b a ⨯+== 表示。
1). 消元过程对1,2,,1k n =-(1) 选主元,找{},1,,k i k k n ∈+ 使得 ,max k i k ik k i na a ≤≤= (2) 如果,0k i k a =,则矩阵A 奇异,程序结束;否则执行(3)。
(3) 如果k i k ≠,则交换第k 行与第k i 行对应元素位置,k kj i j a a ↔,,,1j k n =+ 。
(4) 消元,对,,i k n = ,计算/,ik ik kk l a a =对1,,1j k n =++ ,计算.ij ij ik kj a a l a =-2). 回代过程(1) 若0,nn a =则矩阵奇异,程序结束;否则执行(2)。
(2) ,1/;n n n nn x a a +=对1,,2,1i n =- ,计算,11/n i i n ij j ii j i x a a x a +=+⎛⎫=- ⎪⎝⎭∑2. Jacobi 迭代法2.1 Jacobi 迭代法基本原理Jacobi 迭代法的基本思想是对n 元线性方程组b Ax =,.,n n R b R A ∈∈将其变形为等价方程组f Bx x +=,其中.,,n n n n R x R f R B ∈∈∈⨯B 成为迭代矩阵。
从某一取定的初始向量)0(x 出发,按照一个适当的迭代公式 ,逐次计算出向量f Bx x k k +=+)()1( ( 1,0=k ),使得向量序列}{)(k x 收敛于方程组的精确解.(1)输入1,,,,)0(=k n xb A ε,. (2) )(1,1)0()1(∑≠=-=n j i i j ij i iii x a b a x )1,0(n i = (3)判断 ε≤--≤≤)0()1(10max i i n i x x ,若是,输出1)1(2)1(1,,n x x x ,若否,置1+=k k ,)1()0(i i x x =,)2,1(n i =。
数值分析列主元高斯消去法
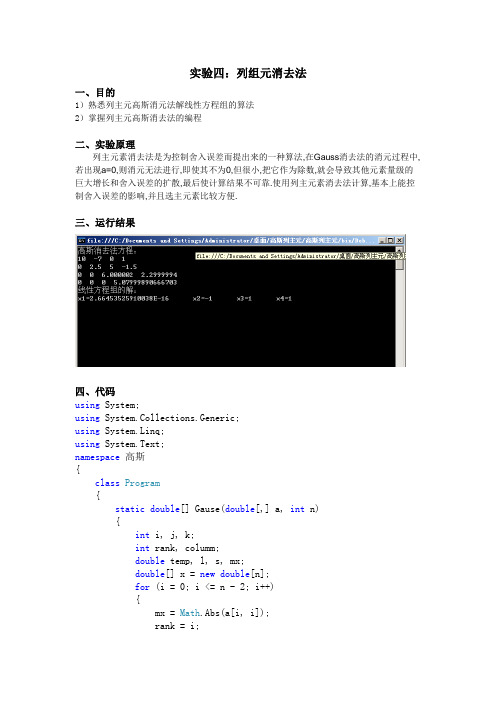
实验四:列组元消去法一、目的1)熟悉列主元高斯消元法解线性方程组的算法2)掌握列主元高斯消去法的编程二、实验原理列主元素消去法是为控制舍入误差而提出来的一种算法,在Gauss消去法的消元过程中,若出现a=0,则消元无法进行,即使其不为0,但很小,把它作为除数,就会导致其他元素量级的巨大增长和舍入误差的扩散,最后使计算结果不可靠.使用列主元素消去法计算,基本上能控制舍入误差的影响,并且选主元素比较方便.三、运行结果四、代码using System;using System.Collections.Generic;using System.Linq;using System.Text;namespace高斯{class Program{static double[] Gause(double[,] a, int n){int i, j, k;int rank, columm;double temp, l, s, mx;double[] x = new double[n];for (i = 0; i <= n - 2; i++){mx = Math.Abs(a[i, i]);rank = i;columm = i;for (j = i + 1; j <= n - 1; j++) //选主元if (Math.Abs(a[j, i]) > mx){mx = Math.Abs(a[j, i]);rank = j;columm = i;}for (k = 0; k <= n; k++) //主元行变换{temp = a[i, k];a[i, k] = a[rank, k];a[rank, k] = temp;} //消元for (j = i + 1; j <= n - 1; j++){l = a[j, i] / a[i, i];for (k = i; k <= n; k++)a[j, k] = a[j, k] - l * a[i, k];}}x[n - 1] = a[n - 1, n] / a[n - 1, n - 1]; //回代方程求解x for (i = n - 2; i >= 0; i--){s = 0;for (j = i + 1; j <= n - 1; j++)s = s + a[i, j] * x[j];x[i] = (a[i, n] - s) / a[i, i];}return x;}static void Main(string[] args){double[,] a = new double[4, 5] { { 10, -7, 0, 1, 8 }, { -3, 2.099999, 6, 2, 5.900001 }, { 5, -1, 5, -1, 5 }, { 2, 1, 0, 2, 1 } };int n = 4;double[] x = new double[n];x = Gause(a, n);Console.WriteLine("高斯消去法方程:");for (int i = 0; i < n; i++){for (int j = 0; j < n; j++)Console.Write(a[i, j].ToString() + " ");Console.WriteLine();}Console.WriteLine("线性方程组的解:");for (int i = 0; i <= n - 1; i++)Console.Write("x" + (i + 1).ToString() + "=" +x[i].ToString() + " ");Console.WriteLine();Console.ReadLine();}}}四、分析通过本次实验的学习,学会根据算法编写基本的相关程序,虽然此次程序模板由老师给予,但认真阅读理解程序有助于今后的学习,再利用计算机中的C语言对高斯列主元消去法可以快速得到线性方程组的解,由简单的线性方程组可以推广到一般n阶线性方程组,这对如何利用高斯列主元消去法解决实际问题有了一定的经验。
列主元素高斯消去法

实验报告题目:列主元素高斯消去法学生姓名陈玉霞学号20111325015学院信息与控制学院专业信息工程(系统工程方向)指导教师殷传洋2013 年11 月18日一、实验目的(1)掌握高斯消去法的基本思路和迭代步骤;(2)培养编程与上机调试能力。
二、实现功能本程序采用GAUSS列主元消去法求解线性方程组。
AX=b.其中A为N阶矩阵,X,b均为N围列向量。
三、算法描述高斯消去法基本思路设有方程组Ax=b,设A是可逆矩阵。
高斯消去法的基本思想就是将矩阵的初等行变换作用于方程组的增广矩阵B [A b],将其中的A变换成一个上三角矩阵,然后求解这个三角形方程组。
四、实验内容X1-0.5*X2+1.5*X3=0.5X2-0.25*X3=0.5X3=-6五、实验步骤(1) 写出增广矩阵A;(2) 选主元;(3) 判断是否奇异;(4) 交换对应行元素;(5) 消元;(6) 回代,计算出X[1], X[2], X[3].六、代码# include<stdio.h># include<math.h># define delta 1e-6#define N 100void main(){int i,j,t,r,n,u,c=0;float p,L,max,s;float X[N];float a[N][N+1];printf("请输入方程的阶数\n"); scanf("%d",&n);printf("输入的原方程系数,中间用空格隔开\n"); for(i=0;i<n;i++) for(j=0;j<n+1;j++)scanf("%f",&a[i][j]);printf("方程系数为\n");for(i=0;i<n;i++){for(j=0;j<n+1;j++){printf("%.2f ",a[i][j]);if(j==n) {printf("\n");}}}for(j=0;j<n-1;j++){{max=fabs(a[j][j]);r=j;}for(i=j+1;i<n;i++)if(fabs(a[i][j])>max){max=a[i][j];r=i;}if(fabs(a[i][j])<delta)printf("矩阵奇异");for(t=j;t<n+1;t++){} p=a[j][t]; a[j][t]=a[r][t]; a[r][t]=p; } for(i=j+1;i<N;i++) { L=a[i][j]/a[j][j]; for(t=j;t<n+1;t++) a[i][t]=a[i][t]-L*a[j][t]; }printf("输出原方程的解为:\n");X[n-1]=a[n-1][n]/a[n-1][n-1];for(i=n-2;i>=0;i--){s=a[i][n];for(j=i+1;j<n;j++)s=s-a[i][j]*X[j];X[i]=s/a[i][i];}for(u=0;u<n;u++)for(j=0;j<n+1;j++){printf("%12f",a[u][j]); c++;if(c%(n+1)==0) printf("\n");}for(i=0;i<n;i++){printf("x(%d)=%.4f\n",i+1,X[i]); if(i==n-1)printf("\n");}}七、实验结果八、实验体会从实验中,我学会了很多,首先要弄懂高斯消去法的原理和计算步骤,使我更加了解Gauss列主元素消去法的实质,掌握了新知识的同时,也为以后的学习打下一个好的基础。
高斯列主元消去法例题

高斯列主元消去法例题高斯列主元消去法是解线性方程组的一种方法,也称为高斯-约旦(Gauss-Jordan)消去法。
它的基本思想是通过矩阵的初等行变换,将矩阵化为简化行阶梯形矩阵,然后根据系数矩阵的行列式是否等于0来求得唯一或无穷多解。
下面以一个例题来讲解高斯列主元消去法的步骤。
例题:解下列线性方程组x1 + 2x2 + 3x3 = 94x1 + 5x2 + 6x3 = 247x1 + 8x2 + 10x3 =40首先,将方程组表示为增广矩阵的形式:1 2 3 | 94 5 6 | 247 8 10| 40接下来,要使用高斯列主元消去法,将增广矩阵化为简化行阶梯形矩阵。
具体步骤如下:1.将第一列中的绝对值最大的元素移到第一行。
7 8 10| 404 5 6 | 241 2 3 | 92.用第一行的首元素消元。
7 8 10| 400 1 -2| 60 -6 -21| -273.将第二列中的绝对值最大的元素移到第二行。
7 8 10| 400 -6 -21| -270 1 -2| 64.用第二行的次元素消元。
7 8 10| 400 1 -2| 60 0 -9| 95.将第三列中的绝对值最大的元素移到第三行。
7 8 10| 400 1 -2| 60 0 -9| 96.用第三行的末元素消元。
7 8 10| 400 1 -2| 60 0 1 | -1现在,我们得到了一个简化行阶梯形矩阵,可以根据系数矩阵的行列式是否等于0来求得唯一或无穷多解。
我们发现,最后一行只有一个非零元素,因此,对应的未知数x3的系数不为0,可以直接利用倒推法求得方程组的解。
7.用第二行解出x2x2 - 2x3 = 6x2 = 2x3 + 68.用第一行解出x1x1 + 8x2 + 10x3 = 40x1 + 8(2x3 + 6) + 10x3 = 40x1 + 26x3 = 8综上所述,该线性方程组的解为:x1 = -26t + 8x2 = 2t + 6x3 = t其中,t为任意常数。
gauss列主元素消去法matlab

高斯列主元素消去法是一种解线性方程组的常用方法,特别在数值分析和线性代数中应用广泛。
在Matlab中,我们可以使用该方法来解决大规模的线性方程组,包括矩阵的求解和矩阵的反转。
一、高斯列主元素消去法的基本原理高斯列主元素消去法是一种基于矩阵消元的方法,它通过一系列的矩阵变换将原始的线性方程组转化为上三角形式,然后再进行回代求解。
这个方法的核心就是通过矩阵的变换来简化原始的线性方程组,使得求解过程更加简单高效。
在Matlab中,我们可以利用矩阵运算和函数来实现高斯列主元素消去法,如`lu`分解函数和`\"`运算符等。
通过这些工具,我们能够快速地求解各种规模的线性方程组并得到准确的结果。
二、高斯列主元素消去法在Matlab中的实现在Matlab中,我们可以通过调用`lu`函数来实现高斯列主元素消去法。
该函数返回一个上三角矩阵U和一个置换矩阵P,使得PA=LU。
通过对U进行回代求解,我们可以得到线性方程组的解。
除了`lu`函数之外,Matlab还提供了一些其他的函数和工具来帮助我们实现高斯列主元素消去法,比如`\"`运算符和`inv`函数等。
通过这些工具的组合使用,我们能够更加灵活地进行线性方程组的求解,并且可以方便地处理特殊情况和边界条件。
三、高斯列主元素消去法的应用与局限性高斯列主元素消去法在实际应用中具有广泛的适用性,特别是对于大规模的线性方程组或者稀疏矩阵的求解。
通过Matlab中的工具和函数,我们可以快速地求解各种规模的线性方程组,并得到高精度的数值解。
然而,高斯列主元素消去法也存在一些局限性,比如对于奇异矩阵或者接近奇异矩阵的情况时,该方法的求解精度可能会下降。
在实际应用中,我们需要结合具体的问题和矩阵特性来选择合适的求解方法,以确保得到准确的结果。
四、个人观点和总结作为一种经典的线性方程组求解方法,高斯列主元素消去法在Matlab 中具有较好的实现和应用效果。
通过对其原理和实现细节的深入理解,我们能够更加灵活地应用该方法,并且能够更好地理解其适用性和局限性。
高斯列主元消元法解线性方程组

高斯列主元消元法解线性方程组一、题目:用Gauss 列主元消去法解线性方程组Ax b =,其中,A=17.031 -0.615 -2.991 1.007 -1.006 0.000-1.000 34.211 -1.000 -2.100 0.300 -1.7000.000 0.500 13.000 -0.500 1.000 -1.5004.501 3.110 -3.907 -61.705 12.170 8.9990.101 -8.012 -0.017 -0.910 4.918 0.1001.000 2.000 3.000 4.500 5.000 21.803⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ 0.230 -52.322 54.000 240.236 29.304 -117.818b ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭T X=(0.907099 -1.961798 3.293738 -4.500708 3.029344 -5.255068)二、原理及步骤分析设nn ij R a A ⨯∈=][)1(,nn Rb b b b ∈=],,,[)1()2(2)1(1 。
若约化主元素),,2,1(0)(n k a k kk =≠,则通过高斯消元法将方程b AX =约化为三角形方程组求解。
如果在消元过程中发现某个约化主元0)(=k kk a , 则第K 次消元就无法进行。
此外,即使所有约化主元全不为零,虽然可以完成方程组的求解,但也无法保证结果的可靠性,因为计算过程中存在舍入误差。
为减少计算过程中的舍入误差对解的影响,在每次消元前,应先选择绝对值尽可能大的元作为约元的主元,如果在子块的第一列中选取主元,则相应方法称为列主元消元法。
相应过程为:(1)选主元:在子块的第一列中选择一个元)(k k i k a 使)(max k ik ni k kk i a a k ≤≤=并将第k 行元与第k i 行元互换。
列主元高斯消去法

列主元高斯消去法简介
【示例范文仅供参考】
---------------------------------------------------------------------- 列主元素消去法是为控制舍入误差而提出来的一种算法,列主元素消去法计算基本上能控制舍入误差的影响。
其基本思想是:在进行第k(k=1,2,...,n-1)步消元时,从第k列的akk 及其以下的各元素中选取绝对值最大的元素,然后通过行变换将它交换到主元素akk的位置上,再进行消元。
列主元消去法仅需矩阵行的交换,因此不发生未知数排列次序的调换。
而全主元消去法则要花费相当多的时间选取主元,且还需记录系数矩阵列交换信息。
其原理是在高斯消去法的消元过程中第k步要求除以akk,为了防止除数为零或除数太小造成的误差过大的问题,在消元开始是先将该列最大元(绝对值)所在行移到消元第一行在除akk,然后消元。
列主元消去法虽然和高斯消去法原理一样,但是列主元消去法可以减小舍入误差,精度比较高,是解决小型稠密矩阵的一个较好的算法。
而高斯消去法虽然编程简单,但是计算量大,而且对于两个相近的解时由于舍入误差的存在,使得结果误差很大。
高斯列主元消去法和直接三角分解法(LU分解)

实验六高斯列主元消去法和直接三角分解法(LU分解)一、实验名称:分别用高斯列主元消去法和直接三角分解法(LU分解)求方程组的解系数矩阵:10 7 8 7 常向量:107 5 6 5 88 6 10 9 67 5 9 10 7精确解为:(-60,102,-27,16)二、试验目的:分别用高斯列主元消去法和直接三角分解法(LU分解)求方程组的解,比较二者不同的特点。
三、算法描述:2、直接三角分解法(LU分解)四、源程序:1、高斯列主元消去法#include <stdio.h>void main(){float a[4][4]={{10,7,8,7},{7,5,6,5},{8,6,10,9},{7,5,9,10}}, y[4],c[4][4],x[4],d[4],m,b; int i,n,j,f;printf("请输入右端项:\n");for(i=0;i<=3;i++)scanf("%f",&y[i]);for(n=0;n<=2;n++){ m=a[n][n]; f=n;for(i=(n+1);i<=3;i++){if(m<a[i][n]){m=a[i][n]; f=i;}}if(f!=n){for(j=0;j<=3;j++){c[n][j]=a[n][j]; a[n][j]=a[f][j];a[f][j]=c[n][j];}d[n]=y[n]; y[n]=y[f]; y[f]=d[n];}for(i=(n+1);i<=3;i++){b=-a[i][n]/a[n][n];for(j=0;j<=3;j++)a[i][j]=a[n][j]*b+a[i][j];y[i]=y[n]*b+y[i];}}x[3]=y[3]/a[3][3];x[2]=(y[2]-a[2][3]*x[3])/a[2][2];x[1]=(y[1]-a[1][3]*x[3]-a[1][2]*x[2])/a[1][1];x[0]=(y[0]-a[0][3]*x[3]-a[0][2]*x[2]-a[0][1]*x[1])/a[0][0];printf("x1的值为%f\nx2的值为%f\nx3的值为%f\nx4的值为%f\n",x[0],x[1],x[2],x[3]);}2、直接三角分解法(LU分解)#include <stdio.h>void main (){float a[4][4]={{10,7,8,7},{7,5,6,5},{8,6,10,9},{7,5,9,10}},y[4], l[4][4],x[4],u[4][4],b[4]; int i,n,j;printf("请输入右端项:");for(i=0;i<=2;i++)scanf ("%f",&b[i]);for (i=0;i<=3;i++){ u[0][i]=a[0][i];l[i][0]=a[i][0]/u[0][0];}for (n=1;n<=2;n++){for(j=0;j<=(3-n);j++){u[n][n+j]=a[n][n+j];for (i=0;i<n;i++)u[n][n+j]=u[n][n+j]-l[n+j][i]*u[i][n]; }if (n=1){l[2][1]=(a[2][1]-l[2][0]*u[0][1])/u[1][1]; l[3][1]=(a[3][1]-l[3][0]*u[0][1])/u[1][1]; } else if (n=2){l[3][2]=(float)(a[3][2]-l[3][0]*u[0][2]-l[3][1]*u[1][2])/u[2][2]; } }for (n=0;n<=3;n++){y[n]=b[n];for (i=0;i<n;i++)y[n]=y[n]-l[n][i]*y[i]; }for (n=3;n>=0;n--){x[n]=y[n];for (i=3;i>n;i--)x[n]=(x[n]-u[n][i]*x[i]);x[n]=x[n]/u[n][n]; }for(i=0;i<=3;i++)printf("x%d的的值为:%f\n",i+1,x[i]); }五、输出结果1、高斯列主元消去法(1)请输入右端项:10 8 6 7X1的值为-59.999584X1的值为101.999306X1的值为-26.999817X1的值为15.999890(2)请输入右端项:5 6 7 8X1的值为-98.999306X1的值为163.998840X1的值为-40.999695X1的值为24.999817六、对算法的理解和改进改变右端项会对结果产生明显的影响,高斯列主元消去法仅考虑依次按列选取主元素,然后按行使之变到主元位置,再进行消去运算,消元结果冲掉A,计算解X冲掉常数项b,则在计算过程中由于右端项的不同解必然不同。
解线性方程组的列主元素高斯消去法和lu分解法

数值试验报告分析一、实验名称:解线性方程组的列主元素高斯消去法和LU 分解法二、实验目的及要求:通过数值实验,从中体会解线性方程组选主元的必要性和LU 分解法的优点,以及方程组系数矩阵和右端向量的微小变化对解向量的影响。
三、算法描述:本次试验采用的是高斯列主元消去法和LU 分解法求解线性方程组的解。
其中,高斯消去法的基本思想是避免接近于零的数作分母;能进行到底的条件:当A 可逆时,列主元Gauss(高斯)消去法一定能进行到底。
优点:具有很好的数值稳定性;具有与顺序Gauss 消去法相同的计算量。
列主元Gauss(高斯)消去法的精度显著高于顺序Gauss(高斯)消去法。
注意:省去换列的步骤,每次仅选一列中最大的元。
矩阵的三角分解法是A=LU,L 是下三角阵,U 是上三角阵,Doolittle 分解:L 是单位下三角阵,U 是上三角阵;Crout 分解:L 是下三角阵,U 是单位上三角阵。
矩阵三角分解的条件 是矩阵A 有唯一的Doolittle 分解的充要条件是A 的前n-1顺序主子式非零;矩阵A 有唯一的Crout 分解的充要条件是A 的前n-1顺序主子式非零。
三角分解的实现是通过(1)Doolittle 分解的实现; (2)Doolittle 分解的缺点:条件苛刻,且不具有数值稳定性。
(3)用Doolittle 分解求解方程组: AX=b LUX=b LY=bA=LU UX=Y ;四、实验内容:解下列两个线性方程组(1) ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--11134.981.4987.023.116.427.199.103.601.3321x x x (2) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----15900001.582012151526099999.23107104321x x x x a 、用你熟悉的算法语言编写程序用列主元高斯消去法和LU 分解求解上述两个方程组,输出Ax=b 中矩阵A 及向量b, A=LU 分解的L 及U ,detA 及解向量x.b 、将方程组(1)中系数3.01改为3.00,0.987改为0.990,用列主元高斯消去法求解变换后的方程组,输出列主元行交换次序,解向量x及detA,并与(1)中结果比较。
列主元高斯消去法的实现

《数值分析课程设计》报告专业:学号:学生姓名:指导教师:一、题目列主元guess消去法求方程的解二、理论列主元高斯消去法是在高斯消去法的基础上而得到的一种比较快速合理的解线性方程组的方法。
它的基本思想是每次在所在列对角线及以下元素中选择绝对值最大的元素作为主元进行消元计算。
使用列主元消去法相对于高斯消去法更能减少舍入误差的影响。
三、方法、算法与程序设计求解Ax=b第一步:写出增广矩阵[A| b];第二步:判断增广矩阵的秩r[A|b]与A的秩r[A]的关系:若r[A|b]= r[A],线性方程组有唯一解;若r[A|b]>r[A],线性方程组没有解;若r[A|b]<r[A],线性方程组有无穷多解;第三步:若|A|≠0,方程组有唯一解法一:求出A-1,x=A-1b法二:利用初等行变换将[A| b]中A化为对角阵计算矩阵行列式:直接调用Det[]函数计算计算矩阵条件数:第一步:求出矩阵的逆矩阵第二步:分别计算矩阵极其逆的无穷范数,一范数和二范数第三步:求解矩阵的条件数Cond(A)∞=||A-1||∞*||A||∞Cond(A)1=||A-1||1*||A||1Cond(A)2=||A-1||2*||A||2=(λmax(A的转置*A)/λmin(A的转置*A))1/2计算机求解第一步:消元对k=1,2,3,……n,进行:步骤1:选主元(第k列中第k个至第n个元素中绝对值较大者)步骤2:将主元所在行与第k行交换步骤3:消元第二步:回代求解流程图如下:k=1,2,……,ni=k+1,k+2,……,nlik =aik/akk得到aikj=k+1,k+2,……,n+1 a ij-a ik*a kj得到a ij三、算例、应用实例用列主元消去法解线性方程组Ax=b⑴ 3.10x1+ 6.03x2+1.99x3=11.27x1+ 4.16x2-1.23x3= 1 ;0.983x1-4.81x2+ 9.34x3=1⑵ 3.00x1+ 6.03x2+ 1.99x3=11.27x1+ 4.16x2-1.23 x3 = 1.0.990x1 -4.81x2+9.34 x3=1分别输出A ,b ,detA,解向量x,⑴中A的条件数。
高斯列主元消去法

问题提出:采用高斯列主元消去法解线性方程组。
算法(公式)推导:高斯顺序消去法有一个最大的缺点就是一旦对角元素为0,就进行不下去了,为了解决这个问题就有了高斯主元消去法。
如果在高斯顺序消去法消去过程进行到第i 步时,先选取a ri ()n r i ≤≤中(即第i 列)绝对值最大的元素,设为第j 行的元素aji ,然后将第i+1行至第n 行中的每一行减去第i 行乘以ii kj a a (k 代表行号),依次进行消元,这样得到的算法叫高斯按列主元消去法。
高斯按列主元消去法的算法步骤介绍如下:1. 将方程组写成以下的增广矩阵的形式: 432144434241343332312423222114131211b b b b a a a a a a a a a a a a a a a a 2. 对k=1,2,3,…..,n-1,令∑==nk s sk pk a a max ,交换增广矩阵的第k 行与第p 行;对j=k+1,K+2,……..,n,计算*km jkjm jm kk a a a a a =-(m=k,k+1,....n)kk jk k j j a a b b b *-=算法结束。
3. 在MATLABE 中编程实现的高斯按列主元消去法函数为:GaussXQLineMain功能:高斯按列主元消去法求线性方程组Ax=b 的解调用格式:[x,XA]=GaussXQLineMain(A,b)其中,A :线性方程组的系数矩阵;B:线性方程组中的常数向量;x:线性方程组的解:XA:消元后的系数矩阵(可选的输出参数)。
高斯列主元消去法用MATLAB实现如下所示:4.其中用到上三角矩阵求解函数:在MATLABE中编程实现的上三角系数矩阵求解函数为:SolveUPTriangle 功能:求上三角系数矩阵的线性方程组Ax=b的解调用格式:x=SolveUpTriangel(A,b)其中,A :线性方程组的系数矩阵;b :线性方程组中的常数向量; X :线性方程组的解;上三角系数矩阵求解函数用MATLAB 实现如下所示:高斯按列主元消去法解线性方程组应用实例:用高斯按列主元消去法求解下列线性方程组的解。
列选主元高斯消去法

列选主元高斯消去法
列选主元高斯消去法是一种常用的线性方程组求解方法,在求解大规模线性方程组时具有较高的数值稳定性和计算效率。
该方法的基本思想是,通过选取主元来消除非主元系数的影响,以减小计算误差。
具体步骤如下:
1. 首先将线性方程组的系数矩阵进行列选主元,即对每一列选取绝对值最大的元素所在的行,然后将该行与第一行交换位置。
2. 对于第一列,将选取的主元所在行除以主元的值,使主元变为1。
3. 利用第一行的主元,通过消去操作将其他行的第一列元素变为零。
具体操作是,对于每一行,将该行与第一行乘以适当的倍数后相减,使得第一列元素为零。
4. 重复以上步骤,对第二列以及其后的列重复进行列选主元和消去操作,直到系数矩阵变成上三角矩阵。
5. 根据上三角矩阵进行回代求解,从最后一行开始,依次代入已求解的变量值,计算出未知数的值。
需要注意的是,在进行列选主元时,要注意避免主元为零或接近零的情况,以免造成计算错误或数值不稳定性。
列选主元高斯消去法可以有效地提高线性方程组的求解精度和计算效率,特别适用于存在较大数值差异或特殊矩阵结构的情况。
然而,在某些情况下,该方法可能会导致数值不稳定性或计算量较大,因此在实际应用中需综合考虑问题的特点和求解需求,选择合适的方法。
高斯列主元素消去法

}
main()
{floata[N][N+1]={{0.101,2.304,3.555,1.183},{-1.347,3.712,4.623,2.137},{-2.835,1.072,5.643,3.035}};//方程组系数
float x[N],max,m,*c,*d;
int k=0,q=0,n=N,i,j;
for(k=0;k<n && q==0;k++)
{
max=max_value(a,n,k);
if(max==0) q=1;
else
{ if(I!=k)
{
for(j=k;j<n+1;j++)
{
c=&a[I][j];
d=&a[k][j];
change(c,d);
}
}
for(i=k+1;i<n;i++)
{
{ float max;
int i;
max=a[k][k];
for(i=k+1;i<n;i++)
if(max<a[i][k])
{
max=a[i][k];
I=i;
}
return(max);
}
void change(float *p,float *q)
{
float temp;
temp=*p; *p=*q; *q=temp;
}
printf("得到的结果如下:\n");
for(i=0;i<n;i++)
printf(" x[%d]=% 6.4f\n",i+1,x[i]);
高斯列主元素消去法

1.183 2.137
2.835x1 1.072x2 5.643x3 3.035
1.4 实验步骤
1.明确实验目标,编写程序 2.运行后分别依次输入方程的阶数、增广矩阵
3.得到试验结果三、程序流程图
总体流程图(一)
定义数组 x[NUMBER],变量 r,k,i,j,celect
(1) 若 ann 0, 则矩阵奇异,程序结束;否则执行(2)。
(2) xn an,n1 / ann ;
n
对 i n 1, , 2,1 ,计算 xi ai,n1 aij xj / aii
j i 1
1.3 实验内容
解方程组
01..130417xx1123..370142xx2234.5.65253xx33
for(j=i;j<n;j++) {
if(j==i) continue; sum=sum+a[i][j]*x[j]; } x[i]=(a[i][n]-sum)/a[i][i]; } printf("最终解得: \n"); for(i=0;i<n;i++) printf("x[%d]=%f\n",i,x[i]); }
for(j=0;j<n+1;j++) scanf("%f",&a[i][j]);
for(k=0;k<n+1;k++) {
t=k; for(i=t+1;i<n;i++)
if((fabs(a[t][k]))<(fabs(a[i][k]))) t=i;
直接三角分解法、高斯消去法、高斯列主元消去法解线性方程组

将高斯消去法的计算结果与实际结果比较可知,高斯消去法的计算,结果也是正确的。
将高斯列主元消去法的计算结果与实际结果比较可知,高斯消去法的计算结果是正确的。
3、同理,根据例4的题目以及给出的A,b的取值,可分别调用直接三角分解法(Doolittle法)、高斯消去法、高斯列主元消去法的函数来求解值;具体的输入以及运行结果如下所示:
如对于直接三角分解法(Doolittle法),有
即(malu为求Doolittle的函数,可直接使用函数名直接调用)
对于高斯消去法和高斯列主元消去法,有
3、编写完函数代码后,便可直接通过定义的函数名,输入相关的取值范围,便可验证书后的例子。具体实验输入和结果看实验数据。
实验内容
编写程序代码,在MATLAB的实验环境下,分别使用直接三角分解法(Doolittle法)、高斯消去法、高斯列主元消去法验证教材书后的P42~P47的例1、例3、例4这3个例子:
由直接三角分解法的计算结果与实际结果比较可知,直பைடு நூலகம்三角分解法的计算结果是显示出来时一个不确定的值NaN,这说明利用直接三角分解法来求解该问题存在着很大的误差,因此解决该类问题,我们将不采用直接三角分解法。
同样由高斯消去法的计算结果与实际结果比较可知,高斯消去法的计算结果也是不确定的值NaN,这说明利用高斯消去法来求解该问题同样也存在着很大的误差。
例1:用Doolittle法解方程组:
例3:用部分选主元的Doolittle法解方程组
例4:用部分选主元的Doolittle法紧凑格式解矩阵方程AX=B,其中
实验数据
1、根据例1的题目以及给出的A,b的取值,可分别调用直接三角分解法(Doolittle法)、高斯消去法、高斯列主元消去法的函数来求解值;具体的输入以及运行结果如下所示:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
printf("得到的结果如下:\n");
for(i=0;i<n;i++)
printf(" x[%d]=% 6.4f\n",i+1,x[i]);
2013-2014(1)专业课程实践论文
题目:高斯列主元素消去法
一、算法理论
1.消元过程:消元结果冲掉 ,行乘数冲掉 ,det存放行列式。
(1) 。
(2)对于 做~ :
按列选主元 ,即确定 使
。
若 ,则输出错误信息;停机。
若 转 ,否则执行换行
消元计算:
。
(3)若 ,则判断 是否等于零:
,则输出“无解”信息;停机。
m=a[i][k]/a[k][k];
for(j=0;j<n+1;j++)
a[i][j]=a[i][j]-a[k][j]*m;
}
}
}
for(i=n-1;i>=0;i--)
{
for(j=i+1;j<n;j++)
a[i][3]=a[i][3]-a[i][j]*x[j];//3为未知函数个数
x[i]=a[i][3]/a[i][i];//3为未知函数个数
return;
}
main()
{floata[N][N+1]={{0.101,2.304,3.555,1.183},{-1.347,3.712,4.623,2.137},{-2.835,1.072,5.643,3.035}};//方程组系数
float x[N],max,m,*c,*d;
int k=0,q=0,n=N,i,j;
for(k=0;k<n && q==0;k++)
{
max=max_value(a,n,k);
if(max==0) q=1;
else
{ if(I!=k)
{
for(j=k;j<n+1;++)
{
c=&a[I][j];
d=&a[k][j];
change(c,d);
}
}
for(i=k+1;i<n;i++)
{
,则输出“非唯一解”,停机。
若 ,则 。
2.回带过程:解冲掉 .
3.输出 及 。 值的大小可以作为方程组是否病态的参考。
二、算法框图
三、算法程序
#include <stdio.h>
#include <math.h>
#define N 3//未知函数个数
int I;
float max_value(float a[N][N+1],int n,int k)
{ float max;
int i;
max=a[k][k];
for(i=k+1;i<n;i++)
if(max<a[i][k])
{
max=a[i][k];
I=i;
}
return(max);
}
void change(float *p,float *q)
{
float temp;
temp=*p; *p=*q; *q=temp;
