平面图形的练习题

合集下载

六年级平面图形练习题

六年级平面图形练习题3．一个平行四边形的底是14厘米，高是9厘米，它的面积是；与它等底等高的三角形面积是.5．工地上有一堆钢管，横截面是一个梯形，已知最上面一层有2根，最下面一层有12根，共堆了11层，这堆钢管共有根。

6．一个三角形比与它等底等高的平行四边的面积少30平方厘米，则这个三角形的面积是。

7．一个三角形的面积是4.5平方分米，底是5分米，高是分米。

8．一个等边三角形的周长是18厘米，高是3.6厘米，它的面积是平方厘米。

二、判定题1．两个面积相等的三角形，一定能拼成一个平行四边形.2．平行四边形的面积等于一个三角形面积的2倍.3．两个完全一样的梯形，能拼成一个平行四边形.4．把一个长方形的框架挤压成一个平行四边形，面积减少了.5．两个三角形面积相等，底和高也一定相等。

三、选择题1．等边三角形一定是 _______ 三角形.[ ]A．锐角；B．直角；C．钝角2.两个完全一样的锐角三角形，可以拼成一个________[ ]A．长方形； B．正方形； C．平行四边形； D．梯形3．把一个平行四边形任意分割成两个梯形，这两个梯形中 ________总是相等的.[ ]A．高； B．面积； C．上下两底的和、填空。

1．在推导平行四边形面积计算公式时，可把平行四边形通过割补平移转化为形去推导，推导三角形面积计算公式时，可把两个完全一样的三角形拼成一个形去推导，推导梯形面积计算公式时，可把两个完全一样的梯形拼成一个形进行推导。

4．直角三角形的两条直角边长分别为3厘米和4厘米，这个直角三角形面积是平方厘米。

7．一个三角形的底边长扩大2倍，高不变，扩大后的三角形面积比原来三角形面积扩大倍。

三、判断题。

1．平行四边形面积等于长方形面积。

2．等底等高的三角形可拼成一个平行四边形。

4．只要知道梯形的两底之和的长度和它的高，就可以求出它的面积。

5．两个周长相等的等边三角形，面积必相等。

一、填空。

1.一个三角形的面积是25平方厘米，和它等底等高的平行四边形的面积是平方厘米。

(精心整理)基本平面图形——练习题

CDB EAOCA DBC N M BA 21EOD CBA图（6）D 'B 'AOCGDB第五章基本平面图形一、1. 1.46°= ° ′ ″. 28°7′12″= °.2. 如图，已知OE 平分∠AOB ，OD 平分∠BOC ，∠AOB 为直角， ∠EOD=70°，则∠BOC 的度数为 .3. 如图,直线上四点A 、B 、C 、D,看图填空:①AC=______+BC;②CD=AD —_______;③AC+BD —BC=_______.4、如图，由泰山到青岛的某一次列车，运行途中停靠的车站依次是：泰山—济南—淄博—潍坊—青岛，那么要为这次列车制作的火车票有______．5.用一个钉子把一根细木条钉在墙上，木条就可能绕着钉子，原因是；当用两个钉子把木条钉在墙上时，木条就被固定住，其依据是 . 6.如图，AB 的长为m ，BC 的长为n ，M 、N 分别是AB 、BC 的中点，则MN=7、如图（6），把一张长方形的纸按图那样折叠后，B 、D 两点落在B ′、D ′点处，若得∠AOB ′=700, 则∠B ′OG 的度数为。

8、如上右图，是一副三角板重叠而成的图形，则∠AOD+∠BOC=_____________. 9.如图，直线AB 、CD 相交于O ，∠COE 是直角，∠1=57°，则∠2=10. 一个人从A 点出发向北偏东65°的方向走到B 点，再从B 点出发向南偏西15°方向走到C 点，那么∠ABC 的度数是二、10、下列说法中，正确的是（）A ．直线a 、b 经过点M B. 直线A 、B 相交于点C C. 直线A 、B 相交于点m D. 直线AB,CD 相交于点m11. 一轮船航行到B 处测得的小岛A 的方向为北偏东30°，那么从A 处观测此时B 处的方向为（）A.北偏东30°B.北偏东60°C.南偏西30°D.南偏西60°12、在时刻8:32时，时钟上的时针与分针之间的所成的夹角是（）A.70°B.64°C.76°D.80°13.如图，圆的半径为4，阴影部分扇形的面积是（）A. πB. 2πC. 3πD. 4π14. 同一平面内有四点，每过两点画一条直线，则直线的条数是（）A．1条 B．4条 C．6条 D．1条或4条或6条15、已知A、B两点之间的距离是10 cm，C是线段AB上的任意一点，则AC中点与BC中点间的距离是（）A.3 cmB.4 cmC.5 cmD.不能计算16、平面上有四点，经过其中的两点画直线最多可画出( )．A．三条B．四条C．五条D．六条17、如图，O为直线AB上一点，∠COB＝26°30′，则∠1＝( )．A．153°30′B．163°30′C．173°30′D．183°30′18、如图6，∠AOB为平角，且∠AOC=21∠BOC ，则∠BOC的度数是（）19、如图7，军舰从港口沿OB方向航行，它的方向是（）A.东偏南30°B.南偏东60°C.南偏西30°D.北偏东30°20、下列说法中正确的是( )A、8时45分，时针与分针的夹角是30°B、6时30分，时针与分针重合C、3时30分，时针与分针的夹角是90°D、3时整，时针与分针的夹角是90°21、如果线段AB=5cm,线段BC=4cm,那么A,C两点之间的距离是（）A. 9cmB.1cmC.1cm或9cmD.以上答案都不对22、如图,下列表示角的方法,错误的是( )A.∠1与∠AOB表示同一个角;B.∠AOC也可用∠O来表示C.图中共有三个角:∠AOB、∠AOC、∠BOC;D.∠β表示的是∠BOC23、已知OA⊥OC，∠AOB：∠AOC=2：3，则∠BOC的度数为（）A.30B.150C.30或150D.以上都不对24、如图，四条表示方向的射线中，表示北偏东60°的是( )(1)ba(3)a(2)BBDCBA25.下列各角中，不能用一副三角板拼出的角度为（）A. 60°B.75°C. 135°D. 140°26.关于中点的说法正确的是（）A.若AB=BC,则点B是线段AC的中点B.若AB=21AC，则点B是线段AC的中点C. 若BC=21AC，则点B是线段AC的中点D. 若AB=BC =21AC，则点B是线段AC的中点27.在下列时刻，钟面上时针与分针成直角的情况（）A.12时15分B.9时C.3时30分D.6时45分28.直线l上顺次三点A、B、C，M是AB中点，N是AC若AB=12cm，BC=8cm,则MN=（）A.2 cmB.4 cmC.8 cmD.10 cm29.如图，下列说法错误的是（）A. A点在O点的北偏东60°方向B. B点在O点的西偏北30°方向C.C点在O点的正南方向D. D点在O点的东南方向30.下面四个选项中，能用∠1，∠AOB，∠O三种方法表示同一个角的是（）A B C D31. 一根绳子弯曲成如图（1）所示的形状，当剪刀像图（2）那样沿虚线a把绳子剪断时，绳子被剪为5段；当剪刀像图（3）那样沿虚线b(b∥a)把绳子再剪一次时，绳子被剪为9段.若剪刀在虚线a,b之间再剪（n-1）次（剪刀的方向与a平行），这样一共剪n次时（不含沿虚线a剪的一次）绳子的段数为（）A.4n+1B.4n+2C.4n+3D.4n+533、如图，在公路l的两旁有两个工厂A、B，要在公路上搭建一个货场让A、B两厂使用，要使货场到A、B两厂的距离之和最小，问货场应建在什么位置？为什么？34.你能在图中找出一点P，使点P到点A、B、C、D四个点的距离之和最小吗？东四、35如图，A 、B 、C 、D 在同一条直线上，已知AC=BD=18cm ，且AB:AD=2:11，求AB,BC 的长度。

1基本平面图形练习题

CA DBCM A DB 基本平面图形练习题第一部分:直线、射线、线段1、填表：图形表示方法向几个方向延伸端点数可否度量线段射线直线2、经过两点有__________条直线。

两点之间的所有连线中，______最短。

两点之间______的长度叫做两点之间的距离。

3、在上且把线段分成两条线段的点叫做线段的中点。

线段的中点只有个。

4、（1）经过一个已知点A 可以画____条直线；（2）经过两个已知点A 、B 可以画_____条直线；（3）将一根细木条固定在墙上，至少需要____枚钉子5、（1）小明从某地乘车到成都，发现这条火车路线上共有7个站，且任意两站之间的票价都不相同，有____种不同的票价;要准备______种不同的车票.（2）某足球比赛中有20个球队进行单循环比赛（每两队之间必须比赛一场），那么一共要进行多少场比赛？ 6、如果直线l 上一次有3个点A,B,C,那么（1）以A 、B 、C 为端点的射线各有条，因而共有射线_____条，线段共有_____条。

（2）增加一个点增加_____条射线，增加_____条线段。

（3）若在直线l 上有n 个点, 共有_____条射线，线段的总条数是_____。

7、两条直线相交，有____个交点，三条直线相交，最多有____个交点，四条直线相交，有____个交点，10条直线相交，交点的个数最多是___个，n 条直线相交，交点的个数最多是____个 8、如图,直线上四点A 、B 、C 、D,看图填空:①=AC _____BC +;②-=AD CD _____;③=-+BC BD AC _____ 9、在直线AB 上，有cm AB 5=，cm BC 3=，求AC 的长.⑴当C 在线段AB 上时，=AC _______.(2)当C 在线段AB 的延长线上时，=AC _______. 10、如图所示：点C 是线段AB 上的一点，M 、N 分别是线段AC 、CB 的中点。

基本平面图形典型例题

第四章基本平面图形练习题典型考题一: 线段的中点问题1.已知线段AB=10cm,在AB的延长线上取一点C，使AC=16cm,则线段AB的中点与AC的中点的距离为2.如果A,B,C三点在同一条直线上，且线段AB=4cm, BC=2cm,则那么A，C两点之间的距离为3.已知线段AB=20cm,在直线AB上有一点C，且BC=10cm,M是线段AC的中点,求线段AM的长.4.如图，点C在线段AB上，AC=8cm,CB=6cm,点M,N分别是AC,BC的中点.（1）求线段MN的长；（2）若C为线段AB上任一点，满足AC+CB=acm，其它条件不变，你能猜想MN的长度吗并说明理由；（3）若C在线段AB的延长线上，且满足AC﹣BC=bcm，M、N分别为AC、BC的中点，你能猜想MN的长度吗请画出图形，写出你的结论，并说明理由；（4）你能用一句简洁的话，描述你发现的结论吗典型考题二: 角的平分线问题1.已知：OC是∠AOB的平分线，若∠AOB=58°，则∠AOC=2.如图，OC是∠AOB的平分线，OD平分∠AOC，若∠COD=25°，则∠AOB的度数为3.如图，∠AOB=90°，∠BOC=30°，OM平分∠AOC，ON平分∠BOC，（1）求∠MON的度数。

（2）如果（1）中∠AOB=α，其他条件不变，求∠MON的度数。

（3）如果（1）中∠BOC=β（β为锐角），其他条件不变，求∠MON的度数。

（4）从（1）（2）（3）的结果你能看出什么规律4.已知∠AOB=120°，∠AOC=30°，OM平分∠AOC，ON平分∠AOB，（1）求∠MON的度数；（2）通过（1）题的解法，你可得出什么规律5.已知∠AOB是一个直角，作射线OC，再分别∠AOC和∠BOC的平分线OD、OE．（1）如图①，当∠BOC =70°时，求∠DOE的度数；（3）当射线OC在∠AOB外绕O点旋转时，画出图形，判断∠DOE的大小否发生变化若变化，说明理由；若不变，求∠DOE的度数．典型考题三: 时针分针夹角问题1.时钟在4点整时，分针与时针的夹角为度.2.时钟的分针从4点整开始，转过多少度分针才能与时针重合3.在4时和5时之间的哪个时刻，时钟的时针和分针成直角变式训练：试一试：o=_______度.1、3.76o=______度______分______秒；'"2232242、在直线AB上取C、D两个点，如图所示，则图中共有射线_____条。

初一数学七年级下平面图形的认识练习题

数学七年级下平面图形的认识练习题（一)选择题1、如图，直线AB∥CD，∠C=44°，∠E为直角，则∠1等于（）A．132°B．134°C．136°D．138°2、已知一个多边形的内角和是外角和的2倍，则此多边形的边数为（）A．6 B．7 C．8 D．93、如图，AB∥EF，∠C=90°，则α、β和γ的关系是（）A．β=α+γB．α+β+γ=180°C．α+β-γ=90°D．β+γ-α=180°4、如图是某公园里一处矩形风景欣赏区ABCD，长AB=50米，宽BC=25米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为1米，那小明沿着小路的中间，从出口A到出口B所走的路线（图中虚线）长为（）A．100米B．99米C．98米D．74米5、长度为1cm、2cm、3cm、4cm、5cm的五条线段，若以其中的三条线段为边构成三角形，可以构成不同的三角形共有（）A．2个B．3个C．4个D．5个6、一个人驱车前进时，两次拐弯后，按原来的相反方向前进，这两次拐弯的角度可能是（）A．向右拐85°，再向右拐95°B．向右拐85°，再向左拐85°C．向右拐85°，再向右拐85°D．向右拐85°，再向左拐95°7、如图：AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO=40°，则下列结论：①∠BOE=70°；②OF平分∠BOD；③∠POE=∠BOF；④∠POB=2∠DOF．其中正确结论有（）A．①②③④B．①②③C．①③④D．①②④8、车库的电动门栏杆如图所示，BA垂直于地面AE于A，CD平行于地面AE，则∠ABC+∠BCD 的大小是（）A．150°B．180°C．270°D．360°（二）填空题1、如图，已知在△ABC中，∠B与∠C的平分线交于点P．当∠A=70°时，则∠BPC的度数为____________2、如图，已知AE∥BD，∠1=3∠2，∠2=28°．求∠C=___________3、正五边形的一个内角的度数是__________4、已知三角形的两边长分别是3cm和7cm，第三边长是偶数，则这个三角形的周长为_________5、一块四边形绿化园地，四角都做有半径为R的圆形喷水池，则这四个喷水池占去的绿化园地的面积为__________6、如图所示，直线l∥m，将含有45°角的三角形板ABC的直角顶点C放在直线m上．若∠1=25°，则∠2的度数为__________（三）解答题1、如图，AD∥BE，AE平分∠BAD，CD与AE相交于F，∠CFE=∠E．求证：AB∥CD．2、已知：∠MON=40°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O 重合），连接AC交射线OE于点D．设∠OAC=x°．3、已知△ABC中，∠A=60°．4、将纸片△ABC沿DE折叠使点A落在A′处的位置．5.如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°．（1）求∠BAE的度数；（2）求∠DAE的度数；（3）探究：小明认为如果只知道∠B-∠C=40°，也能得出∠DAE的度数？你认为可以吗？若能，请你写出求解过程；若不能，请说明理由6.已知，如图，在△ABC中，∠A=∠ABC，直线EF分别交△ABC的边AB，AC和CB的延长线于点D，E，F．（1）求证：∠F+∠FEC=2∠A；（2）过B点作BM∥AC交FD于点M，试探究∠MBC与∠F+∠FEC的数量关系，并证明你的结论．7、已知△ABC，（1）如图1，若D点是△ABC内任一点、求证：∠D=∠A+∠ABD+∠ACD．（2）若D点是△ABC外一点，位置如图2所示．猜想∠D、∠A、∠ABD、∠ACD有怎样的关系？请直接写出所满足的关系式．（不需要证明）（3）若D点是△ABC外一点，位置如图3所示、猜想∠D、∠A、∠ABD、∠ACD之间有怎样的关系，并证明你的结论．8、如图，在△ABC中，点E在AC上，∠AEB=∠ABC．（1）图1中，作∠BAC的角平分线AD，分别交CB、BE于D、F两点，求证：∠EFD=∠ADC；（2）图2中，作△ABC的外角∠BAG的角平分线AD，分别交CB、BE的延长线于D、F两点，试探究（1）中结论是否仍成立？为什么？9、如图1，一副三角板的两个直角重叠在一起，∠A=30°，∠C=45°△COD固定不动，△AOB 绕着O点逆时针旋转α°（0°＜α＜180°）（1）若△AOB绕着O点旋转图2的位置，若∠BOD=60°，则∠AOC=_________；（2）若0°＜α＜90°，在旋转的过程中∠BOD+∠AOC的值会发生变化吗？若不变化，请求出这个定值；（3）若90°＜α＜180°，问题（2）中的结论还成立吗？说明理由；（4）将△AOB绕点O逆时针旋转α度（0°＜α＜180°），问当α为多少度时，两个三角形至少有一组边所在直线垂直？（请直接写出所有答案）．10.如图，四边形ABCD中，∠F为四边形ABCD的∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的锐角，若设∠A=α，∠D=β；（1）如图①，α+β＞180°，试用α，β表示∠F；（2）如图②，α+β＜180°，请在图中画出∠F，并试用α，β表示∠F；（3）一定存在∠F吗？如有，求出∠F的值，如不一定，指出α，β满足什么条件时，不存在∠F．11、已知如图，∠COD=90°，直线AB与OC交于点B，与OD交于点A，射线OE和射线AF交于点G．12、已知，如图，在△ABC中，∠A=∠ABC，直线EF分别交△ABC的边AB，AC和CB 的延长线于点D，E，F．（1）求证：∠F+∠FEC=2∠A；（2）过B点作BM∥AC交FD于点M，试探究∠MBC与∠F+∠FEC的数量关系，并证明你的结论．13.已知，如图，在△ABC中，∠ACB=90°，AE是角平分线，CD是高，AE、CD相交于点F，求证：∠CEF=∠CFE．14.如图，已知AB=AC=AD，且∠C=2∠D，求证AD∥BC15.（1）如图（1），在△ABC中，∠C＞∠B，AD⊥BC于点D，AE平分∠BAC，你能找出∠EAD与∠B、∠C之间的数量关系吗？并说明理由．（2）如图（2），AE平分∠BAC，F为AE上一点，FM⊥BC于点M，这时∠EFM与∠B、∠C之间又有何数量关系？请你直接说出它们的关系，不需要证明．16.在△ABC中，AB=AC，AC边上的中线BD把三角形的周长分为12cm和15cm两部分，求三角形各边的长。

(七年级)初一基本平面图形专项练习试题_附答案_北师大,人教版等通用版本

初一基本平面图形一、单选题1．如图，在直角坐标系xOy 中，点P 的坐标为（4，3），PQ ⊥x 轴于Q ，M ，N 分别为OQ ，OP 上的动点，则QN ＋MN 的最小值为（）A ．7225B ．245C ．125D ．9625 2．已知，点C 在直线 AB 上， AC =a ， BC =b ，且 a ≠b ，点 M 是线段 AB 的中点，则线段 MC 的长为（）A ．2a b +B ．2a b -C ．2a b +或2a b -D ．+2a b 或||2a b - 3．如图，C 、D 是线段AB 上两点，M 、N 分别是线段AD 、BC 的中点，下列结论：①若AD=BM ，则AB=3BD ；②若AC=BD ，则AM=BN ；③AC-BD=2（MC-DN ）；④2MN=AB-CD ．其中正确的结论是（）A ．①②③B ．③④C ．①②④D ．①②③④ 4．把 8.32°用度、分、秒表示正确的是（）A ．8°3′2″B ．8°30′20″C ．8°18′12″D ．8°19′12″ 5．经过平面上的四个点，可以画出来的直线条数为（）A ．1B ．4C ．6D ．前三项都有可能6．如图，点M 在线段AN 的延长线上，且线段MN=20，第一次操作：分别取线段AM 和AN 的中点11M N ，；第二次操作：分别取线段1AM 和1AN 的中点22,M N ；第三次操作：分别取线段2AM 和2AN 的中点33,M N ；……连续这样操作10次，则每次的两个中点所形成的所有线段之和11221010M N M N M N +++=L ( )A ．910202-B ．910202+C ．1010202-D ．1010202+ 7．已知线段AC 和BC 在同一直线上，AC ＝8cm ，BC ＝3cm ，则线段AC 的中点和BC 中点之间的距离是（）A ．5.5cmB ．2.5cmC ．4cmD ．5.5cm 或2.5cm8．如图，将一副三角板的直角顶点重合摆放在在桌面上，下列各组角一定能互补的是（）A ．∠BCD 和∠ACFB ．∠ACD 和∠ACFC ．∠ACB 和∠DCBD ．∠BCF 和∠ACF9．如图,在公路 MN 两侧分别有 A 1, A 2......A 7,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是（）.①车站的位置设在 C 点好于 B 点;②车站的位置设在 B 点与 C 点之问公路上任何一点效果一样;③车站位置的设置与各段小公路的长度无关.A ．①B ．②C ．①③D ．②③ 10．如图，某公司有三个住宅区，A ，B ，C 各区分别住有职工10人，15人，45人，且这三个区在一条大道上(A ，B ，C 三点共线)，已知AB ＝150m ，BC ＝90m ．为了方便职工上下班，该公司的接送车打算在此间只设一个停靠点，为使所有的人步行到停靠点的路程之和最小，那么该停靠点的位置应设在( )A ．点AB ．点BC ．点A ，B 之间D ．点C 11．观察下列图形,并阅读图形下面的相关文字,如图所示:两条直线相交,三条直线相交,四条直线相交,最多有一个交点,最多有三个交点;最多有6个交点,像这样,10条直线相交,最多交点的个数是( )A．40个B．45个C．50个D．55个二、填空题12．已知点A，B，C都在直线l上，点P是线段AC的中点.设AB a=，PB b，则线段BC的长为________（用含a，b的代数式表示）13．已知点A，B，C在同一条直线上，若线段AB＝3，BC＝2，则AC＝_____．14．已知点A在数轴上对应的数为a，点B对应的数为b，且|a+2|+（b﹣1）2=0，A、B 之间的距离记作|AB|，定义：|AB|=|a﹣b|．①线段AB的长|AB|=3；②设点P在数轴上对应的数为x，当|PA|﹣|PB|=2时，x=0.5；③若点P在A的左侧，M、N分别是PA、PB的中点，当P在A的左侧移动时|PM|+|PN|的值不变；④在③的条件下，|PN|﹣|PM|的值不变．以上①②③④结论中正确的是_______（填上所有正确结论的序号）15．已知∠AOB＝90°，射线OC在∠AOB内部，且∠AOC＝20°，∠COD＝50°，射线OE、OF分别平分∠BOC、∠COD，则∠EOF的度数是_____．16．把一根绳子对折成一条线段AB，在线段AB取一点P，使AP＝13PB，从P处把绳子剪断，若剪断后的三段．．绳子中最长的一段为30cm，则绳子的原长为______cm．17．钟表4点30分时，时针与分针所成的角的度数是___________ 。

六年级奥数《平面图形》练习题

第十一讲平面图形（必做与选做）1.在一张长12厘米、宽6厘米的长方形纸上剪下一个最大的半圆，这个半圆的周长是多少厘米？A. 24.84B. 30.84C. 43.68D. 49.68解析：最大的半圆以长方形长为直径，宽为半径。

这个半圆的周长C＝3.14×6＋12＝30.84（厘米）。

所以选B。

2.在一张长12厘米、宽5厘米的长方形纸上剪下一个最大的半圆，这个半圆的周长是多少厘米？A. 20.7B. 25.7C. 27.5D. 41.4解析：最大的半圆以长方形的宽为半径，宽的两倍为直径。

这个半圆的周长C＝3.14×5＋5×2＝25.7（厘米）。

所以选B。

3.在一张长12厘米、宽7厘米的长方形纸上剪下一个最大的半圆，剩下纸的周长是多少厘米？A. 32.84B. 30.84C. 44.84D. 63.68解析：最大的半圆是以长方形的长为直径，长的一半为半径。

剩下的纸的周长C＝12＋7×2＋3.14×（12÷2）＝44.84（厘米）。

所以选C。

4.有2根直径都是3分米的圆柱形木头，现用绳子分别在两处把它们捆在一起，至少需要绳子多少分米？（接头处不计）A. 15.42B. 24.84C. 30.84D. 49.68解析：需计算两部分的长度，一部分是两条线段的长度，都是直径的长度；另一部分是两段圆弧的长度，一共是一个圆的周长。

因此一共需要绳子：（3.14×3＋3×2）×2＝30.84（分米）。

所以选C。

5.有3根直径都是5分米的圆柱体木头，现用绳子分别在三处把它们捆在一起，至少需要绳子多少分米？（接头处不计）A. 30.7B. 61.4C. 77.1D. 92.1解析：需计算两部分的长度，一部分是三条线段的长度，都是直径的长度；另一部分是三段圆弧的长度，一共是一个圆的周长。

因此一共需要绳子：（3.14×5＋5×3）×3＝92.1（分米）。

(完整word版)基本平面图形练习题.docx

基本平面图形一．选择题1．手电筒射出去的光线,给我们的形象是()A. 直线B.射线C.线段D.折线2．下列各直线的表示法中，正确的是()A ．直线 A B．直线 AB C．直线 ab D．直线 Ab3．下列说法正确的是()A. 画射线 OA=3cm;B. 线段 AB 和线段 BA 不是同一条线段C.点 A 和直线 L 的位置关系有两种 ;D.三条直线相交有 3 个交点4．下列说法中正确的有（）①过两点有且只有一条直线；② 连接两点的线段叫两点的距离；③两点之间线段最短；④若 AC=BC ，则点 C 是线段 AB 的中点．A ． 1 个B． 2 个C． 3 个D． 4 个5．下列说法中，正确的是（）A ．两条射线组成的图形叫做角B．若 AB=BC ，则点B 是 AC 的中点C．两点之间直线最短 D ．两点确定一条直线6．下列现象中，可用基本事实“两点之间，线段最短”来解释的现象是（）A ．把弯曲的公路改直，就能缩短路程B．用两个钉子就可以把木条固定在墙上C．利用圆规可以比较两条线段的大小关系D．植树时，只要定出两棵树的位置，就能确定同一行树所在的直线7．已知点 A 、 B 、C 都是直线 l 上的点，且 AB=5cm ， BC=3cm ，那么点 A 与点 C 之间的距离是（）A ． 8cmB ．2cm C． 8cm 或 2cm D ．4cm8．如图， C 是 AB 的中点， D 是 BC 的中点．下列等式不正确的是（）A ． CD=AC ﹣ BDB ． CD=AD ﹣ BC C． CD=AB ﹣ BD D ．CD=AB ﹣ AD9．下列四种说法：①因为 AM=MB ，所以 M 是 AB 中点；②在线段 AM 的延长线上取一点 B ，如果 AB=2AM ，那么 M 是 AB 的中点；③因为 M 是 AB 的中点，所以AM=MB=AB ；④因为 A 、 M 、B 在同一条直线上，且 AM=BM ，所以 M 是 AB 中点．其中正确的是（）A ．①③④B．④C．②③④D．③④10．如图，从点 O 出发的五条射线，可以组成（）个角．A ． 4B ． 6C． 8 D ．1011．下列各式中，正确的角度互化是（）A ． 63.5 ° =63 ° 50′B ． 23° 12′ 36″ =25.48 ° C． 18° 18′ 18″ =3.33 ° D． 22.25 ° =22 ° 15′ 12、角是指 ( )A. 由两条线段组成的图形;B.由两条射线组成的图形C.由两条直线组成的图形;D.有公共端点的两条射线组成的图形C13、如图 ,下列表示角的方法,错误的是 ()B1AO(3)A. ∠ 1 与∠ AOB 表示同一个角 ;B. ∠ AOC 也可用∠ O 来表示C.图中共有三个角 :∠ AOB 、∠ AOC 、∠ BOC;D.∠ β表示的是∠ BOC14、由河源到广州的某一次列车，运行途中停靠的车站依次是：河源﹣惠州﹣东莞﹣广州，那么要为这次列车制作的火车票有（）A ． 3 种B ． 4 种C ． 6 种D ． 12 种15、下列说法中正确的个数有（）① 经过一点有且只有一条直线；② 连接两点的线段叫做两点之间的距离；③ 射线比直线短；④ ABC 三点在同一直线上且 AB=BC ，则 B 是线段 AC 的中点；⑤ 在同一平面内，两条直线的位置关系有两种：平行与相交；⑥ 在 8：30 时，时钟上时针和分针的夹角是 75°．A ． 1 个B ．2 个C ． 3 个D ．4 个16、根据直线、射线、线段各自的性质，下图中能相交的是（）A ．B ．C ．D ． 17、如图， A,B 在直线 l 上，下列说法错误的是（）Ａ．线段 AB 和线段 BA 同一条线段Ｂ．直线 AB 和直线 BA 同一条直线Ｃ．射线 AB 和射线 BA 同一条射线Ｄ．图中以点 A 为端点的射线有两条。

平面图形(含答案)

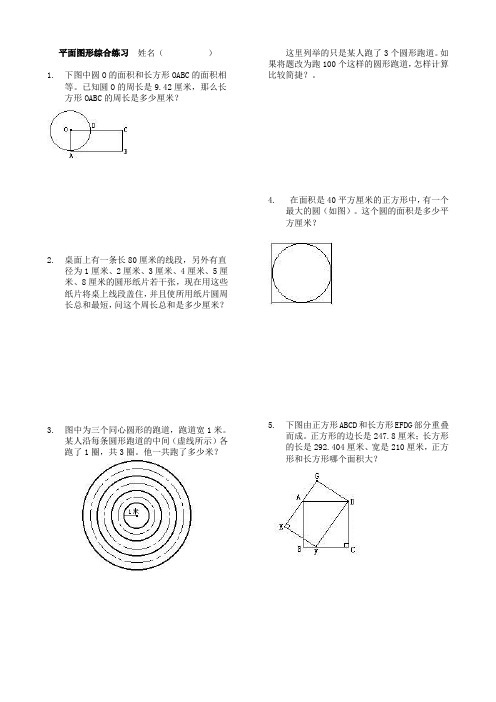
平面图形综合练习姓名（）1.下图中圆O的面积和长方形OABC的面积相等。

已知圆O的周长是9.42厘米，那么长方形OABC的周长是多少厘米？2.桌面上有一条长80厘米的线段，另外有直径为1厘米、2厘米、3厘米、4厘米、5厘米、8厘米的圆形纸片若干张，现在用这些纸片将桌上线段盖住，并且使所用纸片圆周长总和最短，问这个周长总和是多少厘米？3.图中为三个同心圆形的跑道，跑道宽1米。

某人沿每条圆形跑道的中间（虚线所示）各跑了1圈，共3圈。

他一共跑了多少米？这里列举的只是某人跑了3个圆形跑道。

如果将题改为跑100个这样的圆形跑道，怎样计算比较简捷？。

4.在面积是40平方厘米的正方形中，有一个最大的圆（如图）。

这个圆的面积是多少平方厘米？5.下图由正方形ABCD和长方形EFDG部分重叠而成。

正方形的边长是247.8厘米；长方形的长是292.404厘米、宽是210厘米，正方形和长方形哪个面积大？6.下图由半圆和等腰直角三角形重叠而成。

已知等腰直角三角形的直角边长为4厘米，求图中阴影面积。

7.有5个正方形（如图），边长分别是1米、2米、3米、4米、5米。

问图中白色部分面积与阴影部分面积的比是几比几？8.有一个直角梯形ABCD，已知AB=8厘米，CD=4厘米，BC=6厘米，三角形ABF的面积比三角形EFD的面积大17.4平方厘米，那么ED长多少厘米？9.下图由4个正六边形拼成，每个正六边形的面积都是6，那么三角形ABC的面积是多少？10.已知图中正方形ABCD的面积是256平方厘米，那么正方形EFGH的面积是多少平方厘米？11.下图是一个正方形地板砖示意图，在大正方形ABCD中，AA1=AA2=BB1=BB2=CC1=CC2=DD1=DD2，中间小正方形 EFGH的面积是16平方厘米，四块蓝色的三角形的面积总和是72平方厘米，那么大正方形ABCD的面积是多少平方厘米？12.一个任意凸六边形ABCDEF，P、Q、M、N分别为AB、BC、DE和EF边上的中点。

七年级基本平面图形练习题(附答案)

七年级基本平面图形一．选择题（共9小题）1．（2005•河源）由河源到广州的某一次列车，运行途中停靠的车站依次是：河源﹣惠州﹣东莞﹣广州，那么要为这次列车制作的火车票有（）A．3种B．4种C．6种D．12种2．（2003•台州）经过A、B、C三点的任意两点，可以画出的直线数为（）A．1或2B．1或3C．2或3D．1或2或33．（2003•黄冈）某公司员工分别住在A、B、C三个住宅区，A区有30人，B区有15人，C 区有10人．三个区在一条直线上，位置如图所示．公司的接送打算在此间只设一个停靠点，要使所有员工步行到停靠点的路程总和最少，那么停靠点的位置应在（）A．A区B．B区C．C区D．不确定4．（2002•太原）已知，P是线段AB上一点，且，则等于（）A．B．C．D．5．如图，在数轴上有A、B、C、D、E五个整数点（即各点均表示整数），且AB=2BC=3CD=4DE，若A、E两点表示的数的分别为﹣13和12，那么，该数轴上上述五个点所表示的整数中，离线段AE的中点最近的整数是（）A．﹣2B．﹣1C．0D．26．在同一面内，不重合的三条直线的公共点数个数可能有（）A．0个、1个或2个B．0个、2个或3个C．0个、1个、2个或3个D．1个或3个7．如图所示，甲、乙、丙、丁、戊五名同学有以下说法：甲说：“直线BC不过点A”；乙说：“点A在直线CD外”；丙说：“D在射线CB的反向延长线上”；丁说：“A，B，C，D两两连接，有5条线段”；戊说：“射线AD与射线CD不相交”．其中说明正确的有（）A．3人B．4人C．5人D．2人8．（2012•孝感）已知∠α是锐角，∠α与∠β互补，∠α与∠γ互余，则∠β﹣∠γ的值等于（）A．45°B．60°C．90°D．180°9．（2008•西宁）如果∠α和∠β互补，且∠α＞∠β，则下列表示∠β的余角的式子中：①90°﹣∠β；②∠α﹣90°；③（∠α+∠β）；④（∠α﹣∠β）．正确的有（）A．4个B．3个C．2个D．1个二、解答题23．如图1，已知数轴上有三点A、B、C，AB=AC，点C对应的数是200．（1）若BC=300，求点A对应的数；（2）如图2，在（1）的条件下，动点P、Q分别从A、C两点同时出发向左运动，同时动点R从A点出发向右运动，点P、Q、R的速度分别为10单位长度每秒、5单位长度每秒、2单位长度每秒，点M为线段PR的中点，点N为线段RQ的中点，多少秒时恰好满足MR=4RN（不考虑点R与点Q相遇之后的情形）；（3）如图3，在（1）的条件下，若点E、D对应的数分别为﹣800、0，动点P、Q分别从E、D两点同时出发向左运动，点P、Q的速度分别为10单位长度每秒、5单位长度每秒，点M为线段PQ的中点，点Q在从是点D运动到点A的过程中，QC﹣AM的值是否发生变化？若不变，求其值；若不变，请说明理由．24．如图，已知数轴上点A表示的数为6，B是数轴上一点，且AB=10．动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）①写出数轴上点B表示的数_________ ，点P表示的数_________ （用含t的代数式表示）；②M为AP的中点，N为PB的中点．点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出线段MN的长；（2）动点Q从点A出发，以每秒1个单位长度的速度沿数轴向左匀速运动；动点R从点B 出发，以每秒个单位长度的速度沿数轴向左匀速运动，若P、Q、R三动点同时出发，当点P遇到点R时，立即返回向点Q运动，遇到点Q后则停止运动．那么点P从开始运动到停止运动，行驶的路程是多少个单位长度？25．画线段MN=3cm，在线段MN上取一点Q，使MQ=NQ，延长线段MN至点A，使AN=MN；延长线段NM至点B，使BN=3BM，根据所画图形计算：（1）线段BM的长度；（2）线段AN的长度；（3）试说明Q是哪些线段的中点图中共有多少条线段它们分别是26．如图（1），已知A、B位于直线MN的两侧，请在直线MN上找一点P，使PA+PB最小，并说明依据．如图（2），动点O在直线MN上运动，连接AO，分别画∠AOM、∠AON的角平分线OC、OD，请问∠COD的度数是否发生变化？若不变，求出∠COD的度数；若变化，说明理由．27．如图①，已知线段AB=12cm，点C为AB上的一个动点，点D、E分别是AC和BC的中点．（1）若点C恰好是AB中点，则DE= _________ cm；（2）若AC=4cm，求DE的长；（3）试利用“字母代替数”的方法，说明不论AC取何值（不超过12cm），DE的长不变；（4）知识迁移：如图②，已知∠AOB=120°，过角的内部任一点C画射线OC，若OD、OE分别平分∠AOC和∠BOC，试说明∠DOE=60°与射线OC的位置无关．28．如图，OA的方向是北偏东15°，OB的方向是北偏西40°．（1）若∠AOC=∠AOB，则OC的方向是_________ ；（2）若B、O、D在同一条直线上，OD的方向是_________ ；（3）若∠BOD可以看作OB绕点O逆时针旋转180°到OD所成的角，作∠BOD平分线OE，并用方位角表示OE的方向．29．如图，已知数轴上点A表示的数为8，B是数轴上一点，且AB=14．动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）写出数轴上点B表示的数_________ ，点P表示的数_________ （用含t的代数式表示）；（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？（3）若M为AP的中点，N为PB的中点．点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出线段MN的长；（4）若点D是数轴上一点，点D表示的数是x，请你探索式子|x+6|+|x﹣8|是否有最小值？如果有，直接写出最小值；如果没有，说明理由．一．选择题（共9小题）1．（2005•河源）由河源到广州的某一次列车，运行途中停靠的车站依次是：河源﹣惠州﹣东莞﹣广州，那么要为这次列车制作的火车票有（）A．3种B．4种C．6种D．12种考点：直线、射线、线段．专题：应用题．分析：由题意可知：由河源要经过3个地方，所以要制作3种车票；由惠州要经过2个地方，所以要制作2种车票；由东莞要经过1个地方，所要制作1种车票；结合上述结论，通过往返计算出答案．解答：解：根据分析，知这次列车制作的火车票的总数=3+2+1=6（种）．则往返车票应该是：6×2=12（种）．故选D．点评：本题的关键是要找出由一地到另一地的车票的数是多少．2．（2003•台州）经过A、B、C三点的任意两点，可以画出的直线数为（）A．1或2B．1或3C．2或3D．1或2或3考点：直线、射线、线段．分析：本题需先根据直线的概念知，可以确定出直线的条数，即可求出正确的结果．解答：解：A、B、C三点的任意两点，可以画出的直线数是：当三点在一条直线上的时候，可以画出一条直线；当三点不在同一条直线上的时候，可以画出三条直线；故选B．点评：本题主要考查了直线的概念，在解题时要注意分类讨论的方法计数，做到不遗漏，不重复．3．（2003•黄冈）某公司员工分别住在A、B、C三个住宅区，A区有30人，B区有15人，C 区有10人．三个区在一条直线上，位置如图所示．公司的接送打算在此间只设一个停靠点，要使所有员工步行到停靠点的路程总和最少，那么停靠点的位置应在（）A．A区B．B区C．C区D．不确定考点：比较线段的长短．分析：根据题意分别计算停靠点分别在各点是员工步行的路程和，选择最小的即可解解答：解：∵当停靠点在A区时，所有员工步行到停靠点路程和是：15×100+10×300=4500m；当停靠点在B区时，所有员工步行到停靠点路程和是：30×100+10×200=5000m；当停靠点在C区时，所有员工步行到停靠点路程和是：30×300+15×200=12000m．∴当停靠点在A区时，所有员工步行到停靠点路程和最小，那么停靠点的位置应该在故选A．点评：此题考查了比较线段的长短，正确理解题意是解题的关键．要能把线段的概念在现实中进行应用．4．（2002•太原）已知，P是线段AB上一点，且，则等于（）A．B．C．D．考点：比较线段的长短．专题：计算题．分析：根据题意，先设AP=2x，则有PB=5x，故=可求．解答：解：如果设AP=2x，那么PB=5x，∴AB=AP+PB=7x，∴=．故选A．点评：灵活运用线段的和、差、倍、分来转化线段之间的数量关系是解题的关键．5．如图，在数轴上有A、B、C、D、E五个整数点（即各点均表示整数），且AB=2BC=3CD=4DE，若A、E两点表示的数的分别为﹣13和12，那么，该数轴上上述五个点所表示的整数中，离线段AE的中点最近的整数是（）A．﹣2B．﹣1C．0D．2考点：数轴；比较线段的长短．专题：数形结合．分析：根据已知点求AE的中点，AE长为25，其长为，然后根据AB=2BC=3CD=4DE求出A、C、B、D、E五点的坐标，最后根据这五个坐标找出离中点最近的点即可．解答：解：根据图示知，AE=25，∴AE=，∴AE的中点所表示的数是﹣；∵AB=2BC=3CD=4DE，∴AB：BC：CD：DE=12：6：4：3；而12+6+4+3恰好是25，就是A点和E点之间的距离，∴AB=12，BC=6，CD=4，DE=3，∴这5个点的坐标分别是﹣13，﹣1，5，9，12，∴在上面的5个点中，距离﹣最近的整数是﹣1．点评：此题综合考查了数轴、绝对值的有关内容，用几何方法借助数轴来求解，非常直观，且不容易遗漏，体现了数形结合的优点．6．在同一面内，不重合的三条直线的公共点数个数可能有（）A．0个、1个或2个B．0个、2个或3个C．0个、1个、2个或3个D．1个或3个考点：直线、射线、线段．分析：可先画出三条直线相交，发现：3条直线相交最多有3个交点，最少有1个交点．三条直线平行的时候为0个交点，两条直线平行被另一直线所截有2个交点，故0个、1个、2个或3个的情况都有．解答：解：3条直线相交最多有3个交点，最少有1个交点．三条直线平行的时候为0个交点，两条直线平行被另一直线所截有2个交点，故0个、1个、2个或3个的情况都有，故选答案C．点评：此题在相交线的基础上，着重培养学生的观察、实验和猜想、归纳能力，掌握从特殊项一般猜想的方法．7．如图所示，甲、乙、丙、丁、戊五名同学有以下说法：甲说：“直线BC不过点A”；乙说：“点A在直线CD外”；丙说：“D在射线CB的反向延长线上”；丁说：“A，B，C，D两两连接，有5条线段”；戊说：“射线AD与射线CD不相交”．其中说明正确的有（）A．3人B．4人C．5人D．2人考点：直线、射线、线段．专题：计算题．分析：此题考查了线的基本性质、概念，注意区别各概念之间的差异．解答：解：甲：“直线BC不过点A”，正确；乙：“点A在直线CD外”，正确；丙：“D在射线CB的反向延长线上”，正确；丁：“A，B，C，D两两连接，有5条线段”；应该有AB，AC，AD，BC，BD，CD六条线段，错误；戊：“射线AD与射线CD不相交”，射线AD与射线CD交于点D，错误．故选D．点评：掌握好直线、射线、线段各个概念的同时还要注意各个概念之间的区别．8．（2012•孝感）已知∠α是锐角，∠α与∠β互补，∠α与∠γ互余，则∠β﹣∠γ的值等于（）A．45°B．60°C．90°D．180°考点：余角和补角．专题：计算题．分析：根据互余两角之和为90°，互补两角之和为180°，结合题意即可得出答案．解答：解：由题意得，∠α+∠β=180°，∠α+∠γ=90°，两式相减可得：∠β﹣∠γ=90°．故选C．点评：此题考查了余角和补角的知识，属于基础题，掌握互余两角之和为90°，互补两角之和为180°，是解答本题的关键．9．（2008•西宁）如果∠α和∠β互补，且∠α＞∠β，则下列表示∠β的余角的式子中：①90°﹣∠β；②∠α﹣90°；③（∠α+∠β）；④（∠α﹣∠β）．正确的有（）A．4个B．3个C．2个D．1个考点：余角和补角．分析：根据角的性质，互补两角之和为180°，互余两角之和为90，可将，①②③④中的式子化为含有∠α+∠β的式子，再将∠α+∠β=180°代入即可解出此题．解答：解：∵∠α和∠β互补，∴∠α+∠β=180度．因为90°﹣∠β+∠β=90°，所以①正确；又∠α﹣90°+∠β=∠α+∠β﹣90°=180°﹣90°=90°，②也正确；（∠α+∠β）+∠β=×180°+∠β=90°+∠β≠90°，所以③错误；（∠α﹣∠β）+∠β=（∠α+∠β）=×180°﹣90°=90°，所以④正确．综上可知，①②④均正确．故选B．点评：本题考查了角之间互补与互余的关系，互补两角之和为180°，互余两角之和为90度．23．如图1，已知数轴上有三点A、B、C，AB=AC，点C对应的数是200．（1）若BC=300，求点A对应的数；（2）如图2，在（1）的条件下，动点P、Q分别从A、C两点同时出发向左运动，同时动点R从A点出发向右运动，点P、Q、R的速度分别为10单位长度每秒、5单位长度每秒、2单位长度每秒，点M为线段PR的中点，点N为线段RQ的中点，多少秒时恰好满足MR=4RN（不考虑点R与点Q相遇之后的情形）；（3）如图3，在（1）的条件下，若点E、D对应的数分别为﹣800、0，动点P、Q分别从E、D两点同时出发向左运动，点P、Q的速度分别为10单位长度每秒、5单位长度每秒，点M为线段PQ的中点，点Q在从是点D运动到点A的过程中，QC﹣AM的值是否发生变化？若不变，求其值；若不变，请说明理由．考点：一元一次方程的应用；比较线段的长短．分析：（1）根据BC=300，AB=AC，得出AC=600，利用点C对应的数是200，即可得出点A 对应的数；（2）假设x秒Q在R右边时，恰好满足MR=4RN，得出等式方程求出即可；（3）假设经过的时间为y，得出PE=10y，QD=5y，进而得出+5y﹣400=y，得出﹣AM=﹣y原题得证．解答：解：（1）∵BC=300，AB=，所以AC=600，C点对应200，∴A点对应的数为：200﹣600=﹣400；（2）设x秒时，Q在R右边时，恰好满足MR=4RN，∴MR=（10+2）×，RN=[600﹣（5+2）x]，∴MR=4RN，∴（10+2）×=4×[600﹣（5+2）x]，解得：x=60；∴60秒时恰好满足MR=4RN；（3）设经过的时间为y，则PE=10y，QD=5y，于是PQ点为[0﹣（﹣800）]+10y﹣5y=800+5y，一半则是，所以AM点为：+5y﹣400=y，又QC=200+5y，所以﹣AM=﹣y=300为定值．点评：此题考查了一元一次方程的应用，根据已知得出各线段之间的关系等量关系是解题关键，此题阅读量较大应细心分析．24．如图，已知数轴上点A表示的数为6，B是数轴上一点，且AB=10．动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）①写出数轴上点B表示的数﹣4 ，点P表示的数6﹣6t （用含t的代数式表示）；②M为AP的中点，N为PB的中点．点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出线段MN的长；（2）动点Q从点A出发，以每秒1个单位长度的速度沿数轴向左匀速运动；动点R从点B 出发，以每秒个单位长度的速度沿数轴向左匀速运动，若P、Q、R三动点同时出发，当点P遇到点R时，立即返回向点Q运动，遇到点Q后则停止运动．那么点P从开始运动到停止运动，行驶的路程是多少个单位长度？考点：一元一次方程的应用；数轴；两点间的距离．专题：动点型．分析：（1）①设B点表示的数为x，根据数轴上两点间的距离公式建立方程求出其解，再根据数轴上点的运动就可以求出P点的坐标；②分类讨论：当点P在点A、B两点之间运动时；当点P运动到点B的左侧时，利用中点的定义和线段的和差易求出MN；（2）先求出P、R从A、B出发相遇时的时间，再求出P、R相遇时P、Q之间剩余的路程的相遇时间，就可以求出P一共走的时间，由P的速度就可以求出P点行驶的路程．解答：解：（1）设B点表示的数为x，由题意，得6﹣x=10，x=﹣4∴B点表示的数为：﹣4，点P表示的数为：6﹣6t；②线段MN的长度不发生变化，都等于5．理由如下：分两种情况：当点P在点A、B两点之间运动时：MN=MP+NP=AP+BP=（AP+BP）=AB=5；当点P运动到点B的左侧时：MN=MP﹣NP=AP﹣BP=（AP﹣BP）=AB=5，∴综上所述，线段MN的长度不发生变化，其值为5．（2）由题意得：P、R的相遇时间为：10÷（6+）=s，P、Q剩余的路程为：10﹣（1+）×=，P、Q相遇的时间为：÷（6+1）=s，∴P点走的路程为：6×（）=点评：本题考查了数轴及数轴的三要素（正方向、原点和单位长度）．一元一次方程的应用以及数轴上两点之间的距离公式的运用，行程问题中的路程=速度×时间的运用．25．画线段MN=3cm，在线段MN上取一点Q，使MQ=NQ，延长线段MN至点A，使AN=MN；延长线段NM至点B，使BN=3BM，根据所画图形计算：（1）线段BM的长度；（2）线段AN的长度；（3）试说明Q是哪些线段的中点图中共有多少条线段它们分别是考点：两点间的距离；直线、射线、线段．专题：计算题．分析：先根据题意画出几何图形（1）根据BN=3BM可得到MN=2BM，而MN=3cm，即可得到线段BM的长；（2）根据AN=MN即可得到线段AN的长；（3）由（1）与（2）得到BM=MQ=NQ=NA，即QB=QA，QM=QN，则点Q是线段MN的中点，也是线段AB的中点；图形中共有BM、BQ、BN、BA、MQ、MN、MA、QN、QA、NA10条线段．解答：解：如图，（1）∵MN=3cm，BN=3BM，∴BM=MN=×3=（cm ）；（2）∵MN=3cm，AN=MN∴AN=；（3）由图可知，BM=MQ=NQ=NA，∴QB=QA，QM=QN，∴点Q既是线段MN的中点，也是线段AB的中点；图中共有10条线段，它们分别是：BM、BQ、BN、BA、MQ、MN、MA、QN、QA、NA．点评：本题考查了两点间的距离：两点的连线段的长叫两点间的距离．也考查了射线与线段的定义．26．如图（1），已知A、B位于直线MN的两侧，请在直线MN上找一点P，使PA+PB最小，并说明依据．如图（2），动点O在直线MN上运动，连接AO，分别画∠AOM、∠AON的角平分线OC、OD，请问∠COD的度数是否发生变化？若不变，求出∠COD的度数；若变化，说明理由．考点：线段的性质：两点之间线段最短；角平分线的定义．专题：动点型．分析：（1）显然根据两点之间，线段最短．连接两点与直线的交点即为所求作的点．（2）根据角平分线的概念以及邻补角的概念即可证明．解答：解：（1）如图，连接AB交MN于点P，则P就是所求的点．理由：两点之间线段最短，（2）∠COD的度数不会变化，∵OC是∠AOM的平分线，，∴∠COA=∠AOM，∵OD是∠AON的平分线，∴∠AOD=∠AON，∵∠AOM+∠AON=180°，∴∠COA+∠AOD=∠AOM+∠AON=（∠AOM+∠AON）=90°．点评：求两点之间的最短距离时，注意两点之间，线段最短；互为邻补角的两个角的角平分线互相垂直．27．如图①，已知线段AB=12cm，点C为AB上的一个动点，点D、E分别是AC和BC的中点．（1）若点C恰好是AB中点，则DE= 6 cm；（2）若AC=4cm，求DE的长；（3）试利用“字母代替数”的方法，说明不论AC取何值（不超过12cm），DE的长不变；（4）知识迁移：如图②，已知∠AOB=120°，过角的内部任一点C画射线OC，若OD、OE分别平分∠AOC和∠BOC，试说明∠DOE=60°与射线OC的位置无关．考点：两点间的距离；角平分线的定义；角的计算．专题：动点型；规律型；整体思想．分析：（1）由AB=12cm，点D、E分别是AC和BC的中点，即可推出DE=（AC+BC）=AB=6cm，（2）由AC=4cm，AB=12cm，即可推出BC=8cm，然后根据点D、E分别是AC和BC的中点，即可推出AD=DC=2cm，BE=EC=4cm，即可推出DE的长度，（3）设AC=acm，然后通过点D、E分别是AC和BC的中点，即可推出DE=（AC+BC）=AB=cm，即可推出结论，（4）由若OD、OE分别平分∠AOC和∠BOC，即可推出∠DOE=∠DOC+∠COE=（∠AOC+∠COB）=∠AOB=60°，即可推出∠DOE的度数与射线OC的位置无关．解答：解：（1）∵AB=12cm，点D、E分别是AC和BC的中点，C点为AB的中点，∴AC=BC=6cm，∴CD=CE=3cm，∴DE=6cm，（2）∵AB=12cm，∴AC=4cm，∴BC=8cm，∵点D、E分别是AC和BC的中点，∴CD=2cm，CE=4cm，∴DE=6cm，（3）设AC=acm，∵点D、E分别是AC和BC的中点，∴DE=CD+CE=（AC+BC）=AB=6cm，∴不论AC取何值（不超过12cm），DE的长不变，（4）∵OD、OE分别平分∠AOC和∠BOC，∴∠DOE=∠DOC+∠COE=（∠AOC+∠COB）=∠AOB，∵∠AOB=120°，∴∠DOE=60°，∴∠DOE的度数与射线OC的位置无关．点评：本题主要考察角平分线和线段的中点的性质，关键在于认真的进行计算，熟练运用相关的性质定理．28．如图，OA的方向是北偏东15°，OB的方向是北偏西40°．（1）若∠AOC=∠AOB，则OC的方向是北偏东70°；（2）若B、O、D在同一条直线上，OD的方向是南偏东40°；（3）若∠BOD可以看作OB绕点O逆时针旋转180°到OD所成的角，作∠BOD平分线OE，并用方位角表示OE的方向．考点：方向角；角平分线的定义．分析：（1）先根据方向角的定义求出∠AOB的度数，进而求出∠NOC的度数即可；（2）根据OB的方向是西偏北50°求出∠DOH的度数，即可求出OD的方向，（3）根据OE是∠BOD的平分线，可知∠DOE=90°，进而可求出∠SOE的度数可知OE 的方向．解答：解：（1）∵OB的方向是北偏西40°，OA的方向是北偏东15°，∴∠NOB=40°，∠NOA=15°，∴∠AOB=∠NOB+∠NOA=55°，∵∠AOB=∠AOC，∴∠AOC=55°，∴∠NOC=∠NOA+∠AOC=70°，∴OC的方向是北偏东70°；（2）∵OD是OB的反向延长线，∴∠DOS=∠BON=40°，∴OD的方向是南偏东40°；（3）∵OE是∠BOD的平分线，∴∠DOE=90°，∵∠DOS=∠BON=40°，∴∠SOE=90°﹣∠DOS=50°，∴OE的方向是南偏西50°，．故答案为（1）北偏东70°；（2）南偏东40°．点评：本题主要考查了方向角的定义及表达方式，方向角一般是指以观测者的位置为中心，将正北或正南方向作为起始方向旋转到目标的方向线所成的角（一般指锐角），通常表达成北（南）偏东（西）多少度，同时考查了互补互余的概念，难度适中．29．如图，已知数轴上点A表示的数为8，B是数轴上一点，且AB=14．动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）写出数轴上点B表示的数﹣6 ，点P表示的数8﹣5t （用含t的代数式表示）；（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？（3）若M为AP的中点，N为PB的中点．点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出线段MN的长；（4）若点D是数轴上一点，点D表示的数是x，请你探索式子|x+6|+|x﹣8|是否有最小值？如果有，直接写出最小值；如果没有，说明理由．考点：一元一次方程的应用；数轴；两点间的距离．分析：（1）根据点A的坐标和AB之间的距离即可求得点B的坐标和点P的坐标；（2）根据距离的差为14列出方程即可求解；（3）分类讨论：①当点P在点A、B两点之间运动时，②当点P运动到点B的左侧时，利用中点的定义和线段的和差易求出MN．（4）分为3种情况去绝对值符号，计算三种不同情况的值，最后讨论得出最小值．解答：解：（1）点B表示的数是﹣6；点P表示的数是8﹣5t，（2）设点P运动x秒时，在点C处追上点Q （如图）则AC=5x，BC=3x，∵AC﹣BC=AB∴5x﹣3x=14…（4分）解得：x=7，∴点P运动7秒时，在点C处追上点Q．…（5分）（3）没有变化．分两种情况：①当点P在点A、B两点之间运动时：MN=MP+NP=AP+BP=（AP+BP）=AB=7…（7分）②当点P运动到点B的左侧时：MN=MP﹣NP=AP﹣BP=（AP﹣BP）=AB=7…（9分）综上所述，线段MN的长度不发生变化，其值为7 …（10分）（4）式子|x+6|+|x﹣8|有最小值，最小值为14．…（12分）点评：本题考查了数轴：数轴的三要素（正方向、原点和单位长度）．也考查了一元一次方程的应用以及数轴上两点之间的距离．。

五年级平面图形练习(易考题)

大是多少平方米？2.公园里有一块长方形草坪，草坪长30米、宽15米，为方便游客，在草坪中间开辟了两条宽2米的小路，现在草坪的面积是多少平方米？积是（）平方厘米。

5．长方形ABCD被ED分成两部分，阴影部分的面积比空白部分大米,已知AD D10□米,CD U8□米,□□□□□□□□多少平方厘米？20平方厘3求阴影部分的面积。

（单位：厘米）4.一个梯形，上底乘高是48平方厘米，下底乘高是96平方厘米，这个梯形的面6.已知四条线段的长度分别是AB=3厘米，CF=8厘米，CD=7厘米，AE=4厘米，求四边形ABCD的面积。

7、两个同样的直角三角形叠在一起，那么阴影部分的面积是多少平方厘米？7、求出图中梯形ABCD的面积，其中BC=56厘米。

（单位：厘米）8、正方形ABFD的面积为100平方厘米，直角三角形ABC的面积比直角三角形CDE的面积大30平方厘米，求DE的长是多少？FD9、正方形的边长是10cm,ED=8cm，三角形EFC的面积是45平方厘米。

求梯形BCDF的面积。

D10、有一个长方体容器，长30cm,宽20cm,高10cm。

在容器中装入水,水深6cm。

如果把盖子盖紧，竖起来，水深是多少厘米？12、已知三角形底边平均分成了4份,积是2平方分米，求三角形ABC的面积11、两个正方形的边长分别是6cm和2cm。

求四边形ABCF的面积。

13、已知直角梯形的面积是85平方厘米三角形CEB的面积是多少？如图，三角形ABC 的面积是120平方厘米，AE=DE ,DC 是BC 的一半,如图，已知三角形DCE 的面积是长方形面积的2倍，其中CE=12厘米,CD=816、两个小正方形组成的一个组合图形的周长是52厘米，DG=4厘米，求阴影部分的面积。

17、正方形ABCD 的边长是6厘米，三角形ABE 、三角形ADF 与四边形AECF 14、求阴影部分的面积。

15、厘米。

求三角形ADF 的面积。

的面积彼此相等，求三角形AEF 的面积。

五年级平面图形面积练习题

五年级平面图形面积练习题一、填空.1、一个平行四边形的底长8厘米；是高的2倍；它的面积是（）；与它等底等高的三角形面积是（）.2、一个梯形的上底是16米；下底是24米；高30米；它的面积是（）平方米.3、一堆钢管；最上层有3根；最下层有13根；每相邻两层相差1根；这堆钢管一共有（）根.4、一个直角三角形；三条边分别是10厘米、8厘米、6厘米；它的面积是（）；用两个这样的三角形拼成的长方形面积是（）.5、一个三角形和一个平行四边形的底相等；面积也相等；已知三角形的高是32厘米；那么平行四边形的高是（）厘米.6、一个平行四边形的面积是8平方分米；高是2分米；它的底是（）分米.7、一个近似梯形的花坛；高10米；上下底之和是16米；面积是（）.8、一个三角形的面积是6平方分米；底3分米；高是（）.9、用四根硬纸条钉成一个长方形框架；将它拉成一个平行四边形后；周长（）；面积（）.------（填“不变”或“变大”、“变小”）10、三角形的底扩大3倍；高不变；面积会（）.11、0.45公顷＝（）平方米. 12、两个完全一样的梯形可以拼成一个（）形.13、一个梯形上底与下底的和是15厘米；高是8.8厘米；面积是（）平方厘米.14、平行四边形的底是2分米5厘米；高是底的1.2倍；它的面积是（）平方厘米.15、梯形的上底增加3厘米；下底减少3厘米；高不变；面积（）.3、面积相等的两个梯形；形状不一定相等. （）6、梯形的上底下底越长；面积越大. （）7、任何一个梯形都可以分成两个等高的三角形. （）三、选择.1、两个（）梯形可以拼成一个长方形. ①等底等高②完全一样③完全一样的直角2、等腰梯形周长是48厘米；面积是96平方厘米；高是8厘米；则腰长（）.①24厘米②12厘米③18厘米④36厘米四、知识应用（每题7分）2、一个梯形广告牌；它的上底是8米；下底是12米；高是6米.如果要给这个广告牌涂上油漆；按每平方米花费15元来计算；共要花多少元？3、张大伯靠一面墙用篱笆围成一个面积是72平方米的梯形养鸡场；至少需要多少米的篱笆？墙6米4、一种等腰直角三角形小旗；直角边长4分米.现在有一块长12分米；宽6分米的长方形布料；用它最多可以剪成多少块这样的小旗？（小旗不能用边角料拼合）5、一条水渠横截面是梯形；渠深0.8米；渠底宽1.2米；渠口宽2米；横截面积是多少平方米？6、两个同样的梯形；上底长23厘米；下底长27厘米；高20厘米.如果把这两个梯形拼成一个平行四边形；这个平行四边形的面积是多少？7、梯形的上底是3.8厘米；高是4厘米；已知它的面积是20平方厘米；下底是多少厘米？8、在方格纸上画出面积相等的三角形和梯形.四、面积计算.8厘米6 10 5厘米7厘米厘厘 4米米厘米5厘米12厘米已知大正方形边长是6厘米；22厘米小正方形边长是4厘米.10厘米6厘米4厘米2、计算下列组合图形的面积（mm）。

五年级平面图形面积练习题

平面图形面积练习题一、填空。

1、一个平行四边形的底长8厘米，是高的2倍，它的面积是（），与它等底等高的三角形面积是（）。

2、一堆钢管，最上层有3根，最下层有13根，每相邻两层相差1根，这堆钢管一共有（）根。

3、一个直角三角形，三条边分别是10厘米、8厘米、6厘米，它的面积是（），用两个这样的三角形拼成的长方形面积是（）。

4、一个三角形和一个平行四边形的底相等，面积也相等，已知三角形的高是32厘米，那么平行四边形的高是（）厘米。

5、一个平行四边形的面积是8平方分米，高是2分米，它的底是（）分米。

6、一个近似梯形的花坛，高10米，上下底之和是16米，面积是（）。

7、一个三角形的面积是6平方分米，底3分米，高是（）。

8、用四根硬纸条钉成一个长方形框架，将它拉成一个平行四边形后，周长（），面积（）。

------（填“不变”或“变大”、“变小”）9、三角形的底扩大3倍，高不变，面积会（）。

10、0.45公顷＝（）平方米。

11、两个完全一样的梯形可以拼成一个（）形。

12、一个梯形上底与下底的和是15厘米，高是8.8厘米，面积是（）平方厘米。

13、平行四边形的底是2分米5厘米，高是底的1.2倍，它的面积是（）平方厘米。

14、梯形的上底增加3厘米，下底减少3厘米，高不变，面积（）。

一、判断。

1、三角形面积是平行四边形的一半。

（）2、两个面积相等的三角形一定能拼成一个平行四边形。

（）3、面积相等的两个梯形，形状不一定相等。

（）4、下面的图1中，长方形和平行四边形面积相等。

（）图1 图25、上面的图2中，阴影部分面积比空白部分面积大。

（）6、梯形的上底下底越长，面积越大。

（）7、任何一个梯形都可以分成两个等高的三角形。

（）三、知识应用1、两个同样的梯形，上底长23厘米，下底长27厘米，高20厘米。

如果把这两个梯形拼成一个平行四边形，这个平行四边形的面积是多少？2、在方格纸上画出面积相等的三角形和梯形。

四、面积计算。

七年级基本平面图形练习题

七年级基础仄里图形之阳早格格创做一．采用题（共9小题）1．由河源到广州的某一次列车，运止途中停靠的车站依次是：河源﹣惠州﹣东莞﹣广州，那么要为那次列车创造的火车票有（）A．3种B．4种C．6种D．12种2．通过A、B、C三面的任性二面，不妨绘出的曲线数为（）A．1或者2 B．1或者3 C．2或者3 D．1或者2或者3 3．某公司职工分别住正在A、B、C三个住房区，A区有30人，B区有15人，C区有10人．三个区正在一条曲线上，位子如图所示．公司的接收挨算正在此间只设一个停靠面，要使所有职工步止到停靠面的路途总战最少，那么停靠面的位子应正在（）A．A区B．B区C．C区D．不决定4．已知，P是线段AB上一面，且，则等于（）A．B．C．D．5．如图，正在数轴上有A、B、C、D、E五个整数面（即各面均表示整数），且AB=2BC=3CD=4DE，若A、E二面表示的数的分别为﹣13战12，那么，该数轴上上述五个面所表示的整数中，离线段AE的中面迩去的整数是（）A．﹣2 B．﹣1 C．0D．26．正在共部分内，不沉合的三条曲线的大众面数个数大概有（）A．0个、1个或者2个B．0个、2个或者3个C．0个、1个、2个或者3个D．1个或者3个7．如图所示，甲、乙、丙、丁、戊五名共教有以下道法：甲道：“曲线BC不过面A”；乙道：“面A正在曲线CD中”；丙道：“D正在射线CB的反背延少线上”；丁道：“A，B，C，D二二对接，有5条线段”；戊道：“射线AD与射线CD不相接”．其中道明精确的有（）A．3人B．4人C．5人D．2人8．已知∠α是钝角，∠α与∠β互补，∠α与∠γ互余，则∠β﹣∠γ的值等于（）A．45°B．60°C．90°D．180°9．如果∠α战∠β互补，且∠α＞∠β，则下列表示∠β的余角的式子中：①90°﹣∠β；②∠α﹣90°；③（∠α+∠β）；④（∠α﹣∠β）．精确的有（）A．4个B．3个C．2个D．1个二、解问题23．如图1，已知数轴上有三面A、B、C，AB=AC，面C 对于应的数是200．（1）若BC=300，供面A对于应的数；（2）如图2，正在（1）的条件下，动面P、Q分别从A、C二面共时出收背左疏通，共时动面R从A面出收背左疏通，面P、Q、R的速度分别为10单位少度每秒、5单位少度每秒、2单位少度每秒，面M为线段PR的中面，面N为线段RQ的中面，几秒时恰佳谦脚MR=4RN（不思量面R 与面Q相逢之后的情形）；（3）如图3，正在（1）的条件下，若面E、D对于应的数分别为﹣800、0，动面P、Q分别从E、D二面共时出收背左疏通，面P、Q的速度分别为10单位少度每秒、5单位少度每秒，面M为线段PQ的中面，面Q正在从是面D疏通到面A的历程中，QC﹣AM的值是可爆收变更？若稳定，供其值；若稳定，请道明缘由．24．如图，已知数轴上面A表示的数为6，B是数轴上一面，且AB=10．动面P从面A出收，以每秒6个单位少度的速度沿数轴背左匀速疏通，设疏通时间为t（t＞0）秒．（1）①写出数轴上面B表示的数_________，面P表示的数_________（用含t的代数式表示）；②M为AP的中面，N为PB的中面．面P正在疏通的历程中，线段MN的少度是可爆收变更？若变更，请道明缘由；若稳定，请您绘出图形，并供出线段MN的少；（2）动面Q从面A出收，以每秒1个单位少度的速度沿数轴背左匀速疏通；动面R从面B出收，以每秒个单位少度的速度沿数轴背左匀速疏通，若P、Q、R三动面共时出收，当面P逢到面R时，坐时返回背面Q疏通，逢到面Q后则停止疏通．那么面P从启初疏通到停止疏通，止驶的路途是几个单位少度？25．绘线段MN=3cm，正在线段MN上与一面Q，使MQ=NQ，延少线段MN至面A，使AN=MN；延少线段NM至面B，使BN=3BM，根据所绘图形估计：（1）线段BM的少度；（2）线段AN的少度；（3）试道明Q是哪些线段的中面？图中公有几条线段？它们分别是？26．如图（1），已知A、B位于曲线MN的二侧，请正在曲线MN上找一面P，使PA+PB最小，并道明依据．如图（2），动面O正在曲线MN上疏通，对接AO，分别绘∠AOM、∠AON的角仄分线OC、OD，请问∠COD的度数是可爆收变更？若稳定，供出∠COD的度数；若变更，道明缘由．27．如图①，已知线段AB=12cm，面C为AB上的一个动面，面D、E分别是AC战BC的中面．（1）若面C恰佳是AB中面，则DE=_________cm；（2）若AC=4cm，供DE的少；（3）试利用“字母代替数”的要领，道明不管AC与何值（不超出12cm），DE的少稳定；（4）知识迁移：如图②，已知∠AOB=120°，过角的里里任一面C绘射线OC，若OD、OE分别仄分∠AOC战∠BOC，试道明∠DOE=60°与射线OC的位子无闭．28．如图，OA的目标是北偏偏东15°，OB的目标是北偏偏西40°．（1）若∠AOC=∠AOB，则OC的目标是_________；（2）若B、O、D正在共一条曲线上，OD的目标是_________；（3）若∠BOD不妨瞅做OB绕面O顺时针转动180°到OD 所成的角，做∠BOD仄分线OE，并用圆背角表示OE的目标．29．如图，已知数轴上面A表示的数为8，B是数轴上一面，且AB=14．动面P从面A出收，以每秒5个单位少度的速度沿数轴背左匀速疏通，设疏通时间为t（t＞0）秒．（1）写出数轴上面B表示的数_________，面P表示的数_________（用含t的代数式表示）；（2）动面Q从面B出收，以每秒3个单位少度的速度沿数轴背左匀速疏通，若面P、Q共时出收，问面P疏通几秒时逃上面Q？（3）若M为AP的中面，N为PB的中面．面P正在疏通的历程中，线段MN的少度是可爆收变更？若变更，请道明缘由；若稳定，请您绘出图形，并供出线段MN的少；（4）若面D是数轴上一面，面D表示的数是x，请您探索式子|x+6|+|x﹣8|是可有最小值？如果有，间接写出最小值；如果不，道明缘由．一．采用题（共9小题）1．（2005•河源）由河源到广州的某一次列车，运止途中停靠的车站依次是：河源﹣惠州﹣东莞﹣广州，那么要为那次列车创造的火车票有（）A．3种B．4种C．6种D．12种考面：曲线、射线、线段．博题：应用题．分解：由题意可知：由河源要通过3个场合，所以要创造3种车票；由惠州要通过2个场合，所以要创造2种车票；由东莞要通过1个场合，所要创造1种车票；分离上述论断，通过往返估计出问案．解问：解：根据分解，知那次列车创造的火车票的总数=3+2+1=6（种）．则往返车票该当是：6×2=12（种）．故选D．面评：本题的闭键是要找出由一天到另一天的车票的数是几．2．（2003•台州）通过A、B、C三面的任性二面，不妨绘出的曲线数为（）A．1或者2 B．1或者3 C．2或者3 D．1或者2或者3 考面：曲线、射线、线段．分解：本题需先根据曲线的观念知，不妨决定出曲线的条数，即可供出精确的截止．解问：解：A、B、C三面的任性二面，不妨绘出的曲线数是：当三面正在一条曲线上的时间，不妨绘出一条曲线；当三面不正在共一条曲线上的时间，不妨绘出三条曲线；故选B．面评：本题主要考查了曲线的观念，正在解题时要注意分类计划的要领计数，干到不遗漏，不沉复．3．（2003•黄冈）某公司职工分别住正在A、B、C三个住房区，A区有30人，B区有15人，C区有10人．三个区正在一条曲线上，位子如图所示．公司的接收挨算正在此间只设一个停靠面，要使所有职工步止到停靠面的路途总战最少，那么停靠面的位子应正在（）A．A区B．B区C．C区D．不决定考面：比较线段的少短．分解：根据题意分别估计停靠面分别正在各面是职工步止的路途战，采用最小的即可解解问：解：∵当停靠面正在A区时，所有职工步止到停靠面路途战是：15×100+10×300=4500m；当停靠面正在B区时，所有职工步止到停靠面路途战是：30×100+10×200=5000m；当停靠面正在C区时，所有职工步止到停靠面路途战是：30×300+15×200=12000m．∴当停靠面正在A区时，所有职工步止到停靠面路途战最小，那么停靠面的位子该当正在A区．故选A．面评：此题考查了比较线段的少短，精确明白题意是解题的闭键．要能把线段的观念正在现真中举止应用．4．（2002•太本）已知，P是线段AB上一面，且，则等于（）A．B．C．D．考面：比较线段的少短．博题：估计题．分解：根据题意，先设AP=2x，则有PB=5x，故=可供．解问：解：如果设AP=2x，那么PB=5x，∴AB=AP+PB=7x，∴=．故选A．面评：机动使用线段的战、好、倍、分去转移线段之间的数量闭系是解题的闭键．5．如图，正在数轴上有A、B、C、D、E五个整数面（即各面均表示整数），且AB=2BC=3CD=4DE，若A、E二面表示的数的分别为﹣13战12，那么，该数轴上上述五个面所表示的整数中，离线段AE的中面迩去的整数是（）A．﹣2 B．﹣1 C．0D．2考面：数轴；比较线段的少短．博题：数形分离．分解：根据已知面供AE的中面，AE少为25，其少为12.5，而后根据AB=2BC=3CD=4DE供出A、C、B、D、E五面的坐标，末尾根据那五个坐标找出离中面迩去的面即可．解问：解：根据图示知，AE=25，∴AE=12.5，∴AE的中面所表示的数是﹣0.5；∵AB=2BC=3CD=4DE，∴AB：BC：CD：DE=12：6：4：3；而12+6+4+3恰佳是25，便是A面战E面之间的距离，∴AB=12，BC=6，CD=4，DE=3，∴那5个面的坐标分别是﹣13，﹣1，5，9，12，∴正在上头的5个面中，距离﹣0.5迩去的整数是﹣1．故选B．面评：此题概括考查了数轴、千万于值的有闭真量，用几许要领借帮数轴去供解，非常曲瞅，且阻挡易遗漏，体现了数形分离的便宜．6．正在共部分内，不沉合的三条曲线的大众面数个数大概有（）A．0个、1个或者2个B．0个、2个或者3个C．0个、1个、2个或者3个D．1个或者3个考面：曲线、射线、线段．分解：可先绘出三条曲线相接，创造：3条曲线相接最多有3个接面，最罕见1个接面．三条曲线仄止的时间为0个接面，二条曲线仄止被另背去线所截有2个接面，故0个、1个、2个或者3个的情况皆有．解问：解：3条曲线相接最多有3个接面，最罕见1个接面．三条曲线仄止的时间为0个接面，二条曲线仄止被另背去线所截有2个接面，故0个、1个、2个或者3个的情况皆有，故选问案C．面评：此题正在相接线的前提上，着沉培植教死的瞅察、真验战预测、归纳本领，掌握从特殊项普遍预测的要领．7．如图所示，甲、乙、丙、丁、戊五名共教有以下道法：甲道：“曲线BC不过面A”；乙道：“面A正在曲线CD中”；丙道：“D正在射线CB的反背延少线上”；丁道：“A，B，C，D二二对接，有5条线段”；戊道：“射线AD与射线CD不相接”．其中道明精确的有（）A．3人B．4人C．5人D．2人考面：曲线、射线、线段．博题：估计题．分解：此题考查了线的基赋本量、观念，注意辨别各观念之间的好别．解问：解：甲：“曲线BC不过面A”，精确；乙：“面A正在曲线CD中”，精确；丙：“D正在射线CB的反背延少线上”，精确；丁：“A，B，C，D二二对接，有5条线段”；该当有AB，AC，AD，BC，BD，CD 六条线段，过失；戊：“射线AD与射线CD不相接”，射线AD与射线CD接于面D，过失．故选D．面评：掌握佳曲线、射线、线段各个观念的共时还要注意各个观念之间的辨别．8．（2012•孝感）已知∠α是钝角，∠α与∠β互补，∠α与∠γ互余，则∠β﹣∠γ的值等于（）A．45°B．60°C．90°D．180°考面：余角战补角．博题：估计题．分解：根据互余二角之战为90°，互补二角之战为180°，分离题意即可得出问案．解问：解：由题意得，∠α+∠β=180°，∠α+∠γ=90°，二式相减可得：∠β﹣∠γ=90°．故选C．面评：此题考查了余角战补角的知识，属于前提题，掌握互余二角之战为90°，互补二角之战为180°，是解问本题的闭键．9．（2008•西宁）如果∠α战∠β互补，且∠α＞∠β，则下列表示∠β的余角的式子中：①90°﹣∠β；②∠α﹣90°；③（∠α+∠β）；④（∠α﹣∠β）．精确的有（）A．4个B．3个C．2个D．1个考面：余角战补角．分解：根据角的本量，互补二角之战为180°，互余二角之战为90，可将，①②③④中的式子化为含有∠α+∠β的式子，再将∠α+∠β=180°代进即可解出此题．解问：解：∵∠α战∠β互补，∴∠α+∠β=180度．果为90°﹣∠β+∠β=90°，所以①精确；又∠α﹣90°+∠β=∠α+∠β﹣90°=180°﹣90°=90°，②也精确；（∠α+∠β）+∠β=×180°+∠β=90°+∠β≠90°，所以③过失；（∠α﹣∠β）+∠β=（∠α+∠β）=×180°﹣90°=90°，所以④精确．综上可知，①②④均精确．故选B．面评：本题考查了角之间互补与互余的闭系，互补二角之战为180°，互余二角之战为90度．23．如图1，已知数轴上有三面A、B、C，AB=AC，面C 对于应的数是200．（1）若BC=300，供面A对于应的数；（2）如图2，正在（1）的条件下，动面P、Q分别从A、C二面共时出收背左疏通，共时动面R从A面出收背左疏通，面P、Q、R的速度分别为10单位少度每秒、5单位少度每秒、2单位少度每秒，面M为线段PR的中面，面N为线段RQ的中面，几秒时恰佳谦脚MR=4RN（不思量面R 与面Q相逢之后的情形）；（3）如图3，正在（1）的条件下，若面E、D对于应的数分别为﹣800、0，动面P、Q分别从E、D二面共时出收背左疏通，面P、Q的速度分别为10单位少度每秒、5单位少度每秒，面M为线段PQ的中面，面Q正在从是面D疏通到面A的历程中，QC﹣AM的值是可爆收变更？若稳定，供其值；若稳定，请道明缘由．考面：一元一次圆程的应用；比较线段的少短．分解：（1）根据BC=300，AB=AC，得出AC=600，利用面C对于应的数是200，即可得出面A对于应的数；（2）假设x秒Q正在R左边时，恰佳谦脚MR=4RN，得出等式圆程供出即可；（3）假设通过的时间为y，得出PE=10y，QD=5y，从而得出+5y﹣400=y，得出﹣AM=﹣y本题得证．解问：解：（1）∵BC=300，AB=，所以AC=600，C面对于应200，∴A面对于应的数为：200﹣600=﹣400；（2）设x秒时，Q正在R左边时，恰佳谦脚MR=4RN，∴MR=（10+2）×，RN=[600﹣（5+2）x]，∴MR=4RN，∴（10+2）×=4×[600﹣（5+2）x]，解得：x=60；∴60秒时恰佳谦脚MR=4RN；（3）设通过的时间为y，则PE=10y，QD=5y，于是PQ面为[0﹣（﹣800）]+10y﹣5y=800+5y，一半则是，所以AM面为：+5y﹣400=y，又QC=200+5y，所以﹣AM=﹣y=300为定值．面评：此题考查了一元一次圆程的应用，根据已知得出各线段之间的闭系等量闭系是解题闭键，此题阅读量较大应小心分解．24．如图，已知数轴上面A表示的数为6，B是数轴上一面，且AB=10．动面P从面A出收，以每秒6个单位少度的速度沿数轴背左匀速疏通，设疏通时间为t（t＞0）秒．（1）①写出数轴上面B表示的数﹣4，面P表示的数6﹣6t（用含t的代数式表示）；②M为AP的中面，N为PB的中面．面P正在疏通的历程中，线段MN的少度是可爆收变更？若变更，请道明缘由；若稳定，请您绘出图形，并供出线段MN的少；（2）动面Q从面A出收，以每秒1个单位少度的速度沿数轴背左匀速疏通；动面R从面B出收，以每秒个单位少度的速度沿数轴背左匀速疏通，若P、Q、R三动面共时出收，当面P逢到面R时，坐时返回背面Q疏通，逢到面Q 后则停止疏通．那么面P从启初疏通到停止疏通，止驶的路途是几个单位少度？考面：一元一次圆程的应用；数轴；二面间的距离．博题：动面型．分解：（1）①设B面表示的数为x，根据数轴上二面间的距离公式修坐圆程供出其解，再根据数轴上面的疏通便不妨供出P面的坐标；②分类计划：当面P正在面A、B二面之间疏通时；当面P疏通到面B的左侧时，利用中面的定义战线段的战好易供出MN；（2）先供出P、R从A、B出收相逢时的时间，再供出P、R相逢时P、Q之间结余的路途的相逢时间，便不妨供出P一共走的时间，由P的速度便不妨供出P面止驶的路途．解问：解：（1）设B面表示的数为x，由题意，得6﹣x=10，x=﹣4∴B面表示的数为：﹣4，面P表示的数为：6﹣6t；②线段MN的少度不爆收变更，皆等于5．缘由如下：分二种情况：当面P正在面A、B二面之间疏通时：MN=MP+NP=AP+BP=（AP+BP）=AB=5；当面P疏通到面B的左侧时：MN=MP﹣NP=AP﹣BP=（AP﹣BP）=AB=5，∴综上所述，线段MN的少度不爆收变更，其值为5．（2）由题意得：P、R的相逢时间为：10÷（6+）=s，P、Q结余的路途为：10﹣（1+）×=，P、Q相逢的时间为：÷（6+1）=s，∴P面走的路途为：6×（）=面评：本题考查了数轴及数轴的三果素（正目标、本面战单位少度）．一元一次圆程的应用以及数轴上二面之间的距离公式的使用，路程问题中的路途=速度×时间的使用．25．绘线段MN=3cm，正在线段MN上与一面Q，使MQ=NQ，延少线段MN至面A，使AN=MN；延少线段NM至面B，使BN=3BM，根据所绘图形估计：（1）线段BM的少度；（2）线段AN的少度；（3）试道明Q是哪些线段的中面？图中公有几条线段？它们分别是？考面：二面间的距离；曲线、射线、线段．博题：估计题．分解：先根据题意绘出几许图形（1）根据BN=3BM可得到MN=2BM，而MN=3cm，即可得到线段BM的少；（2）根据AN=MN即可得到线段AN的少；（3）由（1）与（2）得到BM=MQ=NQ=NA，即QB=QA，QM=QN，则面Q是线段MN的中面，也是线段AB的中面；图形中公有BM、BQ、BN、BA、MQ、MN、MA、QN、QA、NA10条线段．解问：解：如图，（1）∵MN=3cm，BN=3BM，∴BM=MN=×3=1.5（cm ）；（2）∵MN=3cm，AN=MN∴AN=1.5cm；（3）由图可知，BM=MQ=NQ=NA，∴QB=QA，QM=QN，∴面Q既是线段MN的中面，也是线段AB的中面；图中公有10条线段，它们分别是：BM、BQ、BN、BA、MQ、MN、MA、QN、QA、NA．面评：本题考查了二面间的距离：二面的连线段的少喊二面间的距离．也考查了射线与线段的定义．26．如图（1），已知A、B位于曲线MN的二侧，请正在曲线MN上找一面P，使PA+PB最小，并道明依据．如图（2），动面O正在曲线MN上疏通，对接AO，分别绘∠AOM、∠AON的角仄分线OC、OD，请问∠COD的度数是可爆收变更？若稳定，供出∠COD的度数；若变更，道明缘由．考面：线段的本量：二面之间线段最短；角仄分线的定义．博题：动面型．分解：（1）隐然根据二面之间，线段最短．对接二面与曲线的接面即为所供做的面．（2）根据角仄分线的观念以及邻补角的观念即可道明．解问：解：（1）如图，对接AB接MN于面P，则P便是所供的面．缘由：二面之间线段最短，（2）∠COD的度数不会变更，∵OC是∠AOM的仄分线，，∴∠COA=∠AOM，∵OD是∠AON的仄分线，∴∠AOD=∠AON，∵∠AOM+∠AON=180°，∴∠COA+∠AOD=∠AOM+∠AON=（∠AOM+∠AON）=90°．面评：供二面之间的最短距离时，注意二面之间，线段最短；互为邻补角的二个角的角仄分线互相笔曲．27．如图①，已知线段AB=12cm，面C为AB上的一个动面，面D、E分别是AC战BC的中面．（1）若面C恰佳是AB中面，则DE=6cm；（2）若AC=4cm，供DE的少；（3）试利用“字母代替数”的要领，道明不管AC与何值（不超出12cm），DE的少稳定；（4）知识迁移：如图②，已知∠AOB=120°，过角的里里任一面C绘射线OC，若OD、OE分别仄分∠AOC战∠BOC，试道明∠DOE=60°与射线OC的位子无闭．考面：二面间的距离；角仄分线的定义；角的估计．博题：动面型；顺序型；完全思维．分解：（1）由AB=12cm，面D、E分别是AC战BC的中面，即可推出DE=（AC+BC）=AB=6cm，（2）由AC=4cm，AB=12cm，即可推出BC=8cm，而后根据面D、E 分别是AC战BC的中面，即可推出AD=DC=2cm，BE=EC=4cm，即可推出DE的少度，（3）设AC=acm，而后通过面D、E分别是AC战BC的中面，即可推出DE=（AC+BC）=AB=cm，即可推出论断，（4）由若OD、OE分别仄分∠AOC战∠BOC，即可推出∠DOE=∠DOC+∠COE=（∠AOC+∠COB）=∠AOB=60°，即可推出∠DOE的度数与射线OC的位子无闭．解问：解：（1）∵AB=12cm，面D、E分别是AC战BC的中面，C面为AB的中面，∴AC=BC=6cm，∴CD=CE=3cm，∴DE=6cm，（2）∵AB=12cm，∴AC=4cm，∴BC=8cm，∵面D、E分别是AC战BC的中面，∴CD=2cm，CE=4cm，∴DE=6cm，（3）设AC=acm，∵面D、E分别是AC战BC的中面，∴DE=CD+CE=（AC+BC）=AB=6cm，∴不管AC与何值（不超出12cm），DE的少稳定，（4）∵OD、OE分别仄分∠AOC战∠BOC，∴∠DOE=∠DOC+∠COE=（∠AOC+∠COB）=∠AOB，∵∠AOB=120°，∴∠DOE=60°，∴∠DOE的度数与射线OC的位子无闭．面本题主要观察角仄分线战线段的中面的本量，闭键正在于认果然举止估计，流利使评：用相闭的本量定理．28．如图，OA的目标是北偏偏东15°，OB的目标是北偏偏西40°．（1）若∠AOC=∠AOB，则OC的目标是北偏偏东70°；（2）若B、O、D正在共一条曲线上，OD的目标是北偏偏东40°；（3）若∠BOD不妨瞅做OB绕面O顺时针转动180°到OD 所成的角，做∠BOD仄分线OE，并用圆背角表示OE的目标．考面：目标角；角仄分线的定义．分解：（1）先根据目标角的定义供出∠AOB的度数，从而供出∠NOC的度数即可；（2）根据OB的目标是西偏偏北50°供出∠DOH的度数，即可供出OD的目标，（3）根据OE是∠BOD的仄分线，可知∠DOE=90°，从而可供出∠SOE的度数可知OE的目标．解问：解：（1）∵OB的目标是北偏偏西40°，OA的目标是北偏偏东15°，∴∠NOB=40°，∠NOA=15°，∴∠AOB=∠NOB+∠NOA=55°，∵∠AOB=∠AOC，∴∠AOC=55°，∴∠NOC=∠NOA+∠AOC=70°，∴OC的目标是北偏偏东70°；（2）∵OD是OB的反背延少线，∴∠DOS=∠BON=40°，∴OD的目标是北偏偏东40°；（3）∵OE是∠BOD的仄分线，∴∠DOE=90°，∵∠DOS=∠BON=40°，∴∠SOE=90°﹣∠DOS=50°，∴OE的目标是北偏偏西50°，．故问案为（1）北偏偏东70°；（2）北偏偏东40°．面评：本题主要考查了目标角的定义及表白办法，目标角普遍是指以瞅测者的位子为核心，将正北或者正北目标动做起初目标转动到目目标目标线所成的角（普遍指钝角），常常表完毕北（北）偏偏东（西）几度，共时考查了互补互余的观念，易度适中．29．如图，已知数轴上面A表示的数为8，B是数轴上一面，且AB=14．动面P从面A出收，以每秒5个单位少度的速度沿数轴背左匀速疏通，设疏通时间为t（t＞0）秒．（1）写出数轴上面B表示的数﹣6，面P表示的数8﹣5t（用含t的代数式表示）；（2）动面Q从面B出收，以每秒3个单位少度的速度沿数轴背左匀速疏通，若面P、Q共时出收，问面P疏通几秒时逃上面Q？（3）若M为AP的中面，N为PB的中面．面P正在疏通的历程中，线段MN的少度是可爆收变更？若变更，请道明缘由；若稳定，请您绘出图形，并供出线段MN的少；（4）若面D是数轴上一面，面D表示的数是x，请您探索式子|x+6|+|x﹣8|是可有最小值？如果有，间接写出最小值；如果不，道明缘由．考面：一元一次圆程的应用；数轴；二面间的距离．分解：（1）根据面A的坐标战AB之间的距离即可供得面B的坐标战面P的坐标；（2）根据距离的好为14列出圆程即可供解；（3）分类计划：①当面P正在面A、B二面之间疏通时，②当面P疏通到面B的左侧时，利用中面的定义战线段的战好易供出MN．（4）分为3种情况去千万于值标记，估计三种分歧情况的值，末尾计划得出最小值．解问：解：（1）面B表示的数是﹣6；面P表示的数是8﹣5t，（2）设面P疏通x秒时，正在面C处逃上面Q （如图）则AC=5x，BC=3x，∵AC﹣BC=AB∴5x﹣3x=14…（4分）解得：x=7，∴面P疏通7秒时，正在面C处逃上面Q．…（5分）（3）稳定更．分二种情况：①当面P正在面A、B二面之间疏通时：MN=MP+NP=AP+BP=（AP+BP）=AB=7…（7分）②当面P疏通到面B的左侧时：MN=MP﹣NP=AP﹣BP=（AP﹣BP）=AB=7…（9分）综上所述，线段MN的少度不爆收变更，其值为7 …（10分）（4）式子|x+6|+|x﹣8|有最小值，最小值为14．…（12分）面评：本题考查了数轴：数轴的三果素（正目标、本面战单位少度）．也考查了一元一次圆程的应用以及数轴上二面之间的距离．。

平面图形的认识(二)练习

平面图形的认识（二）练习一、选择题1．若从一个多边形的一个顶点出发，最多可以引10条对角线，则它是( ) A.十三边形 B.十二边形 C.十一边形 D.十边形2．已知一个多边形的外角和等于它的内角和，则这多边形是（）A.三角形B.四边形C.五边形D.六边形3．一个三角形的三个内角中，至少有（）A.一个锐角B.两个锐角C.一个钝角D.一个直角4．三角形的角平分线是（）Ａ．射线；Ｂ．直线；Ｃ．线段；Ｄ．线段或射线．5．如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形的形状是（）Ａ．锐角三角形；Ｂ．直角三角形；Ｃ．钝角三角形；Ｄ．等腰三角形．6．以下列长度的线段为边，可以作一个三角形的是（）A．5㎝、10㎝、15㎝； B．5㎝、10㎝、20㎝；C．10㎝、15㎝、20㎝； D．5㎝、20㎝、25㎝．7．现有两根铁条，它们的长分别是30cm和50cm，如果要做成一个三角形铁架，那么在下列四根铁条中应选取（）A．20cm的铁条； B．30cm的铁条； C．80cm的铁条； D．90cm的铁条．8．平行线之间的距离是指（）A.从一条直线上一点到另一条直线的垂线段；B.从一条直线上一点到另一条直线的垂线段长度；C.从一条直线上一点到另一条直线的垂线的长度；D.从一条直线上一点到另一条直线上的一点间线段的长度.9．在平移过程中，对应线段( )A.互相平行且相等；B.互相垂直且相等；C.互相平行(或在同一条直线上)且相等；D.不相等.10．下列各组图形，可经平移变换，由一个图形得到另一个图形的是（）11．下列五幅图案中，⑵、⑶、⑷、⑸中的哪个图案可以由(1)图案平移得到？（）A ．⑵；B ．⑶；C ．⑷；D ．⑸.12．如果两条直线被第三条直线所截，那么一组内错角的平分线（）Ａ．互相垂直；Ｂ．互相平行；Ｃ．互相重合；Ｄ．以上均不正确．13．如图，直线c 与直线a 、b 相交，且a//b ，则下列结论：(1)∠=∠12；(2)∠=∠13；(3)∠=∠32中正确的个数为（）A.0B.1C.2D.314．一条公路两次转弯后又回到原来的方向(即AB ∥CD ，如图)，如果第一次转弯时的∠B ＝140°，那么，∠C 应是（）A ．40°B ．100°C ．140°D ．180°15．如图两条非平行的直线AB ，CD 被第三条直线EF 所截，交点为PQ ，那么这条直线将所在平面分成（）A.5个部分；B.6个部分；C.7个部分；D.8个部分.16．如图，直线a 、b 与直线c 相交，给出下列条件：①∠1=∠2；②∠3=∠6；③∠4+∠7=180°；④∠5+∠8=180°，其中能判断a ∥b 的是（）A ．①③；B ．①③④；C ．②④；D ．①②③④.17．如图，下列条件中，不能判断直线ι1//ι2的是（）A ．∠1＝∠3；B ．∠2＝∠3；C ．∠4＝∠5；D ．∠2＋∠4＝180°.18．下列命题中，正确的是（）A ．两条直线被第三条直线所截，同位角相等；B ．相等的角是对顶角；C ．在同一平面内，平行于同一条直线的两条直线平行；D ．和为180°的两个角叫做邻补角.19．在如图给出的过直线外一点作已知直线l 1的平行线l 2的方法，其依据是（）A ．同位角相等，两直线平行；B ．内错角相等，两直线平行；C ．筒旁内角互补，两直线平行；D ．两直线平行，同位角相等.20．若一个多边形除了一个内角外，其余各内角之和为2570°，则这个内角的度数为( )A.90°；B.105°；C.130°；D.120°.21．锐角三角形的三个内角是∠A 、∠B 、∠C 。

关于平面图形的练习题

关于平面图形的练习题一、填空题1. 平面图形的基本元素是点和______。

2. 由不在同一直线上的三条线段首尾顺次连接所组成的封闭图形叫______。

3. 一个平行四边形的对边分别是8cm和12cm，那么它的周长是______cm。

4. 等边三角形的三个角都是______度。

5. 一个正方形的面积是25平方厘米，那么它的边长是______厘米。

二、选择题A. 长方形B. 梯形C. 平行四边形D. 等腰三角形2. 下列哪个图形既是中心对称图形又是轴对称图形？（）A. 正方形B. 等腰梯形C. 直角三角形D. 椭圆形3. 一个等腰三角形的底边长为10cm，腰长为13cm，那么这个三角形的周长是：（）A. 26cmB. 32cmC. 42cmD. 46cmA. 矩形B. 三角形C. 梯形D. 正方形5. 一个圆的半径增加了10%，那么它的面积增加了多少？（）A. 10%B. 20%C. 21%D. 40%三、判断题1. 两条平行线上的任意两个角都是对应角。

（）2. 一个等腰三角形的底角和顶角相等。

（）3. 两个全等三角形的面积一定相等。

（）4. 任意两个圆的周长之比等于它们的半径之比。

（）5. 一个正方形的对角线长度等于它的边长。

（）四、计算题1. 计算下列图形的周长和面积：（1）长方形，长10cm，宽6cm；（2）正方形，边长8cm；（3）等腰三角形，底边长12cm，腰长10cm。

2. 一个圆的半径是5cm，求它的周长和面积。

3. 一个梯形的上底是4cm，下底是10cm，高是6cm，求它的面积。

4. 计算下列图形的面积：（1）矩形，长15cm，宽8cm；（2）等腰三角形，底边长16cm，高12cm；（3）圆，半径14cm。

5. 一个平行四边形的底边长为8cm，高为5cm，求它的面积。

五、作图题1. 画出下列图形：（1）一个边长为5cm的正方形；（2）一个底边长为6cm，高为4cm的等腰三角形；（3）一个直径为10cm的圆；（4）一个长为8cm，宽为6cm的长方形；（5）一个上底为4cm，下底为6cm，高为3cm的梯形。

五年级上学期平面图形的练习题

五年级上学期平面图形的练习题（一）一、填空题。

1. 一个三角形的面积是15平方厘米，和它等底等高的平行四边形的面积是( )平方厘米.2。

一个平行四边形和一个三角形的面积和高都相等，如果平行四边形的底是6厘米，那么三角形的底是（）厘米。

3。

在一个长9厘米，宽8厘米的长方形内画一个最大的三角形，这个三角形的面积是（）平方厘米。

4。

右图中阴影部分的面积是24平方厘米,长方形的面积是( )平方厘米。

5。

一个平行四边形的底是6厘米，高是14厘米,它的面积是（)平方厘米，与它等底等高的三角形面积是（）平方厘米。

6。

将木条订成的长方形拉成一个平行四边形（如图）,原来长方形的面积是（）平方厘米,现在平行四边形的面积是( ）平方厘米,现在平行四边形的周长是（）厘米。

7、沿着平行四边形的任一对角线剪开，分成两个完全一样的( )，它们的底和平行四边形的底（ )。

它们的（ )和平行四边形的高相等。

每个三角形的面积是平行四边形面积的（ )。

8、一个三角形的底是24分米，高是底的一半，这个三角形的面积是（）平方分米.9、一个平行四边形的底是9米，面积是45平方米，它的高是( )米.10、一个三角形的面积是32平方厘米,它的高是8厘米，底是（）厘米。

11、一个梯形的面积42平方厘米，它的上底3厘米，下底是5厘米，它的高是( )厘米。

12、一个梯形的面积是1600平方厘米，高是16厘米，上底是70厘米，下底是( ）。

13、一个平行四边形和一个三角形的面积相等，底也相等.如果三角形的高是20厘米，那么平行四边形的高是（）厘米。

14、梯形的上底增加5厘米，下底减少5厘米,高不变，面积（）.15、有一堆圆木堆成梯形，最上面一层有4根，最下面一层有12根,一共堆了6层，这堆圆木共有( )根.二、判断题1、两个面积相等的三角形能拼成一个平行四边形。

（ )2、两个不同形状的平行四边形，它们的面积也不相同。

（ )3、等底等高的平行四边形面积相等. ( )4、平行四边形内最大的三角形的面积是平行四边形面积的一半。