第1、2、3章习题解答

合集下载

工程流体力学习题课1-第2-3-4章-部分习题解答

h 4 = 2H 4 → H =h
2 2 d2
习题3-14解题示意图1
Dr W-X Huang, School of Chemical Engineering, Sichuan University, Chengdu 610065, P.R. China
工程流体力学——习题课(1)——第 2-3-4 章部分习题解答
Fx1 =
y x
H1
D
H2
图 3-26 习题 3-11 附图
1 1 ρ gH1 × ( DL) = × 1000 × 9.8 × 4 × (4 × 10) = 784000 N=784kN 2 2 1 D 1 4 Fx 2 = ρ gH 2 × ( L) = × 1000 × 9.8 × 2 × × 10 = 196000 N=196kN 2 2 2 2
H
h
由此得： H ≥ 122mm + h ≥ 244mm (2) 结合以上正负压操作时结果有：
p / ρ g ≤ h ≤ H − | p| / ρ g
图 3-23 习题 3-8 附图
→ 122mm ≤ h ≤ 178mm
Dr W-X Huang, School of Chemical Engineering, Sichuan University, Chengdu 610065, P.R. China
工程流体力学——习题课(1)——第 2-3-4 章部分习题解答
F1-6
习题 3-8 旋风除尘器如图 3-23 所示，其下端出灰口管段长 H，部分插入水中，使旋风除尘器内部与外界大气隔开，称为水封；同时要求出灰管内液面不得高于出灰管上部法兰位置。设除尘器内操作压力 ( 表压 ) p = −1.2 kPa~ 1.2kPa。净化空气 (1) 试问管段长 H 至少为多少 mm? (2) 若H=300mm，问其中插入水中的部分h应在什么范围？(取水的密度 ρ =1000kg/m3) 含尘解：(1) 正压操作时，出灰管内液面低于管外液面，高差为 h′ = p / ρ g ；为实现水封，出灰管插入深度 h 必须大于此高差，即

人邮社数字电路逻辑设计习题答案

习题参考解答第1章基本知识1．什么是数字信号？什么是模拟信号？（注：所有蓝色标题最后均去掉！）答案：数字信号：指信号的变化在时间上和数值上都是断续的，或者说是离散的，这类信号有时又称为离散信号。

例如，在数字系统中的脉冲信号、开关状态等。

模拟信号：指在时间上和数值上均作连续变化的信号。

例如，温度、交流电压等信号。

2．数字系统中为什么要采用二进制？答案：二进制具有运算简单、物理实现容易、存储和传送方便、可靠等优点。

3．机器数中引入反码和补码的主要目的是什么？答案：将减法运算转化为加法运算，统一加、减运算，使运算更方便。

4．BCD码与二进制数的区别是什么?答案：二进制数是一种具有独立进位制的数，而BCD码是用二进制编码表示的十进制数。

5．采用余3码进行加法运算时，应如何对运算结果进行修正？为什么？答案：两个余3码表示的十进制数相加时，对运算结果修正的方法是：如果有进位，则结果加3；如果无进位，则结果减3。

为了解决四位二进制运算高位产生的进位与一位十进制运算产生的进位之间的差值。

6．奇偶检验码有哪些优点和不足？答案：奇偶检验码的优点是编码简单，相应的编码电路和检测电路也简单。

缺点是只有检错能力，没有纠错能力，其次只能发现单错，不能发现双错。

7．按二进制运算法则计算下列各式。

答案：（1）110001 （2）110.11 （3）10000111 （4）1018．将下列二进制数转换成十进制数、八进制数和十六进制数。

答案：（1）（117）10 ，（165）8 ，（75）16（2）（0.8281）10 ，（0.65）8 ，（0.D4）16（3）（23.25）10 ，（27.2）8 ，（17. 4）169．将下列十进制数转换成二进制数、八进制数和十六进制数（精确到二进制小数点后4位）。

答案：（1）（1000001）2 ，（101）8 ，（41）16（2）（0.0100）2 ，（0.20）8 ，（0.40）16（3）（100001.0101）2 ，（41.24）8 ，（21.50）1610．写出下列各数的原码、反码和补码。

机械原理习题解答(第1-3章)

vB
+
vC2B
=
vC3
+
vC2C3
方向
？？
ω1lAB
？
BC
AB
0
? ∥BC
b
C(C2,C3,C4)
p
C3
C2
d
e
再根据速度影像原理，作△bde ∽ △ BDE 求得d及e，由图可得
b
vD v pd 0.23m / s
C(C2,C3,C4)
p' C '
（3）加速度分析
' C2
3
答：（1）机构所有的瞬心数：K=（N-1）/2=6(6-1)/2=15。（2）求出如下三个瞬心P16，P36，P13，如下图所示。
P23 K（P13） P36
P12 P16
1 / 3 P P / P P 36 13 16 13
3-11 速度多边形和加速度多边形有哪些特性？试标出图中VAB、VBC、VCA及VA、VB、VC的方向？答：速度多边形具有以下特点：（1）作图起点p称为速度多边形的极点p，它代表机构中速度为零的点。（2）在速度多边形中，连接p点和任一点的矢量代表该点在机构图中同名点的绝对速度，其指向是从p点指向该点。
答：速度瞬心是互作平面相对运动的两构件上瞬时相对速度为零的重合点，也就是具有同一瞬时绝对速度的重合点 (即瞬时绝对速度速度相等的重合点)，简称瞬心。若瞬心处的绝对速度为零，则该瞬心称为绝对瞬心，否则称为相对瞬心。 3-2 何为三心定理？何种情况下的瞬心需用三心定理来确定？答：三心定理是指三个彼此作平面平行运动的构件的三个瞬心必位于同一直线上。对于不通过运动副直接相连的两构件间的瞬心位置，需用三心定理来确定。

第123章习题解答

第123章习题解答第1章概述1-02 简述分组交换的要点。

答：（1）报⽂分组，加⾸部（2）经路由器储存转发（3）在⽬的地合并1-03 试从多个⽅⾯⽐较电路交换、报⽂交换和分组交换的主要优缺点。

答：（1）电路交换：端对端通信质量因约定了通信资源获得可靠保障，对连续传送⼤量数据效率⾼。

（2）报⽂交换：⽆须预约传输带宽，动态逐段利⽤传输带宽对突发式数据通信效率⾼，通信迅速。

（3）分组交换：具有报⽂交换之⾼效、迅速的要点，且各分组⼩，路由灵活，⽹络⽣存性能好。

1-17 收发两端之间的传输距离为1000km，信号在媒体上的传播速率为2×108m/s。

试计算以下两种情况的发送时延和传播时延：（1）数据长度为107bit,数据发送速率为100kb/s。

（2）数据长度为103bit,数据发送速率为1Gb/s。

从上⾯的计算中可以得到什么样的结论？解：（1）发送时延：ts=107/105=100s传播时延tp=106/(2×108)=（2）发送时延ts =103/109=1µs传播时延：tp=106/(2×108)=结论：若数据长度⼤⽽发送速率低，则在总的时延中，发送时延往往⼤于传播时延。

但若数据长度短⽽发送速率⾼，则传播时延就可能是总时延中的主要成分。

出现的问题：1 未做完。

2 1-17中的科学计数法不会⽤。

（1）发送时延：ts=107/105=100s传播时延tp=106/(2×108)=（2）发送时延ts =103/109=1µs传播时延：tp=106/(2×108)=1-19 长度为100字节的应⽤层数据交给传输层传送，需加上20字节的TCP⾸部。

再交给⽹络层传送，需加上20字节的IP⾸部。

最后交给数据链路层的以太⽹传送，加上⾸部和尾部⼯18字节。

试求数据的传输效率。

数据的传输效率是指发送的应⽤层数据除以所发送的总数据（即应⽤数据加上各种⾸部和尾部的额外开销）。

半导体物理导论课后习题答案第1-3章

厘米体积中的硅原子数为：原子体密度=8/a3=8/(5.43×108)3=5×1022（个原子/cm3） (2)（111）面为一个边长为 a 2 的等边三角形，
有效原子数为
3
13（顶角原子）
3
12（面心原子）
5 2
个原子
等边三角形的面积为
S
1 2
a
2
2
a
10 2
a2 4
5
第1章
所以，(111)面的原子面密度为
第1章
3.已知Si的晶格常数或单胞的边长a=5.43089 Å, 求：（1）Si的原子体密度。（2）(111)面、(110)面以及(100)面的原子面密度，比较哪个晶面的面密度最大？哪个晶面的面密度最小？
解:(1)每个晶胞中有8个原子，晶胞体积为a3，每个原子所占的空间体积为a3/8，因此每立方
图3
第2章
2. 图中的A、B 分别为两种半导体材料价带中载流子的E-k关系抛物线，其中哪个材料的电子有效质量小？为什么？试确定两种电子的有效质量之比(以自由电子质量为单位) 。
解：由图可知，B材料的能带极值附近的曲率变化较大，故其电子有效质量小。所以，A、B材料的电子有效质量之比为0.26，B材料的电子有效质量小。
Eg h
1.12 4.135 1015
2.711014 (s1)
hc Eg
4.1351015 31017 1.12
1107.1(nm)
第3章
1.掺杂半导体与本证半导体之间有何差异？试举例说明掺杂对半导体的导电性能的影响。
2.试简述杂质在半导体中的几种作用，并分别在能带图上标志出其在半导体中的跃迁过程 3.试说明浅能级杂质和深能级杂质的物理意义及特点。 4.何谓非平衡载流子？非平衡状态与平衡状态的差异何在

电工部分习题解答(1,2,3)

第一章习题解答1-1 在图1-39所示的电路中，若I 1=4A ，I 2=5A ，请计算I 3、U 2的值；若I 1=4A ，I 2=3A ，请计算I 3、U 2、U 1的值，判断哪些元件是电源？哪些是负载？并验证功率是否平衡。

解：对节点a 应用KCL 得 I 1+ I 3= I 2 即4+ I 3=5, 所以 I 3=1A 在右边的回路中，应用KVL 得6⨯I 2+20⨯I 3= U 2，所以U 2=50V 同理，若I 1=4A ，I 2=3A ，利用KCL 和KVL 得I 3= -1A ，U 2= -2V 在左边的回路中，应用KVL 得20⨯I 1+6⨯I 2= U 1，所以U 1=98V 。

U 1，U 2都是电源。

电源发出的功率：P 发=- U 1 I 1- U 2 I 3=-98⨯4-2=-394W 负载吸收的功率：P 吸=2021I +622I +2023I =394W 二者相等，整个电路功率平衡。

1-2 有一直流电压源，其额定功率P N =200W ，额定电压U N =50V ，内阻R o =0.5Ω，负载电阻R L 可以调节，其电路如图1-40所示。

试求：⑴额定工作状态下的电流及负载电阻R L 的大小；⑵开路状态下的电源端电压；⑶电源短路状态下的电流。

解：⑴A U P I N N N 450200===Ω===5.12450N N L I U R ⑵ =⨯+==0R I U U U N N S OC 50+4⨯0.5 = 52V ⑶ A R U I S SC 1045.0520===图1-39 习题1-1图图1-40 习题1-2图1-9 求图1-44所示电路中电阻的电流及其两端的电压，并求图1-44a 中电压源的电流及图1-44 b 中电流源的电压，判断两图中的电压源和电流源分别起电源作用还是负载作用。

解：图1-44a 中，A I R 2=，V U R 2=，电压源的电流A I 2=。

线性代数(第一～三章)习题解答

习题一1．解：(1)31542的逆序数=2+0+2+1+0=5(2)264315的逆序数=1+4+2+1+0+0=8 (3)54321的逆序数=4+3+2+1=10(4))12)(32(135)2)(22(246---n n n n =1+2+3+…(2n －1)＝2)1(+n n 2．解：四阶行列式中含有31a 的项可表示为42142143121)1()1(j j j j j j a a a a τ-，其中421,,j j j 为2，3，4的全排列。

故带有负号的项有：43312412a a a a -，44312213a a a a -，42312314a a a a -3．解：xx x x x x 347165423112展开式中含有4x 的项必须每行都取含x 的项相乘，即41863x x x x x =⋅⋅⋅=，含有3x 的项为x x x x x x ⋅⋅⋅-+⋅⋅⋅-2)1(763)1()1324()4231(ττ3128x -=4．证明：（反证法）假设该行列式不为零，则不为零的元素的个数≥n ，从而为零的元素的个数≤n n -2，与已知行列式中有n n -2个以上元素为零矛盾。

所以该行列式为零。

5．解：（1）2456323652-=⨯-⨯=+ （2）))(())((22222222b ab a b a b ab a b a ba b a b ab a b ab a ++--+-+=+-+++-33b a +=3332)(b b a =--（3）022=bababa （4）45500251190221242513122113-=-----r r r r （5）3711107403112311740532224332453213312213=-----↔-----r r r r r r r r（6）))((0))((0111121212222c b a a c a c c b a a b a b bca ar r r r abc c acb bbca a ++--++-------- 0)(10)(101))(()()(232=++++-----c b a c b a bca aa c ab ac r a b r 提取提取（7）43123524323556485437r r r r --23214123524031102115437r r r r r r -+--3524010002111400---24100011302410000111000524343231－按第一行展开--++-r r r r r r22411＝－按第三列展开（8）132141873754169521321r r r r r ---1226400622069521321r r ---2312226400622043101321r r r r ----346400240043101321r r -----16400240043101321=---（9）4321c c c c xa b c a x c b b c x a c b a x +++----xa b x c b a a x c x c b a bc x x c b a cb a xc b a --++--++--++-++131214 )(r r r r r r x c b a ----++ 提取cx b a a b c a b x a c cb bc a x c b a x c b a -------------++0001)(4223c c c c ++c x b c a x ca c ab x cb c b a x b c a x ca b c a x c b a --+----+----+---+---++-++000001)( 432c c c --cx b c a x c a c a b x cx a b ca b c a x c b a --+----+---++-++-++00000001)( 按第一列展开cx b c a x ca c ab xc x a b x c b a --+-------++--++0|00)())()()(()1()321(x a c b c b a x b c a x x c b a +-++---+----++-=τ ))()()((x c b a x b a c x c a b x c b a ----------++=6．解：(1) 证明：cb a a cb c b a cba cb a ++++++222并提取公因式321c c c ++c b a a b c b a ba++++++21211c)b 2(ac b a c b a bac b a c c c c ++++++--00001)(213123)(2c b a ++=(2)bzay by ax bx az by ax bx az bz ay bxaz bz ay by ax +++++++++5行列式性质bz ay by ax az by ax bx az ay bx az bz ay ax +++++++bz ay by ax bx by ax bx az bz bxaz bz ay by ++++++ 提取公因式bz ay by ax z by ax bx az y bxaz bz ay xa +++++++bzay by ax xby ax bx az z bx az bz ay yb ++++++5行列式性质ay by ax zax bx az y az bz ay x a ++++bz by ax zby bx az ybx bz ay x a ++++bz ay ax xby ax az zbxaz ay y b ++++bz ay by x by ax bx z bxaz bz y b +++y by ax z x bx az y zbzay x a +++2+++00bz ay y xby ax x zbxaz z yb +++25行列式性质y ax z x azy z ay x a 2+y by z x bx y zbzx a 2+ayy x ax x zazz yb 2+bz y x by x zbxz y b 2yxzx z y zy x a 3+++00zy x y xzx z yb 3 1223,c c c c ↔↔第二个行列式y xzx z y z y xb a )(33+ (3)用数学归纳法①当1=n 时，1)11(22x x x D n +===，命题成立；②设k n ≤时命题成立，即k k x k D )1(+=，则1+=k n 时，)1()1(22222100020000002100002100002+⨯+=k k n x x x x x x x x x D=kk x x x x x x x x x x⨯210002000000210000210000222222kk x x x x x x x ⨯-210020000020000122221212)1(22--⋅-+⋅=-=k k k k kx x x k x D x xD 11)2()22(+++=-+k k x k x k k n x n )1(+=综合①、②可得对一切自然数n ，都有n n x n D )1(+=. 7．解：(1)1444414444144441 =n D),,3,2(1n i r r i =+14444144441434343434 ----n n n n)34()34(--n n 提取1444414444141111 )34(,3,2 4 1-=-n ni r r i 300030000301111---)34()3(1--=-n n（2）121212555333321321321321---=n n n n n n n n Dni i c i ,3,2=提取2222224442223213213211111!---n n n n n n n∏≤<≤-nj i j i n 122)(! 式行列利用范德蒙(3)递推法nn n n a a a a a a a a D -------=-+11000010000001100001100001132211112r r +nn n a a a a a a a ------11000100000011000010000113221D n展开按第一列nn n a a a a a a a ------11001000000110000100001143321a -11-a 1Dnn 2=(4)nnn n n n nnn d c d c d c b a b a b a D 111111112----=行取第一行和第拉普拉斯定理n 2nn nnd c b a ．11111111----n n n n d c d c b a b a22)( --n n n n n D c b d a 421111))((-------n n n n n n n n n D c b d a c b d a 可得类似111133331111)())((d c b a c b d a c b d a c b d a n n n n n n n n -------∏=-ni i i i i c b d a 1)((5)na xxxx a x xx x a x x x x a3211,2,1 1-=-+n i c c i inn n a a x x x a x x a a x x x a a x x x a -------- 000000 00 00 001332212,1, 1 -=--n n i r r i ixa a a x x a x a a a x x a a a x xx a n n n n -------------1132321212 000 000002000 020 00∏∏=-+=---+-ni i i n n i i a a x x x a n 2111)2()1()( 展开列按第 ∏∏=-=-++-ni i i ni i x a a x x a 211)2()(8．解：(1)计算系数行列式232142234321212r r r r D --=51050321430-=----5321032143031-+--r r 210321200=－101312173237323211r r r r D --=01240310211=----2321242274331212r r r r D --=311050331450r r -----31105033160r r ---－302321342734321112r r r r D --==----5503215303131103215305r r +---101103212005=-- 所以方程组有唯一解011==D D x ， 322==D Dx ， 133-==DD x (2)计算系数行列式4352323211431121----=D 101110740064112132141312------++r r r r r r 10111010402021104424123------++-r r r r r r6114022111=---展开按c 43513232114711231----=D 24232143r r r r r r +-+01212901919114700610--- 324241212919190610)1(r r c +----+展开按60121290121006101413122224312322211731131r r r r r r D --+----=1421505440001041131c c -------11501440001040131-----390144000104013134---+r r 3900104131)1(434---+展开按c3131r r +303900104001)1(43-=--+41523232174313213--=D 141312223r r r r r r ---2510541042201321-------2423225105410211013212)2(r r r r r -+-------－提取06003300211013212----- 0603302112C 1－－－－展开按36＝－ 13522232714331214--=D 141312223r r r r r r ---5110441024203121----－－－2423251104410121031212)2(r r r r r -+-------－提取61003200121031212----- 613201212C 1---－展开按18= 所以方程组有唯一解1011==D D x ， 522-==D D x ， 633-==D D x ， 344==DDx (3)计算系数行列式5733856155334231=D 343214131222716043307160423133r r r r r r r r r r ++--------17004330150042312004330150001013124---r r r r 64310)1(20204331502331=-⨯+展开按展开按r C3412125738856855364233r r r r D --=24232123230856831304233r r r r r r -++----0100270831301303--13123442320833013)1(r r r r r -+---+展开按600203913-=--57838581556342312=D 022435713022043507130423131131224---------展开按c r r r r r r11420720253232313---+r r r r r 提取12-58338861563343313=D 020453736020045307360433131131224---------展开按c r r r r r r 6=87338561653332314=D 220533316220053303160323131131224---------展开按c r r r r r r122275)1(3220533750212121=-⨯++展开按c r r所以方程组有唯一解111-==D D x ， 222-==D D x ， 133==D D x ， 244==DDx9．解：（1）λλλλ--=3111211D 1232rr c c --λλλλλ----3321022132122332021---+---λλλλλλλ展开按r )2)(2()22)(2()3)(2(2---=--+--=λλλλλλλλ)1()2(2+--=λλ当0=D 时，即时＝－或12λλ=，齐次方程组有非零解. （2）324124122-+--=λλλD 32423601221212---+-----λλλλλr r c cλλλλλλλ--+--+-----2460)1(3223621展开按r [])6)(4)(1()23)(2()6(32-+---++--=λλλλλλ)4)(2)(3(241423-++-=+-=λλλλλλ＋－当0=D 时，即时＝或－或423λλλ=-=，齐次方程组有非零解.习题二1．解：（1）⎪⎪⎪⎭⎫ ⎝⎛---=+776491056532B AB （2）⎪⎪⎪⎭⎫ ⎝⎛------=-4332412332E AB T2．解：（1）⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--000046696432 （2）⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛834231413121342（3）()⎪⎪⎪⎭⎫ ⎝⎛----=-⎪⎪⎪⎭⎫ ⎝⎛-339226113113321 （4）()2321113-=⎪⎪⎪⎭⎫⎝⎛--（5）⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛------777468505642531432321234643755467 （6）()⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛321333231232221131211321x x x a a a a a a a a a x x x()⎪⎪⎪⎭⎫⎝⎛++++++=321333223113332222112331221111x x x x a x a x a x a x a x a x a x a x a)()()(233332233113233222222112133112212111x a x x a x x a x x a x a x x a x x a x x a x a ++++++++=3．解：⎪⎪⎪⎭⎫ ⎝⎛---=210143321TA ， ⎪⎪⎭⎫ ⎝⎛=234112T B(1)⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---=112143213142210143321B A T（2）⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛=124113213142031234112A B T(3)⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛==1165511210143321234112)(TT T A B AB4．解：从321321,,,,x x x y y y 到的线性变换可表示为：⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛321321y y y A x x x ，其中⎪⎪⎪⎭⎫ ⎝⎛---=352143231A ；从321321,,,,y y y z z z 到的线性变换可表示为：⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛321321z z z B y y y ，其中⎪⎪⎪⎭⎫ ⎝⎛=231341652B ，所以从321321,,,,x x x z z z 到的线性变换可表示为：=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛321321z z z AB x x x ⎪⎪⎪⎭⎫ ⎝⎛---352143231⎪⎪⎪⎭⎫ ⎝⎛231341652=⎪⎪⎪⎭⎫ ⎝⎛321z z z ⎪⎪⎪⎭⎫ ⎝⎛--312823111⎪⎪⎪⎭⎫ ⎝⎛321z z z 所以，从321321,,,,x x x z z z 到的线性变换为： ⎪⎩⎪⎨⎧+-=++=+-=32823 321332123211z z z x z z z x z z z x5．解：（1）E A A A f 43)(2+-=⎪⎪⎭⎫ ⎝⎛--=2321⎪⎪⎭⎫ ⎝⎛--2321－3⎪⎪⎭⎫ ⎝⎛--2321E 4+＝⎪⎪⎭⎫⎝⎛8008 (2) 2201310111)(2--=--=x x x x x x f=--=E A A A f 22)(2⎪⎪⎭⎫ ⎝⎛0211⎪⎪⎭⎫ ⎝⎛0211⎪⎪⎭⎫ ⎝⎛-02112E 2-⎪⎪⎭⎫⎝⎛---=01216．（1）∵222))(()(B BA AB A B A B A B A +++=++=+ ∴要使2222)(B AB A B A ++=+，则必须AB BA = (2) ∵22))((B BA AB A B A B A -+-=-+∴要使22))((B A B A B A -=-+，则必须0=+-BA AB ，即AB BA = (3) 当AB BA =时，用数学归纳法证明kk k B A AB =)(①1=k 时，显然kk k B A AB =)(2=k 时，222)()()()(B A B AB A B AB A ABAB AB AB k =====，所以kk k B A AB =)(②设n k =时，有kk k B A AB =)(，则1+=n k 时B BA B A B A B A AB B A AB AB AB AB n n n n n n n n K)()()()()()(1!-+=====B AB B A n n )(1-=21)(B A B A n n -=11)(++===n n n n B A B AB A可见，1+=n k 时，也有k k k B A AB =)(所以，当AB BA =时，对一切正整数k 都有 k k k B A AB =)(7．解：(1) ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛----111122221111n n n n n(2) ∵⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛--100123122∴⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛--为奇数为偶数n n n 2312 10012312 (3) ∵⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛1002101211001100112，⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛1002101211001100113⎪⎪⎪⎭⎫⎝⎛100110011⎪⎪⎪⎭⎫⎝⎛=100310331 =⎪⎪⎪⎭⎫ ⎝⎛41001100113100110011⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛100110011⎪⎪⎪⎭⎫ ⎝⎛=100310331⎪⎪⎪⎭⎫⎝⎛100110011 ⎪⎪⎪⎭⎫ ⎝⎛=100410641 ∴⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫⎝⎛100102)1(1100110011n n n n n8．证明：∵A 、B 为对称矩阵，∴=T A A ，=TB B(1) ∵ AC C C A C AC C T T T T T T T ==)()(∴ AC C T是对称矩阵(2) ∵ ABABA A B A B A ABABA TT T T T T ==)(∴ ABABA 是对称矩阵(3) ∵E E AA TT ==-)(1，=T A A∴==--T T T A A AA )()(11A A E A A T 11)(--== ∴ 11)(--=A A T ∴ 1-A 是对称矩阵9．解：(1) ∵027342≠=∴⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛-23477342173421⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫⎝⎛-23472173421(2) ∵01cos sin sin cos cos sin 22≠=+=-θθθθθθ∴ ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--θθθθθθθθsin cos cos sin 11sin cos cos sin 1⎪⎪⎭⎫⎝⎛-=θθθθsin cos cos sin (3) ∵232132643321532r r r r --01320321110≠-=---- ∴⎪⎪⎪⎭⎫⎝⎛643321532可逆又∵0643211==A ， 3633112=-=A ， 2432113-==A 2645321=-=A ， 3635222-==A ， 1433223=-=A 1325331-==A ， 1315232-=-=A ， 1213233==A ∴⎪⎪⎪⎭⎫ ⎝⎛-----=⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛-1121331206433215323323133222123121111A A A A A A A A A(4) ⎪⎪⎪⎭⎫⎝⎛-------=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛-----11133131121212113123233323133222123121111A A A A A A A A A(5) ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛----1212335123240634332311(6) 把⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=1000210032104321D 分块为⎪⎪⎭⎫ ⎝⎛B C A 0，其中⎪⎪⎭⎫ ⎝⎛=1021A ，⎪⎪⎭⎫ ⎝⎛=1021B ，⎪⎪⎭⎫⎝⎛=3243C ，则01≠==B A D ，∴矩阵D 可逆。

医学高等数学习题解答(1,2,3,6)

第一章函数、极限与连续习题题解(P27)一、判断题题解1. 正确。

设h(x)=f(x)+f(x), 则h(x)= f(x)+f(x)= h(x)。

故为偶函数。

2. 错。

y=2ln x的定义域(0,+), y=ln x2的定义域(,0)∪(0,+)。

定义域不同。

3. 错。

故无界。

4. 错。

在x0点极限存在不一定连续。

5. 错。

逐渐增大。

6. 正确。

设，当x无限趋向于x0,并在x0的邻域内，有。

7. 正确。

反证法：设F(x)=f(x)+g(x)在x0处连续，则g(x) =F(x)f(x)，在x0处F(x)，f(x)均连续，从而g(x)在x=x0处也连续，与已知条件矛盾。

8. 正确。

是复合函数的连续性定理。

二、选择题题解1.2. y=x (C)3. (A)4. (B)5.(B)6. (D)7. 画出图形后知：最大值是3，最小值是10。

(A)8. 设,则，连续，由介质定理可知。

(D)三、填空题题解1.2. 是奇函数，关于原点对称。

3. ,。

4. ,可以写成。

5. 设，，6. 有界，，故极限为0。

7.8. ,而，得c=6, 从而b=6, a=7。

9.10.11. 设u=ex1，12. 由处连续定义，，得：a=1。

四、解答题题解1. 求定义域(1) , 定义域为和x=0(2) 定义域为(3) 设圆柱底半径为r，高为h，则v=r2h, ，则罐头筒的全面积，其定义域为(0,+)。

(4) 经过一天细菌数为，经过两天细菌数为,故经过x天的细菌数为，其定义域为[0,+)。

2. ，，。

3. ,。

4. 证明：。

5. 令x+1=t, 则x=t1。

，所以：。

6. 求函数的极限(1) 原式=。

(2) 原式==。

(3) 原式==。

(4) 原式=。

(5) 原式==。

（P289常见三角公式提示）(6) 原式=，令，则，令，则，，原式=。

(7) 原式=== e3。

(8) 原式=== e2。

(9) 原式==。

(10) 令，则，原式=(填空题11)。

林崇德《发展心理学》(第3版)笔记和课后习题详解-第一章至第三章【圣才出品】

第1章绪论1.1复习笔记一、发展心理学的界说（一）心理学与发展心理学发展心理学是心理学的一个分支。

1．心理学心理学是研究心理活动和行为表现的一门科学。

（1）心理活动与心理现象①心理活动人的心理活动，或称心理，是指人在实践活动和生活活动中，与周围的环境发生交互作用，必然产生的主观活动和行为表现。

②心理现象人的心理现象是指人的心理过程和人格。

a．人的心理过程第一，认知过程：感觉、知觉、注意、记忆、思维和想象等心理活动。

第二，情感过程：人的喜、怒、哀、乐、爱、恶、惧等对周围环境的态度体验。

第三，意志过程：根据既定目的，克服困难，做出努力，并通过行为去处理和变革客观的现实。

b．人格人格（personality），又称个性，是指对待某个事件，不同的人在能力、气质、性格、兴趣、动机和价值观等方面会表现出差异，这种差异既与个人的先天素质有关，也与后天的经验和学习有关。

（2）心理科学的特殊性心理现象与物理现象不同，它不具形体，不能直接观察得到。

心理活动通过人的外部行为，主要是动作和言语表现出来。

①人的行为受到心理活动的支配和调节。

外部行为是人的心理活动的直接表现，心理过程和人格对行为有很大影响。

②人是有意识的高等动物，人的心理非常复杂，人们可以有意识地掩盖自己的某些心理活动。

因此根据直接观察到的行为分析某种心理活动时，必须非常谨慎。

③人心理的复杂性、外部行为的多变性，并不意味着无法研究人的心理活动。

通过较长的时间、全面系统地观察或借助于仪器分析，可以对一个人的心理有所了解。

2．发展心理学发展，一般泛指某种事物的增长、变化和进步。

人的发展指的是人类身心的生长和变化，不同年龄阶段的人有不同的生理和心理特点。

其中，人的心理发展是人类发展的一个重要部分，包括种系心理发展和个体心理发展。

（1）发展心理学的定义发展心理学有广义和狭义之分。

①广义发展心理学是研究种系和个体心理发生与发展的科学。

种系心理发展是指从动物到人类的心理演变过程。

徐景峰《金融数学》1-4章习题解答

《利息理论》习题详解第一章利息的基本概念1.解：（1）)()0()(t a A t A =又()25A t t =+(0)5()2()1(0)55A A t a t t A ∴===++ （2）3(3)(2)11(92 2.318I A A =-=== （3）4(4)(3)0.178(3)A A i A -===2.解：15545(4)(3)(1)100(10.04)0.05 5.2nn n I i A I A i A i i -=∴==+=+⨯=3.证明：（1）123(1)()(2)(1)(3)(2)()(1)m m m m k I A m A m I A m A m I A m A m I A m k A m k ++++=+-=+-+=+-+=+-+-123123()()()()()m m m m k m m m n I I I I A m k A m n m k A n A m I I I I m n +++++++∴++++=+-=+-=++++<令有（2）()(1)()1(1)(1)n A n A n A n i A n A n --==---()1(1)()(1)(1)n n A n i A n A n i A n ∴+=-∴=+-4.证明：（1）112123123(1)(0)(0)(2)(0)(0)(0)(3)(0)(0)(0)(0)()(0)(0)(0)(0)(0)k nk i a a a i a a a i a i a a a i a i a i a n a a i a i a i a i ∴=+=++=+++=+++++第期的单利利率是又(0)1a =123123()1()(0)()1nna n i i i i a n a a n i i i i ∴=+++++∴-=-=++++（2）由于第5题结论成立，当取0m =时有12()(0)n A n A I I I -=+++5.解：（1）以单利积累计算1205003i =⨯1200.085003i ∴==⨯800(10.085)1120∴+⨯=（2）以复利积累计算3120500500(1)i +=+0.074337i ∴=5800(10.074337)1144.97∴+=6.解：设原始金额为(0)A 有(0)(10.1)(10.08)(10.06)1000A +++=解得 (0)794.1A =7.证明：设利率是i ，则n 个时期前的1元钱的当前值为(1)ni +，n 个时期后的1元钱的当前值为1(1)ni +又22211[(1)](1)20(1)(1)n n n ni i i i +-=++-≥++，当且仅当221(1)(1)1(1)n n n i i i +=⇒+=+，0i =即或者n=0时等号成立。

半导体物理导论课后习题答案第1-3章

半导体物理导论课后习题答案第1-3章1.倒格子的实际意义是什么？一种晶体的正格矢和相应的倒格矢是否有一一对应的关系？解答：倒格子的实际意义是由倒格子组成的空间，实际上是状态空间空间，在晶体的X 射线衍射照片上的斑点实际上就是倒格子所对应的点子。

由正格子的基矢(a 1,a 2,a 3)就得到倒格子的矢量(b 1,b 2,b 3)，其中其中Ω是晶格原胞的体积。

由此可以唯一地确定相应的倒格子空间。

显然，倒格子与正格子之间有如下关系：所以一种晶体的正格矢和相应的倒格矢有一一对应的关系。

Ω⨯=Ω⨯=Ω⨯=213132321222a a b a a b a a b πππ，，ij i i πδ2=⋅b a (i,j=1,2,3)2.假设有一立方晶体，画出以下各晶面（1）（100）；（2）（110）；（3）（111）；（4）（100）；（5）（110）；（6）（111）3.已知Si的晶格常数或单胞的边长a=5.43089 Å, 求：（1）Si的原子体密度。

（2）(111)面、(110)面以及(100)面的原子面密度，比较哪个晶面的面密度最大？哪个晶面的面密度最小？解:(1)每个晶胞中有8个原子，晶胞体积为a 3，每个原子所占的空间体积为a 3/8，因此每立方厘米体积中的硅原子数为：原子体密度=8/a 3=8/(5.43×108)3=5×1022（个原子/cm 3）(2)（111）面为一个边长为的等边三角形，有效原子数为等边三角形的面积为个原子（面心原子）（顶角原子）25213313=⨯+⨯4521022212a a a S =⨯⨯=2a所以，(111)面的原子面密度为(110)面为一个边长为的长方形，有效原子数为长方形的面积为所以，(110)面的原子面密度为22524525aa ==等边三角形面积有效原子数2a a ⨯个原子（体对角线原子）（面心原子）（顶角原子）42212414=+⨯+⨯222a a a S =⨯=222224aa ==等边三角形面积有效原子数(100)面为一个边长为的正方形，有效原子数为正方形的面积为所以，(100)面的原子面密度为因此，(111)面的原子面密度∶(110)面的原子面密度∶(100)面的原子面密度为 ∶ ∶ = ∶ ∶1说明(111)面的原子面密度最高，(100)面的原子面密度最低。

数据通信原理(第2版)课后习题 (1~3章)答案

《数据通信原理》（毛京丽等编著，年第二版）习题解答（）１－１　数据通信的定义是什么？画出数据通信系统的基本构成框图，并说明其三大组成部分。

答：数据通信的定义是：依照通信协议，利用数据传输技术在两个功能单元之间传递数据信息，它可实现计算机与计算机、计算机与终端、终端与终端之间的数据信息传递。

数据通信系统的基本构成见教材图—数据通信系统主要由中央计算机系统、数据终端设备（）和数据电路三大部分组成。

数据终端设备：ＤＴＥ相当于人和机器（计算机）之间的接口。

数据电路：数据电路由传输信道（传输线路）及其两端的数据电路终接设备（ＤＣＥ）组成。

数据电路位于ＤＴＥ与计算机系统之间，它的作用是为数据通信提供数字传输信道。

传输信道包括通信线路和通信设备。

ＤＣＥ是ＤＴＥ与传输信道的接口设备。

调制解调器（ｍｏｄｅｍ）是最常见的ＤＣＥ，它是调制器和解调器的结合。

中央计算机系统：中央计算机系统由通信控制器、主机及其外围设备组成，具有处理从数据终端设备输入的数据信息，并将处理结果向相应的数据终端设备输出的功能。

通信控制器（或前置处理机）是数据电路和计算机系统的接口，控制与远程数据终端设备连接的全部通信信道，接收远端ＤＴＥ发来的数据信号，并向远端ＤＴＥ发送数据信号。

主机又称中央处理机，由中央处理单元（ＣＰＵ）、主存储器、输入输出设备以及其他外围设备组成。

其主要功能是进行数据处理。

１－２　什么是数据电路？它的功能是什么？数据电路与数据链路的关系是什么？答：数据电路由传输信道及其两端的数据电路终接设备（）组成，它的作用是为数据通信提供数字传输信道。

数据电路加上两端的传输控制器构成数据链路。

１－３　设数据信号码元时间长度为—，如果采用电平传输，试求数据传信速率和调制速率。

解：，调制速率20072010.09P312DTE DCE 833106S 8 T=83310-6s M=8N Bd =1/T=1200Bd第章概述习题及解答1 l l l l l l l •~•~数据传信速率＝／１－４什么是单工、半双工、全双工数据传输？答：单工传输——传输系统的两端数据只能沿单一方向发送和接收。

电路分析基础第四版课后习题第一章第二章第三章第四章答案

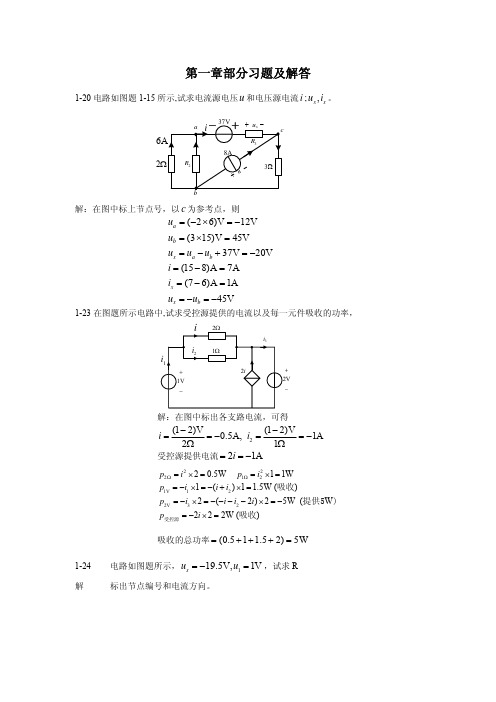
+ 42V
−
i1
18Ω
i2 3Ω
i3
gu
2−5
解
设网孔电流为 i1, i2 , i3 ,则 i3 = −guA = −0.1uA ,所以只要列出两个网孔方程
27i1 −18i2 = 42 −18i1 + 21i2 − 3(−0.1uA ) = 20
因 uA = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
⎪⎩i3 = 4A
第二章部分习题及解答
2-1 试用网孔电流法求图题所示电路中的电流 i 和电压 uab 。
4Ω
1Ω
i2
+
7V
−
i1
2Ω
i3 i
+ 3V
−
解
设网孔电流为 i1, i2 ,i3 ，列网孔方程
⎪⎨⎧3−ii11
− i2 − 2i3 = 7 + 8i2 − 3i3 = 9
⎪⎩−2i1 − 3i2 + 5i3 = −12
解得
i1 = 4.26A uA = (9× 4.26)V = 38.34V i3 = −0.1uA = −3.83A
2-8 含 CCVS 电路如图题 2-6 所示，试求受控源功率。
1Ω i3
5Ω
+
i 4Ω
+
50V i1 −
20Ω i2
15i −
2−6
解
标出网孔电流及方向，
⎧⎪⎨2−52i01i−1 +202i42i−2 −5i43 i=3
50 = −15i
⎪⎩−5i1 − 4i2 +10i3 = 0
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2

第1、2章电路定律与分析方法习题解答

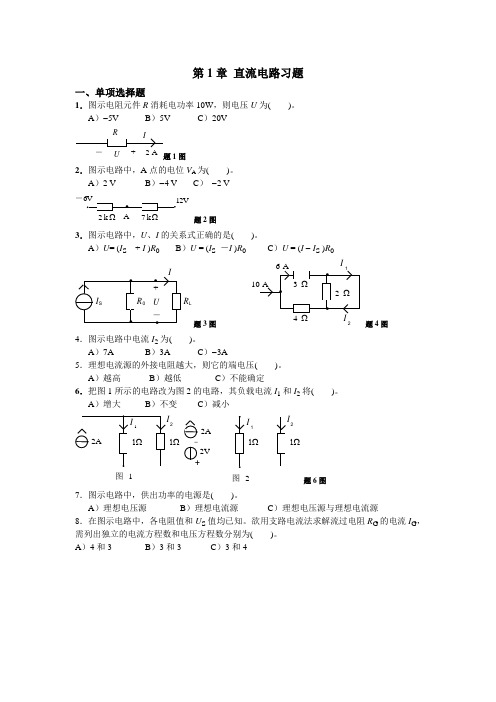
第1章直流电路习题一、单项选择题1．图示电阻元件R 消耗电功率10W ，则电压U 为( )。

A ）-5V B ）5V C ）20VU+题1图2．图示电路中，A 点的电位V A 为( )。

A ）2 V B ）-4 V C ） -2 V－ 2 k 7 k ΩΩ题2图3．图示电路中，U 、I 的关系式正确的是( )。

A ）U = (I S + I )R 0 B ）U = (I S －I )R 0 C ）U = (I - I S )R 0R L题3图I 2题4图4．图示电路中电流I 2为( )。

A ）7AB ）3AC ）-3A5．理想电流源的外接电阻越大，则它的端电压( )。

A ）越高 B ）越低 C ）不能确定6．把图1所示的电路改为图2的电路，其负载电流I 1和I 2将( )。

A ）增大B ）不变C ）减小221Ω2V 2A图 1图 2+题6图7．图示电路中，供出功率的电源是( )。

A ）理想电压源 B ）理想电流源 C ）理想电压源与理想电流源8．在图示电路中，各电阻值和U S 值均已知。

欲用支路电流法求解流过电阻R G 的电流I G ，需列出独立的电流方程数和电压方程数分别为( )。

A ）4和3 B ）3和3 C ）3和4U 4VS题7图S题8图9．在计算线性电阻电路的电压和电流时，用叠加原理。

在计算线性电阻电路的功率时，加原理( )。

A ）可以用 B ）不可以用 C ）有条件地使用10．在图示电路中，已知U S =12V ，I S =2A 。

A 、B 两点间的电压U AB 为( )。

A ）-18VB ）18VC ）-6VU I SS+题10图SA题11图11．在图示电路中，当开关S 闭合时A 点的电位V A ( )。

A ） -3V B ）3V C ）0V12．图示电路中，理想电流源I S1发出的电功率P 为( )。

A ）-3WB ）21WC ）3W4 VS 2题1263ΩΩ题13图13．图示电路中，电流I 是( )。

《电路分析基础》第2版-习题参考答案

《电路分析基础》各章习题参考答案第 1 章习题参考答案1- 1 (1) 50W ; (2) 300 V、25V, 200V、75 V ; (3) 2=12.5 Q R a=100 Q, R4=37.5 Q1- 2 V A=8.5V， V m=6.5V， V B=0.5V， V C=- 12V， V D=-19V， V p=-21.5V， U AB=8V， U BC=12.5，U DA=-27.5V1- 3 电源(产生功率)： A 、 B 元件；负载(吸收功率)： C、 D 元件；电路满足功率平衡条件。

1- 4 (1) V A=1 00V , V B=99V, V C=97V, V D=7V, V E=5V, V F=1V, U AF=99V, U CE=92V, U BE=94V, U BF=98V, U CA=- 3 V；(2) V C=90V, V B=92V , V A=93V, V E=-2V, V F=-6V, V G=- 7V, U AF=99V, U CE=92V, U BE=94V, U BF=98V, U CA=- 3 V1- 5 I 〜0.18A , 6 度，2.7 元1- 6 I=4A， I1=11A，I2=19A1- 7 (a) U=6V, (b) U=24 V, (c) R=5Q, (d) I=23.5A1- 8 (1) i6=-1A ； (2) u4=10V, u6=3 V； (3) P1=-2W 发出, P2 =6W 吸收, P3 =16W 吸收, P4 =-10W 发出, P5 =-7W 发出, P6 =-3W 发出1- 9 I=1A , U s=134V , R~ 7.8Q1- 10 S 断开：U AB=- 4.8V , U AO=- 12V , U BO=-7.2V ;S 闭合：U AB =-12V, U AO =- 12V , U BO=0V1- 11 支路 3，节点 2，网孔 2 ，回路 31- 12 节点电流方程： (A) I1 +I3- I6=0，(B)I6- I5- I7=0，(C)I5 +I 4-I3=0回路电压方程：① I6 R6+ U S5 +I 5 R5- U S3 +1 3 R3=0 ,②-15 R5- U S5+ I 7R7- U S4 =0 ,③-丨3 R3+ U S3 + U S4 + I 1 R2+ I 1 R1=01- 13 U AB=11V , I2=0.5A , l3=4.5A , R3~ 2.4 Q1-14 V A=60V V C=140V V D=90V U AC=- 80V U AD=- 30V U CD=50V1- 15 I1=- 2A I2=3A I3=- 5A I4=7A I5=2A第 2 章习题参考答案2- 1 2.4 Q 5 A2- 2 (1) 4 V 2 V 1 V; (2) 40 mA 20 mA 10 mA2- 3 1.5 Q 2 A 1/3 A2- 4 6 Q 36 Q2- 5 2 A 1 A2- 6 1 A2- 7 2 A2- 8 1 A2- 9 I1 = -1.4 A I2 = 1.6 A I3 = 0.2 A2- 10 I1 = 0 A I2 = -3 A P1 = 0 W P2 = -18 W2- 11 I i = -1 mA , I2 = - 2 mA , E3 = 10 V2- 12 I1 = 6 A , I2 = -3 A , I3 = 3 A2- 13 I1 =2 A , I2 = 1A , I3 = 1 A , I4 =2 A , I5 = 1 A2-14 V a = 12 V , I1 = - 1 A, I2 = 2 A2-15 V a = 6 V , I1= 1.5 A , I2 = - 1 A ,I3 = 0.5 A2-16 V a = 15 V , I1 = - 1 A , I2 =2 A , I3 = 3 A2-17 I1 = -1 A , I2 = 2 A2-18 I1 =1.5 A , I2 = - 1 A , I3 = 0.5 A2-19 I1 =0.8 A , I2 = - 0.75 A , I3 = 2 A , I4 = - 2.75 A , I5 = 1.55 A2-20 I3 = 0.5 A2-21 U o = 2 V , R o = 4 Q, I0 = 0.1 A2-22 I5 = -1 A2-23 (1) I5 = 0 A , U ab = 0 V ; (2) I5 = 1 A , U ab = 11 V2-24 I L = 2 A2-25 I s =11 A , R0 = 2 Q2-26 18 Q, - 2 Q, 12 Q2-27 U = 5 V2-28 I =1 A2-29 U = 5 V2-30 I =1 A2-31 10 V , 180 Q2-32 U0 = 9 V , R0 = 6 Q, U=15 V第3章习题参考答案3- 1 50Hz, 314rad/s, 0.02s, 141V, 100V, 120 °3- 2 200V, 141.4V3- 3 u=14.1si n (314t-60 °V3- 4 (1) ®u1-贏2= 120°(2) ®1 = -90° %= - 210°, %1-屁=120° (不变)3-5 (1) U^50 .^_90 V , U2 =50 .2 -0 V ;(2) U3=100 2 sin (3t+ 45 °)V , U4=100 ■■ 2 sin ( ®t+ 135 °)V3- 6 (1) i 1=14.1 sin ( 72 °)A ; (2) U2=300 sin ( 3—60 °)V3- 7 错误：(1),⑶，(4), (5)3- 8 (1) R； (2) L ； (3) C; (4) R3- 9 i=2.82 sin (10t-30 °)A , Q~ 40 var3- 10 u=44.9sin (3141-135 °V, Q=3.18 var3- 11 (1) I=20A ; (2) P=4.4kW3- 12 (1)I ~ 1.4A , I 1.4 - 30 A ； (3)Q~ 308 var, P=0W ; (4) i~ 0.98 sin (628t-30 °)A3- 13 (1)I=9.67A , I =9.67450 A , i=13.7 sin (314t+150 °) A ; (3)Q=2127.4 var, P=0W;(4) I C=0A3- 14 (1)C=20.3 尸;(2) I L = 0.25A ,l c = 16A第4章习题参考答案4-1 (a) Z =5. 36.87 J, Y =0.2 /36.87 S; (b) Z =2.5 - 2/45 门,Y =0.2.2/45 S4- 2 Y=(0.06-j0.08) S , R~ 16.67 Q, X L=12.5 Q, L~0.04 H4- 3 U R=6 0^0 V U L=80/90 V , U S=100^53.13 V4- 4 卩=2 0 £ 3 6.874-5 Z =100 2^45 ；：■,卩=1^0 A , U R=100^0 V , U L=125/90 V , U C=25/ 90 V4-6 Y =0.25 2^45 S , U =4 “2/0 V ,卩R = .2. 0 A , I L =0.^ 2 / 90 A , I C=1.2.2/90 A4- 7 ll =1 0.「2 4 5，A U S=100 乙90 V4- 8 (a) 30 V ; (b) 2.24 A4- 9 (a) 10 V ; (b) 10 A4- 10 (a) 10 V ; (b) 10 V4- 11 U=14.1 V4- 12 U L1 =15 V , U C2 =8 V , U S=15.65 V4-13 U X1 =100 V, U2 =600 V, X1=10 Q, X2=20 Q, X3=30 Q4- 14 Z =20 .2 45 门，l =2. -45 A , h = 2 0 A , .2/-90 A , U ab=0V 4- 15 (1)1 =£2 A, Z RC=5、2「，Z =5 10 门；(2) R =10 门，X^10'J4- 16 P = 774.4 W , Q = 580.8 var, S = 968 V A-4- 17 l1 = 5 A , l2 = 4 A4-18 I1 = 1 A , I2 =2 A , l =.5. 26.565 A , S =44.72. -26.565 V A4-19 Z=10", I=190A, U R2 =5 2 135 V , P =10 W64-20 a =5X10 rad/s , p= 1000 Q, Q = 100 , l = 2 mA , U R =20 mV , U L = U C = 2 V4-21 30 =104rad/s , p= 100 Q, Q = 100 , U = 10 V, I R = 1 mA , I L = I C = 100 mA4-22 L1 = 1 H , L2 ~ 0.33 H第5章习题参考答案5- 3 M = 35.5 mH5- 4 301 =1000 rad/s ,302 =2236 rad/s5- 5 Z1 = j31.4 Q , Z2 = j6.28 Q 5- 6 Z r = 3+7.5 Q5- 7 M = 130 mH5- 8 “2 二-2/45 A5- 9 U1 = 44.8 V5- 10 M12 = 20 mH , 11 = 4 A5- 11 U2 = 220 V , I1 = 4 A5- 12 n = 1.95- 13 N2 = 254 匝，N3 = 72 匝5- 14 n = 10 , P2 = 31.25 mW章习题参考答案 (1) A 相灯泡电压为零，B 、C 相各位为220V I L = I p = 4.4 A ，U p = 220 V ，U L = 380 V ，P = 2.3 kW (2) I p = 7.62 A ，I L = 13.2 A A 、C 相各为2.2A ，B 相为3.8A U L = 404 V U A N =202/ -47 V cos $ = 0.961 , Q = 5.75 kvar Z =334 28.4 门 (1) I p = 11.26 A , Z = 19.53 / 42.3 °Q; (2) I p = I l = 11.26 A , P = 5.5 kW U l = 391 V i A =22 2sin(・t —53.13 ) A i B =22 .2sin(・t —173.13 ) A i C =22 2 sin(，t 66.87 ) A U V = 160 V (1) 负载以三角形方式接入三相电源 (2) I — =3.8 T 2 -15 A , 1仁 =3.^-2/ 135 A , 仁 =3.8、「2也105 A I A =3.8、. 6/「45 A , I B =3.8I Q 「165 A , I c =3.8.6. 75 A L = 110 mH , C = 91.9 mF 章习题参考答案 P = 240 W, Q = 360 var P = 10.84 W (1) i(t) 4.7sin( t 100 ) - 3sin3 t A (2)I ~ 3.94 A , U ~ 58.84 V , P ~ 93.02 W 0MU m n o L 1 r~2 ------------- 2 u 2(t) m sin(，t —-arctan 1)V , R 2 (丄J 2 z 2 R ' 直流电源中有交流，交流电源中无直流 U 1=54.3 V , R = 1 Q, L = 11.4 mH ;约为 8% , ( L'= 12.33 mH ) 使总阻抗或总导纳为实数(虚部为 0)的条件为尺二& = Rx = ■ L/C G =9.39 折,C 2 =75.13 M F L 1 = 1 H , L 2 = 66.7 mH C 1 = 10 M F, C 2 = 1.25 M F 章习题参考答案第66-16-36-46-56-66-76-86-96-106-116-126-136-146- 15第77- 17-27-37-47-57-67-77-87-97- 10第88- 68-78-8i L(0+) = 1.5mA , U L(0+) = - 15Vh(0+) = 4A, i2(0+) = 1A , U L(0+) = 2V, i1(s)= 3A , i2(^)= 0, U L()= 0 i1 (0+) = 75mA , i2(0+) = 75mA , i3(0+) = 0, U L1 (0+) = 0, U L2(0+) = 2.25V6i c (t)二 2訂 A 4tU L (t) =6e _V u C (t) =10(1 _eg 0t )V , i C (t) =56说*人 500t 貝 u C (t) =115e~ sin(866 亠60 ) V10t 10t 山⑴=12e - V , L(t) =2(1 —e — )A 1 t U R (t) =~U s e 下2C V , U R (3 J - -U S e-V (1) T = 0.1s, (2) u c (t) =10e -0t V , (3) t = 0.1s u C (t) =10 _9e 」°t V 10t _ i L (t) =5e 一 A (a)f(t) =1(t —t 。

液压传动1~9章习题解答

第1~3章作业习题解答1-1/0-1液压千斤顶如图所示。

千斤顶的小活塞直径为15mm ，行程10mm ，大活塞直径为60mm ，重物W 为48000N ，杠杆比为L :l =750:25，试求：1)杠杆端施加多少力才能举起重物W? 2)此时密封容积中的液体压力等于多少? 3)杠杆上下动作一次，重物的上升量。

又如小活塞上有摩擦力175N ，大活塞上有摩擦力2000N ，并且杠杆每上下—次，密封容积中液体外泄0.2cm 3到油箱，重复上述计算。

解 1）4422211d Wd F ππ= N 3000)6015(48000)(22211=⨯==d d W Fl F FL 1=N1007502530001=⨯==L l F F 2）224d W p π=206.0480004⨯⨯=π MPa 98.16=3）22212144h d h d ππ= mm625.010)6015()(212212=⨯==h d d h 又如： 1）442222111d f W d f F ππ+=- N3300175)6015()200048000())((2122121+⨯+=++=f d df W F l F FL 1=N1107502533001=⨯==L l F F 2）222)(4d f W p π+=206.0)200048000(4⨯+⨯=π MPa 69.17=3）l V h d h d +=22212144ππ 44221212d V h d h lππ-=406.0102.001.04015.0262⨯⨯-⨯⨯=-ππmm 554.0m 1054.54=⨯=-1-2/0-2如图所示两液压缸的结构和尺寸均相同，无杆腔和有杆腔的面积各为A 1和A 2，A 1=2A 2，两缸承受负载F 1和F 2，且F 1=2F 2，液压泵流量为q ，试求两缸并联和串联时，活塞移动速度和缸内的压力。

解两缸并联时，由于两缸上作用负载不同，故两缸顺序动作。

大学化学课后习题答案(吉林大学版)第1 2 3 章

第1章化学反应基本规律1.2 习题及详解一．判断题1. 状态函数都具有加和性。

（×）2. 系统的状态发生改变时，至少有一个状态函数发生了改变。

（√）3. 由于CaCO3固体的分解反应是吸热的，故CaCO3的标准摩尔生成焓是负值。

（×）4. 利用盖斯定律计算反应热效应时,其热效应与过程无关,这表明任何情况下,化学反应的热效应只与反应的起,始状态有关,而与反应途径无关。

(×)5.因为物质的绝对熵随温度的升高而增大，故温度升高可使各种化学反应的ΔS大大增加。

（×）6. ΔH, ΔS受温度影响很小，所以ΔG受温度的影响不大。

（×）7. 凡ΔGθ大于零的过程都不能自发进行。

（×）8. 273K，101.325KPa下，水凝结为冰，其过程的ΔS<0, ΔG=0。

(√)9.反应Fe3O4(s)+4H2(g) → 3Fe(s)+4 H2O(g)的平衡常数表达式为2244(/)(/)H OTHp pKp pθθθ=。

（√）10．反应2NO+O2→2NO2的速率方程式是:)()(22OcNOkcv⋅=，该反应一定是基元反应。

（×）二．选择题1. 某气体系统经途径1和2膨胀到相同的终态，两个变化过程所作的体积功相等且无非体积功，则两过程（ B ）A.因变化过程的温度未知，依吉布斯公式无法判断ΔG是否相等B.ΔH相等C.系统与环境间的热交换不相等D.以上选项均正确2. 已知CuCl2(s)+Cu(s)→2CuCl(s) Δr H mΘ(1) =170KJ•mol-1Cu(s)+Cl2(g) → CuCl2(s) Δr H mΘ(2) =-206KJ•mol-1则Δf H mΘ（CuCl,s）应为（D ）KJ.mol-1A.36B. -36C.18D.-183. 下列方程式中,能正确表示AgBr(s)的Δf H mΘ的是( B )A.Ag(s)+1/2Br2(g)→ AgBr(s)B.Ag(s)+1/2Br2(l)→AgBr(s)C.2Ag(s)+Br2(l)→ 2AgBr(s)D.Ag+(aq)+Br-(aq)→ AgBr(s)4. 298K下，对参考态元素的下列叙述中，正确的是（ C ）A.Δf H mΘ≠0，Δf G mΘ＝0，S mΘ＝0B.Δf H mΘ≠0，Δf G mΘ≠0，S mΘ≠0C.Δf H mΘ＝0，Δf G mΘ＝0，S mΘ≠0D.Δf H mΘ＝0，Δf G mΘ＝0，S mΘ＝05. 某反应在高温时能自发进行，低温时不能自发进行，则其（ B ）A.ΔH>0, ΔS<0 ；B. ΔH>0, ΔS>0C.ΔH<0, ΔS<0 ；D.ΔH<0, ΔS>06.1mol气态化合物AB和1mol气态化合物CD按下式反应:AB(g)+CD(g)→AD(g)+BC(g),平衡时,每一种反应物AB 和CD都有3/4mol转化为AD和BC,但是体积没有变化,则反应平衡常数为( B )A.16B.9C.1/9D.16/97.400℃时，反应3H2(g)＋N2(g)→2NH3(g)的K673Θ＝1.66×10-4。

信号系统(第3版)习题解答

《信号与系统》（第3版）习题解析高等教育目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。

1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。

[提示：f ( 2t )表示将f ( t )波形压缩，f (2t )表示将f ( t )波形展宽。

] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解以上各函数的波形如图p1-2所示。

图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。

题1-3图解各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅=t t i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

S R S L S C题1-4图解系统为反馈联接形式。

设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。

数据结构1-4章习题答案

第1章概论习题参考解答一、填空题1、数据的逻辑结构是数据元素之间的逻辑关系，通常有下列4类：（）、（）、（）、（）。

【答】集合、线性结构、树型结构和图状结构。

2、数据的存储结构是数据在计算机存储器里的表示，主要有4种基本存储方法：（）、（）、（）、（）。

【答】顺序存储方法、链接存储方法、索引存储方法和散列存储方法。

二、选择题1、一个算法必须在执行有穷步之后结束，这是算法的（）。

（A）正确性（B）有穷性（C）确定性（D）可行性【答】B。

2、算法的每一步，必须有确切的定义。

也就是说，对于每步需要执行的动作必须严格、清楚地给出规定。

这是算法的（）。

（A）正确性（B）有穷性（C）确定性（D）可行性【答】C。

3、算法原则上都是能够由机器或人完成的。

整个算法好像是一个解决问题的“工作序列”，其中的每一步都是我们力所能及的一个动作。

这是算法的（）。

（A）正确性（B）有穷性（C）确定性（D）可行性【答】D。

三、简答题1、算法与程序有何异同？【答】尽管算法的含义与程序非常相似，但两者还是有区别的。

首先，一个程序不一定满足有穷性，因此它不一定是算法。

例如，系统程序中的操作系统，只要整个系统不遭受破坏，它就永远不会停止，即使没有作业要处理，它仍处于等待循环中，以待一个新作业的进入。

因此操作系统就不是一个算法。

其次，程序中的指令必须是计算机可以执行的，而算法中的指令却无此限止。

如果一个算法采用机器可执行的语言来书写，那么它就是一个程序。

2、什么是数据结构？试举一个简单的例子说明。

【答】数据结构是指数据对象以及该数据对象集合中的数据元素之间的相互关系（即数据元素的组织形式）。

例如，队列的逻辑结构是线性表（先进先出）；队列在计算机中既可以采用顺序存储也可以采用链式存储；对队列可进行删除、插入数据元素以及判断是否为空队列、将队列置空等操作。

3、什么是数据的逻辑结构？什么是数据的存储结构？【答】数据元素之间的逻辑关系，也称为数据的逻辑结构。